Improving the Position Accuracy and Computational Efficiency of UAV Terrain Aided Navigation Using a Two-Stage Hybrid Fuzzy Particle Filtering Method

1  Introduction

Terrain Reference Navigation (TRN) is an advanced navigation technique that enhances the precision of positioning systems by utilizing detailed information about the Earth’s surface. Unlike traditional navigation methods that primarily rely on Global Navigation Satellite Systems (GNSS), TRN integrates various data sources, such as high-resolution topographical maps and terrain features, to improve navigational accuracy and reliability, especially in environments where satellite signals may be weak or obstructed. The concept of TRN has gained significant attention in recent years due to its critical applications in military operations, autonomous vehicles, and aerial robotics. As the demand for accurate navigation systems increases, particularly in urban and challenging terrains, TRN emerges as a viable solution that capitalizes on the natural landscape to assist in localization and navigation. For instance, the ability to correlate terrain data with onboard sensors allows vehicles and aircraft to navigate more effectively in GPS denied environments, making TRN an essential component of modern navigation systems. Recent advancements in sensor technology and machine learning algorithms have further propelled the development of TRN. Research indicates that the integration of Light Detection and Ranging (LIDAR) and photogrammetry with sophisticated data processing techniques can significantly enhance the ability to match terrain features in real time. Moreover, studies show that machine learning models can effectively analyze terrain data to predict and adapt to dynamic navigation challenges, thereby improving the overall performance of navigation systems [1]. The application of TRN is not limited to terrestrial navigation. It plays a crucial role in aerial navigation, particularly for Unmanned Aerial Vehicles (UAVs), where reliable positioning is vital for mission success. The ability of UAVs to utilize terrain data allows them to execute complex flight maneuvers in environments that would otherwise be challenging due to obstructions or changing topography.

As we delve deeper into the mechanisms of Terrain Reference Navigation (TRN), it’s essential to explore its components and operational principles. At its core, TRN relies on the comparison of real-time sensor data with preexisting terrain databases. These databases can include Digital Elevation Models (DEMs), satellite imagery, and other geospatial data, which collectively provide a detailed representation of the navigable area. TRN systems typically integrate various sensors such as Inertial Measurement Units (IMUs), GPS, LIDAR, and cameras. This fusion of data allows for a more comprehensive understanding of the environment and enhances navigational accuracy. The synergy between these sensors helps mitigate the weaknesses of individual systems, especially in scenarios where GPS signals are degraded or unavailable [2]. The core functionality of TRN lies in its ability to match terrain features observed by sensors against those stored in the navigation database. Advanced algorithms, such as point cloud registration and feature extraction techniques, are employed to ensure precise matching, which is critical for real-time navigation. The techniques, including Kalman filtering and particle filtering, are often utilized to refine position estimates continuously. By dynamically adjusting the navigation solution based on the incoming sensor data and terrain information, TRN systems can maintain high levels of accuracy even in changing environments. The versatility of TRN is evident in its applications across multiple domains: In military contexts, TRN offers enhanced navigation capabilities in urban warfare and mountainous terrains where GPS signals may be unreliable. The ability to navigate with high precision can provide a significant tactical advantage. For autonomous ground vehicles, TRN is critical in ensuring safe navigation through complex environments, such as cities or construction zones. By leveraging terrain data, these vehicles can make informed decisions about path planning and obstacle avoidance. UAVs benefit immensely from TRN, particularly in search and rescue operations, surveillance, and agricultural monitoring. The ability to navigate autonomously in GPS denied areas enhances the effectiveness of these missions [3].

The effectiveness of UAV positioning systems depends on two key factors: (1) accuracy of estimated positions and (2) computational efficiency, particularly for real-time applications. The main objective of this paper is to develop a UAV positioning scheme that enhances both aspects. It employs a hybrid two-stage TRN approach, combining an Extended Kalman Filter (EKF) with a fuzzy logic Sequence Importance Resampling (SIR) particle filter. The method features a two-stage fuzzy logic module that dynamically adjusts particle counts in real-time using process noise covariance and a composite terrain feature method. Key contributions include: (1) Reduced Computational Burden: Lower complexity is achieved by minimizing the number of particles in the Particle Filter through a Fuzzy expert system (2) Handling Uncertainties: The Fuzzy Particle Filter improves robustness against noise, efficiently managing uncertainties while maintaining good estimation performance. (3) Positioning Accuracy: The hybrid method of Fuzzy Logic, Particle Filter and Error State Kalman Filter achieves positioning accuracy comparable to traditional Sequential Monte Carlo (SMC) Particle Filter algorithms. (4) System Nonlinearities: The hybrid scheme addresses nonlinearities in aircraft dynamics and terrain maps through appropriate methods. (5) Proposed Nonlinearity Measure: A composite terrain feature metric is presented to assess nonlinearity in the terrain elevation map, enabling the development of a Fuzzy Particle Filter that adjusts the number of particles accordingly.

The rest of the paper is organized as follows: Section 2 reviews recent TAN approaches based on non-linear estimation; Section 3 details the proposed hybrid methods; Section 4 presents simulation results; and Section 5 concludes the paper with future work directions.

2  Related Work

Terrain Reference Navigation (TRN) is a n technique that utilizes terrain features to assist vehicles, particularly in GPS-denied environments. It relies on comparing sensor derived terrain data with pre-stored maps to establish the vehicle’s precise location. The period from the last decade has seen significant advances in TRN technologies, with improvements in sensor accuracy, algorithmic processing, and real-world applications in both military and civilian domains. This literature review covers key developments in TRN, focusing on sensor technologies, algorithms, and integration with other navigation systems.

The roots of TRN lie in early algorithms such as TERrain COntour Matching (TERCOM) and Sandia Inertial Terrain Aided Navigation (SITAN). These algorithms, originally developed in the 1960s and 1970s, remain the foundation of modern TRN systems. Recent studies have focused on improving the computational efficiency of these methods and mitigating their limitations. While TERCOM excels in rapid terrain matching, it struggles with real-time processing, which is crucial for dynamic applications like aircraft navigation. SITAN, while faster and more flexible in real-time, is prone to errors when dealing with large initial position uncertainties or highly variable terrain gradients. These challenges have led to the development of hybrid systems that combine the strengths of both approaches. An innovative approach is highlighted in paper by [4], where the authors introduced a hybrid model that combines deep reinforcement learning with traditional navigation algorithms. The model dynamically adapts its decision making process based on real-time environmental feedback, enabling the UAV to optimize its path while avoiding obstacles. The results indicated a substantial improvement in navigation efficiency. Furthermore, paper in Reference [5] focused on the development of a terrain aware navigation system that leverages geographic information system (GIS) data to inform UAV flight paths. By integrating topographical data into the navigation algorithms, the UAVs were able to adjust their trajectories based on terrain characteristics, such as elevation changes and obstacle locations. This terrain aware strategy not only improved localization accuracy but also enhanced the UAV’s overall operational efficiency, particularly in challenging landscapes.

One of the major drivers of innovation in TRN has been the improvement of sensors. Traditional TRN systems relied heavily on radar altimeters-oriented nadir (directly beneath the vehicle) to collect terrain data. However, nadir-oriented sensors are limited by their narrow field of view, particularly when traversing flat or uniform terrains. To enhance the resilience and navigational capabilities of TRN systems that make use of low-grade Interferometric Radar Altimeters (IRAs), the study in [6] presents a novel particle filter. By combining the immune auxiliary particle filter and the ant colony algorithm, the new particle filter enables the immune system to distinguish between superior and inferior particles through a stochastic process. However, it was reported that the algorithm must possess a wide exploration capability to find a candidate terrain point to track over a large area in the searching mode. A modified terrain-referenced navigation (TRN) algorithm that takes slant range measurement into account is proposed in [7]. The TRN simulations demonstrate that the outcomes rely on the measurement’s angular accuracy as the flight altitude rises. It was found that the TRN results may differ if the flight altitude is too high and erroneous measurements are made since the EKF’s linearization assumption cannot be met. Also, the use of laser-based slant range TRN has also been demonstrated to improve navigation accuracy in complex terrains. The study in [8] investigates a different strategy for TRN that optimizes navigational information by using a gimbaled laser. Using a slant range TRN algorithm to steer a laser optimally can boost overall performance by three to four times. However, steerable Laser TRANs inability to take measurements in inclement weather is one of its few drawbacks. This suggests that steerable TRN might find use where weather disruptions are either nonexistent or have a negligible impact. Additionally, (IRAs) have been integrated into TRN systems to introduce high-resolution, three-dimensional terrain data into navigation algorithms, further improving TRN accuracy. Using IRA’s look angle calculation principle, the authors in [9] derived the “effective look angle” equation and put forth a formula that uses the aircraft’s velocity vector and the effective look angle to determine the relative location of the nearest terrain point. It was claimed that even in windy and high-altitude conditions, TRN performance degradation can be avoided with the suggested approach. Modern TRN technologies increasingly integrate vision-based and inertial navigation systems to enhance performance in GPSdenied environments. Vision-based TRN systems use cameras and computer vision algorithms to extract terrain features from real-time imagery, which is then compared to stored terrain maps. This approach complements radar and laser altimetry by providing visual cues that can help in environments where radar-based methods might fail, such as urban canyons or dense forests. The integration of inertial navigation systems (INS) with TRN has also proven effective. By combining INS with TRN, where the latter serves to correct positional errors over time, researchers have developed systems that are more robust and reliable in environments where GPS is unavailable. The authors in [10] presented the APTAN algorithm which can be utilized even in situations where a GNSS is not available or where it is impossible to assess the roughness of the terrain. Naturally, the error increases over time in scenarios where only pure navigation is carried out and neither the GNSS nor the TRN is available simultaneously.

One of the most prominent applications of TRN is in aerospace. In [11], the improvement of Batch TRN using Mean Removal and Two Step Search Method for the Lunar Lander was suggested. The Inertial Navigation System (INS) and TRN work together to operate a lunar navigation system that uses altimeters and LIDAR to achieve position accuracy for precise lunar landings. The batch process TRN correlation issue brought on by significant position error is significantly lessened by employing the Mean Removal Technique (MRT) method. However, the impacts of sensor noise and uneven terrain were not studied in this paper. TRN is also being applied in the defense sector for autonomous vehicles and unmanned aerial vehicles (UAVs). In these applications, TRN provides a reliable means of navigation in GPSdenied or jammed environments. For example, military UAVs can use TRN to navigate hostile terrain or conduct covert operations without relying on external satellite signals. Furthermore, autonomous ground vehicles are beginning to adopt TRN to enhance their capability in off-road environments, where GPS signals can be weak or unreliable due to natural obstructions like dense vegetation or mountainous terrain. Despite significant advancements, TRN still faces several challenges. One major issue is real-time processing, particularly in complex or rapidly changing environments. Although modern algorithms have improved processing speeds, ensuring that TRN systems can match terrain data to maps in real time remains a challenge for high-speed vehicles such as fighter jets or autonomous cars. Moreover, the reliance on pre-stored maps limits TRN’s effectiveness in environments where terrain data is unavailable or outdated.

Looking forward, researchers are exploring the use of machine learning and neuroinspired algorithms to improve terrain matching accuracy and reduce computational overhead. These approaches have the potential to enhance TRN systems’ ability to adapt to new environments and make real-time decisions with minimal human intervention. Additionally, advances in satellite imaging and remote sensing will likely improve the quality and availability of DEMs, making TRN more applicable in a broader range of environments.

3  The Proposed Method: System Description

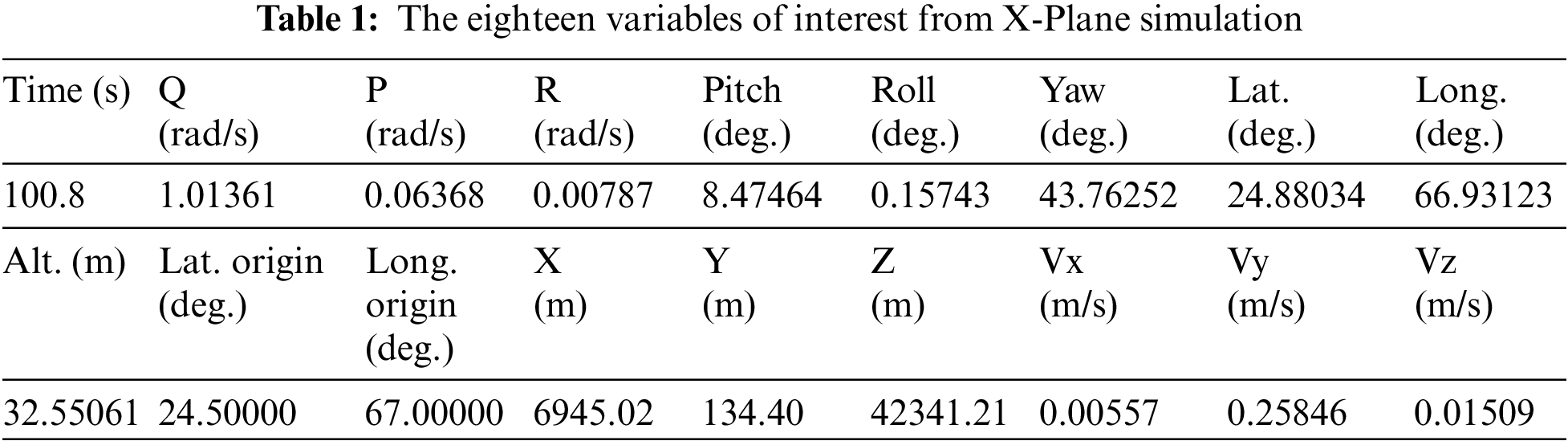
This paper presents two methods for estimating an aircraft’s position. The first method comprises four modules shown in Fig. 1: TERCOM for terrain matching, a Fuzzy Logic module for position prediction, a Particle Filter for estimating non-linear state variables, and an Extended Kalman Filter (ESKF) for height estimation. The Skywalker X8 model was designed using X-Plane software, chosen for its reliability and realism in simulated flight conditions. X-Plane offers features such as data sharing, flight data storage in standard text format, and User Datagram Protocol (UDP) transmission for real-time data access. Sensor data collected from X-Plane was processed in MATLAB, while Mission Planner defined the waypoints for the flight simulation. Table 1 lists eighteen variables generated during the simulation, which serve as inputs for the navigation scheme.

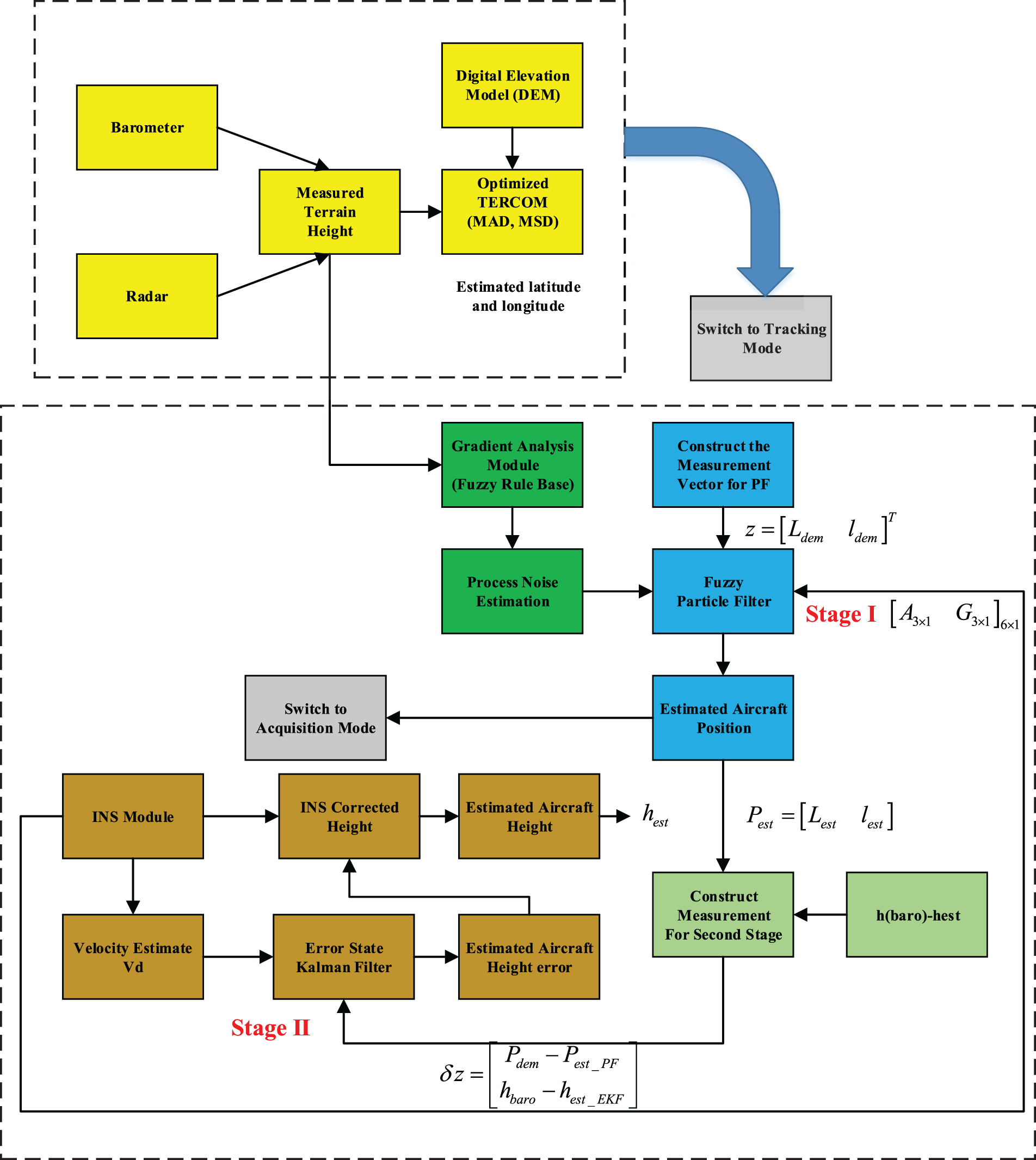
Figure 1: System block diagram

3.1 Terrain Feature Analysis

The terrain feature analysis was performed to construct the Fuzzy Rule Base for the design of the Fuzzy Particle Filter (PF) using the Digital Elevation Model (DEM) of the test region obtained from a specific reference. The terrain is mathematically modeled as a function z = F(x, y) mapping each point (x, y) in a planar domain to an elevation value, with the dataset from Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model (ASTER GDEM) selected for this study, having a resolution of 30 m. Spatial morphometric analysis of the DEM was conducted using MATLAB and Topo-Toolbox software to describe the main terrain features. The direction in which the gradient’s maximum value occurs is referred to as the aspect, and the gradient’s magnitude is referred to as the slope. There are various ways to define a DEM’s gradient [12]. However, the trigonometrical maximum downward gradient is typically taken. The following details pertain to the terrain slope and aspect parameters: Eq. (1) provides the magnitude of the first derivative of the surface function, which can be used to describe the slope of a surface F (x, y) as follows:

S=(∂F∂x)2+(∂F∂y)2(1)

Aspect is defined as the surface’s maximum gradient direction at a specific point. The computation of the aspect, like that of the slope, is done with the estimates of the partial derivatives, i.e., ∂z∂x, and ∂z∂y. This expression is used to obtain aspect:

Aspect=270−3602πatan(∂z∂x,∂z∂y)(2)

By using the raster algebra, to compute the vector mean of the aspect, the x and y direction cosines are calculated as follows:

Cosine(X)=sin(Aspect)(3)

Cosine(Y)=cos(Aspect)(4)

The sum of the direction cosines is then obtained and the final vector mean is computed with raster algebra as follows:

AspectVector=atan(∑Cosine(Y),∑Cosine(X))(5)

3.2 Curvature

The second numerical derivative of the DEM is returned by curvature. The curvature values depend on the plane along which the computations are made, just like the slope computations. Curvature measures can be classified into three main categories: (1) profile curvature, (2) plan curvature, and (3) tangential curvature.

3.3 The Proposed Composite Feature

The second suggested method for creating terrain composite features is one of this work’s main innovations. The four terrain features previously mentioned are combined to create a composite feature that we propose in this paper. The suggested composite terrain feature metric has the following mathematical description:

TFComposite=|Asp|2×[(slope)2+(curv)2zelev](6)

The following benefits are associated with the suggested composite terrain feature metric: (1) Using the combined terrain non-linearity data from multiple terrain morphometric features, it calculates the non-linearity of a terrain region. As a result, this function can be regarded as a “strong” function of non-linearity in the terrain. Thus, we will demonstrate this claim in more detail in the section on simulation results. Secondly, it saves storage space compared to keeping all four terrain feature matrices (slope, aspect, gradient, and curvature). It will be more effective to store a single composite feature in computer memory instead. Table 2 below displays the composite feature’s statistics.

3.4 Two Stage Position Estimation

3.4.1 Stage-I: Fuzzy Based PF Algorithm

The Bayesian Inference is a statistical technique that is applied by the particle filter (PF). This method uses the observations as a form of the probability density function (PDF) to estimate and update the unknown parameters. The PF processes the Bayesian update in a stepwise fashion as shown in Fig. 2.

Figure 2: The major steps in PF filtering method

The two primary stages of the PF are (1) the measurement update (the correction stage) and (2) the time update (i.e., the prediction state), which are similar to the various variations of the Kalman Filter based state estimation method. The PF algorithm’s recursion goes like this:

Time Update:

p(x(k+1)/Z)=∑i=1Nwkiδξi(x(k))(7)

where,

ξki∼p(x(k+1)/x(k)=ξki)(8)

Measurement Update: Obtain the measurement z(k), and calculate the new value of the state vector:

p(x(k)/Z)=∑i=1Nwkiδξk−ix(k)(9)

With the corrected weights:

wki=wk−ip(z(k)/x(k)=ξk−i)∑i=1Nwk−ip(z(k)/x(k)=ξk−)iandξki=ξk−i(10)

During the measurement update step, the particles with lower weights are eliminated to ensure that particle degeneration does not occur. The resampling stage provides the criterion for a sufficient number of particles, which is defined by Eq. (11).

Neffk=1∑i=1Nwki2ε[1,N](11)

The position from the DEM is used to adjust the aircraft’s position in the TAN-based UAV positioning application. The following are the models for the process and observation:

Process Model:

Xk=Xk−1+Vk−1T+Wk−1(12)

Observation Model:

zk=h(Xk)+rk(13)

The position and velocity vectors are represented by the variable “X” in Eq. (12). Eq. (13) contains the observation model. The parameter in Eq. (13), which also displays measurement errors from the barometer, radar altimeter, and digital elevation map, represents the non-linear function of the terrain elevation values at the position. To maximize the computational efficiency of the particle filter method, a two-stage fuzzy expert module (Fig. 3) was proposed to update the particle number in real-time for each iteration. The proposed Fuzzy Inference System (FIS) consists of two cascaded fuzzy logic modules. The first module, FIS-I, uses fuzzified information—specifically the gradient and gradient change rate derived from the extracted terrain features from the stored DEM—to estimate the process noise variable.

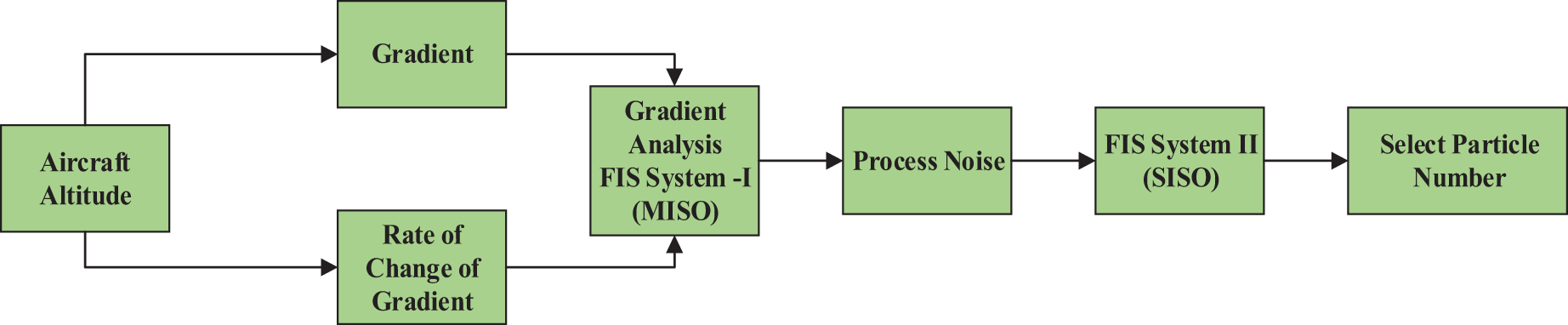
Figure 3: Proposed fuzzy logic module for updating particle number, the first approach

Based on the corresponding terrain height calculated from the TERCOM module, the values of the two features are determined. The following formula is used to calculate the terrain height measurement:

ht=hbaro−hradar(14)

The data pertaining to the process noise variable “σ” is utilized in the second FIS module to update the particle number “N.” First, the crisp inputs in a FIS system are fuzzified by using the membership functions (MFs) over the universe of discourse. Triangular MFs as shown in Fig. 4, are chosen in this work because they are resistant to stochastic noise factors [13]. The rule-base in the FIS expert system’s inference engine is used to determine the value of the output variable or variables. Center-of-Gravity (COG) scheme, is used to calculate the crisp value from the fuzzified output:

zCOG=∫zuA(z).zdz∫zuA(z).dz(15)

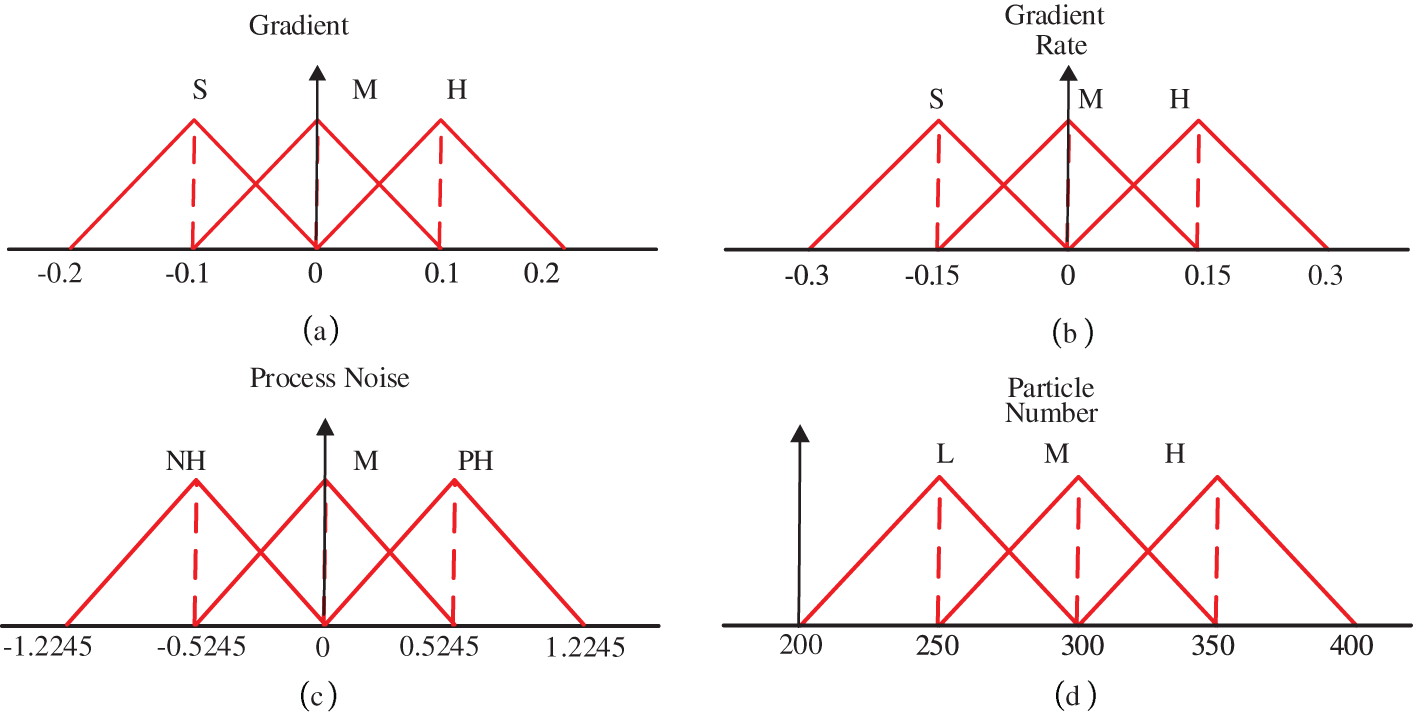
Figure 4: MFs for the input and output variables in FIS-I and FIS-II

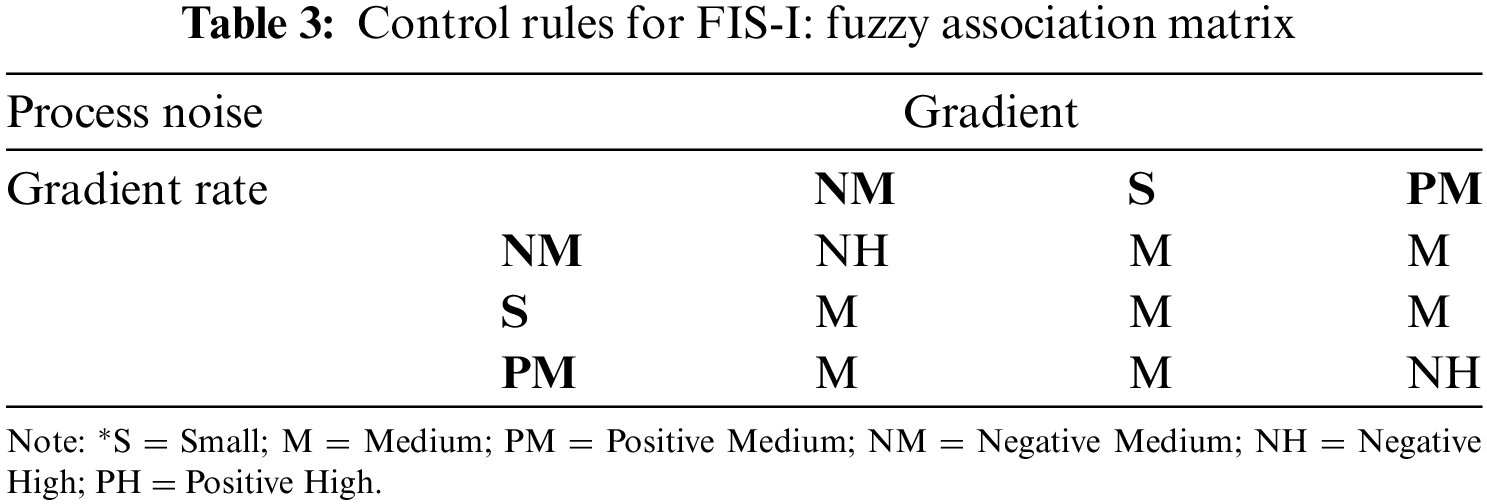
Based on the gradient and gradient-rate information, the following rules exist for process noise variation:

R1: If gradient is small and the gradient rate is small then process noise is Medium.

R2: If gradient is Negative Medium and the gradient rate is Negative Medium then set process noise Negative High.

The input subset is divided into three divisions for gradient and the gradient rate variables, i.e., G = {NM, S, PM}, and GR = {NM, S, PM}. The process noise output subset is also divided into three divisions, i.e., P = {NH, M, PH} and the output for FIS-II is divided into N = {L, M, H}. The rule tables for the two FIS modules are shown in Tables 3 and 4.

The Fuzzy Membership Functions (MFs) for the Input and Output variables in FIS-I and FIS-II are depicted in Fig. 4a–d. For implementing the MFs, triangular membership functions are selected due to their robustness against the noise factors.

3.4.2 Stage-II: Error State Kalman Filter

A variation of Kalman filter is used to estimate the aircraft height, the third state variable, in order to further minimize the computational time and effort of the PF. The aircraft height variable’s state can also be extremely non-linear, much like the aircraft’s latitude and longitude positions. In order to maintain the non-linearity of the height state variable, the ESKF is suggested as an alternative to the traditional linear Kalman Filter in the second stage of the estimation process. The ESKF is more realistic for non-linear systems, much like the EKF. Given that the EKF is susceptible to divergence problems, the ESKF emerges as a viable option for applications utilizing TERCOM technology. The error propagation for the aircraft positions can be obtained as follows by using the dynamic equations of the aircraft position and velocities. The reader is directed to and for a thorough analysis of the ESKF filter framework [14–16].

Application to TRN

The error equations for estimating the aircraft latitude, longitude and the height variable are given as follows:

δL˙=1Rm+hδVN+ρERm+hδh+ρERminRm+h(16)

δl˙=secLRt+hδVE(17)

δh=−δVD(18)

where Rm is the meridian radius of curvature, Rt is the transverse radius of curvature and ρE is the transport rate.

4  Simulation Results

In this section, the Fuzzy Particle Filter simulations are presented to evaluate the proposed design method based on two stage FIS approach to update particle number in real-time.

Test Case-I

The DEM with a resolution of 30 arc-seconds and a size of 1508 × 535 was utilized in the fuzzy particle filter’s implementation. The data on terrain elevation is obtained through the utilization of measurements obtained from the radar altimeter and barometer. FIS-I in the fuzzy particle filter, uses the two terrain features—(1) the gradient, or the slope, and (2) the rate of change of the gradient, which is computed from the corresponding DEM—as inputs to estimate the process noise variable, which is then fed as input to the second FIS, or FIS-II, in order to update the particle number (N) in real-time. The range of the process noise is [−1−1]. It was observed that the number of particles increases with an increase in process noise variation.

The GPS measurements for the aircraft positions were also taken from the X-Plane-based flight simulation in order to validate the suggested system. The estimated latitude and longitude positions of the aircraft are displayed in Fig. 5 along with the performance of the suggested Fuzzy PF system. The red color indicates the reference positions. The corresponding error plot between the estimated and reference positions is displayed in Fig. 6. The reference aircraft latitude and longitude positions are shown in Fig. 5.

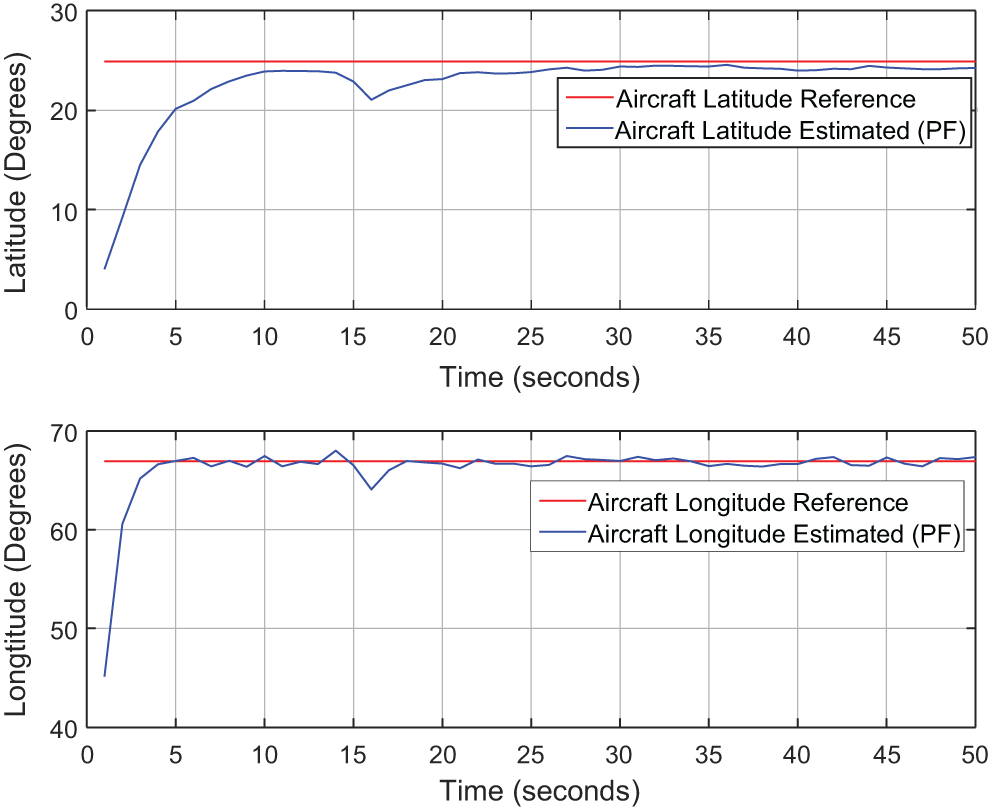
Figure 5: Estimated aircraft positions from fuzzy PF

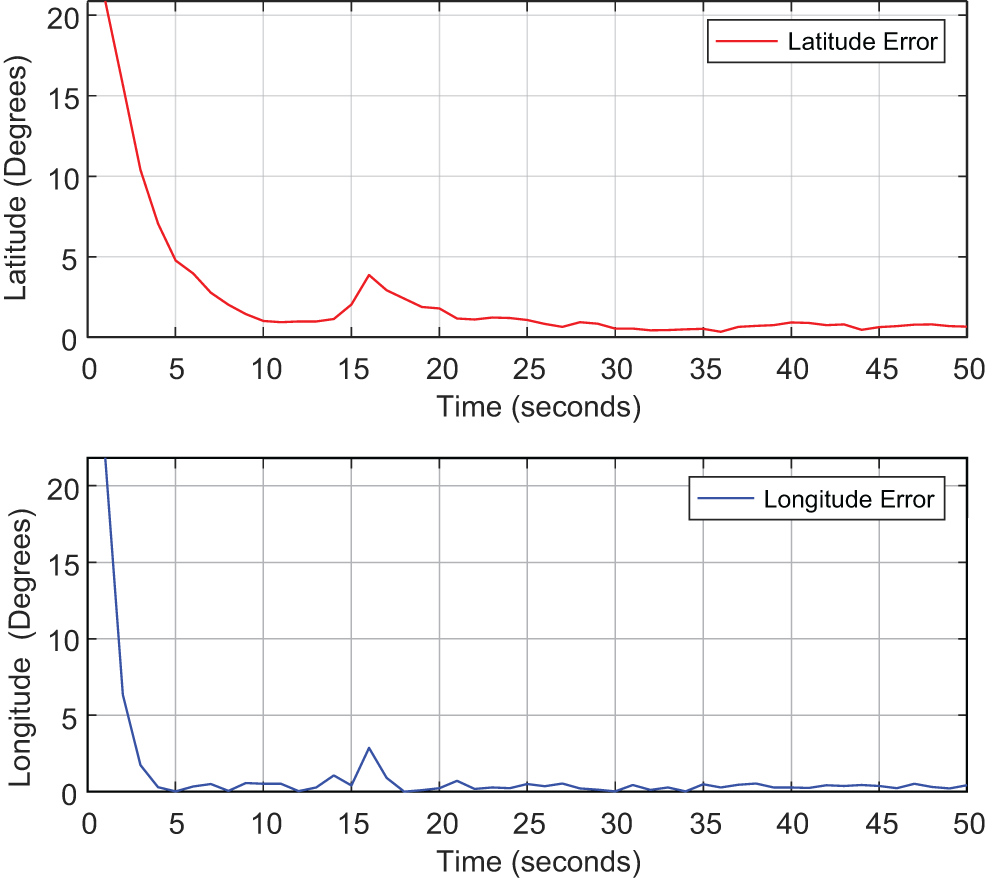
Figure 6: Latitude and longitude error plots

Table 5 displays the mean position errors for the latitude and longitude using the general particle filter and the suggested fuzzy PF. The range [200–400] was used to vary the particle count. In the PF’s resampling step, the effective threshold parameter was set to Neff = 210.

Using the same hardware, the computational time is calculated using the MATLAB tic-toc function. 100, 200, 300, and 1000 particles were used in the simulations to gauge how long it would take to calculate each state variable in PF. The range of the execution time is 2.0 to 15.0 s. It is evident that as the number of particles rises, so does the computational complexity of the PF (as shown in Fig. 7). Additionally, Fig. 8 compares the computational complexity of the two approaches. It is clear from the figure that the suggested Fuzzy Particle Filter performs significantly faster computationally than the generalized Particle Filter. Each calculation in Fuzzy PF has N particle iterations, which are determined by the expert judgment of the suggested Fuzzy Logic module. Unlike the Fuzzy PF, the Error State Kalman Filter (ESKF) was used to estimate the aircraft height variable. To preserve the non-linearity aspect of the aircraft height state variable and yield better estimation results compared to general KF, the ESKF filter is utilized in this paper instead of the conventional Linear KF. Figs. 9 and 10, respectively, show the estimated result for the aircraft height variable and the corresponding height error.

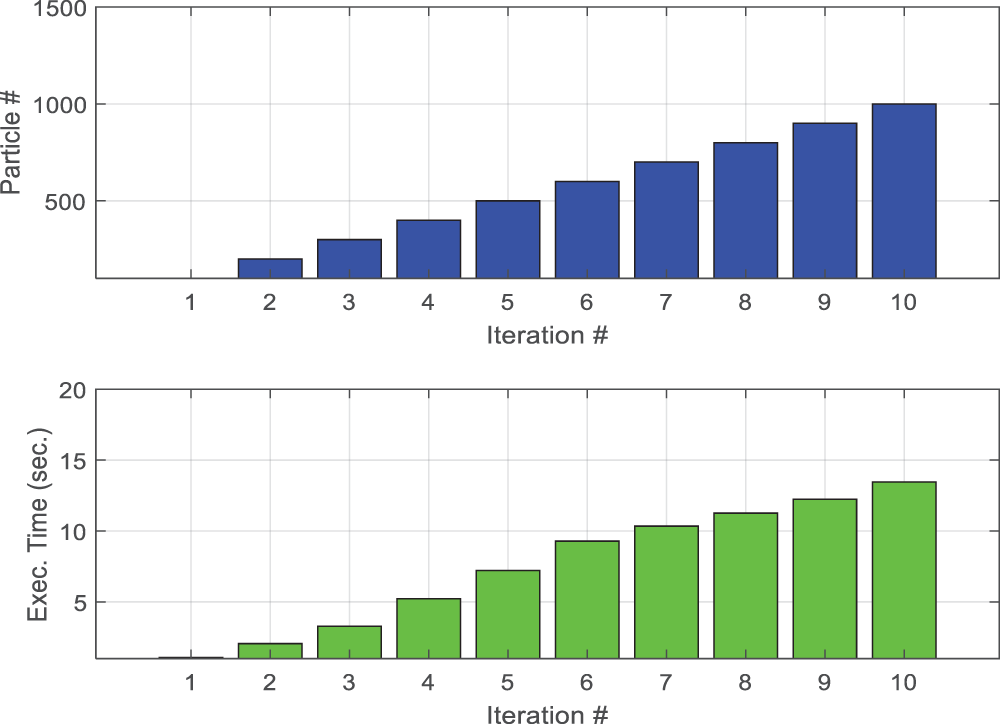
Figure 7: Computational time vs. number of particles

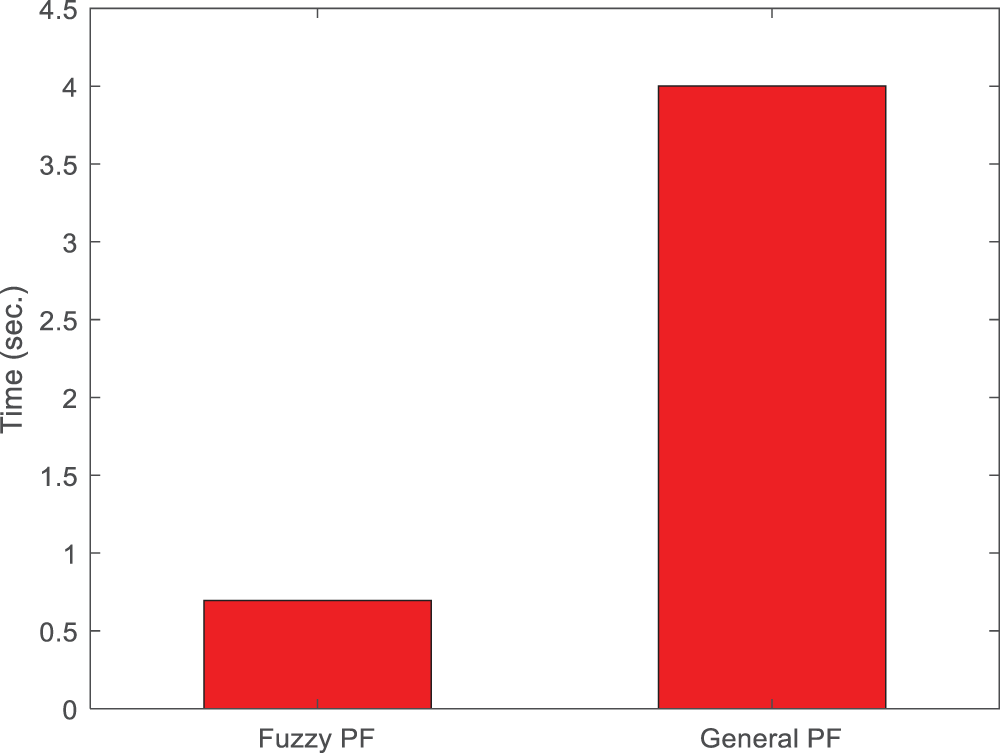
Figure 8: Computational speed: proposed fuzzy PF and the generalized PF

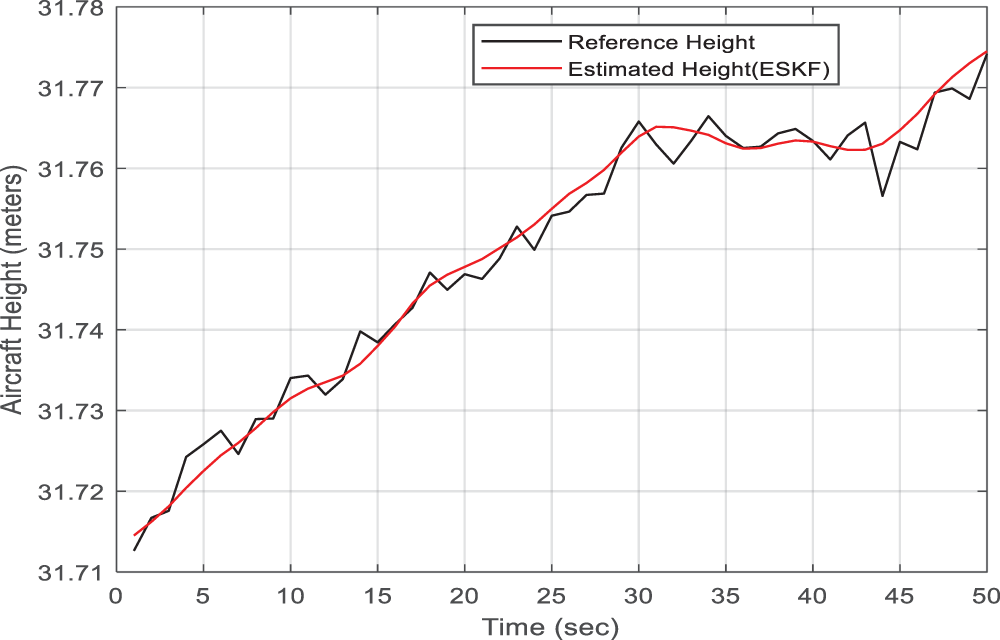
Figure 9: Estimated aircraft height (ESKF)

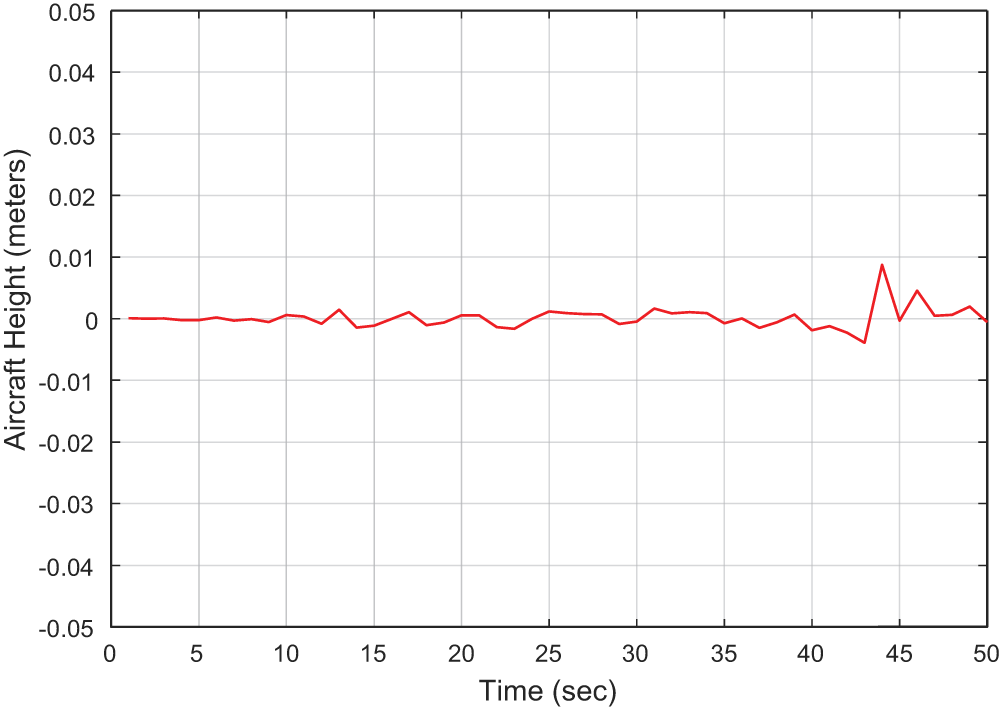
Figure 10: Height error

Test Case-II

Test case II was designed to assess the suggested TF composite method in order to gauge the scheme’s effectiveness. Compared to other DEM features like slope and curvatures, the method’s primary benefit was that it required less memory to store the TF composite fusion matrix alone. Secondly, it takes less time to execute in real time than the previously suggested plan that makes use of each terrain feature independently. The system’s block diagram is shown in Fig. 11.

Figure 11: Proposed TF composite method

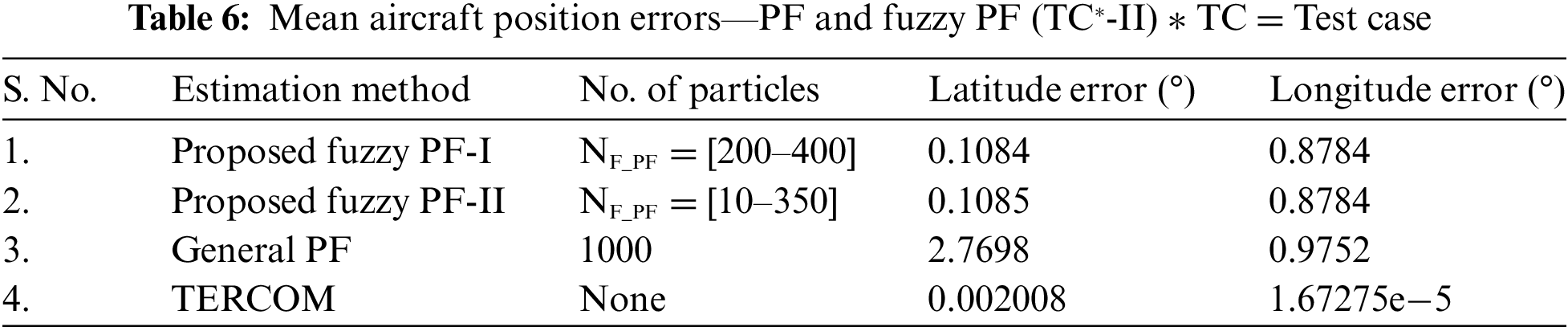
Figs. 12 and 13, respectively, display the membership functions for TF and Particle Number that vary adaptively in the PF algorithm. Fig. 14 displays the estimated positions for latitude and longitude. In Fig. 15, the corresponding errors are shown. The position obtained from the proposed method was validated using GPS based position that was captured during the flight test simulation with X-Plane software. The mean absolute errors between the obtained position and the actual position are reported in the following Table 6.

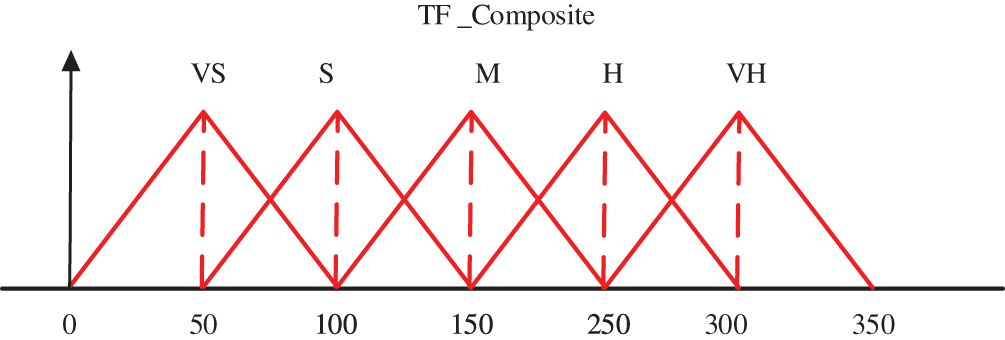
Figure 12: Fuzzy membership functions for proposed TF composite feature (Input)

Figure 13: Fuzzy membership functions for particle number, (Output) (Test-Case-II)

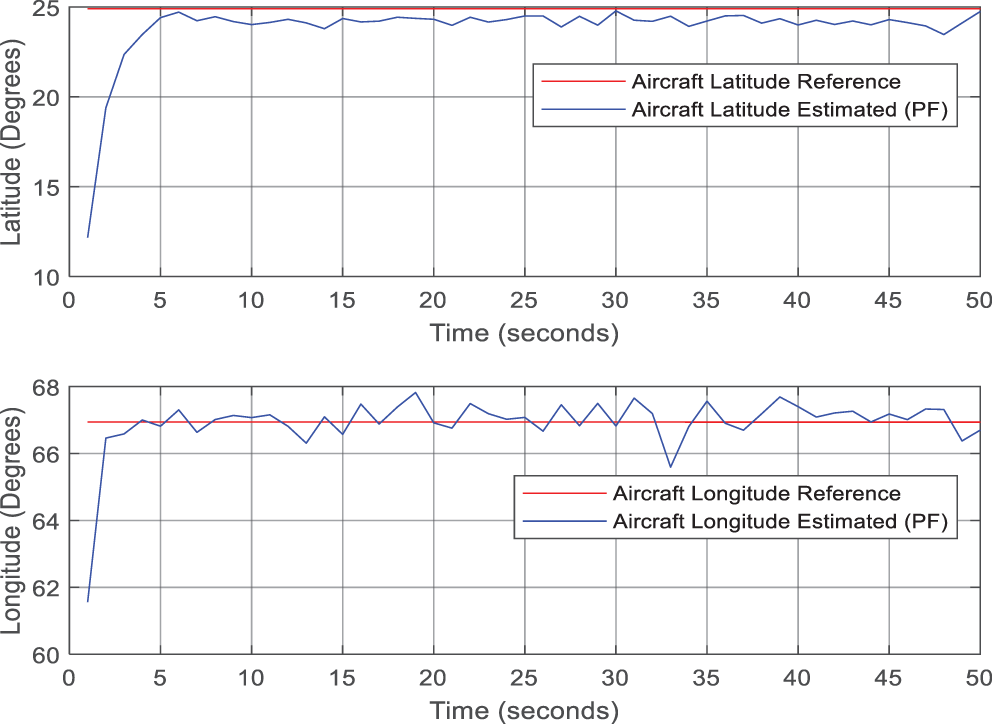
Figure 14: Aircraft latitude and longitude (Test-Case-II)

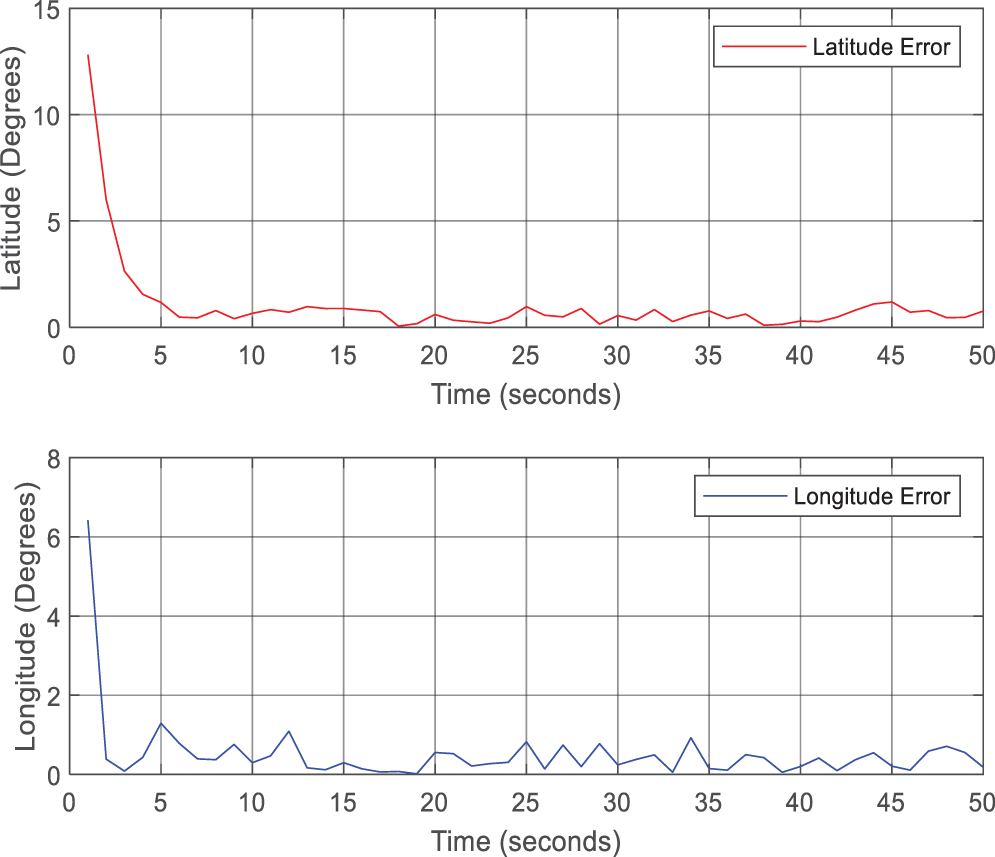
Figure 15: Aircraft latitude and longitude errors (Test-Case-II)

And the fuzzy rules for this system are crafted as follows:

IF TF_Composite is Low then Particle_Nmuber is Low

IF TF_Composite is Medium then Particle_Number is Medium

Another advantage of the second scheme is the computational efficiency; it requires lesser amount of time to produce the position estimate. Comparison is shown in Table 7 and Fig. 16.

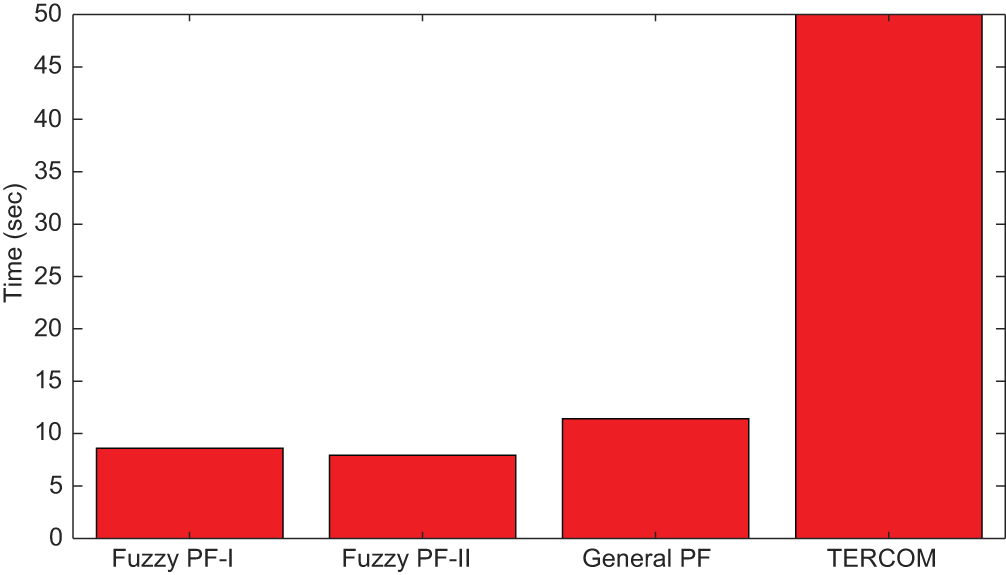
Figure 16: Computational speed: proposed fuzzy PF-I, II and the generalized PF

5  Discussion

The main objective of this study was to design and analyze a hybrid solution that integrates Fuzzy logic with Particle Filters (PF) to enhance position accuracy and computational efficiency in Terrain Reference Navigation (TRN). Various algorithms localize vehicles in TRN, including Particle Filters, Rao-Blackwellized Particle Filters (RBPF), TERCOM, and LSTM networks. Each method has limitations regarding accuracy and computational cost. Particle Filters can be computationally intensive, especially as the number of particles increases, which is challenging for real-time applications in resource-constrained systems like UAVs or submarines [17]. The accuracy of Particle Filters depends on a well-characterized noise model. Poorly defined noise in terrain data can lead to unreliable estimates, and the effectiveness of the filter is influenced by the terrain map’s resolution. Although, RBPF reduces the number of required particles, it remains computationally demanding, especially in high-dimensional state spaces. Its implementation involves partitioning the state space, which can be complex when vehicle motion or terrain interactions are intricate [18]. The TERCOM strategy relies on detailed terrain maps, and its performance decreases with outdated or inaccurate maps. It struggles in featureless terrains like deserts, where distinctive characteristics are minimal [19]. Additionally, deep learning methods such as LSTMs require extensive training data, which is often difficult to obtain. Their complex training process is computationally intensive, complicating real-time adaptation, and they are prone to overfitting issues [20]. In contrast, the proposed method in this study provides good accuracy in terms of mean absolute error while reducing computational costs compared to traditional Particle Filters. It is less complex than RBPF and does not require large training data like LSTM networks, offering acceptable position results even with low-resolution Digital Elevation Models (DEMs), making it advantageous over classical TERCOM.

6  Conclusion

Using a large number of particles in a particle filter typically enhances estimation performance but also significantly increases computational demands, which is a major drawback for real-time positioning applications such as Terrain Aided Navigation (TAN) on Unmanned Aerial Vehicles (UAVs). This paper introduces a hybrid two-stage TAN method designed to address this challenge by combining an Error State Kalman Filter (ESKF) estimator with a fuzzy logic-based Sequential Importance Resampling (SIR) particle filter. The proposed system features a two-stage fuzzy logic module that dynamically adjusts the particle count in real-time, reducing the computational burden associated with traditional particle filters. The study explored two distinct approaches:

1.    Test I: The fuzzy logic module utilized terrain features from the Digital Elevation Model (DEM) to generate appropriate process noise. Adjusting the number of particles based on process noise improved navigation accuracy.

2.    Test II: The module determined optimal values for non-linearity measure parameters, known as TF-Composite feature values. This approach not only enhanced accuracy but also further reduced computational load.

Experimental results showed that the proposed system significantly decreased computational costs while maintaining high tracking accuracy compared to conventional particle filtering methods. Particularly, Test II demonstrated increased computational efficiency, supporting the real-time implementation of the TAN algorithm. One major limitation of the proposed study is the unavailability of high quality (high resolution) DEMs that will further enhance the position accuracy of the algorithm. Another limitation is that in flat areas, the lack of gradient information of terrain results in bad localization accuracy.

Future research will concentrate on several key areas: (1) Validation with Real Flight Data: Testing the proposed system’s performance using actual flight data from aircraft to ensure its effectiveness in real-world scenarios. (2) Enhancing Particle Filtering: Investigating the Takagi-Sugeno Fuzzy Semantic Particle Filtering technique to improve particle diversity and address issues related to particle degradation in particle filters and (3) Adaptive Membership Functions: Exploring the use of adaptive membership functions in Fuzzy Expert Systems to further enhance the accuracy of the system’s estimations.

Acknowledgement: The authors would like to acknowledge the support of Prince Sultan University, Riyadh, Saudi Arabia for paying the Article Processing Charges (APC) of this publication.

Funding Statement: The authors would like to acknowledge the partial research grant provided by National Centre for GIS and Space Applications (NCGSA), Pakistan for the project titled “High Precision Location Identification for Multiple Applications Using Deep Neural Networks by Augmenting GPS with Terrain Knowledge” which enabled us to procure the hardware resources required for the project.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Muhammad Bilal Kadri; methodology, Muhammad Bilal Kadri and Sofia Yousuf; software, Muhammad Bilal Kadri and Sofia Yousuf; validation, Sofia Yousuf and Muhammad Bilal Kadri; formal analysis, Sofia Yousuf and Muhammad Bilal Kadri; investigation, Sofia Yousuf and Muhammad Bilal Kadri; resources, Muhammad Bilal Kadri; data curation, Sofia Yousuf; writing—original draft preparation, Sofia Yousuf; writing—review and editing, Muhammad Bilal Kadri; visualization, Sofia Yousuf and Muhammad Bilal Kadri; supervision, Muhammad Bilal Kadri; project administration, Muhammad Bilal Kadri; funding acquisition, Muhammad Bilal Kadri. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No datasets were used or generated during the current study.

Ethics Approval: No ethics approval was required for this work.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. R. Ali, R. Liu, Y. He, A. Nayyar, and B. Qureshi, “Systematic review of dynamic multi-object identification and localization: Techniques and technologies,” IEEE Access, vol. 9, pp. 122924–122950, 2021. doi: 10.1109/ACCESS.2021.3108775. [Google Scholar] [CrossRef]

2. R. Krishnamurthi, A. Kumar, D. Gopinathan, A. Nayyar, and B. Qureshi, “An overview of IoT sensor data processing, fusion, and analysis techniques,” Sensors, vol. 20, no. 21, 2020, Art. no. 6076. doi: 10.3390/s20216076. [Google Scholar] [PubMed] [CrossRef]

3. A. Bousbaine et al., “Design and implementation of a robust 6-DOF quadrotor controller based on kalman filter for position control,” in Mobile Robot: Motion Control and Path Planning. Cham: Springer International Publishing, 2023, pp. 331–363. [Google Scholar]

4. M. L. Jayaramu, H. N. Suresh, M. S. Bhaskar, D. Almakhles, S. Padmanaban and U. Subramaniam, “Real-time implementation of extended kalman filter observer with improved speed estimation for sensorless control,” IEEE Access, vol. 9, pp. 50452–50465, 2021. doi: 10.1109/ACCESS.2021.3069676. [Google Scholar] [CrossRef]

5. N. L. Schomer, “TerrainAware probabilistic search planning for unmanned aerial vehicles,” Masters thesis, Oregon State Univ., Corvallis, OR, USA, 2024. [Google Scholar]

6. S. Kang and M. J. Yu, “Antmutated immune particle filter design for terrain referenced navigation with interferometric radar altimeter,” Remote Sens., vol. 13, no. 11, 2021, Art. no. 2189. doi: 10.3390/rs13112189. [Google Scholar] [CrossRef]

7. H. C. Jeon, J. N. Lim, and C. G. Park, “Modified sequential processing terrain referenced navigation considering slant range measurement,” IET Radar Sonar Nav., vol. 12, no. 11, pp. 1208–1216, 2018. doi: 10.1049/iet-rsn.2018.5170. [Google Scholar] [CrossRef]

8. J. D. Carroll and A. J. Canciani, “Terrain-referenced navigation using a steerable-laser measurement sensor,” Navigation, vol. 68, no. 1, pp. 115–134, 2021. doi: 10.1002/navi.406. [Google Scholar] [CrossRef]

9. J. Oh, C. K. Sung, J. Lee, S. W. Lee, S. J. Lee and M. J. Yu, “Accurate measurement calculation method for interferometric radar altimeterbased terrain referenced navigation,” Sensors, vol. 19, no. 7, 2019, Art. no. 1688. doi: 10.3390/s19071688. [Google Scholar] [PubMed] [CrossRef]

10. J. Lee, C. K. Sung, J. Oh, K. Han, S. Lee and M. J. Yu, “A pragmatic approach to the design of advanced precision terrainaided navigation for UAVs and its verification,” Remote Sens., vol. 12, no. 9, 2020, Art. no. 1396. doi: 10.3390/rs12091396. [Google Scholar] [CrossRef]

11. P. M. Ku, Y. B. Park, and C. G. Park, “Improvement of batch TRN using mean removal and two step search method for lunar lander,” in 2015 10th Asian Control Conf. (ASCC), IEEE, 2015, pp. 1–6. [Google Scholar]

12. M. Kim, J. Ben-Othman, and H. Kim, “Reconfigurable UAV-aided 3D sustainable surveillance in classified air-spaces,” Veh. Commun., vol. 45, no. 13, 2024, Art. no. 100728. doi: 10.1016/j.vehcom.2024.100728. [Google Scholar] [CrossRef]

13. Y. Kim, K. Hong, and H. Bang, “Utilizing out-of-sequence measurement for ambiguous update in particle filtering,” IEEE Trans. Aerosp. Electron. Syst., vol. 54, no. 1, pp. 493–501, 2017. doi: 10.1109/TAES.2017.2741878. [Google Scholar] [CrossRef]

14. D. Peng, T. Zhou, J. Folkesson, and C. Xu, “Robust particle filter based on Huber function for underwater terrain-aided navigation,” IET Radar Sonar Nav., vol. 13, no. 11, pp. 1867–1875, 2019. doi: 10.1049/iet-rsn.2019.0123. [Google Scholar] [CrossRef]

15. S. Yousuf and M. B. Kadri, “Sensor fusion of INS, odometer and GPS for robot localization,” in 2016 IEEE Conf. Syst., Process Control (ICSPC), IEEE, Dec. 2016, pp. 118–123. [Google Scholar]

16. S. Yousuf and M. B. Kadri, “Information fusion of GPS, INS and odometer sensors for improving localization accuracy of mobile robots in indoor and outdoor applications,” Robotica, vol. 39, no. 2, pp. 250–276, 2021. doi: 10.1017/S0263574720000351. [Google Scholar] [CrossRef]

17. M. Teng et al., “An AUV localization and path planning algorithm for terrain-aided navigation,” ISA Trans., vol. 103, no. 1, pp. 215–227, 2020. doi: 10.1016/j.isatra.2020.04.007. [Google Scholar] [PubMed] [CrossRef]

18. J. Zhang, T. Zhang, and S. Liu, “An outlier-robust Rao-Blackwellized particle filter for underwater terrain-aided navigation,” Ocean Eng., vol. 288, 2023, Art. no. 116006. doi: 10.1016/j.oceaneng.2023.116006. [Google Scholar] [CrossRef]

19. L. A. Catalano, Z. Hu, and H. E. Sevil, “Modeling and analysis of meteorological contour matching with remote sensor data for navigation,” Automation, vol. 3, no. 2, pp. 302–314, 2022. doi: 10.3390/automation3020016. [Google Scholar] [CrossRef]

20. S. Lee and H. Bang, “Terrain contour matching with recurrent neural networks,” in 2018 IEEE Aerosp. Conf., IEEE, 2018, pp. 1–9. [Google Scholar]