 Open Access
Open Access
ARTICLE
Coordinate Descent K-means Algorithm Based on Split-Merge
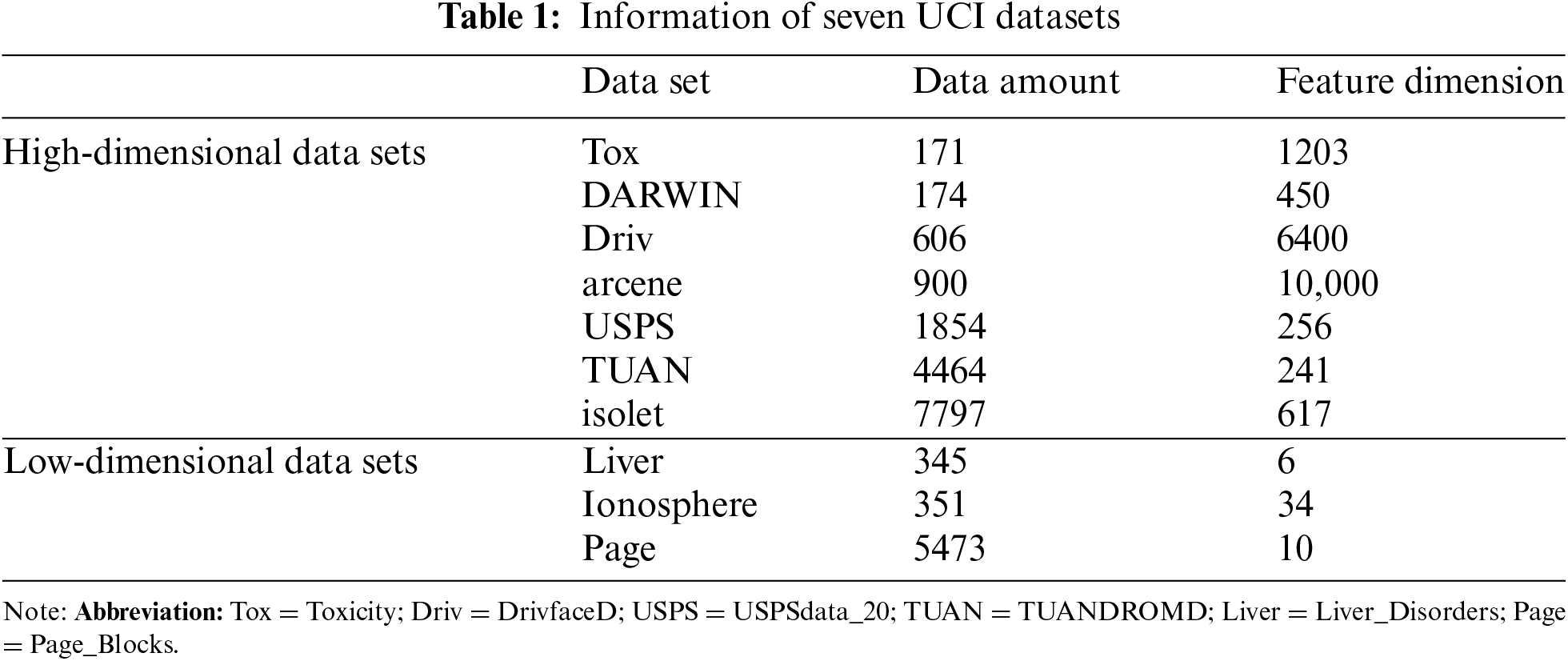
1 College of Computer Science and Technology, Changchun University of Science and Technology, Changchun, 130022, China
2 College of Computer Science and Technology, Jilin Agricultural University, Changchun, 130118, China
* Corresponding Author: Yong Yang. Email:
(This article belongs to the Special Issue: Artificial Intelligence Algorithms and Applications)
Computers, Materials & Continua 2024, 81(3), 4875-4893. https://doi.org/10.32604/cmc.2024.060090
Received 23 October 2024; Accepted 20 November 2024; Issue published 19 December 2024
Abstract
The Coordinate Descent Method for K-means (CDKM) is an improved algorithm of K-means. It identifies better locally optimal solutions than the original K-means algorithm. That is, it achieves solutions that yield smaller objective function values than the K-means algorithm. However, CDKM is sensitive to initialization, which makes the K-means objective function values not small enough. Since selecting suitable initial centers is not always possible, this paper proposes a novel algorithm by modifying the process of CDKM. The proposed algorithm first obtains the partition matrix by CDKM and then optimizes the partition matrix by designing the split-merge criterion to reduce the objective function value further. The split-merge criterion can minimize the objective function value as much as possible while ensuring that the number of clusters remains unchanged. The algorithm avoids the distance calculation in the traditional K-means algorithm because all the operations are completed only using the partition matrix. Experiments on ten UCI datasets show that the solution accuracy of the proposed algorithm, measured by the E value, is improved by 11.29% compared with CDKM and retains its efficiency advantage for the high dimensional datasets. The proposed algorithm can find a better locally optimal solution in comparison to other tested K-means improved algorithms in less run time.Keywords
Clustering is an unsupervised machine-learning method [1] that does not depend on data labels. It has a wide range of applications in many fields [2], such as image segmentation [3], target recognition [4] and feature extraction [5]. Among these applications, the K-means algorithm is one of the most commonly used clustering algorithms due to its simplicity and interpretability [6,7].
The K-means clustering problem is a non-deterministic polynomial-time hardness (NP-hard) problem [8]. The traditional K-means clustering algorithm is a greedy algorithm used to optimize the K-means clustering model. However, its sensitivity to the choice of the initial centroids leads to its tendency to fall into local optimal solutions.
To address this problem, researchers have proposed many improved methods [9−10] for enhancing the solution accuracy1 of the K-means clustering algorithm. Gul et al. proposed the R-K-means algorithm, which uses a two-step process to find the initialization centroids, making the K-means algorithm effective in solution accuracy on large-scale high dimensional datasets [11]. Biswas et al. used the computational geometry for cluster center initialization to make cluster centers uniformly distributed [12]. Layeb et al. proposed two deterministic initialization methods for K-means clustering based on modified crowding distances, which are capable of selecting more uniform initial centers based on the modified crowding distances [13]. Arthur et al. proposed the K-means++ algorithm, which is based on a random seeding technique to make the initialization centroids as dispersed as possible [14]. Lattanzi et al. improved K-means++ by adding a new local search strategy to it, which can optimize the location of the center of bad clusters [15]. Şenol proposed a method to find the optimal initial centers using kernel density estimation so that the initial centroids are distributed in regions with a high density of data points [16]. Reddy et al. selected the initial cluster centers by constructing a Voronoi diagram using the data points, which reduces the problem of the K-means algorithm’s overdependence on initial centroids and improves the convergence time of the subsequent K-means algorithm [17].
In addition to the above methods, a large number of improvements for initialization have been proposed in the literature [18]. The final result of K-means clustering is determined by initialization and iteration. Iteration and initialization are similar. They can both make improvements to the solution accuracy. However, there is little research on iterative processes. Recently, Nie et al. improved the iterative process of the K-means algorithm. They rewrote the objective function of K-means and introduced the Coordinate Descent Method [19,20] to optimize the K-means clustering model. This new algorithm is called the Coordinate Descent Method for K-means (CDKM) algorithm. Experimental results show that under the same initialization conditions, the CDKM algorithm has a more significant improvement in solution accuracy than the K-means algorithm and runs more efficiently on high dimensional datasets [21].
Although CDKM is able to find smaller local optimal solutions than K-means, CDKM is still sensitive to initialization. There is a large room for improvement in the solution accuracy of CDKM. Since selecting the appropriate initial center is not always feasible [21], we attempt to improve its iterative process. Specifically, we introduce the split-merge criterion into CDKM. The split-merge criterion was proposed by Kaukoranta et al. in the iterative split-and-merge algorithm in 1998 [22]. The iterative split-and-merge algorithm aims to optimize codebook generation by utilizing the split-merge criterion. The split-merge criterion is also an excellent operation that can significantly enhance the solution accuracy of K-means. Based on the split-and-merge criterion, many improved algorithms have been proposed, such as the iterative split-and-merge algorithm [22], split algorithm [23], random swap algorithm [24] and I-K-means-+ algorithms [25]. However, the split-merge criterion primarily operates under the original K-means objective function, which may not apply to the CDKM objective function. One of the key strengths of CDKM is its efficiency in high dimensional data. This efficiency arises from its objective function, which eliminates the need for distance calculations during the search process. This feature is not typically available in traditional K-means algorithms and its improved algorithms, such as the algorithms mentioned above [11−14] and the split-merge algorithm [22−25] analyzed earlier.
The challenge is how to apply the split-merge criterion based on the original K-means objective function to the CDKM algorithm, which is based on the CDKM objective function. We propose a Coordinate Descending method for K-means algorithm based on Split-Merge (CDKMSM) algorithm from the perspective of improving the iterative process of CDKM. First, an existing algorithm based on split-merge criterion, specifically, the I-K-means+ algorithm, is modified with the aim of obtaining an excellent solution. Then, the proposed split-merge criterion is converted into a partition matrix operation to make it applicable to the CDKM clustering model. In order to retain the efficiency advantage of the original CDKM under high dimensional data, the proposed algorithm avoids distance computation, and its computation process can be accomplished only by using the partition matrix.
Suppose
where,
where,
The clustering model of K-means can be described as a minimization problem is shown as follows:
CDKM rewrites the K-means clustering problem as Eq. (5) by using the partition matrix.
In Eq. (5),
In order to reduce the amount of calculation, CDKM defines
where,
According to the coordinate descent method and the property of the partition matrix
The variables that need to be updated after the i-th row of
Note: The CDKM method presents new formulas to modify the objective function and replace the original K-means iterative process with a coordinate descent method. These formulas clarify the improvement process and detail the iterative method used in the newly proposed algorithm (Algorithm 1). This paper includes the objective function and iterative process of CDKM, which is why the formulas are presented.

2.2 The Problems of CDKM Algorithm
When the initial center position is not ideal (as shown in the left part of Fig. 1), the initial centers in different regions may be too few or too many. As shown in the right part of Fig. 1, there may be a local optimum problem after CDKM clustering. The datasets in the clusters are too sparse after clustering in regions with too few centers, and the datasets in the clusters are too dense after clustering in regions with too many centers. The division of these clusters is not accurate enough, which leads to the solution accuracy needing to be improved.
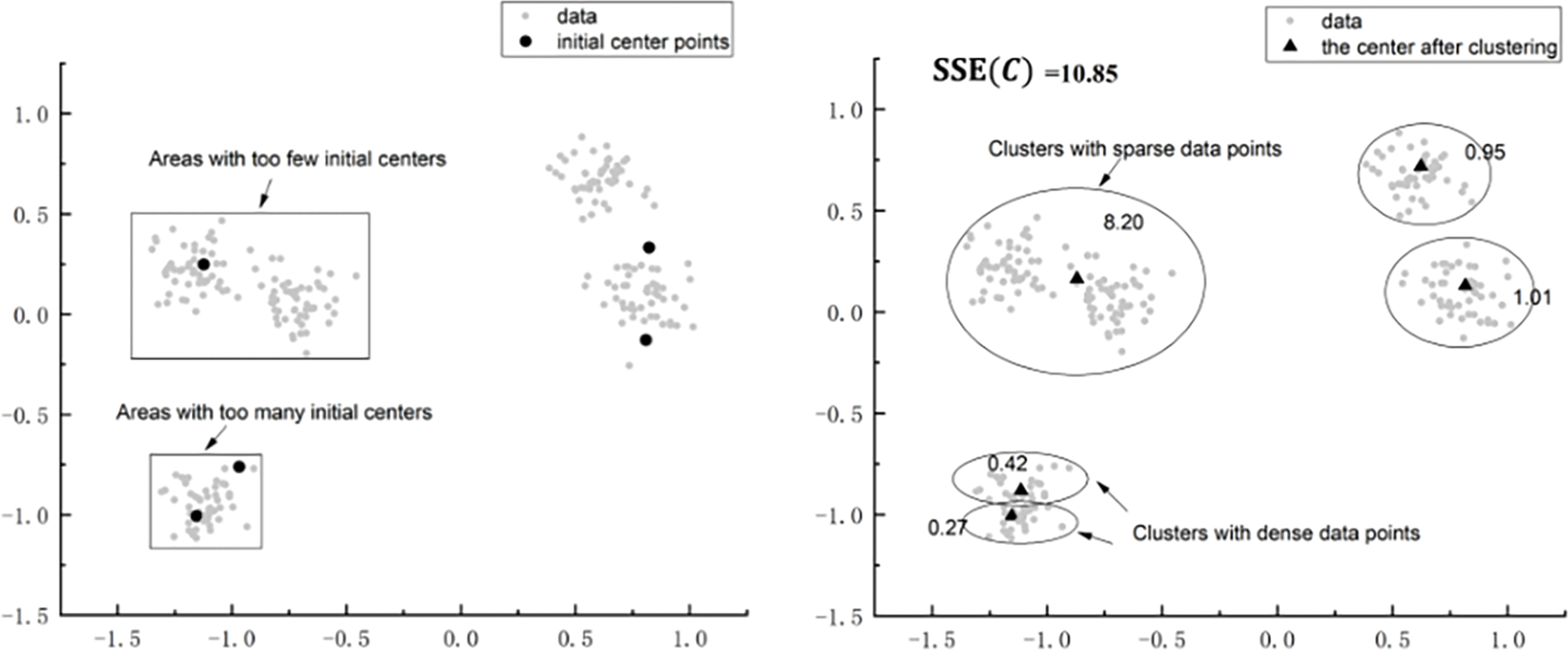
Figure 1: The left part is initial center distribution. The right part is the division of datasets after CDKM clustering
3 Design of Coordinate Descent K-Means Algorithm Based on Split-Merge
For the problem described in Section 2.2, in order to improve the solution accuracy of the CDKM algorithm, we introduce the split-merge criterion and transform it to apply to the clustering model of CDKM. Split-merge criterion has already been introduced in the iterative split-and-merge algorithm in 1998 [22]. The iterative split-and-merge algorithm begins with an initial codebook and enhances it through merge and split operations. Merging small neighboring clusters frees up additional code vectors, which can then be reallocated by splitting larger clusters. We introduce the split-merge criterion for the traditional K-means algorithm in Section 3.1. In Section 3.2, we analyze the shortcomings of the split-merge criterion for the traditional K-means algorithm and introduce the modified method in this paper. Since the split-merge criterion for the traditional K-means and the modified criterion we proposed in Section 3.2 are used to optimize the objective function value
3.1 Split-Merge Criterion for the Traditional K-Means Algorithm
The idea of split-merge criterion has been used to improve K-means, resulting in many proposed algorithms [22−25]. These algorithms generally share a common approach, utilizing split-merge criterion to enhance the original K-means algorithm. In this paper, we build upon one of the more recent split-merge criterion algorithms, specifically the I-K-means-+ algorithm proposed in 2018. It improves the K-means’ solution accuracy by merging two clusters, splitting another cluster, and regrouping in each iteration, which is capable of gradually approaching the global optimal solution. The cluster
where,
3.2 Split-Merge Criterion in This Paper
Since the calculation of the gain value of the I-K-means-+ algorithm (Eq. (11)) is an approximate calculation method, it may produce a misclassification when splitting and merging. So in this paper, the split-merge criterion of the I-K-means-+ algorithm is modified in the expectation of obtaining a solution with higher solution accuracy. We have changed the method of calculating the gain to an exact one, and also improved the method of calculating the cost of the I-K-means-+ algorithm.
The merging strategy in this paper aims to find two clusters that are close to each other, which are too densely populated with datasets, and merge them to minimize the cost is shown as follows [22]:
where,

Figure 2: The left part is the division results corresponding to the original solution
The objective of the splitting criterion presented in this paper is to identify clusters characterized by sparse datasets. Upon splitting such a cluster into two distinct clusters, a significant reduction in the SSE value is observed. Eq. (13) is employed in this study to facilitate an accurate calculation of the gain resulting from splitting [22].
where,
The advantage of this split-merge criterion is that it avoids too dense or sparse division of clusters and improves the solution accuracy.
3.3 Split-Merge Criterion for CDKM Model Optimization
Section 3.2 introduces the improved split-merge criterion, however, this criterion is based on the original K-means model, which is not directly applicable to the CDKM model since the form of the solution and the objective function value of the CDKM are different from the original K-means. Moreover, this criterion needs to adjust the existing centers and redistribute the data points for the split-merge operation, which involves more distance calculations, and the more the centers change, the more the data points need to be calculated, and the higher the time complexity, especially in the high-dimensional dataset, which is even more prominent. To address the above problems, this paper uses the partition matrix to design a new split-merge criterion to make it applicable to the CDKM model and reduce the time complexity at the same time.
1) Merging operation
We perform the merging operation by integrating the two columns of the partition matrix. The split-merge criterion in the previous section used the objective function values of the K-means algorithm for calculating the cost gain, which is modified here to use the CDKM form of the objective function values. The values of the objective function before and after merging are calculated using Eqs. (14) and (15), respectively, and the cost after merging is calculated as clusters using Eq. (16). Where,

Figure 3: Use membership matrix to merge two clusters
2) Splitting operation
First, the gain of each cluster is calculated. Then, the cluster splitting operation is accomplished by splitting the columns of the partition matrix. The specific method is as follows. For each cluster

Figure 4: Using partition matrix to split clusters
The following describes the method of splitting the cluster with the largest gain, i.e., column

Figure 5: Using partition matrix to split clusters
Algorithm 2 is the proposed algorithm in this paper. The following steps provide a clear representation of the algorithm’s workflow, illustrating how it progresses from start to finish. This includes performing the CDKM, followed by the split-merge criterion, and concludes with the final completion of the algorithm.

3.5 Computational Complexity Analysis
Our proposed algorithm is mainly composed of four parts. Let
4.1 Experimental Environment and Experimental Dataset
The hardware experimental platform for all the algorithms used Intel (R) Core (TM) i7-9750H CPU @ 2.60 GHz processor. The results of the split algorithm and random swap algorithm were obtained from the C++ software available at https://cs.uef.fi/ml/software/(data=May.26.2010) (accessed on 19 November 2024), and they were executed in Linux environment. The other algorithms’ codes are written in C++. They were executed in Windows environment. Ten sets of UCI (The University of California, lrvine) data sets are selected in the experiment, which can be downloaded from https://archive.ics.uci.edu/(data=September.30.1985) (accessed on 19 November 2024). The specific data set information is shown in Table 1.
In order to objectively evaluate the clustering performance of each algorithm, the evaluation index adopted in this paper is SSE, and the SSE value of each algorithm is calculated by Eq. (1) and compared. For the algorithms that rewrite the objective function, including CDKM and CDKMSM, we run the algorithm to get its solution first, and then calculate the SSE value of the corresponding K-means model objective function based on this solution.
The experiment compares the results of K-means algorithm (KM), CDKM algorithm [21], split algorithm [23], Random Swap algorithm (RS) [24], I-K-means-+ algorithm (IKM) [25], K-means with new formulation algorithm (KWNF) [26] and CDKMSM algorithm. The K-means algorithm is the original clustering algorithm. The split algorithm is an original algorithm based on splitting. Random swap algorithm is an excellent variant based on the split-merge criterion. The I-K-means-+ algorithm is a modified K-means algorithm based on split-merge criterion. CDKM is a new algorithm that incorporates the coordinate descent method into the iterative process of K-means clustering. CDKM is the algorithm that is to be improved in this paper. The KWNF algorithm is a recent and effective improvement of the K-means algorithm.
In order to verify the effect of the algorithm with different numbers of clusters k, five different values of k are chosen in this paper: 4, 6, 8, 10 and 12, and the corresponding clustering results are counted. For each value of k for each data set, all algorithms run within 50 random times and the results are averaged for comparison. For each algorithm, we used randomized initialization of the centers.
The SSE value is affected by various aspects such as the dataset scale and the dataset size dimension, resulting in large differences in the SSE value for different datasets and k values. By defining a variable to represent the relationship between the SSE values of two algorithms, we can directly compare their clustering performance. It allows us to quantify the difference in performance between the two algorithms. Therefore, in addition to the SSE value (shown in Eq. (1)), we define the following E value, which measures the relative degree of improvement in the solution accuracy of a certain algorithm, named here as “alg1”, with respect to another algorithm “alg2”.
where,
By defining a variable that represents the relationship between the time values of the two algorithms, we can directly compare their clustering performance. This variable serves as a quantitative measure that encapsulates both the execution time and the effectiveness of the clustering results produced by each algorithm. The index for the time of the algorithm we measured by the following T value, which quantifies the percentage speedup of the running time
The SSE results are shown in Table 2, with the optimal and sub-optimal results shown bolded as well as skewed, respectively. The E value of the remaining algorithms as measured against the solution accuracy of the K-means algorithm is shown in Table 3.
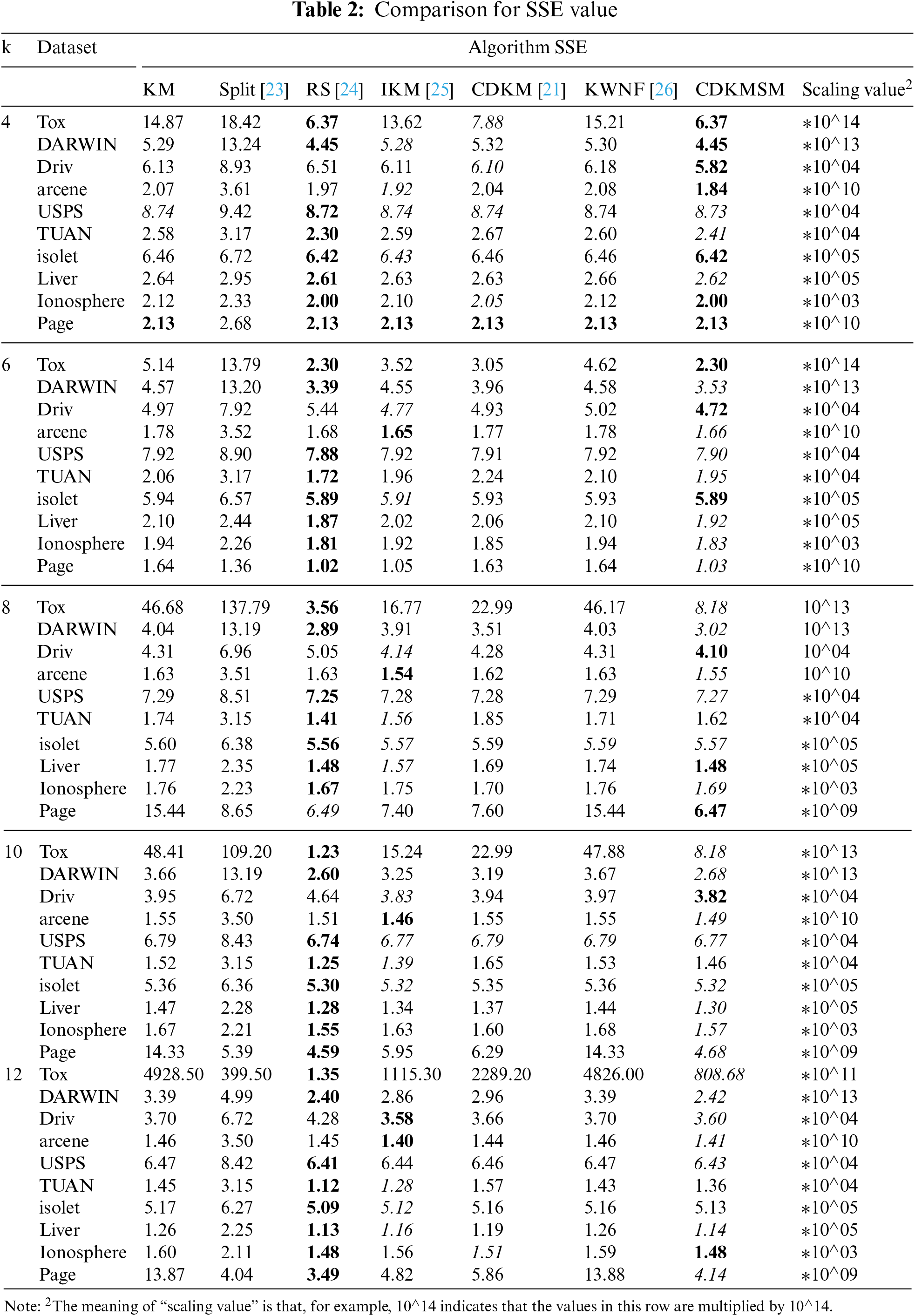
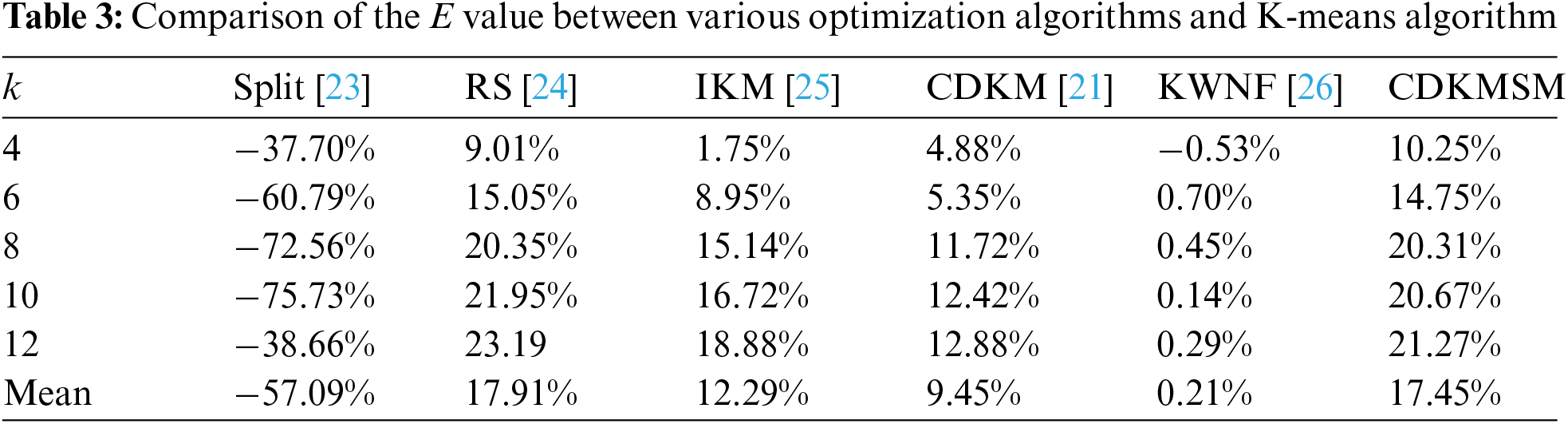
In Table 2, as the number of clusters increases, the sum of squared errors (SSE) typically decreases because more clusters can better capture the data characteristics, resulting in a reduced distance between data points and their cluster centers. Fig. 6 represents the comparison of the E value between each optimization algorithm and the K-means algorithm. Due to the relatively lower solution accuracy of the split algorithm compared to the other algorithms, it was not included in the comparison in Fig. 6. The E value of the CDKM algorithm is 9.45%, the E value of split algorithm, I-K-means-+ algorithm, and KWNF algorithm are −57.09%, 12.29%, and 0.21%, respectively, the E value of the proposed algorithm is 17.45%. The E value of the proposed algorithm is 11.29% with respect to the CDKM algorithm, 35.61%, 7.87%, and 17.39% with respect to the split algorithm, I-K-means-+algorithm, and KWNF algorithm, respectively. As the number of clusters increases, the E value of the proposed algorithm compared to the K-means algorithm gradually increases, indicating that the improvement in the SSE relative to K-means and other tested algorithms apart from the random swap algorithm becomes more and more significant. The solution accuracy of the proposed algorithm has achieved an improvement over the K-means algorithm and other tested K-means optimization algorithms apart from the random swap algorithm. Compared to the K-means algorithm, the E value of the random swap algorithm is 17.91%, which is slightly higher than the E value of the proposed algorithm, which is 17.45%.

Figure 6: Comparison of the E value between each optimization algorithm and K-means algorithm
The runtime results of the algorithm are shown in Table 4 with the optimal and sub-optimal results shown bolded as well as skewed, respectively. Since the split and random swap algorithms were run on Linux system, we did not compare their execution time. As the number of clusters increases, the time gradually increases. Fig. 7 represents the percentage speedup of our proposed algorithm with other algorithms, for the higher dimensional datasets (first seven datasets) at k = 4, 6, 8, 10, 12. The T values of our proposed algorithm compared to another split-merge based K-means improved algorithm I-K-means-+ algorithm are 9.16%, 32.69%, 44.65%, and 50.96%, respectively, 50.51%. Compared to the I-K-means-+ algorithm, the algorithm in this paper operates more efficiently as the value of k increases. Comparing the T value with K-means algorithm and K-means with new formulation algorithm is 11.60% and 89.23%, respectively. As the number of clusters increases, the T value of the proposed algorithm compared to other tested algorithms becomes increasingly larger. It can be concluded that the proposed algorithm still maintains the efficiency advantage of CDKM algorithm in high dimensional data.
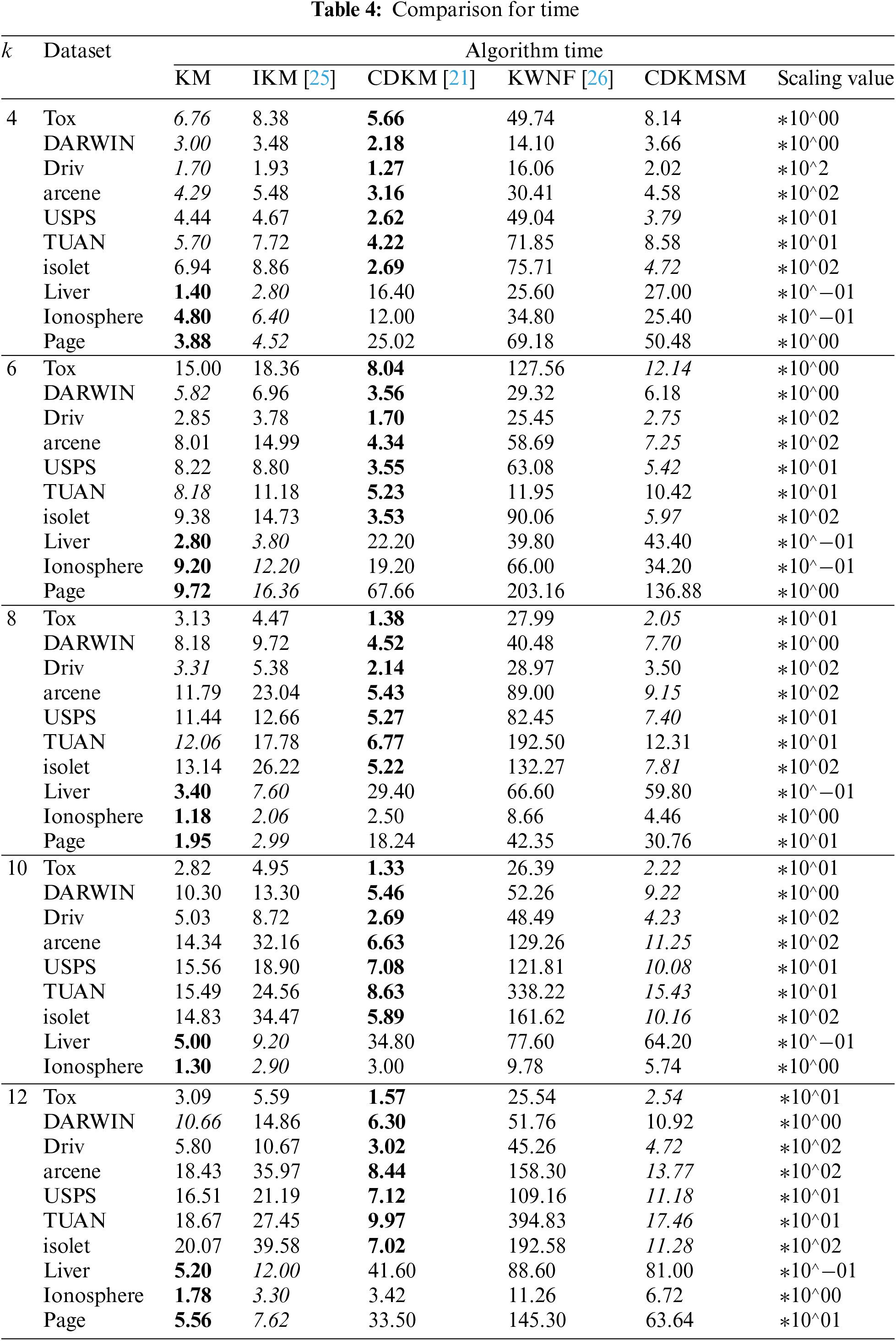

Figure 7: Comparison of T value between the proposed algorithm and other algorithms under high dimensional data
The experimental results show that the solution accuracy of the proposed method is higher than that of the K-means algorithm and the two algorithms based on split-merge, namely split and I-K-means-+. The proposed algorithm improves the solution accuracy of CDKM while retaining its computational efficiency advantage by using partition matrix under high dimensional data. Additionally, it outperforms the recently proposed KWNF algorithm. However, its solution accuracy is slightly lower than that of the random swap algorithm. The random swap algorithm is a variant of the split-merge criterion that incorporates the swap operation into the traditional split-merge criterion. This suggests that the swap operation can effectively improve the solution accuracy, which is a key focus of our future research.
The CDKM algorithm employs a coordinate descent method to optimize the K-means model and improve the solution accuracy of the original K-means algorithm. However, it is sensitive to the initial centers, which makes its solution accuracy not high enough. In this paper, the iterative process of CDKM is modified, and a coordinate descent K-means algorithm based on Split-merge is proposed. The proposed algorithm obtains the partition matrix by CDKM. Then the partition matrix is optimized by the proposed split-merge criterion to improve the solution accuracy. Since the introduced split-merge operations are completed entirely using the partition matrix, which avoids the distance calculation in traditional K-means and related improved algorithms. So, like CDKM, it has an efficiency advantage over other algorithms on high dimensional datasets.
The experimental results show that in terms of solution accuracy. The E value of the proposed algorithm relative to K-means is 17.45%, which is higher than that of the CDKM algorithm (9.45%), and also higher than that of the I-K-means-+ algorithm, split algorithm, and KWNF algorithm. This result indicates that incorporating basic split-merge criterion into the CDKM algorithm can achieve better solution accuracy than traditional split-merge algorithm. We also observed that a variant of the split-merge algorithm, known as the random swap algorithm, has a slight E value advantage (17.91%) over the proposed algorithm (17.45%), which is significantly higher than the other two algorithms, the I-K-means-+ algorithm and the split algorithm, which are based on the basic split-merge criterion. This suggests that the swap operation plays a significant role in further enhancing the solution accuracy of the split-merge criterion. As the number of clusters increases, the proposed algorithm shows increasingly greater improvements in the SSE index compared to both K-means and other tested algorithms apart from the random swap algorithm. In terms of computational efficiency, the proposed algorithm is more efficient on high dimensional data than another split-merge based algorithm, i.e., I-K-means-+ algorithm, and it is also more efficient than other tested algorithms. The percentage of time speedup for the proposed algorithm relative to the time of I-K-means-+, K-means, and the latest KWNF algorithm is 37.59%, 11.60%, and 89.23%, respectively. As the number of clusters increases, the T value of the proposed algorithm gradually increases compared to other algorithms, indicating that its time efficiency improves progressively.
The split-merge criterion can significantly improve the solution accuracy of the K-means algorithm. CDKM model is fundamentally different from the K-means model, direct application of split-merge criterion is not feasible. Therefore, this paper explores the integration of the split-merge criterion into the CDKM clustering model to enhance its solution accuracy. We aim to apply the split-merge criterion, traditionally used in the K-means model, to the CDKM model. In traditional K-means, there are several methods for split-merge operations and subsequent improvements, such as random swap clustering [24], which effectively enhance the solution accuracy of the original K-means model. These represent further advancements built upon the foundation of split-merge. Some effective indexes can measure clustering performance. In our future work, we plan to explore the integration of these advanced methods and indexes into our research. Our goal is to demonstrate the successful application of these methods and to explore the potential of incorporating such traditional methods into the CDKM model in future research.
Acknowledgement: The authors would like to acknowledge the valuable feedback provided by the reviewers.
Funding Statement: This research was funded by National Defense Basic Research Program, grant number JCKY2019411B001. This research was funded by National Key Research and Development Program, grant number 2022YFC3601305. This research was funded by Key R&D Projects of Jilin Provincial Science and Technology Department, grant number 20210203218SF.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Fuheng Qu, Yuhang Shi; data collection: Yuhang Shi; analysis and interpretation of results: Yuhang Shi, Yong Yang, Yating Hu; draft manuscript preparation: Yuhang Shi, Yuyao Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data used in this study are freely available and accessible. The sources of the data utilized in this research are thoroughly explained in the main manuscript.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
1In this paper, when we say that the solution accuracy of solution
References
1. S. Jha, G. P. Joshi, L. Nkenyereya, D. W. Kim, and F. Smarandache, “A direct data-cluster analysis method based on neutrosophic set implication,” Comput. Mater. Contin., vol. 65, no. 2, pp. 1203–1220, 2020. doi: 10.32604/cmc.2020.011618. [Google Scholar] [CrossRef]
2. G. J. Oyewole and G. A. Thopil, “Data clustering: Application and trends,” Artif. Intell. Rev., vol. 56, no. 7, pp. 6439–6475, 2023. doi: 10.1007/s10462-022-10325-y. [Google Scholar] [PubMed] [CrossRef]
3. S. K. Dubey, S. Vijay, and A. Pratibha, “A review of image segmentation using clustering methods,” Int. J. Appl. Eng. Res., vol. 13, no. 5, pp. 2484–2489, 2018. [Google Scholar]
4. M. Jamjoom, A. Elhadad, H. Abulkasim, and S. Abbas, “Plant leaf diseases classification using improved K-means clustering and SVM algorithm for segmentation,” Comput. Mater. Contin., vol. 76, no. 1, pp. 367–382, 2023. doi: 10.32604/cmc.2023.037310. [Google Scholar] [CrossRef]
5. R. Aarthi, K. Divya, N. Komala, and S. Kavitha, “Application of feature extraction and clustering in mammogram classification using support vector machine,” in 2011 Third Int. Conf. Adv. Comput., IEEE, 2011, pp. 62–67. [Google Scholar]
6. M. Ahmed, R. Seraj, and S. M. S. Islam, “The k-means algorithm: A comprehensive survey and performance evaluation,” Electronics, vol. 9, no. 8, 2020, Art. no. 1295. doi: 10.3390/electronics9081295. [Google Scholar] [CrossRef]
7. A. M. Ikotun, A. E. Ezugwu, L. Abualigah, B. Abuhaija, and J. Heming, “K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data,” Inf. Sci., vol. 622, pp. 178–210, 2023. doi: 10.1016/j.ins.2022.11.139. [Google Scholar] [CrossRef]
8. A. K. Jain, “Data clustering: 50 years beyond K-means,” Pattern Recognit. Lett., vol. 31, no. 8, pp. 651–666, 2010. doi: 10.1016/j.patrec.2009.09.011. [Google Scholar] [CrossRef]
9. S. S. Khan and A. Ahmad, “Cluster center initialization algorithm for K-means clustering,” Pattern Recognit. Lett., vol. 25, no. 11, pp. 1293–1302, 2004. doi: 10.1016/j.patrec.2004.04.007. [Google Scholar] [CrossRef]
10. M. E. Celebi, H. A. Kingravi, and P. A. Vela, “A comparative study of efficient initialization methods for the k-means clustering algorithm,” Expert Syst. Appl., vol. 40, no. 1, pp. 200–210, 2013. doi: 10.1016/j.eswa.2012.07.021. [Google Scholar] [CrossRef]
11. M. Gul and M. A. Rehman, “Big data: An optimized approach for cluster initialization,” J. Big Data, vol. 10, no. 1, pp. 120, 2023. doi: 10.1186/s40537-023-00798-1. [Google Scholar] [CrossRef]
12. T. K. Biswas, K. Giri, and S. Roy, “ECKM: An improved K-means clustering based on computational geometry,” Expert Syst. Appl., vol. 212, 2023, Art. no. 118862. doi: 10.1016/j.eswa.2022.118862. [Google Scholar] [CrossRef]
13. A. Layeb, “ck-means and fck-means: Two deterministic initialization procedures for K-means algorithm using a modified crowding distance,” Acta Inform. Prag., vol. 12, no. 2, pp. 379–399, 2023. doi: 10.18267/j.aip.223. [Google Scholar] [CrossRef]
14. D. Arthur and S. Vassilvitskii, “k-means++: The advantages of careful seeding,” Soda, vol. 7, pp. 1027–1035, 2007. [Google Scholar]
15. S. Lattanzi and C. Sohler, “A better k-means++ algorithm via local search,” in Int. Conf. Mach. Learn., PMLR, 2019, pp. 3662–3671. [Google Scholar]
16. A. Şenol, “ImpKmeans: An improved version of the K-means algorithm, by determining optimum initial centroids, based on multivariate kernel density estimation and Kd-tree,” Acta Polytechnica Hungarica, vol. 21, no. 2, pp. 111–131, 2024. doi: 10.12700/APH.21.2.2024.2.6. [Google Scholar] [CrossRef]
17. D. Reddy, P. K. Jana, and I. S. Member, “Initialization for K-means clustering using Voronoi diagram,” Procedia Technol., vol. 4, pp. 395–400, 2012. doi: 10.1016/j.protcy.2012.05.061. [Google Scholar] [CrossRef]
18. E. Baratalipour, S. J. Kabudian, and Z. Fathi, “A new initialization method for k-means clustering,” in 2024 20th CSI Int. Symp. Artif. Intell. Signal Process. (AISP), IEEE, 2024, pp. 1–5. [Google Scholar]
19. S. J. Wright, “Coordinate descent algorithms,” Math. Program., vol. 151, no. 1, pp. 3–34, 2015. doi: 10.1007/s10107-015-0892-3. [Google Scholar] [CrossRef]
20. H. -J. M. Shi, S. Tu, Y. Xu, and W. Yin, “A primer on coordinate descent algorithms,” 2016, arXiv:1610.00040. [Google Scholar]
21. F. Nie, J. Xue, D. Wu, R. Wang, H. Li and X. Li, “Coordinate descent method for k-means,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 5, pp. 2371–2385, 2021. doi: 10.1109/TPAMI.2021.3085739. [Google Scholar] [PubMed] [CrossRef]
22. T. Kaukoranta, P. Fränti, and O. Nevalainen, “Iterative split-and-merge algorithm for VQ codebook generation,” Opt. Eng., vol. 37, no. 10, pp. 2726–2732, Oct. 1998. [Google Scholar]
23. P. Fränti, T. Kaukoranta, and O. Nevalainen, “On the splitting method for VQ codebook generation,” Opt. Eng., vol. 36, no. 11, pp. 3043–3051, Nov. 1997. [Google Scholar]
24. P. Fränti, “Efficiency of random swap clustering,” J. Big Data, vol. 5, no. 13, pp. 1–29, 2018. [Google Scholar]
25. H. Ismkhan, “Ik-means−+: An iterative clustering algorithm based on an enhanced version of the k-means,” Pattern Recognit., vol. 79, pp. 402–413, 2018. [Google Scholar]
26. F. Nie, Z. Li, R. Wang, and X. Li, “An effective and efficient algorithm for k-means clustering with new formulation,” IEEE Trans. Knowl. Data Eng., vol. 35, no. 4, pp. 3433–3443, 2022. doi: 10.1109/TKDE.2022.3155450. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools