RSSI-Based 3D Wireless Sensor Node Localization Using Hybrid T Cell Immune and Lotus Optimization

1  Introduction

A collection of sensors that are dispersed randomly in a particular space is called WSN. The nodes in this network help to monitor and document the surrounding conditions. Moreover, WSN is useful in the healthcare industry, surveillance, and environmental monitoring. The process of finding the sensor node’s physical coordinates is known as node localization. This is complex because without knowing the location, data and information processing are useless. The localization technology in the WSN is broadly utilized in various fields including underwater monitoring, environmental monitoring, and target tracking with the advancement of the Internet, where node localization is regarded as one of the key applications of WSN [1]. The node deployment in 3D fields is required in enormous applications such as agricultural management, environmental monitoring, and healthcare treatment. The network connectivity in 3D fields is more divergent when contrasted with the two-dimensional (2D) scenarios and also the boundary conditions in WSN become more important in 3D localization.

When dealing with sensor nodes in wireless networks, the positioning of nodes is a crucial issue [2]. Various techniques have been implemented to solve this issue, but most of the localization techniques consider the deployment of nodes only in 2D environments [3]. The distance among the sensor nodes while concerned with the Angle of Arrival (AoA) and RSSI is used for the deployment of nodes in the range-based algorithms. RSSI is an indicator used to express the measurement of computing the signal strength received from the nearby nodes. As the distance between the transmitting and receiving nodes increases, the received signal strength starts decreasing. The distance between nodes can be estimated by examining the RSSI measurements. The exploitation of sensor nodes in complex 3D environments including the seabed, air, and mountain surface environment in practical application environments is usually complicated. The blocked communication and low connectivity between nodes are the issues that arise especially in the terrain [4]. Hence, lowering the energy consumption during node localization and attaining high precision in complex 3D and irregular environments have become significant in several research works.

The range-free algorithms are the techniques used for the localization of nodes based on hops [5]. The connectivity between the nodes is determined by these algorithms as the distance among the nodes is one of the imperative constraints. The distance of hops among the reference nodes and sensor nodes is estimated for the appropriate localization of nodes [6]. In WSN, the localization of nodes with a mobile beacon is implemented in distinct research works in existing works, and that is the solution for computing the appropriate node’s position in real time. Three or more signals are received by the unknown nodes from the beacon nodes from various positions and the estimation of locations is done using multi-lateration or tri-lateration algorithms [7]. The precise positioning of static nodes in WSN is accomplished precisely in prior works, but it is quite challenging in the case of moving nodes.

The major contributions of the implemented RSSI-based node localization approach are given in the below points:

•   To present an RSSI-based node localization model in 3DWSN for examining the coordinates of target nodes with the estimated location of anchor nodes that improve the communication performance in wireless networks.

•   To estimate the RSSI value from the transmitted signal using DNN for evaluating the distance between the anchor nodes and the unknown nodes that minimize the computation time.

•   To develop an HTCI-LEO for optimizing the dimension of the target nodes in the x-axis, y-axis, and z-axis and localizing the nodes very effectively to decrease the average localization error.

•   To validate the localization efficiency of the implemented scheme among the traditional models during RSSI estimation and node localization process concerning various performance indices.

The remaining portions of the proposed node localization model in 3DWSN are summarized as follows. Section 2 gives a detailed description of conventional node localization approaches and their features and challenges. The system model and overall processing steps are described in Section 3. The DNN-based RSSI estimation and hybrid heuristic algorithm description are provided in Section 4. The node localization using hybrid algorithms and its objective function is described in Section 5. The experimental validation and the summary of the proposed model are given in Section 6.

2  Related Works

In 2017, Fan et al. [8] have developed a distributed algorithm-based 3D node localization strategy in WSN. Two steps were followed in the node localization procedure segmentation and joint localization. Initially, the approximate convex partitioning method was adapted for dividing the network into various subnetworks. Next, the network segmentation was performed using the spatial convex node recognition strategy, which mainly relied on the connectivity of information. Then, the accurate localization over each subnetwork was carried out with the support of a multidimensional scaling-based mechanism. The empirical results proved that the complex 3-D sensor network has been greatly segmented by this developed approach and the localization rate has been significantly improved.

In 2020, Xu et al. [9] have proposed a multistage collaborative calibration-based hybrid approach for WSN localization, specifically in 3D environments. At first, the Light Gradient Boosting (LGB) method was used based on a cooperative methodology, a regression scheme, and a fine calibration approach for collaborative fusion. The modified version of the Frog-Leaping (FL) strategy and Multi-Communication Radius (MCR) method has been used for combining the distance vector hop and Quadrilateral Shrunk Centroid (QSC) mechanisms. The prediction accuracy of this system was improved via the screening cooperative anchor node strategy and it increased the node density. The fine position of the nodes has been effectively estimated when compared to the conventional algorithms and the adaptability of this model was also high.

In 2023, Wu et al. [10] have offered a hop localization mechanism based on Distance Vector (DV), which was a non-ranging node localization strategy, and its operation was very simple. Moreover, this model didn’t demand any additional experimental components that minimized the implementation cost. In this work, the number of hops in the nodes was decimalized to diminish the errors by integrating the radii of multiple communications 3D WSNs.

In 2022, Singh et al. [11] have proposed a Fuzzy Logic System (FLS)-based range-free approach to determine the Degree Of Irregularity (DOI). The grey wolf with the firefly strategy has been used for the estimation of anisotropic properties. The RSSI has been estimated among the anchor and the unknown nodes to evaluate the appropriate distance based on edge weights. The exact location of the nodes was determined by modeling the edge weights that have been accomplished by the proposed optimization strategy.

In 2023, Wajgi et al. [12] have proposed a localization algorithm based on clustering in a 3D environment. Based on the RSSI at the respective anchor nodes, the sensor nodes were combined as a cluster in WSN. The clusters were effectively formed with the support of the nearest-neighbor clustering strategy. Here, the beacon nodes acted as the heads of the clusters, and the location of the members in the clusters was determined through the local map based on the distance information of RSSI along with AOA. Lastly, the density control strategy has been adapted to reduce the energy dissipation. The experimentation results revealed that the implemented strategy had less computational complexity and was highly energy efficient.

3  System Model of 3D Wireless Sensor Networks

3.1 System Model

An optimal node localization model is developed in WSN using deep learning-based RSSI estimation. For unknown nodes, the range-based algorithms yield a more precise location of data. Based on signal attenuation, the RSSI measures the strength of received signals. The range-based techniques are capable of obtaining more accurate results. Beacon nodes are used in the range-based localization process. The unknown nodes calculate their distances from these beacon nodes by measuring the strength of the signals they receive. RSSI works based on this idea, so it is a good option for performing range-based localization.

The devices in WSN communicate with the adjacent nodes and localization of nodes is significant to offer efficient communication in the network. The localization process is originally performed based on the neighboring node connected to the anchor node that is represented by the term Be and then it will be reversed to the farthest node until the coverage of all the sensor nodes. The total amount of sensor nodes is indicated as O in the network. In 3DWSN, the hop is the important aspect and it is indicated by the term (Be,Oe) that indicates only small amounts of hops are required for the communication link establishment between the nodes Be,Oe. Hence, more than one node is connected in the regions of the overlapping networks.

The RSSI between the nodes Oe and Om is indicated by the term RSem and the distance between the nodes Oe and Om is signified by the term Dtem. The distance among the sensor nodes mainly depends on the factor RSSI. If any difficulties are present in the network, the strength of the signal is weakened and the calculated distance for combining the nodes in WSN is decreased. These are the basic depictions in the proposed node positioning scheme in 3DWSN. The system model of 3D WSN is graphically represented in Fig. 1.

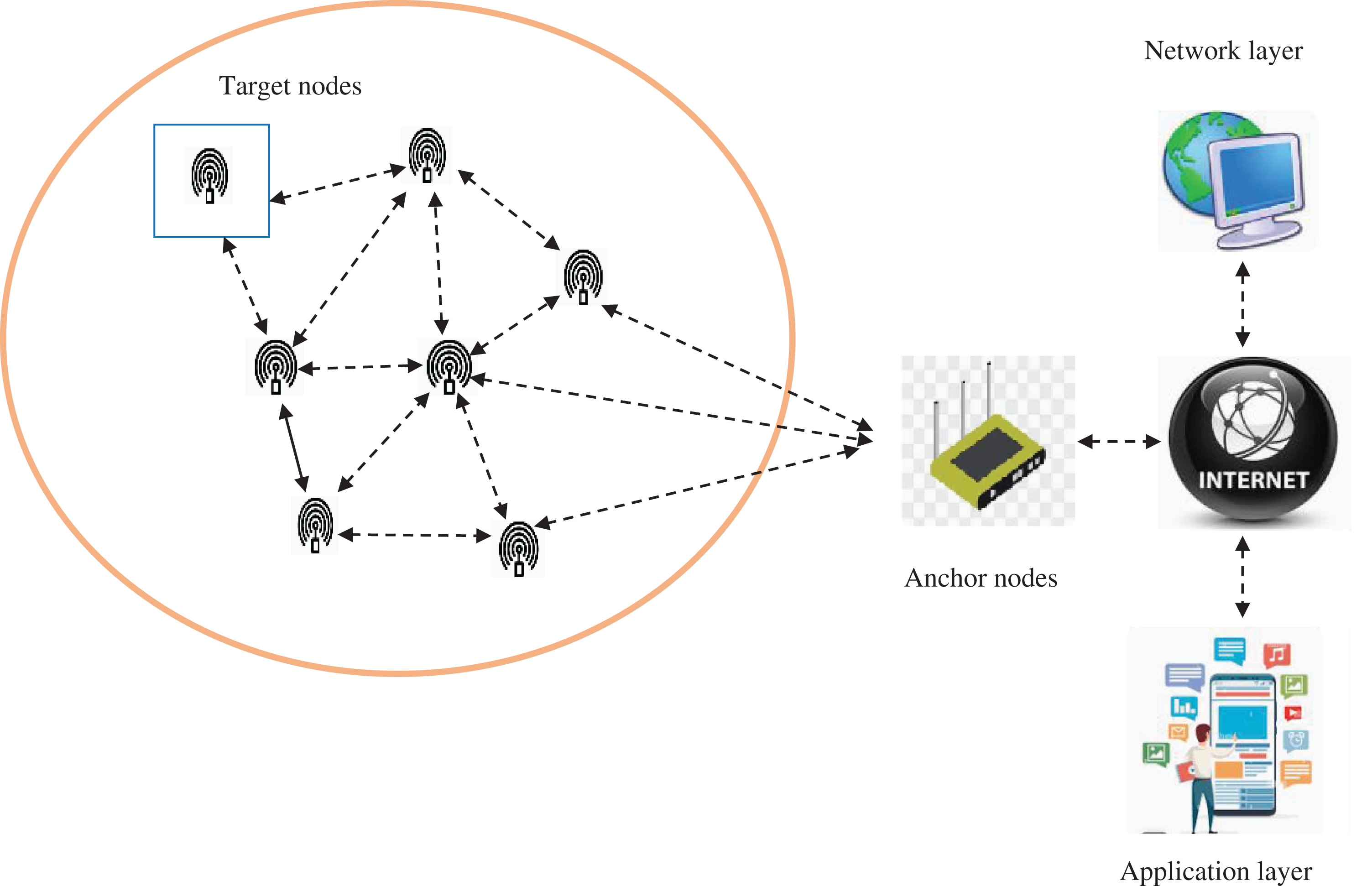
Figure 1: Network model of WSN

3.2 Overall Processing Steps

To develop a node localization model in 3DWSN for determining the unknown node’s position concerning RSSI. This node localization enhances the communication performance in WSN. The steps followed to localize the nodes are schematically visualized in Fig. 2.

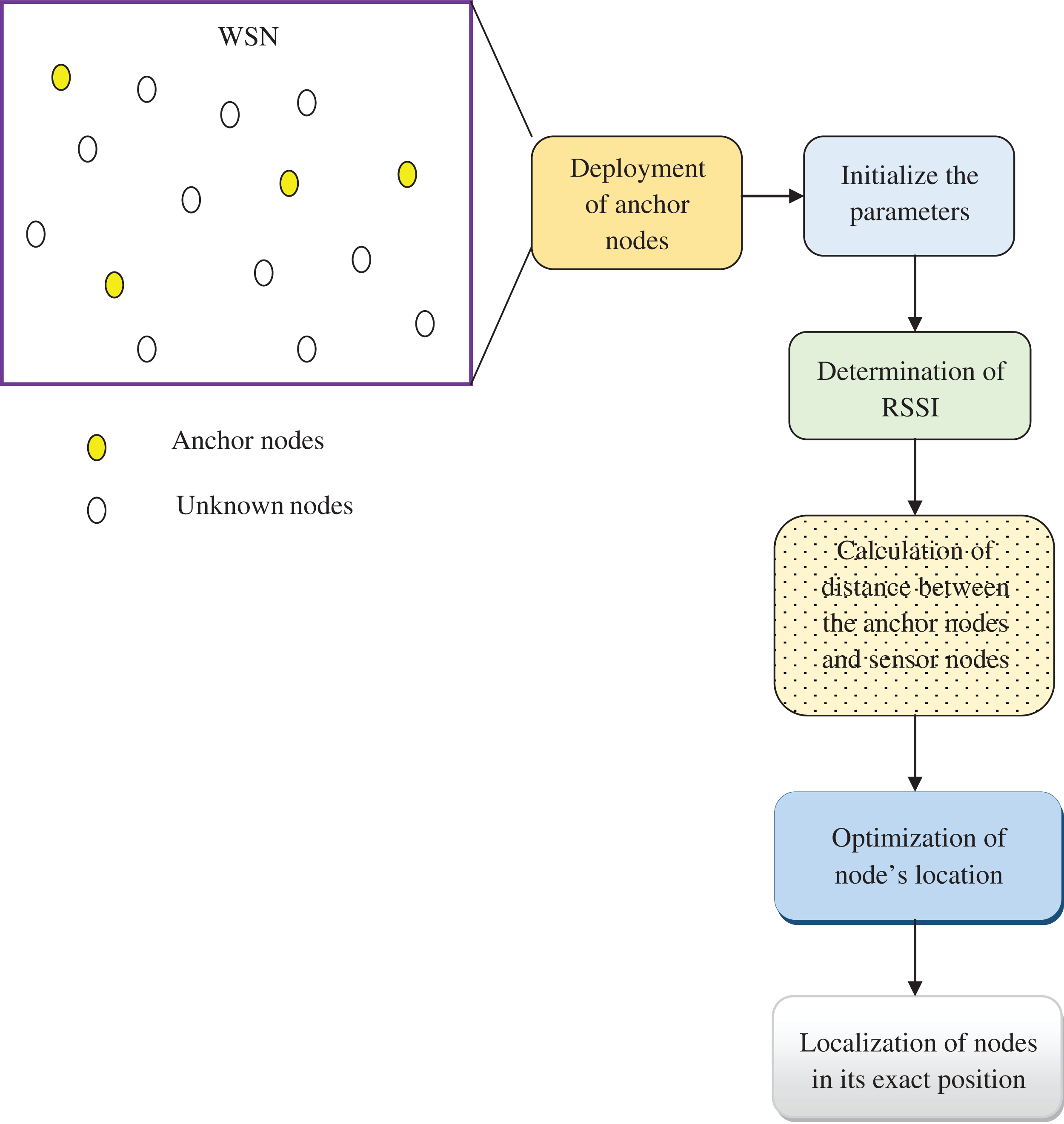
Figure 2: Schematic representation of steps to be followed in node localization

4  Optimization on Node’s Position Using Hybrid Heuristic Mechanism in WSN

4.1 Conventional T Cell Immune Algorithm (TCIA)

The T cell theory [13] is implemented based on immune responses produced via the T cells in the adaptive immune system. The static optimization issues are solved with the adoption of this T cell theory. The T cells endure from their origin in the bone marrow until they become the memory cells in the hematopoietic stem cells. The origination of T cells is from the hematopoietic stem cells in the bone marrow.

In T cells, several subsets are discovered with a distinct function. Following the expressed antigen receptor, the T cells are classified into various populations. In regards to the development level and maturation, the T cells can be partitioned into three groups. The effector cells are the type of cells that can activate the co-simulating signals. The main aim of the proliferation process is cell replication and the aim of discrimination is changing the clone.

4.2 Conventional LEA

Lotus Effect optimization Algorithm (LEA) [14] is a nature-inspired strategy for engineering optimization design. The properties such as the pollination of leaves and lotus flowers are the inspiration for LEA. Two main processes comprised in the LEA are non-biological and biological processes. The pollinators like birds and insects are employed to transform the pollen from one flower to various flowers in biological pollination. This process is considered as the global pollination in the solution space. The dragonfly optimization algorithm is employed for modeling the LEA based on its global pollination process. The self-pollination process in the flowers is considered a non-biological process. These kinds of flowering plants are pollinated due to factors like release in water and wind. Local pollination is used for the extraction and searching of local optimum. For analyzing the association of droplets over the leaves, the double local search is conceded.

The seed-spreading behavior of insects and the behavior of alignment; separation and cohesion are considered for this phase. The main motive of all the swarms is to survive. The behaviors such as attraction towards the sources of the food and distraction from the enemies are considered for updating the individuals and this process is mathematically modeled in Eq. (1).

Mku=−∑l=1RIku−Ilu(1)

The position of the present individual is denoted by Ik with iteration u and evolution index k, the l-th individual in the neighborhood is indicated by the term Il and the total count of neighborhood individuals is represented as R.

The alignment behavior is estimated through Eq. (2).

ALku=∑l=RIlu(2)

For the l-th individual, the velocity of the neighborhood is indicated by the term Il.

The cohesion behavior is evaluated through Eq. (3).

Chku=∑l=RIluR−Iku(3)

The position of the present individual is denoted by Ik with iteration u and evolution index k, and the l-th individual in the neighborhood is denoted by the term Il.

Food source attraction is determined based on Eq. (4).

Fdku=I+u−Iku(4)

The position of the current individual with the evolution index l is represented as Ik, and the food source’s location for the current iteration is signified by the term I+u.

The interruption of the enemy is evaluated via Eq. (5).

Emku=I−u−Iku(5)

The current individual position is indicated as Iku and the position of the enemy is indicated as I−u.

The movement direction of insects is used for demonstrating the direction of movement and the step vector for this process is given in Eq. (6).

ΔIku+1=(mMku+aALku+cChku+fFdku+eEmku)+iwΔIku+1(6)

Here, the separation, alignment, and cohesion coefficients are denoted by the terms m, a, and c, respectively.

The random stochastic behavior of the dragonflies is improved based on the exploration of artificial dragonflies around the search space.

4.3 Proposed HTCI-LEO

The HTCI-LEO algorithm is formed by combining the two different optimization algorithms including TCIA and LEA. The LEA algorithm is developed based on the self-cleaning and super-hydrophobic properties of lotus leaves. It also mimics the dragonfly’s movement in flower pollination during the exploration phase. This algorithm models the movement of water droplets on lotus leaves to identify optimal solutions efficiently. The TCIA algorithm is inspired by the T-cell immune process, which involves attacking pathogens, activating cells, and recognizing antigens. T cells are crucial for the immune system, as it identifies the abnormal and cancer cells.

The HTCI-LEO strategy has been implemented to position the nodes in 3D dimensions to improve the node localization performance with reduced node localization error. High accuracy in the node placements is indicated by a lower average localization error. It serves as a crucial performance metric for assessing and contrasting various localization methods and algorithms. How well node’s predicted positions match their actual placements is measured by this average localization error. Accurate node localization is essential to a WSN’s effective performance. The precise locations of nodes are necessary for several network operations, including data aggregation and routing. To guarantee that nodes are positioned in an effective manner, average localization error must be minimized. This improves the WSN’s overall accuracy and produces higher-quality data for improving user satisfaction. The position of target nodes in the x, y, and z-axis are optimally tuned for examining the appropriate position of the target nodes in the geographical region. These optimal tuning of positions in 3-dimensional TCIA highly decreases the average localization error.

Initially execute the TCIA, and then update the position for attaining the optimal solution y. Then execute the LEA, and then update the position Iku+1. The position attained from the TCIA is denoted by the term Posn1 and the position obtained from the LEA is denoted by Posn2. Based on the updated position of TCIA and LEA, the new HTCI-LEO algorithm is executed and then the position is estimated for getting the best optimal solution. The expression for calculating the new position is given in Eq. (7).

Posn=OLDPosn+STD(Posn1+Posn2)(7)

Here, the term Posn specifies the newly estimated position, Posn1 indicates the position attained from TCIA and the term Posn2 represents the position obtained from the LEA. The convergence rate of the developed HTCI-LEO is greater when compared to traditional TCIA and LEA. This new concept of upgrading the positions based on Eq. (7) helps to rectify the challenges in conventional LEA and TCIA algorithms. By upgrading this position, the algorithm’s strength in obtaining a better optimal solution is improved. Thus, the improved solution helps to enhance the precision of node localization by minimizing the average localization error.

5  Estimation of RSSI Using Deep Network for Localization of Nodes in WSN With Minimized Localization Error

5.1 RSSI Estimation Using DNN

Most of the localization algorithms in 3DWSN use the time difference of arrival rate, angle of arrival, and channel state information. However, our model uses the RSSI for the localization of nodes in their appropriate positions. Initially, the RSSI is estimated with the assumption of no obstacles present within the system.

The entire geographical area of the WSN is divided into multiple grid areas and then the anchor nodes are positioned in an exact location. DNN is a type of neural network that processes data and solves complicated tasks with the help of numerous layers presented in this network. DNNs are utilized in a wide range of tasks including Natural Language Processing (NLP) and computer vision. In addition, tasks like text processing, classification, and image recognition are accomplished using DNN. In this work, the RSSI value is identified using the DNN. For the RSSI identification process, DNNs are selected over K-Nearest Neighbour (KNN), Support Vector Machine (SVM), Random Forest (RF), and AdaBoost mechanisms. Because techniques like KNN do not have better generalization ability. SVMs work well for classification tasks; however, they are not as efficient as DNNs in capturing intricate non-linear patterns. AdaBoost and RF are two ensemble techniques that provide better robustness in detection tasks. However, these techniques require substantial feature learning ability. DNNs outperform conventional algorithms in capturing these intricate and non-linear interactions. Because of variables such as interference, changing environmental circumstances, and multi-path fading, RSSI data frequently contains intricate and non-linear correlations. So, DNN is employed in this work for estimating RSSI.

Initially, the attributes including node names, topology, traversal between nodes, distance matrix, and node coordinates are assigned. Similarly, the target value is also fixed for the RSSI estimation process. The initialized data is received by the DNN and it performs the prediction process to determine the RSSI value that is closer to the target RSSI values. The total number of layers in DNN [15] is indicated by the term ξ, and the neurons present in each layer are indicated by N λ, which lies in the interval between 1≤λ≤ξ. The activation function at the layer λ is indicated as Acλ in which the weight and bias of the model are indicated as Wtλ∈ℜN λ−1×N λ and Bsλ∈ℜN λ, correspondingly. The output of each layer is represented in Eq. (8).

otλ=Acλ(otλ−1×Wtλ+Bsλ)(8)

If λ is the first layer, then otλ−1 is assumed as the input data, and the softmax operation is applied for transfering the logits values zpm to the likelihood score of all values. The possibilities of all RSSI are predicted and it is calculated in the following Eq. (9).

argmaxpmzpmezpm∑∀pm∈Zezpm(9)

Based on the feed-forward process, the mapping function is supported in the proposed scheme and then the RSSI is predicted by this DNN. RSSI estimation using DNN is diagrammatically shown in Fig. 3.

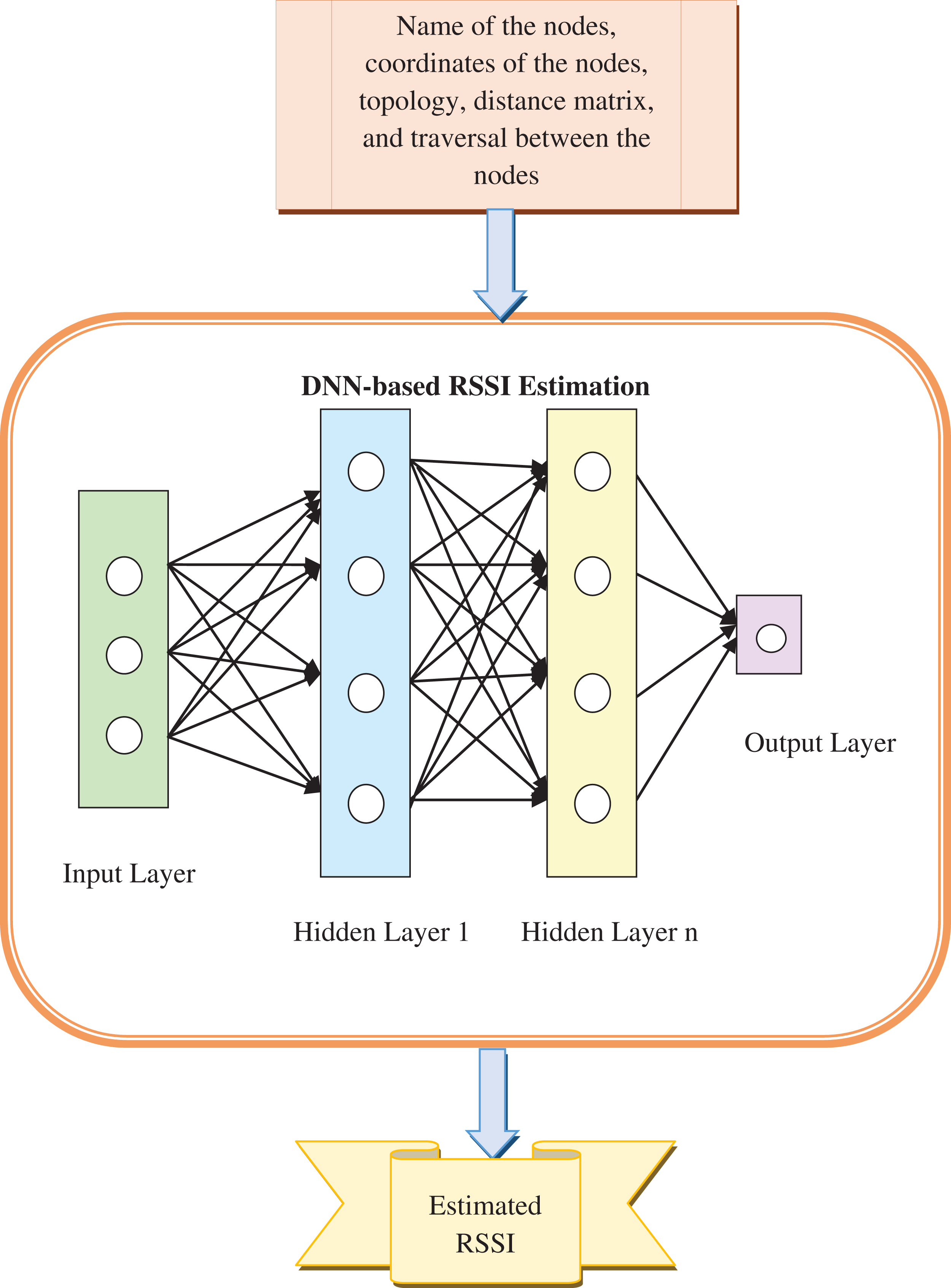
Figure 3: Diagrammatic view of RSSI estimation using DNN

5.2 Node Localization Using Proposed HTCI-LEO

To localize the nodes in 3DWSN, the anchor nodes are positioned in a well-known location. The RSSI is estimated initially by using the DNN. The inputs given to the DNN for training the network are names of the nodes, coordinates of the nodes, topology, distance matrix, and traversal between the nodes. After estimating the RSSI, the node location in the x-axis, y-axis, and z-axis of the unknown nodes are optimized in the sensing region with the support of implemented HTCI-LEO. The optimal preference of 3 dimensions minimizes the average localization error among the anchor as well as unknown nodes in WSN. The distance between the anchor as well as target nodes is calculated to find the target node’s location. For the regular and irregular surfaces, the developed HTCI-LEO performed well while localizing the nodes. The objective function of the developed HTCI-LEO-based node positioning model in WSN is expressed in Eq. (10).

OBf=arg⁡min{NPh,NPj,NPk}(Errloc)(10)

The proposed node localization model’s objective function is indicated as OBf, the minimized localization error is defined as Errloc, and the target nodes’ location to be tuned in x, y, and z-axis are represented as NPh,NPj and NPk, respectively. The average localization error formula between the anchor as well as target nodes is illustrated in Eq. (11).

Errloc=1S∑m=1S(distin−distem)(11)

The average localization error is denoted as Errloc the distance between the sensor and other nodes in the geographical region is defined by distin and the distance between the anchor, as well as the target nodes, is represented as distem.

The node localization process using HTCI-LEO is diagrammatically represented in Fig. 4.

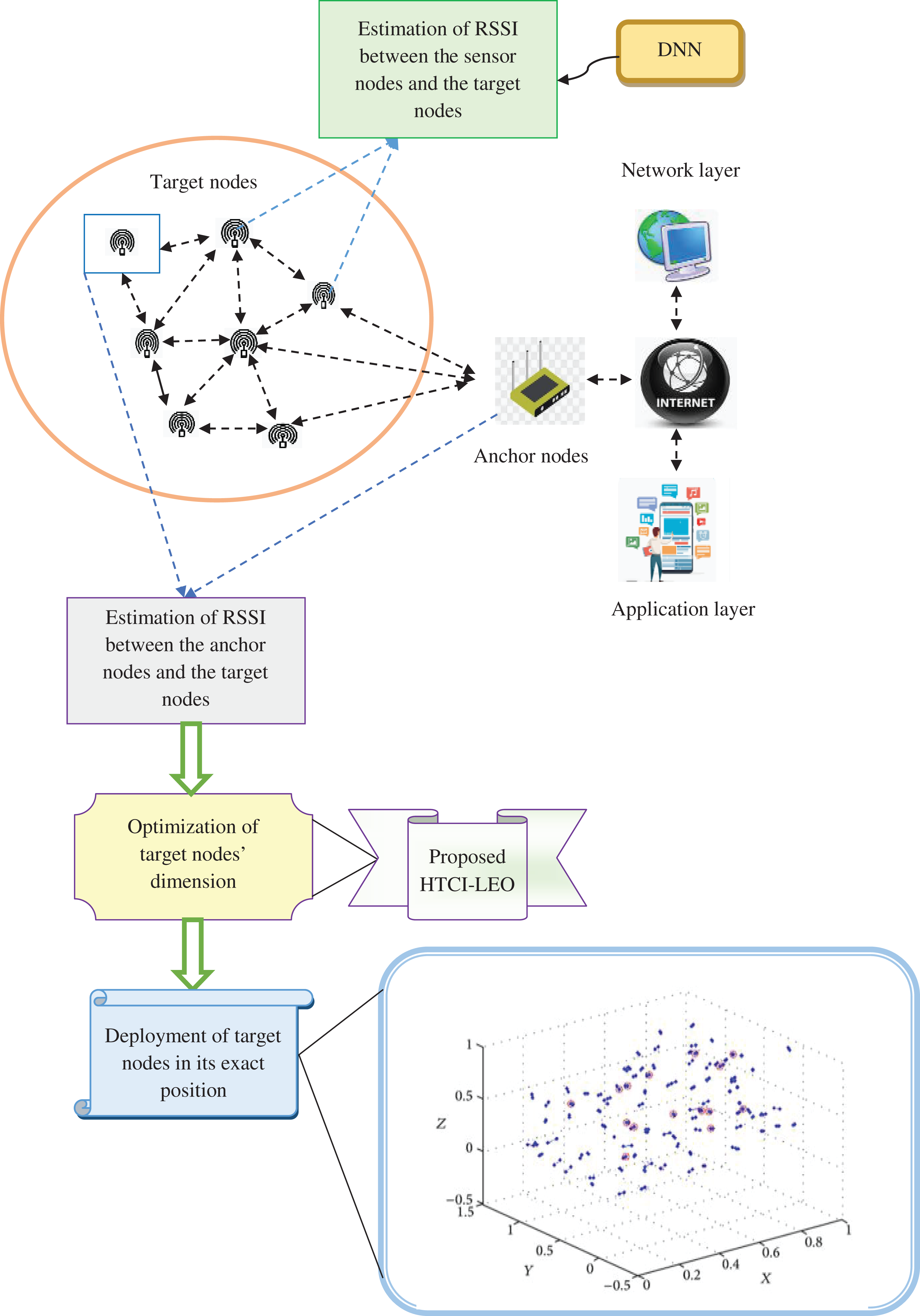
Figure 4: Node localization process using HTCI-LEO in 3DWSN

5.3 Objective Constraints

The RSSI is the significant constraint used for the localization of nodes in 3DWSN. It is calculated through the DNN. The expression for RSSI is given in Eq. (12).

RSSI(distin)=RSSI(distem)−10PLinlog⁡(distindistem)+Gsκ(12)

The received signal strength is indicated by RSSI(distem) at the anchor as well as the target node. Moreover, the path loss index is indicated as PLin, and the RSSI between the sensor as well as other nodes are denoted as RSSI(distin), and the Gaussian random variable is represented by the term Gsκ.

“The distance between the sensor and the other nodes in the network” is denoted as distin.

distin=10RSSI(distin)−RSSI(distem)+Gsκ10PLin(13)

“The distance between the anchor and the target nodes in the network” is denoted as distem and it is expressed in Eq. (14).

distem=(hm−he)2+(jm−je)2+(km−ke)2(14)

Here, the terms (hm,jm,km) represent the anchor nodes’ coordinates and the term (he,je,ke) denotes the target nodes’ coordinates in 3DWSN.

6  Results and Discussion

6.1 Experimental Setup

The MATLAB 2020a software was utilized for the implementation of the presented node localization model in 3DWSN. The number of population considered for the implementation was 10, the chromosome length taken was 3 and the maximum number of iterations assumed was 100 for the experimentation. The 3DWSN was initialized with the parameters like area and amount of anchor nodes. In addition, attributes such as topology, distance matrix, node names, traversal between nodes, and node coordinates were also considered for initialization purposes to predict the required RSSI. The algorithms used for the performance validation were the Elephant Herding T Cell Immune Algorithm (TCIA) [13], Lotus Effect Optimization Algorithm (LEA) [14], Optimization Algorithm (EHO) [16], and Eurasian Oystercatcher Optimization (EOO) [17]. Furthermore, the deep learning-based RSSI prediction outcomes were analyzed with the previous models like KNN [18], SVM [19], AdaBoost [20], and Random Forest [21]. The previously developed node positioning schemes like Compressive sensing [22], Fuzzy logic [23], Linear embedding [24], and Dempster-Shafer Evidence Theory [25] were used for the comparative analysis. The performance metrics such as “Mean Square Error (MSE), Mean Absolute Scaled Error (MAE), and Root Mean Square Error (RMSE)” were considered for the validation of RSSI prediction performance. The overall node localization efficiency was analyzed through the measure of average localization error.

6.2 Evaluation of RSSI Estimation

The performance of RSSI prediction using DNN is analyzed through measures such as MASE, MAE, and RMSE, which are shown in Fig. 5. The learning rate of the model is varied for analyzing the performance of RSSI prediction. By analyzing the results, the RMSE of the proposed DNN-based RSSI prediction model is lowered by 60.41% to KNN, 68.33% to SVM, 55.81% to AdaBoost, and 62.74% to Random Forest for considering the learning rate as 0.21. The measures such as MAE and MASE also performed well in the RSSI prediction and hence the efficiency of the localization in WSN is also increased when compared to the conventional machine learning approaches.

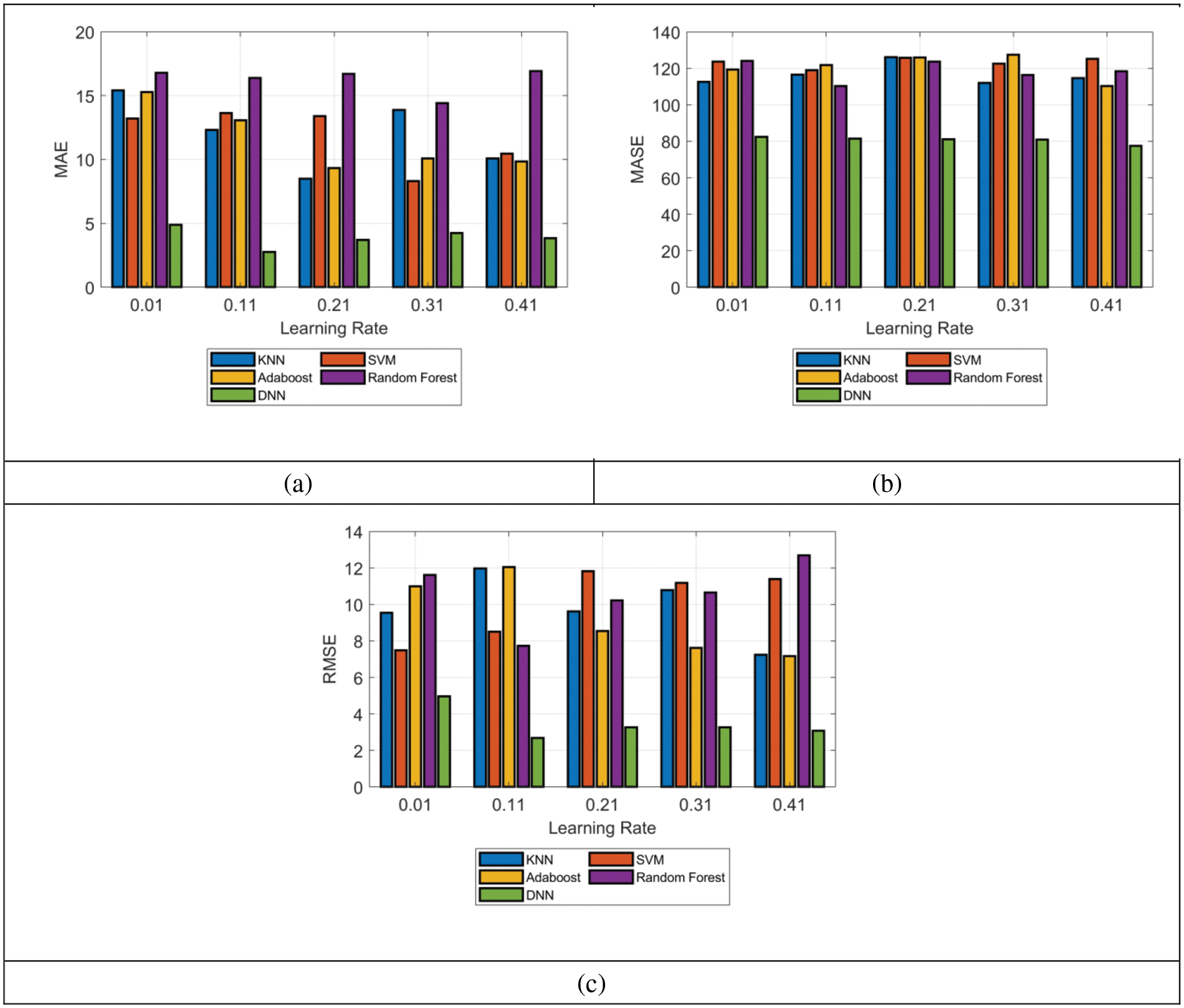
Figure 5: Node performance analysis over RSSI prediction on proposed model among the prior machine learning approaches in regards to “(a) MAE, (b) MASE, and (c) RMSE”

6.3 Performance Evaluation of Average Localization Error and Total Execution Time

The efficiency of the implemented node localization model is analyzed according to average localization error and it is demonstrated in Fig. 6. The total execution time analysis is provided in Fig. 7. The sensor nodes deployed in the WSN and the node density are varied for analyzing the performance of localization. The experimental results show that the total execution time of the DNN-based RSSI prediction model is lowered by 48.52% of EHO, 52.05% of EOO, 64.24% of LEA, and 68.18% of TCIA for considering the number of nodes as 60. The average localization error of the presented scheme is also highly decreased by the variation in the density and number of nodes in the sensing region. Similarly, the performance validation among the recently developed node localization approaches shows effective performance in terms of total execution time and average localization error.

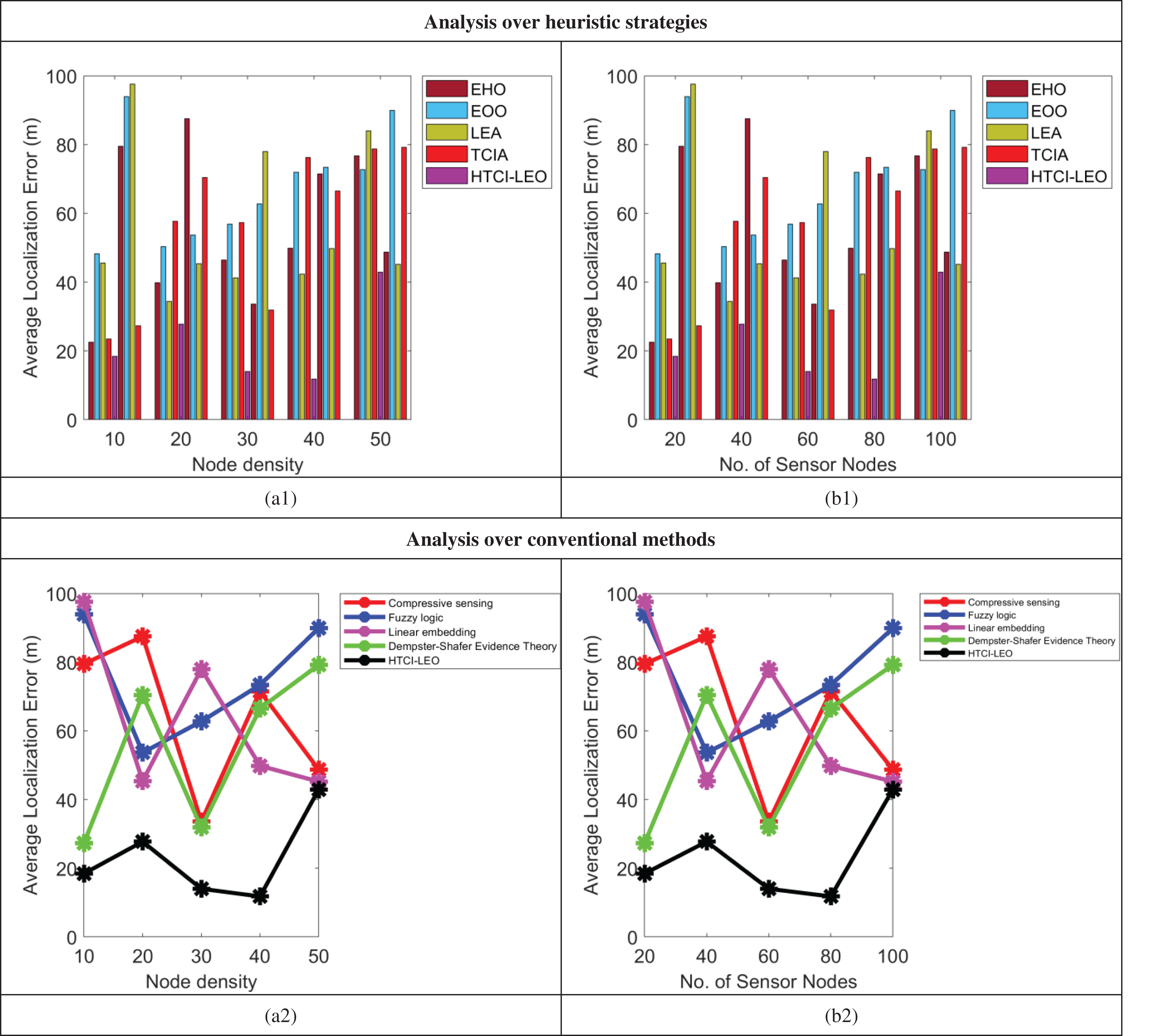
Figure 6: Performance analysis over average localization error on proposed model among 1. heuristic algorithms and 2. methods concerning “(a) Node density, and (b) Number of sensor nodes”

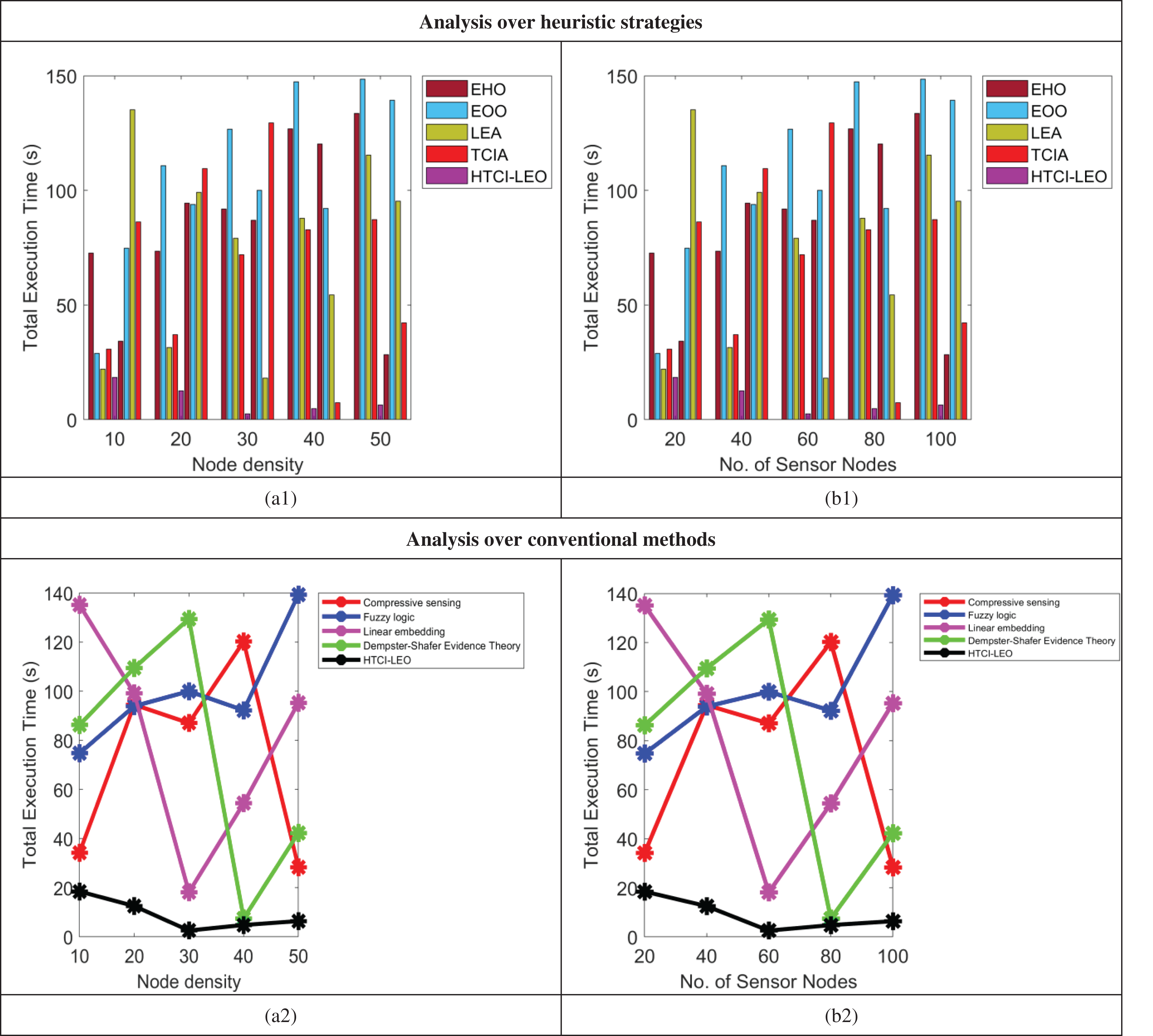
Figure 7: Performance analysis over total execution time on proposed model among heuristic algorithms and methods by concerning “(a) Node density, (b) Number of sensor nodes”

6.4 Numerical Assessment of RSSI Estimation

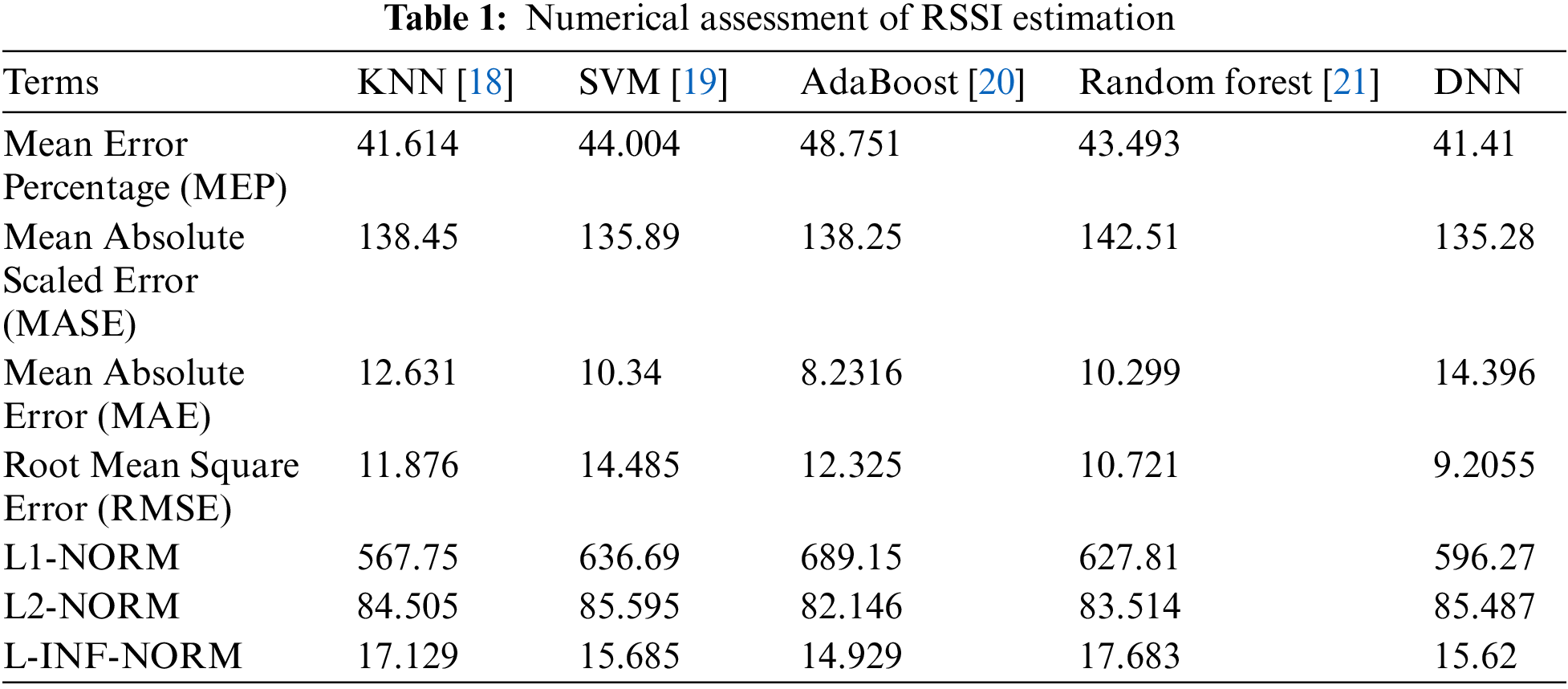
The efficiency of the implemented RSSI estimation process via DNN is verified by the results showcased in Table 1. From the table results, it is confirmed that the RSSI value estimation using DNN is better than other techniques like KNN, SVM, AdaBoost, and random forest. The proposed model attained less MEP, MASE, and MAE values; it proves that the model’s predictions are closer to the actual RSSI values. Lower scores represent less error during the RSSI estimation. Thus, the proposed model is more accurate in predicting the signal strength that is received from the other node. The computational resource requirement of the presented method is very low as it resulted in lower error metrics.

6.5 Convergence Estimation

The convergence performance of the developed hybrid algorithm HTCI-LEO for the node localization process is analyzed among other algorithms and the results are given in Fig. 8. Better convergence is achieved by the suggested HTCI-LEO when compared to EHO, EOO, LEA, and TCIA. The best convergence indicates that the HTCI-LEO algorithm accurately estimates the position of nodes more quickly. Therefore, the overall time needed for localizing nodes is minimized. The bandwidth and energy in WSNs are limited. Therefore, the localization process performed by the developed HTCI-LEO reduces the need for prolonged communications and computations as it converges more quickly than existing algorithms.

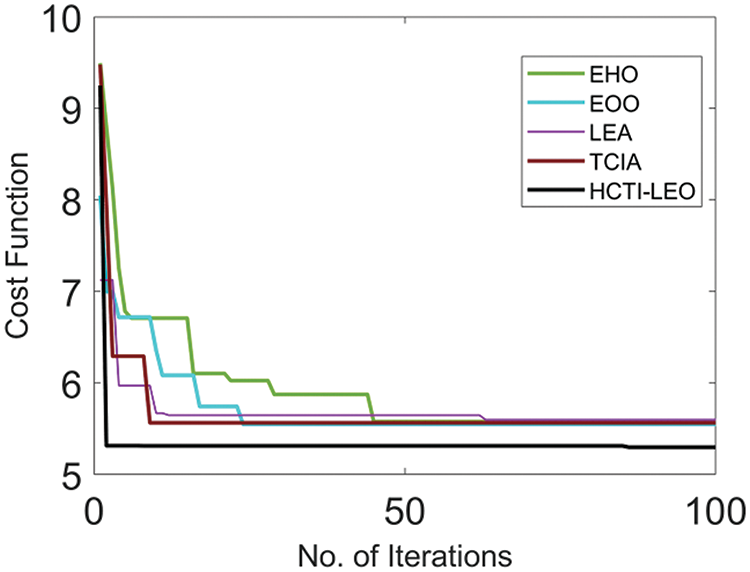
Figure 8: Convergence estimation of the recommended node localization process

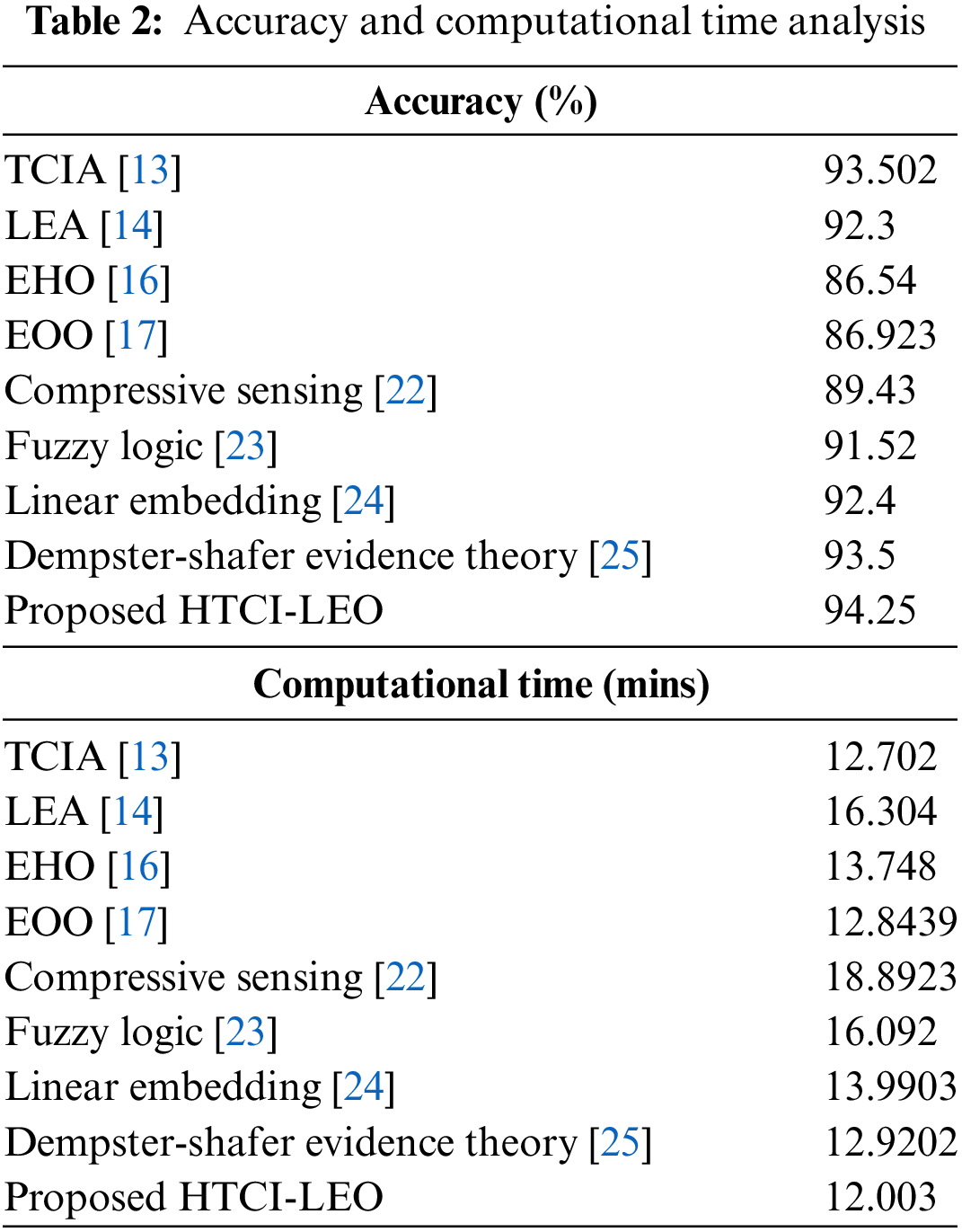
6.6 The Overall Effectiveness of the Proposed Node Localization Model

The overall effectiveness of the proposed node localization model is analyzed concerning accuracy, computation time, and computational complexity. Table 2 provides the accuracy and computational time results. The proposed HTCI-LEO’s accuracy in identifying the location of nodes is 94.25%. This higher accuracy in node localization ensures that nodes are positioned correctly, which is crucial for environmental monitoring tasks. The computational complexity of the suggested model is BigO[MaximumIteration+NumberofPopulation+Chromosomelength+1]. As we can see from the table results, the computational time of the presented model is less than other techniques and algorithms. Therefore, it is proved that the implemented localization process is quicker and requires less processing power.

6.7 Scalability Analysis

The scalability analysis of the suggested HTCI-LEO-based node localization process is visualized in Fig. 9. The proposed model’s performance is stable without any fluctuations even if the number of node counts is increasing. Communication overhead and energy consumption issues do not affect the performance of the developed HTCI-LEO due to its scalable localization process. Moreover, the changes in the network are easily adapted by the proposed model due to its high scalability.

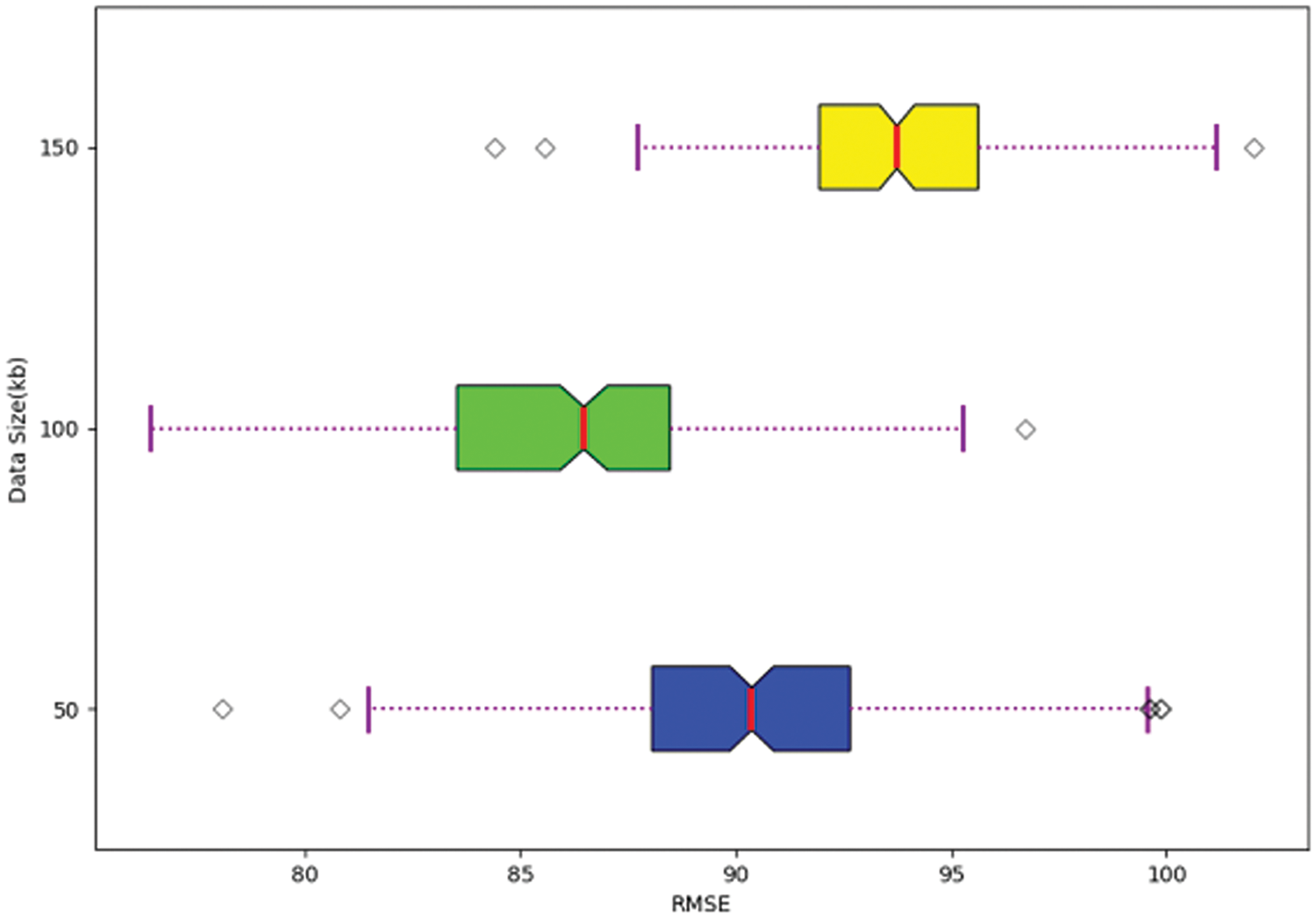
Figure 9: Scalability of the implemented node localization process

7  Conclusion

A node localization model has been implemented in 3DWSN to improve communication performance. The anchor nodes have been situated in a known location and then the position of unknown nodes needed to be estimated. The DNN method has been used for the estimation of RSSI between the sensor and other nodes and then the nodes were localized using the proposed hybrid optimization strategy. The position of nodes in the x, y, and z-axis was optimized using the developed HTCI-LEO that reduced the average localization error in 3DWSN. The efficiency of the presented node localization approach has been validated concerning total computation time and average localization error among the conventional models and the results demonstrated that the average localization error of the implemented model has been greatly decreased by 8.92% of EHO, 39.28% of EOO, 53.57% of LEA, and 3.57% of TCIA for the node density value of 30. The computation time required for the proposed node positioning scheme is very low when compared to other methods. So, the developed node localization scheme performs well in 3DWSN, and hence the communication performance over WSN is greatly increased.

Acknowledgement: All authors sincerely thank all organizations and institutions that have provided data and resources. Thanks to all the members of our research group, their suggestions and support have provided important help and profound impact on our research work.

Funding Statement: The authors present their appreciation to King Saud University for funding this research through the Researchers Supporting Program number (RSPD2024R918), King Saud University, Riyadh, Saudi Arabia.

Author Contributions: Study conception and design: Weiwei Hu; Methodology: Kiran Sree Pokkuluri; Software and validation: Preethi Palanisamy; Formal analysis and investigation: Rajesh Arunachalam; Resources and data curation, Funding acquistion: Bander A. Jabr; Writing—original draft preparation, review and editing, visualization: Yasser A. Ali; Supervision: Preethi Palanisamy. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: This work didn’t utilize any dataset. The work has been validated by initializing the sensor nodes in the WSN.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. P. Singh, A. Khosla, A. Kumar, and M. Khosla, “3D localization of moving target nodes using single anchor node in anisotropic wireless sensor networks,” AEU Int. J. Electron. Commun., vol. 82, no. 8, pp. 543–552, Dec. 2017. doi: 10.1016/j.aeue.2017.10.016. [Google Scholar] [CrossRef]

2. G. Sharma and A. Kumar, “Fuzzy logic based 3D localization in wireless sensor networks using invasive weed and bacterial foraging optimization,” Telecommun. Syst., vol. 67, no. 2, pp. 149–162, 2018. doi: 10.1007/s11235-017-0333-0. [Google Scholar] [CrossRef]

3. S. Soundararajan et al., “Heuristic optimization based node localization and multihop routing scheme with mobile sink for wireless sensor networks,” Wirel. Pers. Commun., vol. 129, no. 4, pp. 2583–2605, 2023. doi: 10.1007/s11277-023-10247-0. [Google Scholar] [CrossRef]

4. P. Raguraman, M. Ramasundaram, and V. Balakrishnan, “Localization in wireless sensor networks: A dimension based pruning approach in 3D environments,” Appl. Soft Comput., vol. 68, pp. 219–232, 2018. doi: 10.1016/j.asoc.2018.03.039. [Google Scholar] [CrossRef]

5. L. A. Villas, D. L. Guidoni, G. Maia, R. W. Pazzi, J. Ueyama and A. A. F. Loureiro, “An energy efficient joint localization and synchronization solution for wireless sensor networks using unmanned aerial vehicle,” Wirel. Netw., vol. 21, pp. 485–498, 2015. doi: 10.1007/s11276-014-0802-2. [Google Scholar] [CrossRef]

6. Y. H. Robinson, S. Vimal, E. G. Julie, K. Lakshmi Narayanan, and S. Rho, “3-dimensional manifold and machine learning based localization algorithm for wireless sensor networks,” Wirel. Pers. Commun., vol. 127, no. 1, pp. 523–541, 2022. doi: 10.1007/s11277-021-08291-9. [Google Scholar] [CrossRef]

7. S. J. Bhat and K. V. Santhosh, “A localization and deployment model for wireless sensor networks using arithmetic optimization algorithm,” Peer-to-Peer Netw. Appl., vol. 15, pp. 1473–1485, 2022. doi: 10.1007/s12083-022-01302-x. [Google Scholar] [CrossRef]

8. J. Fan, Y. Hu, T. H. Luan, and M. Dong, “DisLoc: A convex partitioning based approach for distributed 3-D localization in wireless sensor networks,” IEEE Sens. J., vol. 17, no. 24, pp. 8412–8423, 2017. doi: 10.1109/JSEN.2017.2763155. [Google Scholar] [CrossRef]

9. L. Xu, Z. Li, and X. Li, “A hybrid approach using multistage collaborative calibration for wireless sensor network localization in 3D environments,” IEEE Access, vol. 8, pp. 130205–130223, 2020. doi: 10.1109/ACCESS.2020.3009171. [Google Scholar] [CrossRef]

10. Y. Wu, C. Zhang, L. Tong, and X. Shi, “Location optimization based on improved 3D DV-HOP algorithm in wireless sensor networks,” IEEE Access, vol. 11, pp. 85525–85536, 2023. doi: 10.1109/ACCESS.2023.3303569. [Google Scholar] [CrossRef]

11. P. Singh, N. Mittal, and P. Singh, “A novel hybrid range-free approach to locate sensor nodes in 3D WSN using GWO-FA algorithm,” Telecommun. Syst., vol. 80, pp. 303–323, 2022. doi: 10.1007/s11235-022-00888-0. [Google Scholar] [CrossRef]

12. D. W. Wajgi and J. V. Tembhurne, “A clustering-based 3D localization in wireless sensor networks using RSSI and AoA,” SN Comput. Sci., vol. 4, 2023, Art. no. 682. doi: 10.1007/s42979-023-02139-8. [Google Scholar] [CrossRef]

13. H. Zhang, Y. Zhang, Y. Niu, K. He, and Y. Wang, “T cell immune algorithm: A novel nature-inspired algorithm for engineering applications,” IEEE Access, vol. 11, pp. 95545–95566, 2023. doi: 10.1109/ACCESS.2023.3311271. [Google Scholar] [CrossRef]

14. E. Dalirinia, M. Jalali, M. Yaghoobi, and H. Tabatabaee, “Lotus effect optimization algorithm (LEAA lotus nature-inspired algorithm for engineering design optimization,” J. Supercomput., vol. 80, no. 1, pp. 761–799, 2024. doi: 10.1007/s11227-023-05513-8. [Google Scholar] [CrossRef]

15. Z. Shen, T. Zhang, A. Tagami, and J. Jin, “When RSSI encounters deep learning: An area localization scheme for pervasive sensing systems,” J. Netw. Comput. Appl., vol. 173, 2021, Art. no. 102852. doi: 10.1016/j.jnca.2020.102852. [Google Scholar] [CrossRef]

16. M. Nayak, S. Das, U. Bhanja, and M. R. Senapati, “Elephant herding optimization technique based neural network for cancer prediction,” Inform. Med. Unlocked, vol. 21, 2020, Art. no. 100445. doi: 10.1016/j.imu.2020.100445. [Google Scholar] [CrossRef]

17. A. Salim, W. K. Jummar, F. M. Jasim, and M. Yousif, “Eurasian oystercatcher optimiser: New meta-heuristic algorithm,” J. Intell. Syst., vol. 31, no. 1, pp. 332–344, 2022. doi: 10.1515/jisys-2022-0017. [Google Scholar] [CrossRef]

18. X. Fang, Z. Jiang, L. Nan, and L. Chen, “Optimal weighted K-nearest neighbour algorithm for wireless sensor network fingerprint localisation in noisy environment,” IET Commun., vol. 12, no. 10, pp. 1171–1177, 2018. doi: 10.1049/iet-com.2017.0515. [Google Scholar] [CrossRef]

19. A. Chriki, H. Touati, and H. Snoussi, “SVM-based indoor localization in wireless sensor networks,” in 2017 13th Int. Wirel. Commun. Mobile Comput. Conf. (IWCMC), Valencia, Spain, 2017, pp. 1144–1149. [Google Scholar]

20. R. Al Alawi, “RSSI based location estimation in wireless sensors networks,” in 2011 17th IEEE Int. Conf. Netw., Singapore, 2011, pp. 118–122. [Google Scholar]

21. K. Madhumathi and T. Suresh, “Node localization in wireless sensor networks using multi-output random forest regression,” in Soft Computing for Problem Solving. Singapore: Springer, 2018, pp. 177–186. doi: 10.1007/978-981-15-0184-5_16. [Google Scholar] [CrossRef]

22. Y. Wei, W. Li, and T. Chen, “Node localization algorithm for wireless sensor networks using compressive sensing theory,” Pers. Ubiquit. Comput., vol. 20, pp. 809–819, 2016. doi: 10.1007/s00779-016-0951-7. [Google Scholar] [CrossRef]

23. S. Amri, F. Khelifi, A. Bradai, A. Rachedi, M. L. Kaddachi and M. Atri, “Node localization in wireless sensor networks: A comprehensive survey,” Future Gener. Comput. Syst., vol. 93, pp. 799–813, 2019. doi: 10.1016/j.future.2017.10.023. [Google Scholar] [CrossRef]

24. N. Jain, S. Verma, and M. Kumar, “Adaptive locally linear embedding for node localization in sensor networks,” IEEE Sens. J., vol. 17, no. 9, pp. 2949–2956, 2017. doi: 10.1109/JSEN.2017.2681100. [Google Scholar] [CrossRef]

25. C. Elkin, R. Kumarasiri, D. B. Rawat, and V. Devabhaktuni, “Localization in wireless sensor networks: A dempster-shafer evidence theoretical approach,” Ad Hoc Netw., vol. 54, pp. 30–41, 2017. doi: 10.1016/j.adhoc.2016.09.020. [Google Scholar] [CrossRef]