An Investigation of Frequency-Domain Pruning Algorithms for Accelerating Human Activity Recognition Tasks Based on Sensor Data

1  Introduction

The evolution and advancement of the Internet of Things (IoT) alongside sensor technology persist, permeating various domains. This advancement not only facilitates efficient management and optimization of energy consumption but also enables the integration of sensors, characterized by their compact size and heightened precision, into a myriad of devices and systems, including smartphones and watches. Consequently, the utilization of sensors for Human Activity Recognition (HAR) emerges as a highly promising and advantageous technological avenue [1–3].

By harnessing sensor technology and machine learning algorithms, Human Activity Recognition (HAR) autonomously identifies and categorizes diverse bodily activities across various states, encompassing walking, running, sitting, standing, ascending and descending stairs, among others. This capability finds extensive applications within the realms of healthcare, fitness monitoring, and elderly care, facilitating enhanced monitoring, analysis, and support for individuals in these domains [4–6]. Compared to traditional machine learning algorithms, deep learning methods, especially deep convolutional neural networks (DCNNs), have become the dominant technology for all kinds of activity recognition tasks due to their efficient feature extraction capabilities and excellent classification performance as well as model generalization. It has been shown to be more effective than traditional machine learning methods in inferring activities from sensor data. Although DCNNs have stronger feature learning capabilities, their large-scale model sizes and large and complex model operations require more memory and computational resources, which makes it a challenge to deploy HAR on mobile or wearable devices. In the realm of real-time activity recognition systems, the imperative of low-latency prediction underscores the necessity for research endeavors focused on developing lightweight deep learning models meticulously optimized for mobile devices. Commonly used model lightweighting methods include low-rank decomposition [7], model quantization [8], knowledge distillation [9] and network pruning [10–12]. Among all the compression methods, network pruning is widely explored for its remarkable compression effect and easy implementation.

Presently, the predominant approach in network pruning research involves setting pertinent thresholds based on the characteristics of the output mapping derived from network convolution, thereby facilitating network pruning. Luo et al. [13] introduced an evaluation framework based on filter entropy, where a higher entropy value signifies greater information content and hence, higher importance. Conversely, Lin et al. [14] noted that the average rank of feature mappings produced by individual filters correlates consistently with the average rank of feature mappings collectively, suggesting that higher ranks denote greater contributions to the model. However, unlike image data, human activity datasets comprise heterogeneous data collected from diverse devices’ testing, rendering conventional visual data analysis methods irrelevant. Consequently, a holistic consideration of HAR-related dataset characteristics is imperative for analyzing output feature mappings and selecting an appropriate pruning strategy from an interpretable standpoint, aimed at minimizing network redundancy and achieving lightweighting objectives.

Building upon the aforementioned challenges, this paper undertakes a paradigmshift in data analysis, transitioning from the spatial domain to the frequency domain to glean insights into data features from a frequency-domain perspective. Subsequently, redundant filters are pruned to achieve model lightweighting objectives. Initially, the output feature mapping is converted from the spatial domain to the frequency domain through Discrete Fourier Transform (DFT), enabling the analysis of various frequency components within the feature mapping. Emphasis is then placed on the low-frequency components of the feature mappings in the frequency domain, which typically encapsulate the bulk of energy and correspond to the overarching structure and smooth features of the data. Spectrograms, encompassing the frequency spectrum and magnitude spectrum, are visualized to intuitively analyze their informative properties. Subsequent to assessing the energy distribution of the feature mapping in the frequency domain, specifically focusing on the energy spectral density of low-frequency information, the contribution degree of different filters is ascertained. Subsequently, a threshold is established based on the contribution degree, facilitating the removal of filters with negligible contributions, thereby culminating in the formation of a final lightweight network characterized by reduced network complexity and redundancy. The framework of the traditional pruning framework and our proposed method are shown in Figs. 1 and 2, respectively, encapsulating our primary contributions summarized below.

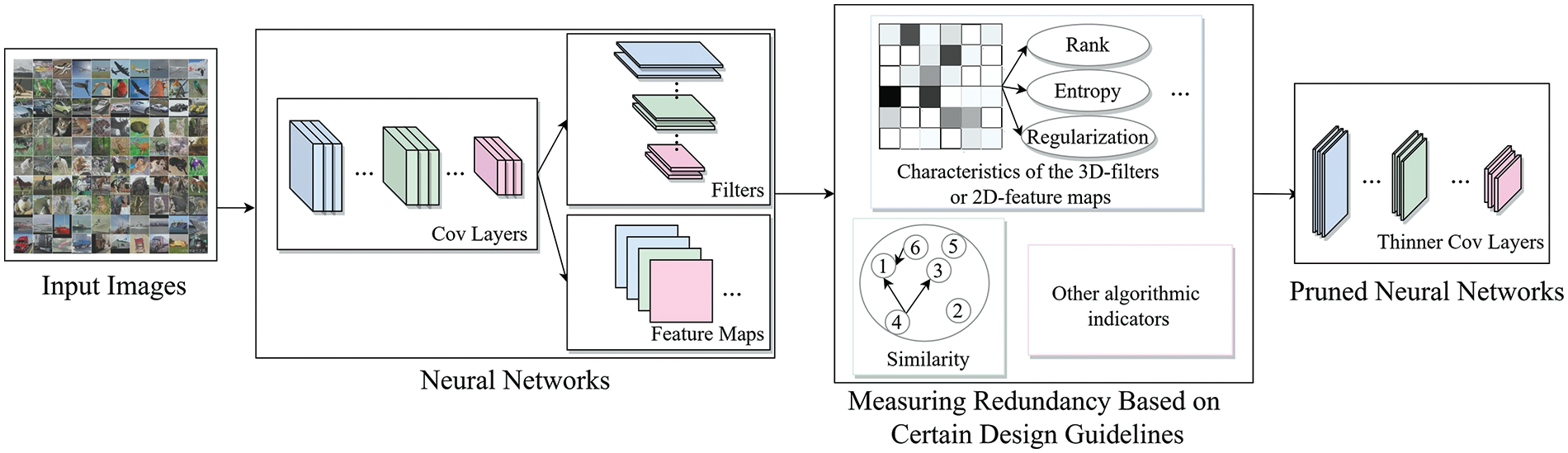
Figure 1: Traditional pruning algorithm process

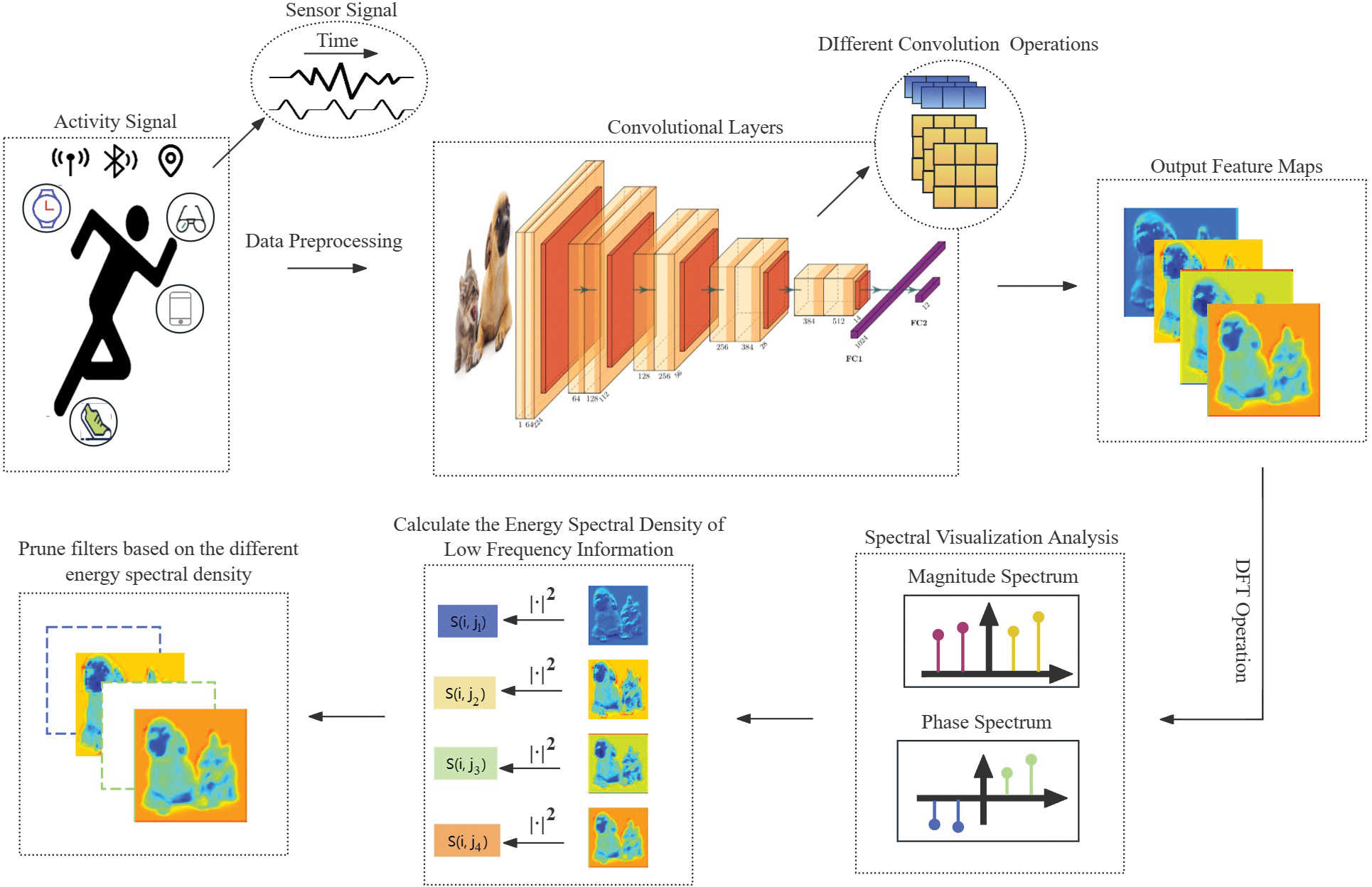
Figure 2: Our frame diagram of a method for processing human activity signals

i) This paper champions the implementation of filter pruning within the spectral realm, recognizing that operations executed in the frequency domain exhibit heightened resilience to perturbations and provide a more conducive environment for the analysis of sensor data, particularly within the purview of Human Activity Recognition (HAR).

ii) The empirical analyses presented herein unequivocally establish the preeminence of examining the energy dispersion of low-frequency components over that of their high-frequency counterparts or a holistic dataset. Such a methodology has proven to be markedly more efficacious in extracting salient information.

iii) Comprehensive experimental procedures, conducted across a variety of benchmark HAR datasets, corroborate the proficiency of our proposed algorithm. It adeptly minimizes memory footprint and preserves computational resources, all the while maintaining the integrity of the model’s performance, thus validating its pragmatic applicability.

The rest of the paper is organized as follows. Section 2 discusses the main network pruning techniques. Section 3 describes the proposed pruning method in detail. Section 4 discusses the experimental design and gives the results. Finally, ablation experiments and conclusions of the study are given in Sections 5 and 6, respectively.

2  Related Work

The rapid development of the DCNNs has revolutionized various computer vision tasks such as image classification [15–18], target detection [19–22] and segmentation [23–25]. Therefore, in the field of HAR, DCNNs are now also widely used in the pursuit of better performance [4,26]. Ronao et al. [27], Yang et al. [28] and others have pioneered the application of DCNN models that can automatically extract features for activity recognition. Although deeper networks exhibit superior performance, their practical implementation is hindered by substantial computational and memory requirements, thereby constraining their applicability in resource-constrained systems such as embedded or mobile devices. Regrettably, recent research has largely neglected Human Activity Recognition (HAR) based on Deep Convolutional Neural Network (DCNN) acceleration. Consequently, addressing the challenge of high resource consumption stemming from intricate and voluminous models is imperative to realize high-speed and accurate mobile devices like sports watches and smart bracelets for human gesture activity recognition. Amidst various model compression techniques such as knowledge distillation, model quantization, and tensor decomposition, network pruning garners significant attention owing to its remarkable compression efficacy and straightforward implementation.

As an early result of neural network pruning, weight pruning [29] increases the sparsity of the network by discriminating the importance of connections based on their weights and pruning unimportant connections. This unstructured pruning [30] requires hardware and Basic Linear Algebra Subprograms (BLAS) library support to achieve substantial performance improvement [31]. On the contrary, structured pruning [32–34] enables efficient computational reasoning and does not require specialized hardware devices; therefore, we focus on the work of structured pruning in practical applications of HAR.

In the realm of structured pruning research, determining filter importance via various metrics stands as a fundamental approach. Li et al. [8] adopt absolute weight sums to gauge filter significance, effectuating network lightening by pruning inconsequential filters. Tang et al. [35] introduce faux features, devoid of truth labels, to aid in redundant filter selection. He et al. [36] posit that filters closer to the geometric median harbor redundant information that can be effectively represented by other filters, advocating for their pruning to diminish model redundancy. Hu et al. [37] assess filter importance based on the percentage of zero-activation values in output feature mapping, thereby guiding pruning decisions. In contrast to solely relying on metric-based approaches to assess filter importance, regularization-based pruning emerges as a prevalent methodology. This approach incorporates the pruning imperative into the training loss of the model, thereby facilitating the generation of adaptive pruning decisions. Liu et al. [38] impose sparsity constraints on the scale factor of the batch normalization layer and select filters from the convolutional layer with the corresponding minimum scale factor for pruning to reduce the model complexity. Singh et al. [39] enhance the correlation between filter pairs by applying regularization to train the model, which reduces the information loss that may be caused by pruning. Ding et al. [40] propose an Auto-Balanced Filter Pruning (AFP) pruning method based on the evaluation of the importance of filters based on the L1 paradigm, which applies positive penalties to the unimportant filters and negative penalties to the important ones using the L2 regularization to achieve the pruning operation. Wang et al. [41] propose an incremental pruning method that applies gradually increasing L2 regularization to unimportant filters during the training process.

Given the protracted training durations and intricate optimization design associated with regularization-based pruning methods, their deployment in Human Activity Recognition (HAR) tasks becomes challenging. Hence, our approach pivots filter screening from the spatial domain to the frequency domain. Herein, filter importance is discerned through spectrogram visualization and energy spectral density values, culminating in the reduction of network redundancy and the attainment of model lightweighting objectives. The effectiveness of the proposed method on three different HAR datasets can be seen from the experimental results in Section 4.

3  Our Method

In this section, the algorithms employed to statistically characterize filters within the domain of Human Activity Recognition (HAR) will be expounded upon, followed by a detailed exposition of the process entailing the removal of redundant filters.

Traditional pruning algorithms are almost always deployed in the spatial domain, and therefore the process design is basically based on the specification of the metrics (Fig. 1). Diverging from conventional filter evaluation methodologies, the approach employed for filter screening has undergone a transformative shift from the customary spatial domain to the frequency domain. This paradigm shift not only affords a lucid comprehension of the contributions rendered by various frequency components and the spectral attributes of the data but also streamlines the statistical analysis of sensor data pertinent to HAR. The schematic depiction of this innovative approach is delineated in Fig. 2. This pioneering methodology adeptly captures both local nuances and overarching global characteristics of the filter. Such discriminative evaluation facilitates the discernment of filters housing redundant information, thereby rendering them prime candidates for elimination. The overarching objective is to effectuate astute model compression, thereby optimizing network sparsity while safeguarding crucial performance metrics.

3.1 Basic Notations

Suppose a DCNNs model has L convolutional layers, denote layer i as Wi, which has the shape of Wi∈Rni×ni−1×k×k, where ni, ni−1 and k denote the number of output channels, the number of input channels and the kernel size of layer i, respectively. After the convolution operation on the input data, the corresponding output mapping Oi of the layer can be denoted as Oi∈Rb×ni×h×w, where b is the batch size and h and w are the height and width of the output mapping of the layer, respectively. Given the j-th filter of the i-th layer, it can be denoted as Wi,j, which has the shape Wi,j∈Rni−1×k×k, where ni−1 represents the number of channels corresponding to this filter. In the convolutional layer, the filters and their output feature mappings are identical in number and index order, and the corresponding output feature mapping Oi,j for each filter can be denoted as Oi,j∈Rb×h×w.

In this section, the algorithms employed for the statistical characterization of filters in the context of Human Activity Recognition (HAR) are meticulously examined, succeeded by an elaborate exposition of the methodology for the excision of superfluous filters. Deviating from traditional techniques for filter assessment, our methodology has experienced a paradigmatic evolution, migrating from the customary spatial domain to the frequency domain. This novel transition affords a lucid comprehension of the contributions derived from diverse frequency components and the spectral properties of the data, while simultaneously expediting the streamlined statistical analysis of sensor data pertinent to HAR. The schematic depiction of this cutting-edge approach is presented in Fig. 2.

This pioneering methodology adeptly captures both localized nuances and overarching global characteristics of the filter. Such discriminative evaluation facilitates the identification of filters harboring redundant information, thus designating them as prime candidates for elimination. The overarching objective is to effectuate judicious model compression, thereby optimizing network sparsity while preserving crucial performance metrics.

3.2 Frequency-Domain Analysis for Convolutional Neural Networks

Previous endeavors in pruning have predominantly concentrated on spatial manipulation, wherein unimportant filters are pruned based on intrinsic properties of the filters or their corresponding feature mappings. In stark contrast to these conventional methodologies, our approach pioneers a novel perspective by shifting the pruning paradigm to the frequency domain. Specifically, given a convolutional neural network model with an output feature mapping corresponding to the j-th filter in layer i Oi,j∈Rb×h×w, we first transform it from the spatial domain to the frequency domain by means of a discrete Fourier transform, denoted as F(Oi,j):

F(Oi,j)=DFT(Oi,j)(1)

The utilization of 2D Discrete Fourier Transform (2D-DFT) serves as a pivotal tool in transitioning data from the spatial domain to the frequency domain, thereby enabling operations such as feature extraction. Our primary focus lies in sensor data, particularly in the context of HAR. Upon undergoing DFT, the original 2D matrix data undergoes decomposition into a series of complex frequency domain components. This transformation not only facilitates a deeper understanding of the spectral properties inherent in the data but also empowers us to analyze the energy distribution across different frequencies within the original dataset. By discerning the contribution of data at various frequencies, we are equipped to conduct a more comprehensive and insightful analysis.

More specifically, for an output feature mapping matrix like Oi,j, Oi,j(x,y){(x,y)|1≤x≤h,1≤y≤w} can be regarded as the representation of each matrix element in the spatial domain in the output feature mapping corresponding to the j-th filter of the i-th layer. Then, its discrete Fourier transform process can be memorized as:

F(Oi,j)(u,v)=∑x=1h∑y=1wOi,j(x,y)e−i2π(uxh+vyw)(2)

where F(Oi,j)(u,v) represents the frequency-domain representation of the matrix elements obtained by the discrete Fourier transform, and each element contains a complex value where the real part represents the magnitude of the data and the imaginary part represents the phase of the data.

As previously stated, this study will focus on analyzing the low-frequency components of the matrix following the Discrete Fourier Transform (DFT) and visualize its spectral representation to discern the analytical features. Once the matrix has undergone 2D-DFT, the predominant energy and informational content are typically concentrated within the low-frequency spectrum of the transformed domain. This is manifested by an increased signal concentration in the central regions of the spectral data. Within the frequency domain, low-frequency components correspond to the overall distributions and relationships within the data, including changes and discontinuities between data points. Conversely, high-frequency components elucidate the finer details of the data and the statistical features of the local regions of the data points. The methodology for extracting information from the low-frequency components of the data can be summarized as follows:

Flow(Oi,j)(u,v)={F(Oi,j)(u,v)if u<τu and v<τv0otherwise(3)

where τu and τv are used to determine the thresholds for which frequency components are retained. By setting a suitable threshold, it is possible to select the low-frequency components to be retained in the frequency domain and the high-frequency components to be set to zero.

3.3 Filter Pruning Based on Energy Spectral Density of Low-Frequency Components

To quantify the discrepancy in low-frequency information encapsulated within different filters, we advocate for an analysis aimed at comprehending the energy concentration of the data within this frequency range, expressed in terms of the energy spectral density. This metric serves as a pivotal indicator, shedding light on the frequency-domain characteristics and thus facilitating the measurement of filter importance. The energy spectral density of low-frequency data can be written as:

Elow(Oi, j)=1M∑u∑v|Flow(Oi, j)(u,v)|2(4)

where Elow(Oi,j) represents the average value of the energy spectral density of the low-frequency information in the frequency domain space, corresponding to the j-th filter of the i-th layer. m represents the number of low-frequency data elements in this feature mapping after a two-dimensional DFT. High energy spectral density indicates the presence of significant frequency components or a concentrated energy distribution within the data, suggesting potential impact on signal characteristics and behavior. Conversely, low energy spectral density signifies minimal variations or energy concentration at frequencies of lesser significance. We advocate for spectral visualization of all frequency domain data, encompassing both magnitude and phase spectra, during the quantization process. This comprehensive approach allows for a thorough analysis of energy distribution across various frequency components. By juxtaposing the energy spectral density with spectral imagery, we gain insights into the properties of the data implied in the frequency domain, thus enhancing our understanding based on energy spectral density analysis. Specifically, the matrix element F(Oi,j)(u,v) in the complex matrix F(Oi,j) is defined by:

F(Oi,j)(u,v)=A(Oi,j)(u,v)+iB(Oi,j)(u,v)(5)

where A(Oi,j)(u,v) and B(Oi,j)(u,v) denote the real and imaginary parts, respectively, through which we can use to compute their magnitude and phase spectra, respectively:

M(Oi,j)(u,v)=A(Oi,j)(u,v)2+B(Oi,j)(u,v)2(6)

Φ(Oi,j)(u,v)=atan2(B(Oi,j)(u,v),A(Oi,j)(u,v))(7)

where M(Oi,j)(u,v) and ϕ(Oi,j)(u,v) denote the magnitude and phase at position (u,v) in the frequency domain, respectively. When we quantize the frequency domain data by using the energy spectral density values, we visualize the magnitude and phase spectra of all elements of the frequency domain matrix by using Eqs. (6) and (7) from which we cannot only observe the characteristics and trends of the overall data, but also statistically generalize them to look for the laws embedded in the spectral maps of the HAR data in the frequency domain, so as to generalize the special problems and explore the general solutions of this type of problems.

Ultimately, we empirically establish a threshold to retain filters associated with high energy values, while filtering out those associated with low energy values. This strategic approach aims to minimize model accuracy loss while fulfilling the objective of model lightweighting. The comprehensive pruning process based on the frequency domain is elucidated in Algorithm 1.

4  Experiments

In this section, we meticulously assess the performance of the proposed frequency domain-based pruning algorithm across a diverse array of HAR benchmark datasets. In order to delineate the advantages of our method, we juxtapose its outcomes with those of the conventional importance-based pruning approach. Furthermore, a series of ablation experiments are conducted to provide additional validation of the method’s efficacy.

4.1 Benchmark Datasets

In recent years, the burgeoning advancement of Human Activity Recognition (HAR) has led to a proliferation of publicly available benchmark datasets, which are extensively employed in research endeavors. Typically, these datasets comprise raw data collected from wearable sensors or cell phone sensors, facilitating the determination of user behavioral patterns and other states. To ensure a fair and unbiased performance comparison with other algorithms, and to enhance the generalizability of our proposed algorithm, we conduct a comprehensive evaluation across three prominent HAR benchmark datasets: UCI-HAR, WISDM, and PAMAP2. These datasets have gained widespread recognition as benchmarks [42,43], boasting considerable citation rates and are freely accessible for download from the Internet. Detailed information regarding these datasets is provided in Table 1.

UCI-HAR [44]: The dataset comprises data collected from 30 volunteers aged between 19 and 48 years old. The recorded exercise data encompassed x, y, and z accelerometer data (representing linear acceleration) and gyroscope data (denoting angular velocity) sourced from a smartphone. The data were sampled at a frequency of 50 Hz, yielding 50 data points per second. Volunteers engaged in one of six standard activities: Walking, Walking Upstairs, Walking Downstairs, Sitting, Standing, and Laying. Movement data were recorded using specialized cell phone software. The dataset was partitioned in a randomized manner, with a training set to test set ratio of 5:2.

WISDM [45]: Developed by the WISDM research team at Fordham University, this dataset encompasses daily activity data recorded by the accelerometer integrated into a smartphone. It captures information pertaining to six distinct daily activities: Walking, Running, Walking Upstairs, Walking Downstairs, Sitting, and Standing. Each activity is undertaken by a different user with the phone securely fastened to the body. The dataset is partitioned into two segments, with 80% allocated as a training set and 20% designated as a test set.

PAMAP2 [46]: The Physical Activity Monitoring dataset encompasses data from 18 distinct physical activities, such as Walking, Cycling, and Playing Soccer, among others. These activities were performed by 9 subjects wearing 3 inertial measurement units along with heart rate monitors. The data were recorded at a frequency of 100 Hz during the experiment. Similar to previous datasets, we partitioned the dataset in an 8:2 ratio, allocating 80% for model training and reserving 20% for testing purposes.

4.2 Experimental Settings

This subsection focuses on the implementation details of the experiments, including the model framework used in our experiments, the different hyperparameter settings for different datasets during training, and the introduction of evaluation metrics for the performance of the algorithms.

Architectures and Parameter Settings: In constructing the model framework, in order to increase the likelihood of deploying it in mobile devices and for a fair comparison with the previous work [27,28,47], we constructed a CNNs backbone model with five convolutional layers and one fully connected layer as a baseline. The number of filters in the convolutional layers are 64, 128, 256, 384 and 512, respectively. It is worth noting that we use different convolutional kernel sizes for each dataset due to the different preprocessing processes for different datasets, resulting in different data sizes. For both the UCI-HAR dataset and the PAMAP2 dataset, our convolution kernel size is set to 3 × 3, while the convolution kernel size for the WISDM dataset is set to 7 × 1.

Training and Fine-Tuning Configurations: In the process of pre-training the model, since the number of samples in the three different datasets is similar, we set the batch size to 64 and train the model for 200 epochs. The initial learning rate is set to 0.1, and for every 50 epochs, the learning rate decreases to 10% of the original. For the pruned model, a total of 100 epochs are needed for fine-tuning, and the batch size, momentum, weight decay, and initial learning rate are set to 64, 0.9, 0.0005 and 0.01, respectively, and the learning rate is adjusted to 10% of the original after every 30 epochs.

Evaluation Metrics: Our experiments use three different metrics to fully evaluate the pruning effect:

1) Model Accuracy after Pruning. The accuracy of the model before pruning is given by Baseline in the table of experimental results, and the accuracy after pruning is given by Pruned, and Accdrop is also a visual representation of the difference in accuracy before and after pruning.

2) Pruned FLOPs. This is given by Flops in the table, and expresses the amount of reduction in the floating-point operations. A larger reduction means faster inference.

3) Pruned Parameters. This is given by Params in the table and expresses the reduction of parameters, where a larger reduction means a smaller model size.

All experiments were implemented in the PyTorch [48] framework and performed on a single NVIDIA RTX 3060 GPU.

4.3 Visualization Analysis of Spectrograms

This section delves into the visualization and analysis of spectrograms derived from data across various Human Activity Recognition (HAR) datasets within the frequency domain. Specifically, after isolating the low-frequency information components from the data, we opted to utilize the energy spectral density value as our filtering metric for the removal of redundant filters. This choice stems from the versatility of energy spectral density, which not only allows for numerical visualization of energy concentration but also unveils intrinsic frequency-domain characteristics of the data. Furthermore, by visualizing spectrograms of data with differing energy values, such as magnitude and phase spectra, we gain insights into underlying characteristics, enabling the extraction of more universally applicable conclusions or patterns.

Illustratively, employing our model as a case study, we sample the output feature mapping of the final convolutional layer across various datasets and subject it to a two-dimensional Discrete Fourier Transform (2D-DFT) transform to compute energy spectral density values. It is noteworthy that our approach involves visualizing and comparing data with both the highest and lowest energy values within each dataset. This deliberate choice aids in more effectively exploring features and patterns, as depicted in Fig. 3.

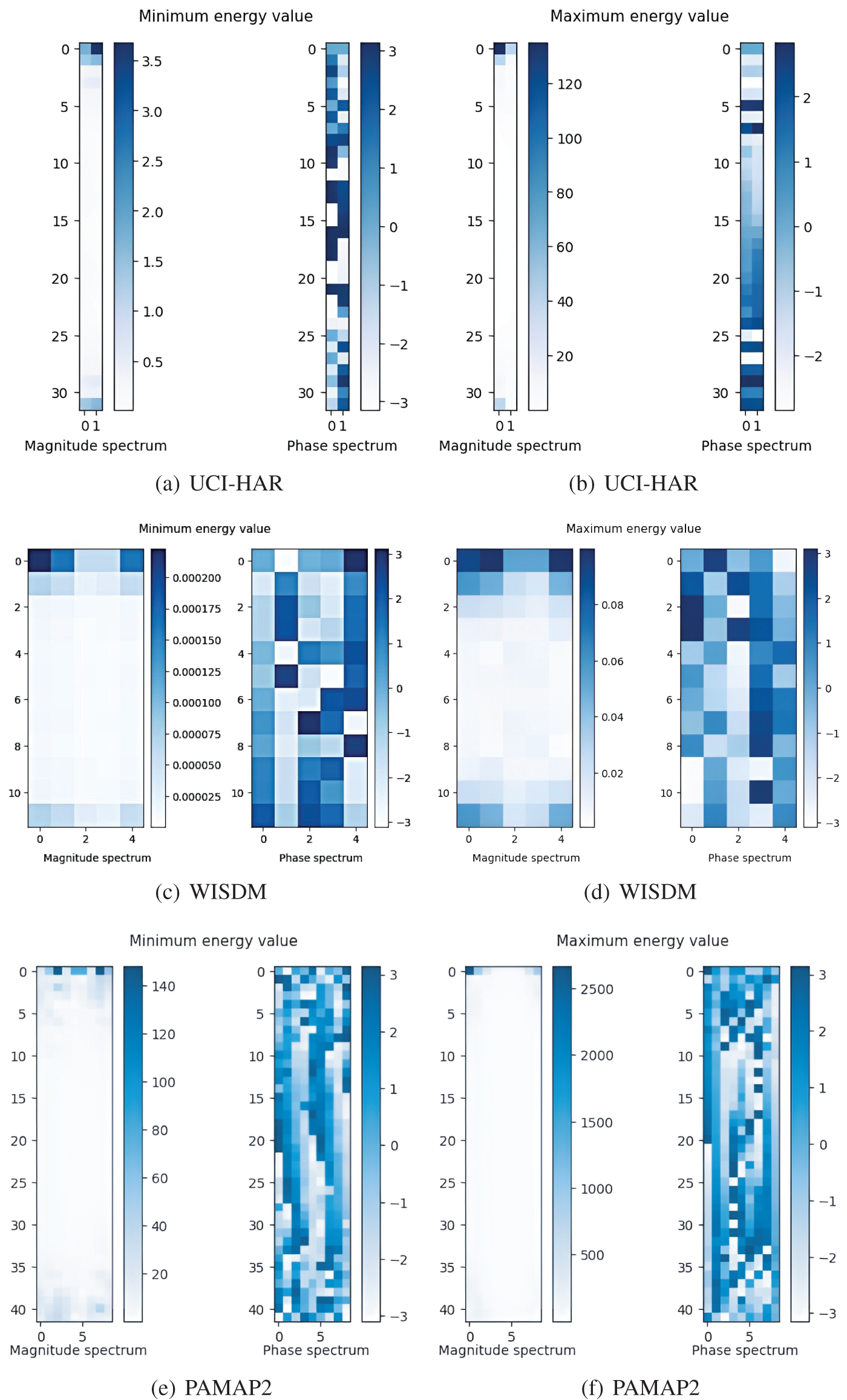
Figure 3: Visualization of sample spectra with different energy values

The provided figure showcases spectrograms depicting data with the highest and lowest energy values across three distinct datasets. Variations in spectrogram sizes denote discrepancies in original data sizes and sampling settings across the datasets.

Magnitude Spectrum Analysis: Within the magnitude spectrum, distinct colors signify different magnitude values, with darker and brighter shades representing higher magnitudes, while lighter hues denote lower magnitudes. Across all datasets, data with elevated energy values exhibit relatively high magnitudes, whereas data with low energy values correspond to diminished magnitudes. Notably, irrespective of energy values, magnitude spectra manifest elevated magnitudes only at specific frequencies, with lower magnitudes prevailing across other frequencies. This observation suggests sparse distribution of data in the frequency domain, with energy concentration primarily occurring at select frequencies. In essence, this sensor-type HAR data displays low amplitude across most data elements post 2D-DFT transform, with energy predominantly concentrated at specific frequencies, indicative of discernible energy concentration.

Phase Spectrum Analysis: Contrary to the magnitude spectrum, the distribution of phase values across the three datasets appears markedly heterogeneous, regardless of energy spectral density values. Each frequency exhibits a mix of large and small phase values, devoid of any discernible pattern. This suggests intricate and varied phase information within data elements in the frequency domain, potentially encompassing phase variations across multiple frequencies. Consequently, HAR sensor data of this nature demonstrates complex dynamic characteristics and time-varying attributes, with data elements at different times or frequencies exhibiting disparate phase magnitudes. Consequently, in practical applications, comprehensive analysis of data within the context of specific scenarios and data characteristics is imperative.

4.4 Results and Analysis

During our experiments, we used our own parameter settings as described above to pre-train our model, which may lead to differences in metrics such as the initial accuracy and the number of floating-point operations of our model compared to the model used in our previous work. Therefore, we have analyzed and summarized the specific difference values of different metrics as shown in the Table 2 below.

The initial baseline models exhibit nearly identical parameter counts, indicating consistency in model design and similar representation and generalization capabilities. This consistency is advantageous for subsequent experimental comparisons. Notably, our baseline model demonstrates markedly superior training accuracy on both the WISDM and PAMAP2 datasets, underscoring its enhanced feature learning and representation capabilities. Furthermore, in the comparison of floating-point operations, our baseline model demonstrates lower complexity on both the UCI-HAR and WISDM datasets. However, it exhibits higher complexity solely on the PAMAP2 dataset. The results of our pruning algorithm on three different datasets are given in Tables 3–5, respectively.

UCI-HAR. To ensure the robustness and validity of our experiments, we set the pruning threshold to vary within the range of 0.6 to 0.75, with an incremental step of 0.05. When the pruning threshold is set at 0.6, our algorithm achieves a compression of 83.67% in FLOPs and 83.46% in model parameter counts, without any loss of accuracy. This performance outperforms the results in both metrics of the ABCSearch-0.5 algorithm [49] and all three metrics of the Liu algorithm [38]. This indicates that our method not only achieves substantial model compression and efficiency improvement but also maintains competitive accuracy. When the pruning threshold is raised to 0.7, our algorithm performs even better, reducing FLOPs and the number of parameters by 90.73% and 90.53%, respectively. This outcome is significantly superior to other algorithms. Notably, at this threshold, the model’s accuracy does not decrease; instead, it increases by 0.14%. This increase in accuracy suggests that our pruning algorithm enhances the model’s generalization performance to a certain degree and effectively addresses the issue of overfitting.

WISDM. The experimental results on the WISDM dataset also demonstrate the competitiveness and excellent performance of our pruning algorithm. When the pruning threshold is set to 0.6, it outperforms other methods, including Liu et al.’s [38], Wang et al.’s [52], and Han et al.’s [53], with only a 0.05% decay in model accuracy. It achieves 83.72% compression in FLOPs and 83.46% compression in parameters. This finding highlights the effectiveness of our method in balancing model complexity and parameter optimization while sustaining high model accuracy.

After adjusting the threshold to 0.7, our method achieves a leading edge. It not only obtains higher FLOPs compression (90.77%) and model compression (90.53%) compared to the ABCSearch-0.7 method (89.42% and 88.70%), but it also only sacrifices 0.13% of the model’s accuracy.

PAMAP2. Unlike the other two datasets, the PAMAP2 dataset not only has a wider variety of human activities, but also brings a more complex amount of floating-point computations to the model. This poses a challenge for the deployment of the pruning algorithm, but the experimental results summarized above intuitively demonstrate the effectiveness and superiority of our algorithmic structure. For example, with the pruning threshold set to 0.65, our pruning algorithm achieves 87.50% compression of FLOPs while coordinating 86.71% compression of the number of parameters. At this time, the model accuracy is only lost by 0.38%, and this result is significantly better than Ma et al.’s [54] and Zeng et al.’s [26].

As the pruning threshold is adjusted to 0.7, our algorithm continues to show a distinct advantage. It achieves a higher compression rate in both FLOPs (90.74%) and parameters (90.05%), surpassing the performance of ABCSearch-0.7, with a minimal sacrifice in accuracy of just 0.67%. This further validates the effectiveness of our pruning architecture, especially when compared to traditional importance-based pruning methods. However, when the pruning threshold is increased to 0.75, the model experiences a more significant decay in accuracy of 1.62%. This indicates that there is a limit to the compression that can be achieved without negatively impacting the model’s performance, suggesting that excessive parameter reduction can lead to a point where the model’s efficacy is compromised.

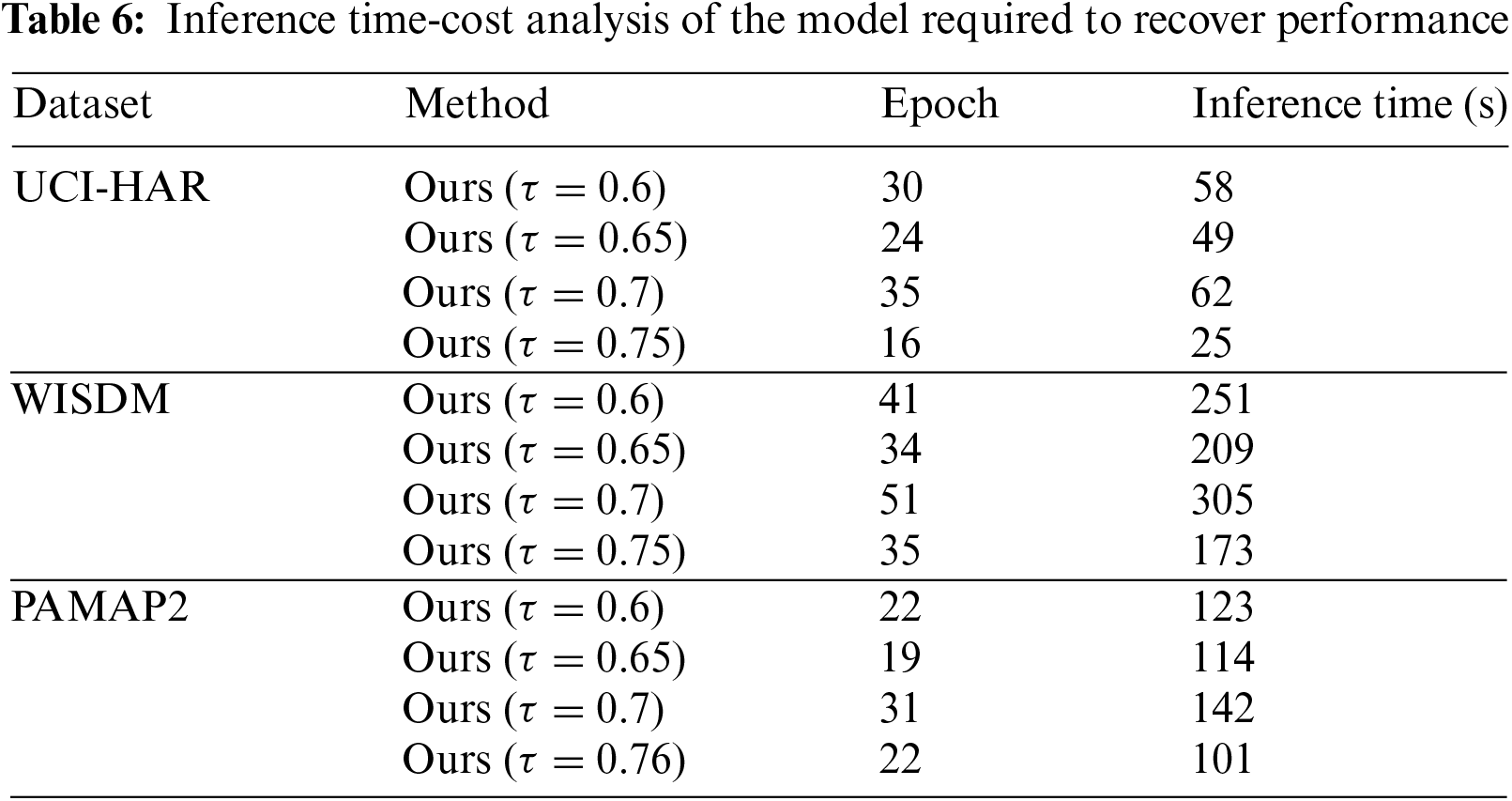
Excessive lightweighting of the model may also lead to an increase in inference time. To verify whether the time recovery cost of model performance increases with the degree of pruning, we counted the number of fine-tuning rounds required to recover most of the performance of the model at different degrees of lightweighting (as shown in Table 6).

In addition, our threshold selection focuses on the overall architecture of the complete model, i.e., the number of channels in each convolutional layer, aiming to search for the optimal number of channels retained in each layer and prune them by the algorithm. Therefore, in order to further show the specific impact our algorithm has on the model, we made a statistical comparison of the number of channels in each layer before and after model lightening.

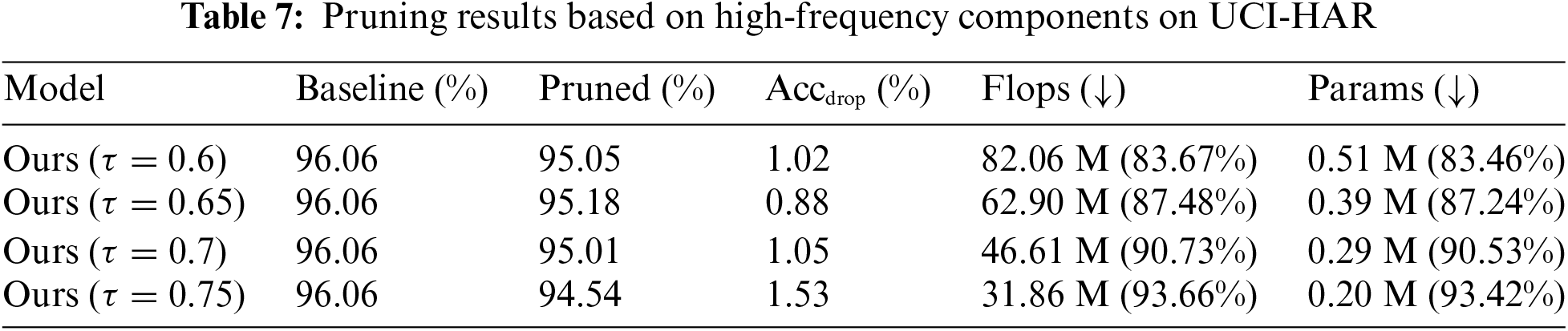
Fig. 4 shows specifically the impact on the model before and after applying the pruning algorithm. The horizontal axis represents each layer of the five-layer network and the vertical axis indicates the number of filters retained in each layer at different pruning rates. As can be seen, the original model is actually highly redundant, so there is no fatal impact on the model performance when the lightweighting algorithm is applied to greedily discard convolutional layer channels.

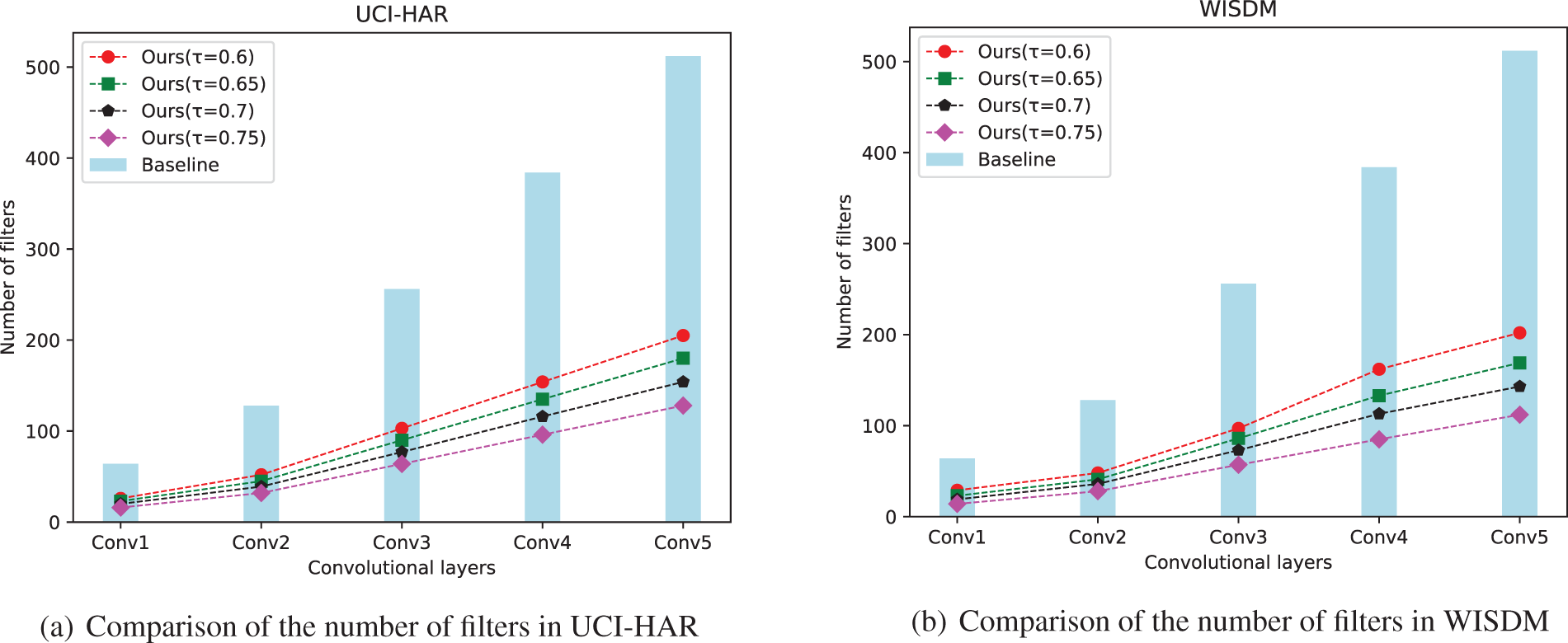
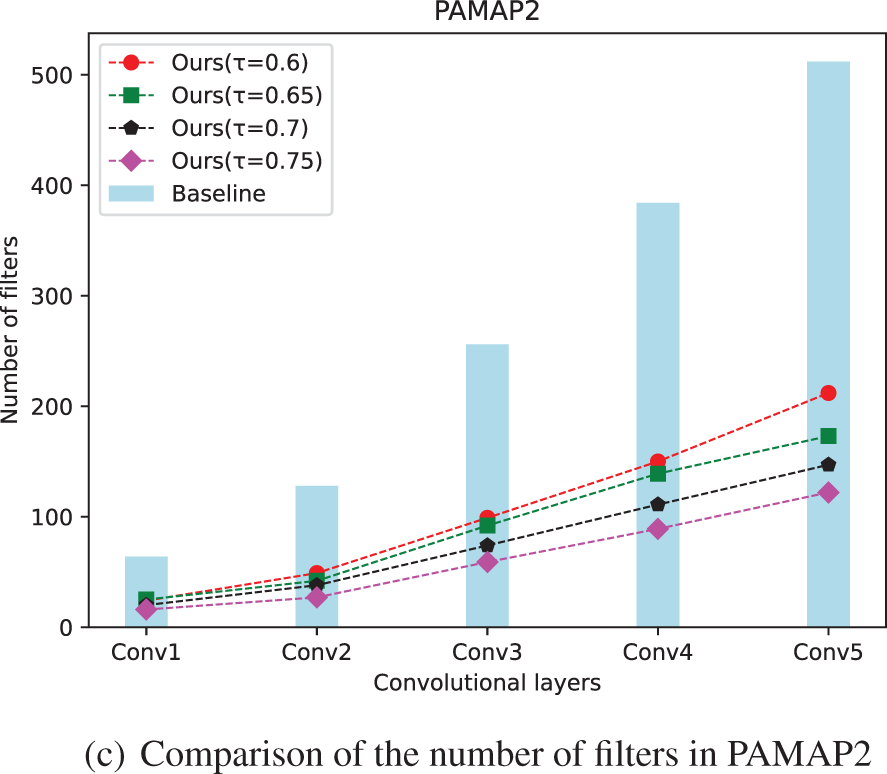
Figure 4: Comparison of the number of filters in each layer before and after pruning

In summary, our experiments underscore the importance of finding the right balance between model compression and accuracy maintenance. Our pruning algorithm has proven to be more effective and competitive in the field of human activity recognition (HAR) than current conventional pruning algorithms. It successfully achieves a higher degree of compression while keeping the reduction in accuracy to a minimum, highlighting its potential for practical applications in deploying efficient and accurate models.

5  Ablation Study

5.1 The Comparison of Different Frequency Representations

For datasets like HAR, frequency domain information provides valuable insights into movement characteristics and patterns of change across various frequencies in human activity data. Specifically, low-frequency components typically correspond to overarching trends and gradual changes in movement, reflecting activities like walking, jogging, or other slow and sustained movements over extended periods. Conversely, high-frequency components capture rapid changes and intricate details, representing actions such as acceleration, deceleration, turning, jumping, and similar movements. Generally, low-frequency features carry more informative value than high-frequency features in vision tasks [55], a principle that extends to sensor data tasks like HAR.

To scrutinize the impact of different frequency components on the pruning efficacy, we conducted evaluations using varying frequency information across three HAR datasets. Subsequently, we compared and analyzed the results. Initially, we devised experiments utilizing the energy density value of high-frequency components as the pruning index. The overall algorithmic performance is summarized in Tables 7–9.

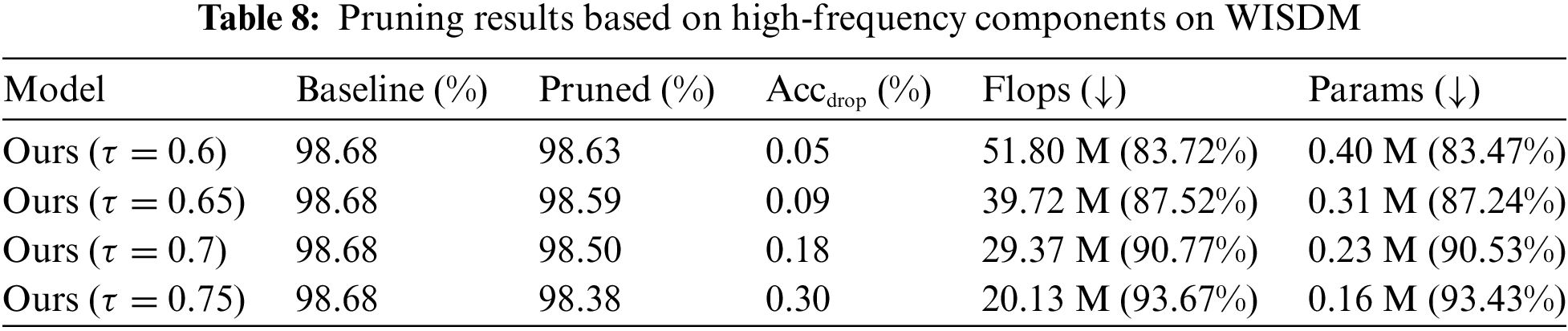
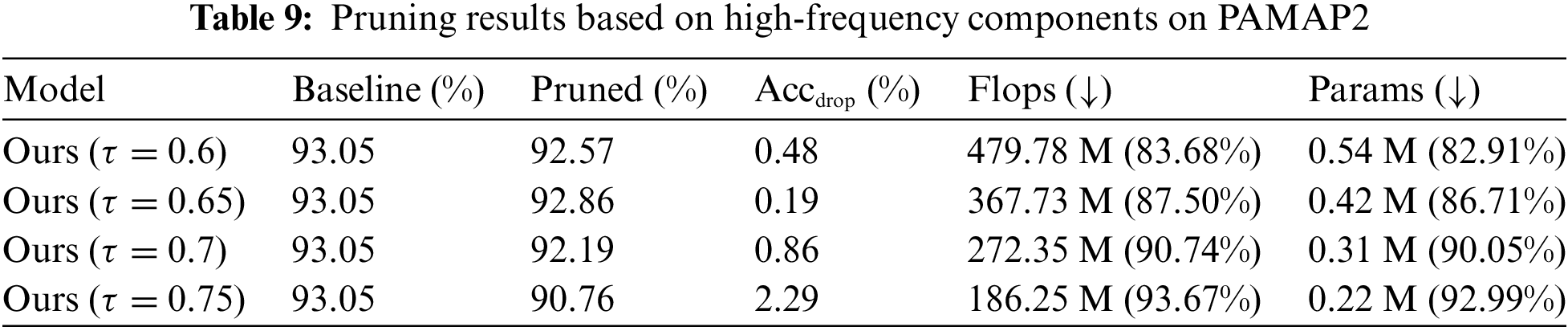
A discernible reduction in model accuracy is observed across all three datasets, with the effect being particularly pronounced in the PAMAP2 dataset. Here, a model accuracy decline of 2.29% is noted when employing a pruning threshold of 0.75. A similar, significant decrease exceeding 1% in model accuracy is observed in the UCI-HAR dataset, and this trend continues as the threshold is increased. In contrast, the algorithm performs more effectively in the WISDM dataset, showing only a minimal deviation from the baseline results obtained using low-frequency data. Nonetheless, this also underscores the algorithm’s sensitivity to the characteristics of different datasets, indicating a lack of robust generalization. In summary, while utilizing the high-frequency information component as a pruning criterion yields notable reductions in model FLOPs and parameters, it leads to a substantial loss in model performance. The approach demonstrates a lack of robustness across various datasets and fails to achieve an effective balance between model accuracy and compression.

Given that the low-frequency component of data such as HAR, mapped to the frequency domain, typically reflects motion tendencies and slower changes, whereas the high-frequency component signifies fast changes and detailed textures, it may be advantageous to achieve more favorable experimental outcomes by considering both components. Building on this premise, we conducted experiments to evaluate the energy spectral density of the overall information as an index. The results and analysis are detailed in Tables 10–12.

In order to make the experimental effects of these three different pruning strategies more intuitive, we visualize the model accuracy performance brought by these three strategies on different datasets, as shown below.

Fig. 5 clearly demonstrates that the low-frequency strategy holds a distinct advantage within the UCI-HAR dataset, yielding superior model performance. In contrast, the distinction between the high-frequency strategy and the overall frequency domain information strategy is less pronounced, with both showing reduced model accuracy. Within the WISDM dataset, both low-frequency and high-frequency strategies perform commendably, with only a marginal decrease in model accuracy. However, the overall frequency domain information strategy underperforms, exhibiting a significant drop in model performance compared to the other two strategies. In the PAMAP2 dataset, the performance of the three strategies is initially comparable, with no clear advantage for any single approach. Notably, at a pruning threshold of 0.65, the overall frequency domain information strategy outperforms the others, achieving a notable increase in model accuracy by over 0.5%.

Figure 5: Comparison of model accuracy under different pruning strategies

Upon evaluating the performance of the three strategies across various datasets, the results using the overall frequency domain information as an indicator diverge from expectations. In the UCI-HAR dataset, model accuracy experiences a significant decline, dropping by 1.70% at its lowest point, indicating a detrimental impact on performance due to pruning with this algorithm. In the WISDM dataset, employing a pruning threshold of 0.65 leads to the most severe performance degradation among all experimental outcomes, with a 2.73% decrease in model accuracy. Conversely, in the PAMAP2 dataset, the same threshold results in a 0.57% increase in model accuracy. However, as the pruning intensity increases, model performance suffers a substantial decline, with the lowest accuracy recorded at 91.71%, representing a loss of 1.33% in accuracy.

In summary, these experiments highlight the efficacy of the strategy that utilizes the energy spectral density values of low-frequency HAR data, outperforming strategies that rely on high-frequency components or overall frequency domain information. The high-frequency component strategy demonstrates lower stability, robustness, and generalization ability, making it more vulnerable to data variations and potentially overlooking critical action features, thus reducing recognition accuracy. On the other hand, the overall frequency domain information strategy increases computational and model complexity and is more susceptible to interference from invalid signals and noise. Furthermore, integrating both low- and high-frequency information may complicate the model, heightening the risk on unknown data and leading to unstable performance. The superior experimental outcomes of the low-frequency information-focused strategy suggest that it more effectively captures essential action features and patterns, thereby providing a more accurate characterization of overall action features in the HAR task.

5.2 The Differences in Selecting Redundant Filters among Different Strategies

After analyzing the experiments conducted with three different pruning strategies, a notable observation emerged. While the performance gap among these strategies is evident in the evaluation index of model accuracy, distinguishing between them becomes challenging when considering the evaluation indexes of FLOPs reduction and model parameter compression. It is evident that all three strategies demonstrate commendable model lightweighting performance, with minimal discernible differences in FLOPs reduction and model parameter compression. The disparity primarily manifests in the model performance post-pruning, where the redundant filters identified by each strategy vary, thereby influencing model performance differently.

To visually depict this discrepancy, we implemented a pruning ratio of 0.7 to filter the filters in the first layer of the convolutional network. Subsequently, we visualized the differences in the redundant filters selected by the three strategies across different datasets, as illustrated in Fig. 6.

Figure 6: The differences among the three strategies in the selection of redundant filters in different datasets

Fig. 6 displays heat maps illustrating the performance of three distinct strategies: the low-frequency component strategy (denoted as Algo-Low), the high-frequency component strategy (denoted as Algo-High), and the overall frequency-domain information strategy (denoted as Algo-Overall). Each heatmap represents the performance of these strategies in filter selection, with the horizontal axis representing the filter index ranging from 0 to 63. The vertical axis visually indicates whether the algorithm has selected the filter corresponding to that index, with purple bars denoting affirmative selections and white bars indicating negative selections.

It is evident that each of the three strategies exhibits noticeable differences in filter selection across various datasets. Instances arise where all three strategies identify a filter as redundant, while in other cases, only one strategy deems a filter redundant. The disparate choices of redundant filters by different strategies contribute to divergent model performances.

6  Conclusions

In this study, we introduce a novel network pruning algorithm that transitions from the conventional spatial domain to the frequency domain. This algorithm aims to streamline the network model by utilizing the characteristics of data in the frequency domain to judiciously select filters. The algorithm’s core concept is anchored in sensor data, such as that used in Human Activity Recognition (HAR), where a two-dimensional Discrete Fourier Transform (DFT) is applied to transition the data into the frequency domain. Subsequently, features are meticulously analyzed by visualizing the spectrograms of various frequency components to identify potential data patterns. The algorithm places particular emphasis on low-frequency components, utilizing their energy spectral density values as a criterion for evaluating and pruning redundant filters. Furthermore, we conduct extensive experiments to evaluate and validate the proposed algorithm by varying the pruning ratios. These experiments, performed on multiple standard HAR benchmarks, demonstrate the algorithm’s effectiveness in accelerating activity inference. Additionally, our approach surpasses existing methodologies in reducing Floating Point Operations (FLOPs) and model parameters, all while maintaining high activity recognition performance. These findings are instrumental in facilitating the implementation of deep models across a range of resource-constrained mobile devices. In future research, we intend to further optimize our algorithm and explore synergies with other neural network compression techniques, such as network quantization and knowledge distillation. This endeavor seeks to develop more efficient lightweight models capable of expediting the practical deployment of deep models in mobile HAR applications.

Acknowledgement: We thank the journal’s editors and anonymous reviewers for many helpful comments and Shao Labs for hardware support.

Funding Statement: This research is supported by National Natural Science Foundation of China (Nos. 61902158 and 62202210).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jian Su, Haijian Shao; data collection: Jian Su, Xing Deng; analysis and interpretation of results: Haijian Shao, Yingtao Jiang; draft manuscript preparation: Jian Su, Haijian Shao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data will be made available by the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. A. Andrade-Ambriz, S. Ledesma, M. -A. Ibarra-Manzano, M. I. Oros-Flores, and D. -L. Almanza-Ojeda, “Human activity recognition using temporal convolutional neural network architecture,” Expert. Syst. Appl., vol. 191, 2022, Art. no. 116287. doi: 10.1016/j.eswa.2021.116287. [Google Scholar] [CrossRef]

2. A. K. Panja, A. Rayala, A. Agarwala, S. Neogy, and C. Chowdhury, “A hybrid tuple selection pipeline for smartphone based human activity recognition,” Expert. Syst. Appl., vol. 217, 2023, Art. no. 119536. doi: 10.1016/j.eswa.2023.119536. [Google Scholar] [CrossRef]

3. S. R. Sekaran, P. Y. Han, and O. S. Yin, “Smartphone-based human activity recognition using lightweight multiheaded temporal convolutional network,” Expert. Syst. Appl., vol. 227, 2023, Art. no. 120132. doi: 10.1016/j.eswa.2023.120132. [Google Scholar] [CrossRef]

4. A. Bulling, U. Blanke, and B. Schiele, “A tutorial on human activity recognition using body-worn inertial sensors,” ACM Comput. Surv., vol. 46, pp. 1–33, 2014. doi: 10.1145/2499621. [Google Scholar] [CrossRef]

5. W. S. Lima, H. Bragança, and E. J. P. Souto, “Nohar-novelty discrete data stream for human activity recognition based on smartphones with inertial sensors,” Expert Syst. Appl., vol. 166, 2021, Art. no. 114093. doi: 10.1016/j.eswa.2020.114093. [Google Scholar] [CrossRef]

6. D. Zhang et al., “Fine-grained and real-time gesture recognition by using IMU sensors,” IEEE Trans. Mob. Comput., 2023, vol. 22, no. 4, pp. 2177–2189. doi: 10.1109/TMC.2021.3120475. [Google Scholar] [CrossRef]

7. Z. Shen, Z. He, and X. Xue, “Meal: Multi-model ensemble via adversarial learning,” in Proc. AAAI Conf. Artif. Intell., vol. 33, no. 1, pp. 4886–4893, 2019. doi: 10.1609/aaai.v33i01.33014886. [Google Scholar] [CrossRef]

8. H. Li, A. Kadav, I. Durdanovic, H. Samet, and H. P. Graf, “Pruning filters for efficient convnets,” 2017. doi: 10.48550/arXiv.1608.08710. [Google Scholar] [CrossRef]

9. N. Aghli and E. Ribeiro, “Combining weight pruning and knowledge distillation for CNN compression,” in 2021 IEEE/CVF Conf. Comput. Vis. Pattern Recognit. Workshops (CVPRW), 2021, pp. 3185–3192. doi: 10.1109/CVPRW53098.2021.00356. [Google Scholar] [CrossRef]

10. S. Guo, Y. Wang, Q. Li, and J. Yan, “DMCP: Differentiable markov channel pruning for neural networks,” 2020. doi: 10.48550/arXiv.2005.03354. [Google Scholar] [CrossRef]

11. H. Wang, R. Mo, Y. Chen, W. Lin, M. Xu and B. Liu, “Pedestrian and vehicle detection based on pruning yolov4 with cloud-edge collaboration,” Comput. Model. Eng. Sci., vol. 137, pp. 1–23, 2023. doi: 10.32604/cmes.2023.027603. [Google Scholar] [CrossRef]

12. J. Liu, H. J. Shao, X. Deng, and Y. T. Jiang, “Exploiting similarity-induced redundancies in correlation topology for channel pruning in deep convolutional neural networks,” Int. J. Comput. Appl., vol. 45, no. 5, pp. 379–390, 2023. doi: 10.1080/1206212X.2023.2218061. [Google Scholar] [CrossRef]

13. J. -H. Luo and J. Wu, “An entropy-based pruning method for CNN compression,” 2017. doi: 10.48550/arXiv.1706.05791. [Google Scholar] [CrossRef]

14. M. Lin et al., “HRank: Filter pruning using high-rank feature map,” 2020. doi: 10.48550/arXiv.2002.10179. [Google Scholar] [CrossRef]

15. A. Krizhevsky, I. Sutskever, and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” Commun. ACM, vol. 60, pp. 84–90, 2012. doi: 10.1145/3065386. [Google Scholar] [CrossRef]

16. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” 2015. doi: 10.48550/arXiv.1409.1556. [Google Scholar] [CrossRef]

17. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” 2015. doi: 10.1109/CVPR.2016.90. [Google Scholar] [CrossRef]

18. G. Huang, Z. Liu, L. Van der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” 2018. doi: 10.1109/CVPR.2017.243. [Google Scholar] [CrossRef]

19. R. Girshick, J. Donahue, T. Darrell, and J. Malik, “Rich feature hierarchies for accurate object detection and semantic segmentation,” 2014. doi: 10.1109/CVPR.2014.81. [Google Scholar] [CrossRef]

20. S. Ren, K. He, R. Girshick, and J. Sun, “Faster R-CNN: Towards real-time object detection with region proposal networks,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 6, pp. 1137–1149, 2017. doi: 10.1109/TPAMI.2016.2577031. [Google Scholar] [PubMed] [CrossRef]

21. B. Singh, M. Najibi, and L. S. Davis, “SNIPER: Efficient multi-scale training,” 2018. doi: 10.48550/arXiv.1805.09300. [Google Scholar] [CrossRef]

22. Q. Mu, Q. Yu, C. Zhou, L. Liu, and X. Yu, “Improved YOLOv8n model for detecting helmets and license plates on electric bicycles,” Comput. Mater. Contin., vol. 80, no. 1, pp. 449–466, 2024. doi: 10.32604/cmc.2024.051728. [Google Scholar] [CrossRef]

23. E. Shelhamer, J. Long, and T. Darrell, “Fully convolutional networks for semantic segmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 4, pp. 640–651, 2017. doi: 10.1109/TPAMI.2016.2572683. [Google Scholar] [PubMed] [CrossRef]

24. Z. Zhu, M. Xu, S. Bai, T. Huang, and X. Bai, “Asymmetric non-local neural networks for semantic segmentation,” in 2019 IEEE/CVF Int. Conf. Comput. Vis. (ICCV), 2019, pp. 593–602. doi: 10.1109/ICCV.2019.00068. [Google Scholar] [CrossRef]

25. M. Gao, F. Zheng, J. J. Yu, C. Shan, G. Ding and J. Han, “Deep learning for video object segmentation: A review,” Artif. Intell. Rev., vol. 56, pp. 457–531, 2022. doi: 10.1007/s10462-022-10176-7. [Google Scholar] [CrossRef]

26. M. Zeng et al., “Understanding and improving recurrent networks for human activity recognition by continuous attention,” 2018. doi: 10.1145/3267242.3267286. [Google Scholar] [CrossRef]

27. C. A. Ronao and S. -B. Cho, “Human activity recognition with smartphone sensors using deep learning neural networks,” Expert. Syst. Appl., vol. 59, pp. 235–244, 2016. doi: 10.1016/j.eswa.2016.04.032. [Google Scholar] [CrossRef]

28. J. Yang, M. N. Nguyen, P. P. San, X. Li, and S. Krishnaswamy, “Deep convolutional neural networks on multichannel time series for human activity recognition,” in Int. Joint Conf. Artif. Intell., 2015. [Google Scholar]

29. B. Hassibi and D. G. Stork, “Second order derivatives for network pruning: Optimal brain surgeon,” in Proc. 5th Int. Conf. Neural Inform. Process. Syst., San Francisco, CA, USA, Morgan Kaufmann Publishers Inc., 1992, pp. 164–171. [Google Scholar]

30. A. Aghasi, A. Abdi, N. H. Nguyen, and J. K. Romberg, “Net-trim: Convex pruning of deep neural networks with performance guarantee,” in Neural Information Processing Systems. Red Hook, NY, USA: Curran Associates Inc., 2016. doi: 10.48550/arXiv.1611.05162. [Google Scholar] [CrossRef]

31. Y. He, G. Kang, X. Dong, Y. Fu, and Y. Yang, “Soft filter pruning for accelerating deep convolutional neural networks,” 2018. doi: 10.48550/arXiv.1808.06866. [Google Scholar] [CrossRef]

32. Z. You, K. Yan, J. Ye, M. Ma, and P. Wang, “Gate decorator: Global filter pruning method for accelerating deep convolutional neural networks,” in Advances in Neural Information Processing Systems, H. Wallach, H. Larochelle, A. Beygelzimer, F. d’ Alché-Buc, E. Fox and R. Garnett, Eds., Red Hook, NY, USA: Curran Associates, Inc., 2019, vol. 32. doi: 10.48550/arXiv.1909.08174. [Google Scholar] [CrossRef]

33. J. Li, H. Shao, X. Deng, and Y. Jiang, “Efficient filter pruning: Reducing model complexity through redundancy graph decomposition,” Neurocomputing, vol. 599, 2024, Art. no. 128108. doi: 10.1016/j.neucom.2024.128108. [Google Scholar] [CrossRef]

34. J. Li, H. Shao, S. Zhai, Y. Jiang, and X. Deng, “A graphical approach for filter pruning by exploring the similarity relation between feature maps,” Pattern Recognit. Lett., vol. 166, pp. 69–75, 2023. doi: 10.1016/j.patrec.2022.12.028. [Google Scholar] [CrossRef]

35. Y. Tang et al., “Scop: Scientific control for reliable neural network pruning,” 2021. doi: 10.48550/arXiv.2010.10732. [Google Scholar] [CrossRef]

36. Y. He, P. Liu, Z. Wang, Z. Hu, and Y. Yang, “Filter pruning via geometric median for deep convolutional neural networks acceleration,” in 2019 IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), 2019, pp. 4335–4344. doi: 10.1109/CVPR.2019.00447. [Google Scholar] [CrossRef]

37. H. Hu, R. Peng, Y. Tai, and C. Tang, “Network trimming: A data-driven neuron pruning approach towards efficient deep architectures,” 2016. doi: 10.48550/arXiv.1607.03250. [Google Scholar] [CrossRef]

38. Z. Liu, J. Li, Z. Shen, G. Huang, S. Yan and C. Zhang, “Learning efficient convolutional networks through network slimming,” 2017. doi: 10.48550/arXiv.1708.06519. [Google Scholar] [CrossRef]

39. P. Singh, V. K. Verma, P. Rai, and V. P. Namboodiri, “Leveraging filter correlations for deep model compression,” 2020. doi: 10.48550/arXiv.1811.10559. [Google Scholar] [CrossRef]

40. X. Ding, G. Ding, J. Han, and S. Tang, “Auto-balanced filter pruning for efficient convolutional neural networks,” in AAAI Conf. Artif. Intell., 2018. doi: 10.1609/aaai.v32i1.12262. [Google Scholar] [CrossRef]

41. H. Wang, C. Qin, Y. Zhang, and Y. Fu, “Neural pruning via growing regularization,” 2021. doi: 10.48550/arXiv.2012.09243. [Google Scholar] [CrossRef]

42. K. Chen, D. Zhang, L. Yao, B. Guo, Z. Yu and Y. Liu, “Deep learning for sensor-based human activity recognition: Overview, challenges, and opportunities,” ACM Comput. Surv., vol. 54, no. 4, pp. 1–40, May 2021. doi: 10.1145/3447744. [Google Scholar] [CrossRef]

43. L. M. Dang, K. Min, H. Wang, M. J. Piran, C. H. Lee and H. Moon, “Sensor-based and vision-based human activity recognition: A comprehensive survey,” Pattern Recognit., vol. 108, 2020, Art. no. 107561. doi: 10.1016/j.patcog.2020.107561. [Google Scholar] [CrossRef]

44. D. Anguita, A. Ghio, L. Oneto, X. Parra, and J. L. Reyes-Ortiz, “Human activity recognition on smartphones using a multiclass hardware-friendly support vector machine,” in Ambient Assisted Living and Home Care, J. Bravo, R. Hervás and M. Rodríguez, Eds., Berlin, Heidelberg: Springer, 2012, pp. 216–223. doi: 10.1016/j.patcog.2020.107561. [Google Scholar] [CrossRef]

45. J. R. Kwapisz, G. M. Weiss, and S. Moore, “Activity recognition using cell phone accelerometers,” SIGKDD Explor., vol. 12, pp. 74–82, 2011. doi: 10.1145/1964897.1964918. [Google Scholar] [CrossRef]

46. A. Reiss and D. Stricker, “Introducing a new benchmarked dataset for activity monitoring,” in 2012 16th Int. Symp. Wearable Comput., 2012, pp. 108–109. doi: 10.1109/ISWC.2012.13. [Google Scholar] [CrossRef]

47. M. Zeng et al., “Convolutional neural networks for human activity recognition using mobile sensors,” in 6th Int. Conf. Mobile Comput., Appl. Serv., 2014, pp. 197–205. doi: 10.4108/icst.mobicase.2014.257786. [Google Scholar] [CrossRef]

48. A. Paszke et al., “PyTorch: An imperative style, high-performance deep learning library,” 2019. doi: 10.48550/arXiv.1912.01703. [Google Scholar] [CrossRef]

49. J. Liang, L. Zhang, C. Bu, D. Cheng, H. Wu and A. Song, “An automatic network structure search via channel pruning for accelerating human activity inference on mobile devices,” Expert. Syst. Appl., vol. 238, 2024, Art. no. 122180. doi: 10.1016/j.eswa.2023.122180. [Google Scholar] [CrossRef]

50. Y. Dong et al., “Evidential reasoning with hesitant fuzzy belief structures for human activity recognition,” IEEE Trans. Fuzzy Syst., vol. 29, no. 12, pp. 3607–3619, 2021. doi: 10.1109/TFUZZ.2021.3079495. [Google Scholar] [CrossRef]

51. A. Ignatov, “Real-time human activity recognition from accelerometer data using convolutional neural networks,” Appl. Soft Comput., vol. 62, pp. 915–922, 2018. doi: 10.1016/j.asoc.2017.09.027. [Google Scholar] [CrossRef]

52. X. Wang et al., “Deep convolutional networks with tunable speed accuracy tradeoff for human activity recognition using wearables,” IEEE Trans. Instrum. Meas., vol. 71, pp. 1–12, 2022. doi: 10.1109/TIM.2021.3132088. [Google Scholar] [CrossRef]

53. C. Han, L. Zhang, Y. Tang, W. Huang, F. Min and J. He, “Human activity recognition using wearable sensors by heterogeneous convolutional neural networks,” Expert. Syst. Appl., vol. 198, 2022, Art. no. 116764. doi: 10.1016/j.eswa.2022.116764. [Google Scholar] [CrossRef]

54. H. Ma, W. Li, X. Zhang, S. Gao, and S. Lu, “AttnSense: Multi-level attention mechanism for multimodal human activity recognition,” in Int. Joint Conf. Artif. Intell., 2019. doi: 10.24963/ijcai.2019/431. [Google Scholar] [CrossRef]

55. K. Xu, M. Qin, F. Sun, Y. Wang, Y. Chen and F. Ren, “Learning in the frequency domain,” 2020. doi: 10.1109/CVPR42600.2020. [Google Scholar] [CrossRef]