Secure Transmission Scheme for Blocks in Blockchain-Based Unmanned Aerial Vehicle Communication Systems

1  Introduction

As distinguished by low cost and high flexibility [1–3], there has been a growing interest in utilizing unmanned aerial vehicles (UAVs) for wireless communications and networking [4]. UAVs can act as mobile communications base stations or network relay nodes [5], providing services, extending network coverage, and improving connectivity in remote or disaster-stricken areas [6], and hence widely used in military, commercial, scientific research, and agriculture [7,8]. Integrating blockchain technology with UAVs can significantly enhance the capabilities of blockchain-based UAV communication systems in data collection, transmission, and storage. Blockchain ensures that the data collected by UAVs is stored in a secure and immutable manner, making it tamper-proof and easily traceable. A Smart Collaborative Evolvement (SCE) scheme is proposed for Virtual Group Creation (VGC) in the customized industrial Internet of Things [9]. This is achieved through the decentralized and cryptographic nature of blockchain, where data is divided into blocks that are linked and secured using cryptographic hashes [10]. However, one of the challenges faced during the implementation of this system is the vulnerability of the blocks to eavesdropping by malicious external nodes during the publishing process [11,12]. Addressing this issue is crucial for maintaining the integrity and confidentiality of the data transmitted and stored by UAVs using blockchain technology.

These potential threats can not only lead to mission failure but also pose significant security risks [13–15]. Traditional encryption techniques can address some aspects of UAV network security, but efficiently solving the underlying complex mathematical problems is necessary, which poses certain limitations for simple devices [16]. Therefore, physical layer security (PLS) can be employed to address security issues in blockchain-based UAV communication systems [17–20]. PLS does not rely on traditional encryption algorithms; instead, it utilizes the characteristics of signal transmission and the physical properties of communication systems to protect communication content from eavesdropping [21,22]. The design of appropriate communication protocols and signal processing techniques allows for the effective prevention of information leakage and tampering while enhancing the security of UAV communication networks [23–25]. A new consensus protocol called Proof of Channel (PoC) utilizes the natural characteristics of wireless communication and develops a permission BLOWN protocol for single-hop wireless networks under the adversarial SINR model [26]. This paper studies a secure transmission scheme for blocks in blockchain-based UAV communication systems to prevent the information contained in blocks from being completely eavesdropped during transmission.

1.1 Motivation and Contributions

As previously stated, most literature only investigates the security performance of UAV communication at the physical layer without considering that messages within blocks may also be susceptible to eavesdropping during transmission. The data was securely stored in the blockchain to prevent tampering during transmission, but cannot prevent eavesdropping during block publishing. Current physical layer security methods only target the bit stream and do not consider communication systems where the transmission unit is a block with a finite length related to a blockchain system’s performance. In a blockchain system, longer block lengths can delay data transmission and increase storage and processing demands. Longer blocks take more time to propagate, which increases confirmation times. Additionally, they consume more storage space and computational resources, burdening nodes with limited resources. Conversely, shorter block lengths can result in frequent block generation, thereby increasing the burden on transmission and processing. This, in turn, can lead to redundancy and reduced efficiency in the blockchain system. Therefore, block length design should strike a balance between transaction processing efficiency, network propagation speed, and system resource consumption.

According to the abovementioned, this paper explores a secure block transmission scheme for blocks in blockchain-based UAV communication systems. It aims to guarantee that over half of the legitimate nodes can accurately receive the entire block information during the communication process. Our approach utilizes blockchain technology due to its unique ability to provide decentralized, secure, and tamper-resistant data management. For Unmanned Aerial Vehicle (UAV) systems, these attributes are crucial for ensuring data integrity and security, especially in environments where trust cannot be established between parties, such as drones or ground stations. Additionally, it ensures that no eavesdropper can access the complete block information. If the eavesdropper receives only part of the block information, it cannot decode the private information contained in the block intended for transmission. We consider both the physical layer security of the UAV network and the performance of the blockchain. We utilize jamming UAVs to transmit jamming signals to prevent eavesdropping by external malicious nodes, reduce the quality of the eavesdropping channel, and consequently enhance the security performance of the legitimate channel. The trajectory and power of the UAV, along with the block length, are jointly optimized to maximize the average minimum secrecy rate (AMSR) and the performance of the blockchain while considering the constraints of UAV maneuverability and the maximum power.

In summary, the main contributions of this paper are as follows:

•   Firstly, we consider the secure communication of a block with a finite length in blockchain-enabled UAV communication systems. Putting the information into a blockchain block for transmission ensures that the information is not tampered with. However, current physical layer security methods only target the bit stream and do not consider communication systems where the transmission unit is a block. We aim to prevent eavesdroppers from accessing the entire block information during communication. In addition, we consider the delay caused by block generation and transmission to determine an appropriate block length. This approach differs from previous studies focusing solely on the physical layer to ensure secure information transmission.

•   We design a joint optimization problem to improve the security performance of the block transmission and the performance of the blockchain itself by adjusting the trajectory and power of the UAV, along with the block length.

•   The proposed optimization problem is non-convex and challenging to solve directly. Therefore, we first decompose the original problem into non-convex subproblems and then use a first-order approximation to transform these subproblems into convex problems. Finally, an alternating iteration algorithm based on the successive convex approximation (SCA) technique is used to solve these problems.

The simulation results demonstrate the superiority and effectiveness of our alternating algorithm in improving the AMSR for secure block transfer in UAV-assisted blockchain communication systems. When considering blockchain performance, an optimal block size can be determined. When blockchain performance is not considered, the block size defaults to the maximum value, and long blocks may result in transmission delays.

1.2 Related Works

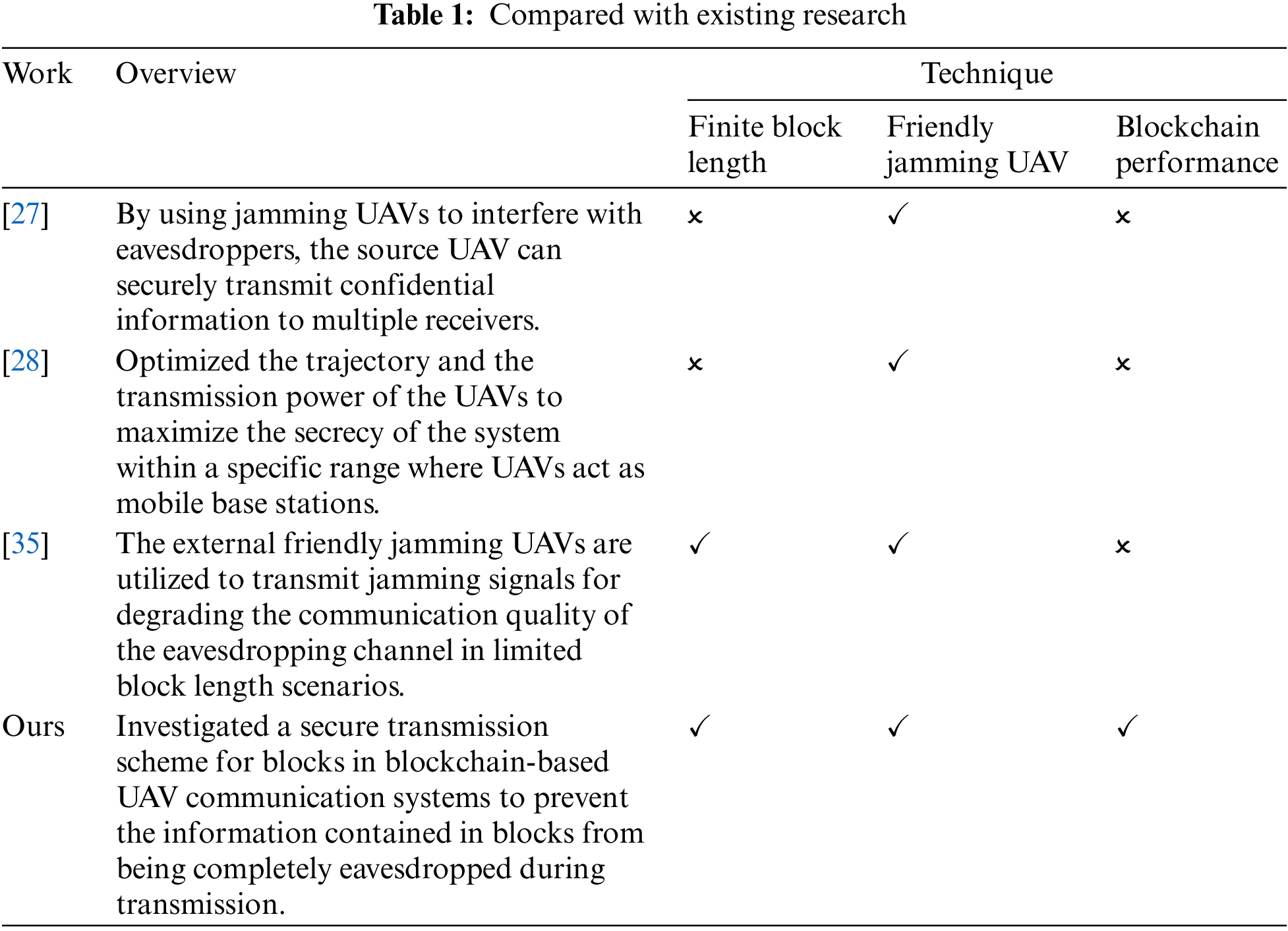
1) PLS for UAV communication systems: In [27], the communication performance between UAVs and ground devices is enhanced by jointly optimizing the trajectory of UAVs and communication network resources. Using jamming UAVs to interfere with eavesdroppers, the source UAV can securely transmit confidential information to multiple receivers [27]. The authors in [28] propose optimizing the trajectory and transmission power of the UAVs to maximize the system’s secrecy within a specific range where UAVs act as mobile base stations. To ensure communication security between a transmitter and a receiver, a series of covert communications with UAV networks has been employed [29,30] to prevent malicious users from discovering the occurrence of communication. When the allowed delay is short or strict concealment requirements are in place, the work [31] demonstrates that randomly altering the transmission power can strengthen the performance of covert communication. With delay constraints, the authors in [32] investigate covert communication over an Additive White Gaussian Noise (AWGN) channel. Notably, the works as mentioned above assume infinite block lengths, which is impractical in real-world scenarios. Due to constraints such as data transmission rates, energy consumption, signal interference, attenuation, and transmission delays, it is generally necessary to limit the block size to ensure communication quality and energy efficiency [33]. It is impossible to transmit data packets of infinite block length within sufficiently small time slots, and such packets may cause delays during transmission. Therefore, it is necessary to consider finite block-length data packets to overcome these issues. Under the practical scenario of finite block length, a method is proposed to maximize secure UAV communication’s average effective secrecy rate by jointly optimizing the UAV trajectory and transmission power [34]. The external friendly jamming UAVs are utilized in [35] to transmit jamming signals to degrade the communication quality of the eavesdropping channel in limited block length scenarios. To understand better, we have compared our findings with existing research in Table 1.

2) Blockchain communication systems: Blockchain technology can be used to guarantee the secure recording and transmission of data [36]. The blockchain is formed by dividing data into blocks and linking these blocks sequentially. Each block contains information derived from the preceding block. The most significant characteristic of blockchain is its immutability, which ensures the integrity and reliability of data. This feature has led to the widespread adoption of blockchain technology across various industries [37]. Once data is recorded on the blockchain, it is not easy to alter, ensuring data integrity and security through encryption and consensus algorithms. These characteristics make blockchain technology particularly suitable for applications requiring high trust, data security, and transparency. There is a significant amount of research on applying blockchain technology to the Internet of Vehicles (IoV) [38–40]. To effectively prevent unauthorized data access, consortium blockchain, and smart contracts enable secure data storage and sharing within the vehicular edge network [41]. A lightweight blockchain security protocol is used to support secure storage and communication in software-defined networking (SDN) [42]. Utilizing blockchain technology to construct a UAV network, UAVs can be deployed to provide services and act as nodes in the blockchain network [43]. These UAVs can exchange computing resources with each other and obtain necessary resources from edge computing nodes. In [44], the data collection process based on blockchain utilizes UAVs as relays to gather information from the Internet of Things (IoT) and securely store it in the blockchain on the mobile edge computing (MEC) server. In [45], the authors combine the delegated Byzantine fault tolerance (DBFT) consensus mechanism from the blockchain with the Multi-point Relay (MPR) mechanism to introduce a trusted network framework for UAV self-organizing networks. In [46], the authors design a reputation-based consensus protocol to accommodate weak connectivity environments and enhance consensus efficiency, aiming to encourage honest behavior among UAVs.

The rest of the paper is organized as follows. Section 2 proposes a model for a UAV-assisted blockchain communication system and presents the AMSR maximization problem. Section 3 employs an alternating optimization algorithm based on successive approximation and SCA techniques to solve the optimal AMSR problem. Section 4 presents simulation results obtained through comparison with other schemes, which validate the superiority and effectiveness of the proposed algorithm. Finally, Section 5 gives the conclusion and discussion of the whole paper.

2  System Model and Problem Formulation

This section will introduce the system model and propose the AMSR maximization problem.

2.1 Transmission Model

As illustrated in Fig. 1, we study a secure block transmission method in a blockchain-based UAV (Unmanned Aerial Vehicle) communication system. This system is designed for a downlink transmission scenario involving four key entities: the source UAV (UAV-B), the jamming UAV (UAV-J), the ground receiver (GR), and the eavesdropper (EVE). In this scenario, the source UAV (UAV-B) transmits sensitive or classified information to the ground receiver (GR). However, during the transmission, there is a risk that the eavesdropper (EVE) may intercept and attempt to decode this information. To reduce the risk of the eavesdropper successfully decoding the intercepted information, we introduce a jamming UAV (UAV-J) into the system. The jamming UAV (UAV-J) continuously emits jamming signals aimed at the eavesdropper (EVE) to disrupt its ability to decode the transmitted information. This approach enhances the security of the communication link between the source UAV and the ground receiver.

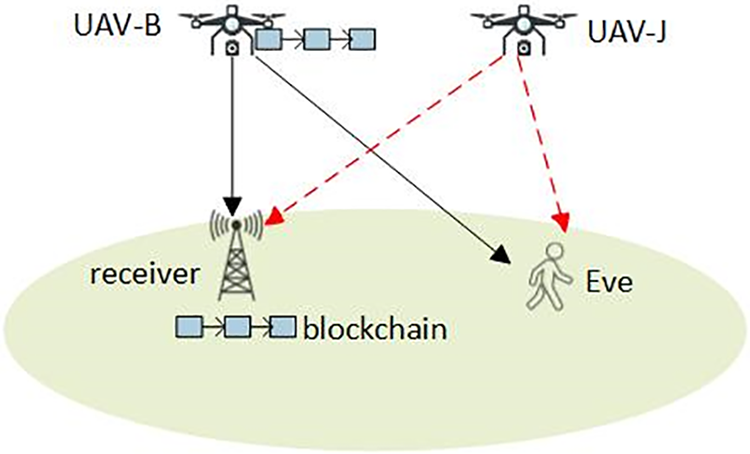
Figure 1: Blockchain-based UAV communication systems

Additionally, all messages are stored on a blockchain to secure the transmitted information further. Blockchain technology provides a secure and immutable record of the transmitted data, ensuring that the integrity of the information is maintained and preventing unauthorized tampering. For effective transmission and jamming, we assume that the locations of both the ground receiver (GR) and the eavesdropper (EVE) are known to the UAVs in the system. This setup aims to ensure secure data transmission in UAV networks by combining physical layer security (jamming) with blockchain technology for data integrity.

In the UAV transmission model, the UAV flies horizontally at a fixed altitude H, which is the minimum altitude to avoid obstacles, and has a flight period T. The flight period T is divided into I equal-length time slots of τ, i.e., T=Iτ. Since the time slots τ are sufficiently small, we assume that the position of the UAV remains approximately constant during the transmission phase of each time slot, but the position changes in different time slots. We use a 3D coordinate system to describe the position of the UAV and define the coordinates of the UAV at the τ-th time slot as qu[τ]=[x(τ), y(τ), H]T. Let the maximum speed of the UAV be Vmax, and then the maximum distance traveled in each time slot τ is L=Vmax. Thus, the mobility constraint of the UAV can be expressed as

‖qu[τ+1]−qu[τ]‖≤L,(1)

‖⋅‖ denotes the Euclidean distance. This constraint indicates that the distance the UAV moves between adjacent time slots cannot exceed the maximum allowable flight distance L.

Similarly, we can define the minimum distance dmin between UAV-B and UAV-J as

‖qB[τ]−qJ[τ]‖≥dmin.(2)

This constraint avoids collisions between UAVs.

The UAV-B and the ground node act as the legitimate sender and receiver, respectively. The UAV to the ground node communication channels can be modeled as a Rayleigh fading channel.

gu,g[τ]=δu,g[τ]du,g−α[τ], g∈G={m, k}, u∈U={B,J},(3)

where gu,g is the channel coefficient between UAVu and ground node g, δu,g is the channel gain after Rayleigh fading and varies randomly for each time slot [47]. The path loss exponent α is usually in the range of 2–4, and we take 2 here. And du,g is the instantaneous distance between the node u and the node g, that is, the distance between UAVu and ground node g at the time slot τ, which can be expressed as du,g=‖qu[τ]−qg‖.

Let PB[τ] and PJ[τ] represent the transmit power of UAV-B and UAV-J, respectively, when sending information to the ground node at the time slot τ. We denote their average transmit power as P¯B[τ] and P¯J[τ], respectively. In practice, the transmit power is often subject to peak constraints, denoted as PB,MAX and PJ,MAX, respectively. Consequently, the transmit power can be constrained as follows:

0≤PB[τ]≤PB, MAX,(4a)

1T∑τ=1TPB[τ]≤PB¯[τ],(4b)

0≤PJ[τ]≤PJ, MAX,(4c)

1T∑τ=1TPJ[τ]≤PJ¯[τ].(4d)

2.2 Secrecy Rate

According to the above transmission model, the instantaneous Signal to Interference plus Noise Ratio (SINR) of the link at the time slot τ when UAV-B transmits a message to the ground receiver m is given by

rB,m[τ]=(PB[τ]ρB,m[τ])/‖qB[τ]−qm‖2(PJ[τ]ρJ, m[τ])/‖qJ[τ]−qm‖2,(5)

where ρB,m[τ]=δB,m[τ]σ2, δB,m is the channel gain after Rayleigh fading, and the channel gain varies randomly for each time slot. Similarly, ρJ, m[τ]=δJ, m[τ]σ2, δJ, m represents the channel gain following the occurrence of Rayleigh fading between the UAV-J and the ground receiver m. And σ2 denotes the noise power of the additive Gaussian white noise (AWGN).

For the wiretap channel, the instantaneous SINR of the link between UAV-B and the eavesdropper k is given by

rJ,k[τ]=(PB[τ]ρB,k[τ])/‖qB[τ]−qk‖2(PJ[τ]ρJ,k[τ])/‖qJ[τ]−qk‖2,(6)

At the time slot τ, the achievable rate (bps/Hz) from the UAV-B to the ground receiver m can be expressed as

Rm[τ]=log2⁡(1+rB,m[τ]).(7)

Similarly, the achievable rate (bps/Hz) by the eavesdropper k can be expressed as

Rk[τ]=log2⁡(1+rJ,k[τ]).(8)

When the transmission rate is lower than the secure transmission rate and the confidential information is sufficiently long, the error probability during transmission can be minimized. However, when the information length is finite, decoding errors and information leakage at the ground receiver are unavoidable [48]. Therefore, at the time slot τ, the secrecy rate Rsecm for the ground receiver m can be expressed as

Rsecm[τ]=[[Rm[τ]−Rk[τ]]−Vm[τ]lQ−1(ε)ln2−Vk[τ]lQ−1(η)ln2]+,(9)

where [x]+ is defined as the maximum of x and 0. Additionally, Vm[τ]lQ−1(ε)ln2 denotes the constraint on the probability of decoding error ϵ for ground receivers and Vk[τ]lQ−1(η)ln2 denotes the secrecy constraint on information leakage η. Here, l denotes the length of the block, and Vx[τ]=1−(1+rx[τ])−2, where x∈{m, k}, represents the channel dispersion, which measures the randomness of the channel relative to a deterministic channel with the same capacity. Channel dispersion reflects the randomness of a channel relative to a deterministic channel and determines how closely the channel capacity can be approached under finite block length conditions. A more significant channel dispersion indicates greater randomness in the channel. The function Q−1(⋅) represents the inverse of the Gaussian Q-function. It is utilized in communication systems and signal processing to determine thresholds for achieving optimal performance at a given error rate or leakage probability, defined as Q(x)=∫x∞12πe−t22dt.

2.3 The Performance of a Blockchain

The block size affects two key metrics: block generation time and transmission latency [49]. The block generation time refers to the time required to create a new block. Transmission delay refers to the time required for a newly created block to propagate through the network to all nodes. A larger block size can accommodate more transactions, reducing block generation time. However, a larger block size also requires more time for transmission. In contrast, smaller block sizes can reduce transmission time but may increase the total block generation time because more blocks are needed to process all transactions in the memory pool. Therefore, optimizing the block size is necessary.

The time required to create the block is represented by

Tg=Smeml(Toverhead+l/StMerklet×TMerkle),(10)

where Smem represents the size of the memory pool, while l denotes the block size. Consequently, the number of blocks is represented as Smem/l. We denote St as the size of an individual transaction, so l/St represents the transaction count within a block. Let Merklet symbolize the transaction count within a Merkle tree, which is typically maintained as a constant value, and TMerkle represent the time required for the construction of the Merkle tree. In addition, and Toverhead denotes the extra overhead time.

The time for the transmission latency of a block can be expressed as

Td=h⋅(Tp+lR),(11)

where Tp represents the processing time, and R denotes the transmission rate of the node. It is assumed that R is equal for every node in the blockchain system.

Accordingly, the overall objective function concerning a block performance can be expressed as follows:

F(l)=ρTd+(1−ρ)Tg,(12)

where ρ is the assigned weight. The greater the weight ρ, the shorter the latency time and the longer the block generation time. Hence, given a weight ρ, we can find the optimal block length.

2.4 Optimization Problem

To facilitate the description, we define Qu={qu[τ]|u∈{B, J}, ∀τ} to represent the position of UAVs. Different weights ω and 1−ω are assigned to the secrecy rate Rsecm and the block performance F(l). Then, the overall optimization problem can be expressed as (P1):

maxPB,PJ,QB,QJ,l⁡min[ω(1T∑τ=1TRsecm[τ])−(1−ω)F(l)]+,(13a)

s.t. Eqs. (1),(2),(4a),(4b),(4c),(4d),(13b)

rB,m[τ]≥β1, ∀τ,(13c)

Rsecm[τ]≥β2, ∀τ,(13d)

0≤l≤lmax,(13e)

where the constraints (1) and (2) represent the mobility and position constraints of the UAVs. The constraints (4a) and (4b) are for the UAVs’ power constraints. Constraints (13c) and (13d) indicate that for reliable message transmission and successful block generation, rB,m must exceed the threshold β1, and the secrecy rate Rsecm must be greater than the threshold β2. Constraint (13e) indicates that the block length should be less than the maximum value.

3  Proposed Alternating Algorithm

In this section, we utilize an alternating optimization algorithm based on successive approximation and SCA techniques to solve the proposed AMSR maximization problem while considering the blockchain’s performance.

The non-convex nature of the optimization problem makes it challenging to solve. To ensure convergence and efficacy in maximizing the AMSR with the performance of the blockchain, and achieve a locally optimal solution to the optimization problem, this work employs an efficient alternating optimization algorithm [35].

By introducing the slack variables Tg={tg[τ], ∀τ} and Mg={mg[τ], ∀τ}, omiting min and [x]+, the original optimization problem (P1) is reformulated as (P2):

maxPB,PJ,QB,QJ,l⁡[ω(1T∑τ=1TR¯secm[τ])−(1−ω)F(l)],(14a)

s.t. Eqs. (1),(2),(4a)−(4d),(13c)−(13e),(14b)

tg[τ]≥(PB[τ]ρB,g[τ])/‖qB[τ]−qg‖2(PJ[τ]ρJ,g[τ])/‖qJ[τ]−qg‖2, g∈{m, k}, ∀τ,(14c)

mg2[τ]≥1−(1+tg[τ])−2, g∈{m, k}, ∀τ,(14d)

mg[τ]≥0, g∈{m, k}, ∀τ,(14e)

R¯secm[τ]=[log2(1+PB[τ]ρB,m[τ]/‖qB[τ]−qm‖2PJ[τ]ρJ, m[τ]/‖qJ[τ]−qm‖2)−log2(1+tk[τ])]−mm[τ]Q−1(ε)ln2−mk[τ]Q−1(η)ln2.(15)

where the constraint (14c) transforms the problem into a more manageable form. The constraints (14d) and (14e) ensure the smooth operation of the iterative algorithm proposed below. In addition, the constraints (14c) and (14d) are set with an equal sign, ensuring that (P1) and (P2) are equivalent. And the secrecy rate can be enhanced by decreasing Tg and Mg.

Problem (P2) is still a non-convex and highly complex problem to solve due to the non-concave nature of the objective function (14a) concerning both Pu and Qu, as well as the non-convex constraints (14c) and (14d). To solve it, we divide the optimization problem (P2) into the following five subproblems: (1) the position optimization for UAV-B, (2) the position optimization for UAV-J, (3) the length optimization for blocks, (4) the power optimization for UAV-B, and (5) the power optimization for UAV-J.

3.1 Position Optimization for the UAV-B

This subsection will optimize UAV-B’s position while maintaining UAV-B’s power, UAV-J’s position, power, and block length constant. As a result, the subproblem is represented by (P3a):

maxQB,Tg,Mg⁡[ω(1T∑τ=1TR¯secm[τ])−(1−ω)F(l)],(16a)

s.t. Eqs. (1),(2),(13c),(13d),(14c),(14d),(14e).(16b)

Because the constraints (14c) and (14d) are non-convex, and the objective function (16a) is non-convex, problem (P3a) remains non-convex. We will then focus on transforming problem (16a) into a convex optimization problem. Define Cm=PB[τ]ρB,m[τ]PJ[τ]ρJ, m[τ]/∥qJ[τ]−qm∥2, R¯secm[τ] can be expressed as

R¯secm[τ]=log2⁡(1+Cm‖qB[τ]−qm‖2)−log2⁡(1+tk[τ])−mm[τ]Q−1(ε)ln2l−mk[τ]Q−1(η)ln2l.(17)

We introduce the slack variables Lg={lg[τ], ∀τ}, g∈{m, k}, and rewrite the constraint (14c) equivalently as

tg(τ)≥Cmlg(τ),(18a)

lg[τ]≥‖qB[τ]−qg‖2, g∈{m, k}.∀τ.(18b)

The above (18a) is a convex constraint and the term ∥qB[τ]−qg∥2 in (18b) serves as a lower bound of a convex function. Therefore, we can convert the first-order Taylor expansion into a convex constraint. For a given initial feasible point q^u[τ], (18b) can be expressed as

lg[τ]≥‖q^B[τ]−qg‖2+2‖q^B[τ]−qg‖(qB[τ]−q^B[τ]), g∈{m, k}, ∀τ.(19)

where (19) is a convex constraint now.

Similarly, the non-convex constraint (14d) can be converted into a convex constraint by applying the first-order Taylor expansion. With the initial feasible points represented by the symbols with t^g[τ] and m^g[τ], g∈{m, k}, the constraint (14d) can be restated as follows:

m^g2[τ]+2m^g[τ](mg[τ]−m^g[τ])≥1−(1+t^g[τ])−2+2(1+t^g[τ])−3(tg[τ]−t^g[τ]), g∈{m, k}.∀τ.(20)

For (17), we can see that R¯secm[τ] is a convex function concerning ∥qB[τ]−qg∥2 and tg[τ]. By using feasible points q^B[τ] and t^k[τ], we can employ the first-order approximation technique to construct a lower bound for R¯secm[τ] as below:

R¯secm[τ]≥R~sec1m[τ]=log2⁡(1+Cm‖q^B[τ]−qm‖2)−Cm(‖qB[τ]−qm‖2−‖q^B[τ]−qm‖2)ln2‖q^B[τ]−qm‖2(‖q^B[τ]−qm‖2+Cm)−log2⁡(1+t^k[τ])−(tk[τ]−t^k[τ])ln2(1+t^k[τ])−mm[τ]Q−1(ϵ)ln2l−mk[τ]Q−1(η)ln2l.(21)

Thus, our optimization problem can be finally expressed as (P3b):

maxQB,Tg,Mg, Lg⁡[ω(1T∑τ=1TR~sec1m[τ])−(1−ω)F(l)],(22a)

s.t. Eqs. (1),(2),(13c),(13d),(14e),(18a),(19),(20).(22b)

The subproblem (P3b) is a standard convex optimization problem that can be effectively solved using techniques such as CVX [50].

3.2 Position Optimization for the UAV-J

In this subsection, we optimize the position of the UAV-J while maintaining the position and power of UAV-B, the power of UAV-J, and the block length constant. Then, the corresponding sub-problem can be expressed as (P4a):

maxQJ,Tg,Mg⁡[ω(1T∑τ=1TR¯secm[τ])−(1−ω)F(l)],(23a)

s.t. Eqs. (1),(2),(13c),(13d),(14c)−(14e).(23b)

Define C1=PB[τ]ρB,k[τ]∥qB[τ]−qk∥2 and C2=PJ[τ]ρJ,k[τ]. The objective function R¯secm[τ] can be reformulated as

R¯secm[τ]=log2⁡(1+tm[τ])−log2⁡(1+C1C2∥qJ[τ]−qk∥2)−mm[τ]Q−1(ε)ln2l−mk[τ]Q−1(η)ln2l.(24)

The second term in (24) is identified as a non-convex function. By utilizing the first-order Taylor expansion on the feasible point ∥q^J[τ][τ]−qk∥2, we obtain

R¯secm[τ]≥R~sec2m[τ]=log2⁡(1+tm[τ])−log2⁡(1+C1C2∥q^J[τ]−qk∥2)−C1C2(∥qJ[τ]−qk∥2−∥q^J[τ]−qk∥2)ln2(C1∥q^J[τ]−qk∥2+C2+∥q^J[τ]−qk∥2)(C2∥qJ[τ]−qk∥2)−mm[τ]Q−1(ε)ln2l−mk[τ]Q−1(η)ln2l.(25)

Accordingly, the optimization problem can be finally expressed as (P4b):

maxQJ,Tg,Mg, Lg⁡[ω(1T∑τ=1TR~sec2m[τ])−(1−ω)F(l)],(26a)

s.t. Eqs. (1),(2),(13c),(13d),(14e),(18a),(18),(20).(26b)

At this stage, our position optimization for the UAV-J has been transformed into a standard convex optimization problem (P4b) that can be solved using the CVX tool.

3.3 Blocklength Optimization

In this subsection, we optimize the block length l, while maintaining the positions and powers of the UAV-B and UAV-J. Consequently, the corresponding sub-problem can be expressed as (P5a):

maxl[ω(1T∑τ=1TRsecm[τ])+(1−ω)F(l)],(27a)

s.t. Eqs. (13c),(13d),(27b)

0≤l≤lmax.(27c)

The block length affects the secrecy rate in the physical layer transmission process and influences the blockchain’s performance. Therefore, it is necessary to optimize the block length l in both the secrecy rate R¯secm[τ] and the function F(l).

Define r1[τ]=log2⁡(1+PB[τ]ρB,m[τ]/∥qB[τ]−qm∥2PJ[τ]ρJ, m[τ]/∥qJ[τ]−qm∥2), r2[τ]=log2⁡(1PB[τ]ρB,k[τ]/∥qB[τ]−qk∥2PJ[τ]ρJ,k[τ]/∥qJ[τ]−qk∥2), N1[τ]=mm[τ](Q−1(ε))ln⁡2, N2[τ]=mk[τ](Q−1(η))ln⁡2, the objective function R¯secm[τ] can be simplified to

=ω(r1[τ]−r2[τ]−(N1[τ]+N2[τ])l)−(1−ω)F(l).(28)

The objective function is concave. Therefore, we can directly formulate the optimization problem as (P5b):

maxl[ω(1T∑τ=1TR~sec3m[τ])−(1−ω)F(l)],(29a)

s.t. Eqs. (13c),(13d),(29b)

0≤l≤lmax.(29c)

The problem (P5b) is a standard convex optimization problem that can be solved using the CVX tool.

3.4 Power Optimization for UAV-B

In this subsection, we will optimize the power PB of UAV-B while keeping the positions of UAV-B and UAV-J unchanged, as well as the power PJ and the block length constant. Therefore, the corresponding sub-problem can be written as (P6a):

maxPB,Tg,Mg⁡[ω(1T∑τ=1TR¯secm[τ])−(1−ω)F(l)],(30a)

s.t. Eqs. (4a)−(4d),(13c),(13d),(14c)−(14e).(30b)

Defining A1[τ]=gB,g2[τ]PJ[τ]gJ,g2[τ], the second term of R¯secm[τ], log2⁡(1+t^k[τ]), can be reformulated by utilizing its convex lower bound through a first-order Taylor expansion with a feasible point. Thus, we obtain

R¯secm[τ]≥R~sec4m[τ]=log2⁡(1+A1[τ]PB[τ])−log2⁡(1+t^k[τ])−(tk[τ]−t^k[τ])ln2(1+t^k[τ])−mm[τ](Q−1(ε))ln2l−mk[τ](Q−1(η))ln⁡2l.(31)

Therefore, the corresponding subproblem can be written as (P6b):

maxPB,Tg,Mg⁡[ω(1T∑τ=1TR~sec4m[τ])−(1−ω)F(l)],(32a)

s.t. Eqs. (4a)−(4d),(13c),(13d),(14c),(14e),(20).(32b)

After such an approximation, the power optimization for the UAV-B subproblem has been transformed into a standard convex optimization problem (P6a), which can be optimally solved using CVX.

3.5 Power Optimization for UAV-J

In this subsection, we will optimize the power PJ of UAV-J while keeping the positions of UAV-B and UAV-J unchanged, as well as the power PB of UAV-B and the block length constant. Therefore, the corresponding sub-problem can be written as (P7a):

maxPJ,Tg,Mg⁡[ω(1T∑τ=1TR¯secm[τ])−(1−ω)F(l)],(33a)

s.t. Eqs. (4a)−(4d),(13c),(13d),(14c)−(14e)(33b)

When constraints (14c) and (14d) are set to equality, the optimization problem is equivalent to (P1), enabling AMSR to obtain the optimal solution. Define B1=PB[τ]gB,k2[τ]gJ,k2[τ], R¯secm[τ] can be rewritten as

R¯secm[τ]=log2⁡(1+tm[τ])−log2⁡(1+B1[τ]PJ[τ])−mm[τ]Q−1(ε)ln⁡2l−mk[τ]Q−1(η)ln⁡2l.(34)

Obviously, due to the non-concavity of the second term of the objective function R¯secm[τ] and the non-convexity of constraint (14d), the problem (P7a) represents a non-convex optimization problem. Therefore, we use a first-order Taylor expansion to obtain a lower bound, and constraint (14) can be addressed using (20). Then we have

R¯secm[τ]≥R~sec5m[τ]=log2⁡(1+tm[τ])+log2⁡(PJ[τ])−log2⁡(B1[τ]+P^J[τ])−PJ[τ]−P^J[τ]ln⁡2(B1[τ]+P^J[τ])−mm[τ]Q−1(ε)ln⁡2l−mk[τ]Q−1(η)ln⁡2l.(35)

Therefore, the power optimization problem for UAV-J can be rewritten as (P7b):

maxPJ,Tg,Mg⁡[ω(1T∑τ=1TR~sec5m[τ])−(1−ω)F(l)],(36a)

s.t. Eqs. (4a)−(4d),(13c),(13d),(14c),(14e),(20).(36b)

The problem (P7b) is a convex optimization problem, which can be efficiently solved using techniques such as CVX.

3.6 Proposed Alternating Algorithm

We transformed the trajectory optimization, power optimization, and block length optimization subproblems into convex optimization problems in the preceding subsections. In this subsection, we utilize an alternating iterative algorithm to solve these subproblems with the specific algorithm outlined in Algorithm 1. We observe that each iteration only requires the solution of convex optimization problems with polynomial complexity of O(N3.5), making Algorithm 1 feasible in practice. Since the value of AMSR does not decrease in each iteration and the objective value is bounded, we can ensure that Algorithm 1 converges.

4  Numerical Results

In this section, we validate the effectiveness of the proposed alternating optimization algorithm, in which we jointly consider the performances of the secure transmission and the blockchain itself. This algorithm jointly optimizes the trajectory of the UAVs, block length, and power of the UAVs (JTBP). To demonstrate the effectiveness of the proposed algorithm, we consider the following two benchmark schemes:

BPFT: Joint optimization of block length and UAV power while keeping the UAV trajectory fixed.

TFBP: Optimization of the UAV trajectory while keeping the block length and UAV power fixed.

The specific simulation parameters are provided in Table 2.

In Fig. 2, we illustrate the performance of AMSR under various schemes with iteration numbers for task durations of 30 and 25 s, respectively, to confirm the rapid convergence of Algorithm 1 and effectiveness. This also highlights the advantages of our joint optimization strategy. As can be seen from the figure, AMSR is non-decreasing during all iterations of the algorithm. Our proposed JTBP algorithm achieves the best AMSR performance among all methods. At the same number of iterations, the AMSR performance of the JTBP method is significantly better than that of other algorithms. As shown in Fig. 2a,b, the AMSR of JTBP is approximately 17% higher than that of BPFT and about 35% higher than that of TFBP. Fig. 2 indicates that optimizing resource allocation (the block length and power) with a fixed trajectory is more important than optimizing the trajectory with fixed resources. However, the joint design of the two yields better results.

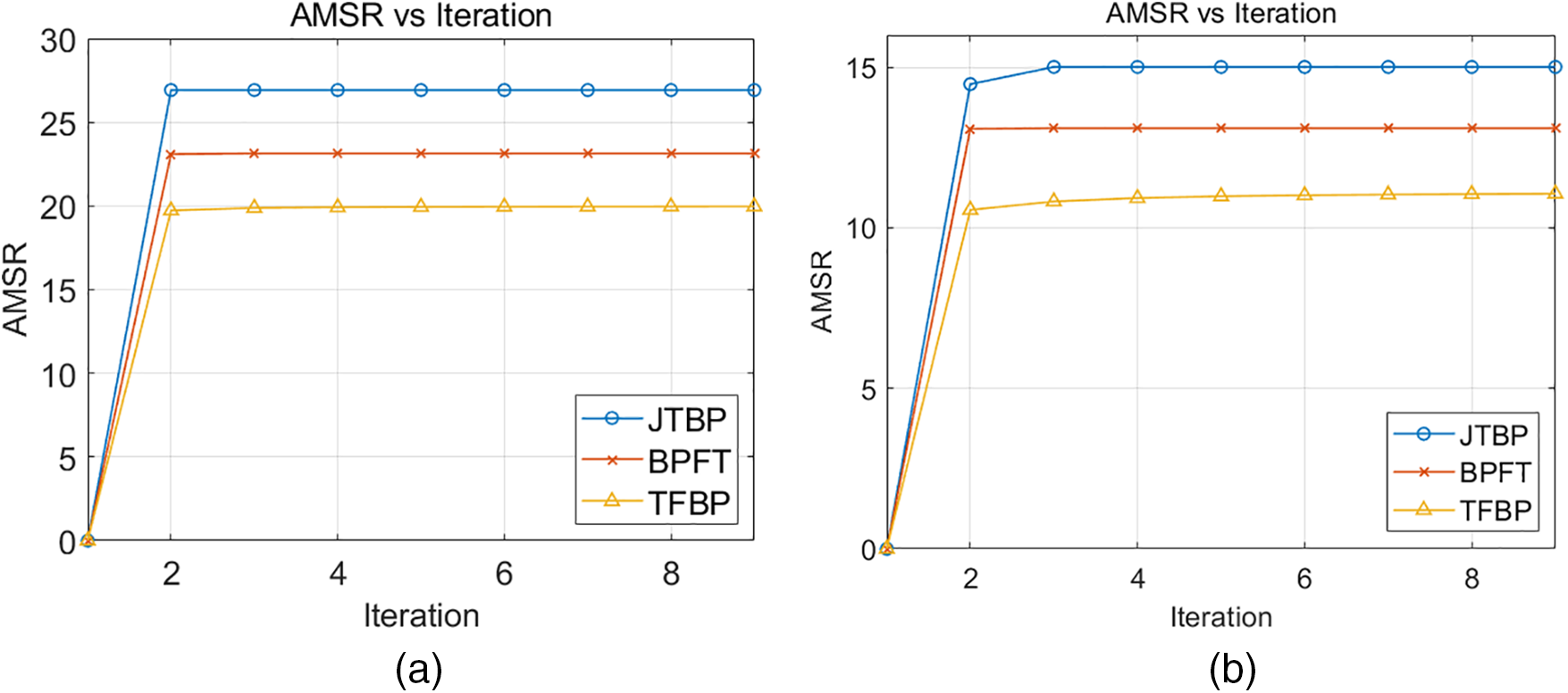
Figure 2: Comparison of AMSR for different schemes at various periods T, where T = 30 s for (a), and T = 25 s for (b)

Furthermore, as intuitively shown in Fig. 2a,b, when the task duration decreases from 30 to 25 s, the AMSR performance decreases. This indicates that the task duration is directly proportional to the AMSR performance. As the task duration increases, the time the UAV remains at the receiver’s position also increases, thereby enhancing the total amount of secure information transmitted by the UAV. Thus, it improves the performance of AMSR and the security of information transmission.

Similarly, Fig. 3 illustrates that throughout the iteration process of all algorithms, the total utility function exhibits a comparable trend to the changes in AMSR. It can be seen that the total utility function value of our proposed method is higher than that of the other two methods. This highlights the advantage of joint optimization of blockchain performance and physical layer secure transmission performance.

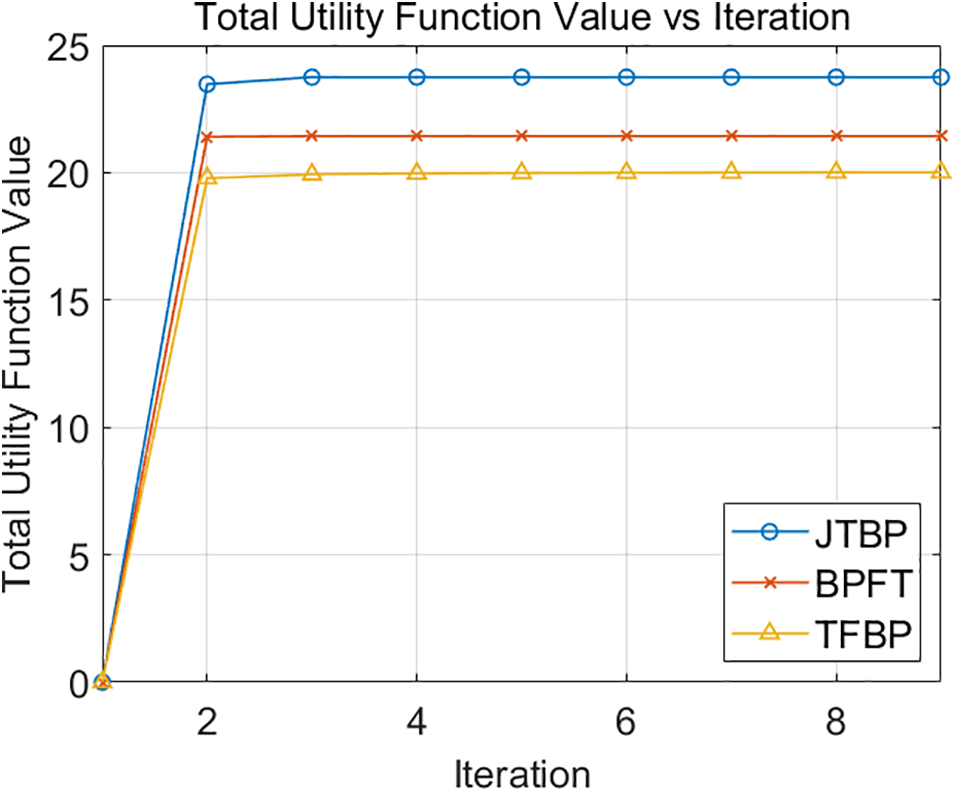
Figure 3: Comparison of the total utility function for different schemes at T = 30 s

Fig. 4 illustrates the flight trajectory of the UAVs. The initial and final positions of UAV B/J, as well as the positions of the receiver and the eavesdropper, are indicated by the symbols ◊, △, ◼, ▴, respectively. Before the optimization process, the initial flight route of UAV-B is defined as a straight-line trajectory from the initial to the final position. Fig. 4a,b illustrates the flight trajectories of the UAVs under various schemes for different flight periods. From Fig. 4a, it can be seen that the trajectories of UAV-B and UAV-J are similar under different schemes. When T = 30 s, the UAVs first accelerate towards the receiver’s position, then hover above the receiver for as long as possible to ensure the optimal AMSR performance before finally flying to the final position. As illustrated in Fig. 4a, in the JTBP scheme, UAV-B is positioned closer to the GR, whereas UAV-J is situated closer to Eve. This configuration results in a greater distance between UAV-B and the eavesdropper Eve, which enables UAV-J to increase interference with Eve’s eavesdropping activities, thereby enhancing communication security. In Fig. 4b, due to insufficient task time for UAV-B to reach the receiver GR, UAV-B should fly to the final position at maximum speed to ensure communication performance within the task time T. The trajectories of the UAVs under the two different schemes are similar.

Figure 4: Comparison of UAV flight trajectories at different periods T, where T = 30 s for (a), and T = 25 s for (b)

Fig. 5 illustrates the speed variations of UAV-B and UAV-J during the flight. Fig. 5a shows that the speed of UAV-B initially increases and then decreases, reaching a minimum when it is near the receiver. This strategy aims to optimize communication efficiency and security. In the initial stage, increasing the speed can quickly bring the UAV closer to the receiver to transmit confidential messages rapidly. When the UAV approaches the receiver, reducing its speed allows UAV-B to stay near the receiver for as long as possible. This can optimize the performance of AMSR, thereby enhancing the reliability and confidentiality of communication. Before reaching the final destination, gradually increasing the speed ensures that the UAV can depart promptly after completing the communication. Fig. 5b illustrates that the speed of UAV-J also exhibits an initial increase, followed by a subsequent decrease, reaching a minimum near the eavesdropper. Initially, increased speed allows the jamming UAV to approach the eavesdropper rapidly. As the jamming UAV nears the eavesdropper, reducing the speed can increase the duration and effectiveness of the jamming, making it more difficult for the eavesdropper to obtain confidential information. After completing the jamming task, gradually increasing the speed again can ensure that the UAV withdraws promptly to prevent detection by the eavesdropper.

Figure 5: Flight speeds of UAV-B and UAV-J vary over a time period of T = 25 s, where UAV-B for (a) and UAV-J for (b)

Fig. 6 illustrates the AMSR values obtained with and without optimizing blockchain performance during the optimization process. As shown in Fig. 6, ω=1 indicates that the blockchain performance is not considered during the optimization process. When ω=0.8, the blockchain performance is considered with a weight of 0.2. We can see from the figure that the value of AMSR without considering the blockchain performance is greater than the value of AMSR when considering the blockchain performance. When the blockchain performance is not considered, the block length is always maximized because the more significant the block, the more information is transmitted, resulting in a higher AMSR value. After considering the blockchain performance, increasing the block length may lead to higher network latency. Moreover, if the block length is too short, it might result in longer transaction confirmation times and increased transaction fees. Therefore, the block length is not simply maximized. In conclusion, our study method may result in an AMSR value lower than that when blockchain performance is not considered. This is because we need to find an optimal block length that balances the network latency and transaction congestion.

Figure 6: Comparison of secrecy rates with and without blockchain performances

Fig. 7 compares block lengths with and without optimizing the blockchain performance during the optimization process. When ω=1, the blockchain performance is not considered during the optimization process. From the figure, it can be observed that in the absence of consideration for the blockchain performance, the block length is maximized at each timeslot to ensure the optimal AMSR value. When ω=0.8, the impact of the blockchain performance is considered with a weight of 0.2. In this instance, the optimization process considers the time delay associated with the creation and propagation of blocks during information transmission. Consequently, an optimal block size is considered. The figure shows that when the blockchain performance is considered, the block length is not maximized at every time slot. The block size is the smallest when closest to the receiver. When the UAV is farther away from the ground receiver, larger block sizes may be needed to ensure the communication signal covers a sufficient range. Consequently, the block size varies in each time slot to optimize the AMSR value while minimizing block creation and transmission delays. This dynamic adjustment approach better balances the conflicting requirements of blockchain performance and AMSR optimization, resulting in a more robust and efficient overall system performance.

Figure 7: Comparison of block lengths with and without blockchain performances

Fig. 8 shows the variation of transmission power of UAVs with time slots. In Fig. 8a, UAV-B’s power decreases initially and then increases, reaching its minimum when close to the receiver. This strategy helps to reduce the risk of eavesdropping. Higher power levels ensure reliable transmissions over greater distances when the UAV is far from the receiver. In Fig. 8b, UAV-J’s power also decreases initially and then increases, reaching its minimum when close to the eavesdropper. This strategy aims to maximize interference with potential eavesdroppers. By increasing power when far from the eavesdropper, the interference UAV ensures that the jamming signal covers a broader area, making it more difficult for the eavesdropper to obtain precise information. UAV-B and UAV-J achieve optimized power control to address secure communication through these strategies. UAV-B adjusts its power during transmission to balance signal reliability and communication security, thereby reducing the risk of eavesdropping. UAV-J dynamically adjusts its power to maximize the interference with potential eavesdroppers, ensuring information security. This flexible power control method enhances the UAV communication system’s efficiency and improves its security and anti-jamming capabilities in complex environments.

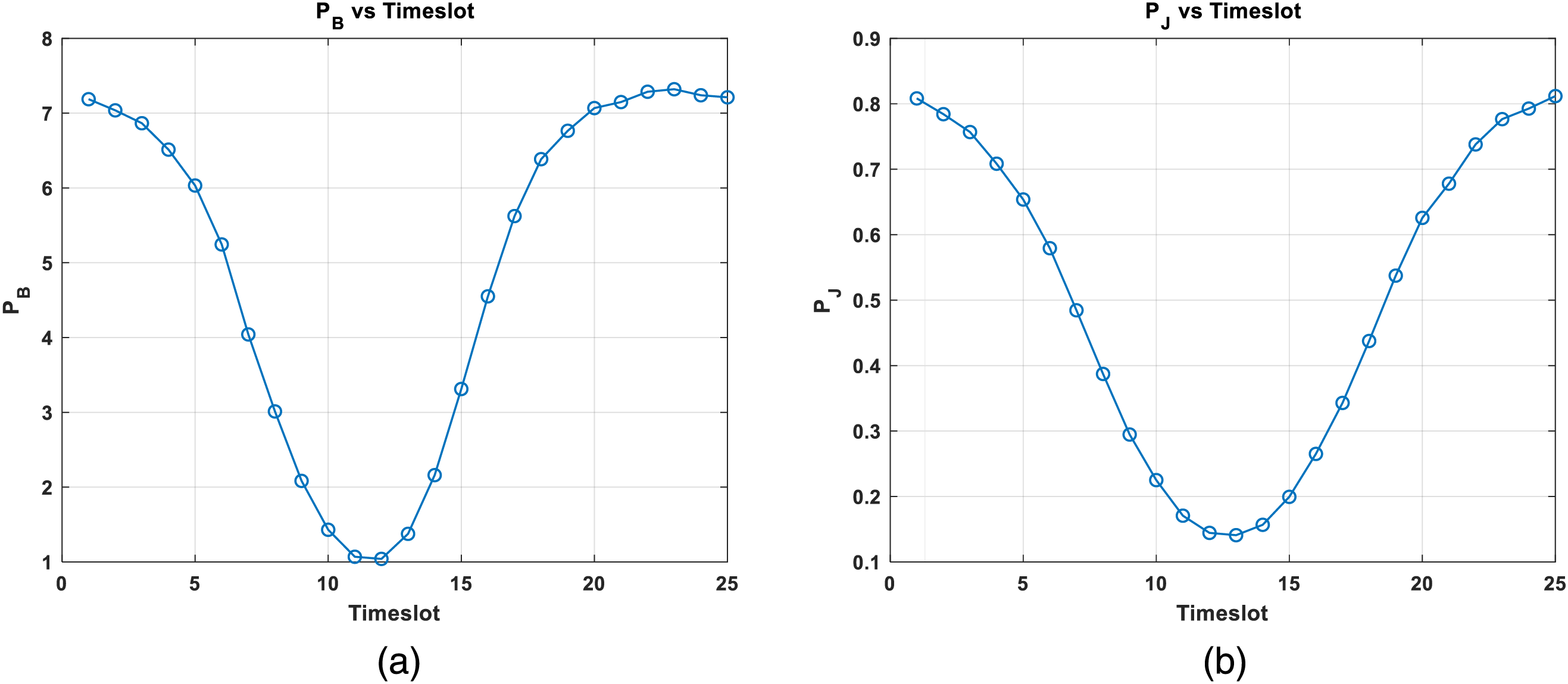
Figure 8: The variation of transmission power of UAV-B and UAV-J in T = 25 s with time slots, where UAV-B for (a) and UAV-J for (b)

5  Conclusion

In this paper, a method for secure block transmission in UAV-assisted blockchain communication systems was investigated. The objective is to prevent the information within blocks from being fully eavesdropped during transmission. It is paramount to ensure that at least 50% of valid nodes can accurately receive complete block information during communication while preventing eavesdroppers from accessing complete block information. Furthermore, the performance of the blockchain was considered. A block that is too large may result in transmission delays, while a block that is too short may lead to transaction congestion and longer confirmation times. Therefore, maximizing AMSR is achieved through the joint design of UAV trajectory, transmission power, and block length. However, the resulting optimization problem is non-convex, making it challenging to solve directly. Consequently, the optimization problem was decomposed into three subproblems: trajectory optimization, transmission power optimization, and block length optimization. Subsequently, these subproblems were reformulated as convex optimization problems using first-order approximation techniques. Finally, an alternating iterative algorithm based on SCA techniques was employed to solve these subproblems iteratively. The results of the simulations demonstrate that the proposed scheme achieves a superior secure communication performance and blockchain performance compared to benchmarks. Our current research primarily relies on simulation results to demonstrate the feasibility and performance of the model. In our future research, we plan to expand our work to include real-time experiments, focusing on aspects such as energy consumption, scalability, and potential interference with other communication systems further to enhance the robustness and reliability of the system.

Acknowledgement: The authors would like to thank editors and reviewers for their valuable work.

Funding Statement: This work is supported in part by the National Key R&D Program of China under Grant 2022YFB3104503; in part by the China Postdoctoral Science Foundation under Grant 2024M750199; in part by the National Natural Science Foundation of China under Grants 62202054, 62002022 and 62472251; in part by the Fundamental Research Funds for the Central Universities under Grant BLX202360.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ting Chen, Xin Fan; formula derivation: Shuna Jiang, Jianchuan Xia; data collection: Xiujuan Zhang; analysis and interpretation of results: Chuanwen Luo, Yi Hong; draft manuscript preparation: Ting Chen, Shuna Jiang, Xin Fan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Readers can access the data used in this study by contacting the corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. N. Kato et al., “Optimizing space-air-ground integrated networks by artificial intelligence,” IEEE Wirel. Commun., vol. 26, no. 4, pp. 140–147, Aug. 2019. doi: 10.1109/MWC.2018.1800365. [Google Scholar] [CrossRef]

2. A. Fotouhi et al., “Survey on UAV cellular communications: Practical aspects, standardization advancements, regulation, and security challenges,” IEEE Commun. Surv. Tutor., vol. 21, no. 4, pp. 3417–3442, Dec. 2019. doi: 10.1109/COMST.2019.2906228. [Google Scholar] [CrossRef]

3. C. Luo, M. N. Satpute, D. Li, Y. Wang, W. Chen and W. Wu, “Fine-grained trajectory optimization of multiple UAVs for efficient data gathering from WSNs,” IEEE/ACM Trans. Netw., vol. 29, no. 1, pp. 162–175, Feb. 2021. doi: 10.1109/TNET.2020.3027555. [Google Scholar] [CrossRef]

4. Q. Wu, Y. Zeng, and R. Zhang, “Joint trajectory and communication design for multi-UAV enabled wireless networks,” IEEE Trans. Wirel. Commun., vol. 17, no. 3, pp. 2109–2121, Mar. 2018. doi: 10.1109/TWC.2017.2789293. [Google Scholar] [CrossRef]

5. D. -H. Tran, V. -D. Nguyen, S. Chatzinotas, T. X. Vu, and B. Ottersten, “UAV relay-assisted emergency communications in IoT networks: Resource allocation and trajectory optimization,” IEEE Trans. Wirel. Commun., vol. 21, no. 3, pp. 1621–1637, Mar. 2022. doi: 10.1109/TWC.2021.3105821. [Google Scholar] [CrossRef]

6. Z. Su, Y. Wang, Q. Xu, and N. Zhang, “LVBS: Lightweight vehicular blockchain for secure data sharing in disaster rescue,” IEEE Trans. Dependable Secur. Comput., vol. 19, no. 1, pp. 19–32, Jan.–Feb. 2022. doi: 10.1109/TDSC.2020.2980255. [Google Scholar] [CrossRef]

7. Z. Ullah, F. Al-Turjman, and L. Mostarda, “Cognition in UAV-aided 5G and beyond communications: A survey,” IEEE Trans. Cogn. Commun. Netw., vol. 6, no. 3, pp. 872–891, Sep. 2020. doi: 10.1109/TCCN.2020.2968311. [Google Scholar] [CrossRef]

8. H. Wu, X. Tao, N. Zhang, and X. Shen, “Cooperative UAV cluster-assisted terrestrial cellular networks for ubiquitous coverage,” IEEE J. Sel. Areas Commun., vol. 36, no. 9, pp. 2045–2058, Sep. 2018. doi: 10.1109/JSAC.2018.2864418. [Google Scholar] [CrossRef]

9. F. Song, Y. Ma, I. You, and H. Zhang, “Smart collaborative evolvement for virtual group creation in customized industrial IoT,” IEEE Trans. Netw. Sci. Eng., vol. 10, no. 5, pp. 2514–2524, 1 Sep.–Oct. 2023. doi: 10.1109/TNSE.2022.3203790. [Google Scholar] [CrossRef]

10. X. Fan and Y. Huo, “Blockchain based dynamic spectrum access of non-real-time data in cyber-physical-social systems,” IEEE Access, vol. 8, pp. 64486–64498, 2020. doi: 10.1109/ACCESS.2020.2985580. [Google Scholar] [CrossRef]

11. Y. Zhou et al., “Improving physical layer security via a UAV friendly jammer for unknown eavesdropper location,” IEEE Trans. Veh. Technol., vol. 67, no. 11, pp. 11280–11284, Nov. 2018. doi: 10.1109/TVT.2018.2868944. [Google Scholar] [CrossRef]

12. W. Wang, H. Tian, and W. Ni, “Secrecy performance analysis of IRS-aided UAV relay system,” IEEE Wirel. Commun. Lett., vol. 10, no. 12, pp. 2693–2697, Dec. 2021. doi: 10.1109/LWC.2021.3112752. [Google Scholar] [CrossRef]

13. M. T. Mamaghani, X. Zhou, N. Yang, and A. L. Swindlehurst, “Secure short-packet communications via UAV-enabled mobile relaying: Joint resource optimization and 3D trajectory design,” IEEE Trans. Wirel. Commun., vol. 23, no. 7, pp. 7802–7815, Jul. 2024. doi: 10.1109/TWC.2023.3344802. [Google Scholar] [CrossRef]

14. X. Fan, Y. Wang, G. Li, Y. Huo, and Z. Tian, “Hybrid uplink-downlink NOMA for secure coordinated multi-point networks,” in 2021 IEEE Int. Conf. Commun. Workshops, Montreal, QC, Canada, 2021, pp. 1–6. [Google Scholar]

15. X. Fan and Y. Huo, “Security analysis of cooperative jamming in Internet of Things with multiple eavesdroppers,” in 2019 IEEE Glob. Commun. Conf., Waikoloa, HI, USA, 2019, pp. 1–6. doi: 10.1109/GLOBECOM38437.2019.9014015. [Google Scholar] [CrossRef]

16. A. Kumar, A. S. Yadav, S. S. Gill, H. Pervaiz, Q. Ni and R. Buyya, “A secure drone-to-drone communication and software defined drone network-enabled traffic monitoring system,” Simul Model. Pract. Theory., vol. 120, 2022, Art. no. 102621. doi: 10.1016/j.simpat.2022.102621. [Google Scholar] [CrossRef]

17. Y. Zou, J. Zhu, X. Wang, and V. C. M. Leung, “Improving physical-layer security in wireless communications using diversity techniques,” IEEE Netw., vol. 29, no. 1, pp. 42–48, Jan.–Feb. 2015. doi: 10.1109/MNET.2015.7018202. [Google Scholar] [CrossRef]

18. Y. Zhou, F. Zhou, H. Zhou, D. W. K. Ng, and R. Q. Hu, “Robust trajectory and transmit power optimization for secure UAV-enabled cognitive radio networks,” IEEE Trans. Commun., vol. 68, no. 7, pp. 4022–4034, Jul. 2020. doi: 10.1109/TCOMM.2020.2979977. [Google Scholar] [CrossRef]

19. H. Zhang, J. Zhang, and K. Long, “Energy efficiency optimization for NOMA UAV network with imperfect CSI,” IEEE J. Sel. Areas Commun., vol. 38, no. 12, pp. 2798–2809, Dec. 2020. doi: 10.1109/JSAC.2020.3005489. [Google Scholar] [CrossRef]

20. W. Wang et al., “Joint precoding optimization for secure SWIPT in UAV-aided NOMA networks,” IEEE Trans. Commun., vol. 68, no. 8, pp. 5028–5040, Aug. 2020. doi: 10.1109/TCOMM.2020.2990994. [Google Scholar] [CrossRef]

21. X. Fan, L. Huang, Y. Huo, C. Hu, Y. Tian and J. Qian, “Space power synthesis-based cooperative jamming for unknown channel state information,” in Int. Conf. Wirel. Algorithms, Syst. Appl., Springer, 2017, pp. 483–495. doi: 10.1007/978-3-319-60033-8_42. [Google Scholar] [CrossRef]

22. X. Fan and Y. Huo, “Cooperative secure transmission against collusive eavesdroppers in Internet of Things,” Int. J. Distrib. Sens. Netw., vol. 16, no. 6, 2020, Art. no. 155014772093346. doi: 10.1177/1550147720933464. [Google Scholar] [CrossRef]

23. H. Dang-Ngoc et al., “Secure swarm UAV-assisted communications with cooperative friendly jamming,” IEEE Internet Things J., vol. 9, no. 24, pp. 25596–25611, Dec. 15, 2022. doi: 10.1109/JIOT.2022.3197975. [Google Scholar] [CrossRef]

24. H. Lei et al., “Safeguarding UAV IoT communication systems against randomly located eavesdroppers,” IEEE Internet Things J., vol. 7, no. 2, pp. 1230–1244, Feb. 2020. doi: 10.1109/JIOT.2019.2953903. [Google Scholar] [CrossRef]

25. X. Jiang et al., “Covert communication in UAV-assisted air-ground networks,” IEEE Wirel. Commun., vol. 28, no. 4, pp. 190–197, Aug. 2021. doi: 10.1109/MWC.001.2000454. [Google Scholar] [CrossRef]

26. M. Xu, F. Zhao, Y. Zou, C. Liu, X. Cheng and F. Dressler, “BLOWN: A blockchain protocol for single-hop wireless networks under adversarial SINR,” IEEE Trans. Mob. Comput., vol. 22, no. 8, pp. 4530–4547, Aug. 1, 2023. doi: 10.1109/TMC.2022.3162117. [Google Scholar] [CrossRef]

27. X. Zhou, Q. Wu, S. Yan, F. Shu, and J. Li, “UAV-enabled secure communications: Joint trajectory and transmit power optimization,” IEEE Trans. Veh. Technol., vol. 68, no. 4, pp. 4069–4073, Apr. 2019. doi: 10.1109/TVT.2019.2900157. [Google Scholar] [CrossRef]

28. G. Zhang, Q. Wu, M. Cui, and R. Zhang, “Securing UAV communications via trajectory optimization,” in IEEE Glob. Commun. Conf., Singapore, 2017, pp. 1–6. doi: 10.1109/GLOCOM.2017.8254971. [Google Scholar] [CrossRef]

29. Y. Su, S. Fu, J. Si, C. Xiang, N. Zhang and X. Li, “Optimal hovering height and power allocation for UAV-aided NOMA covert communication system,” IEEE Wirel. Commun. Lett., vol. 12, no. 6, pp. 937–941, Jun. 2023. doi: 10.1109/LWC.2023.3238510. [Google Scholar] [CrossRef]

30. P. Wu, X. Yuan, Y. Hu, and A. Schmeink, “Joint power allocation and trajectory design for UAV-enabled covert communication,” IEEE Trans. Wirel. Commun., vol. 23, no. 1, pp. 683–698, Jan. 2024. doi: 10.1109/TWC.2023.3281730. [Google Scholar] [CrossRef]

31. S. Yan, B. He, X. Zhou, Y. Cong, and A. L. Swindlehurst, “Delay-intolerant covert communications with either fixed or random transmit power,” IEEE Trans. Inf. Forensic. Secur., vol. 14, no. 1, pp. 129–140, Jan. 2019. doi: 10.1109/TIFS.2018.2846257. [Google Scholar] [CrossRef]

32. F. Shu, T. Xu, J. Hu, and S. Yan, “Delay-constrained covert communications with a full-duplex receiver,” IEEE Wirel. Commun. Lett., vol. 8, no. 3, pp. 813–816, Jun. 2019. doi: 10.1109/LWC.2019.2894617. [Google Scholar] [CrossRef]

33. M. Oh, J. Park, and J. Choi, “Joint optimization for secure and reliable communications in finite blocklength regime,” IEEE Trans. Wirel. Commun., vol. 22, no. 12, pp. 9457–9472, Dec. 2023. doi: 10.1109/TWC.2023.3270925. [Google Scholar] [CrossRef]

34. Y. Wang et al., “UAV-enabled secure communication with finite blocklength,” IEEE Trans. Veh. Technol., vol. 69, no. 12, pp. 16309–16313, Dec. 2020. doi: 10.1109/TVT.2020.3042791. [Google Scholar] [CrossRef]

35. H. Han, Y. Huang, H. Hu, Y. Pan, Q. An and J. Si, “Mobile jammer enabled secure UAV communication with short packet transmission,” AEU-Int. J. Electron. Commun., vol. 157, 2022, Art. no. 154434. doi: 10.1016/j.aeue.2022.154434. [Google Scholar] [CrossRef]

36. R. Beck et al., “Blockchain technology in business and information systems research,” Bus Inf. Syst. Eng., vol. 59, pp. 381–384, 2017. doi: 10.1007/s12599-017-0505-1. [Google Scholar] [CrossRef]

37. S. Ammous, “Blockchain technology: What is it good for?,” Commun. ACM, vol. 63, no. 1, pp. 46–53, 2019. doi: 10.1145/3369752. [Google Scholar] [CrossRef]

38. L. He et al., “Blockchain-based vehicular edge computing networks: The communication perspective,” Sci. China Inf. Sci., vol. 66, 2023, Art. no. 172301. doi: 10.1007/s11432-022-3658-7. [Google Scholar] [CrossRef]

39. D. Das, S. Banerjee, P. Chatterjee, U. Ghosh, and U. Biswas, “Blockchain for intelligent transportation systems: Applications, challenges, and opportunities,” IEEE Internet Things J., vol. 10, no. 21, pp. 18961–18970, Nov. 2023. doi: 10.1109/JIOT.2023.3277923. [Google Scholar] [CrossRef]

40. B. Ghimire, D. B. Rawat, and A. Rahman, “Efficient information dissemination in blockchain-enabled federated learning for IoV,” IEEE Internet Things J., vol. 11, no. 9, pp. 15310–15319, May 2024. doi: 10.1109/JIOT.2023.3346296. [Google Scholar] [CrossRef]

41. J. Kang et al., “Blockchain for secure and efficient data sharing in vehicular edge computing and networks,” IEEE Internet Things J., vol. 6, no. 3, pp. 4660–4670, Jun. 2019. doi: 10.1109/JIOT.2018.2875542. [Google Scholar] [CrossRef]

42. L. Vishwakarma, A. Nahar, and D. Das, “LBSV: Lightweight blockchain security protocol for secure storage and communication in SDN-enabled IoV,” IEEE Trans. Veh. Technol., vol. 71, no. 6, pp. 5983–5994, Jun. 2022. doi: 10.1109/TVT.2022.3163960. [Google Scholar] [CrossRef]

43. Z. Chang et al., “Blockchain-empowered drone networks: Architecture, features, and future,” IEEE Netw., vol. 35, no. 1, pp. 86–93, Jan./Feb. 2021. doi: 10.1109/MNET.011.2000202. [Google Scholar] [CrossRef]

44. A. Islam and S. Y. Shin, “BUAV: A blockchain-based secure UAV-assisted data acquisition scheme in Internet of Things,” J. Commun. Netw., vol. 21, no. 5, pp. 491–502, Oct. 2019. doi: 10.1109/JCN.2019.000050. [Google Scholar] [CrossRef]

45. X. Jian, P. Leng, Y. Wang, M. Alrashoud, and M. S. Hossain, “Blockchain-empowered trusted networking for unmanned aerial vehicles in the B5G era,” IEEE Netw., vol. 35, no. 1, pp. 72–77, Jan./Feb. 2021. doi: 10.1109/MNET.011.2000177. [Google Scholar] [CrossRef]

46. Y. Wang, Z. Su, Q. Xu, R. Li, T. H. Luan and P. Wang, “A secure and intelligent data sharing scheme for UAV-assisted disaster rescue,” IEEE/ACM Trans. Netw., vol. 31, no. 6, pp. 2422–2438, Dec. 2023. doi: 10.1109/TNET.2022.3226458. [Google Scholar] [CrossRef]

47. F. Ayaz, Z. Sheng, I. W. -H. Ho, D. Tian, and Z. Ding, “Blockchain-enabled FD-NOMA-based vehicular network with physical layer security,” in Proc. IEEE 95th Veh. Technol. Conf., Helsinki, Finland, 2022, pp. 1–6. [Google Scholar]

48. H. -M. Wang, Q. Yang, Z. Ding, and H. V. Poor, “Secure short-packet communications for mission-critical IoT applications,” IEEE Trans. Wirel. Commun., vol. 18, no. 5, pp. 2565–2578, May 2019. doi: 10.1109/TWC.2019.2904968. [Google Scholar] [CrossRef]

49. B. A. Aygün and H. Arslan, “Block size optimization for PoW consensus algorithm-based blockchain applications by using whale optimization algorithm,” Turk J. Electr. Eng. Comput. Sci., vol. 30, no. 2, pp. 406–419, 2022. doi: 10.3906/elk-2105-217. [Google Scholar] [CrossRef]

50. M. Grant and S. Boyd, “CVX: Matlab software for disciplined convex programming, Version 2.2,” Jan. 2020. Accessed: Jun. 13, 2024. [Online]. Available: http://cvxr.com/cvx [Google Scholar]