Improved IChOA-Based Reinforcement Learning for Secrecy Rate Optimization in Smart Grid Communications

Abbreviations

1  Introduction

The smart grid (SG) represents a transformative leap in energy management, integrating advanced digital technology into the traditional power grid to enhance efficiency [1–3], reliability, and sustainability [4]. As an integral component of this modernization, communication technologies play a pivotal role, facilitating real-time data exchange and control across various grid components [5]. Within this context, non-orthogonal multiple access (NOMA) has emerged as a significant advancement, offering a paradigm shift in SG communications [6]. NOMA stands out by enabling multiple users to share the same frequency resources, thereby drastically increasing spectral efficiency and network capacity [7]. This is particularly crucial in SG environments, where the need to simultaneously connect a multitude of devices, such as smart meters (SMs) and renewable energy sources, is ever-growing. By efficiently managing these dense and diverse communication demands, NOMA not only addresses the scalability challenges of the SG but also contributes to the overall optimization of energy distribution and consumption, heralding a new era of intelligent energy management [8].

Security concerns in SG are paramount, given the critical nature of energy infrastructure and the sensitive data involved in its operation [9]. As SGs become increasingly interconnected and reliant on wireless communications, they become vulnerable to various cyber threats [10–12]. One notable security threat in the SG neighborhood area networks (NAN) is the risk of eavesdropping and impersonation attacks. For instance, an attacker might position themselves as an eavesdropper within the communication range of a neighborhood gateway (NG) and the SMs it controls. By intercepting the communication, the attacker could gain unauthorized access to confidential information, such as consumption data or control commands. More alarmingly, they could impersonate the NG, sending fraudulent signals or commands to the SMs. Such an attack could lead to severe consequences, including the disruption of power distribution, manipulation of billing data, or even causing physical damage to the grid infrastructure. This scenario underscores the critical need for robust security mechanisms in SG communications, to prevent unauthorized access and ensure the integrity and reliability of the energy supply chain [13].

The importance of secrecy performance analysis in designing security schemes for SG communications cannot be overstated [14–16], particularly in the context of emerging technologies like NOMA. Secrecy performance analysis is crucial for evaluating how well a communication system can protect against unauthorized interception and ensure the confidentiality of transmitted data [16–18]. A key metric in this analysis is the secrecy capacity, which is defined as the maximum rate at which information can be reliably transmitted to the intended receiver while ensuring that an eavesdropper gains negligible information [19–21]. In NOMA SG communication, optimizing secrecy capacity poses a unique challenge. NOMA systems are inherently designed to allow multiple users to share the same frequency resources, which increases the complexity of maintaining secure communications [22,23]. The shared spectrum means that the signals intended for legitimate users can be more susceptible to interception by eavesdroppers. Optimizing secrecy capacity in this context involves not only enhancing the signal strength at the intended receivers but also minimizing the information leakage to potential eavesdroppers [24,25]. This requires sophisticated strategies that can dynamically adapt to the varying channel conditions and user positions typical in SG environments, ensuring robust and secure communication against the backdrop of NOMA’s spectral efficiency benefits [26–28].

There is limited research on applying deep learning (DL) and reinforcement learning (RL) models to improve secrecy in NOMA communication systems. Ali et al. [14] developed advanced resource allocation strategies for future communication systems, focusing on maximizing the total transmission rate within a restricted power budget and ensuring a necessary power differential among users for effective NOMA deployment. They introduced a deep neural network (DNN) framework to determine a combined power allocation strategy for both source and relay nodes. To support the training and validation of the DNN, they also obtained an optimal solution using convex optimization methods, which served as a benchmark to evaluate the DNN solution’s effectiveness. It was found that the DNN solution delivers promising outcomes in terms of both sum rate and computational efficiency.

Given the notable gap in SG literature regarding the lack of a robust secrecy performance optimization scheme in NOMA communications, this paper introduces a pioneering approach based on RL to fortify this critical aspect. Recognizing the complexity and dynamism inherent in SG communication systems, especially under the NOMA paradigm, our research proposes leveraging the adaptive and predictive capabilities of RL. RL is selected over other machine learning (ML) methods for secrecy optimization in SG communications due to its distinct capabilities in handling dynamic and complex environments. Unlike static ML models like K-nearest neighbors (KNN), support vector machine (SVM), RL excels in adapting to evolving network conditions by continuously learning optimal policies through interactions with the environment, making it particularly suited for the unpredictable nature of SGs. Additionally, RL’s proficiency in sequential decision making allows it to optimize long-term secrecy performance by considering the future implications of current actions, which is crucial for maintaining secure communication over time. This novel approach is specifically designed to enhance the secrecy capacity rate, a vital metric of secrecy performance, in NOMA communications within SG environments. By employing RL algorithms, our method aims to adjust communication strategies intelligently and dynamically in response to varying network conditions and potential security threats. This allows for the optimization of secrecy capacity rates, ensuring that sensitive data transmitted across the SG remains secure from eavesdroppers and malicious actors. Our research, therefore, stands at the forefront of addressing a critical, yet previously unexplored, aspect of SG communications, offering a significant contribution to the advancement of secure and resilient SG networks.

The training process of a fully connected neural network, commonly used in RL, is a critical phase where the network learns to approximate the optimal policy for decision-making. In RL, a fully connected neural network, also known as a deep Q network (DQN) when used in Q-learning, is often responsible for mapping states to action values. The quality of this mapping directly influences the agent’s ability to make intelligent decisions that maximize the cumulative reward over time. The importance of the training process lies in its ability to capture the complex relationships between the actions, the state of the environment, and the received rewards. Proper training ensures that the neural network generalizes well to unseen states, enabling the RL agent to perform well across the entire state space of the problem. Motivated by the need for efficient and effective training of the fully connected layers in the RL network, we employ an improved chimp optimization algorithm (IChOA) to update the parameters of the neural network, which is inspired by the intelligent hunting behavior of chimpanzees in nature.

The choice of combining RL with IChOA to enhance secrecy performance in SGs is driven by the need to address the complex and dynamic nature of SG communication environments, particularly under the NOMA paradigm. SGs are characterized by their high connectivity and reliance on wireless communication, which inherently increases the risk of eavesdropping and other security threats. RL offers a robust framework for optimizing secrecy capacity by dynamically adapting communication strategies to counteract these threats, ensuring that sensitive data remains secure. However, the effectiveness of RL heavily depends on the efficiency of its training process, where the optimization of neural network parameters plays a crucial role in determining the agent’s ability to make intelligent decisions under varying network conditions. The integration of IChOA into the RL framework is justified by its ability to enhance the training process, specifically by improving the convergence speed and robustness of the learned policies. This combination allows the RL agent to learn more effective policies faster and with greater accuracy, thereby improving the overall secrecy performance. By comparing the proposed IChOA-RL method against other state-of-the-art DL and ML algorithms, the paper demonstrates that this approach not only surpasses traditional methods in terms of scalability, accuracy, and convergence but also provides a more effective solution for the specific challenges of optimizing secrecy in SG communications.

1.1 Related Works

Several research efforts have focused on investigating the physical layer security (PLS) performance of SG communications in recent years. Campongara et al. [29] explored the benefits of hybrid power line communication (PLC)/wireless channels for improving PLS in low-bit-rate applications. They derived mathematical formulations for the average secrecy capacity (ASC) and secrecy outage probability (SOP), revealing the advantages of hybrid PLC/wireless models in enhancing PLS when eavesdroppers utilize a single data communication interface. Salem et al. [30] delved into the PLS of cooperative relaying PLC systems with artificial noise. They derived expressions for ASC, highlighting the potential of cooperative relaying to significantly enhance the security of PLC systems. Building on this, Salem et al. [31] extended their study to consider PLS in correlated log-normal cooperative PLC networks. Their work analyzed the impact of background and impulsive noise components, providing mathematical insights into ASC and SOP under various network scenarios.

Odeyemi et al. [32] introduced a dynamic wide area network (WAN) for SGs featuring a friendly jammer to enhance network secrecy. They derived closed-form expressions for connection SOP and ASC, showcasing the network’s enhanced security performance. Atallah et al. [33] investigated PLS performance in wireless sensor networks within SG environments. They considered the impact of destination-assisted jamming on secrecy performance metrics and derived analytical expressions for SOP, revealing the potential for significant improvement in security using jamming techniques. El-Shafie et al. [34] studied the influence of wireless network’s PLS and reliability on demand-side management in SGs. Their work explored the tradeoff between security and reliability, proposing artificial-noise-aided schemes and encoding strategies to enhance security and reliability in SG. Mohan et al. [35] examined PLS in low-frequency PLC systems, focusing on ASC and SOP. They considered both the independent and correlated log-normal channel distributions, incorporating the impact of impulsive noise and various network parameters.

Kaveh et al. [18] delved into the application of reconfigurable intelligent surfaces (RIS) to enhance the PLS in SG communications. The research addresses the vulnerabilities of SG communication links to eavesdropping and unauthorized access, proposing RIS as a solution to improve secrecy performance. By integrating RIS with reflecting elements in the SG environment, alongside SMs, neighborhood gateways, and potential eavesdroppers, the authors derive closed-form expressions for SOP and ASC. They analyze the signal-to-noise ratio (SNR) distributions at both the gateway and the eavesdropper, providing a comprehensive evaluation of the impact of various system parameters. Their asymptotic analysis under high-SNR conditions, supported by Monte Carlo simulations, validates that RIS can significantly enhance the secrecy performance of SG communications, outperforming conventional scenarios without RIS. Faheem et al. [36] introduced a framework utilizing smart contracts within a Solana blockchain-based industrial wireless sensor network (BCWSN), referred to as the advanced Solana blockchain (ABC), specifically designed for distributed energy resources (DERs) in SGs. This ABC framework facilitates robust and secure real-time control and monitoring of DERs within the SGs. Performance evaluations and security analyses demonstrated that the ABC scheme is secure, dependable, and efficient for lightweight data sharing between DERs in SGs.

However, while some studies have focused on analyzing the secrecy performance in SG communications under various system and channel conditions, there has been limited research on developing optimization approaches specifically aimed at optimizing the secrecy rate in SG. Mensi et al. [37] investigated the security challenges posed by the Internet of Things (IoT) and bidirectional communications in SG environments. Given the increasing data transmission demands due to the proliferation of IoT devices, the study emphasizes the need for high data rate technologies like Sub-6 GHz, millimeter-wave (mmWave), and massive multiple-input multiple-output (MIMO). The authors address the vulnerabilities of IoT-enabled SGs to eavesdropping and jamming attacks, proposing a hybrid beamforming design to enhance secrecy capacity. Unlike previous methods that increase secrecy capacity through random power augmentation or system combiner settings, this research utilizes the Gradient Ascent algorithm to optimize the beamforming strategy, considering both fixed and variable transmit power scenarios. The study’s numerical results validate the efficacy of their approach, highlighting its potential for improving security in SG communications. Although the work by Mensi has proposed a method to optimize secrecy performance in SG, there remains a need for developing a more robust optimization approach to enhance the secrecy rate in SG. The Gradient Ascent Algorithm, as used by Mensi, can get stuck in local minima. Therefore, a novel approach with a stronger capability for exploration and exploitation in such problem environments would likely yield a more optimal secrecy rate.

1.2 Paper Contributions

•   This study introduces a new IChOA-RL model aimed at optimizing secrecy performance for secure NOMA communication within an SG. The IChOA is used to optimize the parameters (weights and biases) of the RL.

•   In the proposed IChOA, a new V-shaped transfer function is introduced to enhance the ChOA. The primary benefit of IChOA is its proficiency in balancing exploration and exploitation.

•   The effectiveness of the proposed IChOA-RL model is evaluated by comparing it with various advanced ML algorithms, such as recurrent neural network (RNN), long short-term memory (LSTM), KNN, SVM, improved crow search algorithm (I-CSA), and grey wolf optimizer (GWO).

•   The evaluation of the results utilizes multiple criteria such as the scalability of the NOMA communication system, accuracy, coefficient of determination (R2), root mean square error (RMSE), and convergence curves. Simulation results indicate that the IChOA-RL model surpasses other models in performance. The use of IChOA in the training process of neural networks shows that it can significantly speed up learning and convergence to optimal policies, ensuring efficient power resource utilization while maintaining high security levels.

1.3 Main Objectives of the Study

•   Enhance secrecy performance in SG Communications: This study aims to develop a novel RL framework, integrated with an IChOA, to optimize the secrecy capacity rate in SG NAN. By leveraging advanced RL algorithms, the framework seeks to intelligently adapt to dynamic communication environments, ensuring secure NOMA SG communication.

•   Improve training efficiency and convergence: Another key objective is to improve the training efficiency and convergence properties of the RL network through the integration of the IChOA. This integration is expected to enable the RL agent to learn more robust policies faster compared to standard algorithms, thereby enhancing the overall performance in complex SG environments.

•   Compare and validate performance: The study also aims to extensively compare and validate the performance of the proposed IChOA-RL method against several state-of-the-art ML algorithms, including RNN, LSTM, KNN, SVM, I-CSA, and GWO. The objective is to demonstrate significant improvements in secrecy capacity rates, scalability, accuracy, R², RMSE, and convergence trends under various network conditions.

1.4 Paper Organization

The organization of our paper is as follows. In Section 2, we present the detailed architecture of the studied system model and formulate the specific problem of optimizing the secrecy capacity rate. This section also introduces our novel RL-based approach, explaining how it addresses the challenges identified in the problem formulation. Section 3 demonstrates the effectiveness of our proposed solution through rigorous simulation scenarios and provides a comparative analysis with existing methods. Finally, Section 4 summarizes our key findings and discusses their implications for the future of secure SG communications.

2  Research Method and Modeling

This section delineates the proposed RL technique aimed at optimizing the secrecy rate within the established SG NOMA communication system. In the context of RL, the IChOA is utilized to optimize the weights and biases of the fully connected neural network. It updates the network parameters in a way that the resultant policy maximizes the expected rewards.

2.1 System Model and Problem Formulation

The system under consideration is an SG NOMA communication model designed for secure message broadcasting from an NG to a set of K SMs under its control in an NAN, indexed by SM1, SM2,…,SMk. The NG serves as a central hub that uses NOMA to transmit critical control messages to the SMs, which are the end-users of the grid. The system is under the threat of an eavesdropper (Eve) attempting to intercept the communications. The NOMA protocol employed allows multiple SMs to be served simultaneously over the same frequency band by exploiting the power domain. Each SM is assigned a different power level based on the channel state information (CSI), which is assumed to be perfectly known at the NG. The signals are superimposed when transmitted by the NG and are separated at the receiver side using successive interference cancellation (SIC), which requires the SMs to decode and subtract signals not intended for them before decoding their own.

The channel between the NG and each SM (hm), as well as between the NG and Eve (he), is subject to Rayleigh fading, characterized by a probability density function of the signal’s amplitude. This fading model is appropriate for environments where multiple scattered paths exist without a line of sight. The channel coefficients are modeled as complex Gaussian random variables with zero mean and unit variance, representing the rapid changes in the amplitude and phase of the signals due to multipath propagation. The SG environment is dynamic, with the channel conditions varying due to factors such as physical obstructions, weather changes, and varying electrical load. We assume NG is a multi-antenna user while SMs and Eve are single-antenna users. Fig. 1 depicts the studied system model in this paper.

Figure 1: The studied SG NOMA communication system model

Assuming, without loss of generality, that the users are ordered by their channel gain magnitudes, we have an ordered sequence from the weakest to the strongest channel gain relative to the eavesdropper’s channel. In this NOMA setup, the NG broadcasts signals using a superposition coding strategy that combines the power-scaled messages of all SMs, where γi represents the power allocation coefficient for the i-th SM, and p denotes the total transmission power available at the NG. Each SM’s message, Si, is normalized such that the expected value of the message’s power is unity. Following the NOMA protocol, we order the power allocation coefficients such that γ1≥γ2≥…≥γk, with the sum of these coefficients equaling unity. The received signal at the i-th SM, yi, and at the eavesdropper, ye, are expressed as Eqs. (1) and (2).

yi=hmi(∑k=1KγkPSk)+ni(1)

ye=he(∑k=1KγkPSk)+ne(2)

where ni and ne are the zero-mean additive white Gaussian noise (AWGN) components affecting the i-th SM and the eavesdropper respectively, both modeled as N(0,σ2). Following the principles of NOMA, each SM in the system, specifically the i-th SM, employs the SIC method to accurately detect their dedicated messages. This is executed by sequentially decoding messages intended for SMs with inferior channel gains-namely, any k-th SM where |hmi|2<|hmk|2-and then removing these decoded messages from the overall SNR of the received signals. Conversely, signals meant for users with superior channel gains compared to the i-th SM are treated as noise. To guarantee the effective application of SIC at the i-th SM’s receiver, it is a prerequisite that the data rate at which the i-th SM decodes the k-th SM’s message (Rk⟶i) must not fall below the target data rate (Rk~) set for the k-th SM. When the i-th SM successfully decodes its own message, the achievable data rate for this user, denoted as Ri and expressed in bits per second per Hertz (b/s/Hz), is calculated using Eq. (3).

log2⁡(1+ρ|hi|2γi1+ρ|hi|2∑k=i+1Kγk)(3)

where ρ represents the signal power to noise power ratio at the receiver, and γi is the power allocation coefficient for i-th SM.

In addressing the eavesdropper’s capabilities, the approach taken is to apply the SIC method to discern the messages intended i-th authorized SM. This user can decode at a rate represented by Re(i). It is acknowledged that the eavesdropper might be among the NOMA user group or an external entity; hence, the formula for Re(i) will vary accordingly and will be elaborated upon in subsequent sections. The secrecy rate i-th NOMA SM is defined as achievable when there exists an encoding strategy that can provide both reliable communication to the intended user and complete secrecy from the eavesdropper. The secrecy rate i-th authorized SM, denoted as RSi, is the excess rate at which i-th SM can communicate over the eavesdropper’s decoding rate and is mathematically represented as Eq. (4).

RSi=[Ri−Re(i)]+(4)

where Ri is the SM’s achievable rate as previously defined, and the operation [x]+ signifies the positive part of x, calculated as max(0,x). This definition is fundamental to ensure that a non-negative secrecy rate is maintained, providing a metric for secure communication.

We proceed under the assumption that complete CSI for all bona fide SMs is accessible to NG, and likewise, the CSI of the eavesdropper is also known. It is important to note that, through the use of SIC, the SM with the superior channel gain is capable of decoding the transmissions intended for other NOMA SMs that possess weaker channel gains. Therefore, in a scenario where there exists an internal adversary, the only SM that can achieve a secrecy rate greater than zero is the SM with the highest channel gain, identified as i-th SM. In the most adverse situation, where the penultimate user, or (i−1)-th SM, is the eavesdropper aiming to intercept i-th SM’s messages, the secrecy rate for every legitimate SM can be represented as Eq. (5).

RSi={log2⁡(1+ρ|hK|2γK)−log2⁡(1+ρ|hK−1|2γK)i=K0, Otherwise(5)

According to [28], in the worst-case scenario, the analytical expression for the i-th SM’s secrecy rate under the condition of asymptotically high SNR, that is, as ρ approaches infinity, can be delineated as Eq. (6).

RSi=1βilog2⁡(i(i−1)Γ(1−βi)×∑s=0i−2(i−2s)(−1)s2F1[1−βi,22−βi;−1−s])(6)

where Γ(.) and F12[.,..;.] show the Gamma function and the generalized hyper-geometric function, respectively. The main objective of this paper is to maximize the secrecy rate in Eq. (6) by using a novel RL technique.

2.2 Basic ChOA

The ChOA is a meta-heuristic technique that draws inspiration from the way chimpanzees forage for food and resources. Introduced in 2020 by Khishe and Mosavi, this algorithm emulates the foraging patterns of chimpanzees, including their social interactions and learning processes. ChOA models the collaborative hunting strategy of chimpanzees, where they exhibit roles such as the driver, chaser, blocker, and attacker. In a coordinated hunting strategy, different roles are played by chimpanzees [38–40]. Driver chimps focus on tracking prey without directly approaching it, primarily to monitor its movements and pinpoint its location. Barrier chimps, often positioned in trees, strategically place themselves to create impediments that hinder the prey’s progress, effectively steering it away from certain escape routes. Chaser chimps leverage their speed and agility to quickly close in on the prey, enhancing the prospects of a successful catch. Lastly, attacker chimps evaluate the prey’s behavior to anticipate possible escape paths, positioning themselves to reroute the prey towards the chasers, thus boosting the chances of capture. These roles are translated into explorative and exploitative steps in the algorithm to find the best solutions. Fig. 2 shows two primary stages of the hunting procedure. ChOA is known for its balance between exploration, to find new potential areas in the search space, and exploitation, to refine the solutions in promising areas. Eqs. (7)–(11) outline the formulas used for driving and chasing the prey.

d=|cXprey(t)−mXchimp(t)|(7)

Xchimp(t+1)=Xprey(t)−ad(8)

a=2fr1−f(9)

c=2r2(10)

m=Chaotic_value(11)

where Xprey(t) is the prey’s position vector; Xchimp(t) denotes the chimp’s position vector; r1 and r2 are the random vectors ∈[0,1]; a,c, and m are the coefficient vectors; m indicates a chaotic vector; and f is the dynamic vector ∈[0,2.5].

Figure 2: Hunting process in basic ChOA

During the hunting phase, chimpanzees initially locate their prey with the help of blockers, drivers, and chaser chimps. The prey’s position is subsequently determined by barrier, attacker, chaser, and driver chimps, while other chimpanzees adjust their positions in response to the prey. These stages are expressed in Eqs. (12)–(14).

{dAttacher=|c1XAttacher−m1X|dBarrier=|c2XBarrier−m2X|dChaser=|c3XChaser−m3X|dDriver=|c4XDriver−m4X|(12)

{X1=XAttacher−a1(dAttacher)X2=XBarrier−a2(dBarrier)X3=XChaser−a3(dChaser)X4=XDriver−a4(dDriver)(13)

X(t+1)=X1+X2+X3+X44(14)

where XAttacher presents the best search agent, XBarrier is the second-best search agent, XChaser denotes the third-best search agent, XDriver is the fourth-best search agent, and X(t+1) is the updated position of each chimp. Fig. 3 illustrates the position updating mechanism in the basic ChOA. This figure demonstrates how different roles assigned to chimpanzees influence the movement towards the prey during the optimization process.

Figure 3: Position updating in basic ChOA

Ultimately, once the hunt is over, all chimpanzees converge to attack the prey, driven by sexual motivation, irrespective of their roles. These sexual motivations are represented using chaotic maps, as shown in Eq. (15).

Xchimp(t+1)={Xprey(t)−adifμ<0.5Chaotic_valueifμ≥0.5(15)

where μ is the random number ∈ [0, 1].

2.3 Improved ChOA

The creation of a new binary version of the ChOA is motivated by the growing need for more robust and adaptable optimization algorithms in various fields such as science, engineering, and industry. Originally inspired by chimpanzees’ social hunting tactics, the standard ChOA has been effective in solving continuous optimization problems. However, its effectiveness in dealing with discrete variables is limited. This limitation underscores the necessity to improve the ChOA framework to adequately address discrete optimization challenges through a binary adaptation. As a result, there is an ongoing effort among researchers and industry professionals to enhance or develop new techniques that increase the efficiency and effectiveness of optimization processes.

Binary encoding streamlines the representation of variables, especially in optimization scenarios where variables are discrete. By using a binary format, ChOA avoids the necessity for continuous parameter adjustments, facilitating its application across different problem areas. The binary encoding of ChOA typically results in lower computational complexity compared to its continuous variable counterpart. This decrease in complexity can lead to quicker convergence and reduced computational demands, making ChOA more practical for addressing optimization challenges, particularly in scenarios with extensive solution spaces.

In binary algorithms, the transfer function plays a pivotal role in transitioning from a continuous to a discrete search space, where it handles binary decision variables. This function is vital because it enables the algorithm to switch between binary states, accommodating scenarios where traditional algorithms primarily handle continuous variables. The design of this function is critical to the algorithm’s approach in navigating the search space, balancing the discovery of new opportunities (exploration) and focusing on promising solutions (exploitation). The ongoing development and enhancement of this transfer function are crucial for developing a successful binary meta-heuristic algorithm, as they significantly influence its search efficiency and convergence capabilities. Accordingly, our paper introduces a novel V-shaped transfer function to adapt the ChOA algorithm. In the suggested IChOA, the position update equation is defined as Eq. (16). To achieve this, a novel V-shaped transfer function is utilized as shown in Eq. (17).

Xdt+1={(Xdt)−1if R<T(X1+X2+X3+X44)Xdt otherwise (16)

T(x)=|32πarctan⁡(3π5x+φ)|(17)

where, Xdt+1 presents the updated binary position at t+1 iteration; Xdt denotes the binary position at t iteration; (Xdt)−1 is the complement of Xdt; R is a random number ∈[0,1]; T(x) is the V-shaped transfer function; and φ is a threshold number ∈[π10,π5]. This modification contributes to reduced computational complexity and faster convergence rates, particularly when dealing with large solution spaces or problems with binary constraints.

2.4 The Proposed RL Technique

The primary goal of the RL algorithm is to dynamically adjust the power allocation coefficients γi for each SM in a way that maximizes the secrecy rate against a sophisticated eavesdropper. The RL framework is modeled as a Markov decision process (MDP), where at each decision epoch, the system state includes the current CSI of all SMs and the eavesdropper, represented by their respective channel gains |hmi|2 and |he|2. The action space consists of possible power allocation vectors γ=[γ1,γ2,…,γk] within the power budget set by the NG’s total transmission power P.

MDP provides a structured way to model an environment in which an agent interacts and makes decisions over time. The core components of an MDP are states, actions, transition functions, reward functions, and policies. In the MDP framework, a state represents a specific situation or configuration of the environment. For SG communications, a state could encompass various factors such as the current security level, network traffic, and channel conditions. Actions are the decisions or moves that the agent can make in each state, such as adjusting transmission power or changing encryption parameters to enhance security. These actions lead to transitions between states, which are governed by the transition function. This function provides the probabilities of moving from one state to another, given a particular action, effectively modeling the dynamics of the environment.

The reward function is another critical component of the MDP framework. It assigns a numerical value to each state-action pair, representing the immediate feedback or benefit of taking a specific action in a given state. In the context of secrecy optimization in SGs, rewards could reflect improvements in the secrecy capacity rate, better energy efficiency, or other performance metrics. The MDP framework is particularly well-suited to problems like secrecy optimization in SGs because it explicitly accounts for the sequential nature of decision-making and the stochastic nature of the environment. By modeling the problem as an MDP, the RL agent can systematically explore different strategies and learn to make decisions that enhance security and efficiency over time. This approach contrasts with traditional machine learning methods, which may not fully capture the temporal and probabilistic aspects of the problem, making RL a powerful tool for optimizing secrecy rates in SG communications.

The RL agent’s objective is to learn a policy π that selects actions to maximize the cumulative discounted secrecy rate over time, defined as Eq. (18) [41].

RSπ=E[∑t=0∞δtRSi(t)](18)

where E[.] is the expectation operator, RSi(t) is the instantaneous secrecy rate at time t, and δ is a discount factor that prioritizes immediate rewards. We propose to utilize a DQN due to its ability to handle high-dimensional state spaces. The DQN comprises a neural network that approximates the optimal action-value function Q∗(s,a). The network is trained iteratively using experience replay and target networks to stabilize learning. The experiences (s,a,r,s′) are stored in a replay buffer, where s′ is the new state after taking action a in state s and receiving reward r.

The reward at each time step is designed to reflect the improvement in secrecy rate. Therefore, if the action taken at time t leads to an increase in the secrecy rate from RSi(t−1) to RSi(t), the reward r(t) is given by the difference RSi(t)−RSi(t−1). This incentivizes the agent to pursue actions that enhance security. The DQN agent is trained over a series of episodes. In each episode, the environment is initialized with a random state, and the agent iteratively selects actions based on ϵ-greedy policy to explore the action space and exploit the current best-known policy. The performance of the trained agent is evaluated by its ability to maintain a high secrecy rate over a separate validation set of channel realizations. The RL agent’s learned policy is expected to adeptly allocate power among the SMs, accounting for the dynamic nature of the SG environment and the potential internal threat posed by an eavesdropper. By doing so, the algorithm ensures that k-th SM, which has the highest risk of information leakage, maintains a secure channel. The proposed RL, with its adaptive power allocation strategy, promises a significant enhancement in the security of SG communications. By optimizing the power distribution in real-time, the network’s overall secrecy performance is bolstered, ensuring the integrity and confidentiality of critical control messages within the SG NAN. By integrating the IChOA into the training process, the RL agent is expected to learn more robust policies faster and with better convergence properties compared to standard algorithms. This can lead to improved performance in complex SG environments, where the agent must make decisions that enhance the security and efficiency of the network.

In the proposed IChOA-RL, the IChOA enhances the RL framework by optimizing key hyper-parameters such as weights, biases, learning rate, ε-greedy parameters, and batch size. By leveraging advanced search mechanisms inspired by chimpanzee behavior, IChOA effectively balances exploration and exploitation within the hyper-parameter space. This process allows for the fine-tuning of weights and biases, leading to more accurate neural network mappings and improved decision-making in complex environments like SGs. Additionally, IChOA dynamically adjusts the learning rate to ensure efficient convergence, optimizes the ε-greedy parameter to maintain a balanced exploration-exploitation trade-off, and selects an optimal batch size that balances computational efficiency with learning stability. The integration of IChOA into the RL framework results in a synergistic optimization of these parameters, considering their interdependencies to maximize overall performance. This holistic approach not only accelerates the convergence of the RL agent but also enhances the robustness of the learned policies, making the agent better equipped to handle the complexities and dynamism of SG communications. Ultimately, IChOA’s optimization process significantly improves the efficiency and effectiveness of RL training, leading to more reliable and secure SG operations.

3  Simulation Results and Analysis

The simulation environment is configured to evaluate the secrecy rate performance of an SG NOMA communication system under various ML and RL algorithms. The setup includes an NG transmitting to several SMs in the presence of an eavesdropper. The number of SMs K=3 unless otherwise mentioned. The performance metrics are assessed against the power allocation coefficient (γk in dB) and the total transmission power (P in mW). The algorithms compared with our proposed IChOA-RL in the simulation include traditional ML approaches like standard ChOA, GWO, LSTM, RNN, KNN, SVM, and standard RL model. The selection of comparison algorithms in this study was carefully made to ensure a comprehensive evaluation of the proposed IChOA-RL approach. These algorithms were chosen for their relevance to SG communications, their diversity in representing both traditional ML and advanced optimization techniques, and their proven track records in tasks such as classification, prediction, and optimization. The scope of potential values for each parameter during the simulation process has been extensive; however, due to pragmatic constraints, it is necessary to choose and exhibit a limited set of diverse parameter instances. Table 1 provides a snapshot of this selection, shedding light on the experimental process by emphasizing the specific parameter values that, in certain instances, either enhanced or diminished the performance of the algorithm.

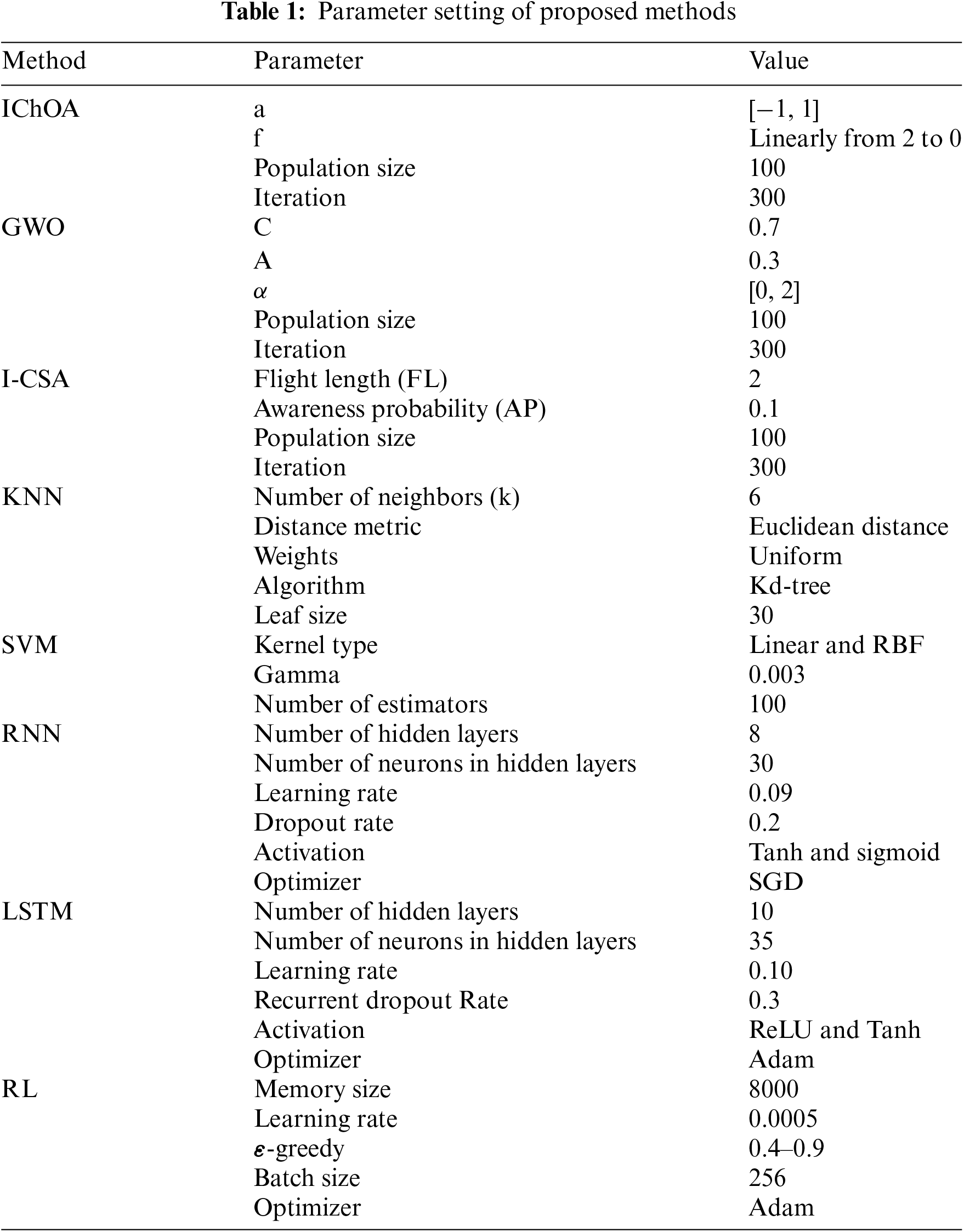
Calibrating parameters for ML algorithms is critical for achieving peak performance and demands careful consideration. It entails identifying the best combinations of parameter values for the algorithms to function efficiently. Establishing these optimal settings is crucial before proceeding with the performance evaluation of the algorithm. In this research, we adopt a systematic trial-and-error approach for parameter tuning, methodically adjusting each parameter separately and monitoring its impact while maintaining all other variables constant. For instance, in an algorithm with multiple parameters such as the number of hidden layers, or iteration, we analyze each parameter independently to assess its effect on the algorithm’s performance. Although there are numerous possible variations for each parameter, practical constraints require us to select and demonstrate a limited range of different parameter scenarios. For our simulations, we utilized OpenAI Gym as the primary simulation environment for training the RL agents. Additionally, we integrated TensorFlow to implement the neural network components of the RL algorithm. To incorporate and evaluate the proposed evolutionary algorithm for updating the fully connected layers in this paper, we employed the distributed evolutionary algorithms in python (DEAP) library.

Fig. 4 presents a detailed analysis of the secrecy rate’s dependency on the power allocation coefficient γk, as represented in decibels (dB), across various algorithmic strategies. In this figure, the proposed IChOA-RL approach consistently outperforms the other methods, showcasing a superior secrecy rate across the entire γk range. This suggests that the IChOA-RL’s optimization process is effectively enhancing the RL agent’s ability to allocate power in a way that maximizes the secrecy rate, regardless of the power coefficient’s magnitude. The RL method alone shows notable improvement over the traditional ML techniques of RNN, LSTM, KNN, and SVM, which indicates the inherent advantage of adaptive learning in dynamic environments. However, KNN and SVM, despite being less dynamic, provide a baseline performance that, while not scaling as well with increased γk, still contributes to our understanding of the impact of power allocation on secrecy. The graph also indicates a diminishing return on the secrecy rate as the power allocation coefficient increases, particularly for KNN and SVM, suggesting a threshold beyond which increasing power does not yield proportional secrecy gains. Overall, the performance trends in Fig. 4 highlight the effectiveness of integrating advanced optimization techniques like IChOA with RL in enhancing secure communications in SG NOMA communication.

Figure 4: Secrecy rate vs. the power allocation coefficient across various algorithms

Fig. 5 provides an insightful illustration of how the secrecy rate varies under the proposed IChOA-RL approach with the power allocation coefficient γk for different quantities of NOMA SMs, designated as K. The curves represent four distinct scenarios, with K taking on values of 6, 10, 14, and 18, respectively. As can be seen in this figure, when γk increases, a corresponding incremental rise in the secrecy rate is observed for each scenario, which aligns with the theoretical understanding that a higher power allocation coefficient enhances the signal’s robustness against potential eavesdropping, thus improving secrecy.

Figure 5: Secrecy rate under the proposed IChOA-RL approach vs. the power allocation coefficient for different numbers of NOM SMs

Notably, the rate at which the secrecy rate increases with γk is more pronounced as the number of SMs, K, grows. This indicates a multiplicative effect of NOMA’s power domain exploitation when more SMs are present; essentially, the system can better differentiate between the intended signal and potential eavesdropping attempts. The scenario with K = 18 SMs achieves the lowest secrecy rate, suggesting that a larger network of SMs can utilize the intrinsic properties of NOMA more effectively, translating into superior secure communication capabilities. This could be due to the lesser complexity and reduced efficacy in channel use when fewer SMs are involved. These trends collectively highlight the effectiveness of NOMA in enhancing secure communications, particularly as the number of participating SMs in the network increases.

Fig. 6 delves into the relationship between the total transmission power, denoted by P and measured in milliwatts (mW), and the resulting secrecy rate, offering a comparative analysis across different algorithmic approaches. As the transmission power increases, all techniques exhibit an upward trend in secrecy rate, indicative of the direct correlation between transmission power and the ability to maintain secure communications. The IChOA-RL technique demonstrates a clear superiority, achieving higher secrecy rates at any given power level. This suggests that the IChOA’s sophisticated optimization algorithm significantly refines the RL agent’s power allocation decisions, leading to more effective secrecy enhancements.

Figure 6: Secrecy rate vs. the NG’s transmission power across various algorithms

Notably, the slope of the IChOA-RL curve is steeper than that of the other methods, especially in the mid-range of the power spectrum, indicating a more efficient conversion of increased power into higher secrecy rates. This efficiency is a critical advantage in real-world applications where power resources are limited and must be used judiciously. The RNN, LSTM, KNN, and SVM methods, while showing improvements with increased power, plateau sooner than the RL-based approaches, revealing the limitations of static models in leveraging additional power for secrecy. The GWO-RL, I-CSA-RL, ChOA-RL, and RL curves, while outperforming the traditional ML models, still lag behind the IChOA-RL, underscoring the impact of the improved optimization algorithm on RL’s adaptability and performance. Fig. 6 finally illustrates not only the beneficial impact of higher transmission power on secrecy rates but also underscores the enhanced performance that can be achieved by a more powerful algorithm.

In this paper, the results were evaluated using three metrics: accuracy, R2, and RMSE. The coefficient of determination quantifies the correlation between observed and predicted values, with values ranging from 0 to 1. A value of one signifies perfect correlation, whereas a value of zero indicates no correlation between the observed and predicted values. Eqs (19)–(21) provide the formulas for calculating R2, RMSE, and Accuracy.

R2=[1N∑i=1N[(Pi−P¯)(Oi−O¯)]σpσo]2(19)

RMSE=(1N∑i=1N[Pi−Oi]2)12(20)

Accuracy=TP+TNTP+FN+FP+TN(21)

where N is the number of observations; Pi is the calculated parameter; Oi is the observed parameter; P¯ is the average calculation parameter; O¯ is the average observations parameter; σp is the standard deviation of calculations; σo is the standard deviation of observations; TN = true negative; TP = true positive; FN = false negative; and FP = false positive.

Table 2 displays R2, accuracy and runtime results for various evolutionary architectures designed to secure NOMA communication in SGs. The data clearly indicate that the IChOA-RL architecture outperforms the others in terms of both R2 and accuracy, not just in the training set but also in the validation set. The IChOA-RL architecture achieved accuracy levels of 97.41% in the testing set and 98.86% in the training set. When it is stated that the IChOA-RL architecture has the highest R2 value, it implies that this architecture most accurately captures and explains the variations in the problem. In other words, it fits the actual data points best and offers the most reliable predictive power among the architectures evaluated. The I-CSA-RL, GWO-RL, ChOA-RL, and RL models also recorded relatively strong performance. Conversely, the LSTM, RNN, SVM, and KNN algorithms demonstrated lower effectiveness. When comparing the runtime across the different methods, IChOA-RL demonstrates a significant advantage with a runtime of 724 s, making it the most efficient among the advanced algorithms evaluated. In contrast, I-CSA-RL, GWO-RL, and ChOA-RL require substantially more time, with runtimes of 985, 1024, and 896 s, respectively, indicating higher computational demands. Traditional methods like RNN, LSTM, SVM, and KNN show moderate runtimes ranging from 869 to 941 s, with the standard RL method being relatively faster at 659 s. This comparison highlights IChOA-RL’s efficiency in delivering high performance without incurring excessive computational costs.

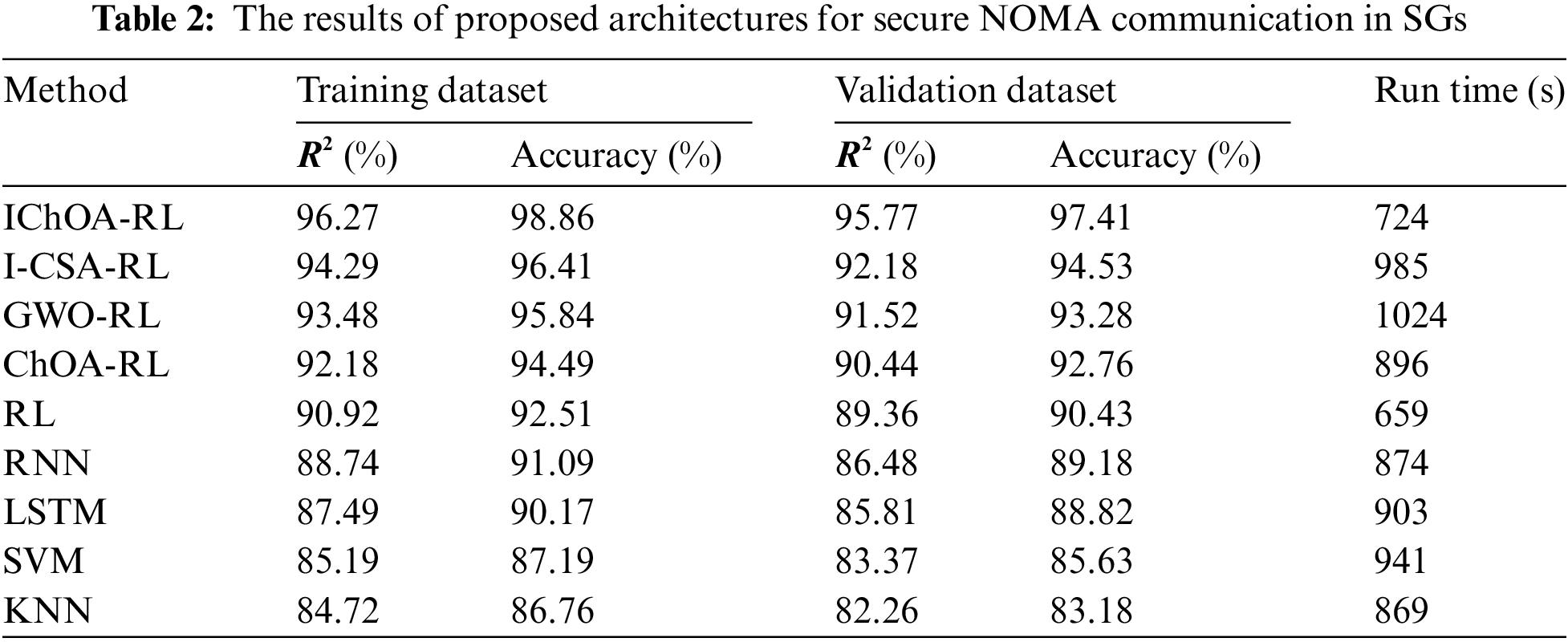
These results highlight the successful training of these architectures with meta-heuristic algorithms, which have effectively optimized their operational efficiency. Moreover, these architectures consistently demonstrate high accuracy across different hybrid RL structures in both testing and training datasets. This consistent performance suggests that the meta-heuristic algorithms used in the training processes have delivered reliable and uniform results across various models and datasets. The RMSE metric is used to evaluate the performance of the models presented in Table 3. The results clearly show that the IChOA-RL surpasses its competitors, highlighting its effectiveness for the problem at hand. This model enhances the RL network by efficiently updating its weight and bias vectors through the integration of IChOA. The IChOA effectively tunes the parameters, enabling the RL network to more accurately detect and model the patterns and relationships in the data. According to Fig. 7, the IChOA-RL converges more quickly than the others. By the 100th epoch, it almost reaches the lowest RMSE score, while the RMSE scores for the other architectures remain higher. Additionally, the IChOA-RL shows exceptional stability and swift convergence as epoch’s progress. The significant initial drop in RMSE for the model showcases a strong capacity for learning, and its sustained low error rate suggests it generalizes well across the dataset. In contrast, other models gradually improve but fail to achieve the low RMSE scores of the IChOA-RL. For example, SVM and KNN exhibit a slower reduction in RMSE. Other architectures like I-CSA-RL, GWO-RL, ChOA-RL, RL, RNN, and LSTM show moderate learning speeds. They manage to lower the RMSE to a commendable level, yet their convergence trajectories indicate they may need additional epochs to potentially equal the performance of IChOA-RL.

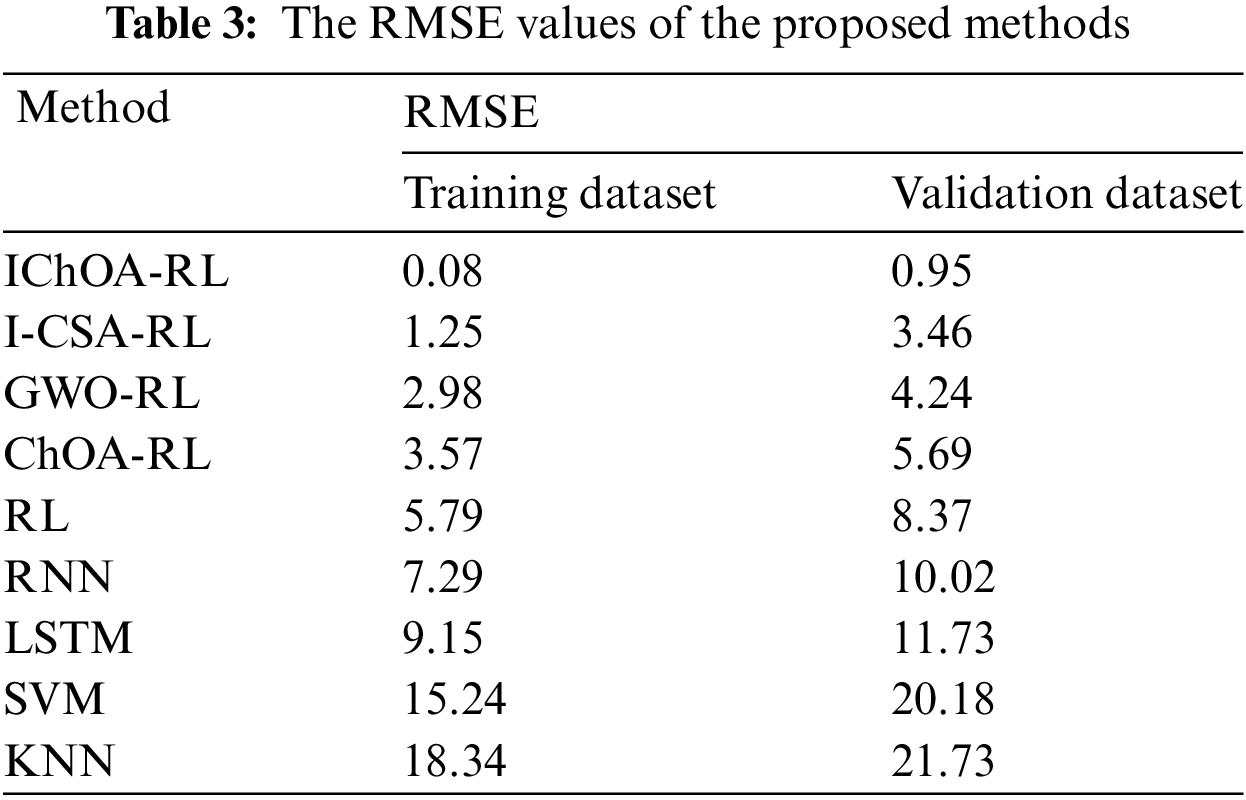
Figure 7: The convergence curve of proposed methods

The computational complexity of the proposed RL technique primarily hinges on the intricacies of the RL algorithm itself and the optimization process facilitated by the IChOA. RL, particularly in environments modeled as MDPs, involves substantial computational effort due to the need to explore and learn optimal policies through interactions with the environment. The computational complexity of a DQN technique involves several key components, including the neural network architecture, the number of states, the number of actions, and the number of iterations required for convergence. Integrating the IChOA into this framework adds another layer of computational complexity. IChOA enhances the training process by optimizing the parameters of the RL network, leading to more robust policy learning. The complexity of IChOA, like other meta-heuristic algorithms, depends on the population size, the number of iterations, and the computational cost of evaluating the fitness function. In this paper, the total computational complexity (C) of the proposed IChOA-RL model is calculated as Eqs. (22)–(24).

CRL=T.O(B.N.M)(22)

CIChOA=O(P⋅D)+G⋅O(P⋅F)+G⋅O(PlogP)+G⋅O(P⋅U)(23)

C=H.CRL+H.CIChOA(24)

where CRL is the computational complexity of RL, CIChOA is the computational complexity of IChOA, T is the total number of iterations for convergence, B is the mini-batch size used during training, N is the total number of neurons in the neural network, M is the average number of connections per neuron, P is the population size, G is the number of generations, F is the complexity of the fitness function, D is the number of dimensions, U is the complexity of updating positions for one individual, and H denotes the number of times the IChOA process is invoked within the DQL training process. The proposed IChOA-RL technique effectively addresses scalability challenges in smart grid implementations by integrating the IChOA for efficient training, enabling rapid convergence and adaptive policy updates in response to real-time data. This approach optimizes resource use, ensuring the method can operate within the constraints of existing smart grid infrastructure, from high-power servers to lower-power edge devices. Extensive simulations validate the method’s ability to maintain high performance and adaptability across various network conditions and scales, demonstrating its robustness in managing large-scale smart grid networks. This scalability is essential for widespread deployment in complex smart grid environments, where efficient resource management and dynamic adaptability are crucial.

4  Conclusions

This paper has presented an in-depth exploration of a novel RL-based strategy for optimizing secrecy performance in an SG environment utilizing NOMA communication. By integrating IChOA to adjust the parameters of a fully connected neural network within the RL framework, we have demonstrated a significant enhancement in the secrecy rates across a range of operational scenarios. The IChOA-RL model was compared against eight other ML architectures. The IChOA-RL model achieved the highest accuracy, recording 97.41% on the validation datasets, making it the most effective approach. Our simulation results have conclusively shown that the IChOA-RL method outperforms traditional ML approaches such as RNN, LSTM, KNN, and SVM, as well as standard RL techniques. The robustness of IChOA-RL was particularly evident in its superior performance at higher power allocation coefficients and transmission power levels, showcasing its potential for practical implementation in real-world SG systems. The scalability of the NOMA communication system was also put to the test, giving insights into the relationship of the number of NOMA SMs with the utilization of the power domain for enhancing secrecy rates, as indicated by the higher slopes in the secrecy rate curves as the number of SMs. This finding underscores the importance of considering user density in designing secure SG communications. Furthermore, the study has contributed to the body of knowledge by highlighting the critical role of sophisticated optimization algorithms in RL. The application of IChOA to the training process of the neural network has been shown to significantly accelerate learning and convergence to optimal policies, ensuring efficient use of power resources while maintaining high levels of security.

Implementing the proposed IChOA-RL technique in real-world SG environments faces several challenges. The significant computational complexity and resource demands of the hybrid method require substantial processing power and memory, making real-time applications potentially costly and impractical. Scalability is also a concern, as the SG’s vast network size demands efficient handling without performance degradation or exponential computational increases. Ensuring real-time adaptability and convergence is crucial, as the RL algorithm must quickly adapt to the dynamic conditions of the SG to maintain optimal performance. Integration with existing SG systems poses further challenges, requiring seamless incorporation without disrupting current operations while ensuring interoperability and regulatory compliance. While the paper addresses some of the practical challenges associated with implementing the IChOA-RL approach in SG environments, there are additional considerations that future research could explore in greater depth. These include real-time processing requirements, data quality issues, energy consumption, and security concerns. Addressing these challenges through innovative solutions and rigorous testing will be essential to realize the full benefits of the proposed method in enhancing the security and efficiency of SG communications.

Moreover, the IChOA-RL method may face difficulties in converging to a global optimum in highly complex or non-convex problem spaces, particularly if the initial conditions or parameter settings are not well-tuned. This is a common challenge shared with other evolutionary algorithms and advanced optimization methods like RL, RNN, LSTM, SVM, KNN, GWO, and I-CSA, which also require careful parameter tuning and can suffer from premature convergence or getting trapped in local optima. However, compared to these algorithms, IChOA-RL’s advantage lies in its ability to adapt more dynamically to changing conditions, albeit at the cost of potentially higher computational demands. In summary, while the IChOA-RL method offers superior performance in terms of adaptability and scalability, its limitations include increased computational requirements and the need for careful tuning to ensure convergence, challenges that are also in other state-of-the-art ML algorithms. Additionally, several unresolved questions regarding the IChOA and RL underscore the need for further investigation in this field. Future studies on the IChOA should delve into refining the algorithm’s specific parameters and thresholds. Such research could involve detailed assessments of how parameter variations affect the algorithm’s rate of convergence, the quality of solutions, and computational efficiency. Researchers might consider employing strategies like meta-heuristic parameter tuning or adaptive adjustments to dynamically optimize parameters during the process. Meanwhile, the development of RL models is likely to evolve towards overcoming the challenge posed by the scarcity of labeled data. This shift may lead to a stronger focus on semi-supervised and unsupervised learning methods. Future efforts could also examine the integration of IChOA into these learning frameworks to better leverage unlabeled data, thus enhancing the performance and generalization capabilities of RL models.

Acknowledgement: None.

Funding Statement: The work described in this paper has been developed within the project PRESECREL. We would like to acknowledge the financial support of the Ministerio de Ciencia e Investigación (Spain), in relation to the Plan Estatal de Investigación Científica y Técnica y de Innovación 2017–2020.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Mehrdad Shoeibi, Mohammad Mehdi Sharifi Nevisi, Sarvenaz Sadat Khatami, Diego Martín; data collection: Mehrdad Shoeibi, Mohammad Mehdi Sharifi Nevisi, Sina Aghakhani; analysis and interpretation of results: Mehrdad Shoeibi, Sarvenaz Sadat Khatami, Sepehr Soltani; draft manuscript preparation: Mehrdad Shoeibi, Mohammad Mehdi Sharifi Nevisi, Diego Martín, Sina Aghakhani; supervision: Diego Martín. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. Docquier, Y. Q. Song, V. Chevrier, L. Pontnau, and A. Ahmed-Nacer, “Performance evaluation methodologies for smart grid substation communication networks: A survey,” Comput. Commun., vol. 198, no. 4, pp. 228–246, 2023. doi: 10.1016/j.comcom.2022.11.005. [Google Scholar] [CrossRef]

2. M. Kaveh, M. R. Mosavi, D. Martín, and S. Aghapour, “An efficient authentication protocol for smart grid communication based on on-chip-error-correcting physical unclonable function,” Sustain. Energy, Grids Netw., vol. 36, 2023, Art. no. 101228. [Google Scholar]

3. S. Li, Y. Wu, Y. Zhang, S. Duan, and J. Xu, “Privacy transmission via joint active and passive beamforming optimization for RIS-Aided NOMA-IoMT networks,” IEEE Trans. Consum. Electron., vol. 70, no. 1, pp. 2290–2302, 2024. doi: 10.1109/TCE.2024.3349618. [Google Scholar] [CrossRef]

4. S. Aghapour, M. Kaveh, M. R. Mosavi, and D. Martín, “An ultra-lightweight mutual authentication scheme for smart grid two-way communications,” IEEE Access, vol. 9, pp. 74562–74573, 2021. doi: 10.1109/ACCESS.2021.3080835. [Google Scholar] [CrossRef]

5. M. Alonso, H. Amaris, D. Alcala, and R. D. M. Florez, “Smart sensors for smart grid reliability,” Sensors, vol. 20, no. 8, 2020, Art. no. 2187. doi: 10.3390/s20082187. [Google Scholar] [PubMed] [CrossRef]

6. E. S. Hassan and A. S. Elsafrawey, “Cooperative secrecy techniques for improving physical layer security in NOMA-based PLC networks,” IETE Tech. Rev., vol. 40, no. 6, pp. 755–766, 2023. doi: 10.1080/02564602.2023.2167741. [Google Scholar] [CrossRef]

7. S. Miri, M. Kaveh, H. S. Shahhoseini, M. R. Mosavi, and S. Aghapour, “On the security of an ultra-lightweight and secure scheme for communications of smart metres and neighbourhood gateways by utilisation of an ARM Cortex-M microcontroller,” IET Inf. Secur., vol. 17, no. 3, pp. 544–551, 2023. doi: 10.1049/ise2.12108. [Google Scholar] [CrossRef]

8. S. Mounchili and S. Hamouda, “Pairing distance resolution and power control for massive connectivity improvement in NOMA systems,” IEEE Trans. Vehicular Technol., vol. 69, no. 4, pp. 4093–4103, 2020. doi: 10.1109/TVT.2020.2975539. [Google Scholar] [CrossRef]

9. F. R. Ghadi, M. Kaveh, and D. Martín, “Performance analysis of RIS/STAR-IOS-aided V2V NOMA/OMA communications over composite fading channels,” IEEE Trans. Intell. Veh., vol. 9, no. 1, pp. 279–286, 2023. doi: 10.1109/TIV.2023.3337898. [Google Scholar] [CrossRef]

10. M. Zeng, A. Yadav, O. A. Dobre, and H. V. Poor, “Energy-efficient joint user-RB association and power allocation for uplink hybrid NOMA-OMA,” IEEE Internet Things J., vol. 6, no. 3, pp. 5119–5131, 2019. doi: 10.1109/JIOT.2019.2896946. [Google Scholar] [CrossRef]

11. X. Tian et al., “Power allocation scheme for maximizing spectral efficiency and energy efficiency tradeoff for uplink NOMA systems in B5G/6G,” Phys. Commun., vol. 43, 2020, Art. no. 101227. doi: 10.1016/j.phycom.2020.101227. [Google Scholar] [CrossRef]

12. F. Fang, Z. Ding, W. Liang, and H. Zhang, “Optimal energy efficient power allocation with user fairness for uplink MC-NOMA systems,” IEEE Wirel. Commun. Lett., vol. 8, no. 4, pp. 1133–1136, 2019. doi: 10.1109/LWC.2019.2908912. [Google Scholar] [CrossRef]

13. M. Ghiasi et al., “A comprehensive review of cyber-attacks and defense mechanisms for improving security in smart grid energy systems: Past, present and future,” Elect. Power Syst. Res., vol. 215, 2023, Art. no. 108975. doi: 10.1016/j.epsr.2022.108975. [Google Scholar] [CrossRef]

14. Z. Ali, G. A. S. Sidhu, F. Gao, J. Jiang, and X. Wang, “Deep learning based power optimizing for NOMA based relay aided D2D transmissions,” IEEE Trans. Cogn. Commun. Netw., vol. 7, no. 3, pp. 917–928, 2021. doi: 10.1109/TCCN.2021.3049475. [Google Scholar] [CrossRef]

15. M. Kaveh and M. R. Mosavi, “A lightweight mutual authentication for smart grid neighborhood area network communications based on physically unclonable function,” IEEE Syst. J., vol. 14, no. 3, pp. 4535–4544, 2020. doi: 10.1109/JSYST.2019.2963235. [Google Scholar] [CrossRef]

16. L. Yang et al., “Secrecy performance analysis of RIS-aided wireless communication systems,” IEEE Trans. Vehicular Technol., vol. 69, no. 10, pp. 12296–12300, 2020. doi: 10.1109/TVT.2020.3007521. [Google Scholar] [CrossRef]

17. D. Wang et al., “Uplink secrecy performance of RIS-based RF/FSO three-dimension heterogeneous networks,” IEEE Trans. Wirel. Commun., vol. 23, no. 3, pp. 1798–1809, 2023. doi: 10.1109/TWC.2023.3292073. [Google Scholar] [CrossRef]

18. M. Kaveh, Z. Yan, and R. Jäntti, “Secrecy performance analysis of RIS-aided smart grid communications,” IEEE Trans. Ind. Inform., vol. 20, no. 3, pp. 5415–5427, 2024. doi: 10.1109/TII.2023.3333842. [Google Scholar] [CrossRef]

19. H. Lei et al., “Secrecy outage performance analysis for uplink CR-NOMA systems with hybrid SIC,” IEEE Internet Things J., vol. 10, no. 15, pp. 13181–13195, 2023. doi: 10.1109/JIOT.2023.3261308. [Google Scholar] [CrossRef]

20. F. R. Ghadi, F. J. López-Martínez, W. P. Zhu, and J. M. Gorce, “The impact of side information on physical layer security under correlated fading channels,” IEEE Trans. Inf. Forensics Secur., vol. 17, pp. 3626–3636, 2022. doi: 10.1109/TIFS.2022.3212198. [Google Scholar] [CrossRef]

21. Y. Pei, X. Yue, C. Huang, and Z. Lu, “Secrecy performance analysis of RIS assisted ambient backscatter communication networks,” IEEE Trans. Green Commun. Netw., vol. 8, no. 3, p. 1, 2024. doi: 10.1109/TGCN.2024.3365692. [Google Scholar] [CrossRef]

22. M. Kaveh, F. Rostami Ghadi, R. Jäntti, and Z. Yan, “Secrecy performance analysis of backscatter communications with side information,” Sensors, vol. 23, no. 20, 2023, Art. no. 8358. doi: 10.3390/s23208358. [Google Scholar] [PubMed] [CrossRef]

23. V. L. Nguyen, D. B. Ha, V. T. Truong, D. D. Tran, and S. Chatzinotas, “Secure communication for RF energy harvesting NOMA relaying networks with relay-user selection scheme and optimization,” Mob. Netw. Appl., vol. 27, no. 4, pp. 1719–1733, 2022. doi: 10.1007/s11036-022-01929-3. [Google Scholar] [CrossRef]

24. C. E. Garcia, M. R. Camana, and I. Koo, “Ensemble learning aided QPSO-based framework for secrecy energy efficiency in FD CR-NOMA systems,” IEEE Trans. Green Commun. Netw., vol. 7, no. 2, pp. 649– 667, 2022. doi: 10.1109/TGCN.2022.3219111. [Google Scholar] [CrossRef]

25. S. Thakur and S. Thakor, “Secrecy performance optimization of SWIPT wireless networks in partial secrecy regime,” IEEE Trans. Green Commun. Netw., 2024. doi: 10.1109/TGCN.2024.3464241. [Google Scholar] [CrossRef]

26. Z. Chu et al., “Secrecy rate optimization for intelligent reflecting surface assisted MIMO system,” IEEE Trans. Inf. Forensics Secur., vol. 16, pp. 1655–1669, 2020. doi: 10.1109/TIFS.2020.3038994. [Google Scholar] [CrossRef]

27. G. Sharma, N. Pandey, A. Singh, and R. K. Mallik, “Secrecy optimization for diffusion-based molecular timing channels,” IEEE Trans. Mol., Biol. Multi-Scale Commun., vol. 7, no. 4, pp. 253–261, 2021. doi: 10.1109/TMBMC.2021.3054907. [Google Scholar] [CrossRef]

28. W. Yu, A. Chorti, L. Musavian, H. V. Poor, and Q. Ni, “Effective secrecy rate for a downlink NOMA network,” IEEE Trans. Wirel. Commun., vol. 18, no. 12, pp. 5673–5690, 2019. doi: 10.1109/TWC.2019.2938515. [Google Scholar] [CrossRef]

29. A. Camponogara, H. V. Poor, and M. V. Ribeiro, “The complete and incomplete low-bit-rate hybrid PLC/wireless channel models: Physical layer security analyses,” IEEE Internet Things, vol. 6, no. 2, pp. 2760–2769, 2019. doi: 10.1109/JIOT.2018.2874377. [Google Scholar] [CrossRef]

30. A. Salem, K. M. Rabie, K. A. Hamdi, E. Alsusa, and A. M. Tonello, “Physical layer security of cooperative relaying power-line communication systems,” in 2016 Int. Symp. Power Line Commun. App. (ISPLC), Bottrop, Germany, 2016, pp. 185–189. [Google Scholar]

31. A. Salem, K. A. Hamdi, and E. Alsusa, “Physical layer security over correlated log-normal cooperative power line communication channels,” IEEE Access, vol. 5, pp. 13909–13921, 2017. doi: 10.1109/ACCESS.2017.2729784. [Google Scholar] [CrossRef]

32. K. O. Odeyemi, P. A. Owolawi, and O. O. Olakanmi, “Secure transmission in smart grid dynamic wide area network by exploiting full-duplex jamming scheme,” Trans. Emerg. Telecomm. Technol., vol. 34, no. 1, 2023, Art. no. e4657. doi: 10.1002/ett.4657. [Google Scholar] [CrossRef]

33. M. Atallah, M. S. Alam, and G. Kaddoum, “Secrecy analysis of wireless sensor network in smart grid with destination assisted jamming,” IET Commun., vol. 13, no. 12, pp. 1748–1752, 2019. doi: 10.1049/iet-com.2018.5344. [Google Scholar] [CrossRef]

34. A. El-Shafie, D. Niyato, R. Hamila, and N. Al-Dhahir, “Impact of the wireless network’s PHY security and reliability on demand-side management cost in the smart grid,” IEEE Access, vol. 5, pp. 5678–5689, 2017. doi: 10.1109/ACCESS.2017.2695520. [Google Scholar] [CrossRef]

35. V. Mohan, A. Mathur, V. Aishwarya, and S. Bhargav, “Secrecy analysis of PLC system with channel gain and impulsive noise,” in 2019 IEEE 90th Veh. Tech. Conf. (VTC2019-Fall), Honolulu, HI, USA, 2019, pp. 1–6. [Google Scholar]

36. M. Faheem, H. Kuusniemi, B. Eltahawy, M. S. Bhutta, and B. Raza, “A lightweight smart contracts framework for blockchain-based secure communication in smart grid applications,” IET Gen., Trans. Distrib., vol. 18, no. 3, pp. 625–638, 2024. doi: 10.1049/gtd2.13103. [Google Scholar] [CrossRef]

37. N. Mensi, D. B. Rawat, and E. Balti, “Gradient ascent algorithm for enhancing secrecy rate in wireless communications for smart grid,” IEEE Trans. Green Commun. Netw., vol. 6, no. 1, pp. 107–116, 2021. doi: 10.1109/TGCN.2021.3093821. [Google Scholar] [CrossRef]

38. J. Wang, M. Khishe, M. Kaveh, and H. Mohammadi, “Binary chimp optimization algorithm (BChOAA new binary me-ta-heuristic for solving optimization problems,” Cognit. Comput., vol. 13, no. 5, pp. 1297–1316, 2021. doi: 10.1007/s12559-021-09933-7. [Google Scholar] [CrossRef]

39. M. Aljebreen et al., “Binary chimp optimization algorithm with ML based intrusion detection for secure IoT-assisted wireless sensor networks,” Sensors, vol. 23, no. 8, 2023, Art. no. 4073. doi: 10.3390/s23084073. [Google Scholar] [PubMed] [CrossRef]

40. M. Kaveh and M. S. Mesgari, “Application of meta-heuristic algorithms for training neural networks and deep learning architectures: A comprehensive review,” Neural Process. Lett., vol. 55, no. 4, pp. 4519–4622, 2022. doi: 10.1007/s11063-022-11055-6. [Google Scholar] [PubMed] [CrossRef]

41. A. K. Shakya, G. Pillai, and S. Chakrabarty, “Reinforcement learning algorithms: A brief survey,” Expert. Syst. Appl., vol. 231, no. 7, 2023, Art. no. 120495. doi: 10.1016/j.eswa.2023.120495. [Google Scholar] [CrossRef]