 Open Access
Open Access
ARTICLE
DAUNet: Detail-Aware U-Shaped Network for 2D Human Pose Estimation
1 College of Information and Artificial Intelligence, Nanchang Institute of Science and Technology, Nanchang, 330108, China
2 School of Electrical and Information Engineering, Wuhan Institute of Technology, Wuhan, 430205, China
3 School of Computer Science and Technology, Hubei Business College, Wuhan, 430079, China
* Corresponding Author: Zhenhua Xiao. Email:
Computers, Materials & Continua 2024, 81(2), 3325-3349. https://doi.org/10.32604/cmc.2024.056464
Received 23 July 2024; Accepted 07 October 2024; Issue published 18 November 2024
Abstract
Human pose estimation is a critical research area in the field of computer vision, playing a significant role in applications such as human-computer interaction, behavior analysis, and action recognition. In this paper, we propose a U-shaped keypoint detection network (DAUNet) based on an improved ResNet subsampling structure and spatial grouping mechanism. This network addresses key challenges in traditional methods, such as information loss, large network redundancy, and insufficient sensitivity to low-resolution features. DAUNet is composed of three main components. First, we introduce an improved BottleNeck block that employs partial convolution and strip pooling to reduce computational load and mitigate feature loss. Second, after upsampling, the network eliminates redundant features, improving the overall efficiency. Finally, a lightweight spatial grouping attention mechanism is applied to enhance low-resolution semantic features within the feature map, allowing for better restoration of the original image size and higher accuracy. Experimental results demonstrate that DAUNet achieves superior accuracy compared to most existing keypoint detection models, with a mean PCKh@0.5 score of 91.6% on the MPII dataset and an AP of 76.1% on the COCO dataset. Moreover, real-world experiments further validate the robustness and generalizability of DAUNet for detecting human bodies in unknown environments, highlighting its potential for broader applications.Keywords
The primary objective of two-dimensional human pose estimation is to detect anatomical key points, such as elbows and wrists, or specific parts of the human body. This technique represents a vital research area within computer vision, playing a significant role in comprehending human behavior. It shows great application potential in many fields, such as human movement recognition, medical assistance, virtual reality, and security monitoring. Therefore, the research and implementation of human pose estimation technology have emerged as both a central focus and a significant challenge in computer vision.
Compared with the estimation of local human poses, the estimation of whole-body poses faces more challenges. The most commonly used methods for pose estimation include two frameworks, the top-down and bottom-up methods [1]. Heatmaps are the dominant method for top-down critical point detection [2]. This study focuses on single-person pose estimation in top-down 2D images, which is fundamental to other related challenges in computer vision. Fig. 1 shows the basic flow of key point detection under the deep learning framework. In node detection, RGB images containing people are first input into a deep convolutional neural network to generate key point heatmaps. Dense heatmaps are generated with sliding window convolutions and multiresolution inputs. During training, the joint coordinates are encoded by a two-dimensional Gaussian distribution. Subsampling reduces the computational burden, restoring the resolution after heatmap prediction. Finally, the key point location is determined via coordinate decoding. Pose recognition relies on feature extractors, which are responsible for extracting useful features from the input images, and regressors, which are responsible for predicting the specific coordinates of each key point. Feature extractors generally use pre-trained deep convolutional neural network models such as U-Net [3] or ResNet [4] to obtain image feature representations. The regressors utilize a combination of convolutional neural networks and fully connected layers to effectively analyze and process image features, ultimately enabling the accurate prediction of key point coordinates.
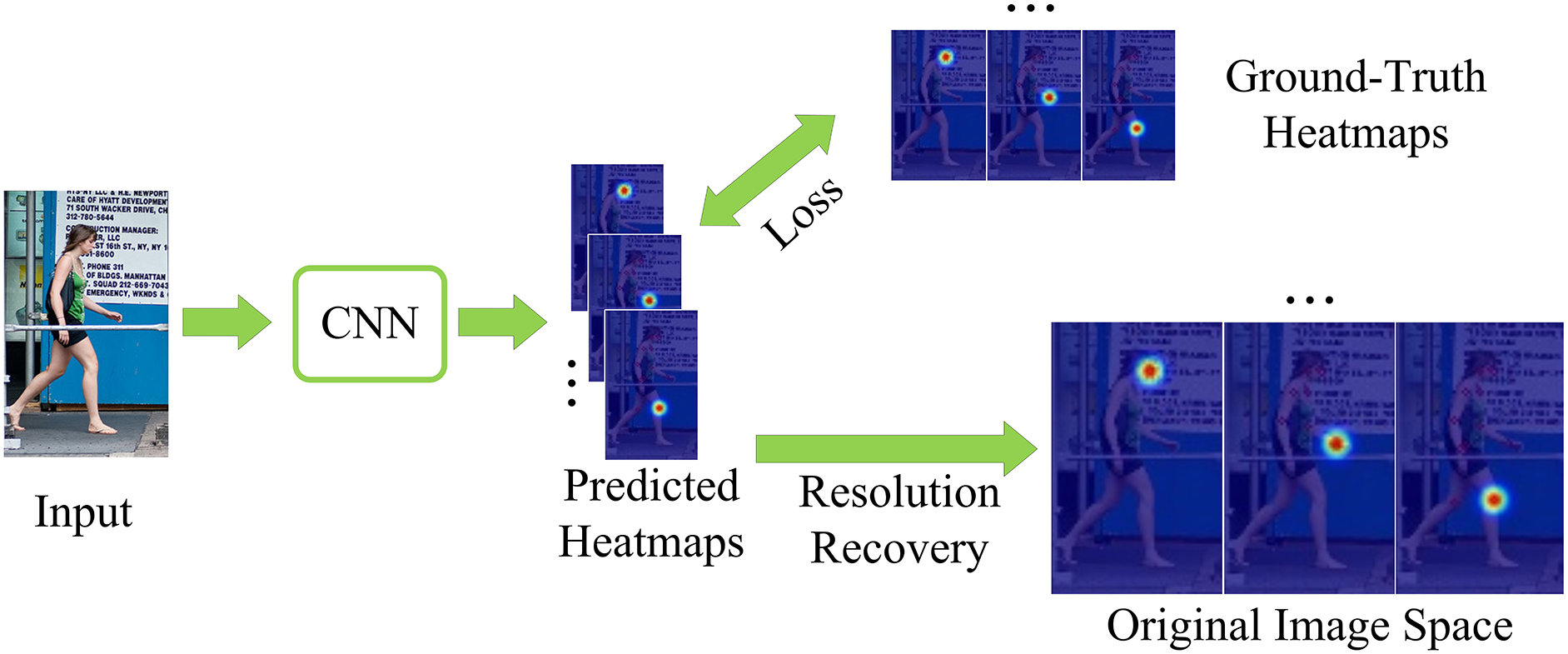
Figure 1: A flow chart of a human pose estimation network. The model needs to be run in a low-resolution image space to reduce the calculation cost, and corresponding resolution restoration needs to be carried out during testing to obtain the prediction of key point coordinates in the original image space
Recent advancements in pose estimation are categorized into 3D pose estimation and 2D pose estimation. In the realm of 3D pose estimation, Ha’s work [5] stands out with notable achievements. This approach leverages internal spatiotemporal non-locality to capture meaningful semantic features for effective pose recognition. Hourglass [6] is considered a relatively simple and classic algorithm in 2D pose recognition because it uses multiple stacked hourglass modules for attitude estimation. Each module consists of downsampling and upsampling processes, the former by convolution and pooling downsampling and the latter by upsampling and jump joins to integrate features. It can effectively extract and integrate multiscale features. However, the downsampling process will lead to information loss, resulting in a certain error in keypoint detection. The CPN (Cascaded Pyramid Network) [7] includes GlobalNet [8] for the initial detection of key points and RefineNet for further refinement of difficult key points by combining ResNet and FPN (Feature Pyramid Network) [9]. The accuracy of the attitude estimation is improved. However, the processing is complicated, and the perception of low-resolution features after downsampling is not sensitive. HRNet (High Resolution Network) [10] maintains high-resolution features throughout the entire process through parallel multiresolution branches and gradually adds low-resolution branches. The potential information loss of high-resolution features is avoided. The resolution information positioning accuracy is improved. However, the network structure is relatively complex, with high computational and storage costs. MSPN (Multi Stage Pose Network) [11] improves the multistage structure by using cross-stage feature fusion and supervision to reduce information loss. Using the GlobalNet module in each stage, multistage refinement and cross-stage fusion improve the estimation accuracy, reduce information loss, and alleviate gradient vanishing problems. However, there although feature information loss, network redundancy, and insensitivity to low-resolution features may appear as separate issues, they are intrinsically interrelated in the context of human pose estimation. Feature information loss and network redundancy directly impact the model’s ability to effectively interpret low-resolution inputs. For instance, information loss due to downsampling can lead to inaccuracies in keypoint detection, while network redundancy can exacerbate computational inefficiencies. These interconnected challenges collectively affect the performance and accuracy of pose estimation models. Addressing these issues together is crucial for improving the model’s overall effectiveness and efficiency.
To address the aforementioned issues, this paper introduces a novel U-shaped network architecture inspired by the ResNet network, as shown in Fig. 2. Partial convolution and strip pooling strategies are implemented in each network block through a series of high to low resolution subnets. In contrast to traditional convolutions, partial convolutions concentrate on processing specific regions of the feature map, thereby minimizing computational resource consumption while maximizing the preservation of image feature information. Strip pooling is a novel pooling method that uses elongated nuclei in one dimension to capture remote relationships and narrow nuclei in the other dimension to focus on the local context, effectively preventing interference from irrelevant information. This design enables the network to synthesize context information at the global and local levels, allowing for more accurate analysis of the scene than with traditional square pooled windows.
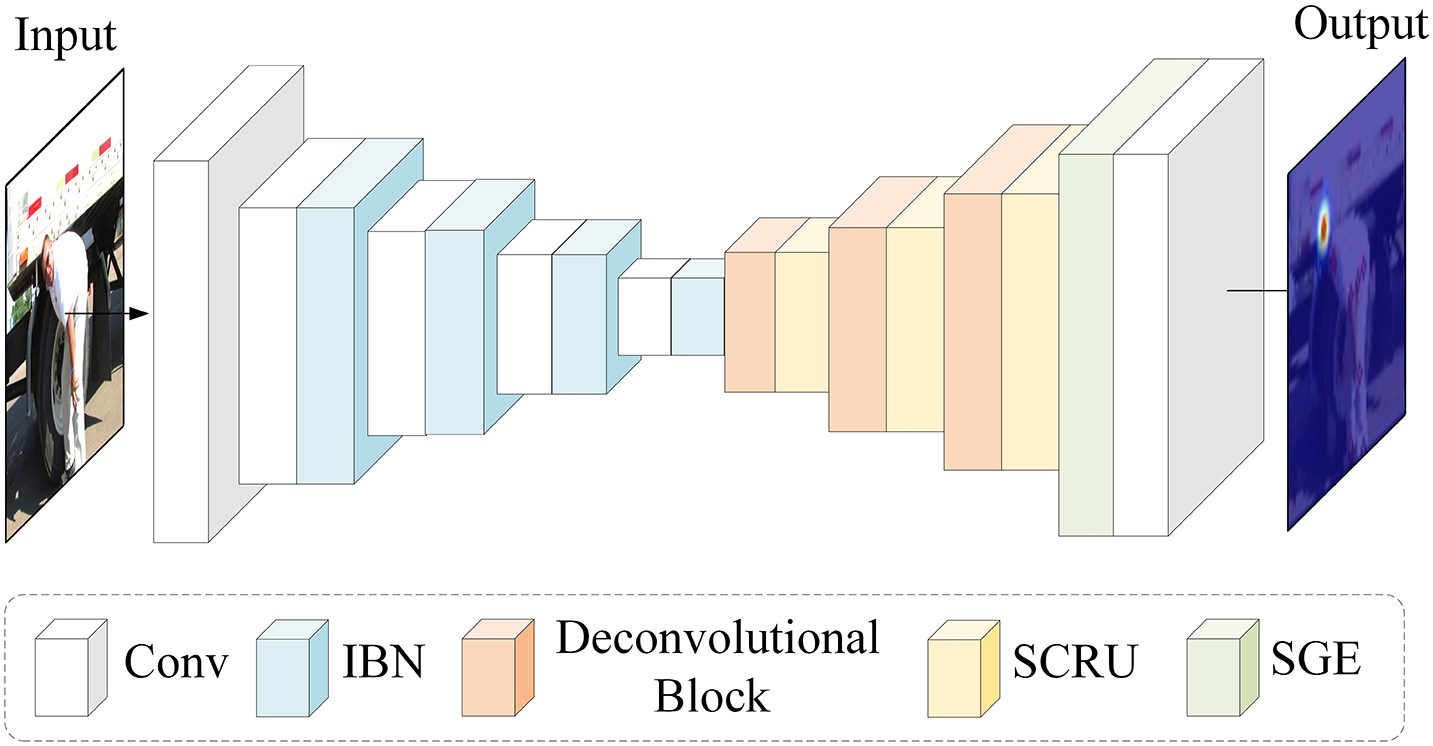
Figure 2: Overall network structure of DAUNet
The feature mapping of deep convolutional neural networks contains redundancy in both the spatial and channel dimensions. To tackle this issue, we sequentially merge the spatial rebuild unit (SRU) and channel rebuild unit (CRU) and apply them to the feature map restoration network architecture.
After the downsampling process, the loss of the original detailed information of the feature map is inevitable, especially in an image where the background is dominant and the figure is small. To generate precise semantic features at the correct spatial locations within the original image, we incorporated the spatial group enhancement attention mechanism following upsampling in the deconvolution module to improve the richness of the feature map. This attention mechanism is particularly effective for detecting small objects and can provide a more robust and evenly distributed feature representation in space, thus showing significant advantages in the detection of small objects.
The primary contributions of this study can be summarized as follows:
1: We designed a human key point detection network and enhanced the feature extraction module by integrating advanced partial convolution and strip pooling to maintain the integrity of the original feature information.
2: To reduce redundancy in the channel and spatial dimensions during the upsampling process, we systematically integrate the SRU and CRU in the feature mapping’s spatial and channel dimensions.
3: For small targets with low resolution, based on optimizing the network in the first two modules, we employ a spatial group enhancement attention mechanism to significantly improve the representational power of the feature maps after restoring the original features.
2.1 Prediction of Key Human Points Based on Heatmap Regression
The objective of human pose estimation is to identify the spatial locations of human joints within images captured in natural environments, thereby constructing the human skeletal framework. Convolutional neural networks (CNNs) excel at this task [12]. At present, most attitude detection methods are based on heatmap regression [2] to detect joint nodes. This approach produces a probability distribution map for each joint, from which the position with the highest probability is chosen as the predicted location of the joint. The heatmap takes into account not only the context clues but also the uncertainty of the target location, reducing the risk of overfitting the model during training by providing spatially supported features in the ground truth. However, a significant challenge of using heatmap representation is that the computational cost doubles as the input image resolution increases. This escalation in computational demand constrains the CNN model’s capacity to effectively handle high resolution images. To reduce the computational burden, the human body boundary frame is often downsampled, and the arbitrarily large resolution image is converted into a smaller feature map for processing.
Once the heatmap prediction is completed, the predicted coordinates must be converted to the coordinate space of the original image through a process of resolution recovery. Since heatmaps are typically smaller than network inputs, direct use of the coordinates of the maximum points introduces quantization errors. To mitigate this problem, the coordinate decoding process usually includes manual offset operations. In practical reasoning, the coordinates of the maximum point are often post-processed to reduce the quantization error. For example, in the Hourglass model, the second largest value point of the predicted coordinates is shifted by 1/4 of a pixel; in HRNet, the actual offset is 1/4 of the gradient at the maximum point.
Heatmap representation has become an effective method for locating key points in human posture recognition and has quickly become within the mainstream of coordinate representation. Current research focuses on designing more efficient network architectures for regression heatmap supervision, including improved designs such as pyramid residual learning, deconvolution upsampling, and high-resolution representation retention. These methods are designed to enhance model performance while maintaining sensitivity to the details and retention of high-resolution features.
2.2 Two Paradigms for Human Pose Estimation: Top-Down and Bottom-Up
In the field of human posture recognition, the top-down approach is a common and classic strategy. This approach begins by identifying the bounding boxes for each person within the image, followed by performing individual pose estimation within those bounding boxes. Early CNN methods directly predicted the key point location for single-person attitude estimations, but these methods gradually surpassed the heat-map-based estimation methods. Previous studies, like Luvizon et al. [13], used the softmax operation to read joint locations from heatmaps in single-person 2D pose estimation. MaskR-CNN [14] extends FasterR-CNN [15] by adding an attitude estimation branch parallel to the original boundary frame recognition branch. Modern top-down pose estimation networks include CCAM-Person [16], FDAPose [17], YH-Pose [18], and others. Although these methods have been successful in achieving high accuracy and precision, they often require additional computational costs in detecting the human frame.
In contrast, the bottom-up approach adopts a markedly different strategy. It begins by detecting all body joints across individuals in the image and then groups these joints to form complete human figures. This method performs pose detection and grouping simultaneously, eliminating the need for prior detection of human body bounding boxes. Typical bottom-up approaches include Openpose [19], PersonLab [20], and PifPaf [21]. Openpose uses a two-branch multilevel network, one branch for heatmap prediction and one branch for grouping. It uses the grouping method of the partial affinity field to complete the grouping by calculating the line integral between two key points and grouping the key points by the maximum integral. Other methods, such as PersonLab, group key points by directly learning the two-dimensional offset domain of each pair of key points, or PifPaf, locate body parts by using a part strength field and associate body parts with each other by using a part association field to form a complete human posture. The bottom-up method has high robustness and can effectively deal with complex scenes and occlusions, so it shows advantages in some specific scenes. However, this method has the disadvantages of slow calculation and high cost for real-time monitoring.
Attention models have revolutionized the field of computer vision by markedly improving performance across various tasks such as image classification and object detection. By enabling models to concentrate on the most critical parts of an image, these models not only enhance accuracy but also bolster the overall robustness of the systems. This targeted focus helps in more precise identification and analysis, leading to superior outcomes in visual recognition tasks. Self-attention methods provide a way to calculate feature context by calculating the weighted sum of all the positions in an image. This approach is especially effective in generative tasks and sequence modeling because it captures the global context, not just the local information. In terms of the gesture detection attention mechanism, feature grouping learning can be traced back to AlexNet, whose convolutional groups can better learn feature representations and allocate models to more GPU resources [22]. SENet [23] represents a highly optimized lightweight attention mechanism that specifically emphasizes the significance of each channel. This is accomplished by calculating the importance score for each channel and then calibrating the feature map from these scores. This channel-level attention mechanism empowers the network to concentrate on features rich in informative content while diminishing the impact of less relevant features. GCNet [24] combines the advantages of nonlocal operations and SE modules to create a more effective global context module. This has achieved convincing results in tasks such as object detection that require global contextual information. SKNet [25] introduces a dynamic kernel selection mechanism that uses multiscale group convolution to select suitable convolution kernels. This method significantly improves classification performance with a small increase in computational complexity and parameters, making it particularly suitable for learning multiscale features. Beyond channel-level attention, BAM [26] and CBAM [27] introduce spatial attention mechanisms. These advanced modules incorporate attention strategies across both the channel and spatial dimensions, improving the performance of the model by highlighting the key points in each dimension. Our network integrates a minimal lightweight attention mechanism called SGE, which is a key aspect of its lightweight nature. Traditional attention mechanisms often substantially increase computational overhead and parameter count, but our lightweight attention mechanism significantly reduces additional computation and memory consumption while preserving model performance. This design further optimizes network efficiency, ensuring high effectiveness and practicality in real-world applications.
3 A Detail-Aware U-Shaped Network for 2D Human Pose
This paper investigates key point detection for human pose estimation using heatmaps. Human posture detection aims to recognize the human body within a given image, locate the joint coordinates, and construct a skeleton diagram of the human body. To do this, we construct a regression model that maps the image to the coordinates, and we use the heatmap as a representation of the node coordinates during training and testing. We use image datasets labeled with joint coordinates and convert these coordinates into heatmaps that serve as learning targets for model training. We employ the same body detection approach utilized in SimpleBaseline [28] to track postures across frames. In the prediction stage, we parse the heatmap generated by the model back into the original coordinate space of the image to obtain the position of the final node.
Fig. 2 illustrates the comprehensive network architecture of DAUNet. It is a single-stage U-shaped structure that includes an improved concatenated feature extraction module, SGE, several residual blocks, and upsampling operators. This streamlined structure not only reduces the number of model parameters but also lowers computational complexity, thereby enhancing processing efficiency. The key point prediction network is suitable for any type of input mode, and the key point position of the human posture is generated by the heatmap.
This paper utilizes the standard coordinate decoding method. Specifically, for a heatmap predicted by the trained model, we first identify the coordinates corresponding to the maximum activation (m) and the second highest activation (s). Subsequently, the node’s position is predicted as follows:
where
Initially, the image is scaled to match the input dimensions required by the target network, and then feature extraction is carried out through the improved subsampling module based on partial convolution and strip pooling. To easily recover and retain spatial features after the convolution operation, we use a self-defined upper sampling layer to upsample the feature graph. Then, the feature map is deconvolved (upsampled), and space rebuild and channel rebuild are carried out to reduce the feature redundancy. In addition, to retain the local fine feature information, we capture the global space-dependent information through a lightweight attention mechanism after upsampling. Finally, we recover the original image through a standard convolution layer so that we can obtain the key point prediction graph with the same image size at the output end as the input end.
3.1.1 Improved Bottleneck Using Partial Convolution and Strip Pooling
The bottleneck module is one of the fundamental modules in ResNet and is used to construct deep neural networks. In the task of designing fast key point estimation networks, many works currently focus on the depth of stacked neural networks. However, we observed that as the depth increases, the prediction performance does not necessarily improve to a certain extent but rather increases the number of floating-point operands (FLOPS), increasing network latency. Moreover, repeated downsampling in pose estimation can lead to a significant reduction in the preservation of original feature details.
ResNet is similar to GoogLeNet [29], but the difference is that large convolution kernel downsampling (7×7Conv) is directly adopted for the first convolution layer, followed by MaxPooling for further downsampling. The first block of each phase undertakes the functions of changing dimensions and downsampling. It is worth noting that Stage 1 does not downsample because MaxPooling has been completed and uses 1×1Conv (a BottleNeck structure). In the downsampled block, the second 1×1Conv increases the dimension, and then a 3×3Conv is downsampled. In a BottleNeck that is not subsampled, the first 1×1Conv decreases its dimension, and the second 1×1Conv increases its dimension. The other path is subsampled by the pooling layer and subsequently increased in dimension, which is similar to DenseNet’s TransitionBlock structure [30].
However, in the downsampling process, both average pooling and maximum pooling have some limitations. Average pooling averages the pixel values in each pooling window, which may lead to the loss of some details. Especially when there are large feature variations or textures, average pooling may not effectively retain the important features. The maximum pooling keeps only the maximum value in the pooling window and erases some subtle feature information. In some cases, this can affect the performance of the model, especially when detailed key point location information is needed. Therefore, inspired by recent work [31,32], we propose a reconstructed subsampling module, IBN, in which we use custom partial convolution and strip pooling to extract spatial features more efficiently by reducing feature loss and simultaneously improving the model’s fitness.
Here, we describe how our rebuilt module works. As shown in Fig. 3, compared with traditional convolution and grouping convolution, partial convolution is more focused on processing the local region of the input image rather than the whole image, The subset of channels selected for convolution is typically continuous.
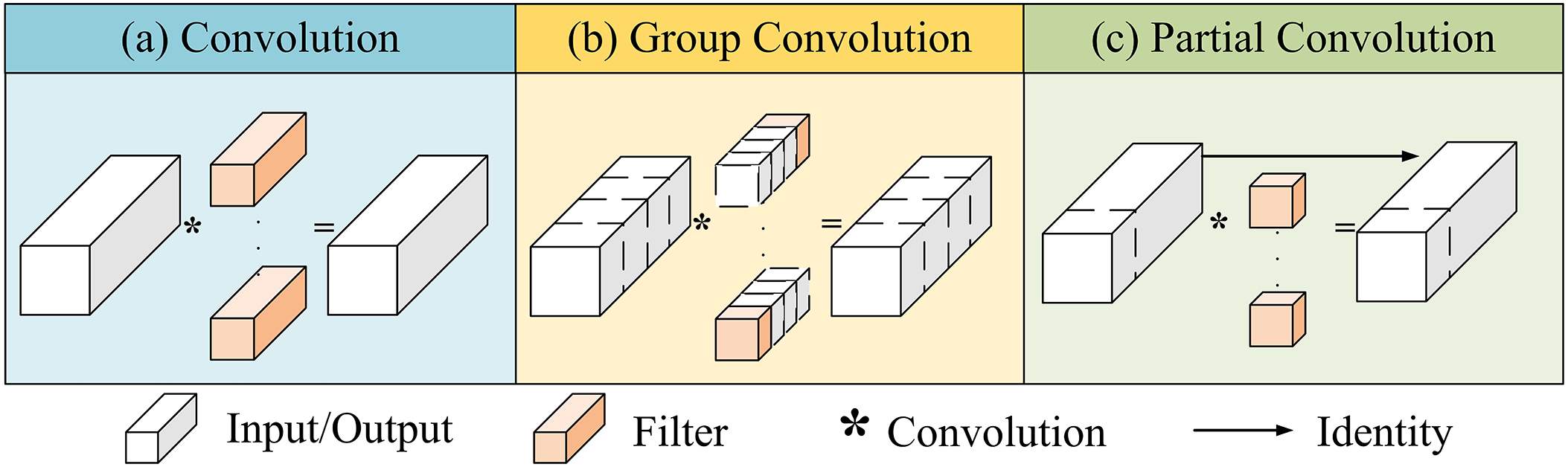
Figure 3: Contrast diagram of local convolution with conventional and packet convolution. Local convolution applies filters to a few input channels while remaining unchanged
When implementing this method, we first determine the number of channels in the partial convolutional layer and then define a partial convolutional layer using a 3 × 3 sized kernel. In the forward propagation process, we use segmentation and concatenation methods. This means that we divide the input tensor into two parts according to the specified number of channels, apply partial convolution operations on one part, and finally concatenate the two processed tensors together. In panel (c) of Fig. 3, we apply convolution to the first continuous subset of channels, while the unprocessed channels are preserved and passed to subsequent layers. This approach allows later convolutional layers to utilize the unprocessed channels, ensuring that information flows through all channels and preventing the loss of important data. This method simplifies the memory access pattern, reducing the number of floating-point operations (GFLOPs) and the memory access requirements of the model. This approach helps preserve the spatial information of the input image because the convolution kernel at each position operates only with pixels in a local region. This processing method ensures that partial convolution only extracts spatial features from some input channels while keeping other channels unchanged, thus ensuring that the channel count for both the input and output feature maps remains constant without compromising generality. The detailed formula is given by:
where
Fig. 4 depicts the structure of our stripe pooling method, where
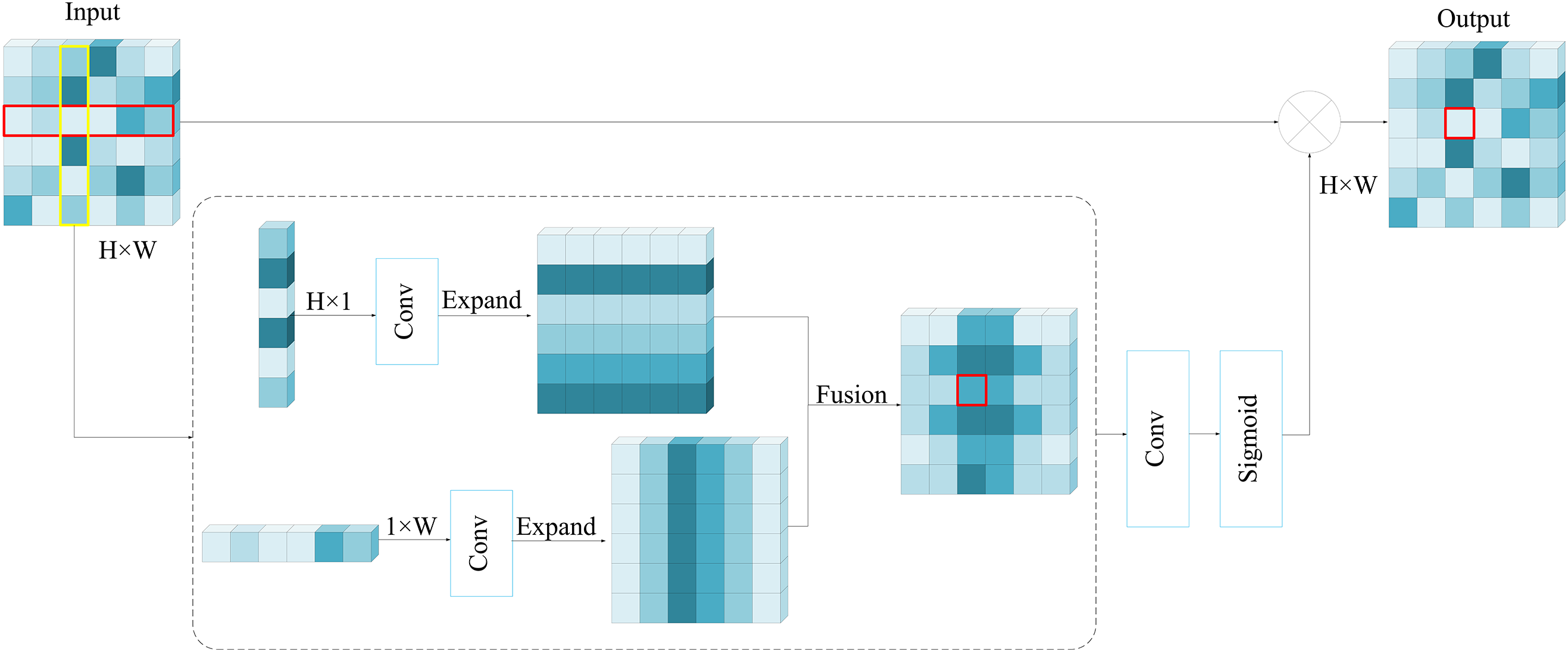
Figure 4: Structure diagram of ribbon pooling module
The horizontal ribbon pooling can be expressed as:
Vertical ribbon pooling can be expressed as:
This gives us
Then, the output z is calculated as:
where
In Fig. 4, we link the output tensor to every position indicated by the red and yellow boxes. In contrast to average pooling, which operates on a global scale, strip pooling emphasizes handling local regions. Additionally, unlike attention modules that demand substantial computational resources, strip pooling offers a more efficient and lightweight alternative.
3.1.2 Space/Channel Rebuild Unit
Fig. 5 illustrates the design of the reduced space rebuild unit and the channel rebuild unit introduced in this paper.
Figure 5: De-redundant structure combining spatial rebuild unit (SRU) and channel rebuild unit (CRU)
In a general U-shaped network, downsampling operations usually occur in the first half of the network, while upsampling operations occur in the second half of the network. The downsampling operation diminishes the spatial dimensions of the feature map through pooling or convolution, while the upsampling operation increases the spatial resolution of the feature map by deconvolution or interpolation. Typically, the network loses some details during downsampling and attempts to recover the lost information during upsampling. Therefore, during the upsampling stage, there may be a certain degree of redundancy in the feature map. This is because downsampling reduces the spatial extent of the feature map while upsampling increases the spatial dimension of the feature map, which may cause certain information in the feature map to be copied or duplicated.
To leverage spatial redundancy, we introduce a spatial rebuild unit (SRU) with separation and rebuild operations, using the scale factor in group normalization to assess feature map information [33]. We obtain normalized input features by subtracting the mean ρ and then dividing by the standard deviation α, where λ is a small constant added to ensure numerical stability, ρ and α represent the mean and standard deviation of X, and φ and μ are learnable affine transformations.
We utilize the learnable parameter
Then, the weights of the Wφ-reweighted feature maps are scaled to the range (0, 1) using the sigmoid function and regulated by a threshold. The complete procedure for deriving W is described by the following formula:
Finally, we get two weighted features,
To reduce space redundancy, we perform cross-reconstruction addition operations to save space and generate richer feature representations. Then, the reconstructed features
where
To utilize channel redundancy, we introduce a channel rebuild unit (CRU) and adopt a splitting conversion fusion strategy. First, the input feature is divided into the
After segmentation and expansion, the detailed spatial feature
The process of up-transformation can be detailed as:
where
where
To dynamically combine the output features
Next,
Finally, under the guidance of the feature importance vectors β1 and β2, The upper feature Y1 and the lower feature Y2 are merged along the channel axis to derive the channel-thinned feature Y:
In summary, we achieve the goal of reducing feature redundancy by arranging the SRU and CRU in order, merging them into one SCRU module, and adding them after each upsampling module.
3.1.3 Lightweight Spatial Grouping Attention
The attention mechanism in the field of node detection mainly covers spatial attention and channel attention. In this paper, to boost the semantic capacity of the feature groups, the spatial attention acquisition module, Spatial Groupwise Enhance (SGE), is integrated into the node detection network. The network architecture is illustrated in Fig. 6.

Figure 6: Structure diagram of lightweight SGE module
First, divide the feature map into G groups along the channel dimension, we focus on the vector representation of a certain set of features, called
For each position, we measure the similarity ci between the global semantic feature g and the local feature xi, and we have:
To avoid bias in coefficients across different samples, we perform spatial normalization of c.
where ɛ is a constant introduced to ensure numerical stability. Meanwhile, the parameters γ and β are calculated for each coefficient.
Finally, the original feature vector
All the enhanced features make up the final feature set:
The mean square error (MSE) serves as a prevalent measure for assessing the accuracy of predictions in human pose estimation challenges and is often defined as Joints MSE Loss in key point prediction. The calculation of the MSE loss forward equation begins by calculating the square error (SE) between the model prediction (A) and the actual true value (Y):
Next, we determine the sum of squared errors (SSE). Here,
This operation sums all the elements of the SE (A, Y) matrix, which has dimensions N × C. The errors between rows are aggregated by multiplying
During backpropagation, the gradient of the MSE loss relative to the model output (A) needs to be calculated to update the model parameters:
Therefore, the MSE loss function is defined as:
where A is the model prediction value. Y is the true value. N is the number of samples in the batch. C is the output dimension of each sample.
The experimental platform of this paper is Ubuntu 20.04. The programming environments used were PyTorch 1.14.1 and Cuda 11.8, and the system comes with an NVIDIA Tesla A100 40G GPU. We have verified the performance of DAUNet through a large number of experiments. All the experiments are performed on open human pose datasets, and classical benchmark models such as Hourglass and Openpose are selected for comparison. The performance of the proposed modules is studied, and the effectiveness of key point detection in an actual environment is evaluated.
4.2 Datasets and Experimental Setup
We used the public human pose datasets MPII [35] and COCO [36] to train and validate our approach. The MPII Human Posture Dataset is the most advanced benchmark for evaluating human joint posture estimates. The images for this dataset were systematically collected using an established taxonomy of daily human activity. The dataset contains 410 human activities and approximately 25k images, including more than 40k human objects, all labeled with 16 points of information; these images were extracted from YouTube videos. The data include verification and test sets for single-frame single-person poses, single-frame multiperson poses, and video multiperson poses, and most methods use a single-frame multiperson pose test set. The COCO Pose dataset is widely used in pose recognition by Microsoft. It contains approximately 80 types of images and more than 250,000 labeled images, covering a wide variety of complex gestures and movements. Each image shows the location of up to 17 key points on the whole body, such as the head, limbs, and hands. The dataset is suitable for training and evaluating pose estimation, action recognition, pose generation, and other tasks.
In the MPII dataset, the Percentage of Correct Key Points (PCK) quantifies the proportion of accurately identified key points by assessing normalized distances against a predefined threshold. This metric employs the head diameter as a scaling factor for normalization. Additionally, the variant known as PCKh evaluates key point accuracy after this normalization process, providing a refined measure of precision in detecting key points relative to the head diameter.
where i is the key point ID, k is the k-th threshold Tk, p is the detected p-th object,
The evaluation indices of key point detection in the COCO dataset simulate the target detection evaluation indices, and the average precision (AP) and average recall rate (AR) are used for evaluation. Its objective is to define key similarity (Object Keypoint Similarity, OKS) to measure similarity matching and real forecast stances, and more than 10 OKS threshold average precisions (APs) are used as its main index.
where p indicates a specific test object in the ground truth, while pi signifies the key point for an individual. dpi denotes the Euclidean distance between the key point ID of i in the current set of tested key points and the key point ID of i in the ground truth key point p for the human body.
The similarity measure OKS between the reference key points and the detected key points is computed as a scalar value. An artificial threshold T is then applied, allowing the calculation of the AP based on the OKS across all images:
In COCO datasets, the key point detection and instance segmentation evaluation methods use AR indicators, which denote the average proportion of detected predictions relative to the actual number. AR ranks the prediction boxes in order of confidence from high to low, calculates the number of real boxes covered by the prediction boxes at each position, multiplies the ratio between the score and the number of real boxes by 1 or 0, and then averages the ratio between the score of all prediction boxes and the number of real boxes to obtain the AR value. The formula for determining the recall is given by:
where TP (true positive) indicates true cases. FN (false negative) stands for false counterexample. The average recall rate AR is used to average the recall rate of all the categories, specifically, to take the largest recall rate for different IoUs and then average them.
4.3 Experimental Results and Analysis
For the MPII dataset, we used a two-stage top-down detection method. That is, the detector is first used to detect the human instance, and then the detection key point is predicated on the detected object.
Our algorithm comprises the following steps: human body detection and propagation, human body pose estimation, and pose association between adjacent frames. We adjust the height or width of the human detection box to maintain a fixed aspect ratio (4:3 height to width), and subsequently crop the box from the image to resize it to a fixed dimension of 256 × 256. We use the Adam optimizer. The batch size is set to 128, and the learning process follows this setting. The basic learning rate is set to 1e-3, and the momentum is 0.9. As shown in Fig. 7, and the loss decreases to 4.2e-4 and 3.9e-4 at the 100th and 200th iterations, respectively. The accuracy (mean) increases to 90% at 130 iterations. The accuracy of each joint is basically similar to the overall accuracy; the highest effect is achieved approximately 130 times, and the training process is finished in 200 cycles.

Figure 7: Network training on MPII dataset
By convention, a quarter shift in the direction from the highest heating value response to the second highest response on the heatmap is the position of the predicted key point.
Because each key point reflects different areas in the image, it is difficult for the model to locate each type of key point. We reimplemented the other methods by using ResNet-50 as the backbone with an input size of 256 × 256 for comparison with our DAUNet. As shown in Table 1 and Fig. 8, for the shoulder, elbow, wrist, knee, and ankle, which are relatively smaller than the other types of key areas, DAUNet has greater accuracy than the other methods, reaching average accuracies of 96.9, 92.6, 87.9, 87.9 and 83.7, respectively. The proposed DAUNet achieves competitive performance with a relatively small number of GFLOPs compared to other networks with similar parameter counts. The reduced number of floating-point operations leads to enhanced model performance, enabling the extraction of more useful features from low-resolution semantic attention through multiple interactions. This results in increasingly focused attention, with more accurate predictions of key point locations in small regions. Although the accuracy of the head, hip, and other parts was slightly different, the mean (PCKh@0.5) of the verification set had the preferable score of 91.6.

Figure 8: Visual result of network node verification on MPII valid set
The testing process is almost identical to the testing process in MPII, where the human detection box is resized to maintain a 4:3 aspect ratio; thereafter, the box is extracted from the image and subsequently resized to 256 × 192 pixels. The data augmentation scheme and the coordinate decoding strategy are consistent with MPII, Our method employs the Adam optimizer and the batch size is set to 128. In the experiment, as shown in Fig. 9, the model was trained for 200 rounds, the initial learning rate was set at 1e-3 and the momentum was 0.9, which attenuated to 3.8e-4 and 3.4e-4 in the 100th and 200th rounds, respectively. Our method also uses a top-down detection method (Openpose in the table is a bottom-up paradigm). The PR curve indicates that as the recall increases, the precision significantly decreases, especially noticeable when the recall approaches 0.7. This suggests that to capture more positive samples, the model also includes more misclassified negative samples, resulting in reduced precision. The model performs better at low recall, identifying some positive samples with higher precision, but precision drops rapidly as recall increases. Tables 2 and 3 show how DAUNet compares to other networks on COCO’s validation and test sets.

Figure 9: Network training on the COCO dataset
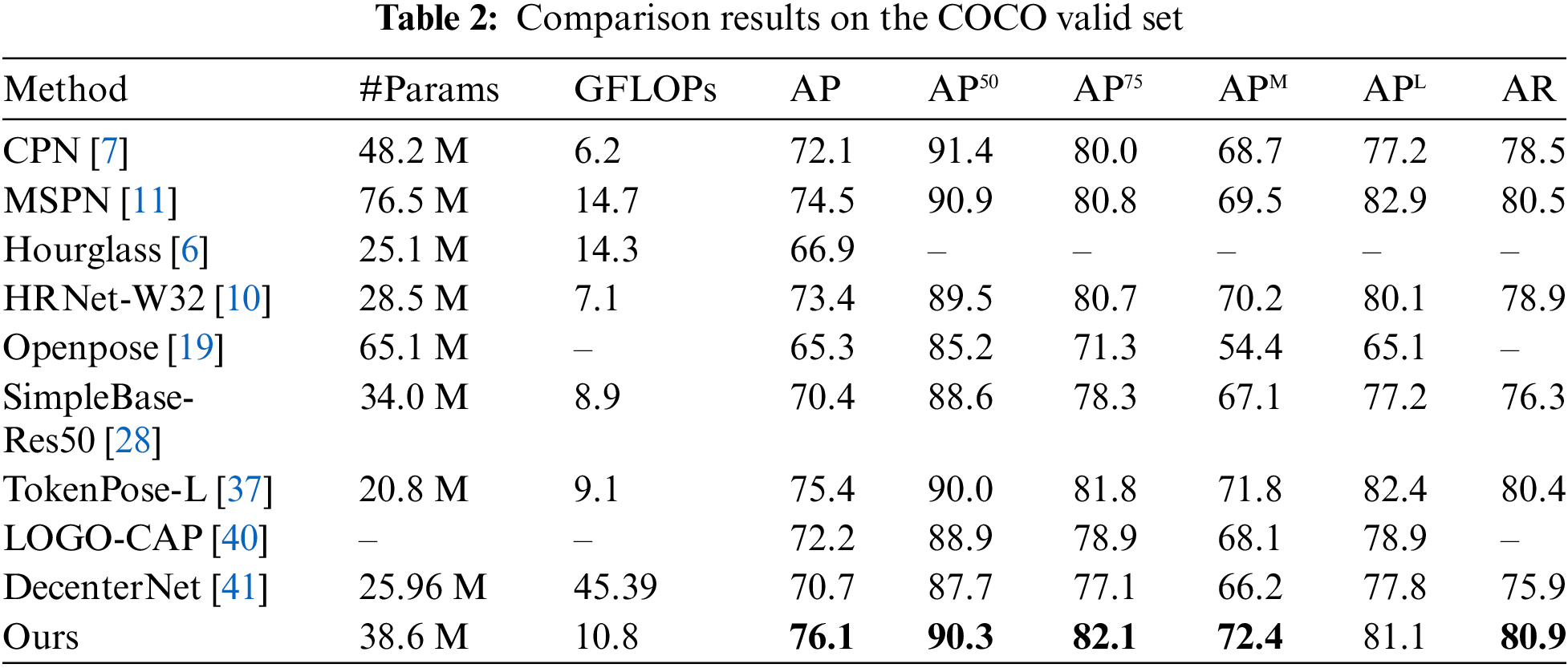
Table 2 and Fig. 10 present the results of this method alongside other leading techniques evaluated on the COCO validation set. The DAUNet proposed in this paper is pre-trained in the convolutional network part but not in the attention mechanism part.

Figure 10: Visual result of the network node verification on the COCO valid set
From Table 2, it can be seen that DAUNet’s average accuracy (AP) and average recall (AR) have increased by 0.7% and 0.5%, respectively, compared to the highest-scoring token pose. We believe that the model complexity remains within an acceptable range. Despite a slight increase in the number of parameters (#Params) and computations (GFLOPs), DAUNet still exhibits the best performance on the COCO dataset overall. Since DAUNet reduces feature redundancy for low resolutions, it uses partial convolution for the downsampling of high-resolution images to improve the recognition of low-resolution images and can eliminate the inaccuracy of upsampling fusion through an attention mechanism after subsequent upsampling. This results in a 0.6% improvement in APM performance. Compared with TokenPose, although TokenPose has a slightly higher score in APL, TokenPose uses a self-attention interaction to capture and embed key point markers to complete the interactive fusion of deep features, and the parameters and computation amount of the attention mechanism used are greater than those of the lightweight spatial attention mechanism used in this paper.
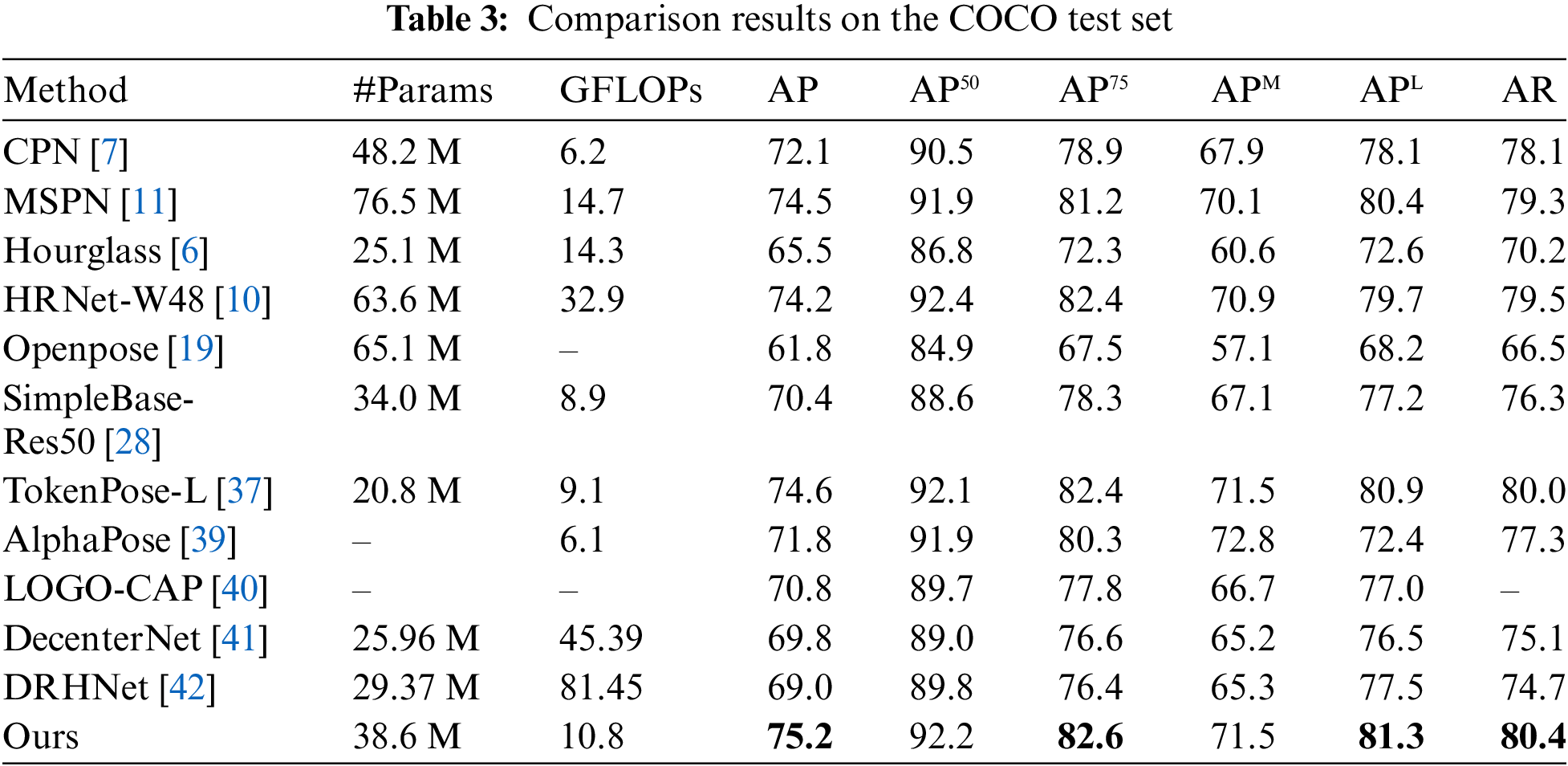
Table 3 and Fig. 11 show DAUNet’s performance on the COCO test set, where it outperforms other methods, particularly those using Transformer architectures, with a 0.6% higher average precision (AP) and 0.4% higher average recall (AR), despite increased parameters and computational complexity. DAUNet excels by leveraging low-resolution global semantic information, and spatial attention, enhancing the spatial distribution of semantic features. Its partial convolution and strip pooling methods effectively retain image features, achieving superior results, especially in the APM index. Nowadays, most pose estimation networks are leaning towards complex attention structures and high computational loads. The increase in floating-point operations and parameter count for DAUNet is acceptable given its impact on model complexity relative to the final results. Overall, DAUNet demonstrates superior performance compared to other networks. It achieves better experimental results by increasing only the quantity of parameters and the computational load and has a good overall performance.

Figure 11: Visual result of network node verification on COCO test set
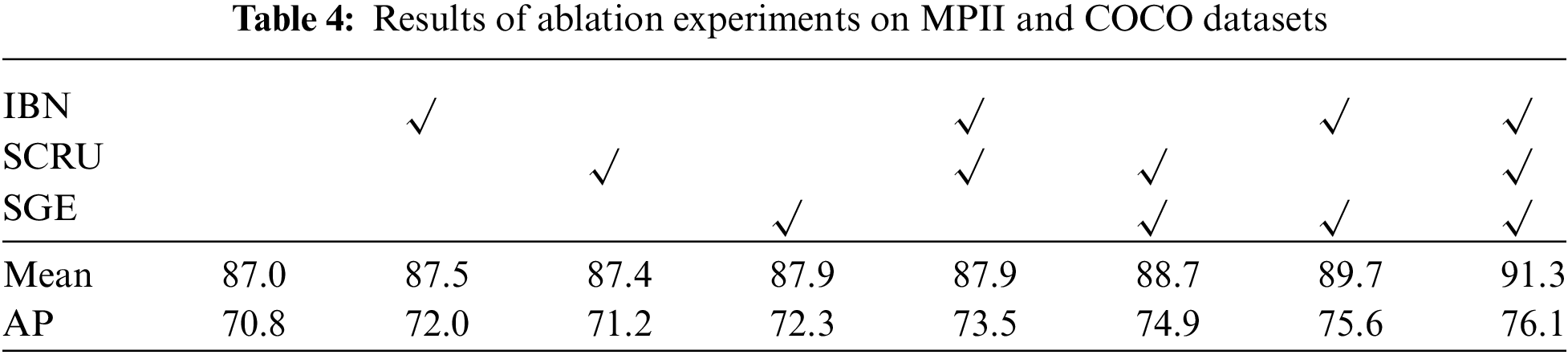
In this section, we consider taking a deeper look at the different modules in DAUNet from the following three perspectives to understand their performance impact on the overall network. The MPII and COCO datasets were compared, and the evaluation criteria were the mean and AP.
The three submodules in DAUNet are crucial for improving the performance of the network, and the accuracy is enhanced to some degree. In the ablation experiment, DAUNet achieved the greatest improvement in performance after the fusion of all the modules. In the experiments using a single module, it is found that each additional module can partly improve the performance of the model. Table 4 shows the improved IBN module achieves 0.5% accuracy on the MPII dataset and a 1.2% improvement in the AP on COCO. A decrease in the redundancy of features at the back of the network resulted in a 0.4% accuracy improvement on the MPII dataset and a 0.4% AP improvement on the COCO dataset. The addition of a lightweight attention mechanism alone resulted in the greatest improvement, with a 0.9% increase in accuracy on the MPII dataset and a 1.5% increase in AP on the COCO dataset.
In terms of computational efficiency, achieving better prediction results with fewer floating-point operations is a significant advantage of our network. As seen in Table 5, the network’s computational load is significantly reduced with the inclusion of the IBN module. This is because the improved IBN module uses partial convolution and strip pooling, which effectively matches or even exceeds the performance of traditional convolution and average pooling while reducing computational costs. As indicated in Fig. 12 incorporating the improved IBN module allows the network to generate heatmap center points for the left-hand joints, indicating that reducing feature loss through partial convolution and strip pooling enhances prediction performance. Adding the IBN and SCRU modules further improves the clarity of left-hand detection and increases accuracy, demonstrating that spatial and channel reconstruction units reduce redundancy and improve model precision. Finally, the addition of the SGE attention module enables each feature set to independently enhance its learned semantic representation, leading to more focused key point detection and higher accuracy for small joints in low-resolution images. These modules help our model accurately locate the precise positions of every detail key point in human posture.


Figure 12: Comparison of ablation experiment heat maps in the COCO dataset, where None means that no module is added, and the others are heatmap prediction renderings of key points of a module added in turn
Based on the above ablation experiments, we can find that both the IBN module and SCRU module can effectively improve the key point detection capability, laying the foundation for the SGE module to play a role. After adding the SGE module, the accuracy of low-resolution detail key points is further improved, and the detection precision has reached a satisfactory level.
4.5 Generalization and Detection in Real-World Scenarios
Inspired by Wang’s work [43], we utilized a subset of the NTU-60 pose dataset to evaluate the generalization capability of our model. Specifically, we extracted 5000 video sequence frames from various categories within the x-sub validation data, using the skeletal points as ground truth. Our model achieved an accuracy of 90.9% on the x-sub validation set, demonstrating robust generalization performance.
We used the Microsoft Azure Kinect DK RGB-D camera for the deployment experiment of the model to obtain an image of the full field coverage of the test target human body. We use the trained prediction model in a separate thread that communicates via a camera and computer; it transmits images and makes predictions. The results of the experiment are illustrated in Fig. 13, which reveals good and accurate predictions for clear pose images, motion-blurred pose images, and images with partial pose occlusions. Our key point detection model can be easily applied to other hardware platforms and other practical scenarios and has good robustness and generalizability.

Figure 13: Prediction results of the model in a real scenario
This paper proposes a U-shaped key point detection network based on an improved ResNet subsampling structure and spatial grouping mechanism, designs and implements residual blocks for image subsampling processing and proposes a node detection model that removes spatial redundancy and channel redundancy after deconvolution and adds a lightweight spatial grouping attention mechanism. Experiments on two classical datasets show that the model can effectively predict the correct key point image from a large number of images containing people, and the accuracy rate is significantly improved, which improves the key point detection performance in human poses. Although DAUNet performs well in some scenarios, we found that improved sample detection under relaxed conditions leads to more false positives. This trade-off may be due to complex backgrounds, pose variations, or inconsistent bounding box sizes. Key point detection under long-term occlusions also needs improvement. Future work could enhance training data diversity with varied poses and backgrounds, increase model complexity, and explore methods like multi-view images or temporal information to better infer key points of occluded body parts.
Acknowledgement: The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.
Funding Statement: This research was supported by the Natural Science Foundation of Hubei Province of China under grant number 2022CFB536, the National Natural Science Foundation of China under grant number 62367006, and the 15th Graduate Education Innovation Fund of Wuhan Institute of Technology under grant number CX2023579.
Author Contributions: Conceptualization, Xi Li and Yuxin Li; methodology, Yuxin Li; software, Zhenhua Xiao; validation, Xi Li, Yuxin Li and Zhenghua Huang; formal analysis, Yuxin Li; investigation, Lianying Zou; resources, Xi Li; data curation, Xi Li; writing—original draft preparation, Yuxin Li; writing—review and editing, Yuxin Li and Zhenghua Huang; visualization, Yuxin Li; project administration, Xi Li. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data presented in this study are available on request from the corresponding author. Data are not publicly available due to privacy considerations.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. Bulat and G. Tzimiropoulos, “Human pose estimation via convolutional part heatmap regression,” presented at the 14th Eur. Conf. Comput. Vis. (ECCVAmsterdam, The Netherlands, Oct. 11–14, 2016. [Google Scholar]
2. J. J. Tompson, A. Jain, Y. LeCun, and C. Bregler, “Joint training of a convolutional network and a graphical model for human pose estimation,” presented at the 27th Adv. Neural Inf. Process. Syst. (NeurIPSMontreal, QC, Canada, Dec. 8–13, 2014. [Google Scholar]
3. O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional networks for biomedical image segmentation,” presented at the 18th Int. Conf. Med. Image Comput. Comput.-Assist. Interv. (MICCAIMunich, Germany, Oct. 5–9, 2015. [Google Scholar]
4. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” presented at the IEEE Conf. Comput. Vis. Pattern Recognit. (CVPRLas Vegas, NV, USA, Jun. 26–30, 2016, pp. 770–778. [Google Scholar]
5. M. H. Ha, “Top-heavy CapsNets based on spatiotemporal non-local for action recognition,” J. Comput. Theories Appl., vol. 2, no. 1, pp. 39–50, 2024. doi: 10.62411/jcta.10551. [Google Scholar] [CrossRef]
6. A. Newell, K. Yang, and J. Deng, “Stacked hourglass networks for human pose estimation,” presented at the 14th Eur. Conf. Comput. Vis. (ECCVAmsterdam, The Netherlands, Oct. 11–14, 2016, pp. 483–499. [Google Scholar]
7. Y. Chen, Z. Wang, Y. Peng, Z. Zhang, G. Yu and J. Sun, “Cascaded pyramid network for multi-person pose estimation,” presented at the IEEE Conf. Comput. Vis. Pattern Recognit. (CVPRSalt Lake City, UT, USA, Jun. 18–22, 2018, pp. 7103–7112. [Google Scholar]
8. R. Wang, C. Huang, and X. Wang, “Global relation reasoning graph convolutional networks for human pose estimation,” IEEE Access, vol. 8, pp. 38472–38480, 2020. doi: 10.1109/ACCESS.2020.2973039. [Google Scholar] [CrossRef]
9. G. Ghiasi, T. -Y. Lin, and Q. V. Le, “NAS-FPN: Learning scalable feature pyramid architecture for object detection,” in IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Long Beach, CA, USA, Jun. 16–20, 2019, pp. 7036–7045. [Google Scholar]
10. K. Sun, B. Xiao, D. Liu, and J. Wang, “Deep high-resolution representation learning for human pose estimation,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRLong Beach, CA, USA, Jun. 16–20, 2019, pp. 5686–5696. [Google Scholar]
11. W. Li et al., “Rethinking on multi-stage networks for human pose estimation,” 2019, arXiv:1901.00148. [Google Scholar]
12. Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proc. IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. doi: 10.1109/5.726791. [Google Scholar] [CrossRef]
13. D. C. Luvizon, H. Tabia, and D. Picard, “Human pose regression by combining indirect part detection and contextual information,” Comput. Graph., vol. 85, no. 1, pp. 15–22, 2019. doi: 10.1016/j.cag.2019.09.002. [Google Scholar] [CrossRef]
14. K. He, G. Gkioxari, P. Dollár, and R. Girshick, “Mask R-CNN,” presented at the IEEE Int. Conf. Comput. Vis. (ICCVVenice, Italy, Oct. 22–29, 2017, pp. 2961–2969. [Google Scholar]
15. S. Ren, K. He, R. Girshick, and J. Sun, “Faster R-CNN: Towards real-time object detection with region proposal networks,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 6, pp. 1137–1149, 2016. doi: 10.1109/TPAMI.2016.2577031. [Google Scholar] [PubMed] [CrossRef]
16. C. Dong and G. Du, “An enhanced real-time human pose estimation method based on modified YOLOv8 framework,” Sci. Rep., vol. 14, 2024, Art. no. 8012. doi: 10.1038/s41598-024-58146-z. [Google Scholar] [PubMed] [CrossRef]
17. S. Zhou et al., “Human pose estimation based on frequency domain and attention module,” Neurocomputing, vol. 604, no. 10, 2024, Art. no. 128318. doi: 10.1016/j.neucom.2024.128318. [Google Scholar] [CrossRef]
18. Q. X. Dong et al., “YH-Pose: Human pose estimation in complex coal mine scenarios,” Eng. Appl. Artif. Intell., vol. 127, no. 6, 2024, Art. no. 107338. doi: 10.1016/j.engappai.2023.107338. [Google Scholar] [CrossRef]
19. Z. Cao, T. Simon, S. -E. Wei, and Y. Sheikh, “Realtime multi-person 2D pose estimation using part affinity fields,” presented at the IEEE Conf. Comput. Vis. Pattern Recognit. (CVPRHonolulu, HI, USA, Jul. 21–26, 2017, pp. 7291–7299. [Google Scholar]
20. G. Papandreou, T. Zhu, L. -C. Chen, S. Gidaris, J. Tompson and K. Murphy, “Person pose estimation and instance segmentation with a bottom-up, part-based, geometric embedding model,” presented at the Eur. Conf. Comput. Vis. (ECCVMunich, Germany, Sep. 8–14, 2018, pp. 269–286. [Google Scholar]
21. S. Kreiss, L. Bertoni, and A. Alahi, “PifPaf: Composite fields for human pose estimation,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRLong Beach, CA, USA, Jun. 16–20, 2019, pp. 11977–11986. [Google Scholar]
22. A. Krizhevsky, I. Sutskever, and G. E. Hinton, “ImageNet classification with deep convolutional neural networks,” Commun. ACM, vol. 60, no. 6, pp. 84–90, 2017. doi: 10.1145/3065386. [Google Scholar] [CrossRef]
23. J. Hu, L. Shen, and G. Sun, “Squeeze-and-excitation networks,” presented at the IEEE Conf. Comput. Vis. Pattern Recognit. (CVPRSalt Lake City, UT, USA, Jun. 18–22, 2018, pp. 7132–7141. [Google Scholar]
24. Y. Cao, J. Xu, S. Lin, F. Wei, and H. Hu, “Non-local networks meet squeeze-excitation networks and beyond,” presented at the IEEE/CVF Int. Conf. Comput. Vis. Workshops (ICCV WorkshopsSeoul, Republic of Korea, Oct. 27–28, 2019, pp. 12–13. [Google Scholar]
25. X. Li, W. Wang, X. Hu, and J. Yang, “Selective kernel networks,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRLong Beach, CA, USA, Jun. 16–20, 2019, pp. 510–519. [Google Scholar]
26. J. Park, S. Woo, J. -Y. Lee, and I. S. Kweon, “BAM: Bottleneck attention module,” 2018, arXiv:1807.065144. [Google Scholar]
27. S. Woo, J. Park, J. -Y. Lee, and I. S. Kweon, “CBAM: Convolutional block attention module,” presented at the Eur. Conf. Comput. Vis. (ECCVMunich, Germany, Sep. 8–14, 2018, pp. 3–19. [Google Scholar]
28. B. Xiao, H. Wu, and Y. Wei, “Simple baselines for human pose estimation and tracking,” presented at the Eur. Conf. Comput. Vis. (ECCVMunich, Germany, Sep. 8–14, 2018, pp. 466–481. [Google Scholar]
29. C. Szegedy et al., “Going deeper with convolutions,” presented at the IEEE Conf. Comput. Vis. Pattern Recognit. (CVPRBoston, MA, USA, Jun. 7–12, 2015, pp. 1–9. [Google Scholar]
30. G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” presented at the IEEE Conf. Comput. Vis. Pattern Recognit. (CVPRHonolulu, HI, USA, Jul. 21–26, 2017, pp. 4700–4708. [Google Scholar]
31. J. Chen et al., “Run, don’t walk: Chasing higher FLOPS for faster neural networks,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRVancouver, BC, Canada, Jun. 18–24, 2023, pp. 12021–12031. [Google Scholar]
32. Q. Hou, L. Zhang, M. -M. Cheng, and J. Feng, “Strip pooling: Rethinking spatial pooling for scene parsing,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRSeattle, WA, USA, Jun. 13–19, 2020, pp. 4003–4012. [Google Scholar]
33. Y. Wu and K. He, “Group normalization,” presented at the Eur. Conf. Comput. Vis. (ECCVMunich, Germany, Sep. 8–14, 2018, pp. 3–19. [Google Scholar]
34. O. Russakovsky et al., “ImageNet large scale visual recognition challenge,” Int. J. Comput. Vis., vol. 115, no. 3, pp. 211–252, 2015. doi: 10.1007/s11263-015-0816-y. [Google Scholar] [CrossRef]
35. M. Andriluka, L. Pishchulin, P. Gehler, and B. Schiele, “2D human pose estimation: New benchmark and state of the art analysis,” presented at the IEEE Conf. Comput. Vis. Pattern Recognit. (CVPRColumbus, OH, USA, Jun. 23–28, 2014, pp. 3686–3693. [Google Scholar]
36. T. -Y. Lin et al., “Common objects in context,” presented at the Eur. Conf. Comput. Vis. (ECCVZurich, Switzerland, Sep. 6–12, 2014, pp. 740–755. [Google Scholar]
37. Y. Li et al., “TokenPose: Learning keypoint tokens for human pose estimation,” presented at the IEEE/CVF Int. Conf. Comput. Vis. (ICCVMontreal, QC, Canada, Oct. 11–17, 2021, pp. 11313–11322. [Google Scholar]
38. G. Ning, Z. Zhang, and Z. He, “Knowledge-guided deep fractal neural networks for human pose estimation,” IEEE Trans. Multimed., vol. 20, no. 5, pp. 1246–1259, 2017. doi: 10.1109/TMM.2017.2762010. [Google Scholar] [CrossRef]
39. H. -S. Fang et al, “AlphaPose: Whole-body regional multi-person pose estimation and tracking in real-time,” presented at the IEEE/CVF Conf. Comp. Vision Patt. Recogn. (CVPRNew Orleans, LA, USA, Jun. 19–24, 2022. [Google Scholar]
40. N. Xue, T. Wu, G. -S. Xia, and L. Zhang, “Learning local-global contextual adaptation for multi-person pose estimation,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRNew Orleans, LA, USA, Jun. 19–24, 2022, pp. 13065–13074. [Google Scholar]
41. Z. Geng, K. Sun, B. Xiao, Z. Zhang, and J. Wang, “Bottom-up human pose estimation via disentangled keypoint regression,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRNashville, TN, USA, Jun. 19–25, 2021, pp. 14676–14686. [Google Scholar]
42. Y. Dang, J. Yin, L. Liu, Y. Sun, Y. Hu and P. Ding, “DHRNet: A dual-path hierarchical relation network for multi-person pose estimation,” 2024, arXiv:2404.14025. [Google Scholar]
43. Y. Wang et al., “BCCLR: A skeleton-based action recognition with graph convolutional network combining behavior dependence and context clues,” Comput. Mater. Contin., vol. 78, no. 3, pp. 4489–4507, 2024. doi: 10.32604/cmc.2024.048813. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF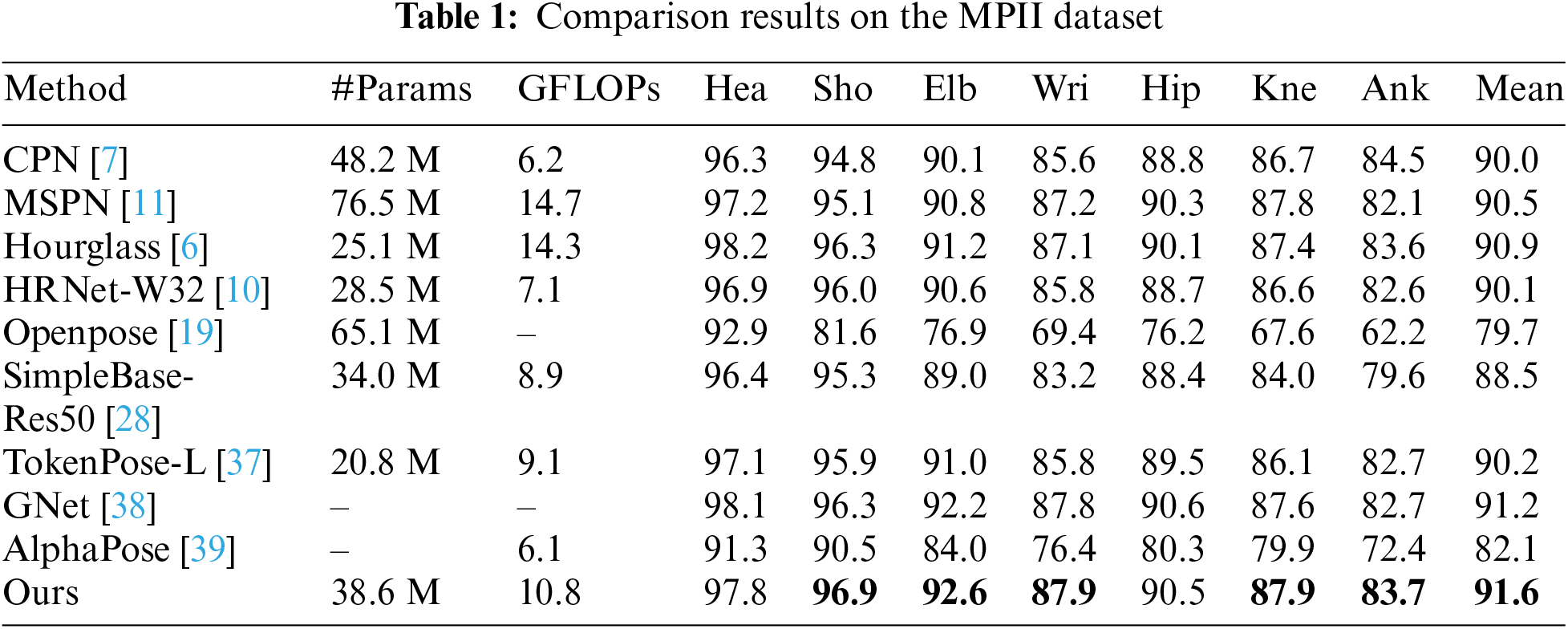
 Downloads
Downloads
 Citation Tools
Citation Tools