 Open Access
Open Access
ARTICLE
HGNN-ETC: Higher-Order Graph Neural Network Based on Chronological Relationships for Encrypted Traffic Classification
Key Laboratory of Aerospace Information Security and Trusted Computing, Ministry of Education, School of Cyber Science and Engineering, Wuhan University, Wuhan, 430072, China
* Corresponding Author: Xiya Guo. Email:
Computers, Materials & Continua 2024, 81(2), 2643-2664. https://doi.org/10.32604/cmc.2024.056165
Received 15 July 2024; Accepted 27 September 2024; Issue published 18 November 2024
Abstract
Encrypted traffic plays a crucial role in safeguarding network security and user privacy. However, encrypting malicious traffic can lead to numerous security issues, making the effective classification of encrypted traffic essential. Existing methods for detecting encrypted traffic face two significant challenges. First, relying solely on the original byte information for classification fails to leverage the rich temporal relationships within network traffic. Second, machine learning and convolutional neural network methods lack sufficient network expression capabilities, hindering the full exploration of traffic’s potential characteristics. To address these limitations, this study introduces a traffic classification method that utilizes time relationships and a higher-order graph neural network, termed HGNN-ETC. This approach fully exploits the original byte information and chronological relationships of traffic packets, transforming traffic data into a graph structure to provide the model with more comprehensive context information. HGNN-ETC employs an innovative k-dimensional graph neural network to effectively capture the multi-scale structural features of traffic graphs, enabling more accurate classification. We select the ISCXVPN and the USTC-TK2016 dataset for our experiments. The results show that compared with other state-of-the-art methods, our method can obtain a better classification effect on different datasets, and the accuracy rate is about 97.00%. In addition, by analyzing the impact of varying input specifications on classification performance, we determine the optimal network data truncation strategy and confirm the model’s excellent generalization ability on different datasets.Keywords
At present, traffic encryption has been the most important protection technology for network transmission information. In 2019, it was reported that the global hypertext transfer protocol secure (HTTPS) page load increased from 39% to more than 80% in just four years [1,2]. However, while effectively protecting data confidentiality and privacy through encryption technology, malicious behavior traffic sent by attackers will also be hidden, resulting in security problems such as malware activities [3], data leakage [4], and vulnerability intrusion [5]. There are also many malicious software that use encryption technologies such as transport layer security (TLS) to avoid the firewall and intrusion detection system intercept, which brings new challenges to traditional traffic classification methods [6].
Before traffic encryption became commonplace, port-based approaches and deep packet [7] inspection techniques were extensively recognized and employed. These methods analyze source and destination ports, source and destination addresses, and protocol types, classifying the types of applications based on their port numbers. In addition, methods based on statistical characteristics and behavioral characteristics were also commonly used in traditional traffic classification [8–11]. However, these methods are ineffective in the face of attacks from cryptographic payloads, and a series of issues such as communication delay, resource consumption, and privacy disclosure have emerged. In recent years, many traffic classification studies have used machine learning (ML) methods and achieved good classification results [12]. However, machine learning methods require manual statistical extraction of features from raw data before use, and then input of already defined features [13]. Therefore, a lot of effort has been spent on the characteristic statistics of flow-level network traffic rather than packet-level network traffic [14–17].
Thanks to the continuous development of neural networks, many traffic classification methods using ML have also achieved certain results [18–20]. However, these methods cannot handle the traffic data converted to non-Euclidean space well, leaving much valuable information unusable for classification tasks. To solve the above problems, graph neural networks (GNNs) are used in traffic classification tasks. Some methods use GNNs to classify traffic, and consider the adjacency relationship between packets and packet raw bytes in the network traffic but ignore the chronological relationship between packets [21]. There are also some GNN-based network traffic classification methods [22,23] which use GNNs with lower dimensions. These methods do not make full use of node information and only make use of partial information. Higher-order information in the graph structure is ignored in these methods.
To make full use of all kinds of valid information in encrypted traffic and enhance the generalization ability of the classification model, we propose HGNN-ETC. Our HGNN-ETC first considers the raw bytes of packets and the chronological relationship between packets and maps the network traffic into a graph that preserves both the raw bytes and the chronological relationship. Specifically, we take the first ten packets of each session as nodes, the original bytes of each packet as attributes, and the chronological relationship between packets as edges. Next, we use the higher-order generalization of GNN to fully utilize the feature information of the graph and effectively classify the traffic according to the type of service and application. Higher-order GNN uses multi-level graph convolution operations and can consider higher-order graph structures of multiple scales, to obtain better classification results. The network architecture design details are presented in Section 3. In the experimental part, we utilize the dataset USTC-TK2016 and ISCXVPN2016, which contains both encrypted and unencrypted traffic, to verify that our model can achieve higher classification accuracy and stronger generalization ability. We also conducted experiments on different input specifications to determine the optimal input specification. The results of the experiment showed that HGNN-ETC performs better than other methods in different datasets, with the best classification accuracy reaching 97%.
The following three points summarize the main contributions of our work:
1. We propose a novel encryption traffic classification method called HGNN-ETC based on higher-order GNN. The higher-order information of the graph is retained by higher-order GNN, which effectively improves the accuracy of classification and the generalization ability of the model.
2. We improve the feature extraction features of encrypted traffic, make full use of the packet raw bytes and chronological relationship features, and provide more potential feature information for encrypted traffic classification to improve the accuracy of the classification results of the model.
3. Finally, we conducted experiments on ISCXVPN2016 and USTC-TK2016 datasets to demonstrate that HGNN-ETC has better classification accuracy and generalization ability. The effectiveness of each module was verified by ablation experiments with different inputs.
The remainder of this paper is organized as follows. In Section 2, we summarize the relevant work in the field of traffic classification. In Section 3, we describe the data processing method, the graph construction method, and the classifier we designed based on a higher-order GNN. In Section 4, we evaluate our proposed model on two datasets and compare our results with the state-of-the-art methods. In Section 5, we summarize our work and propose directions for our future work.
More and more researchers are using deep learning (DL) methods for various studies, including network traffic classification, as various neural networks have matured [24]. DL can automatically extract the main features of the input data, omitting the step of manual selection of features, which also makes the DL method adapt to the scene with new categories. With the advantages of automatic feature extraction and end-to-end classification, some researchers have attempted to apply DL to encrypted traffic classification. In Table 1, we summarize specific information about DL-based classification methods, including methods, years, and datasets.
Convolutional neural networks (CNN) and long short-term memory (LSTM) are common DL methods, and many studies have used these models for data feature extraction and propagation. In the work of Yao et al. [25], the authors combined LSTM with a self-attention mechanism to focus on important flows in the flow sequence. The model based on CNN proposed in the work of Wang et al. [26] used a one-dimensional vector to represent each stream or session, which achieves better classification results than the C4.5 method. As an improvement, in the work of Wang et al. [27], the author used a two-dimensional CNN to classify traffic named 2DCNN. The FS-Net designed by Liu et al. [28] used a multi-layer encoder-decoder structure to dig deep into the latent sequence features of the stream and introduces a reconstruction mechanism to improve the effectiveness of the features. Wang et al. [29] proposed a new model that combines a variational autoencoder (VAE), LSTM, and deep residual network (DRN) to enhance the processing power of the original unbalanced dataset and improve the identification accuracy of encrypted traffic. Huang et al. [30] used recurrent neural network’s (RNN) variant model to extract temporal features and combined it with the TextCNN model to extract local multi-receptive field spatial features, to improve the accuracy of classification.
From the above-related work, we can see that many researchers are keen to use the CNN model because the CNN is very efficient in solving problems in Euclidean images. Therefore, many studies have used the Euclidean form of network traffic data to train models [26]. However, the basic data structures adopted in these studies are still limited to grid or sequence data. Therefore, some researchers have introduced graphical models to deal with unstructured data for traffic classification.
2.2 Graph Neural Networks Methods
Some researchers try to associate the network traffic with non-Euclidean data, and convert the traffic into a directed graph representation, to retain the information contained in the traffic more completely and use the information for classification. However, traditional deep learning networks (such as CNN) make it difficult to process such non-Euclidean data, so many studies use GNN to process such information.
As shown in Table 1, some recent works have studied how to use GNN for flow-based traffic classification and achieved some results. Pang et al. [21] proposed a chain graph model of traffic named CGNN to maintain a chain combination sequence for application identification. The application identification is carried out by capturing the causality of raw network traffic data. Shen et al. [22] proposed a graph structure called Traffic Interaction Graph (TIG) to represent encrypted decentralized application (DApp) flows, transformed DApp fingerprinting into a graph classification problem, and designed a powerful GNN-based classifier. Zheng et al. [31] proposed an encrypted malicious traffic detection method based on a graph convolutional network (GCN) called GCN-ETA, which considers the statistical features (internal information) of network flows and the structural information (external connections) between them. Huoh et al. [23] collected the raw bytes, metadata, and packet relationships of traffic, and then used GNNs for classification. Diao et al. [32] proposed a novel DL framework called EC-GCN for classifying encrypted traffic based on multi-scale graph convolutional neural networks. It learns representative spatiotemporal traffic features hidden in the traffic time series and then classifies them in a unified framework. The TC-GNN proposed by Hu et al. [33] used the Graph Convolutional Network (GCN) to learn the potential application representation of the packets by converting network packets into undirected graphs to achieve high-precision traffic classification. Han et al. [34] proposed DE-GNN, a model that handles packet headers and payloads separately and employs a hierarchical structure to comprehensively study fine-grained cryptographic traffic classification.
Although the above methods based on GNNs have made some accomplishments, these methods also have some shortcomings, such as single feature recognition and insufficient generalization ability. For example, Pang et al. [21] only considered the adjacency relationship between packets and packet raw bytes in the network traffic but did not consider the time relationship between packets. The computational complexity of some methods [32] is higher when the amount of data is large. There are also GNN-based methods such as TC-GNN [33] and DE-GNN [34] that are built with lower-order GNN. These methods use the locality of nodes to complete the classification task and do not make full use of the higher-order information embedded in the structure required for graph classification. As a result, the generalization ability of the method is mediocre and may not be effective in generalizing to other invisible traffic types.
To overcome the limitations of relevant methods, we propose an innovative encryption traffic classification method based on higher-order graph neural networks. By constructing a novel traffic graph model, we transform network traffic into graph structure, and integrate the chronological relationship between data packets based on the original byte information, to provide rich context information for the model. In addition, we have significantly improved the traditional low-order GNN and developed a higher-order GNN model, which can deeply mine and utilize higher-order information of graphs to improve classification accuracy and model generalization ability.
In this section, we will detail the design process of the encryption stream classification method. We first introduce the process of processing the data and then constructing it into a graph and then introduce the GNN model we used for classification. The entire flow of HGNN-ETC is shown in Fig. 1.
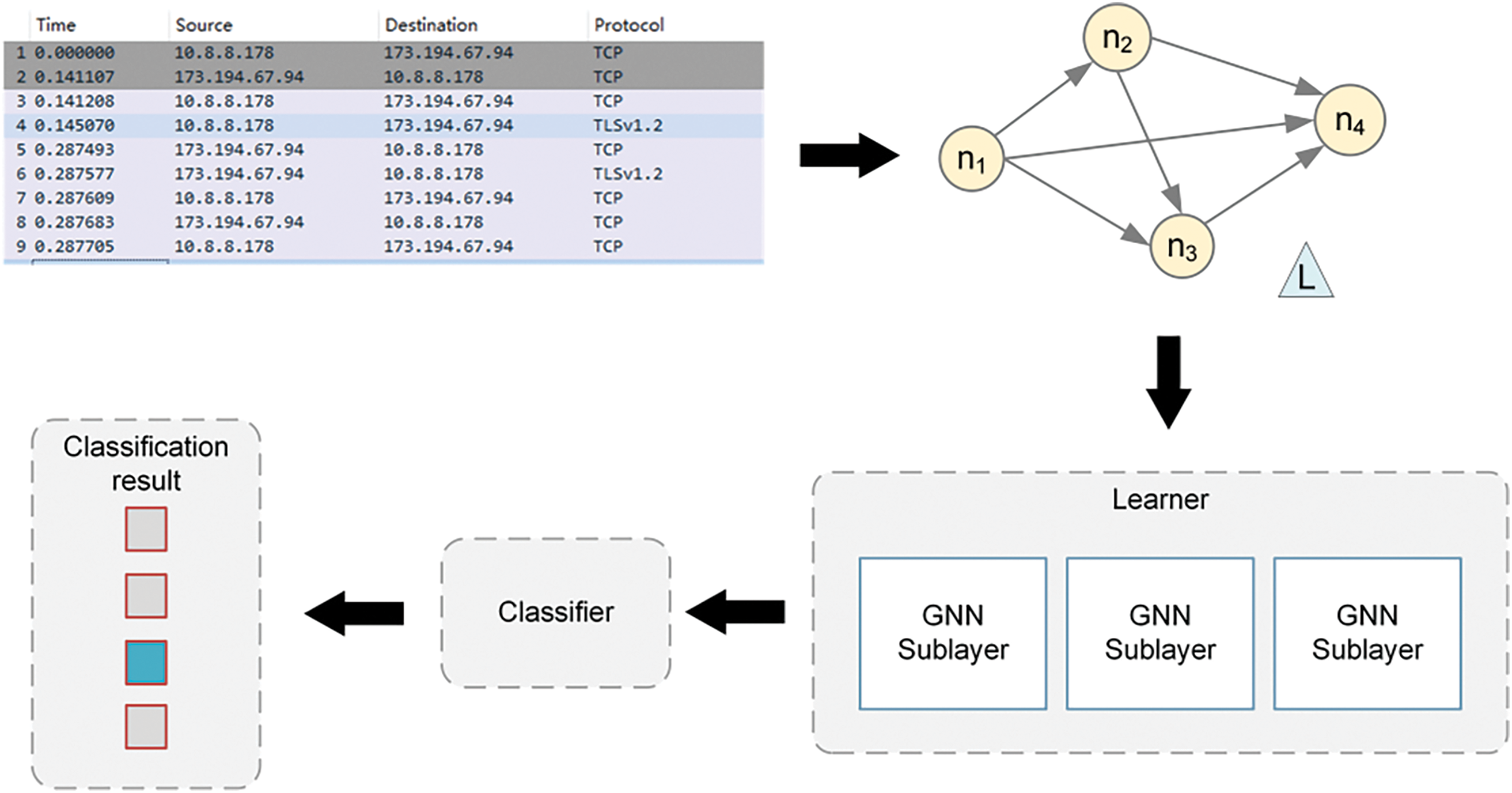
Figure 1: Overall framework of method
It has been shown that using bi-directional flows, such as sessions, performs better than unidirectional flows when performing classification tasks. Therefore, bi-directional flows are also used in our work. Many mainstream network traffic datasets are captured from servers, so the pcap file contains a large number of raw packets. Before using this dataset, we preprocess it in the following three steps:
1. We split the original pcap file into sessions using the traffic processing tool SplitCap. If the crawled traffic files have the suffix pcapng, they are converted to pcap files before being split.
2. To ensure that the information obtained is valid and remove the disturbing information, we remove the relevant data in the traffic. Network traffic data is collected at the second data link layer in the open system interconnection (OSI) model, which contains the physical information of the transmission link. We remove Ethernet headers that contain media access control (MAC) addresses because Ethernet headers are only used for local network Layer 2 (L2) addressing and do not play a role in classification tasks. Then the source internet protocol address (IP) and the destination address IP of the network layer are anonymized to improve the effectiveness of our scheme, such as Wang et al. [27].
3. Finally, the pcap files are converted to their original byte format, and the complete raw data are used as the network input. In traffic files, packets are the units that make up each bi-directional data stream, and a packet is composed of a byte stream, which has a maximum size determined by the maximum transmission unit (MTU), typically 1500 bytes. The quantitative results of previous work [25,26,35] show that entering the full raw data into the network will result in more accurate classification results. To use more valid information in the classification task, we convert all the information in the packet to raw bytes, and the ones that are less than the MTU will be filled. The value of each byte is then normalized so that it falls within the interval [0, 1].
After packet preprocessing, we transform each packet into a graph consisting of nodes and edges. In the network, a session refers to all packets consisting of bidirectional flows. When we build the graph, we model the packets in the session as nodes in the graph, and the chronological relationships between the packets are used to build the directed edges between the nodes. In the approach [25], the network input of the model is to intercept the first ten packets in the bi-directional stream. Peng et al. [36] showed that the first five to seven packages are most suitable for classification. We utilize the first 1500 bytes of the first ten packets in the stream. If the number of packets in a stream is greater than ten, it is intercepted, and less than ten, it is filled with zero. In this way, each graph represents a session, where the ten nodes are the first ten packets in the session, and each node has a feature vector of 1500 length that represents the original data of 1500 bytes in the packet. Nodes are connected by chronological relationships. Finally, each graph has a label that is used to learn the classification. The flow of the whole graph construction is shown in Fig. 2.
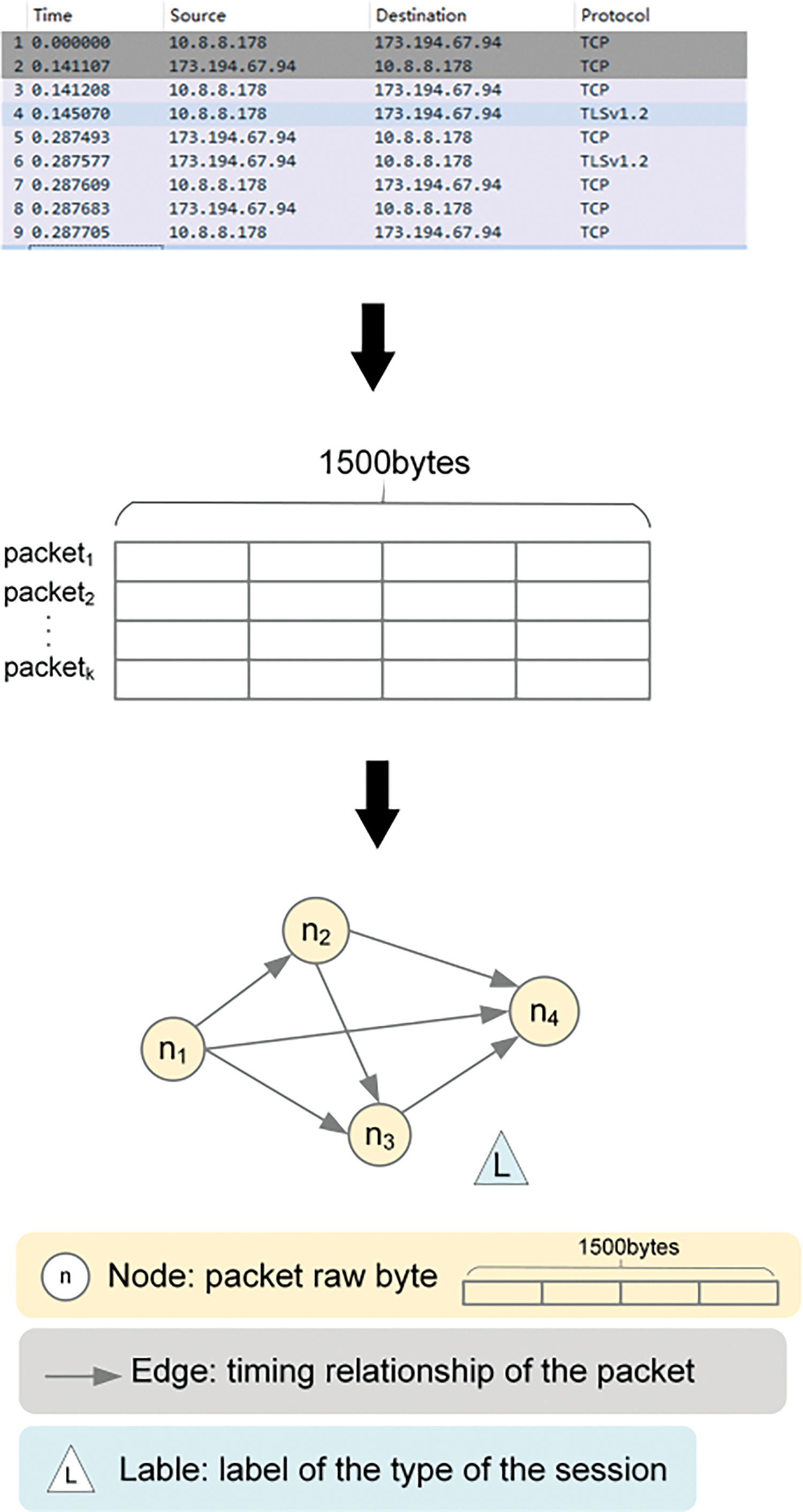
Figure 2: The process of mapping traffic into a graph
1. Nodes: We define each packet as a node in the graph, represented by ni, where i represents the serial number of the node, for example, the 10th node is defined as n10. Each node has a row vector of 1500 (MTU size) length as its attribute, and the data in the row vector is the packet raw bytes normalized to [0, 1].
2. Edges: After obtaining nodes, the set of directed edges between vertices is extracted based on the chronological relationship between packets. In our approach, the edges are built based on the timestamp order of the nodes. Specifically, for each node, we compare its timestamp against the timestamps of other nodes, ensuring that nodes with earlier timestamps always point to nodes with later timestamps. This construction method can not only reflect the time series of events but also effectively capture the time-dependence relationship between nodes, to improve the model’s processing ability of time information. Fig. 3 illustrates how directed edges are used to connect nodes when the number of packets is 3 and 4. In the subsequent calculation of the network model, the pointing relationship between nodes is used to aggregate and update information, so that the network can obtain a better classification effect.
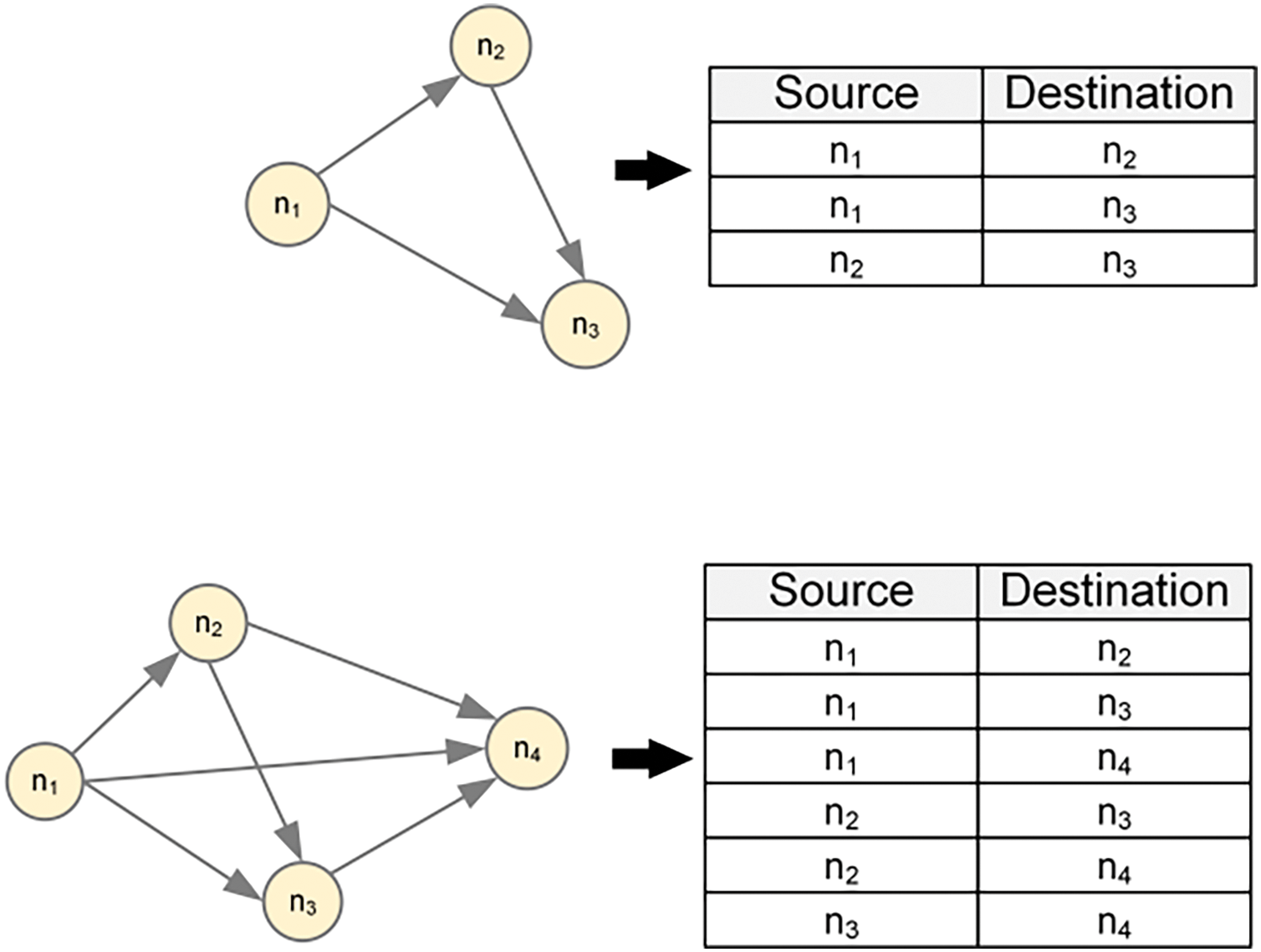
Figure 3: Instances of the construction of edges between nodes
3. Labels: Finally, each graph has a label that corresponds to the category of the application or service type to which it belongs. After the session is built as a graph, we assign labels to the session based on the type it belongs to, so that subsequent learners can learn from it.
3.3.1 Higher-Order Graph Neural Networks
k-GNNs [37] is a higher-order generalization of GNNs based on the Weisfeiler-Leman graph isomorphism heuristic (1-WL), which can obtain higher-order structure information in the graph. We use V(G) and E(G) to represent the node set and edge set of the graph G. For a given k, let [V(G)]k be a subset of V(G) and let v = {v1, ..., vk} denotes a set of k nodes, And v is defined as a node in the graph whose neighborhood can be defined as follows:
In layman’s terms, the neighbors of v are k-sets that have only k −1 nodes in common with v. The neighborhood of v can be divided into local neighborhood NL(v) and global neighborhood NG(v). All elements of t ∈ N(v) form the local neighborhood NL(v). The global neighborhood NG(v) then is defined as N(v)\NL(v). Based on the above definition, the propagation formula of k-GNN is defined as follows:
where σ is the nonlinear activation function, W is the weight matrix and f (t−1)k(v) is The eigenvector of the set of nodes s at layer t −1.
For the second part of this propagation formula, we can separate and aggregate the local domain and the global domain. In addition, considering the extensibility and overfitting of GNN, local k-GNNs were produced, where the global neighborhood of s was omitted. Therefore, the feature propagation formula of layer t > 0 becomes:
In Section 2, we introduce the existing works that use DL and GNNs for classification, but these methods have certain limitations. In this section, we introduce the knowledge and principles of higher-order GNNs, which can better model higher-order relationships between data and achieve more powerful feature extraction and classification capabilities.
Our architecture is shown in Fig. 4 where our model is built using an input-learner-classifier-output architecture. The construction of the learner refers to the k-GNN described by Morris et al. [37]. We choose k as 3, which means that the learner consists of three sub-layers, each of which has a dimension of 128. The input graph goes through graph convolution, normalization, and pooling operations. A vector representation of the graph is generated for each sub-layer based on the node features computed by concatenation of the global average pooling (GAP) value and the global maximum pooling (GMP) value. Concatenation is used to concatenate the results before they are fed into the classifier. The classifier consists of dense layers and dropout layers. Finally, the data is entered into the soft-max classification and a predicted label is assigned to each graph.
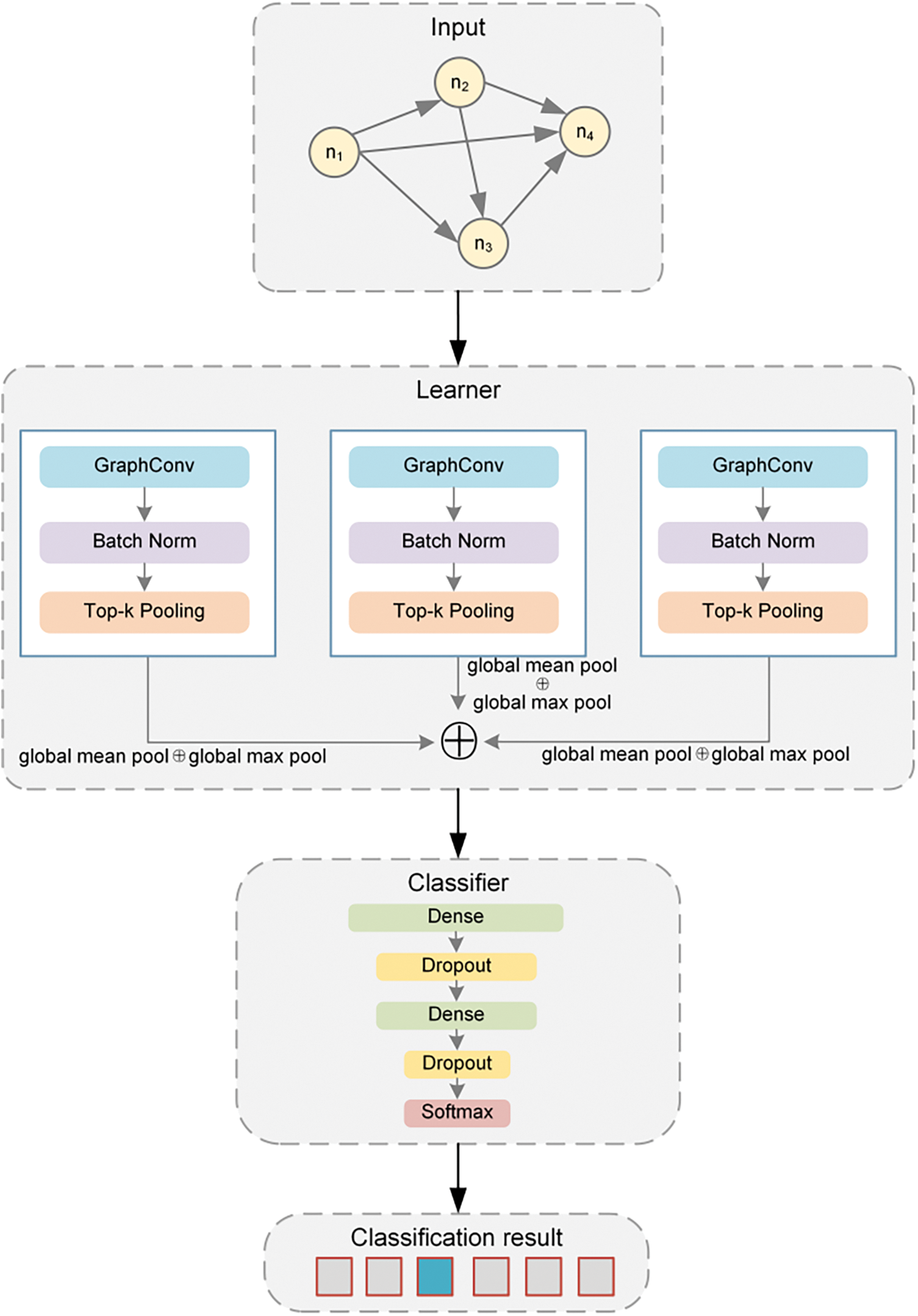
Figure 4: Network model for graph classification
In the learner, each graph convolution layer contains 128 neurons to solve the problem of information loss during the learning phase. This is followed by a Batch Normalization (BN) layer that normalizes the value of each feature, reduces the internal covariate shift, and can also reduce overfitting in convolutional neural networks. The last layer of the learner is a top-K pooling layer for dimensionality reduction. The top-K pooling layer usually preserves the topological structure information of the graph when performing node feature selection. This means that the selected node features will usually correspond to the adjacency relations of the graph, thus preserving the local structure information of the graph and helping the model to better understand the topology of the graph. The top-K pooling layer can also reduce the overall dimension of the graph, thus making our model more robust. GMP can highlight key features, while GAP pays more attention to the extraction of overall information. Therefore, we take two kinds of data from each sublayer to concatenate as output. The three sublayers produce three embeddings, which are connected in series and fed into the classifier.
The classifier consists of dense layers, dropout layers, and a classification function. Dense layers can be used to map and transform the node features of a graph to map the node feature space to a higher or lower dimensional space or to map the node feature space to another feature space. By randomly discarding neuron outputs, dropout layers can effectively enable the model to understand the graph data more deeply and represent graph data, thereby improving the accuracy of graph classification. In the classifier, we first map with a dense layer with input 256 and output 128, then use a dropout layer to deal with overfitting, then map with a dense layer with input 128 and output 64, then use a dropout layer, and finally use a soft-max classifier to predict the classification label.
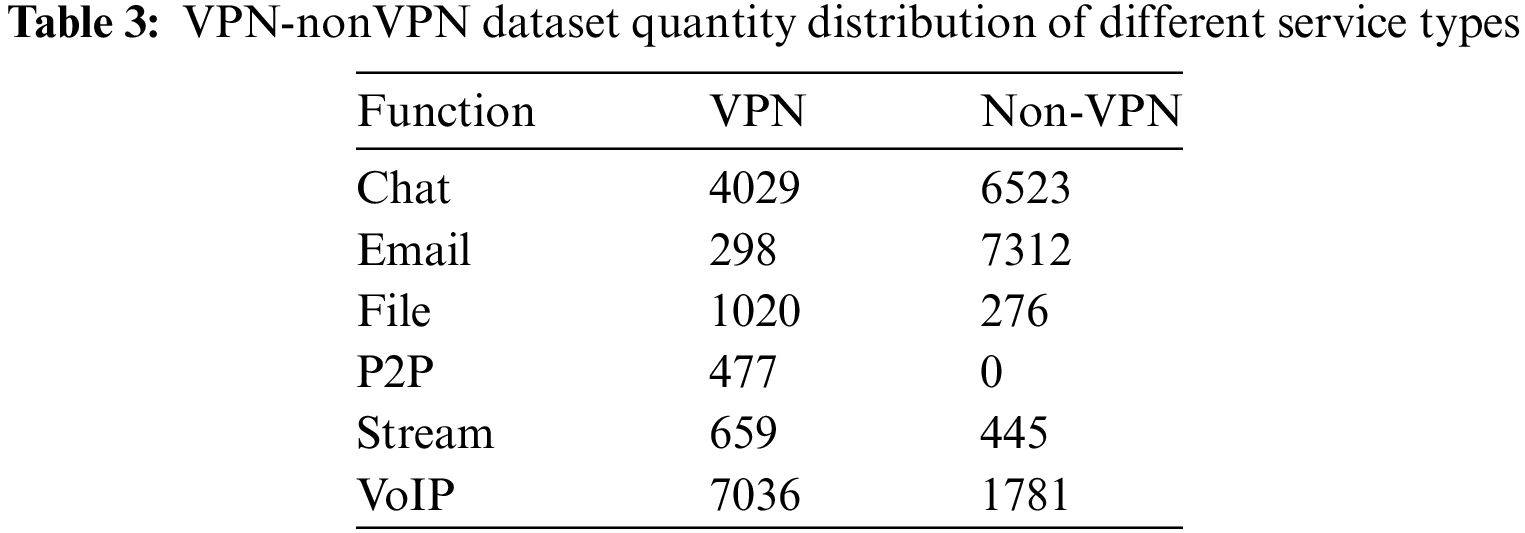
In our study, we first chose to use the ISCX VPN-nonVPN dataset [38] for our experiments. A virtual private network (VPN) is a way of encrypting communication services to bypass censorship as well as access geo-locking services. By using traffic capture tools, both regular and VPN sessions are captured in the dataset, so there are a total of 14 traffic categories, generating a total of 28 GB of data. The specific application sources for both datasets are shown in Table 2. Table 3 shows the quantity distribution of VPN-nonVPN data by service type. The second dataset is USTC-TK2016 [27], which is divided into malicious traffic and normal traffic. There are 10 types of traffic, including 8 types of applications, as shown in Table 4. After the preprocessing of the pcap file is completed, the traffic dataset is divided into the training set, the verification set, and the test set according to the ratio of 8:1:1.


4.2.1 Experimental Environment
The following specifications are used for development, training, and testing. PyTorch with a Python3.9 backend is used to generate plots, build, train, and test our model. The processor is a 12th-generation Intel (R) Core (TM) i7-12700KF with 32 GB of physical memory.
We evaluate our model using four standard classification metrics. Accuracy is often used to measure the accuracy of a model. However, since real-world datasets are often imbalanced, classification accuracy is not a complete measure of how good a model is. Therefore, we also selected precision, recall, and F1-score as the evaluation criteria of the model. In addition, we report the confusion matrix of experimental results, which helps us understand and analyze the performance of the model through intuitive visualizations. The four criteria are calculated as follows:
where TP is the number of true positive samples, FN is the number of false negative samples, FP is the number of false positive examples, and TN is the number of true negative examples.
4.2.3 Evaluation Metrics Parameter Setting
For the hyperparameter setting, we set the learning rate to 0.0003, decay rate to 0.00001, batch to 1024, epoch to 500, and use the cross-entropy loss function. We set up five-fold cross-validation to evaluate the predictive performance of the model, to reduce overfitting to some extent, and to obtain as much valid information as possible from the limited data. For the design of the loss function, we choose the cross-entropy loss function, the specific function is as follows:
where y is a matrix of true labels, yi, c representing the true labels of sample i on class c (usually 1 or 0).
4.3 Experiment Comparing Performance of Different Models
In the first part of the experiment, we compare our proposed method with the existing network traffic classification methods. In order to ensure the fairness of the experiment, we use the same method in the process of data processing. The network parameters of the comparison method in our paper are all the optimal parameters proposed by the author, and the relevant parameters of the packet or session are as consistent as possible with our methods. In addition, since data are mostly imbalanced in the real world, we do not choose to unify the size of different categories of datasets in our experiments to simulate the real-world situation. Therefore, we should not only focus on accuracy when evaluating the classification effect, because it cannot be used as a good indicator to measure the result in the case of unbalanced samples. The related works we compare are as follows:
1. 1DCNN [26] used the first 785 bytes of the packet’s raw data as a feature and then used one-dimensional CNN for encrypted traffic classification, a method called 1DCNN.
2. In AM-LSTM [25], the first 1500 bytes of the first 10 packets in a bidirectional flow are used as the network input, and the LSTM is combined with the self-attention mechanism to focus on the important flows in the flow sequence.
3. In deep packet [19], the author only selected information effective for classification as features and then used two-layer CNN, a Max-Pooling layer, and three full connection layers to build a classifier to classify encrypted network traffic by application.
4. In GNN-Flow [23], the author collected the raw information about traffic and the relationship between packets and then converted the traffic data into a graph structure. GNN is then used to classify the traffic converted to a graph.
5. 2DCNN [27] uses the same data processing method as 1DCNN and also uses the CNN model as the classifier. The difference is that 2DCNN used a two-dimensional CNN to classify the image.
6. CGNN [21] combines GCN with GNN. By introducing adaptive weights and multi-level information fusion mechanism into the graph convolution layer, this method enhances the modeling ability of complex relationships between nodes. Its input node size is also 1500 bytes.
7. FS-Net [28] is unique in that it is characterized by the length of the packet rather than its content. Multi-layer bidirectional gated recurrent unit (bi-GRU) encoder and multi-layer bi-GRU decoder are used to process the features and then classify them.
4.3.2 Performance Comparison on the ISCX VPN-nonVPN Dataset
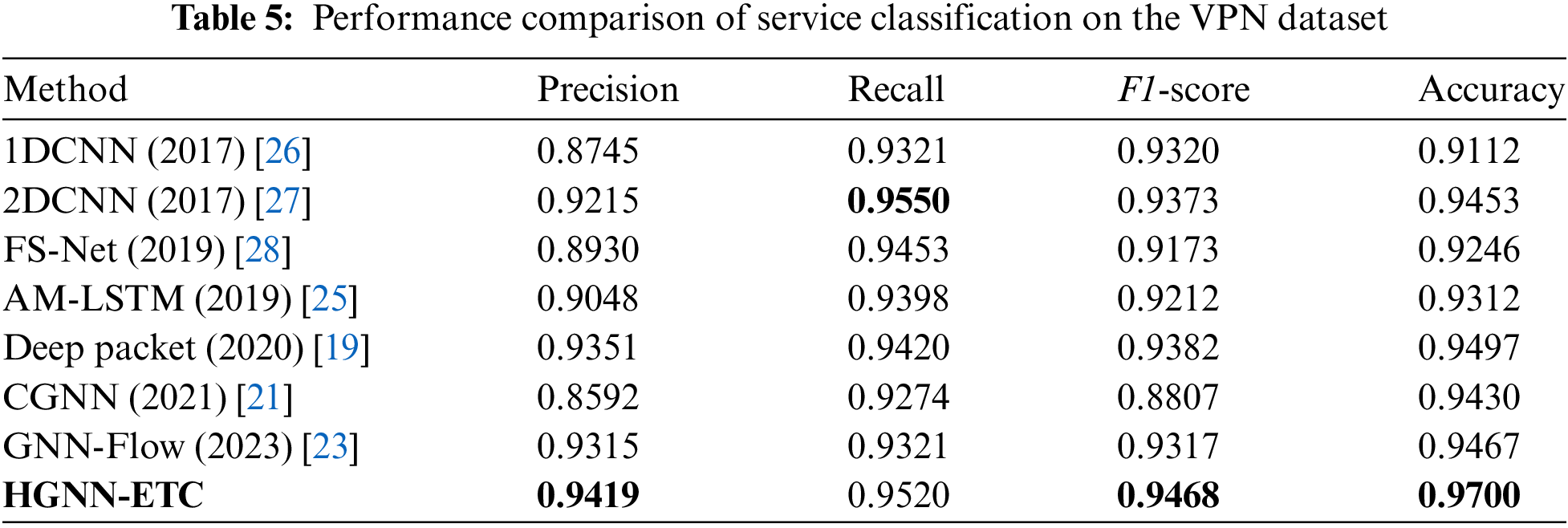
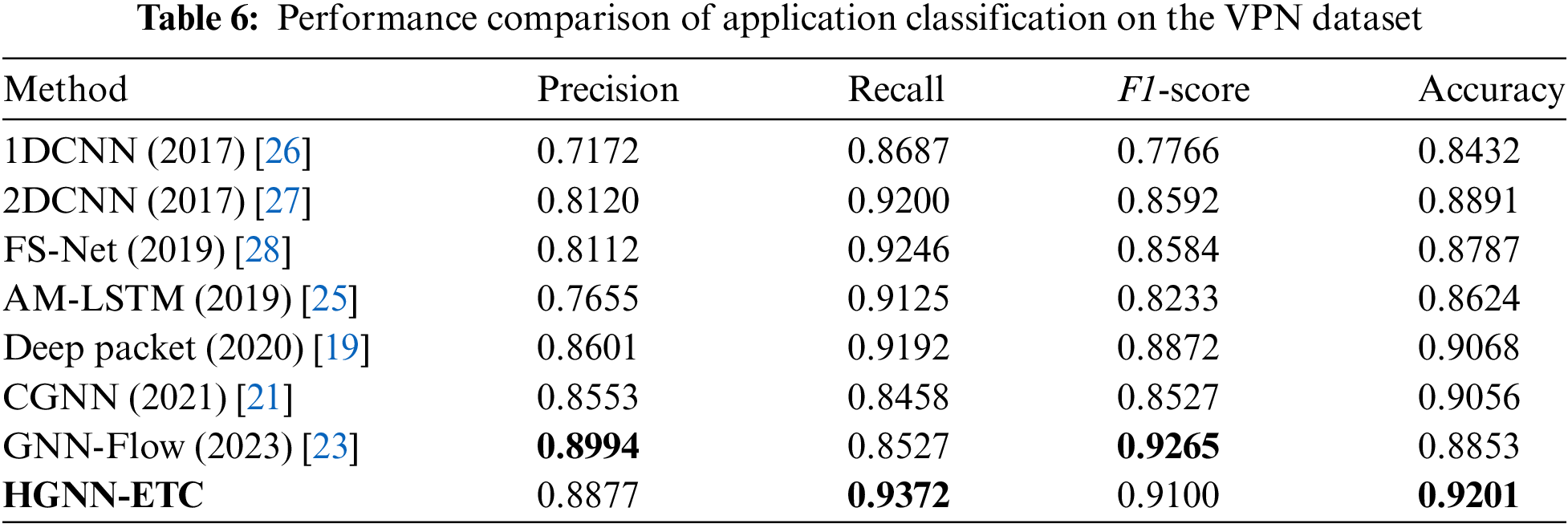
We divide this part of the experiment into three small experiments, including service classification on the VPN dataset, application classification on the VPN dataset, and service classification on the non-VPN dataset. In Table 5, we list the experimental results of the VPN dataset set classified by service. We can see that HGNN-ETC can obtain better results than the existing advanced methods. We achieved an accuracy of 97%, which demonstrates the excellent effectiveness of our approach in encrypted traffic. In Table 6, we list the experimental results of the VPN dataset set classified by application. Similar to the results in Table 5, HGNN-ETC maintains a good classification effect, but the classification effect of other methods declines.
For non-VPN data, we can see from Table 7 that HGNN-ETC can still obtain an accuracy greater than 92% over other methods, which proves that HGNN-ETC has good generalization ability. Although the classification effect of non-VPN data is slightly worse than that of VPN data, HGNN-ETC still makes use of the characteristic information of unencrypted traffic to a certain extent. 1DCNN [26] and AM-LSTM [25] have poor results in all three experiments. This is because GNNs have no constraint on the format of network input. When the network traffic converted into a graph is input into the network, the data contained in the traffic can be fully utilized. However, the input format of the CNN or LSTM model is fixed and the number of packets must be the same, which cannot make full use of the information in the packets, leading to an unsatisfactory classification effect. In addition, the results of some GNN-based methods are not as good as HGNN-ETC, because HGNN-ETC can obtain and aggregate more information in the classification process, to improve the classification effect. Figs. 5–7 show the confusion matrix of HGNN-ETC in three experiments.
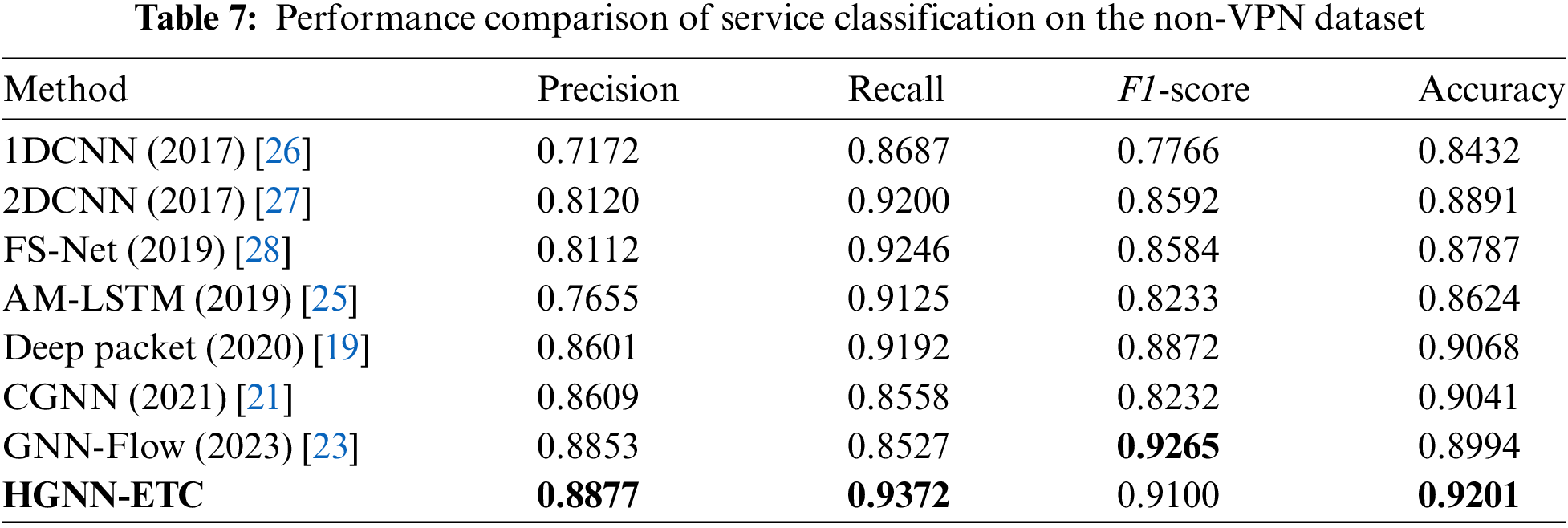
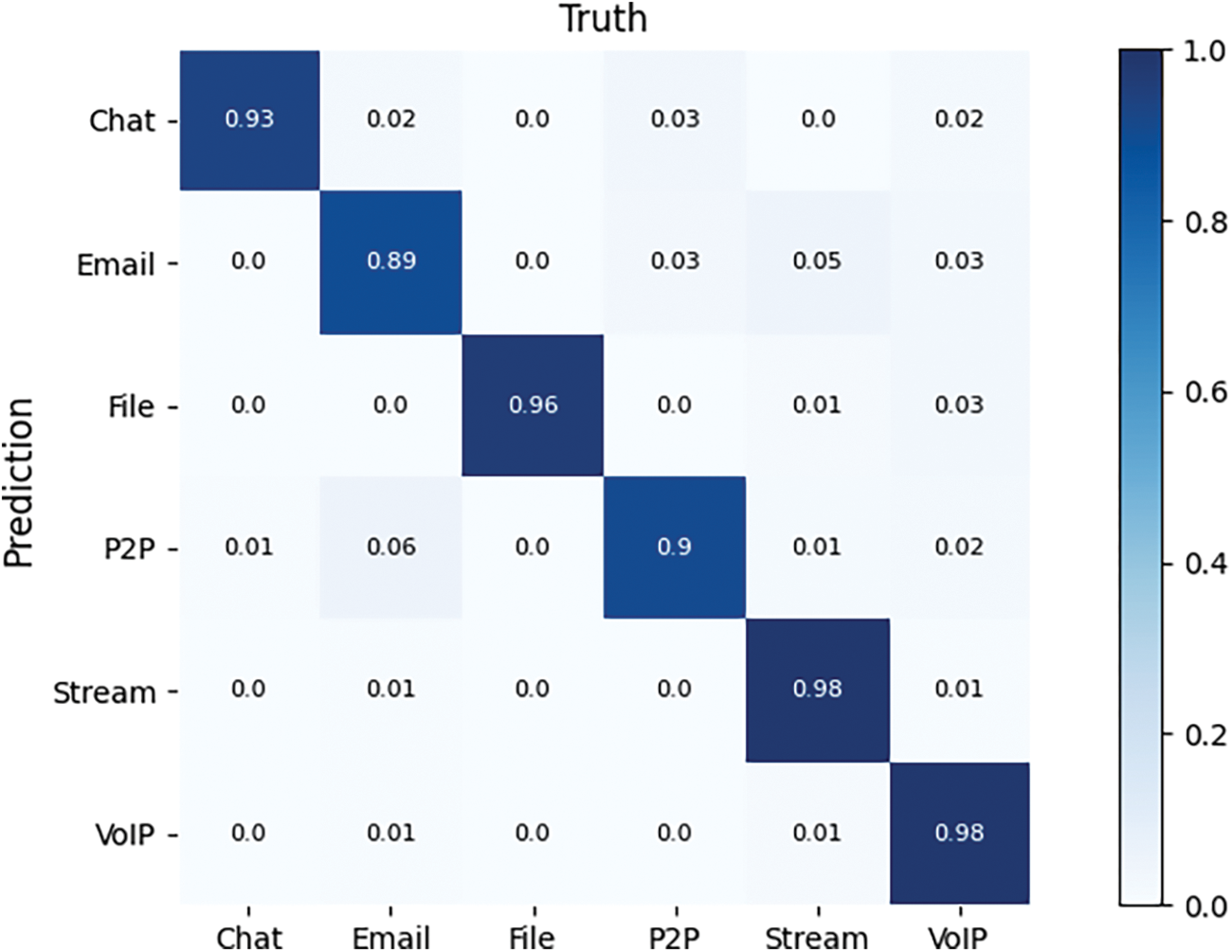
Figure 5: Confusion matrix for VPN dataset service classification
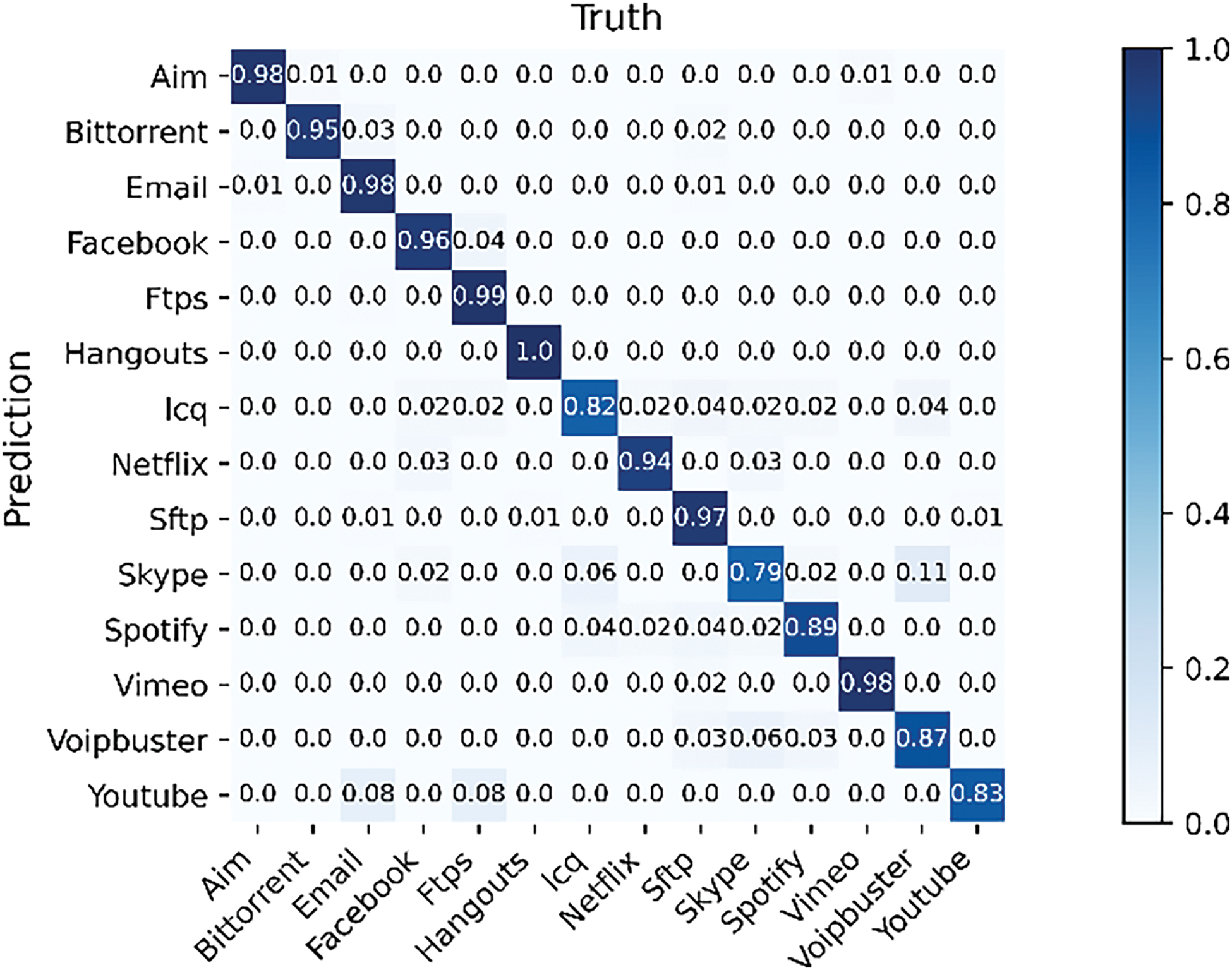
Figure 6: Confusion matrix for VPN dataset application classification
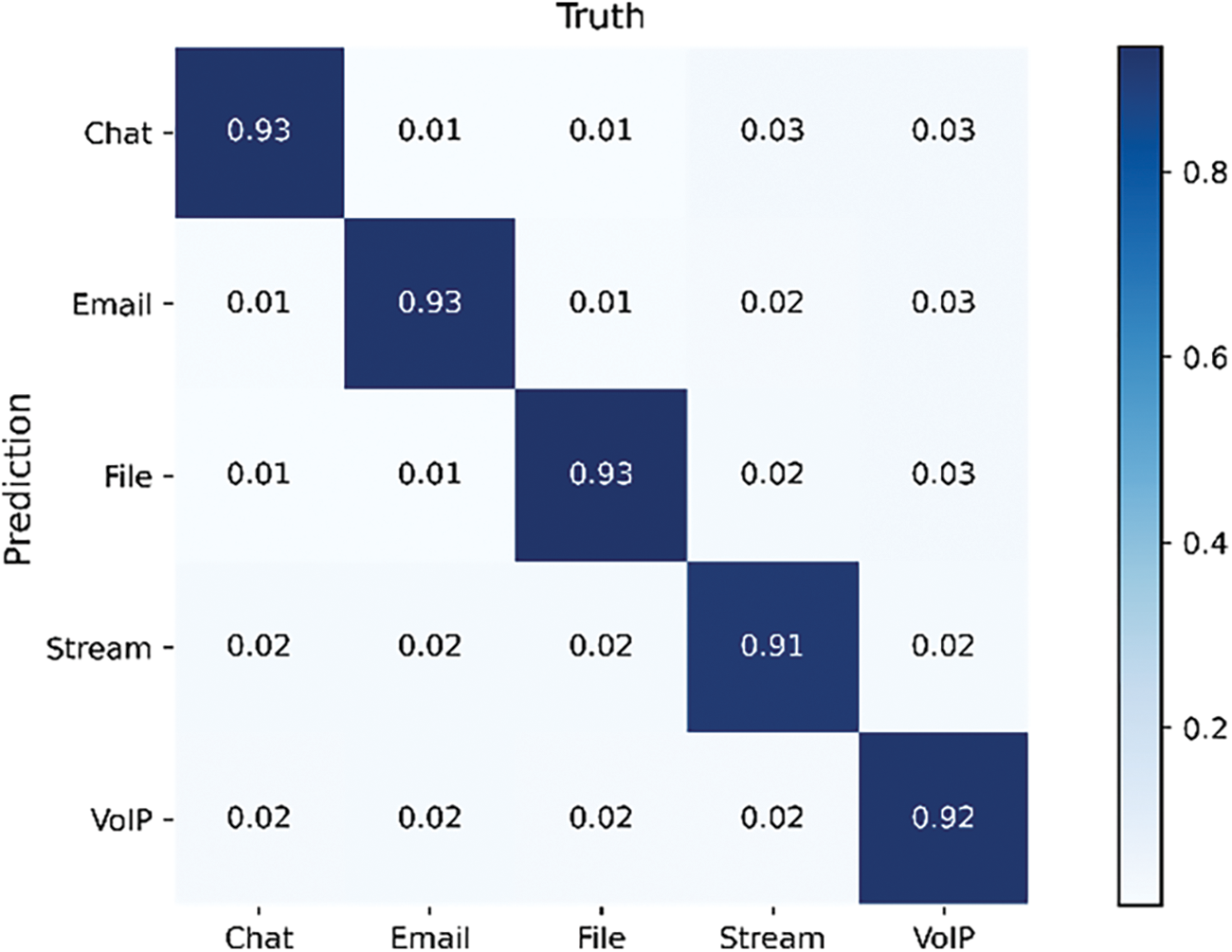
Figure 7: Confusion matrix for non-VPN dataset service classification
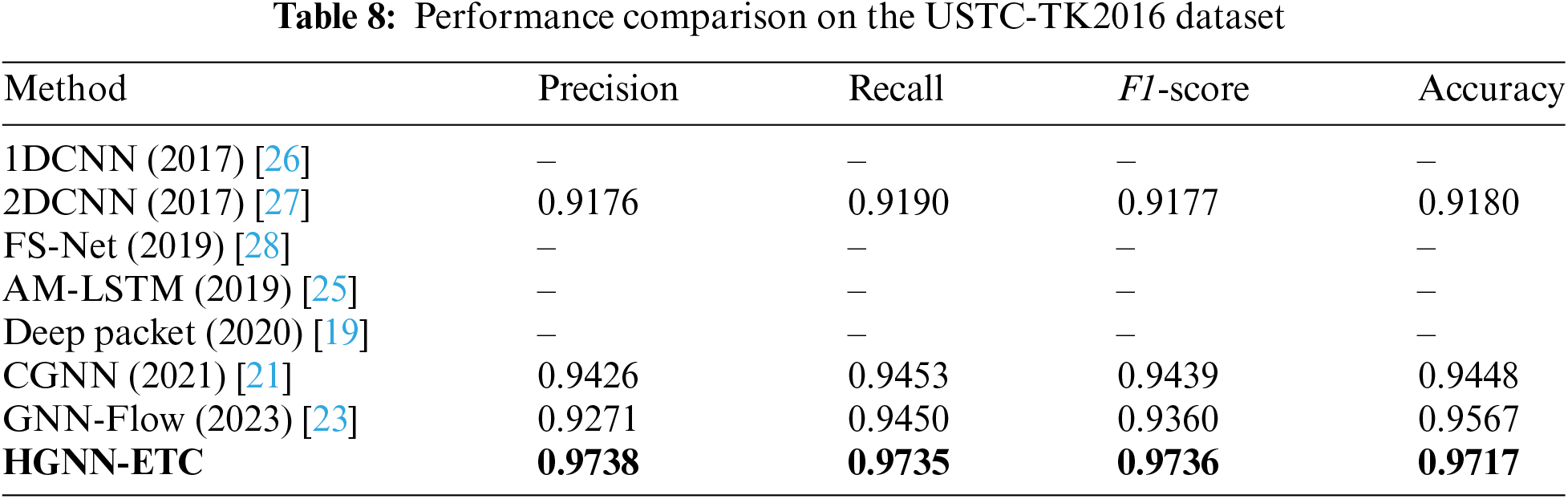
4.3.3 Performance Comparison on the USTC-TK2016 Dataset
In the USTC-TK2016 dataset, we focus on the malicious traffic section and classify it according to the malicious type. The classification results are shown in Table 8. HGNN-ETC performs better than other methods in handling the classification task of malicious traffic. The above experimental results fully prove the superiority of our proposed HGNN-ETC method in the task of encrypted traffic classification. By comparing with other existing methods, it is obvious that HGNN-ETC achieves the best classification effect on multiple datasets. The accuracy is about 97%. This not only demonstrates the superior performance of the method in specific scenarios but also shows its consistency and robustness under different datasets and multiple classification criteria, further demonstrating the strong generalization ability of HGNN-ETC in processing diverse traffic data.
4.4 Comparison Experiment of Different Inputs
In this part of the experiment, we design 4 experiments and implement them on both VPN and non-VPN datasets. We test the effect of different inputs on the classification performance, so there are some differences in the input of each study, including the attribute length of nodes, edges, and nodes. In Experiment 1, we use as input the number of nodes and attribute sizes designed in the proposed scheme. In Experiment 2 we test the optimal feature length to investigate the best generalization. Therefore, we do not change the number of nodes, but only change the attribute size, reducing the feature vector by nearly half. In addition, in Experiment 3, we only use nodes containing 1500 bytes of raw data as network inputs. With Study 3, we can also compare the performance differences between our model and the DL-based model (including CNN and LSTM), because their network inputs are consistent with those of Study 3. In Experiment 4, to evaluate the influence of the number of nodes in each graph on the classification results, we take all the data packets of each session as the network input of nodes, and the length of each data packet attribute is still fixed as 1500.
Table 9 shows the results of four experiments for VPN traffic. In Experiment 1, HGNN-ETC achieves the best results, the input of the network is to take 10 packets as nodes, and each node attribute size is 1500. In Experiments 2 and 4, we change the number of nodes and the length of node attributes respectively, and although the classification effect is lower than that of our proposed method to a certain extent, it can also get a good classification effect. In Experiment 3, where we trained only on raw bytes, we achieved the lowest classification accuracy among the four experiments, yet still reached 92%. Compared with DL, CNN [27] and LSTM [1] models, which only use raw bytes, can also achieve similar classification results.
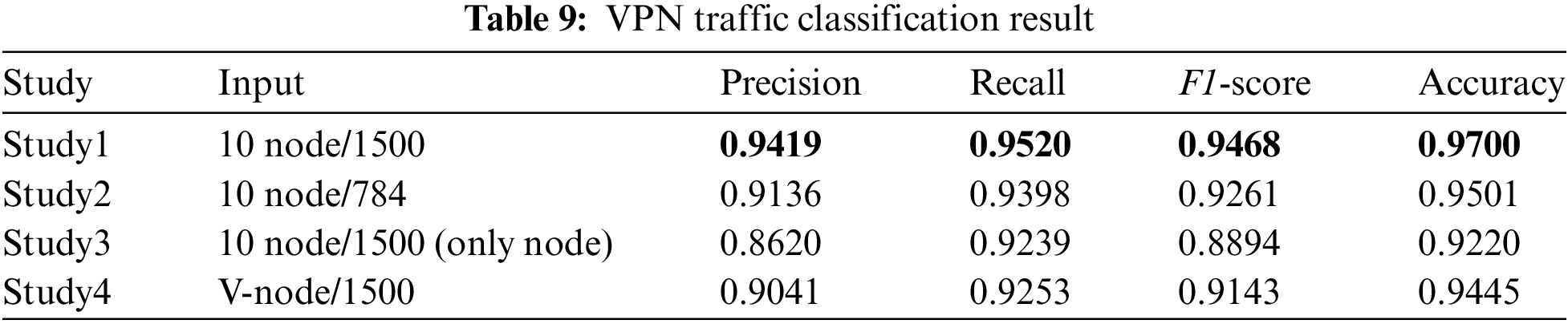
Table 10 shows the results for the non-VPN traffic classification task. Experiment 1 still produces the best results among the four experiments. The results of Experiment 2 are quite different from those of the VPN dataset, obtaining an accuracy of only about 66%. The reason for this result may be that the classification of unencrypted traffic is more dependent on the original attribute of the packet, and when we truncate the attribute, the classification effect will be greatly affected. Secondly, another reason may be that the imbalance of the dataset leads to the unsatisfactory classification result of a certain kind of traffic, thus affecting the overall classification effect. For Experiment 3, the classification effect of the model with only input nodes recently also drops to some extent, but it is a little better than Experiment 2. In the results of Experiment 4, if the number of nodes is not fixed, it cannot achieve a good classification effect. Together with the results of Experiment 2, it can be concluded that for non-VPN datasets, the truncation and unfixing of the input dimension have a greater impact on the classification effect.
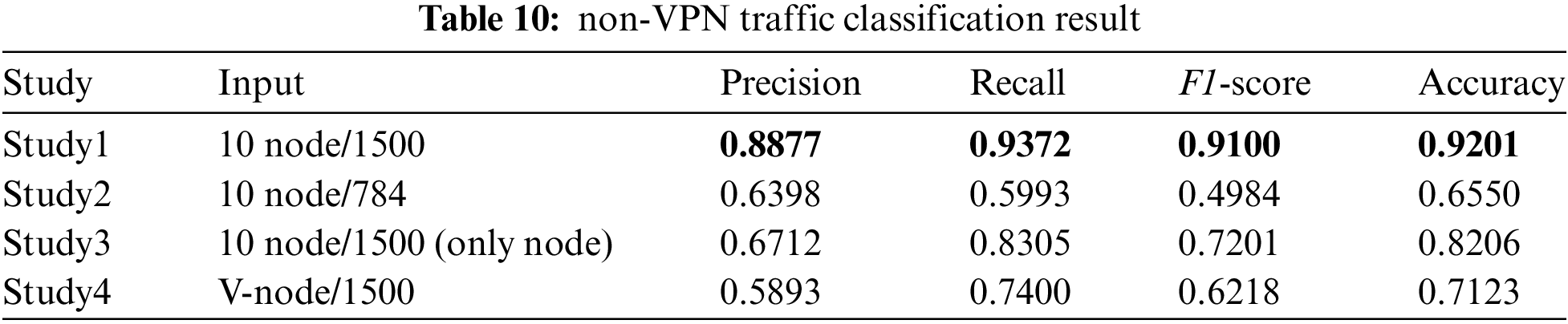
In summary, HGNN-ETC maintains the best accuracy in both datasets. The above experiments prove that the construction of the graph, the selection of the number of points, and the selection of the node attribute dimension in our scheme are all optimal. Figs. 8 and 9 show the confusion matrix of experimental results for the two datasets.
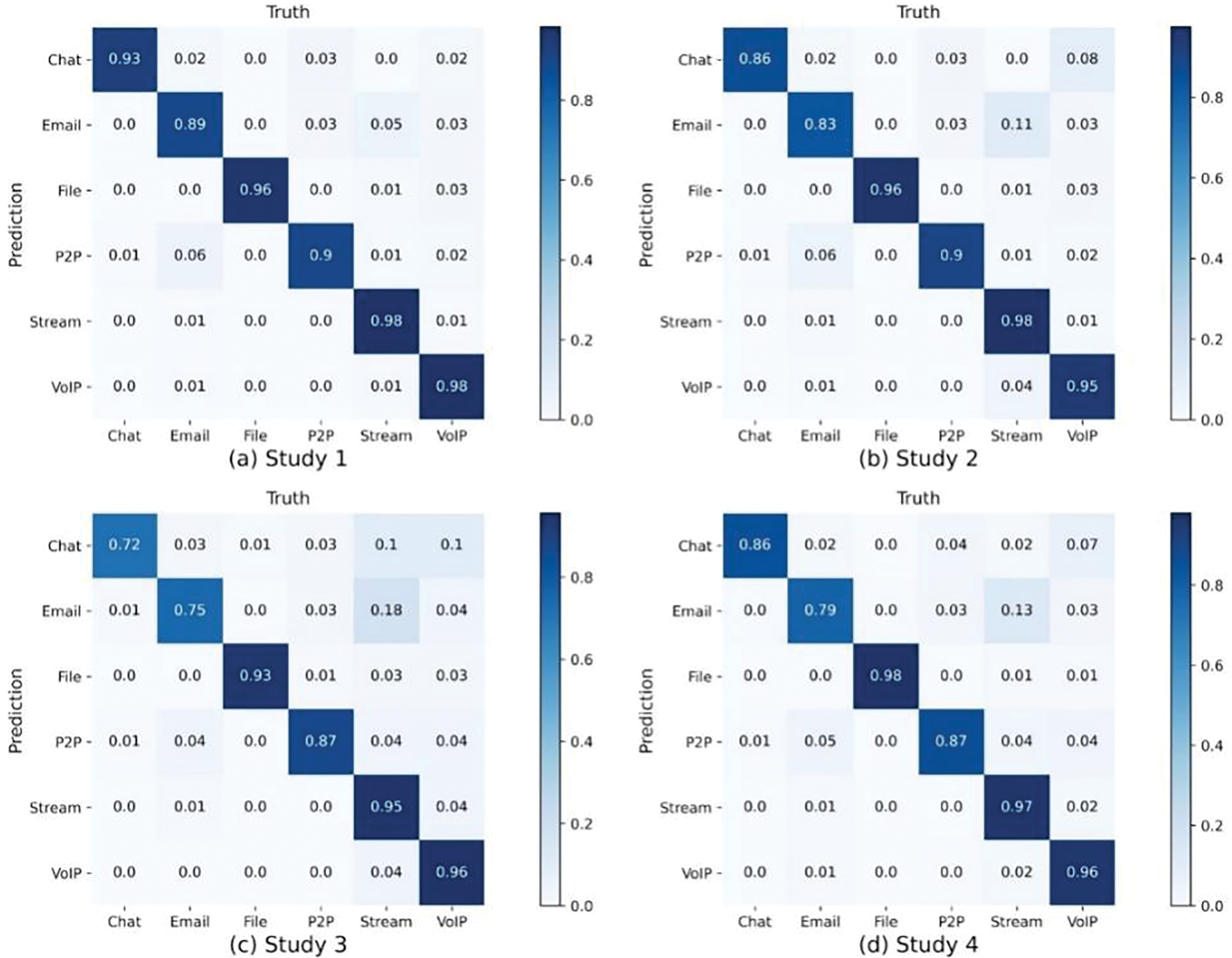
Figure 8: Confusion matrix for VPN dataset
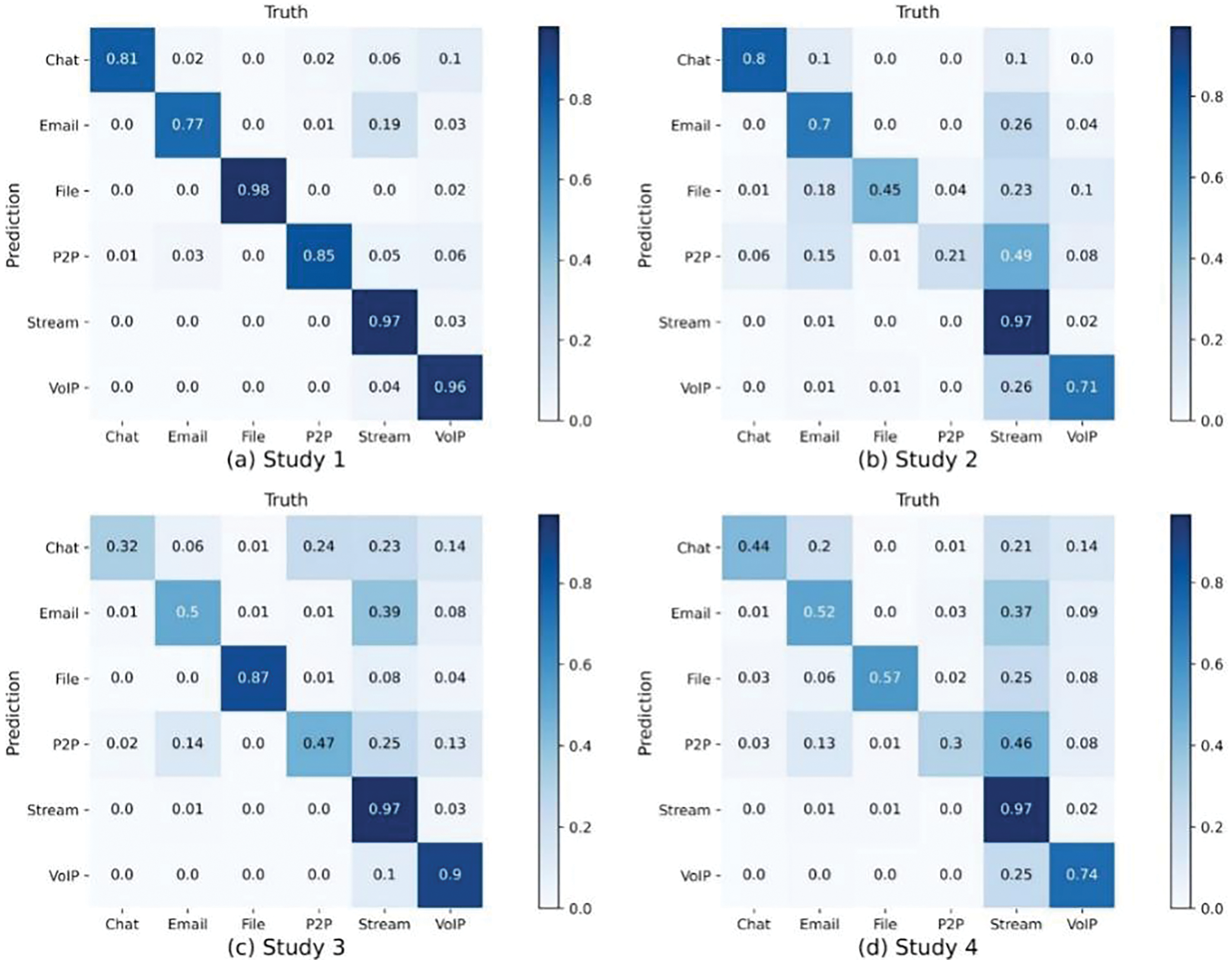
Figure 9: Confusion matrix for non-VPN dataset
In this paper, we design a novel traffic classification method based on higher-order GNN named HGNN-ETC. Since classification models based on DL typically operate on Euclidean data, they may face limitations when dealing with data structures that do not conform to grid or sequence formats. To solve the traffic classification problem geometrically, we use graph structure to represent the network traffic, which retains the original byte information and time information of the traffic. Graphs visualize the relationship between or among multiple entities, which is more effective in maintaining data integrity. We define packets in a session as nodes in the graph and chronological relationships of packets as edges. Each node has a property consisting of 1500 bytes of raw bytes. We can then feed the labeled graph into the classification model for training and classification. HGNN-ETC is built based on k-GNN. Its advantage is that it can better retain the vertex and structure information of the graph suitable for classification, and complete better aggregation of adjacent node information. During the experiment, we choose different datasets for testing, and the imbalance of the data is retained to verify the generalization ability of HGNN-ETC. We first compare with the existing state-of-the-art work and prove that our proposed method outperforms the existing state-of-the-art methods on both VPN and non-VPN data, and shows the best generalization strength for all datasets. The experimental results show that HGNN-ETC is effective and advanced for traffic classification tasks. In addition to this, we also do a series of ablation experiments for different inputs, such as changing the number of nodes, attribute length, etc. At the same time, the experimental results show the influence of different types of truncations on traffic classification results and also prove the rationality of the graph construction method designed in our method.
Current methods still have limitations in feature extraction, and it is difficult to accurately capture important information in complex data. In addition, the adaptability and generality of the existing algorithms have not been fully verified in different application scenarios. In the future, we will focus on improving feature extraction methods and exploring novel deep learning and machine learning models to adapt to all types of data. We plan to apply these methods to other areas such as traffic analysis, natural language processing, and more. In addition, we aim to develop fine-grained graph structures that will fully harness the potential of GNNs for efficient feature extraction and dimensionality reduction, thereby driving advancements in related methodologies.
Acknowledgement: The authors thank all reviewers for their valuable feedback and suggestions.
Funding Statement: This work was supported in part by the National Key Research and Development Program of China (No. 2022YFB4500800) and the National Science Foundation of China (No. 42071431).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Rongwei Yu, Xiya Guo; data collection: Rongwei Yu, Xiya Guo; analysis and interpretation of results: Rongwei Yu, Xiya Guo, Peihao Zhang; draft manuscript preparation: Xiya Guo, Peihao Zhang and Kaijuan Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Publicly available datasets were analyzed in this study. These datasets can be found here: https://www.unb.ca/cic/datasets/ (accessed on 19 September 2024) and https://github.com/yungshenglu/USTC-TFC2016 (accessed on 19 September 2024).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. E. Papadogiannaki and S. Ioannidis, “A survey on encrypted network traffic analysis applications, techniques, and countermeasures,” ACM Comput. Surv., vol. 54, no. 6, pp. 1–35, Jul. 2021. doi: 10.1145/3457904. [Google Scholar] [CrossRef]
2. Cisco, “Encrypted traffic analytics,” Accessed: Oct. 10, 2019. [Online]. Available: https://www.cisco.com/c/dam/en/us/td/docs/solutions/CVD/Campus/eta-design-guide-2019oct.pdf. [Google Scholar]
3. B. Anderson and D. A. McGrew, “Identifying encrypted malware traffic with contextual flow data,” in Proc. AISec. ACM, New York, NY, USA, 2016, pp. 35–46. doi: 10.1145/2996758.2996768. [Google Scholar] [CrossRef]
4. K. Thomas et al., “Data breaches, phishing, or malware?: Understanding the risks of stolen credentials,” in Proc. CCS. ACM, New York, NY, USA, 2017, pp. 1421–1434. doi: 10.1145/3133956.3134067. [Google Scholar] [CrossRef]
5. G. Pellegrino, M. Johns, S. Koch, M. Backes, and C. Rossow, “Deemon: Detecting CSRF with dynamic analysis and property graphs,” in Proc. CCS. ACM, New York, NY, USA, 2017, pp. 1757–1771. doi: 10.1145/3133956.3133959. [Google Scholar] [CrossRef]
6. Z. Cao, G. Xiong, Y. Zhao, Z. Li, and L. Guo, “A survey on encrypted traffic classification,” in Applications and Techniques in Information Security, Berlin, Heidelberg: Springer, 2014, pp. 73–81. [Google Scholar]
7. R. T. El-Maghraby, N. M. A. Elazim, and A. M. Bahaa-Eldin, “A survey on deep packet inspection,” in Proc. 12th Int. Conf. Comput. Eng. Syst. (ICCES), Cairo, Egypt, 2017, pp. 188–197. doi: 10.1109/ICCES.2017.8275301. [Google Scholar] [CrossRef]
8. T. Karagiannis, K. Papagiannaki, and M. Faloutsos, “BLINC: Multilevel traffic classification in the dark,” in Proc. ACM SIGCOMM Comput. Commun., New York, NY, USA, 2005, vol. 35, pp. 229–240. [Google Scholar]
9. A. L. Buczak and E. Guven, “A survey of data mining and machine learning methods for cyber security intrusion detection,” IEEE Commun. Surv. Tut., vol. 18, no. 2, pp. 1153–1176, 2016. doi: 10.1109/COMST.2015.2494502. [Google Scholar] [CrossRef]
10. V. Chandola, A. Banerjee, and V. Kumar, “Anomaly detection: A survey,” ACM Comput. Surv., vol. 41, no. 3, pp. 1–58, Jul. 2009. doi: 10.1145/1541880.1541882. [Google Scholar] [CrossRef]
11. P. Garcia-Teodoro, J. Díaz-Verdejo, G. Maciá-Fernández, and E. Vázquez, “Anomaly-based network intrusion detection: Techniques, systems and challenges,” Comput. Secur., vol. 28, no. 1–2, pp. 18–28, 2009. doi: 10.1016/j.cose.2008.08.003. [Google Scholar] [CrossRef]
12. B. Anderson and D. McGrew, “Machine learning for encrypted malware traffic classification: Accounting for noisy labels and non-stationarity,” in Proc. 23rd ACM SIGKDD Inter. Conf. Knowled. Discover. Data Mining, New York, NY, USA, 2017, pp. 1723–1732. [Google Scholar]
13. A. Azab, M. Khasawneh, S. Alrabaee, K. R. Choo, and M. Sarsour, “Network traffic classification: Techniques, datasets, and challenges,” Digit. Commun. Netw., vol. 10, no. 3, pp. 676–692, Jun. 2024. doi: 10.1016/j.dcan.2022.09.009. [Google Scholar] [CrossRef]
14. A. H. Lashkari, G. Draper-Gil, M. S. I. Mamun, and A. A. Ghorbani, “Characterization of Tor traffic using time based features,” in Proc. 3rd Int. Conf. Inform. Syst. Secur. Priv., 2017, pp. 253–262. [Google Scholar]
15. Z. Zhang, Y. Chen, and L. Wang, “Deep learning for VPN traffic classification: A comparative study,” IEEE Access, vol. 9, pp. 123456–123467, 2021. [Google Scholar]
16. O. Barut, R. Zhu, Y. Luo, and T. Zhang, “TLS encrypted application classification using machine learning with flow feature engineering,” in Proc. 10th Int. Conf. Commun. Netw. Security, New York, NY, USA, 2020, pp. 32–41. [Google Scholar]
17. A. Jenefa et al., “A robust deep learning-based approach for network traffic classification using CNNs and RNNs,” in Proc. 4th Int. Conf. Signal Process. Commun. (ICSPC), Coimbatore, India, 2023, pp. 106–110. [Google Scholar]
18. M. Alzahrani, H. Alhassan, and A. Alharthi, “A survey on network traffic classification techniques: current trends and future directions,” IEEE Access, vol. 9, pp. 123456–123478, 2021. doi: 10.1109/ACCESS.2021.3091234. [Google Scholar] [CrossRef]
19. M. Lotfollahi, M. Jafari Siavoshani, R. Shirali Hossein Zade, and M. Saberian, “Deep packet: A novel approach for encrypted traffic classification using deep learning,” Soft Comput., vol. 24, pp. 1999–2012, 2020. doi: 10.1007/s00500-019-04030-2. [Google Scholar] [CrossRef]
20. Z. Zou, J. Ge, H. Zheng, Y. Wu, C. Han and Z. Yao, “Encrypted traffic classification with a convolutional long short-term memory neural network,” in Proc. IEEE 20th Int. Conf. High Perform. Comput. Commun.; IEEE 16th Int. Conf. Smart City; IEEE 4th Int. Conf. Data Sci. Syst. (HPCC/SmartCity/DSS), 2018, pp. 329–334. [Google Scholar]
21. B. Pang, Y. Fu, S. Ren, Y. Wang, Q. Liao and Y. Jia, “CGNN: Traffic classification with graph neural network,” 2021, arXiv:2110.09726. [Google Scholar]
22. M. Shen, J. Zhang, L. Zhu, K. Xu, and X. Du, “Accurate decentralized application identification via encrypted traffic analysis using graph neural networks,” IEEE Trans. Inf. Forensics Secur., vol. 16, pp. 2367–2380, 2021. doi: 10.1109/TIFS.2021.3050608. [Google Scholar] [CrossRef]
23. T. -L. Huoh, Y. Luo, P. Li, and T. Zhang, “Flow-based encrypted network traffic classification with graph neural networks,” IEEE Trans. Netw. Serv. Manag., vol. 20, no. 2, pp. 1224–1237, Jun. 2023. doi: 10.1109/TNSM.2022.3227500. [Google Scholar] [CrossRef]
24. S. Rezaei and X. Liu, “Deep learning for encrypted traffic classification: An overview,” IEEE Commun. Mag., vol. 57, no. 5, pp. 76–81, May 2019. doi: 10.1109/MCOM.2019.1800819. [Google Scholar] [CrossRef]
25. H. Yao, C. Liu, P. Zhang, S. Wu, C. Jiang and S. Yu, “Identification of encrypted traffic through attention mechanism based long short term memory,” IEEE Trans. Big Data, vol. 8, no. 1, pp. 241–252, Feb. 2022. doi: 10.1109/TBDATA.2019.2940675. [Google Scholar] [CrossRef]
26. W. Wang, M. Zhu, J. Wang, X. Zeng, and Z. Yang, “End-to-end encrypted traffic classification with one-dimensional convolution neural networks,” in Proc. 2017 IEEE Int. Conf. Intell. Secur. Inf. (ISI), Beijing, China, Jul. 2017, pp. 43–48. [Google Scholar]
27. W. Wang, M. Zhu, X. W. Zeng, X. Z. Ye, and Y. Q. Sheng, “Malware traffic classification using convolutional neural network for representation learning,” in Proc. 2017 Int. Conf. Inform. Netw. (ICOIN), Da Nang, Vietnam, 2017, pp. 712–717. [Google Scholar]
28. C. Liu, L. He, G. Xiong, Z. Cao, and Z. Li, “FS-Net: A flow sequence network for encrypted traffic classification,” in Proc. IEEE INFOCOM 2019—IEEE Conf. Comput. Commun., Paris, France, 2019, pp. 1171–1179. doi: 10.1109/INFOCOM.2019.8737507. [Google Scholar] [CrossRef]
29. H. Wang, J. Yan, and N. Jia, “A new encrypted traffic identification model based on VAE-LSTM-DRN,” Comput. Mater. Contin., vol. 78, no. 1, pp. 569–588, 2024. doi: 10.32604/cmc.2023.046055. [Google Scholar] [CrossRef]
30. H. Huang, X. Zhang, Y. Lu, Z. Li, and S. Zhou, “BSTFNet: An encrypted malicious traffic classification method integrating global semantic and spatiotemporal features,” Comput. Mater. Contin., vol. 78, no. 3, pp. 3929–3951, 2024. doi: 10.32604/cmc.2024.047918. [Google Scholar] [CrossRef]
31. J. Zheng, Z. Zeng, and T. Feng, “GCN-ETA: High-efficiency encrypted malicious traffic detection,” Secur. Commun. Netw., vol. 2022, 2022, Art. no. 4274139. doi: 10.1155/2022/4274139. [Google Scholar] [CrossRef]
32. Z. Diao et al., “EC-GCN: A encrypted traffic classification framework based on multi-scale graph convolution networks,” Comput. Netw., vol. 224, 2023, Art. no. 109614. doi: 10.1016/j.comnet.2023.109614. [Google Scholar] [CrossRef]
33. G. Hu, X. Xiao, M. Shen, B. Zhang, X. Yan and Y. Liu, “TCGNN: Packet-grained network traffic classification via Graph Neural Networks,” Eng. Appl. Artif. Intell., vol. 123, 2023, Art. no. 106531. doi: 10.1016/j.engappai.2023.106531. [Google Scholar] [CrossRef]
34. X. Han, G. Xu, M. Zhang, Z. Yang, Z. Yu and W. Huang, “DE-GNN: Dual embedding with graph neural network for fine-grained encrypted traffic classification,” Comput. Netw., vol. 245, 2024, Art. no. 110372. doi: 10.1016/j.comnet.2024.110372. [Google Scholar] [CrossRef]
35. T. -L. Huoh, Y. Luo, and T. Zhang, “Encrypted network traffic classification using a geometric learning model,” in Proc. IFIP/IEEE Int. Symp. Integr. Netw. Manage. (IM), Bordeaux, France, 2021, pp. 376–383. [Google Scholar]
36. L. Peng, B. Yang, Y. Chen, and T. Wu, “How many packets are most effective for early stage traffic identification: An experimental study,” China Commun., vol. 11, no. 9, pp. 183–193, Sep. 2014. doi: 10.1109/CC.2014.6969782. [Google Scholar] [CrossRef]
37. C. Morris et al., “Weisfeiler and Leman go neural: Higher-order graph neural networks,” Proc. AAAI Conf. Arti. Intell., vol. 33, no. 1, pp. 4602–4609, 2019. doi: 10.1609/aaai.v33i01.33014602. [Google Scholar] [CrossRef]
38. G. Draper-Gil, A. H. Lashkari, M. S. I. Mamun, and A. A. Ghorbani, “Characterization of encrypted and VPN traffic using time-related features,” in Proc. ICISSP, 2016, pp. 1–8. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF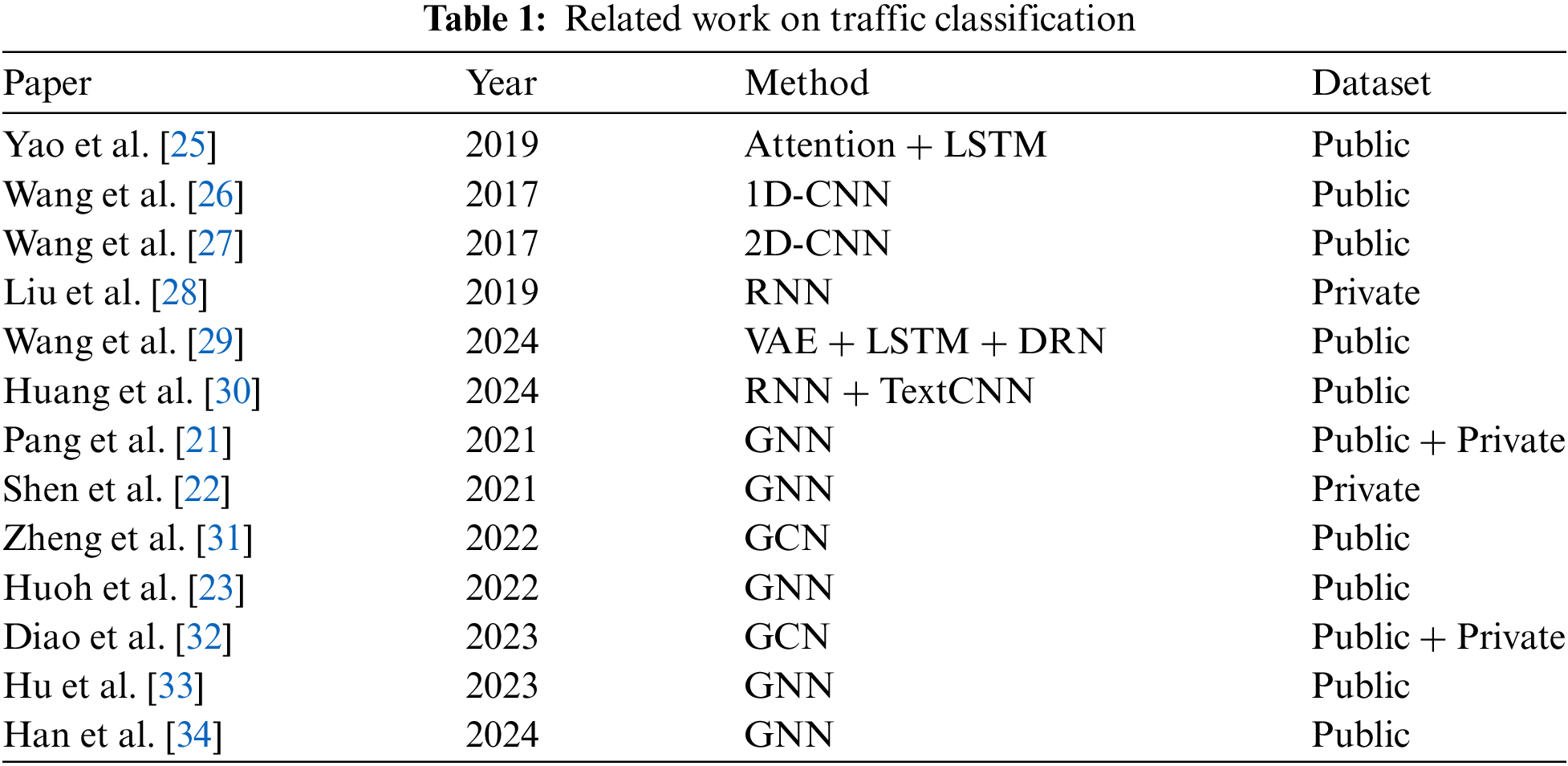
 Downloads
Downloads
 Citation Tools
Citation Tools