Automatic Fetal Segmentation Designed on Computer-Aided Detection with Ultrasound Images

1  Introduction

Fetal head circumference (HC) measurement is a critical parameter in prenatal care, used to assess gestational age and monitor fetal growth. Accurate and consistent measurement of HC is essential for identifying potential developmental issues and ensuring timely interventions. However, traditional methods of measuring HC in 2D ultrasonography images are often reliant on the expertise of sonographers, which can lead to variability in measurements due to human error, especially in regions with limited access to highly trained professionals.

Pregnant women commonly utilize ultrasound imaging [1], a non-intrusive, real-time, and affordable imaging modality, for surveillance and screening purposes. However, the operator’s skill in capturing ultrasound images is crucial; in addition, the images often exhibit reduction, speckle, and artifacts such as silhouettes and impacts, which can complicate their interpretation. Statistical values of the fetus, especially the crown-rump length (CRL) as well as the circumference of the head (HC), are frequently computed during an ultrasound screening test to identify the age of gestation (GA) and to track the fetus’s growth. The recommendations dictate that we evaluate HC in a transverse slice of the skull using a central midline echo, disrupted in the anterior third by the hollow of the septum pellucidum, and visible in both the posterior and anterior lobes of the lateral ventricles. Hand-taking of the biometric measures results in inter-and intra-observer heterogeneity. Due to the absence of intra-observer variability, it is not affected by inconsistencies between different observers, a precise automated structure might minimize gauging time and variability. Developing nations account for 99 percent of all maternal fatalities worldwide. However, early skilled treatment and later labor can save the lives of women and neonatal babies [2]. Inappropriately, there is still a chronic scarcity of well-trained sonographers in low-resource circumstances. Furthermore, most pregnant women in certain countries lack access to ultrasonography screening [3].

One of the primary challenges in fetal HC measurement is the variability in image quality and fetal positioning, which can significantly affect the accuracy of manual measurements. Inconsistent imaging conditions, such as low contrast or noise, further complicate the task of identifying the fetal skull and determining the precise boundaries for measurement. Additionally, the manual nature of the process is time-consuming and susceptible to inter-and intra-operator variability, leading to potential discrepancies in gestational age estimation.

One significant challenge is the scarcity of trained sonographers, particularly in developing countries. According to the World Health Organization (WHO), approximately 810 women die daily from preventable causes related to pregnancy and childbirth, with 94% of these deaths occurring in low-resource settings. The lack of trained healthcare professionals, including sonographers, exacerbates these outcomes, as many regions suffer from a critical shortage of skilled personnel capable of performing accurate fetal measurements. For instance, in Sub-Saharan Africa, there is an estimated shortfall of 2.4 million health workers, including those trained in ultrasonography.

Additionally, the variability in image quality and fetal positioning presents another challenge, significantly affecting the accuracy of manual measurements. Studies have shown that inter-operator variability can lead to differences in fetal HC measurements by as much as 10%, which can translate into inaccurate assessments of gestational age and potential mismanagement of pregnancy. Inconsistent imaging conditions, such as low contrast or noise, further complicate the task of identifying the fetal skull and determining precise boundaries for measurement. Moreover, current automated solutions, while showing promise, often struggle with generalizability across different trimesters and diverse patient populations. Limited datasets, particularly in the later stages of pregnancy when head molding can occur, train many existing models. This lack of comprehensive training data can result in models that perform well in controlled settings but fail to maintain accuracy in real-world clinical environments.

Addressing these challenges requires a robust and reliable system capable of consistently identifying and measuring fetal HC across varying conditions and stages of pregnancy. Our research aims to create such a system by using advanced machine learning techniques and a lot of training data to make a computer-aided detection (CAD) model that gets around the problems with current methods and gives accurate, automated measurements of fetal HC.

Inexperienced human observers may benefit from the assistance of an automated system in achieving an accurate measurement. In this work, our focus is on monitoring the HC, as it holds the potential for calculating the GA and tracking the fetus’s development. In addition, the embryonic head is more visible than the embryonic abdomen. Systems for automatic HC measurement have used the randomized Hough transform [4,5], Haar-like features [6–9], multilevel thresholding [10], circular shortest paths [11], boundary fragment models [12], semi-supervised on region graphs [13], active contouring [14,15], intensity-based features [16], and text on created features [4]. Fig. 1 displays the ultrasound fetal head images from the public HC18 dataset.

Figure 1: Ultrasound fetal head images from the public HC18 dataset

Despite the positive outcomes of these methods, their evaluation began with a limited collection of data, ranging from 10 to 175 examination images. In addition, few of the above studies employed fetal pictures after all three trimesters of pregnancy. We present a framework that was built using 999 ultrasound scans from the HC18 challenge data source. This framework was then tested against a large, unbiased set of 335 ultrasound pictures taken at different stages of pregnancy. We built the proposed quantitative structure to be as quick and vigorous as possible, and then we contrasted its outcomes with approaches suggested in the available literature.

2  Literature Review

The study [4] demonstrated a texton-based supervised technique that enables precise measurements of the femur and fetal heads (BPD, OFD, HC). It is useful for tracking fetal growth during pregnancy since it has time and financial advantages over earlier techniques. It is useful for tracking fetal growth during pregnancy since it has time and financial advantages over earlier techniques. It is used to calculate the fetal gestation period (GA) by assessing its total weight and percentage, as well as to detect abnormal fetal development patterns. The texton map is a monochromatic image used to generate similar primitives. Following the last stage, it is clear that the overall precision of both of the professionals for the fetus is greater than 97%, with a variance of not as much as 1%, then all the additional metrics (accuracy, responsiveness, uniqueness) readings remain close to 99%.

Another study [11] utilized computer-aided detection (CAD) to calculate the fetus’s head diameter from 2D ultrasonography images. The Radboud University Healthcare Center’s Section of Obstetrics in Nijmegen, the Netherlands, is where the ultrasonography photographs of the HC originate. The CAD approach is divided into two steps: initially, to recognize the fetus skull, Haar-like characteristics remained extracted as of ultrasonography scans, then employed for training a forest-based classifier. We determine the HC in the second step using the Hough transform, adaptive software design, and an elliptical fit. We programmed the CAD structure on 999 pictures and then verified its applicability in a different set of tests on 335 images across all trimesters. The GA variance between the baseline and CAD structures averaged 0.6 4.3, 0.4 4.7, and 2.5 12.4 days, respectively. To get a vibrant picture of the fetus’s development, investigators gathered 1334 2D photos of 551 pregnant females. The accuracy of this learning was substantially higher than that of earlier investigations.

The study [13] employed CNN to enhance the understanding of brain categorization, while U-net also played a similar role in enhancing comprehension. We digitally resized all photos to 256 × 256 around the center of the mask’s head area (512 × 512). This guarantees that the brain region is visible in every new image. Massive databases had never been formerly used, but this research emphasizes their importance. This document also includes a CNN network centered on the U-Net concept. In Computerized 2D Fetal of MRI Information that Utilizes a Deep U-Net 13, the suggested technique generated much better results than the original U-Net’s with its enhancements.

The study [14] endeavored to enhance the useful image of the fetus offers only 3D ultrasonography scan to identify and then quantify multiple fatal frameworks in a first-trimester fetal examination. Because the initial trimester is critical for assessing fetus growth, ultrasonography at this period is similarly required to identify the embryo’s gestational age. In addition, deep learning and image processing techniques are used to carry out semantic categorization of the fetus, which is also used for biometrics monitoring. The objective of the project was to create an entirely autonomous biometric structure that would employ Foetal ultrasonography during critical initial trimesters. This three-dimensional ultrasonography determination will be used in embryo dividing in the future; nevertheless, there are limits in both global and regional information that determination eventually takes an influence on proceeding development.

According to the study [15], prenatal ultrasonography is a standard examination performed throughout pregnancy. It is used to calculate the fetal head circumference, determine gestational age, screen the fetus’ development, and then assess the overall health of the newborn. This non-invasive procedure provides valuable information to healthcare professionals and helps ensure a healthy pregnancy and delivery. They utilized the HC18 challenge data source, which includes 999 three-dimensional ultrasonography pictures and observations. Their focus was on the fetal HC dimension, specifically utilizing the fetal skull edge and the fetal skull. They updated the network to utilize U-Net because of its exceptional performance in biological image processing. The technique remains based entirely on the HC18 grand challenge dataset, which comprises 2D ultrasonography pictures after numerous pregnancy trimesters. Because the ultrasound picture of the skull is fuzzy and inaccurate, measuring the fetal head can be challenging. They used a deep learning U-net model approach toward dividing up the skull of the embryo for fetal HC measurement; consequently, the doctor might accurately measure the HC and make a further diagnosis. This work is trustworthy and effective to some level; however, there are certain imperfections in this research. Minor details that may have been previously overlooked can be identified using prenatal ultrasonography. These details may not require an in-depth understanding of picture segmentation techniques. Besides, one broad information consumption has been employed consequently aimed at image segmentation; that is one of the major issues due to research limitations. Rather than having multiple defects, this model is 96% right, meaning that it outperforms other networks. The system also predicts blurry pictures accurately, with a 3 mm reduced mean difference. In this experiment, researchers obtain 2D representations of prenatal ultrasound scans.

The studies [17–21] closely align with our research as it uses an ensemble transfer learning approach for fetal head analysis. It covers segmentation, as well as predictions for gestational age and weight, which are critical aspects of fetal development. Given its focus on the same dataset (HC18) and similar goals, this study is particularly relevant. The methodology and results of this study highlight the similarities in objectives, discuss the differences in techniques used (e.g., transfer learning), and evaluate the outcomes.

The measurement of fetal head circumference (HC) has been a focal point of research in prenatal care, with various methods developed to improve accuracy and reliability. We can broadly categorize these methods into manual, semi-automated, and fully automated approaches, each offering unique advantages and limitations. Traditionally, HC measurement in ultrasonography has relied on manual techniques performed by trained sonographers. While widely used, this approach is prone to significant inter-and intra-operator variability. A study by Sarris et al. [22] found that manual measurements could differ by up to 10% between operators, leading to inconsistent estimations of gestational age and potential mismanagement of pregnancy. Additionally, manual methods are time-consuming and heavily reliant on the skill and experience of the sonographer, which poses a challenge in low-resource settings where trained professionals are scarce. Semi-automated methods, developed to reduce variability and enhance efficiency, integrate manual input with automated tools for boundary detection. These methods, such as those described by Wang et al. [23], often use edge detection algorithms to assist sonographers in identifying the boundaries of the fetal head. While semi-automated techniques can reduce the time required for measurements and improve consistency, they still rely on significant manual intervention, limiting their scalability and introducing the potential for error if the initial boundary detection is inaccurate. In recent years, fully automated approaches have gained attention, particularly with the advent of deep learning and advanced image processing techniques. Yang et al. [24] suggested models using convolutional neural networks (CNNs) that show promise in accurately separating fetal head images and measuring HC with little help from humans. These methods, however, often struggle with generalizability across diverse datasets and varying image quality. A critical limitation identified in several studies is the lack of robustness in handling different fetal head shapes and orientations, particularly in the later stages of pregnancy. Furthermore, the training of many existing models on relatively small and homogenous datasets raises concerns about their performance in real-world clinical settings.

The strength of fully automated methods lies in their potential to provide consistent and rapid measurements without the need for extensive manual input, which is particularly valuable in resource-limited settings. However, their current limitations in generalizability and robustness highlight the need for further development and validation. On the other hand, manual and semi-automated methods, while more adaptable to varying conditions, suffer from issues of variability and dependence on operator expertise. Although recent advancements in automated HC measurement have demonstrated significant potential, there is a need for more comprehensive models that can address the challenges of variability and generalizability. Existing literature often focuses on the performance of these models in controlled environments, with limited exploration of their application in diverse clinical settings. Our research aims to fill this gap by developing a fully automated system that leverages extensive training data from all trimesters of pregnancy, ensuring robustness and accuracy across different fetal head shapes and orientations. Various machine learning models, notably convolutional neural networks (CNNs) like U-Net, commonly used for biomedical image segmentation, comprise existing approaches. For example, the U-Net model fine-tuned with a pre-trained MobileNet V2 has shown high accuracy in segmenting fetal head images, achieving a pixel accuracy of 97.94% on the HC18 dataset (grand-challenge.org, accessed on 15 September 2023).

Performance under different conditions: U-Net models, including variations like U-Net++ and U-Net with pre-trained backbones (e.g., MobileNetV2), have shown different levels of success in fetal head circumference (HC) measurement. For instance, a U-Net++ model achieved a Dice Similarity Coefficient (DSC) of 0.94 on the HC18 dataset, which indicates high accuracy in boundary delineation of the fetal head. However, its performance varied depending on image quality and gestational age, with a decrease in accuracy for low-contrast images from the third trimester. Traditional methods like edge detection combined with the Hough transform have been used to identify the fetal skull’s elliptical shape in ultrasound images. While these methods are computationally efficient, they often struggle with noisy images or those with unclear boundaries. In one study, an edge detection algorithm achieved an accuracy of 85% in segmenting the fetal head, but its performance dropped to around 70% in images with lower resolution or higher noise levels (grand-challenge.org).

CNN-based approaches, particularly those using transfer learning, have demonstrated robustness in various conditions. For instance, a CNN model that was fine-tuned on the HC18 dataset got an average absolute error (MAE) of 1.2 mm in HC measurement. This meant that it worked better than traditional methods in a range of situations, such as when the fetal head was in different positions and the image quality was poor. However, the model’s performance was less reliable in cases with extreme fetal head orientations, where the MAE increased to 3.5 mm. Semi-automated methods, which combine manual input with algorithmic assistance, as shown in Table 1, have shown promise in reducing variability. A method combining manual boundary initialization with a region-growing algorithm achieved a mean DSC of 0.88. This approach was particularly effective in images from the second trimester, where manual input helped guide the algorithm in cases of ambiguous boundaries. However, in the third trimester, the method’s reliance on manual input led to increased operator dependency, affecting overall reliability (grand-challenge.org).

Including these specific performance metrics and comparative insights will provide a better understanding of how different approaches handle various challenges in fetal head circumference measurement. This detailed analysis will also underline the significance of research in addressing the limitations observed in existing methods.

3  Research Objective

The goal of this study was to use CAD to conduct unsupervised segments on 2D ultrasonography pictures for HC. We planned to train the framework using a training dataset that included 2D ultrasonography pictures. Examination of the training procedure with the authentication dataset first, then with the testing dataset. Another goal of the investigation was to evaluate the efficiency of the segmentation approach.

4  Paper Outline

This study begins with an introduction that covers the fundamentals of fetal head and autonomous segmentation methods. The study challenges highlighted how we obtained data for the search. The literature survey section covered the views and methodologies of various scholars. In the background study section, we referenced the research-related studies. In the study methodology part, we provided a workflow comprising a system model, data collection, and data preparation. The second component includes annotation and masking, grayscale conversion, scaling, and normalizing. Following the grayscale output, we test and segment the data. We then computed and analyzed the head circumference and length measurement in the model implementation and performance metrics section. The results section provides an explanation of the CAD system’s HC classification output. We then discuss the limitations and future directions of our research.

5  Background Study

For the past few decades, computer-aided detection (CAD) has served as a key area of study. CAD makes use of machine learning approaches to evaluate imaging and/or non-imaging medical data and determine the pregnant woman’s fetal growth, which may subsequently be utilized to help physicians make decisions. For the past few decades, computer-aided detection (CAD) has been a key area of study.

“Detection” and “Diagnosis,” accordingly, are two critical areas of CAD investigation [11]. The method to locate the lesion in the image is known as detection. Its goal is to lessen the observational load on medical professionals. The term “Diagnosis” refers to the technique used to identify probable ailments. It intends to give more assistance to clinicians. “Detection” and “Diagnosis” are commonly used in CAD systems. The area of concern is separated after the usual tissues in the “Detection” phase, and the lesion is analyzed toward providing an evaluation in the “Diagnosis” phase.

Fig. 2 displays the ultrasonic CAD system, which includes “Detection” and “Diagnosis.” Picture preprocessing, picture segmentation, feature extraction, and lesion classification are the four stages of the ultrasonic CAD system.

Figure 2: Basic CAD framework flowchart

5.1 Why an Ultrasound Image?

Ultrasound has numerous other medical usages beyond tracking fetal growth throughout pregnancy. This technology allows for the imaging of the heart, blood vessels, eyes, thyroid, brain, breast, abdominal organs, skin, and muscles. It is useful for identifying a range of medical disorders in various medical disciplines because of its adaptability and non-invasiveness.

5.2 Biometric Parameter

CRL (crown-rump length) delivers the most precise result, aimed at assessing the GA of a fetus aged 8 to 12. After thirteen weeks, the most reliable approach for detecting GA is the HC method [11]. Identification of these sections is necessary to test for prenatal diseases. Though, due to operator dependence, US images have a number of faults, including motion blurring, acoustic or sound shadows, boundary uncertainty, noise, reduction, low signal-to-noise ratio, and impacts [10]. As a consequence, these objects provide inaccurate feedback and conclusions [10]. Identifying anatomical features, inconsistencies, and measurement mistakes becomes harder as the outcome.

5.3 Autonomous Segmentation

The orientation of the fetus, the ultrasound device, maternal tissue, the expertise of the experts, and other factors all have a role in the inability to detect ideal features. Therefore, automated recognition is necessary for the measurement of biometric parameters. Additionally, an independent method can excerpt the Region of Interest (ROI) through the intended and anticipated outcomes [2]. This approach can therefore quickly and accurately section and measure fetal sections. This tactic significantly boosts the effectiveness of the workflow.

6  Materials and Methods

The suggested system aims to perform fetal fragmentation using U-Net architecture, thereby identifying various fetal biometric characteristics. In order to accomplish this, the model must be created as a procedure that accepts 2D ultrasonography images (sourced publicly available data from https://hc18.grand-challenge.org/, accessed on 15 September 2023) as the inputs, executes methodical feature extraction using those images, then undertakes image segmentation with regard to the fetus’s two primary parts: the head and belly. Depending on the type of picture, ellipses, lines, or polynomial curves remain fitted and hooked on the sectioned area after categorizations have been completed.

This technique will segment input pictures in order to estimate gestational age and evaluate fetal growth with head circumference (HC). The deployment of the approach may be separated into two works that will be executed sequentially: the initial is edge detection and recognition, and the other is object fitting. Fig. 3 shows the workflow of system model.

Figure 3: Workflow of system model

This process has the following five stages.

6.1 Data Preprocessing

The professionals annotated 2D head datasets from the photos that were gathered. The following step is to create masks from these photos. Again, the experts did not pre-annotate the remaining photographs. As a result, these photographs will be properly tagged by utilizing annotation software. Then resize; the majority of the photos have huge pixel values and are therefore unsuitable for feeding into the suggested design. Consequently, we will scale the photos to reduce their pixel values. We will adjust the resized photos to enhance the quality of the original images.

6.1.1 Annotation and Masking

The first step in our preliminary processing technique was to create mask pictures of the dataset. We had to manually markup 2D photo renderings of the head employing a marking tool that outputs the data in JSON format comprising the details of the ellipse. We advanced the requirements to produce mask pictures based on the JSON Mask information. To achieve this goal, we used OpenCV’s fillPoly() function.

We labeled the unprocessed images in the two-dimensional dataset. We used the contour lines from the annotated photographs to match and fill the ellipse form for the purpose of creating mask representations of the data. We investigated the Hough transform technique and then utilized OpenCV for together boundary spotting and elliptical adaptation to accomplish elliptical fitting. Fig. 4 presents a comprehensive comparison between the annotated image and the created mask image.

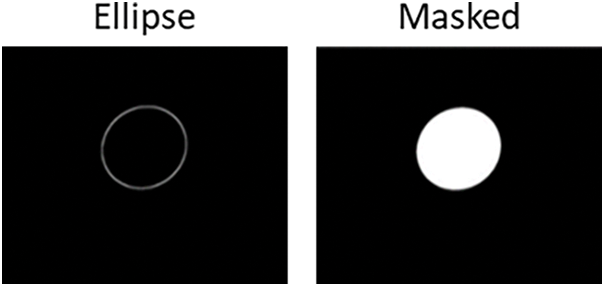
Figure 4: Automated image and generated mask image

6.1.2 Turning to Grayscale

We have #2563 fetus data points in 2D with varying pixel sizes. Between the 2563 photos, 2D images contain a single channel for grayscale pictures. To ensure uniformity across all of the information, we transformed them all into grayscale pictures using OpenCV’s bgr2gray technique.

6.1.3 Resizing

Considering the majority of the pixels within our data set are greater than 500 × 500, we downsized the image to 256 × 256 to avoid over-fitting our CAD model. After channel conversion and scaling, the picture data’s final dimension is 256 × 256 × 1, which will be used for the remainder of the classification job method. To resize the data, we utilized the Scikit-image library’s transform Resize() function. Fig. 5 shows the original image and resized grayscale image.

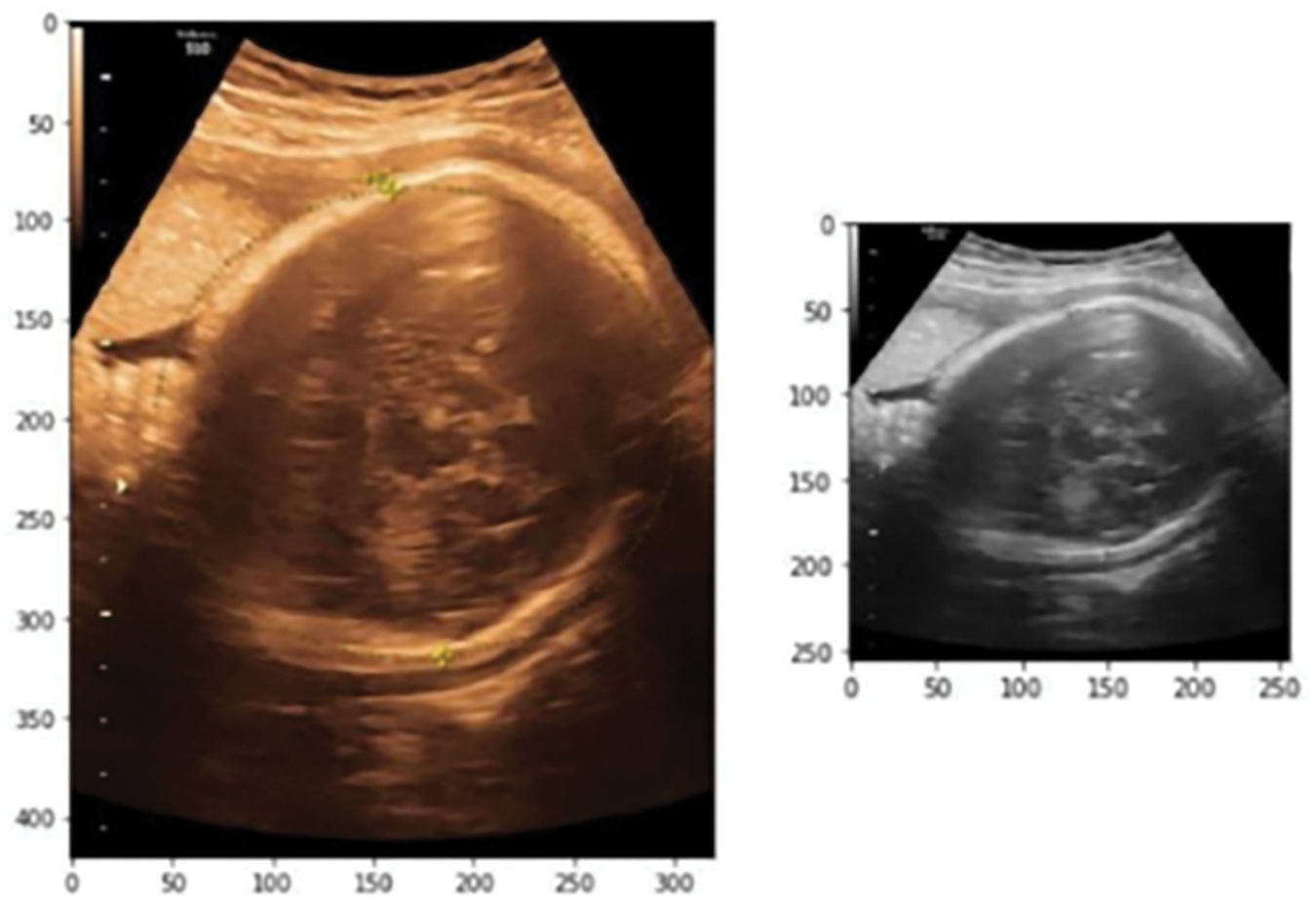
Figure 5: Original image and resized grayscale image

6.1.4 Normalization

Normalized all of the training and testing unprocessed data by dividing it by 255, then we stored the result in an array as a floating-point number. When dealing with masked data, we standardized it by reducing it by its mean value and then saved it. It’s stored in an array with the floating-point values 0.0 and 1.0, where 1 represents the white-colored emphasized area and 0.0 represents the black background.

6.2 Splitting

Once all of the essential pre-processing procedures have been completed, the picture determination will be divided into training, validation, and testing information.

6.3 Training

For training, the original pictures, then matching masked pictures, will be determined and provided to the model for fitting. The model will begin to learn its segmentation technique. We have 999 fetal data points in total, 236 of which are in 2D. In order to train and evaluate the system, we divided the 335 photos into two groups. From each of them, we set aside 80% of the photos for training the system and the other twenty percent for testing and result prediction.

The initial training and assessment data must be accurately mapped in order for the system to function. We pulled 25% out of the 80% of the information that we preserved to train the model. We divided the training information from the validation results using the train_test_split() function. The validation dataset determines if the training is contributing to the issue of model overfitting by assessing the results of the fitted model. We use the validation dataset to tune the model parameters. The testing sample is necessary for the final algorithm’s performance evaluation. Since the model kept the test results hidden throughout the training phase, the testing dataset can provide an unbiased evaluation of the model’s final outcome.

6.4 Testing

The U-Net architecture will divide the testing photos into their appropriate categories. Following training using annotated photos, the model determination foresees the segmentation of a piece of these fetal components based on the type of testing imaginings.

6.5 Fitting and Measurement

Fitting and Measurement: After segmentation, the model will fit an ellipse, line, or polynomial curve to the segmented region, depending on the type of image. We will use the elliptical fitting to measure the circumferences of the head and abdomen. We will later utilize this information to determine the gestational age.

7  Model Implementation and Performance Metrics

7.1 Head Circumference & Length Measurement

The measurement of head circumference defines the likelihood of fetal health concerns or complications and governs the monitoring procedure. For instance, rapid head growth can identify hydrocephalus or water on the brain. Again, abnormally delayed head growth could indicate a cephalic, or smaller-than-expected, head. First, we determined the contours of the head; subsequently, we used the Hough transform method to get the center points; and last, we utilized ellipse fitting to determine the short and long axes.

7.1.1 Finding Contours

We use the OpenCV function FindContours to identify contours in images. Images should be processed prior to guaranteeing proper contour detection. To find contours, we utilized the OpenCV library’s.findContour() function. This enabled us to detect and readily locate the limits of the infant’s head and abdomen in a picture.

7.1.2 Haar-Like Features

Haar-like features are a common choice for object detection, particularly in real-time applications like ultrasound imaging, due to their computational efficiency. These features are well-suited for detecting edges, lines, and rectangles, making them effective in capturing the contours of the fetal head in ultrasound images. They are particularly advantageous in scenarios where the focus is on distinguishing between light and dark areas, which is crucial in ultrasound images where the contrast between the fetal head and the surrounding tissue is significant. Additionally, Haar-like features can be quickly computed using an integral image, which enhances the speed of detection without compromising accuracy (grand-challenge.org). The effectiveness of Haar-like features in medical imaging, specifically for detecting anatomical structures, is supported by studies such as the work by Viola et al. [25], who demonstrated their use in real-time face detection.

7.1.3 The Random Forest

The random forest algorithm is chosen due to its robustness against overfitting and its ability to handle high-dimensional data, which is common in image processing tasks. This method is particularly effective when working with a large number of Haar-like features, as it can efficiently select the most relevant features while ignoring redundant ones. Random forests also offer the advantage of interpretability, allowing for an understanding of which features are most influential in detecting the fetal head. This is important in medical applications, where the interpretability of the model can aid in clinical decision-making (GitHub). Breiman’s [26] seminal work on random forests highlights their efficacy in various pattern recognition tasks.

7.1.4 Dynamic Programming

The selection of dynamic programming stems from its efficiency in solving optimization problems, particularly for tasks like fitting an ellipse to the detected fetal head. This method breaks down the problem into simpler subproblems, and then solves them recursively to find the optimal path or solution. In the context of ellipse fitting, dynamic programming helps minimize the error between the detected boundary of the fetal head and the ideal elliptical shape, ensuring that the measurements of the head circumference are as accurate as possible (grand-challenge.org). Bellman’s [27] work on dynamic programming provides the foundational theory that underpins its application in various optimization problems, including those in image processing.

7.1.5 Hough Transform Method

Hough Transform Method: Apparently, the key stage in ellipse recognition is detecting the center point. A common method is to find the center of the line in the picture that connects two locations with tangents parallel to each other. The midpoint may be the ellipse center if these two sites are on it. The HT method can rely on this regulation as its foundation. We used the Hough transform method to fit ellipses and get the center point. The Hough transform is a robust technique for detecting shapes within images, particularly when the shape can be represented parametrically, such as an ellipse. Its ability to identify shapes despite the presence of noise and partial occlusions makes it ideal for detecting the fetal head, which may not always be fully visible or clearly defined in ultrasound images. The Hough transform works by transforming the image space into a parameter space, where the desired shape (ellipse) corresponds to a peak in this space. This method is particularly effective in medical imaging, where precision in detecting anatomical shapes is critical (grand-challenge.org). Image processing literature has widely cited. Duda et al. [28] worked on the Hough transform, particularly in applications involving the detection of geometric shapes.

7.1.6 Ellipse Fitting

Ellipse Fitting: An ellipse in ultrasound images closely approximates the shape of the head, making elliptical fitting crucial for accurately measuring the fetal head circumference. This technique allows for precise measurement by ensuring that the best-fit ellipse closely follows the detected contour of the fetal head. By applying an elliptical fit, the method reduces measurement errors that could arise from irregular or partial shapes, ensuring consistent and reliable measurements across different images. Fitzgibbon et al. [29] offered a thorough method for least-squares ellipse fitting, widely utilized in diverse image analysis tasks, including medical imaging.

Using the center as a guide, we established the long and short axes of the ellipse. For the ellipse to then obtain the x, y coordinates as well as the long and short axes, we utilized the OpenCV library’s.fitEllipse() function.

We then used the parameters of both the short and long axes in the respective formulae to calculate the head circumference as show in Eqs. (1) and (2).

h=(a−b)2(a+b)2(1)

HC=π(a+b)(1+3h10+4−3h)(2)

We included the expected and true measurements of the first ten forecasted pictures of head circumference in Table 2. When we compared our predicted values to the original ones, we saw tiny discrepancies in the numbers of EHC and HC, which is why we got mistakes. The Table 2 shows that the mistakes differ from picture to image. In picture 4, in the preceding example, the actual head assessment is 6.8 cm, whereas the anticipated head circumference (HC) is 7.61 cm. This results in a prediction error of (7.61–6.8) = 0.81 cm. The overall mean error found while assessing head circumference is 0.571 cm. This indicates that, on average, there is a 0.571 cm difference between the projected and actual head circumferences.

7.2 Performance Metrics

Performance Metrics: To prevent overfitting, we gradually removed 50% of the information from each layer through both up-and down-sampling. Throughout the modeling procedure, the ReLu activation was employed in each layer to avoid the vanishing gradient issue, then the padding was preserved by way of “same.” The Adam optimizer was also utilized to optimize the technique. We set the learning rate at 0.0001. We set the total number of batches at 5, with 150 periods and fifteen phases per epoch. The picture classification and segmentation prompted an increasing number of researchers to recognize the potential for performance enhancement brought about by employing deep learning in the ultrasonic CAD system. The research randomly selected a training group of 137 instances. The models would assist medical personnel in tracking the development and health of the fetus during pregnancy.

Fig. 6 shows a scatter plot with a line graph depicting fetal head circumference (in millimeters) as it relates to gestational age (in weeks). The data points likely represent individual measurements, and the graph includes percentile curves, typically the 5th, 50th, and 95th percentiles, indicating the range within which most measurements fall at different gestational ages. The x-axis represents the gestational age in weeks, ranging from around 15 to 40 weeks. The y-axis represents the head circumference in millimeters, ranging from 100 mm to over 350 mm. The three curves (5th, 50th, and 95th percentiles) show how fetal head circumference typically increases as the pregnancy progresses. The 50th percentile line indicates the median head circumference at each gestational age. The 95th percentile shows the upper range, while the 5th percentile shows the lower range, indicating the spread of normal variations in fetal head circumference. Deviations from these percentiles can indicate potential health issues such as intrauterine growth restriction (IUGR) or macrosomia. Consistently low or high measurements (falling outside the 5th or 95th percentiles) may prompt further investigations. For computer-aided detection (CAD) systems, such a graph could serve as a benchmark for validating the accuracy of automated head circumference measurements. The comparison of CAD-derived measurements to established percentiles helps ensure that the system can reliably measure and interpret fetal growth.

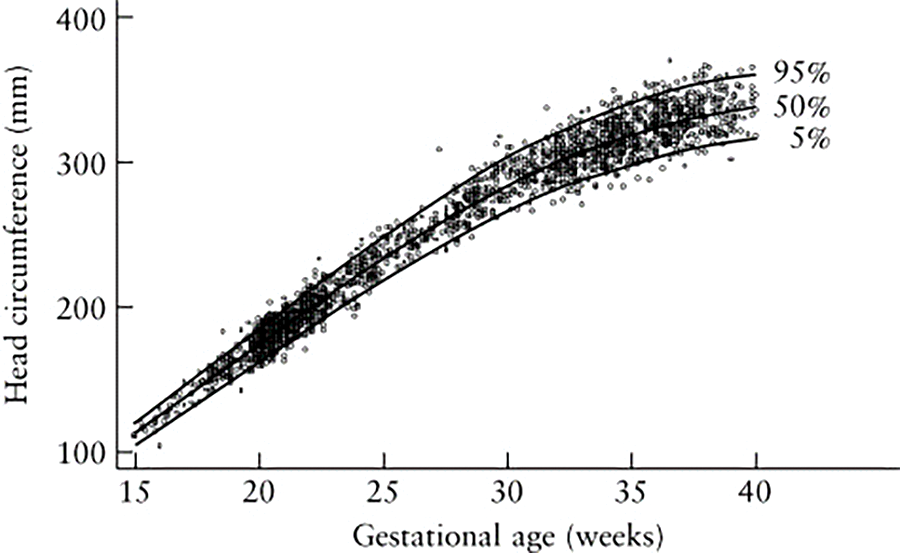
Figure 6: Shows the measurement of GA and HC in relation to the data

7.2.1 Dice Similarity Coefficient

The “Dice Similarity Coefficient” (DSC) performance statistic measures the precision of picture segmentation algorithms. It measures how much of an image’s divided sections actually overlap their expected counterparts. DSC values vary from 0 to 1, with higher numbers indicating more accurate segmentation. It is usual practice to use the Dice Similarity Coefficient (DSC) to measure how closely a predicted segmentation matches a reference ground-truth mask. An analytical technique used to compare two sets of data is called a “dice coefficient.”

The equation for this concept is shown in Eq. (3), where C and D are two sets.

DSC(C,D)=2∗(C∩D)/(C+D)(3)

A set with vertical bars either side refers to the cardinality of the set, i.e., the number of elements in that set; e.g., |C| means the number of elements in set C.

∩ is used to signify the intersection of two groups; and means the elements that are mutual to both sets.

7.2.2 Hausdorff Distance

Hausdorff Distance (HD) is a performance metric that evaluates the dissimilarity between expected and ground-truth segmentations in medical imaging and image processing tasks. It measures the maximum distance between the boundaries of two sets. We determine the average Hausdorff distance between two finite feature sets, X and Y as shown in Eq. (4).

dADH(X,Y)=(1X∑x∈Yminy∈Yd(x,y)+1Y∑x∈Yminx∈Xd(x,y))/2(4)

The directional average Hausdorff distance between points set X and Y is calculated by dividing the total amount of minimum distances between all points in X by the total amount of points in Y. The pointed average Hausdorff length from X and Y with the directed average Hausdorff distance between Y and X can be used to compute the average Hausdorff distance. In the domain of medical picture segmentation, the point sets X and Y refer to the voxels of the ground truth and the segmentation process, respectively. It is possible to determine the average Hausdorff distance in millimeters or voxels among the ground truth of the segmentation voxel sets. Eq. (4) can be expressed more succinctly as shown in Eq. (5).

Average Hausdorff distance =(GtoSG+StoGS)/2(5)

Eq. (5) as follows: GtoS is the pointed average Hausdorff distance between the ground truth and the segments, StoG is the pointed average Hausdorff distance between the segmentation and the ground truth, and G and S are the numbers of voxels in each component.

7.2.3 DF or HC Difference

DF or HC difference Frequently used to evaluate the effectiveness of segmentation algorithms, the DF efficiency statistic measures the difference between the boundaries of a segmented item and a fitted model. A performance indicator known as “Distance to Fit” (DF) or “Head Circumference (HC) Difference” quantifies the discrepancy between a model’s estimated segmented head circumference and the actual ground truth head circumference. It offers information about the precision of the segmentation method used to measure head circumference.

The complete variance between the assessed HC and the actual HC is used to determine the DF or HC difference as shown in Eq. (6).

DF=|Estimated HC−Ground Truth HC|(6)

Considering the assumed and ground truth HC values were more precisely aligned, a smaller HC differential indicates a higher degree of HC assessment accuracy. By measuring the absolute difference between the estimated and real HC values, the HC difference measurement helps to figure out how accurate and reliable HC estimation methods or models are. Table 3 summarizes the result of proposed system.

In the context of the first trimester, the Dice Similarity Coefficient (DSC%) for the training set was around 94%, with a variation of approximately ±6.5. Similarly, for the test set, the DSC% was approximately 94.8%, with a variation of about ±5.5. Regarding the Hausdorff Distance (HD mm), the model’s performance on the training set resulted in an average distance of 2.0 mm, with a variation of around ±2.5. In contrast, on the test set, the Hausdorff distance was about 1.6 mm on average, with a variation of approximately ±2.1. For the Distance to Fit (DF mm), during training, the average distance was −0.5 mm, accompanied by a variation of approximately ±6.7. In the test set, the average distance to fit was nearly −0.1 mm, with a variation of around ±6.3.

In the context of the second trimester, the Dice Similarity Coefficient (DSC%) achieved a high-performance level, with an average of 97.8% for both the training and test sets. The training set DSC variation was around ±1.7, while for the test set, it was approximately ±1.3. For the Hausdorff Distance (HD mm), the model demonstrated excellent accuracy. The average distance for the training set was 2.0 mm, with a narrow variation of about ±0.8. Similarly, on the test set, the average HD was 2.1 mm, with a slightly larger variation of around ±1.4. Regarding the Distance to Fit (DF mm), the model’s performance was also favorable. In the training set, the average distance was 0.8 mm, with a variation of approximately ±2.5. For the test set, the average DF was 0.9 mm, and the variation was slightly larger at around ±3.8.

For the third trimester, in terms of the Dice Similarity Coefficient (DSC%), the model exhibited strong performance. In the training set, the average DSC was 97%, with a small variation of approximately ±1.8. Similarly, for the test set, the average DSC was slightly higher at 97.5%, with a similar variation of around ±1.8. Regarding the Hausdorff Distance (HD mm), the model demonstrated reasonably accurate results. The training set’s average HD was 3.5 mm, with a variation of about ±2.2. On the test set, the average HD was slightly lower at 3.2 mm, and the variation was again around ±1.8. For the Distance to Fit (DF mm), the model’s performance varied. In the training set, the average distance was 1.1 mm, with a larger variation of approximately ±6.3. In contrast, on the test set, the average DF was lower at 0.7 mm, with a similar variation of around ±6.1.

8  Results of Segmented Image Analysis

We trained our data using an effective model, achieving an amazing training accuracy of 0.95, thereby ensuring an effective study. This high accuracy shows that the model was successful in identifying trends and connections in the data. We still need to confirm the model’s dependability and generalizability through additional analysis and validation.

We used a methodical approach to conducting our investigation. From marked-up photos, we produced ground truth images, and we preprocessed the information by normalizing and scaling it. We jointly created our dataset and model. We then divided the data, allocating 20% for training and the remaining 80% for testing. We further separated the training data into 25% for validation and 75% for training. Then, we fed the matching ground reality or mask photos into our model. We fed this data into the model, which in turn produced annotated images with precise segmentations. We were able to create a trustworthy model using this method and confirm its performance using a different test set.

Fig. 7 shows that the fetal head circumference’s three images unprocessed, projected, and actual—appear in succession. When compared to its ground realities, the projected image’s bounds are a little haphazard, with a particularly small discrepancy in the top right and bottom left corners. These might be the result of different head circumference bounds across images, despite the fact that our model correctly predicted the form. However, the oval shape of both photos is 90% comparable, which is enough to identify an embryonic head circumference.

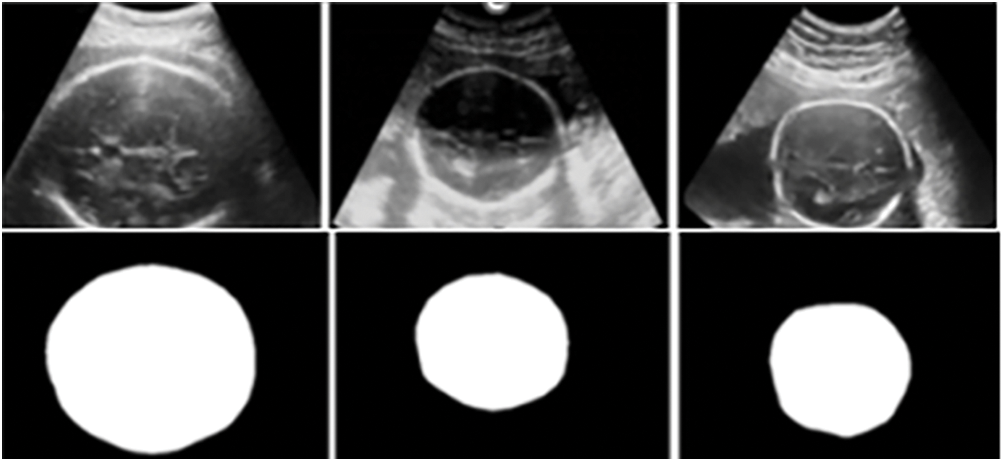
Figure 7: HC measurement data

9  Limitations of Research

Our model still has a few flaws that need to be addressed, as seen by the difference between training and validation loss, though we were able to decrease and endure a loss of 0.16 during the training phase, and ultimately there had been a 0.16 data loss in addition. Further research is necessary to identify the cause of the data loss and ensure the model’s performance and accuracy remain unaffected. For training to produce the best results, monitoring data integrity is essential; losing 0.26 data in the validation phase is quite unsatisfactory. From the latter half of the period to the end, the disparity widens. As a result, our model continues to improve, even though it learns accurately and quickly during the training phase but inadequately during the validation phase. This means that at the end of the validation step, our model falls victim to an overfitting situation. In conclusion, we believe that the dataset we are using to train our model is too small for the complexity of the model based on our assumptions. This leads to a loss in performance between the training and validation phases. We propose to increase the dataset size in order to overcome this problem and enhance our findings. This should result in improved performance overall and help to close the gap between training and validation loss.

10  Future Work

We aim to improve our model in the future by addressing issues such as overfitting and restricted generality. By lowering the model’s layer count, we hope to improve performance using the available data without manually expanding the dataset. This strategy will improve the model’s segmentation capabilities and increase its effectiveness and efficiency for practical applications.

11  Conclusion

This study proposes a completely unsupervised CAD-based fetus segmentation method for 2D ultrasonography pictures. Biomedical photos often feature a symmetrical layout. We will divide these images into segments, and then fit an ellipse, circle, or line to the segmented region based on the images. We can use these forms to identify various biometric characteristics. We will evaluate the model’s effectiveness during the testing phase by conducting comparison experiments and examinations. Therefore, we can divide ultrasound pictures using this architecture to identify different fetal biometrics. These biometrics determine the health of the fetus. As a result, an independent fetal fragmentation technique using CAD would make it easier to determine fetal biometric parameters efficiently, leading to the identification of defects relating to fetal health. This will enable the healthcare professionals to decide on suitable clinical actions. We believe our technology, adaptable to various clinical settings, will offer a potent solution to numerous pregnancy-related risks.

Acknowledgement: We would like to thank SRM Institute of Science and Technology for their support and contributions to this research.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: conceptualization, data collection, data analysis, writing—original draft, editing: Mohana Priya Govindarajan; review: Sangeetha Subramaniam Karuppaiya Bharathi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The dataset used in this study was obtained from https://hc18.grand-challenge.org/ (accessed on 15 September 2023) and is available at Zenodo, “DOI: 10.5281/zenodo.1322001.” The data is publicly accessible.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Cornthwaite et al., “Management of impacted fetal head at cesarean birth: A systematic review and meta-analysis,” Acta Obstet. Gynecol. Scand., vol. 103, no. 9, pp. 1702–1713, Sep. 2024. doi: 10.1111/aogs.14873. [Google Scholar] [PubMed] [CrossRef]

2. C. -W. Wang, “Automatic entropy-based femur segmentation and fast length measurement for fetal ultrasound images,” in 2014 Int. Conf. Adv. Robot. Intell Syst. (ARIS), Taipei, Taiwan, 2014, pp. 1–5. doi: 10.1109/ARIS.2014.6871490. [Google Scholar] [CrossRef]

3. O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional networks for biomedical image segmentation,” Med. Image Comput. Comput.-Ass. Intervent.–MICCAI 2015, Munich, Germany, Oct. 2015, vol. 9351, pp. 234–241. doi: 10.1007/978-3-319-24574-4_28. [Google Scholar] [CrossRef]

4. L. Zhang, X. Ye, T. Lambrou, W. Duan, N. Allinson and N. Dudley, “A supervised texton based approach for automatic segmentation and measurement of the fetal head and femur in 2D ultrasound images,” Phys. Med. Biol., vol. 61, no. 3, pp. 1095–1115, Jan. 2016. doi: 10.1088/0031-9155/61/3/1095. [Google Scholar] [PubMed] [CrossRef]

5. J. Jang, Y. Park, B. Kim, S. M. Lee, J -Y. Kwon and J. K. Seo, “Automatic estimation of fetal abdominal circumference from ultrasound images,” IEEE J. Biomed. Health Inform., vol. 22, no. 5, pp. 1512–1520, Sep. 2018. doi: 10.1109/JBHI.2017.2776116. [Google Scholar] [PubMed] [CrossRef]

6. J. Zhang, C. Petitjean, P. Lopez, and S. Ainouz, “Direct estimation of fetal head circumference from ultrasound images based on regression CNN,” in Proc. Third Conf. Med. Imag. Deep Learn., PMLR, Sep. 2020, vol. 121, pp. 914–922. [Google Scholar]

7. J. Zhang, C. Petitjean, and S. Ainouz, “Segmentation-based vs. regression-based biomarker estimation: A case study of fetus head circumference assessment from ultrasound images,” J. Imaging, vol. 8, no. 2, 2022, Art. no. 23. doi: 10.3390/jimaging8020023. [Google Scholar] [PubMed] [CrossRef]

8. T. Ghi and A. Dall’Asta., “Sonographic evaluation of the fetal head position and attitude during labor,” Am. J. Obstet. Gynecol., vol. 230, no. 3, pp. S890–S900, 2024. doi: 10.1016/j.ajog.2022.06.003. [Google Scholar] [PubMed] [CrossRef]

9. L. N. LaGrone, V. Sadasivam, A. L. Kushner, and R. S. Groen, “A review of training opportunities for ultrasonography in low and middle income countries,” Trop Med. Int Health, vol. 17, no. 7, pp. 808–819, Jul. 2012. doi: 10.1111/j.1365-3156.2012.03014.x. [Google Scholar] [PubMed] [CrossRef]

10. Y. Zeng, P. H. Tsui, W. Wu, Z. Zhou, and S. Wu, “Fetal ultrasound image segmentation for automatic head circumference biometry using deeply supervised attention-gated V-Net,” J. Digit. Imag., vol. 34, no. 1, pp. 134–148, Feb. 2021. doi: 10.1007/s10278-020-00410-5. [Google Scholar] [PubMed] [CrossRef]

11. T. L. van den Heuvel, D. de Bruijn, C. L. de Korte, and B. V. Ginneken, “Automated measurement of fetal head circumference using 2D ultrasound images,” PLoS One, vol. 13, no. 8, Aug. 23, 2018, Art. no. e0200412. doi: 10.1371/journal.pone.0200412. [Google Scholar] [PubMed] [CrossRef]

12. H. Lamba, “Understanding semantic segmentation with UNET,” 2019. Accessed: Sep. 30 2023. [Online]. Available: https://towardsdatascience.com/understanding-semantic-segmentationwith-unet-6be4f42d4b47 [Google Scholar]

13. A. Rampun, D. Jarvis, P. Armitage, and P. Griffiths, “Automated 2D fetal brain segmentation of mr images using a deep U-Net,” Lect. Notes Comput. Sci., vol. 12047, pp. 373–386, Nov. 2019. [Google Scholar]

14. H. Ryou, M. Yaqub, A. Cavallaro, A. Papageorghiou, and J. Noble, “Automated 3D ultrasound image analysis for first trimester assessment of fetal health,” Phys. Med. Biol., vol. 64, no. 18, Aug. 2019. doi: 10.1088/1361-6560/ab3ad1. [Google Scholar] [PubMed] [CrossRef]

15. D. Qiao and F. Zulkernine, “Dilated squeeze-and-excitation U-Net for fetal ultrasound image segmentation,” in 2020 IEEE Conf. Comput. Intell. Bioinform. Computat. Biol. (CIBCB), Via del Mar, Chile, 2020, pp. 1–7. doi: 10.1109/CIBCB48159.2020.9277667. [Google Scholar] [CrossRef]

16. J. J. Cerrolaza et al., “Deep learning with ultrasound physics for fetal skull segmentation,” in 2018 IEEE 15th Int. Symp. Biomed. Imag. (ISBI 2018), Washington, DC, USA, 2018, pp. 564–567. doi: 10.1109/ISBI.2018.8363639. [Google Scholar] [CrossRef]

17. J. Shao, S. Chen, J. Zhou, H. Zhu, Z. Wang, and M. Brown, “Application of U-Net and optimized clustering in medical image segmentation: A review,” Comput. Model. Eng. Sci., vol. 136, no. 3, pp. 2173–2219, 2023. doi: 10.32604/cmes.2023.025499. [Google Scholar] [CrossRef]

18. Z. Sobhaninia et al., “Fetal ultrasound image segmentation for measuring biometric parameters using multi-task deep learning,” in 2019 41st Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. (EMBC), Berlin, Germany, 2019, 6545–6548. doi: 10.1109/EMBC.2019.8856981. [Google Scholar] [PubMed] [CrossRef]

19. Y. Yang, P. Yang, and B. Zhang, “Automatic segmentation in fetal ultrasound images based on improved U-Net,” J. Phys.: Conf. Ser., vol. 1693, no. 1, Dec. 2020, Art. no. 012183. doi: 10.1088/1742-6596/1693/1/012183. [Google Scholar] [CrossRef]

20. M. Saii and Z. Kraitem, “Determining the gestation age through the automated measurement of the bi-parietal distance in fetal ultrasound images,” Ain Shams Eng. J., vol. 9, no. 4, Nov. 2017. doi: 10.1016/j.asej.2017.08.008. [Google Scholar] [CrossRef]

21. M. Alzubaidi, M. Agus, U. Shah, M. Makhlouf, K. Alyafei and M. Househ, “Ensemble transfer learning for fetal head analysis: From segmentation to gestational age and weight prediction,” Diagnostics, vol. 12, no. 9, Sep. 15, 2022, Art. no. 2229. doi: 10.3390/diagnostics12092229. [Google Scholar] [PubMed] [CrossRef]

22. I. Sarris et al., “Intra-and interobserver variability in fetal ultrasound measurements,” Ultrasound Obstetr. Gynecol, vol. 39, no. 3, pp. 266–273, 2012. doi: 10.1002/uog.10082. [Google Scholar] [PubMed] [CrossRef]

23. L. J. Wang et al., “Automatic fetal head circumference measurement in ultrasound using random forest and fast ellipse fitting,” IEEE J. Biomed. Health Inform., vol. 22, no. 1, pp. 215–223, 2018. doi: 10.1109/JBHI.2017.2703890. [Google Scholar] [PubMed] [CrossRef]

24. C. Yang et al., “A new approach to automatic measure fetal head circumference in ultrasound images using convolutional neural networks,” Comput. Biol. Med., vol. 147, Aug. 2022, Art. no. 105801. doi: 10.1016/j.compbiomed.2022.105801. [Google Scholar] [PubMed] [CrossRef]

25. P. Viola and M. Jones, “Rapid object detection using a boosted cascade of simple features,” Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. (CVPR), vol. 1, pp. 511–518, 2001. doi: 10.1109/CVPR.2001.990517. [Google Scholar] [CrossRef]

26. L. Breiman, “Random Forests,” Mach. Learn., vol. 45, no. 1, pp. 5–32, 2001. doi: 10.1023/A:1010933404324. [Google Scholar] [CrossRef]

27. R. Bellman, Dynamic Programming. Princeton University Press, 1957. Accessed: Sep. 30 2023. [Online]. Available: https://books.google.com.au/books?id=wdtoPwAACAAJ [Google Scholar]

28. R. Duda and P. Hart, “Use of the Hough transformation to detect lines and curves in pictures,” Commun. ACM, vol. 15, no. 1, pp. 11–15, 1972. doi: 10.1145/361237.361242. [Google Scholar] [CrossRef]

29. A. Fitzgibbon, M. Pilu, and R. B. Fisher, “Direct least-squares fitting of ellipses,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 21, no. 5, pp. 476–480, 1999. doi: 10.1109/34.765658. [Google Scholar] [CrossRef]