Adaptive Nonlinear PD Controller of Two-Wheeled Self-Balancing Robot with External Force

1  Introduction

Nowadays, two-wheeled self-balancing (TWSB) robots have become increasingly popular and are attracting more attention. TWSB robots are widely utilized in a variety of applications, particularly transport and exploration [1]. According to the inverted pendulum technique, whenever the angle of inclination away from the pivot point changes, the TWSB robot’s wheels speed up or slow down in order to maintain the robot’s balance. The TWSB robot is an underactuated mechanical system with high-order, multivariable, nonlinear, and tightly coupled components. As a result, numerous scientists are interested in conducting research and development on the TWSB robot [1–5].

The proportional derivative (PD) and proportional integral derivative (PID) controllers have been available for a long time and so far are the most commonly used control methods. The PD and PID control algorithms have been well received by engineering and research thanks to their straightforward form, the apparent physical significance of each parameter in the controller, and facilitative tuning. Although control theory and technology are developed over a long period of time, these controllers continue to play a significant role in control engineering. In [6], Mudeng et al. used a PID controller as a control system in a self-balancing robot with an inverted pendulum-like operating principle. In [7], a PID controller was developed to balance the TWSB robot in a standing stance and receive orders through Bluetooth signals to follow an intended trajectory. In order to improve the control performance, different types of nonlinear PD and PID (NPD and NPID) controllers have been introduced and successfully deployed. Zhou et al. [8] developed a nonlinear PI/PD control for a wind energy conversion system (WECS). In order to regulate contour tracking in machining applications and guarantee the quality of the finished product, Ouyang et al. [9] proposed a nonlinear PD (NPD) control rule in the position domain. Chen et al. [10] proposed a random averaging approach to investigate randomly stimulated single-degree-of-freedom (SDOF) highly nonlinear systems with fractional-order PD controllers that provide delayed feedback. For control of other nonlinear systems as in [11–15], many scientists have applied NPD/NPID controllers. They do, however, run into problems when it comes to standardized control systems. Generally, PD/PID and NPD/NPID operate well for linear or almost linear application systems. It performs poorly if the controlled system is nonlinear, time-varying, or has a significant time delay. In [16], an NPD controller was developed for redundantly actuated cable-driven parallel robots. Although the NPD controller is applicable to nonlinear systems, it also has some problems to solve. The problem mainly with the NPD controller [16] is the tuning of its parameters. In this work, the author used a trial-and-error approach to determine the appropriate parameters. Therefore, the controller’s efficacy was constrained, and in some cases, it may have performed poorly or been unstable. To solve this problem, a different control parameter optimization method is needed to achieve better performance.

Recently, many authors have designed controllers for TWSB robots using artificial intelligence. Anisimov et al. [17] built a TWSB robot with an intelligent system that makes use of an adaptation fuzzy controller and the Mamdani algorithm modified by relation models. Zhao et al. [18] presented several non-singleton general type-2 fuzzy logic controllers for a mobile TWSB robot that was under-actuated to increase the system’s capacity to prevent interference. In [19], Nguyen et al. proposed the global finite-time active disturbance rejection controller for tracking control of robots with uncertainties. In [20], the non-negative adaptive mechanism based on an adaptive nonsingular fast terminal sliding mode control strategy was developed to track the robot’s trajectories at high speeds and finite time in the presence of uncertainties and disturbances. Nguyen et al. [21] proposed a controller technique that combines sliding mode control and a chattering-free neural network. This control strategy adjusts for the system’s nonlinearity by updating the sliding mode condition parameter online, hence eliminating tracking errors. Sliding mode control, fuzzy logic systems and neural networks are useful tools for dealing with unknown nonlinearities. To the TWSB robot system, there are many other fuzzy and neural network controllers [22–24] that are developed, these systems run pretty steadily and meet the specified goals. It can be shown that robust tracking control strategies based on computational intelligence such as neural networks and fuzzy systems have been proposed above and are suitable for the TWSB robot system. In addition, some neural network structures applied to mobile robots and underactuated systems can be considered in [25–27]. In [25], Hassan et al. applied a neural network-based controller to wheeled mobile robots. The results demonstrated that the controller effectively handled parameter uncertainties and external disturbances, significantly improving the trajectory tracking accuracy and overall performance compared to traditional control methods. In [26], Yang et al. applied an adaptive neural network-based controller to uncertain underactuated systems and achieved good performance results. Ji et al. in [27] developed a sliding mode control method that incorporates a Radial Basis Function (RBF) neural network. This approach was designed to handle a class of underactuated systems experiencing bounded unknown disturbances as well as sensor and actuator faults. The RBF neural network was used to estimate the unknown functions within the system, providing robust compensation for disturbances. However, because of the complicated training requirements for fuzzy rules or neural weights, computational intelligences always require a significant amount of computation. The implementation of them might then be computationally demanding. Within this paper, an adaptive nonlinear proportional derivative (ANPD) controller is proposed to control the TWSB system with external force. Some other methods to control the TWSB system such as using neural networks in [28]. The main difference lies in the use of adaptive neural networks for the TWSB system in the mentioned paper, focusing on real-time adaptation and adaptive neural networks to learn and adjust control parameters based on data and changing environments. While ANPD controller uses non-linear PD parameters optimized for the specific dynamic model of the controller, focusing on precise control. The advantages of an ANPD controller come from its straightforward construction, which excels in transient response and disturbance rejection. The PID controllers use fewer resources compared to other intelligent control strategies and can be easily integrated into TWSB systems. The simplicity of the ANPD controller is based on its straightforward mathematical formulation and ease of implementation. It requires only a few tuning parameters to control and clearly defined physical meanings of these each control parameter. The control parameters setting of the ANPD controller is selected by a genetic algorithm [29–31], which helps the system to quickly reach a stable equilibrium. The control law has been verified to be stable according to the Lyapunov theory [32–33]. In addition, the efficacy of the proposed control law has been demonstrated via experiments and comparison with related control algorithms. The performance of the ANPD controller, PD controller, and NPD controllers [16] are compared to demonstrate efficacy. The experiment results indicate that, compared with the conventional PD and NPD controllers, the proposed ANPD controller can provide better trajectory tracking accuracy of the position and angle of the TWSB robot system. The experiments also provide a full description of how to tune the control settings.

The organization of the paper has five sections. Following the introduction, Section 2 shows the dynamic model of the TWSB robot. Section 3 presents the design of the NPD controller, where the proposed controller’s entire design process is thoroughly explained. In Section 4, numerical simulation and experimental results are provided to show the robust control performance of the proposed approach. Finally, Section 5 draws conclusions.

2  Dynamic Model of the TWSB Robot

Generally, the TWSB robot system has many complex constraints. This season mainly presents the robot’s ideal assumptions, kinematics analysis, and a dynamic model as in [34].

2.1 Kinematic Analysis Model

Consider a TWSB robot as shown in Fig. 1. We assume that the mass of the left wheel equals the right wheel, and they are denoted by M. The wheel’s radius is denoted by R. The two wheels are separated by L=2l. The middle portion of the robot, which is separate from the wheels, is a cylinder with a mass of Mc and a radius of Rc that is attached to the center axes of the two wheels. The robot’s centroid is on the central axes and the distance between it and the axes of the two wheels is denoted by h. The robot will veer off the vertical axis after a disturbance, with an α-pitch angle. The angle at which the robot will rotate around the central axis is β. For the robot to keep its balance, torque Ml and Mr must be applied to the left and right wheels, respectively. The wheels rotary with angles φ1 and φ2.

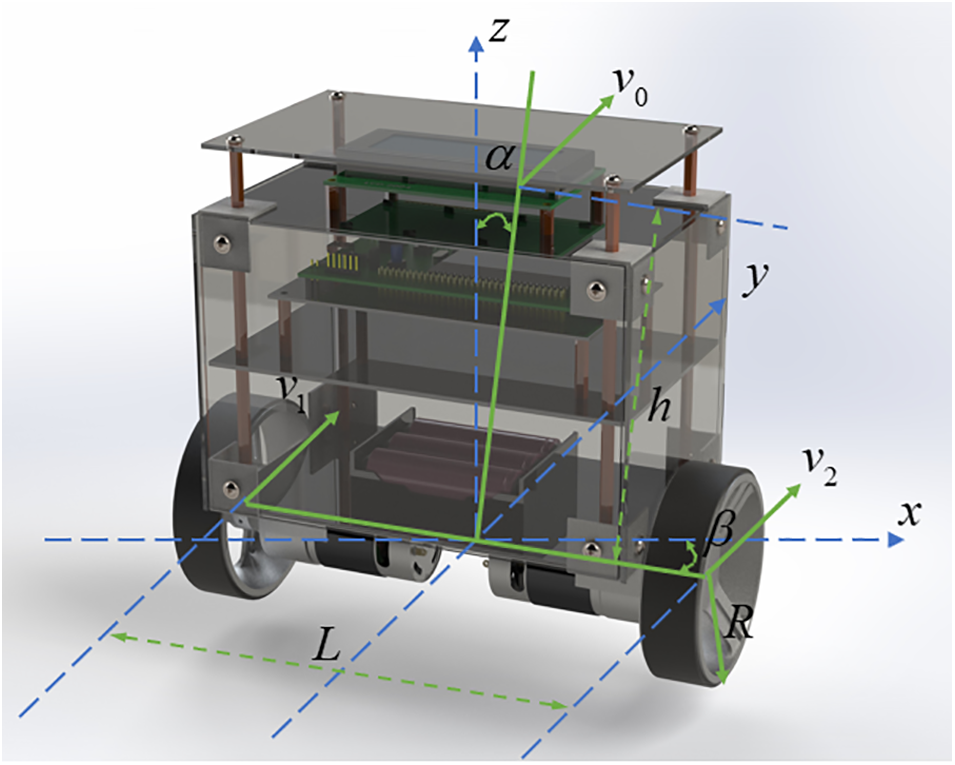
Figure 1: The two-wheeled self-balancing robot structure

The linear velocity of the left and right wheels is v1 and v2, respectively. The left wheel rotates at a rate of Rφ˙1 around the center axis. Similarly, the left wheel rotates at a rate of Rφ˙2 around the center axis. Jl and Jr are the moments of inertia of the left and right wheels, respectively. Two wheels rotate around their absolute instantaneous center of velocity is θ. So, the following mathematical formulas are established:

v1=Rφ˙1,(1)

v2=Rφ˙2,(2)

v0=v1+v22,(3)

β˙=|v1+v2|L,(4)

where L=2l.

The left and right wheel’s kinetic energy are calculated as follows:

T1=12Mv12+12Jl(v1R)2,(5)

T2=12Mv22+12Jr(v2R)2,(6)

where the moment of the inertia is Jl=Jr=MR2. Let’s vc denotes the cylinder’s centroid speed. The body moves by rotating at a rate of v0 around its absolute instantaneous center of velocity and at a rate of hα˙ around its central axis. The moment of inertia is Jc. Both v0 and hα˙ have the angle is α. Afterward, the following equation is formed from the vector correlation,

vc2=v02+(hα˙)2+2v0hα˙cos⁡α.(7)

The intermediate component’s kinetic energy is

T3=12Mcvc2+12Jcα˙2,(8)

where

Jc=43Mch2.(9)

Based on the equations above, the TWSB robot’s total kinetic energy is determined below:

T=T1+T2+T3.(10)

After the simplification, it is rewritten as:

T=MR2(φ˙12+φ˙22)+Mc8R2(φ˙1+φ˙2)2+12McRh(φ˙1+φ˙2)α˙cos⁡α+76Mch2α2.(11)

The total potential energy of the robotic system is calculated as follows, using the ground as a reference surface:

V=2MgR+Mcg(hcos⁡α+R).(12)

2.2 Dynamic Analysis Model

Following the TWSB robot shown in Fig. 1, we replace the system’s entire kinetic and potential energy to get its Lagrange operator.

L=T−V=MR2(φ˙12+φ˙22)+Mc8R2(φ˙1+φ˙2)2+12McRh(φ˙1+φ˙2)α˙cos⁡α+76Mch2α2−2MgR−Mcg(hcos⁡α+R).(13)

The Lagrange equation is

Q1=ddt(∂L∂q˙1)−∂L∂q1(i=1,2,3,…,k).(14)

where Q1 is the corresponding generalized force, L=T−Ve, and qi is the generalized coordinate. We select the left wheel’s angle φ1, the right wheel’s angle φ2, and the pitch angle α as the generalized coordinates for this system. The output torques of the left and right motors Ml and Mr correspond to the generalized forces.

Place the Lagrange operator in the equation and then arrange the variables, we have

J(q)q¨+f(q,q˙)q˙+G(q)=τ+Ξ(q,q˙,q¨),(15)

where the generalized coordinates are

q=[φ1,φ2,α]T,(16)

τ=[Ml,Mr,0]T,(17)

Ξ(q,q˙,q¨)=[Ξ1(q,q˙,q¨)Ξ2(q,q˙,q¨)Ξ3(q,q˙,q¨)],z∈Rn.(18)

J(q)=[2MR2+Mc4R2Mc4R2Mc2Rhcos⁡αMc4R22MR2+Mc4R2Mc2Rhcos⁡αMc2Rhcos⁡αMc2Rhcos⁡α73Mch],(19)

f(q,q˙)=[00−12McRhα˙sin⁡α00−12McRhα˙sin⁡α000],(20)

G(q)=[00−Mcghsin⁡α].(21)

3  ANPD Control Design

This section describes the proposed ANPD controller design. Firstly, it presents the basic structure of the NPD controller. Secondly, the control law of the proposed ANPD controller is designed based on the kinematic equation of the TWSB robot system, and the stability of the proposed control law is proven. Lastly, the GA algorithm is applied to quickly determine the proposed controller gain parameters.

3.1 Structure of NPD Controller

The linear PD controller takes the following form:

uL(t)=kpe(t)+kde˙(t),(22)

where kp and kd are the positive-definite matrices of proportional and derivative constant parameters, respectively, and e(t) is the system error.

Similar to the linear PD controller in structure, the nonlinear PD (NPD) controller can be any control structure of the following:

uN(t)=kp(⋅)e(t)+kd(⋅)e˙(t).(23)

where kp(⋅) and kd(⋅) are the time-varying proportional and derivative gains, respectively, which may be influenced by the state of the system, the input, or other factors.

For robotic applications, a number of NPD controllers have recently been presented as in [7–10]. When compared to linear PD controllers for robot control, the NPD controller provides better trajectory tracking and disturbance rejection capabilities.

3.2 ANPD Controller for the TWSB Robot

The ANPD controller proposed in this research is created by fusing a genetic algorithm and a nonlinear PD controller. On the basis of the dynamic model (15), and the NPD controller structure (23), the ANPD controller’s control law may be expressed as follows:

τe=J(q)q¨d+F(q,q˙)q˙d+G(q)+Kp(e)e+Kd(e˙)e˙,(24)

where q˙d and q¨d represent the end-intended effector’s acceleration and velocity. According to the various functions, the control legislation (24) may be separated into three parts. The first part is the dynamics compensation defined by the intended trajectory, which is expressed as follows:

τe1=J(q)q¨d+F(q,q˙)q˙d.(25)

The tilt angle compensation is the second part, which is expressed as follows:

τe2=G(q).(26)

The error elimination, which is the third part, which is expressed as follows:

τe3=Kp(e)e+Kd(e˙)e˙,(27)

where e=qed−qe is the position error of the position and angle of the TWSB robot system, Kp(e) and Kp(e) are symmetric, positive definite matrices of time-varying gains. Kp(e) and Kd(e˙) can be expressed as

Kp(e)=diag(kp|λ1|c1−1,kp|λ2|c1−1),(28)

Kd(e˙)=diag(kd|γ1|c2−1,kd|γ2|c2−1),(29)

where kp and kd are the positive constant gains, that can be derived from the structure of the NPD controller (23) as follows:

kp(e)={kp|e|c1−1|e|>δ1kpδ1c1−1|e|≤δ1,(30)

kd(e˙)={kd|e˙|c2−1|e˙|>δ2kdδ1c2−1|e˙|≤δ2.(31)

The following guidelines are used to determine the variables λn,γn, n=1,2: if |en|>δ1, then λn=en, else λn=δ1; if |e˙n|>δ2, then γn=e˙n, else γn=δ2; c1, c2, δ1 and δ2 are the intended parameters that should be adjusted in use.

The structure of the ANPD controller is shown in Fig. 2. There are two ANPD control loops. The outer control loop is responsible for calculating the setpoint value of the position to give the output value and updating that value into the input for the inner control loop. The inner control loop is responsible for calculating the angle value updated from the outer loop to give the control signal to the TWSB.

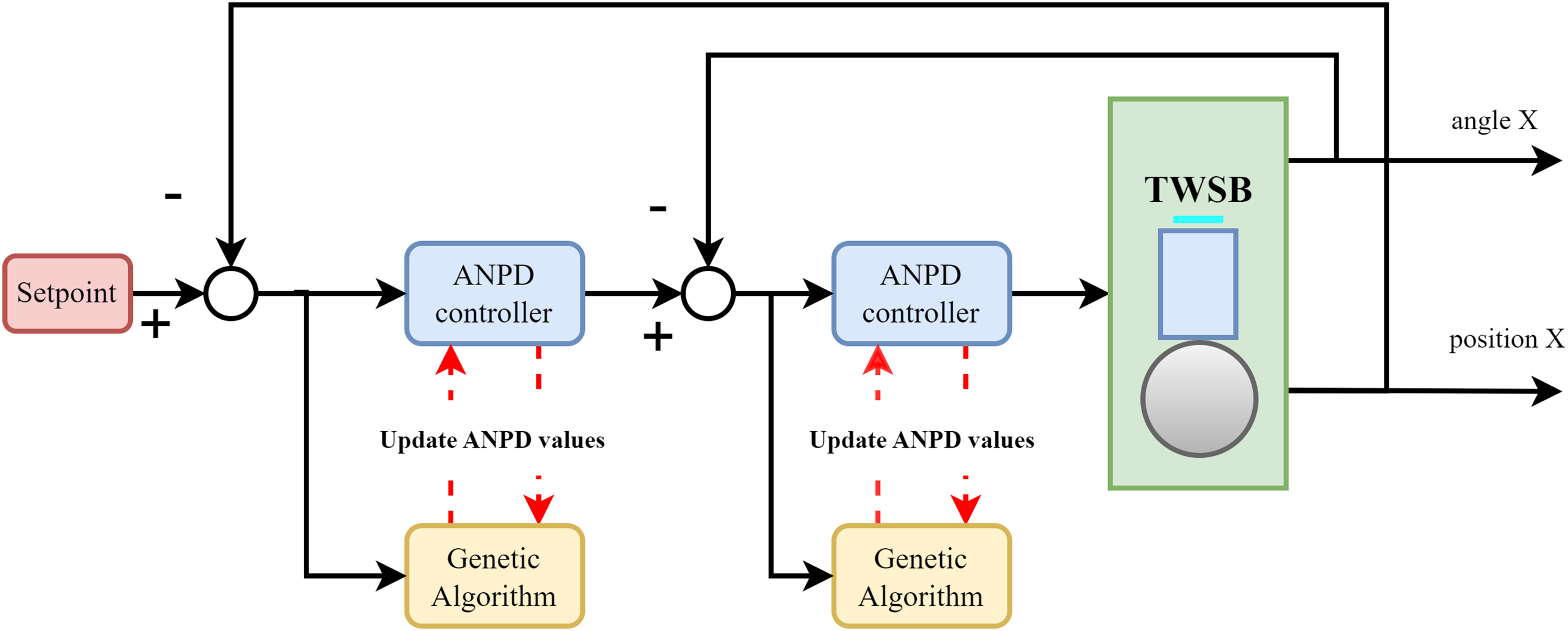
Figure 2: ANPD controller structure

The TWSB robot system driven by the ANPD controller’s asymptotic stability will be demonstrated in the sections that follow (24). We will start by presenting two important lemmas.

Lemma 1 [16] Let c(.) be a class K function and g(.) a continuous function. If g(λ)≥c(|λ|) ∀λ∈R, then ∫0λg(ω)dω>0, ∀λ≠0∈R and ∫0λg(ω)dω→∞ as |λ|→∞.

Lemma 2 Consider the continuous diagonal matrix Kp: Kp(e)=[kp1(e1)00kp2(e2)]. Assume that there exist class K functions ci(.) such that: λkpn(λ)≥cn(|λ|), λ∈R, n=1,2 then ∫0eμTKp(μ)dμ>0, ∀e≠0∈R and ∫0eμTKp(μ)dμ→∞ as e→∞.

Next, we will give a brief proof for Lemma 2. Define g(en)=kpn(en)en. Lemma 1 leads to the following constrain:

∫0eng(μn)dμn>0,∀en≠0∈R,(32)

which is equivalent to:

∫0enKpn(μ)μndμn>0,∀en≠0∈R.(33)

As a result, the function ∫0eμTKp(μ)dμ is positive definite. Lemma 1 also guarantees that the above integral is radially unbounded with respect to e, which means that ∫0eμTKp(μ)dμ→∞ as |e|→∞.

Theorem 1. The TWSB robot system controlled by the ANPD control rule (27) is asymptotically stable if the nonlinear gains Kp(e) and Kd(e˙) are determined by (28) and (29), respectively.

Proof Choose the Lyapunov function candidate as

V(e,e˙)=12e˙TJee˙+∫0eμTKp(μ)dμ,(34)

where

∫0eμTKp(μ)dμ=∫0e1μ1Kp1(μ1)dμ1+∫0e2μ2Kp2(μ2)dμ2.(35)

The workspace complies with the dynamic system’s structural properties (15) for the following: Je is a symmetric and positive definite matrix; J˙e−2Fe is the skew-symmetric matrix. Therefore, the first term in (34) is positive definite. Furthermore, the integral term can be regarded as potential energy generated by the controller’s position error-driven component. Next, the second term in (34) will be determined whether is positive definite. Considering kpn(en) is defined as

kpn(en)={kpn|en|c1−1|en|>δkpnδnc1−1|en|≤δn.(36)

Define class k functions cn(.) as

cn(|en|)={ϕnen|e|c1−1|en|>δ1ϕnenδnc1−1|en|≤δ1andkpn>ϕn>0.(37)

The integral term in (34) is a radically unbounded positive definite function, according to Lemma 2. V(e,e˙) is therefore a positive function. As a result of differentiating V(t) according to time as follows:

V˙(e,e˙)=e˙TJee¨+12e˙TJ˙ee˙+eTKp(e)e˙.(38)

The closed-loop system equation is expressed as follows by fusing the control rule (24), and the dynamic model (15):

Jee¨+Fee˙+Kp(.)e+Kd(.)e˙=0.(39)

The following results are obtained by multiplying both sides of (39) by e˙T and then entering the resulting equation into (38):

V˙(e,e˙)=−e˙TKd(.)e˙+12e˙T(J˙e−2Fe)e˙.(40)

Taking the structural J˙e−2Fe attribute into consideration, one can have e˙T(J˙e−2Fe)e˙=0.

V˙(e,e˙)=−diag(kd|γ1|c2−1,kd|γ2|c2−1)e˙2,(41)

where kd is the positive constant gain, therefore V˙(e,e˙) is a semi-negative definite matrix. Combined with (34), and (41), the law control (24) of the TWSB robot system is uniformly stable.

3.3 Parameter Optimization

Optimization algorithms are important for optimizing controller parameters. Studies such as [35] have demonstrated the effectiveness of genetic algorithms in optimizing PID controller parameters for complex systems like continuous stirred tank reactors. This method efficiently improves system stability and performance compared to traditional tuning methods. Similarly, the study in [36] illustrates the application of FOPID controllers in improving idle speed control performance in internal combustion engines. This approach enhances control precision and robustness, showcasing the advantages of fractional-order control in automotive applications.

The genetic algorithm (GA) employs a stochastic global search technique based on the concepts of natural selection and genetically modified offspring [26]. According to Darvin’s “survival of the fittest” principle, GA works on a population of alternative solutions to arrive at a solution that is becoming closer to reality. Prior to the start of GAs, persons or current approximations are represented as strings known as chromosomes, which are constructed over some alphabets, such that the genotype (chromosome value) is uniquely mapped on the decision variable (phenotypes) domain. Each chromosome, which is made up of a number of genes encoded using binary codes, may be viewed as a potential solution to the difficulties. The population of the upcoming generation is built on a set of chromosomes similar to this one. According to GA, chromosomes in one generation are driven to develop into a superior one through reproduction, crossover, mutation, and fitness function [25–27].

1) Reproduction: The method of choosing the most advantageous chromosomes to pass on to the offspring. It decides how often a specific individual is selected for reproduction and, as a result, the number of offspring an individual will have.

2) Crossover: Chromosomes from the randomly chosen group of parents are switched during crossover to create offspring.

3) Mutation: In mutation, a probability dictated by the mutation rate leads to the alteration of a set of randomly chosen genes on the parent chromosomes.

The objective function defines the process of separating undesirable chromosomes from the rest and choosing those that are most suitable for reproduction. Typically, the objective function is converted into a measure of relative fitness using the fitness function [27]. Thus,

J(y)=ρ{j(y)}.(42)

where J(y) represents the resultant relative fitness and (y) is the objective function, and ρ converts the objective function’s value to a nonnegative integer. Only a specific number of chromosomes are chosen and passed on to the following generation based on the fitness function value. GA is frequently terminated after a predetermined number of generations, and then the problem definitions are tested against the best member of the population. GA is very different from conventional search and optimization techniques. The following list includes the main distinctions.

1) GA doesn’t just look at one point; it looks at a population of points concurrently.

2) GAs is not reliant on supplementary knowledge or derived information; the objective function and associated fitness levels are the only factors influencing the search’s direction.

3) GAs employs probabilistic transition rules as opposed to deterministic ones.

4) Instead of working directly with the parameter set, GAs encodes it (except where real-valued individuals are used).

To find the optimal parameters for the NPD controller, the objective function is selected as: J=min[E1(i)+E2(i)]. The required parameters for searching the factor for an ANPD controller are shown in Table 1.

4  Numerical Simulation and Experiment

This section presents the numerical simulation and experimental results. The system structure and performance evaluation are detailed.

4.1 Numerical Simulation

The simulations in this portion make use of a TWSB robot [1] as shown in Fig. 1 to demonstrate the effectiveness of the proposed controller. The kinematic parameters of the TWSB robot system are M=0.3(kg), R=0.05(m), Mc=0.1(kg), Rc=0.01(m), l=0.09(m), h=0.12(m), g=9.81 (m/s2).

In order to show how performance has improved, the proposed controller is contrasted with the PD controller and the NPD controller [16]. The parameters are set as follows: c1=0.5, c2=1.1. The coefficients of the proposed controller and PD controller are selected through the GA algorithm as follows: kp1=39.14, kd1=67.29, kp2=29.93, kd2=6.2. The parameter of the NPD controller is simulated according to the value in [16]. The simulations are run in MATLAB/Simulink, the simulation time is set as 10 s, and the sampling time is set as 0.01 s.

The effectiveness of the proposed controller is assessed using two distinct examples to test the trajectory tracking simulations. In Case 1, we simulate the proposed controller operation when there are no external forces. This is the initial evaluation as well as a comparison point for the fault situations that follow. In Case 2, we supply an external force impact on the robot as follows: Ξ(q,q˙,q¨)=[00Ξ3(q,q˙,q¨)]T, where Ξ3(q,q˙,q¨)=23π180×exp⁡(−(t−3)20.53)(rad/s). This external force is shown in Fig. 3. This case depicts the controller’s response when the system is subjected to an external force.

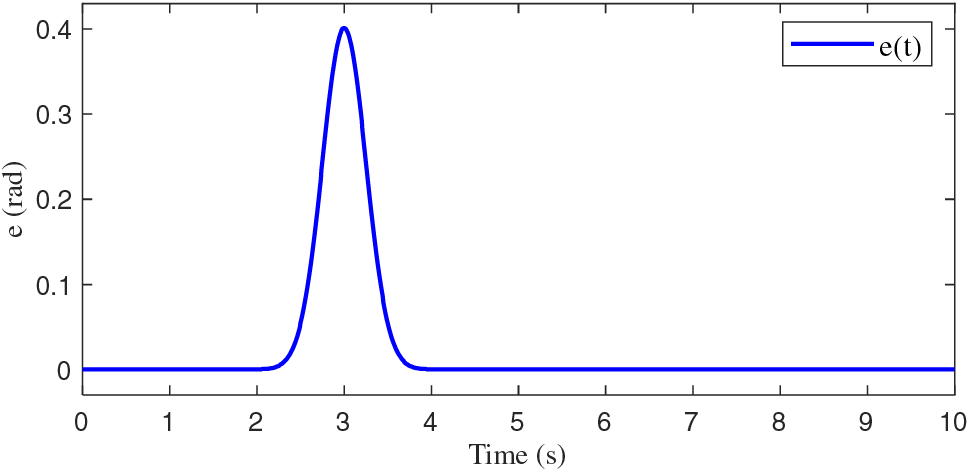
Figure 3: The external force

The simulation outcomes are shown in Figs. 4 and 5. The tracking inaccuracy of the angle and position in Case 1 is depicted in Figs. 4a and 5a. It is obvious to observe that NPD and ANPD controllers have met Balancing requirements. Meanwhile, the PD controller oscillates unstably and tends to collapse. Especially, ANPD controllers perform smooth tasks significantly more. Figs. 4b and 5b show the values of tracking inaccuracy of the angle and position during Case 2. When encountering an external force, the proposed controller is capable of bringing the system back to the desired equilibrium. Besides, the proposed controller performs fast tasks significantly more efficiently. Fig. 6 presents the values of tracking control signal u during both simulation cases. It is obvious that the ANPD controller’s graph line is more even and less variable in both cases. Based on the simulation results, it has initially been shown that the ANPD controller is optimal and more efficient than the PD and NPD [16] controllers.

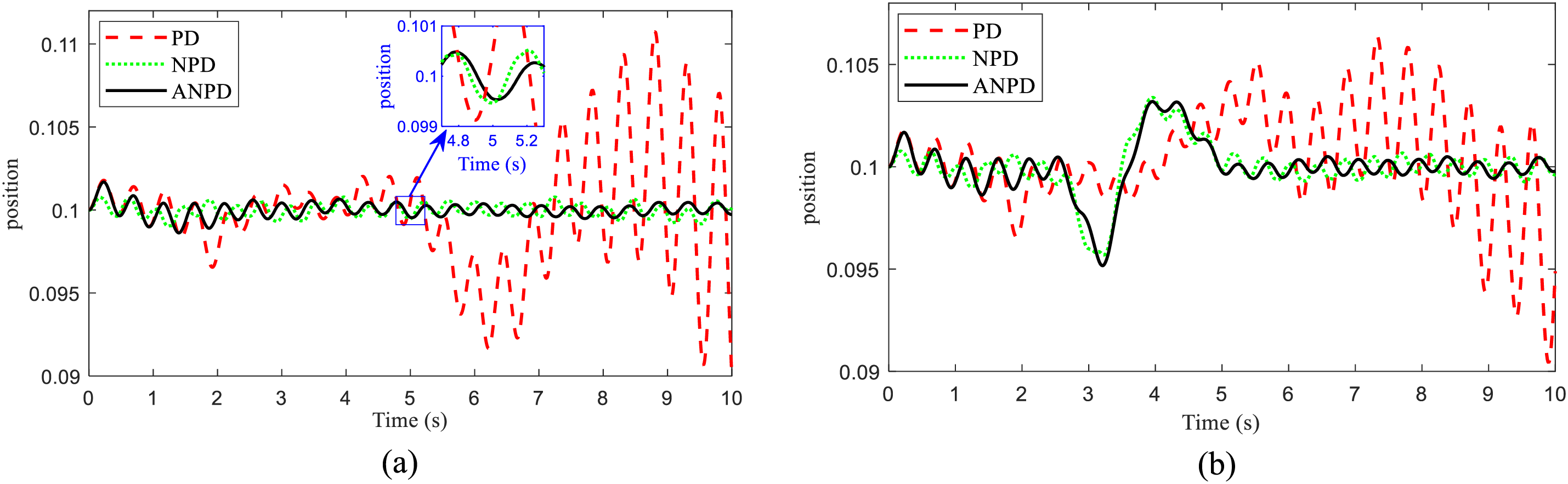
Figure 4: The position response of TWSB robot in simulation: (a) Case 1, (b) Case 2

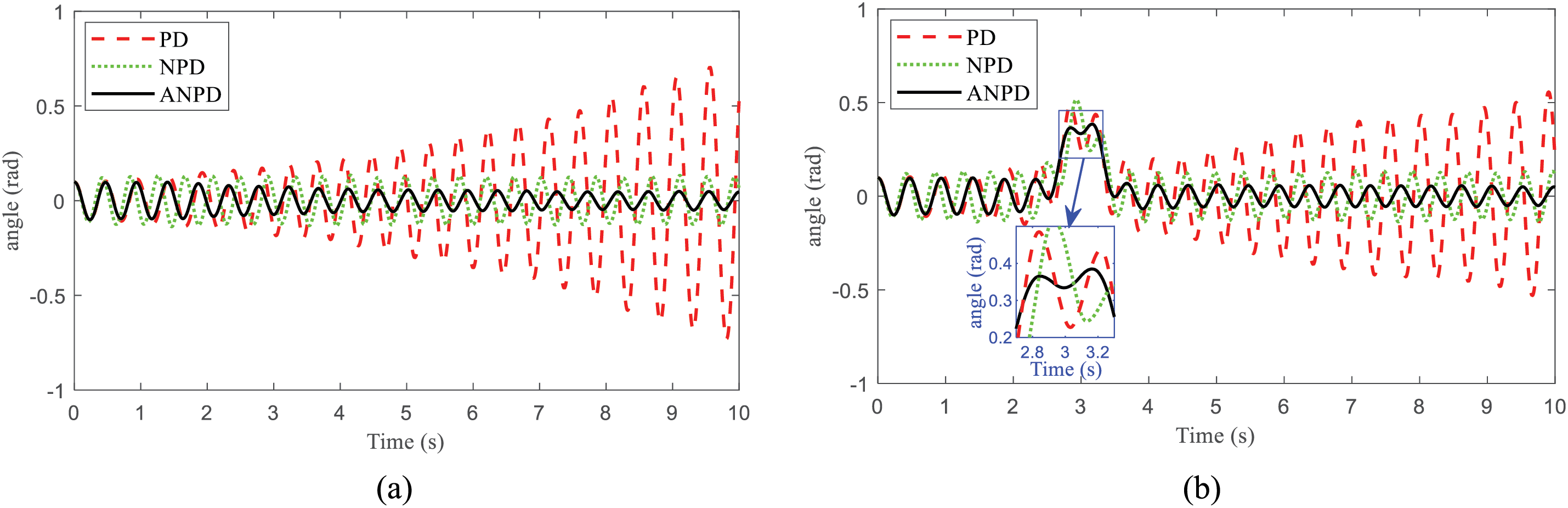
Figure 5: The angle response of TWSB robot in simulation: (a) Case 1, (b) Case 2

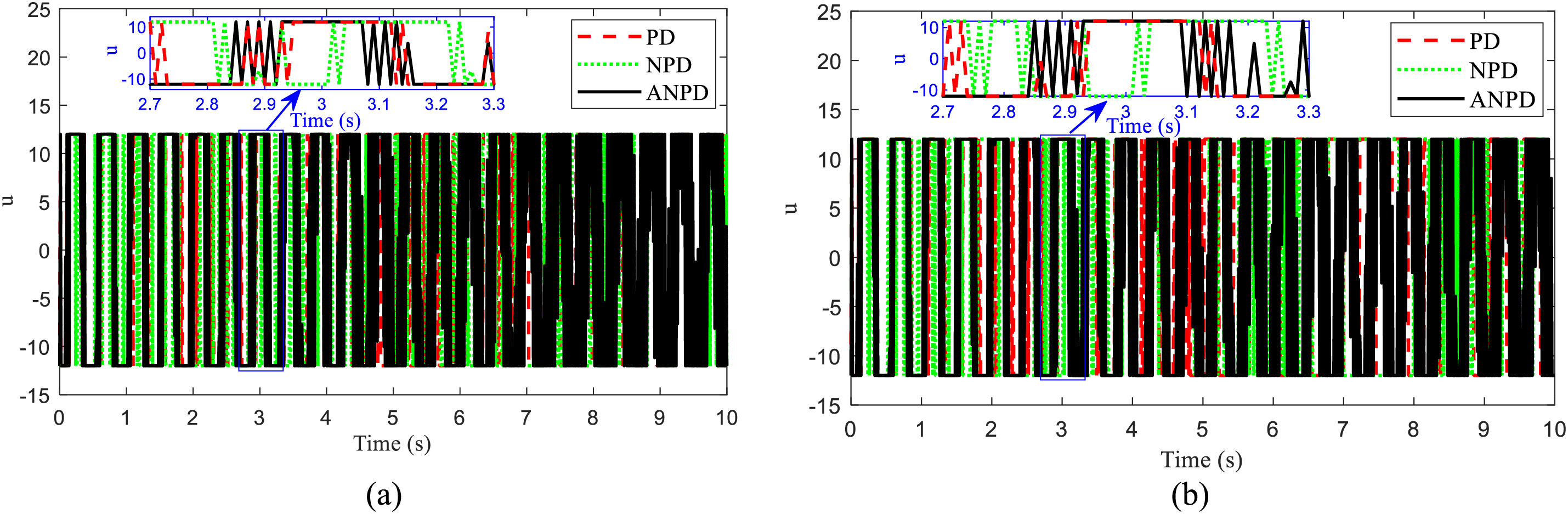
Figure 6: The signal control response of TWSB robot in simulation: (a) Case 1, (b) Case 2

To see more clearly the superiority of the ANPD controller, we choose the control parameter set that has not been optimized by GA as follows: c1=0.5, c2=1.1, kp1=50, kd1=77, kp2=59, kd2=3. The simulations run in 2 cases: without external forces and subject to external forces as in the simulations case when the parameter set is optimized by GA.

Fig. 7a,b shows position control under normal and noisy conditions. Under normal conditions, the PD controller is unstable with significant fluctuations, the NPD controller is more stable but not optimal, and the ANPD controller has minimal fluctuations and superior stability. Under noisy conditions, the PD controller’s performance worsens significantly, the NPD controller handles noise better but still has disturbances, and the ANPD controller remains robust and effective. Fig. 8a,b shows angle control under normal and noisy conditions. The PD controller performs poorly with significant oscillations, the NPD controller reduces oscillations but still has noticeable fluctuations, and the ANPD controller has the least oscillations and quickest settling time. Under noisy conditions, the PD controller is highly sensitive to noise, the NPD controller shows improved resistance but still significant oscillations, and the ANPD controller demonstrates superior noise resistance. Fig. 9a,b shows control signals for the PD, NPD, and ANPD controllers. The PD controller is highly erratic, the NPD controller has some variability, while the ANPD controller is stable and consistent. The inset highlights the ANPD controller’s superior precision and reliability.

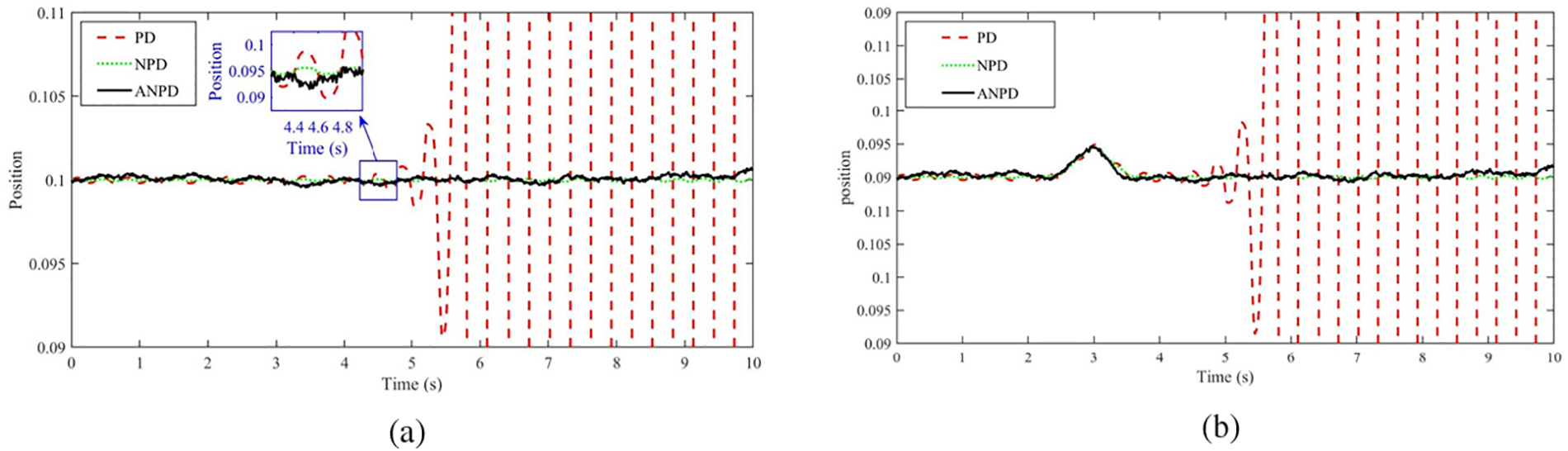
Figure 7: The position response of TWSB robot in simulation without GA: (a) Case 1, (b) Case 2

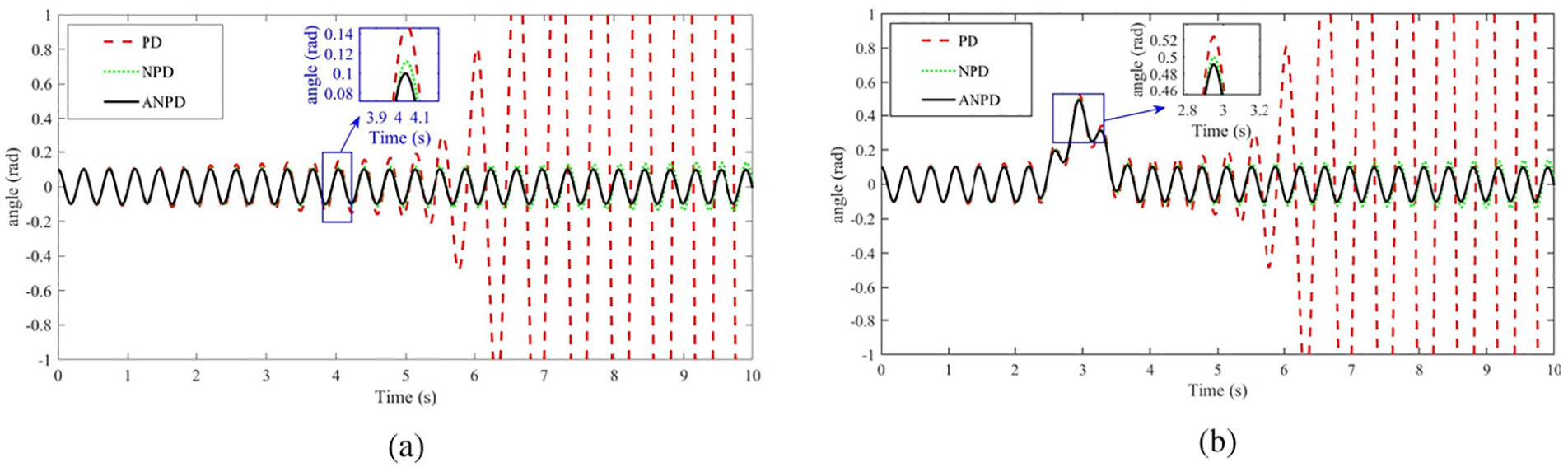
Figure 8: The angle response of TWSB robot in simulation without GA: (a) Case 1, (b) Case 2

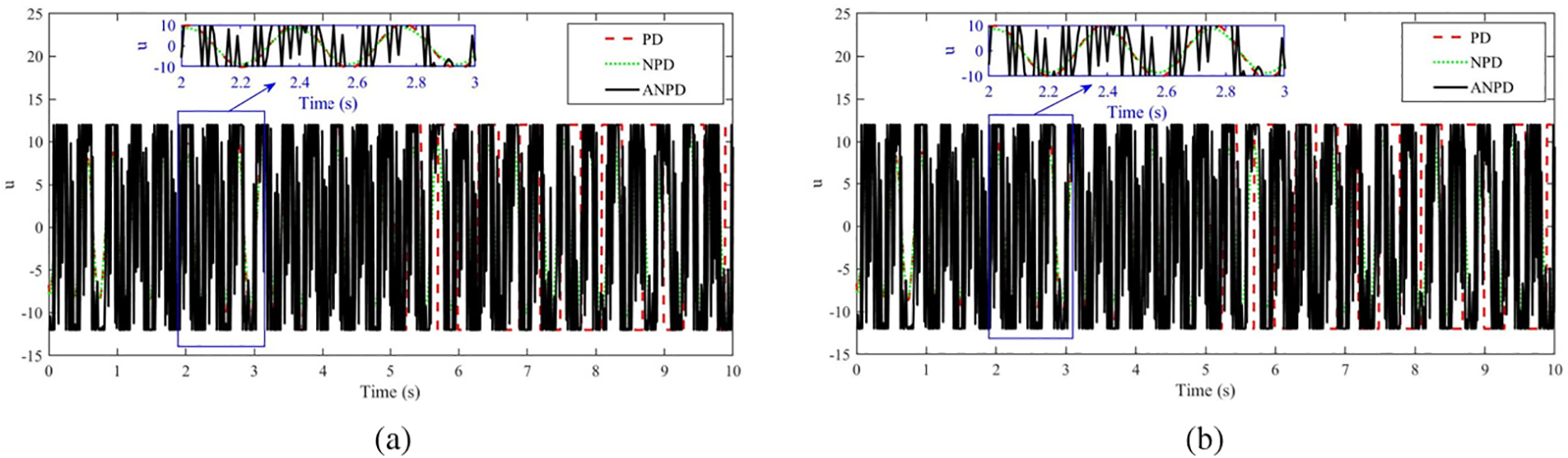
Figure 9: The signal control response of TWSB robot in simulation without GA: (a) Case 1, (b) Case 2

4.2 Experiment

In this section, in order to further confirm the efficiency of the proposed controller, certain experimental findings are given. An image of the reality of the TWSB robot system is shown in Fig. 10. Fig. 11 presents the important parts of the TWSB robot.

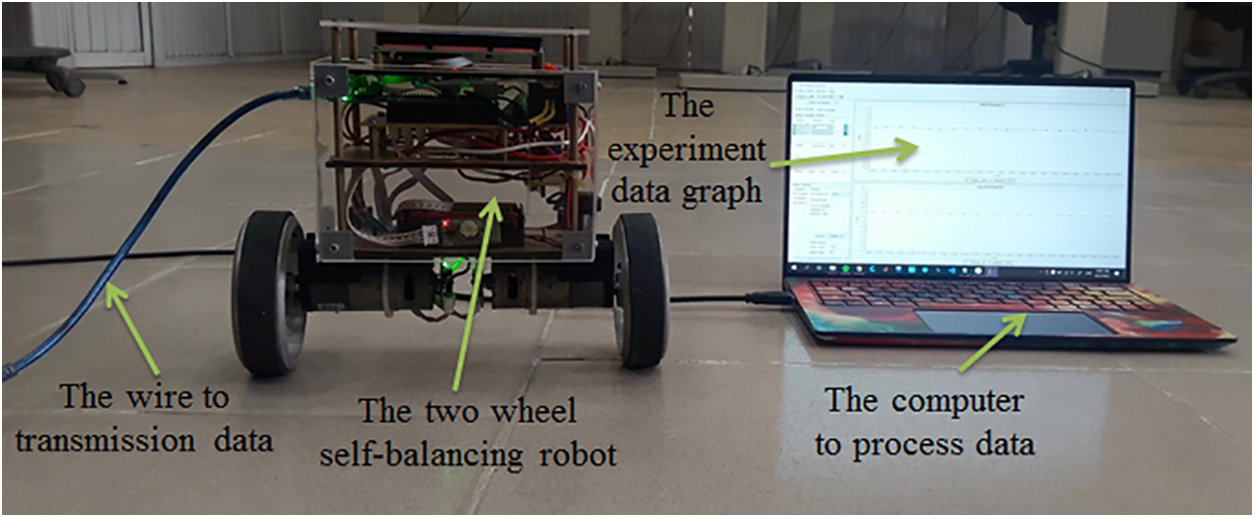
Figure 10: The TWSB robot system

Figure 11: The details of important components of TWSB

TWSB robot has two direct current servo motors with a limit voltage is 12 volts. Two soft rubber-coated hard wheels are used for the movement of the robot with a mass parameter of 0.03 kg and a radius parameter of 0.05 m. The kinematic parameters of the TWSB robot system are provided in Section 4.1 including the total robot mass is 3 kg, height is 0.22 m and width is 0.1 m. We program the NPD controller with Keilc V5, and the algorithms run on an STM32f4 Discovery board at 100MHZ. The real-time system utilized for control has a 1 ms sample rate.

The maximum velocity, maximum acceleration, and jerk for the TWSB robot in the experiment are 0.5(m/s),0.1(m/s2), and 0.4(m/s2), respectively. The dynamic parameters in (25), the tilt angle parameters in (26), and the error elimination parameters in (27), which are used to implement the controller (24), are adjusted and established by the real tests as follows: c1=0.1, c2=0.3. The experimental values for the dynamic parameters are chosen to be nominal values.

To show the improvement in different cases of the proposed controller, we tested in two cases as follows. In Case 1, we gave the system work on its balance on a less slippery surface. The system is turn controlled by PD, NPD, and ANPD controllers. In Case 2, the initial conditions of the three controllers are still tested similarly to Case 1, it is shown in Fig. 12. However, we employ an m=0.4(kg) item of mass to exert an external force on the system while it is self-balancing. This helps us compare the ability to bring the system to the equilibrium point of the three controllers.

Figure 12: The TWSB robot is attached to an external item. (a–d) The TWSB robot in different interference situations

The position and angle responses in experiments of the TWSB robot system at two conditions are shown in Figs. 13 and 14. The results of Case 1 are shown in Figs. 13a and 14a. Similarly, the results of Case 2 are shown in Figs. 13b and 14b. The simple PD controller cannot meet the most basic requirements when applied to a nonlinear system like a TWSB robot system. The NPD [16] controller can make the system self-balancing, but the system fluctuates quite a lot and moves a lot to balance. Furthermore, the NPD controller is unreliable and unable to restore the system’s equilibrium when it is subjected to noise. The proposed ANPD controller solves all the above problems. When there is interference, the system oscillates very little and rapidly recovers to the equilibrium position, which also ensures that the TWSB robot system operates steadily. Fig. 15 presents the values of tracking control signal during both simulation Cases 1 and 2. The experimental results also show that the control signal of the ANPD controller is better than that of the PD and NPD [16] controllers.

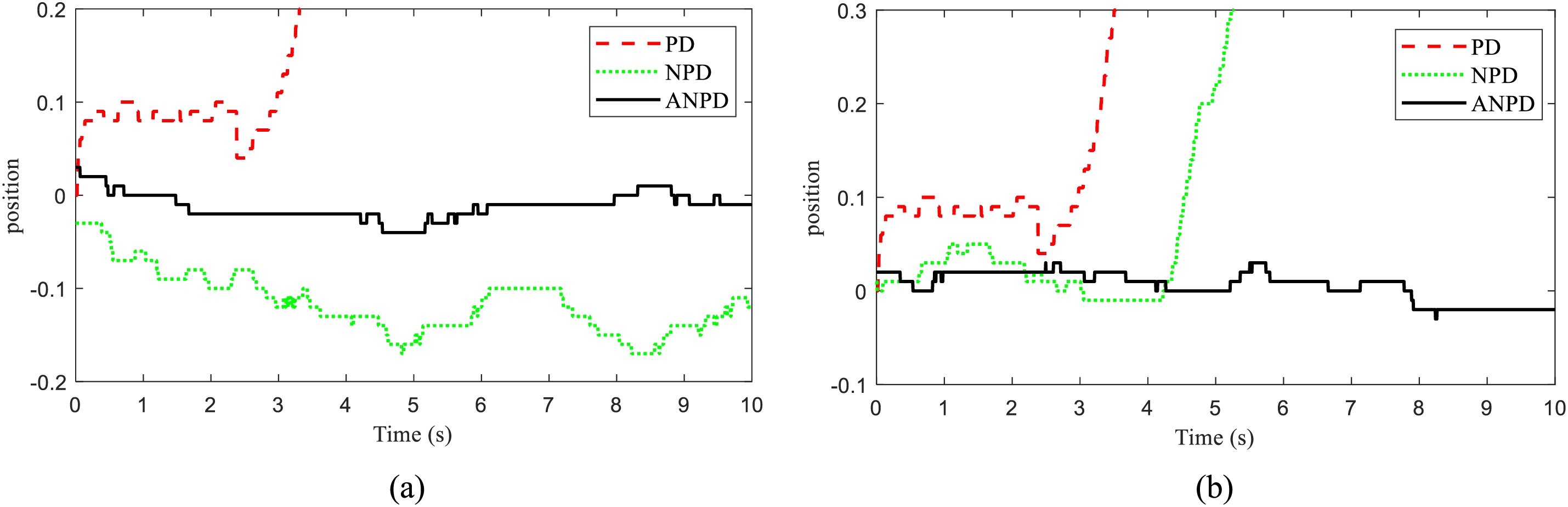
Figure 13: The position of TWSB robot in experiment: (a) Case 1, (b) Case 2

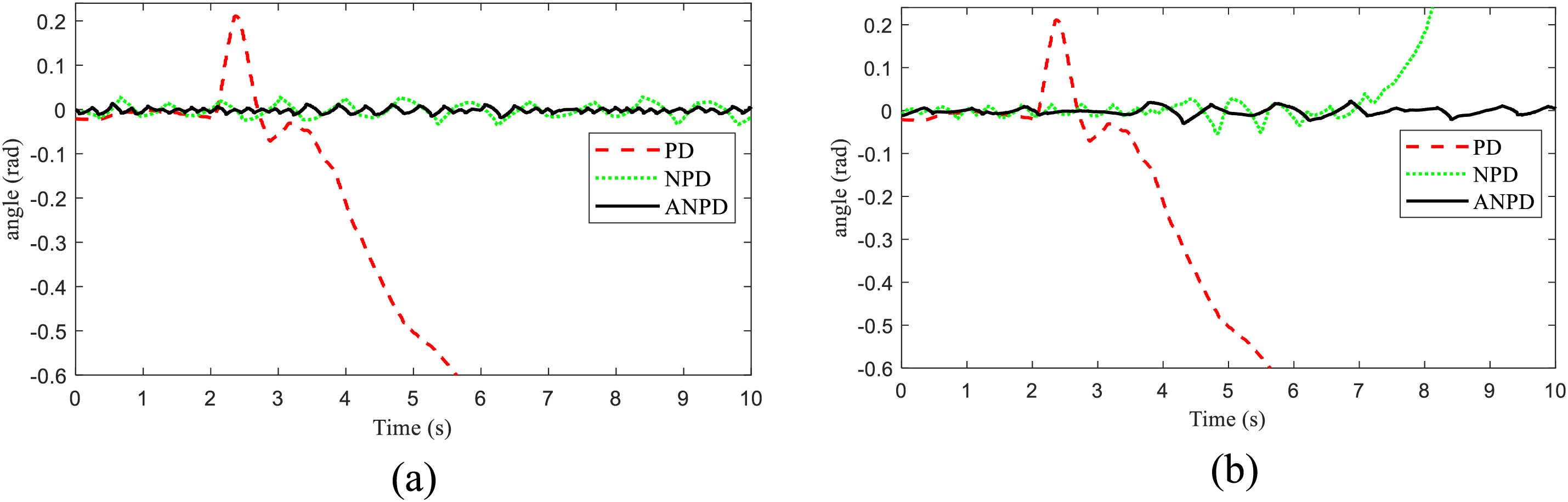
Figure 14: The angle response of TWSB robot in experiment: (a) Case 1, (b) Case 2

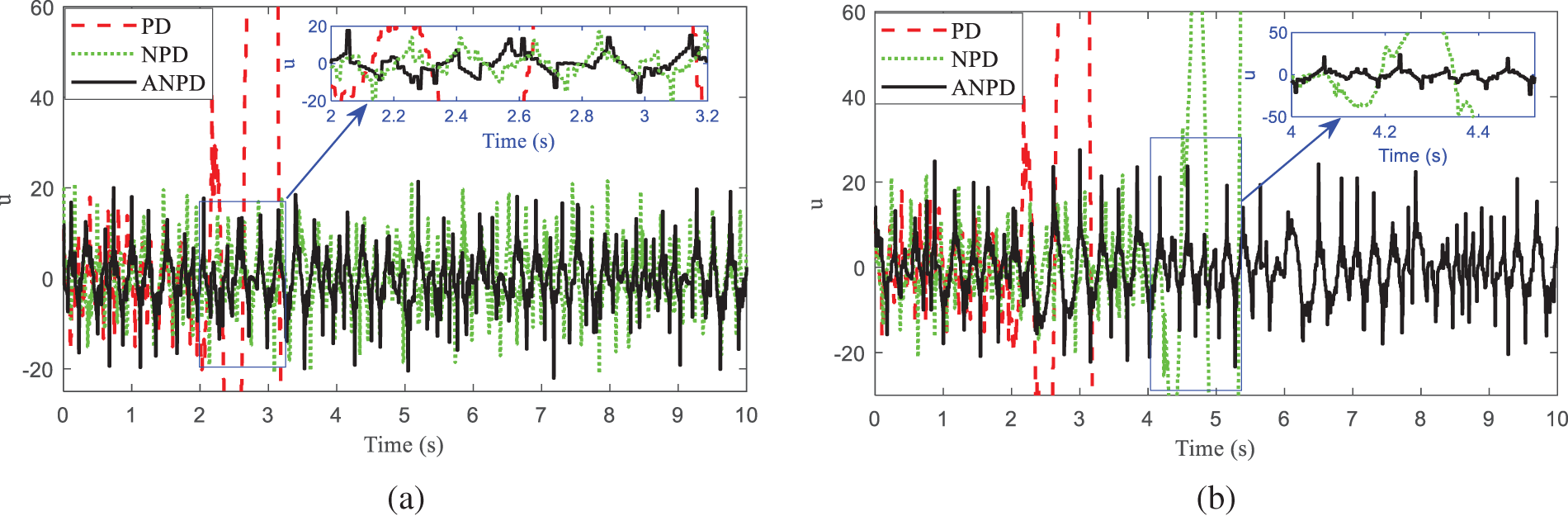
Figure 15: The control signal u of TWSB robot in experiment: (a) Case 1, (b) Case 2

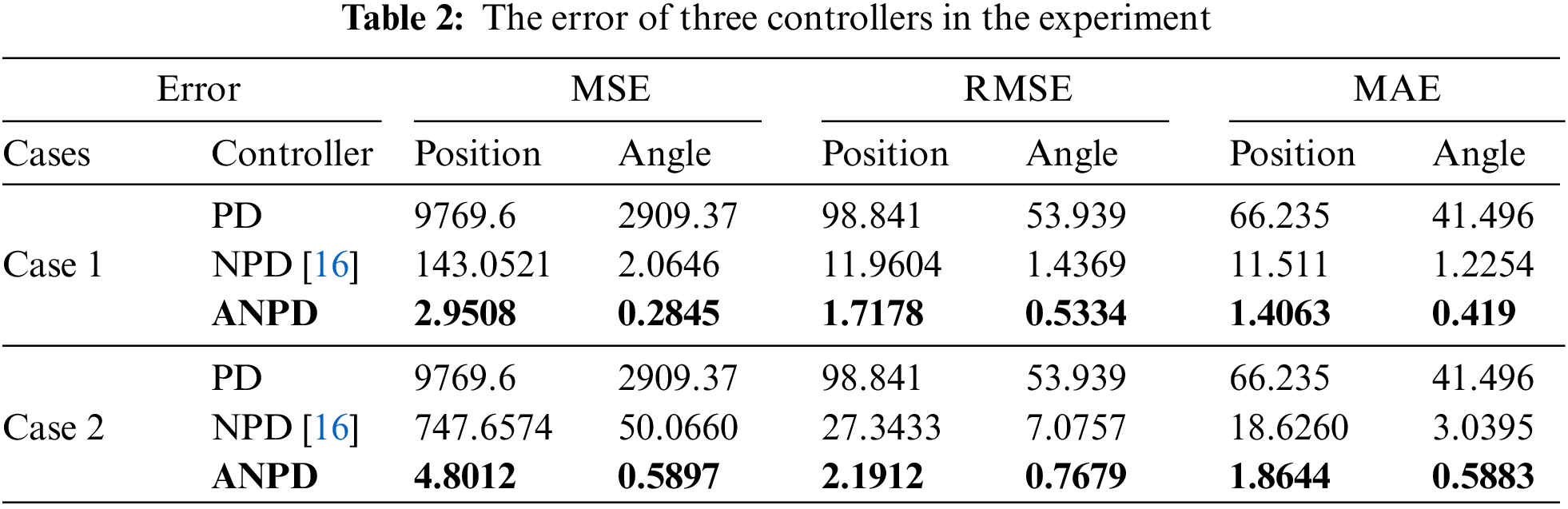
Table 2 provides the assessments of errors, including Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Mean Absolute Error (MAE). The proposed ANPD controller has about 97.94%, 85.64%, and 87.78% respectively position tracking improvements than the NPD [16] controller. With the angle tracking, the ANPD controller has about 86.22%, 62.88%, and 65.81% respectively improvements over the NPD [16] controller. As a result, the proposed ANPD controller produces better control performance than the others.

5  Conclusion

This paper delivers our findings on an adaptive nonlinear PD control approach for the TWSB robot’s dynamics model. The ANPD controller has been successfully developed by combining the nonlinear PD controller with the genetic algorithm. The design of the control law for the proposed ANPD controller is based on the kinematic equation of the TWSB robot system. The suggested controller’s initial parameters are determined by a genetic algorithm, demonstrating the ANPID controller’s simplicity. This combination entirely solves the difficulty of choosing the most appropriate parameters. The adaptive control law is updated continuously during operation to handle the real-time estimation of the external force. The stability of the system is proven using the Lyapunov theory. Simulation results show that ANPD adheres to the desired trajectory well, with a fast and stable response time when the system has been noisy. Furthermore, experimental results have confirmed the applicability of the ANPD controller to the actual system. The error comparison table shows a significant improvement in the proposed controller compared to the previous ones. Generally, the proposed ANPD controller is a simple and effective method, easy to apply to nonlinear systems such as TWSB robots, promising to provide many practical applications. In the future, the system will be evaluated with effects such as parameter uncertainty and time delay, which can significantly affect the system’s performance. In addition, the ANPD controller will also be used in other nonlinear systems to evaluate the performance. And then, various artificial intelligence approaches can be used to improve the effectiveness of ANPD control.

Acknowledgement: The authors express grateful thankfulness to the Shibaura Institute of Technology, Japan.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Van-Truong Nguyen and Dai-Nhan Duong; Methodology, Van-Truong Nguyen and Dai-Nhan Duong; Software, Dai-Nhan Duong; Formal analysis, Dinh-Hieu Phan; Investigation, Thanh-Lam Bui; Resources, Xiem HoangVan; Data curation, Van-Truong Nguyen; Writing—original draft, Van-Truong Nguyen and Dai-Nhan Duong; Writing—review & editing, Van-Truong Nguyen and Phan Xuan Tan; Visualization, Xiem HoangVan; Funding, Phan Xuan Tan; Supervision, Van-Truong Nguyen; Project administration, Phan Xuan Tan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author, Van-Truong Nguyen.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. I. Jmel, H. Dimassi, S. H. Said, and F. M'Sahli, “Adaptive observer-based sliding mode control for a two-wheeled self-balancing robot under terrain inclination and disturbances,” Math. Probl. Eng., vol. 2021, no. 7, pp. 1–15, 2021. doi: 10.1155/2021/8853441. [Google Scholar] [CrossRef]

2. L. Guo, S. A. A. Rizvi, and Z. Lin, “Optimal control of a two-wheeled self-balancing robot by reinforcement learning,” Int. J. Robust Nonlin. Control, vol. 31, no. 6, pp. 1885–1904, 2021. doi: 10.1002/rnc.5058. [Google Scholar] [CrossRef]

3. Á. Odry, R. Fullér, I. J. Rudas, and P. Odry, “Fuzzy control of self-balancing robots: A control laboratory project,” Comput. Appl. Eng. Educ., vol. 28, no. 3, pp. 512–535, 2020. doi: 10.1002/cae.22219. [Google Scholar] [CrossRef]

4. C. Iwendi, M. A. Alqarni, J. H. Anajemba, A. S. Alfakeeh, Z. Zhang and A. K. Bashir, “Robust navigational control of a two-wheeled self-balancing robot in a sensed environment,” IEEE Access, vol. 7, pp. 82337–82348, 2019. doi: 10.1109/ACCESS.2019.2923916. [Google Scholar] [CrossRef]

5. F. Ünker, “Proportional control moment gyroscope for two-wheeled self-balancing robot,” J. Vib. Control, vol. 28, no. 17–18, pp. 2310–2318, 2022. doi: 10.1177/10775463211009988. [Google Scholar] [CrossRef]

6. V. Mudeng, B. Hassanah, Y. T. K. Priyanto, and O. Saputra, “Design and simulation of two-wheeled balancing mobile robot with pid controller,” Int. J. Sustain. Transp. Technol., vol. 3, no. 1, pp. 12–19, 2020. doi: 10.31427/IJSTT.2020.3.1.3. [Google Scholar] [CrossRef]

7. A. Y. Zimit, H. J. Yap, M. F. Hamza, I. Siradjuddin, B. Hendrik and T. Herawan, “Modelling and experimental analysis two-wheeled self balance robot using PID controller,” in Int. Conf. Computat. Sci. Appl., Cham, Springer, 2018, pp. 683–698. [Google Scholar]

8. F. Zhou and J. Liu, “Pitch controller design of wind turbine based on nonlinear PI/PD control,” Shock Vib., vol. 2018, no. 1, pp. 1–14, 2018. doi: 10.1155/2018/7859510. [Google Scholar] [CrossRef]

9. P. R. Ouyang, V. Pano, J. Tang, and W. H. Yue, “Position domain nonlinear PD control for contour tracking of robotic manipulator,” Robot. Comput. Integr. Manuf., vol. 51, no. 11, pp. 14–24, 2018. doi: 10.1016/j.rcim.2017.11.017. [Google Scholar] [CrossRef]

10. L. Chen, X. Liang, W. Zhu, and Y. Zhao, “Stochastic averaging technique for SDOF strongly nonlinear systems with delayed feedback fractional-order PD controller,” Sci. China Technol. Sci., vol. 62, no. 2, pp. 287–297, 2019. doi: 10.1007/s11431-018-9326-2. [Google Scholar] [CrossRef]

11. O. Saleem and K. Mahmood-ul-Hasan, “Robust stabilisation of rotary inverted pendulum using intelligently optimised nonlinear self-adaptive dual fractional-order PD controllers,” Int. J. Syst. Sci., vol. 50, no. 7, pp. 1399–1414, 2019. doi: 10.1080/00207721.2019.1615575. [Google Scholar] [CrossRef]

12. J. Moreno-Valenzuela, R. Pérez-Alcocer, M. Guerrero-Medina, and A. Dzul, “Nonlinear PID-type controller for quadrotor trajectory tracking,” IEEE/ASME Trans. Mechatron., vol. 23, no. 5, pp. 2436–2447, 2018. doi: 10.1109/TMECH.2018.2855161. [Google Scholar] [CrossRef]

13. J. Guerrero, J. Torres, V. Creuze, A. Chemori, and E. Campos, “Saturation based nonlinear PID control for underwater vehicles: Design, stability analysis and experiments,” Mechatronics, vol. 61, no. 4, pp. 96–105, 2019. doi: 10.1016/j.mechatronics.2019.06.006. [Google Scholar] [CrossRef]

14. A. M. Agwa, M. Abdeen, and S. M. Shaaban, “Optimal FOPID controllers for LFC including renewables by bald eagle optimizer,” Comput. Mater. Contin., vol. 73, no. 3, pp. 5525–5541, 2022. doi: 10.32604/cmc.2022.031580. [Google Scholar] [CrossRef]

15. R. Farkh, M. T. Quasim, K. Al Jaloud, S. Alhuwaimel, and S. T. Siddiqui, “Computer vision-control-based CNN-PID for mobile robot,” Comput. Mater. Contin., vol. 68, no. 1, pp. 1065–1079, 2021. doi: 10.32604/cmc.2021.016600. [Google Scholar] [CrossRef]

16. B. Zhang, W. Shang, S. Cong, and Z. Li, “Coordinated dynamic control in the task space for redundantly actuated cable-driven parallel robots,” IEEE/ASME Trans. Mechatron., vol. 26, no. 5, pp. 2396–2407, 2020. doi: 10.1109/TMECH.2020.3038852. [Google Scholar] [CrossRef]

17. D. N. Anisimov, T. S. Dang, and V. N. Dinh, “Development of a microcontroller-based adaptive fuzzy controller for a two-wheeled self-balancing robot,” Microsyst. Technol., vol. 24, no. 9, pp. 3677–3687, 2018. doi: 10.1007/s00542-018-3825-2. [Google Scholar] [CrossRef]

18. T. Zhao, Q. Yu, S. Dian, R. Guo, and S. Li, “Non-singleton general type-2 fuzzy control for a two-wheeled self-balancing robot,” Int. J. Fuzzy Syst., vol. 21, no. 6, pp. 1724–1737, 2019. doi: 10.1007/s40815-019-00664-4. [Google Scholar] [CrossRef]

19. V. T. Nguyen, C. Y. Lin, S. F. Su, W. Sun, and M. J. Er, “Global finite time active disturbance rejection control for parallel manipulators with unknown bounded uncertainties,” IEEE Trans. Syst., Man, Cybern.: Syst., vol. 51, no. 12, pp. 7838–7849, 2021. doi: 10.1109/TSMC.2020.2987056. [Google Scholar] [CrossRef]

20. V. T. Nguyen, “Non-negative adaptive mechanism-based sliding mode control for parallel manipulators with uncertainties,” Comput. Mater. Contin., vol. 74, no. 2, pp. 2771–2787, 2023. doi: 10.32604/cmc.2023.033460. [Google Scholar] [CrossRef]

21. V. T. Nguyen, C. Y. Lin, S. F. Su, and Q. V. Tran, “Adaptive chattering free neural network based sliding mode control for trajectory tracking of redundant parallel manipulators,” Asian J. Control, vol. 21, no. 2, pp. 908–923, 2019. doi: 10.1002/asjc.1789. [Google Scholar] [CrossRef]

22. V. T. Nguyen, S. F. Su, A. T. Nguyen, and V. T. Nguyen, “Adaptive nonsingular fast terminal sliding mode tracking control for parallel manipulators with uncertainties,” in 2019 Int. Conf. Syst. Sci. Eng. (ICSSE), Dong Hoi, Vietnam, 2019, pp. 522–525. [Google Scholar]

23. V. T. Nguyen, X. T. Vu, and H. B. Giap, “Adaptive neural network hierarchical sliding-mode control for pendubot based genetic algorithm optimization,” in Intelligent Systems and Networks, Vietnam, 2022, pp. 574–580. [Google Scholar]

24. A. Chhotray and D. R. Parhi, “Navigational control analysis of two-wheeled self-balancing robot in an unknown terrain using back-propagation neural network integrated modified DAYANI approach,” Robotica, vol. 37, no. 8, pp. 1346–1362, 2019. doi: 10.1017/S0263574718001558. [Google Scholar] [CrossRef]

25. N. Hassan and A. Saleem, “Neural network-based adaptive controller for trajectory tracking of wheeled mobile robots,” IEEE Access, vol. 10, no. 4, pp. 13582–13597, 2022. doi: 10.1109/ACCESS.2022.3146970. [Google Scholar] [CrossRef]

26. T. Yang, H. Chen, N. Sun, and Y. Fang, “Adaptive neural network output feedback control of uncertain underactuated systems with actuated and unactuated state constraints,” IEEE Trans. Syst. Man Cybern. Syst., vol. 52, no. 11, pp. 7027–7043, 2022. doi: 10.1109/TSMC.2021.3131843. [Google Scholar] [CrossRef]

27. N. Ji and J. Liu, “Sliding mode control based on RBF neural network for a class of underactuated systems with unknown sensor and actuator faults,” Int. J. Syst. Sci., vol. 51, no. 16, pp. 3539–3549, 2020. doi: 10.1080/00207721.2020.1817615. [Google Scholar] [CrossRef]

28. I. Gandarilla, J. M. Cháirez, V. Santibáñez, C. A. Avelar, and J. M. Valenzuela, “Trajectory tracking control of a self-balancing robot via adaptive neural networks,” Eng. Sci. Technol. Int. J., vol. 35, 2022, Art. no. 101259. doi: 10.1016/j.jestch.2022.101259. [Google Scholar] [CrossRef]

29. S. N. Sivanandam and S. N. Deepa, “Genetic algorithms,” in Introduction to Genetic Algorithms, Berlin, Heidelberg: Springer, 2008, pp. 15–37. [Google Scholar]

30. S. Mirjalili, “Genetic algorithm,” in Evolutionary Algorithms and Neural Networks, Cham: Springer, 2019, pp. 43–55. [Google Scholar]

31. S. Katoch, S. S. Chauhan, and V. Kumar, “A review on genetic algorithm: Past, present, and future,” Multimed. Tools Appl., vol. 80, no. 5, pp. 8091–8126, 2021. doi: 10.1007/s11042-020-10139-6. [Google Scholar] [PubMed] [CrossRef]

32. H. Ahmadi and A. Kazemi, “The Lyapunov-based stability analysis of reduced order micro-grid via uncertain LMI condition,” Int. J. Electr. Power Energy Syst., vol. 117, 2020, Art. no. 105585. doi: 10.1016/j.ijepes.2019.105585. [Google Scholar] [CrossRef]

33. Y. Chow, O. Nachum, E. Duenez-Guzman, and M. Ghavamzadeh, “A lyapunov-based approach to safe reinforcement learning,” in Adv. Neural Inf. Process. Syst., vol. 31, 2018. [Google Scholar]

34. S. Kim and S. Kwon, “Dynamic modeling of a two-wheeled inverted pendulum balancing mobile robot,” Int. J. Control Autom. Syst., vol. 13, no. 4, pp. 926–933, 2015. doi: 10.1007/s12555-014-0564-8. [Google Scholar] [CrossRef]

35. A. Jayachitra and R. Vinodha, “Genetic algorithm based PID controller tuning approach for continuous stirred tank reactor,” Adv. Artif. Intell., vol. 2014, no. 15, pp. 1–8, 2014. doi: 10.1155/2014/791230. [Google Scholar] [CrossRef]

36. Y. Yang, H. H. Zhang, W. Yu, and L. Tan, “Optimal design of discrete-time fractional-order PID controller for idle speed control of an IC engine,” Int. J. Powertrains, vol. 9, pp. 79–95, 2020. doi: 10.1504/IJPT.2020.108412. [Google Scholar] [CrossRef]