A Novel Filtering-Based Detection Method for Small Targets in Infrared Images

1  Introduction

Imaging technology encompasses both visible light and infrared imaging. Visible light travels in straight lines and has limited penetration. It is also susceptible to the influence of environmental factors in its surroundings. Infrared imaging, in contrast, offers advantages including superior penetration, high concealment, extended working distances, robust anti-interference capabilities, and longer operational periods compared to visible light imaging. Consequently, the utilization of infrared imaging technology for detecting small targets has been widely applied in military early warning, missile tracking, precision guidance, and other sectors [1–5]. However, due to the extended distances involved in infrared imaging, targets often occupy fewer pixels, resulting in a lack of corresponding shape and texture details [6]. Moreover, challenges arise from factors such as intricate and varying backgrounds, a low signal-to-noise ratio, and substantial interference from bright pixels, all of which considerably complicate infrared small target detection [7]. Consequently, the technique of detecting infrared small targets remains highly challenging.

Algorithms for detecting infrared small targets are primarily categorized into two groups: multi-frame detection based on spatio-temporal filters and single-frame detection based on spatial filters. Multi-frame detection involves processing multiple frames, resulting in complex and time-consuming algorithms that demand significant amounts of computational resources. This type of approach thus finds better applications in scenes with static backgrounds and lower real-time requirements [8]. It is noteworthy that much of the multi-frame detection methodology is built upon the foundations of single-frame detection methods [9]. Single-frame detection algorithms generally perform detection based on the spatial information of small targets. Such approaches often require less computational loads, resulting in shorter detection time, heightened detection flexibility, and broader applicability. Consequently, single-frame detection methods have gained substantial favor among scholars [10]. Single-frame detection methods can be primarily categorized into four types: those based on background estimation models, low-rank sparse decomposition models, the utilization of human vision mechanisms, and the application of deep learning models.

1.1 Related Work

At present, models for infrared small target detection algorithms based on single-frame images are mainly categorized into four types: background estimation models, low-rank sparse decomposition models, human vision mechanism models, and deep learning models.

Detection methods based on the background estimation model assume that the background undergoes gradual changes and neighboring pixels exhibit high correlations. However, a target serves as a critical element in disrupting this correlation, allowing for the separation of the subtly evolving background and the significantly salient small target through their differences. Notable techniques within this category encompass maximum mean/maximum median filtering [11], two-dimensional least mean square (TDLMS) filtering [12], morphology-based TOP-HAT transform [13], high-pass filtering [14], and wavelet transform [15]. Cao et al. [16] utilized the maximum inter-class variance method to improve morphological filtering. These methods offer swift execution, yet they grapple with challenges in attenuating high-frequency noise [17], leading to less-than-optimal detection outcomes.

Unlike background estimation models, infrared small target detection methods based on low-rank sparse decomposition exhibit superior background suppression capabilities. These methods decompose infrared images into three components: background, target, and noise. The target component is assumed to be sparse, the background is low-rank, and the noise follows a zero-mean Gaussian distribution. This approach formulates small target detection as a robust principal component analysis (RPCA) problem [18]. Gao et al. [19] proposed the Infrared Patch Image (IPI) model, which improved the characterization of the background’s low-rank property. Subsequently, Guo et al. [20] developed the Reweighted IPI (ReWIPI) model, and Zhang et al. [21] introduced the Non-convex Rank Approximation Model (NRAM). Furthermore, multi-subspace methods have been explored, such as the Stable Multisubspace Learning (SMSL) model [22] and the Improved Self-regularization Weighted Sparse (SRWS) model [23], which extract clutter and constrain the background through multiple subspaces. However, these methods are computationally complex and heavily rely on the sparsity of the target.

Detection methods based on human visual mechanisms are inspired by the human visual system, treating small targets in infrared images as salient regions to be enhanced, while background areas are treated as irrelevant and suppressed. This increases the contrast between the target and its surrounding background. The Local Contrast Measure (LCM), proposed by Chen et al. [24], is a classic method that has been refined over time. Wei et al. [25] proposed the Multiscale Patch-based Contrast Measure (MPCM), and Han et al. [26] introduced the Relative Local Contrast Measure (RLCM), which suppresses background clutter through ratio and difference forms. Han et al. [27] further developed the multiscale Tri-Layer Local Contrast Measure (TLLCM), which enhances the target before calculating local contrast. Other advancements include the Weighted Strengthened Local Contrast Measure (WSLCM) [28] and the Global Contrast Measure (GCM) [29]. However, when background edges or high-intensity pixel noise are present in the image, these algorithms often struggle to effectively distinguish between the target, background, and noise.

With the continuous development of artificial intelligence, methods based on deep learning are becoming increasingly prominent. They have shown significant advancements [30–34], with superior accuracy and robustness compared to traditional methods. However, this does not mean that traditional methods can be completely abandoned, and only deep learning methods can be studied in the future. Both traditional methods and deep learning-based methods have promising prospects in the field of infrared small target detection. In the future, traditional methods and deep learning techniques can be combined to leverage the benefits of traditional methods, such as lower computational complexity and higher interpretability, along with the strengths of deep learning methods, such as robust learning capabilities and adaptability to various environments.

In this paper, a new infrared small target detection algorithm based on a novel filter kernel is proposed, departing from the traditional detection algorithm. This method features a simple structure akin to the background estimation model, yet it excels in eliminating high-frequency noise and enhancing detection accuracy. The detailed model architecture is presented in Section 2. Although the algorithm proposed in this paper falls short of the detection performance achieved by current deep learning methods, it offers a valuable framework for future researchers to build upon.

This study focuses on single-frame infrared small target detection, which is critical in scenarios requiring real-time processing or when computational resources are limited. While multi-frame and sequence-based detection methods have their merits, they are beyond the scope of this work.

1.2 Motivation

The Gaussian filter kernel is a type of filter characterized by a high center weight and low edge weight, commonly known as a Gaussian low-pass filter. Its principle is based on the properties of the Gaussian function, wherein a two-dimensional space, the weight assigned to each pixel is inversely related to its distance from the center pixel—the closer the pixel, the higher the assigned weight. This filter is effective in removing noise and smoothing details in the image. However, due to its suppression of high-frequency information, it also tends to blur small targets in infrared imagery, causing the pixel values of these targets to become more similar to the surrounding background, thus reducing the visibility of the small targets. The Difference of Gaussian (DoG) method, as proposed in literature [35], is an edge and contour detection technique that operates by subtracting the results of two Gaussian low-pass filters applied at different scales. This approach enhances the high-frequency components, effectively highlighting the edges and contours within the image.

Additionally, existing Gaussian filters also include the Gaussian high-pass filter, characterized by high edge weights and low center weights. This filter enhances high-frequency information within the image and accentuates target edges by subtracting the results of low-pass filtering. The theoretical foundation of the Gaussian high-pass filter is thoroughly discussed in the literature [36], where the Gaussian Local Contrast Measure (GLCM) is introduced. The GLCM model enables adaptive filtering based on target size by combining Gaussian high-pass and low-pass filters (i.e., Gaussian kernel and anti-Gaussian kernel), providing a flexible approach to target detection and contrast enhancement.

However, the classical anti-Gaussian kernel (as defined in Eq. (1)) may exhibit suboptimal filtering performance due to its insufficient convergence rate. To address this limitation, we introduce an improved filtering method with enhanced convergence characteristics.

g(x,y)=12πσ2(1−e−(x−x0)2+(y−y0)22σ2).(1)

The general infrared small target detection methods based on background estimation often result in residual background clutter and high-frequency noise even after preprocessing and threshold segmentation. To address these challenges, an additional step involves selecting the results derived from threshold segmentation to isolate the ultimate target for detection.

Drawing from the above considerations, this paper presents an innovative infrared small target detection approach. The contributions are outlined as follows:

1) A novel filter kernel model, the transformed Gaussian filter kernel, has been designed. By calculating the difference between the transformed Gaussian filter results and the Gaussian high-pass filter results, this method effectively highlights small targets, enhances background suppression, and increases the contrast and differentiation between the target and the background.

2) To further enhance detection accuracy and minimize false alarms, an approach that selects targetsafter threshold segmentation is introduced. This technique involves cluster analysis.

The subsequent sections are structured as follows: Section 2 elaborates on the construction of the filter kernel and the detection process as proposed in this paper. Section 3 details the composition of the datasets along with the comprehensive presentation of experimental results and data analysis. Finally, Section 4 provides a summarized overview of the paper.

2  The Proposed Approach

The infrared small target detection algorithm proposed in this paper is mainly divided into three steps, as shown in Fig. 1. The initial step involves acquiring a different image. In this phase, the original infrared image containing a small target undergoes processing using both the constructed transformed Gaussian filter and the Gaussian low-pass filter. Subsequently, the outcomes of these two processes are subtracted to yield a difference image. The second step entails adaptive threshold segmentation. This phase effectively eliminates the majority of background noise from the different images, along with other minor clutter, through the application of adaptive threshold selection. This step serves to ascertain whether a pixel point is classified as belonging to a small target or not. In the final step, areas for small targets are generated through the application of the fuzzy C-mean clustering algorithm to the threshold-segmented image, effectively isolating the small targets. Upon completing these three steps, the desired small target image is obtained. Nonetheless, the parameterization of each of these steps remains to be determined. Optimal detection outcomes can only be achieved by selecting suitable and universally applicable parameters. This study exclusively addresses infrared small target detection using single-frame images. Detection methods based on infrared image sequences are not within the scope of this paper.

Figure 1: Flowchart of the proposed infrared small target detection algorithm

2.1 Construction of the Transformed Gaussian Filter Kernel

The Gaussian low-pass filter effectively blurs small targets in the image by smoothing the pixel values, causing the target area to gradually resemble the surrounding background. This process diminishes the prominence of the small target within the image. While this filtering helps reduce high-frequency noise, it may also lower the contrast between the target and background, potentially impacting detection accuracy. In contrast, the Gaussian high-pass filter sharpens small, blurred targets by enhancing high-frequency components, thereby emphasizing edges and details. The core principle involves preserving high-frequency information while suppressing low-frequency components, thus improving the visibility of small targets. These two filters are often used as complementary operations in image processing: the Gaussian low-pass filter for noise reduction and the Gaussian high-pass filter for target enhancement, as illustrated in Fig. 2.

Figure 2: Gaussian filtering model 3D drawing

However, experimental results indicate that directly applying the Gaussian low-pass and high-pass filters to infrared small target images and computing their difference does not yield optimal detection performance at the target locations. This suboptimal outcome may be attributed to the Gaussian high-pass filter’s amplification of high-frequency noise, which insufficiently enhances the contrast between the target and the background. Consequently, using the difference between these two filters as a detection strategy results in less effective detection performance.

To address this issue, a novel transform Gaussian filter kernel is proposed as a replacement for the traditional Gaussian high-pass filter kernel. The transform Gaussian filter kernel enhances the features of small targets through an asymmetric weight distribution. Specifically, the filter’s weights increase progressively from the center towards the periphery, with higher weights assigned to regions farther from the center. This design amplifies the pixel contrast within the target area, thereby improving target detection performance.

Assume the center of the filter kernel is located at (0, 0), with the surrounding square template having a size of 2d. Let the position of a pixel be denoted as (x, y), and the distance from the center as r=x2+y2. Based on this setup, the weight of each pixel in the transformed Gaussian filter kernel is defined by the following equation:

ω(x,y)=12πse−(r−d)22s2,(2)

where s represents the standard deviation of the transformed Gaussian filter kernel.

Fig. 2 displays the 3D representation of the constructed transformed Gaussian filter model. The figure reveals that the transformed Gaussian filter exhibits a more pronounced transition from the center to the periphery compared to the Gaussian high-pass filter. This heightened contrast enhances the prominence of the central image region, rendering the small target more discernible and visually accentuated.

The transform Gaussian filter kernel assigns higher weights to pixels farther from the center by incorporating a distance factor r−d. Unlike traditional Gaussian high-pass filters, which typically apply uniform enhancement across all distances, this design allows the proposed method to more effectively highlight small target features, thereby improving detection performance.

Gaussian high-pass filtering enhances image details by removing low-frequency components and retaining high-frequency details and edges. However, this method is sensitive to high-frequency noise, which can lead to unstable detection results when processing noisy or low-contrast images, ultimately affecting the accurate detection of small targets. In contrast, the transform Gaussian filter makes small targets in the central area of the image more prominent through a carefully designed weight distribution. This approach not only preserves the details of small targets but also effectively suppresses background noise, thereby significantly improving the contrast and saliency of the targets. The design not only enhances the brightness and contrast of small targets visually but also achieves stronger noise suppression and target prominence functionally, providing a more stable and accurate solution for infrared small target detection.

2.2 Finding Parts of an Image that May Be Small Targets

In infrared images, the area of interest typically corresponds to small targets. These small targets appear as “dots” in grayscale images, usually consisting of fewer than 80 pixels, although slightly larger targets may exceed this pixel count. A common characteristic of these small targets is that their pixel values are highest at the center and gradually decrease towards the periphery. This pixel distribution closely resembles the shape of a Gaussian function [36]. Consequently, Gaussian filters have been widely used in infrared small target detection.

The Gaussian low-pass filter is commonly used for noise reduction by smoothing the image, suppressing high-frequency noise, and emphasizing the target’s low-frequency information. In contrast, the Gaussian high-pass filter enhances edge and detail information by amplifying the high-frequency components in the image. In this paper, we first apply the Gaussian high-pass filter to process the original image. Let I represent the original infrared image of size m × n. After convolution with the Gaussian filter template, the resulting processed image can be expressed as:

I1=I∗G(x,y),(3)

where I1 represents the pixel value of the original image after Gaussian filtering, while G(x,y) denotes the Gaussian high-pass filter kernel characterized by a high center weight and low edge weight. Its mathematical expression is given by:

G(x,y)=12πσ2e−(x−x0)2+(y−y0)22σ2,(4)

where (x0,y0) denotes the coordinates of the Gaussian filter kernel’s center, and σ represents the standard deviation of the Gaussian distribution, which determines the spread range of the filter kernel.

Next, the original image was convolved with the transform Gaussian filter template to produce the image processed by the transform Gaussian filter. The resulting calculation is as follows:

I2=I∗ω(x,y),(5)

where I2 represents the pixel value of the image after the original image is computed by a transformed Gaussian filter.

Due to the significant difference in the pixel value magnitudes of the original image after applying the two filters, directly computing their difference may render the filtering results with smaller pixel values ineffective. Therefore, it is necessary to standardize the two filtered images before performing the difference operation. The Gaussian filtering results are standardized first, with the calculation process as follows:

I1′(x,y)=I1(x,y)−I1minI1max−I1min(1≤x≤m,1≤y≤n),(6)

where I1min and I1max represent the minimum and maximum pixel values in the image processed by the Gaussian filter, respectively. Similarly, the results of the transformed Gaussian filtering are standardized, with the calculation formula as follows:

I2′(x,y)=I2(x,y)−I2minI2max−I2min(1≤x≤m,1≤y≤n).(7)

This standardization ensures that both filtering results are brought to the same scale, thereby enhancing the accuracy and effectiveness of the difference calculation.

To illustrate, consider an infrared small target image containing two small targets. Upon processing and normalization by Gaussian high-pass filtering and transformed Gaussian filtering, a 3D map is generated. This map is depicted in Fig. 3. Upon examination of the figure, it becomes apparent that the pixel values within the small target region, as processed by the transformed Gaussian filter outlined in this study, are notably higher compared to those processed by the Gaussian high-pass filter. This discrepancy suggests that the transformed Gaussian filter kernel introduced in this paper yields significantly enhanced results for small target enhancement. A detailed experimental comparison of the two filters is given in Section 3.4.

Figure 3: Comparison of the results of Gaussian high-pass and transformed Gaussian filtering of the original image containing two small targets

Fig. 4 shows the results obtained by the proposed approach in the detection of small targets in an infrared image. By subtracting the results of the two aforementioned filter normalization processes and then taking the absolute value, we derive a difference image denoted as D. This difference image’s 3D representation is illustrated in Fig. 4f.

Figure 4: 3D map of the original image and the processing results of each part of the image: (a) original image, (b) 3D map of the original image, (c) 3D map of the transformed Gaussian filtering processing results, (d) 3D map of the Gaussian filtering processing results, (e) the results of the small target detection, (f) 3D map of the difference image, (g) 3D map of the denoised image, (h) 3D map of the clustered image

D=|I2′−I1′|.(8)

Upon comparing Fig. 4b,f, it becomes evident where the small target is situated. In contrast, the background clutter appears more uniform in the original image. The process of applying the transformed Gaussian filter and Gaussian filter, followed by subtraction, is akin to undergoing two closely related filtering stages before computing the difference. As a result, the background clutter in the different images is subdued and not as prominent, sharply contrasting with the distinct small target area.

In the process of determining the position of a small target in an image, the selection of several hyperparameters is crucial, including the sizes of the two filter templates and the setting of the filter standard deviation. Using three infrared small target images as examples, we studied the relationship between the standard deviation and filter template size for both Gaussian low-pass filters and transform Gaussian filters and their effects on target enhancement. Additionally, we conducted a detailed sensitivity analysis of these hyperparameters. The results are presented in Tables 1 to 4, where the data represent the contrast value between the target area and the surrounding background area. Specifically, I1 represents the result of the original image after Gaussian low-pass filtering, I2 represents the result after transforming Gaussian filtering, and D represents the differential image.

Table 1 illustrates the effect of the standard deviation of Gaussian low-pass filtering on the contrast ratio. As shown in Table 1, the contrast ratio increases with the standard deviation, indicating that Gaussian filtering enhances image smoothing. However, from the contrast values of the difference images in the 2nd and 3rd plots, it is evident that a larger standard deviation is not always better; it must be optimized in conjunction with the parameter settings of the transform Gaussian filter to achieve the best results. Table 2 presents the effect of the Gaussian low-pass filter template size on contrast. As the filter template size increases, the smoothing effect improves, leading to higher contrast in the differential image. However, if the template is too large, it can result in the loss of target details. Therefore, it is essential to strike a balance between smoothing and detail retention.

Table 3 illustrates the effect of the standard deviation of the transformed Gaussian filter on contrast. Within the standard deviation range of 0.5 to 6, the contrast value between the target region and the surrounding background region, after processing with the transformed Gaussian filter and in the differential image, exhibits minimal change. This indicates that the detection algorithm proposed in this paper is not particularly sensitive to the standard deviation of the transformed Gaussian filter, thereby enhancing the algorithm’s robustness in practical applications. Table 4 depicts the effect of the size of the transformed Gaussian filter template on contrast. As the filter template size increases, the contrast value of the I2 image gradually decreases, reducing the prominence of the target. In differential images, the contrast value will reach a maximum saturation point. Therefore, the smaller the filter template, the better the prominence effect on the target.

The standard deviation of the Gaussian low-pass filter determines the smoothness of the image. Generally, if the target is small or the noise level is high, a larger standard deviation should be selected to achieve better smoothing; otherwise, a smaller standard deviation is sufficient. The standard deviation of the transformed Gaussian filter dictates the degree of target enhancement. A larger standard deviation results in better enhancement of the target. If the edge information of the small target is weak or the background is more complex, a larger standard deviation is advisable; otherwise, a smaller standard deviation can be used. However, the final detection effect is determined by the difference image of the two filtering results, so the template size with the best difference image effect should be selected based on the above principles.

Gaussian low-pass filtering is primarily used to smooth the image and remove noise and fine details, so the filter template size should be as large as possible to retain the overall structure of the target. On the other hand, the transformed Gaussian filter is designed to enhance high-frequency information and highlight the edge details of the target. Therefore, the template size should be kept as small as possible to preserve the fine details of the target.

2.3 Adaptive Thresholding Segmentation

Alongside the presence of small targets within the different images, one encounters background noise and minor clutter. To address this, the paper employs the adaptive threshold segmentation method to assess, pixel by pixel, whether it qualifies as part of the small target region. Specifically, if a pixel’s value surpasses a predetermined threshold, it is categorized as foreground; otherwise, it is assigned to the background. Denoting the candidate target image as It this threshold segmentation process is expressed as represented in Eq. (9).

{It(x,y)=D(x,y)D(x,y)≥ThIt(x,y)=0D(x,y)<Th,(9)

the adaptive threshold Th is defined as follows:

Th=μD+kεD,(10)

where μD and εD are the mean and standard deviation of the difference values D for all pixels, respectively, and k is the influence factor for threshold, which is usually constant.

Observing Fig. 4g, it becomes evident that the denoised difference image effectively eliminates the majority of background noise. The residual noisy pixel values that persist are comparatively closer in magnitude to the pixel values of the small target. Nevertheless, these remaining noisy pixels lack the distinct prominence exhibited by the small target.

2.4 Image Clustering Process to Extract Small Targets

Following the aforementioned steps, Fig. 4g demonstrates that the most prominent aspect of the image is the desired final small target, closely followed by the presence of other minor noises. Consequently, the entire image’s pixels can be classified into three distinct categories. The first comprises the small target pixel region, the second encompasses the area containing other noise, and the third pertains to the background noise and other minor noise regions that were eliminated during the threshold segmentation process. To effectively separate the small targets from these categories, the method of clustering is employed. The remaining foreground section, once threshold segmentation is completed, is subjected to clustering. This process clusters pixels belonging to the same target, facilitating the isolation of the small targets to be detected.

The fuzzy C-mean clustering algorithm is employed to refine the objective function, thereby determining the degree of association between each sample point and all the class centers. This affiliation degree governs the classification of sample points, automating the process of sample data categorization. Each sample is assigned an affiliation function indicating its connection to each cluster. Subsequently, the samples are categorized based on the magnitude of their affiliation values. The mathematical representation of the objective function is presented in Eq. (11).

Jm=∑i=1N∑j=1Cuijm‖xi−cj‖2,1≤m<∞,(11)

where m is the number of clusters of clustering, which is set to 2 in this paper, N is the total number of pixels, C is the number of clustered pixel centers, xi denotes the ith pixel value, cj denotes the jth clustering center, uij denotes the affiliation degree of the pixel value xi to the clustering center cj, and the expressions of uij and cj are as follows:

uij=1∑k=1C(‖xi−cj‖‖xi−ck‖)2m−1,(12)

cj=∑i=1Nuijmxi∑i=1Nuijm.(13)

After several iterations, the value of the affiliation matrix uij obtained from two similar iterations is compared, and the iteration is terminated if it does not exceed a very small set constant.

Based on the preceding analysis, the outlook can be broadly divided into three components. In the pursuit of enhancing the resilience of the ultimate detection outcomes, this study configures the number of clustered pixel centers as 4. This selection effectively aids in the improved filtration of noise that closely aligns with the value of small target pixels, thereby leading to more optimal detection results.

3  Experimental Results and Analysis

To demonstrate the detection prowess of the algorithm proposed in this paper, this section conducts qualitative and quantitative analyses. The paper starts by presenting the parameter configurations of the baseline method along with details about the employed dataset. Following this, an introduction to various evaluation metrics is provided. Subsequently, the ideal parameter settings for the proposed method are outlined. The paper proceeds with a comprehensive comparison between the proposed approach and the baseline method. Finally, a thorough complexity analysis of the proposed method is presented, accompanied by a comparative assessment of the runtime performance across each detection method. All experiments were executed on a computer equipped with a 3.70 GHz Intel Core i5-12600K Central Processing Unit (CPU), and 16.0 GB Random Access Memory (RAM), and the code was implemented using Matrix Laboratory (MATLAB) 2023a software. The experiment of the deep learning method adopts Ubuntu18.04 operating system, Pytorch 1.8.0 deep learning framework, 11.1.1 version of Compute Unified Device Architecture (CUDA).

3.1 Parameter Setting

The algorithm proposed in this paper is compared with four traditional methods: TOP-HAT [13], LCM [24], MPCM [25], and RLCM [26]. Additionally, we also compare it with the Dense Nested Attention Network (DNANet) [30], which is a deep learning-based approach. Although these traditional methods are not recent, they remain authoritative within the detection field. This paper introduces a novel filter kernel that is more concise than many of the leading detection algorithms developed in recent years. The parameters for the baseline methods were configured according to the authors’ recommendations, as detailed in Table 5.

The datasets for the four sequences are sourced from [37–39]. These datasets encompass images captured in three distinct scenarios: air, land, and sea. They include a diverse range of attributes, including varying levels of signal heterogeneity, single and multi-target instances, and small targets characterized by pixel counts below 80. Additionally, slightly larger targets with pixel counts exceeding 80 are also incorporated. Comprehensive details regarding the datasets for each of the four sequences are provided in Table 6.

3.2 Evaluation Indicators

Three metrics have been selected to assess the detection capabilities of the proposed method. These quantitative evaluation criteria include Signal-to-Clutter Ratio Gain (SCRG), Background Suppression Factor (BSF), and Contrast Gain (CG). These metrics serve to evaluate both the global background suppression capability and the local target enhancement capability. The mathematical expressions for these metrics are as follows:

SCRG=SCRoutSCRin,(14)

where SCRin and SCRout represent the SCRG of the original and processed images, respectively, and SCR has the value of:

SCR=|μt−μb|σb,(15)

where μt denotes the mean gray value of the target region, and μb and σb denote the mean gray value and standard deviation of the local neighborhood, respectively.

BSF=σinσout,(16)

where σin and σout represent the standard deviation of the original and processed images, respectively.

CG=CONoutCONin,(17)

where CONin and CONout represent the contrast of the input and output images, respectively, and the value of CON is

CON=|μt−μb|,(18)

where μt and μb have the same meaning as in Eq. (15).

Higher values of SCRG and BSF reflect the algorithm’s effectiveness in enhancing targets while suppressing background interference. Similarly, greater values of CG indicate the algorithm’s superior proficiency in detecting small infrared targets.

To assess detection accuracy, the Probability of Detection (PD) and False-Alarm Rate (FA) are employed. These metrics are visually depicted through the Receiver Operating Characteristic Curve (ROC) [40]. In the ROC curve, the horizontal axis represents FA, while the vertical axis signifies PD. The PD and FA values for various algorithms across different thresholds are determined by adjusting thresholds. The mathematical expressions for PD and FA are as follows:

PD=number of true detectionsnumber of actual targets,(19)

FA=number of false pixels detectionnumber of total pixels in images.(20)

3.3 Parameterization of the Proposed Method

The proposed method involves determining five key parameters: the template size and standard deviation for transformed Gaussian filtering, the template size and standard deviation for Gaussian low-pass filtering, and the hyperparameter k. The hyperparameter k is uniformly set to 8. The selection of these parameters is significantly influenced by factors such as varying sizes of small targets, distinct intensities, and varying background complexities found in real infrared images. To achieve enhanced small target visibility and effective blurring, the experimental trials conducted on real infrared images employed a 2×2 template for transformed Gaussian filtering to retain intricate target details, while a 13×13 template was chosen for Gaussian low-pass filtering to eliminate noise and retain the overall target information. Through extensive experimentation, it has been established that altering the template size of Gaussian low-pass filtering 13×13 yields minimal overall result variations. However, the dimensions of the template for transformed Gaussian filtering significantly influence the outcomes. The specific settings for the filtering standard deviations corresponding to Seq1–4 are meticulously presented in Table 7.

3.4 Comparison of Algorithms

To compare the effectiveness of the transform Gaussian filter proposed in this paper with the original Gaussian high-pass filter in highlighting small targets, Fig. 5 presents four comparison images. These images include 3D maps of the difference images obtained by processing with the Gaussian high-pass filter and Gaussian low-pass filter, as well as 3D maps of the difference images obtained by processing with the transform Gaussian filter and Gaussian low-pass filter. A 3D map is created based on the location and intensity of each pixel in an image, where its x and y axes represent the location of a pixel and its z-axis describes pixel intensity. To ensure a fair comparison, the parameters for the Gaussian low-pass filter are kept consistent. As clearly illustrated in Fig. 5, the difference image generated by the Gaussian high-pass filter retains excessive background clutter, and the small targets are not effectively enhanced. This contrasts significantly with the different images produced by the transform Gaussian filter, which demonstrates superior performance. Therefore, the combination of the original Gaussian high-pass filter and Gaussian low-pass filter does not achieve the desired effect in highlighting small targets in infrared images, leading to suboptimal detection results. In contrast, the method proposed in this paper shows significantly better performance in this regard.

Figure 5: Comparison of Gauss high-pass filter and transform Gauss filter on different images, where peaks in 3D maps indicate the pixels that are detected to be in a small target region (Small targets are marked by red circles)

To facilitate a comparison of detection capabilities across different algorithms, Figs. 6 and 7 illustrate the performance of diverse methods on distinct images. Analyzing the sample images in Fig. 6, it becomes evident that the LCM method yields the least favorable performance among the algorithms considered. It merely leads to target “inflation,” failing to effectively suppress background or enhance targets. The RLCM method exhibits an improvement compared to LCM, proving more effective on images with simpler backgrounds. However, it remains susceptible to background clutter and displays numerous false target points in images with intricate backgrounds. The MPCM method displays superior performance solely on the seventh image while being impacted by background noise and clutter. The TOP-HAT algorithm similarly excels on images with isolated backgrounds but encounters challenges posed by edges and potent clutter. In contrast, the approach outlined in this paper excels in both background suppression and target enhancement. Although its performance on the fourth image isn’t as pronounced as that of the RLCM method, it offers a unique advantage in detecting intricate target shapes. Notably, the RLCM method tends to overly constrict targets, leading to the detection of only a few pixels, whereas the proposed method captures the target’s shape more comprehensively.

Figure 6: Significance maps for different algorithms, where peaks in 3D maps suggest pixels that are determined to be in a small target region by an approach

Figure 7: Plot of detection results for different algorithms, where the identified areas for small targets are marked by red circles

Fig. 7 presents the conclusive detection outcomes attained by various algorithms. In this depiction, red circles are employed to indicate the location and quantity of small targets. An observation from the figure reveals that both the LCM and TOP-HAT algorithms yield a higher count of false alarm points in their detection outcomes. Particularly, the LCM algorithm even demonstrates a prevalence of false alarm blocks, consequently exhibiting a lower success rate in detection. Notably, the LCM and MPCM algorithms exhibit blocky detection outcomes, indicative of a block-like effect. This phenomenon is noticeable when detecting images with multiple targets, where scenarios consist of both high-contrast targets against the background and low-contrast targets against the background. During the detection of images containing multiple targets, a scenario involving both high-contrast targets against the background and low-contrast targets against the background often arises. In such cases, the LCM, RLCM, MPCM, and TOP-HAT algorithms are limited to detecting solely those high-contrast targets, while missing out on the low-contrast ones. In contrast, both the proposed method and DNANet are capable of detecting both types of targets, significantly enhancing the overall detection success rate. In addition, the proposed method significantly enhances background clutter suppression through two key operations: threshold segmentation and clustering analysis. During the threshold segmentation phase, the adaptively determined threshold allows for a clearer distinction between the target and the background, effectively reducing the likelihood of low-contrast targets being obscured by background interference. The subsequent clustering analysis further strengthens this effect by isolating noise points from true targets, leading to more stable and accurate detection results. These two operations together provide efficient filtering of background noise, thereby considerably reducing the false alarm rate. As a result, the detection system not only performs well in complex backgrounds but also maintains high accuracy and reliability in multi-target scenarios, significantly improving the overall detection performance.

Table 8 presents the SCRG, BSF, and CG metrics associated with diverse algorithms across the four sequences. In each row, the most exceptional result is highlighted through bolding, while the second-ranked result is denoted by a horizontal line. Notably, the LCM method attains the most favorable CG outcomes across the four sequences, albeit displaying comparatively inferior SCRG and BSF performances. The RLCM method stands out in Seq2 and Seq3, demonstrating commendable background suppression and target enhancement capabilities. However, its performance falters in terms of CG. The MPCM and TOP-HAT methods, as indicated by the table data, prove less efficacious in detection. The proposed method performs exceptionally well on the Seq2 and Seq3 datasets, achieving the best detection results. This demonstrates the method’s strong adaptability and robustness, effectively suppressing background clutter and enhancing target features. Although its performance on the Seq1 and Seq4 datasets is relatively less impressive compared to Seq2 and Seq3, its background suppression and target enhancement capabilities remain satisfactory. Notably, in scenarios with complex backgrounds, the proposed method maintains a good balance between the false alarm rate and detection accuracy, ensuring effective target capture.

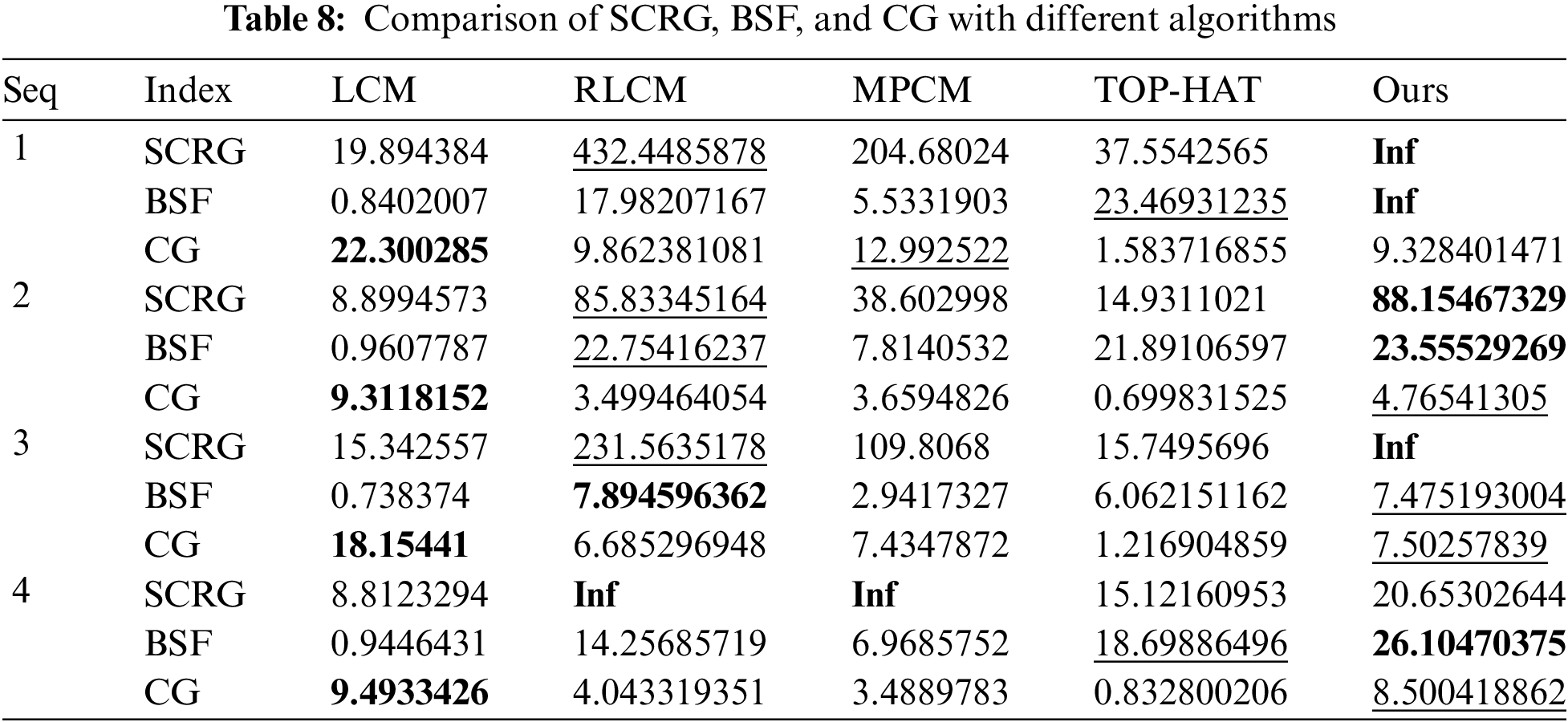
Fig. 8 illustrates the comparative ROC curves of all methods across the four real IR image sequences. Observing the graph, it’s evident that the LCM method exhibits the poorest performance, manifesting the highest FA and the lowest PD. Nevertheless, its performance on Seq3 marginally surpasses that of the RLCM method. Overall, the RLCM method delivers better results than the LCM method. Contrarily, the TOP-HAT method outperforms the RLCM method across three sequences. The MPCM method showcases relatively higher PD and lower FA, only slightly trailing behind the performance of the approach proposed in this paper. The method proposed in this paper outperforms several traditional detection approaches, consistently achieving a high probability of detection (PD) across various threshold settings. Its robustness and stability are superior, demonstrating stronger adaptability and reliability in complex environments. Compared with the traditional method of state of the arts (SOTA) detection method, the detection accuracy of the four sequences is increased by 2.06%, 0.95%, 1.03%, and 1.01%, respectively, and the false alarm rate is reduced, thus providing a more effective and robust solution.

Figure 8: ROC curves for Seq1–4

However, among all methods evaluated, the deep learning-based approach, DNANet, exhibits the best overall performance. The ROC curve of DNANet is significantly higher than that of the proposed method, indicating that DNANet delivers superior detection performance in infrared small target detection, achieving a higher detection rate at lower false alarm rates. Nevertheless, deep learning methods typically require extensive training data, intricate model architectures, and substantial computational resources. In contrast, the proposed method offers advantages in terms of simplicity, lower computational cost, and scalability. It can be effectively combined with other detection methods, providing a more practical and efficient solution in resource-constrained environments.

3.5 Complexity Analysis and Runtime Comparison

A concise overview of the time complexity analysis of the presented method is provided below. The time consumption primarily originates from two key aspects: the transformed Gaussian filtering involving Gaussian low-pass filtering processing and the subsequent clustering analysis. Assuming an input image denoted as I∈Rm×n, with a transformed Gaussian filtering template represented as n1×n1, a Gaussian low-pass filtering template as n2×n2, and a specified iteration count denoted as k. Consequently, the complexity of the filtering stage can be represented as O(mn(n12+n22)), while the clustering stage’s complexity can be denoted as O(kmnC). The overall complexity of the process is captured by O(mn(n12+n22+kC)).

Runtime comparisons among different methods on the Seq2 dataset are presented in Table 9. It’s worth noting that the proposed method distinguishes itself by incorporating a clustering analysis stage after threshold segmentation, setting it apart from the baseline methods. Consequently, Table 9 provides a separate breakdown of results, considering both cases with and without the cluster analysis stage. The table provides a clear overview of the time requirements for each method. Notably, the TOP-HAT method exhibits the quickest execution time. Similarly, the proposed method demonstrates a swift execution when the cluster analysis stage is absent. The LCM and MPCM methods closely follow in terms of time consumption. The RLCM method exhibits progressively increased time consumption. On the other hand, the proposed method’s execution time becomes comparatively longer upon the inclusion of the cluster analysis stage. However, this additional stage significantly enhances accuracy and reduces false alarm rates. The performance of small target detection can thus be significantly improved by incorporating the additional stage of clustering.

It’s important to highlight that the time spent in the cluster analysis stage is visibly influenced by the image size. The time required for the clustering analysis phase is significantly influenced by the size of the image. To demonstrate this, we selected images with three different resolutions: 128 × 128, 256 × 256, and 640 × 512 pixels, with 40 images for each resolution. We calculated the average time spent on clustering analysis per image. The results are shown in Table 10. As illustrated in Table 10, the time required for processing a single image increases significantly when a large number of pixels need to be processed. This is because the time consumed by clustering analysis is strongly correlated with the number of initial samples; the larger the number of initial samples, the more time each iteration requires.

4  Conclusion and Prospect

In this paper, we propose a novel method for infrared small target detection, introducing a new transform Gaussian filter kernel. The approach follows three key steps. First, the difference image is generated by subtracting the filtering results from the newly designed transform Gaussian filter and the traditional Gaussian filter. Second, an adaptive thresholding technique is applied to identify small target pixels, effectively suppressing most background noise. Finally, fuzzy C-means clustering is utilized to eliminate false positives and extract small targets.

Experimental results demonstrate that the proposed method outperforms traditional techniques, particularly in low signal-to-noise ratio (SNR) and low signal-to-clutter ratio (SCR) environments, achieving better detection rates with fewer false alarms. While deep learning methods generally achieve higher accuracy, the proposed method offers significant advantages, including simplicity, lower data dependency, reduced computational requirements, and strong portability, making it a practical choice for many real-world applications.

Despite these strengths, the proposed method sometimes splits a single small target into two closely adjacent targets. This issue arises due to the transform Gaussian filter, which, during the enhancement process, emphasizes the edges of small targets but fails to enhance the central region effectively. This can cause positional shifts in the different images, leading to the division of a single target into two. Future work should focus on addressing this issue by considering the shape characteristics of small targets to reduce or eliminate positional deviations.

Currently, the proposed algorithm is tailored for single-frame infrared small target detection, where it performs effectively. However, its application in multi-frame or sequence-based detection has not yet been explored. In complex backgrounds or low SNR environments, single-frame detection may be less robust compared to methods that utilize temporal information. Future research could extend this algorithm to multi-frame scenarios, leveraging temporal data to further enhance detection performance.

Acknowledgement: The authors are grateful for the constructive comments and suggestions from the anonymous reviewers on an earlier version of the paper.

Funding Statement: This work is fully supported by the Funding of Jiangsu University of Science and Technology, under the grant number: 1132921208.

Author Contributions: Sanxia Shi contributed to the research method, and was responsible for data collection and analysis and algorithm implementation. Yinglei Song contributed to the proposal of research methods and was responsible for the design of the research. All authors participated in writing, reviewing and editing the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets for the paper are sourced from [38–40]. The rest of the data is available at https://github.com/wawawa-sou/111.git (accessed on 09 September 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Gao, L. Wang, Y. Xiao, Q. Zhao, and D. Meng, “Infrared small-dim target detection based on Markov random field guided noise modeling,” Pattern Recogn., vol. 76, no. 12, pp. 463–475, Apr. 2018. doi: 10.1016/j.patcog.2017.11.016. [Google Scholar] [CrossRef]

2. P. Du and A. Hamdulla, “Infrared small target detection using homogeneity-weighted local contrast measure,” IEEE Geosci. Remote Sens. Lett., vol. 17, no. 3, pp. 514–518, Mar. 2020. doi: 10.1109/LGRS.2019.2922347. [Google Scholar] [CrossRef]

3. S. S. Rawat, S. K. Verma, and Y. Kumar, “Review on recent development in infrared small target detection algorithms,” in Proc. Comput. Sci., Gurugram, India, 2020, pp. 2496–2505. [Google Scholar]

4. J. Du et al., “A spatialoral feature-based detection framework for infrared dim small target,” IEEE Trans. Geosci. Remote Sens., vol. 60, no. 2, pp. 1–12, 2022. doi: 10.1109/TGRS.2021.3117131. [Google Scholar] [CrossRef]

5. X. Lu, X. Bai, S. Li, and X. Hei, “Infrared small target detection based on the weighted double local contrast measure utilizing a novel window,” IEEE Geosci. Remote Sens. Lett., vol. 19, pp. 1–5, 2022. doi: 10.1109/LGRS.2022.3194602. [Google Scholar] [CrossRef]

6. C. Kwan and B. Budavari, “A high-performance approach to detecting small targets in long-range low-quality infrared videos,” SignalImage Video Process, vol. 16, no. 1, pp. 93–101, Feb. 2022. doi: 10.1007/s11760-021-01970-x. [Google Scholar] [CrossRef]

7. K. Qian, S. Rong, and K. Cheng, “Anti-interference small target tracking from infrared dual waveband imagery,” Infrared Phys. Technol., vol. 118, Nov. 2021, Art. no. 103882. doi: 10.1016/j.infrared.2021.103882. [Google Scholar] [CrossRef]

8. E. Zhao, L. Dong, and J. Shi, “Infrared maritime target detection based oniterative corner and edge weights in tensordecomposition,” IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens., vol. 16, pp. 1–16, 2023. doi: 10.1109/JSTARS.2023.3298479. [Google Scholar] [CrossRef]

9. F. Chen, C. Bian, and X. Meng, “Infrared small target detection using homogeneity-weighted local patch saliency,” Infrared Phys. Technol., vol. 133, no. 10, Sep. 2023, Art. no. 104811. doi: 10.1016/j.infrared.2023.104811. [Google Scholar] [CrossRef]

10. X. Sun, W. Xiong, and H. Shi, “A novel spatiotemporal filtering for dim small infrared maritime target detection,” in Proc. Int. Symp. Electr., Electron. Inf. Eng. (ISEEIE), Chiang Mai, Thailand, 2022, pp. 195–201. [Google Scholar]

11. S. D. Deshpande, M. H. Er, R. Venkateswarlu, and P. Chan, “Maxmean and max-median filters for detection of small targets,” Proc. SPIE, vol. 3809, pp. 74–83, Oct. 1999. doi: 10.1117/12.364049. [Google Scholar] [CrossRef]

12. M. M. Hadhoud and D. W. Thomas, “The two-dimensional adaptiveLMS (TDLMS) algorithm,” IEEE Trans. Circuits Syst., vol. 35, no. 5, pp. 485–494, May 1988. doi: 10.1109/31.1775. [Google Scholar] [CrossRef]

13. X. Bai and F. Zhou, “Analysis of new top-hat transformation and theapplication for infrared dim small target detection,” Pattern Recogn., vol. 43, no. 6, pp. 2145–2156, Jun. 2010. doi: 10.1016/j.patcog.2009.12.023. [Google Scholar] [CrossRef]

14. X. Wang, Z. Peng, P. Zhang, and Y. He, “Infrared small target detectionvia nonnegativity-constrained variational mode decomposition,” IEEE Geosci. Remote Sens. Lett., vol. 14, no. 10, pp. 1700–1704, Aug. 2017. doi: 10.1109/LGRS.2017.2729512. [Google Scholar] [CrossRef]

15. H. Wang and Y. Xin, “Wavelet-based contourlet transform and kurtosismap for infrared small target detection in complex background,” Sensors, vol. 20, no. 3, Feb. 2020, Art. no. 755. doi: 10.3390/s20030755. [Google Scholar] [PubMed] [CrossRef]

16. M. Cao and D. Sun, “Infrared weak target detection based on improved morphological filtering,” in 2020 Chin. Control Decis. Conf. (CCDC), Hefei, China, 2020, pp. 1808–1813. doi: 10.1109/CCDC49329.2020.9164372. [Google Scholar] [CrossRef]

17. M. Zhang, L. Dong, H. Zheng, and W. Xu, “Infrared maritime smalltarget detection based on edge and local intensity features,” Infrared Phys. Technol., vol. 119, no. 4, Dec. 2021, Art. no. 103940. doi: 10.1016/j.infrared.2021.103940. [Google Scholar] [CrossRef]

18. S. Yao, Y. Chang, and X. Qin, “A coarse-to-fine method for infrared small target detection,” IEEE Geosci. Remote Sens. Lett., vol. 16, no. 2, pp. 256–260, Feb. 2019. doi: 10.1109/LGRS.2018.2872166. [Google Scholar] [CrossRef]

19. C. Gao, D. Meng, Y. Yang, Y. Wang, X. Zhou and A. G. Hauptmann, “Infrared patch-image model for small target detection in a single image,” IEEE Trans. Terahertz Sci. Technol., vol. 22, no. 12, pp. 4996–5009, Sep. 2013. doi: 10.1109/TIP.2013.2281420. [Google Scholar] [PubMed] [CrossRef]

20. J. Guo, Y. Wu, and Y. Dai, “Small target detection based on reweightedinfrared patch-image model,” IET Image Process., vol. 12, no. 1, pp. 70–79, Jan. 2018. doi: 10.1049/iet-ipr.2017.0353. [Google Scholar] [CrossRef]

21. L. Zhang, L. Peng, T. Zhang, S. Cao, and Z. Peng, “Infrared small targetdetection via non-convex rank approximation minimization joint l2, 1norm,” Remote Sens., vol. 10, no. 11, 2018, Art. no. 1821. doi: 10.3390/rs10111821. [Google Scholar] [CrossRef]

22. X. Wang, Z. Peng, D. Kong, and Y. He, “Infrared dim and smalltarget detection based on stable multisubspace learning in heterogeneousscene,” IEEE Trans. Geosci. Remote Sens., vol. 55, no. 10, pp. 5481–5493, Aug. 2017. doi: 10.1109/TGRS.2017.2709250. [Google Scholar] [CrossRef]

23. T. Zhang, Z. Peng, H. Wu, Y. He, C. Li and C. Yang, “Infraredsmall target detection via self-regularized weighted sparse model,” Neurocomputing, vol. 420, no. 12, pp. 124–148, Jan. 2021. doi: 10.1016/j.neucom.2020.08.065. [Google Scholar] [CrossRef]

24. C. L. P. Chen, H. Li, Y. Wei, T. Xia, and Y. Y. Tang, “A local contrast method for infrared small target detection,” IEEE Trans. Geosci. Remote Sens., vol. 52, no. 1, pp. 574–581, Jan. 2014. doi: 10.1109/TGRS.2013.2242477. [Google Scholar] [CrossRef]

25. Y. Wei, X. You, and H. Li, “Multiscale patch-based contrast measure for infrared small target detection,” Pattern Recogn., vol. 58, no. 1, pp. 216–226, Oct. 2016. doi: 10.1016/j.patcog.2016.04.002. [Google Scholar] [CrossRef]

26. J. Han, K. Liang, B. Zhou, X. Zhu, J. Zhao and L. Zhao, “Infrared small target detection utilizing the multiscale relative local contrast measure,” IEEE Geosci. Remote Sens. Lett., vol. 15, no. 4, pp. 612–616, Apr. 2018. doi: 10.1109/LGRS.2018.2790909. [Google Scholar] [CrossRef]

27. J. Han, S. Moradi, I. Faramarzi, C. Liu, H. Zhang and Q. Zhao, “A local contrast method for infrared small-target detection utilizing a tri-layer window,” IEEE Geosci. Remote Sens. Lett., vol. 17, no. 10, pp. 1822–1826, Oct. 2019. doi: 10.1109/LGRS.2019.2954578. [Google Scholar] [CrossRef]

28. J. Han et al., “Infrared small target detection based on the weighted strengthened local contrast measure,” IEEE Geosci. Remote Sens. Lett., vol. 18, no. 9, pp. 1670–1674, Jul. 2020. doi: 10.1109/LGRS.2020.3004978. [Google Scholar] [CrossRef]

29. Y. Tang, K. Xiong, and C. Wang, “Fast infrared small target detection based on global contrast measure using dilate operation,” IEEE Geosci. Remote Sens. Lett., vol. 20, no. 6, pp. 1–5, 2023. doi: 10.1109/LGRS.2023.3233958. [Google Scholar] [CrossRef]

30. D. Ren, J. Li, M. Han, and M. Shu, “DNANet: Dense nested attention network for single image dehazing,” in IEEE Int. Conf. Acoust., Speech Signal Process., Toronto, ON, Canada, 2021, pp. 2035–2039. doi: 10.1109/ICASSP39728.2021.9414179. [Google Scholar] [CrossRef]

31. M. Zhang et al., “RKformer: Runge-kutta transformer with random-connection attention for infrared small target detection,” in Proc. ACM Int. Conf. Multimed., Lisboa, Portugal, 2022, pp. 1730–1738. [Google Scholar]

32. M. Zhang, K. Yue, J. Zhang, Y. Li, and X. Gao, “Exploring feature compensation and cross-level correlation for infrared small target detection,” in Proc. ACM Int. Conf. Multimed., Lisboa, Portugal, 2022, pp. 1857–1865. [Google Scholar]

33. R. Kou et al., “Infrared small target segmentation networks: A survey,” Pattern Recogn., vol. 143, Nov. 2023, Art. no. 109788. doi: 10.1016/j.patcog.2023.109788. [Google Scholar] [CrossRef]

34. X. Tong et al., “MSAFFNet: A multi-scale label-supervised attention feature fusion network for infrared small target detection,” IEEE Trans. Geosci. Remote Sens., vol. 61, pp. 1–16, 2023. doi: 10.1109/TGRS.2023.3279253. [Google Scholar] [CrossRef]

35. P. Fan, W. Zhang, P. Kong, Q. Gao, M. Wang and Q. Dong, “Infrared dim target detection based on visual attention,” Infrared Phys Technol., vol. 55, no. 6, pp. 513–521, Nov. 2012. doi: 10.1016/j.infrared.2012.08.004. [Google Scholar] [CrossRef]

36. P. Fan, W. Zhang, P. Kong, Q. Gao, M. Wang and Q. Dong, “Infrared Dim and Small Target detection based onsample data,” in Int. Conf. Control Autom. Inf. Sci. (ICCAIS), Xi’an, China, 2021, pp. 532–536. [Google Scholar]

37. B. Hui et al., “A dataset for infrared detection and tracking of dim-small aircraft targets underground/air background,” Chin Sci. Data., vol. 5, no. 3, pp. 291–302, Aug. 2020. doi: 10.11922/sciencedb.902. [Google Scholar] [CrossRef]

38. Y. Dai, Y. Wu, F. Zhou, and K. Barnard, “Attentional local contrast networks for infrared small target detection,” IEEE Trans. Geosci. Remote Sens., vol. 59, no. 11, pp. 9813–9824, Nov. 2021. doi: 10.1109/TGRS.2020.3044958. [Google Scholar] [CrossRef]

39. M. Zhang, R. Zhang, Y. Yang, H. Bai, J. Zhang and J. Guo, “ISNet: Shape matters for infrared small target detection,” in Proc IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, 2022, pp. 867–876. [Google Scholar]

40. C. -I. Chang, “An effective evaluation tool for hyperspectral targetdetection: 3D receiver operating characteristic curve analysis,” IEEE Trans. Geosci. Remote Sens., vol. 59, no. 6, pp. 5131–5153, Jun. 2020. doi: 10.1109/TGRS.2020.3021671. [Google Scholar] [CrossRef]