Two-Stage Client Selection Scheme for Blockchain-Enabled Federated Learning in IoT

1  Introduction

In recent years, the application of Internet of Things (IoT) technology in communication, healthcare, and smart cities has been increasing, generating a large amount of data. Many companies can use this massive amount of data to train the artificial intelligence (AI) models they need. The more data the company collects, the more accurate the model it trains. However, the data usually comes from different IoT devices, such as smartphones, personal laptops, robots, drones, various sensors, and so on. These IoT devices have limited resources, and we often call them resource-constrained devices. Due to limited resource availability, training these edge devices with large dataset is not feasible [1]. They don’t have the capacity to handle massive amounts of data, so large companies will collect data from massive devices to train their models, but some users may not want companies to obtain their own local data to train models, which raises data privacy concerns and results in some valuable data not being used well. At a time when data is listed as the fifth factor of production, a privacy-protecting AI solution must be built to maximize the value of data.

Federated learning (FL) is a promising approach that trains AI models while preserving the privacy of user data. FL offers several advantages for IoT applications, including enhanced data privacy, reduced latency in network communication, and improved learning quality [2]. Despite its theoretical appeal, FL faces practical challenges when deployed in real-world scenarios. One major issue is the assumption of a trusted environment where all participants are honest and trustworthy. In reality, FL is often deployed in untrusted domains where participants may act maliciously, uploading fake models during training, thus affecting the training rate and the accuracy of the final model. Additionally, FL lacks a robust incentive mechanism, which is crucial for encouraging users to contribute their local data and computational resources for model training. Without proper incentives, users may be reluctant to participate, leading to a lack of motivation and potentially skewed model training. Furthermore, FL has been found to have certain privacy vulnerabilities, such as model inversion attacks [3], property inference attacks [4], and membership inference attacks [5]. These challenges highlight the need for a secure, incentive-compatible, and privacy-preserving FL solution.

The emergence of blockchain [6] technology offers a potential solution to some of the challenges faced by FL. Blockchain enables decentralized data storage and processing without the need for third-party intermediaries. The nodes within a blockchain, often referred to as miners, contribute computational and storage resources to the system and are rewarded with block rewards. Blockchain’s characteristics, such as security, transparency, incentive mechanisms, traceability, and distribution, seem to complement FL, potentially addressing some of the shortcomings in FL’s application process. At present, blockchain based FL (BCFL) architecture has been a hot research direction [7,8]. However, current research on BCFL primarily focuses on security aspects, with limited exploration of client selection schemes within the BCFL framework. Based on the three key issues of BCFL, namely decentralization, incentive mechanism and client selection [9]. This paper will research the client selection issue.

Because blockchain is an open platform, with the characteristics of openness and transparency, clients can freely access the data on the blockchain, which will give users privacy concerns. For example, if an FL task is placed on blockchain, how will the task publisher know which client data satisfies the FL task requirements? Without client filtering, FL training simply cannot continue. At the same time, FL task publishers may not want their FL tasks to be seen by all nodes on the blockchain, preferring to send encrypted FL tasks to the blockchain. In addition, because of the limited resources, some clients may not fully participate in all training processes. Empirical observations [10] show that increasing the number of participants in each round (that is, increasing the total number of trained models in the absence of training failures) may improve the convergence rate. However, task publishers are not always nodes with rich storage, communication, and computing resources like cloud server, so it is impossible for them to establish connections with all candidate clients. Each round requires selecting a suitable set of clients to participate in model training. Therefore, a suitable client selection algorithm is of great significance in BCFL architecture.

This paper introduces a two-stage client selection scheme for BCFL that addresses the aforementioned challenges. In the first stage, we employ attribute-based encryption (ABE) to select clients that meet the FL task requirements, ensuring the privacy of client attributes. In the second stage, we utilize a reinforcement learning algorithm to further refine the selection of clients for local model aggregation, enhancing the efficiency of the FL training process. Our contributions are as follows:

(1) We design the BCFL architecture for IoT, where task publishers issue FL tasks on the blockchain, and nodes with the necessary data for the FL task apply to participate in the training. The outcomes are recorded on the blockchain, ensuring transparency and traceability.

(2) We develop a client selection algorithm based on ABE for the initial selection, allowing task publishers to encrypt FL tasks and broadcast them on the blockchain. Clients possessing the relevant attributes can decrypt and access the training tasks, ensuring that only those meeting the task requirements are selected.

(3) For the second stage, we propose a client selection scheme based on the Proximal Policy Optimization (PPO) algorithm, considering factors such as data quality, communication capabilities, and fairness in the training process. This approach aims to select clients that contribute to the efficient and effective training of the global model.

2  Related Work

A security aggregation protocol [11] is proposed to ensure the confidentiality of gradient while supporting client exit workflow, and a new blockchain architecture is designed to make global gradient verification resistant to potential attacks. Some studies [12–14] have shown the number of clients selected in each epoch has a significant impact on the convergence rate. Peng et al. proposed VFchain [15] that selects a committee through the blockchain to aggregate the model for the FL process and design a blockchain authentication data structure to provide auditability for the FL process. At present, most of the FL research based on blockchain focuses on the security direction, and there are few researches on the client selection scheme under the framework of BCFL. Yu et al. proposed an innovative solution [16] for the verification of federated learning aggregation results. This method uses zero-knowledge proof technology to design an efficient verification circuit to reduce the computational burden of IIoT devices in the verification process. Although EV-FL has made significant progress in verifying weight aggregation, the EV-FL approach is computatively expensive during the initialization phase, which can affect the overall efficiency of the system, especially in large-scale IIoT networks. Li et al. proposed that SVFLC [17] solves the problem of gradient leakage by designing a privacy protection method and defends the collusion attacks of semi-honest users. SVFLC’s extensive experimental results on real-world datasets show high efficiency, but SVFLC schemes are computatively expensive during the initialization phase, which can affect the overall efficiency of the system, especially in large-scale IIoT networks.

Fraboni et al. [18] introduced cluster sampling for client selection and demonstrated that cluster sampling leads to better customer representation and reduces the variance of the random aggregation weights of clients. In [18], two different clustering methods are provided to achieve customer clustering based on sample size and model similarity. Compared with the standard sampling method, the model aggregation based on cluster sampling always has better training convergence and variability. Balakrishnan et al. [19] proposed federated averaging with diverse clients selection algorithm, selecting a small number of different clients that carry representative gradient information, and only transmitting these updates to the server. Taking inspiration from the structure of classical artificial intelligence methods, the active federated learning (AFL) [20] framework is proposed, with the aim of selecting an optimized subset of clients based on a value function that reflects the usefulness of the data for that user during each training session. Cho et al. [21] proposed power-of-choice, which has the flexibility to balance convergence rate and solution bias.

Blockchain data sharing technology based on ABE has also developed in recent years. A new blockchain-based trusted security ciphertext policy and attribute hiding access control scheme TrustAccess [22] is proposed, which ensures the privacy of policies and attributes while realizing trusted access. Zhang et al. [23] focused on privacy protection of ciphertext policies in CP-ABE schemes, by designing appropriate ciphertext and key structures as well as access structures to protect privacy information in access policies. This paper draws on the ideas of the above research to share a global model of FL on blockchain using ABE technology.

3  Preliminaries

3.1 Attribute-Based Encryption (ABE)

ABE was first proposed in [24]. It is a cryptographic solution that solves the access control requirements in the cloud computing data sharing scenario. Only keys that satisfy access control conditions can decrypt ciphertext and obtain plaintext. Otherwise, garbled characters are obtained. ABE is mainly divided into CP-ABE [25] and KP-ABE [26] schemes.

3.2 Proximal Policy Optimization (PPO)

Trust region policy optimization algorithm (TRPO [27]) is a policy gradient algorithm in reinforcement learning. By limiting the kullback-leibler divergence (or the range of policy change), TRPO avoids the problem in each iteration. Large change of policy parameters. PPO algorithm [28] is an improvement on the basis of TRPO, which is simpler and less computational in practice. This kind of algorithm needs to be updated in each iteration, so the calculation is large, but from the performance of the actual application, the performance of this kind of algorithm is more stable and easier to converge. Compared with the policy gradient algorithm, the confidence region optimization algorithm is more stable, more robust to hyperparameters, and has higher sample efficiency.

4  System Model

This section consists of three parts, the overall system architecture, the first phase of client selection based on ABE, and the second phase of client selection based on reinforcement learning. The system architecture is shown in Fig. 1. The system architecture consists of the following entities:

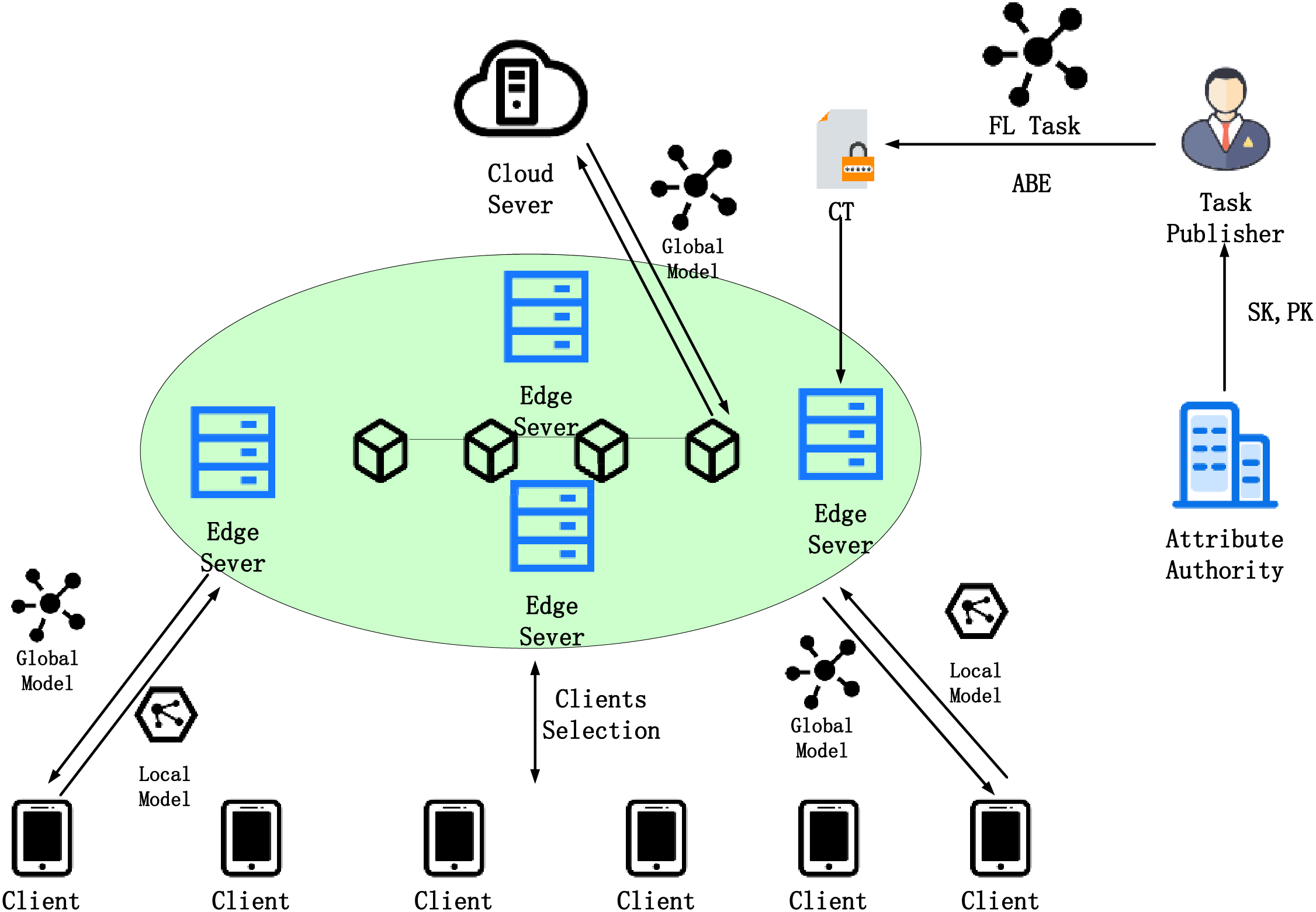
Figure 1: System architecture

Task Publisher. The task publisher (TP) encrypts the FL task through an attribute policy to generate ciphertext CT and then sends it to the blockchain. The clients that satisfy the attribute policy can obtain the FL task.

Attribute Authority. Attribute authorities (AA) are responsible for generating attribute keys for Clients.

IoT Devices. IoT devices hold the data needed for FL tasks. The clients that satisfy the FL task access policy train the model using local data. The CT contains a bloom filter [29], through which IoT device can know whether they have attributes that satisfy the policy. Clients that satisfy the policy can decrypt the encrypted model.

Edge Nodes. Edge nodes have computing and storage capabilities, are full nodes in the blockchain, and store the global model which has been attribute-based encrypted. The main function of the blockchain is to record data usage (which edge nodes trained the global model uploaded by the task publisher and which clients participated in the model training); Select nodes that participate in FL training; Provide incentives to eventually form a market for data trading. Edge nodes are also responsible for aggregating local models uploaded by clients.

Cloud Server. The cloud server mainly obtains the local model from the blockchain and aggregates the model to get the global model.

The workflow of our scheme is as follows:

(1) AA generates attribute keys for clients with certain attributes. Attribute keys are used to decrypt FL tasks issued by task publishers.

(2) The FL task publisher designs the attribute policy according to the attributes of the data required for the training task, encrypts the global model through the attribute policy, and generates the ciphertext of the FL task.

(3) The TP publishes the FL task to the blockchain, and the client can judge whether its own data satisfies the attribute policy of the task. If it satisfies the attribute policy, the client can provide the proof of satisfying the attribute policy to the edge node.

(4) Each edge node collects candidate clients that satisfy the FL task and forms a candidate client set. Each edge node has a candidate client set.

(5) Clients, edge nodes, and cloud server begin the FL training process. The edge node obtains the clients participating in each training round through the client selection algorithm of the second stage according to its own candidate client set.

(6) The selected clients train the global model with local dataset and upload the trained models to the edge node. In this step, the selected client may be offline.

(7) Each edge node collects the local model of the client, and then uploads the aggregated model together with other edge nodes to the cloud server, which carries out further model aggregation, finally gets the updated global model, and then sends the global model to all edge nodes.

(8) Repeat Steps (5)–(7) for client, edge node and cloud server to finally get the trained global model. The client participating in the training is recorded on the blockchain.

4.1 First Stage Client Selection Based on ABE

Firstly, the clients with relevant training data are selected as candidate clients through the first step of client selection. Access policy privacy protected by ABF (attribute bloom filters) in [30]. We apply this approach to our system to filter out clients that meet the FL task attribute policy. By joining a global identity document (GID), each identity has its own GID stored on the blockchain. Clients only need to prove that they satisfy certain attribute policy, thus providing models to the edge nodes.

GlobalSetup(1з) → (PK, MSK). First input the security parameters з, operation Global Setup(1з), obtain the global public parameter GP and the public key of the edge nodes.

GP={p, G, g, e}(1)

PK={g, h, e(g, g)α, gβ, LABF, H1(), H2(), …, Hk(), GID}(2)

p is the order of subgroups G. e is a bilinear mapping. g in the PK is the generator of G, and h is a random element in G. α and β are random integer, the PK contains k hash functions that are used to create an ABF during the encryption phase.

KeyGen(PK,MSK,S) → SK. KeyGen algorithm selects the attribute set of DU, and generates the attribute private key SK to DU. S is attribute name and IS is the index of the attribute name. Select a random number d and we can get

K=gαgβd(3)

K′=gd(4)

Kx=(gSρ(x)h)d(5)

SK=(S, K, K′, {Kx}x∈IS)(6)

Encrpty(m, PK, (M, ρ)) → (CT, M, ABF). The encryption algorithm is divided into two substeps, the first substep encrypts the global model into ciphertext, and the second substep is to generate ABF.

a. Enc (m, PK, (M, ρ)) → CT. DO encrypts the model with PK, embedding the attribute value V=(attVρ(1), attVρ(2), …,attVρ(l)) in the ciphertext. Then select random numbers T=(tVρ(1), tVρ(2),…, tVρ(l))∈ZNl for each attribute, and a random vector v=(s, y2, y3, …, yN,)T, s is the secret value to be shared. M is the access matrix and ρ is the mapping between the access matrix row number and the attribute name and then calculate λt=Mi as the component of the shared secret value s of Mi where i∈[1, l], l is the number of attributes, Mi is line i of M, and the final output is CT.

CT={C=me(g, g)αs, C′=gs, Ci=gαλi(gtρ(i)h)−s}(7)

b. ABFBuild (M, ρ) → ABF. First create a long enough array, initialize all the values in the array to 0, which completes the initialization of ABF. Then accesses the corresponding attribute and its row number for each row in the matrix to form Se={i||atte}i∈[1,l].The elements in Se are concatenated by attribute name i and attribute value atte. Then expand the line number and number of digits. The element in Se is sorted in ABF. Select a random k-1 λ bit string rek=re1⊕re2⊕…⊕rek−1⊕e, selected k different hash functions for each attribute name. The k bit string obtained through (k, k) sharing is stored in k hash locations. Combine all elements in Se by Eq. (8) to get the l+1 element el+1.

el+1=∑i=1lei(8)

Use the (k, k) share of element el+1 as with other e elements, obtain rl+11, rl+12, …, rl+1k. This maps the user attributes to the ABF. In this way, the attributes of DO who meet the attribute policy are mapped to specific locations in the ABF, thus selecting users who meet the FL task while protecting attribute privacy. With ABF, it is possible to prevent the disclosure of sensitive information on the blockchain and prevent data leakage to unauthorized participants. ABF ensures that all eligible clients have the opportunity to participate in model training, helping to achieve a fair distribution of resources and opportunities.

Remarks: hash collisions may occur in ABF, as shown in the following Fig. 2. The position of H2(ei) is first written to ri2, H1(ej) is mapped to the same position, then rj1 will overwrite ri2, and we set ri2=rj1, so that ei=ri1+rj1+ri3 can be recovered normally.

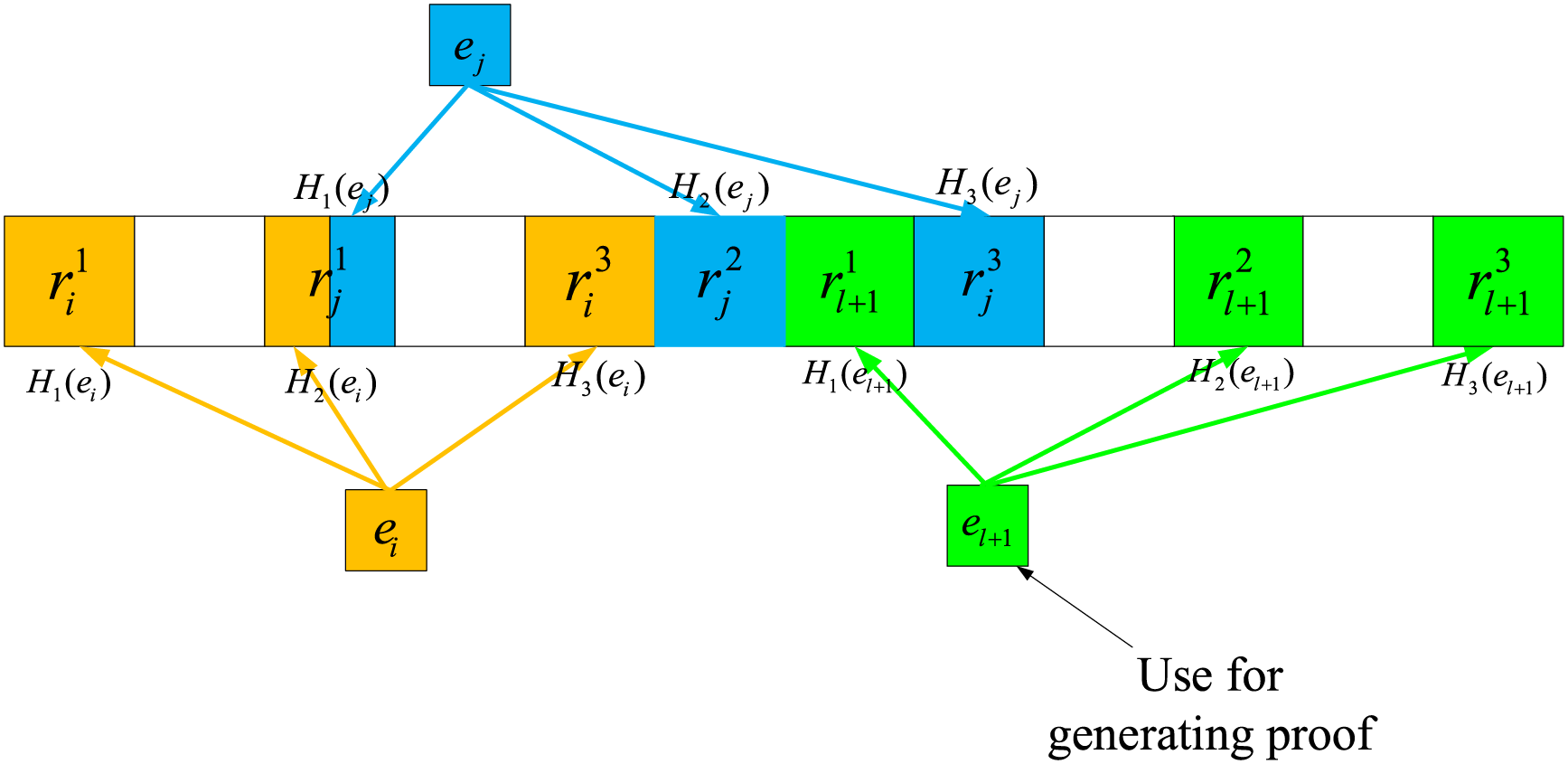
Figure 2: Example of ABF

Decrypt (PK, SK, CT) → m. In the decryption phase of the tradition ciphertext policy CP-ABE, any DU that satisfies the access policy can recover message.

a. ABFQuery (S*, ABF, PK) → ρ. S* is the attribute set of DU, and k hash values of attribute names are calculated to obtain the index in ABF. The element e is reverted according to Eq. (9).

e=re1⊕re2⊕⋯⊕rek−1⊕rek=re1⊕re2⊕⋯⊕rek−1⊕re1⊕re2⊕⋯⊕rek−1⊕rek⊕e(9)

Finally we can recovery ρ′=(rownum, attn)attn∈S∗. When all e is obtained by Eq. (9), we can get el+1 as Eq. (8). The client can then generate the proof as Eq. (10).

proof={GID, signature, {rl+11, rl+12, …, rl+1k}}(10)

The GID corresponds to each proof one by one. The client uses the private key to sign the GID to get the signature. The edge node can verify the signature through the public key corresponding to the GID.

b. Dec (SK, CT, A) → m or ⊥. If the DU satisfies the access policy, then the coefficient is calculated {ωi∈Zp}i∈I makes

∑i∈IωiMi=(1, 0, …, 0)(11)

So we get

∑i∈Iωiλi=s(12)

Decryption process is

W=e(C′,K)e(∏i=1lCi,K′)e(C′,∏i=1lKρ(i))(13)

m=CW(14)

Only if tρ(i)=sρ(i) Eq. (15) is valid.

m=CW=me(g,g)αse(g,g)αs(15)

Then DU gets the global model m.

Client selection (proof) → client set. A client that obtains the FL training task need to prove to the blockchain node that it satisfies the access policy of the FL task, so it needs to provide proof that it can participate in the FL task, and the blockchain node verifies the proof sent by the client to get the subset of candidate clients. At the Decrypt stage, the client calculates el+1 to get the corresponding index in ABF, and then gets {rl+11, rl+12, …,rl+1k} from the index. The client generates the proof.

The GID corresponds to each proof one by one. The client uses the private key to get the signature. The edge node can verify the signature through the public key corresponding to the GID. {rl+11, rl+12, …, rl+1k} is the (k, k) share of the element el+1, the blockchain node verifies that {rl+11,rl+12, …, rl+1k} can pass the ABF and, if so, adds the client that provides the proof to the training task.

Using ABE for the first phase of client selection has the following advantages:

Access control: ABE provides fine-grained access control, ensuring that only clients that conform to specific attribute policies can decrypt and access related federated learning tasks. This access control mechanism enhances data security and compliance.

Data privacy protection: Through ABE, the client’s local data and gradient information are protected during the upload process, preventing data from being intercepted and abused during transmission.

Improve system transparency: The use of ABE increases the transparency of the system because clients can verify that they are eligible to participate in a specific task, which helps build user trust in the system.

Enhance the scalability of the system: ABE allows the system to flexibly deal with the participation of different clients, so that the system can dynamically adjust the collection of participating clients according to the task requirements, thus improving the scalability and flexibility of the system.

Promote fairness: ABE ensures that all eligible clients have the opportunity to participate in model training, helping to achieve a fair distribution of resources and opportunities.

Lower participation threshold: ABE simplifies the participation process of clients, so that even resource-constrained devices can participate in federated learning, lowering the technical threshold for participation in federated learning.

Prevent data leakage: With ABF, it is possible to prevent the disclosure of sensitive information on the blockchain and prevent data leakage to unauthorized participants.

Improve system transparency: ABF allows clients to verify that they are eligible to participate in a specific task, increasing the transparency of the system and user trust in the system.

Reduced communication overhead: ABF reduces communication overhead by reducing the amount of data that needs to be transmitted, making the federated learning process more efficient.

4.2 Security Analysis

The ABE scheme in this paper should meet two requirements: (1) No other node on the blockchain can obtain the attribute name and (2) no proof can be forged. A client that does not satisfy the training task attribute requirements cannot obtain the relevant attributes of the training task. The clients can launch a dictionary attack to obtain the attribute name in the training task, but each attribute name corresponds to multiple attribute values, and the attribute values are embedded in the ciphertext. Therefore, the client participating in the training will not expose its own attribute values. The proof={GID, signature, {rl+11, rl+12, …, rl+1k}} contains three pieces of information, the GID is public information, and attacker cannot forge the {rl+11, rl+12, …, rl+1k}, the attacker would need to obtain {e1, …, el} without all the relevant attribute keys. It is not possible to get el+1 as well. Therefore, the attacker cannot participate in FL task by forging the proof.

4.3 Second Stage Client Selection Based on Reinforcement Learning

ABE initially filters the clients that satisfy the task requirements with privacy, but these clients are not completely trusted, and edge nodes are required to further screen these massive clients, so that the more clients with high-quality data, the better. Edge nodes are aggregated in one step to obtain a local aggregation model, and multiple edge nodes are further aggregated on the blockchain, that is, global aggregation.

How does the edge node filter the clients that satisfy the attribute? Consider the following factors: data quality, communication capability. If we only consider the data quality and ignore the communication ability, the training time may become longer and the efficiency will be affected. If only communication capability is considered and data quality is ignored, the training model may be inefficient due to low quality dataset. Therefore, both client data quality and communication capability must be taken into account.

But data quality and communication capabilities are not a priori. In this paper each edge node selects the clients by reinforcement learning (RL) method, which needs to consider communication delay and data quality. RL can learn the fastest client subset by interacting with the environment. In RL, the player performs a possible action and receives a corresponding reward from the environment. By performing this process iteratively, the player learns the rewards for each action, and ultimately the optimal action.

Edge node and client subset are represented by player and action, respectively. The reward includes communication delay and model accuracy. The client communication delay is expressed as whether the client is offline or not in this paper. Data quality is judged by model accuracy, and edge nodes use test dataset to calculate the accuracy of each model.

4.3.1 Problem Formulation

Some studies [10,31] mentioned that the accuracy of FL is related to the size of client data, the more data the better the training effect. However, due to privacy concerns, the size, label distribution and size of client data are unknowable, so one way is translating the size of client data into the number of clients [32]. However, the dataset size of the client is often unknowable, so increasing the number of clients does not necessarily increase the size of the dataset. In this paper, the problem is directly transformed into the size of global model accuracy. The utility function is as Eq. (16).

μ(smt)=1Nc∑n=1Nλnt(16)

where Nc is the total number of candidates selected by the first stage client, and λnt is the precision of the client N on the test dataset after the integer t. For an edge node, the bandwidth resources are limited, and the clients that can be selected are also limited. In the later stage, clients with higher data quality are selected according to the previous selection results. The rate of convergence is also related to efficiency, and the communication delay of the client is reduced, but the convergence rate is not necessarily reduced.

Client selection rate. The delay of each client is different, and some clients may be offline due to network state fluctuations and other reasons, so each round of edge nodes needs a deadline as the longest waiting time, and clients that fail to upload the local model after the deadline cannot participate in the training.

Client selection rate. In order to ensure that each client is selected throughout the training process, it is required that the probability of each client being selected is greater than β, so for a client:

lim1T∑t=1TE[xt,n]≥β, n∈N(17)

where xt,n is a binary variable, indicating whether the client n is selected in the t round.

Bandwidth constrain. Assuming that the bandwidth budget for each edge node is B, and assuming that the number of candidate clients is large, and the bandwidth of edge nodes is limited so it is impossible to select all clients to participate in FL training. The average bandwidth resource allocated to limited clients is

bnt~=Bm|smt|(18)

where bnt is the bandwidth allocated by client n. The sum of the client bandwidth for each alternative cannot exceed Bm.

∑n=1stbnt≤Bm(19)

Ideally, edge nodes should allocate limited bandwidth to clients with high data quality.

Training model accuracy constraints. In order to ensure data quality, the model trained by the client should be higher than a certain precision, otherwise it will be abandoned, and the number of abandoned should be recorded, affecting the probability of the client being selected later. The precision constraint is expressed as Eq. (20).

H(ωnt,Dtest)≥θt(20)

θt=(θt−1+θt−2)/2(21)

where θt is the minimum accuracy required by the t round, because the accuracy of the model in the early stage of training is not too high, so θt also changes with t. As the task publisher can only obtain the accuracy of the test dataset, while the training accuracy is only known by the client themselves. The threshold is the average accuracy of the selected clients in the adjacent two rounds. The purpose is to eliminate some clients with substandard data quality.

Then, the underlying problem with the above constraints is formulated as Eq. (22).

maxμ(st),st⊆CABEs.t.lim1T∑t=1TE[xt,n]≥β,n∈N∑n=1stbn≤BmH(ωnt,Dtest)≥θt(22)

4.3.2 Reinforcement Learning Client Selection Policy

The following describes the state space, action space, reward and policy functions in PPO:

State space. The state consists of a four-dimensional vector of characteristics of all n selected clients, including the test accuracy (TA), offline rate (OR), selection rate (SR) and the number of times selected until round t−1.

st={p1t, p2t, …, pnt}(23)

pit={TAi(t−1), ORi(t−1), SRit−1, ∑k=0t−1xk, n}(24)

Assume the total number of FL training rounds is R, then selection rate SRi(t−1) can be calculated by

SRi(t−1)=∑k=0t−1xk,nR(25)

Offline rate ORi(t−1) can be calculated by

ORit−1=∑k=0t−1αk,nR(26)

where αk,n is the number of times the client n participated in FL training in k rounds and αk,n≤xk,n.

Action space. The action space is the entire client collection. Edge nodes select a subset of clients st each round.

A={st|st⊆CABE}(27)

CABE is the candidate client selected in the first stage. This paper assumes that there are a large number of client nodes to be selected and a small number of clients per round. Therefore, the action space is large.

Reward. During the training process, we need to consider three issues: whether the training accuracy rate can meet the requirements, whether the selected results can satisfy the fairness, and whether the impact of offline clients can be reduced. Taking the above three factors into consideration, the reward function in this paper is defined as Eq. (28).

rew={λ1TA−λ2SRminn∈N(SRn)<χλ1TA−λ3ORminn∈N(SRn)≥χ(28)

χ is the minimum client selection rate. At first the edge node is in the exploration stage, and every client should be selected as far as possible until the selection rate of each client is greater than χ. Then the edge node has a certain knowledge of the training effect of each client. At this time, it is necessary to consider the impact of offline clients on training. Once the client is selected by the edge node but does not send the local model to the edge node within the deadline, the client will be judged as an offline node, and OR will be increased. As a penalty item, the more times a client is offline, the smaller the probability of being selected later. λ1, λ2, λ3 are reward coefficients, and the corresponding reward on the client will increase exponentially with TA, SR and OR. If λ1 is too large, the client selection process will completely follow the model accuracy, and the client with higher test accuracy will be preferred, which will lead to the loss of diversity of training data. λ1 Too small and you lose the ability to weed out malicious or poor data quality clients. λ2 plays an important role in the pre-training exploration stage. In order to select as many clients as possible early on, λ2 reduces the subsequent rewards for selected clients. So adjusting the value of λ2 can adjust the speed of the previous exploration. λ3 limits the selection rate of clients that go offline too many times in the later part of the training, but considering that some clients with better data quality may go offline due to network problems, this value should not be set too high. If some FL tasks require that the number of times the node is not too high, it can be adjusted to λ3.

Policy. Output a feasible client selection action with any state as input. The policy function is to determine the specific probability of taking any possible action in the state of time step t, so πθ can be regarded as a probability density function. This probability distribution can be used to sample the actual policy action. Where θ determines the shape of the probability distribution.

πθ(a|s)=P(a|s, θ)(29)

Reinforcement learning training process. The edge nodes first observe the characteristics of the clients. Edge nodes execute actions based on policy, selected clients will participate in subsequent FL training. After that, the policy network can be updated based on state. The state-action function is defined as Eq. (30).

Qπ(s,a)=Eπ[∑k=0∞γkr(st+k,at+k)|st=s,at=a](30)

The state value function is

Vπ(s)=Eπ[∑k=0∞γkr(st+k,at+k)|st=s,at=a](31)

Advantage function is

Aπold(s,a)=Qπ(s,a)−Vπ(s)(32)

πθold indicates the policy that was not updated. The advantage function is a measure of how bad a current state or action is relative to the expected value. The objective function of PPO algorithm is

J(θ)=Est,at[clipPPO(ϑt(θ)Aπθold(st,at)](33)

where

clipPPO(ϑt(θ))={1−εϑt(θ)≤1−ε1+εϑt(θ)≥1+εϑt(θ)otherwise(34)

The clip range of PPO is

Ω{ϑ(θ)|1−ε≤ϑt(θ)≤1+ε}(35)

The amplitude of each gradient update is limited, thus improving stability. Policy probability ratio is

ϑt(θ)=[(πθ(at|st))/(πθold(at|st))](36)

According to the accuracy of the clients selected in the last round and the offline status update the policy, the edge nodes will prefer to select the clients with better training results in the later training period.

The two-stage client selection algorithm is shown in Algorithm 1.

5  Performance Evaluation and Discussion

This simulation mainly considers the performance of each algorithm when some clients are offline. Simulation parameters are set as follows: the experiment environment is python, ubuntu 20.04, The CPU is Intel(R) Xeon(R) Silver 4210R CPU @ 2.40 GHz, and the GPU is GeForce RTX 3060 Lite Hash Rate. The FL model aggregation algorithm uses FedAvg algorithm [10], the local learning rate of the client is 0.1, the neural network uses CNN network, batchsize is set to 20, the total round is set to 1000, the number of clients selected in each round is set to 10. The dataset used is FederatedEMNIST [33], FederatedEMNIST is one of the opensource datasets in FL Benchmark LEAF. The dataset is divided based on EMNIST, which can be divided by IID (Independent Identically Distribution) or non-IID (non-Independent Identically Distribution). The non-IID partition is based on different writers. Therefore, a more realistic non-IID distribution can be achieved.

The number of candidate clients selected in the first phase is divided into three groups: 400, 500, and 600. The client numbers are 1 to 400, 1 to 500, and 1 to 600, respectively. Due to the bandwidth limitations of the edge nodes, we set the number of selected clients per round to 10. Set the top 10% clients as offline clients, that is, they do not participate in training when they are selected. Clients numbered 10% to 40% are semi-offline clients, and there is a 50% probability that they will not participate in training. Clients numbered 40% to 50% are clients that add gaussian noise, which mean value is 0 and the standard deviation is 0.08, to the model to protect privacy. Clients numbered 50% to 60% are clients that add some gaussian noise, which mean value is 0 and the standard deviation is 0.013, to the local model making their local models less accurate to simulate clients with poor data quality. Clients numbered 60% to 100% are online clients, they do not add noise to the model, and they do not offline. The comparison algorithms we selected are random, cluster [18], AFL [20] and pow-d [21]. The random algorithm selects 10 candidates completely at random. In PPO algorithm, λ1, λ2, and λ3, in Eq. (28) are set to 425, 225 and 150, respectively. An excessively high reward coefficient in the PPO algorithm can result in issues like erratic strategy behavior and inadequate exploration, while an overly low reward coefficient can cause a sluggish learning pace, excessively cautious strategies, and difficulty in identifying pivotal actions. Consequently, the optimal balance of reward coefficients is achieved through iterative experimentation and fine-tuning.

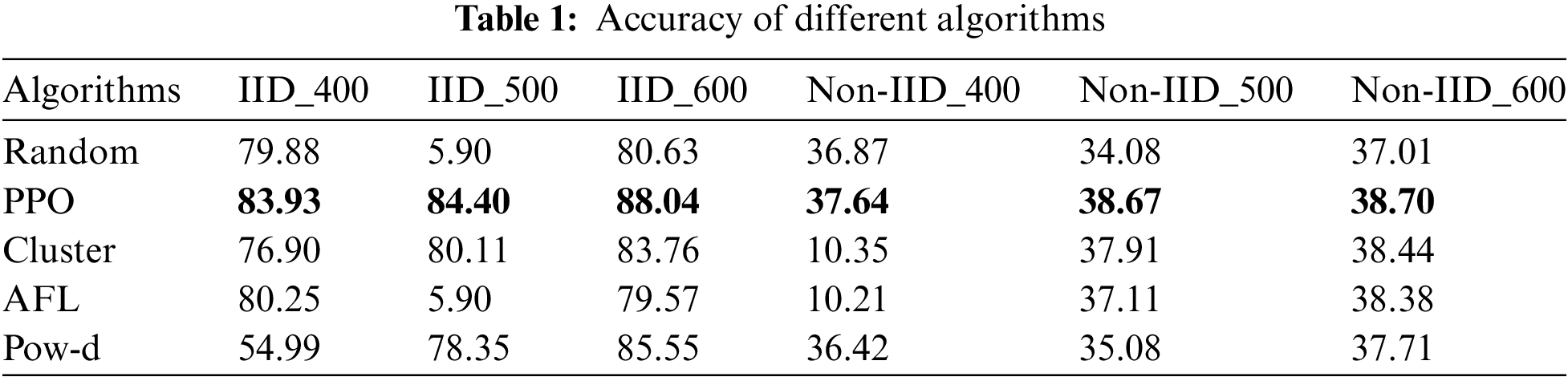
The accuracy of different algorithms when the total number of clients is 400, 500 and 600 is shown in Fig. 3. Table 1 shows the maximum accuracy of the global model on the test set of different algorithms under different conditions, and we bold the values with the highest accuracy. In Fig. 3a–c, PPO algorithm training process is relatively stable, and finally can converge to a higher accuracy. When the Random algorithm is trained to 392 and 217 rounds in Fig. 3a,c, respectively, the accuracy of the global model begins to decline sharply, and there is no improvement in the subsequent training process, and the accuracy rate finally stays at 5.90%. Due to the presence of noisy clients within the simulation environment, the accumulation of noise to a certain threshold can significantly disrupt the parameters of the global model, leading to a marked deterioration in its accuracy. However, our proposed scheme incorporates the consideration of such noise during the client selection phase, thereby preventing any abrupt decline in the model’s performance. Cluster, pow-d and AFL also show this sudden decline in accuracy when there are different numbers of candidate clients, so except PPO algorithm, the other algorithms are poor in robustness and are easily affected by noise in the model.

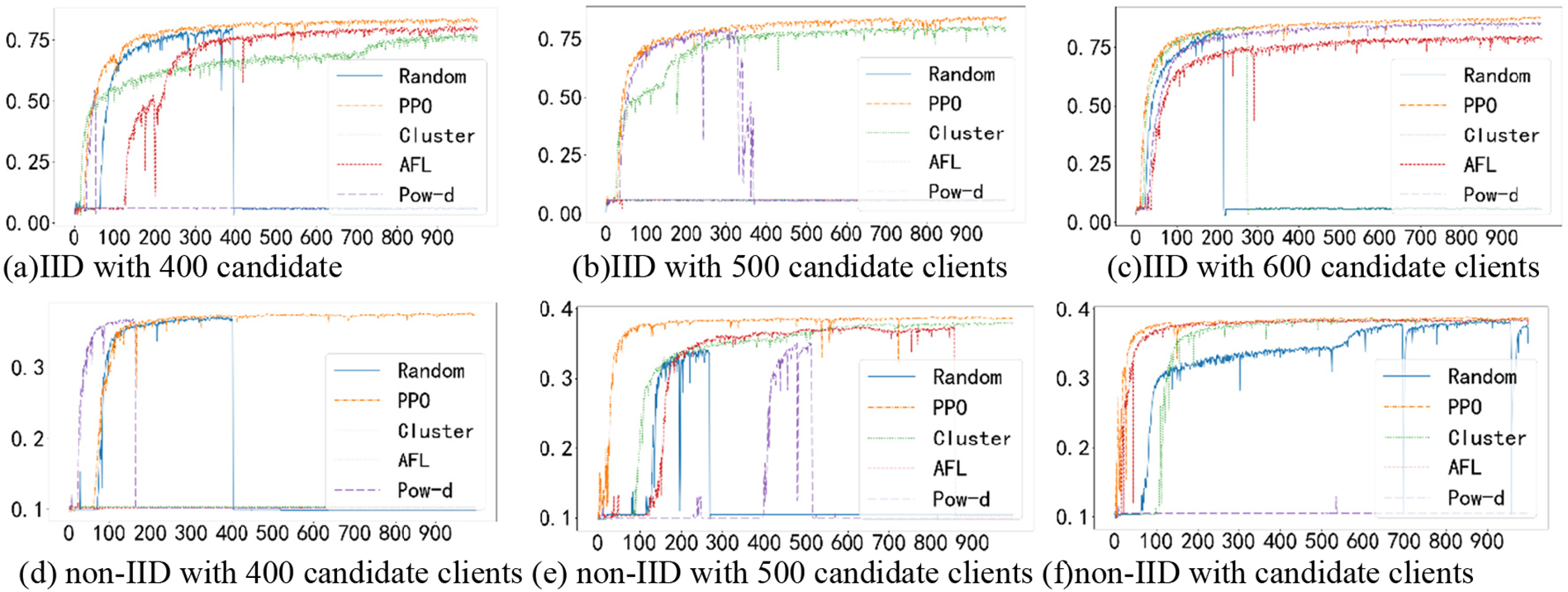
Figure 3: Performance comparison with different number of candidate clients

In Fig. 3d–f, PPO algorithm can reach 37.64%, 38.67% and 38.70% accuracy respectively in FederatedEMNIST_non-IID dataset, but other algorithms still have the phenomenon that they cannot be trained or their accuracy suddenly declines during training. The Cluster algorithm cannot be trained only when the total number of clients is 400, while the AFL and Random algorithms can only be trained when the total number of clients is 600, and the pow-d algorithm cannot be trained when the total number of clients is different. We can observe that regardless of the total number of clients, our scheme always performs best in both datasets.

5.1 Client Selection Times

In our experiment, the client data quality is different, some clients may be online all the time but the data quality is not necessarily high, while some clients are semi-offline but may have higher quality data. The purpose is to obtain the optimal global model by client selection when there are offline clients, semi-offline clients and noise models. By experiments, we found that the effects obtained by different client selection algorithms are very different. Below, we take the client selection distribution in Fig. 3b as an example to compare the relationship between different client selection distributions and the final training results. We divide clients into offline, semi-offline, differential privacy and low quality. Fig. 4 shows the distribution of client selection times corresponding to Fig. 3b. Table 2 shows the corresponding data in Fig. 4. The offline and semi-offline clients of PPO have the fewest selection times showed in Fig. 4, so they also have higher training efficiency. The low data quality clients selected by PPO and Cluster are the least, so the training effect of these two algorithms in Fig. 3b is also better than other algorithms. However, the number of online clients selected by PPO is the largest, so the final result of PPO algorithm is also better than Cluster algorithm.

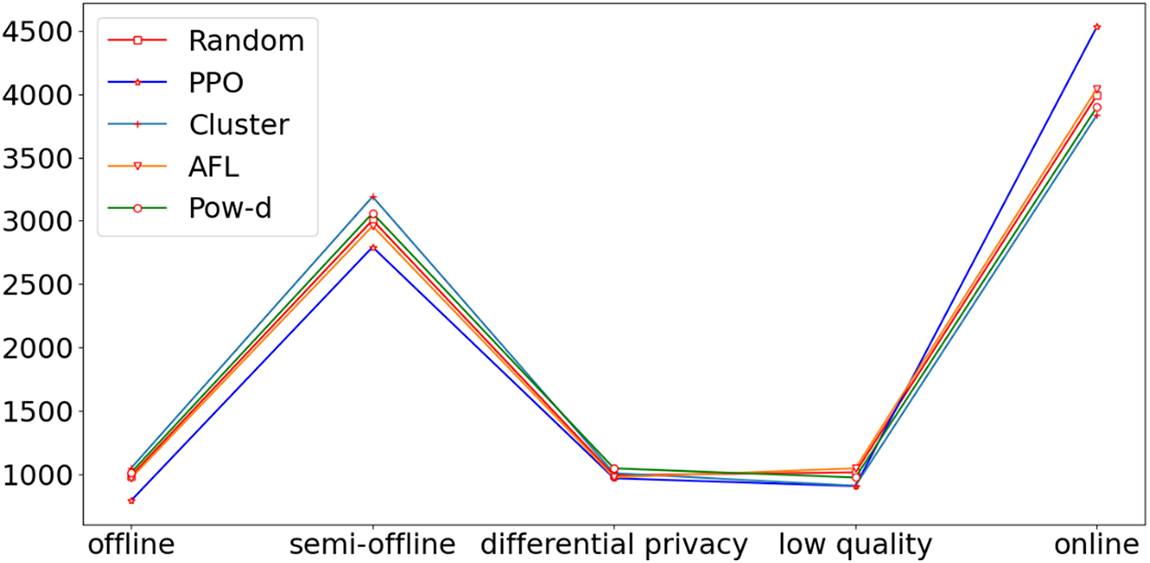
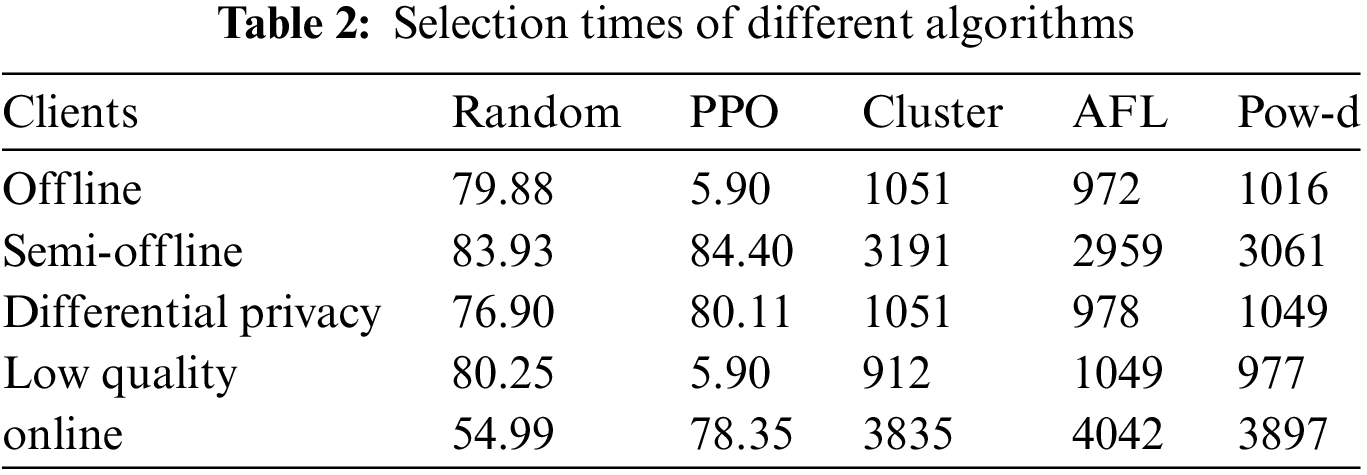
Figure 4: Clients selection distribution

5.2 Operating Efficiency

Finally, we compare the execution efficiency of each algorithm. Fig. 5 shows the training time of each algorithm with 400, 500, 600 clients. As can be seen from Fig. 5, random, cluster and pow-d algorithms have faster execution rate, but their training results are not good. AFL had the longest training time, while PPO had lower training time than AFL but higher training time than random, cluster and pow-d. With the increase of the total number of clients, the execution time of PPO is increased by 21.25% and 23.24%, respectively.

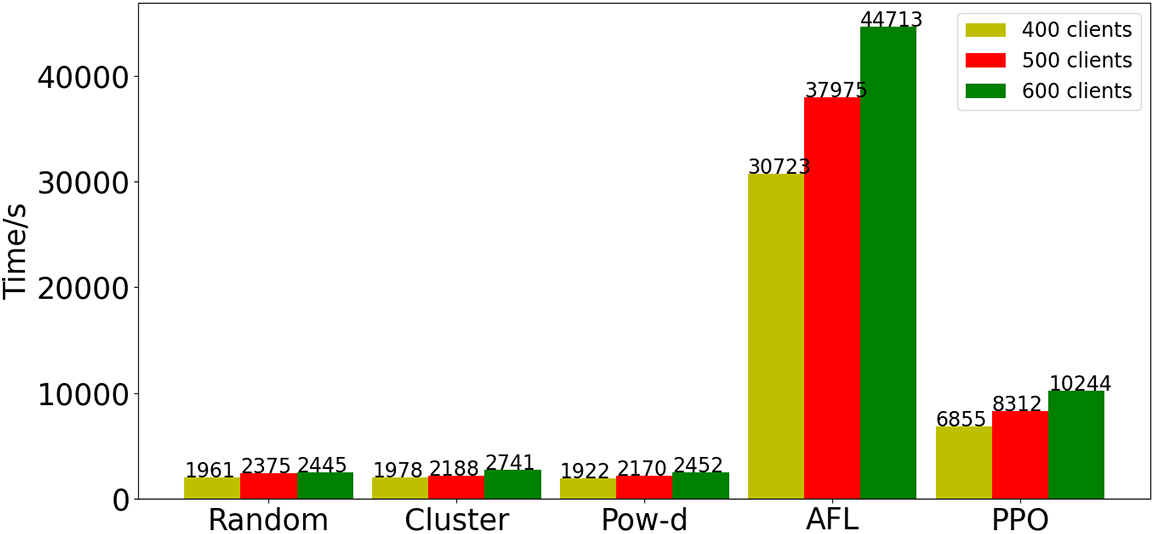
Figure 5: The execution time of different algorithms

5.3 Increase Bandwidth

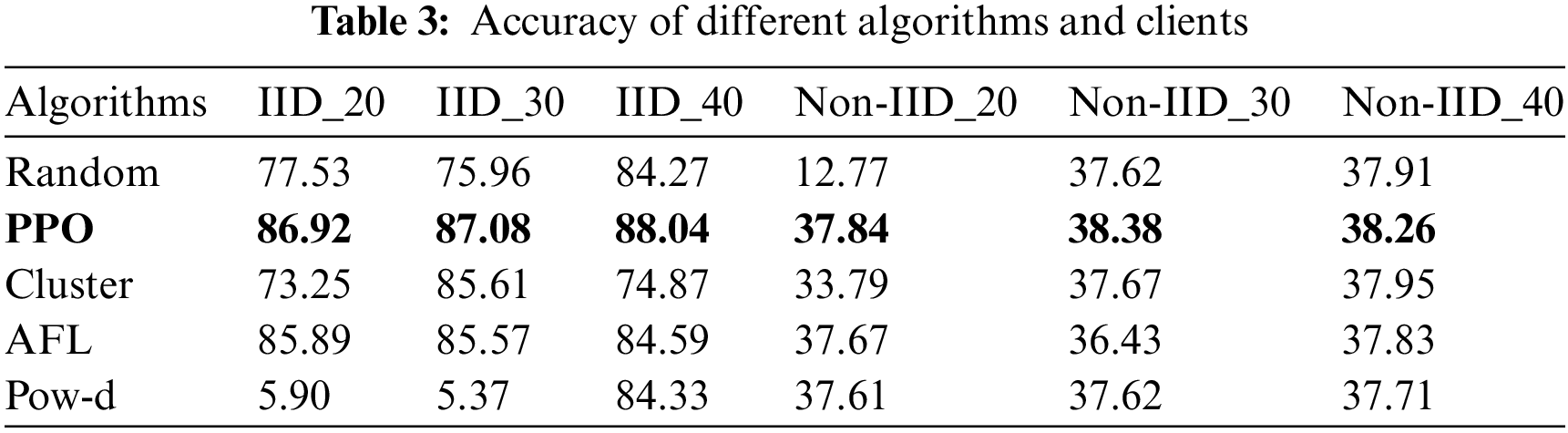
We increase the bandwidth so that each round of client selection is 20, 30, 40, and then test the accuracy of each client selection algorithm. It can be seen from Fig. 6 and Table 3, as the bandwidth of edge nodes increases, the number of clients selected in each round also increases, and the model accuracy rate obtained by each client selection algorithm is on the rise as a whole, and the accuracy rate of our scheme is always the highest. Therefore, improving bandwidth is a feasible method in the client selection algorithm. When the number of selected clients reaches 40, the accuracy of each algorithm is not much different, and the performance is relatively close, which is understandable, because when the bandwidth is high to a certain extent, the edge node can select all the client nodes, this time there is no need for client selection. The main function of our scheme is that when the edge nodes have limited clients to choose from and the communication quality and data quality of each client are different, the client with better communication ability and data quality is selected through each round of client training information, and the global model with better performance is finally obtained. It is worth noting that choosing as many clients as possible per round is not necessarily a good choice. As shown in Figs. 3 and 6, when the local model of the client contains noise, the accuracy of some client selection algorithms will suddenly decline in a certain round. Therefore, we can consider dynamically adjusting the number of selected clients in each round of training, and how this number changes with the previous training effect is our future research focus.

Figure 6: Performance comparison with different number of selected clients

6  Conclusion

This paper designs the two-stage client selection algorithm in the BCFL architecture. In the first stage, a client selection scheme based on ABE is adopted to select clients with FL task data. How to reasonably match different datasets and attributes of the clients is our future research direction. In the second stage, a client selection scheme based on PPO is used to train the global model. The experiment shows that our scheme can select clients with good communication ability and data quality from a great deal of candidate clients to participate in FL, thereby obtaining a better global model. The main implications of this paper for IoT and federated learning are as follows:

Data Privacy and Security Redefined: The integration of attribute-based encryption (ABE) and blockchain technology redefines data privacy and security in IoT deployments. By enabling encrypted data access based on specific attributes, the proposed scheme mitigates the risk of data breaches and unauthorized access, which is a significant advancement in the field.

Enhanced Model Training Dynamics: The adoption of the Proximal Policy Optimization (PPO) algorithm for client selection introduces a dynamic approach to model training in federated learning. This method ensures that only clients with high-quality data contribute to the global model, thereby enhancing the overall training dynamics and the accuracy of AI models.

Incentivization of Data Contribution: The natural alignment with blockchain’s financial attributes paves the way for creating incentive mechanisms that reward data contribution and participation in the federated learning process. This could revolutionize how data is valued and exchanged in IoT ecosystems.

In our simulation, the number of clients selected per round is constant. In the future, we will continue to conduct deep research and consider dynamically adjusting the number of clients selected per round to make BCFL more practical. Blockchain is gradually becoming an important technology for data trading and sharing, and the research in this paper will help customers make full use of data value in smart cities, smart healthcare and other scenarios in the future.

Despite its potential, our scheme does have limitations that require further research. As the number of IoT devices grows, the scheme’s ability to scale while maintaining efficiency and security will be crucial. Our scheme does not address the incentive mechanisms necessary to encourage participation in the FL process, which is crucial for the scheme’s practical adoption. Moving forward, we aim to address these limitations by following methods. Investigating scalable blockchain solutions that can handle a large number of IoT devices. Developing dynamic client selection strategies that adapt to the changing data landscape. Exploring incentive mechanisms to motivate participation in the FL process. In conclusion, our two-stage client selection scheme for BCFL shows promise in securing and enhancing federated learning tasks. However, continued research is necessary to overcome the challenges and fully realize the potential of decentralized AI training in IoT environments.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xiaojun Jin, Pengyi Zeng; data collection: Chao Ma; analysis and interpretation of results: Song Luo; draft manuscript preparation: Yifei Wei. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated during and analyzed during the current study are available from the corresponding author on reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Imteaj, U. Thakker, S. Wang, J. Li, and M. H. Amini, “A survey on federated learning for resource-constrained IoT devices,” IEEE Internet Things J., vol. 9, no. 1, pp. 1–24, Jul. 2021. doi: 10.1109/JIOT.2021.3095077. [Google Scholar] [CrossRef]

2. D. C. Nguyen, M. Ding, P. N. Pathirana, A. Seneviratne, J. Li and H. V. Poor, “Federated learning for internet of things: A comprehensive survey,” IEEE Commun. Surveys & Tutorials, vol. 23, no. 3, pp. 1622–1658, Apr. 2021. doi: 10.1109/COMST.2021.3075439. [Google Scholar] [CrossRef]

3. F. Matt, S. Jha, and T. Ristenpart, “Model inversion attacks that exploit confidence information and basic countermeasures,” in Proc. 22nd ACM SIGSAC Conf. Comput. Commun. Security, Denver, CO, USA, Oct. 2015, pp. 1322–1333. doi: 10.1145/2810103.2813677. [Google Scholar] [CrossRef]

4. K. Ganju, Q. Wang, W. Yang, C. A. Gunter, and N. Borisov, “Property inference attacks on fully connected neural networks using permutation invariant representations,” in Proc. 2018 ACM SIGSAC Conf. Comput. Commun. Security, 2018, pp. 619–633. doi: 10.1145/3243734.3243834. [Google Scholar] [CrossRef]

5. R. Shokri, M. Stronati, and C. Song, “Membership inference attacks against machine learning models,” in 2017 IEEE Symp. on Security and Privacy (SP), San Jose, CA, USA, IEEE, 2017, pp. 3–18. doi: 10.1109/SP.2017.41. [Google Scholar] [CrossRef]

6. N. Satoshi, “Bitcoin: A peer-to-peer electronic cash system,” Accessed: Oct. 31, 2008. [Online]. Available: https://assets.pubpub.org/d8wct41f/31611263538139.pdf [Google Scholar]

7. A. Qammar, A. Karim, H. Ning, and J. Ding, “Securing federated learning with blockchain: A systematic literature review,” Artif. Intell. Rev., vol. 56, no. 5, pp. 3951–3985, 2023. doi: 10.1007/s10462-022-10271-9. [Google Scholar] [PubMed] [CrossRef]

8. D. Li et al., “Blockchain for federated learning toward secure distributed machine learning systems: A systemic survey,” Soft Comput., vol. 26, no. 9, pp. 4423–4440, 2022. doi: 10.1007/s00500-021-06496-5. [Google Scholar] [PubMed] [CrossRef]

9. Y. Qu, M. P. Uddin, C. Gan, Y. Xiang, L. Gao and J. Yearwood, “Blockchain-enabled federated learning: A survey,” ACM Comput. Surv., vol. 55, no. 4, pp. 1–35, 2022. doi: 10.1145/3524104. [Google Scholar] [CrossRef]

10. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. Y. Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Proc. 20th Int. Conf. Artif. Intell. Stat., PMLR, 2017, pp. 1273–1282. doi: 10.48550/arXiv.1602.05629. [Google Scholar] [CrossRef]

11. C. Fang, Y. Guo, J. Ma, H. Xie, and N. D. Y. Wang, “A privacy-preserving and verifiable federated learning method based on blockchain,” Comput. Commun., vol. 186, pp. 1–11, 2022. doi: 10.1016/j.comcom.2022.01.002. [Google Scholar] [CrossRef]

12. J. Wang, S. Wang, R. R. Chen, and M. Ji, “Local averaging helps: Hierarchical federated learning and convergence analysis,” 2010. doi: 10.48550/arXiv.2010.12998. [Google Scholar] [CrossRef]

13. L. Liu, J. Zhang, S. Song, and K. B. Letaief, “Hierarchical quantized federated learning: Convergence analysis and system design,” 2021. doi: 10.48550/arXiv.2103.14272. [Google Scholar] [CrossRef]

14. S. Luo, X. Chen, Q. Wu, Z. Zhou, and S. Yu, “HFEL: Joint edge association and resource allocation for cost-efficient hierarchical federated edge learning,” IEEE Trans. Wirel. Commun., vol. 19, no. 10, pp. 6535–6548, 2020. doi: 10.1109/TWC.2020.3003744. [Google Scholar] [CrossRef]

15. Z. Peng et al., “VFChain: Enabling verifiable and auditable federated learning via blockchain systems,” IEEE Trans. Netw. Sci. Eng., vol. 9, no. 1, pp. 173–186, 2021. doi: 10.1109/TNSE.2021.3050781. [Google Scholar] [CrossRef]

16. H. Yu, R. Xu, H. Zhang, Z. Yang, and H. Liu, “EV-FL: Efficient verifiable federated learning with weighted aggregation for industrial IoT networks,” IEEE/ACM Trans. Netw., vol. 32, no. 2, pp. 1723–1737, 2023. doi: 10.1109/TNET.2023.3328635. [Google Scholar] [CrossRef]

17. N. Li, M. Zhou, H. Yu, Y. Chen, and Z. Yang, “SVFLC: Secure and verifiable federated learning with chain aggregation,” IEEE Internet Things J., vol. 11, no. 8, pp. 13125–13136, 2023. doi: 10.1109/JIOT.2023.3330813. [Google Scholar] [CrossRef]

18. Y. Fraboni, R. Vidal, L. Kameni, and M. Lorenzi, “Clustered sampling: Low-variance and improved representativity for clients selection in federated learning,” in Int. Conf. Machine Learning., PMLR, 2021, pp. 3407–3416. doi: 10.48550/arXiv.2105.05883. [Google Scholar] [CrossRef]

19. R. Balakrishnan, T. Li, T. Zhou, N. Himayat, V. Smith and J. Bilmesn, “Diverse client selection for federated learning via submodular maximization,” in Int. Conf. Learn. Represent., 2022. doi: 10.48550/arXiv.2107.11728. [Google Scholar] [CrossRef]

20. J. Goetz, K. Malik, D. Bui, S. Moon, H. Liu and A. Kumar, “Active federated learning,” 2019. doi: 10.48550/arXiv.1909.12641. [Google Scholar] [CrossRef]

21. Y. Cho, J. Wang, and G. Joshi, “Client selection in federated learning: Convergence analysis and power-of-choice selection strategies,” 2020. doi: 10.48550/arXiv.2010.01243. [Google Scholar] [CrossRef]

22. S. Gao, G. Piao, J. Zhu, X. Ma, and J. Ma, “TrustAccess: A trustworthy secure ciphertext-policy and attribute hiding access control scheme based on blockchain,” IEEE Trans. Vehicular Technol., vol. 69, no. 6, pp. 5784–5798, 2020. doi: 10.1109/TVT.2020.2967099. [Google Scholar] [CrossRef]

23. Z. Zhang and X. Ren, “Data security sharing method based on cp-abe and blockchain,” J. Intell. Fuzzy Syst., vol. 40, no. 2, pp. 2193–2203, 2021. doi: 10.3233/JIFS-189318. [Google Scholar] [CrossRef]

24. A. Sahai and B. Waters, “Fuzzy identity-based encryption,” in Adv. Cryptol.–EUROCRYPT 2005: 24th Annu. Int. Conf. Theor. Appl. Cryptogr. Tech., Aarhus, Denmark, Springer, 2005, pp. 457–473. doi: 10.1007/11426639_27. [Google Scholar] [CrossRef]

25. J. Bethencourt, A. Sahai, and B. Waters, “Ciphertext-policy attribute based encryption,” in 2007 IEEE Symp. Security Privacy (SP’07), Berkeley, CA, USA, IEEE, 2007, pp. 321–334. doi: 10.1109/SP.2007.11. [Google Scholar] [CrossRef]

26. V. Goyal, O. Pandey, A. Sahai, and B. Waters, “Attribute-based encryption for fine-grained access control of encrypted data,” in Proc. 13th ACM Conf. Comput. Commun. Security, 2006, pp. 89–98. doi: 10.1145/1180405.1180418. [Google Scholar] [CrossRef]

27. J. Schulman, S. Levine, P. Abbeel, M. Jordan, and P. Moritz, “Trust region policy optimization,” in Int. Conf. Mach. Learn., Lille, France, PMLR, 2015. doi: 10.48550/arXiv.1502.05477. [Google Scholar] [CrossRef]

28. J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” 2017. doi: 10.48550/arXiv.1707.06347. [Google Scholar] [CrossRef]

29. B. H. Bloom, “Space/time trade-offs in hash coding with allowable errors,” Commun. ACM, vol. 13, no. 7, pp. 422–426, 1970. doi: 10.1145/362686.362692. [Google Scholar] [CrossRef]

30. L. Zhang, J. Wang, and Y. Mu, “Privacy-preserving flexible access control for encrypted data in internet of things,” IEEE Internet Things J., vol. 8, no. 19, pp. 14731–14745, 2021. doi: 10.1109/JIOT.2021.3071553. [Google Scholar] [CrossRef]

31. T. Nishio and R. Yonetani, “Client selection for federated learning with heterogeneous resources in mobile edge,” in ICC, 2019-2019 IEEE Int. Conf. Commun. (ICC), Shanghai, China, 2019. doi: 10.1109/ICC.2019.8761315. [Google Scholar] [CrossRef]

32. J. Kuang, M. Yang, H. Zhu, and H. Qian, “Client selection with bandwidth allocation in federated learning,” in 2021 IEEE Glob. Commun. Conf. (GLOBECOM), Madrid, Spain, 2021, pp. 1–6. doi: 10.1109/GLOBECOM46510.2021.9685090. [Google Scholar] [CrossRef]

33. S. Caldas et al., “Leaf: A benchmark for federated settings,” 2018. doi: 10.48550/arXiv.1812.01097. [Google Scholar] [CrossRef]