An Enhanced Integrated Method for Healthcare Data Classification with Incompleteness

1  Introduction

Classification is a supervised learning technique that includes two phases: the training cycle and the testing cycle. In the training cycle, a given dataset is provided with the labels for the different output classes. The training cycle trains a classification algorithm for the given input-output data, thus building a classifier. In the testing cycle, the classifier assigns a new test data point to the number of classes/labels. Classification has wide applications in several fields such as data mining [1,2], pattern recognition [3,4], mathematical expression recognition [5,6], machine learning [7], and healthcare [8].

Most of the classification algorithms available in the literature work well under the assumption of complete data; however, it becomes quite challenging to classify incomplete data.

It is impossible to avoid missing values in real practice for several reasons, such as human error while collecting the data or tabulating it, machine failure or incomplete surveys, etc. Incomplete data can be a problem in a lot of different areas, like social science [9], medicine [10], and remote sensing [11].

During social surveys, some people may refuse to answer certain questions, resulting in incomplete data collection. Remote sensing is another example where only a small number of sensors can be used in certain areas. A method to filling missing data and removing outliers for remote sensing data was proposed in [12]. Medical datasets are widely acknowledged to be incomplete owing to challenges in both data collection and integration. These datasets usually have a lot of missing data because it is often impractical to test all patients. In a questionnaire given to a population, the chances of encountering missing data are high because individuals may intentionally skip certain questions regarding their medical conditions. This incompleteness often stems from various other factors such as manual data entry processes, inaccuracies in measurements, or errors in equipment. For example, some of prenatal records at a birth center are missing, it might be due to imperfect procedures, measurements that aren’t accurate, or equipment malfunctions. The presence of incompleteness in medical data poses significant obstacles for achieving accurate classification. As a result, it is critical to ensure proper management of missing data.

Healthcare information is characterized by significant levels of noise, strong relationships between variables, and a large number of dimensions, posing significant obstacles to conventional classification approaches. As a result, it’s crucial to develop sophisticated models to enhance the performance of healthcare data classification. An analysis of machine learning-based algorithms for missing data imputation is performed [13]. A novel approach is presented to healthcare data classification using the Convolutional Neural Network (CNN) model [8]. Electronic health records as the source of data for data mining and analysis of various health conditions are explored, where imputation of missing data was performed using patients’ similarities [14], and sematic parsing [15].

Managing missing data correctly is essential for providing accurate predictions in clinical studies. The simplest strategy is to remove the missing sample entirely if any one of the features of the sample data is missing. However, the problem with this strategy is the loss of information on account of the complete removal of the data samples. Also, this approach is applicable only when the proportion of missing data is minimal, usually below 10%.

Another popular strategy is filling the missing feature using any statistical method, thereby completing the data before applying any traditional classification algorithm [16,17]. This process of filling in missing features in incomplete data is known as Data Imputation. Statistical methods include several imputation methods such as mean, median, hot-deck imputation and regression analysis [6]. Numerous studies have shown that data imputation results in improved accuracy. However, integrating imputation into classification algorithm presents challenges as it results in increase in imputation time of missing values, especially in the testing cycle where the samples are processed individually. It is important to address this issue of higher computational cost in imputing missing values in the testing cycle without loss of classification accuracy [16,17]. This paper presents two insights on addressing the computational burden associated with imputing missing values during the testing cycle without compromising the classification accuracy of these imputation methods. Additionally, it explores several imputation approaches to enhance classification accuracy for incomplete data. Numerous scientists have created deep learning (DL)–driven methods for estimating missing features [18].

Clustering is a machine learning technique (unsupervised) used to group patterns in a dataset based on some predefined similarity metrics. It has been extensively used in several applications such as anomaly detection [19], document clustering [20], and genome sequencing [21]. A new method for filling in missing data in medical datasets by combining advanced clustering techniques and regularized regression with L2 regularization is discussed [22]. A productive method for imputing missing features and categorizing health information by grouping medical records based on their class characteristics is explored [23]. In IoT settings, the data sets often contain missing information. These missing values make the classifier ineffective for classification. Researchers introduced a method for estimating missing data and identifying anomalies in IoT settings through machine learning techniques [24].

For data mining applications, the classification model requires labeled data for the training phase. Data labeling has always been an expensive and time-consuming task. Several algorithms have been proposed in the literature where clustering has been used for building a classifier, without considering the class labels [25,26]. Support Vector Machine (SVM) regression and a two-level classification process to improve the performance of machine learning models for diabetes classification is introduced [27,28].

A significant amount of research has been conducted on the use of imputation and clustering techniques, particularly in the context of improving data analysis and machine learning processes. Clustering methods have also been extensively explored for labeling data in classification tasks, helping to enhance model performance. In our work, we have integrated imputation, clustering, and classification in a unified approach. By first imputing missing data, we ensure completeness, and then apply clustering to identify meaningful patterns and groups within the data. Finally, classification techniques are employed to assign labels based on these identified clusters, offering a more structured and efficient workflow for predictive modeling.

1.1 Contributions

This paper introduces new approaches to enhance the effectiveness and efficiency of imputation for classification tasks involving incomplete data. The main contributions of this paper include the following:

a. A critical review of various statistical imputation methods for the classification of incomplete data.

b. Integration of clustering with imputation for the estimation of missing features to enhance the classification accuracy.

c. A new nearest center-based approach for the imputation of incomplete data during the testing phase of classification is presented.

1.2 Organization

The rest of the paper is structured as follows: Section 2 briefly explains the related literature on various statistical imputation methods and the clustering techniques for incomplete data. Section 3 presents the proposed methodology of various schemes adopted for the classification of incomplete data. Experimental design is elaborated upon in Section 4. Results and discussion are presented in Section 5, followed by conclusions and future scope in Section 6.

2  Related Literature

Since the classification requires complete data, some imputation technique is required to impute the missing values/features of the incomplete data. The aim is to provide a complete overview of various statistical methods used for imputation of incomplete data. In addition to statistical methods, an overview of some variants of Fuzzy c-means (FCM)-based clustering strategies used for the imputation of missing data is provided. Lastly, an overview of missingness mechanisms is described.

2.1 Imputation Methods

Imputation techniques are statistical methods, used to find the missing values or features of a data sample by replacing it with an “imputed value”. The imputed value makes the data complete for any data analysis method. Imputation techniques make use of information present in the data to assess the missing information. Imputation techniques are broadly categorized into two categories: (i) Single imputation, where the missing data points are replaced with a single value determined by methods such as mean, median, linear interpolation and regression; (ii) Multiple imputation where the missing feature is replaced by several imputed values. This approach can help keep datasets usable and prevent the problems that come with removing incomplete records. However, it can also affect the accuracy of the original data in several ways, such as introducing bias, reducing variance, distorting correlations, making the model more dependent, losing information, increasing complexity, and causing false confidence. To lessen the negative effects, it’s crucial to take hold of the reasons behind the missing data, select the right imputation techniques, assess the consequences, and be transparent while dealing with missing data. Though multiple imputation is supposed to perform better than single imputation but found to be computationally expensive [16].

This paper investigates three popularly used single imputation methods namely mean, nearest neighbor and linear interpolation. The most straightforward statistical imputation method involves using mean imputation for continuous variables. It is generally used as a baseline method wherein the missing features of an observed data are substituted by the mean of remaining available features of the observed data. Another widely used imputation method is the k-nearest neighbor imputation method [29,30]. Using the values calculated from the k-nearest observed data, the missing values are imputed based on the k-nearest classification principle. The k-nearest neighbor imputation method is effective for missingness completely at random (MCAR) and missing at random (MAR) data but struggles with Missing not at random (MNAR) data due to inherent biases. Its performance is highly dependent on the choice of distance metric and the proper tuning of parameters. Understanding the nature of the missing data and the underlying patterns is crucial to leveraging the strengths of Nearest Neighbor Imputation (NNI) effectively. Another statistical imputation technique, known as interpolation, is also explored. In the literature, three interpolation techniques are available: Linear interpolation, Quadratic interpolation, and Cubic interpolation. Among these, Linear interpolation is the simplest and it imputes the missing values of incomplete data by considering linearity between the data points. The imputation of missing features is based on the straight-line concept in the linear interpolation imputation technique [31–33]. Alam et al. [34] have explored imputation techniques for addressing missing values in ordinal data, focusing on how these methods can enhance the validity of clustering and classification analyses in their research. Very few research papers have reported the experimental results on linear interpolation imputation and therefore this technique is included in the comparative study for the classification of incomplete data.

2.2 Clustering Methods for Incomplete Data

Clustering is an unsupervised learning algorithm used for partitioning the data to find groups of similar data based on some similarity measure. Similar measures may be taken as distance, density, etc. Despite the requirement for complete data in clustering, significant efforts have been dedicated to clustering incomplete data. Fuzzy c-means is one of the most used clustering algorithm that partitions a set of objects into fuzzy clusters by minimizing a distance-based objective function

J=∑i=1p∑j=1kuijm‖Ok−vp‖2(1)

where Ok={ok1,ok2,…okl,…oks} vp is the pth cluster prototype, uij is the fuzzy partition matrix that represents the degree of belonginess of data Ok to the pth cluster. uij∈[0,1] and satisfy the condition ∑i=1puij=1

for j=1,2…k

Hathway et al. [35] proposed four strategies based on the FCM algorithm for handling incomplete data in clustering namely Whole data strategy (WDS), Partial distance Strategy (PDS), Optimal control Strategy (OCS), and Nearest Prototype Strategy (NPS).

Let the incomplete data be represented as

O={o1,o2,…,om,,,,,ok}∈Rs

Ok={ok∈O|Okisacompletedatum}Om={om∈O|Omisanincompletedatum}

e.g., let O=[2334?8641?1623442?] be an incomplete data set.

Here Ok=[231483612] and Om=[3?6?2444?] “?” represents the missing feature.

The Whole Data Strategy (WDS) is a straightforward technique that is only applied when a minimal percentage of data is incomplete, usually less than 10%. This strategy is often referred to as the list-wise elimination strategy. However, cluster memberships of incomplete data vectors in Om are determined based on the partial distance from each incomplete datum to each of the computed cluster centers. The WDS technique offers cluster center updates and memberships from the data vector in Ok. Following is the formula for calculating partial distances:

Dki=s∑l=1sIlk∑l=1s(okl−vil)2Ilk(2)

where

Ilk={01ifokl∈omisamissingattributeifokl∈omisavailable

The Partial Distance Strategy (PDS) calculates the partial distance between the incomplete datum and the cluster centers using the available attributes in Om and ignores the missing features, as shown in Eq. (2). The following formula is used to update the cluster centers:

vil=∑j=1k(uijmIlkOkl)∑j=1kuijmIlk(3)

PDS is suggested when the level of missing features is large in the given dataset with the goal that WDS can’t be justified.

The third methodology, known as the Optimal Control Strategy (OCS), is considered the most effective among all the approaches, as it addresses missing features during the clustering process. Similar to the Nearest Prototype Strategy (NPS), missing values are replaced with the attribute values of the closest cluster centers before clustering. The missing features are treated as additional features, and the objective function in Eq. (1) is further improved with respect to these missing traits. During clustering, missing traits are determined as follows:

Okl=∑i=1p(uijmvil)∑i=1puijm(4)

The OCS is slightly altered in the Nearest Prototype Strategy (NPS). Here, in the clustering process, the missing attributes are substituted with the relevant attribute values of the closest cluster center according to the following expression:

Oklt=vilt where Dik=min{D1k,D2k,…,Dpk}(5)

Okl∈Om are the missing attributes and Dik is the partial distance between the incomplete datum and the cluster centers using the available attributes in Om and ignore the missing features.

While existing clustering-based imputation methods can address incomplete data problems to a certain extent, there is always room for improvement through the exploration of new approaches. In the literature, a few papers have explored the linear interpolation imputation technique before applying clustering [31–33], but the impact of this integrated approach on the classification accuracy of incomplete data remains unexplored. Further, Yosboon et al. [36] in the work explored optimized multiple data partitions for cluster-wise imputation of missing values in gene expression data to handle missing values.

To the best of our knowledge, there seems to be a lack of research investigating the utilization of clustering to enhance the effectiveness of classification in scenarios involving incomplete data and linear interpolation imputation.

2.3 Missingness Mechanism

A missingness mechanism refers to the process or pattern through which data becomes missing in a dataset. Understanding the missingness mechanism is crucial for accurately handling missing data in statistical analysis. There are three main missingness mechanisms: MCAR, MAR, and MNAR [16]. These mechanisms illustrate the connections between observed variables and the likelihood of data being missing.

According to MCAR, the likelihood of data being missing is unrelated to both observed and unobserved data. Essentially, missingness occurs randomly and independently of any other variables or factors in the dataset. In other words, there are no systematic differences between the missing and observed data.

In this mechanism, the probability of data being missing depends only on observed data but not on the missing data itself. In other words, once we account for observed variables, the probability of missingness is constant across all levels of missing data. MAR implies that the missing data can be predicted by the observed data.

Enders et al. [37] asserted that the MCAR mechanism can only be empirically tested. Even though a large number of MCAR tests have been utilized in numerous kinds of research linked to this field, they often have low power and could be seen as a highly strict assumption that is unlikely to be met in actual life. However, because they rely on unobserved data, the MAR and NMAR mechanisms are impossible to validate. In [32], various techniques for effectively handling missing values in datasets are examined, with a particular focus on how these methods can improve classification outcomes using machine learning approaches.

3  Classification of Incomplete Data: Various Approaches

To enhance the effectiveness and efficiency of classifying incomplete data, a novel integrated method is proposed in this study. This approach combines imputation, clustering, and classification techniques. The outcomes of this new method with the conventional approach, which involves imputation followed by classification are compared. Both approaches have two cycles: training and testing. The testing cycle employs the classifier that was created during the training process to categorize new instances.

3.1 Traditional/Classical Approaches

The traditional approach involves imputing missing values through some imputation method. Fig. 1 depicts the flowchart illustrating the various steps involved in utilizing imputation for the classification of data with missing values. Initially, the data is split into two parts: training data and testing data, in a 70:30 ratio. During the training cycle, an imputation technique is applied to impute the missed values, thus rendering the data complete. Subsequently, the imputed training data is utilized to build a classifier using a chosen classification algorithm. In the testing cycle, when a new instance is presented, it is directly classified if the instance is complete; otherwise, its missing values are imputed by using an imputation method. Finally, the newly completed instance is classified by the trained classifier. Among several imputation methods available in the literature, three imputation methods, i.e., mean, nearest neighbor, and linear interpolation methods are utilized. Naïve Bayes classifier [38] is employed for building the classifier. Different classical imputation techniques have been used in applications such as trauma injury [39], 24-h activity pattern [40], and breast cancer [41]. A survey on imputation techniques on medical research is available in [42].

Figure 1: Illustration of a traditional approach to classifying missing data (Imputation + Classification)

3.2 Proposed Approach: Integrating Imputation, Clustering and Classification

The integration of imputation with clustering techniques uses the specific details and connections in the data, resulting in more precise and reflective imputations. Consequently, this boosts the effectiveness of classification models by offering them a dataset that is more thorough and well-organized. Different clustering techniques are available in the literature [43–45]. The accuracy of classification models is frequently enhanced when compared to conventional approaches that either eliminate missing data or employ less complex imputation strategies. Fig. 2 shows the core steps of this proposed approach. It consists of three steps described below:

Step 1: In the proposed approach, the first step involves filling the data by an imputation method. The linear interpolation method is used for the imputation of missing features in the training data.

Step 2: After imputation of missing data, clustering is applied to the complete data. IterativeFCM (IFCM) clustering algorithm is applied to the imputed training data to create groups of data instances [32,33]. Clustering plays a multifaceted role in classification:

(i) Through clustering, the labels of the unlabeled data points can be inferred based on the clusters provided by it, thereby improving the clustering accuracy.

(ii) The missing values are further updated during the clustering method, thereby improving the imputation process.

(iii) In case some missing values are detected during the testing cycle, clustering helps in identifying/imputing those missing values.

Step 3: Clustering provides labeled data based on the inherent clusters present and this information is further fed to Naïve Bayes classifier to build the classifier.

Figure 2: Illustration of proposed approach of classifying missing data (Imputation + Clustering+ Classification)

During the testing phase, a new instance is checked for completeness. If found complete, it is directly fed to the classifier for classification. If found incomplete, the data is imputed by the nearest prototype strategy as given in Eq. (5) and then fed to the classifier for classification.

The detailed algorithm of the proposed approach is explained below:

4  Experiment Designs

To validate our strategy, comprehensive experiments using real data from the UCI repository [47] are carried out. Five complete datasets are chosen, and one incomplete dataset is suitable for classification. Table 1 presents the basic details of these datasets, which include Iris, Ecoli, Ionosphere, Glass, thyroid dataset, and Wisconsin Breast Cancer dataset. Out of these six datasets, we have used two medical datasets, the thyroid and Wisconsin Breast Cancer datasets. The Wisconsin Breast Cancer dataset is an incomplete real-world data set with 16 naturally occurring missing values. The primary characteristics of the selected datasets encompass the number of observations, variables, and categories, alongside their completeness status.

In-depth tests to determine the efficacy and efficiency of the proposed approach are conducted. In contrast to current benchmark approaches that generally integrate imputation and classification, our proposed method incorporates imputation and clustering before classification. The framework of the proposed method is shown in Fig. 2. For preprocessing, three imputation techniques—mean imputation, nearest neighbor, and linear interpolation techniques are employed. Mean Imputation (MI) is used to impute missing values by taking the mean value of remaining attributes. NNI [29] identifies the closest neighbors and imputes the incomplete feature utilizing the mode, median, or mean of the selected neighbors.

Linear Interpolation Imputation, a state-of-the-art technique, attempts to predict missing data directly by fitting a straight line between the two data points, finding the missing feature using the straight-line condition, and imputing the missing values of incomplete data. An iterative Fuzzy c-means clustering is used to cluster data [46] for all cases. The Naïve Bayes algorithm is used to implement the classification.

Data is divided randomly, allocating 70% of the data as training samples and the remaining 30% as test samples. For the datasets without missing values, the missing rate ranging from 10% to 50% with a step size of 10% is randomly selected. Additionally, 20 trials are carried out to obtain an average. To ensure accurate comparison and study of results, the same sample of data was generated for each trial and utilized for all computations. Subsequently, the results were determined by averaging over all independent experiments. The hyperparameters used for initializing the clustering algorithms include m=2,no.ofiterations=100,∈=0.0001 and cluster centers were initialized randomly and optimized using iteration process of IFCM. The software environment consists of Matlab 2023a running on a 64-bit PC equipped with an Intel(R) Celeron(R) 2957U CPU clocked at 1.40 GHz and 4.00 GB RAM for the implementation of all algorithms.

5  Results and Discussions

In the case of evaluating statistical imputation techniques for the process of classification or clustering, the emphasis is on how well the imputed data aids in the desired process. Various performance evaluation metrics were employed to compare different approaches as discussed above. The metrics utilized include Classification accuracy, Precision, Recall or sensitivity and Specificity and their mathematical formulas are provided below:

Accuracy=TP+TNTotal(12)

Precision=TPTP+FP(13)

Recall or Sensitivity=TPTP+FN(14)

Specificity=TNTN+FP(15)

Abbreviations and their details:

Different approaches are represented by following abbreviations:

Tables 2 and 3 present the comparison results of various performance metrics for five real datasets: Iris, Ecoli, Ionosphere, Glass dataset and Thyroid medical dataset, at a 10% missing rate whereas Table 4 represents Wisconsin Breast Cancer dataset which is an incomplete real-world dataset. The findings demonstrate that our proposed method consistently outperforms other stated methods in terms of performance.

As per the findings in Table 2, when we compare the results of traditional approaches, the classification accuracy and precision with interpolation imputation methods are much better than other two approaches, followed by nearest neighbor imputation method. When clustering is integrated with the imputation method, classification accuracy increases for all three approaches as compared to the traditional approach whereas when imputation is solely employed with the classifier, the precision achieved with the linear interpolation imputation method yields superior results across all five datasets followed by nearest neighbor imputation. However, incorporating clustering alongside imputation aids in enhancing the outcomes, and the results given by our proposed method “Clust-LI” is significantly better than all other methods.

Table 3 showcases the average recall (sensitivity) and specificity values of various algorithms, respectively. Once more, it is evident that the proposed approach outperforms others across all cases. Table 4 provides the performance metrics for the Wisconsin Breast Cancer dataset, a real-life incomplete dataset. The proposed approach exhibits slightly superior classification accuracy compared to all other methods. Additionally, performance on other metrics is either comparable or slightly better than the next best method, which involves integrating nearest neighbor imputation with IFCM.

Based on the results the performance metrics for the Iris, Glass, and Thyroid datasets are notably better compared to the Ecoli and Ionosphere datasets. This disparity can be attributed to several factors including size and the balanced distribution of the data concerning different number of cluster groups present. Iris, Glass, and Thyroid datasets are relatively small and well-balanced datasets with 2–3 distinct classes resulting into more reliable and stable clustering/classification results. The Ecoli and Ionosphere dataset include a greater number of instances and continuous features resulting into the problem of class imbalance, which can negatively impact performance metrics.

To delve deeper into the impact of varying missing rates on performance, the effectiveness of various classifiers across missing rates ranging from 10% to 50% is examined. Fig. 3 illustrates the trend analysis of the effect of missing rates on accuracies across different datasets. While the results exhibit a decline with an increase in missing values, it is apparent that the accuracy of our proposed method consistently surpasses other methods in all cases.

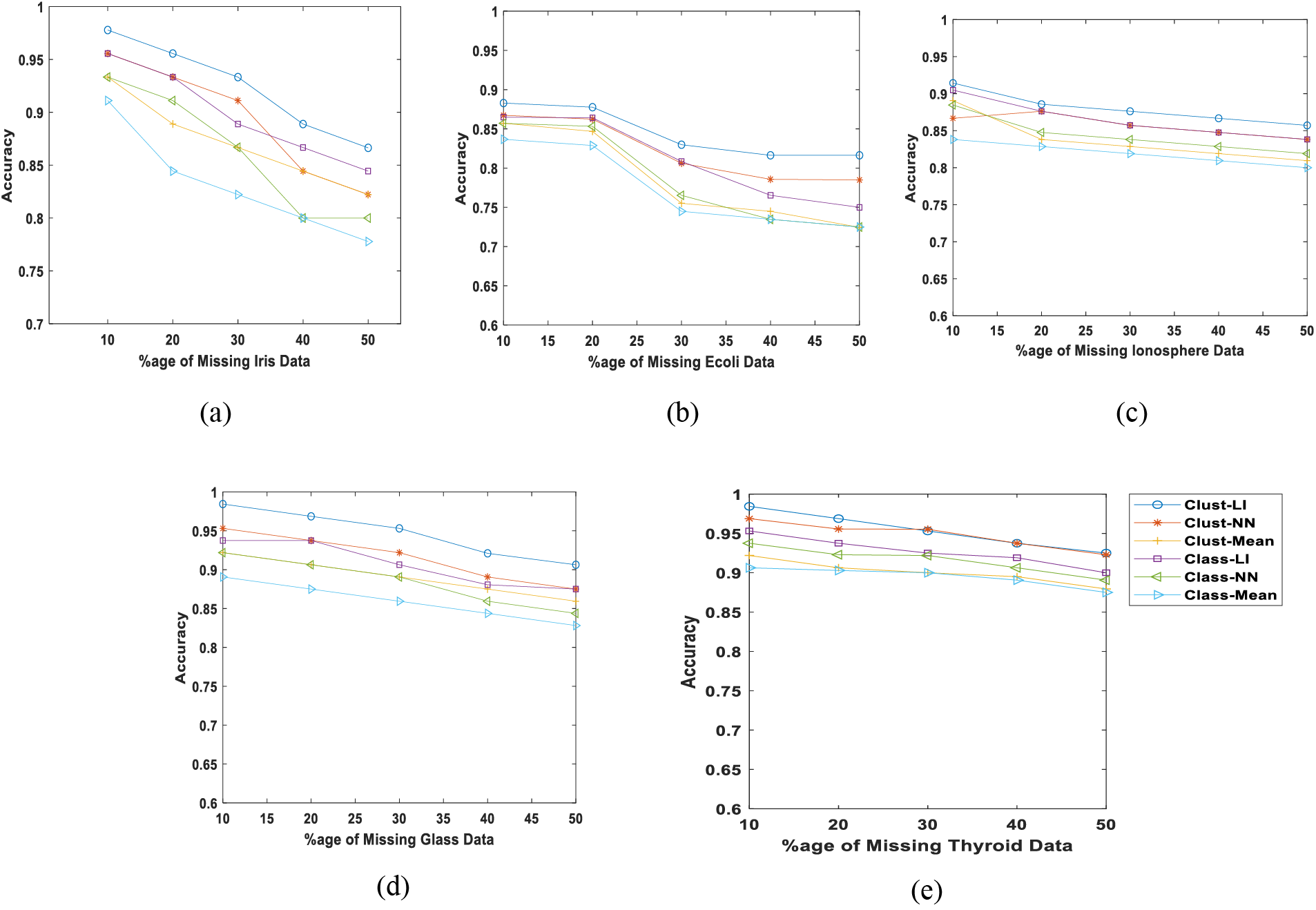
Figure 3: Average classification accuracies with different missing rates (a) Iris data (b) Ecoli data (c) Ionosphere (d) Glass data (e) Thyroid data

As shown in Fig. 3a, the missing percentage escalates from 10% to 50% in the Iris dataset, the classification accuracy decreases from 97% to 87% when applying our proposed approach. Conversely, utilizing the “Class-Mean” method yields the lowest accuracy of 77% among all methods. Notably, the “Class-LI” approach produces the next best results with an accuracy of 85%, indicating that the linear interpolation method outperforms all other imputation methods considered in this study.

Fig. 3b illustrates the impact of varying missing percentages on the classification accuracy for the Ecoli dataset. Once more, the results reinforce the assertion of the superiority of our proposed approach, with a slight decrease in accuracy from 87% to 84%. Notably, at a 50% missing rate, the “Class-Mean,” “Class-NN,” and “Clust-Mean” approaches yield identical accuracies. The second-best results are demonstrated by the “Clust-NN” approach, achieving approximately 80% accuracy, significantly lower than our proposed method. Similarly, Fig. 3c,e shows the proposed algorithm outperforms the other algorithms when the missing rate is increased from 10% to 50%.

To verify the accuracy and efficiency of the proposed algorithm, boxplots are employed to analyze datasets with 30% missing data in Figs. 4 and 5, respectively. When conducting a box plot analysis of our proposed algorithm in classification tasks, two performance metrics: accuracy and precision are described. Within each boxplot, the median is depicted as a central line, the 25th and 75th percentiles as the lower and upper quartiles, and outliers are marked with a plus sign. It can be seen that the proposed Clust-LI algorithm consistently provides the highest level of accuracy and precision across all the datasets compared to alternative algorithms. Notably, the width of the box plot for our proposed algorithm remains consistently lower than that of others, showing its reliability in managing of missing features.

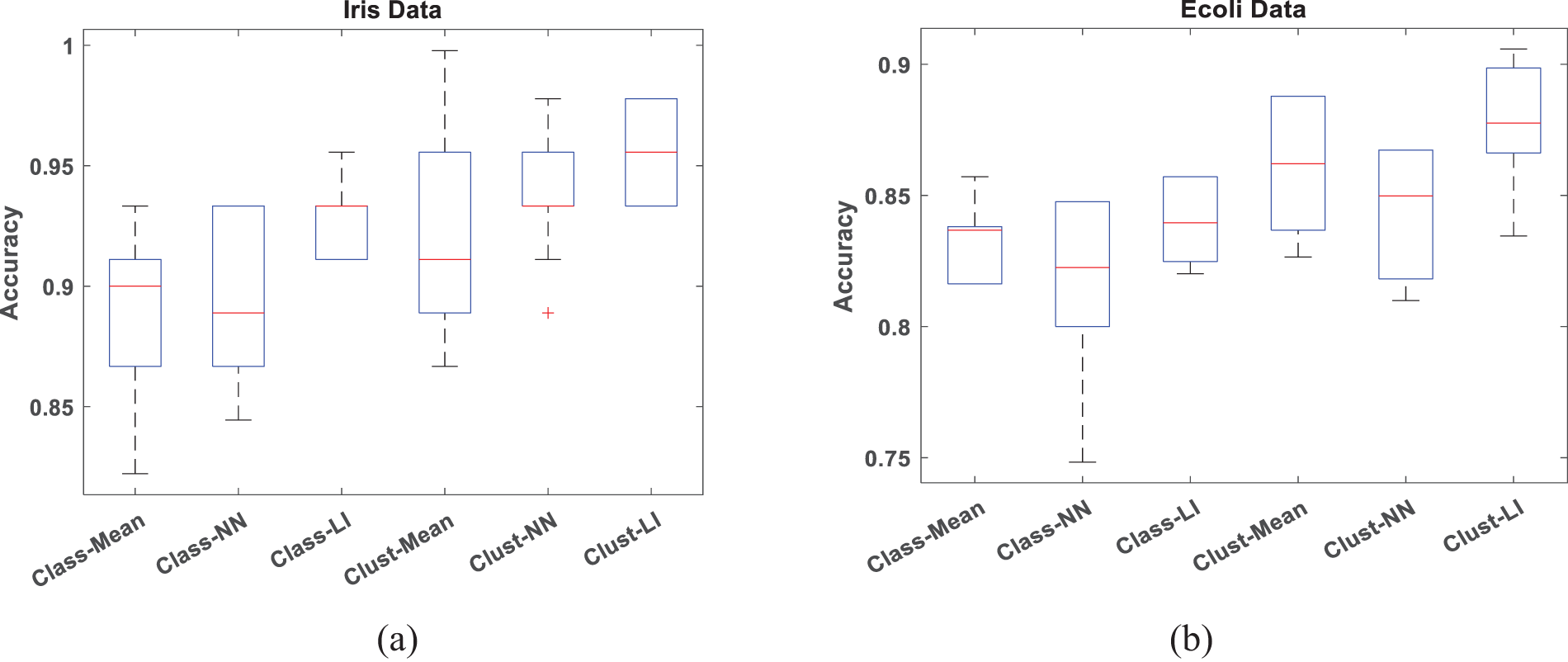
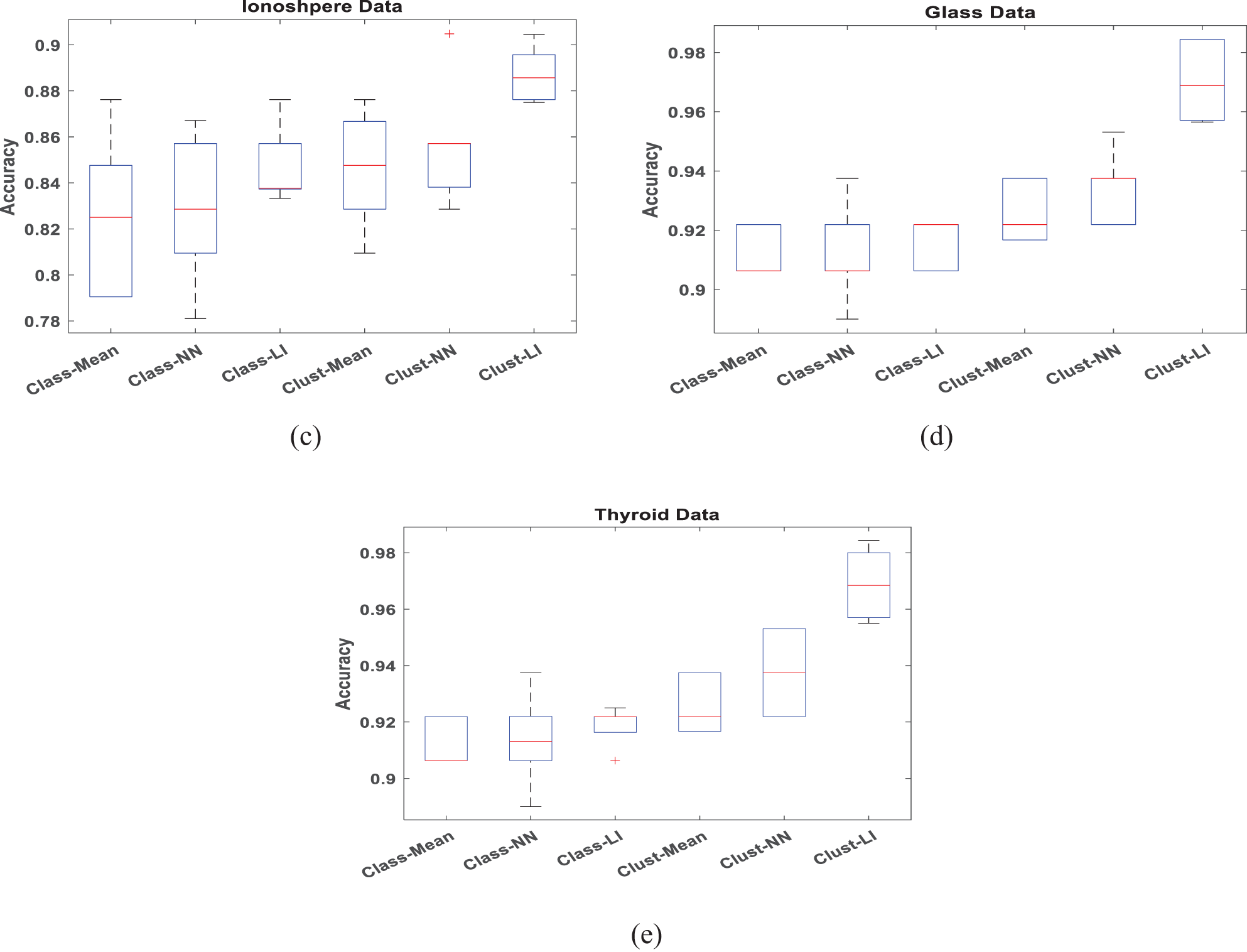
Figure 4: Box plot for classification Accuracy with 30% missing rate (a) Iris data (b) Ecoli data (c) Ionosphere (d) Glass data (e) Thyroid data

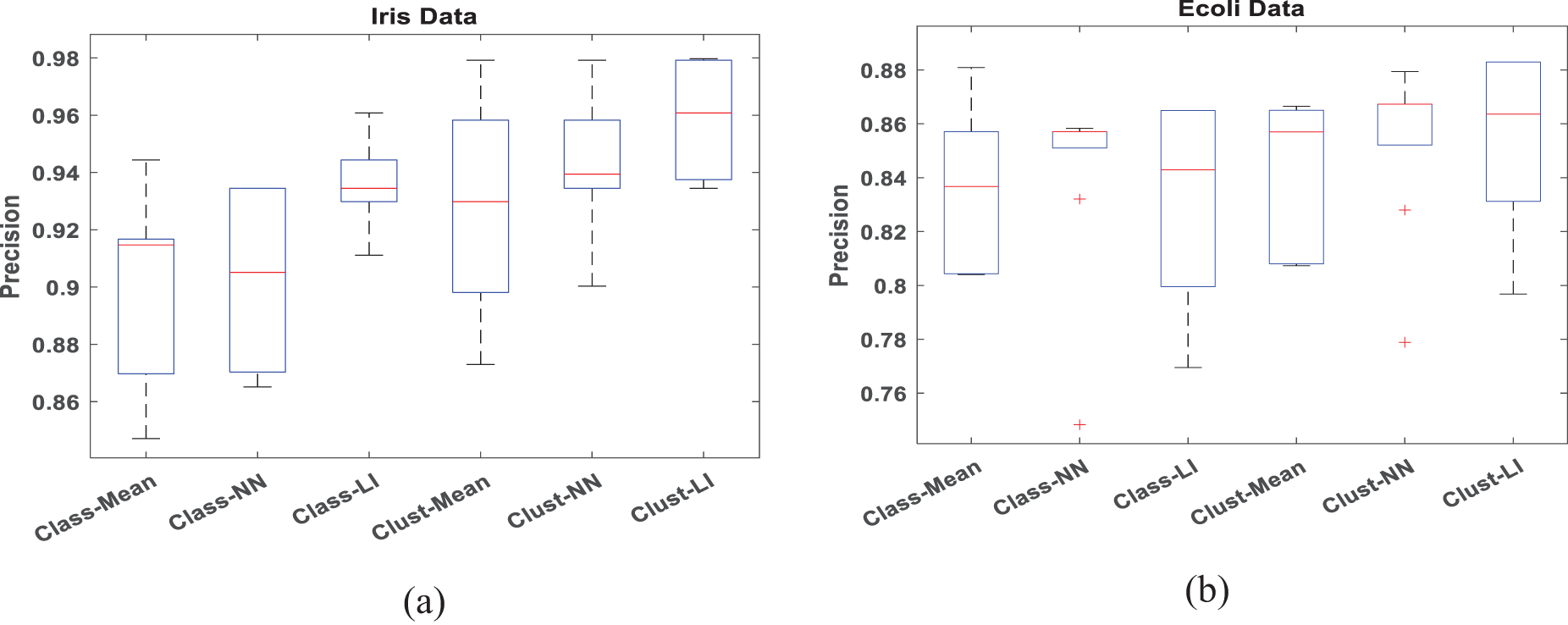
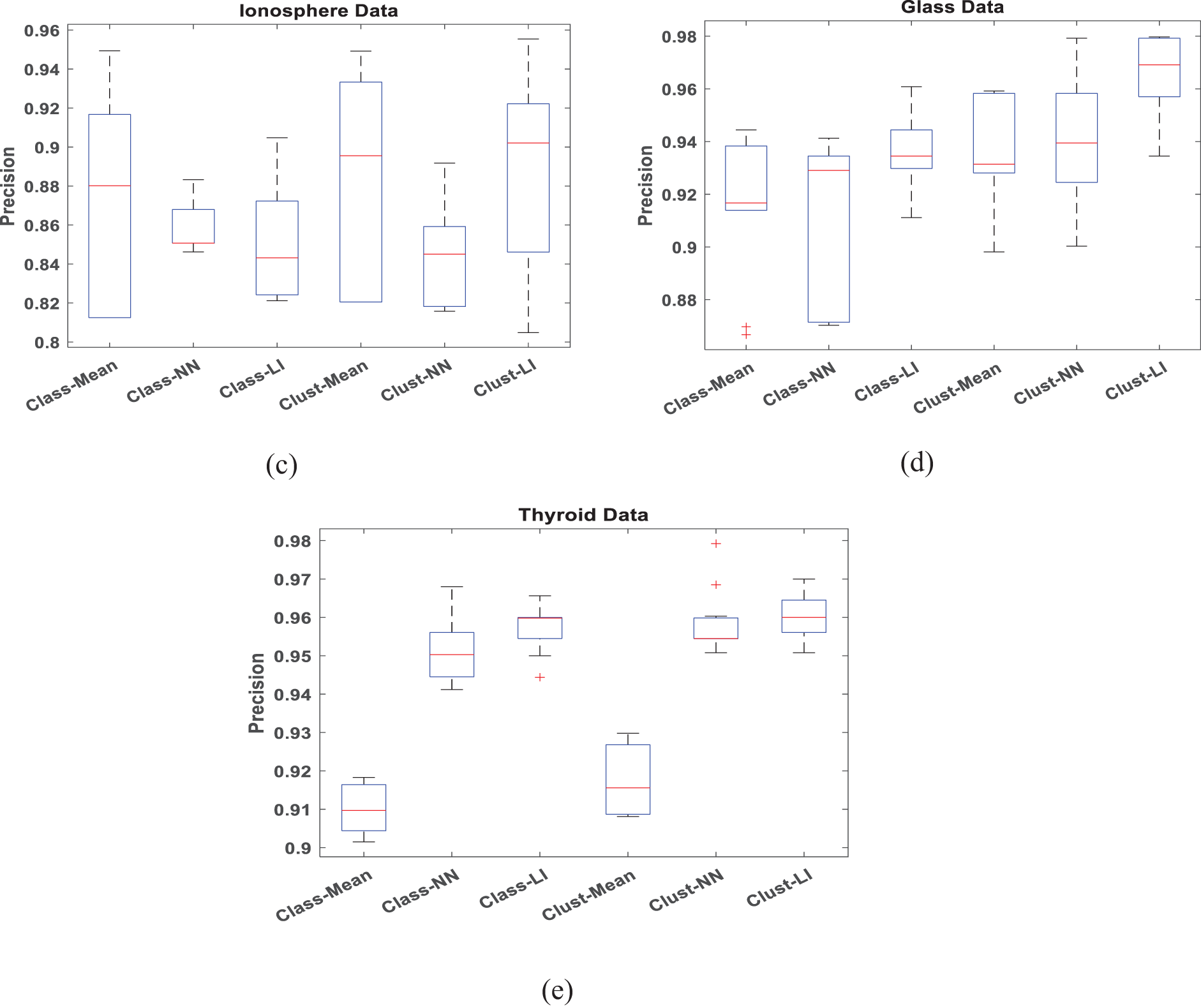
Figure 5: Box plot for Precision with 30% missing rate (a) Iris data (b) Ecoli data (c) Ionosphere (d) Glass data (e) Thyroid data

Lastly, we have done statistical analysis on the accuracy of the clustering algorithms (10% missing) based on the confidence interval to check the variability of the results across multiple trials. We have calculated the accuracy of the different algorithms over 20 trials. The outcome of the results is shown in Table 5. As can be seen from the table, our proposed approach is giving the best results on accuracy with minimum variability for multiple trials as well.

6  Conclusions and Future Scope

Incomplete data sets with missing attribute values may influence the decision-making results when analyzing them. The missing value imputation is commonly used to solve the problem of incomplete data sets. In this paper, a new algorithm to enhance the efficiency and effectiveness of classification with incomplete data is proposed. The proposed algorithm (Clust-LI) is composed of two modules. The first module focuses on the linear interpolation imputation method, which aims to produce better imputation results than mean and NN imputation methods. The second module uses an iterative Fuzzy c-means clustering algorithm on the imputed dataset and it further improves the missing values update. This updated dataset is used in the training process to build a classifier. In the testing phase, clustering is used to reduce the number of instances used for imputation.

During the comparison experiments, our proposed method is compared with some classical approaches and different combinations of imputation methods with the IFCM clustering. Different scales of data sets are taken, and some data are randomly removed to get different missing rates. Our experimental results show that integrating the IFCM clustering with the linear interpolation imputation achieves higher accuracy than other stated methods. Furthermore, the integration of the clustering with the imputation not only accelerates the imputation but also improves the classification accuracy.

There are certain limitations to our proposed work. For this study, we focused solely on continuous data. However, we plan to include categorical and ordinal data in future research. Secondly, we have assumed that the missing data is missing completely at random (MCAR). This approach yields reliable and unbiased estimates, unlike the challenges posed by missing data analysis under the Missing Not at Random (MNAR) mechanism, where the distribution of missing values is influenced not only by the observed values but also by the unobserved values.

There are several clustering algorithms available in the literature that can effectively handle incomplete datasets. These algorithms could be explored in future research. Further, to enhance the process of imputation, the integration of feature selection into imputation techniques for classification using incomplete data will be explored along with clustering techniques. Future research will incorporate the experimental results on large datasets considering imputation speed and the impact of overfitting.

Acknowledgement: None.

Funding Statement: The work is supported by the Researchers Supporting Project number (RSP2024R34), King Saud University, Riyadh, Saudi Arabia.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Sonia Goel, Meena Tushir, Jyoti Arora, Tripti Sharma; data collection: Sonia Goel, Meena Tushir, Deepali Gupta, Ali Nauman; analysis and interpretation of results: Jyoti Arora, Tripti Sharma, Ghulam Muhammad; draft manuscript preparation: Sonia Goel, Meena Tushir, Jyoti Arora; review of manuscript: Deepali Gupta, Ali Nauman, Ghulam Muhammad; supervision: Deepali Gupta, Ali Nauman, Ghulam Muhammad; funding acquisition: Ghulam Muhammad. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data can be made available upon request to Sonia Goel (email: soniagoel@msit.in).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. W. Ngai, L. Xiu, and D. C. Chau, “Application of data mining techniques in customer relationship management: A literature review and classification,” Expert Syst. Appl., vol. 36, no. 2, pp. 2592–2602, 2009. doi: 10.1016/j.eswa.2008.02.021. [Google Scholar] [CrossRef]

2. J. Gola et al., “Advanced microstructure classification by data mining methods,” Comput. Mater. Sci., vol. 148, no. 1, pp. 324–335, 2018. doi: 10.1016/j.commatsci.2018.03.004. [Google Scholar] [CrossRef]

3. K. Riesen and H. Bunke, “IAM graph database repository for graph based pattern recognition and machine learning,” in Struct., Syntactic, Stat. Pattern Recognit.: Orlando, FL, USA, 2008, pp. 287–297. [Google Scholar]

4. K. Hattori and M. Takahashi, “A new edited k-nearest neighbor rule in the pattern classification problem,” Pattern Recognit., vol. 33, no. 3, pp. 521–528, 2000. doi: 10.1016/S0031-3203(99)00068-0. [Google Scholar] [CrossRef]

5. V. Kukreja, “Recent trends in mathematical expressions recognition: An LDA-based analysis,” Expert Syst. Appl., vol. 213, 2023, Art. no. 119028. [Google Scholar]

6. V. Kukreja and Sakshi, “Machine learning models for mathematical symbol recognition: A stem to stern literature analysis,” Multimed. Tools Appl., vol. 81, no. 20, pp. 28651–28687, 2022. doi: 10.1007/s11042-022-12644-2. [Google Scholar] [CrossRef]

7. S. F. Sabbeh, “Machine-learning techniques for customer retention: A comparative study,” Int. J. Adv. Comput. Sci. Appl., vol. 9, no. 2, pp. 273–281, 2018. [Google Scholar]

8. L. Wang and K. Zuo, “Medical data classification assisted by machine learning strategy,” Comput. Math. Methods Med., vol. 2022, no. 1, 2022, Art. no. 9699612. doi: 10.1155/2022/9699612. [Google Scholar] [PubMed] [CrossRef]

9. J. L. Peugh and C. K. Enders, “Missing data in educational research: A review of reporting practices and suggestions for improvement,” Rev. Educ. Res., vol. 74, no. 4, pp. 525–556, 2004. doi: 10.3102/00346543074004525. [Google Scholar] [CrossRef]

10. M. W. Heymans and J. W. R. Twisk, “Handling missing data in clinical research,” J. Clin. Epidemiol., vol. 151, no. 2, pp. 185–188, 2022. doi: 10.1016/j.jclinepi.2022.08.016. [Google Scholar] [PubMed] [CrossRef]

11. S. Wei, Y. Luo, X. Ma, P. Ren, and C. Luo, “MSH-Net: Modality-shared hallucination with joint adaptation distillation for remote sensing image classification using missing modalities,” IEEE Trans. Geosci. Remote Sens., vol. 61, pp. 1–15, 2023, Art. no. 4402615. [Google Scholar]

12. Q. Chen, P. Gong, D. Baldocchi, and G. Xie, “Filtering airborne laser scanning data with morphological methods,” Photogramm. Eng. Remote Sensing, vol. 73, no. 2, pp. 175–185, 2007. doi: 10.14358/PERS.73.2.175. [Google Scholar] [CrossRef]

13. S. T. Rizvi, M. Y. Latif, M. S. Amin, A. J. Telmoudi, and N. A. Shah, “Analysis of machine learning based imputation of missing data,” Cybern. Syst., pp. 1–15, 2023. doi: 10.1080/01969722.2023.2247257. [Google Scholar] [CrossRef]

14. A. Jazayeri, O. S. Liang, and C. C. Yang, “Imputation of missing data in electronic health records based on patients’ similarities,” J. Healthcare Inform. Res., vol. 4, no. 3, pp. 295–307, 2020. doi: 10.1007/s41666-020-00073-5. [Google Scholar] [PubMed] [CrossRef]

15. Q. Li, T. You, J. Chen, Y. Zhang, and C. Du, “LI-EMRSQL: Linking information enhanced Text2SQL parsing on complex electronic medical records,” IEEE Trans. Reliab., vol. 73, no. 2, pp. 1280–1290, 2023. [Google Scholar]

16. R. J. Little and D. B. Rubin, Statistical Analysis with Missing Data, 2nd ed. New Jersey, NJ, USA: John Wiley & Sons, 2019. [Google Scholar]

17. A. Farhangfar, L. A. Kurgan, and W. Pedrycz, “A novel framework for imputation of missing values in databases,” IEEE Trans. Syst., Man, Cybern.-A: Syst. Humans, vol. 37, no. 5, pp. 692–709, 2007. doi: 10.1109/TSMCA.2007.902631. [Google Scholar] [CrossRef]

18. M. Liu et al., “Handling missing values in healthcare data: A systematic review of deep learning-based imputation techniques,” Artif. Intell. Med., vol. 142, no. 24, 2023, Art. no. 102587. doi: 10.1016/j.artmed.2023.102587. [Google Scholar] [PubMed] [CrossRef]

19. G. Pu, L. Wang, J. Shen, and F. Dong, “A hybrid unsupervised clustering-based anomaly detection method,” Tsinghua Sci. Technol., vol. 26, no. 2, pp. 146–153, 2020. doi: 10.26599/TST.2019.9010051. [Google Scholar] [CrossRef]

20. N. Shah and S. Mahajan, “Document clustering: A detailed review,” Int. J. Appl. Inf. Syst., vol. 4, no. 5, pp. 30–38, 2012. doi: 10.5120/ijais12-450691. [Google Scholar] [CrossRef]

21. A. Tomović, P. Janičić, and V. Kešelj, “n-Gram-based classification and unsupervised hierarchical clustering of genome sequences,” Comput. Methods Programs Biomed., vol. 81, no. 2, pp. 137–153, 2006. doi: 10.1016/j.cmpb.2005.11.007. [Google Scholar] [PubMed] [CrossRef]

22. G. Nagarajan and L. D. Babu, “Missing data imputation on biomedical data using deeply learned clustering and L2 regularized regression based on symmetric uncertainty,” Artif. Intell. Med., vol. 123, no. 6, 2022, Art. no. 102214. doi: 10.1016/j.artmed.2021.102214. [Google Scholar] [PubMed] [CrossRef]

23. U. Yelipe, S. Porika, and M. Golla, “An efficient approach for imputation and classification of medical data values using class-based clustering of medical records,” Comput. Electr. Eng., vol. 66, no. 12, pp. 487–504, 2018. doi: 10.1016/j.compeleceng.2017.11.030. [Google Scholar] [CrossRef]

24. R. Vangipuram, R. K. Gunupudi, V. K. Puligadda, and J. Vinjamuri, “A machine learning approach for imputation and anomaly detection in IoT environment,” Expert Syst., vol. 37, no. 5, 2020, Art. no. 12556. doi: 10.1111/exsy.12556. [Google Scholar] [CrossRef]

25. R. F. Brøndum, T. Y. Michaelsen, and M. Bøgsted, “Regression on imperfect class labels derived by unsupervised clustering,” Brief. Bioinform., vol. 22, no. 2, pp. 2012–2019, 2021. doi: 10.1093/bib/bbaa014. [Google Scholar] [PubMed] [CrossRef]

26. M. I. Lopez, J. M. Luna, C. Romero, and S. Ventura, “Classification via clustering for predicting final marks based on student participation in forums,” in Int. Conf. Educ. Data Mining (EDM), Chania, Greece, Jun. 19–21, 2012. [Google Scholar]

27. A. Palanivinayagam and R. Damaševičius, “Effective handling of missing values in datasets for classification using machine learning methods,” Information, vol. 14, no. 2, 2023, Art. no. 92. doi: 10.3390/info14020092. [Google Scholar] [CrossRef]

28. L. Ren, T. Wang, A. S. Seklouli, H. Zhang, and A. Bouras, “Missing values for classification of machine learning in medical data,” in Int. Conf. Artif. Intell. Big Data, IEEE, 2022, pp. 101–106. [Google Scholar]

29. P. J. García-Laencina, J. L. Sancho-Gómez, A. R. Figueiras-Vidal, and M. Verleysen, “K nearest neighbours with mutual information for simultaneous classification and missing data imputation,” Neurocomputing, vol. 72, no. 7, pp. 1483–1493, 2009. doi: 10.1016/j.neucom.2008.11.026. [Google Scholar] [CrossRef]

30. S. Zhang, “Nearest neighbor selection for iteratively kNN imputation,” J. Syst. Softw., vol. 85, no. 11, pp. 2541–2552, 2012. doi: 10.1016/j.jss.2012.05.073. [Google Scholar] [CrossRef]

31. N. M. Noor, M. M. Al Bakri Abdullah, A. S. Yahaya, and N. A. Ramli, “Comparison of linear interpolation method and mean method to replace the missing values in environmental data set,” in Materials Science Forum. Trans Tech Publications Ltd., 2015, vol. 803, pp. 278–281. doi: 10.4028/www.scientific.net/MSF.803.278. [Google Scholar] [CrossRef]

32. S. Goel and M. Tushir, “Different approaches for missing data handling in fuzzy clustering: A review,” in Recent Advances in Electrical & Electronic Engineering, 2020, vol. 13, no. 6, pp. 833–846. doi: 10.2174/2352096512666191127121710. [Google Scholar] [CrossRef]

33. S. Goel and M. Tushir, “A new imputation-based incomplete data-driven fuzzy modeling for accuracy improvement in ubiquitous computing applications,” Int. J. Pervasive Comput. Commun., vol. 17, no. 4, pp. 426–442, 2021. doi: 10.1108/IJPCC-03-2021-0069. [Google Scholar] [CrossRef]

34. S. Alam, M. S. Ayub, S. Arora, and M. A. Khan, “An investigation of the imputation techniques for missing values in ordinal data enhancing clustering and classification analysis validity,” Decis. Anal. J., vol. 9, no. 6, 2023, Art. no. 100341. doi: 10.1016/j.dajour.2023.100341. [Google Scholar] [CrossRef]

35. R. J. Hathaway and J. C. Bezdek, “Fuzzy c-means clustering of incomplete data,” IEEE Trans. Syst., Man, Cybern., B (Cybern.), vol. 31, no. 5, pp. 735–744, 2001. doi: 10.1109/3477.956035. [Google Scholar] [PubMed] [CrossRef]

36. S. Yosboon, N. Iam-On, T. Boongoen, P. P.Keerin, and K. Kirimasthong, “Optimised multiple data partitions for cluster-wise imputation of missing values in gene expression data,” Expert Syst. Appl., vol. 257, no. 1, 2024, Art. no. 125040. doi: 10.1016/j.eswa.2024.125040. [Google Scholar] [CrossRef]

37. C. K. Enders and A. N. Baraldi, “Missing data handling methods,” in The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test Development, 2018, pp. 139–185. [Google Scholar]

38. F. J. Yang, “An implementation of naive bayes classifier,” in Int. Conf. Computat. Sci. Computat. Intell., Las Vegas, NV, USA, IEEE, 2018, pp. 301–306. doi: 10.1109/CSCI46756.2018.00065. [Google Scholar] [CrossRef]

39. K. I. Penny and T. Chesney, “Imputation methods to deal with missing values when data mining trauma injury data,” in Int. Conf. Inf. Technol. Interfaces, Cavtat, Croatia, IEEE, 2006, vol. 2, pp. 213–218. doi: 10.1109/ITI.2006.1708480. [Google Scholar] [CrossRef]

40. L. Weed, R. Lok, D. Chawra, and J. Zeitzer, “The impact of missing data and imputation methods on the analysis of 24-hour activity patterns,” Clocks Sleep, vol. 4, no. 4, pp. 497–507, 2022. doi: 10.3390/clockssleep4040039. [Google Scholar] [PubMed] [CrossRef]

41. J. M. Jerez et al., “Missing data imputation using statistical and machine learning methods in a real breast cancer problem,” Artif. Intell. Med., vol. 50, no. 2, pp. 105–115, 2010. doi: 10.1016/j.artmed.2010.05.002. [Google Scholar] [PubMed] [CrossRef]

42. R. P. Hayati, K. J. Lee, and J. A. Simpson, “The rise of multiple imputation: A review of the reporting and implementation of the method in medical research,” BMC Med. Res. Methodol., vol. 15, pp. 1–14, 2015. [Google Scholar]

43. R. Chauhan, H. Kaur, and M. A. Alam, “Data clustering method for discovering clusters in spatial cancer databases,” Int. J. Comput. Appl., vol. 10, no. 6, pp. 9–14, 2010. doi: 10.5120/1487-2004. [Google Scholar] [CrossRef]

44. Y. Ban et al., “Micro-directional propagation method based on user clustering,” Comput. Inform., vol. 42, no. 6, pp. 1445–1470, 2023. doi: 10.31577/cai_2023_6_1445. [Google Scholar] [CrossRef]

45. H. H. Huang, J. Shu, and Y. Liang, “MUMA: A multi-omics meta-learning algorithm for data interpretation and classification,” IEEE J. Biomed. Health Inform., vol. 28, no. 4, pp. 2428–2436, 2024. doi: 10.1109/JBHI.2024.3363081. [Google Scholar] [PubMed] [CrossRef]

46. S. Goel and M. Tushir, “A new iterative fuzzy clustering approach for incomplete data,” J. Stat. Manag. Syst., vol. 23, no. 1, pp. 91–102, 2020. doi: 10.1080/09720510.2020.1714150. [Google Scholar] [CrossRef]

47. K. Bache and M. Lichman, “UCI machine learning repository,” 2013. Accessed: Jul. 20, 2024. [Online]. Available: https://archive.ics.uci.edu/datasets [Google Scholar]