V2I Physical Layer Security Beamforming with Antenna Hardware Impairments under RIS Assistance

1  Introduction

In the future, the Internet of Vehicles (IoV) will play an important role in mobile communication. With the development of beyond 5G and 6G technologies, the demand for ultra-high reliability and ultra-low latency will become even more urgent. IoV will carry large volumes of security- and privacy-sensitive data, so security communication between vehicles is becoming increasingly critical [1,2]. Physical layer security (PLS) communication technology is one of the important means to improve the security of IoV communication [3].

PLS communication technologies for IoV typically include physical layer key generation, radio resource management, cooperative jamming, and multi-antenna technology. Physical layer key generation technology mainly utilizes the randomness and stability of channel characteristics to generate keys through specific algorithms, which are used to encrypt and decrypt communication data in IoV. Keys’ distribution and management are carried out through secure protocols to ensure that only authorized devices can obtain and use the keys [4]. Radio resource management technology typically allocates transmission power and channel resources, which generally include centralized resource allocation and distributed resource allocation. In traditional centralized resource allocation methods, the physical layer security transmission rate (PLSTR) is often maximized by employing two-stage optimization methods, however, it is prone to increased transmission latency [5,6]. Distributed resource allocation methods can reduce the time overhead by allowing each vehicle to individually choose resources for optimization, where each vehicle can sense the signal and interference levels of its neighboring vehicles [7]. Cooperative jamming technology is mainly used in time-division duplex (TDD) systems [8]. In the first stage, when the legitimate user sends information to the relay node, the roadside unit (RSU) acts as a cooperative jammer to send interference signals to interfere with eavesdropping users. In the second stage, when the relay node forwards information to the RSU, the legitimate user acts as a cooperative jammer. Both stages use cooperative jamming signals to increase the PLSTR of the legitimate user. Multi-antenna technology for enhancing PLS communication in vehicular networks generally includes beamforming and precoding, introducing artificial noise (AN), and transmitting antenna selection. Multi-antenna technology can fully utilize the spatial degrees of freedom to optimize the transmit precoding based on the channel state information (CSI) so that a directional signal beam is formed to maximize the PLSTR. Although transmit precoding can help PLS communication, its performance is often dependent on the optimization results of the precoding matrix [9,10]. To further weaken the eavesdropping channel’s eavesdropping ability, AN is intentionally introduced into the eavesdropping channel to ensure that legitimate users remain unaffected. If the number of legitimate user’s antennas exceeds the number of eavesdropping user’s antennas, the AN at the eavesdropping user cannot be eliminated, thereby weakening the signal-to-interference-plus-noise ratio (SINR) at the eavesdropping user, achieving PLS communication [11,12]. However, the objective of these methodologies is to optimize the transceiver or only encrypt the signal itself for passive adaptation to the wireless transmission channel, without necessitating active alterations or reconstruction of the channel to improve the PLSTR.

In recent years, reconfigurable intelligent surface (RIS) technology has transformed the challenge of passive adaptation to wireless channels by enabling active reconfiguration of line-of-sight virtual links. This advancement has led to significant improvements in signal enhancement, coverage of blind spots, and various other aspects. RIS consists of a large number of simple, low-power electronic units arranged in an array that can be controlled by flexible digital circuits to perform signal reflection functions. By manipulating the circuits of these units, it is possible to adjust the phase, amplitude, or frequency of incident electromagnetic wave signals, allowing the reflected waves to form beams directed toward desired locations. Due to its low power consumption, cost-effectiveness, and flexible controllability, research on RIS-assisted mobile and wireless communication has made substantial progress. Areas such as channel modeling and information acquisition [13,14], simultaneous wireless information and power transfer [15,16], multi-antenna transmission and beamforming technologies [17], cognitive radio communication assistance [18], and physical layer security communications under RIS support have all garnered increasingly extensive and in-depth investigation [19].

In the design of RIS-assisted PLS, when the transmitter communicates with the receiver over a vulnerable communication link, a RIS can be strategically deployed to leverage the characteristics of the line-of-sight virtual channel. This deployment aims to enhance the signal-to-noise ratio (SNR) at the receiver by mitigating fading effects and ensuring channel stability. Additionally, it serves to limit the amount of information that eavesdroppers can extract from encrypted messages by introducing multipath fading across the channel. Research on PLS with RIS assistance has been conducted in various network scenarios and system models. Notable studies [20–22] have explored PLS transmission challenges with RIS support in THz systems, Non-Orthogonal Multiple Access (NOMA) networks, and satellite communication systems, respectively. Furthermore, investigations into performance indicators, methodologies, and optimization problems are progressively advancing. Literature [23] proposed a novel approach by virtually dividing RIS units into two segments to improve expected signal strength for legitimate users while enhancing artificial noise influence for illegitimate users through distinct phase shift configurations in each segment. To achieve this objective, two optimization problems were defined: one aimed at jointly optimizing both division ratios and SNR of transmit power. A closed-form solution was subsequently provided under constraints pertaining to both legitimate and illegitimate user rate limits. Literature [24] proposed a secure and energy-efficient transmission scheme assisted by RIS under the SNR constraints of both legitimate users and eavesdroppers, with the objective of minimizing transmit power. This scheme was realized through the joint optimization of the transmitter’s beamforming weights and the phase shift coefficients of the RIS. To address the non-convex nature of this problem, the original optimization challenge was approximated as a second-order cone programming (SOCP) problem. In literature [25], efforts were made to enhance system PLSTR, taking into account varying quality of service (QoS) requirements and time-varying channel conditions. A joint optimization problem involving base station (BS) beamforming and RIS reflected beamforming was established. For non-convex optimization problems characterized by high dynamic complexity that are challenging to solve, a deep reinforcement learning-based secure beamforming method was proposed to derive optimal strategies for counteracting eavesdroppers in dynamic environments.

All these research findings indicate that RIS technology offers significant advantages in supporting PLS communication. However, none of these studies have considered scenarios related to the IoV, particularly regarding beamforming challenges for PLS communication amidst coexisting V2I and V2V communications.

There is significant potential for utilizing RIS technology to enhance PLS communication in vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) systems within the IoV. Literature [26] examined the effects of deployment location and the number of RIS units on the PLSTR in two RIS-assisted vehicular communication models: V2I and V2V. However, this study did not address scenarios where V2I and V2V share spectrum resources, nor did it propose a joint beamforming algorithm. Literature [27] suggested partitioning the RIS units into two segments, with one segment functioning as a reflection surface while the other acts as a relay. Closed-form expressions for average secrecy capacity were derived separately for both segments, allowing for comparative analysis. Nonetheless, this investigation overlooked the design of PLS beamforming algorithms despite comparing the secrecy transmission rates between RIS-enhanced systems and traditional relays. Literature [28] explored both V2V and vehicle-to-RIS communication contexts, deriving closed-form expressions for the probability of secure transmission interruption in scenarios involving eavesdropping users. This work demonstrated that employing RIS can significantly improve PLSTR in vehicular networks; however, it inadequately addressed aspects related to V2I links by failing to analyze cascaded channels or provide an appropriate beamforming algorithm. Moreover, collectively these studies have neglected non-ideal conditions such as hardware impairments affecting transceiver antennas. In practice, radio frequency (RF) components inevitably encounter hardware limitations that result in imperfect operational conditions due to factors like phase noise, quantization errors, amplified noise, and nonlinearity. Current research indicates that distortion noise arising from hardware impairments can be effectively modeled using additive Gaussian noise [29]. Consequently, this serves as our primary motivation for further research.

With the aforementioned motivation, this paper examines a scenario in which V2I, V2V, and eavesdropping users coexist within a RIS-assisted IoV system. It proposes a robust beamforming method for the V2I user’s PLSTR, taking into account hardware impairments present in the transmit antenna. The primary contributions of this work are as follows:

(1) A PLS communication model is established with the assistance of RIS, where V2I, V2V, and eavesdropping users coexist. The proposed problem model aims to maximize the PLSTR for V2I users while adhering to constraints imposed by hardware impairments in the V2I base station antenna and the SINR of V2V users. The noise resulting from hardware damage in the antennas combines with useful signals and is transmitted through a reflected channel via RIS, thereby affecting both the received signal-to-noise ratio of V2I users and that of eavesdropping users. This interaction poses significant challenges in addressing the maximization problem for PLSTR among V2I users.

(2) This paper proposes an alternating optimization algorithm for the non-convex optimization problem involving coupled variables. The approach utilizes relaxed variables, first-order Taylor expansion, and semi-definite relaxation techniques. The challenge of solving the coupled variables is decomposed into two sub-problems, each of which is ultimately transformed into an equivalent convex optimization problem through sophisticated mathematical methods. The transmitted precoding of the V2I base station and the reflection phase shift matrix of the RIS are jointly optimized to maximize the secure transmission rate for V2I users.

(3) The PLS transmission simulation scenario is established with the support of RIS to facilitate the coexistence of three types of vehicles in a two-lane environment. The simulation results are compared against traditional algorithms and non-robust algorithms, highlighting the superiority of the proposed algorithm. Furthermore, the advantages conferred by robust algorithms in PLS transmission for vehicular networks are discussed, accompanied by simulation results and an analysis of how relevant system parameters—such as vehicle speed, number of antennas, and quantity of RIS reflective units—affect PLSTR.

Note that some key abbreviations used throughout the paper are listed in Table 1.

2  System Model

This paper investigates the maximization of downlink PLSTR under RIS-assisted V2I communication in IoV systems. In this system, both V2V and V2I communications coexist, with the base station’s transmitting antenna suffering from hardware impairments as depicted in Fig. 1. The model considers the scenario where the base station (denoted as B) transmits information to V2I vehicles (denoted as C), while V2V vehicles share spectrum resources with V2I. It is assumed that spectrum resource allocation has been completed, such that each spectrum resource is exclusively used by a pair of V2I and V2V devices. The transmitter (denoted as Dt) of a V2V vehicle sends information to its corresponding receiver (denoted as Dr). An eavesdropping vehicle (denoted as E) aims to intercept the information transmitted from the base station to the V2I vehicle.

Figure 1: IoV downlink transmission scenario aided by RIS

A simple and low-power reactive RIS is deployed on buildings alongside roads, which can be flexibly adjusted through an RIS controller controlled by the base station based on channel conditions to enhance useful signal strength, suppress interference signals, and mitigate eavesdropping attempts. This study assumes that perfect channel estimation results are available at the base station, however, detailed research on channel estimation falls outside the scope of this paper. The focus of this work is on downlink MISO communication, where the base station is equipped with M antennas, the vehicle transmitter/receiver has a single antenna, and the RIS consists of N reflective units. The reflection coefficient for the n th unit is denoted as ϕn=ejθn, where θn∈[0,2π] represents the phase shift. Here we assumed that the amplitude of the reflection coefficient is 1, which indicates that the incident signal seems to be specular reflected, and it only changes in phase, but the amplitude does not change.

According to the system description in Fig. 1, the communication links can be categorized into three types: links associated with V2I, links related to V2V, and links relevant to eavesdropping users. Specifically, the communication link gain between base station B and RIS is denoted as channel H∈CN×M, where the symbol Ci×j represents a set of complex matrices of size i×j. Other communication links, such as from base station B to V2I vehicle C, from B to Dr and from B to E are respectively denoted as hc∈CM×1, hd∈CM×1 and he∈CM×1. The channels from V2V transmitter Dt to RIS, from Dt to C and from Dt to Dr are denoted as g∈CN×1, gc∈C and gd∈C. The channels from RIS to C, from RIS to Dr and from RIS to E are denoted as fc∈CN×1, fd∈CN×1 and fe∈CN×1, respectively.

Assume that a symbol s∈C satisfying E(ss∗)=1 is transmitted from B to C, define the transmitted precoding vector w∈CM×1, then the signal transmitted from B is x=ws+mt, where mt∈CM×1 describing the noise caused by hardware impairments in BS transmit antennas, the noise at each antenna is assumed to follow an independent and identically distributed Gaussian distribution, i.e., mt∼CN(0,μtdiag~(wwH)), where μt≥0 is the ratio of the hardware impairments noise power to the transmitted signal power for each antenna [29], diag~(A) represents generating a diagonal matrix whose diagonal elements are the diagonal elements of the matrix A. Similarly, assume that Dt sends sd∈C satisfying E(sdsd∗)=1 to Dr. The Dt transmitter equipped with a single antenna requires no precoding.

According to the above model, the received signal at vehicle C includes a direct path signal from B, hardware impairment noise from the direct path, reflected signal from the RIS and hardware impairment noise from the reflected path, as well as V2V interference signal and thermal noise, which can be expressed as yc=(hcH+fcHΨH)(ws+mt)+(gc+fcHΨg)sd+nc, where Ψ=diag(ϕ1,ϕ2,⋯,ϕN) is RIS reflection coefficient matrix and nc∼CN(0,σc2) is Gaussian noise at the receiver of C.

Similarly, the received signal of the V2V vehicle Dr includes V2V direct path signal, reflected signal through RIS, V2I signal, interference from hardware impairments and thermal noise. This can be expressed as yd=(gd+fdHΨg)sd+(hdH+fdHΨH)(ws+mt)+nd, where nd∼CN(0,σd2) is Gaussian noise at the receiver of Dr. The received signal from eavesdropper E includes eavesdropped V2I target signals, hardware damage noise, V2V interference signals and thermal noise, which can be represented as ye=(heH+feHΨH)(ws+mt)+(ge+feHΨg)sd+ne, where ne∼CN(0,σe2) is Gaussian noise at the receiver of E.

Therefore, the SINRs of vehicle C and vehicle Dr can be given by SINRc=|(hcH+fcHΨH)w|2|(hcH+fcHΨH)mt|2+|gc+fcHΨg|2+σc2 and SINRd=|gd+fdHΨg|2|(hdH+fdHΨH)w|2+|(hdH+fdHΨH)mt|2+σd2, respectively. The SINR of eavesdropper E is SINRe=|(heH+feHΨH)w|2|ge+feHΨg|2+|(heH+feHΨH)mt|2+σe2. Thus, the V2I’s information transmission rate is Cc=log2⁡(1+SINRc) bit/s/Hz and the eavesdropping rate of the vehicle E is Ce=log2⁡(1+SINRe) bit/s/Hz. Then the PLSTR of the vehicle C can be given by Csec=max{0,Cc−Ce}.

3  Problem Formulation

This paper investigates the maximization problem of PLSTR for V2I user C when there are hardware impairments to the transmitting antenna at the base station. The V2V communication require a minimum SINR, there are limitations on the total power transmitted by the multi-antenna base station and on the phase shift range of RIS units. Based on these considerations, an optimization problem P1 can be formulated.

P1:maxw,Ψ Csec(1a)

s.t.|gd+fdHΨg|2|(hdH+fdHΨH)w|2+|(hdH+fdHΨH)mt|2+σd2≥γ(1b)

‖w‖2≤Pmax(1c)

|ϕn|=1,n=1,2,⋯,N(1d)

mt∼CN(0,μtdiag~(wwH))(1e)

where the vector w that is transmitted precoding and the matrix Ψ that is RIS’s reflection coefficient are two variables to be optimized. Constraint (1b) is the SINR requirement for V2V vehicles, taking into account the hardware impairments of the base station’s transmit antenna, where γ denotes the SINR threshold. Constraint (1c) is related to the total power constraint of the base station, with Pmax representing the maximum available transmitted power of B. Constraint (1d) imposes a phase shift constraint on RIS units, given that reflected phases range from 0 to 2π, it follows that the reflection coefficient ϕn has a modulus of one. Lastly, constraint (1e) pertains to noise distribution constraints associated with hardware impairments in base station transmit antennas.

Problem P1 is not only a non-convex optimization challenge but also involves interdependent variables, making it difficult to solve and even more challenging to attain the global optimal solution. One potential approach to address this issue is through alternate optimization, which decouples the variables using an alternating method and subsequently solves the subproblems independently. The specific procedure involves initially solving for variable w while keeping variable Ψ a fixed, followed by solving for variable Ψ with variable w held constant. These two steps are alternated until the algorithm converges, ultimately yielding the optimal solution for both variables. Each iteration addresses a non-convex subproblem, which can be effectively resolved using appropriate mathematical techniques.

To facilitate the alternating optimization, problem P1 is first transformed into an equivalent form where the hardware impairments constraint can be absorbed. Denote ϕ=[ϕ1,ϕ2,⋯,ϕN]T, then fcHΨ=ϕHdiag(fcH), Let z=[ϕ1,ϕ2,⋯,ϕN,1]T and denote G~x=(diag(fxH)HhxH), G¯x=(diag(fxH)ggx) where x={c,d,e}, then SINRc, SINRd, SINRe can be rewritten by SINRc=wHG~cHzzHG~cwIc(w,z), SINRd=zHG¯dG¯dHzId(w,z) and SINRe=wHG~eHzzHG~ewIe(w,z), where Ic(w,z)=μtzHG~cdiag~(wwH)G~cHz+zHG¯cG¯cHz+σc2, Id(w,z)=wHG~dHzzHG~dw+μtzHG~ddiag~(wwH)G~dHz+σd2 and Ie(w,z)=μtzHG~ediag~(wwH)G~eHz+zHG¯eG¯eHz+σe2. Then, we have Cc=log2⁡(Ic(w,z)+wHG~cHzzHG~cwIc(w,z)) and Ce=log2⁡(Ie(w,z)+wHG~eHzzHG~ewIe(w,z)).

The objective function reveals that when the eavesdropping rate exceeds the V2I information transmission rate, the V2I PLSTR may become zero. In such cases, power control methods can be implemented at the base station to halt V2I communication. Consequently, joint beamforming is excluded from the algorithm’s design, focusing solely on scenarios where the eavesdropping rate remains below the vehicle-to-infrastructure (V2I) transmission rate. Thus, optimization problem P1 can be equivalently transformed into P2.

P2:maxw,zCc−Ce(2a)

s.t.zHG¯dG¯dHzId(w,z)≥γ(2b)

‖w‖2≤Pmax(2c)

z∈𝒮,𝒮={z||zn|2=1,1≤n≤N,zN+1=1}(2d)

The variables to be solved have been changed to w and z. Due to the non-convex objective function and coupled variables in problem P2, it can be further equivalently transformed into a simple form by introducing slack variables p=[p1,p2,p3,p4]T. Let

{log2⁡(Ic(w,z)+wHG~cHzzHG~cw)≥p1(3a)log2⁡(Ic(w,z))≤p2(3b)log2⁡(Ie(w,z)+wHG~eHzzHG~ew)≤p3(3c)log2⁡(Ie(w,z))≥p4(3d)(3)

so that Cc≥p1−p2, Ce≤p3−p4. The problem P2 becomes P3, as follows:

P3:maxw,z,pp1−p2−p3+p4(4a)

s.t.zHG¯dG¯dHzId(w,z)≥γ(4b)

‖w‖2≤Pmax(4c)

z∈𝒮(4d)

(3a)∼(3d)(4e)

In problem P3, the new variable p is not coupled with the original variables w and z, so the following two parts provide alternating solutions only for the two variables w and z. In solving for w, the method of introducing relaxation variables and first-order Taylor expansion was used to convert the optimization problem into an equivalent SOCP problem. In the process of solving for z, the method of semi-definite relaxation (SDR) and first-order Taylor expansion was used to convert the optimization problem into an equivalent semi-definite programming (SDP) problem.

4  Alternating Optimization Algorithm

The following two subsections provide a comprehensive procedure for the alternating optimization of the two variables.

4.1 Solve for the Transmitted Precoding

In this subsection, we solve for the base station’s precoding vector w under the assumption that the RIS reflection coefficient z is fixed. The original problem P3 can be then reformulated as problem P4.

P4:maxw,pp1−p2−p3+p4(5a)

s.t.zHG¯dG¯dHzId(w,z)≥γ(5b)

‖w‖2≤Pmax(5c)

(3a)∼(3d)(5d)

The non-convex constraint (5d) in problem P4 still needs to be further transformed. First, the convexification process of the constraint (5d) is presented, followed by the explicit expression of the SINR constraint (5b).

By using the equation relationship yHdiag~(xxH)y=xHdiag~(yyH)x, we can obtain zHG~xdiag~(wwH)G~xHz=wHdiag~(G~xHzzHG~x)w. Therefore, given z, the Ic(w,z), Id(w,z), and Ie(w,z) in equations (5b) and (5d) can be respectively transformed into

{Ic(w)=μtwHdiag~(G~cHzzHG~c)w+zHG¯cG¯cHz+σc2(6a)Id(w)=wHG~dHzzHG~dw+μtwHdiag~(G~dHzzHG~d)w+σd2(6b)Ie(w)=μtwHdiag~(G~eHzzHG~e)w+zHG¯eG¯eHz+σe2(6c)(6)

For constraint (5d), we can firstly transform (3a)~(3d) into following equivalent form by introducing the variable rw=[rw1,rw2,rw3,rw4]T.

(3a)(3b)⇒{log2⁡(rw1)≥p1(7a)Ic(w)+wHG~cHzzHG~cw≥rw1(7b)log2⁡(rw2)≤p2(7c)Ic(w)≤rw2(7d)(7)

(3c)(3d)⇒{log2⁡(rw3)≤p3(8a)Ie(w)+wHG~eHzzHG~ew≤rw3(8b)log2⁡(rw4)≥p4(8c)Ie(w)≥rw4(8d)(8)

It can be seen that (7a), (7d), (8b) and (8c) are convex constraints, while (7b), (7c), (8a) and (8d) are non-convex constraints. Non-convex constraints can be handled using an asymptotically convex approximation method. Here, the first-order Taylor expansion is used for this purpose.

Let A1=μt diag~(G~cHzzHG~c)+G~cHzzHG~c. Then, the first-order Taylor expansion of wHA1w can be obtained as wHA1w≥2Re{(w(t))HA1w}−(w(t))HA1w(t). Therefore, using the lower bound for approximation, (7b) is equivalent to

2Re{(w(t))HA1w}−(w(t))HA1w(t)+zHG¯cG¯cHz+σc2≥rw1(9)

where w(t) represents the tth iteration result of the w.

Observe (7c), and a first-order Taylor expansion can be used to obtain an upper bound as log2⁡(rw2)≤log2⁡(rw2(t))+rw2−rw2(t)rw2(t)ln⁡2

Using upper bounds for approximation, (7c) is equivalent to

log2⁡(rw2(t))+rw2−rw2(t)rw2(t)ln⁡2≤p2(10)

Similarly, using the first-order Taylor expansion, (8a) is equivalent to

log2⁡(rw3(t))+rw3−rw3(t)rw3(t)ln⁡2≤p3(11)

And (8d) is equivalent to

2Re{(w(t))HA2w}−(w(t))HA2w(t)+zHG¯eG¯eHz+σe2≥rw4(12)

where A2=μtdiag~(G~eHzzHG~e).

For constraint (5b), substituting (6b) into (5b) will yield

(5b)⇒wHA3w+γσd2≤zHG¯dG¯dHz(13)

where A3=γG~dHzzHG~d+γμtdiag~(G~dHzzHG~d).

Finally, the optimization problem P4 can be rewritten as follows P5.

P5:maxw,p,rwp1−p2−p3+p4(14a)

s.t.(7a)(7d)(8b)(8c),(9)∼(13)(14b)

‖w‖2≤Pmax(14c)

Problem P5 is an SOCP problem that can be solved using convex optimization tools such as CVX.

4.2 Solve for the RIS Reflection Coefficient

In this section, we analyze the problem of finding the optimal RIS reflection coefficient vector z given the transmit precoding w. The initial problem P3 can be reformulated as problem P6.

P6:maxz,pp1−p2−p3+p4(15a)

s.t.zHG¯dG¯dHzId(w,z)≥γ(15b)

z∈𝒮(15c)

(3a)∼(3d)(15d)

Problem P6 is a non-convex problem, and the non-convexity mainly arises from the non-convex constraints (15c) and (15d). Upon simplifying and substituting the expressions of the objectives or constraints in the problem, the non-convex problem can be reformulated as the convex optimization problem through techniques such as convex approximation and semidefinite relaxation.

For constraint (15c), define E=zzH, then (15c) can be equivalently transformed as

z∈𝒮⇒{E≽0,rank(E)=1,diag~(E)=IN+1}(16)

For constraint (15d), by introducing slack variables re=[re1,re2,re3,re4]T, (3a)~(3d) can be equivalently transformed as follows:

(3a)(3b)⇒{log2⁡(re1)≥p1(17a)Ic(z)+wHG~cHzzHG~cw≥re1(17b)log2⁡(re2)≤p2(17c)Ic(z)≤re2(17d)(17)

(3c)(3d)⇒{log2⁡(re3)≤p3(18a)Ie(z)+wHG~eHzzHG~ew≤re3(18b)log2⁡(re4)≥p4(18c)Ie(z)≥re4(18d)(18)

where (17a) and (18c) are convex constraints, which do not need to be transformed. Other inequality constraints need to be further transformed.

First, Ic(z) can be simplified as Ic(z)=zHB1z+σc2=Tr(B1E)+σc2, where B1=μtG~cdiag~(wwH)G~cH+G¯cG¯cH, then Ic(z)+wHG~cHzzHG~cw=zHB2z+σc2=Tr(B2E)+σc2, where B2=B1+G~cwwHG~cH. Similarly, Ie(z) can be simplified as Ie(z)=zHB3z+σe2=Tr(B3E)+σe2, where B3=μtG~ediag~(wwH)G~eH+G¯eG¯eH, then we have Ie(z)+wHG~eHzzHG~ew=zHB4z+σe2=Tr(B4E)+σe2, where B4=B3+G~ewwHG~eH. Therefore, (17b), (17d), (18b) and (18d) can be converted into linear inequalities as follows:

(17b)⇒Tr(B2E)+σc2≥re1(19)

(17d)⇒Tr(B1E)+σc2≤re2(20)

(18b)⇒Tr(B4E)+σe2≤re3(21)

(18d)⇒Tr(B3E)+σe2≥re4(22)

By using the first-order Taylor expansion, the non-convex constraints (17c) and (18a) can be transformed into convex constraints, which can be expressed as follows:

(17c)⇒log2⁡(re2(t))+re2−re2(t)re2(t)ln⁡2≤p2(23)

(18a)⇒log2⁡(re3(t))+re3−re3(t)re3(t)ln⁡2≤p3(24)

For constraint (15b), the following transformation can be easily obtained.

(15b)⇒Tr(B5E)+γσd2≤0(25)

where B5=γG~dHwwHG~d+γμtG~ddiag~(wwH)G~dH−G¯dG¯dH.

Finally, problem P6 can be equivalently rewritten as problem P7.

P7:maxE,p,rep1−p2−p3+p4(26a)

s.t.(17a)(18c),(19)∼(25)(26b)

{E≽0,rank(E)=1,diag~(E)=IN+1}(26c)

To solve problem P7, we can first ignore the constraint rank(E)=1 and relax it into an SDP problem. The SDP problem constitutes a convex optimization problem that can be effectively addressed utilizing the convex optimization toolbox, CVX. However, the optimal solution E∗ obtained by solving the SDP problem may not satisfy rank(E∗)=1. Therefore, we can use the Gaussian randomization method to find the optimal z∗ that satisfies rank(E)=1. The steps for determining z∗ using Gaussian randomization are shown in Algorithm 1.

4.3 Comprehensive Analysis of Algorithm and the Complexities

For the convenience of understanding, a flow chart is provided in Fig. 2 to summarize the key steps of the whole optimization procedure. Based on the solution processes of the two subproblems in Sections 4.1 and 4.2, the comprehensive algorithm for problem P1 is described as Algorithm 2. From the algorithm, it can be seen that the algorithm designed to address the two subproblems primarily involves the implementation of SOC constraints and matrix inversion, resulting in 𝒪(M3)+𝒪(N3) complexity characteristic of the algorithm.

Figure 2: The key steps and methodologies diagram

However, the current physical layer security beamforming algorithm based on solving convex optimization problems also has some defects, such as the input parameters of the algorithm cannot be adapted to the environment or system requirements adaptively, and the model-based algorithm cannot adapt well to the heterogeneous and complex vehicular network environment, which requires the use of reinforcement learning or deep learning methods to study the more complex PLS problems in the vehicular network. Reinforcement learning or deep learning has been proven to have great application potential in wireless communication and networks [30–32] and deep learning has been applied well in semantic spectrum sharing and edge computing in vehicular network [33,34]. It is expected that using deep learning or reinforcement learning to study the PLS beamforming problem under the assistance of RIS will also have good results.

5  Simulation Results

To assess the feasibility and efficacy of the algorithm, a dual-lane vehicular network simulation scenario is established, where the positions of the BS, RIS, and vehicles are described in the Cartesian coordinate system. Specifically, the positions of the BS and RIS are (x=0,y=0) and (x=8,y=0), respectively, while the positions of the vehicles are randomly distributed within the same communication cell with a width of 8 m, vehicle positions vary randomly as they move. The average vehicle speed is denoted as v, with an average inter-vehicle spacing of 2.5v. Unless specified otherwise in the text, all other simulation parameters are set according to Table 2. Based on the beam steering capability of RIS, we posit that all channels linked to the RIS are Rician channels, such as H, g, fc and fe, while all other channels are classified as Rayleigh channels. A Rician channel can be articulated in the following unified framework f=ρd−α(κ1+κfLoS+11+κfNLoS), where d is the distance between transceiver, ρ represents the path loss at a reference distance of 1 m, α denotes the path loss exponent, κ signifies the Rician fading factor, fNLoS refers a non-line-of-sight random scattering path, characterized by a standard complex Gaussian distribution. Conversely, fLoS pertains to the line-of-sight component described by the antenna array response. The Rayleigh channel can be uniformly represented by the following equation g=ρd−αg^, where g^ indicates a random scattering path also modeled as a standard complex Gaussian distribution.

Figs. 3–7 show the convergence, superiority, and performance of the proposed algorithm concerning different system parameters.

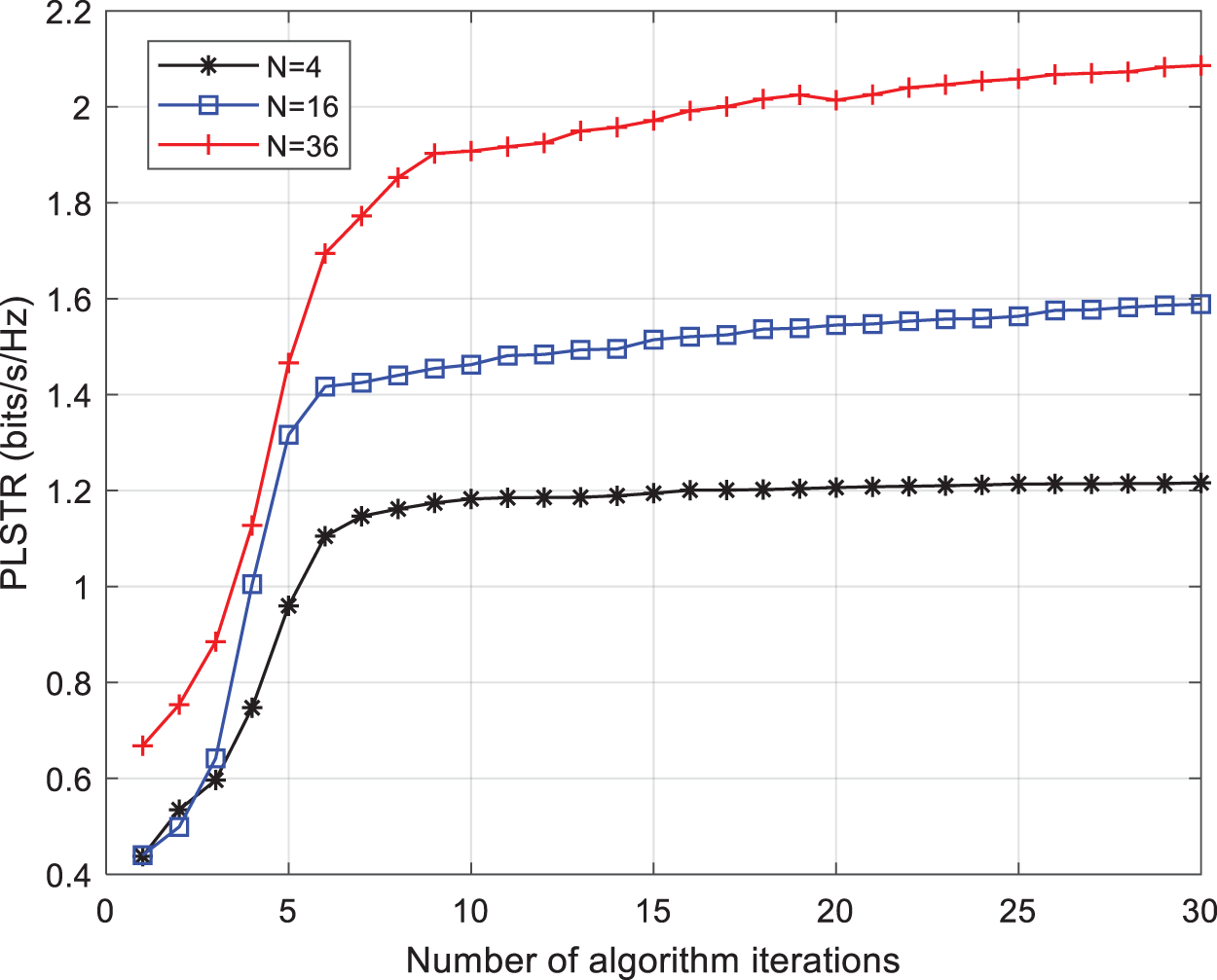
Figure 3: Algorithm convergence

Figure 4: Impact of the number of RIS reflection units on the PLSTR

Figure 5: Comparison between different algorithms

Figure 6: Impact of the maximum transmit power of the base station on the PLSTR

Figure 7: Impact of vehicle speed and hardware impairments distortion factor on PLSTR

Fig. 3 provides the convergence of the proposed algorithm. When solving the problem using the proposed algorithm with different numbers of RIS reflective units, such as N = 4, 16, and 36, the solution converges to a stable state within about 20 iterations, indicating good convergence of the algorithm. Fig. 4 illustrates the impact of the number of RIS reflective units and the maximum transmit power of the BS on the PLSTR under different numbers of transmit antennas at the BS. As the number of RIS reflective units increases, there is a gradual improvement in the PLSTR. Specifically, when the base station’s antenna count is 4, increasing the number of RIS reflective units from 10 to 50 results in an almost 2 dB enhancement in secure transmission rate. The increased number of RIS reflective units allows for more flexible control over reflection coefficients, leading to stronger reflection beamforming effects and improved PLSTR. Furthermore, as indicated by both solid and dashed lines in the figure, an increase in base station antenna count further amplifies PLSTR. This demonstrates that multiple antennas bring about noticeable gains in multiplexing and diversity.

Fig. 5 illustrates the comparative performance analysis between the proposed robust algorithm and various benchmark algorithms, including those that do not consider robustness. In this comparison, the total transmit power of the base station is limited to 1.5 W (approximately 31.76 dBm). The “Our proposed-robust” algorithm refers to the algorithm proposed in this paper, which takes into account potential hardware impairments to the base station antennas. The “Random RIS phase-robust” algorithm involves randomly assigning phase coefficients to the RIS reflection matrix, with transmit precoding obtained through the proposed method in this paper. The “CMA (Channel matching algorithm)-robust” involves using idealized transmit precoding at the base station and designing it based on singular value decomposition of channel gain matrices, while obtaining phase coefficients for the RIS reflection matrix using our proposed optimization method. The “NoRIS-robust” algorithm considers hardware impairments to BS antennas but does not utilize RIS assistance. The “Joint optimization-nonrobust” algorithm utilizes our proposed method for solving both base station transmit precoding and RIS reflecting coefficients matrix but does not take into account potential hardware impairments to base station antennas during its design process.

From Fig. 5, it is evident that our proposed robust algorithms designed for hardware impairments to base station antennas outperform CMA algorithms and also exhibit superior performance compared to the “Rand RIS phase” algorithm or algorithm without RIS support. Furthermore, they achieve an average performance improvement of 0.7 dB over a non-robustly designed algorithm.

Fig. 6 further illustrates the relationship between the maximum transmit power of the base station, path loss coefficient, and PLSTR. A larger maximum transmit power at the base station results in a higher PLSTR. This is due to the increased V2I vehicle communication rate as a result of higher base station transmit power. Additionally, leveraging RIS for eavesdropping path suppression prevents an escalation in eavesdropping rates, thereby leading to an increase in PLSTR.

Furthermore, performance results under different path loss coefficients are compared in the figure. When observing the three curves at αB2E = 3.75, it is evident that as the path loss coefficient αB2C between base stations B and C decreases, V2I’s PLSTR increases. Similarly, when observing the three curves at αB2C = 3.75, it can be observed that as the path loss coefficient αB2E between base stations B and E decreases, V2I’s PLSTR decreases due to an increase in V2I eavesdropping rates resulting from reduced path loss coefficients between B and E.

Fig. 7 illustrates the influence of vehicle speed on the PLSTR of the proposed robust algorithm under various hardware impairment noise power ratios, with the base station’s total power limited to 1.5 W (approximately 31.76 dBm). As previously mentioned, the Doppler frequency shift in this simulation system does not induce fast fading, and variations in vehicle speed primarily affect inter-vehicle spacing. According to our hypothesis, higher vehicle speeds result in greater inter-vehicle spacing, leading to increased path loss between V2V and V2I and reduced mutual interference. Simultaneously, eavesdropping vehicles experience weakened received signal power, and combined with RIS control, V2I’s PLSTR gradually increases. However, as vehicle speed rises, this growth trend will gradually stabilize due to PLSTR being capped at a level that does not exceed the V2I information transmission rate. Additionally, it is evident from the figure that the hardware distortion factor μt of the transmitting antenna has a substantial impact on performance. When this factor decreases from 0.05 to 0.01, PLSTR correspondingly increases.

6  Conclusion

This paper investigates the issue of robust physical-layer security transmission in V2I and V2V coexisting networks aided by the RIS. It mathematically models the hardware impairments to base station transmit antennas and addresses the problem of maximizing the PLSTR for V2I. By jointly optimizing the transmitted precoding and RIS reflection phase shift matrix, a robust optimization algorithm is proposed, which enhances the V2I’s PLSTR in the presence of hardware impairments to transmit antennas. The proposed algorithm demonstrates fast convergence and can achieve an average performance improvement of 0.7 dB over a non-robustly designed algorithm. Furthermore, increasing the number of RIS reflective units from 10 to 50 results in an almost 2 dB enhancement in secure transmission rate.

Based on the research methodology in this paper, future studies should continue to investigate robust beamforming methods under the presence of quantization errors introduced by AD conversion at the base station and phase shift noise caused by RIS reflection. To adapt to more flexible and variable scenarios and handle complex big data models, utilizing reinforcement learning or deep learning to design robust PLS beamforming algorithms with RIS assistance will also be one of our research priorities in the future.

Acknowledgement: Thanks to the editors for the revision of the grammar and format of the full text, and thanks to the anonymous reviewers for their professional and constructive suggestions.

Funding Statement: This research was funded by the Key Research and Development Plan of Jiangsu Province, grant number BE2020084-2 and the National Key Research and Development Program of China, grant number 2020YFB1600104.

Author Contributions: The authors confirm their contribution to the paper as follows: conceptualization and investigation: Tiecheng Song and Zerong Tang; modeling and methodology: Zerong Tang; simulation, Zerong Tang and Jing Hu; writing—original draft preparation: Zerong Tang; writing—review and editing: Tiecheng Song and Jing Hu; funding acquisition: Tiecheng Song. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: If the reader needs relevant data, please contact the author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Mejri, J. Ben-Othman, and M. Hamdi, “Survey on VANET security challenges and possible cryptographic solutions,” Veh. Commun., vol. 1, no. 2, pp. 53–66, 2014. doi: 10.1016/j.vehcom.2014.05.001. [Google Scholar] [CrossRef]

2. S. Zeadally, R. Hunt, Y. S. Chen, A. Irwin, and A. Hassan, “Vehicular ad hoc networks (VANETS): Status, results, and challenges,” Telecommun. Syst., vol. 50, no. 4, pp. 217–241, 2012. doi: 10.1007/s11235-010-9400-5. [Google Scholar] [CrossRef]

3. X. Luo, Y. Liu, H. Chen, and Q. Guo, “Physical layer security in intelligently connected vehicle networks,” IEEE Netw., vol. 34, no. 5, pp. 232–239, 2020. doi: 10.1109/MNET.011.1900628. [Google Scholar] [CrossRef]

4. Z. Wang et al., “A reliable physical layer key generation scheme based on RSS and LSTM network in VANET,” IEEE Internet Things J., vol. 11, no. 1, pp. 692–707, 2024. doi: 10.1109/JIOT.2023.3286120. [Google Scholar] [CrossRef]

5. Y. Wu et al., “Secrecy-driven resource management for vehicular computation offloading networks,” IEEE Netw., vol. 32, no. 3, pp. 84–91, 2018. doi: 10.1109/MNET.2018.1700320. [Google Scholar] [CrossRef]

6. Q. Wu, W. Wang, P. Fan, J. Wang, and K. B. Letaief, “URLLC-awared resource allocation for heterogeneous vehicular edge computing,” IEEE Trans. Veh. Technol., vol. 73, no. 8, pp. 11789–11805, 2019. doi: 10.1109/TVT.2024.3370196. [Google Scholar] [CrossRef]

7. H. Ye, G. Y. Li, and B. -H. F. Juang, “Deep reinforcement learning based resource allocation for V2V communications,” IEEE Trans. Vehicular Technol., vol. 68, no. 4, pp. 3163–3173, 2019. doi: 10.1109/TVT.2019.2897134. [Google Scholar] [CrossRef]

8. D. Wang, P. Ren, Q. Du, L. Sun, and Y. Wang, “Security provisioning for MISO vehicular relay networks via cooperative jamming and signal super position,” IEEE Trans. Veh. Technol., vol. 66, no. 12, pp. 10732–10747, 2017. doi: 10.1109/TVT.2017.2703780. [Google Scholar] [CrossRef]

9. X. Zhang and M. Vaezi, “Deep learning based precoding for the MIMO Gaussian wiretap channel,” in Proc. IEEE GLOBECOM, Waikoloa, HI, USA, 2019, pp. 1–6. [Google Scholar]

10. F. Qamar, S. H. A. Kazmi, K. A. Z. Ariffin, M. Tayyab, and Q. N. Nguyen, “Multi-antenna array-based massive MIMO for B5G/6G: State of the art, challenges, and future research directions,” Information, vol. 15, no. 8, 2024, Art. no. 442. doi: 10.3390/info15080442. [Google Scholar] [CrossRef]

11. Y. Liu, H. -H. Chen, and L. Wang, “Secrecy capacity analysis of artificial noisy MIMO channels—An approach based on ordered eigenvalues of Wishart matrices,” IEEE Trans. Inform. Forensic. Secur., vol. 12, no. 3, pp. 617–630, 2017. doi: 10.1109/TIFS.2016.2627219. [Google Scholar] [CrossRef]

12. C. Wang, Z. Li, X. Xia, J. Shi, J. Si and Y. Zou, “Physical layer security enhancement using artificial noise in cellular vehicle-to-everything (C-V2X) networks,” IEEE Trans. Veh. Technol., vol. 69, no. 12, pp. 15253–15268, 2020. doi: 10.1109/TVT.2020.3037899. [Google Scholar] [CrossRef]

13. Z. Peng et al., “Two-stage channel estimation for RIS-aided multiuser mmWave systems with reduced error propagation and pilot overhead,” IEEE Trans. Signal Process., vol. 71, pp. 3607–3622, 2023. doi: 10.1109/TSP.2023.3317729. [Google Scholar] [CrossRef]

14. Y. Zhu, Y. Liu, Q. Wu, C. You, and Q. Shi, “Channel estimation by transmitting pilots from reconfigurable intelligent surface,” IEEE Trans. Wirel. Commun., vol. 23, no. 4, pp. 3328–3343, 2023. doi: 10.1109/TWC.2023.3307450. [Google Scholar] [CrossRef]

15. Q. Wu and R. Zhang, “Joint active and passive beamforming optimization for intelligent reflecting surface assisted SWIPT under QoS constraints,” IEEE J. Sel. Areas Commun., vol. 38, no. 8, pp. 1735–1748, 2020. doi: 10.1109/JSAC.2020.3000807. [Google Scholar] [CrossRef]

16. C. Pan et al., “Intelligent reflecting surface aided MIMO broadcasting for simultaneous wireless information and power transfer,” IEEE J. Select. Areas Commun., vol. 38, no. 8, pp. 1719–1734, 2020. doi: 10.1109/JSAC.2020.3000802. [Google Scholar] [CrossRef]

17. W. Tang et al., “MIMO transmission through reconfigurable intelligent surface: System design, analysis, and implementation,” IEEE J. Select. Areas Commun., vol. 38, no. 11, pp. 2683–2699, 2020. doi: 10.1109/JSAC.2020.3007055. [Google Scholar] [CrossRef]

18. J. Ge, Y. -C. Liang, S. Li, and Z. Bai, “RIS-enhanced spectrum sensing: How many reflecting elements are required to achieve a detection probability close to 1?” IEEE Trans. Wireless Commun., vol. 21, no. 10, pp. 8600–8615, 2022. doi: 10.1109/TWC.2022.3167474. [Google Scholar] [CrossRef]

19. J. Chen, Y. -C. Liang, Y. Pei, and H.Guo, “Intelligent reflecting surface: A programmable wireless environment for physical layer security,” IEEE Access, vol. 7, pp. 82599–82612, 2019. doi: 10.1109/ACCESS.2019.2924034. [Google Scholar] [CrossRef]

20. J. Qiao, C. Zhang, A. Dong, J. Bian, and M. -S. Alouini, “Securing intelligent reflecting surface assisted terahertz systems,” IEEE Trans. Veh. Technol., vol. 71, no. 8, pp. 8519–8533, 2022. doi: 10.1109/TVT.2022.3172763. [Google Scholar] [CrossRef]

21. W. Wang et al., “Beamforming and jamming optimization for IRS-aided secure NOMA networks,” IEEE Trans. Wireless Commun., vol. 21, no. 3, pp. 1557–1569, Mar. 2022. doi: 10.1109/TWC.2021.3104856. [Google Scholar] [CrossRef]

22. Q. T. Ngo, K. T. Phan, A. Mahmood, and W. Xiang, “Physical layer security in IRS-assisted cache-enabled satellite communication networks,” IEEE Trans. Green Commun. Netw., vol. 7, no. 4, pp. 1920–1931, 2023. doi: 10.1109/TGCN.2023.3280118. [Google Scholar] [CrossRef]

23. S. Arzykulov, A. Celik, G. Nauryzbayev, and A. M. Eltawil, “Artificial noise and RIS-aided physical layer security: Optimal RIS partitioning and power control,” IEEE Wireless Commun. Lett., vol. 12, no. 6, pp. 992–996, 2023. doi: 10.1109/LWC.2023.3256001. [Google Scholar] [CrossRef]

24. Y. Kawai and S. Sugiura, “QoS-constrained optimization of intelligent reflecting surface aided secure energy-efficient transmission,” IEEE Trans. Veh. Technol., vol. 70, no. 5, pp. 5137–5142, 2021. doi: 10.1109/TVT.2021.3075685. [Google Scholar] [CrossRef]

25. H. Yang, Z. Xiong, J. Zhao, D. Niyato, L. Xiao and Q. Wu, “Deep reinforcement learning-based intelligent reflecting surface for secure wireless communications,” IEEE Trans. Wireless Commun., vol. 20, no. 1, pp. 375–388, 2021. doi: 10.1109/TWC.2020.3024860. [Google Scholar] [CrossRef]

26. A. U. Makarfi, K. M. Rabie, O. Kaiwartya, X. Li, and R. Kharel, “Physical layer security in vehicular networks with reconfigurable intelligent surfaces,” in Proc. VTC2020-Spring, Antwerp, Belgium, 2020, pp. 1–6. [Google Scholar]

27. N. Mensi and D. B. Rawat, “On the performance of partial RIS selection vs. partial relay selection for vehicular communications,” IEEE Trans. Veh. Technol., vol. 71, no. 9, pp. 9475–9489, 2022. doi: 10.1109/TVT.2022.3177130. [Google Scholar] [CrossRef]

28. Y. Ai, F. A. P. deFigueiredo, L. Kong, M. Cheffena, S. Chatzinotas and B. Ottersten, “Secure vehicular communications through reconfigurable intelligent surfaces,” IEEE Trans. Veh. Technol., vol. 70, no. 7, pp. 7272–7276, 2021. doi: 10.1109/TVT.2021.3088441. [Google Scholar] [CrossRef]

29. E. Bjärnson, J. Hoydis, M. Kountouris, and M. Debbah, “Massive MIMO systems with non-ideal hardware: Energy efficiency, estimation, and capacity limits,” IEEE Trans. Inform. Theory, vol. 60, no. 11, pp. 7112–7139, 2014. doi: 10.1109/TIT.2014.2354403. [Google Scholar] [CrossRef]

30. W. Jiang, “Cellular traffic prediction with machine learning: A survey,” Expert. Syst. Appl., vol. 201, 2022, Art. no. 117163. doi: 10.1016/j.eswa.2022.117163. [Google Scholar] [CrossRef]

31. W. Jiang, “Graph-based deep learning for communication networks: A survey,” Comput. Commun., vol. 185, no. 1, pp. 40–54, 2022. doi: 10.1016/j.comcom.2021.12.015. [Google Scholar] [CrossRef]

32. Q. Wu, W. Wang, P. Fan, Q. Fan, H. Zhu and K. B. Letaief, “Cooperative edge caching based on elastic federated and multi-agent deep reinforcement learning in next-generation networks,” IEEE Trans. Netw. Serv. Manag., vol. 21, no. 4, pp. 4179–4196, 2024. doi: 10.1109/TNSM.2024.3403842. [Google Scholar] [CrossRef]

33. Z. Shao et al., “Semantic-aware spectrum sharing in internet of vehicles based on deep reinforcement learning,” 2024, arXiv:2406.07213. [Google Scholar]

34. C. Zhang et al., “Distributed deep reinforcement learning based gradient quantization for federated learning enabled vehicle edge computing,” IEEE Internet Things J., 2024. doi: 10.1109/JIOT.2024.3447036. [Google Scholar] [CrossRef]