Computation Offloading in Edge Computing for Internet of Vehicles via Game Theory

1  Introduction

In recent years, the Internet of Things (IoT) [1–4] technology has enabled a wide range of applications across various aspects of daily life. According to the latest report of Cisco Visual Networking Index (VNI), the number of global IoT devices has reached 26 billion [5]. As the proliferation of IoT devices continues, the vast interconnection of these devices generates a substantial amount of task data, posing significant challenges to traditional data collection and processing methods. Additionally, the implementation of centralized device management and control has become increasingly impractical in this environment.

One of the most important subsets of the Internet of Things (IoT) is the Internet of Vehicles (IoV). It is essential for tackling the problems caused by the increasing traffic on roads and the various needs of the modern environment. With a focus on safety, efficiency, and entertainment, the IoV significantly impacts the management of densely populated roadways and evolving user needs, drawing considerable attention from researchers and various industry sectors [6–8].

However, the rapid expansion of the IoV has resulted in a substantial rise in terminal devices and a substantial increase in data traffic [9–11]. According to the research report released by Intel, the data volume of autonomous vehicles has reached an astonishing 4000 GB [12]. Faced such a massive volume of data, relying solely on the limited local computing resources of the IoV is inadequate. In order to overcome these difficulties, traditional cloud computing-based IoV has surfaced, which makes it easier to transfer vehicle operations to the cloud by utilizing cutting-edge communication technology. This approach enables vehicles to offload specific tasks for computation in the cloud while simultaneously performing local task computation, effectively mitigating the constraints imposed by limited computing resources within vehicles [13,14]. However, cloud computing paradigms are not suitable for all application requirements, particularly in the context of IoV.

To overcome these challenges, mobile edge computing (MEC) technology has been introduced into the IoV. MEC brings cloud computing capabilities closer to the network’s edge, thereby reducing transmission delays and providing more resources for processing computing tasks. This proximity enables MEC to handle the dynamic and high-speed nature of vehicular networks more effectively than traditional cloud computing models. MEC can offload tasks to nearby edge servers, thus minimizing latency and ensuring more efficient use of network resources. One of the primary challenges with cloud computing is the latency associated with data transmission to and from distant cloud servers. For delay-sensitive applications in IoV, such as real-time navigation and collision avoidance systems, this latency can be detrimental. Furthermore, when the offloading task is too intensive, network congestion and excessive resource utilization can occur, further exacerbating the problem. Current optimization methods such as Ant Colony Optimization (ACO) [15], Firefly Algorithm (FA) [16], and Simulated Annealing (SA) [17] have been extensively applied to address resource allocation and task offloading issues. However, these schemes struggle to quickly adapt to dynamic networks resulting from changes in network topology or user demands.

Consider a real-time navigation system in a smart city. Traditional cloud computing requires data to be sent to a distant server, processed, and then sent back to the vehicle, causing delays. With MEC, the data can be processed at a nearby edge server, providing instantaneous updates and directions to the driver, thereby enhancing the driving experience and safety.

Certain studies mainly examine the options of doing all computations locally, using the vehicle’s internal processing power, or sending all duties to adjacent MEC servers. However, in the task-intensive IoV environment, limited by computing resources and the maximum delay, these approaches often fail to meet user needs. Resource scheduling in the Internet of Vehicles is mainly carried out in two ways: vehicle-to-vehicle (V2V) and vehicle-to-roadside infrastructure (V2R). Task offloading is essentially accomplished by trading communication resources for computing resources. With the growing prevalence of data generation at the network edge, processing data locally becomes more efficient. Typically, the task offloading process involves three steps: task delivery, task execution, and result retrieval. The edge computing environment represents an innovative network architecture that enables task execution on edge servers close to the vehicle, thereby minimizing data communication response times. Interference poses challenges for mobile users seeking optimal data rates. However, suboptimal offloading decisions may impact overall system performance. Efficient management of interference, considering the dynamic needs of mobile users and maximizing data rates, is crucial for ensuring optimal computational offloading strategies. This, in turn, affects energy efficiency and data transfer time adversely. In such scenarios, leveraging MEC for task offloading may not effectively enhance the experience of mobile users. Efficient task offloading strategies in mobile wireless networks are pivotal for enhancing wireless access efficiency. The synergy of the MEC task offloading strategy is instrumental in efficiently utilizing resources [18].

In this paper, we selected the Artificial Bee Colony (ABC) algorithm due to its distinctive suitability for the dynamic and distributed nature of IoV environments. The ABC algorithm is particularly adept at real-time adaptability, enabling it to respond expeditiously to frequent alterations in network topology and resource availability. This capability is of paramount importance for maintaining optimal system performance in IoV. Furthermore, it operates with minimal computational overhead, rendering it an optimal choice for resource-constrained edge devices that are prevalent in vehicular networks.

Furthermore, the ABC algorithm’s intrinsic scalability and decentralized structure render it highly resilient in the context of dynamic network conditions, such as fluctuating signal quality and intermittent connectivity. In contrast to distributed deep learning algorithms, which necessitate substantial computational resources and stable communication links, the ABC algorithm is both cost-effective and resilient, offering a balanced solution that optimizes task offloading and resource allocation in IoV scenarios. These advantages make the ABC algorithm an optimal choice for enhancing the efficiency and reliability of vehicular networks.

Game theory is essential to the IoV’s resource allocation. Game models help cars realize spectrum allocation techniques, increase spectrum efficiency, and make the best judgments possible given the limited spectrum, computer resources, and energy available. These models can also be used to optimize communication decisions between vehicles to ensure congestion control and load balancing of the network. The cooperative game model, for instance, analyzes strategies for vehicle cooperation in sharing information, sensor data, and task offloading. The competitive game model is employed to study resource competition and strategy selection among vehicles [19]. An increasing number of studies adopt partial task offloading, dynamically dividing computing tasks into two parts: one remains local, and the other is offloaded to the MEC server for processing. The tasks offloaded to the MEC server involve purchasing computing resources, meaning that the volume of tasks offloaded and the unit price of computing resources directly impact the overall system revenue. Moreover, recent advancements in privacy-preserving schemes such as privacy-preserving reputation updating scheme (PPRU) [20] and privacy-preserving trust management scheme (PPTM) [21] have highlighted the growing importance of efficient and secure task offloading and resource allocation mechanisms in vehicular networks.

Despite the advantages of MEC, several bottlenecks remain in task offloading and resource allocation in IoV environments. Current challenges include the dynamic nature of vehicular networks, where vehicle mobility causes frequent changes in network topology and communication links. This dynamic environment makes it difficult to maintain stable and efficient task offloading strategies. Additionally, the heterogeneity of vehicle capabilities and the varying demands of different applications further complicate resource allocation.

By leveraging a game-theoretic approach for task offloading and resource allocation in MEC-enabled IoV environments, our proposed solution addresses these bottlenecks. By modeling the interaction between vehicles and edge servers as a multi-master and multi-slave double-layer game, we can optimize both task offloading decisions and resource pricing strategies. The proposed scheme employs a distributed artificial bee colony algorithm to achieve game equilibrium, ensuring efficient and fair resource allocation. This method offers a reliable solution for IoV applications by enhancing system utility and convergence speed while also accommodating the dynamic character of vehicular networks. While Reinforcement Learning (RL) is an effective tool for learning from historical data, adapting to new settings frequently necessitates large computational resources and extensive training.

In the context of a vehicle edge computing network, in this paper, we investigate task offloading and resource allocation schemes in the IoV. Using game theory and an ABC distribution technique, it provides an edge computing network architecture in the IoV with the goal of maximizing overall revenue. The key contributions of this paper can be summarized as follows:

1. To maximize system revenue, an edge computing network task offloading architecture is constructed in the Internet of Vehicles scenario, and revenue models for vehicles and MEC servers are established, respectively.

2. Based on the game theory, the resource allocation decision-making scheme of the interaction between the pricing of MEC server computing resources and the size of vehicle task offloading is constructed as a game model, and according to the Brouwer fixed point theorem, it is proved that there is a Nash equilibrium and the convergence is guaranteed.

3. A distributed task offloading algorithm for artificial bee colonies based on swarm intelligence global optimization is proposed, which aims to deal with complex game problems and optimize the utility of the overall system. The simulation outcomes reveal that, in contrast to existing methods, the proposed scheme demonstrates superior optimization performance. Specifically, the total revenue achieved by this scheme surpasses ACO by approximately 8.98%, FA by 9.17%, and SA by 9.84%.

In summary, game-theoretic model we proposed for task offloading in MEC-enabled IoV environments addresses the limitations of traditional cloud computing models and overcomes the current bottlenecks in resource allocation. By minimizing latency, optimizing resource utilization, and adapting to the dynamic vehicular environment, our solution significantly enhances the performance and reliability of IoV applications.

This paper is organized as follows: Section 2 provides related works. Following this, Section 3 outlines the foundational framework for our investigation. Subsequently, Section 4 introduces and elucidates a novel algorithm designed to optimize task distribution in the IoV context. Moving forward, Section 5 presents findings obtained through rigorous simulations, shedding light on the algorithm’s effectiveness and potential areas for improvement. We conclude the paper in Section 6.

2  Related Work

Due to the high mobility of vehicles, edge computing solutions tailored for IoV face the challenge in maintaining low latency. To mitigate this issue, a wireless and computation allocation scheme is proposed [22], which transformed the resource allocation problem into a convex problem. However, this solution failed to account for the maximum tolerable delay for users, resulting in limited practicality. Similarly, Wang et al. [23] identified that the task offloading process is susceptible to the mutual interference of multiple channels. Consequently, the problem of computational offloading in multiple vehicles simultaneously was reformulated as a game-theoretic problem, leading to the proposal of distributed computational offloading algorithms to reduce the computational overhead of vehicles. Moreover, Wu et al. [24,25] introduced collaborative allocation algorithms designed to optimize both wireless and MEC computational resources. These algorithms aim to minimize the overall delay within the vehicular network while maintaining reliable communication. Unfortunately, they focused predominantly on the limitations of system resources themselves, overlooking the users’ requirements for low latency. Mkiramweni et al. [26] introduced a MEC-assisted vehicular network intended to facilitate vehicles receiving processed tasks from roadside units (RSU). This scheme established a potential game framework centered on vehicle offloading decisions, with the objective of minimizing computational overhead. Furthermore, Liu et al. [18] presented a task offloading strategy employing game theory and developed an algorithm aimed at minimizing system overhead. However, their simulation results focused solely on system overhead and neglected the benefits to users. Hou et al. [19] proposed a joint scheduling scheme to simultaneously optimize wireless resources and computing resources. This scheme tended to prioritize latency reduction while neglecting the revenue of service providers. Zhang et al. [27] proposed a Unmanned Aerial Vehicle (UAV)-assisted Multi-Access MEC system, where a game theory-based scheme was utilized to derive an optimal solution. The scheme considered weighted values, addressing both delay and energy consumption aspects. Jang et al. [28] tackled two optimization challenges in task offloading: full offloading and partial offloading. Their objective was to minimize the energy consumption of the vehicle system by optimizing bit allocation and adjusting the offloading ratio. Nevertheless, user delay was not taken into account in the simulation experiments carried out under this scheme, which raises questions regarding its viability. Chen et al. [29] introduced a distributed task offloading algorithm aimed at optimizing delay and energy consumption. However, this scheme failed to consider the maximum tolerable delay for users in high-density networks.

To address latency during data transmission and reduce energy consumption, Wu et al. [30] proposed a hybrid offloading model that integrates mobile cloud computing and mobile edge computing. However, this scheme overlooked the critical aspect of balancing workloads at the edge nodes. In addition, Zhang et al. [31] introduced a novel joint optimization scheme that focused on the simultaneous optimization of task offloading and resource allocation. Wang et al. [32] developed a MEC-based vehicle-to-everything (V2X) network aimed at reducing delay caused by task offloading by enabling vehicle-to-vehicle (V2V) connections for offloading and modeling this interaction through game theory. Furthermore, Huang et al. [33] integrated task offloading with resource allocation to formulate a dynamic offloading strategy specifically designed for multi-subtasks. This strategy accounts for variations in computing resources across different vehicles, with the goal of minimizing system overhead. While most of the above studies focused on either system overhead or delay and energy consumption of MEC applications, they have largely neglected the specific impact of the interaction between vehicles and edge servers.

While game-theory-based offloading methods have shown significant promise, RL-based approaches have also been explored due to their adaptability and ability to learn from historical data. Jiang et al. [34] developed a RL-based framework for task offloading in vehicular networks, utilizing Q-learning to optimize offloading decisions based on network conditions and resource availability. Luo et al. [35] proposed a deep reinforcement learning (DRL) approach, employing deep Q-networks (DQNs) to enhance task offloading performance in IoV. Their method demonstrated improved adaptability to dynamic environments. Zhao et al. [36] presented a multi-agent reinforcement learning (MARL) algorithm for collaborative task offloading, enabling multiple vehicles learn to cooperatively optimize their offloading strategies. These RL-based methods effectively leverage the ability to store and utilize historical data, which enhances their adaptability to dynamic environments. However, they often necessitate extensive training data and substantial computational resources, presenting challenges for implementation in real-time IoV scenarios.

This paper distinguishes from prior studies by focusing on the intricate interaction dynamics between edge servers and vehicles. To tackle the challenges associated with task offloading and resource allocation, a game-theoretic framework is developed. Our model incorporates crucial factors such as the pricing of computational resources by edge servers and the varying sizes of tasks offloaded by vehicles. Through rigorous analysis, the complex interplay of these elements is examined, revealing the existence of a Nash equilibrium with convergent properties within the game model. The interaction between edge servers and vehicles primarily involves a dynamic decision-making process for task offloading. Vehicles transmit their task requirements, such as data size, computational demands, and environmental sensing data (like location, speed, sensor data), to edge servers. In response, edge servers provide not only resource allocation decisions and processing results but also estimated computation delays, service quality metrics, and dynamic pricing information based on current network conditions and resource availability. Edge servers dynamically adjust their pricing strategies and resource allocation policies based on real-time task loads and resource utilization levels, feeding this information back to the vehicles. This bidirectional feedback loop ensures that edge servers can maximize their revenue by optimizing pricing and resource allocation, while vehicles minimize their operational costs and latency by selecting the most suitable edge server based on the feedback received. Furthermore, to optimize the interaction between edge servers and vehicles and to maximize system revenue, a distributed computing offloading algorithm is proposed. While RL-based methods offer significant benefits, our game-theory-based approach provides stable, predictable solutions that can be quickly recalculated in real-time. This stability is crucial for maintaining optimal performance in the highly dynamic IoV environment.

Our paper leverages the ABC algorithm within a game-theoretic framework to overcome the limitations of previous approaches in IoV contexts. As a swarm intelligence-based method, the ABC algorithm offers distinct advantages, including real-time adaptability, computational efficiency, and scalability. Unlike RL-based methods, which require extensive training, the ABC algorithm quickly adjusts to dynamic network conditions and operates with lower computational overhead, making it particularly well-suited for resource-constrained IoV environments. Its decentralized nature further enhances scalability in distributed settings, where central coordination is often challenging. By incorporating resource pricing and task size variability within a game-theoretic model, our approach optimizes interactions between edge servers and vehicles, ensuring system stability and maximizing revenue. This provides a more practical, efficient, and stable solution compared to RL-based methods, especially in dynamic and resource-constrained IoV environments.

By integrating the ABC algorithm into a game-theoretic framework, our approach effectively balances adaptability, efficiency, and scalability, thereby maximizing system performance and revenue while remaining practical and deployable. This combination makes the ABC algorithm a superior choice for addressing the specific challenges in this study, particularly when compared to more resource-intensive distributed deep learning methods.

3  Task Offloading Model for IoV Based on Game Theory

In this section, we develop a comprehensive task offloading model specifically designed for the IoV leveraging game theory principles. Our goal is to tackle the critical challenges of task offloading and resource allocation by developing a robust framework that can effectively adapt to the dynamic and complex vehicular environment.

3.1 System Model

We consider a vehicular networking scenario at an intersection, as depicted in Fig. 1. An adaptive handoff management method is used to reduce the negative consequences of frequent handovers by dynamically adjusting task offloading decisions based on real-time predictions of handoff events. By incorporating machine learning techniques to predict of handoff occurrences, our model proactively adjusts offloading strategies to sustain optimal performance. Each vehicle traversing the road is equipped with a device capable of processing information and equipped with a wireless transmission module. Additionally, a set of roadside units (RSUs), denoted as M={1, 2,…,M}, are strategically deployed along both sides of the road to facilitate the reception and collection of task processing requests and associated data information, where M denotes the number of RSUs. The set of vehicles within the service scope is defined as N={1, 2,…,N}, where N is the number of vehicles. Each vehicle in N transmits its computing tasks to the nearest RSU. Each RSU is equipped with a Vehicular Edge Computing (VEC) server, which is responsible for offloading the received tasks for complex data computation, processing, and analysis. Without causing ambiguity, the set of VEC servers is also represented by M. Finally, the processed data information is directly transmitted to the moving vehicle to complete the task feedback, as illustrated in Fig. 1. Table 1 summarizes the meanings of the main symbols used in the paper.

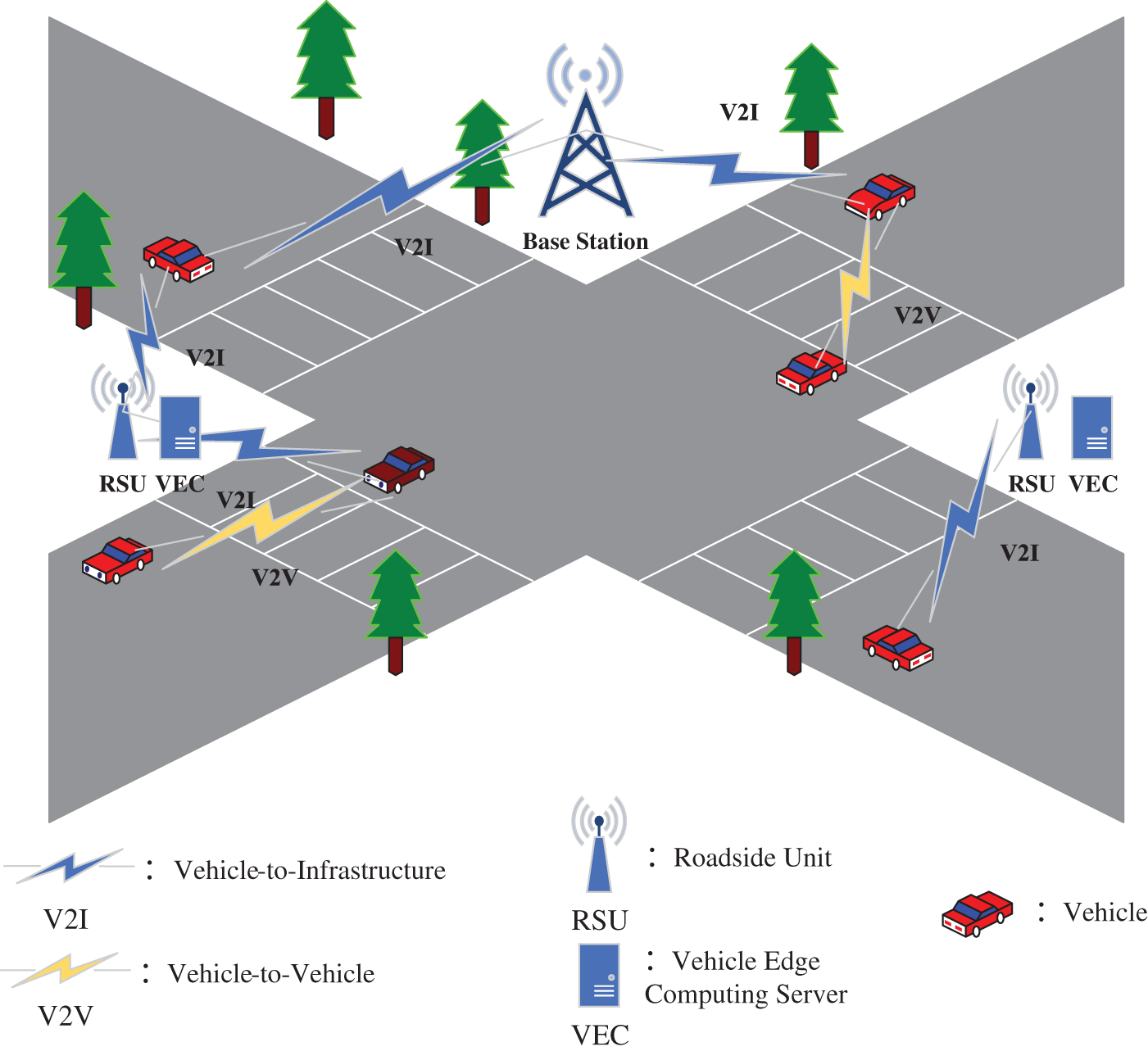
Figure 1: Task offloading architecture in the Internet of Vehicles

In order to analyze the computing task offloading problem more conveniently and intuitively, the computing task is specifically expressed as Di≜(Ri, Li.k, Timax),i∈N, k∈M, where Ri denotes the data volume of the task in vehicle i, Li.k represents the size of the task data offloaded from vehicle i to the VEC server k, Timax denotes the maximum delay allowed by the vehicle i to complete the task.

The upload of task data needs to be transmitted through the channel in the uplink, and the channel model is established in this scenario. For the ideal channel model without interference, the transmission rate ri, k from the vehicle i to the edge server k can be defined according to Shannon’s formula [37] as:

ri, k=Blog2⁡(1+Pihi, k2N0)(1)

where B denotes the bandwidth, Pi is the task uplink transmission power of the vehicle i, hi, k denotes the channel gain between the vehicle i and the VEC server k. The channel state hi, k in a mobile environment is highly dynamic. To accommodate this, our algorithm is designed to frequently update the channel state information based on real-time measurements. This frequent tracking ensures that the offloading decisions remain robust despite the variability in the channel conditions. Moreover, the characteristics for hi, k in a vehicle network are indeed different from an IoT setup on a factory floor. In fact, we explicitly recognize the differences in mobility patterns and channel dynamics between these two scenarios. Our analysis account for these differences by employing a Rayleigh fading channel model, which is well-suited for highly mobile environments like vehicular networks. With orthogonal channels, interference between vehicles is eliminated. Taking into account Rayleigh fading and path loss, N0 represents the noise power spectral density. Rayleigh fading channel model is well suited for urban vehicular environments where there is no direct line of sight between the transmitter and receiver and multipath propagation dominates.

In a mobile environment, the mobility of vehicles causes continuous changes in the channel state, necessitating dynamic updates to the channel model. We have employed the Rayleigh fading channel model, which is particularly suited to environments characterized by dominant multipath propagation, excluding direct line-of-sight transmission. In urban and suburban landscapes, where buildings, trees, and various obstructions frequently interrupt direct communication pathways, multipath phenomena frequently lead to rapid fluctuations in signal strength. The Rayleigh model precisely represents these scenarios by simulating the consequential effects. By continuously monitoring the channel state and adjusting model parameters in real-time, we can more precisely reflect the channel conditions that vehicles encounter during movement. In the case of imperfect Channel State Information (CSI), we employ pilot-based channel estimation algorithms. During this process, vehicles periodically transmit predetermined pilot signals, upon which the receiver (i.e., VEC server) estimates the current channel state information using techniques like least squares estimation. This estimation process takes into account the time-varying characteristics of the channel. By applying filtering methods, the estimation process mitigates the effects of noise, ultimately yielding a more precise CSI. Specifically, when vehicle i communicates with the VEC server k, it periodically transmits known pilot signals over the uplink. Upon receiving these signals, the VEC server employs the least squares method to estimate the current channel gain. By analyzing the series of pilot transmissions, the server is capable of tracking the dynamic nature of the channel and updating the channel model accordingly. Moreover, the Rayleigh fading channel model is adopted as it provides a realistic representation of the rapidly changing, multipath-dominated communication environment typical in vehicular networks. This allows the model to effectively capture the dynamic behavior of wireless channels in such environments, making it highly relevant for our study.

The vehicle i performs dual execution, processing tasks in parallel on both the vehicle and the VEC server k. The required central processing unit (CPU) cycles for processing 1 bit of data is denoted as Ci, and the local CPU frequency of the vehicle i is expressed as floc, i. Consequently, when vehicle i computes its entire task locally, the calculation delay [38] is determined by:

Tloc, i=RiCifloc, i(2)

when the vehicle i elects to offload a segment of its task, specifically Li.k to the VEC server k, the remaining component of the task remains for local computation. This residual task volume is represented as (Ri−Li.k). Consequently, the associated delay for local computation can be expressed as:

tloc, i=(Ri−Li.k)Cifloc, i(3)

when vehicle i offloads tasks to VEC server k, the offloading delay can be divided into two components. The first is the wireless transmission delay involved in sending the task from the vehicle i to the VEC server k. Then the offloading delay is [38]:

toff, i, k=Li.kri, k+Li.kCifi, k(4)

where fi, k denotes the computing resource allocated by the VEC server k to the vehicle i. Taking into account the dynamic allocation and concurrent processing of each task, both locally and on the VEC server, the overall task delay is determined by the maximum of the two delays, Tloc, i and toff, i, k. Therefore, the overall task delay can be expressed as:

Ti, k=max{tloc, i, toff, i, k}(5)

3.2 Problem Modeling

This section employs the multi-master multi-slave two-level game [39] (Two Level Game, TL-G) to model the task offloading procedure. An in-depth analysis is conducted to determine the equilibrium point, focusing on the balance between vehicles and VEC servers. The TL-G represents a non-cooperative framework, where participants aim to optimize their individual performance. In the TL-G, VEC servers serve as leaders, initially devising their optimal strategies and broadcasting them. Meanwhile, all vehicles act as followers, adjusting their strategies based on the strategies communicated by the leaders.

In the VEC network, vehicles offload tasks to the VEC server to leverage their superior computing resources and reduce computing delays. While VEC servers are more computationally efficient than local computing, the vehicle must transfer as many jobs as possible to the VEC server; this adds to the overall cost and reduces the benefits of the vehicle. The VEC servers set a unit price for computing resources, necessitating a careful balance to promote task offloading without imposing excessive costs on vehicles. This dynamic results in a game between the size of offloaded tasks and the unit price of computing resources, involving strategic decisions between the VEC servers and vehicles. Utilizing the TL-G game, where VEC servers lead and vehicles optimize their responses, a non-cooperative game emerges. Each vehicle seeks to maximize its utility by determining optimal offloading strategies, while the VEC server, in turn, devises pricing strategies until an equilibrium is reached. Next, we will analyze and model the optimization problem for the vehicle and the VEC server. Unlike previous approaches that only considered vehicle utility by minimizing delay, our scheme separately addresses the utilities of both vehicles and VEC servers. The vehicle aims to maximize the difference between locally computed latency and partially offloaded latency, while the VEC server seeks to maximize its overall benefit.

3.2.1 Vehicle Side Revenue Model

The selection strategy for vehicles is denoted by X={xi, k, ∀i∈N, ∀k∈M}, A={ai, k, ∀i∈N,∀k∈M} denotes the assignment strategy for offloading. The revenue of each vehicle includes its delay and the fee paid by the VEC server. Therefore, the revenue function [39] of the vehicle i offloading some of its tasks to the VEC server k can be expressed as:

Bi=∑k=1Mxi, k(θilog⁡(Tloc, i−Ti, kai, k+1)−μk, iai, kCi)(6)

where θi is a positive constant, μk, i is the unit price of computing resources charged by the VEC server k to the vehicle i. xi, k is a selection variable, xi, k∈{0, 1}. xi, k=1 indicates that the vehicle i has chosen the VEC server k as its designated server for offloading tasks, while xi, k=0 indicates that it has not selected server k for this purpose.

3.2.2 Service Side Revenue Model

The revenue of VEC servers is defined as the revenue derived from selling computing resources to vehicles, with the objective of maximizing this revenue. To minimize latency, vehicles are inclined to offload a significant amount of tasks to the VEC servers. However, due to the limitation of computing resources, excessive tasks offloading by vehicles to the edge servers can lead to computational overload, thereby reducing the efficiency of the offloading process and increasing the cost associated with it. Consequently, a delicate balance must be struck between minimizing delay and minimizing cost. The revenue [40] of the VEC server k is expressed as:

Bk=∑i=1Nμk, iai, kCi(7)

As the objective of the VEC server is to maximize its revenue, offloading more tasks from the vehicle to the VEC server directly contributes to higher revenue. Given the specified delay constraints, the vehicle will select the optimal VEC server for task offloading. In order to attract vehicles and generate revenue through their data offloading, the VEC servers formulate an appropriate pricing strategy. Therefore, there is competition between vehicles and between VEC servers.

In summary, the total revenue function of the system under the edge computing task offloading architecture, that is, the objective function, is expressed as follows:

B=max{αBi+βBk|(ai, k)}(8)

where α+β=1, 0<α, β<1.

3.2.3 Constructing TL-G Game

The TL-G game aims to find a set of strategies that optimize the offloading of tasks from vehicle i to edge server k, achieving both low cost and high profit objectives. Additionally, it aims to determine the servers that are currently occupied and utilizes these strategies to formulate an effective edge server layout. The layout strategy contains decisions for each vehicle to achieve the goal of low cost and high yield for the system. In this game, the rules of the game determine which edge server k surrounding vehicle i will be selected. A−i=(a1,…,ai−1,ai+1,…,an) represents the collection of allocation decisions made by all vehicles except for vehicle i [23]. This game requires the vehicle i to make a decision ai that maximizes the benefit of the system in order to consider the decisions of other vehicles A−i.

The TL-G game operates under a non-cooperative framework where both the VEC servers and the vehicles aim to optimize their own utility functions. The VEC servers (leaders) set the pricing for computing resources based on their capacity and anticipated demand, while vehicles (followers) decide how much of their computational tasks to offload based on the pricing and the need to minimize their own costs and delays. The goal is to achieve a Nash equilibrium where neither the VEC servers nor the vehicles can unilaterally change their strategy to achieve a better outcome. The equilibrium reflects an optimal balance where the server’s pricing strategy matches the vehicle’s task offloading strategy, given the network’s dynamic conditions.

Therefore, the allocation problem of the server layout is expressed as a game X=(N, Ai, Bi), i∈N, where N is the set of vehicles, Ai is the allocation strategies set of vehicle i, and Bi is the benefit function of the system revenue caused by the allocation decision of vehicle i. t is very important to explore whether there is at least one Nash equilibrium in a game [24], and the Nash equilibrium has the property that the allocation decision of each vehicle i is the best decision for other vehicles. Then according to this property, the Nash equilibrium of the TL-G game can be defined as follows:

Definition 1. (Nash Equilibrium) If the allocation strategy A∗=(a1∗,…,an∗) is a Nash equilibrium of the TL-G game, then no vehicle can further increase its own benefit by changing its allocation decision unilaterally, namely BA−i∗(ai∗)≥BA−i∗(ai),∀ai∈Ai,∀i∈N.

Lemma 1. In Nash equilibrium A∗, the allocation decision ai∗ of each vehicle i must be the optimal choice for the allocation strategy A−i=(a1,…,ai−1,ai+1,…,an) [41].

The existence of a Nash equilibrium in the multi-master and multi-slave double-layer game model is guaranteed (Proof provided in Appendix A).

Definition 2. Let f be a continuous map from a compact convex K⊂IRn set to itself, then there is a point x¯∈K such that x¯=f(x¯). That is, this point is the Nash equilibrium point of the game model.

Lemma 2. The system model has a Nash equilibrium.

The uniqueness of the Nash equilibrium in the proposed game model is established (Proof provided in Appendix B).

Definition 3. Assuming f is twice differentiable, then f is convex if and only if domf is convex, and the Hessian matrix of f is positive semidefinite, ie: ∇2f(x)≥0, ∀x∈domf, otherwise, if ∇2f(x)≤0, ∀x∈domf, f is concave.

Lemma 3. The Nash equilibrium of the system model is unique.

The convergence of the distributed artificial bee colony algorithm to the Nash equilibrium is assured (Proof provided in Appendix C).

4  Heuristic Algorithm Analysis

In this section, we delve into the analysis of heuristic algorithms employed to solve the task offloading and resource allocation problems in the IoV environment. Heuristic algorithms, which take into account the dynamic and intricate structure of vehicle networks, offer effective and workable solutions for optimization issues that would otherwise be too hard to solve computationally. We introduce and evaluate the artificial bee colony algorithm, a swarm intelligence-based method, which is particularly well-suited for distributed and dynamic scenarios.

4.1 Artificial Bee Colony (ABC) Algorithm

After establishing a two-level game model between vehicles and VEC servers and demonstrating the existence of a unique Nash equilibrium point, the model is optimized using the ABC algorithm [40], a heuristic method based on swarm intelligence for global optimization. The main steps of the algorithm are as follows:

(1) Honey source initialization

Let there be nPop nectar sources, where the quality of a nectar source (its ability to attract bees) corresponds to a solution of the function. In this model, the offloading allocation decision ai made by the vehicle i in this model is the solution of the function, also referred to as the fitness value fiti. For these nPop nectar sources, the initial position of each nectar source, xid, is determined according to the following equation:

xid=Ld+rand(0,1)∗(Ud−Ld)(9)

where Ld and Ud represent the upper and lower bound of the traversal, respectively [42].

(2) Updating honey sources

A leader bee searches for a new nectar source around the existing nectar source xid. xidnew is calculated using the following formula:

xidnew=xid+a∗φ(xid−xjd), j≠i(10)

where φ is a random number uniformly distributed in interval [−1, 1], a∗ is the acceleration coefficient (usually 1). When the fitness of the new nectar source xidnew is superior to xid, a greedy selection approach is employed to replace xid with xidnew as the solution to the function. Otherwise, xid is retained.

(3) Follow bees choose lead bees

The leader bee recruits follower bees using a roulette wheel selection method, with the selection probability Pi calculated as follows:

Pi=fiti∑i=1nPopfiti(11)

(4) Generate scout bees

If the nectar source xid fails to be updated to a superior one after trial iterations of search reach the threshold L, it will be discarded, and the corresponding leading bee will transform into a scout bee. Subsequently, the scout bee will randomly generate a new nectar source within the search space to replace xid [43]. The aforementioned process is represented as follows:

xidt+1={Ld+rand(0,1)∗(Ud−Ld),trail⩾Lxidt,trail<L(12)

The flowchart of the ABC algorithm is illustrated in Fig. 2.

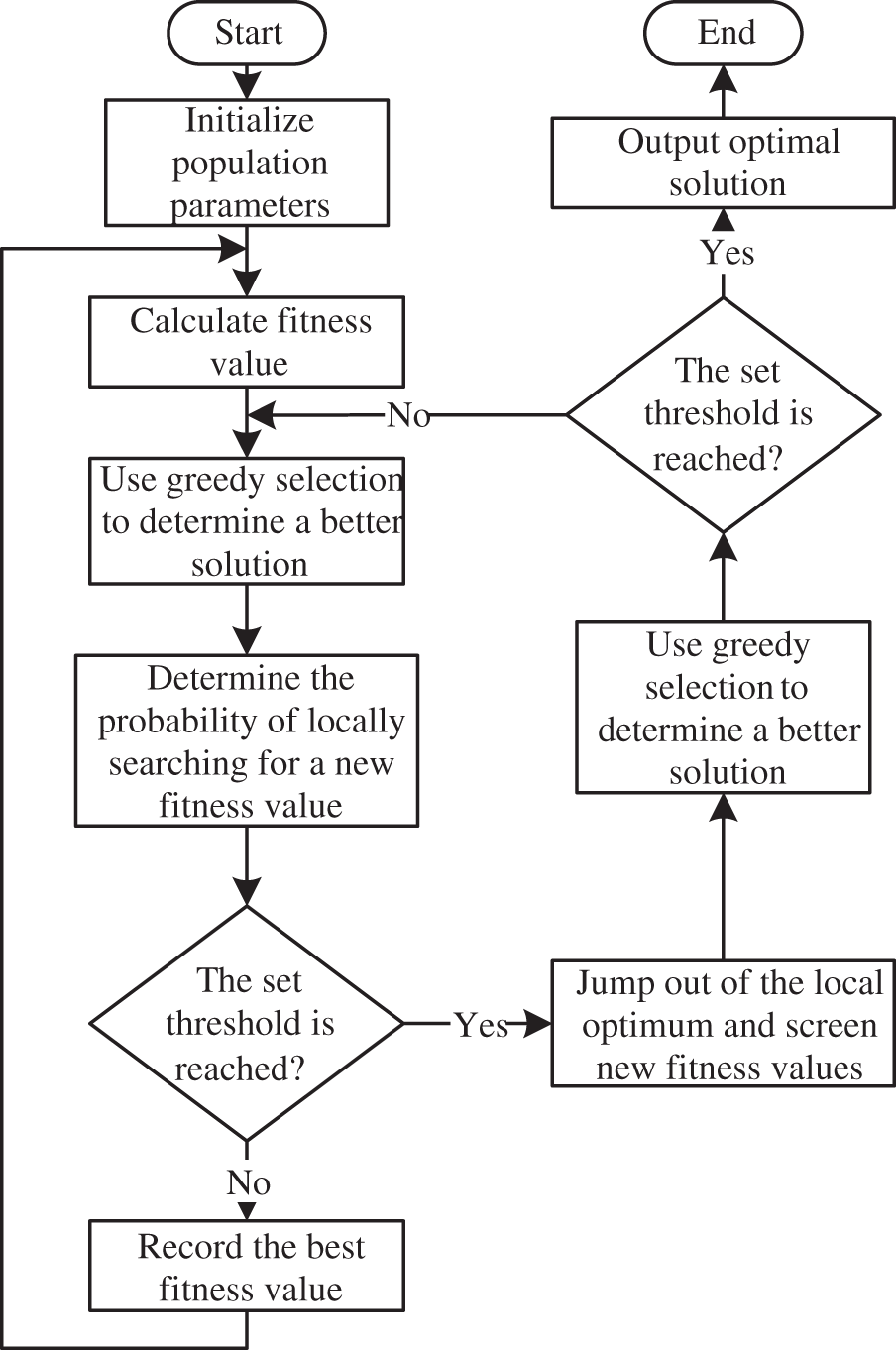
Figure 2: Flow chart of artificial bee colony algorithm

4.2 Specific Application and Analysis

The total cost is defined as the sum of the revenue from both the vehicle side and the VEC server side, which constitutes the target function value. Initially, parameters such as the number of iterations and the number of populations are set. The offloading allocation decision ai is randomly initialized according to the Eq. (9) and bring it into the function to calculate the total cost. A new fitness value is then found around the initial ai using Eq. (10). Here, a greedy selection approach is adopted to determine whether the new fitness value replaces the old one as the solution to the function. Furthermore, based on the probability computed using Eq. (11), a roulette wheel selection approach is utilized to decide whether to carry out the local search for a new fitness function around the initial ai. The pseudocode for the ABC algorithm is provided in Algorithm 1.

Once the number of searches reaches the preset threshold, an evaluation of the optimal solution is evaluated. If a superior fitness value is still not found, the previous ai is discarded, and a new one is selected based on Eq. (12) to replace it. The greedy algorithm is also employed to obtain a superior function solution and its corresponding function value. This process continues until the iteration count reaches the termination condition, at which point the optimal solution is output, and the algorithm terminates.

The time and space complexity of the ABC algorithm are influenced by several factors: the dimension of the problem, the number of individuals in the population, the maximum number of iterations, and the computational cost per iteration. For time complexity, the computational cost per iteration is proportional to the problem dimension N, thus the overall time complexity of the ABC algorithm can be expressed as O(G∗N), where G is the number of iterations and N is the problem dimension. For space complexity, it is jointly determined by the number of individuals in the population and the problem dimension. Therefore, the space complexity of the ABC algorithm is expressed as O(M+N), where M is the number of individuals in the population.

5  Simulation Results and Analysis

In this section, we present the comparative analysis of our proposed game-theory-based task offloading and resource allocation scheme against three widely-used optimization methods: ACO [15], FA [16], and SA [17]. ACO is a probabilistic technique inspired by the foraging behavior of ants. It is particularly effective for combinatorial optimization problems and has been applied to various IoV scenarios due to its ability to find good solutions through iterative improvement. FA is inspired by the flashing behavior of fireflies, where the brightness of a firefly attracts others. It is used for continuous optimization problems and is known for its efficiency in exploring the search space and avoiding local optima. SA is a probabilistic technique that mimics the annealing process in metallurgy. It is used for finding a good approximation of the global optimum of a given function. SA is particularly useful for large search spaces. Comparing our proposed scheme with these well-established methods enhances the credibility of our evaluation.

5.1 Simulation Environment Construction and Parameter Setting

This experiment is simulated on a personal computer (PC) with a 12th Gen Intel(R) Core Trade Mark (TM) i7-12700H processor and 16.0 GB Random Access Memory (RAM) configuration. The platform for simulation is Matlab R2016a. The specific simulation parameter values are shown in Table 2. The parameter values in Table 2 were chosen to reflect typical vehicular network conditions [18,19]: a task size of 500 KB was selected for its relevance to real-time communications, a bandwidth of 10 MHz reflects common conditions in congested environments, and 500 CPU cycles per bit represent the computational demands of encryption algorithms. The local CPU frequency of 1 GHz aligns with standard vehicular on-board units, providing a balance of performance and efficiency. A maximum delay of 2 s is set to meet the latency requirements for safety-critical applications. The noise power spectral density of −174 dBm/Hz corresponds to typical urban noise levels, and the uplink transmission power of 30 dBm is in line with regulatory standards. These selections ensure the simulation accurately represents real-world scenarios and aligns with the research objectives. The initial positions of the vehicle and the edge server are shown in Fig. 3. The edge servers are positioned at a certain distance from each other, while the locations of vehicles are randomly selected based on a Gaussian distribution.

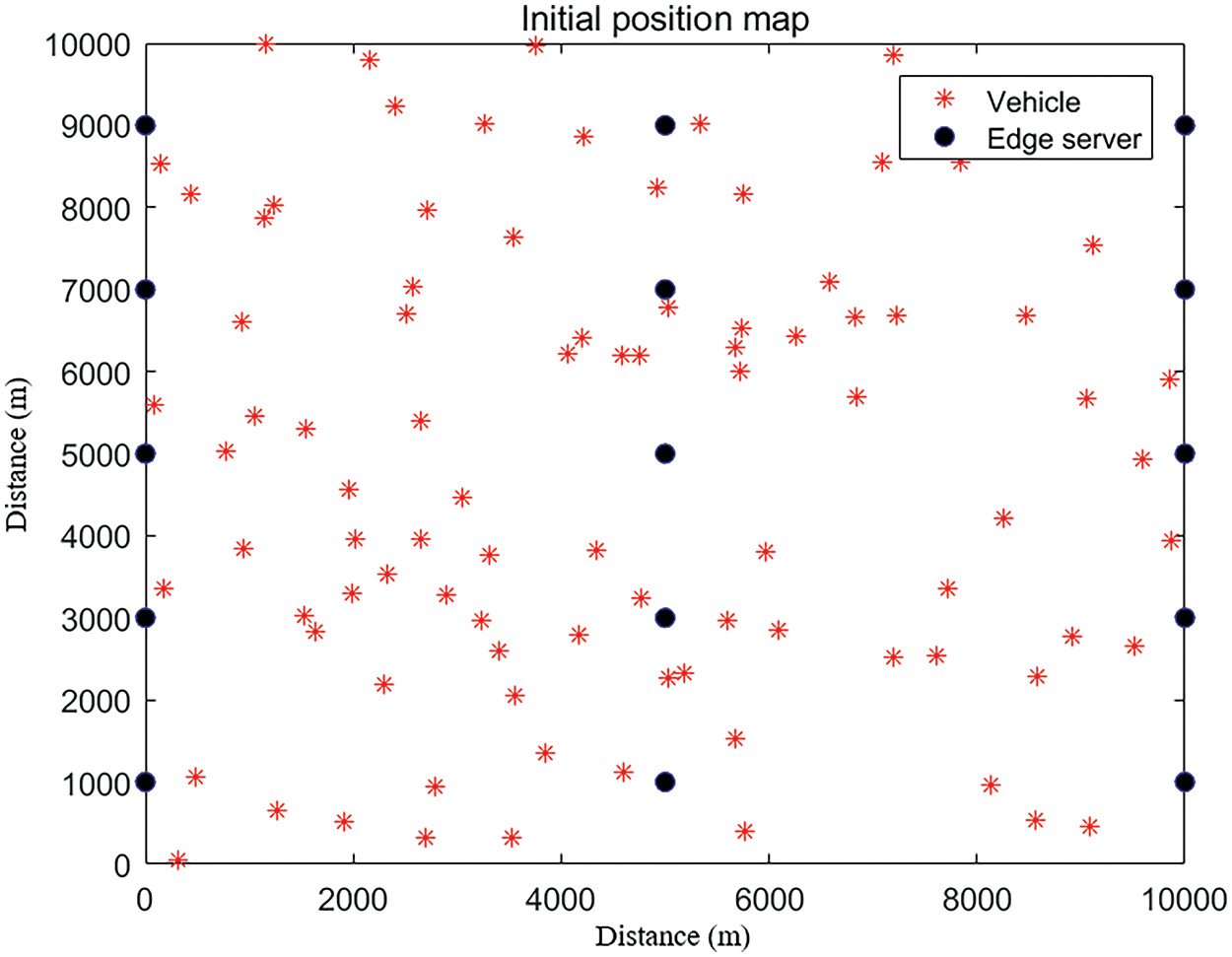
Figure 3: Initial position setting of the simulation scene

5.2 Results Performance Analysis

A correlation between the price of edge server computing resources and the quantity of jobs offloaded by cars was finally established through an iterative optimization process utilizing the artificial bee colony method and a game-theoretic approach aimed at optimizing the benefits of both parties. The pricing of edge server computing resources is shown in Fig. 4. There are a total of 15 edge servers, and the pricing value is between 1.5 and 2.5. Correspondingly, Fig. 5 depicts the number of 1 MB tasks offloaded by all vehicles to each of the 15 servers, with values ranging from 0 to 10.

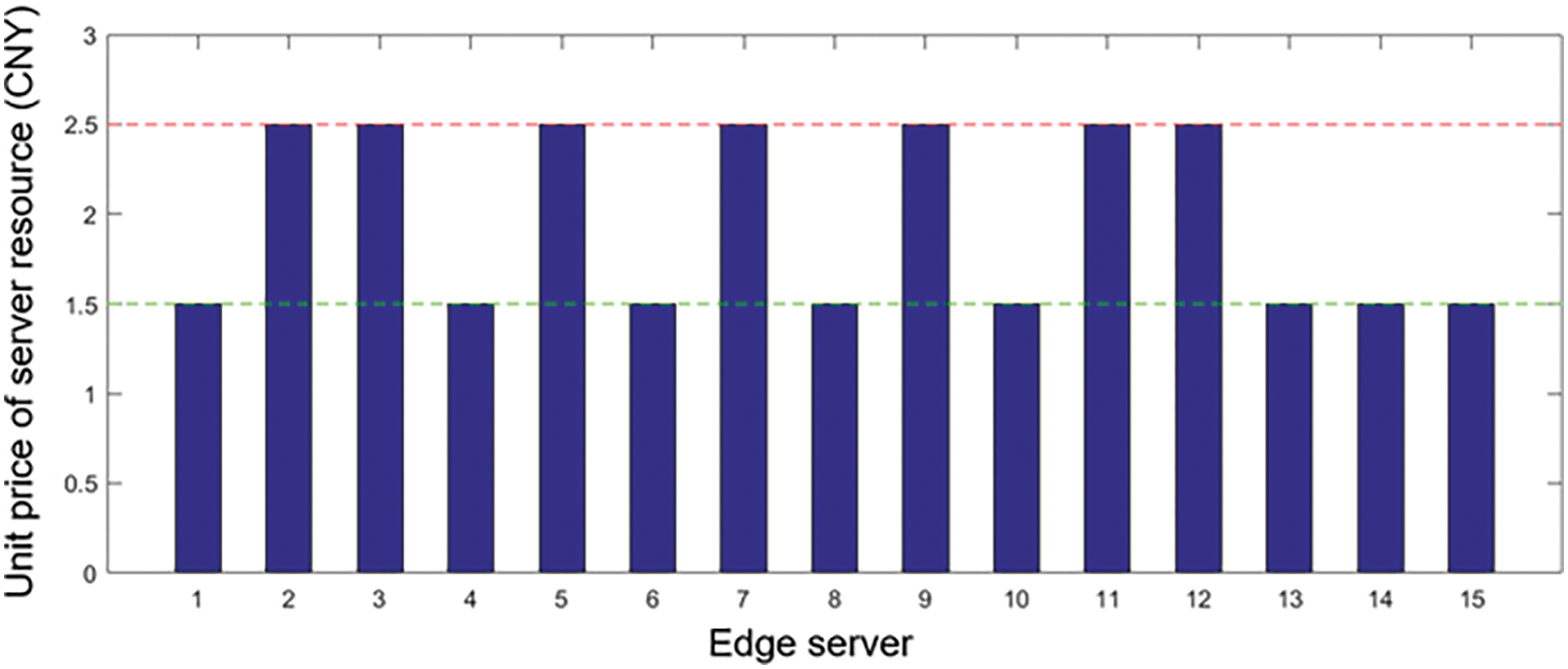
Figure 4: The pricing of edge server resources

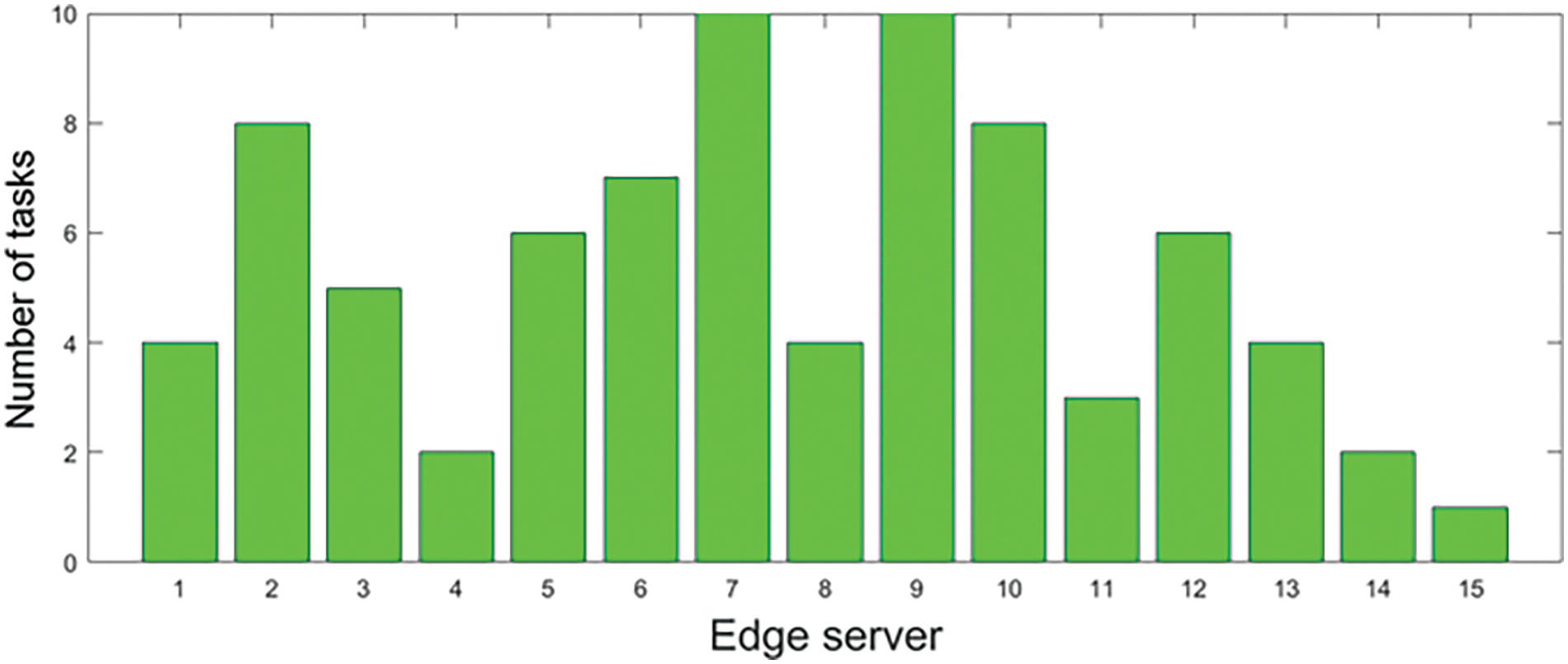
Figure 5: Task volume offloaded by vehicles

Figs. 6 and 7 depict the convergence curves of the total system revenue under three different scenarios, varying numbers of vehicles and edge servers, respectively. The data reveal that the number of participants in the model exhibits a positive correlation trend with the total system revenue. Specifically, with the number of vehicles offloading tasks set to 30, 40, and 50, and the number of edge servers set to 9, 10, and 11, it is evident that, the total system revenue increases with the growth of both the number of vehicles and edge servers.

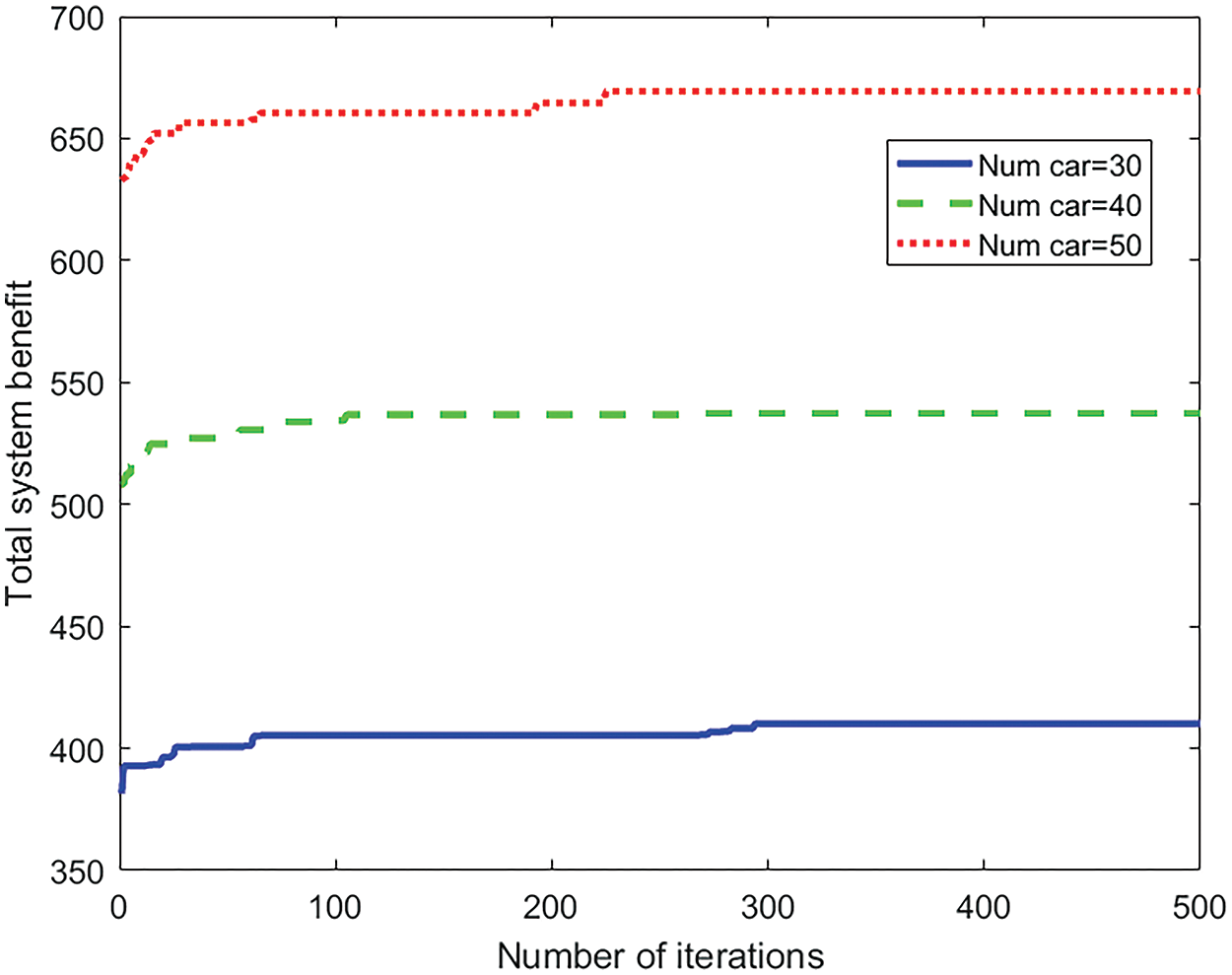
Figure 6: The influence of the number of task vehicles on the total benefit

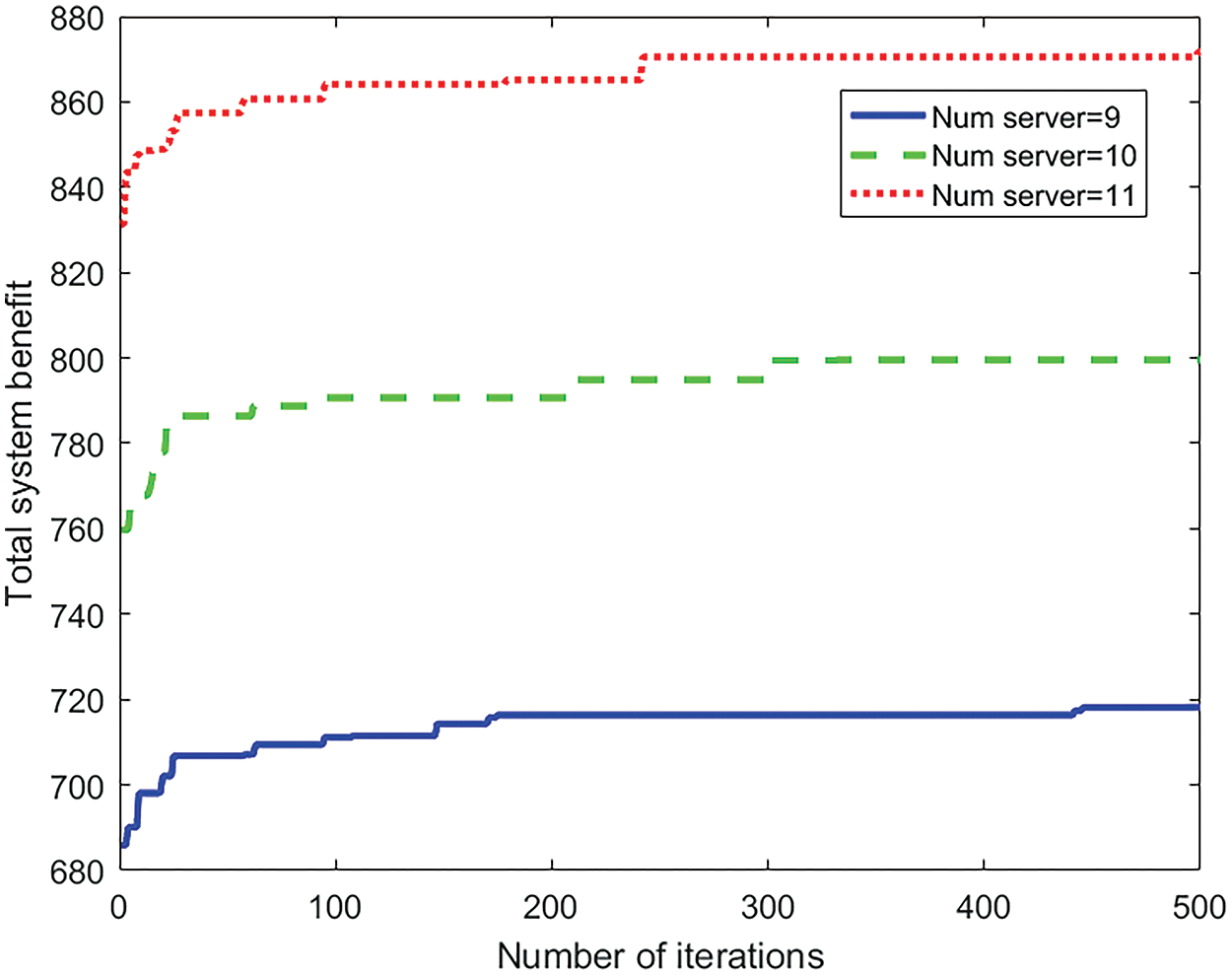
Figure 7: The impact of the number of edge servers on the total benefit

Fig. 8 illustrates the impact of a uniform pricing scheme for edge server computing resources on the total system revenue. With a unified resource unit price set at 1.5, 2.0, and 2.5, respectively, the iterative convergence curves of the total revenue are plotted. It can be observed that changes in the unit price do not significantly affect the total system revenue. This is because, an increase in the uniform unit price can be compensated by adjusting the volume of tasks offloaded by the vehicles to achieve the optimal solution.

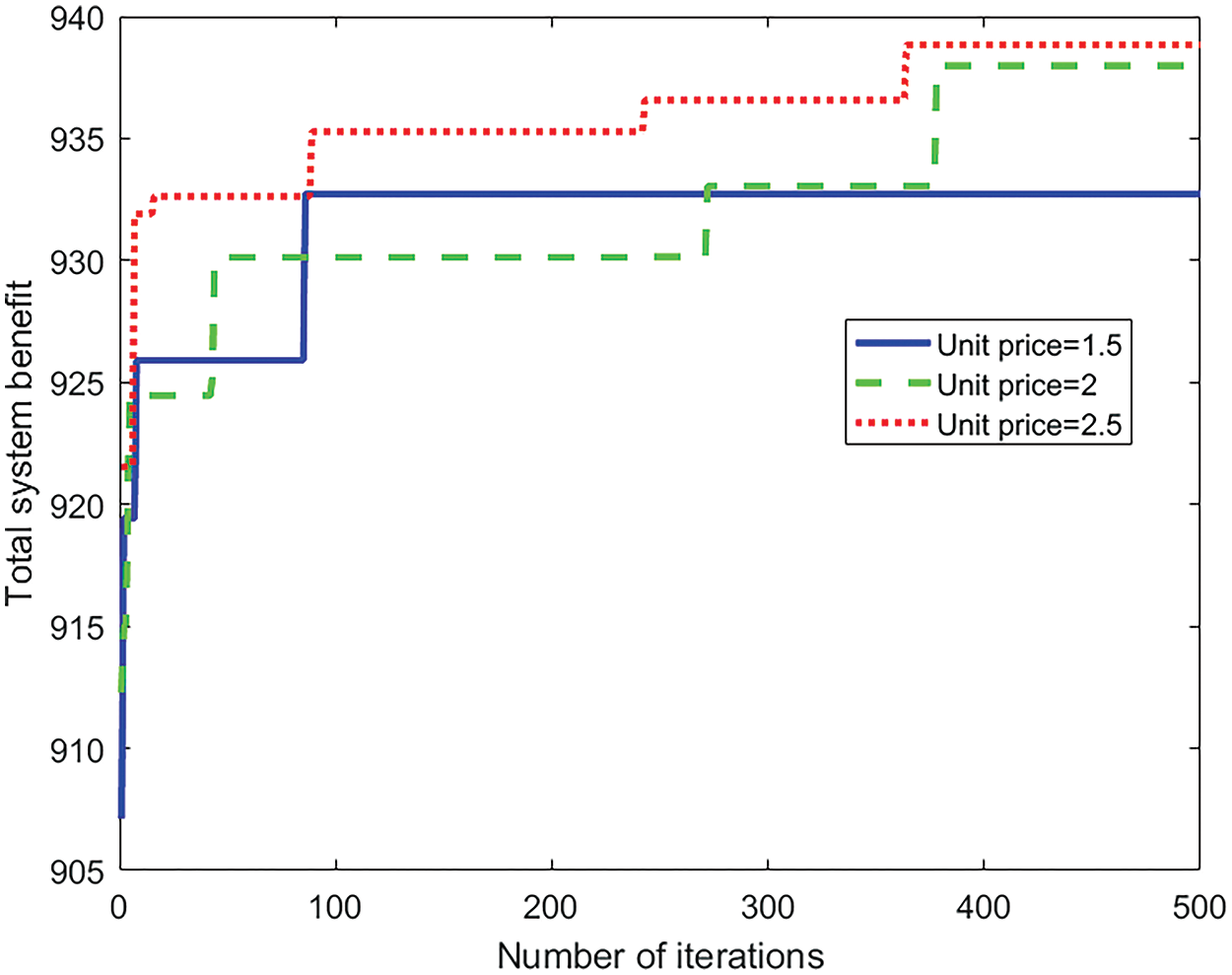
Figure 8: The impact of resource unit price on total benefit

Next, we analyze various task offloading and resource allocation schemes. In the proposed scheme, the VEC servers adopt a non-uniform pricing mechanism, where the prices are dynamically adjusted based on the supply and demand relationship. Vehicles can select the optimal VEC server based on the actual network conditions. As the unit price increases, the cost for vehicles to purchase resources also rises, leading them to favor local computation or purchasing fewer resources, which subsequently results in longer task computation delay.

Fig. 9 illustrates the relationship between different offloading schemes and the system benefit. The ABC algorithm that employs non-uniform pricing achieves convergence approximately at 160 iterations. Under the strategy of non-uniform pricing for computing resources, both the ABC algorithm and greedy algorithm [44] exhibit superior convergence performance. Conversely, the ABC scheme with uniform pricing demonstrates the poorest performance, achieving only 825. If the offloading volume of tasks is fixed, the overall system benefit will still be affected, but the maximum system benefit will be situated between the uniform and non-uniform pricing schemes. In summary, the proposed scheme achieves the optimal overall system benefit with non-uniform pricing.

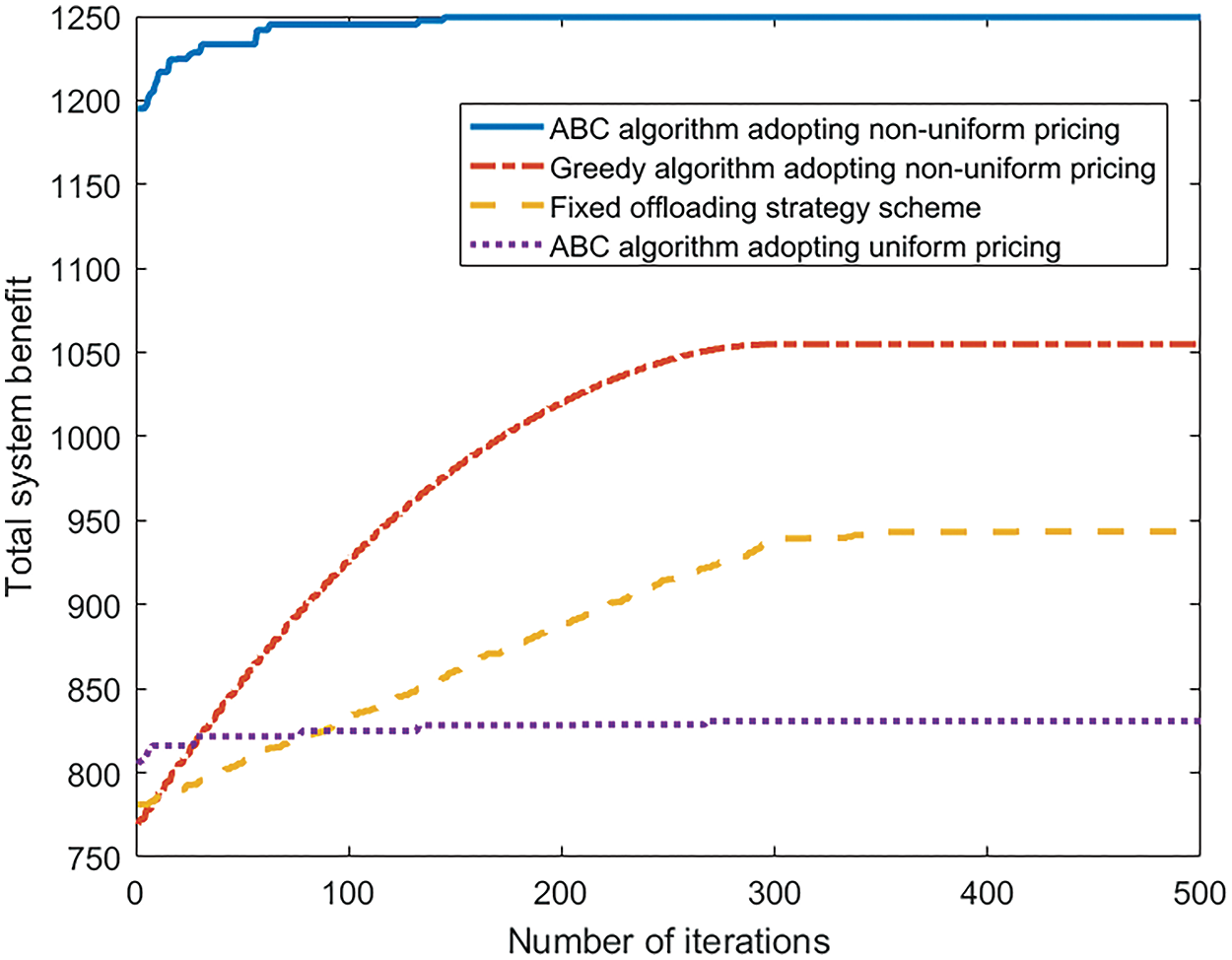
Figure 9: The comparison of the total system benefit

Fig. 10 illustrates the variation curve of system benefits across different iteration counts. It can be observed that as the number of iterations increases, various algorithms tend to converge, resulting in a continuous increase in the overall system benefit. Notably, for varying iteration counts, the ABC algorithm achieves the highest overall system benefit. Additionally, in terms of convergence speed, the ACO algorithm [15] exhibits the fastest convergence rate, followed by the ABC and FA [16] algorithms. The SA algorithm [17] demonstrates the slowest convergence, requiring approximately 350 iterations to converge. Once the overall system benefits stabilize for each algorithm, the ABC algorithm achieves the best total benefit of 1249, outperforming the ACO algorithm by 8.98%, the FA algorithm by 9.17%, and the SA algorithm by 9.84%. Overall, the ABC algorithm demonstrates superior performance in overall system benefit compared to other algorithms.

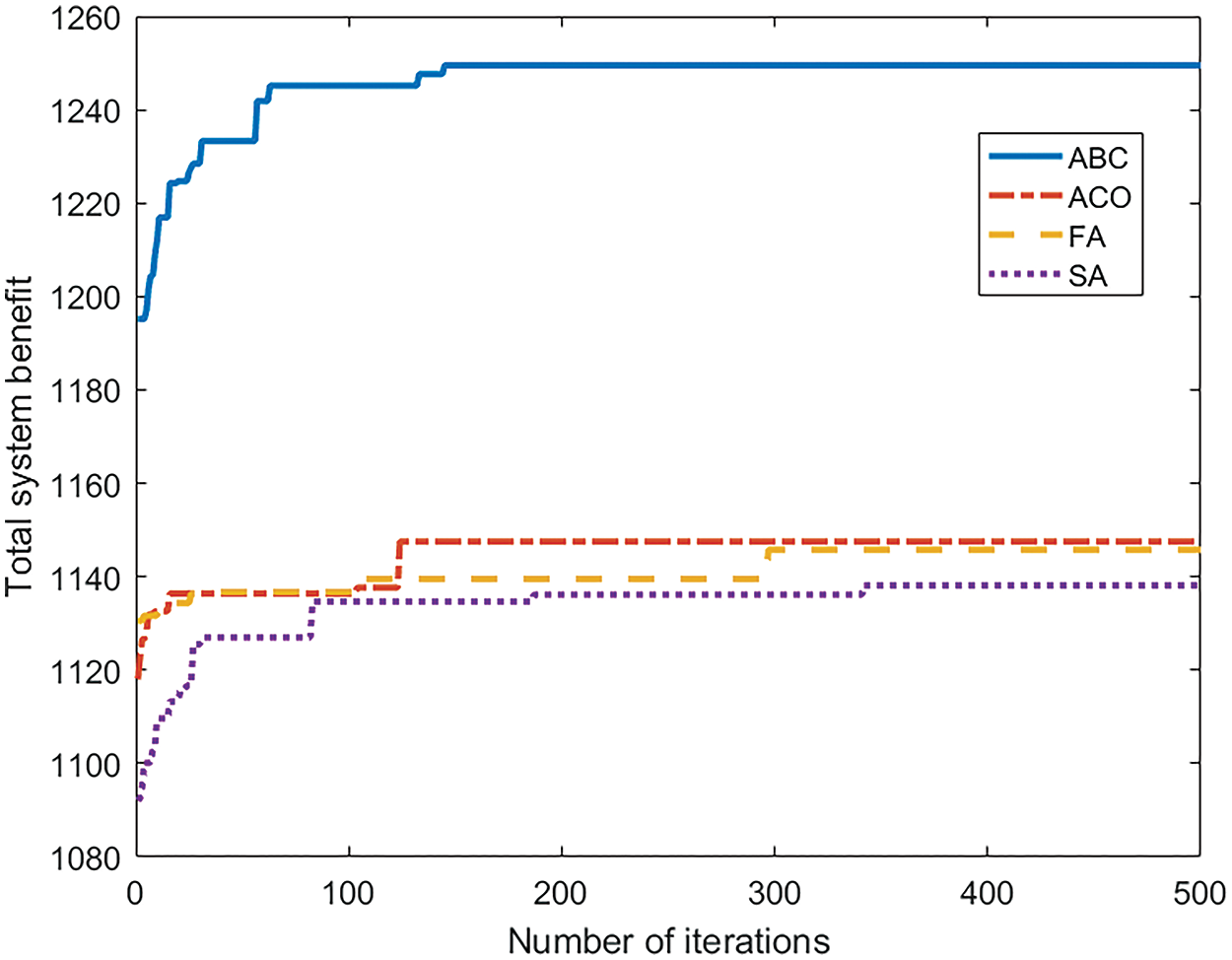
Figure 10: ABC algorithm and performance comparison of each algorithm

6  Conclusion

To enhance the benefits of both the vehicle and the VEC server while meeting the delay constraints of computing tasks, a non-uniform pricing task offloading scheme grounded in a bilateral game is proposed. Initially, considering the scenario of insufficient server computing resources, a partial offloading approach is adopted, and a non-uniform pricing mechanism is applied on the server side to assist the vehicle’s offloading strategy. Subsequently, a two-level game model is constructed based on the maximization of the benefits for both the vehicle and the VEC server, and the existence of Nash equilibrium points is proven using the Brouwer Fixed Point Theorem. Finally, a distributed algorithm based on artificial bee colony is proposed to obtain the equilibrium strategy of the game. Simulation results demonstrate that the proposed scheme improves overall vehicle benefit by approximately 9.84% over SA, 9.17% over FA, and 8.98% over ACO. Additionally, it reduces average task completion delay by 12.5% and decreases overall system cost by 10.3% compared to other approaches.

In summary, the proposed scheme offers significant advantages in optimizing resource allocation and task offloading in MEC-enabled IoV environments, offering a robust and efficient solution for dynamic vehicular networks.

Acknowledgement: The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers and editors, which have improved the presentation.

Funding Statement: This work was supported by the Central University Basic Research Business Fee Fund Project (J2023-027), and China Postdoctoral Science Foundation (No. 2022M722248).

Author Contributions: Study conception and design: Jianhua Liu, Jincheng Wei, Rongxin Luo; data collection: Guilin Yuan, Jiajia Liu; analysis and interpretation of results: Jianhua Liu, Jincheng Wei, Xiaoguang Tu; draft manuscript preparation: Jianhua Liu, Jincheng Wei, Rongxin Luo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. H. Zhang and S. Cheng, “Application of internet of things technology based on artificial intelligence in electronic information engineering,” Mob. Inf. Syst., vol. 2022, no. 1, pp. 1–11, 2022. doi: 10.1155/2022/2888925. [Google Scholar] [CrossRef]

2. T. Xu, Z. Wang, and X. Zhang, “Research on intelligent campus and visual teaching system based on internet of things,” Math. Probl. Eng., vol. 2022, no. 1, pp. 1–10, 2022, Art. no. 4845978. doi: 10.1155/2022/4845978. [Google Scholar] [CrossRef]

3. H. Ji, “Design of distributed collection model of student development information based on internet of things technology,” Secur. Commun. Netw., vol. 2021, no. 1, pp. 1–10, 2021. doi: 10.1155/2021/6505359. [Google Scholar] [CrossRef]

4. K. Zhao and W. Liu, “The design of the exercise load monitoring system based on internet of things,” Math. Probl. Eng., vol. 2022, no. 1, 2022, Art. no. 8011124. doi: 10.1155/2022/8011124. [Google Scholar] [CrossRef]

5. K. Yu, S. Eum, T. Kurita, Q. Hua, and V. P. Kafle, “Information-centric networking: Research and standardization status,” IEEE Access, vol. 7, pp. 126164–126176, 2019. doi: 10.1109/ACCESS.2019.2938586. [Google Scholar] [CrossRef]

6. D. Yin and B. Gong, “Auto-adaptive trust measurement model based on multidimensional decision-making attributes for internet of vehicles,” Wirel. Commun. Mob. Comput., vol. 2022, no. 1, 2022, Art. no. 3537771. doi: 10.1155/2022/3537771. [Google Scholar] [CrossRef]

7. Z. Ma, Y. Wang, J. Li, and Y. Liu, “A blockchain based privacy-preserving incentive mechanism for internet of vehicles in satellite-terrestrial crowdsensing,” Wirel. Commun. Mob. Comput., vol. 2022, 2022, Art. no. 4036491. doi: 10.1155/2022/4036491. [Google Scholar] [CrossRef]

8. Q. Luo, M. Ling, X. Zang, C. Zhai, L. M. Shao and J. Yang, “Modeling analysis of improved minimum safe following distance under internet of vehicles,” J. Adv. Transport., vol. 2022, no. 1, 2022, Art. no. 8005601. doi: 10.1155/2022/8005601. [Google Scholar] [CrossRef]

9. Z. U. A. Akhtar, H. F. Rasool, M. Asif, W. U. Khan, Z. U. A. Jaffri and M. S. Ali, “Driver’s face pose estimation using fine-grained Wi-Fi signals for next-generation internet of vehicles,” Wirel. Commun. Mob. Comput., vol. 2022, no. 1, 2022, Art. no. 7353080. doi: 10.1155/2022/7353080. [Google Scholar] [CrossRef]

10. P. Agbaje, A. Anjum, A. Mitra, E. Oseghale, G. Bloom and H. Olufowobi, “Survey of interoperability challenges in the internet of vehicles,” IEEE Trans. Intell. Transp. Syst., vol. 23, no. 12, pp. 22838–22861, Dec. 2022. doi: 10.1109/TITS.2022.3194413. [Google Scholar] [CrossRef]

11. T. Y. Wu, X. Guo, L. Yang, Q. Meng, and C. M. Chen, “A lightweight authenticated key agreement protocol using fog nodes in social internet of vehicles,” Mob. Inf. Syst., vol. 2021, no. 1, pp. 1–14, 2021. doi: 10.1155/2021/3277113. [Google Scholar] [CrossRef]

12. Intel, “The future of autonomous vehicles: How data and connectivity will transform mobility,” in Intel White Papers, Clara, CA, USA. 2018. Accessed: Jul. 18, 2024. [Online]. Available: https://download.intel.com/newsroom/2021/archive/2016-11-15-editorials-krzanich-the-future-of-automated-driving.pdf [Google Scholar]

13. Q. Li, Y. Andreopoulos, and M. van der Schaar, “Streaming-viability analysis and packet scheduling for video over in-vehicle wireless networks,” IEEE Trans. Veh. Technol., vol. 56, no. 6, pp. 3533–3549, 2007. doi: 10.1109/TVT.2007.901927. [Google Scholar] [CrossRef]

14. S. Zhang, Y. Hou, X. Xu, and X. Tao, “Resource allocation in D2D-based V2V communication for maximizing the number of concurrent transmissions,” in 2016 IEEE 27th Annu. Int. Symp. Personal, Indoor, Mobile Radio Commun. (PIMRC), Valencia, Spain, IEEE, 2016, pp. 1–6. doi: 10.1109/PIMRC.2016.7794859. [Google Scholar] [CrossRef]

15. L. Hu, W. Lei, J. Zhao, and X. Sun, “Optimal weighting factor design of finite control set model predictive control based on multi objective ant colony optimization,” IEEE Trans. Ind. Electron., vol. 71, no. 7, pp. 6918–6928, Jul. 2024. doi: 10.1109/TIE.2023.3301534. [Google Scholar] [CrossRef]

16. R. Nand, B. N. Sharma, and K. Chaudhary, “Stepping ahead firefly algorithm and hybridization with evolution strategy for global optimization problems,” Appl. Soft Comput., vol. 109, 2021, Art. no. 107517. doi: 10.1016/j.asoc.2021.107517. [Google Scholar] [CrossRef]

17. L. Xu et al., “Optimization of 3D trajectory of UAV patrol inspection transmission tower based on hybrid genetic-simulated annealing algorithm,” in Proc. 3rd Int. Symp. New Energy Electr. Technol., Lecture Notes in Electrical Engineering, 2023, vol. 1017, pp. 841–848. doi: 10.1007/978-981-99-0553-9_87. [Google Scholar] [CrossRef]

18. Y. Liu, S. Wang, J. Huang, and F. Yang, “A computation offloading algorithm based on game theory for vehicular edge networks,” presented at the 2018 ICC, Kansas City, MO, USA, May 20–24, 2018. [Google Scholar]

19. Y. Hou, C. Wang, M. Zhu, X. Xu, X. Tao and X. Wu, “Joint allocation of wireless resource and computing capability in MEC-enabled vehicular network,” China Commun., vol. 18, no. 6, pp. 64–76, 2021. doi: 10.23919/JCC.2021.06.006. [Google Scholar] [CrossRef]

20. Z. Liu et al., “PPRU: A privacy-preserving reputation updating scheme for cloud-assisted vehicular networks,” IEEE Trans. Veh. Technol., pp. 1–16, Dec. 2023. doi: 10.1109/TVT.2023.3340723. [Google Scholar] [CrossRef]

21. Z. Liu et al., “PPTM: A privacy-preserving trust management scheme for emergency message dissemination in space–air–ground-integrated vehicular networks,” IEEE Internet Things J., vol. 9, no. 8, pp. 5943–5956, Apr. 15, 2022. doi: 10.1109/JIOT.2021.3060751. [Google Scholar] [CrossRef]

22. M. Zhu, Y. Hou, X. Tao, T. Sui, and L. Gao, “Joint optimal allocation of wireless resource and MEC computation capability in vehicular network,” presented at the 2020 WCNCW, Republic of Korea, Apr. 6–9, 2020. [Google Scholar]

23. H. Wang, T. Lv, Z. Lin, and J. Zeng, “Energy-delay minimization of task migration based on game theory in mec-assisted vehicular networks,” IEEE Trans. Veh. Technol., vol. 71, no. 8, pp. 8175–8188, 2022. doi: 10.1109/TVT.2022.3175238. [Google Scholar] [CrossRef]

24. G. Wu and Z. Li, “Task offloading strategy and simulation platform construction in multi-user edge computing scenario,” Electronics, vol. 10, no. 23, 2021, Art. no. 3038. doi: 10.3390/electronics10233038. [Google Scholar] [CrossRef]

25. J. Chen and T. Li, “Internet of vehicles resource scheduling based on blockchain and game theory,” Math. Probl. Eng., vol. 2022, no. 1, pp. 1–13, 2022. doi: 10.1155/2022/6891618. [Google Scholar] [CrossRef]

26. M. E. Mkiramweni, C. Yang, J. Li, and W. Zhang, “A survey of game theory in unmanned aerial vehicles communications,” IEEE Commun. Surv. Tutorials, vol. 21, no. 4, pp. 3386–3416, 2019. doi: 10.1109/COMST.2019.2919613. [Google Scholar] [CrossRef]

27. K. Zhang, X. Gui, D. Ren, and D. Li, “Energy-latency tradeoff for computation offloading in UAV-assisted multi-access edge computing system,” IEEE Internet Things J., vol. 8, no. 8, pp. 6709–6719, 2020. doi: 10.1109/JIOT.2020.2999063. [Google Scholar] [CrossRef]

28. Y. Jang, J. Na, S. Jeong, and J. Kang, “Energy-efficient task offloading for vehicular edge computing: Joint optimization of offloading and bit allocation,” presented at the 2020 VTC2020-Spring, Antwerp, Belgium, May 25–28, 2020. doi: 10.1109/VTC2020-Spring48590.2020.9128785. [Google Scholar] [CrossRef]

29. M. Chen and Y. Hao, “Task offloading for mobile edge computing in software defined ultra-dense network,” IEEE J. Sel. Areas Commun., vol. 36, no. 3, pp. 587–597, 2018. doi: 10.1109/JSAC.2018.2815360. [Google Scholar] [CrossRef]

30. H. Wu, Z. Zhang, C. Guan, K. Wolter, and M. Xu, “Collaborate edge and cloud computing with distributed deep learning for smart city internet of things,” IEEE Internet Things J., vol. 7, no. 9, pp. 8099–8110, 2020. doi: 10.1109/JIOT.2020.2996784. [Google Scholar] [CrossRef]

31. Y. Zhang, X. Qin, and X. Song, “Mobility-aware cooperative task offloading and resource allocation in vehicular edge computing,” presented at the 2020 WCNCW, Seoul, Republic of Korea, Apr. 6–9, 2020. [Google Scholar]

32. H. Wang, Z. Lin, K. Guo, and T. Lv, “Computation offloading based on game theory in MEC-assisted v2x networks,” presented at the 2021 ICC Workshops, Montreal, QC, Canada, Jun. 14–23, 2021. [Google Scholar]

33. X. Huang, K. Xu, C. Lai, Q. Chen, and J. Zhang, “Energy-efficient offloading decision-making for mobile edge computing in vehicular networks,” EURASIP J. Wirel. Commun. Netw., vol. 2020, no. 1, pp. 1–16, 2020. doi: 10.1186/s13638-020-01848-5. [Google Scholar] [CrossRef]

34. H. Jiang, X. Dai, Z. Xiao, and A. Iyengar, “Joint task offloading and resource allocation for energy-constrained mobile edge computing,” IEEE Trans. Mob. Comput., vol. 22, no. 7, pp. 4000–4015, 2023. doi: 10.1109/TMC.2022.3150432. [Google Scholar] [CrossRef]

35. Q. Luo, T. H. Luan, W. Shi, and P. Fan, “Deep reinforcement learning based computation offloading and trajectory planning for multi-UAV cooperative target search,” IEEE J. Sel. Areas Commun., vol. 41, no. 2, pp. 504–520, 2023. doi: 10.1109/JSAC.2022.3228558. [Google Scholar] [CrossRef]

36. N. Zhao, Z. Ye, Y. Pei, Y. -C. Liang, and D. Niyato, “Multi-agent deep reinforcement learning for task offloading in UAV-assisted mobile edge computing,” IEEE Trans. Wirel. Commun., vol. 21, no. 9, pp. 6949–6960, 2022. doi: 10.1109/TWC.2022.3153316. [Google Scholar] [CrossRef]

37. Y. Li, Z. Liu, and Q. Tao, “A resource allocation strategy for internet of vehicles using reinforcement learning in edge computing environment,” Soft Comput., vol. 27, no. 7, pp. 3999–4009, 2023. doi: 10.1007/s00500-022-07544-4. [Google Scholar] [CrossRef]

38. K. Wang, X. Wang, X. Liu, and A. Jolfaei, “Task offloading strategy based on reinforcement learning computing in edge computing architecture of internet of vehicles,” IEEE Access, vol. 8, pp. 173779–173789, 2020. doi: 10.1109/ACCESS.2020.3023939. [Google Scholar] [CrossRef]

39. X. Li, “A computing offloading resource allocation scheme using deep reinforcement learning in mobile edge computing systems,” J. Grid Comput., vol. 19, no. 1, pp. 1–12, 2021. doi: 10.1007/s10723-021-09568-w. [Google Scholar] [CrossRef]

40. X. J. Wu, D. Hao, and C. Xu, “An improved method of artificial bee colony algorithm,” Appl. Mech. Mater., vol. 101, pp. 315–319, 2012. doi: 10.4028/www.scientific.net/AMM.101-102.315. [Google Scholar] [CrossRef]

41. X. Chen and K. C. Leung, “Non-cooperative and cooperative optimization of scheduling with vehicle-to-grid regulation services,” IEEE Trans. Veh. Technol., vol. 69, no. 1, pp. 114–130, 2020. doi: 10.1109/TVT.2019.2952712. [Google Scholar] [CrossRef]

42. O. P. Verma, N. Agrawal, and S. Sharma, “An optimal edge detection using modified artificial bee colony algorithm,” Proc. Nat. Acad. Sci., India Section A: Phys. Sci., vol. 86, pp. 157–168, 2016. doi: 10.1007/s40010-015-0256-7. [Google Scholar] [CrossRef]

43. A. B. de Souza, P. A. L. Rego, V. Chamola, T. Carneiro, P. H. G. Rocha and J. N. de Souza, “A bee colony-based algorithm for task offloading in vehicular edge computing,” IEEE Syst. J., vol. 17, no. 3, pp. 4165–4176, Sep. 2023. doi: 10.1109/JSYST.2023.3237363. [Google Scholar] [CrossRef]

44. M. Zhang and Y. Zhu, “An enhanced greedy resource allocation algorithm for localized SC-FDMA systems,” IEEE Commun. Lett., vol. 17, no. 7, pp. 1479–1482, Jul. 2013. doi: 10.1109/LCOMM.2013.052013.130716. [Google Scholar] [CrossRef]

45. P. Li et al., “Hierarchically partitioned coordinated operation of distributed integrated energy system based on a master-slave game,” Energy, vol. 214, 2021, Art. no. 119006. doi: 10.1016/j.energy.2020.119006. [Google Scholar] [CrossRef]

46. J. Liu and G. Yu, “Fuzzy Kakutani-Fan-Glicksberg fixed point theorem and existence of Nash equilibria for fuzzy games,” Fuzzy Sets Syst., vol. 447, pp. 100–112, 2022. doi: 10.1016/j.fss.2022.02.002. [Google Scholar] [CrossRef]

47. Y. Liu, C. Xu, Y. Zhan, Z. Liu, J. Guan and H. Zhang, “Incentive mechanism for computation offloading using edge computing: A stackelberg game approach,” Comput. Netw., vol. 129, pp. 399–409, 2017. doi: 10.1016/j.comnet.2017.03.015. [Google Scholar] [CrossRef]

A  Appendix A: Proof of Lemma 1

Lemma 1. In Nash equilibrium A∗, the allocation decision ai∗ of each vehicle i must be the optimal choice for the allocation strategy A−i=(a1,…, ai−1, ai+1,…,an).

Proof. If the decision ai∗ is not optimal choice for the vehicle i under strategy Ai, then there must be another allocation decision ai in strategy Ai that increases the benefit of vehicle i. Therefore, if the vehicle i changes the decision ai∗ to a decision ai, then the vehicle i will obtain a higher benefit, that is, existence BA−i∗(ai∗)<BA−i∗(ai). However, this conclusion is contradicted by BA−i∗(ai∗)≥BA−i∗(ai),∀ai∈Ai,∀i∈N, that is, in the Nash equilibrium, no vehicle can unilaterally change its allocation decision to improve its own benefit.

In the TL-G game model established in this paper, there are two participants, the VEC server and the vehicle, where the VEC server is designated as the leader, while the vehicle serves as the follower. When the vehicle side makes the best response according to the strategy of the VEC server, and the server also gives its own optimal strategy based on this corresponding basis, the game model reaches the Nash equilibrium, that is, none of the task-bearing participants can unilaterally improve the system’s overall revenue by altering their individual strategies. This can be expressed as:

{Bk(μk, i∗)≥Bk(μk, i),∀μk, i∈μBi(ai, k∗, xi, k∗)≥Bi(ai, k, xi, k), ∀ai, k∈A(13)

Before solving the Nash equilibrium point of the system, it is necessary to prove its existence and uniqueness [45]. That is, if the leader’s unique Nash equilibrium is obtained, then the follower will produce a corresponding unparalleled Nash equilibrium, resulting in a singular Nash equilibrium point. Brouwer’s fixed point theorem [46] is used here to prove the existence of the Nash equilibrium of the system.

B  Appendix B: Proof of Lemma 2

Lemma 2. The system model has a Nash equilibrium.

Proof. There are two participants i and k, and the pure strategy space S=Si×Sk of the participants k and i is a finite set, and s=(si, sk) is the pure strategy group, Σ=Σi×Σk is the individual mixed strategy space, which σ=(σi,σk) is a mixed strategy group. Set ∅i, si(σ)=max{0, ui(si, σ−i)−ui(σ)}, the function reflects the tendency of individual i to switch strategies. Define the map f from Σi to Σk, f is a function whose input variable is |Si|×|Sk| dimension and output variable is |Si|×|Sk|, that is, for any σ=(σi, σk)∈Σ, it holds that f(σ)∈Σ.

σi′(si)=σi(si)+∅i, si(σ)∑ai∈Si(σi(ai)+∅i, ai(σ))=σi(si)+∅i, si(σ)1+∑ai∈Si∅i, ai(σ)(14)

where 0≤σi′(st)≤1, and ∑ai∈Siσi′(at)=1. Based on the aforementioned equation, it can be inferred that, for a given strategy k, the utility of i would be higher if σi is changed to si. Given σ, within f(σ), the weight assigned by i to the pure strategy si will be greater, otherwise, it would be smaller. Because Σ it is a compact convex set, but a continuous function, there must be a fixed point σ∗=f(σ∗). If σ∗ is a Nash equilibrium, then σi′(si)=σi(si)+∅i, si(σ)1+∑ai∈Si∅i, ai(σ), ∀ai∈Si, ∅i, ai(σ∗) = 0, i.e., σi′(si)=σ∗(si), σ∗ is a fixed point. That is to say, ∀si∈Si, it holds true that σi′(si)=σi(si)+∅i, si(σ)1+∑ai∈Si∅i, ai(σ). Assuming that given the policy of x∗, σk∗ is actually a pure policy, that is, for a certain ai∈Si, σ∗(ai)=1, it obviously satisfies the requirement of Nash equilibrium. Suppose σ∗ is assigned to more than one pure strategy with positive probability, that is, it is assigned to Ai⊆Si. The utility of an individual i adopting a pure strategy ai∈Ai is that ui(ai, σk∗)=∑sk∈Sσk∗(sk)ui(ai, sk), there exists at least one ai∈Ai such that ui(ai, σk∗)−ui(σ∗)≤0. That is, when the leader adopts a strategy μk, i, the system cannot obtain higher utility by changing the task strategy. Therefore, σ∗ is a Nash equilibrium point, and the system model has a Nash equilibrium.

After proving the existence of Nash equilibrium, we employ the Hessian matrix to assess the convexity or concavity of the function, thereby demonstrating the uniqueness of the Nash equilibrium in the system model. The Hessian matrix is a matrix constructed from the second-order partial derivatives of a multivariate function. The Hessian matrix of function f(x) at point x∗, denoted as H, can be expressed as:

∇2f(x)=[∂2f∂x12∂2f∂x1∂x2⋯∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x2∂x1⋯∂2f∂x2∂xn⋮⋮⋮⋮∂2f∂xn∂x1∂2f∂xn∂x2⋯∂2f∂xn2](15)

C  Appendix C: Proof of Lemma 3

Lemma 3. The Nash equilibrium of the system model is unique.

Proof. The vehicle i selects an appropriate VEC server for partial task offloading, we have:

∂2Bi∂ai, k2=−θixi, k(1ri, k+Cifi, k)2(RiCifloc, i−ai, kxi, kri, k−ai, kCixi, kfi, k+1)2≤0(16)

Then the Hessian matrix formed by the second-order partial derivative of the utility function at point ai, k can be expressed as:

HBi(a)=[∂2Bi∂a1, 12∂2Bi∂a1, 22⋯∂2Bia1, m2∂2Bi∂a2, 12∂2Bi∂a2, 22⋯∂2Bi∂a2, m2⋮⋮⋮⋮∂2Bi∂an, 12∂2Bi∂an, 22⋯∂2Bi∂an, m2]≤0(17)

According to the Definition 3, it is proved that the system model is a convex optimization problem, then the Nash equilibrium of the model is unique [47].