Obstacle Avoidance Capability for Multi-Target Path Planning in Different Styles of Search

1  Introduction

Multi-agent pathfinding (MAPF) is a crucial problem in multi-agent planning. Each agent must move from a starting point to a predetermined destination while avoiding collisions with other agents. This problem has gained significant attention due to the widespread use of AI and robotics. Recent research has demonstrated the effectiveness of MAPF in various applications, including autonomous airplanes towing cars, office and warehouse robots, and other multi-robot systems [1,2]. In a shared environment, MAPF aims to minimize the total completion times for a group of agents while planning collision-free pathways between their start and goal locations. Even though MAPF is NP-hard to solve optimally, the AI community has developed various optimal and approximate suboptimal MAPF planners for fully observable environments. When a central planner has complete knowledge of the surroundings and allows agents to determine their routes collaboratively, critical factors are needed to handle environments to choose the path for mobile robots. These factors are generally divided into global and local categories, applicable in known and unknown environments [3]. The goal of learning-based MAPF approaches is to develop a uniform, decentralized policy that each agent follows based on its local observations. Path planning generally aims not only to avoid fixed obstacles but also to prevent collisions between agents, which can lead to planning failures. Planning for moving paths is somewhat similar to fixed paths but involves treating moving agents as obstacles and planning accordingly [4]. Given that the size of the single-agent observation space is determined by the partially observable scenario, this method can be applied to any number of agents in various settings. However, learning-based MAPF techniques face significant challenges due to the non-stationarity of the environment from the perspective of any single agent. Goal-oriented reinforcement learning with single-agent incentives can make the learning process unpredictable and time-consuming, leading to each agent prioritizing its own goals over teamwork. The two main challenges are determining the best route for each robot and maintaining control of the robots [5]. Although considerable work has been done in the field of robot route planning, much of it focuses on single robots. Some researchers have extended these concepts to multi-robot systems, but coordination remains a significant issue that needs to be addressed fully. Several adjustment techniques have been proposed by researchers [6]. MAPF can be applied in various modern scenarios, such as autonomous straddle carriers, office robots, warehouse robots, unmanned surface vehicles, and self-driving cars. These industrial and service robots are often non-holonomic and designed to resemble cars. Most of the strategies mentioned above rely on the assumption that agents are modeled as disks with rotational capability. In reality, robots with rectangular shapes that resemble cars and have small turning radii are more common. This type of path planning is known as a car-like robot [7,8], or nonholonomic path planning [9].

To prevent collisions between moving agents, solvers use various types of conflicts, such as vertex conflicts and edge conflicts [10]. However, the types of conflicts applied depend on their specific contexts and cannot cover all possible collision scenarios. This research addresses the problem of route planning in a warehouse system with an unknown environment by introducing a successful multi-agent pathfinding approach (MAPP). Conflict-Based Search (CBS) is a re-planning method that generates paths and expands state spaces. A major challenge with many previously implemented methods is their failure when the environment changes frequently. Frequent changes can increase the time required for re-planning and affect the path length. Most methods rely on pre-determined paths, which fail in unknown environments. Although a few algorithms are capable of re-planning paths when environments change frequently, they may still struggle with other factors.

Dynamic route planning aims to avoid both static obstructions and collisions. In real life, dynamic obstacles are always moving, but if their motion trajectory can be analyzed, they can be treated as static obstacles. When this is the case, path planning can proceed as it would for static obstacles. If there is insufficient information about the environment, the robot will use its sensors to gather data about the local surroundings. The A* method [11], and its variations are well-known for finding the shortest path and performing well in static environments. Pathfinding techniques that use incremental search methods, like other algorithms and their variations, reuse previous and incomplete searches. Unlike the A* algorithm, the D* algorithm can quickly handle navigation problems in dynamic environments by combining heuristic and incremental search approaches. However, relying solely on D* may decrease the success rate and increase the time required to reach the goal. In terms of planning time and solution quality, this study proposes a modified Conflict-Based Search (CBS) algorithm. The key points summarized in this study are as follows:

•   A conflict-based search algorithm is introduced to plan the paths of robots in various environments. The proposed method demonstrates high efficiency across different scenarios, including dynamic maps and obstacles, and other factors that may impact the environment. The method offers complete flexibility in improving goal search results and adapting to environmental changes without requiring prior information about the environment.

•   Most dynamic pathfinding techniques perform well with minor map alterations. However, when the map changes too frequently, fixing the path may take longer than replanning, with a slight possibility of path-seeking failures. Abrupt map changes can negatively impact performance, particularly in large areas with numerous moving obstacles.

•   The study aims to develop a path-planning method that supports agents in navigating and avoiding obstacles of various shapes, such as concave, rectangular, and circular. A modified conflict-based search method is proposed for robot path planning in mixed settings. This method performs local route planning independently and selects the best route. It also includes a prejudgment process to reassess neighbors to avoid obstructions and incorporates techniques for robot waiting and circuitous routing. To validate the proposed method, a comparison was made with relevant prior work, and the study also provides a comprehensive definition of the critical elements involved in creating and fine-tuning multi-robot pathways. Experimental results show that the proposed method achieves a high success rate, particularly in terms of avoiding obstacles and reaching goals in record time.

This study section also includes several noteworthy contributions and evaluations of related literature. Section 2 provides an overview of associated works and defines the problem. The proposed solution is discussed in Section 3, and the final analysis is presented in Section 4.

2  Literature Reviews

In this section, this study aims to compile research closely related to the proposed task. Initially, robotic route planning was focused solely on specific industrial production needs. Since then, robotics has gained acceptance across various fields, with evolving robot classifications being used to perform tasks and an increase in work related to route planning algorithms. The history of planning algorithms is extensive, with solutions ranging from heuristic methods to evolutionary and hybrid algorithms to address route-planning problems. Multi-robot systems (MR) are employed to perform complex tasks. While a single robot can handle many streamlined tasks, a multi-robot system is required for performing multiple tasks simultaneously, which presents its challenges. Multiple robots have been used in applications such as dynamic mission planning [2], collaborative construction, multi-tasking assignments, and mapping environment variables, which require distinct architectures to function effectively. Each robot is assigned a unique task, making the management of multiple robots in unpredictable settings more dynamic and complex. In addition to structural obstacles within the environment, there are dynamic barriers created by each robot that affect the others. Multi-agent reinforcement learning (MARL) is a popular area in reinforcement learning, focusing on sequential decision-making where multiple agents share actions and information [12]. The problem becomes evident when planning for a group of mobile robots with multiple locations, similar to traveling salesman problems (MTSP) with one or more depots [13]. For example, Reference [14] proposed a conflict resolution method to help agents verify their speed and movements, while Reference [15] introduced a modified algorithm that avoids re-planning. Additionally, Reference [16] proposed a parallelized algorithm for multi-agent path planning (MAPP). Experimental results from this method, tested in static settings and compared with traditional algorithms, indicate superior performance.

In [17], multi-agent reinforcement learning was used to enable conflict-free automated guided vehicle (AGV) path planning in automated container terminals, though it faced limitations related to kinematic operations and omnidirectional issues. The A* technique is less effective in MAPF situations and requires high environmental model accuracy [18]. Experimental results can be obtained by simulating specific environments using this method [19]. Future work will include experimenting with contemporary methods in highly complex situations and using advanced techniques to enhance performance and reduce complexity. The MAPF-POST algorithm for differential drive robots, proposed in [20], ensures a safe distance between robots, and considers velocity constraints. This includes a generalized version of CBS for large agents occupying multiple grids, combining token-passing mechanisms and SIPP (Speed-Indexed Path Planning) for pickup and delivery scenarios. It also features a roadmap-based planner supporting various movement speeds, alongside a grid-based planner for any-angle moves using a variation of SIPP. Distributed collision avoidance for multiple non-holonomic robots is another research area [21]. Traditional methods such as artificial potential fields, dynamic window techniques, and model predictive control are used for single robots. The decentralized reciprocal velocity obstacle (RVO) algorithm allows robots to avoid collisions while maintaining silence [22]. However, many methods may face issues with complex or high environmental requirements, such as rapid re-planning accuracy and short-term changes [23]. This article focuses on warehousing and industrial applications that use multiple robots to reduce labor-intensive tasks and require highly efficient re-planning in changing environments. A fundamental overview is provided in this regard in Table 1.

2.1 Problem Definition

Traditional Multi-Agent Pathfinding (MAPF) solutions typically assume holonomic agents that can travel in four directions and do not account for the size of the agents. This limitation prevents these solutions from being effectively implemented in real-world multi-agent systems, particularly those involving robot cars. Omnidirectional Robots (O-MAP) present significant challenges for researchers. In practice, various route models, such as circular and asymptotically headed trajectories, apply to different types of robots. A multi-agent pathfinding (MAPF) problem can be defined using a graph G = (V, E) and a set of agents {a1,…, ak}. Time is discretized into steps, and each agent can either wait at its current vertex or move to a neighboring vertex in subsequent time steps. Waiting incurs a unit cost unless an agent is at the final goal. The AI must decide between moving or waiting based on the action that will be taken from the start position. Node conflicts arise when agents ai and aj occupy the same vertex (u,v) at time step t, potentially increasing the total cost of the paths. In a dynamic warehouse challenge involving multiple robots, there is a predefined configuration and specific target positions. The problem can be viewed as an optimization task for robots to find routes that avoid collisions and allow each robot to reach its destination efficiently. Path planning in a multi-robot system requires the creation of collision-free paths with minimal robotic movement. The environment includes static obstacles that robots cannot bypass. The target mission is crucial, as the objective area provides essential information for direction planning. Generally, a multi-robot trajectory planning system involves mapping out goals for each robot to reach. The destination itself becomes an additional obstacle that impacts the final path calculation. Effective goal assignment aims to minimize the length of future paths and the computation time required. Randomly assigning targets can significantly increase both computation time and path length. Therefore, it is preferable to employ a strategy that considers path length in advance, Fig. 1 shows an example of a simulation structure.

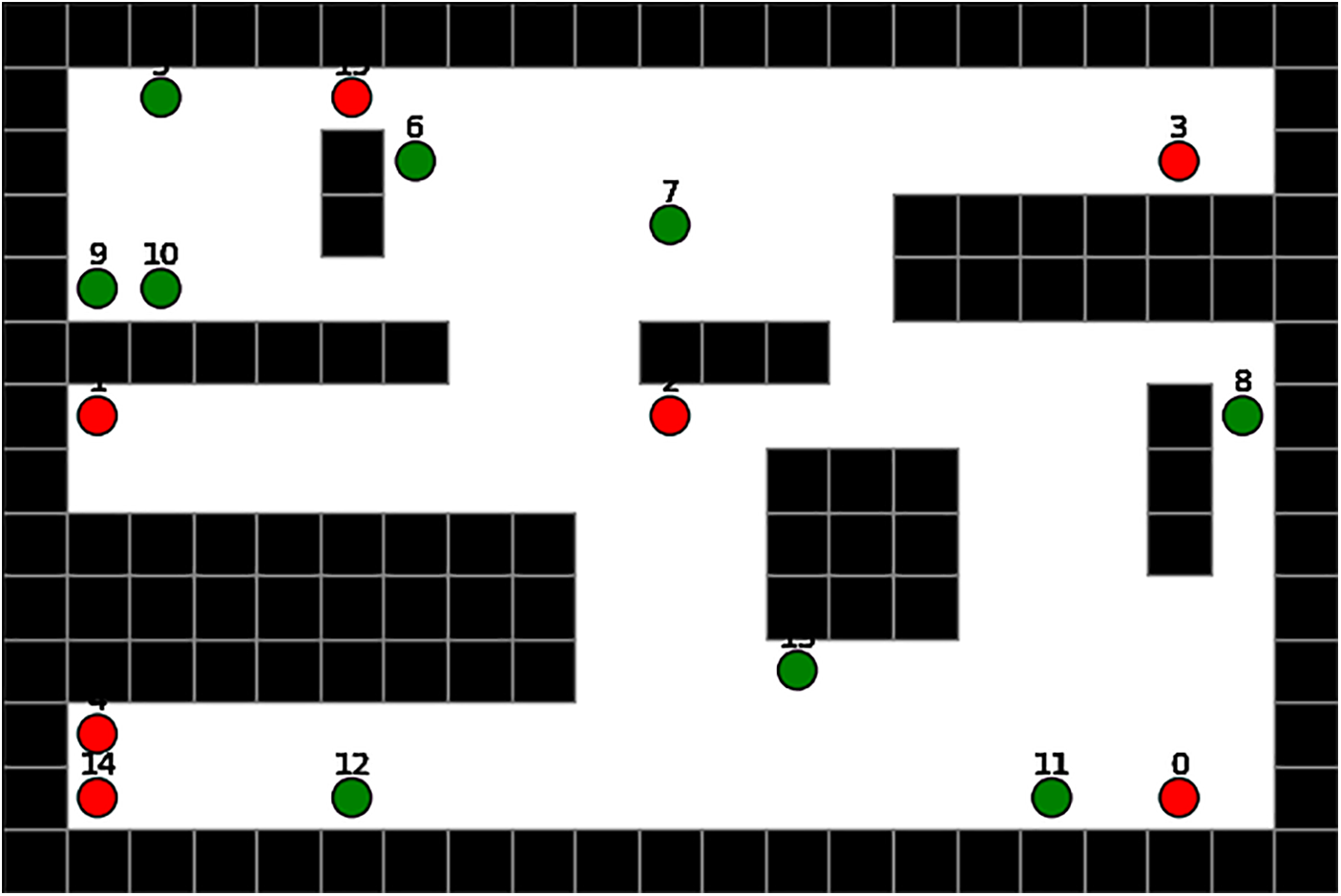
Figure 1: In the simulation, the red block represents the agent, the green block represents the dynamic obstacle, and the black pods represent the static obstacle

2.2 Conflict-Based Search (CBS)

CBS begins by separately planning the shortest paths for all agents, which can be done relatively quickly. These paths are initially designed to avoid collisions. A collision-free solution is sought by detecting and resolving conflicts. If a collision is found between two nodes (e.g., nodes a and b), CBS recursively evaluates two possibilities: one with a restriction preventing node a from being in a cell x at time step t, and another with a restriction preventing node b from being in a cell x at time step t. At the top level of the binary constraint tree, each node N contains a set of constraints. These constraints can be either:

•   A (negative) vertex constraint a,x,ti that prevents node a from being in a cell x at time ti, or

•   A (negative) edge constraint a,x,y,ti that prevents node a from moving from cell x to cell y at time ti.

The root node of the constraint tree starts with an empty set of constraints and a solution composed of the n shortest paths. CBS checks if the solution is collision-free once the node N has been picked for expansion. If it is, node N becomes a goal node, and CBS returns the solution. If not, CBS resolves the collision by choosing one of the conflicting nodes and updating the node N. For instance, if CBS resolves a vertex collision between nodes a and b at cell x at time step t, it ensures that only one of these nodes can be in the cell x at time t. The constraints added are either a,x,ti or b,x,ti. CBS creates two child nodes, each with a set of constraints that reflect these restrictions. Alternatively, if CBS resolves an edge collision at the time step t, it must consider constraints like b,x,y,ti (preventing node b from moving from cell y to cell x at the time t) and a,x,y,ti (preventing node a from moving from cell x to cell y at time t). In the low-level search phase, CBS quickly finds the new shortest path for each node with the newly enforced constraints. For example, a vertex constraint prunes one node in the search tree, potentially intersecting the paths of other nodes but not crossing the environment’s boundaries. Each child node must adhere to the constraints imposed. The separation between all robots and their respective targets is then calculated, choosing the closest point to each robot’s objective. The distance ratio helps identify the best collision-free path. The suggested solution is applied to address challenges in warehouse packaging, where multiple robots share the same environment and have various goals.

To explain more broadly, let’s assume we have a constraint tree, where each node represents a set of constraints that are used to resolve conflicts during pathfinding. In this tree, the root node, referred to as the constraint’s node N, initially contains an empty set of constraints. Imagine a scenario with two agents. The root node N is tasked with finding the shortest paths for both agents. For simplicity, let’s say:

•   Agent 1’s path is represented by [A, B, E],

•   Agent 2’s path is represented by [B, C, D].

These paths are calculated independently of each other, with the total cost of node N being the sum of the individual costs for both agents. Assume the cost of moving between nodes is uniform, and the total cost for node N is 4. During the simulation, observing that a collision will occur at the node C during time step 1 when both agents attempt to occupy the same space. To resolve this conflict, CBS will split the root node N into two child nodes, each imposing a different constraint to avoid collision. In the left child node, a constraint is added to prevent Agent 1 from being at the node C at time step 1. This constraint is represented as [1, C, 1] After adding this constraint, CBS recalculates the shortest path for Agent 1. The new path might be [A, A, C, E], where the agent waits at node A for a one-time step before proceeding. The cost of this new path is now 3 (including the wait time). Agent 2’s path remains unchanged, as it doesn’t need to avoid node C. The total cost of this child node becomes 5 (path cost + wait time). In the right child node, a different constraint is added to prevent Agent 2 from being at the node C at time step 1, represented as [2, C, 1]. Again, CBS recalculates the shortest path for Agent 2, which might be [B, B, C, D] with a wait time at node B. The cost of this new path for Agent 2 also becomes 3. Agent 1’s path remains the same as in the root node. The total cost for this child node also sums up to 5. In this example, both child nodes generated by the CBS algorithm have the same total cost, which is 5. However, the algorithm will select the node that represents a collision-free path as the target node. In this case, since both paths involve different constraints that resolve the collision, either could be selected, depending on other factors like search heuristics or additional constraints. The key takeaway is that CBS systematically imposes constraints to prevent collisions, recalculates paths considering these constraints, and ultimately selects the path with the best cost that also avoids collisions. This process of constraint-based decision-making is visualized in Fig. 2.

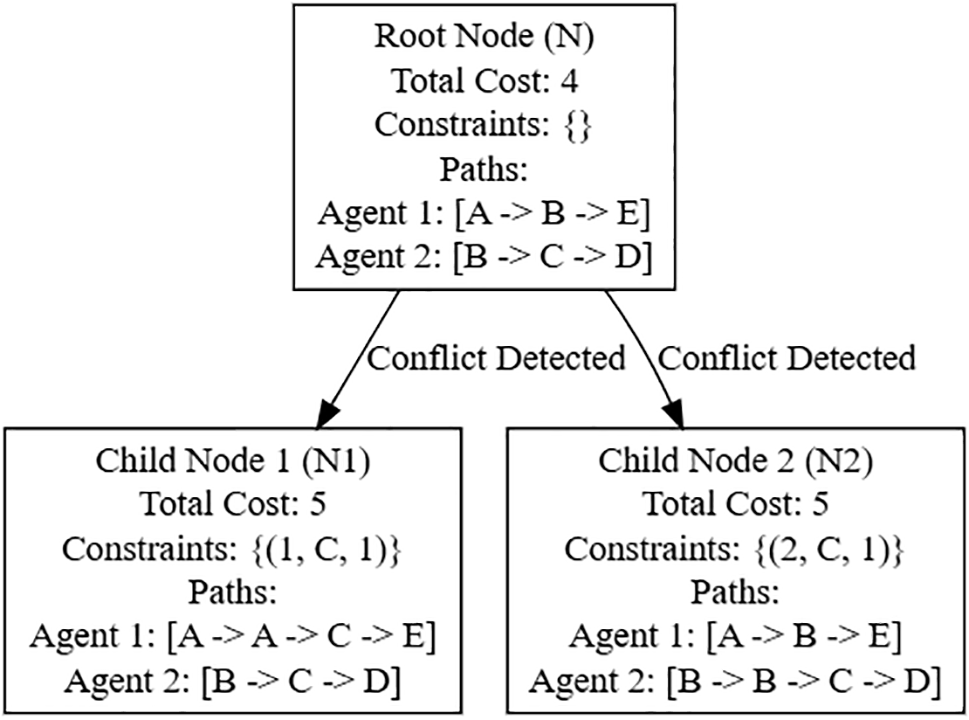
Figure 2: Example of tree node of the multi-agent path

At each stage of the algorithm’s operation, CBS selects the lowest-cost node that leads to the goal. When the algorithm detects a potential collision between two nodes (as previously explained), it splits the parent node into two child nodes, each introducing additional constraints to address the predicted collision. This process, known as node expansion, increases the complexity of the nodes where collisions are expected. When the algorithm evaluates all nodes generated from the collision hypothesis, it assumes the presence of an agent at each vertex during each time step. This assumption is logical and helps in reducing the number of constraints the algorithm needs to apply, which is approximately O(nkC). Typically, constraints are added at each node of the root tree, and the cumulative number of constraints can limit the depth of the parent tree. Consequently, the overall time complexity of the algorithm can be bounded by O(nC*2knC). As discussed earlier, priority plays a crucial role in resolving conflicts and preventing collisions. For instance, consider a scenario where an agent is stuck due to a priority issue. If a low-priority agent holds a resource simultaneously needed by a high-priority agent, it could lead to failure, especially if a medium-priority agent is also present. In such situations, an agent that inherits priority from a higher-priority client must wait to determine if this waiting will yield a successful outcome. If the waiting is justified, the agent can proceed to its target node. However, if the waiting does not resolve the issue, the agent must request a different node excluding those already claimed by agents with higher priority. This priority-based approach ensures that agents with higher priority can navigate more effectively, while lower-priority agents adapt to avoid collisions and resource conflicts. By dynamically adjusting to these constraints, the algorithm can achieve a collision-free path that efficiently guides all agents to their respective goals. Initially, there are no constraints at the root node of the Conflict Tree (CT). This absence of restrictions allows for the free computation of potential paths for all agents. The root node serves as the foundation for expanding the CT, guiding the search for a collision-free solution. In summary, the CT's role in CBS is to methodically explore and validate potential paths while resolving any conflicts that arise. The root node of the CT, which starts without constraints, is progressively expanded as conflicts are detected and resolved. When no further conflicts are found, the CT node is selected as the destination, indicating a successful solution. Ri is a mobile robot where i = 1, to n, that represents the agent ID this representation is done using Eq. (1).

Ci(t)=(xi,yi,t)(1)

If there is a collision between Ri and Rj, the result will be as Eq. (2).

Collision (i,j)→∃t:Ci(t)=Cj(t) where i≠j(2)

The maximum path will be selected after producing the length of the path (µ pl) as in Eq. (3).

µp1=∑i=1, j=1npij(3)

The following equation can be used to express these scenarios numerically to ensure that the solution is optimum. Presenting the free routes after getting the total number of agents inside the map, and then reaching the goal, Eq. (4).

Collision (i,k)=ϕ∀Ri, Rk where, i≠k(4)

First deleting the conflict mobile path if that happened. Second, pl ought to be at a minimum. Consider the following while employing the specified set of ideal pathways (S) for all agents inside the device:

S=[Pij,…]∀i,j where Di,j=1(5)

and min (µ pl) and collision (i,k)= µ for each pair of Ri, Rk robots in the system. The flowchart in Fig. 3 describes the modification of the work structure.

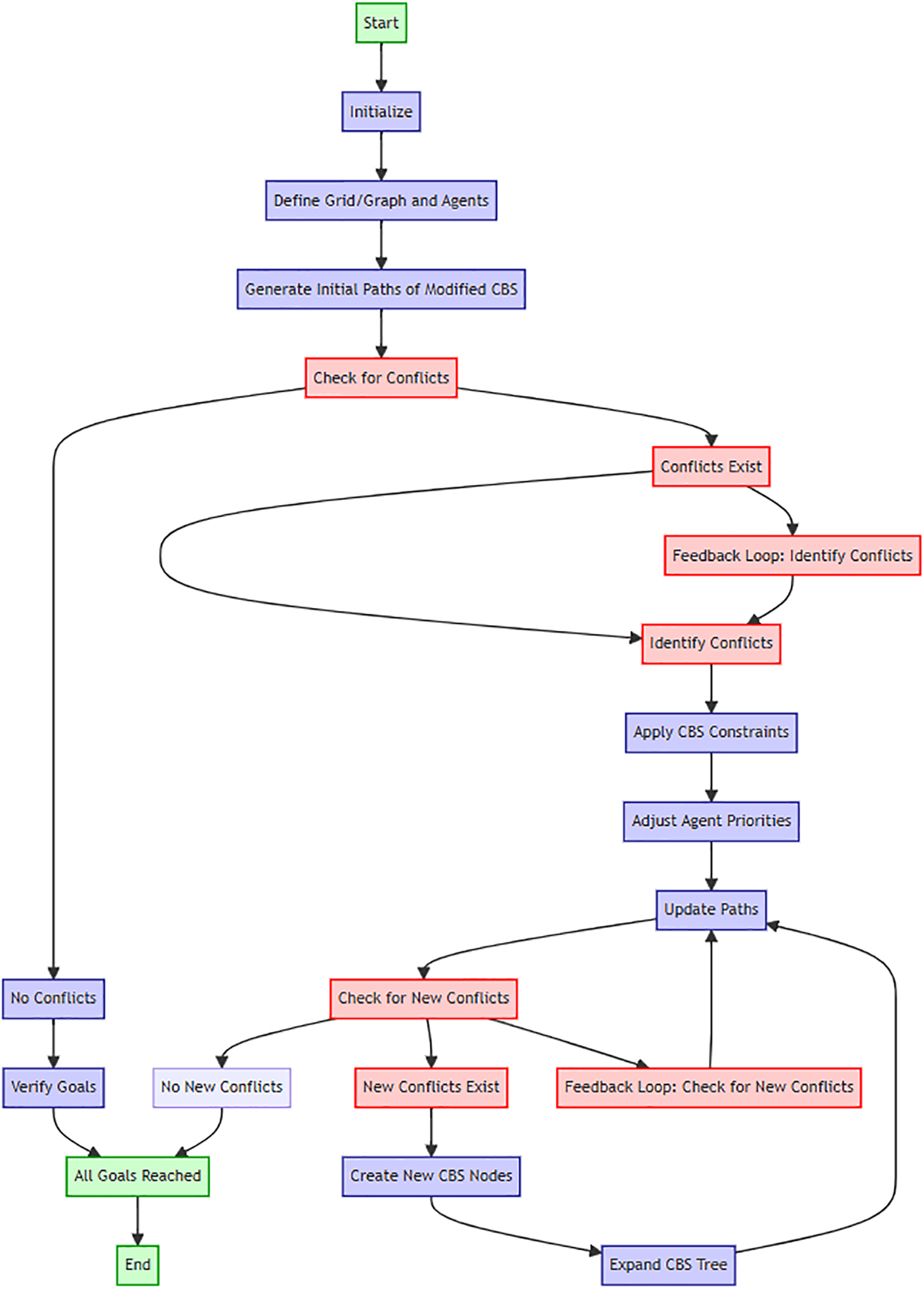
Figure 3: Flowchart of the proposed approach

2.3 General Path Method

The simulation begins with converting the warehouse environment into a node-based graph format, which is essential for applying pathfinding algorithms. Following this, source-to-destination pairs are created using the distance ratio of the destination assignment, which helps in determining the most efficient paths for the robots. A distance metric-based method is then employed to design collision-free routes, ensuring smooth operations in the dynamic warehouse environment. Collision avoidance is addressed using reserved tables, which manage and prevent mutual collisions by reserving paths for each robot. The environment is set up by constructing a habitat with multiple robots, where an input reference map defines the accessible and inaccessible areas. Robots start at predetermined locations and are assigned goals using an intelligent selection approach, resulting in a goal-mapping matrix that facilitates further path planning. Distance ratios for each target are calculated to enhance the evaluation of free space traversed, improving pathfinding efficiency. Finally, the cost of transfers is calculated in a static warehouse setting to ensure cost-effective and optimized paths.

2.4 Simulation Structure

The proposed method is assessed for its efficacy in planning paths for multiple robots across various known and unknown environments, including those with both fixed and moving obstacles. In dynamic settings, each robot is tasked with navigating towards its target while treating other robots as moving obstacles. In these scenarios, red circles represent the robots, green circles denote moving obstacles, and black blocks indicate fixed obstacles. Target assignment in environments such as unknown and warehouse settings is determined by evaluating the cost associated with each path, which includes factors like the total path length and the number of collisions encountered. The cost function is used to assign positions to multiple mobile robots.

For unknown environments, target destinations are often chosen randomly. An example image illustrates a warehouse scenario with multiple robots, detailing their starting positions, goal positions, storage areas, and depots. Fig. 4 demonstrates an example of the target assignment process.

Figure 4: Shows the targets, marked in white, inside the black pods. It also depicts the starting position of each agent’s launch into the environment

3  Simulation Experiments

To evaluate the effectiveness of the proposed method, this study simulated various moving scenarios and obstacles by creating approximately 230 different maps. These maps varied in size and shape, with obstacles including concave, rectangular, and circular forms. The study was divided into three scenarios, each with different complexities. The first scenario involved multiple environments with varying locations and shapes, classified as having medium complexity. In this scenario, agents were tested in unknown environments with multiple dynamic obstacles. The agents were required to navigate through these obstacles and reach their destinations without collisions. An example of this setup is illustrated in Fig. 5.

Figure 5: Different movement of multi-agents in a dynamic environment

Fig. 5 illustrates one of the results obtained from path planning in an environment containing moving targets, with no prior knowledge of the environment type. The primary objective is for the robot to reach its goals in this unknown environment without colliding with any fixed or moving obstacles. The proposed method prioritizes path planning for the robot closest to the goal, taking into account both the time required to reach the goal and the length of the path. After determining both the goal points and starting points, the path length was calculated. Table 2 provides details on the starting positions, goal positions, estimated time to reach the goals, path lengths, agents involved, and map sizes.

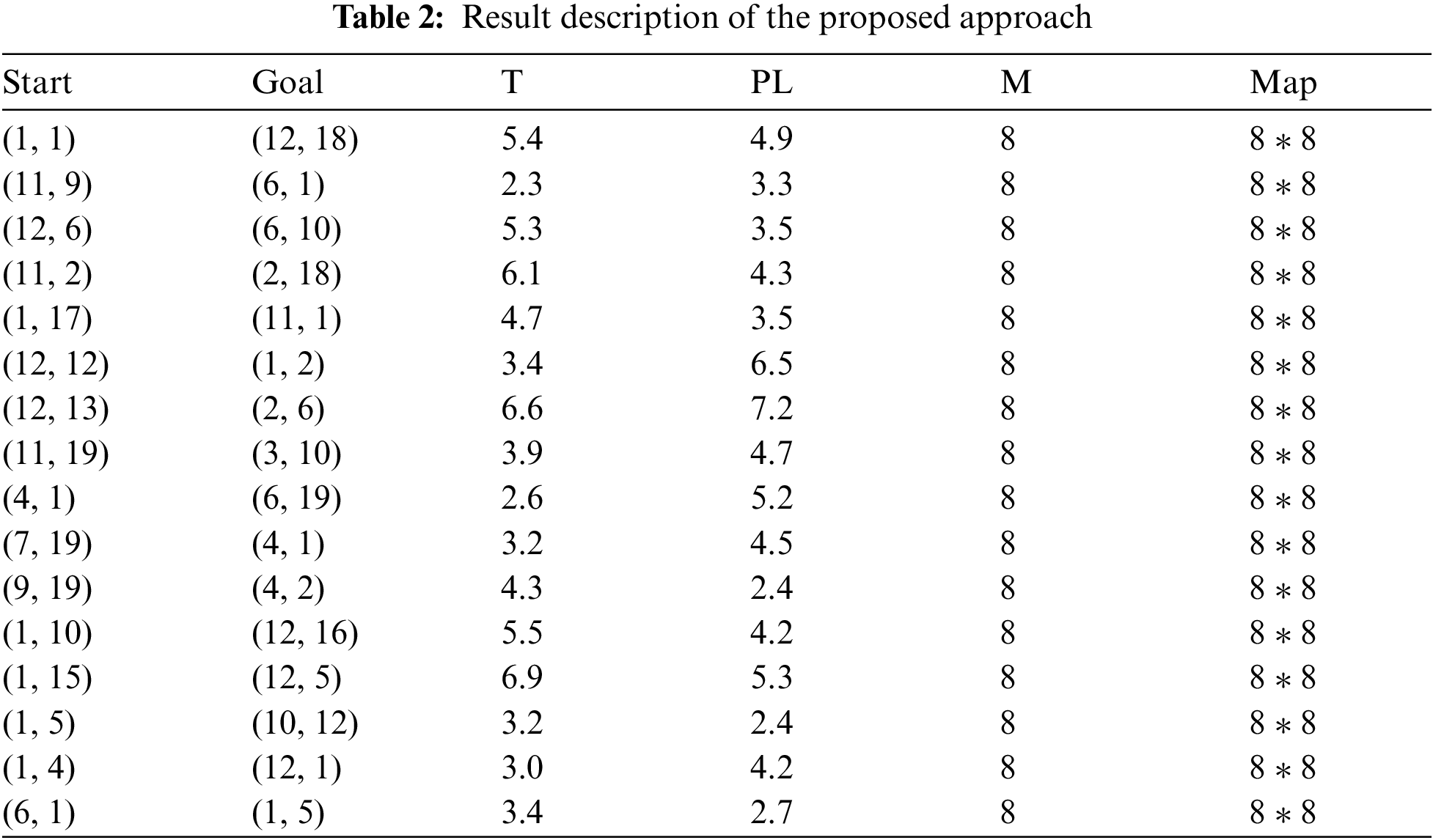
It is evident how the robot’s movement is managed within an unknown environment, with a recorded success rate of reaching the target in a time of 6.9. This success rate varies among robots due to factors such as the time required to avoid collisions or potential waiting caused by priority rules for crossing paths with other robots. Performance analysis largely depends on collision avoidance and priority determination. For instance, if two robots are moving in the same direction and encounter a single exit, the robot that should pass first is determined by the priority mechanism specifically, the robot closest to the goal is given precedence. The second robot will then pass once the first robot has cleared the exit. If a new collision occurs with another robot, the priority will be recalculated based on the closest target, and the same mechanism will be applied. The evaluation of the modified algorithm for multi-agent pathfinding considers different map metrics, including static and dynamic obstacles. In this evaluation, one mobile robot is treated as an agent while other robots are considered moving obstacles. The main goal is for each agent to reach its final destination without colliding with obstacles or other agents. To further test the algorithm, the map size is expanded, and the number of agents and obstacles is increased. Additional examples illustrate the algorithm’s performance in unknown environments with moving obstacles, as shown in Fig. 6 below.

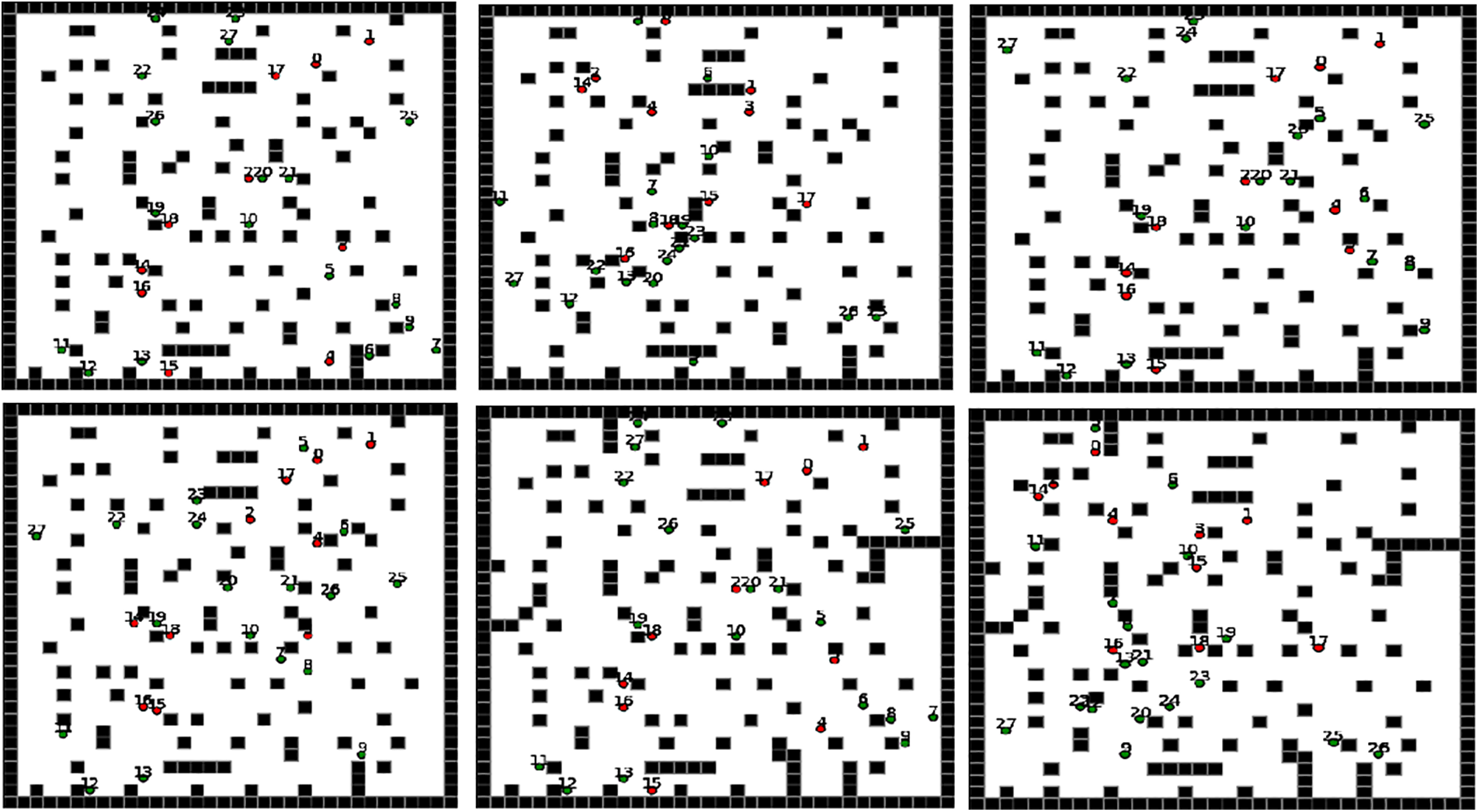
Figure 6: General path planning under an unknown environment

Fig. 6 illustrates the changes that occurred within the work environment. It demonstrates how various factors impact the environment and the robot’s interaction with these changes. As the complexity of the environment increases, previously available paths to the goal may disappear, highlighting the need for continuous path modification. Each time obstacles are added, or paths are altered, the planning calculations are updated accordingly. Changes in the environment, such as the introduction of static obstacles, can affect the path length, travel time, and success rate of reaching the goal. These performance metrics and positional data are detailed in Table 3.

Based on Table 3 and the clear results, several important observations can be made. As the complexity of the environment increases, there is a noticeable rise in the time required to reach the goal and in the length of the robot’s path. Although the time increment is not substantial, it reflects the challenges of navigating through moving obstacles, particularly in unknown environments where many influencing factors are present.

In Phase Two, multi-target scenarios in warehousing present a significant challenge today. Agents need to respond swiftly, and many industrial warehouses can serve as realistic examples for this simulation. Each agent must be assigned specific start and destination positions and navigate the routes ensuring no collisions occur. Several scenarios have been developed to demonstrate how the simulation addresses these challenges effectively see Fig. 7.

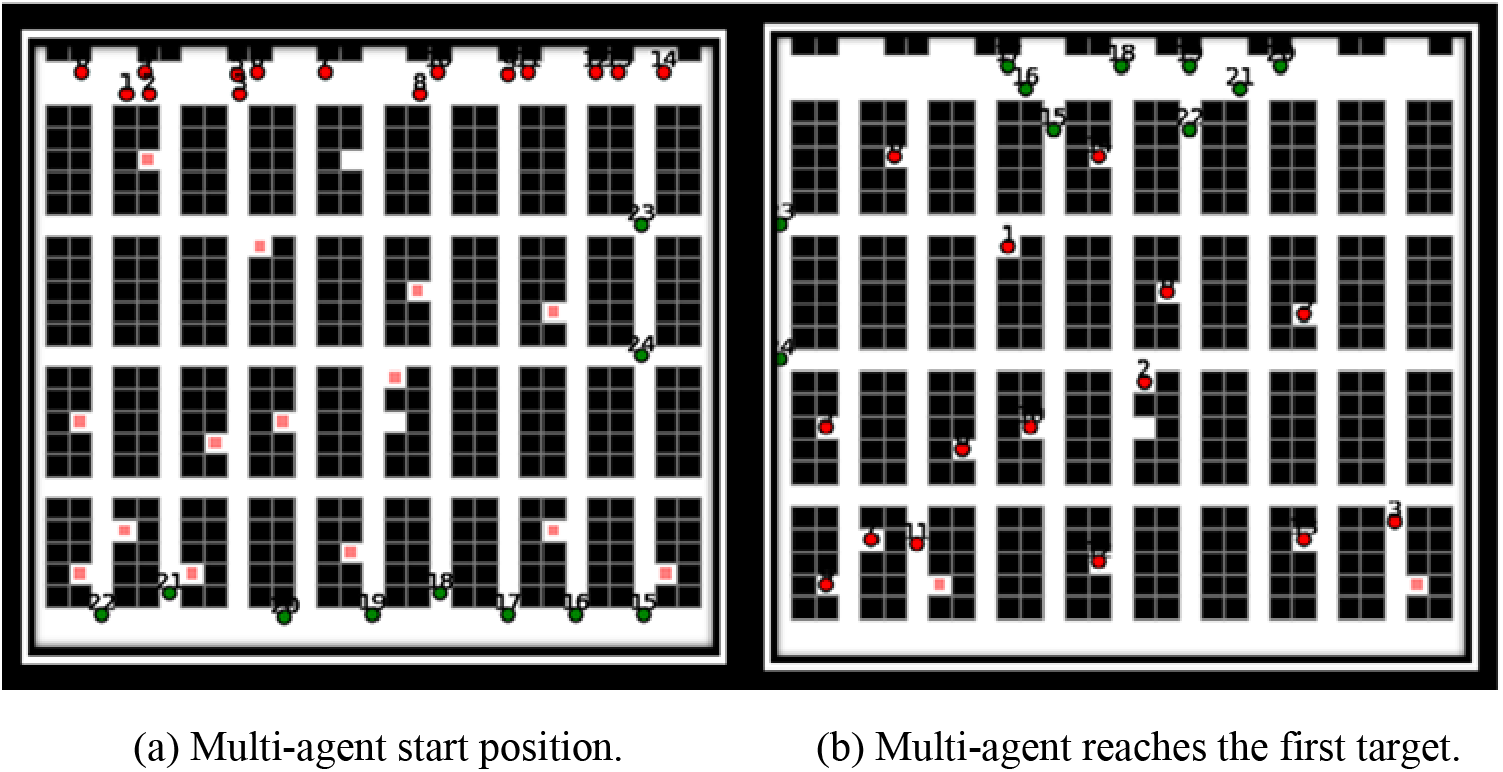
Figure 7: The proposed experiment works first target setting. (a) Multi-agent start position. (b) Multi-agent reaches the first target

Fig. 7a illustrates the initial placement of points and targets within the warehouse. Initially, the robot moves towards its designated target while navigating around moving obstacles in the environment. As shown in Fig. 7b, the robot successfully avoids all obstacles and reaches its target, despite the ongoing movement of the obstacles. Following this, an update on the robots’ status and the generation of new targets within the environment occurs. The robot, having reached its initial goal, now considers this point as its new starting position. Consequently, the robot must re-plan its path to tackle new challenges, including potential increases or decreases in the number of obstacles and changes in target locations. This dynamic testing aims to evaluate the performance of the proposed system under varying conditions. Fig. 8 depicts the results of these environmental changes and the introduction of new goals, highlighting the system’s adaptability and effectiveness in a continually evolving setting.

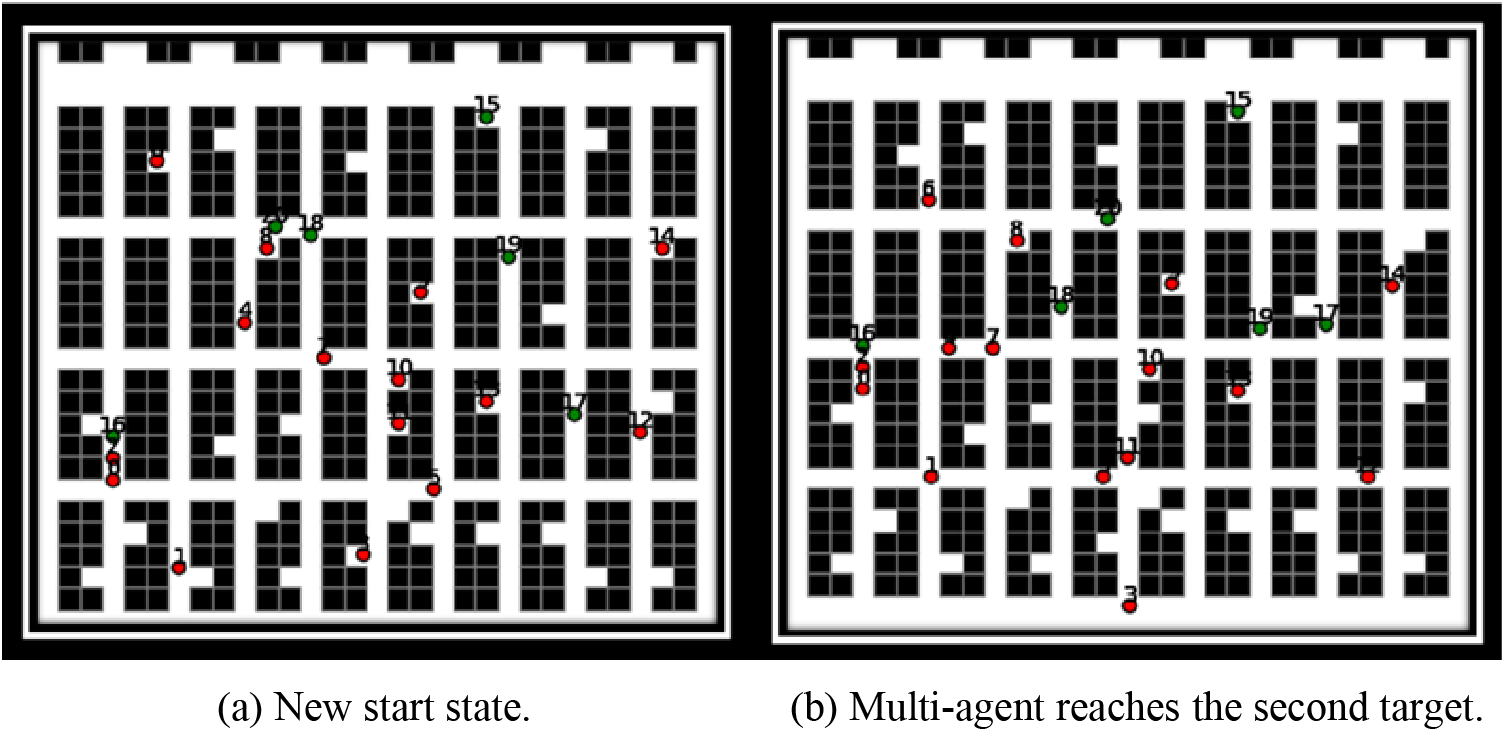
Figure 8: New targets have been assigned. (a) New start state. (b) Multi-agent reaches the second target

Fig. 8a shows the robot starting from a previously reached target, which now serves as its new starting point. After receiving an update with new goals, the robot relies on this initial target point and recalculates its path based on the new targets. Additionally, the number of moving obstacles has decreased. This phase also introduces a new change: new goals are assigned to the robot. The robot must now re-plan its path, considering the updated environment complexity and recalculating priorities, as discussed earlier. In Fig. 8b, you can see that the goals have changed twice. Initially, after reaching the first goal, the robot’s information was updated, and new starting points were established. Subsequently, new goal points were introduced, leading to changes in the environment twice sequentially. The robot must now plan its path again, with the new starting points based on the previously achieved goals. This scenario simulates an environment with varying numbers of moving obstacles, reflecting the dynamic nature of real-world warehouse settings, where targets, worker locations, and obstacle positions can change. The final step involves examining the results of these updates, as illustrated in Fig. 9, which will detail the outcomes of this dynamic planning and adaptation process.

Figure 9: The final destination has been reached by the mobile robot after the pick and delivery operation

Fig. 9 illustrates the final result where the robot reaches its ultimate goal after a series of changes. Initially, the last goal reached was the robot’s original starting point. However, due to updates, the robot had to adjust its goals into two sub-goals. Upon completing these, the robot returned to its original starting point. The simulation involved 28 mobile robots, 520 static blocks, and human workers as moving objects. The results presented in Figs. 7–10 depict the performance of the robots in handling multiple targets. Each robot navigates from the starting state, passes through dynamic obstacles, reaches the first goal, then moves to a new assigned goal, and finally returns to its workstation. The success rate remained consistent across various map selections, demonstrating the robustness of the proposed method. The method effectively managed environments with 50 × 50 maps and maintained a high success rate throughout the simulation. The summary of the experiment changes is detailed in Fig. 10.

Figure 10: Overall system experiment

The following table provides a comparison of all changes in the environment, focusing on time and path length. It also details the changes in target assignments within a warehouse environment. The table outlines the results for three-goal assignments: the first goal represents the agents moving from their starting positions, the second goal involves new targets being assigned to the agents, and the third goal represents further target adjustments. The fourth column of Table 4 illustrates how changes in the path affect the multi-agent system’s performance.

Table 4 provides a detailed comparison of the effects of changing goals across three stages. It highlights the impact on various outcomes, with a focus on a 48 × 48 environment containing numerous static and dynamic obstacles. This table underscores the differences observed in performance based on goal changes. The next results will address the success rate and the effectiveness of avoiding obstacles, particularly in scenarios involving the addition, removal, and modification of obstacles. Figs. 11 and 12 illustrate the performance in handling multiple obstacle changes, including variations in the number of obstacles and the generation of random maps. The proposed method demonstrates versatility in managing different styles of random maps, each with its level of complexity, which can influence the path planning process. Based on testing in various unknown environments, the study concludes that the proposed approach effectively meets the challenges of path planning.

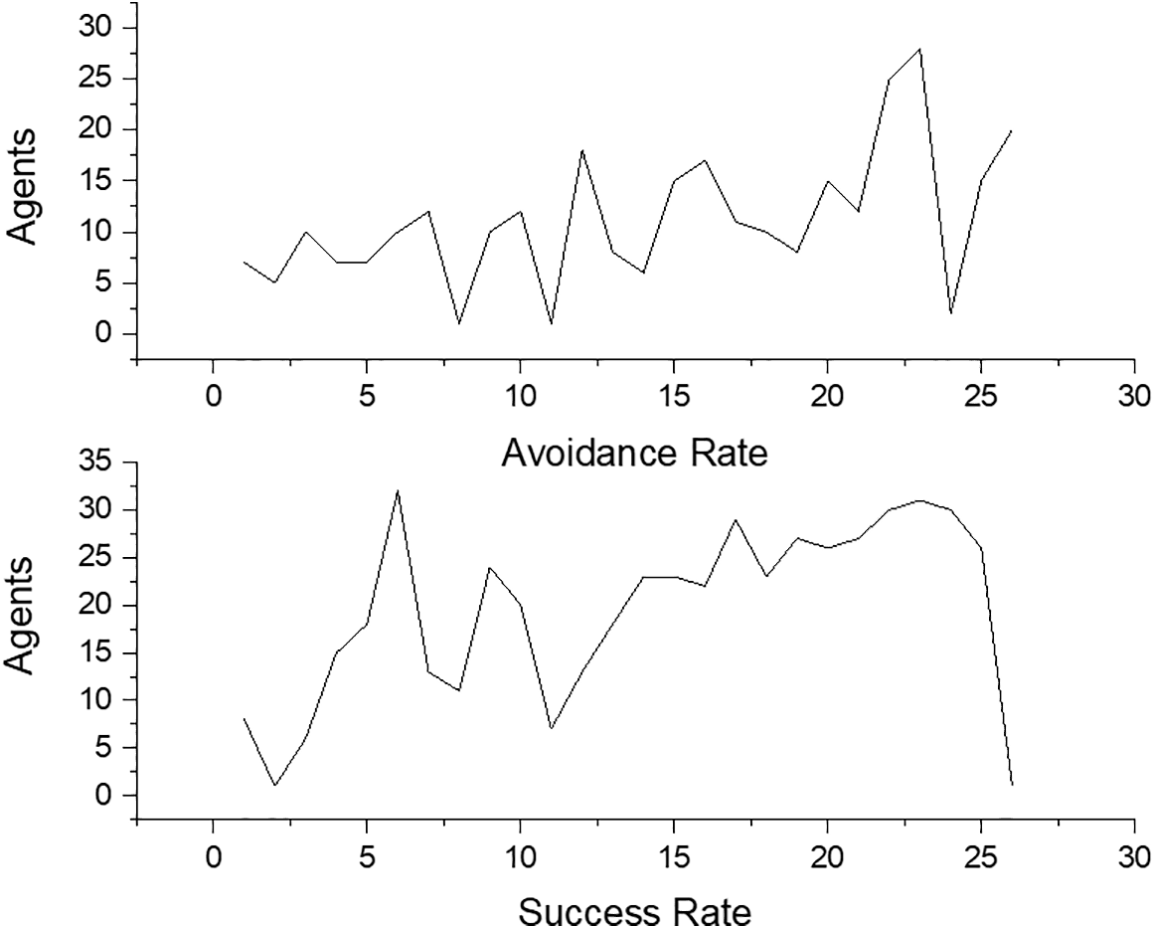
Figure 11: The success rate of our modified algorithm especially when avoiding obstacles in path trajectory

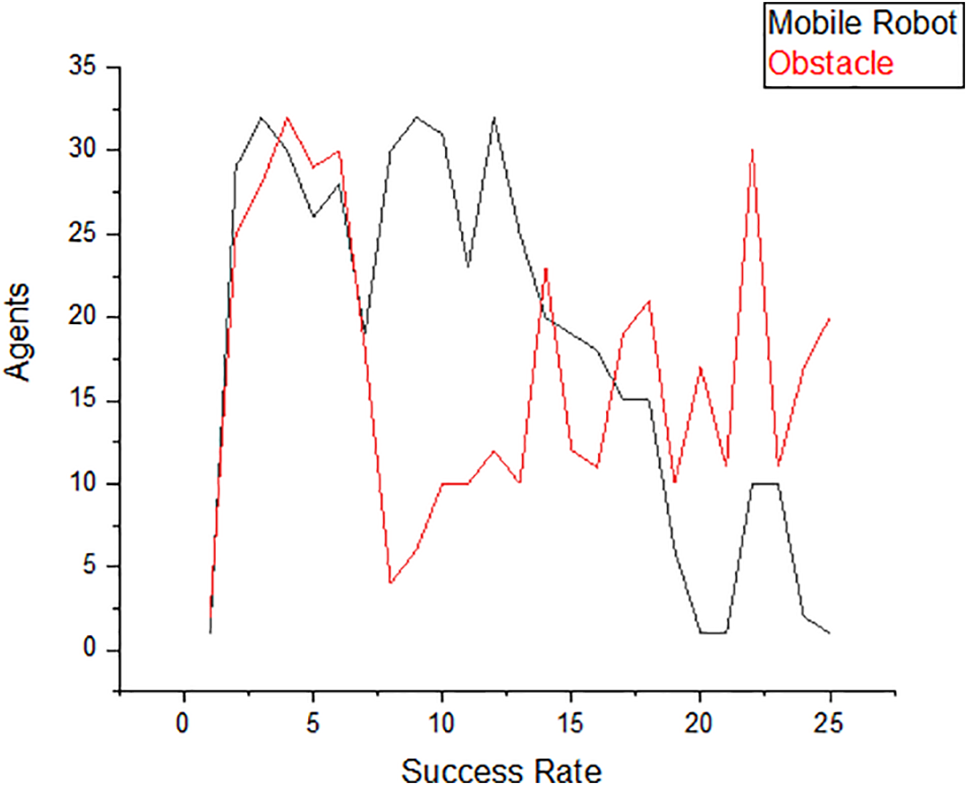
Figure 12: The success rate of avoiding obstacles in path trajectory

Figs. 11–13 illustrate the complete process of obstacle avoidance and the capability of the modified planning method to handle transitions from single to multi-target scenarios. The success rate assessment focuses on evaluating the effectiveness of the proposed method in dynamic environments. Changes in the environment can impact the success of agents in reaching their goals. For instance, in a warehouse setting, while the initial target setting might have a minimal effect, subsequent changes such as introducing a second goal can increase complexity, priority considerations, and costs, which may indirectly influence the success rate. This impact is further observed with additional target settings, reflecting how the method adapts to evolving challenges. In particular, a comparison was made of the proposed method with relevant prior work to validate its high performance as shown in Table 5.

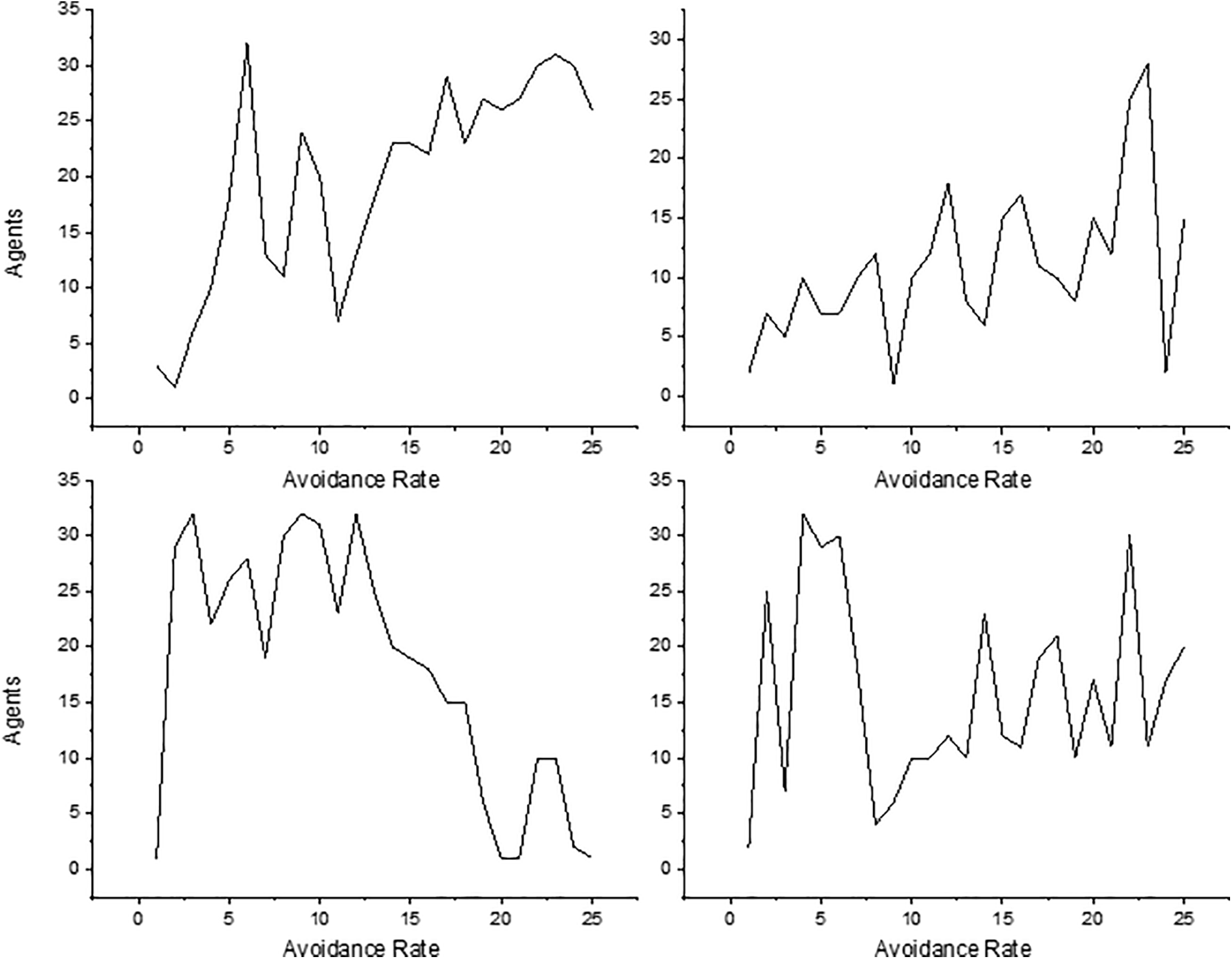
Figure 13: The number of obstacle avoidance average

4  Conclusion

This research evaluated the performance of a modified conflict-based search (CBS) method in various virtual environments to test its effectiveness and adaptability. By progressively increasing the complexity of the environments, starting from simple scenarios and advancing to those with added obstacles, the study demonstrated the method’s high performance. The results indicate that the proposed CBS algorithm effectively handles both static and dynamic environments, adapts to changes, and efficiently manages multiple goals. The method excels in maintaining a high success rate, optimizing path length, and reducing travel time. It successfully navigates environments with varying levels of complexity and is capable of managing multiple goals before returning to the base. The proposed approach addresses challenges encountered in previous implementations, showcasing its robustness in both simulated and complex scheduling scenarios, such as in manufacturing plants where resource optimization is crucial. However, the current approach has limitations, including its focus on omnidirectional robots and potential issues related to grid size, response time, and complex planning when applied to real-world scenarios. Future research will explore expanding the approach to 3D paths and industrial environments, aiming to overcome these limitations and enhance practical applicability.

Acknowledgement: This paper extends sincere gratitude to all the reviewers for their invaluable contributions to the field and the editors for their exceptional work in enhancing the quality of this research.

Funding Statement: The authors did not receive any specific funding for this study.

Author Contributions: Study conception and design: Mustafa Mohammed Alhassow, Oguz Ata, Dogu Cagdas Atilla; data collection: Mustafa Mohammed Alhassow; analysis and interpretation of results: Mustafa Mohammed Alhassow, Oguz Ata, Dogu Cagdas Atilla; draft manuscript preparation: Mustafa Mohammed Alhassow, Oguz Ata. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that all data supporting the findings of this study are included in the paper.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Liang and L. Wang, “Applying genetic algorithm and ant colony optimization algorithm into marine investigation path planning model,” Soft Comput., vol. 24, no. 11, pp. 8199–8210, 2020. doi: 10.1007/s00500-019-04414-4. [Google Scholar] [CrossRef]

2. G. Chen, T. Wu, and Z. Zhou, “Research on ship meteorological route based on A-star algorithm,” Math. Probl. Eng., vol. 2021, no. 7, pp. 1–8, 2021. doi: 10.1155/2021/9989731. [Google Scholar] [CrossRef]

3. B. Fu et al., “An improved A* algorithm for the industrial robot path planning with high success rate and short length,” Robot. Auton. Syst., vol. 106, no. 3, pp. 26–37, 2018. doi: 10.1016/j.robot.2018.04.007. [Google Scholar] [CrossRef]

4. H. Lu, M. Zhang, X. Xu, Y. Li, and H. T. Shen, “Deep fuzzy hashing network for efficient image retrieval,” IEEE Trans. Fuzzy Syst., vol. 29, no. 1, pp. 166–176, 2020. doi: 10.1109/TFUZZ.2020.2984991. [Google Scholar] [CrossRef]

5. X. R. Tang, Y. K. Zhu, and X. X. Jiang, “Improved A-star algorithm for robot path planning in a static environment,” J. Phys.: Conf. Ser., vol. 2021, pp. 1792, 2021, Art. no. 012067. [Google Scholar]

6. A. Mavrogiannis, R. Chandra, and D. Manocha, “B-GAP: Behavior-rich simulation and navigation for autonomous driving,” IEEE Robot. Autom. Lett., vol. 7, no. 2, pp. 4718–4725, 2022. doi: 10.1109/LRA.2022.3152594. [Google Scholar] [CrossRef]

7. L. Wen, Y. Liu, and H. Li, “CL-MAPF: Multi-agent path finding for car-like robots with kinematic and spatiotemporal constraints,” Robot. Auton. Syst., vol. 150, 2022, Art. no. 103997. doi: 10.1016/j.robot.2021.103997. [Google Scholar] [CrossRef]

8. M. M. Alhassow, O. Ata, and D. C. Atilla, “Car-Like robot path planning based on voronoi and Q-Learning algorithms,” in 2021 Int. Conf. Eng. Emerg. Technol. (ICEET), Istanbul, Turkey, 2021, pp. 1–4. [Google Scholar]

9. X. Zhang, G. Xiong, Y. Wang, S. Teng, and L. Chen, “D-PBS: Dueling priority-based search for multiple nonholonomic robots motion planning in congested environments,” IEEE Robot. Autom. Lett., vol. 9, no. 4, pp. 638–639, 2024. doi: 10.1109/LRA.2024.3402183. [Google Scholar] [CrossRef]

10. R. D’Andrea, “Guest editorial: A revolution in the warehouse: A retrospective on kiva systems and the grand challenges ahead,” IEEE Trans. Autom. Sci. Eng., vol. 9, no. 4, pp. 638–639, 2012. doi: 10.1109/TASE.2012.2214676. [Google Scholar] [CrossRef]

11. D. Zhang, C. Chen, and G. Zhang, “AGV path planning based on improved A-star algorithm,” in 2024 IEEE 7th Adv. Inf. Technol., Electron. Autom. Control Conf. (IAEAC), Chongqing, China, 2024, pp. 1590–1595. [Google Scholar]

12. K. Zhang, Z. Yang, and T. Başar, “Multi-agent reinforcement learning: A selective overview of theories and algorithms,” in Handbook of Reinforcement Learning and Control, 2021, pp. 321–384. [Google Scholar]

13. D. -H. Cho, D. -S. Jang, and H. -L. Choi, “Memetic algorithm-based path generation for multiple Dubins vehicles performing remote tasks,” Int. J. Syst. Sci., vol. 51, no. 4, pp. 608–630, 2020. doi: 10.1080/00207721.2020.1737263. [Google Scholar] [CrossRef]

14. A. Bakdi, A. Hentout, H. Boutami, A. Maoudj, O. Hachour and B. Bouzouia, “Optimal path planning and execution for mobile robots using genetic algorithm and adaptive fuzzy-logic control,” Robot. Auton. Syst., vol. 89, no. 1, pp. 95–109, 2017. doi: 10.1016/j.robot.2016.12.008. [Google Scholar] [CrossRef]

15. R. Almadhoun, T. Taha, L. Seneviratne and Y. Zweiri, “A survey on multi-robot coverage path planning for model reconstruction and mapping,” SN Appl. Sci., vol. 1, no. 8, pp. 1–24, 2019. doi: 10.1007/s42452-019-0872-y. [Google Scholar] [CrossRef]

16. J. J. Roldán, P. Garcia-Aunon, M. Garzón, J. D. León, J. D. Cerro and A. Barrientos, “Heterogeneous multi-robot system for mapping environmental variables of greenhouses,” Sensors, vol. 16, no. 7, 2016, Art. no. 1018. doi: 10.3390/s16071018. [Google Scholar] [PubMed] [CrossRef]

17. H. Hu, X. Yang, S. Xiao, and F. Wang, “Anti-conflict AGV path planning in automated container terminals based on multi-agent reinforcement learning,” Int. J. Prod. Res., vol. 61, no. 1, pp. 65–80, 2023. doi: 10.1080/00207543.2021.1998695. [Google Scholar] [CrossRef]

18. Y. Jeon and D. Park, “Poster: Adaptive astar algorithm for calculation time reduction of autonomous vehicle’s pathfinding,” in 2024 IEEE Veh. Netw. Conf. (VNC), IEEE, 2024. [Google Scholar]

19. J. Li, Z. Chen, D. Harabor, P. J. Stuckey, and S. Koenig, “MAPF-LNS2: Fast repairing for multi-agent path finding via large neighborhood search,” Proc. AAAI Conf. Artif. Intell., vol. 36, no. 9, pp. 10256–10265, 2022. doi: 10.1609/aaai.v36i9.21266. [Google Scholar] [CrossRef]

20. W. Hönig, S. Kiesel, A. Tinka, J. W. Durham, and N. Ayanian, “Persistent and robust execution of MAPF schedules in warehouses,” IEEE Robot. Autom. Lett., vol. 4, no. 2, pp. 1125–1131, Apr. 2019. doi: 10.1109/LRA.2019.2894217. [Google Scholar] [CrossRef]

21. T. Guo and J. Yu, “Decentralized lifelong path planning for multiple ackerman car-like robots,” 2024, arXiv:2402.11767. [Google Scholar]

22. I. Solis, J. Motes, R. Sandström, and N. M. Amato, “Representation-optimal multi-robot motion planning using conflict-based search,” IEEE Robot. Autom. Lett., vol. 6, no. 3, pp. 4608–4615, Jul. 2021. doi: 10.1109/LRA.2021.3068910. [Google Scholar] [CrossRef]

23. A. Zanardi, P. Zullo, A. Censi, and E. Frazzoli, “Factorization of multi-agent sampling-based motion planning,” in 2023 62nd IEEE Conf. Decis. Control (CDC), IEEE, 2023. [Google Scholar]

24. Q. Lin and H. Ma, “SACHA: Soft actor-critic with heuristic-based attention for partially observable multi-agent path finding,” IEEE Robot. Autom. Lett., vol. 8, no. 1, pp. 1–8, 2023. doi: 10.1109/LRA.2023.3292004. [Google Scholar] [CrossRef]

25. L. Chang, L. Shan, C. Jiang, and Y. Dai, “Reinforcement-based mobile robot path planning with improved dynamic window approach in an unknown environment,” Auton. Robots, vol. 45, no. 1, pp. 51–76, 2021. doi: 10.1007/s10514-020-09947-4. [Google Scholar] [CrossRef]

26. E. S. Low, P. Ong, and C. Y. Low, “A modified Q-learning path planning approach using distortion concept and optimization in a dynamic environment for an autonomous mobile robot,” Comput. Ind. Eng., vol. 181, no. 6, 2023, Art. no. 109338. doi: 10.1016/j.cie.2023.109338. [Google Scholar] [CrossRef]

27. F. H. Ajeil, I. Ibraheem, A. Azar, and A. J. Humaidi, “Autonomous navigation and obstacle avoidance of an omnidirectional mobile robot using swarm optimization and sensors deployment,” Int. J. Adv. Robot. Syst., vol. 17, no. 3, 2020. doi: 10.1177/1729881420929498. [Google Scholar] [CrossRef]

28. G. Fragapane, R. de Koster, F. Sgarbossa, and J. O. Strandhagen, “Planning and control of autonomous mobile robots for intralogistics: Literature review and research agenda,” Eur. J. Oper. Res., vol. 294, no. 2, pp. 405–426, 2021. doi: 10.1016/j.ejor.2021.01.019. [Google Scholar] [CrossRef]

29. J. Yuan, H. Wang, C. Lin, D. Liu, and D. Yu, “A novel GRU-RNN network model for dynamic path planning of mobile robot,” IEEE Access, vol. 7, pp. 15140–15151, 2019. [Google Scholar]

30. H. Tang, “Multi-robot material delivery in industrial parks based improved on A* algorithm,” Highl. Sci. Eng., Technol., vol. 46, pp. 280–288, 2023. [Google Scholar]

31. J. Li, W. Ruml, and S. Koenig, “EECBS: A bounded-suboptimal search for multi-agent pathfinding,” Proc. AAAI Conf. Artif. Intell., vol. 35, no. 14, 2021. [Google Scholar]

32. R. Cui, J. Guo, and B. Gao, “Game theory-based negotiation for multiple robots task allocation,” Robotica, vol. 31, no. 6, pp. 923–934, 2013. doi: 10.1017/S0263574713000192. [Google Scholar] [CrossRef]

33. D. Zhang, H. Maei, X. Wang, and Y. Wang, “Deep reinforcement learning for visual object tracking in videos,” 2017, arXiv:1701.08936. [Google Scholar]

34. Q. Wu, H. Lin, Y. Jin, Z. Chen, S. Li and D. Chen, “A new fallback beetle antennae search algorithm for path planning of mobile robots with collision-free capability,” Soft Comput., vol. 24, no. 3, pp. 2369–2380, 2020. doi: 10.1007/s00500-019-04067-3. [Google Scholar] [CrossRef]

35. R. Chandra and D. Manocha, “GamePlan: Game-theoretic multi-agent planning with human drivers at intersections, roundabouts, and merging,” IEEE Robot. Autom. Lett., vol. 7, no. 2, pp. 2676–2683, 2022. doi: 10.1109/LRA.2022.3144516. [Google Scholar] [CrossRef]

36. M. M. Alhassow, O. Ata, and D. C. Atilla, “Multi-agents path planning for a mobile robot in a dynamic warehouse environment,” in Int. Conf. Comput., Intell. Data Analyt., Springer, 2022. [Google Scholar]

37. Q. Li, F. Gama, A. Ribeiro, and A. Prorok, “Graph neural networks for decentralized multi-robot path planning,” in 2020 IEEE/RSJ Int. Conf. Intell. Robots Syst. (IROS), Las Vegas, NV, USA, IEEE, 2020. [Google Scholar]