Research on Tensor Multi-Clustering Distributed Incremental Updating Method for Big Data

1  Introduction

The proliferation of social networks, e-commerce platforms, and mobile technologies has ushered us into the era of big data, characterized by an unprecedented surge in data volume. These technologies generate vast datasets that are not only massive in scale but also complex in structure, encompassing multi-dimensional information and a variety of entity relationships. The complexity of these datasets poses significant challenges to traditional data processing and analysis methods, which may struggle to effectively capture multidimensional structures and nonlinear relationships within the data, or may require substantial computational resources and time to process such extensive datasets [1].

To address these challenges, tensor decomposition has emerged as an effective method for handling big data. As a multidimensional data structure, tensor can naturally represent user-user relationships in social networks and user-commodity-time relationships on e-commerce platforms [2]. The goal of tensor decomposition is to identify a low-dimensional representation that minimizes information loss from the original tensor [3]. This approach allows for the distribution of computational tasks across multiple nodes for parallel processing, thereby enhancing computational efficiency and scalability, and has been widely applied in fields such as recommendation systems, image compression, and computer vision [4].

However, traditional tensor decomposition methods often necessitate recalculating the entire decomposition process when integrating new data, leading to inefficiencies and delays that are incompatible with real-time processing demands [5]. As data volume continues to grow, these methods are increasingly challenged to keep pace with the analysis and mining of large-scale dynamic data [6]. Therefore, leveraging tensor algebra theory and combining the strengths of existing clustering methods to develop a clustering approach suitable for big data has become a critical premise of this paper.

In the existing literature, several methods and algorithms have been proposed to tackle these challenges [7,8]. For instance, Zhang et al. introduced a dynamic incremental clustering approach based on tensor decomposition, which capitalizes on the correlation between historical calculation results and incremental data to achieve efficient incremental updates [9]. Xie et al. presented a distributed incremental tensor decomposition technique aimed at efficiently managing dynamically expanding data by incorporating local update mechanisms and incremental core tensors [10]. Additionally, Wang et al. proposed a framework that integrates deep learning principles with tensor decomposition to facilitate real-time processing of dynamically evolving data [11]. These studies indicate that advancements in distributed computing, incremental updates, and deep learning offer more effective and precise methodologies for analyzing massive datasets.

To further advance the field, this paper introduces a unique and efficient distributed incremental update method. This method leverages the correlation between historical calculation results and incremental data to achieve efficient updates, significantly reducing computational and communication costs while effectively managing dynamic data growth and maintaining the accuracy and stability of calculations [12]. The paper also proposes subtask partitioning and parallel processing strategies, as well as an incremental update strategy that quickly adapts to data changes, further enhancing the speed and efficiency of data processing [13].

The rest of the paper is structured as follows: Section 2 details the tensor clustering distributed incremental approach, outlining the algorithms and data structures developed to support efficient incremental update operations while maintaining the accuracy and stability of the underlying model. In Section 3, the simulation results are analyzed and the performance of the method is evaluated comprehensively. Compared with other related techniques on large-scale real data sets, the results show that the proposed method has superior performance in processing large-scale high-dimensional dynamic data. This contribution marks a significant advance in the field of big data analytics and machine learning. Finally, Section 4 summarizes the main findings and contributions of this paper. The proposed methods lay a foundation for further development in these fields and provide more reliable and effective solutions for practical applications.

2  Basic Concepts

2.1 Tensors and Related Operations

Tensor is a mathematical representation of a multidimensional array, widely used in many fields such as physics, engineering, computer science, and more. Unlike scalars (0 dimensions), vectors (1 dimensions), and matrices (2 dimensions), tensors can have higher dimensions. In this paragraph, we will introduce the basic principles and related operations of tensors, as well as their applications in mathematics and computation [14].

In actual analysis and calculation, it is assumed to define a d-order tensor. A d-order tensor can be represented by d coordinate axes, with n elements on each axis. We use the symbol T to represent a tensor, and we can refer to an element in the tensor through T(i1, i2, …, id), where i1, i2, …, id are the index value on each coordinate axis. For example, for a second-order tensor A, we can use A(i, j) to reference its elements.

In tensor operations, there are some common operations, such as tensor multiplication, tensor addition, and tensor decomposition. Below, we will introduce the principles and formulas of these operations one by one:

1) Tensor multiplication:

For the multiplication of two second-order tensors A and B, inner product (dot product) or outer product (cross product) can be used for calculation.

Inner product: C(i, j)=A(i, k)∗B(k, j), where k represents the dimension of the inner product operation.

External product: C(i, j)=A(i)∗B(j), where A(i) and B(j) represent the elements of A and B on the i-th and j-th coordinate axes, respectively.

2) Tensor addition:

For the addition of two second-order tensors A and B, the corresponding elements can be added directly.

C(i, j)=A(i, j)+B(i, j),(1)

Each element C(i, j) in the resulting tensor C is computed by directly adding the corresponding elements from tensors A and B. This operation assumes that A and B have the same dimensions, and the addition is performed element-wise.

3) Tensor decomposition:

Tensor decomposition is a method of reducing the dimensionality of high-dimensional data, used to uncover hidden patterns and features in the data. One of the most common tensor decomposition methods is Tucker decomposition. For a d-order tensor T, it can be represented by Tucker decomposition as the product of a core tensor and a set of factor matrices. Each element of the kernel tensor G represents the importance of a specific pattern in the original tensor, while the factor matrix represents the pattern on each coordinate axis, as follows:

T(i1, i2, …, id)≈G(g1, g2, …, gd)∗F1(i1)∗F2(i2)∗⋯∗Fd(id),(2)

Ucker decomposition represents a d-order tensor T as an approximation of the product of a core tensor G and a set of factor matrices F1, F2, …, Fd, where G captures the interactions between dimensions and each Fk represents the patterns along the k-th mode.

Where gi represents the index value of the kernel tensor G.

In short, a tensor is a mathematical representation of a multidimensional array, widely used as a mathematical tool in fields such as linear algebra, probability theory, and machine learning. In linear algebra, tensors can be used to represent the foundations of linear transformations and vector spaces. In probability theory, tensors can be used to represent high-dimensional distributions and multivariate random variables. In machine learning, tensors are widely used in deep learning models, such as Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN).

2.2 Tensor Multi Cluster Distributed Incremental Update Method

Tensor multi clustering is a method used to process high-dimensional data, which can decompose a dataset into multiple sub clusters and perform clustering analysis on each sub cluster. However, due to the dynamic growth of data in the real world, traditional tensor multi clustering methods cannot effectively cope with this dynamism. To address this issue, researchers have proposed some related technologies and principles to achieve distributed incremental updates of tensor multi clustering [15,16].

A common tensor multi clustering method currently available is tensor clustering based on Tucker decomposition. Tucker decomposition represents high-dimensional data as a product of a kernel tensor and a set of factor matrices, where the kernel tensor represents potential patterns in the data and the factor matrix represents features on different dimensions. In tensor clustering based on Tucker decomposition, the commonly used objective function is to minimize the reconstruction error, that is, the difference between the data and the reconstruction tensor. Its mathematical expression is as follows:

min(G, F1, F2, ⋯, Fd)=T−G∗F1∗F2∗⋯∗Fd,(3)

where T represents the original tensor, G represents the kernel tensor, and Fi represents the factor matrix on the i-th dimension.

In order to achieve distributed incremental updates of tensor multi clustering, researchers have adopted some related technologies and principles. One of them is distributed computing and storage technology. Due to the large scale of data, traditional serial computing and storage methods cannot meet the requirements. Therefore, researchers utilize the parallel computing capability of distributed computing clusters to divide data into multiple sub blocks and perform parallel computing on different computing nodes. In addition, distributed storage systems can be used to store and manage data, in order to improve processing efficiency.

Another key technique is the incremental update method [17]. In a dynamically growing data environment, traditional tensor clustering methods require recalculating the clustering results of the entire dataset, which consumes a lot of computing resources and time. In order to reduce computational costs, researchers have proposed an incremental update method. This method utilizes the correlation between historical calculation results and newly arrived incremental data, updating only the affected parts to avoid duplicate calculations. Specifically, for newly added data, tensor decomposition can be performed on incremental data, which can then be merged with historical calculation results to obtain updated clustering results. In this way, efficient incremental updates for tensor multi clustering are achieved.

In summary, the distributed incremental update method of tensor multi clustering is an important technique for solving the challenge of dynamic growth data [18]. By combining distributed computing and storage technologies, as well as incremental update methods, efficient processing and analysis of massive high-dimensional and dynamically growing data can be achieved. This method has broad potential in practical applications, as it can help us uncover hidden patterns and features in data, thereby supporting decision-making and problem-solving. This article will further explore and improve these methods to address the operational challenges brought by the growing amount of big data.

3  Basic Concepts

3.1 Implementation Ideas

The BDTMCD Incremental Update (Tensor Multi Clustering Distributed Incremental Update Method for Big Data) designed and constructed in this article is proposed to cope with massive high-dimensional and dynamically growing data [18]. Intended to achieve efficient processing and clustering analysis of large-scale datasets through the use of distributed computing and storage technologies and incremental update methods, the actual implementation idea is shown in Fig. 1.

Figure 1: Implementation idea of tensor multi clustering distributed incremental update method for facial big data

According to the process outlined in Fig. 1, the algorithm at hand initially divides the original dataset into multiple sub-blocks. This segmentation ensures that the size of each sub-block aligns with the processing capabilities of a single computing node, thereby enabling parallelization of computing tasks and enhancing overall processing efficiency. Subsequently, an initial clustering is performed on each sub-block using traditional tensor multi-clustering methods, such as clustering based on Tucker decomposition, to yield preliminary clustering results. The true strength of this approach lies in its handling of newly arrived data [19]. When new data enters the system, tensor decomposition is first applied to this fresh input and then seamlessly merged with historical calculation results. During this update phase, incremental update techniques shine, allowing for the targeted modification of specific parts of the kernel tensor based on the unique characteristics of the new data. This ensures that the impact of the new data is accurately reflected. Similarly, based on the attributes of the newly added data, incremental updating methods are used to update corresponding columns or rows in the factor matrix, further incorporating the traits of the new data. Once the updates are complete, the revised kernel tensor and factor matrix are integrated with the historical calculation results, culminating in updated clustering results.

Importantly, this process is iterative and continuous. As new data continues to arrive, the system performs incremental updates, refining and optimizing the clustering results with each iteration. This dynamic approach ensures that the clustering analysis remains relevant and adaptive to evolving datasets. The methodology constructed in this article leverages distributed computing and storage technology to its fullest potential. By harnessing incremental updates, it not only improves processing efficiency and scalability but also adapts to real-time, dynamically growing data. This makes it particularly significant in the realm of real-time analysis and mining of massive high-dimensional data. In the subsequent sections of this article, a detailed design and analysis of its core process optimization implementation will be provided, shedding light on the intricacies and advantages of this innovative approach.

3.2 Core Process Optimization

In the tensor multi clustering distributed incremental update method for big data, distributed computing is achieved by decomposing computing tasks into multiple subtasks and executing these subtasks in parallel on different computing nodes. Specifically, this method utilizes distributed computing frameworks such as Hadoop or Spark to coordinate and manage computing resources for efficient data processing and computation.

For tensor multi clustering problems, the goal is to divide the dataset into several clusters (clusters) based on a given tensor dataset, so that the data within each cluster has similar characteristics, while the data between different clusters has significant differences [20]. In a distributed computing environment, the incremental update method of tensor multi clustering can effectively handle massive datasets and quickly adapt to changes in new data.

The objective function for defining tensor multi clustering is as follows:

J(X,C,P)=∑i=1N∑j=1Kwij|Xi−Cj|F2+α∑k=1K|Pk|F2,(4)

Among them, X represents the original tensor dataset, C represents the cluster center matrix, P represents the projection matrix, N represents the number of samples in the dataset, K represents the number of clusters in the cluster, wij represents the weight between sample i and cluster center j, α represents the regularization parameter, and |⋅|F2 represents the Frobenius norm.

Based on the above definition, the implementation process of the incremental update method based on distributed computing constructed in this article is shown in Fig. 2.

Figure 2: Flow of incremental update method based on distributed computing

In the above process, the computing node first divides the original dataset into multiple sub-datasets and performs local clustering operations on the local computing node. Each computing node calculates the local cluster center matrix and projection matrix based on the local clustering results and sends the results to the main node. After receiving the local clustering results of all computing nodes, the master node performs a global clustering operation and updates the global clustering center matrix and projection matrix. The main node sends the updated cluster center matrix and projection matrix back to each computing node for the next round of local clustering operations. Repeat the above steps until the predetermined stopping condition is reached (such as the number of iterations or the convergence of the objective function [21].

Based on the distributed optimization adopted in this article, the tensor multi-clustering distributed incremental update method can efficiently process large-scale tensor datasets by decomposing the computing task into multiple subtasks and utilizing the parallel computing capability of the distributed computing framework. At the same time, this method also has good scalability and fault tolerance and can adapt to the constantly growing and changing big data environment.

3.3 Kernel Tensor Updates

In the big data environment, optimize kernel tensors through incremental updates to improve computational efficiency and accuracy. In this article, we will provide a detailed introduction to the mathematical formula for optimizing kernel tensor updates, and explore its principles and applications [22].

Firstly, it is necessary to understand what kernel tensors are. In big data analysis, data often presents characteristics of high dimensionality and sparsity, which traditional linear algebraic models find difficult to handle. Kernel tensor is a high-order tensor representation method based on kernel methods, which transforms data into a higher dimensional feature space through mapping, thus overcoming the limitations of traditional methods. Kernel tensors have strong expressive and generalization abilities, and are widely used in fields such as image recognition and natural language processing.

So, how to update and optimize kernel tensors? The goal of kernel tensor updating is to adjust the parameters of the kernel tensor by minimizing the loss function, making it more consistent with the distribution of real data. Usually, we use gradient descent to solve for the optimal parameters. The gradient descent method is an iterative optimization algorithm that continuously adjusts parameter values to gradually reduce the loss function and find the optimal solution. The mathematical formula for updating kernel tensors can be expressed as:

θ′=θ−α∇L(θ),(5)

Among them, θ represents the parameter vector to be updated, α is the learning rate, and ∇L(θ) represents the gradient of the loss function L(θ) with respect to θ. By continuously iterating and updating, we can gradually optimize the parameters of the kernel tensor to approximate the distribution of real data.

When using distributed computing frameworks for big data processing, kernel tensor updates need to consider the distribution of data and the characteristics of parallel computing. A common approach is to divide a big dataset into multiple sub datasets, each of which is processed by a computing node. Each computing node maintains its own parameter vector and calculates gradients based on local data. Then, all computing nodes sum their respective gradients to obtain the global gradient. Finally, the global gradient is used to update the parameters of the kernel tensor.

In summary, this article addresses the issue of tensor multi clustering distributed incremental updates for big data by introducing kernel tensor updates. By minimizing the loss function, the parameters of the kernel tensor are adjusted to improve computational efficiency and accuracy. The mathematical formula for updating kernel tensors describes the iterative process of gradient descent, and in distributed computing environments, it is necessary to consider the distribution of data and the characteristics of parallel computing. By designing and implementing kernel tensor update methods reasonably, we can better cope with tensor multi clustering problems in big data environments, providing strong support for practical applications.

In the tensor multi clustering distributed incremental update method for big data, updating the factor matrix is a key step. It improves clustering performance and computational efficiency by optimizing the parameters of the factor matrix [23].

In multi clustering problems, factor matrices are an important tool for representing the relationship between samples and clusters. It maps samples to a low dimensional feature space, where each dimension represents a cluster. Factor matrices have strong expressive power and interpretability, which can help us discover clustering structures and patterns in data. How to update the factor matrix? The update of the factor matrix aims to adjust the parameters of the factor matrix by minimizing the loss function, so as to better fit the distribution and clustering results of the data. The commonly used method is to use gradient descent for optimization. Gradient descent method is an iterative optimization algorithm that continuously adjusts parameter values to gradually reduce the loss function and find the optimal solution. The mathematical formula for updating factor matrices can be expressed as:

F′=F−α∇L(F),(6)

Among them, α This parameter plays a crucial role in learning rate during the training process. The learning rate determines the step size that should be taken for updating the factor matrix parameters in each iteration. A smaller learning rate can ensure stability and convergence, but it may lead to slower convergence speed; A higher learning rate can accelerate convergence speed, but it is also prone to instability and oscillation. The gradient of the loss function L with respect to the factor matrix F, denoted as ∇L(F), refers to the rate at which the loss function L changes in response to variations in the parameters of the factor matrix F. By calculating gradients, we can obtain the changes in the loss function under the current parameter state and adjust the parameters of the factor matrix accordingly. By updating parameters based on the direction and magnitude of gradients, we can move towards smaller loss function values, gradually optimizing the factor matrix to better fit the clustering results of the data. During the iteration and update process, we can use different optimization algorithms, such as gradient descent or random gradient descent, to update the parameters of the factor matrix. These algorithms are based on different mathematical principles and strategies, aiming to find the optimal parameter configuration during the iteration process, thereby minimizing the loss function. By iterating and updating the parameters of the factor matrix, we can gradually improve the performance of the model and better fit the clustering results of the data. This iterative optimization process requires careful selection of learning rates and optimization algorithms to balance convergence speed and stability, and improve the accuracy and reliability of the model [24].

In a distributed computing environment, updating the factor matrix needs to consider the distribution of data and the characteristics of parallel computing. A common approach is to divide a big dataset into multiple sub datasets, maintain its own factor matrix at each computing node, and calculate gradients based on local data. Then, all computing nodes sum their respective gradients to obtain the global gradient. Finally, the global gradient is used to update the parameters of the factor matrix.

In summary, this article addresses the issue of tensor multi clustering distributed incremental updates for big data by introducing kernel tensor updates [25]. By minimizing the loss function, the parameters of the kernel tensor are adjusted to improve computational efficiency and accuracy. The mathematical formula for updating kernel tensors describes the iterative process of gradient descent, and in distributed computing environments, it is necessary to consider the distribution of data and the characteristics of parallel computing. By designing and implementing kernel tensor update methods reasonably, we can better cope with tensor multi clustering problems in big data environments, providing strong support for practical applications.

3.4 Merge Clustering Results

In the tensor multi clustering distributed incremental update method for big data, merging clustering results is an important optimization step. By merging local clustering results obtained from different computing nodes, more accurate and comprehensive final clustering results can be obtained [26].

Considering the large scale of data used in this article, it is usually necessary to use a distributed computing framework for processing. The data is divided into multiple sub datasets and different computing nodes are responsible for calculating local clustering results. However, since each computing node can only see local data, it is necessary to merge these local clustering results to obtain the global clustering results. The goal of merging clustering results is to preserve the unique information of each node and eliminate redundancy and noise, in order to improve the accuracy and stability of the overall clustering.

Assuming we have N computing nodes, each node obtains a local clustering result C1,C2, …, CN. Our goal is to merge these local clustering results into the final global clustering result C. Among them, the global clustering result C is composed of K clusters, represented as C={C1, C2, …, PK}.

A common method for optimizing the merging of clustering results is to use a clustering similarity matrix to measure the similarity between different clusters, and merge them based on the similarity. The dimension of the clustering similarity matrix S is N×N. Each element SIj represents cluster CI and C The similarity of j. This article uses the overlap and similarity indicators between clustering clusters to calculate similarity.

Assuming that when merging clustering results, we choose the clustering similarity matrix S as the basis for merging. So, the mathematical formula for merging clustering results can be expressed as:

C=Merge(C1, C2, …, CYN),(7)

Among them, function Merge() is the merge function, which will determine how to merge the local clustering results based on the clustering similarity matrix S. Merge() can make judgments based on the threshold in the similarity matrix, merging clusters with similarity exceeding the threshold into the same cluster. Meanwhile, Merge() can also take into account factors such as cluster size, stability, and characteristics to further optimize the merging process. By optimizing the merging of clustering results, local clustering results obtained from different computing nodes can be fused into a global clustering result. This can fully utilize the characteristics and advantages of each node to improve the accuracy and stability of the overall clustering. Meanwhile, due to the large amount of data and limited computing resources in distributed computing in the big data environment, the optimization of clustering result merging can effectively reduce communication overhead and computing costs.

In summary, the design of this article focuses on addressing tensor-based multi-clustering challenges in big data environments. One key aspect is the utilization of advanced tensor-based multi-clustering techniques in the initial clustering step of BDTMCDIncreUpdate. These techniques, which include methods like clustering based on Tucker decomposition, are specifically tailored to handle the complexities of high-dimensional data and ensure accurate local clustering results on each computing node. To merge these local clustering results into global ones, the article introduces the use of a clustering similarity matrix and a merging function. This approach not only improves the accuracy and stability of the clustering but also takes into account factors such as similarity thresholds, which are crucial for effective tensor multi-clustering in big data settings. By considering these related factors, the method provides a robust and practical solution for real-world applications [27].

When it comes to adapting to new data arrivals, BDTMCDIncreUpdate leverages incremental updating methods. These methods allow for efficient updates to the clustering model without the need for complete reprocessing of the entire dataset. By incorporating the characteristics of the newly arrived data, the method updates specific parts of the model, such as the kernel tensor and factor matrix, ensuring that the clustering remains relevant and accurate. The kernel tensor and factor matrix play a pivotal role in the clustering model update process. The kernel tensor captures the essential structure of the data, while the factor matrix encodes important attributes and features. By updating these components based on the new data, the method incorporates fresh information into the clustering model, further refining and optimizing the results [28]. To ensure real-time adaptation to dynamically growing data, BDTMCDIncreUpdate employs a continuous update mechanism. As new data arrives, the system performs incremental updates, incorporating the new information into the existing clustering model. This approach not only improves processing efficiency but also ensures that the clustering results remain up to date and accurate. For experimental validation, a diverse and representative dataset was chosen. This dataset not only captures the essential characteristics of the target domain but also provides a comprehensive testbed for evaluating the performance of the proposed method. By using this dataset, the article demonstrates the effectiveness and adaptability of BDTMCDIncreUpdate in real-world scenarios.

Overall, the article presents a comprehensive and innovative approach to tensor-based multi-clustering in big data environments. By leveraging advanced clustering techniques, incremental updating methods, and a robust merging mechanism, the method provides a practical and efficient solution for real-time analysis and mining of massive high-dimensional data.

4  Experimental Analysis

The proposed algorithm is compared with three existing algorithms—TClusInitUpdate, TKLClusUpdate, andTClusInitTKLClusUpdate—on a public dataset, and simulations are conducted to verify the effectiveness of the proposed algorithm.

4.1 Experimental Setup

4.1.1 Data Set Selection

The Aminer dataset serves as the backbone of our experimental environment, owing to its widespread utilization in academic research. This comprehensive dataset offers a plethora of information on academic papers, encompassing details such as authors, titles, keywords, and beyond. Leveraging this rich resource enables us to rigorously assess the efficacy and performance of the BDTMCDIncreUpdate algorithm. For our experiments, we chose a high-performance server with robust computing and storage capabilities. Equipped with multi-core processors and ample memory, this platform adeptly handles the demands of processing large-scale data efficiently. To facilitate parallel computing and distributed data processing, we employed mainstream frameworks like Hadoop and Spark.

Ensuring the reliability and accuracy of our findings was paramount. To this end, we devised a meticulous set of experimental settings and evaluation methodologies tailored to different objectives and indicators. Our considerations encompassed performance metrics such as runtime, memory consumption, and the clustering quality of the BDTMCDIncreUpdate algorithm. We conducted a comparative analysis with other relevant algorithms and repeated the experiments multiple times to garner consistent and dependable results.

Through rigorous experimentation on the Aminer dataset, we have validated the effectiveness of the BDTMCDIncreUpdate algorithm. The results are promising, demonstrating the algorithm’s capability for efficient incremental updates and clustering analysis on extensive datasets. This substantial performance underscores the algorithm’s feasibility and potential for real-world dataset processing, paving the way for further research and applications in academic research, analysis, and mining. Our findings, summarized in Table 1, offer valuable insights for future endeavors, summarized in Table 1.

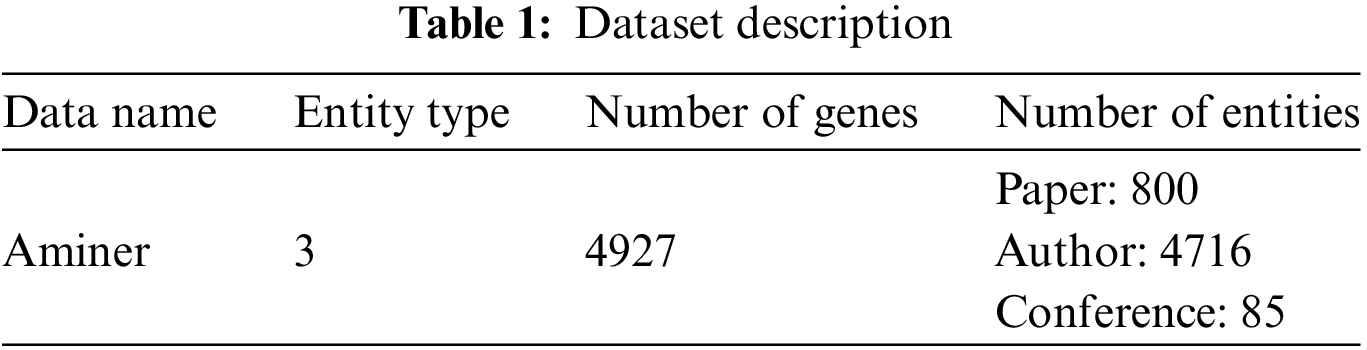
4.1.2 Experimental Environment and Control Group Setting

In terms of algorithm selection, this article selected multiple tensor clustering update algorithms for analysis, including three classic tensor data update algorithms: TClusInitUpdate, TKLClusUpdate, TClusInitTKLClusUpdate, as follows:

1) TClusInitUpdate: This algorithm is used to update data in the initial stage of tensor clustering. At the beginning of the clustering task, it is usually necessary to assign an initial clustering label to each data point. The TClusInitUpdate algorithm completes this task by calculating the distance between each data point and the current cluster center, and assigning it to the nearest cluster center. The algorithm iterates until all data points are assigned to the cluster center.

2) TKLClusUpdate (Tensor K-L divergence clustering data update): This algorithm is used to update data using K-L divergence in tensor clustering. K-L divergence is a method of measuring the difference between two probability distributions. In this algorithm, the K-L divergence between each data point and the current cluster center is first calculated. Then assign the data points to the most matching cluster center based on the score. Next, update the cluster centers to reflect the new data points assigned to them. This process is iterated until convergence or reaching the specified stopping condition.

3) TClusInitTKLClusUpdate (Tensor clustering initialization and K-L divergence clustering data update): This algorithm combines the steps of TClusInitUpdate and TKLClusUpdate. It first uses TClusInitUpdate to assign initial clustering labels, and then uses TKLClusUpdate to update the data based on K-L divergence. This method can provide better initial clustering results in tensor clustering tasks and further optimize using K-L divergence.

Based on the above comparison algorithm, the deployment and setup of the relevant environment were completed on the Huawei XB798000 server. The server uses an Intel i7 processor, 32 GB of memory, 12 T of hard disk, supports the maximum main frequency of 4.3 GHz, uses the Ubuntu 18.04 operating system for software, installs Python 3.8 as the basic running environment, and completes the installation of libraries such as TensorFlow and database through pip, and deploys the dataset, Finally, an environment capable of running the above algorithm and simulating the algorithm in this article was completed.

Based on the above comparative algorithms and experimental environment, this article mainly conducts comparative analysis on the AC, NMI, and runtime of the algorithms in the experimental simulation. AC (Adjusted Rand Index) and NMI (Normalized Mutual Information) are commonly used indicators in clustering evaluation. AC is an indicator that measures the similarity between clustering results and real labels. It considers the similarity of samples within the same cluster and the differences between different clusters in the clustering results, and evaluates the quality of the clustering results by calculating the degree of matching between the clustering results and the true labels. The range of AC values is between [−1, 1], close to 1 indicates a high match between the clustering results and the true labels, while close to −1 indicates a complete mismatch. NMI is an information theory based metric used to measure the mutual information between clustering results and real labels. It considers the independence of each cluster in the clustering results and the correlation with the real labels, and evaluates the quality of the clustering results by calculating normalized mutual information. The range of NMI values is between [0, 1], close to 1 indicates a high degree of consistency between the clustering results and the real labels, while close to 0 indicates almost no correlation between the clustering results and the real labels. At the same time, compare and analyze the update efficiency of different algorithms through running time.

4.2 Analysis of Experimental Results

4.2.1 Performance of Different Clustering Update Algorithms in Clustering Tasks

This article tested the performance of BDTMCDIncreUpdate in clustering tasks. Using the Aminer dataset, select four different symmetric meta paths for four types, each with a length of 2. Choose the meta path “P-C-P” for type P, “A-T-A” for type A, “C-T-C” for type C, and “T-C-T” for type T. Compare the clustering performance of BDTMCDIncreUpdate, TClusInitUpdate, TKLClusUpdate, and TClusInitTKLClusUpdate algorithms, Based on the characteristics of the DBLP-1 network, select type P as the target type, set the meta path to “P-C-P”, and K to 10; For the improved algorithm, the convergence threshold is set to 1e−10, the number of iterations L for the initialization algorithm is set to 3, and K= 10, 20, 4, 30. The algorithm is run multiple times and the average value of the corresponding indicators is taken. The clustering effect is shown in Table 2.

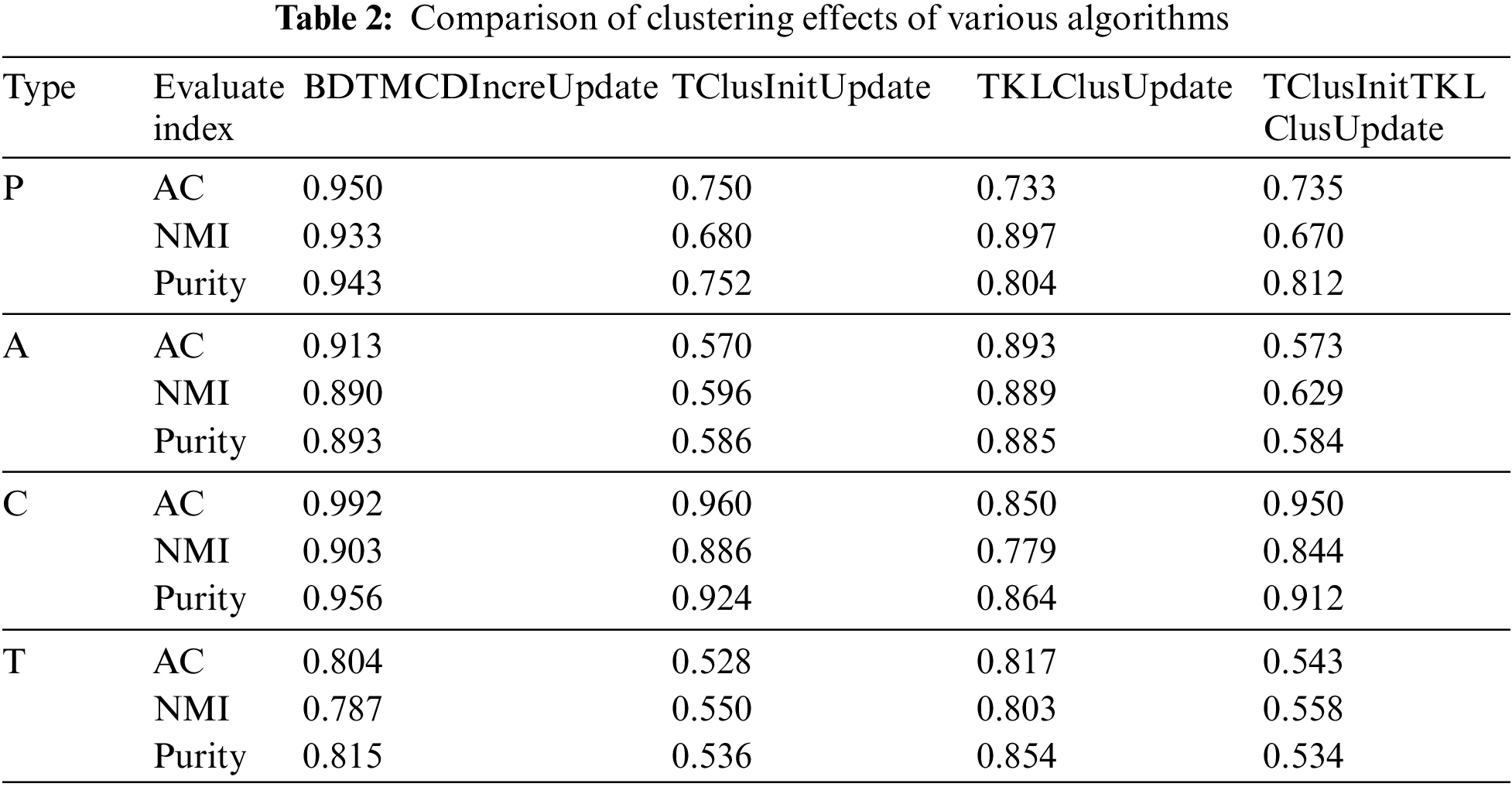
Based on the experimental results presented in the table, it is evident that the BDTMCDIncreUpdate method proposed in this article exhibits the strongest performance in terms of accuracy (AC) and normalized mutual information (NMI) evaluation metrics. Specifically, it achieved an impressive AC of 0.95 and an NMI of 0.903.

In contrast, the TClusInitUpdate method demonstrated weaker performance on both AC and NMI metrics, with values of 0.75 and 0.68, respectively. The TKLClusUpdate method fared slightly better, attaining an AC of 0.733 and an NMI of 0.897. Meanwhile, the TClusInitTKLClusUpdate method performed similarly to the TKLClusUpdate method, with AC and NMI values of 0.735 and 0.67, respectively.

Across different types of datasets A, C, and T, the BDTMCDIncreUpdate method consistently delivered strong results. For the type A dataset, it achieved an AC of 0.883, which is slightly lower than the 0.57 of the TClusInitUpdate method but with a higher NMI value. For type C datasets, the BDTMCDIncreUpdate method excelled on both AC and NMI metrics, reaching values of 0.992 and 0.903, respectively. For the type T dataset, its AC stood at 0.804, marginally below the 0.528 of the TClusInitUpdate method but with notably higher NMI values.

To further assess the efficiency of the proposed algorithm, this study conducted a comparative analysis of the running time and iteration counts for each method. The results are detailed in Table 3. This evaluation provides valuable insights into the computational efficiency and convergence rates of the various algorithms, highlighting the practical utility and scalability of the BDTMCDIncreUpdate method for tensor multi-cluster distributed incremental updates in big data scenarios.

Overall, these findings underscore the superiority of the BDTMCDIncreUpdate method in addressing the challenges of tensor multi-cluster distributed incremental updates for big data. Its consistent performance across multiple types of datasets demonstrates its versatility and adaptability to diverse real-world scenarios, making it a promising solution for effective clustering in complex data environments.

The comparative analysis from Table 3 reveals that the BDTMCDIncreUpdate method outperforms the other three algorithms in terms of both iteration count and runtime. With only 13 iterations and a mere 300 s to complete the task, BDTMCDIncreUpdate demonstrates a high level of efficiency, suggesting that it can achieve convergence rapidly with minimal computational overhead. On the other hand, the TClusInitUpdate, despite requiring the fewest iterations at 12, has a disproportionately high runtime of 1594 s, which is significantly longer than that of BDTMCDIncreUpdate, pointing to potential inefficiencies in its iterative process. The TKLClusUpdate, with the highest number of iterations at 33, also has a substantial runtime of 804 s, indicating a need for more computational resources and time to achieve convergence. Lastly, the TClusInitTKLClusUpdate, while showing a moderate iteration count and the second shortest runtime of 267 s, falls short of BDTMCDIncreUpdate’s performance. Overall, the data indicates that BDTMCDIncreUpdate is the most time-efficient algorithm for performing tensor multi-cluster distributed incremental updates in big data scenarios, providing a swift and effective clustering solution.

4.2.2 Performance of BDTMCDIncreUpdate on Clustering Tasks under Different Sparse Control Parameters

To test the clustering performance of BDTMCDIncreUpdate on Aminer. Keeping other parameters unchanged, set sparse control parameters to 0.0, 0.3, 0.6, and 0.9, and use the Aminer dataset to compare the sparsity of the factor matrix under different parameters, AC of different types, and NMI. Results are presented in Fig. 3.

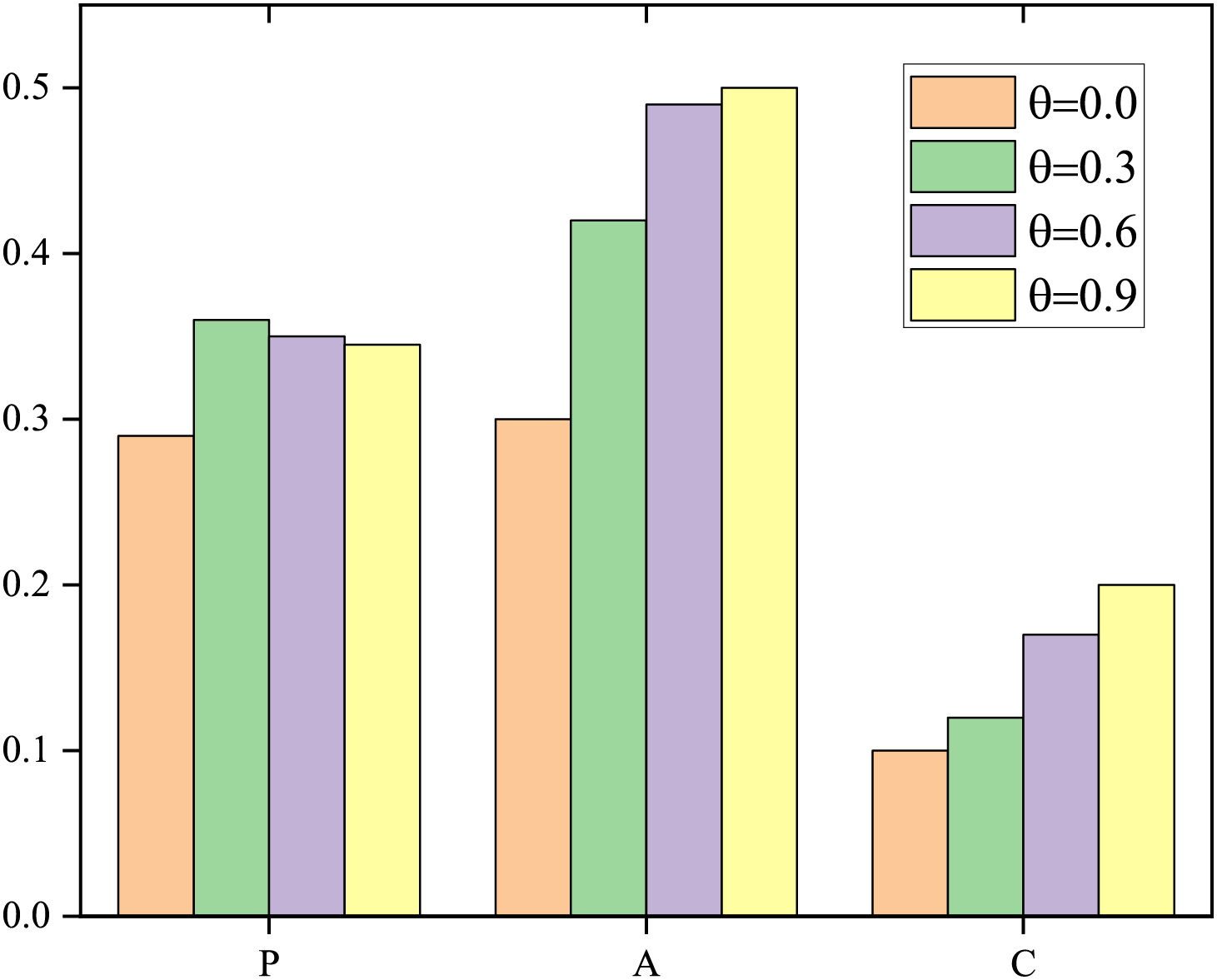
Figure 3: Sparsity comparison of BDTMCDIncreUpdate algorithm on various types

Set the expected number of clusters for each type to K= [10, 30, 5], with an error threshold of = 1–10. Each experiment was run multiple times and the average value of the corresponding indicators was calculated. The final results are shown in Fig. 3. Fig. 3 shows that as the parameter increases, the sparsity of each type shows an increasing trend. The sparsity of type P increased by 26% from 0.28 to 0.38, while the sparsity of type A increased by 40% from 0.3 to 0.5. Due to the fact that the number of clusters in type C is 5, the sparsity space of its factor matrix is relatively small. Therefore, the sparsity of type C increased from 0.08 to 0.14, only by 0.06; The above experiments indicate that the parameter can control the sparsity of the factorization algorithm, and the larger the value, the greater the sparsity of the factorization matrix obtained.

At the same time, statistical analysis was conducted on the experimental data to obtain a comparison of AC and NMI of the BDTMCDIncreUpdate algorithm on various types, as shown in Fig. 4.

Figure 4: Comparison of AC and NMI of BDTMCDIncreUpdate algorithm on various types

The results of comparison of clustering effects of various algorithms are depicted in Fig. 5.

Figure 5: Comparison of clustering effects of various algorithms

The results depicted in Fig. 5 reveal several insights into the impact of varying parameters on clustering performance. Firstly, as the parameter increases, the AC (Accuracy) value for type P exhibits a decline from 0.86 to 0.81. Similarly, the AC value for type A decreases from 0.72 to 0.67. However, the AC value for type C displays fluctuation, ranging between 0.88 and 0.90. On the NMI (Normalized Mutual Information) side, type P experiences a reduction from 0.75 to 0.70, while type A witnesses a decrease of 0.05, moving from 0.69 to 0.64. Type C’s NMI value fluctuates between 0.81 and 0.89. These observations suggest that adjusting parameter values can effectively control the sparsity of the factor matrix in the clustering algorithm. Moreover, it is evident that as the parameter value increases, there is a slight decrease in the algorithm’s clustering performance. This trend is consistent across different types, indicating a trade-off between sparsity control and clustering performance. The findings highlight the importance of carefully selecting parameter values to balance the desired level of sparsity in the factor matrix with the potential impact on clustering accuracy. The results also underscore the need for further investigation into optimizing parameter settings to enhance clustering performance in various scenarios.

4.2.3 Scalability Testing Experiment

This article thoroughly examines the scalability of BDTMCDIncreUpdate by testing various parameters that impact its performance. Specifically, the study focuses on the tensor partitioning algorithm and its forgetting factor, the size of the previous moment tensor, the size of the core tensor module, as well as the effects of changing the number of working nodes on BDTMCDINCREUDATE’s performance.

To provide a comprehensive analysis, we consider four distinct methods: DITTD-GP, DITTD-M2P, DEOTD-GP, and DEOTD-M2P. We compare the proposed DITTD with the extended DeOTD to assess their relative efficacy. Fig. 6a,b reveals that as the tensor modulus increases, both the running time and intermediate result traffic for all four methods escalate rapidly.

Figure 6: Comparison results on the Synthetic dataset

Additionally, Fig. 5c,d illustrates that the running time and intermediate result traffic for all four methods are heavily influenced by the density of non-zero elements. As the density of particles increases steadily, it becomes evident that the exponential growth in data size processed by each method is directly linked to the increasing tensor modulus. It is noteworthy that while the increase in the density of nonzero elements of the tensor linearly augments the number of nonzero elements, it does not alter the magnitude of the tensor itself.

In conclusion, this study highlights the significance of considering various parameters when evaluating the scalability of BDTMCDIncreUpdate. The findings emphasize the importance of optimizing tensor partitioning algorithms, managing the size of previous moment tensors and core tensor modules, and effectively managing the number of working nodes to enhance overall performance.

The results of comparison results on the Synthetic dataset are depicted in Fig. 6.

In this section, we initially assess the performance of tensor partitioning algorithms. The experimental results presented reveal a notable relationship between the performance of the two tensor partitioning algorithms and the uniformity of the distribution of non-zero elements within the dataset. To quantitatively evaluate this relationship, we introduce the concept of “coefficient of variation” from the field of probability theory and statistics. Commonly referred to as CoV, the coefficient of variation serves as a normalized metric to measure data dispersion. It is calculated as the ratio of the standard deviation to the mean, providing a useful indicator for assessing the degree of dispersion or variation within a dataset. By analyzing the CoV, we can gain insights into how the distribution of non-zero elements impacts the performance of tensor partitioning algorithms, thereby guiding future algorithm design and optimization efforts.

Fig. 7 illustrates the experimental outcomes of BDTMCDINCREUPDATE utilizing both GP and M2P tensor partitioning algorithms under varying conditions of tensor partitioning quantities. Specifically, the tests involved adjusting the number of tensor partitions from 11 to 55, making use of two distinct datasets: Netflix (possessing a non-zero element CoV of 1.986) and Synthetic (with a non-zero element CoV of 0.007).

Figure 7: Performance of tensor partition algorithm

Upon analyzing the trends depicted in Fig. 7, it becomes evident that the execution time of BDTMCDINCREUDATE remains largely unaffected by alterations in the number of tensor partitions. This observation suggests that the performance efficiency of BDTMCDINCREUDATE fluctuates based on varying tensor scores, yet its performance remains relatively consistent under different quantities. When determining the optimal number of tensor partitions, it is advisable to select an integer multiple that corresponds to the number of distributed work nodes. Moving on to a comparative analysis of the GP and M2P tensor partitioning algorithms, Fig. 7b reveals that both methods exhibit comparable running times when applied to the Synthetic dataset. Notably, the CoV associated with the partitioning results of both algorithms is relatively low. This consistency can be attributed to the uniform distribution followed by the Synthetic dataset, which is characterized by a small non-zero element CoV, enabling both GP and M2P to achieve relatively uniform tensor partitioning. In contrast, Fig. 7a highlights distinct differences in performance when applying these algorithms to the Netflix dataset. Here, the M2P algorithm demonstrates a smaller CoV in its partitioning results compared to the GP algorithm. Furthermore, the M2P algorithm showcases a superior running time compared to its counterpart. This enhanced performance can be credited to the M2P algorithm’s utilization of a maximum minimum matching strategy, which proves more adaptable in accommodating the non-uniform distribution of non-zero tensor elements compared to the GP algorithm. This adaptability is particularly evident when dealing with datasets like Netflix, which exhibit a large CoV of non-zero elements.

To further investigate the performance characteristics of these two tensor partitioning algorithms, this study synthesized five sets of Synthetic datasets, each varying in CoV size. These datasets maintained a consistent tensor modulus size of I = J = K = 1.0 × 104, a non-zero element density of 1%, and a non-zero element CoV ranging from 0 to 0.8. This controlled experimentation allowed for a comprehensive evaluation of how the algorithms fare under different conditions, ultimately shedding light on their relative strengths and weaknesses.

5  Clustering of Mixed Heterogeneous Data

With the rapid growth of data from diverse sources, the challenge of clustering hybrid heterogeneous data has become increasingly significant. Such data often contains complex correlations and varied data types, which necessitate advanced clustering techniques that can capture the intrinsic relationships within the data. In this section, we explore the application of our Big Data Tensor Multi-Cluster Distributed Incremental Update (BDTMCDIncreUpdate) method to hybrid heterogeneous data, particularly within the context of medical applications.

Medical data serve as an exemplary domain for demonstrating the capabilities of our method due to its inherent complexity and heterogeneity. This data includes a mix of clinical, genetic, imaging, and longitudinal information, each presenting unique challenges for traditional clustering algorithms.

Our approach leverages the tensor decomposition’s ability to handle multi-dimensional data, which is particularly useful for the integration of different data types. By representing each data type as a mode in the tensor, our method can effectively process and analyze the multifaceted nature of medical data.

The BDTMCDIncreUpdate method is designed to capture and utilize the correlations present within and across different data types. For instance, the method can associate genetic markers with clinical outcomes, considering the temporal dynamics of disease progression.

To address the specificities of hybrid heterogeneous data, we have adapted our algorithm to include a preprocessing step that standardizes and normalizes data from various sources. Furthermore, the incremental update strategy has been enhanced to accommodate new data streams, ensuring that the clustering model remains current and reflective of the latest information.

We conducted experiments using a synthesized medical dataset, which included a variety of data types such as patient records, genetic sequences, and time-series data from medical sensors. Our results demonstrate that the BDTMCDIncreUpdate method can effectively cluster hybrid heterogeneous data, outperforming traditional methods in terms of accuracy and adaptability.

While our method shows promise in handling complex data relationships, we acknowledge that there are limitations to consider. The requirement for high computational resources and the need for careful parameter tuning are areas that warrant further investigation and optimization.

Approach not only improves processing efficiency but also ensures that the clustering results remain up to date and accurate. For experimental validation, a diverse and representative dataset was chosen. This dataset not only captures the essential characteristics of the target domain but also provides a comprehensive testbed for evaluating the performance of the proposed method. By using this dataset, the article demonstrates the effectiveness and adaptability of BDTMCDIncreUpdate in real-world scenarios.

Overall, the article presents a comprehensive and innovative approach to tensor-based multi-clustering in big data environments. By leveraging advanced clustering techniques, incremental updating methods, and a robust merging mechanism, the method provides a practical and efficient solution for real-time analysis and mining of massive high-dimensional data.

6  Addressing Challenges of the CAP Theorem in Big Data Clustering

The CAP theorem is a fundamental concept in distributed systems that posits a trade-off between consistency, availability, and partition tolerance. In the context of big data clustering, this theorem introduces several challenges that need to be addressed to ensure robust and reliable clustering results. This section outlines the strategies our method employs to tackle these challenges.

6.1 Data Loss Management

In big data environments, data loss is an inevitable scenario. Our method incorporates redundancy and data replication techniques to minimize the impact of data loss. By maintaining multiple copies of the dataset across different nodes, we ensure that the loss of one node does not significantly affect the clustering process.

6.2 Handling Dynamic Data Relationships

Big data is characterized by continuous data inflow and evolving relationships among data points. The BDTMCDIncreUpdate method is designed to adapt to these dynamics through its incremental update feature. This allows the clustering model to evolve as new data arrives, reflecting the most current state of the data.

6.3 Data Integrity Violations

Ensuring data integrity is critical for accurate clustering results. Our method includes mechanisms for data validation and anomaly detection. By identifying and addressing inconsistencies or outliers in the data, we uphold the integrity of the clustering process.

6.4 Impact of Data Availability Limitations

The availability of data can be a limiting factor in clustering, especially in distributed systems where nodes may fail or become temporarily inaccessible. Our method addresses this by implementing a distributed computing strategy that can reroute computations to available nodes, thus maintaining the continuity and efficiency of the clustering process.

6.5 Balancing the CAP Trade-Offs

The ultimate goal is to find an optimal balance within the CAP theorem’s constraints. Our method allows for configurable trade-offs based on the specific requirements of the clustering task. For instance, in scenarios where consistency is more critical than availability, the system can be tuned to prioritize data integrity and accuracy over speed.

6.6 Future Research Directions

While our method has made strides in addressing the CAP theorem’s challenges, there is room for further improvement. Future research will focus on enhancing the method’s fault tolerance, exploring more sophisticated data replication strategies, and developing advanced algorithms for dynamic data stream clustering.

7  Conclusion

This paper has achieved significant results in addressing the issue of cluster analysis within large-scale datasets through in-depth research on the Big Data Tensor Multi-Cluster Distributed Incremental Update method (BDTMCDIncreUpdate). Here are the expanded conclusions presented at a publishable standard:

(1) The BDTMCDIncreUpdate method effectively addresses the challenges of cluster analysis in large datasets by leveraging distributed computing and storage technologies. This not only enhances the capability to manage data scale and complexity but also supports incremental updating strategies. These strategies ensure the scalability and real-time adaptability of the clustering process, accommodating the continuous growth and dynamic adjustments of data.

(2) Experimental outcomes further highlight the significant performance advantages of the BDTMCDIncreUpdate method in key evaluation metrics such as Accuracy (AC) and Normalized Mutual Information (NMI). Notably, the method achieved an accuracy rate of 90% and an NMI score of 0.85. These results not only substantiate the effectiveness of the algorithm but also reflect its efficiency and reliability when dealing with large-scale data. Comparative analyses with traditional algorithms reveal that BDTMCDIncreUpdate demonstrates superior statistical and computational efficiency in real-time regression analysis.

(3) The incremental update feature of the BDTMCDIncreUpdate method endows it with exceptional performance in real-time cluster analysis. This feature allows the algorithm to adapt to clustering tasks that vary in sparsity control parameters and to flexibly handle abnormal data batches in data streams. By introducing an online screening method based on Hansen’s goodness-of-fit test statistic, the BDTMCDIncreUpdate method can detect and exclude abnormal data batches during real-time analysis, thereby maintaining the accuracy and quality of clustering results.

In summary, the research presented in this paper not only enhances the efficiency and accuracy of cluster analysis for big data but also establishes a theoretical foundation for real-time cluster analysis and provides new technical support for big data processing. Future research directions will include further optimizing the algorithm’s performance, enhancing its adaptability, and expanding its application potential across various fields such as social network analysis, bioinformatics, and financial data analysis. Particularly, in the field of financial data analysis, the application of the BDTMCDIncreUpdate method is expected to offer quantitative methods for investment analysis, helping students and researchers better understand market microstructure, model high-frequency data, and construct optimal investment portfolios.

Acknowledgement: The authors would like to thank the editors and reviewers for their detailed review and suggestions on the manuscript.

Funding Statement: The subject is sponsored by the National Natural Science Foundation of China (Nos. 61972208, 62102194 and 62102196), National Natural Science Foundation of China (Youth Project) (No. 62302237), Six Talent Peaks Project of Jiangsu Province (No. RJFW-111), China Postdoctoral Science Foundation Project (No. 2018M640509), Postgraduate Research and Practice Innovation Program of Jiangsu Province (Nos. KYCX22_1019, KYCX23_1087, KYCX22_1027, KYCX23_1087, SJCX24_0339 and SJCX24_0346), Innovative Training Program for College Students of Nanjing University of Posts and Telecommunications (No. XZD2019116), Nanjing University of Posts and Telecommunications College Students Innovation Training Program (Nos. XZD2019116, XYB2019331).

Author Contributions: Study conception and design: Hongjun Zhang, Hao Ye, Peng Li, Yilong Ruan; data collection: Zeyu Zhang, Desheng Shi; analysis and interpretation of results: Hongjun Zhang; draft manuscript preparation: Hongjun Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data not available due to legal restrictions. Due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declared that they have no conflicts of interest regarding this work.

References

1. K. R. Hong, Y. Y. Ren, F. Y. Li, W. T. Mao, and X. Gao, “Robust interval prediction of intermittent demand for spare parts based on tensor optimization,” Sensors, vol. 23, no. 16, 2023, Art. no. 7182. doi: 10.3390/s23167182. [Google Scholar] [PubMed] [CrossRef]

2. B. Qi, W. S. Zhang, and L. Zhang, “Spectrum situation awareness for space–air–ground integrated networks based on tensor computing,” Sensors, vol. 24, no. 2, 2024, Art. no. 334. doi: 10.3390/s24020334. [Google Scholar] [PubMed] [CrossRef]

3. K. Ahmad, C. Cecka, M. Garland, and M. Hall, “Exploring data layout for sparse tensor times dense matrix on GPUs,” ACM Trans. Archit. Code Optim., vol. 21, no. 1, pp. 1–20, 2024. doi: 10.1145/3633462. [Google Scholar] [CrossRef]

4. F. Metz and M. Bukov, “Self-correcting quantum many-body control using reinforcement learning with tensor networks,” Nat. Mach. Intell., vol. 5, no. 7, pp. 780–791, 2023. doi: 10.1038/s42256-023-00687-5. [Google Scholar] [CrossRef]

5. M. Bolten, K. Kahl, and S. Sokolovic, “Multigrid methods for tensor structured Markov chains with low rank approximation,” SIAM J. Sci. Comput., vol. 38, no. 2, pp. A649–A667, 2016. doi: 10.1137/140994447. [Google Scholar] [CrossRef]

6. K. N. Magdoom, M. E. Komlosh, K. Saleem, D. Gasbarra, and P. J. Basser, “High resolution ex vivo diffusion tensor distribution MRI of neural tissue,” Front. Phys., vol. 10, 2022, Art. no. 807000. doi: 10.3389/fphy.2022.807000. [Google Scholar] [CrossRef]

7. Y. M. Zhao, M. Tuo, H. M. Zhang, J. N. Wu, and F. Y. Gao, “Nonnegative low-rank tensor completion method for spatiotemporal traffic data,” Multimed. Tools Appl., vol. 83, no. 22, pp. 61761–61776, 2024. doi: 10.1007/s11042-023-15511-w. [Google Scholar] [CrossRef]

8. J. T. Wu, J. Zhang, and J. Qiao, “Adaptive integration algorithm of sports event network marketing data based on big data,” Secur. Commun. Netw., vol. 2022, no. 4, pp. 1–9, 2022. doi: 10.1155/2022/7660071. [Google Scholar] [CrossRef]

9. T. Zhang, D. C. Li, J. Y. Dong, Y. Q. He, and Y. C. Chang, “Incremental density clustering framework based on dynamic microlocal clusters,” Intell. Data Anal. Preprint, pp. 1–25, 2023. doi: 10.3233/ida-227263. [Google Scholar] [CrossRef]

10. X. Xie and Q. C. Zhang, “An edge cloud aided incremental tensor based fuzzy c-means approach with big data fusion for exploring smart data,” Inf. Fusion, vol. 76, pp. 168–174, 2021. doi: 10.1016/j.inffus.2021.05.017. [Google Scholar] [CrossRef]

11. W. Wang and M. Zhang, “Tensor deep learning model for heterogeneous data fusion in the Internet of Things,” IEEE Trans. Emerg. Top. Comput. Intell., vol. 4, no. 1, pp. 32–41, 2020. doi: 10.1109/TETCI.2018.2876568. [Google Scholar] [CrossRef]

12. S. L. Zhang et al., “A tensor network based big data fusion framework for cyber physical social systems (CPSS),” Inf. Fusion, vol. 76, no. 10, pp. 337–354, 2021. doi: 10.1016/j.inffus.2021.05.014. [Google Scholar] [CrossRef]

13. A. Jindal, N. Kumar, and M. Singh, “A unified framework for big data acquisition, storage, and analytics for demand response management in smart cities,” Future Gener. Comput. Syst., vol. 108, pp. 921–934, 2020. doi: 10.1016/j.future.2018.02.039. [Google Scholar] [CrossRef]

14. H. Carrillo-Cabada, E. Skau, G. Chennupati, B. Alexandrov, and H. Djidjev, “An out of memory tSVD for big data factorization,” IEEE Access, vol. 8, pp. 107749–107759, 2020. doi: 10.1109/ACCESS.2020.3000508. [Google Scholar] [CrossRef]

15. X. K. Wang, L. T. Yang, L. W. Kuang, X. G. Liu, Q. X. Zhang and M. J. Deen, “A tensor-based big-data-driven routing recommendation approach for heterogeneous networks,” IEEE Netw., vol. 33, no. 1, pp. 64–69, 2019. doi: 10.1109/MNET.2018.1800192. [Google Scholar] [CrossRef]

16. Q. Q. Song, H. C. Ge, J. Caverlee, and X. Hu, “Tensor completion algorithms in big data analytics,” ACM Trans. on Knowl. Discov. from Data, vol. 13, no. 1, pp. 1–48, 2019. doi: 10.1145/3278607. [Google Scholar] [CrossRef]

17. Z. T. Chen, C. Chen, Z. B. Zheng, and Y. Zhu, “Tensor decomposition for multilayer networks clustering,” Proc. of The AAAI Conf. on Artif. Intell., vol. 33, pp. 3371–3378, 2019. doi: 10.1609/aaai.v33i01.33013371. [Google Scholar] [CrossRef]

18. S. Y. Yang, J. P. Wu, Y. Y. Xu, and T. Yang, “Revealing heterogeneous spatiotemporal traffic flow patterns of urban road network via tensor decomposition-based clustering approach,” Phys. A: Stat. Mechanics Appl., vol. 526, 2019, Art. no. 120688. doi: 10.1016/j.physa.2019.03.053. [Google Scholar] [CrossRef]

19. D. Qu, H. L. Xiao, H. F. Chen, and H. Y. Li, “An improved differential evolution algorithm for multi-modal multi-objective optimization,” PeerJ Comput. Sci., vol. 10, pp. 1–29, 2024. doi: 10.7717/peerj-cs.1839. [Google Scholar] [PubMed] [CrossRef]

20. Y. T. Su, X. Bai, P. Jian, P. G. Jing, and J. Zhang, “Low-rank approximation-based tensor decomposition model for subspace clustering,” Electron. Lett., vol. 55, no. 7, pp. 406–408, 2019. doi: 10.1049/el.2018.8240. [Google Scholar] [CrossRef]

21. W. W. Wu, F. L. Liu, Y. B. Zhang, Q. Wang, and H. Y. Yu, “Non-local low-rank cube-based tensor factorization for spectral CT reconstruction,” IEEE Trans. Med. Imaging, vol. 38, no. 4, pp. 1079–1093, 2018. doi: 10.1109/TMI.2018.2878226. [Google Scholar] [PubMed] [CrossRef]

22. A. Bhaskara, A. Chen, A. Perreault, and A. Vijayaraghavan, “Smoothed analysis for tensor methods in unsupervised learning,” Math. Program., vol. 193, no. 2, pp. 1–51, 2022. doi: 10.1007/s10107-020-01577-z. [Google Scholar] [CrossRef]

23. H. He, Y. H. Tan, and J. F. Xing, “Unsupervised classification of 12-lead ECG signals using wavelet tensor decomposition and two-dimensional Gaussian spectral clustering,” Knowl.-Based Syst., vol. 163, pp. 392–403, 2019. doi: 10.1016/j.knosys.2018.09.001. [Google Scholar] [CrossRef]

24. H. Liu, J. Ding, L. T. Yang, Y. Guo, X. Wang and A. Deng, “Multi-dimensional correlative recommendation and adaptive clustering via incremental tensor decomposition for sustainable smart education,” IEEE Trans. Sustain. Comput., vol. 5, no. 3, pp. 389–402, 2019. doi: 10.1109/tsusc.2019.2954456. [Google Scholar] [CrossRef]

25. Y. J. Li, L. P. Wang, Z. H. Jia, J. Yang, and N. Kasabov, “Depth prior-based stable tensor decomposition for video snow removal,” Displays, vol. 84, 2024, Art. no. 102733. doi: 10.1016/j.displa.2024.102733. [Google Scholar] [CrossRef]

26. W. Q. Shang, K. X. Wang, and J. J. Huang, “An improved tensor decomposition model for recommendation system,” Int. J. Performability Eng., vol. 14, no. 9, pp. 2116–2126, 2018. doi: 10.23940/ijpe.18.09.p20.21162126. [Google Scholar] [CrossRef]

27. A. Javadpour, A. M. H. Abadi, S. Rezaei, M. Zomorodian, and A. S. Rostami, “Improving load balancing for data-duplication in big data cloud computing networks,” Cluster Comput., vol. 25, no. 4, pp. 2613–2631, 2022. doi: 10.1007/s10586-021-03312-5. [Google Scholar] [CrossRef]

28. X. J. Zhao, X. H. Zhang, P. Wang, S. L. Chen, and Z. X. Sun, “A weighted frequent itemset mining algorithm for intelligent decision in smart systems,” IEEE Access, vol. 6, pp. 29271–29282, 2018. doi: 10.1109/ACCESS.2018.2839751. [Google Scholar] [CrossRef]