An Aerial Target Recognition Algorithm Based on Self-Attention and LSTM

1  Introduction

Aerial target recognition is a very important research aspect of aerial defense. It mainly focuses on how to identify and judge the model, type, and quantity of aerial targets according to the relevant features and attributes [1]. Due to sensor measurement error, noise interference, and other factors, the single sensor has a poor target recognition effect [2]. Using multi-sensor and multi-attribute target recognition methods can effectively improve recognition accuracy and reliability and reduce the uncertainty from sensor measurement [3].

The problem of target recognition can be transformed into a decision-making problem or pattern recognition problem. Correspondingly, the recognition methods based on aerial target features include MADM methods, pattern classification algorithms, and so on. Due to the difficulties in data collection and the influence of uncertainty in data, the recognition algorithm using the MADM method and pattern recognition algorithm once occupied the main position of the target recognition method. However, the recognition method of MADM has the problems of difficult determination of attribute weight, strong subjectivity of measurement setting, and weak environmental adaptability [4]. Pattern classification algorithm needs to define the likelihood function and membership function, which is complex and not widely used [5].

With the improvement of computer hardware level and the development of artificial intelligence technology, target recognition methods based on machine learning have gradually become a research hotspot and have achieved good results [6,7]. In terms of the application of traditional machine learning, the recognition algorithms based on Back Propagation (BP) neural network, K-Nearest Neighbors (KNN), and Support Vector Machine (SVM) have improved the algorithm’s robustness and recognition accuracy [8]. In recent years, deep learning has become a study hot spot of machine learning technology. It has developed rapidly and has been applied to target recognition with significant performance [9,10].

The current target recognition algorithms based on machine learning mostly use the instantaneous features of the target. However, using the target sequence information to improve the recognition effect is barely considered. Moreover, in the research of recognition algorithms based on machine learning, more attention is paid to a single feature, such as one-dimensional range profile and two-dimensional range profile, etc., without using multi-dimensional attributes.

In practical, we can only obtain very few information such as motion characteristics about non-cooperative targets, which is very difficult to be used to identify aerial targets. This paper proposes a recognition algorithm based on self-attention and LSTM to recognize the aerial target with multi-dimensional attributes when there are few or none of actual measurement data.

The innovations of this paper are as follows:

1) A recognition model based on self-attention and LSTM is designed. To improve the accuracy of target recognition, the aerial target is recognized based on continuous measurement data through using the sliding window mechanism.

2) The three-point estimation method is adopted to obtain the probability distribution of each feature of the target, and the data set is constructed for target recognition by sampling, which makes it possible to use the machine learning method when we have none real measured data.

The rest of this paper is organized as follows. Related works are introduced in Section 2. The recognition framework of the method is constructed in Section 3. In Section 4, the generating details of the dataset are provided. The experimental results are analyzed in Section 5. Finally, the conclusions are given in Section 6.

2  Related works

2.1 Application of LSTM in Target Recognition

With the improvement of artificial intelligence technology, aerial target recognition remains an active area. As a very important artificial intelligence technology, Recurrent Neural Network (RNN) can obtain features from sequential data. Therefore, it is used in many domains, such as natural language learning, video data object detection, etc. [11]. The most important models in RNN include LSTM, gated recurrent unit (GRU), etc. They are becoming more and more popular in practical applications [12]. In the domain of target recognition, many researchers have used them for prediction and classification.

LSTM serves as a versatile tool, being employed both as a prediction model and in recognition tasks [13,14], notably for target recognition. An innovative classifier integrating Vectorization based on Feature Engineering with Bidirectional Long Short-Term Memory (Bi-LSTM) has been devised for detecting spam in short text messages (SMS) [15]. Extensive experiments have confirmed that this method surpasses others in terms of precision, recall, F1-measure, and detection accuracy. Furthermore, a hybrid approach combining Bidirectional Long Short-Term Memory (BLSTM) and a Hidden Markov Model (HMM) has been proposed for target recognition [16]. This method excels at capturing multi-domain sequence features from high-resolution range profiles (HRRPs), achieving over 91% recognition accuracy, a lower false positive rate, and heightened recognition confidence compared to cutting-edge technologies. However, its application necessitates a substantial dataset of HRRP samples. A multi-view attention CNN with LSTM to extract and fuse the features from images of synthetic aperture radar (SAR) [17]. It adopts multiple convolutional modules to extract deep features from each single-view SAR image and a spatial attention module to locate the target and suppress the noise. The LSTM module performs feature fusion based on the correlation of features obtained from adjacent azimuths. Experiments have verified the effectiveness of the proposed method on the moving and stationary target recognition dataset. Similarly, the study is based on a large number of SAR images.

Because LSTM can effectively extract features from sequence data, we use LSTM to classify airborne targets using sequence data. Compared with traditional recognition methods based on instantaneous features, this method can improve recognition accuracy.

2.2 Application of Self-Attention

Self-attention is a mechanism that allows models to directly establish relationships between different positions within a sequence. Since its proposal in 2017 [18], the self-attention mechanism has become one of the hotspots in deep learning research in recent years and has been widely applied in fields such as natural language processing, image classification, and object detection [19].

The common use of self-attention mechanism is to model and extract features from sequential data. The self-attention mechanism adaptively learns the weight of each position by calculating the correlation between different positions in the sequence, thereby achieving global modeling and feature extraction of the sequence [20]. Compared to traditional recurrent neural networks (RNNs) and convolutional neural networks (CNNs), self-attention mechanisms can better capture long-range dependencies in sequences, improving the effectiveness of sequence modeling and feature extraction [21]. The sequence modeling and feature extraction algorithm based on the self-attention mechanism has important research significance and application value in the field of sequence data processing. By adaptively calculating the correlation between different positions in the sequence, these algorithms can more accurately model the global dependencies of the sequence and extract useful features.

By introducing the attention mechanism on the basis of LSTM, more efficient information extraction and feature learning can be achieved when processing sequence data. An innovative deep learning model, incorporating the Convolutional Long Short-Term Memory (ConvLSTM) network and a self-attention mechanism, is introduced to recognize polarimetric HRRP. Experimental results have demonstrated the model’s promising performance, showcasing its remarkable potential and effectiveness in accurately identifying and classifying HRRP data [22]. An end-to-end sequence-oriented network architecture has been crafted, seamlessly integrating a streamlined convolutional neural network and a Bi-LSTM network, further enhanced by the incorporation of a self-attention mechanism. This holistic approach is meticulously designed to precisely discern eight diverse intrapulse modulation patterns embedded within radar signals [23]. By introducing a masked multi-head self-attention module into the time-series prediction model based on LSTM, critical information in the sequences is captured and the prediction performance is improved. Teng et al. proposed an aerial target combat intention recognition method based on a gated recurrent unit (GRU) [24]. The proposed method uses a bidirectional gated recurrent units (BiGRU) network for learning air combat characteristics and adaptively assigns characteristic weights using an attention mechanism to improve the accuracy of aerial target combat intention recognition, which can realize intention recognition and prediction.

Taking inspiration from the methods proposed in the aforementioned literature, we propose a method based on self-attention and LSTM. The attention mechanism calculates the weight of each input element and applies the weight to the hidden state of the LSTM, thereby adjusting the LSTM’s attention to the input. This combination retains the learning ability of LSTM and introduces the advantages of the attention mechanism, making the model have stronger feature extraction ability and adaptability when processing sequence data.

2.3 Solutions to the Problem of Little Data Samples Learning

Addressing the challenge of limited data samples in aerial target recognition, various strategies have emerged, including incremental learning, transfer learning, continual learning, and lifelong learning. Within this domain, innovative methods have been widely adopted. For instance, the Class Boundary Exemplar Selection-based Incremental Learning (CBesIL) preserves previous recognition capabilities through class boundary exemplars, outperforming state-of-the-art approaches in multiclass recognition accuracy [25]. An open-set incremental learning method has also been proposed, capable of recognizing and learning new, unknown classes while maintaining high accuracy and efficiency [26]. Another incremental learning approach focuses on extracting more information from old data by appending linear layers to the feature extractor and utilizing distilled labels for training on new data, demonstrating superior performance [27]. In the realm of transfer learning, a deep framework leveraging radar HRRPs has been introduced, enhancing target recognition performance [28]. Additionally, a transfer learning method based on electromagnetic properties from attributed scattering center models has been applied to SAR target recognition, achieving improved classification accuracy [29]. To tackle the overfitting issue due to limited labeled SAR data, a semi-supervised transfer learning method leveraging generative adversarial networks (GANs) has been presented, achieving significant accuracy enhancements over random-initialized CNN models [30]. An incremental learning system for radar signal recognition, adaptable to dataset changes and capable of new class inference, few-shot learning, and knowledge transfer, further underscores the value of these approaches in target recognition [31]. However, it is crucial to note that incremental, continual, and lifelong learning methods inherently rely on previous data or tasks as a foundation for new learning. When confronted with extremely limited or non-existent training data, these methods face significant challenges in aerial target recognition.

To overcome this limitation, we propose a novel dataset generation method grounded in expert knowledge and three-point estimation. This method addresses the difficulty of applying deep learning methods with scarce actual measurement data, offering a promising solution for target recognition in data-scarce environments.

3  Recognition Algorithm Based on Self-Attention and LSTM

3.1 Framework and Recognition Flow

The aerial target recognition framework designed includes a training process and a recognition process. In the training process, the model is trained based on a large number of labeled data, which are the training data, so that the model can classify the new input data. Generally, the real data are used as the training data, but in simulation, when there is a lack of real data, data with a probability distribution similar to the real data can be used as training data. In the recognition process, the unknown data are put into the trained model, and the type of aerial target will be the output. The framework of the proposed algorithm in this paper is shown in Fig. 1.

Figure 1: Framework of the proposed algorithm

In the framework, the recognition model is very important. The target type can be obtained by inputting the target feature vector into the trained model of the algorithm. In practice, the observed value of the target is random due to the influence of target motion and sensor measurement error, and the result of single measurement and recognition will also have certain randomness. Through multiple measurements in continuous time, the influence of this randomness can be greatly reduced. So, the recognition model based on LSTM is designed to improve the recognition performance using the sequence data. Meanwhile, in order to better capture the global dependencies of the sequence, we use self-attention to optimize the initial connection weights of the LSTM, solving the problem of LSTM converging to local optima, thereby improving the recognition performance of the model.

We accumulate sensor measurements using a sliding window mechanism to form a continuous sequence of measurements. Then normalize it and input it into the self-attention layer. The self-attention layer weights the data features and outputs a new sequence. The sequence is put into the corresponding LSTM cells in the recognition model. Then, the output of the LSTM layer is put into the structure combined with the fully connected layer and SoftMax layer to identify the target, and the recognition result is the target type at the leading edge of the sliding window.

The recognition flow of the algorithm proposed in this paper is shown in Fig. 2.

Figure 2: Recognition flow of the proposed algorithm

Suppose that the feature vector of the target obtained by the i th observation is xi={x1,x2,…,xn}, n is feature vector dimension. First, we should choose a sliding window size s, which is larger than or equal to 1. Then, the measurement sequence {xi−s+1,xi−s+2,…,xi} is put into the recognition model, and the output y^i is got, which is the predicted target type in the i th observation. In the next recognition moment, the sliding window with length s and Step 1 slides forward and the output y^i+1will be got, which is the predicted target type in the (i+1)th observation. All subsequent recognition results would be obtained one by one.

The single recognition dataflow of the recognition algorithm is as follows:

3.2 Recognition Model

The recognition model is constructed from LSTM combined with self-attention. Through adaptive weighting, it can better handle global modeling and complex interaction relationships between multi-dimensional vectors when dealing with long sequences, and can improve target recognition ratio and denoise.

Self-attention mechanism is a component of the Transformer, which has the advantage that the weight assigned to each input feature depends on the interaction between the input features. It updates each element of the sequence by integrating global information from the input sequence [32], as shown in Fig. 3.

Figure 3: Self-attention schematic diagram

The input sequence of the recognition model is the normalized time series X={x1,x2,…,xi}. Input it into the Self Attention layer, which calculates the input attention weight A to generate new weight enhanced feature vectors X′={x1′,x2′,…,xi′}. Then input it into the LSTM layer to obtain the final recognition result. The specific description is

X′=AV(1)

A=softmax(QKTdk)(2)

where dk represents the input feature dimension, Q, K and V represent three matrices mapped from the input. Unlike typical attention mechanisms, Q, K and V all come from the same input X.

Q=WqX(3)

K=WkX(4)

V=WvX(5)

where W represent parameter matrices for linear transformations, which can be learned through model training.

LSTM layer consists of a series of LSTM cells, which form a chain structure. LSTM avoids the problem of gradient disappearance, gradient explosion, and long-term dependencies in the training process of long sequence data by using the “gate” mechanism and the concept of cell state [33]. As shown in Fig. 4, the real input of the single LSTM cell includes the current input xt, the output ht−1, and the cell state Ct−1 of the previous cell. In the LSTM cell, there are the forgetting gate ft, the input gate it, the output gate Ot, and cell state Ct. These gates are used to adjust the flow direction of the output. The forgetting gate determines what information is discarded in the cell. The input gate determines how much new information need to be add to the cell. The output gate determines the value the cell outputs.

Figure 4: Structure of LSTM cell

The expression of the forgetting gate ft is [34]

ft=sigmoid(Wf⋅[ht−1,xt]+bf)(6)

where Wf and bf are respectively the weights and offsets of the forgetting gate.

The expression of the input gate it is as follows:

it=sigmoid(Wi⋅[ht−1,xt]+bi)(7)

where Wi and bi are respectively the weights and offsets of the input gate.

The expression of the output gate is as follows:

Ot=sigmoid(Wo⋅[ht−1,xt]+bo)(8)

where Wo and bo are respectively the weights and offsets of the output gate.

The expressions of the output and state of cell are as follows:

ht=Ot⊙tan⁡h(Ct)(9)

Ct=Ct−1⊙ft+it⊙tan⁡h(Wc⋅[ht−1,xt]+bc)(10)

where Wc and bc are respectively the weights and offsets.

In the chain structure of LSTM, the inputs of the next cell are Ct and ht of the current cell [35].

In the method proposed in this paper, the LSTM layer is designed as a one-layer structure that contains s LSTM cells. At t time in a sliding window, the feature vector of the aerial targets is input into the t th LSTM cell.

The LSTM model in this method proposed is used to classify the target. We add a fully connected layer and a SoftMax layer in the last, as shown in Fig. 5.

Figure 5: Structure added in the model

The output of the model is

y^=softmax(WT⋅ht+b)(11)

where W is the weight matrix, and b is the bias.

We suppose that there are K types of targets known, the output feature vector of the LSTM layer is ht={h1,h2,…,hn}. For the each of target type, the predicted value y^i can be described as

y^i=softmax(Wi⋅ht+bi)=e(Wi⋅ht+bi)∑k=1Ke(Wk⋅ht+bk)(12)

In particular, when s=1, the LMST layer has only one LSTM cell. Now, the ht−1 and Ct−1 are zero, the output of the LSTM model can express as

ht=sigmoid(Wo⋅xt+bo)⊙tanh(sigmoid(Wi⋅xt+bi)⊙tanh(Wc⋅xt+bc))(13)

We can see that ht is a nonlinear function when s=1. It also means that the recognition model not only recognizes aerial target through sequential data but also instantaneous data.

In the training process, for the target measurement data set(xj,yj), xj∈Rm, j=0,1,…,l, xj and yj respectively represent the sample feature vector and the sample labels, m and l respectively indicate the sample feature dimensions and the sample number. Put xj into the network for forward propagation to get y^j. For classification tasks, the cross-entropy loss function is commonly used. It can be expressed as

loss=−(yjlog⁡(y^j)+(1−yj)log⁡(1−y^j))(14)

The cross-entropy loss gradually increases as the predicted probability deviates from the actual label. It is also important to note that the cross-entropy loss heavily penalizes those predictions that have high confidence but are wrong.

4  Training Data Generation

In the practice of target recognition, there is often little or none training data due to the difficulty of data collection and category marking. So, it is necessary to simulate the training dataset according to priori knowledge. The simulated dataset is used to train deep learning models, and incremental learning and online learning methods can be adopted to continuously improve the recognition performance of the model.

4.1 The Representation of Uncertainty

Due to the influence of noise caused by sensor measurement and target motion, the target feature data obtained is uncertain. It is a core issue of the training data generation to accurately represent the uncertainty of the measured data of targets. The representation of uncertainty is usually expressed by fuzzy number and probability distribution [36].

The fuzzy number methodology offers a powerful tool to delineate the value range and distribution characteristics of features, effectively capturing the inherent uncertainty in measurements. Employing the triangular fuzzy number as an illustrative case, once its membership function is defined (as outlined in Eq. (12)), it can be succinctly represented by a triplet (a, b, c), where a, b, and c correspond to the lower bound, median, and upper bound, respectively.

However, the representation of fuzzy features and their membership degrees inherently involves numerous human factors, necessitating the adoption of different membership functions tailored to specific scenarios. This variability introduces a challenge: the algorithm based on fuzzy numbers can suffer from reduced flexibility, posing limitations in its application to aerial target recognition tasks.

Probability distribution methodologies predominantly embody the inherent uncertainty in target recognition through the lens of probability density functions. Each target measurement can be conceptualized as a random variable, adhering to a specific probability distribution, a prime example being the triangular distribution. These measurements are often intricately tied to multiple influencing factors, resulting in a composite probability distribution that encapsulates the totality of their individual distributions. Consequently, we frequently regard target features as a composite probability distribution.

To derive this synthetic distribution, various approaches exist, including the unified display method and the expansion method, among others. The unified display method, particularly utilized in this study, harnesses a single distribution density function that flexibly represents diverse distributions by adjusting its parameters. Specifically, leveraging the three-point estimation technique based on the upper and lower bounds as well as the modes of the target feature, we derive the probability density function of the beta distribution. This step culminates in the generation of a training dataset by sampling from this probability distribution, thereby ensuring that the data captures the intricacies and uncertainties inherent in the target recognition process.

4.2 Target Feature Probability Distribution

This paper employs the three-point estimation method to assess the probability distribution of typical target features, drawing from the fundamental principles of the Program Evaluation and Review Technique (PERT) [37]. Three-point estimation serves as a pivotal tool in accurately forecasting progress and costs [38]. To implement this method, one initially establishes the maximum and minimum values, subsequently engaging domain experts to identify the most plausible empirical value, serving as the mode. Typically, the mode corresponds to the value that occurs most frequently within the stipulated maximum and minimum range. Once the maximum, minimum, and mode are determined, the beta distribution is commonly adopted to model the probability distribution of the value under consideration. This choice stems from the beta distribution’s characteristic smooth probability density function, which offers a suitable framework for estimating the likelihood of various outcomes within the specified range.

Beta distribution is very suitable to represent the more complex synthetic probability distribution [39]. Fig. 6 shows the comparison of the beta distribution and other common distributions at the same maximum and median.

Figure 6: Beta distribution and the other distributions

The expectation of beta distribution is as follows:

μij=(aij+4bij+cij)/6(15)

where aij,bij,cij are respectively the minimum, mode and maximum of the j th feature of the i th known target.

Beta distribution has two parameters α,β, and its mode b and expectation μ are

{b=α−1α−β−2μ=αα+β(16)

By substituting the actual mode and expectation into the above formula, the two parameters α,β can be obtained, and then the probability density function of each feature of each type of target can be obtained.

f(xij|α,β)=xα−1(1−xij)β−1∫01μα−1(1−μ)β−1dμ(17)

Then the training data set can be obtained by Monte Carlo simulation according to its probability distribution. The feature of the known target is expressed in the form of beta distribution parameters, and the known target feature set [(αij,βij)]m×n could be established, where (αij,βij) is the beta distribution parameter value of the j th feature of the i th type of known typical target.

4.3 Relationship with MADM

The measurement data pertaining to targets frequently encompass inaccuracies and vague information, rendering MADM grounded in fuzzy information a prevalent and pertinent topic in target recognition research [40–42]. The objective of MADM leveraging fuzzy numbers is to devise an efficient membership function, which meticulously delineates the degree of affiliation of the measurement data to a particular category [43,44]. This article delves into the intricate interplay between our proposed methodology and MADM founded on fuzzy numbers. The innovative algorithm introduced herein endeavors to explore the utilization of probability distributions as a means to generate synthetic data and subsequently train models, particularly in scenarios where procuring vast quantities of authentic data poses significant challenges.

Literature [43] uses triangular fuzzy numbers to represent target features. The membership function of the triangular fuzzy number A(aij,bij,cij) is defined as

μA(x)={x−aijbij−aij,aij≤x≤bijcij−xcij−bij,bij<x≤cij(18)

When multiplying μA(x) by a constant 2/(cij−aij), the following expression would be obtained:

μA(x)2cij−aij=f(x|aij,bij,cij)(19)

We can see that f(x|aij,bij,cij) is the probability density function of triangular distribution with the minimum aij, mode bij and maximum cij. It can be seen that the meaning of triangular fuzzy number is consistent with triangular distribution. Moreover, literature [43] uses the Euclidean distance to measure the similarity between the observed fuzzy number and the known fuzzy number. This process can be equivalent to calculating the probability that the observed value falls in the triangular distribution corresponding to triangular fuzzy numbers. Therefore, it can be said that the method using LSTM and generating data by three-point estimation based on triangular distribution has the same basis as the MADM method using fuzzy numbers, and the effect of the two algorithms is comparable.

Compared with triangular distribution, beta distribution has a smoother probability density curve and higher approximation to the real data distribution. When the three-point estimation method based on beta distribution is to generate data set, the recognition performance is supposed to be further improved.

4.4 Data Set Generation

When ample real data is available for the target recognition task, it can be directly leveraged for model training. Conversely, in scenarios where no measurement data can be procured, the methodology outlined in this section offers a viable solution for data acquisition, which can then be utilized to train the recognition model. For the detection and recognition of aerial targets, a diverse array of sensors and intelligence sources, such as various types of radar and listening equipment, come into play. These sensors are capable of capturing the electromagnetic spectrum characteristics, motion patterns, and other pertinent features of the targets. In practical applications, the information gathered by detection sensors primarily comprises track details and radiation signatures of the aerial targets.

Drawing inspiration from literature [43], this paper selects velocity V (km/h), acceleration A (m/s2), height H (km), and emitter carrier frequency F (GHz) as the key target features. Utilizing the data generation approach detailed in this section, a target feature set is constructed based on these features. This feature set encompasses five distinct types of known, typical targets. The target feature set, established through the normalization of beta distribution values, is presented in Table 1.

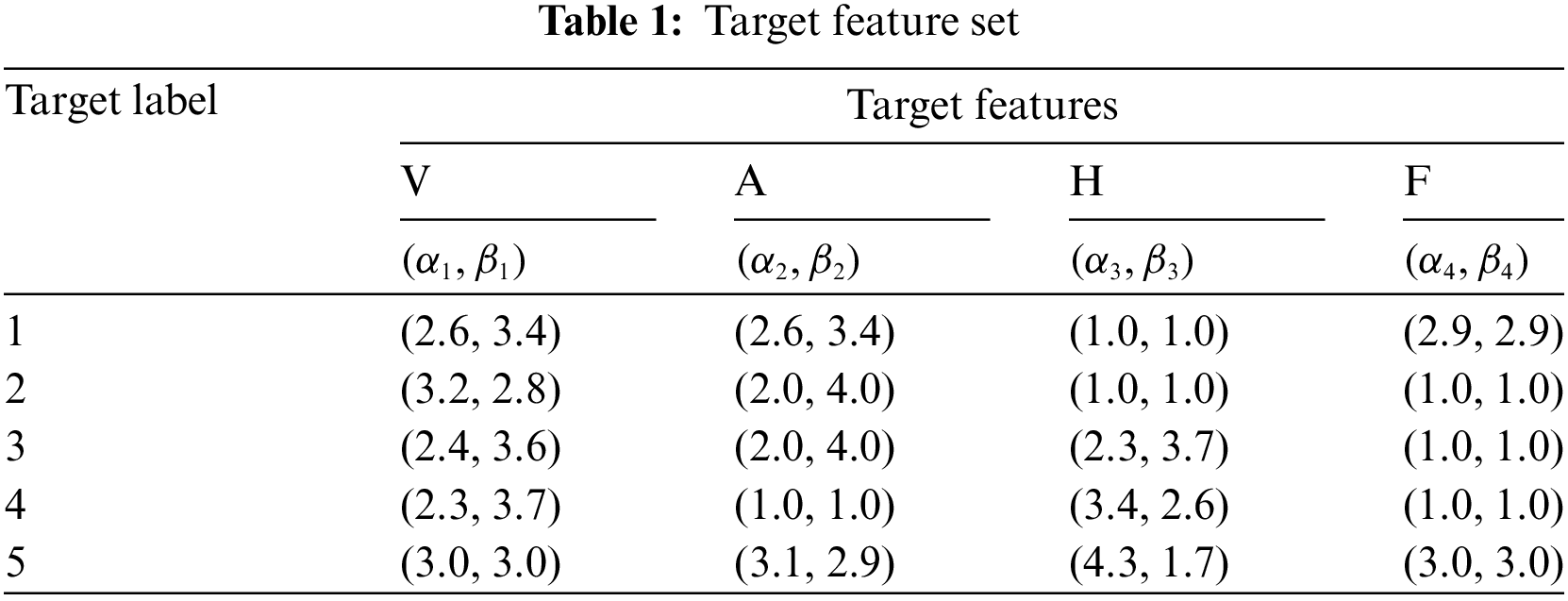
The data set is established with the sampling data according to the target feature set. The dataset is divided into training dataset and testing dataset with the ratio 8:2. In order to test the robustness of the algorithm and the generalization ability of the model, the testing data is not limited to the same distribution as the known target features but is randomly selected within p times of the target feature value range. The sampling number of each typical target is q, and the total number of samples is 5 × q. So, when we take the value of q as 5000, the scale of training dataset and the testing dataset respectively are 20,000 and 5000.

5  Experimental Verification

To verify the effectiveness and practicability of the algorithm, the data have been simulated and the algorithm has been experimented in this paper. The experimental environment is a 64-bit Windows 10 system, the CPU is Intel (R) core (TM) i7-10750h, the CPU @ 2.60 GHz, 2.59 GHz, and the memory has 16 GB. Python language is used to program.

We use accuracy and false alarm as the evaluation indexes.

Accuracy is the ratio of the number of all correctly classified samples to the number of all samples, which can be expressed as

Accuracy=(TP+TN)/(P+N)(20)

where TP is the number of samples that are classified as positive in the positive samples, TN is the number of samples that are classified as negative in the negative samples, P is the number of positive samples, and N is the number of negative samples.

The expression of false alarm ratio is as follows:

falsealarm=FP/(FP+TN)(21)

where FP is the number of samples that are classified as positive in the negative samples.

5.1 Performance Comparison of the Algorithms

MADM is a vital and efficient methodology in the field of target recognition research. At the heart of its success lies the precise determination of feature weights, which is pivotal in assessing the influence of diverse feature values on decision outcomes. However, this particular challenge does not apply to LSTM-based target recognition algorithms, where feature weight optimization is inherently addressed through the network’s learning process. As evidenced by the experiments reported in the literature [43], the application of MADM utilizing fuzzy numbers has demonstrated impressive results in target recognition. Notably, the dataset and parameter values (p and s) employed in this paper align with those used in the cited literature, ensuring a fair comparison. Specifically, when the p value is fixed at 1.2, Table 2 presents a comparative analysis of the recognition performance between the two algorithms, highlighting the changes in recognition efficacy as the s value varies from 2 to 6. This comparison underscores the effectiveness of the fuzzy number-based MADM approach in enhancing target recognition capabilities.

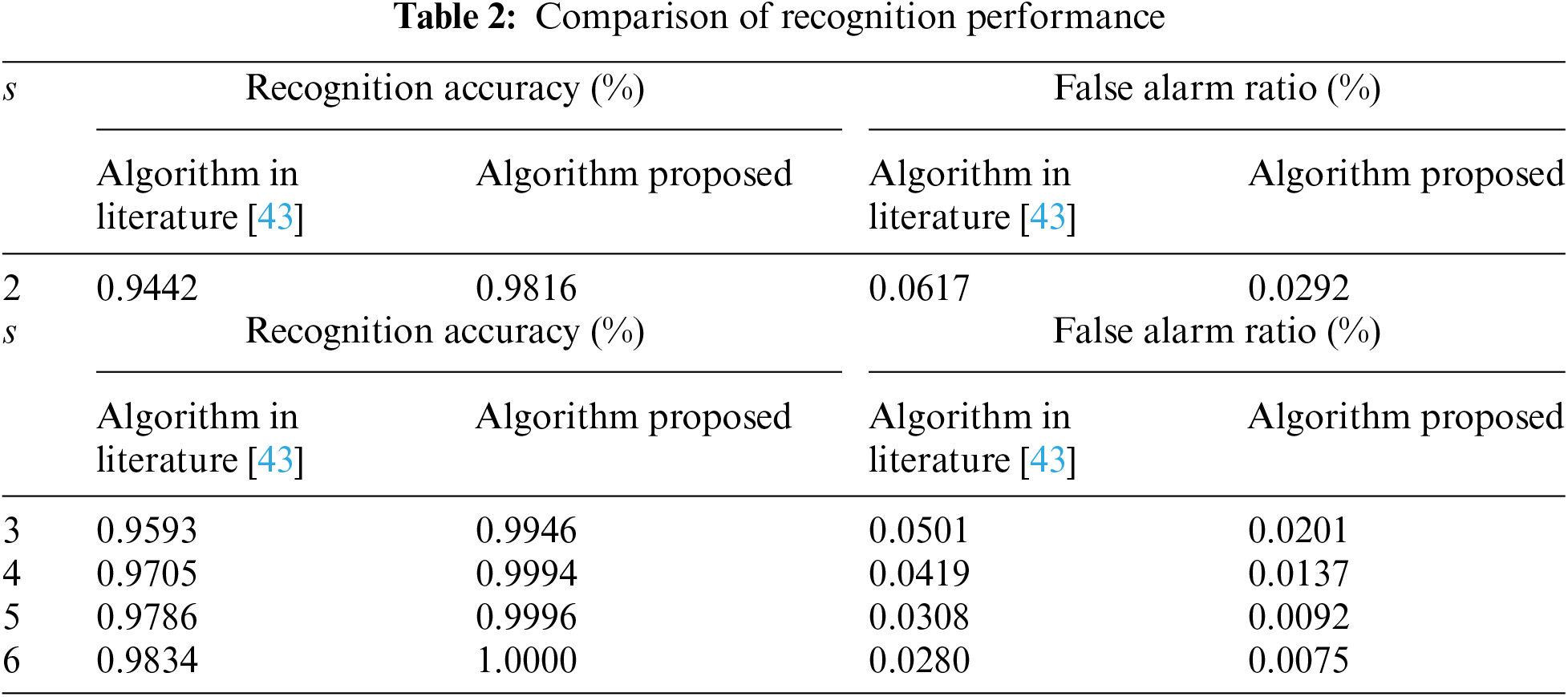
It should be noted that the sliding window size s in this paper is consistent with the meaning of “number of observation groups” in literature [43]. As can be seen from Table 2, compared with the MADM based on fuzzy numbers, the algorithm proposed in this paper has greatly improved recognition accuracy and reduced false alarm rate. Fig. 7 shows the change trend of the recognition accuracy and false alarm ratio of the two algorithms with the sliding window size s changing.

Figure 7: Change trend of recognition accuracy and false alarm ratio

5.2 Robustness Analysis

Robustness stands as a crucial performance metric for target detection algorithms, holding immense significance in practical applications. This robustness is manifested in the algorithm’s ability to withstand errors stemming from target feature measurements and target maneuvers, which is quantitatively represented by the parameter p in this context. Specifically, a p value of 1 signifies that the measured target feature values adhere strictly within their prior distribution range, thereby promising high recognition accuracy. Conversely, as the p value escalates, there is an increased likelihood that measured target feature values will exceed their respective prior distribution boundaries, leading to a deterioration in recognition performance. Table 3 provides an overview of the recognition performance exhibited by the recognition algorithm introduced in this paper, under varying conditions of p and s values.

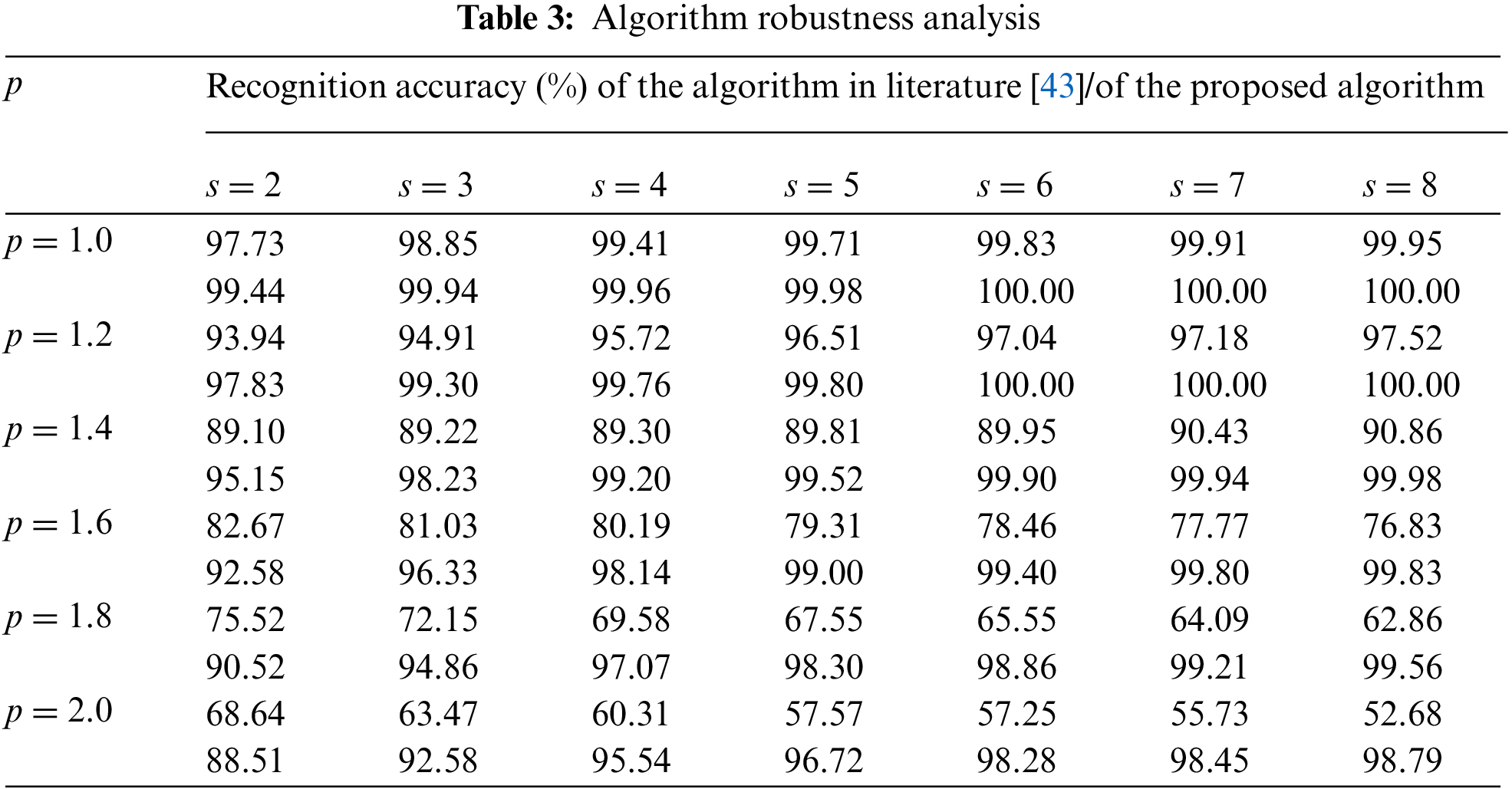
In Table 3, it can be seen that the recognition accuracy of the algorithm proposed in this paper is much higher than the MADM based on fuzzy number. The visualization of recognition performance is shown in Fig. 8.

Figure 8: Comparison of the recognition accuracy of the two algorithms

In the Fig. 8, the blue ring area represents the difference between the recognition accuracy of the two algorithms at the same value. The outer circle area represents the recognition accuracy of the algorithm proposed in the paper, and the inner circle area represents the recognition accuracy of the MADM based on fuzzy number. By observing the change law of the ring area, two change trends can be obtained: First, with the expansion of the range of value, the difference between the two algorithms gradually widens; Second, with the increase of sliding window size, the performance gap between the two algorithms increases gradually. Trend 1 shows that the target recognition algorithm proposed in this paper is more robust than the MADM based on fuzzy number. Trend 2 shows that the performance of target recognition algorithm proposed in this paper is getting better and better by continuous accumulation by sliding window.

The target recognition algorithm based on LSTM proposed can distinguish singular values and show better robustness. It also means that the algorithm proposed has better anti-noise performance. The MADM based on fuzzy number achieves better recognition performance than a single measurement by averaging the measurement sequence. However, when the noise distribution is not Gaussian white noise, this method is no longer effective.

5.3 Influence of Data Set Generation Methods

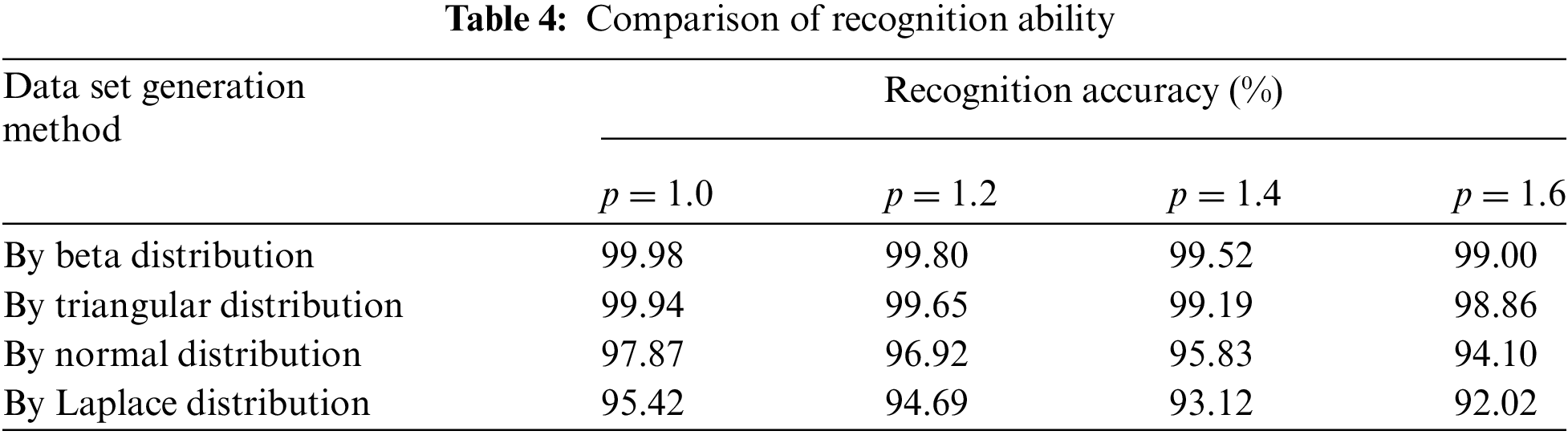
In order to explore the influence of the data generated by different probability distributions on the recognition accuracy, the datasets generated by different probability distribution described in Section 4.2 are used for experimental comparison.

The beta distribution and triangular distribution are determined by the minimum, mode, and maximum values of the data of literature [43]. The normal distribution and Laplace distribution are determined by the maximum and minimum values, that is, the maximum and minimum values are taken as 0.99 quantiles to calculate the mean and standard deviation of the two types of distribution, and then their probability density functions are obtained. Finally, the data set is generated by Monte Carlo simulation.

The algorithm model is trained with the training data sets obtained from the above four probability distributions. Then the recognition accuracies of each model trained are compared. When the sliding window size is 5, the recognition results are shown in Table 4.

5.4 Specific Scenarios Analysis

A simulation scenario has been meticulously designed to evaluate the performance of the trained model. This scenario leverages a flight simulation system to extract aircraft flight data, specifically tailored for an alert patrol mission. The target’s flight trajectory, clearly depicted in Fig. 9a, encompasses the entire duration of the mission, from inception to completion. Throughout this duration, a total of 100 observations were extracted, each serving as a basis for individual target recognition tasks. To ensure optimal recognition performance, a sliding window approach was employed, with an initial window size of 1 that gradually expanded to 8 over the first 8 observation instances. The outcomes of these recognition attempts are visually presented in Fig. 9b, offering a comprehensive view of the model’s performance under varying conditions.

Figure 9: The effect of target recognition. (a) Flight track. (b) Comparison of recognition results [43]

In Fig. 9a, the whole track is divided into three segments according to the change of target motion. In the AB track segment, the target flies to the mission area. In order to achieve the concealment of the action, the electromagnetic spectrum signal is camouflaged, and the emitter carrier frequency F is similar to the Class 4 target. The number of measurements in this track segment is thirty. In the BC track segment, when the target arrives at the mission area, the electromagnetic spectrum signal returns to the normal level. However, in order to achieve the best mission effect, the target flight altitude is always close to the critical value, which is similar to the normal cruise altitude of Class 4 target. The number of measurements in this track segment is forty-seven. In CD track segment, the target is returning, all attribute features return to normal level, and the number of measurements in this track segment is thirty-three.

In Fig. 9b, a notable improvement in target recognition accuracy is evident when comparing our proposed method to the MADM approach based on fuzzy numbers. Specifically, in the AB track segment, our method reduced the number of recognition errors from seven to three. Similarly, in the BC segment, the errors dropped from six to just two. Furthermore, in the CD segment, the MADM approach based on fuzzy numbers incurred one error, whereas our algorithm achieved zero errors. Throughout the entire process, which encompassed one hundred measurements, our method demonstrated a remarkable performance, with a recognition accuracy of 95%. In contrast, the MADM approach based on fuzzy numbers yielded an accuracy of merely 86%, highlighting the superiority of our proposed algorithm in enhancing target recognition precision.

5.5 Discussion

The essence of the algorithm proposed is a data-driven approach, which is currently a popular research method. It is through training a neural network model to fit the data, thereby changing the model and achieving target recognition. The traditional recognition method based on MADM is a model-driven approach, which first sets a certain mathematical model and then judges the data through the model without changing the model itself.

We first verify the superiority of data-driven over model-driven experiments. From the experimental results in Section 5.2, it can be seen that compared with MADM based on fuzzy numbers, the algorithm proposed in this paper greatly improves recognition accuracy and reduces false alarm rates. The reason for the poor performance of MADM based on fuzzy numbers is that it requires manual setting of feature weights, and the subjectivity of manually setting feature weights has a negative impact on classification performance. This is precisely why the data-driven approach outperforms the model-driven approach.

This superiority is also reflected in the experiment in Section 5.3. As can be seen, the algorithm proposed in this paper demonstrates better robustness. The reason is that MADM based on fuzzy numbers uses Euclidean distance to measure the similarity between observed fuzzy numbers and known fuzzy numbers. When the measured target feature values are separated from the original probability distribution region, it is difficult to distinguish them by distance. The algorithm proposed utilizes the powerful nonlinear processing capability of LSTM to solve this problem.

As the literature [43] described, the MADM based on fuzzy number has better performance than other weighting methods and the relative entropy ranking method is improved, which is better than other MADM methods; The similarity index is improved, which is better than other indexes. The effect of the algorithm in this paper is better than the MADM based on fuzzy numbers, which shows that the role of machine learning in eliminating human factors in decision-making is effective.

The data-driven approach relies heavily on data, and the experiment in Section 5.3 verified the impact of training data generated from different probability distributions on recognition accuracy. Of course, in the later stage of the method proposed in this paper, incremental learning can be used to introduce measured data to continue training the model, gradually improving the recognition performance of the target. This is also one of the advantages of the algorithm proposed in this paper, which cannot be achieved by model-driven methods.

The algorithm proposed in this paper is used for the identification of military aircraft. Because the measured data cannot be made public. Therefore, in the experiment in Section 5.4, a simulation data set was used to verify the effectiveness of the algorithm. At the same time, it is also a specific demonstration of the identification process of the proposed algorithm. The experimental results show that our method is superior to the MADM method based on fuzzy numbers.

6  Conclusions

Based on extensive experimentation, the following conclusions can be drawn regarding the target recognition algorithm proposed in this paper:

1) The algorithm exhibits remarkable recognition performance, surpassing the MADM based on fuzzy numbers. Under identical conditions, it achieves an increase in target recognition accuracy by over 3.15% and a reduction in the false alarm rate by at least 3.33%.

2) The proposed algorithm displays exceptional robustness, thanks to the incorporation of self-attention and LSTM. This integration enhances the algorithm’s adaptability to both sensor measurement noise and noise arising from target motion. Consequently, when utilizing the algorithm presented in this paper under identical sliding window conditions, the average decrease in recognition accuracy caused by increased errors is mitigated by 9.2%, underscoring its resilience and reliability.

3) Compared to triangle, normal, and Laplace distributions, the data set generated using the three-point estimation method with the beta distribution more accurately simulates real target features. This makes it highly practical for target recognition applications, particularly in scenarios with limited sample sizes.

Although the proposed algorithm has a good effect in the application of aerial target recognition, we should realize that the data used in this paper is simulation data, and the recognition effect of the training model might be attenuated when it comes to real target. In future study, we can further apply our method on real targets and with a few data, and we can combine incremental learning, transfer learning, continual learning, lifelong learning, and other methods to improve the accuracy of real target recognition.

Acknowledgement: We thank Yinan Zhang for editing the English text of this paper. She is very kind, beautiful and talented.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Futai Liang, Xin Chen; data collection: Song He; analysis and interpretation of results: Futai Liang, Xin Chen, Zihao Song, Hao Lu; draft manuscript preparation: Futai Liang, Song He. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. W. Lu, Y. Zhang, C. Xu, and Y. Huo, “A deep learning-based satellite target recognition method using radar data,” Sensors, vol. 19, no. 9, 2019, Art. no. E2008. doi: 10.3390/s19092008. [Google Scholar] [PubMed] [CrossRef]

2. W. Wang, Z. Tang, Y. Chen, Y. Zhang, and Y. Sun, “Aircraft target classification for conventional narrow-band radar with multi-wave gates sparse echo data,” Remote Sens., vol. 11, 2019, Art. no. 2700. doi: 10.3390/rs11222700. [Google Scholar] [CrossRef]

3. B. Feng, B. Chen, and H. Liu, “Radar HRRP target recognition with deep networks,” Pattern Recognit., vol. 61, no. 10, pp. 379–393, 2017. doi: 10.1016/j.patcog.2016.08.012. [Google Scholar] [CrossRef]

4. P. Dong, H. Wang, and Y. Chen, “GRA-TOPSIS emitter threat assessment method based on game theory,” J. Beijing Univ. Aeronaut. Astronaut., vol. 46, no. 10, pp. 1973–1981, 2020 (In Chinese). doi: 10.13700/j.bh.1001-5965.2019.0543. [Google Scholar] [CrossRef]

5. S. Liu and L. Jin, “A survey on algorithms for automatic target recognition,” Electron. Opt. Control, vol. 10, pp. 1–7, 2016. [Google Scholar]

6. D. Zhao and H. Li, “Radar target recognition based on central moment feature and GA-BP neural network,” Infrared Laser Eng., vol. 8, pp. 394–400, 2018. [Google Scholar]

7. Y. Hao, Y. Bai, and X. Zhang, “Synthetic aperture radar target recognition based on KNN,” Fire Control Command Control, vol. 9, pp. 111–113+118, 2018 (In Chinese). [Google Scholar]

8. T. Bufler and R. Narayanan, “Radar classification of indoor targets using support vector machines, IET Radar,” Sonar Navig., vol. 8, pp. 1468–1476, 2016. [Google Scholar]

9. Y. Xu, H. Sun, J. Chen, L. Lei, K. Ji and G. Kuang, “Adversarial self-supervised learning for robust SAR target recognition,” Remote Sens., vol. 13, no. 20, 2021, Art. no. 4158. doi: 10.3390/rs13204158. [Google Scholar] [CrossRef]

10. Y. Yang, Z. Zhang, W. Mao, Y. Li, and C. Lv, “Radar target recognition based on few-shot learning,” Multimed. Syst., vol. 29, no. 5, pp. 1–11, 2023. doi: 10.1007/s00530-021-00832-3. [Google Scholar] [CrossRef]

11. Y. Yu, X. Si, C. Hu, and J. Zhang, “A review of recurrent neural networks: LSTM cells and network architectures,” Neural Comput., vol. 31, no. 7, pp. 1235–1270, 2019. doi: 10.1162/neco_a_01199. [Google Scholar] [PubMed] [CrossRef]

12. A. Sherstinsky, “Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network,” Phys. D: Nonlinear Phenom., vol. 404, 2022, Art. no. 132306. doi: 10.1016/j.physd.2019.132306. [Google Scholar] [CrossRef]

13. R. Peng, W. Wei, D. Sun, and G. Wang, “A positive-unlabeled radar false target recognition method based on frequency response features,” IEEE Signal Process. Lett., vol. 30, pp. 1067–1071, 2023. doi: 10.1109/LSP.2023.3305192. [Google Scholar] [CrossRef]

14. H. Liu, H. Zhang, and C. Mertz, “DeepDA: LSTM-based deep data association network for multi-targets tracking in clutter,” presented at the 2019 22th Int. Conf. Inf. Fusion (FUSION), Ottawa, ON, Canada, Jul. 2–5, 2019. [Google Scholar]

15. A. L. Rosewelt, N. D. Raju, and S. Ganapathy, “An effective spam message detection model using feature engineering and Bi-LSTM,” presented at the 2022 Int. Conf. Adv. Comput., Commun. Appl. Inf. (ACCAI), Chennai, India, Jan. 28–29, 2022. [Google Scholar]

16. F. Gao, T. Huang, J. Wang, J. Sun, A. Hussain and H. Zhou, “A novel multi-input bidirectional LSTM and HMM based approach for target recognition from multi-domain radar range profiles,” Electronics, vol. 8, no. 5, 2019, Art. no. 535. doi: 10.3390/electronics8050535. [Google Scholar] [CrossRef]

17. C. Wang, X. Liu, J. Pei, Y. Huang, Y. Zhang and J. Yang, “Multiview attention CNN-LSTM network for SAR automatic target recognition,” IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens., vol. 14, pp. 12504–12513, 2021. doi: 10.1109/JSTARS.2021.3130582. [Google Scholar] [CrossRef]

18. A. Vaswani et al., “Attention is all you need,” presented at the 31st Int. Conf. Neural Inf. Process. Syst., Long Beach, CA, USA, Dec. 4–9, 2017. [Google Scholar]

19. S. Jamshidi et al., “Effective text classification using BERT, MTM LSTM, and DT,” Data Knowl. Eng., vol. 151, 2024, Art. no. 102306. doi: 10.1016/j.datak.2024.102306. [Google Scholar] [CrossRef]

20. Z. Li, Z. Hu, W. Luo, and X. Hu, “SaberNet: Self-attention based effective relation network for few-shot learning,” Pattern Recognit., vol. 133, 2023, Art. no. 109024. doi: 10.1016/j.patcog.2022.109024. [Google Scholar] [CrossRef]

21. Z. Huang, M. Liang, J. Qin, S. Zhong, and L. Lin, “Understanding self-attention mechanism via dynamical system perspective,” presented at the 2023 IEEE/CVF Int. Conf. Comput. Vis. (ICCV), Paris, France, 2023, pp. 1412–1422. [Google Scholar]

22. L. Zhang, Y. Li, Y. Wang, J. Wang, and T. Long, “Polarimetric HRRP recognition based on ConvLSTM with self-attention,” IEEE Sens. J., vol. 21, no. 6, pp. 7884–7898, 2021. doi: 10.1109/JSEN.2020.3044314. [Google Scholar] [CrossRef]

23. S. Wei, Q. Qu, X. Zeng, J. Liang, J. Shi and X. Zhang, “Self-attention Bi-LSTM networks for radar signal modulation recognition,” IEEE Trans. Microw. Theory Tech., vol. 69, no. 11, pp. 5160–5172, Nov. 2021. doi: 10.1109/TMTT.2021.3112199. [Google Scholar] [CrossRef]

24. F. Teng, Y. Song, G. Wang, P. Zhang, L. Wang and Z. Zhang, “A GRU-based method for predicting intention of aerial targets,” Comput. Intell. Neurosci., vol. 2021, no. 6, 2021, Art. no. 6082242. doi: 10.1155/2021/6082242. [Google Scholar] [PubMed] [CrossRef]

25. S. Dang, Z. Cao, Z. Cui, Y. Pi, and N. Liu, “Class boundary exemplar selection based incremental learning for automatic target recognition,” IEEE Trans. Geosci. Remote Sens., vol. 58, no. 8, pp. 5782–5792, 2020. doi: 10.1109/TGRS.2020.2970076. [Google Scholar] [CrossRef]

26. S. Dang, Z. Cao, Z. Cui, Y. Pi, and N. Liu, “Open set incremental learning for automatic target recognition,” IEEE Trans. Geosci. Remote Sens., vol. 57, no. 7, pp. 4445–4456, Jul. 2019. doi: 10.1109/TGRS.2019.2891266. [Google Scholar] [CrossRef]

27. C. Hu, M. Hao, W. Wang, Y. Yang, and D. Wu, “Incremental learning using feature labels for synthetic aperture radar automatic target recognition,” IET Radar Sonar Navig., vol. 16, no. 11, pp. 1872–1880, Aug. 2022. doi: 10.1049/rsn2.12303. [Google Scholar] [CrossRef]

28. Y. Wen, L. Shi, X. Yu, Y. Huang, and X. Ding, “HRRP target recognition with deep transfer learning,” IEEE Access, vol. 8, pp. 57859–57867, 2020. doi: 10.1109/ACCESS.2020.2981730. [Google Scholar] [CrossRef]

29. J. Liu, M. Xing, H. Yu, and G. Sun, “EFTL: Complex convolutional networks with electromagnetic feature transfer learning for SAR target recognition,” IEEE Trans. Geosci. Remote Sens., vol. 60, pp. 1–11, 2022. doi: 10.1109/TGRS.2021.3083261. [Google Scholar] [CrossRef]

30. W. Zhang, Y. Zhu, and Q. Fu, “Semi-supervised deep transfer learning-based on adversarial feature learning for label limited SAR target recognition,” IEEE Access, vol. 7, pp. 152412–152420, 2019. doi: 10.1109/ACCESS.2019.2948404. [Google Scholar] [CrossRef]

31. J. Luo, W. Si, and Z. Deng, “New classes inference, few-shot learning and continual learning for radar signal recognition,” IET Radar Sonar Navig., vol. 16, no. 10, pp. 1641–1655, 2022. doi: 10.1049/rsn2.12286. [Google Scholar] [CrossRef]

32. K. Han, A. Xiao, E. Wu, J. Guo, C. Xu and Y. Wang, “Transformer in transformer,” Adv. Neural Inf. Process. Syst., vol. 34, pp. 15908–15919, 2021. [Google Scholar]

33. X. Zhang, Y. Liu, and J. Song, “Short-term orbit prediction based on LSTM neural network,” Syst. Eng. Electron., vol. 44, no. 3, pp. 939–947, 2022. [Google Scholar]

34. A. Kumar, Manish, and U. Satija, “Residual stack-aided hybrid CNN-LSTM-based automatic modulation classification for orthogonal time-frequency space system,” IEEE Commun. Lett., vol. 27, no. 12, pp. 3255–3259, 2023. doi: 10.1109/LCOMM.2023.3328011. [Google Scholar] [CrossRef]

35. Q. Wang, S. Bu, Z. He, and Z. Y. Dong, “Toward the prediction level of situation awareness for electric power systems using CNN-LSTM network,” IEEE Trans. Ind. Inform., vol. 17, no. 10, pp. 6951–6961, 2021. doi: 10.1109/TII.2020.3047607. [Google Scholar] [CrossRef]

36. L. Li, M. Wu, and Z. Li, “Uncertain information processing method in the reliability measurement,” J. Mech. Eng., vol. 8, no. 8, pp. 153–158, 2012. doi: 10.3901/JME.2012.08.153. [Google Scholar] [CrossRef]

37. X. Lei, “Assumption analysis and duration simulation of three-point estimate in PERT technique,” presented at the 2011 Int. Conf. Comput. Manag. (CAMAN), Wuhan, China, May 19–21, 2011. [Google Scholar]

38. B. Gładysz, “Fuzzy-probabilistic PERT,” Ann. Oper. Res., vol. 258, no. 2, pp. 437–452, 2017. doi: 10.1007/s10479-016-2315-0. [Google Scholar] [CrossRef]

39. A. Hernández-Bastida and M. Fernández-Sánchez, “How adding new information modifies the estimation of the mean and the variance in PERT: A maximum entropy distribution approach,” Ann. Oper. Res., vol. 274, no. 1–2, pp. 291–308, 2019. doi: 10.1007/s10479-018-2857-4. [Google Scholar] [CrossRef]

40. G. Ali, H. Alolaiyan, D. Pamučar, M. Asif, and N. Lateef, “A novel MADM framework under q-Rung orthopair fuzzy bipolar soft sets,” Mathematics, vol. 9, no. 13, 2021, Art. no. 2163. doi: 10.3390/math9172163. [Google Scholar] [CrossRef]

41. M. Akram, G. Ali, and J. C. R. Alcantud, “Hybrid multi-attribute decision-making model based on (m, N)-soft rough sets,” J. Intell. Fuzzy Syst., vol. 36, no. 6, pp. 6325–6342, 2019. doi: 10.3233/JIFS-182616. [Google Scholar] [CrossRef]

42. G. Ali and M. N. Ansari, “Multiattribute decision-making under Fermatean fuzzy bipolar soft framework,” Granul. Comput., vol. 7, no. 2, pp. 337–352, 2022. doi: 10.1007/s41066-021-00270-6. [Google Scholar] [PubMed] [CrossRef]

43. H. Zhang, X. Wang, and Y. Xu, “Relative entropy method in target recognition with fuzzy features,” J. Beijing Univ. Aeronaut. Astronaut., vol. 49, no. 12, pp. 3547–3558, 2023 (In Chinese). doi: 10.13700/j.bh.1001-5965.2020.0237. [Google Scholar] [CrossRef]

44. S. Dhanasekar, S. Hariharan, and P. Sekar, “Fuzzy hungarian MODI algorithm to solve fully fuzzy transportation problems,” Int. J. Fuzzy Syst., vol. 5, pp. 1479–1491, 2016. [Google Scholar]