Hierarchical Optimization Method for Federated Learning with Feature Alignment and Decision Fusion

1  Introduction

The rapid proliferation of edge devices has led to massive volumes of data explosion [1]. Deep Neural Networks (DNNs) are commonly used for machine learning tasks and rely on extensive training data for optimal performance [2]. Servers with abundant computing resources can process a large number of application services in parallel [3]. However, as more and more computing tasks are being offloaded to servers for processing, it can lead to privacy and security issues [4]. But due to heightened privacy and security concerns, along with stringent regulatory restrictions, data owners are reluctant to share their raw data with centralized computing centers. Hence, developing algorithms that facilitate efficient communication and safeguard data privacy is crucial for leveraging client data effectively (e.g., data islands and mobile devices). Federated Learning (FL) has emerged as a key distributed machine learning technology to tackle these challenges. FL decouples data collection and model training via multi-party computation and model aggregation [5]. In FL, clients train models locally without sending raw data to the server, addressing privacy issues and enabling collaborative training across decentralized clients and servers [6]. Typically, a central server in FL manages the global model and facilitates aggregation, as like FedAvg [7].

Traditional FL algorithms perform well when client data follows an Independently and Identically Distributed (IID) pattern. However, in real-world scenarios, client data often exhibits varied distributions. This arises due to differences in data contexts, user preferences, generation methods, and sampling techniques. This results in heterogeneous data distributions across clients, known as Non-IID data distribution [8]. This data heterogeneity includes scenarios such as skewed label distributions, imbalanced quantities, and differing feature distributions [9]. For example, hospitals in a region may collaborate to train a disease prediction model. However, due to their different specializations, the distribution of disease categories and data quantities will vary. Specialty hospitals have extensive data in their fields but lack data on other diseases compared to general hospitals. In such scenarios, traditional FL algorithms struggle with convergence, resulting in suboptimal global model performance. Therefore, Personalized Federated Learning (pFL) is needed. The pFL aims to create models tailored to each client’s local data [10]. This approach aligns more closely with each client's specific target tasks and requirements [11].

DNNs-based models consist of a feature extractor for extracting feature embeddings and a classifier (prediction head) for classification tasks. The feature extractor's structure is crucial, while the classifier is more task-specific, as evidenced by the success of deep learning in centralized learning [12,13]. In heterogeneous data scenarios, clients face local learning tasks, highlighting the need to optimize both the feature extractor for improved representation learning and the classifier for accurate decisions. However, in the pursuit of personalization performance, the existing pFL algorithm faces the problems of excessive communication cost and poor scalability in more heterogeneous data scenarios, as well as the defects that global knowledge is not fully utilized.

Therefore, this paper proposes FedFCD, a hierarchical optimization method for federated learning with feature alignment and the fusion of classification decisions. Specifically, FedFCD computes the average Local Feature Representation (LFR) for each class on the client side and aggregates them at the server to train a shared global classification head. The resulting Global Feature Representation (GFR) for each class is then transmitted back to the respective client to guide local model training. A hierarchical and alternating parameter optimization method is employed during local training. Fig. 1 illustrates the overall framework of FedFCD. The key contributions of this work are as follows:

(1)   From the perspective of feature representation, a regularization term is designed for the client-side feature extractor. This term utilizes the knowledge from global feature learning to achieve feature alignment, thereby improving the quality of local feature learning.

(2)   For the classification decision process, this study proposes a late fusion method that combines the output vectors of the global classifier and the local classifier at the decision level. The approach enables the learning of more complex and complementary feature information, enhancing overall decision-making.

(3)   We adopt a hierarchical optimization method to separately optimize parameters the two components of the model. This strategy prevents interference between the representation learning and the decision-making, thereby enhancing the flexibility of FedFCD and reducing unnecessary parameter computations.

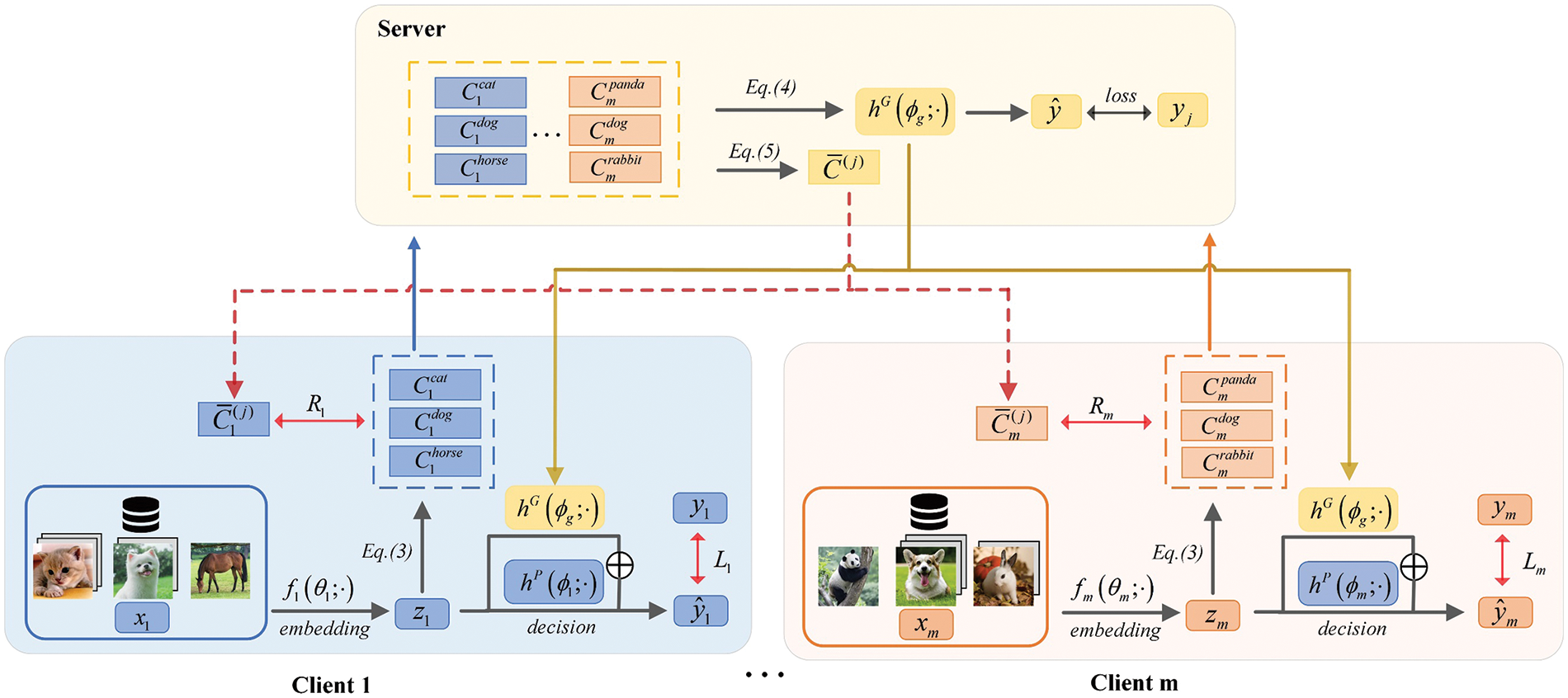
Figure 1: Structure design of FedFCD

The remainder of this article is organized as follows: Section 2 reviews the most relevant works on Personalized Federated Learning (pFL). Section 3 introduces the technical details of FedFCD. Section 4 reports and analyzes the experimental results. Section 5 provides the concluding remarks and future works.

2  Related Works

2.1 Federated Learning in Heterogeneous Data Scenarios

In existing research, numerous methods aim to enhance the performance of global models under Non-IID data distribution. For instance, FedProx [14] introduces an L2 regularization term to the local training objective, which restricts the magnitude of local updates, ensuring that the updated local parameters remain appropriately close to the global model parameters. Karimireddy et al. [15] introduced the SCAFFOLD, which addresses parameter offset correction in local training by introducing update control variables on both the server and client sides. Some efforts have focused on exploring data sharing mechanisms and data augmentation techniques to alleviate the effects of heterogeneous data. Experiments conducted by Zhao et al. [16] demonstrated that sharing 5% of global data in the CIFAR-10 dataset led to a significant improvement in the test accuracy of the global model, by approximately 30%. Additionally, certain studies have tackled the issue from the perspective of model aggregation. The study [17] suggested implementing client aggregation based on model similarity and selecting clients that contribute more to the global model. This approach aims to accelerate convergence and mitigate the impact of data heterogeneity. Different from the above methods, this study focuses on learning a personalized model for each client.

2.2 Personalized Federated Learning

Existing pFL methods encompass a variety of approaches, including local strategies guided by Meta-Learning. This approach is designed to enhance the learning algorithm by exposure to different data distributions [18]. The Model-Agnostic Meta-Learning (MAML) algorithm [19] is renowned for its strong generalization capability and rapid adaptation to new tasks. For example, Per-FedAvg is a variant of the FedAvg algorithm that utilizes MAML [20]. After downloading the global model, clients undergo additional fine-tuning based on their local data distribution to enhance the model's local performance. Fine-grained model aggregation tailored to specific clients is exemplified by FedAMP [21], which evaluates the similarity between clients using an attention-inducing function. This method learns pairwise collaboration relationships among clients with similar data distributions and achieves personalized cloud models for each client through fine-grained weighted aggregation. A similar approach is adopted in the FedFomo [22]. Such methods often rely on heuristics to assess model similarity or accuracy verification, necessitating a trade-off between communication computational overhead and personalization performance.

Combined with the Prototype-Based Learning strategy, the core idea is to store a set of representative samples (prototypes), and then use the prototypes to perform the training task. Tan et al. proposed FedProto [23], where the prototypes of each class of samples are involved in FL communication. The aim of local training on the client is to make the resulting local prototype close enough to the corresponding global prototype. Parameter decoupling methods decompose model parameters into local private parameters and global parameters. For instance, FedRep [13] separates the model into a feature extractor and a classifier, then aggregates the feature extractor parameters on the server, and shares the training of the feature extractor. Similar notable methods in this category include GPFL [24], LightFed [25], FedFC [26] and FedTC [27]. The recently proposed FedGH [28] adopts a similar parameter decomposition approach. The difference is that in FedGH, the local classifier is directly replaced with the global classifier. Different from existing works, we design a regularization term based on feature representation, which reduces communication cost and enriches local features. At the same time, the decision output of the global head is fused to integrate the global knowledge into the local classification task. Finally, the parameters were updated in a hierarchical alternating manner to avoid the interference between feature learning and classifier decision.

3  Proposed Method

3.1 Problem Formulation and Notation

For clarity in formulation, the classic problem as follows: in pFL scenarios, there exists a central server and m clients. The private data distribution on client i is denoted as Pi(x, y), and it differs between clients. The target loss of client i is defined as, where wi represents the personalized model and l(⋅) is the loss function. The optimization objective can be defined as follows:

minW{F(W):=1m∑i=1mE(x, y)∼Pi(x, y)[l(wi; x, y)]}(1)

where W=(w1, w2,…,wm) denotes the collection of all local models. However, the true underlying distribution is inaccessible, and the goal is typically achieved through empirical risk minimization (ERM). The assumption is that ni independent and identically distributed samples are locally obtained from each client, denoted as Di={(xl(i), yl(i))}l=1ni. The set of samples labeled as j is Si(j)={x|(x, y)∈Di and y=l}, and the its empirical distribution is P¯i(x, y). Assuming that the empirical distribution approximates the true distribution, the training objective can be defined as:

w∗=argminw1m∑i=1m[Li(wi)+Ri(wi; Ω)](2)

where Li(wi)=1ni∑i=1nil(wi; xl(i),yl(i)) is the local average loss, Eq. (2) directly seeks to minimize the client’s ERM (plus the regularization term). Typical R(⋅) is a predefined regularization term, and Ω represents some global information captured from the relevant client.

3.2 Method Overview

The DNNs model can be decomposed into the representation layer θ and the final decision layer ϕ. The representation layer, also known as the feature extractor, is responsible for extracting features, while the final decision layer, refers to the classifier head in classification tasks. For client i, its feature extractor is a neural network parameterized by θi, which can be represented as fi:x→Rd, where d is the dimension of embedding. For a given data sample x, the embedding is z=fi(θi; x). For the global and the personalized classifier, each is parameterized by ϕg and ϕi, respectively, and is represented as hG(ϕg; z) and hP(ϕi; z). So, the form of the personalization model for client i is wi={θi, ϕi}. Personalizing certain modules of the model while sharing others is a common approach in pFL. However, previous researches [24–28] overlooked global knowledge when personalizing specific modules and failed to coordinate with modules containing global information. This undoubtedly constrained the model's performance, and excessive personalization increased the complexity of the model parameters. Hence, a hierarchical optimization method based on Feature Alignment and Fusion of Classifier Decisions.

3.3 Feature Alignment

The server needs to recognize the label set C={C(1), C(2),…} of multiple categories, whereas each client typically needs to identify only a subset of these classes. As shown in Fig. 1, the feature embedding representation of a sample is derived by feature extractor. The average embedding of all samples within the same class serves as the LFR of that class, defined as:

Ci(j)=1|Di, j|∑(x, y)∈Di, jfi(θi; x)(3)

where Di,j is a subset of the local data set, representing all training samples belonging to the class. In representation learning [12], a representation denotes the feature embedding vector extracted by feature extractor from an input sample. Inferring the original data solely from the extracted feature representations is challenging when model parameters are unknown. Since the client uploads Ci(j), which is the feature representation after the class average calculation, it further mitigates the risk of privacy disclosure. In specific t-th round communication, client i uploads Ci(j) and its corresponding label yj to the server. The server receives Ci(j) and inputs it into the global classifier to produce a prediction label. The error loss between the predicted labels and the true labels is calculated, and the global classifier parameters are updated:

ϕgt←ϕgt−1−ηϕg∇ϕl(ϕgt−1; Ci(j), yj)(4)

where ηϕg is the learning rate of the global classifier. To improve training efficiency, all clients upload their LFR before training commences. The global prediction head captures representation knowledge from diverse data categories across all clients. Furthermore, the server aggregates the LFR of overlapping classes and computes the corresponding GFR as follows:

C¯(j)=1|mj|∑i∈mj|Di, j|NjCi(j)(5)

where Nj represents the total number of samples of class j, and a represents the set of clients with samples of class j. The concept of GFR bears similarity to the prototype concept in Prototype-Based Learning, which has found wide application in small sample learning [29], contrastive learning [30]. To promote consistency in feature representation, the local feature extractor is updated by considering both supervised learning loss and generalization error. GFR are utilized to represent C¯(j), with regularization terms incorporated into local training objectives. Local representation learning gains from GFR, and the following is the definition of a local regularization term:

Ri(θi; C)=λ⋅1ni∑l=1ni1d‖fi(θi; xl)−C¯yl(j)‖22(6)

where fi(θi;xj) is the LFR of a given data point xj, C¯yj(j) is its corresponding GFR, and λ is a hyperparameter that controls the degree of regularization. Eq. (6) optimizes the representation learning process by aiming to learn more consistent feature representations. It regulates the parameter complexity of the local feature extractor while minimizing local classification error.

3.4 Fusion of Classifier Decisions

In multi-modal feature fusion, decision fusion is a common late-stage method. It involves classifying various modal information as network inputs and then merging them at the decision level. The goal is to capture the significance of multi-branch models, allowing for more comprehensive learning of feature information and improved performance [31]. When a client has limited local data, its personalized classifier may show significant variance. Despite many efforts to improve classification and evaluation performance, challenges remain, such as designing a more flexible classifier that can adapt to complex and diverse data [32]. Inspired by decision fusion, we combine decisions from both local and global sources to co-train a personalized classifier. Unlike previous works [24–27], the FedFCD performs classification decision fusion, which adds global decision information while improving the personalization performance of local classifiers. For client i, the specific process of its decision fusion is shown in Fig. 2.

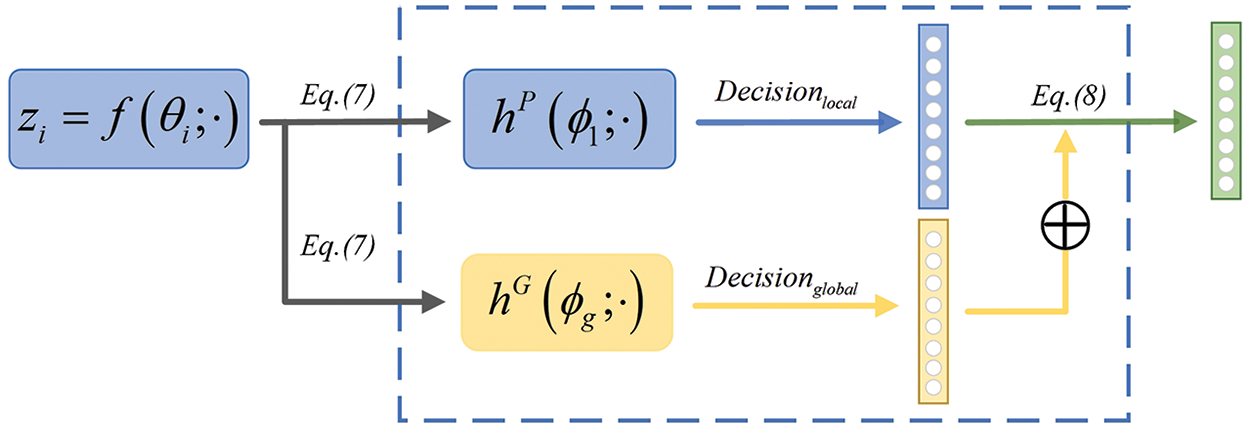
Figure 2: The fusion process of global classifier decision and local classifier decision

In the decision process of the classifier, the feature representation embedding fi(θi; x) is obtained by the feature extractor, and then input into the global classifier ϕg and personalized classifier ϕi respectively to output the global and local classification features:

Decisionglobal=hG(ϕg; fi(θi; x))Decisionlocal=hP(ϕi; fi(θi; x))(7)

where Decisionglobal represents the global classification feature and Decisionlocal represents the local classification feature. The element-based summation method is used to fuse the classification output feature vectors, and the final feature classification output is as follows:

Decision=softmax(Decisionglobal⊕Decisionlocal)(8)

where Decision represents the final classification vector obtained after decision level fusion, and softmax(⋅) represents the Softmax multi-class regression operation. In the classifier decision process, Decisionglobal can be considered an additional component of Decisionlocal, providing global information that cannot be captured by the personalized classifier.

3.5 Hierarchical Optimization

In this subsection, this study presents a hierarchical optimization method that iteratively updates the parameters of the feature extractor and classifier during local training. During the t-th communication round, client i first receives the global feature representation and classifier from the server. This optimization method updates the local model as follows:

Fix ϕi, update θi. During the specific local training process, the parameters of frozen ϕi are not backpropagated. The training samples and the GFR are only used to update θi:

θit←θit−ηf∇θ[l(θit, ϕit; ξk)+Ri(θit; C¯it)](9)

where ηf is the learning rate of the feature extraction layer, ξk represents the mini-batch data, and C¯it is the corresponding global feature representation.

Fix θi, update ϕi. Similarly, the parameters of the feature extraction layer are frozen directly and optimized separately during the classification decision process ϕi:

ϕit←ϕit−ηϕi∇ϕl(θit+1, ϕit; ξk)(10)

where ηϕi represents the learning rate of the classification decision layer. The loss is computed based on the final decision classification results. This method separates the parameter update of the feature extraction layer and the classification decision layer, which ensures the relevance of feature alignment and the effectiveness of decision fusion. Algorithm 1 presents the pseudocode of FedFCD.

4  Test Experimental Results and Discussion

4.1 Experimental Setup

4.1.1 Experimental Data

This paper performs experiments on three benchmark datasets: Fashion-MNIST [33], CIFAR-10 [34], and CIFAR-100 [34]. For each dataset, two scenarios are simulated to represent Non-IID data distribution. The first scenario, known as the Pathological heterogeneous setting (Pat), is the earliest studied federated heterogeneous scenario. In this scenario, each client is randomly assigned 2 class labels from the set of 10 class labels in each Fashion-MNIST/CIFAR-10 dataset (10 classes from the 100 on CIFAR-100). This ensures that the data samples obtained by each client do not overlap [7]. This setup simulates the extreme unevenly distributed data that may be encountered in practical applications. The second scenario is the Practical heterogeneous setting, which uses the probability density function of the Dirichlet distribution [35] to construct the data distribution on the client. Dirichlet distribution controls the heterogeneity of data among clients by a parameterized way, which is simplified as Dir(β). The specific definition and settings are as follows:

Pi(φ1, φ2,…,φc)=τ(∑kβk)∏kτ(βk)∏k=1cτ(βk)φkβk−1(11)

pi(φc)=Pi(φc)∑k=1cPi(φk)(12)

where c represents the number of label categories owned by the local dataset. The pi(φk) represents the proportion of data with category label k on client i: {φ1, φ2,…,φc}∼Dir(β1, β2,…,βc), where the value of β can affect the degree of heterogeneity of the data.

For example, Fig. 3 illustrates a data distribution scenario with 10 clients on the CIFAR-10 dataset. As can be seen from Fig. 3., consider the two cases where β is 0.1 and 1.0, respectively. The smaller the value of β, the more unbalanced the data distribution and the more extreme the degree of data heterogeneity.

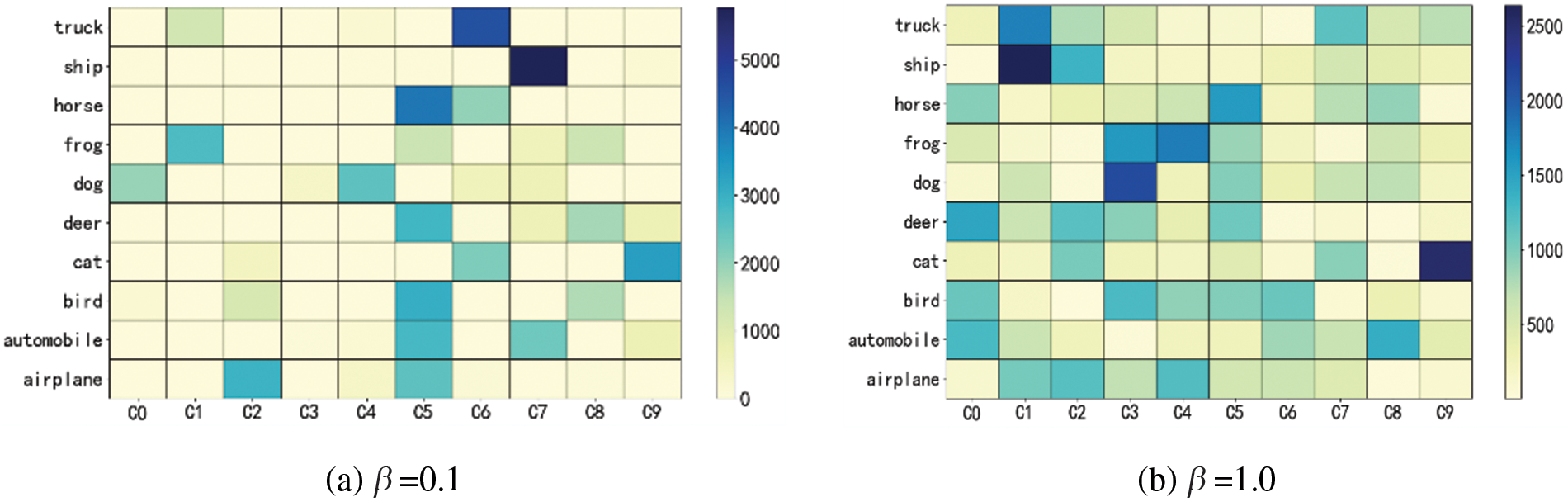
Figure 3: Data distribution of clients at different Non-IID levels

4.1.2 Detail Setup

To simulate personalized client-side data in real-world scenarios, the dataset's training and test sets are combined and shuffled before being distributed to each client in an unbalanced manner. On each client device, 75% of the data is randomly assigned to the training set, while the remaining 25% is allocated to the test set. The evaluation metric relies on the highest average test accuracy attained by each algorithm. In traditional FL algorithms, the assessment focuses on the highest average accuracy achieved by the global model across all clients. In contrast, pFL algorithms prioritize the highest average accuracy achieved by local personalized models across all clients.

Depending on the dataset's characteristics, different DNNs models are selected for training. For relatively simple datasets like Fashion-MNIST, a Multilayer Perceptron (MLP) is utilized. The input image is represented as a 784-dimensional vector, and the network architecture consists of a hidden layer with 100 neurons employing the Rectified Linear Unit (ReLU) activation function. When dealing with the CIFAR-10 dataset, a Convolutional Neural Network (CNN) is employed. The model comprises two convolutional layers, each utilizing 5 × 5 filters with 32 and 64 filters, respectively. Following each convolutional layer is a 2 × 2 max-pooling layer. Subsequently, there exists a fully connected layer with 512 neurons also utilizing the ReLU activation function. To evaluate the algorithm's effectiveness and feasibility on more complex models, particularly considering the inherently intricate image recognition task of the CIFAR-100 dataset, the ResNet-18 deep residual network model [36] is adopted. The network structure is illustrated in Fig. 4.

Figure 4: ResNet-18 model for CIFAR-100 dataset

For all experiments with 20 clients, the default parameter values are as follows: The learning rate for the global classifier is set to 0.01, while the learning rate for hierarchical optimization on the client side is also set to 0.01. To better evaluate the models on each client, the participation rate of clients in each communication round is set to 1. The total number of communication rounds is set to 500, ensuring that all algorithms reach empirical convergence, with no further accuracy gains observed even with additional communication rounds. Considering the feature extraction process varies in difficulty across different datasets, we set λ as 1 for the Fashion-MNIST dataset. For the CIFAR-10 and CIFAR-100 datasets, λ was set to 5. Finally, the parameter β was set to 0.1.

4.2 Contrast Experiment

4.2.1 Compared Algorithms

To conduct a comprehensive comparison, this study conducted experiments involving the following seven algorithms: FedAvg [7], FedProx [14], Pre-FedAvg [20], FedAMP [21], FedProto [23], GPFL [24], and FedGH [28], along with the proposed FedFCD algorithm. For fairness, experiments employed the same data partitioning method, models, and common experimental parameters.

4.2.2 Results and Analysis

Table 1 presents the best average test accuracy of all algorithms in two heterogeneous scenarios. From the specific results, pFL algorithms perform well on the Fashion-MNIST dataset. Although FedAMP demonstrates the best performance, FedFCD remains highly competitive with only marginal differences. On the CIFAR-10 dataset, FedFCD outperforms other pFL methods in both heterogeneous data scenarios, improving the average test accuracy by 1.09% and 2.11%, respectively. On the CIFAR-100 dataset, which has the highest number of categories, FedFCD performs exceptionally well. In both heterogeneous scenarios of this dataset, FedFCD enhances the average accuracy by 6.83% and 4.23% compared to the contrast methods. Even when compared to FedGH, the best-performing method among the contrasts, FedFCD increases the classification accuracy by 3.24% and 1.83%.

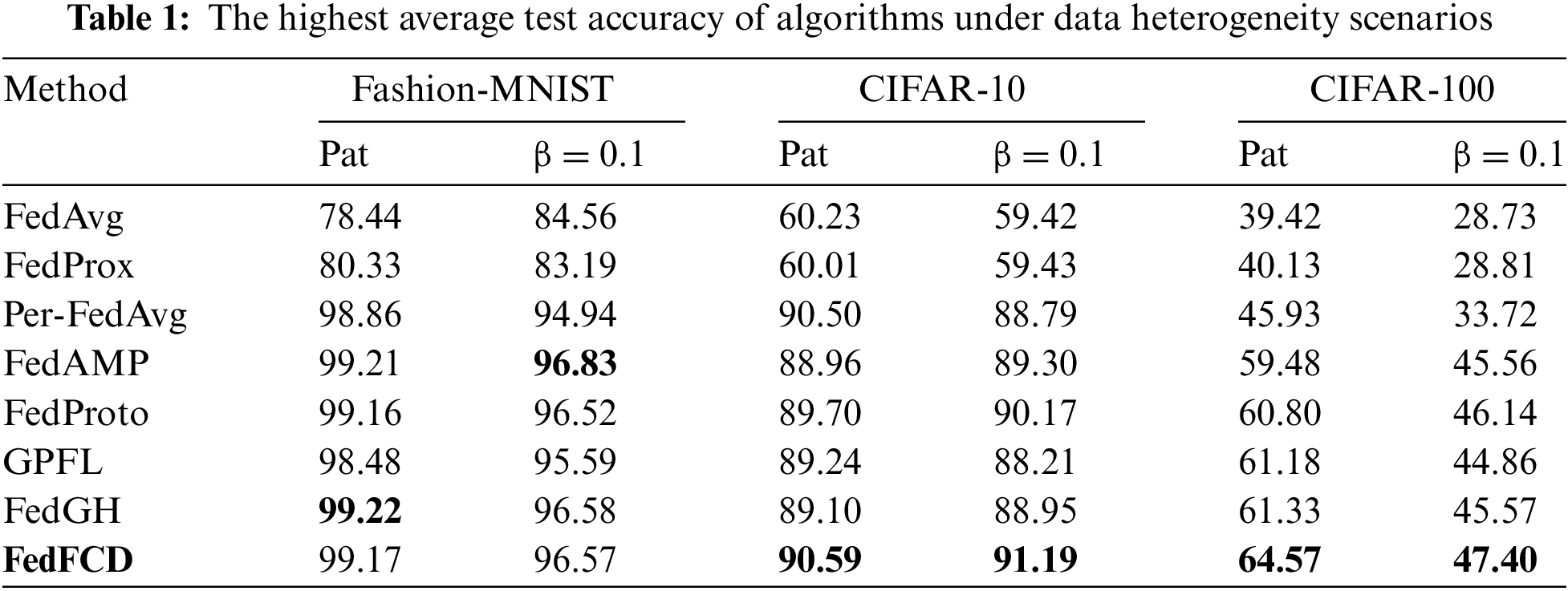
Consequently, FedFCD demonstrates significant advantages under various heterogeneity settings and is more suitable for tasks with a larger number of categories.

4.3 Extended Experiment

4.3.1 Robustness

To investigate the robustness of algorithms in larger-scale federated learning scenarios, this study conducts extended experiments on CIFAR-10. The specific settings are: {(m= 50, ρ= 0.4), (m= 100, ρ= 0.2)}. To ensure fair comparison, the number of participating clients in training was kept consistent in each round (m×ρ= 20). Please review the results in Table 2. In practical heterogeneous settings, traditional FL algorithms are notably impacted, with the best accuracies declining by 3.97% and 4.67%, respectively. However, FedFCD consistently achieves optimal performance. Compared to four personalized algorithms, FedFCD enhances accuracy by 1.01% and 1.71% in the extended settings of pathological heterogeneous scenarios. In practical heterogeneous scenarios, it increases accuracy by 1.5% and 2.11%.

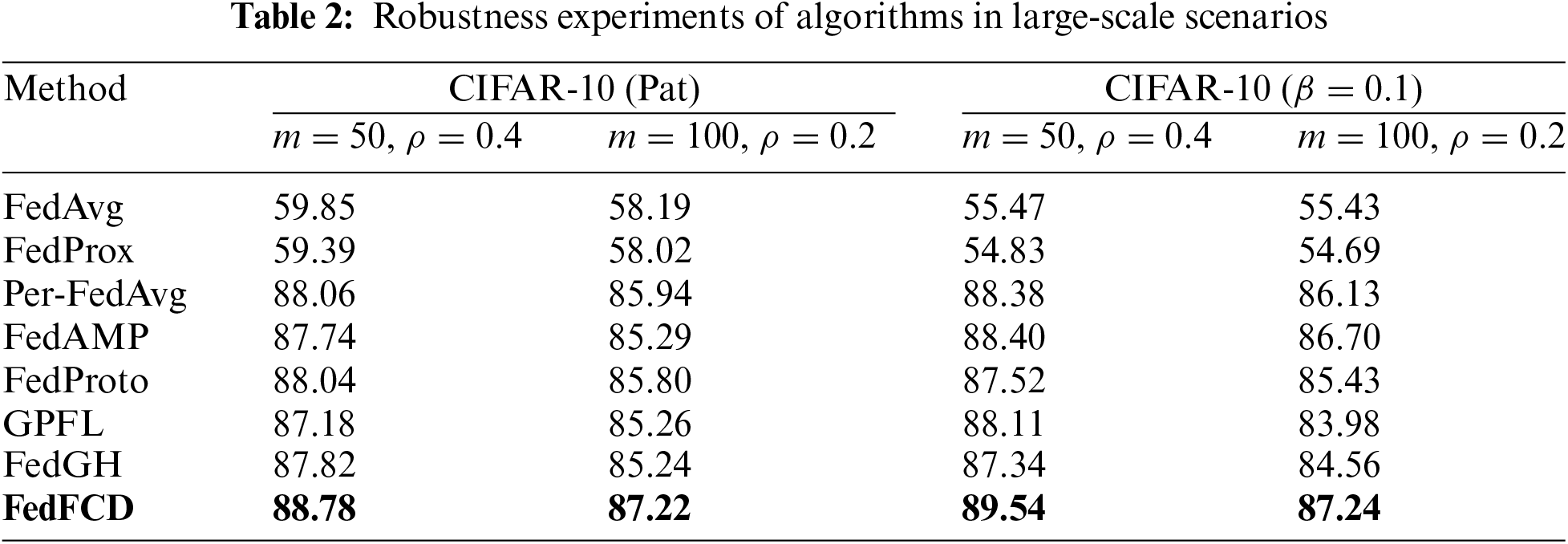
To evaluate the performance of those algorithms in a wider range of heterogeneous scenarios, we tested FedFCD along with two algorithms, FedAMP and FedGH, which performed well in the comparative experiments, on CIFAR-10 under various degrees of Pat conditions. Specifically, in a setup with 20 clients and the participation rate ρ= 1, we distributed {4, 6, 8} classes of samples to each client. The more sample categories a client possesses, the lower the skewness in its label distribution [9]. As depicted in Fig. 5, experimental results reveal that FedFCD achieves the highest model accuracy across different levels of Pat heterogeneity. Compared to the best baseline method, FedAMP, FedFCD improved accuracy by 2.70%, 3.05%, and 2.58%. This underscores the robustness and broad applicability of FedFCD to data with varying degrees of heterogeneity.

Figure 5: Average test accuracy under different degrees of pathological data heterogeneity

4.3.2 Parameter Sensitivity

The global classifier learning rate ηϕg and the regularization coefficient λ are two important hyperparameters. The former affects the prediction head quality learned by the server, while the latter influences the alignment of global and local features. To investigate the sensitivity of these parameters, experiments were conducted in the heterogeneous data scenario of CIFAR-10 (with β= 0.1), setting the number of clients m = 20 and the participation rate ρ= 1. With λ fixed at 5, the candidate set for ηϕg was {0.001, 0.005, 0.01, 0.05, 0.1, 0.5}. With ηϕg fixed at 0.01, the candidate set for λ was {0, 1, 2, 4, 5, 10}. Fig. 6 presents the relationship between average test accuracy and the number of communication rounds for various learning rate settings. Observations from this figure suggest that an optimal learning rate can foster early empirical convergence. For instance, when ηϕg = 0.01, the algorithm can quickly achieve convergence. The varied learning rate values have minimal impact on the model's final performance, indicating that the FedFCD algorithm is not sensitive to this hyperparameter. This insensitivity is due to the use of sparse local average representations in training the global prediction head, which simplifies the training process compared to training a full model. Consequently, the learning rate does not have a decisive influence on performance, demonstrating the robustness of FedFCD to the choice of the learning rate ηϕg.

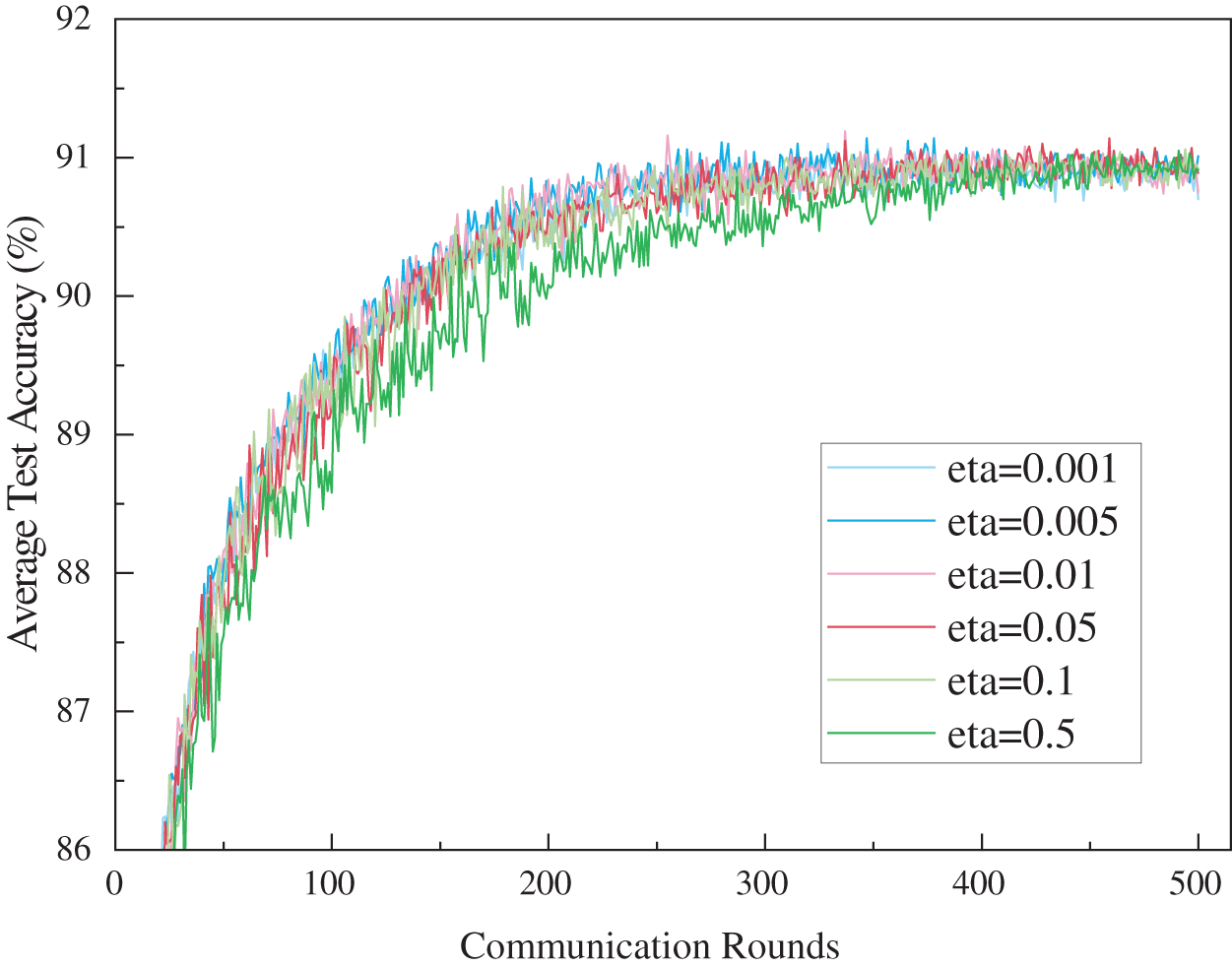
Figure 6: Impact of eta value on average test accuracy

Fig. 7 shows the curves of average test accuracy against the number of communication rounds with varying values of the regularization coefficient. From Fig. 7, it can be observed that when the value of λ is small, the model performance is affected to some extent, and appropriately increasing λ can lead to better results. However, if the value is excessively large, optimal performance cannot be achieved, indicating that FedFCD is somewhat sensitive to this parameter. This is because the value of λ influences the effectiveness of feature alignment, making the selection of an appropriate value crucial. Additionally, it can be observed that when λ = 0 (i.e., without regularization term), there is a significant decrease in average test accuracy compared to other values. This highlights the effectiveness of feature alignment.

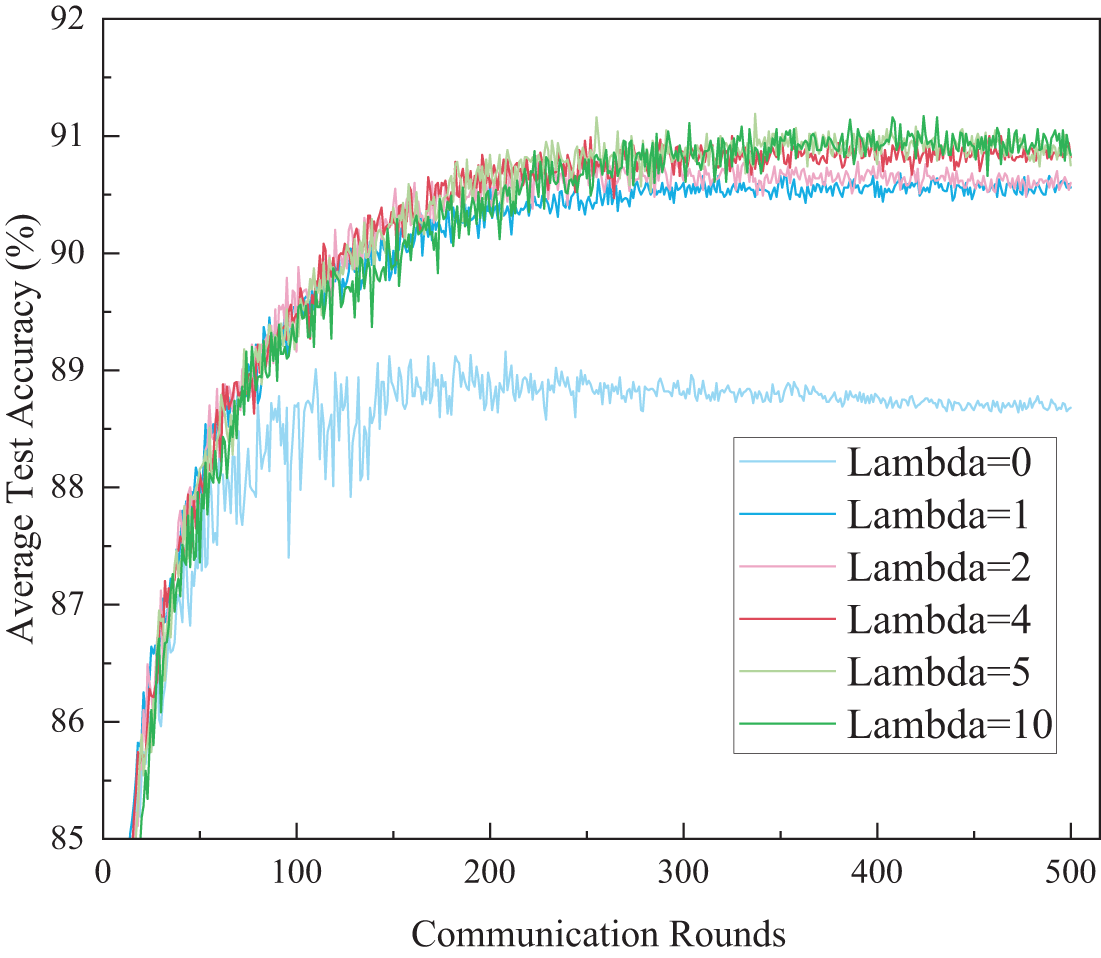
Figure 7: Impact of Lambda value on average test accuracy

4.3.3 Ablation Studies

There are two components and a method in FedFCD, i.e., feature alignment (FA), fashion of decision (FD) and hierarchical optimization (HO). We create some variants to verify the individual efficacy of those factors (“w/o” is short for “without”). In the two heterogeneous data scenarios of the CIFAR-10 dataset, experiments were conducted using the same settings as those in the contrast experiments. As demonstrated in Table 3, both of them can help improve the average test accuracy and the combination of them is able to achieving the most satisfactory model performance.

5  Conclusion and Future Work

Heterogeneous data distribution poses a significant challenge in FL. While pFL methods offer assistance, current research often overlooks the utilization of global knowledge in local learning and neglects the generalization of local classifiers. This paper introduces FedFCD, a pFL algorithm designed to address these issues. FedFCD leverages global feature knowledge to enhance local feature extraction and improves the efficiency of training the global prediction head. Additionally, it employs a hierarchical alternating optimization strategy to optimize the parameters of the model while focusing on both feature extraction and classification decisions.

Experimental results on various benchmark datasets demonstrate that FedFCD constructs efficient personalized federated models. Extended experiments validate its robustness and resilience to parameter variations, effectively handling data heterogeneity in federated learning scenarios. Given the constraints of limited communication and varying computational resources among clients in real-world settings, future research will prioritize federated learning in resource-constrained environments. The goal is to design efficient algorithms tailored to a wider range of federated scenarios.

Acknowledgement: The authors would like to thank Dr. Xinfang Ji for the academic discussions, which contributed to the improvement of this work.

Funding Statement: This research was funded by the National Natural Science Foundation of China (Grant No. 62062001) and Ningxia Youth Top Talent Project (2021).

Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Ke Li; data collection: Ke Li; paper guidance and overall planning: Xiaofeng Wang; analysis and interpretation of results: Ke Li and Hu Wang; draft manuscript preparation: Ke Li, Xiaofeng Wang and Hu Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data incorporated in this study can be accessed by contacting the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present paper.

References

1. Y. Shen, S. Shen, Q. Li, H. Zhou, Z. Wu and Y. Qu, “Evolutionary privacy-preserving learning strategies for edge-based IoT data sharing schemes,” Digit. Commun. Netw., vol. 9, no. 4, pp. 906–919, 2023. doi: 10.1016/j.dcan.2022.05.004. [Google Scholar] [CrossRef]

2. Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, 2015. doi: 10.1038/nature14539. [Google Scholar] [PubMed] [CrossRef]

3. G. Wu, X. Chen, Z. Gao, H. Zhang, S. Yu and S. Shen, “Privacy-preserving offloading scheme in multi-access mobile edge computing based on MADRL,” J. Parallel Distr. Comput., vol. 183, 2024, Art. no. 104775. doi: 10.1016/j.jpdc.2023.104775. [Google Scholar] [CrossRef]

4. G. Wu et al., “Combining Lyapunov optimization with actor-critic networks for privacy-aware IIoT computation offloading,” IEEE Internet Things J., vol. 11, no. 10, pp. 17437–17452, 2024. doi: 10.1109/JIOT.2024.3357110. [Google Scholar] [CrossRef]

5. S. X. Ji et al., “Emerging trends in federated learning: From model fusion to federated x learning,” Int. J. Mach. Learn. Cybern., vol. 15, pp. 1–22, 2024. doi: 10.1007/s13042-024-02119-1. [Google Scholar] [CrossRef]

6. Y. Qu, L. Gao, Y. Xiang, S. Shen, and S. Yu, “FedTwin: Blockchain-enabled adaptive asynchronous federated learning for digital twin networks,” IEEE Netw., vol. 36, no. 6, pp. 183–190, 2022. doi: 10.1109/MNET.105.2100620. [Google Scholar] [CrossRef]

7. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. Y. Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Proc. 20th Int. Conf. Artif. Intell. Stat., Fort Lauderdale, FL, USA, 2017, pp. 1273–1282. [Google Scholar]

8. Z. P. Li, V. Sharma, and S. P. Mohanty, “Preserving data privacy via federated learning: Challenges and solutions,” IEEE Consum. Electron. Mag., vol. 9, no. 3, pp. 8–16, 2020. doi: 10.1109/MCE.2019.2959108. [Google Scholar] [CrossRef]

9. Q. B. Li, Y. Q. Diao, Q. Chen, and B. S. He, “Federated learning on non-IID data silos: An experimental study,” in IEEE Int. Conf. Data Eng., Kuala Lumpur, Malaysia, 2022, pp. 965–978. [Google Scholar]

10. Q. Wu, K. W. He, and X. Chen, “Personalized federated learning for intelligent IoT applications: A cloud-edge based framework,” IEEE Open J. Comput. Soc., vol. 1, pp. 35–44, 2020. doi: 10.1109/OJCS.2020.2993259. [Google Scholar] [PubMed] [CrossRef]

11. P. Kairouz et al., “Advances and open problems in federated learning,” Found. Trends Mach. Learn., vol. 14, no. 1–2, pp. 1–210, 2021. doi: 10.1561/2200000083. [Google Scholar] [CrossRef]

12. Y. Bengio, A. Courville, and P. Vincent, “Representation learning: A review and new perspectives,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 35, no. 8, pp. 1798–1828, 2013. doi: 10.1109/TPAMI.2013.50. [Google Scholar] [PubMed] [CrossRef]

13. L. Collins, H. Hassani, A. Mokhtari, and S. Shakkottai, “Exploiting shared representations for personalized federated learning,” in Proc. 38th Int. Conf. Mach. Learn., Vienna, VIE, Austria, 2021, pp. 2089–2099. [Google Scholar]

14. T. Li et al., “Federated optimization in heterogeneous networks,” in Proc. 1st Adapt. Multitask Learn. Workshop, Austin, TX, USA, 2020, pp. 429–450. [Google Scholar]

15. S. P. Karimireddy et al., “SCAFFOLD: Stochastic controlled averaging for federated learning,” in Proc. 37th Int. Conf. Mach. Learn., Vienna, VIE, Austria, 2020, pp. 5132–5143. [Google Scholar]

16. Y. Zhao et al., “Federated learning with non-IID data,” 2018, arXiv:1806.00582. [Google Scholar]

17. Y. Fraboni, R. Vidal, L. Kameni, and M. Lorenzi, “Clustered sampling: Low-variance and improved representativity for clients selection in federated learning,” in Proc. 38th Int. Conf. Mach. Learn., Vienna, VIE, Austria, 2021, pp. 3407–3416. [Google Scholar]

18. T. Hospedales, A. Antoniou, P. Micaelli, and A. Storkey, “Meta-learning in neural networks: A survey,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 9, pp. 5149–5169, 2021. doi: 10.1109/TPAMI.2021.3079209. [Google Scholar] [PubMed] [CrossRef]

19. C. Finn, P. Abbeel, and S. Levine, “Model-agnostic meta-learning for fast adaptation of deep networks,” in Proc. 34th Int. Conf. Mach. Learn., Sydney, Australia, 2017, pp. 1126–1135. [Google Scholar]

20. A. Fallah, A. Mokhtari, and A. Ozdaglar, “Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach,” in Adv. Neural Inform. Process. Syst., 2020, pp. 3557–3568. [Google Scholar]

21. Y. Huang et al., “Personalized cross-silo federated learning on non-IID data,” in Proc. AAAI Conf. Artif. Intell., Vancouver, BC, Canada, 2021, pp. 7865–7873. [Google Scholar]

22. O. Marfog, G. Neglia, A. Bellet, L. Kameni, and R. Vidal, “Federated multi-task learning under a mixture of distributions,” in Adv. Neural Inform. Process. Syst., 2021, pp. 15434–15447. [Google Scholar]

23. Y. Tan et al., “FedProto: Federated prototype learning across heterogeneous clients,” in Proc. AAAI Conf. Artif. Intell., Vancouver, BC, Canada, 2022, pp. 8432–8440. [Google Scholar]

24. J. Zhang et al., “GPFL: Simultaneously learning global and personalized feature information for personalized federated learning,” in Proc. IEEE/CVF Int. Conf. Comput. Vis., Paris, France, 2023, pp. 5041–5051. [Google Scholar]

25. J. Guo, J. Wu, A. Liu, and N. N. Xiong, “LightFed: An efficient and secure federated edge learning system on model splitting,” IEEE Trans. Parallel Distrib. Syst., vol. 33, no. 11, pp. 2701–2713, 2021. doi: 10.1109/TPDS.2021.3127712. [Google Scholar] [CrossRef]

26. W. H. Chung, Y. C. Chang, C. H. Hsu, C. H. Chang, and C. L. Hung, “Federated feature concatenate method for heterogeneous computing in federated learning,” Comput. Mater. Contin., vol. 75, no. 1, pp. 351–371, 2023. doi: 10.32604/cmc.2023.035720. [Google Scholar] [CrossRef]

27. Y. Liu et al., “FedTC: A personalized federated learning method with two classifiers,” Comput. Mater. Contin., vol. 76, no. 3, pp. 3013–3027, 2023. doi: 10.32604/cmc.2023.039452. [Google Scholar] [CrossRef]

28. L. P. Yi, G. Wang, X. G. Liu, Z. Shi, and H. Yu, “FedGH: Heterogeneous federated learning with generalized global header,” in Proc. 31th Int. Conf. Multimed., Ottawa, ON, Canada, 2023, pp. 8686–8696. [Google Scholar]

29. J. Snell, K. Swersky, and R. Zemel, “Prototypical networks for few-shot learning,” in Adv. Neural Inform. Process. Syst., Long Beach, CA, USA, 2017. [Google Scholar]

30. J. N. Li, P. Zhou, C. Xiong, and S. C. H. Hoi, “Prototypical contrastive learning of unsupervised representations,” 2020, arXiv:2005.04966. [Google Scholar]

31. T. X. Zhou, S. Ruan, and S. Canu, “A review: Deep learning for medical image segmentation using multi-modality fusion,” Array, vol. 3, 2019, Art. no. 100004. doi: 10.1016/j.array.2019.100004. [Google Scholar] [CrossRef]

32. S. Feng, L. Zhao, H. Shi, M. Wang, S. Shen and W. Wang, “One-dimensional VGGNet for high-dimensional data,” Appl. Soft Comput., vol. 135, 2023, Art. no. 110035. doi: 10.1016/j.asoc.2023.110035. [Google Scholar] [CrossRef]

33. H. Xiao, K. Rasul, and R. Vollgraf, “Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms,” 2017, arXiv:1708.07747. [Google Scholar]

34. A. Krizhevsky and G. Hinton, “Learning multiple layers of features from tiny images,” in Handbook of Systemic Autoimmune, 2009. [Google Scholar]

35. N. Wojke and A. Bewley, “Deep cosine metric learning for person re-identification,” in IEEE Winter Conf. Appl. Comput. Vis. (WACV), Lake Tahoe, NV, USA, 2018, pp. 748–756. [Google Scholar]

36. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, 2016, pp. 770–778. [Google Scholar]