Dynamical Artificial Bee Colony for Energy-Efficient Unrelated Parallel Machine Scheduling with Additional Resources and Maintenance

1  Introduction

Scheduling problems and algorithms have been extensively utilized in manufacturing and service industries to enhance production efficiency. As a typical scheduling problem, parallel machine scheduling problem (PMSP) extensively exists in many processes of manufacturing and service including production lines, hospital management systems, computer systems and shipping docks [1,2]. In unrelated parallel machine scheduling (UPMSP), the processing time of a job depends on its assigned machine. UPMSP with various conditions and constraints such as additional resources, maintenance and energy have been well studied and a number of results were obtained in the past decade [3–5].

There are many works on unrelated parallel machine scheduling problems with additional resources (UPMSPR). Ventura et al. [6] proved that the problem with one single type of additional resources is equivalent to the asymmetric assignment problem. Zheng et al. [7] reported a two-stage adaptive fruit fly optimization algorithm (FOA) with a heuristic and knowledge-guided search. Fanjul-Peyro et al. [8] presented two integer linear programming models and three matheuristics. Fleszar et al. [9] gave an efficient mixed-integer linear programming (MILP) model for a lower bound. Zheng et al. [10] proposed a collaborative multi-objective FOA to minimize carbon emissions. Villa et al. [11] developed several heuristics based on resource constraints and assignment rules. Afzalirad et al. [12] presented an integer mathematical programming model and two genetic algorithms for the problem with eligibility restrictions. Vallada et al. [13] applied an enriched scatter search and an enriched iterated greedy with a best-known heuristic and a repair mechanism.

UPMSPR with at least two real-life constraints is also studied, which are non-zero arbitrary release dates and sequence-dependent setup times (SDST) [14], processing resources, setup resources and shared resources [15], and additional resources in processing and setup [16]. Pinar et al. [17] proposed three heuristics and greedy randomized adaptive search procedures for UPMSP with setup times, and additional limited resources in setup.

Preventive maintenance (PM) is often applied to prevent potential failures and serious accidents in parallel machines and UPMSP with PM is frequently addressed. Some real-life constraints such as aging effects [18], multi-resources PM planning [19], deteriorating [20] and SDST [21] are included into UPMSP with PM. Various meta-heuristics including genetic algorithm [20], novel imperialist competitive algorithm (NICA) with an estimation of distribution algorithm [22], a differentiated shuffled frog-leaping algorithm [23], iterated algorithm [24], artificial bee colony (ABC [25]) and adaptive ABC [26].

The increasing environmental and energy pressures result in the increasing attention to energy saving or energy efficiency in manufacturing industries. In recent years, UPMSP with energy has received some attention. Che et al. [27] presented an improved continuous-time MILP model and a two-stage heuristic for UPMSP under time-of-use (TOU) electricity price. Cota et al. [28] proposed a MILP model and a novel math-heuristic algorithm for UPMSP with makespan and total consumption of electricity. Abikarram et al. [29] developed a mathematical optimization model and some analyses for UPMSP with energy cost. Zhang et al. [30] provided a new heuristic evolutionary algorithm to solve UPMSP with tool changes, makespan and total energy consumption. Wang et al. [31] applied a modified artificial immune algorithm to deal with UPMSP with energy, auxiliary resource shared among machines. For UPMSP with TOU electricity tariffs, Saberi-Aliabad et al. [32] presented a MILP model and a number of dominance rules and valid inequalities and Pei et al. [33] proposed an approximate algorithm after the problem is transformed into single machine problems with TOU electricity price. Zhang et al. [34] developed a combinatorial evolutionary algorithm (CEA) for UPMSP with setup times, limited worker resources and learning effect.

As stated above, UPMSPR, UPMSP with PM and UPMSP with energy have attracted attention and have been addressed using metaheuristics like ABC, NICA and FOA etc.; moreover, UPMSP with at least two real-life constraints is often studied [14–17,22–24]; however, UPMSP with additional resources, maintenance and energy is hardly investigated. In many unrelated parallel machine production processes, additional resources and maintenance often exist simultaneously and energy efficiency is important for production with the increasing pressures of environmental protection and energy price. The consideration of these things can result in a high application value of the obtained schedule, so it is essential to solve energy-efficient UPMSP with additional resources and PM.

It also can be found that ABC is an effective method to solve UPMSPR and UPMSP with PM. As a meta-heuristic inspired by the intelligent foraging behavior of honeybee swarm, ABC has some features such as simplicity and ease of implementation, and it has been successfully applied to deal with various production scheduling problems [35–39] and notable advantages of ABC in solving UPMSP [36–40] are proved by computational results. The energy-efficient UPMSP with additional resources and PM is an extended version of the UPMSP. It is still composed of the same sub-problems as UPMSP [36–40]. ABC has some particular features. It also has successfully applied to hand various UPMSP. There are close relations between UPMSP and its extended version. These three things reveal that ABC has potential optimization advantages in solving energy-efficient UPMSP with additional resources and PM, which is why ABC is chosen.

In this study, energy consumption, additional resources and PM are integrated into UPMSP and an effective way is provided for the problem by adding some new dynamical optimization mechanisms into ABC. The main contributions are summarized as follows. (1) Energy-efficient UPMSP with PM and additional resources is considered. (2) The dynamical artificial bee colony (DABC) is presented to minimize makespan and total energy consumption. Three heuristics are used in the initialization. Employed bee swarm and onlooker bee swarm are constructed and computing resources are shifted from the dominated solutions to non-dominated solutions in each swarm when the given condition is met. The dynamical employed bee phase is implemented by computing resource shifting and solution migration. The Dynamical onlooker bee phase involves computing resource shifting and feedback. This phase is applied to dynamically select search operators based on global and neighborhood searches. (3) Many experiments are conducted. The computational results demonstrate that new strategies of DABC are effective and that DABC has promising advantages in solving the considered UPMSP.

The remainder of the paper is organized as follows. Problem description is given in Section 2. Section 3 shows DABC for the considered problem. Section 4 gives numerical experiments on DABC and Section 5 shows the conclusions and some topics of future research are provided.

2  Problem Description

Energy-efficient UPMSP with additional resources and PM is composed of n jobs J1,J2,⋯,Jn and m unrelated parallel machines M1,M2,⋯,Mm. Each job can be processed on any one of m machines. pki is processing time of job Ji on machine Mk. An additional renewable resource is needed for each job. For job Ji processed on Mk, it needs rki units of the additional resource. At most Rmax units of additional resources can be used at any time.

PM is considered. There is a time interval between two consecutive PMs, during which jobs are processed. For Mk, uk is the length of the interval, wk denotes the duration of PM, and the start time of the g−th PM is g×uk

Machine Mk has three modes: processing mode, idle mode and PM mode. ek,iek and pek indicate the energy consumption per unit time when Mk is in processing mode, idle mode and PM mode, respectively.

The mathematical mode of the problem is shown below:

Cmax=max{Cj|j=1,2,⋯,n}(1)

TEC=∑k=1m∑i=1n∫0Cmaxwikt×ekdt+∑k=1m(iek×ipk+pek×tpk)(2)

s.t.∑k=1m∑l=1nxikl=1∀i(3)

∑i=1nxikl≤1∀k,l(4)

bk,1=0 ∀k(5)

zklg×(bk,l+1−bk,l−∑l=1npik×xikl)=0 ∀g(6)

(1−zklg)×(bk,l+1−guk)=0 ∀g(7)

∑k=1m∑i=1n∑lrkixiklwikt≤Rmax ∀t(8)

bi¯=∑k=1m∑l=1nbkl×xikl∀i(9)

Ci=bi¯+∑k=1m∑l=1npik×xikl∀i(10)

xikl∈{0,1}∀k,l(11)

where Ci indicates completion time of job Ji and Cmax is maximum completion time of all jobs, wikt is 1 if job Ji is processed on Mk at time t and 0 otherwise. xikl is 1 if Ji is processed on position l on Mk and 0 otherwise. zklg is 1 if bk,l+∑l=1npik×xikl≤guk and 0 otherwise, bk,l is beginning time of job on position l of machine Mk, ipk,tpk are the total idle time and total maintenance duration, respectively. TEC denotes total energy consumption.

Eqs. (1) and (2) are about objectives. Constraint (3) indicates that job Ji is just needed to be assign to one machine. Constraint (4) denotes that at most one job is assigned to one position of one machine. Constraints ((6), (7)) are about PM. Constraint (8) is related one on additional resource. The last two constraints are about beginning time and completion time of job Ji.

For energy-efficient UPMSP with Cmax and TEC, z≻x means that z dominates x and defined below:

Cmaxz≤Cmaxx, TECz≤TECx, at least one of Cmaxz<Cmaxx, TECz<TECx exists. When z≻x, x≻z are not met, z,x are non-dominated each other. Cmaxx and TECx are makespan and total energy consumption of x.

An illustrative example with 2 machines and 8 jobs is given, the matrix of processing time and matrix of additional resource are provided in Eqs. (12) and (13), e1=2, e2=3, iek=1, pek=5, uk=24, wk=3.

(pki)m×n=(5665244633444533)(12)

(rki)m×n=(5773376534584332)(13)

Fig. 1 shows a schedule, in which 6 (7) as an example indicates job J6 with r16 of 7.

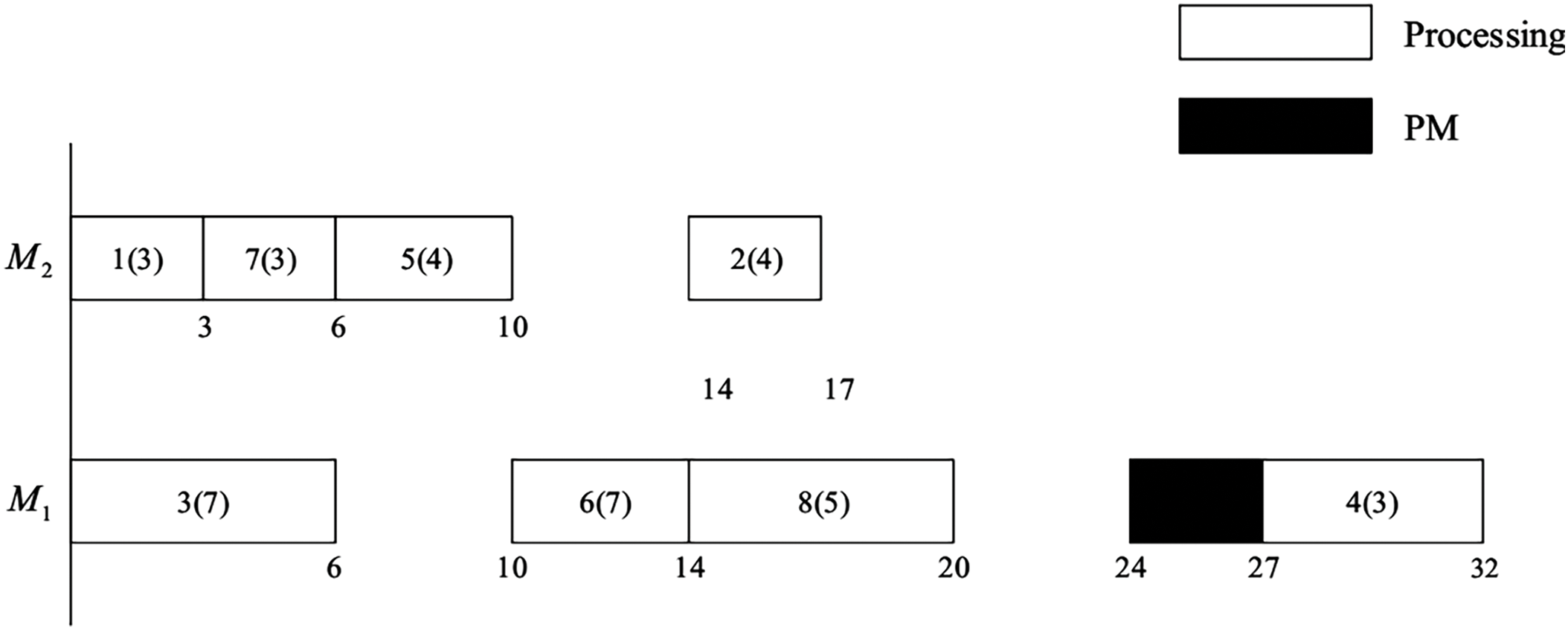
Figure 1: A schedule of example

3  DABC for Energy-Efficient UPMSP with Additional Resource and PM

Dynamical optimization mechanisms such as feedback and competition have been successfully used in ABC to adjust dynamically search operators or search behaviors [41–45]. The search advantages of dynamical mechanisms are tested and proved. In this study, dynamical optimization mechanism is implemented by computing resource shifting, solution migration and feedback.

3.1 Initialization

Lei et al. [26] proposed a two-string representation. For energy-efficient UPMSP with n jobs, m machines, Rmax units of additional resource and PM, its solution consists of a machine assignment string [Mh1,Mh2,⋯,Mhn] and a scheduling string [θ1,θ2,⋯,θn], where Mhi is the assigned machine for job Ji and θi is real number.

The decoding procedure is described as follows:

(1) Obtain job permutation [π1,π2,⋯,πn] by sorting all jobs in ascending order of θi.

(2) Start with π1, for each job πi, assign it to its machine Mhπi according to the first string, decide if job πi can be inserted into idle period and deal with PM as done in paper [16].

For the example in Section 2, a solution consists of [M2,M2,M1,M1,M2,M1,M2,M1] and [0.1,0.3,0.7,0.57,0.62,0.23,0.85,0.41, the obtained job permutation is [1,3,7,5,6,2,8,4], when J6 is allocated on M1, if no additional resource constraint is considered, J6 can be processed between [6,10], however, the sum of the additional resource is 11, the additional resource constraint is violated, so J6 is processed on [10,14]. For J4, if it is processed directly after J8, C4=25>u1, so PM is first executed and then J4 is processed. The obtained schedule is shown in Fig. 1.

β initial solutions are produced by heuristics. Heuristic 1 is used to produce solution x1 and described as follows. For each Ji, min{pki,1≤k≤m} is decided, a machine Mhπi with phii=min{pki} and the smallest phii×ehi are chosen; then a scheduling string is randomly generated. Heuristic 2 is used for solution x2 and shown below. For each job Ji, compute min{pki×ek,1≤k≤m} and then select Mhπi with the smallest phii and phii×ehi=min{pki×ek}. The scheduling string of x2 is also stochastically generated.

Heuristic 3 is used for each of β−2 solutions: randomly produce a scheduling string, for each job Ji, if rand<0.5, then decide a machine Mhπi as done in heuristic 1 for each Ji; else determine a machine Mhπi as done in heuristic 2 for each Ji. Where rand is random number following uniform distribution on [0, 1].

N−β initial solutions are stochastically gotten. Employed bee swarm EB consists of randomly chosen N/2 solutions from P and onlooker bee swarm OB is composed of the remained N/2 solutions.

3.2 Dynamically Employed Bee Phase

Six neighborhood structures are used. 𝒩1 is used to move a randomly chosen job Ji on a machine with the biggest completion time to a machine Mk with the smallest pki×ek. 𝒩2 is similar with 𝒩1, Ji is moved to Mk with the smallest pki in 𝒩2. 𝒩3 is shown below. Decide max{phii×ehi,1≤i≤n} and a job Jj with phjj×ehj=max{phii×ehi} and move Jj to a machine Mk with pkj×ek=min{plj×el,1≤l≤m}. 𝒩4 is adopted to exchange a randomly selected job on a machine Mk with the biggest completion time and a randomly chosen job on a stochastically decided Ml,l≠k. 𝒩5 is shown below. Randomly choose Mk and swap two randomly selected jobs Ji,Jj on Mk, that is, θi,θj are exchanged. 𝒩6 is described as follows. Randomly decide a machine Mk and two randomly selected jobs Ji,Jj on Mk, then insert θi into position j on scheduling string.

Algorithm 1 describes the detailed steps of dynamical employed bee phase, where cni and rankxi indicate the number of searches on a generation and rank of xi decided by non-dominated sorting [46], 𝒩g(x) is the set of neighborhood solutions of x produced by 𝒩g. The set Ω is used to store historical optimization data. When Ω is updated with x, x is added into Ω and all solutions of Ω are compared and all dominated ones are removed.

Global search between xi,y is shown below. Execute two-point crossover on machine assignment strings of xi and a randomly chosen y∈EB, and obtain a new one z, if z≻xi or z,xi are non-dominated each other, then let traili=0, xi is used to renew Ω and z substitutes for xi; otherwise, traili=traili+1, perform two-point crossover on scheduling strings of xi and a randomly selected y∈EB, obtain a new one z and update xi, traili and Ω according to the above condition.

Neighborhood search NS1 on xi is described as follows. Randomly decide 𝒩g, produce z∈𝒩g(xi), update xi, traili and Ω in terms of conditions of global search.

Solution migration is described below. Define Δ={xi∈EB|rankxi=1,It≤traili}, then perform non-dominated sorting on OB, sort all solutions of OB in the ascending order of rank, for some solutions with same rank, sort them in the ascending order of traili, select the first |Δ| solutions, for each chosen solution xi, a multiple neighborhood search is applied and let traili=0.

For solution xi, multiple neighborhood search is executed below. Let g=1, repeat the following steps until g=7: produce a solution z∈𝒩g(xi), if z≻xi or z,xi are non-dominated each other, then z substitutes for xi and let g=7; otherwise g=g+1.

Neighborhood search NS2 on xi is shown as follows. (1) Select the machine Mk with the biggest completion time and randomly choose a job Ji assigned to Mk, Then, repeat the following steps: insert Ji into each possible position on Mk and obtain a solution z until z≻xi. (2) Determine a machine Mk with the biggest energy consumption and randomly select a job Ji on Mk, repeat the following steps: move Ji to Ml,l≠k and obtain a solution z until z≻xi. In NS2, if z≻xi is not met, then traili=traili+1; else traili=0.

In dynamical employed bee phase, some dominated solutions with rankxi>1 have cni=0, and their computing resources are reallocated to non-dominated solutions with rankxi=1. As a result, cni for some solutions exceed 1 and cni of other solutions are 0. This indicates that the search times for solutions are dynamically adjusted based on solution quality. Additionally, solution migration is triggered when all non-dominated solutions satisfy It≤traili. In this case, some best solutions of OB are moved to EB and solutions of EB are dynamically adjusted when the given condition is met, Therefore, dynamic adjustment is applied in both scenarios.

3.3 Dynamical Onlooker Bee Phase

Four search operators SO1−SO4 are given. SO1 is described below. For a solution 0, select a 𝒩g according to an adaptive process and produce a solution z∈𝒩g(xi), if z≻xi, then xi is used to update Ω and z substitutes for xi; if z,xi are non-dominated each other, then z is applied to renew Ω; if xi≻z, then randomly select y∈EB, multiple neighborhood search acts on y and xi is replaced with y.

Adaptive process is depicted below. Choose a neighborhood structure by roulette selection based on Pseg; if rand>Q, then randomly choose a neighborhood structure; suppose 𝒩a is chosen, produce a new solution z∈𝒩a(xi), if z≻xi, then counta=counta+2; if z,xi are non-dominated each other, then counta=counta+1, where Q is threshold.

SO2 is shown as follows. For a solution xi∈OB, let α=0, execute variable neighborhood descent (VND) shown in Algorithm 2, if α=0, then perform multiple neighborhood search on xi.

SO3 is done in the following way. For a solution xi∈OB, randomly choose y∈EB, perform global search between xi,y as done in Lines 3–7 of Algorithm 1; then execute multiple neighborhood search on xi. SO4 has the same steps as SO3; however, y∈Ω in SO4.

In SO1−SO4, when multiple neighborhood search acts on xi, for each z, if xi cannot be replaced with z, then traili=traili+1; otherwise, traili=0.

In SO1, an adaptive process is adopted to select neighborhood structure adaptively, SO2 is an adaptive combination of VND and multiple neighborhood search, SO3, SO3 are combination of global search and multiple neighborhood search.

In onlooker bee phase, for each 𝒩g, set initial countg=1 and define selection probability Pseg.

Pseg=countg/∑l=16countl(14)

Algorithm 3 describes dynamical onlooker bee phase on generation gen, where if SO3 is chosen in Line 4, then y∈EB is randomly decided; if SO4 is selected, then y∈Ω is chosen randomly, in Lines 7, 9, when the chosen operator is executed, the decided y in Line 4 is directly used, EvoOBgen denotes the evolution quality.

EvoOBgen=∑xi∈OBnewxigen(15)

where newxigen is defined below. For xi when an operator SOl acts on xi on generation, gen if new solution z≻xi, then newxigen=newxigen+2; if z,xi are non-dominated each other, newxigen=newxigen+1.

Feedback is dynamical process used in control. In this study, feedback is applied to decide one of SO1−SO4 dynamically, for each xi∈OB, on generation gen, if EvoOBgen−1<EvoOBgen−2, then random select one operator of SO1,SO2 and perform the chosen operator on xi∈OB; otherwise, execute the chosen operator on generation gen−1 on xi∈OB.

In dynamical onlooker bee phase, for each xl, if rankxl>1 and xl≻y, then computing resource of xl is shifted to non-dominated solution xj∈OB, feedback is used to dynamical decide search operator by selecting a new one if EvoOBgen−1<EvoOBgen−2 or using search operator of generation gen−1, that is, search operator on generation gen is decided or affected by evolution on the previous two generations, obviously, computing resource and search operator are dynamically adjusted.

In Algorithm 1, the search operator is combination of global search and neighborhood search NS1, in Algorithm 3, SO3,SO4 are composed of global search and multiple neighborhood search, SO1,SO2 are neighborhood search-based operator; moreover, these operators are dynamically selected by feedback, these operators can be useful to make good balance between exploration and exploitation.

3.4 Algorithm Description

The detailed steps of DABC are shown in Algorithm 4.

Scout phase is described as follows. For each solution xi∈P, if traili≥Limit, then xi is used to update Ω and then replaced with a randomly produced solution and traili=0.

Unlike the previous ABC [36–40], DABC has the following new features. (1) The initial population is produced by three heuristics. (2) Dynamical employed bee phase is implemented by using computing resource shifting and solution migration. (3) Four search operators are used and dynamical onlooker bee phase is performed by applying computing resource shifting and feedback. The above dynamical optimization mechanisms such as solution migration and feedback can decide the number of searches and adjust solutions of swarms and search operator dynamically, as a result, search efficiency can be improved. On the other hand, many new things are required to be implemented when DABC is used, this may be a disadvantage of DABC.

4  Computational Experiments

Extensive experiments are conducted to test the performance of DABC for energy-efficient UPMSP with additional resource and PM. All experiments are implemented by using Microsoft Visual C++ 2019 and run on 8.0 G Random Access Memory 2.30 GHz Central Processing Unit Personal Computer.

4.1 Test Instances, Metrics and Comparative Algorithms

Fanjul-Peyro et al. [8] provided 300 instances, which can be divided into 30 types and the size of each type is depicted as n×m, n∈{8,12,16,20,25,30,50,150,250,350} and m∈{2,4,6}. For each type n×m, five ways are used for generating pki and two ways are applied for rki, 10 instances n×m×1,⋯,n×m×10 are generated. Fanjul-Peyro et al. [8] described seven ways for pki,rki and the related data can be obtained directly from http://soa.iti.es/problem-instances (accessed on 24 May 2024). Rmax=5m. We generate PM data as follows, wk is integer selected from the same interval as pki, uk=round(wk+3.5×maxi=1,2,⋯,n{pki}). Where round(x) is an integer being closet to x.

Metric 𝒞 [47] is used to compare the approximate Pareto optimal set respectively obtained by algorithms.

𝒞(L,B)=|{b∈B:∃h∈L,h≻b}||B|(16)

Metric ρ is the ratio of |{x∈Ωl|x∈Ω∗}| to |Ω∗| [48], where Ωl is non-dominated set of Algorithm l, the reference set Ω∗ consists of the non-dominated solutions in the union of non-dominated sets of all algorithms.

Metric DIR [49] is used to measure the convergence performance by computing the distance of the non-dominated set Ωl relative to a reference set Ω∗.

DIR(Ωl)=1|Ω∗|∑y∈Ω∗min{σxy|x∈Ωl}0(17)

where σxy is the distance between a solution x and a reference solution y in the normalized objective space.

Lei et al. [23] proposed NICA for multi-objective UPMSP with PM. Shahidi-Zadeh et al. [3] presented a multi-objective harmony search (MOHS) for UPMSP. Zhang et al. [34] developed CEA for energy-efficient UPMSP with makespan and total energy consumption. These algorithms can be used to solve energy-efficient UPMSP with additional resource and PM after related steps on additional resource and PM are added into decoding procedure; moreover, they have promising advantages in solving UPMSP, so they are chosen as comparative algorithms.

ABC is used to show the effect of new strategies of DABC. ABC is constructed as follows: in employed bee phase, Lines 1–10 with cni=1 for each xi∈P of Algorithm 1 are executed; in onlooker bee phase, a solution xi∈P is selected by binary tournament and the above Lines 1–10 are executed, scout phase of DABC is adopted in ABC.

4.2 Parameter Settings

DABC has following parameters: N,It,β,R,Q,Limit and stopping condition. Stopping condition is first decided independently as done in [18], we found by experiments that DABC converges well when 0.3n s CPU time reaches. We also obtained that when 0.3n s CPU time is applied, all comparative algorithms also converge fully, so stopping condition is set as 0.3n s CPU time for all algorithms.

An empirical method was used to determine the settings for other parameters by using the instance 50×20×5. Table 1 shows the levels of each parameter. The orthogonal array L27(36) is tested. DABC with each combination runs 10 times on the chosen instance.

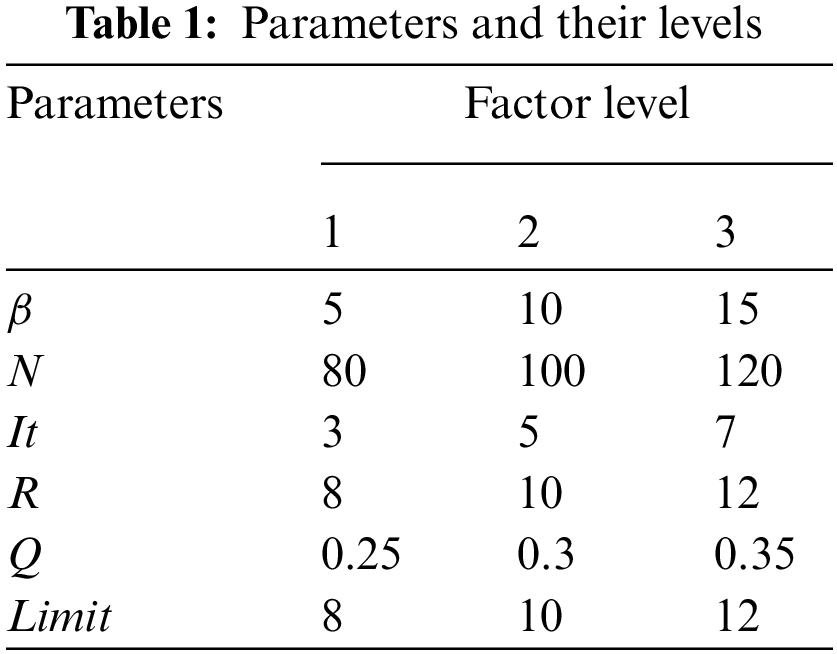
Fig. 2 shows the results of ρ and S/N ratio, which is defined as −10×log10⁡(ρ2). It can be found from Fig. 2 that DABC with following combination N=100,It=5,β=10,R=10,Q=0.3,Limit=10 produces better results than DABC with other combinations, moreover, we tested the above combination on all instances, the results reveal that the above combination is still effective, so the above parameter settings are adopted.

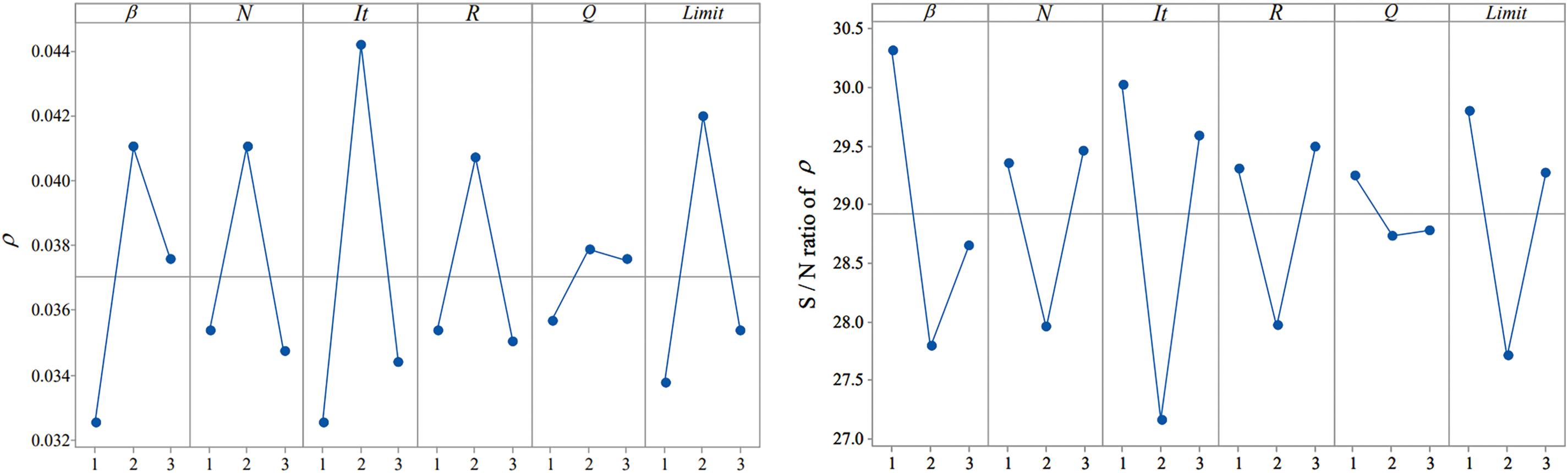
Figure 2: Main effect plot for mean and S/N ratio

ABC has N=100,Limit=10 and the above stopping condition.

Parameter settings of three comparative algorithms are directly selected from References [3,23,34] except that the stopping condition. To compare fairly, all algorithms should be stopped under the same condition, so MOHS, CEA and NICA are given the same stopping condition as DABC. We conducted experiments on other parameters of comparative algorithms, the experimental results show that each comparative algorithm with parameter settings from [3,23,34] can produce better results than the same algorithm with other parameter settings, so the original parameter settings are still used.

4.3 Results and Discussions

DABC, its three comparative algorithms and ABC are compared. Each algorithm randomly runs 10 times for each instance. Tables 2–9 describe the corresponding results of five algorithms. D, A, N, M, C denote DABC, ABC, NICA, MOHS and CEA. Fig. 3 shows the distribution of non-dominated solutions obtained by all algorithms.

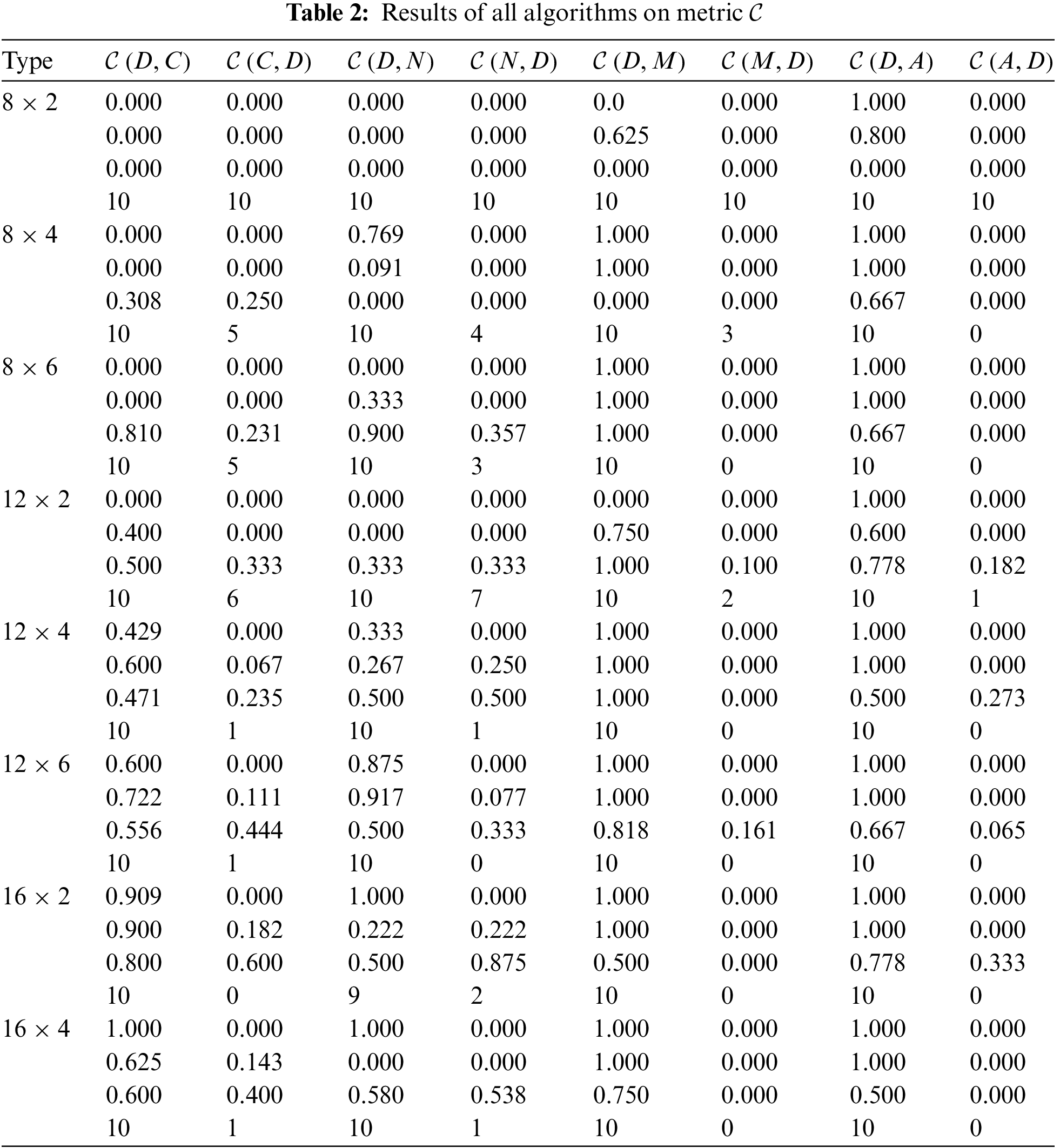
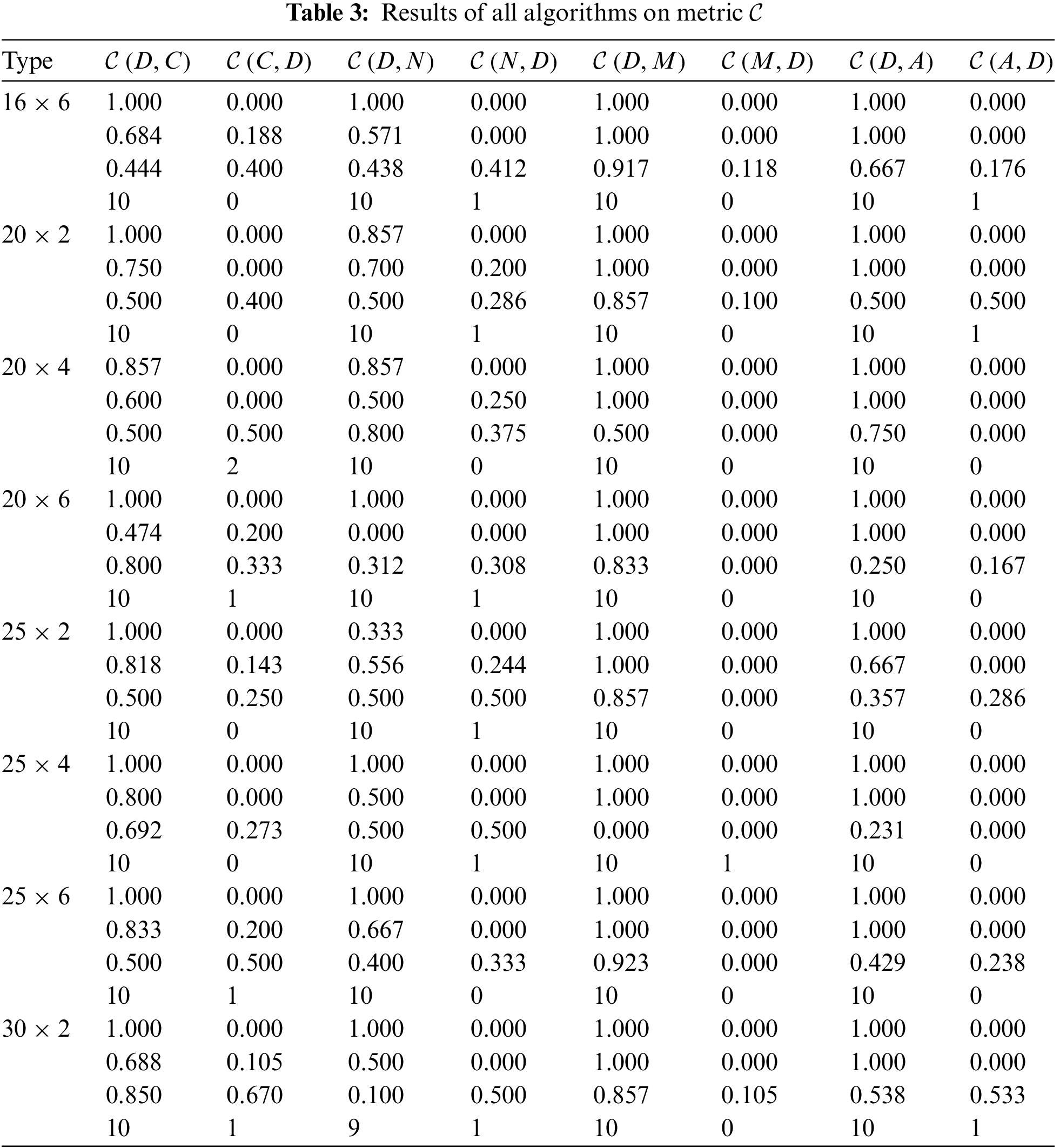
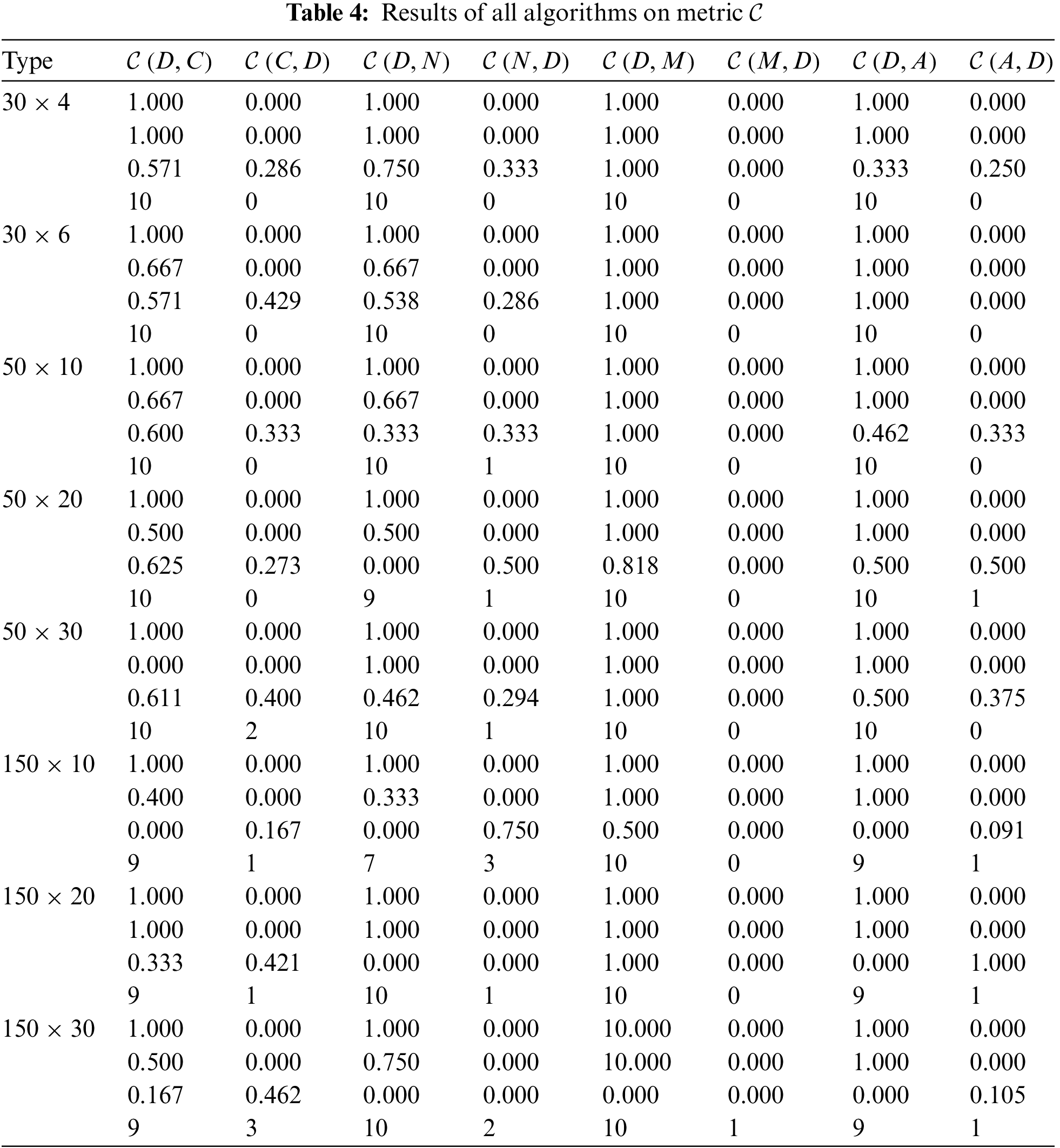
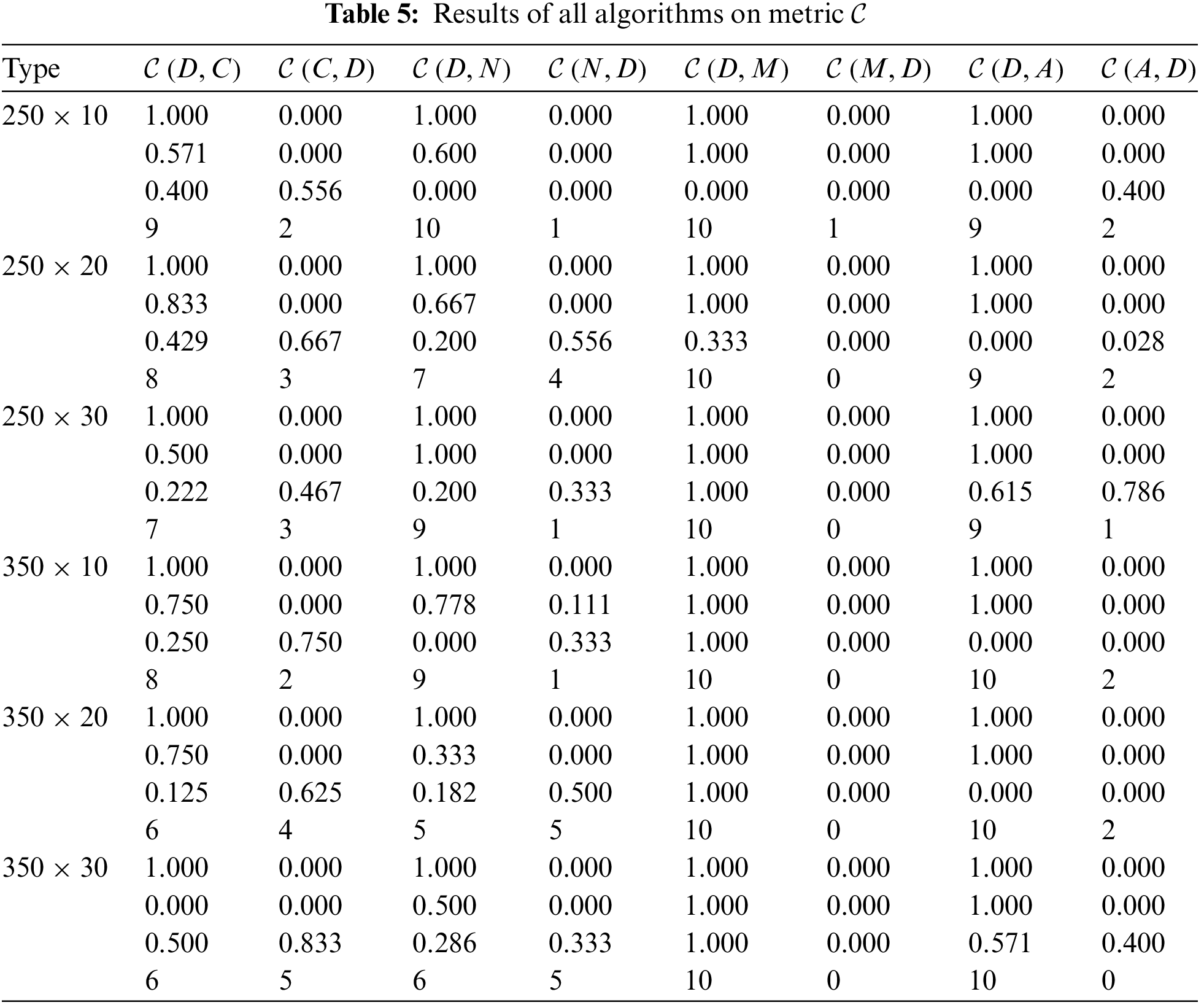
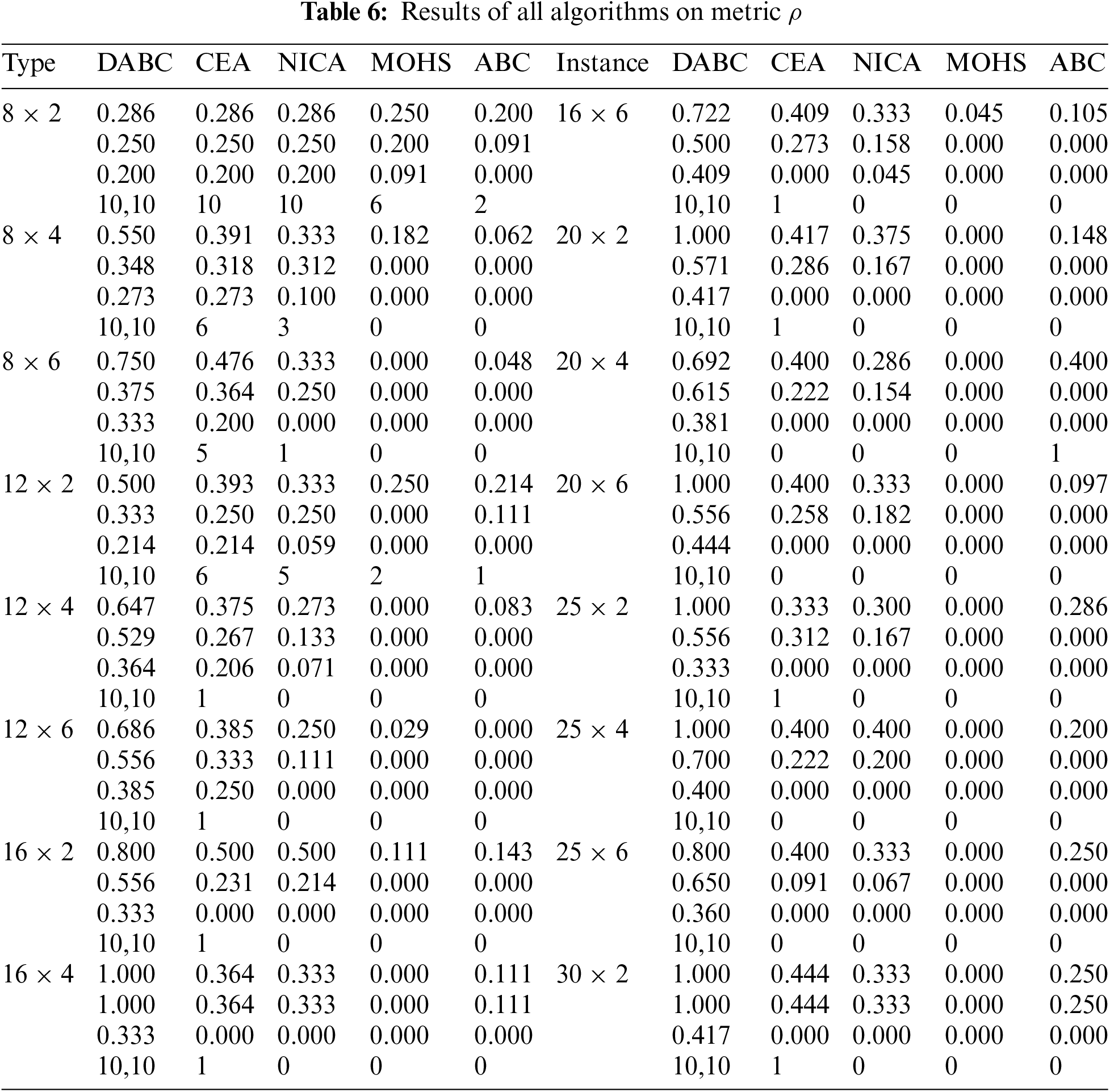
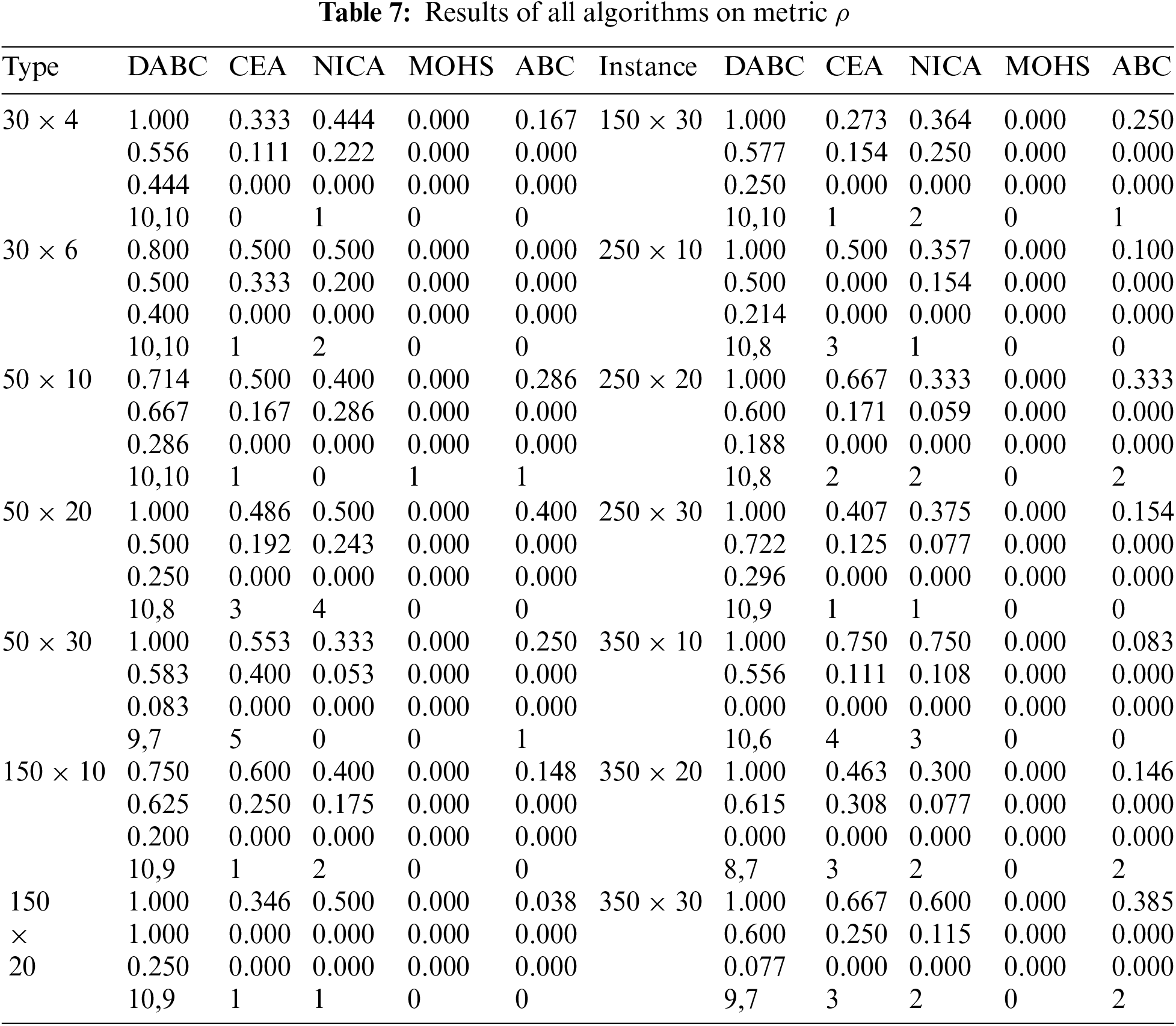
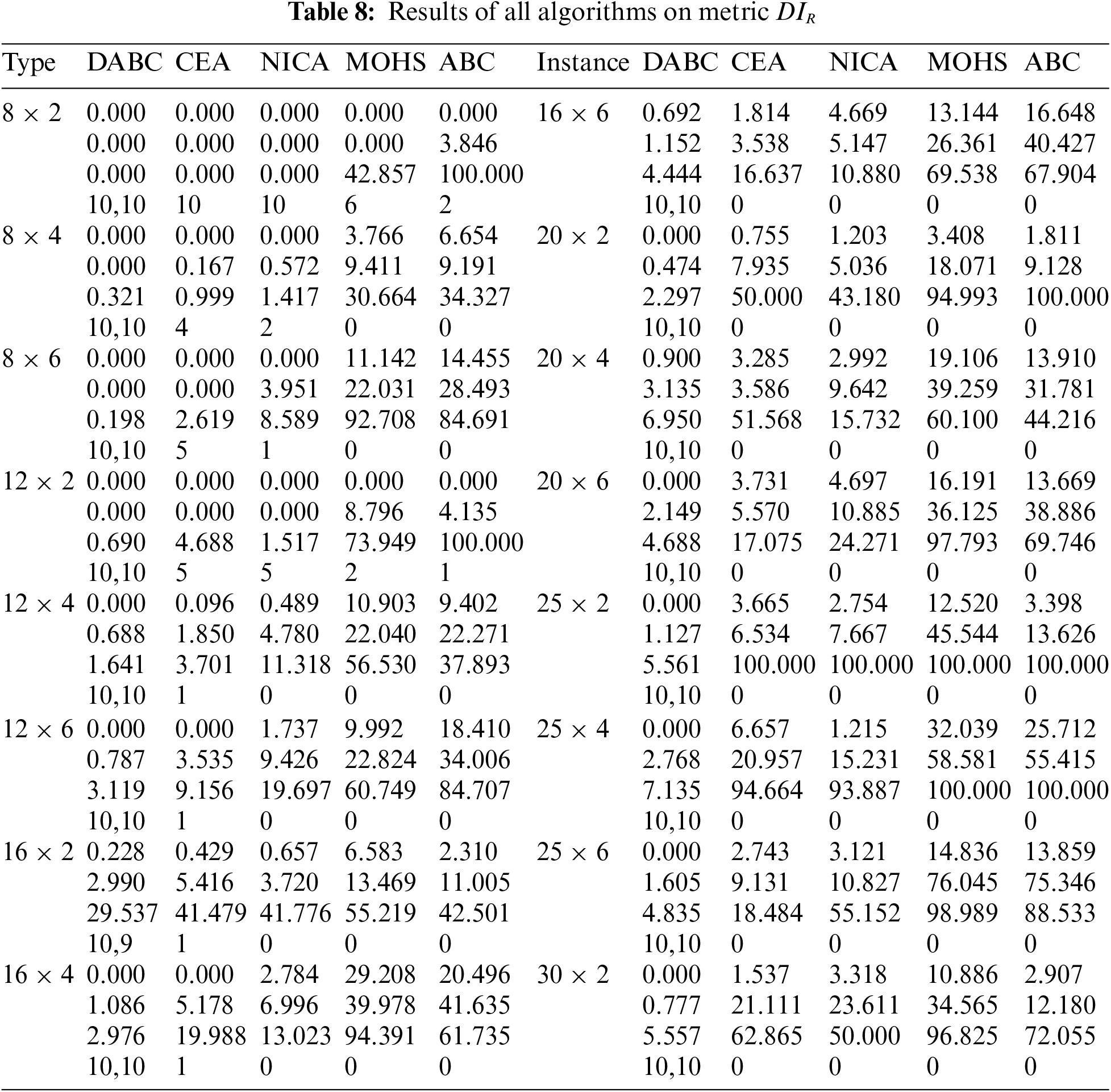
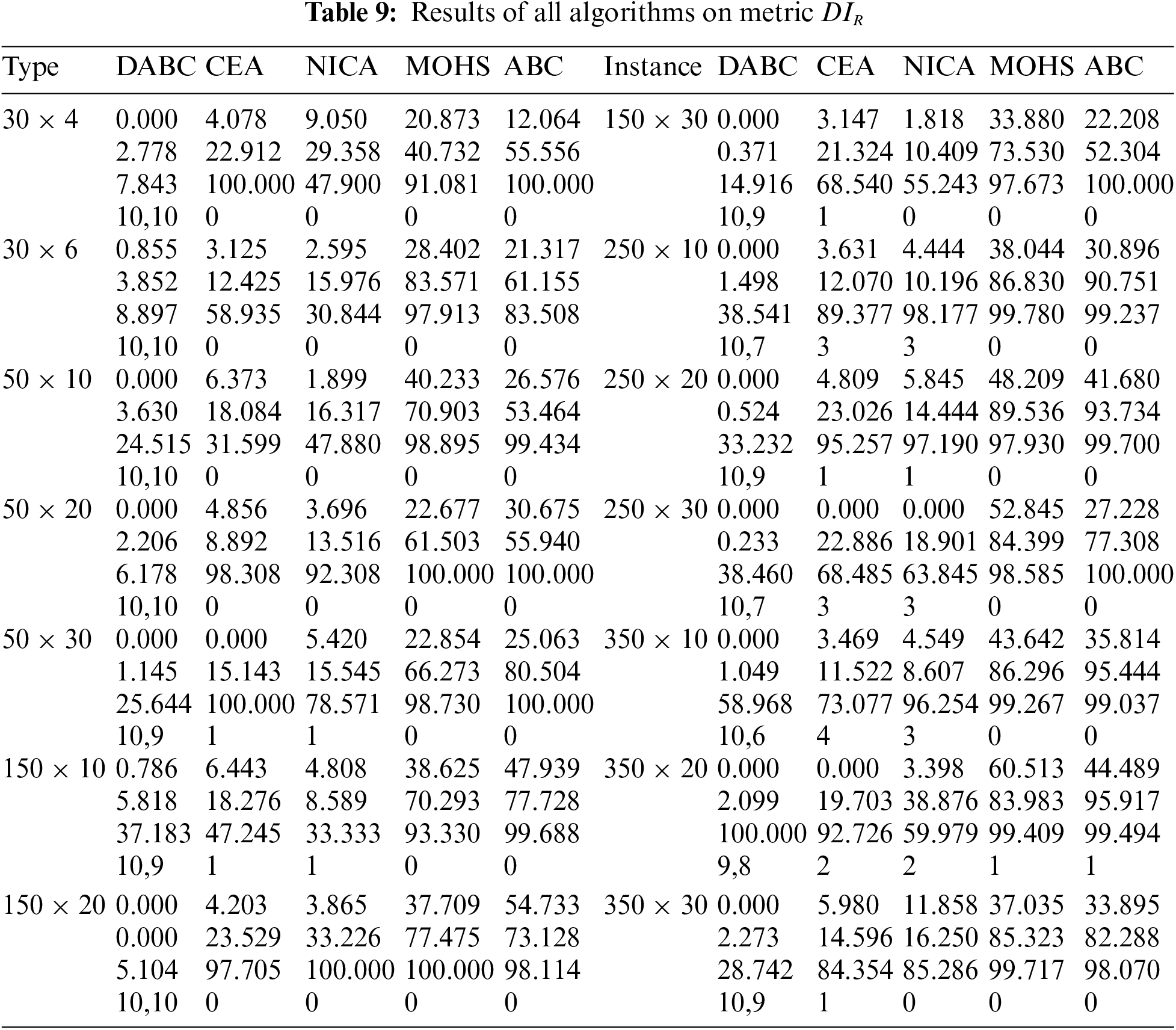
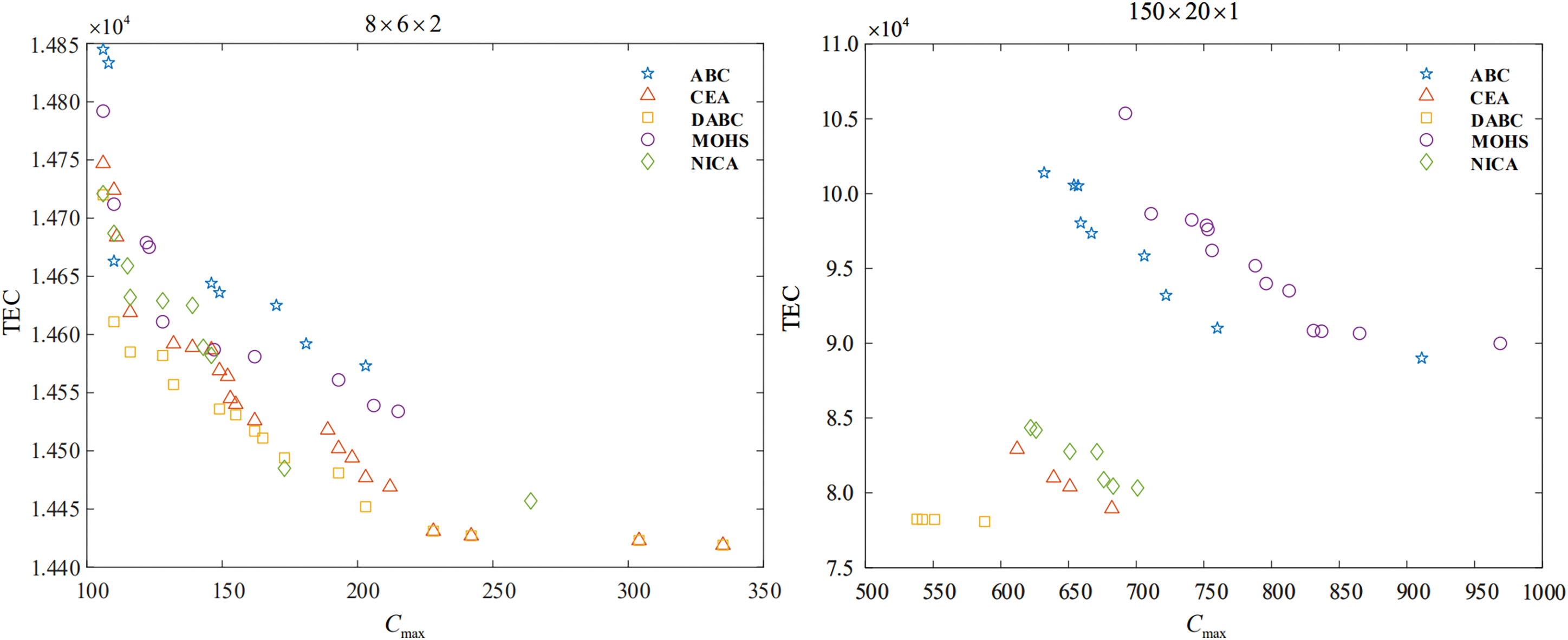
Figure 3: Distribution of non-dominated solutions of five algorithms

An effective way is applied to show results of five algorithms on 300 instances. In Tables 2–5, for each type n×m, four groups of data are given, 𝒞(C,D) and 𝒞(D,C) are computed for each instances, 10 𝒞(C,D) are sorted in the ascending order, the first group is the smallest 𝒞(C,D) and its corresponding 𝒞(D,C), the second is the fifth 𝒞(C,D) and its 𝒞(D,C), the third is the tenth 𝒞(C,D) and its corresponding 𝒞(D,C), let α1=α2=0, for 𝒞(C,D), 𝒞(D,C) of each instance of n×m, if 𝒞(C,D)<𝒞(D,C), then α1=α1+1; if 𝒞(C,D)>𝒞(D,C), then α2=α2+1; if 𝒞(C,D)=𝒞(D,C), then α1=α1+1, α2=α2+1, the fourth group consists of α1,α2.

For type 16×6, 10 pairs of 𝒞(C,D), 𝒞(D,C) are listed below. (0.4, 0.6), (0.143, 0.824), (0.188, 0.684), (0.4, 0.444), (0, 0.125), (0, 0.857), (0.2, 0.333), (0, 1), (0.286, 0.7), (0.25, 0.273), obviously, α1=10, α2=0, which means that 𝒞(C,D) is less than 𝒞(D,C) on 10 instances.

The same way is used to decide four group for 𝒞(D,N),𝒞(N,D) and other columns, αi is defined for the i−th column.

In Tables 6, 7, for each type n×m, 10 results are obtained and sorted in the descending order for each algorithm, the first group of data is the smallest value, the second group is the fifth value and the third group is the worst value, for each instance, a best value between DABC, ABC is decided, if ρ of DABC is equal to the best value, α1=α1+1, if ρ of DABC is better than that of ABC, then α2=α2+1, the first group is composed of α1,α2 for DABC, ABC. The way of α1 is used to decide α3,α4,α5,α6 for CEA, NICA, MOHS, ABC. Four groups of data for each type are decided for Tables 8, 9 in the same way of Tables 6, 7, 10, DIR are sorted in the ascending order.

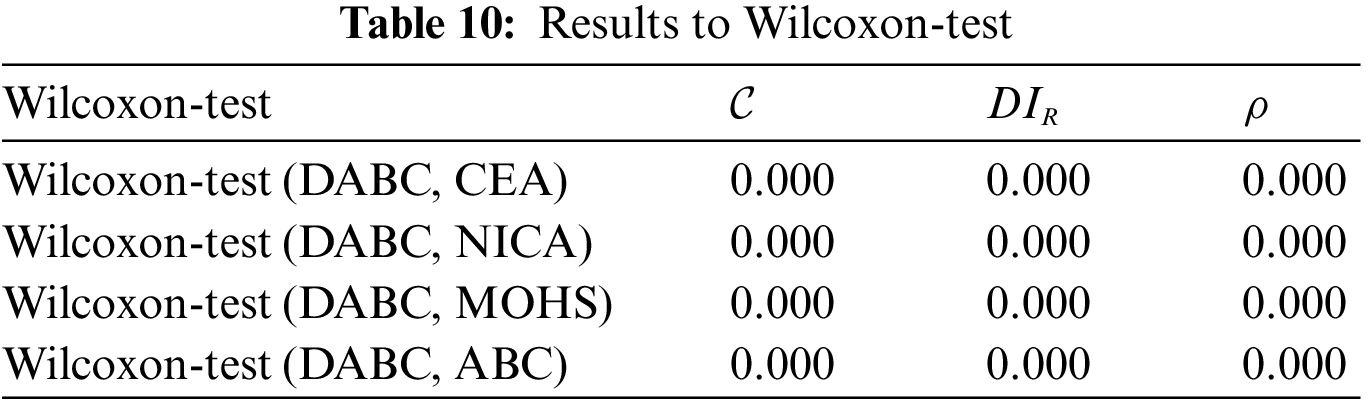
Table 10 gives the results of pair-sample Wilcoxon-test, in which Wilcoxon-test (A, B) means a test conducted to judge whether Algorithm A gives a better sample mean than B and data on columns 2–4 are p-value. A significance level is 0.05. There is significant difference between A and B in the statistical sense if the p-value is less than 0.05.

As shown in Tables 2–5, DABC obtains the smaller value of 𝒞(A,D) and 𝒞(D,A) on 294 instances, ABC has the smaller value of 𝒞(A,D) and 𝒞(D,A) on 20 instances, and DABC generates smaller 𝒞(A,D) than 𝒞(D,A) on 280 instances; moreover, 𝒞(D,A) is equal to 1 on at least 138 instances, that is all solu-tions of ABC are dominated by non-dominated solutions of DABC on these instances. DABC converge significantly better than ABC.

Tables 6, 7 show that ρ of DABC outperforms ABC on more than 280 instances, while ρ of ABC is 0 on more than 177 instances, meaning ABC fails to contribute any members for the set Ω∗. Tables 8, 9 show that DABC obtains smaller DIR than ABC on most of instances. Table 10 and Fig. 3 also reveal that performance differences between DABC and ABC are significant, obviously, the new strategies have positive impact on the performance of DABC, so new strategies are effective.

Tables 2–5 show that DABC produces smaller 𝒞(C,D) than 𝒞(D,C) on 241 instances and obtains 𝒞(D,C) of 1 on at least 31 instances. As shown in Tables 6 and 7, DABC outperforms CEA on 236 instances, with ρ greater than 0.6 on at least 71 instances, that is, members of reference set Ω∗ are mainly produced by DABC. DABC also performs better than CEA on metric DIR because DABC gets better DIR than CEA on 260 instances. The above analyses reveal that DABC provides better results than CEA. Table 10 shows that the performance different between DABC and CEA are significant in the statistical sense. It can be found from Fig. 3 that the obtained non-dominated solutions can dominate most of solutions of other algorithms, thus, DABC performs better than CEA.

As listed in Tables 2–5, DABC has smaller 𝒞(N,D) than 𝒞(D,N) on more than 80% instances, DABC gets bigger ρ than NICA on more than 250 instances, and obtains better DIR than NICA on 270 instances. There are notable performance differences between DABC and NICA; moreover, these differences also can be found in Table 10 and Fig. 3. On the other hand, DABC performs better than MOHS. 𝒞(D,M) is 1 on more than 190 instances and 𝒞(M,D) is 0 on 280 instances, that is, non-dominated solutions of DABC do not dominate by any solutions of MOHS. The notable convergence differences also can be seen from Fig. 3. ρ of MOHS is 0 on 276 instances and MOHS cannot provide any members of Ω∗. Tables 8, 9 show the performance differences between DABC and MOHS on metric DIR. The statistical results in Table 10 also reveals that the performance differences between DABC, MOHS are significant.

The above analyses reveal that DABC performs better than MOHS, NICA and CEA. In DABC, three dynamical adjustment strategies are implemented, which are computing resource shifting, feedback and solution migration. Computing resource shifting can lead to extensive usage of non-dominated solutions, solution migration can increase the diversity of employed bee swarms and feedback based on four operators can result in the dynamical adjustment of the search operators according to search behavior. These strategies can effectively extend exploration ability, keep a high diversity of population and lead to a low possibility of falling local optima, thus, DABC is a promising method for energy-efficient UPMSP with additional resources and PM.

5  Conclusions

Additional resources, maintenance and energy are often considered in UPMSP; however, the existing researches seldom deal with these three things together in UPMSP. In this study, energy-efficient UPMSP with additional resources and PM is addressed, and a new algorithm called DABC is proposed to minimize makespan and total energy consumption. In DABC, some dynamical optimization mechanisms are implemented. The dynamic employed bee phase involves computing resource shifting and solution migration. The dynamical onlooker bee phase is applied by computing resource shifting and feedback. Extensive experiments are conducted on 300 instances. The computational results show that the new strategies such as the dynamical employed bee phase are effective and DABC can provide better results than its comparative algorithms.

UPMSP with several real-life conditions and constraints has attracted some attention. We will focus on UPMSP by involving additional resources, machine eligibility, and SDST, addressing these problems through meta-heuristics combined with new optimization mechanisms such as reinforcement learning and competition among sub-populations. We also handle distributed hybrid flow shop scheduling problems with some practical constraints in the near future. Additionally, distributed assembly scheduling problems involving transportation will be among our future research topics.

Acknowledgement: The authors would like to thank the editors and reviewers for their valuable work, as well as the supervisor and family for their valuable support during the research process.

Funding Statement: This research was funded by the National Natural Science Foundation of China (grant number 61573264).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Deming Lei, Shaosi He; data collection: Yizhuo Zhu; analysis and interpretation of results: Deming Lei, Shaosi He, Yizhuo Zhu; draft manuscript preparation: Deming Lei, Yizhuo Zhu, Shaosi He. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data supporting this study are described in the first paragraph of Section 4.1.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. C. E. Cheng and C. C. S. Sin, “A state-of-the-art review of parallel-machine scheduling research,” Eur. J. Oper. Res., vol. 47, no. 3, pp. 271–292, 1990. doi: 10.1016/0377-2217(90)90215-W. [Google Scholar] [CrossRef]

2. E. Mokotoff, “Parallel machine scheduling problems: A survey,” Asia-Pacific. J. Oper. Res., vol. 18, pp. 193–242, 2011. [Google Scholar]

3. B. Shahidi-Zadeh, R. Tavakkoli-Moghaddam, A. Taheri-Moghadam, and I. Rastgar, “Solving a bi-objective unrelated parallel batch processing machines scheduling problem: A comparison study,” Comput. Oper. Res., vol. 88, no. 6, pp. 71–90, 2017. doi: 10.1016/j.cor.2017.06.019. [Google Scholar] [CrossRef]

4. C. Wang, X. Li, and Y. Gao, “A novel collaborative evolutionary algorithm with two-population for multi-objective flexible job shop scheduling,” Comput. Model. Eng. Sci., vol. 137, no. 2, pp. 1849–1870, 2023. doi: 10.32604/cmes.2023.028098. [Google Scholar] [CrossRef]

5. L. Wang and Y. Qi, “Scheduling an energy-aware parallel machine system with deteriorating and learning effects considering multiple optimization objectives and stochastic processing time,” Comput. Model. Eng. Sci., vol. 135, no. 1, pp. 325–339, 2023. doi: 10.32604/cmes.2022.019730. [Google Scholar] [CrossRef]

6. J. A. Ventura and D. Kim, “Parallel machine scheduling with earliness-tardiness penalties and additional resource constraints,” Comput. Oper. Res., vol. 30, no. 13, pp. 1945–1958, 2003. doi: 10.1016/S0305-0548(02)00118-1. [Google Scholar] [CrossRef]

7. X. L. Zheng and L. Wang, “A two-stage adaptive fruit fly optimization algorithm for unrelated parallel machine scheduling problem with additional resource constraints,” Expert. Syst. Appl., vol. 65, no. 9–12, pp. 28–39, 2016. doi: 10.1016/j.eswa.2016.08.039. [Google Scholar] [CrossRef]

8. L. Fanjul-Peyro, F. Perea, and R. Ruiz, “Models and matheuristics for the unrelated parallel machine scheduling problem with additional resources,” Eur. J. Oper. Res., vol. 260, no. 2, pp. 482–493, 2017. doi: 10.1016/j.ejor.2017.01.002. [Google Scholar] [CrossRef]

9. K. Fleszar and K. S. Hindi, “Algorithms for the unrelated parallel machine scheduling problem with a resource constraint,” Eur. J. Oper. Res., vol. 271, no. 3, pp. 839–848, 2018. doi: 10.1016/j.ejor.2018.05.056. [Google Scholar] [CrossRef]

10. X. L. Zheng and L. Wang, “A collaborative multiobjective fruit fly optimization algorithm for the resource constrained unrelated parallel machine green scheduling problem,” IEEE Trans. Syst. Man Cyber. Syst., vol. 48, no. 5, pp. 790–800, 2018. doi: 10.1109/TSMC.2016.2616347. [Google Scholar] [CrossRef]

11. F. Villa, E. Vallada, and L. Fanjul-Peyro, “Heuristic algorithms for the unrelated parallel machine scheduling problem with one scarce additional resource,” Expert. Syst. Appl., vol. 93, pp. 28–38, 2018. doi: 10.1016/j.eswa.2017.09.054. [Google Scholar] [CrossRef]

12. M. Afzalirad and M. Shafipour, “Design of an efficient genetic algorithm for resource-constrained unrelated parallel machine scheduling with machine eligibility restrictions,” J. Intell. Manuf., vol. 29, no. 2, pp. 423–437, 2018. doi: 10.1007/s10845-015-1117-6. [Google Scholar] [CrossRef]

13. E. Vallada, F. Villa, and L. Fanjul-Peyro, “Enriched metaheuristics for the resource unrelated parallel machine scheduling problem,” Comput.Oper. Res., vol. 111, pp. 415–424, 2019. [Google Scholar]

14. I. M. Al-Harkan and A. A. Qamhan, “Optimize unrelated parallel machine scheduling problems with multiple limited additional resources, sequence-dependent setup times and release date constraints,” IEEE Access, vol. 7, pp. 171533–171547, 2019. doi: 10.1109/ACCESS.2019.2955975. [Google Scholar] [CrossRef]

15. L. Fanjul-Peyro, “Models and an exact method for the unrelated parallel machine scheduling problem with setups and resources,” Expert Syst. Appl. X, vol. 5, 2020, Art. no. 100022. [Google Scholar]

16. A. Lopez-Esteve, F. Perea, and J. C. Yepes-Borrero, “GRASP algorithm for the unrelated parallel machines scheduling problem with additional resources during processing and setups,” Int. J. Prod. Res., vol. 61, no. 17, pp. 6013–6029, 2023. doi: 10.1080/00207543.2022.2121869. [Google Scholar] [CrossRef]

17. Y. Pinar and T. Y. Seyda, “Constraint programming approach for multiresource-constrained unrelated parallel machine scheduling problem with sequence-dependent setup times,” Int. J. Prod. Res., vol. 60, no. 7, pp. 2212–2229, 2022. doi: 10.1080/00207543.2021.1885068. [Google Scholar] [CrossRef]

18. D. L. Yang, T. C. E. Cheng, S. J. Yang, and C. J. Hsu, “Unrelated parallel machine scheduling with aging effects and multi-maintenance activities,” Comput. Oper. Res., vol. 39, no. 7, pp. 1458–1464, 2012. doi: 10.1016/j.cor.2011.08.017. [Google Scholar] [CrossRef]

19. S. J. Wang and M. Liu, “Multi-objective optimization of parallel machine scheduling integrated with multi-resources preventive maintenance planning,” J. Manuf. Syst., vol. 37, no. 7, pp. 182–192, 2015. doi: 10.1016/j.jmsy.2015.07.002. [Google Scholar] [CrossRef]

20. A. Gara-Ali, G. Finke, and G. Espinouse, “Parallel-machine scheduling with maintenance: Praising the assignment problem,” Eur. J. Oper. Res., vol. 252, no. 1, pp. 90–97, 2016. doi: 10.1016/j.ejor.2015.12.047. [Google Scholar] [CrossRef]

21. O. Avalos-Rosales, F. Angel-Bello, A. lvarez, and Y. Cardona-Valds, “Including preventive maintenance activities in an unrelated parallel machine environment with dependent setup times,” Comput. Ind. Eng., vol. 123, pp. 364–377, 2018. doi: 10.1016/j.cie.2018.07.006. [Google Scholar] [CrossRef]

22. M. Wang and G. H. Pan, “A novel imperialist competitive algorithm with multi-elite individuals guidance for multi-object unrelated parallel machine scheduling problem,” IEEE Access, vol. 7, pp. 121223–121235, 2019. doi: 10.1109/ACCESS.2019.2937747. [Google Scholar] [CrossRef]

23. D. M. Lei and T. Yi, “A novel shuffled frog-leaping algorithm for unrelated parallel machine scheduling with deteriorating maintenance and setup time,” Symmetry, vol. 13, no. 9, 2021, Art. no. 1574. doi: 10.3390/sym13091574. [Google Scholar] [CrossRef]

24. J. H. Pang, Y. C. Tsai, and F. D. Chou, “Feature-extraction-based iterated algorithm to solve the unrelated parallel machine problem with periodic maintenance activities,” IEEE Access, vol. 9, pp. 139089–139108, 2021. doi: 10.1109/ACCESS.2021.3118986. [Google Scholar] [CrossRef]

25. D. M. Lei and M. Y. Liu, “An artificial bee colony with division for distributed unrelated parallel machine scheduling with preventive maintenance,” Comput. Ind. Eng., vol. 141, no. 6, 2020, Art. no. 106320. doi: 10.1016/j.cie.2020.106320. [Google Scholar] [CrossRef]

26. D. M. Lei and S. S. He, “An adaptive artificial bee colony for unrelated parallel machine scheduling with additional resource and maintenance,” Expert. Syst. Appl., vol. 205, no. 2, 2022, Art. no. 117577. doi: 10.1016/j.eswa.2022.117577. [Google Scholar] [CrossRef]

27. A. Che, S. B. H. Zhang, and X. Q. Wu, “Energy-conscious unrelated parallel machine scheduling under time-of-use electricity tariffs,” J. Clean. Prod., vol. 156, no. 2, pp. 688–697, 2017. doi: 10.1016/j.jclepro.2017.04.018. [Google Scholar] [CrossRef]

28. L. P. Cota, V. N. Coelho, F. G. Guimaraes, and M. J. F. Souza, “Bi-criteria formulation for green scheduling with unrelated parallel machines with sequence-dependent setup times,” Int. Trans. Oper. Res., vol. 28, no. 2, pp. 996–1017, 2021. doi: 10.1111/itor.12566. [Google Scholar] [CrossRef]

29. J. B. Abikarram, K. McConky, and R. Proano, “Energy cost minimization for unrelated parallel machine scheduling under real time and demand charge pricing,” J. Clean. Prod., vol. 208, no. 1, pp. 232–242, 2019. doi: 10.1016/j.jclepro.2018.10.048. [Google Scholar] [CrossRef]

30. L. K. Zhang, Q. W. Deng, G. L. Gong, and W. W. Han, “A new unrelated parallel machine scheduling problem with tool changes to minimise the total energy consumption,” Int. J. Prod. Res., vol. 58, no. 22, pp. 6826–6845, 2020. doi: 10.1080/00207543.2019.1685708. [Google Scholar] [CrossRef]

31. Z. Wang and T. Y. Liu, “A novel multi-objective scheduling method for energy based unrelated parallel machines with auxiliary resource constraints,” IEEE Access, vol. 7, pp. 168688–168699, 2019. doi: 10.1109/ACCESS.2019.2954601. [Google Scholar] [CrossRef]

32. H. Saberi-Aliabad, M. Reisi-Nafchi, and G. Moslehi, “Energy-efficient scheduling in an unrelated parallel-machine environment under time-of-use electricity tariffs,” J. Clean. Prod., vol. 249, no. 2, 2020, Art. no. 119393. doi: 10.1016/j.jclepro.2019.119393. [Google Scholar] [CrossRef]

33. Z. Pei, M. Z. Wan, Z. Z. Jiang, Z. T. Wang, and X. Dai, “An approximation algorithm for unrelated parallel machine scheduling under TOU electricity tariffs,” IEEE Trans. Auto. Sci. Eng., vol. 18, no. 2, pp. 743–756, 2020. doi: 10.1109/TASE.2020.2995078. [Google Scholar] [CrossRef]

34. L. K. Zhang, Q. W. Deng, R. H. Lin, G. L. Gong, and W. W. Han, “A combinatorial evolutionary algorithm for unrelated parallel machine scheduling problem with sequence and machine-dependent setup times, limited worker resources and learning effect,” Expert. Syst. Appl., vol. 175, 2021, Art. no. 114843. doi: 10.1016/j.eswa.2021.114843. [Google Scholar] [CrossRef]

35. J. Q. Li, Q. K. Pan, and K. Z. Gao, “Pareto-based discrete artificial bee colony algorithm for multi-objective flexible job shop scheduling problem,” Int. J. Adv. Manuf. Techno., vol. 55, no. 9-12, pp. 1159–1169, 2011. doi: 10.1007/s00170-010-3140-2. [Google Scholar] [CrossRef]

36. K. C. Ying and S. W. Lin, “Unrelated parallel machine scheduling with sequence and machine-dependent setup times and due date constraints,” Int. J. Innov. Comput., vol. 8, pp. 3279–3297, 2012. [Google Scholar]

37. K. C. Ying and S. W. Lin, “ABC-based manufacturing scheduling for unrelated parallel machines with machine-dependent and job sequence-dependent setup times,” Comput. Oper. Res., vol. 51, no. 5, pp. 172–181, 2014. doi: 10.1016/j.cor.2014.05.013. [Google Scholar] [CrossRef]

38. E. Caniyilmaz, B. Benli, and M. S. Ilkay, “An artificial bee colony algorithm approach for unrelated parallel machine scheduling with processing set restrictions, job sequence-dependent setup times, and due date,” Int. J. Adv. Manuf. Technol., vol. 77, no. 9–12, pp. 2105–2115, 2015. doi: 10.1007/s00170-014-6614-9. [Google Scholar] [CrossRef]

39. S. J. Lu, X. B. Liu, J. Pei, M. T. Thai, and P. M. Pardalos, “A hybrid ABC-TS algorithm for the unrelated parallel-batching machines scheduling problem with deteriorating jobs and maintenance activity,” Appl. Soft Comput., vol. 66, no. 2, pp. 168–182, 2018. doi: 10.1016/j.asoc.2018.02.018. [Google Scholar] [CrossRef]

40. D. M. Lei, Y. Yuan, and J. C. Cai, “An improved artificial bee colony for multi-objective distributed unrelated parallel machine scheduling,” Int. J. Prod. Res., vol. 59, no. 17, pp. 5259–5271, 2020. doi: 10.1080/00207543.2020.1775911. [Google Scholar] [CrossRef]

41. J. Q. Li and Y. Q. Han, “A hybrid multi-objective artificial bee colony algorithm for flexible task scheduling problems in cloud computing system,” Cluster Comput., vol. 23, no. 4, pp. 2483–2499, 2020. doi: 10.1007/s10586-019-03022-z. [Google Scholar] [CrossRef]

42. T. Meng and Q. K. Pan, “A distributed heterogeneous permutation flowshop scheduling problem with lot-streaming and carryover sequence-dependent setup time,” Swarm Evol. Comput., vol. 60, no. 9, 2021, Art. no. 100804. doi: 10.1016/j.swevo.2020.100804. [Google Scholar] [CrossRef]

43. D. W. Gong, Y. Y. Han, and J. Y. Sun, “A novel hybrid multi-objective artificial bee colony algorithm for blocking lot-streaming flow shop scheduling problems,” Knowl-Based Syst., vol. 148, pp. 115–130, 2018. [Google Scholar]

44. J. Wang, D. M. Lei, and J. C. Cai, “An adaptive artificial bee colony with reinforcement learning for distributed three-stage assembly scheduling with maintenance,” Appl. Soft Comput., vol. 117, no. 2, 2022, Art. no. 108371. doi: 10.1016/j.asoc.2021.108371. [Google Scholar] [CrossRef]

45. J. Wang, H. T. Tang, and D. M. Lei, “A feedback-based artificial bee colony algorithm for energy-efficient flexible flow shop scheduling problem with batch processing machines,” Appl. Soft Comput., vol. 153, no. 1, 2024, Art. no. 111254. doi: 10.1016/j.asoc.2024.111254. [Google Scholar] [CrossRef]

46. K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. Evolu. Comput., vol. 6, no. 2, pp. 182–197, 2002. doi: 10.1109/4235.996017. [Google Scholar] [CrossRef]

47. E. Zitzler and L. Thiele, “Multi-objective evolutionary algorithms: A comparative case study and the strength Pareto approach,” IEEE Trans. Evolu. Comput., vol. 3, no. 4, pp. 257–271, 1999. doi: 10.1109/4235.797969. [Google Scholar] [CrossRef]

48. D. M. Lei, “Pareto archive particle swarm optimization for multi-objective fuzzy job shop scheduling problems,” Int. J. Adv. Manuf. Tech., vol. 37, no. 1–2, pp. 157–165, 2008. doi: 10.1007/s00170-007-0945-8. [Google Scholar] [CrossRef]

49. J. D. Knowles and D. W. Corne, “On metrics for comparing nondominated sets,” in Proc. ICAIS, New York, NY, USA, 2002, pp. 711–716. [Google Scholar]