Improved Harris Hawks Algorithm and Its Application in Feature Selection

1  Introduction

Recent years have witnessed significant advancements in the fields of machine learning and data mining, leading to the creation of numerous feature-rich data sets [1]. Additionally, the scale of global data has shown a trend of rapid growth. Numerous redundant, pointless, and noisy features can be found in these raw data sets [2]. These erroneous characteristics will lengthen the algorithm’s execution time [3], lower its classification accuracy [4], and cause overfitting [5]. In the age of big data, determining the ideal feature combination has grown in importance as a research area [6].

The issues can be successfully resolved by feature selection as a machine learning data preprocessing technique [7]. By removing unnecessary features and condensing the amount of input, feature selection increases classification accuracy and speeds up the execution of machine learning algorithms [8]. Feature selection can be categorized into three types—embedded, wrapped, and filtered—based on its integration with the learner [9]. Lower classification accuracy results from the filtering method’s lack of consideration for the complementarity and mutual exclusion of features, albeit having less computing overhead [10]. The wrapper method examines each feature subset after using a classifier to train the chosen feature subset. Essentially a specific wrapper method, the embedded method mixes the learning algorithm model’s training phase with the selection process. Nevertheless, it can be challenging to conduct an enumeration search on the feature subset using the wrapper method when the data has a large number of features. Therefore, how to perform effective feature selection has become a research hotspot. In recent times, numerous researchers have employed swarm intelligence optimization algorithms as a search mechanism for wrapped feature selection [11], including HHO [12], Ant Colony Optimization [13] (ACO), Sparrow Search Algorithm [14] (SSA), Particle Swarm Optimization [15] (PSO), Grey Wolf Optimizer [16] (GWO), Whale Optimization Algorithm [17] (WOA), etc., which can efficiently find satisfactory feature subsets within acceptable timeframes, thereby effectively enhancing the efficiency of feature selection [18]. In [19], Long et al. improved the escape energy factor update strategy using a sine function and applied the enhanced HHO to feature selection problems. In [20], a multiswarm particle swarm optimization (PSO) approach combined with collaborative search PSO (CS-PSO) is introduced to address the issue of feature selection. In [21], a dynamic Salp swarm algorithm is introduced for feature selection, which effectively improves the effectiveness of feature selection. Consequently, utilizing swarm intelligence optimization techniques in feature selection helps to efficiently discover optimal feature combinations.

The HHO demonstrates superior search capabilities compared to the others. HHO [12] is a new swarm intelligence optimization algorithm proposed by Heidari in 2019, which simulates the hunting behaviour of hawks in nature to solve optimization problems. Research conducted in previous studies [22] demonstrates that the HHO is highly effective in addressing practical challenges. However, the algorithm also has many common problems of swarm intelligence optimization algorithms [23], such as the imbalance between exploration and exploitation [24], low population diversity [25], and insufficient deep exploitation capabilities [26]. In order to address these issues, numerous researchers have enhanced the HHO methodology using various approaches. In [26], the Sine Cosine algorithm is integrated into the HHO, which provides an effective search strategy for the feature selection problem of high-dimensional data sets. The experimental results show that this method can produce better search results without increasing the computational cost. In [27], the Salp Swarm Algorithm is embedded in the HHO, which improves the search ability of the optimizer and expands its application range. In [28], the HHO population is divided into different levels, and the excellent individuals are exploited locally. An enhanced HHO algorithm (EHHO) is proposed for the feature selection task. The experimental results show that this method can obtain better convergence speed and accuracy, and the performance is better than the HHO in the case of fewer features. In [19], an improved HHO (LIL-HHO) is proposed, which uses the escape energy parameter strategy and the improved position search equation and uses the lens imaging learning method to enhance the population diversity. The above algorithm can effectively improve the optimization performance of the algorithm by integrating the sine cosine algorithm, embedding the Salp Swarm Algorithm, and performing local exploitation after stratification. Nonetheless, upon evaluating the aforementioned enhancement strategies on various test functions, it has been observed that the solution capacity of the HHO still possesses potential for additional refinement.

This study proposes three strategies aimed at enhancing the HHO algorithm by addressing three distinct aspects: a population initialization method grounded in opposition-based learning, an escape energy factor update strategy that addresses the equilibrium between exploration and exploitation, and a deep exploitation strategy integrating variable neighbourhood search and mutation operator. Firstly, this study designs a population initialization strategy that utilizes opposition-based learning to enhance population diversity during population initialization. Secondly, this paper studies the escape energy factor update strategy of the HHO and finds an imbalance between the exploration and exploitation of the HHO. This paper designs an escape energy factor update strategy that fully considers the balance between exploration and exploitation to balance exploration and exploitation of the HHO. Finally, to avoid the algorithm becoming trapped in local optima and improve its global optimization ability, this paper designs a deep exploitation strategy combining variable neighbourhood search and mutation operator, which improves the profound exploitation ability of the HHO.

To assess the efficacy of the enhanced strategies presented in this study, IHHO and a variety of well-known similar algorithms (HHO, PSO, SSA, OOA, DBO) are used to solve the famous 23 benchmark test functions [29]. The experimental findings indicate that the problem-solving capability of the IHHO surpasses that of other algorithms. This demonstrates that the enhancement strategy proposed in this paper markedly elevates the performance of the HHO algorithm.

In addition, to address the challenges of low classification accuracy, low feature selection efficiency, and slow response speed when using a supervised machine learning model to classify and predict high-dimensional data [30], this study designs a feature selection method based on IHHO (IHHO-FS). This paper compares the feature selection methods using all features (Full Features), feature selection approach utilizing IHHO (IHHO-FS), feature selection approach utilizing HHO (HHO-FS), feature selection approach utilizing PSO (PSO-FS), feature selection approach utilizing SSA (SSA-FS), feature selection approach utilizing OOA (OOA-FS) and feature selection approach utilizing DBO algorithm (DBO-FS) on eight datasets to evaluate the effectiveness and applicability of IHHO-FS. The findings from the experiments indicate that IHHO-FS dramatically reduces the computational cost of the classification model (reduces the data dimension), improves the efficiency of feature selection, and improves the classification accuracy. IHHO-FS stands out among many algorithms and is very competitive. Consequently, the enhanced approach to Harris Hawks Optimization proposed in this study demonstrates significant efficacy. IHHO-FS is highly effective for feature selection tasks, significantly enhancing the classification accuracy of various classifiers while also decreasing their response times.

2  Harris Hawks Optimization

HHO is an innovative swarm intelligence algorithm proposed by Heidari in 2019. It is inspired by the natural hunting strategies of hawks and aims to address optimization challenges. Harris’ hawks often work together while foraging, employing coordinated raids in which multiple hawks simultaneously dive at prey from various angles to catch them by surprise. The HHO algorithm delineates hawk hunting behavior into three distinct stages: the global exploration stage, the transition stage from global exploration to local exploitation, and the local exploitation phase. In this algorithm, the positions of the hawks are treated as candidate solutions, while the position of the prey represents the current best candidate solution.

2.1 Exploration Phase

Hawks hunt with keen eyes to track and detect prey. Their waiting and observation time may be up to a few hours, and through two equal probability strategies to hunt. In the HHO algorithm, the hawks’ position is considered a candidate solution, and the location of the prey is the current best candidate solution. The position update method of hawks in the exploration stage is shown in Eq. (1).

X(t+1)={Xrand(t)−r1|Xrand(t)−2r2X(t)|q≥0.5(Xrabbit(t)−Xm(t))−r3(LB+r4(UB−LB))q<0.5(1)

In Eq. (1), X(t+1) denotes the revised location of the hawks. Xrabbit(t) represents the optimal position within the current population. X(t) represents the present location of the hawks. Xrand(t) denotes the position of a hawk randomly selected from the current population. Xm(t) represents the average position of the current population, which is defined as shown in Eq. (2). LB and UB represent the boundary of the exploration space, that is, the lower and upper bounds of the range of variable values. r1,r2,r3,r4,q are random numbers between (0, 1). The average position of hawks is as follows:

Xm(t)=1N∑i=1NXi(t)(2)

In Eq. (2), N denotes the aggregate count of hawks, while t refers to the present iteration count.

2.2 Transition from Exploration to Exploitation

The HHO algorithm is capable of transitioning from the exploration phase to the exploitation phase, dynamically adjusting its exploitation strategies based on the escape energy exhibited by the prey. In escape behavior, the escape energy of prey will be significantly reduced. The HHO algorithm models the escape energy of the prey as shown in Eq. (3). The escape energy of the prey is shown in Fig. 1 (left). In Eq. (3), E represents the escape energy of the prey, T denotes the highest number of iterations, and E0 signifies the initial energy value, which is randomly selected within the range of (−1, 1). Enter the exploration phase when |E|≥1. Otherwise, enter the exploitation phase. In Fig. 1, t indicates the iteration count, while E denotes the escape energy of the prey.

E=2E0(1−tT)(3)

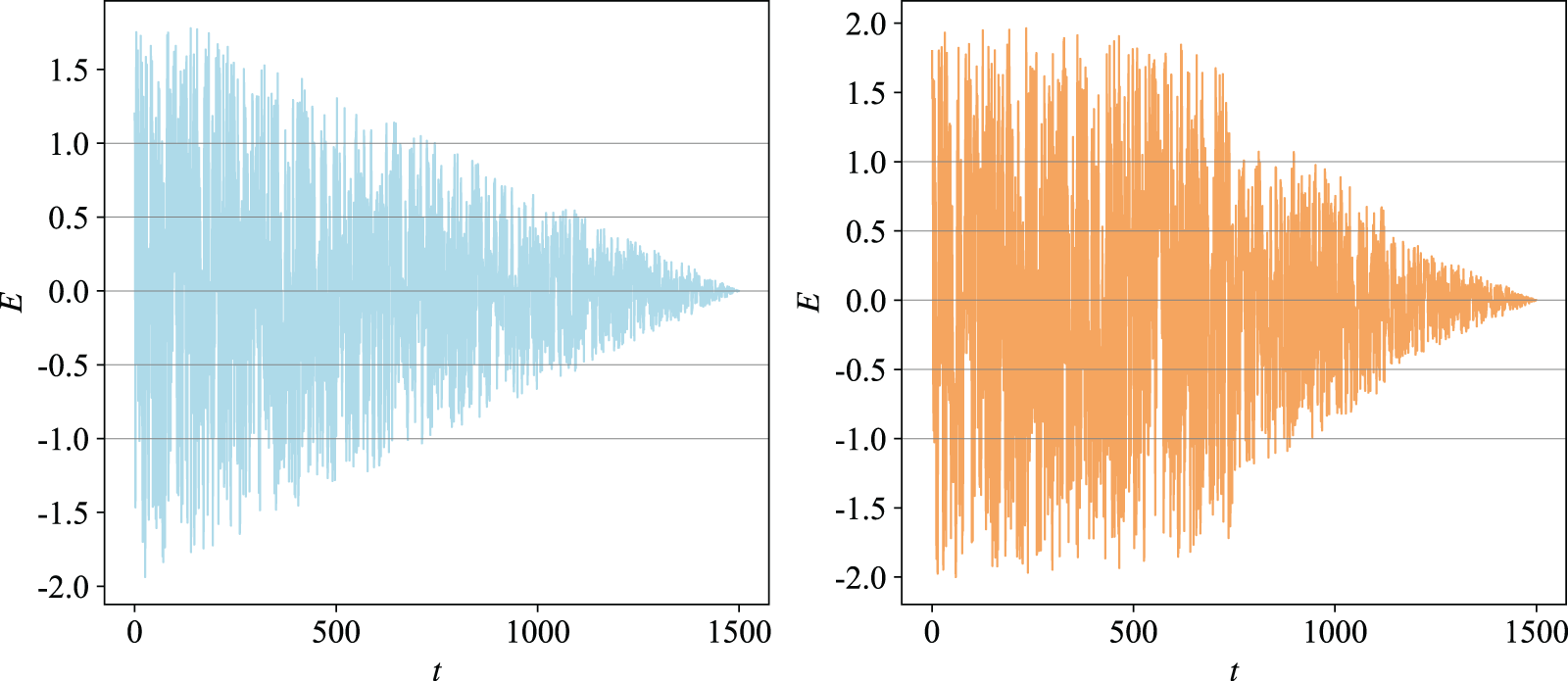
Figure 1: Changes in escape energy of prey under two strategies (left HHO, right IHHO)

2.3 Exploitation Phase

In the hawks hunting behavior, based on the prey’s escape behavior and the Harris’ hawks’ pursuit strategy, the HHO algorithm uses four strategies in the exploitation phase to simulate the hawks’ attack behavior and update its position. The choice of hunting strategy mainly depends on the escape energy E and escape probability r of prey. The escape energy factor E allows HHO to switch between soft and hard besiege. When |E|≥0.5, soft besiege is performed. When |E|<0.5, a hard besiege is performed. r is the opportunity for the prey to escape successfully (r<0.5) or unsuccessfully (r≥0.5). During the exploitation phase, four besiege strategies can be identified: Hard besiege, and Hard besiege with progressive rapid dives, Soft besiege, Soft besiege with progressive rapid dives. The specific descriptions of the aforementioned four siege strategies can be found in the original paper [12].

3  Improved Harris Hawks Optimization

In the HHO, the initial population is established through random generation, and the stage of the Harris’ hawks is determined according to the escape energy factor E (when |E|≥1, it enters the exploration phase. Otherwise, it enters the exploitation phase). The exploitation strategy adopted by the Harris’ hawks is determined by E and r.

Firstly, a greater diversity within the population provides the algorithm with an increased amount of relevant information [31]. However, the HHO algorithm uses a random method to generate the initial population during population initialization, resulting in insufficient population diversity. Secondly, the update method of the escape energy factor E will affect the balance between exploration and exploitation of the HHO algorithm. In Fig. 1 (left), it can be seen that the number of times |E|≥1 during the iteration process is significantly smaller than the number of times |E|<1. Therefore, in the HHO algorithm, the escape energy factor update method cannot ensure the balance between exploration and exploitation. Then, the profound exploitation ability of the algorithm in the later stage can affect the convergence accuracy of the algorithm. Simultaneously, the exploitation ability of the HHO algorithm is insufficient. Consequently, this study introduces three strategies aimed at enhancing the HHO algorithm: Firstly, a population initialization approach grounded in opposition-based learning; secondly, an escape energy factor adjustment strategy designed to balance exploration and exploitation; and thirdly, a deep exploitation method that combines variable neighborhood search with a mutation operator. The basic principle of the IHHO is illustrated in Fig. 2.

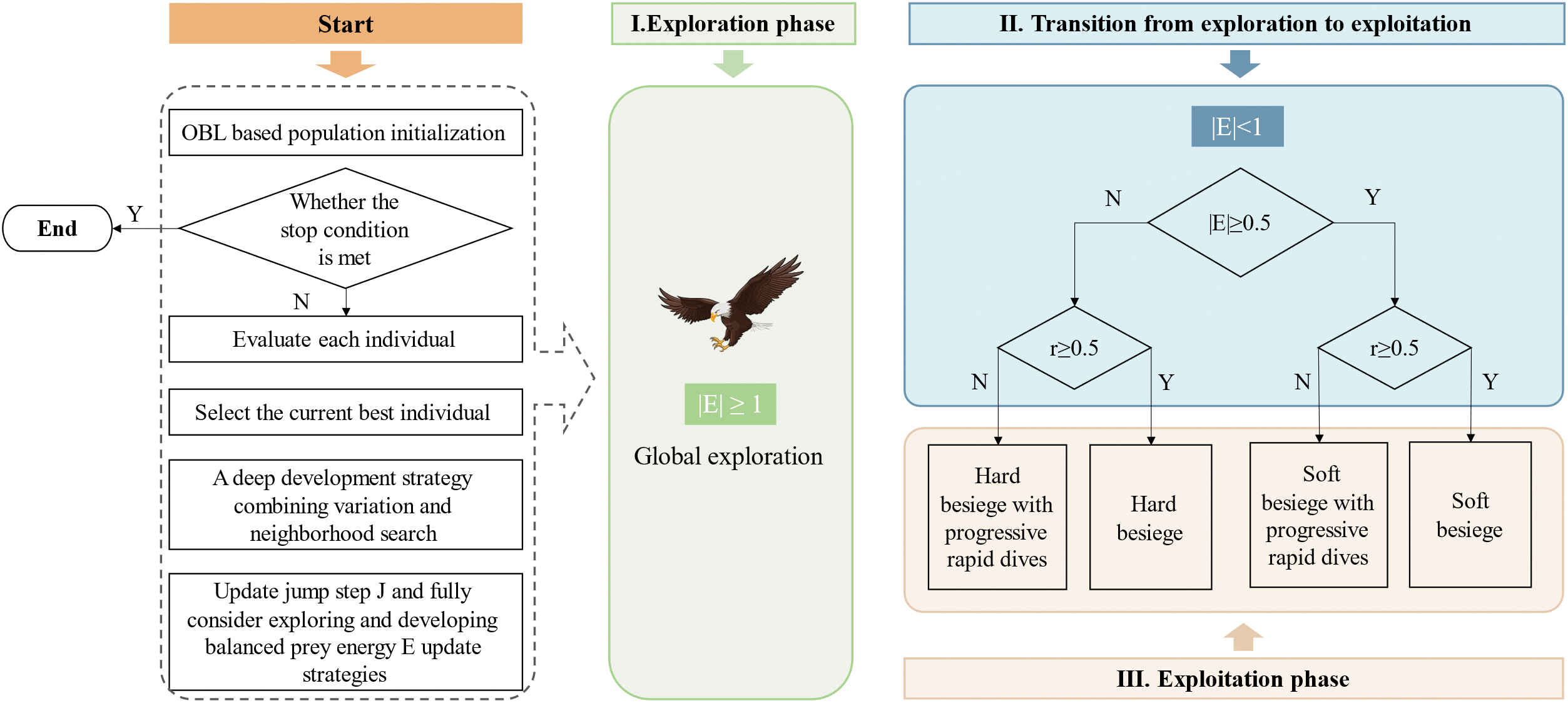
Figure 2: The schematic diagram of the IHHO algorithm

3.1 A Population Initialization Strategy Based on Opposition-Based Learning

Haupt et al. [32] pointed out that the diversity of the initial population of swarm intelligence optimization algorithms can affect their solving accuracy and convergence speed, and the diversity of the initial population will lay the foundation for the algorithm to conduct a global search. However, the HHO algorithm randomly generates an initial population, which cannot guarantee the diversity of the initial population and effectively extract useful information from the search space, thus affecting the search efficiency of the algorithm to a certain extent. The opposition-based learning (OBL) strategy was proposed by Tizhoosh [33] in 2005 and is a new technology that has emerged in the field of intelligent computing in recent years. It has been effectively utilized in swarm intelligence optimization techniques, including PSO and Differential Evolution (DE) algorithms.

Define 1. Opposite point. Suppose that there exists a number x between [l,u], then the opposite point of x is defined as x′=l+u−x. Extending the definition of the opposite point to d-dimensional space, let p=(x1,x2,⋯,xd) be a point in d-dimensional space, where xi∈[li,ui],i=1,2,⋯,d, then the opposite point is p′=(x1′,x2′,⋯,xd′), where xi′=li+ui−xi.

This study incorporates an OBL strategy into the HHO for the purpose of initializing the population, thereby enhancing its diversity. The procedure is outlined as follows: Initially, generate n individuals at random within the permissible domain. Secondly, generate n opposite points based on opposition-based learning. Then, remove from the set of 2n individuals (formed by n individuals and n opposite points) any individuals that are not within the feasible domain. Finally, select the top−n individuals with the highest fitness from the remaining individuals as the initial population.

3.2 An Escape Energy Factor Update Strategy That Addresses the Equilibrium between Exploration and Exploitation

Although all the current metaheuristic algorithms vary greatly, a common feature can be found in their search process during optimization, that is, they can be divided into two stages: exploitation and exploration [34]. Exploration entails that the algorithm must traverse the entire search space in a manner that maximizes randomness, thereby mitigating the risk of converging to a local optimum. The exploitation should have good local exploitation ability, and find a better solution based on the better solution found in the exploration phase. In the process of optimization and solving, algorithms often exhibit randomness in their selection for exploration and exploitation. Many studies [35] have shown that maintaining a balance between exploitation and exploration of metaheuristic algorithms can effectively enhance their problem-solving ability. Therefore, it is necessary to establish a reasonable balance mechanism between exploitation and exploration. In the HHO algorithm, when |E|≥1, it enters the exploration phase, and when |E|<1, it enters the exploitation phase. As illustrated in Fig. 1 (left), during the iterative process, the instances where |E|≥1 are notably fewer compared to those where |E|<1, that is, the number of explorations is significantly less than the number of exploitations (i.e., weak exploration ability and strong exploitation ability). This study enhances the HHO algorithm by developing an update strategy for the escape energy factor, which comprehensively addresses the equilibrium between exploration and exploitation capabilities. This balance is articulated in Eq. (4).

E={2E0[1−(tT)2]t<int(T3)2E0[1−(tT)32]int(T3)≤t<int(T2)2E0(1−tT)int(T2)≤t≤T(4)

Furthermore, this study conducts a comparative analysis of the prey escape energy for HHO and IHHO, illustrated in Fig. 1. Fig. 1 clearly illustrates that in the IHHO algorithm, the frequency of explorations and exploitations within the algorithm are more closely aligned, indicating that the balance between exploitation and exploration of the IHHO algorithm has been improved, which shows the effectiveness of the escape energy factor update strategy that fully considers the balance between exploitation and exploration.

3.3 A Deep Exploitation Strategy Integrating Variable Neighbourhood Search and Mutation Operator

This paper designs a deep exploitation strategy that integrates variable neighbourhood search and mutation operator to improve the local exploitation ability of the IHHO. As the number of iterations rises, the algorithm’s population quality is continuously improved and then stabilized. When the population’s quality tends to be stable, the position of the prey changes little or no longer changes. At this time, the learning ability of the algorithm is limited, and it is not easy to search for a better position. Therefore, in each iteration, it is necessary to improve the exploitation ability of the algorithm. This paper improves the quality of prey in each generation by deeply exploiting the location of prey in each generation, providing more practical information for the algorithm, and then improving the algorithm’s local exploitation ability.

The variable neighbourhood search (VNS) algorithm has good search performance, solid global search ability, simplicity, and ease of implementation, and its applicability is extensive. It is often applied in the search process of metaheuristic algorithms. Therefore, this paper designs two neighbourhood search operators: mutation operator and perturbation operator. The two operators together constitute the VNS algorithm. The VNS algorithm is applied to improve the exploitation ability of the Harris Hawk optimization algorithm.

After each iteration, the variable neighbourhood search algorithm starts the search from the first hawk (i.e., the current global best position). Once a better position than the current global best position is found, stop the search immediately, update the current global best position, and proceed to the next iteration. If the search for a complete neighbourhood space has yet to find a better position than the current global best position, proceed directly to the next iteration. In each iteration, more local exploitation operations are added, which can improve the local exploitation ability of the IHHO, thereby improving its performance.

Mutation operator. The inspiration for designing a mutation operator comes from the Genetic Algorithm, which can obtain better candidate solutions with a certain probability through mutation; that is, a favourable mutation occurs. The purpose of designing the mutation operator is to extensively search the current global best position and prevent the algorithm from falling into the local optimum. Firstly, define the number of mutations. Secondly, define a mutation operator, which randomly selects a particular dimension to undergo mutation and generate a neighbour solution. If there is an improvement in the neighbour solution, return the neighbour solution information and stop the search. If there is no improvement in the neighbour solution, continue searching.

Perturbation operator. The perturbation operator can perform a refined search near the current global optimal position with a very small movement amplitude. Firstly, define a list of moving steps, steps=[10−3,10−4,10−5,10−6,10−7,10−8,10−9]. Secondly, traverse the 1st,5th,10th,15th,…,i dimensions of the current solution (i is a multiple of 1 or 5), and move each dimension in turn according to the step size in the moving step list to obtain a new candidate solution. The evaluation function value f1 of the new candidate solution is calculated immediately, and if f1>f (f is the current optimal function value), the search continues; if f1<f, the search is stopped and the new candidate solution information is recorded. Finally, if a new candidate solution is found, the relevant information is returned.

4  A Feature Selection Method Based on Improved Harris Hawk Optimization Algorithm

Feature selection constitutes a challenging combinatorial optimization task [36,37], selecting the best feature combination from all available features. Through feature selection, it is possible to achieve the goal of using as few features as possible to achieve the highest classification accuracy [38]. The swarm intelligence optimization algorithm can find a better approximate solution in an acceptable time and is often used in feature selection problems [39]. This paper proposes a feature selection approach utilizing the IHHO to solve this complex combinatorial optimization problem.

In the feature selection problem, each individual within the population of the IHHO algorithm is represented as a vector of dimension d, where d corresponds to the total number of original features present in the dataset. When the IHHO algorithm initializes the population, each dimension of the individual x is a random number between [0,1], that is, xi∈[0,1]. When xi∈[0,0.5], the feature is not selected; when xi∈(0.5,1], the feature is selected. Because the purpose of feature selection is to use as few features as possible to obtain the highest classification accuracy possible, it is necessary to consider both the number of features and the classification accuracy when evaluating the quality of individuals. Therefore, the evaluation function of the individual is defined as:

f=alpha∗sd+beta∗(1−score(D))(5)

In Eq. (5), alpha and beta are moderators, alpha∈[0,1], beta∈[0,1], and alpha+beta=1. s represents the quantity of features selected by the individual. d is the dimension of the individual, that is, the number of all features in the data set. score(D) represents the classification accuracy corresponding to the selected feature subset. Therefore, the smaller the f, the better the quality of the individual. Because the core of the classification problem is the classification accuracy, this paper takes alpha=0.02, beta=0.98. The definition of classification accuracy is shown in Eq. (6). In Eq. (6), TP refers to True Positives; TN denotes True Negatives; P represents Positives; and N signifies Negatives.

score(D)=TP+TNP+N(6)

5  Experiment and Analysis

The core focus of this chapter comprises two main aspects: firstly, the validation of the performance of the IHHO algorithm, and secondly, the confirmation of the effectiveness of the feature selection method based on the IHHO algorithm. To evaluate the efficacy of the IHHO algorithm, this study applies the IHHO, HHO, PSO, SSA, OOA, and DBO to solve 23 renowned benchmark test functions. The experimental results are then subjected to thorough analysis. This paper employs KNN as the underlying classifier and conducts a comparative analysis of seven feature selection methods to ascertain the effectiveness of IHHO-FS (The classifier’s classification accuracy serves as the evaluation metric for these feature combinations. Thus, one of the classifier’s roles in this paper is to provide assessment criteria for feature selection methods. Consequently, the choice of classifier is not restricted to KNN, various classifiers such as decision trees or random forests are viable options). The comparison involves methods using all features (Full Features), feature selection approach utilizing the IHHO (IHHO-FS), feature selection approach utilizing the HHO (HHO-FS), feature selection approach utilizing the PSO (PSO-FS), feature selection approach utilizing the SSA (SSA-FS), feature selection approach utilizing the OOA (OOA-FS), and feature selection approach utilizing the DBO (DBO-FS).

5.1 The Performance Test Experiment of IHHO

To evaluate the performance of IHHO, this paper uses IHHO, HHO, PSO, SSA, OOA, and DBO respectively to solve the famous 23 benchmark test functions [29]. Firstly, the solution process of IHHO is qualitatively analyzed from the perspectives of search history (population position change), the trajectory of the first hawk, and the average fitness and convergence. Then, the test results of each algorithm on 23 benchmark functions are quantitatively analyzed in detail. All experimental programs in this section are implemented using Python 3.9.15 on computers with Windows 10 64-bit Pro and 64 GB of memory. The total population size for all algorithms is set to 200, with the number of iterations fixed at 1500. The other parameter settings are detailed in Table 1. Each algorithm runs 10 times independently on each benchmark test function, and use the algorithm’s average performance as the result data.

5.1.1 Benchmark Function

23 benchmark functions, which were initially put out by Yao et al. [29] and are frequently used for assessing the performance of different metaheuristic algorithms, are chosen as testing functions in this article. A thorough overview of the definitions, dimensions, domains, optimal solutions, and optimal values of these 23 functions was given by Xin Yao. Kindly consult [29] for more details. In the domain of swarm intelligence optimization algorithms, these 23 functions are frequently employed to evaluate algorithm performance and are considered authoritative benchmarks. Moreover, these 23 benchmark function types are highly diverse, encompassing fixed-dimensional multimodal functions, unimodal functions, and multimodal functions. They facilitate comprehensive testing of algorithm performance, thereby preventing algorithms from overfitting to specific individual benchmark functions or classes of benchmark functions.

5.1.2 Qualitative Analysis

To qualitatively analyze the solving performance of IHHO, this study examines four widely recognized metrics within the discipline [12]: search history (population position change), the trajectory of the first hawk, the average fitness of the population, and the optimal fitness value within the population. The 23 benchmark functions are classified into three distinct categories: Unimodal Test Functions, Multimodal Test Functions, and Multimodal Test Functions with Fixed Dimensions. This paper selects 1 benchmark functions from each category for display and analysis. The search history diagram consists of black, yellow, and red points, representing the population’s initial, intermediate, and final state, respectively. In the first hawk trajectory diagram, the x-axis denotes the number of iterations, while the y-axis indicates the value of the first-dimensional variable associated with the first hawk. Similarly, in the average fitness diagram for the population, the x-axis represents the number of iterations, and the y-axis reflects the average fitness value of the population. For the best fitness diagram, also referred to as the convergence curve, the x-axis again signifies the number of iterations, whereas the y-axis displays the optimal fitness value observed within the population.

Fig. 3 shows the qualitative analysis results of IHHO on f1, f9 and f14. The first column in Fig. 3 represents the search history. The black, yellow, and red points represent the population distribution at the beginning, middle transition, and end of the iteration. It is evident that the population undergoes a gradual convergence process, transitioning from its initially scattered state (depicted by black points) to an intermediate stage (depicted by yellow points) throughout the iteration process, ultimately culminating in convergence towards the final red point. The findings indicate that the initial population of the IHHO algorithm exhibits strong diversity, and that the IHHO algorithm possesses notable convergence capabilities. The second column in Fig. 3 represents the Trajectory of 1st hawk. It can be seen that the position curve of the first hawk fluctuates rapidly and even fills the entire search space. As the number of iterations increases, the amplitude of the position change of the first hawk gradually decreases. This shows that IHHO is transitioning from the exploration phase to the local exploitation phase. Finally, the position of the first hawk is very stable, indicating that IHHO continues to exploit the potential area and converges to the optimal position. The third column in Fig. 3 represents the average fitness of all hawks, which shows that the average fitness value of the population shows a decreasing trend in fluctuations, and the decrease is fast first and then slow, indicating that the population quality of the IHHO algorithm continues to improve in slight fluctuations and eventually tends to be stable. The fourth column in Fig. 3 represents the convergence curve. It is evident that as the number of iterations increases, the optimal fitness value of the population initially declines rapidly before stabilizing, suggesting that IHHO is effective in swiftly identifying the optimal solution. At the same time, it also reflects that the algorithm has a good balance between exploration and exploitation, which gives it strong optimization ability when solving problems.

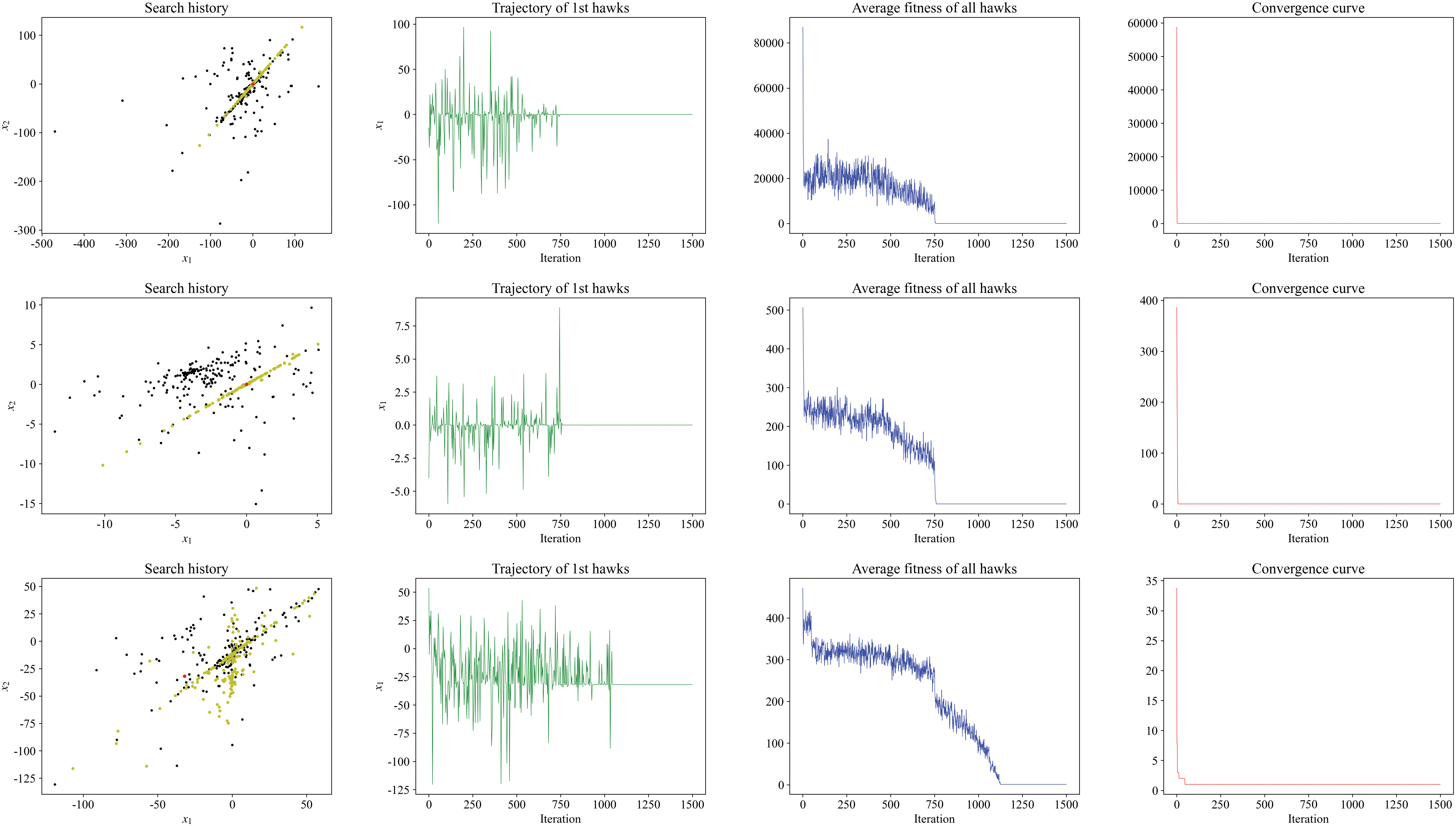
Figure 3: Results of qualitative analysis for IHHO applied to various benchmark test functions

By analyzing the search history, trajectory of the first individual, average fitness value of the population, and convergence curve of IHHO in solving benchmark test functions, it is evident that the IHHO algorithm exhibits notable features of substantial population diversity and rapid convergence rate. Moreover, the unimodal function serves as a measure of the algorithm’s exploitation capabilities, while the multimodal function is utilized to assess its exploration capabilities. The IHHO demonstrates remarkable efficacy in addressing both unimodal and multimodal functions, suggesting that the algorithm possesses robust exploration and exploitation abilities, with a notable equilibrium between the two.

5.1.3 Quantitative Analysis

In this study, the algorithms IHHO, HHO, PSO, SSA, OOA, and DBO are executed 10 times on 23 benchmark functions, yielding a total of 10 experimental outcomes for each algorithm across all benchmark functions. The resulting data are subjected to further processing and analysis.

(1) A comparative analysis of numerical results

Quantitative analysis indicators that can be used to evaluate algorithm performance include maximum error value, minimum error value, median error, mean error value (MEV), time cost, and standard deviation (Std). This article uses MEV, time cost, and Std as quantitative analysis indicators to evaluate the performance of the IHHO algorithm. Because the experimental results show that the time cost of each algorithm is very close, this article will not provide a detailed analysis of the time cost. In Table 2, MEV and Std for each algorithm after solving 23 classic benchmark functions are recorded, and the solving performance of each algorithm is ranked on each benchmark function. Furthermore, Table 2 concludes with a summary of the frequency with which each algorithm secures the top position, along with the average ranking and Friedman ranking for each algorithm. Table 2 provides a detailed record of the experimental findings of IHHO and five other metaheuristic algorithms on 23 classic test functions. The IHHO algorithm secured the top position on 17 occasions, whereas the PSO algorithm achieved first place 8 times. The SSA attained this ranking 4 times, followed by the HHO algorithm with 3 victories. Both the OOA and DBO algorithms each achieved first place once. In addition, the Friedman ranking of the IHHO algorithm is first, indicating that its solving ability is outstanding and far superior to other algorithms.

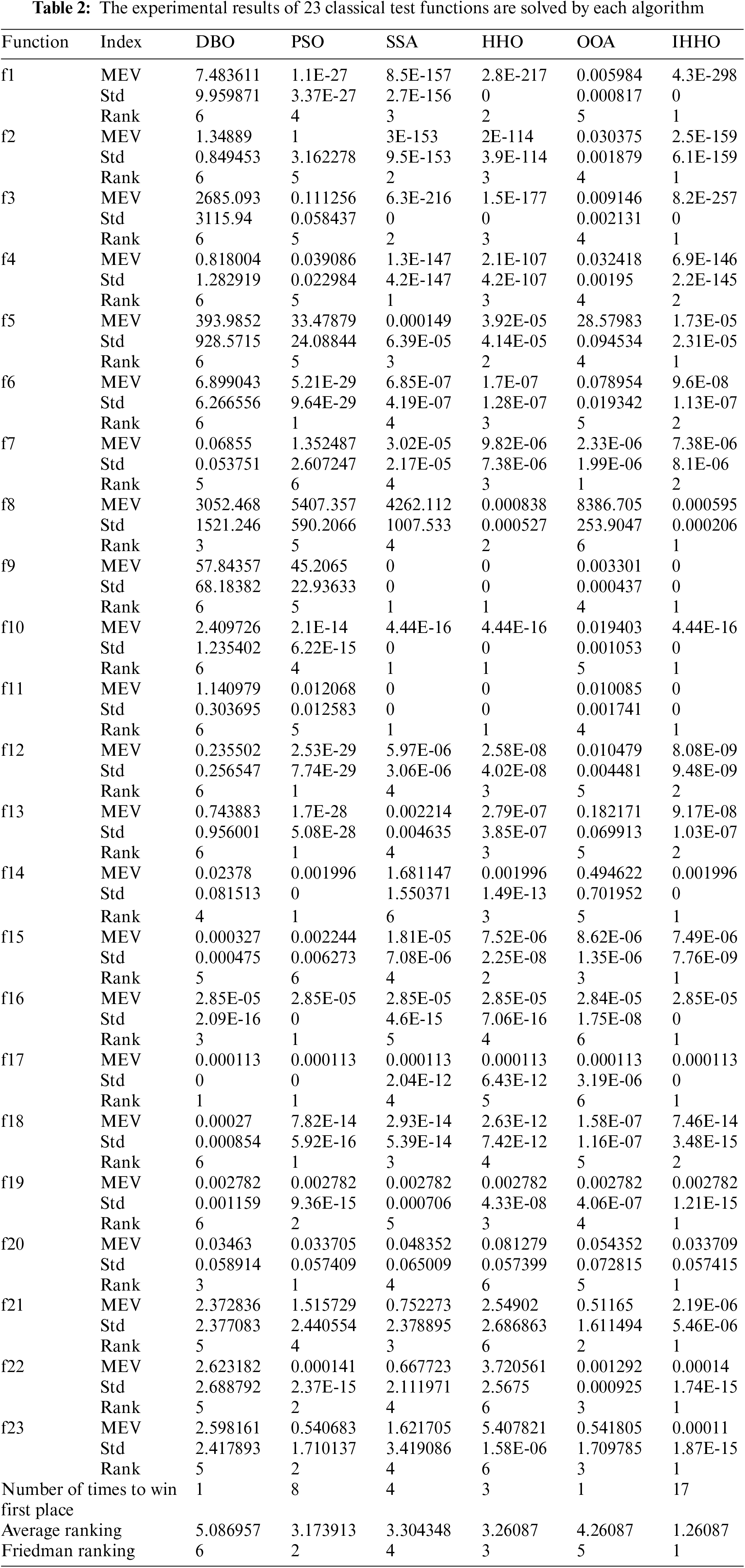
To further analyze the exploitation and exploration ability of the IHHO, this paper presents the experimental results of each algorithm on unimodal and multimodal benchmark test functions. In the evaluation of the seven unimodal benchmark test functions, the IHHO algorithm achieves the top ranking on four occasions. In contrast, the OOA algorithm secures the first position once, as do the SSA and PSO algorithms, while the remaining algorithms do not attain the highest rank. This demonstrates that the IHHO algorithm is particularly effective in addressing unimodal functions, showcasing exceptional capabilities in exploration and exploitation. In the evaluation of 16 multimodal benchmark functions, the IHHO algorithm achieved the top position on 13 occasions, while the PSO secured first place 7 times. The SSA ranked first 3 times, the HHO achieved this position twice, and the DBO algorithm attained the top position once. Notably, the OOA did not achieve any first-place rankings. These findings suggest that the IHHO demonstrates superior efficacy in addressing multimodal functions, highlighting its robust exploration capabilities. Therefore, the exploration and exploitation ability of the IHHO is powerful, and its comprehensive performance is outstanding.

Additionally, Table 3 records the Wilcoxon test results of the IHHO algorithm and five other algorithms across 23 benchmark test functions. From Table 3, it is observed that the p-values between IHHO and the other algorithms are all less than 0.05, indicating significant differences between the experimental results of the IHHO algorithm and those of the other algorithms at the 0.05 significance level.

(2) Convergence comparative analysis

From the above results, IHHO has excellent solving performance, outperforming the remaining five advanced algorithms in most problems, and has strong competitiveness. Concurrently, this paper draws the convergence curve of each algorithm on all test functions, as shown in Fig. 4. By comparison, we can see that different algorithms have significant differences in search speed and accuracy. On 23 classical benchmark functions, IHHO has faster convergence speed and higher convergence accuracy, which has obvious advantages compared with other algorithms. The comprehensive performance of the IHHO is good and has strong competitiveness.

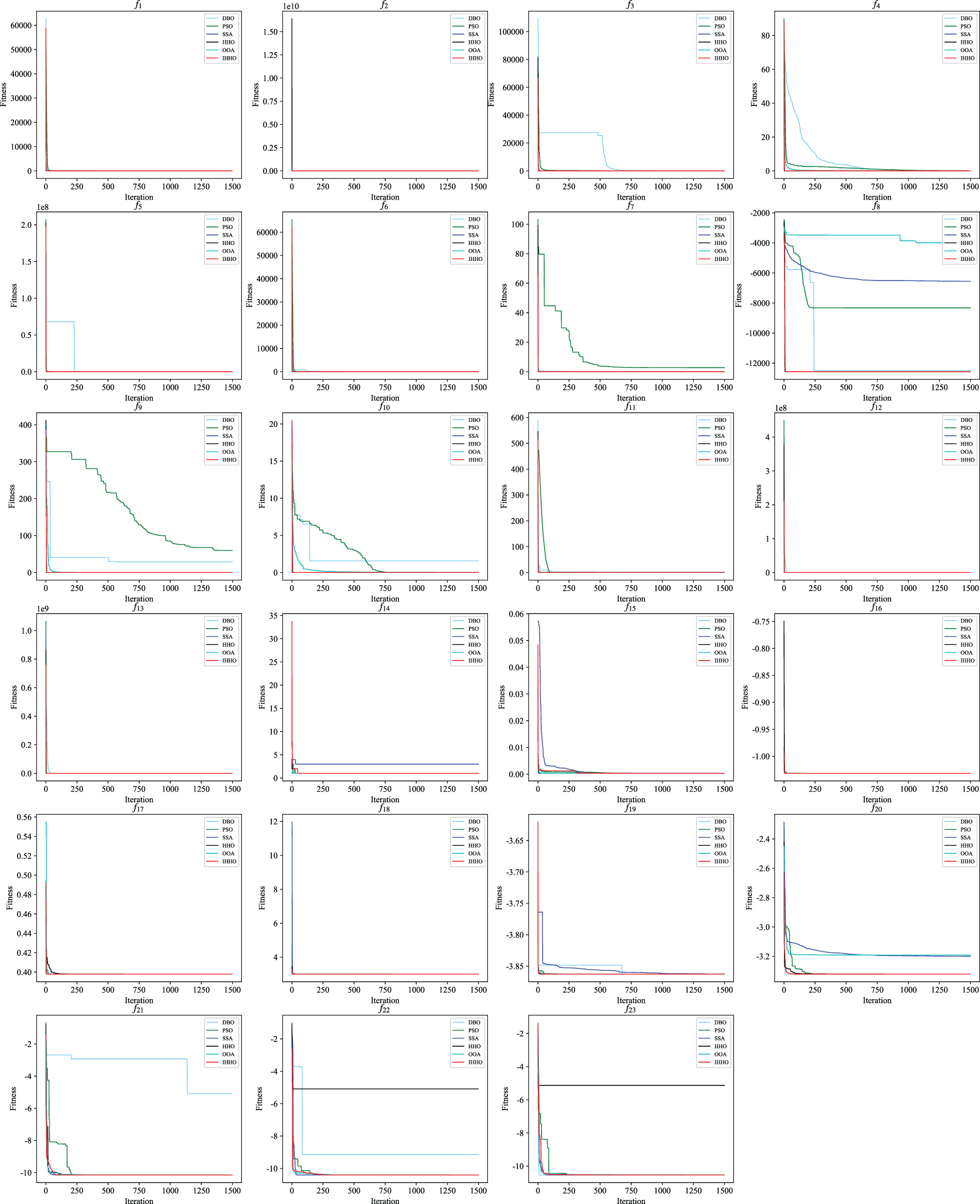
Figure 4: The convergence curves of each algorithm on 23 classical test functions

(3) Robustness analysis

This section presents a comparative analysis of the robustness of IHHO and other algorithms, illustrating box plots of the performance of the six algorithms across various test functions, as shown in Fig. 5. Fig. 5 illustrates notable variations in both solution accuracy and robustness across the various algorithms. Across the first seven unimodal functions, SSA, OOA, HHO, and IHHO exhibit high robustness and precision, demonstrating clear advantages. Across the subsequent 16 multimodal functions, the robustness of the IHHO algorithm significantly surpasses that of the other algorithms, maintaining consistently strong performance across different benchmark test functions, showcasing its remarkable stability in solution capability.

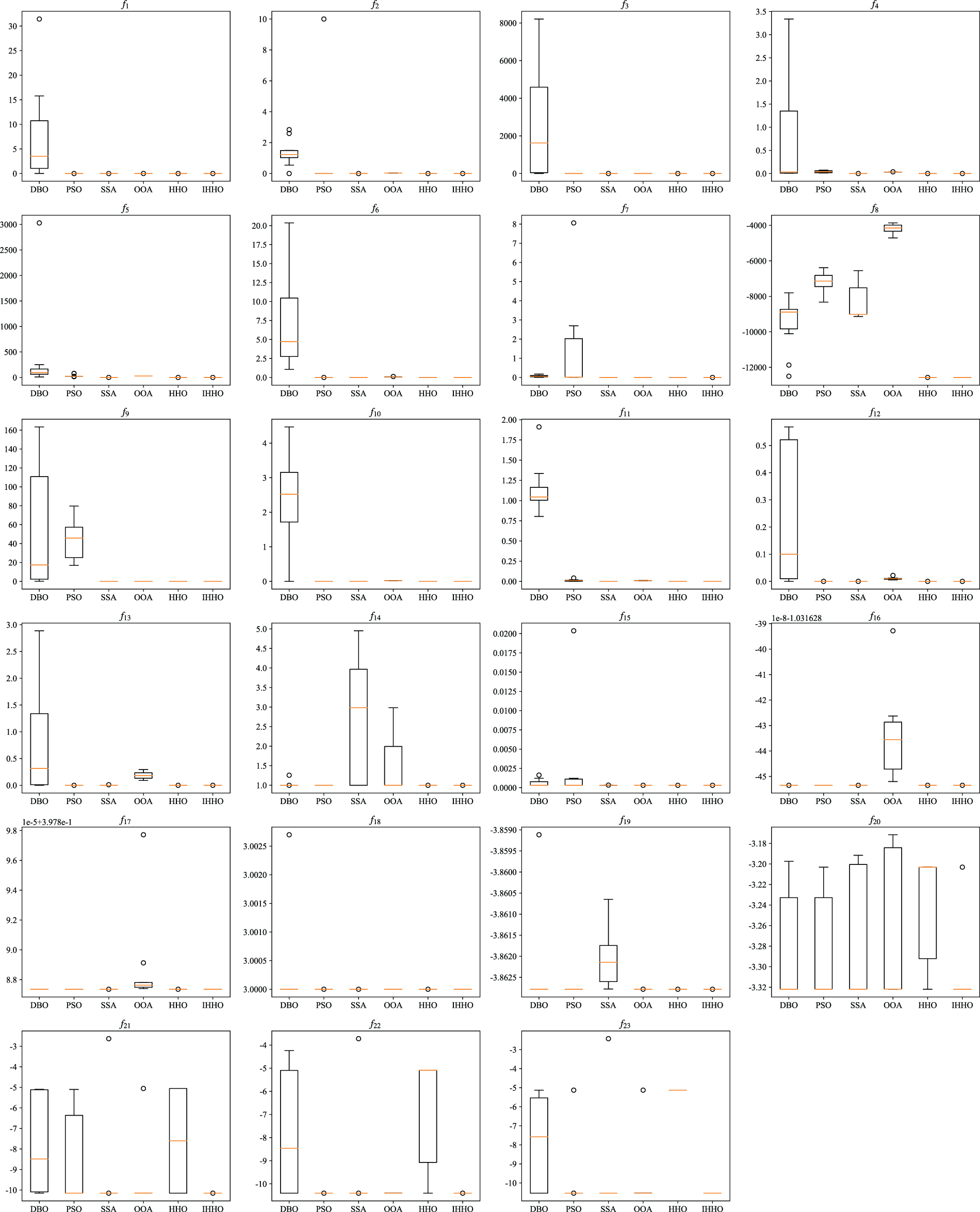
Figure 5: Box plots of various algorithms across 23 classical benchmark functions

5.2 The Effectiveness of the Feature Selection Method Based on IHHO

All experiments described in this section were conducted using Python 3.9.15 on a Windows 10 64-bit Pro system with 64 GB of RAM. The population size for all algorithms was set to 100, and the number of iterations was set to 150. Each algorithm is executed independently for ten trials on every data set, with the average of the experimental results computed to serve as the final outcome. Furthermore, to mitigate feature selection overfitting, this study employed k-fold cross-validation techniques to evaluate the efficacy of feature selection, using the mean accuracy across each fold as the final outcome.

5.2.1 Datasets

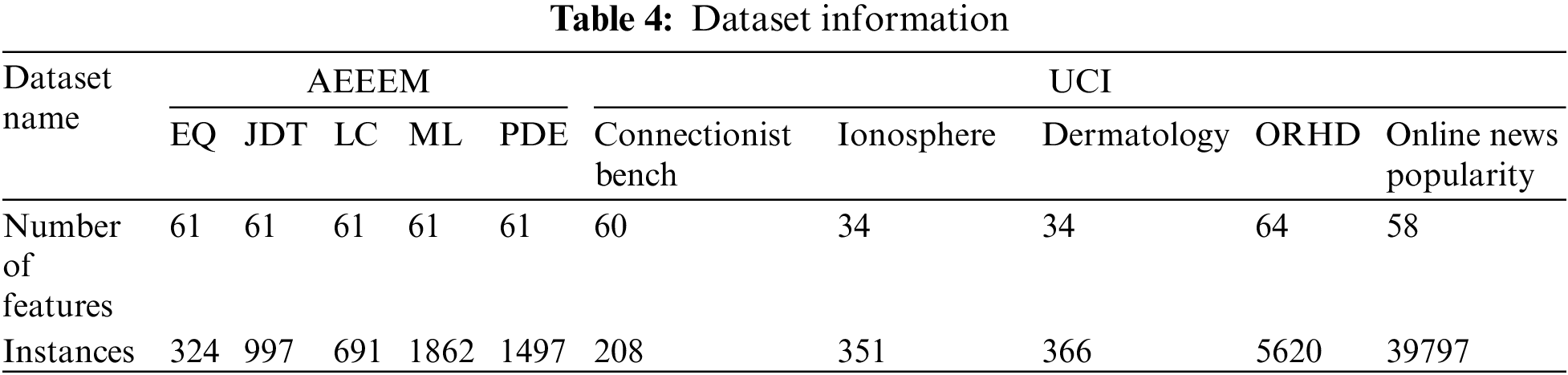
This article uses five datasets from AEEEM [40] and five datasets from publicly available UCI machine learning databases to measure the effectiveness of IHHO-based feature selection methods. These datasets are publicly accessible and are frequently utilized to assess the efficacy of feature selection methods, as demonstrated in Table 4.

5.2.2 Comparative Analysis

This paper uses KNN as the primary classifier to compare and analyze Full Features, IHHO-FS, HHO-FS, PSO-FS, SSA-FS, OOA-FS, and DBO-FS on ten classical datasets to evaluate the effectiveness and performance of IHHO-FS. Each scheme is run independently 10 times, with the final results presented in Table 5, which include the average classification accuracy (score), average number of features (features), and average function values (f).

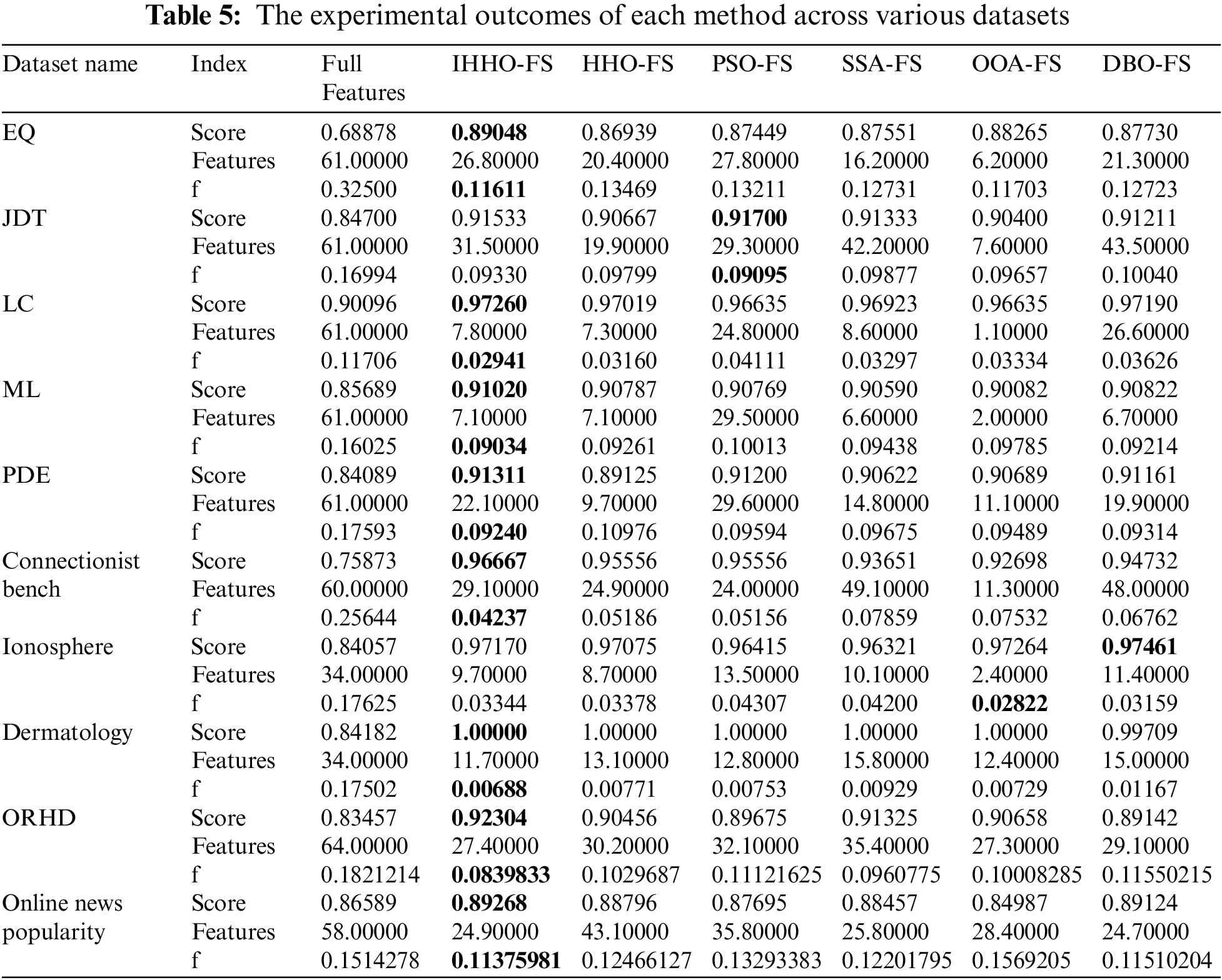
The higher the classification accuracy, the higher the accuracy of the scheme. The lower the number of features used, the lower the computational cost of the scheme. The lower the value of the evaluation function, the better the overall effect of the scheme. Table 5 provides a detailed record of score, features, and f of the above seven methods on ten datasets. The highest classification accuracy and minimum evaluation function values on each dataset are also highlighted in bold.

Comparing the Full Features column and IHHO-FS column in Table 5, it can be seen that the feature selection approach utilizing the IHHO can significantly improve the classification accuracy of the model, reduce the number of features used, and lower the evaluation function value, indicating that IHHO-FS is very effective. In addition, on the eight datasets of EQ, LC, ML, PDE, Connectivity Bench, Dermatology, ORHD, and Online News Popularity, IHHO-FS has the highest classification accuracy and the lowest evaluation function value. On the JDT and Ionosphere datasets, although IHHO-FS is not the best, its performance is also excellent, ranking among the top in comprehensive performance. This indicates that IHHO-FS not only effectively improves model performance but also stands out among numerous algorithms and is highly competitive. Therefore, IHHO-FS can improve the classification accuracy of the classification model, reduce the number of features used by the model (that is, reduce the data dimension), reduce the evaluation function value, and show strong competitiveness in many schemes. It can provide an efficient feature selection method for various supervised machine learning models.

Furthermore, this study performs a comparative assessment of the robustness of IHHO-FS and five additional feature selection techniques, as demonstrated in Fig. 6. Fig. 6 presents box plots of ten experimental results across various datasets for the six feature selection methods. It is evident from Fig. 6 that significant differences exist among the methods in terms of solution accuracy and robustness. Across the EQ, JDT, LC, ML, CB, ORHD, ONP, and Ionosphere datasets, IHHO-FS demonstrates high robustness and clear advantages. Moreover, on other datasets, IHHO-FS also exhibits robust performance. Therefore, applying IHHO to feature selection problems ensures the robustness of the model.

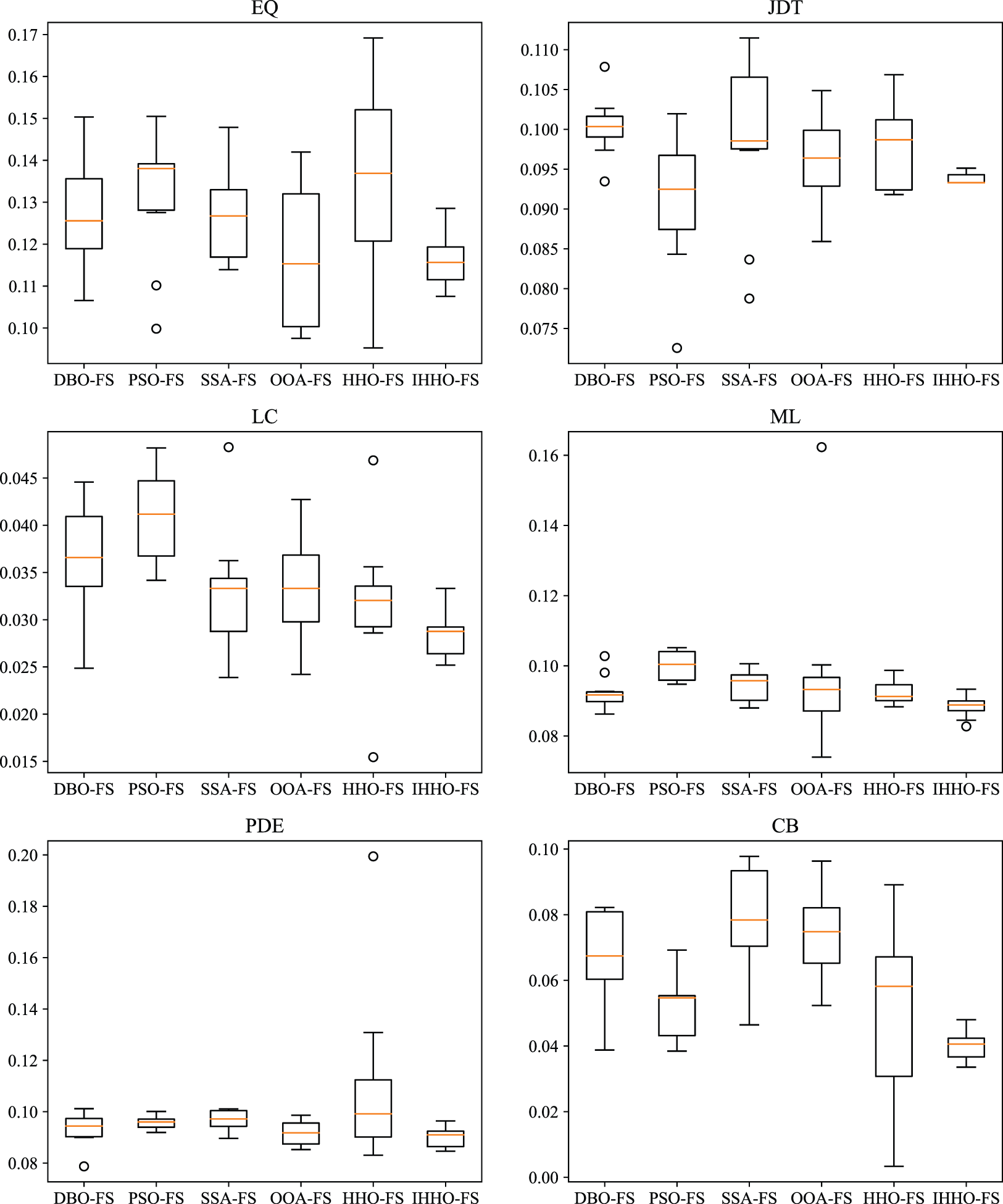
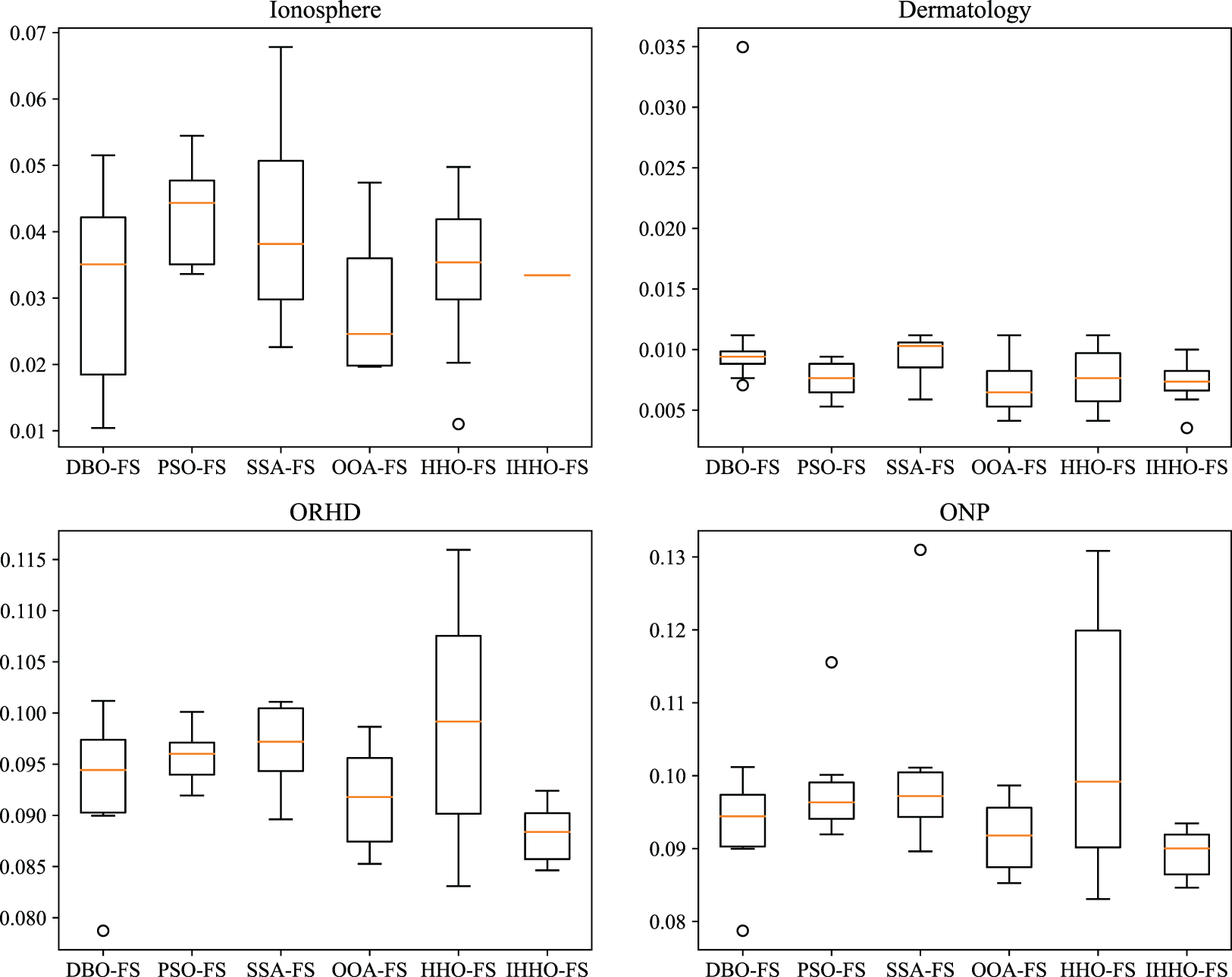
Figure 6: Box plots of various schemes across 10 classical datasets

6  Conclusion

To address the issues of uneven exploration and exploitation capabilities, limited population diversity, and inadequate deep exploitation in the Harris Hawks Optimization algorithm, this paper introduces three strategies designed to enhance its performance. One approach involves a population initialization method utilizing opposition-based learning to enhance diversity. Another strategy focuses on updating an escape energy factor to maintain a balance between exploration and exploitation capabilities within the algorithm. Lastly, a deep exploitation strategy combines variable neighborhood search with a mutation operator to boost the algorithm’s exploitation efficiency, thereby enhancing its convergence speed and accuracy.

Furthermore, to address the issues of inefficient feature selection and slow response times in classification models, this study proposes a feature selection technique using an enhanced Harris Hawks Optimization algorithm. This method effectively identifies suitable feature combinations within a reasonable timeframe, significantly lowering the computational costs associated with classification models (through data dimensionality reduction) and enhancing the overall efficiency of feature selection.

This paper uses IHHO, HHO, PSO, SSA, OOA, and DBO to solve the famous 23 benchmark functions to assess the efficacy of the IHHO. The results from the experiments show that the IHHO outperforms other algorithms in terms of solving ability. This suggests that the enhancements proposed in this paper successfully boost the performance of the HHO. This study employs KNN as the main classifier to evaluate Full Features, IHHO-FS, HHO-FS, PSO-FS, SSA-FS, OOA-FS, and DBO-FS across eight well-established datasets, aiming to assess the performance of the feature selection technique grounded in the IHHO. The findings indicate that IHHO-FS enhances the classification model’s accuracy while also decreasing data dimensionality, outperforming the other methods analyzed. It shows that IHHO-FS can find the appropriate feature combination quickly, efficiently, and accurately, which significantly improves the efficiency of feature selection and provides a new and efficient feature selection method.

Drawing from the preceding analysis, IHHO has outstanding problem-solving performance and can solve various optimization problems quickly and accurately. In addition, IHHO can efficiently select and search for satisfactory feature combinations, providing an effective technical method for feature selection. In the future, we aim to enhance the computational efficiency of the IHHO algorithm. We plan to explore the integration of parallel and distributed computing techniques to increase the solution speed, ultimately broadening the applicability of IHHO-FS to ultra-high-dimensional data sets. Furthermore, we will delve deeper into enhancing the discrete optimization capability of IHHO, thus augmenting the practical applicability of IHHO-FS.

Acknowledgement: Special thanks to those who have contributed to this article, such as Zipeng Zhao, and Yu Wan. They not only provided many effective suggestions, but also encouraged us.

Funding Statement: This study was supported by the National Natural Science Foundation of China (grant number 62073330) and constituted a segment of a project associated with the School of Computer Science and Information Engineering at Harbin Normal University.

Author Contributions: All authors contributed to the topic research and framework design of the paper. Qianqian Zhang, Yingmei Li and Shan Chen were responsible for data collection and the gathering and summarization of references. Qianqian Zhang and Jianjun Zhan handled the innovative algorithm design, experimental design and analysis and visualization of experimental results. The initial draft was written by Qianqian Zhang, with all authors providing revisions for earlier versions. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: For questions regarding data availability, please contact the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Cuesta, C. Lancho, A. Fernández-Isabel, E. L. Cano, and I. Martín De Diego, “CSViz: Class separability visualization for high-dimensional datasets,” Appl. Intell., vol. 54, no. 1, pp. 924–946, 2024. doi: 10.1007/s10489-023-05149-4. [Google Scholar] [CrossRef]

2. T. França, A. M. B. Braga, and H. V. H. Ayala, “Feature engineering to cope with noisy data in sparse identification,” Expert Syst. Appl., vol. 188, no. 1, 2022, Art. no. 115995. [Google Scholar]

3. R. Xu, M. Li, Z. Yang, L. Yang, K. Qiao and Z. Shang, “Dynamic feature selection algorithm based on Q-learning mechanism,” Appl. Intell., vol. 51, no. 1, pp. 1–12, 2021. doi: 10.1007/s10489-021-02257-x. [Google Scholar] [CrossRef]

4. S. Liang, Z. Liu, D. You, W. Pan, J. Zhao and Y. Cao, “PSO-NRS: An online group feature selection algorithm based on PSO multi-objective optimization,” Appl. Intell., vol. 53, no. 12, pp. 15095–15111, 2023. doi: 10.1007/s10489-022-04275-9. [Google Scholar] [CrossRef]

5. K. Yin, A. Xie, J. Zhai, and J. Zhu, “Dynamic interaction-based feature selection algorithm for maximal relevance minimal redundancy,” Appl. Intell., vol. 53, no. 8, pp. 8910–8926, 2023. doi: 10.1007/s10489-022-03922-5; [Google Scholar] [CrossRef]

6. P. Qiu, C. Zhang, D. Gao, and Z. Niu, “A fusion of centrality and correlation for feature selection,” Expert Syst. Appl., vol. 241, no. 1, 2024, Art. no. 122548. doi: 10.1016/j.eswa.2023.122548. [Google Scholar] [CrossRef]

7. L. Sun, Y. Ma, W. Ding, and J. Xu, “Sparse feature selection via local feature and high-order label correlation,” Appl. Intell., vol. 54, no. 1, pp. 565–591, 2024. doi: 10.1007/s10489-023-05136-9. [Google Scholar] [CrossRef]

8. S. Zhuo, J. Qiu, C. Wang, and S. Huang, “Online feature selection with varying feature spaces,” IEEE Trans. Knowl. Data Eng., vol. 36, no. 9, pp. 1–14, 2024. doi: 10.1109/TKDE.2024.3377243. [Google Scholar] [CrossRef]

9. H. M. Abdulwahab, S. Ajitha, and M. A. N. Saif, “Feature selection techniques in the context of big data: Taxonomy and analysis,” Appl. Intell., vol. 52, no. 12, pp. 13568–13613, 2022. doi: 10.1007/s10489-021-03118-3. [Google Scholar] [CrossRef]

10. R. Jiao, B. Xue, and M. Zhang, “Learning to preselection: A filter-based performance predictor for multiobjective feature selection in classification,” IEEE Trans. Evol. Comput., vol. 28, no. 1, pp. 1–15, 2024. doi: 10.1109/TEVC.2024.3373802. [Google Scholar] [CrossRef]

11. S. Zhang, K. Liu, T. Xu, X. Yang, and A. Zhang, “A meta-heuristic feature selection algorithm combining random sampling accelerator and ensemble using data perturbation,” Appl. Intell., vol. 53, no. 24, pp. 29781–29798, 2023. doi: 10.1007/s10489-023-05123-0. [Google Scholar] [CrossRef]

12. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja and H. Chen, “Harris hawks optimization: Algorithm and applications,” Fut. Gen. Comput. Syst., vol. 97, no. 1, pp. 849–872, 2019. [Google Scholar]

13. D. Yilmaz Eroglu and U. Akcan, “An adapted ant colony optimization for feature selection,” Appl. Artif. Intell., vol. 38, no. 1, 2024, Art. no. 2335098. doi: 10.1080/08839514.2024.2335098. [Google Scholar] [CrossRef]

14. J. Xue and B. Shen, “A novel swarm intelligence optimization approach: Sparrow search algorithm,” Syst. Sci. Control Eng., vol. 8, no. 1, pp. 22–34, 2020. doi: 10.1080/21642583.2019.1708830. [Google Scholar] [CrossRef]

15. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. ICNN’95-Int. Conf. Neural Netw., Perth, WA, Australia, Nov. 1995, pp. 1942–1948. [Google Scholar]

16. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, no. 1, pp. 46–61, 2014. doi: 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

17. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 1, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

18. J. Too, A. R. Abdullah, and N. Mohd Saad, “A new quadratic binary harris hawk optimization for feature selection,” Electronics, vol. 8, no. 10, 2019, Art. no. 1130. doi: 10.3390/electronics8101130. [Google Scholar] [CrossRef]

19. W. Long, J. Jiao, M. Xu, M. Tang, T. Wu and S. Cai, “Lens-imaging learning Harris hawks optimizer for global optimization and its application to feature selection,” Expert Syst. Appl., vol. 202, no. 1, 2022, Art. no. 117255. doi: 10.1016/j.eswa.2022.117255. [Google Scholar] [CrossRef]

20. S. X. Y. X. Tang, “Sensitive feature selection for industrial flotation process soft sensor based on multiswarm PSO with collaborative search,” IEEE Sens. J., vol. 24, no. 10, pp. 17159–17168, 2024. doi: 10.1109/JSEN.2024.3381837. [Google Scholar] [CrossRef]

21. M. Tubishat et al., “Dynamic salp swarm algorithm for feature selection,” Expert Syst. Appl., vol. 164, no. 1, 2021, Art. no. 113873. doi: 10.1016/j.eswa.2020.113873; [Google Scholar] [CrossRef]

22. M. A. Al-Betar, M. A. Awadallah, A. A. Heidari, H. Chen, H. Al-Khraisat and C. Li, “Survival exploration strategies for Harris hawks optimizer,” Expert Syst. Appl., vol. 168, no. 1, 2021, Art. no. 114243. doi: 10.1016/j.eswa.2020.114243. [Google Scholar] [CrossRef]

23. A. G. Hussien et al., “Recent advances in harris hawks optimization: A comparative study and applications,” Electronics, vol. 11, no. 12, 2022, Art. no. 1919. doi: 10.3390/electronics11121919. [Google Scholar] [CrossRef]

24. H. M. Alabool, D. Alarabiat, L. Abualigah, and A. A. Heidari, “Harris hawks optimization: A comprehensive review of recent variants and applications,” Neural Comput. Appl., vol. 33, no. 1, pp. 8939–8980, 2021. doi: 10.1007/s00521-021-05720-5. [Google Scholar] [CrossRef]

25. M. Shehab et al., “Harris hawks optimization algorithm: Variants and applications,” Arch. Comput. Methods Eng., vol. 29, no. 7, pp. 5579–5603, 2022. doi: 10.1007/s11831-022-09780-1. [Google Scholar] [CrossRef]

26. K. Hussain, N. Neggaz, W. Zhu, and E. H. Houssein, “An efficient hybrid sine-cosine Harris hawks optimization for low and high-dimensional feature selection,” Expert. Syst. Appl., vol. 176, no. 1, 2021, Art. no. 114778. doi: 10.1016/j.eswa.2021.114778. [Google Scholar] [CrossRef]

27. Y. Zhang, R. Liu, X. Wang, H. Chen, and C. Li, “Boosted binary Harris hawks optimizer and feature selection,” Eng. Comput., vol. 37, no. 1, pp. 3741–3770, 2021. doi: 10.1007/s00366-020-01028-5. [Google Scholar] [CrossRef]

28. L. Peng, Z. Cai, A. A. Heidari, L. Zhang, and H. Chen, “Hierarchical Harris hawks optimizer for feature selection,” J. Adv. Res., vol. 53, no. 1, pp. 261–278, 2023. doi: 10.1016/j.jare.2023.01.014. [Google Scholar] [PubMed] [CrossRef]

29. X. Yao, Y. Liu, and G. Lin, “Evolutionary programming made faster,” IEEE Trans. Evol. Comput., vol. 3, no. 2, pp. 82–102, 1999. doi: 10.1109/4235.771163. [Google Scholar] [CrossRef]

30. Y. Xue, H. Zhu, and F. Neri, “A feature selection approach based on NSGA-II with ReliefF,” Appl. Soft Comput., vol. 134, no. 1, 2023, Art. no. 109987. doi: 10.1016/j.asoc.2023.109987. [Google Scholar] [CrossRef]

31. H. Cui et al., “Enhanced harris hawks optimization integrated with coot bird optimization for solving continuous numerical optimization problems,” Comput. Model. Eng. Sci., vol. 137, no. 2, pp. 1–41, 2023. doi: 10.32604/cmes.2023.026019. [Google Scholar] [CrossRef]

32. R. L. Haupt and S. E. Haupt, “The binary genetic algorithm,” in Practical Genetic Algorithms. New York, NY, USA: John Wiley & Sons, Ltd, 2003, pp. 27–50. [Google Scholar]

33. H. R. Tizhoosh, “Opposition-based learning: A new scheme for machine intelligence,” in Int. Conf. Comput. Intell. Model., Control Automat. Int. Conf. Intell. Agents, Web Technol. Internet Comm. (CIMCA-IAWTIC’06), Vienna, Austria, IEEE, Nov. 2005, pp. 695–701. [Google Scholar]

34. S. Shadravan, H. R. Naji, and V. K. Bardsiri, “The sailfish optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems,” Eng. Appl. Artif. Intell., vol. 80, no. 1, pp. 20–34, 2019. doi: 10.1016/j.engappai.2019.01.001. [Google Scholar] [CrossRef]

35. M. Braik, A. Sheta, and H. Al-Hiary, “A novel meta-heuristic search algorithm for solving optimization problems: Capuchin search algorithm,” Neural Comput. Appl., vol. 33, no. 7, pp. 2515–2547, 2021. doi: 10.1007/s00521-020-05145-6. [Google Scholar] [CrossRef]

36. M. Ghaemi and M. -R. Feizi-Derakhshi, “Feature selection using forest optimization algorithm,” Pattern Recognit., vol. 60, no. 1, pp. 121–129, 2016. doi: 10.1016/j.patcog.2016.05.012. [Google Scholar] [CrossRef]

37. S. Tabakhi, P. Moradi, and F. Akhlaghian, “An unsupervised feature selection algorithm based on ant colony optimization,” Eng. Appl. Artif. Intell., vol. 32, no. 1, pp. 112–123, 2014. doi: 10.1016/j.engappai.2014.03.007. [Google Scholar] [CrossRef]

38. J. Li et al., “Feature selection: A data perspective,” ACM Comput. Surv., vol. 50, no. 6, pp. 1–45, 2017. doi: 10.1145/3136625. [Google Scholar] [CrossRef]

39. Z. Sadeghian, E. Akbari, H. Nematzadeh, and H. Motameni, “A review of feature selection methods based on meta-heuristic algorithms,” J. Experiment. Theor. Artif. Intell., vol. 35, no. 1, pp. 1–51, 2023. doi: 10.1080/0952813X.2023.2183267. [Google Scholar] [CrossRef]

40. M. D’Ambros, M. Lanza, and R. Robbes, “An extensive comparison of bug prediction approaches,” in 2010 7th IEEE Working Conf. Mining Softw. Reposit. (MSR 2010), Cape Town, South Africa, IEEE, May 2010, pp. 31–41. [Google Scholar]