DeepSurNet-NSGA II: Deep Surrogate Model-Assisted Multi-Objective Evolutionary Algorithm for Enhancing Leg Linkage in Walking Robots

1  Introduction

The advent of robotics, particularly in domains requiring nuanced physical interaction with the environment, has necessitated the development of sophisticated design and optimization strategies. One of the critical challenges in robotics is the design of leg linkages for walking robots, which plays a pivotal role in achieving efficient horizontal propulsion. Traditional design methodologies often fall short when faced with the multi-faceted objectives that such a task entails, including but not limited to energy efficiency, stability, and adaptability to various terrains [1]. Consequently, there has been a growing interest in leveraging advanced computational techniques to address these challenges. Among these, the use of multi-objective evolutionary algorithms (MOEAs) has emerged as a particularly promising avenue, providing a framework for navigating the complex trade-offs inherent in robotic design [2]. However, despite the potential of MOEAs, their application in this context is not without limitations, chief among them being the computational expense associated with evaluating the performance of a vast number of design alternatives.

In response to these challenges, the integration of surrogate models into the optimization process has been proposed as a means to alleviate the computational burden. Surrogate models, by approximating the fitness landscape, enable a more efficient exploration of the design space, reducing the need for exhaustive simulation or physical prototyping [3]. Deep learning, with its remarkable ability to capture complex patterns and relationships, offers a compelling foundation for constructing such surrogate models [4]. The integration of deep learning-based surrogate models with MOEAs holds the promise of significantly enhancing the efficiency and efficacy of the optimization process, yet its practical implementation in the context of robotic leg linkage design remains underexplored.

This research introduces DeepSurNet-NSGA, a novel framework that combines a deep surrogate model with the Non-dominated Sorting Genetic Algorithm (NSGA), specifically tailored for the optimization of leg linkage designs in walking robots. The NSGA, a widely recognized MOEA, is renowned for its effectiveness in handling multi-objective optimization problems, offering a balanced exploration and exploitation of the search space [5]. By augmenting NSGA with a deep learning-based surrogate model, DeepSurNet-NSGA II aims to overcome the computational challenges traditionally associated with such optimization tasks, facilitating a more efficient and nuanced exploration of the design space.

The potential of surrogate-assisted MOEAs in streamlining the design and optimization process has been highlighted in various fields, from aerospace engineering to renewable energy systems [6–8]. In these contexts, surrogate models have been instrumental in reducing computational costs while maintaining or even enhancing the quality of the solutions obtained. Building upon this foundation, DeepSurNet-NSGA seeks to extend these benefits to the domain of robotic design, where the complexity of the design objectives and constraints poses a significant challenge.

Furthermore, the proposed framework is distinguished by its emphasis on deep learning for the development of the surrogate model. Recent advancements in deep learning methodologies have significantly expanded their applicability and effectiveness across a broad range of domains [9]. In particular, the capacity of deep learning models to learn from data and to generalize from it makes them exceptionally suited for capturing the intricacies of the fitness landscape in robotic design optimization [10]. This is a critical aspect of DeepSurNet-NSGA, as the accuracy and predictive power of the surrogate model directly impact the efficiency and effectiveness of the optimization process.

The application of DeepSurNet-NSGA II to the optimization of leg linkage in walking robots represents a significant step forward in the pursuit of more sophisticated and capable robotic systems. By addressing the dual challenges of computational efficiency and optimization effectiveness, this research contributes to the broader field of robotics, opening new avenues for the design and development of advanced robotic systems. In doing so, it underscores the critical role of advanced computational techniques, such as deep learning and evolutionary algorithms, in pushing the boundaries of what is possible in robotics.

2  Related Works

The exploration and application of multi-objective optimization strategies in the realm of robotics have been extensive, reflecting a rich tapestry of approaches and methodologies aimed at enhancing robotic design and functionality. The related works in this domain highlight a progression from traditional optimization techniques to more sophisticated, computationally driven methods, underscoring the evolution of the field towards more efficient and effective solutions.

One of the foundational aspects of robotics optimization, particularly in the context of legged locomotion, has been the application of evolutionary algorithms (EAs). These algorithms mimic natural selection processes to iteratively improve design solutions [11]. The NSGA-II method and its subsequent iterations have been pivotal in this regard, offering robust frameworks for navigating the complex trade-offs between multiple objectives [12]. These algorithms have been successfully applied in various aspects of robotics, including the optimization of legged robot structures for enhanced mobility and efficiency [13–15].

Despite the effectiveness of EAs in handling multi-objective problems, their application is often hampered by the high computational cost associated with evaluating a large number of potential solutions. This challenge has led to the integration of surrogate models as a means to approximate the fitness landscape, thereby reducing the need for exhaustive evaluations [16]. Surrogate models, particularly those based on polynomial regression, Gaussian processes, and machine learning, have demonstrated considerable success in reducing the computational load while maintaining optimization quality [17]. However, these models often struggle to capture the highly complex and nonlinearity in robotic design problems.

The advent of deep learning has introduced new possibilities for surrogate model development. With their capacity for high-dimensional data representation and pattern recognition, deep learning models have shown great promise in accurately approximating complex fitness landscapes [18]. The application of deep learning-based surrogate models in the optimization of aerodynamic designs and material properties has illustrated their potential to significantly enhance the efficiency of evolutionary optimization processes [19].

In the context of legged robotics, the design and optimization of leg linkages stand out as a particularly challenging problem, given the intricate interplay between mechanical design, energy efficiency, and environmental adaptability. Previous studies have explored various optimization strategies, including gradient-based methods and traditional EAs, to improve the design of leg linkages [20–22]. However, these approaches often fail to adequately address the multi-objective nature of the problem or to efficiently explore the vast design space.

The concept of Deep Surrogate Model-Assisted Multi-Objective Evolutionary Algorithms (DSM-MOEAs) represents a novel integration of deep learning-based surrogate models with MOEAs. This approach aims to leverage the strengths of both methodologies to optimize complex systems more effectively. Preliminary applications of DSM-MOEAs in fields such as renewable energy optimization and structural design have demonstrated their potential to significantly improve optimization outcomes [23]. However, the implementation of DSM-MOEAs in robotic leg linkage design remains relatively unexplored, highlighting a gap in the current literature and a compelling opportunity for advancement.

Additionally, the environmental and operational adaptability of legged robots, a critical aspect of their design optimization, poses additional challenges. The need to ensure that optimized designs are not only efficient but also capable of navigating a variety of terrains has led to the exploration of adaptive optimization strategies [24]. These strategies, which dynamically adjust optimization objectives based on environmental feedback, represent an advanced frontier in robotic design optimization.

In summary, the related works in the optimization of legged robotics underscore a trajectory from traditional evolutionary algorithms towards more sophisticated, surrogate-assisted approaches. The integration of deep learning-based surrogate models with MOEAs, exemplified by the proposed DeepSurNet-NSGA framework, marks a promising advancement in the field. Nonetheless, the exploration of this integration in the specific context of leg linkage design optimization remains nascent, presenting a fertile ground for further research. Additionally, the consideration of metrics such as burstiness and perplexity, alongside the adaptation to varying environmental conditions, highlights the multi-dimensional complexity of the optimization challenge and the need for innovative, comprehensive solutions.

3  Materials and Methods

The development of leg-linkage designs for walking robots that enable the foot’s center to follow a straight-line trajectory offers significant benefits, notably in terms of energy conservation and streamlined control mechanisms [25–27]. A model illustrating the legged robot’s horizontal movement system is depicted in Fig. 1a, where feet F1 and F2 are in the supporting phase (touching the ground), and F3 and F4 are in the transferring phase (swinging) [28–30]. The concept of employing straight-line mechanisms to advance walking machines has been a fruitful avenue of exploration since Chebyshev introduced the “lambda mechanism” in 1878 [31]. This mechanism, shown in Fig. 1b as a four-bar linkage ABCD with a coupler point E, creates a horizontal straight line as the crank AB undergoes rotation exceeding 180 degrees, denoted by the crank rotation angle and the initial crank angle. Previous research has applied the Sobol-Statnikov method for the multi-criteria optimal design of bar linkages, utilizing a “LP-tau generator” based on random searches and trial tables [32,33]. Fig. 1c illustrates a three-dimensional model of the horizontal propulsion mechanism of the legged robot, highlighting its complex structural integration and mechanical linkages. This visual representation is instrumental in understanding the spatial configuration and the engineering design principles applied. Fig. 1d further elaborates on the 3D model by focusing on specific components such as joints and actuators, providing a detailed view of the assembly and the functional aspects of the propulsion system. This detailed visualization aids in comprehending the operational dynamics and potential stress points within the mechanism.

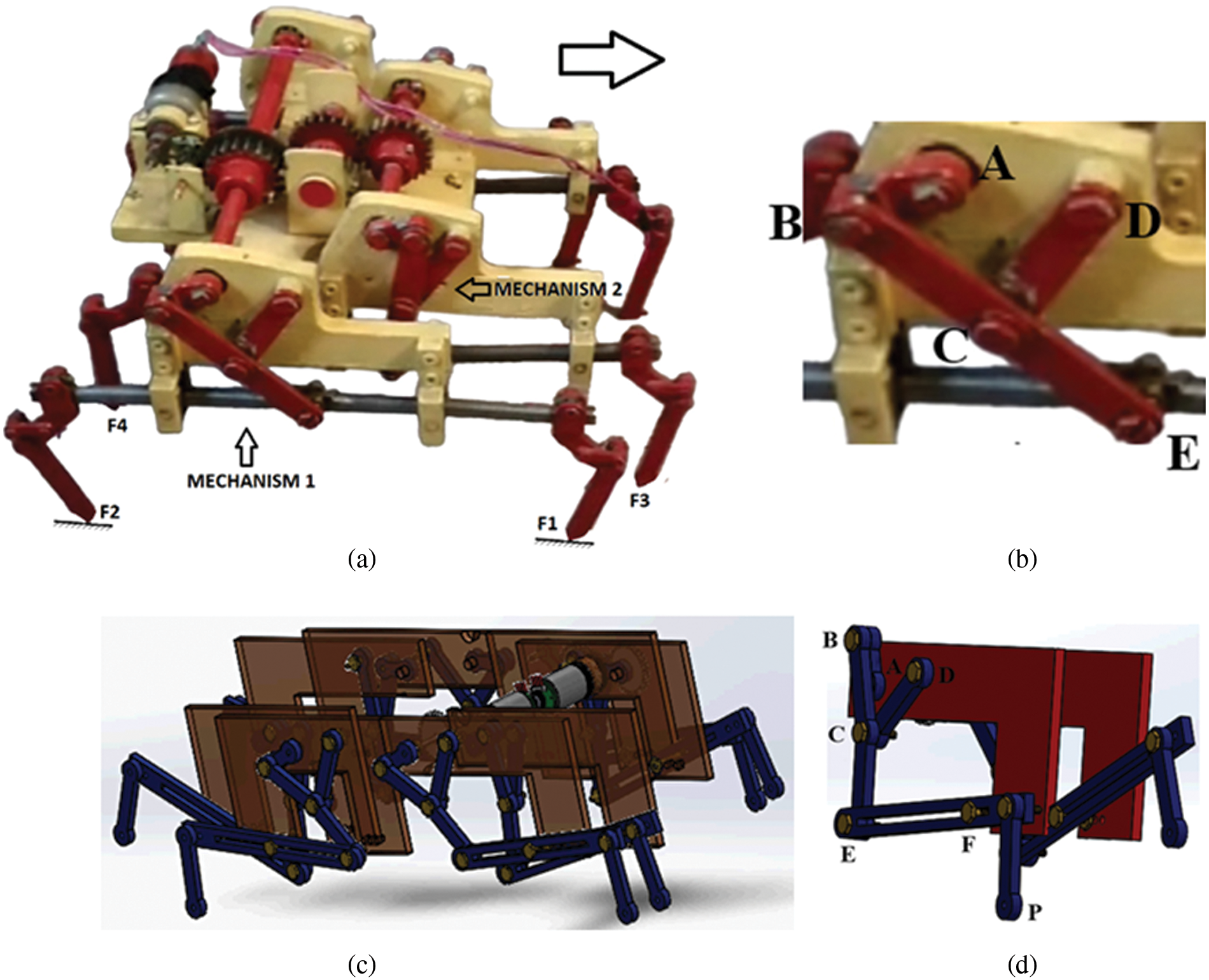
Figure 1: Model of the horizontal propulsion system for the legged robot (a, b) and 3D model (c, d)

The primary design objectives focused on achieving high precision in the generated output movement (criterion c1) and optimizing the force transmission angle (criterion c2). Additional objectives included extending the crank rotation angle ΔΦ beyond 180 degrees to ensure overlapping support phases for alternating legs (criterion c3) [34] and reducing the sum of the mechanism’s link lengths to minimize its overall dimensions (criterion c4).

Design parameters p1 = rAB, p2 = lBC, p3 = lCD, p4 = ϕ0 were adjusted within predefined limits through a “random LP-tau sequence generator” [35], while six specific parameters x1, …, x6 were identified to satisfy the main criterion c1. The design challenge was formulated as a minimization problem, aiming to reduce the design error δi, which is the discrepancy between the actual Ei and desired positions Ei∗ of the foot center E:

δ=∑I=1nδI2=>minxE,yE,Sx,Sy(1)

δ2≡‖EiEi∗‖22(2)

To achieve criterion c1, an analytical solution for variables x1,…,x6 was derived by solving a system of six linear equations.

Ax=b(3)

with the matrix A and vector b

A=[EA1A2A1TE12EA2T12E1N∑i=1NkiE](4)

E=[1001],(5)

A1=[−1N∑i=1Ncos⁡βi−1N∑i=1Nsin⁡βi1N∑i=1Nkisin⁡βi−1N∑i=1Nkicos⁡βi](6)

A2=[−1N∑i=1Nkicos⁡βi−1N∑i=1Nkisin⁡βi1N∑i=1Nkisin⁡βi−1N∑i=1Nkicos⁡βi](7)

b=[b1,b2,…,b6]Tb1=−1N∑i=1N(XBicos⁡βi+YBisin⁡βi)b2=1N∑i=1N(XBisin⁡βi−YBicos⁡βi)b3=1N∑i=1NXBib4=1N∑i=1NYBib5=1N∑i=1NkiXBib6=1N∑i=1NkiYBi(8)

with adjustments made to parameters p1, …, p4 using the LPτ-sequence method within set constraints [0.175 ≤ p1 ≤ 0.500; 0.410 ≤ p2 ≤ 1.200; 0.530 ≤ p3 ≤ 1.200; 40° ≤ p4 ≤ 100°.].

For each set of parameters p1,…, p4 the following conditions are imposed:

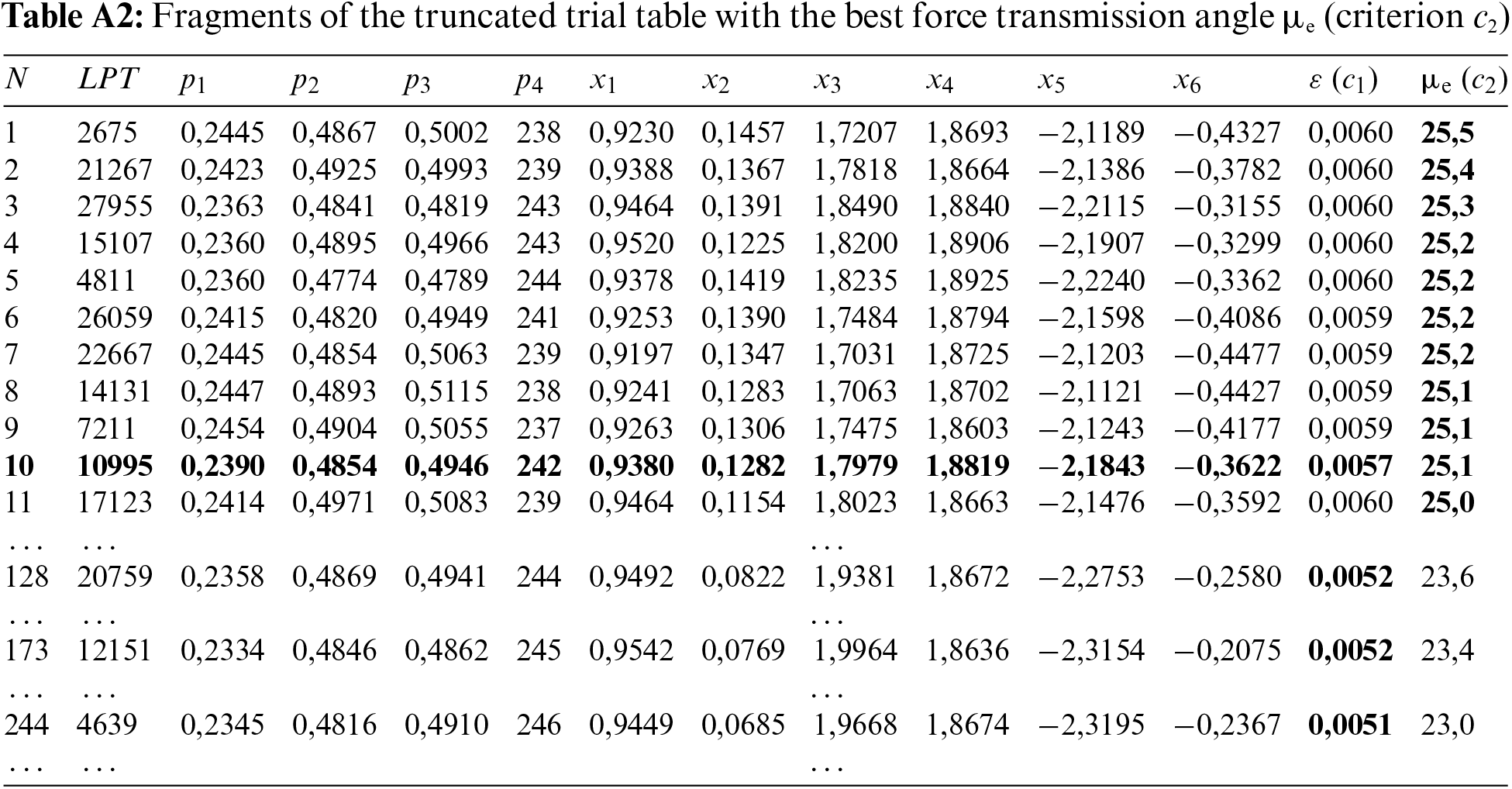
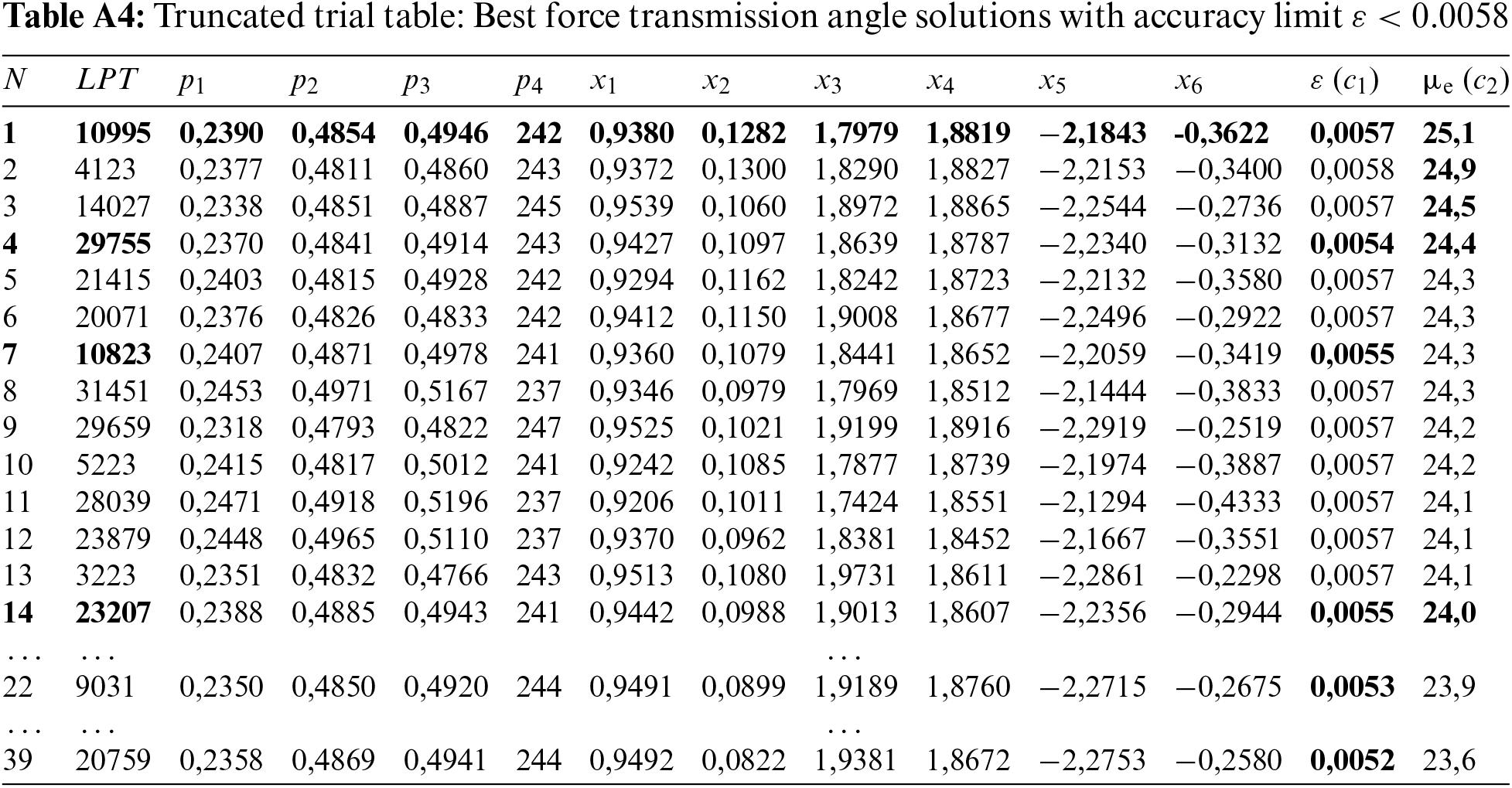
The least favorable value µe of the force transmission angle µi was identified. Six synthesis parameters X = [x1, …, x6]T were calculated by resolving a system of linear equations. The greatest divergence from the intended trajectory (with an error ε=maxi=1..N‖EiEi∗‖22) was determined. These findings were documented in a trial table included in Appendix A.

3.1 Multi-Objective Optimization

Managing trial tables can be exceedingly time-consuming, particularly when dealing with design criteria that are inherently at odds. The complexity escalates when the number of design criteria increases to three or four. Efforts to improve accuracy (criterion c1) can inadvertently compromise the effectiveness of force transmission (criterion c2), and the reverse is also true. To navigate these conflicts, a balanced approach is necessary, which led to our decision to adjust the parameter ΔΦ. Consequently, we also began to modify this parameter within its designated range, introducing it as a fifth variable, p5 = ΔΦ. An excerpt from the updated trial table is presented in Table A2 (Appendix A), while the complete version, containing 2384 entries, is available in Appendix A. Our objective was to identify the top 100 solutions positioned on the Pareto optimal front. To achieve this, we employed the NSGA method, aiming to efficiently resolve the challenge presented by the competing design criteria.

The core of this study revolves around a multi-objective optimization problem (MOP) integral to the design of leg-linkages for walking robots, aiming to reconcile conflicting design objectives to achieve an optimal blend of efficiency, functionality, and compactness. The problem is articulated within a mathematical framework, underpinned by a set of design objectives, constraints, and variables. The MOP is formalized as follows:

Let X={x1,x2,…,xn} represent the set of design variables with n variables, and each xi is bounded by a predefined range [xi,min,xi,max]. The objective of the optimization is to find the set of X that optimizes the following set of objective functions F(X)={f1(X),f2(X),…,fm(X)}, where m is the number of objectives. These functions are defined as:

f1(X): Accuracy of the foot’s center following a straight-line trajectory, aiming to minimize the deviation from the desired path. The deviation is quantified by the design error σ, which is the distance between the actual and desired positions of the foot’s center across a series of discrete points along the path.

f2(X): Force transmission angle, seeking to maintain this angle within optimal bounds to ensure efficient power transmission and mechanical advantage.

f3(X): Crank rotation angle ΔΦ, corresponding to the support phase of the leg’s step cycle. This angle should exceed 180 degrees to allow for overlapping support phases of two alternating legs, maximizing this parameter enhances stability and gait efficiency.

f4(X): Overall dimensions of the mechanism, represented by the sum of the mechanism link lengths. Minimizing this sum is crucial for creating a compact, lightweight design conducive to energy efficiency and portability.

The multi-objective optimization problem can thus be formulated as:

Minimize F(X)={f1(X), f2(X), f3(X), f4(X)}(9)

Subject to the constraints: [0.175 ≤ p1 ≤ 0.500; 0.410 ≤ p2 ≤ 1.200; 0.530 ≤ p3 ≤ 1.200; 40° ≤ p4 ≤ 100°, ΔΦ > 180°].

where p1, p2, p3, φ0, and ΔΦ are design parameters subject to optimization within their respective bounds.

The optimization aims to identify a set of Pareto optimal solutions, representing the best trade-offs among the conflicting objectives. This is achieved through the application of the Non-dominated Sorting Genetic Algorithm (NSGA), which sorts the potential solutions based on Pareto dominance, facilitating the selection of the most promising design configurations.

This problem statement encapsulates the theoretical and mathematical underpinnings of the optimization challenge at the heart of this study, setting the stage for the application of sophisticated algorithms to navigate the intricacies of robotic leg-linkage design.

3.2 Deep Surrogate Model-Assisted NSGA

The proposed Deep Surrogate Model-Assisted Non-dominated Sorting Genetic Algorithm (DeepSurNet-NSGA) integrates the efficiency of deep learning-based surrogate models with the robust optimization capabilities of the NSGA. This approach aims to address complex multi-objective optimization problems, such as the design of robotic leg linkages, by enhancing the exploration and exploitation of the search space while significantly reducing computational costs. Below is a detailed description of the proposed algorithm’s workflow that illustrated in Fig. 2.

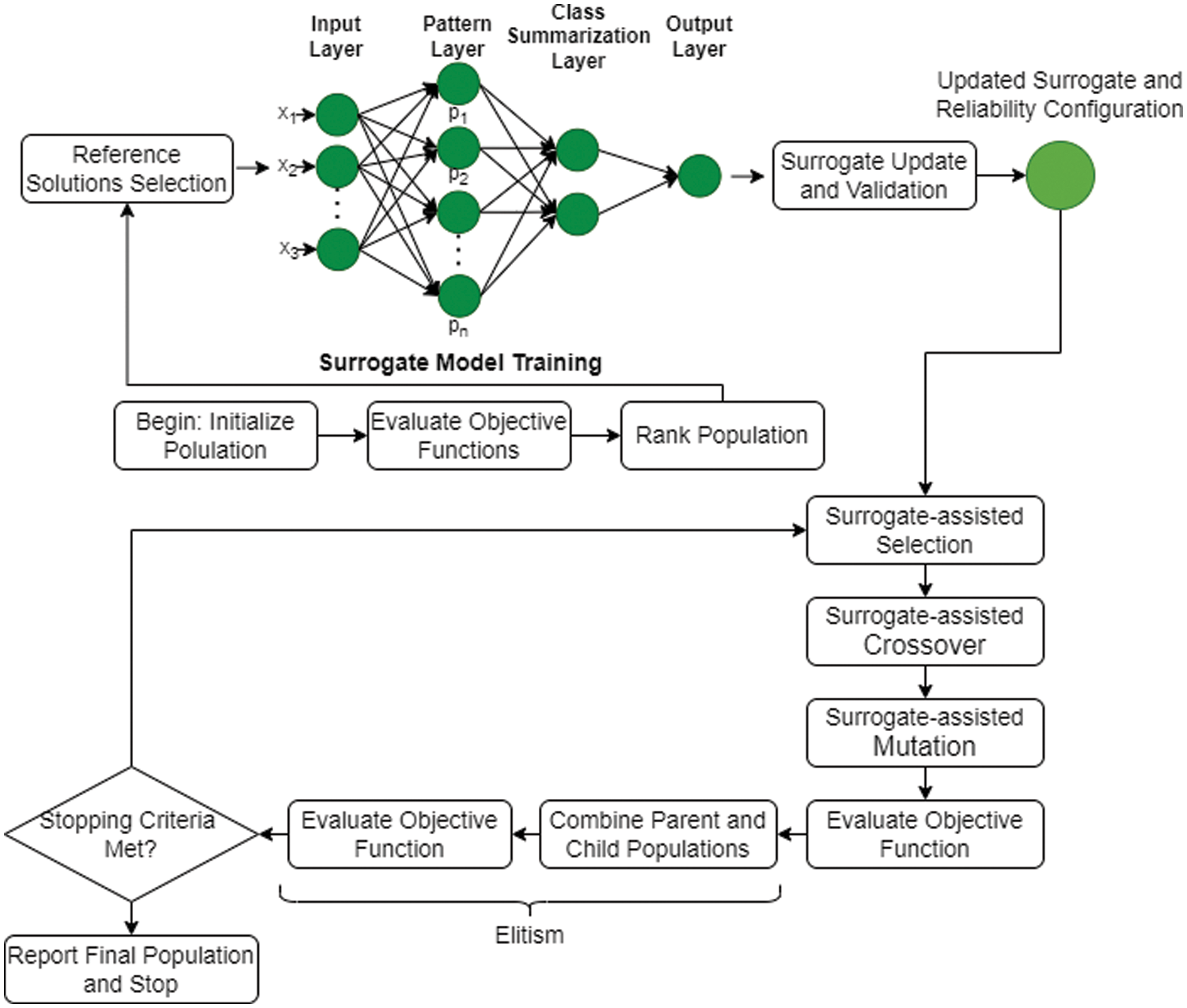
Figure 2: Flowchart of the proposed model

We have advanced a streamlined one-dimensional Convolutional Neural Network (Conv1D) to create a surrogate model linking process parameters with product quality attributes, as illustrated in Fig. 3. This model functions as a mechanism for managing multi-objective optimization of quality attributes through its input parameters.

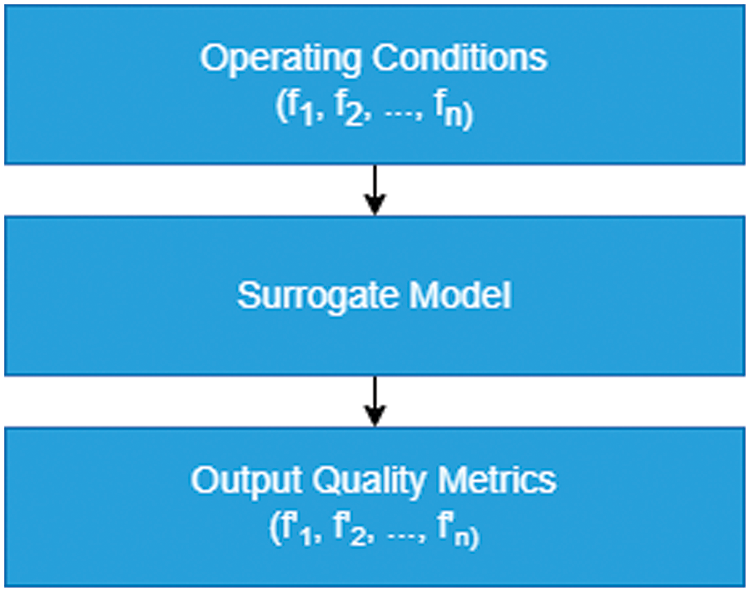
Figure 3: Application of deep surrogate model

The proposed surrogate deep learning model is structured to map input features to output predictions efficiently, using a sequence of convolutional and normalization layers. The architecture of this model is depicted in Fig. 4. The input data is first processed by a one-dimensional convolutional (1D Conv) layer to extract local patterns, followed by batch normalization to stabilize and accelerate training. This process is repeated with another 1D Conv layer and batch normalization, after which a ReLU activation function is applied to introduce non-linearity. A third 1D Conv layer and batch normalization are again followed by a ReLU activation. The extracted features are then downsampled using max pooling, which reduces the spatial dimensions while retaining essential information. Finally, a fully connected layer maps the processed features to the output, completing the model architecture.

Figure 4: 1D convolutional neural network surrogate model

wf=γwσ2+ε(10)

bf=γb−μσ2+ε+β(11)

Lastly, the neural network architecture optimization involves configurable hyperparameters such as the quantity of filters, the dimensions of convolution kernels, and the dilation rate. These parameters allow for fine-tuning the model to achieve optimal performance.

The Deep Surrogate Model-Assisted NSGA-II (DeepSurNet-NSGA) initiates with the generation of an initial solution population, which is then subjected to objective function evaluations to assess performance. This is followed by the application of Non-dominated Sorting to rank the solutions based on Pareto dominance. A subset of these solutions is selected to train a deep learning-based surrogate model, which is subsequently validated and updated to enhance prediction accuracy. This surrogate model is then employed to assist in the selection, crossover, and mutation processes, enabling an efficient exploration of the design space with reduced computational demand. Periodic evaluations of new solutions using actual objective functions ensure the model’s accuracy. The algorithm applies elitism to merge and select the top-performing individuals from the combined parent and offspring populations. This cycle repeats until predefined stopping criteria are met, at which point the algorithm concludes by presenting a final set of Pareto-optimal solutions, effectively balancing the computational efficiency provided by surrogate modeling with the robust optimization capabilities of NSGA.

3.3 Baseline Design for the Proposed Method

To effectively evaluate the performance of the proposed DeepSurNet-NSGA II, it is essential to establish a robust baseline. The baseline model will serve as a point of reference, allowing for a clear comparison of the improvements offered by our method. Below, we outline the key components and steps involved in designing the baseline model.

Baseline Model: Standard NSGA-II. The standard NSGA-II is chosen as the baseline model. NSGA-II is a well-established multi-objective optimization algorithm widely used for its efficiency and effectiveness in handling complex optimization problems. The key steps involved in implementing the NSGA-II baseline are as follows:

1. Initialization: Generate an initial population of solutions randomly within the defined parameter space. Each solution represents a potential configuration of the leg linkage design.

2. Evaluation: Compute the objective function values for each solution in the population. The objectives include minimizing the RMSE and MAE, and maximizing the CC, to ensure high prediction accuracy and reliability.

3. Non-dominated Sorting: Arrange the solutions according to Pareto dominance. Solutions are classified into multiple fronts, with the first front comprising non-dominated solutions, the second front including solutions dominated solely by those in the first front, and continuing in this manner.

4. Crowding Distance Calculation: Calculate the crowding distance for each solution within each front to ensure diversity among the solutions. The crowding distance helps maintain a spread of solutions across the Pareto front.

5. Employ binary tournament selection, utilizing rank and crowding distance, to choose parent solutions for the subsequent generation.

6. Crossover and Mutation: Apply genetic operators such as crossover and mutation to generate offspring solutions. These operators introduce variability and help explore the search space.

7. Merge the parent and offspring populations, then select the leading solutions through non-dominated sorting and crowding distance to establish the new population.

8. Termination: Repeat the evaluation, sorting, selection, crossover, mutation, and replacement steps until a predefined number of generations is reached or convergence criteria are met.

4  Results

The research was conducted using a high-performance computer powered by an Intel Core i5-12400F processor, which features a base clock frequency of 2.5 GHz and a Turbo Boost frequency of 4.4 GHz. This processor, part of the Alder Lake platform, has six cores, an 18 MB L3 cache, and operates with a thermal design power (TDP) of 117 watts, utilizing the LGA1700 socket for optimal performance and reliability. For computational tasks, we employed Python 3.0 and a comprehensive suite of libraries essential for scientific computing and data analysis, including NumPy, SciPy, Matplotlib, Scikit-learn, Pandas, TensorFlow, and Seaborn. These libraries facilitated various aspects of our research, from data processing and statistical analysis to machine learning and visualization, ensuring a robust and efficient workflow.

4.1 Evaluation Parameters

This subsection elaborates on the evaluation indicators employed in our study, justifying their selection and exploring potential alternative metrics. The primary evaluation metrics used are Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Correlation Coefficient (CC). These indicators were chosen due to their robust ability to quantify the accuracy and reliability of the predictive models, facilitating a comprehensive assessment of model performance.

RMSE is a widely used metric that measures the average magnitude of the errors between predicted and observed values. It is particularly useful in highlighting significant errors, as it squares the deviations, thus giving more weight to larger discrepancies. This makes RMSE a crucial indicator in applications where larger errors can have a substantial impact on the system’s overall performance. MAE, on the other hand, provides a straightforward measure of the average absolute errors, offering a clear and interpretable indication of the model’s prediction accuracy. Unlike RMSE, MAE does not amplify larger errors, making it more robust to outliers. The Correlation Coefficient (CC) measures the strength and direction of the linear relationship between predicted and observed values.

RMSE=1n∑i=1n(yi−y^i)2(12)

where yi represents the observed values, y^i represents the predicted values, and n is the number of observations.

MAE=1n∑i=1n|yi−y^i|(13)

The Correlation Coefficient is calculated using the following formula:

CC=n∑i=1nyiy^i−∑i=1nyi∑i=1ny^i(n∑i=1nyi2−(∑i=1nyi)2)((n∑i=1ny^i2−(∑i=1ny^i)2))(14)

4.2 Experiment Results

Fig. 5 unfolds a graphical illustration of the relationships between five unique parameters, presenting a detailed analysis of their complex interrelations and mutual influences. This visual representation aids in the examination of the subtle interactions and correlations that bind these parameters together, playing a critical role in the understanding of their combined effects on overall outcomes. Thus, Fig. 5 becomes a pivotal analytical instrument, shedding light on the detailed and possibly non-linear connections among the parameters. This, in turn, supports the development of hypotheses and analytical frameworks, paving the way for future investigations into the mechanisms at play behind these observed relationships.

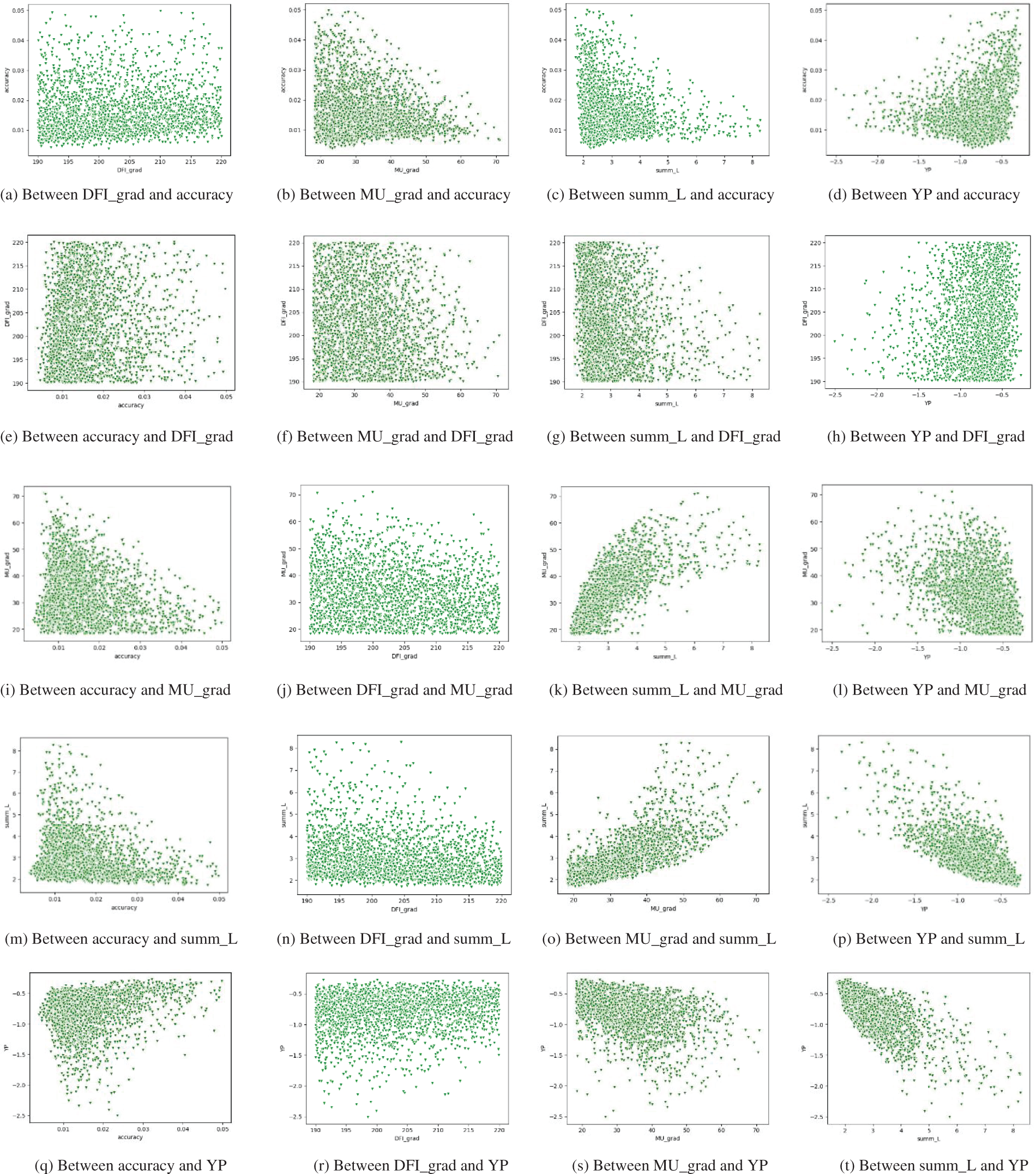
Figure 5: Dependencies between parameters

Fig. 6 presents a clear empirical relationship between actual data collected from a sample table and the outcomes generated through the application of the Deep SurNet-NSGA method. In this figure, red dots are used to mark the actual data points, collected from a comprehensive sampling table, while blue dots illustrate the solutions derived within the framework of Pareto optimality. There is a notable strong correlation between these datasets, highlighting the accuracy and effectiveness of the Deep SurNet-NSGA method in closely mirroring real-world data scenarios.

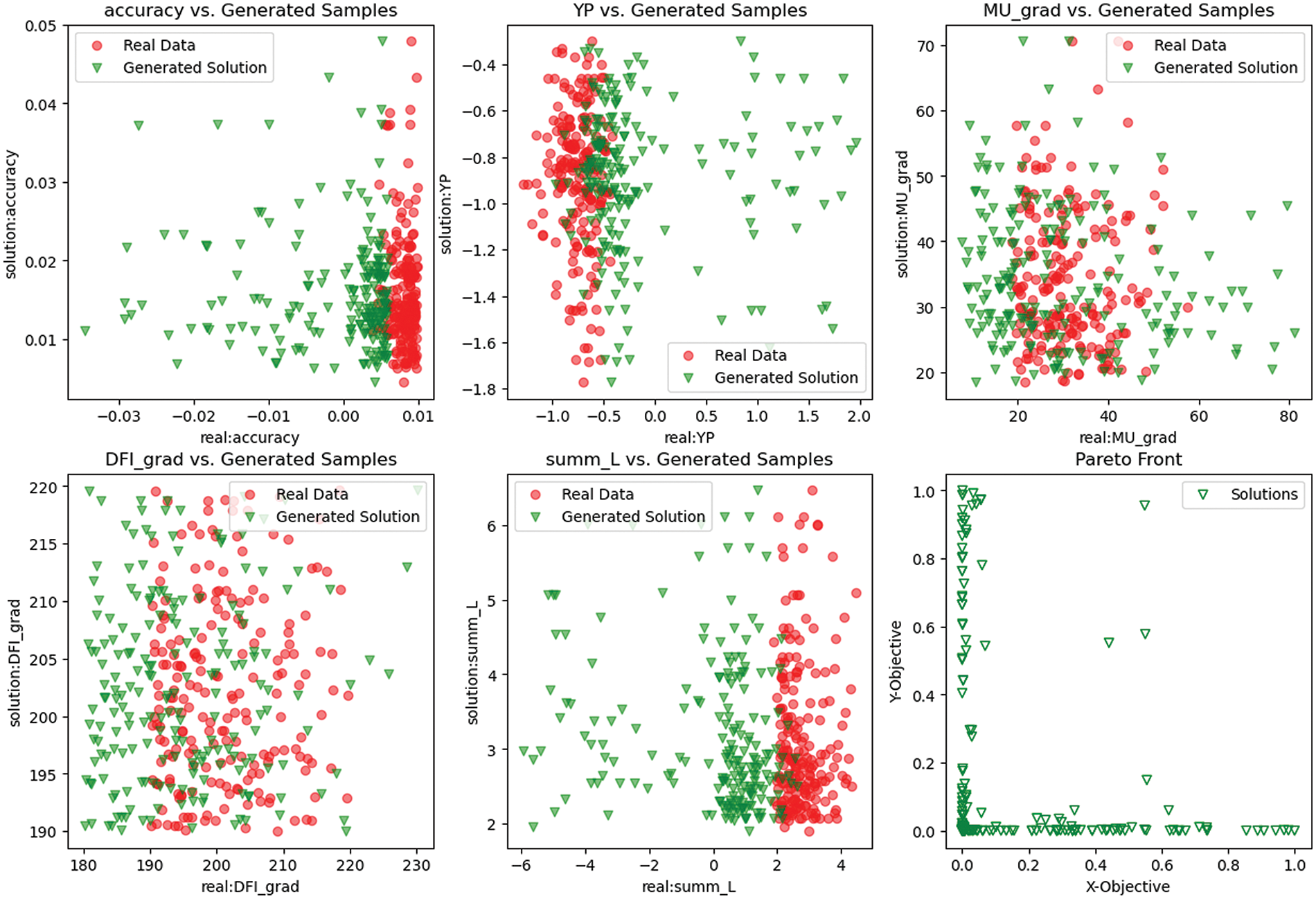
Figure 6: Obtained results (Comparison of the real data and the generated solutions by the Deep SurNet-NSGA approach)

Furthermore, the concluding section of Fig. 6 reveals the Pareto front, achieved via the meticulous implementation of the Deep SurNet-NSGA algorithm. This visual display not only delineates the non-dominated solutions within the objective space but also accentuates the algorithm’s adeptness in exploring the solution space to approximate the genuine Pareto front accurately. The identification of the Pareto front is significant, representing a set of optimal solutions where none can be considered better than another across all objectives simultaneously. This showcases the critical trade-offs among the various objectives being considered.

Hence, the correlation demonstrated and the elucidation of the Pareto front in Fig. 6 validate the practical effectiveness of the Deep SurNet-NSGA approach in navigating the intricate terrains of multi-objective optimization problems. This approach aids in the enhancement of decision-making processes, grounded on a detailed and computational analysis of potential solutions.

Fig. 7 elucidates the positioning of solutions that align with the Pareto-optimal frontier, identified through a combination of empirical research and the deployment of the Deep SurNet-NSGA. This figure uses a visual scheme where solutions pinpointed by the NSGA-II are highlighted in blue, while outcomes from direct experimental activities are marked in red. The observable strong correlation between these varied sets of data vividly attests to the accuracy and dependability of the approach utilized. It showcases the effectiveness of the Deep SurNet-NSGA algorithm in generating solutions that closely align with those derived from empirical experiments, underlining the algorithm’s significant role in aligning theoretical models with practical experimental findings.

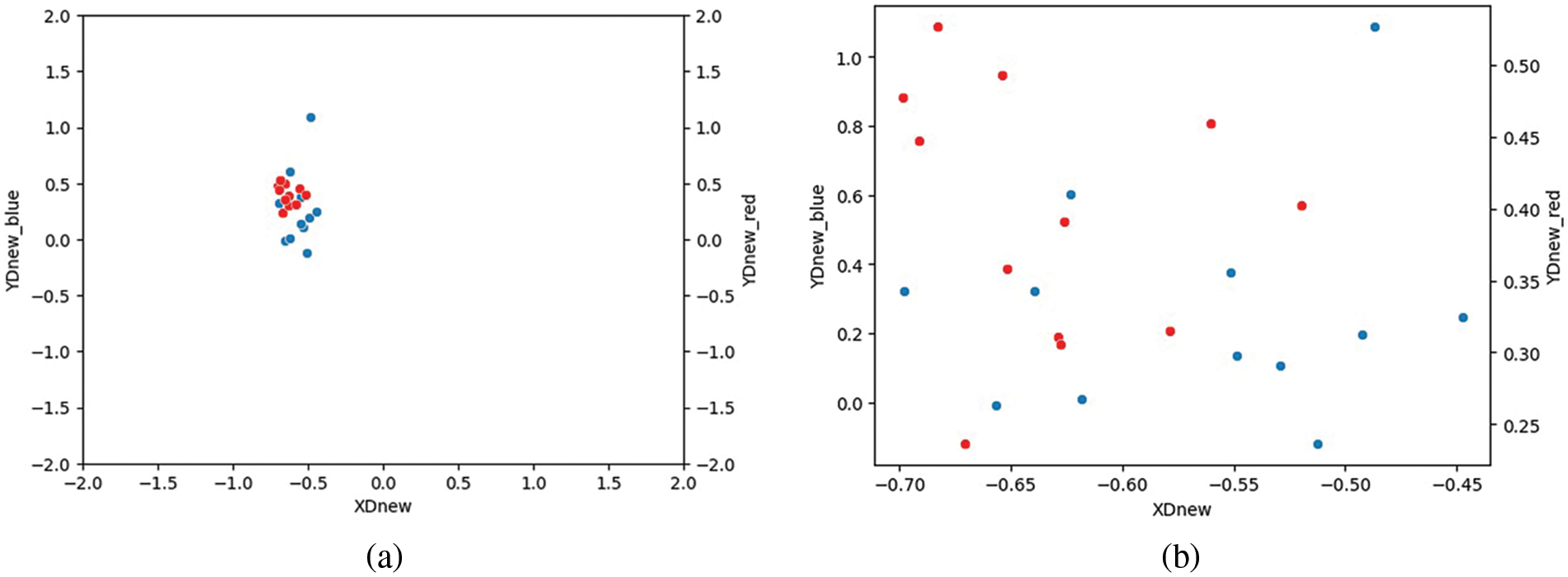
Figure 7: Comparison between practical solutions and the obtained results (Red dots are the practical solutions; blue dots are the obtained results). (a) Scatter plot across the entire space, (b) Scatter plot within a limited space

Fig. 8 provides a comprehensive comparison of the convergence behavior of two algorithms, NSGA-II and SurNet-NSGA, under similar operational conditions, revealing distinct performance dynamics. The NSGA-II model, depicted in Fig. 8a, exhibits incomplete convergence, stabilizing around a value of 0.9 after 4000 iterations, which can be attributed to factors such as parameter sensitivity, an imbalance between exploration and exploitation, reduced population diversity, and inefficiencies in the selection mechanism. Conversely, the SurNet-NSGA model, shown in Fig. 8b, achieves near-ideal convergence at a value close to 1 within just 1500 iterations, thanks to advanced search mechanisms, improved exploitation capabilities, adaptive parameter settings, and robust diversity maintenance. These differences in convergence behavior have significant implications: SurNet-NSGA demonstrates greater computational efficiency and resource utilization, making it more suitable for real-time or resource-constrained applications. It also provides higher quality solutions and better scalability for complex problems or larger search spaces. The superior convergence characteristics of SurNet-NSGA highlight its potential as a preferred choice for applications requiring precise and timely solutions, emphasizing the importance of selecting and customizing optimization algorithms based on their convergence performance. This analysis underscores the critical advantages of SurNet-NSGA in achieving efficient and high-quality results, guiding its application in various optimization tasks.

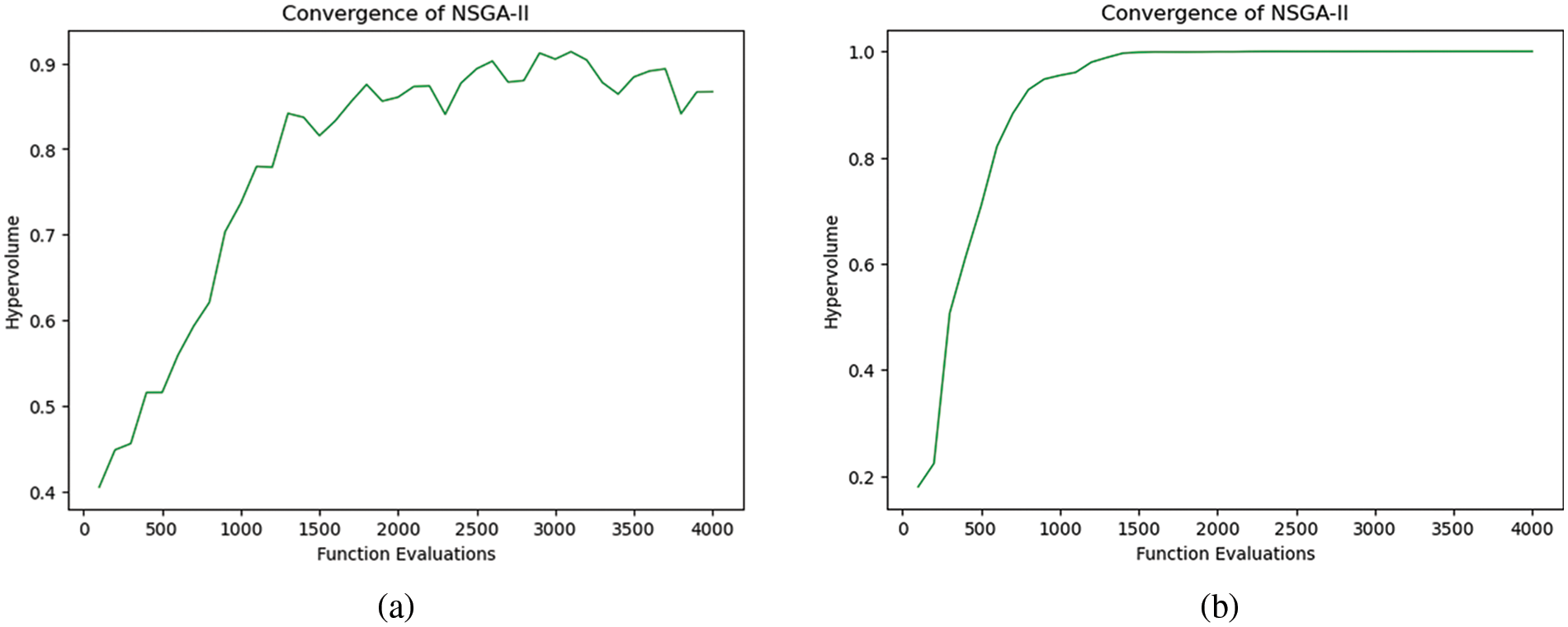
Figure 8: Convergence of the proposed model before and after the application of the surrogate model. (a) Convergence of NSGA-II, (b) Convergence of surrogate assisted NSGA-II

4.3 Comparative Analysis of Obtained Results

Table 1 provides a comparative analysis of the proposed model against several existing models, highlighting its advantages. The proposed model demonstrates superior performance, as evidenced by its low error rates and high Correlation Coefficient, indicating its accuracy and reliability. Compared to other models, such as the deep learning model with surrogate-assisted feature selection, the ANN surrogate model, the multi-output regression algorithm-based NSGA II, and the CNN-BiGRU model, the proposed model consistently shows better results across all evaluated metrics. This underscores the proposed model’s effectiveness in providing precise predictions and maintaining high-quality outputs, making it a more robust solution for multi-objective optimization tasks.

5  Discussion

Here it aims to encode and present the results provided by DeepSurNet-NSGA II utilization in multi-objective optimization of robotic-leg linkage’s design into a broader perspective. In this section, we conduct a thorough analysis of the outcomes to assess the algorithm’s performance, its capability to efficiently integrate deep learning based surrogate models, and comprehend the impact of these developments on the overall design process efficiency and effectiveness. In addition, this part identifies and discusses the methodological advances incorporated into this study that could set standards for the forthcoming process stages. Along this, we look at the shortcomings in our strategy and state areas for future research; there, we suggest using different optimization methods which would allow the techniques to be more reliable and applicable for various tasks. Through this discussion, we eventually would be able to produce an informative discussion on the main idea behind our work with its robotic design and optimization techniques contribution.

5.1 Key Findings and Implications

Deep learning of surrogate models has been incorporated into the NSGA-II framework which was confirmed by the results obtained as such provokes significant reduction in computational time and quality of solutions. The proposed method was able to express the Pareto-optimal frontier with utmost accuracy. As a result, the complexity of nonlinear optimization function can be dramatically reduced which is typically a major computational task. Particularly in robotics, this brings down expenses connected with functional complexity and several stages of tests. They might rise out of control. One of the most attractive features of the research is the proficiency of DeepSurNet-NSGAII in navigating the intricate spatial optimisation with a great sensitivity. The simulated system not only suggested approaches that are optimized in the computational level but also closely corresponded to the experimental data as an indicator of the reliability of the algorithm in real workplace. It is true that this alignment is critical for the practical realization of a theoretical model that must be adapted to be the base design and for practical robustness in the real world.

5.2 Methodological Innovations

This approach frames the framework in a broadly deep learning perspective by incorporating recent findings in machine learning, including deep learning schemes. Utilization of the emulation of fitness constructor as the replica of robotic leg linkage design is a unique strategy. On the other hand, the main complications are the need for intense computations that reduce the number of function evaluations to their minimum possible and this is the aim of this algorithm. The application in practice to the solutions for single objective vs. multi objective optimization—wherein the efficiency airplane is the the case of this one analogous to the multi objective problem—proves that the researchers are aware about the complex nature of the design problem. It, moreover, can be considered as a trailblazer for the future development of machine learning in various complex system optimization situations and some others can utilize this blueprint.

5.3 Limitations and Future Work

Though results are positive, the investigation possesses not the absence of restrictions. This is another constraint to be taken into consideration and that is the quality of data used for training the substitute models; all the possible inaccuracies in the initial data set can eventually lead to worst design outputs. Furthermore, this study does not detail the legged robot leg design itself, which is the most significant and challenging aspect of the project. Besides the applicability of the model to other types of robotic systems or even to the branches of other engineering fields, the model could be used for confirmation of its accuracy and for improvement. Next research might find few of the following areas interesting. Secondly, evaluating the algorithm on different sorts of environments and robots from different bases as well can give a clear overview pertaining to its versatility and robustness. Another factor which may advance the surrogate models is improving their self-convergence and precision to make the final optimum more predictable. In addition, the integration of one or two more artificial neural networks such as the reinforcement learning system with unsupervised learning algorithms will enhance the pathways through which complex systems optimized can be done more effectively.

6  Conclusion

In conclusion, this research has demonstrated the significant efficacy of the Deep Surrogate Model-Assisted Non-dominated Sorting Genetic Algorithm II (DeepSurNet-NSGA II) in tackling complex multi-objective optimization problems, specifically in robotic leg-linkage design. The empirical investigations and theoretical analyses underscore the robustness, precision, and computational efficiency of the proposed algorithm. Critical results include a high degree of correlation between empirical outcomes and algorithmic predictions, validating the method’s reliability. The integration of deep learning-based surrogate models within the NSGA-II framework has markedly enhanced the algorithm’s ability to approximate the Pareto-optimal frontier accurately while substantially reducing computational overhead. This advancement is evidenced by the graphical representations, which highlight the algorithm’s adeptness in navigating intricate design spaces and yielding practically viable solutions. Key developments include enhanced optimization efficiency through reduced computational demands, superior predictive accuracy, and effective surrogate model integration. These contributions collectively establish a robust foundation for future research, suggesting potential refinements in surrogate models and exploration of alternative evolutionary algorithms. The demonstrated potential of DeepSurNet-NSGA II positions it as a pivotal tool for optimizing complex systems, extending its applicability beyond this study to broader engineering and design optimization contexts.

Acknowledgement: Not applicable.

Funding Statement: This study was funded by the research project “BR18574136—Development of deep learning methods and intellectual analysis for solving complex problems of mechanics and robotics”.

Author Contributions: Conceptualization, Sayat Ibrayev; methodology, Sayat Ibrayev, Arman Ibrayeva, and Batyrkhan Omarov; software, Zeinel Momynkulov; data curation, Sayat Ibrayev; writing—original draft preparation, Sayat Ibrayev, Batyrkhan Omarov, and Arman Ibrayeva; writing—review and editing, Batyrkhan Omarov; supervision, Sayat Ibrayev; discussion, Sayat Ibrayev, Batyrkhan Omarov, and Zeinel Momynkulov. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Dataset available in supporting materials.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. I. Navarro et al., “SoRTS: Learned tree search for long horizon social robot navigation,” IEEE Robot. Autom. Lett., vol. 9, pp. 1–8, Jan. 2024. doi: 10.1109/LRA.2024.3370051. [Google Scholar] [CrossRef]

2. A. A. Shaikh, A. K. Mukhopadhyay, S. Poddar, and S. Samui, “Toward robust and accurate myoelectric controller design based on multi-objective optimization using evolutionary computation,” IEEE Sens. J., vol. 24, no. 5, pp. 6418–6429, Mar. 2024. doi: 10.1109/JSEN.2023.3347949. [Google Scholar] [CrossRef]

3. H. Wu, Y. Jin, K. Gao, J. Ding, and R. Cheng, “Surrogate-assisted evolutionary multi-objective optimization of medium-scale problems by random grouping and sparse gaussian modeling,” IEEE Trans. Emerg. Top. Comput. Intell., pp. 1–16, Jan. 2024. doi: 10.1109/TETCI.2024.3372378. [Google Scholar] [CrossRef]

4. A. Mazumdar and V. Kyrki, “Hybrid surrogate assisted evolutionary multi-objective reinforcement learning for continuous robot control,” in Lecture Notes in Computer Science. Springer, Cham, Jan. 2024, vol. 14635, pp. 61–75. doi: 10.1007/978-3-031-56855-8_4. [Google Scholar] [CrossRef]

5. M. Fan, Y. Li, J. Shen, K. Jin, and J. Shi, “Multi-objective optimization design of recycled aggregate concrete mixture proportions based on machine learning and NSGA-II algorithm,” Adv. Eng. Softw., vol. 192, Jun. 2024, Art. no. 103631. doi: 10.1016/j.advengsoft.2024.103631. [Google Scholar] [CrossRef]

6. M. Cheng, X. Zhao, M. Dhimish, W. Qiu, and S. Niu, “A review of data-driven surrogate models for design optimization of electric motors,” IEEE Trans. Transp. Electrif., Jan. 2024. doi: 10.1109/TTE.2024.3366417. [Google Scholar] [CrossRef]

7. A. Şumnu, İ. H. Güzelbey, and O. Öğücü, “Aerodynamic shape optimization of a missile using a multi-objective genetic algorithm,” Int. J. Aerosp. Eng., vol. 2020, pp. 1–17, Jun. 2020. doi: 10.1155/2020/1528435. [Google Scholar] [CrossRef]

8. T. Guo, Y. Mei, K. Tang, and W. Du, “A knee-guided evolutionary algorithm for multi-objective air traffic flow management,” IEEE Trans. Evol. Comput., vol. 28, no. 4, pp. 994–1008, Aug. 2024. doi: 10.1109/tevc.2023.3281810. [Google Scholar] [CrossRef]

9. S. F. Ahmed et al., “Deep learning modelling techniques: Current progress, applications, advantages, and challenges,” Artif. Intell. Rev., vol. 56, pp. 13521–13617, Apr. 2023. doi: 10.1007/s10462-023-10466-8. [Google Scholar] [CrossRef]

10. X. Zhou et al., “Multi-strategy competitive-cooperative co-evolutionary algorithm and its application,” Inf Sci., vol. 635, pp. 328–344, Jul. 2023. doi: 10.1016/j.ins.2023.03.142. [Google Scholar] [CrossRef]

11. B. Doerr and Z. Qu, “A first runtime analysis of the NSGA-II on a multimodal problem,” IEEE Trans. Evol. Comput., vol. 27, no. 5, pp. 1288–1297, Oct. 2023. doi: 10.1109/TEVC.2023.3250552. [Google Scholar] [CrossRef]

12. B. Omarov, S. Ibrayev, A. Ibrayeva, B. Amanov, and Z. Momynkulov, “Optimal leg linkage design for horizontal propel of a walking robot using non-dominated sorting genetic algorithm,” IEEE Access, vol. 12, pp. 97207–97225, Jan. 2024. doi: 10.1109/ACCESS.2024.3354384. [Google Scholar] [CrossRef]

13. G. Li, J. Wang, Z. Li, G. G. Yen, Q. Qi and J. Xing, “Multi-objective optimization of a lower limb prosthesis for metabolically efficient walking assistance,” IEEE Trans. Autom. Sci. Eng., pp. 1–16, Jan. 2024. doi: 10.1109/TASE.2024.3432572. [Google Scholar] [CrossRef]

14. Y. Wang et al., “Multi-objective energy consumption optimization of a flying-walking power transmission line inspection robot during flight missions using improved NSGA-II,” Appl. Sci., vol. 14, no. 4, Feb. 2024, Art. no. 1637. doi: 10.3390/app14041637. [Google Scholar] [CrossRef]

15. V. Esfahanian, M. Javad Izadi, H. Bashi, M. Ansari, A. Tavakoli and M. Kordi, “Aerodynamic shape optimization of gas turbines: A deep learning surrogate model approach,” Struct. Multidiscip. Optim., vol. 67, no. 1, Dec. 2023, Art. no. 2. doi: 10.1007/s00158-023-03703-9. [Google Scholar] [CrossRef]

16. R. Dubey, S. Hickinbotham, M. Price, and A. Tyrrell, “Local fitness landscape exploration based genetic algorithms,” IEEE Access, vol. 11, pp. 3324–3337, 2023. doi: 10.1109/ACCESS.2023.3234775. [Google Scholar] [CrossRef]

17. A. Marrel and B. Iooss, “Probabilistic surrogate modeling by Gaussian process: A review on recent insights in estimation and validation,” Reliab Eng. Syst. Saf., vol. 247, Mar. 2024, Art. no. 110094. doi: 10.1016/j.ress.2024.110094. [Google Scholar] [CrossRef]

18. J. A. Barbero-Aparicio, A. Olivares-Gil, J. J. Rodríguez, C. García-Osorio, and J. F. Díez-Pastor, “Addressing data scarcity in protein fitness landscape analysis: A study on semi-supervised and deep transfer learning techniques,” Inf. Fusion, vol. 102, Feb. 2024, Art. no. 102035. doi: 10.1016/j.inffus.2023.102035. [Google Scholar] [CrossRef]

19. Y. Sun, U. Sengupta, and M. Juniper, “Physics-informed deep learning for simultaneous surrogate modeling and PDE-constrained optimization of an airfoil geometry,” Comput. Methods Appl. Mech. Eng., vol. 411, Jun. 2023, Art. no. 116042. doi: 10.1016/j.cma.2023.116042. [Google Scholar] [CrossRef]

20. Á. Belmonte-Baeza, J. Lee, G. Valsecchi, and M. Hutter, “Meta reinforcement learning for optimal design of legged robots,” IEEE Robot. Autom. Lett., vol. 7, no. 4, pp. 12134–12141, Oct. 2022. doi: 10.1109/LRA.2022.3211785. [Google Scholar] [CrossRef]

21. S. Ibrayev, A. Ibrayeva, A. Rakhmatulina, A. Ibrayeva, B. Amanov and N. Imanbayeva, “Multicriteria optimization of lower limb exoskeleton mechanism,” Appl. Sci., vol. 13, no. 23, Nov. 2023, Art. no. 12781. doi: 10.3390/app132312781. [Google Scholar] [CrossRef]

22. J. Zhang, L. Cheng, C. Liu, Z. Zhao, and Y. Mao, “Cost-aware scheduling systems for real-time workflows in cloud: An approach based on genetic algorithm and deep reinforcement learning,” Expert. Syst. Appl., vol. 234, Dec. 2023, Art. no. 120972. doi: 10.1016/j.eswa.2023.120972. [Google Scholar] [CrossRef]

23. G. Chen, H. Zhang, H. Hui, and Y. Song, “Deep-quantile-regression-based surrogate model for joint chance-constrained optimal power flow with renewable generation,” IEEE Trans. Sustain. Energy., vol. 14, no. 1, pp. 657–672, Jan. 2023. doi: 10.1109/TSTE.2022.3223764. [Google Scholar] [CrossRef]

24. T. S. Vaquero et al., “EELS: Autonomous snake-like robot with task and motion planning capabilities for ice world exploration,” Sci. Robot., vol. 9, no. 88, Mar. 2024, Art. no. eadh8332. doi: 10.1126/scirobotics.adh8332. [Google Scholar] [PubMed] [CrossRef]

25. S. Ibrayev, A. Ibrayeva, N. Jamalov, A. Ibrayev, Z. Ualiyev and B. Amanov, “Optimal synthesis of walking robot leg,” Mech Based Des. Struct. Mach., vol. 52, pp. 1–21, Mar. 2023. doi: 10.1080/15397734.2023.2189938. [Google Scholar] [CrossRef]

26. M. Chen, Q. Li, S. Wang, K. Zhang, H. Chen and Y. Zhang, “Single-leg structural design and foot trajectory planning for a novel bioinspired quadruped robot,” Complex, vol. 2021, pp. 1–17, Jan. 2021. doi: 10.1155/2021/2574025. [Google Scholar] [CrossRef]

27. F. Hou, J. Yuan, K. Li, and Z. Wang, “Design and analysis of a multi-configuration wheel-leg hybrid drive robot machine,” Int. J. Adv. Robot. Syst., vol. 20, no. 2, Mar. 2023. doi: 10.1177/17298806231163828. [Google Scholar] [CrossRef]

28. H. Du et al., “A review of shape memory alloy artificial muscles in bionic applications,” Smart Mater. Struct., vol. 32, no. 10, Aug. 2023, Art. no. 103001. doi: 10.1088/1361-665x/acf1e8. [Google Scholar] [CrossRef]

29. S. M. Song, V. J. Vohnout, K. J. Waldron, and G. L. Kinzel, “Computer-aided design of a leg for an energy efficient walking machine,” Mech Mach. Theory., vol. 19, no. 1, pp. 17–24, Jan. 1984. doi: 10.1016/0094-114X(84)90005-3. [Google Scholar] [CrossRef]

30. H. Sun, C. Wei, Y. Yao, and J. Wu, “Analysis and experiment of a bioinspired multimode octopod robot,” Chin J. Mech. Eng., vol. 36, no. 1, Nov. 2023, Art. no. 142. doi: 10.1186/s10033-023-00963-w. [Google Scholar] [CrossRef]

31. E. A. Dijksman, “Watt-1 linkages with shunted chebyshev-dyads, producing symmetrical 6-bar curves,” Mech. Mach. Theory, vol. 16, no. 2, pp. 153–165, Jan. 1981. doi: 10.1016/0094-114X(81)90061-6. [Google Scholar] [CrossRef]

32. H. -B. Zhou, X. Yue, Y. -X. Deng, and Z. -C. Qin, “Design and analysis of an adjustable Stephenson-III closed-chain leg mechanism and its application in multi-legged robot,” Proc. Inst. Mech. Eng., vol. 237, no. 19, pp. 4529–4545, Feb. 2023. doi: 10.1177/09544062231152182. [Google Scholar] [CrossRef]

33. C. Yan, K. Shi, H. Zhang, and Y. Yao, “Simulation and analysis of a single actuated quadruped robot,” Mech. Sci., vol. 13, no. 1, pp. 137–146, Mar. 2022. doi: 10.5194/ms-13-137-2022. [Google Scholar] [CrossRef]

34. Z. Zhang, Q. Yang, X. Liu, C. Zhang, and J. Liao, “Modeling, comparison and evaluation of one-DOF six-bar bioinspired jumping leg mechanisms,” Adv Mech. Eng., vol. 13, no. 2, Feb. 2021. doi: 10.1177/1687814021992954. [Google Scholar] [CrossRef]

35. A. Kapsalyamov, S. Hussain, N. A. T. Brown, R. Goecke, M. Hayat and P. K. Jamwal, “Synthesis of a six-bar mechanism for generating knee and ankle motion trajectories using deep generative neural network,” Eng Appl. Artif. Intell., vol. 117, Jan. 2023, Art. no. 105500. doi: 10.1016/j.engappai.2022.105500. [Google Scholar] [CrossRef]

36. R. Espinosa, F. Jiménez, and J. Palma, “Surrogate-assisted and filter-based multi-objective evolutionary feature selection for deep learning,” IEEE Trans. Neural Netw. Learn. Syst., vol. 35, pp. 1–15, Jan. 2023. doi: 10.1109/TNNLS.2023.3234629. [Google Scholar] [PubMed] [CrossRef]

37. I. Kerdan and D. Gálvez, “Artificial neural network structure optimisation for accurately prediction of exergy, comfort and life cycle cost performance of a low energy building,” Appl. Energy., vol. 280, Dec. 2020, Art. no. 115862. doi: 10.1016/j.apenergy.2020.115862. [Google Scholar] [CrossRef]

38. S. Li, Z. Qian, and J. Liu, “Multi-output regression algorithm-based non-dominated sorting genetic algorithm II optimization for L-shaped twisted tape insertions in circular heat exchange tubes,” Energies, vol. 17, no. 4, Feb. 2024, Art. no. 850. doi: 10.3390/en17040850. [Google Scholar] [CrossRef]

39. Z. Zheng, D. Chen, Y. Wang, and L. Zhuang, “Remaining useful life indirect prediction of lithium-ion batteries using CNN-BiGRU fusion model and TPE optimization,” AIMS Energy, vol. 11, no. 5, pp. 896–917, Sep. 2023. doi: 10.3934/energy.2023043. [Google Scholar] [CrossRef]

Appendix A