Adaptive Update Distribution Estimation under Probability Byzantine Attack

1  Introduction

With rapid technological advancements, the emergence of sensor networks [1], the Internet of Things [2], and distributed systems [3,4] has presented unprecedented opportunities for data acquisition and information interaction. This influx of information offers immense potential for understanding and optimizing complex systems [5]. However, it also brings forth new challenges. In this age of information explosion, the efficient estimation of system parameters [6,7] has become a focal point of attention.

Distributed parameter estimation, a prominent research area in the fields of information science and engineering, strives to develop methods capable of extracting information about the state or characteristics of a system from distributed data sources [8,9]. Differing from traditional centralized estimation methods, distributed parameter estimation achieves inference of system parameters by leveraging observational data from multiple nodes scattered throughout the network [10–12]. The uniqueness of distributed networks lies in their adaptability to large-scale, dynamically changing environments, coupled with robustness and real-time capabilities. Consequently, the application of distributed networks is becoming increasingly widespread.

In distributed networks, the most representative algorithm is undoubtedly the diffusion least mean square (DLMS) algorithm because of its excellent adaptive capability and stable performance. Due to these advantages, the distributed DLMS algorithm has gained widespread adoption. For instance, in [13], a detailed derivation of the DLMS algorithm under Gaussian noise is presented, along with the algorithm’s convergence conditions. Based on this, Reference [14] considers pulse noise and proposes a distributed algorithm with the maximum correntropy criterion. These algorithms consider data fusion without delay. However, in some instances, communication delays may exist in the network. Therefore, Reference [15] investigates this scenario and provides insights into its data fusion methodology and performance analysis. These applications primarily focus on single-task parameter estimation. As applications become more complex, the occurrence of multi-task parameter estimation becomes more frequent. In [16], the authors investigate a multi-task distributed network that considers multiple parameter estimations and propose an adaptive multi-task parameter estimation algorithm. Besides, Reference [17] further studies the asynchronous sampling of multi-task estimation problem and then proposes a distributed estimation algorithm with asynchronous data fusion under a secure estimation environment. Despite the considerable expansion of these studies into various scenarios, it is noteworthy that they all assume the distributed network is normal. When a distributed network is invaded by attackers [7,18,19], it leads to the contamination of certain data, rendering it malicious. If there is no secure action to address these malicious data in the network, it cannot work properly. In other words, the network will estimate incorrect parameters [14,16,17]. In recent years, an increasing number of strategies have been designed to counteract intrusion attacks. In [19], the research focuses on attacks targeting sensing and communication processes and proposes a secure distributed estimation algorithm. In [20], the impact of a false data injection attack is investigated, and a data cross-validation strategy is designed. Apart from these attacks, there is another common type in real-life scenarios: Byzantine attacks. This attack is more prevalent and easier for attackers in daily life. The characteristics of such attacks have been studied in [21,22]. To mitigate the impact of Byzantine attack, a distributed estimation algorithm with a sign adaptation function gradient in DLMS (SA-DLMS) algorithm is proposed in [23], aiming to balance the abnormal gradient errors caused by Byzantine attacks and the errors from various abnormal data.

However, despite the numerous proposed counter-strategies against the Byzantine attack, most researchers still focus on this scenario where the Byzantine attack occurs throughout the entire process. In other words, the Byzantine attack is present throughout the entire algorithm execution. This attack model does not align with the intention of attackers in real-world situations. The occurrence probability of an attack should be random and determined by the attackers. Differing from these studies, this paper primarily investigates a type of probability Byzantine (PB) attack based on real-life scenarios. Furthermore, their existing secure algorithms typically rely on additional detection mechanisms to identify Byzantine attack, thereby increasing the operational burden and energy consumption of distributed nodes. Moreover, their algorithms may not necessarily optimize the performance of the detection algorithm. To address these issues, this paper designs an adaptive penalty strategy to mitigate the impact of PB attack. Subsequently, an adaptive distributed estimation algorithm with adaptive fusion weights is designed based on this strategy. Through mathematical analysis and simulations, it is evident that regardless of whether the network is under PB attack or what the probability of attack is, the proposed algorithm can consistently achieve optimal estimation.

The main contributions of this paper are concluded as:

1) A probability Byzantine attack whose probabilistic attack model adheres to a Bernoulli distribution, more aligned with the real-life scenario, is studied.

2) An adaptive update distributed estimation algorithm is proposed, which incorporates an adaptive penalty strategy and adaptive fusion weight, to mitigate the impact of PB attack.

3) Mathematical analyses of the proposed algorithm are conducted to ascertain why it can effectively mitigate PB attacks, and its effectiveness is further validated through experiments.

The remaining part of the paper is organized as follows. In Section 2, the distributed network model is presented, and the PB attack model is proposed. In Section 3, the adaptive update algorithm with penalty mechanism and adaption fusion weight is designed. The convergence analysis of mathematical behavior is achieved in Section 4, and the simulation experiments are done in Section 5. In the last, Section 6 concludes the conclusion of this paper.

2  Network Model and Probability Byzantine Attack Model

Consider a distributed network composed of V nodes. Each node v is capable of communicating with its neighboring nodes, and this set of communicating neighbor nodes is denoted as Nv. Since a node v has access to and can utilize its own information, it is assuredly a member of the set Nv. At each time instant t, every node can sense an expected scalar signal yv(t) along with a regression vector signal uv,t whose dimension is M×1. The mathematic relation [13,20,24,25] between them can be got through a linear expression

yv(t)=uv,tTx∘+nv(t),(1)

where x∘(M×1) represents the unknown and interest variable to be estimated, (⋅)T denotes the transpose of a vector, and nv(t) is a Gaussian additive and independent noise with the mean of 0 and the variance of σn,v2.

In traditional Byzantine attack [18,26], the form of attack involves arbitrarily changing sensed data from normal data to malicious data that is unknown and different. This can be expressed by

yv(t)={yvmal(t),if node vis invaded by attackyvnor(t), otherwise ,(2)

where yvnor(t) is the normal data, and yvmal(t) is the malicious data. In these traditional studies, they consider the case that if a node is compromised by a Byzantine attack, then the data of this node is tampered with for the entire sensing time. Therefore, if node v is compromised by the attacker, then its sensing data yv(t) must become malicious data yvmal(t).

In our real life, since the attacker can intrude into the nodes and tamper with the data, it must be a smarter kind of decision maker. In order to maximize data contamination, the attacker must be capable of inducing prolonged adverse effects with a certain amount of stored energy. That is, the attacker employs a more energy-efficient method to induce data contamination while maintaining the capability to sustain the attack for a longer duration. Consequently, in this paper, we study a stochastic Byzantine attack with a probabilistic form, which is more intelligent. Differing from (2), PB attack can be expressed as

yv(t)=(1−qv)yvnor(t)+qvyvmal(t),s.t.qv∼B(T,p),(3)

where qv∈{0,1} decides the state of node v with probability p controlled by Byzantine attacker, T is the number of all iterations, and B(T,p) is a Binomial distribution with T independent trials and probability p of success. When attacker invades the node v and then its data is tampered with, one has qv=1 and yv(t)=yvmal(t); otherwise, qv=0 and yv(t)=yvnor(t).

Noting the attack form (3), if the attacker selects a suitable attack probability p, it can cause more persistent data contamination with less energy. When such a PB attack occurs in the network, the distributed network without any adaption mechanism will fail to estimate the desired signal x∘. The conventional approaches to handling the malicious data involve implementing a detection mechanism to identify them. While these approaches could get the good performance, they rely on additional detection schemes. Implementing such detection mechanisms not only increases the computational load and energy consumption of the estimation algorithm but also diminishes the estimation efficiency of the distributed nodes. To improve the situation, we introduce an adaptive update with penalty term in the data update formula to counter PB attack, which can effectively weaken the impact of the attack without adding extra burden to the distributed estimation algorithm.

3  Proposed Adaptive Update Algorithm

In this section, the distributed estimation algorithm is first introduced. Based upon this distributed algorithm, the adaptive update with penalty term strategy is designed. Furthermore, an adaptive weight fusion mechanism is proposed to enhance the algorithm’s estimation capabilities.

3.1 Distributed Estimation Algorithm

In the distributed network described in this paper, each node exchanges information exclusively with neighbor nodes within the set Nv. In this context, from (1), it is clear that if node v seeks to attain the more accurate estimation, it needs to fuse the information transmitted by its neighboring nodes. Therefore, to estimate the unknown parameter, the following loss function Jv(xv,t) [27] can be got:

Jv(xv,t)=∑j∈NvE‖yj(t)−uj,tTxv,t‖22,(4)

where xv,t is the estimation of node v at time t, and E(⋅) is the expectation operator.

Based on the cost function Jv(xv,t), a negative gradient update strategy can be employed to yield the distributed DLMS algorithm. The distributed DLMS algorithm comprises two fundamental steps: adaptation and combination. In the adaptation step, each node v utilizes data {yv(t),uv,t} to attain the intermediate estimate ϕv,t by the negative gradient update. In the combination step, each node v collects the intermediate estimate ϕj,t generated by neighboring nodes during the adaptation step to fuse and generate a new estimate xv,t+1. These two steps can be summarized as the adaptation then combination (ATC) strategy [28]. The ATC strategy of the DLMS algorithm can be expressed as

{ϕv,t=xv,t+μvuv,tev,v(t)xv,t+1=∑j∈Nvcj,vϕj,t,(5)

where

ev,v(t)=yv(t)−uv,tTxv,t,(6)

and μv is the step-size of node v and cj,v is the information fusion weight from node v to node j, which are non-negative real constants. Observing (5), the intermediate estimation ϕj,t and estimation xv,t+1 are approximate to the interest parameter x∘, but the estimation xv,t+1 is closer to x∘ than ϕj,t. The fusion weight needs to satisfy the following condition [13,29,30]:

cj,v=0,ifj∉Nv,andcj,v≥0,ifj∈Nv.(7)

In other References [13,20], the information fusion weight cj,v can be determined by the communication relation among nodes. For instance, methods such as the Metropolis rule and the nearest neighbor rule offer methodologies for establishing these weights, which can be denoted as

cj,v={1/max(|Nv|,|Nj|), if j∈Nv∖{v}1−∑ℓ∈Nv∖{v}cℓ,v, if j=v0, otherwise ,(8)

and

cj,v={1|Nv|, if j∈Nv0, otherwise ,(9)

where |Nv| denotes the degree of node v, which is the number of neighbors of node v. The Metropolis rule can determine the information weight based on the degree, while the nearest neighbor rule averages the weight across all neighbors. Differing from above rules, to derive a better estimation performance, a new information fusion rule with penalty term can be designed and can provide an adaptive weight in the following part.

3.2 Secure Distributed Estimation with Adaptive Update

Based on the above Section 2, it can be observed that in the presence of a PB attack, there is a significant data deviation between the perceived data and normal data. In contrast, normal data typically incurs relatively small errors, which is primarily influenced by noise nv(t). However, in general, the influence of noise is more filtered compared to PB attack. Therefore, from this point, a penalty term can be designed based on the different to counteract the impact of PB attack.

In the presence of PB attack, such penalty terms manifest minimal data updates, or even remain devoid of updates, whereas in the context of tolerable data differentials that may be caused by noise, they exhibit conventional data updates. Within the domain of difference-based penalty functions, prevalent exemplars include the Geman-McClure function, the Cauchy function, and the Huber function. The responsiveness of these functions to differentials is delineated in Fig. 1. The corresponding parameters of Cauchy function and Huber function are set as 0.9.

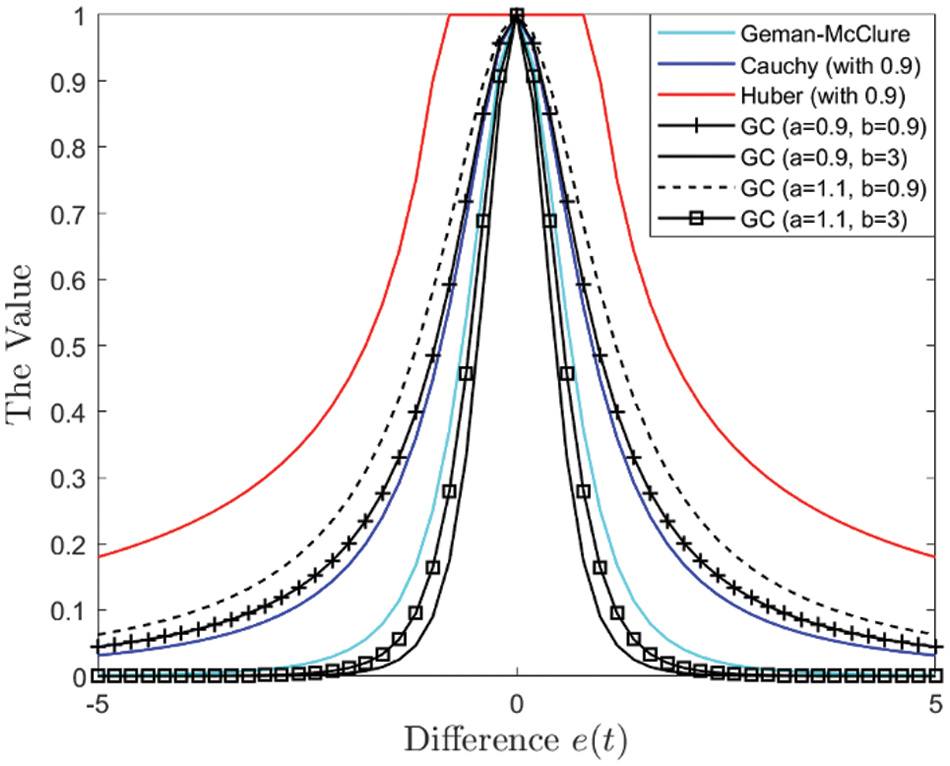
Figure 1: The reactions of difference under different functions

Based on the Geman-McClure function and the Cauchy function, an adaptive penalty term function can be devised and named as GC. Its mathematical formulation is expressed by the following equation:

GC(e(t))=1(1+(e(t)a)2)b,(10)

where e(t) denotes the difference, and a and b are the adjustable parameter. From the Fig. 1, it is found that the penalty term with GC function can obtain the best performance under the appropriate parameters a and b.

Combining with the penalty term (10), the adaptive negative gradient update with penalty term can be designed as follows:

GC(ev,v(t))uv,tev,v(t).(11)

In other References [7,18,19,31], because the data may be tampered with by PB attack, the adaptation step could not fuse the neighbor information{yj(t),uj,t}(j∈Nv). However, noting (11), the designed penalty term can serve as a robust measure to counteract contamination from adversarial or tainted data, which means that the adaptation step with fusion strategy can be obtained as

ϕv,t=xv,t+μv∑j∈Nvcj,v′GC(ej,v(t))uj,tej,v(t),(12)

where

ej,v(t)=yj(t)−uj,tTxv,t,(13)

and cj,v′ is the fusion weight. Since the penalty term GC(ej,v(t)) has been used to weaken the impact of PB attack, the fusion weight cj,v′ can be got by the Metropolis rule (8) or the nearest neighbor rule (9).

Combining with the intermediate estimation ϕv,t, the combination step can be got as

xv,t+1=∑j∈Nvcj,v″(t)ϕj,t,(14)

where cj,v′′(t) is a new adaptive fusion weight and will be changing over iteration t.

The adaptive weight cj,v′′(t) is necessary to fuse the different variables, because the intermediate estimation ϕj,t from node j may contain the malicious impact. If node j is invaded by PB attack and there is the missing detection, the ϕj,t would interfere the fusion performance.

Since one has owned the neighboring information {yj(t),uj,t} and the intermediate estimation ϕj,t(j∈Nv) in combination step, the adaptive weight cj,v′′(t)$  can be designed as

cj,v″(t)=[ej,v(t)]−2∑ℓ∈Nv[eℓ,v(t)]−2,(j∈Nv).(15)

Therefore, we can derive the distributed adaptive update DLMS (AU-DLMS) algorithm with penalty term as follows:

{ϕv,t=xv,t+μv∑j∈Nvcj,v′GC(ej,v(t))uj,tej,v(t)xv,t+1=∑j∈Nvcj,v″(t)ϕj,t,(16)

and the proposed algorithm has been also summarized in Table 1.

4  Convergence Analysis of Mathematical Behavior

Convergence analysis is a crucial aspect for estimation algorithms to reach their optimal solutions. In this section, we will derive the convergence analyses of the proposed AU-DLMS algorithm from both mean and mean square behaviors. To better analyze this mathematical process, we first examine the convergence status of the normal nodes. Subsequently, based on the convergence status of these normal nodes, we analyze the situation of the malicious nodes invaded by PB attack.

According to the PB attack model (3), when node v and its neighbors are normal, one has qj=0 and yj(t)=yjnor(t)(j∈Nv). Hence, subtracting x∘ from both sides of (16) yields

{ϕv,t−x∘=xv,t+μv∑j∈Nvcj,v′GC(ej,v(t))uj,tej,v(t)−x∘xv,t+1−x∘=∑j∈Nvcj,v″(t)ϕj,t−x∘.(17)

To facilitate expression, we introduce the following formulas [32]:

ϕ^v,t=ϕv,t−x∘,(18)

and

x^v,t=xv,t−x∘.(19)

Therefore, Formula (17) can be written as

{ϕ^v,t=x^v,t+μv∑j∈Nvcj,v′GC(ej,v(t))uj,tej,v(t)x^v,t+1=∑j∈Nvcj,v″(t)ϕ^j,t.(20)

Because of yjnor(t)=uv,tTx∘+nv(t), according to (1), one yields

{ϕ^v,t=x^v,t−μv∑j∈Nvcj,v′GC(ej,v(t))uj,tuj,tTx^v,t+μv∑j∈Nvcj,v′GC(ej,v(t))uj,tnj(t)x^v,t+1=∑j∈Nvcj,v″(t)ϕ^j,t.(21)

Under the expectation E(⋅), because the noise is independent of other variables, it can obtain

Ex^v,t+1=E∑ℓ∈Nvcℓ,v″(t)(IM−μℓ∑j∈Nℓcj,ℓ′GC(ej,ℓ(t))uj,tuj,tT)x^ℓ,t.(22)

where IM is the matrix with M×M. If (22) can get the mean stability, the coefficient of variable x^ℓ,t lies in (−1, 1), which means the coefficient matrix satisfies the following condition:

ρ(∑ℓ∈Nvcℓ,v″(t)(IM−μℓ∑j∈Nℓcj,ℓ′GC(ej,ℓ(t))uj,tuj,tT))<1.(23)

where ρ(⋅) is the spectral radius.

Based on the operational property of the spectral radius and the characteristic of fusion weight (7) from Formula (23), we can have

ρ(IM−μv∑j∈Nvcj,v′GC(ej,v(t))uj,tuj,tT)<1.(24)

If Formula (24) can hold, the following condition need to be satisfied:

−1<λmax(IM−μv∑j∈Nvcj,v′GC(ej,v(t))uj,tuj,tT)<1.(25)

Based on Formula (25), we can get the following convergence condition:

0<μv<1λmax(∑j∈Nvcj,v′GC(ej,v(t))uj,tuj,tT).(26)

From Fig. 1, it is found that  GC(ej,v(t))≤1, must hold for j∈Nv, since Formula (26) can be denoted as

0<μv<1λmax(∑j∈Nvcj,v′uj,tuj,tT).(27)

Therefore, when step-size μv is small enough to satisfy the step Formula (27), the mean stability of normal node v can be got [19], which means that the proposed algorithm can make the normal nodes estimate the normal parameter. Besides, when the step Formula (27) is satisfied, the estimation error (21) can be zero as t→+∞. Furthermore, based on (21), it is easy to get that when μv is sufficiently small, the mean-square deviation (MSD) E‖x^v,t‖22 will converge to a higher order infinitesimal of μv under t→+∞ [7,19].

When node v is invaded by PB attack, combining with (3) can yield qv=1 and yv(t)=yvmal(t). In order to simplify analysis, the expression yv(t)=yvmal(t) can be written as

yvmal(t)≜yvnor(t)+y~v(t),(28)

where y~v(t) denotes the difference from the normal value yvnor(t).

Under Formula (28), the relation (21) becomes

{ϕ^v,t=x^v,t−μv∑j∈Nvcj,v′GC(ej,v(t))uj,tuj,tTx^v,t+μv∑j∈Nvcj,v′GC(ej,v(t))uj,tnj(t)−μv∑j∈Nvcj,v′GC(ej,v(t))uj,ty~j(t)x^v,t+1=∑j∈Nvcj,v″(t)ϕ^j,t.(29)

Similarly, one has the following expectation operation:

Ex^v,t+1=E∑ℓ∈Nvcℓ,v″(t)(IM−μℓ∑j∈Nℓcj,ℓ′GC(ej,ℓ(t))uj,tuj,tT)x^ℓ,t−E∑ℓ∈Nvcℓ,v″(t)(μv∑j∈Nℓcj,ℓ′GC(ej,ℓ(t))uj,ty~j(t))..(30)

Comparing Formulas (21) and (30), it can be observed that their difference lies in the following term:

Z≜E∑ℓ∈Nvcℓ,v″(t)(μv∑j∈Nℓcj,ℓ′GC(ej,ℓ(t))uj,ty~j(t)).(31)

Therefore, as long as the behavior of Z can be analysis, the convergence behaviour of malicious node can be obtained.

Based on the characteristic of fusion weight (7), the convergence behavior of variable Z is mainly determined by the following term:

Z~≜Eμv∑j∈Nvcj,v′GC(ej,v(t))uj,ty~v(t).(32)

Combining with (10), one has

Z~≈E∑j∈Nvcj,v′uj,tμvy~j(t)(1+(y~j(t)+nv(t)+uj,tTx^v,ta)2)b(33)

When the node v is attacked by PB attack, y~v(t) is obviously larger than nv(t). Meanwhile, in order to make each node converge to the ideal estimation, the step-size condition must be satisfied. Based on the above analyses, x^v,t will be close to a higher order infinitesimal about μv, and then uj,tTx^v,t will approximate to zero with t→∞. Hence, the Formula (33) can be further approximate to

Z~≈E∑j∈Nvcj,v′uj,tμvy~j(t)(1+(y~j(t)a)2)b.(34)

Let

G(y~v(t))≜μvy~v(t)(1+(y~v(t)a)2)b.(35)

Therefore, (34) can be denoted as

Z~≈E∑j∈Nvcj,v′uj,tG(y~j(t)).(36)

In order to make analysis convenient, the function G(y~v(t)) can be depicted in Fig. 2. It is obvious that due to the proposed penalty mechanism, G(y~j(t))(j∈Nv) would be sufficiently small in the properly adjustable parameter and can be a higher order infinitesimal about μv. Combining with (36), it is obtained that Z~ is also a higher order infinitesimal about μv, which means that the variable Z (31) will be a sufficiently small term when the condition (27) is satisfied. Meanwhile, it is concluded that the malicious node can achieve the mean stability under the proposed penalty term. Similarly, the second moment of Z is definitely a higher order infinitesimal about μv, so the MSD of malicious node will converge. Hence, the proposed penalty term can weaken the impact of the malicious data, and it will make the malicious node converge to the efficient estimation.

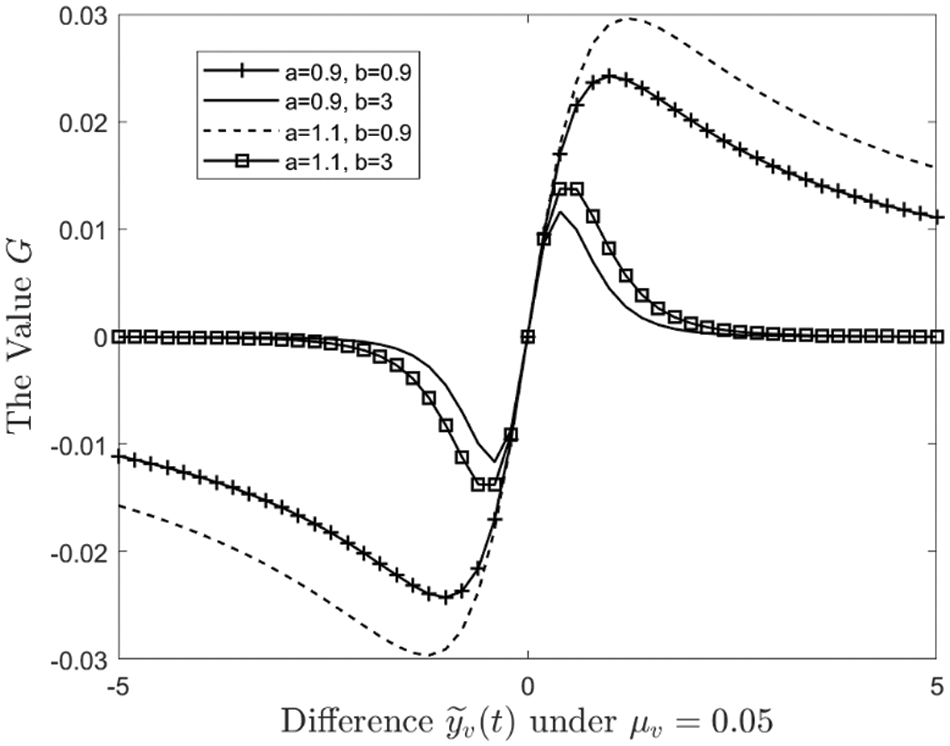
Figure 2: The function G under μv=0.05 with the different parameters

Based on all above analysis, when node v is the normal node with all normal neighbors or the malicious node, it always obtains the mean and mean-square stability and must converge. That is, if node v is the normal node with malicious neighbor node or the malicious node with malicious neighbor node, it still gets the mean and mean-square stability. It is concluded that the proposed penalty mechanism is effective against PB attack, and AU-DLMS algorithm can estimate the accuracy parameter.

5  Experimental Simulation

In this section, to assess the efficacy of the proposed AU-DLMS algorithm in mitigating the impact of malicious attack nodes invaded by PB attack on the network, MSD and excess mean square error (EMSE) [13,18,31] are employed as the metric to gauge algorithm performance. At time t, based on the definition of MSD E‖x^v,t‖22, the MSD(t) for the entire network is defined as

MSD(t)=1V∑v=1VE‖x^v,t‖22,(37)

and the EMSE for the entire network is viewed as

EMSE(t)=1V∑v=1VE‖uv,tTx^v,t‖22.(38)

In simulations, the distributed network is composed of V=30 nodes and is shown in Fig. 3. All results of simulations are based on the average of 150 Monte Carlo experiments. The PB attack invades some nodes that are marked by the red color in Fig. 4. Meanwhile, each node v can not know the attack prior information, and uniformly set the following parameters: μv=0.05, M=3, and cj,v′ obtained by (9). Besides, combining the above convergence analysis and Fig. 2, it is obvious that when the adjustable parameters a and b are set as 0.09 and 3, respectively, the influence of PB attack can be minimal, so the proposed AU-DLMS algorithm can obtain the best secure performance. Fig. 5 shows the additive noise variance σn,v2 and the vector variance σu,v2.

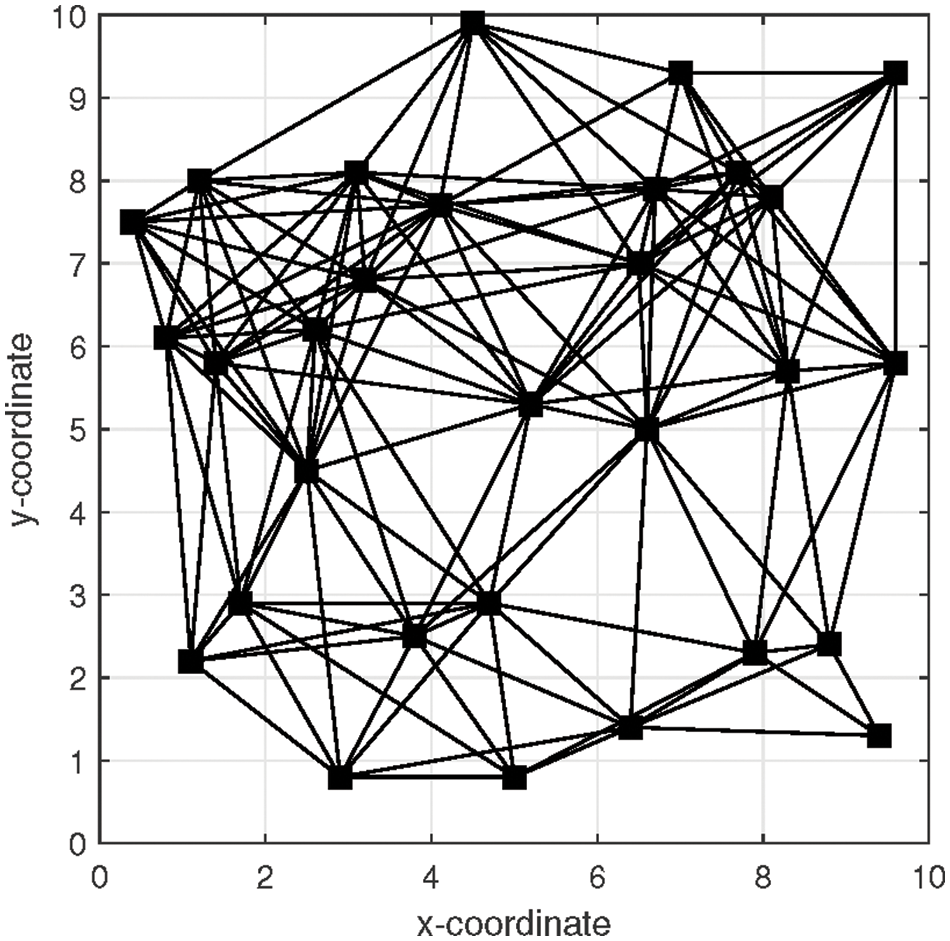
Figure 3: The distributed network

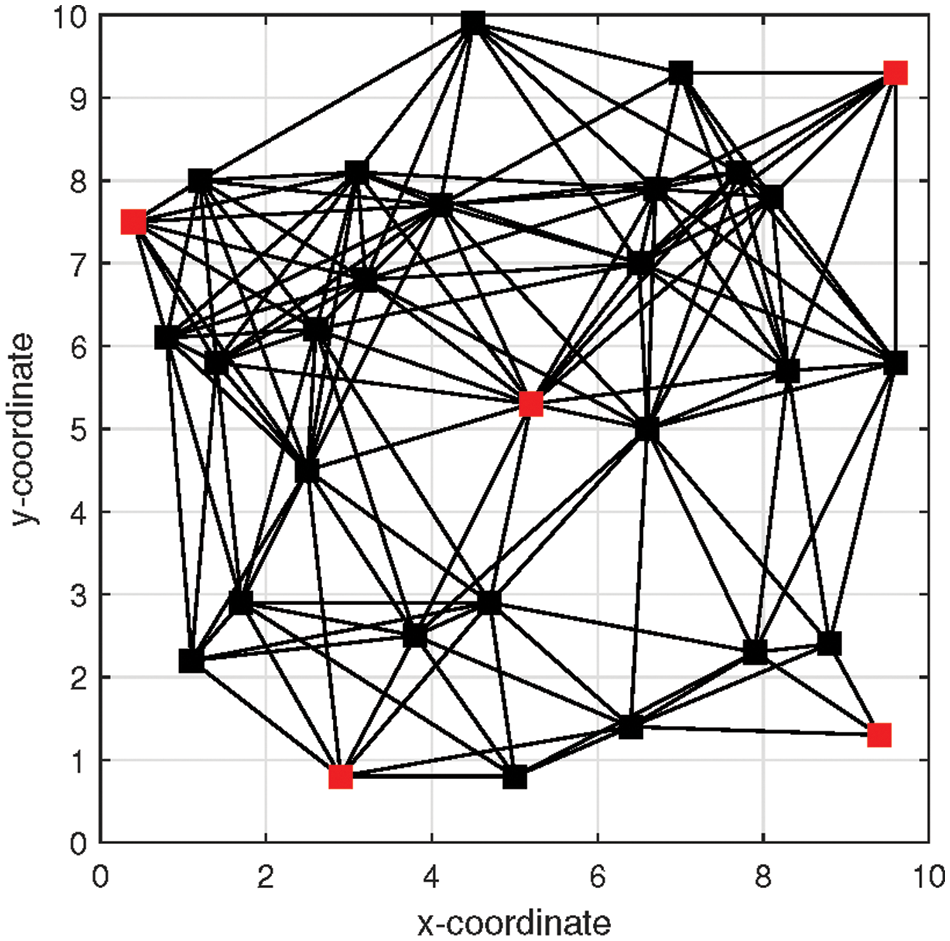
Figure 4: The distributed network under PB attack

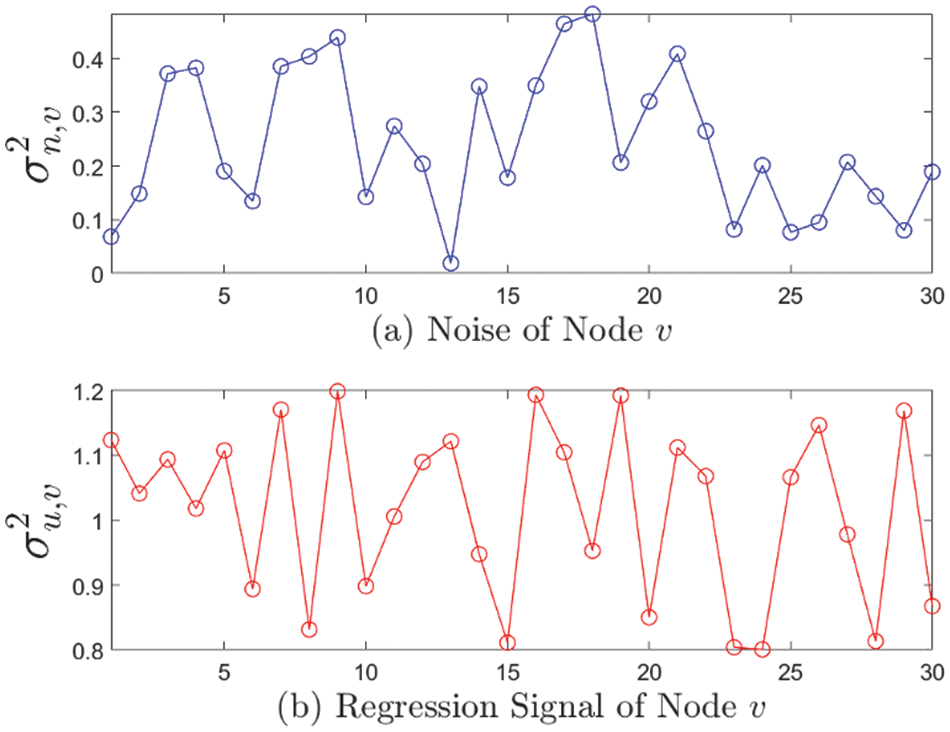
Figure 5: The variance of noise and regression signal

In the experimental simulations, to thoroughly demonstrate the performance of the proposed AU-DLMS algorithm, two sets of probabilistic experiments are conducted in the following parts. In the first set of experiments, these nodes invaded by PB attack are consistently subjected to attacks, implying that the PB attack probability is a complete probability. Subsequently, in the following set of experiments, these nodes invaded by PB attack are modeled according to a Binomial distribution.

In the first experiment, the attack probability of all malicious nodes is set to 1. That is, Byzantine attackers continuously expends energy to carry out consecutive attacks. Fig. 6 depicts transient MSD of different algorithms, and Fig. 7 shows the steady MSD of different nodes of different algorithms. Observing Figs. 6 and 7, it is evident from the NC-LMS algorithm curve that the performance of the five malicious nodes is markedly poor, while the other nodes maintain normal performance. Furthermore, it is observed that the DLMS algorithm exhibits significantly degraded performance when facing attacks without the implementation of security strategies. From these two curves, it is discernible that although the nodes intruded by attackers are minimal, such malicious behavior can exert a network-wide performance impact through cooperation among nodes. The SA-DLMS [23] algorithm demonstrates a certain level of adversarial resilience against PB attacks, but there still exist discernible performance fluctuations. Across both figures, it is apparent that the proposed AU-DLMS algorithm exhibits commendable stability in the face of attacks. Moreover, it is noticeable that the design of penalty mechanism can effectively enhance and improve estimation performance regardless of the presence of PB attack.

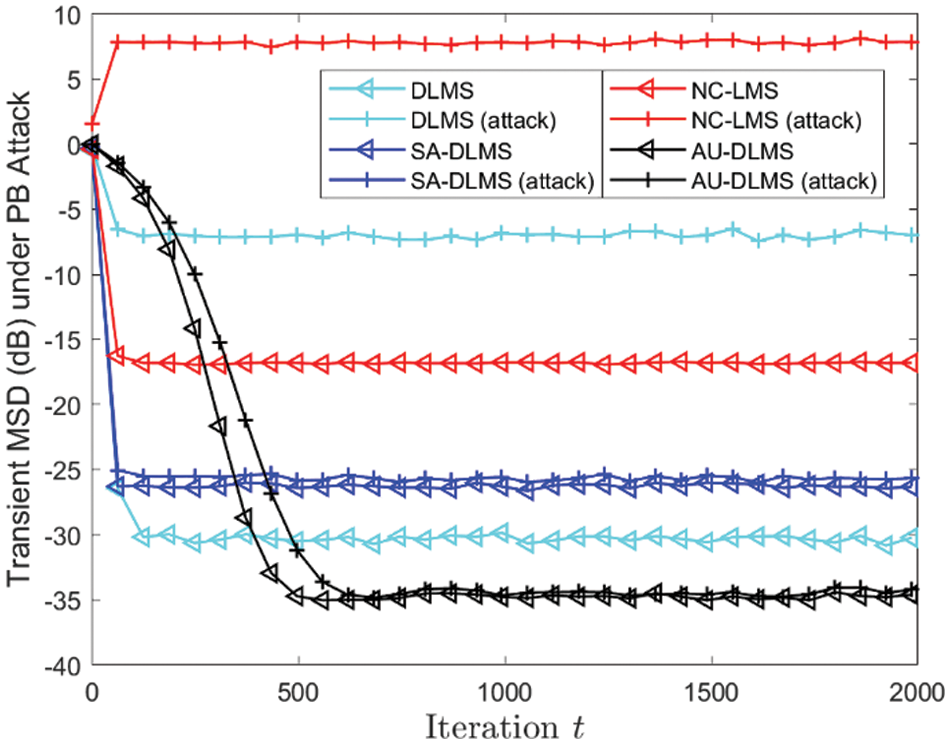
Figure 6: Transient MSD of different algorithms under PB attack with pv=1

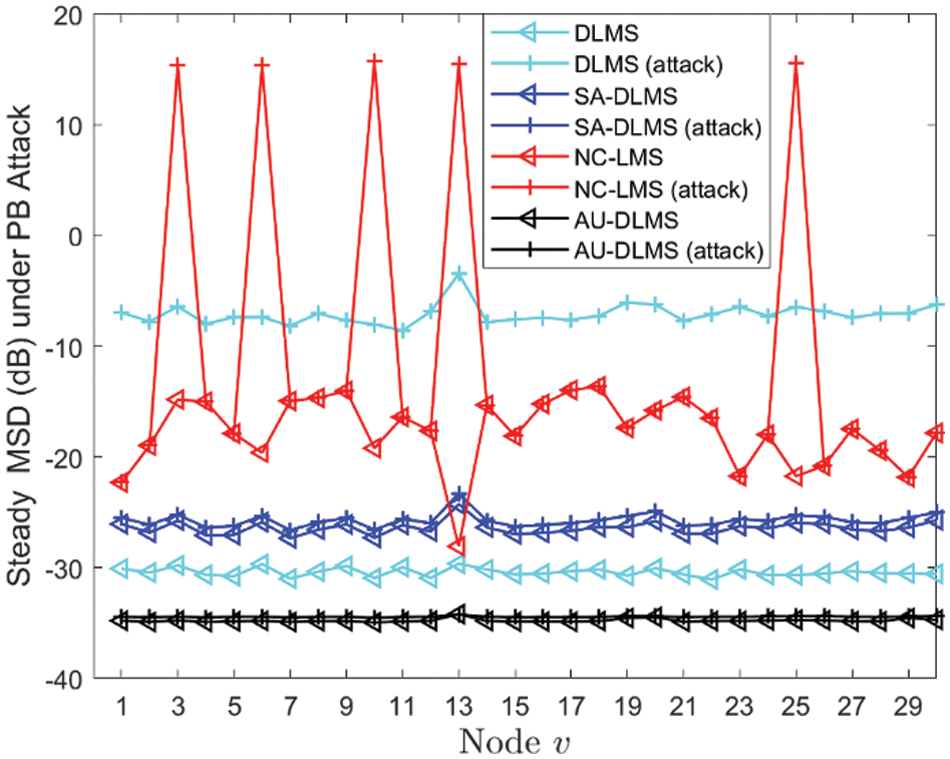
Figure 7: Steady MSD of different nodes of different algorithms under PB attack with pv=1

Fig. 8 depicts transient EMSE of different algorithms, and Fig. 9 shows the steady EMSE of different nodes of different algorithms. From these two figures, it can be observed that the EMSE performance of all curves aligns consistently with the MSD performance. It is also evident that the proposed AU-DLMS algorithm stands out as the optimal algorithm among all, irrespective of the presence of attacks.

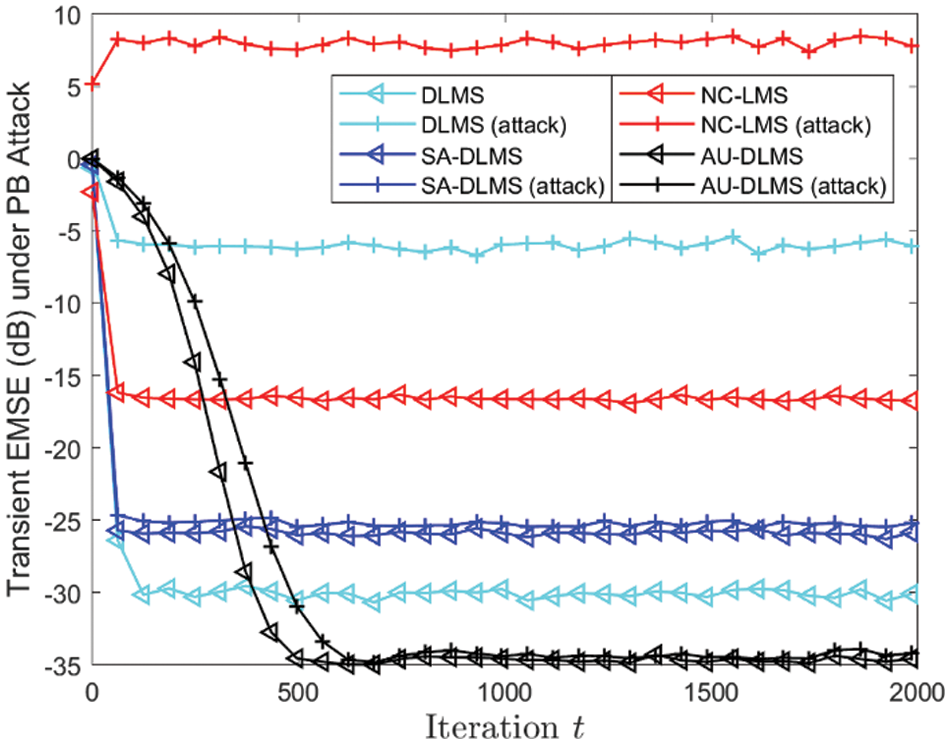
Figure 8: Transient EMSE of different algorithms under PB attack with pv=1

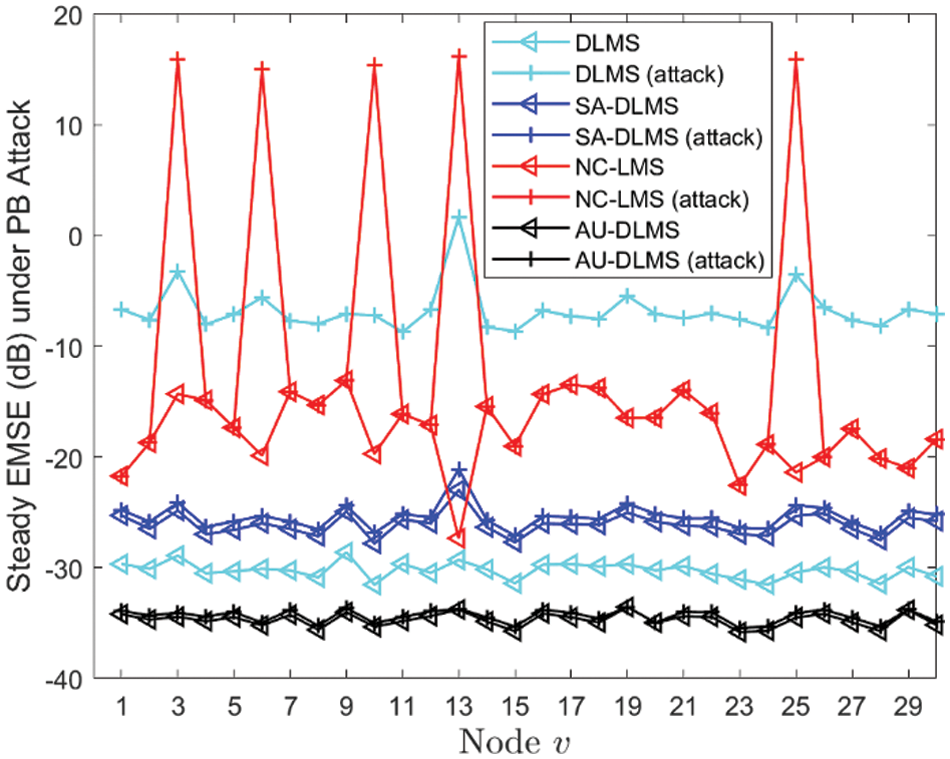
Figure 9: Steady EMSE of different nodes of different algorithms under PB attack with pv=1

In the second experiment, the attack probabilities for all malicious nodes are set to follow a Binomial distribution. The probabilities of nodes being attacked are set as 0.5, 0.6, 0.7, 0.8, and 0.9, respectively. Fig. 10 depicts transient MSD of different algorithms with different pv s, and Fig. 11 shows the steady MSD of different nodes of different algorithms with different pv s. From Figs. 10 and 6, it can be observed that the DLMS algorithm exhibits some performance fluctuations when attackers employ probability attack with pv<1. In Figs. 10 and 11, under different probabilities of Byzantine attack, both DLMS and NC-LMS algorithms consistently demonstrate poor performance. While the SA-DLMS algorithm shows some resilience against such attacks, it still falls short of achieving optimal estimation. The proposed AU-DLMS algorithm not only improves the original estimation performance and attains optimal estimates but also exhibits minimal impact when facing PB attack.

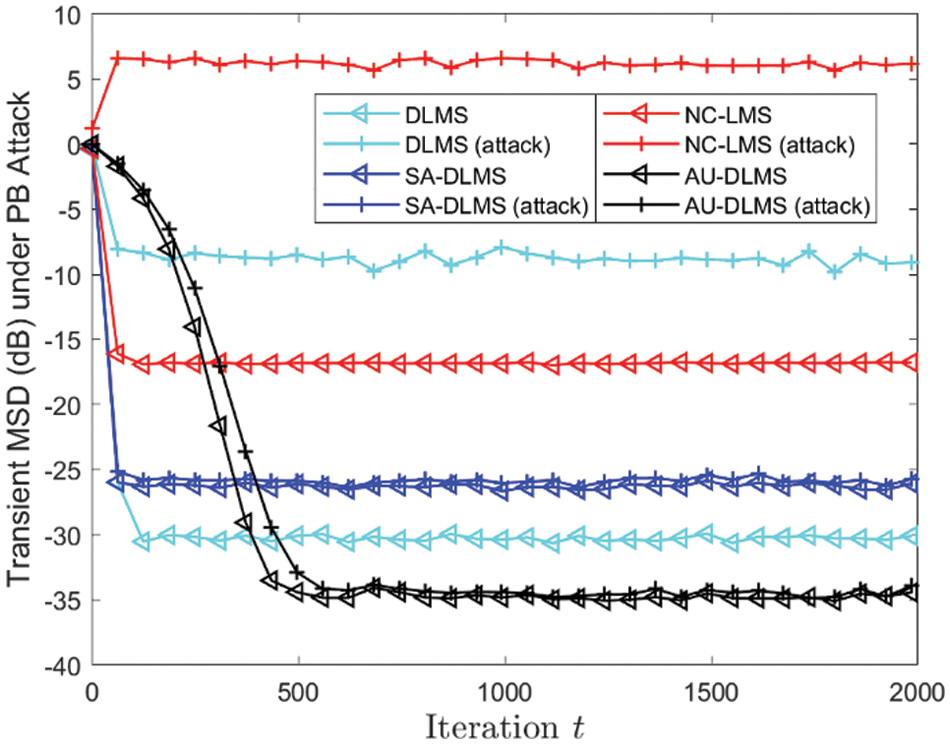
Figure 10: Transient MSD of different algorithms under PB attack with different pv: 0.5, 0.6, 0.7, 0.8, and 0.9

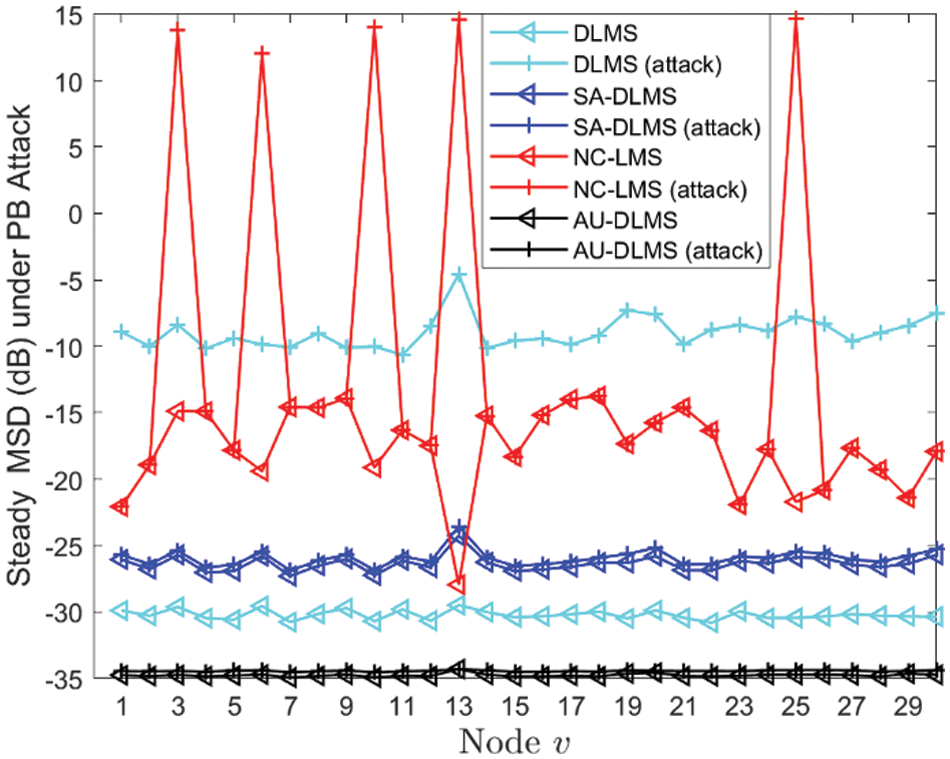
Figure 11: Steady MSD of different nodes of different algorithms under PB attack with different pv: 0.5, 0.6, 0.7, 0.8, and 0.9

Fig. 12 depicts transient EMSE of different algorithms with different pv s, and Fig. 13 shows the steady EMSE of different nodes of different algorithms with different pv s. From these two figures, it can be observed that all algorithms experience slight performance fluctuations in terms of the EMSE metric. However, the proposed AU-DLMS algorithm is still capable of estimating the optimal parameter and maintaining the highest estimation accuracy. From Fig. 13, it is also found that all nodes can obtain the interesting parameter and there is not much fluctuation among them.

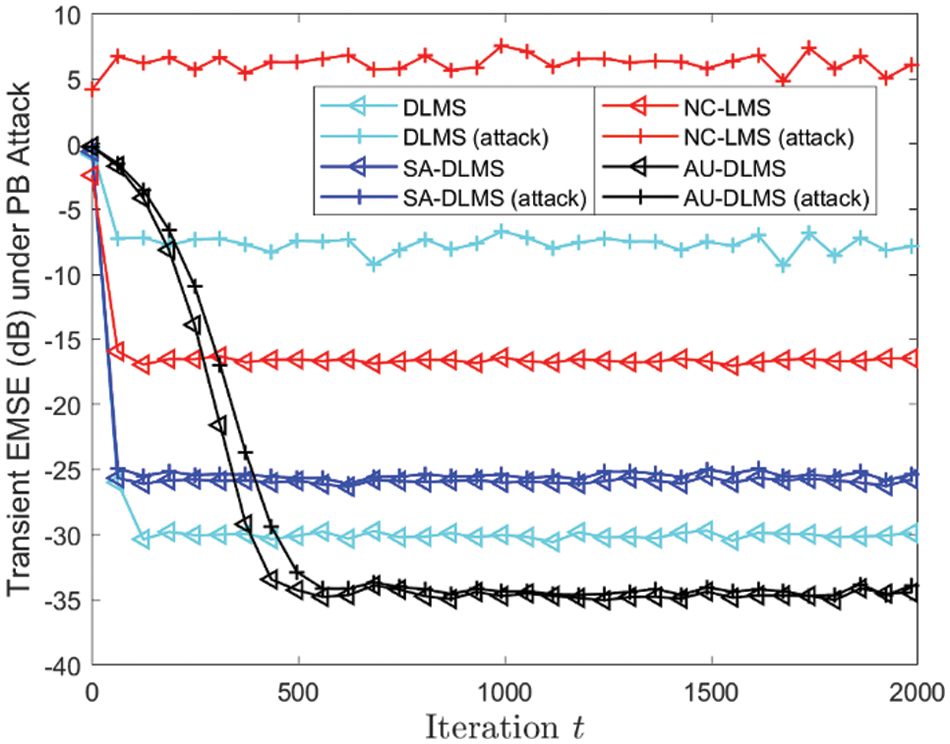
Figure 12: Transient EMSE of different algorithms under PB attack with different pv: 0.5, 0.6, 0.7, 0.8, and 0.9

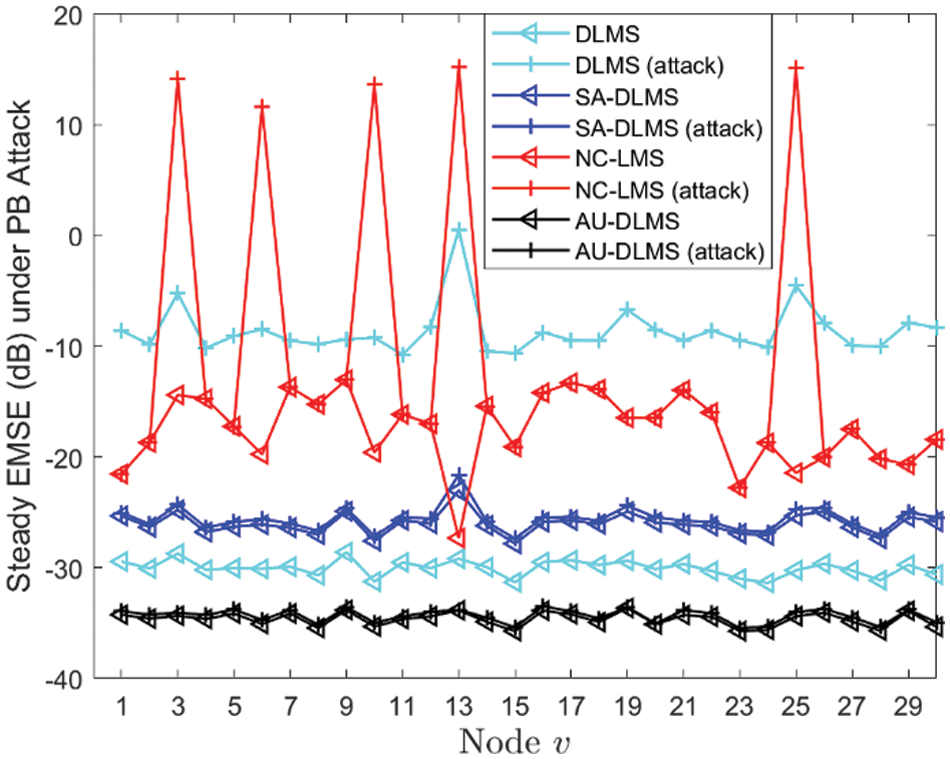
Figure 13: Steady EMSE of different nodes of different algorithms under PB attack with different pv: 0.5, 0.6, 0.7, 0.8, and 0.9

From all the simulation experiments, it is evident that even when attackers employ Byzantine attacks with certain probabilities, it can still have a detrimental impact on their estimation algorithms. This implies that attackers can utilize such probabilistic attack to inflict more enduring malicious effects. Therefore, employing the penalty strategy designed in this paper not only effectively mitigates these impacts but also improves the original estimation performance, which proves the effectiveness of the designed strategy. Hence, it can be considered that the proposed AU-DLMS algorithm exhibits superior advantages in distributed parameter estimation.

6  Conclusion

In this paper, a probability Byzantine attack is investigated, simulated by a Bernoulli distribution, which closely resembles real-life scenarios. To reduce energy consumption and alleviate the burden on distributed nodes, a penalty strategy is devised in the adaptation step. Subsequently, an adaptive fusion weight method is proposed to combine all intermediate estimations in the combination step. Through convergence analysis, a stability condition can be derived, ensuring the convergence of the distributed AU-DLMS algorithm if the step size satisfies this condition. Furthermore, the rationale behind the efficacy of this penalty item in weakening the attack has been analyzed. Simulation experiments have also been presented to validate the performance of the proposed algorithm. Through these simulations, it becomes evident that the AU-DLMS algorithm enhances estimation performance under normal network conditions and effectively mitigates the impact of PB attacks.

Future directions will include: (1) considering the design of the secure method for false data injection attacks and bad communication attacks; (2) considering the presence of the impulse noise; (3) considering the energy efficiency of the node.

Acknowledgement: We thank all the members who have contributed to this work with us.

Funding Statement: This work was not supported in part by any funding.

Author Contributions: The authors confirm contribution to the paper as follows. Gang Long: Study conception, design, and draft manuscript preparation; Zhaoxin Zhang: Simulation, analysis, interpretation of results and draft manuscript preparation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Xia et al., “A trust-based reliable confident information coverage model of wireless sensor networks for intelligent transportation,” IEEE Trans. Vehicular Technol., vol. 72, no. 7, pp. 9542–9554, 2023. doi: 10.1109/TVT.2023.3253131. [Google Scholar] [CrossRef]

2. L. Hu, Z. Chen, Y. Jia, M. Wang, and T. Q. Quek, “Asymptotically optimal arrival rate for IoT networks with AoI and peak AoI constraints,” IEEE Commun. Lett., vol. 25, no. 12, pp. 3853–3857, 2021. doi: 10.1109/LCOMM.2021.3119350. [Google Scholar] [CrossRef]

3. F. Ullah, G. Srivastava, S. Ullah, and L. Mostarda, “Privacy-Preserving federated learning approach for distributed malware attacks with intermittent clients and image representation,” IEEE Trans. Consumer Electron., vol. 70, no. 1, pp. 4585–4596, Jan. 2023. doi: 10.1109/tce.2023.3342644. [Google Scholar] [CrossRef]

4. Y. Hua, F. Chen, S. Duan, and J. Wu, “Distributed data-selective DLMS estimation under channel attacks,” IEEE Access, vol. 7, pp. 83863–83872, 2019. doi: 10.1109/ACCESS.2019.2925009. [Google Scholar] [CrossRef]

5. F. Ullah, G. Srivastava, S. Ullah, K. Yoshigoe, Y. Zhao, “NIDS-VSB: Network intrusion detection system for VANET using spark-based big data optimization and transfer learning,” IEEE Trans. Consum. Electron., vol. 70, no. 1, pp. 1798–1809, Feb. 2024. doi: 10.1109/TCE.2023.3328320. [Google Scholar] [CrossRef]

6. H. Zayyani, “Robust minimum disturbance diffusion LMS for distributed estimation,” IEEE Trans. Circuits Syst. II: Express Briefs, vol. 68, no. 1, pp. 521–525, 2020. [Google Scholar]

7. F. Wan, T. Ma, Y. Hua, B. Liao, and X. Qing, “Secure distributed estimation under Byzantine attack and manipulation attack,” Eng. Appl. Artif. Intell., vol. 116, no. 1, 2022, Art. no. 105384. doi: 10.1016/j.engappai.2022.105384. [Google Scholar] [CrossRef]

8. Y. Hua, F. Wan, H. Gan, and B. Liao, “One-step asynchronous data fusion dlms algorithm,” IEEE Commun. Lett., vol. 25, no. 5, pp. 1660–1664, 2021. doi: 10.1109/LCOMM.2021.3049965. [Google Scholar] [CrossRef]

9. F. Ullah, S. Ullah, G. Srivastava, and J. C. Lin, “IDS-INT: Intrusion detection system using transformer-based transfer learning for imbalanced network traffic,” Digit. Commun. Netw., vol. 10, no. 1, pp. 190–204, Mar. 2023. doi: 10.1016/j.dcan.2023.03.008. [Google Scholar] [CrossRef]

10. F. Chen, S. Deng, Y. Hua, S. Duan, L. Wang and J. Wu, “Communication-reducing algorithm of distributed least mean square algorithm with neighbor-partial diffusion,” Circuits, Syst., Signal Process., vol. 39, no. 9, pp. 4416–4435, 2020. doi: 10.1007/s00034-020-01374-1. [Google Scholar] [CrossRef]

11. Z. Xu, Y. Liu, and C. Li, “Distributed semi-supervised learning with missing data,” IEEE Trans. Cybern., vol. 51, no. 12, pp. 6165–6178, 2020. doi: 10.1109/TCYB.2020.2967072. [Google Scholar] [PubMed] [CrossRef]

12. Y. Hua, F. Wan, B. Liao, Y. Zong, S. Zhu and X. Qing, “Adaptive multitask clustering algorithm based on distributed diffusion least-mean-square estimation,” Inf. Sci., vol. 606, no. 4, pp. 628–648, 2022. doi: 10.1016/j.ins.2022.05.074. [Google Scholar] [CrossRef]

13. F. S. Cattivelli and A. H. Sayed, “Diffusion LMS strategies for distributed estimation,” IEEE Trans. Signal Process., vol. 58, no. 3, pp. 1035–1048, 2009. doi: 10.1109/TSP.2009.2033729. [Google Scholar] [CrossRef]

14. F. Chen, X. Li, S. Duan, L. Wang, and J. Wu, “Diffusion generalized maximum correntropy criterion algorithm for distributed estimation over multitask network,” Digit. Signal Process., vol. 81, no. 4–5, pp. 16–25, 2018. doi: 10.1016/j.dsp.2018.02.008. [Google Scholar] [CrossRef]

15. F. Hua, R. Nassif, C. Richard, H. Wang, and A. H. Sayed, “Diffusion LMS with communication delays: Stability and performance analysis,” IEEE Signal Process. Lett., vol. 27, pp. 730–734, 2020. doi: 10.1109/LSP.2020.2990086. [Google Scholar] [CrossRef]

16. J. Chen, C. Richard, and A. H. Sayed, “Multitask diffusion adaptation over networks,” IEEE Trans. Signal Process., vol. 62, no. 16, pp. 4129–4144, 2014. doi: 10.1109/TSP.2014.2333560. [Google Scholar] [CrossRef]

17. Y. Hua, H. Gan, F. Wan, X. Qing, and F. Liu, “Distributed estimation with adaptive cluster learning over asynchronous data fusion,” IEEE Trans. Aerosp. Electron. Syst., vol. 59, no. 5, pp. 5262–5274, Oct. 2023. [Google Scholar]

18. J. Li, W. Abbas and X. Koutsoukos, “Resilient distributed diffusion in networks with adversaries,” IEEE Trans. Signal Inf. Process. Over Netw., vol. 6, pp. 1–17, 2019. [Google Scholar]

19. Y. Liu and C. Li, “Secure distributed estimation over wireless sensor networks under attacks,” IEEE Trans. Aerosp. Electron. Syst., vol. 54, no. 4, pp. 1815–1831, 2018. doi: 10.1109/TAES.2018.2803578. [Google Scholar] [CrossRef]

20. Y. Hua, F. Wan, H. Gan, Y. Zhang, and X. Qing, “Distributed estimation with cross-verification under false data-injection attacks,” IEEE Trans. Cybern., vol. 53, no. 9, pp. 5840–5853, 2023. doi: 10.1109/TCYB.2022.3197591. [Google Scholar] [PubMed] [CrossRef]

21. B. Kailkhura, Y. S. Han, S. Brahma, and P. K. Varshney, “Distributed Bayesian detection in the presence of Byzantine data,” IEEE Trans. Signal Process., vol. 63, no. 19, pp. 5250–5263, 2015. doi: 10.1109/TSP.2015.2450191. [Google Scholar] [CrossRef]

22. J. Wu et al., “Analysis of Byzantine attack strategy for cooperative spectrum sensing,” IEEE Commun. Lett., vol. 24, no. 8, pp. 1631–1635, 2020. doi: 10.1109/LCOMM.2020.2990869. [Google Scholar] [CrossRef]

23. J. Ni, J. Chen, and X. Chen, “Diffusion sign-error LMS algorithm: Formulation and stochastic behavior analysis,” Signal Process., vol. 128, no. 8, pp. 142–149, 2016. doi: 10.1016/j.sigpro.2016.03.022. [Google Scholar] [CrossRef]

24. B. Chen, L. Xing, J. Liang, N. Zheng, and J. C. Principe, “Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion,” IEEE Signal Process. Lett., vol. 21, no. 7, pp. 880–884, 2014. doi: 10.1109/LSP.2014.2319308. [Google Scholar] [CrossRef]

25. F. Wan, Y. Hua, B. Liao, T. Ma, and X. Qing, “Distributed estimation with novel adaptive data selection based on a cross-matching mechanism,” Circuits Syst., Signal Process., vol. 42, no. 10, pp. 6324–6346, 2023. doi: 10.1007/s00034-023-02410-6. [Google Scholar] [CrossRef]

26. D. Yin, Y. Chen, R. Kannan, and P. Bartlett, “Byzantine-robust distributed learning: Towards optimal statistical rates,” in Int. Conf. Mach. Learn, PMLR, Stockholm, Sweden, 2018, pp. 5650–5659. [Google Scholar]

27. H. Zayyani, F. Oruji, and I. Fijalkow, “An adversary-resilient doubly compressed diffusion LMS algorithm for distributed estimation,” Circuits Syst., Signal Process., vol. 41, no. 11, pp. 6182–6205, 2022. doi: 10.1007/s00034-022-02072-w. [Google Scholar] [CrossRef]

28. V. Shumovskaia, M. Kayaalp, and A. H. Sayed, “Distributed decision-making for community structured networks,” in Proc. IEEE Int. Conf. Acoust., Speech Signal Process (ICASSP), Seoul, Republic of Korea, 2024, pp. 9316–9320. [Google Scholar]

29. B. Chen, L. Xing, H. Zhao, N. Zheng, and J. C. Principe, “Generalized correntropy for robust adaptive filtering,” IEEE Trans. Signal Process., vol. 64, no. 13, pp. 3376–3387, 2016. doi: 10.1109/TSP.2016.2539127. [Google Scholar] [CrossRef]

30. Y. Hua, L. Hu, and F. Chen, “An adaptive malicious punishment over secure distributed estimation under attacks,” in 2018 IEEE 4th Int. Conf. Comput. Commun. (ICCC), Chengdu, China, 2018, IEEE, 2018, pp. 2195–2199. [Google Scholar]

31. Y. Hua, F. Chen, S. Deng, S. Duan, and L. Wang, “Secure distributed estimation against false data injection attack,” Inf. Sci., vol. 515, no. 8, pp. 248–262, 2020. doi: 10.1016/j.ins.2019.12.016. [Google Scholar] [CrossRef]

32. F. Chen, T. Shi, S. Duan, L. Wang, and J. Wu, “Diffusion least logarithmic absolute difference algorithm for distributed estimation,” Signal Process., vol. 142, no. 5, pp. 423–430, 2018. doi: 10.1016/j.sigpro.2017.07.014. [Google Scholar] [CrossRef]