African Bison Optimization Algorithm: A New Bio-Inspired Optimizer with Engineering Applications

1  Introduction

There are lots of complex computational problems in the fields of scientific computing, socioeconomics, and engineering which exhibit a high degree of non-linearity, non-differentiability, discontinuity, and high complexity [1]. In many cases, the conventional optimization algorithms that rely on analysis are inadequate for solving these problems. As a result, many new metaheuristic optimization algorithms are explored to overcome the above problems.

Nature has evolved over billions of years through genetic evolution to perfectly demonstrate its efficiency and magic. Meanwhile, humans have learned a great scale from natural systems to develop new algorithms and models for solving complex problems [2–4]. Nature-inspired metaheuristic optimization algorithms can be categorized into four groups, biological evolution-based, natural physics-based, human-based, and biological swarm-based approaches (See Fig. 1).

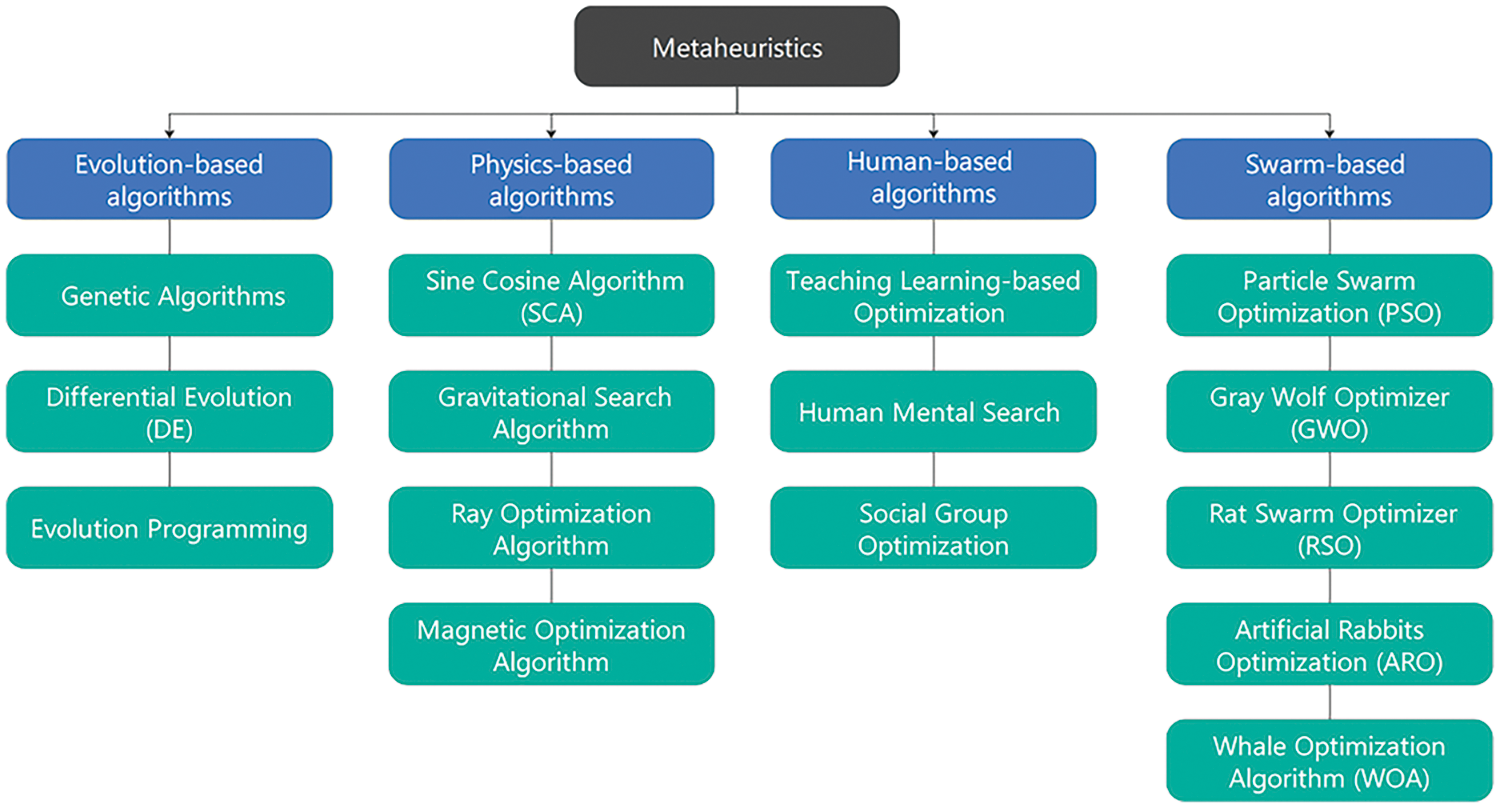
Figure 1: Metaheuristics classification

Evolution-based algorithms mimic natural evolutionary processes, including reproduction, mutation, recombination, and selection. Genetic Algorithms [5] stand out as a popular technique that draws inspiration from Darwin’s theory of evolution and simulates its principles. Other popular algorithms are Differential Evolution (DE) [6] and Evolution Programming [7].

Physics-based algorithms are derived from fundamental principles of the natural world. These physical phenomena are represented by objects such as sound, light, force, electricity, magnetism, and heat. The most popular algorithm is the Sine Cosine Algorithm (SCA) [8]. Other popular algorithms are Gravitational Search Algorithm [9], and Magnetic Optimization Algorithm [10].

Human-based algorithms draw inspiration from a variety of human activities, including cognition and physical behaviors. There are teaching-learning based optimization [11], Human Mental Search [12], and Social Group Optimization [13].

Swarm-based algorithms emulate the social behaviors exhibited by animals. Among these techniques, Particle Swarm Optimization (PSO) [14], Whale Optimization Algorithm (WOA) [15], and Gray Wolf Optimizer (GWO) [16] have gained tremendous popularity. In recent years, new algorithms such as Flower Pollination Algorithm (FPA) [17], Chimp Optimization Algorithm (CHOA) [18], Rat Swarm Optimizer (RSO) [19], Tunicate Swarm Algorithm (TSA) [20], Reptile Search Algorithm (RSA) [21], and Artificial Rabbits Optimization (ARO) [22] are proposed.

All swarm-based optimization algorithms share common properties: exploration and exploitation. The tradeoff between exploration and exploitation has been a central issue in the field of evolutionary computation and optimization research. It is crucial for minimizing computational costs and achieving efficient results. Therefore, optimization algorithms must possess the capability to explore the global space and exploit local regions. The No Free Lunch (NFL) states that there is no algorithm that can solve all optimization problems well [23]. In other words, an algorithm can have brilliant results in a specific class of problems but fails to solve other problems.

The above-mentioned facts inspire us to propose a novel algorithm with swarm intelligence characteristics for solving optimization problems. In this paper, the proposed African Bison Optimization (ABO) algorithm is inspired by the survival behaviors of African bison, including foraging, jousting, mating, and eliminating from the herd. As far as we know, these behaviors are proposed for the first time, and there is no similar study in the literature. The African Buffalo Optimization algorithm models the organizational skills of African buffalos by two basic sounds, waaa and maaa when they are finding food sources [24]. Although the African buffalo and bison are related species, ABO proposed in this paper is based on completely different principles.

The main contributions of this paper can be summarized as follows:

•   A swarm-based African Bison Optimization (ABO) is proposed and the survival strategies of bison are investigated and modeled mathematically.

•   The proposed ABO is implemented and tested on 23 benchmark test functions.

•   The performance of ABO is compared with some classical and latest optimizers.

•   The efficiency of ABO is examined for solving the real-world engineering problems with constraints.

The rest of the paper is arranged as follows: Section 2 shows the biological characteristics of the African bison and introduces the proposed ABO algorithm. In Section 3, the performance and efficiency of ABO are tested by using benchmark test functions. The results of the algorithm on five constrained real-world engineering problems are discussed in Section 4. Section 5 provides a comprehensive conclusion of the study, along with future research directions.

2  African Bison Optimization Algorithm

2.1 African Bison

African bison is a genus of animals in the even-toed ungulates, bovidae, with five subspecies. As shown in Fig. 2, it has characteristics of a broad chest, strong limbs, a large head, and long horns. The African bison is widely distributed throughout most of sub-Saharan Africa. Their habitats are extensive, including open grasslands, savannas with drinking water, and lowland rainforests.

Figure 2: African Bison in nature

African bison are social animals, and only old or injured individuals will be broken away from the herd. The strongest bison becomes the leader and enjoys the right to eat the best grains. African bison cannot live without water, so they are rarely far away from water. They often hide in the shade, or dip in pools or mud to keep their bodies at a cooler temperature. To drink and feed, African bison often live near water. When food and water are plentiful, they will soak their entire body in water and reduce activities significantly to avoid high temperatures. Jousting and Mating take place in the rainy season when the temperature is comfortable and the food is abundant. Parts of the survival behaviors of the African bison described above are shown in Figs. 3–5.

Figure 3: Foraging behavior

Figure 4: Bathing behavior

Figure 5: Jousting behavior

2.2 Mathematical Model and Algorithm

This subsection focuses on the mathematical modeling of foraging, jousting, mating, and eliminating of African bison herd, and provides a detailed description of ABO.

2.2.1 Initialization

In the initialization part, a uniformly distributed population is generated by random initialization, and this approach can be implemented by the following equation:

Xi=Xmin+rand∗(Xmax−Xmin)(1)

where Xi is the position of i-th individual, rand is a random number in the range from 0 to 1, and Xmin and Xmax are the lower and upper bounds of the problem, respectively.

In Eq. (2), the members of the bison population are represented through a population matrix. In this matrix, each row represents a potential solution, while the columns correspond to the suggested values for the variables of the problem.

X=[X1⋮Xi⋮XN]=[x1,1⋯x1,j⋯x1,d⋮⋱⋮⋮xi,1⋯xi,j⋯xi,d⋮⋮⋱⋮xN,1⋯xN,j⋯xN,d](2)

where X is the population matrix, N and d represent population size and individual dimension, respectively. xi,j is the j-th dimension of the i-th individual.

In ABO, each individual is metaphorically represented as a bison, serving as a potential solution to the given problem. The fitness values are determined by using a vector in Eq. (3).

F=[F1⋮Fi⋮FN]=[F(X1)⋮F(Xi)⋮F(XN)](3)

where Fi is the fitness value of the i-th individual. F is the vector of these fitness values.

2.2.2 Cluster and Finding the Best Individual

In ABO, the population is divided into two subgroups with the same size N/2: male and female (See Fig. 6). In the herd, the position of the best individual also represents the place where the richest food source is located in. Therefore, we define the best position as the location of the richest food source and it is denoted as XGbest (See Fig. 7).

Figure 6: Examples of population grouping

Figure 7: The definition of the best individual

2.2.3 Defined the Satiety Rate and Temperature

African bison are very sensitive to temperature. When the temperature is high and food is plentiful, they soak their body in the water and reduce activities. They tend to breed during the rainy season when the temperature is suitable and food is plentiful. Individuals are competing for the right to mate. Inspired by above behaviors, we use the satiety rate (S) and temperature (Q) to balance the exploration and exploitation in ABO, and defined by Eqs. (4) and (5):

S=2∗sin((3t/2T)∗π)(4)

Q=cos(−((T−t)/T)∗π/2)(5)

where the S is used for the balance of the exploration and exploitation phase, which has values from −2 to 2. Q is used for the balance of the development phase and it has values from 0 to 1. The current and maximum number of iterations are denoted by t and T, respectively.

2.2.4 Exploration Phase

If |S|< Threshold_1 (Threshold_1 = 0.5), it means that the individuals are hungry. They will randomly update their position to find food. This behavior happens in the male and female subgroups and is modeled by Eqs. (6) and (7):

Xit+1=(Xrandt∗S)+A∗((Xmax−Xmin)∗R1)∗R23(6)

A=cos((Frand/Fi)∗π)∗R3(7)

where Xrandt is the current position of a random individual, R1 and R2 are random numbers between [−1, 1], respectively. A represents the bison’s ability to find food. Frand and Fi are fitness values of random and current one, respectively. R3 is a random number between [−5, 5].

2.2.5 Exploration Phase

If |S|≥ Threshold_1, it means that food and water are enough. The bison will be bathing, jousting, mating, and eliminating according to the temperature level (Q).

If Q≥ Threshold_2 (Threshold_2 = 0.6), it means that food and water are enough but the temperature is high. The bison will soak their body in water and reduce activities to avoid high temperatures. We define this behavior as bathing behavior. It is represented by Eq. (8) in the male and female subgroups:

Xit+1=2∗(XGbestt−Xit)∗R4+exp(R5∗Q5)∗cos(Q∗2π)(8)

where XGbestt is the best position in the herd, R4 and R5 are the random numbers between [0, 2], respectively.

If Q < Threshold_2, it means that food and water are enough and the temperature is suitable for surviving. Then, the herd enters the jousting stage, and the winner has the right to mate.

The bison jousting behavior is represented by Eqs. (9) and (10) in the male and female subgroups:

J=XSbestt−XSbestt∗(rand∗Xit2)∗(cos(Xit)+sin(Xit))∗R65(9)

Xit+1=XSbestt−J∗R7(10)

where J is the fighting power of bison in the population. R6 is a random number between [−0.01, 0.01], R7 is a random number between [0, 2], and XSbestt denotes the position of the best individual in the male or female subgroup.

The mating behavior of male bison is represented by Eqs. (11) and (12):

MM=cos(Fi_f/Fi_m)(11)

Xi_mt+1=Xi_mt+sin(2π∗R8)∗R8∗MM∗(Xi_mt−Xi_ft)(12)

where MM is the mating ability of male individuals, Fi_m and Fi_f are the fitness values of the current male and female individual, respectively. Xi_mt and Xi_ft denote the current position in the male and female population, respectively. R8 is a random number between [0, 1].

The mating behavior of female bison is achieved by the following expressions:

MF=sin(Fi_m/Fi_f)(13)

Xi_ft+1=Xi_ft+cos(2π∗R9)∗R9∗MF∗(Xi_ft−Xi_mt)(14)

where MF is the mating ability of female individuals and R9 is a random number between [0, 1].

The eliminating behavior means the aged or injured individuals will consciously detach themselves from the herd, thus allowing the entire population to remain at the highest level of competence. This behavior is represented by the following Eq. (15):

Xworstt=Xmin+R10∗(Xmax−Xmin)(15)

where Xworstt represents the eliminating of the old or injured individuals from the population. R10 is a random number between [0, 1].

2.2.6 The ABO Pseudo-Code

The above behaviors are mathematically modeled in this paper to construct ABO. To show the iterative process of ABO more clearly, Algorithm 1 gives the pseudo-code of the algorithm.

2.3 Computational Complexity

The complexity of an algorithm is determined by the population size (n), number of iterations (T), and problem dimensionality (d). The computational complexity of ABO can be summarized into the following three stages: the initialization of the population, the calculation of the fitness, and the position update of the individuals. It can be expressed as: O(ABO) = O(Initialization) + O(Function evaluation) + O(Location update of the individuals) = O(n + Tn + Tnd).

2.4 Parameters Threshold_1 and Threshold_2 Sensitivity Analysis

The Threshold_1 and Threshold_2 are the key parameters to balance the exploration and exploitation stages of ABO. This section analyzes the sensitivity of the parameter Threshold_1 and Threshold_2 by setting different values. The results are shown in Table 1, where the Threshold_1 and Threshold_2 are set to (0, 0.4), (0.5, 0.6), (1, 0.8) and (2, 1), respectively. The performance of (0.5, 0.6) is the best compared with others.

2.5 The Survival Behaviors Analysis

ABO is inspired by the survival behaviors of the African bison. The foraging behavior drives the individuals to search for local optimal solutions randomly. The bathing behavior enables the individuals to fully explore near the local optimal solutions, thus improving the quality of the solution. Through jousting and mating behavior, the population can produce better individuals, so that ABO can converge to the optimal value faster. The worst individual in the population is eliminated and replaced by the elimination behavior, so the whole population can always maintain diversity in the iteration.

3  Experimental Results and Discussion

This section presents the results of experiments conducted on 23 benchmark functions to demonstrate the performance superiority of ABO. The experimental results of ABO are compared with those of nine other metaheuristic optimization algorithms.

3.1 Benchmark Test Functions

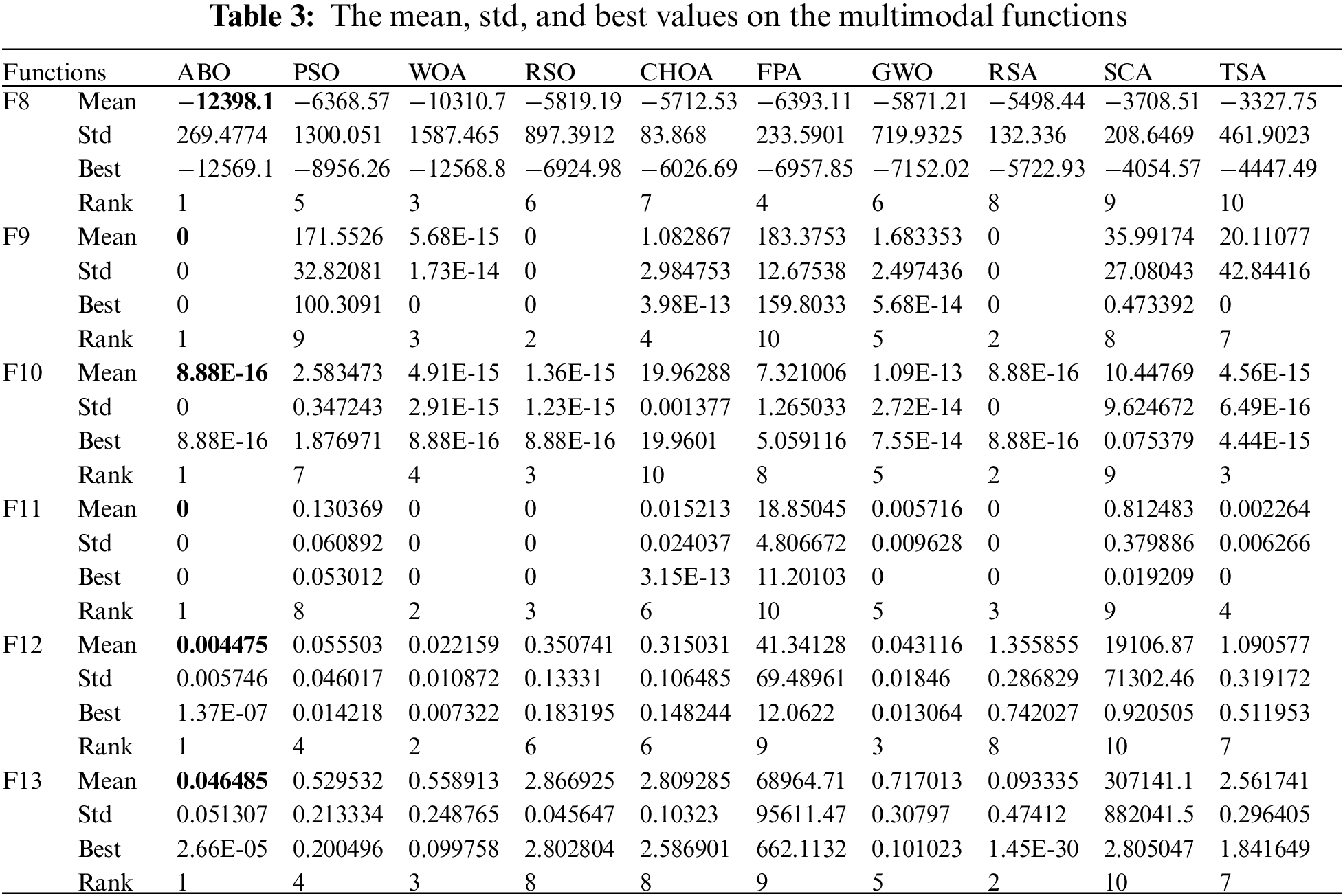
To comprehensively evaluate the performance of ABO in terms of optimization, we test it on 23 benchmark functions. These functions can be classified into three main categories: Unimodal, Multimodal, and Fixed-dimension multimodal [25]. The presence of a single global optimum in Unimodal (F1–F7) benchmark functions serves as a valuable test for evaluating the exploration capability of the algorithm under consideration. The optimization algorithms’ diversification capabilities are shown by using the Multimodal (F8–F13) and Fixed-dimension multimodal (F14–F23) benchmark functions. Details about these functions can be found in [15].

3.2 Experimental Setup

The parameters of the other algorithms (PSO, GWO, CHOA, SCA, RSA, FPA, WOA, RSO, and TSA) are derived from the corresponding papers. The experimentation process and algorithms have been carried out on an i5 processor operating at 2.60 GHz and 16 GB of RAM.

3.3 Performance Comparison

To ensure an equitable comparison, we maintain a consistent population size of 30 individuals across all optimization algorithms and perform 500 generations. The mean, std, best result, and ranking after 30 independent runs of each algorithm are presented in Tables 2–4, where the ranking is determined based on the mean.

According to Table 2, the mean, std, and best of ABO on F1–F4 are all zero, which indicates that the algorithm can accurately find the global optimum of these functions each time. For F5 and F6, ABO can achieve significantly better optimal solutions than other algorithms. On F7, ABO is similarly competitive, with optimization results next only to TSA and RSA. The results demonstrate that ABO has significant advantages in exploitation compared to other algorithms.

According to the experimental results in Tables 3 and 4, ABO achieves very competitive results. On F8–F13, F15, and F20–F23, the optimization results of ABO are better than other algorithms, and the ranking is 1. On the other functions, the proposed algorithm also achieves satisfactory results, and the optimization performance is better than most algorithms. These results illustrate that ABO has excellent performance in terms of exploration capability.

3.4 Convergence Analysis

Fig. 8 shows the convergence curves of ABO with the other algorithms on benchmark test functions. It can be seen that ABO has three different convergence behaviors. In the early stages, it explores fully the given search space, allowing the highest convergence efficiency. In the second stage, the algorithm initiates iterative processes aimed at approaching the optimal solution until reaching the maximum allowed number of iterations. The last stage is the iterative process of rapid convergence of ABO, where it finds the optimal solution to the benchmark test problem through full exploration and exploitation. The above analysis show that ABO achieves a good balance of exploration and exploitation than other metaheuristic optimization algorithms.

Figure 8: Convergence plots for various benchmark functions

3.5 Statistical Testing

In addition to utilizing standard statistical measures such as mean and standard deviation, we have also employed the Wilcoxon sum rank test for further analysis and comparison [26]. It is used to assess whether ABO’s results statistically significantly differ from that of other competing algorithms. In this paper, the sample size of the Wilcoxon sum rank test is 30 and the confidence interval is 95%. The significance of an algorithm can be determined by examining its p-value. If the p-value of a algorithm is lower than 0.05, it signifies that the algorithm exhibits statistical significance when compared to the other algorithms under consideration. Table 5 shows the Wilcoxon sum rank test for the 23 benchmark test functions. From the experimental results of the table, it can be obtained that the p-value obtained from the comparison of ABO with the other algorithms is much less than 0.05 in general for all the benchmark functions. It can be shown that ABO has a significant difference compared with other algorithms.

4  Engineering Problems

In this section, ABO is tested also with five constrained engineering design problems: Pressure vessel design, Rolling element bearing design, Tension/compression spring design, Cantilever beam design, and Gear train design. Mathematical models of these engineering design problems can be found in the corresponding literature. For the constraint problem, this paper uses the widely used penalty function method to deal with the constraints [22]. To ensure an equitable comparison, we maintain a consistent population size of 30 individuals across all optimization algorithms and perform 500 generations.

4.1 Pressure Vessel Design Problem

The pressure vessel design is an engineering problem initially presented by Kannan and Kramer [22]. As shown in Fig. 9, this design challenge involves the optimization of a pressure vessel’s manufacturing cost, encompassing expenses related to materials, forming processes, and welding. The primary objective is to minimize the overall cost of producing the pressure vessel while ensuring it meets all design constraints and performance requirements.

Figure 9: Pressure vessel design

We use ABO to optimize the problem and compare the experimental results with other algorithms. The results presented in Table 6 illustrate the statistical outcomes of the algorithms in terms of the optimal and variables. By utilizing ABO, it is possible to obtain the optimal function value of f1= 6285.942, with corresponding structure variables x= (0.8140874, 0.4987349, 41.91206, 179.0077). The results show that ABO can find the optimal design of the pressure vessel problem with the lowest manufacturing cost compared with other algorithms.

4.2 Rolling Element Bearing Design

The design of rolling element bearings is a well-known engineering benchmark problem introduced by Rao and Tiwari in 2007. This problem aims to maximize the dynamic load-carrying capacity of rolling bearings, as illustrated in Fig. 10. The problem is framed by ten constraints and ten design variables.

Figure 10: Rolling element bearing design

Table 7 shows the optimal values and optimal variables obtained by these algorithms on this problem. ABO can obtain the optimal function value f2=−85380.5266 with the structure variables x= (125.6417, 21.40225, 11, 0.515001, 0.5154961, 0.4021139, 0.6181131, 0.3026727, 0.03466326, 0.6025443). The outcomes reveal that ABO can identify the optimal configuration for the design of rolling element bearings, maximizing their dynamic load-carrying capacity.

4.3 Tension/Compression Spring Design Problem

The design problem introduced by Arora focuses on tension/compression spring design. This design problem, as depicted in Fig. 11, provides a visual representation of the optimization process for the spring design. The primary goal is to minimize the weight of the spring while ensuring it meets specific constraints, including minimum deflection, vibration frequency, and shear stress.

Figure 11: Tension spring design

The comparison results between ABO and other algorithms are given in Table 8. The superiority of ABO is evident as it attains the optimal solution with the variables set at x= (0.0518975, 0.36175, 11), resulting in an objective function value of f3= 0.012666.

4.4 Cantilever Beam Design

The cantilever beam design is given in Fig. 12. The design objective of the problem is to minimize the weight of the cantilever beam and the constraint is to satisfy a vertical displacement constraint [22]. It consists of five hollow members. Each unit is defined by distinct variables with a specific thickness, thus rendering this design problem to encompass five decision variables.

Figure 12: Cantilever beam design

Table 9 presents the optimized outcomes obtained from ABO as well as other competing methods. Notably, ABO achieves the optimal function value of f4=1.3422 by utilizing the structure variables x= (5.8506, 5.4175, 4.4818, 3.6739, 2.0867). The conclusion that can be drawn is that ABO finds the optimal set of structural parameters for the cantilever beam design.

4.5 Gear Train Design

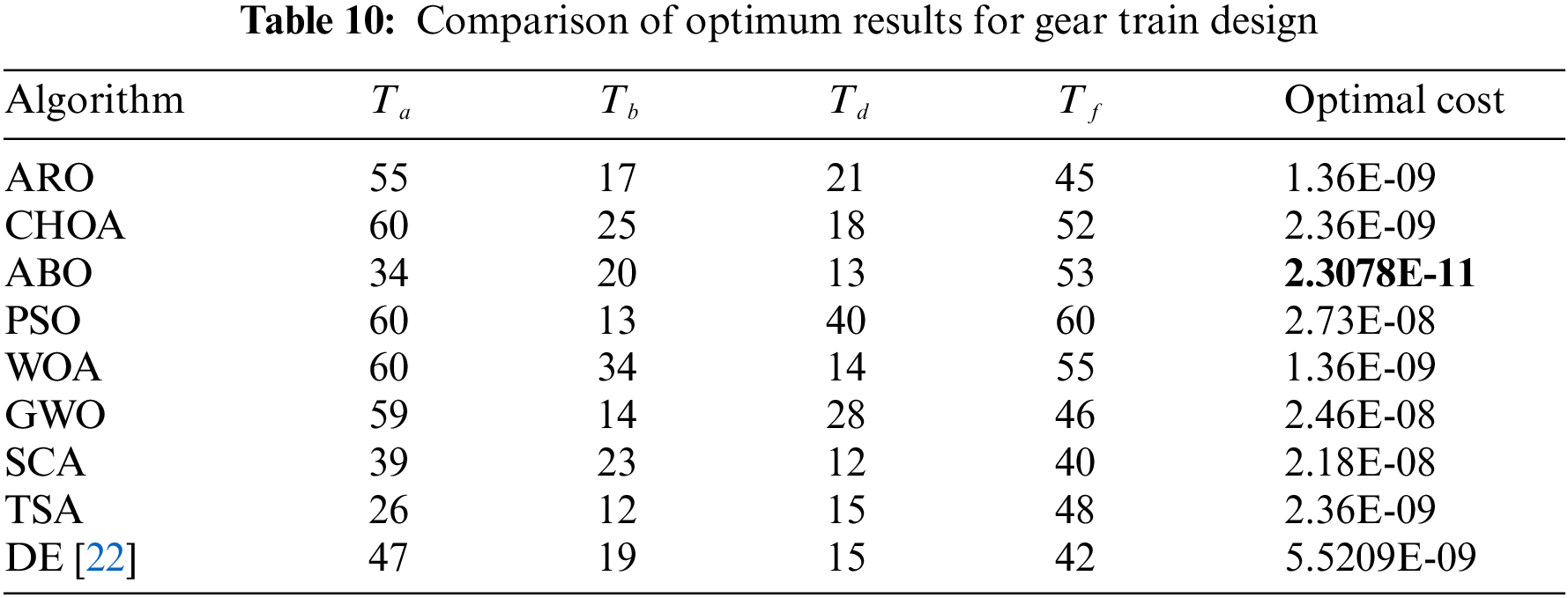
The last engineering design problem is the gear train design [11]. As shown in Fig. 13, this problem has four integer decision variables, where Ta, Tb, Td, and Tf represent the number of teeth of four different gears, respectively. Its objective is to minimize the transmission ratio cost of the gear train. The transmission ratio is given as Tb/Ta⋅Td/Tf.

Figure 13: Gear train design

The comparison results obtained by ABO and other optimizers are given in Table 10. The optimal gear parameters obtained by the ABO optimization for this problem are x= (34, 20, 13, 53) and the transmission ratio is f5= 2.3078E−11. The results demonstrate that ABO outperforms other algorithms in identifying the optimal design for the gear train, effectively minimizing the cost of transmission ratio.

5  Conclusion

In this paper, a new metaheuristic optimization algorithm based on biological population, named ABO, is proposed. ABO mimics the foraging, jousting, mating, and eliminating behaviors of the African bison herd while introducing the parameters S and Q to balance the exploration and exploitation phases. To test the ability of ABO in global exploration and local exploitation, it is tested on 23 benchmark test functions and five constrained real-world engineering problems.

The experimental results of ABO demonstrate its superiority and the ability to solve real-world engineering problems, especially when compared to other existing algorithms. In future work, ABO could be further developed and modified to explore other aspects. One direction is to combine ABO with other algorithms to extend it to more fields, such as neural networks, image processing, etc. Another direction is to expand ABO into a multi-objective optimization tool. Incorporating multi-objective optimization capabilities could greatly enhance the utility of ABO, making it well-suited for solving complex problems with multiple objectives.

Acknowledgement: None.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China (Grant No. U1731128); the Natural Science Foundation of Liaoning Province (Grant No. 2019-MS-174); the Foundation of Liaoning Province Education Administration (Grant No. LJKZ0279); the Team of Artificial Intelligence Theory and Application for the financial support.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jian Zhao, Kang Wang; data collection: Jian Zhao; analysis and interpretation of results: Jian Zhao, Kang Wang, Jiacun Wang; draft manuscript preparation: Kang Wang, Jian Zhao, Xiwang Guo, Liang Qi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. C. Fu, “Optimization via simulation: A review,” Ann. Oper. Res., vol. 53, pp. 199–247, 1994. doi: 10.1007/BF02136830. [Google Scholar] [CrossRef]

2. X. Cui, X. Guo, M. Zhou, J. Wang, S. Qin and L. Qi, “Discrete whale optimization algorithm for disassembly line balancing with carbon emission constraint,” IEEE Robot. Autom. Lett., vol. 8, no. 5, pp. 3055–3061, 2023. doi: 10.1109/LRA.2023.3241752. [Google Scholar] [CrossRef]

3. C. Lu, L. Gao, and X. Li, “Chaotic-based grey wolf optimizer for numerical and engineering optimization problems,” Memetic Comp., vol. 12, pp. 371–398, 2020. doi: 10.1007/s12293-020-00313-6. [Google Scholar] [CrossRef]

4. C. Lu, L. Gao, and J. Yi, “Grey wolf optimizer with cellular topological structure,” Expert. Syst. Appl., vol. 107, pp. 89–114, 2018. doi: 10.1016/j.eswa.2018.04.012. [Google Scholar] [CrossRef]

5. J. H. Holland, “Genetic algorithms,” Sci. Am., vol. 267, no. 1, pp. 66–73, 1992. doi: 10.1038/scientificamerican0792-66. [Google Scholar] [CrossRef]

6. R. Storn and K. Price, “Differential evolution: A simple and efficient heuristic for global optimization over continuous spaces,” J. Glob. Optim., vol. 11, no. 4, pp. 341–359, 1997. doi: 10.1023/A:1008202821328. [Google Scholar] [CrossRef]

7. D. Corne and M. A. Lones, Evolutionary Algorithms. Cham: Springer International Publishing, 2018,pp. 409–430. [Google Scholar]

8. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowl. Based Syst., vol. 96, pp. 120–133, 2016. doi: 10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

9. E. Rashedi, H. Nezamabadi-Pour, and S. Saryazdi, “GSA: A gravitational search algorithm,” Inf. Sci., vol. 179, no. 13, pp. 2232–2248, 2009. doi: 10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

10. M. -H. Tayarani-N and M. -R. Akbarzadeh-T, “Magnetic-inspired optimization algorithms: Operators and structures,” Swarm Evol. Comput., vol. 19, pp. 82–101, 2014. doi: 10.1016/j.swevo.2014.06.004. [Google Scholar] [CrossRef]

11. R. V. Rao, V. J. Savsani, and D. Vakharia, “Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems,” Comput.-Aided Design, vol. 43, no. 3, pp. 303–315, 2011. doi: 10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]

12. E. K. Mousavirad, “Human mental search: A new population-based metaheuristic optimization algorithm,” Appl. Intell., vol. 47, no. 4, pp. 850–887, 2017. doi: 10.1007/s10489-017-0903-6. [Google Scholar] [CrossRef]

13. N. Satapathy, “Social group optimization (SGO): A new population evolutionary optimization technique,” Complex Intell. Syst., vol. 2, no. 4, pp. 173–203, 2016. doi: 10.1007/s40747-016-0022-8. [Google Scholar] [CrossRef]

14. R. Poli, J. Kennedy, and T. Blackwell, “Particle swarm optimization,” Swarm Intell., vol. 1, no. 1, pp. 33–57, 2007. doi: 10.1007/s11721-007-0002-0. [Google Scholar] [CrossRef]

15. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

16. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, 2014. doi: 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

17. X. S. Yang, Flower Pollination Algorithm for Global Optimization. Berlin, Heidelberg: Springer, 2012,pp. 240–249. [Google Scholar]

18. M. Khishe and M. Mosavi, “Chimp optimization algorithm,” Expert. Syst. Appl., vol. 149, pp. 113–338, 2020. doi: 10.1016/j.eswa.2020.113338. [Google Scholar] [CrossRef]

19. G. Dhiman, M. Garg, A. Nagar, V. Kumar, and M. Dehghani, “A novel algorithm for global optimization: Rat swarm optimizer,” J. Ambient Intell. Humaniz. Comput., vol. 12, no. 8, pp. 8457–8482, 2021. doi: 10.1007/s12652-020-02580-0. [Google Scholar] [CrossRef]

20. S. Kaur, L. K. Awasthi, A. Sangal, and G. Dhiman, “Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization,” Eng. Appl. Artif. Intell., vol. 90, pp. 103–541, 2020. doi: 10.1016/j.engappai.2020.103541. [Google Scholar] [CrossRef]

21. L. Abualigah, M. A. Elaziz, P. Sumari, Z. W. Geem, and A. H. Gandomi, “Reptile search algorithm (rsa): A nature-inspired meta-heuristic optimizer,” Expert. Syst. Appl., vol. 191, pp. 116–158, 2022. doi: 10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]

22. L. Wang, Q. Cao, Z. Zhang, S. Mirjalili, and W. Zhao, “Artificial rabbits optimization: A new bio-inspired algorithm for solving engineering optimization problems,” Eng. Appl. Artif. Intell., vol. 114, 2022, Art. no. 105082. doi: 10.1016/j.engappai.2022.105082. [Google Scholar] [CrossRef]

23. F. A. Hashim and A. G. Hussien, “Snake optimizer: A novel meta-heuristic optimization algorithm,” Knowl. Based Syst., vol. 242, pp. 108–320, 2022. doi: 10.1016/j.knosys.2022.108320. [Google Scholar] [CrossRef]

24. J. B. Odili, M. N. M. Kahar, and S. Anwar, “African buffalo optimization: A swarm-intelligence technique,” Procedia Comput. Sci., vol. 76, pp. 443–448, 2015. doi: 10.1016/j.procs.2015.12.291. [Google Scholar] [CrossRef]

25. X. S. Yang, A New Metaheuristic Bat-Inspired Algorithm. Berlin, Heidelberg: Springer, pp. 65–74, 2010. [Google Scholar]

26. F. Wilcoxon, Individual Comparisons by Ranking Methods. New York: Springer, 1992, pp. 196–202. [Google Scholar]

27. J. P. Savsani and V. Savsani, “Passing vehicle search (PVS): A novel metaheuristic algorithm,” Appl. Math. Model., vol. 40, no. 5, pp. 3951–3978, 2016. doi: 10.1016/j.apm.2015.10.040. [Google Scholar] [CrossRef]

28. M. Dorigo, M. Birattari, and T. Stutzle, “Ant colony optimization,” IEEE Comput. Intell. Mag., vol. 1, no. 4, pp. 28–39, 2006. doi: 10.1109/MCI.2006.329691. [Google Scholar] [CrossRef]