PSMFNet: Lightweight Partial Separation and Multiscale Fusion Network for Image Super-Resolution

1  Introduction

Single image super-resolution (SISR) seeks to generate a high-resolution (HR) image from its low-resolution (LR) counterpart by recovering lost information. The swift advancement of high-speed internet transmission has led to a surge in high-quality data, such as high-definition images and videos, resulting in the extensive application of SISR across various domains [1]. Consequently, devising an efficient and potent SR technique is crucial for enhancing the visual experience.

The progress of deep learning (DL) has led to the emergence of various SISR approaches that exhibit outstanding performance. The SRCNN [2] achieved superior performance compared to traditional methods using only three convolutional layers. On the basis of residual learning, the VDSR [3] was developed to a depth of 20 layers, while RCAN [4] goes a step further to 400 layers. These networks have achieved impressive performance, but their most significant drawback is the high computational cost, which is not conducive to the practical needs of resource-limited devices. On the other hand, the introduction of Transformer architecture has further developed the field of image restoration. For example, SwinIR [5] achieved more advanced performance than CNN models at the time. Although these models require high computational costs, they have also demonstrated the importance of non-local feature interactions in image reconstruction.

To reduce model parameters and complexity, many lightweight SR networks have been proposed. These networks have employed various strategies to achieve high efficiency, including lightweight module design [1–3], neural network architecture search [4,5] structural reparameterization [6,7], knowledge distillation [8–10] and attention mechanisms [11–15]. They have implemented efficient architecture and modules to significantly reduce the parameters and complexity of the model, but there is still redundancy in the convolution operation. By reducing unnecessary calculations and developing more effective modules, we can construct a more efficient SR model.

Motivated by the aforementioned observations, this paper has proposed a novel lightweight SR network, called partial separation and multiscale fusion network (PSMFNet). By optimizing convolution operations and introducing multiscale feature modulation, it achieves a favorable balance between performance and complexity. Specifically, PSMFNet uses partial convolution (PConv) [16] to construct its basic modules, which reduces a significant amount of calculation redundancy while maintaining feature extraction capability. PConv is advantageous for efficient SR. Moreover, the implementation of long-range dependencies and attention mechanisms can effectively boost the performance of SR networks. In this paper, a multi-scale feature fusion block (MFFB) is proposed to achieve this goal. The MFFB combines a multi-scale spatial feature modulation mechanism and spatial attention enhancement group to deeply explore features in both spatial and channel directions, resulting in better image detail restoration. This paper also proposes an efficient inverse residual block (EIRB) to enhance the extraction of local contextual information.

The specific contributions of this paper are as follows:

Standard convolutions, including grouped convolutions, often involve redundant computations. In order to improve the utilization of convolutions and ensure reconstruction effectiveness, local convolutions are introduced to construct basic modules, demonstrating their effectiveness for super-resolution tasks;

Multiscale feature information is crucial for image reconstruction. In order to address the issue of single-feature extraction, a multiscale feature fusion block is proposed to capture more representative features in both spatial and channel directions. It is combined with effective inverse residual blocks to compensate for the weak local contextual information interaction capability of the network;

In this paper, EIRB and MFFB have been merged into a lightweight feature enhancement block (LFEB) and used to construct PSMFNet. Benchmark dataset evaluations indicate that our PSMFNet strikes an advantageous balance between its performance and the complexity of the model.

2  Related Work

2.1 Deep Learning-Based Image Super-Resolution

With the introduction of the groundbreaking SRCNN [17] network, deep learning has experienced substantial progress in the domain of super-resolution. For example, VDSR [18] has achieved better performance by deepening the network layer. EDSR [19] showed that batch normalization (BN) layers are unnecessary for SR tasks and remove them to enhance the expressive power of model. CARN [20] incorporated dense connections into the network to offset the loss resulting from recursive networks. Lately, image SR tasks have exhibited superior performance compared to CNN models when utilizing the ViT [21] architecture. SwinIR [22] introduces a baseline model based on the Swin Transformer and incorporates it as the feature extraction module in the composite model. The powerful feature extraction capability enables the model to achieve outstanding performance. The GRL [23] network architecture utilizes self-attention mechanism and integrates channel feature information to model image features at different levels of global, regional, and local scopes, leading to improved image restoration results. However, these methods [22,24–27] have brought expensive computational costs along with their excellent performance, making deployment on resource-constrained devices more challenging. This has also prompted developers to develop more efficient SR methods.

2.2 Efficient Image Super-Resolution

Aiming to lower the computational cost associated with the model, many effective SR methods utilizing CNN have been introduced [28,29]. FSRCNN [30] adopted a post-upsampling method to reduce complexity while maintaining performance. ESPCN [31] developed a sub-pixel convolution that directly transforms LR images into HR images at the end, thereby reducing time complexity. PAN [14] proposed a pixel attention approach that greatly reducing the parameters and achieving better SR performance. IMDN [9] developed an information distillation block to separate and refine features, thereby enhancing the restoration of image details. RFDN [10] reevaluated the network structure of IMDN and introduced a shallow residual block as the foundational module of RFDN. By incorporating feature distillation connections, RFDN achieved a lighter architecture compared to IMDN. ShuffleMixer [32] explored image feature extraction from a different perspective by employing large convolutions and channel-wise shuffle operations instead of stacking multiple small-kernel convolutions. It also introduces Fused-MBConvs to enhance local connectivity, effectively restoring image details. RLFN [33] simplified the feature aggregation operation of RFDN by employing three layers of standard convolution for residual connections, enhancing the learning of local features and significantly improving the model’s runtime. FMEN [34] designed a high-frequency attention block to enhance image details, and applied structural reparameterization to reduce feature fusion and further accelerate network inference speed. BSRN [35] built the model based on blueprint separable convolution [36], reducing redundant operations in depthwise convolution (DWConv) but also increasing inference time. To incorporate the benefits of ViT, SAFMN [37] proposed a lightweight spatially adaptive feature modulation module to learn long-range dependencies from multiscale features. The above methods have made improvements to the model in different aspects, but there is still room for trade-offs.

3  Method

3.1 Network Architecture

The architecture of Partial Separation and Multiscale Fusion Network (PSMFNet) that has been proposed in this paper is shown in Fig. 1. The PSMFNet is composed of three primary components: Shallow feature extraction, multiple stacked lightweight feature enhancement modules (LFEB), and an image reconstruction module. In the initial segment, a 3 × 3 convolutional layer is employed to extract shallow features from the input image. In this paper, the ILR has been represented as an input to PSMFNet, and the operation can be represented as:

F0=Hsfe(ILR)(1)

where Hsfe(⋅) denotes the module for extracting shallow features, and F0 is the extracted shallow features. A stack of LFEBs is then utilized to extract deep features from F0. This process can be denoted as:

Fn=HLFEBn(Fn−1)=HLFEBn((HLFEBn−1(…HLFEB0(F0)))(2)

where HLFEBn(⋅) denotes the n-th LFEB function, while Fn−1 and Fn represent the input and output features of the n-th LFEB, respectively.

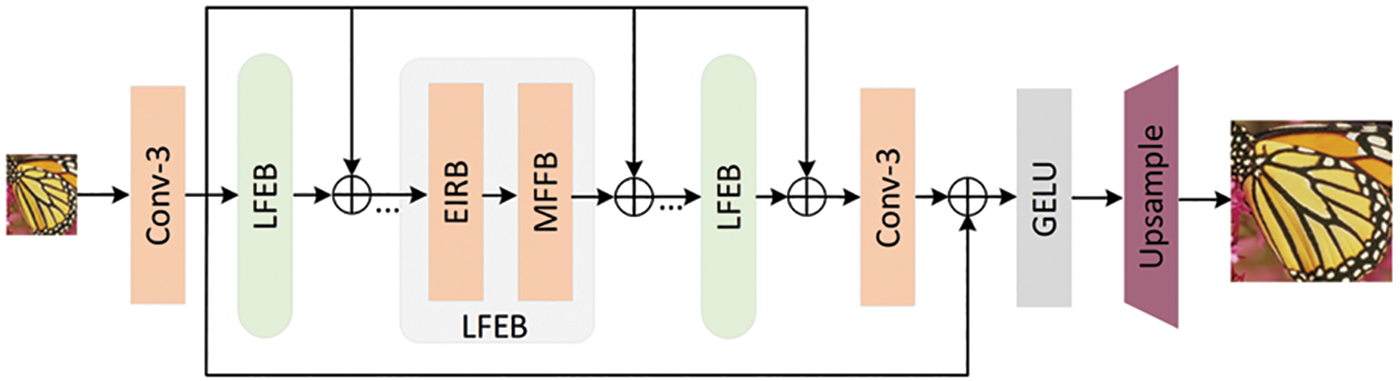
Figure 1: The architecture of partial separation and multiscale fusion network (PSMFNet)

Subsequently, in this paper, 3 × 3 convolutional layers have been used to smooth the extracted depth feature maps and introduce long jump connections before image reconstruction. Finally, the image reconstruction module is employed to produce the final output ISR, which can be depicted as:

ISR=Hrec(Hsmooth(Fn)+F0)(3)

where Hrec(⋅) denotes the image reconstruction module function, encompassing a 3 × 3 convolutional layer and a sub-pixel convolution [31] operation. Hsmooth(⋅) represents the 3 × 3 convolutional operation. We optimized the model using the L1 loss function, which can be expressed as:

L1(ISR,IHR)=∑i=1m|ISR−IHR|(4)

where IHR denotes the ground-truth image. The L1 loss calculates the sum of the absolute differences between the actual values and the target values. In image super-resolution tasks, the goal is to make the generated image as close as possible to the real high-resolution image. The L1 loss calculates the error between the values at corresponding pixel positions in the super-resolved and high-resolution images.

3.2 Efficient Inverted Residual Block

In previous work, MobileNetv2 [3] proposed a depthwise convolution-based inverted residual block. Although the introduction of depthwise convolution (DWConv) [2] reduces the computational complexity and parameters of the model, expanding the channels increases the time required for convolutional operations. Recently, a novel approach [16] has been developed, which utilizes an efficient module based on PConv. This module directly connects to the inverted residual block after PConv, eliminating the DWConv in the residual block and reducing the computational burden of convolution, resulting in faster inference speed.

Given an input I∈RH×W×C1, convolution operation is performed on it using a kernel of size k × k, resulting in an output O∈RH×W×C2. In standard convolution, the number of floating point operations is:

FLOPsregular=k2×H×W×C1×C2(5)

From Fig. 2, it is evident that when r is 4, which means one-fourth of the input features undergo convolution, the FLOPs of local convolution is:

FLOPsPConv=k2×H×W×C14×C24(6)

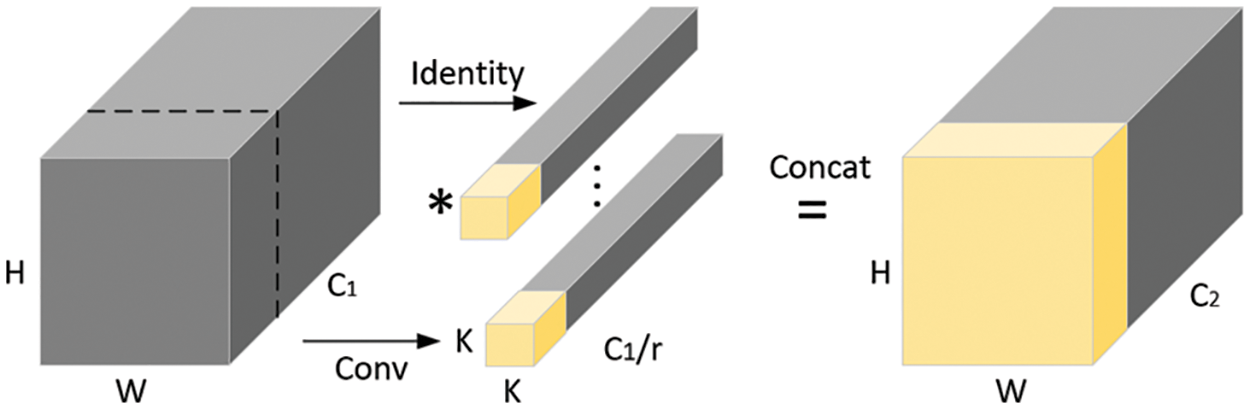
Figure 2: Partial convolution

In general, the number of output channels in convolution matches the number of input channels. In this scenario, the FLOPs of local convolution is only 1/16 of the standard convolution.

This module has been further optimized in this paper according to specific SR tasks. The batch normalization layer has been shown to potentially cause unexpected artifacts in image reconstruction [19,38], so we removed it. Additionally, GELU [39] has become the preferred choice for recent SR methods [22,35,37]. As shown in Fig. 3, given the input feature Fin, the entire structure can be described by as:

Fshortcut=Fin(7)

FEIRB=HEIRB(Fin)+Fshortcut(8)

where Fshortcut denotes the shortcut operation, HEIRB(⋅) denotes the EIRB function, and FEIRB represents the output feature of EIRB.

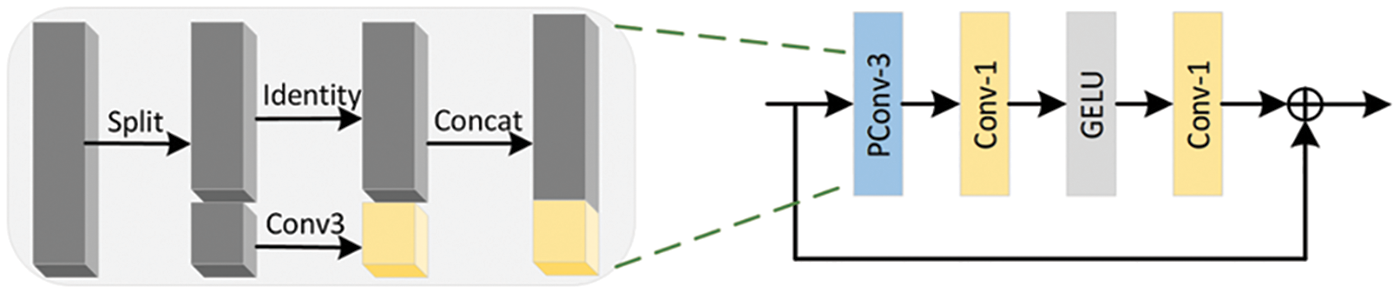
Figure 3: The structure of EIRB. Partial convolution (PConv) only extracts features through convolution on a portion of the input channels, without affecting the remaining channels

3.3 Multiscale Feature Fusion Block

Self-attention mechanisms [23–25] have the ability to capture long-range dependencies within neural networks and boost model performance. However, the adoption of self-attention mechanisms leads to a marked increase in parameters and computational complexity. Some researchers have proposed alternative approaches to self-attention mechanisms, such as the utilization of large convolutional kernels [40] or spatially adaptive feature modulation [37]. All of these methods share a common feature of utilizing DWConv, which results in a reduction of the feature extraction ability. Moreover, they frequently neglect the channel information of the image, which results in incomplete information for image reconstruction. Therefore, in this paper, we have proposed a lightweight multiscale feature fusion block (MFFB) that explores important features in the spatial and channel domains while learning long-range dependencies. As illustrated in the Fig. 4, MFFB focuses on a wider range of pixel information, ensuring the reconstruction of image details as much as possible.

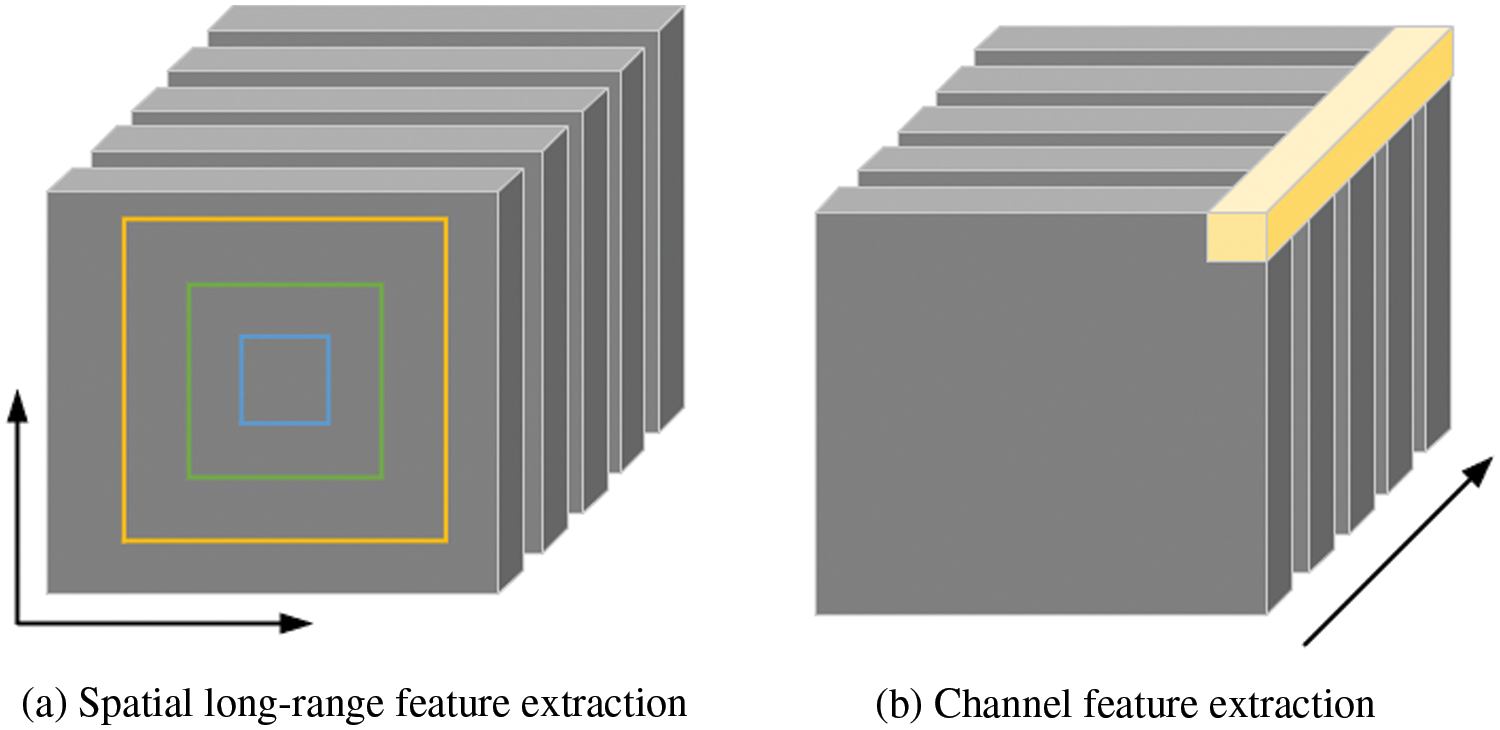
Figure 4: Multi-scale feature fusion

The MFFB primarily consists of multiscale spatial feature modulation (MSFM) block and channel attention enhancement group (CAEG). As shown in Fig. 5, the MFFB divides the features output by EIRB into three parts for processing. In the first part, spatial features are extracted from a long-range perspective through MSFM. Firstly, the features undergo channel split operations, and then each feature component is sent to different levels of spatial feature extraction channels. This procedure can be expressed as:

[Fd0,Fd1,Fd2,Fd3]=Split(FEIRB)F0=Hpconv(Fd0)Fi=↑2i(Hpconv(↓12i(Fdi))),1≤i≤3(9)

where Split(⋅) represents channel split operation. Hpconv(⋅) represents the PConv operation. ↑2i represents upsampling the feature map to the original input size using nearest neighbor interpolation. ↓12i represents downsampling the input feature to a size of 12i. In this paper, we have concatenated features from different spatial levels, aggregated them using 1 × 1 convolution and activated them nonlinearly using GELU. This procedure can be expressed as:

Fpart1=GELU(Hpwconv(Concat([Fd0,Fd1,Fd2,Fd3])))(10)

where Fpart1 represents the output of MSFM, Hpwconv(⋅) and Concat(⋅) denote pointwise convolution (PWConv) and concatenation operations, respectively. In the second part, this paper has used Partial Convolutional Enhancement Group (PCEG) consisting of 3 × 3 PConv and PWConv to filter the input features and the process can be formulated as follows:

Fpart2=HPCEG(FEIRB)(11)

where Fpart2 denotes the output of PCEG, and HPCG(⋅) denotes the PCEG function. In the final part, CAEG is used to prevent the loss of channel information. CAEG consists of two parts, and in order to obtain useful channel information from deeper layers, we use PCEG for feature enhancement before CA [11]. This procedure can be formulated as:

Fpart3=HCA(HPCEG(FEIRB))(12)

where Fpart3 denotes the output of CAEG, and HCA(⋅) denotes the CA function.

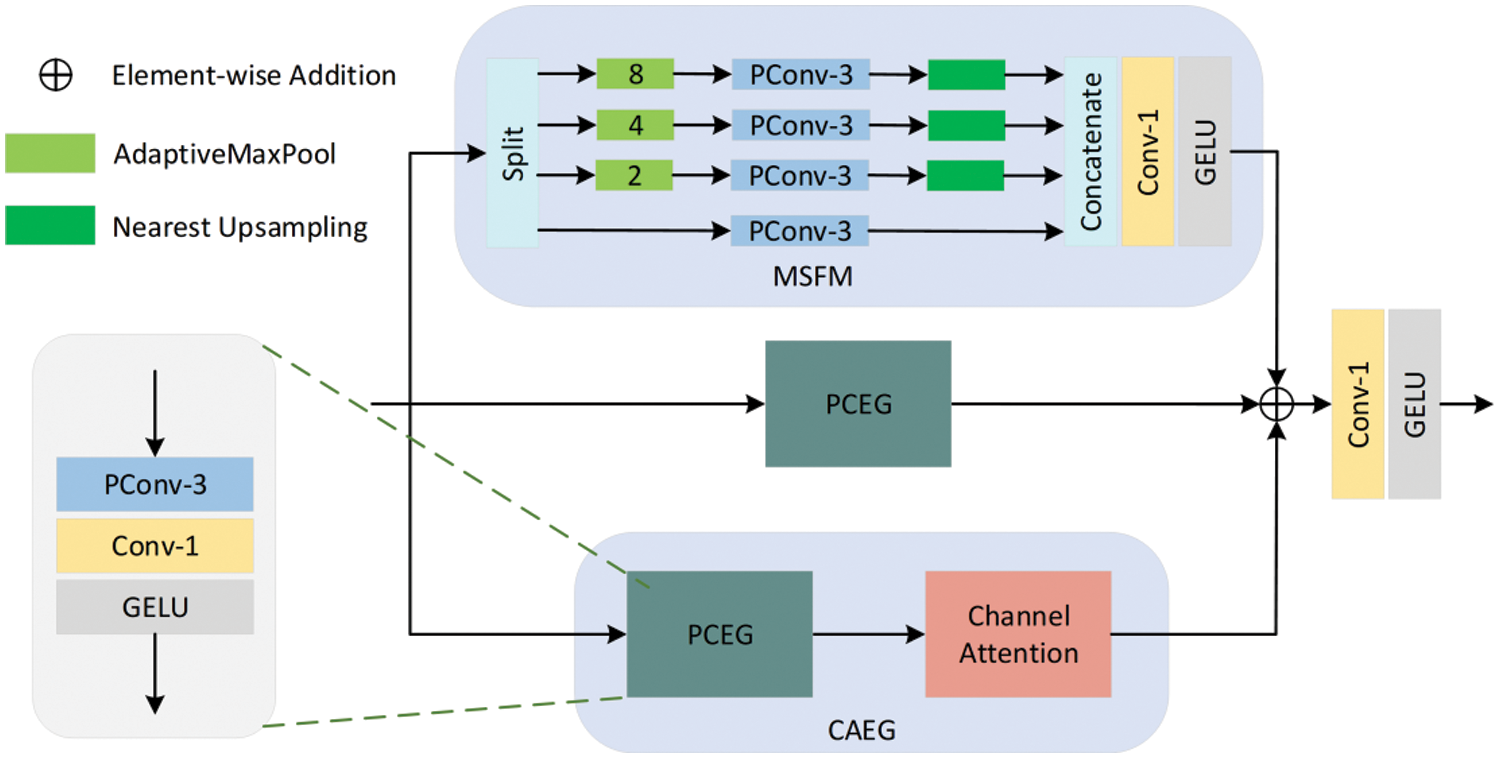
Figure 5: Global feature fusion block (MFFB)

After obtaining representative features, in this paper, they have been aggregated using 1 × 1 convolution method and normalized using GELU nonlinear function. The feature aggregation is formulated as:

FMFFB=GELU(Hpwconv(Fpart1+Fpart2+Fpart3))(13)

where FMFFB denotes the output of MFFB.

3.4 Image Reconstruction Module

The high-resolution images obtained by networks like SRCNN through bicubic interpolation may lead to increased time complexity. Therefore, in this paper, the PixelShuffle operation is used to upsample images.

As shown in Fig. 6, After the feature extraction module, a convolutional layer is utilized to generate r × r channel feature maps, where r represents the upsampling factor. Subsequently, PixelShuffle is employed to reorganize the r × r channel feature maps into an upsampled image of size W × r, H × r, where W and H denote the width and height of the low-resolution image, respectively.

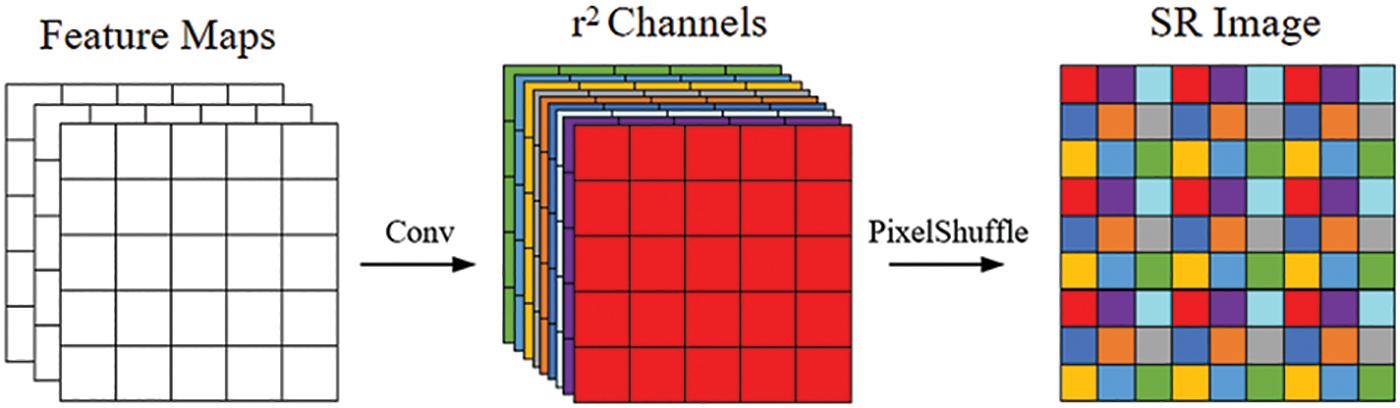
Figure 6: Image reconstruction module

4  Experiment

4.1 Datasets and Metrics

The training image collection consists of 800 images originating from DIV2K [41] and 2650 images derived from Flickr2K [19]. In this paper, our model has been evaluated using five commonly used benchmark datasets: Set5 [42], Set14 [43], BSD100 [44], Urban100 [45], and Manga109 [46].

Set5 and Set14 contain 5 and 14 test images, respectively, covering a variety of scenes and content. These images are used to comprehensively evaluate the performance of algorithms in different scenarios and settings. BSD100 contains 100 test images with higher complexity and diversity, designed to evaluate algorithms in real-world scenarios. Urban100 is a super-resolution reconstruction dataset tailored for urban landscapes, comprising 100 test images typically featuring buildings, streets, and cityscapes to assess algorithm performance in urban environments. Manga109 is a super-resolution reconstruction dataset specifically curated for manga images, which often exhibit unique styles and details, aimed at evaluating algorithm performance in handling manga-style images.

In this paper, Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) [47] have been used as evaluation metrics. All PSNR and SSIM values are computed on the Y channel of images converted to the YCbCr color space. Given the ground-true image IHR and the super-resolution image ISR, PSNR is defined as:

PSNR(IHR,ISR)=10log10⁡maxvalue2MSE(14)

where

MSE=1M×N∑i=1M∑j=1N(ISR(i,j)−IHR(i,j))2(15)

MaxValue represents the maximum pixel value, and M and N respectively denote the height and width. The definition of SSIM is as follows:

SSIM(IHR,ISR)=(2μhrμsr+c1)(2σhr⋅sr+c2)(μhr2+μsr2+c1)(σhr2+σsr2+c2)(16)

The variables μhr and μsr represent the mean grayscale value, σhr and σsr is the variance of the image, and σhr⋅sr is the covariance of the image. c1=(K1L)2 and c2=(K2L)2 are two constant terms, where L represents the range of pixel values.

4.2 Implementation Details

During the data augmentation process for training, this paper applied random rotations of 90, 180, and 270 to the images, as well as horizontal flipping. Furthermore, this paper randomly extracted 64 patches of 48 × 48 pixels from the LR images to serve as training inputs for the model. The model in this paper needs to balance the accuracy and complexity of the model. When the number of LFEB is 9, Param (K) is 435, FLOPs (G) is 24.5, and Acts (M) is 270, which is obviously higher than the current advanced SR method such as ShuffeMixer and does not meet the lightweight requirements. When LFEB is 7, Param (K) is 353, FLOPs (G) is 19.9, Acts (M) is 212, and the reconstruction quality cannot be guaranteed. Therefore, the number of LFEB selected in this paper is 8, which can improve the quality of image reconstruction as much as possible under the premise of lightweight. The proposed PSMFNet consists of 8 LFEBs with a channel number of 64, and PConv preserves three-quarters of the channels. This paper utilized the Adam [48] optimizer with β1=0.9 and β2=0.999 to solve the proposed model. The iteration quantity is fixed at 1 × 106. The initial learning rate is configured at 5 × 10−4, which is updated by the Cosine Annealing scheme [49]. All experiments are conducted using the Pytorch framework on a GeForce RTX 3090 GPU.

4.3 Ablation Study

This paper conducted extensive ablation experiments in this section to further evaluate the effectiveness of each component of PSMFNet. We trained all experiments based on ×4 PSMFNet with the same settings.

4.3.1 Effectiveness of the Partial Convolution

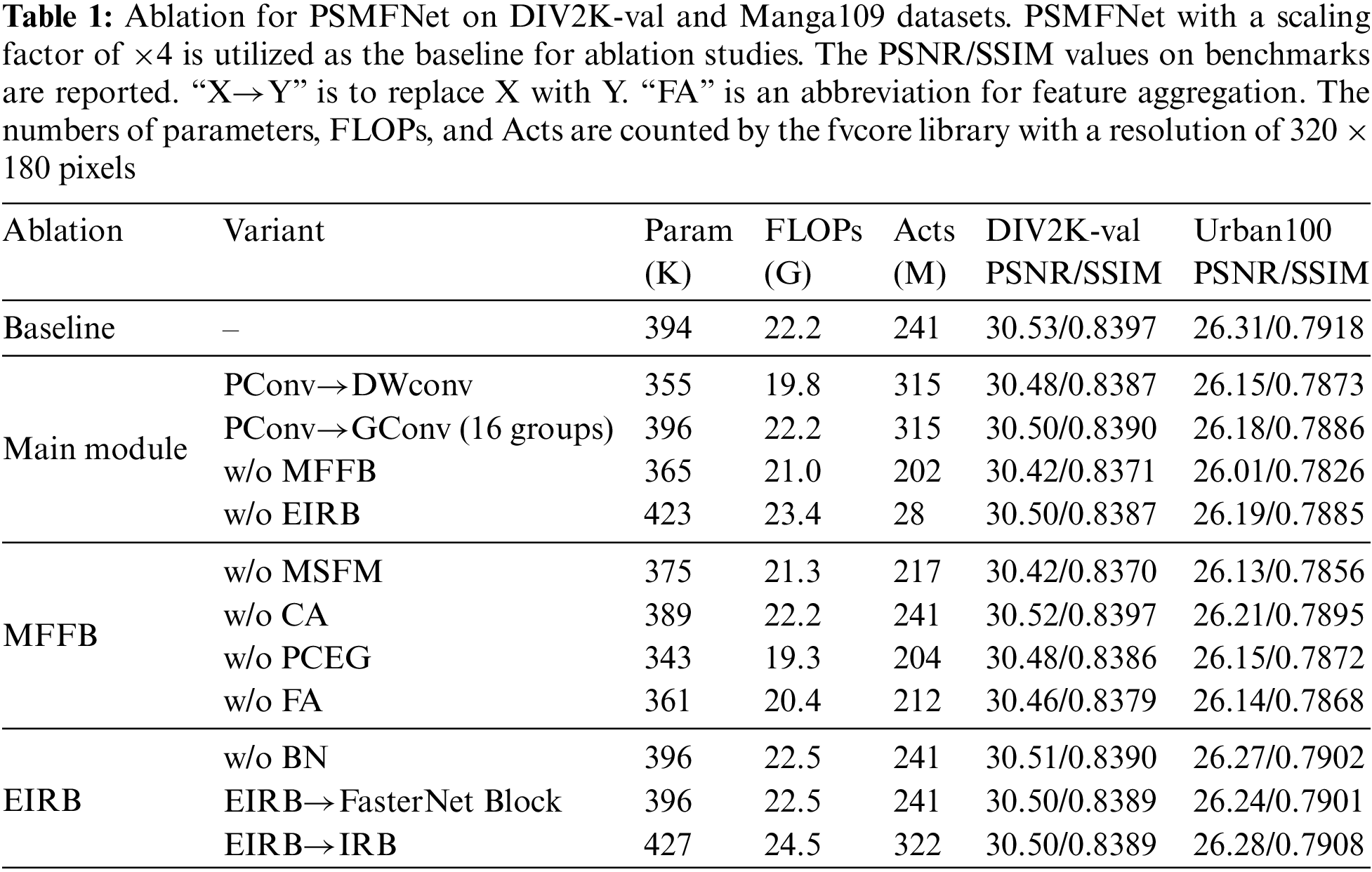
Unlike DWConv [2] and group convolution (GConv) [50], PConv only performs convolution on a portion of the input channels, while the remaining channels are preserved. Compared to standard convolution, PConv has fewer parameters and FLOPs, while also possessing superior spatial feature extraction capabilities compared to DWConv and GConv. As shown in Table 1, when PConv was replaced with DWConv in the backbone network, the PSNR decreased by 0.05 and 0.16 dB on the DIV2K-val and Urban100 datasets, respectively. Similarly, when GConv was used, the PSNR decreased by 0.03 and 0.13 dB on the same datasets after replacing PConv with DWConv in the backbone network. The experimental results demonstrate that PConv not only maximizes the feature extraction capabilities, but also positively contributes to subsequent modeling through the preserved features.

4.3.2 Effectiveness of the Lightweight Feature Enhancement Block

This paper visualized the feature maps in Fig. 7 to illustrate the effectiveness of LFEB. LFEB consists of two modules, MFFB and EIRB, which explore global and local features, respectively. To verify their importance, this paper conducted the following experiments: (1) Using only two MFFB blocks in LFEB, and (2) using only two EIRB blocks in LFEB. The reason for doing this is to ensure that the models have similar parameters and achieve a fairer comparison. In Table 1, w/o EIRB indicates the use of only two MFFBs in LFEB, while w/o MFFB indicates the use of only two EIRBs in LFEB. Table 1 shows that using only MFFB resulted in a decrease of 0.03 and 0.12 dB in PSNR on the DIV2K-val and Urban100 datasets, respectively, while using only EIRB resulted in a decrease of 0.11 and 0.3 dB in PSNR on the same datasets. As shown in Fig. 8, The decrease in performance indicates that using only GFFB or EIRB alone will result in the loss of some useful information, leading to a decrease in image reconstruction quality. However, using both modules simultaneously can fuse rich features and improve model performance.

Figure 7: Illustration of learned deep features from the LFEB ablation: (a) Input image; (b) Shallow features of input images; (c) The feature map after obtaining global information by MFFB; (d) The feature map after the supplementation of local information by EIRB

Figure 8: Effect of the MFFB and the EIRB in the LFEB for SISR

4.3.3 Effectiveness of the Efficient Inverse Residual Block

Compared to the FasterNet Block [16], the EIRB has made modifications by removing the BN layer [51]. Additionally, this paper have utilized the GELU [39] activation function to better suit the SR task. This paper will conduct a sequence of ablation experiments to show its ability to effectively extract local contextual information.

As shown in Table 1, this paper replaced EIRB with FasterNet Block, and the PSNR on the Urban100 dataset decreased by 0.07 dB. This performance decrease was due to the influence of the BN layer and activation function. When this paper replaced EIRB with IRB [3], although the performance only decreased by 0.03 dB after channel expansion through the inverse residual block, the corresponding parameter count and FLOPs increased by nearly 30 K and 2.0 G, respectively, and the activations (Acts) also increased by nearly 80 M. It can be observed that the expansion of channels in the inverse residual block leads to a significant convolutional computational burden. Additionally, a performance decrease of 0.04 dB was observed when a BN layer was added after the first PWConv. Therefore, the improved EIRB has a more efficient performance.

4.3.4 Effectiveness of the Multiscale Feature Fusion Block

The MFFB primarily consists of a multiscale spatial feature modulation block and channel attention enhancement group. As shown in Fig. 9, this module enables the model to integrate more diverse features. Here, this paper delved deeper into this module to uncover the reasons behind its effectiveness.

•   Multiscale spatial feature modulation. Here, “w/o MSFM” in Table 1 indicates that we replaced the MSFM in the MFFB with a PConv of kernel size 3 × 3. Without modulation of spatial features, a decrease of 0.18 dB in PSNR values was observed on the Urban100 dataset. It is evident that the lack of learning spatial long-range dependency features has a significant impact on performance;

•   Channel attention enhancement group. When only used CA [11] without PCEG to filter features, a decrease of 0.16 dB in PSNR values was observed on the Urban100 dataset. If only PCEG is left, MFFB lacks channel information, leading to a decrease in image modeling ability and a 0.1 dB decrease in PSNR value on the dataset;

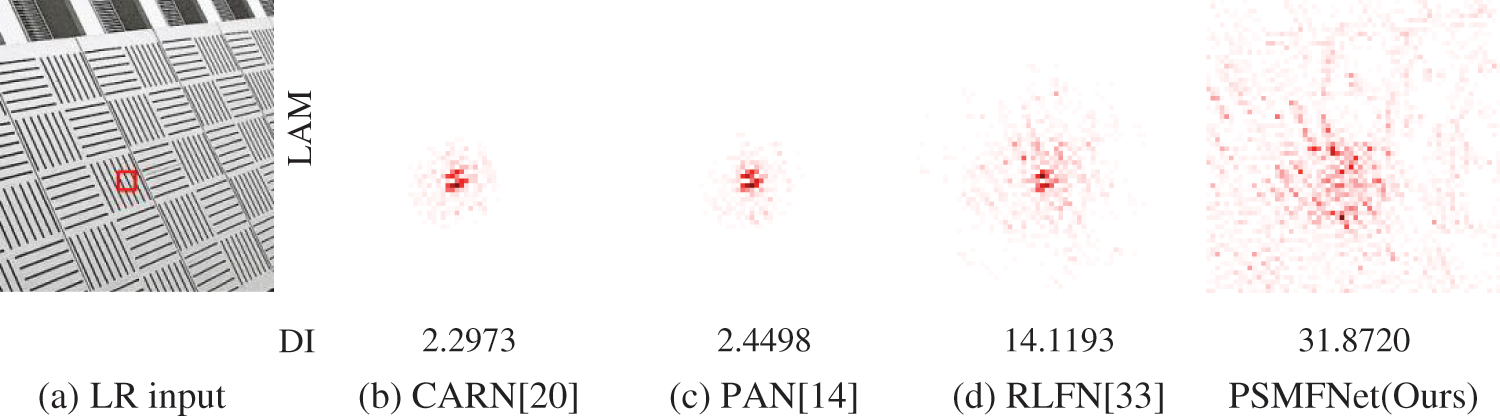
Figure 9: Comparison of local attribution maps (LAMs) [52] and diffusion indices (DIs) [52] between PSMFNet and other efficient SR models. The LAM outcomes highlight the significance of each pixel in the input LR image when processing the patches denoted by red boxes in SR. The DI value reflects the range of pixels involved. A larger DI value corresponds to a broader attention range. The proposed method can utilize more feature information

Feature aggregation. This paper used 1 × 1 convolution to aggregate spatial and channel information. After feature aggregation, the PSNR on the Urban100 dataset increased by 0.17 dB, demonstrating the necessity of aggregating spatial and channel features.

4.4 Comparisons with State-of-the-Art Methods

To gauge the performance of PSMFNet, this paper conducted a comparison with multiple state-of-the-art lightweight image super-resolution approaches, including SRCNN [17], ESPCN [31], VDSR [18], LapSRN [53], CARN [20], IDN [8], IMDN [9], PAN [14], LAPAR-A [54], RFDN [10], ShuffleMixer [32], RLFN [33]. Fig. 10 shows that PSMFNet achieves comparable performance at lower complexity.

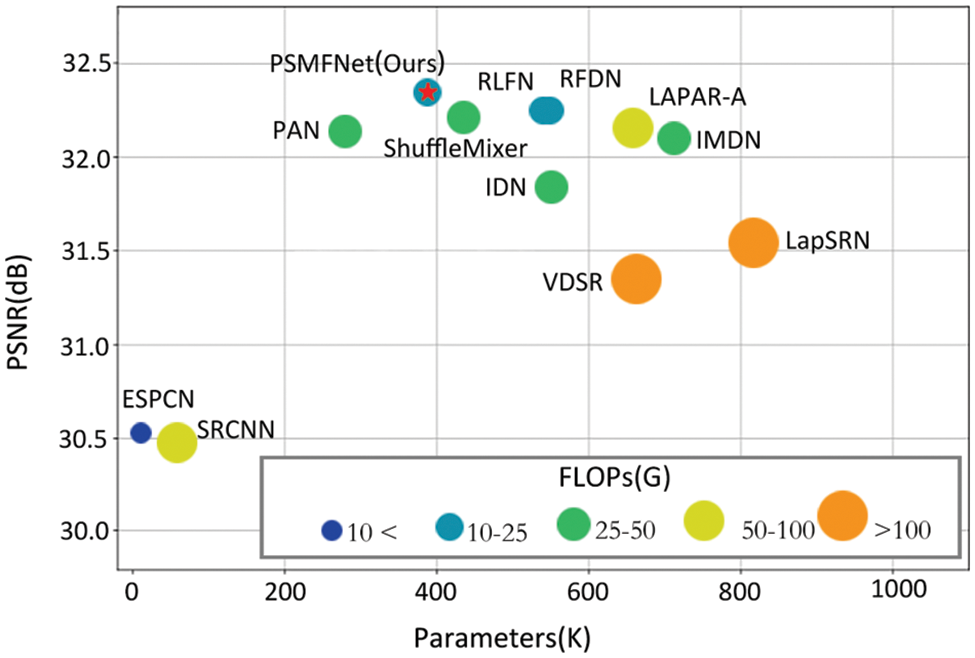
Figure 10: The complexity and performance of proposed PSMFNet model are compared with other lightweight methods on the Set5 dataset for ×4 SR

4.4.1 Quantitative Comparisons 1

The quantitative comparison findings for various upscaling factors on five benchmark datasets are presented in Table 2. Along with the PSNR/SSIM indicators, this paper also included the number of parameters (Params) and floating-point operations (FLOPs). Benefiting from the simple yet efficient structure, the proposed PSMFNet achieved comparable performance with fewer parameters. Taking the example of ×4 SR on the Urban100 dataset, PSMFNet has approximately 75% fewer parameters than CARN, 28% fewer parameters than RFDN, and 27% fewer parameters than RLFN. The results of quantitative comparison show that PSMFNet achieves the highest accuracy with fewer parameters.

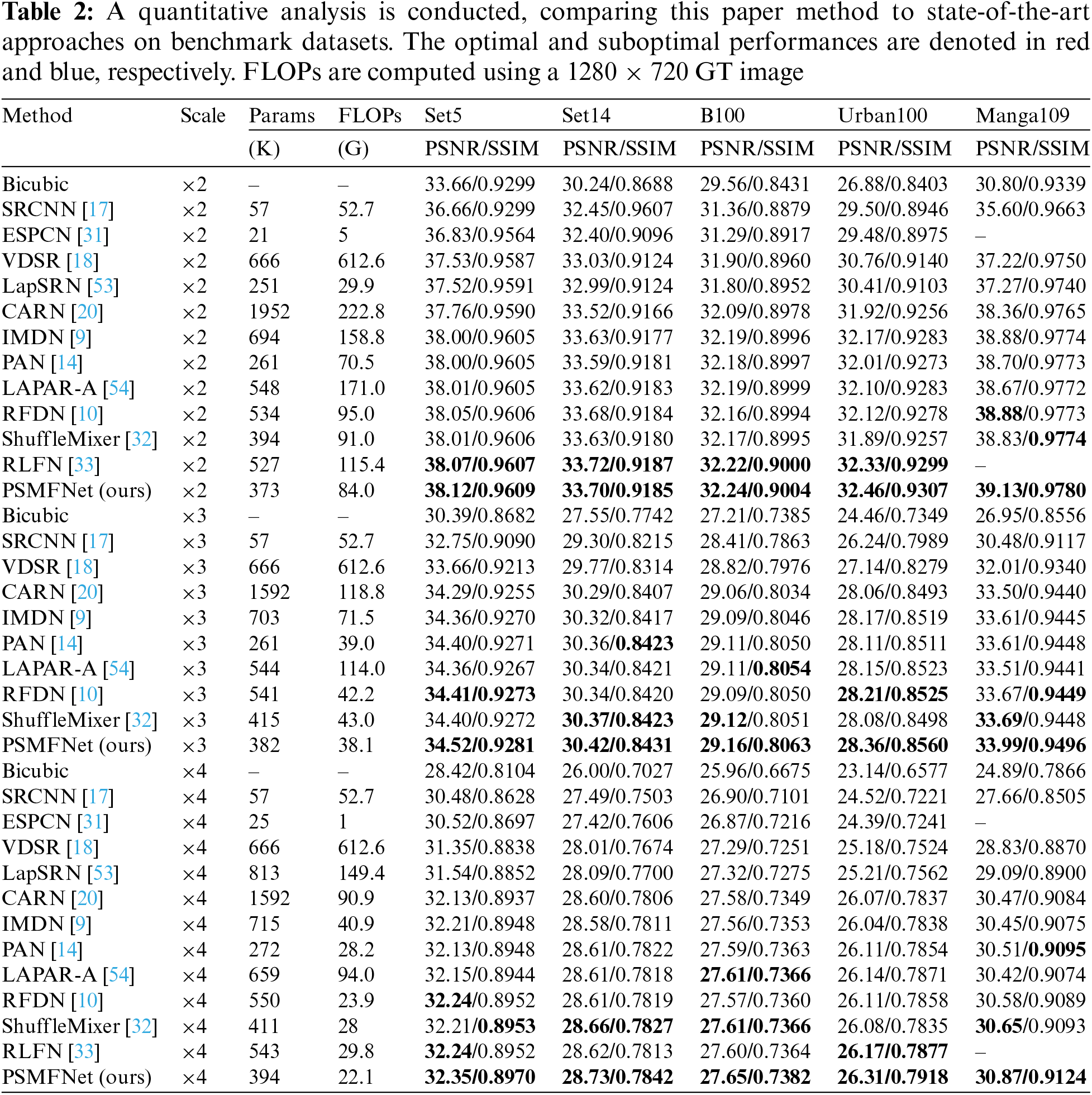
4.4.2 Quantitative Comparisons 2

In addition to quantitative evaluation, this paper conducted a qualitative analysis of proposed PSMFNet by comparing it with state-of-the-art methods through visual comparison. It can be observed in Fig. 11 that the images restored by PSMFNet exhibit superior performance in terms of texture details. The results validate that the proposed PSMFNet, which utilizes multiscale feature fusion, can explore deeper and more effective features.

Figure 11: Visual comparisons for ×4 SR on the Urban100 dataset

Urban100 is a dataset primarily focused on urban landscapes. To validate the performance of the model in other scenarios, images from the Set14, Manga109, and B100 datasets were selected for visualization, as shown in Fig. 12.

Figure 12: visual comparisons of ×4 SR on other SR datasets

4.4.3 Memory and Running Time Comparisons

To further validate the efficiency of PSMFNet, this paper compared it with five representative efficient SR methods, including CARN [21], IMDN [13], PAN [17], RFDN [14], and RLFN [51]. This paper conducted tests on the DIV2K-val ×4 dataset and recorded the maximum GPU memory consumption (GPU Mem) and average running time (Avg.Time) during the inference process to further validate the performance of PSMFNet. A comparison of memory consumption and runtime has been presented in Table 3, where PSMFNet’s GPU consumption is only 30% of that of the CARN series and 37% of that of IMDN; Compared with PAN, our method has a similar running speed but significantly reduces GPU memory consumption. To fully leverage the advantages of Partial Convolution, this paper employed Pointwise Convolution to enhance the fusion of features. However, Pointwise Convolution is a computationally intensive operation in convolutional neural networks, which may impact the utilization of hardware resources and consequently affect the execution speed of tasks. This leads to certain drawbacks in terms of runtime compared to RFDN and RLFN. Tables 2 and 3 demonstrate that proposed PSMFNet achieves a favorable balance between model complexity and performance.

5  Conclusion

In this paper, a simple and efficient model has been proposed to solve the problem of efficient image super-resolution, which is called Partial Separation and Multiscale Fusion Network (PSMFNet). The lightweight feature enhancement module (LFEB), based on partial convolution (PConv), is constructed as the basic module of PSMFNet. The efficient and lightweight architecture design effectively reduces redundant convolution operations. This module consists of a multiscale feature fusion block (MFFB) and an efficient inverse residual block (EIRB). This paper designed MFFB can aggregate spatial and channel features and learn long-range dependencies, while EIRB supplements the model with local contextual information extraction. By modeling the image at multiple levels, including local, global, channel, and spatial levels, PSMFNet fully leverages the rich feature information in the image. The wide-ranging experimental results indicate that our PSMFNet offers a more competitive performance using a smaller number of parameters relative to the state-of-the-art efficient SR approaches.

Acknowledgement: We would like to express our sincere gratitude to all those who have contributed to this research project in various ways.

Funding Statement: This research was funded by Guangdong Science and Technology Program under Grant No. 202206010052, Foshan Province R & D Key Project under Grant No. 2020001006827 and Guangdong Academy of Sciences Integrated Industry Technology Innovation Center Action Special Project under Grant No. 2022GDASZH-2022010108.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Shuai Cao , Jianan Liang; data collection: Jinglun Huang; analysis and interpretation of results: Zhishu Yang, Yongjun Cao; draft manuscript preparation: Shuai Cao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Jianan Liang, upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflict of interest to report regarding the present study.

References

1. J. Shu, S. Wang, S. Yu, and J. Zhang, “CFSA-Net: Efficient large-scale point cloud semantic segmentation based on cross-fusion self-attention,” Comput. Mater. Contin., vol. 77, no. 3, pp. 2677–2697, 2023. doi: 10.32604/cmc.2023.045818. [Google Scholar] [CrossRef]

2. C. Dong, C. C. G. Loy, K. M. He, and X. O. Tang, “Learning a deep convolutional network for image super-resolution,” in Proc. ECCV, Zurich, Switzerland, 2014, pp. 184–199. [Google Scholar]

3. J. Kim, J. K. Lee, and K. M. Lee, “Accurate image super-resolution using very deep convolutional networks,” in Proc. CVPR, Las Vegas, USA, 2016, pp. 1646–1654. [Google Scholar]

4. Y. Zhang, K. Li, K. Li, L. Wang, and B. Zhong, “Image super-resolution using very deep residual channel attention networks,” in Proc. ECCV, Munich, Germany, 2018, pp. 294–310. [Google Scholar]

5. J. Y. Liang, J. Z. Cao, and G. L. Sun, “SwinIR: Image restoration using swin transformer,” in Proc. ICCV, Montreal, Canada, 2021, pp. 1833–1844. [Google Scholar]

6. J. Si and S. Kim, “PP-GAN: Style transfer from korean portraits to ID photos using landmark extractor with GAN,” Comput. Mater. Contin., vol. 77, no. 3, pp. 3119–3138, 2023. doi: 10.32604/cmc.2023.043797. [Google Scholar] [CrossRef]

7. Y. Harjoseputro, I. Yuda, and K. P. Danukusumo, “MobileNets: Efficient convolutional neural network for identification of protected birds,” Int. J. Adv. Sci., Eng. Inf. Technol., vol. 10, no. 6, pp. 2290–2296, 2020. [Google Scholar]

8. M. Sandler, A. Howard, M. Zhu, and A. Zhmoginov, “MobileNetV2: Inverted residuals and linear bottlenecks,” in Proc. CVPR, Salt Lake, USA, 2018, pp. 4510–4520. [Google Scholar]

9. D. H. Song, C. Xu, X. Jia, and Y. Y. Chen, “Efficient residual dense block search for image super-resolution,” in Proc. AAAI, New York, USA, 2020, pp. 12007–12014. [Google Scholar]

10. X. Chu, B. Zhang, H. Ma, R. Xu, and Q. Li, “Fast, accurate and lightweight super-resolution with neural architecture search,” in Proc. ICPR, Milan, Italy, 2021, pp. 59–64. [Google Scholar]

11. N. Ullah, J. A. Khan, S. Almakdi, M. S. Alshehri, and M. Al Qathrady, “A lightweight deep learning-based model for tomato leaf disease classification,” Comput. Mater. Contin., vol. 77, no. 3, pp. 3969–3992, 2023. doi: 10.32604/cmc.2023.041819. [Google Scholar] [CrossRef]

12. Y. Wang, “Edge-enhanced feature distillation network for efficient super-resolution,” in Proc. CVPRW, New Orleans, LA, USA, 2022, pp. 776–784. [Google Scholar]

13. Z. Hui, X. Wang, and X. Gao, “Fast and accurate single image super-resolution via information distillation network,” in Proc. CVPR, Salt Lake, USA, 2018, pp. 723–731. [Google Scholar]

14. Z. Hui, X. Gao, Y. Yang, and X. Wang, “Lightweight image super-resolution with information multi-distillation network,” in Proc. ACM, Aizu Wakamatsu, Tokyo, Japan, 2019, pp. 2024–2032. [Google Scholar]

15. J. Liu, J. Tang, and G. Wu, “Residual feature distillation network for lightweight image super-resolution,” in Proc. ECCV, 2020, pp. 2359–2368. [Google Scholar]

16. S. Balatti, S. Ambrogio, R. Carboni, and V. Milo, “Physical unbiased generation of random numbers with coupled resistive switching devices,” IEEE Trans. Electron Devices, vol. 63, no. 5, pp. 2029–2035, 2016. doi: 10.1109/TED.2016.2537792. [Google Scholar] [CrossRef]

17. J. Liu, W. J. Zhang, Y. T. Tang, and J. Tang, “Residual feature aggregation network for image super-resolution,” in Proc. CVPR, Seattle, USA, 2020, pp. 2356–2365. [Google Scholar]

18. H. Zhao, X. Kong, J. He, Y. Qiao, and C. Dong, “Efficient image super-resolution using pixel attention,” in Proc. ECCV, 2020, pp. 56–72. [Google Scholar]

19. H. Zang, Y. Zhao, C. Niu, and H. Zhang, “Attention network with information distillation for super-resolution,” Entropy, vol. 24, no. 9, 2022, Art. no. 1226. doi: 10.3390/e24091226. [Google Scholar] [PubMed] [CrossRef]

20. J. Chen, S. H. Kao, H. He, and W. Zhuo, “Run, don’t walk: Chasing higher FLOPS for faster neural networks,” arXiv:2303.03667, 2023, doi: 10.48550/arXiv.2303.03667. [Google Scholar] [CrossRef]

21. N. Ahn, B. Kang, and K. A. Sohn, “Fast, accurate, and lightweight super-resolution with cascading residual network,” in Proc. ECCV, Munich, Germany, 2018, pp. 256–272. [Google Scholar]

22. F. Y. Kong, M. X. Li, and S. W. Liu, “Residual local feature network for efficient super-resolution,” in Proc. CVPRW, New Orleans, USA, 2022, pp. 765–775. [Google Scholar]

23. J. Gu and C. Dong, “Interpreting super-resolution networks with local attribution maps,” in Proc. CVPR, 2021, pp. 9195–9204. [Google Scholar]

24. B. Lim, S. Son, H. Kim, and S. Nah, “Enhanced deep residual networks for single image super-resolution,” in Proc. CVPRW, Hawaii, USA, 2017, pp. 1132–1140. [Google Scholar]

25. Z. Liu, Y. T. Lin, Y. Cao, and H. Hu, “Swin Transformer: Hierarchical vision transformer using shifted windows,” in Proc. ICCV, Montreal, Canada, 2021, pp. 9992–10002. [Google Scholar]

26. S. W. Zamir, A. Arora, S. Khan, and M. Hayat, “Restormer: Efficient transformer for high-resolution image restoration,” in Proc. CVPR, New Orleans, USA, 2022, pp. 5718–5729. [Google Scholar]

27. J. Zhang, Y. Zhang, J. Gu, and Y. Zhang, “Accurate image restoration with attention retractable transformer,” arXiv:2210.01427, 2022, doi: 10.48550/arXiv.2210.01427. [Google Scholar] [CrossRef]

28. S. Shi, J. Gu, and L. Xie, “Rethinking alignment in video super-resolution transformers,” in Proc. NeurIPS, New Orleans, LA, USA, 2022, pp. 36081–36093. [Google Scholar]

29. X. Chen, X. Wang, and J. Zhou, “Activating more pixels in image super-resolution transformer,” arXiv.2205.04437, 2022, doi: 10.48550/arXiv.2205.04437. [Google Scholar] [CrossRef]

30. Y. Tai, J. Yang, and X. Liu, “Image super-resolution via deep recursive residual network,” in Proc. CVPR, Hawaii, USA, 2017, pp. 2790–2798. [Google Scholar]

31. Y. Tai, J. Yang, X. Liu, and C. Xu, “MemNet: A persistent memory network for image restoration,” in Proc. ICCV, Venice, Italy, 2017, pp. 4549–4557. [Google Scholar]

32. C. Dong, C. C. Loy, and X. O. Tang, “Accelerating the super-resolution convolutional neural network,” in Proc. ECCV, Amsterdam, Netherlands, 2016, pp. 391–407. [Google Scholar]

33. W. Shi, J. Caballero, F. Huszar, and J. Totz, “Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network,” in Proc. CVPR, Las Vegas, USA, 2016, pp. 1874–1883. [Google Scholar]

34. Z. C. Du, D. Liu, J. Liu, and J. Tang, “Fast and memory-efficient network towards efficient image super-resolution,” in Proc. CVPRW, New Orleans, LA, USA, 2022, pp. 852–861. [Google Scholar]

35. Z. Y. Li, Y. Q. Liu, X. Y. Chen, and H. M. Cai, “Blueprint separable residual network for efficient image super-resolution,” in Proc. CVPRW, New Orleans, LA, USA, 2022, pp. 832–842. [Google Scholar]

36. D. Haase and M. Amthor, “Rethinking depthwise separable convolutions: How intra-kernel correlations lead to improved mobilenets,” in Proc. CVPR, Seattle, SEA, USA, 2020, pp. 14588–14597. [Google Scholar]

37. L. Sun, J. Dong, J. Tang, and J. Pan, “Spatially-adaptive feature modulation for efficient image super-resolution,” arXiv:2302.13800, 2023, doi: 10.48550/arXiv.2302.13800. [Google Scholar] [CrossRef]

38. X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu and C. Dong, “ESRGAN: Enhanced super-resolution generative adversarial networks,” in Proc. ECCV, 2019, pp. 63–79. [Google Scholar]

39. D. Hendrycks and K. Gimpel, “Gaussian error linear units (GELUs),” arXiv:1606.08415, 2016, doi: 10.48550/arXiv.1606.08415. [Google Scholar] [CrossRef]

40. Y. Li et al., “Efficient and explicit modelling of image hierarchies for image restoration,” arXiv:2303.00748, 2023, doi: 10.48550/arXiv.2303.00748. [Google Scholar] [CrossRef]

41. M. H. Guo, C. Z. Lu, Z. N. Liu, and M. M. Cheng, “Visual attention network,” arXiv:2202.09741, 2022, doi: 10.48550/arXiv.2202.09741. [Google Scholar] [CrossRef]

42. E. Agustsson and R. Timofte, “NTIRE 2017 challenge on single image super-resolution: Dataset and study,” in Proc. CVPRW, New Orleans, LA, USA, 2017, pp. 1122–1131. [Google Scholar]

43. M. Bevilacqua, A. Roumy, C. Guillemot, and A. Morel, “Low-complexity single image super-resolution based on nonnegative neighbor embedding,” in Proc. BMVC, Surrey, UK, 2012, pp. 1–10. [Google Scholar]

44. R. Zeyde, M. Elad, and M. Protter, “On single image scale-up using sparse-representations,” in Proc. CS, Avignon, France, 2010, pp. 711–730. [Google Scholar]

45. D. Martin, C. Fowlkes, D. Tal, and J. Malik, “A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics,” in Proc. ICCV, Vancouver, Canada, 2001, pp. 416–423. [Google Scholar]

46. J. B. Huang, A. Singh, and N. Ahuja, “Single image super-resolution from transformed self-exemplars,” in Proc. CVPR, Boston, MA, USA, 2015, pp. 5197–5206. [Google Scholar]

47. Y. Matsui, K. Ito, Y. Aramaki, A. Fujimoto, and T. Ogawa, “Sketch-based manga retrieval using manga109 dataset,” Multimed. Tools Appl., vol. 76, no. 1, pp. 21811–21838, 2016. [Google Scholar]

48. Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Trans. on Image Process., vol. 13, no. 4, pp. 600–612, 2004. doi: 10.1109/TIP.2003.819861. [Google Scholar] [PubMed] [CrossRef]

49. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv:1412.6980, 2014, doi: 10.48550/arXiv.1412.6980. [Google Scholar] [CrossRef]

50. I. Loshchilov and F. Hutter, “SGDR: Stochastic gradient descent with warm restarts,” arXiv:1608.03983, 2016. [Google Scholar]

51. Y. Ioannou, D. Robertson, R. Cipolla, and A. Criminisi, “Deep roots: Improving CNN efficiency with hierarchical filter groups,” in Proc. CVPR, Hawaii, USA, 2017, pp. 5977–5986. [Google Scholar]

52. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. ICML, Lille, France, 2015, pp. 448–456. [Google Scholar]

53. W. S. Lai, J. B. Huang, N. Ahuja, and M. H. Yang, “Deep laplacian pyramid networks for fast and accurate super-resolution,” in Proc. CVPR, Hawaii, HI, USA, 2017, pp. 5835–5843. [Google Scholar]

54. W. Li, K. Zhou, L. Qi, N. Jiang, J. Lu and J. Jia, “LAPAR: Linearly-assembled pixel-adaptive regression network for single image super-resolution and beyond,” in Proc. NeurIPS, New Orleans, LA, USA, 2020, pp. 20343–20355. [Google Scholar]

55. L. Sun, J. Pan, and J. Tang, “ShuffleMixer: An efficient convnet for image super-resolution,” in Proc. NeurIPS, New Orleans, LA, USA, 2022, pp. 17314–17326. [Google Scholar]