Service Function Chain Deployment Algorithm Based on Multi-Agent Deep Reinforcement Learning

1  Introduction

In recent years, with the explosive growth of mobile data traffic and the emergence of various new services and application scenarios in 5G networks, Network Function Virtualization (NFV) technology has gained widespread attention from academia and industry due to its ability to decouple 5G network functions from underlying hardware, enabling flexible and elastic resource management and resource sharing. By orchestrating Service Function Chains (SFC) in a specific order, NFV provides end-to-end network services and achieves soft-hard decoupling of network element functions. NFV manages the traditional middlebox as a specific Virtual Network Functions (VNFs). VNFs alone cannot provide complex network functions. When network operators receive new SFC requests, they need to represent data processing services as a collection of virtual nodes and virtual links, while ensuring resource constraints such as latency and bandwidth are met. Traffic must then pass sequentially through the predefined order of virtual nodes. Since the resource demand of SFC is dynamically changing, it is necessary to select the physical general servers and physical links that satisfy the service demand from the limited physical resources to be deployed in order to meet the changing service demand. Based on limited resources and under the conditions of prioritizing various network resources, how to save resource consumption, reduce operating costs, and efficiently realize SFC deployment has become an urgent problem in NFV.

Currently, SFC mapping optimization is a key research topic in the field of NFV. Based on diverse service demands and network environments, the researchers have set appropriate optimization criteria and designed and developed various algorithms to solve these problems. Early heuristic algorithms, although able to provide solutions quickly, relied on manually set rules and were difficult to adapt to the dynamic changes in the network environment. Liu et al. [1] proposed a dynamic programming-based algorithm to optimize SFC deployment costs under resource constraints. Cao et al. [2] utilized sorting, greedy, and shortest path algorithms to map virtual resources to the physical network, optimizing the mapping process. However, this method does not fully account for the order and dependencies among VNFs. In contrast, artificial intelligence algorithms that combine reinforcement learning and deep learning can learn near-globally optimal strategies through interaction with the environment. Agents acquire high-dimensional data through interactions, utilize deep learning for environmental state perception and feature representation, and then make decisions through reinforcement learning. This process maps the current state to the agent’s actions, guiding the agent to adopt optimal strategies to reach target positions.

The deployment of SFC is essentially the allocation process of physical network resources, in order to improve the efficiency of network resource orchestration, a large number of scholars have carried out in-depth research on efficient deployment methods for SFC. Current heuristic methods or mathematical model methods for SFC deployment have the problem of over-optimizing a single resource (latency or bandwidth) and easily falling into local optimality, resulting in a significant increase in overhead, unstable performance, and reduced service quality. Aiming at the above problems, this paper proposes a muti-agent deep deterministic policy gradient optimization algorithm for SFC deployment (MADDPG-SD) that effectively improves the request acceptance rate and reduces the SFC deployment costs and end-to-end transmission latency while satisfying the performance requirements and resource capacity constraints. Within the NFV domain, reusing initialized VNF eliminates bandwidth consumption between two VNF and reduces SFC latency [3]. Considering that network services have specific requirements for customized VNFs, reusing existing VNFs cannot meet service requirements, therefore, this paper conducts research in a scenario that does not include reuse. Specifically, this paper makes the following contributions:

•   This paper analyzes the shortcomings in SFC deployment, such as poor strategy coordination in single-agent deployment strategies and a tendency to fall into local optima.

•   This paper establishes a costs minimization model for service function chain deployment under user latency requirements and resource capacity constraints. And model the dynamic problem as a Markov decision process (MDP).

•   Combining action and state information from other intelligences and storing them together in the current intelligence’s experience playback pool is used to centrally train the Critic network, where each intelligence is allowed to learn its state and action value functions separately.

The rest of this paper is organized as follows. Section 2 provides an overview of related work previously conducted by other researchers. Section 3 presents the network architecture, optimization objective, and formula description for SFC deployment. Section 4 describes the MADDPG-SD deployment methodology and algorithmic training steps in detail. Section 5 describes the design of the simulation experiments and analyzes the results. Section 6 summarizes and concludes this paper.

2  Related Work

In the NFV environment, a network function node can deploy multiple instances of different network functions, the orchestration of various functions can be modeled as service function chaining problem [4]. With the advancement of NFV technology, the deployment of SFCs tailored to service requests has become a hot topic in academic research, attracting widespread attention. SFC deployment is proven to be an NP-hard problem [5]. The existing SFC deployment methods mainly take costs, energy consumption, load balancing and end-to-end delay as optimization objectives, and are divided into service function chain deployment methods based on mathematical programming model, heuristic algorithm and artificial intelligence algorithm. Bari et al. [6] provided a dynamic programming-based heuristic to solve virtual network function assignment problem in order to reduce network operating costs. Reddy et al. [7] proposed a novel optimization model based on the concept of robustness to deal with uncertainties in the traffic demand and as a consequence in the resource requirements of the VNFs while fulfilling individual average roundtrip delay bounds for each chain of VNFs. Jemaa et al. [8] introduced VNF placement and provisioning optimization strategies over an edge-central carrier cloud infrastructure taking into account Quality of Service (QoS) requirements (i.e., response time, latency constraints and real-time requirements) and using queuing and QoS models. As the scale of the underlying network continues to expand, the applicability and time efficiency of the above methods become lower and lower.

Heuristic algorithms offer greater flexibility, computational efficiency, and practicality in addressing the service function chain deployment issue compared to mathematical planning model algorithms. To optimize the resource utilization, Li et al. [9] designed a two-stage heuristic solution T-SAT to solve the integer linear programming model and minimize the number of physical machines used. Rankothge et al. [10] proposed a resource allocation algorithm for VNFs based on genetic algorithms and conducted a comprehensive analysis of the initial placement of VNFs and how to scale them to adapt to traffic changes. Zhang et al. [11] devised an algorithm that constructs subsets of candidate base nodes and candidate base paths prior to embedding, significantly reducing the execution time of mapping without compromising performance. Nonetheless, heuristic methods lack rigorous theoretical validation, often resulting in convergence towards local optimal solutions.

The advantage of artificial intelligence algorithms over heuristic methods lies in their ability to learn strategies that approximate global optimality through interaction with the environment, thereby demonstrating superior performance in practical applications. Zhu et al. [12] introduced a deep reinforcement learning-based cross-domain mapping algorithm for service function chaining within a centralized orchestration framework. This approach models the segmentation of SFC requests as a Markov decision process, facilitating cross-domain SFC deployment. However, the algorithm overlooks disparities in resource requirements among different VNF types, leading to excessive complexity. Luo et al. [13] presented an online scaling algorithm that dynamically adjusts VNF instance deployment to optimize operational, maintenance, and deployment costs. Regrettably, this algorithm neglects consideration of request latency. In order to solve the problem of automatic fault recovery in SFC, Avgeris et al. [14] proposed a distributed solution that supports reinforcement learning in a seamless manner in real time. Qu et al. [15] proposed a reliability-aware method that combines VNF deployment with routing optimization, reducing resource consumption through backup sharing. However, while using the backup mechanism to improve reliability, it also increases the link length of the SFC, which to some extent increases the SFC latency. Yang et al. [16] used the Deep Q-Network (DQN) algorithm to maximize the overall energy efficiency of communication and computing within the mobile edge computing server and sensor by jointly optimizing the allocation of channels and computing resources, effectively reducing the total energy consumption of the system while ensuring accuracy. Chen et al. [17] combined deep neural networks and Markov decision process reinforcement learning networks to establish a service function chain migration mechanism based on a Double Deep Q-Network (DDQN) to achieve online migration decisions and avoid overestimation. Nonetheless, this approach necessitates the selection of optimal policies at each time step, which may not fully ensure service quality for swiftly incoming service requests. Therefore, Schneider et al. [18] proposed a centralized Deep Reinforcement Learning (DRL) framework. However, during interaction with the network, this approach relies on delayed state information and requires periodic updates to forwarding rules.

In conclusion, heuristic algorithms are prone to fall into local optimality and unstable performance. Single-agent deep policy gradient algorithms lack coordination and may have unstable gradients and poor adaptability to the environment. Multi-agents provide more efficient, flexible and robust solutions than single agents in SFC resource deployment problems through parallel processing, distributed decision-making, optimized resource sharing, and improved learning efficiency. This paper uses multiple agents to jointly find the optimal strategy. Through collaboration and information sharing between agents, it can comprehensively consider multiple performance indicators and resource constraints, thereby finding a more global and efficient SFC deployment solution, which can achieve positive results in improving request acceptance rate, reducing deployment costs, and shortening end-to-end latency.

3  System Model and Problem Description

3.1 System Model

The NFV architecture comprises an application layer [19], a virtualization layer, and an infrastructure layer, as illustrated in Fig. 1. The application layer is tasked with creating SFC to fulfill network service requests, thereby delivering specific services to users. The virtualization layer handles network state monitoring and the analysis of underlying network loads. The infrastructure layer provides SFC with instantiated physical resources, which include general-purpose servers, compute resources, and link bandwidth resources. The NFV infrastructure depicted in the figure includes physical nodes and links within the NFV network. NFV orchestration management is crucial in gathering relevant information about VNF, such as resource requirements and successor VNF on the SFC. Based on the current network state and service deployment policies, it devises fast and efficient VNF deployment solutions. Table 1 lists key notations that will be used in the following of the paper.

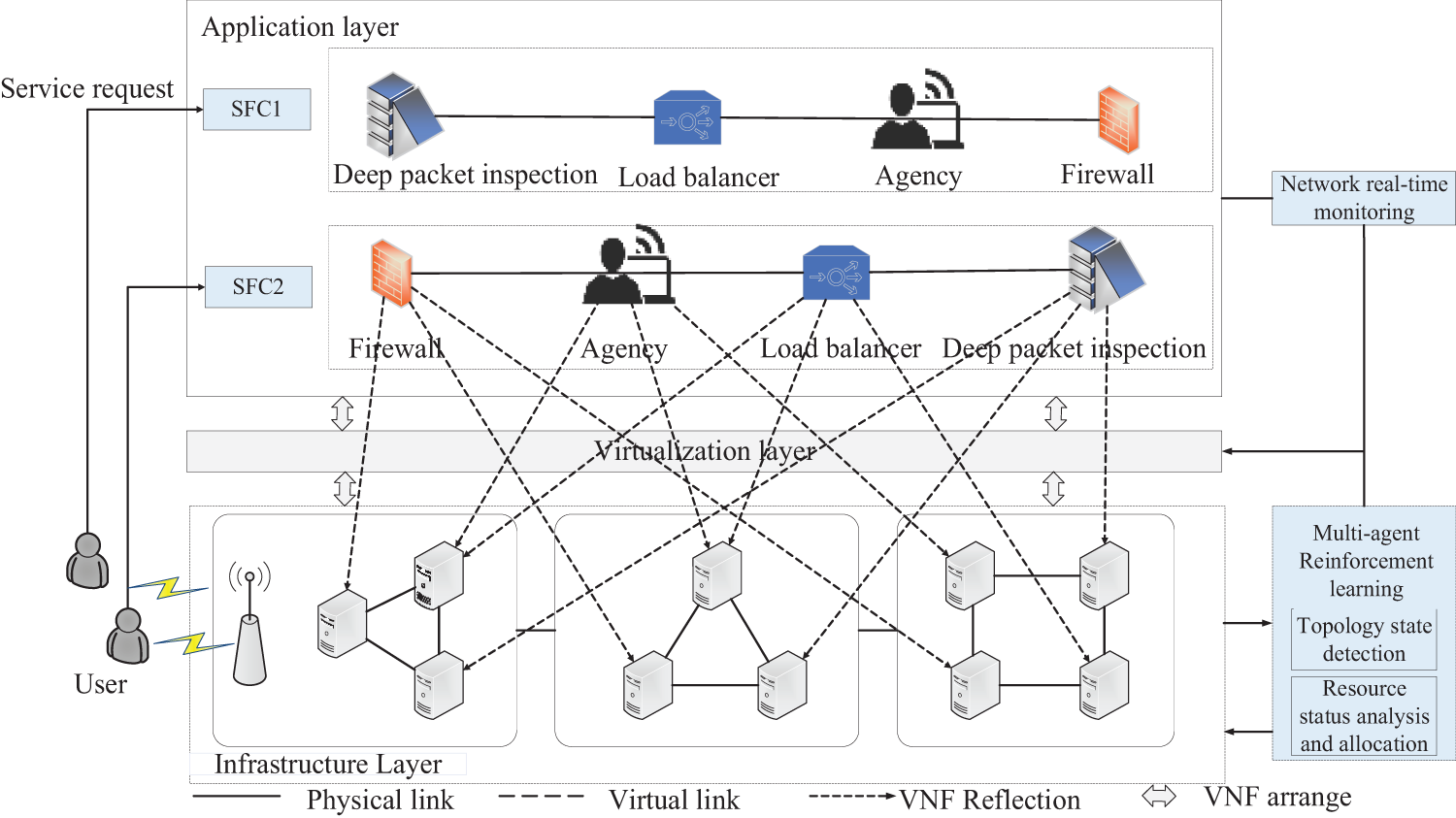
Figure 1: NFV architecture

First, the underlying physical network of the infrastructure network is represented as an undirected graph G=(V,E), where V denotes the set of physical nodes, i.e., servers, and E denotes the set of connection links between each pair of physical nodes. For any physical node v∈V, Cnv denotes its total CPU resource, and two neighboring physical servers a,b∈V, ab denotes the physical link connecting a and b, with its limited bandwidth resources represented as Babs. Each server can deploy multiple VNF with sufficient resources. Considering the energy consumption issue and the convenience of managing the servers, Tvalue is set as the server resource threshold to ensure that each node’s resource consumption does not exceed 90% of its total resources [20].

One SFC request can be represented as a directed graph G=(N,L), with S denoting the set of service function chain requests. The i−th SFC is represented as Gi=(Ni,Li), where Ni denotes the VNF of the service request, including common network functions such as firewalls, proxy services, load balancers, NAT, deep packet inspection, and customized VNF, and Li represents the set of virtual links on the SFC. For randomly arriving service requests, a set of ordered VNF must be processed. The SFC needs to arrange VNF instances in sequence as VNF1, VNF2, ..., VNFn. Define a binary Boolean variable xi,jn=0,1, When the j−th VNF Nii,j of the i−th SFC is successfully deployed on the physical server n∈N, xi,jn=1, otherwise, xi,jn=0. Define a binary Boolean variable yi,je=0,1. When the j−th virtual link li∈Li of the i−th SFC is successfully deployed on the physical link e∈E, yi,je=1, otherwise, yi,je=0.

3.2 Problem Description

In the paper, the SFC end-to-end latency is defined to include two parts, service processing latency and service transmission latency, and the end-to-end latency is denoted by Ttotal, with service processing latency represented by Dm, and transmission latency represented by Dtr, which can be described by Eq. (1) and Eq. (2). ⋎i represents the end-to-end maximum tolerable latency of the SFC. Processing latency refers to the time required to handle the SFC at network nodes, occurring only at nodes with computing resources. The average data sent in time slot t must not exceed ωm, the maximum data a user can send at once is ηm, and the service rate coefficient β indicates the amount of data a single CPU can process per second.

Dm=∑m∈Nii,jxi,jn(t)ωmt+ηmCnmβ(1)

Dtr=ωmt+ηmBes(2)

At time slot t, the total latency constraint for SFC requests is given as Eq. (3).

Ttotal=Dm+Dtr<⋎i(3)

The SFC deployment costs encompass two aspects: the energy consumption costs incurred by deploying VNF operations when the server is active and the energy consumption costs incurred when the server is in standby mode after VNF deployment, as given in Eq. (4).

Ct=∑i∈Ni∑n∈N(xi,jnλi,j+onfnyi,jeλi,j)(4)

As exhibited in Eq. (4), λi,j represents the energy consumption costs of deploying VNF, on denotes the duration of occupancy, and 0≤fn≤1 signifies the percentage of energy consumption costs when the server is in standby mode post-VNF deployment.

The SFC request acceptance rate refers to the ratio of successfully deployed SFCs to the actual number of network service requests over a given period, as given in Eq. (5).

Ra=limT→∞ns(T)nq(T)(5)

As exhibited in Eq. (5), ns(T) and nq(T) represent the number of service requests successfully processed and the total number of requests received within the 0→T time interval, respectively.

The paper aims to minimize the deployment cost of SFC and reduce service latency, as demonstrated in Eq. (6).

Here, ξα and ξβ represent weighted parameters, where the weighting coefficients ξα,ξβ satisfy ξα,ξβ∈(0,1) and ξα+ξβ=1.

min(ξαTtotal+ξβCt)(6)

The SFC deployment problem in this paper can be formulated as follows: how to rationalize the mapping of VNF as well as to get the minimized deployment costs and the minimized end-to-end latency with limited network resources such as bandwidth resources and CPUs. The objective function and constraints are given as Eq. (7).

minξαTtotal+ξβCts.t.C1:xi,jn(t)={0,1},∀i∈S,∀j∈Gi,∀n∈VC2:yi,je(t)={0,1},∀i∈S,∀j∈Gi,∀e∈EC3:∑n∈VNi,jn(t)=1,∀i∈S,∀j∈GiC4:∑e∈ELi,je(t)=1,∀i∈S,∀j∈GiC5:∑i∈S∑j∈Gixi,jn(t)Cnv≤Cmv,∀m∈VC6:∑i∈S∑j∈Giyi,je(t)Babs≤Bnms,∀nm∈LiC7:Ttotal<⋎i,∀i∈S(7)

As exhibited in Eq. (7), C1 indicates that the virtual node mapping satisfies the binary variable constraints. C2 indicates that the link mapping satisfies the binary variable constraints. C3 indicates that a virtual node in a virtual network service function chain can be mapped to only one physical node. C4 indicates that a virtual link in a virtual network service function chain can be mapped to only one physical link. C5 ensures that the CPU resource requirement of the SFC does not exceed the available resources of the deployed physical node. C6 ensures that the bandwidth resources of the SFC are less than the available resources of the link. C7 indicates that each SFC meets the latency requirements.

4  MADDPG-SD Deployment Methodology

4.1 MADDPG-SD Algorithm Description

The MADDPG-SD algorithm employs the principle of centralized learning training and distributed execution, making it applicable to complex large-scale network environments that cannot be handled by traditional reinforcement learning algorithms, where each set of Actor networks and Critic networks is an intelligent agent. The Actor network is responsible for selecting actions based on the current state, while the Critic network is responsible for evaluating the value of these actions and learning them using the strategies of the other intelligences, i.e., each intelligence approximates the strategy of the other intelligences by one function. While traditional reinforcement learning algorithms have to use the same information data for both learning and application, the MADDPG-SD algorithm allows the use of some of the global information for learning, but only local information for application decisions.

The MADDPG-SD algorithm is a multi-agent deep reinforcement learning algorithm designed for environments where multiple agents learn and perform tasks collaboratively. Each agent has its own policy, and their actions influence each other. MADDPG-SD aims to maximize the expected cumulative reward by training multiple agents while accounting for the presence and behavior of other agents. During training, a central controller coordinates the policy updates of multiple agents, gathering state information and actions from all agents. This information is used to train a global policy or value function. Each agent possesses a local Actor network to select actions and relies on a global Critic network to evaluate the effectiveness of the joint actions of all agents. Through this iterative process, each agent continuously learns and refines its strategy, enhancing cooperation in the multi-agent environment. The MADDPG-SD algorithm is capable of handling continuous action spaces, and the structure of the algorithm is shown in Fig. 2.

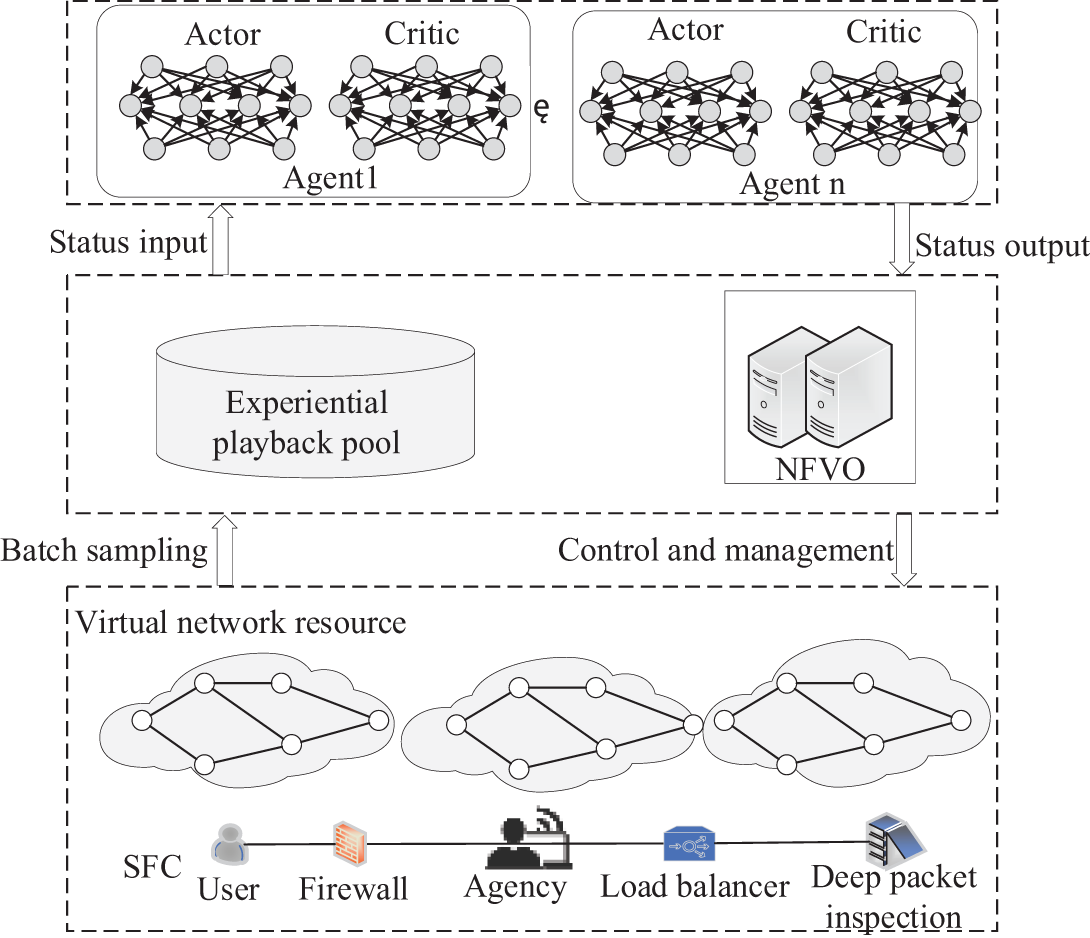
Figure 2: Structure of the MADDPG-SD algorithm

Each intelligence computes the forward propagation of its own Critic network by stitching the states of all intelligences, including itself, such as current network load, resources used by the server, etc., into a state vector s={s1,s2,…,sn}, splice all intelligent agent actions into an action vector a={a1,a2,…,an}, (s,a) serves as an input to the Online Critic network and outputs a one-dimensional Q-value, which is Qϕi(s,a), by playing back the samples it is possible to calculate Qϕi(s′,a′). The mean square error (MSE) loss function for both is constructed in terms of the temporal difference error, and the gradient descent is utilized in order to update the parameter ϕi. The loss function and the gradient are shown in Eqs. (8) and (9).

minϕiLoss=minϕiE(s,a,r,s′,d)∼D[((Qϕi(s,a)−(ri+γ(1−di)Qϕi(s′,a′)))⏟J(ϕi)2](8)

∇ϕiJ(ϕi)==∇ϕiE(s,a,r,s′,d)∼D[(Qϕi(s,a)−(ri+γ(1−di)Qϕi(s′,a′)))2](9)

where a′={μθ~(s1′),μθ~(s2′),…,μθ~(sN′)}, to compute the action taken by the next state intelligence. The parameters are then updated using gradient descent. In computing the forward propagation of its own Actor, each intelligence takes as input to the Online Actor network only its own local state vector s={s1,s2,…,sn}, and outputs a deterministic action ai, which is μθi(si). Next, the MSE loss function for the temporal difference error is calculated and the gradient is computed with respect to parameter θi. The loss function and gradient are shown in Eqs. (10) and (11).

minθiLoss=minθi−Es∼D[Qϕi(s,a)](10)

∇θiJ(θi)=−Es∼D[∂Qϕi∂θi]=−Es−D[Qϕi(s,a)∂μθi(si)μθi(si)∂θi](11)

4.2 Mapping of Deployment Issues

Deep reinforcement learning can be described using a Markov decision process. By making online decisions and continuously sampling, it acquires immediate reward values to evaluate the value function of the current state. This approach simulates the stochastic policies and returns achievable by the agent to obtain the optimal SFC deployment strategy. Under long-term iteration, the states observed by the intelligences are random, and part of the intelligences’ states depend on the actions taken by the intelligences, thus modeling the VNF deployment process as MDP{S,A,P,R,γ}, where S is the state space, A is the action space, P is the state transfer probability, R is the reward function, and γ∈[0,1] is the discount factor for future rewards.

•   State space S

Define the state st∈S as st={M(t),W(t)}, where M(t)={∂c(t),∂b(t),dt} denotes the SFC mapping state, ∂c(t) denotes the physical resources required by the VNF, ∂b(t) denotes the bandwidth resources required by the SFC, dt denotes the total latency of the service function chain from the source node to the current state, W(t)={μc(t),μb(t)t}μc(t)μb(t)t denotes the physical network state, μc(t) denotes the remaining available resources of the server node, and μb(t)t denotes the remaining available bandwidth resources of the physical link. Based on the real-time availability of computational resources across physical nodes, the deployment locations and resource allocations for each VNF within the current SFC are determined. Consequently, the environmental state observed by each VNF of the SFC is defined by the remaining computational resources across all physical nodes in the infrastructure.

•   Action space A

The agent performs action a upon the arrival of a service request at a node. In this paper, the action at time slot t is defined as at=knt. If node n can process the service request within time slot t, then knt=0, otherwise, knt=1.

•   State transfer probability P

Pa(s,s′)=E(st+1=s′|S=st,A=at) represents the probability that the execution of the operation of deploying the VNF by the intelligent agent when the environment is in the state st at time slot t leads to the transformation of the environment into s′ at moment t+1.

•   Reward function R

In this paper, the objective is to minimize the SFC end-to-end latency as well as the deployment costs, then the reward function can be defined as the VNF its own deployment costs and the negative value of the latency, as shown in Eq. (12).

Rreward=−(ξα∑iTtotalγ+ξβ∑iCtγ)(12)

4.3 Training Process

In deep reinforcement learning, the Actor-Critic algorithm combines the Actor and Critic strategies to optimize the decision-making process through agent-environment interaction. The Actor is responsible for selecting actions, while the Critic evaluates the value of the selected actions. The Critic is extended to learn from the policies of other agents, enabling each agent’s policy gradient to incorporate a Critic that uses the global policy as input. This means that each agent approximates the policies of other agents through a function approximation. In this paper, the process of handling a service request is divided into multiple time slots, denoted by T={1,2,…,t}, with each time slot t representing a link mapping processing cycle. Each agent possesses its own policy network and requires a centralized controller for policy network training during the training phase. During operation, each agent interacts with the environment independently and makes decisions based on its own observed states using its policy network. Each agent independently deploys its own policy network π(ai|si;θi) and configures its parameters θi. The input to the policy network is the agent’s individual state si. Each agent’s decision ai is independent of the states of other agents s.The central controller hosts n value networks, denoted as q(s,a;wi). These value networks have identical structures, but their parameters wi are typically different. The input to the value network q consists of all s and all a. The central controller obtains the states s and actions a of all agents. During training, the central controller is aware of all agents’ states, actions, and rewards. The multi-intelligent body training process is shown in Fig. 3.

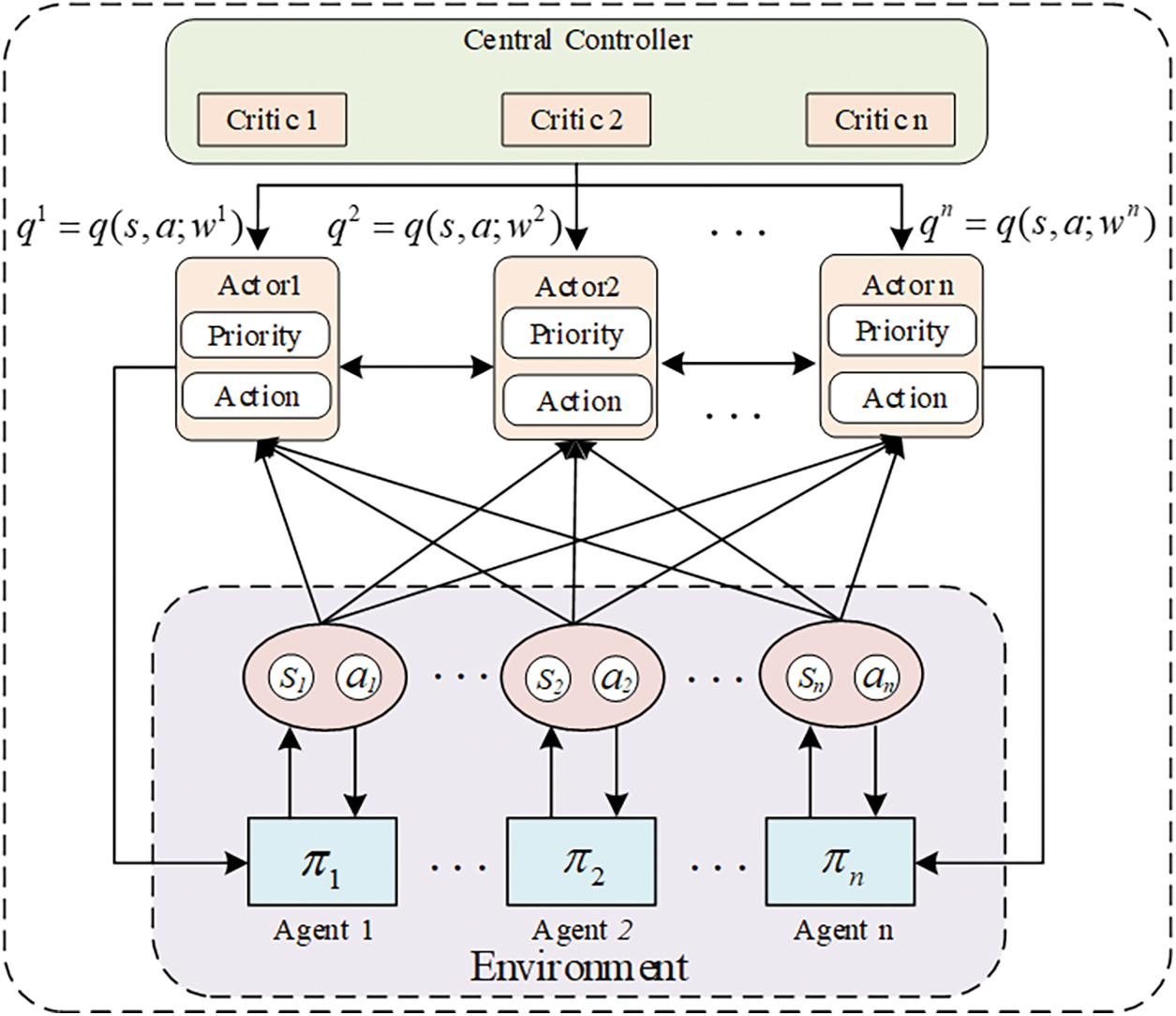
Figure 3: Multi-agent training process

The pseudocode of our proposed intelligent framework, which includes local training and aggregation training, is described in Algorithm 1. Learning effectiveness and stability are improved by using an independent Actor-Critic architecture for each intelligence and considering the policy information of other intelligences during training.

5  Simulation Experiment Design and Result Analysis

5.1 Simulation Experiment Environment Design

In order to verify the validity of the models and methods proposed in this paper, the simulation experiments are run on a device with rows of i5-12490F CPU @ 3.00 GHz, 16 GB-DDR4 RAM and GTX-3070 graphics card based on Python 3.6.12 and tensorflow-gpu-2.4.0 platforms. In order to validate the performance of the proposed algorithm, it is compared with the DQN [21], DDPG [22] and PG [23] algorithms in terms of performance in terms of latency, request acceptance rate and deployment costs. To mitigate the impact of randomness, the average of 100 simulation test results is used as the final test outcome. The number of VNF instances deployed on each node is uniformly distributed between [2,5]. In this simulation experiment, the set of network service function requests includes all SFC requests within one time period t. Each SFC request consists of 2 to 5 types of network functions, with a total of 5 types of VNF. The CPU and memory resources required for the normal operation of each VNF are randomly distributed between [10,20], and the bandwidth requirements for virtual links are uniformly distributed between [10,20]. The arrival times of SFC requests follow a Poisson distribution, with an average of 5 arrivals per time period. The service time for each request is a random number between [10,50]. For the MADDPG-SD algorithm, during training, the neural network employs the Adam optimizer and ReLU activation function, comprising two fully connected hidden layers with 128 neurons each. The learning rates for both the Actor and Critic are set to 0.001, the batch size is set to 128, the replay buffer size is 10,000, and the discount factor is set to 0.95. The parameter settings in the simulation are shown in Table 2.

5.2 Analysis of Experimental Results

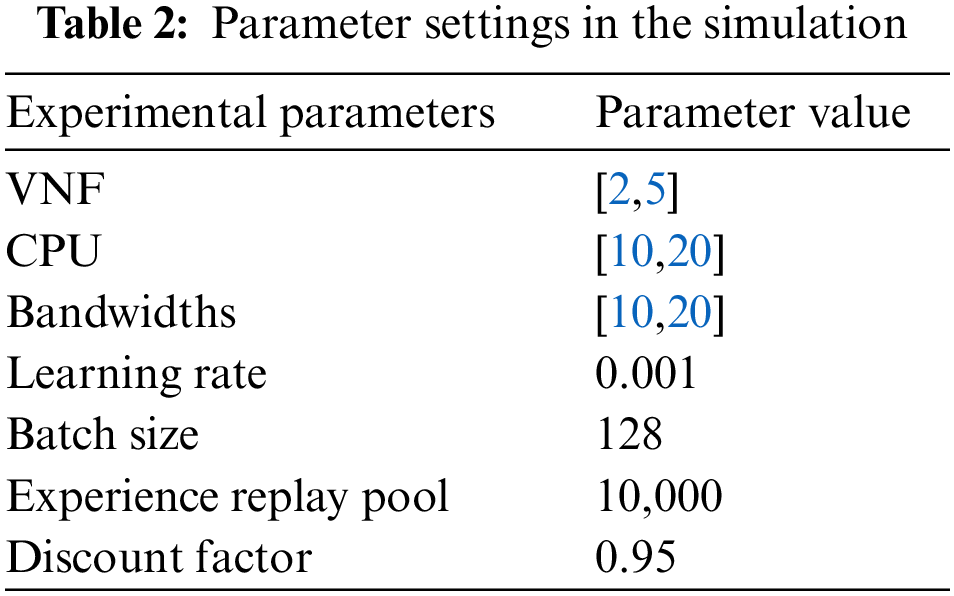
Fig. 4 shows convergence of the MADDPG-SD algorithm in the simulation experiment environment of this paper. As the training iterations increase, the overall average reward of the MADDPG-SD algorithm tends to stabilize. In the pre-training period, since the MADDPG-SD algorithm needs to provide the global information of the virtual network function for centralized training, the convergence is more volatile, and the algorithm convergence tends to be stabilized by periodically updating the target network parameters to stabilize the training.

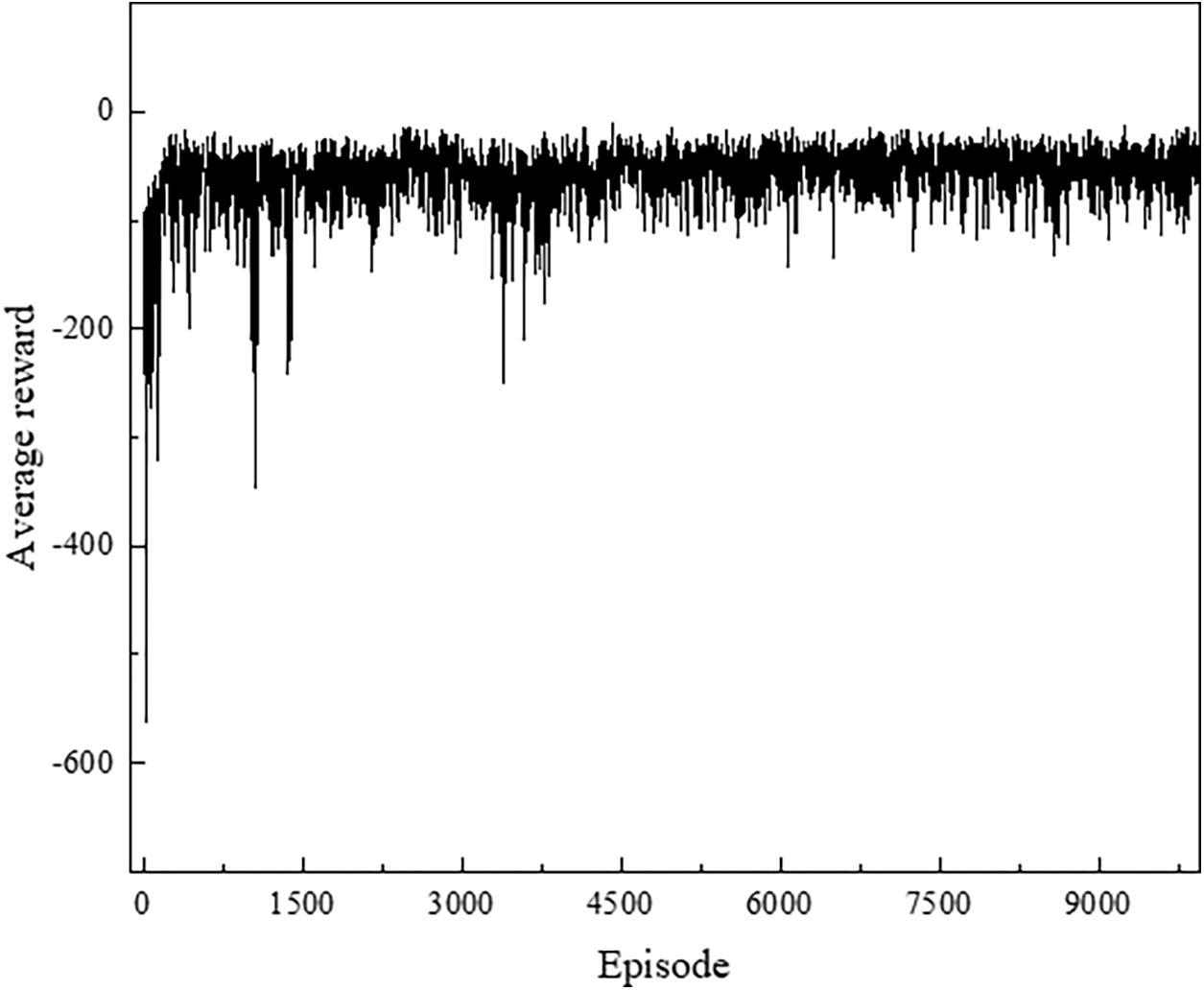
Figure 4: Convergence of MADDPG-SD algorithm

(1) System End-to-End Latency Performance Comparison

Using the number of service function chain requests as a variable, Fig. 5 illustrates the end-to-end latency comparison of various service function chains, it can be seen that as the number of service function chain requests continues to increase, the amount of data that needs to be processed also gradually increases, and the time used to process the data also increases. The end-to-end latency of all four algorithms increases accordingly. However, the MADDPG-SD algorithm excels in achieving balanced network resource allocation, exhibiting a markedly lower increase in end-to-end latency compared to the DDPG, DQN, and PG algorithms. This algorithm leverages a centralized Critic to aggregate data from all Actors, facilitating neural network updates that enable Actors to make informed decisions under the Critic’s guidance. By integrating global information, the MADDPG-SD algorithm ensures stable and smooth updates, ultimately attaining a globally optimal solution.

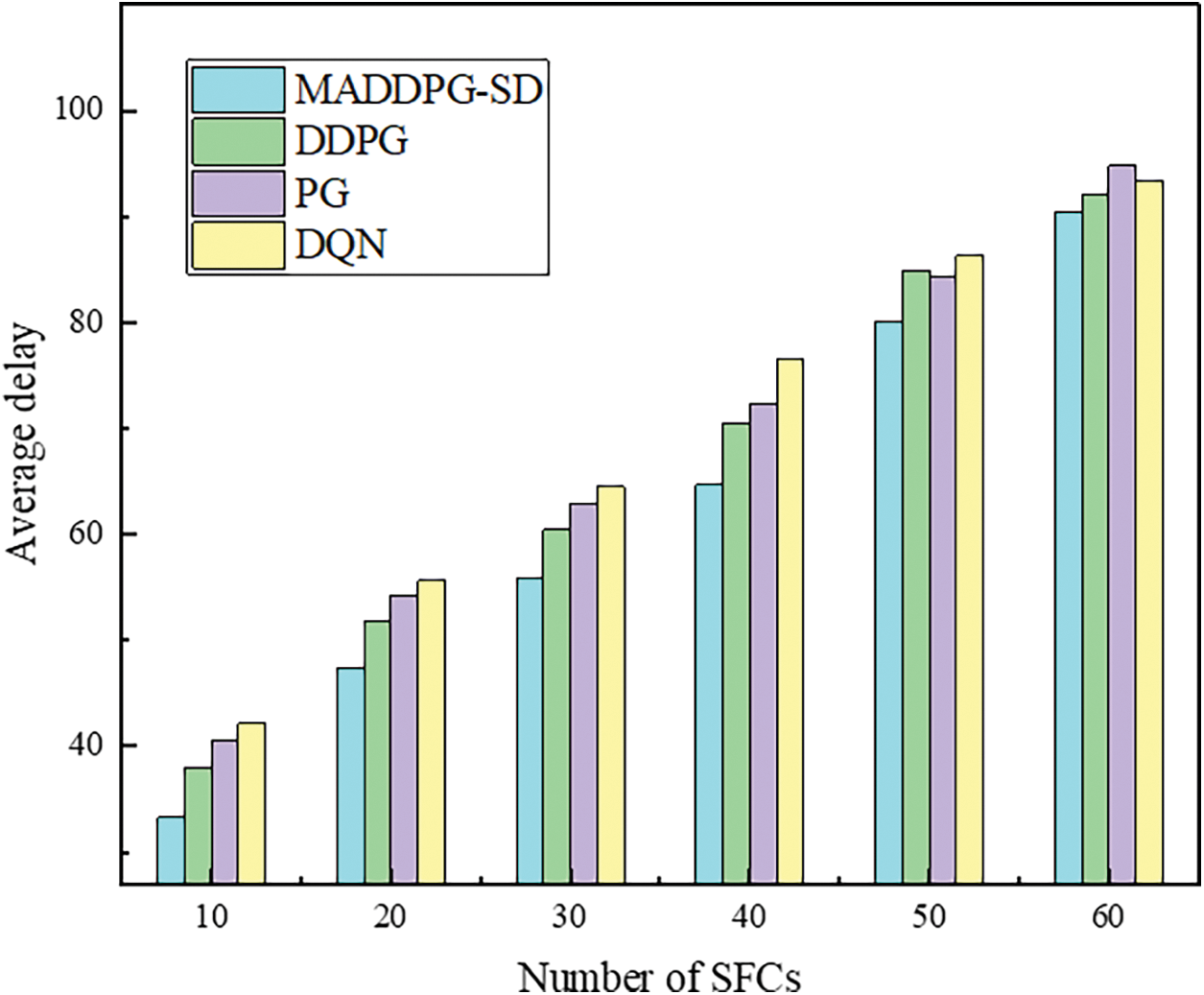
Figure 5: System end-to-end latency comparison

In the training process of this article, in order to better simulate the actual network environment and conduct effective research under limited resources, the case of 30 SFCs was selected to verify the delay distribution. The distribution of the counts of training rounds reaching a certain latency is shown in Fig. 6, where MADDPG-SD has a large statistic of small latency bias and the maximum latency is the lowest compared to the other algorithms, indicating that the algorithm has an advantage in the general trend of latency increase. After an in-depth analysis of the experimental data distribution, the MADDPG-SD end-to-end latency bias has a large statistic and the end-to-end latency is the lowest compared to other algorithms, which reveals that the MADDPG-SD algorithm has a significant stability in terms of latency control for SFC deployment. The MADDPG-SD algorithm enhances network resource allocation by minimizing latency deviations and fluctuations, thereby significantly improving overall network performance. By integrating policy gradient methods with entropy regularization, the algorithm enables agents to rapidly adapt their strategies to real-time network conditions, effectively managing dynamic changes in the network environment.

Figure 6: End-to-end latency with 30 SFCs

(2) System Deployment Request Acceptance Rate Performance Comparison

The request acceptance rates under different request intensities are shown in Fig. 7. The figure illustrates that the acceptance rates of all four algorithms decline as SFC requests arrive and the physical network resources are progressively occupied, leading to subsequent service requests being rejected. However, as the number of SFC requests increases, the rate of decline in acceptance for MADDPG-SD is noticeably smaller than that for the PG, DQN, and DDPG algorithms. The PG algorithm, which does not consider the resource status of underlying server nodes and links in its deployment strategy, frequently overuses certain central links and nodes, resulting in local congestion and the fastest rate of decline. At the end of time step t, MADDPG-SD achieves the highest acceptance rate of 72.17%. This indicates that the proposed algorithm effectively coordinates the allocation of underlying resources, allowing for the reasonable distribution of resources to each SFC within a resource-constrained physical network, thereby deploying more SFC requests and exhibiting an advantage in request acceptance rate.

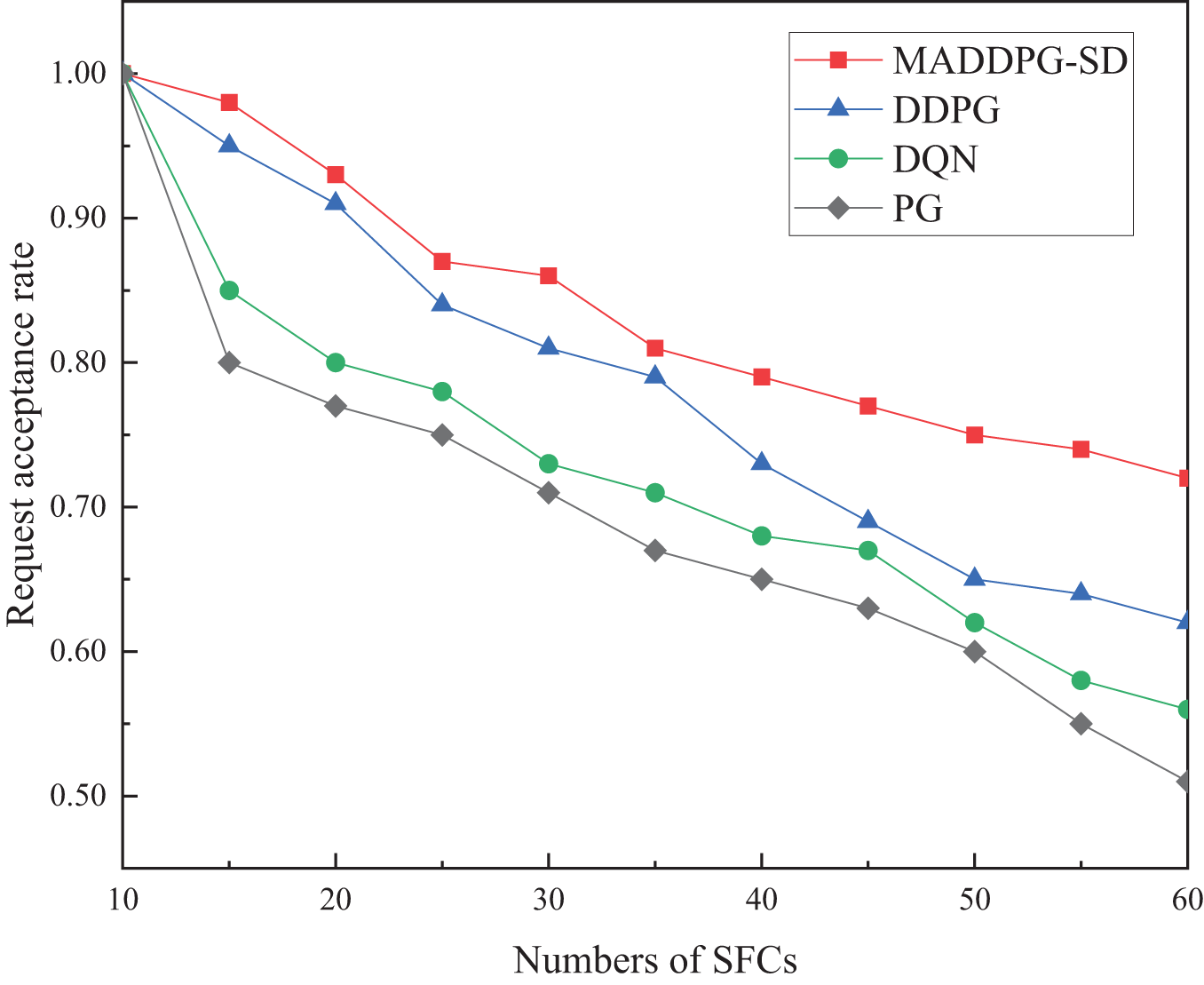
Figure 7: Request acceptance rate

(3) Comparison of Total System Deployment Costs Performance

The deployment costs of the MADDPG-SD, DDPG, DQN, and PG algorithms under varying numbers of SFC requests are depicted in Fig. 8. The DQN and DDPG algorithms typically select the superior action based on the current state during execution. However, centralized algorithms tend to prioritize fulfilling the needs of front-row users in resource allocation, neglecting global optimality, which leads to diminished rewards for back-row users. Conversely, the MADDPG-SD algorithm employs a centralized platform to harness global network information, simplifying the learning process while enabling agents to make independent decisions based on local observations within a distributed environment. This architecture comprehensively considers the needs of all users, aiming for a globally optimal solution, thereby discovering more efficient deployment strategies for SFC.

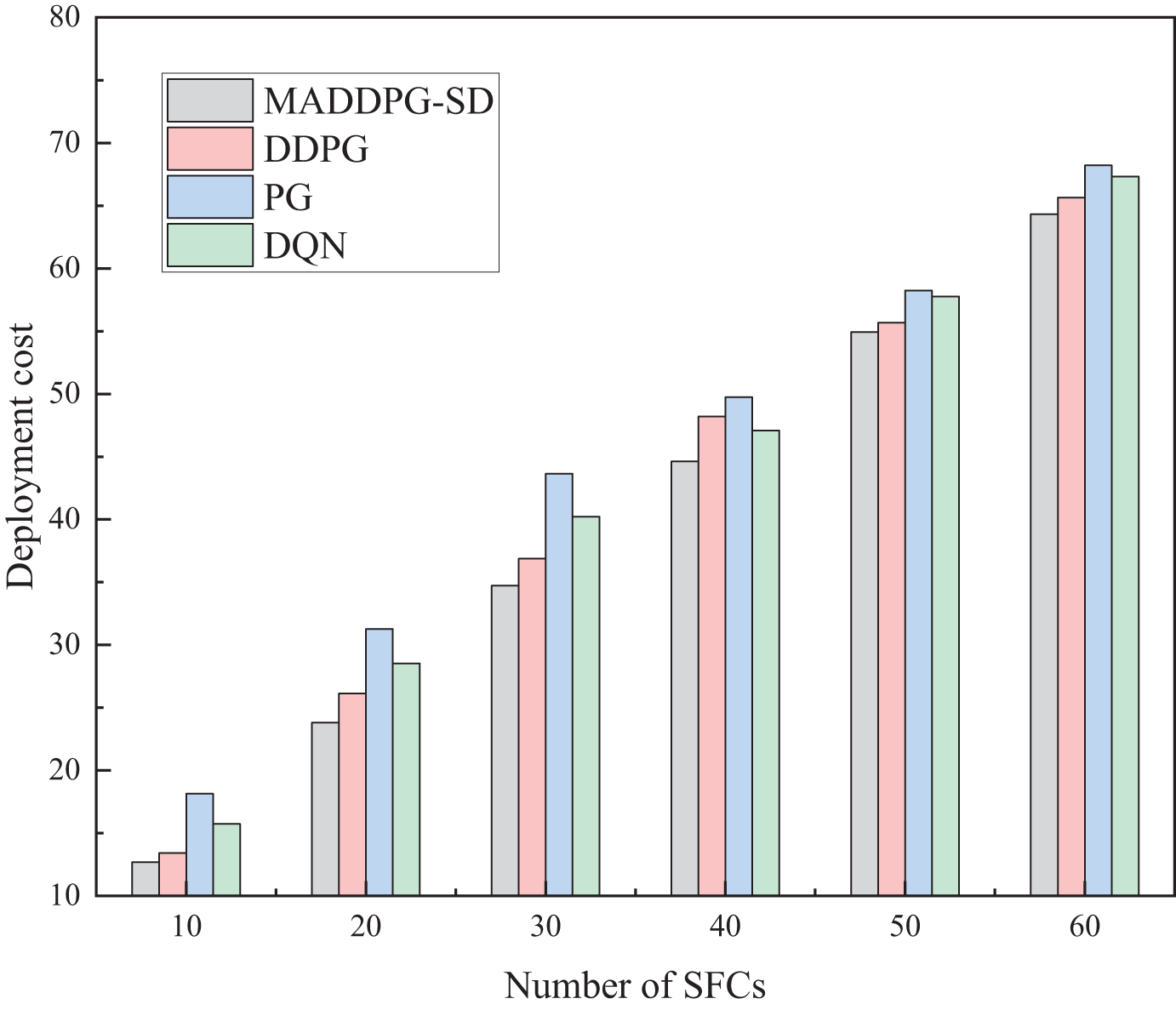
Figure 8: Comparison of total system deployment costs

Similarly, when selecting a quantity of 30 SFCs, the distribution of deployment costs was verified, and the distribution of training round counts reaching a certain deployment cost is shown in Fig. 9. Comparatively, the MADDPG-SD algorithm shows a larger statistical frequency of lower deployment costs and achieves the lowest maximum deployment costs among the algorithms. By leveraging the differences in state value functions to adjust the next action in each time slot, the MADDPG-SD algorithm can identify the globally optimal actions and obtain correspondingly higher reward values, resulting in lower deployment costs compared to the other algorithms.

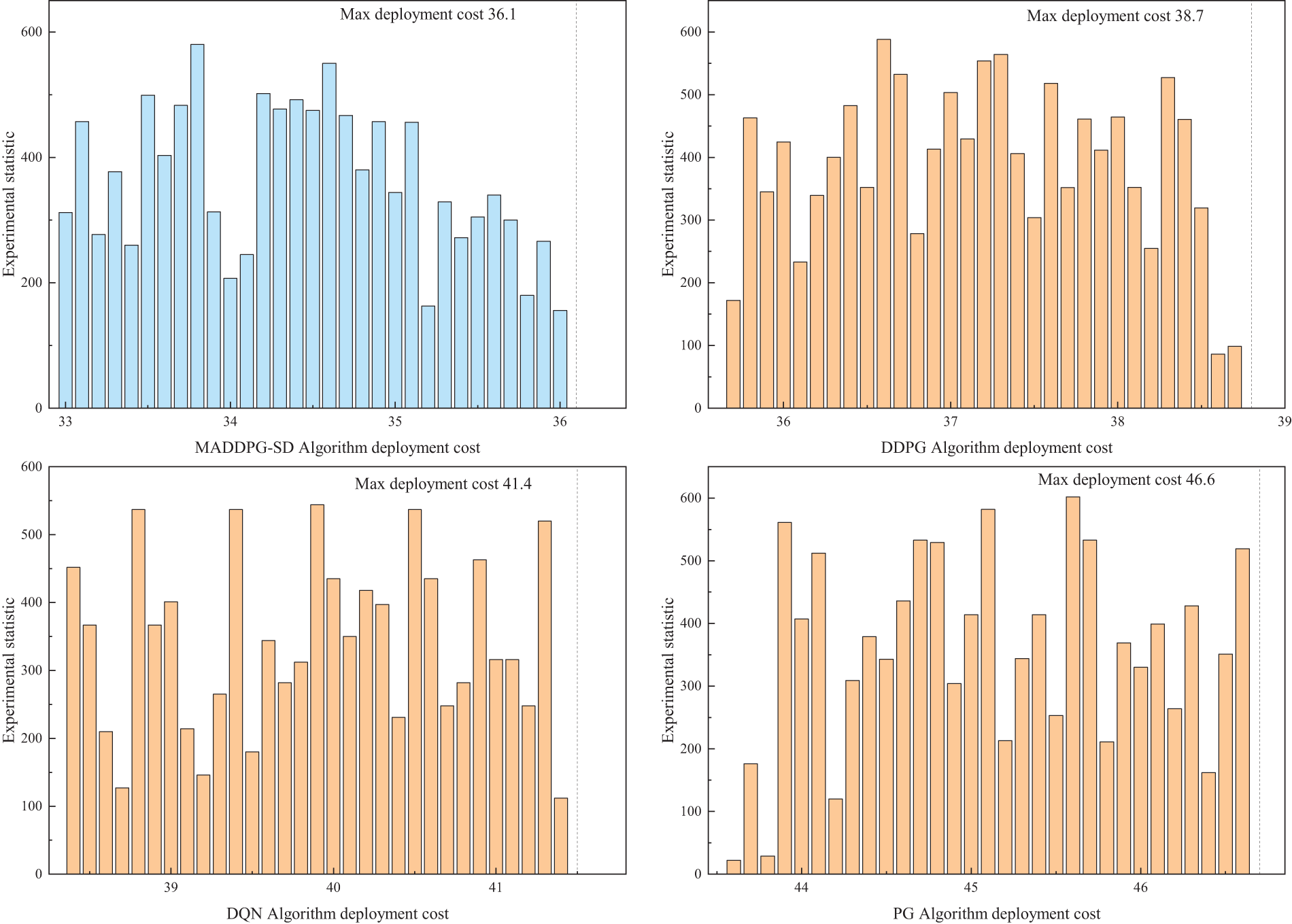
Figure 9: Deployment costs with 30 SFCs

A comprehensive comparison of deployment costs and total system latency reveals that as the number of SFC requests increases, both deployment costs and total system latency rise across all four algorithms. However, since the PG algorithm optimizes only for latency without considering the VNF deployment costs, it results in the highest deployment costs due to suboptimal resource allocation. The DQN algorithm, which optimizes both latency and the operational costs associated with deployment failures, has a higher total latency than the PG algorithm. Additionally, because the DQN algorithm is suited for discrete action spaces, it performs significantly worse than the DDPG and MADDPG-SD algorithms in optimizing latency and VNF deployment costs, as the action space in this study is continuous. The MADDPG-SD algorithm, building upon the DDPG algorithm, characterizes the exploration rate of each time slot action through state value function differences, enabling it to find more optimal actions and thus achieve better reward values. Consequently, the proposed algorithm results in lower deployment costs and total system latency.

6  Conclusion

This paper proposes the MADDPG-SD algorithm with the optimization objectives of improving the request acceptance rate, reducing latency and cost. The algorithm constructs a multi-agent deep strategic gradient SFC optimization model and transforms the SFC deployment optimization problem into a Markov decision process to adapt to the dynamic network environment. The multi-agent collaboration mechanism promotes mutual coordination of intelligence to achieve effective deployment of SFC and ultimately achieve a near-optimal deployment strategy. Although the algorithm performs well in a simulated environment, the non-stationarity problem in the multi-agent environment will lead to instability in algorithm training, so its scalability in large-scale 5G networks in the real world remains to be fully verified. Our future researches will include the integration between the computing power network and AI-based intelligent systems to make our services more robust, secure and efficient.

Acknowledgement: The authors would like to express their heartfelt gratitude to the editors and reviewers for their detailed review and insightful advice.

Funding Statement: The financial support from the Major Science and Technology Programs in Henan Province (Grant No. 241100210100), National Natural Science Foundation of China (Grant No. 62102372), Henan Provincial Department of Science and Technology Research Project (Grant No. 242102211068), Henan Provincial Department of Science and Technology Research Project (Grant No. 232102210078), the Stabilization Support Program of The Shenzhen Science and Technology Innovation Commission (Grant No. 20231130110921001), and the Key Scientific Research Project of Higher Education Institutions of Henan Province (Grant No. 24A520042) is acknowledged.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Wanwei Huang, Qiancheng Zhang; data collection: Yaoli Xu; analysis and interpretation of results: Tao Liu, Dalei Zhang; draft manuscript preparation: Qiancheng Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Liu, J. Pei, P. Hong, and D. Li, “Cost-efficient virtual network function placement and traffic steering,” presented at the IEEE Int. Conf. Commun., Shanghai, China, May 20–24, 2019. [Google Scholar]

2. H. Cao, Y. Zhu, G. Zheng, and L. Yang, “A novel optimal mapping algorithm with less computational complexity for virtual network embedding,” IEEE Trans. Netw. Serv. Manag., vol. 15, no. 1, pp. 356–371, Mar. 2018. doi: 10.1109/TNSM.2017.2778106. [Google Scholar] [CrossRef]

3. W. Huang, H. Tian, X. Zhang, M. Huang, S. Li and Y. Li, “An improved resource allocation method for mapping service function chains based on A3C,” IET Commun., vol. 18, no. 5, pp. 333–343, Mar. 2024. doi: 10.1049/cmu2.12740. [Google Scholar] [CrossRef]

4. X. Chen, T. Wu, and M. Afzal, “Multi-path service function chaining for mobile surveillance of animal husbandry,” Comput. Mater. Contin., vol. 71, no. 1, pp. 1959–1971, 2022. doi: 10.32604/cmc.2022.022344. [Google Scholar] [CrossRef]

5. D. Zhao, J. Ren, R. Lin, S. Xu, and V. Chang, “On orchestrating service function chains in 5G mobile network,” IEEE Access, vol. 7, pp. 39402–39416, 2019. doi: 10.1109/ACCESS.2019.2895316. [Google Scholar] [CrossRef]

6. F. Bari, S. R. Chowdhury, R. Ahmed, R. Boutaba, and O. C. M. B. Duarte, “Orchestrating virtualized network functions,” IEEE Trans. Netw. Serv. Manag., vol. 13, no. 4, pp. 725–739, 2016. doi: 10.1109/TNSM.2016.2569020. [Google Scholar] [CrossRef]

7. V. S. Reddy, A. Baumgartner, and T. Bauschert, “Robust embedding of VNF/service chains with delay bounds,” presented at 2016 IEEE Conf. Netw. Funct. Virtualization Softw. Defined Netw., Palo Alto, CA, USA, Nov, 2016, pp. 7–10. [Google Scholar]

8. F. B. Jemaa, G. Pujolle, and M. Pariente, “QoS-aware VNF placement optimization in edge-central carrier cloud architecture,” in presented at 2016 IEEE Global Commun. Conf., Washington, DC, USA, Dec, 2016, pp. 4–8. [Google Scholar]

9. D. Li, P. Hong, K. Xue, and J. Pei, “Virtual network function placement considering resource optimization and SFC requests in cloud datacenter,” IEEE Trans. Parallel Distrib. Syst., vol. 29, no. 7, pp. 1664–1677, Jul. 2018. doi: 10.1109/TPDS.2018.2802518. [Google Scholar] [CrossRef]

10. W. Rankothge, F. Le, A. Russo, and J. Lobo, “Optimizing resource allocation for virtualized network functions in a cloud center using genetic algorithms,” IEEE Trans. Netw. Serv. Manag., vol. 14, no. 2, pp. 343–356, Jun. 2017. doi: 10.1109/TNSM.2017.2686979. [Google Scholar] [CrossRef]

11. Q. Zhang, X. Qiu, and X. Zhu, “A novel resource optimization algorithm for dynamic networks combined with NFV and SDN,” in Wirel. Satellite Syst.: 10th EAI Int. Conf., WiSATS 2019, Harbin, China, Springer, Jan. 12–13, 2019, pp. 283–296. [Google Scholar]

12. G. Zhu, Q. Li, and S. Liang, “Cross-domain mapping algorithm of service function chain based on deep reinforcement learning,” (in Chinese), Appl. Res. Comput., vol. 38, no. 6, pp. 1834–1837, 2021. doi: 10.19734/j.issn.1001-3695.2020.08.0246. [Google Scholar] [CrossRef]

13. Z. Luo and C. Wu, “An online algorithm for VNF service chain scaling in datacenters,” IEEE/ACM Trans. Netw., vol. 28, no. 99, pp. 1–13, 2020. doi: 10.1109/TNET.2020.2979263. [Google Scholar] [CrossRef]

14. M. Avgeris, A. Leivadeas, and I. Lambadaris, “Reinforcement learning-enabled auctions for self-healing in service function chaining,” presented at 2023 IEEE Int. Conf. Commun. Workshops, Rome, Italy, May 28–Jun. 01, 2023. [Google Scholar]

15. L. Qu, M. Khabbaz, and C. Assi, “Reliability-aware service chaining in carrier-grade softwarized networks,” IEEE J. Sel. Areas Commun., vol. 36, no. 3, pp. 558–573, 2018. doi: 10.1109/JSAC.2018.2815338. [Google Scholar] [CrossRef]

16. Z. Yang, H. Mei, W. Wang, D. Zhou, and K. Yang, “Joint resource allocation for emotional 5G IoT systems using deep reinforcement learning,” Int. J. Mach. Learn. Cybern., vol. 12, no. 12, pp. 3517–3528, Aug. 2021. doi: 10.1007/s13042-021-01398-2. [Google Scholar] [CrossRef]

17. Z. Chen, G. Feng, Y. He, and Y. Zhou, “Deep reinforcement learning based migration mechanism for service function chain in operator networks,” (in Chinese), J. Electr. Inf. Technol., vol. 42, no. 9, pp. 2173–2179, Sep. 2020. [Google Scholar]

18. S. Schneider et al., “Self-driving network and service coordination using deep reinforcement learning,” in 2020 16th Int. Conf. Netw. Service Manag., Izmir, Turkey, Nov. 2–6, 2020. [Google Scholar]

19. J. Zu, G. Hu, J. Yan, and S. Li, “Resource management of service function chain in NFV enabled network: A survey,” J. Comput. Res. Dev., vol. 58, no. 1, pp. 137–152, 2021. doi: 10.7544/issn1000-1239.2021.20190823. [Google Scholar] [CrossRef]

20. L. Tang, S. Li, Y. Du, and Q. Chen, “Deployment algorithm of service function chain based on multi-agent soft actor-critic learning,” (in Chinese), J. Electr. Inf. Technol., vol. 45, no. 8, pp. 2893–2901, 2023. doi: 10.11999/JEIT220803. [Google Scholar] [CrossRef]

21. W. Wu, S. Kao, and F. Chang, “An efficient virtualized network function deployment scheme for service function chain using deep Q-network,” Int. J. Commun. Syst., vol. 35, no. 6, Apr. 2022, Art. no. e5084. doi: 10.1002/dac.5084. [Google Scholar] [CrossRef]

22. Y. Liu, Y. Lu, X. Li, W. Qiao, Z. Li and D. Zhao, “SFC embedding meets machine learning: Deep reinforcement learning approaches,” IEEE Commun. Lett., vol. 25, no. 6, pp. 1926–1930, Jun. 2021. doi: 10.1109/LCOMM.2021.3061991. [Google Scholar] [CrossRef]

23. G. Li, H. Zhou, B. Feng, Y. Zhang, and S. Yu, “Efficient provision of service function chains in overlay networks using reinforcement learning,” IEEE Trans. Cloud Comput., vol. 10, no. 1, pp. 383–395, Jan. 2022. doi: 10.1109/TCC.2019.2961093. [Google Scholar] [CrossRef]