Fuzzy Multi-Criteria Decision Support System for the Best Anti-Aging Treatment Selection Process through Normal Wiggly Hesitant Fuzzy Sets

1  Introduction

As the skin grows, it loses its natural elasticity and appears thin, broken, and wrinkled. There are usually two types of skin aging: natural aging and mild aging. The former mainly indicates body aging, which is due to factors such as genetic, mediating, endocrine, and protective functions of suppressors. The latter is due to frequent changes in the role of Ultraviolet (UV) rays, weather, and environmental pollution that accelerate the natural aging process. Three types of processes can be summarized based on the process of skin maturation. This usually includes protection from external environmental factors, repair of infrared-induced free radical damage, and the use of personal care products to enhance skin appearance. This study investigates anti-aging cosmetics and examines both internal and external skin development techniques.

Aging is a natural and inevitable phenomenon. But the bar set by the beauty industry is driving people to aspire to look younger. A young-looking skin can be achieved through surgical and non-surgical processes. Various factors such as UV rays, poor eating and sleeping habits, pollution, and blue light cause rapid aging of the skin. The skin care industry mainly focuses on the protection of the skin from harmful UV rays from the sun. Now, a variety of products and treatments are available in the market for delaying the sagging and wrinkling of the skin. Chemicals such as hyaluronic acids, retinoids, polyphenols, amino acids peptides, etc., are available in the market to hydrate and prevent skin from wrinkling. They can also boost collagen formation which is responsible for the elasticity in the skin. To create anti-aging products, regular pigmentation modulators are essential. While some products and treatments can significantly lessen or delay the symptoms of skin damage, it is more accurate to think of reducing the overall appearance of aged skin. While these modern techniques can be used to improve the quality of the skin, it is to be noted that every product that is available on the market is not as safe and effective as it claims. Several cosmetic products claim they can reduce the clinical symptoms of skin damage, but there are not many reliable, double-blind, placebo-controlled scientific clinical trials to support these claims.

This study focuses on anti-aging treatments such as Microdermabrasion, laser resurfacing, chemical peel, dermal fillers, and Botox injections. These techniques focus on the regeneration of skin and enhance collagen production. This reduces wrinkles, fades acne scars, and provides healthy and luminous skin. It is to be noted that these techniques differ both in terms of methodology and results. Therefore, it is important to choose, based on experience, the ideal technique that will deliver the best results for the skin. The selection of an optimal technique involves ambiguities and uncertainty that arise during the conversion of real-life scenarios into mathematical models. This necessitates the need for a fuzzy decision-making environment. Decision makers (DMs) can provide several assessment values for membership and non-membership degrees using the Pythagorean Hesitant Fuzzy Set (PHFS). In this study, the Normal Wiggly Pythagorean Hesitant Fuzzy Set (NWPHFS) is proposed to comprehensively mine the uncertain preferences from original Pythagorean hesitant fuzzy information, since many cognitive preferences of DMs may be hidden in the evaluation information and cannot be fully expressed. While providing the original assessment data, NWPHFS can assist DMs in more precisely expressing their potentially useful preferences for things. The names of the acronyms defined in this paper are given in the Table 1.

2  Related Works

Adhami et al. [1] considered a versatile behavior uncertain problem and extended the reluctant fuzzy Pythagorean algorithm to solve the considered problem. A decision-making approach is proposed with fuzzy Pythagorean value, which contains a set of preferable values for the limb, also nonmember phases of all objective activities in ambiguously hesitant environments. Energy-saving technologies (ESTs) help bridge the gap between energy sources by saving more energy for use when required. Thus, the evaluation of technologies on energy-saving options is extremely important and is seen as a multiple-decision problem. Colak et al. [2] presented a case study on ESTs using a hesitant fuzzy approach. Krishankumar et al. [3] discovered a goal, which was to propose a novel method of presenting findings in the framework of Interval Value Probability Liability (IVPHFS). The weight information environment is completely unknown. Green suppliers for a big baking firm were chosen to ensure structural compatibility. By linking Spearman’s sensitivity analysis with the weight and classification values, the structure is efficient, practical, and systematic for rational decision making in the hesitant fuzzy environment. Gül et al. [4] has presented interval valued-neutrosophic environment for the drone selection problem. Kumar et al. [5] helped a secure online application to last longer. For optimising the lifespan of a secure online application, a security life cycle measurement evaluation is crucial. As a result, the goal of this research is to look at the security capabilities of a web application in order to optimize security efforts for a certain life cycle. This study uses the Hybrid Assurance Group, the Analytical Hierarchy Process (AHP), and a hybrid approach to the Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS) based on a hesitant fuzzy environment. The effectiveness of the combined Hesitant Fuzzy-AHP-TOPSIS strategy has been carefully tested. The implanted tip’s personal safety is graded. The initiative seeks to make a significant contribution to the advancement of safety and will help security experts. Ali et al. [6] have established distance and similarity measures for normal wiggly dual hesitant fuzzy sets and successfully applied the developed method in the detection of diseases in the medical field. The application of the fuzzy sets in a hypothetical war environment has been established by Xia et al. [7] in the normal wiggly probabilistic hesitant fuzzy environment. Zhang et al. [8] have made use of the normal wiggly hesitant fuzzy-based multi-criteria method in the evaluation of electric vehicle charging location. Zindani et al. [9] have evaluated the agro-waste fibers under normal wiggly hesitant fuzzy environments and have presented a tool to design optimal parameters that can be used to evaluate the green products. A failure mode and effect analysis model based on Normal Wiggly Hesitant Fuzzy Set (NWHFS) was demonstrated by Zhang et al. [10] for the risk analysis of the electric bus systems. Xian et al. [11] have proposed an aggregation operator for the Pythagorean fuzzy environment and developed an algorithm to suggest optimal routes for travelers that could reduce the time, cost, and distance during their travel.

Zhou et al. [12] have evaluated the risk associated with the power transformer parts under the hesitant fuzzy environment using the improved hesitant fuzzy weighted averaging operator. Jeon et al. [13] have studied the probabilistic hesitant fuzzy environment in India’s strategies during the COrona VIrus Disease-19 (COVID-19) pandemic. Feng et al. [14] proposed an adequate technical concept of the environmental aspects that occur when products are primarily designed with the product life cycle model in mind. The VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method has been used to prove this selected application. Joshi [15] have presented a novel framework as a criterion for ambiguous entropy in images. With the VIKOR approach, a novel and efficient R-Norm picture of ambiguous information action has been created. Khan et al. [16] focused on expanding the traditional VIKOR technique as in case of Multi-Criteria Decision Making (MCDM) situations that involve ambiguous Pythagorean data. Compromise resolution is essentially decided by VIKOR’s compromise categorization approach, which provides the “majority” the most “group utility” and the “opponent” the least “individual regret,” making it an excellent tool for resolving MCDM situations. Li et al. [17] provide a novel approach to choosing the finest machine tool. Decision Making Trial and Evaluation Laboratory (DEMATEL) and VIKOR were utilized to choose a suitable alternative using a new unified MCDM model that was built. Ren et al. [18] suggested a combination approach called VIKOR-AHP, which is utilized to tackle the Artificial Intelligence (AI) selection strategy problem. Finally, a literature review on the selection of AI strategy proves the technique’s application and use. Table 1 lists various reviews of literature studies that are relevant to our planned investigation. Ali et al. [19] have proposed r, s, t-spherical fuzzy set, which is an extension of the t-spherical fuzzy set and defined the basic operational laws, distance measures, score, and accuracy functions and has combined the fuzzy set with VIKOR method. A VIKOR method based on the Pythagorean hesitant fuzzy decision-making method has been proposed by Zhang et al. [20] to obtain compromise alternatives based on regret theory. Singh et al. [21] proposed an Intuitionistic fuzzy-based Entropy-VIKOR method and analyzed similarity and dissimilarity measures for the extended VIKOR method. Abdul et al. [22] analyzed renewable energy technologies based on the Integrated Delphi-AHP-VIKOR approach towards sustainable energy resources. A literature review on various MCDM methods is given in the Table 2.

Fletcher [28] provided an indisputably strong relationship between contemporary anti-aging technologies and several social science-related biological aging studies. Traditional conceptions of ecological and chronological aging were challenged, and researchers tried to enhance functions as people aged and aged more sophisticatedly. From the cross-sectional approach of Rajan-Rankin et al. [29], this theoretical study investigates the intersections between race and old age. It looks at cultural archaeology (particularly aging simulation studies) and post-colonial approaches to aging as ideological lenses for understanding aging national bodies, with a focus on the body and transportation. Rostkowska et al. [30] have discussed extensively the properties of the skin, factors affecting skin aging, and Invasive and non-invasive methods for skin aging treatment. It also reveals the active ingredients in cosmetics that help delay skin aging. Liang et al. [31] have deeply analyzed the skin architecture and has studied the aging of the skin on a molecular level. Goberdan et al. [32] have experimented with Dermabrasion treatment on Dry, hyperpigmented, photodamaged, or acne-prone/oily skin and have shown long-term improvement in the skin. Markiewicz-Tomczyk et al. [33] have studied that chemical peeling can improve hydration of the skin and reduce wrinkles. Nanda et al. [34] have studied the application of lasers in the treatment of Keratoacanthomas. McKenzie et al. [35] have studied the effects of botulinum toxin and dermal fillers on the skin of color (Asian, Black, Latinx) population and have concluded that these treatments provide a higher satisfaction degree for the patients.

2.1 Motivation

The research work is aimed to choose the best alternative among the available anti-aging treatments. The MCDM method is processed to get results after performing various tests. In MCDM techniques, criterion selection is the most critical factor in determining the validity of the proposed results.

Uncertainty is represented using fuzzy sets, specifically the Pythagorean Fuzzy Set (PFS), which extends the membership function (m.f.) and non-membership function (n.m.f.) from Intuitionistic Fuzzy Set (IFS) and Hesitant Fuzzy Sets (HFS) utilized in ordinary fuzzy sets. A collection of hesitant ambiguities aids in resolving the uncertainties inherent in human cognition.

In this study, we propose an extended NWHFS derived from HFS. The NWHFS addresses the deep and latent hesitant thoughts that decision-makers encounter, thereby aiding in their resolution. This approach enables the derivation of a clear and definitive solution. By combining Pythagoras fuzzy sets with NWHFS, we improved the decision-making process for anti-aging treatments. Common MCDM methods, such as weight detection and alternative ranking, were utilized in this study.

To find this utility, we have used the entropy weight detection method and VIKOR alternative ranking system. The VIKOR method assumes that choosing an alternative is not biased with DM while making decisions. The result of this method is that they do not like an exchange not between wishes and possibilities but between the different interests of the decision-makers. Thus the best alternative is selected using NWPHFS.

2.2 Research Contributions

The contributions of this research are summarized as follows: Section 2 contains definitions of fuzzy sets, including the proposed set definitions and operations. Section 3 provides details of the applications selected for the study and a complete description of the chosen alternatives. Section 4 outlines the algorithm for the NWHPFS, an extension of the HFS proposed in this research, and includes the algorithm for the VIKOR method, selected as part of the MCDM approach. Section 5 illustrates the selection of the best alternative by presenting an illustrative example of the chosen application and the proposed set. Finally, Section 7 concludes with the method proposed and a summary of the findings related to the proposed set.

3  Preliminaries

Definition 3.1. According to [36], let Υ, a fixed set, the following expression is denoted as PFS (Pythagorean Fuzzy Set), P∈ Υ:

P={⟨υ, hf(υ), gf(υ)⟩/υ∈Υ}(1)

The functions hf(υ) and gf(υ) belongs to [0, 1]. Here, hf(υ)-membership degree (m. d.) and gf(υ)-non-membership degree (n.m.d.) of P. 0≤(hf(υ)2)+(gf(υ)2)≤1 is the condition of PFS. πf(υ)=1−(hf(υ))2−(gf(υ))2, an indeterminacy degree of q to P.

Definition 3.2. In accordance with [36], The Hesitant Pythagorean Fuzzy Set (HPFS), P~ on Υ is,

P~={⟨υ, hpf(υ), gpf(υ)⟩/υ∈Υ}(2)

Here, the two set hpf(υ)-m.d. and gpf(υ)-n.m.d. ∈ [0, 1]. The m.f. and n.m.f. satisfies with (hpf+)2+(gpf+)2 lies between [0, 1], where 0≤hpf≤1, 0≤gpf≤1, here, hpf, gpf∈υ∈Υ where,

hpf+=maxhpf∈υ{hpf}(3)

gpf+=maxgpf∈υ{gpf}(4)

for all υ∈Υ.

Definition 3.3. In [26], An Intuitionistic Hesitant Fuzzy Set (IHFS), the function B∈ Υ is with hpf, m.f. and gpf, n.m.f. is applied to Υ, returns ⊂[0, 1], the IHFS can be expressed,

B={⟨υ, hpf(υ), gpf(υ)rangle/υ∈Υ}(5)

where hpf(υ) and gpf(υ) in [0, 1], let υ∈Υ, an element in B, then the condition must be met,

Max(hpf(υ))+Min(gpf(υ))≤1(6)

Min(hpf(υ))+Max(gpf(υ))≤1(7)

Here, the IHFS element is hpf(υ) and gpf(υ).

Definition 3.4. Let P1=(hpf1, gPf1) and P2=(hpf2, gpf2) are two PHFS elements. Some operation laws between P1 and P2 may be shown below:

1.

P1⊕P2=⋃ϑ1∈hpf1,ϑ2∈hpf2,φ1∈gPf1,φ2∈gpf2{(ϑ1)2+(ϑ2)2−(ϑ1)2(ϑ2)2,{φ1, φ2}}(8)

2.

P1⊗P2=⋃ϑ1∈hpf1,ϑ2∈hpf2,φ1∈gPf1,φ2∈gpf2{{ϑ1, ϑ2},(φ1)2+(φ2)2−(φ1)2(φ2)2}(9)

3.

P1n=⋃ϑ1∈hpf1,φ1∈gPf1{ϑ1n,1−(1−φ12)n}, n>0(10)

4.

nP1=⋃ϑ1∈hPf1,φ1∈gPf1{1−(1−ϑ12)n, φ1n}, n>0(11)

4  Some Basic Preliminaries of NWHPFS

Definition 4.1. According to [26], fE~(υ) and fE~(υ) ′ are the Normal Wiggly Triangular Hesitant Pythagorean Fuzzy Set (NWTHPFS), a function, P~ on Υ provides some different NWTPHF-Number Set (NWTHPFN).

P~={⟨υ, fE~(υ), fE~ ′(υ)⟩/υ∈Υ}(12)

The Triangular Hesitant Pythagorean Fuzzy Set (THPFS) is represent as fE~(υ) and fE~ ′(υ). The THPFS gives some different counts of NWTHPFN.

fE~(υ)={P(τi)}⇒{P(τiL, τiM, τiU)/P(τi)∈fE~(υ), i=1, 2,…,#fE~(υ)}(13)

fE~ ′(υ)={P(υi)}⇒{P(υiL, υiM, υiU)/P(υi)∈fE~ ′(υ), i=1, 2,…,#fE~ ′(υ)}(14)

Here, the triangular NWHPFS are denoted as P(τi) and P(υi). Then, the triangular lower, middle, and upper values are denoted as P(τiL≤τiM≤τiU) and P(υiL≤υiM≤υiU). The total number of NWHPFN is #fE~(υ) and #fE~ ′(υ).

Definition 4.2. According to [26], let, the hesitant Pythagorean fuzzy element hpf={ϑ1, ϑ2,ϑ3,…,ϑ#h} and gpf={φ1, φ2, φ3,…,φ#g}. Then, the set of mean values is,

h¯pf=1#h∑i=1#hϑi(15)

g¯pf=1#g∑i=1#gφi(16)

Definition 4.3. As per [26], let the Standard Deviation can be addressed with m.d.-(h^) and n.m.d.-(g^).

σhpf=1#h∑i=1#h(ϑi−h¯pf)(17)

σgpf=1#h∑i=1#g(φi−g¯pf)(18)

The m.f., n.m.f. h^ and g^ satisfy the equations,

f~(ϑi)=σhpfe(ϑi−h¯pf)22σh¯pf2(19)

f~(φi)=σgpfe(φi−g¯pf)22σg¯pf2(20)

The Pythagorean wiggly ranges of ϑi and φi are denoted the interval [ϑi−f~(ϑi),ϑi+f~(ϑi)] and [φi−f~(φi), φi+f~(φi)].

Definition 4.4. In [26], let a Real Preference Degrees (rpd) are,

rpd(h~pf)={∑i=1#h~ϑi~(#hpf~−i#hpf~−1)if hpf<0.51−∑i=1#h~ϑi~(#hpf~−i#hpf~−1)if hpf>0.50.5if hpf=0.5(21)

rpd(g~pf)={∑i=1#g~φi~(#gpf~−i#gpf~−1)if gpf<0.51−∑i=1#g~φi~(#gpf~−i#gpf~−1)if gpf>0.50.5if gpf=0.5(22)

Definition 4.5. Let the HFS H = {⟨υ, h^(υ)⟩/υ∈Υ}, a Υ’s reference set. The set NWHPFS on P~ ′ implies,

p~  ′={⟨υ, p(h^(υ)), p(g^(υ)), ζ(p(h^(υ))), ζ(p(g^(υ)))⟩υ∈Υ}(23)

Here, the possible NWHPFS’s m.f. and n.m.f. are represented (p(h^(υ))) and (p(g^(υ))), respectively. The Normal Wiggly Hesitant Pythagorean Fuzzy Element (NWHPFE) are ζ(p(h^(υ))), ζ(p(g^(υ))), for all υ∈Υ. Then, we get the equation as,

ζ(p(h^(υ)))={ϑ1~, ϑ2~,…,ϑ~#p(h^(υ))} ={max(ϑi−f~(ϑi), 0),(2rpd(p(h~(υ)))−1)f~(ϑi) +ϑi,min(ϑi+f(ϑi)~, 1)},(24)

p(h^(υ)) value is ϑi. Likewise,

ζ(p(g^(υ))) ={φ1~, φ2~,…,φ~#p(g^(υ))}={max(φi−f~(φi), 0), (2rpd(p(g~(υ)))−1)f~(φi) +φi,min(φi+f(φi)~, 1)},(25)

p(g^(υ)) value is φi.

Definition 4.6. Let NWHPFE is {⟨υ, p(h^(υ)), p(g^(υ)), ζ(p(h^(υ))), ζ(p(g^(υ)))⟩υ∈Υ}, the score function ⟨υ, p(h^(υ)), ζ(p(h^(υ)))⟩ and ⟨υ, p(g^(υ)), ζ(p(g^(υ)))⟩ is,

SNWPHF(⟨υ, p(h^(υ)), p(g^(υ)), ζ(p(h^(υ))), ζ(p(g^(υ)))⟩) =[μ(h¯pf−σhpf)+(1−μ)(1#p(h^(υ))∑i=1#p(h^(υ))ϑi¯~−σϑ~i) −μ ′(Pg¯−σPg^)+(1−μ ′)(1#P(g^(υ))∑i=1#P(g^(υ))φi¯~−σφ~i)](26)

where,

ϑi¯~=ϑiL+ϑiM+ϑiU3(27)

φi¯~=φiL+φiM+φiU3,(28)

σϑi¯~=(ϑiL)2+(ϑiM)2+(ϑiU)2−(ϑiLϑiM)−(ϑiLϑiU)−(ϑiMϑiU),(29)

σφi¯~=(φiL)2+(φiM)2+(φiU)2−(φiLφiM)−(φiLφiU)−(φiMφiU).(30)

Now, ϑ, φ∈(0, 1).

4.1 Operation Laws of NWHPFEs

Let B1=⟨{h^1, g^1}, {ζ(h^1), ζ(g^1)}⟩ and B2=⟨{h^2, g^2}, {ζ(h^2), ζ(g^2)}⟩ are two NWHPFEs, then,

1.

B1⊕B2=⟨⋃ϑ1∈h^1, ϑ2∈h^2, φ1∈g^1, φ2∈g^2(ϑ1+ϑ2−ϑ1ϑ2, φ1φ2),⋃ϑ1∈ζ(h^1), ϑ2∈ζ(h^2), φ1∈ζ(g^1), φ2∈ζ(g^2)(ϑ1˘⊕ϑ2˘, φ1˘⊕φ2˘)⟩(31)

2.

B1⊗B2=⟨⋃ϑ1∈h^1, ϑ2∈h^2, φ1∈g^1, φ2∈g^2(ϑ1+ϑ2−ϑ1ϑ2, φ1φ2), ⋃ϑ1∈ζ(h^1), ϑ2∈ζ(h^2), φ1∈ζ(g^1), φ2∈ζ(g^2)(ϑ1˘⊗ϑ2˘, φ1˘⊗φ2˘)⟩(32)

3.

B1n=⟨⋃ϑ1∈h^1, φ1∈g^1(ϑ1n, 1−(1−φ1)n),⋃ϑ1∈ζ(h^1), φ1∈ζ(g^1)(ϑ˘1n, φ˘1n)⟩(33)

4.

nB1=⟨⋃ϑ1∈h^1, φ1∈g^1(1−(1−ϑ1)n, φ1n),⋃ϑ1∈ζ(h^1), φ1∈ζ(g^1)(nϑ˘1n, nφ˘1n)⟩(34)

Here, n>0, ϑ1˘⊕ϑ2˘ is the basic operational addition rule of triangular fuzzy set and ϑ1˘⊗ϑ2˘ goes with the triangular fuzzy set multiplication rules. Both of the rules are given as follows:

1.

ϑ1˘⊕ϑ2˘={τ1L, τ1M, τ1U}⊕{τ2L, τ2M, τ2U}={τ1L+τ2L, τ1M+τ2M, τ1U+τ2U},(35)

2.

ϑ1˘⊗ϑ2˘={τ1L, τ1M, τ1U}⊗{τ2L, τ2M, τ2U}={τ1Lτ2L, τ1Mτ2M, τ1Uτ2U},(36)

3.

ϑ1n˘={(τ1L)n, (τ1M)n, (τ1U)n}(37)

4.

nϑ1˘={nτ1n, nτ2M, nτ1U}(38)

Also, φ1˘⊕φ2˘ is satisfies the same rules as ϑ1˘⊕ϑ2˘ and φ1˘⊗φ2˘ is satisfies the same rules as ϑ1˘⊗ϑ2˘. φ1n˘ is is satisfying the same rules as ϑ1n˘ and nφ1˘ satisfies the same rules as nϑ1˘.

5  Anti-Aging Treatments

1. Dermabrasion or Microdermabrasion

Microdermabrasion is a subtle yet effective procedure that restores overall skin tone and texture. It significantly improves skin texture affected by conditions such as sun exposure, melasma, fine lines, wrinkles, age spots, pimples, and other skin issues. Microdermabrasion is generally safe for a variety of skin types and tones. This peeling procedure employs a rotary tool to remove the outer layers of the skin. It is popular among individuals seeking to enhance the appearance and radiance of their skin, addressing concerns like fine lines, acne scars, and sun damage. During the procedure, the dermatologist will first use an anesthetic to numb the skin and then remove the outer layer. Patients can typically recover at home following the treatment.

2. Laser Resurfacing

Laser therapy, also known as light therapy, is an anti-aging treatment that utilizes the power of light to repair and regenerate skin cells. This technique involves directing intense and focused rays of light through the skin to target damaged areas. Commonly referred to as laser peeling or laser ablation, this procedure is popular for its effectiveness in improving skin texture and appearance.

3. Chemical Peel

Chemical peeling is a skin restorative procedure that involves applying acidic chemical solutions to the face. This method removes the outer layers of skin and smooths the skin’s surface, resulting in a reduction of fine lines. Many chemical peels have a gel-like consistency and can be used not only on the face but also on other areas such as the neck, arms, and chest. After the chemical application, the skin develops controlled blisters that eventually shed, leading to improved texture. This treatment enhances the appearance of fine wrinkles, acne scars, and skin discoloration by removing dead skin cells from the surface.

4. Dermal Fillers

As people age, it is natural for the skin to lose elasticity, suppleness, and moisture, leading to the development of wrinkles. Commonly affected areas include the cheeks, nose, eyes, mouth, and jaws. To enhance the skin’s appearance, smooth tissue is applied to targeted areas. For medical or cosmetic procedures, needle points are used for infusions. An antibiotic substance is applied to disinfect the area, and an anesthetic agent is used to ensure patient comfort during the procedure. Subsequently, a filler—typically hyaluronic acid or a collagen-stimulating agent—is injected using a fine needle. The reaction to the injection can vary among patients, with some experiencing a slight odor or a burning sensation from the filler.

5. Botox Injections

Botox, also known as botulinum neurotoxin, is a toxin injected into the skin to temporarily paralyze muscle activity. This intervention helps prevent the formation or worsening of wrinkles. Botulinum neurotoxin is a protein that targets presynaptic nerve cells at neuromuscular junctions. It functions by inhibiting the release of the neurotransmitter acetylcholine, which leads to reduced muscle contraction. By entering the muscles and blocking nerve signals to these tissues, Botox diminishes muscular function, resulting in a smoother appearance.

6  Problem Formulation-Proposed Method

This section proposes an extended VIKOR method with NWHPFS. The calculation method of the proposed method and procedure for its improvement are also provided. The decision matrix is formulated based on the knowledge of the experts in this field and the linguistic measurement is fixed within the interval [0, 1] and satisfies the conditions of NWHPFS. The research methodology of the NWHPFs-VIKOR method is given in the Fig. 1.

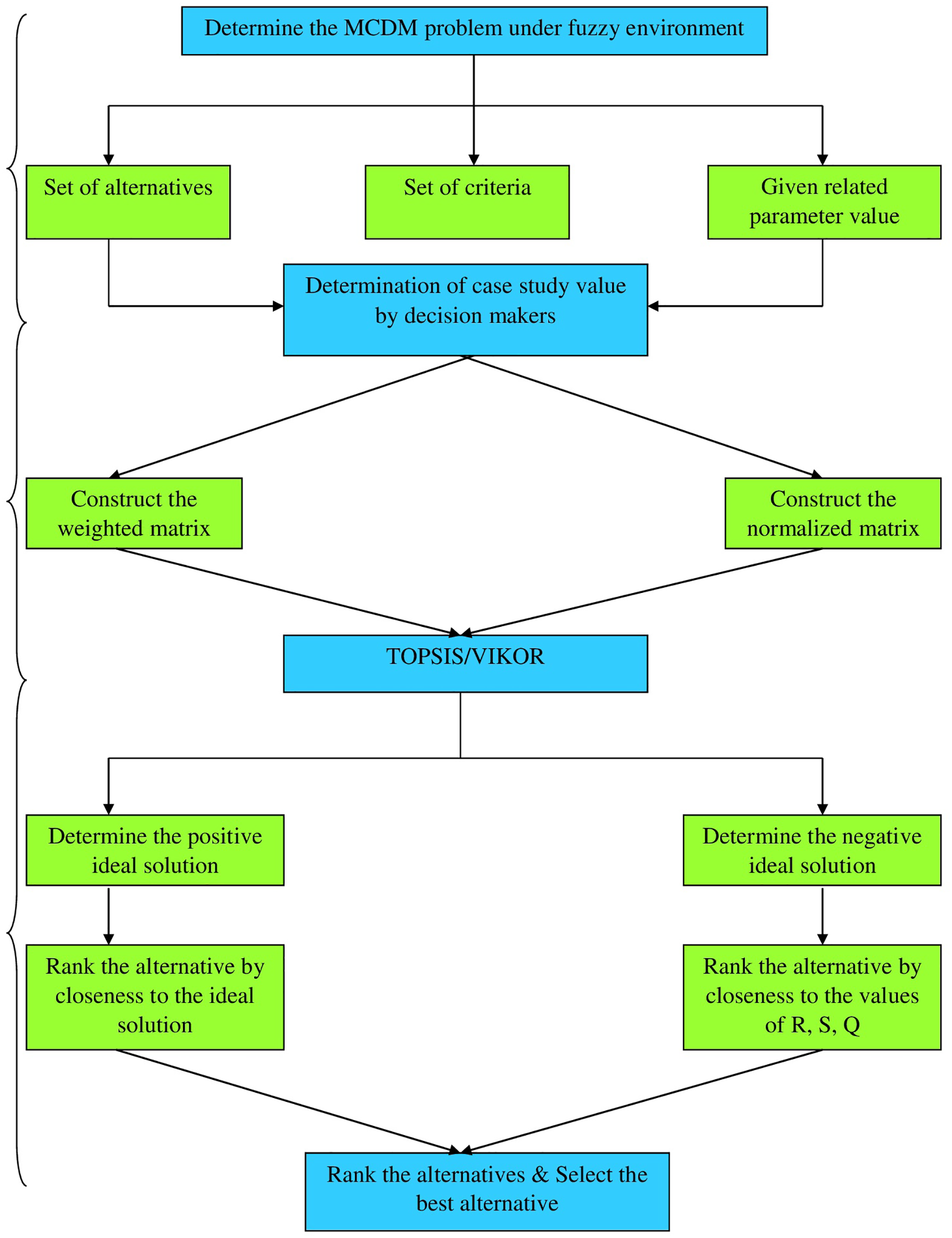
Figure 1: The mathematical procedure for NWHPF-VIKOR method

Here, we define the alternative is Ai(i=1, 2, 3,…,n). The criteria are define as Rj(j=1, 2, 3,…,m). The following expression represents the NWHPFE:

p~(Hij)={[ζ(p(h^(υij))), ζ(p(g^(υij)))]/p(h^(υij)), p(g^(υij))∈Υ}(39)

Step 1:

Define the NWHPFS decision matrix. Experts determine the values for the MCDM issue. The value of NWHPFS is represented in the Table 3 below:

H~=p~(Hij)={[p(h^(υij)), p(g^(υij))]/ζ(p(h^(υij))), ζ(p(g^(υij)))∈Υij}(40)

Step 2:

The score function is determined using the following equation. Such an equation has both membership and non-membership functions. The score function equation contains both standard deviation and mean values. The membership score function and non-membership score functions of ⟨p(h^ij), ζp(h^ij)⟩, ⟨p(g^ij), ζp(g^ij)⟩ is,

SNWPHF(⟨υ, p(h^(υ)), p(g^(υ)), ζ(p(h^(υ))), ζ(p(g^(υ)))⟩)=[μ(h¯pf−σh^pf)+(1−μ)(1#p(h^(υ))∑i=1#p(h^(υ))ϑi¯~−σϑ~i)−μ′(g¯pf−σg^pf)+(1−μ′)(1#p(g^(υ))∑i=1#p(g^(υ))φi¯~−σφ~i)](41)

Step 3:

By using weighted entropy, we calculate the criteria weight values.

E(A)=1−∑i=1m∑j=1n[ζ(p(h^(υij)))+ζ(p(g^(υij)))]2=0.(42)

To determine the entropy matrix E, we use H~ relative to the end matrix.

E=[E11E12…E1nE21E22…E2n……⋱…Em1Em2…Emn]

E~ is the normalized entropy matrix. The following equation is used to calculating the normalized entropy matrix E~.

Eij~=Eijmax{Ei1, Ei2…,Ein}(43)

Here, m and n represent the alternatives and criteria for 1≤i,j≤m,n. The criteria weights are denoted as Wj. The following equation is used to calculate the weight values. The weight value is calculated with the values of the criteria.

Wj=(1−ej)∑j=1n(1−ej), (1≤j≤n).(44)

In above equation n represent the number of indicators and 0≤Wj≤1, ∑j=1nWj=1.

Step 4:

The Positive Ideal Solution (PIS) and Negative Ideal Solutions (NIS) of NWHPFS must be computed in Step 4. The PIS and NIS of NWHPFS are indicated by V^+ and V^−, respectively.

V^+={([maxζ(p(h^(υij))), minζ(p(g^(υij)))]/p(h^ij)∈ζ(p(h^(υij))), p(g^ij)∈ζ(p(g^(υij))))([minζ(p(h^(υij))), maxζ(p(g^(υij)))]/p(h^ij)∈ζ(p(h^(υij))), p(g^ij)∈ζ(p(g^(υij))))}(45)

V^−={([minζ(p(h^(υij))), maxζ(p(g^(υij)))]/p(h^ij)∈ζ(p(h^(υij))), p(g^ij)∈ζ(p(g^(υij))))([maxζ(p(h^(υij))), minζ(p(g^(υij)))]/p(h^ij)∈ζ(p(h(υij))), p(g^ij)∈ζ(p(g^(υij))))}(46)

Step 5:

The decision maker’s utility values are Θi, and the decision maker’s view about personal frustration is Φi, as computed by the following equation. The wide majority utility ratings are then represented by Θi. The individual regret values are denoted by the letter Φi.

Θj=∑j=1nWj(V~j+−V~ij)(V~j+−V~j−),(47)

Φj=max{Wj(V~j+−V~ij)(V~j+−V~j−)}(48)

Step 6:

Calculate the value of ℵi. Here ℵi represents the index value. The following equation is used for calculating the index value:

ℵi=vΘi−Θ−Θ+−Θ−+(1−v)Φi−Φ−Φ+−Φ−,(49)

Θ+=minΘj, Θ−=maxΘj,(50)

Φ+=minΦj, Φ−=maxΦj,(51)

Here, v is the maximum group utility compromise solution. The value, v=(0.5).

Step 7:

The utility measure values and the regret measure are used to rank the options. The options are ordered by the index value. The descending order of each value in Θ, Φ and ℵ is an alternate ranking. The compromise solution ℵ[i] is used to pick alternatives, and the rules that follow are dependent on the compromise solution.

C1: Acceptable advantage

The alternative advantages are calculated by using this equation ℵ(A2)−ℵ(A1)≥(1n−1), where 1n−1=DG. The alternative ranking lists are sorted. The first place is ℵ(A1), the second place is ℵ(A2) alternative.

C2: Acceptable stability

When, the regret measure Φ and utility measure Θ ranking is based on v. Here the best value of v=0.5. Every alternative value is stable.

If conditions C1 do not satisfy the requirement, we have to move on to the following consolation solution:

•   The regret measure R2 is not satisfied the condition, if the alternative A[1] and alternative A[2].

•   The regret measure R1 does not satisfy the condition, if the alternative sequence is A[1],…,A[n]. Here, the equation ℵ(An)−ℵ(A1)≤(1n−1) is A[n] evaluated.

7  Illustrative Example

Anti-aging therapy helps to make our appearance look younger. These treatments can cause a variety of side effects. So the treatment we choose should be tailored to the nature of the skin. Choosing a good treatment can fix the problems that occur in our skin. Here, we have selected five types of non-surgical anti-aging treatments and selected the best one of them. The five types of anti-aging treatments including microdermabrasion or dermabrasion, laser resurfacing anti-aging skin treatments, chemical peel, dermal fillers, and botox injections are considered for this proposed problem.

We choose the finest among these alternative types based on the attributes of the specified parameters. The best solutions are those that fulfill all of the safety and risk requirements, as well as the investment cost, customer satisfaction, and side effects criteria. The hierarchical tiers of the selected options, as well as the criterion, are depicted in the Fig. 2. For the proposed mathematical logical method, we provide results of the NWHPF combination of two different MCDM techniques.

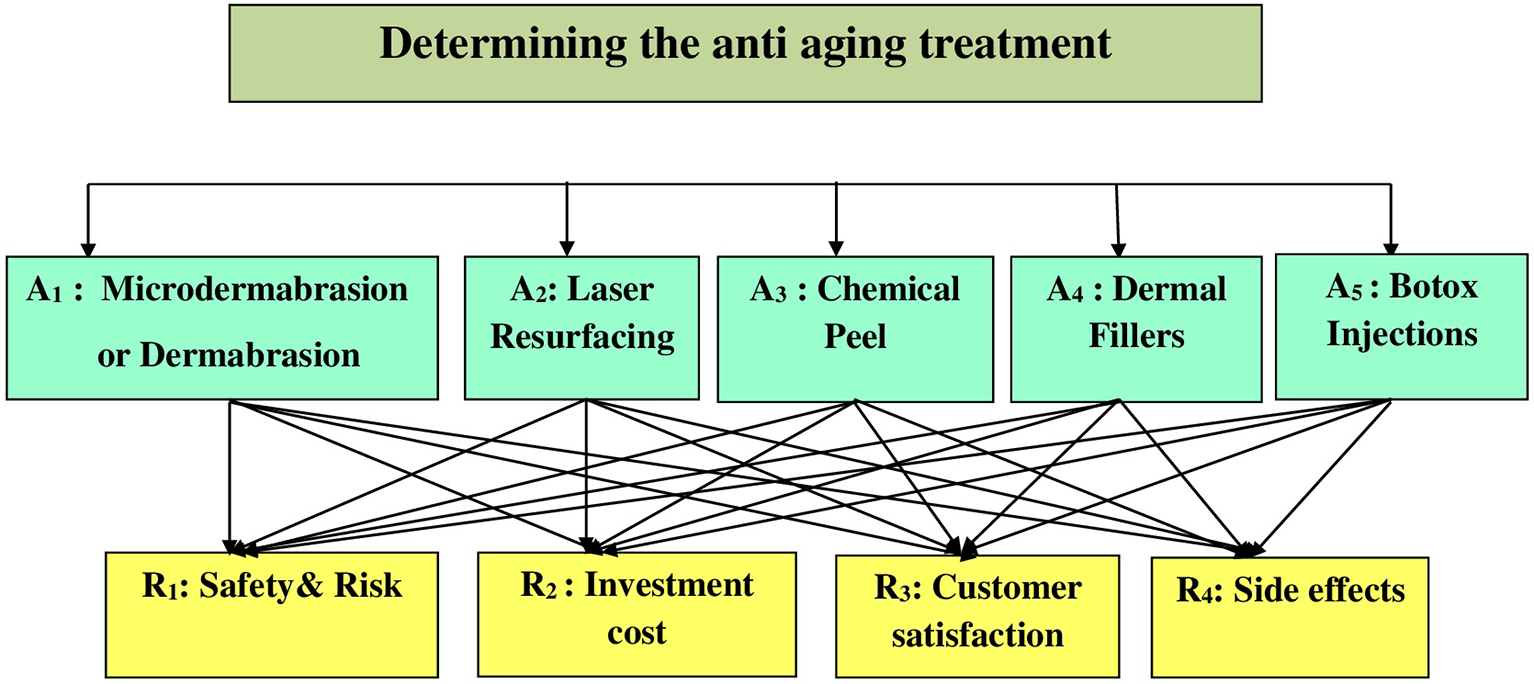
Figure 2: Hierarchical determination of the proposed problem

Using the MCDM process, we have now determined the value of the suggested set. We have incorporated the decision matrix values along with the criteria for the selected applications. The utility of such a matrix is determined by whether it allows the policymaker to remember the deep thoughts that come to mind. In this approach, the decision maker’s minor reservations are explained. Both m.d. and n.m.d. are included in the NWHPFS matrix value. The Pythagorean set provides a concise answer by focusing just on membership and non-membership. The Table 4 displays the NWHPFDM values. The NWHPF matrices value must be computed using Eq. (22). The choice matrix is made up of Ai(i=1, 2,…,m), which stands for options, and Rj(j=1, 2,…,n), which stands for criteria.

Eq. (23) is used to construct the score function of NWHPF m.d. and n.m.d., and the results are shown in the Table 5.

The NWHPF’s unique score value is represented in the Table 6. This score value is utilized to determine the MCDM’s additional techniques and the process of selecting the optimal anti-aging treatment. Fig. 3 depicts the NWHPF score value.

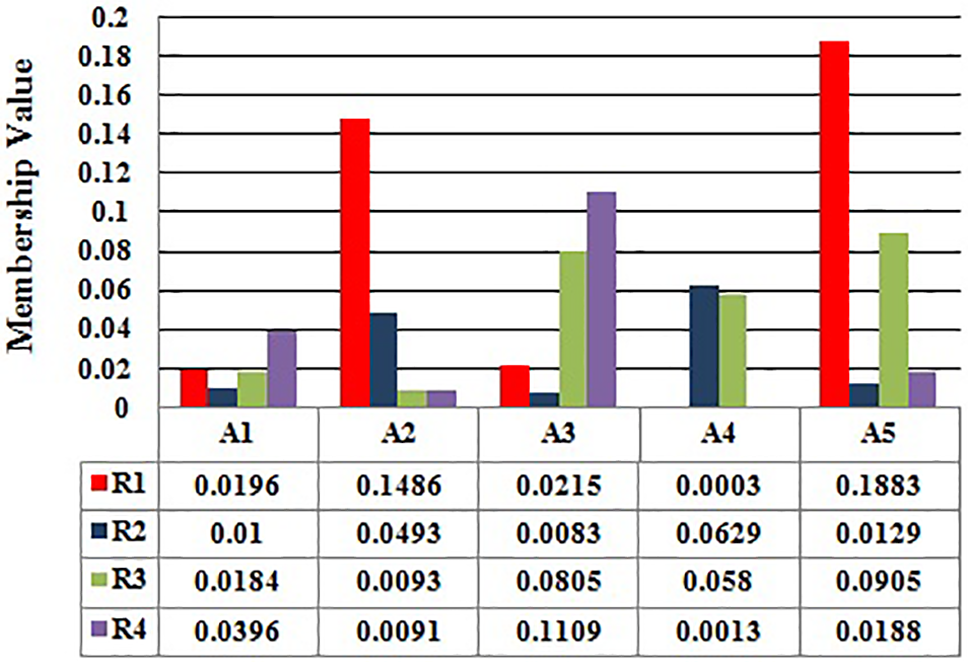
Figure 3: The score value of NWHPF

The normalized score value is calculated using score values. The Table 7 lists the normalized score values, which are seen in the Fig. 4.

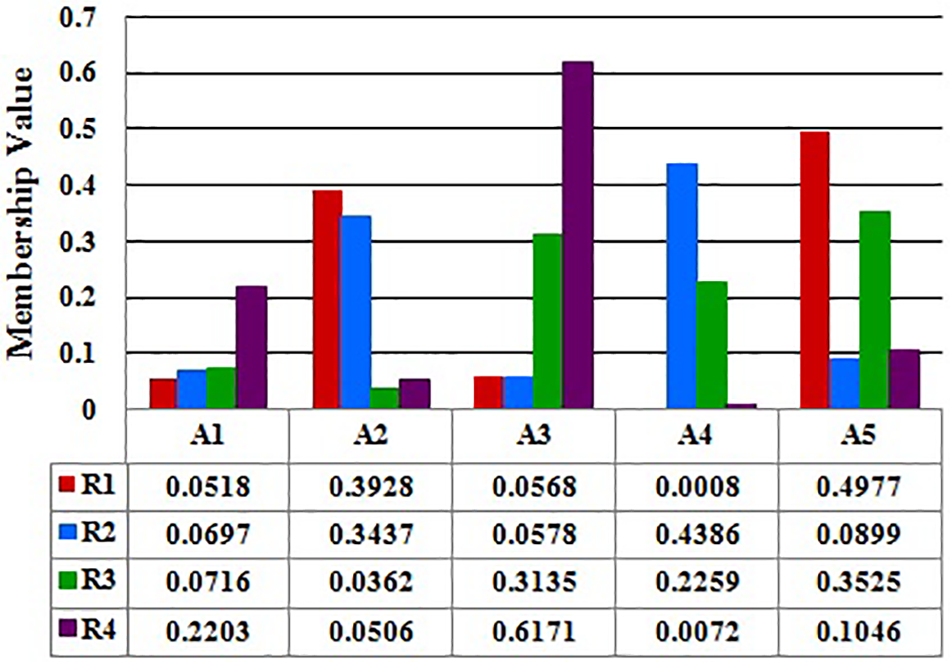
Figure 4: The normalized score value NWHPF

By using score values we have to determine the weighted entropy. By using Eq. (24) we determined the weighted entropy value. The Table 8 represents the weighted entropy values. The Fig. 5 represents the weighted criteria value of NWHPFS. The sum of the weighted criteria value is always 1.

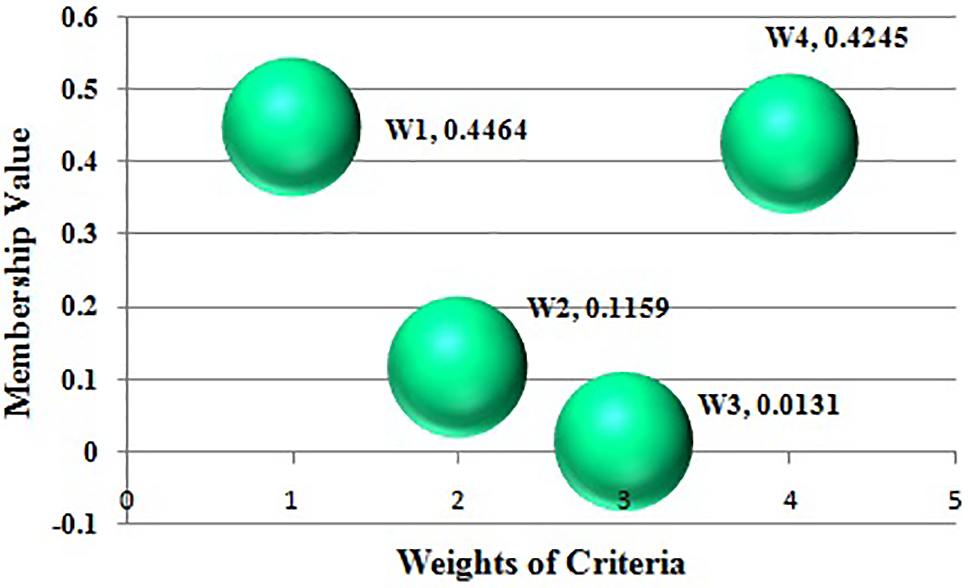
Figure 5: The weighted criteria value of NWHPF

By using the normalized score matrix, the PIS and NIS of (27) and (28) are calibrated and represented in Figs. 6 and 7.

V^+={0.1883, 0.0629, 0.0905, 0.1109}(52)

V^−={0.0003, 0.0083, 0.0093, 0.0013}(53)

Figure 6: PIS of NWHPF

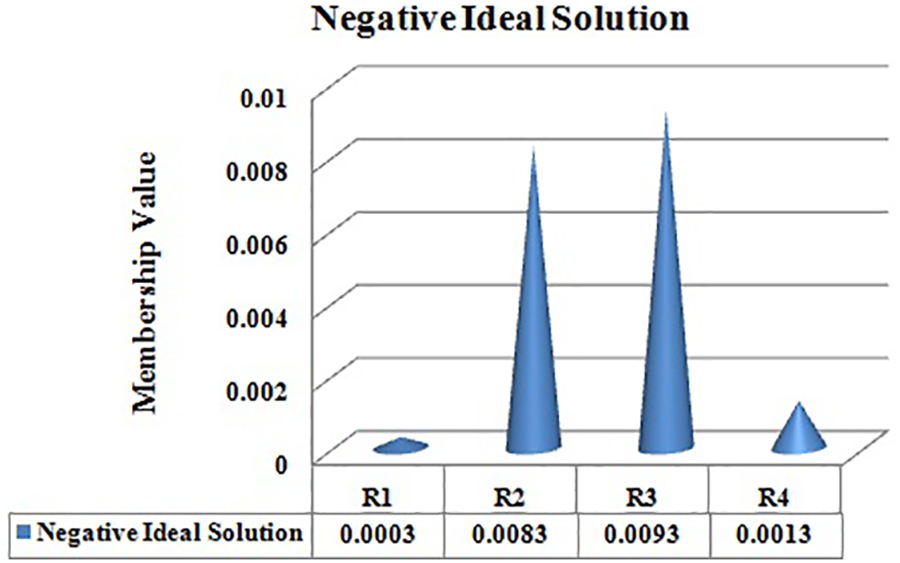
Figure 7: PIS of NWHPF

The utility measures matrix is calculated by using (29) and demonstrated in the Table 9.

Now we can calculate regret measures from (30). The Fig. 8 represents the result of utility and regret measure.

Θ1=0.8232, Θ2=0.5392, Θ3=0.5106, Θ4=0.5812Θ5=0.2823.(54)

Figure 8: The result of utility and regret measure

Now regret measures (Φ) are calculated by using (23).

Φ1=0.3395, Φ2=0.2567, Φ3=0.3356, Φ4=0.3783Φ5=0.1510.(55)

Now for each alternative, index (ℵi) value been calculated by using Eq. (31).

ℵ1=0.9150, ℵ2=0.4703, ℵ3=0.6172, ℵ4=0.7766ℵ5=0.(56)

Sort the ℵ values in decreasing order to rank the alternatives, which means,

A5>A2>A3>A4>A1

Here, A5 is best anti-aging treatment for skin. The final results of regret measure (Φi), utility measure (Θi) and index value (ℵi) are tabulated in the Table 10 and shown in the Fig. 9.

Figure 9: The result of VIKOR method

7.1 Comparative Analysis

Since MCDM is a vast and developing field, there many viable MCDM methods that can be applied to the discussed problem. A comparative analysis is performed to compare and contrast the proposed method with existing MCDM methods. The proposed method is compared with the other MCDM methods such as Weighted Aggregated Sum Product Assessment (WASPAS), Evaluation based on Distance from Average Solution (EDAS), Additive Ratio Assessment (ARAS), Multi-Attributive Border Approximation area Comparison (MABAC), Improved Deviation Objectivity based on Criteria Importance through Intercriteria Correlation (IDOCRIW). The ranking results of these methods are given in Table 11. Fig. 10 shows the results of the comparative analysis approaches in accordance with other existing MCDM methodologies.

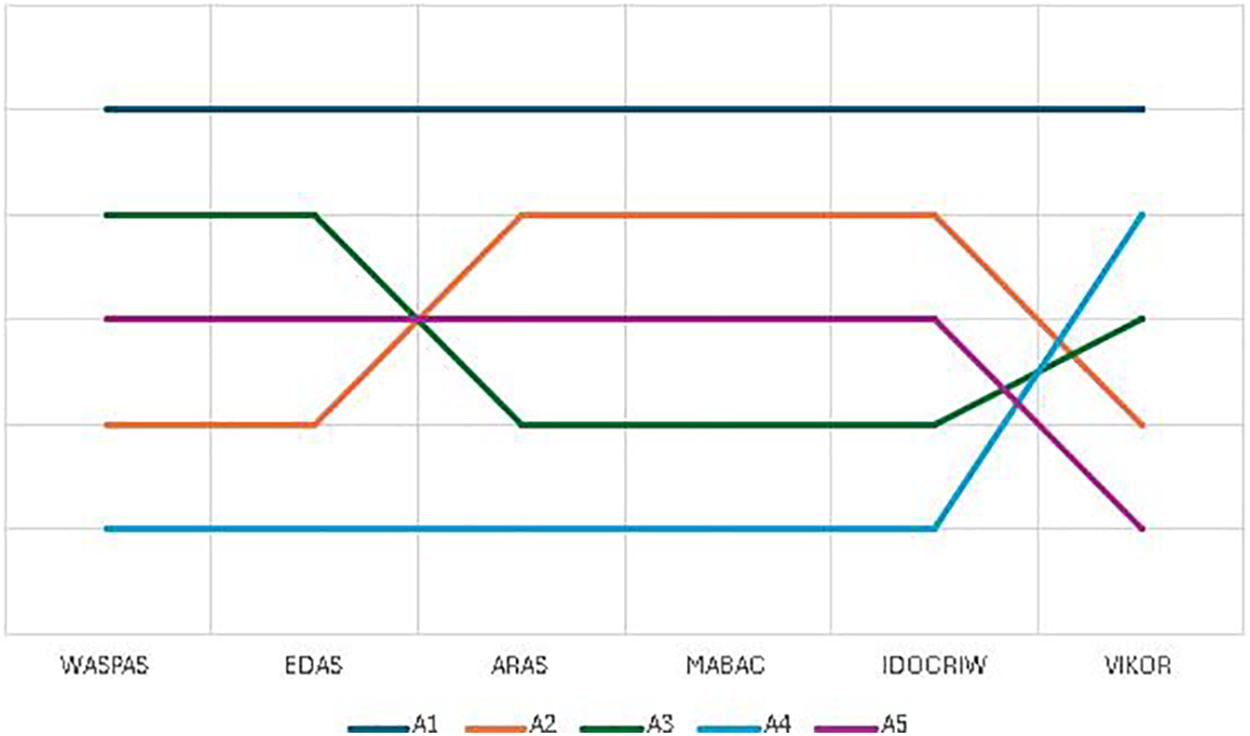
Figure 10: Comparative analysis

Furthermore, the ranking outcomes of NWHPFS-MCDM approaches show minor deviations when compared to other techniques. The smallest difference is owing to the fact that criterion weights play an important role in MCDM problems. In this situation, the weighting of the criteria reflects the relative importance of the criterion.

Spearman’s rank correlation analysis is performed to analyze the monotonicity of the results obtained from the proposed NWHPFS-VIKOR method. The decision matrix is formed based on expert opinions which could not be captured by generalized assumptions that are used in the other MCDM methods. This results in the low correlation of VIKOR with other methods as shown in the Fig. 11.

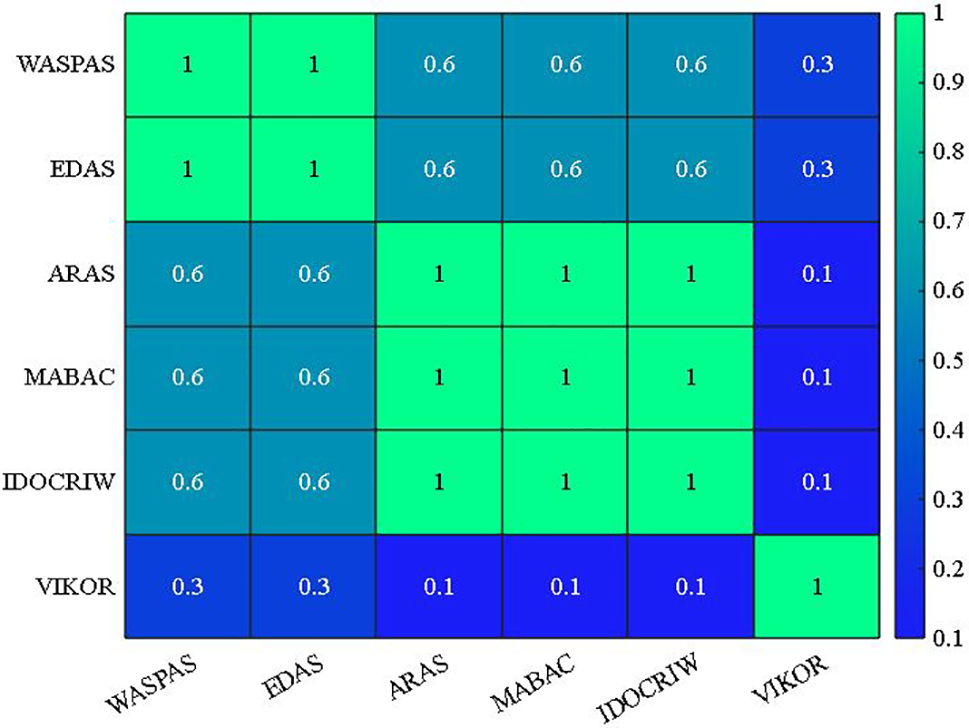
Figure 11: Spearman correlation analysis

7.2 Sensitive Analysis

The robustness and reliability of any proposed model can be verified using the sensitive analysis. The sensitive analysis is performed by varying the weights of the criteria to check the performance of the model in each scenario. In this study, the criteria R1 and R3 are considered to be beneficial and the remaining are considered as cost criteria.

1.    Case 1: Each criterion is assumed to have equal weights, thus each criterion assumes a weight of 0.25. The ranking of the alternatives is as follows: A5 > A3 > A1 > A4 > A2.

2.    Case 2: The beneficial criteria is assumed to have 70 percent weightage and while the cost criteria is assumed to have 30 percent weightage. Thus the criteria R1 and R3 assume a value of 0.35 and R2 and R4 assume a value of 0.15, respectively. The preference order of the alternatives is given as: A5 > A3 > A4 > A2 > A1.

This implies that the change in weights of the criteria, i.e., the change in the influence exerted by the criteria in ranking the alternatives does not adversely affect the overall ranking. This shows the proposed model can perform well under different scenarios making it ideal for real-world applications.

8  Conclusion

Anti-aging medicine is defined as the early identification, prevention, and therapy of age-related disorders in the medical and commercial communities. It’s not the same as treating the aging process, and there are a variety of procedures and treatments available right now. Based on performance, along with utility values, regret values, and index values, the VIKOR method offers a compromise option. This mathematical model is more suitable for evaluating anti-aging medicines in this regard. The HFS is used to deal with the unstable set theory’s issue of uncertainty. HFS asked decision-makers for their thoughts on alternative criteria. We utilized the NWHFS as an expansion of the HFS. The greater information about the policymakers was delivered via a NWHFS. An MCDM is employed to an anti-aging medication in the usual wiggly reluctant fuzzy environment in this study work. Using VIKOR in a hesitant fuzzy environment, we have concluded that the optimum anti-aging treatment for the identified condition is based on our numerical evaluation. We conclude that botox injection is the best anti-aging therapy based on a ranking methodology. Further, the robustness and reliability of the method are analyzed using sensitive analysis. The comparison of the suggested methodology to current ranking systems revealed that it is consistent with other approaches. These offered procedures are the most effective anti-aging therapy options.

8.1 Limitations and Future Implications

There are a few limitations that the presented study must overcome. This study analyses five widely known anti-aging treatments based on expert opinion. While expert opinions offer insightful insights into the problem, the mindset and emotions toward these anti-aging therapies remain unknown. In the future, the sentiments of people in selected cities can be conducted to ensure better accuracy in the present study. This proposed methodology analyzes the treatment techniques based on four major generalized criteria. This study could be further expanded by introducing sub-criteria to further scrutinize the treatment technologies. Due to the robustness of the presented method, this methodology can be applied to various fields such as robot selection, supply chain, site selection, and much more. Further, VIKOR is an objective method, a hybrid methodology combining VIKOR with a subjective method could bring a new perspective by analyzing both sides of the same coin. The NWHFS set can be combined with various other MCDM methods to accurately quantify the ambiguities and inconsistencies that often arise during the conversion of real-world problems into a mathematical model.

Acknowledgement: This work was supported by Department of Mathematics, Bharathiar University, Coimbatore, India and National Research Foundation (NRF) of Korea grant.

Funding Statement: This work is funded by the Korean Government (MSIT) Grant NRF-2022R1C1C1006671.

Author Contributions: Daekook Kang: Investigation, Resources, Validation, Visualization, Funding acquisition, Writing—review and Editing. Ramya Lakshmanaraj: Writing—original draft, Data curation, Resources, Visualization, Writing—review and Editing. Samayan Narayanamoorthy: Conceptualization, Data curation, Formal analysis, Supervision, Investigation, Methodology, Validation, Visualization, Writing—original draft, Writing—review and Editing. Navaneethakrishnan Suganthi Keerthana Devi: Data curation, Writing—review and Editing. Samayan Kalaiselvan: Validation, Editing and Visualization. Ranganathan Saraswathy: Validation, Visualization, and Editing. Dragan Pamucar: Validation, Visualization, Writing—review and Editing. Vladimir Simic: Validation, Visualization, Writing—review and Editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The study utilizes secondary data, which is available with the authors and can be made available upon public request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Y. Adhami and F. Ahmad, “Interactive Pythagorean-hesitant fuzzy computational algorithm for multiobjective transportation problem under uncertainty,” Int. J. Manage. Sci. and Eng. Manage., vol. 15, no. 4, pp. 288–297, 2020. doi: 10.1080/17509653.2020.1783381. [Google Scholar] [CrossRef]

2. M. Colak and İ. Kaya, “Multi-criteria evaluation of energy storage technologies based on hesitant fuzzy information: A case study for Turkey,” J. En. Storage., vol. 28, no. 3, 2020, Art. no. 101211. doi: 10.1016/j.est.2020.101211. [Google Scholar] [CrossRef]

3. R. Krishankumar, K. S. Ravichandran, A. H. Gandomi, and S. Kar, “Interval-valued probabilistic hesitant fuzzy set-based framework for group decision-making with unknown weight information,” Neural Comp. App., vol. 33, no. 7, pp. 2445–2457, 2021. doi: 10.1007/s00521-020-05160-7. [Google Scholar] [CrossRef]

4. A. Y. Gül, E. Cakmak, and A. E. Karakas, “Drone selection for forest surveillance and fire detection using interval valued neutrosophic edas method,” Facta Universitatis, Ser.: Mech. Eng., 2024. doi: 10.22190/FUME231028008G. [Google Scholar] [CrossRef]

5. R. Kumar, A. I. Khan, Y. B. Abushark, M. M. Alam, A. Agarwal and R. A. Khan, “A knowledge-based integrated system of hesitant fuzzy set, AHP and TOPSIS for evaluating security-durability of web applications,” IEEE Access, vol. 8, pp. 48870–48885, 2020. doi: 10.1109/ACCESS.2020.2978038. [Google Scholar] [CrossRef]

6. J. Ali and M. Naeem, “Distance and similarity measures for normal wiggly dual hesitant fuzzy sets and their application in medical diagnosis,” Sci. Rep., vol. 12, 2022, Art. no. 13784. doi: 10.1038/s41598-022-16078-6. [Google Scholar] [CrossRef]

7. J. Xia, M. Chen, and W. Fang, “Normal wiggly probabilistic hesitant fuzzy set and its application in battlefield threat assessment,” Int. J. Fuzzy Syst., vol. 25, pp. 145–167, 2023. doi: 10.1007/s40815-022-01371-3. [Google Scholar] [CrossRef]

8. P. Zhang, Z. Zhang, D. Gong, and X. Cui, “A novel normal wiggly hesitant fuzzy multi-criteria group decision making method and its application to electric vehicle charging station location,” Expert. Syst., vol. 223, no. 9, 2023, Art. no. 119876. doi: 10.1016/j.eswa.2023.119876. [Google Scholar] [CrossRef]

9. D. Zindani, S. R. Maity, and S. Bhowmik, “Extended TODIM method based on normal wiggly hesitant fuzzy sets for deducing optimal reinforcement condition of agro-waste fibers for green product development,” J. Clean. Prod., vol. 301, 2021, Art. no. 126947. doi: 10.1016/j.jclepro.2021.126947. [Google Scholar] [CrossRef]

10. P. Zhang, Z. Zhang, and D. Gong, “An improved normal wiggly hesitant fuzzy FMEA model and its application to risk assessment of electric bus systems,” Appl. Intell., vol. 54, pp. 6213–6237, 2024. doi: 10.1007/s10489-024-05458-2. [Google Scholar] [CrossRef]

11. S. Xian, D. Ma, H. Guo, and X. Feng, “Route intelligent recommendation model and algorithm under the Pythagorean hesitant fuzzy linguistic environment,” Comp. Appl. Math., vol. 42, 2023, Art. no. 110. doi: 10.1007/s40314-023-02249-2. [Google Scholar] [CrossRef]

12. B. Zhou, J. Chen, Q. Wu, D. Pamučar, W. Wang and L. Zhou, “Risk priority evaluation of power transformer parts based on hybrid FMEA framework under hesitant fuzzy environment,” Facta Universitatis, Ser.: Mech. Eng., vol. 20, no. 2, pp. 399–420, 2022. doi: 10.22190/FUME220223013Z. [Google Scholar] [CrossRef]

13. J. Jeon et al., “A probabilistic hesitant fuzzy MCDM approach to evaluate India’s intervention strategies against the COVID-19 pandemic,” Socio-Econ. Plan. Sci., vol. 89, no. 4, 2023, Art. no. 101711. doi: 10.1016/j.seps.2023.101711. [Google Scholar] [CrossRef]

14. Y. Feng, Z. Hong, G. Tian, Z. Li, J. Tan and H. Hu, “Environmentally friendly MCDM of reliability-based product optimisation combining DEMATEL-based ANP, interval uncertainty and Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR),” Infor. Sci., vol. 442–443, pp. 128–144, 2018. doi: 10.1016/j.ins.2018.02.038. [Google Scholar] [CrossRef]

15. R. Joshi, “A Novel decision-making method using R-Norm concept and VIKOR approach under picture fuzzy environment,” Expert. Sys. with App., vol. 147, 2020, Art. no. 113228. doi: 10.1016/j.eswa.2020.113228. [Google Scholar] [CrossRef]

16. M. S. A. Khan, S. Abdullah, A. Ali, and F. Amin, “An extension of VIKOR method for multi-attribute decision-making under Pythagorean hesitant fuzzy setting,” Gra. Comp., vol. 4, pp. 421–434, 2019. doi: 10.1007/s41066-018-0102-9. [Google Scholar] [CrossRef]

17. H. Li, W. Wang, L. Fan, Q. Li, and X. Chen, “A novel hybrid MCDM model for machine tool selection using fuzzy DEMATEL, entropy weighting and later defuzzification VIKOR,” Appl. Soft. Comp., vol. 91, 2020, Art. no. 106207. doi: 10.1016/j.asoc.2020.106207. [Google Scholar] [CrossRef]

18. Z. Ren, Z. Xu, and H. Wang, “The strategy selection problem on artificial intelligence with an integrated VIKOR and AHP method under probabilistic dual hesitant fuzzy information,” IEEE Access, vol. 7, pp. 103979–103999, 2019. doi: 10.1109/ACCESS.2019.2931405. [Google Scholar] [CrossRef]

19. J. Ali and M. Naeem, “r, s, t-spherical fuzzy VIKOR method and its application in multiple criteria group decision making,” IEEE Access, vol. 11, pp. 46454–46475, 2023. doi: 10.1109/ACCESS.2023.3271141. [Google Scholar] [CrossRef]

20. N. Zhang, Y. Zhou, J. Liu, and G. Wei, “VIKOR method for Pythagorean hesitant fuzzy multi-attribute decision-making based on regret theory,” Eng. Appl. Artif. Intell., vol. 126, 2023, Art. no. 106857. doi: 10.1016/j.engappai.2023.106857. [Google Scholar] [CrossRef]

21. A. Singh and S. Kumar, “Intuitionistic fuzzy entropy-based knowledge and accuracy measure with its applications in extended VIKOR approach for solving multi-criteria decision-making,” Granul. Comput., vol. 8, pp. 1609–1643, 2023. doi: 10.1007/s41066-023-00386-x. [Google Scholar] [CrossRef]

22. D. Abdul, W. Q. Jiang, A. Tanveer, and M. Sameeroddin, “Comprehensive analysis of renewable energy technologies adoption in remote areas using the integrated delphi-fuzzy AHP-VIKOR approach,” Arab. J. Sci. Eng., vol. 49, pp. 7585–7610, 2024. doi: 10.1007/s13369-023-08334-2. [Google Scholar] [CrossRef]

23. A. Guleria and R. K. Bajaj, “A robust decision making approach for hydrogen power plant site selection utilizing (R, S)-Norm Pythagorean Fuzzy information measures based on VIKOR and TOPSIS method,” Int. J. Hydro. En., vol. 45, no. 38, pp. 18802–18816, 2020. doi: 10.1016/j.ijhydene.2020.05.091. [Google Scholar] [CrossRef]

24. P. Liu, H. Xu, and Y. Geng, “Normal wiggly hesitant fuzzy linguistic power Hamy mean aggregation operators and their application to multi-attribute decision making,” Comp. Ind. Eng., vol. 140, 2019, Art. no. 106224. doi: 10.1016/j.cie.2019.106224. [Google Scholar] [CrossRef]

25. A. Liu, X. Ji, H. Lu, and H. Liu, “The selection of 3PRLs on self-service mobile recycling machine: Interval-valued Pythagorean hesitant fuzzy best-worst multi-criteria group decision-making,” J. Cle. Prod., vol. 230, pp. 734–750, 2019. doi: 10.1016/j.jclepro.2019.04.257. [Google Scholar] [CrossRef]

26. S. Narayanamoorthy, L. Ramya, D. Baleanu, J. V. Kureethara, and V. Annapoorani, “Application of normal wiggly dual hesitant fuzzy sets to site selection for hydrogen underground storage,” Int. J. Hydrogen En., vol. 44, no. 54, pp. 28874–28892, 2019. doi: 10.1016/j.ijhydene.2019.09.103. [Google Scholar] [CrossRef]

27. G. Wei, J. Wang, C. Wei, Y. Wei, and Y. Zhang, “Dual hesitant Pythagorean fuzzy hamy mean operators in multiple attribute decision making,” IEEE Access, vol. 7, pp. 86697–86716, 2019. doi: 10.1109/ACCESS.2019.2924974. [Google Scholar] [CrossRef]

28. J. R. Fletcher, “Anti-aging technoscience & the biologization of cumulative inequality: Affinities in the biopolitics of successful aging,” J. Aging Stu., vol. 55, 2020, Art. no. 100899. doi: 10.1016/j.jaging.2020.100899. [Google Scholar] [CrossRef]

29. S. Rajan-Rankin, “Race, embodiment and later life: Re-animating aging bodies of color,” J. Aging Stud., vol. 45, pp. 32–38, 2018. doi: 10.1016/j.jaging.2018.01.005. [Google Scholar] [CrossRef]

30. E. Rostkowska, E. Poleszak, K. Wojciechowska, and K. Dos Santos Szewczyk, “Dermatological management of aged skin,” Cosmetics, vol. 10, no. 2, 2023, Art. no. 55. doi: 10.3390/cosmetics10020055. [Google Scholar] [CrossRef]

31. Y. Liang, W. Su, and F. Wang, “Skin ageing: A progressive, multi-factorial condition demanding an integrated, multilayer-targeted remedy,” Clin. Cosmet. Investig. Dermatol., vol. 16, pp. 1215–1229, 2023. doi: 10.2147/CCID.S408765. [Google Scholar] [CrossRef]

32. L. T. Goberdhan, K. Schneider, E. T. Makino, and R. C. Mehta, “Combining diamond-tip dermabrasion treatments and topical skincare in participants with dry, hyperpigmented, photodamaged or acne-prone/oily facial skin: A clinical usage study,” Clin. Cosmet. Investig. Dermatol., vol. 16, pp. 2645–2657, 2023. doi: 10.2147/CCID.S423688. [Google Scholar] [CrossRef]

33. A. Markiewicz-Tomczyk, E. Budzisz, and A. Erkiert-Polguj, “A subjective and objective assessment of combined methods of applying chemical peels and microneedling in antiaging treatments,” J. Clin. Med., vol. 12, no. 5, 2023, Art. no. 1869. doi: 10.3390/jcm12051869. [Google Scholar] [CrossRef]

34. R. Nanda and J. L. Cohen, “Spontaneous resolution of eruptive papules following ablative laser resurfacing—Case report and review of laser-associated eruptive keratoacanthomas,” J. Cosmet. Dermatol., vol. 23, no. 6, pp. 1936–1939, 2024. doi: 10.1111/jocd.16182. [Google Scholar] [CrossRef]

35. S. McKenzie, J. Wang, A. C. Mora Hurtado, P. Uppal, S. C. Taylor and N. Elbuluk, “Cosmetic injectables in skin of color: A review of uses, safety, and effectiveness of neuromodulators and dermal fillers,” J. Cosmet. Dermatol., vol. 23, no. 7, pp. 2345–2360, 2024. doi: 10.1111/jocd.16297. [Google Scholar] [CrossRef]

36. C. Yang, Q. Wang, W. Peng, J. Zhang, and J. Zhu, “A normal wiggly Pythagorean hesitant fuzzy bidirectional projection method and its application in EV power battery recycling mode selection,” IEEE Access, vol. 8, pp. 62164–62180, 2020. doi: 10.1109/ACCESS.2020.2984242. [Google Scholar] [CrossRef]