 Open Access
Open Access
ARTICLE
Q-Learning-Assisted Meta-Heuristics for Scheduling Distributed Hybrid Flow Shop Problems
1 Institute of Systems Engineering, Macau University of Science and Technology, Macau, 99078, China
2 Department of Electronics and Computer Science, Koszalin University of Technology, Koszalin, 75-453, Poland
* Corresponding Author: Kaizhou Gao. Email:
(This article belongs to the Special Issue: Recent Advances in Ensemble Framework of Meta-heuristics and Machine Learning: Methods and Applications)
Computers, Materials & Continua 2024, 80(3), 3573-3589. https://doi.org/10.32604/cmc.2024.055244
Received 21 June 2024; Accepted 13 August 2024; Issue published 12 September 2024
Abstract
The flow shop scheduling problem is important for the manufacturing industry. Effective flow shop scheduling can bring great benefits to the industry. However, there are few types of research on Distributed Hybrid Flow Shop Problems (DHFSP) by learning assisted meta-heuristics. This work addresses a DHFSP with minimizing the maximum completion time (Makespan). First, a mathematical model is developed for the concerned DHFSP. Second, four Q-learning-assisted meta-heuristics, e.g., genetic algorithm (GA), artificial bee colony algorithm (ABC), particle swarm optimization (PSO), and differential evolution (DE), are proposed. According to the nature of DHFSP, six local search operations are designed for finding high-quality solutions in local space. Instead of random selection, Q-learning assists meta-heuristics in choosing the appropriate local search operations during iterations. Finally, based on 60 cases, comprehensive numerical experiments are conducted to assess the effectiveness of the proposed algorithms. The experimental results and discussions prove that using Q-learning to select appropriate local search operations is more effective than the random strategy. To verify the competitiveness of the Q-learning assistedmeta-heuristics, they are compared with the improved iterated greedy algorithm (IIG), which is also for solving DHFSP. The Friedman test is executed on the results by five algorithms. It is concluded that the performance of four Q-learning-assisted meta-heuristics are better than IIG, and the Q-learning-assisted PSO shows the best competitiveness.Keywords
Distributed production and manufacturing affect the efficiency and competitiveness of enterprises and are important components of intelligent manufacturing systems [1]. Distributed flow shop scheduling is an important problem in distributed production and manufacturing. The study of distributed flow shop scheduling problems holds practical application value and significance [2]. Distributed flow shop scheduling refers to industries that have multiple workshops in different geographical locations. These workshops need to be managed to process and manufacture products. In the distributed flow shop scheduling problems, the workpieces are assigned to different workshops, the resources are allocated for workpieces, and the workpieces are sequenced in each workshop, to optimize one or more production targets. Reasonable and efficient distributed scheduling can reduce cost, improve industrial competitiveness, and fully utilize resources [3].
The hybrid flow shop scheduling problem (HFSP) refers to a production facility that consists of multiple stages, each of which includes one or more parallel machines. HFSP is extensively present in many manufacturing industries, such as steel, textile, petrochemicals, and electronics and each factory represents a HFSP environment [4,5]. HFSP can be considered a combination of flow shop scheduling problem (FSP) and parallel machine scheduling [6]. To enhance the efficiency of the flow shop, in the traditional HFSP, jobs are processed by a single factory that utilizes one or more parallel machines for production at each stage. Therefore, numerous scholars have conducted extensive research on HFSP and have proposed various methods to address the issue, including the exact methods [7], heuristics [8], and meta-heuristics [9]. HFSP is a typical flow shop scheduling problem. It combines the characteristics of both classic flow shop and parallel machine scheduling and is an non-deterministic polynomial (NP-hard) problem [10].
The manufacturing problem with multiple hybrid flow plants is called DHFSP. DHFSP combines distributed production and HFSP, which is more complex and presents greater optimization challenges compared to HFSP. Compared to distributed production and HFSP, DHFSP has less studied. However, DHFSP is a common issue in manufacturing, particularly in semiconductor manufacturing. This issue holds significant research importance. Fig. 1 shows a semiconductor manufacturing process with two distinct workshops. All semiconductors begin with wafers. The raw materials used to make wafers are processed to produce finished wafers, followed by the application of oxidation protection. After completing the aforementioned steps, photo etching, etching, and thin film deposition are carried out on the wafer to create the circuit and micro-devices. Finally, the interconnection process is carried out to connect the circuits on the wafer, and the preliminary manufacturing of the semiconductor is completed.

Figure 1: The diagram of DHFSP in semiconductor manufacturing
In the recent development, DHFSP has garnered significant thinking and has yielded numerous results [11–15]. Meta-heuristics are widely utilized to solve DHFSP. The artificial bee colony algorithm (ABC) is widely used to resolve the discrete harmony search and firefly algorithm (DHFSP). Li et al. [16] improved the ABC (IABC) minimization algorithm to solve DHFSP, the IABC uses a two-stage encoding approach and a machine-selected decoding approach. The hybrid search strategy combines the benefits of simulated annealing (SA) and retention mechanisms to enhance the performance of ABC. In [17], a hybrid ABC method with mixed domain operation and a multiple critical plant exchange strategy is proposed. The self-adaptive ABC (SABC) is introduced to address the DRCHFS, the algorithm considers resource constraints and machine allocation in decoding and introduces a new initialization strategy that considers the maximum completion time of the work piece [18]. There are also numerous studies utilizing other meta-heuristic algorithms. Hao et al. found an improved crossover operator based on Partial Mapping Crossover (PMX) to enhance the performance of the brain storm optimization Algorithm (BSO) [19]. A hybrid multi-objective iterated greedy with a new integration initialization strategy by incorporating four heuristic rules is introduced by Lu et al. [20] to solve an energy-aware problem of DHFSP. Li et al. [21] classified groups to implement different evolutionary strategies becomes a multi-group cooperative evolutionary mechanism, increasing the diversity of solutions. In [22], Cai et al. introduced a novel shuffled frog-leaping algorithm (FLA) with memeplex quality designed, selecting new memeplex by evaluating the quality of each memeplex. Wu utilizes particle swarm optimization (PSO) in conjunction with the leapfrog algorithm to address production management issues in manufacturing facilities [23]. It combines the variation and crossover ideas of genetic algorithms.
With the wide application of reinforcement learning (RL), there is an increasing amount of research to solve DHFSP using reinforcement learning. Using RL and an effective solution selection strategy based on decomposition can help in selecting appropriate improved operators [24], which is advantageous for both the convergence and diversity of solutions. Q-learning, as a kind of RL, is often used to solve the distributed flow shop scheduling problem. Zhang et al. [25] proposed a meta-reinforcement learning-based meta-heuristic (MRLM). The search operator is trained to construct the initial learning model, and then Q-learning is utilized to learn and assimilate feedback for selecting the search operator. In order to expedite the convergence of the algorithm, it is common to design multiple domain structures. Currently, many studies combine Q-learning to select the domain structure more effectively [26,27]. In literature [28], Luo et al. used Q-learning to select the most effective strategy among the six domain structures designed to accelerate convergence. A training algorithm based on genetic algorithms is proposed by Liu et al. [29]. Combined with a genetic algorithm, a target evaluation strategy for each workshop state is proposed, and the Deep Q-Network (DQN) is enhanced to ensure stability during training. Zhao et al. [30] proposed a knowledge-driven cooperative scatter search algorithm. To enhance the exploration ability and search efficiency of the algorithm, Q-learning is design to select disturbance strategies. The aforementioned research demonstrates that combining Q-learning to enhance algorithm performance is feasible and effective. There is few existing research on applying Q-learning to solve DHFSP. It is a challenge that design Q-learning to effectively enhance the performance of algorithms to solve the DHFSP. This paper introduces meta-heuristics integrates Q-learning to solve DHFSP.
The main contributions of this study are shown as follows:
(1) A mathematical model is developed for solving the DHFSP.
(2) Six local search schemes are designed based on the nature of DHFSP to improve the performance of four meta-heuristics.
(3) A learning strategy is proposed to assist the algorithms find the best local search strategy during iterations.
The rest of this study consists of the following. In Section 2, we introduce the DHFSP and establish a mathematical model. In Section 3, the proposed algorithms and the improvement strategies are presented. In Section 4, experiments are conducted to validate the effectiveness of the proposed strategies. Finally, Section 5 summarizes this work, and future directions are given.
2 Problem Description and Model
In this section, the specific process of DHFSP is introduced. There is a set of jobs that need to be processed in factories. Each factory has stages. Each job must include all processing steps. Each stage has one or more machines. The denote the number of machines at stage in factory. When a machine is available on the production stage, the next job can be processed on this machine. The optimization objective is to minimize the maximum completion time among all factories (makespan). The makespan is crucial for optimizing resource utilization and achieving high productivity.
Parameters:
| Number of factories. | |
| Number of stages in each factory. | |
| Number of jobs. | |
| Index for factories. | |
| Index for stages. | |
| Index for jobs. | |
| Index for machines. | |
| The number of machines at stage | |
| The beginning time of job j in stage g. | |
| The processing time of job j in stage g. | |
| The completion time of job j in stage g. | |
| The makespan of a schedule. | |
| 1 if job | |
| 1 if job | |
| 1 if job |
The target of the problem is to minimize the makespan as follows:
On the basis of the notations described, the mathematical model of DHFSP is as follows:
Constraint (2) states that each job assigned to one factory cannot be assigned to another. Constraint (3) indicates that the current operation can only be performed after its previous operation is complete. Constraint (4) indicates that all jobs must go through all operations, and when a machine starts an operation, the operation cannot be assigned to other machines. Constraints (5) and (6) describe that a task can only be processed on one machine, and when a machine starts an operation, it cannot perform other operations. Constraint (7) stipulates that the start time of each operation will not be less than 0. Constraint (8) means that when multiple parallel machines are idle, the previous machine is given priority.
In this section, we present the encoding and decoding methods, four meta-heuristics, local search operations, and Q-learning. Then, we propose a method for selecting local search operations using Q-learning during iterations and introduce the framework of the proposed algorithms.
DHFSP can be divided into the following steps: (1) assign jobs to several factories, (2) assign jobs to multiple machines within each factory, and (3) sort jobs on machines. There are widely used encoding methods for HFSP in [31]. In this study, the solution of DHFSP is encoded and decoded by the method in [32]. Set a solution


Figure 2: The Gantt chart of one solution for the example is in Table 1
Many meta-heuristics are utilized to solve production scheduling problems. In this study, we select four algorithms: ABC, differential evolution (DE), PSO, and genetic algorithm (GA). These four algorithms are most commonly used to solve DHFSP problems, and most studies have confirmed that they have better performance in solving DHFSP. Fig. 3 illustrates the four algorithms’ framework. First, the initial population is randomly generated, and the mass of the initial population is calculated, which represents the current optimal solution by default. Then enter the iteration, and update the optimal solution by comparing the fitness values according to meta-heuristics respective population updating strategies. The fitness value is used to assess the quality of the current solutions generated by the four meta-heuristics. In the DHFSP, the fitness value is makespan.

Figure 3: Algorithm flow framework
The GA is a computational model that simulates the biological evolution process by mimicking natural selection and the genetic mechanisms of Darwinian evolution. GA is now commonly used in optimizing problems across various engineering fields. In GA, each solution is considered a chromosome. In each generation, new chromosomes are created through three operations crossover, mutation, and selection, using the parent chromosome from the previous generation.
The PSO simulates the process of hunting birds and fish in nature. Its principle of seeking the global optimal solution to a problem through group collaboration is now widely applied in optimization problems across various engineering fields.
The DE is based on population evolution. The fundamental operations of DE include mutation, crossover, and selection. The DE generates new individuals through the mutation operation based on the difference. Compared with the GA, DE retains the global search strategy based on population, utilizes real number coding, employs simple variation operations based on differences, and implements a one-to-one competitive survival strategy to simplify genetic operations.
The ABC simulates the behavior of bees searching for honey sources in nature and seeks the optimal solution through the division of labor and information sharing. A nectar source stands for a feasible solution, and the quantity of nectar in each source reflects the fitness of that solution. ABC exhibits strong global search ability and local optimization capability, making it well-suited for function optimization problems. Compared with other heuristic algorithms, it has fewer control parameters and higher robustness.
The meta-heuristics are easy to implement and converge quickly. However, the algorithms may easily fall into a situation where they reach a local optimum during the iteration process. To enable the algorithm to escape from a local optimal solution, this paper develops six local search methods based on the nature of the concerned problems. In DHFSP, set the factory with the maximum
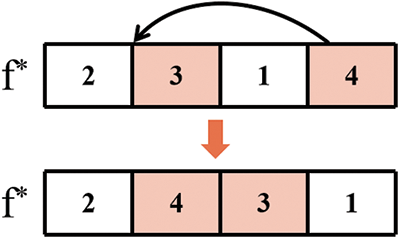
Figure 4: Critical factory insertion
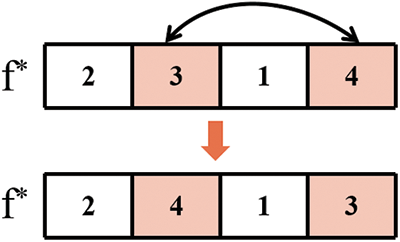
Figure 5: Critical factory swap
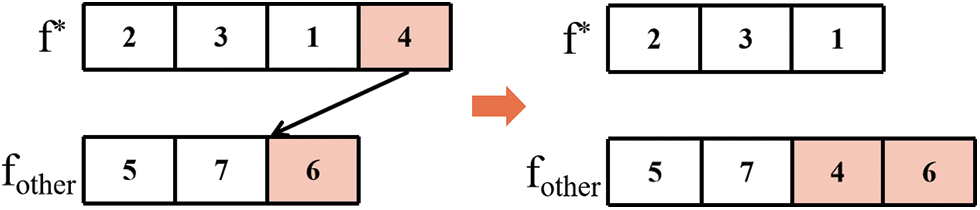
Figure 6: Critical factory and other factory insertion
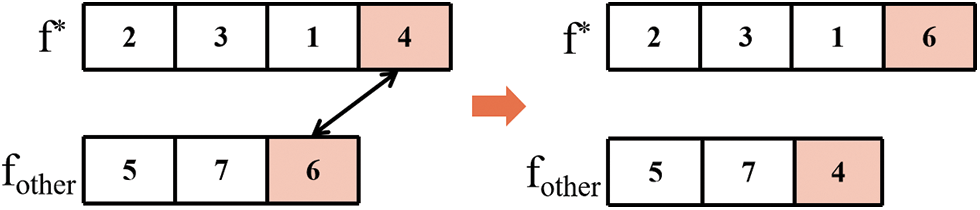
Figure 7: Critical factory and other factory swap
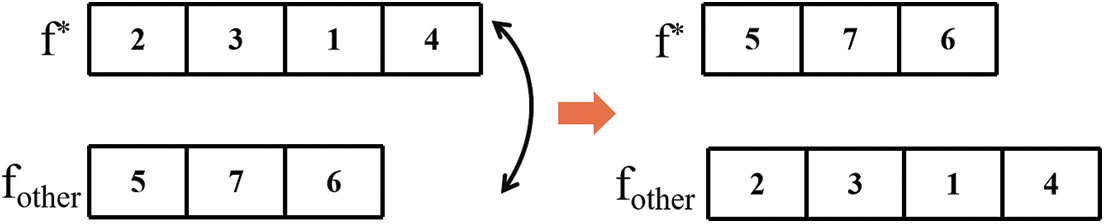
Figure 8: Critical factory and other factory sequence exchange
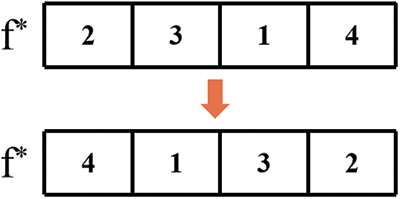
Figure 9: Critical factory opposite sequence
Critical Factory Insertion (Fig. 4): Select a job in the
Critical Factory Swap (Fig. 5): Select two jobs randomly in the
Critical Factory and Other Factory Insertion (Fig. 6): Select a job at random in both the
Critical Factory and Other Factory Swap (Fig. 7): Select a job at random in both the
Critical Factory and Other Factory Sequence Exchange (Fig. 8): Exchange job sequences for
Critical Factory Opposite Sequence (Fig. 9): Reverse the sequence of jobs in
The
RL is a field of machine learning. In RL, agents acquire tactics to optimize rewards or accomplish particular objectives through their engagements with the environment. RL focuses on how agents make decisions in an environment to maximize cumulative rewards. Learners will take actions in the environment and receive rewards based on their actions. Through feedback, the agent will eventually obtain the optimal policy. The policy aims to maximize his reward for actions and interactions with the environment. The framework of RL is depicted in Fig. 10.
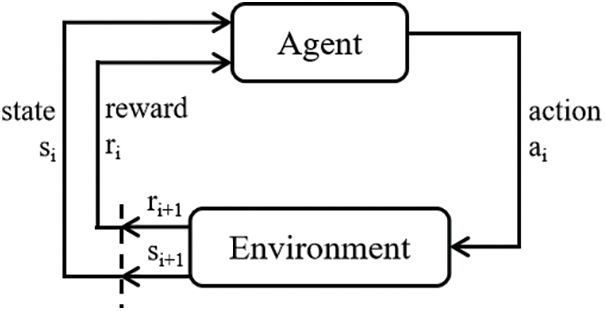
Figure 10: The framework of reinforcement learning
Q-learning is a form of RL. In Q-learning, positive behavior is rewarded, while negative behavior is punished. Q-learning introduces new components within the framework of reinforcement learning. Q-values represent the value of acting in its current state. Q-learning uses Q-values to determine the optimal action. The updated formula for Q-values is as follows:
where
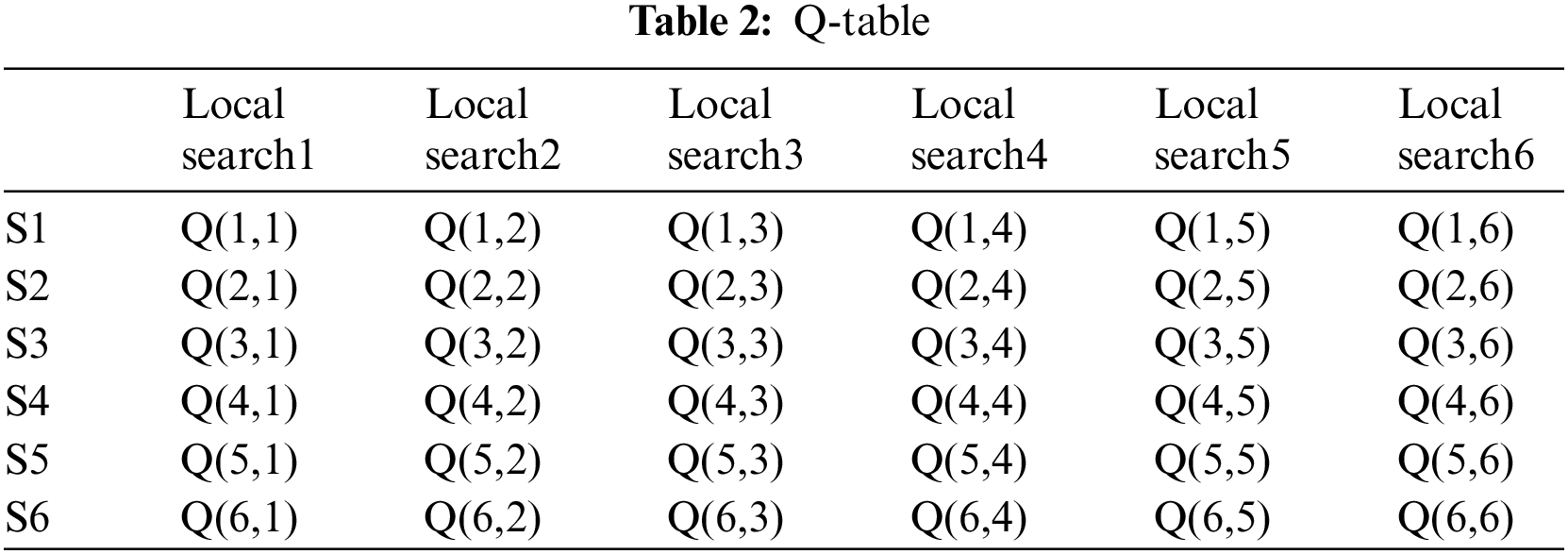
Q-table is used to store Q-values. The Q-table contains a list of rewards for the optimal behavior in each state within a specific environment. It can aid in understanding the outcomes of various behaviors in different scenarios. Once an agent makes in deciding the environment, the corresponding Q-value in the Q-table will be updated. Through continuous iteration and receiving more feedback, the Q-table will become more accurate, allowing the agent to make better decisions toward achieving the optimal solution. The Q-table for local search selection during iterations is shown in Table 2, where both rows and columns are set to local search operators. At the beginning, the Q-value of each local search in the Q-table is the same. With each iteration, the Q-value of each local search is updated. Compare the Q-values and choose the local search that receives the best feedback in the current state.
4 Computational Results and Discussions
In this section, we compare the performance of Q-learning-assisted meta-heuristics and the classical meta-heuristics on a standard data set. To further verify the performance of the proposed algorithms, we also execute the Friedman test to compare the Q-learning-assisted meta-heuristics and one existing high-performance algorithm.
In this study, we take 60 instances with different scales,
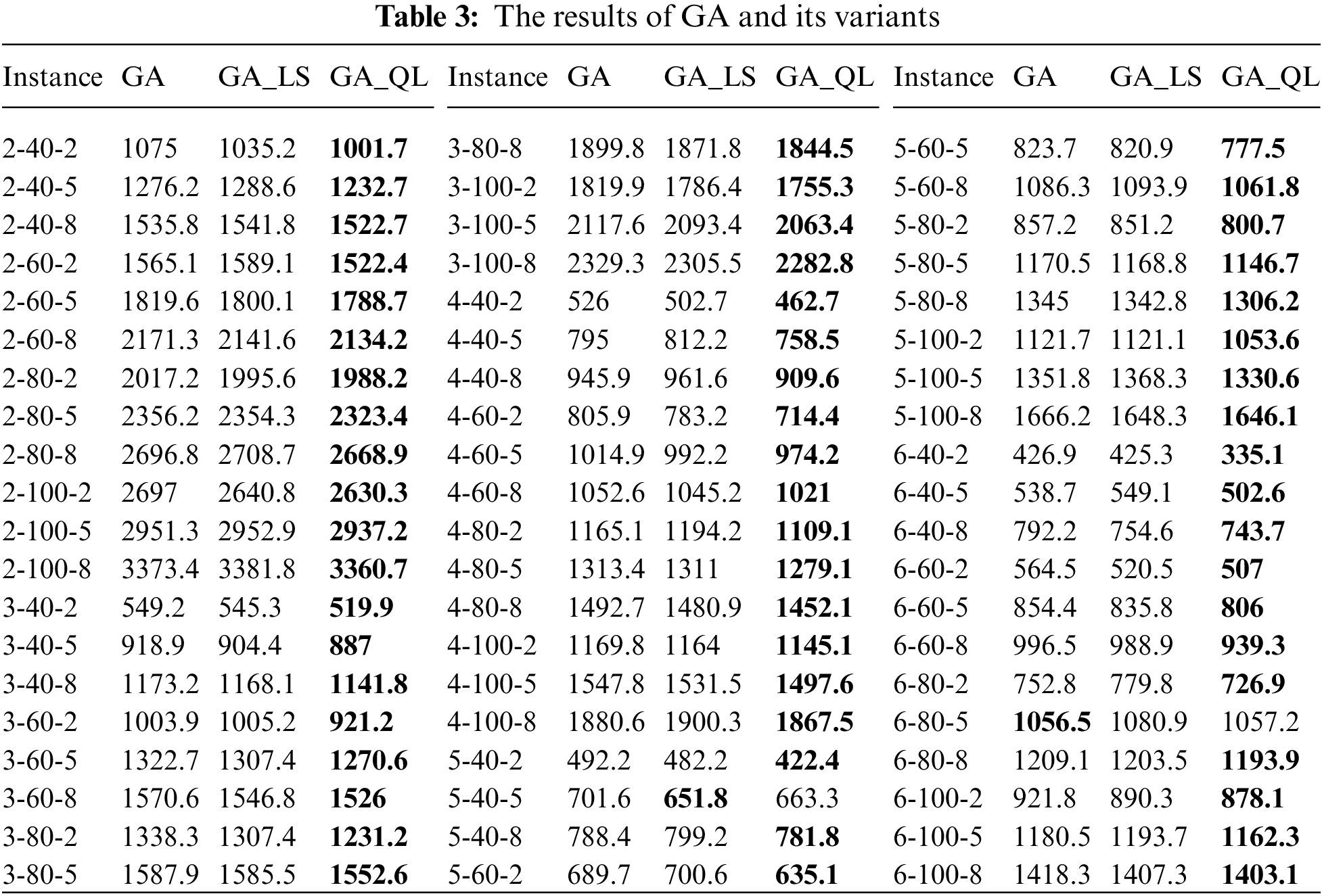
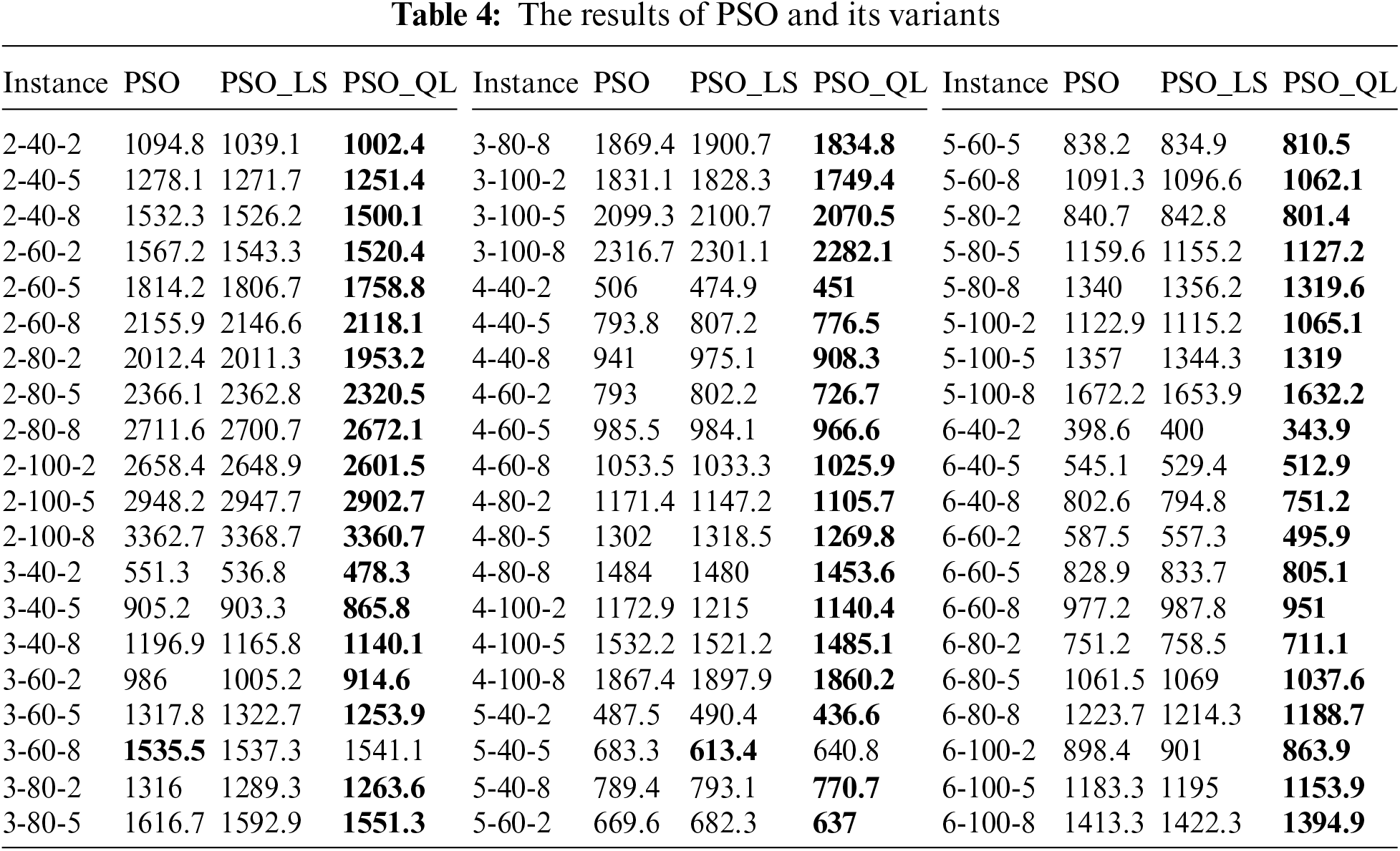
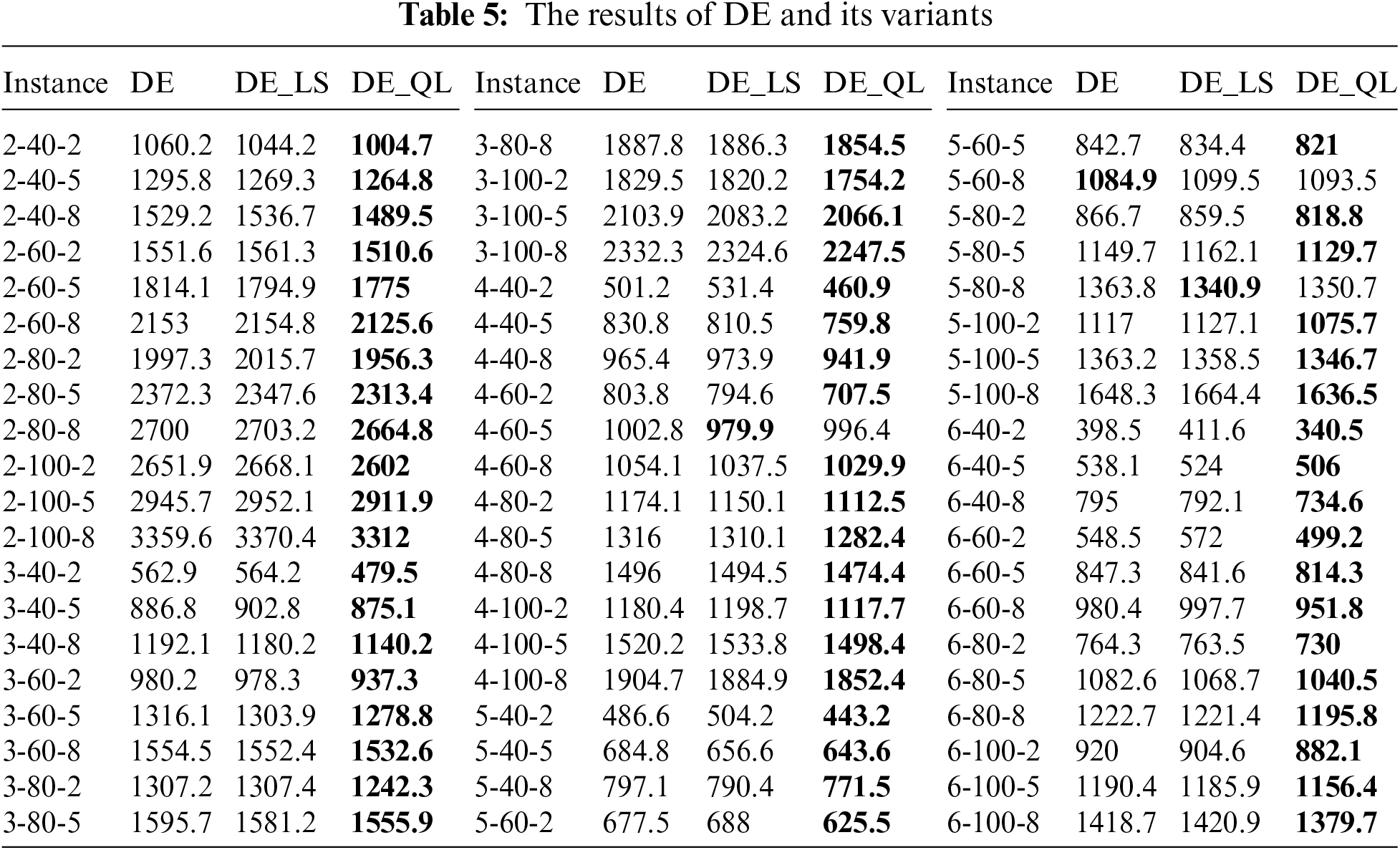
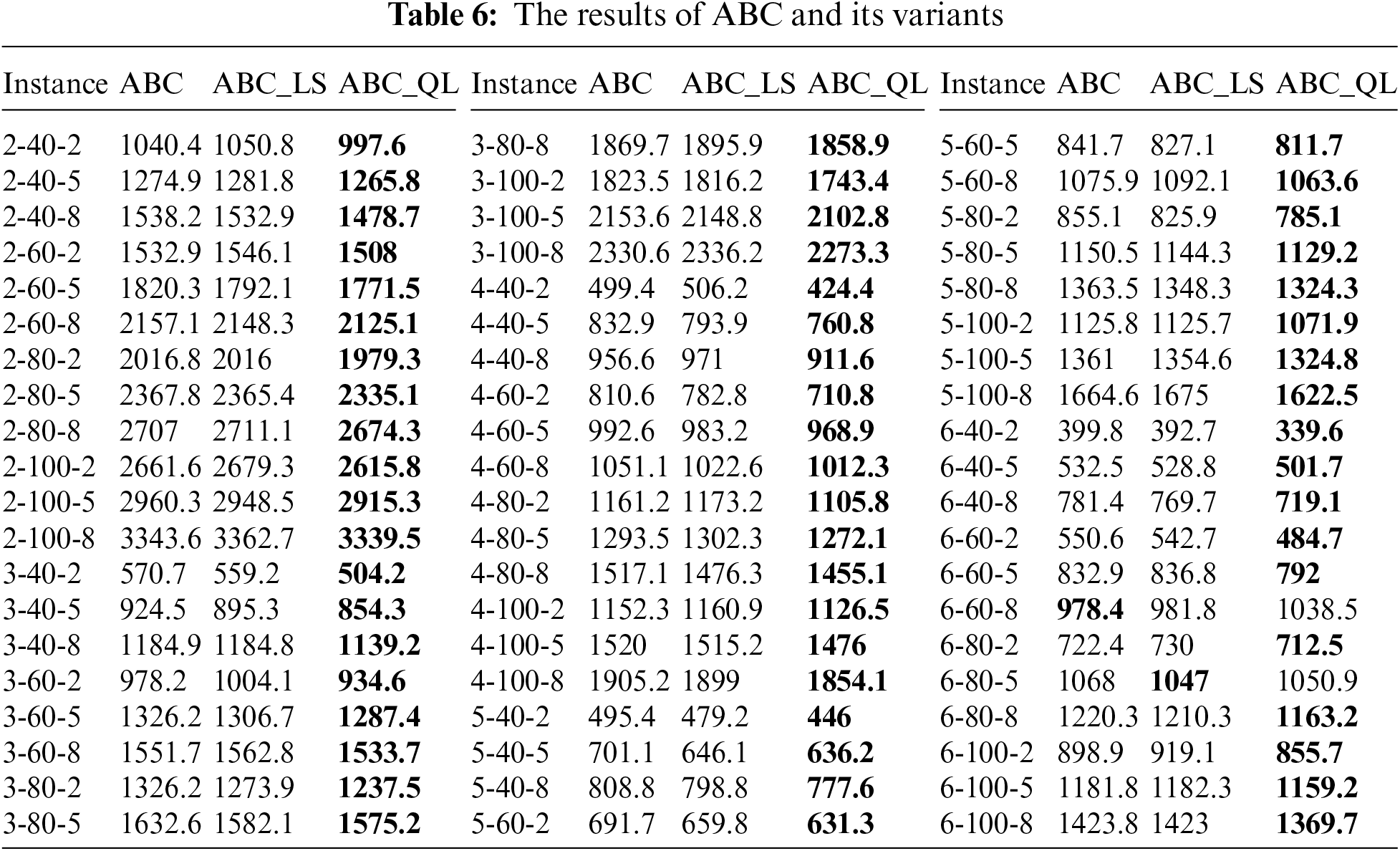
To assess the performance of the proposed enhancement strategies, four basic meta-heuristics, four meta-heuristics with random local search operation selection, and four meta-heuristics with Q-learning-based local search operation selection are compared in respective groups. The results of four fundamental meta-heuristics, with random selection local search, and with Q-learning-based local search are shown in Tables 3–6. The experimental results consist of the average values in ten runs by four meta-heuristics and their variants across 60 examples. The best minimum values are highlighted in bold. From Tables 3–6, it can be seen that the results of the local search based on Q-learning have the most optimal solutions for each algorithm. It means that using Q-learning to enhance the meta-heuristics for solving DHFSP is effective.
Coefficient of Variation (CV) is the coefficient of variation, which is used to measure the degree of variation in experimental results. It is particularly useful when comparing data sets with different units or scales, as it standardizes the standard deviation relative to the mean.
where Avg is the average of the results in 10 runs for one instance and SD is the standard deviation. The CV values of four meta-heuristics and their variants are shown in Table 7. All of four meta-heuristics the best CV are GA_QL, PSO_QL, DE_QL and ABC_QL.

In this section, we conduct the Friedman test on four meta-heuristics combined with Q-learning and improved iterated greedy algorithm (IIG) [33] to compare their performance. The reason for choosing IIG is that the comparison of the IIG algorithm with IG_VND [34], GA, IG [35], and iterated local search (ILS) [36] shows that the IIG algorithm has the best performance. The results of the Friedman test are reported in Table 8. The asymptotic significance (Asymp. Sig.) is 0.000, which is less than the specified significance level of 0.05. It means that there are significant differences among the five algorithms. The ranks of the five algorithms are shown in Fig. 11. The algorithm with a smaller rank value has better performance. From Fig. 11, we can see that PSO_QL has the smallest rank value (2.175), indicating the most competitiveness of the PSO_QL. The distribution by ranks of five algorithms is depicted in Fig. 12. Through the rank value and rank distribution of the Friedman test, it can be obtained that the PSO_QL is the most competitive one among the five algorithms.
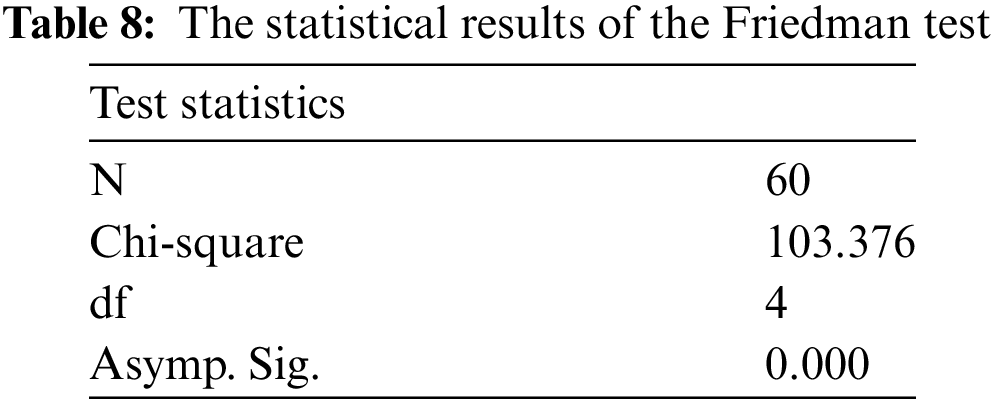
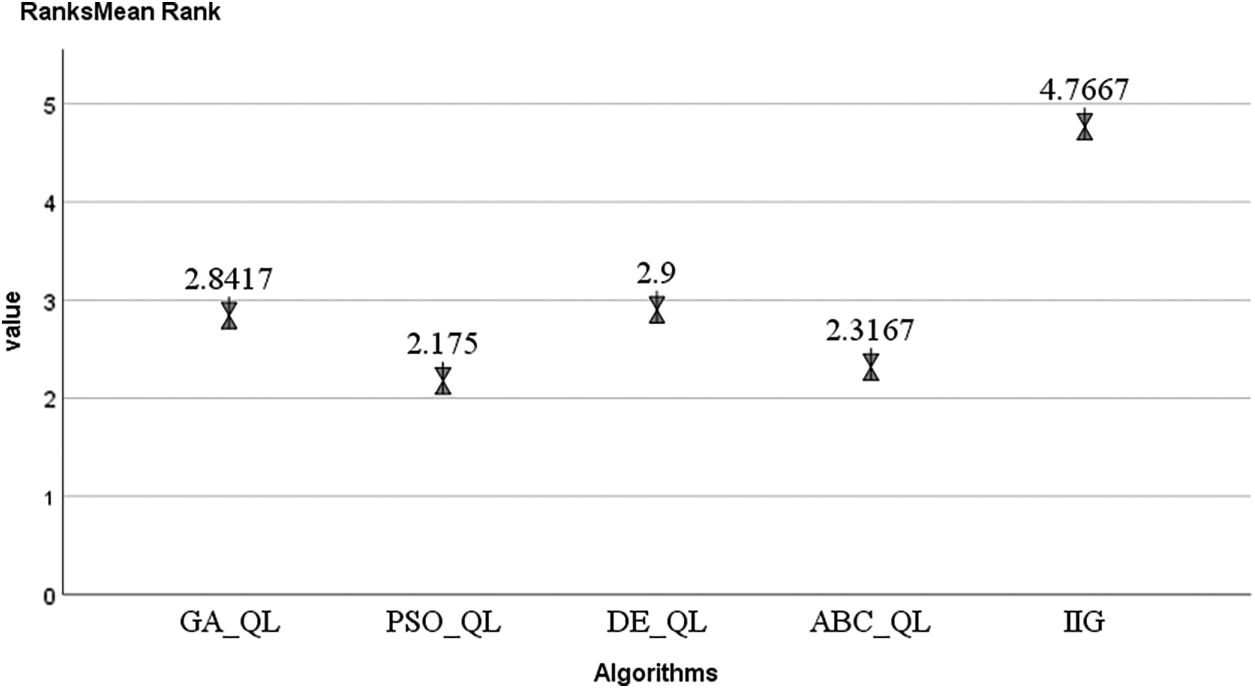
Figure 11: The rank value of algorithms

Figure 12: The distribution by ranks of algorithms
5 Conclusions and Future Directions
This paper introduces the integration of Q-learning and meta-heuristics to address DHFSP. Four meta-heuristics (GA, PSO, DE, ABC) are utilized, and six local search strategies are developed to avoid algorithms falling into local optimality based on the feature of DHFSP. The meta-heuristics combine Q-learning to select six types of local searches to choose the appropriate local search strategy more efficiently. In the experiments, 60 different examples are used to analyze algorithms’ performances. The experimental results show that the PSO_QL exhibits the highest competitiveness among all the compared algorithms.
Based on this work, the following issues are planned to be addressed in the future. (1) In DHFSP, multiple optimization goals are considered, including energy efficiency and cost. (2) Consider comparing Q-learning with other reinforcement learning methods, such as Sarsa. (3) There are many complex situations in the actual shop, such as job setup time. We will consider adding more constraints to the concerned DHFSP problems.
Acknowledgement: None.
Funding Statement: This study is partially supported by the Guangdong Basic and Applied Basic Research Foundation (2023A1515011531), the National Natural Science Foundation of China under Grant 62173356, the Science and Technology Development Fund (FDCT), Macau SAR, under Grant 0019/2021/A, Zhuhai Industry-University-Research Project with Hongkong and Macao under Grant ZH22017002210014PWC, the Key Technologies for Scheduling and Optimization of Complex Distributed Manufacturing Systems (22JR10KA007).
Author Contributions: Study conception and design: Qianyao Zhu and Kaizhou Gao; data collection: Qianyao Zhu; analysis and interpretation of results: Qianyao Zhu; draft manuscript preparation: Qianyao Zhu; review and editing: Kaizhou Gao and Adam Slowik. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. B. T. Wang, Q. -K. Pan, L. Gao, Z. -H. Miao, and H. -Y. Sang, “Modeling and scheduling a constrained flowshop in distributed manufacturing environments,” J. Manuf. Syst., vol. 72, pp. 519–535, 2024. [Google Scholar]
2. S. Wang, X. Li, L. Gao, and J. Li, “A multi-disjunctive-graph model-based memetic algorithm for the distributed job shop scheduling problem,” Adv. Eng. Inform., vol. 60, 2024, Art. no. 102401. doi: 10.1016/j.aei.2024.102401. [Google Scholar] [CrossRef]
3. A. M. Fathollahi-Fard, L. Woodward, and O. Akhrif, “A distributed permutation flow-shop considering sustainability criteria and real-time scheduling,” J. Ind. Inf. Integr., vol. 39, 2024, Art. no. 100598. doi: 10.1016/j.jii.2024.100598. [Google Scholar] [CrossRef]
4. D. Lei, J. Zhang, and H. Liu, “An adaptive two-class teaching-learning-based optimization for energy-efficient hybrid flow shop scheduling problems with additional resources,” Symmetry, vol. 16, no. 2, 2024, Art. no. 203. doi: 10.3390/sym16020203. [Google Scholar] [CrossRef]
5. M. Geetha, R. Chandra Guru Sekar, M. K. Marichelvam, and Ö. Tosun, “A sequential hybrid optimization algorithm (SHOA) to solve the hybrid flow shop scheduling problems to minimize carbon footprint,” Processes, vol. 12, no. 1, 2024, Art. no. 143. doi: 10.3390/pr12010143. [Google Scholar] [CrossRef]
6. C. -C. Lin, Y. -C. Peng, Y. -S. Chang, and C. -H. Chang, “Reentrant hybrid flow shop scheduling with stockers in automated material handling systems using deep reinforcement learning,” Comput. Indus. Eng., vol. 189, no. 3, 2024, Art. no. 109995. doi: 10.1016/j.cie.2024.109995. [Google Scholar] [CrossRef]
7. O. Moursli and Y. Pochet, “A branch-and-bound algorithm for the hybrid flowshop,” Int. J. Prod. Econ., vol. 64, pp. 113–125, 2000. doi: 10.1016/S0925-5273(99)00051-1. [Google Scholar] [CrossRef]
8. L. Hidri and A. Gharbi, “New efficient lower bound for the hybrid flow shop scheduling problem with multiprocessor tasks,” IEEE Access, vol. 5, pp. 6121–6133, 2017. doi: 10.1109/ACCESS.2017.2696118. [Google Scholar] [CrossRef]
9. B. Khurshid, S. Maqsood, Y. Khurshid, K. Naeem, and Q. S. Khalid, “A hybridization of evolution strategies with iterated greedy algorithm for no-wait flow shop scheduling problems,” Sci. Rep., vol. 14, no. 1, 2024, Art. no. 2376. doi: 10.1038/s41598-023-47729-x. [Google Scholar] [PubMed] [CrossRef]
10. M. Y. Wang, S. P. Sethi, and S. L. van de Velde, “Minimizing makespan in a class of reentrant shops,” Oper. Res., vol. 45, no. 5, pp. 702–712, 1997. doi: 10.1287/opre.45.5.702. [Google Scholar] [CrossRef]
11. Y. Zhu, Q. Tang, L. Cheng, L. Zhao, G. Jiang and Y. Lu, “Solving multi-objective hybrid flowshop lot-streaming scheduling with consistent and limited sub-lots via a knowledge-based memetic algorithm,” J. Manuf. Syst., vol. 73, no. 5, pp. 106–125, 2024. doi: 10.1016/j.jmsy.2024.01.006. [Google Scholar] [CrossRef]
12. Z. Shao, W. Shao, J. Chen, and D. Pi, “A feedback learning-based selection hyper-heuristic for distributed heterogeneous hybrid blocking flow-shop scheduling problem with flexible assembly and setup time,” Eng. Appl. Artif. Intell., vol. 131, no. 4, 2024, Art. no. 107818. doi: 10.1016/j.engappai.2023.107818. [Google Scholar] [CrossRef]
13. G. Ziadlou, S. Emami, and E. Asadi-Gangraj, “Network configuration distributed production scheduling problem: A constraint programming approach,” Comput. Indus. Eng., vol. 188, no. 10, 2024, Art. no. 109916. doi: 10.1016/j.cie.2024.109916. [Google Scholar] [CrossRef]
14. B. Khurshid and S. Maqsood, “A hybrid evolution strategies-simulated annealing algorithm for job shop scheduling problems,” Eng. Appl. Artif. Intell., vol. 133, 2024, Art. no. 108016. doi: 10.1016/j.engappai.2024.108016. [Google Scholar] [CrossRef]
15. J. Wang, H. Tang, and D. Lei, “A feedback-based artificial bee colony algorithm for energy-efficient flexible flow shop scheduling problem with batch processing machines,” Appl. Soft Comput., vol. 153, no. 1, 2024, Art. no. 111254. doi: 10.1016/j.asoc.2024.111254. [Google Scholar] [CrossRef]
16. Y. Li, X. Li, L. Gao, and L. Meng, “An improved artificial bee colony algorithm for distributed heterogeneous hybrid flowshop scheduling problem with sequence-dependent setup times,” Comput. Indus. Eng., vol. 147, no. 2, 2020, Art. no. 106638. doi: 10.1016/j.cie.2020.106638. [Google Scholar] [CrossRef]
17. Y. Li et al., “A discrete artificial bee colony algorithm for distributed hybrid flowshop scheduling problem with sequence-dependent setup times,” Int. J. Prod. Res., vol. 59, no. 13, pp. 3880–3899, 2020. doi: 10.1080/00207543.2020.1753897. [Google Scholar] [CrossRef]
18. X. -R. Tao, Q. -K. Pan, and L. Gao, “An efficient self-adaptive artificial bee colony algorithm for the distributed resource-constrained hybrid flowshop problem,” Comput. Indus. Eng., vol. 169, no. 18, 2022, Art. no. 108200. doi: 10.1016/j.cie.2022.108200. [Google Scholar] [CrossRef]
19. J. -H. Hao, J. -Q. Li, Y. Du, M. -X. Song, P. Duan and Y. -Y. Zhang, “Solving distributed hybrid flowshop scheduling problems by a hybrid brain storm optimization algorithm,” IEEE Access, vol. 7, pp. 66879–66894, 2019. doi: 10.1109/ACCESS.2019.2917273. [Google Scholar] [CrossRef]
20. C. Lu, J. Zhou, L. Gao, X. Li, and J. Wang, “Modeling and multi-objective optimization for energy-aware scheduling of distributed hybrid flow-shop,” Appl. Soft Comput., vol. 156, no. 1, 2024, Art. no. 111508. doi: 10.1016/j.asoc.2024.111508. [Google Scholar] [CrossRef]
21. X. Li, Q. Zhao, H. Tang, S. Yang, D. Lei and X. Wang, “Joint scheduling optimisation method for the machining and heat-treatment of hydraulic cylinders based on improved multi-objective migrating birds optimisation,” Manuf. Syst., vol. 73, pp. 170–191, 2024. [Google Scholar]
22. J. Cai, D. Lei, and M. Li, “A shuffled frog-leaping algorithm with memeplex quality for bi-objective distributed scheduling in hybrid flow shop,” Int. J. Prod. Res., vol. 59, no. 18, pp. 5404–5421, 2021. doi: 10.1080/00207543.2020.1780333. [Google Scholar] [CrossRef]
23. M. Wu, “Application of particle swarm optimisation algorithm incorporating frog-leaping algorithm in optimal scheduling for production management in manufacturing plant,” Int. J. Interact. Des. Manuf., vol. 286, no. 1, 2024, Art. no. 32. doi: 10.1007/s12008-024-01767-5. [Google Scholar] [CrossRef]
24. J. -J. Wang and L. Wang, “A cooperative memetic algorithm with learning-based agent for energy-aware distributed hybrid flow-shop scheduling,” IEEE Trans. Evol. Comput., vol. 26, no. 3, pp. 461–475, Jun. 2022. doi: 10.1109/TEVC.2021.3106168. [Google Scholar] [CrossRef]
25. Z. Zhang, Z. Shao, W. Shao, J. Chen, and D. Pi, “MRLM: A meta reinforcement learning-based metaheuristic for hybrid flow-shop scheduling problem with learning and forgetting effects,” Swarm Evol. Comput., vol. 85, no. 1, 2024, Art. no. 101479. doi: 10.1016/j.swevo.2024.101479. [Google Scholar] [CrossRef]
26. H. Yu, K. Gao, N. Wu, M. Zhou, P. N. Suganthan and S. Wang, “Scheduling multiobjective dynamic surgery problems via Q-learning-based meta-heuristics,” IEEE Trans. Syst. Man, Cyber.: Syst., vol. 54, no. 6, pp. 3321–3333, Jun. 2024. [Google Scholar]
27. F. Q. Wang, Y. P. Fu, K. Z. Gao, Y. X. Wu, and S. Gao, “A Q-learning-based hybrid meta-heuristic for integrated scheduling of disassembly and reprocessing processes considering product structures and stochasticity,” Complex Syst. Model. Simul., vol. 4, no. 4, pp. 184–209, 2024. doi: 10.23919/CSMS.2024.0007. [Google Scholar] [CrossRef]
28. C. Luo, W. Gong, F. Ming, and C. Lu, “A Q-learning memetic algorithm for energy-efficient heterogeneous distributed assembly permutation flowshop scheduling considering priorities,” Swarm Evol. Comput., vol. 85, 2024, Art. no. 101497. doi: 10.1016/j.swevo.2024.101497. [Google Scholar] [CrossRef]
29. Y. Liu, F. Zhang, Y. Sun, and M. Zhang, “Evolutionary trainer-based deep Q-network for dynamic flexible job shop scheduling,” IEEE T. Evolut. Comput., doi: 10.1109/TEVC.2024.3367181. [Google Scholar] [CrossRef]
30. F. Zhao, G. Zhou, T. Xu, N. Zhu, and Jonrinaldi, “A knowledge-driven cooperative scatter search algorithm with reinforcement learning for the distributed blocking flow shop scheduling problem,” Expert Syst. App., vol. 230, 2023, Art. no. 120571. doi: 10.1016/j.eswa.2023.120571. [Google Scholar] [CrossRef]
31. Q. -K. Pan, L. Gao, X. -Y. Li, and K. -Z. Gao, “Effective metaheuristics for scheduling a hybrid flowshop with sequence-dependent setup times,” Appl. Math. Comput., vol. 303, pp. 89–112, 2017. doi: 10.1016/j.amc.2017.01.004. [Google Scholar] [CrossRef]
32. K. -C. Ying and S. -W. Lin, “Minimizing makespan for the distributed hybrid flowshop scheduling problem with multiprocessor tasks,” Expert Syst. Appl., vol. 92, no. 2, pp. 132–141, 2018. doi: 10.1016/j.eswa.2017.09.032. [Google Scholar] [CrossRef]
33. C. Lu, J. Zheng, L. Yin, and R. Wang, “An improved iterated greedy algorithm for the distributed hybrid flowshop scheduling problem,” Eng. Optim., vol. 56, no. 5, pp. 792–810, 2023. doi: 10.1080/0305215X.2023.2198768. [Google Scholar] [CrossRef]
34. B. Naderi and R. Ruiz, “The distributed permutation flowshop scheduling problem,” Comput. Oper. Res., vol. 37, pp. 754–768, 2010. doi: 10.1016/j.cor.2009.06.019. [Google Scholar] [CrossRef]
35. H. Oztop, M. F. Tasgetiren, D. T. Eliiyi, and Q. K. Pan, “Metaheuristic algorithms for the hybrid flowshop scheduling problem,” Comput. Oper. Res., vol. 111, no. 1, pp. 177–196, 2019. doi: 10.1016/j.cor.2019.06.009. [Google Scholar] [CrossRef]
36. W. S. Shao, D. C. Pi, and Z. S. Shao, “Local search methods for a distributed assembly no-idle flow shop scheduling problem,” IEEE Syst. J., vol. 13, no. 2, pp. 1945–1956, 2019. doi: 10.1109/JSYST.2018.2825337. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools