Enhanced UAV Pursuit-Evasion Using Boids Modelling: A Synergistic Integration of Bird Swarm Intelligence and DRL

1  Introduction

In recent years, Unmanned Aerial Vehicles (UAVs) [1–3] have seen increasingly widespread applications across various fields, including military reconnaissance, logistics delivery, and agricultural monitoring. These applications typically involve complex and dynamic environments, necessitating precise environmental awareness and intelligent decision-making capabilities for UAVs. As intelligent perception and decision-making technology rapidly advances, the UAV pursuit-evasion task has emerged as a pivotal area of research. As shown in Fig. 1, in a typical UAV pursuit-evasion scenario, multiple UAVs are strategically deployed to efficiently track and intercept a moving target, which employs evasive maneuvers to avoid capture, within a dynamic and often adversarial environment [4–6]. The target, which employs evasive maneuvers to avoid capture, navigates within a dynamic and often adversarial environment. In this illustration, UAV #1, UAV #2, UAV #3, and UAV #4 work in coordination, using their respective sensors and communication systems to maintain real-time updates on the target’s position and trajectory. This complex interaction underscores the importance of advanced control algorithms and robust communication protocols in managing multi-UAV operations in pursuit-evasion tasks.

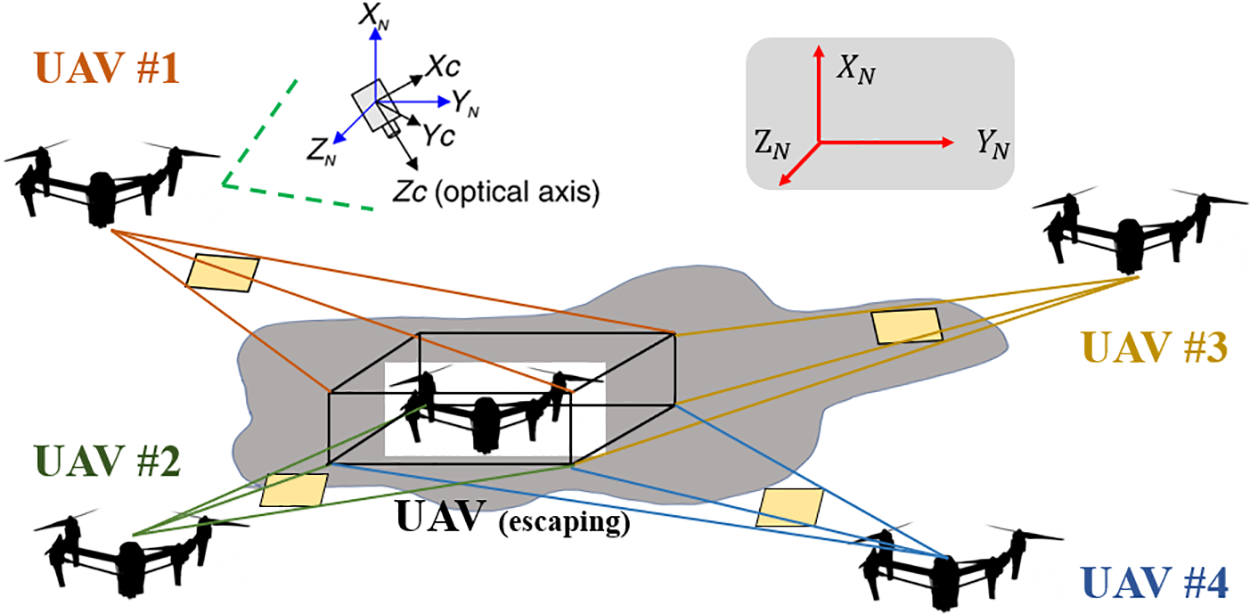
Figure 1: The diagrams of typical UAV pursuit-evasion scenes

Deep reinforcement learning (DRL)-based intelligent decision-making approaches [5,7,8] have achieved remarkable advancements in UAV pursuit-evasion problem, showcasing its immense potential in handling high-dimensional data and continuous action spaces. However, despite their success in various simulated environments, applying these DRL algorithms to real-world UAV pursuit-evasion tasks presents a host of challenges. Specifically, reinforcement learning optimization [9] solely based on reward feedback struggles to impart the innate behavioral advantages observed in biological populations to decision models. For UAVs, emulating the flocking behavior patterns of birds presents a valuable and promising decision-making strategy. Moreover, obtaining a large number of training samples for DRL learning is not only costly and time-consuming but also poses potential safety risks, especially involving complex scenarios like UAVs with high degrees of freedom and unpredictable flight paths. Additionally, real-time obstacle avoidance demands that the algorithms respond and adjust quickly during flight, which further complicates their design and computational requirements. UAVs must cope with constantly changing obstacles and complex terrains, meanwhile quickly respond and adjust during high-speed flight to meet real-time obstacle avoidance demands. However, existing intelligent decision-making algorithms often do not adequately account for these dynamic factors, which can lead to collisions or failures in path planning during actual operations.

Swarm Intelligence Algorithms [2,10], such as the Wolf Pack [11], the Ant Colony [12], the Bee Colony [13], and the Whale Optimization Algorithms [14], optimize problems by emulating the collective behaviors observed in nature, without relying on sample-based learning processes, which have demonstrated notable advantages and efficacies in specific scenarios. Al Baroomi et al. [15] proposed the Ant Colony Optimization (ACO) algorithm, which has shown significant potential in path planning for UAV navigation. The ACO algorithm simulates ant behavior, using pheromone trails and attractive heuristics to help UAVs navigate safely and efficiently in dynamic environments. Chen et al. [16] addressed the task allocation problem for heterogeneous multi-UAVs with different payloads by proposing an improved Wolf Pack Algorithm (WPA), namely a chaotic wolf pack algorithm based on enhanced Stochastic Fractal Search (MSFS-CWPA). They divided complex combat tasks into three subtasks: reconnaissance, strike, and evaluation and introduced Gaussian walking in Stochastic Fractal Search (SFS) after chaos optimization into the WPA through an adaptive mechanism. Chen et al. [17] proposed an Environment-adaptive Bat Algorithm (EABA) to address the path planning problem of UAVs in complex environments. The EABA enhances its convergence ability and avoids local extrema by integrating particle swarm optimization (PSO) for adaptive convergence adjustments, significantly surpassing the traditional Bat Algorithm (BA) and PSO algorithm. Furthermore, Particle Swarm Optimization (PSO) has shown significant potential in UAV pursuit-evasion tasks. Zhang et al. [18] proposed a PSO-optimized M3DDPG (PSO-M3DDPG) algorithm for multi-UAV pursuit-evasion, which combines the PSO algorithm with the M3DDPG algorithm. Experimental simulations demonstrate the improved response speed and capture success rate of PSO-M3DDPG by dynamically adjusting global and local information.

However, their performance often falls short when dealing with highly dynamic and complex environments. In contrast, the Boids model [19], a superior efficient algorithm that simulates the collective motion of biological groups such as flocks of birds or schools of fish, is frequently used in the study of flocking behavior in low-latency and distributed systems.

Specifically, the existing challenges in UAV pursuit-evasion includes:

1. High Cost and Safety Risks in Sample Acquisition: UAV pursuit-evasion faces the high cost and safety risks associated with acquiring training samples. UAVs, especially those with high degrees of freedom and unpredictable flight paths, require substantial amounts of data for effective training. This process is not only costly but also poses safety risks during data collection.

2. Dynamic and Complex Environments: UAV pursuit-evasion tasks occur in highly dynamic and complex environments that demand real-time obstacle avoidance and adaptive decision-making. Previous algorithms do not adequately account for these dynamic factors, leading to potential collisions in path planning during actual operations.

3. Existing Limitations in Complex Scenarios: While swarm intelligence algorithms like Wolf Pack [11], Ant Colony [15], and Bee Colony [13] have shown effectiveness in specific scenarios, they often falls short in highly dynamic and complex environments. They optimize problems by emulating collective behaviors observed in nature but struggle to maintain efficacy when environmental complexity increases.

Inspired by the birds’ swarm intelligent behavior [10,19], we integrate this Boids model together with the Apollonian Circles algorithm [20] to mainstream deep reinforcement learning approaches [7,8] to address the abovementioned issues. Our research aims to tackle the specific challenges in UAV pursuit-evasion tasks and presents a robust solution that reduces training costs and enhances the adaptability and robustness of UAVs in real-world applications.

Specifically, we introduce a novel bio-inspired swarm intelligence and DRL-based hybrid intelligent control framework, named the Boids-based Pursuit-Evasion (Boids-PE). Boids-PE combines the Boids model [19], which simulates the swarm intelligence behaviors of bird flocks, with deep reinforcement learning to enhance intelligent decision-making in UAV pursuit tasks. This addresses the challenges of obstacle avoidance and navigation in complex terrains, and the ability to maintain formation. The integration of the Boids model with the Apollonian Circles algorithm addresses significant challenges in UAV pursuit-evasion tasks. This hybrid approach leverages the Boids model’s simplicity and robustness in maintaining formation and avoiding collisions while enhancing it with the Apollonian Circles algorithm’s capability to calculate optimal geometric paths. This combination effectively resolves issues of collision avoidance among UAVs in the same group and improves long-distance tracking and capture efficiency. Overall, the proposed Boids-PE combines bio-inspired swarm intelligence with advanced reinforcement learning techniques to overcome the limitations of existing algorithms, reduce training costs, and enhance the adaptability and robustness of UAVs in pursuit-evasion tasks.

Additionally, we have developed simulated environments based on the Pybullet physics engine [21] specifically for the Boids-PE algorithm in UAV pursuit-evasion tasks, addressing the challenge of acquiring training samples. In these virtual environments, UAVs can undergo extensive preliminary training to gather experience and data, and then be fine-tuned for real-world deployment. This not only reduces the cost of sample collection but also accelerates the training process and enhances training efficiency. Through extensive sample training and iterative learning, the DRL-driven UAVs system can better adapt to complex dynamic environments [1,5,6,22]. To further enable UAVs to learn more effective pursuit-evasion strategies, we introduced a self-play training method [23,24] in our Boids-PE. This technique allows UAVs to alternately train against each other, continually enhancing their performance in pursuit-evasion scenarios. Through this, UAVs not only learn effective strategies but also continuously adapt and optimize their behavior in response to changing environments, demonstrating higher adaptability and flexibility.

Extensive simulated experiments prove that the above enhancements and strategies significantly improve the overall effectiveness of the UAVs’ pursuit decision-making, making Boids-PE reduce the learning costs associated with collecting training samples and the high computational demands during real-world deployment. The code implementations for Boids-PE are accessible on GitHub via: https://github.com/albert-jin/Boids-PE (accessed on 7 August 2024).

2  Related Works

2.1 UAV Pursuit-Evasion and Existing Pursuit-Evasion Methods

UAV decision control research has extensively explored traditional methods relying on detailed dynamic modeling and game theory [1,3,4,6], such as differential games [25]. These methods, while theoretically capable of providing precise strategies, pose significant challenges in mathematical modeling and computational complexity due to their reliance on complex partial differential equations. To address the UAV pursuit-evasion problems, researchers often transform them into optimization problems solved using various algorithms like genetic algorithms [1], Bayesian inference [26], and bio-inspired optimization [2]. Bio-inspired optimization algorithms [11,13,14], like Particle Swarm Optimization (PSO) [22] and Wolf Pack Algorithm [11], draw inspiration from collective behaviors in nature, simulating phenomena such as bird flocking or fish schooling to find optimal or near-optimal solutions to problems.

Recent advancements in UAV pursuit-evasion have emerged rapidly, showcasing a multitude of cutting-edge approaches. For instance, Camacho et al. [9,27] proposed a framework for multi-player aerial robotic pursuit-evasion games. They focused on devising effective pursuit and evasion strategies and interaction mechanisms in environments with multiple UAVs and targets. Sun et al. [4] explored cooperative pursuit-evasion problems in multi-UAV systems under partial observation conditions. They introduced an algorithm that enables multiple UAVs to collaborate and track targets effectively despite incomplete information. Vlahov et al. [5] presented a model for optimizing UAV pursuit-evasion strategies using deep reinforcement learning. Their study focused on how UAVs can achieve efficient target tracking and evasion through autonomous learning and optimization in dynamic and complex environments. Weintraub et al. [6] investigated the game theoretic approaches to UAV pursuit-evasion and thus proposed a UAV swarm pursuit-evasion model based on optimal control theory. Their model concentrated on developing optimal pursuit and evasion strategies within a UAV swarm to achieve effective target tracking and capture. Optimal control methods, while theoretically robust, can be challenging to implement in real-time or effectively in practical applications due to their complexity. de Souza et al. [28] introduced a decentralized deep reinforcement learning (DRL) approach for multi-agent pursuit scenarios involving non-holonomic constraints. Utilizing the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm [29], their method trains multiple homogeneous pursuers to independently capture a faster evader within a bounded area. The approach emphasizes local information and group rewards, employing curriculum learning to enhance training efficiency and effectiveness. In the context of UAV pursuit-evasion research, the TD3 algorithm [29] lies in its use of the TD3 algorithm to address control challenges encountered in dynamic UAV pursuit-evasion tasks. The UAV pursuit-evasion model can benefit from the insights provided by this study, particularly in terms of optimizing control strategies using reinforcement learning techniques like TD3, which could enhance UAV performance in highly dynamic and unpredictable environments.

As the number of UAVs or environmental complexity rises, the computational resources become prohibitively large and time-consuming. To overcome this, researchers employ realistic simulation environments to gather training data, facilitating the learning of effective strategies that can be fine-tuned for real-world applications. Transfer learning is also applied to reduce the need for samples and training time for new tasks, thus accelerating the learning process. Integrating advanced technologies such as reinforcement learning, deep learning, transfer learning, and self-play training significantly enhances UAV decision-making capabilities. Future research will focus on improving the generalization, adaptability, and robustness of algorithms while prioritizing safety, operational efficiency, and minimizing training costs.

2.2 Bio-Inspired Swarm Optimization Algorithms

Bio-inspired optimization algorithms, such as Particle Swarm Optimization (PSO) and Wolf Pack Algorithm, draw inspiration from collective behaviors in nature, like bird flocking or fish schooling, to find optimal or near-optimal solutions to problems. These algorithms simulate natural phenomena to optimize various aspects of UAV control and decision-making.

In addition to PSO and Wolf Pack Algorithm, other bio-inspired technologies have been developed to enhance UAV performance. For example, Genetic Algorithms (GA) mimic the process of natural selection to solve optimization problems, while Ant Colony Optimization (ACO) simulates the foraging behavior of ants to find the shortest paths. These algorithms have been applied to various UAV tasks, such as path planning, resource allocation, and task scheduling, showcasing their versatility and effectiveness.

Focusing on Particle Swarm Optimization (PSO), the related algorithm has proven particularly effective in UAV applications. For instance, Zhang et al. [18] presented an enhanced algorithm, PSO-M3DDPG, which combines Particle Swarm Optimization (PSO) with Mini-Max Multi-agent Deep Deterministic Policy Gradient (M3DDPG) to address the pursuit-evasion problem in UAVs. The PSO algorithm optimizes the experience sample set, improving the learning efficiency and convergence speed of the M3DDPG algorithm and validating its effectiveness in multi-UAV pursuit-evasion environments.

Additionally, Li et al. [30] introduced a bio-inspired neural network (BINN) approach to address real-time evasion in dynamic and complex environments. The BINN uses a neurodynamic shunting model to generate evasive trajectories without formulating the problem as a differential game. It is topologically organized to handle only local connections, enabling real-time adjustments to moving and sudden-change obstacles, demonstrating its effectiveness and efficiency in handling complex pursuit-evasion scenarios.

Despite their effectiveness, these optimization algorithms face limitations when scaling up the number of UAVs or increasing environmental complexity, as the required computational resources and time can become prohibitive. Thus, there is a continuous effort to improve the efficiency and scalability of these algorithms to handle larger and more complex scenarios.

2.3 Deep Reinforcement Learning

To address these challenges, artificial intelligence (AI) approaches, including expert systems [3,31], neural networks [32–34], especially deep reinforcement learning [3,5,8,9], have been increasingly explored for UAV countermeasure tasks in recent years. Deep reinforcement learning (DRL), which combines the strengths of reinforcement learning and deep learning, has demonstrated exceptional performance across various domains, notably in autonomous flight and decision control for UAVs. It trains agents based on learnable neural network models to make decisions through rewards and penalties, enabling UAVs to autonomously learn pursuit and evasion strategies without human intervention.

For instance, Wang et al. [35] proposed a novel interception strategy for high-speed maneuvering targets using the Deep Deterministic Policy Gradient (DDPG) algorithm [36]. By reshaping the reward function and focusing on relative position information and path angle, they trained an interception policy that approximates the optimal control model for maneuvering target interception. Ye et al. [37] presented a study on a classical pursuit-evasion problem where the pursuer attempts to capture a faster evader in a bounded area. They utilized game theory to model the multi-agent pursuit-evasion game and demonstrated that the game model has a Nash equilibrium. Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm [36] is adapted to seek the equilibrium, and simulation examples illustrated its effectiveness in a dynamic multi-agent pursuit-evasion system. Chen et al. [38] introduced the TaskFlex Solver (TFS), which combines reinforcement learning and curriculum learning to address multi-agent pursuit problems in diverse and dynamic environments. TFS significantly improves training efficiency and adaptability in both 2D and 3D scenarios by using a curriculum learning framework.

Reinforcement learning has brought significant advancements to UAV pursuit-evasion tasks. Techniques that based on various Multi-Agent Reinforcement Learning, and Hierarchical Reinforcement Learning help UAVs to autonomously learn and adapt to complex and dynamic environments, enabling UAVs to make decisions with minimal human intervention. These DRL techniques enhance UAVs’ capability to execute effective pursuit and evasion strategies, making them more efficient and resilient in real-world scenarios. We anticipate even greater innovations in UAV countermeasure tasks, driven by the continuous evolution of DRL algorithms and applications.

3  Our Model: Biods-PE

3.1 Framework Architecture Modeling

Inspired by the intelligent behavior of bird swarm [2,10,19], we introduce a hybrid control framework for UAV pursuit and escape tasks, combining deep reinforcement learning (DRL) with Bird Swarm Intelligence, named the “Boids Model-based DRL Approach for Pursuit and Escape” (Boids-PE). Boids-PE leverages DRL to address the adaptive capability issues inherent in traditional frameworks. By incorporating birds behaviors (Boids Model) [19] into the Apollonian circle algorithm, the framework enables UAVs to effectively avoid obstacles and maintain formation, thereby enhancing their practical application.

In the specific modeling of UAV pursuit and escape tasks, as shown in Fig. 2, Boids-PE employs a hierarchical modeling strategy. The high level is responsible for intelligent decision-making through reinforcement learning algorithms, named deep reinforcement learning module (DRL module), while the low level is controlled by a fine-tuned mechanism based on the Boids model and the Apollonian circle algorithm [20], named bio-inspired behavior module. When the agent gathers environmental information, it utilizes a combination of bio-inspired control algorithms and high-level reinforcement learning decisions to generate final actions, such as rotor speed or position adjustments for the UAVs. These actions are then transmitted to the control module, which converts them into specific control commands like throttle adjustments. Our code is now available on Github: https://github.com/albert-jin/Boids-PE (accessed on 7 August 2024).

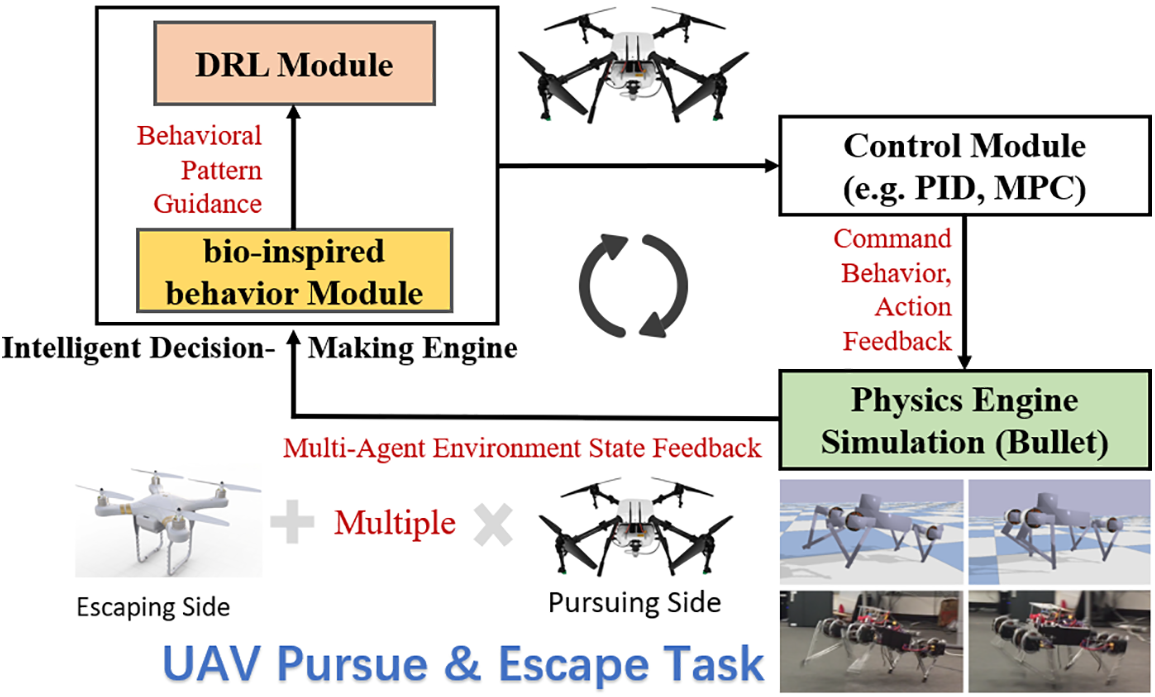
Figure 2: The overall architecture of Boids-PE

In Biods-PE, UAVs make intelligent decisions by perceiving multi-agent environments and optimizing the decision-making network of DRL. UAVs leverage the superiority of the bio-inspired behavior module, which incorporates self-adaptive avian flight behavior preferences, to further enhance decision-making. After high-level decision-making, fine control is carried out by the low-level control module, utilizing the Pybullet physics engine [21] for environment state inference.

Specifically, DRL algorithms such as Proximal Policy Optimization (PPO) [39] and Deep Deterministic Policy Gradient (DDPG) [8,36] are adopted in Boids-PE, with a particular emphasis on the DDPG algorithm. This algorithm combines the policy gradient method and Q-learning within an actor-critic architecture. The actor network generates the strategy (deterministic actions), while the critic network evaluates the strategy (action value). DDPG uses experience replay and target networks to stabilize the training process, making it an effective tool for solving complex control tasks in the field of deep reinforcement learning. Next, we will systematically illustrate the competitive DDPG reinforcement learning algorithm.

3.2 The Integration of Apollonian Circles Algorithm, Boids Model and DRL

The integration of the Apollonian Circles algorithm, Boids model, and DRL forms a comprehensive and synergistic control framework for UAV pursuit-evasion tasks.

Firstly, utilizing the Apollonian Circles algorithm, pursuer UAVs calculate optimal paths to encircle the evader effectively. This geometric strategy minimizes the evader’s escape routes, thereby enhancing capture efficiency. Specifically, the Apollonian Circles, a geometric concept introduced by the ancient Greek mathematician Apollonius of Perga, plays a crucial role in optimizing UAV pursuit-evasion strategies. These circles are defined as loci of points where the ratio of distances to two fixed points A and B is constant. Formally, for any point on the Apollonian Circle, the ratio d(P,A)d(P,B)=k, where k is a constant, holds true.

In UAV pursuit-evasion missions, Apollonian Circles are utilized to optimize the path planning of multiple UAVs working together in pursuit. By leveraging the geometric properties of Apollonian Circles, the pursuing UAVs can precisely calculate the optimal encirclement paths, effectively reducing the escape options available to the evading UAV. Specifically, in complex three-dimensional environments, the Apollonian Circles algorithm helps the pursuing UAVs determine ideal paths around the evading target, forming a dynamic encirclement. This geometric strategy minimizes the evading UAV’s available routes, gradually trapping it in a confined space. Therefore, we believe that Apollonian Circles not only improve the efficiency of pursuit in UAV pursuit-evasion scenarios but also significantly reduce the evading UAV’s ability to exploit environmental complexity for evasion, contributing to more effective capture and superior path planning strategies.

By incorporating the Apollonian Circles algorithm into our UAV control framework, we leverage geometric properties to enhance the efficiency and effectiveness of pursuit strategies. This method allows pursuing UAVs to utilize precise geometric positioning to encircle and capture evading targets more effectively, thereby increasing the overall system performance.

To further augment the capabilities of the UAV swarm, we integrate the Boids model into our framework. The Boids model, inspired by the flocking behavior of birds, involves three primary behavioral rules:

1. Separation (fPP): This rule ensures that UAVs maintain a safe distance from each other to avoid collisions. It acts as a repulsive force between the UAVs.

2. Cohesion (fPE): This rule steers UAVs towards the average position of their neighbors, helping to maintain group coherence.

3. Alignment (fPA): This rule aligns the direction of each UAV with the average direction of its neighbors, promoting coordinated movement.

These behaviors are combined into a single control force F=K1fPP+K2fPE+K3fPA, where K1,K2, and K3 are weighting factors that balance the influence of each behavior. By implementing the Boids model, UAVs are endowed with robust formation maintenance and obstacle avoidance capabilities, which are crucial for swarm effectiveness in dynamic environments. The Boids model ensures that UAVs maintain formation integrity and avoid collisions. The decentralized control provided by the Boids model makes the swarm scalable and robust, allowing for efficient coordination without a central controller.

Finally, based on these bio-inspired low-level action schemes, the DRL component, particularly the DDPG algorithm, allows UAVs to learn optimal strategies through continuous interaction with the environment. The actor-critic architecture of DDPG, combined with experience replay and target networks, stabilizes the learning process and improves the UAVs’ decision-making capabilities in dynamic and complex scenarios.

As shown in Fig. 3, this flowchart illustrates the overall information flow and implementations of technique integrations in our Boid-PE. From this figure, the workflow in the UAV pursuit-evasion framework is as follows:

1.    State Observation: Each UAV gathers information about its own state (position, velocity, etc.) and the states of its neighbors and the target. This information is essential for decision-making and control processes.

2.    High-Level Decision Making: One is Self-Play Training, in which pursuer and evader UAVs alternately train their strategies through self-play, continuously improving their performance by adapting to each other’s tactics. The other is Action Generation (DDPG), where the actor network generates control actions based on the current state and high-level decisions and the critic network evaluates the actions and provides feedback for policy improvement. Experience replay stores past experiences and samples them to stabilize the learning process, ensuring the UAVs learn effectively from diverse scenarios.

3.    Low-Level Control Execution: Boids Model Application: UAVs apply Boids rules to determine initial adjustments for maintaining formation and avoiding collisions. This is critical for swarm behavior and coordination; Apollonian Circles Calculation: Pursuer UAVs use the Apollonian Circles algorithm to determine optimal encirclement paths, effectively trapping the evader through geometric strategies.

4.    Interaction and Learning: 1. Environment Interaction: UAVs execute commands based on the high-level and low-level decisions, leading to state transitions that impact future decisions; 2. Reward Calculation: Rewards are calculated based on the effectiveness of the actions taken, guiding the learning and ensuring that UAVs optimize their strategies.

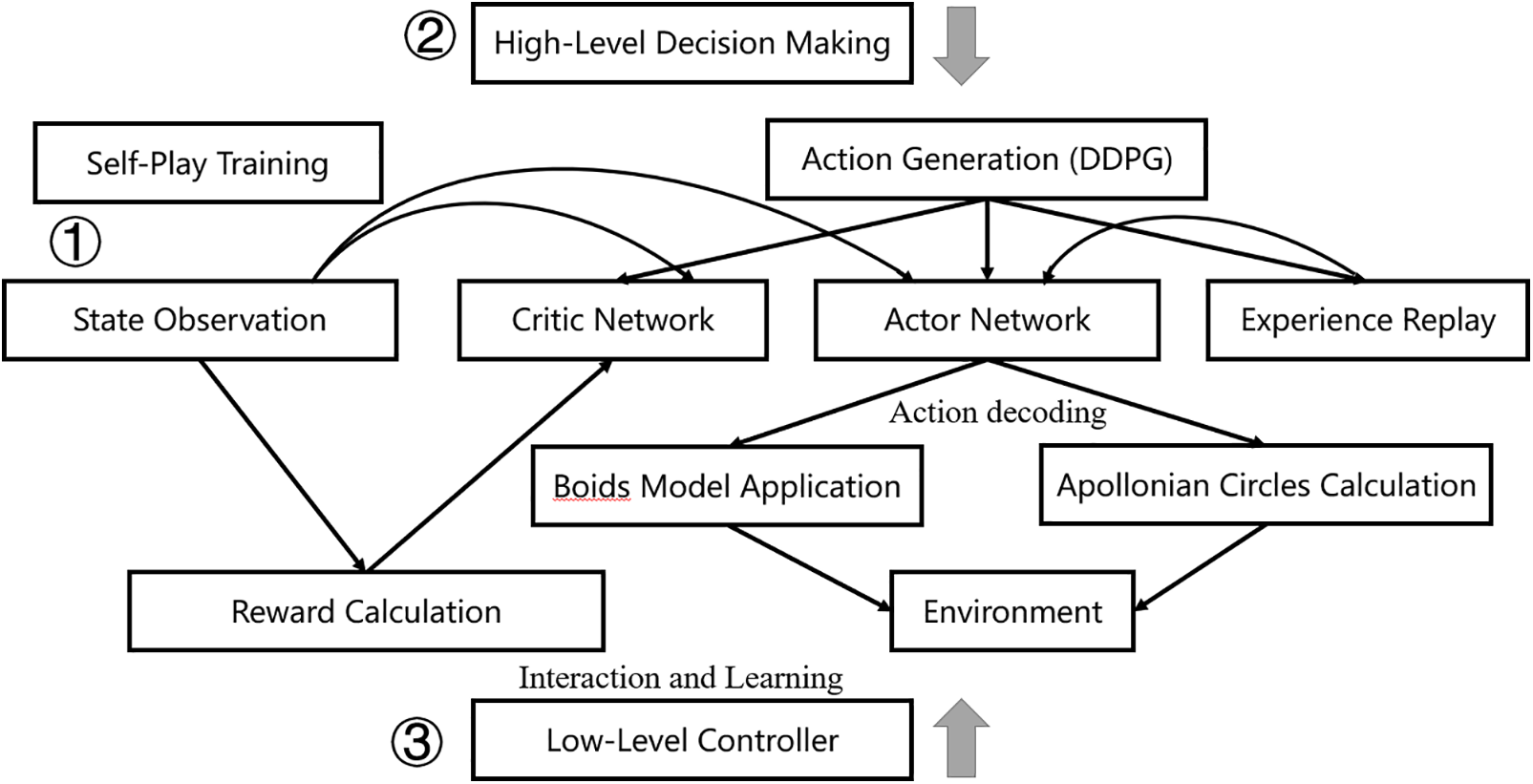
Figure 3: The integration diagram of Apollonian Circles algorithm, Boids model and DRL in our proposed Boids-PE

Overall, this synergistic approach leverages geometric strategies for encirclement, decentralized control for formation maintenance, and adaptive learning for strategic decision-making, significantly enhancing the effectiveness and reliability of UAV operations in dynamic environments.

3.3 Deep Reinforcement Learning Algorithm (DDPG)

The Deep Deterministic Policy Gradient (DDPG) algorithm [8,36] is a model-free, off-policy actor-critic algorithm that combines the strengths of policy gradient methods and Q-learning. The algorithm process of DDPG is depicted in Fig. 4. DDPG is particularly effective for solving continuous action space problems, which are common in complex control tasks.

Figure 4: The diagram of DDPG algorithm

DDPG algorithm belongs to classic Actor-Critic architecture, which contains Actor Network (Generates deterministic actions based on the current policy. The output of the actor network is the action a = π (s ∣ θπ), where s is the state and θπ represents the parameters of the actor network.) and Critic Network (Evaluates the value of the actions generated by the actor. The critic network estimates the Q-value Q(s, a ∣ θQ), where θQ represents the parameters of the critic network.). And the critic network is updated by minimizing the loss function in Eq. (1); the actor network is updated using the deterministic policy gradient in Eq. (2).

L(θQ)=E[(r+γQ′(s′,π′(s′∣θπ′)∣θQ′)−Q(s,a∣θQ))2](1)

∇θπJ≈E[∇aQ(s,a∣θQ)∣a=π(s∣θπ)∇θπ(s∣θπ)](2)

Moreover, DDPG uses a replay buffer to store transitions (s, a, r, s′), which are sampled randomly during training. This helps break the correlation between consecutive samples and stabilizes the training process. And DDPG employs target networks for both the actor and critic, which are slowly updated to match the weights of the main networks. This technique reduces the risk of divergence during training. The target networks are denoted as θπ′ and θQ′. The learning process of DDPG involves updating both the local and global action-value functions, optimizing the policy function for each agent, and ultimately refining the strategies used by the UAVs.

Overall, the combination of experience replay, target networks, and an actor-critic framework of DDPG makes it a powerful tool for solving complex control tasks, such as those encountered in UAV pursue and escape scenarios.

3.4 Self-Play Training

As we all know, reinforcement learning training requires agents to interact with their environment, resulting in self-play technique’s significant potentials [23,24]. Here, to further enhance the performance of pursuit-escape UAVs, we propose a self-play training framework as shown in Fig. 5. A typical example of self-play originates from the Go-playing AI, AlphaZero. Inspired by AlphaZero, we enhance the performance of our pursuit UAVs by dynamically switching training objectives through self-play.

Figure 5: The illustration of the learning procedure self-play training mechanism. We conducted a demonstration using two UAVs, designated #5027 (responsible for Pursuing) and #9373 (responsible for Escaping). During each training round, the decision networks for pursuing and escaping are alternated, as indicated by the vertical arrows. The colored curved arrows represent the optimization of decision network parameters through training samples

As shown in Fig. 5, the UAV #9373 and UAV #5027 continuously optimize their pursuit strategies through mutual self-play, resulting in significant improvements in both efficiency and performance, ultimately achieving highly effective pursuit strategies.

Specifically, initially, the training focuses on the escape UAV #9373 reaching a fixed position, ensuring a certain distance is maintained between the pursuing, escaping UAVs #5027, and #9373. Subsequently, the pursuing UAV #5027 undergoes training in a manner consistent with non-self-play experimental designs. Once the pursuing UAV #5027 achieves repeated success in capturing the escaping UAV #9373, the training shifts back to refining the escape UAV #9373’s strategy. If the pursuing UAV #5027 fails to successfully capture the escaping UAV #9373, its training resumes. This process is controlled by a set total number of training steps, after which the training halts. This self-play training methodology [23,24] ensures that the UAVs #5027 and #9373 continuously improve their strategies in an ever-changing environment, significantly enhancing their performance and adaptability.

Fig. 6 visually represents the self-play training framework, detailing each decision point and training step comprehensively. As depicted, the training begins by initializing the UAVs’ parameters and positions. Initially, the escaping UAV is trained to reach a fixed position, ensuring it can achieve and maintain this predetermined location. The process then checks whether the escaping UAV can consistently reach this fixed position N times. If successful, the training proceeds to the next step; otherwise, the escaping UAV is retrained until it meets the criteria.

Figure 6: Training process flowchart for pursuit-evasion UAVs within a self-play framework

Subsequently, the focus shifts to training the chasing UAV to effectively follow the escaping UAV. This phase evaluates whether the chasing UAV can successfully capture the escaping UAV N times. If the chasing UAV achieves this, the training advances to developing the escaping UAV’s evasion strategies. If not, the chasing UAV is retrained to enhance its pursuit capabilities. The final step involves training the escaping UAV to evade capture and enter a designated safe area N times. Successful training is indicated when the escaping UAV consistently reaches the safe area; otherwise, the escaping UAV continues to be trained until it meets this objective.

In summary, the self-play framework involves continuous iterations between training the chasing and escaping UAVs. By continuously adapting to each other’s tactics, both UAVs significantly enhance their performance and adaptability. This iterative method ensures robust and efficient UAV operations in real-world scenarios, ultimately leading to improved strategy development and execution.

3.5 State Space and Action Space Modeling for UAV Pursuit-Evasion

To consider practical applications, assume that each UAV communicates with a ground station, which sends decision information to each UAV. The ground station can access all UAVs’ information, with each UAV’s observation data forming part of the overall environmental state, comprised of the state information of N UAVs. Each UAV makes decisions based on its observation data, which is derived from sensor-acquired dynamic information. Traditional control methods such as PID [40], and MPC [41] are then utilized to control the UAVs based on the decision information. The state transitions in the environment are inferred through the Bullet physics engine. The position, speed, and other information of the pursuing and fleeing UAVs influence the decision-making process.

Since UAV pursuit-evasion is a continuous control task, with the ultimate goal of determining the rotor speed of the UAV, the action space of the UAV can be directly defined as [P0,P1,P2,P3]n, representing the speeds of the four rotors of the UAV. This definition of the action space outputs the rotor speeds directly, obviating the need for traditional control methods like PID. Considering the complexity of tasks, solely controlling rotor speed can be challenging. Thus, the action space of the UAV is defined as [vx,vy,vz,vm]n, representing the velocity components in three dimensions and the magnitude of the velocity. When the action space is defined by speed or position, traditional control methods such as PID are required for control, with high-level decision-making and low-level control.

Formally, we now further illustrate the action space using formulas. Specifically, the action space of the UAV can be defined as controlling its rotor speeds or velocity components:

1.    Rotor speeds (Pn): Directly defined as [P0,P1,P2,P3]n, representing the speeds of the four rotors.

2.    Velocity (Vn): Defined as [vx,vy,vz,vm]n, representing the velocity components in three dimensions and the magnitude of the velocity.

The action space is typically restricted to the range of [−1, 1] to ensure flight safety and task completion.

Based on the agent’s state, reinforcement learning algorithms are employed to determine the velocity for the next time step. This velocity is then converted into motor speed or final throttle size using traditional control methods like PID. When defining the action space for the UAV, it is crucial to consider the safety of the UAV during flight. This involves limiting the maximum speed or rotor speed of the UAV. Typically, the action space is restricted to the range of [−1, 1]. This range will be further converted to obtain the UAV’s actual speed or rotor speed. Different types of rewards will be set for training based on various scene tasks. This paper will initially focus on constructing simple tasks, including one-on-one pursuit and evasion tasks and many-to-one pursuit and evasion tasks, to explore the performance of reinforcement learning in these scenarios.

More specifically, the state space of each UAV can be formally defined through the following equations. The state information of each UAV includes the following aspects:

1.    Position (xn): The three-dimensional coordinates of the n-th UAV.

2.    Quaternion (qn): The quaternion representing the UAV’s orientation.

3.    Angular velocities (rn,pn,jn): Representing the roll, pitch, and yaw angular velocities of the UAV, respectively.

4.    Velocity (x˙n): The linear velocity of the UAV.

In summary, the state vector for each UAV can be expressed as: sn=[xn,qn,rn,pn,jn,xn]. The overall environmental state information is composed of the state information of N UAVs, i.e., S=[s1,s2,s3,…,sN].

For clarity, we have summarized the experimental parameters in Table 1. This will serve as a comprehensive reference for readers to accurately replicate the experiment.

3.6 Reward Settings for UAV Pursuit-Evasion

In the experiments, we set up two main pursuit-evasion scenarios: one-on-one UAV pursuit-evasion and many (multiple)-to-one UAV pursuit-evasion. The rewards for these two scenarios differ, as detailed below.

For the one-on-one pursuit-evasion scenario, where one pursuing UAV competes against one evading UAV, the action space in the three-dimensional environment is quite large. Therefore, appropriate rewards are set to guide the UAV’s movement. The following reward functions are established as follows (Eq. (3)):

{rt1=dt−1−dtrt=krt1+rt2+rt3,(3)

where the rt2=−R(dt>Df) and the rt3=Rf(dt<Dn).

In this formula, rt—The total reward obtained by the pursuing UAV at time t, where rt1, rt2, and rt3 represent rewards under different conditions; rt1—The difference in distance to the evading UAV between two consecutive time steps, reflecting the process of continuously approaching the evading UAV; rt2—When the distance between the two UAVs is large, indicating the evading UAV is in an advantageous position, a small reward is given to the pursuing UAV during this process.

When the distance between the pursuing UAV and the evading UAV is less than a certain threshold, it is considered a successful pursuit, and the pursuing UAV receives a significant reward. In this experiment, rt1 is consistently used to guide the agent to overcome the sparse reward problem. The reward function for the evading UAV is the inverse of that for the pursuing UAV. Based on the above reward settings, we conduct the one-on-one pursuit model experiment.

For the multiple-on-one pursuit-evasion scenario, multiple pursuing UAVs should cooperate with each other to collaboratively capture the evading UAV, thereby completing the pursuit task. Inspired by the Boids model [19], the reward function for the UAVs can be composed of the following aspects: First, the pursuing UAVs should not be too close to each other to prevent collisions. Second, the UAVs should maintain a certain formation while advancing towards the target. Third, the pursuing UAVs should effectively encircle the evading UAV.

To achieve the behaviors of the bio-inspired control algorithm (Boids model) during this process, appropriate reward functions need to be set to guide reinforcement learning. Based on this, our designed reward function includes two aspects: local rewards and global rewards. Specifically, the local rewards are composed of obstacle avoidance between the pursuing UAVs, maintaining formation among the pursuing UAVs, and each UAV approaching the target position. The local reward for each UAV, considering obstacle avoidance and maintaining formation among the pursuing UAVs, is formulated as follows (Eqs. (4)–(6)):

r1(dij)={−Rr(dij≤x1)−adij(dij>x1),(4)

r2(die)=βdie+α,(5)

ri=∑j≠ik1r1(dij)+k2r2(die),(6)

where the die represents the distance between each pursuing UAV and the evading UAV. dij denotes the distance between two pursuing UAVs. This local reward setup guides the UAVs to maintain formation and prevent collisions. ri denotes the local reward.

Simultaneously, by setting a global reward, the center of the pursuing UAV swarm is guided to coincide as closely as possible with the position of the evading UAV. Based on this, the global reward is defined as shown in Eq. (7):

rg=ρdce+γ,(7)

where the dce denotes the distance from the center of the pursuing UAVs to the evading UAV; the rg is the global reward.

4  Experiments and Analysis

This section focuses on modeling one-on-one and many-to-one pursuit-evasion scenarios based on the aforementioned Boids-PE model. Through a series of experiments and systematic analysis, the decision-making superiority and intelligence of the Boids-PE model are validated.

4.1 Experimental Setting and Environment Modelling

For environment construction, we use the PyBullet physics engine [21] to construct the experimental environment and evaluate on the Boids-PE model. The experimental platform performs inference based on the Bullet physics engine. To make it more realistic, we include factors such as collisions, drag, and ground effects to closely resemble real physical scenarios. The Boids-PE model also supports sensor and visual information as inputs for decision-making and control [32]. Considering the impact of collisions and other factors, this three-dimensional simulation environment closely approximates real flight test scenarios. Since this platform requires setting the control and simulation frequency manually, the simulation frequency is often based on the current action to predict the state at the next time step.

The platform has an established low-level UAV model, upon which the environment needs to be built, including scene elements (such as whether there are obstacles, initial positions, and attitudes of the UAVs). We present the basic platform settings in Table 2. In this paper, we construct one-on-one and many-to-one pursuit-evasion tasks. In the one-on-one task, a single pursuing UAV learns how to effectively track and capture an evading UAV in three-dimensional space. The many-to-one model increases the number of pursuing UAVs, which not only increases the complexity of the strategies but also introduces the issue of collaboration between UAVs. Each pursuing UAV needs to learn how to cooperate with other UAVs to more effectively capture the evader.

In this experiment, we primarily selected efficiency and reliability as the key performance indicators for UAV pursuit and evasion tasks, based on their importance in practical applications. Efficiency determines whether a UAV can successfully complete the pursuit task within a limited time, while reliability pertains to the system’s stability and the success rate of the task.

Additionally, for the specific measurement methods, we utilized the UAV capture success rate within a specified time as the efficiency metric. Specifically, a successful capture is considered when the distance between the two UAVs is less than 3 cm and this condition is maintained for more than 5 s. If the above success conditions are not met within 20 s, it is considered a capture failure. This standard directly reflects the UAV’s ability to complete tasks within a given timeframe, offering high operability and practical value. In our experimental design, by comparing different pursuit scenarios and examining the inclusion of self-play methods, we comprehensively evaluated the UAV’s performance in various complex environments. These comparative experiments reveal the UAV’s adaptability and flexibility in changing conditions.

Overall, we chose efficiency and reliability as the primary performance indicators based on the practical needs and application background of UAV pursuit and evasion tasks. These metrics, measured by the capture success rate within a specified time and various experimental scenarios, can comprehensively and objectively evaluate the performance of UAV systems, providing a feasible solution for the practical application of UAV pursuit tasks.

4.2 One-on-One Pursuit and Evasion Results and Analysis

In the one-on-one pursuit-evasion scenario where UAVs move only in a one-dimensional space, the movement information of the UAVs is shown in Fig. 7. In this figure, the red line represents the evading UAV, while the green line represents the pursuing UAV. As illustrated in Fig. 7, the evading UAV reaches a fixed position and then stops moving. The pursuing UAV, which has been trained through reinforcement learning, successfully completes the pursuit. The closer the green line gets to the red line, the better the pursuing UAV demonstrates its advantage, ultimately leading to a successful interception.

Figure 7: One-on-one (One-dimensional) pursuit-evasion UAV movement information. The red curve represents the evading UAV information, while the others represent the pursuing UAV information. The closer the curves are, the better the advantage shown by the pursuing UAV

In the one-on-one (one-dimensional) scenario, the pursuing UAV trained through reinforcement learning successfully captures the evading UAV. The experimental results of the one-on-one (one-dimensional) scenario using the self-play training method [23,24] are shown in Fig. 8. Initially, the pursuing UAV successfully captures the evading UAV. The evading UAV then adjusts its strategy and manages to escape. Throughout the process, it can be observed that both UAVs continuously adjust their positions. Due to their close proximity, this results in noticeable horizontal displacement.

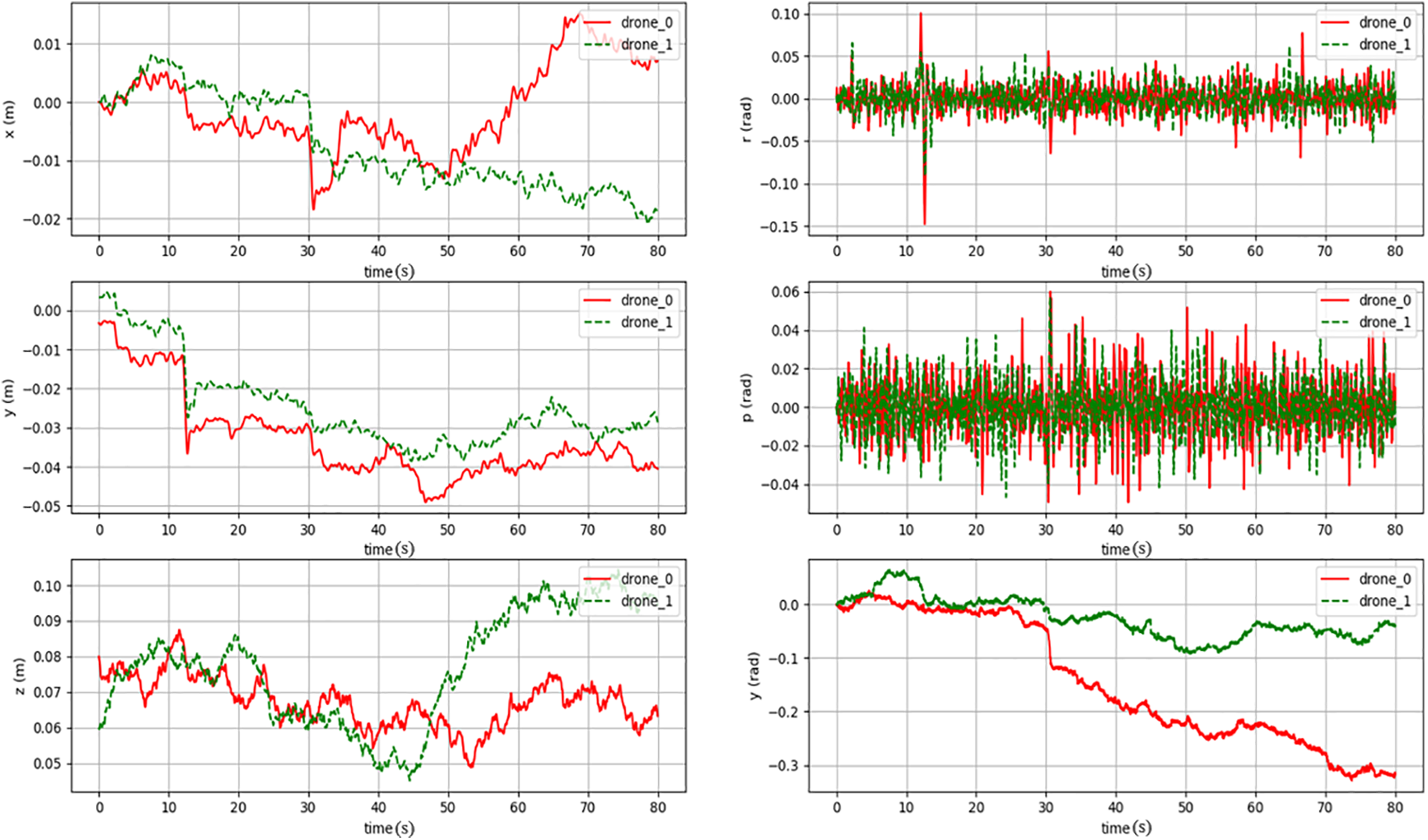
Figure 8: One-on-one (One-dimensional) pursuit-evasion UAV movement information under a self-play learning framework

In summary, from these flight pursuit trajectories, it can be seen that UAVs based on the Boids-PE model possess strong autonomous decision-making capabilities and flexible adaptability. The self-play training method [23,24] enables the pursuing UAV to continuously optimize its strategy to adapt to the evasive UAV’s changing behaviors. In the one-on-one pursuit-evasion scenario, the pursuing UAV not only successfully completes the initial pursuit task through reinforcement learning but also quickly responds and re-engages in capture when the evading UAV adjusts its strategy. This decision-making mechanism enhances the UAV’s execution efficiency and task success rate in complex dynamic environments, fully demonstrating the Boids-PE model’s significant potential and advantages in controlling UAV group behaviors.

Fig. 9 illustrates the pursuit-evasion process of UAVs under the self-play framework within the Boids-PE model. We further conduct experiments in three-dimensional space. During this process, it can be observed that the pursuing UAV continuously approaches the evading UAV in the x, y, and z directions, while the evading UAV quickly attempts to escape. Due to the large action space in three-dimensional space, the combination of reinforcement learning and the self-play method [23,24] ultimately enables the pursuing UAV to learn an effective strategy.

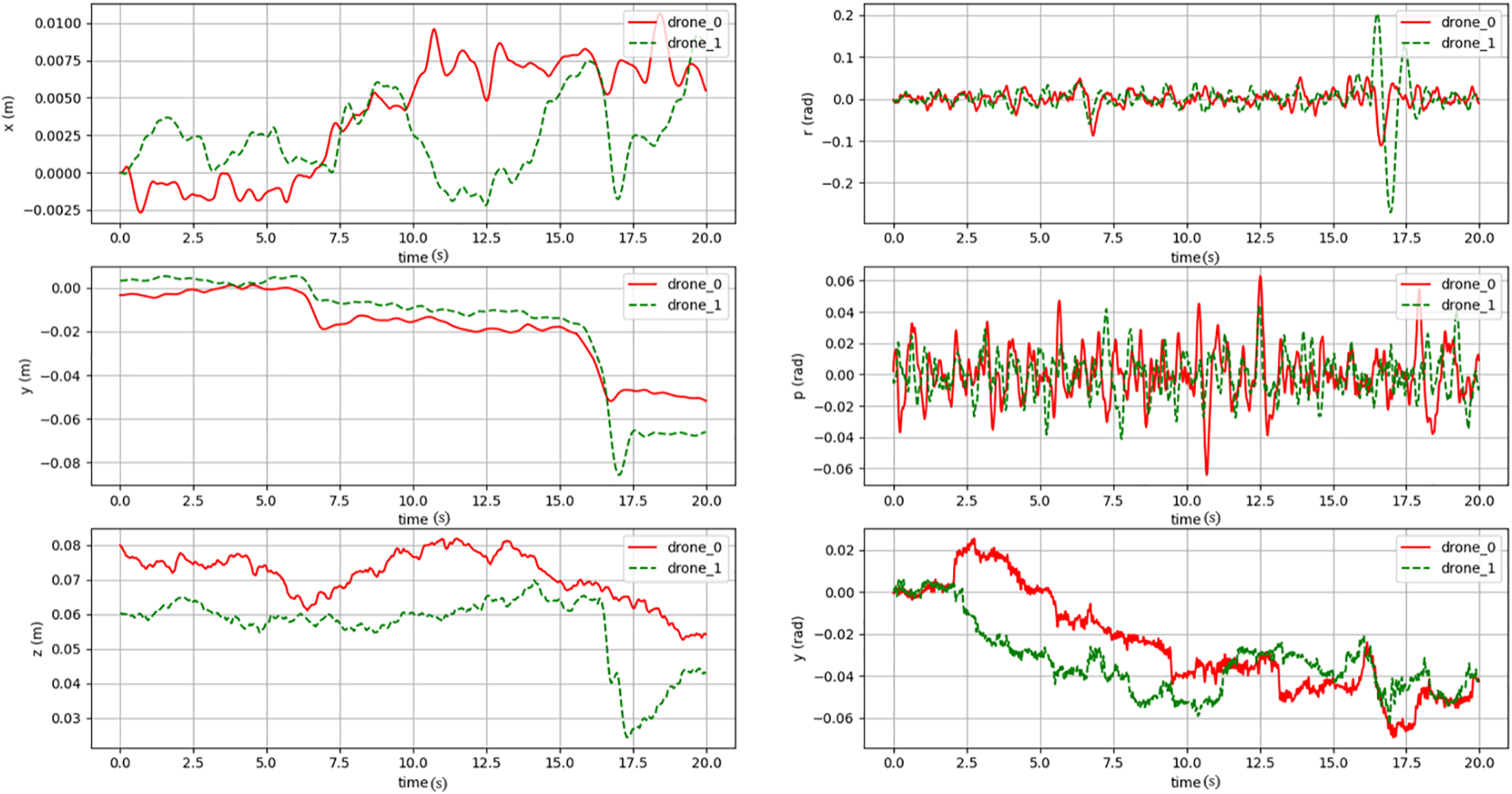
Figure 9: One-on-one (Three-dimensional) pursuit-evasion UAV movement information under the Boids-PE model self-play learning framework

The above illustrates the performance of Boids-PE’s hybrid swarm intelligence-based deep reinforcement learning in one-on-one pursuit-evasion scenarios, with experiments conducted in both one-dimensional and three-dimensional spaces. From the above we can observe that in the one-dimensional space, scenarios with and without self-play training are included. Compared to the scenarios without self-play training, the introduction of self-play training significantly enhances the adaptability of the pursuing UAV.

Especially through experiments in three-dimensional space, the advantages brought by the self-play training framework [23,24] are significant, with the pursuing UAVs demonstrating excellent adaptability throughout the process. The combination of reinforcement learning and self-play methods in three-dimensional space enabled the pursuing UAVs to learn more effective pursuit strategies, showcasing the robustness and potential of the Boids-PE model in complex environments. This comprehensive approach emphasizes the model’s ability to handle dynamic interactions and continuously improve through adaptive learning, making it highly suitable for real-world applications where environmental variables are constantly changing.

The self-play training method in the Boids-PE model enables the chasing UAV to continually optimize its strategy to adapt to the changing behaviors of the escaping UAV. This not only demonstrates the model’s adaptability in dynamic environments but also underscores the importance of the self-play approach in enhancing UAVs’ autonomous decision-making and flexible response capabilities.

To study the performance comparison between strategies with and without self-play in one-on-one scenarios, we fixed the strategy of the evading UAV to be either random or other rule-based strategies. We then controlled the pursuing UAV trained under the self-play framework and the pursuing UAV not trained under the self-play framework to chase the evading UAV. A successful capture is considered when the distance between the two UAVs is less than 3 cm and this condition is maintained for more than 5 s. If the above success conditions are not met within 20 s, it is considered a capture failure.

Based on this, for each independent UAV pursuit and evasion experiment, we conducted 5 independent random tests, each lasting 20 s. The number of successful captures within 20 s was recorded, as shown in Tables 3–5.

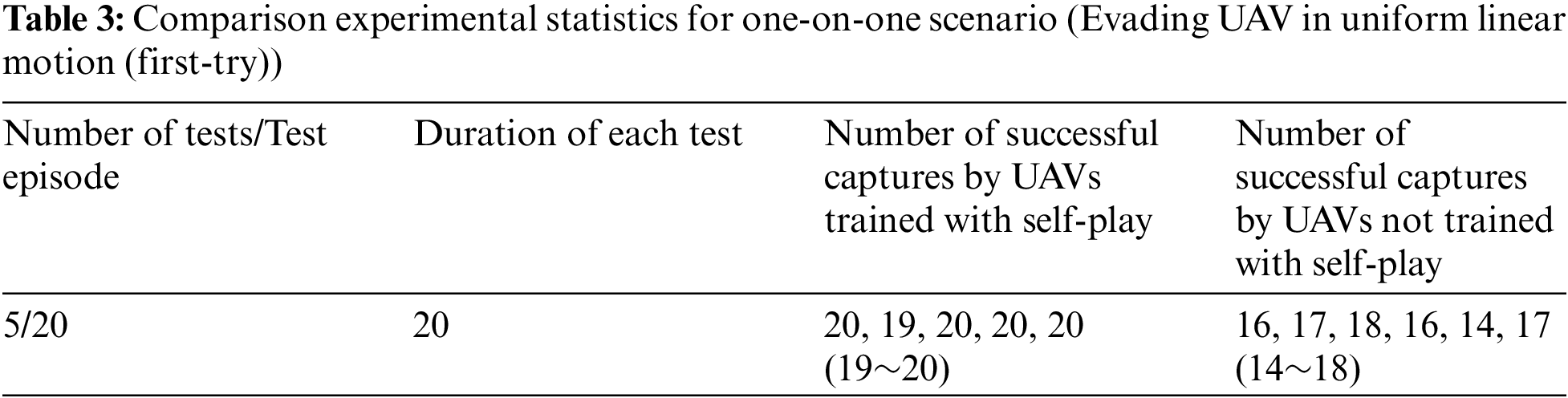
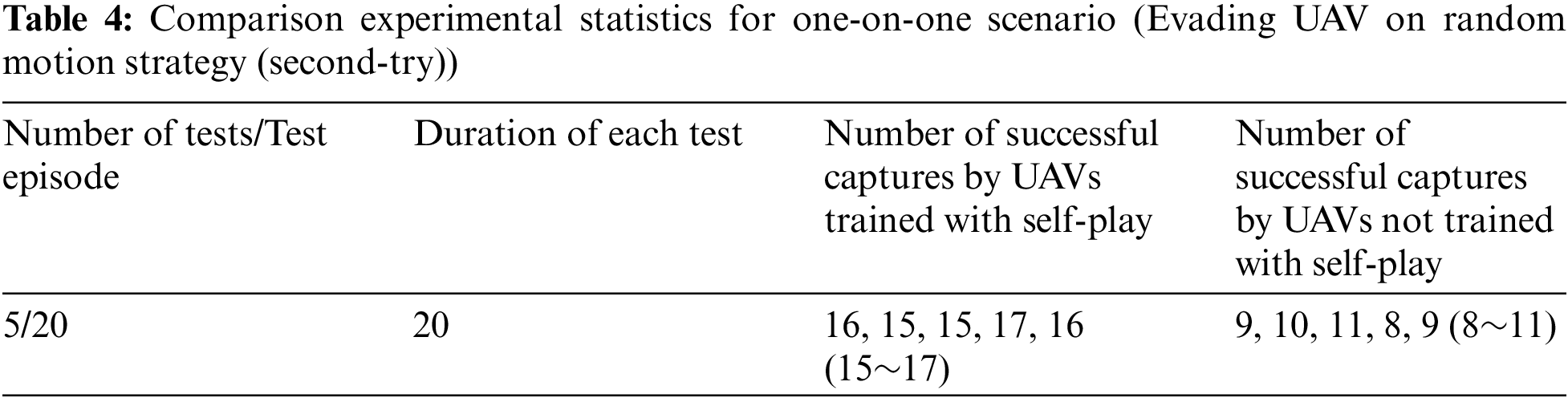
Based on the statistics in Table 3, for the scenario where the evading UAV follows a simple uniform linear motion, the UAVs trained under the self-play framework achieved successful captures in all 20 tests. In contrast, the UAVs not trained with self-play successfully captured the target around 14~18 times, losing the target about 2~6 times. In Table 4, for the scenario where the evading UAV follows a random strategy, the UAVs trained under the self-play framework successfully captured the target about 15~17 times, while those not trained with self-play succeeded only less than 5 times. Based on this, the self-play training framework has certain advantages: Its pursuit strategies are more generalized and have demonstrated better performance across different scenarios.

We further included evading UAVs with self-play trained strategies into the test scenarios. Using the same setup, the experimental results are shown in Table 5, which summarizes the number of successful captures. In Table 5, the success rate (about 6~9 times) of UAVs trained with self-play is higher than those not trained with self-play (about 3~5 times). Compared to the previous two scenarios, the evading UAVs trained with self-play have enhanced evasion strategies, making them more difficult to capture.

These results indicate that the Boids-PE framework combined with self-play training [23,24] has a distinct advantage. Its capture strategy shows stronger generalization and performs well across different scenarios. The advantages of the self-play framework within the Boids-PE were demonstrated: 1. Enhanced Adaptability: successfully capturing targets across different evasion strategies, whether in uniform linear motion or random motion scenarios; 2. Higher Success Rate: UAVs trained with the self-play framework achieved significantly higher success rates compared to those not trained with self-play; 3. Improved Generalization: The self-play training of Boids-PE enhances the UAVs to develop generalized strategies that perform well across various scenarios, based on the consistent success in different test conditions.

In summary, through these experiments, we can observe that UAVs employing the Boids-PE model exhibit strong autonomous decision-making abilities and flexible adaptability in one-dimensional chase-escape scenarios. The self-play training method allows the chasing UAV to not only successfully complete the initial chase task through reinforcement learning but also to quickly respond and resume the chase when the escaping UAV adjusts its strategy. This decision-making mechanism significantly improves the execution efficiency and task success rate of UAVs in complex dynamic environments, fully showcasing the notable potential and advantages of the Boids-PE model in controlling the behavior of UAV swarms.

4.3 One-on-One Pursuit and Evasion Process Visualization

To better demonstrate the effectiveness of the Boid-PE model in UAV pursuit-evasion scenarios, we recorded several typical pursuit-evasion videos. These videos (accessible via the link in Fig. 10) showcase a one-on-one UAV pursuit-evasion experiment conducted in a three-dimensional space. At the beginning of the video, two UAVs are moving within the 3D space, with one serving as the evading UAV and the other as the pursuing UAV. Through reinforcement learning and self-play training, the pursuing UAV gradually learns effective pursuit strategies, continuously closing in on the evading UAV.

Figure 10: One-on-one (3D) Boid-PE pursuit-evasion UAV motion process recording (Please visit the link: Here) (Accessed on 7 August 2024)

In the video, it can be observed that the evading UAV attempts to escape by changing its position, but the pursuing UAV quickly adjusts its strategy and follows closely. In the x, y, and z directions, the pursuing UAV demonstrates agile maneuverability and quick response capabilities. As time progresses, the pursuing UAV gradually gains the upper hand, reducing the distance to the evading UAV. his video demonstrates that, in a complex three-dimensional space, the combination of reinforcement learning and self-play methods can significantly enhance the performance of UAVs in pursuit-evasion tasks, ultimately leading to successful capture.

Through this, the pursuing UAVs can significantly enhance its performance in pursuit tasks, demonstrating the model’s strong adaptability and flexibility in dynamic and complex environments.

4.4 Multiple-on-One Pursuit and Evasion Results and Analysis

In the many (multiple)-to-one pursuit-evasion scenario, Fig. 11 illustrates the process of using the Boids Model-based Apollonian Circles improved algorithm, which is based on the improved Boids model [19], to capture an evading UAV moving in a straight line. The positional data of both the pursuing and evading UAVs reveal several effective strategies employed during the pursuit:

1.    Formation Maintenance: The pursuing UAVs maintain a cohesive formation throughout the chase, ensuring they do not collide with each other and can coordinate their movements effectively.

2.    Encirclement of the Target: The pursuing UAVs successfully implement a strategy to surround the evading UAV, which is crucial in preventing its escape. This encirclement strategy ensures that the evading UAV has limited options for maneuvering, increasing the likelihood of capture.

3.    Escape Prevention: The coordinated effort of the pursuing UAVs to position themselves strategically around the evading UAV minimizes the chances of the target breaking free. This highlights the effectiveness of the algorithm in controlling and limiting the evading UAV’s movements.

4.    Advancement towards the Target: The pursuing UAVs consistently move towards the evading UAV, reducing the distance between them over time. This demonstrates the UAVs’ ability to adapt their paths dynamically to close in on the target.

Figure 11: The movement records of the UAVs in the pursuit-evasion scenario using the improved Apollonian Circles algorithm based on Boids model. The red curve represents the evading UAV, while the other curves represent the pursuing UAVs. The closer the other curves are to the red curve in each dimension, the better the advantage shown by the pursuing UAVs

These strategies collectively showcase the robustness and efficacy of the Boids-PE model in dynamic and complex pursuit-evasion tasks, particularly in scenarios involving multiple pursuers. The ability to maintain formation, advance towards, and encircle the target, while preventing its escape, demonstrates a high level of coordination and strategic planning facilitated by the self-play training framework [23,24].

In summary, Boids-PE demonstrates significant advantages in managing dynamic and complex pursuit-evasion tasks through its self-play training framework. Particularly in scenarios involving multiple pursuers, the model showcases a high level of coordination and strategic planning ability, with the self-play training framework enhancing team collaboration and strategy execution. The model’s capability to handle dynamic and unpredictable environments highlights its potential in practical applications. Especially in tasks requiring high maneuverability, precision, and coordination, the Boids-PE model effectively improves the operational capability and success rate of UAVs. These capabilities make the Boids-PE model not only theoretically significant but also demonstrate broad practical application prospects.

In the many-to-one pursuit-evasion scenario, Fig. 12 illustrates the movement information of UAVs under reinforcement learning decisions not guided by an intelligent algorithm. The positional data of both the pursuing UAVs and the evading UAV (drone_0) reveal that initially, the evading UAV attempts to escape in the y and z directions. However, the pursuing UAVs quickly manage to encircle it. This leads to a state of oscillation, where the UAVs maintain their positions while trying to keep the evading UAV contained. Due to the complexity introduced by the three-dimensional space, the pursuing UAVs, under non-intelligent algorithm guidance, have learned a basic encirclement strategy.

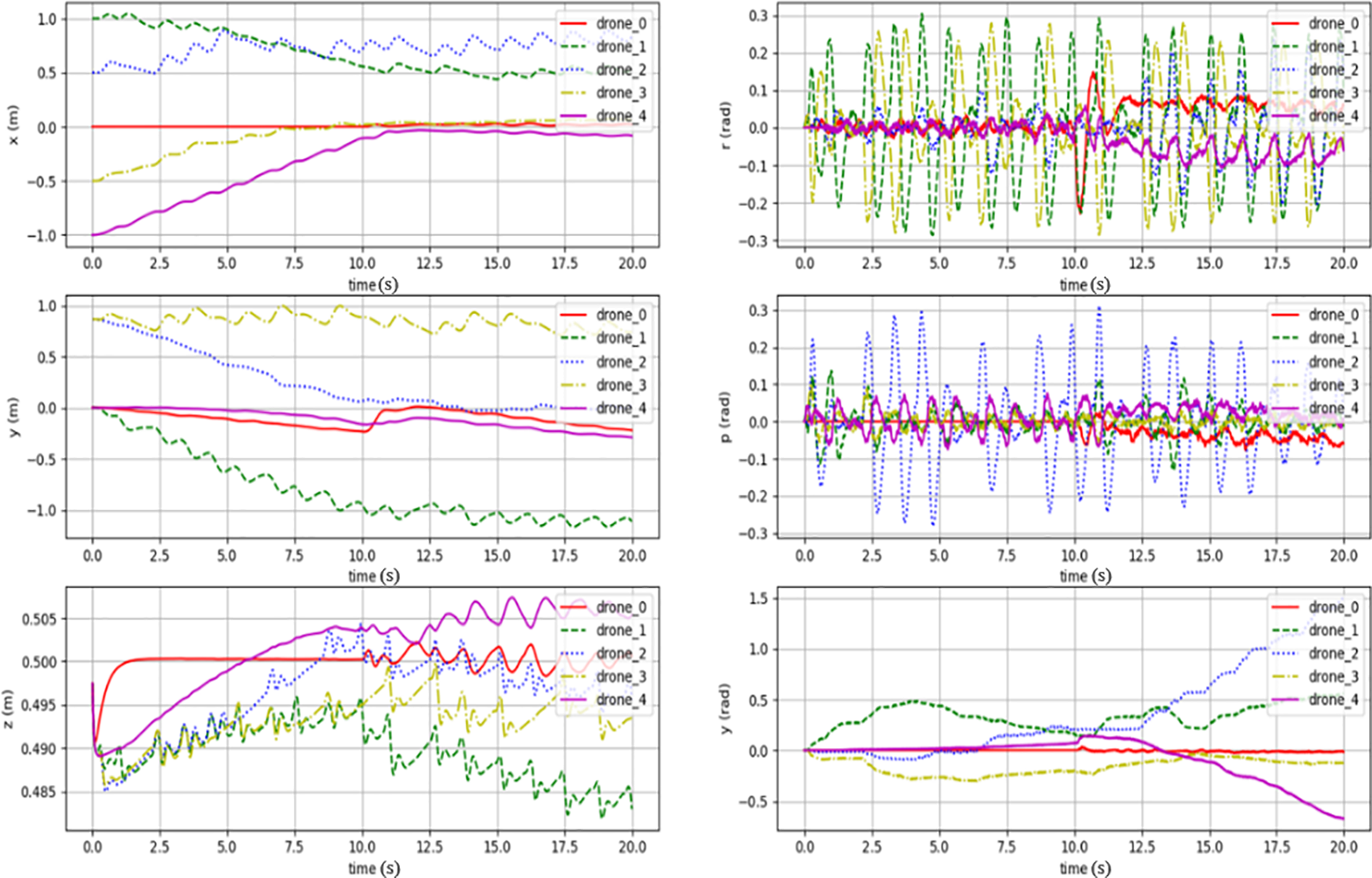
Figure 12: The movement information of pursuit-evasion UAVs reinforcement learning decisions within the Boids-PE model under many-to-one pursuit-evasion scenario

Overall, the Boids-PE model allows UAVs to better predict and react to the evading UAV’s movements, significantly reducing the time to capture and increasing the success rate. This model’s ability to handle dynamic and unpredictable environments showcases its potential for real-world applications, where agility and precision are crucial, highlighting its clear advantage over non-intelligent algorithm-guided methods.

4.5 Multiple-on-One Pursuit and Evasion Process Visualization

To better demonstrate the effectiveness of the Boid-PE model in multi-UAV pursuit-evasion scenarios, we recorded several typical pursuit-evasion videos. These videos (accessible via the link in Fig. 13) showcase a multi-UAV pursuit-evasion experiment conducted in a three-dimensional space. At the beginning of the video, five UAVs are moving within the 3D space, with one serving as the evading UAV and the remaining four as the pursuing UAVs.

Figure 13: One-on-one (3D) Boid-PE pursuit-evasion UAV motion live recording (Please visit the link: Here) (accessed on 7 August 2024)

Through reinforcement learning and self-play training, the pursuing UAVs gradually learn effective pursuit strategies, working collaboratively to constantly approach the evading UAV. In the video, it can be observed that the evading UAV attempts to escape by changing its position and trajectory, but the pursuing UAVs quickly adjust their strategies and cooperate to encircle it. In the x, y, and z directions, the pursuing UAVs exhibit agile maneuverability and quick response capabilities, coordinating seamlessly with each other.

As time progresses, the pursuing UAVs gradually gain the upper hand, reducing the distance to the evading UAV through cooperation and forming effective encirclement strategies. This video demonstrates that, in a complex three-dimensional space, the combination of reinforcement learning and self-play methods can significantly enhance the performance of UAV teams in pursuit-evasion tasks, ultimately leading to successful capture.

5  Comparative Results with SOTA Baselines

Based on our extensive experiments in one-on-one and multiple-on-one pursuit-evasion scenarios, we conducted a comparative analysis of our proposed Boids-PE model against several state-of-the-art (SOTA) baselines: PSO-M3DDPG, DualCL, RL-CombatA3C, and batA3C.

PSO-M3DDPG [18] is a multi-agent reinforcement learning model designed to improve the training efficiency and convergence of algorithms for complex pursuit-evasion problems. It combines the Mini-Max-Multi-agent Deep Deterministic Policy Gradient (M3DDPG) algorithm with Particle Swarm Optimization (PSO) to address challenges such as sparse sample data and instability in convergence. By leveraging these techniques, PSO-M3DDPG achieves better performance and faster convergence in simulated multi-agent pursuit-evasion tasks, demonstrating its effectiveness through experimental simulations.

DualCL (Dual Curriculum Learning Framework) [38] is a method for multi-UAV pursuit-evasion tasks designed to handle the challenge of capturing an evader in diverse environments. Traditional heuristic algorithms often struggle with providing effective coordination strategies and can underperform in extreme scenarios, such as when the evader moves at high speeds. In contrast, reinforcement learning (RL) methods have the potential to develop highly cooperative capture strategies but face difficulties in training due to the vast exploration space and the dynamic constraints of UAVs.

RL-CombatA3C [5] is a state-of-the-art algorithm developed to optimize UAV pursuit-evasion tactics using Reinforcement Learning (RL) in one-on-one aerial combat scenarios. It employs the Asynchronous Actor-Critic Agents (A3C) algorithm with deep neural networks to learn and refine effective interception maneuvers. The model is trained in simulation and validated through live-flight tests, demonstrating its ability to transfer learned behaviors from virtual environments to real-world applications.

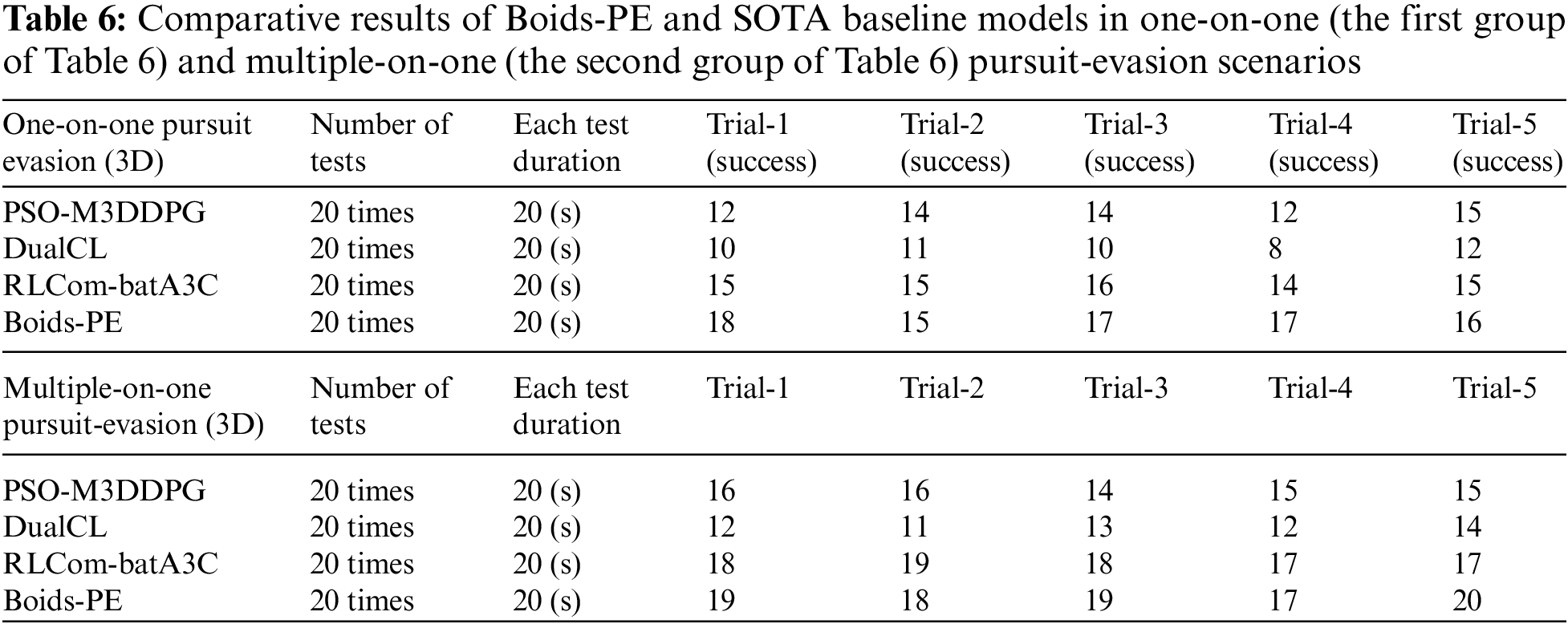
For both the one-on-one and multiple-on-one pursuit-evasion scenarios, we conducted five independent trials, with each trial consisting of 20 rounds of pursuit-evasion. The efficiency of each model was measured based on the UAV capture success rate within a specified time frame. Specifically, a successful capture was considered when the distance between the pursuing UAV and the evading UAV was less than 3 cm, and this condition was maintained for more than 5 s. If these success conditions were not met within 20 s, it was considered a capture failure. The results are summarized in Table 6 with two sub-tables, which includes the number of successful captures by UAVs within a set duration.

5.1 One-on-One Pursuit-Evasion (3D) Results

For the one-on-one pursuit-evasion scenario, the Boids-PE model outperformed all other models in terms of the number of successful captures across multiple trials. The detailed results are as follows:

The PSO-M3DDPG model achieved a consistent performance across all trials, showing an average of 13 successful captures. The DualCL model, although efficient, showed slightly lower performance with an average of 10 successful captures. RL-CombatA3C displayed robust performance with an average of 15 successful captures. The batA3C model demonstrated moderate performance with an average of 13 successful captures. In contrast to these baselines, our proposed Boids-PE model significantly outperformed the others with an average of 17 successful captures.

These highlight the superior performance of Boids-PE, attributed to its effective combination of swarm intelligence and deep reinforcement learning, enabling better decision-making and strategy adaptation in dynamic environments.

5.2 Multiple-on-One Pursuit-Evasion (3D) Results

As shown the second group of Table 6, in the multiple-on-one pursuit-evasion scenario, Boids-PE again showed superior performance, which is detailed as follows:

Firstly, PSO-M3DDPG achieved an average of 14 successful captures, demonstrating solid performance but falling short in more complex multi-agent scenarios. DualCL maintained an average of 12 successful captures, indicating some difficulty in coordination among multiple UAVs. RL-CombatA3C performed well with an average of 17 successful captures, showing strong adaptability in multi-agent settings. The batA3C model had an average of 13 successful captures, consistent with its performance in simpler scenarios. Our Boids-PE excelled with an average of 19 successful captures, showcasing its effectiveness in managing complex interactions and coordination among multiple pursuing UAVs.

The Boids-PE model’s superior performance can be attributed to several key factors. Firstly, the utilization of swarm intelligence algorithms plays a crucial role. By leveraging the simple yet effective rules of the Boids model—separation, alignment, and cohesion—Boids-PE maintains stable formations and prevents collisions, which is essential in dynamic environments. These fundamental behaviors allow the UAVs to operate cohesively and efficiently, providing a solid foundation for complex maneuvers required during pursuit-evasion tasks. The self-play training method itself is a significant contributor to the model’s success. By training UAVs in both pursuit and evasion roles, the method ensures that each UAV can anticipate and counter the strategies of its opponents. This dynamic training environment fosters greater adaptability and responsiveness, allowing UAVs to refine their tactics continuously and perform better in real-world applications.

In comparison, the PSO-M3DDPG algorithm, which combines Particle Swarm Optimization (PSO) with the M3DDPG algorithm, aims to enhance training efficiency and convergence. While it achieves better performance and faster convergence in simulated multi-agent pursuit-evasion tasks, it struggles with sparse sample data and instability in convergence, which limits its effectiveness in more complex or dynamic real-world scenarios. RL-CombatA3C, designed for optimizing UAV pursuit-evasion tactics in one-on-one aerial combat scenarios, uses the Asynchronous Actor-Critic Agents (A3C) algorithm with deep neural networks. Although it demonstrates its ability to transfer learned behaviors from virtual environments to real-world applications, its performance in more complex multi-agent environments may not be as robust due to its specific focus on one-on-one scenarios. DualCL, intended for multi-UAV pursuit-evasion tasks, addresses the challenges of capturing an evader in diverse environments. While traditional heuristic algorithms struggle with effective coordination in extreme scenarios, such as high-speed evasion, DualCL shows potential by leveraging reinforcement learning. However, it faces difficulties in training due to the vast exploration space and dynamic constraints of UAVs, which can hinder its overall effectiveness in comparison to the Boids-PE model.

In conclusion, the Boids-PE model demonstrates exceptional performance and robustness in UAV pursuit-evasion tasks, providing a significant improvement over existing methods. Its ability to handle dynamic and complex environments highlights its potential for practical applications, offering a reliable and efficient solution for UAV pursuit-evasion missions.

6  Discussions

The remarkable performance of the Boids-PE model in UAV pursuit and evasion tasks can be attributed to several key factors. Firstly, the introduction of swarm intelligence algorithms allows UAVs to achieve complex group behaviors through simple rules such as separation, alignment, and cohesion. This approach enables the UAVs to maintain stable and efficient formations when facing dynamic and complex pursuit scenarios, thereby improving the success rate of the pursuit.

Secondly, the integration of deep reinforcement learning techniques endows UAVs with a high degree of adaptability and decision-making capability in pursuit tasks. Through extensive simulation experiments and self-play training, UAVs can continuously adjust and optimize their strategies in changing environments. This process not only enhances the execution efficiency and reliability of the UAVs but also enables them to improve their performance through self-learning, even in the absence of large amounts of labeled data.

Experimental results demonstrate that the proposed method significantly increases the success rate of pursuit UAVs in both one-on-one and many-on-one environments. This result is primarily due to the following factors:

1.    Self-Play Training Method: Through the self-play training framework, the pursuit and evasion UAVs alternately train, gradually enhancing their respective strategies and performance. This allows the UAVs to continuously learn and improve their strategies in simulated adversarial environments, thereby increasing their adaptability and responsiveness.

2.    Reward Function Design: The carefully designed reward functions not only consider the success rate of the pursuit but also incorporate practical needs such as obstacle avoidance and formation maintenance. This multi-dimensional reward setting enables the UAVs to comprehensively improve various capabilities during training.

3.    Environmental Diversity: In the experimental design, by comparing different pursuit scenarios, including uniform linear motion and random motion strategies, we comprehensively evaluated the UAVs’ performance in various complex environments. This diverse experimental environment enhances the generalization capability of UAVs, making them perform better in practical applications.

In summary, our proposed Boids-PE demonstrates exceptional performance in UAV pursuit and evasion tasks by integrating swarm intelligence algorithms with deep reinforcement learning techniques. The success of this model is attributed not only to the innovative design of the model itself but also to the carefully crafted self-play training method and reward functions, enabling UAVs to learn and optimize their strategies in dynamically complex environments.

7  Conclusions

We introduce a novel model, Boids Model-based deep reinforcement learning (DRL) Approach for Pursuit and Escape (Boids-PE), for UAV pursuit-evasion tasks, a novel approach that cleverly integrates the Boids model, inspired by bird flocking behavior, with DRL techniques. This model effectively addresses multiple challenges in UAV pursuit-evasion missions. Through a meticulously designed self-play training framework and reward functions, this method goes beyond traditional approaches by considering practical needs such as obstacle avoidance. By setting appropriate rewards, UAVs are guided to emulate biological behaviors and continuously improve their pursuit-evasion performance through self-play training. Boids-PE significantly enhances the execution efficiency and reliability of UAV missions. Moreover, the research provides new insights into cooperation and competition in multi-agent systems. Through extensive simulation training and self-play learning, UAVs can rapidly accumulate experience in a safe, risk-free environment. The learned strategies can then be transferred to real-world applications, demonstrating strong adaptability and robustness.

Future work will focus on further improving the algorithm’s generalization capabilities and its ability to handle more complex environments. Continued exploration will aim at enabling UAVs to make effective decisions in more open and dynamic settings, and at enhancing UAV autonomy and intelligence through advanced reinforcement learning techniques, such as multi-modal learning and meta-reinforcement learning.

Acknowledgement: The authors extend their sincere gratitude to Xi’an Jiaotong University, China Electroncs Technology Group Corporation (CETC), and Beihang University for providing the vital support needed to complete this research project. The corresponding author of this paper is Biao Zhao. The authors extend their gratitude to the editors and anonymous reviewers for their insightful discussions and perceptive feedback, which greatly improved the quality of this work.

Funding Statement: This work was supported by no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author Contributions: The authors confirm contributions to this paper as follows: Conceptualization, Methodology, Formal analysis, Writing—original draft, Project administration, Investigation, Validation, Formal analysis, Writing—review & editing: Weiqiang Jin, Software, Investigation, Visualization, Conceptualization, Project administration: Xingwu Tian, Validation: Bohang Shi, Writing—review & editing, Supervision: Biao Zhao, Haibin Duan, and Hao Wu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data openly available in a public repository. Full code to replicate this experiments are available from Github: https://github.com/albert-jin/Boids-PE (accessed on 7 August 2024). The other used materials will be made available on request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Chen, Y. Tian, and T. Jiang, “Cooperative task assignment of a heterogeneous Multi-UAV system using an adaptive genetic algorithm,” Electronics, vol. 9, no. 4, 2020, Art. no. 687. doi: 10.3390/electronics9040687. [Google Scholar] [CrossRef]

2. N. K. Long, K. Sammut, D. Sgarioto, M. Garratt, and H. A. Abbass, “A comprehensive review of shepherding as a bio-inspired swarm-robotics guidance approach,” IEEE Trans. Emerg. Top. Comput. Intell., vol. 4, no. 4, pp. 523–537, 2020. doi: 10.1109/TETCI.2020.2992778. [Google Scholar] [CrossRef]

3. Y. Li, S. Zhang, F. Ye, T. Jiang, and Y. Li, “A UAV path planning method based on deep reinforcement learning,” in Proc. 2020 IEEE USNC-CNC-URSI N. Am. Radio Sci. Meet. (Joint AP-S Symp.), 2020, pp. 93–94. doi: 10.23919/USNC/URSI49741.2020.9321625. [Google Scholar] [CrossRef]

4. X. Sun, B. Sun, and Z. Su, “Cooperative pursuit-evasion game for Multi-AUVs in the ocean current and obstacle environment,” presented at the 2023 Intell. Robot. Appl., Singapore, Springer Nature Singapore, 2023, pp. 201–213. doi: 10.1007/978-981-99-6489-5_16. [Google Scholar] [CrossRef]

5. B. Vlahov, E. Squires, L. Strickland, and C. Pippin, “On developing a UAV pursuit-evasion policy using reinforcement learning,” presented at the 2018 17th IEEE Int. Conf. Mach. Learn. Appl. (ICMLA), Orlando, FL, USA, 2018, pp. 859–864. doi: 10.1109/ICMLA.2018.00138. [Google Scholar] [CrossRef]

6. I. E. Weintraub, M. Pachter, and E. Garcia, “An introduction to pursuit-evasion differential games,” presented at the 2020 Ame. Control Conf. (ACC), Denver, CO, USA, 2020, pp. 1049–1066. doi: 10.23919/ACC45564.2020.9147205. [Google Scholar] [CrossRef]

7. V. Mnih et al., “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533, 2015. doi: 10.1038/nature14236. [Google Scholar] [PubMed] [CrossRef]

8. T. P. Lillicrap et al., “Continuous control with deep reinforcement learning,” 2016, arXiv:1509.02971. [Google Scholar]

9. R. Camacho, A. Talebpour, M. Naeem, H. Azimi, and B. Piccoli, “Aerial robotic pursuit-evasion games with multiple players,” 2019, arXiv.1912.02728. [Google Scholar]

10. M. Schranz, M. Umlauft, M. Sende, and W. Elmenreich, “Swarm robotic behaviors and current applications,” Front Robot. AI., vol. 7, 2020, Art. no. 36. doi: 10.3389/frobt.2020.00036. [Google Scholar] [PubMed] [CrossRef]

11. H. -S. Wu and F. -M. Zhang, “Wolf pack algorithm for unconstrained global optimization,” Math. Probl. Eng., vol. 2014, no. 1, 2014, Art. no. 465082. doi: 10.1155/2014/465082. [Google Scholar] [CrossRef]

12. M. Dorigo and G. Di Caro, “Ant colony optimization: A new meta-heuristic,” presented at the 1999 Congr. Evol. Comput.-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 1999, vol. 2, pp. 1470–1477. doi: 10.1109/CEC.1999.782657. [Google Scholar] [CrossRef]

13. D. Teodorovic, P. Lucic, G. Markovic, and M. D. Orco, “Bee colony optimization: Principles and applications,” presented at the 2006 8th Sem. Neural Netw. Appl. Electr. Eng., Belgrade, Serbia, 2006, pp. 151–156. doi: 10.1109/NEUREL.2006.341200. [Google Scholar] [CrossRef]

14. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 12, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

15. B. Al Baroomi, T. Myo, M. R. Ahmed, A. Al Shibli, M. H. Marhaban and M. S. Kaiser, “Ant colony optimization-based path planning for UAV navigation in dynamic environments,” presented at the 2023 7th Int. Conf. Automation, Control Robots (ICACR), Kuala Lumpur, Malaysia, Oct. 14–16, 2023. doi: 10.1109/ICACR59381.2023.10314603. [Google Scholar] [CrossRef]

16. H. Chen, J. Xu, and C. Wu, “Multi-UAV task assignment based on improved wolf pack algorithm,” presented at the 2020 Int. Conf. Cyberspace Innov. Adv. Technol., Guangzhou, China, Dec. 28–30, 2020. doi: 10.1145/3444370.3444556. [Google Scholar] [CrossRef]

17. Z. Chen, J. Zhong, X. Lan, G. Ma, and W. Xu, “Environment-adaptive bat algorithm for UAV path planning,” presented at the 2022 Chin. Automat. Congress (CAC), Chengdu, China, Nov. 25–27, 2022. doi: 10.1109/CAC57257.2022.10055819. [Google Scholar] [CrossRef]

18. Y. Zhang et al., “Multi-UAV pursuit-evasion gaming based on PSO-M3DDPG schemes,” Complex Intell. Syst., 2024. doi: 10.1007/s40747-024-01504-1. [Google Scholar] [CrossRef]

19. L. Bajec, N. Zimic, and M. Mraz, “The computational beauty of flocking: Boids revisited,” Math Comput. Model. Dyn. Syst., vol. 13, no. 4, pp. 331–347, 2007. doi: 10.1080/13873950600883485. [Google Scholar] [CrossRef]

20. R. E. Barnhill, “Apollonius’ problem: A study of solutions and applications,” Am. Math. Mon., vol. 82, no. 4, pp. 328–336, 1975. doi: 10.2307/2318786. [Google Scholar] [CrossRef]

21. E. Coumans and Y. Bai, “PyBullet, a python module for physics simulation in robotics, games, and machine learning,” 2016. Accessed: Aug. 07, 2024. [Online]. Available: http://pybullet.org [Google Scholar]

22. S. Alaliyat, R. Oucheikh, and I. Hameed, “Path planning in dynamic environment using particle swarm optimization algorithm,” presented at the 2019 8th Int. Conf. Model. Simul. Appl. Optim. (ICMSAO), Amwaj Islands, Bahrain, 2019, pp. 1–5. doi: 10.1109/ICMSAO.2019.8880434. [Google Scholar] [CrossRef]

23. D. Silver et al., “Mastering the game of Go with deep neural networks and tree search,” Nature, vol. 529, no. 7587, pp. 484–489, 2016. doi: 10.1038/nature16961. [Google Scholar] [PubMed] [CrossRef]

24. D. Silver et al., “Mastering the game of Go without human knowledge,” Nature, vol. 550, no. 7676, pp. 354–359, 2017. doi: 10.1038/nature24270. [Google Scholar] [PubMed] [CrossRef]

25. N. Chen, L. Li, and W. Mao, “Equilibrium strategy of the pursuit-evasion game in three-dimensional space,” IEEE/CAA J. Autom. Sinica., vol. 11, no. 2, pp. 446–458, Feb. 2024. doi: 10.1109/JAS.2023.123996. [Google Scholar] [CrossRef]

26. S. A. Wu, R. E. Wang, J. A. Evans, J. B. Tenenbaum, D. C. Parkes and M. Kleiman-Weiner, “Too many cooks: Bayesian inference for coordinating multi-agent collaboration,” presented at the Top. Cognit. Sci., 2021, vol. 13, no. 2, pp. 414–432. doi: 10.1111/tops.12525. [Google Scholar] [PubMed] [CrossRef]

27. M. Wei, G. Chen, J. B. Cruz, L. S. Haynes, K. Pham and E. Blasch, “Multi-pursuer multi-evader pursuit-evasion games with jamming confrontation,” J. Aer. Comput., Inf., Commun., vol. 4, no. 3, pp. 693–706, 2007. doi: 10.2514/1.25329. [Google Scholar] [CrossRef]

28. C. de Souza, R. Newbury, A. Cosgun, P. Castillo, B. Vidolov and D. Kulić, “Decentralized multi-agent pursuit using deep reinforcement learning,” IEEE Robot. Autom. Lett., vol. 6, no. 3, pp. 4552–4559, Jul. 2021. doi: 10.1109/LRA.2021.3068952. [Google Scholar] [CrossRef]

29. O. E. Egbomwan, S. Liu, and H. Chaoui, “Twin delayed deep deterministic policy gradient (TD3) based virtual inertia control for inverter-interfacing DGs in microgrids,” IEEE Syst. J., vol. 17, no. 2, pp. 2122–2132, Jun. 2023. doi: 10.1109/JSYST.2022.3222262. [Google Scholar] [CrossRef]

30. J. Li and S. X. Yang, “Bio-inspired neural network for real-time evasion of multi-robot systems in dynamic environments,” Biomimetics, vol. 9, no. 3, 2024, Art. no. 176. doi: 10.3390/biomimetics9030176. [Google Scholar] [PubMed] [CrossRef]

31. E. Camci and E. Kayacan, “Game of drones: UAV pursuit-evasion game with type-2 fuzzy logic controllers tuned by reinforcement learning,” presented at the 2016 IEEE Int. Conf. Fuzzy Syst. (FUZZ-IEEE), Vancouver, BC, Canada, 2016, pp. 618–625. doi: 10.1109/FUZZ-IEEE.2016.7737744. [Google Scholar] [CrossRef]

32. M. Kouzeghar, Y. Song, M. Meghjani, and R. Bouffanais, “Multi-target pursuit by a decentralized heterogeneous UAV swarm using deep multi-agent reinforcement learning,” 2023, arXiv:2303.01799. [Google Scholar]

33. M. Zamanipour, “Novel Information-theoretic Game-theoretical Insights to Broadcasting in Internet-of-UAVs,” 2022, arXiv:2201.01843. [Google Scholar]

34. V. K. Kaliappan, H. Yong, A. Budiyono, and D. Min, “Linear velocity based predictive control design and experiment for pursuit-evasion of a multiple small scale unmanned helicopter,” in Converg. Hybrid Inf. Technol.: 5th Int. Conf., ICHIT 2011, Daejeon, Republic of Korea, Berlin Heidelberg, Springer, Sep. 22–24, 2011. [Google Scholar]

35. X. Wang, Y. Cai, Y. Fang, and Y. Deng, “Intercept strategy for maneuvering target based on deep reinforcement learning,” presented at the 2021 40th Chin. Control Conf. (CCC), Shanghai, China, Jul. 26–28, 2021. doi: 10.23919/CCC52363.2021.9549458. [Google Scholar] [CrossRef]

36. E. H. Sumiea et al., “Deep deterministic policy gradient algorithm: A systematic review,” Heliyon, vol. 10, no. 9, 2024, Art. no. e30697. doi: 10.1016/j.heliyon.2024.e30697. [Google Scholar] [PubMed] [CrossRef]

37. J. Ye, Q. Wang, B. Ma, Y. Wu, and L. Xue, “A pursuit strategy for multi-agent pursuit-evasion game via multi-agent deep deterministic policy gradient algorithm,” presented at the 2022 IEEE Int. Conf. Unmanned Syst. (ICUS), Guangzhou, China, Nov. 18–20, 2022. doi: 10.1109/ICUS55513.2022.9986838. [Google Scholar] [CrossRef]

38. J. Chen et al., “A dual curriculum learning framework for Multi-UAV pursuit-evasion in diverse environments,” 2024, arXiv:2312.12255. [Google Scholar]

39. J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” 2017, arXiv:1707.06347. [Google Scholar]

40. K. J. Åström and R. M. Murray, “PID controllers: Theory, design, and tuning,” IEEE Trans. Control Syst. Technol., vol. 16, no. 4, pp. 755–776, 2008. doi: 10.1109/TCST.2007.916255. [Google Scholar] [CrossRef]

41. J. M. Maciejowski, “Model predictive control: Theory and practice–A survey,” Automatica, vol. 39, no. 3, pp. 447–457, 2002. doi: 10.1016/S0005-1098(02)00207-0. [Google Scholar] [CrossRef]