A Path Planning Algorithm Based on Improved RRT Sampling Region

1  Introduction

Path planning algorithms that are now widely studied include heuristic search based on the A* algorithm [1], online path planning Dijkstra star (D*) [2], Ant Colony algorithm [3] and others. Research on A* algorithm is also endless, A* algorithm integrates the Artificial Potential Field (APF) [4] method, through the gravitational field for node expansion to guide the repulsive field in the obstacle, so that the algorithm can obtain the effective path more quickly. Benefits of the Rapidly Exploring Random Tree (RRT) algorithm [5], such as global search having great randomness, make the RRT algorithm not easily trapped in local optima interference. The RRT algorithm is widely applied in real-time planning [6], finding effective paths in limited time, etc., so RRT algorithms are widely studied and applied by researchers. However, the classic RRT algorithm has the weakness in not being able to guarantee the optimal path because of its great randomness, random search without direction in the whole graph range [7], which leads to the high computational intricacy of the algorithm, and it has great difficulties in dealing with the narrow channel because it must be expanded at each node of the tree, and so on.

In recent years, many researchers have been working on fusing the algorithm with other algorithms to improve the performance of RRT algorithms. RRT* and A* algorithm [8] are fused to optimize the path step by step using the heuristic idea of the A* algorithm, but the algorithm requires a lot of computation, and the efficiency obtained is not satisfactory. RRT and the Probabilistic Roadmap Method algorithm (PRM) [9] are combined in order to improve the global and local properties of the RRT algorithm, but the two algorithms are of different natures, and the fusion of both of them has a greater complexity of strategy. RRT and simulated annealing algorithm are fused. The fusion of RRT and Simulated Annealing algorithm (SA) [10,11] is mainly to prevent the RRT algorithm from falling into local optimum, but the optimization process of simulated annealing is more complicated and time consuming. Wei et al. [12] proposed an enhanced sparrow search algorithm (MSSA) that applies a Cauchy-Gaussian perturbation to the optimal position of the SSA algorithm to improve its ability to jump out of the local optimum. The fusion of RRT and Genetic Algorithm (GA) [13] mainly makes the paths diversified, but the genetic algorithm [14,15] is very computationally intensive, which is more time-consuming. RRT incorporates the Particle Swarm Optimization (PSO) algorithm [16] to optimize the initial path of the intelligent swarm. The branch of the A* algorithm is the D* algorithm, which is mainly applied to path planning in dynamic environments. Researchers have proposed a variety of optimization strategies to improve the performance of the D* algorithm [17], such as the inclusion of a multi-objective optimization technique, which allows the algorithm to acquire paths under a variety of constraints, which is particularly important for real-world application scenarios. Ant colony algorithms in bionic algorithms are also widely studied, and researchers have fused ant colony algorithms and genetic algorithms to form a hybrid optimization algorithm in the latest research, which can perform better for more complex environments. These hybrid algorithms perform excellently in logistics and distribution.

To improve the RRT algorithm effectively, this paper adds more obstacles to the map to test the superiority of this paper’s algorithm, and it conducts several experiments in different complex maps to ensure that the algorithm does not have accidents. In summary, under the premise of existing research results, this paper proposes a feedback bias sampling strategy, the feedback bias strategy can avoid the random tree falling into the local optimum, and solve the problem of inefficiency of the search in complex environments. For the randomness of the search, it aims to restrict the sampling area of the random tree, and this restriction on the sampling area can limit the search area to a large extent. The inverse optimization strategy is introduced to remove redundant nodes from the initial paths obtained to reduce the path cost. Finally, auxiliary nodes are used to optimize the cubic Bessel curve to ensure the robot’s smooth operation.

The contributions of this paper can be outlined as follows:

(1) To improve the efficiency of random tree sampling, an improved feedback bias sampling is used.

(2) To avoid ineffective searching of random trees in redundant spaces, an extension strategy to limit the growth of random trees is designed.

(3) In order to solve the issues of obtaining an initial path with a large number of inflection points, a reverse optimization strategy is introduced to remove redundant nodes from the initial path.

(4) To ensure smooth operation in the real environment of the robot, auxiliary nodes are used to optimize the cubic Bezier curves.

2  Related Works

In recent years, researchers have addressed the limitations of the classic RRT algorithm, such as slow search pace and randomness. Many scholars have improved the traditional RRT algorithm with various effects. Some researchers have proposed increasing the dynamic step leader for the RRT algorithm to add a motion step to adjust the fixed step size so that the step size converges in the vicinity of the obstacle, shortening the path length. Kuffner et al. [18] proposed the RRT* algorithm, which introduces a re-selection of the parent node strategy, which leads to the node being carried out by the selection of the nearest node, so that the path obtained reaches a shorter path. The researcher proposed a regional sampling adjustment, which restricts the region of the path search and allows the random tree to search for paths in a controlled range, this method effectively improves the shortcomings of the randomness of the search algorithm. Kang et al. [19] proposed a more efficient RRT-connect algorithm which searches for the random tree with simultaneous starting and ending points, and two trees at the same time path search, this method greatly improves the effective path search speed. In response to the problems of blind search in the classic RRT algorithm and its improved algorithms, an improved RRT-Connect algorithm [20,21] was proposed, which solves the problems of slow expansion and slow convergence by setting an adaptive step-size strategy and utilizing the method of fixed sampling function.

Proposed an improved RRT* algorithm (ATS-RRT*) [22], an algorithm that uses triangular region sampling to improve the RRT* algorithm. Xu et al. [23] proposed to make the robotic robot avoid obstacles, find the optimal path, and complete the automatic charging and docking, maintaining the global integrity and path optimality. The authors proposed an enhanced Informed-RRT* algorithm [24–26] to address the blind spots in path planning. This algorithm employs an adaptive growth strategy and an elliptic region variable weight sampling strategy. Generate multiple initial paths and consider communication between sampling and target points, which accelerates initial path planning and enhances the discovery rate of viable paths. Suggested a strategy for local path replanning to address path discontinuities, which render the planned path practically unviable. The unidirectional random tree extension cannot satisfy the need, the Bidirectional RRT (Bi-RRT) algorithm [27,28] is also based on the same principle. An improved artificial potential field method for generating guidance nodes in complex orchard environments [29] has been designed in the literature. Extend-RRT [30] is based on the RRT algorithm by introducing a goal-oriented sampling strategy for the target, which point increases the sampling rate for the target point, and when the random tree searches near the target point, the random tree has the probability to directly connect the target point. Huang et al. [31], by introducing a bias strategy, the path is reduced by bias near the obstacle when the random tree is expanded. Then, the path stretching strategy is introduced to simplify the original path and smooth it. The literature extracts high-precision 3D crack features and verifies [32] the effectiveness of the improvement by comparing the measurements with those of the traditional method. It provides a reliable basis for studying robot path planning in 3D environment.

To sum up, some problems of RRT need to be solved urgently, such as undesirable random expansion paths and time-consuming acquisition paths. There are also many solutions to the problem of slow random tree expansion, which can guide the direction of random tree expansion, try to make the step size and iteration speed more suitable for the map, which can accelerate the expansion of random tree. There are many tools to optimize the path, Zhang et al. [33] proposed a tracking control method combined with the actual operation of the robot to map the generated nodes into Bessel curve points for path smoothing. B-spline, Bessel curve and trigonometric methods have been used to smooth the paths to make them more compatible with robots in real life applications.

2.1 Basic RRT Algorithm

The RRT algorithm relies on a sampling-based path planning strategy. The specific implementation is shown as follows: First, the starting point serves as the root node and is incorporated into the RRT. Then, a random point is generated and randomly sampled in the configuration space, and a new node closest to the configuration space is found as an extension node in the RRT. Check if the extended node crashes with obstacles or if the generated node is in an obstacle by collision detection. If yes, the node is discarded and an extension node is regenerated, verify if the extension node intersects with any obstacles by collision detection, and if there is no collision, add the node to the random tree. Finally, check whether the extended node is tied to the goal point or not, if the generated random point is objected to the target point, then the algorithm is terminated, otherwise, continue with the previous step. The principle of the RRT algorithm is shown in Fig. 1.

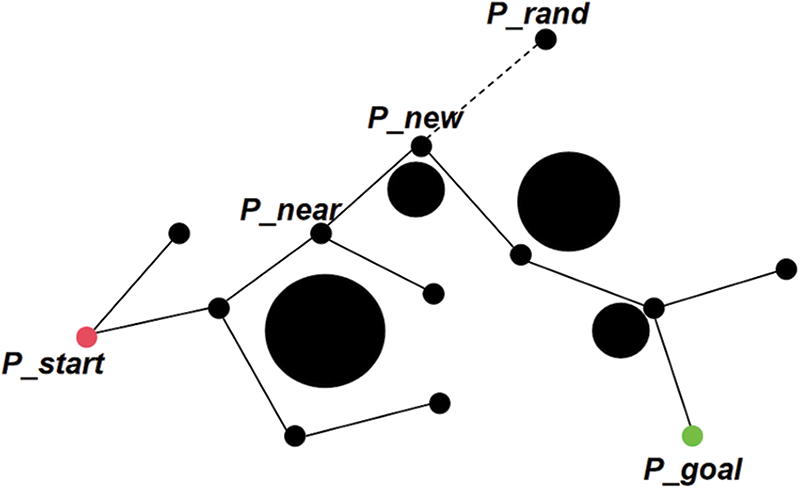
Figure 1: Schematic diagram of RRT expansion

It can be seen from Fig. 1 that the starting point is P_start, the endpoint is P_goal, and the obstacle in the middle is an obstacle. A node P_rand is randomly generated in the map, and a point P_nearest nearest P_rand is found among the known nodes, and two points P_nearest and P_rand are connected. According to the set step E, a new node with step E in the direction from P_nearest to P_rand is detected. If there is, then name this point P_new. If two points, P_nearest and P_rand, are connected and the intermediate point does not pass the collision detection, the P_rand point is discarded, and the point is searched again. After finding the P_new point, add the node to the tree. After several searches, an RRT tree is obtained. In the last search, if the distance between the newly generated node P_new and the end point P_goal is found to be less than a certain extreme value, the search is stopped, and P_new is directly connected to the endpoint P_goal to generate a feasible path.

Therefore, to solve this issue, this article improves the traditional RRT algorithm to obtain a shorter, smoother, and more advantageous path for the robot’s motion.

2.2 Basic RRT* Algorithm

The primary difference between the RRT* algorithm and the RRT algorithm is the introduction of the reconnecting parent node strategy, as can be seen in Fig. 2a, the cost required for each node to get to the next node, expanding a new node, Qnew, to form a circle, and all nodes within the circle can be used as the parent nodes of Qnew. It can be seen that the minimum parent node cost of Qnew is 3. Connecting this point, the path after reconnecting the parent nodes is shown in Fig. 2b.

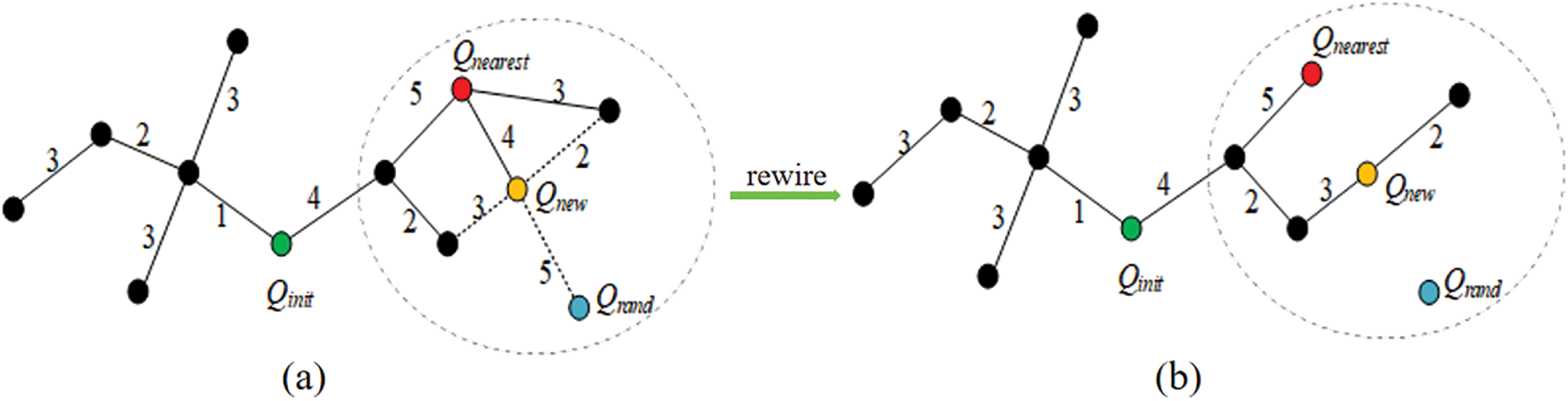
Figure 2: RRT* rewire parent node strategy

3  Method

3.1 Feedback Bias Sampling Strategy

Using feedback bias sampling, the random tree is guaranteed to return an angle information after expanding to an obstacle, and the angle information affects the expansion of the next node of the random tree. The feedback bias sampling strategy can significantly enhance the performance of the algorithm by dynamically adjusting the sampling probability based on feedback. During the execution of the algorithm, feedback is collected on the validity, quality and density of the sampling points. New paths can be explored by shifting the sampling focus to unsearched regions or regions around existing paths. If a region has a high density of sampling points but no optimized paths are found, then that local minimum region is sampled less, thus reducing the frequency of exploration. The specific impacts include: (1) Improving Sample Efficiency: By adjusting the sampling probability through feedback signals, the algorithm becomes more likely to select samples that have previously generated high feedback. This enhances the utilization efficiency of samples. (2) Reducing Invalid Samples: The strategy reduces the number of samples with low feedback, preventing the waste of computational resources on invalid or sub-optimal samples. (3) Accelerating Learning of High-Quality Strategies: Biased sampling allows the algorithm to identify and learn high-quality strategies or model parameters more quickly, thus speeding up the convergence of the training process. (4) Dynamic Adaptation: The sampling probability is dynamically adjusted through feedback signals during different training phases, making the algorithm more adaptable. This accelerates overall convergence and increases stability in complex or changing environments. The specific principle is shown in Fig. 3.

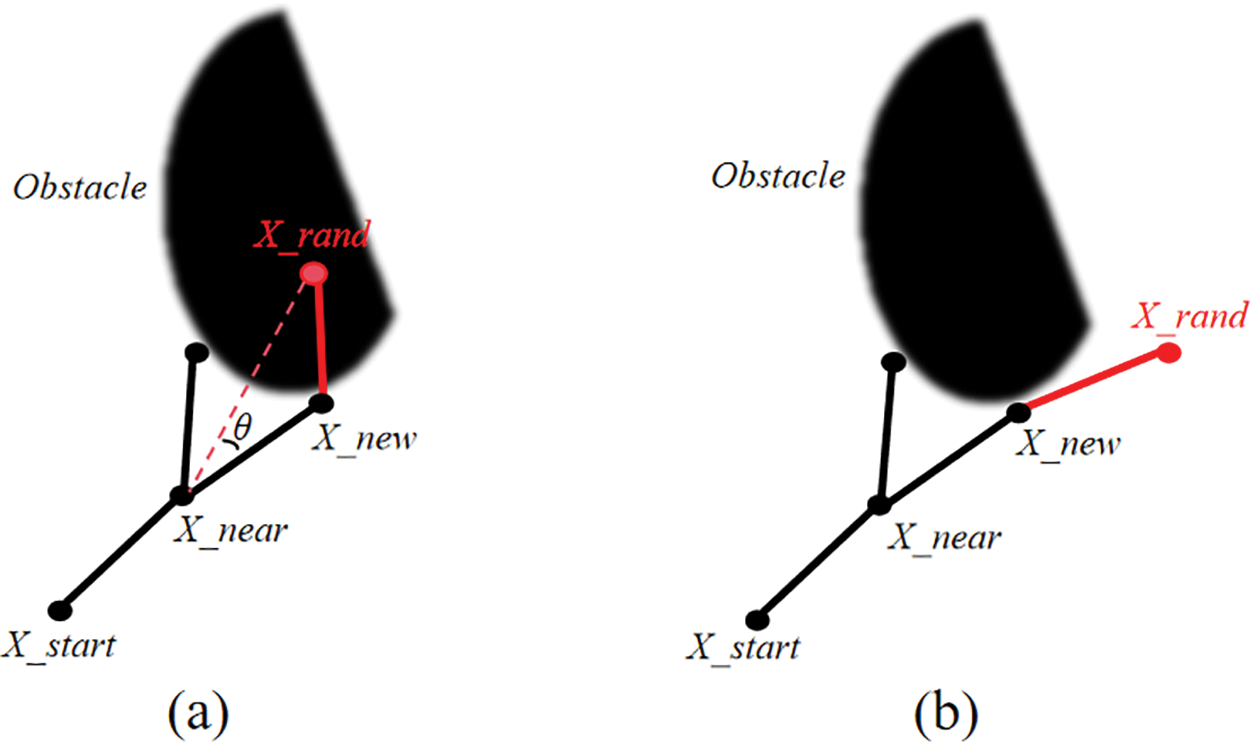
Figure 3: Feedback bias sampling strategy. (a) shows a randomized tree expansion hitting an obstacle. (b) shows the node choosing the direction of expansion after receiving feedback (red dots)

As shown in Fig. 3a, the starting point is X_start, when the node X_near expands a child node X_new, the node X_new generates a random point X_rand, if the random point X_rand is not collision-detected and the node is temporarily within the obstacle, X_new obtains the information of the random point X_rand within the obstacle to form the angle θ, the node X_new discards the extended area to the left and right of the angle θ and re-selects the extended area. This step is repeated until the X_rand extension is not within the obstacle, as shown in Fig. 3b, and the random tree from the X_new node is re-selected with an X_rand.

The specific θ angle is calculated as shown in Eq. (1). Where the coordinates of X_new are assumed to be (x_new,y_new) and the coordinates of Y_rand are assumed to be (x_rand,y_rand).

θ=arctan(y_rand−y_new,x_rand−x_new)(1)

An offset value will be generated randomly when the root node encounters obstacles when searching for random points, as shown in Eq. (2). To ensure the search area, the offset value should not be too large.

B=Rand(−0.1,0.01)(2)

In summary, compared with the traditional random sampling, the feedback bias sampling can avoid the expansion of the random tree for some obstacle areas due to the introduction of angle information, which not only reduces the time of obtaining the path, but also reduces the number of expansion nodes.

3.2 Principle of Restricted Area

To tackle this problem, this paper proposes a search method to improve the search scope of the RRT algorithm across the entire graph area. The design idea of the algorithm is: To take the line connecting a Fast search for the starting point of a randomized tree and the endpoint of the random tree search as the horizontal axis of the coordinate axis and expand a certain angle to the simultaneous left and right with the horizontal axis as the center, which can be changed with the complexity of the environment, and the angle information should be adjusted a little bit larger in the complex environment to avoid getting into a loop in the narrow space. The search for effective paths is carried out within the designed angle, thus discarding some unnecessary search space. This significantly enhances the algorithm’s efficiency. Limiting the search area of the algorithm, as illustrated in Fig. 4.

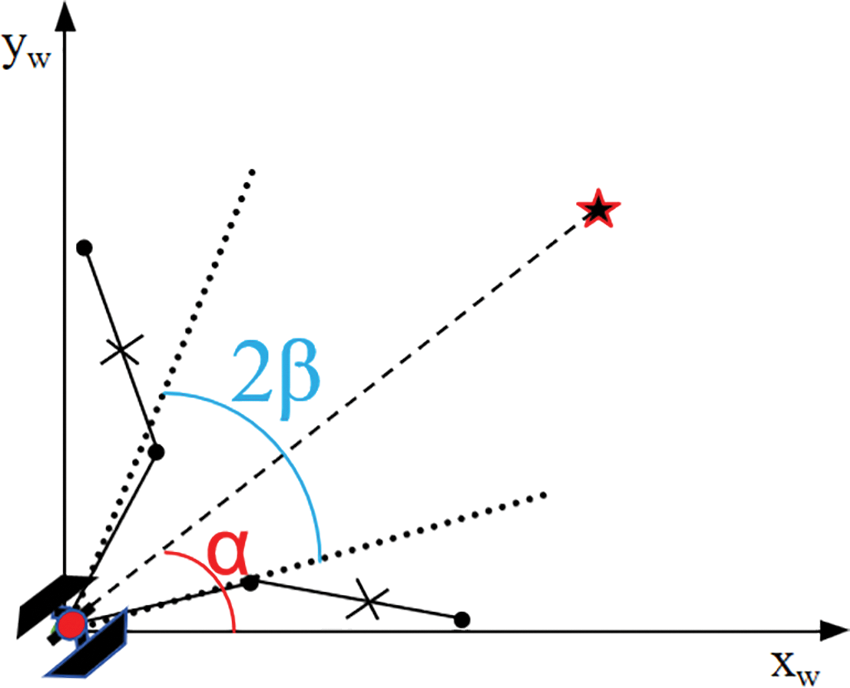
Figure 4: Restricted search area strategy

Enhances the RRT algorithm’s exploration range. Let’s assume the coordinates of the starting point for the random tree search are (x1, y1) and the coordinates of the endpoint of the random tree search are (x2, y2). The distance L between the start and end points is calculated according to Eq. (3), and L is limited between L and the set step size E according to Eq. (4).

L=((x2−x1)2+(y2−y1)2)(3)

L=min(L,E)(4)

From the graph it can be observe that the red ray represents the horizontal coordinate axis, as shown in Eq. (5), the information about the angle between the line segment connecting the start and end points and the horizontal coordinate axis is α.

α=actan2((y2−y1),(x2−x1))(5)

The θ angle is set according to the actual situation of the map. In this paper, the θ angle is set to π/6, which needs to be calculated because it needs to be ensured that each expansion has to calculate the angle limited by the line connecting the expanded random tree node and the root node must be ensured to be at the preset θ. When the angle formed by the random node and the root node is larger than θ, the angle is restricted to be θ angle; when the angle is smaller than −θ angle, the angle is restricted to be −θ angle; and when the angle information is in the range between the −θ and θ angles. It is guaranteed that the search direction angle is also for θ angle. The specific θ angle information is shown in Eq. (6).

β={π6,β>π6π6,−π6≤β≤π6π6,β<−π6(6)

According to this improvement, the search range of the map can be greatly reduced, which is a major advantage in scenes with a lot of blank areas. The use of a dynamic step-size strategy allows the sampling step to adjust the search step with dense or sparse obstacles. Although there is a limitation on the sampling area, there is still the problem of low sampling efficiency, which can be solved by randomized biased sampling.

3.3 Reverse Optimization Strategy

After using the angle restriction, the searched path still has many inflection points and redundant nodes, next the initial path is reverse optimized using the reverse optimization strategy to make the path shorter. First, path traversal and evaluation are the core components of the inverse optimization strategy. The algorithm begins at the end of the path and traverses each point towards the starting point. Each traversed path point undergoes a detailed evaluation based on criteria such as its impact on the overall path length and its effect on obstacle avoidance. Second, identifying redundant points is a crucial step in path simplification. Through evaluation, points that serve a redundant role in the path can be identified. These redundant points are typically those that, if removed, do not significantly impact the path’s effectiveness. After identifying these points, the algorithm determines whether they should be removed or merged with neighboring points. Finally, during the process of removing or merging redundant points, the algorithm performs a series of operations to ensure the path’s connectivity and validity. This involves recalculating connections between remaining points to maintain a continuous and feasible path that adheres to all planning constraints. The specific principle is shown in Fig. 5.

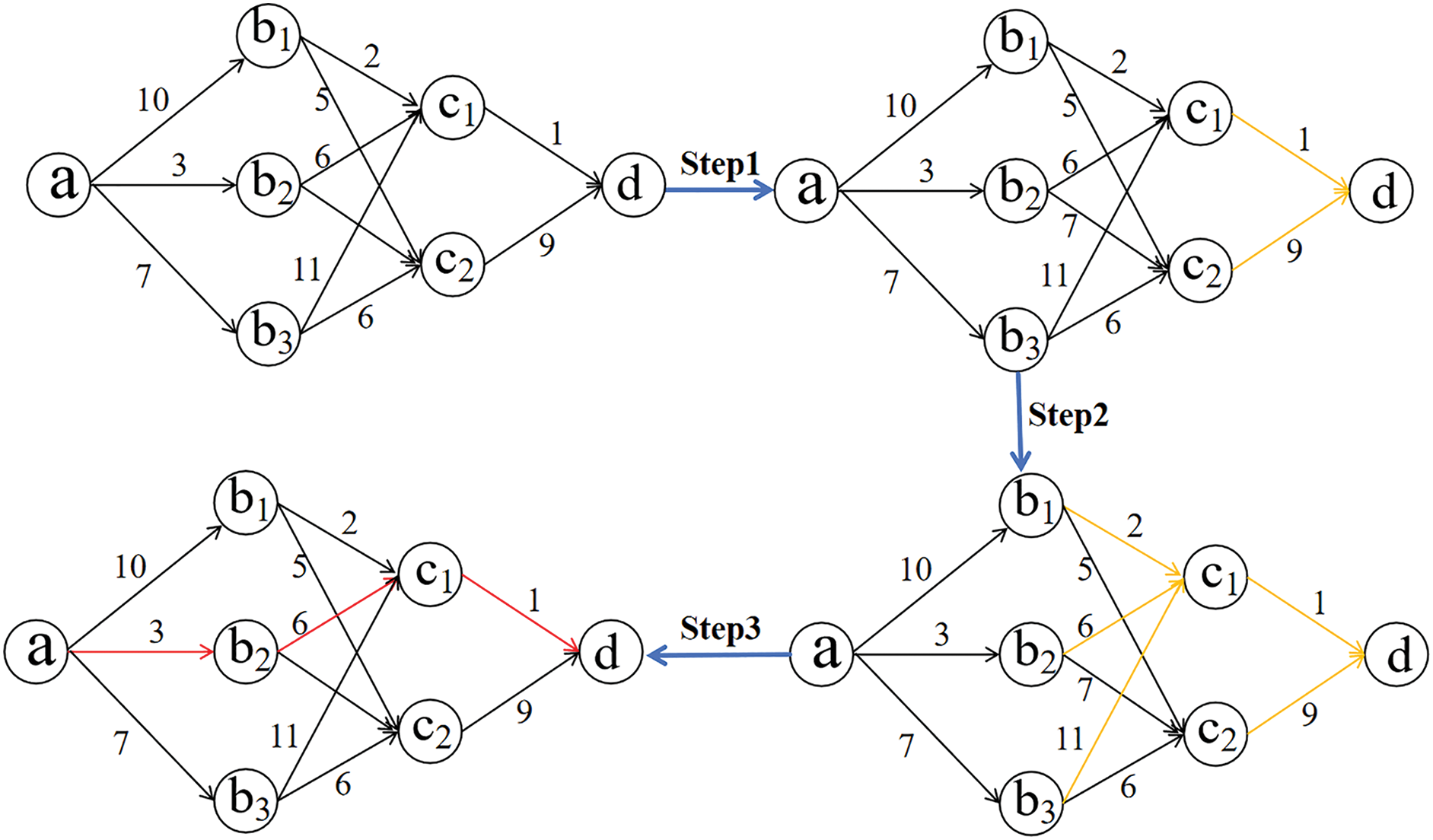
Figure 5: Steps in the realization of reverse optimization

The principle of the algorithm is that the points in each stage must find all the paths to reach the end point, and the figure shows that the existing path map can be split into three steps. The third stage goes from point d to point c, is indicated by the lower right corner 3 of F in Eqs. (7) and (8), which expresses the minimum distance for c1 and c2 to reach the end point d, respectively.

F3(c1)=1(7)

F3(c2)=9(8)

The second stage is all the paths from point b to point c, of which there are 6 paths in total. Among them, Eq. (9) delegates the cost of the path from point b1 to the end point via c1 and c2, respectively, the shortest path is from point b1 to point c1 to point d, and the minimum cost is 3.

F2(b1)=min{h(b1,c1)+F3(c1)h(b1,c2)+F3(c2)}=3(9)

Eq. (10) delegates the cost of the path from point b2 to the end point via c1 and c2, respectively, and the shortest path is from point b2 to point c1 to point d, with a minimum cost of 7. Eq. (11) is the same, and the minimum cost from point b3 is 12.

F2(b2)=min{h(b2,c1)+F3(c1)h(b2,c2)+F3(c2)}=7(10)

F2(b3)=min{h(b3,c1)+F3(c1)h(b3,c2)+F3(c2)}=12(11)

The first stage is from the starting point a to b to find the path a total of three feasible paths, after the calculation can be seen from the point a through the point b2 through the c1 and finally arrive at the end point d is the shortest path, it can be noted that the minimum cost of this map is 10.

F1(a)=min{h(a,b1)+F2(b1)h(a,b2)+F2(b2)h(a,b3)+F2(b3)}=10(12)

The use of the inverse optimization strategy in the improved RRT algorithm, which further reduces the path length after obtaining the initial path, results in a significant reduction in cost compared to the initial path.

3.4 Auxiliary Point Optimization for Cubic Bessel Curves

After the redundant points are removed from the path by inverse optimization, there are still some inflection points in the path, which is not optimized for the smooth movement of the robot in the actual movement process. In order to solve this problem, the sampling optimized cubic Bessel curves are smoothed for the path. B-spline curves require more control points and node vectors, along with complex calculations, consuming additional storage and computational resources. In contrast, Bezier curves, defined by fewer control points, offer intuitive shape adjustments and are computationally efficient for real-time applications. Polynomial fitting curves suit simpler, smoother datasets but struggle with complex shapes or those with many inflection points. Bezier curves can effectively describe complex shapes by adding control points or splicing segments, making them versatile for tasks like path planning. Therefore, in this paper, we take Bessel curves to smooth the paths. Under the premise of avoiding obstacles, the optimized Bessel curve can balance the curvature of the path in the path generation process. By adjusting the position and number of auxiliary points, the curvature of the path at the bend can be effectively controlled to avoid unnecessary bends. In dynamic environments, the position and movement of obstacles may affect the feasibility of the path. The optimized Bessel curve can adjust the path in time to cope with the changes in obstacle positions through the intelligent placement of auxiliary points, thus improving the robustness and reliability of path planning. The specific schematic diagram is shown in Fig. 6.

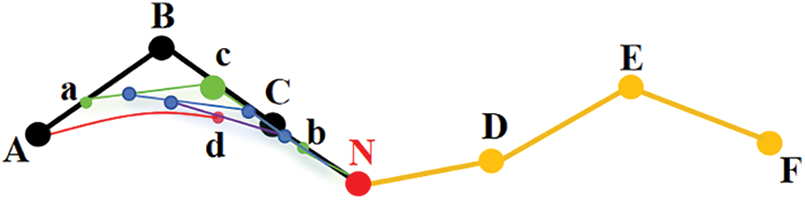
Figure 6: Auxiliary point optimization for cubic Bessel curves

The cubic Bezier curve needs four points, which are represented as A, B, C and point N in the figure, and the starting point of the next section of the cubic Bezier curve should coincide with the end point of the previous section of the Bezier curve, and the selection of auxiliary points is one of the most important parts of the optimization of the cubic Bezier curve, and the selection of auxiliary points should satisfy the following conditions: [I] The point N should be at the same level with the straight line BC; [II] The point N should not be in between the line segments BC again; [III] The distance of the point N and the point C meets the Eq. (13). [IV] The distance of the point N and the point C is smaller than or equal to the distance between the BC, which meets the Eq. (14).

||dCN||≤||dND||(13)

dCN=n×dBC,n∈(0,1](14)

The formula for the Bessel curve is shown below:

P(t)=∑i=0nn!(n−1)!×i!(1−t)n−i×ti×π,t∈[0,1](15)

The cubic Bezier curve is chosen in the paper, with n equal to 3.

3.5 Auxiliary Point Optimization for Cubic Bessel Curves Overall

To ensure that the improved algorithm has a higher, while keeping the practicality, and to ensure that a smoother path can be obtained after solving the problem of solving the slower random tree search, this paper proposes an improved FS-RRT based on the RRT algorithm, and its overall improvement module is shown in Fig. 7. First of all, for the random tree random sampling there are a lot of uncertainty and slow problems, the article will replace the random sampling, the use of feedback bias sampling strategy, this sampling strategy can be better for the obstacle information to capture, to avoid other nodes for the obstacle to re-detect. Secondly, to improve the sampling efficiency of the random tree, the expansion mechanism of the random tree is improved, and each expansion node is restricted to expand within the effective region to avoid searching for redundant space. Then, in order to achieve shorter paths, the initial paths obtained are preliminarily optimized using the inverse optimization strategy to remove useless, redundant nodes. Finally, to satisfy the smooth movement of the robot in practical applications, the simplified path is smoothed using an optimized cubic Bessel curve, and the increase of auxiliary points can avoid the problem of the path crossing the obstacles when optimizing the path using the Bessel curve.

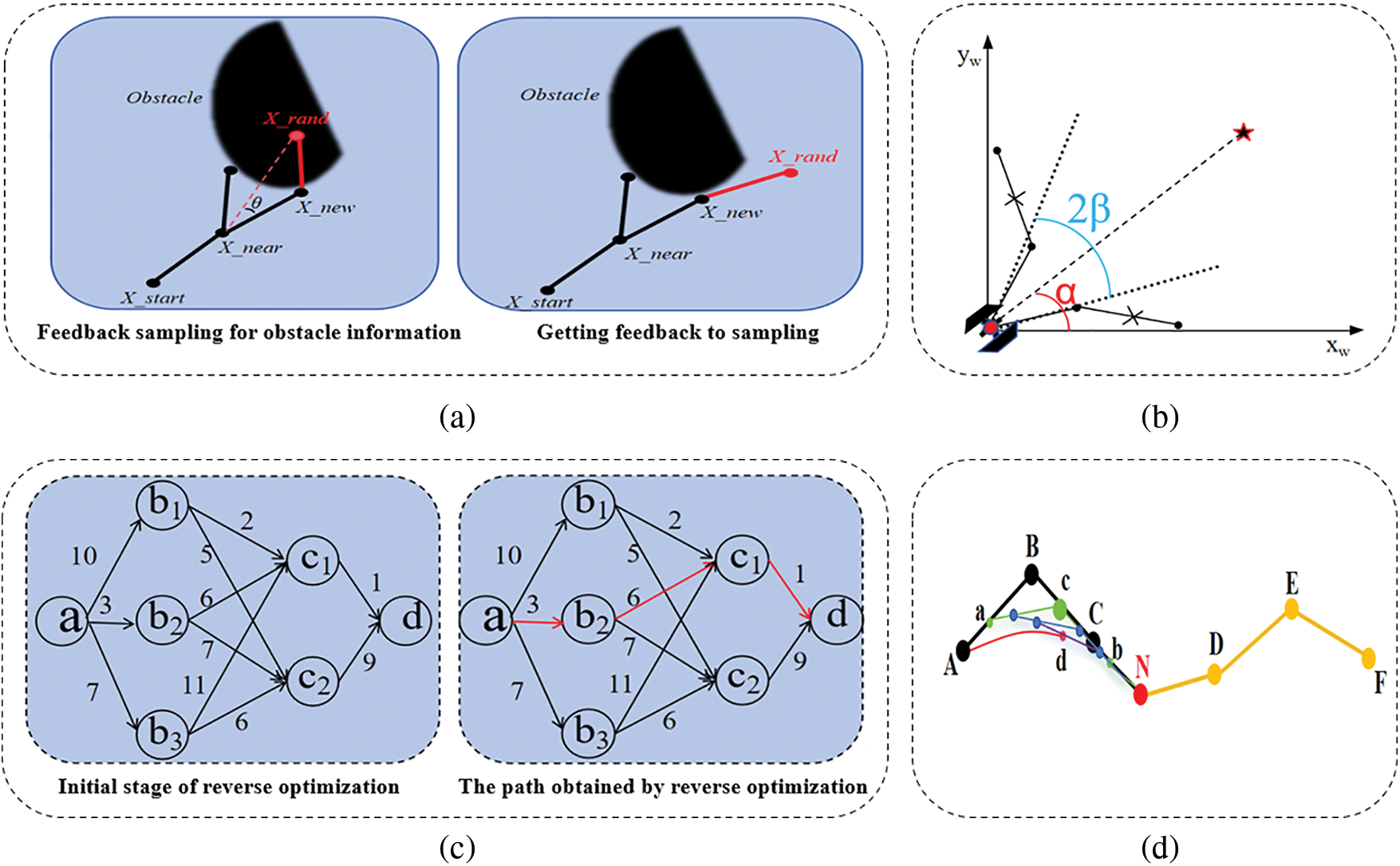
Figure 7: Schematic diagram of the four parts of the FS-RRT improvement. (a) Feedback bias sampling strategy. (b) Principle of restricted area. (c) Reverse optimization strategy. (d) Auxiliary point optimization for cubic Bessel curves

4  Experiments

4.1 Experimental Conditions

4.1.1 Experimental Environments Set

To confirm the effectiveness of the improved algorithm in this paper, the 12th generation Intel(R) Core (TM) i5-12500H 2.50 GHz hardware platform is used in this paper, running a 64-bit operating system and 16 GB RAM in the same environment. The software platform is MATLAB2018b programming platform. The experiments were conducted with green color as the random tree for searching and black color as the path for finding. Four algorithms, RRT, RRT*, Extend-RRT and FS-RRT, are selected for experimental comparison in the same environment. In this paper, RRT, RRT*, and Extend-RRT algorithms are chosen for comparative experiments due to their distinct strengths: the rapid exploration capability of RRT, the path optimization proficiency of RRT*, and the adaptability and real-time performance of Extend-RRT. By selecting these algorithms as benchmarks, we can comprehensively evaluate the performance and applicability of the improved algorithms across various scenarios.

Due to FS-RRT introducing a dynamic step-size strategy, the step-size of the FS-RRT algorithm is not fixed at 2 m but varies flexibly between 1.5 and 2.5, which speeds up the search of the randomized tree in the space with fewer obstacles and enables a more detailed search of the path in dense obstacle environments. Three different maps were used in the experiments to ensure that the algorithm is comparable to other comparative algorithms in both complex and austere environments. To avoid chance, the data obtained from the experiments are averaged over 100 experiments.

4.1.2 Experimental Data Set

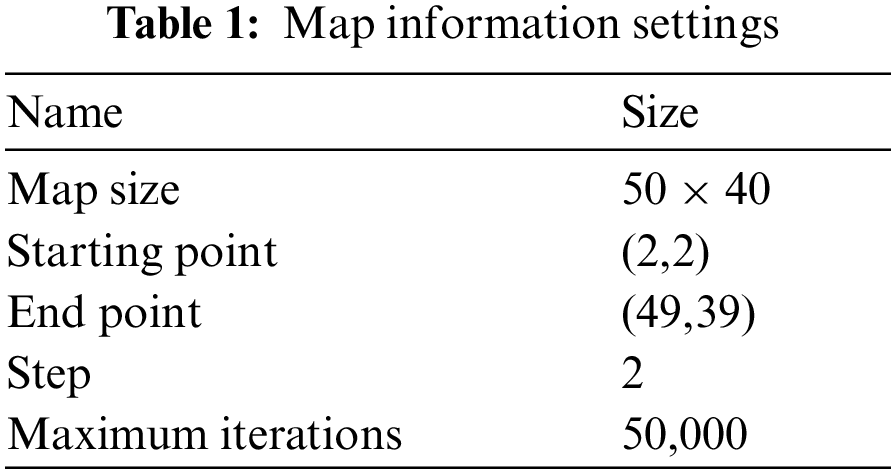
The Map information settings for this study is shown in Table 1.

4.2 Three Types of Complex Map Information

Build three different maps of varying complexity as shown in Fig. 8 below. From left to right are Map 1, Map 2 and Map 3.

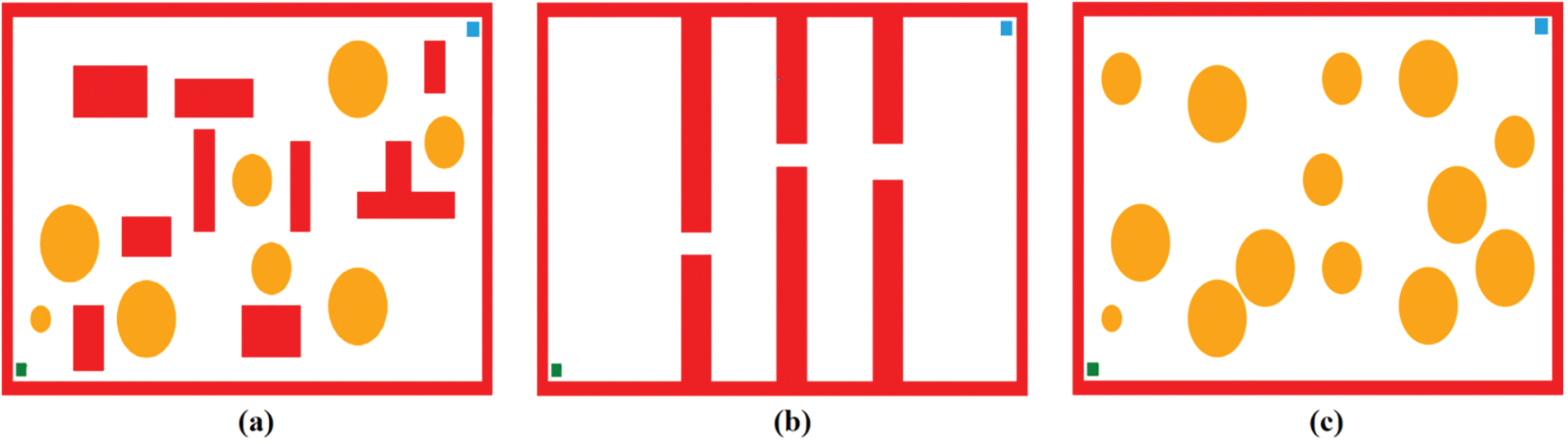
Figure 8: Different environmental map models: (a) Map 1; (b) Map 2; (c) Map 3. In three maps, the starting point is represented by a green square, and the goal point is represented by a blue square

4.3 Experimental Results

4.3.1 Multi-Obstacle Environment Testing

To verify the improved algorithm’s performance, the RRT, RRT*, and Extend-RRT algorithms are selected as comparisons, and experiments are carried out in the same environment. To verify the reliability of FS-RRT and other algorithms in an environment with many obstacles, more obstacles are set up in Fig. 9, and 100 groups of experiments are conducted to avoid the chance of the algorithm. The summary of experimental data is shown in Table 2. In Fig. 9, a black curve is used to represent the path that was eventually found, a red line is used to represent the extended branches of the random tree and a cyan is used to represent the nodes of each extension. The experimental data results are shown in Table 2.

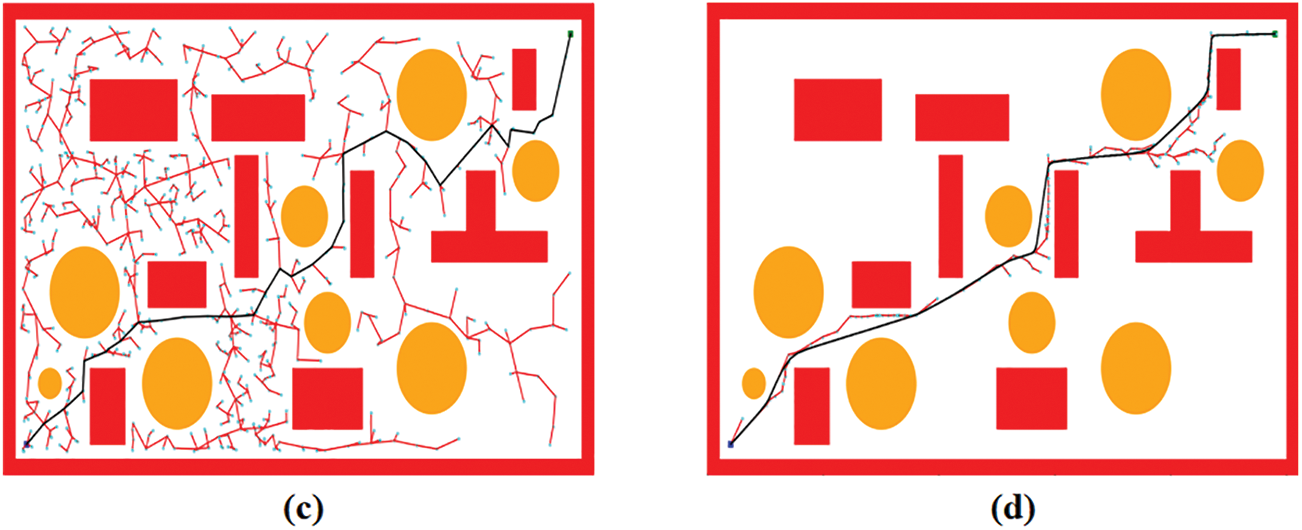
Figure 9: Performance of the four algorithms in the environment with many obstacles. The red line represents the expansion of the random tree, the cyan dot represents the expansion node, and the black line represents the final path to be found. (a) RRT. (b) RRT*. (c) Extend-RRT. (d) FS-RRT

By comparing the four planning results in Fig. 9, it can be concluded that FS-RRT has the best performance in searching paths in an environment with more obstacles. In addition, Fig. 9d shows the sampling point distribution of the improved algorithm in the complex obstacle environment, which is because the feedback bias sampling strategy restricts the expansion direction of the random tree and leads the random tree to tend to grow towards the target point.

Table 2 shows that the planning success rate of the four algorithms in this map reaches 100%, and the cost is shortened by 17.9% compared with RRT*. In terms of node expansion, the replacement random sampling strategy makes the expansion nodes far less than the other three algorithms.

4.3.2 Narrow Environment Testing

A relatively narrow obstacle environment is set up in Map 2 to verify the reliability as well as the performance of the FS-RRT algorithm in a relatively narrow environment. Four algorithms are used to conduct 100 experiments in the same environment, respectively, and the final experimental results are taken as the average of the results of 100 experiments, the specific experimental results are shown in Table 3.

Fig. 10 shows the experimental results of the four algorithms in the narrow obstacle environment, from the experimental results of the graph can be seen, RRT, RRT* and Extend-RRT three algorithms for the left blank area for a large number of redundant search, FS-RRT algorithm because of the introduction of the area restriction strategy and feedback sampling strategy for the obstacles to be able to have the information storage and the search direction is always towards the target point direction greatly saves the search time and improves the efficiency of path acquisition.

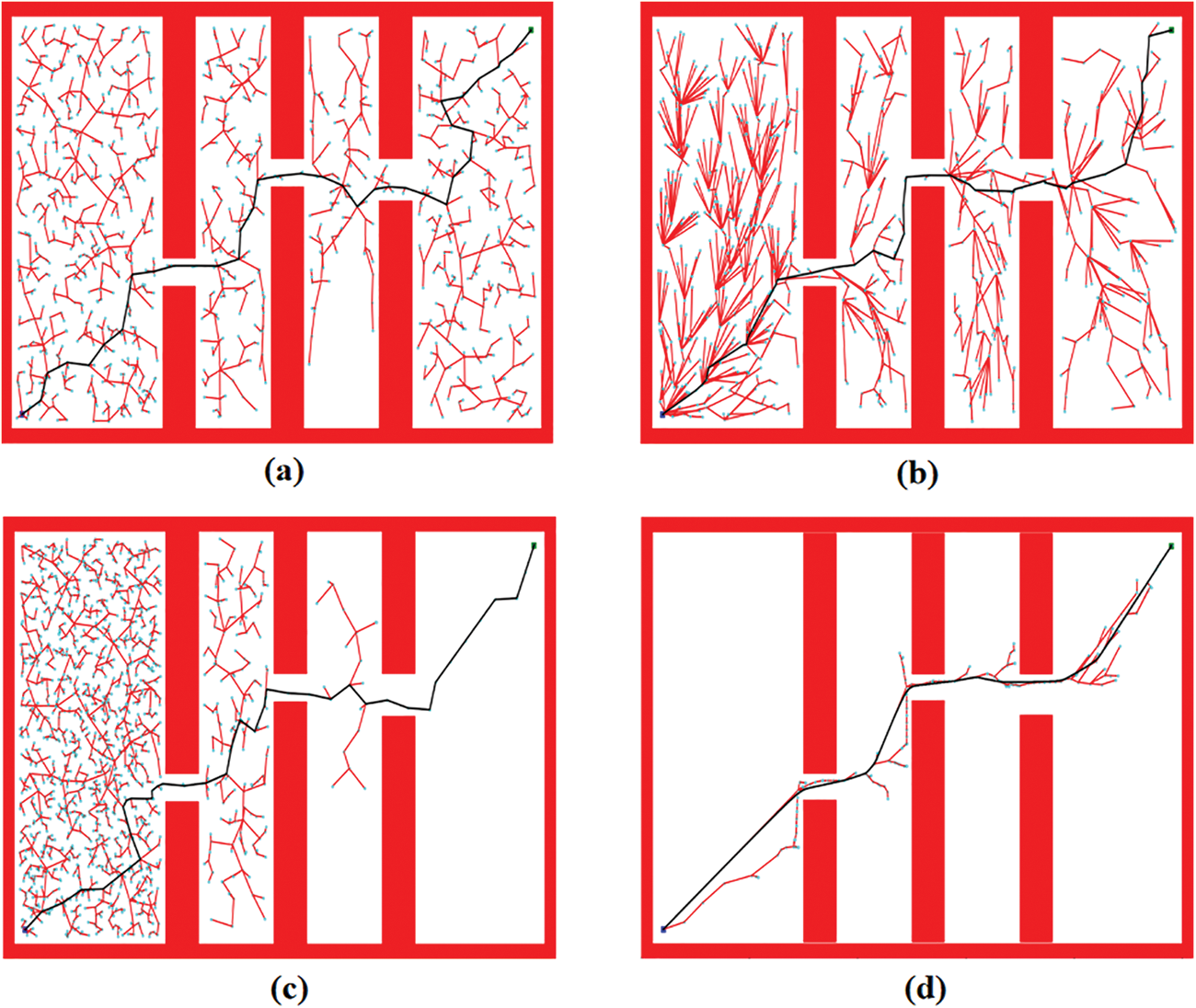
Figure 10: Performance of the four algorithms in the narrow environment. The red line represents the expansion of the random tree, the cyan dot represents the expansion node, and the black line represents the final path to be found. (a) RRT. (b) RRT*. (c) Extend-RRT. (d) FS-RRT

From the data in Table 3, it can be seen that the Extend-RRT algorithm does not perform very well in Map 2, with a planning failure rate of 2%, while the other three algorithms have a success rate of 100% when conducting 100 experiments. The Extend-RRT algorithm planning consumes the longest time in terms of path acquisition time. The FS-RRT algorithm has a mean time reduction of about 42% compared to the RRT* algorithm. With respect to path costs, the FS-RRT algorithm reduces 12.19%, 17.10%, and 15.93% when compared to the RRT*, RRT, and Extend-RRT algorithms, respectively. From the average path search nodes, the FS-RRT algorithm has the highest efficiency in searching the least number of nodes.

4.3.3 Easy Environment Testing

In order to test that the algorithms can perform well in most environments, a simple environment of Map 3 is built for performance testing, and 100 experimental comparisons are carried out using four algorithms in the same environment, and the experimental results are shown in Table 4.

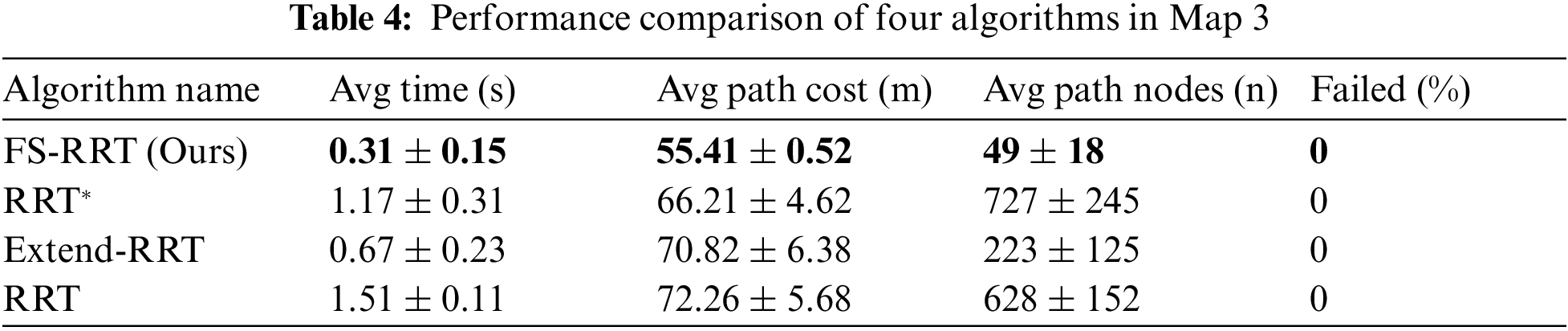
In simple environments, in terms of path acquisition time, all four algorithms successfully acquire paths in a very short time. FS-RRT has a very significant improvement in path cost compared to the other three algorithms, and there is not much difference in path length between Extend-RRT and RRT algorithms. The FS-RRT is 16.3% shorter compared to the RRT* algorithm. The improved algorithm and have 21.7% and 23.3% shorter path lengths compared to the RRT and Extend-RRT. FS-RRT performs the best with the least number of nodes around 50, and RRT* and RRT have more node extensions. Fig. 11 shows the experimental results of the four algorithms in the simple obstacle environment,

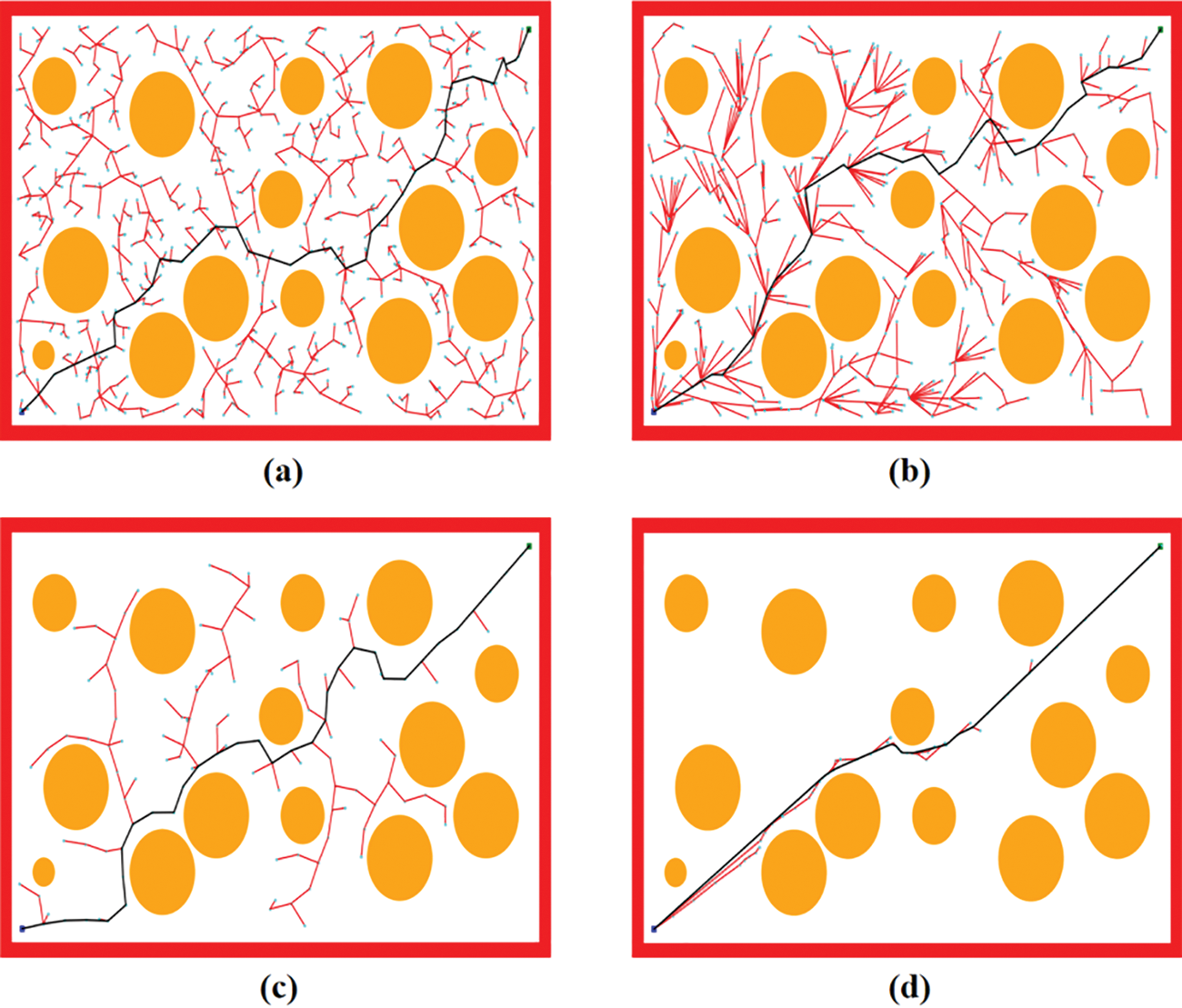
Figure 11: Performance of the four algorithms in the easy environment. The red line represents the expansion of the random tree, the cyan dot represents the expansion node, and the black line represents the final path to be found. (a) RRT. (b) RRT*. (c) Extend-RRT. (d) FS-RRT

From Fig. 12a, it can be seen that in relatively complex environments, including circular and rectangular obstacles in Map 1, FS-RRT converges faster, and although the RRT algorithm has a longer initial path length, the path cost is relatively shorter compared to the RRT* and Extend-RRT algorithms after convergence. From Fig. 12b, it can be seen that the Extend-RRT algorithm is still changing after the other three algorithms’ path costs have levelled off. It can be seen that the Extend-RRT algorithm does not perform well in narrow obstacle environments, and the FS-RRT algorithm converges quickly at 0.63. From Fig. 12c, the four algorithms converge relatively fast in simple environments, but the path length of the FS-RRT algorithm stabilizes at about 55 m.

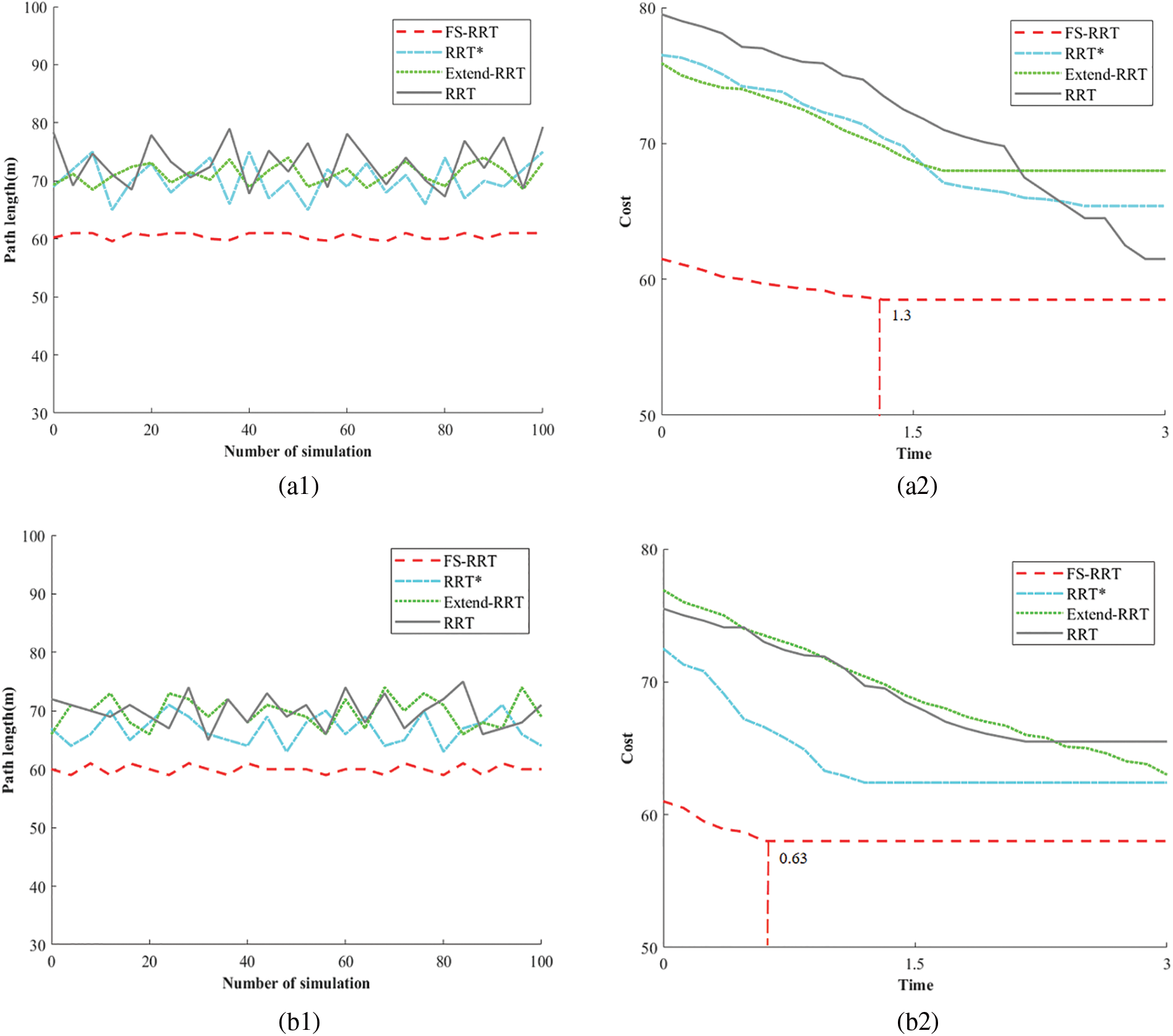
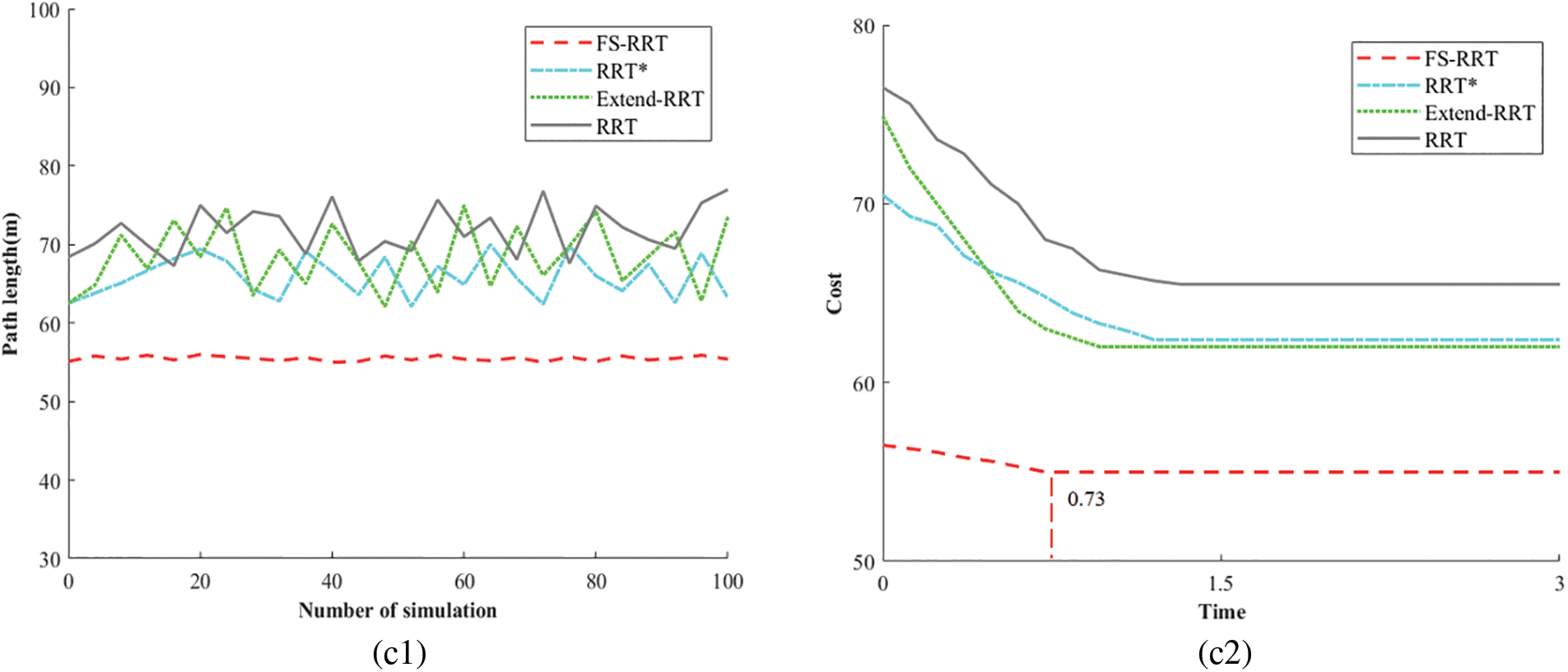
Figure 12: Comparison of data from three maps. (a1) Trends in numbers of simulation and path length in Map 1. (a2) Time and path cost trends in Map 1. (b1) Trends in numbers of simulation and path length in Map 1. (b2) Time and path cost trends in Map 1. (c1) Trends in numbers of simulation and path length in Map 1. (c2) Time and path cost trends in Map 1

4.3.4 Dynamic Environment Testing

To test that the improved algorithms do not only have better performance in static environments, an additional dynamic map is set up to test the performance of the FS-RRT algorithm in dynamic environments in comparison with the other three algorithms. The experimental results are shown in Table 5. Fig. 13 shows the experimental results of the four algorithms in the dynamic obstacle environment.

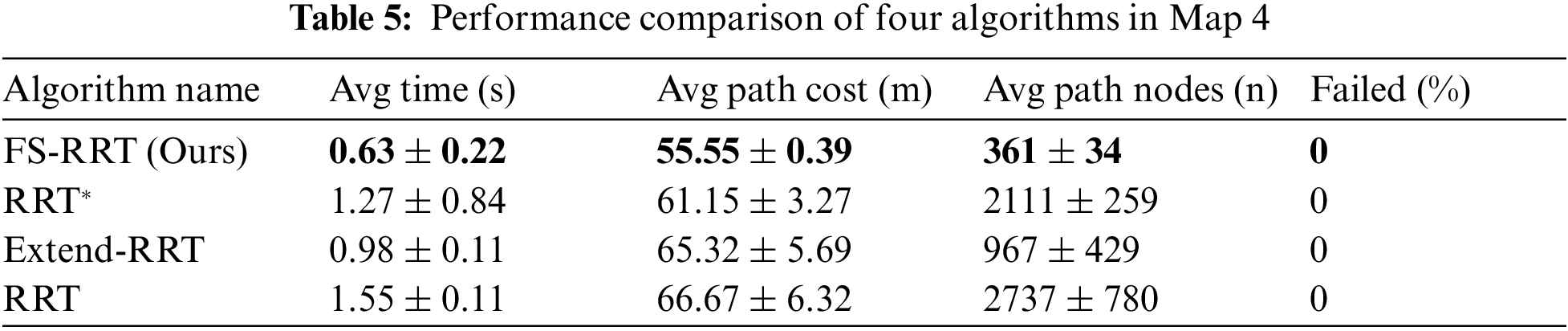
Figure 13: Performance of the four algorithms in the easy environment. The red line represents the expansion of the random tree, the cyan dot represents the expansion node, and the black line represents the final path to be found. (a) RRT. (b) RRT*. (c) Extend-RRT. (d) FS-RRT

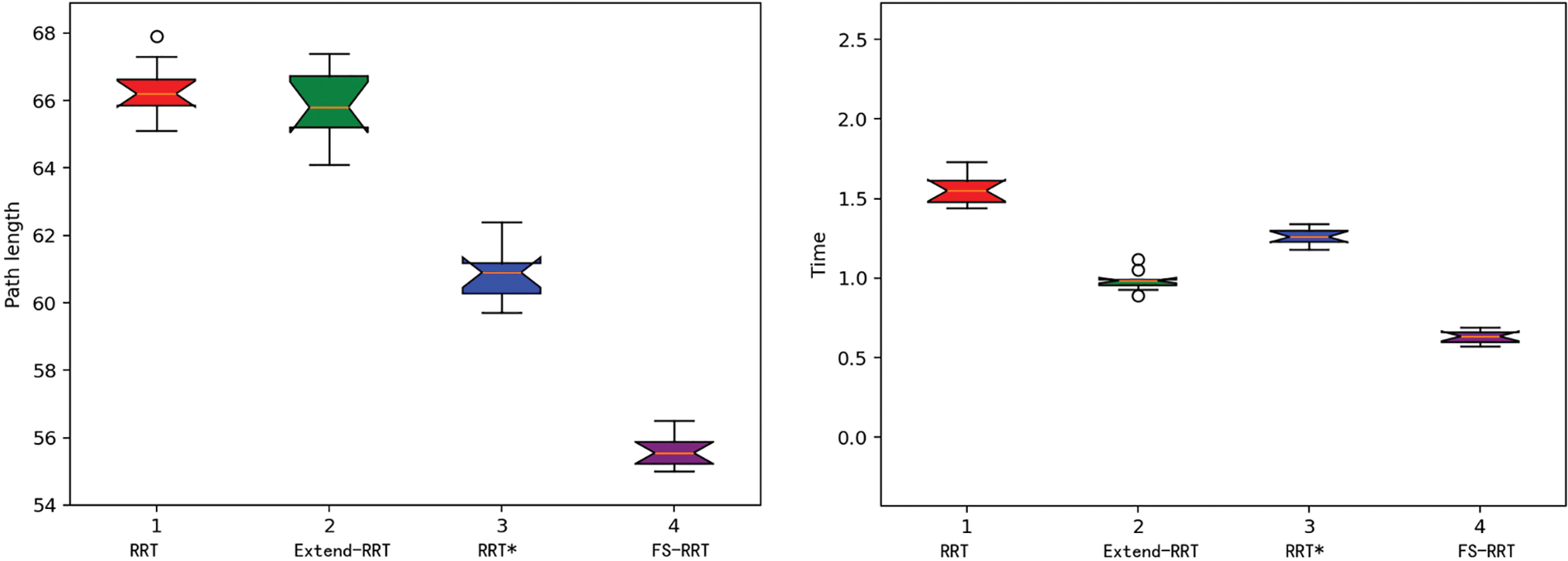
Figure 14: Comparison of data from Map 4

From the data in Table 4, it can be seen that all four algorithms have 100% success rate in path planning in dynamic environment. The RRT algorithm takes the longest time to acquire the path and spends the largest path cost. In terms of path length, FS-RRT is 9.15% and 14.95% shorter than RRT* and Extend-RRT algorithms, respectively. FS-RRT also spends the least number of nodes searching for each path acquisition, which saves a lot of searching time. The FS-RRT algorithm reduces 50.39% and 35.71% in terms of time spent compared to RRT* and Extend-RRT, respectively.

As can be seen in Fig. 14, on the left is a comparison of the performance of the four algorithms in terms of path length after 100 experiments. It can be seen that Extend-RRT is the four algorithms with the largest variation in path length, the improved algorithm is almost around 55 in terms of path length, and the RRT algorithm has the largest variation. The right-hand side of Fig. 14 shows a comparison of the performance of the four algorithms in terms of time. It can be seen that Extend-RRT acquires the path faster than RRT and RRT*, but the time is sometimes spent a lot, and FS-RRT acquires the path in almost the same time around 0.6 s.

5  Conclusion

A restricted search algorithm FS-RRT is proposed to improve the extension strategy of the RRT algorithm. Firstly, to address the problem of inefficient planning due to random sampling of RRT, it is proposed to use feedback biased sampling to guide the growth direction of random trees. Second, for the direction of random number expansion toward the surroundings, restrict the node expansion of the random tree so that the random tree expands toward the direction of the target point. Then, for the initial path obtained with many sharp corners, the sampling inverse optimization strategy is used to simplify the path initially. Finally, sampling auxiliary points optimizes the cubic Bessel curve to smooth the path and achieve smooth operation in practice. Experiments show that FS-RRT performs better than mainstream algorithms. Although the overall performance of FS-RRT is better, the performance in the dynamic environment has yet to be discovered, which will be the main work of the following research. FS-RRT is primarily designed for static environments and may struggle to adapt to dynamic changes. To address this limitation, integrating a real-time path optimization mechanism can dynamically adjust paths based on environmental fluctuations. As the search space expands, the enhanced algorithm may necessitate more iterations and optimization steps to achieve high-quality paths. However, it maintains superiority over mainstream algorithms in terms of path acquisition time and length. In increasingly complex environments with more obstacles or dynamic changes, FS-RRT requires additional computational resources to ensure path effectiveness and quality. This may involve incorporating more sophisticated path optimization strategies into the algorithm design or increasing the density of sampling points to manage the complexities effectively.

Acknowledgement: The authors gratefully acknowledge the support of Shaanxi Province’s Key Research and Development Plan.

Funding Statement: Funding for this research was provided by Shaanxi Province’s Key Research and Development Plan (No. 2022NY-087).

Author Contributions: The authors contributed to this paper as follows: study planning and design by Zihao Wang and Xiangkui Jiang; numerical map construction by Zihao Wang and Chao Dong; data analysis and interpretation by Zihao Wang and Xiangkui Jiang; and first draft writing by Zihao Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used and analyzed during this study are available from the corresponding authors upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. Liu, L. Zhang, S. K. Wang, T. W. Niu, Y. K. Xu and J. Cao, “Research on path planning of mobile robot based on DWA-IMP-A* algorithm,” Key Laborat. Intell. Control Decision Complex Syst., vol. 8, pp. 103–108, 2023. [Google Scholar]

2. Y. Y. Long et al., “Path planning method based on D* lite algorithm for unmanned surface vehicles in complex environments,” China Ocean Eng., vol. 35, pp. 372–383, 2021. doi: 10.1007/s13344-021-0034-z. [Google Scholar] [CrossRef]

3. X. Jia, C. Tang, X. Zhang, and J. Liu, “Research on dual robot collaboration method based on improved double ant colony algorithm,” Ind. Robot, vol. 51, no. 3, pp. 424–435, 2024. doi: 10.1108/IR-12-2023-0316. [Google Scholar] [CrossRef]

4. H. Wu et al., “Research on vehicle obstacle avoidance path planning based on APF-PSO,” Proc. Inst. Mech. Eng., vol. 237, no. 6, pp. 1391–1405, 2023. doi: 10.1177/09544070221088364. [Google Scholar] [CrossRef]

5. R. Mashayekhi, M. Y. I. Idris, M. H. Anisi, and I. Ahmedy, “Hybrid RRT: A semi-dual-tree RRT-based motion planner,” IEEE Access, vol. 8, pp. 18658–18668, 2020. doi: 10.1109/Access.6287639. [Google Scholar] [CrossRef]

6. Z. J. Hao, P. S. Guo, G. Wang, G. Peng, W. Ping and H. Peng, “Path planning of unmanned vehicles in narrow and long space based on improved RRT algorithm,” Glob. Position. Syst., vol. 4, pp. 81–90, 2023. [Google Scholar]

7. Z. Liang, W. Xin, and Z. J. Feng, “Many obstacles’ scenarios improved RRT path planning algorithm,” Comput. Eng. Design, vol. 44, pp. 1706–1713, 2023. [Google Scholar]

8. J. Braun, T. Brito, J. Lima, P. G. Costa, P. Costa and A. Y. Nakano, “A comparison of A* and RRT* algorithms with dynamic and real time constraint scenarios for mobile robots,” in Proc. 9th Int. Conf. Simulat. Model. Methodol. Technol. Appl., Prague, Czech Republic, Jul. 29–31, 2019, pp. 398–405. [Google Scholar]

9. X. Zhou, X. Wang, Z. Xie, J. Gao, F. Li and X. Gu, “A Collision-free path planning approach based on rule guided lazy-PRM with repulsion field for gantry welding robots,” Robot. Auton. Syst., vol. 174, 2024, Art. no. 104633. doi: 10.1016/j.robot.2024.104633. [Google Scholar] [CrossRef]

10. K. Shi, Z. Wu, B. Jiang, and H. R. Karimi, “Dynamic path planning of mobile robot based on improved simulated annealing algorithm,” J. Franklin Inst., vol. 360, no. 6, pp. 378–4398, 2023. [Google Scholar]

11. H. Wang, P. Zhang, and W. Wang, “Research on robot path planning based on simulated annealing algorithm,” J. Artif. Intell. Pract., vol. 6, no. 7, pp. 29–36, 2023. [Google Scholar]

12. X. Wei, Y. Zhang, H. Song, H. Qin, and G. Zhao, “Research on evacuation path planning based on improved sparrow search algorithm,” Comput. Model. Eng. Sci., vol. 139, no. 2, pp. 1295–1316, 2024. doi: 10.32604/cmes.2023.045096. [Google Scholar] [CrossRef]

13. I. Q. Mudassar, M. Ahmad, S. Rauf, and D. Irfan, “RDF query path optimization using hybrid genetic algorithms: Semantic web vs. data-intensive cloud computing,” Int. J. Cloud Appl. Comput., vol. 12, no. 1, pp. 1–16, 2022. [Google Scholar]

14. X. Wang, “Genetic RRT: Asymptotically optimal sampling-based path planning via optimization of genetic algorithm,” Highlights Sci., Eng. Technol., vol. 43, pp. 215–222, 2023. doi: 10.54097/hset.v43i.7423. [Google Scholar] [CrossRef]

15. W. Zheng, Y. Li, S. Li, Y. Sun, and Y. Yang, “Research on task path planning method for substation inspection robot and UAV based on genetic algorithm,” Int. Symp. Sensors. Mechatron. Automat. Syst., vol. 12981, pp. 1120–1125, 2024. [Google Scholar]

16. A. Malik and M. Pohan, “The development of a path planning algorithm combining the rapidly-exploring random tree algorithm and the particle swarm optimization algorithm,” J. Eng. Sci. Technol., vol. 17, no. 6, pp. 3742–3754, 2022. [Google Scholar]

17. M. Dakulović and I. Petrović, “Two-way D∗ algorithm for path planning and replanning,” Robot. Auton. Syst., vol. 59, no. 5, pp. 329–342, 2011. doi: 10.1016/j.robot.2011.02.007. [Google Scholar] [CrossRef]

18. J. J. Kuffner and S. M. LaValle, “RRT-connect: An efficient approach to single-query path planning,” in IEEE Int. Conf. Robot. Autom., San Francisco, CA, USA, Apr. 24–28, 2000, pp. 995–1001. [Google Scholar]

19. J. G. Kang, D. W. Lim, Y. S. Choi, W. J. Jang, and J. W. Jung, “Improved RRT-Connect algorithm based on triangular inequality for robot path planning,” Sensors, vol. 21, 2021, Art. no. 333. doi: 10.3390/s21020333. [Google Scholar] [PubMed] [CrossRef]

20. Z. Tu, W. Zhuang, Y. Leng, and C. Fu, “Accelerated Informed RRT*: Fast and asymptotically path planning method combined with RRT*-Connect and APF,” in IEEE Int. Conf. Intell. Robot. Appl., Singapore, Jul. 5, 2023, pp. 279–292. [Google Scholar]

21. H. Zhang, Y. Tang, and Z. Zhu, “A novel motion planning algorithm based on RRT-Connect and bidirectional approach for Free-Floating space robot,” in Int. Conf. Intell. Robot. Appl., Singapore, Jul. 5, 2023, pp. 304–316. [Google Scholar]

22. Z. Zhang, Y. Jia, Q. Su, X. Chen, and B. Fu, “ATS-RRT*: An improved RRT* algorithm based on alternative paths and triangular area sampling,” Adv. Robot., vol. 37, no. 10, pp. 605–620, 2023. doi: 10.1080/01691864.2023.2174817. [Google Scholar] [CrossRef]

23. C. Xu, H. Zhu, H. Zhu, J. Wang, and Q. Zhao, “Improved RRT∗ algorithm for automatic charging robot obstacle avoidance path planning in complex environments,” Comput. Model. Eng. Sci., vol. 137, no. 3, pp. 2567–2591, 2023. doi: 10.32604/cmes.2023.029152. [Google Scholar] [CrossRef]

24. L. Yuan, J. Zhao, W. Li, and J. Hou, “Improved Informed-RRT* based path planning and trajectory optimization for mobile robots,” Int. J. Precis. Eng. Manuf., vol. 24, pp. 435–446, 2023. doi: 10.1007/s12541-022-00756-6. [Google Scholar] [CrossRef]

25. K. Min-Cheol and J. Song, “Informed RRT* with improved converging rate by adopting wrapping procedure,” Intell. Serv. Robot., vol. 11, pp. 53–60, 2018. doi: 10.1007/s11370-017-0242-9. [Google Scholar] [CrossRef]

26. Z. Liu, J. Cui, F. Meng, H. Xie, Y. Dan and B. Lin, “Research on intelligent ship route planning based on the adaptive step size informed-RRT* algorithm,” J. Mar. Sci. Appl., pp. 1–11, 2024. doi: 10.1007/s11804-024-00433-2. [Google Scholar] [CrossRef]

27. H. Fan, J. Huang, X. Huang, H. Zhu, and H. Su, “BI-RRT*: An improved path planning algorithm for secure and trustworthy mobile robot’s systems,” Heliyon, vol. 10, no. 5, 2024, Art. no. 38455527. [Google Scholar]

28. P. Xin, X. Wang, X. Liu, Y. Wang, Z. Zhai and X. Ma, “Improved directional RRT* algorithm for robot path planning,” Sensors, vol. 26, 2023, Art. no. 36679837. [Google Scholar]

29. L. Ye, F. Wu, X. Zou, and J. Li, “Path planning for mobile robots in unstructured orchard environments: An improved kinematically constrained bi-directional RRT approach,” Comput. Electron. Agric., vol. 215, 2023, Art. no. 108453. doi: 10.1016/j.compag.2023.108453. [Google Scholar] [CrossRef]

30. J. Huang et al., “FAEL: Fast autonomous exploration for large-scale environments with a mobile robot,” IEEE Robot. Autom. Lett., vol. 8, no. 3, pp. 1667–1674, 2023. doi: 10.1109/LRA.2023.3236573. [Google Scholar] [CrossRef]

31. Y. Huang and C. Jin, “Path planning based on improved RRT algorithm,” in 2023 2nd Int. Symp. Control Eng. Robot. (ISCER), Hangzhou, China, Feb. 17–19, 2023, pp. 136–140. [Google Scholar]

32. K. Hu, Z. Chen, H. Kang, and Y. Tang, “3D vision technologies for a self-developed structural external crack damage recognition robot,” Autom. Constr., vol. 159, 2024, Art. no. 105262. doi: 10.1016/j.autcon.2023.105262. [Google Scholar] [CrossRef]

33. Z. Zhang, C. Ai, S. Li, Y. Xue, G. Ren and Q. Zhang, “Path planning and tracking control method based on bessel curve,” in IEEE World Conf. Mech. Eng. Intell. Manuf., Ma’anshan, China, Nov. 18–20, 2022, pp. 511–514. [Google Scholar]