An Efficient and Secure Privacy-Preserving Federated Learning Framework Based on Multiplicative Double Privacy Masking

1  Introduction

In recent years, machine learning has rapidly developed and has become an indispensable tool in various academic disciplines [1]. With machine learning, people can efficiently complete a variety of complex tasks [2]. However, as the scale of data continues to grow and awareness of privacy increases, traditional centralized machine learning methods are facing greater challenges [3]. Scientific researchers have gained a deeper understanding of data security, and laws have been established to regulate data protection. Notable examples include the Cybersecurity Law of the People’s Republic of China implemented in 2017, the General Data Protection Regulation (GDPR) passed by the European Union in 2018, and the California Consumer Privacy Act (CCPA) enacted in the United States in 2020. Due to legal restrictions, machine learning faces a new dilemma as data acquisition becomes increasingly challenging. In this context, data privacy protection has emerged as a significant area of research [4]. Personal privacy data is no longer as freely accessible as it was in the past [5]. Data-holding institutions cannot directly share data with computing bodies, leading to a bottleneck period in the development of machine learning. This phenomenon is referred to as “data islands” [6].

Federated learning (FL), as a distributed machine learning approach, effectively addresses issues related to data privacy and centralization by training models on local devices and aggregating the updated model parameters [7]. In 2016, McMahan et al. [8,9] innovatively proposed the concept of FL, introducing a distributed, privacy-preserving machine learning architecture. This framework allows multiple parties to collaboratively train models without the need to share their local private data with others. By disseminating the trained models, we achieve a training outcome that is equivalent to what would have been attained if the private data had been shared directly. This approach markedly diminishes the risk of breaches in data privacy and concurrently reduces the training expenses for diverse institutions.

Nowadays, the privacy protection performance of FL has been enhanced and has been applied in many fields. Yazdinejad et al. [10] proposed a privacy-preserving federated learning model that integrates internal audit, additive homomorphic encryption, and Gaussian mixture models. This model effectively defends against poisoning attacks and optimizes computational and communication costs. Compared to full homomorphic and other encryption technologies, it better ensures accuracy and privacy. Yang et al. [11] proposed a novel training paradigm called Secure Federated Learning (SFL), which embeds watermarks into the parameters of deep neural network models to protect the intellectual property of federated models, aiming to address the challenges of data privacy and model intellectual property protection.

Badr et al. [12] introduced a privacy-preserving and communication-efficient smart grid energy prediction scheme based on FL, utilizing a deep learning model that combines Long Short-Term Memory networks (LSTM) and Convolutional Neural Networks (CNN) to forecast future changes in grid energy while ensuring the security of user data. Zhou et al. [13] presented a paper on a privacy-aware asynchronous FL framework based on peer-to-peer networking for secure and resilient decentralized model training in modern mobile robotic systems within 5G and beyond networks. This framework includes a reputation-aware coordination mechanism, a communication mechanism based on secret sharing, and a secure stochastic gradient descent (SGD) scheme, which can effectively enhance security. Xu et al. [14] proposed a multi-source data privacy protection method that combines homomorphic encryption and blockchain. This effectively solves the difficult problem of privacy protection for heterogeneous data in media communication, significantly shortens the processing time, and compared to k-anonymity and differential privacy technologies, it demonstrates lower encryption and decryption time consumption and widespread application potential. Despite the fact that these studies have enhanced the privacy protection performance of FL systems, some of the schemes currently in use still pose risks of privacy leakage.

Based on the aforementioned studies, to further enhance the privacy protection performance and reduce communication overhead in FL systems, a new privacy protection method is proposed and applied to FL systems. The contributions of this research are as follows:

1) Enhanced privacy protection performance. By using an improved dual privacy masking protocol, it ensures that malicious participants or curious servers cannot obtain or analyze any private information from the uploaded data.

2) Increased computational efficiency. By employing the proposed TQRR (Top-Q-Random-R) gradient selection algorithm, the volume of data that needs to be encrypted is significantly reduced, thereby drastically decreasing the time required for computation.

3) Reduced communication overhead. The algorithm efficiently selects the privacy gradients uploaded by various participants, significantly reducing communication overhead while maintaining the accuracy of the model.

The structure of this article is as follows. Section 2 reviews the latest advancements in FL for privacy protection. In Section 3, we introduce the relevant technologies and algorithms used in the proposed scheme. Section 4 describes the threat model, elaborates on the proposed algorithm, and provides a complete system model. In Section 5, we conduct a performance evaluation and discussion of the proposed system framework. Section 6 provides a systematic summary of the article.

2  Related Works

To enhance the privacy protection performance of FL systems, scholars have continuously proposed new privacy protection methods since the advent of FL. Chen et al. [15] proposed a privacy-preserving and traceable FL framework by improving the aggregation architecture and combining blockchain with the Inter Planetary File System (IPFS) to achieve privacy protection of shared data and model traceability in industrial Internet of Things applications. Wang et al. [16] introduced a privacy-preserving federated learning (PPFL) framework, proposing a user grouping mechanism to balance time consumption and training cycles, for model training in intelligent medical systems. Experimental results show that the size of the public key set and the number of users participating in training have a certain impact on the time for signature and verification, and the framework provides privacy protection and efficient performance for FL in intelligent medical systems. Song et al. [17] proposed an Efficient Privacy-Preserving Data Aggregation (EPPDA) scheme for FL, which employs encryption and data aggregation techniques to protect user privacy. This scheme aims to address the problem of user privacy leakage in FL. In response to the consumer smart environments driven by the Internet of Things, Namakshenas et al. [18] proposed a federated learning scheme based on quantum center verification and additive homomorphic encryption. This effectively addresses the privacy challenges at the client side. Experimental validation on multiple datasets has proven the scheme to be efficient and accurate, significantly enhancing the security and privacy protection of consumer IoT.

However, traditional FL faces issues such as high communication overhead and insufficient privacy protection during the model aggregation process, which necessitates further optimization. Ma et al. [19] introduced a PPFL scheme based on multi-key homomorphic encryption (HE), highlighted the privacy issues associated with FL, discussed existing privacy protection methods, and proposed a PPFL scheme based on this encryption approach. This scheme can prevent information leakage and collusion between devices, thereby enhancing the privacy protection performance of FL. Zhang et al. [20] discussed the application of PPFL based on HE in the Internet of Things (IoT) healthcare systems, and proposed a PPFL framework based on HE. This framework allows for model training and updates in a distributed environment while protecting user data privacy. Nguyen et al. [21] proposed a framework that combines secure aggregation with defense mechanisms to address attacks from users. By delegating the execution of defense mechanisms to users and using zero-knowledge proof protocols to verify their correctness, the framework integrates secure aggregation with defense mechanisms. It also introduced a new secure aggregation protocol that can tolerate malicious users and semi-honest servers while maintaining privacy and liveness. However, the efficiency of its verification still needs to be improved.

3  Preliminaries

3.1 Federated Learning

FL is a machine learning approach designed to train models through collaborative learning from multiple distributed data sources without sharing the original data [7–9]. In FL, individual devices or data centers train models locally, then send the updated model parameters or gradients to a central server for aggregation in order to produce a global model. This method helps to address data privacy and security concerns, as there is no need to share original data between different devices. Additionally, FL can reduce the amount of data transmission, alleviate the burden on the central server, and is adaptable to various network conditions and devices [8,9]. The basic model of FL is illustrated in Fig. 1.

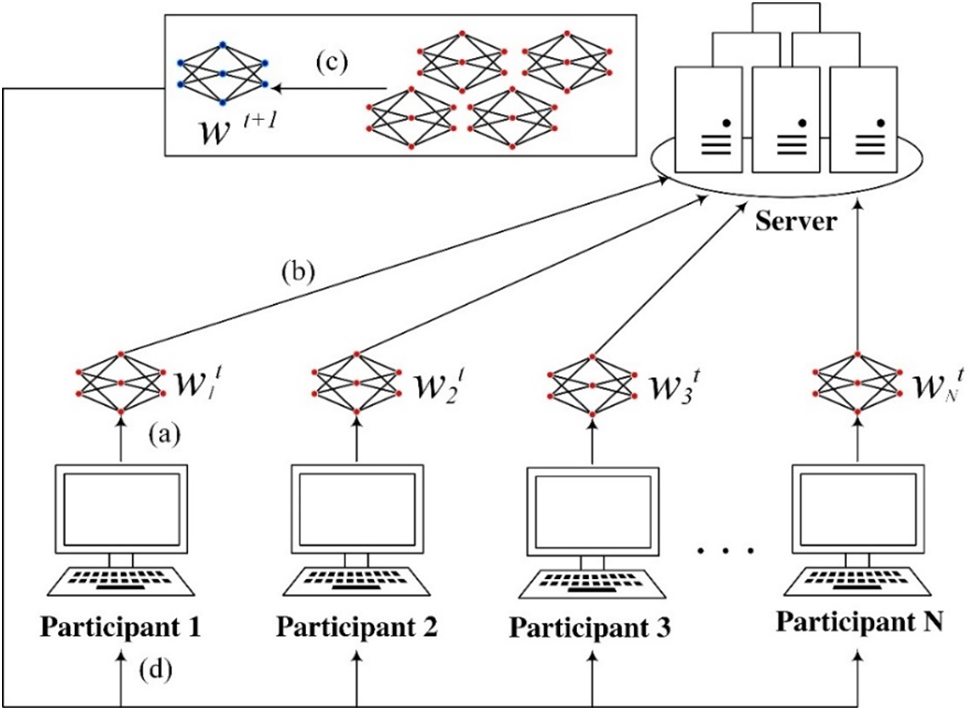
Figure 1: Federal learning framework

Given a network consisting of N participants, where each participant Pi has a private dataset Di, with data distributions that may differ from those of other participants. FL aims to collaboratively learn a global model w, minimizing the loss function L(θ), while minimizing the risk of data sharing and privacy leakage. L(θ) is defined as follows:

L(θ)=∑i=1NMiMLi(θ)(1)

where θ is the parameter of the model, M is the total number of samples from all participants, Mi is the number of samples from participant Pi, and Li(θ) is the loss function of participant Pi, defined as follows:

Li(θ)=∑(xi,yi)∈Dil(f(xi;θ),yi)(2)

where f(xi;θ) represents the model’s prediction for sample xi, yi is the label corresponding to sample xi, and l is the loss function.

In Fig. 1, the participants and the server collectively complete the following steps in one round of the iteration process:

a) Local Training: Participants use local data Di to train their local model parameters. Let wit represent the local model parameters of participant Pi after the t-th round of training.

b) Upload Local Model: All participants upload their local model parameters wit to the central server.

c) Model Aggregation: Upon receiving all updates, the central server executes a model aggregation algorithm, combining the participants’ model parameters into the global model parameters wt+1 for the (t+1)-th iteration.

d) Model Update: The central server sends the updated global model parameters wt+1 to each participant. Each participant then uses the global model parameters wt+1 to update their local model.

The process is carried out over several iterative rounds until a predetermined stopping condition or convergence criterion is met. The goal of FL is to collaboratively learn a global model while maximizing the protection of the privacy and data security of the participants.

3.2 Homomorphic Encryption

HE is a cryptographic technique that possesses a unique property allowing for certain operations to be performed on ciphertexts while they are still encrypted. The results, once decrypted, are identical to those obtained if the same operations had been performed on the plaintext [22]. This characteristic enables computations to be carried out without revealing the original data, thereby making it possible to protect data privacy.

A complete HE algorithm consists of the following three parts:

1) Key Generation (KeyGen): The key generation algorithm is a probabilistic algorithm that takes a security parameter 1λ as input and outputs a key pair. This key pair includes a public key pk and a private key sk, where pk is the public parameter used for encryption, and sk is the private parameter used for decryption. It can be represented as follows:

(pk,sk)←KeyGen(1λ)(3)

2) Encryption (Enc): The encryption algorithm accepts the public key pk and plaintext m as inputs, and outputs ciphertext c. In HE, this algorithm requires that the operations during the encryption process maintain homomorphic properties with respect to operations between ciphertexts. It is represented as follows:

c=Enc(pk,m)(4)

3) Decryption (Dec): The decryption algorithm accepts the private key sk and ciphertext c as inputs, and outputs plaintext m. The decryption algorithm needs to ensure that the correct plaintext is obtained from the correct ciphertext decryption. It is represented as follows:

m=Dec(sk,c)(5)

Homomorphic encryption’s homomorphic property refers to the characteristic where operations performed on ciphertexts, once decrypted, yield results equivalent to those obtained by performing the same operations directly on the plaintexts. Homomorphism can be categorized into additive homomorphism and multiplicative homomorphism, each satisfying the following two equations, respectively:

Dec (sk,c1⊗c2)=m1+m2(6)

Dec (sk,c1⊕c2)=m1×m2(7)

where m1 and m2 are plaintexts, and c1 and c2 are the corresponding ciphertexts.

3.3 Shamir Secret Sharing

Shamir proposed a secret sharing (SS) scheme based on polynomial interpolation algorithm in 1979 [23]. It assumes that a secret s is kept by n users, and only more than m users can recover the original secret s. The scheme mainly consists of two parts:

Secret splitting: The secret s is divided into n secret shares, and initially a polynomial is constructed as follows:

G(x)=s+e1x1+e2x2+⋯+em−1xm−1mod p(8)

In this setup, p is a prime number greater than s. Assign n pairs of distinct (xi,yi) to n users, then publicly disclose the prime p and destroy G(x). Each user is responsible for keeping their own (xi,yi) confidential.

Secret Reconstruction: Utilizing the Lagrange Interpolation Formula

G(x)=∑i=1myi(∏j≠i1≤j≤nx−xjxi−xj)modp(9)

when x=0, G(0)=0, by substituting m pairs of (xi,yi) into Eq. (9), the secret s can be reconstructed.

3.4 Top-K Gradient Selection Algorithm

The Top-K gradient selection algorithm is a method used for gradient compression and sparse gradient transmission, commonly employed in distributed machine learning or model training to reduce communication overhead and enhance training efficiency [24]. This algorithm assists in selecting only the most critical gradients for transmission during gradient updates, thereby reducing the amount of communication and computation required.

The basic steps of the Top-K gradient selection algorithm are as follows:

1. Calculate gradients: In each training iteration, compute the gradients of model parameters.

2. Sort gradients: Sort all gradients by their absolute values to determine the largest K gradients.

3. Select Top-K gradients: Choose the largest K gradients, which are considered the most important gradients, and transmit them to other nodes or the central node for model updating.

4. Gradient compression: For the selected Top-K gradients, perform gradient compression to reduce communication overhead. Common compression methods include truncating gradient precision, using fixed-point integer representation, and employing differential coding.

5. Update model: Use the transmitted Top-K gradients to update model parameters.

The main advantage of the Top-K gradient selection algorithm is the reduction of communication and computation overhead, especially in distributed machine learning, where it can decrease the amount of communication and enhance training efficiency.

4  Our System Framework

In this section, we will introduce the system’s threat model, the proposed new algorithm, the system’s workflow, and the roles of various entities.

4.1 Threat Model

In the FL system discussed in this paper, both the server and the participants are set up under a semi-honest threat model [8,25]. This means that while the server and participants will follow the protocol steps during the execution process, they may attempt to acquire private information about other participants’ data by analyzing the transmitted information. Under the semi-honest threat model, attempts might be made to obtain additional information about the data during the communication process, but they will not maliciously tamper with or damage the execution of the protocol. Typically, there are two main risks involved:

Message Eavesdropping: Semi-honest entities may eavesdrop on messages transmitted over the communication channel, attempting to obtain gradient updates or model parameters transmitted by other participants. This could potentially leak private information about other participants’ data.

Model Inversion: Semi-honest entities may try to infer other participants’ model updates or data distribution information from the communication process, in order to reconstruct or infer data characteristics without accessing the original data.

The limitations of the traditional double masking scheme are as follows: 1. The traditional double masking scheme supports additive aggregation, which is feasible for the federated averaging algorithm, but it results in errors for other algorithms that require weighted averaging. 2. In common double masking schemes, the masks used in each training round need to be generated through Diffie-Hellman (DH), leading to significant computational and communication overhead, thus increasing the overall cost of federated learning. 3. The traditional double masking scheme faces the risk of delay attacks when a user drops offline.

Our improved scheme combines multiplicative double masking with homomorphic encryption, ensuring the confidentiality of private gradients during aggregation while retaining the homomorphic properties of homomorphic encryption, facilitating more complex homomorphic aggregations. Additionally, we propose a method for reusing DH by encrypting the DH-generated masks with the AES encryption algorithm, allowing for the reuse of DH-generated masks and reducing the computational and communication overhead caused by DH exchanges. Since homomorphic encryption is maintained throughout the process, privacy gradients remain confidential even in the face of delay attacks.

4.2 Proposed Algorithm

4.2.1 Multiplicative Double Privacy Mask

A single mask is a method that adds an additional mask on top of the privacy gradient to conceal private information and removes the mask through computation during the decryption phase to achieve privacy-preserving computation. To mitigate the risk of accidental participant disconnection, which may result in the compromise of a single mask and subsequent exposure of private information, a double masking scheme is implemented by applying an additional mask over the initial one [26].

Single-layer Mask Generation: Firstly, number all N participants. Any two participants Pi and Pj, generate the first layer of privacy mask parameter Xi,j through the Diffie-Hellman (DH) key exchange protocol (where i and j correspond to the numbers of the participants). If i>j, then the mutual privacy mask parameter between participants Pi and Pj is Xi,j. During the k-th round of training, the privacy mask undergoes AES [27] encryption k times. The privacy mask for participant Pi in the k-th round is the product ai=∏i>jEncAESk(Xi,j)∏i<jEncAESk(Xi,j)−1 of its mask parameters with all other participants.

Dual Mask Generation: Each participant Pi generates their own mask bi and utilizes the Shamir SS algorithm to obtain N−1 shares, which are then distributed to the other participants.

Removing the mask: Since for any two participants Pi and Pj, the product of the first layer of masks contains two factors EncAESk(Xi,j) and EncAESk(Xi,j)−1, which are multiplicative inverses of each other, the product is 1. Therefore, after multiplying all the first layer masks together, the product is 1, which effectively removes the mask. For the second layer of masks, bi is obtained through secret reconstruction, and then the second layer of masks is eliminated.

4.2.2 Homomorphic Encryption Algorithm Based on Double Privacy Mask

This paper combines the Paillier HE algorithm with multiplicative double masking to form the following encryption algorithm.

Key Generation (KeyGen): Select large prime numbers p and q, and compute n=p×q. Then calculate the least common multiple u of p−1 and q−1. Choose g such that g is coprime with n2 and L(gumodn2) is coprime with n, where L(x)=(x−1)/n. Here, (n,g) represents the public key, and u represents the private key.

Encryption (Enc): For a message m that needs encryption, ensure 0≤m≤n. Randomly select r, ensuring 0≤r≤n. Compute the ciphertext:

c=gm×rnmodn2(10)

Adding a Mask: The ciphertext c is multiplied by a double mask to obtain caibi.

Removing the Mask: After the ciphertext aggregation in the service area, the mask must be removed before decryption. Since the product of the first layer masks of any two participants Pi and Pj contains two factors EncAESk(Xi,j) and EncAESk(Xi,j)−1, which are multiplicative inverses of each other, their product equals 1. Therefore, after multiplying all the first layer masks together, the product is 1, and the mask can be eliminated. For the second layer mask, bi is obtained through secret reconstruction, and then the second layer mask is removed. The aggregated ciphertext message is as follows:

∏1≤i≤Nciaibi=∏1≤i≤Ncibi(11)

In the equation, A equals B, thus it is eliminated. Subsequently, using the secret reconstruction of all bi, the process of eliminating the second layer of masking is as follows:

∏1≤i≤Ncibi/∏1≤i≤Nbi=∏1≤i≤Nci(12)

Decryption (D):

m=L(cumodn2)×μmodn(13)

In the equation, μ=(L(gumodn2))−1modn.

Due to the additive homomorphic property of the Paillier HE algorithm [28], the value m=m1+m2+⋯mN obtained by decrypting c=c1×c2×⋯cN=∏1≤i≤Nci represents the result after aggregation.

4.2.3 TQRR (Top-Q-Random-R) Gradient Selection Algorithm

This algorithm addresses the flaw in the Top-K algorithm process where some gradients may never be updated, thereby affecting the overall accuracy of the model. We have made corresponding improvements by dividing the gradient selection into two parts: one part consists of the gradients ranked in the top Q by absolute value, and the other part consists of R randomly selected gradients after excluding the top Q gradients. Assuming the total gradient count in the model is s, the range for Q is between 0.15s and 0.4s, and the range for R is between 0.05s and 0.35s, with the sum of Q and R not exceeding 0.7s. We have made this setting because when Q is less than 0.15s, the critical gradients updated in each training round are too few, which may lead to model distortion. Moreover, when the sum of Q and R exceeds 0.7s, the savings in computational and communication overhead during the training process are not significantly advantageous compared to traditional approaches. The parameter R can be adjusted based on actual conditions (e.g., R=0.05s) to enhance the accuracy of the model.

In a system where the total number of model parameters is s (Q<s,R<s), the specific algorithmic process is shown in Fig. 2.

Figure 2: The code of TQRR algorithm

To illustrate the advantages of the TQRR algorithm with a simple example, suppose the total number of model gradients is s, Q is set to 0.15s, and R is set to 0.1s. Then in the traditional scheme, participants need to encrypt and upload all privacy gradients, which requires a large computational overhead and communication volume. However, in each round of our training process, participants only need to encrypt and transmit a quarter of the gradients and privacy gradients. Therefore, the computational overhead and communication overhead of the participants are effectively reduced, and the number of privacy gradients received by the server is also greatly reduced, which also reduces the computational and communication load of the server.

4.3 Workflow of the System

A cycle of the system process includes local training of participants, local gradient encryption, mask addition and upload, server aggregation of gradients, mask removal, and participant download of aggregated gradient updates to the local model. When a sufficient number of training cycles have been completed or when the trained model has reached the expected performance, the FL process ends at this point. The process is shown in Fig. 3.

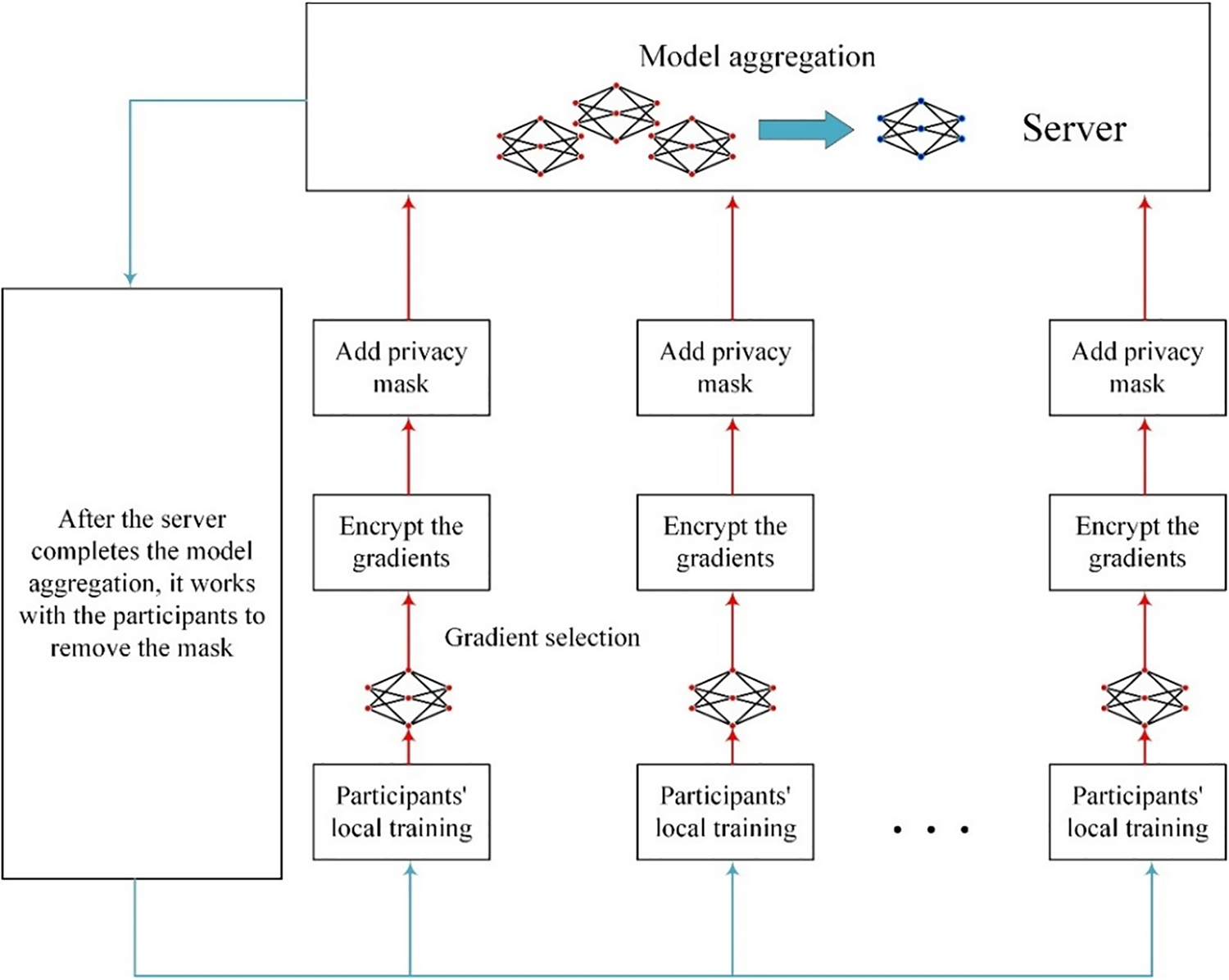
Figure 3: Scheme architecture

First, the participants initialize the parameters and use local data for training to obtain a local model. The TQRR gradient selection algorithm is used to select an appropriate number of gradients (e.g., top 15% gradients, random 5% gradients). The gradients are then homomorphically encrypted, followed by the addition of dual privacy masks, and then uploaded to the server.

Upon receiving the privacy gradients uploaded by the participants, the server eliminates the first layer of privacy masking while aggregating the private gradients. Subsequently, it collaborates with the participants to reconstruct bi, removing the second layer of privacy masking, thereby obtaining the final aggregated result.

All participants download the aggregated results from the server, decrypt the privacy gradients locally, and then update the local model to begin the next round of training. The FL process ends when the training expectations are met or after the maximum training rounds have been completed.

4.4 Participants

The participants in this system mainly act as trainers, allowing all participants to use the results of training with others’ data to improve local models while ensuring privacy.

At the initial stage, the participants cooperate with the server to complete the initialization, and then they are responsible for completing the training locally. All uploaded gradients have undergone HE and double masking locally, ensuring that the data is always transmitted and processed in an encrypted state within the system, thus ensuring privacy and security.

After the server completes the aggregation, the participants assist the server in removing the privacy masks and download the aggregated results to update the local gradients.

4.5 Servers

The server in this system mainly plays a role in aggregating operations and coordinating decryption. After receiving the encrypted messages from the participants, it uses the properties of HE to securely aggregate them. At the same time as completing the aggregation, the first layer of privacy masking is eliminated, and then the participants jointly reconstruct and eliminate the second layer of masking. The gradients encountered by the server are all encrypted, ensuring that even a semi-honest server has no possibility of obtaining the privacy data of the participants.

5  Experimental Evaluation

The benchmark testing platform in this study uses a computer with an Intel Core i5-12600KF CPU and an Nvidia GeForce RTX3060Ti GPU. The training process is accelerated using the Pytorch platform with cuda version 11.4. The effectiveness of learning is validated using public datasets such as MNIST and CIFAR-10. To compare communication efficiency, we simulated a local area network with a rate of 2.5 Gbps to implement FL. The model parameters were optimized using the Adam optimizer [29], with a weight decay of 1e-8, a learning rate of 0.001, and a batch size of 50 for parameter optimization. This study primarily evaluates our approach from the following aspects.

5.1 Computing Overhead

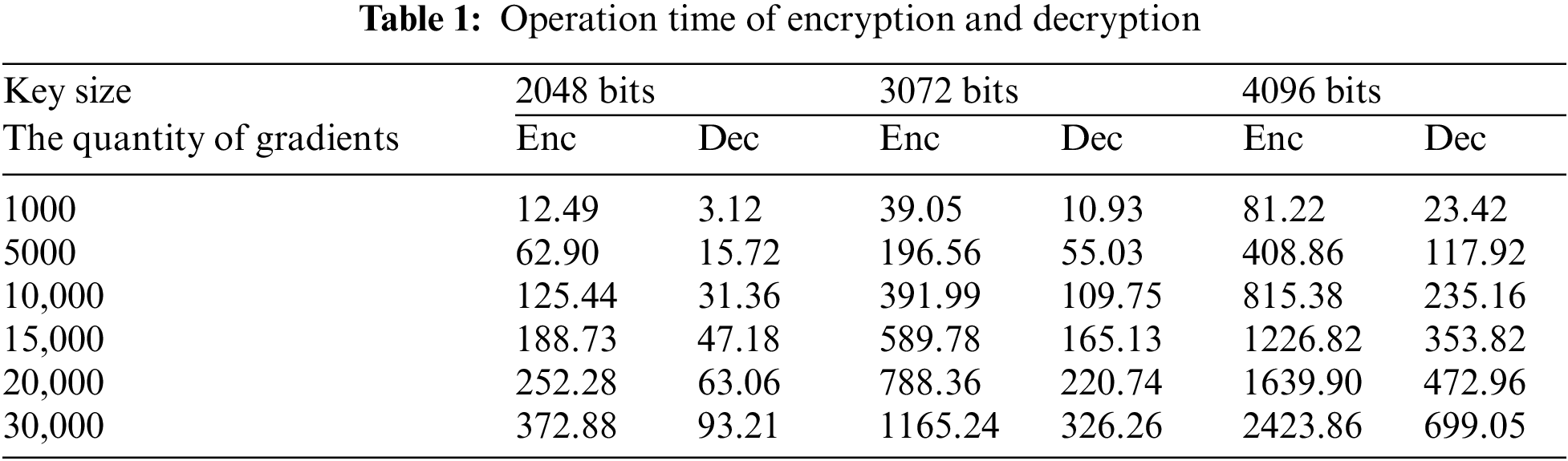
Firstly, we consider the computational cost. We have tested the encryption and decryption processes with a varying number of gradients under the conditions of key lengths of 2048 bits, 3072 bits, and 4096 bits. The number of gradients tested ranged from 1000 to 30,000. Given that the gradient values in each set are unequal, to ensure more objective and accurate results, each set of experiments was run ten times, and the average computation time was taken as the standard. The computation times are shown in Table 1.

To ensure the security of the cryptographic scheme, the key length is generally selected to be 3072 bits. In Figs. 4 and 5, we compared our scheme with those in References [30] and [31]. The results show that the encryption time of our scheme is reduced by 51.78% and 80.01%, respectively, and the decryption time is reduced by 51.96% and 80.42%, respectively. This is mainly because our scheme utilizes the TQRR gradient selection algorithm, which efficiently filters and randomly selects the gradients that need to be encrypted. This significantly reduces the number of gradients that need to be encrypted and uploaded in each round of training. For instance, in this example, TQRR selects the top 15% of gradients with the largest absolute values, and then randomly selects an additional 5% of gradients for encryption and upload. As a result, the number of gradients encrypted during the actual training process is only a quarter of the original amount, thus substantially reducing the computation time.

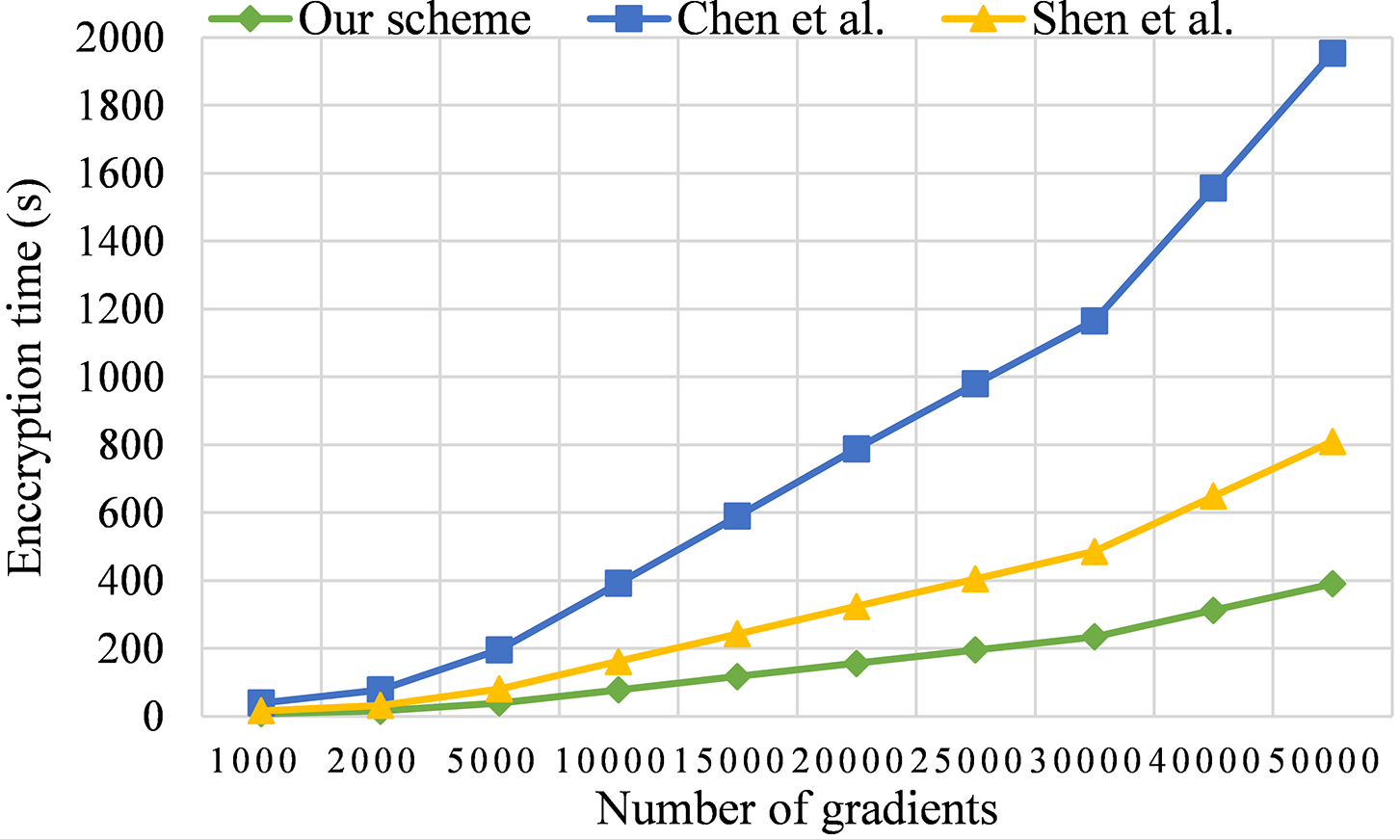
Figure 4: Encryption time [30,31]

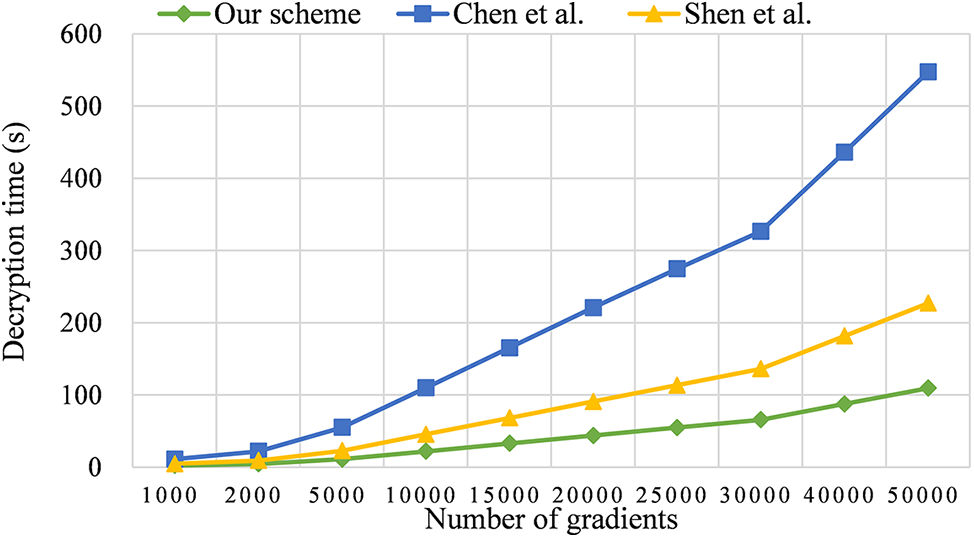
Figure 5: Decryption time [30,31]

5.2 Accuracy

Subsequently, we validated our scheme on the MNIST and CIFAR-10 datasets. In this experiment, we employed the SEER model proposed by Goyal et al. [32], using Adam as the parameter optimizer with a learning rate of 0.001 and set the number of epochs to 20, achieving an accuracy of 98.98%. Fig. 6 presents the confusion matrix from the final test results on the MNIST dataset.

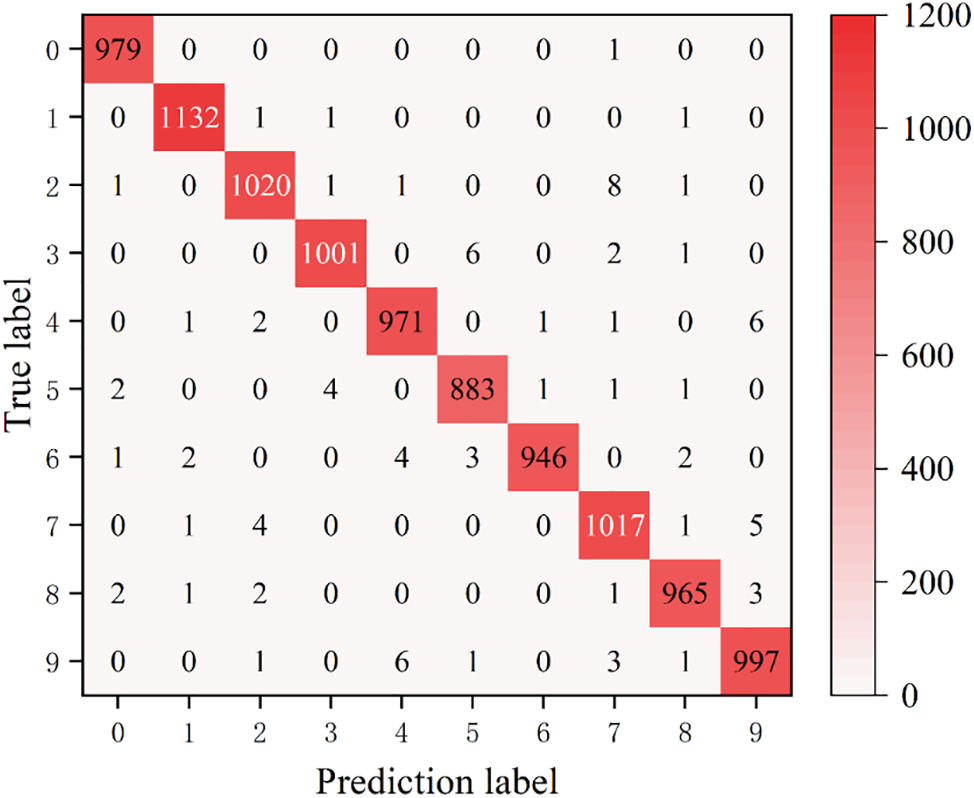
Figure 6: Confusion Matrix of validation results on MNIST dataset

In experiments conducted on the CIFAR-10 dataset, our approach was compared with the traditional Top-K scheme and the method described in Reference [30]. The experimental parameters were set as follows: the model used was Resnet-50, and the optimization method was momentum gradient descent with a momentum of 0.9. Our approach employed the TQRR gradient selection algorithm with the Top gradient ratio set at 15%, and random gradient ratios of 5% and 10%. The test accuracy and loss are displayed in Figs. 7 and 8, respectively. It can be observed that compared to the Top-K algorithm, our accuracy has improved. Additionally, as the proportion of random gradients increases, the accuracy also improves. Compared to Reference [30], our scheme achieved an accuracy of 97.44%, which is essentially on par with it, lagging only one training cycle in convergence, but with a significantly reduced amount of communication.

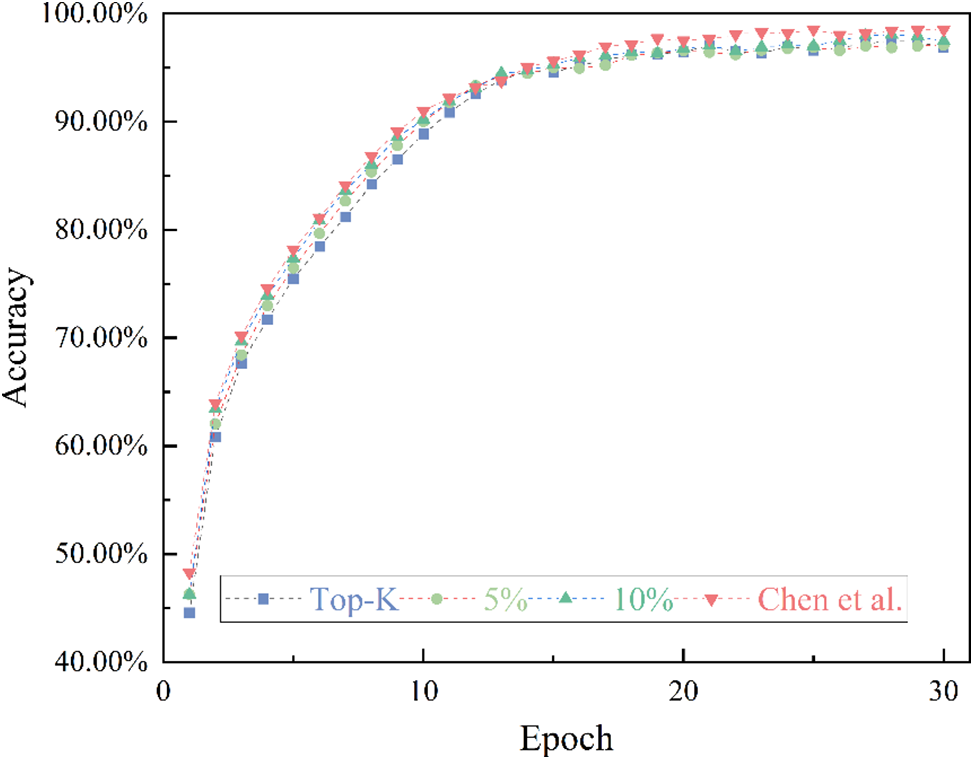
Figure 7: Accuracy on CIFAR-10 datasets under different scheme conditions [30]

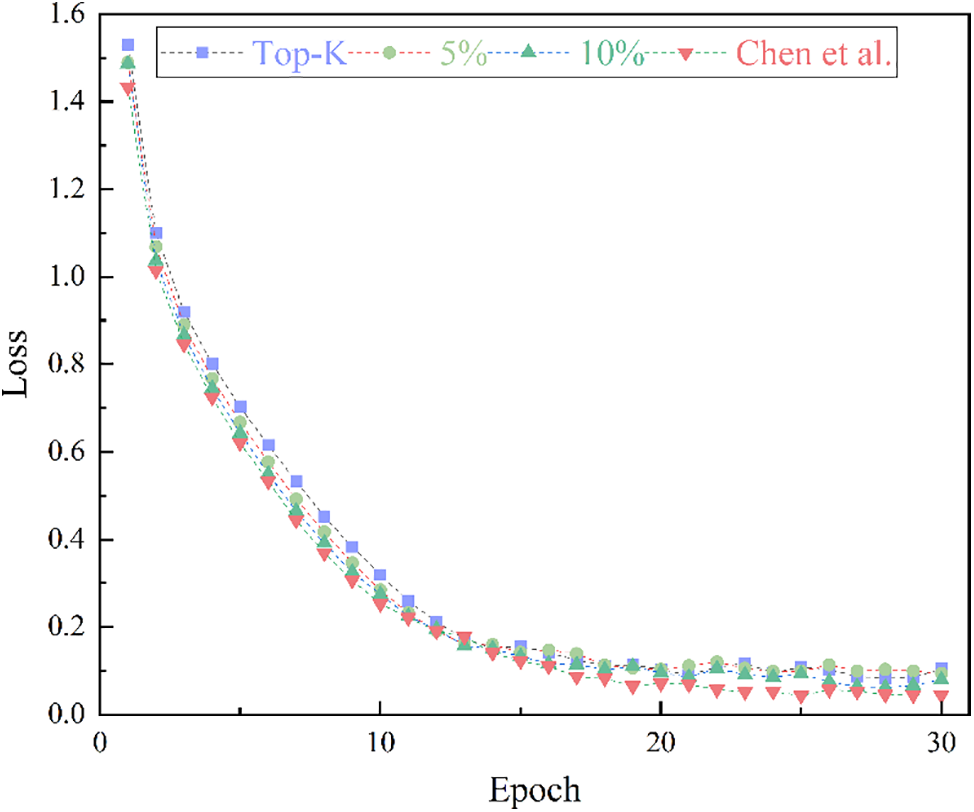
Figure 8: The loss on CIFAR-10 dataset varies with epoch under different conditions [30]

Additionally, to verify the universality of our method, we tested the accuracy of our approach on three datasets: MNIST, CIFAR-10, and SVHN, and compared it with recent works. The results, where Q=0.2s and R=0.2s, are shown in Fig. 9. It can be observed that our accuracy is almost identical to that of PPFDL [33], PEPFL [30], and the study documented in [34], and slightly higher than that of PFLS [35]. This validates that our scheme does not negatively impact accuracy while protecting the privacy of the participants.

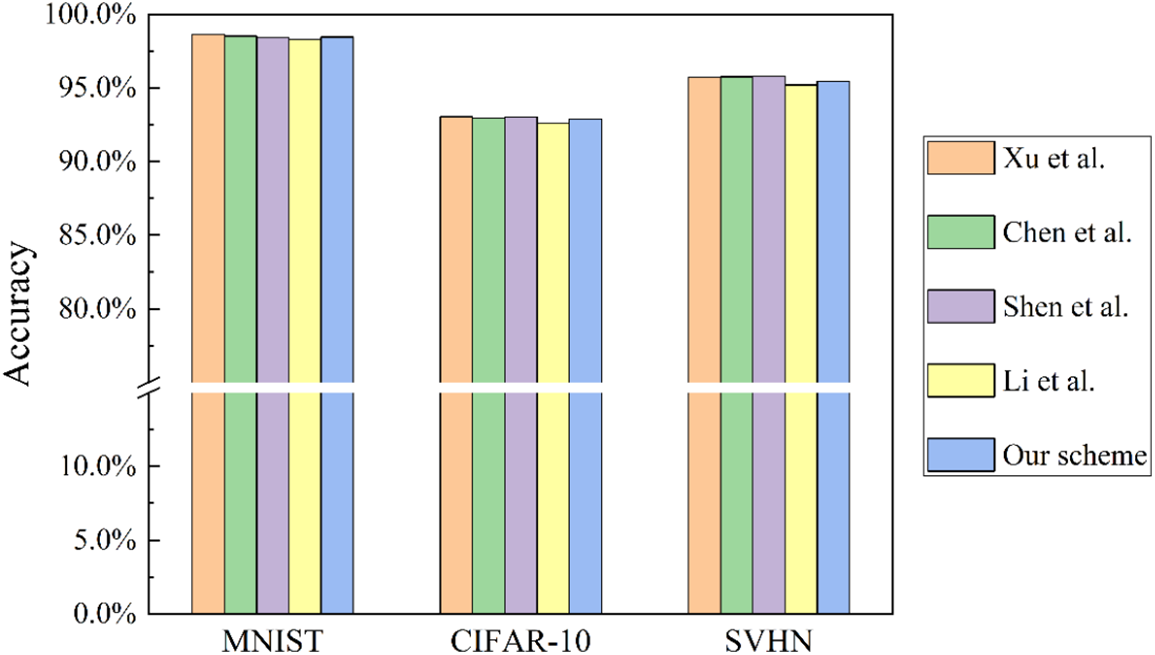
Figure 9: Comparison of accuracy of different schemes [30,33–35]

Accordingly, we have verified the accuracy of the model under various Q and R conditions. The results in Fig. 10 show that the accuracy tends to increase as Q gradually increases. However, the number of random gradients, R, does not show a clear pattern of influence on accuracy.

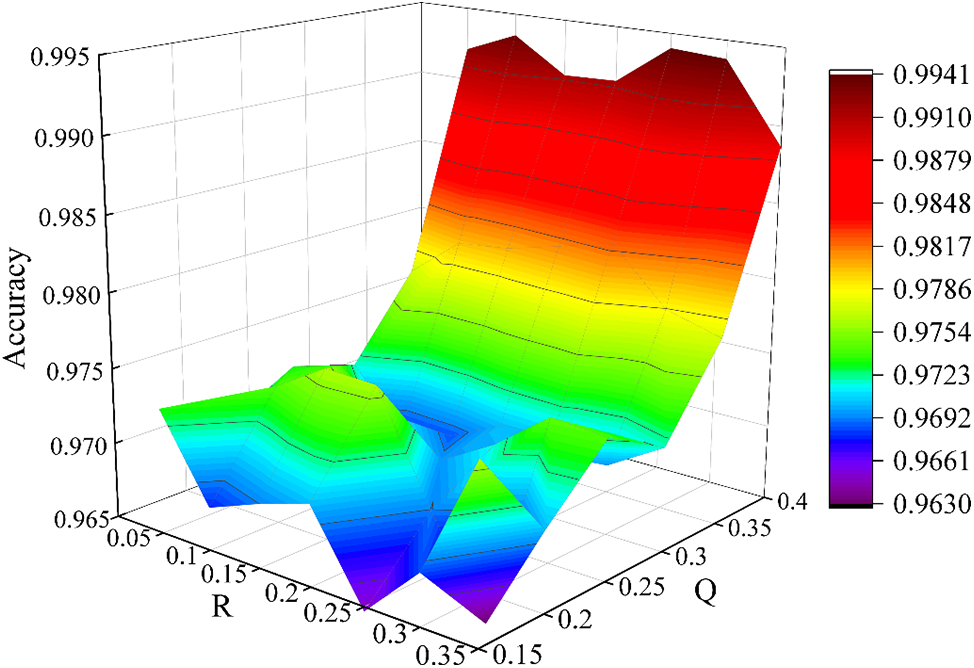
Figure 10: The influence of TOP gradient quantity and random gradient quantity on accuracy

To further verify the impact of our solution on model accuracy, we used LSTM to predict temperature on the Daily Climate dataset. The Daily Climate dataset consists of daily climate data from Delhi city from 2013 to 2017, including information on date, average temperature, humidity, wind speed, and air pressure. The training period was set to 500 cycles with a learning rate of 0.001 and a batch size of 64. The prediction results during the testing process are shown in Fig. 11. At this point, the Mean Squared Error (MSE) is 2, and it can be observed that the predicted values largely coincide with the actual values, confirming that our solution does not adversely affect the model’s performance.

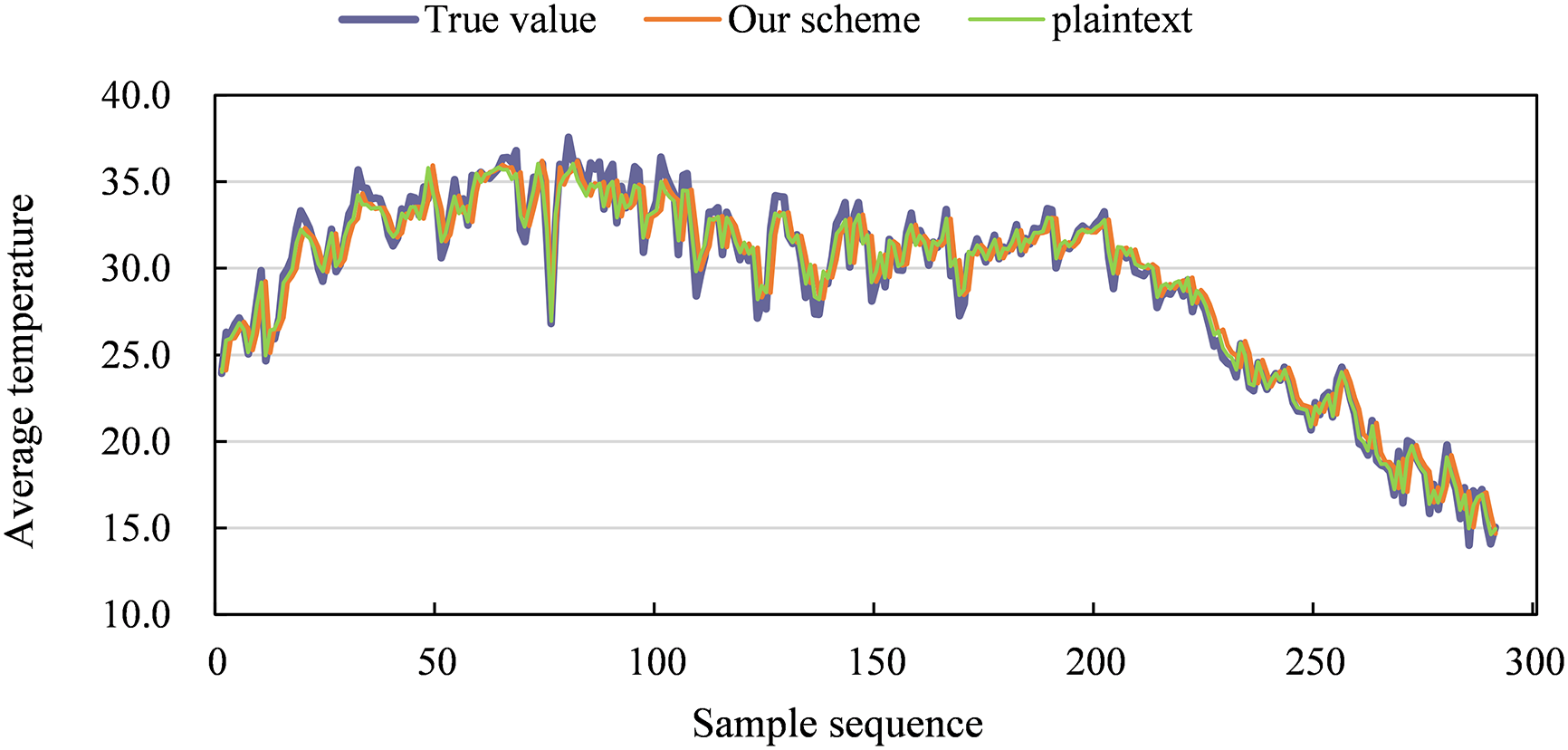
Figure 11: The comparison between our scheme and plaintext

5.3 Communication Overhead

Next, we will explore the impact of the number of participants on the communication overhead. Taking the small neural network model LeNet-5 [36] as an example, it has a total of 44,306 learnable parameters. With the top gradient ratio at 15%, and random gradient ratios at 5%, 10%, and 15%, the number of participants increases from 10 to 100. As shown in Fig. 12, when the ratio of random gradients is fixed, the communication overhead increases non-linearly with the number of participants. When the number of participants is fixed, an increase of 5% in the ratio of random gradients results in a commensurate increase in communication overhead, which corresponds to the added communication cost of the increased random gradients.

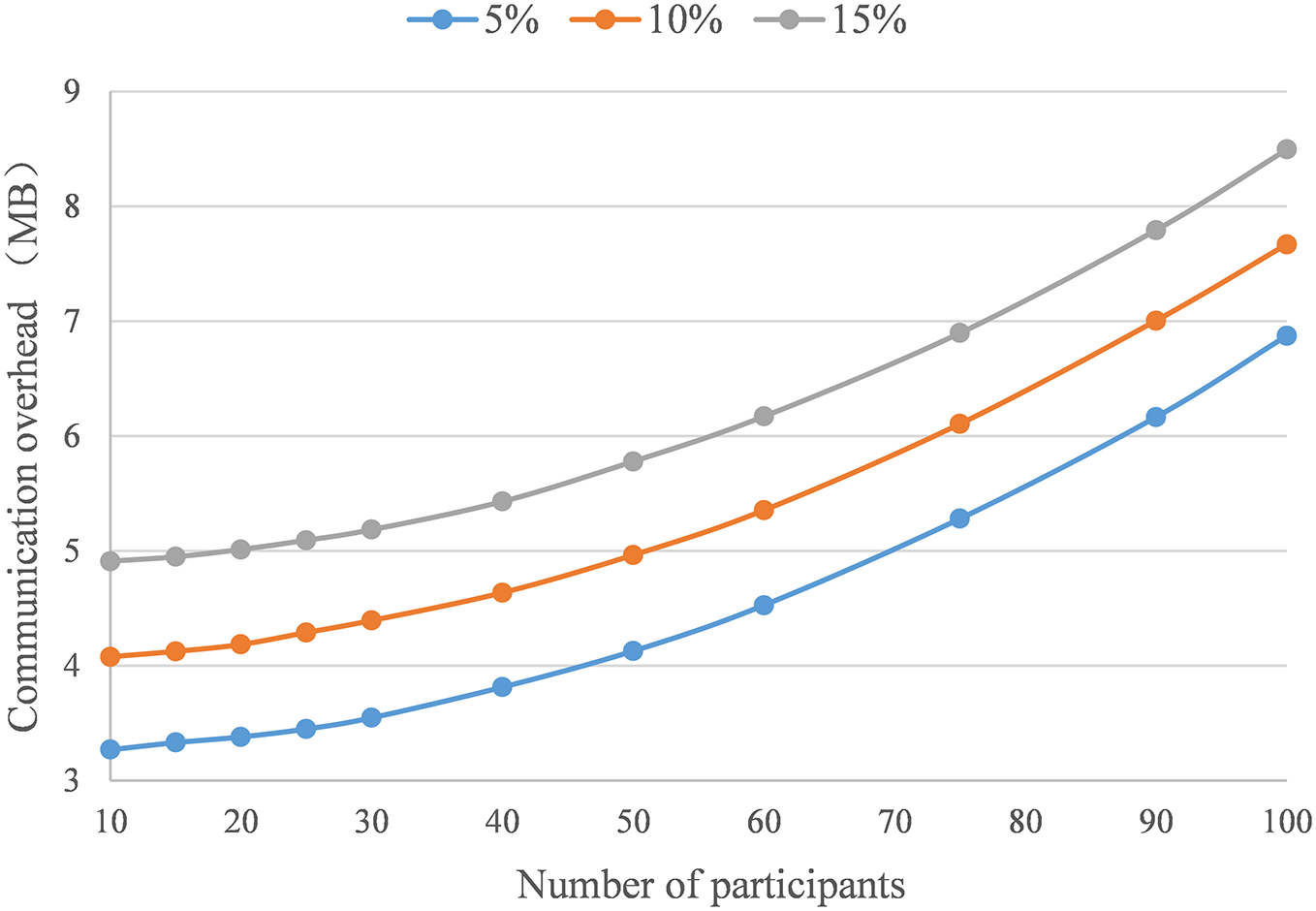
Figure 12: The communication overhead varies with the number of participants

We tested the relationship between the communication volume, the number of participants, and the proportion of stochastic gradients during the learning process to reflect the impact of these factors on communication overhead. Under the conditions where the top gradient ratio is 15%, the stochastic gradient ratio increases from 5% to 20%, and the number of participants increases from 10 to 100, the experimental results are shown in Fig. 13. It can be seen that as the number of participants increases, the communication volume for negotiating keys among participants also increases; the increase in the proportion of stochastic gradients leads to an increase in the number of gradients that participants need to encrypt and upload, which in turn causes an increase in communication overhead. Compared to the Top-K algorithm, our approach slightly increases the communication volume but accelerates the convergence of the model and improves the accuracy of the model. Compared to MaskCrypt [37], when the stochastic gradient ratio is set to 5%, our approach reduces the communication volume by 78.56%, and even when the stochastic gradient ratio is set to 20%, our approach still reduces the communication volume by 50.21%. When the proportion of random gradients is 20%, the method in References [38] and [34] have communication overheads that are respectively 113.34% and 153.65% higher than our scheme.

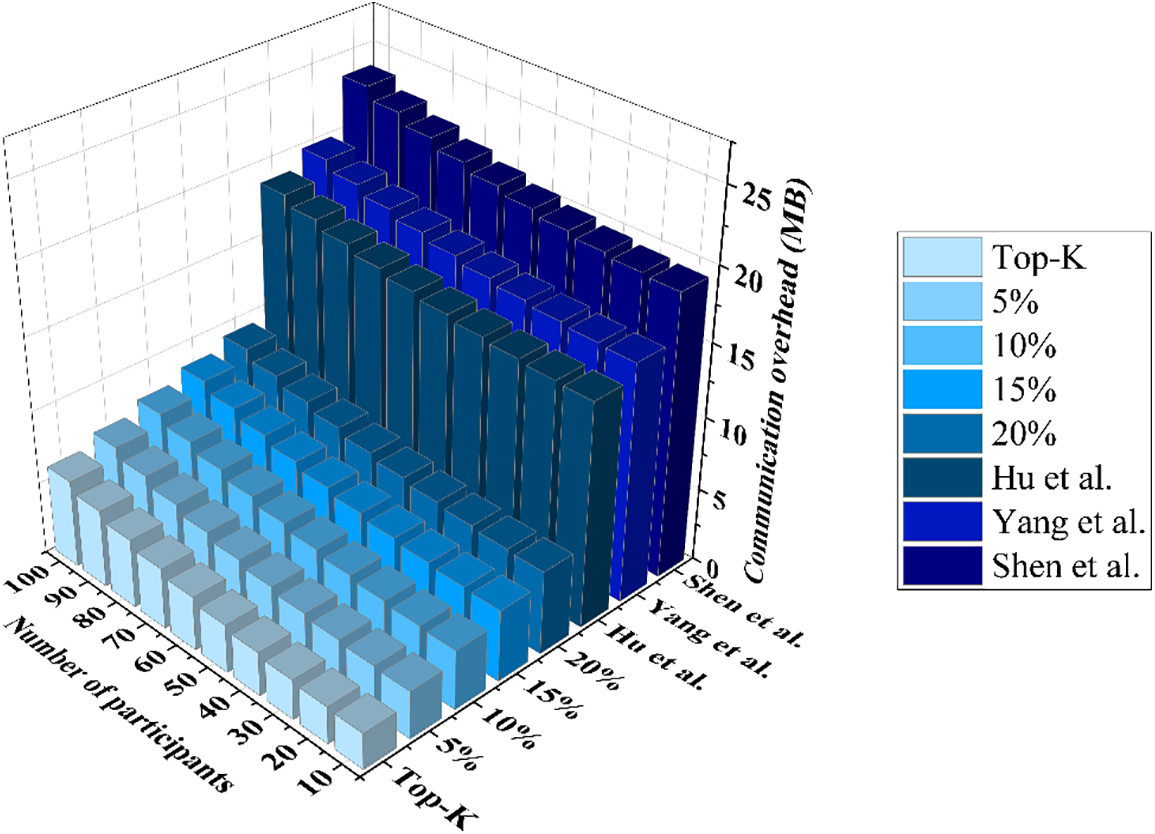
Figure 13: The relationship between communication overhead and the number of participants and the proportion of random gradients [34,37,38]

From the results above, it can be observed that as the number of participants increases, both computational costs and communication volume gradually increase. When the number of participants significantly increases, the computational overhead of calculating the local encrypted gradient and the communication volume for uploading the privacy gradient remain unchanged for each participant. However, the communication volume for exchanging keys and generating masks with other participants increases. For the server, although the computational complexity of the aggregation process is limited, the increase in computational overhead for the aggregation operation is still acceptable. Nevertheless, the communication overhead required to receive the privacy gradients from participants significantly increase. In cross-institutional federated learning systems with fewer participants, these increased costs are still within a tolerable range. However, for cross-device federated learning with a large number of participants, this increase in costs will significantly reduce the system’s usability. We propose a potential solution: when the number of participants surpasses a predefined threshold, an additional intermediate layer can be introduced between the server and participants to establish a tiered federated learning system. This approach effectively mitigates the computational and communication burden on both the participants and the server.

6  Conclusion

This paper improves the traditional additive double-masking scheme to a multiplicative dual-mask scheme that is more suitable for homomorphic addition aggregation, and integrates it with the Paillier HE algorithm. This ensures that servers cannot obtain private information from the encrypted data uploaded by participants, effectively enhancing the privacy protection performance of FL. Subsequently, the TQRR algorithm is proposed on the basis of the Top-K gradient selection algorithm. This algorithm eliminates the adverse impact of certain gradients that are never updated on the model, accelerates model convergence, and improves the final accuracy. Since the TQRR algorithm only requires the encryption and upload of a portion of the gradients to achieve a training effect that is essentially the same, the time spent on encryption and decryption is reduced by more than 51.78% and 80.01% compared to the methods in References [30] and [31], respectively, and the communication overhead is reduced by more than 64.87% compared to Reference [38]. This paper enhances the framework of FL from multiple perspectives including security performance, computational overhead, and communication volume, making FL more secure and efficient in practical applications.

Acknowledgement: The authors wish to express their appreciation to the reviewers and editors for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Nos. 62172436, 62102452), the National Key Research and Development Program of China (2023YFB3106100, 2021YFB3100100), and the Natural Science Foundation of Shaanxi Province (2023-JC-YB-584).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Cong Shen, Tanping Zhou; data collection: Cong Shen, Yiming Zhang; analysis and interpretation of results: Cong Shen, Wei Zhang; draft manuscript preparation: Cong Shen, Lingling Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used to support the findings of this study are publicly available on Internet as follows: MNIST: http://yann.lecun.com/exdb/mnist/ (accessed on 5 August 2024); CIFAR-10: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 5 August 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Gheisari et al., “Deep learning: Applications, architectures, models, tools, and frameworks: A comprehensive survey,” CAAI Trans. Intell. Technol., vol. 8, no. 3, pp. 581–606, Sep. 2023. doi: 10.1049/cit2.12180. [Google Scholar] [CrossRef]

2. S. Jabeen, X. Li, M. S. Amin, O. Bourahla, S. Li and A. Jabbar, “A review on methods and applications in multimodal deep learning,” ACM Trans. Multimed. Comput. Commun. Appl., vol. 19, no. 2s, pp. 1–41, Jun. 2023. doi: 10.1145/3545572. [Google Scholar] [CrossRef]

3. M. Rigaki and S. Garcia, “A survey of privacy attacks in machine learning,” ACM Comput. Surv., vol. 56, no. 4, pp. 1–34, Apr. 2024. doi: 10.1145/3624010. [Google Scholar] [CrossRef]

4. J. Zhou et al., “PPML-Omics: A privacy-preserving federated machine learning method protects patients’ privacy in omic data,” Sci. Adv., vol. 10, no. 5, Feb. 2024, Art. no. eadh8601. doi: 10.1126/sciadv.adh8601. [Google Scholar] [PubMed] [CrossRef]

5. S. Z. El Mestari, G. Lenzini, and H. Demirci, “Preserving data privacy in machine learning systems,” Comput. Secur., vol. 137, no. 2, 2024, Art. no. 103605. doi: 10.1016/j.cose.2023.103605. [Google Scholar] [CrossRef]

6. A. Das, T. Castiglia, S. Wang, and S. Patterson, “Cross-silo federated learning for multi-tier networks with vertical and horizontal data partitioning,” ACM Trans. Intell. Syst. Technol., vol. 13, no. 6, pp. 1–27, Dec. 2022. doi: 10.1145/3543433. [Google Scholar] [CrossRef]

7. C. Zhang, Y. Xie, H. Bai, B. Yu, W. Li and Y. Gao, “A survey on federated learning,” Knowl.-Based Syst., vol. 216, no. 1, Mar. 2021, Art. no. 106775. doi: 10.1016/j.knosys.2021.106775. [Google Scholar] [CrossRef]

8. J. Konečn, H. B. McMahan, F. X. Yu, P. Richtrik, A. T. Suresh and D. Bacon, “Federated learning: Strategies for improving communication efficiency,” 2016, arXiv:161005492. [Google Scholar]

9. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. Y. Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Artif. Intell. Statistics, PMLR, 2017, pp. 1273–1282. [Google Scholar]

10. A. Yazdinejad, A. Dehghantanha, H. Karimipour, G. Srivastava, and R. M. Parizi, “A robust privacy-preserving federated learning model against model poisoning attacks,” IEEE Trans. Inf. Forensics Secur, vol. 19, pp. 6693–6708, 2024. doi: 10.1109/TIFS.2024.3420126. [Google Scholar] [CrossRef]

11. Q. Yang et al., “Federated learning with privacy-preserving and model IP-right-protection,” Mach Intell. Res., vol. 20, no. 1, pp. 19–37, 2023. doi: 10.1007/s11633-022-1343-2. [Google Scholar] [CrossRef]

12. M. M. Badr et al., “Privacy-preserving and communication-efficient energy prediction scheme based on federated learning for smart grids,” IEEE Internet Things J., vol. 10, no. 9, pp. 7719–7736, 2023. doi: 10.1109/JIOT.2022.3230586. [Google Scholar] [CrossRef]

13. X. Zhou et al., “Decentralized P2P federated learning for privacy-preserving and resilient mobile robotic systems,” IEEE Wirel. Commun., vol. 30, no. 2, pp. 82–89, 2023. doi: 10.1109/MWC.004.2200381. [Google Scholar] [CrossRef]

14. Z. Xu and S. Cao, “Multi-source data privacy protectionmethod based on homomorphic encryption and blockchain,” Comput. Model. Eng. Sci., vol. 136, no. 1, pp. 861–881, 2023. doi: 10.32604/cmes.2023.025159. [Google Scholar] [CrossRef]

15. J. Chen, J. Xue, Y. Wang, L. Huang, T. Baker and Z. Zhou, “Privacy-preserving and traceable federated learning for data sharing in industrial IoT applications,” Expert. Syst. Appl., vol. 213, 2023, Art. no. 119036. doi: 10.1016/j.eswa.2022.119036. [Google Scholar] [CrossRef]

16. W. Wang, X. Li, X. Qiu, X. Zhang, V. Brusic and J. Zhao, “A privacy preserving framework for federated learning in smart healthcare systems,” Inf. Process. Manag., vol. 60, no. 1, 2023, Art. no. 103167. doi: 10.1016/j.ipm.2022.103167. [Google Scholar] [CrossRef]

17. J. Song, W. Wang, T. R. Gadekallu, J. Cao, and Y. Liu, “Eppda: An efficient privacy-preserving data aggregation federated learning scheme,” IEEE Trans. Netw. Sci. Eng., vol. 10, no. 5, pp. 3047–3057, 2022. doi: 10.1109/TNSE.2022.3153519. [Google Scholar] [CrossRef]

18. D. Namakshenas, A. Yazdinejad, A. Dehghantanha, and G. Srivastava, “Federated quantum-based privacy-preserving threat detection model for consumer internet of things,” IEEE Trans. Consum. Electron., pp. 1, 2024. doi: 10.1109/TCE.2024.3377550. [Google Scholar] [CrossRef]

19. J. Ma, S. Naas, S. Sigg, and X. Lyu, “Privacy-preserving federated learning based on multi-key homomorphic encryption,” Int. J. Intell. Syst., vol. 37, no. 9, pp. 5880–5901, Sep. 2022. doi: 10.1002/int.22818. [Google Scholar] [CrossRef]

20. L. Zhang, J. Xu, P. Vijayakumar, P. K. Sharma, and U. Ghosh, “Homomorphic encryption-based privacy-preserving federated learning in iot-enabled healthcare system,” IEEE Trans. Netw. Sci. Eng., vol. 10, no. 5, pp. 2864–2880, 2022. doi: 10.1109/TNSE.2022.3185327. [Google Scholar] [CrossRef]

21. T. Nguyen and M. T. Thai, “Preserving privacy and security in federated learning,” IEEE ACM Trans. Netw., vol. 32, no. 1, pp. 1–11, 2023. doi: 10.1109/TNET.2023.3302016. [Google Scholar] [CrossRef]

22. A. Acar, H. Aksu, A. S. Uluagac, and M. Conti, “A survey on homomorphic encryption schemes: Theory and implementation,” ACM Comput. Surv., vol. 51, no. 4, pp. 1–35, Jul. 2019. doi: 10.1145/3214303. [Google Scholar] [CrossRef]

23. A. Shamir, “How to share a secret,” Commun. ACM., vol. 22, no. 11, pp. 612–613, 1979. doi: 10.1145/359168.359176. [Google Scholar] [CrossRef]

24. S. Shi et al., “A distributed synchronous SGD algorithm with global top-k sparsification for low bandwidth networks,” in 2019 IEEE 39th Int. Conf. Distr. Comput. Syst. (ICDCS), Dallas, TX, USA, IEEE, 2019, pp. 2238–2247. [Google Scholar]

25. T. Veugen, F. Blom, S. J. De Hoogh, and Z. Erkin, “Secure comparison protocols in the semi-honest model,” IEEE J. Sel. Top. Signal Process, vol. 9, no. 7, pp. 1217–1228, 2015. doi: 10.1109/JSTSP.2015.2429117. [Google Scholar] [CrossRef]

26. K. Bonawitz et al., “Practical secure aggregation for privacy-preserving machine learning,” presented at the CCS’17, Dallas, TX, USA, Oct. 30–Nov. 3, 2017. [Google Scholar]

27. J. Daemen and V. Rijmen, “AES proposal: Rijndael,” 1999. Accessed: August 5, 2024. https://www.cs.miami.edu/home/burt/learning/Csc688.012/rijndael/rijndael_doc_V2.pdf [Google Scholar]

28. P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” in Advances in Cryptology—EUROCRYPT’99, J. Stern, Ed., Berlin, Heidelberg: Springer Berlin Heidelberg, 1999, vol. 1592, pp. 223–238. doi: 10.1007/3-540-48910-X_16 [Google Scholar] [CrossRef]

29. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” 2014, arXiv:14126980. [Google Scholar]

30. Y. Chen, B. Wang, H. Jiang, P. Duan, Y. Ping and Z. Hong, “PEPFL: A framework for a practical and efficient privacy-preserving federated learning,” Digit. Commun. Netw., vol. 10, no. 2, pp. 355–368, 2022. doi: 10.1016/j.dcan.2022.05.019. [Google Scholar] [CrossRef]

31. C. Shen and W. Zhang, “Privacy enhanced federated learning via privacy masks and additive homomorphic encryption,” presented at the NaNA 2023, Qingdao, China, Aug. 18–22, 2023. [Google Scholar]

32. P. Goyal et al., “Vision models are more robust and fair when pretrained on uncurated images without supervision,” 2022, arXiv:220208360. [Google Scholar]

33. G. Xu, H. Li, Y. Zhang, S. Xu, J. Ning and R. H. Deng, “Privacy-preserving federated deep learning with irregular users,” IEEE Trans. Dependable Secure Comput, vol. 19, no. 2, pp. 1364–1381, 2020. doi: 10.1109/TDSC.2020.3005909. [Google Scholar] [CrossRef]

34. C. Shen, W. Zhang, T. Zhou, and L. Zhang, “A security-enhanced federated learning scheme based on homomorphic encryption and secret sharing,” Mathematics, vol. 12, no. 13, 2024, Art. no. 1993. doi: 10.3390/math12131993. [Google Scholar] [CrossRef]

35. X. Li, M. Wen, S. He, R. Lu and L. Wang, “A privacy-preserving federated learning scheme against poisoning attacks in smart grid,” IEEE Internet Things J., vol. 11, no, pp. 16805–16816, 2024. doi: 10.1109/JIOT.2024.3365142. [Google Scholar] [CrossRef]

36. Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proc. IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. doi: 10.1109/5.726791. [Google Scholar] [CrossRef]

37. C. Hu and B. Li, “MASKCRYPT: Federated learning with selective homomorphic encryption,” IEEE Trans. Dependable Secure Comput, pp. 1–14, 2024. doi: 10.1109/TDSC.2024.3392424. [Google Scholar] [CrossRef]

38. W. Yang, B. Liu, C. Lu, and N. Yu, “Privacy preserving on updated parameters in federated learning,” in Proc. ACM Turing Celebration Conf., Hefei, China, ACM, May 2020, pp. 27–31. doi: 10.1145/3393527.3393533. [Google Scholar] [CrossRef]