 Open Access
Open Access
ARTICLE
Multi-Objective Optimization of Multi-Product Parallel Disassembly Line Balancing Problem Considering Multi-Skilled Workers Using a Discrete Chemical Reaction Optimization Algorithm
1 College of Information and Control Engineering, Liaoning Petrochemical University, Fushun, 113000, China
2 Department of Computer Science and Technology, Shandong University of Science and Technology, Qingdao, 266590, China
3 Department of Computer Science and Software Engineering, Monmouth University, West Long Branch, NJ 07764, USA
4 Research Center of the Economic and Social Development of Henan East Provincial Joint, Shangqiu Normal University, Shangqiu, 476000, China
5 Department of Computer Science, New Jersey City University, Jersey City, NJ 07305, USA
* Corresponding Authors: Zhiwei Zhang. Email: ; Liang Qi. Email:
(This article belongs to the Special Issue: Recent Advances in Ensemble Framework of Meta-heuristics and Machine Learning: Methods and Applications)
Computers, Materials & Continua 2024, 80(3), 4475-4496. https://doi.org/10.32604/cmc.2024.048123
Received 28 November 2023; Accepted 30 April 2024; Issue published 12 September 2024
Abstract
This work investigates a multi-product parallel disassembly line balancing problem considering multi-skilled workers. A mathematical model for the parallel disassembly line is established to achieve maximized disassembly profit and minimized workstation cycle time. Based on a product’s AND/OR graph, matrices for task-skill, worker-skill, precedence relationships, and disassembly correlations are developed. A multi-objective discrete chemical reaction optimization algorithm is designed. To enhance solution diversity, improvements are made to four reactions: decomposition, synthesis, intermolecular ineffective collision, and wall invalid collision reaction, completing the evolution of molecular individuals. The established model and improved algorithm are applied to ball pen, flashlight, washing machine, and radio combinations, respectively. Introducing a Collaborative Resource Allocation (CRA) strategy based on a Decomposition-Based Multi-Objective Evolutionary Algorithm, the experimental results are compared with four classical algorithms: MOEA/D, MOEAD-CRA, Non-dominated Sorting Genetic Algorithm II (NSGA-II), and Non-dominated Sorting Genetic Algorithm III (NSGA-III). This validates the feasibility and superiority of the proposed algorithm in parallel disassembly production lines.Keywords
Nowadays, with the rapid development of the economy, various industries produce large quantities of end-of-life (EOL) products. Initially, most EOL products are treated by incineration and burial, which negatively impact the environment. Moreover, EOL products cannot be reused, causing a great waste of resources [1,2]. Disassembly is one of the important steps of product resource recovery. Parts of EOL products can be remanufactured by disassembly [3]. There is less impact on the environment, and the waste of resources is reduced simultaneously.
In the past, for the Disassembly Line Balancing Problem (DLBP), most scholars [4–6] mainly study a single disassembly line, which is widely used. A single disassembly line can be divided into two types: a linear disassembly line and a U-shaped disassembly line. The linear disassembly line comprises one disassembly line, where workers disassemble on one side of the workstation. Bentaha et al. [7] consider the stochastic partial benefit-oriented DLBP (SP-DLBP) in the presence of hazardous parts. They use an AND/OR graph to model the precedence relationships between disassembly alternative schemes and tasks, aiming to maximize the generated profits. Compared to linear disassembly lines, the U-shaped disassembly line offers greater flexibility, with workers positioned in the middle and able to disassemble EOL products on both sides of the workstation. The U-shaped disassembly line has attracted numerous researchers due to its unique advantages. Li et al. [8] optimize the single-objective U-shaped disassembly line model with mixed-integer programming using a local iterative neighborhood search algorithm and compare it with the CPLEX solver to verify its performance.
In actual production and life, a parallel disassembly line can be used to completely separate different EOL products during disassembly, reduce the disassembly difficulty, and improve the workstation’s utilization rate. This work introduces the Parallel Disassembly Line Balancing Problem (PDLBP). A parallel disassembly line refers to the arrangement of two or more disassembly lines in parallel, enabling the simultaneous disassembly of various products and effectively enhancing disassembly efficiency and production line flexibility. Since the introduction of PDLBP, there has been relatively little research on this problem. Hezer et al. [9] propose a solution method based on the shortest path model of the network and establish a PDLBP mathematical model to minimize the number of chemical stations.
DLBP can be divided into two types. The first type is where the number of workstations is uncertain, and each workstation has a fixed cycle. The second type is where the number of workstations is determined, and the cycle of workstations is uncertain. Wang et al. [10] study the two-sided DLBP with the number of workstations determined, establishe the mathematical model of the problem, and design a variable neighborhood leapfrog algorithm. The proposed algorithm uses variable neighborhood search to improve population local search efficiency. Under the condition that the number of disassembly line workstations is fixed, Wang et al. [11] establish the optimization model of the Class II DLBP with the goal of the minimum beat time and the assignment of balancing tasks on the workstation and proposes a parallel dynamic neighborhood depth search algorithm to solve the problem. This work studies the second type of DLBP.
Multi-product means that EOL products can be combined in pairs or other forms of single-product combination, and multiple products can be disassembled simultaneously. Yin et al. [12] propose a multi-objective hybrid-driven algorithm (HDA) based on a three-tier encoding method and heuristic rules to address the balanced problem of synchronously disassembling multiple products across multiple robot workstations (MPRPDLBP). Precise mixed-integer programming models are established, targeting cycle time, energy consumption, and an improved hazard index. Guo et al. [13] propose a disassembly line balance control method for random multi-product robots, which can solve the DLBP of multi-objective and multi-product robots and give a better solution.
Among many studies on DLBP, only very few pay attention to multi-skilled workers. In actual production, qualified operation skills of workers are the premise to ensure work quality and product quality, and also the basis for enterprises to produce on time and within budget. Simultaneously, through the rational allocation of multi-skilled workers, enterprises help reduce labor costs, address the issue of insufficient emergency production personnel, respond flexibly to emergencies to ensure the normal operation of production operations, improve the flexibility and versatility of the production line, and enhance the overall productivity level of the enterprise [14–18]. This work introduces multi-skilled workers, who are arranged on workstations to disassemble EOL products. The different skills required for each task in the disassembly of each product lead to more diversified disassembly sequences.
This work proposes a multi-product parallel disassembly-line-balancing problem considering multi-skilled workers (MPDMW). As MPDMW is a discrete problem, heuristic algorithms typically address such problems [19–22]. In recent years, researchers have explored various methods to solve DLBP [23–25]. Table 1 summarizes the literature above. However, a Multi-Objective Discrete Chemical Reaction Optimization (MDCRO) algorithm has not yet been applied to address this problem. Chemical Reaction Optimization (CRO) is a recent swarm intelligence optimization algorithm. It draws inspiration from chemical reactions in the natural world. It simulates the interactions between molecules in chemical reactions to seek minimal potential energy. In just a few years, CRO has successfully addressed many complex problems. We choose to employ CRO to solve MPDMW because CRO possesses robust global search capabilities, adaptability, and parallelism. This algorithm conducts a global search by simulating chemical reactions, avoiding being trapped in local optima. The adaptability allows for dynamic adjustments in the search strategy, enhancing convergence speed. The parallelism fully utilizes computational resources, accelerating the solving process. We attempt to use it to address MPDMW. The main contributions of this paper are as follows:
1. This work introduces a new problem, MPDMW. To address this problem, a mixed-integer linear programming mathematical model is established to maximize profits and minimize workstation cycles.
2. The use of MDCRO to solve MPDMW is proposed for the first time. Among them, we design a three-segment coding structure. Four reactions, decomposition reaction, synthesis reaction, intermolecular ineffective collision reaction, and wall ineffective collision reaction, are designed to achieve the evolution of molecular individuals and enhance the algorithm’s capability for optimal solution search.
3. In order to verify the feasibility and superiority of MDCRO, we compare the algorithm with Non-dominated Sorting Genetic Algorithm II (NSGA-II) [26], Non-dominated Sorting Genetic Algorithm III (NSGA-III) [27], and Multi-Objective Evolutionary based on Decomposition (MOEA/D) [28], and collaborative resource allocation (CRA) strategy for MOEA/D (MOEA/D-CRA) [29]. Experimental results show the effectiveness of MDCRO in solving MPDMW.

The following content arrangement is outlined in this paper. Section 2 describes MPDMW and its mathematical model. Section 3 introduces MDCRO. Section 4 analyzes experimental results. Section 5 summarizes the work and discusses future research directions.
2 Problem Statement and Formulation
In actual production and life, a parallel disassembly line can be used to completely separate different EOL products during disassembly, reduce the disassembly difficulty, and improve the workstation’s utilization rate. This work puts forward MPDMW. Multi-product means that EOL products can be combined in pairs or other single products in various forms to form multi-products for disassembly simultaneously. The multi-skilled worker means that each worker has different skills. The multi-skilled worker is assigned to the workstation to disassemble EOL products. The different skills required for each task in disassembling each product lead to the allocation disassembly sequence becoming more diverse, and there are often many complex task allocation problems. Enterprises can reduce labor costs through the reasonable distribution of multi-skilled workers. Solve the problem of insufficient emergency production personnel. Flexible response to emergencies to ensure the normal operation of production operations. Improve the production line’s flexibility and the enterprise’s overall productivity level. A parallel disassembly line is placed in two or more parallel disassembly lines and can disassemble various products synchronously, effectively improving disassembly efficiency and production line flexibility. According to the mathematical model established by MPDMW, the following assumptions are made:
• Each worker has multiple skills.
• One task corresponds to one workstation.
• The cost per unit of time is workstation-specific.
• The disassembly task satisfies the known precedence and conflict constraints.
• No matter which workstation the task is assigned, it has nothing to do with workers and time.
Through the AND/OR graph of the flashlight in Fig. 1, different disassembly sequences can be obtained, but these sequences must meet certain constraints to ensure that the disassembly sequence is correct and feasible. In the AND/OR graph, subassemblies are represented by nodes, and the index of each subassembly is indicated by an integer within angle brackets. Directed edges between linked subassemblies depict each disassembly task. It is easy to observe that this product consists of 15 subassemblies and 10 disassembly tasks.
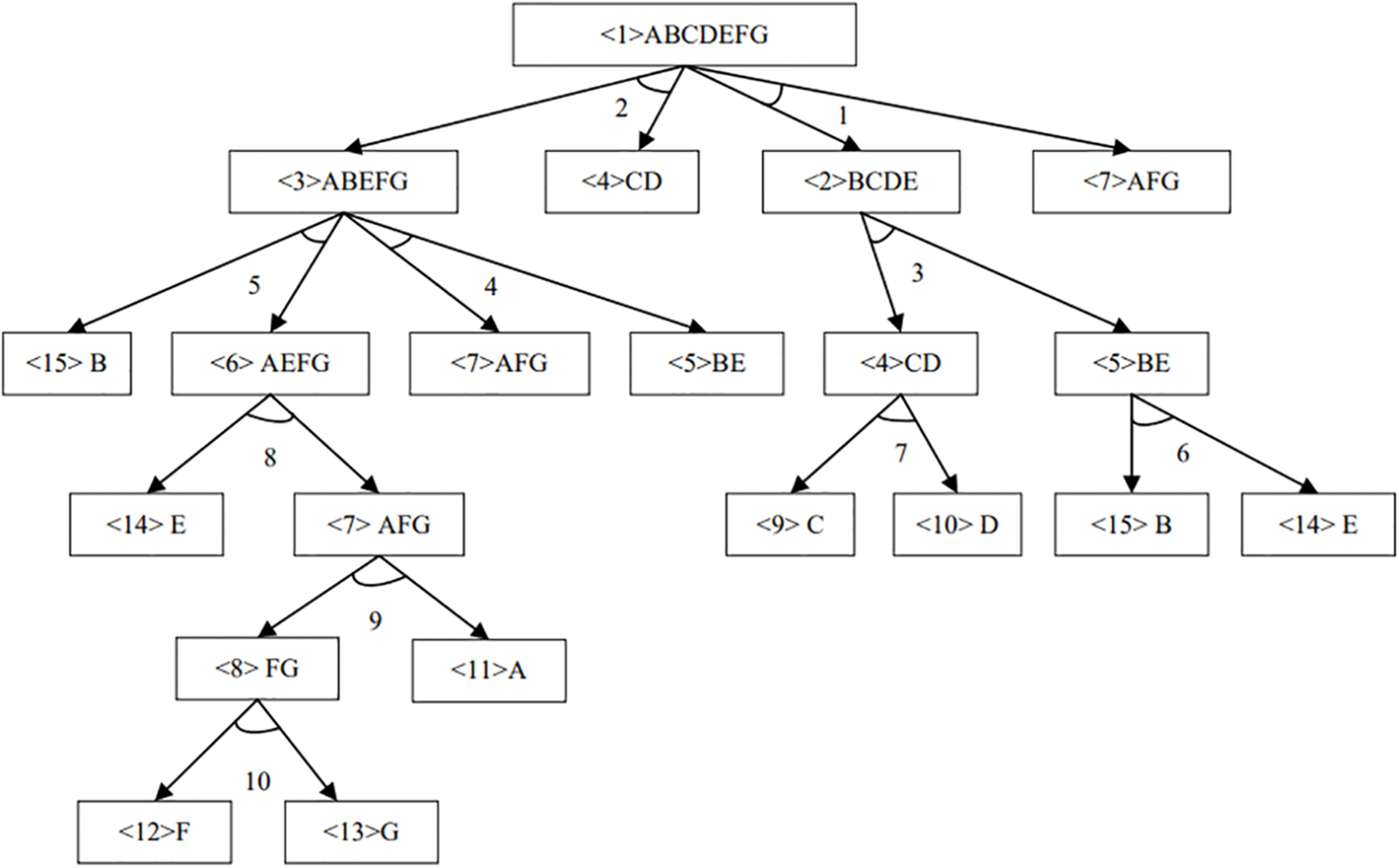
Figure 1: AND/OR graph of a flashlight
In order to describe the problem more deeply and systematically, four relation matrices, S, D, A, and B, are introduced in this paper to describe relevant constraint relations. The detailed definition of the matrix is as follows.
The disassembly precedence relation matrix
Disassembly incidence matrix
The matrix of workers and skills
1) Disassemble the ballpoint pen and radio for the multi-skilled worker and skill matrix below. The abscissa represents the multi-skilled workers required for disassembly, and the ordinate represents the skills required for the disassembly task composed of 10 skills.
Disassembly task and disassembly task skill matrix
2) Disassemble the ballpoint pen and radio for the disassembly task and the disassembly task required the skill matrix below. The abscissa represents that the disassembly task consists of 43 disassembly tasks, and the ordinate represents that the skills required by the disassembly task consist of 10 skills.
In MPDMW, a feasible disassembly task sequence is obtained, and it is reasonably allocated to each workstation according to the required skills of the disassembly task and the workers’ skills. This work aims to reduce costs, improve workstation utilization, and meet the environmental requirements of disassembly enterprises.
Notations used in the model to be presented are summarized as follows:
Sets:
| Set of products. | |
| Set of tasks. | |
| Set of subassemblies. | |
| Set of workstations. | |
| Set of line workers. | |
| Set of skills. |
Parameters:
| Worker | |
| Disassemble the matrix of skill | |
| Disassembly line serial number | |
| Number of disassembly tasks on disassembly line | |
| | Disassembly time of skill |
| The cost of hiring workers. | |
| The recovery value of disassembled component | |
| A big enough number. | |
| Workstation cycle time. | |
| An element of the precedence matrix | |
| Precedence matrix for product | |
| The incidence matrix of product | |
| An element in the | |
| The matrix of workers |
Decision variables:
We formulate the optimization problem of MPDMW as:
The objective function (1) represents the maximum profit from the disassembly of EOL products, composed of three parts: the total recovery value of disassembly EOL products, the total cost of disassembly, and the total cost of workers. (2) represents the minimization cycle time. Constraint (3) guarantees that only one worker can be assigned to each workstation on each side. Constraint (4) indicates that a person can be assigned to at most one side of the workstation. Constraint (5) indicates that each task can only be assigned to one side of a workstation. Constraint (6) indicates that each enabled workstation must be assigned at least one task. Constraint (7) indicates that a workstation that is not enabled cannot be assigned tasks. Constraint (8) ensures that each assigned task must be executed. Constraint (9) represents the relationship between skills and workers’ tasks. Constraint (10) ensures that the task can only be executed if it is assigned to the workstation side. Constraint (11) ensures that the task can only be performed if the worker is assigned to the workstation and has this skill. Constraint (12) indicates that the processing time of each workstation does not exceed the cycle time. Constraint (13) indicates that tasks on the demolition line must meet the precedence relation. Constraints (14) and (15) indicate that the feasible disassembly sequence must satisfy the conflict relation. Constraint (16) represents the range of decision variables.
The inspiration for CRO comes from the interactions among molecules during chemical reactions, thereby attaining the minimum molecular potential energy [30]. Many past studies indicate that CRO performs excellently in solving optimization problems, which is why we chose this method [31–33]. In CRO, molecules possess kinetic and potential energy, denoted as and, respectively. Represents the objective value of the disassembly sequence while signifying the molecule’s ability to escape local optima. We make some improvements to its four reactions. The flowchart of MDCRO is illustrated in Fig. 2.
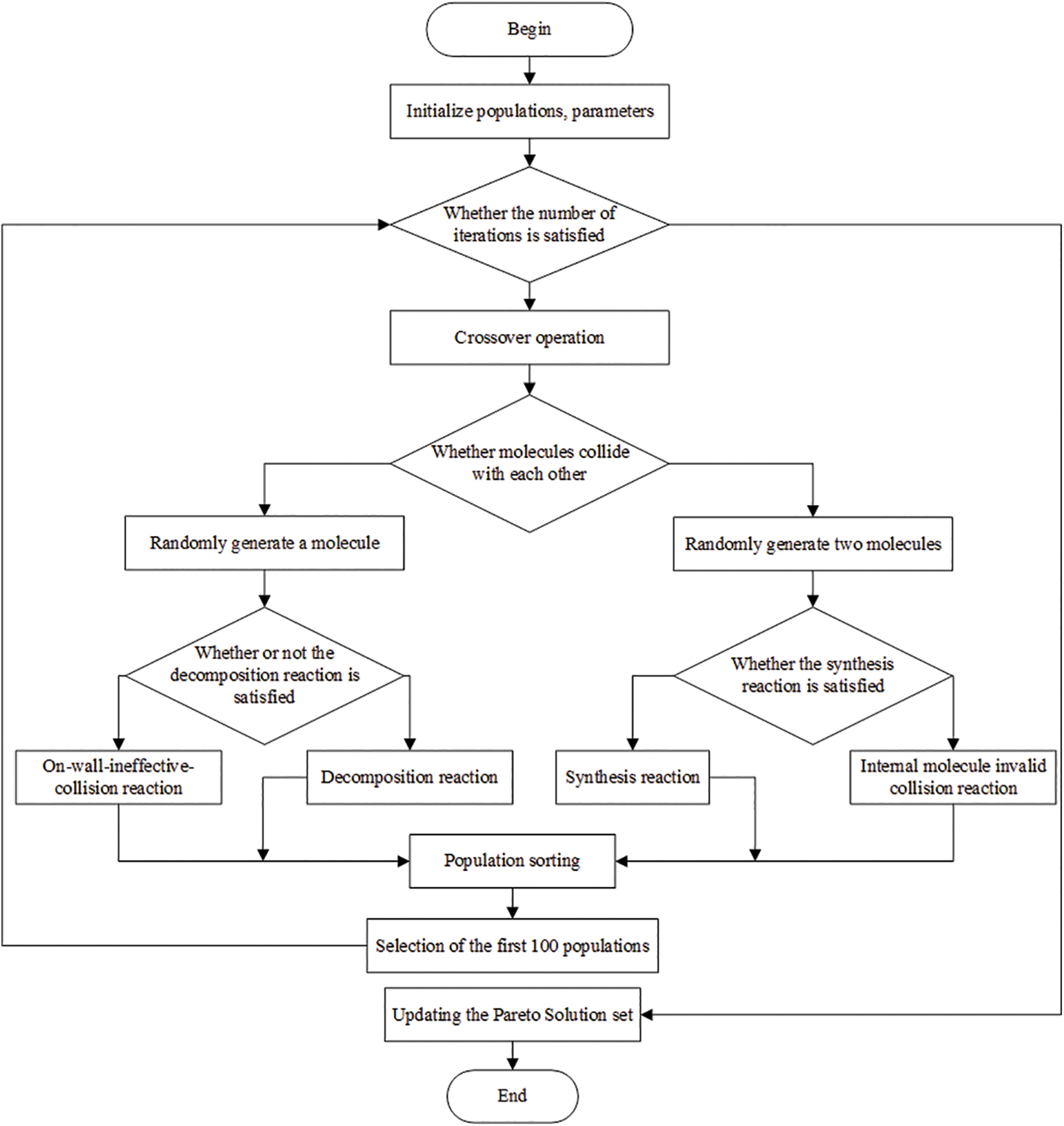
Figure 2: Flowchart of MDCRO
The three-segment idea

Figure 3: Coding process of a case
After the coding of the solution is completed, it needs to be decoded. The idea of decoding is to assign tasks to each workstation based on the fixed number of workstations. The decoding process of the parallel disassembly line is to assign feasible task sequences to each workstation. The allocation principle allocates disassembly tasks to each workstation. In the allocation process, the cycle time of each workstation is minimized. Fig. 4 shows the specific assignment of the task sequence at the workstation. Task 2 takes 10 s, task 14 takes 6 s, and task 11 takes 8 s. Assigned to workstation 1, Workstation 1 has a cycle time of 24 s. Task 16 has a time of 5 s, task 6 has a time of 7 s, task 8 has a time of 9 s, and workstation 2 has a cycle time of 21 s. Task 43 time is 4 s, Task 17 time is 5 s, task 18 time is 7 s, task 29 time is 5 s, task 10 time is 4 s, and workstation 3 cycle time is 25 s.
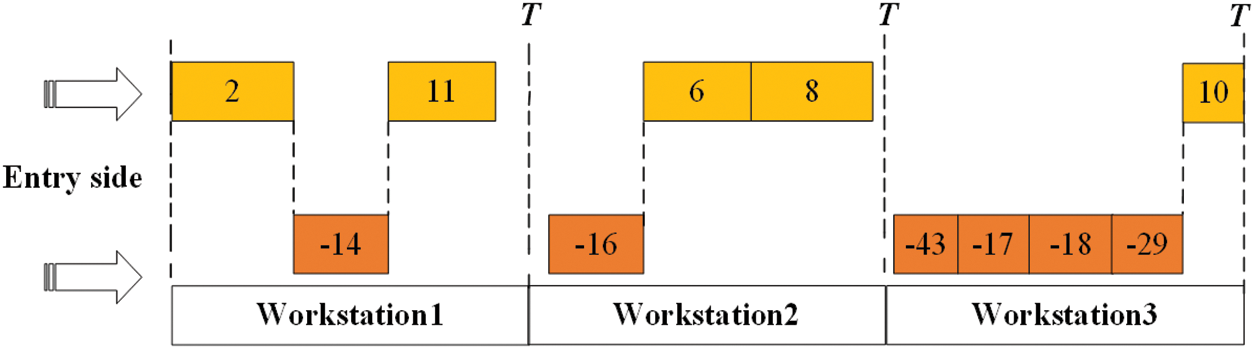
Figure 4: Decoding process of a case
According to the above allocation, the cycle of each workstation can be minimized. Three workstations are required to complete the disassembly to optimize the two objective functions.
This work uses the AND/OR graph of two products, ballpoint pen and radio, to illustrate the encoding and decoding of parallel disassembly lines. Fig. 5 describes the disassembly process of these two products on the parallel disassembly line. For illustration purposes, the feasible disassembly sequence it forms is {2, −14, −16, −43, −17, −18, 11, 6, −29, 8, 10}. The numbers in the disassembly sequence represent the corresponding disassembly tasks. The numbers prefixed with “−” indicate that the current task is disassembling the radio and assigned to the lower disassembly line. The numbers without prefix symbols indicate that the current task disassembles the ballpoint pen and is assigned to the upper disassembly line. For instance, −14 denotes that task 14 for the radio is allocated to the lower disassembly line, while 2 signifies that task 2 for the ballpoint pen is assigned to the upper disassembly line. The required skills refer to the skills needed to perform each disassembly task, and only workers possessing those specific skills can execute the disassembly. For example, task −14 corresponds to skill 4, meaning skill level 4 is necessary to accomplish task −14. At this moment, Worker 1 happens to have skill level 4, thus enabling the allocation of task −14 to Worker 1’s lower disassembly line station for disassembly.
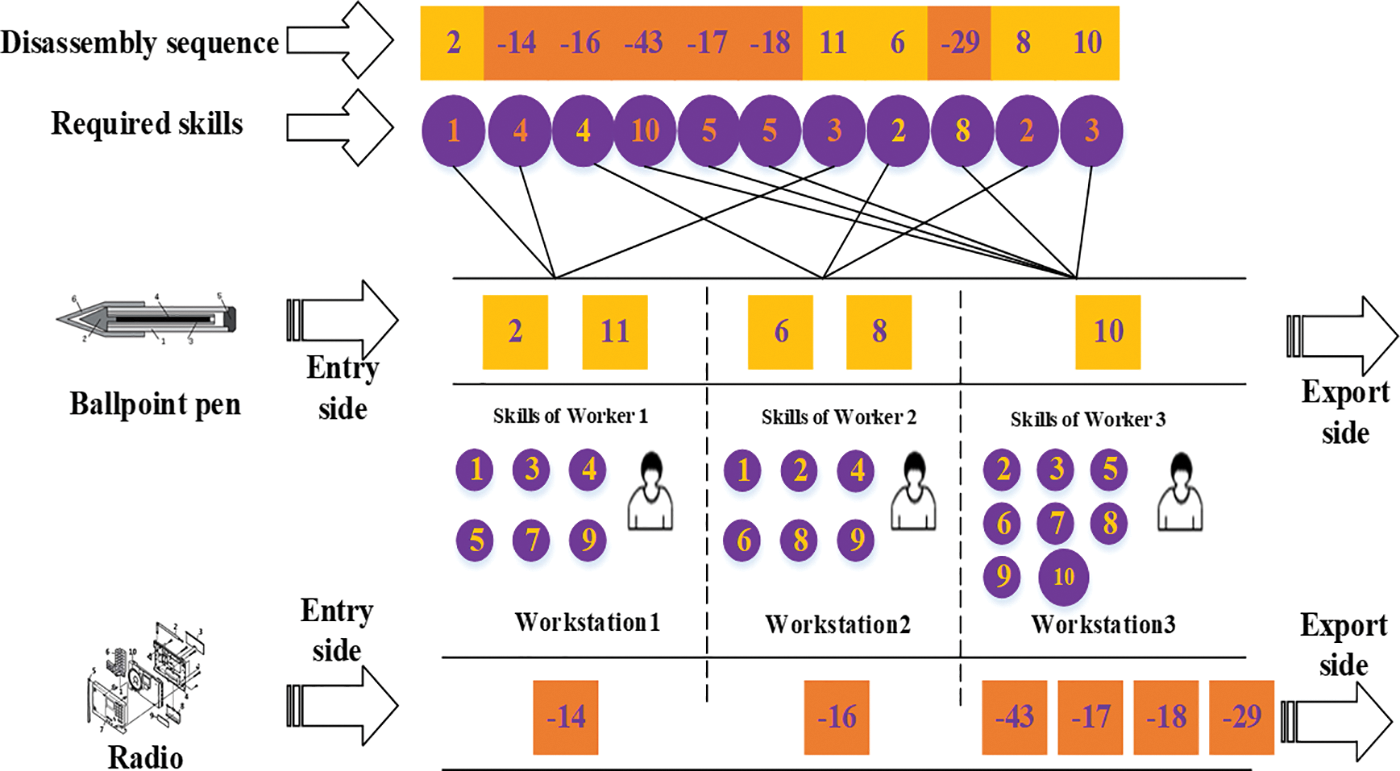
Figure 5: Distribution process of a case
3.3 Synthesis Reaction Search Strategy
Synthesis reaction is the process of two or more molecules colliding to form a single molecule. As shown in Fig. 6. The steps are as follows:
Step 1: Randomly select two molecules from the population and judge whether the kinetic energy of each molecule of the two molecules is greater than the threshold for the decomposition reaction. If the conditions are met, a synthesis reaction will occur. Currently, the number of molecular collisions at each position (
Step 2: Give the molecule at
Step 3: Give StartChildent1 the {−11, −13, 3, 6, −17, −18, 7, −19} at positions {0, 2, 4, 6, 8, 10, 12, 14} in the Father.
Step 4: Give {2, −21, −40, 9, 6, −17, 10} at positions {1, 3, 5, 7, 9, 11, 13} in the Mother to the corresponding {1, 3, 5, 7, 9, 11, 13} in StartChildren1.
Step 5: When the sequence is added to StartChildren1 by the Father and the Mother individuals, respectively, the two are conducted by polling. If the sequence added does not exist in StartChildren1, it will be added; otherwise, it will not be added. For example, when the Mother individual adds sequence {6, −17}, If this sequence is found to already exist in StartChildren1, these two sequences cannot be added. The corresponding current index is also added.
Step 6: If the size of the current index is smaller than the length of the Father, then add the sequence of the corresponding index in the Father and the sequence does not exist in StartChildren1, then add the sequence to StartChildren1 and then give the fully allocated sequence to StartChildren2.
Step 7: If the size of the current index is smaller than the length of the Mother, add the sequence of the corresponding index in the Mother, and it does not exist in StartChildren1, then add the sequence to StartChildren1.
Step 8: Because it is so multi-objective here in calculating the potential energy, we introduced the thought of weight, combined with the actual reasonable weight distribution, due to the first goal being profit, the second being the workstation cycle, are essential for decision making, so we are here to set their weights are 0.5, calculation, draw the corresponding potential energy. To see if this reaction can happen.
Step 9: If the sum of the kinetic energy plus the potential energy of the Father and the Mother is greater than the potential energy of the StartChildren2 solution, this reaction can occur. The synthesis reaction is complete, and the next iteration is performed.
Step 10: Check and adjust the newly generated sequence of StartChildren2 to meet the constraints of precedence and conflict relationships.
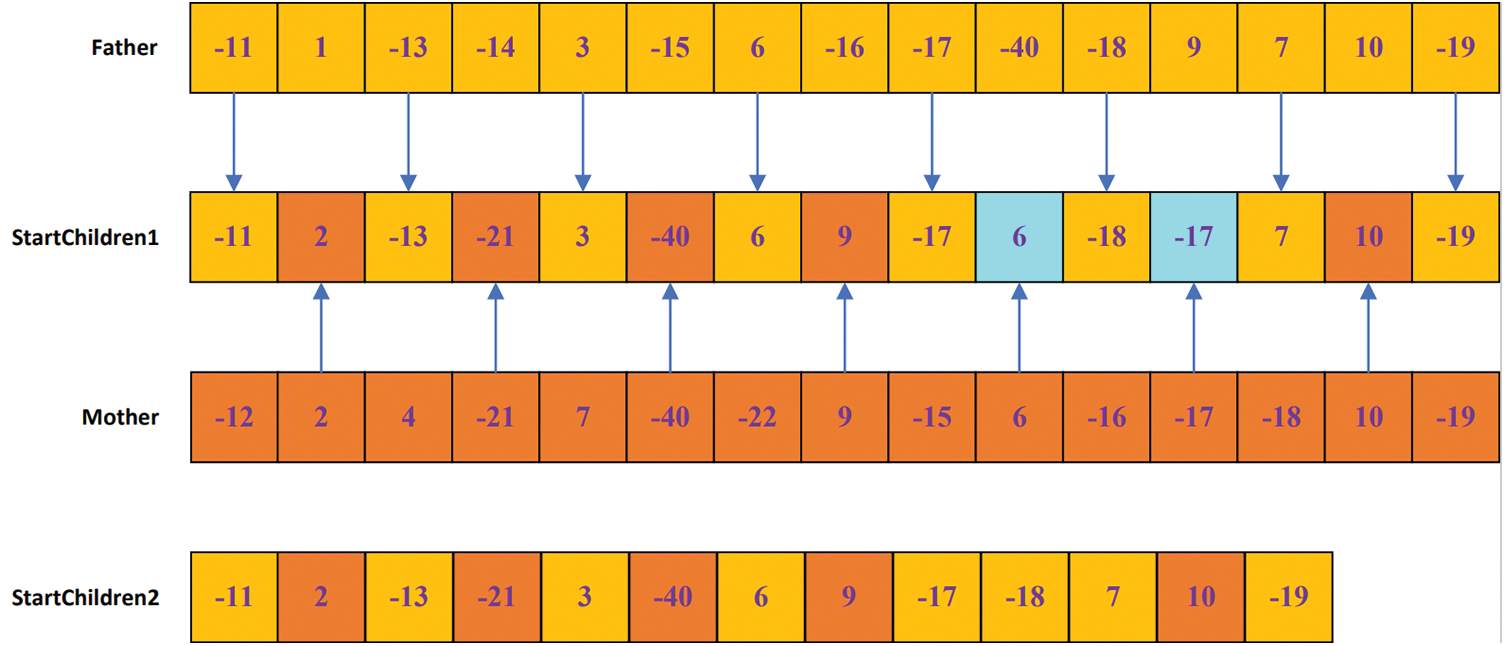
Figure 6: Synthesis reaction
3.4 Internal Molecule Invalid Collision Reaction Search Strategy
In this reaction, two or more molecules collide with each other without changing their structure. Here, two molecules are taken as examples, as shown in Figs. 7 and 8, and the steps are as follows:
Step 1: Randomly select two molecules from the population and judge whether these two molecules meet the threshold for synthesis. An ineffective internal molecular collision reaction will occur if they do not meet the conditions. At this time, the molecular collision times of each position (
Step 2: Give the molecule at
Step 3: Generate two random numbers
Step 4: Assign {−15, 1} and {10, −39, −41, −43, −42, 11, −22} in the Father to the corresponding position of the Child 1. The middle blue part of Child 1 is filled with 0.
Step 5: Traverse the Mother individual and add the elements not in Child 1 to the 0 part of Child 1. In Fig. 7, fill {−14, 3, −16, −17, −18} into the corresponding position of Child 1, and {−19, −30, 6} in Mother individual into the opposite end of Child 1.
Step 6: If the Mother does not complete the 0 in Child 1 in Step 5, the Father will be randomly selected from the middle of
Step 7: Give {−14, 1, 3} and {11, −22} in the Mother to Child 2, and fill the middle blue part of Child 2 with 0.
Step 8: Traverse the individual Father and add the elements not found in Child 2 to the 0 part of Child 2. As shown in Fig. 8, fill {−15, 6, −24, −27, −32, 10, −39, −41, −43} into the corresponding position of Child 2, and {−42} in the individual Father is added to the opposite end of Child 2.
Step 9: If the Father does not complete the 0 in Child 2 in Step 8, the Mother will be randomly selected from the middle of
Step 10: Check and adjust the newly generated sequence of Child 1 and Child 2 to meet the constraints of precedence and conflict relationships.
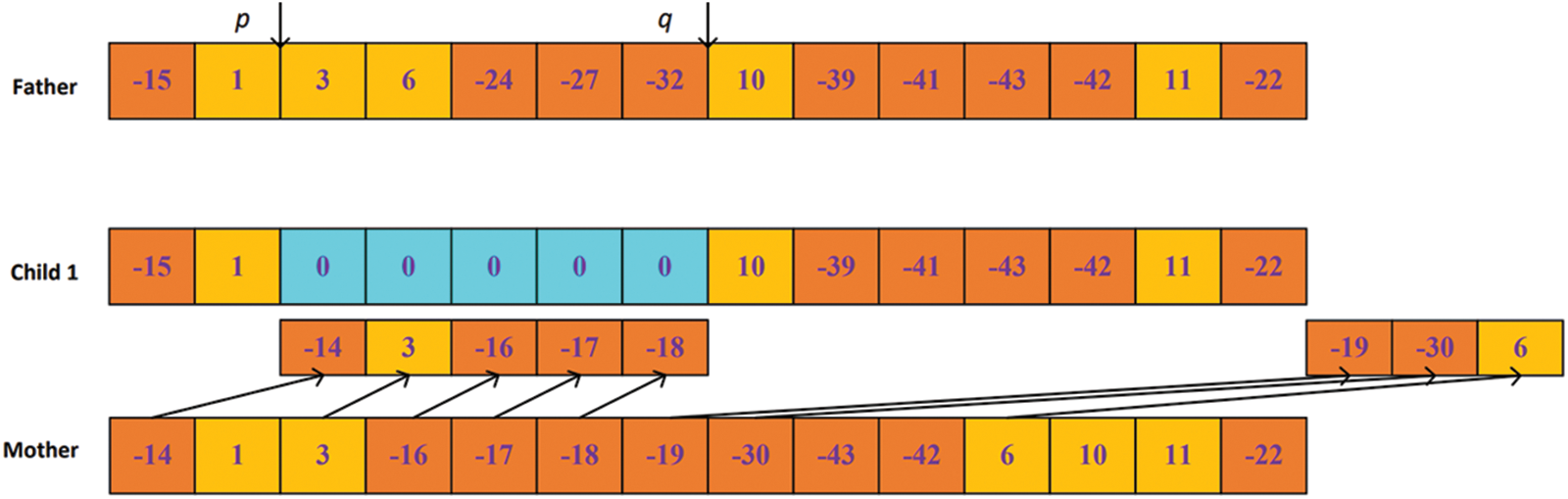
Figure 7: Example 1 of an internal molecular null collision reaction
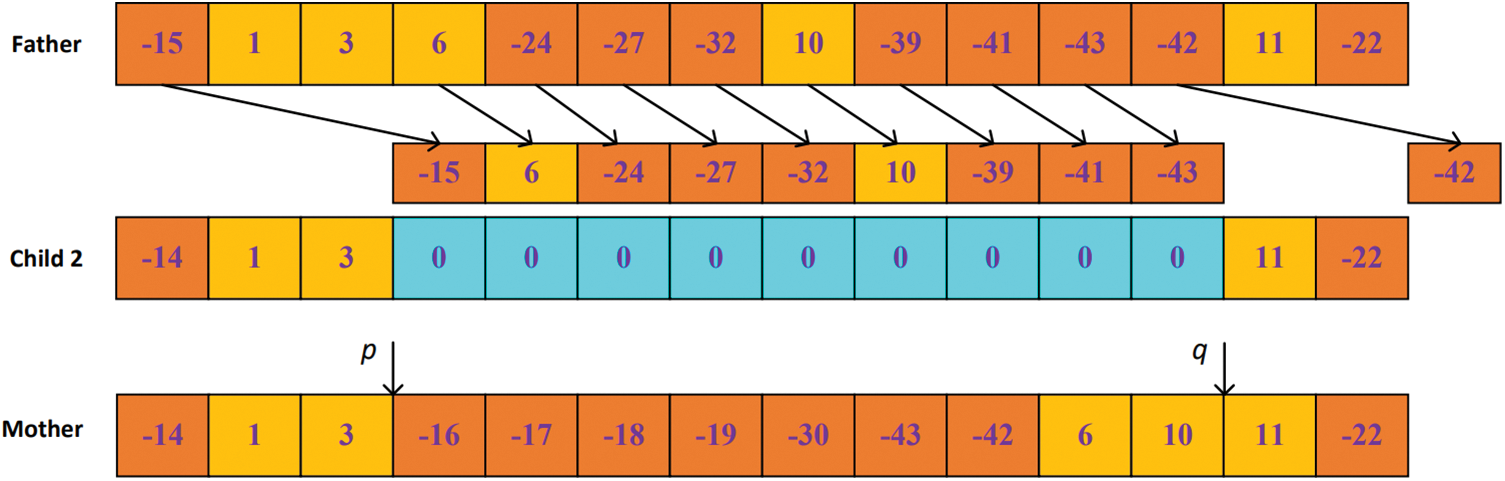
Figure 8: Example 2 of an internal molecular null collision reaction
3.5 On-Wall-Ineffective-Collision Reaction Search Strategy
The molecules hit the wall, and the structure of the molecule doesn’t change very much. This reaction is an example of a reaction in which one molecule forms another.
Step 1: As shown in Fig. 9, generate two random numbers
Step 2: If
Step 3: Swap the disassembly tasks at positions
Step 4: Check and adjust the disassembly sequence, turn it into a feasible solution, and calculate the objective function.
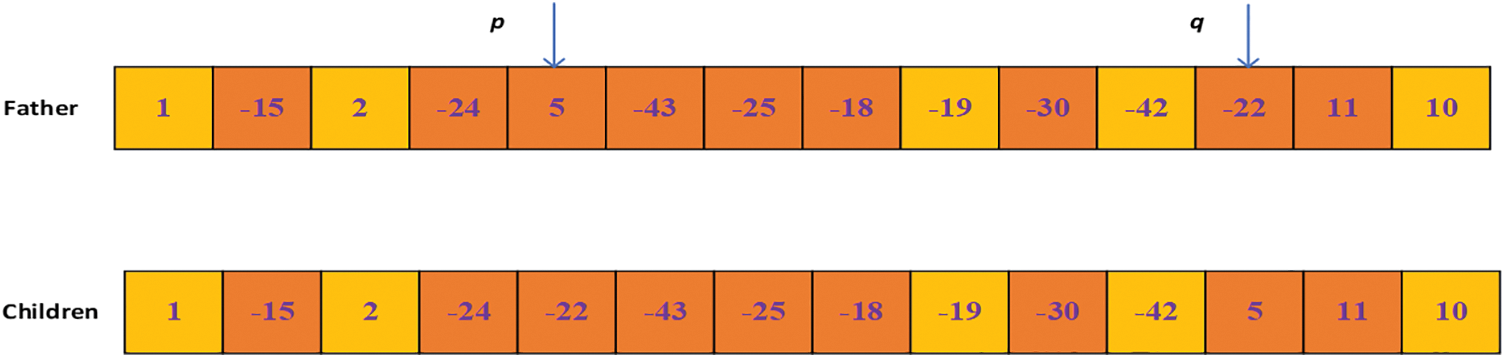
Figure 9: On-wall-ineffective-collision reaction
3.6 Decomposition Reaction Strategy
Decomposition reaction refers to the decomposition of one molecule into two or more molecules. The specific steps are shown in Fig. 10.
Step 1: The operation of new molecule 1 is: the loop starts from 0 and ends with the length/2 of the parent task sequence.
Step 2: Once a cycle, a random number will be generated. If the number is greater than 0.5, Step 3 will be repeated three times.
Step 3: Randomly generate a task. If the task is larger than 13, multiply by −1. If the task is not in the sequence, add it to the sequence.
Step 4: Perform Step 1 until the loop ends. The new individual is Children1.
Step 5: The operation of new molecule 2 is: the loop starts at length/2 of the parent task sequence and stops at the length of the parent task sequence.
Step 6: Once a cycle, a random number will be generated. If the number is greater than 0.5, Step 7 will be repeated three times.
Step 7: Randomly generate a task. If the task is larger than 13, multiply by −1. If the task is not in the sequence, add it to the sequence.
Step 8: Go to Step 5 until the loop ends. The new individual is Children2.
Step 9: Check and adjust the disassembly sequence, turn it into a feasible solution, and calculate the objective function.
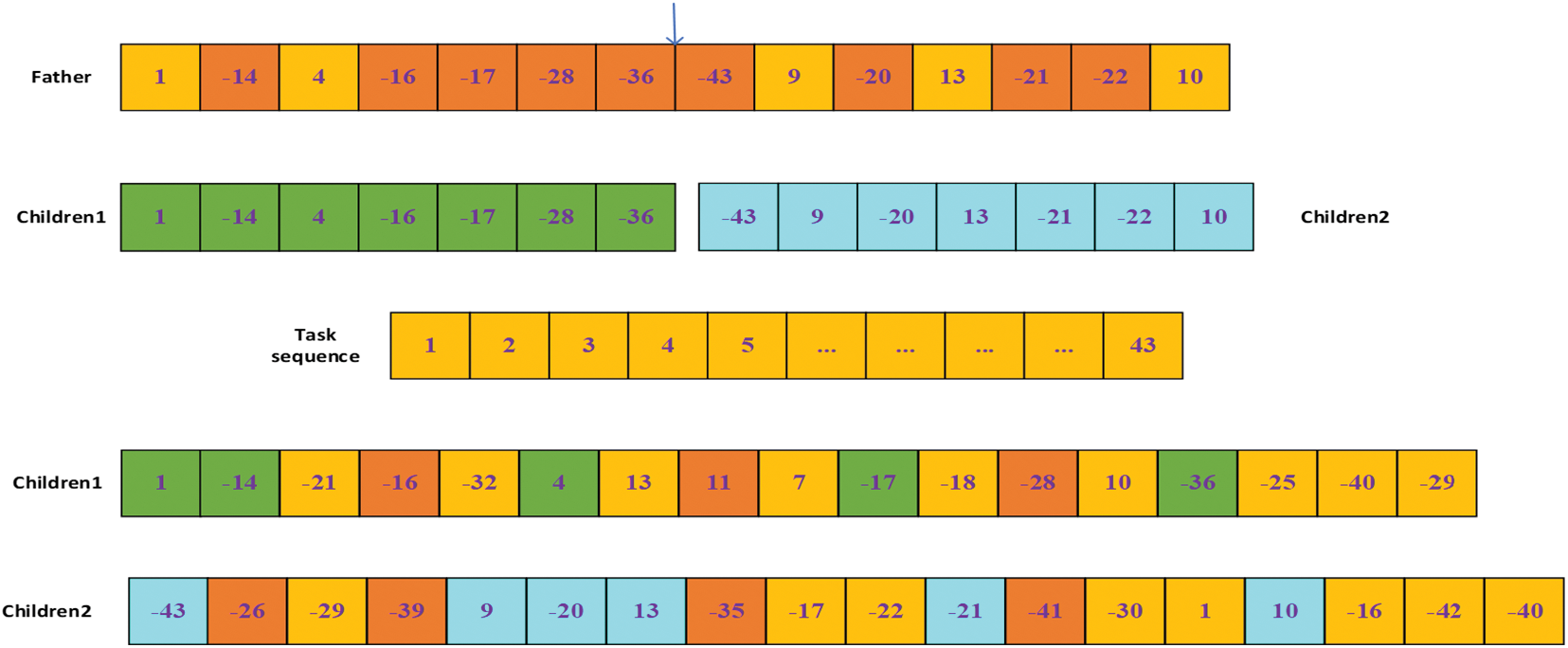
Figure 10: Decomposition reaction
In this paper, multi-product composed of a Ballpoint pen and radio (BR), flashlight and radio (FR), washing machine and radio (WR) are used as experimental cases to verify the feasibility of MDCRO in solving MPDMW, and NSGA-II, MOEA/D, NSGA-III and MOEAD-CRA are selected to solve MPDMW together to study the advantages and disadvantages of the five algorithms in solving this problem. The reason for choosing these metaheuristic methods lies in their unique strengths in multi-objective optimization. For instance, MOEA/D exhibits problem decomposition capabilities, MOEAD-CRA incorporates a control variable adjustment mechanism, NSGA-II utilizes non-dominated sorting and crowding distance calculation, and NSGA-III introduces layered non-dominated sorting. These characteristics contribute to effectively addressing the complex objectives and constraints of the problem. To ensure the accuracy and correctness of the experiment, all the algorithms are compared under the condition of complete fairness.
Among the experimental parameters, the molecular collision rate is set as 0.5, the synthesis threshold is 10, the energy loss rate is 0.3, the crossover rate of NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA
4.2 Model Validation and Analysis
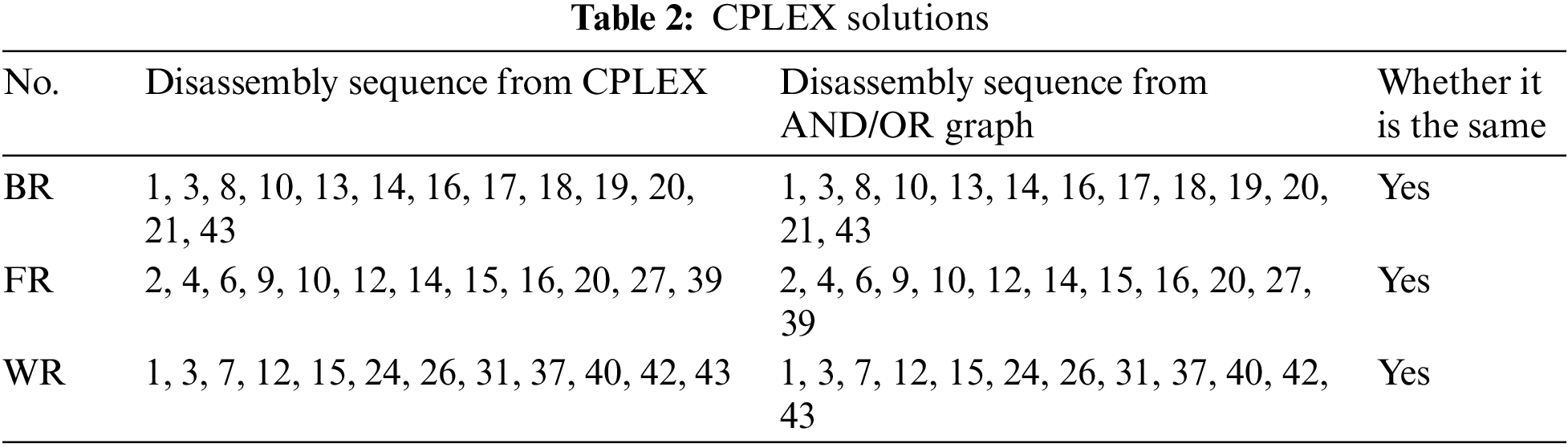
To verify the correctness of the model, the CPLEX solver is used for the first time to solve the established model. Since CPLEX does not support multi-objective optimization, only one objective can be optimized. Therefore, when verifying the model, the maximum profit is taken as the goal to solve. As can be seen from Table 2, comparing the sequence obtained by CPLEX solving BR, FR, AND WR with the AND/OR graph composed of actual cases, it can be seen whether the sequence is a feasible solution, thus verifying the correctness of the established model. To verify the feasibility and superiority of MDCRO, the algorithm is compared with NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA. The experimental results show that MDCRO is superior to the other four algorithms in solving MPDMW.
To analyze the performance of MDCRO in solving MPDMW compared with other algorithms, IGD-metric [34], Hypervolume-metric [35], and Epsilon-metric are used for comparison. Verification is done using the t-test. The t-test is a statistical method used to compare whether the means of two samples are significantly different. It assesses whether the difference in means between two samples is likely due to random factors or if it reflects a true difference in population means. When calculating the objective function, we try to find the maximization of profit and the minimization of workstation cycle time, so the value of the first objective function is multiplied by −1 to facilitate the comparison of results.
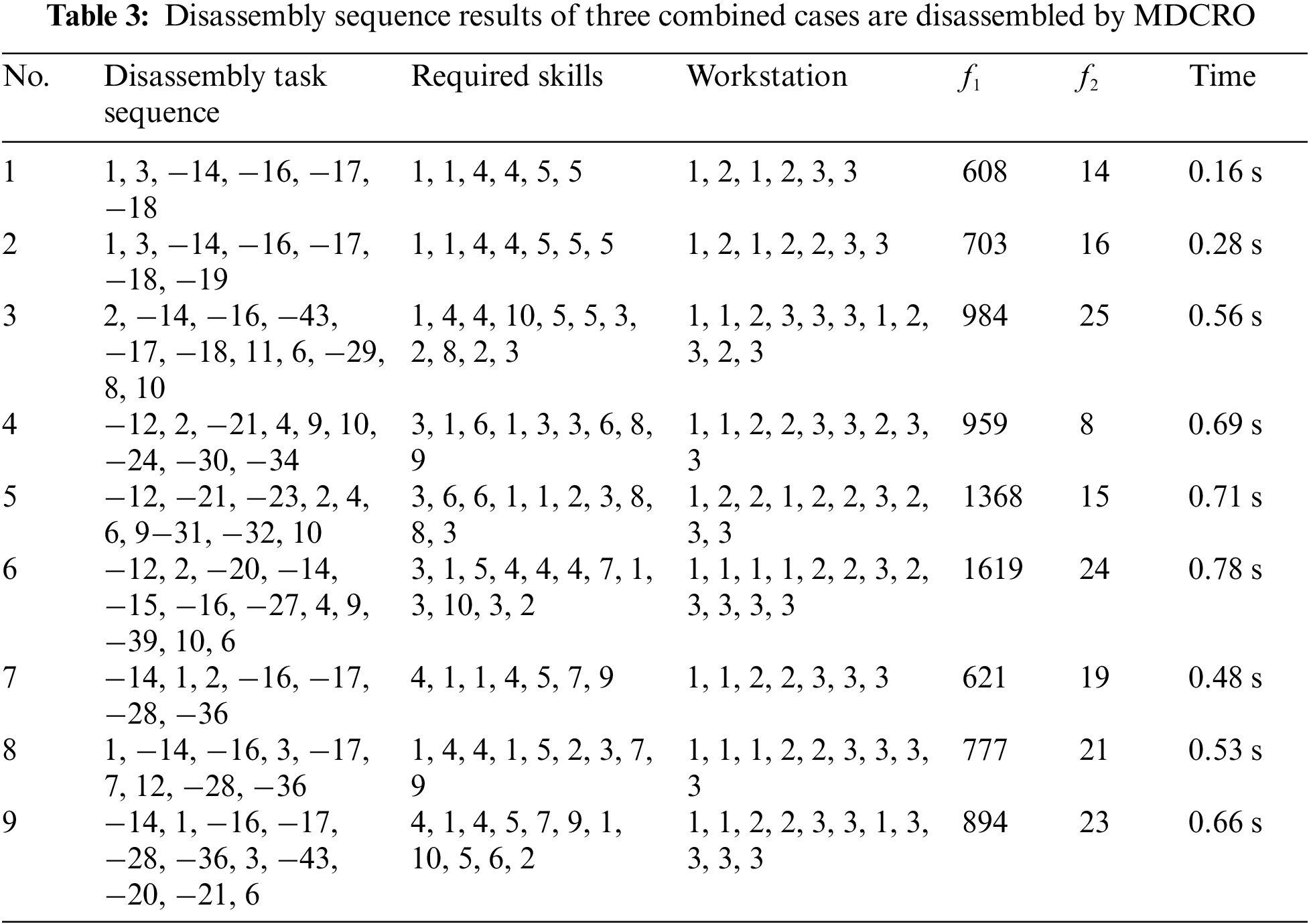
Through experiments, MDCRO can provide a feasible solution for MPDMW. Table 3 shows the nine non-dominated solutions obtained by MDCRO solving the above three combination cases. Among them, numbers 1–3 refer to the disassembly sequence obtained when BR is disassembled, numbers 4–6 refer to the disassembly sequence obtained when FR is disassembled, and numbers 7–9 refer to the disassembly sequence obtained when WR is disassembled. The disassembly sequence represents the sequence of feasible tasks for disassembling the above multi-product, and the required skills represent the skills required for disassembling the corresponding tasks. Workstation allocation represents the allocation of disassembly tasks between workstations, with
In order to conduct an in-depth study on the performance of MDCRO, this paper chooses NSGA-II, MOEA/D, NSGA-III, MOEAD-CRA, and MDCRO to conduct an in-depth study around MPDMW. For multi-product cases composed of BR, FR, and WR under the condition of the same implementation parameters, The performance gap of five algorithms under different population sizes is studied.
Table 4 shows the IGD index results obtained by the five algorithms when the population is 100, 200, and 300. The experimental results indicate that MDCRO’s IGD index significantly outperforms NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA in the three multi-product combination cases mentioned above. It’s only in the case of a population size of 200 that the disassembly of WR is not as effective as NSGA-III.
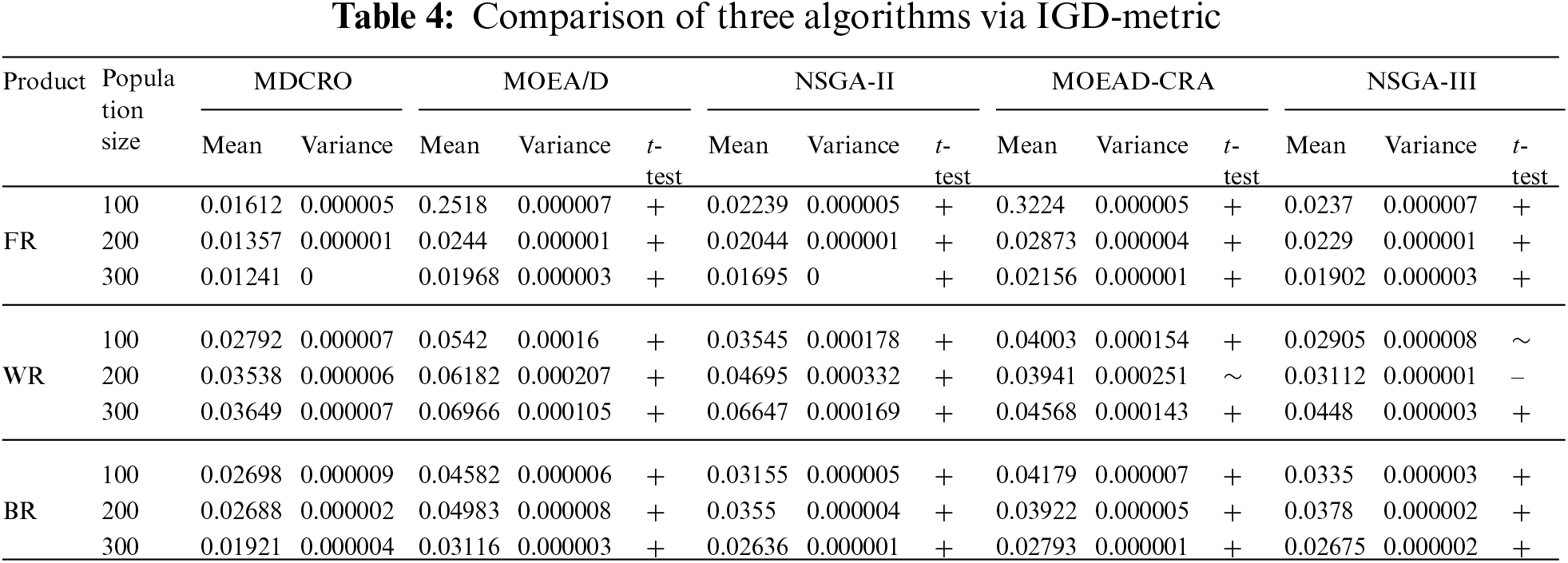
Table 5 shows the Hypervolume index obtained by five algorithms when the population is 100, 200, and 300 for analysis. The Hypervolume index can comprehensively evaluate the convergence and distribution of non-dominant solution sets. The experimental results show that the Hypervolume index of MDCRO is slightly lower than that of NSGA-II except when the product BR is disassembled and the population size is 100 and 200. The disassembly Hypervolume index of MDCRO of the above three combinations is significantly higher than that of NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA.
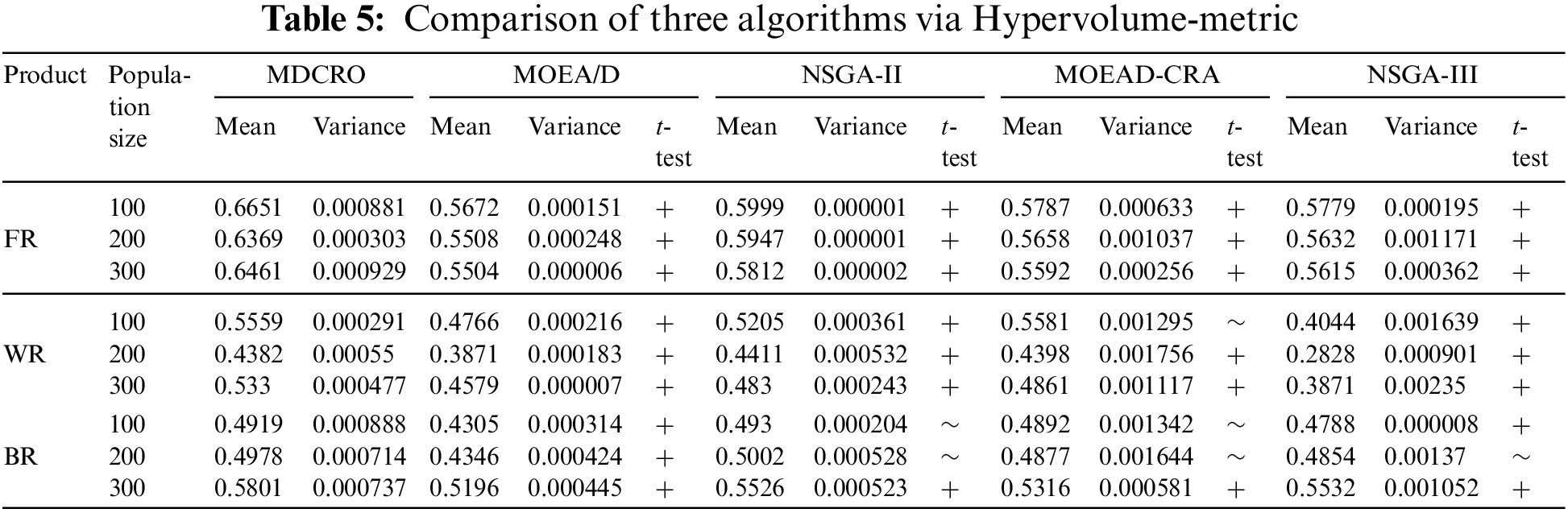
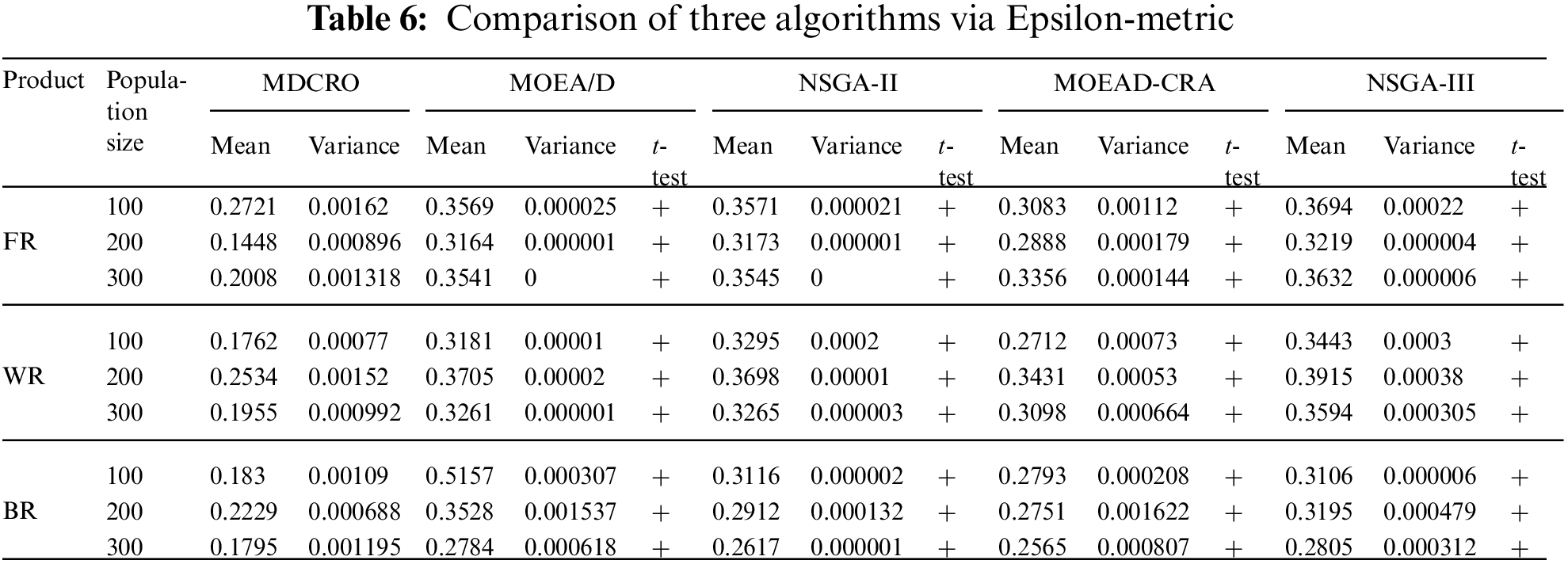
Table 6 provides the Epsilon index obtained by five algorithms for population sizes of 100, 200, and 300, along with the corresponding analysis. The Epsilon index can measure the approximation degree of the solution. According to the results of the Epsilon index, the disassembly values of the above three composite products by MDCRO are significantly lower than those of NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA.
In order to further verify the superiority of MDCRO in the processing of MPDMWS, the performance of MDCRO is shown by the box graph more intuitively. Fig. 11 shows MDCRO has a better Hypervolume-metric, IGD-metric, and Epsilon-metric when removing WR. Experimental results and analysis show that the MDCRO algorithm is superior to NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA in solving MPDMW.
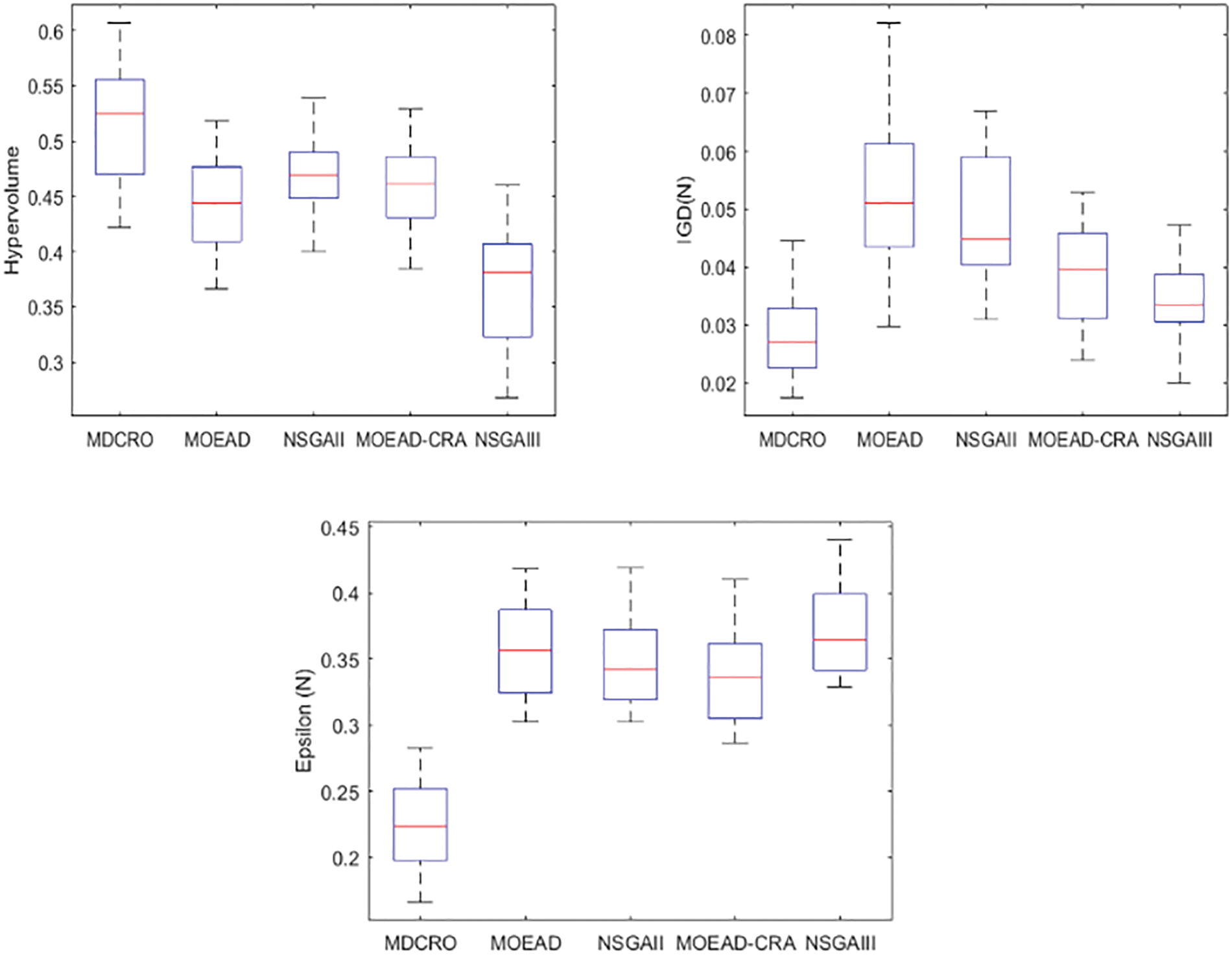
Figure 11: IGD-metric E-metric Hypervolume-metric compare boxplots of WR
As shown in Fig. 12, when the profit is less than 1500, there is little difference between the solutions of the five algorithms. However, when the profit reaches 1500, the feasible solution cannot be found by other algorithms at all. MDCRO can still find a feasible solution. The results show that MDCRO performs well in depth and breadth of solution. As a result, MDCRO has a broader distribution in solving MPDMW than NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA.
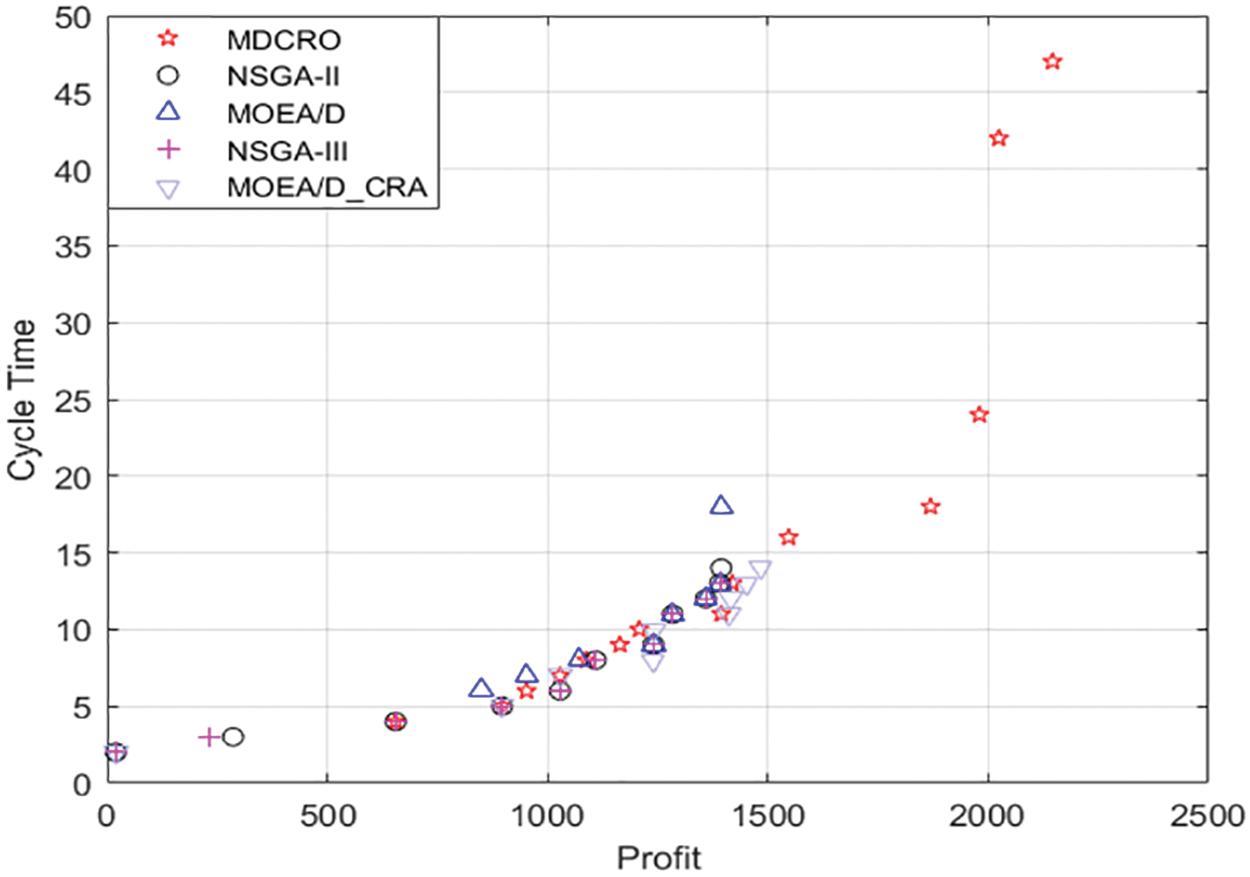
Figure 12: FR set disassembly result
This paper investigates MPDMW, introducing multi-skilled workers to dismantle EOL products. It proposes MPDMW, establishes the corresponding mathematical model, and presents mathematical models for maximizing disassembly profit and minimizing workstation cycle time. The MDCRO is designed to solve this problem. In MDCRO, a three-segment encoding structure represents the disassembly task. The corresponding encoding and decoding modes are designed, and the synthesis reaction, decomposition reaction, internal molecule invalid collision reaction, and wall invalid collision reaction are improved. The experimental results demonstrate the effective applicability of the model and algorithm for the efficient operation of parallel disassembly lines. The results show that MDCRO outperforms NSGA-II, MOEA/D, NSGA-III, and MOEAD-CRA, providing non-dominated solution sets.
In our future work, we plan to continue exploring different types of disassembly lines and combine additional optimization strategies [36,37] to enhance MDCRO for addressing multi-objective DLBP. Additionally, we will explore the application of reinforcement learning in solving such problems [38].
Acknowledgement: The authors gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Study conception and design: Xiwang Guo, Shujin Qin, Liang Qi; data collection: Zhiwei Zhang, Jinrui Cao; analysis and interpretation of results: Liangbo Zhou; draft manuscript preparation: Liangbo Zhou, Jiacun Wang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this article and are available from the corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. X. Guo et al., “Human–robot collaborative disassembly line balancing problem with stochastic operation time and a solution via multi-objective shuffled frog leaping algorithm,” IEEE Trans. Autom. Sci. Eng., vol. 21, no. 3, pp. 4448–4459, 2023. doi: 10.1109/TASE.2023.3296733. [Google Scholar] [CrossRef]
2. Y. Gao, Y. Feng, Q. Wang, H. Zheng, and J. Tan, “A multi-objective decision making approach for dealing with uncertainty in eol product recovery,” J. Clean. Prod., vol. 204, pp. 712–725, 2018. doi: 10.1016/j.jclepro.2018.09.080. [Google Scholar] [CrossRef]
3. A. Gungor, S. M. Gupta, K. Pochampally, and S. V. Kamarthi, “Complications in disassembly line balancing,” in Environ. Conscious Manuf., SPIE, 2001, vol. 4193, pp. 289–298. [Google Scholar]
4. Z. Zhang, K. Wang, L. Zhu, and Y. Wang, “A pareto improved artificial fish swarm algorithm for solving a multi-objective fuzzy disassembly line balancing problem,” Expert. Syst. Appl., vol. 86, pp. 165–176, 2017. doi: 10.1016/j.eswa.2017.05.053. [Google Scholar] [CrossRef]
5. S. Agrawal and M. Tiwari, “A collaborative ant colony algorithm to stochastic mixed-model u-shaped disassembly line balancing and sequencing problem,” Int. J. Prod. Res., vol. 46, no. 6, pp. 1405–1429, 2008. doi: 10.1080/00207540600943985. [Google Scholar] [CrossRef]
6. K. Wang, L. Gao, and X. Li, “A multi-objective algorithm for u-shaped disassembly line balancing with partial destructive mode,” Neural Comput. Appl., vol. 32, no. 16, pp. 12715–12736, 2020. doi: 10.1007/s00521-020-04721-0. [Google Scholar] [CrossRef]
7. M. L. Bentaha, O. Battaïa, and A. Dolgui, “Chance constrained programming model for stochastic profit-oriented disassembly, line balancing in the presence of hazardous parts,” in Adv. Prod. Manag. Syst. Sustain. Prod. Serv. Supply Chains: IFIP WG 5.7 Int. Conf., APMS 2013, State College, PA, USA, Springer, Sep. 9–12, 2013, pp. 103–110. [Google Scholar]
8. Z. Li, I. Kucukkoc, and Z. Zhang, “Iterated local search method and mathematical model for sequence-dependent U-shaped disassembly line balancing problem,” Comput. Ind. Eng., vol. 137, 2019, Art. no. 106056. doi: 10.1016/j.cie.2019.106056. [Google Scholar] [CrossRef]
9. S. Hezer and Y. Kara, “A network-based shortest route model for parallel disassembly line balancing problem,” Int. J. Prod. Res., vol. 53, no. 6, pp. 1849–1865, 2015. doi: 10.1080/00207543.2014.965348. [Google Scholar] [CrossRef]
10. S. W. Wang, G. X. Xu, and J. Liu, “Modeling and optimizing the two-sided disassembly line balancing problem of type II,” (in Chinese), Oper. Res. Manag. Sci., vol. 31, no. 8, pp. 51–56, 2022. [Google Scholar]
11. K. Wang, X. Li, and L. Gao, “Modeling and optimization of multi-objective partial disassembly line balancing problem considering hazard and profit,” J. Clean. Prod., vol. 211, no. 10, pp. 115–133, 2019. doi: 10.1016/j.jclepro.2018.11.114. [Google Scholar] [CrossRef]
12. T. Yin, Z. Zhang, Y. Zhang, T. Wu, and W. Liang, “Mixed-integer programming model and hybrid driving algorithm for multi-product partial disassembly line balancing problem with multi-robot workstations,” Robot. Comput. Integr. Manuf., vol. 73, 2022, Art. no. 102251. doi: 10.1016/j.rcim.2021.102251. [Google Scholar] [CrossRef]
13. X. Guo, Z. Zhang, L. Qi, S. Liu, Y. Tang and Z. Zhao, “Stochastic hybrid discrete grey wolf optimizer for multi-objective disassembly sequencing and line balancing planning in disassembling multiple products,” IEEE Trans. Autom. Sci. Eng., vol. 19, no. 3, pp. 1744–1756, 2021. doi: 10.1109/TASE.2021.3133601. [Google Scholar] [CrossRef]
14. B. Małachowski and P. Korytkowski, “Competence-based performance model of multi-skilled workers,” Comput. Ind. Eng., vol. 91, no. 5, pp. 165–177, 2016. doi: 10.1016/j.cie.2015.11.018. [Google Scholar] [CrossRef]
15. T. Ling, “Study on the training of multi-skilled workers in order to meet Chinese manufacturing 2025,” Res. Technol. Econ. Manag., vol. 6, pp. 30–35, 2016. [Google Scholar]
16. J. Lian, C. Liu, W. Li, and Y. Yin, “A multi-skilled worker assignment problem in seru production systems considering the worker heterogeneity,” Comput. Ind. Eng., vol. 118, no. 3, pp. 366–382, 2018. doi: 10.1016/j.cie.2018.02.035. [Google Scholar] [CrossRef]
17. L. Qi, Y. Su, M. Zhou, and A. Abusorrah, “A state-equation-based backward approach to a legal firing sequence existence problem in petri nets,” IEEE Trans. Syst. Man Cybern., Syst., vol. 53, no. 8, pp. 4968–4979, 2023. doi: 10.1109/TSMC.2023.3241101. [Google Scholar] [CrossRef]
18. D. Xiang, S. Lin, X. Wang, and G. Liu, “Checking missing-data errors in cyber-physical systems based on the merged process of petri nets,” IEEE Trans. Ind. Inform., vol. 19, no. 3, pp. 3047–3056, 2022. doi: 10.1109/TII.2022.3181669. [Google Scholar] [CrossRef]
19. S. Gao, M. Zhou, Y. Wang, J. Cheng, H. Yachi and J. Wang, “Dendritic neuron model with effective learning algorithms for classification, approximation, and prediction,” IEEE Trans. Neural Netw. Learn. Syst., vol. 30, no. 2, pp. 601–614, 2018. doi: 10.1109/TNNLS.2018.2846646. [Google Scholar] [PubMed] [CrossRef]
20. A. H. Khan, X. Cao, S. Li, V. N. Katsikis, and L. Liao, “BAS-ADAM: An ADAM based approach to improve the performance of beetle antennae search optimizer,” IEEE/CAA J. Autom. Sinica, vol. 7, no. 2, pp. 461–471, 2020. doi: 10.1109/JAS.2020.1003048. [Google Scholar] [CrossRef]
21. Z. Zhao, Q. Jiang, S. Liu, M. Zhou, X. Yang and X. Guo, “Energy, cost and job-tardiness-minimized scheduling of energy-intensive and high-cost industrial production systems,” Eng. Appl. Artif. Intell., vol. 133, no. 6, 2024, Art. no. 108477. doi: 10.1016/j.engappai.2024.108477. [Google Scholar] [CrossRef]
22. K. Wang, X. Li, L. Gao, P. Li, and S. M. Gupta, “A genetic simulated annealing algorithm for parallel partial disassembly line balancing problem,” Appl. Soft Comput., vol. 107, 2021, Art. no. 107404. doi: 10.1016/j.asoc.2021.107404. [Google Scholar] [CrossRef]
23. E. Özceylan, C. B. Kalayci, A. Güngör, and S. M. Gupta, “Disassembly line balancing problem: A review of the state of the art and future directions,” Int. J. Prod. Res., vol. 57, no. 15–16, pp. 4805–4827, 2019. doi: 10.1080/00207543.2018.1428775. [Google Scholar] [CrossRef]
24. Y. Fu, M. Zhou, X. Guo, L. Qi, and K. Sedraoui, “Multiverse optimization algorithm for stochastic biobjective disassembly sequence planning subject to operation failures,” IEEE Trans. Syst., Man, Cybern.: Syst., vol. 52, no. 2, pp. 1041–1051, 2021. doi: 10.1109/TSMC.2021.3049323. [Google Scholar] [CrossRef]
25. P. Liang, Y. Fu, K. Gao, and H. Sun, “An enhanced group teaching optimization algorithm for multi-product disassembly line balancing problems,” Complex Intell. Syst., vol. 8, no. 6, pp. 4497–4512, 2022. doi: 10.1007/s40747-021-00478-8. [Google Scholar] [CrossRef]
26. K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. Evol. Comput., vol. 6, no. 2, pp. 182–197, 2002. doi: 10.1109/4235.996017. [Google Scholar] [CrossRef]
27. Q. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Trans. Evol. Comput., vol. 11, no. 6, pp. 712–731, 2007. doi: 10.1109/TEVC.2007.892759. [Google Scholar] [CrossRef]
28. W. Wang, S. Dai, W. Zhao, and C. Wang, “Multi-objective optimization of hexahedral pyramid crash box using MOEA/D-DAE algorithm,” Appl. Soft Comput., vol. 118, 2022, Art. no. 108481. doi: 10.1016/j.asoc.2022.108481. [Google Scholar] [CrossRef]
29. Q. Kang, “A collaborative resource allocation strategy for decomposition-based multiobjective evolutionary algorithms,” IEEE Trans. Syst., vol. 49, no. 12, pp. 2416–2423, 2018. [Google Scholar]
30. A. Y. S. Lam and V. O. K. Li, “Chemical-reaction-inspired metaheuristic for optimization,” IEEE Trans. Evol. Comput., vol. 14, no. 3, pp. 381–399, 2010. doi: 10.1109/TEVC.2009.2033580. [Google Scholar] [CrossRef]
31. J. Xu, A. Y. Lam, and V. O. Li, “Chemical reaction optimization for task scheduling in grid computing,” IEEE Trans. Parallel Distrib. Syst., vol. 22, no. 10, pp. 1624–1631, 2011. doi: 10.1109/TPDS.2011.35. [Google Scholar] [CrossRef]
32. Y. Fu, M. Zhou, X. Guo, and L. Qi, “Artificial-molecule-based chemical reaction optimization for flow shop scheduling problem with deteriorating and learning effects,” IEEE Access, vol. 7, pp. 53429–53440, 2019. doi: 10.1109/ACCESS.2019.2911028. [Google Scholar] [CrossRef]
33. T. K. Truong, K. Li, and Y. Xu, “Chemical reaction optimization with greedy strategy for the 0–1 knapsack problem,” Appl. Soft Comput., vol. 13, no. 4, pp. 1774–1780, 2013. doi: 10.1016/j.asoc.2012.11.048. [Google Scholar] [CrossRef]
34. L. Allou, D. Zouache, K. Amroun, and A. Got, “A novel epsilon-dominance Harris Hawks optimizer for multi-objective optimization in engineering design problems,” Neural Comput. Appl., vol. 34, no. 19, pp. 17007–17036, 2022. doi: 10.1007/s00521-022-07352-9. [Google Scholar] [CrossRef]
35. H. Jiang, J. Yi, S. Chen, and X. Zhu, “A multi-objective algorithm for task scheduling and resource allocation in cloud-based disassembly,” J. Manuf. Syst., vol. 41, no. 4, pp. 239–255, 2016. doi: 10.1016/j.jmsy.2016.09.008. [Google Scholar] [CrossRef]
36. Z. Zhao, S. Liu, M. Zhou, and A. Abusorrah, “Dual-objective mixed integer linear program and memetic algorithm for an industrial group scheduling problem,” IEEE/CAA J. Autom. Sinica, vol. 8, no. 6, pp. 1199–1209, 2021. doi: 10.1109/JAS.2020.1003539. [Google Scholar] [CrossRef]
37. C. Xia and C. Li, “Property preservation of petri synthesis net based representation for embedded systems,” IEEE/CAA J. Autom. Sinica, vol. 8, no. 4, pp. 905–915, 2021. doi: 10.1109/JAS.2020.1003003. [Google Scholar] [CrossRef]
38. H. Li, K. Gao, P. -Y. Duan, J. -Q. Li, and L. Zhang, “An improved artificial bee colony algorithm with q-learning for solving permutation flow-shop scheduling problems,” IEEE Trans. Syst., Man, Cybern.: Syst., vol. 53, no. 5, pp. 2684–2693, 2022. doi: 10.1109/TSMC.2022.3219380. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools