PARE: Privacy-Preserving Data Reliability Evaluation for Spatial Crowdsourcing in Internet of Things

1  Introduction

The proliferation of intelligent, connected Internet of Things (IoT) devices brings convenience to people and facilitates data collection. This collected data can provide robust support for personalized services, urban sensing, and training models [1–5]. IoT is already relevant and plays an essential role in people’s lives. The number of IoT endpoint links in China reached over 6.2 billion, with a market size of over 3.5 trillion RMB in 2023 (www.askci.com, accessed on 26 February 2024). Therefore, studying spatial crowdsourcing (SC) data collection tasks in IoT is particularly significant and has become a popular research topic.

As depicted in Fig. 1, a general SC data collection system consists of three parts: task requesters (TRs), task workers (TWs), and the SC server. TRs post SC data collection tasks through the SC server. At the same time, TWs get paid to complete tasks utilizing powerful IoT devices. However, TWs submit data containing private information about themselves, such as location, health indicators, etc. TWs may be reluctant to participate in SC data collection tasks due to concerns about disclosing sensitive information. On the other hand, TRs are also concerned about the authenticity and accuracy of the data submitted by TWs and certainly do not want to pay for inaccurate data. In addition to the reliability of the SC server, the concerns of TRs and TWs are a vital issue constraining the development of SC in IoT. Consequently, a reasonable system needs features that protect TWs’ privacy and evaluate the data quality. In general, a privacy-preserving data reliability evaluation system faces the following challenges.

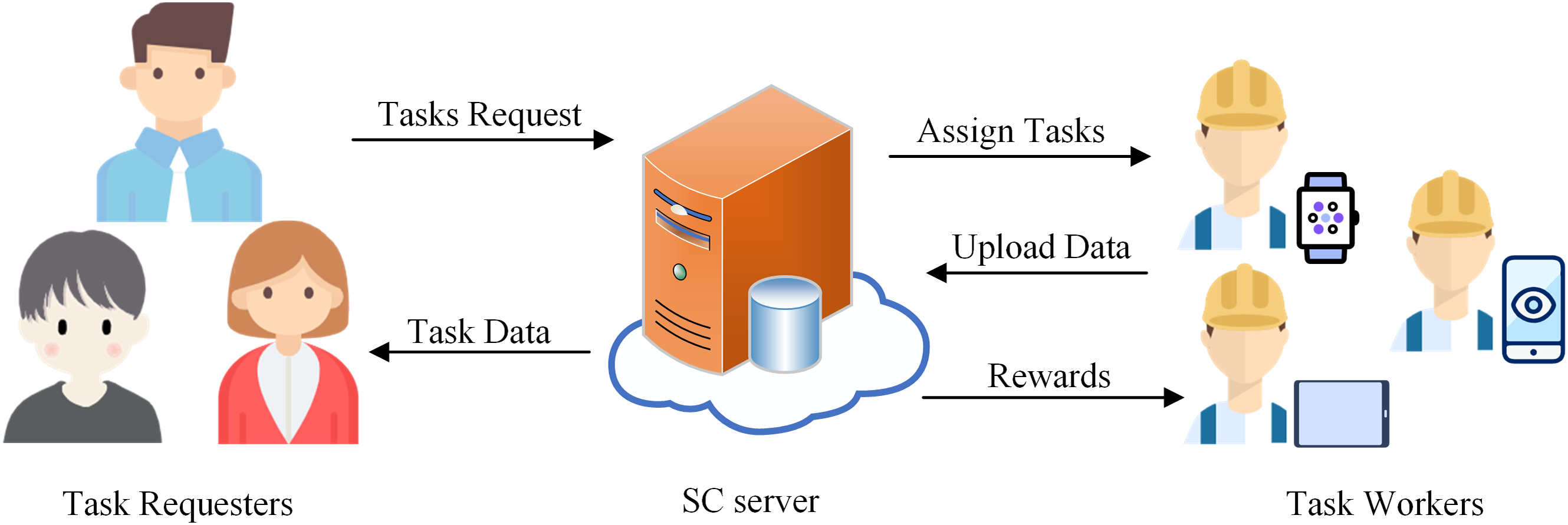
Figure 1: General SC data collection system

Challenge 1: Data Privacy and Security. When collecting data for SC tasks, it is vital to ensure the privacy and security of the data before exchanging it for rewards because such data is typically associated with the privacy and interests of TWs. TWs strongly desire to prevent their private information from leaking and secure their data from anyone until obtaining rewards. Furthermore, only the TR can access the data after payment. This approach prevents data leakage and the possibility of TRs cancelling or terminating the task and refusing to pay if they obtain the data content in advance. Methods based on credit [6], pseudonym [7,8], anonymity [9–11], and blockchain [12–16] have been proposed to address privacy-preserving problems. However, most of these methods do not consider the needs of TRs. TRs also vigorously desire to validate data before paying the reward to prevent TWs from cheating on the payment by submitting false data. Therefore, it is essential to have verifiable and traceable data without revealing sensitive information to meet the needs of TRs and TWs. The differing requirements of TRs and TWs create a conflict between data validity verification and data security. Hence, having a verifiable and traceable data storage and transmission format without revealing sensitive information is challenging and essential during the task process.

Challenge 2: Screening Criteria with Privacy-Preserving. The determination of screening criteria represents a pivotal procedure in assessing data quality. The efficacy of the screening criteria directly correlates with the quality of the screened data. Typically, the screening criteria are derived from the analysis of uploaded data. Specifically, the detection criteria can be developed by aggregating the uploaded data. Correct data originate from measuring the same or similar object, thus tending to cluster around a specific value. Conversely, erroneous data will deviate from this value by a considerable margin. In plaintext data, these aggregated areas are clearly observable. However, TWs’ uploaded data should be processed to protect their privacy. The processed data have been distorted, making it challenging to distinguish them from erroneous data, affecting the accuracy of the screening criteria. So, presetting screening criteria without relying on uploaded data was proposed [17]. However, presetting criteria relies heavily on historical data and defeats the original purpose of collecting data. Furthermore, TWs are concerned that TRs may obtain data under the guise of verifying it without paying for it. Consequently, they are unwilling to provide even the vaguest data for TRs to utilize. Instead, they prefer that the data be encrypted or rendered unknowable to complete the standard setting. The TWs’ concerns regarding the privacy and security of the data make determining screening criteria a challenging problem.

Challenge 3: Data Filtering with Privacy-Preserving. The data filtering process can be achieved by comparing the original data in its unencrypted form, provided the relevant filtering criteria have been established. However, in light of the need to safeguard the data, TWs would prefer to complete the validation process without disclosing their data, which makes screening data challenging. Data privacy protection solutions for TWs typically involve disturbing [18–20] or encrypting [21–23] their data. These treatments of data make data screening difficult, particularly as disturbing data results in a change in the data size. This alteration in size can result in data at the boundary of the filter entering or falling out of the filter range, making it impossible to infer whether the original data is within the filter interval. In the case of encrypted data, it is necessary to design a reasonable security protocol. The protocol can ensure that the data transmitted and processed during the screening process is not leaked.

To address the above challenges, we propose a privacy-preserving data reliability evaluation for SC data collection tasks called PARE. PARE guarantees the privacy, integrity, and non-repudiation of data uploaded by TWs through the blockchain-empowered Paillier homomorphic upload mechanism. Furthermore, utilizing the Paillier homomorphic cryptosystem, PARE can determine assessment criteria and assess the data without knowing it. Our contributions are threefold as follows:

1)   We propose a blockchain and Paillier-based data structure for uploading and storing data. This structure protects the privacy and security of TWs’ data. It supports data validation and traceability after completing the data collection task.

2)   We present a method for determining screening criteria for privacy data. The method can select reasonable data for the screening criteria without knowing the exact value.

3)   We propose a screening protocol for privacy data. The protocol enables the screening of privacy data without knowing its precise value, thereby ensuring the data’s security during the screening process.

The rest of this paper is organized as follows. Section 2 introduces the related work. Section 3 describes the system model, threat model, Design goals, and Preliminaries. We introduce the details of PARE in Section 4. Section 5 analyzes the security of PARE. Section 6 demonstrates the performance of PARE through theoretical and experimental analyses. Finally, we conclude this paper in Section 7.

2  Related Work

In this section, we briefly review related work regarding privacy protection and data reliability based on the different concerns of TWs and TRs.

2.1 Privacy-Preserving Technologies in Data Collection Tasks

TWs are the main participants in data collection tasks. Whether the privacy of their information is protected affects their willingness to participate in data collection tasks. As a result, several schemes have been proposed to protect data privacy, such as pseudonyms, anonymity, and perturbance. Yang et al. [10] proposed a way to collect and anonymize data without a trusted third party. Razak et al. [7] addressed data privacy leakage and proposes biometric authentication and pseudonym creation techniques to protect data from data storage and access rights. Tan et al. [8] proposed a degree of anonymity to assess the level of privacy protection. However, the purpose of pseudonyms and anonymity only interrupt the connection between the data and the owner and do not treat the data protectively.

Wang et al. [11] combined k-anonymity and ε-differential privacy preservation techniques to propose a two-stage auction algorithm based on trust and privacy sensitivity to protect TWs’ privacy. Differential privacy preservation is a method of preprocessing data to achieve privacy preservation. Because differential privacy protection requires the addition of noise to achieve protection, this has the potential to reduce the usability of the collected data. So, it is usually used to process location information that is not very sensitive to accuracy [18,19]. Ma et al. [20] realized this problem and proposed a stochastic perturbation method to purify the dataset, where the perturbations come from the remaining samples in the same dataset. These methods do protect the TWs’ privacy to a certain extent. However, they do not consider the security of the data. In a data collection mission, data is an asset that must be protected from easy access.

Consequently, many encryption methods [17,21–23] have been proposed to protect users’ privacy. In order to render the encrypted information usable, all of these methods employ homomorphic encryption in conjunction with the design of a set of secure computational protocols. These methods protect the data but make data quality verification very difficult.

2.2 Data Quality-Assured Methods in Data Collection Tasks

TRs are publishers of data collection tasks. They focus on the reliability of the collected data, which also affects their willingness to issue tasks. Therefore, the study on safeguarding data quality is another research point.

Incentive mechanisms serve to motivate TWs to provide high-quality data. Li et al. [6] proposed a credit-based privacy-preserving incentive scheme whereby TWs earn credit points by uploading data. Peng et al. [24] proposed data quality-based incentives that reward TWs based on their performance and contribution. Yang et al. [25] introduced long-term reputation while considering data quality and filters anomalous data with outlier detection techniques. Alsheikh et al. [26] identified a contradiction between data and privacy levels and proposes a profit maximization model. Blockchain technology is also employed in data quality assurance methodologies because it can guarantee the traceability and integrity of data. Nguyen et al. [12] provided complete protected data using blockchain. Moreover, based on this, an ant colony optimization algorithm is proposed for secure and reliable IoT data sharing. Li et al. [13] considered the transaction problem of anonymized data arising from the collection of TWs’ data by the SC server and uses deniable ring signatures with Monroe Coin to solve the transaction dispute problem of data sharing under anonymity. Zhang et al. [14] proposed an efficient and privacy-preserving blockchain-based incentive scheme for quality awareness by designing smart contracts, matrix decomposition, and proxy re-encryption techniques. The above methods do not consider validating data quality while protecting TWs’ privacy or only consider judging data reliability based on TWs’ credit. Zhao et al. [17] proposed a zero-knowledge model for data reliability assessment, which can validate data while protecting privacy without disclosing data. However, this data reliability assessment requires a preset detection range. Hence, it is still necessary to design a method to validate data that protects user privacy and does not disclose data.

3  Problem Formulation and Preliminaries

3.1 System Model

As depicted in Fig. 2, our system has a Key Generation Center (KGC), a TR, TWs, and a SC server. KGC is a trusted organization that generates and distributes public and private keys. TR publishes data collection tasks and is willing to pay for valid data. TWs want to get paid to collect data. SC server is a platform for connecting and protecting TWs and TR. It matches the tasks initiated by TR with suitable TWs. Also, it ensures that TW gets paid and TR gets the available data. In particular, the general flow of a SC data collection task is described below, with implementation detailed in Section 4.

1)   Distribute key: KGC generates public and private keys and distributes them to TR, TWs, and the SC server if needed.

2)   Task requests and rewards: A TR sends the task requests and rewards to the SC server.

3)   Assign task: The SC server broadcasts or publishes the task requests and value of rewards to recruit TWs.

4)   Upload data: TWs collect and upload data to the SC server according to the task requirements.

5)   Data filtering: The SC server completes data filtering with the help of TR.

6)   Transmit data and rewards: The SC server transmits data to TR and rewards to TWs, respectively.

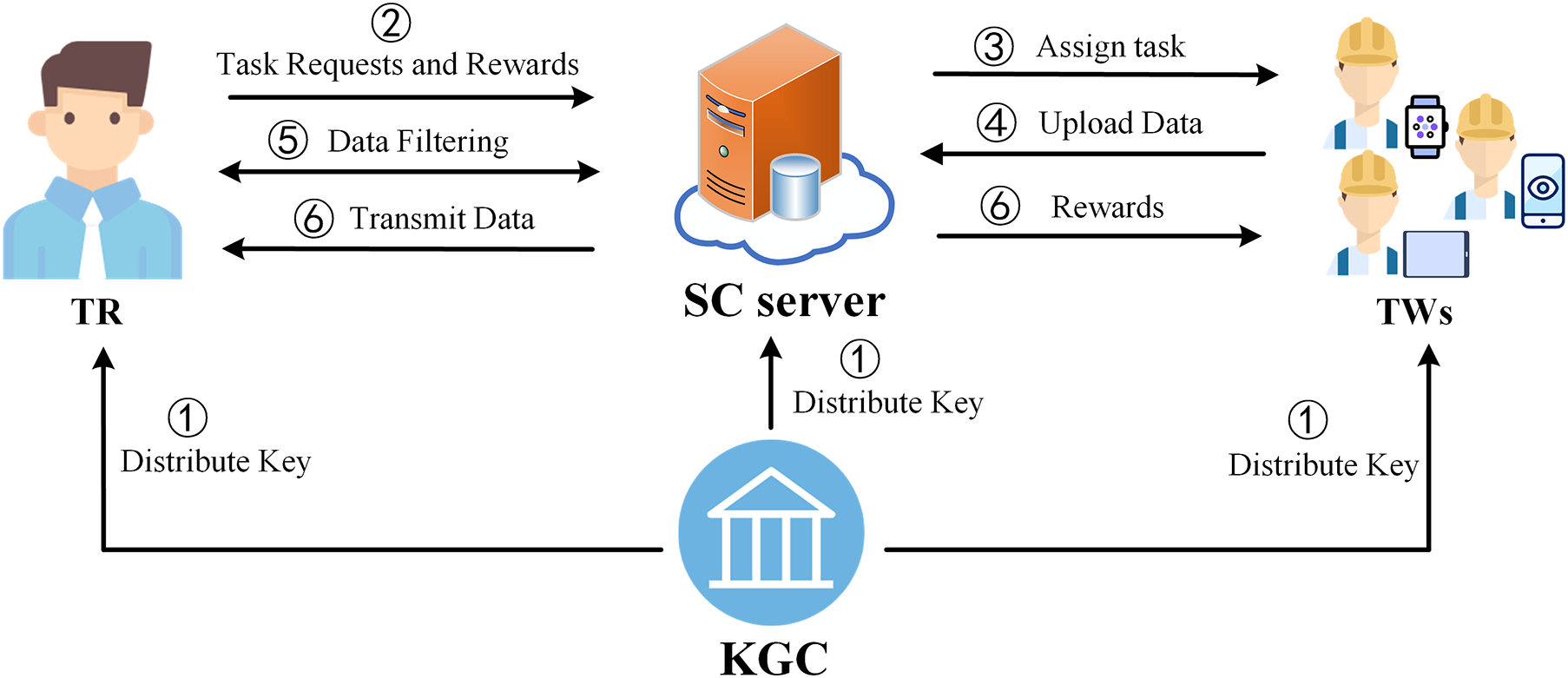
Figure 2: System model of PARE

3.2 Threat Model and Design Goals

In our system, the SC server is semi-honest, just like [17,21,27]. The SC server executes commands as required by the protocol. However, it is also curious about the data and tries to get its contents. Moreover, TRs and TWs are untrusted. So, in PARE, threats come from three primary sources: TRs, TWs, and the SC server. The threats are described in detail below.

SC server is where the data uploaded by TWs is stored and filtered. While storing and filtering data, the SC server will try to obtain the data content.

TWs upload collection data to earn a payment. Collecting this data requires proximity to the acquisition target and the appropriate collection device. However, some TWs will upload fictitious data to get paid.

TRs are data purchasers. However, it is first necessary to ensure that TRs will pay for the data when acquired. Secondly, TRs must be unable to access the data content throughout the filtering process. To prevent them from finding an excuse to refuse payment after obtaining the data.

Considering the above threats, some design goals are below:

Privacy. The information submitted by TWs contains much personal information. It should be ensured that the information is kept private throughout the process until it receives payment, and only TR gets that information.

Verifiability. While protecting privacy, TWs upload information that can be verified as true or false. Some TWs will upload actual data, while others want to upload fictitious data to get rewarded. We need to identify fictitious data while protecting the privacy of actual data.

Non-repudiation. TWs cannot deny the data they uploaded. If falsified data is detected, TWs who uploaded that data cannot deny their uploading behaviour and uploaded data.

3.3 Preliminaries

Paillier cryptosystem [28] is a homomorphic cryptosystem used for cipher operations, which contains additive homomorphism and scalar-multiplicative homomorphism properties. The specific implementation and properties are described below:

Key Generation: Let p and q be randomly independent of large prime numbers. Calculate N=pq and λ=lcm(p−1, q−1), and select random integer g where g∈ZN2∗, and then compute μ=(L(gλmodN2))−1modN, where the function L is defined as L(x)=x−1N. pk=(g, N) and sk=(λ, μ) are the public key and private key.

Encryption: Given a message m∈ZN to be encrypted, it is encrypted by the public key pk to 𝒞=⟦m⟧pk=gm⋅rNmodN2, where r is a selected random integer r∈ZN∗.

Decryption: Given a ciphertext to be decrypted, it is decrypted by the private key sk to m=Dsk(𝒞)=L(𝒞λmodN2)⋅μmodN.

The additive homomorphism and scalar-multiplicative homomorphism properties are listed as follows where x, y∈ZN and encrypted by the same pk.

⟦x⟧pk⋅⟦y⟧pk=⟦x+y⟧pk(1)

⟦x⟧pky=⟦x⋅y⟧pk(2)

4  Design of PARE

In this section, we describe the details of PARE’s implementation of data filtering without knowing the values of the collected data. Firstly, we introduce an overview of PARE. Secondly, we address a data format that is private, verifiable, and traceable during upload and storage. Finally, based on this format, we describe the methodology for determining data screening criteria and the data screening process.

4.1 Overview of PARE

The system model previously described has provided an initial understanding of PARE. This section will describe the main program flow. Furthermore, as illustrated in Fig. 3, a data collection example will demonstrate the data transfer process and the issues that must be addressed afterward.

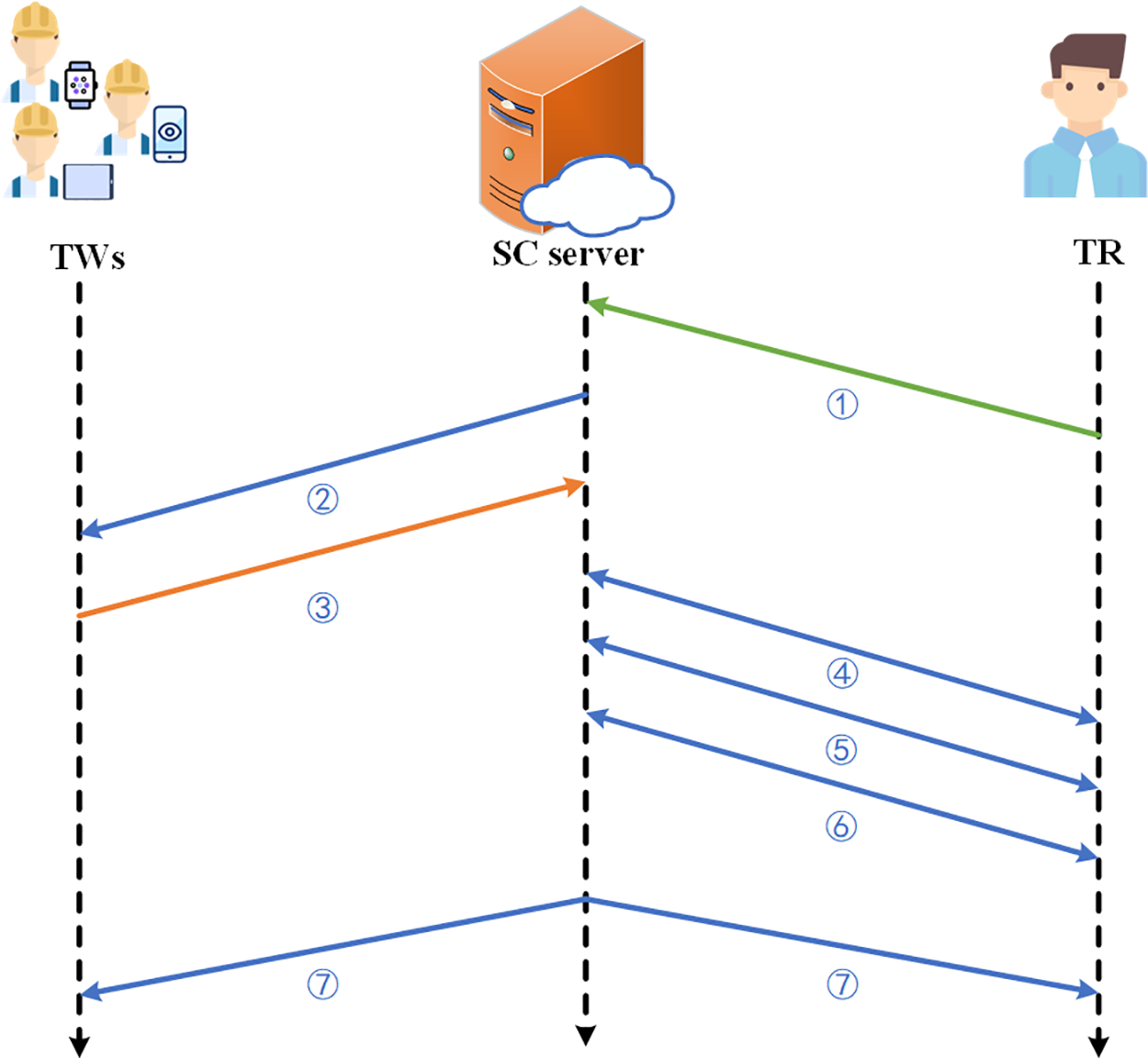
Figure 3: Scheme process of PARE

① A TR requests a public-private key pair (pkR, skR) from KGC and sets up the task requirements Tr, data requirements Dr, and rewards R. Then upload the {pkR, Tr, Dr, R} to the SC server. Then, the SC server builds the blockchain header based on the task information uploaded by TR, creates the task ID, and publishes the task.

② Interested TWs download this information from the SC server.

③ After completing the data collection task, TWs use the pkR to encrypt the collected data and the required data elements item by item ⟦data⟧={⟦time⟧,⟦lng⟧,⟦lat⟧,⟦data1⟧,⟦data2⟧,…}, calculate the packed ciphertext’s hash value H(⟦data⟧), and upload the hash value with TW’s signature and ciphertext data ⟦data⟧ to the SC server to wait for verification.

④ The SC server uploads the encrypted data hash H(⟦data⟧) to the blockchain after verification based on the order in which TWs upload the data. After completing the data collection, the SC server determines the correct data to calculate the data screening criteria with the help of TR. Subsection 4.3 details this data selection process and rationale.

⑤ Based on the selected data, the SC server calculates the screen criteria. Subsection 4.4 describes in detail the process of calculating the screening criteria.

⑥ The SC server completes the data evaluation based on the screening criteria with the support of TR. Subsection 4.4 describes this approach.

⑦ The SC server rewards TWs passed data validation and sends the TR the validated data.

4.2 Data Upload and Store Mechanism

In the data collection task, the security and reliability of the data during transmission and storage are paramount. In particular, the data format must align with the objectives of data confidentiality and verifiability throughout the process. To address this issue, we propose a data upload model that balances privacy with reliability by combining consortium blockchain and Paillier cryptosystem. Blockchain technology utilizes the hash function and digital signature to ensure traceability and data integrity, providing reliable data. Using Paillier’s ciphertext computability can simultaneously guarantee the confidentiality of data and facilitate subsequent data verification.

As illustrated in Fig. 4, the blockchain header on the SC server is constructed based on the task information uploaded by the TR. The header includes the TR’s task information and the TR’s signature for this information. The TW, who is willing to complete the task, encrypts the data using the TR’s public key after completing the task. Each piece of data is encrypted based on the level of granularity required for validation or computation, such as time, longitude, latitude, temperature, humidity, or other factors. Subsequently, the TW calculates and signs the entire encrypted packet’s hash value. He then uploads the hash value of the packet and his signature to the SC server. The SC server verifies that the hash value and signature are correct based on the uploaded encrypted message. If correct, it uploads the hash value and TW’s signature to the blockchain. In the meantime, the specific encrypted data is stored on the SC server and is not made public.

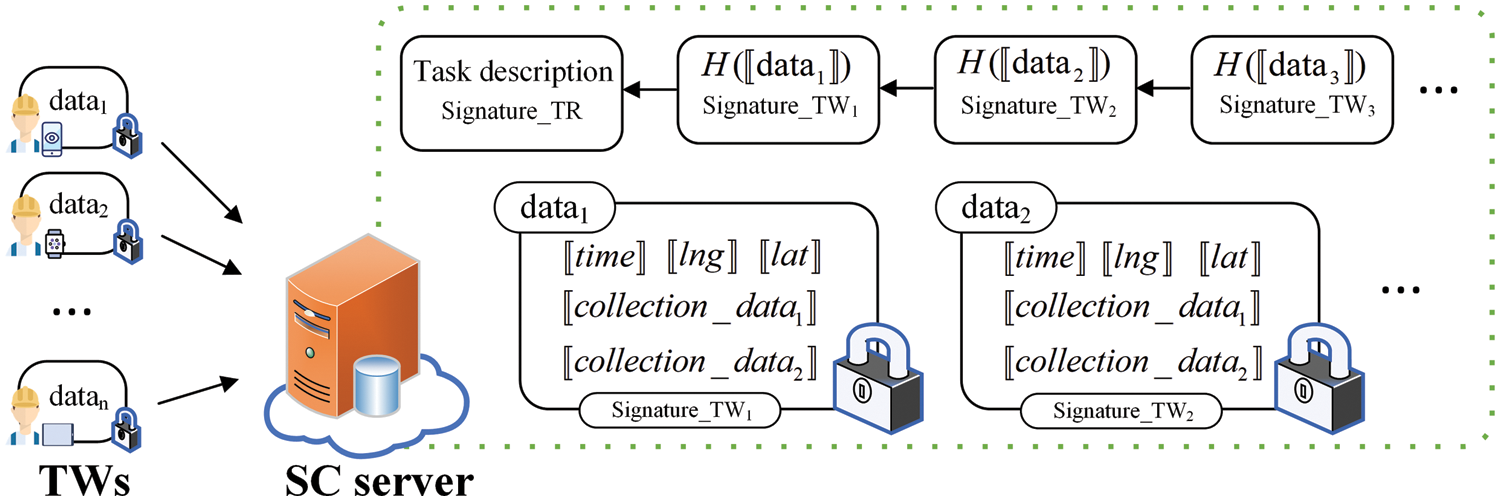
Figure 4: Data upload and store format

This method of data upload addresses privacy concerns while ensuring data non-repudiation. On the one hand, task descriptions that do not reveal private information are signed by TR before being uploaded to the SC server, thus ensuring non-repudiation of task requirements. On the other hand, the data collected by TWs is encrypted and stored on the SC server. As the encrypted data is not public, the SC server only has the ciphertext, and the TR only has the private key, so neither can get the data content. In turn, disclosing encrypted data hashes and signatures facilitates the inspection and identification of data in subsequent data transfers.

4.3 Determination of Data Screening Criteria

Once encrypted data collection has been completed, a challenging question arises: how can these encrypted data be evaluated? Specifically, this problem is to develop a judgment standard based on the collected encrypted data. Since the data is a record of measurements of the same object or a class of similar objects, these correct measurements should be clustered around a point or within a minimal interval. According to the law of large numbers and the central limit theorem, they should obey the Gaussian distribution approximately when enough data is collected.

As shown in Fig. 5, for values obeying the same distribution, the probability of being within one times the variance of the mean is 0.683, the probability of being within twice the variance of the mean is 0.954, and the probability of being within three times the variance of the mean is 0.997. Therefore, we can complete data screening based on mean and variance.

Figure 5: Gaussian distribution

Nevertheless, in the case of encryption, it becomes difficult to distinguish when correctly measured data is mixed with the wrong data. We illustrate this with an example of temperature collection. {15, 16, 28, 15, 14, 15, 16, 15, 32, 15} is a set of collected temperature data. Under plaintext, we can easily conclude that {28, 32} is the wrong data. By choosing {15, 16, 15, 14, 15, 16, 15, 15}, we can quickly get the mean to be 15.125 and the variance to be 0.36. Under ciphertext, we do not know the exact value. So, we can only choose the whole set to calculate. The mean value obtained is 18.1, and the variance is 36.49. It is evident that the selection of erroneous data will result in a significant shift in the mean and variance.

Since each value is unknowable in encrypted data, we cannot intuitively choose the correct data to calculate the mean and variance. Therefore, we need to face two challenges. One is how to select the correct data. The other one is calculating the mean and variance based on these correct data without revealing them.

Although the exact value of the data in the ciphertext is unknown, the size relationship between the values can be obtained by comparison. Given the considerations above, we propose a correct data selection idea. We sort the encrypted data items to be examined from smallest to largest. Due to the centralized nature of the correct data, they will be distributed centrally at a specific location in that queue. As illustrated in Fig. 6, the square section represents the correct data, while the grid represents the incorrect data. The two extreme cases are represented by a and b. In case a, the incorrect data are all smaller than the correct data. In case b, the incorrect data are all larger than the correct data. Combining these two extreme cases shows that when the correct data is greater than 50%, the overlap in the middle must be the correct data. For this reason, we need to ensure the overall quality of the data received by screening and validating the IP address and the task location.

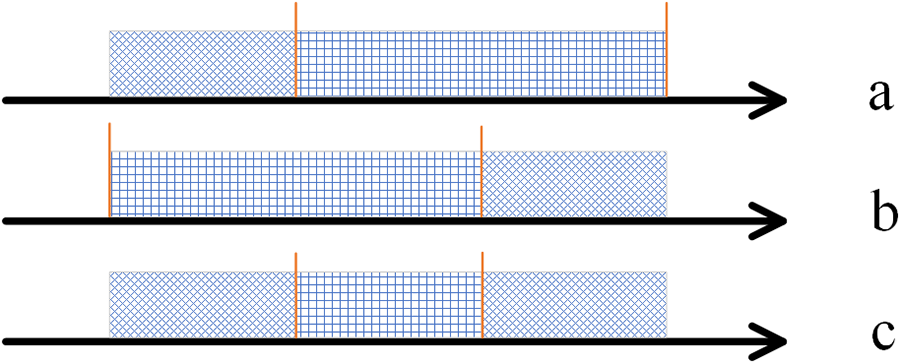
Figure 6: Ordered queue possibility

In order to get a queue of encrypted data sorted from smallest to largest, we design Privacy-Preserving Comparison (PPC) and Shortcut Sorting (SS) methods. In PPC, let ⟦x⟧ and ⟦y⟧ be two ciphertexts to be compared at the SC server. R is a random integer ranging from 1 to 128. The SC server randomly calculates ⟦x⟧−R⋅⟦y⟧R or ⟦x⟧R⋅⟦y⟧−R. When calculating ⟦x⟧−R⋅⟦y⟧R, it means that ⟦R(y−x)⟧. When calculating ⟦x⟧R⋅⟦y⟧−R, it means that ⟦R(x−y)⟧. Let A be a random large integer, and both x and y are much smaller than it. The SC server initially transmits the value of A to the TR. Subsequently, it transmits ⟦x⟧−R⋅⟦y⟧R⋅⟦A⟧ or ⟦x⟧R⋅⟦y⟧−R⋅⟦A⟧ to the TR. The TR receives the data, decrypts them, and then compares the size of the received number with A. If it is greater than A, it returns 1; if it is less than A, it returns −1; if it is equal to A, it returns 0. The SC server can get the size relationship between the x and y based on the return value and the previously randomly selected format.

With the help of TR and PPC, the SC server can get an ordered queue of encrypted data. The time consumption of moving the encrypted data is trivial compared to the time consumption of comparing the encrypted data. Therefore, we want to get ordered queues with as few comparisons as possible. Due to the asynchronous nature of TWs completion task, the SC server can sort the data uploaded earlier and insert the data received later into that ordered queue. In other words, the SC server can get the ordered sequence by comparing the two data once it receives them. Then, depending on the order of the received data, the SS algorithm is used repeatedly until the whole ordered sequence is obtained.

4.4 Process of Data Screening

Based on the work in Section 4.3, we can obtain the correct data sequence; let the correct data sequence be {x1, x2, x3,..., xn}. Denoting the Paillier encryption of x as ⟦x⟧, for this sequence, the mean X¯ is calculated as follows:

[[∑i=1nXi]]=∏i=1n[[Xi]]=[[nX¯]](3)

X¯=1n∑i=1nXi=1nD(⟦nX¯⟧)(4)

In order to obtain the mean value of this set of sequences, we need the TR to help decrypt ⟦nX¯⟧. We devise a dynamic perturbation (DP) method to prevent the leak of the mean value in the process. We add a random perturbation factor ci to each corresponding xi. In order to make the degree of perturbation large enough, the range of ci is an integer from 1 to 1024. This value range can also vary according to the measurements.

M=[[X1+C1]]⋅[[X2+C2]]⋅…⋅[[Xn+Cn]]=∏i=1n[[Xi]]⋅[[∑j=1nCj]](5)

The SC server calculates M based on Eq. (5) and sends it to the TR. The TR decrypts the value, encrypts it with the SC server’s public key, and sends it back. After receiving the data, the SC server subtracts the perturbation data ∑j=1nCj to find the mean value X¯. The following section discusses the safety of this perturbation method in detail. Based on the mean, the SC server can calculate the variance using the following equation:

[[(n−1)σX2]]=∏i=1n[[(Xi−X¯)2]]=∏i=1n([[Xi2]]⋅[[X¯2]]⋅[[Xi]]−2X¯)(6)

σX2=1n−1∑i=1n(Xi−X¯)2=1n−1D(⟦(n−1)σX2⟧)(7)

In Eq. (4), the mean value X¯ of the sequence may yield decimals due to the division involved. In order to satisfy Paillier’s requirement, we align the mean value towards the data item, i.e., after determining the exact number of decimal places, we zoom in on it to make it an integer. The mean value X¯ can be considered a constant in server-side calculations. Therefore, all parameters in Eq. (6) can be obtained without compromising privacy. [[X¯2]] is an encryption of the mean square by the TR’s public key; ⟦Xi2 ⟧ can be uploaded by the TW in advance; ⟦Xi⟧−2X¯ can be calculated from ⟦Xi⟧ previously uploaded by the TW. Hence, the ciphertext variance can then be derived based on Eq. (6). Similar to before, after perturbing it using Eq. (5), the variance can be obtained with the TR’s help using Eq. (7).

After obtaining the mean and variance, we can use PPC to determine whether the values fall within the interval [X¯−3σX2, X¯+3σX2]. Based on the Central Limit Theorem, the probability that data belonging to the same distribution fall within this interval is 99.7%. Based on this, we consider the data falling within this interval valid and can be rewarded for the task.

5  Security Analysis

This section analyses the security of protocols and algorithms in PARE, including data format, PPC, DP, and PARE system security.

Theorem 1. The data uploaded by TWs in PARE is secure, verifiable, and traceable as long as the Paillier cryptosystem is secure.

Proof. TWs encrypt the data item with the TR’s public key and then upload them to the SC server for storage. The SC server stores the ciphertext, which is encrypted using Paillier and inaccessible to the public. Therefore, only the SC server can crack the ciphertext. Consequently, if the Paillier cryptosystem is secure, the SC server cannot access the ciphertext content without TR’s private key. Consequently, the uploaded encrypted data storage is secure.

TWs transmit the encrypted data, along with the signature of the hash of that encrypted data, to the SC server. If the Paillier cryptosystem is secure, the signature of the TW is unforgeable. Subsequently, the SC server can verify the data with the TWs’ public key when data has been received. After the exchange of data and rewards is complete, the TR can also verify the data received with the hash value recorded on the blockchain. The record on the blockchain can also be used as a basis for traceability. Consequently, the data is verifiable and traceable.

Theorem 2. The PPC and DP methods in PARE are secure as long as the Paillier cryptosystem is secure.

Proof. The security of the PPC and DP methods is consistent with the security of the ciphertext operation equation, ⟦A+B⟧=⟦C⟧. The SC server calculates the ciphertext ⟦A+B⟧ and passes the resultant ciphertext ⟦C⟧ after perturbation to the TR, who decrypts ⟦C⟧ and shares the content with the SC server. If Paillier is secure, the TR and SC server can only get the value of C. A+B=C can be viewed as a binary equation with an infinite number of solutions, i.e., the values of A and B cannot be inferred from C. Therefore, the PPC and DP methods are safe.

Furthermore, for TR, he gets a set of size relations and perturbated mean and variance. With the previous corollary, TR cannot infer the mean and variance before perturbation. For the TR wishing to collect data, obtaining the size relations and distortion data with perturbation is meaningless. The SC server can obtain the no perturbated mean and variance, and whether this will harm the system will be discussed in Theorem 3.

Theorem 3. The PARE system remains secure even if the SC server obtains the size relation, mean, and variance.

Proof. We discuss this in two parts. When passing a size relation, the SC server only receives the value representing the size relation. It does not have access to the specific difference between the two data. If Paillier is secure, the SC server cannot access information other than this size relation. When passing the mean and variance, since the SC server adds the perturbations, it can easily remove them, i.e., obtain D([[∑i=1nXi]]) and D([[∑i=1n(Xi−X¯)2]]). However, the SC server is insufficient to find every Xi because this is equivalent to an n-membered equation with infinite solutions. However, the SC server can indeed forge data that fulfills the requirements based on this information. However, the data submission record already exists on the blockchain. There is no way for the SC server to modify the blockchain to add this forged data. Therefore, even if the SC server can access this information, the PARE system is still secure.

6  Performance Analysis

In this section, we first describe our experimental environment and the dataset. Then, we show the computation overhead in PARE. Finally, we analyze the performance of our scheme in comparison with similar research schemes.

6.1 Dataset and Experiment Setting

Dataset. To evaluate the performance of PARE, we used a real dataset published online by the CRAWDAD Team, CROWD_TEMPERATURE [29]. CROWD_TEMPERATURE is outdoor temperature data collected by taxis in Rome, Italy. The dataset contains 5030 records, each with Taxi ID, Date, Time, Latitude, Longitude, and Temperature. We simulate a data collection task to capture the temperature of Roman Street (12.365308–12.627256 E and 41.7902–41.9951 N) at 15:00–18:00 on 14th January. We take 100 data from the dataset as the correct data. In our experiment, for these 100 data, the latitude and longitude records were set as the collection location, the temperature records were considered the collected temperature, and the time records were considered the collection time. In this case, the latitude and longitude are accurate to 1 metre (5 decimal places), the temperature is accurate to 0.01°C, and the time is accurate to 1 s. We have scaled them all to integers to satisfy the program and converted the time to seconds.

Configuration. In order to evaluate the efficacy and efficiency of PARE, we implemented the PARE scheme in Java. The experimental machine is a personal computer (PC) with a Core i7 CPU (1.80 GHz) and a smartphone with Kirin 990 CPU and 8 GB RAM. We used the mobile phone to simulate TR and TWs and the PC to simulate the SC server.

6.2 Computational Overhead Evaluation

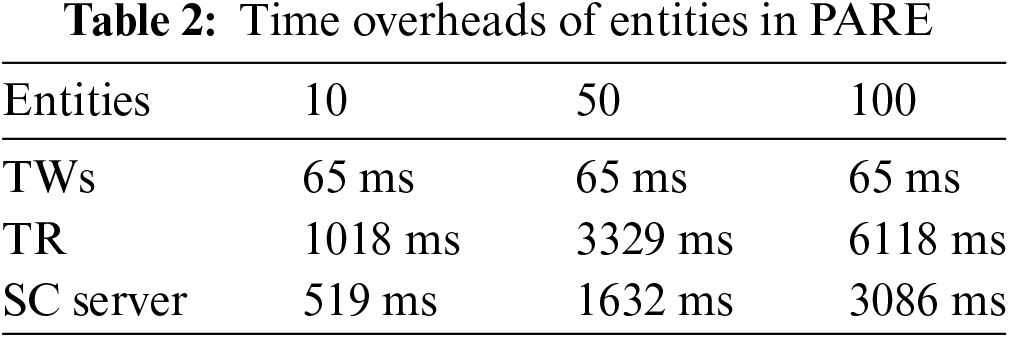
We theoretically analyze the computational overhead of the TR, TWs, and SC server from a protocol design perspective. TPE represents the time spent in pallier encryption. TPD represents the time spent in pallier decryption. The time consumption for exponentiation, multiplication, division, comparison, and hash are denoted as exp, mul, div, comp, and hash, respectively. The number of encrypted minimum data units per TW is m, the total number of TWs is n, and the number of TWs selected to compute the mean and variance is t. TWs need to compute the ciphertext of each minimum data unit, the ciphertext packet hash, and the hash’s encryption. So, the computational overhead per TW is (m+1)⋅TPE+1⋅hash.

In the process of mean and variance, for n data size ordering, the SC server needs to compare ∑i=2n[log⁡i] times, and TR needs to decrypt ∑i=2n[log⁡i] times per data unit. Afterward, based on this ordered sequence, the SC server’s overhead to compute mean is (t+1)⋅mul+1⋅TPD+1⋅sub+1⋅div+1⋅TPE, and the computational overhead of TR is 1⋅TPD+1⋅TPE. The computational overhead of the SC server to compute the variance is t⋅(4⋅mul+1⋅exp+1⋅TPE)+1⋅mul+1⋅sub+1⋅div+1⋅TPE+1⋅TPD and the computational overhead of TR is 1⋅TPD+1⋅TPE.

Finally, the remaining n-t data need to be filtered, with each data compared no more than two times per data unit. The computational overhead of the SC server is 2⋅mul+2⋅exp+2⋅(n−t)comp and the computational overhead of TR is 2⋅(n−t)⋅TPD. So, in the PARE scheme, the computational overheads of TR, TW, and the SC server are shown in Table 1. We take 80% correctness, i.e., the selected number of data in the ordered queue from 20% to 80%, to test the actual time overhead of PARE. As shown in Table 2, we test 10, 50, 100 pieces of data.

6.3 Performance Evaluation

In order to assess the effectiveness and accuracy of PARE, we define two metrics: a correctness rate and a false selection rate. The correctness rate, denoted by CR, is the probability that the correct data is selected. The false selection rate, denoted by FSR, is the probability that the wrong data is selected.

CR=number of correct data selectednumber of correct data×100%(8)

FSR=number of error data selectednumber of error data×100%(9)

The larger the value of CR, the smaller the probability of correct data being missed. The objective is to select as much correct data as possible while avoiding including a significant number of erroneous data points. The FSR indicator indicates the probability of erroneous data being selected in this model. A lower probability value is indicative of an effective screening effect.

Among the 100 correct data previously selected, we extracted 90, 80, 70, 60 data respectively and generated random error data to make up 100. In order to evaluate the screening effect of PARE, we select PACE [17] and Randm as the control group. PACE filters data based on intervals, which are defined as ranges of 100 correct data points. Both PARE and Randm screen the data to determine whether the data falls within [X¯−3σX2, X¯+3σX2]. Unlike PARE’s sorting and selecting the data for calculation, Randm selects data randomly to calculate the mean and variance.

As shown in Figs. 7 and 8, the experiment is repeated 100 times. The corresponding CR and FSR will be calculated, and their average values will be taken. PACE, constrained by the limitations of the dataset, selects 100 data boundaries of the day as its filtering criteria. This setting makes PACE the optimal filtering scheme, as it is backcasting the criteria through the results. In the real world, given that historical data can only be used as a reference, the actual data is bound to be biased, resulting in inferior outcomes. It can be observed that all three schemes exhibit high CR when the correctness of the filtered data is high. However, as the correctness of the data decreases, so does their CR. PACE is devoid of any effect among the schemes above, given that it is optimal. PARE has a data selection mechanism that reduces its impact. However, the Randm is randomly selected. As the data correctness rate decreases, the probability of it selecting the incorrect data to formulate the filtering criteria increases, resulting in a corresponding decrease in the CR. Similarly, since the Randm lacks data selection criteria, it exhibits a high rate of FSR, which decreases as the data correctness rate increases. In contrast, PARE and PACE maintain a very low rate of FSR.

Figure 7: CR with different rates of correct data

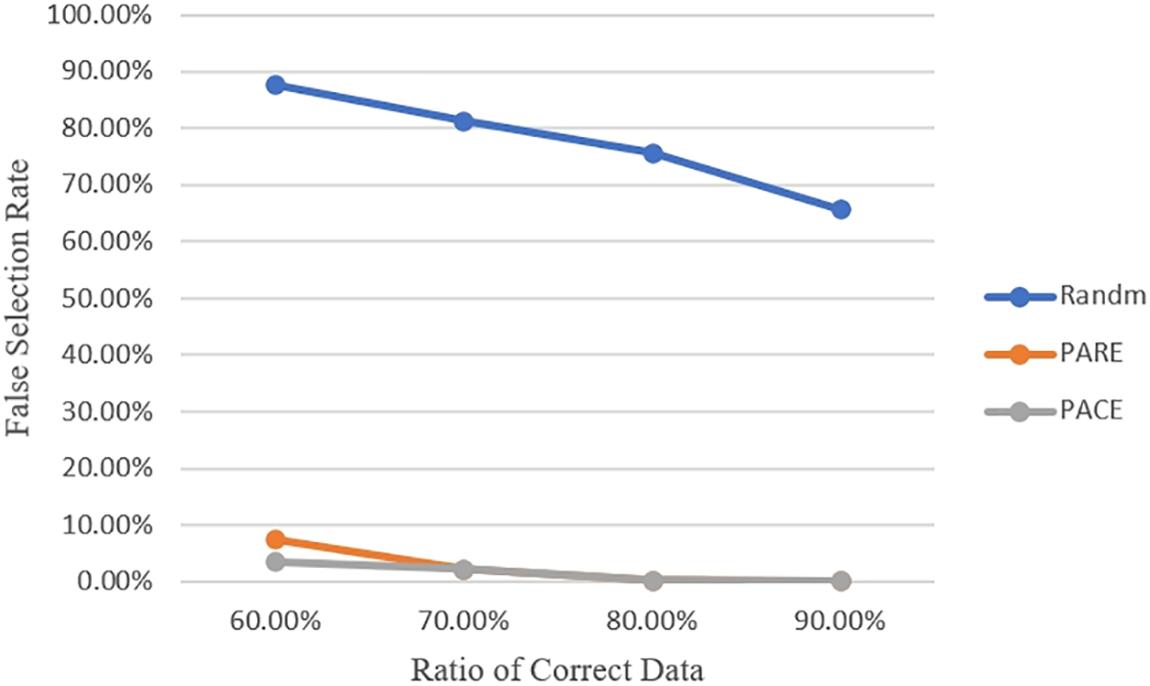
Figure 8: FSR with different rates of correct data

7  Conclusion

In this paper, we propose a data reliability evaluation scheme, which designs a form of data uploading and storage that combines blockchain and Paillier homomorphism in response to the conflict between data protection and data validation. We also designed a method to develop screening criteria based on the uploaded data without knowing the specific values. It is shown through experiments that the scheme can achieve a high level of correct data screening results. Although it is possible to filter the data using IP address and task location, the filtering criteria cannot be actively adjusted. In future work, the inclusion of sentinel data may be considered for important data collection tasks to filter and evaluate the data dynamically. Furthermore, this paper considers the case of single aggregation data. However, research on the multi-aggregation case is also necessary.

Acknowledgement: The authors appreciate the valuable comments from the reviewers.

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant 62233003 and the National Key Research and Development Program of China under Grant 2020YFB1708602.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Peicong He, Yang Xin, Yixian Yang; data collection: Peicong He; analysis and interpretation of results: Peicong He; draft manuscript preparation: Peicong He. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The CROWD_TEMPERATURE datasets used in this paper can be accessed at https://ieee-dataport.org/open-access/crawdad-queensucrowdtemperature (accessed on 14 October 2023).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Plageras, K. Psannis, C. Stergiou, H. Wang, and B. Gupta, “Efficient IoT-based sensor big data collection-processing and analysis in smart buildings,” Future Gener. Comput. Syst., vol. 82, pp. 349–357, 2018. doi: 10.1016/j.future.2017.09.082. [Google Scholar] [CrossRef]

2. M. Ghahramani, M. Zhou, and G. Wang, “Urban sensing based on mobile phone data: Approaches, applications, and challenges,” IEEE/CAA J. Automatica Sinica, vol. 7, no. 3, pp. 627–637, 2020. doi: 10.1109/JAS.2020.1003120. [Google Scholar] [CrossRef]

3. C. Hu, C. Zhang, D. Lei, T. Wu, X. Liu and L. Zhu, “Achieving privacy-preserving and verifiable support vector machine training in the cloud,” IEEE Trans. Inf. Forensics Secur., vol. 18, pp. 3476–3491, 2023. doi: 10.1109/TIFS.2023.3283104. [Google Scholar] [CrossRef]

4. C. Zhang, C. Hu, T. Wu, L. Zhu, and X. Liu, “Achieving efficient and privacy-preserving neural network training and prediction in cloud environments,” IEEE Trans. Depend. Secur. Comput., vol. 20, no. 5, pp. 4245–4257, 2022. doi: 10.1109/TDSC.2022.3208706. [Google Scholar] [CrossRef]

5. A. Yazdinejad, A. Dehghantanha, G. Srivastava, H. Karimipour, and R. Parizi, “Hybrid privacy preserving federated learning against irregular users in next-generation Internet of Things,” J. Syst. Archit., vol. 148, pp. 103088, 2024. doi: 10.1016/j.sysarc.2024.103088. [Google Scholar] [CrossRef]

6. Q. Li and G. Cao, “Providing privacy-aware incentives in mobile sensing systems,” IEEE Trans. Mob. Comput., vol. 15, no. 6, pp. 1485–1498, 2016. doi: 10.1109/TMC.2015.2465375. [Google Scholar] [CrossRef]

7. S. Razak, N. Nazari, and A. Al-Dhaqm, “Data anonymization using pseudonym system to preserve data privacy,” IEEE Access, vol. 8, pp. 43256–43264, 2020. doi: 10.1109/ACCESS.2020.2977117. [Google Scholar] [CrossRef]

8. X. Tan, J. Zheng, C. Zou, and Y. Niu, “Pseudonym-based privacy-preserving scheme for data collection in smart grid,” Int. J. Ad Hoc Ubiquitous Comput., vol. 22, no. 2, pp. 120–127, 2016. doi: 10.1504/IJAHUC.2016.077203. [Google Scholar] [CrossRef]

9. J. Wang, Y. Luo, S. Jiang, and J. Le, “A survey on anonymity-based privacy preserving,” presented at 2009 EBISS, Wuhan, China, May 23–24, 2009, pp. 1–4. doi: 10.1109/EBISS.2009.5137908. [Google Scholar] [CrossRef]

10. Z. Yang, S. Zhong, and R. Wright, “Anonymity-preserving data collection,” presented at KDD05, Chicago, IL, USA, Aug. 21–24, 2005, pp. 334–343. doi: 10.1145/1081870.1081909. [Google Scholar] [CrossRef]

11. Y. Wang, Z. Cai, X. Tong, Y. Gao, and G. Yin, “Truthful incentive mechanism with location privacy-preserving for mobile crowdsourcing systems,” Comput. Netw., vol. 135, pp. 32–43, 2018. doi: 10.1016/j.comnet.2018.02.008. [Google Scholar] [CrossRef]

12. B. Nguyen et al., “Privacy preserving blockchain technique to achieve secure and reliable sharing of IoT data,” Comput. Mater. Contin., vol. 65, no. 1, pp. 87–107, 2020. doi: 10.32604/cmc.2020.011599. [Google Scholar] [CrossRef]

13. T. Li, H. Wang, D. He, and J. Yu, “Blockchain-based privacy-preserving and rewarding private data sharing for IoT,” IEEE Internet Things J., vol. 9, no. 16, pp. 15138–15149, 2022. doi: 10.1109/JIOT.2022.3147925. [Google Scholar] [CrossRef]

14. C. Zhang, M. Zhao, L. Zhu, W. Zhang, T. Wu and J. Ni, “FRUIT: A blockchain-based efficient and privacy-preserving quality-aware incentive scheme,” IEEE J. Sel. Areas Commun., vol. 40, no. 12, pp. 3343–3357, 2022. doi: 10.1109/JSAC.2022.3213341. [Google Scholar] [CrossRef]

15. C. Zhang, M. Zhao, J. Liang, Q. Fan, L. Zhu and S. Guo, “NANO: Cryptographic enforcement of readability and editability governance in blockchain databases,” IEEE Trans. Depend. Secur. Comput., vol. 21, no. 4, pp. 3439–3452, Jul.–Aug. 2024. doi: 10.1109/TDSC.2023.3330171. [Google Scholar] [CrossRef]

16. A. Yazdinejad, A. Dehghantanha, R. M. Parizi, M. Hammoudeh, H. Karimipour and G. Srivastava, “Block hunter: Federated learning for cyber threat hunting in blockchain-based IIoT networks,” IEEE Trans. Ind. Inform., vol. 18, no. 11, pp. 8356–8366, 2022. doi: 10.1109/TII.2022.3168011. [Google Scholar] [CrossRef]

17. B. Zhao, S. Tang, X. Liu, and X. Zhang, “PACE: Privacy-preserving and quality-aware incentive mechanism for mobile crowdsensing,” IEEE Trans. Mob. Comput., vol. 20, no. 5, pp. 1924–1939, 2020. doi: 10.1109/TMC.2020.2973980. [Google Scholar] [CrossRef]

18. H. To, G. Ghinita, and C. Shahabi, “A framework for protecting worker location privacy in spatial crowdsourcing,” Proc. VLDB Endowment, vol. 7, no. 10, pp. 919–930, 2014. doi: 10.14778/2732951.2732966. [Google Scholar] [CrossRef]

19. L. Zhang, X. Lu, P. Xiong, and T. Zhu, “A differentially private method for reward-based spatial crowdsourcing,” presented at Appl. Tech. Inf. Secur.: 6th Int. Conf., Beijing, China, Nov. 4–6, 2015. [Google Scholar]

20. C. Ma, L. Yuan, L. Han, M. Ding, R. Bhaskar and J. Li, “Data level privacy preserving: A stochastic perturbation approach based on differential privacy,” IEEE Trans. Knowl. Data Eng., vol. 35, no. 4, pp. 3619–3631, 2021. doi: 10.1109/TKDE.2021.3137047. [Google Scholar] [CrossRef]

21. B. Zhao, S. Tang, X. Liu, X. Zhang, and W. Chen, “iTAM: Bilateral privacy-preserving task assignment for mobile crowdsensing,” IEEE Trans. Mob. Comput., vol. 20, no. 12, pp. 3351–3366, 2020. doi: 10.1109/TMC.2020.2999923. [Google Scholar] [CrossRef]

22. K. Gai, M. Qiu, and H. Zhao, “Privacy-preserving data encryption strategy for big data in mobile cloud computing,” IEEE Trans. Big Data, vol. 7, no. 4, pp. 678–688, 2017. doi: 10.1109/TBDATA.2017.2705807. [Google Scholar] [CrossRef]

23. P. He, Y. Xin, B. Hou, and Y. Yang, “PKGS: A privacy-preserving hitchhiking task assignment scheme for spatial crowdsourcing,” Electronics, vol. 12, no. 15, pp. 3318, 2023. doi: 10.3390/electronics12153318. [Google Scholar] [CrossRef]

24. D. Peng, F. Wu, and G. Chen, “Data quality guided incentive mechanism design for crowdsensing,” IEEE Trans. Mob. Comput., vol. 17, no. 2, pp. 307–319, 2017. doi: 10.1109/TMC.2017.2714668. [Google Scholar] [CrossRef]

25. S. Yang, F. Wu, S. Tang, X. Gao, B. Yang and G. Chen, “On designing data quality-aware truth estimation and surplus sharing method for mobile crowdsensing,” IEEE J. Sel. Areas Commun., vol. 35, no. 4, pp. 832–847, 2017. doi: 10.1109/JSAC.2017.2676898. [Google Scholar] [CrossRef]

26. M. Alsheikh, D. Niyato, D. Leong, P. Wang, and Z. Han, “Privacy management and optimal pricing in people-centric sensing,” IEEE J. Sel. Areas Commun., vol. 35, no. 4, pp. 906–920, 2017. doi: 10.1109/JSAC.2017.2680845. [Google Scholar] [CrossRef]

27. C. Zhang, X. Luo, J. Liang, X. Liu, L. Zhu and S. Guo, “POTA: Privacy-preserving online multi-task assignment with path planning,” IEEE Trans. Mob. Comput., vol. 23, no. 5, pp. 5999–6011, 2023. doi: 10.1109/TMC.2023.3315324. [Google Scholar] [CrossRef]

28. P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” presented Adv. Cryptol.—EUROCRYPT ’99: Int. Conf. Theor. Appl. Cryptogr. Tech., Prague, Czech Republic, May 2–6, 1999, pp. 223–238. [Google Scholar]

29. M. A. Alswailim, H. S. Hassanein, and M. Zulkernine, “CRAWDAD queensu/crowd_temperature,” in IEEE Dataport, Nov. 6, 2022. doi: 10.15783/C7CG65. [Google Scholar] [CrossRef]