A Novel Quantization and Model Compression Approach for Hardware Accelerators in Edge Computing

1  Introduction

The new era of the IoT enables a smart society by interconnecting cyberspace with the physical world. At the same time, artificial intelligence (AI) is widely spread in a variety of business sectors and industries. A number of revolutionary applications in computer vision, games, speech recognition, medical diagnostics, and many others are reshaping our everyday lives. Traditionally, IoT devices would send data to a centralized cloud server for processing and analysis. However, this approach can lead to delays due to data transmission and processing times. To address this issue, edge computing in IoT devices is proposed, referring to the practice of processing data closer to its source on the edge of the network, near the devices that generate the data. This approach aims to minimize latency, reduce bandwidth usage, enhance privacy and security, and improve overall system efficiency. By deploying computing resources closer to where data is generated, it enables faster decision-making, critical for applications that require real-time responses (e.g., industrial automation, autonomous vehicles, and healthcare monitoring).

Despite the myriad advantages inherent in edge computing, it grapples with multifaceted challenges. The foremost challenge lies in resource constraints. Edge devices often have limited computational power, memory, and storage capacity compared to centralized servers. This restricts the complexity and scale of computations that can be performed at the edge. Therefore, edge computing in IoT devices calls for not only low-power chips for energy efficient processing at the edge but also a model with low latency and less accuracy reduction. To address this issue, a variety of low-precision quantization methods are emerged to reduce model size and arithmetic complexity.

Quantization attempts to reduce data bit-width in IoT devices’ local computing, shrink model size for memory saving, and simplify the operations for compute acceleration. Low-precision quantization has caught plenty of attention, wherein inference acceleration is to substitute intricate 32-bit floating-point (FP32) multiplication for fewer-bit multiplication. An integer-arithmetic inference framework is introduced to quantize full-precision weights and activations into 8-bit integer values, while bias parameters remain 32-bit to maintain baseline accuracy [1]. The performance of this approach is demonstrated on Qualcomm Hexagon and Advanced Reduced Instruction Set Computer (RISC) Machine (ARM) New Engine for Next Generation Objects (NEON) hardware platforms, achieving up to 50% latency reduction and −1.8% accuracy loss on objection detection tasks. To close the accuracy gap between the low-bit and FP32 model, fixed-point quantization is proposed, where the fractional length is optimized during retraining to enforce different layers adapting to different mantissa [2]. While a lot of effective quantization schemes have been published in recent years targeting different domains and applications, we in this paper primarily focus on low-precision (e.g., 3–6 bit) approaches that are hardware-friendly in the perspective of less computational resource demand, memory efficiency, and low inference latency.

On the one hand, extreme low-precision quantization is an intriguing area of research that converts full-precision values into representations using a minimal number of bits, thus requiring the least computation. Learned Step Size Quantization Plus (LSQ+) improves low-bit quantization via learning optimal offsets and using better initialization for parameters [3]. A block mini-float representation is proposed to reduce the expensive training at FP32 precision by a narrow floating-point format (e.g., 4–8 bit), which shows Residual Networks (ResNet) with 6-bit on ImageNet has no accuracy loss, achieving 16× energy reduction compared to FP32 model [4]. Likewise, Progressive-Freezing Iterative Training (PROFIT) adapting a novel training method is introduced for efficient model architecture (e.g., MobileNet) at extremely low precision [5].

On the other hand, the PoT paradigm is widely explored and serves as a promising approach to bridging the gap between computing acceleration and accuracy degradation. PoT introduces bit-shifting operations in computation in order to achieve higher numerical resolution. In earlier works, group-wise PoT quantization with iterative retraining is adopted to quantize the pre-trained FP32 model into its low-precision representation, where weights are quantized uniformly [6]. A learning approach with adaptive FP32 hyper-parameters is utilized to select suitable clipping and scaling factors, which provides the advantage for the quantizer to tolerate the scale of quantization input [7]. It is proved that for extremely low precision (less than 4-bit), uniform quantizer suffers from great accuracy loss whereas non-uniform quantizer is more robust and adaptive to different input distributions [8]. A non-uniform PoT scheme is introduced in conjunction with re-parameterization (e.g., FP32 scaling) on clipping function for which the threshold is effectively optimized to adapt to the dynamics of weight and activation distribution in retraining [8]. In contrast, the quantization approach in Deepshift retrains the FP32 model and converts weights to shift-arithmetic units as quantized values directly, which incorporates two distinct stages for the transformation. First, logarithmic transformation and nearest-rounding operation maps FP32 models to their low-precision counterparts. Second, a learning strategy for bit-shift operations is used to directly learn low-bit weights which are successively optimized throughout the retraining process, and activations are quantized by a customized floating-point scheme due to serious loss of accuracy [9]. Furthermore, a quantization framework adapting trainable look-up tables (LUTs) is proposed to learn dictionaries and assessment matrices for quantization projection, in which different quantization schemes (including PoT) can be realized by different configurations, and low-precision models are obtained via dictionaries and assignment matrices, while it resorts to fixed-point activations to gain higher accuracy [10].

However, general researches based on the PoT scheme require substantial bit-wise operations and rely heavily on either computational/memory-expensive FP32 hyper-parameters or fixed-point quantization on activations to achieve acceptable accuracy performance [8–10]. With the abundance of bit-shifting and high-precision parameters, the computing hardware takes a lot of cycles to complete, and inference latency would become a bottleneck limiting both the utilization and throughput of hardware. Therefore, the achievable performance of existing PoT schemes on inference acceleration and memory efficiency is sub-optimal, especially on IoT devices with edge computing.

To achieve low-latency inference and resource/memory-efficient computation at the edge of the IoT, we propose an end-to-end efficient inference approach that encapsulates Internetworking Operating System-Cisco (IOS)-PoT quantization, two-stage model compression, and P-LUT inference. To address the practical needs of IoT scenarios, a hardware accelerator with our approach is developed using Verilog Hardware Description Language (HDL) and deployed on Field Programmable Gate Array (FPGA) platforms with a camera. First, the 32-bit width values from the original model undergo IOS-PoT quantization. Then, we use Verilog HDL to efficiently develop register-transfer level (RTL-level) hardware code for the accelerator and deploy the inference method on the Xilinx KV260 FPGA platform. This process is illustrated in Fig. 1. IOS-PoT replaces all FP32 hyper-parameters with only few-bit integers. The main contributions of this paper are summarized as follows:

1.    We present an end-to-end quantization and efficient inference approach, realized by hardware-friendly IOS-PoT quantization, model compression, and P-LUT, which is dedicated to effectively deploying deep neural models on edge learning devices with limited resources and power budget, and implementing efficient acceleration infrastructure.

2.    To shrink the model size, IOS-PoT quantization and two-stage model compression are proposed to map a full-precision model to low bit-width representation, where a jointly designed distribution-loss regularizer is introduced to minimize the mismatch problem between quantization inputs and outputs, and signed-Huffman (S-Huff) is introduced for improving memory efficiency.

3.    To reduce the bottleneck of computing latency and hardware-resource overhead, P-LUT inference is proposed to substitute matrix multiplication with only value indexing and addition, in which P-LUT is shared among low-precision weights and activations at inference. Furthermore, an inference accelerator prototype based on the P-LUT scheme for convolution operations on FPGA is developed.

Figure 1: The architecture of quantization and model compression for hardware accelerators in edge computing

2  Related Work

Due to the complex architecture, Deep Neural Networks (DNNs) suffer from huge memory consumption and computation powers as well as considerable inference latency. As embedded computing systems are rapidly proliferating every aspect of human endeavor today, these drawbacks pose a huge challenge to deploying deeper models on edge platforms. To address this issue, a bulk of works have emerged, while allowing for tolerable performance degradation. Existing works include but are not limited to network pruning, low-precision quantization, and weight compression.

2.1 Weight Compression

Weight compression refers to reducing the memory requirement of model parameters, in which efficient encoding schemes are usually employed to decrease memory access and storage size. A network compression pipeline is introduced, which combines pruning, quantization, weight sharing, and Huffman coding to achieve a remarkable compression ratio. Pruning attains the highest compression ratio around 10×, while quantization and encoding provide an additional 2×∼4× [11]. Vector quantization achieves a good balance between model size and recognition accuracy by applying k-means clustering algorithms to weights, which has proved to be most effective for densely connected layers [12,13]. Some prior works on model compression are mainly targeted at efficient inference for edge platforms [14–16].

2.2 PoT Quantization

Assume that a pre-trained full-precision (e.g., 32-bit floating-point) convolutional neural network (CNN) is represented by {Wl:1≤l≤L}, where Wl denotes weights of the lth layer, and L indicates the number of layers in the network. Kernels in a convolutional layer are indicated by a 4D tensor Wl∈RCout×Cin×K×K, where Cin and Cout are input and output channels, and K constitutes the kernel size. The quantized weights are represented by:

W~l=∏Ω(δ,b)⌊Wl,δ⌉(1)

where δ is a real number and represents the clipping range, ⌊⋅⌉ stands for the nearest-round operation, and the clipping function ⌊.,δ⌉ constraints weights to [−δ,δ]. ∏(⋅) projects elements of Wl onto low-precision quantization levels. Ω(δ,b) refers to quantization levels which all weights can be projected onto, where b is the bit-width for each quantized weight of W~l.

In order to boost hardware efficiency and lower latency at the inference phase for DNNs, uniform PoT quantization is introduced by restricting all weights to be PoT values or zeros as shown:

Ω(δ,b)=δ×{0,±2−2b−1+1,±2−2b−1+2,…,±2−1,±1}(2)

As PoT quantization is non-uniform, it has a good resolution for weight approximation owing to the exponential property. Quantization levels are represented by PoT values, which means that multiplication operations between a PoT number 2r and an operand m are simply realized by bit manipulation rather than computationally intensive operations such as digital multipliers. The intricate multiplication operations replaced with bit-wise shifting are represented mathematically as:

2rm={m,if r=0m≪r,if r>0m≫r,if r<0(3)

where ≪ and ≫ denote left and right shift operation, respectively.

2.3 Distribution Regularizer

Quantization which maps high-precision numbers to low-precision representations is inherently leading to deviations. In quantized neural networks (QNNs), the objective is to ensure acceptable prediction accuracy is achieved, on which the degree of quantization errors has a direct impact. A variety of methods for optimizing quantization loss to achieve good final accuracy are emerged [17–20]. A distribution-loss function is proposed to minimize the Kullback-Leibler (KL) divergence between full-precision and quantized binary models [21]. The compensated-DNN approach in QNNs is developed in [22], where they optimize QNNs’ retraining by first-order derivative approximation on quantization errors with well-structured compensation values that are computationally inexpensive. A more recent approach (named Vector Quantization (VecQ)) introduces vectorized quantization with vector loss to mitigate quantization disturbances [23], which has proved to be more adaptive. Besides, distribution loss can be applied to data distribution of input samples, where it approximates the fluctuation dynamics of inputs, e.g., a clustering algorithm employing this type of distribution loss to learn the statistical characteristics of input data [24].

2.4 LUT Inference

One approach in literature to achieve PoT quantization is via learning look-up tables (weight assignment tensors and dictionaries) [10]. It has captured a broad range of different quantization schemes as the learning dynamics can easily be updated by pre-set configurations, e.g., binary and ternary models. Despite its flexibility in realizing different quantization schemes, the achievable PoT quantization scheme relies on substantial bit-shifting at the inference phase. In [25], LUT resources in FPGA are used as the fundamental logic for performing DNN computations, where matrix multiplications are implemented with either XNOR logic or complex K-input boolean operations. This method effectively utilizes FPGA native resources to address area and resource efficiency problems of DNN inference.

To summarize, our approach has three distinctions compared with previous methods. (1) With IOS-PoT, tensor scaling at runtime is simply achieved by bit-shifting operation, omitting division operations as in prior PoT methods. (2) We utilize a two-stage compression pipeline to reduce memory requirement, where the S-Huff encoding and decoding hardware are leveraged to reduce memory footprint at inference. (3) In our product look-up table (P-LUT) scheme, multiplications are not required at runtime. Thus, indexing and addition are two main operations for computing matrix products, breaking the bottleneck of computation latency and hardware-resource overhead.

3  Proposed Approach

The proposed method consists of IOS-PoT quantization, distribution-loss regularizer, model compression, and P-LUT inference scheme (illustrated in Fig. 2). Firstly, IoT devices collect data and centrally train models to get FP32 weights and activation. Secondly, IOS-PoT is developed to quantize FP32 weights and activations to fully PoT representations, with joint optimization on distribution loss to reduce quantization errors. Thirdly, model compression techniques are introduced to relieve memory requirements. Finally, the P-LUT inference scheme built on our quantization and compression framework is proposed for accelerating inference on edge computing devices of IoT.

Figure 2: The architecture of the proposed approach

3.1 Integer-Only Scalar Power-of-Two Quantization

IOS-PoT quantization is introduced to remove the computation overhead arising from the adoption of FP32 scaling parameters, for which the required arithmetic operations are mere bit-shift and addition. Quantization is performed on weights and activations to project full-precision values onto low-precision representations during the forward pass, and then the prediction accuracy is calculated, while FP32 weights and gradients are kept for gradient descent during the backward pass.

To avoid matrix multiplication involving full precision numbers at inference, the quantized model is subject to full PoT representation in IOS-PoT. For low-bit projection, the clipping threshold is defined as δk where k is predefined, and δ is a learnable parameter, instead of clipping inputs directly to [−k,k]. This new version has better range representation ability and more robust to quantization errors. The scaling operation of quantization input is utilized to assist minimizing the gap between quantization levels and inputs, as seen in [7]. Since the scaling operation is based on a real number δ which is not computationally efficient, a transformation is introduced to restrict it to a PoT value. Hence, the scaling operation is simple bit-shifting. In the quantization procedure, all weights/activations are scaled down, and subsequently projected to low-bit PoT levels. Then, the learned parameter δ, k, and low-bit PoT weights are stored. At the inference stage, weights/activations multiply by PoT coefficient 2⌊log2|δ|⌉ to approximate the FP32 values, where ⌊⋅⌉ and |⋅| refer to the nearest rounding and absolute value operation, respectively. Therefore, FP32 numbers are not included, and all multiplications are realized by bit-wise operations, which substantially relieves the computational complexity and inference latency. To simplify explanation, unsigned weights for quantization (quantization on activations follows the same approach) are only considered in subsequent discussions.

In IOS-PoT quantization, each level is defined by the equation as shown below:

Ω(λ,d×m)={λ×{∑i=1mpi}},where p_i∈{{0,2−(i),2−(i+m),…,2−(i+(2k−2)m)(4)

where λ controls the magnitude of each PoT term contribution. The bit-width for each pi is determined by d, and m refers to the number of addition operations. Thus, the final bit-width for quantized weight is represented by d×m.

Considering the quantization flow during retraining, the clipping function is firstly performed on weights with a PoT scaling factor 2⌊log2⁡|δ|⌉, and [−δk,δk] is the clipping range. Secondly, weights are projected to low-precision PoT levels. Finally, quantized weights in conjunction with coefficients are saved. The IOS-PoT quantization formula is shown:

W~l=𝒬m(Wl;δ;dm)=2⌊log2⁡|δ|⌉×∏Ω(λ,d×m)Clamp(Wl2⌊log2|δ|⌉,δk)(5)

where Wl is the input weight tensor in lth layer, and W~l is the quantized output tensor. d×m is the bit-width for each w~ of W~l, δ is the learned scaling factor, and k is the predefined threshold. Clamp is the clipping function.

Stochastic gradient descent (SGD) is applied to jointly optimize the scaling factor δ and weights during retraining. Gradients remain in a floating point in the backward pass for updating weight parameters. As gradients of the projection function are zeros almost everywhere, a straight-through estimator (STE) [26] is adopted for the back-propagation. To simplify the illustration, let denote Θ=2⌊log2⁡|δ|⌉, so the gradient of δ is calculated as:

∂W~∂δ={Θδ×sign(WΘ),if |W|>δkΘδ×∏Ω(λ,d×m)(WΘ)−Wδ,if |W|≤δk(6)

where W is the full-precision weight tensor. W~ is the weight tensor after quantization. Note that gradients of weights that exceed the clipping threshold are considered, so both clipping and projection errors are taken into account to optimize retraining.

3.2 Distribution-Loss Regularizer

A regularizer on distribution loss is developed to alleviate the mismatch between full-precision and low-precision weights. Gradients of weights during backpropagation do not always contribute to diminishing the gap between quantized outputs and inputs, leading to severe accuracy degradation and model divergence. By employing distribution loss, the mismatch problem is steadily reduced.

Consider a general non-linear DNN consisting of L layers. Let W1, W2,..., WL denote full-precision weights in 1 to L layers, respectively. Likewise, A1, A2,..., AL represent full-precision activations. The regularizer for both weights and activations is expressed as:

ℛm(W;A)=∑l=1L[Wl−𝒬(Wl;δw;dmw)]2+[Al−𝒬(Al;δa;dma)]2(7)

where m refers to the number of PoT terms for each quantization level, and δw and dmw are the clipping threshold and bit-width for quantized weights. Similarly, δa and dma are the clipping threshold and bit-width for quantized activations.

In addition, a learnable hyper-parameter η is introduced for the regularizer, which controls trade-offs between objective loss and the magnitude of penalty. Conventionally, this parameter is set to a constant factor before training. However, this strategy is not optimal. Hence, a penalty term, −log(c×η) for (c×η)>0, is designed as an automatic optimization to seek a good trade-off solution during retraining. Therefore, the final objective loss function to optimize is represented by:

𝒞(X;W;A)=E(X;𝒬(W;δw);𝒬(A;δa))+ηℛ(W;A)−log(c×η)(8)

where 𝒬(W;δw) and 𝒬(A;δa) are low-precision weights and activations in a quantized layer, whose clipping thresholds are δw and δa, respectively. E(X;𝒬(W;δw);𝒬(A;δa)) is the target loss function evaluated on training dataset X. η is the learnable coefficient, and c denotes the magnitude of penalty. In back propagation, the calculation of gradients for η is shown as:

∂𝒞(X;W;δw;A;δa)∂η=ℛ(W;A)−1η(9)

3.3 Model Compression and P-LUT Inference

Model compression and inference schemes based on P-LUT are designed jointly with the IOS-PoT quantization scheme, to facilitate reducing computations and memory requirements, and to enable efficient implementations of specialized accelerators. Ahead of deployment, codebooks of low-precision weights and activations are generated and compressed by S-Huff with the sign-encoding technique. At runtime inference, codebooks are unpacked and loaded onto memory banks while activations are quantized to low precision by special hardware logic in real time.

3.3.1 Compression

Weight sharing and S-Huff encoding methods constitute the first stage for weight reduction, while the last stage (named post compression) is implemented by a standard compression algorithm. In IOS-PoT quantization, weights and activations are projected onto low bit-width quantization levels with different optimized integer scaling parameters. We observe that a great deal of zeros exist in weights. To remove inconsequential memory storage, the sign bit is separated from weight values, and for weights whose values are zero, only sign bits are kept. Hence, weight sharing and Huffman encoding are applied to non-zero weights exclusively to generate a lightweight model. Then, PoT quantization levels are effectively encoded to produce P-LUT for inference. Post compression based on traditional compression algorithm is adopted to reduce the size of generated codebooks, e.g., Lempel-Ziv-Markov chain Algorithm (LZMA) [27]. This compression stage enables less requirement of storage and internet bandwidth, which is suitable for networked edge learning applications. As the algorithm is identical to a fine file compressor, it does not affect prediction accuracy.

To sum up, the compression flow is realized by a two-stage pipeline: (1) Weight sharing and S-Huff encoding, (2) Specialized compressing algorithm. The details are illustrated in Fig. 2.

3.3.2 P-LUT Inference

Matrix multiplication is fundamental in realizing DNN computation, in which the complexity of multiplication determines inference latency and energy efficiency. For the classic PoT scheme, matrix multiplication requires a substantial amount of bit-shifting and addition operations, e.g., LUT-Net which adopts look-up tables for mapping full-precision model to PoT representation directly [10]. In our work, an efficient inference approach for matrix multiplication is carried out by using offline P-LUT codebooks, which is made possible by the novel IOS-PoT quantization together with effective indexing techniques on shared quantization levels of low precision. The P-LUT of the low-bit-width matrix product is 2-dimensional and computed offline. Thus, only 2 indexing and 1 addition necessitate complete multiplication between 2 operands. To illustrate the matrix multiplication between weights and activations built upon P-LUT, assume both weights and activations are quantized to 3-bit precision (1-bit sign and 2-bit value) by IOS-PoT. For clarification, let’s define W and A as 2 matrices shown:

W=[0181412]2×2A=[12141812]2×2(10)

Matrix product obtained via P-LUT is equivalent to the values obtained from standard multiply-add accumulations (MACs), more efficient, and only at the small cost of extra memory space. The matrix multiplication performed upon P-LUT is exemplified in Fig. 3. Low precision codebooks are generated by the first compression stage after the quantization retraining is converged. Then, each low bit-width value in the codebook is multiplied by the remaining values of the same codebook to generate the product matrix which serves as the final P-LUT codebooks for inference. Since the P-LUT codebook is symmetric, only half of the storage is required. For matrix multiplication, indexing operations on codebooks are carried out by W and A, and subsequent additions are executed to obtain the final product. Taken the vector multiplication between the first row of W and the first column of A for example, the indices of the 2 vectors are (0,1) and (3,1), and their product indices are (0,3) and (1,1), respectively. With performing indexing in product LUT by the product indices and one addition operation, the result is obtained 164=0+164.

Figure 3: Matrix multiplication with product Look-UP table

To assess the memory overhead and computation efficiency of P-LUT, an analysis is presented.

Given 4-bit quantized weights and activations (1-bit for sign and 3-bit for value), the dimension of the product matrix of P-LUT is 8×8=23×23, where each element of the matrix is represented by 32-bit fixed-point in the design. Since a single P-LUT matrix is shared among all layers at inference, the negligible memory cost of P-LUT is 2048-bit in total. For computation assessment, let assume the quantized PoT weight and activation is w=(2−1+2−3) and a=(2−4+2−3), respectively. The multiplication of w and a can be represented by w×a=2−5+2−4+2−7+2−6. As the product in P-LUT is computed offline, the cost of computation is a single operation. By contrast, the bit-shifting PoT approach is prohibitively expensive, with up to 25 operations.

4  Experiments

Comprehensive experiments are conducted to justify the efficacy of the proposed approach with comparisons to prior methods. Furthermore, the datasets we select are closely with the IoT scenario. Firstly, image classification tasks on CIFAR10/100 and ImageNet datasets are selected for evaluation [28,29], with the ResNet model architectures. Secondly, facial expression recognition experimented on the RAF-DB dataset is also employed for comparison [30], with novel self-attention to verify the robustness of quantization methods towards extremely low bit-width. Finally, the hardware efficiency of the proposed P-LUT inference is evaluated and compared with conventional bit-shifting PoT schemes and general-purpose platforms, central processing unit (CPU), and graphics processing unit (GPU).

4.1 Evaluation Metrics

32-bit floating-point models are trained from scratch as the baseline metrics for performance evaluation. The accuracy performance is evaluated based on Top-1 and Top-5 metrics as following the conventional assessment standards [9,11]. For indicators of compression rate, it is defined as:

CR=SPSN(11)

where CR is the compression rate. SP and SN refers to the original and compressed size.

To assess computational complexity, a bit-operation scheme is employed to calculate the amount of computation under different low bit-width, as introduced in [8,31] where 1 FIXOPS is defined as the operations between 8-bit weight and 8-bit activation, consuming 64 binary operations in a quantized scheme. The FIXOPS for the multiplication between 2 FP32 real numbers is calculated as 16=32×328×8, whereas the addition between them is viewed as 1 FIXOPS. Open-source tools [32] are also used to calculate computations of DNN models.

4.2 Datasets and Implementation Details

4.2.1 CIFAR10

The CIFAR10 dataset consists of 60,000 RGB (Red, Green, Blue) images, and the size of each image is 32×32 with 10 classes including airplanes, automobiles, birds, cats, deers, dogs, frogs, horses, ships, and trucks. The dataset is partitioned into two sub-datasets, with 500,000 images for the training dataset and 10,000 images for validation, respectively. Normal data augmentation is applied: padding of 4 pixels on each side of the images, random cropping, and random horizontal flipping.

4.2.2 CIFAR100

The CIFAR100 is similar to the CIFAR10 but has a lot more image categories. Image classification on CIFAR100 is more challenging. There are 100 classes which are grouped into 20 super-classes, each of which comes with a “fine” label (the class to which it belongs), and a “coarse” label (the super-class to which it is closely related). Each class is comprised of 600 images, with 500 images used for training and 100 images for testing.

4.2.3 ImageNet

ImageNet (ILSVRC12) is a much more difficult task to deal with, which contains approximately 1.2 million training and 50 k validation 256×256 images with 1000 categories. Random cropping and random horizontal flipping were used as augmentation methods in the retraining stage. In the experiment, 224×224 center cropping is used for evaluation.

4.2.4 RAF-DB (Real-World Affective Faces Database)

RAF-DB contains 30,000 facial images annotated with basic or compound expressions by 40 trained human coders. In the experiment, only images with six basic expressions (neutral, happiness, surprise, sadness, anger, disgust, fear) and neutral expressions are used which leads to 12,271 images for training and 3068 images for testing. All images are resized to 224×224 for both training and testing.

4.2.5 Implementation Details

DNN models are simulated under the Pytorch framework, and all models with full precision are trained from scratch as initialization. The quantization for low bit-width starts with pre-trained models, and then iteratively retrains low-bit weights to recover accuracy loss. Weight normalization is adopted before quantization to assist stabilizing weight distribution [33]. Both weights and activations are converted into the same low bit-width. Since the first and last layers are sensitive towards low-bit quantization, the proposed quantization scheme adopts a higher precision quantization algorithm (i.e., fixed-point quantization with 8 bit-width) for these two layers, as following the convention [34,35]. For the compression of weight parameters, we calculate the weight size based on the same low precision scheme for all comparison methods under quantization, e.g., 4-bit width achieves 4× memory efficiency as compared to 32-bit precision. The details of hardware platform are as follows: CPU running on Intel Core (TM) i3-2120 3.30 GHz, and GPU running on NVIDIA RXT3060 12 GB.

4.3 Ablation Study

In this section, the proposed approach is quantitatively analyzed from both software and inference hardware aspects. Firstly, the efficacy and influence of IOS-PoT quantization and model compression are validated on ResNet18 with the CIFAR100 dataset. Secondly, the inference efficiency and performance of different hardware implementations built on the FPGA platform are thoroughly investigated.

4.3.1 IOS-PoT Quantization

The right part of Fig. 4 gives details of weight distribution to show the effectiveness of the IOS-PoT quantization scheme. FP32 is presented in (a). The effect of the FP32 scalar is illustrated in (b) for which the numerical values of quantization levels are irregular, and it requires more bit-width to reserve accurate precision when performing computation, e.g., 0.719 and 1.079. Therefore, this leads to requiring floating-arithmetic hardware designs, which is energy inefficient.

Figure 4: Distribution difference between FP32 and Integer scaling factors. (a) FP32 weight. (b) FP32 scalar. (c) Integer scalar

In contrast, the quantization levels from integer scalar exhibit regularities of simple PoT terms, e.g., −1.5=−(21+2−1) and 2.0=21, such that the computations for these numerical values can be exclusively implemented by shift-add logic, and the proposed P-LUT inference design as illustrated in Fig. 3. To realize efficient inference based on a bit-shifting scheme, the multiplication between weight values of 1.5 and 2.5, for instance, can be achieved with only addition and bit-wise operations. A simple example in Eq. (12) illustrates the computation procedure, where the computations on exponents are performed by shifting, e.g., 2−1=(1≫1) and 2=(1≪1).

1.5×2.5=(20+2−1×21+2−1)=2+2−1+1+2−2(12)

4.3.2 Distribution-Loss Regularizer

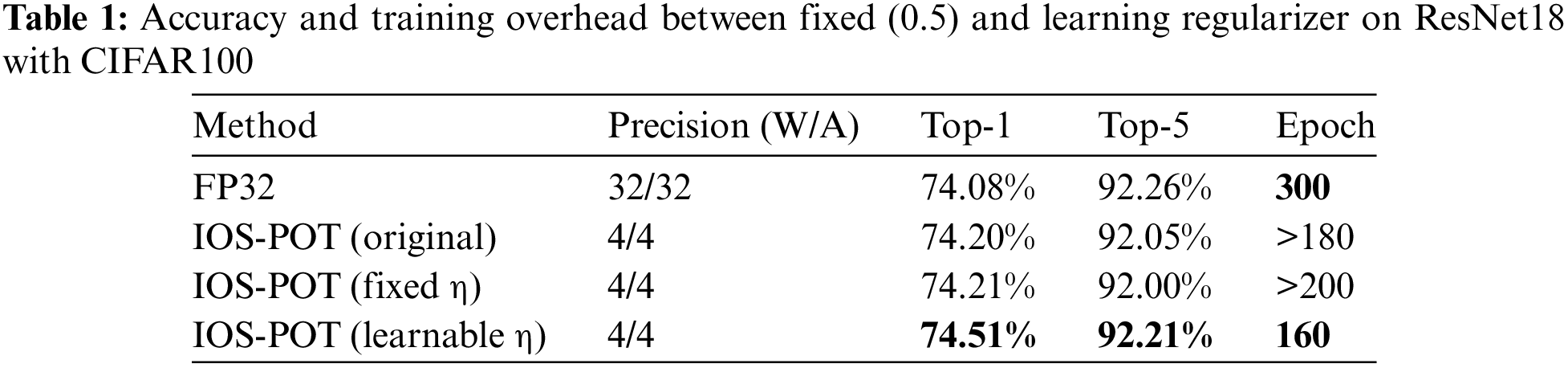
The impact of distribution-loss regularizers is carefully investigated on ResNet18. Different settings are demonstrated in the experiment, i.e., no regularization applied (a), fixed-parameter (b), and the proposed approach choosing a learning strategy (c). The retraining settings are as: 0.04 for learning rate with a decay factor of 0.1 at epoch (60, 120, 160, 200, and 260), 300 epochs of total training, and 128 for batch size. The coefficient λ in the proposed method is initialized to 1, and the coefficient η of the distribution-loss regularizer is set to ex with 5 for c.

The results are plotted based on convergence curves (retraining, testing Top-1 and Top-5 accuracy), in Fig. 5. It is evident from the figure that the regularization almost has no impact on training convergence, and instead, its influence has a direct impact on the validation performance. There exist large fluctuations under quantization retraining if no regularization is applied, as shown in Fig. 5a of the graph. A conventional approach to set the regularization coefficient η with a fixed value (e.g., 0.1, 0.5, and 0.8) causes disturbance as shown in Fig. 5b. By contrast, a stable convergence with a learnable η for validation dataset is achieved, shown in Fig. 5c.

Figure 5: Retraining convergence curves with distribution-loss regularizer. (a) Original. (b) Fixed η (0.1, 0.5, and 0.8). (c) Learnable η

From the graph, the observation is that stable convergence achieved by learnable regularization offers the benefits of reducing retraining overhead without losing prediction accuracy. The training overhead and accuracy results are presented in Table 1. One interesting fact is that the accuracy of fixed regularization is almost identical to no-regularization and that no-regularization has fewer quantization disturbances than fixed regularization with less training overhead (20 epochs less). The reason is that a fixed regularization is not flexible enough to accommodate quantization errors at different training stages. Hence, a learnable approach solves this problem. IOS-PoT with learnable regularization achieves 0.3% improvement in Top-1 accuracy and saves 40 epochs on retraining.

4.3.3 Analysis of Compression Efficiency

To demonstrate the efficacy of the proposed model compression, a comprehensive investigation regarding Huffman encoding is presented on ResNet18 after retraining converged, where FP32, Non-Huffman which only considers low bit-width weights without using additional compression methods, and S-Huff approach are compared under APoT and the proposed IOS-PoT scheme. Furthermore, the performance of two-stage model compression is analyzed. Table 2 gives the baseline of FP32 weights on three convolution layers, in which weights and zero weights represent the total weight parameters and zero weights, respectively. We use KB to express the memory consumption of parameters in convolution layers, with 3-bit (2-bit value and 1-bit sign) precision for quantization.

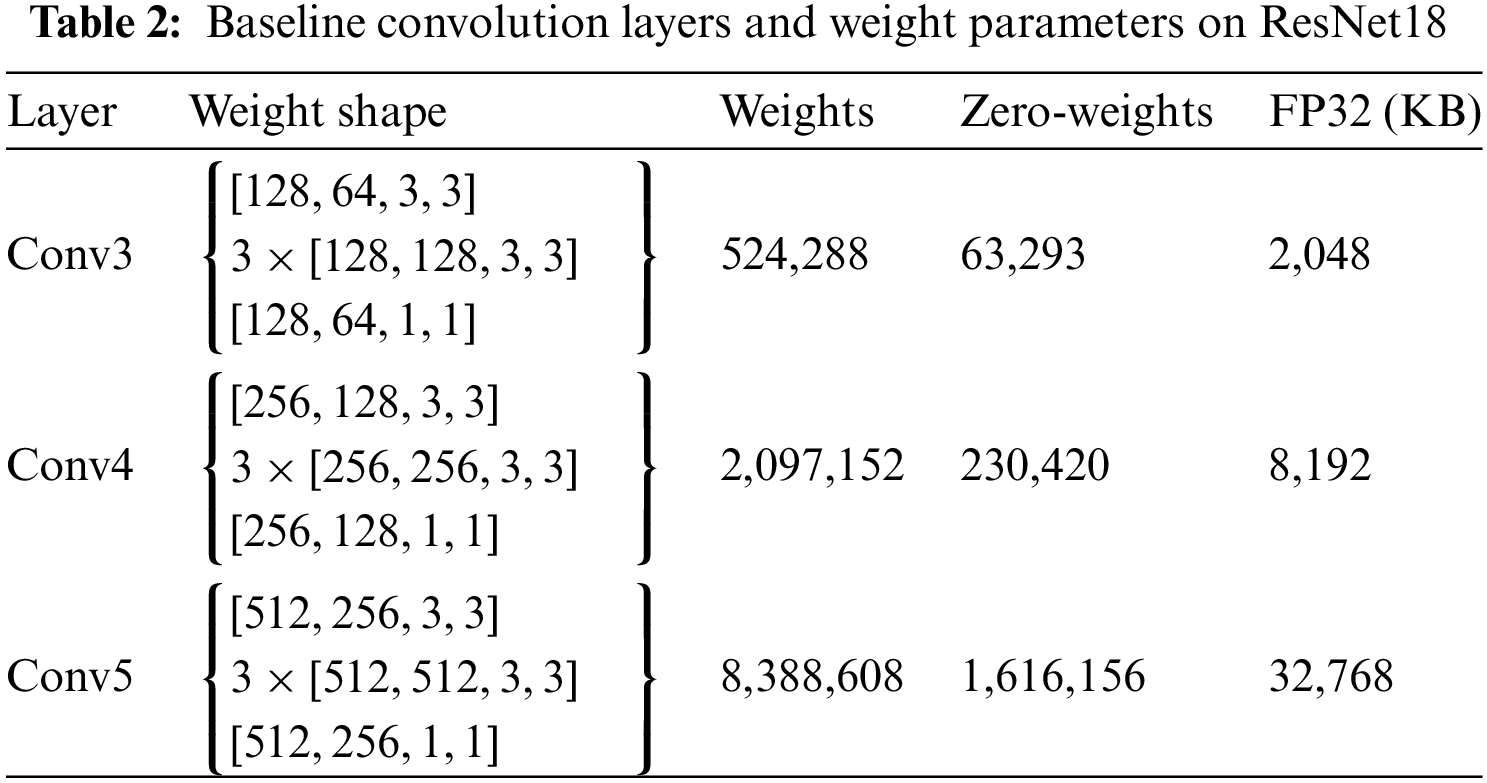
We find that a great deal of weights tend to be zeros when the quantized model is converged, and thus, employing an efficient encoding method to reduce the memory consumption of these weights is of significant importance. This fact is evidenced in Table 2 of our experiment, where the number of zero weights is steadily increasing as layers have more neurons. Therefore, we further improve the compression rate of Huffman encoding by introducing S-Huff which removes zero-valued weights, with performance results shown in Fig. 6, where both Huffman and Non-Huffman enjoy further improvement. To evaluate with/without Huffman encoding, the memory usage of APoT and the IOS-PoT scheme is obtained on three convolution layers, where APoT follows conventional PoT without sign encoding. The results indicate that IOS-PoT gains 1.5×∼2× improvement for memory saving over APoT with/without Huffman when layers have more parameters.

Figure 6: Weight reduction on 4-bit precision and two-stage compression on ResNet18

4.3.4 Hardware Efficiency of P-LUT and SHIFT Scheme

The utilization of hardware resources for P-LUT and bit-shifting (SHIFT) arithmetic is simulated on Xilinx KV260 FPGA whose available resources are presented in Table 3. For fairness in comparison of computational efficiency, only LUT resources of FPGA are enabled for simulation, with benchmarks of LUT utilization after post-synthesis (SYNTH.) and post-implementation (IMPLI.). Different kernel sizes (3×3 and 7×7) for convolution operations are named: Conv3 × 3 and Conv7 × 7. Then, 3 types of processing engines (PE) for simulation are built, P-LUT PE, SHIFT PE, and SHIFT FP32 SCALAR PE (FP32 scaling parameters used), respectively. The LUT’s consumption of these PEs is shown in Fig. 7, where the usage of hardware resources for the SHIFT scheme tends to be exponentially larger than P-LUT as the total number of PEs increases (PE4 × 4 represents the total of 16 PE units). The resource-efficient capability of the P-LUT approach owes to the shared strategy on their look-up tables. The SHIFT saves resources approximately 110 compared to SHIFT FP32 SCALAR which requires more logic to carry out floating-point operations.

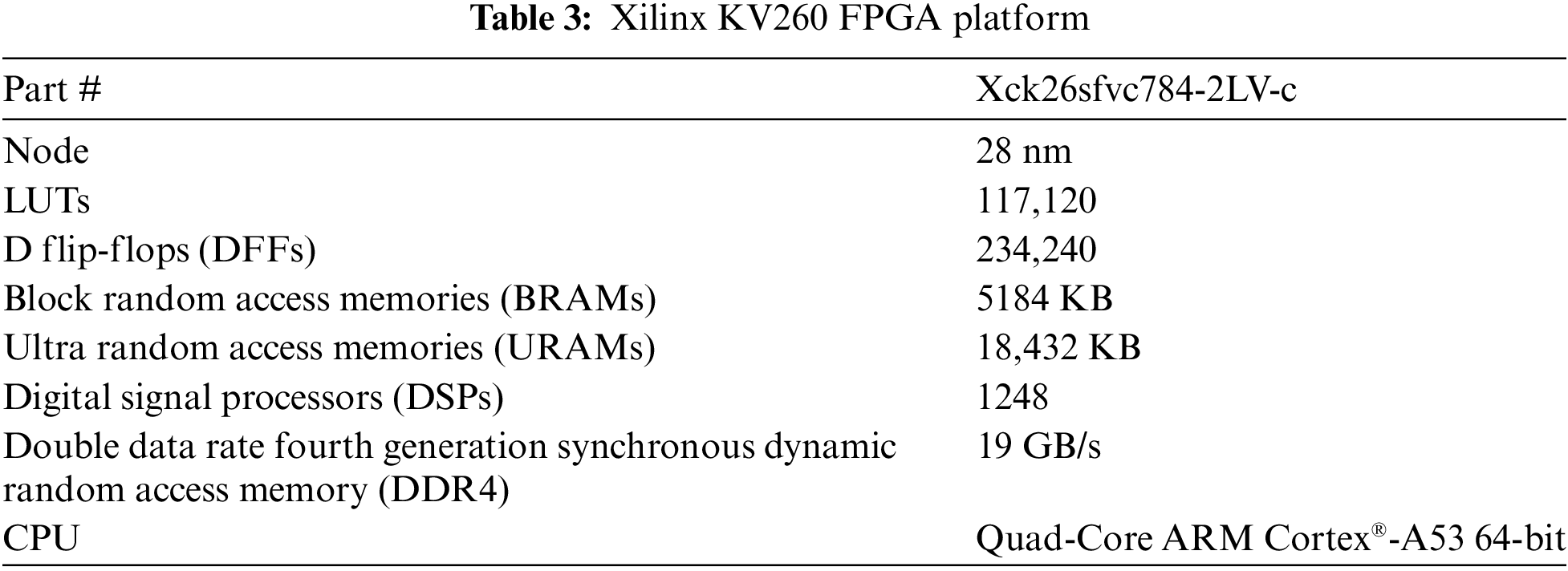
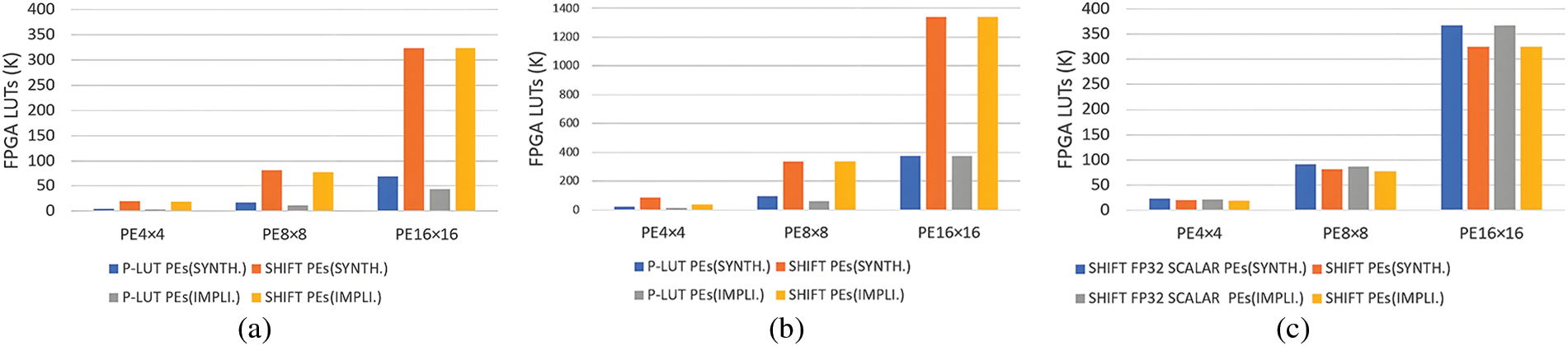
Figure 7: Consumption of FPGA LUTs for different inference schemes, P-LUT PE, SHIFT PE, and SHIFT FP32 SCALAR PE. (a) Conv3 × 3. (b) Conv7 × 7. (c) Conv3 × 3 (FP32 Scalar)

4.4 CIFAR10/100

We first compare the proposed method with prior PoT methods on CIFAR datasets, where residual deep neural models are used for performance evaluation. Then, experiments on efficient model architectures (e.g., SqueezeNet and ShuffleNetV2) are analyzed and compared with state-of-the-art (SOTAs) approaches to further examine the quantization method.

4.4.1 ResNets

The performance of ResNet20 (RES20) and ResNet56 (RES56) on CIFAR10 is investigated, while ResNet18 is experimented on the CIFAR100 dataset [36,37]. Compared PoT methods include APoT, Learned Quantization Net (LQ-Net), DeepShift, and PACT which we implement following their original works, [7–9,38]. Among them, DeepShift uses a higher-precision (8-bit fixed-point) for activation quantization in the experiment as following their original work, due to the large accuracy drop. The initial settings of hyper-parameters for all methods are the following: an initial learning rate of 0.04, retraining 300 epochs, and 128 for batch size. The learning rate starts from 0.04 with a decay factor of 0.1 at epochs (60, 120, 160, 200, and 260). The standard SGD optimization is used with a momentum of 0.9 and weight decay of 0.0004. For the proposed IOS-PoT, the retraining is 260 epochs (less overhead than compared methods). The coefficient λ of the projection function is initialized with 1. For our distribution-loss regularizer, the coefficient η is set to ex with 5 for c. Instead of learning η directly, we choose to learn x as ex is always positive which is easier for backpropagation.

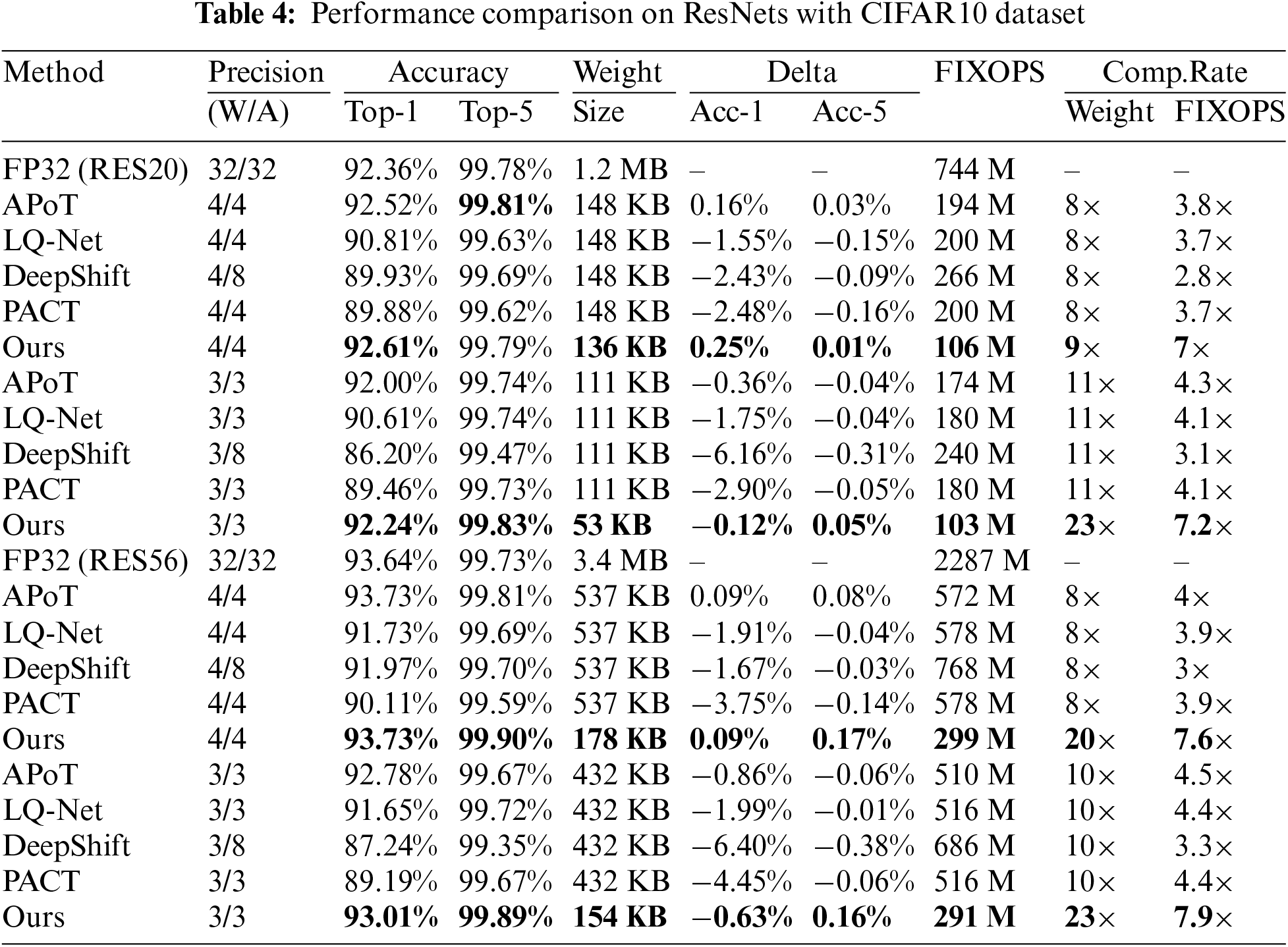
The results on CIFAR10/100 are given in Tables 4 and 5, with notations: Method, Precision W/A (bit-width for weights and activations), Accuracy (Top-1 and Top-5), Weight Size, Delta (Acc-1 and Acc-5 impact), FIXOPS (the number of operations), and Comp.Rate (compression rate on weights and FIXOPS, respectively). Some observations can be summarized as follows:

1.    The proposed approach achieves the most promising compression rate among all selected PoT methods with a negligible loss in prediction accuracy compared to the full-precision baseline model. On ResNet20/56 with 3-bit precision, our method achieves 23× weight size reduction which is 2-fold the compression rate other methods achieve, whereas an average of 1.5× improvement is obtained on ResNet18. It should be pointed out that previous methods (APoT, LQ-Net, DeepShift, and Production Analysis Control Technique (PACT)) are among the categories of conventional PoT, where the compression strategy on weights and computations follows the standard bit-shifting. In terms of computational efficiency, the proposed inference scheme is 2×∼3× faster than prior works, and nearly 8× faster than the baseline model on 3-bit precision.

2.    Most of the Top-1 and Top-5 performances of the proposed approach surpass others, while few exceptions do exist, wherein our method only introduces accuracy loss of less than 0.2%, e.g., Top-1 accuracy of APoT outperforming the proposed approach by 0.06% on ResNet18 under 5-bit precision. Among the tested methods, APoT is ranked as the second best algorithm to achieve competitive accuracy performance, while PACT and DeepShift result in substantial accuracy drop under low-precision such as 3-bit, causing more than a 3% decline in Top-1 accuracy. Overall, the proposed quantization scheme maintains good accuracy with almost no loss of accuracy while achieving a significant reduction in both memory requirement and computation overhead. Our method is still accuracy competitive even under extreme low-precision (e.g., 3/4-bit), gaining huge improvement in acceleration efficiency.

4.4.2 EfficientNets

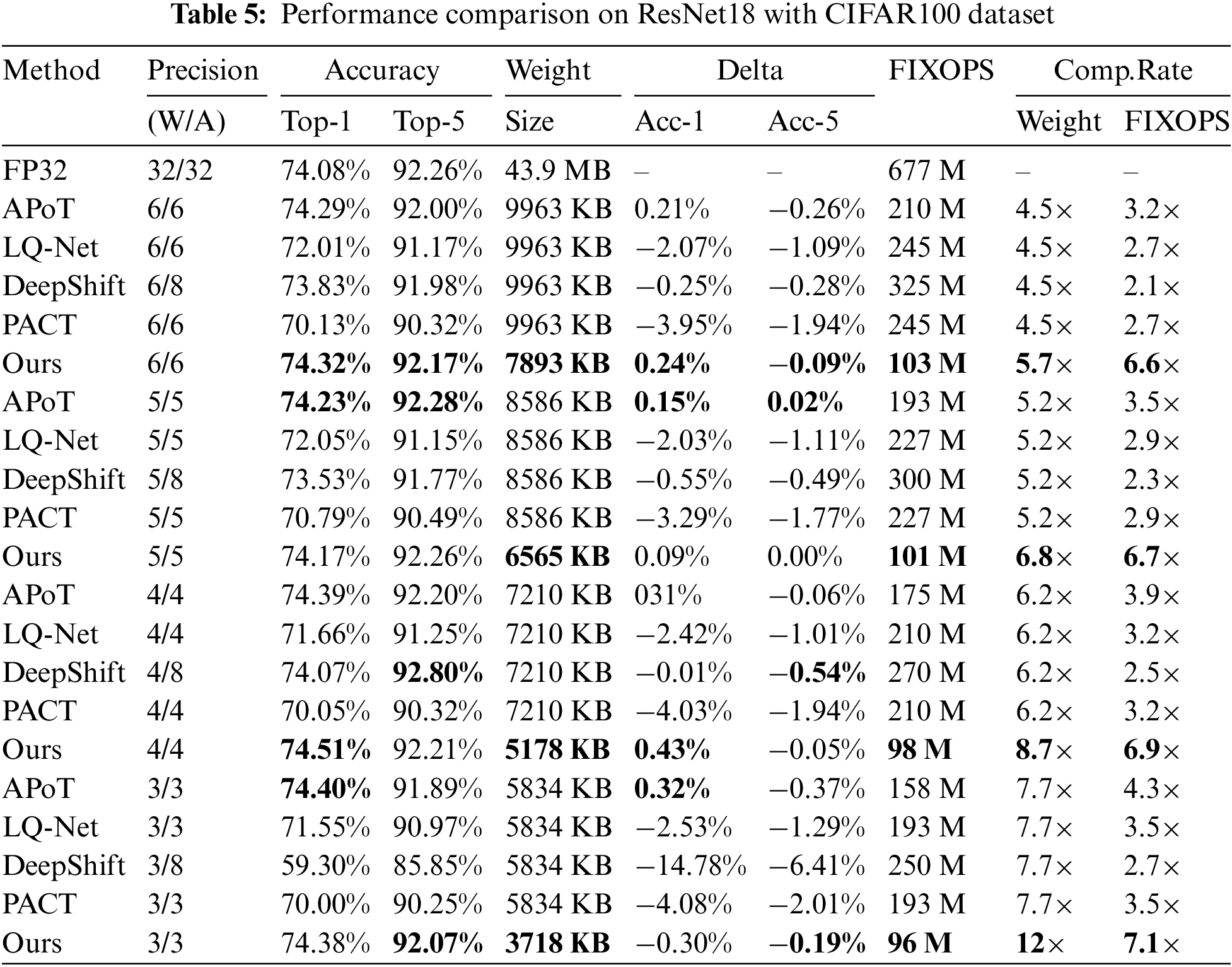
Quantization of efficient neural architectures is often a challenging task, and experiments on such architectures are vitally important for low-precision quantization research. To verify the performance, experiments are performed on CIFAR100, where SqueezeNet and ShuffleNetV2 DNN models are selected and quantized under 3/4-bit precision, [39,40]. SOTA methods, including block-mini float (BM-float) and PROFIT, are compared [4,5]. The experiment starts with training the FP32 model for 300 epochs as the baseline and applying it to initializing low-precision models, where experimental settings in the previous section are adopted for retraining. In the experiment, the first/last layer of DNN models is not quantized for all methods following [4], due to the significant performance impact.

The performance evaluation is presented in Table 6. Overall, the proposed quantization outperforms state-of-the-art (SOTA) approaches by a large margin for the reduction of computation and memory requirement on all tested models, with slight accuracy loss in comparison to compared methods.

For computation efficiency, our approach on average is two orders of magnitude with respect to others (6× to FP32 model), while the memory requirement is reduced by a factor of 1.5× (5×∼7× for FP32 model). The accuracy degradation is more severe on ShuffleNetV2, which indicates that the architecture has fewer redundant features, and is more sensitive to low-precision quantization, resulting in a large accuracy gap between the FP32 baseline and quantized model. Our quantization still achieves better accuracy than BM-float and PROFIT as shown in the table. For the BM-float method, the accuracy decrease is dramatic in 3-bit precision (−24% loss), which shows that fewer bits of exponent and mantissa are difficult for the method to converge. On SqueezeNet, PROFIT slightly outperforms the proposed approach for prediction accuracy, e.g., 0.03% and 0.26% improvement for 4-bit and 3-bit, respectively.

4.5 ImageNet

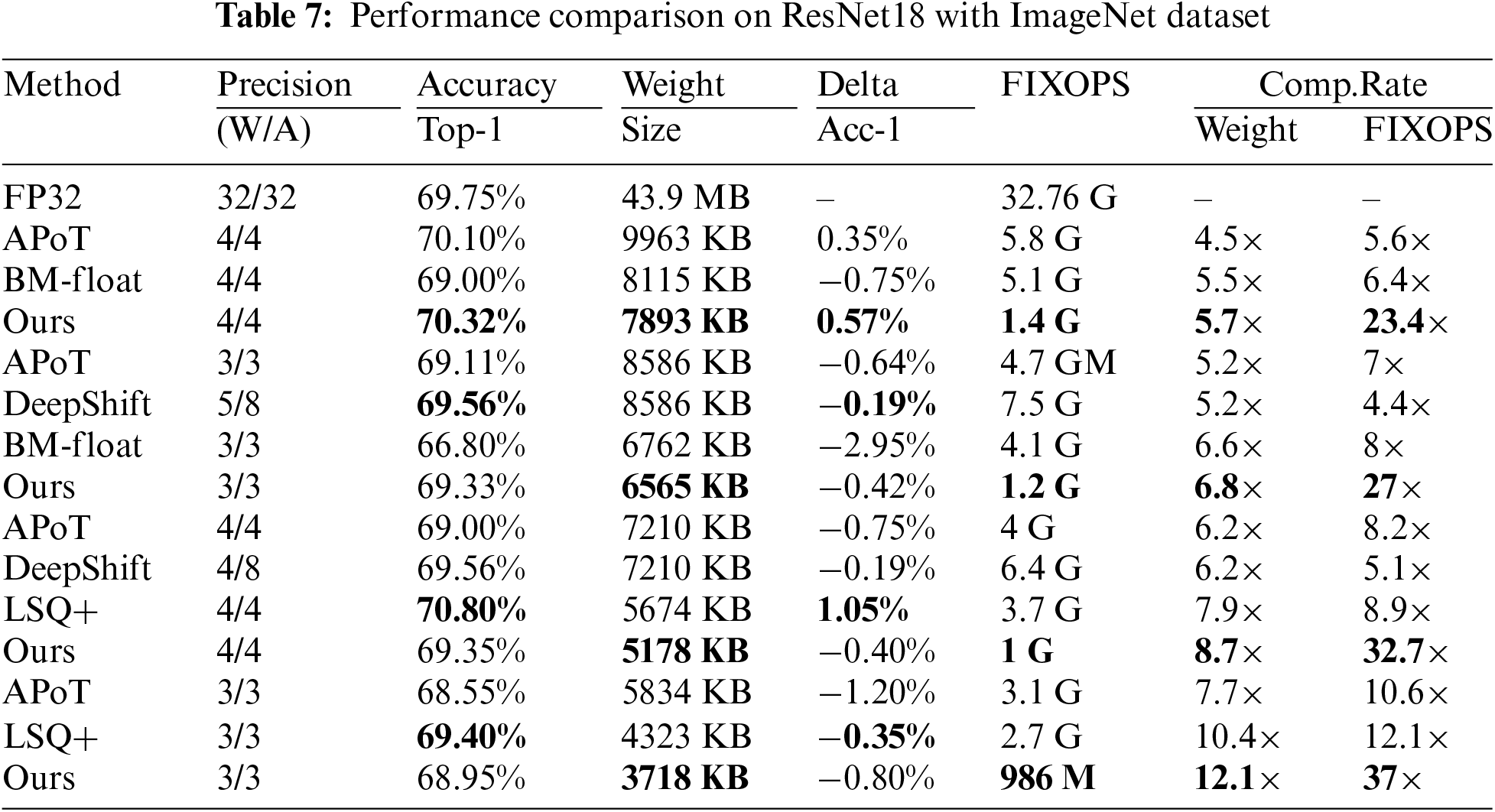
Experiments on representative ImageNet datasets are also conducted. In this experiment, the proposed approach is evaluated on a commonly used ResNet18 neural network, with a comparison to newly published SOTA methods in the literature, e.g., block-mini float (BM-float) [4], LSQ+ [2]. The performance of the FP32 model is selected as the baseline, while other selected methods are for comparison. Different low-precision quantization (e.g., 6, 5, 4, and 3 bit) is tested and validated. It should be pointed out that DeepShift utilizes 8-bit precision for activation quantization for all experiments as following its original work, due to the instability of its quantization causing retraining divergence. We use a pre-trained FP32 model (training from scratch with 120 epochs) as the initialization for all quantized models, where initialization settings are the following: a learning rate of 0.04 with a decay factor of 0.1, training for 60 epochs, and 128 for batch size. The SGD optimization is set with a momentum of 0.9 and weight decay of 0.0004. The settings for our distribution-loss regularizer are the same as those of the CIFAR experiments in this paper. Due to the huge size of the ImageNet dataset and the computation cost of training, a more powerful hardware facility is used, with details: NVIDIA A10 GPU 24 GB, Intel(R) Xeon(R) Gold 6342 CPU @ 2.80 GHz.

Table 7 shows the performance details of the compared approaches, including APoT, DeepShift, BM-float, and LSQ+, where accuracy (Top-1), model size, accuracy drop (Delta), computation cost (FIXOPS), and compression rate of model size and computations, are rigorously examined. The accuracy performance in the original papers of BM-float, DeepShift, and LSQ+, is referenced in the comparison experiment. We can observe from experimental results that our method even in low-precision (e.g., 5, 4, and 3-bit) still achieves acceptable Top-1 accuracy (less than 1% loss), while it improves the accuracy by 0.57% at 6-bit precision, compared to the baseline. The compression ratio on our model size outperforms SOTAs by 1×∼2×, while the reduction of computation overhead is more promising, several orders of magnitude higher than others (3×∼7×). Among the compared methods, DeepShift is inferior to others in terms of the performance on computation cost due to 8-bit precision for activations.

4.6 RAF-DB

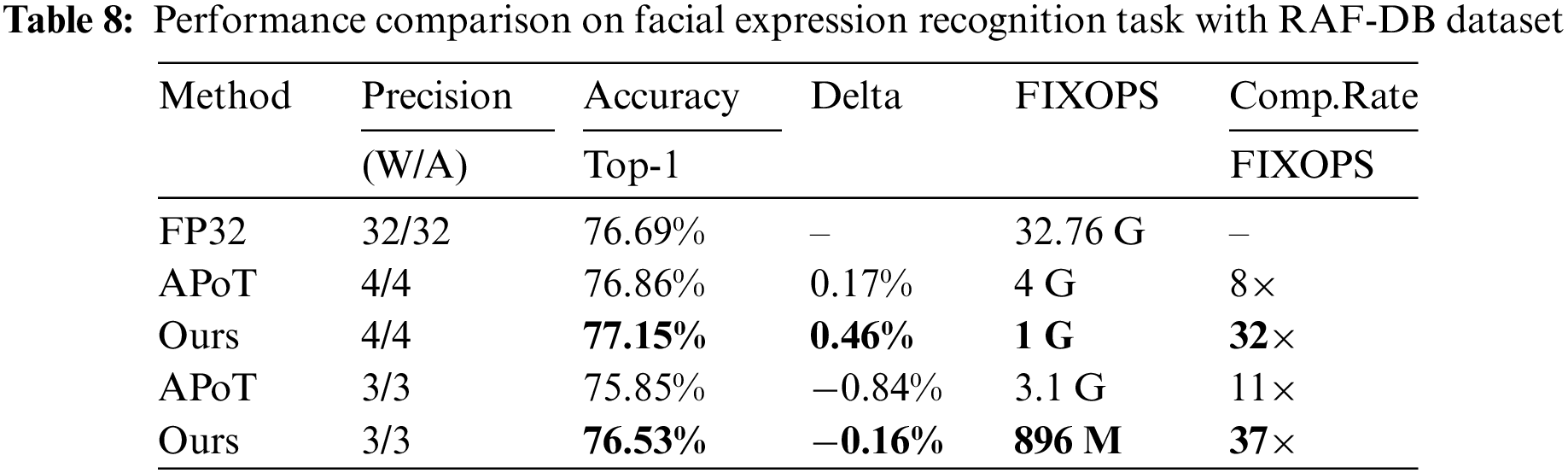
Furthermore, a task on facial expression recognition is used to validate the robustness of quantization methods, with Self-Cure-Network [41] on the RAF-DB dataset, where the experimental settings are the same as in the CIFAR experiment. Performance results on 4-bit and 3-bit precision are illustrated in Table 8. Our method outperforms APoT on both Top-1 and FIXOPS, with accuracy improvement by 0.46% over the baseline model on 4-bit while introducing −0.16% on 3-bit. Regarding FIXOPS, the proposed approach achieves 32× and 37× computation speedup, which is nearly 4-fold of APoT.

4.7 Hardware and Inference Simulation

In this section, we target implementing an efficient CNN accelerator. The hardware accelerator of the proposed P-LUT inference scheme is developed on the Xilinx KV260 FPGA platform by using Verilog HDL. Then, the efficiency of our implementation is evaluated and compared against a conventional bit-shifting scheme (adopted by prior PoT methods), as well as general-purpose computing hardware (Intel Core (TM) i3-2120 3.30 GHz and NVIDIA RXT3060 12 GB).

The overall architecture of the P-LUT accelerator is shown in Fig. 8, which is implemented to support 4-bit precision of 3×3 convolution. It consists of the P-LUT Complex, input/output buffer, S-Huff decoder, double Line-Buffer for input feature/weight, controller, Advanced eXtensible Interface (AXI), and Direct Memory Access (DMA). P-LUT Complex is the core computing engine and is designed to support 8 input/output channels in parallel computation, where each channel processes 8 convolutions (3×3) in the pipeline. Hence, a total of 64 convolutions (3×3) in parallel are achieved for high throughput. In the design, a double buffer for input/output is also used to cache data from external memory to hide the latency of data transfer (4-byte bus). The S-Huff decoder is particularly developed to decode compressed weights for reducing memory footprint. To evaluate the efficacy of P-LUT, a PoT-SHIFT accelerator adapting the same top design is constructed for performance comparison, in which the S-Huff decoder is omitted. With skillful design practices, the two accelerators are synthesized by Xilinx Vivado electronics design automation tools (2021.1 version) and run at 300 MHz frequency.

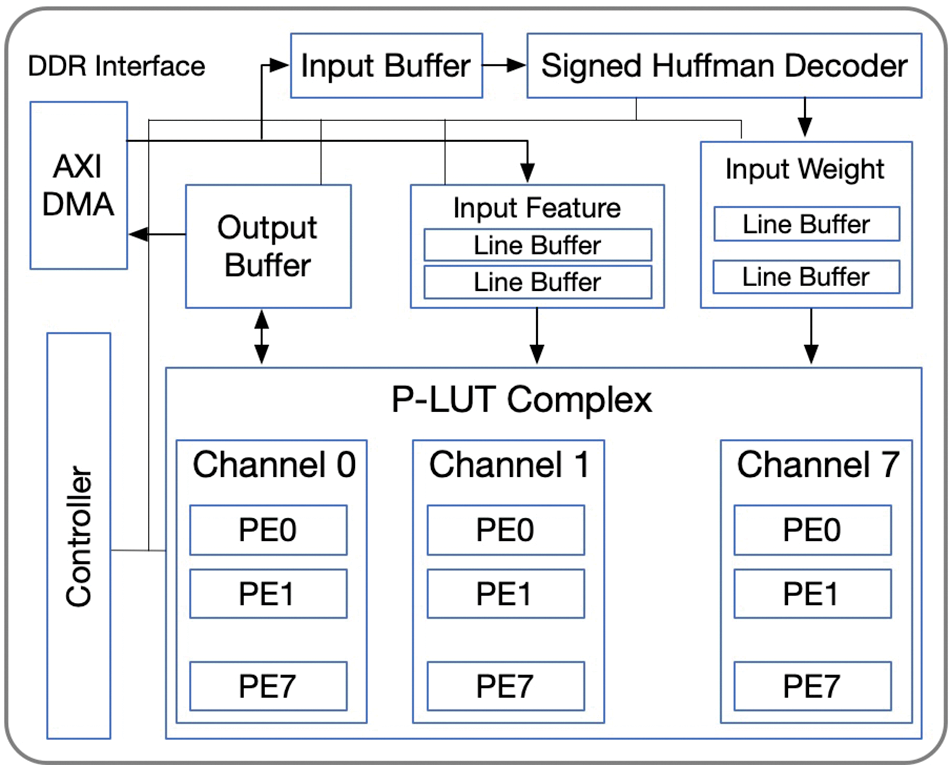
Figure 8: The P-LUT accelerator architecture

The performance of memory footprint, decoding overhead of S-Huff, and computation efficiency of the proposed accelerator benchmarks on ResNet18 with ImageNet dataset, where the convolution operations are performed on the CNN accelerator, and ARM CPU manages the transfer and control schedule. Overall, P-LUT achieves 2× more resource efficiency, reduces memory footprint by 1.45×, and 3× more computation efficiency, in comparison to PoT-SHIFT. The resource utilization of the P-LUT and PoT-SHIFT accelerator on FPGA is given in Table 9. Indicators on LUT and D flip-flop (DFF) resources show that the P-LUT scheme is 2× more resource-efficiency than PoT-SHIFT, while the cost on LUTRAM and BRAM incurs 101 and 21, due to the circuitry of the S-Huff. From Table 10, the S-Huff decoder reduces memory access by roughly 1.45× compared to PoT-SHIFT. The latency cost of the S-Huff decoder is 218, 1139, and 4134 µs for Conv3/4/5. Although the latency overhead of the S-Huff decoder is inevitable, this cost can be amortized by using a double buffer as in our architecture. We use the on-board power meter with Xilinx xmutil command tools to measure the power consumption of the whole device. Table 11 demonstrates the performance results of latency, computation efficiency (Giga Operations Per Second (GOPS)/W), and power usage of different platforms. In terms of latency, P-LUT hardware is approximately 4× faster than PoT-SHIFT, and 20× than CPU, whereas GPU outperforms all others due to its massive parallel computing ability (20× faster than ours). For computation efficiency, P-LUT achieves 3× greater than PoT-SHIFT, 225× than CPU, and 2× than GPU.

5  Conclusion

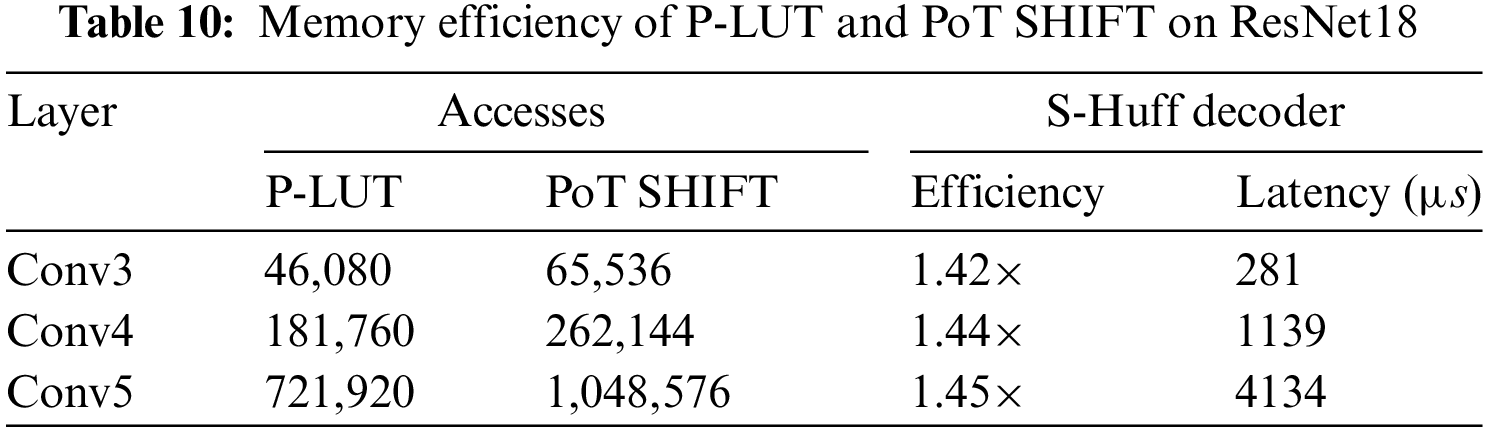
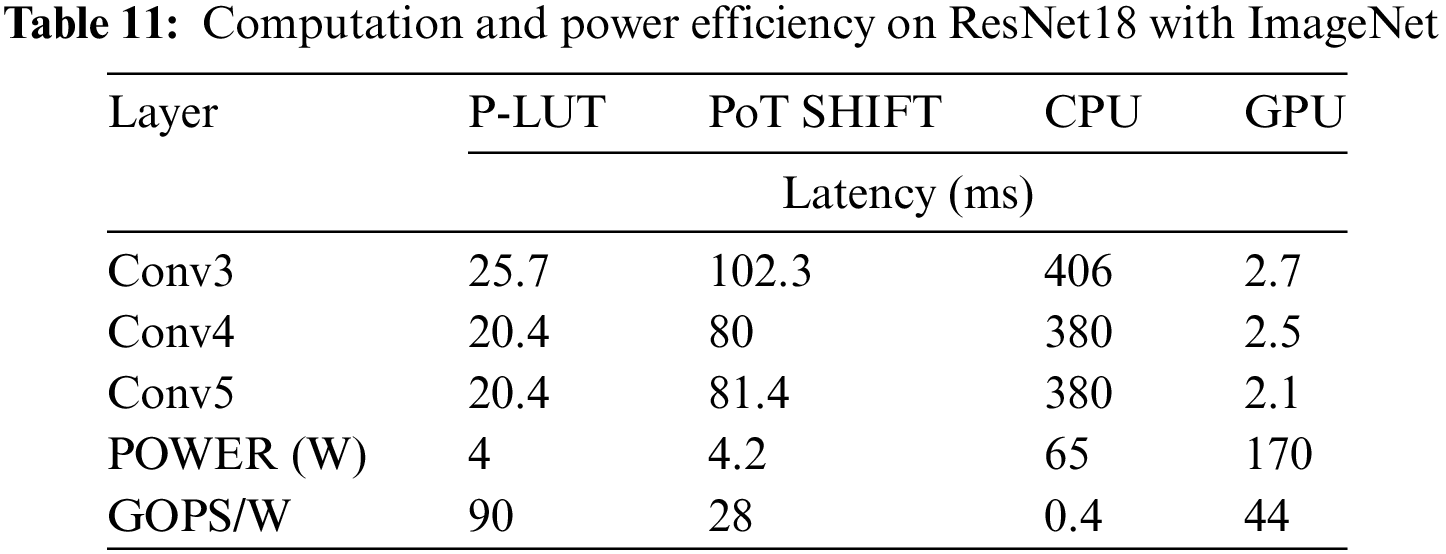
In this paper, we expounded the superiority and limits of edge computing on IoT devices, investigated PoT quantization based on bit-shifting logic, and discovered that the computation and memory efficiency of prior schemes is not optimal, and difficult for AI models applying to resource-limited edge computing devices with intensive communications in IoT scenario. To tackle this challenge, we proposed a P-LUT inference approach with IOS-PoT quantization and compression techniques. We found that the mismatch problem between quantization inputs and outputs can be mitigated by employing a tailored distribution-loss regularizer which assists in quantization convergence. Efficient inference is achieved by P-LUT with weight sharing and S-Huff encoding, which reduces memory footprint and eliminates multiplication operations for acceleration. Comprehensive experiments were conducted on ResNets and efficient architectures (i.e., ShuffleNetV2 and SqueezeNet). With CIFAR10/100, ImageNet, and RAF-DB datasets to validate the efficacy of the proposed approach. Our approach outperformed existing PoT and SOTA methods by several orders of magnitude in weight and computation reduction, achieving 2×∼10× improvement while achieving competitive prediction accuracy. Additionally, we implemented a P-LUT accelerator for convolution operations on the Xilinx KV260 FPGA platform and evaluated the performance against the bit-shifting approach, ×86 CPU, and GPU. Performance results proved that the P-LUT accelerator reduces memory footprint by 1.45×, is 3× more power efficiency and 2× resource efficiency than the prior bit-shifting scheme, and is 225× and 2× more efficient than CPU and GPU, respectively.

Acknowledgement: The authors would like to acknowledge the financial support of State Key Laboratory of Intelligent Vehicle Safety Technology, Chongqing Municipal Education Commission, and the technical support of Foresight Technology Institute, Chongqing Changan Automobile Co., Ltd., and School of Computer Science and Engineering, Chongqing University of Science and Technology.

Funding Statement: This work was supported by Open Fund Project of State Key Laboratory of Intelligent Vehicle Safety Technology by Grant with No. IVSTSKL-202311, Key Projects of Science and Technology Research Programme of Chongqing Municipal Education Commission by Grant with No. KJZD-K202301505, Cooperation Project between Chongqing Municipal Undergraduate Universities and Institutes Affiliated to the Chinese Academy of Sciences in 2021 by Grant with No. HZ2021015 and Chongqing Graduate Student Research Innovation Program by Grant with No. CYS240801.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Fangzhou He, Dingjiang Yan, Jie Li; data collection: Dingjiang Yan, Ke Ding, Jiajun Wang, Mingzhe Chen; analysis and interpretation of results: Fangzhou He, Dingjiang Yan, Jie Li; draft manuscript preparation: Fangzhou He. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets that support the findings of this study are openly available and have been cited from reference.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. Jacob et al., “Quantization and training of neural networks for efficient integer-arithmetic-only inference, Quantization and training of neural networks for efficient integer-arithmetic-only inference,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, Jun. 18, 2018, pp. 2704–2713. [Google Scholar]

2. Q. Jin et al., “F8Net: Fixed-point 8-bit only multiplication for network quantization,” arXiv preprint arXiv:2202.05239, 2022. [Google Scholar]

3. Y. Bhalgat, J. Lee, M. Nagel, T. Blankevoort, and N. Kwak, “LSQ+: Improving low-bit quantization through learnable offsets and better initialization,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. Workshops, Seattle, WA, USA, Jun. 14, 2020, pp. 696–697. [Google Scholar]

4. S. Fox, S. Rasoulinezhad, J. Faraone, D. Boland, and P. Leong, “A block minifloat representation for training deep neural networks,” in Int. Conf. Learn. Represent., May 3, 2021. [Google Scholar]

5. E. Park and S. Yoo, “Profit: A novel training method for sub-4-bit mobilenet models,” in Comput. Vis.–ECCV 2020: 16th Eur. Conf., Glasgow, UK, Springer, Aug. 23–28, 2020, pp. 430–446. [Google Scholar]

6. A. Zhou, A. Yao, Y. Guo, L. Xu, and Y. Chen, “Incremental network quantization: Towards lossless cnns with low-precision weights,” arXiv preprint arXiv:1702.03044, 2017. [Google Scholar]

7. J. Choi, Z. Wang, S. Venkataramani, P. I. -J. Chuang, V. Srinivasan and K. Gopalakrishnan, “PACT: Parameterized clipping activation for quantized neural networks,” arXiv preprint arXiv:1805.06085, 2018. [Google Scholar]

8. Y. Li, X. Dong, and W. Wang, “Additive powers-of-two quantization: An efficient non-uniform discretization for neural networks,” arXiv preprint arXiv:1909.13144, 2019. [Google Scholar]

9. M. Elhoushi, Z. Chen, F. Shafiq, Y. H. Tian, and J. Y. Li, “Deepshift: Towards multiplication-less neural networks,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Nashville, TN, USA, Jun. 20, 2021, pp. 2359–2368. [Google Scholar]

10. F. Cardinaux et al., “Iteratively training look-up tables for network quantization,” IEEE J. Sel. Top. Signal Process., vol. 14, no. 4, pp. 860–870, May 2020. doi: 10.1109/JSTSP.2020.3005030. [Google Scholar] [CrossRef]

11. S. Han, H. Mao, and W. J. Dally, “Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding,” arXiv preprint arXiv:1510.00149, 2015. [Google Scholar]

12. Y. Gong, L. Liu, M. Yang, and L. Bourdev, “Compressing deep convolutional networks using vector quantization,” arXiv preprint arXiv:1412.6115, 2014. [Google Scholar]

13. Y. Choi, M. El-Khamy, and J. Lee, “Universal deep neural network compression,” IEEE J. Sel. Top. Signal Process., vol. 14, no. 4, pp. 715–726, 2020. doi: 10.1109/JSTSP.2020.2975903. [Google Scholar] [CrossRef]

14. Y. Ko, A. Chadwick, D. Bates, and R. Mullins, “Lane compression: A lightweight lossless compression method for machine learning on embedded systems,” ACM Trans. Embedded Comput. Syst. (TECS), vol. 20, no. 2, pp. 1–26, 2021. doi: 10.1145/3431815. [Google Scholar] [CrossRef]

15. K. Bhardwaj, C. -Y. Lin, A. Sartor, and R. Marculescu, “Memory- and communication-aware model compression for distributed deep learning inference on IoT,” ACM Trans. Embedded Comput. Syst. (TECS), vol. 18, no. 5s, pp. 1–22, 2019. [Google Scholar]

16. M. Samragh, M. Javaheripi, and F. Koushanfar, “EncoDeep: Realizing bit-flexible encoding for deep neural networks,” ACM Trans. Embedded Comput. Syst. (TECS), vol. 19, no. 6, pp. 1–29, 2020. doi: 10.1145/3391901. [Google Scholar] [CrossRef]

17. N. Yang, Z. Zheng, and T. Wang, “Model loss and distribution analysis of regression problems in machine learning,” in Proc. 2019 11th Int. Conf. Mach. Learn. Comput., Zhuhai, China, Feb. 22, 2019, pp. 1–5. [Google Scholar]

18. T. Hu and Y. Lei, “Early stopping for iterative regularization with general loss functions,” J. Mach. Learn. Res., vol. 23, pp. 1–36, 2022. [Google Scholar]

19. W. Wan, Y. Zhong, T. Li, and J. Chen, “Rethinking feature distribution for loss functions in image classification,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, Jun. 18, 2018, pp. 9117–9126. [Google Scholar]

20. D. Li, Y. Liu, and L. Song, “Adaptive weighted losses with distribution approximation for efficient consistency-based semi-supervised learning,” IEEE Trans. Circuits Syst. Video Technol., vol. 32, no. 11, pp. 7832–7842, 2022. doi: 10.1109/TCSVT.2022.3186041. [Google Scholar] [CrossRef]

21. S. Zhang, F. Ge, R. Ding, H. Liu, and X. Zhou, “Learning to binarize convolutional neural networks with adaptive neural encoder,” in 2021 Int. Joint Conf. Neur. Netw. (IJCNN), Shenzhen, China, IEEE, Jul. 18, 2021, pp. 1–8. [Google Scholar]

22. S. Jain, S. Venkataramani, V. Srinivasan, J. Choi, P. Chuang and L. Chang, “Compensated-DNN: Energy efficient low-precision deep neural networks by compensating quantization errors,” in Proc. 55th Annu. Des. Automat. Conf., San Francisco, CA, USA, Jun. 24, 2018, pp. 1–6. [Google Scholar]

23. C. Gong, Y. Chen, Y. Lu, T. Li, C. Hao and D. Chen, “VecQ: Minimal loss DNN model compression with vectorized weight quantization,” IEEE Trans. Comput., vol. 70, no. 5, pp. 696–710, 2020. doi: 10.1109/TC.2020.2995593. [Google Scholar] [CrossRef]

24. Z. Wang, Y. -H. Shao, L. Bai, C. -N. Li, and L. -M. Liu, “General plane-based clustering with distribution loss,” IEEE Trans. Neural Netw. Learn. Syst., vol. 32, no. 9, pp. 3880–3893, 2020. doi: 10.1109/TNNLS.2020.3016078. [Google Scholar] [PubMed] [CrossRef]

25. E. Wang, J. J. Davis, P. Y. Cheung, and G. A. Constantinides, “LUTNet: Rethinking inference in fpga soft logic,” in 2019 IEEE 27th Annu. Int. Symp. Field-Programmable Custom Comput. Mach. (FCCM), San Diego, CA, USA, Apr. 28, 2019, pp. 26–34. [Google Scholar]

26. Y. Bengio, N. Léonard, and A. Courville, “Estimating or propagating gradients through stochastic neurons for conditional computation,” arXiv preprint arXiv:1308.3432, 2013. [Google Scholar]

27. A. Lempel and J. Ziv, “Lempel-ziv–markov chain algorithm,” Accessed: Dec. 7, 2023. [Online]. Available: https://en.wikipedia.org/wiki/Lempel-Ziv-Markov_chain_algorithm [Google Scholar]

28. A. Krizhevsky and G. Hinton, “Learning multiple layers of features from tiny images,” Accessed: Dec. 7, 2023. 2009. [Online]. Available: http://www.cs.utoronto.ca/~kriz/learning-features-2009-TR.pdf [Google Scholar]

29. J. Deng, W. Dong, R. Socher, L. J. Li, K. Li and L. Fei-Fei, “ImageNet: A large-scale hierarchical image database,” in 2009 IEEE Conf. Comput. Vis. Pattern Recognit., Miami Beach, FL, USA, Jun. 22, 2009, pp. 248–255. [Google Scholar]

30. S. Li, W. Deng, and J. Du, “Reliable crowdsourcing and deep locality-preserving learning for expression recognition in the wild,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, Jul. 22, 2017, pp. 2852–2861. [Google Scholar]

31. Z. Liu, B. Wu, W. Luo, X. Yang, W. Liu and K. -T. Cheng, “Bi-real Net: Enhancing the performance of 1-bit CNNs with improved representational capability and advanced training algorithm,” in Proc. Eur. Conf. Comput. Vis. (ECCV), Munich, Germany, Sep. 8, 2018, pp. 722–737. [Google Scholar]

32. V. Sovrasov, “ptflops: A flops counting tool for neural networks in pytorch framework,” Accessed: Dec. 7, 2023. 2020. [Online]. Available: https://github.com/sovrasov/flops-counter.pytorch [Google Scholar]

33. T. Salimans and D. P. Kingma, “Weight normalization: A simple reparameterization to accelerate training of deep neural networks,” in Adv. Neur. Inf. Process. Syst., Barcelona, Spain, Dec. 5, 2016, vol. 29. [Google Scholar]

34. S. Jung et al., “Learning to quantize deep networks by optimizing quantization intervals with task loss,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, Jun. 16, 2019, pp. 4350–4359. [Google Scholar]

35. D. Miyashita, E. H. Lee, and B. Murmann, “Convolutional neural networks using logarithmic data representation,” arXiv preprint arXiv:1603.01025, 2016. [Google Scholar]

36. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, Jun. 30, 2016, pp. 770–778. [Google Scholar]

37. Y. Idelbayev, “Proper ResNet implementation for CIFAR10/CIFAR100 in PyTorch,” Accessed: Dec. 7, 2023. 2020. [Online]. Available: https://github.com/akamaster/pytorch_resnet_cifar10 [Google Scholar]

38. D. Zhang, J. Yang, D. Ye, and G. Hua, “LQ-Nets: Learned quantization for highly accurate and compact deep neural networks,” in Proc. Eur. Conf. Comput. Vis. (ECCV), Munich, Germany, Sep. 8, 2018, pp. 365–382. [Google Scholar]

39. F. N. Iandola, S. Han, M. W. Moskewicz, K. Ashraf, W. J. Dally and K. Keutzer, “SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 mb model size,” arXiv preprint arXiv:1602.07360, 2016. [Google Scholar]

40. N. Ma, X. Zhang, H. -T. Zheng, and J. Sun, “ShuffleNet v2: Practical guidelines for efficient CNN architecture design,” in Proc. Eur. Conf. Comput. Vis. (ECCV), Munich, Germany, Sep. 8, 2018, pp. 116–131. [Google Scholar]

41. K. Wang, X. Peng, J. Yang, S. Lu, and Y. Qiao, “Suppressing uncertainties for large-scale facial expression recognition,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, Jun. 13, 2020, pp. 6897–6906. [Google Scholar]