A Feature Selection Method Based on Hybrid Dung Beetle Optimization Algorithm and Slap Swarm Algorithm

1  Introduction

With the development of the information industry, science and technology, and the gradual maturity of modern collection technology, thousands of applications have produced a huge amount of data information, and various data information also provides a guarantee for the development of technology. At the same time, the data analysis and processing are also faced with a big challenge, because the data dimension is too large to get more valuable information. Therefore, dimension reduction is very important in the process of data pre-processing [1].

FS extracts a significant portion of features from the original dataset and uses predetermined assessment metrics to eliminate characteristics that are unnecessary, redundant, or noisy in order to reduce dimension. In contrast to Feature Extraction, which also performs the function of dimension reduction, Feature Extraction accomplishes this through the creation of new feature combinations, while FS does not need to modify original features, so FS has been widely used in text mining and other fields [2]. FS can be divided into three types: filter, wrapper, and embedded. When selecting features, the filter method can select important features based on the internal relationship between features without combining the learning method. Although this method is simple, it usually has low classification accuracy [3]. The wrapper approach evaluates the quality of selected features by combining them with a machine learning model, and the evaluation process is achieved by searching for subsets of features repeatedly until certain stopping conditions are met or the desired optimal subset of features is obtained. This method can obtain higher classification accuracy, but at the same time has greater computational complexity. The embedded method is to embed feature selection into learner training. Compared with the wrapper, it saves more time, but easily increases the training burden of the model.

An increasing number of algorithms have been used in the field of FS as a result of the ongoing development of meta-heuristic algorithms [4]. The meta-heuristic algorithm is an optimization algorithm generated by simulating physical phenomena or biological behaviors in nature. Thanks to the advantages of the simple model, easy implementation, and high robustness, meta-heuristics have been successfully implemented in several optimization domains. Nevertheless, as stated by the No Free-Lunch (NFL) theorem [5], it is impossible for any method to successfully solve every optimization issue, which also encourages researchers to innovate and improve the algorithm constantly, so as to apply the optimization algorithm to a broader field. In the field of FS, Song et al. [6] considered that the particle updating mechanism and population initialization strategy adopted by the traditional Particle Swarm Optimization (PSO) did not consider the characteristics of the FS problem itself, which limited its performance in dealing with high-dimensional FS problems. So they proposed a Bare-Bones Particle Swarm Optimization (BBPSO) based on mutual information. By combining with the K nearest neighbor (KNN) classifier, the effectiveness of the proposed algorithm was verified on multiple datasets, and the classification accuracy was greatly improved. A better binary Salp Swarm Algorithm (SSA) for FS was developed by Faris et al. [7]. To enhance the algorithm’s exploration performance, crossover operators were added and continuous SSA was transformed into binary form using various transfer functions. The suggested method’s higher performance was confirmed when compared to the other 5 algorithms over 22 UCI (University of California Irvine) datasets. Emary et al. [8] proposed a binary Grey Wolf Optimization for FS, which binarized the continuous algorithm through the S-type transfer function and verified the method on multiple datasets. It has provided an important reference value for the subsequent improvement of Grey Wolf Optimization for FS. Mafarja et al. [9] proposed two improved Whale Optimization Algorithm for FS, which demonstrated better classification performance through verification on UCI datasets and comparison with other algorithms. Researchers have also proposed many hybrid optimization algorithms and applied them to FS problems. Enhanced Chaotic Crow Search and Particle Swarm Optimization (ECCSPSOA), a hybrid binary introduced by Adamu et al. [10] accomplished the organic merger of Particle Swarm Optimization and Crow Search Algorithm and included the opposition-based learning technique. The algorithm’s search space was enlarged, and several chaotic initialization procedures were employed to enhance its optimization efficiency, resulting in significant improvements. For high-dimensional imbalanced data containing missing values, a particle swarm optimization-based fuzzy clustering FS algorithm (PSOFS-FC) was proposed by Zhang et al. [11]. It shows superiority over state-of-the-art FS methods in handling high-dimensional unbalanced data with missing values by exhibiting remarkable classification performance on several public datasets. To solve high-dimensional FS issues, Song et al. [12] suggested a variable-size cooperative coevolutionary particle swarm optimization method (VS-CCPSO) and evaluated it against six other algorithms on twelve datasets. The experimental results demonstrated that the algorithm is more advantageous in handling high-dimensional FS problems. In addition, literature [13–15] also proposed different hybrid algorithms for FS, provides new ideas and directions for the application of swarm intelligence optimization algorithms in feature selection.

Dung Beetle Optimization (DBO) [16], as a new meta-heuristic algorithm, shows strong optimization ability in the benchmark function, but there are also problems such as easy to entrap in local optima and exploration and exploitation ability imbalance. Therefore, a hybrid Dung Beetle Optimization is proposed in this paper. The original rolling dung beetle update is replaced with the salp swarm method, which has a unique leader and follower mechanism and enhances the algorithm’s capacity to explore the solution space. Subsequently, the population is initialized using chaotic mapping, augmenting the DBO’s population diversity. Finally, the mutation operator is added to stealing population position updates in the DBO to improve the ability of the algorithm to jump from local optima. By converting the improved DBO into binary form through transfer function, a Hybrid Binary Chaotic Salp Swarm Dung Beetle Optimization (HBCSSDBO) is proposed and applied to FS. The main motivation for the decision to merge DBO and SSA was the strong merit-seeking capability of DBO and the unique leader, and follower search mechanism of SSA. The complementary advantages of the algorithms are realized. The goal of merging these two algorithms is to create a hybrid feature selection algorithm that is more effective. The following highlights this paper’s primary contributions:

•   Introducing a unique feature selection approach for dung beetle optimization in hybrid salp swarms. Combining the salp swarm optimization method with the dung beetle optimization algorithm makes good use of the features that make each approach distinct.

•   Using this hybrid algorithm combined with a KNN classifier greatly improves classification accuracy.

•   The effectiveness of the hybrid algorithm as applied to the FS problem is explored by comparing it with four better-known meta-heuristics on 16 UCI benchmark test datasets, and by employing a variety of evaluation criteria as well as multiple perspectives from high, medium, and low dimensionality.

•   The Friedman test was employed to see whether there was a significant difference between the outcomes produced from the comparison approach and the suggested hybrid feature selection method.

2  Relate Works

2.1 Dung Beetle Optimization

Dung Beetle Optimization (DBO) is a new swarm intelligence optimization algorithm inspired by simulating the social behavior of dung beetles in nature. In this algorithm, the original author divided the dung beetle population into four different agents (ball-rolling dung beetles, brood balls, small dung beetles, and stealing dung beetles) according to a certain proportion to simulate different dung beetle behaviors. The specific proportion division is shown in Fig. 1.

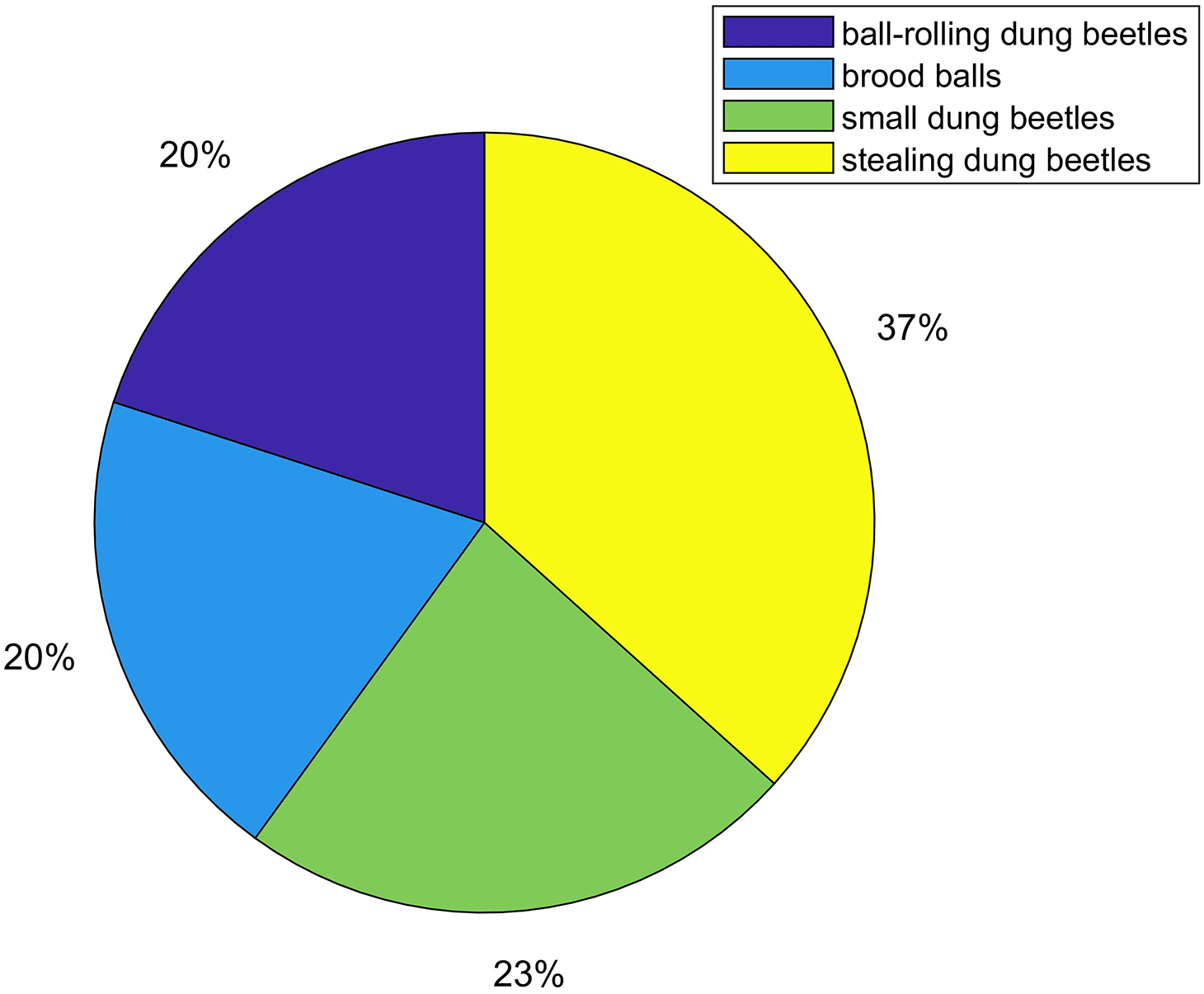
Figure 1: Proportion division of dung beetle population

2.1.1 Dung Beetle Ball Rolling Behavior

To keep the ball moving in a straight course, dung beetles in the wild must pay attention to astronomical signals. The locations of the beetles are continually shifting as they roll. The mathematical model of dung beetles’ ball-rolling is shown in Eq. (1):

x(t+1)=xi(t)+α×k×xi(t−1)+b×Δx,Δx=∣xi(t)−Xw∣(1)

where xi(t) is the position of the i-th dung beetle in the t-th iteration, α is a natural coefficient, assigned −1 or 1, k represents the deflection coefficient and k ∈ (0, 0.2), b represents a random constant and b∈ (0, 1). Xw denotes the global worst position.

A dung beetle must dance to figure out its new course when it comes across an obstruction that prevents it from moving ahead. This dancing behavior is described as follows:

xi(t+1)=xi(t)+tan⁡(θ)|xi(t)−xi(t−1)|(2)

from |xi(t)−xi(t−1)| in the above formula, we can see that the position update of dung beetles is affected by current and historical data. Where θ∈ [0, π], it is important to note that the dung beetle’s location will not be updated if θ is 0, π/2 or π.

2.1.2 Brood Balls

Dung beetles roll their balls to a secure spot, conceal them, and then lay their eggs to create a safer habitat for their larvae. In order to replicate the locations where female dung beetles deposit their eggs, the following boundary selection approach is suggested:

Lb∗=max(X∗×(1−R), Lb),Ub∗=min(X∗×(1+R), Ub)(3)

where X∗ represents the local optimal value, the problem’s lower and upper limits are denoted by Lb and Ub, respectively. R=1−t/Tmax, and Tmax is the maximum number of iterations. Lb∗ and Ub∗ are the lower and upper boundaries of the spawning area, respectively. As can be seen from the above formula, the spawning boundary is dynamically determined by the R value, so the position of the brood ball is also dynamically updated, as shown below:

Xi(t+1)=X∗+b1×(Xi(t)−Lb∗)+b2×(Xi(t)−Ub∗)(4)

where b1 and b2 represent two independent 1 × D random vectors, D is the dimension of the optimization problem.

2.1.3 Small Dung Beetles

The ideal foraging region is first determined to direct tiny dung beetles to forage, and the foraging border is specified as follows in order to mimic the foraging behavior of these insects:

Lbb=max(Xb×(1−R), Lb),Ubb=min(Xb×(1+R), Ub)(5)

where Xb represents the global optimal position, Lbb and Ubb represent the lower and upper optimal foraging boundary, respectively. Thus, the location of the little dung beetle is updated as follows:

xi(t+1)=xi(t)+C1×(xi(t)−Lbb)+C2×(xi(t)−Ubb)(6)

where C1 is a random number that follows a normal distribution, C2 represents a random number belonging to (0, 1).

2.1.4 Stealing Dung Beetles

Certain dung beetles in the wild take dung balls from other dung beetles. The following is an updated position of the thief:

xi(t+1)=Xb+S×g×(∣xi(t)−X∗∣+∣xi(t)−Xb∣)(7)

where S is a constant, g is a 1 × D random vector.

2.2 Salp Swarm Algorithm (SSA)

In 2017, Mirjalili et al. introduced a novel intelligent optimization technique called the Salp Swarm Algorithm (SSA) [17]. SSA, a relatively new swarm intelligence optimization method, mimics the swarm behavior of salps traveling and feeding in a chain in the deep sea. They often exhibit their chain activity as discrete units that are joined end to end and move sequentially. The first person in the salp chain is the only one who is considered the leader; the others are followers. A leader directs the followers to walk in a chain behavior toward food at each iteration. The situation of slipping into local optimum is much reduced while traveling since the leader performs global exploration while the following completely conducts local exploitation. The leader’s position is updated as follows:

xj1={Fj+c1((ubj−lbj)×c2+lbj)c3≤0Fj−c1((ubj−lbj)×c2+lbj)c3>0(8)

where Fj represents the position of the food, ubj and lbj are the upper and lower bounds, respectively, c2 and c3 are two random number between [0, 1], xj1 is the position of the leader. c1 is a very important parameter in the algorithm, which controls the balance between global exploration and local exploitation, and its expression is as follows:

c1=2e−(4ttmax)2(9)

where t is the current iteration number, tmax is the maximum iteration. After the leader’s position is updated, the followers’ position is updated as follows:

xji=12(xji+xji−1)(10)

where xji is the position of the j-th individual in the i-th iteration, and the value of i is greater than 1.

3  The Proposed Algorithm

The FS problem is a binary problem with an upper bound of 1 and a lower bound of 0. Obviously, the continuous DBO cannot deal with this problem, so we convert the continuous algorithm into binary form through Eq. (11) [18,19], so as to search in the solution space.

xi(t+1)={1if11+e(−10∗(xi(t)−0.5))>r0otherwise(11)

where r is the random number in [0, 1].

To address the imbalance between exploration and exploitation and the tendency for local optima to easily stagnate in the current DBO, this paper adopts the following strategies to improve the original DBO.

3.1 Chaotic Mapping

Chaos is an aperiodic phenomenon with asymptotic self-similarity and orderliness. Due to its unique randomness, ergodicity, and complexity, it is widely used as a global optimization processing mechanism to effectively avoid the dilemma of local optima in the process of data search optimization in the field of decision system design [20]. In recent years, chaotic strategies have been widely used in intelligence optimization algorithms.

In order to solve problems such as low population diversity and unsatisfactory search results in the random initialization stage of DBO, the Bernoulli chaotic mapping method is introduced. It makes the dung beetle populations traverse solution space better in the initialization phase, and improves the overall optimal search performance. The histogram of the Bernoulli chaotic mapping sequence is depicted in Fig. 2, and its expression is as follows:

xi+1={xi/(1−a),xk∈(0,1−a](xi−1+a)/a,xi∈(1−a, 1)(12)

where a is control factor, 0.479 is used to achieve better mapping results in this paper.

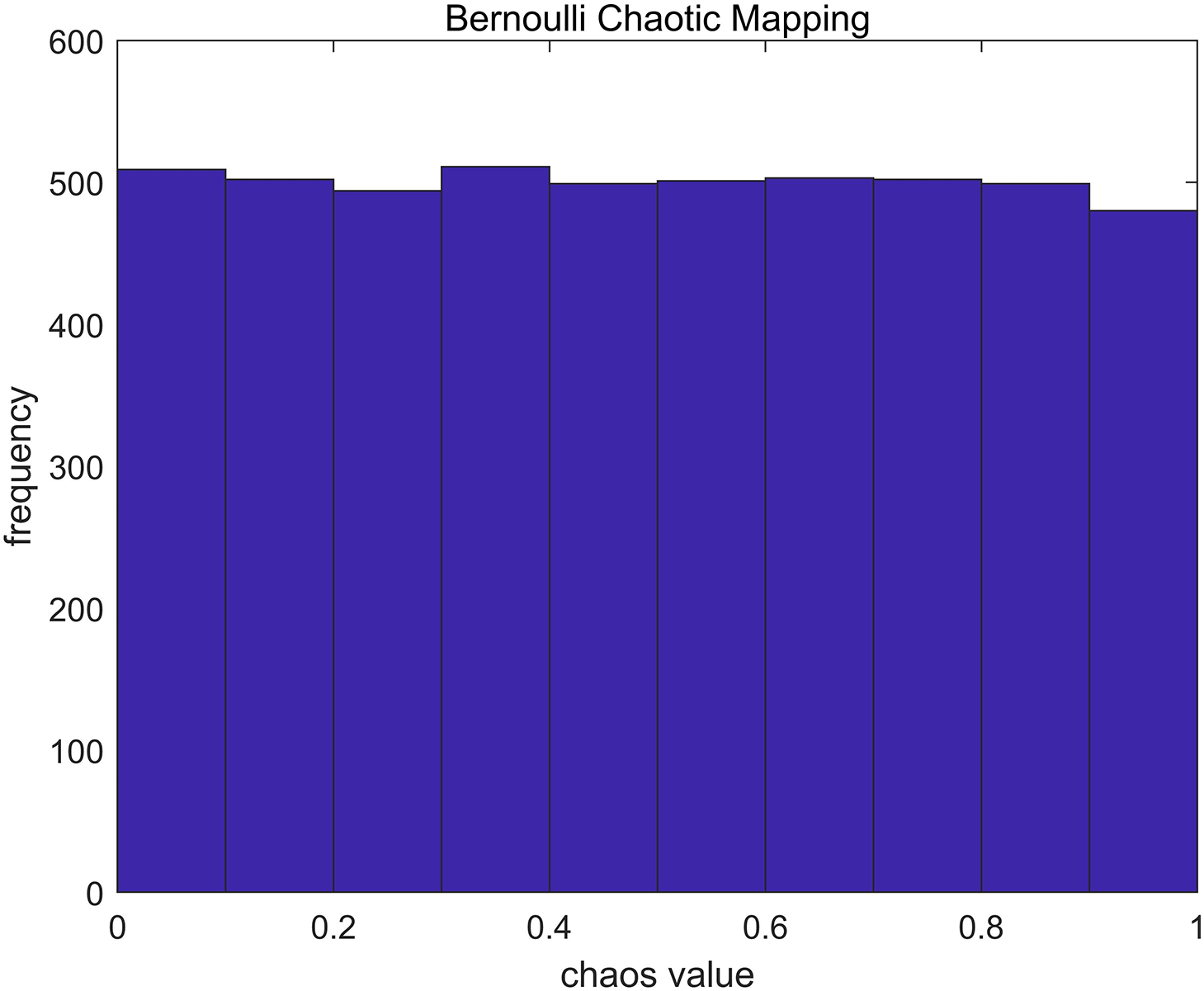
Figure 2: Histogram of the Bernoulli chaotic mapping sequence

3.2 Improved Ball-Rolling Dung Beetles

The ball-rolling dung beetle plays an important role in the DBO, and its updated position has a crucial impact on the global exploration of the algorithm in the solution space. Moreover, SSA has a unique leader and follower mechanism, strong global exploration ability, and a simple structure to implement. Thus, in order to enhance the algorithm’s capacity for global exploration, we include SSA into DBO to update the location of the ball-rolling dung beetle. Simultaneously, the original SSA is improved upon and the Levy flight strategy is introduced to the leader position update in order to disrupt the ideal position, hence facilitating a larger exploration of the solution space by the algorithm. Levy flight strategy [21] is a random behavior strategy used to simulate step size and direction during a random walk or search. The leader’s position in the improved SSA is updated as follows:

xj1={Levy.∗Fj+c1((ubj−lbj)×c2+lbj)c3≤0Levy.∗Fj−c1((ubj−lbj)×c2+lbj)c3>0(13)

The aforementioned variables have been explained above, where the calculation formula of Levy flight operator is shown as follows:

Levy=(s1, s2,⋯,sn),si=μ|v|1λ,i=1, 2,⋯,n(14)

where v follows the standard normal distribution (the mean is 0 and the variance is 1), μ follows Gaussian distribution (the mean is 0 and the variance is σμ), and σμ is calculated as Eq. (15):

σμ=[Γ(1+λ)×sin(π×λ2)Γ(1+λ2)×λ×2λ−12]1λ(15)

where λ falls in the (1, 3), and the value in this paper is 1.5, Γ(x) is the gamma function.

3.3 Mutation Operator

The behavior of the stolen dung beetle is precisely around the dung ball (global optimal location), which aims to address the issue that DBO is prone to be trapped in local optima. As a result, it plays a significant role in the capacity of DBO to exploit situations locally. In order to prevent the stealing dung beetle from stopping forward search due to finding the local optimal position, a mutation operator is added to the position update of the stealing dung beetle. After each stealing dung beetle position update is completed, mutation operation is carried out with a certain probability p, which can effectively ensure that the DBO is not easily trapped in local optima, and enhance the local exploitation ability of the DBO. When p > rand, the inverse operation is performed on the current individual, otherwise it remains unchanged, as shown in Fig. 3. The probability p is calculated as follows:

p=0.9+−0.9∗(t−1)M−1(16)

where t and M represent the current and maximum iterations, respectively.

Figure 3: Mutation of stealing dung beetle in DBO

By enhancing the DBO using the aforementioned tactics, the algorithm’s capacity to break out of local optima is effectively increased, its scope for global exploration is broadened, and a healthy balance between its capabilities for local exploitation and global exploration is struck. The flow chart applied to FS specifically is shown in Fig. 4. The following is the specific process of HBCSSDBO feature selection methods:

1.   Import the data and divide it into training and test sets. Determine the fitness function and the parameter initialization settings.

2.   Initialization of chaotic mapping for dung beetle populations according to Eq. (12).

3.   Using an enhanced SSA to update a rolling dung beetle’s location within a DBO.

4.   The p-value at the moment of the stealing dung beetle’s position update determined whether to carry out a mutation operation. The locations of breeding dung beetles, tiny dung beetles, and stealing dung beetles were updated in accordance with Eqs. (4), (6), and (7), respectively.

5.   The characteristics that are iteratively chosen are supplied into the KNN classifier for training after the dung beetle population is binarized based on the transfer function.

6.   Calculate the fitness value corresponding to the selected feature, if t < Tmax, then return to step three.

7.   Output results.

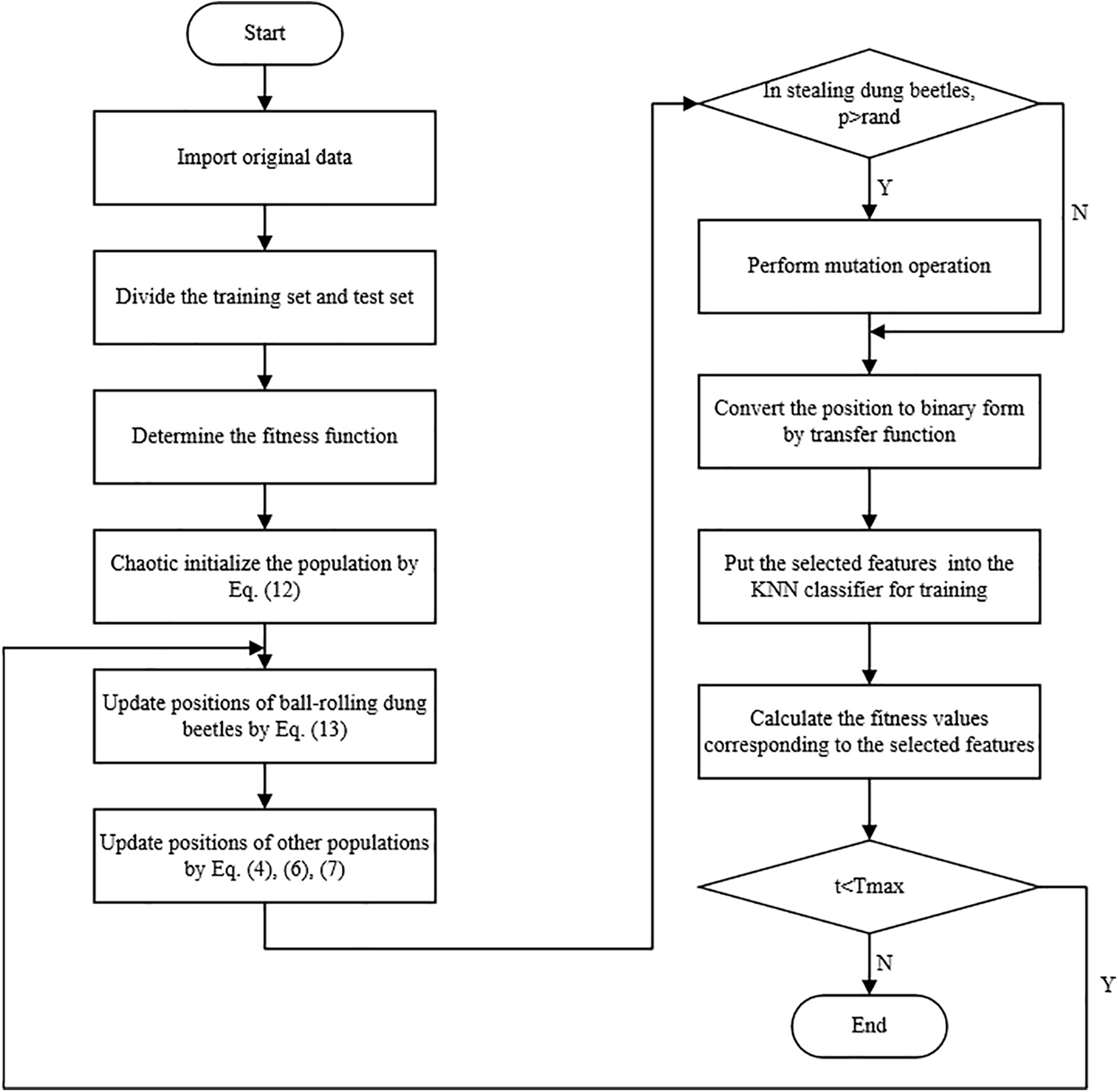
Figure 4: Flow chart

3.4 Fitness Function

Choosing the lowest feature subset from the original features and increasing classification accuracy are the two goals of the multi-objective optimization problem known as the FS problem. Based on the foregoing, the fitness function of the FS issue is determined to be as follows in order to attain a balance between the two objectives [22].

fitness=αρR(D)+β|X||N|(17)

where ρR(D) represents the classification error rate by KNN classifier, |X| represents the number of feature subsets obtained from algorithm optimization, the total number of features in the dataset is represented by the symbol |N|. α and β are used to achieve the balance between classification accuracy and the number of feature subsets, and α∈ [0, 1], β=1−α.

4  Experimental Results

4.1 Datasets

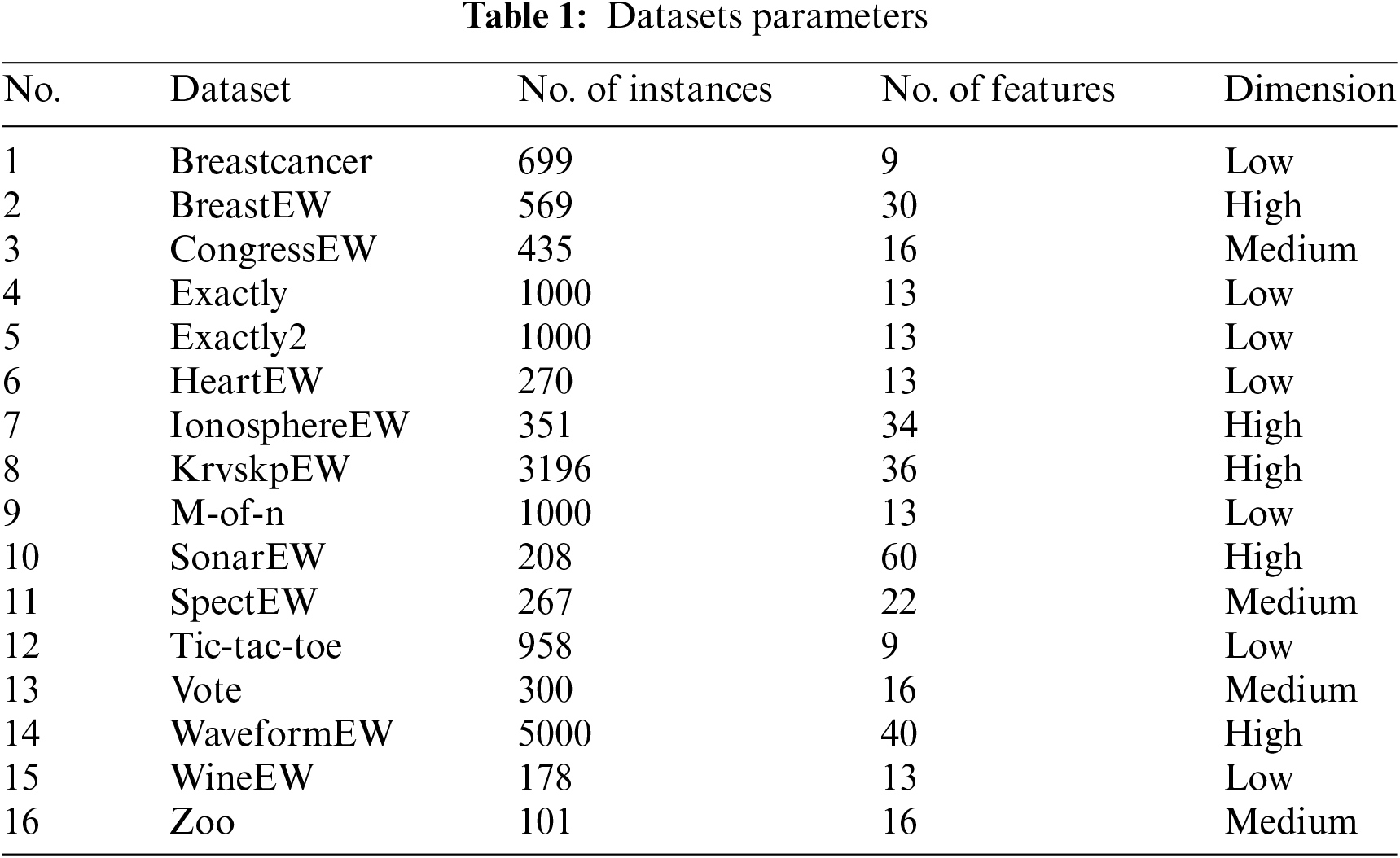
The performance of the HBCSSDBO method for FS is verified in this study using 16 standard datasets that are all taken from the UCI Machine Learning Repository [23]. Table 1 displays each dataset’s parameters, which are categorized into three groups based on the number of features in each dataset: low, medium, and high dimensions.

4.2 Parameter Settings

One supervised learning technique that classifies new instances based on how far they are from the training set is the K nearest neighbor (KNN) approach [24]. It is widely used in pattern recognition, artificial intelligence, and other fields, so this paper selects KNN as a classifier combined with HBCSSDBO to apply to the FS problem and K = 5. Experiments have shown that when K is set to 5, better classification results can be obtained on numerous datasets [25]. By applying K-fold cross-validation, the dataset is divided into K segments. The test set is comprised of one segment, while the training set is made up of the other (K-1) segment, whose data segments are randomly shuffled.

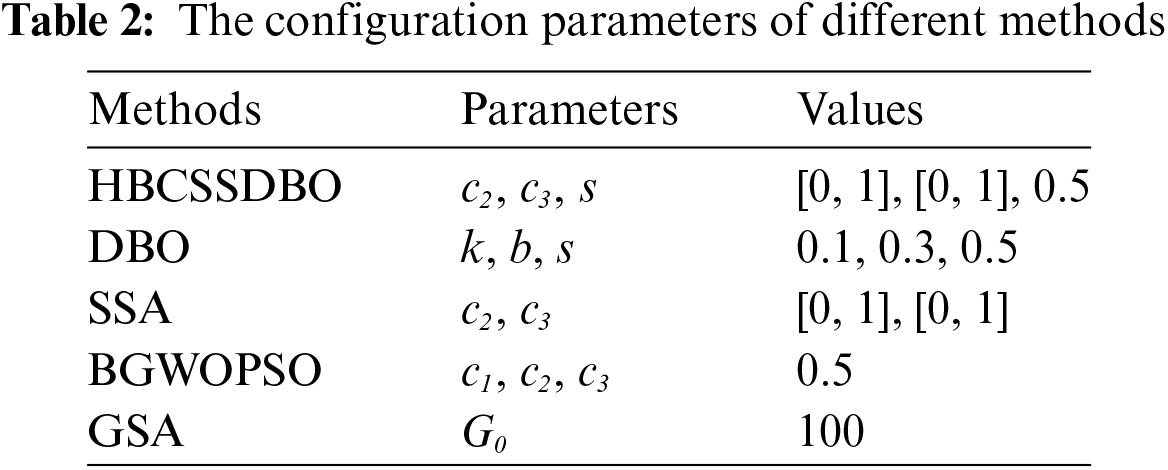
Intel(R) CoreTMi7-6700 machine with 3.4 GHz CPU (Central Processing Unit) and 8 GB of RAM (random access memory) was used to run the HBCSSDBO algorithm and other comparative algorithms. The comparison algorithms include the original DBO [16], SSA [17], hybrid Gray Wolf Particle Swarm Optimization (BGWOPSO) [26], and Gravity Search Algorithm (GSA) [27]. The parameters in each algorithm can be found in Table 2, and the comparison algorithm is converted into binary form by Eq. (11) to ensure the comparability and fairness of the experiment to the greatest extent possible. It is noteworthy that every algorithm’s population number in this work is set consistently at 30, the number of iterations at 100, the upper and lower bounds of the search at 1, and the number of independent operations at 10. For the value of the weight parameter α in the fitness function is 0.99 [28].

4.3 Experimental Evaluation Indices

To validate the suggested approach, a variety of evaluation indices are used in this study, including average classification accuracy (in %), mean fitness value, best and worst fitness values, fitness value variation, average number of picked features, and average computational time. The following formula is used to determine the index:

(1)   Average classification accuracy

Acc=1N∑k=1NFK(18)

where FK is the highest classification accuracy for the K-th run, N is the number of runs.

(2)   Mean fitness value

Fit=1N∑k=1NFK∗(19)

where FK∗ is the best fitness value for the K-th run.

(3)   The best fitness value

Max=min1≤K≤NrFK∗(20)

(4)   The worst fitness value

Min=max1≤K≤NrFK∗(21)

(5)   Fitness value variance

STD=1N−1∑K=1N(FK∗−Fit)2(22)

(6)   Average number of selected features

SIZE=1N∑k=1NTK∗(23)

where TK∗ is the number of selected features at the K-th run.

(7)   Average computational time

Avgtime=1N∑k=1NtimeK(24)

where timeK is the time of running the algorithm for the K-th time.

5  Experimental Results and Discussion

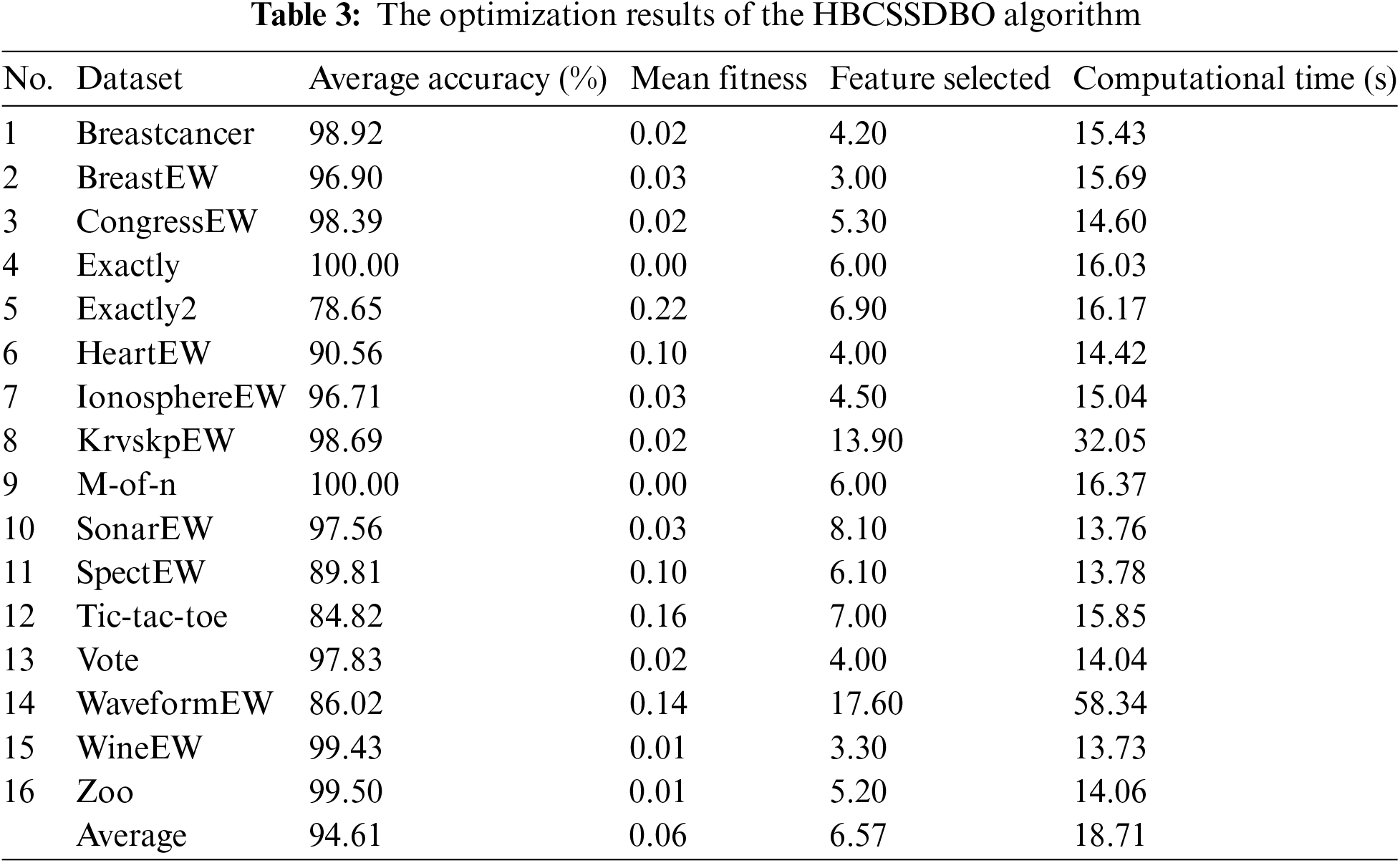
The outcomes of using the HBCSSDBO algorithm on 16 datasets are displayed in Table 3. The computed time, mean fitness, average accuracy (in%), and feature selection are among the outcomes. Ten runs of the method were performed for each dataset. Among these, the algorithm gets the best accuracy of 100% on the datasets M-of-n and Exactly. On the WineEW and Zoo datasets, it also achieves more than 99% accuracy, followed by more than 98% accuracy on the Breastcancer and CongressEW datasets. With respect to the total number of characteristics picked, the BreastEW dataset has the fewest features chosen—just three. Secondly, KrvskpEW and WaveformEW have the highest amount of features picked (13.9 and 17.6, respectively), while WineEW has the fewest features selected (3.3). In terms of computational time, WineEW, SonarEW, and SpectEW datasets spend the least time, with 13.73, 13.76, and 13.78 s, respectively.

The original DBO and the original SSA are compared, respectively, to confirm the efficacy of fusion, and this process is done to validate the hybrid algorithm’s usefulness. To confirm the algorithm’s improved performance, the hybrid Gray Wolf Particle Swarm Optimization method and the Gravity Search algorithm are chosen for comparison. The running results of each algorithm are shown in Tables 4 to 10. The results are average accuracy, average number of selected features, average fitness value, average best fitness value, average worst fitness value, variance of fitness value, and average computational time, respectively, and the optimal value is bolded. Each algorithm runs independently 10 times.

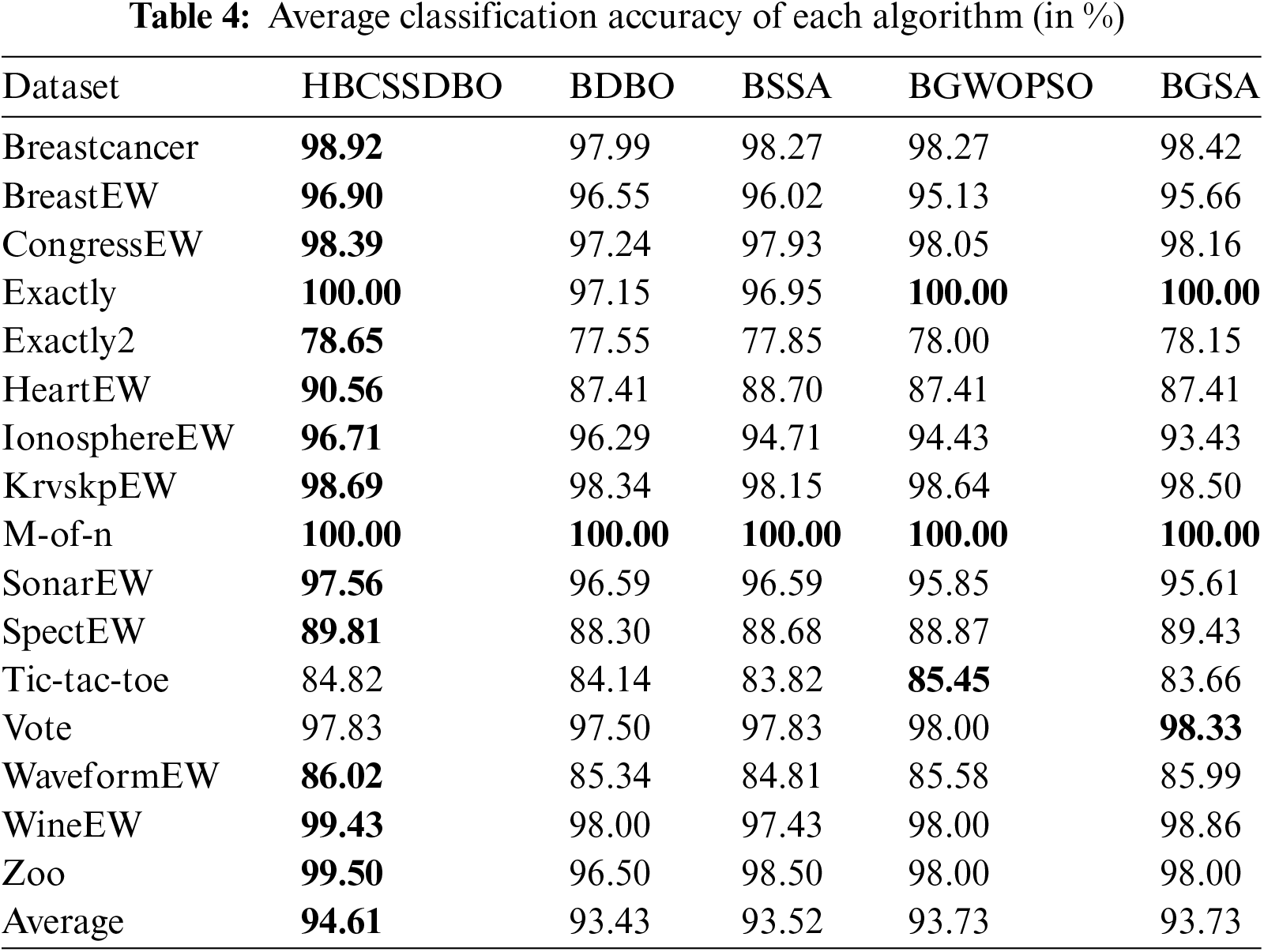
As shown in Table 4, the classification accuracy of HBCSSDBO on 14 datasets is higher than that of other comparative algorithms, and the average classification accuracy on all datasets is as high as 94.61%, which is 1.18%, 1.09%, 0.88%, and 0.88% higher than that of BDBO (Binary Dung Beetle Optimization), BSSA (Binary Salp Swarm Algorithm), BGWOPSO (Binary Grey Wolf Optimization Particle Swarm Optimization), and BGSA (Binary Gravitational Search Algorithm), respectively. The proposed hybrid method, original DBO, and SSA all have 100% classification accuracy on the M-of-n dataset; on the Vote dataset, the hybrid approach and SSA have 97.83% classification accuracy. In addition to the above two datasets, the classification accuracy of the HBCSSDBO is superior to the two original algorithms. The feasibility and effectiveness of the hybrid algorithm are proven. The accuracy of HBCSSDBO, BGWOPSO, and BGSA is 100% on Exactly and M-of-n datasets, and the proposed algorithm only lags behind these two algorithms on Tic-tac-toe and Vote datasets. To sum up, HBCSSDBO has higher classification accuracy.

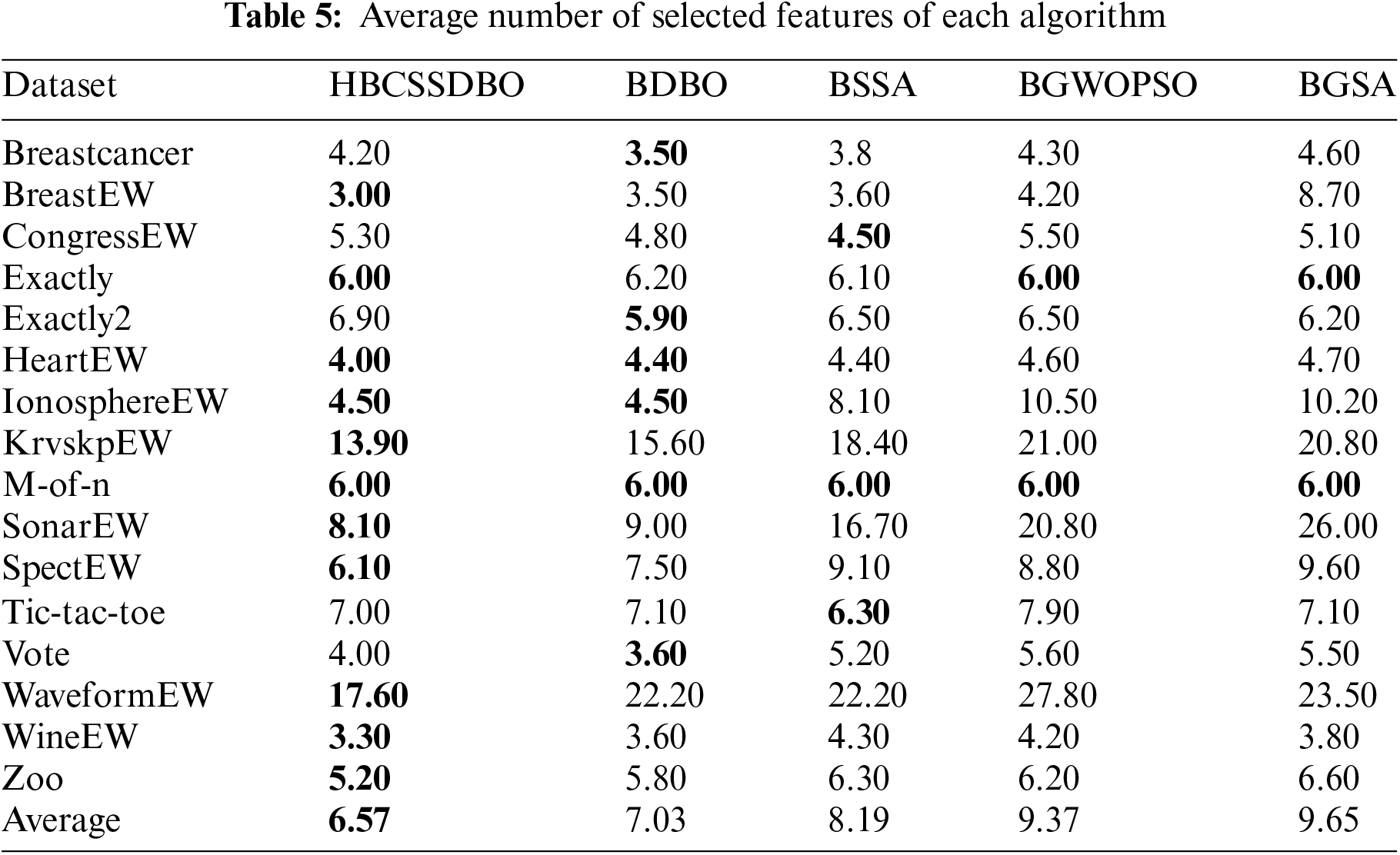
Table 5 shows that, out of all the comparable methods, the suggested approach ranks highest with an average of 6.57 selected features across all datasets. Its number of selected features on only 5 datasets lags behind other comparative algorithms and is in a leading position on the other 11 datasets. Combined with the analysis of the FS accuracy, it has been demonstrated that the suggested algorithm performs better while using FS.

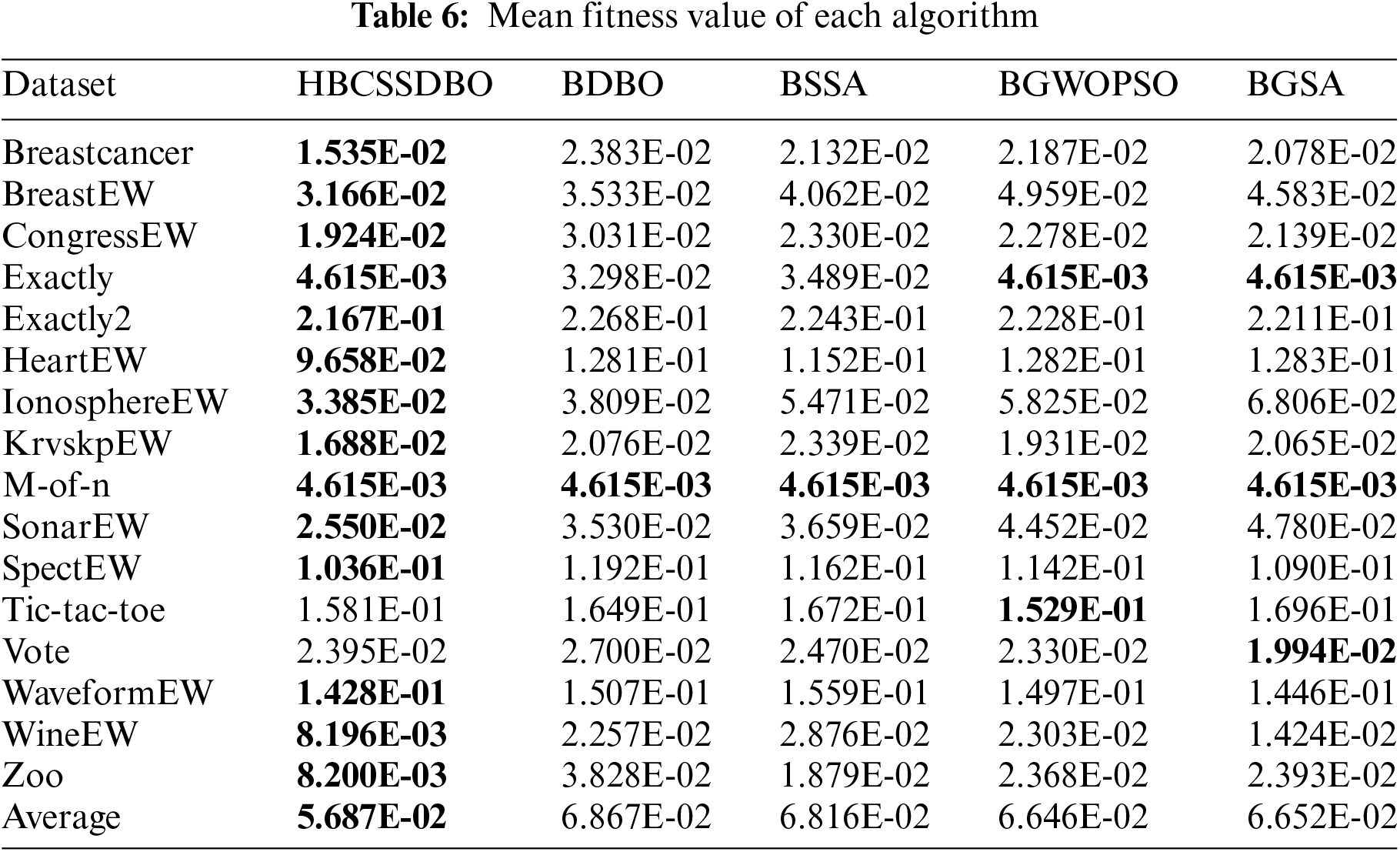
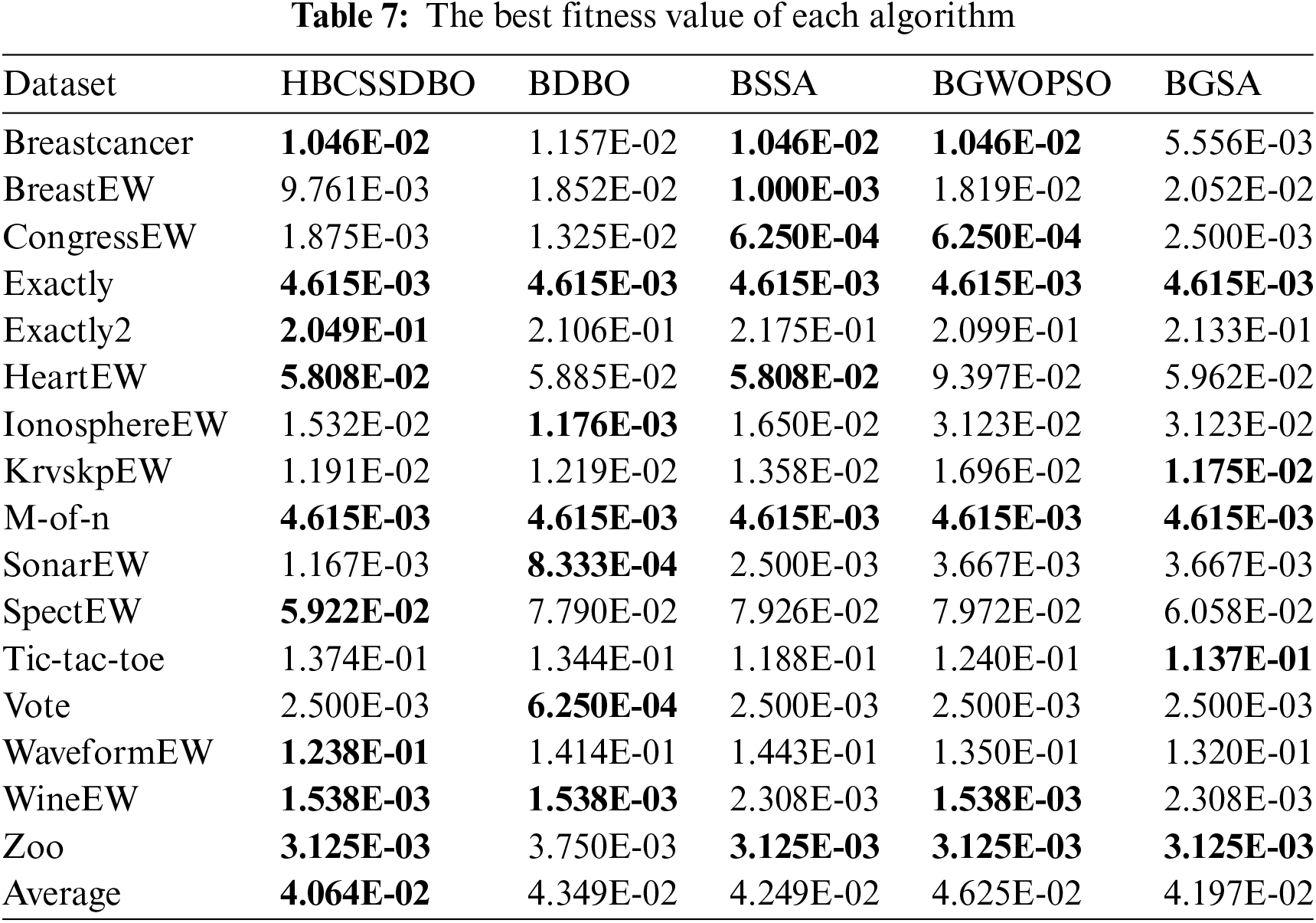
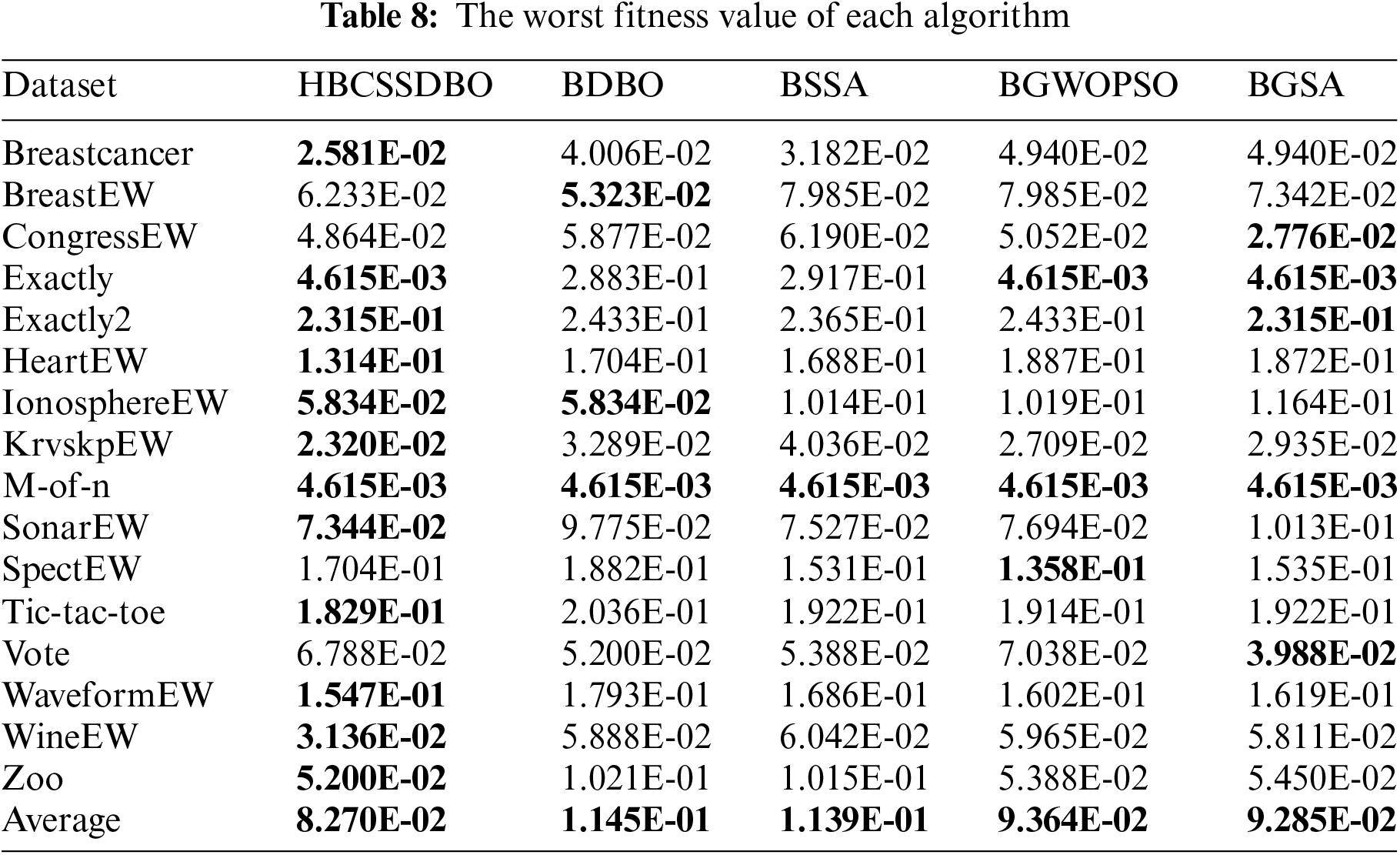
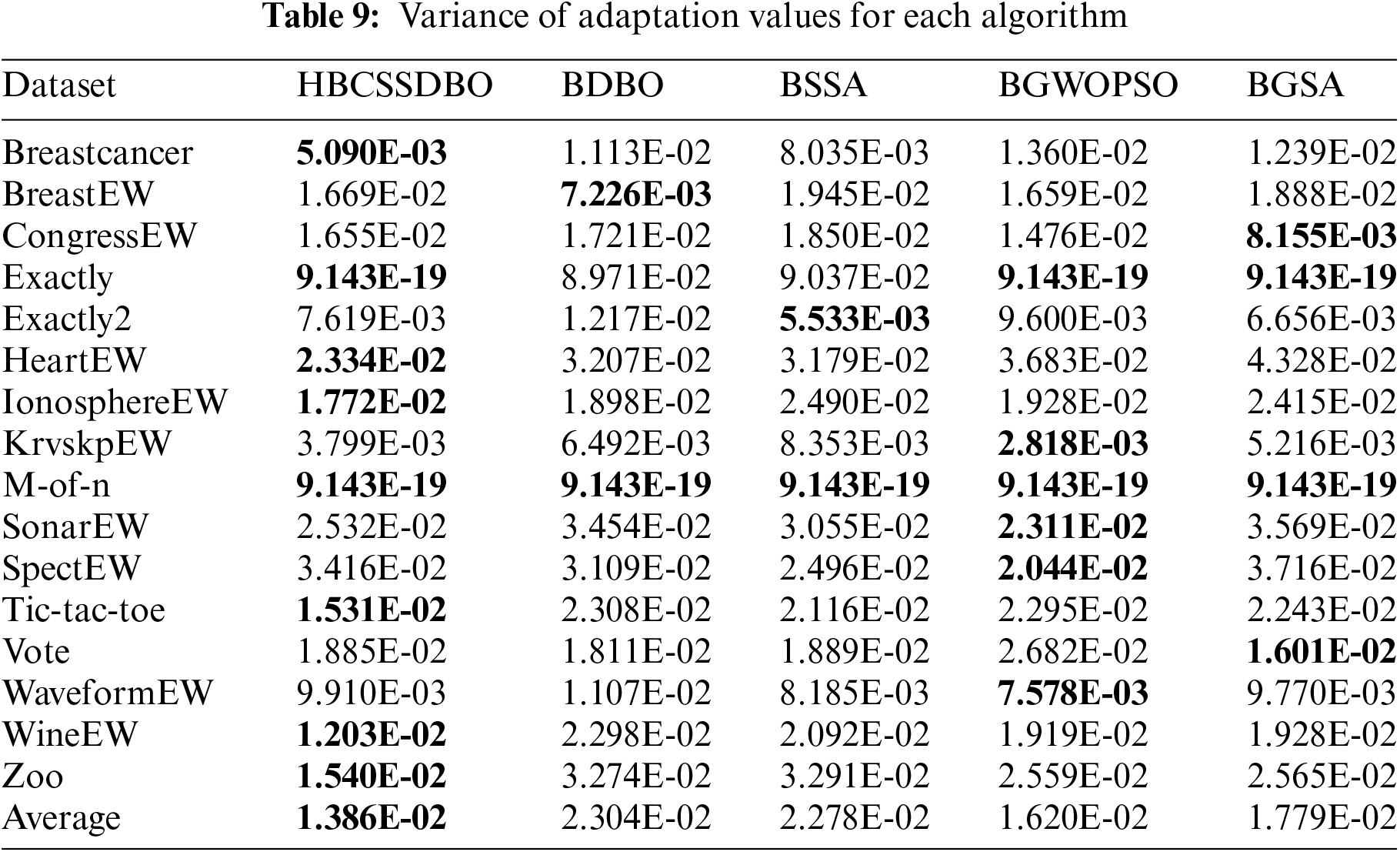
When comparing the average fitness, the best and worst fitness, and the variance of different algorithms, the results are displayed using scientific counting, and the optimal results are bolded in order to prevent data differences from being too minor and challenging to see. Table 6 shows that compared to other comparison algorithms, HBCSSDBO has a higher average fitness value across all datasets. Based on the aforementioned analysis, the proposed algorithm shows stronger optimization ability. However, in Table 7, the best fitness value found by the HBCSSDBO on all datasets is superior to other algorithms, which shows that the algorithm has a stronger optimization breadth and verifies the improvement of the global exploration ability in the algorithm improvement strategy. Moreover, this is still the case in Table 8, where the worst fitness value found by the HBCSSDBO is smaller than other algorithms on 12 datasets. It is proved that the HBCSSDBO is less prone to stagnate in local optima. Combined with the variance of fitness value in Table 9, the variance obtained on half of the datasets is smaller than other algorithms. For datasets Exactly, KrvskpEW, SonarEW, WineEW, etc., although the variance of the proposed algorithm is not optimal, it is still at the forefront of many algorithms, which shows that HBCSSDBO has better robustness.

Table 10 illustrates this, even though the HBCSSDBO only obtains a faster time on six datasets., such as Exactly, KrvskpEW, SpectEW, Vote, WaveformEW, and WineEW, the average time of HBCSSDBO running in 16 datasets is ahead of other algorithms. Furthermore, in other datasets, the computing speed of HBCSSDBO is also at the forefront of many algorithms. The hybrid algorithm is composed of the original DBO and the original SSA, but it does not consume more computing time, which proves the rationality of the proposed algorithm.

The suggested technique performs better than other comparable algorithms in each of the aforementioned seven assessment indices. When compared to the BDBO feature selection approach, the HBCSSDBO feature selection method improves the average prediction accuracy and average number of chosen features on the entire dataset by 1.18% and 7.2%, respectively. It is evident from the aforementioned study of the average classification accuracy and the average number of features chosen that the suggested approach is capable of selecting the best subset of characteristics while also guaranteeing a high classification accuracy. The suggested method has significantly improved in terms of depth of optimization search and exploration ability as well as robustness, according to the examination of the variance, the best fitness value, and the optimal fitness. These results justify the fusion algorithm, i.e., the embedded SSA algorithm leader and follower mechanisms effectively help the dung beetle individuals better explore the solution space, while the mutation operator and chaotic initialization mapping population ensure that the algorithm does not easily fall into the local optimum and guarantee the diversity of the population, respectively. Furthermore, the hybrid algorithm is guaranteed to be efficient because the suggested approach does not result in any extra time overhead when compared to the two original methods in terms of running time.

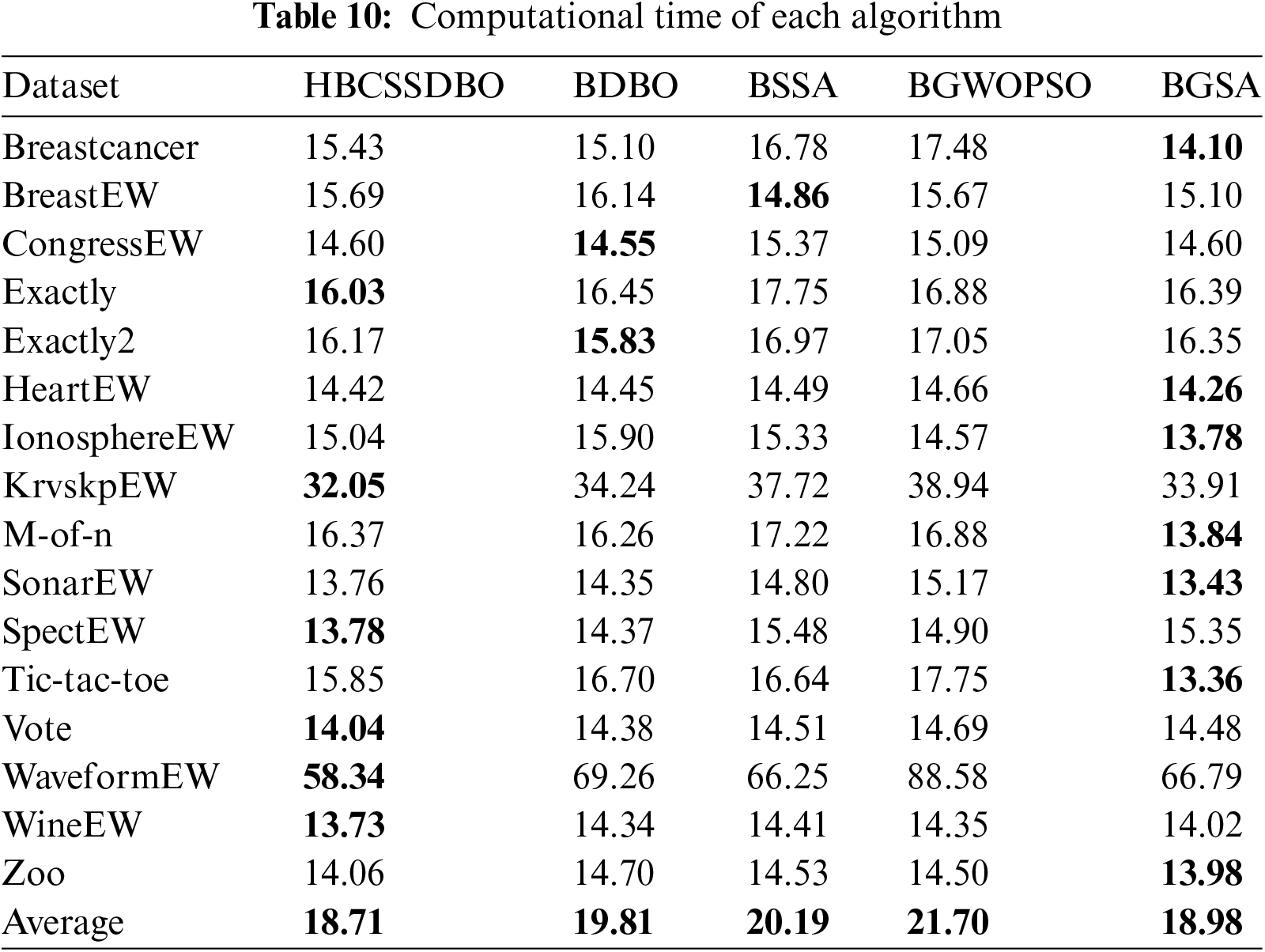
The datasets are split into three datasets of different dimensions based on the varying number of features, namely high dimensional datasets, medium dimensional datasets, and low dimensional datasets, in order to further assess the effectiveness of the suggested approach. Specific corresponding information is given in Table 1. In order to more intuitively verify the superiority of the proposed algorithm, the average classification accuracy (in %) and the average number of selected features obtained by each algorithm are presented in the form of bar charts according to three different dimensions, and the specific results are shown in Figs. 5–7. As can be seen from Fig. 5, on high dimensional datasets, HBCSSDBO is ahead of other comparative algorithms in terms of classification accuracy and number of selected features, which also indicates that HBCSSDBO can use fewer features to obtain higher classification accuracy, showing strong optimization ability. Fig. 6a shows that, for the medium-dimensional datasets, HBCSSDBO’s classification accuracy trails BGSA only in the Vote dataset. Fig. 6b shows that, in the Vote and CongressEW datasets, the number of selected features is marginally higher than the original DBO. It is still in the leading position compared with other algorithms. Fig. 7a shows that all methods work well and achieve high classification accuracy for low-dimensional datasets. Still, it is evident that HBCSSDBO outperforms other algorithms in the majority of datasets. However, as Fig. 7b illustrates, the suggested technique does not choose as many features as other algorithms do—at least not as much as it does for large dimensional datasets.

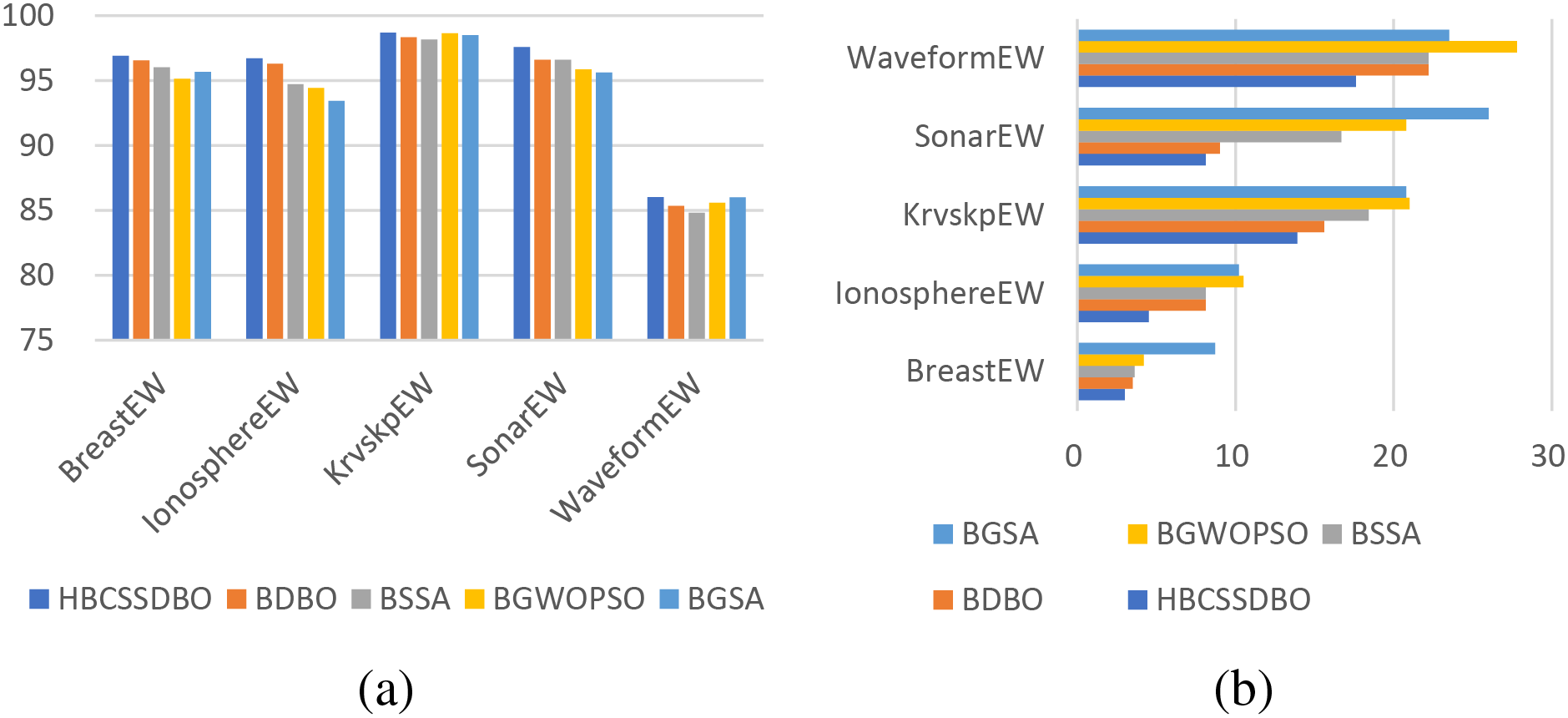
Figure 5: Average classification accuracy (a) and number of selected features (b) for high-dimensional datasets

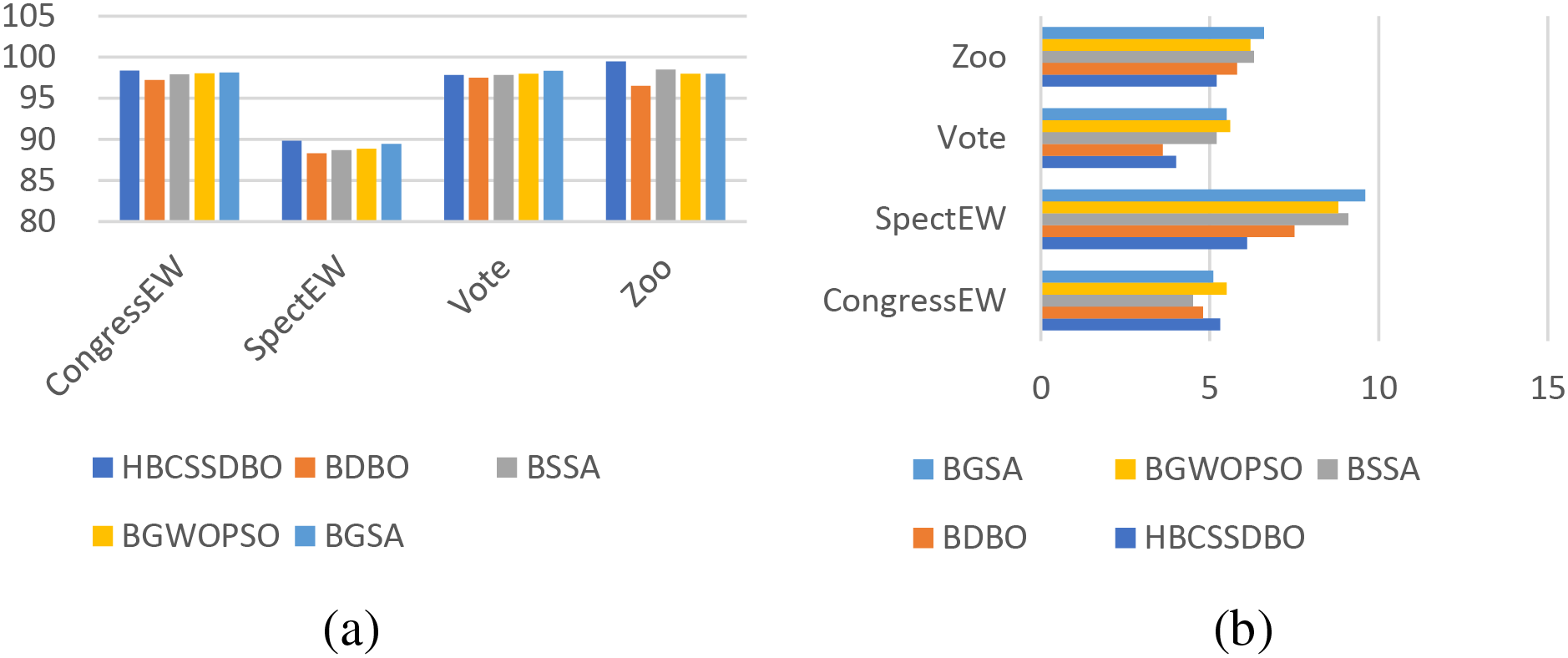
Figure 6: Average classification accuracy (a) and number of selected features (b) for medium dimensional datasets

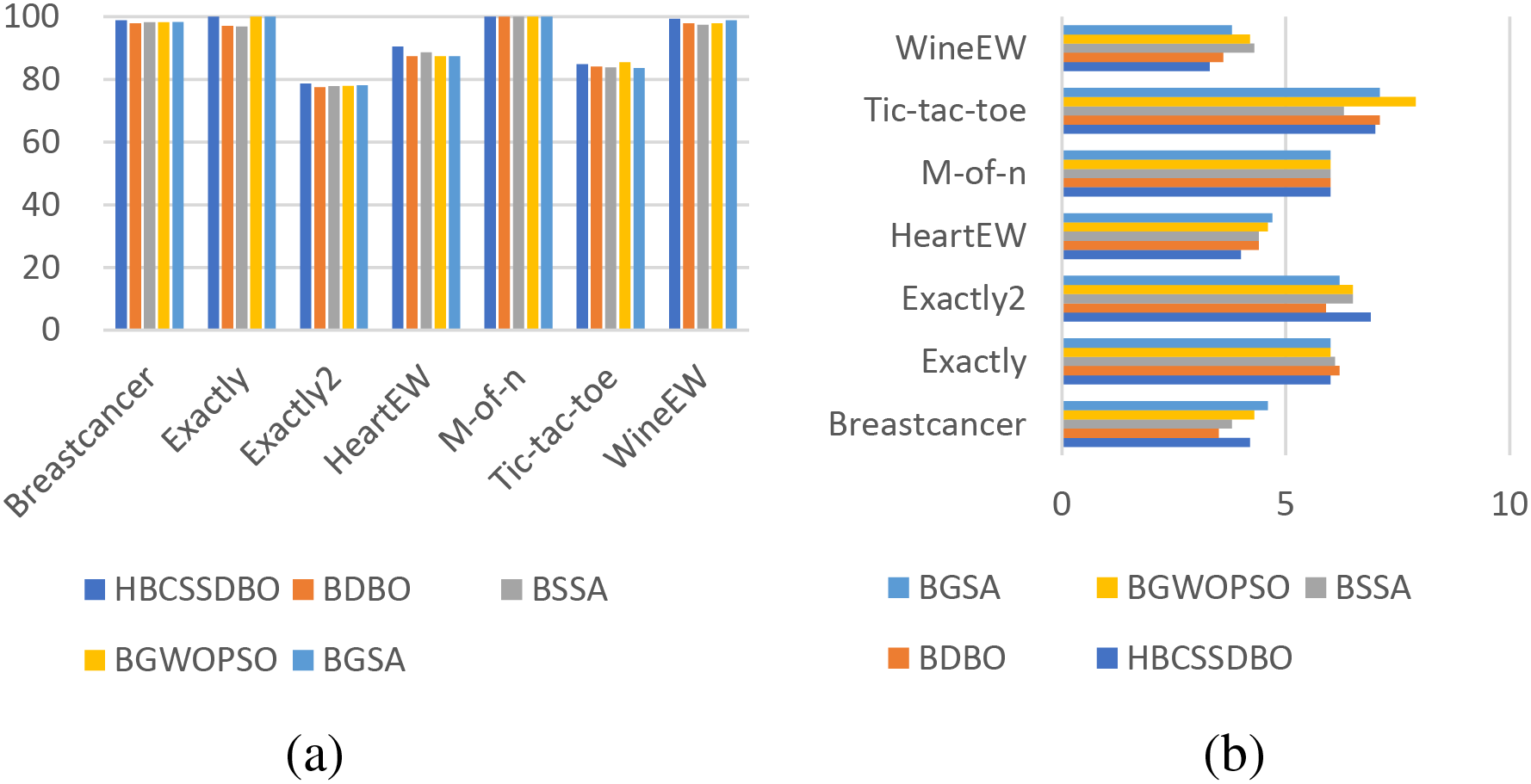
Figure 7: Average classification accuracy (a) and number of selected features (b) for low dimensional datasets

To sum up, HBCSSDBO can obtain higher classification accuracy when applied to FS, can extract feature subsets more effectively from original datasets, especially in medium and high dimensional datasets, and does not perform poorly on low dimensional datasets. Overall, it is still ahead of the comparative algorithms.

To assess the statistical significance of the earlier obtained results, the experimental data were subjected to a Friedman test [11]. Where 5% was used as the significance level for this test. Table 11 displays the test’s findings.

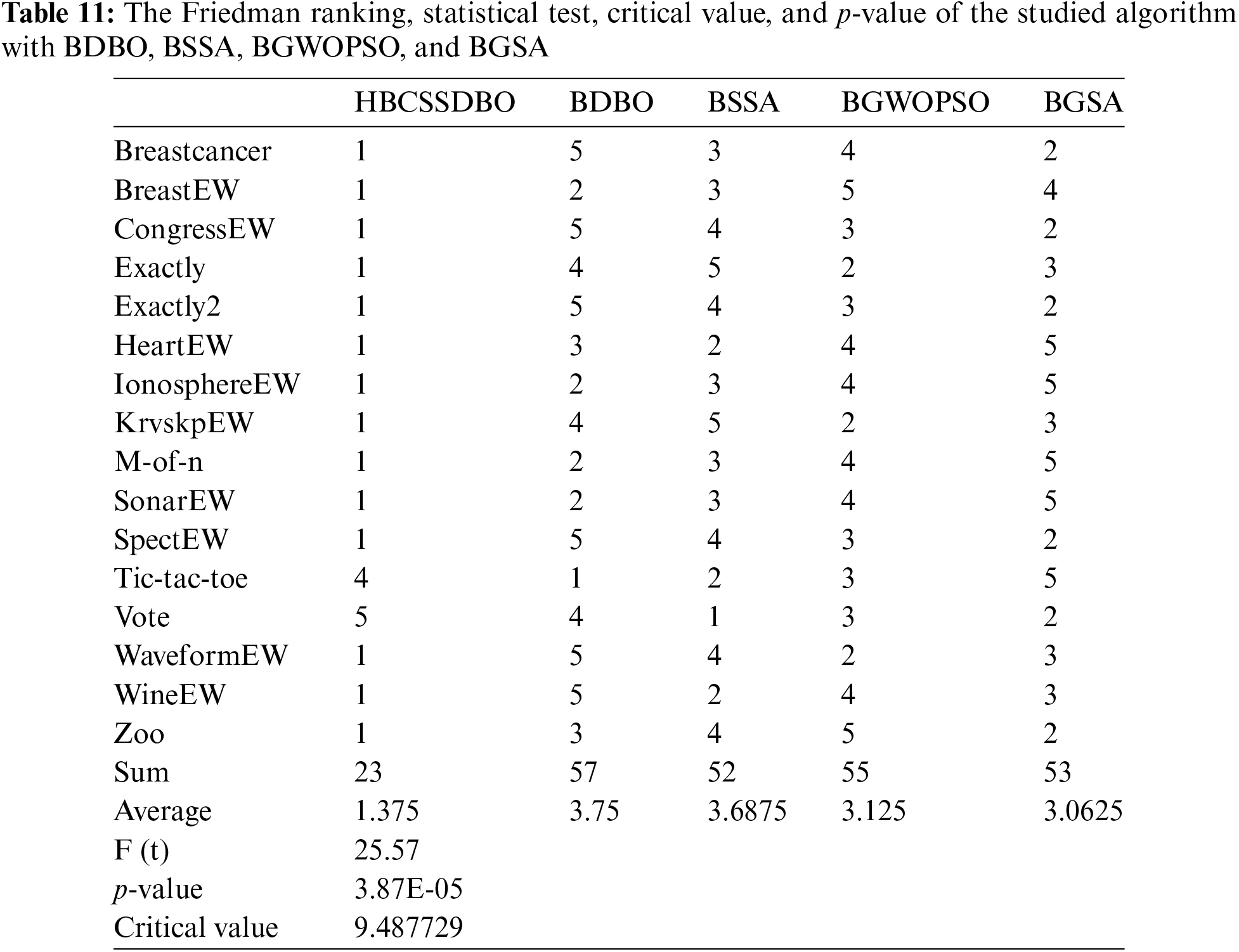
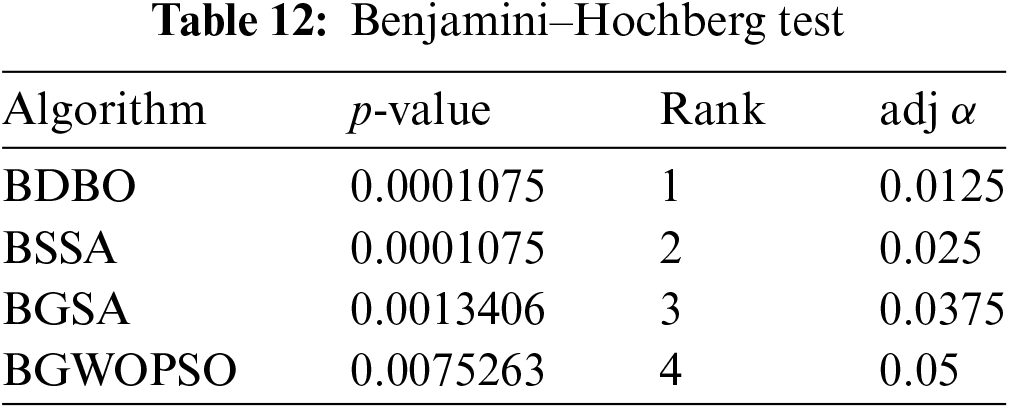
A pairwise Benjamin-Hochberg post hoc test with adjusted p value using HBCSSDBO as a control algorithm was significant for HBCSSDBO vs. BDBO (p= 0.000107511, adj = 0.0125), HBCSSDBO vs. BSSA (p = 0.000107511, adj = 0.025), HBCSSDBO vs. BGSA (p = 0.001340641, adj = 0.0375) and HBCSSDBO vs. BGWOPSO (p = 0.007526315, adj = 0.05). Specific results are shown in Table 12. Consequently, it is evident from the statistical analysis findings above that there is a substantial difference between the other analyzed methods and the suggested approach.

6  Conclusions

In this paper, HBCSSDBO, a new hybrid algorithm, is proposed to solve the feature selection problem. The method combines the respective features of DBO and SSA, realizes the organic integration of the two algorithms, and effectively solves the feature selection challenge. The average fitness value, average classification accuracy, average number of selected features, variance of fitness value, average running time, and optimal and worst fitness values are the seven-evaluation metrics that are used to assess the performance and stability of the proposed method on 16 UCI datasets. In addition, HBCSSDBO is compared with four meta-heuristic feature selection methods, which include BDBO, BSSA, BGWOPSO, and BGSA. Based on several assessment criteria, the trial findings indicate that HBCSSDBO is the best option. Its average classification accuracy is 94.61%, and it has an average of 6.57 chosen features. In the analysis of the method in terms of the optimal and worst fitness values as well as the variance of the fitness values, we can see that the hybrid method has a great improvement in both the optimization searching accuracy and robustness. In addition, the hybrid method does not incur more time loss in terms of running time. These results show that HBCSSDBO is more competitive in solving the feature selection problem. The final statistical test verifies the significant effectiveness of the method.

In our future research, we will explore the application of the proposed method to the feature selection problem in different domains such as data mining, medical applications, engineering applications, and so on. We will try to combine machine learning algorithms other than KNN to study the performance of the HBCSSDBO method.

Acknowledgement: We thank the Liaoning Provincial Department of Education and Shenyang Ligong University for financial support of this paper.

Funding Statement: This research was funded by the Short-Term Electrical Load Forecasting Based on Feature Selection and optimized LSTM with DBO which is the Fundamental Scientific Research Project of Liaoning Provincial Department of Education (JYTMS20230189), and the Application of Hybrid Grey Wolf Algorithm in Job Shop Scheduling Problem of the Research Support Plan for Introducing High-Level Talents to Shenyang Ligong University (No. 1010147001131).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Wei Liu; data collection: Wei Liu; analysis and interpretation of results: Tengteng Ren; draft manuscript preparation: Tengteng Ren. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

Ethics Approval: This article does not contain any research involving humans or animals.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. Dokeroglu, A. Deniz, and H. E. Kiziloz, “A comprehensive survey on recent metaheuristics for feature selection,” Neurocomputing, vol. 494, pp. 269–296, 2022. doi: 10.1016/j.neucom.2022.04.083. [Google Scholar] [CrossRef]

2. T. H. Pham and B. Raahemi, “Bio-inspired feature selection algorithms with their applications: A systematic literature review,” IEEE Access, vol. 11, pp. 43733–43758, 2023. doi: 10.1109/ACCESS.2023.3272556. [Google Scholar] [CrossRef]

3. N. Khodadadi et al., “BAOA: Binary arithmetic optimization algorithm with K-nearest neighbor classifier for feature selection,” IEEE Access, vol. 11, pp. 94094–94115, 2023. doi: 10.1109/ACCESS.2023.3310429. [Google Scholar] [CrossRef]

4. M. Rostami, K. Berahmand, E. Nasiri, and S. Forouzandeh, “Review of swarm intelligence-based feature selection methods,” Eng. Appl. Artif. Intell., vol. 100, pp. 104210, 2021. doi: 10.1016/j.engappai.2021.104210. [Google Scholar] [CrossRef]

5. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Trans. Evol. Comput., vol. 1, no. 1, pp. 67–82, 1997. doi: 10.1109/4235.585893. [Google Scholar] [CrossRef]

6. X. Song, Y. Zhang, D. Gong, and X. Y. Sun, “Feature selection using bare-bones particle swarm optimization with mutual information,” Pattern Recognit., vol. 112, pp. 107804, 2021. doi: 10.1016/j.patcog.2020.107804. [Google Scholar] [CrossRef]

7. H. Faris et al., “An efficient binary salp swarm algorithm with crossover scheme for feature selection problems,” Knowl. Based Syst., vol. 154, pp. 43–67, 2018. doi: 10.1016/j.knosys.2018.05.009. [Google Scholar] [CrossRef]

8. E. Emary, H. M. Zawbaa, and A. E. Hassanien, “Binary grey wolf optimization approaches for feature selection,” Neurocomputing, vol. 172, pp. 371–381, 2016. doi: 10.1016/j.neucom.2015.06.083. [Google Scholar] [CrossRef]

9. M. Mafarja and S. Mirjalili, “Whale optimization approaches for wrapper feature selection,” Appl. Soft Comput., vol. 62, pp. 441–453, 2018. doi: 10.1016/j.asoc.2017.11.006. [Google Scholar] [CrossRef]

10. A. Adamu, M. Abdullahi, S. B. Junaidu, and I. H. Hassan, “An hybrid particle swarm optimization with crow search algorithm for feature selection,” Mach. Learn. Appl., vol. 6, pp. 100108, 2021. doi: 10.1016/j.mlwa.2021.100108. [Google Scholar] [CrossRef]

11. Y. Zhang, Y. H. Wang, D. W. Gong, and X. Y. Sun, “Clustering-guided particle swarm feature selection algorithm for high-dimensional imbalanced data with missing values,” IEEE Trans. Evol. Comput., vol. 26, no. 4, pp. 616–630, 2021. doi: 10.1109/TEVC.2021.3106975. [Google Scholar] [CrossRef]

12. X. F. Song, Y. Zhang, Y. N. Guo, X. Y. Sun, and Y. L. Wang, “Variable-size cooperative coevolutionary particle swarm optimization for feature selection on high-dimensional data,” IEEE Trans. Evol. Comput., vol. 24, pp. 882–895, 2020. doi: 10.1109/TEVC.2020.2968743. [Google Scholar] [CrossRef]

13. R. A. Ibrahim, A. A. Ewees, D. Oliva, M. Abd. Elaziz, and S. Lu, “Improved salp swarm algorithm based on particle swarm optimization for feature selection,” J. Ambient Intell. Humaniz. Comput., vol. 10, pp. 3155–3169, 2019. doi: 10.1007/s12652-018-1031-9. [Google Scholar] [CrossRef]

14. M. Abdel-Basset, W. Ding, and D. El-Shahat, “A hybrid Harris Hawks optimization algorithm with simulated annealing for feature selection,” Artif. Intell. Rev., vol. 54, no. 1, pp. 593–637, 2021. doi: 10.1007/s10462-020-09860-3. [Google Scholar] [CrossRef]

15. A. A. Abdelhamid et al., “Innovative feature selection method based on hybrid sine cosine and dipper throated optimization algorithms,” IEEE Access, vol. 11, pp. 79750–79776, 2023. doi: 10.1109/ACCESS.2023.3298955. [Google Scholar] [CrossRef]

16. J. Xue and B. Shen, “Dung beetle optimizer: A new meta-heuristic algorithm for global optimization,” J. Supercomput., vol. 79, no. 7, pp. 7305–7336, 2023. doi: 10.1007/s11227-022-04959-6. [Google Scholar] [CrossRef]

17. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris and S. M. Mirjalili, “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Adv. Eng. Softw., vol. 114, pp. 163–191, 2017. doi: 10.1016/j.advengsoft.2017.07.002. [Google Scholar] [CrossRef]

18. S. Wang, Q. Yuan, W. Tan, T. Yang, and L. Zeng, “SCChOA: Hybrid sine-cosine chimp optimization algorithm for feature selection,” Comput. Mater. Contin., vol. 77, no. 3, pp. 3057–3075, 2023. doi: 10.32604/cmc.2023.044807. [Google Scholar] [CrossRef]

19. E. S. M. El-Kenawy, M. M. Eid, M. Saber, and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. doi: 10.1109/ACCESS.2020.3001151. [Google Scholar] [CrossRef]

20. B. Alatas, E. Akin, and A. B. Ozer, “Chaos embedded particle swarm optimization algorithm,” Chaos Solit. Fractals, vol. 40, no. 4, pp. 1715–1734, 2009. doi: 10.1016/j.chaos.2007.09.063. [Google Scholar] [CrossRef]

21. H. Haklı and H. Uğuz, “A novel particle swarm optimization algorithm with levy flight,” Appl. Soft Comput., vol. 23, pp. 333–345, 2014. doi: 10.1016/j.asoc.2014.06.034. [Google Scholar] [CrossRef]

22. E. Emary, H. M. Zawbaa, and A. E. Hassanien, “Binary ant lion approaches for feature selection,” Neurocomputing, vol. 213, pp. 54–65, 2016. doi: 10.1016/j.neucom.2016.03.101. [Google Scholar] [CrossRef]

23. A. Frank, “UCI machine learning repository,” 2010. Accessed: Oct. 01, 2023. [Online]. Available: http://archive.ics.uci.edu/ml [Google Scholar]

24. S. Zhang, X. Li, M. Zong, X. Zhu, and R. Wang, “Efficient kNN classification with different numbers of nearest neighbors,” IEEE Trans. Neural Netw. Learn. Syst., vol. 29, no. 5, pp. 1774–1785, 2017. doi: 10.1109/TNNLS.2017.2673241. [Google Scholar] [PubMed] [CrossRef]

25. M. M. Mafarja and S. Mirjalili, “Hybrid whale optimization algorithm with simulated annealing for feature selection,” Neurocomputing, vol. 260, pp. 302–312, 2017. doi: 10.1016/j.neucom.2017.04.053. [Google Scholar] [CrossRef]

26. Q. Al-Tashi, S. J. A. Kadir, H. M. Rais, S. Mirjalili, and H. Alhussian, “Binary optimization using hybrid grey wolf optimization for feature selection,” IEEE Access, vol. 7, pp. 739496–739508, 2019. doi: 10.1109/ACCESS.2019.2906757. [Google Scholar] [CrossRef]

27. E. Rashedi, H. Nezamabadi-Pour, and S. Saryazdi, “GSA: A gravitational search algorithm,” Inf. Sci., vol. 179, no. 13, pp. 2232–2248, 2009. doi: 10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

28. I. Aljarah, M. Mafarja, A. A. Heidari, H. Faris, Y. Zhang and S. Mirjalili, “Asynchronous accelerating multi-leader salp chains for feature selection,” Appl. Soft Comput., vol. 71, pp. 964–979, 2018. doi: 10.1016/j.asoc.2018.07.040. [Google Scholar] [CrossRef]