Sec-Auditor: A Blockchain-Based Data Auditing Solution for Ensuring Integrity and Semantic Correctness

1  Introduction

As data volumes continue to surge, an increasing number of users are opting to store their data in the cloud. Remarkably, 46% of European companies have adopted cloud-based solutions as their primary data storage method, according to a Forbes report. The similar report forecasts that the cloud will accommodate more than 100 zettabytes of data by 2025 [1]. Nevertheless, when a user performs cloud data operations such as uploading, modifying, deleting, the semantic correctness of the data can be compromised. For instance, when a teacher uploads students’ scores to the educational administration system, he might accidentally upload a data entry with a score below 0 due to an operational error. Furthermore, the integrity of cloud data can also be jeopardized by equipment failures, hacker attacks, etc. Even worse, the cloud service vendor may choose to conceal these facts from users to safeguard their reputation. Ensuring the integrity and semantic correctness of cloud data has become a paramount concern that users must prioritize.

To validate data integrity, a third-party auditor (TPA) performs audits on cloud data on behalf of data owners. While there are data auditing solutions emerging, TPA requires access to all the data for auditing, resulting in high bandwidth costs [2–6]. For example, Company A intends to audit 1 TB of cloud data, and their network bandwidth is restricted to 20 MB/s. Under these conditions, Company A will require approximately 15 h to retrieve the entire dataset, which may be unacceptable for time-sensitive applications. To address the aforementioned issues, Atenese et al. first proposed the provable data possession (PDP) scheme in 2007. The scheme enables TPA to verify the cloud data without retrieving them [7]. The PDP scheme is implemented through a challenge-response protocol that involves transmitting a small, constant amount of data. This approach can significantly reduce bandwidth costs. Considering the role of TPA, existing PDP schemes can be categorized into two categories: private PDP schemes [8,9] and public PDP schemes [10–14]. In a private PDP scheme, data verification operations can only be performed by the user who possesses the private key of the data owner. On the other hand, a public PDP scheme permits any entity with access to public information to verify data integrity. Since we mainly focus on data auditing operations for the cloud data, an open data environment, our concern lies with the public PDP scheme.

Existing PDP schemes can only verify data integrity, but cannot validate semantics correctness. To address this issue, we propose a novel data auditing solution, Sec-Auditor, which ensures both data integrity and semantic correctness of the cloud data. The system model of integrating Sec-Auditor into the cloud is illustrated in Fig. 1. When a user uploads, modifies, or deletes their data, a data validation engine employs a predefined rule to verify the semantics of the data. Only verified data or operations are allowed to be sent to the cloud. There are numerous data validation engines emerging, such as those by [15] and [16], so we will not discuss them in the manuscript due to page limits. Each user is assigned a corresponding rule, and Sec-Auditor allows users to update their own rules. After the user uploads data to the cloud, Sec-Auditor can routinely or sporadically perform data auditing operations using file authenticators containing the hash value corresponding to the aforementioned rule. Successfully passing data verification signifies that the cloud data remains not only intact but also adheres to the specified rules governing its semantic correctness. Conversely, failure in verification indicates data corruption. Notably, the bandwidth consumed during the data verification process is independent of the amount of data being audited.

Figure 1: System model of integrating Sec-Auditor into the cloud

The contributions of this study are as follows:

1.    We introduce a novel data auditing solution, Sec-Auditor, capable of guaranteeing both the data integrity and semantic correctness of cloud data. Furthermore, during the data auditing process, the consumed bandwidth remains unaffected by the volume of data being audited.

2.    Sec-Auditor facilitates public auditing, allowing any entity with access to public information to verify cloud data. This standout feature makes the new scheme well-suited for open data environments, such as the cloud. Additionally, Sec-Auditor empowers users to customize their own rules, broadening its applicability to a wider range of fields.

3.    Finally, we analyze the correctness and security of Sec-Auditor, and then conduct an assessment of its performance. The results demonstrate its superior efficiency.

The paper is structured as follows: Section 2 provides related work. Section 3 presents the notations and preliminaries. In Section 4, we discuss the system model, including the system framework, design goals and the algorithm model. In Section 5, we present the technical implementation and includes the correctness analysis. Then, we prove the security analysis of Sec-Auditor in Section 6. In Section 7, we evaluate the performance of the proposed scheme. Finally, we offer concluding remarks in Section 8.

2  Related Work

Traditional data integrity audit schemes rely on technologies such as Message Authentication Code (MAC) [17,18] and hash functions [19]. Take hash functions as an example. To conduct an audit, an auditor should access the data from the cloud, calculate the hash value, and subsequently compare it with the locally stored counterpart. However, in the aforementioned process, the auditor needs to obtain all the audited data through the network, resulting in high communication costs. To address this issue, the PDP scheme was proposed. This scheme enables a client who has stored data on an untrusted server to verify data integrity without retrieving the entire data set. This innovative approach employs a challenge/response protocol, which facilitates the transmission of a small, fixed amount of data and effectively reduces network communication overhead [7].

The PDP scheme can detect a certain proportion of corrupted data, but cannot recover them. To address this issue, Juels et al. proposed a new proof of retrievability (PoR) scheme based on pseudorandom-permutation primitives [20]. The PoR scheme can not only detect but also recover those corrupted data stored on an untrusted server with a high probability. Shacham et al. introduced a public compact PoR scheme that is based on BLS signatures [21]. Notably, both the client’s query and the server’s response in this scheme are exceptionally concise. Yang et al. proposed an identity-based PoR scheme for compressed cloud storage, which also supports public auditing [14]. Xu et al. proposed an efficient and practical PoR scheme, which is based on strong Diffie-Hellman assumption [22]. Paterson et al. presented a multiple-server PoR scheme that ensures data security under specified security assumptions and safeguards data confidentiality [23]. Han et al. introduced a novel PoR scheme as an alternative to the Proof of Work (PoW) consensus mechanism in the blockchain [24]. Both PoR and PDP employ the challenge-response protocol for verifying data integrity, thereby circumventing the need to transmit all the audited data.

As discussed earlier, existing PDP schemes are primarily categorized into two types: public PDP schemes and private PDP schemes. The public PDP scheme can be particularly well-suited for the cloud. Wang et al. first introduced an identity-based public PDP scheme which relies on the public key generator (PKG) to calculate the user’s private key [25]. Yu et al. proposed a new PDP scheme designed to withstand key exposure [11]. A novel public PDP scheme in conjunction with a data supervision platform for validating data compliance was proposed by Wang et al. in 2023 [16]. However, the aforementioned schemes should rely on a trusted third-party node to generate or maintain users’ public and private keys. In the event of the node’s destruction due to network attacks, equipment failure, etc., the entire PDP scheme will become unavailable. To address the issue, Wang et al. proposed a novel PDP scheme without the necessity of a centralized node to maintain users’ keys, thus eliminating a single point of failure [26]. Most existing PDP schemes, such as those mentioned in this section, can only support data integrity auditing. To verify data semantics, the auditor still needs to access all the audited data and utilizes the given rules to verify semantic correctness, which can incur high bandwidth costs. For the first time, we introduce a new PDP scheme named Sec-Auditor, capable of validating both data integrity and semantics by transmitting small, fixed-size data through the network.

3  Notations and Preliminaries

3.1 Notations

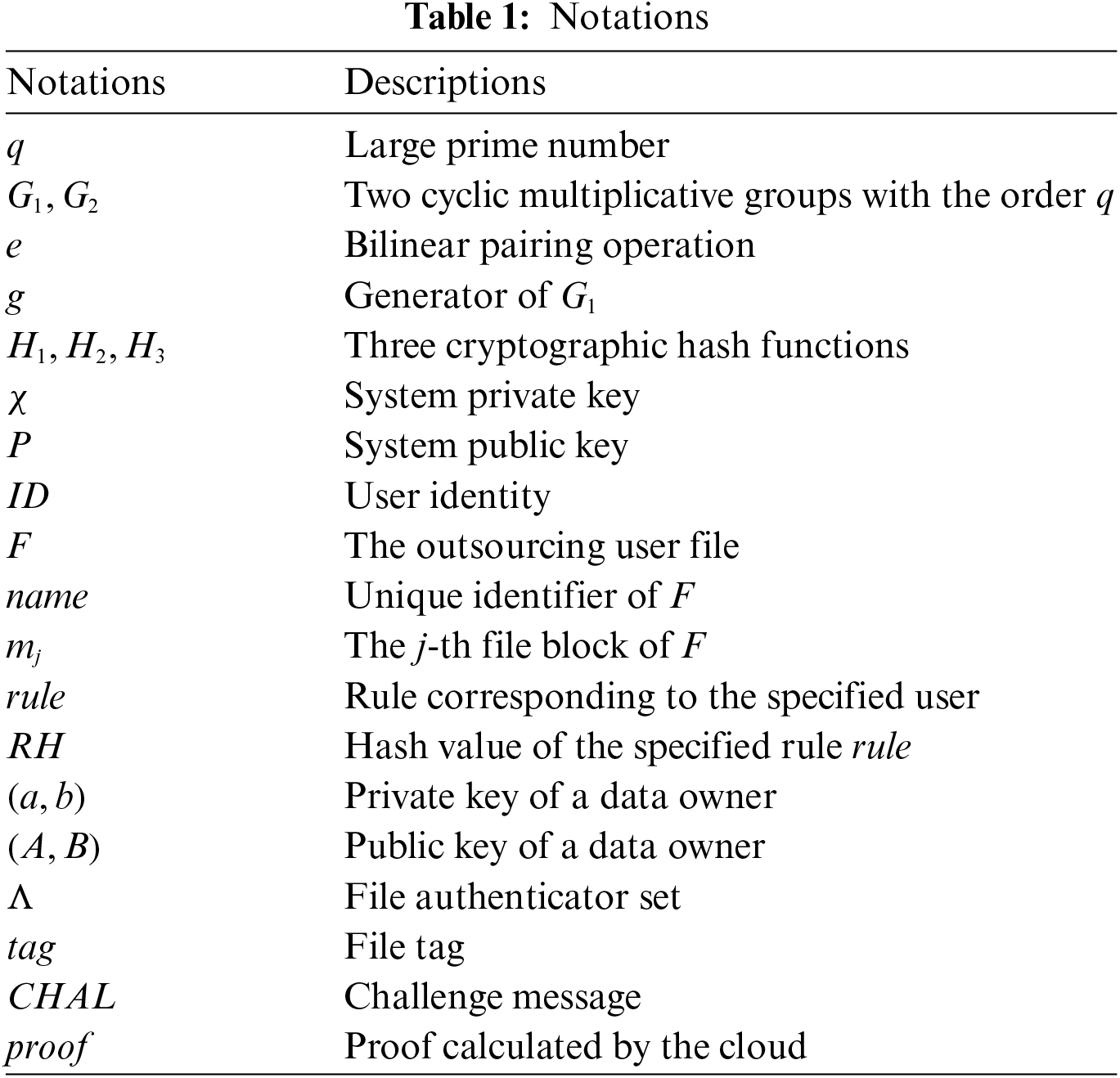
To improve readability, we have presented the main notations used in the paper as listed in Table 1.

3.2 Bilinear Pairing

Our proposed data auditing solution, Sec-Auditor, is constructed using bilinear pairings, which will be discussed in this section. Let G1 and G2 be two cyclic multiplicative groups with the order q, and g is the generator of G1. Let e:G1×G1→G2 be a bilinear pairing, which satisfies the following properties [27]:

Bilinearity: ∀g1,g2∈G1, x,y∈Zq∗, e(g1x,g2y)=e(g1,g2)xy.

Non-degeneracy:e(g,g)≠1.

Computability: ∀g1,g2∈G1, e(g1,g2) can be efficiently solved.

3.3 Computational Hard Problems

Computational Diffie-Hellman (CDH) Problem: For α∈Zq∗, υ∈Zq∗, given g,gα,gυ∈G1, output gαυ∈G1. The CDH assumption in G1 holds if an algorithm γ solves the CDH hard problem in polynomial time with a negligible advantage AdvCDH(γ)=Pr[γ(g,gα,gυ)=gαυ].

Discrete Logarithm (DL) Problem: Given g,gα∈G1, output α. The DL assumption in G1 holds if an algorithm γ solves the CDH hard problem in polynomial time with a negligible advantage AdvDL(γ)=Pr[γ(g,gα)=α].

4  System Model

4.1 System Framework

Fig. 2 illustrates the framework of Sec-Auditor, which comprises five entities: User, Key Generation Center (KGC), Blockchain, Cloud, TPA. Initially, the Setup algorithm is executed by KGC to calculate the system’s private key along with public parameters. Subsequently, the user collaborates with KGC to generate their private and public keys by executing the GenKey algorithm. Sec-Auditor ensures that KGC cannot access the user’s private key. In the StorF algorithm, the user divides his file into fixed-sized blocks, calculates their respective file authenticators, and outsources both the blocks and authenticators to either the cloud or blockchain. TPA employs the Chal algorithm to create a challenge and transmits it to the cloud. Upon receiving the challenge, the cloud executes the Resp algorithm to obtain the proof and sends it back to TPA. In the Verf algorithm, TPA verifies the proof and determines the data integrity and semantic correctness of the audited files. Sec-Auditor also allows the user to update his rule through performing the UptRule algorithm. We will describe the five evolving entities of Sec-Auditor in the following section.

Figure 2: System framework of Sec-Auditor

User: Each user is assigned with a specific rule to verify the semantic accuracy of his files. It should be noted that the rule is known to both the user and KGC. Although the user must compute his private key with the assistance of the KGC, he does not want the KGC to deduce the key from the key generation procedure. When the user outsources, modifies, or deletes a particular file, Sec-Auditor should validate its semantic accuracy. Sec-Auditor also provides the user with the option to encrypt their files for privacy protection. Importantly, this operation does not have any adverse effects on the accuracy of subsequent data auditing tasks.

KGC: KGC is in charge of generating system public parameters and calculates the user’s private and public keys in coordination with the user. Additionally, KGC assists in updating the user’s rule.

Blockchain: Blockchain is a distributed ledger technology comprised of a network of computing nodes. In the context of Sec-Auditor, blockchain can be implemented using either a consortium blockchain or a public blockchain. While current blockchain implementations face security threats like the 51% attack and the decentralized autonomous organization (DAO) attack, researchers have proposed corresponding countermeasures [28]. Therefore, it is assumed that data on the blockchain cannot be corrupted.

TPA: TPA is responsible for auditing the integrity and semantic accuracy of those cloud data. Since Sec-Auditor supports public auditing, TPA can perform the auditing procedure without requiring the data owners’ private key.

Cloud: Cloud offers extensive storage capacity for storing users’ data. However, cloud data are vulnerable to destruction due to equipment failures or malicious behaviors of cloud service providers, so Sec-Auditor is proposed to verify the data. Upon receiving the challenge issued by TPA, the cloud calculates the corresponding proof and transmits it back to TPA. Subsequently, TPA verifies the proof to determine whether the cloud data are intact or not. We assume that the cloud will perform the specified data verification procedure.

4.2 Design Goals

The proposed data auditing solution, Sec-Auditor, may encounter the following security threats: 1. When a user generates his keys, KGC may deduce the user’s private key and employ it to impersonate the user for outsourcing his files or generating proof for corrupted data in the cloud. 2. When a user performs file operations such as uploading, modifying, or deleting, the semantics of the data may be compromised or altered. 3. Cloud service vendors may falsify proof for locally stored data due to concerns such as their own reputation. To address the aforementioned threats, Sec-Auditor should achieve the following objectives:

Correctness: When all entities within Sec-Auditor can faithfully execute the specified algorithms, the response generated by the cloud can successfully pass TPA verification.

Auditing soundness: When the integrity of cloud data are compromised, the cloud cannot generate the correct proof for TPA.

Public auditing: TPA can conduct data auditing operations on cloud data without requiring access to the data owners’ private keys.

4.3 Algorithm Model

Sec-Auditor consists of seven algorithms: Setup, GenKey, StorF, Chal, Resp, Verf and UptRule. Detailed descriptions of these algorithms will be provided in the following part:

Setup: KGC runs the algorithm to generate the system private key χ and public parameters {e,G1,G2,q,g,H1,H2,H3,P}.

GenKey: A user with the identity IDi collaborates with KGC to execute the algorithm and calculate his private key (ai,bi) and public key (Ai,Bi). Throughout this process, KGC is not able to deduce the user’s private key.

StorF: The algorithm is run by a user to outsource his data to the cloud. For the outsourcing file F, the user computes the file tag and authenticators. Then, the user transmits the file tag to the blockchain, and authenticators to the cloud.

Chal: During the data auditing procedure, TPA generates a challenge CHAL and the corresponding public value C, which are then transmitted to the cloud.

Resp: Upon receiving CHAL and C, the cloud generates the proof, which will then be sent to TPA for verification.

Verf: The algorithm is executed by TPA to validate the received proof. If the verification procedure fails, it indicates that the cloud data are not intact.

UptRule: The algorithm is employed by both the user and KGC to replace the user’s current assigned rule rule with a new one rule′.

5  Proposed Scheme

5.1 Description of Sec-Auditor

For the proposed Sec-Auditor, the user should divide the outsourcing file F into n blocks. Consequently, the file F can be represented as {m1,…,mj,…,mn}, where q is a large prime number, and each mj∈Zq∗. When the user performs actions such as outsourcing, modifying, and deleting data, the cloud may employ a data validation engine to assess semantic accuracy. If the verification fails, the cloud will reject the user’s request. It is worth noting that numerous such engines emerging [15,16], though we will not discuss them here due to space constraints.

1) Setup: In this algorithm, KGC computes the system private key, the system public key, and public parameters.

•   KGC selects a bilinear map e:G1×G1→G2, where G1 and G2 are two multiplicative cyclic groups with prime order q, and g is the generator of G1.

•   KGC chooses three hash functions H1:{0,1}∗×G1×G1→Zq∗, H2:{0,1}∗→Zq∗, H3: {0,1}∗→G1.

•   KGC selects a random number χ∈Zq∗ as the system private key, and calculates the public key P=gχ.

•   KGC publishes those public parameters {e,G1,G2,q,g,H1,H2,H3,P}.

2) GenKey: The user collaborates with KGC to generate his own public and private keys.

•   Assuming the current user’s identity is IDi. The user chooses a random number ai∈Zq∗ and calculates Ai=gai. Subsequently, the user sends ⟨IDi,Ai⟩ to KGC.

•   KGC chooses a random number ri∈Zq∗, and calculates Bi=gri, RH=H3(rule), bi=ri+χH1(IDi,Ai+Bi,RH), where rule is the rule corresponding to the user IDi. KGC sends Bi, bi and RH to the user via the secure channel.

•   Upon receiving Bi, bi and RH, the user should verify these data with the equation gbi=BiPH1(IDi,Ai+Bi,RH). If the verification fails, KGC is required to retransmit the corresponding data. Conversely, the user obtains his private key (ai,bi) along with public key (Ai,Bi).

3) StorF: The user stores files, authenticators, file tags, and other data in either the cloud or on the blockchain. It is important to emphasize that a data validation engine has verified the semantic correctness of these files. Failure in verification will halt subsequent procedures. Sec-Auditor provides users with the option to encrypt their files for privacy protection. The user can choose to encrypt his file first and then carry out the StorF algorithm.

•   Assuming the unique identifier of file F is name. The user should divide the file F into n blocks, and calculates the file authenticator Tj=gmj(ai+bi) for each data block mj. Subsequently, the user can obtain the file authenticator set Λ={Tj}1≤j≤n.

•   The user calculates Zi=AiBiPH1(IDi,Ai+Bi,RH) and δ=H2(IDi||Ai||Bi||name||n||Zi).

•   The user computes the file tag tag=IDi||Ai||Bi||name||n||Zi||δ, and sends tag to the blockchain, along with {F,Λ} sent to the cloud.

•   Upon receiving tag, blockchain employs IDi to verify whether the user is authorized to store data. If authorized, the blockchain proceeds to validate whether δ is equal to H2(IDi||Ai||Bi||name||n||Zi). If it is, tag is stored on the blockchain; otherwise, the algorithm terminates. The steps described above are presented in Algorithm 1.

•   When the cloud receives {F,Λ} from the user, it will store these values locally.

4) Chal: TPA generates the challenge and transmits it to the cloud.

•   TPA should obtain tag for the file name from blockchain. If the aforementioned operation fails, the algorithm exits.

•   Upon receiving tag, TPA checks whether δ is equal to H2(IDi||Ai||Bi||name||n||Zi). If the verification fails, the algorithm exits.

•   TPA generates CHAL={i,vi}I={1,…,c},i∈I corresponding to the file name. TPA selects a random number υ∈Zq∗, and calculates C=gυ.

•   TPA sends the challenge CHAL and C to the cloud.

5) Resp: Upon receiving the challenge, the cloud generates the proof corresponding to the locally stored data and sends it back to TPA.

•   Upon receiving CHAL and C, the cloud calculates ρ=∑i∈I⁡mivi, σ=∏i∈I⁡Tivi.

•   The cloud sends the proof proof=⟨ρ,σ⟩ to TPA. In fact, a cloud device can utilize the locally stored data to calculate the values of Δρi and Δσi, and then submit them to TPA for aggregation to obtain ρ=∑i=1ν⁡Δρi and σ=∏i=1ν⁡Δσi, where ν represents the number of devices storing files. By adopting this parallelization strategy, the Resp algorithm can be accelerated.

6) Verf: TPA verifies the response message from the cloud, and determines whether the cloud data are intact or not.

•   Upon receiving the proof proof=⟨ρ,σ⟩, TPA verifies the equation e(συ,g)=e(Zi,Cρ). If the verification fails, the cloud data are not intact.

7) UptRule: The user collaborates with the KGC to update his assigned rule.

•   Assuming that the new rule for the user IDi is rule′. The user calculates RH′=H3(rule′), and sends <IDi,Ai,Bi,RH′,RH,bi> to KGC via a secure channel.

•   Upon receiving <IDi,Ai,Bi,RH′,RH,bi>, KGC should determine whether the user IDi is allowed to perform the UptRule algorithm. If not, the program exits. KGC calculates bi′=bi−χH1(IDi,Ai+Bi,RH)+χH1(IDi,Ai+Bi,RH′), and then sends bi′ to the user IDi via the secure channel.

•   Upon receiving bi′, the user should verify the correctness with the equation gbi′=BiPH1(IDi,Ai+Bi,RH′). If the verification fails, the program exits. Afterwards, the user obtains his private key (ai,bi′) along with public key (Ai,Bi). The user then calculates Zi′=AiBiPH1(IDi,Ai+Bi,RH′), δ′=H2(IDi||Ai||Bi||name||n||Zi′), tag′=IDi||Ai||Bi||name||n||Zi′||δ′. Then, the user retrieves his data from the cloud and calculates Tj′=gmj(ai+bi′) for each data block to obtain the file authenticator set Λ′={Tj′}1≤j≤n. tag′ is stored in the blockchain, and Λ′ is stored in the cloud. The data verification operation performed on the blockchain is shown in Algorithm 1.

5.2 Correctness Analysis

We first prove that after performing the UptRule algorithm, the user’s public key remains unchanged. Since Ai=gai, and ai remains unchanged, Ai keeps constant after performing the UptRule algorithm. In addition, since bi′=ri′+χH1(IDi,Ai+Bi,RH′), we can obtain ri′=bi′−χH1(IDi,Ai+Bi,RH′). On the other hand, due to bi′=bi−χH1(IDi,Ai+Bi,RH)+ χH1(IDi,Ai+Bi,RH′)=ri+χH1(IDi,Ai+Bi,RH)−χH1(IDi,Ai+Bi,RH)+χH1(IDi,Ai +Bi,RH′)=ri+χH1(IDi,Ai+Bi,RH′), we can obtain ri′=bi′−χH1(IDi,Ai+Bi,RH′)=ri and gri′=Bi=gri=Bi′. We can infer that the user’s public key keeps constant after performing the UptRule algorithm.

Then we will prove that in the GenKey algorithm, the verification equation gbi=BiPH1(IDi,Ai+Bi,RH) holds. Since bi=ri+χH1(IDi,Ai+Bi,RH), Bi=gri, P=gχ, we can obtain gbi=gri+χH1(IDi,Ai+Bi,RH)=grigχH1(IDi,Ai+Bi,RH)=BiPH1(IDi,Ai+Bi,RH).

Next we will prove that in the Verf algorithm, the verification equation e(συ,g)=e(Zi,Cρ) holds. Since σ=∏i∈I⁡Tivi, Tj=gmj(ai+bi), we can obtain e(συ,g)=e(gai+bi,g∑j∈I(mjvj)υ). Since C=gυ, bi=ri+χH1(IDi,Ai+Bi,RH), Ai=gai, Bi=gri, P=gχ, Zi=AiBiPH1(IDi,Ai+Bi,RH), we can obtaine(συ,g)=e(gai+ri+χH1(IDi,Ai+Bi,RH),Cρ)=e(Zi,Cρ).

Finally, we will prove that in the UptRule algorithm, the verification equation gbi′=Bi PH1(IDi,Ai+Bi,RH′) holds. Since bi′=bi−χH1(IDi,Ai+Bi,RH)+χH1(IDi,Ai+Bi,RH′), bi=ri+χH1(IDi,Ai+Bi,RH), and bi′=bi−χH1(IDi,Ai+Bi,RH)+χH1(IDi,Ai+Bi,RH′)=ri+χH1(IDi,Ai+Bi,RH)−χH1(IDi,Ai+Bi,RH)+χH1(IDi,Ai+Bi,RH′)=ri+χH1(IDi,Ai+Bi,RH′), we can obtain gbi′=gri+χH1(IDi,Ai+Bi,RH′)=BiPH1(IDi,Ai+Bi,RH′).

6  Security Analysis

Theorem 1 (Auditing soundness): In the proposed solution, Sec-Auditor, if the cloud data are corrupted, the cloud cannot produce the correct proof that would successfully pass the verification conducted by TPA.

Proof. First, we assume that the data stored on the blockchain are immutable. Then, we utilize the game between the adversary λ and the challenger Φ, as described in [27], to prove the theorem. In particular, if the adversary λ fails to construct a proof that can pass TPA’s verification with a non-negligible probability, Sec-Auditor satisfies audit soundness.

Game 0: The challenger Φ performs the Setup algorithm and obtains public parameters {e,G1,G2,q,g,H1,H2,H3,P}. Then, for user IDi, the challenger Φ performs the GenKey algorithm to generate the user’s private key (ai,bi) and public key (Ai,Bi). The challenger Φ then sends these public parameters and (Ai,Bi) to the adversary λ. For the outsourcing file F={m1,…,mj,…mn}, where mj∈Zq∗, the adversary λ sends the file F to the challenger Φ, who can then perform the StorF algorithm. Once the challenger Φ obtains the file authentication set Λ and the file tag tag corresponding to file F, Φ sends them to the adversary λ. When auditing the file F, the challenger Φ calculates the challenge (CHAL,C), and sends them to λ. Then, λ generates the corresponding proof proof and sends it to the challenger Φ. Finally, Φ verifies the proof proof. If the verification is successful, the adversary λ wins the game.

Game 1: The challenger Φ and the adversary λ perform an interaction similar to Game 0. The difference is that when performing the StorF algorithm, the challenger Φ stores the file tag tag in the list List. The adversary λ attempts to forge a new file tag tag and pass the verification of the challenger Φ. If the adversary successfully forges the file tag tag, which does not exist in the list List, the adversary λ wins the game.

Analysis: When the challenger Φ executes the StorF algorithm, the file tag tag will be stored on the blockchain. The smart contract then performs the data verification operation on the file tag tag. If the adversary λ successfully forges a new and different file tag tag, it implies that the data stored on the blockchain can be tampered with, which contradicts the premise that the data on the blockchain are safe. Based on this analysis, it can be concluded that for Game 1, the proposed algorithm ensures that tag is safe during the interaction between the adversary λ and the challenger Φ, and the adversary λ cannot forge tag.

Game 2: In this game, the challenger Φ and the adversary λ perform an interaction similar to Game 1. The difference is that when performing the Resp algorithm, the challenger Φ records all response to the adversary λ. If the adversary λ forges a different proof proof′ and can pass the verification of challenger Φ, λ wins the game.

Analysis: If the cloud data are intact and the correct proof for the challenge CHAL is proof=⟨ρ,σ⟩, the equation e(συ,g)=e(Zi,Cρ) should hold. For the corrupted cloud file F′={m1′,…,mj′,…mn′}, if λ forges a proof proof′=⟨ρ′,σ′⟩, the equation e(σ′υ,g)=e(Zi,Cρ′) should hold. It is obvious that ρ′≠ρ, or σ′=σ. Since ρ=∑i∈Imivi, ρ′=∑i∈Imi′vi, we can obtain

e(συ,g)=e(Zi,C∑i∈Imiυi)(1)

e(σ′υ,g)=e(Zi,C∑i∈Imi′υi)(2)

Let Δmi=mi−mi′. We divide the Eq. (1) by the Eq. (2), and obtain

e((σ/σ′)υ,g)=e(Zi,C∑i∈I(Δmiυi))(3)

Since σ=∏i∈ITiυi, we can obtain

e(∏i∈I(Ti/Ti′)υυ′,g)=e(Zi,C∑i∈I(Δmiυi))(4)

We complete the proof based on the CDH problem on G1. Let a=ai∈Zq∗, ϕ∈G1, ϕa∈G1 and ψ∈G1. If the adversary can forge the proof, the challenger Φ can calculate ψa with non-negligible probability.

When the user outsources his file to the cloud, the challenger Φ obtains file authenticators by executing the StorF algorithm. Let g=ϕψ, b=σ∈Zq∗, and H1(IDi,Ai+Bi,RH)=(−ri/b) We have Tj=gmj(a+bi)=(ϕψ)mj(a+ri+b(−ri/b))=(ϕψ)mja, and Tj′=(ϕψ)mj′(a+ri+χH1(IDi,Ai+Bi,RH)) =(ϕψ)mj′a. From the Eq. (4), we have e(Zi,C∑i∈I(Δmiυi))=e(∏i∈I(Ti/Ti′)υυi,g)=e(∏ (ϕψ)Δmiaυυi,g)= e((ϕψ)aυ∑i∈I(Δmiυi),g)=e(Zi,gυ∑i∈I(Δmiυi))=e(Ziυ∑i∈I(Δmiυi),g). Then, we obtain (ϕψ)a=Zi=AiBiPH1(IDi,Ai+Bi,RH)=AiBiP(−ri/b), and ψa=ϕ−aAiBiP(−ri/b).

When b=0, the challenger Φ can not solve the CDH problem with a negligible probability of 1/q. If the difference between the adversary’s probabilities of winning Game 2 and Game 1 is not negligible, the challenger Φ can solve the CDH problem.

Game 3. In this game, the challenger Φ and the adversary λ perform an interaction similar to Game 2. Φ should record all his responses to λ. If λ can forge a different proof proof′, where ρ≠∑i∈Imivi, and proof′ can pass the validation of Φ, λ wins the game.

Analysis: We assume that the correct proof is ⟨ρ,σ⟩, and the forged one by λ is ⟨ρ′,σ′⟩. Game 2 has proven σ=σ′. Since both proof and proof′ can pass the verification of the challenger Φ, the equation e(συ,g)=e(σ′υ,Cρ)=e(Zi,Cρ)=e(Zi,Cρ′) should hold. Since ρ=∑i∈Imivi, we can obtain Cρ=C∑i∈Imivi=Cρ′=C∑i∈Imi′vi, C∑i∈IΔmivi=1.

We complete the proof based on the DL problem on G1. Given ϕ∈G1 and ψ∈G1, if the adversary can forge the proof, the challenger Φ can calculate η∈Zq∗ that satisfies ψ=ϕη with a non-negligible probability.

The challenger Φ selects two random numbers θ∈Zq∗ and ς∈Zq∗, and sets C=ϕθψς. We can obtain

C∑i∈IΔmivi=(ϕθψς)∑i∈IΔmivi=ϕθ∑i∈IΔmiviψς∑i∈IΔmivi=1. Then we have

ψ=ϕ−θ∑i∈IΔmiυiς∑i∈IΔmiυi=ϕ−θς(5)

The condition for the Eq. (5) to hold is ς≠0 with a probability of 1−1/q. If the difference between the adversary’s probabilities of success in Game 3 and Game 2 is non-negligible, the challenger can solve the DL hard problem on G1. Therefore, the differences between the above games are negligible. Due to page limitations, we will no longer provide the proof, and authors can refer to the literature [27] for further details.

Based on the above analysis, the adversary cannot forge the proof that can pass the challenger’s verification with a non-negligible probability, and Sec-Auditor can guarantee that the cloud cannot forge a correct proof.

Theorem 2 (Detectability): Assuming that the files stored in the cloud are segmented into n blocks, of which υ blocks are corrupted. For the new proposed data auditing solution Sec-Auditor, TPA chooses c blocks to verify. The probability of detecting at least one of those corrupted file blocks is 1−(n−υn)c.

Analysis: Assuming Γ is the number of corrupted file blocks detected by TPA, P(Γ≥1) is the probability of detecting that the entire file is damaged. We can obtain

P(Γ≥1)=1−P(Γ=0)=1−n−υn×⋯×n−c+1−υn−c+1.

Since n−j−1−υn−j−1≤n−j−υn−j, we can obtain 1−(n−υn)c≤P(Γ≥1)≤1−(n−c+1−υn−c+1)c. Sec-Auditor can detect data corruption with a high probability by sampling a fixed number of file blocks, regardless of the total size of the cloud data being audited. For instance, if υ=0.01n, TPA can request 460 blocks to achieve a probability P(Γ≥1) of at least 99%, and 300 blocks to achieve a probability of at least 95%.

7  Evaluations

7.1 Security Attributes Analysis

In this section, we analyze several crucial security attributes, including public auditing, data integrity, and semantic correctness. We selected comparison schemes proposed in recent years. Table 2 presents the comparison results for these security attributes. Our scheme, as well as schemes [14,26,27,29], supports public auditing, whereas scheme [9] supports private auditing. The comparison results also demonstrate that our proposed scheme can simultaneously support both data integrity and semantic correctness.

7.2 Performance Evaluation

To evaluate the performance of Sec-Auditor, we deployed it on a personal computer and conducted tests to measure its actual execution time. In read-world application scenarios, the execution results of Sec-Auditor are influenced not only by the computational complexity of the algorithm but also by network latency, the blockchain’s consensus protocol, and other variables. To enhance our assessment of the algorithm’s performance, we intend to eliminate network latency in subsequent experiments. The configurations for this evaluation are as follows: Central processing unit (CPU): Intel i5-12500H; Random access memory (RAM): 16.0 GB; Blockchain platform: Quorum 2.0; Operation system: Ubuntu 18.04 LTS; Programming language: Java 1.7.0; Blockchain consensus protocol: Quorum byzantine fault tolerance (QBFT); Number of blockchain virtual nodes: 3, as recommended in [29]. In the following evaluations, the datasets are randomly generated to mask differences in execution time caused by diverse data types.

Initially, we need to determine the optimal block size, as it could affect the computational overhead associated with the StorF, Chal, and Resp algorithms. We set the file size, consisting of n blocks, to be 3456 bytes, and the number of challenged file blocks to be n/2. We will conduct tests to explore the relationship between the combined execution times of the above three algorithms and the file block size, aiming to pinpoint the optimal file block. The results are demonstrated as Fig. 3. From these results, we can infer that the optimal block size is 16 bytes, with a corresponding execution time of 1.4 s.

Figure 3: Determine the optimal block size

Next, in order to assess the execution time of each algorithm within Sec-Auditor, we configured the block size to 16 bytes, with 180 challenged file blocks. The results are as presented in Fig. 4. Notably, the StorF and UptRule algorithms within the proposed solution accounts for the majority of the total processing time. In practical applications, the UptRule algorithm is executed less frequently compared to the StorF algorithm. Consequently, we will not assess the performance of the UptRule algorithm. In order to enhance the performance of Sec-Auditor, we need to accelerate the StorF algorithm. Despite this, the StorF algorithm in Sec-Auditor still outperforms the scheme [27], as illustrated in Fig. 5. This superiority is attributed to the fact that the scheme [27] should perform more time-consuming bilinear pairing operations.

Figure 4: Execution time of each algorithm for Sec-Auditor

Figure 5: Performance comparison of the StorF algorithm

Once the user outsources the data to the cloud, the subsequent system will routinely or sporadically perform data auditing operations based on the system’s configuration. These operations entail the execution of the algorithms Chal, Resp, and Verf. Throughout the data’s lifecycle, these three algorithms may be frequently executed. To analyze the execution efficiency of these algorithms, we conducted an evaluation to examine the relationship between their execution times and the number of challenged file blocks. In this evaluation, we utilized a total of 20,000 file blocks and configured the file block size to be 16 bytes. The experimental results are presented in Fig. 6. These results indicate that the Resp algorithm requires more time compared to the other two ones. Since the cloud operates as a distributed storage system, user data are distributed across numerous storage nodes. When performing the Resp algorithm, individual storage nodes can leverage their local data to compute a local proof, which is subsequently submitted to TPA for aggregation. This implementation can effectively accelerate the Resp algorithm.

Figure 6: Performance comparison of the data audit phase

8  Conclusions

We propose a new data auditing solution called Sec-Auditor, capable of simultaneously verifying both data integrity and semantic correctness. Sec-Auditor also supports public auditing, allowing anyone with access to public information to conduct data audits. This feature makes Sec-Auditor highly adaptable to the cloud. What is more, the user in Sec-Auditor is assigned with a specific rule that is utilized to verify the semantic accuracy, and can be allowed to update his own rule as needed. We conduct a comprehensive analysis of Sec-Auditor’s correctness and security, along with performance evaluations to demonstrate its efficiency. In the future, we plan to deploy Sec-Auditor in a broader range of application scenarios and optimize its efficiency.

Acknowledgement: The author would like to express gratitude to Bu Fande from Feisuan Technology Company for his diligent and dedicated efforts in conducting experiments.

Funding Statement: This research was supported by the Qinghai Provincial High-End Innovative and Entrepreneurial Talents Project.

Author Contributions: Guodong Han conceived the study, contributed to the investigation, development, and coordination, and drafted the original manuscript. Hecheng Li, the corresponding author, conducted the experiments and analyzed the data in the study. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Hecheng Li, upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. I. A. Moşescu, R. G. Chivu, I. C. Popa, and F. Botezatu, “Creating value with big data in marketing,” in Int. Conf. Bus. Excell., Rome, Italy, 2021, pp. 129–140. [Google Scholar]

2. C. Zhang, C. Xu, J. Xu, Y. Tang, and B. Choi, “Gem^2-tree: A gas-efficient structure for authenticated range queries in blockchain,” in 2019 IEEE 35th Int. Conf. Data Eng. (ICDE), Macao, China, 2019, pp. 842–853. [Google Scholar]

3. H. Wang, C. Xu, C. Zhang, and J. Xu, “vChain: A blockchain system ensuring query integrity,” in Proc. 2020 ACM SIGMOD Int. Conf. Manag. Data, Portland, OR, USA, 2020, pp. 2693–2696. [Google Scholar]

4. J. Wang et al., “Data secure storage mechanism of sensor networks based on blockchain,” Comput. Mater. Contin., vol. 65, no. 3, pp. 2365–2384, Jul. 2020. doi: 10.32604/cmc.2020.011567. [Google Scholar] [CrossRef]

5. J. Gao et al., “ChainDB: Ensuring integrity of querying off-chain data on blockchain,” in Proc. 2022 5th Int. Conf. Blockchain Technol. Appl., Xi’an, China, 2022, pp. 175–181. [Google Scholar]

6. T. V. Doan, Y. Psaras, J. Ott, and V. Bajpai, “Toward decentralized cloud storage with IPFS: Opportunities, challenges, and future considerations,” IEEE Int. Comput., vol. 26, no. 6, pp. 7–15, Sep. 2022. doi: 10.1109/MIC.2022.3209804. [Google Scholar] [CrossRef]

7. G. Ateniese et al., “Provable data possession at untrusted stores,” in Proc. 14th ACM Conf. Comput. Commun. Secur., Alexandria, VA, USA, 2007, pp. 598–609. [Google Scholar]

8. H. Wang, K. Li, K. Ota, and J. Shen, “Remote data integrity checking and sharing in cloud-based health internet of things,” IEICE Trans. Inf. Syst., vol. 99, no. 8, pp. 1966–1973, May 2016. doi: 10.1587/transinf.2015INI0001. [Google Scholar] [CrossRef]

9. H. Wang, Q. Wang, and D. He, “Blockchain-based private provable data possession,” IEEE Trans. Depend Secure Comput., vol. 18, no. 5, pp. 2379–2389, Oct. 2019. doi: 10.1109/TDSC.2019.2949809. [Google Scholar] [CrossRef]

10. H. Wang, D. He, J. Yu, and Z. Wang, “Incentive and unconditionally anonymous identity-based public provable data possession,” IEEE Trans. Serv. Comput., vol. 12, no. 5, pp. 824–835, Nov. 2016. doi: 10.1109/TSC.2016.2633260. [Google Scholar] [CrossRef]

11. J. Yu and H. Wang, “Strong key-exposure resilient auditing for secure cloud storage,” IEEE Trans. Inf. Forensics Secur., vol. 12, no. 8, pp. 1931–1940, Apr. 2017. doi: 10.1109/TIFS.2017.2695449. [Google Scholar] [CrossRef]

12. W. Shen, G. Yang, J. Yu, H. Zhang, F. Kong and R. Hao, “Remote data possession checking with privacy-preserving authenticators for cloud storage,” Future Gener. Comput. Syst., vol. 76, no. 4, pp. 136–145, Nov. 2017. doi: 10.1016/j.future.2017.04.029. [Google Scholar] [CrossRef]

13. K. He, J. Chen, Q. Yuan, S. Ji, D. He and R. Du, “Dynamic group-oriented provable data possession in the cloud,” IEEE Trans. Depend. Secure Comput., vol. 18, no. 3, pp. 1394–1408, Jul. 2019. doi: 10.1109/TDSC.2019.2925800. [Google Scholar] [CrossRef]

14. Y. Yang, Y. Chen, F. Chen, and J. Chen, “An efficient identity-based provable data possession protocol with compressed cloud storage,” IEEE Trans. Inf. Forensics Secur., vol. 17, pp. 1359–1371, Mar. 2022. doi: 10.1109/TIFS.2022.3159152. [Google Scholar] [CrossRef]

15. N. B. Truong, K. Sun, G. M. Lee, and Y. Guo, “GDPR-compliant personal data management: A blockchain-based solution,” IEEE Trans. Inform. Forensic Secur., vol. 15, pp. 1746–1761, Oct. 2019. doi: 10.1109/TIFS.2019.2948287. [Google Scholar] [CrossRef]

16. L. Wang, Z. Guan, Z. Chen, and M. Hu, “Enabling integrity and compliance auditing in blockchain-based GDPR-compliant data management,” IEEE Internet Things J., vol. 10, no. 23, pp. 20955–20968, Jun. 2023. doi: 10.1109/JIOT.2023.3285211. [Google Scholar] [CrossRef]

17. F. Ramadhani, U. Ramadhani, and L. Basit, “Combination of hybrid cryptography in one time pad (OTP) algorithm and keyed-hash message authentication code (HMAC) in securing the whatsapp communication application,” J. Comput. Sci. Inf. Technol. Telecommun. Eng., vol. 1, no. 1, pp. 31–36, Mar. 2020. doi: 10.30596/jcositte.v1i1.4359. [Google Scholar] [CrossRef]

18. Y. Ogawa, S. Sato, J. Shikata, and H. Imai, “Aggregate message authentication codes with detecting functionality from biorthogonal codes,” in 2020 IEEE Int. Symp. Inf. Theory (ISIT), Los Angeles, CA, USA, 2020, pp. 868–873. [Google Scholar]

19. A. K. Chattopadhyay, A. Nag, J. P. Singh, and A. K. Singh, “A verifiable multi-secret image sharing scheme using XOR operation and hash function,” Multimed. Tools Appl., vol. 80, no. 28-29, pp. 35051–35080, Jul. 2020. doi: 10.1007/s11042-020-09174-0. [Google Scholar] [CrossRef]

20. A. Juels and B. S. Kaliski Jr, “PORs: Proofs of retrievability for large files,” in Proc. 14th ACM Conf. Comput. Commun. Secur., Alexandria, VA, USA, 2007, pp. 584–597. [Google Scholar]

21. H. Shacham and B. Waters, “Compact proofs of retrievability,” J. Cryptol., vol. 26, no. 3, pp. 442–483, Sep. 2012. doi: 10.1007/s00145-012-9129-2. [Google Scholar] [CrossRef]

22. J. Xu and E. C. Chang, “Towards efficient proofs of retrievability,” in Proc. 7th ACM Symp. Inform., Comput. Commun. Secur., Seoul, Republic of Korea, 2012, pp. 79–80. [Google Scholar]

23. M. B. Paterson, D. R. Stinson, and J. Upadhyay, “Multi-prover proof of retrievability,” J. Math. Cryptol., vol. 12, no. 4, pp. 203–220, Sep. 2018. doi: 10.1515/jmc-2018-0012. [Google Scholar] [CrossRef]

24. C. Han, G. J. Kim, O. Alfarraj, A. Tolba, and Y. Ren, “ZT-BDS: A secure blockchain-based zero-trust data storage scheme in 6g edge iot,” J. Int. Technol., vol. 23, no. 2, pp. 289–295, Mar. 2022. doi: 10.53106/160792642022032302009. [Google Scholar] [CrossRef]

25. H. Wang, Q. Wu, B. Qin, and J. Domingo-Ferrer, “Identity-based remote data possession checking in public clouds,” IET Inf. Secur., vol. 8, no. 2, pp. 114–121, Mar. 2014. doi: 10.1049/iet-ifs.2012.0271. [Google Scholar] [CrossRef]

26. L. Wang, Z. Guan, Z. Chen, and M. Hu, “An efficient and secure solution for improving blockchain storage,” IEEE Trans. Inf. Forensics Secur., vol. 18, pp. 3662–3676, Jun. 2023. doi: 10.1109/TIFS.2023.3285489. [Google Scholar] [CrossRef]

27. Y. Zhang, J. Yu, R. Hao, C. Wang, and K. Ren, “Enabling efficient user revocation in identity-based cloud storage auditing for shared big data,” IEEE Trans. Depend. Secure Comput., vol. 17, no. 3, pp. 608–619, Apr. 2018. doi: 10.1109/TDSC.2018.2829880. [Google Scholar] [CrossRef]

28. J. Leng, M. Zhou, J. L. Zhao, Y. Huang, and Y. Bian, “Blockchain security: A survey of techniques and research directions,” IEEE Trans. Serv. Comput., vol. 15, no. 4, pp. 2490–2510, Nov. 2020. doi: 10.1109/TSC.2020.3038641. [Google Scholar] [CrossRef]

29. L. Wang, M. Hu, Z. Jia, Z. Guan, and Z. Chen, “SStore: An efficient and secure provable data auditing platform for cloud,” IEEE Trans. Inf. Forensics Secur., vol. 19, pp. 4572–4584, Apr. 2024. doi: 10.1109/TIFS.2024.3383772. [Google Scholar] [CrossRef]