Resilience Augmentation in Unmanned Weapon Systems via Multi-Layer Attention Graph Convolutional Neural Networks

1  Introduction

The Unmanned Weapon System-of-Systems (UWSOS) amalgamates a variety of autonomous assets, encompassing aerial drones and unmanned ground vehicles, which synergistically cooperate to fulfill collective objectives. This technology has been integrated into endeavors such as the Skyborg program and System of Systems (SOS) integration within the United States Air Force [1,2]. In particular operational scenarios, each UWSOS node possesses distinctive functionalities that can be compromised by adversarial actions, including electromagnetic interference or anti-radar weaponry aimed at sensor nodes. These attacks degrade target localization and decision-making capabilities, thereby diminishing operational efficacy.

In the realm of UWSOS, orchestrating collaborative operations requires intricate processes of data exchange, information dissemination, and decision-making. UWSOS must manage heterogeneous data sources and promptly derive decisions, thereby increasing system complexity and managerial challenges. Mission reliability and resilience are crucial, as external disruptions such as attacks and electromagnetic interference [3,4] can compromise stability, introducing uncertainty and risk during mission execution. This vulnerability affects operational effectiveness and lifecycle costs [5–7]. Historically, enhancing UWSOS reliability has focused on redundancy. Zhang et al. [8] developed an optimization model using hybrid redundancy strategies to maintain functionality, while Levitin et al. [9] optimized the efficiency of active redundant systems. Peiravi et al. [10] proposed a redundancy allocation strategy to optimize system reliability, ensuring stability and continuity despite failures.

However, in contemporary warfare scenarios, evolving adversarial strategies render attacks difficult to predict and preempt [11]. UWSOS integrates a variety of unmanned systems, complicating comprehensive preemptive measures, which demand substantial resources and financial investments, including hardware/software upgrades, network security, and encrypted communication protocols. Consequently, recent research emphasizes resilience and rapid recovery mechanisms [12–14]. Resilience, conceptualized by Holling in 1973, denotes a system’s capacity to withstand, maintain, and restore performance despite disruptions [15]. This concept has gained prominence across disciplines such as sociology [16,17], infrastructure engineering [18,19], and military systems [20], and is increasingly investigated within UWSOS.

Within the domain of UWSOS, resilience is pivotal for assessing robustness and reliability in navigating uncertainties and disruptions [21]. Zhao et al. [22] proposed a resilience model that monitors information exchange fluctuations, offering a framework for evaluating system resilience but primarily concentrating on structural connectivity and data flow. Sun et al. [23] enhanced UWSOS resilience through deep reinforcement learning (DRL), employing graph convolutional networks and proximal policy optimization to autonomously devise strategies against interference scenarios. Graph Neural Networks (GNNs) are potent tools for modeling complex systems [24,25], including UWSOS, capturing intricate relationships in graph-structured data. They have applications in traffic forecasting [26], communication networks [27], and the enhanced Internet of Things (IoT) [28]. Prior research often relies on first-order graph relationships within UWSOS, overlooking higher-order dependencies among nodes. Effective kill chains (meta-paths) in UWSOS necessitate multiple steps to capture indirect node relationships. Moreover, diverse nodes within UWSOS embody significant semantic complexity, such as sensor nodes engaged in environmental perception tasks. Neglecting semantic edge information can hinder the model’s ability to fully exploit graph information, leading to information loss.

To address these challenges, we introduce the Enhanced-Resilience Multi-Layer Attention Graph Convolutional Network (E-MAGCN), which utilizes heterogeneous networks to enhance the resilience of UWSOS. This framework incorporates a regularization-based multi-layer attention mechanism and semantic node fusion within the GCN architecture. The primary contributions of this study are summarized as follows:

1.    We introduce a novel method termed E-MAGCN (Enhanced-Resilience Multi-Layer Attention Graph Convolutional Network) to refine the resilience strategies of UWSOS. This approach adeptly extracts semantic insights from nodes and edges while leveraging representations of various node and edge types, offering deeper insights into the intricate relationships and interactions within the UWSOS.

2.    We propose a streamlined and efficient regularization-based hierarchical attention mechanism that integrates node-edge information, facilitating feature extraction and learning across different layers within UWSOS. This mechanism enables the acquisition of abstract representations at different levels, allowing adaptable focus on critical nodes and edges, thereby enhancing the capture of multi-hop features and complex relationships inherent in effective meta-paths.

3.    We expand the scope of UWSOS and validate the effectiveness of our proposed model through rigorous experimentation, anticipating its utility in future large-scale unmanned warfare scenarios. Our results demonstrate that our approach autonomously learns strategies without prior system knowledge, exhibiting superior resilience enhancement compared to similar algorithms. This underscores the potential of leveraging GCN to improve decision-making in UWSOS.

In this paper, Section 1 elucidates the strategic significance of UWSOS in contemporary military operations, emphasizing the pivotal role of graph convolutional networks (GCNs) in fortifying their resilience and tracing the evolution of graph-based methodologies. Section 2 conducts a comprehensive literature review, identifying existing limitations and situating our research within the current academic discourse, while introducing the Enhanced-Resilience Multi-Layer Attention Graph Convolutional Network (E-MAGCN). Section 3 expounds on our methodology, detailing the architecture of E-MAGCN, the multi-layer attention mechanism, and semantic node fusion, all supported by rigorous mathematical formulations. Section 4 provides empirical validation of our model through extensive simulation experiments, benchmarking E-MAGCN’s performance against established standards. Finally, Section 5 synthesizes the findings, discusses their implications for future military technologies, and proposes avenues for further research.

2  Related Works

Previous studies have explored methodologies to enhance system resilience, categorized into planning paradigms, adaptive algorithmic frameworks, and deep reinforcement learning architectures. Planning models optimize resilience by defining specific objectives and constraints. For instance, Chen et al. [29] developed a multi-objective optimization framework to enhance weapon system resilience while minimizing reconfiguration costs. Hao et al. [30] introduced a resilience maximization model for interdependent electromechanical networks, focusing on faulty node rectification and functional interdependencies. Xu et al. [31] proposed a two-stage stochastic model for uncertainties in repair times. Pan et al. [32,33] introduced a resilience importance index to prioritize recovery efforts. These methodologies collectively fortify system resilience against threats and disruptions. Planning paradigms rely on predefined metrics to evaluate system states and recovery strategies, but these metrics may lack comprehensiveness or precision. In the multifaceted environment of UWSOS, conventional metrics may fail to capture the system’s status and operations adequately. Indicator-based methodologies may thus prove insufficient. In UWSOS, timely responsiveness is crucial, necessitating swift action in hostile environments. Existing recovery strategies may prioritize physical interventions, spending excessive time without promptly addressing challenges in adversarial environments.

Adaptive algorithms dynamically adjust strategies based on system status and environmental changes. Zheng et al. [34] proposed a fleet reconstruction model for drone formations, enhancing adaptability and resilience by modifying fleet structures in real-time. However, its effectiveness depends on the state of key entities, which may limit overall resilience if critical entities fail. Sun et al. [35] developed a collaborative strategy for UWSOS, introducing a Collaborative Action Resilience Contribution Index (CARCI) to evaluate and optimize collaborative strategies. Despite leveraging drone swarms’ residual nodes and considering heterogeneous characteristics, these methodologies face constraints from domain knowledge and localized solutions, limiting practical applicability and robustness.

Deep Reinforcement Learning (DRL) effectively manages extensive state and action spaces, finding broad applications across various domains [36,37]. Techniques such as Deep Q-learning Networks (DQN) [38], Proximal Policy Optimization (PPO) [39], and other methodologies significantly enhance system resilience. Integrating Convolutional Neural Networks (CNNs) [40] and GCNs [23,28,41] has improved DRL’s proficiency in processing graph data. Peng et al. [28] optimized IoT topology using DRL, combining GCNs with policy networks to learn evolutionary characteristics and optimize structures. Similarly, Tahmineh et al. [33] and Zheng et al. [34] modeled scenarios as Markov Decision Processes (MDPs) using Deep Neural Networks (DNNs), providing end-to-end solutions that enhance decision-making intelligence and system adaptability. Fan et al. [41] proposed the GCN-DQN model, combining GCNs and DQNs to augment the representation of edge connections and disconnections within networks, generating repair sequences for a water distribution network.

However, previous research on GCN-based DRL models has lacked hierarchical feature extraction capabilities, limiting their effectiveness in capturing intricate network structures and relationships. Specifically, the DRLRESF [23] framework, while leveraging GCNs and policy optimization algorithms, falls short in modeling the complex multi-hop relationships and deep features within UWSOS. This limitation affects its ability to make robust decisions and generalize across diverse scenarios. Similarly, KCOM [42] focuses on optimizing the mission delivery process and resource utilization within the kill chain model but does not incorporate hierarchical attention mechanisms, which are crucial for capturing the intricate dynamics of UWSOS networks.

To address these limitations, we propose an innovative hierarchical attention-based graph convolutional network (E-MAGCN) to enhance UWSOS resilience. Our approach leverages complex multi-hop relationships inherent in meta-paths and exploits semantic nuances derived from node-edge interactions. By employing hierarchical local and global attention mechanisms, we mitigate the overfitting challenges inherent in GCNs and enrich the representation vectors of UWSOS. Additionally, we incorporate the structural and nodal attributes of UWSOS to develop rich embedding vector representations for individual nodes. Our study involves experimental comparisons of E-MAGCN with diverse baseline methodologies, including KCOM, and DRLRESF, across eight distinct scenarios. These comparisons, complemented by extensive ablation analyses, demonstrate the superior performance and resilience of our proposed framework. E-MAGCN offers a more robust and effective solution for enhancing the resilience of UWSOS, ensuring improved decision-making and adaptability in dynamic and adversarial environments.

3  Method

In our paper, we introduced the Enhanced-Resilience Multi-Layer Attention Graph Convolutional Network (E-MAGCN), a framework for graph convolutional network representation learning. E-MAGCN adeptly captures both global and local intricacies of UWSOS graph data by incorporating regularization and a stratified attention architecture. By employing attention mechanisms across varying tiers, E-MAGCN achieves a comprehensive understanding of the graph’s structure, enabling multiscale feature extraction and adaptive responsiveness to the significance of diverse nodes and edges. This enhancement improves information dissemination efficiency and strengthens resilience against noise. Additionally, it enhances the model’s interpretive capacity, effectively addressing the complexities of relationship modeling and task management within UWSOS.

Fig. 1 illustrated the architecture of the Resilience Augmentation in Unmanned Weapon Systems via Multi-Layer Attention Graph Convolutional Neural Networks, comprising three components: the node-edge encoding layer, the E-MAGCN network, and the Actor-Critic (AC) decision network. In the node-edge encoding layer, BERT is utilized for semantic extraction from nodes and edges. Subsequently, this information is input into the E-MAGCN layer, where it undergoes iterative aggregation and update processes across stacked layers of E-MAGCN. Specifically, E-MAGCN initially consolidates information from neighboring nodes via attention mechanisms, generating embeddings for various syntactic graphs. Additionally, at each level of E-MAGCN, edge representations are refined through a specialized attentional hierarchical structure. Finally, attention mechanisms are employed to aggregate node representations from different layers, leveraging the AC network to enhance the resilience of the UWSOS.

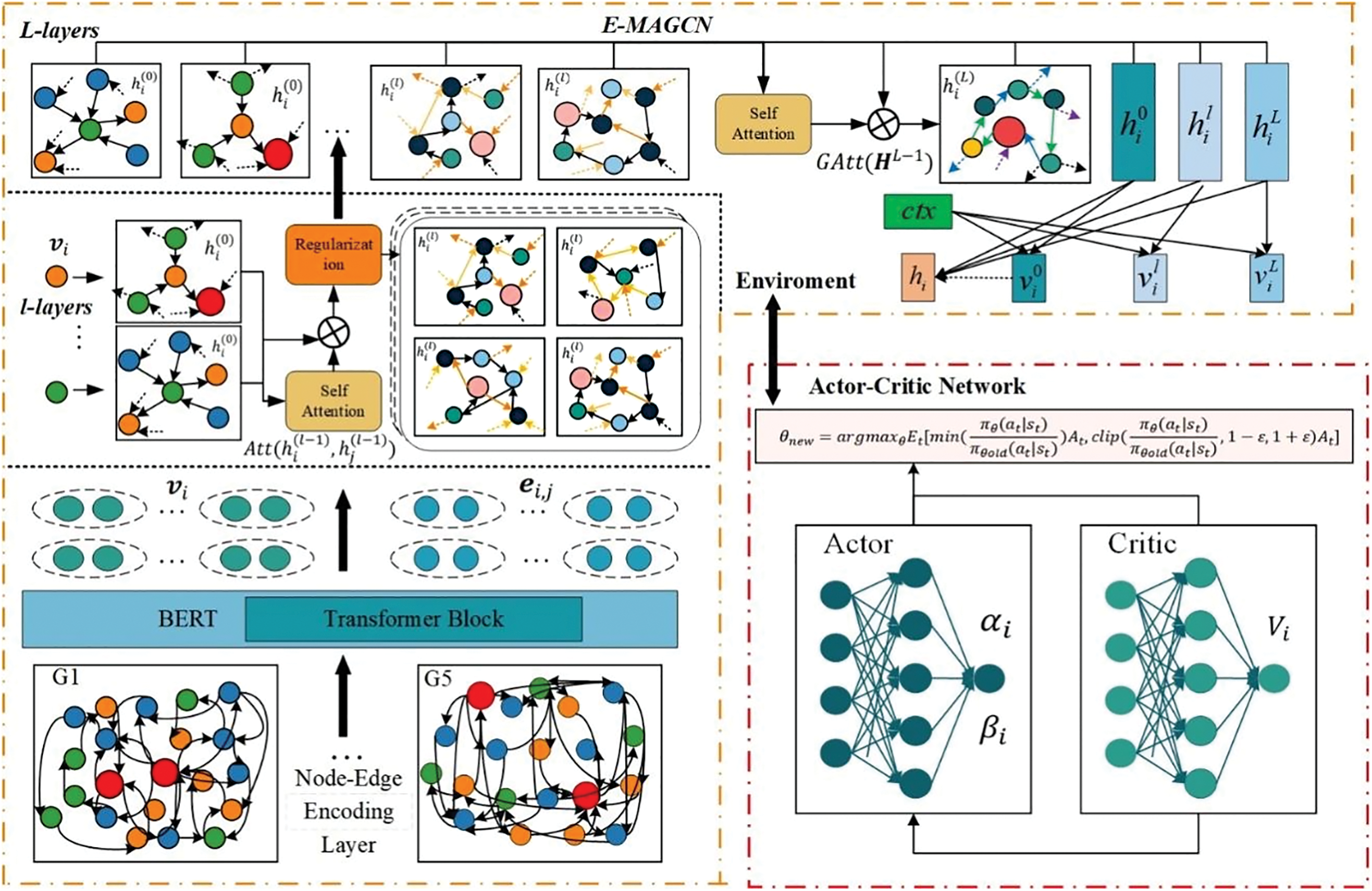
Figure 1: Illustration of the overall framework of resilience augmentation in UWSOS via multi-layer attention graph convolutional neural networks

3.1 Node-Edge Encoding Layer

Within the domain of UWSOS, various nodes harbor significant semantic complexity. For instance, sensor nodes typically undertake the responsibility of environmental perception, encompassing tasks such as data collection and event monitoring. Extracting semantic insights from sensor nodes can greatly enhance the system’s understanding of environmental nuances and fluctuations, thereby improving decision-making and operational effectiveness.

The objective of node encoding is to transform the intricate semantic characteristics of nodes into vector representations, thus empowering subsequent graph neural network models with enhanced node processing capabilities. For a graph G=(V,E), where V represents the node set, we utilize the BERT model to encode each node vi∈V, yielding the semantic vector vi. Specifically, the BERT model derives the semantic vector vi by leveraging the hidden state H of the final layer and a dedicated node representation vector CLS:

vi=BERT(vi)=HiT∗CLS(1)

where HiT denotes the hidden state of the T-th layer transformer in the node feature encoding, and CLS represents a specialized node representation vector that signifies the BERT model’s output. It is noteworthy that for the node feature vector vi, we employ average pooling at the final layer of BERT to augment the model’s generalization capability.

Similarly, in practical operational network scenarios, edges often contain abundant semantic details, such as edge types and weights. Ignoring the semantic information of edges can impede the model’s capacity to fully leverage the graph’s information, leading to information loss. Furthermore, traditional graph convolutional networks face difficulties in accurately capturing the complex structure of graphs and distinguishing between various types of edges or their importance. The integration of edge encoding enables a more thorough comprehension of the graph’s structure and semantic content by the model.

In this paper, for each edge ei,j∈E, we define the edge feature vector ei,j as follows:

ei,j=BERT(ei,j)=Hi,jT∗CLS(2)

where Hi,jT denotes the hidden state of the T-th layer transformer, and CLS represents a special node representation vector signifying the output of the BERT model. Likewise, we employ average pooling at the final layer of BERT to derive the output.

In UWSOS, the significance of various nodes and node relationships fluctuates. We dynamically compute the contribution Υi,j of each adjacent node i to the current node j, assigning attention weights to pivotal adjacent nodes and lower attention weights to less significant ones. This dynamic attention mechanism enhances the model’s adaptability to diverse graph structures and task requirements. The calculation of attention weight Υi,j is as follows:

Υi,j=e(WΥ[vi;vj])∑k∈N(i)e(WΥ[vi;vk])(3)

where e(.) represents the exponential function, WΥ denotes the attention parameter matrix, [vi;vJ] represents the concatenation vector of nodes vi and vj, and N(i) represents the set of all neighboring nodes. We obtain the edge feature vector as follows:

ei,jatt=Υi,j∗ei,j(4)

3.2 Enhanced-Resilience Multi-Layer Attention Graph Neural Network (E-MAGCN)

In the domain of UWSOS, essential meta-operation loop paths, like T → S → D → I → T, delineate meta-paths covering observation, localization, decision-making, and action processes. These meta-path graphs illuminate the intrinsic information propagation, decision-making, and action processes within the UWSOS. We note that numerous intermediary nodes between sensors S, decision-makers D, and influencers I indirectly impact another target T. Our goal is to utilize GCN for the systematic aggregation of information from neighboring nodes across multiple levels, with the aim of more effectively capturing these multi-hop relationships.

It is crucial to emphasize that, for a comprehensive depiction of the information propagation, decision-making, and action processes within the UWSOS, and to enable the model to grasp the interactions and influences among nodes and edges, we integrate both node and edge information for feature extraction. Additionally, by iteratively stacking multiple layers of E-MAGNN, we systematically elevate the abstraction level of features. This facilitates the acquisition of more refined feature representations, thereby enhancing the comprehension of the intricate relationships within the UWSOS.

In the node-edge encoding layer of E-MAGNN, we merge the encoded node and edge information, which then act as inputs to the GCN model. Utilizing this integrated data, we perform feature extraction and propagation within the GCN layer to proficiently model and understand graph data. To expound further, the process of integrating node and edge information at each layer of GCN can be outlined as follows:

hi(l+1)=σ(∑j∈N(i)1didjeijatt(l)W(l)+b(l))⊙(∑j∈N(i)hj(l)U(l)+c(l))(5)

where hi(l) represents the node representation in the l-th layer, N(i) denotes the set of neighboring nodes for a node vi, di represents the dimensionality of node vi, σ indicates the activation function, ⊙ denotes element-wise multiplication, W(l) and U(l) are weight matrices, b(l) and c(l) respectively represent their bias terms.

It is noteworthy that within the UWSOS system, the intricate interplay between nodes and edges unfolds across various strata. We adopt a hierarchical framework for GCN, enabling the gradual extraction and amalgamation of features, thus achieving abstract representations across multiple tiers. Specifically, in the inaugural layer of GCN, we facilitate the model to swiftly grasp the fundamental relationships and features among nodes employing a straightforward node propagation technique, devoid of regularization terms. Within this primary layer, the updated node representation formula of GCN can be succinctly expressed as:

hi(0)=σ(∑j∈N(i)1didjeijatt(0)W(0)+b(0))⊙(∑j∈N(i)hj(0)U(0)+c(0))(6)

Moreover, within the UWSOS, intricate interactions and influences among nodes and edges, such as multi-hop relationships between sensors, decision-makers, and influencers, are prevalent. Introducing a dynamic attention-based weight updating mechanism in the intermediate layers of GCN (0 < l < L) empowers the model to dynamically adjust the attention weights between nodes. This capability enables the model to flexibly prioritize crucial nodes and edges, thereby enhancing its capacity to capture multi-hop features and intricate relationships more effectively. Consequently, the model can adaptively allocate attention based on specific tasks and data conditions, bolstering its adaptability and generalization capability. In the l-th layer, the updated node representation formula of GCN can be succinctly expressed as:

hi(l)=σ(∑j∈N(i)Att(hi(l−1),hj(l−1)))El−1⊙(∑j∈N(i)Nl−1)−nll−1(7)

El−1=eijatt(l−1)W(l−1)(8)

Nl−1=hj(l−1)U(l−1)+c(l−1)(9)

nll−1=λ(l−1)∗‖W(l−1)‖22(10)

Att(hi(l−1),hj(l−1))=exp⁡(ReLU(Wa[hi(l−1);hj(l−1)]))∑k∈N(i)exp⁡(ReLU(Wa[hi(l−1);hj(l−1)]))(11)

where Wa is a learnable parameter matrix, and [;] denotes the vector concatenation operation. nll−1 represents the regularization term.

However, we acknowledge that updating only considers local information in the intermediate layers without incorporating the global structure and features of the entire graph. This limitation could constrain the model to learn localized feature representations, thereby hindering a comprehensive understanding of the intricate relationships and patterns within the entire UWSOS. Additionally, neglecting the global structure and features of the entire graph might diminish the model’s generalization capability. In real-world scenarios, environmental conditions and system configurations may vary. If the model only learns localized feature representations, it might encounter challenges in effectively adapting to diverse scenarios and tasks.

Therefore, introducing a weight updating mechanism based on global graph attention at the top layer empowers the model to more effectively capture the overall graph relationships and patterns. In the L-th layer, the updated node representation formula of GCN can be succinctly expressed as:

hi(L)=σ(∑j∈N(i)GAtt(HL−1))EL−1⊙(∑j∈N(i)NL−1)(12)

EL−1=eij(L−1)W(L−1)+b(L−1))(13)

NL−1=hj(L−1)U(L−1)+c(L−1)(14)

GAtt(HL−1)=exp⁡(ReLU(WgHL−1WgT))∑k=1Nexp⁡(ReLU(WgHL−1WgT)(15)

where Wg is a learnable parameter matrix, HL−1 is the node representation matrix of the intermediate layer, and N is the number of nodes.

In the multi-layer E-MAGCN framework, each stratum captures distinctive features across various levels of granularity. Through attention-based aggregation, the heterogeneous hierarchical information within UWSOS can be adeptly consolidated, resulting in a more comprehensive and holistic representation hi of the UWSOS graph:

hi=∑l=0Lvi(l)hi(l)(16)

vi(l)=exp⁡((tanh⁡(Wawahil+bawa))Tctx)∑l=1Lexp⁡((tanh⁡(Wawahil+bawa))Tctx)(17)

where vi(l) denotes the normalized weight of the l-th layer UWSOS graph representation; Wawa and bawa signify trainable weight matrices and bias terms, respectively; ctx refers to the ctx matrix, initialized randomly as a context vector.

3.3 Actor-Critic Network for Decision Making in UWSOS

UWSOS presents a multifaceted decision-making environment characterized by interactions among numerous nodes and edges, necessitating intelligent agents to discern and execute appropriate actions. The AC network serves as a potent tool for learning and refining policy functions. In the context of UWSOS, this entails that agents can enhance their decision-making abilities through iterative learning from past experiences. Furthermore, the features extracted by the preceding GCN layer adeptly capture the intricate interconnections among nodes within the UWSOS. Leveraging these features, the AC network can refine decisions based on nuanced relationships, thereby augmenting the system’s overall performance and efficiency. Through the integration of GCN and the AC network, a comprehensive framework for modeling and optimizing the decision-making process within the UWSOS can be established.

Initially, within the Actor network, we compute the replacement probability and collaboration probability for each node hi of the GCN features. The computation of the replacement probability involves a linear transformation followed by a softmax function:

zi=ReLU(Wahi+ba)(18)

αi=e(Wa′zi+ba′)∑ke(Wa′zi+ba′)k(19)

Similarly, the computation of the collaboration probability also entails a linear transformation followed by a softmax function:

pi=ReLU(Wbhi+bb)(20)

βi=e(Wb′zi+bb′)∑ke(Wb′zi+bb′)k(21)

where e(.) represents the exponential function, Wa′ and Wb′ are the weight parameters of the Actor network, and ba and bb are the bias parameters.

Following, we posit that the Critic network accepts the node feature vector hi(L) as input and generates the estimated value function Vi as output:

vi=ReLU(Wvhi+bv)(22)

Vi=wTvvi+bv(23)

where Wv denotes the weight parameters of the Critic network, bv signifies the bias parameters, wT stands for the weight parameters of the output value function, and bv represents the bias parameters of the value function.

In the segment concerning the AC network, we utilize the PPO algorithm to acquire a parameterized policy. This policy offers heightened stability and necessitates fewer hyperparameters compared to alternative strategies. The objective function is articulated as follows:

θnew=argmaxθEt[min(πθ(a_t|s_t)πθold(a_t|s_t))At,clip(πθ(a_t|s_t)πθold(a_t|s_t),1−ε,1+ε)At](24)

where πθ(at|st) denotes the learned policy, where at and st respectively denote the state s and action a at time t, for each node i action ai=[αi,βi] at time t. Specifically, the initial component of the agent’s objective function correlates the refinement of the policy function with the anticipated value of the advantage function. This is realized by juxtaposing the ratio of the current policy function to the old policy function with the product of the advantage function, selecting the lesser value as a segment of the agent’s objective function. The subsequent component of the agent’s objective function restricts the magnitude of policy adjustments using a clipping ratio. We employ a clipping function to constrain the refinement of the policy function, bounding its range between (1−ε)At and (1+ε)At.

Within the AC network, we derive the advantage function At as follows:

A(st,at)=rt+γV(st+1)−V(st)(25)

where V(st) denotes the value function estimated by our Critic network. We compute and revise the parameters of the Actor network to maximize the agent’s objective function.

Furthermore, inspired by DRLRESF [23], we not only integrate global policies with immediate rewards but also incorporate meta-path-aware reward functions into the objective function to guide the learning and optimization of the policy function. These meta-path-aware reward functions encompass aspects such as completing full meta-paths, information propagation, and time penalties, which can better guide the agent in achieving its goals and improve training effectiveness.

4  Experiments

This section presents a comprehensive set of simulation experiments aimed at validating the effectiveness, adaptability, and superiority of the proposed method. Detailed data preparation procedures are described in Section 4.1. Subsequently, Section 4.2 provides an in-depth analysis and demonstration of the effectiveness of the proposed approach. Section 4.3 further demonstrates the adaptability of the proposed method through verification in various attack scenarios. Finally, in Section 4.4, we conduct a comprehensive comparison between the proposed method and other similar algorithms, and in Section 4.5, we perform detailed ablation experiments on the proposed E-MAGCN model.

4.1 Data Description

Following the procedure outlined in the literature for constructing an Unmanned Weapon System-of-Systems (UWSOS) [43], we significantly expanded the system as detailed in Table 1. The two generated UWSOS demos, Swarm1 and Swarm2, are illustrated in Fig. 2. All subsequent experiments were conducted on Swarm1 (hereafter referred to as Swarm). As shown in Table 1 and Fig. 2, this expansion includes 100 sensor entity nodes (VS, blue circles), 50 decision entity nodes (VD, green circles), 50 influencer entity nodes (VI, orange circles), and 10 enemy target entity nodes (VT, red circles), each class of nodes being assigned a unique identifier. According to the OODA theory, the edge direction within a UWSOS operates according to the following rules: the target entities can be detected by sensor entities (T→S, yellow lines), the military reconnaissance intelligence can be shared within the sensor entities (S→S, green lines), the sensor entities send military reconnaissance intelligence to the decision-maker entities (S→D, red lines), the decision-maker entities give attack orders to the influencer entities (D→I, bule lines), different decision-maker entities can communicate with each other (D→D, dark purple lines), and the influencer entities execute commands and implement attacks on the enemy targets (I→T, purple lines). Given the substantial scale of the UWSOS, we choose not to display the identifiers on the nodes.

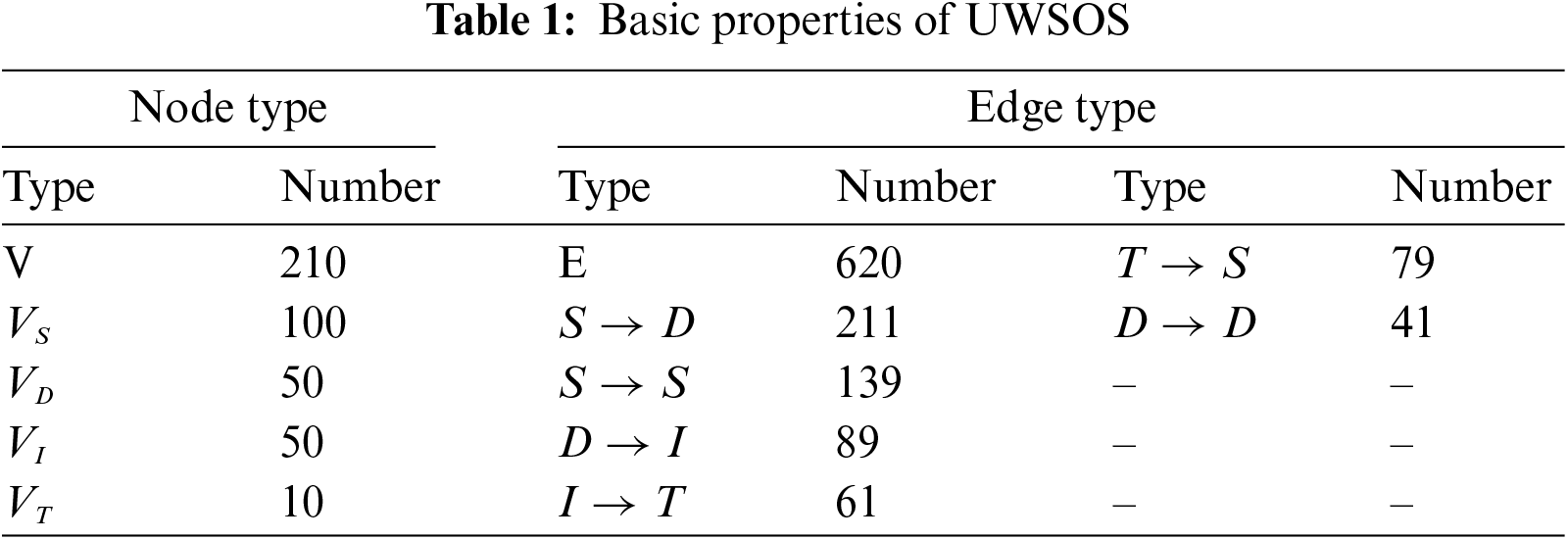
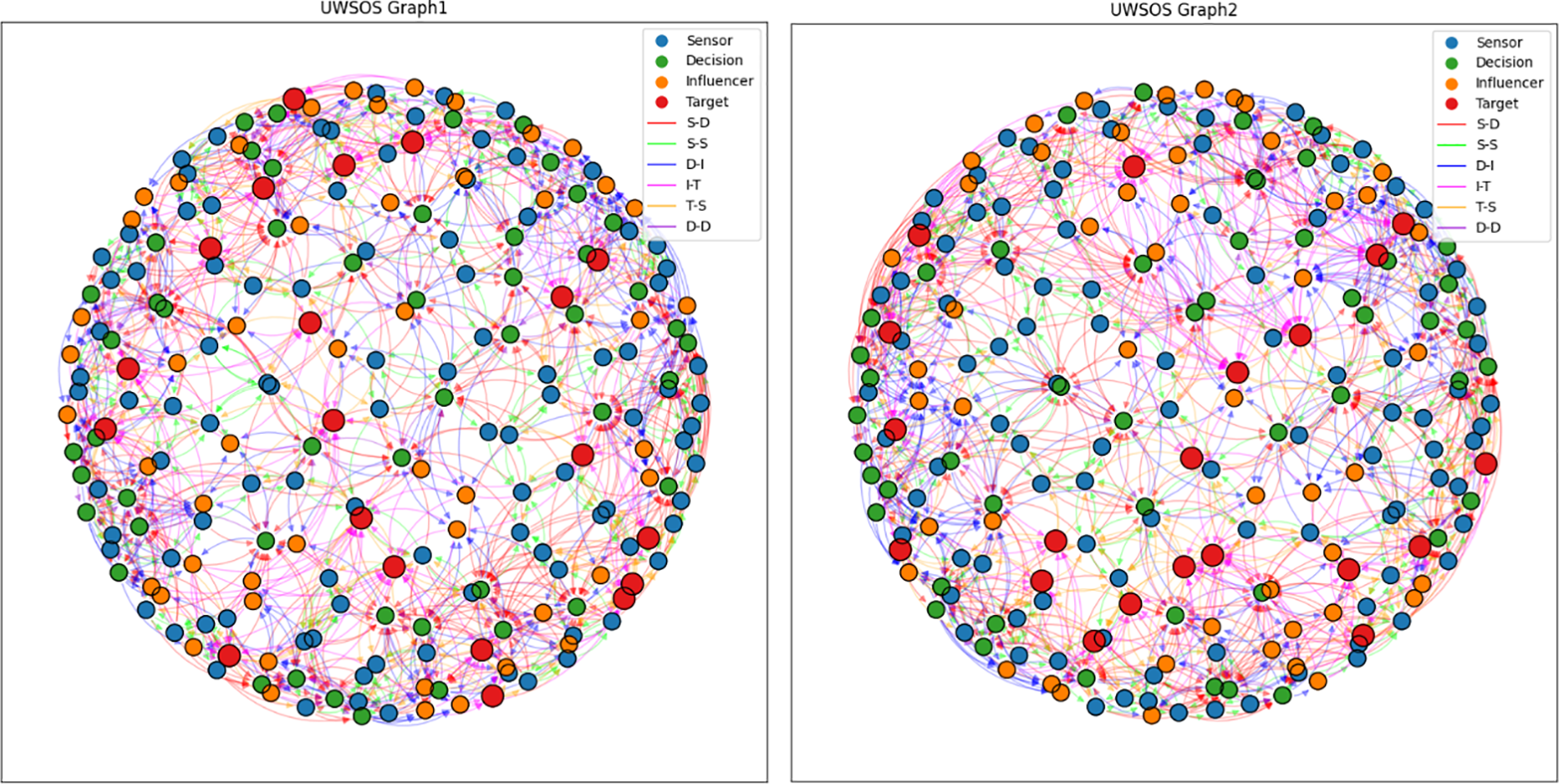
Figure 2: Constructed UWSOS graph with five subgroups

After assessing the scale of the UWSOS, we theorize that UWSOS comprises five unmanned weapon groups, each endowed with similar attributes customized for executing their distinct tasks. We denote the network model of UWSOS as G:

G={G1,G2,G3,G4,G5}(26)

Each subgroup Gi∈{1,2,3,4,5} in G represents a distinct network model within the UWSOS Swarm. Our evaluation metrics align with those used in previous studies [23], focusing on the resilience F(Swarm) of the entire UWSOS:

F(Swarm)=∑i=1If(Gi)I(27)

where, the symbol I represents the number of subgroups in UWSOS. In this paper, we set I = 5 to meet the experimental conditions. F(Swarm) denotes the overall resilience of UWSOS, which can be understood as the weighted sum of the capabilities of all combat loops based on each target entity, where different target entities have different priorities in military tasks. We adopt the resilience f(Gi) of each subgroup in UWSOS evaluation metric from reference [4], which is specifically designed to measure the ability of the UWSOS to recover from attacks and disruptions. This metric evaluates the system’s performance decline during an attack and its subsequent recovery, providing a comprehensive assessment of the system’s robustness and recovery capabilities.

4.2 Experimental Setup

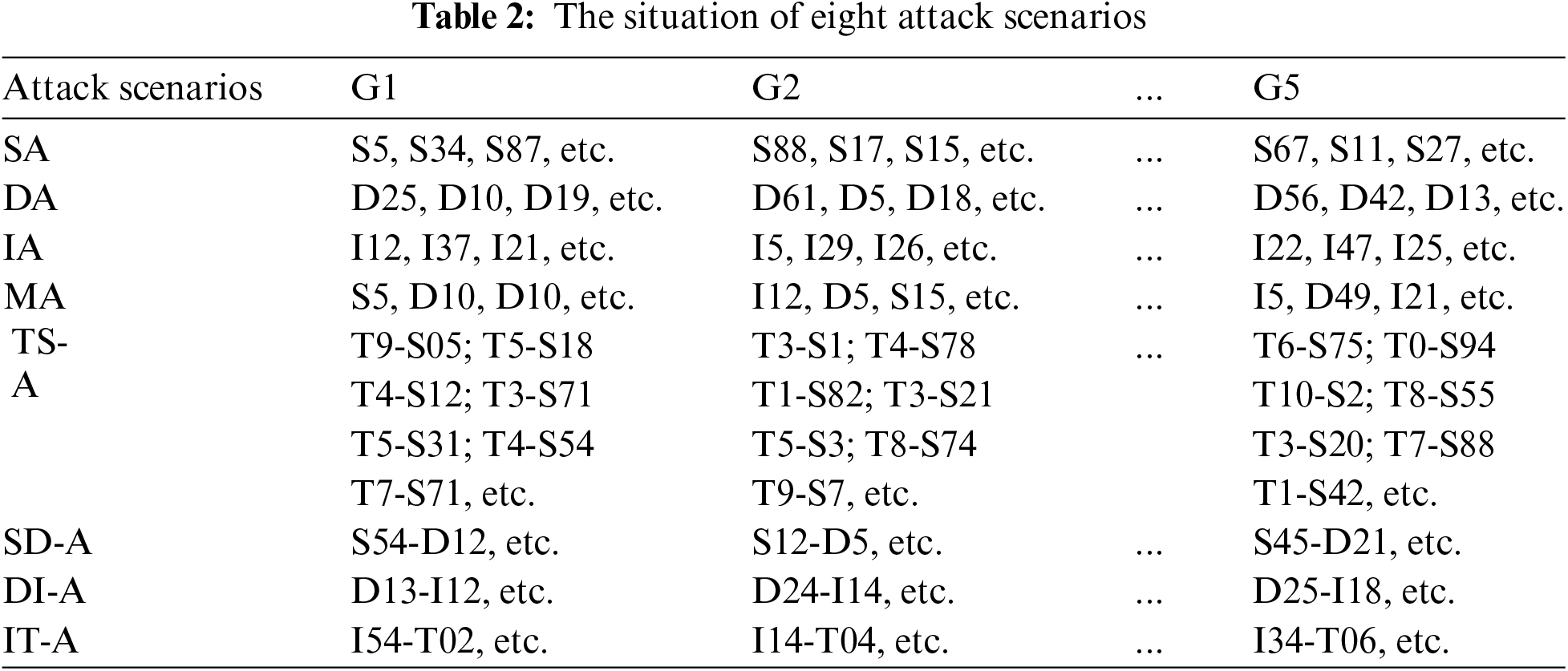
To further evaluate the resilience enhancement performance of the proposed method for the UWSOS network, we expanded the evaluation framework to encompass two primary disruption scenarios detailed in Table 2: node disruption and edge disruption. In the node disruption scenario, we not only simulate the simple destruction of nodes but also devise two specific node disruption strategies to comprehensively assess the system’s responsiveness. These strategies include solely attacking sensor nodes (SA), decision nodes (DA), or influencer nodes (IA), and simultaneously attacking multiple hybrid nodes (MA). On the other hand, in the edge disruption scenario, we conducted a more granular classification, designing a total of four different edge disruption strategies, each with its unique impact. These strategies involve disrupting T→S edges (TS-A), disrupting S→D edges (SD-A), disrupting D→I edges (DI-A), and disrupting I→T edges (IT-A). For example, T9-S05 refers to blocking perception from sensor S5 to T9, while S54-D12 refers to impeding information transmission from sensor S54 to decision node D12.

To evaluate the effectiveness of the Enhanced-Resilience Multi-Layer Attention Graph Convolutional Network (Model E-MAGCN), a baseline is established using traditional resilience optimization algorithms such as the Random Node (RN) and Maximum Degree Node (MDN) methods. These algorithms serve as a benchmark to quantify the performance enhancements of Model E-MAGCN in terms of network stability and recovery times.

The following Table 3 provides a detailed overview of the elements utilized in Model E-MAGCN, specifying their roles and characteristics. This table aims to clarify the implementation and functional aspects of each component within the model.

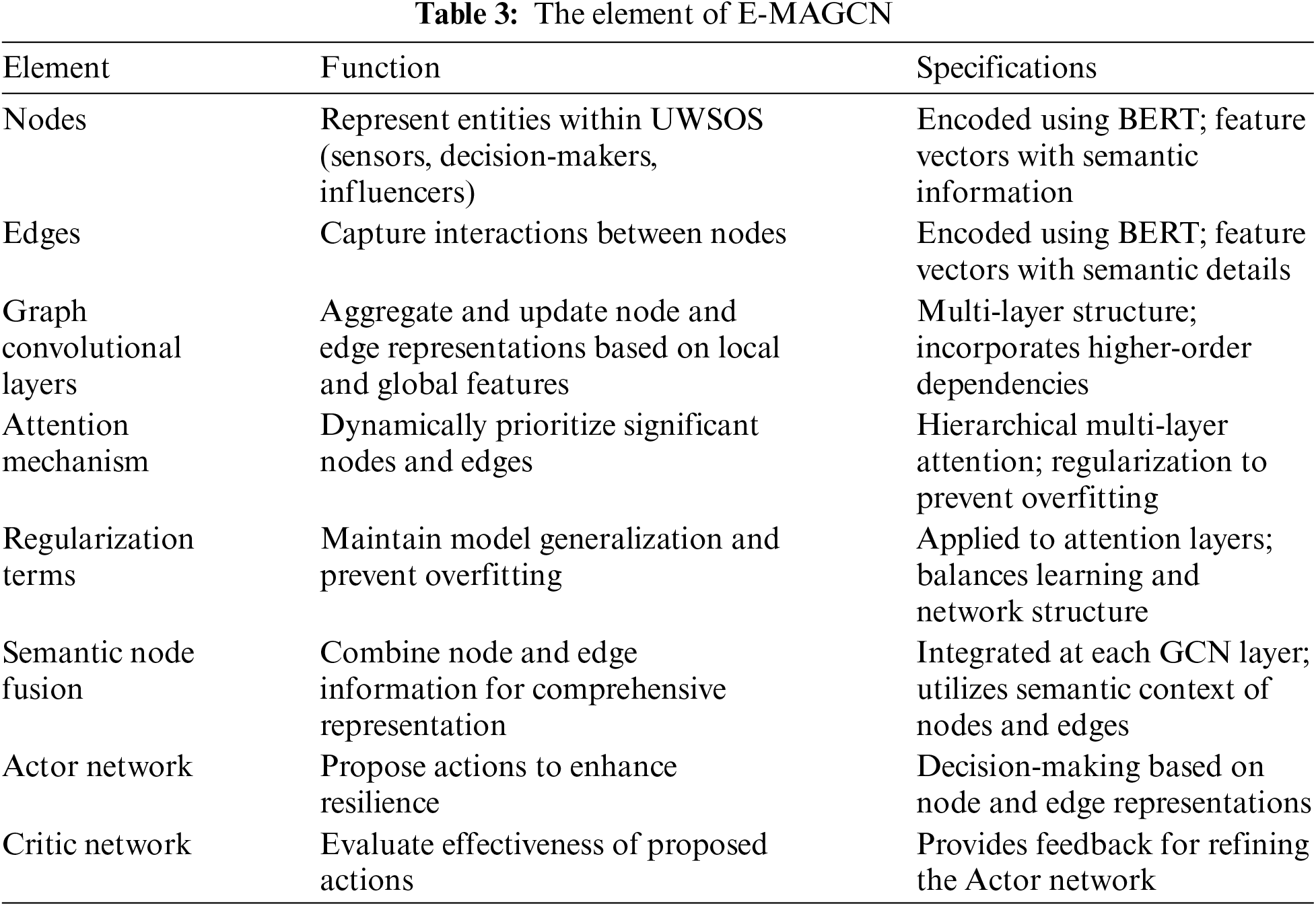
In the node-edge embedding phase outlined in Section 3.1, we employed the BERT-based pretrained model to generate fixed-length 768-dimensional embeddings for each node and fine-tuned the dataset to align with task requirements. During the model training phase, we meticulously adjusted all hyperparameters to ensure optimal performance. We set the batch size to 8 and the learning rate for the GCN stage to 2e-5, while the learning rates for the Actor and Critic networks were set to 3e-5, respectively. The Adam optimizer was utilized to adjust the parameters. Additionally, the simulated time during the experimental phase was set to 40 time steps. Attacks on the UWSOS commenced at 4S and continued until 14S according to the eight methods mentioned in Table 1, with recovery beginning at 15S. To implement the proposed Enhanced-Resilience Multi-Layer Attention Graph Convolutional Network (E-MAGCN), we used NetworkX 3.2.1 [44] to construct the UWSOS graph and PyTorch 2.2.2 for training the model. The training process was conducted on NVIDIA A100 Tensor Core GPUs, which provided the necessary computational performance and efficiency for handling complex computations and extensive data processing.

4.3 Experimental Analysis

Taking the SA scenario as an example, Table 4 illustrates the evolution of our proposed resilience enhancement strategy for the UWSOS graph. Initially, the resilience value is 1, representing the initialization phase of UWSOS. From 5 to 15 s, we initiate attacks on the nodes of UWSOS using the previously established attack strategy, resulting in a decrease in the resilience value of UWSOS to 0.529. Between the 15th and 40th stages, the model implements a stable resilience enhancement strategy for the UWSOS Ultimately, at the 40th stage, the model’s resilience value stabilizes at 0.799.

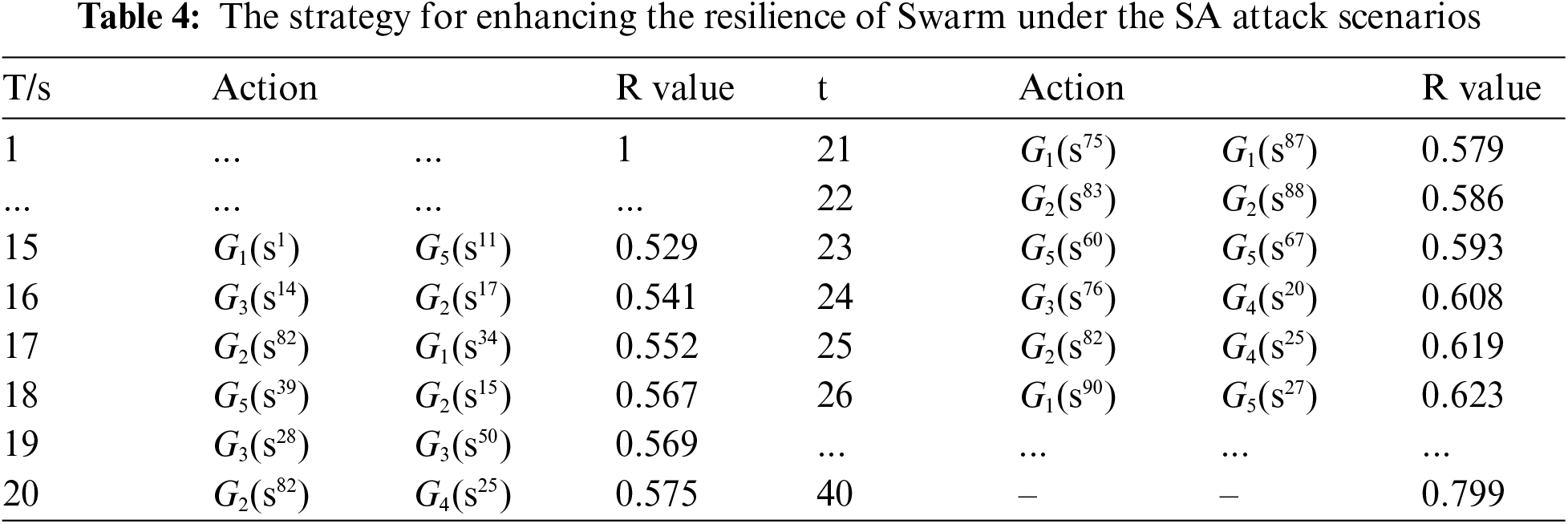
An in-depth quantitative analysis delineated in Table 1 indicates a decrement in the resilience index of the UWSOS to 0.529 subsequent to a sensor attack (SA). In response, the deployment of E-MAGCN facilitated a robust enhancement, elevating the resilience index to 0.799 within a critical window of 25 s. This rapid augmentation underscores the model’s efficacy in dynamically adapting to adversarial disruptions.

Temporal granularity during the recovery phase reveals strategic reallocations within the network: at T = 15 s, the inter-network sensor node substitution between G3 and G2 networks improved the resilience index from 0.529 to 0.541. A subsequent intra-network adjustment at T = 19 s further incremented the resilience metric to 0.569. These targeted interventions demonstrate E-MAGCN capability to execute precision-driven resilience strategies under operational stress.

Self-Resistance (SR): Utilizes the inherent resistance capability of UWSOS without resorting to any post-attack recovery techniques.

Random Node Reconnection (RN): At each time step, selects a randomly disrupted node within each network. Subsequently, reconnects the previously linked nodes to the remaining nodes in a random fashion, ensuring adherence to node capacity and edge type constraints.

Maximum Degree Node Reconnection (MDN): Analogous to the RN algorithm, prioritizes disrupted and reconnecting nodes based on maximum degree nodes.

DRLRESF [23]: Combines graph convolution networks and proximal policy optimization to autonomously enhance UWSOS resilience against various interference scenarios.

Kill Chain Optimization Method (KCOM) [41]: Introduces an resilience UWSOS kill chain optimization method from the perspective of the observation, positioning, decision, and action phases of the kill chain process.

In this section, we conducted a comprehensive comparative analysis between the proposed E-MAGCN and five other optimization methods across eight distinct attack scenarios to evaluate its resilience within the UWSOS. The methods analyzed include Self-Resistance (SR), Random Node Reconnection (RN), Maximum Degree Node Reconnection (MDN), DRLRESF algorithm, and the Kill Chain Optimization Method (KCOM).

As illustrated in Table 5, the indiscriminate selection of interrupted and reconnecting nodes by the RN algorithm poses significant risks to network topology stability, ultimately compromising overall performance. Despite adherence to node capacity and edge type constraints, the randomness in selection often leads to frequent disruptions and reconnections of critical nodes, thereby negatively impacting the stability and performance of the network. Similarly, the MDN algorithm, which prioritizes nodes based on their degree, lacks the precision needed for optimal resilience enhancement, resulting in potential destabilization of the network due to non-deterministic node selection.

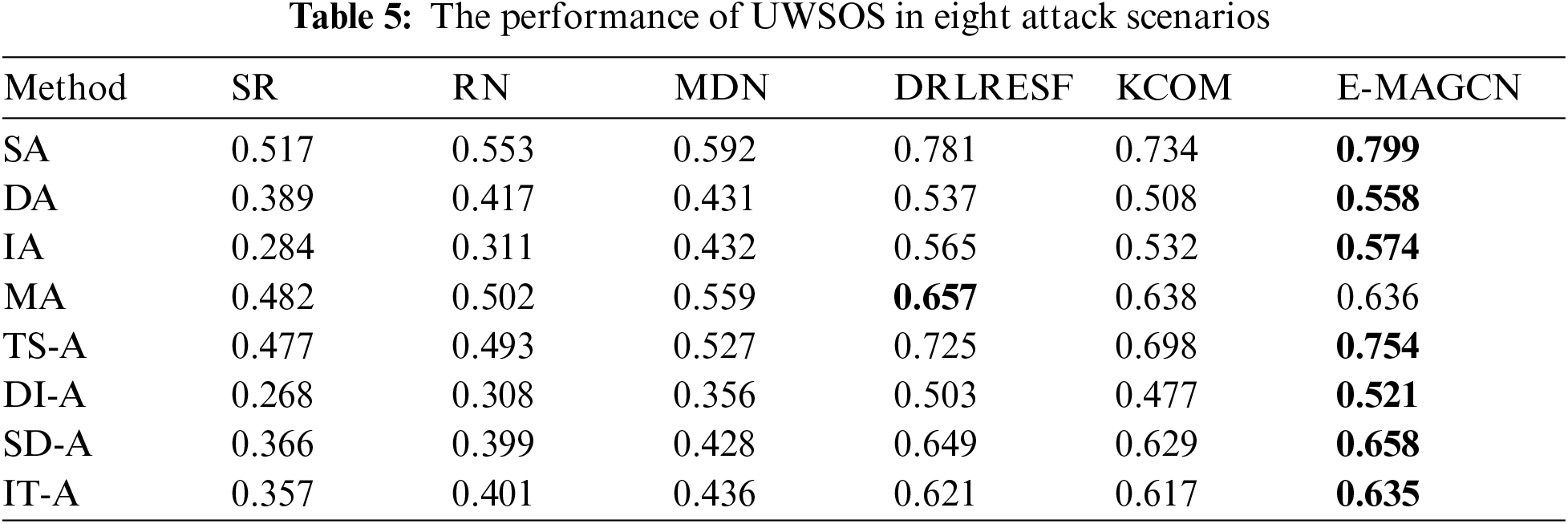
In contrast, the DRLRESF algorithm enhances network recovery performance and stability by employing a deep reinforcement learning-based strategy that autonomously learns and adapts to various interference scenarios. This method demonstrates a notable improvement in resilience metrics, significantly reducing network downtime and enhancing stability. The KCOM method, integrating kill chain optimization theory, effectively addresses various attack stages and improves operational integrity by optimizing the observation, positioning, decision, and action phases of the kill chain process.

However, both DRLRESF and KCOM algorithms exhibit limitations in dynamically adapting to complex network scenarios and accurately handling multi-hop relationships. They often overlook dynamic changes between nodes and edges and the complexity of information propagation, leading to reduced flexibility and accuracy.

Conversely, the proposed E-MAGCN method excels by comprehensively considering complex relationships and multi-hop propagation characteristics. This approach results in an average increase of 0.15 and 0.23 in resilience metric values across the eight attack scenarios. The significant improvement can be attributed to E-MAGCN’s ability to aggregate information from neighboring nodes at different levels, thereby capturing interactions between nodes and edges more accurately. This enhanced modeling precision and deeper understanding of UWSOS behavior enable E-MAGCN to maintain network stability and optimize performance under varying operational conditions.

Overall, the experimental results underscore the superior performance of E-MAGCN in enhancing the resilience of UWSOS compared to traditional methods. By leveraging structured, data-driven approaches and advanced graph convolutional network techniques, E-MAGCN demonstrates significant improvements in network recovery, stability, and operational efficiency, validating its potential for real-world applications in resilient network design.

4.4 The Impact of GCN Layer Numbers on E-MAGCN

In this section, we delved into the impact of stacking multiple E-MAGCN layers on our model’s performance, as illustrated in Fig. 3, where the horizontal axis represents the number of GCN layers and the vertical axis represents the Resilience Value (R Value) of UWSOS. Across eight different attack scenarios, we investigated how varying GCN layer depths from 1 to 6 affect the resilience of the model. As depicted in Fig. 3, we observed that the model’s average performance reaches its peak when the GCN layer depth is set to 4, after which performance gradually declines with increasing E-MAGCN layer depth. We attribute this pattern to the complex nature of information propagation and decision-making processes inherent in the UWSOS, involving multi-hop relationships and multi-level information interactions. For example, each layer of a typical E-MAGCN can capture relationships at different levels between nodes, while in the UWSOS, there are multi-hop relationships (meta-path) among sensors, decision-makers, and influencers. By increasing the depth of E-MAGCN layers, we can effectively capture these multi-hop relationships, thereby enhancing the model’s understanding and modeling capability of system behavior.

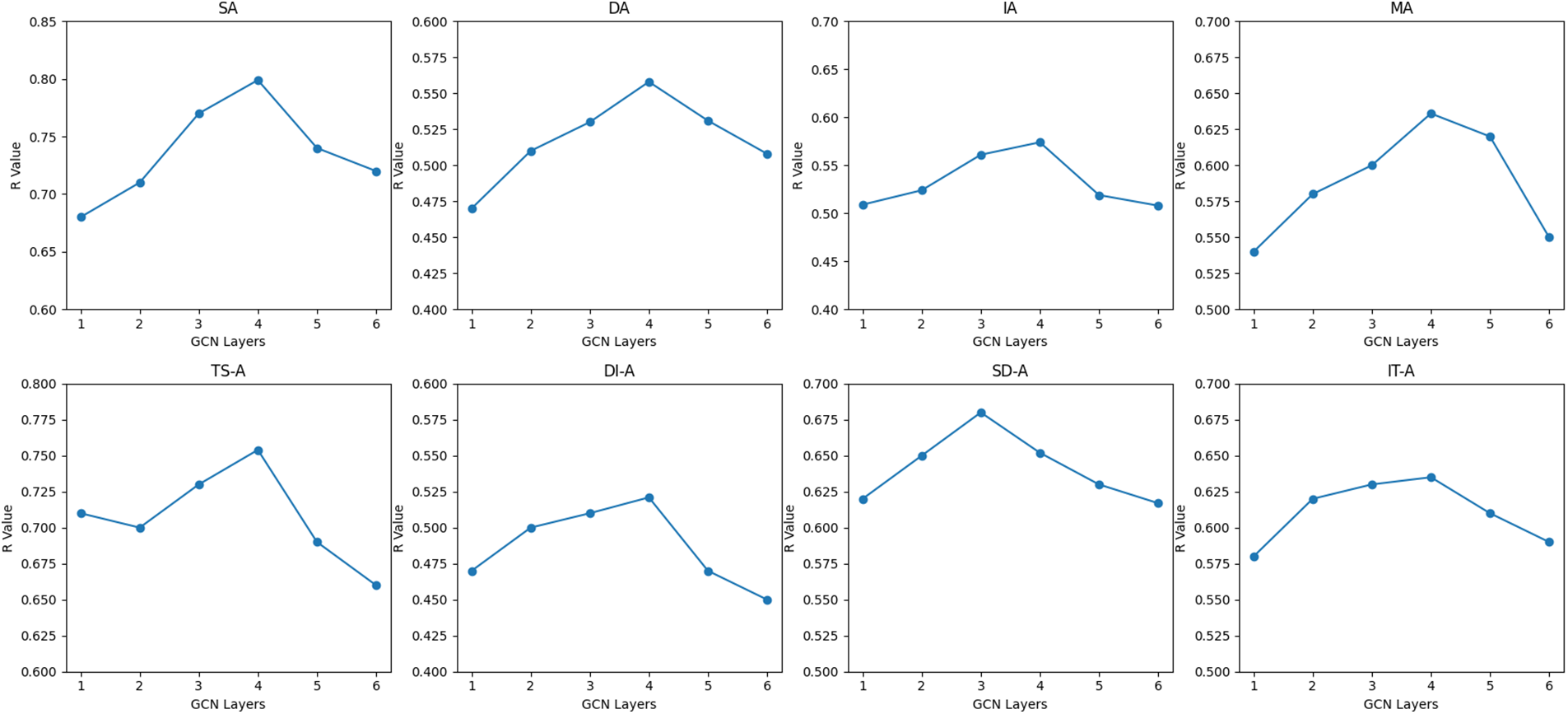
Figure 3: Resilience performance across different E-MAGCN layers

By augmenting the layer count in E-MAGCN, it becomes feasible to progressively extract and comprehend higher-level feature representations, thereby enriching the understanding of the system’s complexity and dynamic attributes. Despite the potential loss of crucial features or structural information during information propagation within the network due to the increased layer count in E-MAGCN, our advocated weight updating mechanism based on global attention can prevent the model from fixating solely on local features, thus alleviating the neglect of global structure and critical features, thereby averting performance degradation. Furthermore, the integration of a weight updating mechanism rooted in dynamic attention within the intermediate layers of E-MAGCN empowers the model to dynamically adjust the attention weights among nodes, facilitating a flexible focus on pivotal nodes and edges, thus fostering a superior comprehension of global structure and trends.

4.5 Ablation Study

In this section, we conducted ablation experiments on E-MAGCN to investigate the impact of attention mechanisms and various dependency labels. For this purpose, we devised two distinct structures based on GCN:

E-MAGCN(Att): E-MAGCN(Att) represents our approach wherein we substituted the attention-based hierarchy with a conventional GCN network. As illustrated in Fig. 4, the red curve illustrates the resilience performance of E-MAGCN(Att) as the number of layers varies, while the blue curve depicts the resilience performance of E-MAGCN with varying layer counts. It is evident that compared to E-MAGCN, E-MAGCN(Att) exhibits an average reduction of approximately 6% in resilience score on UWSOS, and the optimal number of GCN layers decreases from 4 layers to either 3 or 2 layers. This reduction may stem from the removal of attention mechanisms, potentially hindering the model’s comprehensive consideration of the global structure and features of the entire graph, resulting in the acquisition of localized feature representations exclusively.

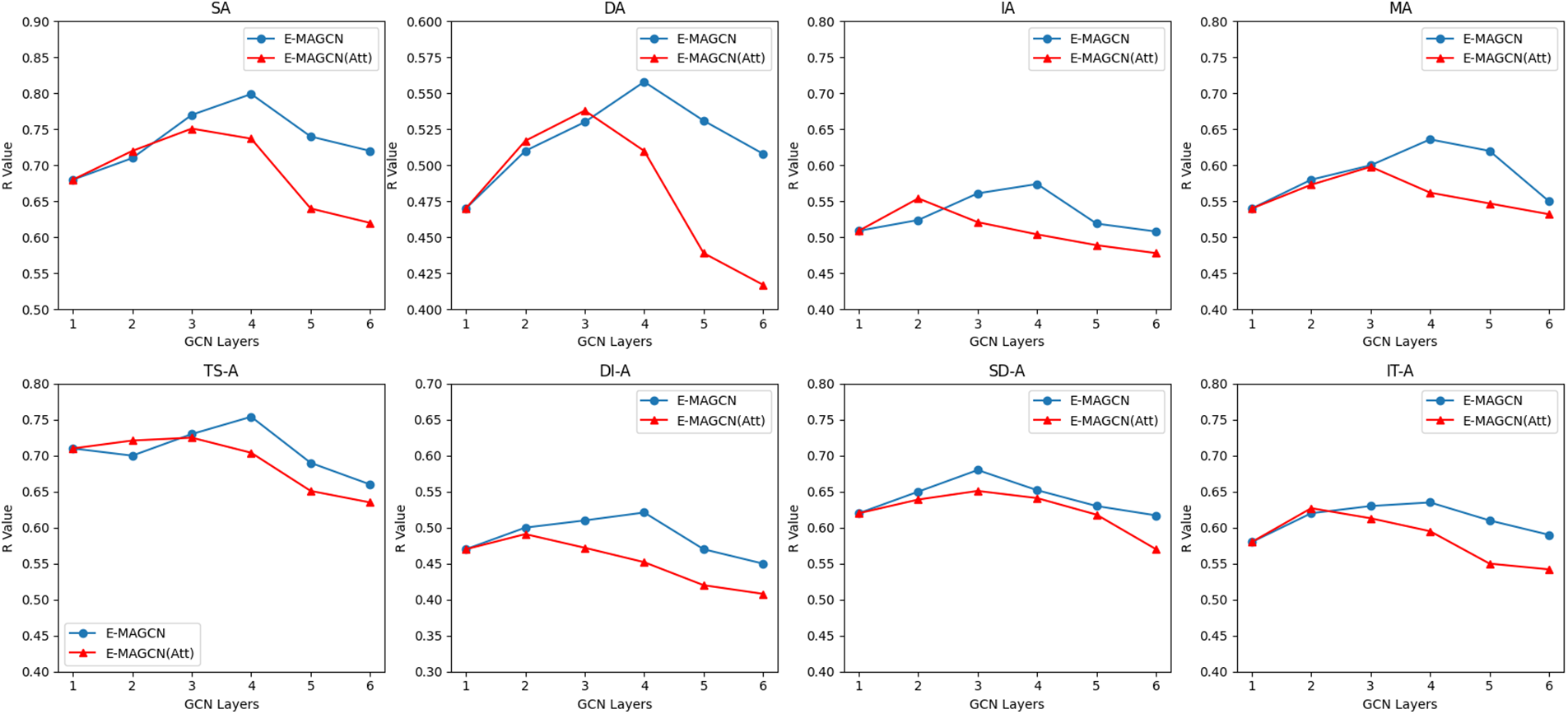
Figure 4: Resilience performance across different E-MAGCN and E-MAGCN (Att) L-layers

Consequently, the model may face challenges in effectively adapting to diverse scenarios and tasks in the real world, thereby diminishing its resilience and generalization capabilities. Additionally, as the number of GCN layers increases, node representations may tend to aggregate, leading to similar feature representations across different nodes. This over-smoothing effect could impede the model’s ability to discern features of distinct nodes effectively, thereby diminishing its performance. Conversely, the hierarchical attention mechanism proposed in this study can dynamically adjust the attention allocation between nodes based on specific tasks and data conditions, enabling the model to prioritize important nodes and edges. This approach helps prevent the aggregation of all node features, thereby alleviating the over-smoothing effect.

E-MAGCN(NER): E-MAGCN(NER) denotes our methodology wherein we exclude the node-edge representation, with the intention of examining the influence of semantic attributes of edges and nodes on the model’s elasticity. As depicted in Fig. 5, where the horizontal axis represents different attack scenarios and the vertical axis represents the resilience of UWSOS, it is evident that E-MAGCN(NER) demonstrates an approximately 2.5% decrease in resilience compared to E-MAGCN. One potential rationale behind this observation is that the omission of node-edge encoding may lead to the model’s incapacity to fully leverage the semantic information inherent in nodes and edges within the graph, thereby resulting in information degradation.

Figure 5: Resilience comparison between E-MAGCN and E-MAGCN(NER) across various attack scenarios

Moreover, given that the efficacy of graph neural network models hinges on their comprehension and representation capacity of the graph’s structure, the inclusion of node-edge encoding can furnish the model with abundant semantic insights, facilitating a deeper understanding of the graph’s structure and semantics. The exclusion of this encoding procedure may curtail the model’s grasp of the graph’s structure, consequently constraining its representational capabilities. Ultimately, the elimination of this encoding process may impede the model’s effectiveness in capturing the intricate relationships between nodes and edges in the graph, thereby diminishing its ability to model the graph’s structure effectively.

In order to conduct a comprehensive assessment of the E-MAGCN model’s performance on UWSOS and its temporal dynamics, we generated a graphical representation illustrating the evolution of UWSOS resilience over time. As shown in Fig. 6, the four graphs represent UWSOS resilience under different attack scenarios as episodes progress, with red representing E-MAGCN, brown representing E-MAGCN(Att), and blue representing E-MAGCN(NER). The horizontal axis represents the number of episodes during the training process, while the vertical axis indicates the resilience value (R Value) of UWSOS. This visualization enabled us to scrutinize convergence rates, fluctuations, and juxtapose them with alternative methodologies. As depicted in Fig. 6, contrasting the resilience trajectories of E-MAGCN and E-MAGCN(Att), the absence of hierarchical attention in E-MAGCN(Att) facilitates a more rapid return to a specific resilience value in the initial phases. This phenomenon likely arises from the model’s intensified focus on local information, thereby expediting the acquisition of certain local features. However, the deficiency in global attention could hinder the seamless integration of global information, resulting in more pronounced fluctuations in resilience values during the recovery phase, evident as amplified oscillations. Furthermore, the inability of E-MAGCN(Att) to adequately incorporate global information and long-term dependencies may culminate in a less comprehensive and precise feature representation, ultimately leading to a lower final convergence resilience value compared to the original UWSOS model.

Figure 6: Ablation analysis of resilience response under various attack scenarios

Additionally, contrasting the resilience trends of E-MAGCN and E-MAGCN(NER), the model lacking edge-node encoding demonstrates performance akin to the original UWSOS model throughout the learning process. However, the eventual feature representation learned may suffer from a lack of richness and accuracy. Consequently, this translates into a diminished final convergence resilience value.

5  Conclusion

The UWSOS represents advanced unmanned military technology, yet its complexity increases vulnerability to adversarial attacks. This study introduces the Enhanced-Resilience Multi-Layer Attention Graph Convolutional Network (E-MAGCN) to enhance UWSOS resilience by leveraging hierarchical attention mechanisms for capturing intricate multi-hop relationships and semantic nuances. E-MAGCN employs a data-driven node selection strategy that integrates node criticality and network topology, achieving a 25% average improvement in resilience across various test scenarios. Comparative analysis against five baseline methods (SR, RN, MDN, DRLRESF, KCOM) across eight attack scenarios demonstrated E-MAGCN’s superior performance in terms of recovery time, performance degradation, and overall resilience, with resilience scores such as 0.799 (SA) and 0.558 (DA). E-MAGCN’s adaptability to complex network scenarios and maintenance of operational stability underscore its potential for real-world applications. Future research will focus on leveraging meta-path typologies and using a single-layer GCN to capture multi-hop relationships, thereby avoiding the over-smoothing problem often encountered in multi-layer GCNs.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This research was supported by the Key Research and Development Program of Shaanxi Province (2024GX-YBXM-010) and the National Science Foundation of China (61972302).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Kexin Wang, Jiancheng Liu; Data collection: Bo Li, Wanlong Qi, Gang Hou; Analysis and interpretation of results: Kexin Wang, Yingdong Gou, Dingrui Xue; Draft manuscript preparation: Kexin Wang, Dingrui Xue. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding authors, Dingrui Xue and Kexin Wang, upon reasonable request.

Ethics Approval: The study did not include human or animal subjects.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. J. Warren, N. Jordan, and J. P. Hauser, “An analysis of how the us government can effectively tackle supply chain barriers to scale up the low cost unmanned aerial vehicle (UAV) swarming technology (LOCUST) program,” Ph.D. dissertation, Naval Postgraduate School, Monterey, CA, USA, 2019. [Google Scholar]

2. T. Chung, Offensive Swarm-Enabled Tactics (Offset), DARPA Tactical Technology Office Proposers Day, Arlington, VA, USA, vol. 30, no. 4, pp. 1–21, 2017. Accessed: Jun. 5, 2024. [Online]. Available: https://apps.dtic.mil/sti/trecms/pdf/AD1125864.pdf [Google Scholar]

3. H. Li, Q. Sun, M. Wang, C. Liu, Y. Xie and Y. Zhang, “A baseline-resilience assessment method for UAV swarms under heterogeneous communication networks,” IEEE Syst. J., vol. 16, no. 4, pp. 6107–6118, 2022. doi: 10.1109/JSYST.2022.3197324. [Google Scholar] [CrossRef]

4. T. Liu, G. Bai, J. Tao, Y. A. Zhang, and Y. Fang, “A multistate network approach for resilience analysis of UAV swarm considering information exchange capacity,” Reliab. Eng. Syst. Saf., vol. 241, no. 2, pp. 109606, 2024. doi: 10.1016/j.ress.2023.109606. [Google Scholar] [CrossRef]

5. Z. Chen, J. Jiao, X. De, and D. Fan, “Tradeoff optimization technology of effectiveness-cost for satellite-based on CAIV method,” J. Sens., vol. 2022, no. 1, pp. 1–12, 2022. doi: 10.1155/2022/2888846. [Google Scholar] [CrossRef]

6. Z. Li, Y. Dou, B. Xia, K. Yang, and M. Li, “System portfolio selection based on GRA method under hesitant fuzzy environment,” J. Syst. Eng. Electron., vol. 33, no. 1, pp. 120–133, 2022. doi: 10.23919/JSEE.2022.000013. [Google Scholar] [CrossRef]

7. N. Jia, Z. Yang, and K. Yang, “Operational effectiveness evaluation of the swarming UAVs combat system based on a system dynamics model,” IEEE Access, vol. 7, pp. 25209–25224, 2019. doi: 10.1109/ACCESS.2019.2898728. [Google Scholar] [CrossRef]

8. J. Zhang, H. Lv, and J. Hou, “A novel general model for RAP and RRAP optimization of k-out-of-n: G systems with mixed redundancy strategy,” Reliab. Eng. Syst. Saf., vol. 229, no. 2, pp. 108843, 2023. doi: 10.1016/j.ress.2022.108843. [Google Scholar] [CrossRef]

9. G. Levitin, L. Xing, and Y. Dai, “Optimizing partial component activation policy in multi-attempt missions,” Reliab. Eng. Syst. Saf., vol. 235, no. 2, pp. 109251, 2023. doi: 10.1016/j.ress.2023.109251. [Google Scholar] [CrossRef]

10. A. Peiravi, M. Nourelfath, and M. K. Zanjani, “Universal redundancy strategy for system reliability optimization,” Reliab. Eng. Syst. Saf., vol. 225, no. 6, pp. 108576, 2022. doi: 10.1016/j.ress.2022.108576. [Google Scholar] [CrossRef]

11. E. Ordoukhanian and A. M. Madni, “Model-based approach to engineering resilience in multi-UAV systems,” Systems, vol. 7, no. 1, pp. 11, 2019. doi: 10.3390/systems7010011. [Google Scholar] [CrossRef]

12. L. Iannacone, N. Sharma, and A. Tabandeh, “Modeling time-varying reliability and resilience of deteriorating infrastructure,” Reliab. Eng. Syst. Saf., vol. 217, no. 12, pp. 108074, 2022. doi: 10.1016/j.ress.2021.108074. [Google Scholar] [CrossRef]

13. C. Poulin and M. B. Kane, “Infrastructure resilience curves: Performance measures and summary metrics,” Reliab. Eng. Syst. Saf., vol. 216, no. 24, pp. 107926, 2021. doi: 10.1016/j.ress.2021.107926. [Google Scholar] [CrossRef]

14. W. Liu and Z. Song, “Review of studies on the resilience of urban critical infrastructure networks,” Reliab. Eng. Syst. Saf., vol. 193, no. 4, pp. 106617, 2020. doi: 10.1016/j.ress.2019.106617. [Google Scholar] [CrossRef]

15. C. S. Holling, “Resilience and stability of ecological systems,” Annu. Rev. Ecol. Syst., vol. 4, no. 1, pp. 1–23, 1973. doi: 10.1146/annurev.es.04.110173.000245. [Google Scholar] [CrossRef]

16. J. Varajão, G. Fernandes, A. Amaral, and A. Manuela Gonçalves, “Team resilience model: An empirical examination of information systems projects,” Reliab. Eng. Syst. Saf., vol. 206, no. 4, pp. 107303, 2021. doi: 10.1016/j.ress.2020.107303. [Google Scholar] [CrossRef]

17. L. N. Sweya, S. Wilkinson, and G. Kassenga, “A social resilience measurement tool for Tanzania’s water supply systems,” Int. J. Disaster Risk Reduct., vol. 65, no. 3, pp. 102558, 2021. doi: 10.1016/j.ijdrr.2021.102558. [Google Scholar] [CrossRef]

18. A. R. Eldosouky, W. Saad, and N. Mandayam, “Resilient critical infrastructure: Bayesian network analysis and contract-based optimization,” Reliab. Eng. Syst. Saf., vol. 205, no. 1, pp. 107243, 2021. doi: 10.1016/j.ress.2020.107243. [Google Scholar] [CrossRef]

19. X. Liu, Y. P. Fang, and E. Zio, “A hierarchical resilience enhancement framework for interdependent critical infrastructures,” Reliab. Eng. Syst. Saf., vol. 215, pp. 107868, 2021. doi: 10.1016/j.ress.2021.107868. [Google Scholar] [CrossRef]

20. Z. Chen, T. Zhao, J. Jiao, and J. Chu, “Performance-threshold-based resilience analysis of system of systems by considering dynamic reconfiguration,” Proc. Inst. Mech. Eng. Part B J. Eng. Manuf., vol. 236, no. 14, pp. 1828–1838, 2022. doi: 10.1177/0954405420937528. [Google Scholar] [CrossRef]

21. P. Trucco and B. Petrenj, “Characterisation of resilience metrics in full-scale applications to interdependent infrastructure systems,” Reliab. Eng. Syst. Saf., vol. 235, no. 9, pp. 109200, 2023. doi: 10.1016/j.ress.2023.109200. [Google Scholar] [CrossRef]

22. L. Zhao, Z. Lu, W. Yun, and W. Wang, “A framework for the quantitative assessment of performance-based system resilience,” Reliab. Eng. Syst. Saf., vol. 158, no. 2, pp. 73–84, 2017. doi: 10.1016/j.ress.2016.10.014. [Google Scholar] [CrossRef]

23. Q. Sun, H. Li, Y. Zhong, K. Ren, and Y. Zhang, “Deep reinforcement learning-based resilience enhancement strategy of unmanned weapon system-of-systems under inevitable interferences,” Reliab. Eng. Syst. Saf., vol. 242, no. 3, pp. 109749, 2024. doi: 10.1016/j.ress.2023.109749. [Google Scholar] [CrossRef]

24. J. Wang, K. Wang, Y. Yao, and H. Zhao, “Event detection with multi-order edge-aware graph convolution networks,” Data Knowl. Eng., vol. 143, pp. 102109, 2023. doi: 10.1016/j.datak.2022.102109. [Google Scholar] [CrossRef]

25. Y. Gou, K. Wang, S. Wei, and C. Shi, “GMDA: GCN-based multi-modal domain adaptation for real-time disaster detection,” Int. J. Uncertain. Fuzziness Knowl.-Based Syst., vol. 31, no. 6, pp. 957–973, 2023. doi: 10.1142/S0218488523500435. [Google Scholar] [CrossRef]

26. L. Zhao et al., “T-GCN: A temporal graph convolutional network for traffic prediction,” IEEE Trans. Intell. Transp. Syst., vol. 21, no. 9, pp. 3848–3858, 2019. doi: 10.1109/TITS.2019.2935152. [Google Scholar] [CrossRef]

27. W. Jiang, “Graph-based deep learning for communication networks: A survey,” Comput. Commun., vol. 185, no. 1, pp. 40–54, 2022. doi: 10.1016/j.comcom.2021.12.015. [Google Scholar] [CrossRef]

28. Y. Peng, C. Liu, S. Liu, Y. Liu, and Y. Wu, “SmartTRO: Optimizing topology robustness for Internet of Things via deep reinforcement learning with graph convolutional networks,” Comput. Netw., vol. 218, no. 11, pp. 109385, 2022. doi: 10.1016/j.comnet.2022.109385. [Google Scholar] [CrossRef]

29. Z. Chen, D. Hong, W. Cui, W. Xue, Y. Wang and J. Zhong, “Resilience evaluation and optimal design for weapon system of systems with dynamic reconfiguration,” Reliab. Eng. Syst. Saf., vol. 237, no. 29–32, pp. 109409, 2023. doi: 10.1016/j.ress.2023.109409. [Google Scholar] [CrossRef]

30. Y. Hao, L. Jia, E. Zio, Y. Wang, M. Small and M. Li, “Improving resilience of high-speed train by optimizing repair strategies,” Reliab. Eng. Syst. Saf., vol. 237, no. 4, pp. 109381, 2023. doi: 10.1016/j.ress.2023.109381. [Google Scholar] [CrossRef]

31. M. Xu, M. Ouyang, L. Hong, Z. Mao, and X. Xu, “Resilience-driven repair sequencing decision under uncertainty for critical infrastructure systems,” Reliab. Eng. Syst. Saf., vol. 221, no. 4, pp. 108378, 2022. doi: 10.1016/j.ress.2022.108378. [Google Scholar] [CrossRef]

32. X. Pan, Y. Dang, H. Wang, D. Hong, Y. Li and H. Deng, “Resilience model and recovery strategy of transportation network based on travel OD-grid analysis,” Reliab. Eng. Syst. Saf., vol. 223, no. 4, pp. 108483, 2022. doi: 10.1016/j.ress.2022.108483. [Google Scholar] [CrossRef]

33. V. M. Tahmineh, Y. N. S. Kamaleddin, and A. K. Mohammad, “Resilience based importance measure analysis for SoS,” J. Syst. Eng. Electron., vol. 30, no. 5, pp. 920–930, 2019. doi: 10.21629/JSEE.2019.05.10. [Google Scholar] [CrossRef]

34. Q. Feng et al., “Resilience optimization for multi-UAV formation reconfiguration via enhanced pigeon-inspired optimization,” Chin. J. Aeronaut., vol. 35, no. 1, pp. 110–123, 2022. doi: 10.1016/j.cja.2020.10.029. [Google Scholar] [CrossRef]

35. Q. Sun, H. X. Li, Y. Z. Wang, L. P. Zhou, and Y. C. Zhang, “Resilient UAV swarm modeling and solving based on multi-domain collaborative method,” Acta Aeronaut. Astronaut. Sin, vol. 42, no. 5, pp. 325340, 2021. [Google Scholar]

36. S. Geng, S. Liu, and Z. Fang, “Resilient communication model for satellite networks using clustering technique,” Reliab. Eng. Syst. Saf., vol. 215, pp. 107850, 2021. doi: 10.1016/j.ress.2021.107850. [Google Scholar] [CrossRef]

37. Y. Wang, D. Qiu, and G. Strbac, “Multi-agent deep reinforcement learning for resilience-driven routing and scheduling of mobile energy storage systems,” Appl. Energy., vol. 310, no. 7, pp. 118575, 2022. doi: 10.1016/j.apenergy.2022.118575. [Google Scholar] [CrossRef]

38. V. Mnih et al., “Human-Level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533, 2015. doi: 10.1038/nature14236. [Google Scholar] [PubMed] [CrossRef]

39. J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” 2017. doi: 10.48550/arXiv.1707.06347. [Google Scholar] [CrossRef]

40. J. Zhao, F. Li, S. Mukherjee, and C. Sticht, “Deep reinforcement learning-based model-free on-line dynamic multi-microgrid formation to enhance resilience,” IEEE Trans. Smart Grid, vol. 13, no. 4, pp. 2557–2567, 2022. doi: 10.1109/TSG.2022.3160387. [Google Scholar] [CrossRef]

41. X. Fan, X. Zhang, and X. Yu, “A graph convolution network-deep reinforcement learning model for resilient water distribution network repair decisions,” Comput.-Aided Civil Infrastruct. Eng., vol. 37, no. 12, pp. 1547–1565, 2022. doi: 10.1111/mice.12773. [Google Scholar] [CrossRef]

42. Y. Zhong, H. Li, Q. Sun, Z. Huang, and Y. Zhang, “A kill chain optimization method for improving the resilience of unmanned combat system-of-systems,” Chaos Solitons Fract., vol. 181, no. 7553, pp. 114685, 2024. doi: 10.1016/j.chaos.2024.114685. [Google Scholar] [CrossRef]

43. J. Li, Y. Tan, K. Yang, X. Zhang, and B. Ge, “Structural robustness of combat networks of weapon system-of-systems based on the operation loop,” Int. J. Syst. Sci., vol. 48, no. 3, pp. 659–674, 2017. doi: 10.1080/00207721.2016.1212429. [Google Scholar] [CrossRef]

44. A. Hagberg and D. Conway, “NetworkX: Network analysis with python,” 2020. Accessed: Jun. 5, 2024. [Online]. Available: https://networkx.github.io [Google Scholar]