Blockchain-Enabled Federated Learning for Privacy-Preserving Non-IID Data Sharing in Industrial Internet

1  Introduction

With the rapid development of Internet of Things technology [1], an increasing number of industrial equipment and sensors can collect and generate data. Data are crucial components of industrial Internet production processes. They record the real-time operational load of end devices and can directly serve the enterprise after analysis and processing. Large-scale data provide essential support for automation, intelligence, and digitization. Because data are a resource that is not limited to a single entity, they have a synergistic impact. This implies that the combined value of multiple data points generally exceeds the sum of their individual values. Therefore, data-sharing and convergence applications benefit the normal business flow and maximization of data value, providing significant resource utilization. Data sharing is also an inevitable trend in big-data development [2]. For example, in the face of widely deployed industrial Internet systems, if the efficient integration of multiple sources of sensory data (such as environmental monitoring, video monitoring, and equipment operation data) from multiple enterprises can be realized, it will make a significant contribution to the production, logistics, and logistical support of enterprises. In addition, enterprises can sell data to other enterprises, allowing the data to flow like blood. Data will be conducive to optimizing the industry structure for all types of enterprises, leading to a sharing economy, thereby creating a new business model and effectively promoting economic development.

Although the industrial Internet is developing rapidly, it faces many challenges [3]. Owing to the lack of a secure and effective data-sharing mechanism, the large volume of data generated by current industrial Internet devices is frequently enjoyed only by data holders, which results in data silos that make full use of the data difficult [4]. According to McKinsey, most industrial Internet companies cannot fully use their data and are reluctant to share them [5]. The current situation of “data silos” has become a bottleneck that restricts the development of big data and makes it challenging to apply data-driven machine learning and deep learning technologies effectively.

During data sharing, problems such as illegal data trading, data leakage, data misuse, and data abuse can lead to user privacy leakage [6]. As people become increasingly aware of information security and privacy protection, data owners are often more reluctant to share their data with third parties directly. Therefore, the effective sharing and utilization of dispersed data while protecting privacy has become an important issue. The traditional centralized approach to data sharing exhibits many problems, such as single points of failure, low data security, and data control in the hands of centralized organizations. In response to these problems, a new distributed machine learning approach known as federated learning (FL) has recently emerged. By distributing the model training process locally among the participants, FL avoids the direct sharing of raw data and protects user privacy. FL is scalable and flexible, which allows it to adapt to different data-sharing scenarios. However, in practice, FL faces several challenges. First, because data from different devices or organizations are usually non-independent and identically distributed (non-IID), reasonably performing aggregation and model updates is a problem that needs to be addressed. Second, there may be trust issues between participants in the FL process, such as false uploads and tampering with data, which may affect the security of the entire system.

FL approaches based on blockchain technology have recently been developed to address these issues. Blockchain has been widely used as a decentralized trust mechanism in various fields. It ensures secure and transparent transactions through distributed ledger technology and allows participants to conduct secure, trustworthy transactions. Combining blockchain technology with FL can create a decentralized and trusted FL framework that enables cross-device and cross-organizational data collaboration and model updates without compromising data privacy. Simultaneously, blockchain technology can guarantee data owners control over their data and restrict data access by other participants to enhance data privacy protection. In this study, we propose a secure sharing mechanism for non-IID data based on FL to protect data privacy. The contributions of this study are as follows.

(1) We apply blockchain technology to FL, enabling decentralized model training and parameter sharing. To reduce the influence of non-IID data, we propose a new strategy for dynamically determining how to update the local model based on the divergence between the global and local models.

(2) We propose a stochastic gradient descent (SGD) algorithm with differential privacy incorporating dynamic gradient clipping. This algorithm safeguards the privacy of the parameters by dynamically adjusting the clipping threshold based on the training progress, which effectively reduces the adverse effects of noise on the model accuracy.

(3) We conducted thorough experiments on the CIFAR-10, MNIST, FASHION-MNIST, and SHAKESPEARE datasets to evaluate the effectiveness of our methods. The experimental results suggest that our proposed strategy significantly improves FL accuracy for non-IID data.

The remainder of this paper is organized as follows. In Section 2, we discuss relevant studies on FL, differential privacy, and non-IID data training. Section 3 describes our proposed system model. Section 4 provides a comprehensive and detailed description of the dynamic local model update and dynamic gradient clipping. The experimental evaluation results and analysis are presented in Sections 5, and 6 concludes the paper.

2  Related Works

2.1 FL

FL is an emerging distributed machine learning paradigm that has received significant attention from academia and industry owing to its use of distributed model inference instead of traditional source data sharing, which can reduce the risk of data privacy breaches. McMahan et al. [7] conducted pioneering research on FL based on distributed training. This approach involves decentralized local training and parameter aggregation, enabling several participants to work together to train a machine learning model without disclosing any data. Okegbile et al. [8] proposed a new validation process based on the quality of trained models during the federated multi-task learning process to guarantee accurate and authorized model evolution in the virtual environment. The proposed framework accelerates the learning process without sacrificing accuracy, privacy and communication costs. This approach can enhance security, privacy and accuracy while reducing the overall connectivity cost. Research [9] investigated a collaborative data-sharing scheme in which multiple data providers and users collaborate to carry out data-sharing tasks through the utilization of blockchain and cloud-edge computing schemes. The spatial distribution of data providers and data users to follow the independent homogeneous Poisson point process, while the transactions generation rate at each node was also modeled using an independent Bernoulli process. This approach can be useful in investigating the performance of any blockchain-enabled data-sharing system. Shayan et al. [10] proposed a fully decentralized peer to peer (P2P) approach to multi-party ML, which uses blockchain and cryptographic primitives to coordinate a privacy-preserving ML process between peering clients. Biscotti is scalable, fault tolerant, and defends against known attacks. Liu et al. [11] presented a novel approach for enhancing privacy in distributed parallel SGD algorithms. Their proposed scheme incorporates differential privacy techniques to ensure the protection of sensitive data. In addition, they introduced an innovative method for dynamically selecting participants, which significantly improves both the efficiency and accuracy of the algorithm. Elayan et al. [12] proposed an FL multi-task learning framework based on deep learning networks to implement a distributed healthcare system, which offers the features of user privacy and automatic training data collection. Zhang et al. [13] presented a secure architecture based on FL to guarantee the security and viability of grid data sharing. Qu et al. [14] proposed a blockchain-based FL scheme with a proof-of-work consensus mechanism that allows all parties to jointly maintain and coordinate the aggregation process of the global model. Chai et al. [15] proposed a hierarchical blockchain architecture to record FL models to reduce storage consumption, and a hierarchical FL algorithm on top of the hierarchical blockchain architecture to improve training accuracy. Various subsequent studies have been conducted to improve its performance in terms of model optimization speed [16,17] cryptographic algorithms [18,19], and system scalability [20].

2.2 Non-IID Data Training

Traditional machine learning models typically assume that the training set is sampled from the same distribution. FL involves different devices that collect varying amounts of data, leading to differences in the collected data. These differences may arise from factors such as different geographical locations, device types, or environmental conditions, resulting in a low correlation between the data and an inability of the model to capture the data characteristics accurately [21]. In [22], the authors provided a real-life situation for the non-IID problem in which the intensity and contrast of medical radiography images obtained for cancer detection varied greatly among medical facilities because of differences in the imaging devices and processes employed in hospitals. Similar scenarios are prevalent in real life because the devices that are involved in FL are often highly heterogeneous. Non-IID data present a significant obstacle to FL. Consequently, the non-IID data of devices must be considered to obtain higher performance [23]. Li et al. [24] proposed a novel FL algorithm Federated Batch Normalization that uses the local batch normalization technique to solve the problem of non-IID data. A global data-sharing approach was proposed in [25] that builds a global IID dataset by collecting a small portion of data from the client to pretrain the initial model and randomly assigns a portion of the data to the client to assist in the training process. However, this approach exhibits security and privacy risks because the data are not encrypted, and the global dataset is untraceable and distributed to clients, which poses a significant threat to user privacy. Li et al. [26] proposed a data redundancy technique for handling non-IID data by sharing local data with trusted nodes to increase the classification job accuracy under non-IID settings.

2.3 Differential Privacy

Differential privacy (DP) techniques do not require a priori knowledge of the attacker and can be proven by rigorous mathematical theory. Dwork et al. [27] introduced the concept of DP and provided a proof of security using a rigorous mathematical derivation. In FL, DP manifests in two forms: local DP (LDP) and central DP (CDP). LDP empowers individuals to apply noise directly to their own data before sharing, thereby safeguarding against the risks of inference and backdoor attacks by obscuring the original data at the source. However, CDP operates under a framework in which a reliable central server introduces noise into the aggregated data, ensuring that the participation of any specific user in the FL training remains indiscernible to potential adversaries.

DP can effectively mitigate various types of attack [28]. Shokri et al. [29] proposed the integration of DP into machine learning models as a potential safeguard against inference attacks on these models. McMahan et al. [30] demonstrated that DP can defend against backdoor tasks. Naseri et al. [31] proved that implementing DP within FL provides robust defense against white-box membership inference attacks. Zhang et al. [32] proposed a novel approach that enhances privacy guarantees by introducing uncertainty while minimizing the impact on the overall model performance. In [33], privacy protection was achieved by introducing Gaussian noise into the gradient following its clipping with a global threshold. However, the specific criteria for determining the threshold were not explicitly outlined. Truex et al. [34] introduced LDP-Fed, which integrates an LDP component to add noise to the parameters of the local participants.

The incorporation of DP creates ambiguity within the uploaded parameters, potentially affecting the model efficacy. Balancing privacy and model quality remains a challenge.

3  System Model

This section discusses the system architecture of the scheme and processes involved in the data sharing.

3.1 System Architecture

Fig. 1 shows a common FL scenario for the industrial Internet, including industrial data providers, requesters, and blockchain.

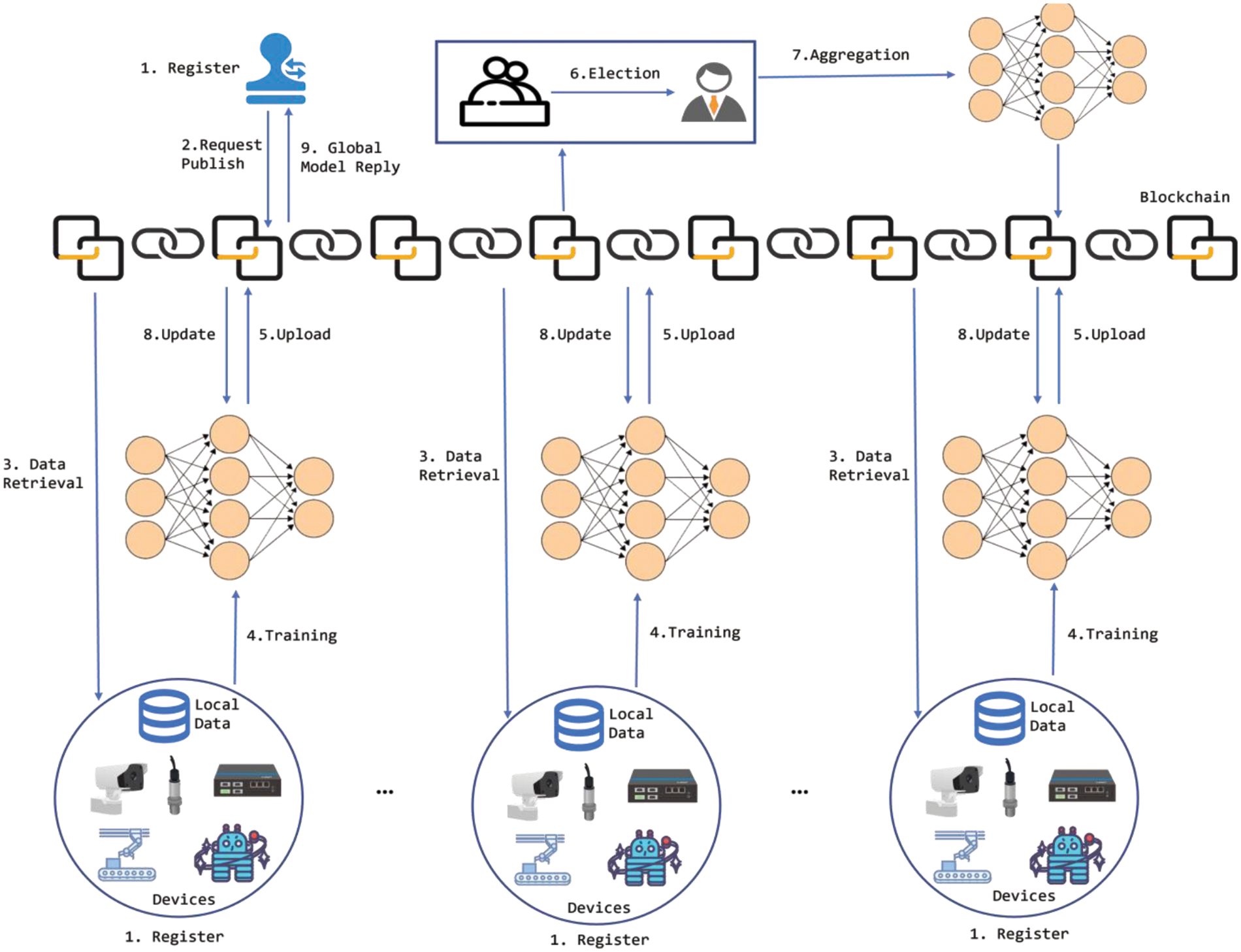
Figure 1: System framework

(1) Data requester: The data requester issues data-sharing requests, obtains the results of joint learning of all data providers, and pays the associated fees to the data providers involved in the task.

(2) Data provider: This is the owner of the industrial Internet data, which participates in data sharing as an FL node to help to train more accurate machine learning models.

(3) Blockchain: The blockchain is used to replace the global aggregation server in traditional FL, providing registration, data retrieval, and node evaluation services for data participants. It is responsible for recording the entire data sharing process, achieving data traceability, and improving data security.

3.2 System Workflow

As shown in Fig. 1, the data-sharing process can be divided into nine main stages, as follows:

(1) Registration: All participants must register with the blockchain platform and assign the corresponding public and private keys to share data.

(2) Data request publish: The data requester shares their data needs, including model parameters, transaction methods, and data usage rules when publishing data requirements.

(3) Multiparty data retrieval: Once the data request is published, the data provider has the option to participate in data sharing. If they choose to join, their unique user ID as well as details such as the data type, size, and attributes are securely recorded on the blockchain. Subsequently, the data provider can proceed to download the task data.

(4) Local training: The data provider trains the local model using the initial parameters.

(5) Model upload: The data provider uploads the model parameters to the blockchain platform after the model is trained. DP is used to process the model parameters before uploading them to the blockchain to ensure the privacy of the parameters.

(6) Committee elections: Miners verify the legitimacy of the signature after receiving the data to prevent attackers from tampering with the data notation. Based on the contribution and reputation consensus protocol, leaders are elected and are responsible for aggregating the global gradient and generating new blocks.

(7) Model aggregation: After each data-sharing node completes model training and uploads it to the blockchain, it needs to elect nodes for aggregating the model parameters, uploading the aggregated model parameters to the blockchain, and notifying other nodes. The node with the highest accumulated reputation acts as the leader node, which is responsible for aggregating the model parameters and issuing the data contribution rewards to the corresponding participants. If the current leader completes their round or if a committee member is unavailable, the system will select a new leader based on the reputation of the participants.

(8) Model update: The data provider downloads the new block, obtains the global gradient from it to update the local model, and starts the next round of training from step (4) until the model reaches the specified accuracy or the maximum number of training rounds.

(9) Global model reply: The training stops after the model in step (7) reaches the specified accuracy or the specified number of training rounds. The elected model parameter aggregation node uploads the final model to the blockchain for preservation and notifies the data requester. The data requester obtains the final result. At this point, the data-sharing process is complete.

4  Blockchain-Enabled FL for Non-IID Data Sharing

4.1 Dynamic Local Model Update

The traditional data-sharing method involves sending the local data of all participants to the requester, which can lead to privacy issues. FL offers a better solution by keeping the data in the participating nodes through a sharing model, thereby avoiding the privacy leakage risk. However, when the data among different participants are non-IID, each participant has different data distributions with no or fewer intersections, and the local models uploaded by these participants vary greatly. This can result in a severe bias in the averaged global models, making it difficult to fit the data for all participants and leading to problems such as over-fitting and slow convergence. We develop a novel dynamic local model update (DLMU) method to address the problems caused by non-IID data in which each participant has a different data distribution and is trained to obtain a different local model. In FL, these local models are combined into a global model. However, updating the local model according to the global model can cause it to scatter or converge more slowly if there is a significant difference between the global and local models. Therefore, we consider retaining the local training model of non-IID data to improve the model performance. We develop a specific formula to update the local model based on the dispersion of the global and local models from the previous round. The formula is as follows:

ωiγ=(1−β)⋅ωγ+β⋅ωiγ−1β=min(αi||ωγ−ωiγ−1||,1)(1)

where ωiγ and ωiγ−1 are the local model parameters of participant i in training rounds γ and γ−1, respectively, and ωγ corresponds to the global model parameters in round γ. β measures the decay rate as the divergence between the global and local models, and α is a scaler that adjusts the degree of model divergence by computing the l2-norm of the global and local models.

The scaler α is critical for adjusting DLMU for varying levels of data divergence. The divergence of global and local models fluctuates as the FL settings change, such as with different degrees of non-IID settings, resulting in different divergences. Because the data characteristics remain unknown before training, we propose an autoscaler to compute a personalized αk automatically for each participant. Because each participant has the same local model in the first round, only the local data are different; therefore, we can use the dispersion of the local model after the first round of training and the initial model as the basis for calculating αk. The formula is αk=τ/||W1−W0||, where τ∈[0,1] is a set parameter that is dynamically adjusted depending on the dataset. We calculate αk only once in the earliest round γ=1 in which participant i is sampled for training.

DLMU aims to strike a balance between local and global knowledge by adjusting the weight that is assigned to each depending on the level of divergence. When the divergence is high, more emphasis is placed on retaining local knowledge, which benefits non-IID data. The global model is formed by aggregating local models that represent the collective knowledge of the participants. However, when the model divergence is low, incorporating more global knowledge helps to improve the overall model generalization. We introduce a parameter β to control the balance between local and global knowledge. β=1 indicates that only local knowledge is used, whereas β=0 indicates that only global knowledge is used. Neither of these situations is well adapted to non-IID data. As the model divergence is higher at the beginning of training, selecting a more significant value for τ within the range of 0.5 to 1 is practical. We adopt the default value of τ=0.8 in our experiments. We use a local multi round training approach to minimize interactions with the blockchain. Algorithm 1 presents the detailed process of DLMU.

4.2 Dynamic Gradient Clipping for DP SGD

Data providers train their model on local datasets and must protect the privacy of gradient information before uploading to prevent the use of model parameters to infer private information regarding the data provider [35]. Homomorphic encryption [36] and secret-sharing algorithms [37] are commonly used to protect local gradients; however, they suffer from excessive computational overheads. In contrast, differential privacy techniques are less computationally intensive and more suitable for resource-constrained edge computing devices [38]. In [39], local differential privacy techniques were used to add noise to the original training data to protect privacy; however, this resulted in a significant loss of model accuracy. Another study [40] added Gaussian noise to the gradients after clipping them using a global clipping threshold C to preserve privacy, but did not specify the basis for selecting the threshold C. The value of C is critical for deep learning models; an immense value of C adds excessive noise, whereas a small value of C over-crops the gradients, both of which may result in a severe loss of model accuracy. In [41], the C value was taken as the median of the gradient norm of all devices; however, requiring the server to obtain the explicit gradients of all devices still risks privacy leakage. To this end, this study proposes a dynamic DP-SGD (DDP-SGD) for local differential privacy, drawing on the DP-SGD algorithm, which can flexibly adjust the clipping threshold according to the training process to reduce the negative impact of noise on the model accuracy. Assuming that E epochs are executed locally in each round, we only perform gradient clipping and add noise when the final epoch is executed locally to reduce the impact of DP on the model accuracy. The threshold for gradient clipping is based on the gradient values of the first two epochs and is calculated as follows:

Cr=γCE−1γ+(1−γ)⋅CE−2γγ=|CE−1γ−CE−2γ|CE−1γ(2)

where CE−1γ and CE−2γ are the gradient clipping values of local epochs E−1 and E−2 in rounds r, respectively, and γ measures the trend of the clipping value, which is used to adjust the trend of the gradient clipping by the former two epochs.

As the gradient gradually decreases as training proceeds, the corresponding gradient clipping threshold should also be reduced accordingly. When the model parameters are close to the optimum values, the number of vanes in the aggregated gradient decrease significantly. The above formula considers the magnitude of the first two epochs of the gradient descent and the trend of the gradient descent. It can be used to adjust the gradient clipping boundary effectively and dynamically. The DDP-SGD algorithm is presented in Algorithm 2.

5  Experimental Evaluation

This section presents the simulation results to assess the performance of the proposed schemes, as discussed in Section 4.

5.1 Evaluation Setup

The use of convolutional neural network (CNN) architectures [42] and long short-term memory (LSTM) [43] for local model training was explored. The performance evaluation was conducted on the widely used CIFAR-10, MNIST, FASHION-MNIST, and SHAKESPEARE datasets. CIFAR-10 comprises 50,000 training samples and 10,000 test samples of labeled images, each sized at 32 × 32 pixels. The CIFAR-10 dataset allows for the flexible construction of varying numbers of clients, enabling simulations with unbalanced data and two distinct types of non-IID scenarios: (1) dataset division using the Dirichlet process Dir (α) [44], and (2) dataset division by class, where each client contains N of the 10 available classes [45]. The local datasets of individual users were independently sampled from the CIFAR-10 dataset, with different frequencies applied to each category to capture the non-IID distribution characteristics. The MNIST and FASHION-MNIST datasets contain 70,000 28 × 28 grayscale images of handwritten digits and fashion products, respectively. Both sets contain 60,000 image training sets and 10,000 image test sets. The FEMNIST and SHAKESPEARE datasets emulate realistic scenarios using data that are not identically distributed and are unevenly balanced, as outlined in [46].

We implemented our scheme in Python using Easy FL [47], which is an open-source FL platform. The experiments were conducted on Ubuntu 22.04 with a Xeon (R) Platinum 8358P CPU and GTX 3090 GPU.

We used FedAvg [7] as the benchmark algorithm for all experiments. The default settings included a local epoch of 10 (E=10), batch size of 32 (B=32), total of 100 rounds (R=100), and 10 clients participating in each round. We used SGD with a learning rate of 0.001 (η=0.001) and momentum of 0.8 (momentum=0.8) as the optimizer, and fine-tuned the learning rate for each dataset.

5.2 Performance Evaluation of FL

Figs. 2 and 3 depict the test accuracy of the FL with our proposed DLMU algorithm, where the algorithm in [47] was selected as a baseline. Different divisions of the local datasets with different distributional dispersions were investigated. We compared the accuracy of the models trained on IID and non-IID datasets. We simulated three levels of non-IID with increasing heterogeneity: Dirichlet process (Dir (0.5)), three classes per client (class (3)), and two classes per client (class (2)). These experiments were conducted with 10 selected clients per round. Fig. 2 shows the comparison of DLMU and baseline with different dataset divisions on the CIFAR-10 dataset. As shown in Fig. 2a, for the IID division, the difference in test accuracy between DLMU and the baseline was negligible, from 80.91% to 81.48%. The reason for the limited improvement in our scheme with IID data is that the data among the clients were not significantly different. Consequently, the locally trained models did not differ significantly from one another, making the global model closer to the local models. In addition, as shown in Fig. 2, our scheme achieved a pronounced improvement for non-IID data. For the Dir (0.5) data partition, the accuracy of the baseline was 68.38%, whereas that of our scheme was 76.63%. Similarly, for the class (3) data partition, the accuracy of the baseline was 62.53%, whereas that of ours was 74.93%. For the class (2) data partition, our scheme achieved a more significant improvement in accuracy, from 39.15% in the baseline to 57.14%, which was the most significant improvement among all data segments. The statistical heterogeneity from the first to the highest dataset division was IID, Dir (0.5), class (3), and class (2). Therefore, Fig. 2 shows that as the statistical heterogeneity increased, so did the DLMU algorithm improvement in accuracy for the CIFAR-10 dataset. Table 1 displays the average absolute error of the model training accuracy between two different local update methods on different data partition methods. It can be observed that the average absolute error of the model accuracy continued to increase as the degree of statistical heterogeneity increased. Our proposed scheme showed a significant improvement in test accuracy for FL on non-IID data, particularly when there was a significant distribution divergence. The training accuracy also improved noticeably, particularly for the non-IID data. This improvement was more significant for local nodes with greater differences in data heterogeneity.

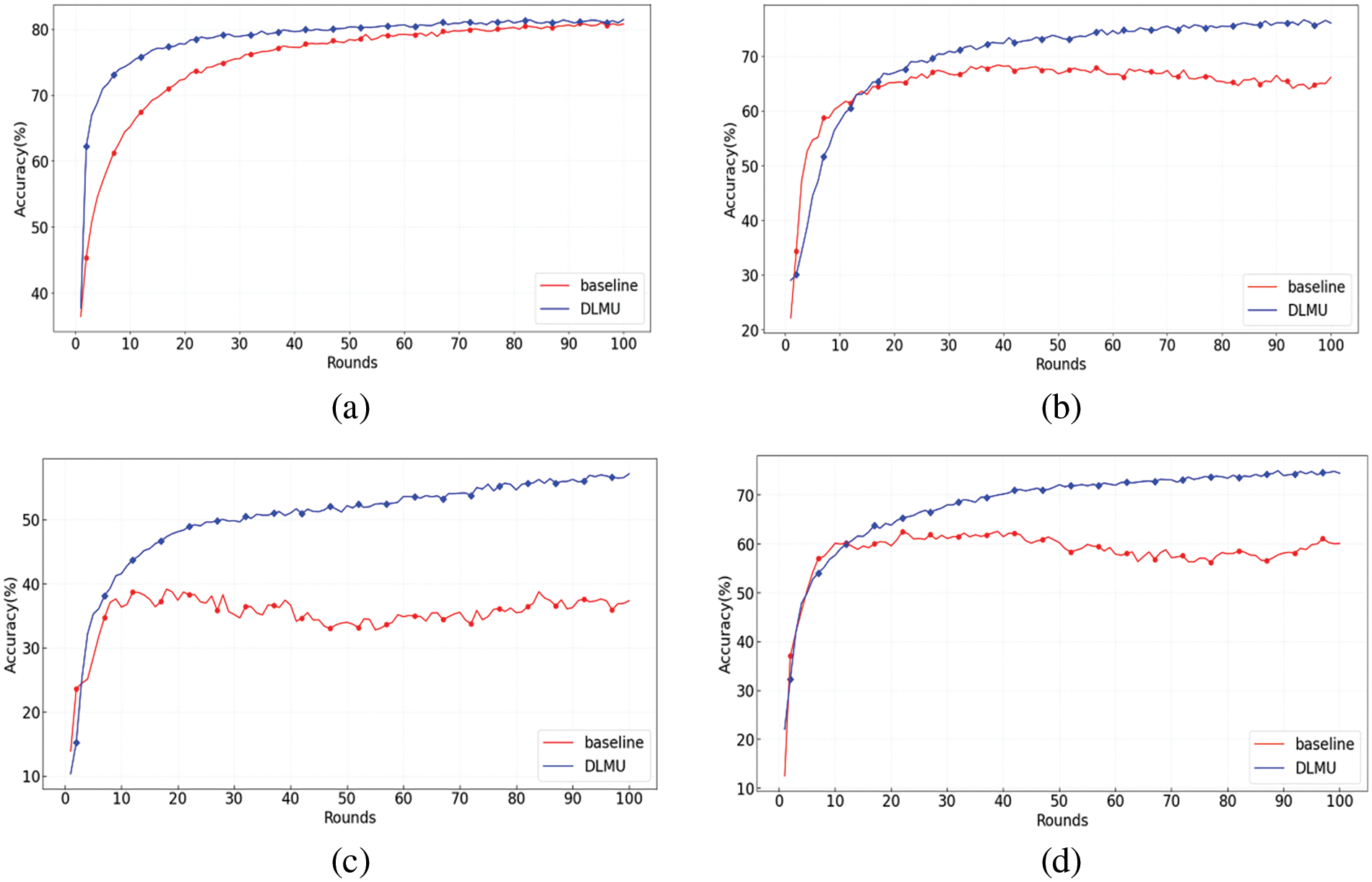
Figure 2: Accuracy comparison of baseline and DLMU with different dataset divisions: (a) IID, (b) Dir (0.5), (c) class (2), and (d) class (3)

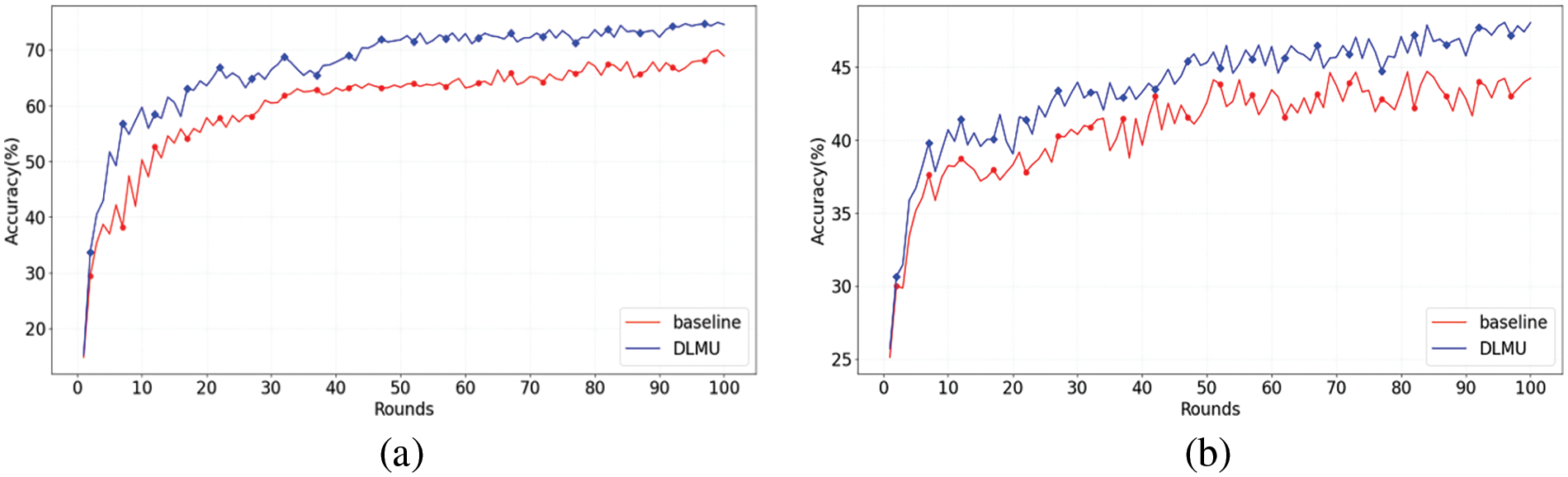
Figure 3: Accuracy comparison of baseline and DLMU with different datasets: (a) FEMNIST and (b) SHAKESPEARE

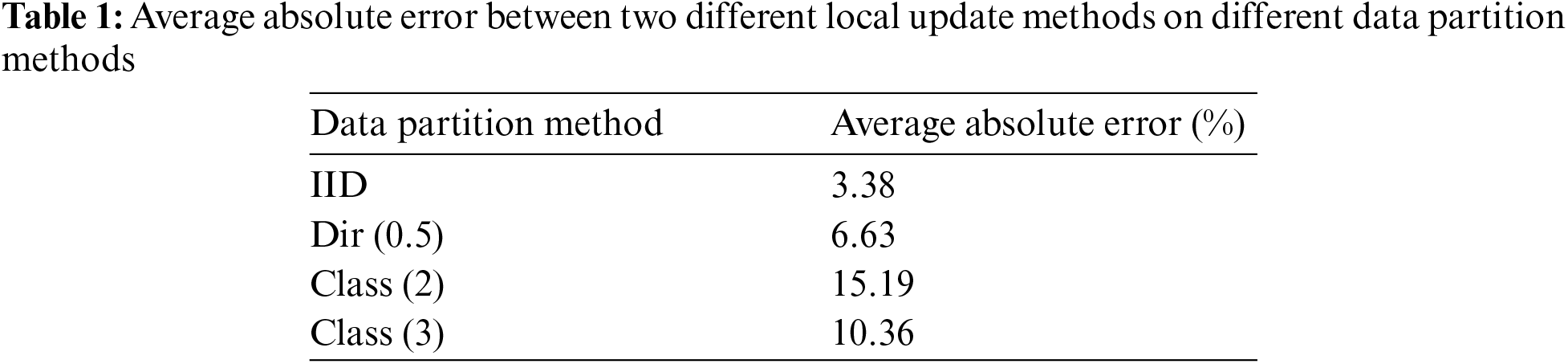
Fig. 3 depicts the accuracy gap between DLMU and the baseline on the FEMNIST and SHAKESPEARE datasets for the non-IID division, respectively. The accuracy gaps were 4.78% and 3.35% for FEMNIST and SHAKESPEARE, respectively. The average absolute error of the model accuracy for FEMNIST was 7.03%, whereas that for SHAKESPEARE was 3.35%. This also proves the effectiveness of the DLMU algorithm.

5.3 Performance Evaluation of Dynamic Gradient Clipping

We performed a DP dynamic gradient clipping analysis using the same experimental setup as described in the previous section. From the analysis in the previous section, it can be observed that the class (2) dataset partitioning was a better test of the effect of data dispersion on the algorithm performance. Therefore, we compared the effects of different privacy budgets with different gradient clipping schemes on the model accuracy in the class (2) dataset partitioning cases. In the following experiments, we enumerate only the cases in which Gaussian noise was added. The dynamic gradient clipping mechanism proposed in this study can easily be generalized to other stochastic optimization algorithms, such as Adam.

The privacy budget ϵ was set to 2, 3, 5, and 10 and σ=1⋅e−5. As shown in Table 2, for all clipping thresholds, the training accuracy decreased owing to noise. Compared to the results of the DP-SGD algorithm, DDP-SGD had a higher accuracy and was essentially the same as the SGD algorithm under a relatively large privacy budget.

As shown in Tables 3 and 4, for all clipping thresholds, the training accuracy decreased. However, the accuracy gap between DDP-SGD and DP-SGD was narrow because of the simplicity of the MNIST and FASHION-MNIST datasets compared with the CIFAR-10 dataset. For CIFAR-10, the complexity and depth of the model indicated that its gradients varied significantly. Consequently, dynamic clipping effectively diminished the gradient variance, which substantially enhanced the precision of the model. Moreover, these findings clarify how employing a static clipping strategy can yield satisfactory precision for straightforward and less complex models.

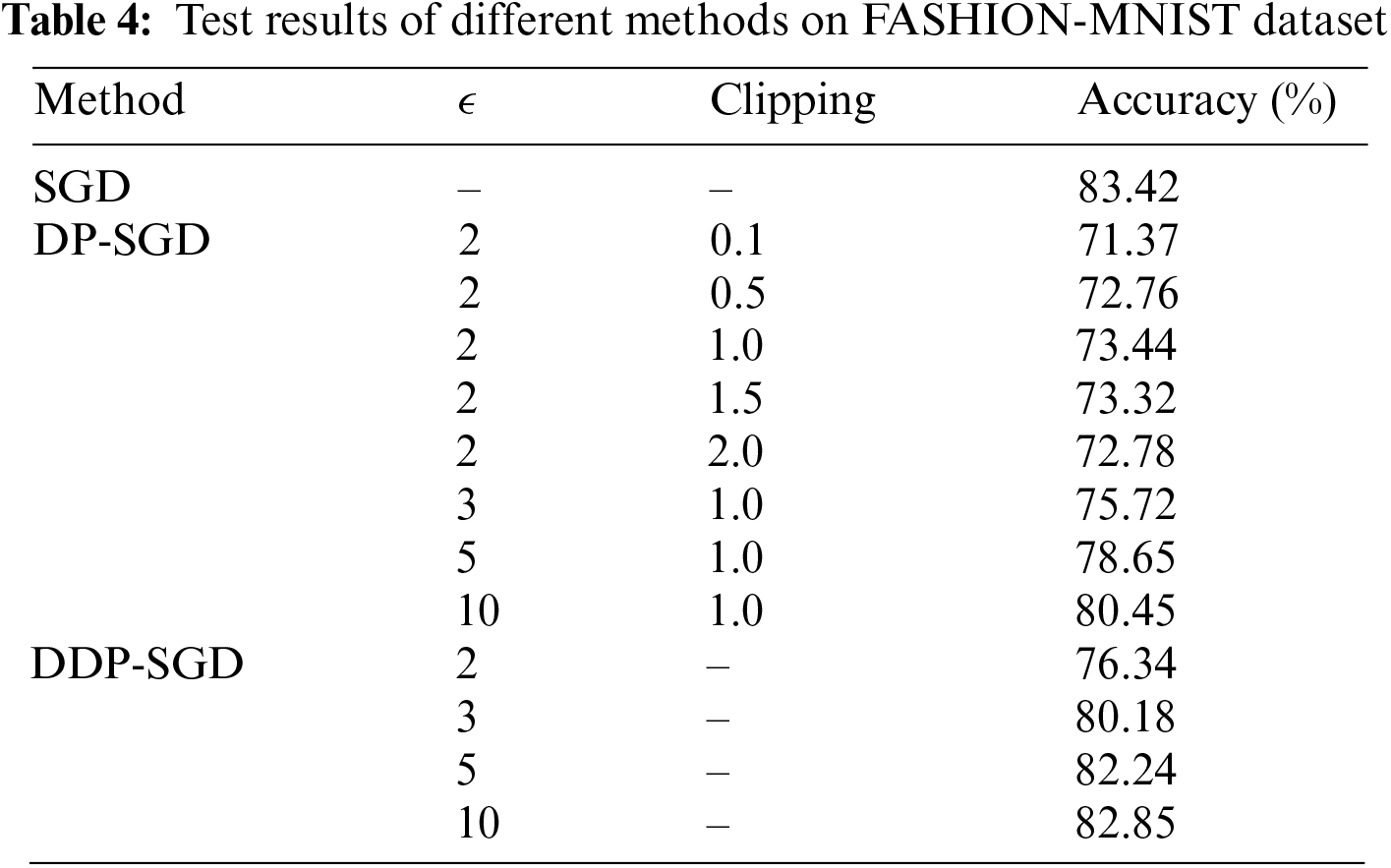
For different ϵ values, dynamic clipping ensured higher model accuracy under different privacy budgets. The DP-SGD algorithm using dynamic clipping could achieve higher accuracy with the same privacy budget, which was slightly lower than that of the original FL algorithm. Therefore, the proposed algorithm is suitable for application scenarios requiring high accuracy and privacy protection.

6  Conclusion

In conclusion, this study addresses the challenges of sharing data while protecting privacy in the industrial Internet through the application of FL and blockchain technology. Traditional machine learning methods are often limited by data availability and privacy concerns, making them unsuitable for decentralized training on non- IID datasets.

To overcome the limitations posed by non-IID data, we have proposed a novel approach that dynamically updates the local model based on the divergence between the global and local models. This dynamic update mechanism significantly improves the accuracy of FL training when there is a relatively large dispersion within the dataset, ensuring better FL performance. Furthermore, to address the potential privacy leakage caused by sharing model parameters, we introduced a dynamic gradient clipping algorithm. This algorithm effectively reduces the impact of noise on model accuracy, thereby enhancing privacy protection without sacrificing significant training performance.

The performance of the proposed scheme was evaluated using commonly opened image datasets. The simulation results confirmed that our approach successfully achieved significant improvements in accuracy while concurrently ensuring privacy preservation and maintaining efficiency. These results offer a promising solution to the challenges of data sharing and privacy protection in the industrial Internet.

Overall, our study contributes to the advancement of FL techniques for data sharing in industrial settings. By leveraging blockchain technology, we can enable secure and private collaboration among data providers while maintaining high accuracy levels. The proposed approach has great potential for facilitating data-driven decision-making processes and fostering innovation in the industrial Internet domain. Future studies should focus on expanding the application of this methodology to different types of datasets and exploring its scalability in larger-scale industrial settings.

Acknowledgement: We would like to extend our sincere appreciation to the editor and reviewers for their valuable feedback and constructive comments, which significantly improved the quality of this paper. Their insightful suggestions have greatly contributed to the refinement of our work.

Funding Statement: This work was supported by the National Key R&D Program of China under Grant 2023YFB2703802; the Hunan Province Innovation and Entrepreneurship Training Program for College Students S202311528073.

Author Contributions: Qiuyan Wang: Writing–original draft, Software, Methodology, Formal analysis. Haibing Dong: Writing–review & editing, Supervision, Funding acquisition. Yongfei Huang: Supervision, Resources, Writing–review. Zenglei Liu and Yundong Gou: Investigation, Writing–review & editing, Data curation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 15 May 2024) and https://github.com/TalwalkarLab/leaf (accessed on 15 May 2024).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. A. E. Houda, B. Brik, A. Ksentini, and L. Khoukhi, “A MEC-based architecture to secure IoT applications using federated deep learning,” IEEE Internet Things Mag., vol. 6, no. 1, pp. 60–63, 2023. doi: 10.1109/IOTM.001.2100238. [Google Scholar] [CrossRef]

2. P. Shojaee, Y. Zeng, M. Wahed, A. Seth, R. Jin and I. Lourentzou, “Task-driven privacy-preserving data-sharing framework for the industrial internet,” in 2022 IEEE Int. Conf. Big Data (Big Data), Osaka, Japan, 2022, pp. 1505–1514. [Google Scholar]

3. K. K. R. Choo, Z. Yan, and W. Meng, “Blockchain in industrial IoT applications: Security and privacy advances, challenges, and opportunities,” IEEE Trans. Ind. Inform., vol. 16, no. 6, pp. 4119–4121, 2020. doi: 10.1109/TII.2020.2966068. [Google Scholar] [CrossRef]

4. H. Xu, W. Yu, D. Griffith, and N. Golmie, “A survey on industrial internet of things: A cyber-physical systems perspective,” IEEE Access, vol. 6, pp. 78238–78259, 2018. doi: 10.1109/ACCESS.2018.2884906. [Google Scholar] [PubMed] [CrossRef]

5. R. Dobbs, J. Manyika, and J. Woetzel, The Internet of Things: Mapping the Value Beyond the Hype. New York: McKinsey & Company, 2015. [Google Scholar]

6. Q. Miao, H. Lin, J. Hu, and X. Wang, “An intelligent and privacy-enhanced data sharing strategy for blockchain-empowered internet of things,” Digit. Commun. Netw., vol. 8, no. 5, pp. 636–643, 2022. doi: 10.1016/j.dcan.2021.12.007. [Google Scholar] [CrossRef]

7. B. McMahan, E. Moore, D. Ramage, S. Hampson, and A. B. Y. Arcas, “Communication efficient learning of deep networks from decentralized data,” Artif. Intell. Stat., pp. 1273–1282, 2017. doi: 10.48550/arXiv.1602.05629. [Google Scholar] [CrossRef]

8. S. D. Okegbile, J. Cai, H. Zheng, J. Chen, and C. Yi, “Differentially private federated multi-task learning framework for enhancing human-to-virtual connectivity in human digital twin,” IEEE J. Sel. Areas Commun., vol. 41, no. 11, pp. 3533–3547, 2023. doi: 10.1109/JSAC.2023.3310106. [Google Scholar] [CrossRef]

9. S. D. Okegbile, J. Cai, and A. S. Alfa, “Performance analysis of blockchain-enabled data sharing scheme in cloud-edge computing-based IoT networks,” IEEE Internet Things J., vol. 9, no. 21, pp. 21520–21536, 2022. doi: 10.1109/JIOT.2022.3181556. [Google Scholar] [CrossRef]

10. M. Shayan, C. Fung, C. J. M. Yoon, and I. Beschastnikh, “Biscotti: A blockchain system for private and secure federated learning,” IEEE Trans. Parallel Distrib. Syst., vol. 32, no. 7, pp. 1513–1525, 2021. doi: 10.1109/TPDS.2020.3044223. [Google Scholar] [CrossRef]

11. C. Liu, S. Guo, S. Guo, Y. Yan, X. Qiu and S. Zhang, “LTSM: Lightweight and trusted sharing mechanism of IoT data in smart city,” IEEE Internet Things J., vol. 9, no. 7, pp. 5080–5093, 2021. doi: 10.1109/JIOT.2021.3110097. [Google Scholar] [CrossRef]

12. H. Elayan, M. Aloqaily, and M. Guizani, “Deep federated learning for IoT-based decentralized healthcare systems,” in Int. Wireless Commun. Mobile Comput. (IWCMC), Harbin, China, 2021, pp. 105–109. doi: 10.1109/IWCMC51323.2021.9498820. [Google Scholar] [CrossRef]

13. X. Zhang, F. Fang, and J. Wang, “Probabilistic solar irradiation forecasting based on variational bayesian inference with secure federated learning,” IEEE Trans. Ind. Inform., vol. 17, no. 11, pp. 7849–7859, 2020. doi: 10.1109/TII.2020.3035807. [Google Scholar] [CrossRef]

14. Y. Qu et al., “Decentralized privacy using blockchain-enabled federated learning in fog computing,” IEEE Internet Things J., vol. 7, no. 6, pp. 5171–5183, 2020. doi: 10.1109/JIOT.2020.2977383. [Google Scholar] [CrossRef]

15. H. Chai, S. Leng, Y. Chen, and K. Zhang, “A hierarchical blockchain-enabled federated learning algorithm for knowledge sharing in internet of vehicles,” IEEE Trans. Intell. Transp. Syst., vol. 22, no. 7, pp. 3975–3986, 2020. doi: 10.1109/TITS.2020.3002712. [Google Scholar] [CrossRef]

16. C. Mwase, Y. Jin, T. Westerlund, H. Tenhunen, and Z. Zou, “Communication-efficient distributed AI strategies for the IoT edge,” Future Gener. Comput. Syst., vol. 131, no. 3, pp. 292–308, Jun. 2022. doi: 10.1016/j.future.2022.01.013. [Google Scholar] [CrossRef]

17. Y. Mao et al., “Communication-efficient federated learning with adaptive quantization,” ACM Trans. Intell. Syst. Technol. (TIST), vol. 13, no. 4, pp. 1–26, 2022. doi: 10.1145/3510587. [Google Scholar] [CrossRef]

18. Z. Shi, Z. Yang, A. Hassan, F. Li, and X. Ding, “A privacy preserving federated learning scheme using homomorphic encryption and secret sharing,” Telecommun. Syst., vol. 82, no. 3, pp. 419–433, 2023. doi: 10.1007/s11235-022-00982-3. [Google Scholar] [CrossRef]

19. B. Pejó and G. Biczók, “Quality inference in federated learning with secure aggregation,” IEEE Trans. Big Data, vol. 9, no. 5, pp. 1430–1437, 2023. doi: 10.1109/TBDATA.2023.3280406. [Google Scholar] [CrossRef]

20. D. Huba et al., “Papaya: Practical, private, and scalable federated learning,” Proc. Mach. Learn. Syst., vol. 4, pp. 814–832, 2022. doi: 10.48550/arXiv.2111.04877. [Google Scholar] [CrossRef]

21. K. Bonawitz et al., “Towards federated learning at scale: System design,” Proc. Mach. Learn. Syst., vol. 1, pp. 374–388, 2019. doi: 10.48550/arXiv.1902.01046. [Google Scholar] [CrossRef]

22. L. Zhao and J. Huang, “A distribution information sharing federated learning approach for medical image data,” Complex Intell. Syst., vol. 9, no. 5, pp. 1–12, 2023. doi: 10.1007/s40747-023-01035-1. [Google Scholar] [PubMed] [CrossRef]

23. Y. He, Y. Chen, X. Yang, H. Yu, Y. H. Huang and Y. Gu, “Learning critically: Selective self-distillation in federated learning on noniid data,” IEEE Trans. Big Data, vol. 99, pp. 1–12, 2022. doi: 10.1109/TBDATA.2022.3189703. [Google Scholar] [CrossRef]

24. X. Li, M. Jiang, X. Zhang, M. Kamp, and Q. Dou, “FedBN: Federated learning on non-IID features via local batch normalization,” 2021. doi: 10.48550/arXiv.2102.07623. [Google Scholar] [CrossRef]

25. Z. Lian, Q. Zeng, and C. Su, “Privacy-preserving blockchain-based global data sharing for federated learning with non-IID data,” in 2022 IEEE 42nd Int. Conf. Distrib. Comput. Syst. Workshops (ICDCSW), Bologna, Italy, 2022, pp. 193–198. doi: 10.1109/ICDCSW56584.2022.00044. [Google Scholar] [CrossRef]

26. K. Li and C. Xiao, “CBFL: A communication efficient federated learning framework from data redundancy perspective,” IEEE Syst. J., vol. 19, no. 4, pp. 5572–5583, 2021. doi: 10.1109/JSYST.2021.3119152. [Google Scholar] [CrossRef]

27. C. Dwork, F. McSherry, and K. Nissim, “Calibrating noise to sensitivity in private data analysis,” J. Priv. Confidentiality, vol. 7, no. 3, pp. 17–51, 2006. doi: 10.29012/jpc.v7i3.405. [Google Scholar] [CrossRef]

28. H. Hu, Z. Salcic, L. Sun, G. Dobbie, P. S. Yu and X. Zhang, “Membership inference attacks on machine learning: A survey,” ACM Comput. Surv., vol. 54, no. 11, pp. 1–37, 2022. doi: 10.48550/arXiv.2103.07853. [Google Scholar] [CrossRef]

29. R. Shokri, M. Stronati, C. Song, and V. Shmatikov, “Membership inference attacks against machine learning models,” in 2017 IEEE Symp. Secur. Priv. (SP), San Jose, CA, USA, 2017, pp. 3–18. doi: 10.48550/arXiv.1610.05820. [Google Scholar] [CrossRef]

30. H. B. McMahan, D. Ramage, K. Talwar, and L. Zhang, “Learning differentially private recurrent language models,” 2017. doi: 10.48550/arXiv.1710.06963. [Google Scholar] [CrossRef]

31. M. Naseri, J. Hayes, and E. De Cristofaro, “Local and central differential privacy for robustness and privacy in federated learning,” 2020. doi: 10.48550/arXiv.2009.035. [Google Scholar] [CrossRef]

32. C. Zhang, S. Ekanut, L. Zhen, and Z. Li, “Augmented multi-party computation against gradient leakage in federated learning,” IEEE Trans. Big Data, vol. 99, no. 22, pp. 1–10, 2022. doi: 10.1109/TBDATA.2022.3208736. [Google Scholar] [CrossRef]

33. N. Ponomareva et al., “How to DP-fy ML: A practical guide to machine learning with differential privacy,” J. Artifi. Intell. Res., vol. 77, pp. 1113–1201, 2023. doi: 10.1613/jair.1.14649. [Google Scholar] [CrossRef]

34. S. Truex, L. Liu, K. H. Chow, M. E. Gursoy, and W. Wei, “LDP-Fed: Federated learning with local differential privacy,” Proc. Third ACM Int. Workshop Edge Syst. Anal. Network., vol. 6, no. 5, pp. 61–66, 2020. doi: 10.1145/3378679.3394533. [Google Scholar] [CrossRef]

35. C. Fu et al., “Label inference attacks against vertical federated learning,” in 31st USENIX Secur. Symp. (USENIX Security 22), Boston, MA, USA, 2022, pp. 1397–1414. [Google Scholar]

36. J. Chen, K. Li, and S. Y. Philip, “Privacy-preserving deep learning model for decentralized vanets using fully homomorphic encryption and blockchain,” IEEE Trans. Intell. Transp. Syst., vol. 23, no. 8, pp. 11633–11642, 2021. doi: 10.1109/TITS.2021.3105682. [Google Scholar] [CrossRef]

37. J. Duan, J. Zhou, and Y. Li, “Privacy-preserving distributed deep learning based on secret sharing,” Inf. Sci., vol. 527, no. 1, pp. 108–127, 2020. doi: 10.1016/j.ins.2020.03.074. [Google Scholar] [CrossRef]

38. G. A. Kaissis, M. R. Makowski, D. Rückert, and R. F. Braren, “Secure, privacy-preserving and federated machine learning in medical imaging,” Nat. Mach. Intell., vol. 2, no. 6, pp. 305–311, 2020. doi: 10.1038/s42256-020-0186-1. [Google Scholar] [CrossRef]

39. R. Shokri and V. Shmatikov, “Privacy preserving deep learning,” in Proc. 22nd ACM SIGSAC Conf. Comput. Commun. Secur. Assoc. Comput. Mach., New York, NY, USA, 2015, pp. 1310–1321. doi: 10.1145/2810103.2813687. [Google Scholar] [CrossRef]

40. M. Abadi et al., “Deep learning with differential privacy,” in Proc. 2016 ACM SIGSAC Conf. Comput. Commun. Secur. (CCS ’16), New York, NY, USA, Association for Computing Machinery, 2016, pp. 308–318. doi: 10.1145/2976749.2978318. [Google Scholar] [CrossRef]

41. R. C. Geyer, T. Klein, and M. Nabi, “Differentially private federated learning: A client level perspective,” 2017. doi: 10.48550/arXiv.1712.07557. [Google Scholar] [CrossRef]

42. A. Krizhevsky, I. Sutskever, and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” Commun. ACM, vol. 66, no. 6, pp. 84–90, 2017. doi: 10.1145/3065386. [Google Scholar] [CrossRef]

43. S. Hochreiter, “Long short-term memory,” Neural Comput., vol. 8, no. 9, pp. 1735–1780, 2010. doi: 10.1007/978-3-642-24797-2_4. [Google Scholar] [CrossRef]

44. H. Wang, M. Yurochkin, Y. Sun, D. Papailiopoulos, and Y. Khazaeni, “Federated learning with matched averaging,” 2020. doi: 10.48550/arXiv.2002.06440. [Google Scholar] [CrossRef]

45. Y. Zhao, M. Li, L. Lai, N. Suda, D. Civin and V. Chandra, “Federated learning with noniid data,” 2018. doi:10.48550/arXiv.1806.00582. [Google Scholar] [CrossRef]

46. S. Caldas et al., “LEAF: A benchmark for federated settings,” 2018. doi: 10.48550/arXiv.1812.01097. [Google Scholar] [CrossRef]

47. W. Zhuang, X. Gan, Y. Wen, and S. Zhang, “EasyFL: A low-code federated learning platform for dummies,” IEEE Internet Things J., vol. 9, no. 15, pp. 13740–13754, 2022. doi: 10.1109/JIOT.2022.3143842. [Google Scholar] [CrossRef]