A Practical Study of Intelligent Image-Based Mobile Robot for Tracking Colored Objects

1  Introduction

Mobile robots are one of the most important research topics in the field of robotic systems. They are still being designed and developed to accomplish service tasks based on the basic structure of wheeled mobile robots. Therefore, they have been applied in many real-life applications, such as industry, entertainment, education, and healthcare [1], as shown in Fig. 1. For example, these applications include indoor cleaning, security patrols, assistance to elderly people, and supplying food and medicaments to COVID-19 patients in hospitals [2,3]. Also, applications of wheeled mobile robots include logistic services of mining and transportation in industrial environments such as ports and warehouses [4]. Recently, autonomous navigation of robots has become essential for the development of autonomous personal vehicles. However, this field of research still has open challenges [5–8].

Figure 1: Applications of mobile robots

To perform autonomous navigation, a robot must be equipped with electronic sensors to allow adaptive interaction with its environment. Therefore, the visual navigation of mobile robots is considered one of the important research topics of robotics in the last years, for instance, indoor mobile robot navigation [9,10], crop picking robots [11], and robotic mobility devices [12]. Vision information can be obtained from a monocular camera to achieve tracking and localization tasks with potential obstacle avoidance [13,14]. Hence, real-time image processing algorithms are required to support the positioning, recognition, and tracking of the robot, based on acquired image measurements and segmentation procedures [15]. In this study, a monocular imaging system as an external surveillance camera has been used to guide the wheeled mobile robot for the colored target location. Moreover, automatic control systems present a main module of the robot navigation system to verify the desired robot performance to reach the target location successfully. These control systems apply adequate input velocities to correctly drive the robot towards its desired destination. However, controlling mobile robots still has open problems because of nonlinear and time-variant multivariable driftless system, motion constraints, delayed closed-loop system, and uncertain variability in applied forces and torques to the robot [16,17]. Therefore, this study presents an adaptive control methodology to handle the possible challenges and difficulties of operating wheeled mobile robots accurately and efficiently.

1.1 Related Work

Mobile robot navigation has been applied in many real-world applications to reduce human workloads using different navigation techniques, including path planning, object detection, and tracking. These navigation techniques were fuzzy logic [15,18], neural networks [19], genetic and evolutionary algorithms [20,21], and/or hybrid methods [22]. Table 1 illustrates a review of previous methods in the literature to control mobile robots. In the last several years, the proportional integral derivative (PID) controller has been proposed as one of the most important control strategies. PID controller uses a control function to apply an accurate and responsive correction [21]. In papers [22–24], different methods have been proposed using PID controllers. For example, the authors in [22] suggested a standard PID controller for solving the path-tracking problem, which was a straightforward solution. However, the proposed controller was designed based on a simple linearized mobile robot model, including an integrator with a delay. In [23], the authors used an optimized standard PID controller for high-speed line tracking. Moreover, in their study, the designed controller was practically implemented and could successfully handle nonlinear and unstable systems. Nevertheless, the authors added an array of ten Infrared reflective sensors to track a non-reflective line using a wired mobile robot. Normey-Rico et al. [24] proposed an adaptive PID control of the leader-follower robots. Their proposed adaptive controller was stable without knowing the speed of the master robot. However, the state feedback linearization method was used to derive the control law of the proposed PID algorithm, nonlinear dynamics of the system are also needed to get complete velocity information of the leader robot. A fuzzy logic controller is another famous control strategy. The fuzzy logic controller uses a mathematical method to analyze logical values, taking on continuous values between 0 and 1 [25]. In papers [26–29], the authors used fuzzy control techniques for navigation. The authors in [26] used a fuzzy logic controller, a successful switching fuzzy logic controller, to track under curvature constraints. However, simulation study and the controller have been used to track only piece-wise linear paths. In [27], the authors used a model-based PI-fuzzy controller to introduce an optimal path-planning solution for four-wheeled omnidirectional mobile robots. Nevertheless, the tuning parameters of the proposed controller are required to obtain practical results for the path planner under external disturbances. Paper [28] proposed a generalized type-2 fuzzy controller, which could handle the uncertainty of the mobile robot better than other fuzzy controllers. Though, the theoretical study was without practical validation. Sanchez et al. [29] proposed an embedded neuro-fuzzy controller. Furthermore, the low-cost field programmable gate array (FPGA)-based embedded controllers have been developed for autonomous car-like robots, and it was validated in both simulation and practical studies. However, the developed controller did not consider the presence of disturbances in complex robotic systems. More different methods and techniques were used in the papers [30–32]. An adaptive neural network controller method was proposed in [30]. Moreover, this robust intelligent controller could handle nonlinear and unknown characteristics of nonholonomic electrically driven mobile robots. In [31], a parallel compact cuckoo search algorithm was proposed. This new bio-inspired optimization algorithm was proposed for the path planning of unmanned robots in a complex three-dimensional (3D) environment. Garcia et al. [32] suggested an ant colony optimization with a fuzzy cost function evaluation method. In addition, this proposed novel path planning method was used to avoid static and dynamic obstacles, named simple ant colony optimization distance and memory (SACOdm). However, the practical validation was not conducted in the theoretical study in papers [30–32]. Further details can be found in [1,23].

1.2 Contributions of This Study

According to the above previous studies, it is obvious that many computer-based simulation results have been demonstrated in these studies without including the practical implementation of mobile robots. In addition, artificial intelligence and automatic control techniques play an important role in enhancing the performance of mobile robot navigation. Therefore, this paper aims to develop an efficient and well-controlled mobile robot to reach colored target objects based on real-time image processing and fuzzy-tuning PID controller in different practical scenarios.

The remainder of this article is structured as follows: Section 2 describes the main hardware and software components of our proposed robotic system with adaptive fuzzy logic-based tuning of the PID controller. Section 3 shows the practical results and comparative evaluation of this study. A detailed discussion about our mobile robot navigation system for solving colored object localization is followed by conclusions and future work in Sections 4 and 5, respectively.

2  Materials and Methods

2.1 Materials

The system used in this research is conceptually illustrated in Fig. 2. The system consists of three main components: a mobile robot, a notebook, and an IP camera. All these components communicate together over a Wi-Fi network established by an access point. The mobile robot used in this study is called Adeept RaspTank (Fig. 3a). It is a two-motor drive robot tank equipped with 4-degree-of-freedom (DOF) robot arm and some sensors that are irrelevant to this research. The robot is controlled by a Raspberry PI 3 B+ board (Fig. 3b) with a 64-bit quad-core processor, 1 GB RAM, and many other capabilities including support for Wi-Fi connectivity. The overhead video is shot using a V380 IP camera (Fig. 3c) capable of producing an HD 720 p video and supporting Wi-Fi connectivity.

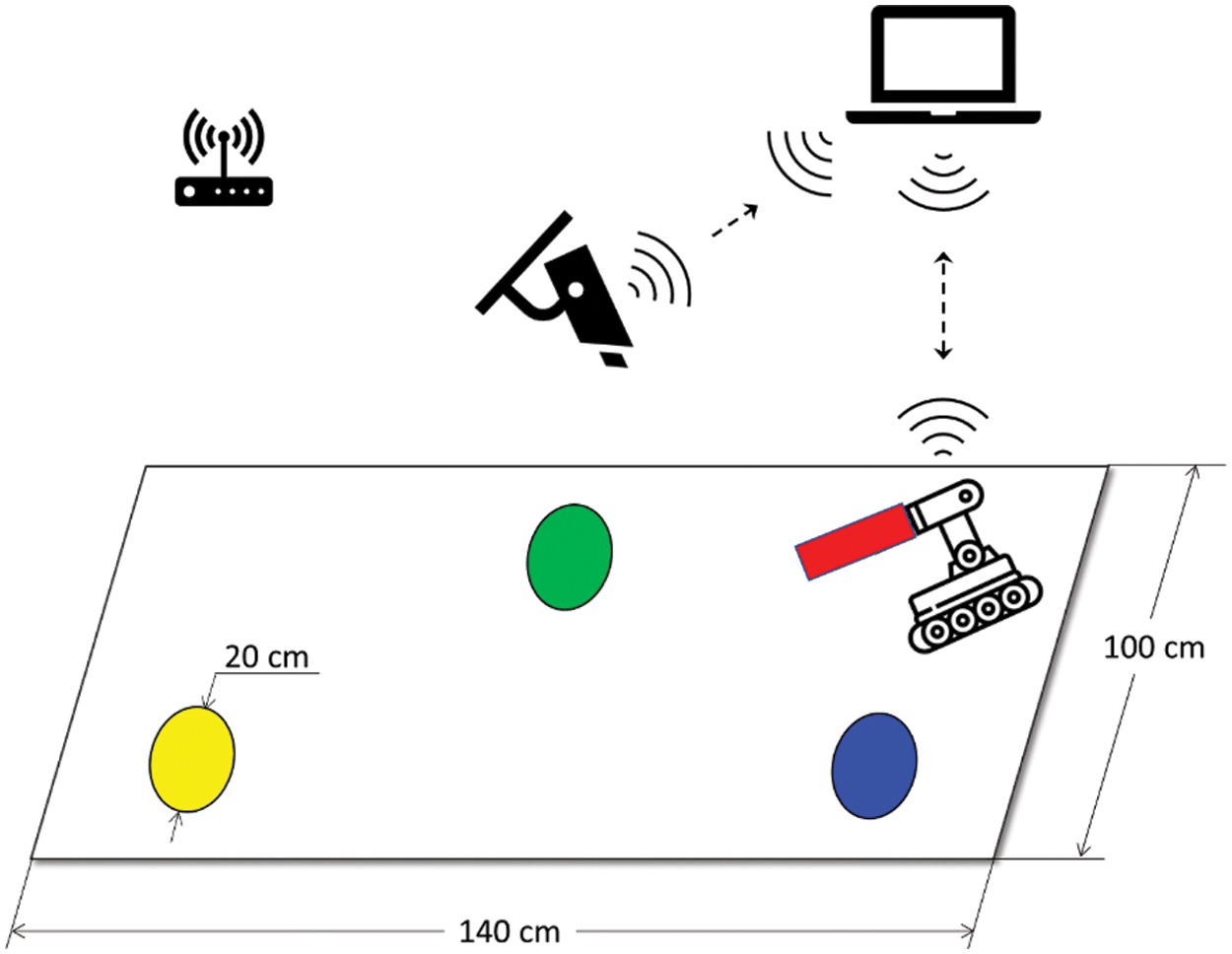
Figure 2: Schematic diagram of the proposed robotic system for tracking colored objects

Figure 3: Main hardware components of the system: (a) Mobile robot; (b) Raspberry PI; and (c) IP camera

The software is split into two parts. The first part of the software is the desktop application that runs on the notebook. This application is a multi-threaded program implemented in Python and does most of the heavy lifting in the system. The application provides a user interface that allows the choosing of the order in which the colored regions are visited by the robot and displays robot status updates in real-time. The main thread of the application processes each video frame received from the camera in real-time to identify the position/orientation of the robot and the position of the target region (to be visited next by the robot). The image processing is done in this part using the Python OpenCV library [33]. More details about this part will come later in Section 2.2. Other threads of the desktop application are used to communicate and exchange information with all other parts of the system (i.e., mobile phone, camera, and robot). The second part of the software is the program that runs on the Raspberry PI board in the robot. This program is also implemented in Python. Its two main purposes are: (1) to establish a communication channel with the desktop application through which the robot receives the commands and status updates (such as its position, orientation, etc.), and (2) to control the robot motors accordingly. The program utilizes the Python libraries provided by the robot manufacturer to interface with the hardware. It also implements various control methods (including proportional integral differential (PID) and fuzzy control) to derive the motors signals. Further details about these control methods are provided in the following sections.

2.2 Methods

2.2.1 Colored Object Detection

The algorithm used to segment out a colored region/object in an image and identify its position is implemented in Python and the OpenCV library [33]. The algorithm has the following steps:

•   Color space conversion: The image is converted from the Red-Green-Blue (RGB) space to the Hue-Saturation-Value (HSV) space (using the cvtColor() method). In the HSV space, the color information is separated from the intensity information and hence it becomes easier to identify specific colors.

•   Smoothing: The HSV image is smoothed with Gaussian Blurring (using the GaussianBlur() method) to reduce the noise and details.

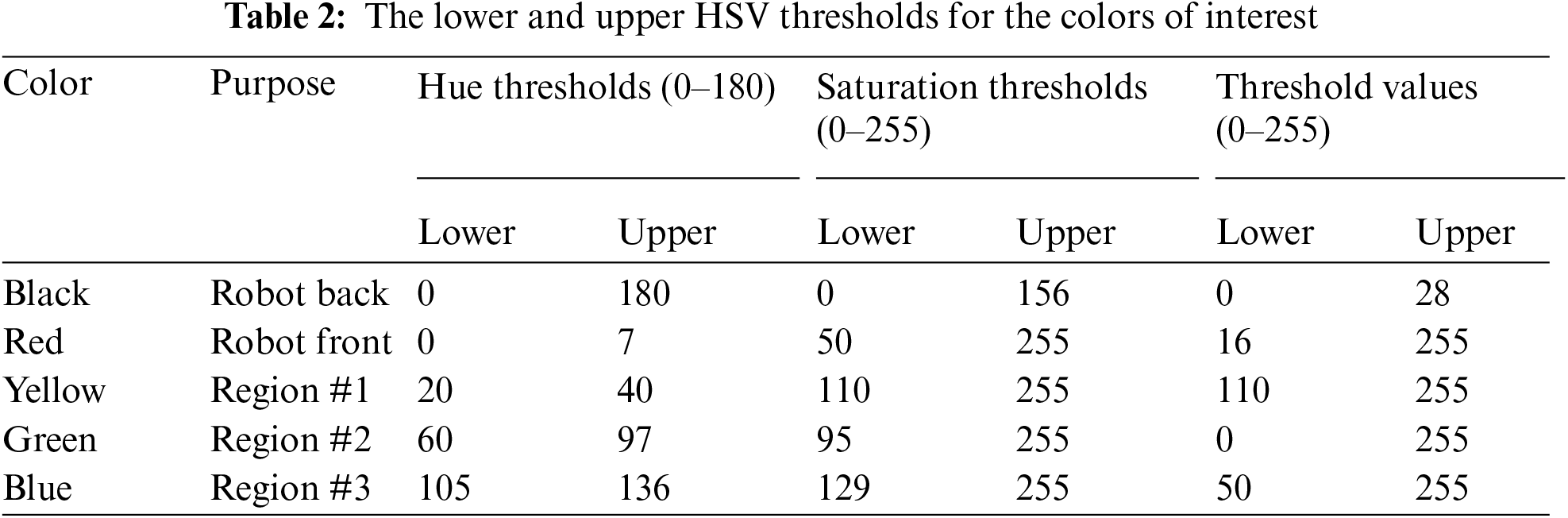
•   Thresholding: the smoothed image is thresholded using a mask that captures the lower and upper limits of the HSV color space of interest (using the inRange() method). The lower and upper thresholds for the colors of interest are experimentally chosen and fine-tuned to the camera position/orientation and the lighting conditions. Table 2 includes the HSV thresholds used in this study.

•   Contour detection: the contour of the colored region of interest is identified (using the findContours() method).

•   Position detection: the center of the colored region of interest is detected by calculating the weighted average of all the pixels within the contour (using the moments() method).

The positions of the three colored regions are identified using the previous algorithm. The algorithm is also used to identify the positions of the front and back regions of the robot. The orientation of the robot is determined by calculating the inclination of the straight line that connects the centers of the front and back regions.

2.2.2 PID Control

The basic control law of PID structure [34] is given by

u(t)=Kpe(t)+Ki∫0te(τ)dτ+Kdde(t)dt(1)

where the error signal e(t) is the difference between the targeted and measured trajectories. The PID controller gains are Kp, Ki, and Kd. In the above control law expression (1), the first term, Kpe(t), presents the proportional control action, which is proportional to the error signal. The second term is the integral control action to eliminate any steady-state error. The last term is the derivative control action. It works as a predictor using the change rate of error signals. Although the derivative control term is used to accelerate the controlled system time response, it is highly sensitive to unwanted noise signals.

2.2.3 Custom PID Control

The main idea behind this control strategy is to engage the PID controller for a specific period te and then disengage it for another period td and repeat that process continuously. The values of the periods te and td are fine-tuned and experimentally determined to reduce the possibility of robot overshooting while having an acceptable overall performance (i.e., rotational and linear speeds). The average values of te and td are 1.0 and 0.3 s, respectively.

2.2.4 Fuzzy Logic Control

The main structure of the fuzzy control system is composed of four successive stages, i.e., the fuzzification, the fuzzy inference engine linked with the knowledge rule-base, and the defuzzification [35], as depicted in Fig. 4. In the fuzzification stage, crisp input signals, i.e., error signals e(t) and Δe(t) are associated with fuzzy sets including a membership function μ=[0,1] with a specific universe of discourse for inputs. The knowledge rule-base includes a group of fuzzy if-then statements as follows [36]:

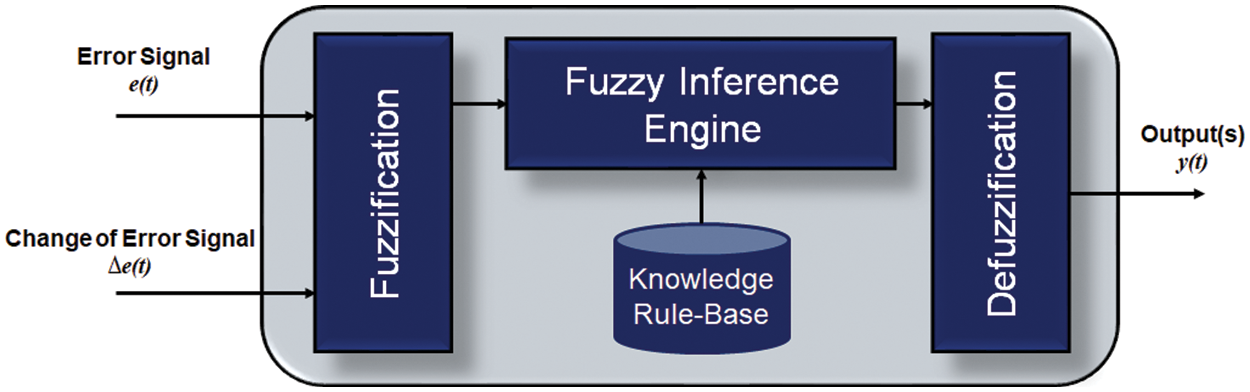
Figure 4: Main structure of a fuzzy control system

R(k):IF x1 is C1k and … and xn is Cnk Then y1 is D1k and … and ym is Dmk(2)

where Cnk and Dmk are the linguistic variables of the fuzzy sets. The total number of if-then rules is k=1,2,…,K. The fuzzy inputs and outputs are x=(x1,…,xn)T, and y=(y1,…,ym)T, respectively. Then, fuzzy inference gives a nonlinear mapping from input to output fuzzy sets based on the above if-then rules. In the last stage, the defuzzification is executed to convert the linguistic results of the fuzzy inference engine to crisp output, yi, as

yi=∑j=1K(∏j=1nμC1k(xj))y¯ik∑j=1K(∏j=1nμC1k(xj)),i=1,2,…, m(3)

where μC1k is the input membership function. y¯ik is the crisp output for the fuzzy set μDik(yi) to achieve the maximum value of one. Utilizing fuzzy logic is advantageous for controlling robots because of its powerful linguistic representations to mimic the knowledge of experienced operators in the presence of uncertain dynamical parameters of the robot [15]. However, human thinking is not the optimal control action of robots. Therefore, the designed fuzzy logic control has been used to achieve the adaptive PID control system of our proposed mobile robot.

2.2.5 Developed Image-Based Robot Tracking

Fig. 5 depicts the schematic diagram of our developed image-based mobile robot for tracking colored objects. A Wi-Fi camera is used to acquire real-time 2D positioning of colored objects. Then, the acquired image is sent remotely to a laptop for measuring the distance, dm, and orientation, θm, between the current position of the mobile robot and the targeted object. The aim of controlling the robot is to achieve the desired distance, dd, and the desired orientation, θd, at zero or the center of colored objects, as shown in Fig. 5. Assuming the shape of all targeted objects is a circle in this study.

Figure 5: Schematic diagram of developed image-based mobile robot for tracking colored objects using Wi-Fi camera

Two fuzzy-PID controllers have been developed to control the distance and orientation of the mobile robot. As depicted in Fig. 6, the generated control action of the fuzzy-PID controller is Vcontrol, which is the voltage drop on the differential motor drive of robot wheels. The inputs of each fuzzy-PID controller are the error and the change of error of both distance and orientation. Their range values are scaled from −1 to +1. The proposed fuzzy tuner provides online adjustments, ΔKp, ΔKi, and ΔKd for the corresponding PID control gains, Kp, Ki, and Kd, respectively. The triangular membership functions, namely negative (N), zero (Z), and positive (P) for fuzzification and defuzzification stages are shown in Fig. 7. The fuzzy tunning rules of ΔKp, ΔKi, and ΔKd are similar for two PID controllers, as illustrated in Table 3.

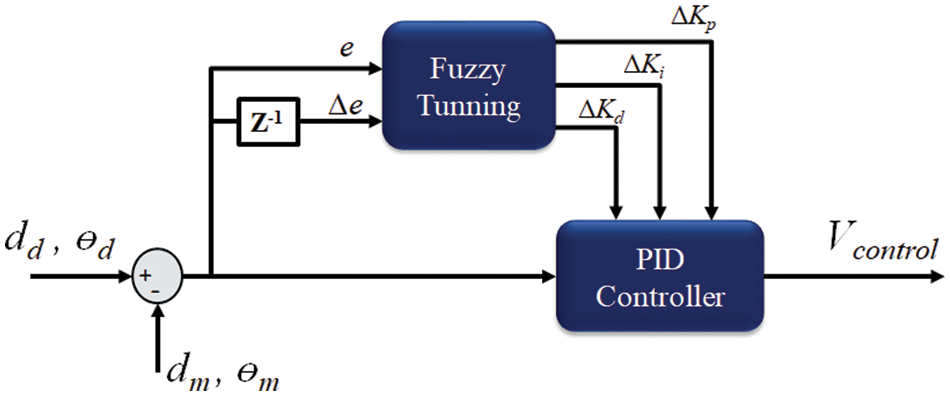
Figure 6: Block diagram of developed fuzzy-PID controller for the distance and orientation of the mobile robot

Figure 7: Triangular membership functions negative (N), positive (P), and zero (Z) for fuzzy inputs and outputs

3  Experimental Results

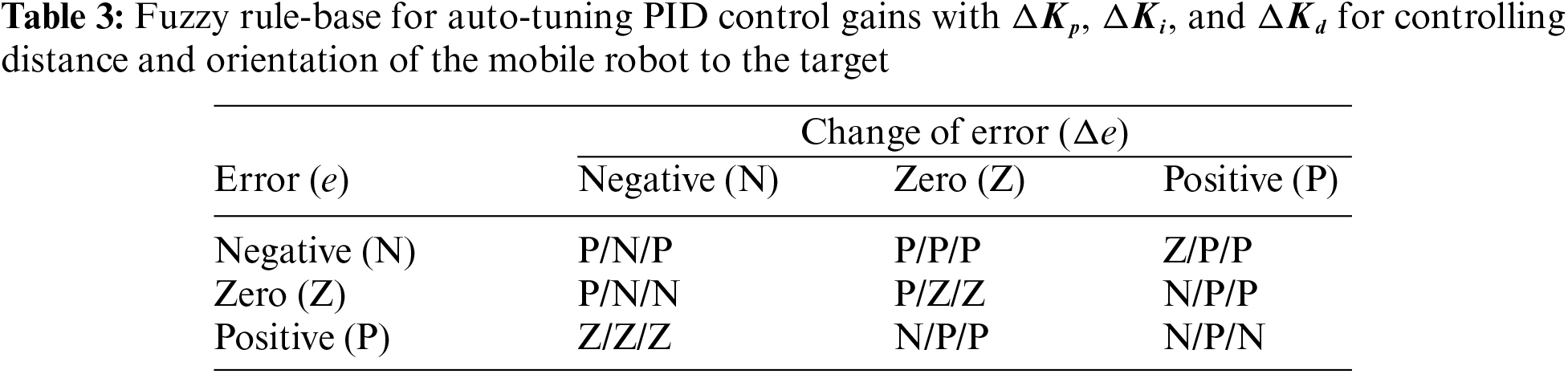
Fig. 8 depicts the experimental setup of this study, as described above in Section 2. The robot operates in a 140 cm × 100 cm rectangular workspace. The size of the workspace is selected such that it is both large enough for the robot (whose dimensions are: 20 cm × 15 cm) to maneuver within and small enough to match the viewing angle of the camera. The colored regions are chosen to be circular shapes to allow being approached from any direction with equal advantage. They are located as far as possible from each other with enough space left for the robot to turn upon reaching the boundaries of the workspace.

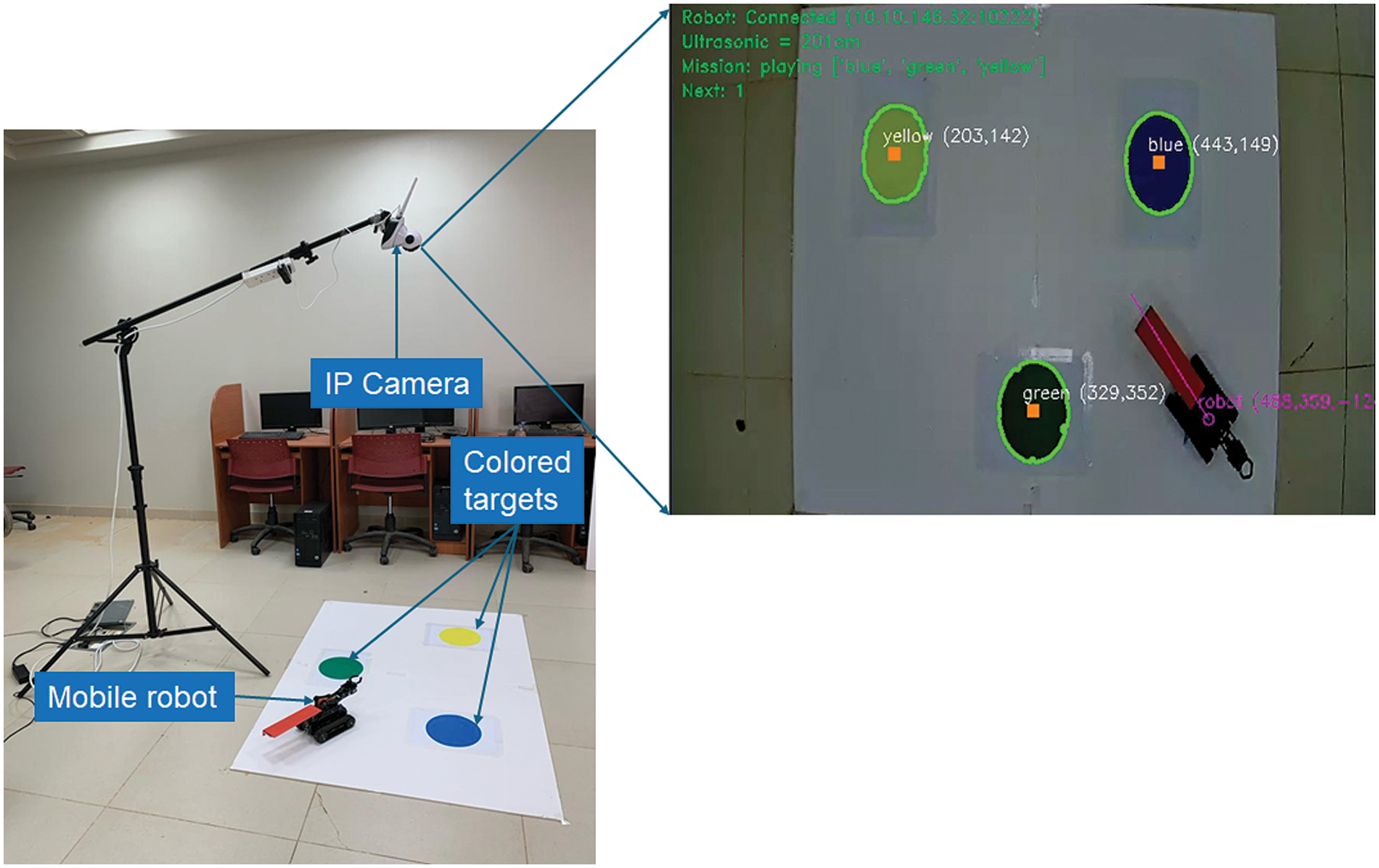
Figure 8: Experimental setup of proposed image-based robot tracking with a processed acquired frame of IP camera to localized colored targets and controlled mobile robot

The experiments of this study have been conducted in twelve different scenarios of our controlled robot for tracking colored objects. In each scenario, the robot begins its trip from a common starting location and visits three colored regions in a specified order. Visually, the robot is ordered to follow a three-step trajectory in each scenario. For instance, in the first scenario, the robot moves from the starting location (S) to the blue region (B) as a first step, and then from the blue region (B) to the green region (G) as a second step, and finally from the green region (G) to the yellow region (Y) as a third step. A picture of the workspace when the robot is about to start to follow one of the scenarios is presented in Fig. 8.

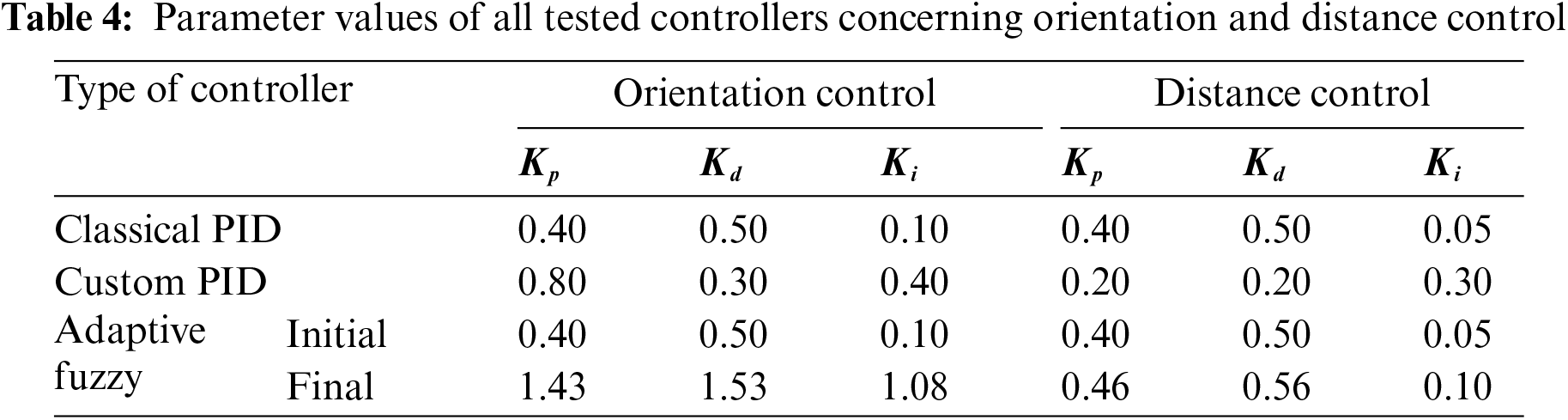
Each experimental scenario is run once for each controller of interest, namely, classical PID, adaptive fuzzy, and custom PID. The parameter values of all tested controllers are illustrated in Table 4, including orientation and distance control, as depicted above in Fig. 5. All controller gains are fixed during the experiments, but adaptive fuzzy control modifies these gains automatically to achieve accurate performance results.

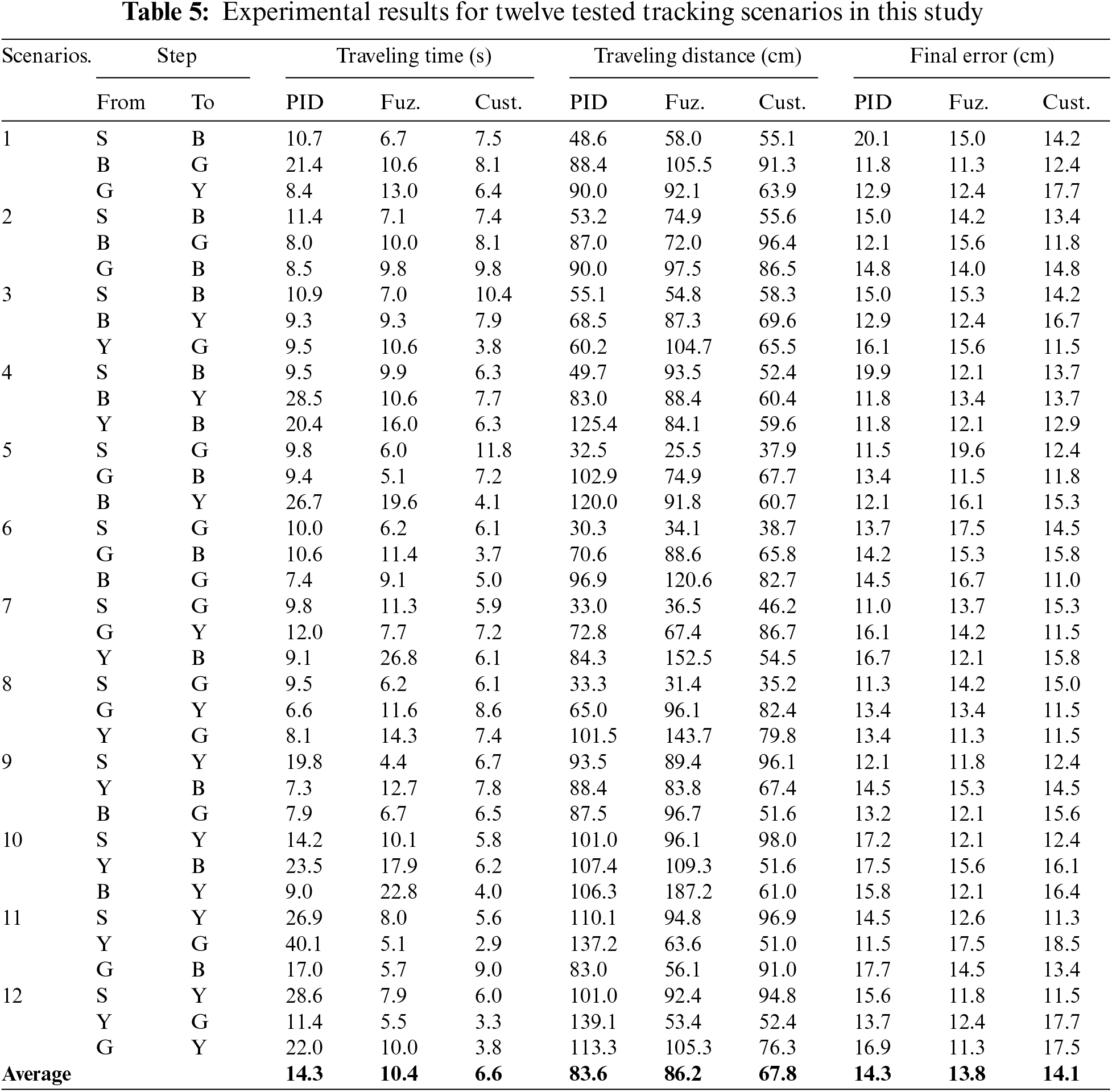
In each experiment, three performance metrics are measured for each step: the traveling time, the traveling distance, and the final error. The traveling time is measured in seconds and refers to the time taken by the robot to reach the destination of the current stage. The traveling distance (measured in centimeters) refers to the length of the path followed by the robot to reach the destination of the current step. The final error (measured in centimeters) is defined as the distance between the center of the robot and the center of the destination region at the end of the current step. Table 5 illustrates the evaluation results obtained by running the twelve different scenarios that are considered in this study with each of the three controllers. A comparison between the performance of the three controllers is visualized in Fig. 8. On average, the custom controller achieves less traveling-time and distance. However, when the fuzzy controller is engaged, the robot tends to become more accurate and get relatively closer to the center of the target region.

4  Discussion

The above practical results demonstrated different successful scenarios of our proposed image-based mobile robot for tracking colored objects. The mobile robot has been controlled using three control methods, which are classical PID, fuzzy control, and custom PID. As shown in Fig. 9, classical PID control achieved the worst results in this study. Therefore, it is not sufficient for the tracking tasks of the mobile robot. In contrast, the proposed fuzzy controller, as given in Fig. 5, achieved the best minimal error among the other two controllers with the longest traveling-distance to the colored targets, as shown in Fig. 9. In addition, our custom PID control achieved the shortest traveling-time and distance path to reach the targets.

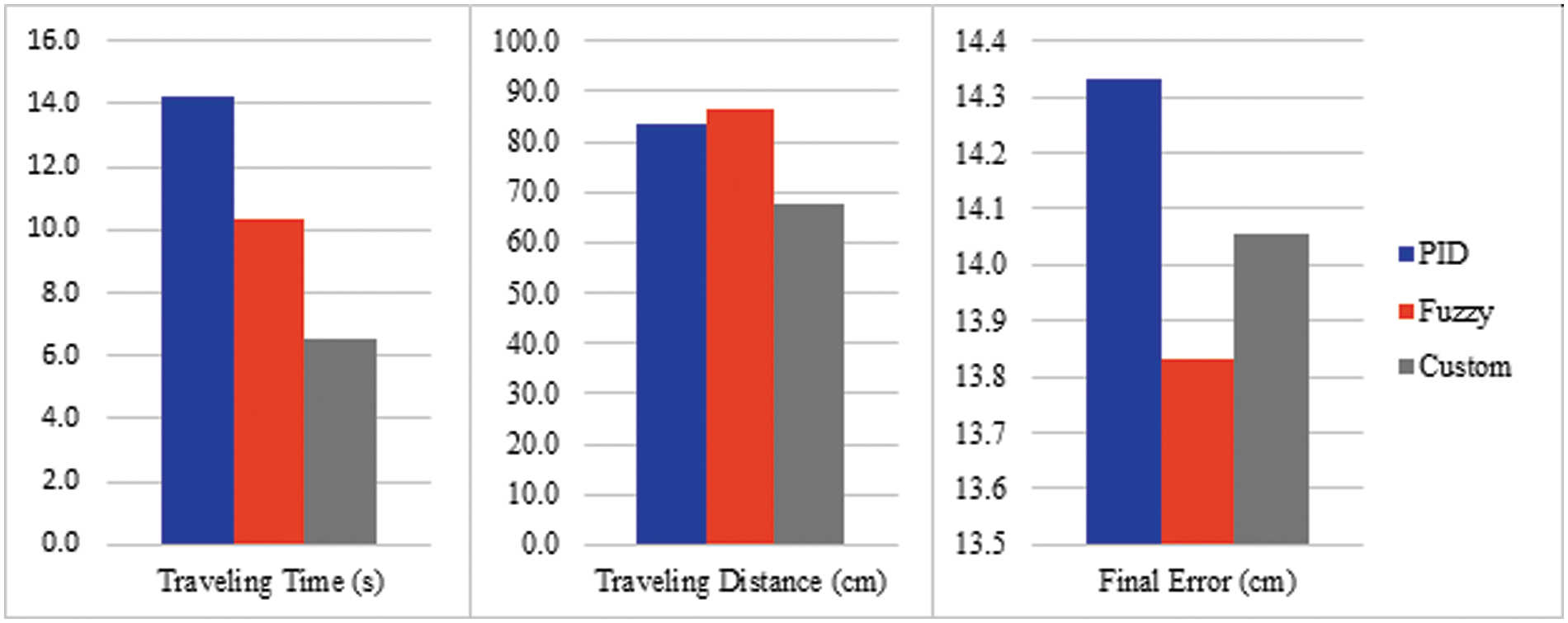
Figure 9: Comparing the three performance metrics (traveling time, traveling distance, and final error) for PID, fuzzy, and custom PID controllers

In Table 5, three evaluation metrics, namely traveling-time, distance, and final error have been applied to evaluate the control performance of the image-based mobile robot. Twelve scenarios of three colored object combinations have been tested by the controlled image-based robot tracking, as depicted in Fig. 8. Classical PID control could not handle these tracking tasks successfully, resulting in the longest traveling-time of 14.3 s, traveling-distance of 83.2 cm and the final error of 14.3 cm. Nevertheless, adaptive fuzzy PID control (see Fig. 6) achieved the best accurate results with the minimum final error of 13.8 cm to reach the colored targets successfully. The impact of the fuzzy rule base plays an important role in adapting PID control gains (see Tables 3 and 4), achieving the best average errors. However, it requires more time and a traveling distance of 86.2 cm to reach these targets because of cost computations, as illustrated in Table 5. The proposed custom PID is a simpler rule-based controller than fuzzy control. It is efficient to save both time and traveling distance of 6.6 s and 14.3 cm, respectively, but its final error is relatively high (14.1 cm) because of the designed non-linear if-then rules to operate the mobile robot. For both proposed intelligent controllers, the designed mobile robot tracker achieved better performance in tracking RGB-colored objects than classical PID control because of their adaptive features to handle the targeted robot tasks like experienced human operators instead of traditional mathematical approaches, as given in Table 5 and Fig. 9.

The control performance of the proposed image-based mobile robot can be enhanced by using other fuzzy control schemes, such as Type-2 and intuitionistic fuzzy approaches [37,38]. Also, integrated bio-inspired optimization techniques with robot controllers have been proposed to estimate the optimum path [39]. Additionally, optimal extremum machine learning (ELM) with a firefly optimization algorithm can be applied to overcome the decoupling problem between the camera coordinates and the image moment features for a vision-based robotic system [40]. However, these advanced approaches require more cost computations by extending the hardware resources including the memory size and processors for practical applications. Therefore, the proposed fuzzy and custom PID controllers are still valid to achieve good performance of image-based mobile robot tracking, as presented in Fig. 9.

5  Conclusion and Future Work

In this paper, we presented a new intelligent mobile robot to accomplish multi-tasks by tracking objects in a real experimental field. This development was achieved by using real-time image processing, fuzzy-tuning and custom PID controllers. The proposed approach was used to recognize and segment a colored object in an image. The adaptive fuzzy logic achieved an accurate tracking result as a practical intelligent controller. In general, our developed multi-purpose robotic system’s promising results can be employed in various applications to reduce human workloads in different environments, such as delivering medical tablets for patients with infectious diseases [41].

For future work, this research can be extended to track different colored shapes with changing the floor color [42], such as industrial robots for painting applications or tracking balls and trajectory prediction using sports robots [43,44]. Also, we aim to improve the performance of developed image-based robot controllers by implying various lighting disturbances of reflection and shadows. Adding obstacles and moving colored targets will also be considered in the prospects of this study.

Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at Shaqra University for funding this research work through the Project Number (SU-ANN-2023016).

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at Shaqra University for funding this research work through the Project Number (SU-ANN-2023016).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mofadal Alymani, Mohamed Esmail Karar, Hazem Ibrahim Shehata; data collection: Mofadal Alymani, Mohamed Esmail Karar, Hazem Ibrahim Shehata; analysis and interpretation of results: Mofadal Alymani, Mohamed Esmail Karar, Hazem Ibrahim Shehata; draft manuscript preparation: Mofadal Alymani, Mohamed Esmail Karar, Hazem Ibrahim Shehata. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The code of this study is available upon request to the corresponding author, Mohamed Esmail Karar (mekarar@ieee.org).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Cebollada, L. Payá, M. Flores, A. Peidró, and O. Reinoso, “A state-of-the-art review on mobile robotics tasks using artificial intelligence and visual data,” Expert. Syst. Appl., vol. 167, pp. 114195, 2020. [Google Scholar]

2. Z. H. Khan, A. Siddique, and C. W. Lee, “Robotics utilization for healthcare digitization in global COVID-19 management,” Int. J. Environ. Res. Public Health, vol. 17, no. 11, pp. 3819, 2020. doi: 10.3390/ijerph17113819. [Google Scholar] [PubMed] [CrossRef]

3. M. E. Karar, Z. F. Khan, H. Alshahrani, and O. Reyad, “Smart IoMT-based segmentation of coronavirus infections using lung CT scans,” Alex. Eng. J., vol. 69, pp. 571–583, 2023. doi: 10.1016/j.aej.2023.02.020. [Google Scholar] [CrossRef]

4. N. Pedemonte et al. “FASTKIT: A mobile cable-driven parallel robot for logistics,” in A. Grau, Y. Morel, A. Puig-Pey, and F. Cecchi (Eds.Advances in Robotics Research: From Lab to Market: ECHORD++: Robotic Science Supporting Innovation, Cham: Springer International Publishing, 2020, pp. 141–163. [Google Scholar]

5. M. B. Alatise and G. P. Hancke, “A review on challenges of autonomous mobile robot and sensor fusion methods,” IEEE Access, vol. 8, pp. 39830–39846, 2020. doi: 10.1109/ACCESS.2020.2975643. [Google Scholar] [CrossRef]

6. L. Wijayathunga, A. Rassau, and D. Chai, “Challenges and solutions for autonomous ground robot scene understanding and navigation in unstructured outdoor environments: A review,” Appl. Sci., vol. 13, no. 17, pp. 9877, 2023. doi: 10.3390/app13179877. [Google Scholar] [CrossRef]

7. G. Ge, Z. Qin, and X. Chen, “Integrating WSN and laser SLAM for mobile robot indoor localization,” Comput. Mater. Contin., vol. 74, no. 3, pp. 6351–6369, 2023. doi: 10.32604/cmc.2023.035832. [Google Scholar] [CrossRef]

8. R. Farkh, H. Marouani, K. A. Jaloud, S. Alhuwaimel, M. T. Quasim, and Y. Fouad, “Intelligent autonomous-robot control for medical applications,” Comput. Mater. Contin., vol. 68, no. 2, pp. 2189–2203, 2021. doi: 10.32604/cmc.2021.015906. [Google Scholar] [CrossRef]

9. T. Ran, L. Yuan, and J. B. Zhang, “Scene perception based visual navigation of mobile robot in indoor environment,” ISA Trans., vol. 109, pp. 389–400, 2020. doi: 10.1016/j.isatra.2020.10.023. [Google Scholar] [PubMed] [CrossRef]

10. Z. Alenzi, E. Alenzi, M. Alqasir, M. Alruwaili, T. Alhmiedat and O. M. Alia, “A semantic classification approach for indoor robot navigation,” Electronics, vol. 11, no. 13, pp. 2063, 2022. doi: 10.3390/electronics11132063. [Google Scholar] [CrossRef]

11. Y. Ma, W. Zhang, and W. S. Qureshi, “Autonomous navigation for a wolfberry picking robot using visual cues and fuzzy control,” Inf. Process. Agric., vol. 8, no. 11, pp. 15–26, 2020. [Google Scholar]

12. A. Boyali, N. Hashimoto, and O. Matsumoto, “A signal pattern recognition approach for mobile devices and its application to braking state classification on robotic mobility devices,” Robot. Auton. Syst., vol. 72, pp. 37–47, 2015. doi: 10.1016/j.robot.2015.04.008. [Google Scholar] [CrossRef]

13. J. R. García-Sánchez et al. “Tracking control for mobile robots considering the dynamics of all their subsystems,” Exp. Implement. Complex., vol. 2017, pp. 5318504, 2017. [Google Scholar]

14. Y. Tang, S. Qi, L. Zhu, X. Zhuo, Y. Zhang and F. Meng, “Obstacle avoidance motion in mobile robotics,” J. Syst. Simul., vol. 36, no. 1, pp. 1–26, 2024. [Google Scholar]

15. M. E. Karar, “A simulation study of adaptive force controller for medical robotic liver ultrasound guidance,” Arab. J. Sci. Eng., vol. 43, no. 8, pp. 4229–4238, 2018. doi: 10.1007/s13369-017-2893-4. [Google Scholar] [CrossRef]

16. F. Rubio, F. Valero, and C. Llopis-Albert, “A review of mobile robots: Concepts, methods, theoretical framework, and applications,” Int. J. Adv. Robot. Syst., vol. 16, no. 2, 2019. doi: 10.1177/1729881419839596. [Google Scholar] [CrossRef]

17. N. H. Singh and K. Thongam, “Mobile robot navigation in cluttered environment using spider monkey optimization algorithm,” Iran. J. Sci. Technol. Trans. Electr. Eng., vol. 44, no. 4, pp. 1673–1685, 2020. doi: 10.1007/s40998-020-00320-w. [Google Scholar] [CrossRef]

18. C. H. Sun, Y. J. Chen, Y. T. Wang, and S. K. Huang, “Sequentially switched fuzzy-model-based control for wheeled mobile robot with visual odometry,” Appl. Math. Model., vol. 47, pp. 765–776, 2017. doi: 10.1016/j.apm.2016.11.001. [Google Scholar] [CrossRef]

19. D. Qin, A. Liu, D. Zhang, and H. Ni, “Formation control of mobile robot systems incorporating primal-dual neural network and distributed predictive approach,” J. Franklin Inst., vol. 357, no. 17, pp. 12454–12472, 2020. doi: 10.1016/j.jfranklin.2020.09.025. [Google Scholar] [CrossRef]

20. H. Qu, K. Xing, and T. Alexander, “An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots,” Neurocomputing, vol. 120, pp. 509–517, 2013. doi: 10.1016/j.neucom.2013.04.020. [Google Scholar] [CrossRef]

21. B. Song, Z. Wang, and L. Zou, “An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve,” Appl. Soft Comput., vol. 100, pp. 106960, 2020. [Google Scholar]

22. M. S. Gharajeh and H. B. Jond, “Hybrid global positioning system-adaptive neuro-fuzzy inference system based autonomous mobile robot navigation,” Robot. Auton. Syst., vol. 134, pp. 103669, 2020. doi: 10.1016/j.robot.2020.103669. [Google Scholar] [CrossRef]

23. M. N. A. Wahab, S. Nefti-Meziani, and A. Atyabi, “A comparative review on mobile robot path planning: Classical or meta-heuristic methods?” Annu. Rev. Control, vol. 50, pp. 233–252, 2020. doi: 10.1016/j.arcontrol.2020.10.001. [Google Scholar] [CrossRef]

24. J. E. Normey-Rico, I. Alcalá, J. Gómez-Ortega, and E. F. Camacho, “Mobile robot path tracking using a robust PID controller,” Control Eng. Pract., vol. 9, no. 11, pp. 1209–1214, 2001. doi: 10.1016/S0967-0661(01)00066-1. [Google Scholar] [CrossRef]

25. V. Balaji, M. Balaji, M. Chandrasekaran, M. K. A. A. Khan, and I. Elamvazuthi, “Optimization of PID control for high speed line tracking robots,” Proc. Comput. Sci., vol. 76, pp. 147–154, 2015. doi: 10.1016/j.procs.2015.12.329. [Google Scholar] [CrossRef]

26. D. Shen, W. Sun, and Z. Sun, “Adaptive PID formation control of nonholonomic robots without leader’s velocity information,” ISA Trans., vol. 53, no. 2, pp. 474–480, 2014. doi: 10.1016/j.isatra.2013.12.010. [Google Scholar] [PubMed] [CrossRef]

27. G. P. Moustris and S. G. Tzafestas, “Switching fuzzy tracking control for mobile robots under curvature constraints,” Control Eng. Pract., vol. 19, no. 1, pp. 45–53, 2011. doi: 10.1016/j.conengprac.2010.08.008. [Google Scholar] [CrossRef]

28. E. Hashemi, M. Ghaffari Jadidi, and N. Ghaffari Jadidi, “Model-based PI-fuzzy control of four-wheeled omni-directional mobile robots,” Robot. Auton. Syst., vol. 59, no. 11, pp. 930–942, 2011. doi: 10.1016/j.robot.2011.07.002. [Google Scholar] [CrossRef]

29. M. A. Sanchez, O. Castillo, and J. R. Castro, “Generalized Type-2 Fuzzy Systems for controlling a mobile robot and a performance comparison with interval Type-2 and Type-1 Fuzzy Systems,” Expert. Syst. Appl., vol. 42, no. 14, pp. 5904–5914, 2015. doi: 10.1016/j.eswa.2015.03.024. [Google Scholar] [CrossRef]

30. I. Baturone, A. Gersnoviez, and Á. Barriga, “Neuro-fuzzy techniques to optimize an FPGA embedded controller for robot navigation,” Appl. Soft Comput., vol. 21, pp. 95–106, 2014. doi: 10.1016/j.asoc.2014.03.001. [Google Scholar] [CrossRef]

31. P. C. Song, J. S. Pan, and S. C. Chu, “A parallel compact cuckoo search algorithm for three-dimensional path planning,” Appl. Soft Comput., vol. 94, pp. 106443, 2020. doi: 10.1016/j.asoc.2020.106443. [Google Scholar] [CrossRef]

32. M. A. P. Garcia, O. Montiel, O. Castillo, R. Sepúlveda, and P. Melin, “Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation,” Appl. Soft Comput., vol. 9, no. 3, pp. 1102–1110, 2009. doi: 10.1016/j.asoc.2009.02.014. [Google Scholar] [CrossRef]

33. A. F. Villán, Mastering Opencv 4 with Python: A Practical Guide Covering Topics from Image Processing, Augmented Reality to Deep Learning with Opencv 4 and Python 3.7. Birmingham, UK: Packt Publishing, 2019. [Google Scholar]

34. C. C. Yu, Autotuning of PID Controllers: Relay Feedback Approach. London: Springer, 2013. [Google Scholar]

35. N. Siddique and H. Adeli, Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing. West Sussex, UK: Wiley, 2013. [Google Scholar]

36. S. Xu and B. He, “Robust adaptive fuzzy fault tolerant control of robot manipulators with unknown parameters,” IEEE Trans. Fuzzy Syst., pp. 1–11, 2023. doi: 10.1109/TFUZZ.2023.3244189. [Google Scholar] [CrossRef]

37. F. Cuevas, O. Castillo, and P. Cortes, “Towards a control strategy based on type-2 fuzzy logic for an autonomous mobile robot,” in O. Castillo and P. Melin (Eds.Hybrid Intelligent Systems in Control, Pattern Recognition and Medicine, Cham: Springer International Publishing, 2020, pp. 301–314. [Google Scholar]

38. D. Kang, S. A. Devi, A. Felix, S. Narayanamoorthy, S. Kalaiselvan, D. Balaenu, and A. Ahmadian, “Intuitionistic fuzzy MAUT-BW Delphi method for medication service robot selection during COVID-19,” Oper. Res. Perspect., vol. 9, pp. 100258, 2022. doi: 10.1016/j.orp.2022.100258. [Google Scholar] [CrossRef]

39. R. H. M. Aly, K. H. Rahouma, and A. I. Hussein, “Design and optimization of PID controller based on metaheuristic algorithms for hybrid robots,” in 2023 20th Learn. Technol. Conf. (L&T), Jeddah, Saudi Arabia, 2023, pp. 85–90. [Google Scholar]

40. Z. Zhou, J. Wang, Z. Zhu, and J. Xia, “Robot manipulator visual servoing based on image moments and improved firefly optimization algorithm-based extreme learning machine,” ISA Trans., vol. 143, pp. 188–204, 2023. doi: 10.1016/j.isatra.2023.10.010. [Google Scholar] [PubMed] [CrossRef]

41. C. Ohneberg et al., “Assistive robotic systems in nursing care: A scoping review,” BMC Nurs., vol. 22, no. 1, pp. 72, 2023. doi: 10.1186/s12912-023-01230-y. [Google Scholar] [PubMed] [CrossRef]

42. J. Gijeong, L. Sungho, and K. Inso, “Color landmark based self-localization for indoor mobile robots,” in Proc. 2002 IEEE Int. Conf. Robot. Automat. (Cat. No. 02CH37292), Washington, DC, USA, 2002, vol. 1, pp. 1037–1042. [Google Scholar]

43. H. A. Gabbar and M. Idrees, “ARSIP: Automated robotic system for industrial painting,” J. Comput. Des. Eng., vol. 12, no. 2, pp. 27, 2024. doi: 10.3390/technologies12020027. [Google Scholar] [CrossRef]

44. Y. Yang, D. Kim, and D. Choi, “Ball tracking and trajectory prediction system for tennis robots,” J. Comput. Des. Eng., vol. 10, no. 3, pp. 1176–1184, 2023. doi: 10.1093/jcde/qwad054. [Google Scholar] [CrossRef]