Scene 3-D Reconstruction System in Scattering Medium

1  Introduction

In the field of computer graphics, the Neural Radiance Fields (NeRF) technology, proposed by Mildenhall and others [1], has garnered widespread attention for its ability to model and represent the surfaces of objects in three-dimensional scenes using deep learning and neural network models. Compared to traditional graphics rendering methods, NeRF offers superior performance in terms of detail accuracy and precision. Especially in the three-dimensional reconstruction of underwater scenes, the application of NeRF technology is of significant importance to the development and management of underwater resources, marine scientific research and protection, and the advancement of marine tourism. However, the physical environment targeted by NeRF is a clean air medium. For a medium that absorbs or flashes light, such as water, the volume rendering equation not only has a volume meaning for the object, but also the external environment will affect the rendering.

In contrast to clear air conditions, when the medium involves absorption or scattering (e.g., haze, fog, smoke, and all aquatic habitats), the volume rendering equation takes on a true volumetric meaning, as the entire volume, not just objects, contributes to the image intensity. Since the NeRF model estimates color and density at every point in the scene, it lends itself to perfect general volume rendering when an appropriate rendering model is used. The choice of water as a scattering medium is due to its prominent light scattering characteristics in image acquisition. The light scattering characteristics in water manifest as the interaction of light rays with water molecules and suspended particles, causing the light to scatter in different directions. The way light propagates in water, including scattering, absorption, and refraction, makes it an ideal model for studying and understanding the behavior of light in scattering media. Due to the relative ease of conducting image capture underwater, water is commonly used as a typical scattering medium for experimental research.

Our proposed underwater scene reconstruction system uses an improved 3D reconstruction method of neural radiation field optimized by multi-resolution hash coding [2] to achieve model construction and rendering. The flowchart of the system is shown in Fig. 1. This coding method based on hash search only needs a small scale neural network to achieve the effect of a fully connected network without loss of accuracy. Based on a multi-level voxel search structure, the weight search of data is realized, so that the weight optimization and data calculation can be controlled step by step in different levels of the corresponding sub-regions. In this way, for weight optimization, too many ineffective calculation processes can be avoided. In image preprocessing, water’s absorption of light is different in different spectral regions and has obvious selectivity. The selective absorption of light by water makes the color of the underwater object change with the increase of its depth. At the same time, when the light propagates in water, it is affected by the medium particles and deviates from the original direction of linear propagation, which is called the scattering of light by water. This phenomenon will reduce the contrast of the image and make the imaging system unable to receive useful information. The image enhancement method we used has good performance on UICQE [3], UIQM [4] and SCM [5] indicators, which can effectively restore the original color of the image, improve the image quality and ensure the consistency of color correction.

Figure 1: Our method has five parts, image enhancement is the preprocessing part, mainly to enhance the clarity of the underwater image, to facilitate the subsequent 3D reconstruction, the next stage, the position estimation module is to obtain the image position information as an input to the 3D reconstruction, after the next stage of keyframe filtering to conserve the arithmetic resources, and finally 3D reconstruction, which can be rendered from an arbitrary point of view of this 3D model

This paper proposes an improved underwater 3D reconstruction system aimed at achieving rapid and high-quality 3D reconstruction. Our main contributions include:

•   We propose an enhancement method for underwater video images that combines the Contrast Limited Adaptive Histogram Equalization (CLAHE) algorithm with Bayesian Retinex enhancement technology, effectively restoring the original color of the images and improving image quality.

•   We develop a keyframe selection method based on pose and image quality, which optimizes resource utilization and reduces the impact of dynamic objects on the reconstruction results.

•   We improve the 3D reconstruction process using a neural radiance field (NeRF) based on multi-resolution hash coding, achieving efficient and accurate model construction and rendering with a small-scale neural network. A small-scale neural network is capable of delivering the performance of a fully connected network without compromising accuracy. Based on a multi-level voxel search structure, we implement weight search for data, avoiding ineffective calculations.

•   This paper establishes a unified system for the 3D reconstruction of underwater scenes. Experiments show that our underwater scene reconstruction method significantly improves reconstruction efficiency and ensures high-quality reconstruction results compared to other methods.

2  Related Work

2.1 Underwater Image Enhancement

In underwater optical imaging, the inherent properties of water, such as significant light absorption and scattering, result in the exponential attenuation of light propagation underwater. Conventional imaging systems used in underwater settings often suffer from high noise levels, pronounced color aberrations, and distortions, leading to poor image quality. In previous work, numerous underwater image enhancement methods have been proposed to address these challenges.

Treibitz et al. [6] combined information from different lighting frames to achieve optimal contrast for each region in the output image. Fu et al. [7] introduced a variational framework for image enhancement based on retinex, which effectively solves the problems of color, exposure, and blur in underwater imaging. Hitam et al. [8] extended the Contrast Limited Adaptive Histogram Equalization (CLAHE) method to underwater image enhancement, using a mixture of CLAHE on RGB and HSV color models and combining the results using Euclidean norm, significantly improving the visual quality of underwater images. Akkaynak et al. [9] presented the first method that recovers color with their revised model, using RGBD images high image enhancement effect has been achieved. Islam et al. [10] presented a conditional generative adaptive network-based model for real-time underwater image enhancement evaluate perceived image quality by developing an objective function based on global content, color, local texture, and style information of the perceived image. The Five A + Network (FA + Net) proposed by Jiang et al. [4] is an efficient and lightweight real-time underwater image enhancement network that achieves real-time enhancement of 1080P images.

Given the effectiveness of the physical models used in underwater image processing and the inherent characteristics of underwater images, we propose a method that combines the CLAHE algorithm with the Retinex enhancement technique for underwater image enhancement. CLAHE processes images in blocks, building upon the adaptive histogram equalization algorithm while introducing a threshold to limit contrast, mitigating the problem of noise amplification. Linear or bilinear interpolation is used to optimize transitions between blocks, resulting in a more harmonious appearance. Multiscale processing is applied to enhance brightness and color representation.

The Retinex algorithm, known for its effectiveness in enhancing brightness and contrast in underwater images, decomposes the image into local and global components for enhancement. The local component refers to an adaptive neighborhood for each pixel in the image, while the global component encompasses the entire image. The Retinex algorithm decomposes the value of each pixel into two parts: reflectance and illumination. It then enhances the reflectance values of each pixel to improve image contrast and brightness. Finally, the enhanced reflectance values are multiplied by the illumination values to obtain the final image.

2.2 Keyframe Filtering

The selection of keyframes plays a pivotal role in various computer vision and robotics applications, particularly in the context of visual SLAM (Simultaneous Localization and Mapping) and 3D reconstruction. This section provides an overview of related works in keyframe selection, highlighting the different approaches and strategies employed in the field.

Klein et al. [11] and Mur-Artal et al. [12] relied on camera pose information for keyframe selection, often considering motion and loop closure. Konolige et al. [13] introduced mutual information-based keyframe selection. These maximize information gain, using metrics like mutual information. Revaud et al. [14] proposed quality-driven selection, considering sharpness and overall image quality. Combining pose and quality criteria, Dubé et al. [15] aimed for accuracy and image quality balance, considering visual saliency and pose for keyframe selection. Our proposed keyframe selection module extends and innovates upon these existing works by simultaneously considering both pose information and image quality, offering a unique perspective on keyframe filtering in the context of underwater scene reconstruction. In the following sections, we will delve into the details of our approach and present experimental results showcasing its effectiveness.

2.3 Underwater Reconstruction

NeRF (Neural Radiance Fields), as a very hot emerging computer vision technology, aims to generate realistic 3D scene reconstruction and rendering. In 2020, Mildenhall et al. [1] first proposed the NeRF technology, which has attracted a lot of attention in academia and industry. Its core idea is to use a neural network to represent the radiation field (radiance field) of each point in a 3D scene, and train the network to estimate the color and depth values of each point. In recent years, a large number of NeRF-related improvements have been proposed, mainly focusing on improving the training efficiency, rendering quality, and expanding the application areas, etc. NeRF++ [16] by Zhang et al. further improves the rendering quality and efficiency of NeRF by introducing techniques such as regularization and local feature extraction, etc. Pumarola et al. proposed D-NeRF [17], which extends the application of NeRF from static scenes to dynamic scenes, and realizes the modeling and rendering of dynamic objects. Based on the consideration of reconstruction efficiency and quality, we use Instant-NGP (Instant Neural Graphics Primitives) to realize fast and high-quality 3D reconstruction. Instant-NGP proposes a coding method that allows the use of a small-scale network to implement NeRF without loss of accuracy. The network is augmented by a multiresolution hash table of feature vectors, performing optimizations based on stochastic gradient descent. The multi-resolution structure facilitates GPU parallelism and is able to reduce computation by eliminating hash conflicts. The implementation improves NeRF’s time overhead in hours to seconds.

For 3D reconstruction of scenes with specular effects and reflections, there is also recent challenging work that focuses on optimizing the stability of NeRF as well as expanding the scenarios in which it can be used. NeRF-W [18] is able to learn and render reconstructed images containing transient objects, but also guarantees separation from the static network without introducing artifacts to the representation of the static scene. A secondary voxel radiation field incorporating a data-dependent uncertainty field is utilized to reduce the impact of transient objects on the static scene representation. NeRF-ReN [19] focuses on the 3D reconstruction of reflective scenes, and proposes the use of separate transmission and reflection neural radiation fields in complex reflective scenes. By dividing the scene into transmission and reflection components, a new parametric definition is proposed that can handle reflection as well as specular scenes well.

For the 3D reconstruction of underwater scenes, laser scanning, structured light projection, and underwater sonar are currently used. Our proposed method for underwater 3D reconstruction mainly works by preprocessing the optical images captured by a monocular camera, and then the enhanced images are used for subsequent reconstruction work. SeaThru-NeRF, proposed by Daniel Levy et al. [20] in 2023, develops a new rendering model for nerf in scattering media based on the SeaThru image imaging model. The idea of SeaThru-NeRF’s underwater 3D reconstruction method has similarities with our method. In the subsequent 3D reconstruction experimental part, we mainly compare with SeaThru-NeRF in terms of rendering quality, training effect, etc., to demonstrate the superiority and efficiency of our method.

3  A Rapid Underwater Scene Reconstruction System

3.1 Underwater Image Enhancement

Due to issues such as refraction and scattering of light in water, the collected underwater images often suffer from blurriness and a bluish or purplish color cast. To address this problem, our algorithm aims to enhance the original underwater images, improving clarity and color restoration. Conventional enhancement methods often result in significant variations in enhancement effects due to the temporal changes in different regions of underwater video frames. In contrast, our proposed method ensures consistency in enhancement within the same region and maintains spatial and temporal continuity between adjacent regions. conventional enhancement methods are not suitable for underwater video enhancement because of the significant variations in enhancement effects caused by the temporal changes in different regions over time, which severely affects the user experience. However, the Contrast Limited Adaptive Histogram Equalization (CLAHE) algorithm divides the image into 4×4 small regions for individual enhancement. It employs bilinear interpolation in the central region, ensuring consistency in enhancement within the same region and maintaining spatial and temporal continuity between adjacent regions. Subsequently, we apply the Bayesian Retinex algorithm for fine-tuning the color. For color correction, we employ the Bayesian Retinex algorithm, which first utilizes color correction methods to remove color casts and restore naturalness. Then, a multi-level gradient prior is established based on the color-corrected image. Color correction involves statistical methods to handle color shifts and can be calculated using the following formula:

Uc=2552×(1+Sc−Mcμ⋅Vc)(1)

For an underwater RGB image, when c(R,G,B), is computed for each of the three channels of the degraded underwater image S, Mc is the mean of the image S, and Vc is the variance of the image S. μ is the parameter that regulates the underwater enhancement saturation, and for each color channel, we usually set it to 2.5. After the aforementioned computational processing, a constant calibration is applied to each color channel. Subsequently, the Bayesian Retinex image enhancement is performed. Using Bayesian inference, the Bayesian Retinex enhancement model simultaneously enhances the illumination component L and the reflectance component R. The formulation of the posterior distribution in the Bayesian Retinex model can be expressed as:

p(I,|L)∝p(L|I,R)p(I)p(R)(2)

Meanwhile, the parameter p introduces a multi-order gradient prior to design p(R) in order to obtain a more complete underwater image structure. p in the first- and second-order gradients of the reflectivity, the image structure is richer, resulting in finer details. In pursuit of better spatial smoothness of illumination, a Gaussian distribution with zero mean and variance is used to model the first-order gradient prior of illumination, which is modeled as:

p1=N(▽I|0,σ321)(3)

Also for the second-order gradient prior, for the approximation of the segmented linear component of the illumination, another Gaussian distribution with zero mean and variance σ42 is used to model the second-order derivative prior of the illumination:

p2=N(△I|0,σ421)(4)

Ultimately, the priori p(I) is modeled as:

p(I)=p1(I)p2(I)(5)

The final illumination adjustment is a fine-tuning operation performed on the environment, using an effective gamma correction to adjust the luminosity. In this context, Ie represents the final adjusted illumination image, I is the input image, and W is a weight correction factor used to perform gamma correction, with γ being the parameter for gamma correction. The correction can be expressed as follows:

Ie=W(IW)1γ(6)

The channel Le of the final image is calculated as:

Le=Ie⋅R(7)

3.2 Keyframe Filtering Based on Pose and Image Quality

Keyframe selection is a critical step in our approach, aiming to identify representative frames from a multitude of images while minimizing their impact on the subsequent 3-D reconstruction module. Diverging from conventional keyframe selection methods that rely solely on pose or image entropy criteria, our method combines both pose information and image sharpness to filter keyframes. This novel approach allows us to consider image quality alongside the appropriateness of keyframe placement.

Pc=[Rt01]=[r1,1r1,2r1,3t1r2,1r2,2r2,3t2r3,1r3,2r3,3t30001](8)

where R is a 3×3 rotation matrix representing the camera’s orientation. t is a 3×1 translation vector representing the camera’s position. The bottom-right element is always 1 to maintain correct matrix multiplication.

We calculate the angular difference and displacement between cameras using the following formulas:

θΔ=arccos⁡(1−0.5(R13−R13′2)+(R23−R23′2)+(R33−R33′2))(9)

DisΔ=(R14−R14′2)+(R24−R24′2)+(R34−R34′2)(10)

Here, we use the camera-to-world (c2w) format for the pose matrices.

Additionally, we compute the image sharpness using the Laplacian operator to identify keyframes with higher quality in noisy datasets. We calculate the keyframe importance parameter as follows:

I=w1×sharpness+w2×DisΔ+(1−w1−w2)×θΔ(11)

Here, w1 and w2 are weights that determine the contribution of sharpness and motion changes to the importance score, respectively. “Sharpness” measures the clarity of the image using the Laplacian operator. DisΔ represents the translational displacement of the camera between frames, while θΔ captures the rotational change in the camera’s pose. We use a weighted average of sharpness and the angular difference with displacement to strike a balance between image quality and quantity.

3.3 3D Reconstruction Based on Instant-NGP

3.3.1 Neural Radiance Fields (NeRFs)

Neural Radiance Fields (NeRFs) is a groundbreaking advancement in the field of 3D visual reconstruction. NeRFs was initially proposed by Mildenhall et al. in 2020 to address the challenging task of scene reconstruction and view synthesis from 2D images.

In essence, the original NeRF can be understood as a Multilayer Perceptron (MLP) that primarily consists of fully connected layers instead of convolutional layers. Its purpose is to learn a static 3D scene, often parameterized through the $MLPfθ:(x,d)⟶(c,σ)$. The NeRF function takes as input a continuous representation of the scene, which is a 5D vector containing a spatial 3D coordinate point x=(x,y,z) and the direction d=(θ,ϕ) from that coordinate position. The output of the function is the RGB color coordinates c=(r,g,b) of the 3D point and the corresponding opacity or density value =σ at that location. The neural network can be represented as follows:

Fθ:(x,d)→(c,σ)(12)

The voxel density σ(x) can be understood as the probability that a ray traveling through space will be terminated by an infinitesimal particle at x. This probability is differentiable and can be approximated as the opacity of the point at that location. Since the points on the observed ray of the camera along a particular direction are continuous, the color of the corresponding pixel in the imaging plane of that camera can be understood as the color integral of the point through which the corresponding ray passes can be expressed as:

C(r)=∫tntfT(t)⋅σ(r(t))⋅c(r(t),d)dt(13)

By labeling the origin of a ray as o and the direction of the ray (i.e., the camera viewpoint) as d, the ray can be represented as r(t)=o+td, with the proximal and distal boundaries of t as tn and tf, respectively.

Where T(t) denotes the cumulative transparency of the section of the ray from tn to t, i.e., the probability that the ray has not been stopped by hitting any particle from tn to t, is denoted as:

T(t)=exp(−∫tntσ(r(s))ds(14)

In practical scenario applications, it is not possible to do the NeRF to estimate continuous 3D information, so a numerical approximation method, i.e., uniform random sampling method, is used, whose i sampling point can be expressed as:

ti=U[tn+i−1N(tf−tn),tn+iN(tf−tn)](15)

The first step is to deal with the region on the ray that needs to be integrated by dividing the region into N parts, and numerical approximation of each small region ensures that the continuity of the adopted position, and simplifies the above color equation to:

C^(r)=∑i=1NTi⋅(1−exp(−σi⋅δ i))⋅ci(16)

where the distance Ti between neighboring come sampling points can be expressed as:

Ti=exp(−∑j=1i−1σjδj)(17)

The rendering principle of NeRF is to sample and sum for each ray emitted by the camera. Hence NeRF’s pain point: it is slightly less efficient. This is because arithmetic is still consumed for regions where rendering is not effective.

Ultimately the training loss of NeRF is directly determined with the L2 loss of the rendering result, which can be expressed as:

L=∑r∈RN[∥Cc^(r)−C(r)∥22−∥Cf^(r)−C(r)∥22](18)

3.3.2 Instant-NGP (Instant Neural Gradient Prediction)

Instant-NGP [3] is an innovative approach that addresses the challenge of gradient prediction in neural networks, particularly in the context of underwater scene reconstruction. It plays a fundamental role in enhancing the training stability and efficiency of our system.

Gradient Prediction Network (GPN). Instant-NGP introduces a Gradient Prediction Network (GPN), denoted as 𝒩GPN, which is a neural network responsible for predicting gradients. The GPN takes the network’s current state W and an input sample x as input and predicts the gradient ∇ℒ(W,x)with respect to the loss function ℒ. This can be expressed as:

∇ℒ(W,x)=𝒩GPN(W,x)(19)

Instantaneous Gradient Updates. Once the gradient is predicted by the GPN, it is used to update the network’s parameters W immediately. This enables the network to adapt rapidly to changing conditions, such as variations in underwater scenes. The instantaneous gradient update can be formulated as:

Wnew=Wold−α⋅∇ℒ(Wold,x)(20)

where α is the learning rate.

Our Underwater 3-D Reconstruction module is powered by the innovative Instant-NGP (Instant Neural Gradient Prediction) algorithm. This algorithm plays a pivotal role in accelerating the reconstruction process compared to traditional methods, such as Seathru-NeRF.

In the context of our underwater scene reconstruction system, the Underwater Reconstruction module harnesses the power of Instant-NGP to achieve both efficiency and accuracy. By incorporating this algorithm, we can reconstruct 3-D underwater scenes in a timely manner without compromising the quality of the reconstructions. This is paramount for tasks such as underwater navigation, environmental monitoring, and scientific exploration, where real-time or near-real-time feedback is essential.

In the following section (Section 5), we will present the experimental results and discuss the performance of our Underwater Reconstruction module in detail, showcasing how Instant-NGP contributes to the success of our system in accurately capturing the intricacies of underwater environments.

4  Experiments and Results

4.1 Video Data

The video data used in our study was obtained through underwater diving exploration, capturing real-world underwater scenes. Meanwhile, we also used the Dataset of Real-world Underwater Videos of Artifacts (DRUVA) collected by Zhang et al. [16] in shallow sea waters. The dataset we collected ourselves collected a total of 241 and 231 individual images, corresponding to two different underwater scenes. These images were captured using the GoPro HERO BLACK camera and recorded at a resolution of 1280 × 720 pixels, providing a nearly 360 degree azimuth view of the diver’s activity around the artifacts. The DRUVA dataset was collected using the GoPro Hero 10 camera. This dataset contains video sequences of 20 different artificial artifacts in shallow water, with divers obtaining nearly 360 degree directional views around the artifacts.

4.2 Evaluation Metrics

In this section, we outline the evaluation metrics used to assess the performance of our underwater scene reconstruction system, focusing on two key modules: the Underwater Enhancement module and the Underwater 3-D Reconstruction module.

4.2.1 Underwater Enhancement Evaluation Metrics

We use three indicators for evaluating underwater images.

UIQM (Underwater Image Quality Measure) is used to evaluate the quality of restored underwater images. UIQM is a no-reference underwater image quality assessment metric inspired by the human visual system. It addresses the degradation mechanisms and imaging characteristics of underwater images by employing three distinct measures: the Underwater Image Colorfulness Measure (UICM), the Underwater Image Sharpness Measure (UISM), and the Underwater Image Contrast Measure (UIConM) These measures are combined linearly to represent the UIQM. The higher the value of UIQM, the better the color balance, sharpness, and contrast of the image are considered to be. The specific formula is expressed as:

UIQM=c1×UICM+c2×UISM+c3×UIConM(21)

UICQE (Underwater Image Color Quality Enhancement) [3] UICQE is a metric designed to evaluate the color enhancement quality of underwater images. It assesses the system’s ability to improve the color fidelity and vibrancy of underwater scenes. Higher UICQE scores indicate superior color enhancement performance. Let Ip be the pixel values of an image in CIELab space, p=1…N. The image has N pixels. Ip=[Ip,ap,bp]. CI is the chroma. The underwater colour image quality evaluation metric UCIQE for image I in CIELab space is defined as:

UCIQE=c1×σc+c2×conl+c3×μs(22)

where σc is the standard deviation of chroma, conl is the contrast of luminance and μs is the average of saturation, and c1,c2,c3 are weighted coefficients.

SCM (Scene Consistency Metric) to evaluate in order to quantify the consistency of the color correction, we compute the average standard deviation of the intensity-normalized RGB values of the pixels tracked through the scene. We need to find a set of SYRF features P between consecutive frames of an underwater image, track the pixel x corresponding to the feature x∈P through the corrected image, and finally calculate the standard deviation of the pixel RGB values. This metric is used to measure the consistency of image correction methods between different views within the same scene. The specific formula is:

SCM=1N∑x∈P∑xi∈x(xi−μx)2Nx(23)

4.2.2 Underwater 3-D Reconstruction Evaluation Metric

We use a similar metric as Levy et al. which is widely used in the field of 3-D reconstruction.

PSNR (Peak Signal-to-Noise Ratio) PSNR is a fundamental metric for evaluating the fidelity of 3-D reconstructed scenes compared to ground truth data. It quantifies the level of noise and distortion present in the reconstructed 3-D models. A higher PSNR value implies a closer match to the ground truth, indicating superior reconstruction accuracy.

PSNR=10⋅log10⁡(MAX2MSE)(24)

In this formula, PSNR stands for Peak Signal-to-Noise Ratio, MAX represents the maximum possible pixel value in the image (typically 255 for 8-bit grayscale images), and MSE denotes the Mean Squared Error, which measures the mean squared difference between the original image and the reconstructed image. PSNR is used to assess the quality of image reconstruction, with higher values indicating greater similarity between the reconstructed and original images.

Structural Similarity Index (SSIM) [21], as mentioned earlier, is also used in this context to evaluate the similarity between the reconstructed 3-D models and the ground truth. It assesses the preservation of structural details in the 3-D reconstructions.

SSIM(x,y)=(2μxμy+C1)(2σxy+C2)(μx2+μy2+C1)(σx2+σy2+C2)(25)

In this formula:

x and y are the two input images being compared.

μx and μy represent the mean values of x and y, respectively.

σx2 and σy2 denote the variances of x and y, respectively.

σxy represents the covariance between x and y.

C1 and C2 are small constants added to avoid division by zero. Typically, C1=(k1L)2 and C2=(k2L)2 are used, where L is the dynamic range of pixel values in the images (e.g., 255 for 8-bit images), and k1 and k2 are constants to control the impact of C1 and C2.

4.3 Experimental Information

Our experiments were conducted on a high-performance server equipped with a NVIDIA RTX 4090 GPU with 24 GB of GPU memory and a Intel(R) Xeon(R) Platinum 8352V CPU @ 2.10 GHz. after testing, in the 3D reconstruction module, we set the aabb_scale parameter to 32 to achieve the best training effect. Retain the default values for other parameters.

4.4 Result and Discussion

4.4.1 Underwater Image Enhancement

Table 1 shows our experimental results, where we evaluated various methods using different evaluation metrics on the dataset. We conducted experiments on seven different scenarios (self collected datasets 1–122, 1–195, self collected datasets 2–004, 2–100, DRUVA195, 229, 272) to evaluate the performance of different methods in underwater 3D reconstruction. For each scenario, we considered eight image enhancement methods: CLAHE, Fusion, RGHS, Seatru, UCM, FUNIE-GAN, FA+, and our proposed method. The evaluation metrics used include UIQM and SCM, and measuring UIQM aims to quantify image quality, with higher values usually being better. The measurement of UCM aims to quantify the consistency of color correction, and the higher the value, the better. Based on the experimental results, it can be observed that our method is competitive in Dataset 1 and Dataset 2, with a small gap compared to the optimal indicator method. In the case of DRUVA, our method UIQM performs the best, 0.141 higher than the second highest CLAHE method. Please note that the final choice of method may depend on the specific circumstances and application requirements, as different methods may have strengths in different aspects. Overall, the experimental results suggest that our method is competitive in some scenarios but may not necessarily be the best choice in all situations. Fig. 2 shows enhanced underwater images using different methods on three datasets: self-collected dataset 1, self-collected dataset 2, and the DRUVA dataset.

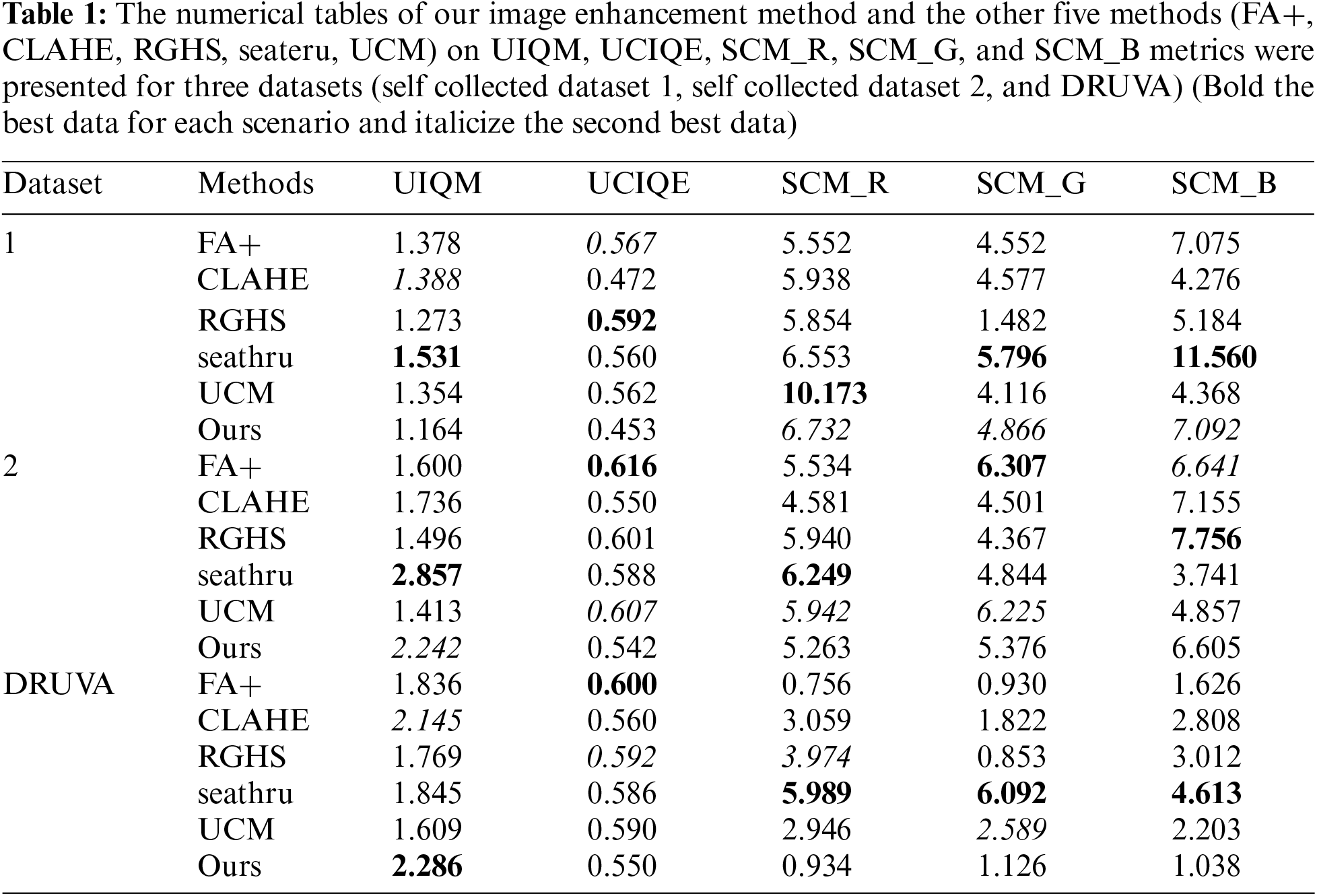
Figure 2: Enhanced images on self collected dataset 1, self collected dataset 2, and DRUVA dataset

4.4.2 Underwater Reconstruction

Table 2 shows our experimental results, comparing Seathu-NeRF with the methods we proposed using different evaluation metrics on our self collected dataset 1. In terms of PSNR, our method achieved the highest score of 18.40 (highlighted in bold), with metric values exceeding that of Seatru-NeRF 3.43, indicating excellent performance in image fidelity. For SSIM, our method values are only slightly lower than SeaThru NeRF 0.0010, indicating better structural similarity with live images. These results indicate that our method provides a good balance between runtime efficiency and reconstruction quality, making it suitable for practical applications. However, the choice between these two methods may depend on specific use cases and priorities. Overall, our method has shown promising results in both PSNR and SSIM, demonstrating their effectiveness in underwater scene reconstruction. Our method outperforms Seathru-NeRF in terms of PSNR, indicating more accurate pixel-wise reconstruction and better noise reduction, but slightly lags in SSIM due to less effective preservation of structural and textural details crucial for perceptual quality. Fig. 3 shows the comparison of our rendering performance with seathu NeRF on self collected dataset 1 and DRUVA.

Figure 3: Comparison of rendering performance between our method and seathru-NeRF on self collected dataset 2 and DRUVA

5  Conclusion and Future Work

5.1 Conclusions

Our image enhancement method relies on the chunking concept of CLAHE and Bayesian Retinex, which avoids a series of problems caused by abrupt color changes, and our approach ensures the continuity of image data. We employ the Colmap visual tool to obtain bitmap information from the original image frames, which offers higher robustness. Meanwhile, our keyframe filtering module is highly efficient, greatly saving computational resources and concurrently enhancing the efficiency of the entire system. The Instant-NGP method we selected, which utilizes hash coding, makes NeRF 3D reconstruction more efficient. As a result, the overall performance of our system is superior.

5.2 Limitations

While our method achieves good reconstruction results with low computational time, it is important to note that, as an image enhancement rather than image restoration approach, there is still room for improvement in terms of color fidelity. Additionally, during our experiments, we observed that the omission of modeling underwater imaging effects still leads to the formation of artifacts during training. Therefore, we consider optimizing the existing method to enhance reconstruction color accuracy and quality as a future avenue of research.

Future work will explore more advanced image restoration techniques to further enhance color accuracy. We have observed that neglecting the modeling of underwater imaging effects can lead to the formation of artifacts during the training process. Therefore, future research will focus on more accurately simulating these effects to improve reconstruction quality. Our method requires prior extraction of the image’s bitmap information, which may be challenging in complex scenes. We plan to investigate automated bitmap information extraction techniques to enhance the system’s robustness.

5.3 Future Work

In the future, we will continue to optimize our existing methods, particularly in improving reconstruction color accuracy and overall quality. We plan to apply our proposed method to a broader range of underwater scenes, including those with more challenging lighting and medium conditions. We will also explore the application of our method to 3D reconstruction in other scattering media, such as foggy environments or smoke-filled scenarios. The research presented in this paper not only advances the development of underwater 3D reconstruction technology but also provides valuable references for research in related fields, such as robotic navigation and environmental monitoring.

Acknowledgement: We would like to express our deepest gratitude to all those who have contributed to the completion of this work. Special thanks to the academic community for providing valuable insights and resources. Our school and funding support have played an important role in this research. Finally, we appreciate the opportunity and encouragement that have made this effort possible.

Funding Statement: This work was supported by the Key Research and Development Program of Hainan Province (Grant Nos. ZDYF2023GXJS163, ZDYF2024GXJS014), National Natural Science Foundation of China (NSFC) (Grant Nos. 62162022, 62162024), the Major Science and Technology Project of Hainan Province (Grant No. ZDKJ2020012), Hainan Provincial Natural Science Foundation of China (Grant No. 620MS021), Youth Foundation Project of Hainan Natural Science Foundation (621QN211).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Zhuoyifan Zhang, Lu Zhang; data collection: Liang Wang; analysis and interpretation of results: Lu Zhang, Liang Wang. Haoming Wu; draft manuscript preparation: Lu Zhang, Liang Wang. Haoming Wu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used in this study are the DRUVA dataset and self collected dataset. The DRUVA dataset that supports the results of this study was proposed in the “Self supervised monocular underwater depth recovery, image recovery, and real ocean video dataset”, IEEE International Conference on Computer Vision (ICCV), Paris, France, pp. 12248–12258, October 2023. The self collected dataset supporting the results of this study can be obtained from the corresponding author (Haoming Wu) upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. Müller, A. Evans, C. Schied, and A. Keller, “Instant neural graphics primitives with a multiresolution hash encoding,” ACM Trans. Graph., vol. 41, no. 4, pp. 102:1–102:15, 15, Jul. 2022. doi: 10.1145/3528223.3530127. [Google Scholar] [CrossRef]

2. M. Yang and A. Sowmya, “An underwater color image quality evaluation metric,” IEEE Trans. on Image Process., vol. 24, no. 12, pp. 6062–6071, 2015. doi: 10.1109/TIP.2015.2491020. [Google Scholar] [PubMed] [CrossRef]

3. J. Zhou et al., “WaterHE-NeRF: Water-ray Tracing neural radiance fields for underwater scene reconstruction,” arXiv preprint arXiv:2312.06946, 2023. [Google Scholar]

4. J. Jiang et al., “Five A+ network: You only need 9K parameters for underwater image enhancement,” arXiv preprint arXiv:2305.08824, 2023. [Google Scholar]

5. T. Treibitz and Y. Y. Schechner, “Turbid scene enhancement using multi-directional illumination fusion,” IEEE Trans. on Image Process., vol. 21, no. 11, pp. 4662–4667, 2012. doi: 10.1109/TIP.2012.2208978. [Google Scholar] [PubMed] [CrossRef]

6. X. Fu, P. Zhuang, Y. Huang, Y. Liao, X. P. Zhang and X. Ding, “A retinex-based enhancing approach for single underwater image,” in Proc. IEEE Int. Conf. Image Process. (ICIP), Paris, France, Oct. 27–30, 2014, pp. 4572–4576. doi: 10.1109/ICIP.2014.7025927. [Google Scholar] [CrossRef]

7. M. S. Hitam, W. N. J. H. W. Yussof, E. A. Awalludin, and Z. Bachok, “Mixture contrast limited adaptive histogram equalization for underwater image enhancement,” in Proc. Int. Conf. Comput. Appl. Technol. (ICCAT), Jan. 20–22, 2013, pp. 1–5. doi: 10.1109/ICCAT.2013.6522017. [Google Scholar] [CrossRef]

8. D. Akkaynak and T. Treibitz, “Sea-Thru: A method for removing water from underwater images,” presented at the IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPRLong Beach, CA, USA, Jun. 16–20, 2019, pp. 1682–1691. [Google Scholar]

9. M. J. Islam, Y. Xia, and J. Sattar, “Fast underwater image enhancement for improved visual perception,” IEEE Robot. Autom. Lett., vol. 5, no. 2, pp. 3227–3234, 2020. doi: 10.1109/LRA.2020.2974710. [Google Scholar] [CrossRef]

10. G. Klein and D. Murray, “Parallel tracking and mapping for small AR workspaces,” in Proc. IEEE/ACM Int. Symp. Mixed Augmented Reality (ISMAR), Nara, Japan, Nov. 13–16, 2007, pp. 225–234. [Google Scholar]

11. R. Mur-Artal, J. M. M. Montiel, and J. D. Tardos, “ORB-SLAM: A versatile and accurate monocular slam system,” IEEE Trans. Robot., vol. 31, no. 5, pp. 1147–1163, 2015. doi: 10.1109/TRO.2015.2463671. [Google Scholar] [CrossRef]

12. K. Konolige and M. Agrawal, “FrameSLAM: From bundle adjustment to real-time visual mapping,” IEEE Trans. Robot., vol. 24, no. 5, pp. 1066–1077, 2008. doi: 10.1109/TRO.2008.2004832. [Google Scholar] [CrossRef]

13. J. Revaud, P. Weinzaepfel, Z. Harchaoui, and C. Schmid, “EpicFlow: Edge-preserving interpolation of correspondences for optical flow,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Boston, MA, USA, Jun. 7–12, 2015, pp. 1164–1172. [Google Scholar]

14. R. Dubé, D. Dugas, E. Stumm, J. Nieto, R. Siegwart and C. Cadena, “SegMatch: Segment based place recognition in 3D point clouds,” in Proc. IEEE Int. Conf. Robot. Autom. (ICRA), Singapore, May 29–Jun. 3, 2017, pp. 5266–5272. [Google Scholar]

15. B. Mildenhall, P. P. Srinivasan, M. Tancik, J. T. Barron, R. Ramamoorthi and R. Ng, “NeRF: Representing scenes as neural radiance fields for view synthesis,” Commun. ACM, vol. 65, no. 1, pp. 99–106, 2021. doi: 10.1145/3503250. [Google Scholar] [CrossRef]

16. K. Zhang, G. Riegler, N. Snavely, and V. Koltun, “NeRF++: Analyzing and improving neural radiance fields,” arXiv preprint arXiv:2010.07492, 2020. [Google Scholar]

17. A. Pumarola, E. Corona, G. Pons-Moll, and F. Moreno-Noguer, “D-NeRF: Neural radiance fields for dynamic scenes,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Nashville, TN, USA, Jun. 19–25, 2021, pp. 10318–10327. [Google Scholar]

18. R. Martin-Brualla, N. Radwan, M. S. M. Sajjadi, J. T. Barron, A. Dosovitskiy and D. Duckworth, “NeRF in the wild: Neural radiance fields for unconstrained photo collections,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Nashville, TN, USA, Jun. 19–25, 2021, pp. 7206–7215. [Google Scholar]

19. Y. C. Guo, D. Kang, L. Bao, Y. He, and S. H. Zhang, “NeRFReN: Neural radiance fields with reflections,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), New Orleans, LA, USA, Jun. 19–24, 2022, pp. 18409–18418. [Google Scholar]

20. D. Levy et al., “SeaThru-NeRF: Neural radiance fields in scattering media,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Vancouver, BC, Canada, Jun. 18–22, 2023, pp. 56–65. [Google Scholar]

21. Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Trans. on Image Process., vol. 13, no. 4, pp. 600–612, 2004. doi: 10.1109/TIP.2003.819861. [Google Scholar] [PubMed] [CrossRef]