Multi-Level Image Segmentation Combining Chaotic Initialized Chimp Optimization Algorithm and Cauchy Mutation

1  Introduction

With the widespread application of various medical images in auxiliary medicine, computer-aided diagnosis has attracted increasing attention [1]. In medical image processing, image segmentation can effectively assist doctors in completing medical diagnoses or surgical treatments, especially for patients with milder conditions. The main issues of early diagnosis with medical images included blurred or imprecise localization of lesion regions [2]. At the same time, there may be significant gaps in the professional level of doctors. Computer assisted medical image segmentation not only avoids misdiagnosis caused by these gaps but also improves the efficiency of diagnosis and treatment [3]. To enhance the accuracy and timeliness of medical image segmentation, academics increasingly apply image thresholding and swarm intelligence optimization algorithm (IOA) in the field of multi-level medical image segmentation [1,3].

Image thresholding divides an image into two or more non-overlapping regions according to a vector of thresholds and the image’s gray level. While the length of the thresholds’ vector is 1, image thresholding can only divide the image into two regions: foreground and background. When its length exceeds 2, the image is divided into more and better-defined regions. However, as the number of thresholds increases, the corresponding calculations also rise exponentially, so swarm IOA is an effective solution [4,5]. To facilitate the application of IOA in multilevel image segmentation, a variety of objective functions to evaluate the segmentation quality are applied [6], including Kapur entropy, Otsu, minimum cross-entropy [7,8], etc.

In the objective function selection, Li et al. [9] compared and analyzed the effectiveness of fuzzy Kapur and Otsu based on the improved fuzzy Coyote Optimization Algorithm (IFCOA). Through visual and quantitative data analysis of natural and medical image segmentation, it concluded that the IFCOA based on fuzzy Kapur achieved better segmentation effect. Li et al. [10] improved the Satin Bowerbird Optimizer (SBO) through various strategies and also applied fuzzy Kapur to perform multi-level segmentation on plant images, by comparing the experimental results with the segmentation effects of discrete Grey Wolf Optimizer (GWO) and fuzzy Coyote Optimization Algorithm (FCOA), it was found that the ISBO has better segmentation performance. Rajinikanth et al. [11] analyzed and compared the application of fuzzy Shannon, fuzzy Kapur and Otsu in multilevel image thresholding. Based on the analysis and comparison of four benchmark medical image data sets (ETIS, ClinicDB, Kvasir and CV2020), the fuzzy Kapur has better clinical application in accuracy, precision and sensitivity. Similarly, Rajinikanth et al. [12] compared and analyzed the effectiveness of Kapur and Tsallis in multi-level segmentation of grayscale and color images. Through extensive experimental comparisons, both objective functions achieved better results and outperformed other similar methods. Wu et al. [13] applied Kapur as the fitness function and compare it with seven other similar methods through evaluation indices such as PSNR and FSIM. The experiments demonstrated that it has dependable performance in multilevel image segmentation. Karakoyun et al. [14] transform the single objective function commonly applied in Kapur and Otsu thresholding into multi-objective functions. Through the experimental analysis of standard data sets, the multi-objective function is superior to other single objective functions and can achieve better image segmentation quality. Renugambal et al. [15] used Kapur combining Water Cycle (WC) and Moth Flame Optimization Algorithm (MFOA) to complete the optimal segmentation of gray matter, white matter, and cerebrospinal fluid in brain medical images, and it has been verified that the Kapur has better segmentation efficiency.

On the application of swarm IOA in multilevel image segmentation, Yan et al. [16] improved the Whale Optimization Algorithm (WOA) based on Kapur to perform multi-level segmentation on hydrological images, and compared the experimental results with algorithms such as Bat Algorithm (BA), Flower Polarization Algorithm (FPA), then discover that WOA can effectively reduce computational complexity, improve segmentation accuracy and effectiveness. Zhu et al. [17] proposed a multi strategy learning Manta Ray Foraging Optimization Algorithm (MRFO). The MRFO selected a skip learning strategy to improve the convergence speed, proposed a behavior selection strategy to judge the current state of the race, and integrated the Tent and Gaussian mutation to avoid the MRFO falling into local optima. Selecting the CEC2017 test function and comparing the segmentation results with 8 algorithms such as PSO, it was found that the MRFO has better advantages and quality in image thresholding. Ewees et al. [18] fused the Artificial Bee Colony (ABC) with the Sine Cosine Algorithm (SCA) to form an improved algorithm (ABCSCA). The Otsu was applied to perform thresholding segmentation experiments on 19 images, and the PSNR and SSIM were used as measurement indicators to compare the segmentation performance of the ABCSCA with eight other algorithms such as SSA and GWO, it was found that the ABCSCA has better performance in terms of convergence speed, robustness and vision. Duan et al. [19] improved the Cuckoo Search Algorithm (ICS) by parameter adaptive and dynamic weighted random walk strategy. Six benchmark test images were subjected to segmentation experiments, and the experimental results compared with other algorithms confirmed that the ICS had better performance. In the field of medical image segmentation, Panda et al. [20] fused Cuckoo Search (CS) and Squirrel Search Algorithm (SSA), combined with the normalized local variance to correct the gray histogram, and achieved better image thresholding effect in the CEC 2005 standard medical image dataset. Ramadas et al. [21] improved Differential Evolution (DE) through mutation strategy for segmentation and diagnosis of brain medical images. Compared with the traditional Kapur scheme, the DE not only significantly reduced the calculation time, but also greatly improved the image segmentation quality. Wu et al. [22] proposed an improved Sparrow Search Algorithm (SSA) which integrated nonlinear inertial weights and Levy flight strategy. The SSA used a two-dimensional maximum entropy to segment classical and medical images, and compared with the WOA, PSO, GWO and other algorithms, the results showed that the SSA has better performance in terms of convergence speed, robustness and visual effect.

The various ideas for improving the global search ability of swarm IOA and avoiding local optima in its iterations can be summarized into two respects: (1) Improving the initialization mode of its population. At the beginning of the swarm IOA, the initial population with higher dispersion and stronger randomness is provided, to improve the optimal search ability and accelerate the convergence speed. (2) Optimizing the renewal strategy of the individual population. A mechanism to update the population of IOA is the most important means to avoid it falling into local optima. Theoretically, with the continuous iteration of the IOA, the final optimal solution is closer to the ideal one. However, if the IOA cannot continuously produce better solutions in its iteration, it easily falls into local optima. Therefore, this paper seeks to improve CHOA based on the above two key improvement directions, and to verify its segmentation effect in natural and medical images.

The CHOA is a swarm IOA proposed by Khishe et al. [23], which has simple principles, fewer parameters, and can be easily deployed and implemented. And the independent development of four type chimps in CHOA ensures the global search ability. However, there is still a risk of reverting to local optima in its iteration [24]. In this paper, Sin chaotic sequence is selected for population initialization to improve the quality of the initial individuals. In the process of population location updating, Cauchy mutation is introduced to reduce the risk of local optima in iteration, and thus form an improved CHOA developed by chaos initialization and Cauchy mutation (CICMCHOA). The main contributions are summarized as follows:

1.    In order to improve the initial population diversity and convergence performance of the CHOA, the random initialization mode of CHOA was improved by Sin chaotic initialization in CICMCHOA.

2.    The population update strategy of CHOA has been improved by utilizing Cauchy mutation. this not only avoids the CHOA falling into local optima but also enhances its global search ability and image segmentation performance.

3.    By combining fuzzy logic and fuzzy membership functions through fuzzy Kapur, this work explored the global optimization ability of CICMCHOA and improved the quality of image segmentation.

4.    The effectiveness of CICMCHOA in natural and medical image segmentation has been validated through extensive visual and data analysis, the experimental results were compared with those of the ISBO [10], ABCSCA [18], ICS [19] and classical meta-heuristic algorithm-DE in [7,8,21].

The rest of this paper is organized as follows. Section 2 briefly introduces the formation mechanism of CHOA and its mathematical modeling process. The CICMCHOA improved by Sin Chaos initialization and Cauchy mutation is provided in Section 3. In Section 4, the experimental results and detailed discussion are presented to illustrate the performance of CICMCHOA. Finally, the conclusion of CICMCHOA is presented in Section 5.

2  Description and Modeling of Chimp Optimization Algorithm

In the CHOA [23], according to wild social behavior and cooperative hunting processes, the initial chimp population is divided into four types with different responsibilities: attacker, barrier, chaser and driver. In practical applications, the attacker chimps represent the optimal solution to the problem. The barrier, chaser and driver chimps represent the three sub-optimal solutions in turn. Each type completes its own tasks of attacking, blocking, chasing and driving, and finally realizes the hunt through division of labor and cooperation. At the same time, the chimp population will be stimulated by external conditions such as sexual motivation and food, and chaos will follow their successful hunting. This mechanism ensures the further optimization and elimination development of the CHOA.

The basic steps of CHOA are as follows: assume there are N chimp individuals in a chimp population, where Xi represents the current position (threshold) of the chimps. The position updating process of the chimps driving and chasing prey is shown in Eq. (1).

Xc(t+1)=Xp(t)−D⋅A(1)

D=|CXp(t)−mXc(t)|(2)

where XP(t) is the prey position vector in the optimization process, XP(t) is the chimp (hunter) position vector, D represents the distance between the chimps and the prey, t represents the number of iterations during the operation of the CHOA. A,C and m are coefficient vectors, and their calculation formulas are shown in Eqs. (3)–(5).

A=2f⋅rand1−f(3)

C=2⋅rand2(4)

m=Chaotic_value(5)

rand1 and rand2 respectively represent a random number within the range [0,1], thus A and C is a random number inside [0,2], indicating the effects of prey location on chimp individual location. In Eq. (3), the variable f is a convergence constraint, its value decreases non-linearly from 2.5 to 0 in the iterative process of the CHOA. In calculating the update positions of four type chimps (the attacker, barrier, chaser and driver), f is calculated by fA,fB,fC and fD separately in Eqs. (6)–(9). In Eq. (5), m is the chaotic vector generated by the chaotic map, representing the degree to which the chimps are excited to hunt. In the hunting process, the chaotic vector in Eq. (5) represents the degree of chaos. To better reflect its impact on the CHOA, it is updated according to different formulas in different chimp populations, as shown in Eqs. (6)–(9).

fA=1.95−2t1/4/T1/3(6)

fB=1.95−2t1/3/T1/4(7)

fC=(−3t3/T3)+1.5(8)

fD=(−2t3/T3)+1.5(9)

In Eqs. (6)–(9), fA,fB,fC and fD respectively represent the updating strategies of the parameter f in four types (the attacker, barrier, chaser and driver chimps). t and T respectively represent the current number of iterations and the preset maximum number of iterations in turn.

In the exploration stage, CHOA simulates the predation process of chimps in nature. The attacker chimps representing the optimal solution complete the last attack on the prey, and the barrier, chaser and driver chimps occasionally participate in the attack behavior while completing their respective tasks. To improve the convergence speed, the CHOA model assumes that the barrier, chaser and driver chimps can also determine the location of the prey. Therefore, other chimps need to complete the iterative updating of their locations according to the location of the first four types of chimps, as shown in Eqs. (10)–(12).

{DA=|C1XA−m1X|DB=|C2XB−m2X|DC=|C3XC−m3X|DD=|C4XD−m4X|(10)

{Temp1=XA−A1DATemp2=XB−A2DBTemp3=XC−A3DCTemp4=XD−A4DD(11)

X(t+1)=(Temp1+Temp2+Temp3+Temp4)/4(12)

where XA,XB,XC and XD respectively represent the position vectors of the attacker, barrier, chaser and driver (i.e., the threshold vectors), and X(t+1) represent the updated position vectors of the current chimps in iteration.

3  The Improved CHOA (CICMCHOA)

3.1 Selection and Analysis of Chaos Parameter (m) in CHOA

The selection of parameter m is not described in detail in [23], neither are the strategies of parameter selection in other relevant literature, or only one single chaotic strategy is used. Therefore, this paper introduces 10 different chaotic maps (Chebyshev, Circle, Gauss/mouse, Iterative, Logistic, Piecewise, Sine, Singer, Sinusoidal and Tent), and seeks a better parameter selection scheme through experimental comparison. The detailed data comparison, analysis and discussion will be provided in Section 4.1.

3.2 Population Initialization Based on Sin Chaotic

The results of swarm IOA are to an extent controlled by the initial value of the initial population. The original CHOA initializes the population in a random way, which will lead to poorer initial solution quality, less population diversity and stronger distribution randomness in some cases. These problems will directly affect the global optimization ability of the CHOA in the subsequent optimization steps. Chaotic variables are used to improve the initial solution of the IOA because of their ergodicity, randomness and uniform distribution, and improve the quality of the initial population [10,17].

In commonly used methods of chaos initialization, Tent and Logistic chaotic models display limited map iterations. The distribution of Tent map is too uniform, which reduces the diversity of initial population. The distribution of logistic map also tends to be uniform and can only produce a small number of singular solutions, contributing less to population diversity. Sin chaotic model by comparison, is a framework with infinite-collapse, with more even distribution while ensuring the differentiation of the initial population. Therefore, this paper uses Sin chaotic map to initialize the population. The Sin chaotic map can be expressed as:

{xn+1=sin⁡πxn,n=0,1,2,…,N−1≤xn≤1,xn≠0(13)

In Eq. (13), to avoid a fixed or zero value between [−1, 1], the initial value of xn is set to a real number not equal to 0.

After the initial population generated by Sin chaotic map, several N dimensional solutions Xi,j,(i=1,2,3,…,N;j=1,2,3,…,d) are obtained. Then, the generated initial solutions are arranged according to the fitness function, and four of the optimal solutions are selected as the attacker, barrier, chaser and driver chimps of the population, to complete the initialization process based on the Sin chaotic map.

3.3 Position Updating Strategy Integrating Cauchy Mutation

As can be seen from Eq. (11), other chimp individuals in the population converge to the optimal solution according to the guidance of the decision-making bodies of attacker, barrier, chaser and driver chimps. However, if the four types of individuals as population decision makers fall into local optima, the full population may easily do so too, thus reducing population diversity, optimization range and accuracy. To address this issue, this paper proposes Cauchy mutation strategy to increase the diversity of the population, improve the global search ability of the CHOA and avoid the problem of ‘pre-maturing’. The standard Cauchy distribution function is shown in Eq. (14).

f(x)=1π(1x2+1)(14)

From the probability density distribution of Cauchy function, it can be seen that the function obtains the maximum at the coordinate origin, and the absolute value of the maximum is relatively small (only between 0.30 and 0.35), to ensure that the mutated chimp individuals will not spend much time exploring the surrounding area, and to improve the global search performance of the CHOA without increasing its complexity. Therefore, making full use of the disturbance ability of Cauchy strategy can improve the diversity of the population, escape of local optima, and improve the global search ability of the CICMCHOA. The improved optimal solution is obtained by Eq. (15), cauchy(0,1) represents the Cauchy operator, calculated by Eq. (14).

Xi,jt+1=Xbest(t)+cauchy(0,1)⊕Xbest(t)(15)

Although Cauchy Mutation can effectively increase the diversity of the population, it can conversely reduce the convergence speed of the CHOA. To balance conflicts between convergence speed and population diversity, a probability variable P is introduced into the improved scheme in this paper, as shown in Eq. (16). While a random number generated by CICMCHOA exceeds P, the Cauchy perturbation is used to prevent the CICMCHOA falling into local optima. Otherwise, the Cauchy perturbation strategy is ignored.

P=−Exp(titermax)20+θ(16)

θ is the adjustment parameter which is set to 0.05, Exp is an exponential function based on the natural constant e. Finally, the position updating strategy of the CICMCHOA changes into:

X(t+1)=Xbest+Xbest∗cauchy(0,1), if rand(1)>P(17)

4  Analysis and Comparison of Experimental Results

4.1 Experiment Preparation and Parameter Setting

In order to verify the practicality of the CICMCHOA in the field of image segmentation, this paper selects four benchmark test images to analyze and compare the segmentation effects of the CICMCHOA and CHOA, and then selects six distinct kinds of medical images to investigate the effectiveness of CICMCHOA in medical image segmentation. In addition to comparison with the CHOA, it is also fully compared and analyzed with the DE [7,8,21], ISBO [10], ABCSCA [18], and ICS [19]. In this paper, the number of test thresholds (NTT) is set to 2–5, respectively, and the number of iterations to 10000. According to [9,10], Kapur is the most widely used objective function in medical segmentation, and the comparison works [10,18,19] also uses fuzzy Kapur as the optimization objective. Therefore, this paper continues to take the same objective function, using PSNR [25] and FSIM [26] to compare the differences between CICMCHOA and other algorithms in segmentation effect. The experimental environment runs on Windows 10 (64-bit) with AMD R9 processor, 32 GB RAM and Matlab 2016a. The experimental parameter values of CICMCHOA are shown in Table 1, the parameters of the comparative works follow their original parameter settings.

In Table 1, the search agent number (SAN) represents the number of chimps, m is the chaotic parameter in Eq. (5), NTT is the number of preset thresholds, Iteration is the maximum number of iterations. To prove the rationality of parameter selection in Table 1, the effects of different parameters in brain image segmentation are analyzed in Tables 2–5.

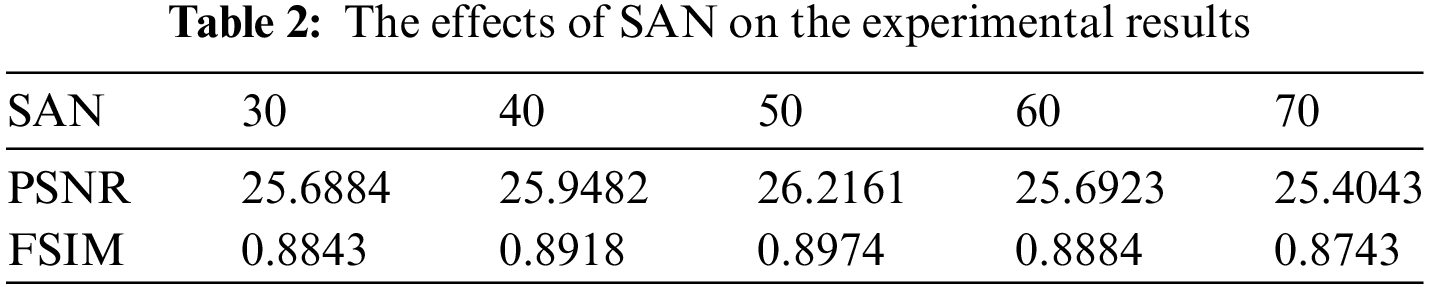
Table 2 compares brain images in different SAN conditions through PSNR and FSIM. To analyze the effects of SAN on the experimental results, the NTT is fixed to the maximum of 5. Other parameters remain consistent with the original CHOA. From the experimental comparison, we can see that when the SAN is set to 50, the optimal values of PSNR and FSIM are obtained.

In Tables 3 and 4, the effects of m adopting different chaotic map strategies on the experimental results are illustrated, and the SAN is fixed to 50, the NTT is set to 5, other parameters remain consistent with the original CHOA. From the data comparison, it can be concluded that the image segmentation effect arrived the best when the parameter m is “Iterative”.

Table 5 illustrates the effects of different iterations on the experimental results. The optimal values of other parameters from Tables 2 to 4 are selected. It can be seen from the data comparison that when the Iteration is set to 1000, the values of PSNR and FSIM are the highest, and continuing to increase the number of iterations cannot visibly improve the image segmentation effect.

4.2 Natural Segmentation Results Based on CICMCHOA

This paper selects four different benchmark test images to analyze and compare the segmentation effects of CHOA and CICMCHOA. In Figs. 1 and 2, the visual effects of multi-level segmentation are presented.

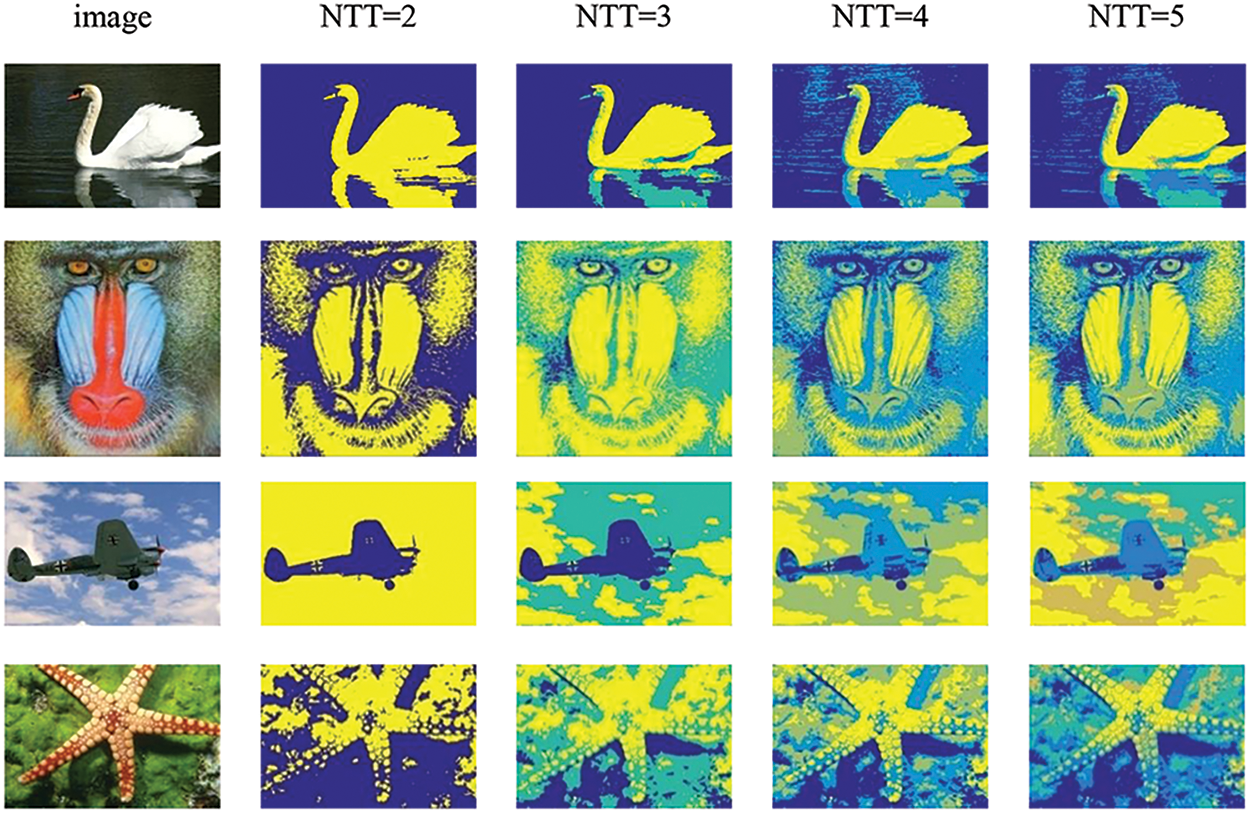
Figure 1: Natural image segmentation based on CHOA

Figure 2: Natural image segmentation based on CICMCHOA

From Figs. 1 and 2, it is difficult to see the difference in segmentation effect based on CHOA and CICMCHOA. Therefore, the PSNR and FSIM used for each image at different thresholds are recorded in Table 6.

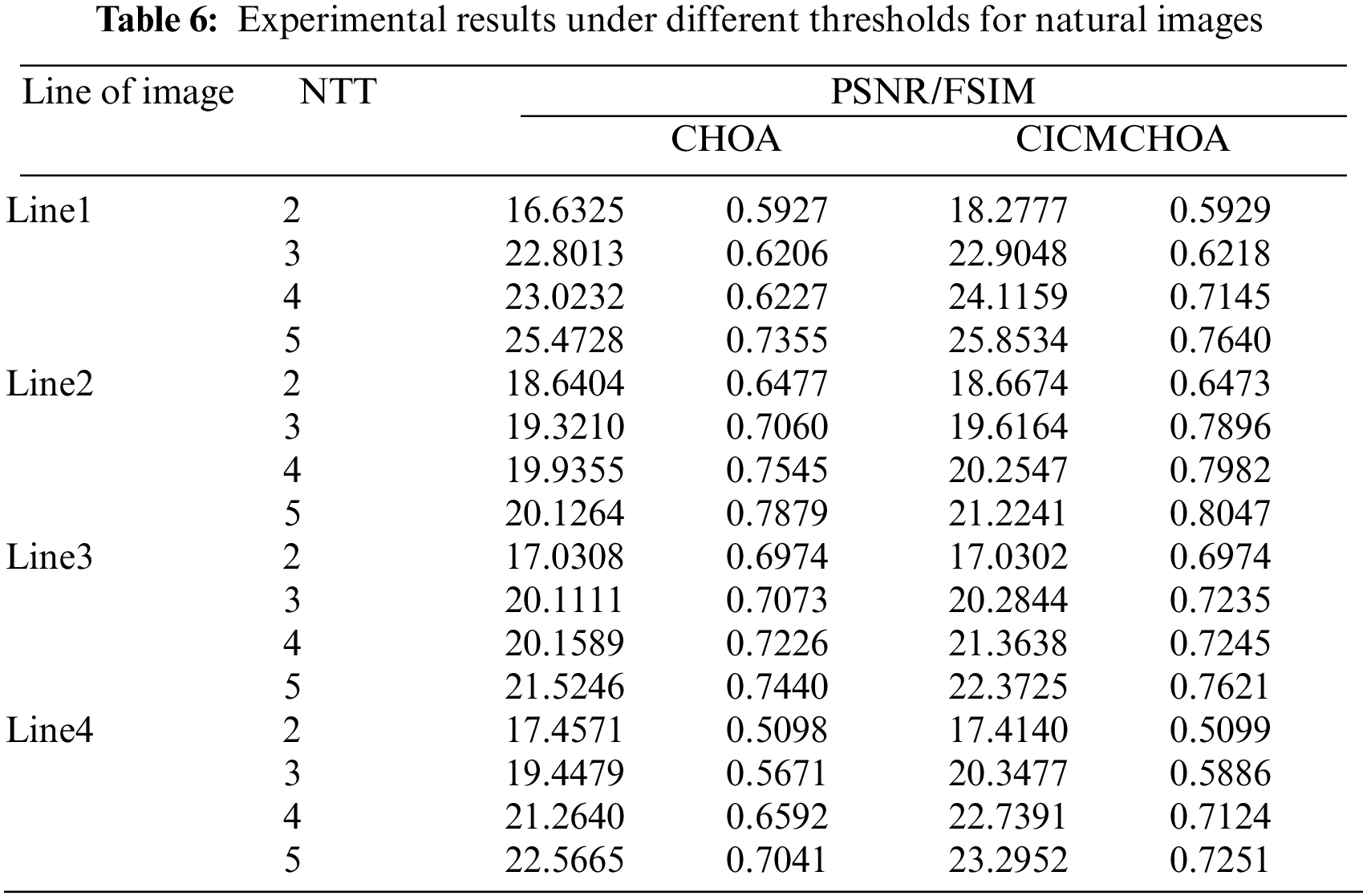
Based on PSNR, it can be seen from Table 6 that except for the case where the NTT in Line3 and Line4 are 2, the segmentation effect of CICMCHOA is not ideal. In other cases, the segmentation effect is better than the CHOA. FSIM also has similar comparative results, proving that the CICMCHOA proposed in this paper can effectively improve the quality of image segmentation.

4.3 Medical Segmentation Results Based on CICMCHOA

Based on six distinct kinds of medical images, this paper uses CICMCHOA to optimize fuzzy Kapur to obtain the optimal thresholds, and then completes the thresholding segmentation. Figs. 3 and 4 respectively show the original medical image and the visual segmentation results with different NTT.

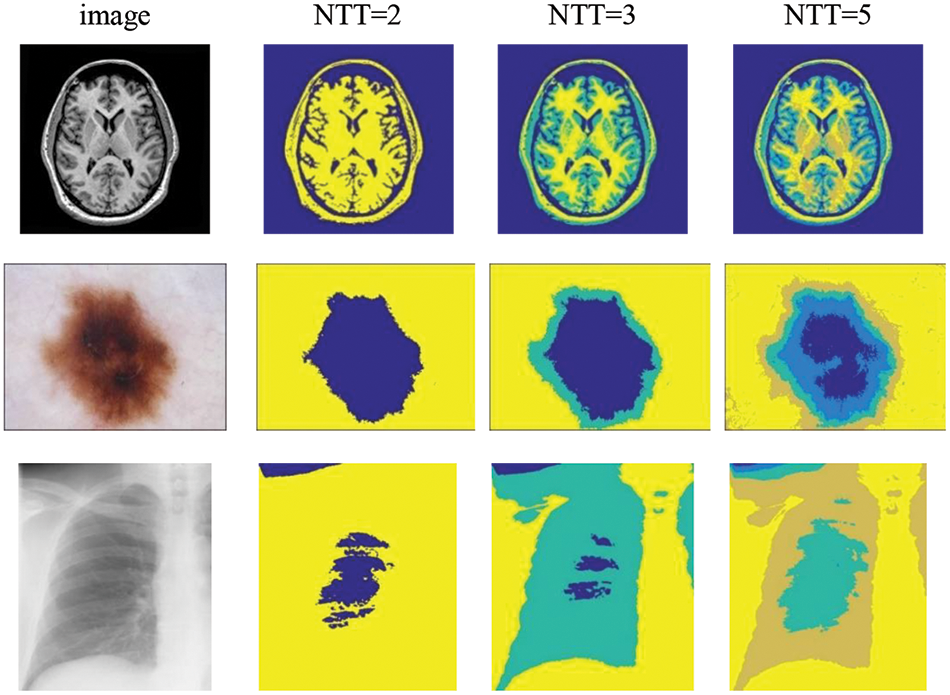
Figure 3: Medical image segmentation based on CICMCHOA (part 1)

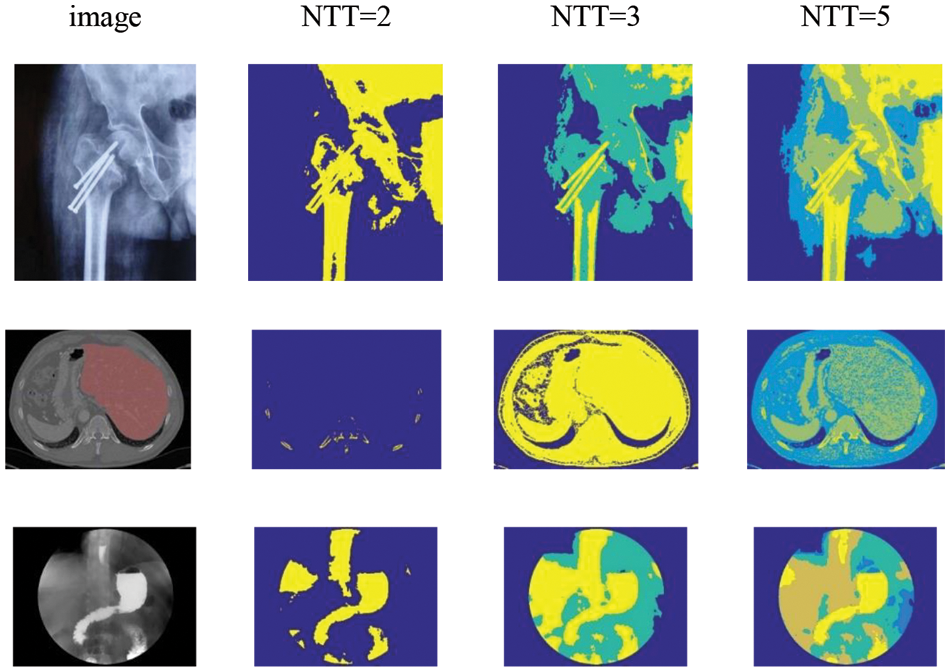
Figure 4: Medical image segmentation based on CICMCHOA (part 2)

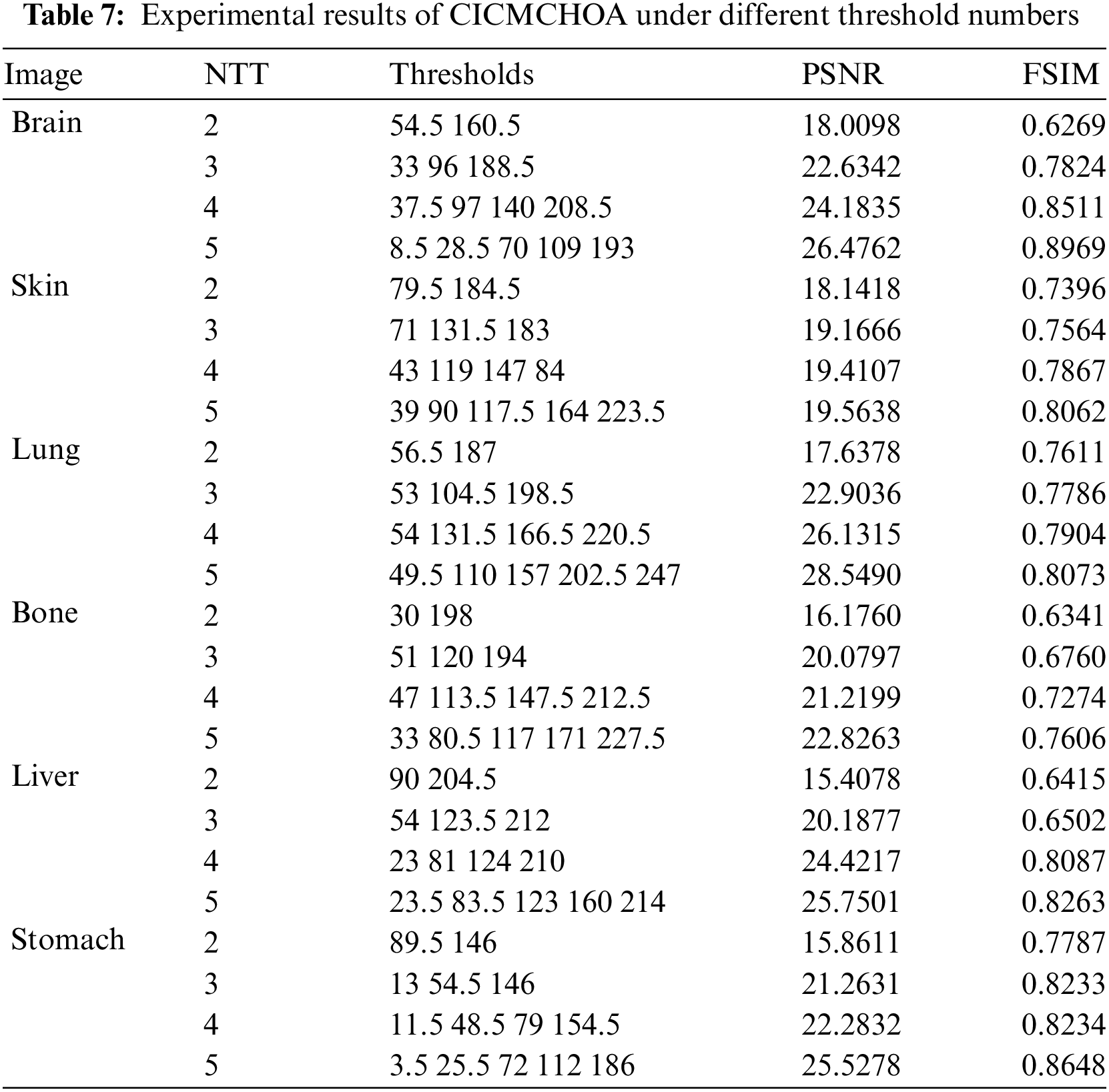
From the visual segmentation results illustrated in Figs. 3 and 4, we can observe that when the NTT is 2, the CICMCHOA can effectively locate and segment the anterior background or the lesion area. When the NTT increases to 3 and then to 5, the details of image segmentation are better defined, which can effectively assist doctors in medical diagnosis. Compared with the segmentation results presented in the references [10,18,19], the CICMCHOA in this paper has the same visual effect and is difficult to distinguish. Therefore, the Thresholds, PSNR and FSIM obtained in the segmentation of six medical images are given in Table 7. A more detailed comparative analysis is provided in next section.

4.4 Comparison and Analysis of Similar Algorithms

To more specifically and definitively compare the performance of the CICMCHOA, this paper takes PSNR as the evaluation standard and compares the segmentation effectiveness of CICMCHOA, CHOA, DE, ISBO, ABCSCA and ICS in medical images through the measured data, as shown in Table 8.

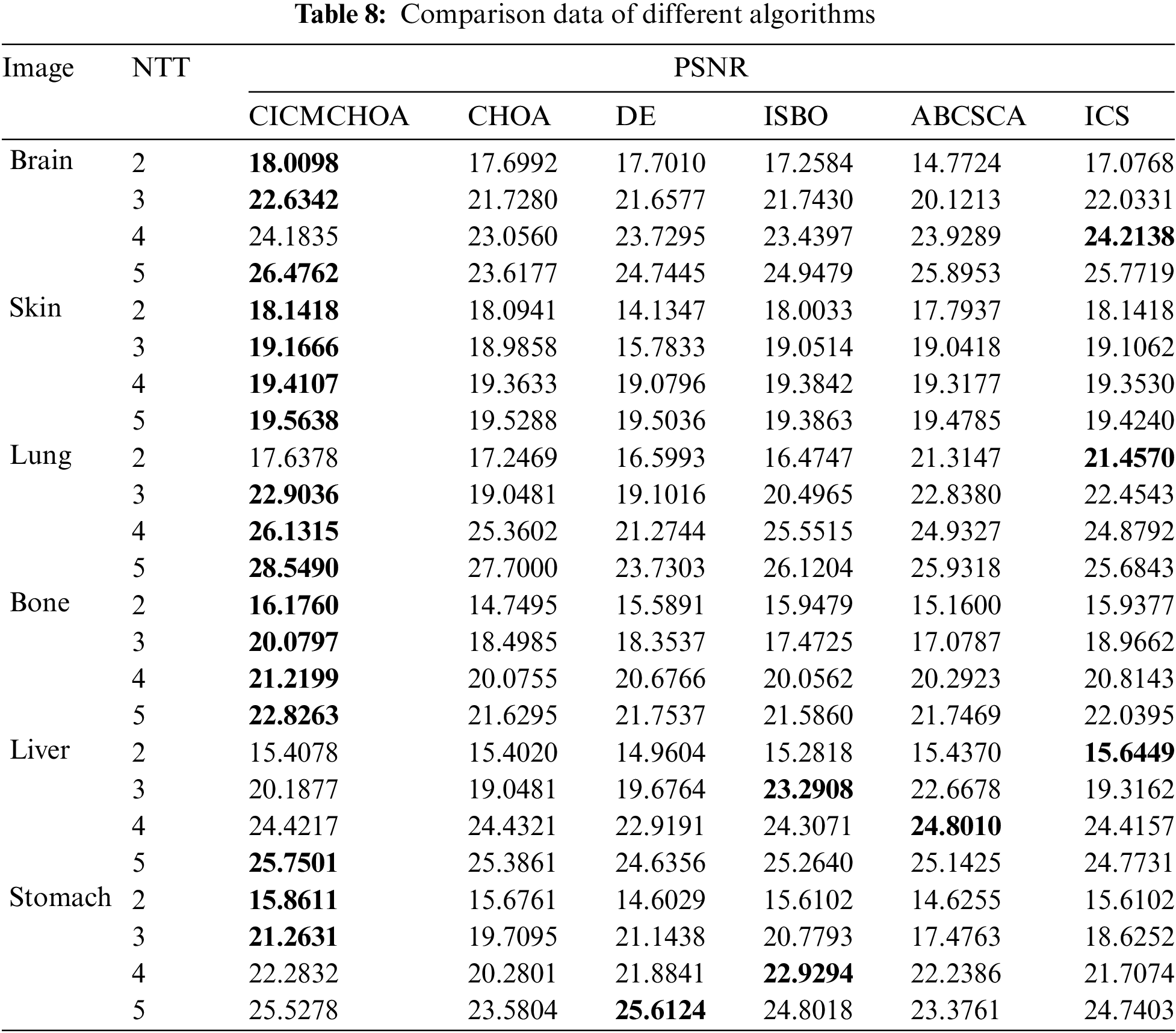
From the comparison of the data in Table 8, the CICMCHOA is superior to the CHOA in medical image thresholding. The most obvious improvement occurs on figure “Lung” when the NTT is 3, the PSNR increases by 3.8555. In the case of NTT = 4 in figure “liver”, the effect of CICMCHOA is lower than that of CHOA, but it is only 0.0104 lower. Overall, The CICMCHOA is 20.2% higher than the CHOA at the maximum. All data taken together, the mean PSNR of CICMCHOA increases byabout 5%.

Compared with DE, the segmentation effect of the CICMCHOA improves by 28% at the maximum, an average increase of 7.7%. Compared with ISBO, the CICMCHOA improves by 15% at the maximum, an average increase of 3%. Compared with ABCSCA, CICMCHOA is slightly weaker than the ABCSCA in the “Lung” when the NTT is 2, in the “Liver” when the NTT is 2,3,4. In other cases, the effects of CICMCHOA are stronger than those of ABCSCA. Overall, compared with ABCSCA, CICMCHOA increases by 4.3%. Compared with the ICS, the CICMCHOA performs slightly lower than the ICS in the “Brain” with NTT = 4, the “Lung” and “Liver” with NTT = 2. On the whole, the CICMCHOA is 2.2% higher than the ICS. Therefore, the improved strategy of CICMCHOA significantly improves the optimization effectiveness of CICMCHOA in medical image segmentation, and outperforms the other similar algorithms.

5  Conclusions

To meet the needs of natural and medical image segmentation, this paper uses the Sin chaotic to improve the random initialization strategy of CHOA. This not only improves the diversity of the initial population, but also reduces the risk of the CHOA falling into local optima. In the process of population position updating, the small disturbance ability of Cauchy mutation strategy is fully utilized to improve the probability of population mutation, further reduce the probability of CHOA falling into local optima, and balance the global search ability and local exploration ability of CICMCHOA. Finally, taking the fuzzy Kapur as the objective function, different kinds of natural and medical images are selected and compared with CHOA, DE, ISBO, ABCSCA and ICS, respectively. From the comparison results, the CICMCHOA shows better segmentation effect in medical image segmentation. In the future, we shall conduct in-depth exploration in the selection, fusion, and optimization of fuzzy objective functions, as well as integration with other IOA, to further improve the performance of CHOA in image segmentation.

Acknowledgement: Thanks for the support and help of the team when writing the paper. Thanks to the reviewers and experts of your magazine for their valuable opinions on the article revision. This has provided great inspiration when writing.

Funding Statement: This work is supported by Natural Science Foundation of Anhui under Grant 1908085MF207, KJ2020A1215, KJ2021A1251 and 2023AH052856, the Excellent Youth Talent Support Foundation of Anhui under Grant gxyqZD2021142 and the Quality Engineering Project of Anhui under Grant 2021jyxm1117, 2021kcszsfkc307, 2022xsxx158 and 2022jcbs043.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shujing Li, Linguo Li, Zhangfei Li; data collection: Wenhui Cheng, Chenyang Qi; analysis and interpretation of results: Zhangfei Li, Shujing Li, Linguo Li, Wenhui Cheng; draft manuscript preparation: Zhangfei Li, Shujing Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in P. Arbelaez et al. at https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/resources.html (accessed on 10/01/2023). The remaining data that support the findings of this study are available from the corresponding author, Linguo Li, upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Pare, A. Kumar, G. K. Singh, and V. Bajaj, “Image segmentation using multilevel thresholding: A research review,” IJST-T Electr. Eng., vol. 44, no. 1, pp. 1–29, Mar. 2020. doi: 10.1007/s40998-019-00251-1. [Google Scholar] [CrossRef]

2. E. H. Houssein, G. M. Mohamed, I. A. Ibrahim, and Y. M. Wazery, “An efficient multilevel image thresholding method based on improved heap-based optimizer,” Sci. Rep, vol. 13, no. 1, pp. 1–36, Jun. 2023. doi: 10.1038/s41598-023-36066-8. [Google Scholar] [PubMed] [CrossRef]

3. M. Juneja et al., “Survey of denoising, segmentation and classification of magnetic resonance imaging for prostate cancer,” Multimed. Tools Appl., vol. 80, no. 19, pp. 29199–29249, Aug. 2021. doi: 10.1007/s11042-021-11044-2. [Google Scholar] [CrossRef]

4. F. S. Xiong, Z. Q. Zhang, Y. Ling, and J. Zhang, “Image thresholding segmentation based on weighted Parzen-window and linear programming techniques,” Sci. Rep, vol. 12, no. 1, pp. 1–16, Aug. 2022. doi: 10.1038/s41598-022-17818-4. [Google Scholar] [PubMed] [CrossRef]

5. S. Singh, N. Mitta, D. Thakur, H. Singh, D. Oliva and A. Demin, “Nature and biologically inspired image segmentation techniques,” Arch Comput. Method. E, vol. 29, no. 3, pp. 1415–1442, May 2021. doi: 10.1007/s11831-021-09619-1. [Google Scholar] [CrossRef]

6. M. Amiriebrahimabadi, Z. Rouhi, and N. Mansouri, “A comprehensive survey of multi-level thresholding segmentation methods for image processing,” Arch. Comput. Methods Eng., vol. 2024, pp. 1–51, Mar. 2024. doi: 10.1007/s11831-024-10093-8. [Google Scholar] [CrossRef]

7. J. Chen et al., “Multi-threshold image segmentation based on an improved differential evolution: Case study of thyroid papillary carcinoma,” Biomed. Signal Proces., vol. 85, no. 1, pp. 1–12, Aug. 2023. doi: 10.1016/j.bspc.2023.104893. [Google Scholar] [CrossRef]

8. A. K. Bhandari, “A novel beta differential evolution algorithm-based fast multilevel thresholding for color image segmentation,” Neural Comput. Appl., vol. 32, no. 9, pp. 4583–4613, Oct. 2020. doi: 10.1007/s00521-018-3771-z. [Google Scholar] [CrossRef]

9. L. Li, L. Sun, Y. Xue, S. Li, X. Huang and R. F. Mansour, “Fuzzy multilevel image thresholding based on improved coyote optimization algorithm,” IEEE Access, vol. 9, pp. 33595–33607, Apr. 2021. doi: 10.1109/ACCESS.2021.3060749. [Google Scholar] [CrossRef]

10. L. Li, S. Qian, Z. Li, and S. Li, “Application of improved satin bowerbird optimizer in image segmentation,” Front. Plant Sci., vol. 13, pp. 1–12, May 2022. doi: 10.3389/fpls.2022.915811. [Google Scholar] [PubMed] [CrossRef]

11. V. Rajinikanth, S. M. Aslam, S. Kadry, and O. Thinnukool, “Semi/Fully automated segmentation of gastric-polyp using aquila-optimization algorithm enhanced images,” Comput. Mater. Contin., vol. 70, no. 2, pp. 4087–4105, Sep. 2022. doi: 10.32604/cmc.2022.019786. [Google Scholar] [CrossRef]

12. V. Rajinikanth, S. Kadry, R. G. Crespo, and E. Verdu, “A study on RGB image multi-thresholding using Kapur/Tsallis entropy and moth-flame algorithm,” Int. J. Interact. Multi., vol. 7, no. 2, pp. 163–171, Dec. 2021. doi: 10.9781/ijimai.2021.11.008. [Google Scholar] [CrossRef]

13. B. Wu, L. Zhu, J. Cao, and J. Wang, “A hybrid preaching optimization algorithm based on kapur entropy for multilevel thresholding color image segmentation,” Entropy, vol. 23, no. 12, pp. 1–12, Dec. 2021. doi: 10.3390/e23121599. [Google Scholar] [PubMed] [CrossRef]

14. M. Karakoyun, S. Gulcu, and H. Kodaz, “D-MOSG: Discrete multi-objective shuffled gray wolf optimizer for multi-level image thresholding,” Eng. Sci. Technol., vol. 24, no. 6, pp. 1455–1466, Dec. 2021. doi: 10.1016/j.jestch.2021.03.011. [Google Scholar] [CrossRef]

15. A. Renugambal and K. S. Bhuvaneswari, “Kapur’s entropy based hybridised WCMFO algorithm for brain MR image segmentation,” IETE J. Res., vol. 9, no. 5, pp. 1–20, Jul. 2023. doi: 10.1016/j.jestch.2021.03.011. [Google Scholar] [CrossRef]

16. Z. Yan, J. Zhang, Z. Yang, and J. Tang, “Kapur’s entropy for underwater multilevel thresholding image segmentation based on whale optimization algorithm,” IEEE Access, vol. 9, pp. 41294–41319, Jul. 2021. doi: 10.1109/ACCESS.2020.3005452. [Google Scholar] [CrossRef]

17. D. Zhu, C. Zhou, Y. Qiu, Y. Tang, and S. Yan, “Kapur’s entropy underwater image segmentation based on multi-strategy manta ray foraging optimization,” Multimed. Tools Appl., vol. 82, no. 14, pp. 21825–21863, Jun. 2023. doi: 10.1007/s11042-022-14024-2. [Google Scholar] [CrossRef]

18. A. A. Ewees, M. Abd Elaziz, M. A. A. Al-Qaness, H. A. Khalil, and S. Kim, “Improved artificial bee colony using sine-cosine algorithm for multi-level thresholding image segmentation,” IEEE Access, vol. 8, pp. 26304–26315, Feb. 2020. doi: 10.1109/ACCESS.2020.2971249. [Google Scholar] [CrossRef]

19. L. Duan, S. Yang, and D. Zhang, “Multilevel thresholding using an improved cuckoo search algorithm for image segmentation,” J. Supercomput., vol. 77, no. 7, pp. 6734–6753, Jul. 2021. doi: 10.1007/s11227-020-03566-7. [Google Scholar] [CrossRef]

20. R. Panda, L. Samantaray, A. Das, S. Agrawal, and A. Abraham, “A novel evolutionary row class entropy based optimal multi-level thresholding technique for brain MR images,” Expert. Syst. Appl., vol. 168, no. 2, pp. 1–13, Apr. 2021. doi: 10.1016/j.eswa.2020.114426. [Google Scholar] [CrossRef]

21. M. Ramadas and A. Abraham, “Detecting tumours by segmenting MRI images using transformed differential evolution algorithm with kapur’s thresholding,” Neural Comput. Appl., vol. 32, no. 10, pp. 6139–6149, May 2020. doi: 10.1007/s00521-019-04104-0. [Google Scholar] [CrossRef]

22. D. Wu and C. Yuan, “Threshold image segmentation based on improved sparrow search algorithm,” Multimed. Tools Appl., vol. 81, no. 23, pp. 33547, Sep. 2022. doi: 10.1007/s11042-022-13334-9. [Google Scholar] [CrossRef]

23. M. Khishe and M. R. Mosavi, “Chimp optimization algorithm,” Expert. Syst. Appl., vol. 149, no. 1, pp. 1–15, Jul. 2020. doi: 10.1016/j.eswa.2020.113338. [Google Scholar] [CrossRef]

24. H. Jia, K. Sun, W. Zhang, and X. Leng, “An enhanced chimp optimization algorithm for continuous optimization domains,” Complex Intell. Syst., vol. 8, no. 1, pp. 65–82, Feb. 2022. doi: 10.1007/s40747-021-00346-5. [Google Scholar] [CrossRef]

25. W. A. H. Jumiawi and A. El-Zaart, “Improving minimum cross-entropy thresholding for segmentation of infected foregrounds in medical images based on mean filters approaches,” Contrast Media Mol. Imaging, vol. 1, pp. 1–13, Mar. 2022. doi: 10.1155/2022/9289574. [Google Scholar] [PubMed] [CrossRef]

26. Q. Liu, N. Li, H. Jia, Q. Qi, and L. Abualigah, “Modified remora optimization algorithm for global optimization and multilevel thresholding image segmentation,” Mathematics, vol. 10, no. 7, pp. 1–11, Apr. 2022. doi: 10.3390/math10071014. [Google Scholar] [CrossRef]