Dynamic Offloading and Scheduling Strategy for Telematics Tasks Based on Latency Minimization

1  Introduction

With the evolution of information and communication technology and the rapid iteration of technological industrial changes, the integration of emerging technologies such as the Internet of Vehicles, artificial intelligence, and 5G technology is accelerating towards intelligent and networked upgrades, giving rise to a large number of intelligent application services such as autonomous driving and real-time image and video-assisted navigation [1,2]. These emerging technologies require a large amount of computing and storage resources to process real-time complex tasks, posing great challenges to low latency and high rate communication. Currently, due to the limited capabilities of vehicles themselves and the high latency problem of traditional cloud computing long-distance transmission, they can no longer meet the huge computing resource requirements in the Internet of Vehicles.

The emerging Internet of Vehicles (IoV) supports several types of communication, including Vehicle-to-Vehicle (V2V), Vehicle-to-Cloud (V2C), and Vehicle-to-Infrastructure (V2I). V2C utilizes remote cloud resources to provide significant computational support, but has high transmission latency [3]. Although V2V reduces the latency caused by distance, it cannot provide strong support for a large number of real-time tasks due to the limited resources of vehicles. V2I moves remote servers to the vicinity of Road Side Units (RSUs) to provide the nearest service support for vehicles on the road, overcoming the limitations of vehicle resources and reducing the response delay of computational tasks. V2I is essentially the fusion of IoV and edge computing, and is an application scenario of Vehicular Edge Computing (VEC), which has significant advantages in improving task transmission efficiency and enhancing real-time interaction experience. The process of offloading latency-sensitive or computationally intensive tasks from vehicles to edge nodes is called task offloading, while resource allocation maximizes the utilization of edge servers or nodes to provide high-performance application services with limited resources. Optimizing task offloading and resource allocation is the core issue of VEC, but there are several challenges, such as frequent changes in the network topology due to the vehicles’ motion, heterogeneity of application services for different users in terms of delay tolerance, and the increasing data volume of vehicle tasks, which burdens the computation of IoV and urgently needs to consider optimization problems of task offloading and computation [1]. Currently, most work focuses on offloading tasks to roadside units based on the V2I mode, but as computational tasks become more complex and data volumes grow, edge servers can become overloaded, resulting in a significant increase in task queuing delay and a decrease in system performance [2]. With the continuous iteration of intelligent technology in IoV, the computational and storage capabilities of vehicles are constantly improving [3]. By using V2V networks as a supplement to V2I task offloading, the overall computational capacity of the system can be effectively expanded, and the load of RSUs can be alleviated [4].

With the continuous increase in the scale of vehicles in IoV, using traditional heuristic algorithms or swarm intelligence-related models lacks active learning ability and cannot adapt well to dynamic vehicle environments. If traditional optimization algorithms are used to solve the task offloading and resource allocation problems in IoV, the computational complexity will increase exponentially. Based on the above challenges, the emerging and rapidly developing technology of reinforcement learning provides a new approach to solving these problems. By regarding vehicles or edge nodes as intelligent agents and utilizing the communication cooperation between agents in reinforcement learning to learn the optimal strategy, the dynamic allocation of resources, power selection, and task offloading decisions in IoV can be effectively solved.

This article is based on the aforementioned research background and focuses on the difficulties and challenges faced in the context of the IoV, specifically the problems of task offloading and resource allocation in dynamic IoV scenarios. The article explores the collaboration between V2I and V2V communication modes in resource allocation. By introducing a multi-agent reinforcement learning algorithm in the IoV dynamic model, efficient task offloading and resource allocation can be achieved.

Our main contributions of this paper are summarized as follows:

1.    In this paper, we study the problem of task computation offloading for vehicular networking, where computationally intensive vehicular tasks are offloaded to vehicles with remaining computational resources. In the problem, we take into account the computational capabilities, communication boundaries and communication delays of the vehicles, aiming to optimize the task offloading decision so that the average task completion time is minimized.

2.    In this paper, we propose a deep reinforcement learning-based dynamic offloading and scheduling scheme for Internet of Vehicles tasks to achieve dynamic decision-making for task offloading during non-uniform movement between vehicles. Simulation results show that the algorithm proposed in this paper can intelligently learn the optimal offloading strategy from the interaction with the dynamic network environment.

The remainder of this paper is organized as follows. Section 2 presents related works. Section 3 formulates the Internet of Vehicles task offloading problem. In Section 4, we propose a solution algorithm based on deep reinforcement learning. Numerical results are presented in Section 5. Section 6 concludes this paper.

2  Related Work

In order to ensure the demand for service quality or experience quality of users and effectively improve the network capacity of the vehicular ad hoc network (VANET) system, researchers have proposed various resource scheduling and allocation methods in the VANET communication network. Meanwhile, mobile edge computing (MEC) is also increasingly integrated into the resource scheduling of VANET.

Ning et al. [5] modeled the architecture of wireless communication and edge computing in vehicular networks using deep reinforcement learning and built an intelligent offloading system to maximize user experience quality. Xin Li’s team [6] studied a dynamic wireless resource allocation strategy in a multi-layered vehicle edge cloud computing framework to better adapt to vehicle task offloading scenarios. Wang et al. [7] used DQN network to solve the network time-varying problem caused by vehicle mobility and designed a task offloading strategy for vehicular edge computing scenarios. Chen et al. [8] proposed a task offloading scheme that relies only on V2V cooperative communication by fully exploring the idle resources of aggregated vehicles. They formulated task execution as a Min-Max problem between a single task and multiple vehicles, and used the particle swarm optimization algorithm to solve the problem. Additionally, the authors [9] proposed a distributed task offloading strategy based on DQN for the limited resources of edge servers, aiming to minimize the task execution time of vehicles. Wang et al. [10] studied the collaboration offloading problem in vehicular networks and proposed a heuristic algorithm for minimizing the average task completion time by considering the randomness of vehicle movement speed and channel conditions in vehicular networks.

In order to enhance network performance, an increasing number of researchers are exploring the integration of V2V and V2I communication, specifically aiming to improve the capacity performance of V2I links while satisfying the constraints of V2V link latency and reliability.

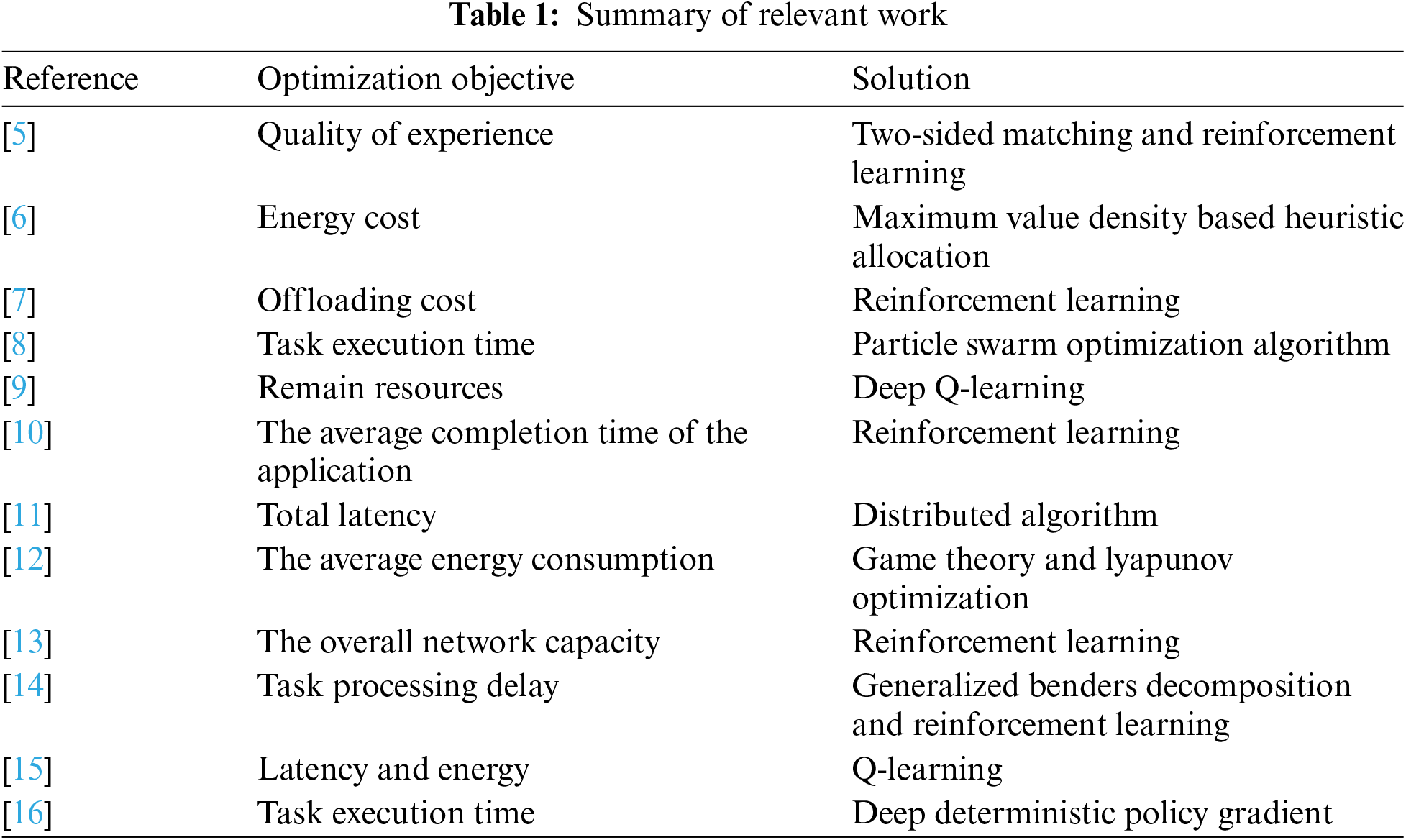
The research team of Wang et al. [11] studied how to achieve joint unloading of mobile vehicles and proposed an unloading architecture and efficient joint unloading strategy that supports V2I communication in a vehicle network that supports joint V2V communication, with the goal of minimizing total delay. The task allocation ratio of the unloading part was considered to find the minimum total delay result. In addition, Lei Feng’s team [12] proposed a joint computing and URLLC resource allocation strategy for co-V2I-assisted V2X networks to adapt to large-scale fading slow-changing channel conditions while ensuring network stability, where the V2I and V2V links do not interfere with each other and occupy different frequencies. Yang et al. [13] proposed an efficient ETAC method to improve learning efficiency and convergence speed, while satisfying V2I link QoS, ensuring low latency requirements for V2V links, and maximizing the overall network capacity through joint task selection, resource allocation, and power control. In [14], the authors consider the joint network selection and computational offloading optimization problem in a multi-service vehicular edge computing environment aiming to minimize the overall latency and energy consumed in an IoV scenario and propose a cooperative q-learning based offloading algorithm. In [15], the authors propose a joint task offloading and resource allocation scheme for a docked mobile vehicle-assisted edge computing scenario based on multi-device, parked and mobile vehicles, which is covered by a base station equipped with an edge server. The tasks of the devices can be offloaded both to the base station and further from the base station to the vehicle. In [16], the authors propose a task offloading scheme for IoV edge computing architecture based on reinforcement learning computing to achieve fast processing of tasks, taking into account the explosive growth of data streams, the rapid increase in the number of vehicles, and the increasing scarcity of spectrum resources, which makes it impossible for the vehicle terminals to perform efficient computations. The relevant research work is summarized in Table 1.

Based on the above literature review, there are still some issues in resource scheduling in the Internet of Vehicles. Firstly, most of the studies did not consider the dynamic mobility environment in the resource scheduling process. Although some studies have addressed the unloading problem of moving vehicles or considered the impact of vehicle speed changes, most of them are based on two assumptions: vehicles are traveling at a constant speed or are relatively stationary during task unloading. The unloading decisions made in these scenarios do not take into account the dynamic decision-making problems in the complex and real-time changing Internet of Vehicles environment, which is unrealistic. Secondly, most of the current research on using reinforcement learning to solve Internet of Vehicles task unloading problems adopts single-agent reinforcement learning algorithms. However, in actual Internet of Vehicles scenarios, there are a large number of vehicles, and the real-time changes and dynamic environment of vehicles will exponentially increase the dimensions of state and action spaces, which can easily lead to the problem of dimension explosion during actual training and affect the final unloading results.

3  System Model and Problem Formulation

We construct task offloading model for vehicular networks, which takes into account scenarios where tasks cannot be split, multiple vehicles are involved with a single base station. As illustrated in Fig. 1, the constructed model uses V={Vs,Vt} to represent the vehicles in the considered scenario, where Vs denotes the service vehicles represented by the set Vs={vs1,vs2,…,vsm}, and m represents the number of service vehicles; Vt denotes the task vehicles represented by the set Vt={vt1,vt2,…,vtn}, and n represents the number of task vehicles; E denotes the base station, which also refers to the edge server. The model is built in the scenario of a busy crossroads where vehicles are on a dual-carriageway, and the road is all within the coverage range of a base station. Vehicles communicate with each other through the DESC communication technology, establishing connections with the base station through designated channels. Some important notations are listed in Table 2.

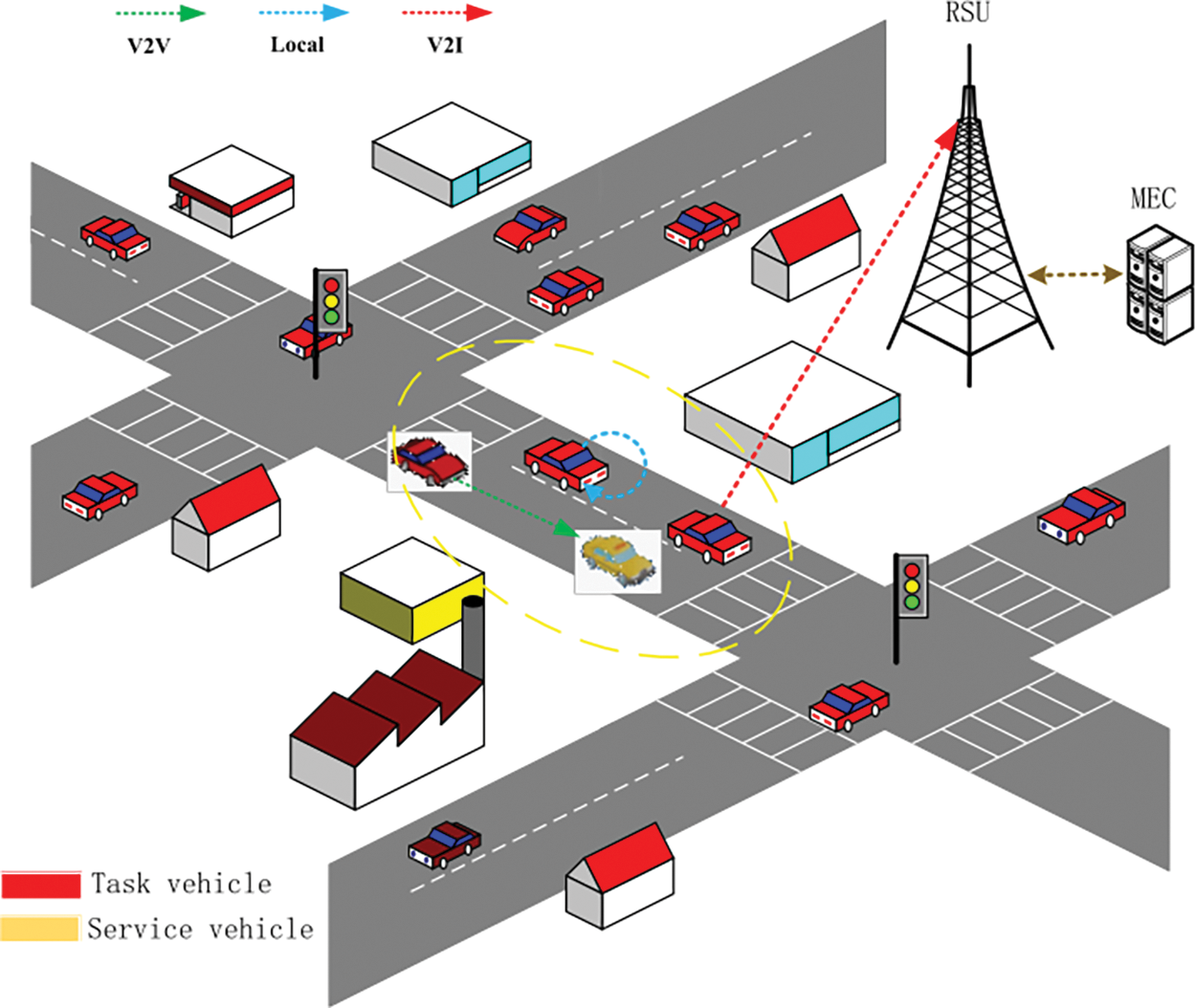
Figure 1: Task offload model in IoV

3.1 Communication Model

As the distance that vehicles move during task offloading between vehicles is very limited and the channel state changes only slightly, and the duration of information exchange and data transmission between vehicles and the base station is usually at the millisecond level, the vehicular network topology can be considered as stable and unchanging during the process of resource scheduling and task offloading. In vehicular communication, the orthogonal frequency-division multiple access (OFDMA) technology is adopted, and the task vehicles connected to the same service vehicle or the base station are mutually interference-free. When tasks need to be offloaded to service vehicles or the base station, the task data or the offloaded task computing instructions need to be transmitted through the wireless link. The communication models for these two scenarios are considered as follows.

1) Unload to Service Vehicles: Assuming the wireless channel for uploading task data between the task vehicle and the service vehicle is an additive white Gaussian noise channel, and since the tasks in the model considered in this paper are indivisible, the formula for calculating the data wireless transmission rate R is given by:

Rtnsm=Blog2⁡(1+Ptn|hn~|2dn−α(t)σn2),(1)

where B represents the wireless bandwidth of the system, Ptn represents the transmission power of the task vehicle, which is the uplink transmission power, σn represents the noise power, hn~ is the channel fading coefficient between the task vehicle and the service vehicle, dn−α(t) represents the transmission path loss, and α is the path loss index. Due to the movement of vehicles, dn(t) represents the time-varying distance between the task vehicle and the service vehicle during the task offloading and transmission process. For this model, it is assumed that the speed of the task vehicle tn and the service vehicle sm are vs and vt, respectively, and the initial distance is d0. The formula for calculating dn(t) is given by:

dn(t)=|d0+(vs−vt)t|2.(2)

The above formula assumes that d0 is not equal to zero, as two vehicles cannot travel at the same position. In addition, the tasks studied in this paper are delay-sensitive, with a delay typically in the order of milliseconds. Vehicles on the road generally travel at high speeds, assuming a speed of 50 ms. The relative speed between the two vehicles is 50 km/h, resulting in a time-varying distance of 0.695 m. However, this value can be ignored because at a relative speed of 50 km/h, the minimum safe distance between vehicles should not be less than 50 m. Therefore, the following formula is obtained:

dn(t)=|d0|,d0≠0.(3)

Assuming the amount of data unloaded to the service vehicle is D, the delay in data transmission can be calculated as follows:

tdata(sm,tn)=DRtnsm=DBlog2⁡(1+Ptn|hn~|2|d0|−ασn2).(4)

During the unloading process, there is also the uploading of calculation instructions related to task unloading. The size of these instructions is usually tens to hundreds of bits, so their delay can be ignored compared with the delay in data transmission. After receiving the calculation instructions, the service vehicle will also undergo a transformation of its own state (such as coordinate transformation), which depends on the data received from the task vehicle. The formula for this process is as follows:

tntran=DMtranFn,(5)

where Mtran represents the computational intensity of the state transformation, and Fn represents the CPU cycle of the service vehicle, which remains relatively stationary during the actual calculation process of the task. Due to continuous upgrading of vehicle equipment and enhancement of wireless transmission technology, the uploading of task data and the perception of the service vehicle almost occur simultaneously. In order to minimize the unloading time, the smaller value between tdata and ttran is generally taken. Therefore, the transmission time from the task vehicle to the service vehicle can be represented as:

tupload_v(sm,tn)=min{tdata(sm,tn),tntran}.(6)

2) Unload to Service Base Station: Assuming that the transmission power of the uplink channel during the unloading process from the task vehicle to the base station is PE and the noise power is σE, according to Eq. (1) , the wireless upload rate from the task vehicle sm to the base station E can be obtained:

RtnE=Blog2⁡(1+PE|hE~|2dE−α(t)σE2),(7)

where dE represents the time-varying distance between the task vehicle and the base station, which is related to the unloading time, the initial position and the movement speed of the task vehicle. Therefore, we have:

dE(t)=|d0−vst|2+H02,(8)

where d0 represents the initial distance between the task vehicle and the base station, H0 represents the height of the base station. Similarly, due to the high-speed movement of the vehicle, the effect of millisecond-level displacement changes on dE(t) is negligible. Therefore, dE(t) becomes:

dE(t)=|d0|2+H02.(9)

Therefore, as each time slot of the task unloading process, the variation of the time-varying distance can be regarded as a constant. Thus, Eq. (6) can be rewritten as:

RtnE=Blog2⁡(1+PE|hE~|2(|d0|2+H02)−α/2σE2).(10)

Similarly, with reference to Eqs. (4) and (5), the data transmission delay tdata(E,tn) and state transition delay tEtran of task unloading to the base station can be obtained:

tdata(E,tn)=DRtnE=DBlog2⁡(1+PE|hE~|2(|d0|2+H02)−α/2σE2),(11)

tEtran=DMtranFE,(12)

where FE represents the CPU cycle of the MEC server in the base station. Similar to unloading to the service vehicle, in order to minimize the unloading time, the minimum value of the transmission delay and the state transition delay is generally taken. Therefore, the unloading delay of the task to the base station can be represented as:

tupload_E(E,tn)=min{tdata(E,tn),tEtran}.(13)

3.2 Computation Model

Once the computing task is generated on the task vehicle and enters decision-making, it will be executed locally or unloaded to the surrounding service vehicles or base station for execution based on the strategy and task size selection.

When a task is executed locally or offloaded to a service vehicle, tvcomp represents the execution delay on the vehicle, D represents the task size, Fv represents the CPU cycle of the vehicle, and M represents the computational intensity of the task (cycles/bit), i.e., the computational resources required per bit of input data. Since the resource configuration of the task vehicle and the service vehicle is not consistent, Fv is also different

tvcomp=DMFv.(14)

When tasks are offloaded to the base station, tEcomp represents the time delay for task execution on the base station, where FE represents the CPU cycle of the base station’s MEC server and fcomp represents the proportion of computing resources allocated to the task in this time slot compared to the total MEC resources. Therefore, the calculation delay of the task on the base station can be expressed as:

tEcomp=DMFEfcomp.(15)

Considering the above communication and computation models, the calculation methods for the time delay of the three task offloading modes considered in this paper can be expressed as follows:

{Tlocal=tvcompTV2V=tupload_v(sm,tn)+tvcompTV2I=tupload_E(E,tn)+tEcomp.(16)

3.3 Dynamic Constraint Model

As this paper considers the scenario of a two-lane road in the vehicular ad hoc network, vehicles may unload their tasks onto a service vehicle traveling in the opposite direction. The relative speed between the two vehicles can reach more than 200 km/h. For a time slot with a large amount of task data, the delay from unloading to the service vehicle and then back to the result transmission can be significant. Assuming a delay of 0.5 s, the relative distance between the two vehicles increases by more than 28 meters. Assuming the maximum distance for effective communication between vehicles is DistV2Vmax, this distance must be taken into account. If the initial distance between the task vehicle and the unloading service vehicle approaches the maximum distance, then during the task unloading and transmission process, the distance between the two vehicles is very likely to exceed DistV2Vmax, resulting in the inability of the calculation result to be returned normally and the failure of the task unloading and transmission. This process is referred to as the communication boundary problem in this paper.

In response to the dynamic situation caused by the rapid movement of vehicles, this paper proposes a dynamic constraint condition, which is expressed as follows:

d0s+vrsTV2V<DistV2Vmax.(17)

Regarding the unloading of tasks from the vehicle to the base station, it is stipulated that the maximum distance allowed for effective communication between the vehicle and the base station is DistV2Imax. Assuming the initial distance between the task vehicle and the base station is d0E, and the relative velocity of the task vehicle with respect to the base station during the time slot is vrE, the following equation can be derived:

d0E+vrETV2I<DistV2Imax.(18)

Under the dynamic model constraints mentioned above, after the vehicle executes the unloading strategy and obtains the unloading target, it does not immediately perform the unloading action. Instead, it evaluates whether the above constraints are satisfied based on the task volume of the time slot, the location of the vehicle and base station sensed by the environment, and the speed of other vehicles. If the constraints are satisfied, it immediately performs the current unloading action and awaits the result. Otherwise, the current target is removed, and the unloading strategy searches for a suboptimal unloading target until a new target that satisfies the constraints is found. Since this evaluation is performed locally and has minimal computation, the delay can be ignored.

3.4 Problem Formulation

The communication model, computation model, and dynamic constraint model for vehicle-to-base-station joint offloading in vehicular networks have been presented above. This section focuses on establishing the task offloading and resource scheduling problem for vehicular networks based on the described system model. In order to achieve the offloading of computational tasks in a dynamic scenario, to meet the computational resource demands of vehicular network tasks, a multi-constraint problem with the objective of minimizing the average completion time Tave of system tasks can be formulated.

minTave(Vs,Vt,E)=minn∈N1n{∑tlocal+∑tV2V+∑tV2I}s.t.{C1:∑i∈MrTi≤RtotalC2:∑j∈mCijs≤CiC3:Ti∈[60,200]C4:∑i∈Nficomp≤1.C5:ficomp∈[0,1]C6:(3−17)C7:(3−18)(19)

In Eq. (20) , constraint C1 indicates that the total amount of computing resources in the model system is greater than or equal to the comprehensive computing resources required for unloading tasks in each time slot; constraint C2 means that the total amount of computing resources required for tasks accepted by each service vehicle does not exceed the maximum computing resources owned by the service vehicle itself; constraint C3 indicates the range of task sizes considered in the model, with different types of tasks corresponding to different size intervals (in MB); constraints C4 and C5 limit the proportion of computing resources required for tasks unloaded to the base station, and finally constraints C6 and C7 represent the dynamic constraint model. The optimization problem above is a non-linear programming problem and has NP-hard characteristics, so the following will use multi-agent deep reinforcement learning methods to solve this problem.

4  TDO-MADDPG Algorithm

4.1 Markov Decision Process Model

Appropriate decisions are made at the beginning of each period for task offloading of the vehicle based on the current resources in the system, thus maximizing the long term rewards [17]. At the beginning of the training phase, as the vehicle moves, the task vehicle will make appropriate actions based on the currently explored environmental situation and receive appropriate environmental rewards. During the training process, those beneficial strategies will be accumulated until the end of the training, then the task vehicle in this system will make the best scheduling and task offloading using the position changes of the service vehicle and the base station. For task offloading of task vehicles in this scenario, each task vehicle is defined as an agent, and each agent learns one of its own policies that guides its optimal strategy during task offloading to minimize the average processing delay of the task. The Markov decision process can be defined as (S,A,R). The definitions of each part are presented separately below.

(1) State

The global state space is made up of the state spaces of multiple task vehicles, and the state space si of a task vehicle vti can be represented as:

S={s1,…,si,sN},si={D,loci,Dists,DistE},(20)

where D and loci denote the task vehicle The size of this unloaded task and the vehicle location, Dists and DistE represent the set of distances from each service vehicle and the distance from the base station. Each agent cannot know the complete state space of the environment, the intelligence obtains the state information of the environment through the observation function, and participates in the training of the optimal overall rewards based on partial observations.

(2) Action

Since tasks are not split in the model considered in this section and it is guaranteed that the unloaded tasks can be processed in each time slot, each task vehicle can only unload a single task. The global action space is composed of the action spaces of multiple task vehicles, and each task vehicle agent executes its own actions synchronously in each time slot without sequential order, i.e., the system executes a joint action. The global action space and the action space of the task vehicles are defined as:

A={a1,…ai,…,aN},ai={Vs,E},Vs={vs1,…,vsm},(21)

where Vs denotes the set of service vehicles offloaded by the task vehicle, {vs1,…,vsm} and E denote whether they are offloaded to the corresponding service vehicle or base station. From the above action space, it can be seen that as the number of vehicles increases, the dimension of the global action space also increases dramatically.

(3) Reward

The model is trained in such a way that each task-vehicle agent continuously maximizes its own long-term reward by interacting with the environment, and makes the global reward converge to the optimal value of the system. For high-speed moving vehicles in the IoV network, the tasks are latency-sensitive, and the system goal of minimizing the average processing latency of the tasks is made clear during the Markov model construction process, which is essentially to minimize the task execution latency of the system. Here the latency of vehicle task processing in the system is included in the reward function in each time slot, defining the overall reward of the system as Rt. Because the goal of this paper is to minimize the objective function, the reward value should be negative. From the communication model and computation model above, Rt mainly includes the communication delay ricomm and computation delay ricomp during the unloading process of the task vehicle. Let the system reward for each time slot be rt, which represents the weighted sum of the delay of the unloading process of each task vehicle in that time slot:

rt=∑i∈Nρiti=∑i∈Nρi(ricomm+ricomp),∑ρi=1.(22)

where ρi denotes the reward weighting factor of each agent in that time slot, then the overall reward of the system shall be the sum of the rewards of each time slot, which can be expressed as:

Rt=−(Rcomm+Rcomp)=−(∑i∈lrti)=−(∑i∈l∑j∈Nρi(rji,comm+rji,comp)).(23)

4.2 Algorithm Design

The framework of the task dynamic offloading and scheduling scheme for vehicular networks based on MADDPG is shown in Fig. 2. Each task vehicle agent obtains experience through interaction with the environment, and then uses the feedback experience to guide its own behavior strategy. Multiple agents jointly explore the vehicular network environment and replay experiences based on the experience replay pool to break the correlation between samples and update the main network parameters and target network parameters of each agent until the model system converges to a stable state. In order to optimize the overall objective function, the agents here have a completely cooperative relationship and share the same reward mechanism. At the same time, the implementation process of this scheme is divided into two stages: centralized training and distributed execution. In the training stage, the agent obtains a reward with the goal of reducing system latency, and then updates its corresponding Actor network and Critic network to adjust it to the optimal strategy. In the execution stage, each agent obtains a local observation state based on the observed local environmental state, and then makes the optimal offloading strategy based on the trained network.

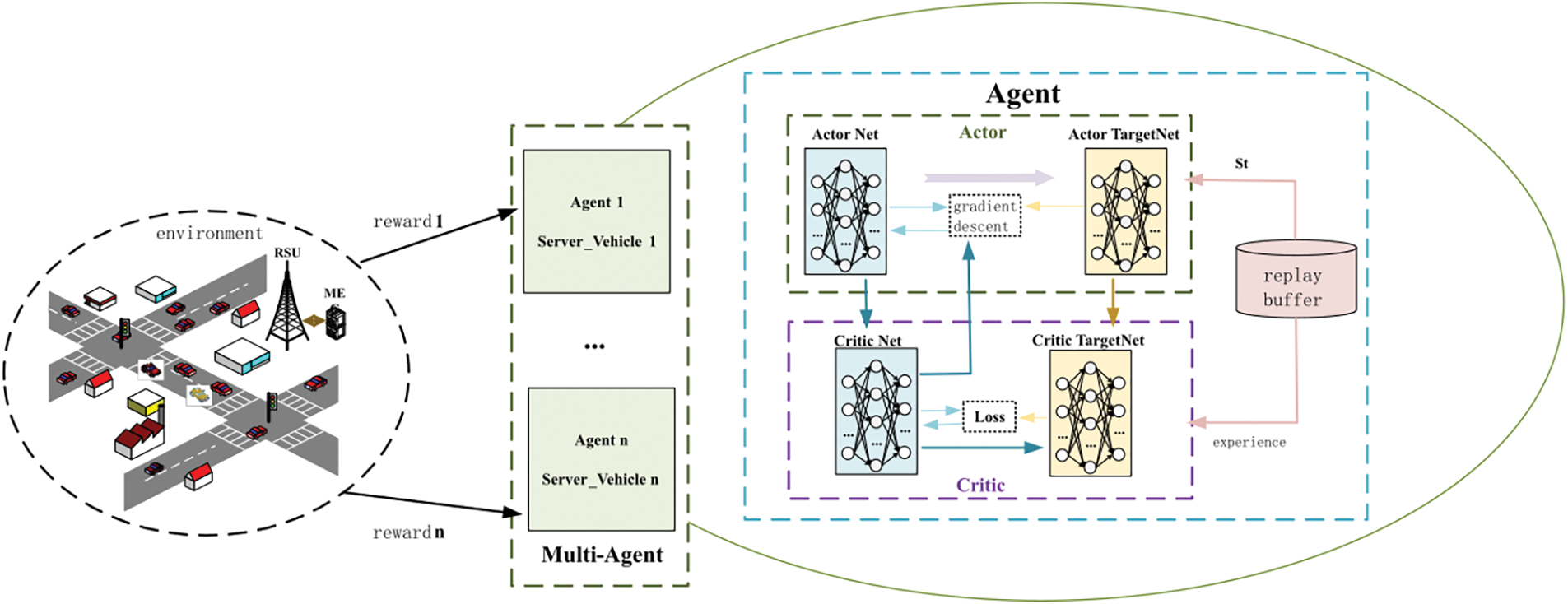
Figure 2: TDO-MADDPG framework

Algorithm 1 shows the training process of the TDO-MADDPG algorithm, which includes the recovery of experience and the use of experience for network updates. During the experience collection process, only when the experience recovery pool is full, a set of randomly selected experiences is started for training, and at the end of the sub-training round, each task vehicle intelligence is softly updated for its respective target network. For each training round the average delay of the system tasks is minimized as the optimization objective, and the computational resources of the system are used as the constraints, and it is also assumed that the topology of the whole car network is kept relatively stable during the offloading process of the tasks, which ensures the reliability and stability of the data transmission to a certain extent.

5  Simulation Analysis

This section establishes a real-time dynamic environment for task offloading and resource allocation in vehicular ad hoc networks and conducts convergence analysis of the TDO-MADDPG algorithm. The effectiveness of the proposed solution is evaluated through an analysis of the average task completion time. The algorithm’s performance is trained and analyzed with respect to parameters, vehicle numbers, and task size. Finally, the algorithm is compared and discussed with DDPG, MADDPG, ATE (All Tasks for Edge), and ATSV (All Tasks for Server Vehicles) algorithms under the same scenario, evaluating convergence and average task completion time to demonstrate the advantages of the optimal strategy.

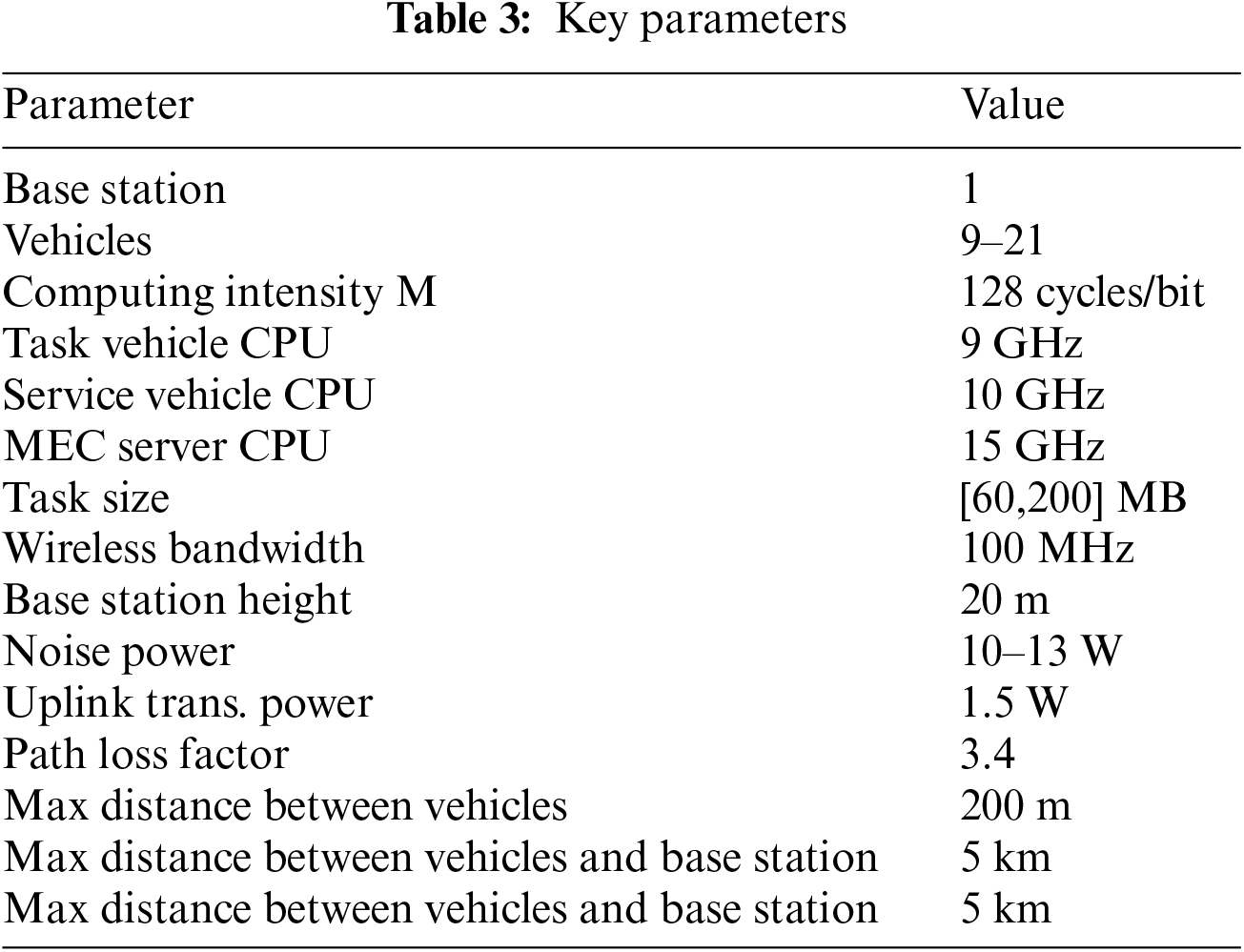
The simulation in this paper is implemented using Python and Pytorch, running on Ubuntu 18.04.6 operating system with Nvidia GeForce RTX 3080 graphics card. The vehicle movements are based on the CRAWDAD [18] publicly available autopilot trajectory dataset. The Python version used is 3.6. The task size interval is [60,200] MB, divided into 15 types of tasks (sizes correspond to 60, 70, ..., 200 MB), where different sizes represent different types of vehicle tasks. Some key parameters are listed in Table 3.

5.1 Recycling Pool Training

Training was conducted on the algorithm with regards to the size of the experience pool and the size of the sampled data clusters, in order to investigate their impact on the convergence of the algorithm. As shown in Figs. 3 and 4, batch_size represents the size of the randomly sampled data cluster during the training process, while buffer_size represents the capacity of the experience replay pool.

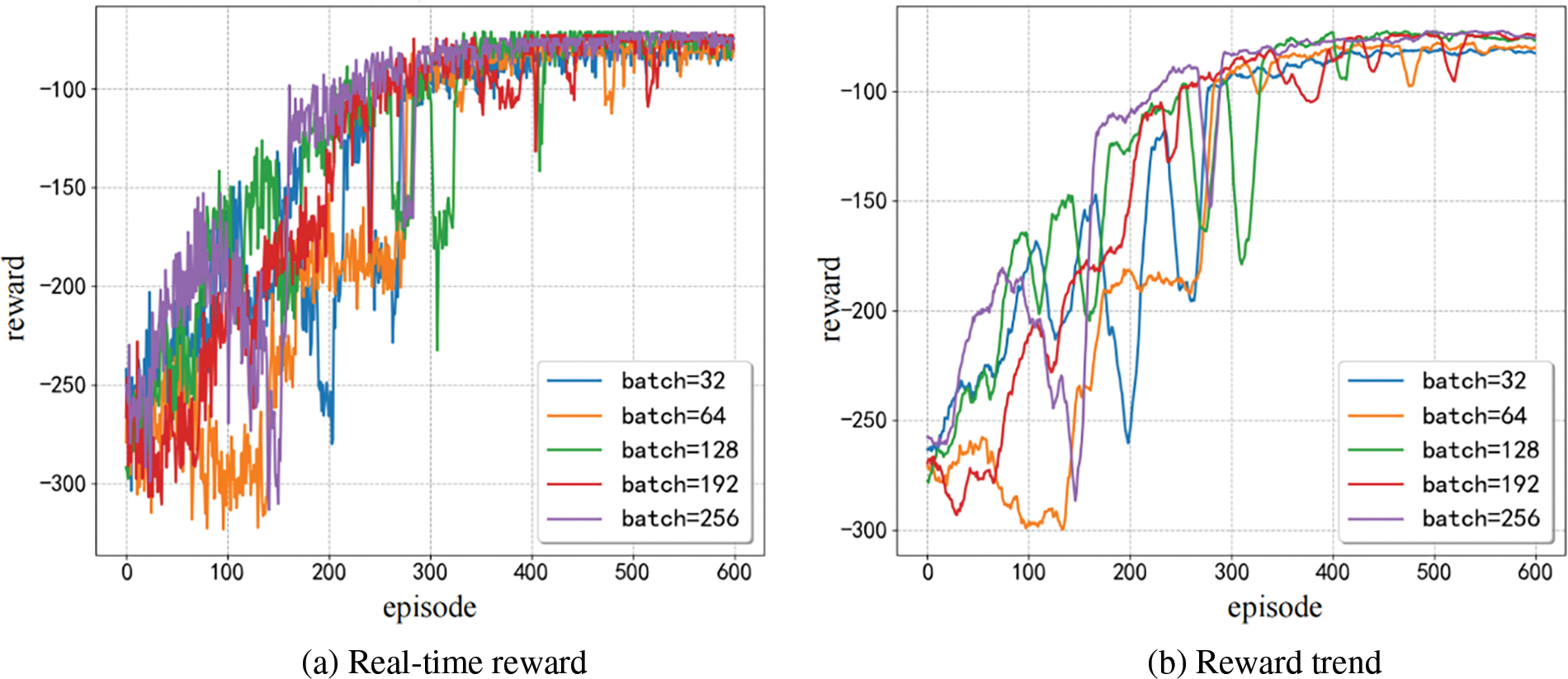
Figure 3: Different batch_size

Figure 4: Different buffer_size

As shown in Fig. 3, the main training is based on the batch_size of the training data cluster randomly sampled from the experience pool, while the buffer_size is fixed at 4096. It can be seen from the figure that the smaller the batch_size, the greater the fluctuation of the reward value in the early stage. This is because the system randomly samples the experience set of batch_size from the experience pool for training each time. If the batch_size is too small, the sampled experience may be relatively poor, and the resulting reward will fluctuate in the opposite direction. According to the trend of the different curves in the figure, it can be seen that different data cluster sizes do not ultimately affect the convergence speed of the algorithm, but they will affect the fluctuation of the algorithm’s reward value in the early stage of training.

5.2 Vehicles Number Training

Fig. 5 shows the impact of different buffer sizes on the convergence performance of the algorithm in this paper, with a fixed batch size of 256. It can be seen from the graph that the buffer size has the greatest influence on the convergence value and speed of the algorithm. When the buffer size is set to 512, the length of the task queue in this scenario is only 100, and the number of task cars is 7, which means that the task queue cannot fully cover the experience of multi-agent training for one round. It is easy to fall into a local optimal solution, and therefore the reward under this condition is the smallest. As shown in the graph, as the buffer size becomes larger, the fluctuations during the algorithm training process become less and less. This is because when the buffer size is large enough, it can store more optimal experiences during the later stages of training, which is more conducive to convergence of training.

Figure 5: Different vehicles number

Fig. 5 shows the convergence performance of the proposed TDO-MADDPG algorithm in the given scenario with varying numbers of vehicles, while keeping the task size constant. As revealed by the simulation parameters, an increase in the number of vehicles also leads to an increase in the number of task vehicles, i.e., an increase in the number of system agents. It can be observed that with an increase in the number of training iterations, the reward values gradually increase and eventually stabilize at a convergent value. At the same time, it can also be seen that with a continuous increase in the number of vehicles, the probability of reward value fluctuation is higher in the initial stages of the algorithm’s operation. This is because an increase in the number of vehicles adds to the action and state spaces in the model environment, thereby making the environment more unstable. Fig. 6 shows the change of the average task completion time of the TDO-MADDPG algorithm with different number of vehicles.

Figure 6: Different vehicles number

5.3 Task Size Training

Fig. 7 shows the changes in task reward and average completion time under different task volumes for unloading. The four curves represent different task volumes, with small indicating a task volume of [60,120], medium indicating a task volume of [80,140], big indicating a task volume of [90,180], and bigger indicating a task volume of [120,200]. According to the reward convergence Fig. 7a, it can be seen that as the task volume increases, the convergence speed of the algorithm slows down. When the data volume is relatively small, the convergence state is reached after 100 rounds of training, and the average completion time of the task is relatively small, at 0.064 s. This is because when the data volume is small, the local computing power of the task car is sufficient to process these data, so the intelligent agent tends to choose to process the task locally to reduce the system overhead. As the task volume continues to increase, most of the task data will exceed the local computing capacity, and the proportion of tasks unloaded to the service car through V2V or to the base station through V2I will gradually increase. As shown in Fig. 7b, when the data volume becomes very large, continuous unloading to the service car will cause the data to time out without being processed, resulting in greater losses, so task unloading will mainly be to the base station, and the average completion time of the task will increase to 0.1109 s. From the completion time of processing the bigger level of data in Fig. 7c, it can be observed that when the data volume far exceeds the vehicle’s own processing limit, the average completion time of the task remains basically unchanged, because at this time, the task will choose to unload to the base station for processing.

Figure 7: Different task size (a) convergence (b) task completion time (c) task completion time

5.4 Comparative Analysis

To verify the superiority of the proposed algorithm in this paper, this section compares the algorithm with MADDPG, DDPG, unloading all tasks to the base station ATE, and unloading all tasks to the service vehicle ATSV in the same scenario, highlighting the performance advantages of the proposed algorithm. For the MADDPG approach, the dynamic decision-making process during vehicle operation is not considered, and the unloading target is generated based on the algorithm’s own decisions, and the unloading action is directly executed. For the ATE approach, the vehicle unloads all tasks to the base station during dynamic movement, without considering local computing and unloading to the service vehicle. In the ATSV approach, the vehicle’s tasks are not considered for the base station, only local computing and unloading to neighboring service vehicles are considered.

Fig. 8 shows the convergence of reward values and comparison with other algorithms for the dynamic offloading and scheduling algorithm based on TDO-MADDPG, under the same task and vehicle conditions. It can be observed that the convergence speed of TDO-MADDPG is comparable to that of MADDPG, but the convergence reward value of TDO-MADDPG is better. This is because TDO-MADDPG considers dynamic decision-making, excludes edge cases where the communication distance may be exceeded during the offloading process, and optimizes the global reward value. It can be seen from the figure that the reward convergence speed of the offloading strategy based on DDPG is much faster than that of the multi-agent strategy, reaching convergence at around 200 times. However, the final convergence reward value of the scheduling strategy proposed in this paper using TDO-MADDPG is much better. The reason is that in the centralized training mode, each agent has a separate policy, limited by the locally observed environmental state, and trained based on the reward feedback from the environment, which slows down the convergence speed of the overall system strategy. At the same time, due to the limitation of service vehicle resources, in the early stages of training, the strategies assigned by agents can usually lead to resource competition, resulting in a decrease in the convergence performance of the multi-agent. With the increase of training times, each agent will gradually improve its action decision-making towards maximizing the overall system reward, and finally reach the state of overall convergence. In contrast, the single-agent algorithm based on DDPG has no global reward constraints, and the algorithm cannot grasp the global state of the system. Each agent maximizes its own reward, which may lead to fluctuation of reward convergence and finding a global suboptimal solution rather than the global optimal solution, resulting in a lower reward value than that obtained by applying TDO-MADDPG or MADDPG algorithm. Furthermore, it can be observed that the DDPG algorithm has a large fluctuation, which is caused by the non-stationarity of the concurrent exploration and learning process of multiple agents, and the changes of other agents affect the environment for the agent itself, thereby affecting the dynamic change of the agent’s state space.

Figure 8: Comparison of different schemes

From Fig. 8, it can be seen that different schemes have different convergence reward situations. Generally speaking, the ATSV scheme has the smallest reward value, as unloading all tasks to the base station will result in significant latency. This scheme is used as a benchmark for comparative analysis. The DDPG scheme is second, and as analyzed earlier, the final convergence value of this scheme may not be the global optimal solution, but a local optimal solution. The ATE scheme is third, with a relatively small reward value. Due to limited resources of the service vehicles, there may be resource competition resulting in incomplete task processing. For the MADDPG scheme, as analyzed earlier, there may be edge cases, so the reward value is not yet optimal. Therefore, based on the comparison of the convergence situation of different schemes, the TDO-MADDPG algorithm proposed in this paper has the optimal final convergence reward value and can also quickly iterate to a convergence state, indicating that this algorithm is more competitive in this scenario. The following will use more specific data to compare the performance advantages of this algorithm.

As shown in Fig. 9, we present a comparison of the average completion time of tasks using different schemes for different numbers of vehicles. It can be observed that the average completion time of tasks for AESV and ATE schemes almost remains unchanged, regardless of the number of vehicles. From the figure, it can be seen that regardless of the variation in the number of vehicles, the TDO-MADDPG algorithm has the least average completion time for unloading tasks. For instance, when the number of vehicles is 12, the task average completion time of this algorithm is 7 ms faster than that of MADDPG, with a performance improvement of 7.6%, and it is significantly higher than the other three schemes, improving the performance of DDPG, ATSV, and ATE by 51.1%, 28.2%, and 80.4%, respectively. This demonstrates the superiority and robustness of the TDO-MADDPG algorithm in terms of latency performance and confirms the excellence of this scheme.

Figure 9: Average completion time of tasks in different schemes

6  Conclusion

This article focuses on the vehicular ad hoc network environment for fast-moving vehicles, and combines multi-agent reinforcement learning algorithms with the computation resources of service vehicles and base stations to achieve the optimization goal of minimizing the average task completion time. The dynamic task offloading and resource scheduling problems are studied. In a simulated environment, the proposed algorithm is verified and analyzed through dynamic decision-making, task offloading, and resource scheduling. The feasibility of the algorithm is verified through convergence verification and training analysis of relevant parameters. In addition, the training results show that the algorithm can achieve optimal convergence performance and lower average task processing time for different numbers of vehicles and tasks, demonstrating its stability and good performance. Finally, the proposed algorithm is compared and analyzed with four different methods, and even with an increase in the number of vehicles, it still achieves the lowest average task completion time, indicating its obvious performance advantages. The comprehensive simulation experiment performance verifies that the proposed algorithm has excellent performance advantages. In our future work, we will further consider the security and privacy of vehicular computation offloading and design secure task offloading schemes for Internet of Vehicles.

Acknowledgement: The authors would like to express our sincere gratitude and appreciation to each other for our combined efforts and contributions throughout the course of this research paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yu Zhou, Yun Zhang, Guowei Li, Hang Yang, Wei Zhang, Ting Lyu and Yueqiang Xu; data collection and analysis: Yu Zhou, Yun Zhang, Guowei Li, Wei Zhang and Yueqiang Xu; draft manuscript preparation: Yueqiang Xu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. W. Fan et al., “Joint task offloading and resource allocation for vehicular edge computing based on V2I and V2V modes,” IEEE Trans. Intell. Transport. Syst., vol. 24, no. 4, pp. 4277–4292, Apr. 2023. doi: 10.1109/TITS.2022.3230430. [Google Scholar] [CrossRef]

2. Q. Wu, S. Wang, H. Ge, P. Fan, Q. Fan and K. B. Letaief, “Delay-sensitive task offloading in vehicular fog computing-assisted platoons,” in IEEE Trans. Netw. Serv. Manag., 2024. doi: 10.1109/TNSM.2023.3322881. [Google Scholar] [CrossRef]

3. X. Xu, Y. Xue, X. Li, L. Qi, and S. Wan, “A computation offloading method for edge computing with vehicle-to-everything,” IEEE Access, vol. 7, pp. 131068–131077, 2019. [Google Scholar]

4. Q. Wu, W. Wang, P. Fan, Q. Fan, J. Wang and K. B. Letaief, “URLLC-Awared Resource Allocation for Heterogeneous Vehicular Edge Computing,” in IEEE Trans. Veh. Technol., 2024. doi: 10.1109/TVT.2024.3370196. [Google Scholar] [CrossRef]

5. Z. Ning, P. Dong, X. Wang, J. J. P. C. Rodrigues, and F. Xia, “Deep reinforcement learning for vehicular edge computing: An intelligent offloading system,” ACM Trans. Intell. Syst. Technol., vol. 10, no. 6, pp. 1–24, 2019. doi: 10.1145/3317572. [Google Scholar] [CrossRef]

6. X. Li, Y. Dang, M. Aazam, X. Peng, T. Chen and C. Chen, “Energy-efficient computation offloading in vehicular edge cloud computing,” IEEE Access, vol. 8, pp. 37632–37644, 2020. doi: 10.1109/ACCESS.2020.2975310. [Google Scholar] [CrossRef]

7. K. Wang, X. Wang, X. Liu, and A. Jolfaei, “Task offloading strategy based on reinforcement learning com-puting in edge computing architecture of internet of vehicles,” IEEE Access, vol. 8, pp. 173779–173789, 2020. doi: 10.1109/ACCESS.2020.3023939. [Google Scholar] [CrossRef]

8. C. Chen et al., “Delay-optimized V2V-based computation offloading in urban vehicular edge computing and networks,” IEEE Access, vol. 8, pp. 18863–18873, 2020. doi: 10.1109/ACCESS.2020.2968465. [Google Scholar] [CrossRef]

9. C. Chen, Y. Zhang, Z. Wang, S. Wan, and Q. Pei, “Distributed computation offloading method based on deep reinforcement learning in ICV,” Appl. Soft Comput., vol. 103, pp. 107–108, 2021. doi: 10.1016/j.asoc.2021.107108. [Google Scholar] [CrossRef]

10. Z. Wang, D. Zhao, M. Ni, L. Li, and C. Li, “Collaborative mobile computation offloading to vehicle-based cloudlets,” IEEE Trans. Vehicular Technol., vol. 70, no. 1, pp. 768–781, 2021. doi: 10.1109/TVT.2020.3043296. [Google Scholar] [CrossRef]

11. H. Wang, X. Li, H. Ji, and H. Zhang, “Federated offloading scheme to minimize latency in MEC-enabled vehicular networks,” in 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 2018, pp. 1–6. [Google Scholar]

12. L. Feng, W. Li, Y. Lin, L. Zhu, S. Guo and Z. Zhen, “Joint computation offloading and URLLC resource allocation for collaborative MEC assisted cellular-V2X networks,” IEEE Access, vol. 8, pp. 24914–24926, 2020. doi: 10.1109/ACCESS.2020.2970750. [Google Scholar] [CrossRef]

13. H. Yang, X. Xie, and M. Kadoch, “Intelligent resource management based on reinforcement learning for ultra-reliable and low-latency IoV communication networks,” IEEE Trans. Veh. Technol., vol. 68, no. 5, pp. 4157–4169, 2019. doi: 10.1109/TVT.2018.2890686. [Google Scholar] [CrossRef]

14. S. S. Shinde and D. Tarchi, “Collaborative reinforcement learning for multi-service internet of vehicles,” IEEE Internet Things J., vol. 10, no. 3, pp. 2589–2602, 2023. doi: 10.1109/JIOT.2022.3213993. [Google Scholar] [CrossRef]

15. W. Fan, J. Liu, M. Hua, F. Wu, and Y. Liu, “Joint task offloading and resource allocation for multi-access edge computing assisted by parked and moving vehicles,” IEEE Trans. Vehicular Technol., vol. 71, no. 5, pp. 5314–5330, May 2022. doi: 10.1109/TVT.2022.3149937. [Google Scholar] [CrossRef]

16. M. Zhang, “Development of analytical offloading for innovative internet of vehicles based on mobile edge computing,” J. Grid Comput., vol. 22, no. 1, pp. 1–12, 2024. doi: 10.1007/s10723-023-09719-1. [Google Scholar] [CrossRef]

17. Q. Wu, S. Shi, Z. Y. Wan, Q. Fan, P. Y. Fan and C. Zhang, “Towards V2I age-aware fairness access: A DQN based intelligent vehicular node training and test method,” Chin. J. Electron., vol. 32, no. 6, pp. 1230–1244, Nov. 2023. doi: 10.23919/cje.2022.00.093. [Google Scholar] [CrossRef]

18. S. Farthofer, M. Herlich, C. Maier, S. Pochaba, J. Lackner and P. Dorfinger, “CRAWDAD dataset,” 2022. Accessed: 18 Jan. 2022. [Online]. Available: srfg/lte-4g-highway-drive-tests-salzburg[EB] [Google Scholar]