 Open Access
Open Access
ARTICLE
Securing the Internet of Health Things with Certificateless Anonymous Authentication Scheme
Department of Computer Science and Information Systems, College of Applied Sciences, AlMaarefa University, Riyadh, 13713, Saudi Arabia
* Corresponding Author: Nisreen Innab. Email:
(This article belongs to the Special Issue: Cybersecurity Solutions for Wireless Sensor Networks in IoT Environments )
Computers, Materials & Continua 2024, 80(2), 2237-2258. https://doi.org/10.32604/cmc.2024.049608
Received 12 January 2024; Accepted 06 June 2024; Issue published 15 August 2024
Abstract
Internet of Health Things (IoHT) is a subset of Internet of Things (IoT) technology that includes interconnected medical devices and sensors used in medical and healthcare information systems. However, IoHT is susceptible to cybersecurity threats due to its reliance on low-power biomedical devices and the use of open wireless channels for communication. In this article, we intend to address this shortcoming, and as a result, we propose a new scheme called, the certificateless anonymous authentication (CAA) scheme. The proposed scheme is based on hyperelliptic curve cryptography (HECC), an enhanced variant of elliptic curve cryptography (ECC) that employs a smaller key size of 80 bits as compared to 160 bits. The proposed scheme is secure against various attacks in both formal and informal security analyses. The formal study makes use of the Real-or-Random (ROR) model. A thorough comparative study of the proposed scheme is conducted for the security and efficiency of the proposed scheme with the relevant existing schemes. The results demonstrate that the proposed scheme not only ensures high security for health-related data but also increases efficiency. The proposed scheme’s computation cost is 2.88 ms, and the communication cost is 1440 bits, which shows its better efficiency compared to its counterpart schemes.Keywords
The Internet of Health Things (IoHT) is a networked system that incorporates various biomedical devices, including smart wearables, implants, and ingestible electronics. These devices are integrated with appropriate software applications to facilitate the collection, analysis, and dissemination of physiological data through the internet [1,2]. Physiological data often encompasses many health-related indications such as blood pressure, chest sounds, body temperature, respiration rate, electrocardiogram (ECG), patient posture, breathing rate, and other vital parameters [3–7]. In addition, IoHT systems could be used to update environmental factors such as patient care settings, room conditions, laboratory shift timings, treatment durations, and staff-to-patient ratios. The health information system maintains computerized records of patients’ environmental conditions and health-related information, accessible to medical professionals anytime the patient enters the hospital.
Privacy and security issues often occur in IoHT systems because biomedical sensors and user-customized devices are frequently involved in internet-based communication. The typical IoHT system architecture is shown in Fig. 1 [8]. To provide secure connectivity in an IoHT system, the primary security challenge is validating the integrity of data transmitted across an unsecured wireless link. The second security concern is ensuring receiver anonymity, which means that only the sender is aware of the identities of the receivers. An intruder can, for instance, intercept communication between biomedical devices and sensors to steal or forge health-related data. This system may also be susceptible to the “greedy behavior attack,” one of the most aggressive DoS attacks. It attempts to prevent authorized nodes from accessing the communication channel [9]. Unfortunately, most IoHT devices have low processing and storage capabilities, making it impossible for them to execute complex cryptographic computations to protect against such attacks. The majority of public key cryptosystems mentioned in the literature require a lot of computation, making them unsuitable for IoHT systems.

Figure 1: A typical architecture of IoHT system
To secure IoHT systems, authentication mechanisms based on the digital signature system can be implemented [10]. This mechanism uses a shared key to provide not just authentication and privacy but also the other three primary requirements of confidentiality, integrity, and non-repudiation [11]. Two of the most common authentication mechanisms used in public-key cryptosystems are Identity-Based Cryptography (IBC) and Public Key Infrastructure (PKI). It is essential in the PKI setting to have a reliable unforgeable connection between a user’s identity and their public keys. Because of this, a Certificate Authority (CA) that gives each link its signature is required. With certificates, the CA limits the public key to serve as the identification of a participant [12]. Problems with certificates expiring, being distributed, and being stored are only a few of the drawbacks of PKI systems. As an alternative, IBC is promoted as a means of cutting down on the cost of managing public keys [13]. The trustworthy Private Key Generator (PKG) has direct knowledge of the private keys of the participants, which is at the cost of private key escrow problems [14,15]. The issue of key escrow in authentication methods can be solved by using a certificateless cryptosystem with a signature strategy. Additionally, there is the problem of receiver anonymity, which means that only the sender knows who the receivers are. Fortunately, this obstacle can be circumvented by using anonymous authentication.
Motivation and Contributions
Authentication schemes are usually built using computing-based cryptographic operations like bilinear pairing, Rivest-Shamir-Adleman (RSA), and ECC, and then evaluated to see how well the proposed scheme works. These operations, on the other hand, have high computation and communication costs. As a result, HECC, an enhanced variant of ECC that employs 80-bit keys, identities, and certificate sizes to give the same level of security as ECC, bilinear pairing, and RSA [16], can be employed. As a result, for resource-constrained devices in IoHT systems, HECC would be a preferable alternative. This work provides a one-of-a-kind IoHT solution called the certificateless anonymous authentication scheme. The scheme is based on the HECC concept and has a small key size. The following are some of the key contributions of the undertaken research work:
1. We propose an efficient anonymous authentication scheme in certificateless settings for IoHT systems.
2. To overcome constraints such as low processing capabilities associated with biomedical devices and sensors, the proposed scheme uses a public-key cryptography method based on the HECC concept.
3. The proposed scheme is secure against various attacks in both formal and informal security analyses. The formal study makes use of the Real-or-Random (ROR) model.
4. Lastly, we show that the proposed scheme has lower costs for both computation and communication than relevant existing schemes.
The following section outlines the organizational structure of the remaining portions of the article. The literature review is further discussed in Section 2. In Section 3, we provide the preliminary information. The CAA plan under consideration is included in Section 4. Section 5 of the document encompasses the security analysis. Section 6 of the document encompasses a comprehensive performance assessment analysis, while Section 7 presents conclusions and future work.
This section focuses on the security and privacy concerns of the IoHT system while using an authentication scheme. Also, we have given the limitations of the scheme, which appear in this section’s literature review in Table 1. Chen et al. [17] proposed a telemedicine information system authentication scheme based on dynamic identity. According to the authors, their scheme overcomes the problem of user anonymity. Jiang et al. [18] pointed out that the Chen et al.’s scheme did not ensure user anonymity or untraceability, which could lead to identity guessing and tracking attacks. They presented an updated strategy for maintaining user anonymity, saying their scheme could survive any attack. On the other hand, Kumari et al. [19] revealed that Jiang et al.’s scheme is vulnerable to several attacks, including password guessing, impersonation, DoS attacks, and even improper login request verification.
Chen et al. [20] proposed an authentication scheme for medical data interchange in the cloud environment to prevent security issues and safeguard patients’ health data. Neither patient privacy nor message authentication were ensured by the proposed scheme, as shown by the work proposed by Chiou et al. [21]. Therefore, they improved the cloud-based healthcare system’s privacy authentication process. Patients’ privacy was not protected in Mohit et al.’s [22] analysis of the method reported in Chiou et al.’s scheme, which they found could be compromised by attacks from stolen mobile devices. To strengthen healthcare security and reduce its burdensome complexity, they designed a lightweight two-factor authentication solution using cloud computing. It was pointed out by Li et al. [23] that the scheme proposed by Mohit et al. is susceptible to the forged inspection report and cannot guarantee patient anonymity or data confidentiality.
Saeed et al. [24] proposed an online/offline certificateless signature approach in wireless body area networks based on the internet of things to build a heterogeneous remote anonymous authentication mechanism. However, Liao et al. [25] demonstrated that the approach of Saeed et al. is vulnerable to a forgery attack in which no information other than public system parameters is required. He et al. [26] proposed anonymous authentication for WBAN and shown that their scheme is both secure and efficient when compared to its counterpart schemes. Kasyoka et al. [27] proposed an ECC-based authentication scheme for WBANs. The proposed scheme was both certificateless and pairing-free. The authors of the presented scheme of Kasyoka et al. claimed that their scheme is efficient in terms of communication cost and running time. Liu et al. [28] introduced a novel and efficient anonymous authentication scheme for WBANs that ensures that doctors and patients are legal in a secure manner.
All of the above-mentioned solutions involve the use of cryptographic techniques; these schemes are mostly based on ECC and bilinear pairing, both of which have prohibitively expensive communication and computation costs. However, the proposed scheme is based on the concept of HECC, a more sophisticated form of ECC. HECC uses an 80-bit key size, which is half as large as ECC’s key size, but it still offers the same level of security as ECC and bilinear pairing.
This section explains some of the key concepts and materials that will be used in constructing the proposed scheme.
In 1989, Koblitz introduced a group law for the Jacobian of a Hyperelliptic curve (HE). It is defined by the Jacobian of genus £s and is based on the discrete logarithm Problem.
It typically has n£s points, where n is the number of Jacobian components. Under the Decisional Diffie-Hellman assumption, the HE-based authentication and key management scheme is completely safe. HE curves are a particular subclass of elliptic curves in algebra, which can be viewed as a generalization. For a HE, we have:
(HE): ∅2+h(Δ)∅=f(Δ), where f(Δ) denotes a monic polynomial and his degree defined over Fieldn as 2£s+1 and h(Δ) represents a polynomial that is defined over Fieldn, which may be equal or less from £s.
3.2 Hyperelliptic Curve Deffie-Hellman (HEDH) Problem
Suppose the random triple (𝒟, V.𝒟, U.𝒟) of the HEDH Problem is given, then to compute the value V.U.𝒟 is called HEDH problem, where V,U are belongs to Fieldn.
3.3 Hyperelliptic Curve Discrete Logarithm (HEDL) Problem
Suppose the random tuple (𝒟, V.𝒟) of the HEDL Problem is given, then to compute the value V.𝒟 is called the HEDL problem, where V belongs to Fieldn. The symbols used in the scheme are illustrated in Table 1.
In this section, the network model is provided first, followed by the construction and correctness of the proposed scheme.
Depending on the requirements, the network model of IoHT systems can be implemented in several topologies; one such networking architecture is shown in Fig. 2. Wearable Biomedical Devices (WBD), Network Manager (NMGR)/Service Provider, Application Provider (APDR), and IoT gateway are all included in this network model. Each entity’s function is described as follows:

Figure 2: Proposed network model
1. APDR: The APDR will assess a patient’s health and generate health-related information. Following this, it sends its encrypted identity along with a public number send (EIds, ηs) over an un-secure channel to NMGR/Service Provider for registration. Upon receiving (EIds, ηs), NMGR/Service Provider can compute the secret key as SK, recover the user the identity IDs using decryption method, and send the encrypted version of partial private key (PrIds) to APDR. Then APDR first decrypt PrIds and set his public key pair as (ηs, ξs) and private key pair as (δs, χs).
2. WBD: To register WBD, the user compute and send (EIdr,ηr) to NMGR/Service Provider via un-secure channel. Upon receiving (EIdr, ηr), NMGR/Service Provider can compute the secret key SK, recover IDr, then compute and PrIds by using un-secure network to the identity (IDr). Then a user with identity (IDr), Then a user with identity (IDr), first recover (χr, ξr), set his public key pair as (ηr, ξr) and private key pair as (δr, χr). When WBD gets a partial private key from NMGR/Service Provider and a digital signature from APDR with a key management request, it generates its own private and public keys before verifying the digital signature. If the signature verification procedure is successful, WBD will produce a secret key, encrypt health-related data with it, and send it to the APDR.
1. NMGR/Service Provider: When NMGR/Service Provider receives identity from both WBD and APDR, this entity will act as a key generation canter in certificateless cryptography and will be responsible for creating the partial private key for both WBD and APDR.
2. IoT Gateway: The IoT gateway router can be used to connect any things that communicate using wireless technologies.
4.2 Construction of the Proposed Scheme
The proposed scheme has been constructed on the basis of the following phases and all the symbols used in the construction is included in Table 2.
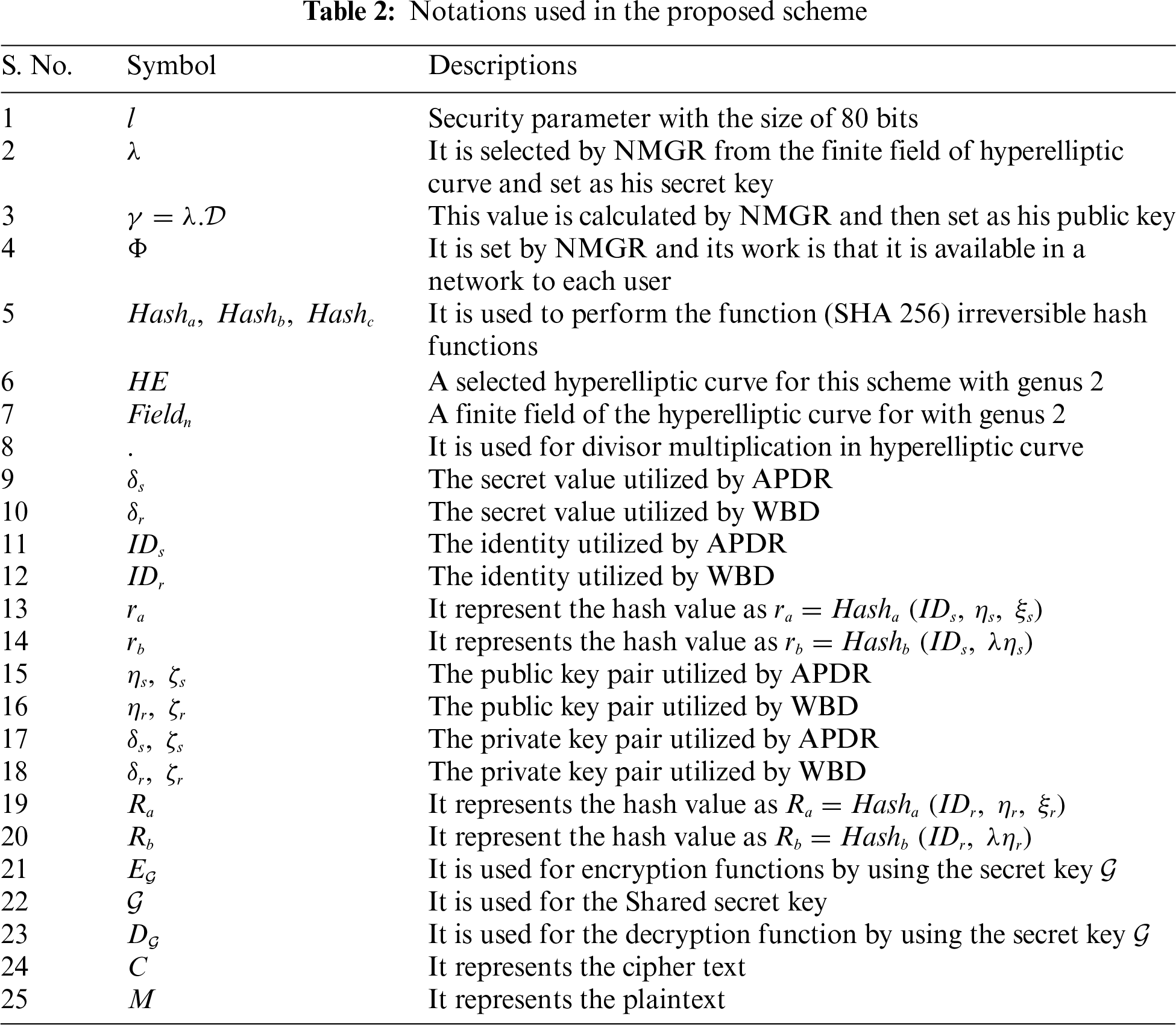
i. Initialization
Given an 80-bit hyper elliptic curve parameter l for the security of the proposed scheme, NMGR selects λ and computes γ=λ.𝒟 as a private and public key. It then set Φ={γ, 𝒟, Hasha, Hashb, Hashc, HE, Fieldn}, where γ denotes the public key of NMGR, 𝒟 is the divisor over HE, Hasha, Hashb, and Hashc are one way cryptographic hash functions with size of 512 bits, HE is a selected hyper elliptic curve with genus 2, and Fieldn is the finite field over HE order n=80 bits, respectively. Then, NMGR disclosed Φ to the network and keep private λ.
ii. Registration Phase
In this phase, APDR and WBD will be registered using the following steps:
1. Fig. 3 shows the registration process of APDR, in which the user selects δs, computes ηs=δs.𝒟, compute SK=δs.γ, encrypt the identity (IDs) as EIds=ESK(IDs), and send (EIds, ηs) to NMGR via un-secure channel. Upon receiving (EIds, ηs), NMGR can compute the secret key as SK=ηs.λ, decrypt the identity as IDs=DSK(EIds), select ζs and compute ξs=ζs.𝒟 and ra=Hasha (IDs, ηs, ξs), and then process χs=ζs.+ra.λ. Finally, encrypt the tuple (χs, ξs) as PrIds=ESK(χs, ξs) and by using un-secure network delivered to the identity (IDs). Then a user with identity (IDs), first decrypt PrIds as (χs, ξs)=DSK (PrIds), set his public key pair as (ηs, ξs) and private key pair as (δs, χs).
2. Fig. 4 shows the registration process of WBD, in which the user selects δr and computes ηr=δr.𝒟 for the identity (IDr), compute RK=δr.γ, encrypt the identity (IDr) as EIdr=ERK(IDr) and send (EIdr, ηr) to NMGR via secure channel. Upon receiving (EIdr, ηr), NMGR can compute the secret key as SK=ηr.λ and decrypt the identity as IDr=DSK(EIdr), then select ζr, compute ξr=ζr.𝒟, rb=Hasha(IDr, ηr, ξr), and then process χr=ζr + rb.λ. Finally, it encrypts the tuple (χr, ξr) as PrIds=ESK(χr, ξr) and by using un-secure network delivered to the identity (IDs). Then a user with identity (IDr), Then a user with identity (IDr), first decrypt PrIds as (χr, ξr)=DSK(PrIds), set his public key pair as (ηr, ξr) and private key pair as (δr, χr).

Figure 3: Application provider registration

Figure 4: Wearable biomedical devices registration
iii. Authentication and Key Management
Fig. 5 represents the flow of proposed scheme, in which the application provider generates the signature for mutual authentication with WBD by using the following steps:

Figure 5: Mutual authentication phase of proposed scheme
• The APDR can compute ω=υ.𝒟, where 𝒟 is the divisor of hyper elliptic curve.
• Compute rb=Hasha(IDr, ηr, ξr) and K=υ(ηr+ξr+rb.γ)
• Calculate 𝒢=Hashb(ω, IDr, IDs, ηs, ξs) and φ=δs+υ/𝒢+δs+χs, then send (φ, ω) to WBD.
• Upon reception (φ, ω), the receiver computeK=(δr+χr)ω, where δr denotes the secret value of WBD.
• Also, compute 𝒢=Hashb (ω, IDr, IDs,ηs, ξs), ra=Hasha(IDs, ηs, ξs), and φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω, if the equality of φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω is satisfied, then the mutual authentication can be done between sender and WBD, where ηs, ξs denotes the public key pair of application provider.
• The WBD set the secret key as K=(δr+χr)ω and done the encryption of a message as C=Hashc(K) ⊕ (M), where ⊕ denotes the encryption function which encrypt the message (M) using the secrete key K and finally send C to application provider.
• After reception of (C), the application provider performs decryption function as M=(Hashc(K)⊕C), for the recovery of plaintext.
As a receiver of (φ, ω), the WBD accepts only this pair when the following equation is satisfied:
φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω=φ(ηs+ξs+ra.γ+𝒢.𝒟)=φ(δs.𝒟+ζs.𝒟+ra.λ.𝒟+𝒢.𝒟)=φ(δs+ζs+ra.λ+𝒢).𝒟=(δs+υ/𝒢+δs+χs)(δs+δs+χs+𝒢).𝒟=(δs.𝒟+υ.𝒟)=ηs+ω
Also, WBD can process its secret key as followed:
K=(δr+χr)ω=(δr+χr)υ.𝒟=(δr+ζr+rb.λ)υ.𝒟=(δr.𝒟+ζr.𝒟+rb.λ.𝒟)υ=υ(ηr+ξr+rb.γ)=K.
In this section, we provide the provable security based on Random Oracle Model (ROM) and informal security analysis, which are as follows.
5.1 Provable Security Analysis
Here, we are going to prove the confidentiality and unforgeability of our proposed scheme against the following two types of attackers by using the ROM.
Outsider Attacker (ξOUA): ξOUA is also known as a key replacement attacker, has the ability to replace user public keys but lacks access to the master key. ξOUA has access to Hasha Query, Hashb Query, Hashc Query, Public Key Queries, Partial Private Key Queries, Private Key Queries, Replace Public Key Queries, Sender Query, and Receiver Query.
Insider Attacker (ξISA): The Insider Attacker (ξISA), also known as a malevolent NMGR attacker, is one who has access to the master key but is unable to replace the public keys. ξISA has access to Hasha Query, Hashb Query, Hashc Query, Public Key Queries, Private Key Queries, Sender Query, and Receiver Query.
So, keeping in view the capabilities of the above attackers (ξOUA, ξISA), we have included Theorems 1 and 2 to prove the confidentiality of our proposed scheme. Then, by using Theorems 3 and 4, we have proved that our proposed scheme is unforgeable against (ξOUA, ξISA). The following are the proofs of theorems:
Theorem 1-Confidentiality: Suppose the outsider attacker (ξOUA), with his advantages OUAξ, wants to break IND-CAA-CCA-I with help of helper called HOUA and his task is to solve HEDH Problem with advantage as followed: OUAξ/(Qnq+1)2, where Qnq denotes the number of private key extract query, partial private key extract query, and sender query, respectively.
Proof: Suppose the random triple (𝒟, VOUA.𝒟, UOUA.𝒟) of HEDH Problem is given to HOUA and his task to compute H=VOUA.UOUA.𝒟. The following sub steps represents the processing of Theorem 1:
Setup: Given an 80 bit hyper elliptic curve parameter l for the security of the proposed scheme, the HOUA set γ=VOUA.𝒟 and Φ={γ, 𝒟, Hasha, Hashb, Hashc, HE,Fieldn}. Then, (HOUA disclosed Φ to the ξOUA). Not that, here HOUA has no access to λ.
Hasha Query: ξOUA chooses the identity IDi and sends out Hasha oracle queries to HOUA. HOUA checks to see if there is a tuple (IDi, ηi, ξi, ri), in list LHasha, if the condition is met, HOUA return with ri to ξOUA, else, it select Ri from {0, 1} such that [Ri=1]=1/(Qnq+1), and do the following steps.
• If Ri=0, then it picks ri randomly, send it to ξOUA, and update the list LHasha with the values ri and Ri=0.
• If Ri=1, then it set ri=P, send it to ξOUA, and update the list LHasha with the values ri and Ri=1.
Hashb Query: ξOUA chooses the identity IDi and sends out Hashb oracle queries to HOUA. HOUA checks to see if there is a tuple (ω, ηi, ξiIDi, 𝒢i), in list LHashb, if the condition is met, HOUA return with 𝒢i to ξOUA, else, it returns 𝒢i of its choice and add (IDi, 𝒢i) into the list LHashc.
Hashc Query: ξOUA chooses the identity IDi and sends out Hashc oracle queries to HOUA. HOUA checks to see if there is a tuple (Ki), in list LHashb, if the condition is met, HOUA return with Ki to ξOUA, else, it returns Ki of its choice and add (IDi, Ki) into the list LHashc.
Public Key Queries: ξOUA chooses the identity IDi and sends out Public Key oracle queries to HOUA. HOUA check (ηi, ξi) in the list LpKq, if it is existing, then it delivers (ηi, ξi) to ξOUA, otherwise the following two conditions should consider:
1. If Ri=0, HOUA compute ηi=δi.𝒟, ξi=ζi.𝒟, and χi=ζi+Hasha (IDi, ηi, ξi). s where δi, ζi, s is the randomly chosen numbers from hyper elliptic curve Jacobian group. Then, HOUA send (ηi, ξi) to ξOUA and update the list LpKq with (ηi, ξi) and (δi, χi).
2. If Ri=1, HOUA compute ηi=δi.𝒟 and ξi=ζi.𝒟, where δi, ζi is the randomly chosen numbers from hyper elliptic curve Jacobian group. Then, HOUA send (ηi, ξi) to ξOUA and update the list LpKq with (ηi, ξi) and (δi, ζi).
Partial Private Key Queries: ξOUA chooses the identity IDi and sends out Partial Private Key oracle queries to HOUA. Then HOUA check (χi, ξi) in the list LpRKq, if available, HOUA will send (χi, ξi) to ξOUA. Otherwise, the following two conditions should consider:
1. If Ri=0, HOUA call Public Key Queries, get (χi,ξi) and send it to the ξOUA.
2. If Ri=0, HOUA will not further processed this game and stop the simulation.
Private Key Queries: ξOUA chooses the identity IDi and sends out Private Key oracle queries to HOUA. Then HOUA check (χi, ξi) in the list LpRiKq, if available, HOUA will send (χi, δi) to ξOUA. Otherwise, the following two conditions should consider:
1. If Ri=0, HOUA call Public Key Queries, get (χi, δi) and send it to the ξOUA.
2. If Ri=0, HOUA will not further processed this game and stop the simulation.
Replace Public Key Queries: ξOUA choose (ηi/, ξi/) and send to HOUA. Upon reception (ηi/, ξi/), HOUA replaces ηi, ξi on (ηi/, ξi/) and adds into the list LRP.
Sender Query: As a response of this query, HOUA examines of the value Rs by using the following computations:
• If Rs=0, HOUA pick (χi, δi) from LpRiKq, if it is not available in LpRiKq, then it call Private Key Queries, obtain (χi, δi), perform the algorithmic steps as made by APDR, and generate (φ, ω). Finally, HOUA will delivered (φ, ω) to ξOUA.
• If Rs=1, HOUA will stop simulation of this process.
Receiver Query: HOUA examines Rr and Rs responds as follows when ξOUA queries for sender signature and encryption:
• If Rr and Rs=0, HOUA pick (χi, δi) from LpRiKq, if it is not available in LpRiKq, then it call Private Key Queries, obtain (χi,δi), perform the alogorithmic steps as made by WBD during signature verifications and APDR decryption of ciphertext, and generate (M). Finally, HOUA will delivered (M) to ξOUA.
• If Rs=1, HOUA pick the value Ki, compute M=(Hashc(K)⊕C), and send M to ξOUA.
• If Rr=1, HOUA compute φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω, where ra and 𝒢 is selected randomly.
Challenge: ξOUA send (MOUA1, MOUA2) and (IDs∗, IDr∗) to HOUA, decides on Rr∗, and do the following steps:
• If Rr∗=0, HOUA stop the simulation.
• If Rr∗=1, HOUA compute ω∗=UOUA.𝒟, obtained Ki∗ from LHashc, select φ∗ randomly, g∗ from {0, 1}, compute C∗=Hashc(Ki∗) ⊕ (Mg∗), and send (ω∗, φ∗, C∗) to ξOUA.
Guess: After performing the same number of queries as performed above, ξOUA outputs with a guess value g/ from {0, 1} of g∗. Then, HOUA can perform the following two steps:
• In the event that any steps of the simulation are avoided, HOUA chooses g from {0, 1} at random as its best guess for the solution of (H=(VOUA.UOUA.𝒟)).
• Otherwise, if g/=g∗, HOUA return δr∗ and ζr∗ from LpKq, further the processing at challenge step will not be aborted and we have Rr∗=1 and rr∗=L. So, HOUA obtains (ω∗, φ∗, Ki∗) and check the equation: K∗−(δr∗+ζr∗)ω∗L=H, is hold. If yes, HOUA return g=1, otherwise it returns g=0.
Note that, HOUA has no knowledge about χr∗=ζr∗+rr.λ, γ=VOUA.𝒟, and λ=VOUA, so λ is not accessible for HOUA. In the challenge phase, ω∗=UOUA.𝒟; it means that UOUA=υ, which is not known to HOUA. In a situation, if (ω∗, φ∗, C∗) valid then we can get:
K∗−(δr∗+ζr∗)ω∗L=UOUA(ηr∗+ξr∗+rr∗.γ)−(δr∗+ζr∗)ω∗L=UOUA(ηr∗+ξr∗+rr∗.γ)−(δr∗+ζr∗)ω∗L=UOUA(ηr∗+ξr∗+rr∗.γ)−(δr∗+ζr∗)UOUA.𝒟L=UOUA(δr∗.𝒟+ζr∗.𝒟+rr∗.VOUA.𝒟)−(δr∗+ζr∗)UOUA.𝒟L=UOUA(δr∗.𝒟+ζr∗.𝒟+L.VOUA.𝒟)−(δr∗+ζr∗)UOUA.𝒟L=UOUA.𝒟(δr∗+ζr∗+L.VOUA)−(δr∗+ζr∗)UOUA.𝒟L=UOUA.𝒟[(δr∗+ζr∗+L.VOUA)−(δr∗+ζr∗)]L=UOUA.𝒟[(L.VOUA)]L=VOUA.UOUA.𝒟=H, if it is holds, for the answer of H, HOUA will return g=1, otherwise it returns g=0.
Probability Analysis: In the above game, let Pr[HOUA Sucess] denote HOUA's probability of solving H=(VOUA.UOUA.𝒟), and Pr[ξOUASucess] denote ξOUA’s probability of doing so. If the process of this game is stop at any stage, then for the answer of H=(VOUA.UOUA.𝒟) and HOUA will select g from {0, 1} as his guess. So, the Pr[HOUASucess]=12 and Pr[ξOUASucess]=12+OUAξ. We have the following computations: Pr[HOUASucess]=Pr[HOUASucess|Stop]Pr[Stop]+Pr[HOUASucess|↼Stop]Pr[↼Stop] =12Pr[Stop]+Pr[ξOUASucess]Pr[↼Stop]=12(1−Pr[↼Stop])+(12+OUAξ)Pr[↼Stop]=12−(OUAξPr[↼Stop]).
On the other hand, if each of the independent events listed below occurs, HOUA will not terminate.
EOUA1: During Private Key Queries and Partial Private Key Queries Ri=0, EOUA2: During Sender Queries Rs=0, and EOUA3: During Challenge Phase Rr∗=0.
So, the probability of EOUA3=1/(Qnq+1) and (EOUA1,EOUA2)=1−Qnq/(Qnq+1), then we have (EOUA1, EOUA2, EOUA3)=(1/(Qnq+1))=1/(Qnq+1)2.
Finally, we can get: Pr[HOUASucess]>=12+OUAξ/(Qnq+1)2.
Theorem 2-Confidentiality: Suppose the insider attacker (ξISA), with his advantages ISAξ, wants to break IND-CAA-CCA-I with help of helper called HOUA and his task is to solve HEDH Problem with advantage as followed: Pr[HOUASucess]>=12+ISAξ/(Qnq+1)2, where Qnq denotes the number of private key extract query, partial private key extract query, and sender query, respectively.
Proof: Suppose the random triple (𝒟, VOUA.𝒟, UOUA.𝒟) of HEDH Problem is given to HOUA and his task to compute H=VOUA.UOUA.𝒟. The following sub steps represents the processing of Theorem 2:
Setup: Given an 80-bit hyper elliptic curve parameter ℓ for the security of the proposed scheme, the HOUA set γ=λ.𝒟 and Φ={γ, 𝒟, Hasha, Hashb, Hashc, HE, Fieldn}. Then, HOUA disclosed Φ to the ξISA. Not that, here HOUA has access to λ.
Hasha Query, Hashb Query, Hashc Query: ξISA chooses the identity IDi and sends out Hasha, Hashb, Hashc oracle queries to HOUA. HOUA will give respond as like in Theorem 1.
Public Key Queries: ξISA chooses the identity IDi and sends out Public Key oracle queries to HOUA. HOUA check (ηi, ξi) in the list LpKq, if it is existing, then it delivers (ηi, ξi) to ξOUA, otherwise the following two conditions should consider:
• If Ri=0, HOUA compute ηi=δi.𝒟, ξi=ζi.𝒟 and χi=ζi + Hasha(IDi, ηi, ξi).λ where δi, ζi is the randomly chosen numbers from hyper elliptic curve Jacobian group. Then, HOUA send (ηi, ξi) to ξISA and update the list LpKq with (ηi, ξi) and (δi, χi).
• If Ri=1, HOUA compute ηi=δi.𝒟 and ξi=VOUA.𝒟, where δi is the randomly chosen numbers from hyper elliptic curve Jacobian group. Then, HOUA send (ηi, ξi) to ξISA and update the list LpKq with (ηi, ξi) and (δi, ζi).
Private Key Queries: ξISA chooses the identity IDi and sends out Private Key oracle queries to HOUA. Then HOUA check (χi, ξi) in the list LpRiKq, if available, HOUA will send (χi, δi) to ξISA. Otherwise, the following two conditions should consider:
1. If Ri=0, HOUA call Public Key Queries, get (χi, δi) and send it to the ξISA.
2. If Ri=0, HOUA will not further processed this game and stop the simulation.
Sender Query: As a response of this query, HOUA examines of the value Rs by using the following computations:
• If Rs=0, HOUA pick (χi,δi) from LpRiKq, if it is not available in LpRiKq, then it call Private Key Queries, obtain (χi, δi), perform the algorithmic steps as made by APDR, and generate (φ, ω). Finally, HOUA will delivered (φ, ω) to ξISA.
• If Rs=1, HOUA will stop simulation of this process.
Receiver Query: HOUA examines Rr and Rs responds as follows when ξOUA queries for sender signature and encryption:
• If Rr and Rs=0, HOUA pick (χi, δi) from LpRiKq, if it is not available in LpRiKq, then it call Private Key Queries, obtain (χi,δi), perform the alogorithmic steps as made by WBD during signature verifications and APDR decryption of ciphertext, and generate (M). Finally, HOUA will delivered (M) to ξISA.
• If Rs=1, HOUA pick the value Ki, compute M=(Hashc(K) ⊕ C), and send M to ξISA.
• If Rr=1, HOUA compute φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω, where ra and 𝒢 is selected randomly.
Challenge: ξISA send (MOUA1, MOUA2) and (IDs∗, IDr∗) to HOUA, decides on Rr∗, and do the following steps:
• If Rr∗=0, HOUA stop the simulation.
• If Rr∗=1, HOUA compute ω∗=UOUA.𝒟, obtained Ki∗ from LHashc, select φ∗ randomly, g∗ from {0, 1}, compute C∗=Hashc(Ki∗) ⊕ (Mg∗), and send (ω∗, φ∗, C∗) to ξISA.
Guess: After performing the same number of queries as performed above, ξISA outputs with a guess value g/ from {0, 1} of g∗. Then, HOUA can perform the following two steps:
• In the event that any steps of the simulation are avoided, HOUA chooses g from {0, 1} at random as its best guess for the solution of (H=(VOUA.UOUA.𝒟)).
• Otherwise, if g/=g∗ HOUA return δr∗ from LpKq, further the processing at challenge step will not be aborted and we have Rr∗=1 and rr∗=L. So, HOUA obtains (ω∗, φ∗, Ki∗ ) and check the equation: H=K∗−(δr∗+L.λ)ω∗, is hold. If yes, HOUA return g=1, otherwise it returns g=0.
Note that, HOUA has no knowledge about ξi∗=VOUA.𝒟, and ζr∗=VOUA. In the challenge phase, ω∗=UOUA.𝒟; it means that UOUA=υ, which is not known to HOUA. In a situation, if (ω∗, φ∗, C∗) valid then we can get:
K∗−(δr∗+L.λ)ω∗=UOUA(ηr∗+ξr∗+rr∗.γ)−(δr∗+L.λ)ω∗=UOUA(ηr∗+ξr∗+rr∗.γ)−(δr∗+L.λ)UOUA.𝒟=UOUA(δr∗.𝒟+ξr∗+rr∗.γ)−(δr∗+L.λ)UOUA.𝒟=UOUA(δr∗.𝒟+ζr∗.𝒟+rr∗.γ)−(δr∗+L.λ)UOUA.𝒟=UOUA(δr∗.𝒟+ζr∗.𝒟+rr∗.λ.𝒟)−(δr∗+L.λ)UOUA.𝒟=UOUA.𝒟(δr∗+ζr∗+rr∗.λ)−(δr∗+L.λ)UOUA.𝒟=UOUA.𝒟(δr∗+ζr∗+L.λ)−(δr∗+L.λ)UOUA.𝒟=UOUA.𝒟(δr∗+ζr∗+L.λ)−(δr∗+L.λ)=UOUA.𝒟(δr∗+VOUA+L.λ)−(δr∗+L.λ))=UOUA.VOUA.𝒟=H, if it is holds, for the answer of H, HOUA will return g=1, otherwise it returns g=0.
Probability Analysis: In the above game, let Pr[HOUASucess] denote HOUA's probability of solving H=(VOUA.UOUA.𝒟), and Pr[ξISASucess] denote ξISA’s probability of doing so. If the process of this game is stop at any stage, then for the answer of H=(VOUA.UOUA.𝒟) and HOUA will select g from {0, 1} as his guess. So, the Pr[HOUASucess]=12 and Pr[ξISASucess]=12+ISAξ. We have the following computations. Pr[HOUASucess]=Pr[HOUASucess|Stop]Pr[Stop]+Pr[HOUASucess|↼Stop]Pr[↼Stop]=12Pr[Stop]+Pr[ξISASucess]Pr[↼Stop]=12(1−Pr[↼Stop])+(12+ISAξ)Pr[↼Stop]=12−(ISAξPr[↼Stop]).
On the other hand, if each of the independent events listed below occurs, HOUA will not terminate.
EISA1: During Private Key Queries and Partial Private Key Queries Ri=0, EISA2: During Sender Queries Rs=0, and EISA3: During Challenge Phase Rr∗=0.
So, the probability of EISA3=1/(Qnq+1) and (EISA1,EISA2)=1−Qnq/(Qnq+1), then we have (EISA1, EISA2, EISA3)=(1/(Qnq+1)) ( 1−Qnq/(Qnq+1)) =1/(Qnq+1)2.
Finally, we can get:
Pr[HOUASucess]>=12+ISAξ/(Qnq+1)2.
Theorem 3-Unforgeability: Suppose the outsider attacker (ξOUA), with his advantages OUAξ, wants to break the security regarding existentially unforgeable under the adaptive chosen- message attacks (EF-CAA-CMA-I) with help of helper called HOUA and his task is to solve HEDLP Problem with advantage as followed: Pr[HOUASucess]>=12+OUAξ/(Qnq+1)2, where Qnq denotes the number of private key extract query, partial private key extract query, and sender query, respectively.
Proof: Suppose the random triple (𝒟, VOUA.𝒟) of HEDLP Problem is given to HOUA and his task to compute H=VOUA.𝒟. The following sub steps represents the processing of Theorem 3.
Setup: Given an 80 bit hyper elliptic curve parameter l for the security of the proposed scheme, the HOUA set γ=VOUA.𝒟 and Φ={γ, 𝒟, Hasha, Hashb, Hashc, HE, Fieldn}. Then, HOUA disclosed Φ to the ξOUA). Not that, here HOUA has no access to λ.
Queries: The queries which can ask by ξOUA is same as asked in Theorem 1.
Output: After performing all the queries that are done in Theorem 1, ξOUA generate (ω∗, φ∗) from APDR∗ to WBD∗ and C∗ from WBD∗ to APDR∗ on M∗. So, according to forking lemma, ξOUA will generate two valid signature that are (C∗, φ∗, ω∗) and (C∗∗, φ∗∗, ω∗∗), so, we have the following outputs: φ∗(𝒢+δs∗+χs∗)=δs∗+υ and φ∗∗(𝒢/+δs∗+χs∗)=δs∗+υ. So, we have:
φ∗(𝒢+δs∗+χs∗)=φ∗∗(𝒢/+δs∗+χs∗), as Rs∗=1 and rs∗=L, then χr∗=ζr∗ + rs∗.λ, γ=VOUA.𝒟, and λ=VOUA, so λ is not accessible for HOUA. Further, χr∗=ζr∗ + L.VOUA, so we have φ∗(𝒢+δs∗+ζr∗ + L.VOUA)=φ∗∗(𝒢/+δs∗+ζr∗ + L.VOUA).
So, in the above equations, VOUA is unknown to HOUA which is solution for HEDLP Problem.
Probability Analysis: In the above game, let Pr[HOUASucess] denote HOUA's probability of solving H=(VOUA.𝒟), and Pr[ξOUASucess] denote ξOUA’s probability of doing so. So, the Pr[ξOUASucess] ≥ OUAξ. We have the following computations. Pr[HOUASucess]=Pr[↼Stop∩HOUASucess]=Pr[↼Stop].Pr[HOUASucess]=Pr[↼Stop].OUAξ.
On the other hand, if each of the independent events listed below occurs, HOUA will not terminate.
EOUA1: During Private Key Queries and Partial Private Key Queries Ri=0, EOUA2: During Sender Queries Rs=0, and EOUA3: During Challenge Phase Rr∗=0.
So, the probability of EOUA3=1/(Qnq+1) and (EOUA1,EOUA2)=1−Qnq/(Qnq+1), then we have (EOUA1,EOUA2,EOUA3)=(1/(Qnq+1)) (1−Qnq/(Qnq+1)) =1/(Qnq+1)2.
Finally, we can get:
Pr[HOUASucess]>=12+OUAξ/(Qnq+1)2.
Theorem 4-Unforgeability: Suppose the insider attacker (ξISA), with his advantages OUAξ, wants to break the security regarding existentially unforgeable under the adaptive chosen- message attacks (EF-CAA-CMA-II) with help of helper called HOUA and his task is to solve HEDLP Problem with advantage as followed: Pr[HOUASucess]>=12+ISAξ/(Qnq+1)2, where Qnq denotes the number of private key extract query, partial private key extract query, and sender query, respectively.
Proof: Suppose the random triple (𝒟, VOUA.𝒟) of HEDLP Problem is given to HOUA and his task to compute H=VOUA.𝒟. The following sub steps represents the processing of Theorem 4:
Setup: Given an 80-bit hyper elliptic curve parameter ℓ for the security of the proposed scheme, the HOUA set γ=VOUA.𝒟 and Φ={γ, 𝒟, Hasha, Hashb, Hashc, HE, Fieldn}. Then, HOUA disclosed Φ to the ξISA. Not that, here HOUA has access to λ.
Queries: The queries which can ask by ξISA is same as asked in Theorem 2.
Output: After performing all the queries that are done in Theorem 2, ξISAgenerate (ω∗,φ∗) from APDR∗ to WBD∗ and C∗ from WBD∗ to APDR∗ on M∗. So, according to forking lemma, ξOUA will generate two valid signature that are (C∗,φ∗,ω∗) and (C∗∗,φ∗∗,ω∗∗), so, we have the following outputs: φ∗(𝒢+δs∗+χs∗)=δs∗+υ and φ∗∗(𝒢/+δs∗+χs∗)=δs∗+υ. So, we have:
φ∗(𝒢+δs∗+χs∗)=φ∗∗(𝒢/+δs∗+χs∗), as Rs∗=1 and rs∗=L, then χr∗=ζr∗+rs∗.λ, γ=VOUA.𝒟, and λ=VOUA, so λ is not accessible for HOUA. Further, χr∗=ζr∗ + L.VOUA, so we have φ∗(𝒢+δs∗+ζr∗ + L.VOUA)=φ∗∗(𝒢/+δs∗+ζr∗ + L.VOUA).
So, in the above equations, VOUA is unknown to HOUA which is solution for HEDLP Problem.
Probability Analysis: In the above game, let Pr[HOUASucess] denote HOUA's probability of solving H=(VOUA.𝒟), and Pr [ξISASucess] denote ξOUA’s probability of doing so. So, the Pr[ξISASucess] ≥ ISAξ. We have the following computations. Pr[HOUASucess]=Pr[↼Stop∩HOUASucess]=Pr[↼Stop].Pr[HOUASucess]=Pr[↼Stop].ISAξ.
On the other hand, if each of the independent events listed below occurs, HOUA will not terminate.
EISA1: During Private Key Queries and Partial Private Key Queries Ri=0, EISA2: During Sender Queries Rs=0, and EISA3: During Challenge Phase Rr∗=0.
So, the probability of EISA3=1/(Qnq+1) and (EISA1,EISA2)=1−Qnq/(Qnq+1), then we have (EISA1,EISA2,EISA3)=(1/(Qnq+1)) 1−Qnq/(Qnq+1)=1/(Qnq+1)2.
Finally, we can get:
Pr[HOUASucess]>=12+ISAξ/(Qnq+1)2.
5.2 Informal Security Analysis
The proposed scheme is based on hash function and hyper elliptic curve discrete logarithm problem. The two main properties of the hash function are irreversibility and collision resistance. Suppose 𝒟1=χ.𝒟, finding ‘χ is said to be a hyper elliptic curve discrete logarithm problem.
Mutual Authentication: The APDR generates the digital signature for mutual authentication with WBD as φ=δs+υ/𝒢+δs+χs and sends it together with ω to the WBD. When the WBD gets φ and ω, it checks the equation φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω
For authentication, and if the equality of φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω holds, which means that mutual authentication between APDR and the WBD is successfully done. The equality test of φ(ηs+ξs+ra.γ+𝒢.𝒟)=ηs+ω can be seen from Section 3.3.
Signature Unforgeability: In the proposed scheme, the signature generated by the application provider is computed using the formula, φ=δs+υ/𝒢+δs+χs. If an attacker attempts to generate a forge one, then he/she must extract δs, and υ from ηs=δs.𝒟 and ω=υ.𝒟 that are normally equals to process two-time hyper elliptic curve discrete logarithm problem, which is difficult.
Sender Anonymity: To register APDR, the user selects δs, computes ηs=δs.𝒟, compute SK=δs.γ, encrypt the identity (IDs) as EIds=ESK(IDs), and send (EIds, ηs) to NMGR via un-secure channel. Upon receiving (EIds, ηs), NMGR can compute the secret key as SK=ηs.λ and decrypt the identity as IDs=DSK(EIds). From the above discussion it is clear that the attacker has no access to the identity of APDR which play the role of sender. Further, the application provider can compute ω=υ.𝒟, where v and 𝒟 denotes the private number and a divisor on hyper elliptic curve. Compute rb=Hasha(IDr, ηr, ξr) and K=υ(ηr+ξr+rb.γ). Calculate 𝒢=Hashb (ω, IDr, IDs, ηs, ξs) and φ=δs+υ/𝒢+δs+χs, then send (φ, ω) to WBD. It is evident from these calculations that the application provider is not providing the identity of any user via an open channel.
Receiver Anonymity: To register WBD, the user selects δr and computes ηr=δr.𝒟 for the identity (IDr), compute RK=δr.γ, encrypt the identity (IDr) as EIdr=ERK(IDr) and send (EIdr, ηr) to NMGR via un-secure channel. Upon receiving (EIdr, ηr), NMGR can compute the secret key as SK=ηr.λ and decrypt the identity as IDr=DSK(EIdr). From the above discussion it is clear that the attacker has no access to the identity of WBD which play the role of receiver. As a result, the proposed scheme is immune to anonymous communication. From the above discussion we can observed that in our proposed scheme ensures anonymous communication, because the attacker cannot get any access to the identity of any participated user.
Integrity: The WBD set the secret key as K=(δr+χr)ω and done the encryption of a message as C=Hashc(K)⊕(M), where ⊕ denotes the encryption function which encrypt the message (M) using the secrete key K and finally send C to application provider. The attacker cannot modify M, because it must need the secret K, which is not accessible for attacker according to the proof of Theorems 1 and 2. Hence, we can conclude from the discussion our proposed scheme satisfies the integrity property.
This section compares the proposed scheme to other relevant schemes in terms of computation cost, communication cost, memory overhead and security functionalities.
In this section, we compare the proposed approach with the methods presented by Liao et al. [25–28]. The comparison is conducted based on the computational costs. Table 2 provides a summary of the important conclusions obtained from the comparison of computing costs. The computational time for Elliptic Curve Point Multiplication (EMUL) is 0.97 milliseconds, while bilinear pairing (P) takes 14.90 ms. Pairing-based point multiplications (BPM) need 4.31 ms, while exponentials on bilinear pairing (EXP) take 1.25 ms [29–32]. To evaluate the computational cost of the suggested approach, we used the Multi-precision Integer and Rational Arithmetic C Library (MIRACL) [33]. The library does a substantial quantity of tests, potentially reaching up to 1000, on fundamental cryptographic procedures. The simulations are executed on a computing device equipped with an Intel Core i7-4510U CPU operating at a frequency of 2.0 GHz, 8 GB of random-access memory (RAM), and the Windows 7 operating system [34]. The HEMUL is expected to have a processing time of 0.48 milliseconds due to its key size of 80 bits. The analysis of Tables 3 and 4, and Fig. 6 demonstrates that the suggested design exhibits much higher cost-effectiveness in terms of computing.



Figure 6: Comparative analysis based on communication cost (in bits) (Liao et al. [25], He et al. [26], Kasyoka et al. [27], Liu et al. [28])
In this part, the proposed scheme is compared to existing schemes proposed by Liao et al. [25–28] in terms of communication cost. Tables 5 and 6 show the primary conclusions drawn from the comparison. According to the data shown in Fig. 7, choosing the proposed scheme results in a significant reduction in communication costs.
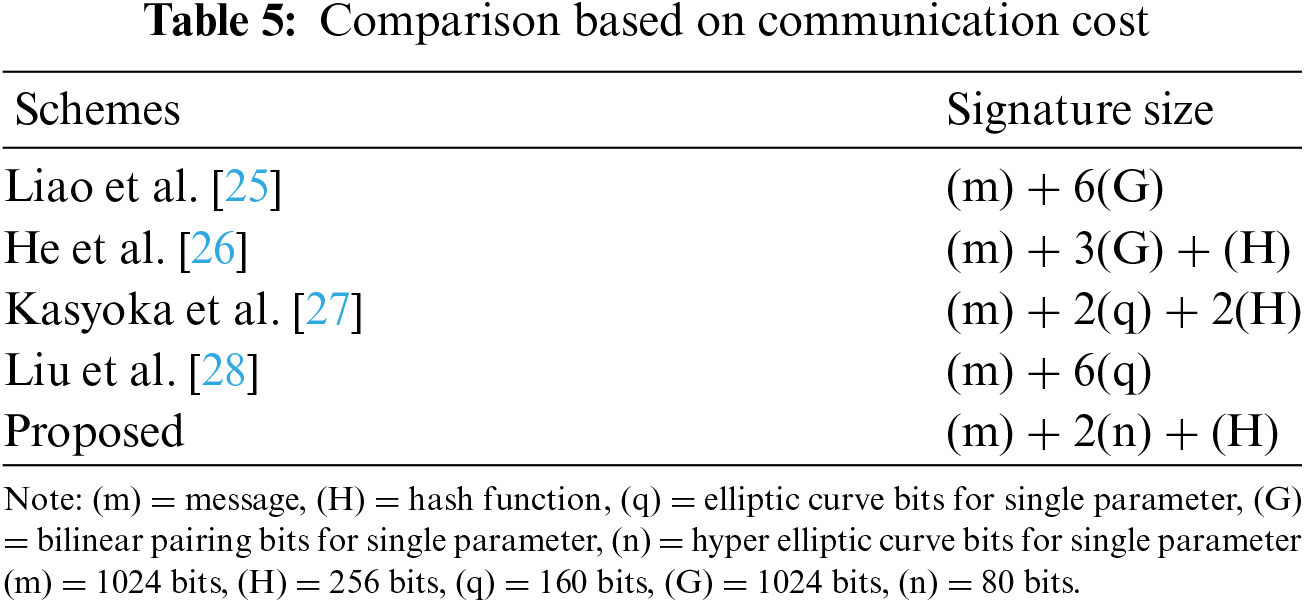


Figure 7: Comparative analysis based on communication cost (in bits) [25–28]
7 Conclusions and Future Works
IoHT systems are used to exchange remote data for a variety of physical activities, including patient monitoring, treatment development, observation and counseling. In IoHT, communication, computing, and interoperability are provided through multiple sensors, actuators, and controllers, resulting in a seamless connection and efficient resource management. Traditional cryptographic techniques, on the other hand, are not practicable for the vast majority of IoHT deployments due to the restrictions of low-power embedded devices. As a result, we proposed the CAA scheme, a security method based on the HECC in this article. The HECC method is effective with small key sizes and can be used in IoHT systems. The security analysis demonstrates the proposed scheme’s efficacy in preventing several cyber-attacks. Second, comparing the proposed scheme with existing schemes is carried out in terms of computation and communication costs. The proposed scheme takes 2.88 ms to compute, compared to 89.21, 68.59, 5.82, and 13.58 ms for Liao et al. [25–28], respectively. Similarly, the proposed scheme’s communication cost is 1440 bits, compared to 7168, 4352, 1856, and 1984 bits for Liao et al. [25–28], respectively. This comparison reveals that the proposed scheme is more efficient than the existing methods in computation and communication costs. In the future, we are intended to consider Genus 3 hyperelliptic curve, which will further improve the proposed scheme efficiency.
Acknowledgement: Nisreen Innab would like to express sincere gratitude to AlMaarefa University, Riyadh, Saudi Arabia, for supporting this research.
Funding Statement: The author received no specific funding for this study.
Availability of Data and Materials: The data supporting the conclusions of this article are included within the article.
Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.
References
1. J. J. P. C. Rodrigues et al., “Enabling technologies for the internet of health things,” IEEE Access, vol. 6, no. 1, pp. 13129–13141, 2018. doi: 10.1109/ACCESS.2017.2789329. [Google Scholar] [CrossRef]
2. S. M. R. Islam, D. Kwak, M. H. Kabir, M. Hossain, and K. S. Kwak, “The internet of things for health care: A comprehensive survey,” IEEE Access, vol. 3, no. 1, pp. 678–708, 2015. doi: 10.1109/ACCESS.2015.2437951. [Google Scholar] [CrossRef]
3. L. Catarinucci et al., “An IoT-aware architecture for smart healthcare systems,” IEEE Internet Things J., vol. 2, no. 6, pp. 515–526, Dec. 2015. doi: 10.1109/JIOT.2015.2417684. [Google Scholar] [CrossRef]
4. Y. Yin, Y. Zeng, X. Chen, and Y. Fan, “The internet of things in healthcare: An overview,” J. Ind. Inf. Integr., vol. 1, no. 1, pp. 3–13, Mar. 2016. doi: 10.1016/j.jii.2016.03.004. [Google Scholar] [CrossRef]
5. C. Dong, Y. Sun, M. Shafiq, N. Hu, Y. Liu and Z. Tian, “Optimizing mobility-aware task offloading in smart healthcare for internet of medical things through multi-agent reinforcement learning,” IEEE Internet Things J., vol. 11, no. 8, pp. 13677–13691, 15 Apr. 2024. doi: 10.1109/JIOT.2023.3338718. [Google Scholar] [CrossRef]
6. B. Farahani, F. Firouzi, V. Chang, M. Badaroglu, N. Constant and K. Ankodiya, “Towards fog-driven IoT eHealth: Promises and challenges of IoT in medicine and healthcare,” Future Gener. Comput. Syst., vol. 78, pp. 659–676, Jan. 2018. doi: 10.1016/j.future.2017.04.036. [Google Scholar] [CrossRef]
7. F. Firouzi et al., “Internet-of-things and big data for smarter healthcare: From device to architecture, applications and analytics,” Future Gener. Comput. Syst., vol. 78, no. 1, pp. 583–586, 2018. doi: 10.1016/j.future.2017.09.016. [Google Scholar] [CrossRef]
8. X. Lin, R. Lu, X. Shen, Y. Nemoto, and N. Kato, “Sage: A strong privacy preserving scheme against global eavesdropping for eHealth systems,” IEEE J. Sel. Areas Commun., vol. 27, no. 4, pp. 365–378, 2009. doi: 10.1109/JSAC.2009.090502. [Google Scholar] [CrossRef]
9. F. S. Sadek, K. Belkadi, A. Abouaissa, and P. Lorenz, “Identifying misbehaving greedy nodes in IoT networks,” Sensors, vol. 21, no. 15, pp. 5127, 2021. doi: 10.3390/s21155127. [Google Scholar] [PubMed] [CrossRef]
10. C. M. Chen, Z. Li, S. A. Chaudhry, and L. Li, “Attacks and solutions for a two-factor authentication protocol for wireless body area networks,” Secur. Commun. Netw., vol. 2021, no. 2021, pp. 1–12. doi: 10.1155/2021/3116593. [Google Scholar] [CrossRef]
11. S. A. Chaudhry, A. Irshad, K. Yahya, N. Kumar, M. Alazab and Y. B. Zekeria, “Rotating behind privacy: An improved lightweight authentication scheme for cloud-based IoT environment,” ACM Trans. Internet Technol., vol. 21, no. 3, pp. 1–19, 2021. [Google Scholar]
12. K. Kim, J. Ryu, Y. Lee, and D. Won, “An improved lightweight user authentication scheme for the internet of medical things,” Sensors, vol. 23, no. 3, pp. 1122, 2023. doi: 10.3390/s23031122. [Google Scholar] [PubMed] [CrossRef]
13. S. Hussain, I. Ullah, H. Khattak, M. A. Khan, C. -M. Chen and S. Kumari, “A lightweight and provable secure identity-based generalized proxy signcryption (IBGPS) scheme for industrial internet of things (IIoT),” J. Inf. Secur. Appl., vol. 58, no. 1, pp. 102625, 2021. doi: 10.1016/j.jisa.2020.102625. [Google Scholar] [CrossRef]
14. C. M. Chen, Z. Chen, S. Kumari, and M. C. Lin, “LAP-IoHT: A lightweight authentication protocol for the Internet of Health Things,” Sensors, vol. 22, no. 14, pp. 5401, Jul. 2022. doi: 10.3390/s22145401. [Google Scholar] [PubMed] [CrossRef]
15. P. Kumar, S. Kumari, V. Sharma, X. Li, A. K. Sangaiah and S. H. Islam, “Secure CLS and CL-AS schemes designed for vanets,” J. Supercomput., vol. 75, no. 6, pp. 3076–3098, 2018. doi: 10.1007/s11227-018-2312-y. [Google Scholar] [CrossRef]
16. I. Ullah, N. U. Amin, M. A. Khan, H. Khattak, and S. Kumari, “An efficient and provable secure certificate-based combined signature, encryption and signcryption scheme for internet of things (IoT) in mobile health (m-health) system,” J. Med. Syst., vol. 45, no. 1, pp. 1–20, 2020. [Google Scholar]
17. H. M. Chen, J. W. Lo, and C. K. Yeh, “An efficient and secure dynamic id-based authentication scheme for telecare medical information systems,” J. Med. Syst., vol. 36, no. 6, pp. 3907–3915, 2012. doi: 10.1007/s10916-012-9862-y. [Google Scholar] [PubMed] [CrossRef]
18. Q. Jiang, J. Ma, Z. Ma, and G. Li, “A privacy enhanced authentication scheme for telecare medical information systems,” J. Med. Syst., vol. 37, no. 1, pp. 9897–9898, 2013. doi: 10.1007/s10916-012-9897-0. [Google Scholar] [PubMed] [CrossRef]
19. S. Kumari, M. K. Khan, and R. Kumar, “Cryptanalysis and improvement of ‘a privacy enhanced scheme for telecare medical information systems’,” J. Med. Syst., vol. 37, no. 4, pp. 1–11, 2013. doi: 10.1007/s10916-013-9952-5. [Google Scholar] [PubMed] [CrossRef]
20. C. L. Chen, T. T. Yang, M. L. Chiang, and T. F. Shih, “A privacy authentication scheme based on cloud for medical environment,” J. Med. Syst., vol. 38, no. 11, pp. 143–216, 2014. doi: 10.1007/s10916-014-0143-9. [Google Scholar] [PubMed] [CrossRef]
21. S. Y. Chiou, Z. Ying, and J. Liu, “Improvement of a privacy authentication scheme based on cloud for medical environment,” J. Med. Syst., vol. 40, no. 4, pp. 101, 2016. doi: 10.1007/s10916-016-0453-1. [Google Scholar] [PubMed] [CrossRef]
22. P. Mohit, R. Amin, A. Karati, G. P. Biswas, and M. K. Khan, “A standard mutual authentication protocol for cloud computing based health care system,” J. Med. Syst., vol. 41, no. 4, pp. 35–50, 2017. doi: 10.1007/s10916-017-0699-2. [Google Scholar] [PubMed] [CrossRef]
23. C. T. Li, D. H. Shih, and C. C. Wang, “Cloud-assisted mutual authentication and privacy preservation protocol for telecare medical information systems,” Comput. Methods Programs Biomed., vol. 157, no. 1, pp. 191–203, 2018. doi: 10.1016/j.cmpb.2018.02.002. [Google Scholar] [PubMed] [CrossRef]
24. M. E. S. Saeed, Q. Liu, G. Tian, B. Gao, and F. Li, “Remote authentication schemes for wireless body area networks based on the internet of things,” IEEE Internet Things J., vol. 5, no. 6, pp. 4926–4944, 2018. doi: 10.1109/JIOT.2018.2876133. [Google Scholar] [CrossRef]
25. Y. Liao, Y. Liu, Y. Liang, Y. Wu, and X. Nie, “Revisit of certificateless signature scheme used to remote authentication schemes for wireless body area networks,” IEEE Internet Things J., vol. 7, no. 3, pp. 2160–2168, 2020. doi: 10.1109/JIOT.2019.2959602. [Google Scholar] [CrossRef]
26. D. He, S. Zeadally, N. Kumar, and J. H. Lee, “Anonymous authentication for wireless body area networks with provable security,” IEEE Syst. J., vol. 11, no. 4, pp. 2590–2601, 2017. doi: 10.1109/JSYST.2016.2544805. [Google Scholar] [CrossRef]
27. P. Kasyoka, M. Kimwele, and S. M. Angolo, “Certificateless pairing-free authentication scheme for wireless body area network in healthcare management system,” J. Med. Eng. Technol., vol. 44, no. 1, pp. 12–19, 2020. doi: 10.1080/03091902.2019.1707890. [Google Scholar] [PubMed] [CrossRef]
28. Y. Liu, Y. Wang, and Z. Peng, “A novel and efficient anonymous authentication for wbans,” Internet Technol. Lett., vol. 1, no. 1, pp. 12–19, 2021. [Google Scholar]
29. M. A. Khan et al., “An online-offline certificateless signature scheme for internet of health things,” J. Healthc. Eng., vol. 2020, pp. 1–10, 2020. doi: 10.1155/2020/6654063. [Google Scholar] [PubMed] [CrossRef]
30. I. Ullah, S. Zeadally, N. U. Amin, M. Asghar Khan, and H. Khattak, “Lightweight and provable secure cross-domain access control scheme for internet of things (IoT) based wireless body area networks (WBAN),” Microprocess. Microsyst., vol. 81, no. 1, pp. 103477, 2021. doi: 10.1016/j.micpro.2020.103477. [Google Scholar] [CrossRef]
31. M. A. Khan et al., “A provable and privacy-preserving authentication scheme for uav-enabled intelligent transportation systems,” IEEE Trans. Ind. Inform., vol. 18, no. 5, pp. 3416–3425, 2022. doi: 10.1109/TII.2021.3101651. [Google Scholar] [CrossRef]
32. M. A. Khan, B. A. Alzahrani, A. Barnawi, A. Al-Barakati, A. Irshad and S. A. Chaudhry, “A resource friendly authentication scheme for space-air–ground-sea integrated maritime communication network,” Ocean Eng., vol. 250, no. 110894, Apr. 2022. doi: 10.1016/j.oceaneng.2022.110894. [Google Scholar] [CrossRef]
33. P. Rastegari, M. Khalili, and A. Sakhaei, “Security analysis and improvement of an access control protocol for wbans,” Int. J. Netw. Security, vol. 25, no. 2, pp. 285–296, 2023. [Google Scholar]
34. S. Yu, A. K. Das, Y. Park, and P. Lorenz, “SLAP-IoD: Secure and lightweight authentication protocol using physical unclonable functions for internet of drones in smart city environments,” IEEE Trans. Vehicular Technol., vol. 71, no. 10, pp. 10374–10388, 2022. doi: 10.1109/TVT.2022.3188769. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools
