CRBFT: A Byzantine Fault-Tolerant Consensus Protocol Based on Collaborative Filtering Recommendation for Blockchains

1  Introduction

The explosion of bitcoin makes blockchain become a potentially revolutionary technology in the information field. The essence of blockchain is a distributed ledger based on a peer-to-peer (P2P) network and cryptography, which is composed of a series of data blocks. Each block contains the previous block’s hash value, and the connection from the original block to the current block forms a chain structure. With the deepening of research, blockchain can help to establish trust relationships among multiple entities in a distributed environment without a trusted third party. Therefore, blockchain promotes the development of cryptocurrency and plays an increasingly important role in scenarios such as the Internet of Things (IoT) and supply chains [1,2].

As the core of blockchain, the consensus protocol determines how all participants in the blockchain reach a consensus on new transactions. According to the selection strategies of the primary, consensus protocols can be divided into Proof-of-X (PoX) and leader-election-based ones [3,4]. Among them, the primary PoX consensus protocol needs to prove that it is qualified to propose new blocks. For example, the Proof-of-Work (POW) in Bitcoin requires all nodes to compete to calculate a hash value that meets specific rules. The node that first finds the target value will immediately record it in a new block and broadcast it to all the nodes in the chain. Then, other nodes will attach the received block to the chain if they consider it to be correct. In addition, the PoX consensus protocols also include Proof-of-Stake (POS), Proof-of-Weight (PoActivity), Proof-of-Space (PoSpace) [5], etc. PoX consensus protocols are widely used, and their availability has been verified in practice. However, such protocols usually have several drawbacks such as low efficiency and lack of fairness [6]. The primary of the leader-election-based consensus protocol (such as Raft [7], Multi-Paxos [8], and PBFT [9,10]) is elected by voting. Such consensus protocols have high throughput and low consensus latency. However, Raft and Multi-Paxos can only tolerate crash faults in the system and cannot handle Byzantine faults. Therefore, Raft and Multi-Paxos cannot ensure the system’s security in a complex network environment.

PBFT is the first Byzantine fault-tolerant consensus algorithm for the asynchronous network environment. It is suitable for blockchain scenarios that require more robust security and consistency. For example, in the earlier version of Hyperledger (v0.6) [11] and FISCO BCOS [12], PBFT is used to ensure that once a block is committed, the block can no longer be replaced or modified. However, with the changing application environment and requirements, the limitations of PBFT are gradually revealed. Firstly, the communication complexity of PBFT will increase with the number of nodes, so it cannot be applied to large-scale blockchain systems requiring high efficiency. Secondly, the security of PBFT is based on the fact that the number of malicious nodes is limited to no more than 1/3 of the total number of nodes. Because of this, the existence of malicious nodes will pose a threat to the system’s security, and PBFT lacks mechanisms to mitigate the impact of them on the system. Finally, once the primary in PBFT crashes or does evil, it will trigger the view-change operation with communication complexity of O(N3), resulting in large computing and communication overhead. PBFT lacks effective means to ensure that the selected primary has high reliability. At present, in view of the above problems, the research on high-performance, high-security, and scalable consensus protocols based on PBFT has become a research hotspot in the field of blockchain.

By introducing the collaborative filtering method [13], this paper proposes a Byzantine fault-tolerant consensus protocol based on Collaborative Filtering Recommendation called CRBFT. CRBFT builds an evaluation system based on collaborative filtering recommendation algorithm between nodes, and then calculates the recommendation credibility based on the recommendation similarity, and takes the latter as the weight factor of the node’s global trust value, which can eliminate the bad influence caused by the unfair evaluation of some malicious nodes, thus ensuring the reliability of the node’s global trust value calculation results. Finally, according to the trust value to give the node the corresponding voting weight, the higher the trust value the greater the voting weight, so as to improve the efficiency of consensus voting. The main contributions are as follows:

a)  A global trust model based on collaborative filtering recommendation is designed for the blockchain system. The global trust value calculator uses the similarity between a node’s recommendation and those of the recommender to determine whether to adopt the recommender’s recommendation. In this way, the recommendation voice of good nodes is amplified, and the impact of cunning malicious nodes on the calculation of global trust value is weakened. In addition, since the number of malicious nodes is limited, malicious nodes are hard to use the similarity factor to fundamentally affect the calculation results of global trust value.

b)  The collaborative filtering recommendation trust model is combined with PBFT, and a new Byzantine fault-tolerant consensus protocol called CRBFT is proposed. In the consensus process, a trust metric is applied to all nodes, and the nodes are assigned the corresponding voting power according to the trust value which can alleviate the influence of malicious nodes on the consensus process. In addition, legitimate consensus messages can obtain votes from honest nodes faster and speed up the consensus-reaching process. This paper also designs and implements a weight random election algorithm to randomly determine the identity of the primary node, thus reducing the probability of an attack due to the primary node being predictable in advance.

c)  The feasibility of CRBFT is validated through theoretical analysis. Then, a blockchain system is constructed to simulate the consensus process, and CRBFT is evaluated in terms of resistance to malicious node attacks, decentralization features, and consensus performance to verify its superiority and reliability.

The rest of this paper is organized as follows. Section 2 briefly reviews some related work. Section 3 presents the relevant background knowledge. Section 4 gives the motivation and design ideas for this paper, as well as a system overview of the CRBFT protocol, and the consensus protocol is proposed in Section 5. Sections 6 and 7 evaluate the safety and performance of CRBFT both theoretically and experimentally. At last, our work is summarized in Section 8.

2  Related Work

To solve the Byzantine general problem in distributed systems, Castro et al. [9] proposed PBFT in 1999, which is the first Byzantine fault tolerance protocol to reduce the algorithm complexity to the polynomial level. Some blockchain platforms adopt PBFT for consensus, but the defects of PBFT also restrict the development of blockchain. As the system size and the number of malicious nodes increase, the system efficiency and security will be significantly reduced. Therefore, in recent years, a large number of improvements for PBFT have been proposed.

Buchman et al. [14] combined PBFT with PoS and proposed a consensus protocol with a reward and punishment mechanism called Tendermint. This protocol has a similar consensus process to PBFT, but the difference is that Tendermint integrates the view-change process with the normal consensus process to reduce the complexity of the protocol. The HoneyBadger [15] consensus protocol proposed by Miller et al. alleviates the bandwidth bottleneck of a single node by segmenting the transaction information. Also, it uses the atomic broadcast protocol to ensure that each node can receive the same messages in the same order. By introducing threshold signature into the consensus process, the HotStuff [16] proposed by Yin et al. decreases the message verification complexity to O(N) and dramatically improves the consensus efficiency. However, HotStuff relies too much on the primary. If the primary does evil and sends inconsistent messages to different replicas, some replicas will be inactivated. Zhang et al. [17] proposed DBFT by establishing the double-response mechanism, which enables replicas to submit requests while sending responses to clients. This protocol avoids additional inconsistency detection and can achieve excellent performance when there are replica failures. The Algorand [18] consensus algorithm proposed by Micali et al. utilizes the verifiable random function to randomly select the proposer and validators of the next block, and the application of PBFT in the public chain improves the scalability of the consensus protocol. However, the actual performance of Algorand will be significantly affected by the stability of the system. SBFT [19] introduces a collector role into the protocol, which is responsible for collecting the consensus messages of replicas. Also, it adopts the BLS threshold signature scheme to aggregate the messages and send them to the client so that the client can complete the whole consensus process after receiving only one reply message, which reduces the network communication overhead effectively. However, the role of the collector will bring centralization problems to SBFT. To reduce the complexity and communication overhead of the consensus algorithm, Li et al. [20] proposed an consensus mechanism called SVBFT based on the reward and punishment strategy. The primary in SVBFT is generated by mutual voting between nodes, and the communication complexity of the whole consensus process is O(N).

Chen et al. [21] utilized feature grouping to divide the nodes into different consensus groups to optimize the structure of large-scale network and proposed a consensus mechanism called FCBFT. Meanwhile, FCBFT utilizes reputation mechanism to enhance the reliability of consensus nodes. However, the node grouping mechanism in FCBFT cannot ensure that each node is divided into a unique organization, which may increase the burden on nodes in the consensus process. To improve consensus efficiency, Gao et al. [22] selected trusted nodes to execute the PBFT protocol by introducing the EigenTrust [23] global trust model into the consensus protocol. However, this scheme only takes the node’s trust as the weight of the recommendation degree, without taking into account the attack of cooperative malicious nodes and may cause the calculation result of the node’s trust value to deviate from the correct value. Zhan et al. [24] utilized the hash function to construct a random selection algorithm and randomly selected some nodes as consensus nodes, which can effectively reduce the size of the consensus group, but cannot reduce the proportion of malicious nodes. To further optimize the consensus efficiency, Li et al. [25] proposed a consensus mechanism called SHBFT to reduce consensus latency by layering consensus nodes. However, as the number of nodes increases, the layered structure will become more complex, which will adversely affect the system’s performance. Lei et al. [26] proposed a reputation-based BFT protocol integrating the reputation model. The protocol selects nodes with a high reputation to execute PBFT to improve consensus efficiency and Byzantine fault tolerance. However, the reputation model in RBFT is only effective in an ideal environment. If the dependent device fails or the operating system has vulnerabilities, the reputation model will not be able to resist the collusion attack from malicious nodes. By presenting the transmission idea of trust relationships in human society, Lv et al. [27] proposed a consensus protocol called CoT based on PageRank. CoT calculates the trust value of each node by constructing the trust relationship graph of the network, and then it selects the node with a high trust value to execute the consensus algorithm. However, due to the congenital disability of PageRank, CoT cannot solve the problem that malicious nodes are exaggerated but normal nodes are belittled. Zhang et al. [28] designed a BFT consensus protocol called LRBP for single-hop wireless network environments, which employs randomized trust election and a voting mechanism based on Boneh-Lynn-Shacham signatures to improve consensus efficiency. Tian et al. [29] designed a consensus protocol called TSBFT in order to overcome the problems of single point of failure and message transmission latency in the traditional BFT-type consensus mechanism, which ensures the security and validity of the scheme by employing the secret election leader protocol and the threshold signature technique. Xiao et al. [30] used a decision tree algorithm to analyze node behavior and designed a new node credit assessment model to select potential non-Byzantine nodes to execute the PBFT protocol.

Due to the complexity of the blockchain network, the current optimized PBFT consensus mechanism based on the trust model is difficult to find out the potential malicious nodes, especially when the malicious nodes conspire with each other, and also affects the result of the trust value calculation of the normal nodes. In addition, the leader election process is crucial for the security of the consensus process, and it is difficult for existing schemes to strike a balance between randomness and node reliability. Therefore, in order to solve the above problems, it is necessary to use a new trust evaluation model to assess the reliability of consensus nodes and combine the node trust value with randomness to provide a reliable and effective support for the leader election.

3  Preliminaries

In this section, the foundation for the design of the consensus protocol in this paper will be briefly described, including the consensus process of PBFT, the collaborative filtering method, and the Spearman correlation coefficient.

3.1 PBFT

PBFT is the first consensus protocol to efficiently solve the Byzantine General problem [31] in the asynchronous network environment. The security of PBFT can be guaranteed only when n⩾3f+1 is satisfied, where n and f represent the total number of nodes and the number of abnormal nodes in the system, respectively. The nodes executing PBFT can be divided into a primary and n−1 replicas.

The primary and the replicas need to go through five stages to reach a consensus on the client’s request. The specific consensus process is shown in Fig. 1. The client first sends a request to the primary, which then signs and endorses the client’s request, constructs a PRE-PREPARE message and broadcasts it to the replica node. After the replica nodes receive the PRE-PREPARE message, they need to verify the consistency of the message with each other, so they need to broadcast the PREPARE message with each other. If more than 2/3 of the nodes adopt the PRE-PREPARE message sent by the primary, then the nodes also broadcast COMMIT message among themselves. Finally, the nodes reply to the client’s request. The detailed implementation can be referred to in the original paper [9,10].

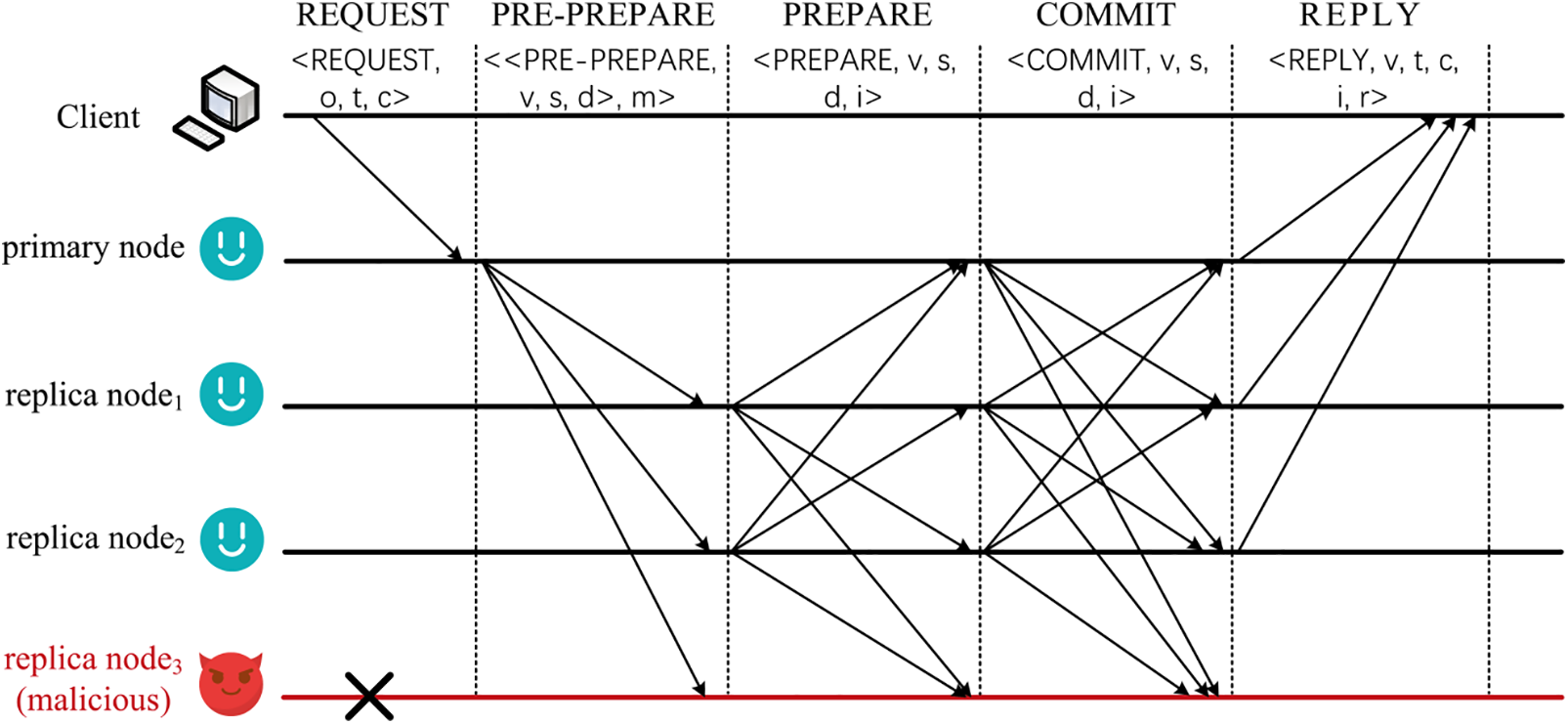
Figure 1: The basic process of PBFT consensus

3.2 Collaborative Filtering

Collaborative filtering is one of the most commonly used methods for recommendation systems [32–34]. Its core idea is to calculate the similarity between users and then make a classification to improve recommendation accuracy. It is based on the assumption that users favoring the same category of items are similar. Fig. 2 illustrates the basic idea of collaborative filtering recommendations. If user A and user C favor the same category of items, they can be considered to have a high degree of similarity. Then, when developing a recommendation strategy, the recommender can recommend the products that user C favors to user A.

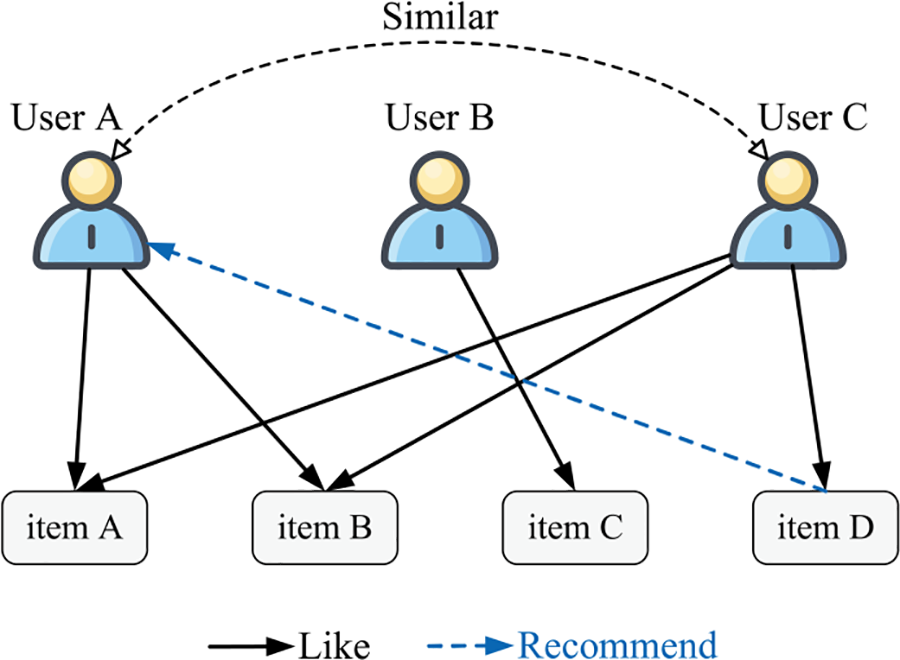
Figure 2: Collaborative filtering recommendation

In this paper, the collaborative filtering mechanism is introduced into the consensus protocol to optimize the calculation of node trust values and improve recommendation accuracy. First, the similarity between nodes is calculated according to the recommendation opinions of nodes. Then, the node utilizes the similarity between its recommendation opinions and those of the recommender as a basis for determining whether to adopt the recommender’s recommendation opinions. It is assumed that good nodes will recommend other nodes in strict accordance with the objective facts, and malicious nodes may give false recommendations to destroy the security of the system. Therefore, the similarity recommendations between good nodes will be relatively high, while that between malicious nodes will be relatively low. The details of the design will be presented in Section 5.1.

3.3 Spearman Correlation Coefficient

ρ=∑i=1n(ℜ(Xi)−ℜ(X)¯)(ℜ(Yi)−ℜ(Y)¯)(∑i=1n(ℜ(Xi)−ℜ(X)¯)2∑i=1n(ℜ(Yi)−ℜ(Y)¯)2)1/2(1)

The Spearman correlation coefficient, proposed by Charles Spearman, is widely employed as a nonparametric measure of correlation [35], and it is one of the oldest statistics based on ranks. It is usually denoted as ρ for data samples. Specify n measurements of two variables as X(X1,…,Xn) and Y(Y1,…,Yn). Then, ℜ(Xi) and ℜ(Yi) respectively represent the rank of Xi and Yi, where each rank is an integer from 1 to n and indicates relative magnitude. The calculation of the Spearman correlation coefficient between X and Y is shown in formula (1), where, ℜ(X)¯ and ℜ(Y)¯ represent the mean value of ℜ(Xi)s and ℜ(Yi)s, respectively. In this paper, the Spearman correlation coefficient is used to calculate the similarity of node recommendation opinions.

4  Motivation, Design Ideas, and System Model

This section describes in detail the motivation and design ideas behind this paper and provides an overview of the system model for the CRBFT protocol.

4.1 Motivation

The prerequisite for PBFT to run successfully is that the number of malicious nodes must be less than one-third of the total number of nodes. However, even if this condition is met, malicious nodes will still pose a threat to the security of the system.

To identify possible malicious nodes, the behavior and type of nodes can be predicted by establishing a trust mechanism [36], but it is not sufficient to rely on the evaluation of certain nodes to calculate the node trust value. This is because the information available to a single node is limited, and it is generally necessary to combine all the reputation information of the target node, i.e., all the other nodes’ evaluations to accurately calculate the trust value of the target node in the network [37]. As investigated in the studies [22,26,27], malicious nodes in the system are identified by building a trust model, but their scheme is still flawed because the evaluation information provided by some nodes in a computer network may be false [38]. Well-disguised malicious spies [39] will deliberately behave well to gain the trust of normal nodes and then exaggerate other malicious nodes, causing the calculation of the node trust value to deviate from the correct one. Therefore, the key to improving the accuracy of trust recommendations is to allow normal nodes to identify the evaluation opinions of malicious nodes in a network environment where trust is lacking.

4.2 Design Ideas

In this paper, the collaborative filtering recommendation designed for consensus protocol is a global trust model. When calculating the trust value of the whole network nodes, the trust value calculator takes the global trust value of the recommender as the weight of the recommender’s recommendation; also, it employs the similarity between its recommendation and the recommender’s as the basis for determining whether to adopt the recommender’s recommendation opinions. The specific idea is that when each good node receives the recommendation opinions of other nodes to the nodes of the whole network, it will calculate the similarity between its recommendation and those given by the recommender. The good node will provide objective recommendation opinions to the nodes of the whole network in strict accordance with the historical interactive information. Therefore, the recommendation opinions between the good nodes have a high similarity, and the malicious nodes may give false recommendation opinions to destroy the system’s security. For example, malicious spies will exaggerate malicious nodes but belittle the good nodes. In this case, the similarity between the good nodes and the malicious nodes is relatively low. Therefore, a good node can identify potential malicious nodes according to the similarity of its recommendation opinions with those of other nodes. Recommendations from malicious nodes will be given a lower weight, while those from good nodes will be given a higher weight. In this way, the recommendation voice of good nodes will be amplified, and the influence of cunning malicious nodes on the calculation of trust value will be weakened.

In addition, PBFT requires that the number of good nodes in the system is at least twice the number of malicious nodes, and the global trust value of any node i is obtained by combining the recommendations of all nodes. Based on this, even if the malicious nodes give a lower weight to the recommendations of good nodes and give a higher weight to the recommendations of other malicious nodes, it is hard to have a fundamental impact on the trust value of the full network node because malicious nodes account for a small number in the system. The resistance of the proposed scheme to malicious nodes will be evaluated through experiments in Section 7.2.

Finally, CRBFT assigns nodes with voting power according to their trust values. And even the node with the lowest trust value will have the right to vote for consensus messages. Meanwhile, the system updates node trust values and voting power periodically. The above design solution has the following three advantages:

a)  The decentralized nature of the blockchain network can be maintained, preventing a small number of nodes from continuously dominating the consensus process of the system and avoiding the evolution of the network in a centralized direction.

b)  Friendly to new nodes that have just joined the system, a new node can actively participate in the consensus process in the current cycle even though it does not have a high trust value, and then the node gains a higher trust value in the next cycle. This can motivate nodes or users.

c)  The voting power of a node is proportional to the node’s trust value, which allows most honest nodes to vote more than malicious nodes, and legitimate consensus messages can obtain votes from honest nodes faster, thus improving consensus efficiency.

4.3 System Model

The blockchain network is an unstructured network that typically uses gossip [40] to disseminate transactions and block data. It ensures that messages sent by each node are eventually received by all nodes so that any two nodes in the system have direct or indirect interaction. The block data and consensus messages are constantly transmitted between nodes because of the need for a consensus process. Attacks against the blockchain are related to messages including broadcasting inconsistent block data and voting information. Therefore, to reduce the impact on the system caused by the unpredictable behavior of malicious nodes, the nodes in CRBFT generate recommendations for other nodes based on historical interaction information, and then the recommendations from the whole network are combined to calculate the global trust value of the nodes, and finally, the corresponding voting power is assigned to the nodes according to their trust values. In this way, malicious nodes will be given little voting power due to their low trust values, thus making it difficult for malicious nodes to influence the consensus process compared to those honest nodes with high voting power.

Fig. 3 illustrates the overall framework of the system. The Monitoring Unit (MU) collects and records the consensus messages transmitted in the network. Then, it updates the recommendation between nodes according to the recorded historical messages when calculating the global trust value of nodes. The proposed scheme embeds the MU in each node. In this way, the failure of the MU on a single node can be avoided. Also, the nodes in the system are allowed to observe the behaviors of other nodes directly, which provides a basis for nodes to generate recommendations. The Global-Trust module in the framework is a global trust value calculation module encoded on all nodes. It is activated when the trust value of all nodes needs to be updated and is responsible for broadcasting recommendation information between nodes and calculating a globally uniform trust value. The lower the trust value, the more likely the node is malicious. Thus, to prevent malicious nodes from being selected as primary nodes, the nodes with higher trust values are divided into candidate primary node groups, while the other nodes are divided into normal groups. Finally, all nodes in the system continue to execute the consensus protocol based on the latest assigned voting power. Section 5.2 will describe in detail the calculation method of node voting power and the candidate node classification strategy.

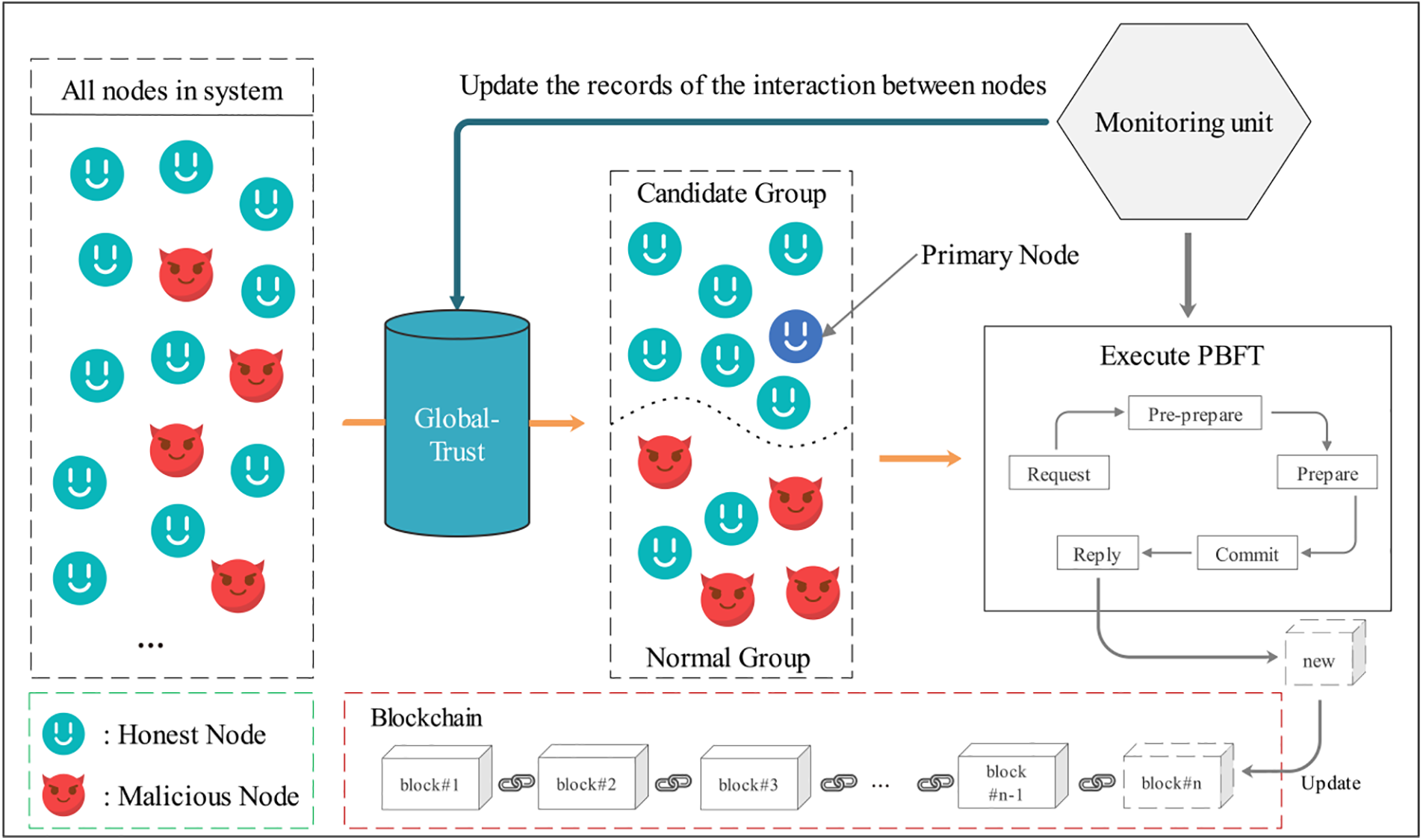
Figure 3: CRBFT framework

5  CRBFT

This section first introduces the collaborative filtering recommendation model in the CRBFT protocol, gives the definition of key information in the model, and describes in detail the calculation of the global trust value of nodes based on the collaborative filtering recommendation model; then, this section introduces the design of the method for calculating the voting power of nodes based on the trust value and the weight random election algorithm, which is used to elect the primary node in each round of the consensus process; finally, this section elaborates on the consensus process of the CRBFT consensus protocol.

5.1 Collaborative Filtering Recommendation

The collaborative filtering recommendation module is the most important part of the CRBFT protocol. Its core function is to periodically update the global trust value of nodes, enhance the ability of honest nodes in the consensus process and weaken the influence of malicious nodes on the system, thus enhancing the security of the blockchain system and improving the consensus efficiency. The definition of key information in the collaborative filtering recommendation module is described in detail below.

5.1.1 Definition

Definition 1. (Local Evaluation): Local evaluation is the evaluation of a node in the system from the perspective of a single node, and its value falls within 0 to 1. The local evaluation of node i and node j is shown in formula (2), where, fij and gij represent the number of unsuccessful and successful interactions between node i and node j, respectively. (fij and gij will be described in detail in Section 5.1.2). The initial value of eij is set to 0.5 according to formula (3).

eij=arccot(fij−gij)/π(2)

Definition 2. (Local Recommendation Vector): The local recommendation vector is calculated from local evaluations, and unlike local evaluations, it reflects the degree to which a node is recommended to all other nodes. For any node i, its local recommendation can be represented as ri=[ri1, ri2,…,rin]. where, rij=eij/2×∑k=1neik, and it denotes the recommendation of node i to j.

Definition 3. (Recommendation Similarity): Recommendation similarity reflects the similarity of the local recommendation vector between any two nodes. This paper adopts the Spearman correlation coefficient to calculate the similarity. For any two nodes i and j, the calculation of the recommended similarity is shown in formula (3), where, ℜ(rik) represents the rank of rik in ri=[ri1, ri2,…,rin], and ℜ(ri)¯ represent the mean value of ℜ(rik)s.

sij=∑k=1n(ℜ(rik)−ℜ(ri)¯)(ℜ(rjk)−ℜ(rj)¯)/2(∑k=1n(ℜ(rik)−ℜ(ri)¯)2∑k=1n(ℜ(rjk)−ℜ(rj)¯)2)1/2+12(3)

Definition 4. (Recommendation Credibility): The recommendation credibility reflects the degree of credibility of a node’s recommendation. If a node’s recommendation is similar to those of the majority nodes, its recommendation has a higher degree of credibility. The method to calculate the node recommendation credibility is shown in formula (4). The recommendation similarity sij between node i and other nodes j is accumulated and then averaged to get ci, which is the recommendation credibility of node i.

ci=∑j=1nsij/n(4)

Definition 5. (Global Recommendation Matrix): As shown in formula (5), the global recommendation matrix R∈Rn×n is derived from the local recommendation of the whole network nodes, where line i represents the local recommendation of node i. This paper assumes that the global recommendation matrix R constructed by all nodes is the same when calculating the global trust value of a node.

R=[r11r12⋯r1nr21r22⋯r2n⋮⋮⋯⋮ri1ri2⋯rin⋮⋮⋯⋮rn1rn2⋯rnn](5)

Definition 6. (Global Trust Vector): The global trust vector is denoted by T=[T1, T2,…,Tn], where Ti is the global trust value of node i, which is calculated by combining the recommendation vectors of the nodes across the network, as shown in formula (6). To obtain more accurate calculation results, formula (6) needs to be called repeatedly to calculate the global trust value of nodes in several iterations until the calculation results converge. It is worth noting that in the initial phase of the system, Ti of any node i is equal to 1/n, and Tj in formula (6) represents the trust value of node j generated during the last iteration.

Ti=∑j=1nsij×cj×Rji×Tj(6)

Since the global trust value of each node is the same in the initial state, the global trust vector T maintained locally by each node is also the same during the subsequent iterative computation of the trust value. Of course, after each global trust value update, the nodes can broadcast among themselves to ensure the consistency of each other’s previously stored T.

The next section describes how to use the above definition to calculate the global trust value of a node and provides the corresponding pseudo-code of the calculation process.

5.1.2 Calculation Method of Global Trust Value of Nodes

According to Definition 1, the local evaluation generated between any two nodes i and j with respect to each other is related to the number of successes and failures of their interactions, and for nodes i and j, the local evaluation update rule is shown below:

•   If j is the primary. If j sends inconsistent messages to i and other nodes, let fij=fij+40 and gij=0. If the block proposed by j is appended to the blockchain, let gij=gij+1.

•   If j is not the primary. If j sends inconsistent messages to i and other nodes, let fij=fij+20 and gij=0. If the message sent by j to i is consistent with the majority of nodes, let gij=gij+0.5. Additionally, if i does not receive a consensus message from j in this round of consensus, let fij=fij+2.5.

Fig. 4 illustrates how the local evaluation changes if the primary node and the other consensus nodes broadcast inconsistent messages. It can be seen that once a node sends a consensus message that is inconsistent with the consensus messages sent by most of the other nodes in the system, the value of the local evaluation of that node by the other nodes decreases dramatically. By comparing the magnitude of the decrease in the red and blue lines in Fig. 4, it can be seen that the primary node suffers a greater penalty than the common consensus node.

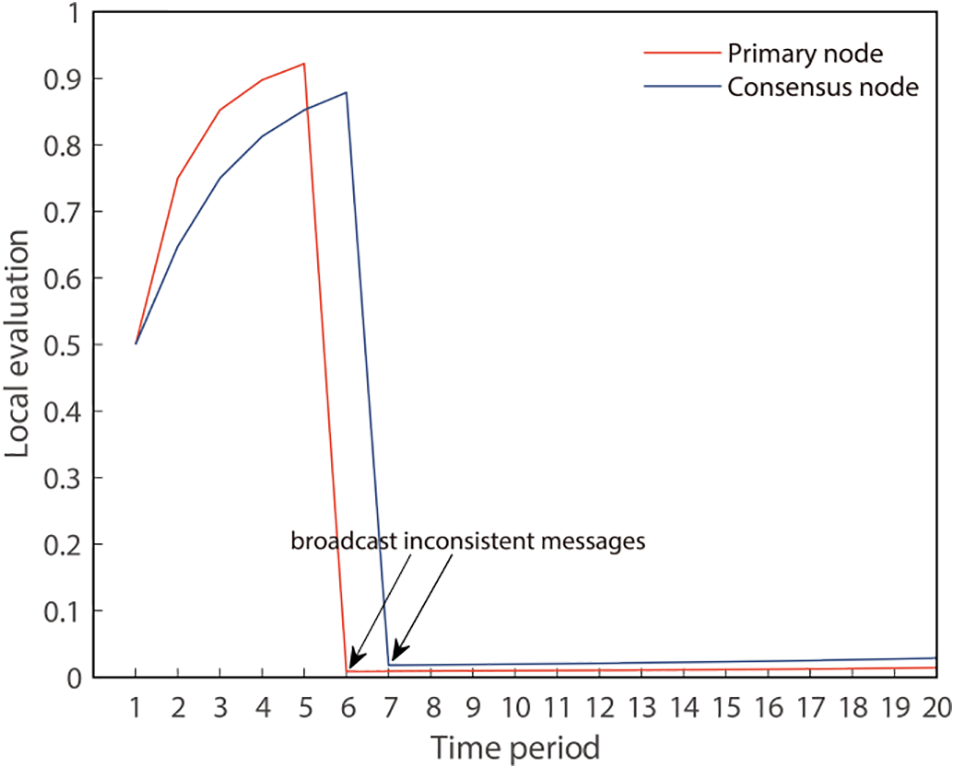
Figure 4: The change of malicious node’s local evaluation

As the consensus process continues, the local evaluation of all nodes in the network is constantly changing, and so is the recommendation degree between any two nodes. This indicates that each node’s global trust value is different at different times. Although obtaining the latest trust value of nodes in real-time will greatly benefit the system security, frequent updating of the global trust value of nodes will cause unnecessary communication and computation overhead. Therefore, this paper adds a trust update cycle mechanism to the CRBFT protocol, and every N rounds of consensus in the system is a cycle. During a cycle, each node in the system only updates its evaluation values f and g to other nodes locally; also, each node does not broadcast its local recommendation vector r to other nodes and will only broadcast it when the cycle is changed. The consensus process will continue only after the global trust values and voting power of all nodes have been updated and a new primary node has been elected. The Algorithm 1 describes the trust value update process, and the detailed node-global trust value update process is shown below:

a)  Each node resets its local evaluation e against other nodes, and then it recalculates the value of e based on the historical interaction information fand g recorded during the previous cycle, followed by the generation of a local recommendation vector r, which is broadcast to other nodes.

b)  When a node receives local recommendation vectors from other n−1 nodes, it will generate the global recommendation matrix R locally and then calculate the similarity of the recommendation vectors between nodes and the recommendation credibility of each node. Finally, the global trust vector T will be computed in iterations through formula (6), as shown in lines 21 to 25 of Algorithm 1.

c)  After obtaining the new global trust value, the node will enter the timeout waiting state to wait for other nodes in the system to complete the update of the global trust value.

5.2 Voting Power and Weight Random Election Algorithm

This section describes how to calculate the voting power of a node based on its trust value and describes a weight random election algorithm, which randomly elects the master node for each round of consensus.

5.2.1 Voting Power

poweri=n−rank(Ti)+1(7)

Different from the PBFT consensus protocol, the CRBFT protocol specifies that nodes with different trust values have different voting power. Eq. (7) gives the method to calculate the voting power of a node. Note that in the initial start-up phase of the system, the voting power of each node is set to 1 for the first cycle because all nodes have equal trust values.

In Eq. (7), n denotes the total number of nodes in the system, and rank(Ti) denotes the ranking of nodes in terms of trust value. The node with the largest trust value has a rank of 1, and conversely, the node with the smallest trust value has a rank of n. The relationship between the total voting power tp and the total number of nodes n in the system can be deduced from Eq. (7) as shown in Eq. (8).

tp=(1+n)n2(8)

5.2.2 Weight Random Election Algorithm

In a consensus protocol based on the primary node election class, the primary node plays a crucial role because it is responsible for proposing new blocks and driving the system to reach consensus. For security reasons, it is necessary to avoid malicious nodes from being elected as primary nodes, and there must be randomness in the election process so that it is difficult for attackers to predict the future primary nodes and launch specific attacks. Based on the above considerations, this section designs a weight random election algorithm based on node voting power, as shown in Algorithm 2. Before each consensus round begins, all nodes in the system run the Algorithm 2 to determine the primary node for the current consensus round.

The system needs to set a voting power threshold t as the input of Algorithm 2. Nodes with voting power greater than t will be selected as primary node candidates, while those with voting power less than t will not be selected as the primary node in the current cycle, but they can still participate in consensus voting. In this paper, the value of t is set to 2n/3, where n denotes the total number of nodes in the system. In addition, the latest block b and a uniform random function rand() are taken as inputs to Algorithm 2. The random function rand() is used to generate a random offset q, with q taking values in (0, sum], where sum denotes the sum of the voting power of all candidate nodes, as shown in line 7 of Algorithm 2. Additionally, Algorithm 2 uses the hash value of block b as the seed for the random function rand(), which ensures that nodes distributed in different parts of the network generate q with a value.

5.3 The Process of CRBFT

The consensus process of CRBFT consists of five phases: Cycle Change, Primary Election, PRE-PREPARE, PREPARE, and COMMIT, as shown in Fig. 5.

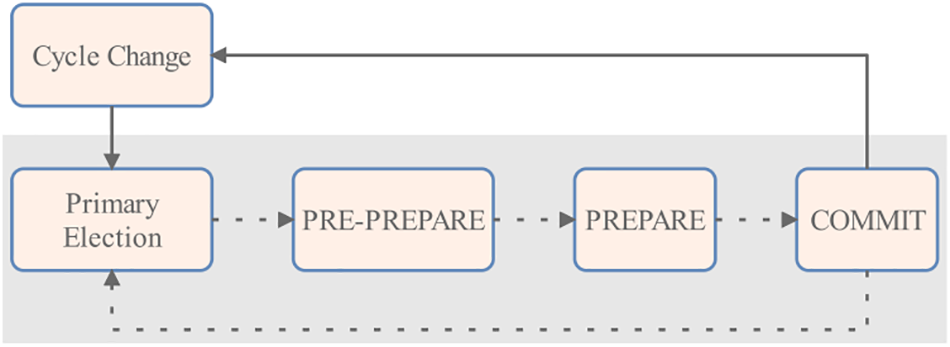
Figure 5: The basic process of CRBFT

Specifically, the Cycle Change phase is equivalent to the node’s trust value update phase, which occurs only at the beginning of each cycle. Then, the remaining four phases occur cyclically within each cycle. The beginning of the Primary Election phase to the end of the COMMIT phase represents the completion of a consensus round. Thus, each round of consensus begins with the re-election of a primary node in the election phase, followed by the primary node proposing a new block in the PRE-PREPARE phase and the other replica nodes verifying the new block in the PREPARE and COMMIT phases. Fig. 6 presents the structure of the consensus messages transmitted in these three phases. The relevant parameters and symbolic descriptions are listed in Table 1.

Figure 6: The structure of the consensus message

Sections 5.1.2 and 5.2.2 describe the process of the Cycle Change phase and the Primary Election phase, respectively, followed by the PRE-PREPARE, PREPARE and COMMIT phases in detail.

PRE-PREPARE: In a blockchain system with c consensus nodes, the primary node p packs the transactions into a new block BlockH. Then, the primary broadcasts a pre-prepare message to other nodes.

PREPARE: Each node checks the pre-prepare message once they receive it from the primary node. If the transactions in the block are all legitimate and the signature of the primary node is correct, the node stores the pre-prepare message locally and broadcasts a prepare message to the other nodes. The replica nodes verify the consistency of prepare messages with each other. If node i receives an inconsistent preparej message from node j, node i will check the signature sigp of the primary node carried in the prepare message of node j, and if it matches the signature in the locally stored pre-prepare message, it indicates that node j has deliberately propagated the inconsistent message; otherwise, it indicates that the primary node has sent different pre-prepare messages to different replica nodes. Furthermore, since the signature cannot be forged, if the verification result of sigp is wrong, it indicates that the other node has deliberately forged the signature of the primary node. This is because if the signature in the pre-prepare message is incorrect, the normal node will not send a prepare message during the PREPARE phase. Once a node receives a prepare message that is equivalent to (2×tp)/3 votes, it will broadcast the commit message.

COMMIT: Once a node receives a commit message, it performs the same checking as that in the PREPARE phase. If a node receives at least (2×tp)/3 voting-power equivalent commit messages, it will append BlockH to the blockchain.

6  Analysis of Consensus CRBFT

6.1 Proof of Feasibility

In the collaborative filtering recommendation scheme, the convergence of the iterative process of calculating the global trust value determines the feasibility of the CRBFT scheme. Here, the feasibility of our proposed scheme is validated.

Theorem 1. The value range of the Spearman correlation coefficient is [−1, 1].

Proof. According to formula (1), ℜ(Xi) and ℜ(Yi) represent the ranks of X and Y, respectively. Therefore, the correlation coefficient between X and Y is calculated as formula (9).

It is clear that the di is the difference between ℜ(Xi) and ℜ(Yi). When X and Y are negatively correlated, for any i∈{1,…,n}, we have ℜ(Xi)+ℜ(Yi)=n+1 and di=|ℜ(Xi)−ℜ(Yi)|=|n+1−2×ℜ(Yi)|. This indicates ∑i=1ndi2=(n−1)n(n+1)/3, and the value of ρ is the smallest at this time, which is equal to 1−2(n−1)n(n+1)/(n3−n)=−1. When X and Y are positively correlated, for any i∈{1,…,n}, we have di=|ℜ(Xi)−ℜ(Yi)|=0, so ∑i=1ndi2=0. It indicates that ρ can achieve the maximum value at this time, which is equal to 1. Thus, Theorem 1 is proved.

ρ=∑i=1n(ℜ(Xi)−ℜ(X)¯)(ℜ(Yi)−ℜ(Y)¯)(∑i=1n(ℜ(Xi)−ℜ(X)¯)2∑i=1n(ℜ(Yi)−ℜ(Y)¯)2)1/2=∑i=1nℜ(Xi)ℜ(Yi)−n((n+1)/2)2{[∑i=1nℜ(Xi)2−n((n+1)/2)2]×[∑i=1nℜ(Yi)2−n((n+1)/2)2]}1/2=12[∑i=1nℜ(Xi)ℜ(Yi)−n(n+1)2/4]n3−n=12∑i=1nℜ(Xi)ℜ(Yi)n3−n−3(n+1)n−1=1−6∑i=1ndi2n3−n(9)

Lemma 1. For any two nodes i and j, their recommendation similarity falls within [0, 1].

Proof. The similarity of recommendation opinions of two nodes can be calculated as formula (10).

sij=∑k=1n(ℜ(rik)−ℜ(ri)¯)(ℜ(rjk)−ℜ(rj)¯)/2(∑k=1n(ℜ(rik)−ℜ(ri)¯)2∑k=1n(ℜ(rjk)−ℜ(rj)¯)2)1/2+12=(ρ(ri,rj)+1)/2(10)

ρ(ri, rj) is the Spearman correlation coefficient between ri and rj. According to Theorem 1, the value range of ρ(ri, rj) is [−1, 1]. So, the value range of (ρ(ri, rj)+1)/2 is [0, 1].

Lemma 2. For any initial vector T, the iterative process on line 21 in Algorithm 1 converges.

Proof. The sufficient condition for the convergence of the above iterative process is max1⩽i⩽n∑j=1n|Rji×sij×cj|<1. According to Lemma 1 and Definition 4, for any i, j∈{1,…,n}, there is 0⩽sij⩽1 and 0≤cj≤1. According to Definition 2 and Definition 5, for any i∈{1,…,n}, there is ∑j=1n|Rij|=∑j=1nrij=∑j=1neij/2∑j=1neij=1/2, so max1⩽i⩽n∑j=1n|Rji×sij×cj|⩽1/2. Therefore, Lemma 2 is proved.

6.2 Proof of Correctness

In this paper, it is assumed that the total number of nodes in the system is n, and in the initial stage of the system, all nodes have a voting power of 1, so the total voting power is tp=n. After the first update of the global trust value of nodes, the total voting power is tp=(1+n)n/2, and the total voting power of a malicious node is always less than one-third of the total voting power.

Lemma 3. For any n≥1, the set of any two nodes with total voting power equal to 2×tp/3 contains at least one identical normal node.

Proof. Since the sum of the voting power of the nodes in the system differs in the initial and subsequent phases, the proof of Lemma 3 will need to consider two cases. (1) In an initial cycle where all nodes have a voting power of 1, let the number of malicious nodes be f and f<n/3. Suppose any two sets S1 and S2, both of which have a voting power of 2n/3, the voting power of these two sets of nodes is summed to 4n/3. Since the sum of the voting power of all nodes is n, the voting power of the set of nodes in the intersection of S1 and S2 is n/3=4n/3−n. Meanwhile, since the total voting power of the malicious nodes is less than n/3, there must be honest nodes in the set of nodes in the intersection of S1 and S2, and Lemma 3 is proved. (2) When the sum of the voting power of all nodes is equal to (1+n)n/2, suppose the total voting power of any two sets of nodes S1 and S2 is equal to (1+n)n/3, and their intersection I=S1∩S2. Since the sum of the voting power of S1 and S2 is 2(1+n)n/3, the sum of the voting power of the nodes in the intersection |I| is equal to (1+n)n/6=2(1+n)n/3−(1+n)n/2, which indicates that there must be more than just malicious nodes in I, because the sum of the voting power of the malicious nodes is less than (1+n)n/6. Thus, Lemma 3 is proved.

Lemma 4. If there is a good node that votes for block b, then all good nodes vote for b.

Proof. Suppose there is a normal node that votes for block b and other normal nodes that vote for block b′. Since the sum of the voting power of the nodes in the system differs in the initial and subsequent phases, the proof of Lemma 4 also needs to consider two cases. (1) In an initial cycle where n nodes all have a voting power of 1, a normal node will submit a block only after it receives 2n/3 votes against the new block. Thus, for two normal nodes that have submitted different blocks, both of them receive 2n/3 votes against b and b′, respectively. According to Lemma 3, any two sets of nodes with voting power equal to 2n/3 contain at least one identical normal node in their intersection, and the same normal node will not vote for different blocks, so the hypothesis does not hold. (2) When the sum of the voting power of all nodes in the system is (1+n)n/2, normal nodes will only submit blocks after they receive voting messages with voting power equal to (1+n)n/3. Thus, for normal nodes that submit two different blocks, they will vote against b and b′ after they receive voting messages with voting power equal to (1+n)n/3. By Lemma 3, for any two sets of nodes with total voting power equal to (1+n)n/3, each contains at least one identical normal node. Again, normal nodes do not vote for two different blocks, so the hypothesis does not hold. Thus, Lemma 4 is proved.

6.3 Discussion

In this section, we theoretically analyze the feasibility and correctness of CRBFT. The calculation of the global trust value of the consensus node involves synthesizing evaluation opinions from nodes across the entire network. Through multiple rounds of matrix iteration operations, all nodes converge to a consistent trust value for the entire network. Lemma 3 proves that this iterative process can achieve convergence. Experimental testing shows no significant relationship between the number of iterations and the number of nodes, with the time consumption generally at millisecond level. In addition, it is crucial to note that the voting power of each node in CRBFT are not uniform like in PBFT. According to Eq. (7), it can be observed that the voting power of all nodes are integers ranging from 1 to n. Assuming that the malicious nodes possess higher voting rights compared to honest nodes, under the condition that the number of malicious nodes does not exceed one-third of the total number of nodes, these malicious nodes collectively hold a total voting power denoted as (n+2n3)⋅n6=518n2, which is less than or equal to (n+1)n3. Consequently, these malicious nodes lack the ability to manipulate the system’s voting outcomes and at worst can only hinder the consensus process without causing a blockchain fork.

7  Experimental Evaluation

In this section, CRBFT is evaluated in terms of resistance to malicious node attacks, decentralization features, and consensus performance, and a comparative analysis with PBFT and Tendermint is provided in terms of consensus performance. Tendermint is an improved consensus algorithm based on PBFT, and there is an open-source project on Github1.

7.1 Simulation Setup

This paper develops a proof concept implementation in Golang (version 1.18.5)2. The whole system includes a stress test module and a consensus module. The former is responsible for generating transactions and sending them to the consensus module, and then the latter verifies and agrees on new transactions. To compare the performance of PBFT and CRBFT, both PBFT and CRBFT are encapsulated in the consensus module, and they can be switched through command-line programs. Multiple nodes are executed on 6 dell workstations equipped with Intel Xeon Gold 6248R CPU (3.00 GHz) and 32 GB memory and running Ubuntu 20.04 operating system. Each node runs the consensus protocol independently in a Docker container. In all experiments performed in this section, the cycle size in the CRBFT protocol was set to 20 rounds of consensus.

7.2 Evaluation of Resistance to Malicious Node Attacks

7.2.1 Types of Malicious Nodes

In this paper, the following malicious node types are used to characterize different malicious behaviors.

(Independently Malicious, IM): When such malicious nodes are elected as consensus nodes, they continuously broadcast inconsistent blocks or voting information. Also, since they never participate in the consensus process correctly, they do not expect good reviews from non-malicious participants.

(Malicious Collectives, MC): When such malicious nodes participate in the consensus process, they always interfere with the consensus process of the system by broadcasting inconsistent blocks or voting information. Different from the IM nodes, such nodes are eager to gain high trust values, so they will exaggerate each other and may degrade other non-malicious nodes.

(Malicious Spies, MS): Such malicious nodes will disguise themselves and participate in the consensus process in an orderly manner to gain the trust of other non-malicious nodes, but they will secretly give other malicious nodes a higher rating and may also degrade non-malicious nodes.

7.2.2 Comparison of Trust Values of Honest and Malicious Nodes

The effectiveness of the collaborative filtering recommendation scheme proposed in discovering and eliminating various malicious nodes determines the effectiveness of CRBFT. This paper sets up 67 good nodes and 33 malicious nodes in the system, and there are three types of malicious nodes as described in Section 7.2.1. To test the resistance of CRBFT to these malicious nodes, the proportion of IM, MC, and MS nodes in malicious nodes is represented as e1, e2, and e3, and then the change in the global trust value of each node is observed in different cycles under situations of (e1 = 50%, e2 = 25%, e3 = 25%), (e1 = 25%, e2 = 50%, e3 = 25%), (e1 = 25%, e2 = 25%, e3 = 50%), and (e1 = 0%, e2 = 0%, e3 = 100%). The experimental results are shown in Fig. 7. The experimental results shown in the figures are the average trust values for each type of node.

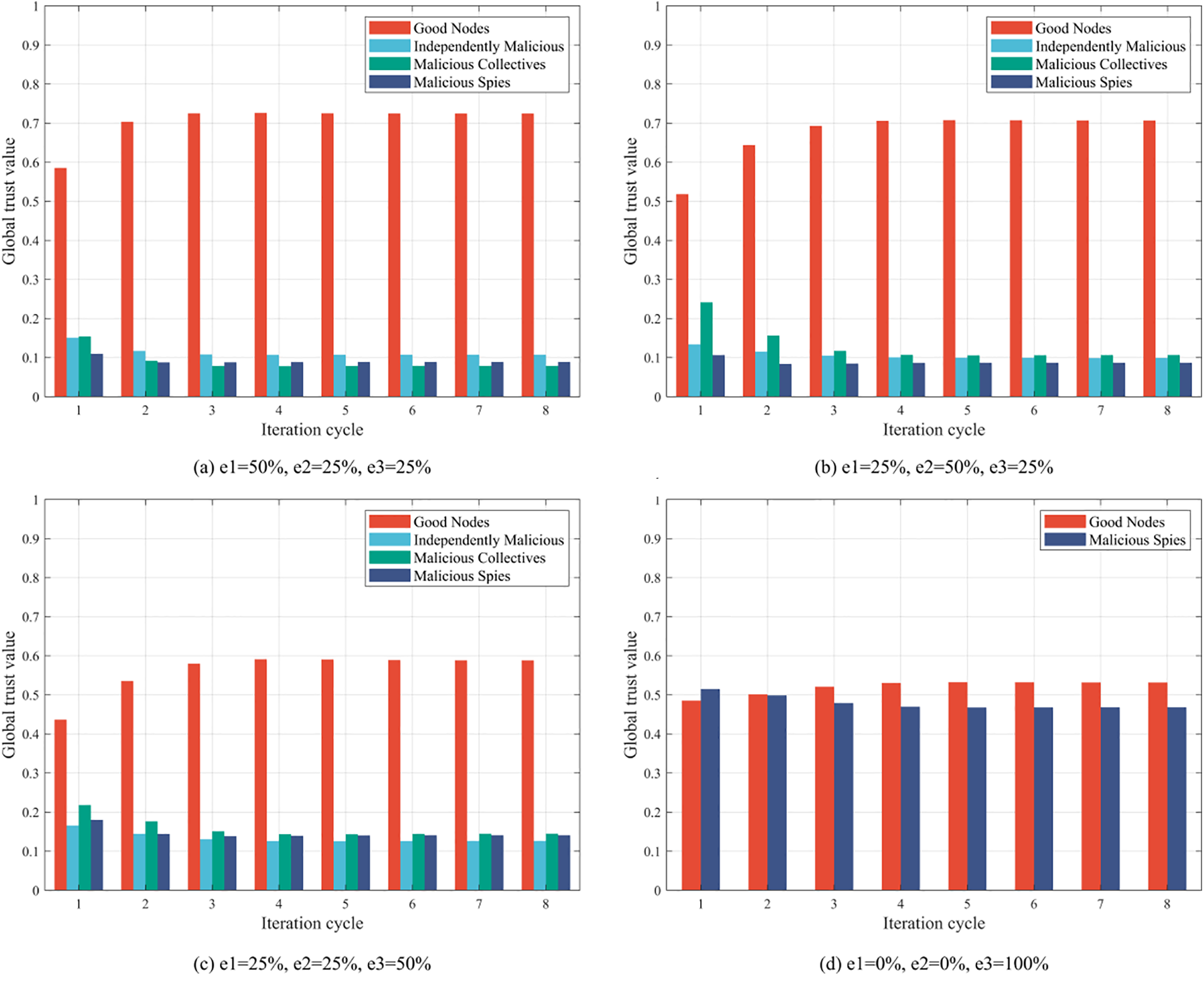
Figure 7: The global trust value of each type of node changes over time in different situations

Fig. 7a–c shows how the global trust values of nodes change over time in different situations. It can be seen that since MS perform well in the system by disguising themselves to gain the trust of good nodes, they support other malicious nodes in the background and deprecate good nodes, and the trust value of good nodes decreases as the number of MS nodes increases. Fig. 7d illustrates the change of trust values of good nodes and MS nodes when there are only such nodes in the system. It is clear that good nodes have lower trust values than MS nodes initially. However, with the system’s continuous operation, there is a significant discrepancy between the recommendation of the MS node and the good node, and the good node will give a lower weight of recommendation. Since MS nodes only account for one-third of the total number of nodes, their impact on the system is limited, and the good node will have higher trust values than MS nodes in the end. MC and IM nodes will not disguise themselves and cannot gain the trust of good nodes. Moreover, their recommendation differs significantly from that of good nodes and will not be adopted by good nodes, so their global trust value is always at a low level.

7.2.3 Comparison of the Voting Power of Honest and Malicious Nodes

PBFT can ensure the security and activity of the system when the number of byzantine nodes in the system does not exceed one-third of the total number of nodes. However, the voting power of both malicious and honest nodes in the system is 1, making the malicious node’s vote on consensus messages as effective as the honest node’s. Thus, it is impossible to give the honest node an advantage over the malicious node in consensus voting, and it is difficult for the honest node to drive the system to consensus more quickly. Therefore, the CRBFT protocol stipulates that the higher the trust value of a node, the greater its voting power; in this way, only a few honest nodes with high voting power can allow the system to reach a consensus quickly. However, achieving an advantage of honest nodes over malicious nodes in terms of voting power, where the voting power of malicious nodes is less than one-third of the total voting power of all nodes in the system, is the key to the safe application of the CRBFT protocol. In this section, the configuration of node types and the size of each type of node in the experiments are the same as those in Section 7.2.2. The change in the share of voting power between honest and malicious nodes in different cycles is observed, and the experimental results are shown in Fig. 8.

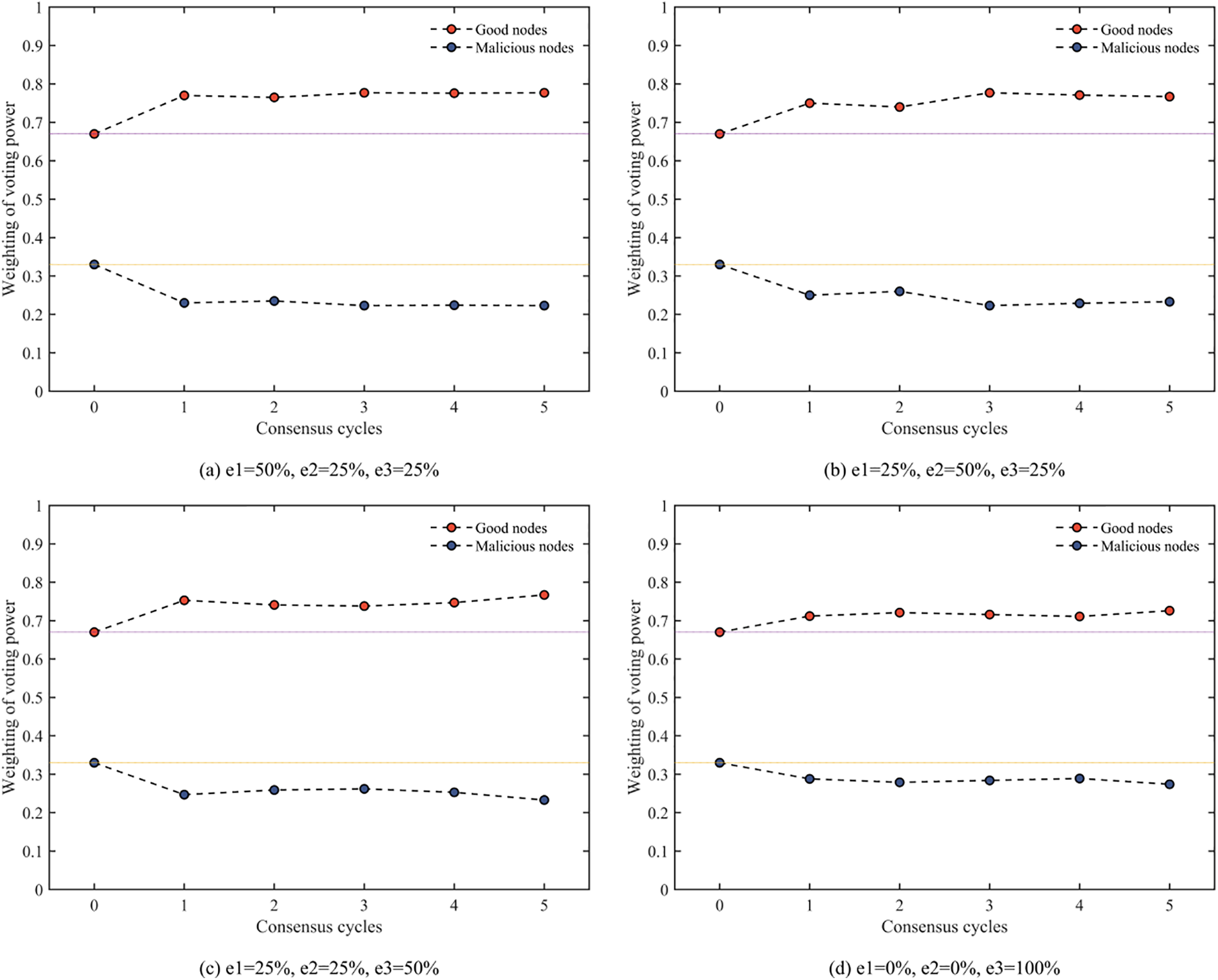
Figure 8: Changes in voting weights of honest and malicious nodes over different cycles

In Fig. 8a, when the nodes of IM, MC, and MS classes account for 50%, 25%, and 25% of the total number of malicious nodes, respectively, the sum of the voting power of all the malicious nodes is significantly less than one-third of the total voting power of the system after multiple rounds of consensus. While the sum of voting power of honest nodes is always higher than two thirds of the total voting power of the system. In Fig. 8b–d, there is an upward trend in the total voting power of malicious nodes as the share of MS class nodes increases. However, in Fig. 8d, even though all malicious nodes are MS class nodes, the total voting power of malicious nodes is still less than one-third of the total voting power of the system.

7.2.4 Comparison with Other Trust Models

To highlight the advantages of the trust model in the CRBFT protocol in terms of its ability to resist malicious node attacks, this paper implements the trust models in the consensus protocols proposed by [22,27], i.e., Eigentrust and Pagerank, respectively, and integrates them into the PBFT consensus protocol, as a control group experiment for CRBFT. The evaluation metric for this experiment is the ratio of the average trust value of honest nodes to the average trust value of malicious nodes α=th/te, where th and te denote the average trust value of honest and malicious nodes, respectively. In this section, the node configuration conditions are the same as those in Section 7.2.2, with 67 honest nodes and 33 malicious nodes. It can be seen from the results in Figs. 7d and 8d that the nodes of the MS class are the most harmful to the system. Therefore, this section considers the variation of the ratio α in the case of MS class nodes of different sizes.

Fig. 9 shows that the trust value of honest nodes decreases with the increase in the number of MS class nodes in all three trust models, but the rate of decrease in CRBFT is significantly smaller than that of the other two models. When all the malicious nodes belong to the MS class, the trust value of honest nodes in CRBFT is generally higher than that of malicious nodes, while the results are reversed in the other two schemes. Therefore, the global trust model in the CRBFT protocol is more reliable in terms of its ability to resist malicious node attacks.

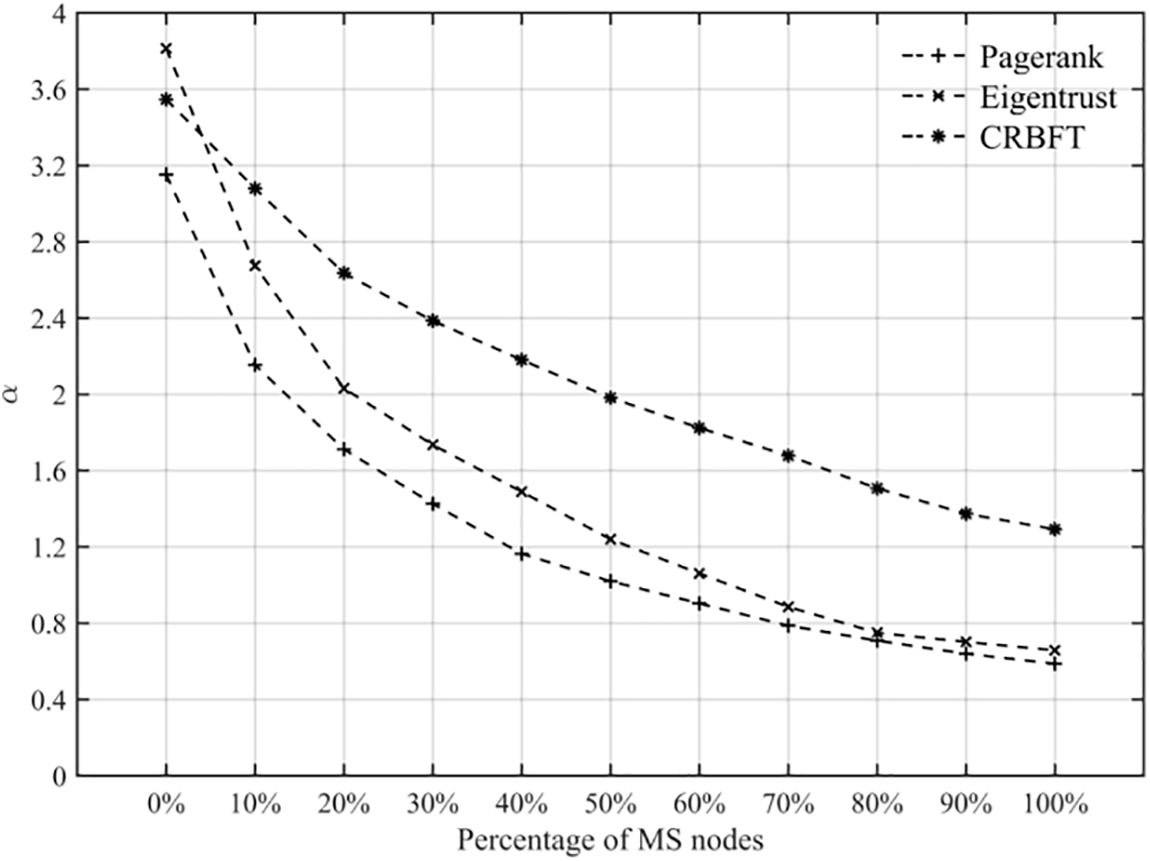
Figure 9: α vs. different percentage of MS nodes

7.3 Evaluation of Decentralized Features

The method of selecting nodes with high trust values to form a consensus group weakens the decentralized nature of the blockchain system, so this paper discards the concept of consensus group and adopts the method of assigning voting power to nodes with different trust values to strengthen the role of honest nodes in the system. Meanwhile, to prevent some nodes with high trust values from continuing to have high voting power after the first trust value update, this paper adopts a memoryless trust value update method, i.e., the global trust value of nodes calculated in the m-th cycle is only related to the evaluation values given by nodes to each other in the (m−1)-th cycle, and it is not related to the evaluation value in the (m−2)-th cycle and all previous cycles. In this paper, to verify that the CRBFT consensus protocol has decentralized properties, the frequency of the nodes in the system selected as master node candidates is taken as the evaluation criterion, and it is calculated in Eq. (11). Here, m denotes the total number of cycles the system operates, and timesi denotes the number of times a node i is selected as a candidate node in m cycles. In this experiment, the total number of cycles m is set to 500.

freqi=timesi/m(11)

Initially, 31 nodes were set up in the system for this experiment, with h and e denoting the proportion of honest and malicious nodes, respectively. Afterward, to verify whether the newly added honest nodes have a chance to become candidates, nodes 32, 33, and 34 were added at the m/4, m/2 and 3m/4 cycles in the system operation phase, respectively, and the frequency of these three nodes becoming candidates was observed. The experimental results are presented in Fig. 10.

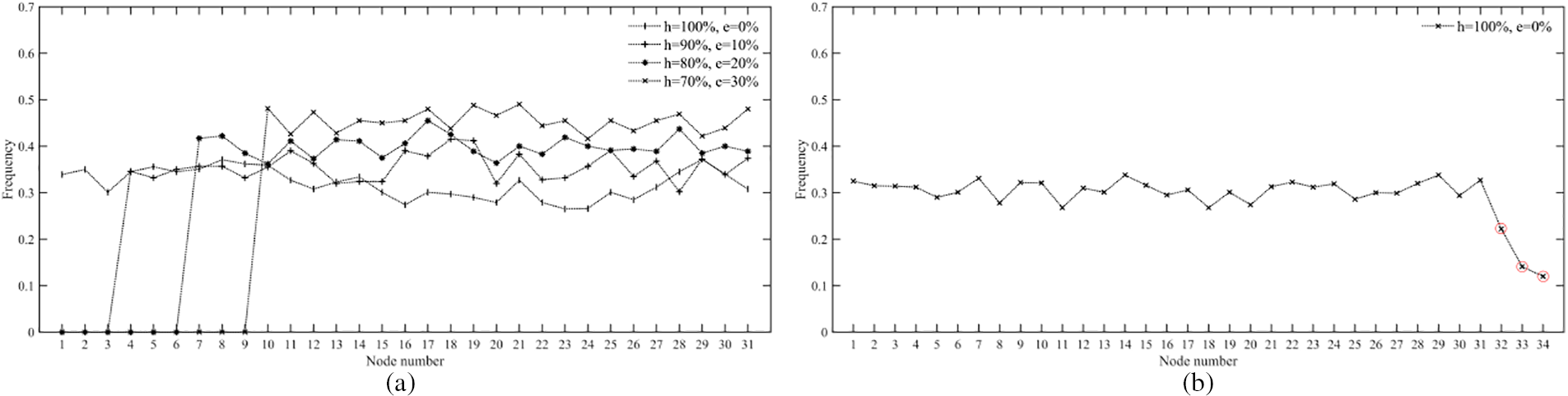
Figure 10: Frequency of each node becoming a candidate node

According to the results in Fig. 10a, the frequency of malicious nodes becoming candidate nodes does not change as the value of e increases and it remains equal to 0 (nodes 1 to 9 are potentially malicious nodes). Also, it is observed that as the proportion of malicious nodes in the system increases, the frequency of each honest node being selected as a candidate node increases. This is because the number of candidate nodes remains the same while the number of honest nodes decreases, so the probability of each honest node taking a turn increases. It can be seen from Fig. 10b that the three new nodes 32, 33 and 34 marked in red in the figure join at the m/4, m/2 and 3m/4 cycles in the system operation phase, respectively, and they all have a chance to become candidate nodes; because these nodes join at a late period, the number of times they become candidate nodes within 500 cycles is relatively small. Therefore, the CRBFT consensus protocol proposed in this paper does not suffer from the problem of centralization.

7.4 Performance Evaluation

This section focuses on evaluating the performance of the CRBFT consensus protocol, including tests on both consensus latency and throughput metrics.

7.4.1 Consensus Latency

Consensus latency refers to the time spent on a new block from being proposed to being confirmed, which reflects the block production efficiency of the system. The lower the consensus latency, the higher the block production efficiency. This paper tests the consensus latency in the way shown in Fig. 11. When the system starts, the consensus module enters the state of waiting for the new transaction. After configuring parameters such as transaction data size and sending method, the stress test module starts sending the transaction to the consensus module. When the consensus module detects that new transaction data arrives, it starts the consensus process and submits new blocks immediately. Then, consensus results are fed back to the stress test module. This paper defines the period from the beginning of consensus on recent transactions in the consensus module to the feedback of consensus results to the stress test module as consensus latency. In the following, the consensus latency of CRBFT will be evaluated from two aspects: the total number of nodes, and the proportion of Byzantine nodes, and the evaluation results are compared with those of PBFT and Tendermint. It should be noted that the consensus latency of the CRBFT protocol shown in the experimental results of this section already considers the time to update the global trust value in the cycle change phase.

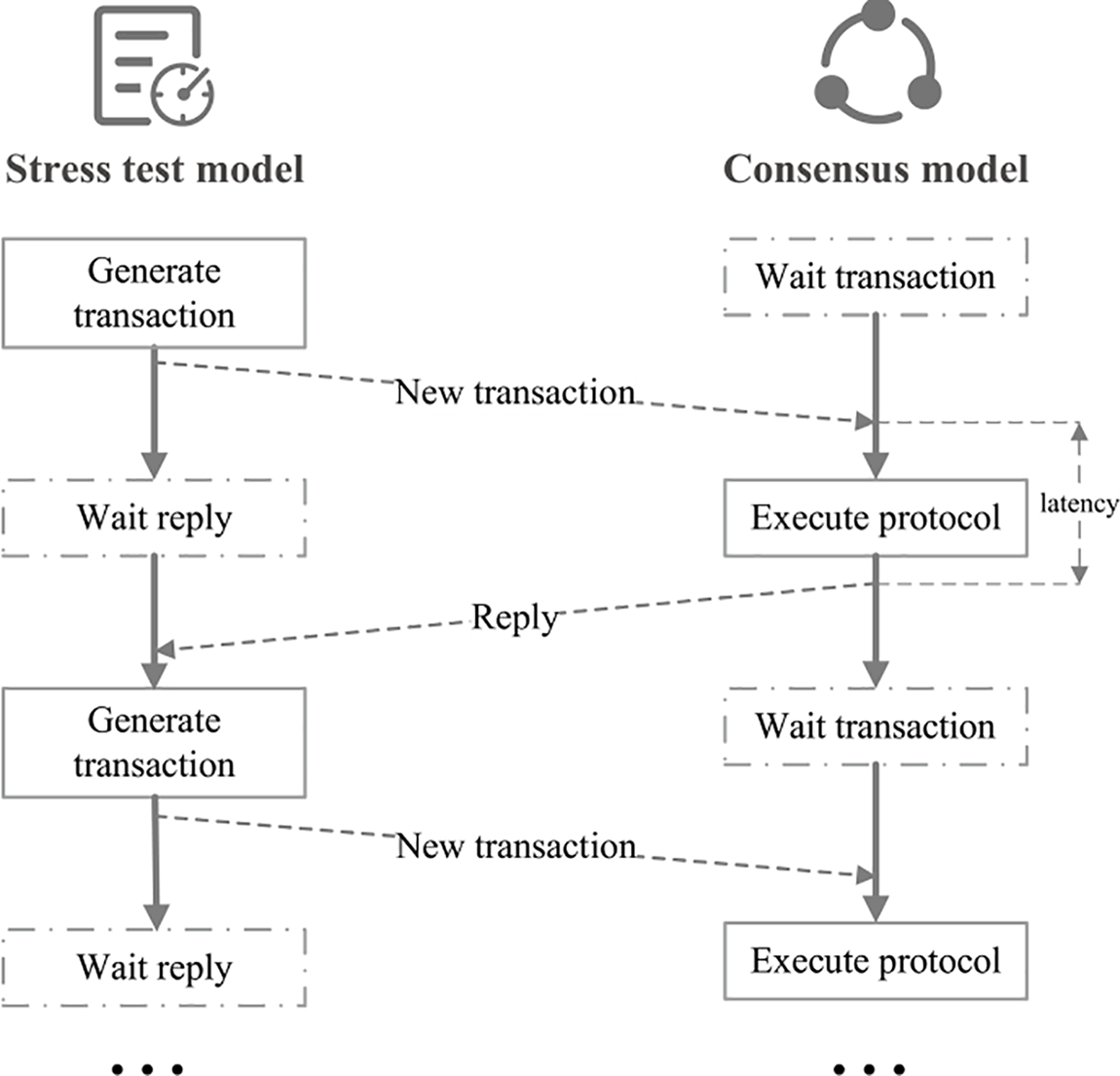
Figure 11: Test process

Fig. 12a shows the consensus latency of CRBFT, PBFT, and Tendermint when the total number of nodes in the system is from 7 to 61. It can be seen that the consensus latency of PBFT, Tendermint, and CRBFT increases with the total number of nodes. However, for CRBFT, after going through a cycle change phase, some of the top-performing honest nodes are given higher voting power, so only a small number of nodes with higher voting power are needed to drive the network to reach consensus quickly and reduce network communication and computational overhead. Thus, the consensus latency growth rate of CRBFT is significantly lower than that of the other two consensus protocols.

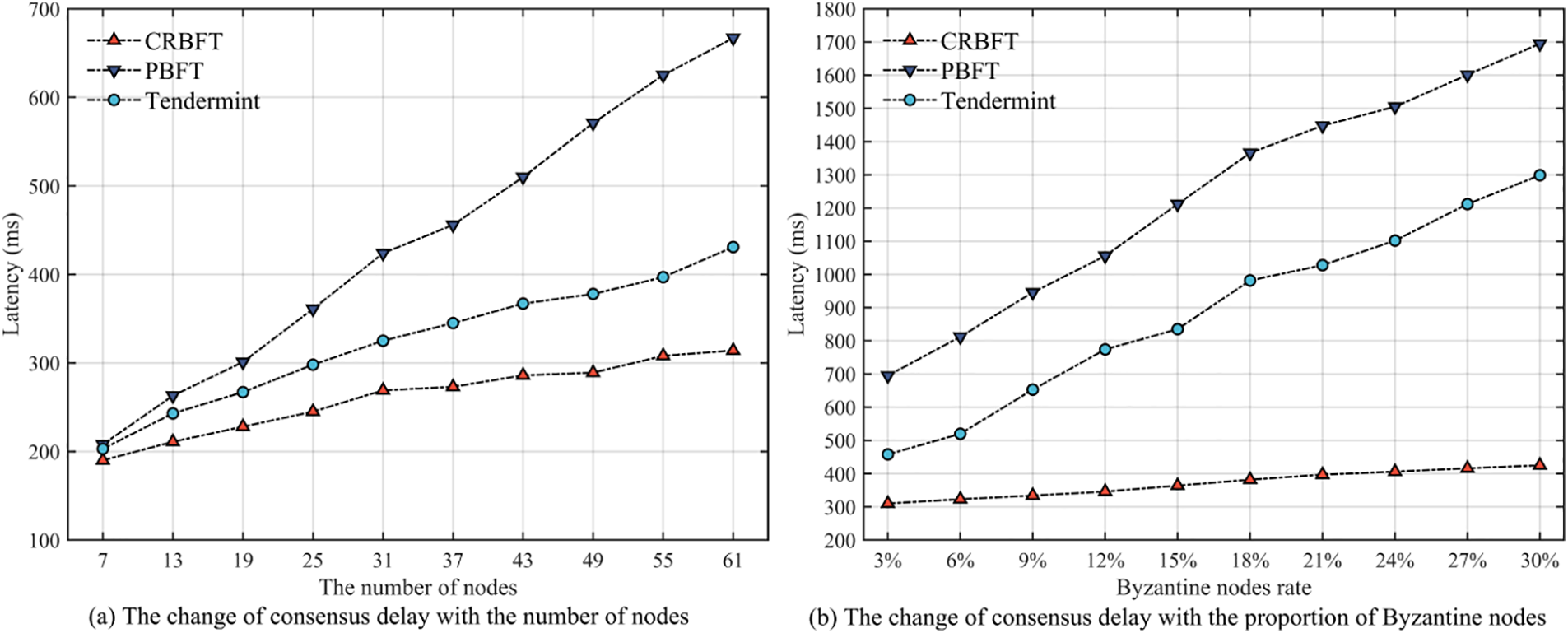
Figure 12: Experiments on consensus latency

Fig. 12b illustrates the consensus latency of CRBFT, PBFT, and Tendermint when the total number of nodes in the system is 61, and malicious nodes account for 3%, 6%, 9%, 12%, 15%, 18%, 21%, 24%, 27%, and 30% of all the nodes, respectively. In our experimental scheme, malicious nodes will perform the following three abnormal operations at a certain probability: (1) Send wrong consensus messages; (2) The message is not sent in time; (3) Ignore the consensus messages arriving locally. The experimental results show that the consensus latency of PBFT and Tendermint is more affected by malicious nodes, while that of CRBFT is less affected by malicious nodes because it can effectively identify malicious nodes in the system.

7.4.2 Throughput

Throughput is used as a measure of how efficiently transactions are packaged. In this section, the stress test module is used to send transaction data to the consensus module continuously. The consensus module temporarily stores the received transactions in the memory pool and then packages the transactions into a block after a short timeout and starts the consensus process. In the following, the impact of the total number of nodes and malicious nodes on the throughput of CRBFT, PBFT, and Tendermint will be evaluated. During testing, the maximum number of transactions that could be stored per block was limited to 3000.

Fig. 13a shows the throughput changes of CRBFT, PBFT, and Tendermint when the total number of nodes in the system is from 7 to 61. The experimental results show that the throughput of CRBFT, PBFT, and Tendermint decreases with the number of nodes. However, according to the experimental results in Section 7.4.1, it is clear that the consensus latency of CRBFT is smaller than that of PBFT and Tendermint, so CRBFT can commit more blocks per unit of time, which makes CRBFT achieve higher throughput than PBFT and Tendermint consistently.

Figure 13: Experiments on throughput

Fig. 13b shows the throughput changes of CRBFT, PBFT, and Tendermint when there are 61 nodes in the system, and malicious nodes account for 3%, 6%, 9%, 12%, 15%, 18%, 21%, 24%, 27%, and 30% of all the nodes, respectively. Obviously, the throughput of PBFT and Tendermint is more affected by the size of the malicious nodes. In contrast, CRBFT can effectively identify malicious nodes in the system and allocate higher voting power to honest nodes to weaken the influence of malicious nodes on the system, so the throughput of CRBFT fluctuates less.

8  Conclusion

Blockchain can provide solutions to many problems in distributed scenarios and it has become a potentially revolutionary technology in the information field. However, with the continuous expansion of the scale of the blockchain system, it is increasingly difficult for the consensus protocol to meet the efficiency requirements of the blockchain system. To address this issue, this paper proposes a Byzantine fault-tolerant consensus protocol called CRBFT based on PBFT and collaborative filtering recommendations. By assigning higher voting power to trusted honest nodes and weakening the voting power of malicious nodes, the protocol reduces the interference of malicious nodes to the system and promotes the consensus efficiency of the system. The experimental results show that CRBFT can effectively identify malicious nodes and reduce their ability to do evil. Meanwhile, CRBFT achieves lower consensus latency and higher throughput than PBFT as the node size and the number of byzantine nodes increase. Therefore, in a large-scale system and complex environment, the scheme proposed in this paper can ensure the security of the blockchain system, effectively improve the system efficiency and scalability, and promote the implementation and application of blockchain technology.

Acknowledgement: The authors would like to thank all the reviewers who participated in the review.

Funding Statement: This work has been supported by the National Natural Science Foundation of China (Grant No. 62102449) awarded to W.J. Wang.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xiangyu Wu; data collection: Qiantao Yang, Na Wang; analysis and interpretation of results: Wenjuan Wang, Aodi Liu; draft manuscript preparation: Xuehui Du, Xiangyu Wu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Xuehui Du, upon reasonable request.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

1https://github.com/tendermint/tendermint/tree/v0.34.11 (accessed on 06/05/2024)

2https://golang.google.cn/dl/go1.18.5.linux-amd64.tar.gz (accessed on 06/05/2024)

References

1. J. Frizzo-Barker, P. A. Chow-White, P. R. Adams, J. Mentanko, D. Ha and S. Green, “Blockchain as a disruptive technology for business: A systematic review,” Int. J. Inf. Manage., vol. 51, pp. 102029, 2020. doi: 10.1016/j.ijinfomgt.2019.10.014. [Google Scholar] [CrossRef]

2. F. Casino, T. K. Dasaklis, and C. Patsakis, “A systematic literature review of blockchain-based applications: Current status, classification and open issues,” Telematics Inform., vol. 36, pp. 55–81, 2019. doi: 10.1016/j.tele.2018.11.006. [Google Scholar] [CrossRef]

3. X. Fu, H. Wang, and P. Shi, “A survey of blockchain consensus algorithms: Mechanism, design and applications,” Sci. China Inf. Sci., vol. 64, no. 2, pp. 121101, Feb. 2021. doi: 10.1007/s11432-019-2790-1. [Google Scholar] [CrossRef]

4. S. Bano et al., “SoK: Consensus in the age of blockchains,” in Proc. 1st ACM Conf. Adv. Financ. Technol., in AFT ’19, New York, NY, USA, Association for Computing Machinery, 2019, pp. 183–198. doi: 10.1145/3318041.3355458. [Google Scholar] [CrossRef]

5. S. Park, A. Kwon, G. Fuchsbauer, P. Gaži, J. Alwen and K. Pietrzak, “SpaceMint: A cryptocurrency based on proofs of space,” in S. Meiklejohn, K. Sako (Eds.Financial Cryptography and Data Security, Berlin, Heidelberg: Springer Berlin Heidelberg, 2018, vol. 10957, pp. 480–499. doi: 10.1007/978-3-662-58387-6_26. [Google Scholar] [CrossRef]

6. B. Lashkari and P. Musilek, “A comprehensive review of blockchain consensus mechanisms,” IEEE Access, vol. 9, pp. 43620–43652, 2021. doi: 10.1109/ACCESS.2021.3065880. [Google Scholar] [CrossRef]

7. D. Ongaro and J. Ousterhout, “In search of an understandable consensus algorithm,” in Proc. 2014 USENIX Conf. USENIX Annu. Tech. Conf. (USENIX ATC’14), Philadelphia, PA, USA, USENIX Association, 2014, pp. 305–320. [Google Scholar]

8. S. Chand, Y. A. Liu, and S. D. Stoller, “Formal verification of multi-paxos for distributed consensus,” in J. Fitzgerald, C. Heitmeyer, S. Gnesi, A. Philippou (Eds.FM 2016: Formal Methods, Cham: Springer International Publishing, 2016, vol. 9995, pp. 119–136. doi: 10.1007/978-3-319-48989-6_8. [Google Scholar] [CrossRef]

9. M. Castro and B. Liskov, “Practical Byzantine fault tolerance,” in OSDI ’99: Proc. Third Symp. Oper. Syst. Design Implement., New Orleans, LA, USA, USENIX Association, 1999, pp. 173–186. [Google Scholar]

10. M. Castro and B. Liskov, “Practical byzantine fault tolerance and proactive recovery,” ACM Trans. Comput. Syst., vol. 20, no. 4, pp. 398–461, Nov. 2002. doi: 10.1145/571637.571640. [Google Scholar] [CrossRef]

11. E. Androulaki et al., “Hyperledger fabric: A distributed operating system for permissioned blockchains,” in EuroSys ’18: Proc. Thirteenth EuroSys Conf., New York, NY, USA, Association for Computing Machinery, 2018. doi: 10.1145/3190508.3190538. [Google Scholar] [CrossRef]

12. H. Li et al., “FISCO-BCOS: An enterprise-grade permissioned blockchain system with high-performance,” in SC ’23 Proc. Int. Conf. High Perform. Comput., Netw., Storage Anal., New York, NY, USA, Association for Computing Machinery, 2023. doi: 10.1145/3581784.3607053. [Google Scholar] [CrossRef]

13. N. Mustafa, A. O. Ibrahim, A. Ahmed, and A. Abdullah, “Collaborative filtering: Techniques and applications,” in 2017 Int. Conf. Commun., Control, Comput. Electron. Eng. (ICCCCEE), Khartoum, Sudan, 2017, pp. 1–6. doi: 10.1109/ICCCCEE.2017.7867668. [Google Scholar] [CrossRef]

14. E. Buchman, J. Kwon, and Z. Milosevic, “The latest gossip on BFT consensus,” arXiv:1807.04938, 2018. Accessed: May 16, 2023. [Online]. Available: https://api.semanticscholar.org/CorpusID:49744920 [Google Scholar]

15. A. Miller, Y. Xia, K. Croman, E. Shi, and D. Song, “The honey badger of BFT protocols,” in CCS ’16: Proc. 2016 ACM SIGSAC Conf. Comput. Commun. Secur., New York, NY, USA, Association for Computing Machinery, 2016, pp. 31–42. doi: 10.1145/2976749.2978399. [Google Scholar] [CrossRef]

16. M. Yin, D. Malkhi, M. K. Reiter, G. G. Gueta, and I. Abraham, “HotStuff: BFT consensus with linearity and responsiveness,” in PODC’19: Proc. 2019 ACM Symp. Princ. Distrib. Comput., New York, NY, USA, Association for Computing Machinery, 2019, pp. 347–356. doi: 10.1145/3293611.3331591. [Google Scholar] [CrossRef]

17. J. Zhang, Y. Rong, J. Cao, C. Rong, J. Bian and W. Wu, “DBFT: A byzantine fault tolerant protocol with graceful performance degradation,” in 2019 38th Symp. Reliab. Distrib. Syst. (SRDS), Lyon, France, 2019, pp. 123–12309. doi: 10.1109/SRDS47363.2019.00023. [Google Scholar] [CrossRef]

18. Y. Gilad, R. Hemo, S. Micali, G. Vlachos, and N. Zeldovich, “Algorand: Scaling byzantine agreements for cryptocurrencies,” in SOSP’17: Proc. 26th Symp. Oper. Syst. Princ., New York, NY, USA, Association for Computing Machinery, 2017, pp. 51–68. doi: 10.1145/3132747.3132757. [Google Scholar] [CrossRef]

19. G. G. Gueta et al., “SBFT: A scalable and decentralized trust infrastructure,” in 2019 49th Annu. IEEE/IFIP Int. Conf. Depend. Syst. Netw. (DSN), Portland, OR, USA, 2019, pp. 568–580. doi: 10.1109/DSN.2019.00063. [Google Scholar] [CrossRef]

20. C. Li, J. Zhang, X. Yang, and L. Youlong, “Lightweight blockchain consensus mechanism and storage optimization for resource-constrained IoT devices,” Inform. Process. Manage., vol. 58, no. 4, pp. 102602, 2021. doi: 10.1016/j.ipm.2021.102602. [Google Scholar] [CrossRef]

21. Y. Chen et al., “An improved algorithm for practical byzantine fault tolerance to large-scale consortium chain,” Inform. Process. Manage., vol. 59, no. 2, pp. 102884, 2022. doi: 10.1016/j.ipm.2022.102884. [Google Scholar] [CrossRef]

22. S. Gao, T. Yu, J. Zhu, and W. Cai, “T-PBFT: An eigentrust-based practical byzantine fault tolerance consensus algorithm,” China Commun., vol. 16, no. 12, pp. 111–123, 2019. doi: 10.23919/JCC.2019.12.008. [Google Scholar] [CrossRef]

23. S. D. Kamvar, M. T. Schlosser, and H. Garcia-Molina, “The eigentrust algorithm for reputation management in P2P networks,” in WWW’03: Proc. 12th Int. Conf. World Wide Web, New York, NY, USA, Association for Computing Machinery, 2003, pp. 640–651. doi: 10.1145/775152.775242. [Google Scholar] [CrossRef]

24. Y. Zhan, B. Wang, R. Lu, and Y. Yu, “DRBFT: Delegated randomization Byzantine fault tolerance consensus protocol for blockchains,” Inf. Sci., vol. 559, pp. 8–21, Jun. 2021. doi: 10.1016/j.ins.2020.12.077. [Google Scholar] [CrossRef]

25. Y. Li, L. Qiao, and Z. Lv, “An optimized byzantine fault tolerance algorithm for consortium blockchain,” Peer-to-Peer Netw. Appl., vol. 14, no. 5, pp. 2826–2839, Sep. 2021. doi: 10.1007/s12083-021-01103-8. [Google Scholar] [CrossRef]

26. K. Lei, Q. Zhang, L. Xu, and Z. Qi, “Reputation-based byzantine fault-tolerance for consortium blockchain,” in 2018 IEEE 24th Int. Conf. Parallel Distrib. Syst. (ICPADS), Singapore, 2018, pp. 604–611. doi: 10.1109/PADSW.2018.8644933. [Google Scholar] [CrossRef]

27. S. Lv, H. Li, H. Wang, and X. Wang, “CoT: A secure consensus of trust with delegation mechanism in blockchains,” in X. Si et al. (Eds.Blockchain Technology and Application, Singapore: Springer Singapore, 2020, vol. 1176, pp. 104–120. doi: 10.1007/978-981-15-3278-8_7. [Google Scholar] [CrossRef]

28. L. Zhang, B. Zhang, and C. Li, “An efficient and reliable byzantine fault tolerant blockchain consensus protocol for single-hop wireless networks,” IEEE Trans. Wireless Commun., vol. 23, no. 3, pp. 1974–1987, Mar. 2024. doi: 10.1109/TWC.2023.3293709. [Google Scholar] [CrossRef]

29. J. Tian, J. Tian, and H. Xu, “TSBFT: A scalable and efficient leaderless byzantine consensus for consortium blockchain,” Comput. Netw., vol. 222, pp. 109541, Feb. 2023. doi: 10.1016/j.comnet.2022.109541. [Google Scholar] [CrossRef]

30. J. Xiao, T. Luo, C. Li, J. Zhou, and Z. Li, “CE-PBFT: A high availability consensus algorithm for large-scale consortium blockchain,” J. King Saud Univ.-Comput. Inf. Sci., vol. 36, no. 2, pp. 101957, 2024. doi: 10.1016/j.jksuci.2024.101957. [Google Scholar] [CrossRef]

31. L. Lamport, R. Shostak, and M. Pease, “The Byzantine generals problem,” in Concurrency: The Works of Leslie Lamport, New York, NY, USA: Association for Computing Machinery, 2019, pp. 203–226. Accessed: Apr. 15, 2023. doi: 10.1145/3335772.3335936. [Google Scholar] [CrossRef]

32. M. Srifi, A. Oussous, A. A. Lahcen, and S. Mouline, “Recommender systems based on collaborative filtering using review texts—A survey,” Information, vol. 11, no. 6, pp. 317, 2020. doi: 10.3390/info11060317. [Google Scholar] [CrossRef]

33. M. Jiang, Z. Zhang, J. Jiang, Q. Wang, and Z. Pei, “A collaborative filtering recommendation algorithm based on information theory and bi-clustering,” Neural Comput. Appl., vol. 31, no. 12, pp. 8279–8287, Dec. 2019. doi: 10.1007/s00521-018-3959-2. [Google Scholar] [CrossRef]

34. Z. Cui et al., “Personalized recommendation system based on collaborative filtering for IoT scenarios,” IEEE Trans. Serv. Comput., vol. 13, no. 4, pp. 685–695, 2020. doi: 10.1109/TSC.2020.2964552. [Google Scholar] [CrossRef]

35. C. C. Aggarwal, “Neighborhood-based collaborative filtering,” in Recommender Systems, Cham: Springer International Publishing, 2016, pp. 29–70. doi: 10.1007/978-3-319-29659-3_2. [Google Scholar] [CrossRef]

36. V. Shankar, G. L. Urban, and F. Sultan, “Online trust: A stakeholder perspective, concepts, implications, and future directions,” J. Strateg. Inf. Syst., vol. 11, no. 3, pp. 325–344, 2002. doi: 10.1016/S0963-8687(02)00022-7. [Google Scholar] [CrossRef]

37. A. Abdul-Rahman and S. Hailes, “Supporting trust in virtual communities,” in Proc. 33rd Annu. Hawaii Int. Conf. Syst. Sci., Maui, HI, USA, 2000, vol. 1, pp. 9. doi: 10.1109/HICSS.2000.926814. [Google Scholar] [CrossRef]

38. J. Riegelsberger, M. A. Sasse, and J. D. McCarthy, “The mechanics of trust: A framework for research and design,” Int. J. Hum. Comput. Stud., vol. 62, no. 3, pp. 381–422, 2005. doi: 10.1016/j.ijhcs.2005.01.001. [Google Scholar] [CrossRef]

39. Z. Su, L. Liu, M. Li, X. Fan, and Y. Zhou, “Reliable and resilient trust management in distributed service provision networks,” ACM Trans. Web., vol. 9, no. 3, pp. 1–37, Jun. 2015. doi: 10.1145/2754934. [Google Scholar] [CrossRef]

40. A. Koloskova, S. U. Stich, and M. Jaggi, “Decentralized stochastic optimization and gossip algorithms with compressed communication,” arXiv:1902.00340, Feb. 01, 2019. Accessed: Apr. 11, 2024. [Online]. Available: http://arxiv.org/abs/1902.00340 [Google Scholar]