Fuzzy Risk Assessment Method for Airborne Network Security Based on AHP-TOPSIS

1  Introduction

With the widespread application of computer network technology in aircraft, an increasing number of aircraft are adopting the ARINC 664 network [1] which is also known as Avionics Full-Duplex Switched Ethernet for data exchange within the aircraft system. Aircrafts utilize the ARINC 664 network for system data interaction, such as the Airbus A380, Boeing 787, and Airbus A350. The ARINC 664 network is based on an extension of the Internet protocol, which effectively improves the rate of data exchange within the aircraft system compared to traditional bus data transmission protocols. The airborne system, ARINC 664 network, and data switching equipment, such as aviation, switch constitute the airborne network. The application of airborne networks in aircraft data communication has greatly improved the rate of data exchange between various aircraft systems, but it has also exposed the airborne system to various information security risks. Hence, conducting an information security risk assessment for airborne networks, analyzing network levels, and identifying key vulnerabilities are necessary to implement targeted security measures and proactively mitigate the impact of information security risks on airborne networks.

Airborne network refers to a computer network used for communication between airborne systems, such as the network connecting the airborne server with the maintenance server. As shown in Fig. 1, The onboard network comprises three subnetworks: the cabin network for providing cabin services, the maintenance network for providing maintenance and critical cabin services, and the limited aircraft network for providing aircraft and critical maintenance services. A maintenance gateway exists between the cabin and maintenance networks, which requires an administrator administration account and password for configuring and updating the network. Meanwhile, an aircraft gateway exists between the maintenance and the limited aircraft network.

Figure 1: Diagram of the airborne network

To effectively address the security issues posed by these information security risks, the FAA released the DO-356A [2], which proposes that information security risk assessments should be conducted on airborne networks to identify the threats faced by these networks and quantitatively assess their impact on aircraft safety. According to the national standard GB/T 20984-2022 [3] for information security risk assessment, the risk assessment should comprehensively analyze the risk level of the assessment object from four aspects: assets, threats, vulnerabilities, and security measures. However, the experts lack in-depth knowledge of the assets, vulnerabilities, threats, and security measures involved due to the confidentiality of the airborne network, which increases the difficulty in accurately evaluating the risk of threat scenarios within the airborne network. Consequently, cognitive uncertainty exists in the risk assessment of airborne network information security. This study focuses on optimizing expert cognitive uncertainty in evaluation to enhance the precision of risk assessment.

2  Related Work

The airborne network serves as the core link for data interaction throughout the aircraft, and its security greatly affects the safety of the aircraft system and the entire aircraft. Therefore, it is necessary to evaluate the security of the airborne network and determine its risk level.

Domestic and international scholars have conducted research on information security risk assessment issues. Humayun et al. [4] conducted a risk assessment targeting the existing threats and vulnerabilities in software, proposing a framework for a secure software development lifecycle based on established practices. Shirvani et al. [5] addressed information security issues in electric vehicles by introducing a framework for electric vehicle security risk assessment. Wang et al. [6] proposed a risk decision evaluation method with weighted criteria to improve express service quality. Tariq et al. [7] proposed an adaptive, robust state estimation method that supports graphical processing units for possible false data injection attacks in the application of 6G technology in smart grid systems. Averyanova et al. [8] analyzed the vulnerabilities in the communication, navigation, control, and monitoring equipment of modern drones, focusing on their existing cybersecurity. They introduced a network threat analysis and evaluation algorithm specifically designed for unmanned aerial system (UAS). However, the assessment of information security in the above fields disregards the uncertainty in the assessment process.

Regarding the information security assessment of airborne networks, Zhang et al. [9] constructed a security assessment method for airborne systems in the airborne network based on the airworthiness requirements of the systems. Li et al. [10] built a security assessment model targeting potential threat stated in new aircraft. Wang et al. [11] proposed an improved FAHP-cloud risk assessment model for airborne networks, provided an indicator system framework for airborne networks. By calculating the similarity between the actual integrated cloud model and the standard cloud model, they classified the risk level of airborne network security. The above papers conducted researches on airborne network information security risk modeling and assessment methods based on potential threats to the network. The proposed indicator system can effectively describe the hierarchical relationship between network assets, threats, and vulnerabilities, but fails to consider the uncertainty of expert cognition in the evaluation process.

Regarding the issue of uncertainty, Li et al. [12] improved the uncertainty caused by insufficient data information, known as poor information uncertainty, to address the uncertainty in the process of assessment. However, they disregarded the issue of cognitive uncertainty inherent in the models. Wang et al. [13] optimized the consistency of solving indicator weights using the AHP but did not consider the cognitive uncertainty that may exist during the assessment process. Zulqarnain et al. [14] combined the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) with AHP, which reduced the influence of expert subjectivity on the results of network security risk measurement. However, these methods were still failed to effectively address the representation problem of expert opinions in the presence of cognitive uncertainty.

Regarding the issue of expert cognitive uncertainty, Klaproth et al. [15] proposed a model-based cognitive assistance method to track the constantly changing needs of pilots in dynamic situations and address the cognitive uncertainty of experts. Yager [16] extended the intuitionistic fuzzy set (IFS) and proposed the Pythagorean fuzzy set (PFS). Compared with IFS, PFS expands the space of PF values, and effectively represents cognitive uncertainty information. Wang et al. [17] combined PFS with fuzzy entropy to improve the cognitive uncertainty of index weight. Zhao et al. [18] integrated PFS and TODIM to investigate the risk attitude and cognitive uncertainty of experts in multi-criteria decision-making problems, thereby enhancing assessment accuracy. Giri et al. [19] integrated PFS with DEMATEL to optimize decision attribute correlation problems in supplier selection problems. Akram et al. [20] combined PFS with VIKOR to improve cognitive uncertainty in the risk prioritization of autonomous vehicles. PFS can effectively optimize cognitive uncertainty in multi-attribute decision-making. Therefore, this study applies PFS to the information security risk assessment of airborne networks for expert cognitive uncertainty optimization.

A fuzzy risk assessment method for airborne network information security based on PF-TOPSIS is first proposed to address the optimization problem of expert cognitive uncertainty in airborne network information security risk assessment. The method integrates TOPSIS and AHP with PFS, employing Pythagorean fuzzy numbers (FPN) to construct AHP pairwise comparison and TOPSIS decision matrices to capture the epistemic uncertainties. With the establishment of an index system for information security risk assessment of airborne networks, PF AHP is utilized to determine the weights of indexes. Subsequently, PF TOPSIS is employed to prioritize threat scenario risks and identify the threat scenario with the highest risk level. This method provides a foundation for the targeted deployment of security measures. Finally, consistency checking is conducted to validate the effectiveness of the proposed method.

The proposed method in this paper has been successfully applied to the evaluation process of airborne networks. Such an application effectively addresses the existing cognitive uncertainty problem in expert review opinions during the information security evaluation of airborne networks for the first time, thereby improving the accuracy of airborne network evaluation results.

3  Methodology

The precise definition of Pythagorean fuzzy sets is presented below:

Definition 1 [15]. Let X be a universe of discourse, x is the element of X. A Pythagorean fuzzy set (PFS) P in X is defined as follows:

P={<x,(μP(x),νP(x))>|x∈X},(1)

where p=(μP(x),νP(x)) denotes the PFN of x, μP(x)∈(0,1) denotes the degree of membership of x to P, and νP(x)∈(0,1) denotes the degree of non-membership of x to P, thereby satisfying the following:

0≤(μP(x))2+(νP(x))2≤1.(2)

The degree of hesitancy of the element x to P is as follows:

πP(x)=1−(μP(x))2−(νP(x))2.(3)

Definition 2 [16]. Let p1=(μ1,ν1), and p2=(μ2,ν2) be two PFNs, and λ>0. The algorithm is as follows:

p1⊕p2=(μ12+μ22−μ12μ22,ν1ν2),(4)

p1⊗p2=(μ1μ2,ν12+ν22−ν12ν22),(5)

λp1=(1−(1−μ12)λ,ν1λ),λ>0.(6)

Definition 3 [16]. Let p1=(μ1,ν1) and p2=(μ2,ν2) be two PFNs. The Euclidean distance measure is then defined as follows:

d(p1,p2)=12(|μ12−μ22|2+|ν12−ν22|2+|π12−π22|2).(7)

Definition 4 [17]. Let P={p1,p2,…,pn} and Q={q1,q2,…,qn} be two PFSs defined in a universe of discourse X={x1,x2,…,xn}. The Pythagorean fuzzy weighted distance measure is then defined as follows:

PFWD(P,Q)=∑j=1nωjd(pj,qj),(8)

where ω=(ω1,ω2,…,ωn)T is the weight vector of xj,(j=1,2,…,n), with ∑j=1nωj=1.

4  Fuzzy Risk Assessment Method for Airborne Network Information Security Based on PF-AHP-TOPSIS

Fig. 2 shows the flow chart of the proposed PF-AHP-TOPSIS based information security fuzzy risk assessment method to realize the information security risk status assessment of the airborne network, and the basic stages are presented as follows:

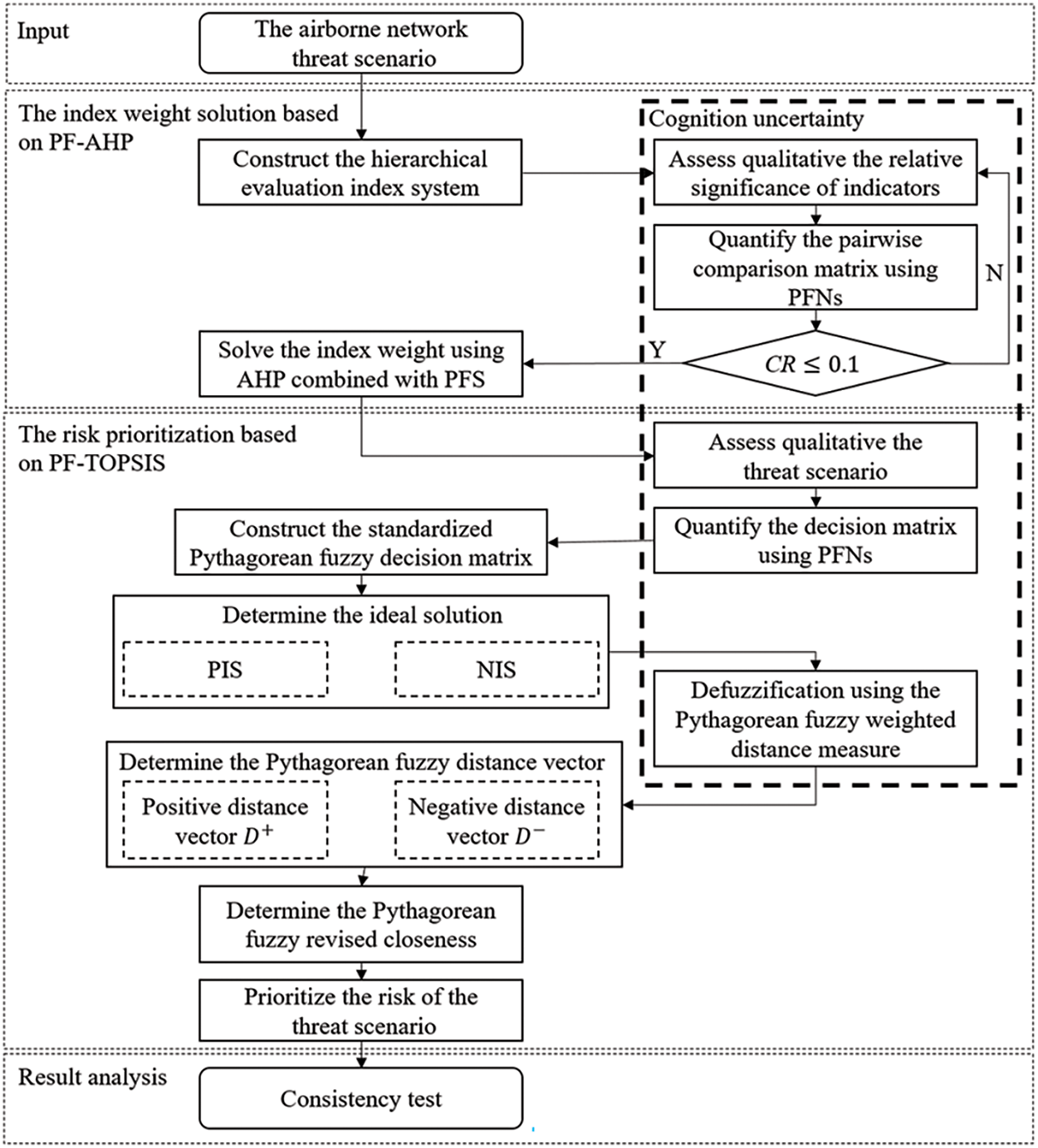
Figure 2: Schematic of the proposed methodology

1) Index weight solution based on PF-AHP. First, the hierarchical evaluation index system for airborne network information security is constructed. Experts then conduct a qualitative assessment to determine the relative significance of the indicators. Pairwise comparison matrices are quantified using PFNs based on the Pythagorean fuzzy AHP language scale, and Pythagorean fuzzy pairwise comparison matrices are established for each layer of indicators. The consistency of the matrix should be examined. If the consistency requirement is not met, then experts should re-evaluate it. Otherwise, proceed to the next step. Finally, the relative and comprehensive weights of each indicator can be determined based on the pairwise comparison matrix and the hierarchical relationship between indicators.

2) Risk prioritization based on PF-TOPSIS. First, the threat scenarios are qualitatively evaluated by experts based on the indicators. Subsequently, decision matrix matrices are quantified using PFSs based on the Pythagorean fuzzy TOPSIS language scale. The decision matrix is standardized to obtain the standardized Pythagorean fuzzy decision matrix. The positive ideal solution (PIS) and the negative ideal solution (NIS) are then determined. The Pythagorean fuzzy positive and negative distance vectors of the threat scenario are computed based on the Pythagorean fuzzy weighted distance measure. The Pythagorean fuzzy revised closeness of the threat scenario is derived by employing the formula. Finally, a risk prioritization of threat scenarios is established.

3) Result analysis. A comparative analysis is conducted between the risk assessment results obtained from the method and those derived from alternative methods to demonstrate the effectiveness of the proposed method. The consistency of the expert group assessment is tested using different assessment methods. The results validate effectiveness of the proposed method optimizing expert cognitive uncertainty in airborne network information security risk assessment.

4.1 Pythagorean Fuzzy Analytic Hierarchy Process (PF-AHP)

The AHP is a widely used method for risk assessment [10]. A hierarchical index system is constructed, and the index weights are determined by evaluating their relative importance. Experts encounter challenges in accurately constructing the pairwise comparison matrix due to the cognitive uncertainty of experts regarding airborne network information security assessment. Therefore, this study integrates AHP with Pythagorean fuzzy theory, thereby introducing PF-AHP. This method is utilized to establish an index system for airborne network information security risk assessment and determine the index weights. The specific steps of PF-AHP are presented as follows:

1) Establish the hierarchical evaluation index system, which comprises the goal, criterion, and indicator levels.

2) Construct the Pythagorean fuzzy pairwise comparison matrix H=(hjk)l×l, based on the fuzzy linguistic quantification presented in Table 1. In this table, hjk=([μjkL,μjkU],[νjkL,νjkU]) represents the relative importance of indicator Aj to Ak relative to indicator A at the upper level.

3) Evaluate the consistency of the Pythagorean fuzzy pairwise comparison matrix H by calculating the consistency index CR using Eq. (9).

CR=CIRI,CI=λmax−ll−1,(9)

where l is the dimension, λmax is the maximum eigenvalue of the Pythagorean fuzzy pairwise comparison matrix H, CI is the consistency index, and RI is the random consistency index. The value is shown in Table 2. If CR<0.1, then the consistency is acceptable. Otherwise, the pairwise comparison matrix H should be reconstructed.

4) Compute the difference matrix D=(djk)l×l, where djk=[djkL,djkU] is calculated using Eqs. (10) and (11).

djkL=μjkL2−νjkU2,(10)

djkU=μjkU2−νjkL2.(11)

5) Determine the interval multiplicative matrix S=(sjk)l×l, where sjk=[sjkL,sjkU] is calculated using Eqs. (12) and (13).

sjkL=1000djkL,(12)

sjkU=1000djkU.(13)

6) Find the determinacy value τ=(τjk)l×l using Eq. (14).

τjk=1−(μjkU2−μjkL2)−(νjkU2−νjkL2).(14)

7) Construct the matrix of weights T=(tjk)l×l based on the interval multiplication matrix S and the determinacy value τ using Eq. (15).

tjk=(sjkL+sjkU2)τjk.(15)

8) Compute the normalized priority weight vector ω=(ω1,ω2,…,ωl)T using Eq. (16).

ωj=∑k=1ltjk∑j=1l∑k=1ltjk.(16)

4.2 Pythagorean Fuzzy Technique for Order Preference by Similarity (PF-TOPSIS)

The TOPSIS is a comprehensive evaluation method proposed by Hwang et al. [21]. The prioritization is achieved by assessing the comprehensive distance between the alternatives with the ideal and worst solutions. This study integrates Pythagorean fuzzy theory with TOPSIS (PF-TOPSIS) to address the cognitive uncertainty of experts in airborne network information security risk assessment, enabling the risk prioritization of threat scenarios for airborne networks. The specific steps of PF-TOPSIS are presented as follows:

1) Construct the Pythagorean fuzzy decision matrix by considering the airborne network threat scenarios and the evaluation index system. Quantify the Pythagorean fuzzy decision matrix based on Table 3. Subsequently, standardize the matrix to obtain the standardized Pythagorean fuzzy decision matrix N=(Aj(xi))m×n shown in Eq. (19).

Standardize the Pythagorean fuzzy decision matrix N′=(Aj′(xi))m×n using Eqs. (17) and (18).

μij=μij′∑i=1m(μij′2+υij′2),(17)

υij=υij′∑i=1m(μij′2+υij′2),(18)

where, μij′∈[0,1] and νij′∈[0,1] denote the degree of membership and non-membership, respectively, before normalization.

N=(Aj(xi))m×n=[p(μ11,ν11)p(μ12,ν12)⋯p(μ1n,ν1n)p(μ21,ν21)p(μ22,ν22)⋯p(μ2n,ν2n)⋮⋮⋱⋮p(μm1,νm1)p(μm2,νm2)⋯p(μmn,νmn)],(19)

where xi(i=1,2,…,m) and Aj(j=1,2,…,n) are the threat scenarios and criteria, respectively, and p(μij,νij) is the Pythagorean fuzzy risk of the threat scenario xi relative to the indicator Aj.

2) Calculate the Pythagorean fuzzy PIS and NIS using Eqs. (20) and (21), respectively.

x+={p(μ1+,ν1+),p(μ2+,ν2+),…,p(μn+,νn+)},(20)

x−={p(μ1−,ν1−),p(μ2−,ν2−),…,p(μn−,νn−)},(21)

μj+=max1≤i≤mμij,νj+=max1≤i≤mνij

μj−=min1≤i≤mμij,νj−=min1≤i≤mνij

3) Compute Pythagorean fuzzy the distance of the threat scenario xi(i=1,2,…,m) using Eqs. (22) and (23).

Di+=PFWD(xi,x+)=∑j=1nωjd(p(μij,νij),p(μj+,νj+)),(22)

Di−=PFWD(xi,x−)=∑j=1nωjd(p(μij,νij),p(μj−,νj−)),(23)

where for i=1,2,…,m, D+=(D1+,D2+,…,Dm+)T denotes the positive distance vector between the threat scenario xi and the PIS x+, D−=(D1−,D2−,…,Dm−)T denotes the positive distance vector between the threat scenario xi and the NIS x−.

4) Find the Pythagorean fuzzy revised closeness vector ξ=(ξ(x1),ξ(x2),…,ξ(xm))T using Eq. (24).

ξ(xi)=Di−Di++Di−.(24)

The risk level of the threat scenario is prioritized based on the Pythagorean fuzzy revised closeness ξ(xi), where the influence of the threat scenario on the airborne network is substantial when the revised closeness ξ(xi) is large.

5  Application

5.1 Analysis of Threat Scenarios in Airborne Networks

As shown in Fig. 2, considering the interaction scenario between passengers and an aircraft airborne network given in DO-356A [2], the risk assessment of the network is conducted using the proposed method.

The onboard network conmprises three subnetworks: the cabin network for providing cabin services, the maintenance network for providing maintenance and critical cabin services, and the limited aircraft network for providing aircraft and critical maintenance services. A maintenance gateway exists between the cabin and maintenance networks, which requires an administrator administration account and password for configuring and updating the network. Meanwhile, an aircraft gateway exists between the maintenance and the limited aircraft network. As shown in Table 4, nine threat scenarios are identified in DO-356A.

5.2 Establishment of the Index System for Airborne Network Information Security

The fundamental components and their interrelationships for conducting information security risk assessment are provided in the national standard GB/T 20984-2022 [3]. Four dimensions, including asset, threat, vulnerability, and security measures, should be considered for the comprehensive analysis of risk assessment. The hierarchical index system for assessing security risks in airborne network information is constructed based on the characteristics of airborne network information security and the airworthiness security standard DO-356A [2]. Fig. 3 illustrates the constructed index system.

Figure 3: Index system of information security risk assessment for airborne network

According to GB/T 20984-2022, confidentiality, integrity, and availability are the crucial security attributes of assets (A1). The value of airborne network assets is reflected the following through three indicators: confidentiality value (B1), integrity value (B2), and availability value (B3). The exploitability of airborne network vulnerability (A2) is assessed by considering the attack vector (B4), privilege required (B5), and attack complexity (B6), in conjunction with the metrics of the common Vulnerability scoring system (CVSS). The threat conditions (A3) of the airborne network, based on the STRIDE model’s common network threats, including denial of service (B7), elevation of privilege (B8), and tampering (B9), are determined to assess their severity of impact on airborne network. Finally, the effectiveness (B10) is utilized to assess the resilience of airborne network security measures (A4) against threats.

5.3 Risk Assessment

The proposed method, which is detailed in Section 3, is applied to prioritize the threat scenario risk in the airborne networks as shown in Fig. 2. The PF-AHP method is initially used to determine the relative and comprehensive weight of the indicators. An expert group comprising five experts E={e1,e2,e3,e4,e5} is invited for analysis. In this case, the expert e1 is selected as an exemplar for analysis.

The experts are requested to qualitatively assess the relative importance of the indicators utilizing the language rating scales provided in Table 1. The Pythagorean fuzzy pairwise comparison matrices for three indicator layers (refer to Tables 5–7) and the criterion layer (refer to Table 8) are obtained. The consistency test of all matrices is conducted in accordance with Eq. (9) to ensure the coherence of expert judgments. The CRs of each matrix are below 0.1, indicating that the consistency level of the matrices was within an acceptable range.

The Pythagorean fuzzy pairwise comparison matrix H=(hjk)3×3 of the criterion layer index A1 is used as an example (refer to Table 5) to illustrate the analysis process. The difference matrix D=(djk)3×3 is calculated based on the upper and lower interval values of membership and non-membership using Eqs. (10) and (11), respectively, as presented in Table 9. Table 10 shows the interval multiplication matrix S=(sjk)3×3 calculated using Eqs. (12) and (13). Table 11 shows that the determined value matrix τ=(τjk)3×3 is computed using Eq. (14). The weighting matrix before normalization T=(tjk)3×3 is constructed using Eq. (15), as shown in Table 12. The relative weights vector ω1, ω2 and ω3 of indicators B1, B2 and B3, respectively, under indicator A1 are determined using Eq. (16), as presented in Table 13.

The above steps are repeated to derive the relative weights ωi for criteria and indicator layers. The comprehensive weights w are computed based on the interrelationship of indicators. Table 13 shows the relative weighs and comprehensive weights of all indicators. The results indicate that availability value B3 is the most crucial indicator with a weight of 0.482, followed by the tampering B9 and denial of service B7 with the weights of 0.123 and 0.099, respectively. The attack complexity B6 is the least important indicator with a weight of 0.008.

Subsequently, the PF-TOPSIS method is employed to assess the risk prioritization of the nine threat scenarios existing in the airborne network using the weighs computed by PF-AHP. Experts qualitatively assess the risk of the threat scenario based on the indicators using the linguistic rating scale in Table 3. The Pythagorean fuzzy decision matrix N=(SCj(xi))9×10 is constructed as shown in Table 14.

The decision matrix is standardized using Eqs. (17) and (18). The PIS vector x+ and NIS vector x− are determined using Eqs. (20) and (21), respectively, and the results are presented as follows:

x+={p(0.220,0.220),p(0.352,0.090),p(0.351,0.099),p(0.361,0.094),p(0.350,0.095),p(0.358,0.080),p(0.328,0.151),p(0.319,0.132),p(0.325,0.130),p(0.065,0.466)}

x−={p(0.066,0.416),p(0.062,0.510),p(0.103,0.493),p(0.149,0.405),p(0.144,0.411),p(0.063,0.451),p(0.066,0.514),p(0.064,0.450),p(0.065,0.441),p(0.324,0.137)}

Table 15 shows the positive distance vector D+ and negative distance vector D− of threat scenarios calculated using Eqs. (22) and (23), respectively. Finally, the revised closeness vector ξ of threat scenarios is computed using Eq. (24), and the results are also presented in Table 15.

A high revised closeness vector ξ substantially affects the threat scenario on the airborne network. Table 16 shows the final risk ranking results of expert e1. The results indicate that the threat scenario with the highest risk is SC9, which involves vulnerabilities (including the weak administrator password for the maintenance gateway and packet filtering vulnerability of the aircraft gateway), threat conditions (including misconfiguration of maintenance gateway and denied aircraft services), and intermediate assets of attack (including maintenance and aircraft gateways). The target asset is the aircraft services.

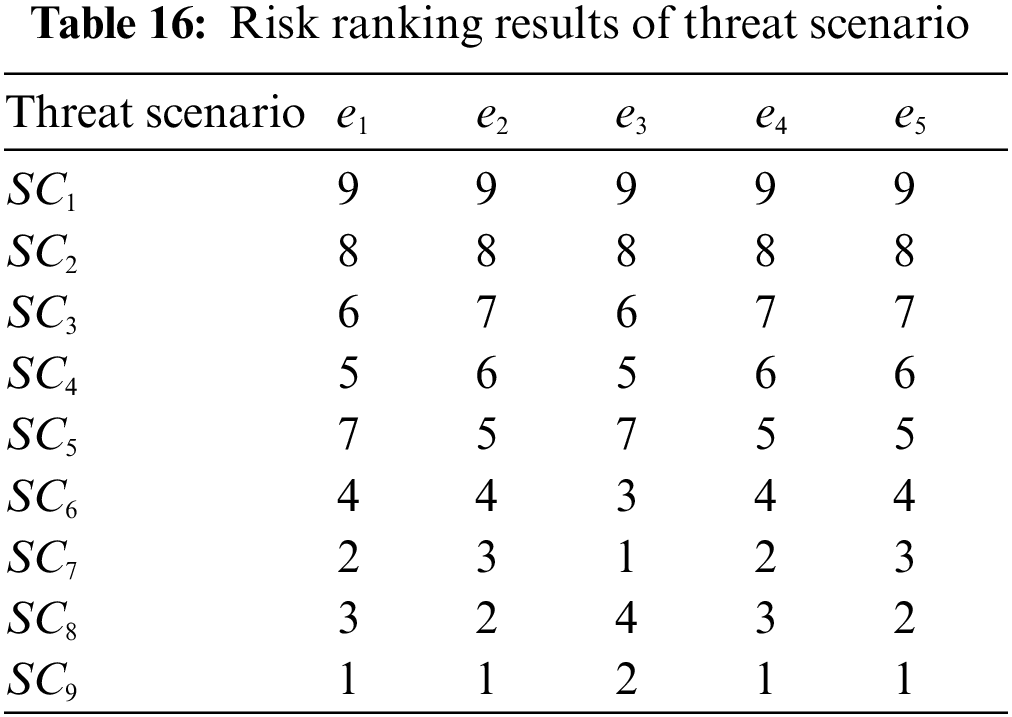
Table 16 and Fig. 4 show the ranking of the risks for nine threat scenarios assessed by five experts. Among them, as concluded by the assessments of four experts, the threat scenario with the highest risk is SC9, while one expert assesses it as SC7.

Figure 4: Ranking of the risk assessment by expert group

5.4 Comparative Analysis

F-AHP-TOPSIS [11], IF-AHP-TOPSIS [16], PF-AHP-VIKOR [22], and PF-AHP-TODIM [23] are used to conduct risk assessment for the information security situation of the airborne network in Fig. 2 and verify the effectiveness of PF-AHP-TOPSIS in optimizing expert cognitive uncertainty for airborne network information security risk assessment. Fig. 5 displays the ranking results for the nine threat scenarios of the five experts using the above method individually.

Figure 5: Ranking results by using different method

The Kendall W coordination coefficient is commonly employed to analyze the consistency of evaluation results among multiple experts. The Kendall W coordination coefficient has a value range of [0,1], indicating a high degree of consistency as the value approaches 1. The coefficient is calculated using Eq. (25).

W=12SK2(N3−N),(25)

where S denotes the sum of squares of the differences between the rank sum and its mean, K denotes the number of groups evaluated for ranking, and N denotes the number of objects.

In comparison with the coefficients obtained using other risk assessment methods, the Kendall W coordination coefficient is used to analyze the consistency of the assessment results of the expert group. Table 17 shows the Kendall W coordination coefficient result using different methods.

The Kendall W coordination coefficient of the assessment results of the expert group exhibits the highest value compared to other methods when employing the PF-AHP-TOPSIS method, as displayed in Table 17. Therefore, the consistency of assessment results is the highest when using the proposed method. Specifically, PF-AHP-TOPSIS exhibits the highest coefficient in comparison with the fuzzy methods F-AHP-TOPSIS and IF-AHP-TOPSIS, demonstrating the effectiveness of Pythagorean fuzzy in addressing the uncertainty of expert epistemic. Simultaneously, compared with the risk assessment methods PF-AHP-VIKOR and PF-AHP-TODIM, the coefficient of PF-AHP-TOPSIS is found to be the highest. This finding reveals the effectiveness of Pythagorean fuzzy combination with AHP and TOPSIS for addressing the uncertainty of expert cognitions in airborne network security risk assessment. The consistency of the results obtained by the PF-AHP-TOPSIS method is the highest when employing different approaches to handle expert group evaluation opinions. Therefore, the effectiveness of the proposed method in optimizing the uncertainty of expert epistemic in airborne network information security risk assessment is demonstrated.

6  Conclusion

With the widespread application of network information technology in airborne network communication, the issue of airborne network information security has become increasingly prominent. Therefore, conducting information security assessments is necessary for airborne networks. However, experts have insufficient knowledge of basic security elements such as assets, threats, and vulnerabilities, due to the confidentiality of airborne networks, leading to cognitive uncertainty. In this study, a fuzzy risk assessment method for airborne network information security based on PF-AHP-TOPSIS is introduced to optimize the expert cognitive uncertainty in airborne network risk assessment. The index system for airborne network information security risk assessment is constructed from the following four perspectives: assets, threat conditions, vulnerabilities, and security measures. This system is based on the national standard of information security assessment and the airworthiness security risk assessment specification in civil aviation. The Pythagoras fuzzy theory is integrated with AHP and TOPSIS to optimize the expert cognitive uncertainty in airborne network information security risk assessment. The Pythagoras fuzzy numbers are used to construct the AHP pairwise comparison and TOPSIS decision matrices, which could not be accurately characterized. The PF-AHP method is employed to determine the index weights, while the PF-TOPSIS method is used to prioritize the risk of threat scenarios in airborne networks. The threat scenario with the most serious risk is then analyzed to provide a foundation for the subsequent implementation of security measures. Finally, a comparison analysis is established to demonstrate the effectiveness of the proposed method in mitigating the impact of expert cognitive uncertainty on risk assessment of airborne network information security. The PF-TOPSIS method assesses risks to airborne networks based on an indicator system for evaluating threat scenarios. However, this method overlooks the relationships between information security elements such as threats, vulnerabilities, and assets. Subsequently, a highly accurate risk assessment of the airborne network can be realized by modeling intrusion paths and conducting an in-depth analysis of the relationships between these information security elements.

In this study, we have not yet explored the issue of security domains within airborne networks. Given the varying security levels across different security domains, developing a network assessment methodology that spans across these domains emerges as a pressing challenge for future research. Additionally, the states of system components and the security risks faced by airborne networks differ during various operational phases of civil aircraft. Therefore, conducting network security risk assessments tailored to each operational phase of civil aircraft is also a subject that warrants further investigation.

Acknowledgement: The authors would like to express their gratitude to the members of the research group for their support.

Funding Statement: This work was supported by the Fundamental Research Funds for the Central Universities of CAUC (3122022076) and National Natural Science Foundation of China (NSFC) (U2133203).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Kenian Wang, Yuan Hong; data collection: Chunxiao Li; draft manuscript preparation: Yuan Hong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data not available due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Aeronautical Radio Inc. Avionics full-duplex switched (AFDX) ethernet: ARINC 664 P7. USA. Accessed: Sep. 1, 2009. [Online]. Available: https://aviation-ia.sae-itc.com/standards/arinc664p7-1-664p7-1-aircraft-data-network-part-7-avionics-full-duplex-switched-ethernet-network [Google Scholar]

2. Radio Technical Commission for Aeronautics, Airworthiness security methods and considerations: RTCA DO-356A. USA. Accessed: Jun. 21, 2018. [Online]. Available: https://standards.globalspec.com/std/10398650/rtca-do-356 [Google Scholar]

3. Standardization Administration of China, Information security technology—Risk assessment method for information security: GB/T 20984-2022. Beijing, China: Standards Press of China, 2022, pp. 6–7. Accessed: Jun. 1, 2023. [Online]. Available: http://c.gb688.cn/bzgk/gb/showGb?type=online&hcno=FDA38AB7D08A715C6B6D69DFDEABB2C0 [Google Scholar]

4. M. Humayun, N. Z. Jhanjhi, M. F. Almufareh, and M. I. Khalil, “Security threat and vulnerability assessment and measurement in secure software development,” Comput. Mater. Contin., vol. 71, no. 3, pp. 5039–5059, 2022. doi: 10.32604/cmc.2022.019289. [Google Scholar] [CrossRef]

5. S. Shirvani, Y. Baseri, and A. Ghorbani, “Evaluation framework for electric vehicle security risk assessment,” IEEE Trans. Intell. Transp. Syst., vol. 25, no. 1, pp. 33–56, Jan. 2024. doi: 10.1109/TITS.2023.3307660. [Google Scholar] [CrossRef]

6. L. Wang, H. Garg, and N. Li, “Pythagorean fuzzy interactive Hamacher power aggregation operators for assessment of express service quality with entropy weight,” Soft Comput., vol. 25, no. 2, pp. 973–993, 2021. doi: 10.1007/s00500-020-05193-z. [Google Scholar] [CrossRef]

7. M. Tariq, M. Ali, F. Naeem, and H. V. Poor, “Vulnerability assessment of 6G-Enabled smart grid cyber-physical systems,” IEEE Internet Things J., vol. 8, no. 7, pp. 5468–5475, Apr. 1, 2021. doi: 10.1109/JIOT.2020.3042090. [Google Scholar] [CrossRef]

8. Y. Averyanova et al., “UAS cyber security hazards analysis and approach to qualitative assessment,” presented at 2020 Int. Symp. Autom., Inf. Comput. (ISAIC 2020), Beijing, China, Dec. 2–4, 2020. [Google Scholar]

9. S. Zhang, D. Kong, and X. Li, “Security risk assessment methodology for airborne system,” (in ChineseComput. Eng. Appl., vol. 49, no. 16, pp. 232–235, 2013. [Google Scholar]

10. G. Li, J. Li, J. Wang, J. Xu, and P. Wang, “A security risk assessment improved model based on threat status for new airborne networks,” Modern Electron. Tech., vol. 42, no. 3, pp. 41–45, 2019. [Google Scholar]

11. J. Wang, J. Li, G. Li, and T. Huang, “An improved FAHP-cloud-based security risk assessment model for airborne networks,” J. Comput. Methods Sci. Eng., vol. 21, no. 2, pp. 277–291, 2021. doi: 10.3233/JCM-204532. [Google Scholar] [CrossRef]

12. J. Li, L. Yan, J. Wang, and T. Fu, “Research on network security risk assessment method based on improved AHP,” presented at 2020 Inter. Symp. Autom., Inf. Comput. (ISAIC 2020Beijing, China, Dec. 2–4, 2020. [Google Scholar]

13. W. Wang, Z. Sun, M. Pan, B. Zhang, Z. Li and L. Ye, “Information security risk assessment method for electric vehicle charging piles based on fuzzy analytic hierarchy process,” Electr. Power, vol. 54, no. 1, pp. 96–103, 2021. [Google Scholar]

14. R. M. Zulqarnain, X. Xin, and M. Saeed, “Extension of TOPSIS method under intuitionistic fuzzy hypersoft environment based on correlation coefficient and aggregation operators to solve decision making problem,” AIMS Math., vol. 6, no. 3, pp. 2732–2755, 2021. doi: 10.3934/math.2021167. [Google Scholar] [CrossRef]

15. O. W. Klaproth, M. Halbrügge, L. R. Krol, C. Vernaleken, T. O. Zander and N. Russwinkel, “A neuroadaptive cognitive model for dealing with uncertainty in tracing pilots’ cognitive state,” Top. Cogn. Sci., vol. 12, no. 3, pp. 1012–1029, 2020. doi: 10.1111/tops.12515. [Google Scholar] [CrossRef]

16. R. R. Yager, “Pythagorean fuzzy subsets,” in Proc. 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, Canada, IEEE, Jun. 24–28, 2013, pp. 57–61. [Google Scholar]

17. L. Wang, Y. Ali, S. Nazir, and M. Niazi, “ISA evaluation framework for security of internet of health things system using AHP-TOPSIS methods,” IEEE Access, vol. 8, pp. 152316–152332, 2020. doi: 10.1109/ACCESS.2020.3017221. [Google Scholar] [CrossRef]

18. M. Zhao, G. Wei, C. Wei, and J. Wu, “Pythagorean fuzzy TODIM method based on the cumulative prospect theory for MAGDM and its application on risk assessment of science and technology projects,” Int. J. Fuzzy Syst., vol. 23, no. 4, pp. 1027–1041, 2021. doi: 10.1007/s40815-020-00986-8. [Google Scholar] [CrossRef]

19. B. C. Giri, M. U. Molla, and P. Biswas, “Pythagorean fuzzy DEMATEL method for supplier selection in sustainable supply chain management,” Expert. Syst. Appl., vol. 193, no. 6, pp. 116396, 2022. doi: 10.1016/j.eswa.2021.116396. [Google Scholar] [CrossRef]

20. M. Akram, F. Ilyas, and H. Garg, “Multi-criteria group decision making based on ELECTRE I method in Pythagorean fuzzy information,” Soft Comput., vol. 24, no. 5, pp. 3425–3453, 2020. doi: 10.1007/s00500-019-04105-0. [Google Scholar] [CrossRef]

21. C. Hwang and K. Yoon, “TOPSIS and VIKOR,” in Multiple Attribute Decision Making: Methods and Applications, 1st ed. Berlin, Germany: Springer, 1981, pp. 69–75. Accessed: Jun. 1, 2023. [Online]. Available: https://link.springer.com/book/10.1007/978-3-642-48318-9 [Google Scholar]

22. G. Bakioglu and A. O. Atahan, “AHP integrated TOPSIS and VIKOR methods with Pythagorean fuzzy sets to prioritize risks in self-driving vehicles,” Appl. Soft Comput., vol. 99, no. 3, pp. 106948, 2021. doi: 10.1016/j.asoc.2020.106948. [Google Scholar] [CrossRef]

23. X. Zhang and Z. Xu, “Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets,” Int. J. Intell. Syst., vol. 29, no. 12, pp. 1061–1078, 2014. doi: 10.1002/int.21676. [Google Scholar] [CrossRef]