Efficient Clustering Network Based on Matrix Factorization

1  Introduction

Due to the potent representation learning capabilities of graph data, Graph Neural Networks (GNNs) have successfully permeated various domains, encompassing node classification [1], graph classification [2], time series analysis, knowledge graphs, and clustering [3]. Within the diverse landscape of graph learning, deep graph clustering [4] emerges as a fundamental yet challenging unsupervised task, marking a recent focal point of research interest. The exploration of deep graph clustering methods encompasses various learning mechanisms. Generative methods leverage generative models to characterize the distribution of graph data, achieving effective clustering of graphs [5–9]. Adversarial methods [10,11] introduce the concept of adversarial training, enhancing clustering performance through the interplay between a generator and a discriminator. Contrastive methods [12–16], on the other hand, propel the development of deep graph clustering by learning the similarity and dissimilarity between samples. Our method falls into the category of multi-view [17] contrastive learning, aligning with the latter approach.

Existing methods generate augmented views of the same nodes through graph augmentation. However, existing studies [18,19] indicate: 1) Due to the inherent characteristics of contrastive learning, sensitivity to noise and incorrect labels can lead to semantic drift and indistinguishable positive samples when inappropriate data augmentation techniques such as edge removal, noise addition, diffusion [13], or masking are used. 2) Due to the computational cost of matrix factorization itself, existing methods still face limitations in handling large sparse datasets. 3) Model pre-training typically requires extensive data for optimal performance. Fine-tuning pre-trained models necessitates large-scale labeled data, which may not be suitable for tasks with limited annotated data. Moreover, due to differences between tasks, transferring pre-trained models to specific tasks can be more complex and challenging.

To address the aforementioned issues, we propose an Efficient Clustering Network based on Matrix Factorization (ECN-MF). The main idea behind this approach is to design a batched low-rank Singular Value Decomposition algorithm and a Mutual Information-Enhanced Clustering Guidance Module. This aims to extract crucial information from the data while better preserving the original information in the embedded data, reducing information loss, and improving the model’s generative capabilities. Specifically, in terms of data augmentation, we introduce a batched low-rank Singular Value Decomposition algorithm that decomposes the attribute matrix of large datasets into smaller modules. This allows better exploration of major variation patterns and important information in sparse and large datasets. In the network architecture, we employ a pseudo-siamese neural network with the same structure but without parameter sharing. This enables the model to better capture unique information from each view, thereby enhancing clustering performance. Additionally, we design a Mutual Information-Enhanced Clustering Guidance Module to ensure better preservation of original data information, reducing information loss, and enhancing the model’s generative capabilities. It brings samples from the same cluster closer while pushing samples from other clusters apart, further improving clustering performance. The main contributions of this work are summarized as follows:

1.    We propose an Efficient Clustering Network based on Matrix Factorization (ECN-MF), which does not require pre-training, thus alleviating the challenges of model pre-training and complex model transfer.

2.    We propose a batched low-rank Singular Value Decomposition (SVD) algorithm to address the resource-intensive nature of the SVD algorithm in large sparse datasets. This method not only avoids losing important information during data augmentation but also effectively extracts latent information from the data.

3.    We designed a Mutual Information-Enhanced Clustering Module (MI-ECM). It enhances the discriminative capability of the network while ensuring better retention of the original data information in the embedded data.

4.    Experimental results demonstrate that our proposed method outperforms existing methods in handling challenges such as large sparse datasets and model transfer complexity.

The remaining sections of this paper are organized as follows. Section 2 reviews relevant literature on matrix factorization and contrastive deep graph clustering. In Section 3, we provide detailed explanations of the symbols used, the batched low-rank Singular Value Decomposition algorithm, our network structure, and the Mutual Information-Enhanced Clustering Guidance Module. Section 4 presents the results of our method tested on five datasets. Finally, Section 5 concludes the paper.

2  Related Work

2.1 Matrix Factorization

Matrix factorization (decomposition) is the process of breaking down a matrix into the product of several matrices. This can involve techniques such as triangular factorization, full rank factorization, orthogonal triangle decomposition, Jordan decomposition, and Singular Value Decomposition. In our case, we primarily utilize Singular Value Decomposition to process data. Singular Value Decomposition allows for the representation of a relatively complex matrix as the product of smaller and simpler matrices. These smaller matrices describe the essential characteristics of the original matrix. Singular Value Decomposition is applicable to any matrix, making it adaptable to the features of current attribute information. It finds applications in various fields such as signal processing, statistics, natural language processing, and more. In recommendation systems, Singular Value Decomposition is widely applied in collaborative filtering and matrix completion algorithms. Through Singular Value Decomposition, a user-item rating matrix can be reduced to a low-dimensional latent factor matrix, extracting latent features of users and items for recommendation purposes.

Singular Value Decomposition has significant potential value in processing raw data. The singular values decrease exponentially with rank, with early singular values much larger than later ones, as shown in Fig. 1. By applying low-rank Singular Value Decomposition to the data, we can capture the essential features of the data, enhance data representation, and improve the performance of multi-view clustering. Based on this, we have optimized and improved the Singular Value Decomposition method to be suitable for large datasets, providing higher computational efficiency and scalability.

Figure 1: (a): Singular values exhibit exponential decay with rank, where the initial singular values are significantly larger than the subsequent ones. (b): All information of X is encoded in all singular values until k. The majority of information is encoded in the first singular vector returned by Singular Value Decomposition

2.2 Contrastive Deep Graph Clustering

In recent years, contrastive learning has achieved remarkable success in the fields of images [20–23] and graphics [24–26], inspiring extensive research on contrastive deep graph clustering methods [12–16]. The clustering performance of these methods is primarily influenced by three key factors: data augmentation, network architecture, and the handling of positive and negative sample pairs. Taking these factors into account, we summarize the distinctions between our proposed ECN-MF and other contrastive deep graph clustering methods.

2.2.1 Data Augmentation

Data augmentation techniques are pivotal in the realm of deep graph-contrastive clustering. Current methods, such as edge removal, diffusion, masking, and noise addition, introduce varying degrees of perturbation to the original data. While these approaches help mitigate over-smoothing during iterative training of graph neural networks, they carry the risk of losing crucial information. Inappropriate data augmentation may lead to semantic drift and indistinguishable positive samples, resulting in suboptimal clustering performance. For instance, reference [13] utilizes diffusion matrices as augmented graphs, while Self-supervised contrastive attributed graph clustering (SCAGC) perturbs graph structure by randomly adding or removing edges. Reference [15] and SCAGC enhance node attributes through attribute perturbation. However, reference [27] has highlighted the risk of semantic drift with improper data augmentation. To address this challenge, we propose a novel enhancement approach. Unlike existing methods, ECN-MF leverages batch low-rank Singular Value Decomposition methods to extract crucial attribute information, filter out noisy data, and construct two augmented views of the same node without compromising the original structure.

2.2.2 Network Architecture

In terms of network architecture, SCAGC, reference [28] uses a shared Graph Convolutional Networks (GCNs) encoder to encode nodes. However, conventional GCNs encoders entangle transformation and aggregation operations during the training process, resulting in high time costs. To address this issue, we employ two separate Multilayer Perceptrons (MLPs) to encode the node attributes of the two views. These two MLPs have the same architecture but do not share parameters, ensuring that the node embeddings for the two views contain different semantic information.

2.2.3 Handling of Positive and Negative Sample Pairs

In contrastive methods, the handling of positive and negative sample pairs is crucial. Contrastive methods bring positive samples together while pushing negative samples apart. Therefore, the quality of positive and negative sample pairs significantly influences the performance of contrastive methods. Specifically, reference [13] generates negative samples by randomly shuffling features and designs the InfoMax loss to maximize cross-view mutual information. Reference [12] distinguishes between similar and dissimilar nodes using cross-entropy loss. Subsequently, SCAGC randomly selects samples from different clusters to improve the quality of negative samples. They also design a contrastive clustering loss to maximize the consistency between representations from the same cluster. Both references [14] and [16] utilize the infoNCE loss to attract positive sample pairs and separate negative sample pairs. While their approaches have shown effectiveness, they still depend on a well-pretrained model to choose high-quality positive and negative samples. To address this issue, we propose a MI-ECM to bring samples from the same cluster closer while pushing samples from different clusters apart, thereby enhancing the discriminative ability of sample pairs.

3  Method

In this section, we introduce a novel Efficient Clustering Algorithm based on Matrix Factorization (ECN-MF). The aim is to enhance clustering performance by leveraging matrix factorization in a way that captures unique information from each view with-out disrupting the original structure. The overall framework of ECN-MF is illustrated in Fig. 2. In the following sections, we will provide a detailed explanation of the pro-posed ECN-MF.

Figure 2: Schematic diagram of the Efficient Clustering Network based on Matrix Factorization. The network consists of three main parts: the batched low-rank Singular Value Decomposition (SVD) on the left, the pseudo-siamese neural network in the middle, and the Mutual Information-Enhanced Clustering Guidance Module on the right. Here, A¯ is the normalized adjacency matrix, X is the attribute matrix, and Xr is its corresponding low-rank attribute matrix. E1 and E2 represent the first and second encoders, Z(L) and Zr(L) represent the embedding information of the first and second encoders. Q is the probability matrix, and P is the target distribution

3.1 Notations and Problem Definition

In an undirected graph G={X,A}, let V={v1,v2,…,vN} be a set containing N nodes with K classes, and E be the set of edges. X∈RN×D represents the attribute matrix, and A∈RN×N represents the original adjacency matrix. The degree matrix is denoted as D=diag(d1,d2,…,dN)∈RN×N, where di=Σ(vi,vj)∈εaij. Normalizing the original adjacency matrix A to A¯∈RN×N is achieved by computing D(−1)(A+I), where I∈RN×N is the identity matrix. Table 1 summarizes these symbols.

3.2 Batch Low-Rank Singular Value Decomposition Algorithm

Recent studies have demonstrated the significant effectiveness of Singular Value Decomposition in handling sparse matrices and dimensionality reduction. Inspired by their success, we introduce the Singular Value Decomposition algorithm, treating attribute information as an independent preprocessing step before training. This approach allows for the effective extraction of latent and essential information from the data while filtering out noise present in the attributes. The method is as follows:

Specifically, given a matrix A∈Rm×n, low-rank Singular Value Decomposition decomposes it into the product of three matrices, where m and n can be any integers:

A=USVT(1)

Here, U∈Rm×r is the left singular vector matrix, containing the structural information of the original data, where r represents the rank of the low-rank. S∈Rm×r is the diagonal matrix containing singular values, typically arranged in descending order, representing the importance of the data. VT∈Rr×n is the right singular vector matrix, containing the feature information of the original data.

Singular Value Decomposition can be applied to decompose any matrix, making it adaptable to the characteristics of current attribute information. We will rewrite Eq. (1) as follows:

Xr=UrSrVrT(2)

Here, Xr∈RN×D represents the low-rank attribute matrix, Ur is the low-rank left singular vector matrix, Sr is the low-rank diagonal matrix, and Vr is the low-rank right singular vector matrix, where VrT is the transpose of Vr.

To adapt to the Singular Value Decomposition in the case of large data, we partition the dataset X={x1,x2,…,xN} into M batches, where each batch batchi consists of B samples, and B is a positive integer, i.e.:

batchi={xi⋅B+1,xi⋅B+2,…,x(i+1)B}(3)

Here, B represents the number of samples included in batchi.

The objective of centralization is to set the mean of the data in each batch to zero. Assuming batchi contains B samples with a mean of μi, centralization is applied to each batch batchi, resulting in the centered batch batchicentered. This process can be mathematically represented as follows:

batchicentered=batchi−μi={xi⋅B+1−μi,xi⋅B+2−μi,…,x(i+1)B−μi}(4)

Here, xi⋅B+2 represents the 2-th sample in batchi, and μi is the mean of batchi. Performing Singular Value Decomposition on each batchicentered yields different low-rank matrices ui,si,vi :

ui∼i+r,si∼i+r,vi∼i+r=SVD(batchicentered)(5)

Here, SVD represents the Singular Value Decomposition algorithm.

We concatenate all low-rank matrices ui,si,vi from each batchicentered to form matrices Ur,Sr,Vr:

Ur={u1,u2,…,ui∗r}

Sr={s1,s2,…,si∗r}(6)

Vr={v1,v2,…,vi∗r}

We perform a descending order sorting on Sr and select the top r values. In other words, we individually sort the real numbers of singular values in descending order and choose the top r singular values. The purpose is to emphasize the significance of singular values, allowing the primary information of attribute matrix X to be represented by a reduced number of singular values or vectors. The aforementioned learning process can be articulated as follows:

Slow=descendingsort(Sr)(7)

Slow_r=TOP(Slow,r)

Next, we will obtain the corresponding vectors of Vr based on the indices selected indices of the singular values Slow_r and form Vlow_r according to Eq. (8):

Vlow_r=f(x)={vi,Slow_r,i match vi0,others(8)

Finally, we reconstruct the low-rank attribute matrix Xr using Ur, Slow_r, Vlow_r according to Eq. (9).

Xr=UrSlow_rVlow_rT(9)

3.3 Pseudo-Siamese Neural Network

In this section, we embed the nodes of both the original and enhanced data into a latent space and design a pseudo-siamese neural network with an encoder that shares the same architecture but has non-shared learnable parameters.

Residual connections allow information to propagate between network layers, aiding in mitigating the vanishing gradient problem, accelerating the training process, and enhancing model performance. In this work, the representations learned by the l-th layer of GCNs can be obtained through the following convolution operation:

Z(l)=∅(A¯Zl−1Wv1l−1+Zl−1)(10)

Zr(l)=∅(A¯Zrl−1Wv2l−1+Zrl−1)

Here, ∅ is the activation function of the fully connected layer, such as Relu [29] or the Sigmoid function. Zl−1 and Zrl−1 represent the embeddings of two views, and Wv1l−1 and Wv2l−1 are the weight matrices corresponding to the encoder’s l-th layer. Additionally, we denote Z(0) as the original data X and Zr(0) as the enhanced data Xr. As shown in Eq. (10), the representations Zl−1 and Zrl−1 will traverse the normalized adjacency matrix A¯ to obtain new representations Z(l) and Zr(l). It is important to note that the input to the first layer of GCNs consists of the original data X and the enhanced data Xr:

Z(1)=∅(A¯XWv11)(11)

Zr(1)=∅(A¯XrWv21)

We denote the embeddings output by the last layer of GCNs as Z(L) and ZrL.

3.4 Mutual Information-Enhanced Clustering Module

To minimize redundancy in embeddings and effectively preserve more discriminative features, we initially optimize the embeddings between cross-view samples using Mean Squared Error (MSE) loss. This ensures that the learned representations are not influenced by irrelevant information, thereby guaranteeing the quality of the latent space for subsequent clustering tasks. The formula is as follows:

LMSE=1n∑i=1n(Z(L)−ZrL)2(12)

Here, Z(L) and ZrL represent the embeddings of the last layer of the graph convolutional network.

Next, we merge the embeddings from the two views for each node as follows:

Z=12(Z(L)+ZrL)(13)

Here, Z∈RN×d represents the node embeddings for clustering.

Finally, by inputting Z into a one-layer Multi-Layer Perceptron (MLP) with a softmax activation function, we convert it into a K-dimensional clustering space, where K represents the number of clusters. The learning process can be expressed as:

Q=softmax(Z)(14)

where Q∈RN×K represents the probability matrix indicating the probability of all N nodes belonging to K clusters. We can view Q as a probability distribution.

Following the acquisition of the clustering probability distribution Q, we refine the data representation by focusing on learning high-confidence data, aiming to strengthen the cohesion within the clustering. Specifically, we aim to reinforce the intra-cluster cohesion by emphasizing representations that are closer to the cluster centers. Therefore, we compute the target distribution P as follows:

Pij=Qij2/fj∑j′Qij′2/fj′(15)

Here, fj=∑iQij is the soft clustering frequency. In the target distribution P, each assignment in Q is squared and normalized to give higher confidence to the assignments. This leads to the following objective function:

LKL(P||Q)=∑xlogP(x)Q(x)(16)

Minimizing the KL divergence loss between the Q and P distributions enables the GCNs module to enhance its ability to learn representations for clustering tasks. This ensures that the data representations around cluster centers become more compact.

In order to aggregate samples within the same cluster while simultaneously separating them from samples in other clusters, we choose to periodically update the top τ probability samples from different clusters. This process enhances the cohesion of positive samples within clusters and improves the discriminative ability of sample pairs, i.e.,

I(xi,j isamongthetopτelements)={1,if qi,jisamongthetopτelements0,otherwise(17)

Here, I(xi,jisamongthetopτelements)=1 indicates that sample xi is most likely to belong to cluster cj, and the label for this sample is recorded as ykey. The number of key samples in each cluster is Nk, and the total number of key samples is C⋅Nk, enhancing the cohesion of positive samples within clusters.

We use the obtained pseudo-labels ykey to constrain the model’s results, i.e.,

LBCE(ykey,y^)=−1C⋅Nk∑i=1C⋅Nk(yikeylog(y^i)+(1−yikey)log(1−y^i))(18)

Here, ykey is the label of the key sample, and y^ is the model’s clustering result.

In summary, the overall loss calculation for ECN-MF is as follows:

L=αLMSE+βLKL+LBCE(19)

Here, α and β are hyperparameters.

The detailed learning procedure of ECN-MF is shown in Algorithm 1.

4  Experiments

4.1 Dataset

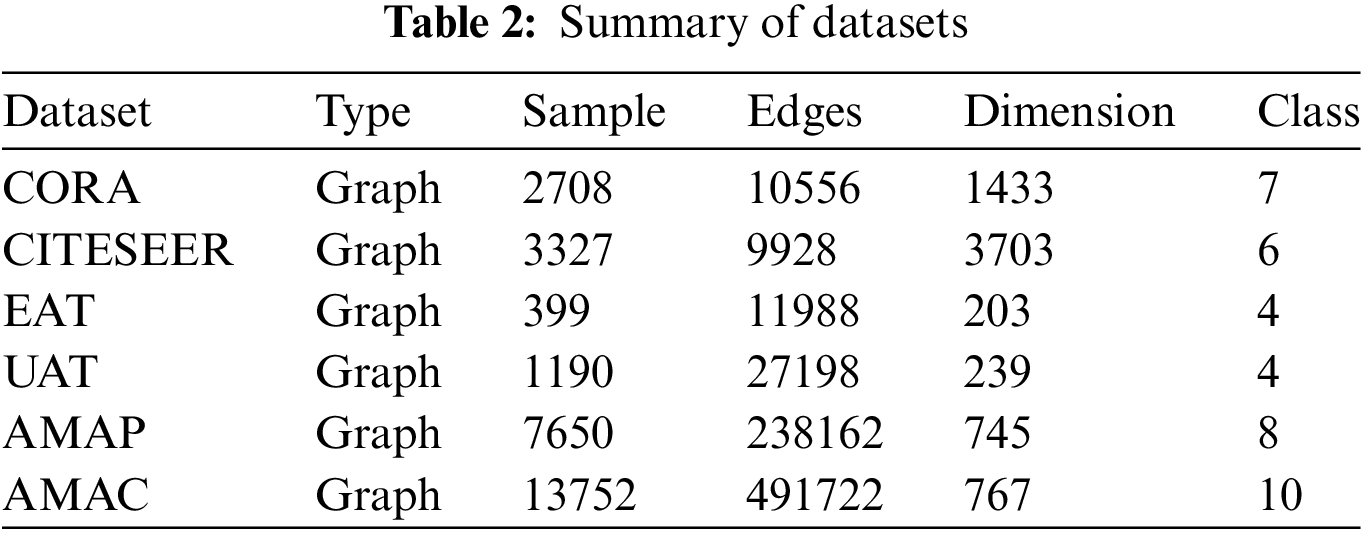
We proposed ECN-MF, which was evaluated on six datasets, including CORA [12] CITESEER [12], European Air Traffic (EAT) [30], United States Air Traffic (UAT) [30], Amazon Photo (AMAP), and Amazon Computer (AMAC). Table 2 provides a brief description of these datasets.

4.2 Experiment Setup

All experimental results were obtained on a high-performance server equipped with an NVIDIA 3090 GPU, 64 GB RAM, and the PyTorch deep learning platform.

4.2.1 Training Procedure

Our network is trained by minimizing the loss in Eq. (19) using the Adam optimizer for 1000 iterations until convergence. After optimization, we directly apply Eqs. (13) and (14) to cluster the node embeddings of the two views and report the final convergence results for four metrics. Following all compared methods and to mitigate the adverse effects of randomness, we repeat the experiments 10 times and report the averages along with the corresponding standard deviations.

4.2.2 Parameter Settings

For the sake of fairness, regarding MCGC [14], we only executed their source code on the graph datasets listed in Table 2. For other baselines, we reproduced the results by adopting the source code with the original settings. In our proposed method, the learning rate of the optimizer is set to 1e-4 for CORA/CITESEER/EAT/AMAP/AMAC and 1e-3 for UAT. The rank r of the attribute matrix is set to 40 for CORA, 50 for CITESEER/EAT, 95 for UAT, 20 for AMAP, and 70 for AMAC. Our encoder consists of two layers of linear MLPs, with dimensions set to 900 for CITESEER, 600 for CORA/EAT/UAT/AMAC, and 800 for AMAP.

4.2.3 Metrics

To validate the superiority of our ECN-MF compared to the baselines, we employed four widely used metrics to evaluate clustering performance, namely Accuracy (ACC), Normalized Mutual Information (NMI), Average Rand Index (ARI), and macro F1-score (F1) [31–33].

4.3 Performance Comparison

To demonstrate the superiority of our proposed ECN-MF, we compared ECN-MF with 13 base- lines. Specifically, a classification method, graphMAE2 [34], is considered. Five deep clustering methods, including AE [35], DEC [36] SSGC [37], SDCN [5], and SAGSC [38], utilize autoencoders for node encoding, followed by clustering on the learned embeddings. Two hard sample mining methods, GDCL [39], and ProGCL [40], are employed. Additionally, five deep graph clustering methods for comparison: MCGC [14], MVGRL [13], AFGRL [27], AutoSSL [41] and SCDGN [42], are incorporated. These methods are designed with contrastive strategies to enhance the discriminative capability of samples.

Table 3 reports the clustering performance of all compared methods on six benchmarks. From these results, we can derive four key observations: 1) Our ECN-MF outperforms other deep clustering methods, attributed to the benefits of contrastive learning in implicitly capturing supervisory information. 2) Compared to contrastive methods, our approach demonstrates superior performance, leveraging an information-enhanced clustering guidance module to better preserve the original data information in the embedded data. It ensures better retention of information and improves the discriminative capability of sample pairs by bringing samples from the same cluster closer and pushing away those from different clusters. 3) Our method achieves the best performance on CITESEER, showcasing the effectiveness of utilizing Singular Value Decomposition to capture latent important information of samples, particularly advantageous in handling sparse matrices. 4) Favorable results on AMAP and AMAC highlight the effectiveness of our batched low-rank singular value decomposition algorithm in handling large datasets. In summary, our method outperforms most others on six datasets with four metrics, validating the effectiveness of our proposed approach in addressing unreasonable data preprocessing and handling positive and negative sample pairs.

4.4 Time Complexity Analysis

Firstly, we perform Singular Value Decomposition on attributes, and the time complexity of calculating the low-rank process to obtain the reconstructed attribute Xr in Fig. 2 is O(batch×BD×r), where r is the rank size, B is the batch size, and D is the dimension. Subsequently, during the training phase, we employ a two-layer residual graph convolutional neural network (GCN) model. The time complexity for computing the two views is O(2NDd+4Ndd), where d is the dimension of the graph convolutional neural network, N is the number of samples, and D is the dimension of the original samples. The time complexity for calculating the mean square error loss function is O(Nd), and N is the number of samples. The time complexity for high confidence selection is O(NK), where K is the number of clusters, and N is the number of samples. The time complexity for computing the target distribution is O(NK), where N is the number of samples. The time complexity for the KL divergence loss function is O(NK), and the time complexity for the cross-entropy loss function is O(NK), where N is the number of samples. Therefore, the overall time complexity of our algorithm is O(batch×BDr+NDd+Ndd+NK+Nd).

4.5 Ablation Studies

In this section, we first experimentally validate the effectiveness of our proposed data augmentation method and periodic update strategy, as shown in Table 4. For simplicity, we denote the Batch low-rank Singular Value Decomposition as B and the periodic update as P. Note that in order to replace the B operation, we use a mask to generate different views of the same node, with a mask rate of 0.5. “(w/o)B & P” represents not using the batch low-rank Singular Value Decomposition operation and periodic update, while B + P indicates the usage of both. Table 4 displays the convergence results after running 1000 epochs. Based on the observed results, we conclude that the performance would degrade without B and P, indicating that these two strategies contribute significantly to the performance improvement.

In Fig. 3, we visualize the accuracy throughout the entire training process until convergence using a line chart. The graph demonstrates that our model exhibits robust performance. Overall, the experimental results validate the effectiveness of B and P.

Figure 3: Accuracy analysis of the proposed batched low-rank Singular Value Decomposition (B) and periodic update (P) on the five datasets is presented. The red line represents the use of batched low-rank Singular Value Decomposition operation and periodic updates, while the blue line represents the absence of batched low-rank Singular Value Decomposition operation and periodic updates. This comparative experiment demonstrates the effectiveness of our proposed method

4.6 Hyperparameter Analysis

In this section, we will analyze the hyperparameters r, α, and β to demonstrate their impact on the dataset. For the rank r, we set the range of values from 10 to 100, and for α and β, we set the range of values from 0.1 to 1.

4.6.1 Analysis of Hyperparameter r

Fig. 4 depicts the performance variation of ECN-MF across the range of r from 10 to 100. Key observations include: 1) Appropriately setting the hyperparameter r can effectively enhance clustering performance. Without adjusting other data settings and only modifying the rank, the model achieves the highest accuracy of 73.13% on CITESEER, 73.61% on CORA, 54.39% on EAT, and 52.94% on UAT. 2) The performance of the hyperparameter r remains relatively stable over a wide range, particularly excelling on sparse datasets such as CITESEER and UAT. 3) Examining the trend in average accuracy, we observe fluctuations and declines in clustering accuracy as the rank increases, particularly on datasets like CORA and EAT. This fluctuation is attributed to the diverse characteristics of the datasets; as the rank increases, the low-rank operation might extract more low-correlation information. 4) ECN-MF requires setting an appropriate rank based on the specific features of the dataset. Nonetheless, the experimental results indicate that the range of rank values can be relatively small, reducing the model’s time complexity even with a smaller rank.

Figure 4: The trend chart of clustering accuracy with varying r on four datasets demonstrates that appropriately setting a low rank reduces the model’s time complexity while effectively enhancing clustering performance

4.6.2 Analysis of Hyperparameters α and β

Fig. 5 illustrates the variation in clustering performance of ECN-MF on the CITESEER dataset across the range of α and β from 0.1 to 1. When modifying only α without adjusting the other parameters, the model achieves a maximum accuracy of 72.25% on CITESEER. Similarly, when modifying only β without adjusting the other parameters, the model achieves a maximum accuracy of 72.22% on CITESEER. It can be observed from the graph that our model is not sensitive to the values of α and β, and both can yield good results.

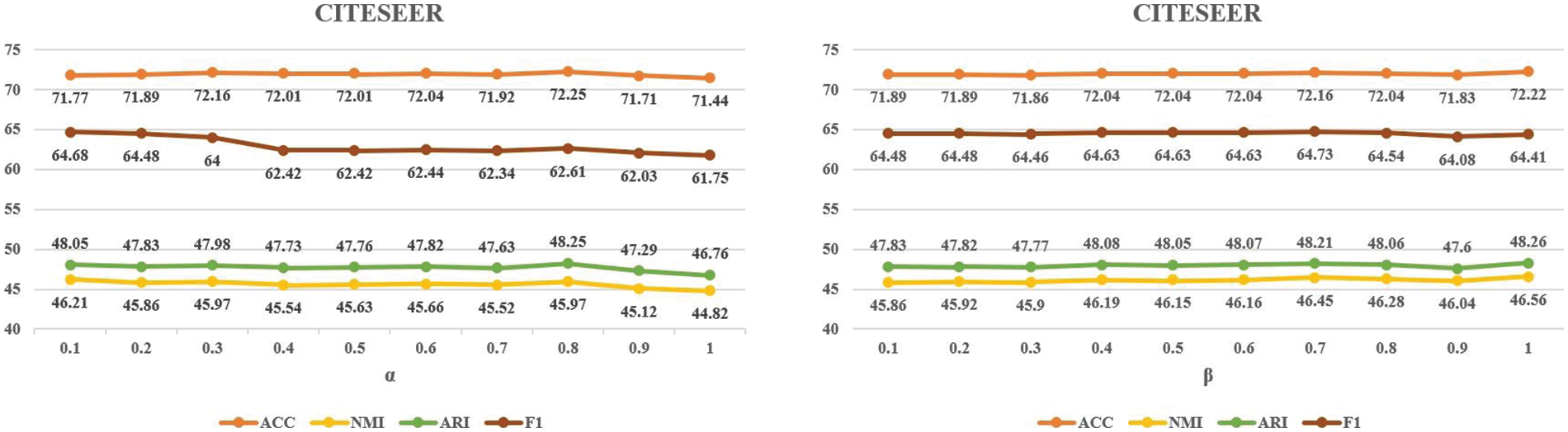
Figure 5: The trend chart of clustering accuracy with varying α and β on the CITESEER dataset, where the horizontal axis represents the values of α and β, and the vertical axis represents the values of the corresponding four evaluation metrics

4.7 Visualization Analysis

To visually showcase the superiority of ECN-MF, we employ the t-SNE algorithm (Maaten and Hinton 2008) to visualize the distribution of the learned clustering embeddings Z in a two-dimensional space. As shown in Fig. 6, ECN-MF can better reveal the intrinsic clustering structure among the data.

Figure 6: 2D visualization of the five datasets. The first row corresponds to the original data, while the second row corresponds to the distribution of ECN-MF. The visualization of partial samples reflects the effectiveness of our method

5  Conclusion

This paper introduces an Efficient Clustering Network based on Matrix Factorization (ECN-MF) to alleviate the negative impact of inappropriate data augmentation and enhance the quality of positive samples. By simplifying the network structure, introducing novel data augmentation methods, and designing a mutual information-enhanced clustering guidance module, ECN-MF improves its capability to handle sparse and large datasets. It brings samples from the same cluster closer while pushing samples from different clusters apart. The results of this study demonstrate the effectiveness and superiority of ECN-MF in addressing the challenges of preprocessing deep graph clustering tasks and handling positive and negative sample pairs. The paper uses hyperparameters to define the rank of the Singular Value Decomposition without special treatment of hard samples. In the future, we hope to explore new avenues of research, including: 1) employing adaptive rank selection for data, accommodating a broader range of datasets; 2) focusing more on challenging samples to enhance data mining and processing capabilities; 3) optimizing loss functions tailored for Singular Value Decomposition and challenging samples to improve clustering performance.

Acknowledgement: The authors would like to acknowledge the valuable feedback provided by the reviewers.

Funding Statement: This work was supported by the Key Research and Development Program of Hainan Province (Grant Nos. ZDYF2023GXJS163, ZDYF2024GXJS014), National Natural Science Foundation of China (NSFC) (Grant Nos. 62162022, 62162024), the Major Science and Technology Project of Hainan Province (Grant No. ZDKJ2020012), Hainan Provincial Natural Science Foundation of China (Grant No. 620MS021), Youth Foundation Project of Hainan Natural Science Foundation (621QN211), Innovative Research Project for Graduate Students in Hainan Province (Grant Nos. Qhys2023-96, Qhys2023-95).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: J. Li; analysis and interpretation of results: J. Li, F. Zeng; draft manuscript preparation: J. Cheng, J. Li, F. Zeng; data collection: Z. Tao, Y. Yang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: After the publication of the paper, the code will be made public on the author’s GitHub.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Berahmand, M. Mohammadi, R. Sheikhpour, Y. Li, and Y. Xu, “WSNMF: Weighted symmetric nonnegative matrix factorization for attributed graph clustering,” Neurocomputing, vol. 566, no. 2, pp. 127041, 2024. doi: 10.1016/j.neucom.2023.127041. [Google Scholar] [CrossRef]

2. K. Berahmand, Y. Li, and Y. Xu, “A deep semi-supervised community detection based on point-wise mutual information,” IEEE Trans. Comput. Soc. Syst., pp. 1–13, 2023. [Google Scholar]

3. E. Pan and Z. Kang, “Multi-view contrastive graph clustering,” Adv. Neural Inf. Process Syst., vol. 34, pp. 2148–2159, 2021. [Google Scholar]

4. C. Wang, S. Pan, R. Hu, G. D. Long, J. Jiang and C. Zhang, “Attributed graph clustering: A deep attentional embedding approach,” in Proc. Twenty-Eighth Int. Joint Conf. Artif. Intell., Macao, China, 2019, pp. 3670–3676. [Google Scholar]

5. D. Bo, X. Wang, C. Shi, M. Zhu, E. Lu and P. Cui, “Structural deep clustering network,” in Proc. web conf. 2020, Taipei, Taiwan, 2020, pp. 1400–1410. [Google Scholar]

6. W. Tu et al., “Deep fusion clustering network,” in Proc. AAAI Conf. Artif. Intell., Vancouver, Canada, 2021, vol. 35, pp. 9978–9987. doi: 10.1609/aaai.v35i11.17198. [Google Scholar] [CrossRef]

7. Z. Peng, H. Liu, Y. Jia, and J. Hou, “Attention-driven graph clustering network,” in Proc. 29th ACM Int. Conf. Multimed., Sichuan, China, 2021, pp. 935–943. [Google Scholar]

8. J. Park, M. Lee, H. J. Chang, K. Lee, and J. Y. Choi, “Symmetric graph convolutional autoencoder for unsupervised graph representation learning,” in Proc. IEEE/CVF Int. Conf. Comput. Vision, Paris, France, 2019, pp. 6519–6528. [Google Scholar]

9. J. Cheng, Q. Wang, Z. Tao, D. Xie, and Q. Gao, “Multi-view attribute graph convolution networks for clustering,” in Proc. Twenty-Ninth Int. Conf. Int. Joint Conf. Artif. Int., Yokohama, Japan, 2021, pp. 2973–2979. [Google Scholar]

10. S. Pan, R. Hu, S. Fung, G. Long, J. Jiang and C. Zhang, “Learning graph embedding with adversarial training methods,” IEEE Trans. Cybern., vol. 50, no. 6, pp. 2475–2487, 2019. doi: 10.1109/TCYB.2019.2932096. [Google Scholar] [PubMed] [CrossRef]

11. Z. Tao, H. Liu, J. Li, Z. Wang, and Y. Fu, “Adversarial graph embedding for ensemble clustering,” in Proc. 28th Int. Joint Conf. Artif. Intell., Macao, China, 2019, pp. 3562–3568. [Google Scholar]

12. G. Cui, J. Zhou, C. Yang, and Z. Liu, “Adaptive graph encoder for attributed graph embedding,” in Proc. 26th ACM SIGKDD Int. Conf. Knowl. Discov. Data Min., California, USA, 2020, pp. 976–985. [Google Scholar]

13. K. Hassani and A. H. Khasahmadi, “Contrastive multi-view representation learning on graphs,” in Int. Conf. Mach. Learn., Vienna, Austria, 2020, pp. 4116–4126. [Google Scholar]

14. W. Xia, S. Wang, M. Yang, Q. Gao, J. Han and X. Gao, “Multi-view graph embedding clustering network: Joint self-supervision and block diagonal representation,” Neural Netw., vol. 145, no. 11, pp. 1–9, 2022. doi: 10.1016/j.neunet.2021.10.006. [Google Scholar] [PubMed] [CrossRef]

15. Y. Liu et al., “Deep graph clustering via dual correlation reduction,” in Proc. AAAI Con. Artif. Intell., Vancouver, Canada, 2022, vol. 36, pp. 7603–7611. [Google Scholar]

16. L. Liu, Z. Kang, J. Ruan, and X. He, “Multilayer graph contrastive clustering network,” Inf. Sci., vol. 613, pp. 256–267, 2022. doi: 10.1016/j.ins.2022.09.042. [Google Scholar] [CrossRef]

17. Y. Yang and H. Wang, “Multi-view clustering: A survey, big data mining and analytics,” Big Data Min. Anal., vol. 1, no. 2, pp. 83–107, 2018. [Google Scholar]

18. X. Cai, C. Huang, L. Xia, and X. Ren, “LightGCL: Simple yet effective graph contrastive learning for recommendation,” in Eleventh Int. Conf. Learn. Rep., 2022, pp. 1–15. [Google Scholar]

19. G. A. Khan, J. Hu, T. Li, B. Diallo, and H. Wang, “Multi-view data clustering via non-negative matrix factorization with manifold regularization,” Int. J. Mach. Learn. Cybern., vol. 13, no. 3, pp. 1–13, 2022. doi: 10.1007/s13042-021-01307-7. [Google Scholar] [CrossRef]

20. T. Chen, S. Kornblith, M. Norouzi, and G. Hinton, “A simple framework for contrastive learning of visual representations,” in Int. Conf. Mach. Learn., Vienna, Austria, 2020, pp. 1597–1607. [Google Scholar]

21. J. Zbontar, L. Jing, I. Misra, Y. LeCun, and S. Deny, “Barlow twins: Self-supervised learning via redundancy reduction,” in Int. Conf. Mach. Learn., 2021, pp. 12310–12320. [Google Scholar]

22. H. Zhong et al., “Graph contrastive clustering,” in Proc. IEEE/CVF Int. Conf. Comput. Vis., 2021, pp. 9224–9233. [Google Scholar]

23. X. Yang, X. Hu, S. Zhou, X. Liu, and E. Zhu, “Interpolation-based contrastive learning for few-label semi-supervised learning,” IEEE Trans. Neural Netw. Learn. Syst., vol. 35, no. 2, pp. 2054–2065, 2022. doi: 10.1109/TNNLS.2022.3186512. [Google Scholar] [PubMed] [CrossRef]

24. Y. You, T. Chen, Y. Sui, T. Chen, Z. Wang and Y. Shen, “Graph contrastive learning with augmentations,” Adv. Neural Inf. Process Syst., vol. 33, pp. 5812–5823, 2020. [Google Scholar]

25. J. Xia, L. Wu, J. Chen, B. Hu, and S. Z. Li, “SimGRACE: A simple framework for graph contrastive learning without data augmentation,” in Proc. ACM Web Conf. 2022, Barcelona, Spain, 2022, pp. 1070–1079. [Google Scholar]

26. P. Bielak, T. Kajdanowicz, and N. V. Chawla, “Graph barlow twins: A self-supervised representation learning framework for graphs,” Knowl. Based Syst., vol. 256, no. 4, pp. 109631, 2022. doi: 10.1016/j.knosys.2022.109631. [Google Scholar] [CrossRef]

27. N. Lee, J. Lee, and C. Park, “Augmentation-free self-supervised learning on graphs,” Proc. AAAI Conf. Artif. Intell., vol. 36, no. 7, pp. 7372–7380, 2022. doi: 10.1609/aaai.v36i7.20700. [Google Scholar] [CrossRef]

28. L. Gong, S. Zhou, W. Tu, and X. Liu, “Attributed graph clustering with dual redundancy reduction,” in IJCAI, 2022, pp. 1–7. [Google Scholar]

29. V. Nair and G. E. Hinton, “Rectified linear units improve restricted boltzmann machines,” in Proc. 27th Int. Conf. Mach. Learn. (ICML-10), Haifa, Israel, 2010, pp. 807–814. [Google Scholar]

30. N. Mrabah, M. Bouguessa, M. F. Touati, and R. Ksantini, “Rethinking graph auto-encoder models for attributed graph clustering,” IEEE Trans. Knowl. Data Eng., pp. 1–31, 2022. [Google Scholar]

31. S. Zhou, et al., “Multiple kernel clustering with neighbor-kernel subspace segmentation,” IEEE Trans. Neural Netw. Learn. Syst., vol. 31, no. 4, pp. 1351–1362, 2019. doi: 10.1109/TNNLS.2019.2919900. [Google Scholar] [PubMed] [CrossRef]

32. S. Wang et al., “Fast parameter-free multi-view subspace clustering with consensus anchor guidance,” IEEE Trans. Image Process., vol. 31, no. 4, pp. 556–568, 2021. doi: 10.1109/TIP.2021.3131941. [Google Scholar] [PubMed] [CrossRef]

33. S. Wang, X. Liu, L. Liu, S. Zhou, and E. Zhu, “Late fusion multiple kernel clustering with proxy graph refinement,” IEEE Trans. Neural Netw. Learn. Syst., vol. 34, no. 8, pp. 4359–4370, 2021. [Google Scholar]

34. Z. Hou et al., “GraphMAE2: A decoding-enhanced masked self-supervised graph learner,” in Proc. ACM Web Conf. 2023, Austin, Texas, USA, 2023, pp. 737–746. [Google Scholar]

35. B. Yang, X. Fu, N. D. Sidiropoulos, and M. Hong, “Towards K-means-friendly spaces: Simultaneous deep learning and clustering,” in Int. Conf. Mach. Learn., Sydney, Australia, 2017, pp. 3861–3870. [Google Scholar]

36. J. Xie, R. Girshick, and A. Farhadi, “Unsupervised deep embedding for clustering analysis,” in Int. Conf. Mach. Learn., New York, USA, 2016, pp. 478–487. [Google Scholar]

37. H. Zhu and P. Koniusz, “Simple spectral graph convolution,” in Int. Conf. Learn. Rep., 2020, pp. 1–15. [Google Scholar]

38. C. Fettal, L. Labiod, and M. Nadif, “Scalable attributed-graph subspace clustering,” Proc. AAAI Conf. Artif. Intell., vol. 37, no. 6, pp. 1–9, 2023. doi: 10.1609/aaai.v37i6.25918. [Google Scholar] [CrossRef]

39. H. Zhao, X. Yang, Z. Wang, E. Yang, and C. Deng, “Graph debiased contrastive learning with joint representation clustering,” in Proc. Thirtieth Int. Joint Conf. Artif. Intell., 2021, pp. 3434–3440. [Google Scholar]

40. J. Xia, L. Wu, G. Wang, J. Chen, and S. Li, “ProGCL: Rethinking hard negative mining in graph contrastive learning,” in Int. Conf. Mach. Learn., Maryland, USA, 2022, pp. 24332–24346. [Google Scholar]

41. W. Jin, X. Liu, X. Zhao, Y. Ma, N. Shah and J. Tang, “Automated self-supervised learning for graphs,” in 10th Int. Conf. Learn. Rep. (ICLR 2022), 2022. [Google Scholar]

42. Y. Ma and K. Zhan, “Self-contrastive graph diffusion network,” in Proc. 31st ACM Int. Conf. Multimed., Ottawa, Canada, 2023, pp. 3857–3865. [Google Scholar]