Distributed Resource Allocation in Dispersed Computing Environment Based on UAV Track Inspection in Urban Rail Transit

Nomenclature

1  Introduction

Urban rail transit, serving as a crucial national infrastructure, holds significant significance in the economic development of a nation. As urban rail transit expands swiftly, the density of road networks has witnessed a continuous rise, safety problems along urban rail transit lines are particularly prominent. Therefore, timely troubleshooting of equipment failures and potential safety hazards along the line is becoming more and more important [1]. To guarantee the safety of urban rail transit operations, concerned urban rail transit entities perform regular inspections of various professions within the urban rail transit system. Many recent urban rail transit safety accidents can be attributed to disasters occurring within the operating environment. Therefore, it is of utmost importance to perform efficient inspections of the urban rail transit operating environment and accurately identify potential hazards and risks. This is critical for ensuring the safety of urban rail transit operations.

The current inspection techniques for urban rail transit primarily involve manual inspections and inspections conducted using rail inspection vehicles. Manual inspection refers to the routine inspection of equipment along the line by using visual inspection or simple inspection tools after professional training. The main feature of rail inspection vehicle inspection is to load the inspection equipment on the rail inspection vehicle and use image processing technology, ultrasonic detection, and laser detection technology to detect faults in key equipment and facilities such as urban rail transit works and power supply. Combining the working principles of the two inspection methods, it can be seen that the two generally have problems such as low efficiency, poor night inspection conditions, low inspection frequency, constraints of comprehensive maintenance skylights, narrow inspection areas, and poor automated analysis capabilities. Moreover, even if various types of inspections are used repeatedly, there are still many dead ends of inspection, and it is difficult to achieve full coverage of inspections. Unmanned Aerial Vehicles (UAVs) offer benefits such as excellent flight maneuverability, low individual flight expenses, extensive surveillance capabilities, and the ability to operate independently of train operations. Using UAVs for urban rail transit inspections can effectively solve the drawbacks of existing methods. It is especially suitable as a supplement and replacement for the current inspection methods of urban rail transit. At present, the UAV inspection method has been widely used in power equipment inspection, engineering survey, geological exploration, fire early warning, highway inspection, and bridge inspection, and has achieved ideal results [2–6], gradually becoming an irreplaceable inspection method. In particular, the power industry has begun to use UAV inspection methods and systems on a large scale. Inspection schemes, route planning, and inspection safety guarantees are becoming more and more mature. It is also necessary to use UAVs to inspect urban rail transit lines and operating environments, it will become a trend [7–9].

Simultaneously, as industrial technology advances rapidly, smart devices are steadily gaining increased computing and communication capabilities while also becoming smaller in size. IoT devices have seamlessly integrated into our daily lives, forming an essential component of our infrastructure [10,11]. However, due to the geographical distribution of equipment (i.e., UAV) is too scattered, computing resources have not been fully utilized. The researchers propose to combine the scattered resources through the network to build a scalable, secure, and robust new system driven by global computing tasks [12]. Nevertheless, the efficient management of extensive computing tasks and real-time monitoring of smart devices entail significant demands on computing paradigms, leading to the emergence of the Dispersed Computing (DCOMP) paradigm [13]. The DCOMP paradigm, as a novel architectural approach, was initially devised to address challenges pertaining to the heterogeneous geographical distribution, collaborative computation, and communication between diverse devices. This is achieved by introducing a dispersed computation layer that serves as a task execution agent, strategically embedded between each network node’s application and resource layers. The primary objectives are to optimize overall performance and network efficiency, as well as enhance the reliability of computing and communication processes [14]. With further research, dispersed computing is defined as connecting devices with general computing and communication properties into a network organism in a wide area, so as to achieve the purpose of device interconnection and capability interoperability. According to the specific requirements of users and applications, computing tasks can automatically access multiple devices with the environment and idle resources from the network, complete the computing tasks in a cooperative way among nodes, and return the computing results [15]. The dispersed computing paradigm, as a new form of dispersed computing, does not aim to replace the existing traditional computing architectures such as cloud computing, mobile cloud computing, fog computing, and mobile edge computing. Instead, it serves as an augmentation and natural progression of these traditional computing paradigms. Its primary objective is to address the evolving requirements of users in the Internet of Everything (IoE) domain, ensuring the fulfillment of increasingly demanding computing quality standards.

The primary contributions of this paper can be summarized as follows:

1) This paper explores a distributed computing environment that utilizes UAV track inspection, comprising multiple mobile users (MUs) and networked computation points (NCPs). One dispersed computing platform exists between the Mus and the NCPs, to achieve task allocation and resource management.

2) The NCPs offer computational resources to mobile users (MUs) based on task requirements, ensuring the timely completion of tasks on the dispersed computing platform. The allocation of computing resources is presented as a binary optimization problem, aiming to minimize energy consumption during task execution.

3) To minimize energy consumption across all the networked computation points (NCPs) in the investigated dispersed computing environment, a Markov decision process (MDP) model is employed. Additionally, a resource allocation approach based on Double Q Network (DDQN) is introduced to determine the optimal allocation strategies.

The paper is presented in the form of the following: Section 2 provides the related works. Section 3 gives the system model. The solutions for the proposed resource allocation problem are provided in Section 4. Numerical simulations are provided in Section 5. Finally, the work in Section 6 is concluded.

2  Related Works

2.1 Resource Allocation for Edge Computing

As commonly understood, the cloud computing paradigm [16] often faces the challenge of geographical distance between a multitude of terminal devices and the centralized cloud center, and cloud computing also consumes substantial bandwidth from the backbone network, leading to network congestion and elevated bandwidth expenses. Mobile cloud computing, as an inherent progression and enhancement of cloud computing, addresses these challenges, but it still encounters challenges related to network congestion and significant computational expenses [17]. Subsequently, fog computing [18–20] was introduced. Compared with mobile cloud computing, fog computing is closer to the user than mobile cloud computing. It can not only provide the resources needed for computing but also provide some other services, such as image recognition. It also faces a lot of security and privacy issues [21,22]. Mobile edge computing (MEC) [23,24] bears a resemblance to fog computing, wherein a versatile computing server is deployed at the network edge, and tasks are likewise transmitted to nearby high-performance servers via wireless links. The difference is that MEC supports user location awareness, and MEC servers belong to mobile operators and are generally deployed on the base station side [25], while fog computing nodes are generally managed by individuals. From the perspective of privacy protection, MEC is relatively more reliable. From the design of MEC paradigm, if the terminal nodes and edge nodes in MEC are not under load for a long time, the computing and communication resources will be idle. Currently, resource allocation has grown into a crucial branch of edge computing.

Liu et al. [26] explored the application of non-orthogonal multiple access (NOMA) technologies to enhance connectivity in IoT networks, enabling energy-efficient mobile edge computing (MEC). Additionally, Yang et al. [27] presented a method of resource allocation in multi-access MEC systems that are designed to minimize mobile device energy consumption while meeting competing deadlines. The scenarios consider a scenario in which several mobile devices with different computing capabilities and energy restrictions offload their MEC tasks to a nearby server. Moreover, Chen et al. [28] analyzed the coordination optimization of computation allocation and resource allocation in edge computing, and proposed a new method: a time attention-deterministic strategy gradient (TADPG) for solving the problem. Zhu et al. [29] presented a synthesis of hybrid NOMA and MEC techniques in their work. They solved the optimization problem with respect to power and time allocation for each group and alleviated latency and energy consumption. The method utilizes a matching algorithm for optimizing power and time allocation to cut down the complexity of the method further. Otherwise, Ali et al. [30] posed the Pow Mig Expand algorithm, based on a comprehensive utility function, which allocates the requests received to the optimal server. In addition, they also introduced the Energy Efficient Intelligent Splitter (EESA) algorithm, which utilizes deep learning to allocate the required energy savings to the most suitable servers. Proposed methods are all using fixed infrastructure and lack scalability, making them unable to flexibly respond to sudden traffic surges or damage caused by disasters or other factors. In order to improve the flexibility of computing networks, recent attention has been focused on mobile device-assisted work. Sun et al. presented a novel system architecture in their work [31] that utilizes unmanned aerial vehicles (UAVs) and multiple Industrial Internet of Things (IIoT) nodes. The proposed architecture enables the direct transmission of resources collected by IoT nodes to the UAV for processing. The main goal of this system is to optimize response time for forest fire monitoring considering some constraints between nodes, i.e., minimize the maximum time. The system proposes a Markov random field-based decomposition (MRF) method and a learning-based collaborative particle swarm optimization (LCPSO) scheme to achieve the optimal allocation. These techniques work together to allocate the resources optimally in the UAV system, facilitating efficient forest fire monitoring. In their work, Chai et al. [32] considered users with task computing needs who may choose to perform edge computing offloading, local computing, or device-to-device offloading. The authors proposed a joint optimization method which wants to minimize costs by dividing the task into small data segments and enabling various computational modes to execute them simultaneously. On a similar note, Wang et al. [33] utilized MEC and D2D communication to facilitate offloading from the core network. They studied the optimal resource allocation strategy in the ICWN (Cognitive Wireless Network Internet) scenario. However, it is worth noting that the assistive technology may involve additional costs. In addition, the above research overlooked the potential untapped resources within the network and the achievement of utilizing neighboring computing nodes. If these factors are considered, it may enhance the efficiency and performance of the system.

2.2 Resource Allocation for Dispersed Computing

Following the emergence of MEC, DCOMP was introduced as a complementary solution, aiming to address this gap and harness the untapped computing resources effectively. The objective is to establish a dispersed and distributed network ecosystem with heterogeneous resources, maximizing the utilization of all available resources within the network and delivering users with enhanced efficiency and reliability in computing services. Dispersed computing possesses distinct advantages compared to other paradigms. The objectives of conventional computing paradigms involve task offloading to either the cloud, which possesses greater computing power, or edge nodes with shorter communication distances. This is done to minimize transmission delays and energy consumption. However, central nodes like fog computing nodes, MEC nodes, or service gateways in cloud computing exhibit limitations [34,35].

With a massive increase in users and tasks, the central node fails, services will be interrupted and tasks will be lost, resulting in a poor user experience. Dispersed computing is an architecture for dispersed resources. In this architecture, nodes with computing power are abstracted as general computing points, and the DCOMP intermediate layer is responsible for security authentication, privacy protection, task decision-making and data routing transmission between nodes [36], and there is no centralized scheduling center. In addition, in a dispersed computing environment, the joining and leaving of nodes are very efficient and transparent. Simultaneously, it also addresses the drawbacks of the cloud computing paradigm, including high delay and high cost, while resolving the limitations of edge computing, such as the limited coverage area of edge nodes and the inability of terminal nodes to collaborate directly.

Indeed, in contrast to mobile edge computing, there has been growing attention to resource allocation in dispersed computing. Several studies [37–39] have emerged in this area, taking into account the presence of idle devices and limited resources within the network. A noteworthy example is the work of Rahimzadeh et al. [37], who introduced SPARCLE. SPARCLE is a scheduling scheme for dispersed computing systems and is designed especially for dispersed computing environments which are provided with a network-aware algorithm for allocating tasks and resources for polynomial time flow processes. The proposed schemes are very useful to optimize resources and improve overall system performance. The collaborative management model for the task resource in a dispersed computing system is proposed by Zhou et al. [38] and focuses on the quantification of dynamic dependencies between the resources occupied in a dispersed computing system and the consumed resources of task requests. This can better understand the resource utilization modes and achieve effective resource allocation. A kind of intelligent controlling mechanism to solve the problem of the overburdened load is brought into the collaborative management model of task resources. These intelligent control technologies aim to dynamically allocate and manage resources to avoid overload and ensure system stability. Through intelligent control, this model can optimize resource allocation and improve the whole performance and reliability of dispersed computing systems. The load-balancing scheduling algorithms and the prioritization-aware resource allocation strategies of the open-source dispersed computing system are studied by Paulos et al. [39]. These strategies are very important and have been integrated into a core feature in middleware. However, the research on resource allocation in dispersed environments is relatively limited to the field of dispersed computing. It is necessary to conduct further exploration and investigation to deepen our understanding of resource allocation in this situation. In addition, considering the limited energy resources of devices and the need to optimize energy consumption, energy cost has become a crucial indicator, especially for mobile devices. Therefore, when designing resource allocation strategies in a dispersed computing environment, special attention should be paid to addressing energy efficiency.

3  System Model and Problem Formulation

In this section, we describe the application scenarios and system models in dispersed computing environments with the goal of minimizing the energy consumption of networked computing nodes.

3.1 Scenario Description

Considering a dispersed computing environment including one dispersed computing platform, N tasks published on the platform by L mobile users, and M networked computation points (NCPs) that can complete the tasks published on the platform using their computing abilities. The platform can publish and assign tasks for the mobile users, and can schedule computing resources of NCPs for various tasks. In the dispersed computing environment, the set of mobile users is denoted by U={u1,u2,…,uL}. Each mobile user publishes the tasks in the platform and requires the computing resources from the NCPs. Assuming the tasks published by user should be completed within a time duration T. In the researched dispersed computing environment, the position of mobile users is assumed to be unchanged with in the time duration for tasks to be completed.

The set of NCPs is given by P={p1,p2,…,pM}, which can provide computing abilities to the tasks in the platform. For each NCP, the available computing resource of NCP j for j=1,2,…,M that can be allocated for the tasks is denoted by cj. By using these computing resources, the NCPs can complete the tasks published on the platform by the mobile users.

The set of tasks published on the platform is denoted by V={v1,v2,…,vN}, which is running on the NCPs. For each computing task vi with i=1,2,…,N, the resources scheduled by the platform is denoted by ri, for i=1,2,…,N. Generally, the tasks wk published by user k will be uniformly treated as the related tasks in the set V={v1,v2,…,vN}. The maximum number of tasks that each mobile user can publish on the platform is given by δ, where 1≤δ≤N, and wk=∑i=1δvi.

Assuming ci,j to denote the computing resources of NCP pj allocated for the task vi. We design a binary variable bi,j to indicated whether the task vi is running on the NCP pj. If bi,j=1, the task vi is executed on NCP pj. If bi,j=0, the task vi is not executed on NCP pj. Then we have ci,j≥∑i=1Nbi,jci,j. In order to achieve load balancing among different NCPs, we assume that the maximum number of tasks that is computed on NCP pj is εj, where εj≥∑i=1Nbi,j. Meanwhile, the maximum number of NCPs working on the same task vi is assumed to be λi, and we have λi≥∑j=1Mbi,j.

3.2 System Model

In the researched dispersed computing environment, we assume all the tasks published by the mobile users should be completed only by the NCPs. The mobile users should publish the computation requirements on the dispersed computing platform. Once the requirements are answered, they should upload the related tasks to the NCPs and wait for the NCPs to complete the corresponding computing tasks. Therefore, for each mobile user, the whole-time duration can be divided into two parts using TDMA. The first part is to upload the computation tasks to the NCPs, where the second part is to complete the computation tasks by the NCPs. The diagram is given in the following figure.

Assuming the transmit power of mobile user is p, and the upload transmission is undertaken on the frequency band with channel bandwidth β. To avoid co-channel interference among different users, we assumed that the task could be uploaded onto the NCP using orthogonal frequency patterns by different users. Then the transmission time for the tasks upload can be written by [32]

τi=vi[βlog(1+pσ2)](1)

Once the tasks are upload to the NCPs, it will be computed by the NCPs. The NCPs should use the limited time to complete the tasks to ensure the real-time satisfaction. The limited time available for computation of task vi in the NCPs is T−τi. Assuming the workload of task vi is given by wi, and the related time for computing the tasks is wi/ci. In order to complete the tasks, the NCPs should contribute their computing abilities, which would bring energy consumption for task due to the control variable ci,j. Therefore, the total cost for computing the task vi in the NCPs can be given by

Ji=(T−τi)ciei=∑j=1M(T−τi)bi,jci,jei,(2)

where ei denotes the unit energy consumption of computation. The gross energy cost for the entire dispersed computing environment can be given:

J=∑i=1N∑j=1M(T−τi)bi,jci,jei.(3)

3.3 Problem Formulation

It follows that we aim at minimizing the consumption of a distributed computing environment and that the minimization problem can be drawn out mathematically as follows:

minbi,j∑i=1N∑j=1M(T−τi)bi,jci,jei,s.t.C1:∑i=1Nbi,jci,j≤cj,C2:∑i=1Nbi,j≤εj,C3:∑j=1Mbi,j≤λi(4)

To eliminate this problem (4) and solve it, the optimal solution to bi,j of the discrete offloading decision is found. In this way, the task offloading in inter-slot time is coordinated under a limited time constraint, and the total computational energy consumed is minimized for a network computing node. It is worth noting that bi,j is a binary variable which is the offloading decision variable and is why the network computing nodes can choose user tasks intelligently. With the increase of mobile users and computing tasks, traditional methods may not adapt to deal with complex scenarios with dynamic characteristics and make intelligent decisions. A method of solution for a certain problem based on reinforcement learning is explored.

4  Proposed Solutions

This paper uses the Markov Decision Process (MDP) model to calculate the optimization problem. The goal is to minimize the network computing nodes’ energy consumption in the dispersed computing environment. Firstly, reward functions, actions and the state within the MDP model are defined. Secondly, a method based on Double Deep Q Network (DDQN) is proposed. This approach effectively addresses the problem of dimensionality by learning the Q function.

4.1 Markov Decision Process Model

State space: The state in the MDP model represents the space of the dispersed computing paradigm. For available resources, on time slot t, the state is decided by ci,j−∑i=1Nbi,jci,j and λi−∑j=1Mbi,j in our proposed system, where the former is the residual available computing resource of network computing nodes and the latter is the maximum number of offloaded nodes. These two parameters are observed to maintain the constraints of computing and resource capacity of network computing nodes. Additionally, if it reaches the suitable state, it is important to consider the energy consumption state Etotali at each time slot t to determine. Therefore, the state vector is defined as (Etotali,cj−∑i=1Nbi,jci,j,λi−∑j=1Mbi,j) at the time node T.

Action: The objective is to select the best action by mapping the state space to the action space. In our proposed dispersed computing environment, agents are responsible for determining the resource allocation of users’ computing tasks in each time period.

Reward: The actions of each agent are motivated by rewards. In the dispersed computing system, the reward function is given as follows to minimize energy consumption. We believe that the best action is produced with the lowest task reward value.

4.2 Markov Decision Process

The MDP problem is effectively solved through dynamic programming or linear programming. However, when dealing with unknown and time-varying state transition probabilities and immediate rewards in discrete time steps, reinforcement learning methods become more suitable for tackling such problems. MDP is commonly used as the theoretical framework for reinforcement learning [40].

We approach the optimization problem by formulating it as an MDP. The agent interacts with the environment through iterative processes and adaptive learning to determine the optimal actions. The agent finds the current state at each time step t which is written as s(t) and chooses an appropriate action a(t) based on the policy π. The action space a is finite, it is the same for state space s. The policy π maps the current state to the corresponding action, providing guidance for decision-making under different states. Subsequently, the agent switches to its next condition s(t+1) based on a switch probability p which receives a reward R. Over the long term, the state value function V represents the cumulative discounted reward R of the agent in state s(t). It quantifies the long-term impact of the policy π in the current state and serves as a measure of the state-value pair.

Now, let us consider the state after executing action a(t) as s(t+1), where the transition probability from s(t) to s(t+1) is denoted as p. By employing the MDP model, the state value function is expressed using temporal differences through the Bellman equation [41]:

V(s(t))=Eπ[(∑t=0∞φRt)|s0=st]=Eπ[(R(st,at)+∑t=1∞φRt)|st=st+1]=R(st,at)+φ∑st+1p(st+1|st,at)Vπ(st+1)(5)

Building upon the aforementioned process, the agent strives to develop an optimal control strategy π that maximizes the expected cumulative discount reward at the current state. This essentially transforms the optimization problem into an optimal state function problem V, as depicted below [41]:

V(s(t))=maxπ[R(st,at)+φ∑st+1p(st+1|st,at)Vπ(st+1)]s.tC1−C3.(6)

Therefore, the optimal strategy is obtained by solving the above problems. The optimal action in state s(t) can be given as [41]

at∗=argmaxatVπ(st,at)(7)

4.3 Solution Based on DDQN

In practical scenarios, the curse of dimensionality often arises when dealing with high-dimensional states and action spaces. To mitigate this issue, this paper proposes a novel DRL algorithm that deviates from traditional Q-learning methods.

In the conventional implementation of a DQN, a single Q network is employed to evaluate actions and is similar to multiple action-value functions, which can be numerous. However, this approach may lead to significant errors and an overestimation of the action-value function, ultimately affecting the choice of the optimal strategy. To address this concern, we adopt the DDQN algorithm. The fundamental principle behind DDQN is to decouple action selection from evaluation by constructing distinct action-value functions.

By updating DNN’s parameters, the DDQN-based approach enhances the approximation of the optimal Q-values. In DDQN, the Q-value expression can be formulated by

Q(s,a)=Q(s,a,θ)(8)

In the DDQN framework, the primary neural network’s weight parameters are denoted as θ. Additionally, it will be discussed for a target network later.

Unlike the general DQN algorithm, the DDQN algorithm incorporates an experience replay buffer. The agent converts relevant experiences into memory tuples (st,at,Rt,s(t+1)) and stores them in the replay buffer at each time step t. The agent utilizes the stored experiences from the buffer which is to train the neural network. It randomly selects a small batch of experiences to fine-tune the neural network and adjust its parameters. This process allows DDQN to leverage randomly chosen previous experiences during each update. Several studies, such as those cited in [41,42], have demonstrated that experience replay improves training efficiency, reduces correlation between training data, and expedites the convergence of DDQN.

In the DDQN algorithm, a target Q-network is introduced. The target Q-network and the Q-network employ different neural network parameters although they have the same neural network structure. The temporal difference signals from the Q-network are received by the target Q-network, while the latter serves as an evaluator for the Q-function.

However, the target Q-network updates its weights periodically instead of continuously. This approach enhances stability and accelerates the learning process.

The agent randomly selects a small batch of sample D with size R from the experience replay buffer to remove temporal correlations in the training data. The loss function L is continuously minimized to approach the target value and improve the accuracy of Q-function approximation during each iteration, as shown below [34]:

L(θ)=E[R(st,at)+φQ(st+1,a∗;θ)−Q(st,at;θ)]2(9)

The structure process and training process of DDQN are illustrated in Fig. 1. The initialization phase involves setting the weights of the neural network and the experience replay buffer’s size. In DDQN, the Q-network and the target Q-network initially share the same weights, denoted as θ=θ′. Next, a neural network is employed to establish the relationship between its corresponding value function Q and each state-action pair. For further details, the decision maker needs to preprocess the allocation strategy of the distributed computing platform adequately.

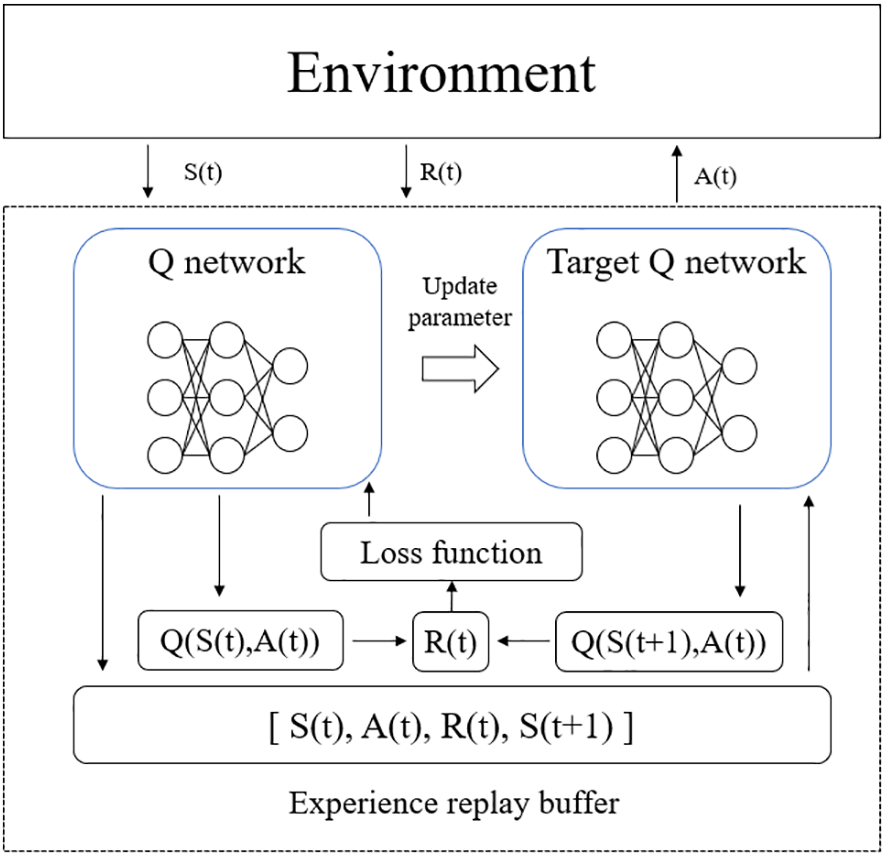
Figure 1: The training process of DDQN

During the training process of each episode, the agent first views the distributed computing platform’s state. Then, to choose the action a for execution, the ε-greedy algorithm is applied. With a probability of ε, the agent randomly selects an action. Otherwise, the state-action pair’s Q-value is estimated using the Q-network to select action a.

Next, the agent accepts the reward value R and the next status by executing action a. It constructs an experience tuple (s,a,R,s) and stores it. The Q-network randomly selects a small batch of samples from the replay buffer using an experience replay mechanism in the training process. Through minimizing the loss function θ, DDQN updates the network parameters. This involves updating the Q-network parameters using Stochastic Gradient Descent (SGD) and calculating the target Q-value. In Algorithm 1, the specific process is provided.

Then, the agent gets the reward value R and the next status by executing action a builds the experience tuple (s,a,R,s), and saves the experience tuple. The Q-network randomly selects small batch samples through an experience replay mechanism in view of the training process. Through minimizing the loss function θ, DDQN renews the network parameters, that is, the algorithm updates the Q-network parameters by taking the Stochastic Gradient Descent (SGD) method for the loss function θ after calculating the target Q-value. Finally, the specific implementation process is provided in Algorithm 1.

5  Numerical Simulations

5.1 Simulation Set

We consider the dispersed computing environment as a smaller area with multiple mobile users and three network computing nodes. We consider user devices that are not computationally capable or cannot meet the demand of computational tasks. Each user has a different size task. Here, we consider two cases: (i) each mobile user has only a single task. The size of tasks per user is randomly distributed in the range of 1–2.5 MB; (ii) each mobile user has multiple tasks. Each mobile user has multiple computing tasks of different types and sizes. The number of tasks per mobile user is randomly distributed in the span of 2–4, and the task’s size is distributed in 0.1–1 MB randomly. The user’s transfer rate is equal to 1 MB/s. In the approach of this paper, the experience replay buffer’s capacity is C = 200 and the selected small batch of samples’ capacity is U = 32. Set The learning rate parameter to lr = 0.01 and set the reward decay parameter to φ = 0.9. The energy consumption of users is decided by the task size of users, i.e., larger tasks consume more energy.

5.2 Performance Analysis

First, the convergence property of the resource allocation method based on DDQN is verified. Fig. 2 illustrates the convergence property of the DDQN-based method which is proposed with a total of 24 user tasks. For the DDQN-based resource allocation method the energy consumption of the system gradually drops while the number of training sets rises. In general, the DDQN-based method with multiple iterations of training is able to converge quickly to a relatively stable value.

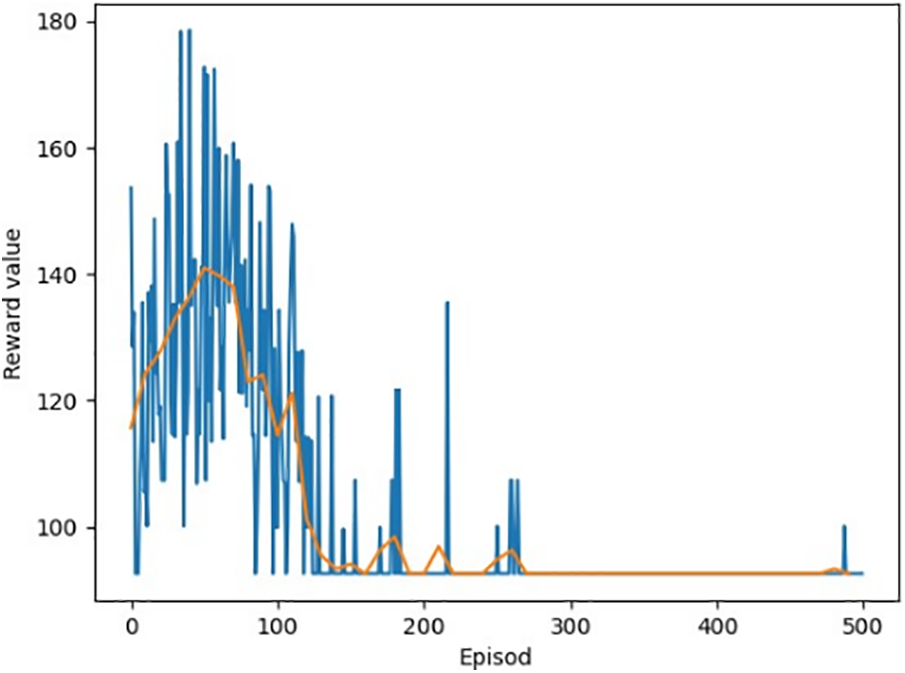
Figure 2: Convergence of the proposed DDQN-based method

5.2.1 One Task per User

Figs. 3–5 show the energy consumption, number of tasks computed, and resource consumption of each dispersed computing platform under different numbers of users, respectively. To be closer to the realistic scenario, each task is selected with a random size. Therefore, the task size is different for each user with the different number of users. It is evident from Fig. 4 that the method based on DDQN is capable of accomplishing tasks across various task quantities. The energy consumption of each network computing node can be observed in Fig. 3. The network computing node 2's energy consumption is low compared to other network computing nodes because of the constraint on the number of offloads of network computing node 2. It is evident from Fig. 5 that with the tasks’ number drop, the computational tasks will be gradually allocated to the nodes with more resources. Network computing node 3 has the most resources compared to the other two nodes and can accommodate the largest number of computational tasks.

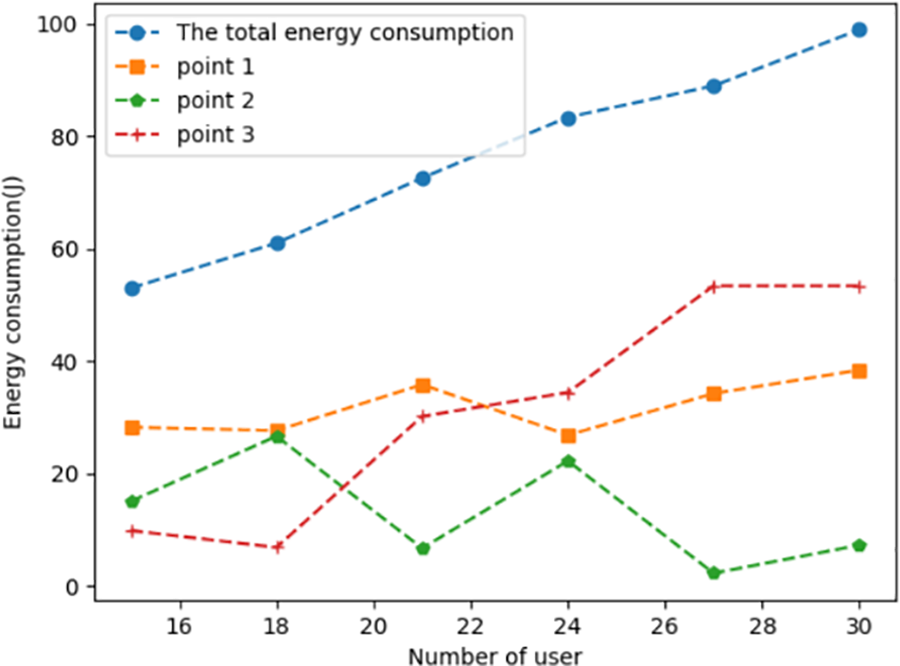
Figure 3: Task energy consumption under different task scales

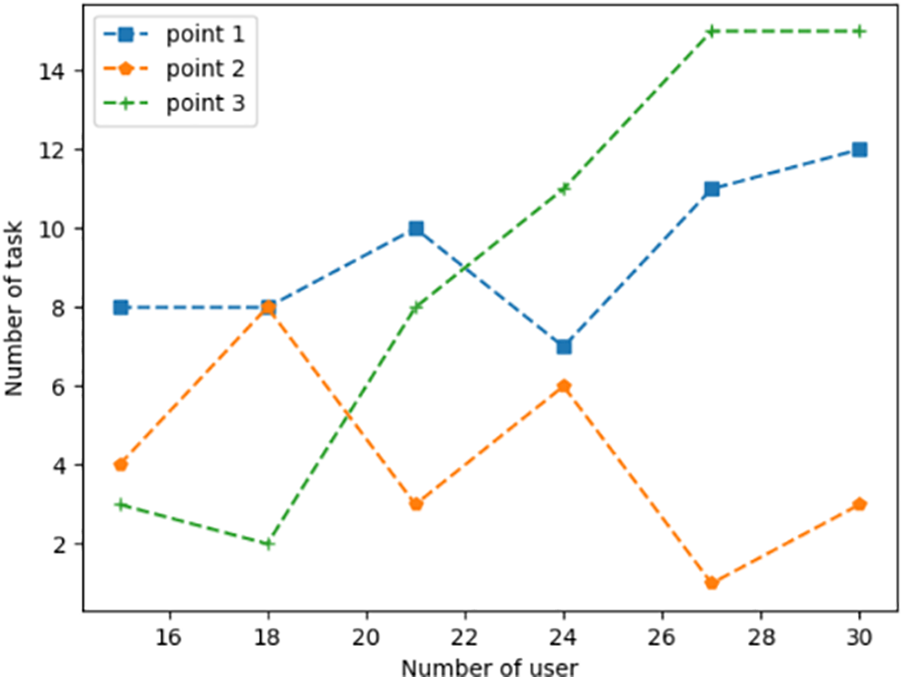
Figure 4: Task allocation under different task scales

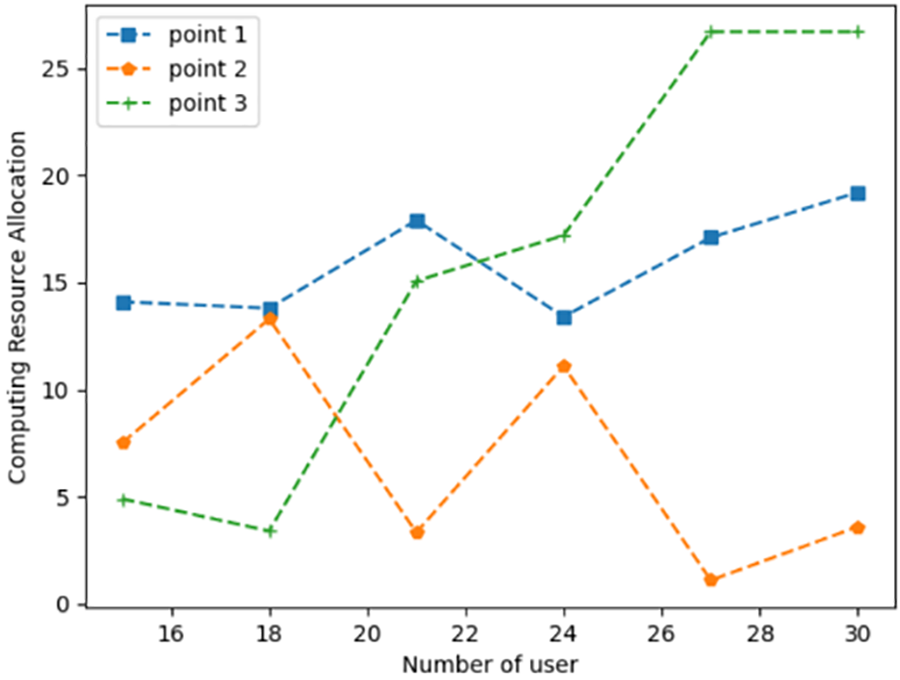
Figure 5: Computing resource consumption under different task scales

5.2.2 Multiple Tasks per User

Figs. 6–8 show that each user has a different number and size of tasks. Since different users have different numbers of tasks, the network nodes need to consider the service count constraint on the user tasks. The number of tasks varies at different numbers of users, i.e., the corresponding number of tasks is [23,29,32,42,46,55]. In Fig. 6, while the number of tasks offloaded rises, multiple network computing nodes are required to collaborate with each other to complete the user’s computing tasks. In Fig. 7, while the number of user tasks rises, task allocation is assigned to the node with more resources remaining to meet the user’s computational tasks. In Fig. 8, when there are fewer tasks, each node satisfies the task demand well. With the increasing number of tasks, the agent gives preference to the network computing nodes with abundant remaining resources.

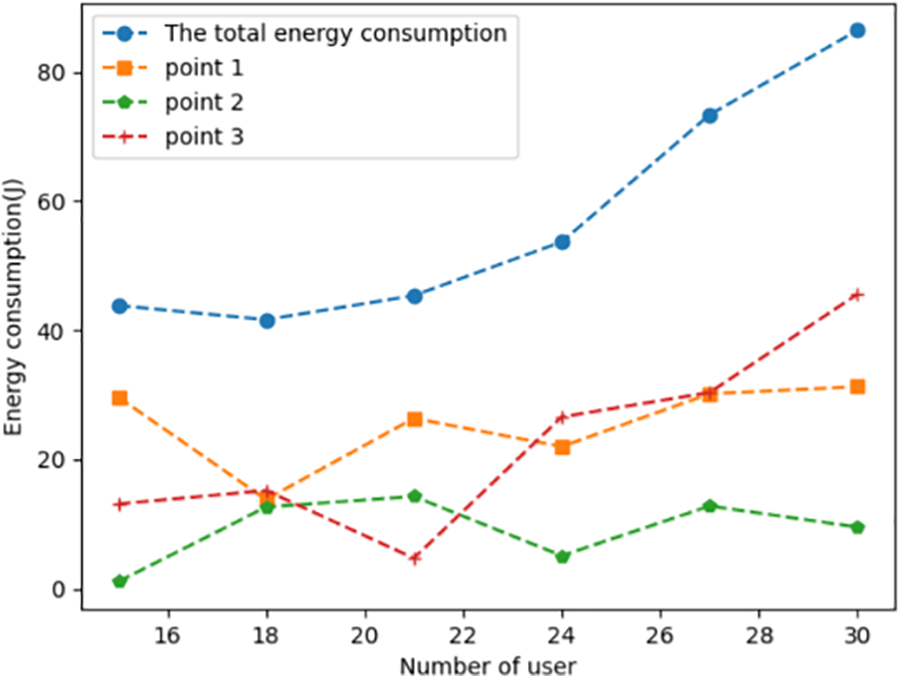
Figure 6: Task energy consumption under different task scales (multiple tasks)

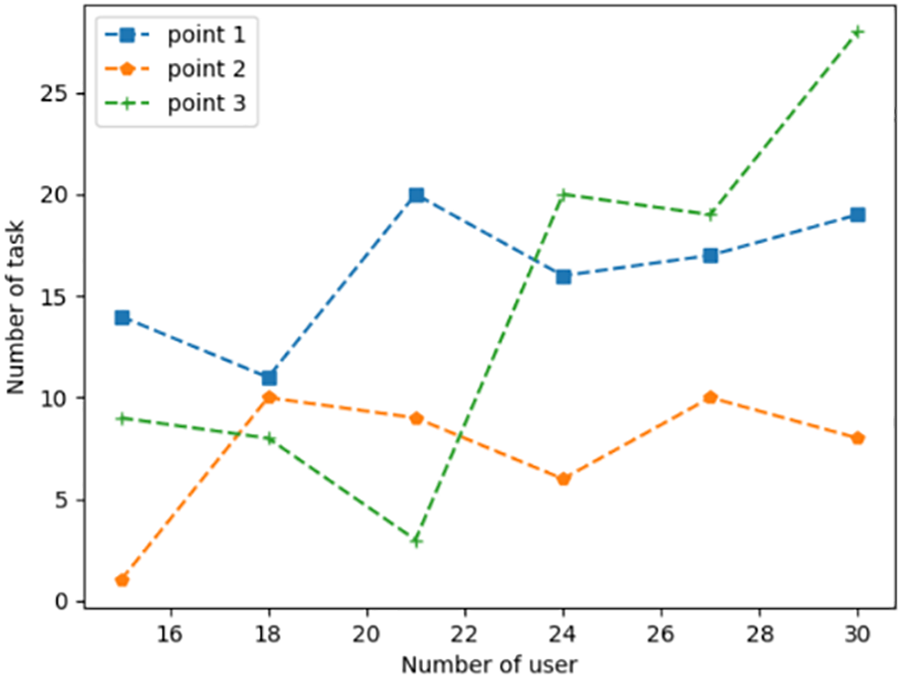
Figure 7: Task allocation under different task scales (multiple tasks)

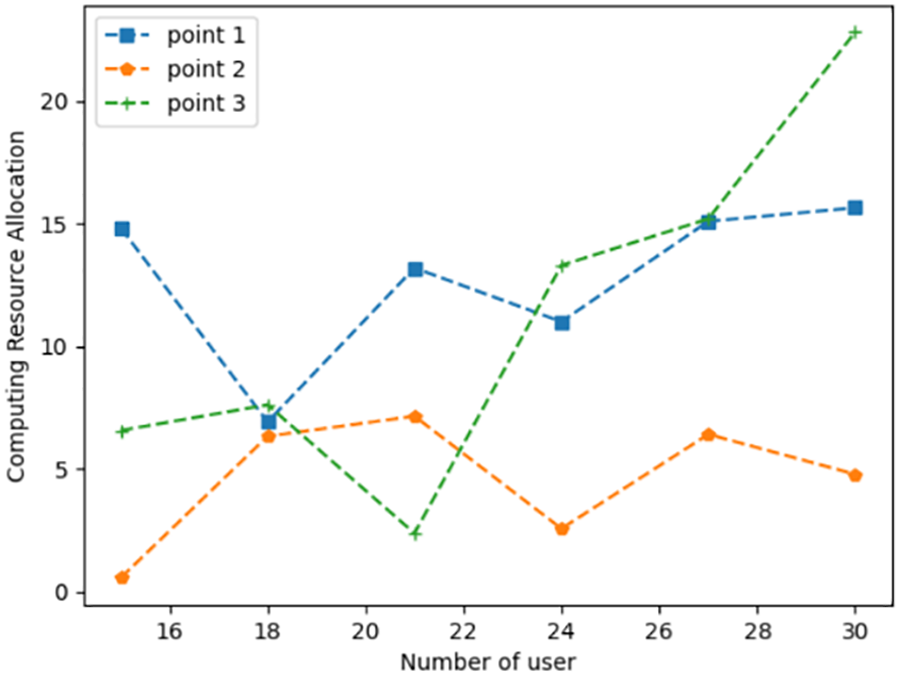
Figure 8: Consumption resource allocation under different task scales (multiple tasks)

In order to further analyze the advantages and disadvantages of the algorithms. We conducted comparison experiments with other algorithms, mainly including the offloading scheme based on random offloading strategy, and the offloading scheme based on dueling DQN (dueling DQN). In the random scheme, the user randomly selects NCPs that satisfy the offloading requirements as offloading nodes. In greedy scheme, the user selects the NCP with the richest computational resources as the offloading node. In dueling scheme, the user offloading policy is obtained based on dueling DQN algorithm. The results of the comparison experiments are shown in Fig. 9. We consider different transmission rates for each node, which ranges from [0.8, 1.2] Mb/s, and the CPU energy consumption per cycle is 2−10. As shown in Fig. 9, we can observe that the algorithm proposed in this paper is able to complete the computation of the task with lower total energy consumption.

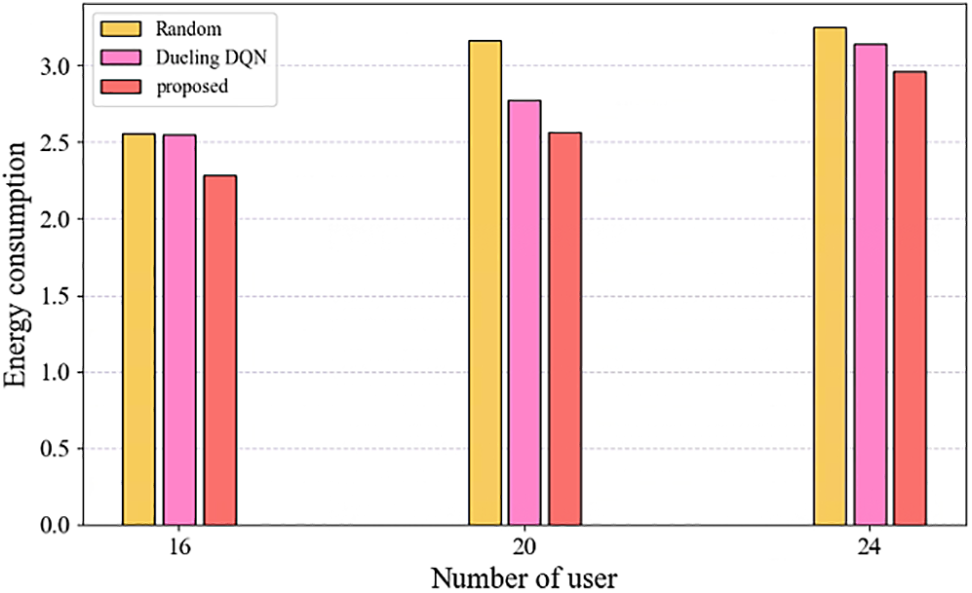
Figure 9: The total energy consumption for the three algorithms to complete the task computing

6  Conclusion

In this paper, we tackle the challenge of allocating resources for multiple users in a dispersed computing environment, where each user has distinct resource requirements and the system conditions vary over time. Our objective is to minimize energy consumption while considering both resource and computational constraints. To tackle this problem, we formulate it as an energy minimization problem with computational constraints and adopt an MDP model to capture the interplay between the dispersed computational resource allocation policy and the system environment. To obtain the optimal policy, we propose an approach based on DDQN. This approach utilizes the capabilities of deep neural networks to approximate optimal Q-values and inform resource allocation decisions. Additionally, we incorporate the experience replay mechanism to mitigate the dimensionality issues caused by action spaces and high-dimensional states. To determine whether our approach is effective, we conduct experimental simulations in various scenarios. The results demonstrate the efficacy of our approach in achieving efficient resource allocation while considering the dynamic nature of the dispersed computing environment.

Acknowledgement: None.

Funding Statement: This work was supported by Beijing Metro Consultancy Corporation Ltd. (the Research on 5G Key Technologies of Urban Rail Transit I).

Author Contributions: Conceptualization, T.G. and J.L.; methodology, T.G., J.L. and S.D.; software, T.G., S.W. and J.L.; validation, T.G., S.D. and J.L.; formal analysis, S.D. and S.W.; investigation, T.G., S.D., S.W. and J.L.; resources, S.D. and S.W.; writing—original draft preparation, T.G. and J.L.; writing—review and editing, T.G., S.D., S.W. and J.L.; visualization, T.G., S.D., S.W. and J.L. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. N. R. AlNaimi, “Rail robot for rail track inspection,” MS thesis, Qatar University, Qatar, 2020. [Google Scholar]

2. S. Siebert and J. Teizer, “Mobile 3D mapping for surveying earthwork projects using an Unmanned Aerial Vehicle (UAV) system,” Autom. Constr., vol. 14, pp. 1–14, 2014. doi: 10.1016/j.autcon.2014.01.004. [Google Scholar] [CrossRef]

3. Y. Zhang, X. Yuan, W. Li, and S. Chen, “Automatic power line inspection using UAV images,” Remote Sens., vol. 9, no. 8, pp. 824, 2017. doi: 10.3390/rs9080824. [Google Scholar] [CrossRef]

4. F. Song, Z. Ai, Y. Zhou, I. You, K. K. R. Choo and H. Zhang, “Smart collaborative automation for receive buffer control in multipath industrial networks,” IEEE Trans. Ind. Inform., vol. 16, no. 2, pp. 1385–1394, 2019. doi: 10.1109/TII.2019.2950109. [Google Scholar] [CrossRef]

5. H. F. Wang, L. Zhai, H. Huang, L. M. Guan, K. N. Mu and G. Wang, “Measurement for cracks at the bottom of bridges based on tethered creeping unmanned aerial vehicle,” Autom. Constr., vol. 119, no. 11, pp. 103330, 2020. doi: 10.1016/j.autcon.2020.103330. [Google Scholar] [CrossRef]

6. X. Gao et al., “Conditional probability based multi-objective cooperative task assignment for heterogeneous UAVs,” Eng. Appl. Artif. Intell., vol. 123, no. 1, pp. 106404, 2023. doi: 10.1016/j.engappai.2023.106404. [Google Scholar] [CrossRef]

7. L. Inzerillo, G. Di Mino, and R. Roberts, “Image-based 3D reconstruction using traditional and UAV datasets for analysis of road pavement distress,” Autom. Constr., vol. 96, pp. 457–469, 2018. doi: 10.1016/j.autcon.2018.10.010. [Google Scholar] [CrossRef]

8. E. Páli, K. Mathe, L. Tamas, and L. Buşoniu, “Railway track following with the AR.Drone using vanishing point detection,” in 2014 IEEE Int. Conf. Autom. Quality Testing, Robot., IEEE, 2014, pp. 1–6. [Google Scholar]

9. F. Flammini, R. Naddei, C. Pragliola, and G. Smarra, “Towards automated drone surveillance in railways: State-of-the-art and future directions,” in Adv. Concepts Intell. Vis. Syst.: 17th Int. Conf., Lecce, Italy, Springer International Publishing, Oct. 24–27, 2016, pp. 336–348. [Google Scholar]

10. F. Song, Y. Ma, I. You, and H. Zhang, “Smart collaborative evolvement for virtual group creation in customized industrial IoT,” IEEE Trans. Netw. Sci. Eng., vol. 10, no. 5, pp. 2514–2524, 2023. doi: 10.1109/TNSE.2022.3203790. [Google Scholar] [CrossRef]

11. J. Manyika et al., The Internet of Things: Mapping the Value Beyond the Hype. vol. 3. New York, NY, USA: McKinsey Global Institute, 2015, pp. 1–24. [Google Scholar]

12. P. Calhoun, “DARPA emerging technologies,” Strateg. Stud. Q., vol. 10, no. 3, pp. 91–113, 2016. [Google Scholar]

13. M. R. Schurgot, M. Wang, A. E. Conway, L. G. Greenwald, and P. D. Lebling, “A dispersed computing architecture for resource-centric computation and communication,” IEEE Commun. Mag., vol. 57, no. 7, pp. 13–19, 2019. doi: 10.1109/MCOM.2019.1800776. [Google Scholar] [CrossRef]

14. C. S. Yang, R. Pedarsani, and A. S. Avestimehr, “Communication-aware scheduling of serial tasks for dispersed computing,” IEEE/ACM Trans. Netw., vol. 27, no. 4, pp. 1330–1343, 2019. doi: 10.1109/TNET.2019.2919553. [Google Scholar] [CrossRef]

15. M. García-Valls, A. Dubey, and V. Botti, “Introducing the new paradigm of social dispersed computing: Applications, technologies and challenges,” J. Syst. Archit., vol. 91, no. 7, pp. 83–102, 2018. doi: 10.1016/j.sysarc.2018.05.007. [Google Scholar] [CrossRef]

16. S. Husain, A. Kunz, A. Prasad, K. Samdanis, and J. Song, “Mobile edge computing with network resource slicing for Internet-of-Things,” in 2018 IEEE 4th World Forum Internet Things (WF-IoT), IEEE, 2018, pp. 1–6. [Google Scholar]

17. A. Alzahrani, N. Alalwan, and M. Sarrab, “Mobile cloud computing: Advantage, disadvantage and open challenge,” in Proc. 7th Euro Am. Conf. Telemat. Inf. Syst., 2014, pp. 1–4. [Google Scholar]

18. A. V. Dastjerdi and R. Buyya, “Fog computing: Helping the Internet of Things realize its potential,” Computer, vol. 49, no. 8, pp. 112–116, 2016. doi: 10.1109/MC.2016.245. [Google Scholar] [CrossRef]

19. F. Song, Z. Ai, H. Zhang, I. You, and S. Li, “Smart collaborative balancing for dependable network components in cyber-physical systems,” IEEE Trans. Ind. Inform., vol. 17, no. 10, pp. 6916–6924, 2020. doi: 10.1109/TII.2020.3029766. [Google Scholar] [CrossRef]

20. Q. Wu, S. Wang, H. Ge, P. Fan, Q. Fan and K. B. Letaief, “Delay-sensitive task offloading in vehicular fog computing-assisted platoons,” IEEE Trans. Netw. Serv. Manag., vol. 21, no. 2, pp. 2012–2026, 2024. doi: 10.1109/TNSM.2023.3322881. [Google Scholar] [CrossRef]

21. A. Alrawais, A. Alhothaily, C. Hu, and X. Cheng, “Fog computing for the internet of things: Security and privacy issues,” IEEE Internet Comput., vol. 21, no. 2, pp. 34–42, 2017. doi: 10.1109/MIC.2017.37. [Google Scholar] [CrossRef]

22. F. Song, Y. T. Zhou, Y. Wang, T. M. Zhao, I. You and H. K. Zhang, “Smart collaborative distribution for privacy enhancement in moving target defense,” Inf. Sci., vol. 479, pp. 593–606, 2019. doi: 10.1016/j.ins.2018.06.002. [Google Scholar] [CrossRef]

23. P. Mach and Z. Becvar, “Mobile edge computing: A survey on architecture and computation offloading,” IEEE Commun. Surv. Tutorials, vol. 19, no. 3, pp. 1628–1656, 2017. doi: 10.1109/COMST.2017.2682318. [Google Scholar] [CrossRef]

24. Q. Wu, W. Wang, P. Fan, Q. Fan, J. Wang and K. B. Letaief, “URLLC-awared resource allocation for heterogeneous vehicular edge computing,” IEEE Trans. Vehicular Technol., pp. 1–16, 2024. doi: 10.1109/TVT.2024.3370196. [Google Scholar] [CrossRef]

25. Y. Mao, C. You, J. Zhang, K. Huang, and K. B. Letaief, “A survey on mobile edge computing: The communication perspective,” IEEE Commun. Surv. Tut., vol. 19, no. 4, pp. 2322–2358, 2017. doi: 10.1109/COMST.2017.2745201. [Google Scholar] [CrossRef]

26. B. Liu, C. Liu, and M. Peng, “Resource allocation for energy-efficient MEC in NOMA-enabled massive IoT networks,” IEEE J. Sel. Areas Commun., vol. 39, no. 4, pp. 1015–1027, 2020. doi: 10.1109/JSAC.2020.3018809. [Google Scholar] [CrossRef]

27. X. Yang, X. Yu, H. Huang, and H. Zhu, “Energy efficiency based joint computation offloading and resource allocation in multi-access MEC systems,” IEEE Access, vol. 7, pp. 117054–117062, 2019. doi: 10.1109/ACCESS.2019.2936435. [Google Scholar] [CrossRef]

28. J. Chen, H. Xing, Z. Xiao, L. Xu, and T. Tao, “A DRL agent for jointly optimizing computation offloading and resource allocation in MEC,” IEEE Internet Things J., vol. 8, no. 24, pp. 17508–17524, 2021. doi: 10.1109/JIOT.2021.3081694. [Google Scholar] [CrossRef]

29. J. Zhu, J. Wang, Y. Huang, F. Fang, K. Navaie and Z. Ding, “Resource allocation for hybrid NOMA MEC offloading,” IEEE Trans. Wirel. Commun., vol. l9, no. 7, pp. 4964–4977, 2020. doi: 10.1109/TWC.2020.2988532. [Google Scholar] [CrossRef]

30. Z. Ali, S. Khaf, Z. H. Abbas, G. Abbas, F. Muhammad and S. Kim, “A deep learning approach for mobility-aware and energy-efficient resource allocation in MEC,” IEEE Access, vol. 8, no. 7, pp. 179530–179546, 2020. doi: 10.1109/ACCESS.2020.3028240. [Google Scholar] [CrossRef]

31. L. Sun, L. Wan, and X. Wang, “Learning-based resource allocation strategy for Industrial IoT in UAV-enabled MEC systems,” IEEE Trans. Industr. Inform., vol. 17, no. 7, pp. 5031–5040, 2021. doi: 10.1109/TII.2020.3024170. [Google Scholar] [CrossRef]

32. R. Chai, J. Lin, M. Chen, and Q. Chen, “Task execution cost minimization-based joint computation offloading and resource allocation for cellular D2D MEC systems,” IEEE Syst. J., vol. 13, no. 4, pp. 4110–4121, 2019. doi: 10.1109/JSYST.2019.2921115. [Google Scholar] [CrossRef]

33. D. Wang, H. Qin, B. Song, X. Du, and M. Guizani, “Resource allocation in information-centric wireless networking with D2D-enabled MEC: A deep reinforcement learning approach,” IEEE Access, vol. 7, pp. 114935–114944, 2019. doi: 10.1109/ACCESS.2019.2935545. [Google Scholar] [CrossRef]

34. F. Song, M. Zhu, Y. Zhou, I. You, and H. Zhan, “Smart collaborative tracking for ubiquitous power IoT in edge-cloud interplay domain,” IEEE Internet Things J., vol. 7, no. 7, pp. 6046–6055, 2019. doi: 10.1109/JIOT.2019.2958097. [Google Scholar] [CrossRef]

35. J. Bellendorf and Z. Á. Mann, “Classification of optimization problems in fog computing,” Future Gener. Comput. Syst., vol. 107, no. 5, pp. 158–176, 2020. doi: 10.1016/j.future.2020.01.036. [Google Scholar] [CrossRef]

36. H. Yang et al., “Dispersed computing for tactical edge in future wars: Vision, architecture, and challenges,” Wirel. Commun. Mob. Comput., pp. 1–31, 2021. doi: 10.1155/2021/8899186. [Google Scholar] [CrossRef]

37. P. Rahimzadeh et al., “SPARCLE: Stream processing applications over dispersed computing networks,” in 2020 IEEE 40th Int. Conf. Distrib. Comput. Syst. (ICDCS), 2020, pp. 1067–1078. [Google Scholar]

38. C. Zhou, C. Gong, H. Hui, F. Lin, and G. Zeng, “A task-resource joint management model with intelligent control for mission-aware dispersed computing,” China Commun., vol. 18, no. 10, pp. 214–232, 2021. doi: 10.23919/JCC.2021.10.016. [Google Scholar] [CrossRef]

39. A. Paulos et al., “Priority-enabled load balancing for dispersed computing,” in 2021 IEEE 5th Int. Conf. Fog Edge Comput. (ICFEC), 2021, pp. 1–8. [Google Scholar]

40. X. Wang et al., “Deep reinforcement learning-based air combat maneuver decision-making: Literature review, implementation tutorial and future direction,” Artif. Intell. Rev., vol. 57, no. 1, pp. 1, 2024. doi: 10.1007/s10462-023-10620-2. [Google Scholar] [CrossRef]

41. N. C. Luong, D. T. Hoang, S. Gong, D. Niyato, and I. K. Dong, “Applications of deep reinforcement learning in communications and networking: A Survey,” IEEE Commun. Surv. Tut., vol. 21, no. 4, pp. 3133–3174, 2019. doi: 10.1109/COMST.2019.2916583. [Google Scholar] [CrossRef]

42. Y. He, N. Zhao, and H. Yin, “Integrated networking, caching, and computing for connected vehicles: A deep reinforcement learning approach,” IEEE Trans. Vehicular Technol., vol. 67, no. 1, pp. 44–55, 2018. doi: 10.1109/TVT.2017.2760281. [Google Scholar] [CrossRef]