Wild Gibbon Optimization Algorithm

1  Introduction

In recent years, the field of optimization has emerged a surge of complex problems, including those with non-linear dynamics [1], intricate constraints [2], and notably, high dimensions. This evolving landscape has brought optimization algorithms into the limelight of scholarly research. The increasing dimensions in various domains such as resource allocation, scheduling, and network design, have catalyzed the emergence of high-dimensional optimization challenges. These challenges are marked by an array of variables, which significantly complicates both analysis and solution process. Compared with other problems, a distinctive aspect of high-dimensional optimization problems is the exponential increase in the search space proportional to the number of decision variables involved.

Metaheuristic algorithms have their roots in the 1960s and 1970s, a period marked by the exploration of heuristic methods derived from observing natural phenomena and human decision-making to tackle complex optimization challenges. These innovative approaches, inspired by the mechanisms of biological evolution, collective behavior of species, and physical processes, were developed to simulate the exploration and learning behaviors found in nature. The aim was to navigate the vast solution spaces of optimization problems efficiently, seeking out optimal or sufficiently good solutions. These algorithms have found widespread application across various fields, notably in engineering design, scheduling problems, network design, and machine learning, where they facilitate resource arrangement, network configuration optimization, and learning model enhancement. The application of metaheuristic algorithms spans a wide array of fields like segmentation [3,4] feature processing [5], vision transformer [6], and multiple-disease detection [7].

Despite their versatility and demonstrated efficacy, metaheuristic algorithms are not without limitations. Challenges include ensuring convergence to global optima in high-dimensional and complex problem spaces, the complexity and sensitivity of algorithm parameters, which can significantly affect performance, and the substantial computational resources required for large-scale problems. Additionally, the lack of a rigorous theoretical foundation for some metaheuristic approaches makes their behavior and efficiency difficult to predict accurately. Nevertheless, the adaptability and success of metaheuristic algorithms in practical applications continue to support their widespread use and ongoing development in the field of optimization, highlighting the balance between their potential and limitations.

To address these challenges, this paper proposes a novel Wild Gibbon Optimization Algorithm (WGOA) based on an analysis of the behavior of wild gibbon populations. The WGOA simplifies the family structure of gibbons to consist of a female, a male, and an offspring, utilizing particles without mass and volume to simulate the behavioral patterns of gibbon populations during foraging and territory acquisition. This search pattern enhances the algorithm’s ability to provide high-precision solutions for high-dimensional optimization problems. The main contributions of the algorithm include the following main points:

•   A community search strategy is proposed in this work. This strategy involves leading the particle swarm with particles that have male gibbon identities to perform global searches. This approach helps in determining the personal optima. This strategy is proposed and developed by the authors to enhance the global search capability of the algorithm.

•   A community competition strategy is proposed in this work. This strategy entails the global optimal group competing with the positions explored by the male gibbons to ensure the superiority of the group’s position. This method is introduced by the authors to improve the algorithm’s convergence towards the global optimum.

•   The combination of the community search strategy and community competition strategy enables the algorithm to conduct broad-scale searches in the initial phases and precise searches in later stages. This integration significantly enhances both the diversity and accuracy of the solution set, ensuring robust and reliable results.

The remainder of this thesis will explain this algorithm in detail. Section 2 introduces related work of this study. Section 3 describes the details of the algorithm. Section 4 shows the contents of the simulations and the results of the experiments. Section 5 summarizes the content of this study and future work.

2  Related work

Metaheuristic algorithms [8–10] are high-level heuristic methods used to find approximate solutions to complex optimization problems. These methods are often inspired by natural phenomena, biological evolution, and behaviors in different species [11–13]. Metaheuristic algorithms have shown great performance in various applications, such as image segmentation [14–16], path planning for mobile robots [17,18], and manufacturing energy optimization problems [19–21]. In recent years, many researchers have developed new metaheuristic algorithms to address these optimization challenges. Su et al. [22] introduced the RIME optimization algorithm (RIME) inspired by the physical phenomenon of rime-ice. The RIME algorithm implements the exploration and exploitation behaviors in the optimization methods by simulating the soft-rime and hard-rime growth process of rime-ice. Song et al. [23] proposed the Phasmatodea population evolution (PPE) algorithm based on the evolution characteristics of the Phasmatodea population. Połap et al. [24] proposed a red fox optimizer (ROF), searching for food, hunting, and developing population while escaping from hunters. These meta-heuristic algorithms have shown good optimization performance in many real-world optimization problems. However, with the further study of these algorithms in the application fields, some researchers have raised some problems of these original meta-heuristic algorithms such as premature convergence [25] and slow convergence speed [26].

To overcome these problems, many scholars have optimized these original algorithms from different aspects. Some scholars have applied the method of adopting new search strategies. Li et al. [27] developed an adaptive particle swarm optimization with decoupled exploration and exploitation (APSO-DEE) to effectively balance exploration and exploitation. The APSO-DEE adopted two novel learning strategies, a local sparseness degree measurement in fitness landscape and an adaptive multi-swarm strategy. Zhang et al. [28] developed a charging safety early warning model for electric vehicles based on the improved grey wolf optimization (IGWO) algorithm. The IGWO improves the classic grey wolf optimization (GWO) algorithm by utilizing a search method based on clustering search results, which can boost wolf diversity and avoid slipping into the local optimum owing to insufficient information exchange among wolves. In the context of optimizing deep learning and evolutionary algorithms, meta-heuristic methods have been integrated with neural networks [29–31] and applied to various optimization problems [32–34]. Tang et al. [35] also proposed a whale optimization algorithm combined with an artificial bee colony (ACWOA) to address the problems of slow convergence and the tendency to fall into local optima in the classic whale optimization algorithm (WOA). Thawkar et al. [36] presented a butterfly optimization algorithm and ant lion optimizer (BOAALO) for breast cancer prediction. The experimental results show that BOAALO outperforms the original butterfly optimization algorithm (BOA) and ant lion optimizer (ALO) in terms of each given statistical measure. Deb et al. [37] proposed a novel meta-heuristic considering the hybridization of chicken swarm optimization (CSO) with ant lion optimization (ALO) for effectively and efficiently coping with the charger placement problem. The amalgamation of CSO with ALO can enhance the performance of ALO, thereby preventing it from getting stuck in the local optima. Emam et al. [38] proposed a modified Reptile search algorithm (mRSA), which combines the RSA algorithm with the Runge kutta optimizer (RUN). The mRSA mitigates the limitations of RSA, which include being stuck in local optima areas and having an insufficient balance between exploitation and exploration.

Despite several improvement measures taken to enhance the effectiveness of meta-heuristic optimization algorithm in solving practical problems, challenges persist in dealing with high-dimensional problems. High-dimensional optimization problems usually involve large-scale sets of parameters or variables, leading to a significant increase in the dimensionality of the solution space. In high-dimensional space, the number of local optimal solutions increases as the solution space expands. This is due to the fact that the solution space of high-dimensional problems is more extensive and the local optimal solutions have more diverse forms in each dimension. The existence of more local optimal solutions in the solution space increases the possibility that the algorithms stay in local optimal solutions during the search process. As a result, the algorithm is more likely to fall into local optima, which in turn increases the difficulty of the problems. Researchers have developed a number of algorithms specifically for high-dimensional optimization problems to address these challenges. MiarNaeimi et al. [39] proposed the Horse herd optimization algorithm (HOA) inspired by the herding behavior of horses for high-dimensional optimization problems. HOA performs well in solving high-dimensional complex problems, due to the large number of control parameters it extracts from the behavior of horses of different ages. Ma et al. [40] proposed a two-stage hybrid ACO for high-dimensional feature selection (TSHFS-ACO). These optimization algorithms can alleviate some of the challenges associated with high-dimensional optimization problems, but there are still limitations. When solving high-dimensional problems, although the two-stage strategy of the TSHFS-ACO can alleviate the algorithm from getting into local optima, there still exist errors in feature selection, which may result in the removal of potentially useful features on the test set, thereby impacting the performance of this model. The HOA has a strong ability to balance the two phases of exploration and exploitation, but it suffers from premature convergence, which limits its effectiveness in finding optimal solutions. Therefore, a novel algorithm based on gibbon territory contention behavior is proposed to solve high-dimensional problems, called the gibbon algorithm.

Zhong et al. [41] introduced the Beluga Whale Optimization (BWO) algorithm, inspired by beluga whale behaviors, which effectively solves optimization problems through self-adaptive mechanisms, Levy flight integration, and competitive performance compared to 15 other metaheuristic algorithms, validated across various benchmark functions and real-world engineering problems. Inspired by African vultures’ foraging and navigation behaviors, Abdollahzadeh et al. [42] introduced the African Vultures Optimization Algorithm (AVOA), demonstrating superior performance in solving optimization problems compared to existing algorithms across various benchmark functions and engineering design problems, supported by statistical evaluation. In addition, to solve high dimensional complex optimization problems, Harris Hawks Optimization (HHO) [43], Dung Beetle Optimizer (DBO) [44], Whale Optimization Algorithm (WOA) [45], Runge Kutta Optimizer (RUN) [46], Krill Herd (KH) [47], Artificial Gorilla Troops Optimizer (GTO) [48], Novel Hippo Swarm Optimization (NHSO) [49] are also proposed.

3  Materials and Methods

3.1 Behavior of Gibbon

The gibbon is one of the primates belonging to the family Hominidae. They are mainly found in the tropical rainforests of South East Asia, including Thailand, Indonesia, Malaysia and Southern China. They are social animals used to living in groups. As such, they generally form family units and colonies within their populations, maintaining the structure and order of the group through social interaction. Family units generally consist of a pair of adult males and females and their minor children. Within a family unit, there may be multiple adult males with certain social hierarchies and competitive relationships, and it is usually the alpha male that dominates the decision-making and defense of the family unit. In order to compete for food resources and habitat environments, they establish their own territories in the forest and defend them. The size of the territory depends on the availability of resources and the number of family units. The quality of territory has a direct impact on gibbon reproduction and survival, thus a particular kind of territorial competition is present in gibbon populations. Family units mark and claim territories through musical calls, which are unique to their species and an important form of communication between them. When competing for territory, the alpha male will roam to determine the distribution of resources and environmental conditions in different territories. This means moving quickly between trees by swinging his long arms to gain a territorial view. In a given area, multiple family units may form a larger group, called a “colony”. There may be some degree of competition or cooperation between the various family units in the herd.

3.2 Wild Gibbon Optimization Algorithm

Inspired by the competition and survival patterns of gibbon populations, the behavior of gibbons was simulated, and the Wild Gibbon Optimization algorithm (WGOA) was designed, which relates the superiority and inferiority process resulting from gibbon population competition to an optimized objective function. During the simulation, it is assumed that the family contains three members: male gibbons, female gibbons, and child gibbons. The physiological factors such as mass and volume of the members are ignored, and they are represented as a point in space, respectively. The value of a gibbon’s preference for a territory depends on the food abundance, and habitat superiority of that territory, which is related to the optimal value of the objective function. The territorial replacement behavior of gibbons arising from population competition is then modeled as a process of solution updating.

In the gibbon family, the male gibbon is considered to be the leader of social behaviors such as territorial conservation and population competition. Male gibbons evaluate their environment by roaming in trees to facilitate locating a superior survival environment. This assessment process is modeled as a search process for solutions and mainly works on local search. Female gibbon is able to maintain the stability of family relationships and therefore can keep the balance during particle updating. Child gibbon can achieve roaming over a larger area of the family territory and can improve the global property in the particle search process. After finding a superior survival environment, male gibbons lead their families to migrate, allowing both male and child gibbons to live around the superior environment.

In simulation experiments, particles without weight and volume are used to simulate the behavior of gibbons. Each particle is endowed with three layers of memory, with the first layer representing male gibbons, the second layer representing female gibbons, and the third layer representing juvenile gibbons. Each particle participates in evolution as a collective entity of a gibbon family. Based on the environmental assessment process and family migration process of the gibbon population, two search strategies are proposed: the community search strategy and the community competition strategy. The cooperation of these two strategies can balance the local search while expanding the search scope, thus avoiding falling into local optimum and improving the search accuracy. The pseudo-code for the basic steps of WGOA is shown in Algorithm 1. The flowchart of WGOA is shown in Fig. 1.

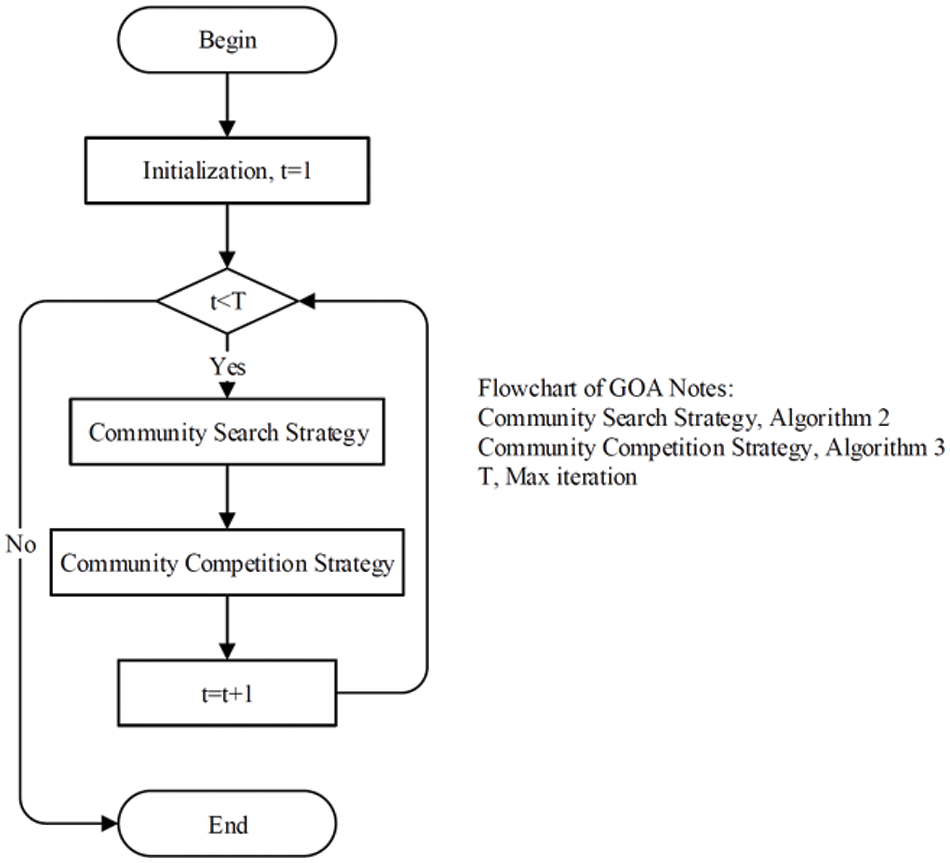
Figure 1: The flowchart of the WGOA

3.3 Community Search Strategy

In the gibbon family, female and child gibbons follow the male gibbon, leading to the elimination of poorer territories due to the dominant role of male gibbons in territory exploration. In the experiments, particles without weight and volume are used to simulate the behavior of gibbons. Within the community search strategy, each particle with three memory layers simulates a gibbon family. Among them, the first layer of memory records the best position, representing male gibbons; the second layer of memory records the second-best position, representing female gibbons; the third layer of memory records the third-best position, representing juvenile gibbons.

In each iteration, the group is searched by the leader particle according to Eq. (1). If the leader particle discovers a better position, the group particles are updated to ensure the superiority of the group’s position. Otherwise, the group particles remain unchanged. This process is completed through Eq. (2). At the same time, the other two particles in the group, represented by the female gibbon and the child gibbon, work to maintain a balance between global and local searches.

α=Gib(ii)t(kk)+BestGibt(ll)2

β=|Gib(ii)t(kk)+BestGibt(ll)|

GibCandidate(ii)t+1(kk,ll)=GD(α,β)(1)

where Gib(ii)t is the position of the iith gibbon in the tth iteration, BestGibt is the best gibbon in the tth iteration, kk = [1, 2, 3] and ll = [1, 2, 3] stand for the memory layer of the Gib and the BestGib, GibCandidate(ii) is the new position that explored by this iteration, and GD() is Gaussian distribution with a mean α and a standard deviation β.

Gib(ii)t+1=Best(3,(GibCandidate(ii)t+1,Gib(ii)t+1))(2)

where Gib(ii)t+1 is the position of the iith gibbon in the (t + 1)th iteration. Best (3, array) is a function used to find the best 3 position form the input array.

The pseudo-code of community search strategy is shown in Algorithm 2. Under this strategy, the information of the particles will be fully utilized, making the global search more efficient.

3.4 Community Competition Strategy

Male gibbons have a stronger fighting ability, allowing them to compete with other families for superior territories. After this competition, the victor will occupy the best territory known so far. According to this modal, in the community competition strategy, the position of the global optimal particle is updated. This strategy maintains three historical best positions to enhance local search. The number of these historical positions matches the number in the particle group of the community search strategy. The global optimal particle group is updated when the leader particle searches for a preferred location. Specifically, the new position found by the leader particle is compared with the current global optimal group positions. If the new position is superior, the global optimal group is updated, thereby ensuring favorable conditions for the group’s position. Following this, the global best particle is updated using Eq. (3).

BestGibCandit+1=Best(Gib(1)t(1),Gib(2)t(1),…,Gib(n)t(1))

BestGibt+1=Best(BestGibCandit+1,BestGibt)(3)

where BestGibCandi(ii)t+1 is the candidate position of the best gibbons in the (t + 1)th iteration, Gib(ii)t(1) is the best memory of the iith gibbon in the tth iteration, BestGibt+1 is the position of the best gibbons in the (t + 1)th iteration. Best (array) is a function used to find the best position form the input array.

The pseudo-code of community competition strategy is shown in Algorithm 3. This strategy improves the diversity of particles while facilitating the local exploration of particles. These two strategies can work together effectively to ensure that the global search range is increased while the search efficiency is improved. This cooperation promotes the balance of local and global search during iteration.

This is followed by an analysis regarding the time complexity. From the pseudo-code of this WGOA, it can be seen that the algorithm mainly consists of particle swarm initialization, community search strategy and community competition strategy. For a particle swarm of size N, the time complexity of the algorithm for random initialization is O(N). In both strategies, only the linear computation with a factor of three is added, which do not increase in computational complexity. Therefore, the time complexity of WGOA is equivalent to the time complexity of the particle swarm algorithm, both being O(N).

4  Results

4.1 Experimental Methods

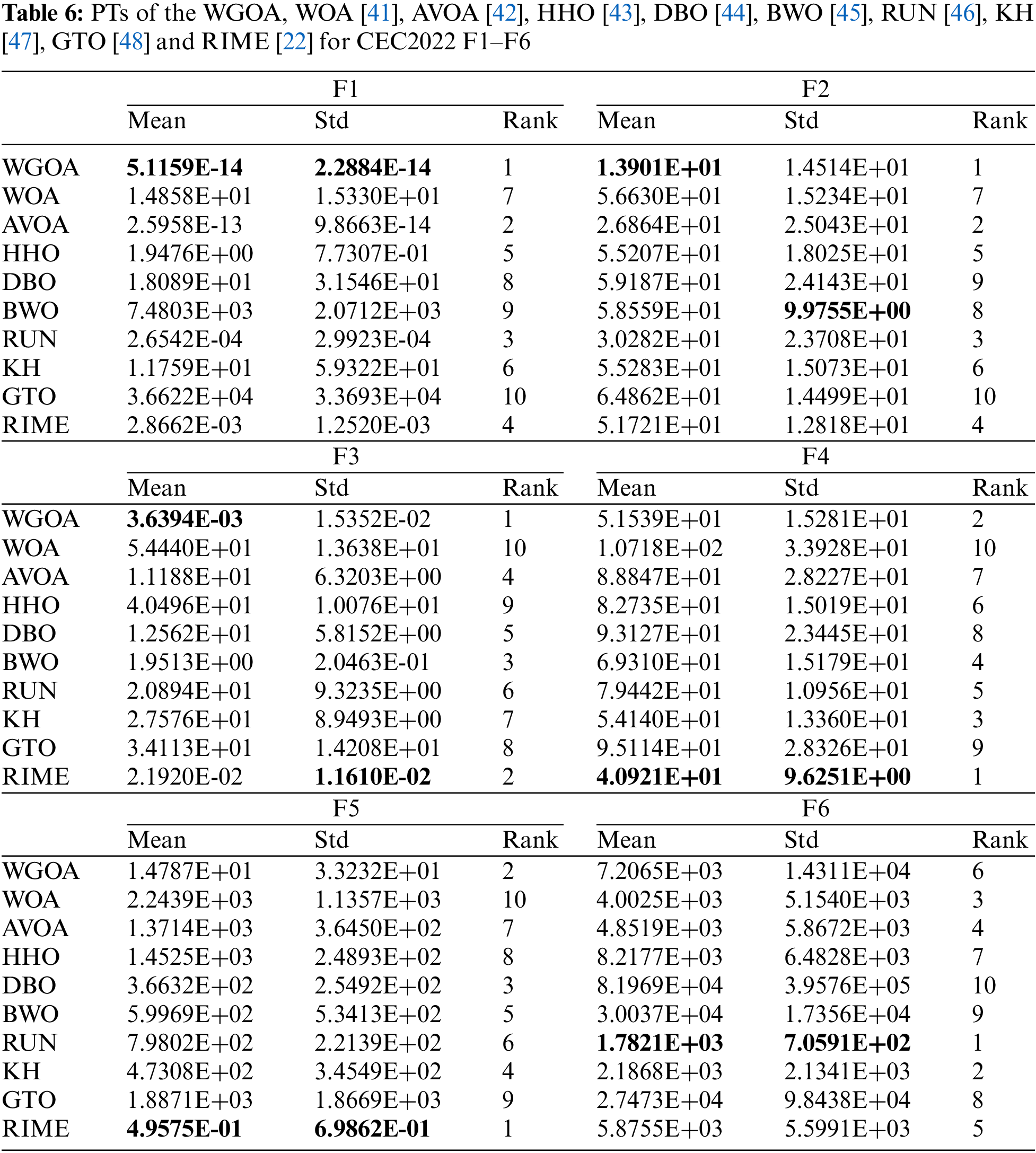
To better show the experimental results, CEC2017 and CEC2022 benchmark functions are selected as the test function. CEC2017 contains 29 test functions, which include uni-modal functions, simple multi-peaked functions, hybrid functions and composite functions. For the uni-modal functions, the algorithm has a low difficulty in finding the optimal value, and these functions have a unique global optimal value, which can show the ability of the algorithm to search globally. Simple multi-peaked functions, hybrid functions and composite functions all have multiple local optima and a unique global optimum. The algorithm is more difficult to find the superiority in these functions. The functions can test whether the algorithm can jump out of the local optimum, has high search efficiency and other comprehensive capabilities. The CEC2022, which contains 13 different benchmark functions, has been recognized for its ability to detect the effectiveness of algorithms in solving high-dimensional optimization problems. To ensure fairness, Function Evaluation Times (FES) are used to evaluate the performance of all algorithms. To show the performance of the WGOA algorithm, 9 excellent meta-heuristics are selected as a control group: Beluga Whale Optimization (BWO) [41], African Vultures Optimization Algorithm (AVOA) [42], Harris Hawks Optimization (HHO) [43], Dung Beetle Optimizer (DBO) [44], Whale Optimization Algorithm (WOA) [45], Runge Kutta Optimizer (RUN) [46], Krill Herd (KH) [47], Artificial Gorilla Troops Optimizer (GTO) [48] and RIME. To ensure equity, all algorithms were employed with their respective optimal parameters. To ensure the fairness of the experiment, the parameters in the algorithm will be consistent with the control group, where the particle population size is 100, every algorithm will stop when it reaches the max fitness-function evaluations (FES) times 100,000. Each group of experiments will be run 30 times independently to reduce the error caused by experimental chance.

4.2 Experimental Results

To compare the experimental and control groups with higher efficiency, we subtract the optimal value obtained by the experimental results from the theoretical optimal value of the function. The smaller the result obtained, the higher the accuracy of the algorithm is indicated. This result will be calculated using Eq. (4) and is denoted as PT.

PT=Practicaloptimum−Theoreticaloptimum(4)

where Practicaloptimum stands for the results obtained by the algorithm after the final iteration, Theoreticaloptimum stands for the theoretical optimum solution.

The MEAN and STD of 30 sets of independent runs are recorded. Numerical results of CEC2017 are shown in Tables 1–5. Numerical results of CEC2022 are shown in Tables 6 and 7. Average rank of the CEC 2017 and CEC2020 are shown in Tables 8 and 9.

The FES-convergence figures of CEC2017 are shown in Figs. 2–7. Friedman test results for the GWOA algorithm and the control group algorithms in CEC2017 and CEC2022 are shown in Fig. 8. The results of The FES-convergence figures of CEC2022 are shown in Figs. 9–11. In Figs. 2–7 and 9–11, the horizontal axis represents the FES, and the vertical axis represents the error.

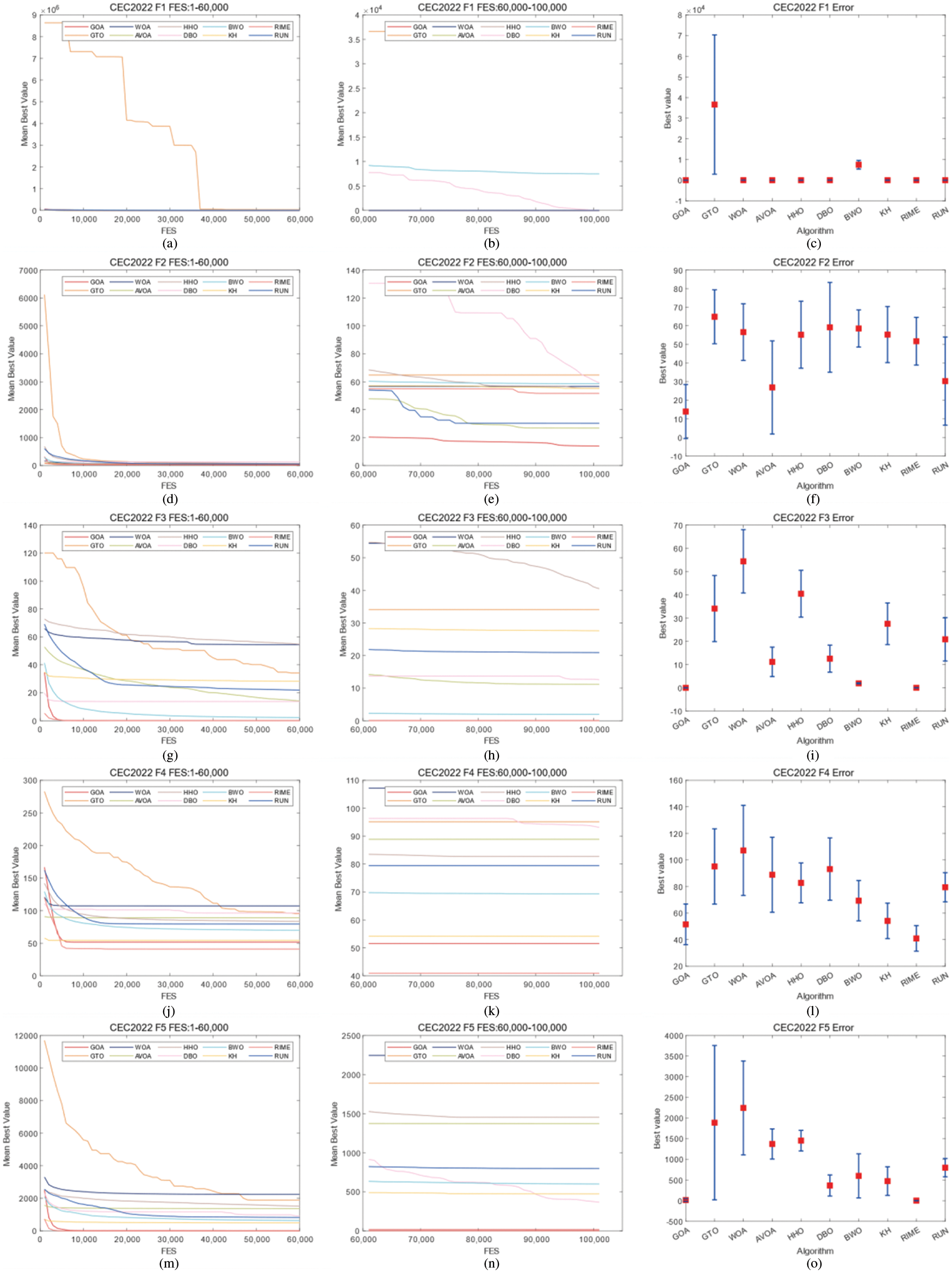
Figure 2: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2017 F1–F5

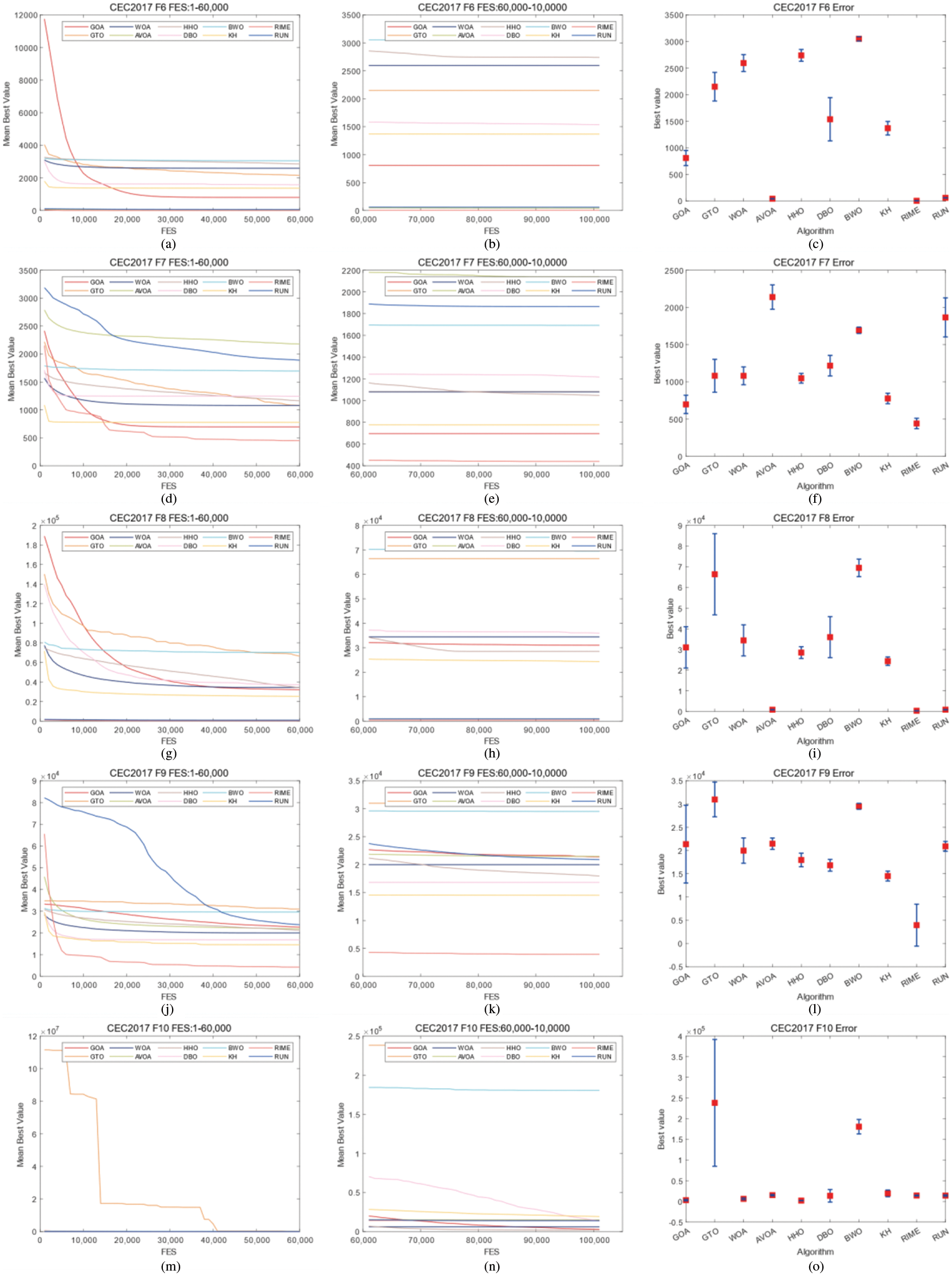
Figure 3: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2017 F6–F10

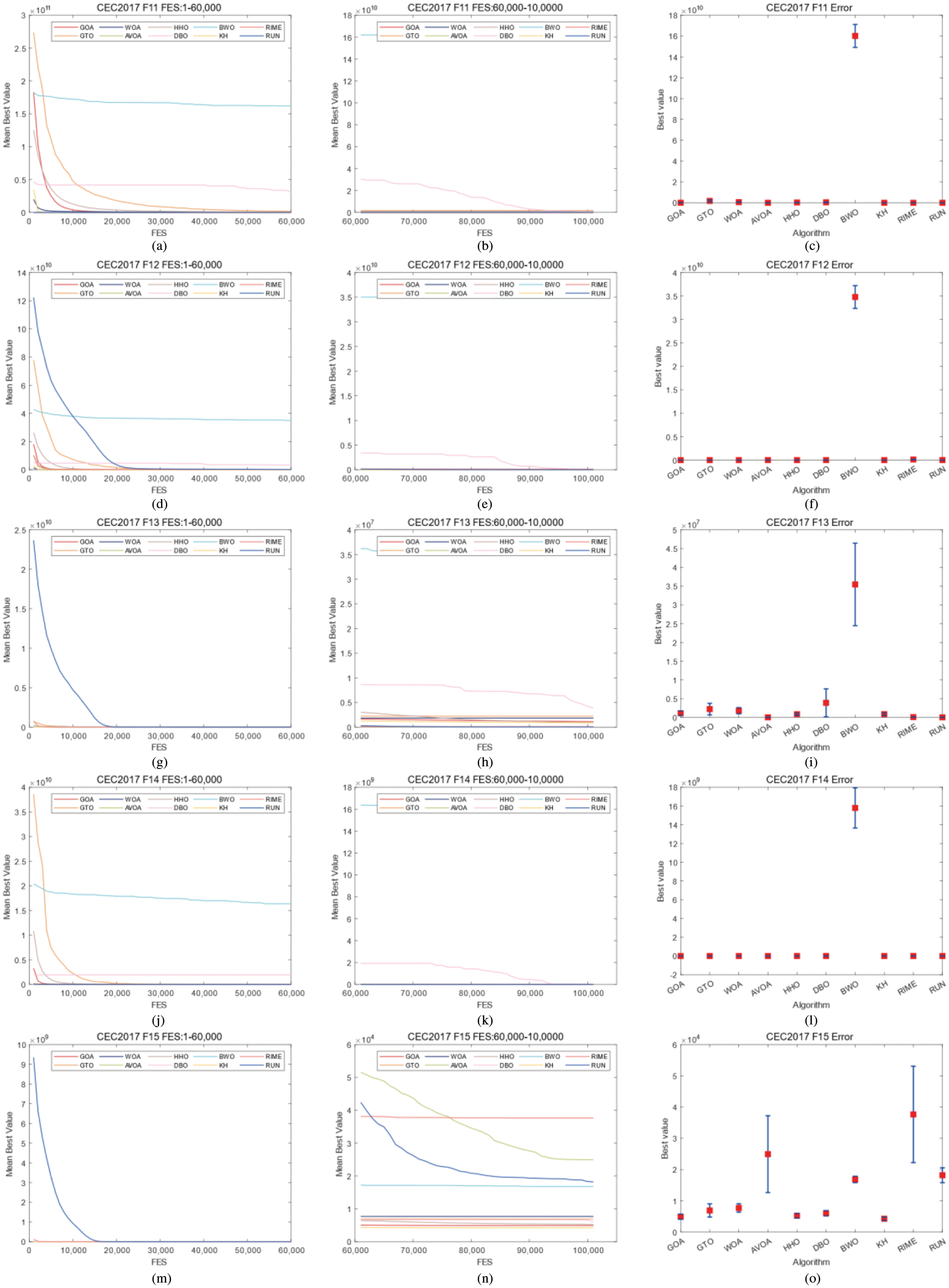
Figure 4: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2017 F11–F15

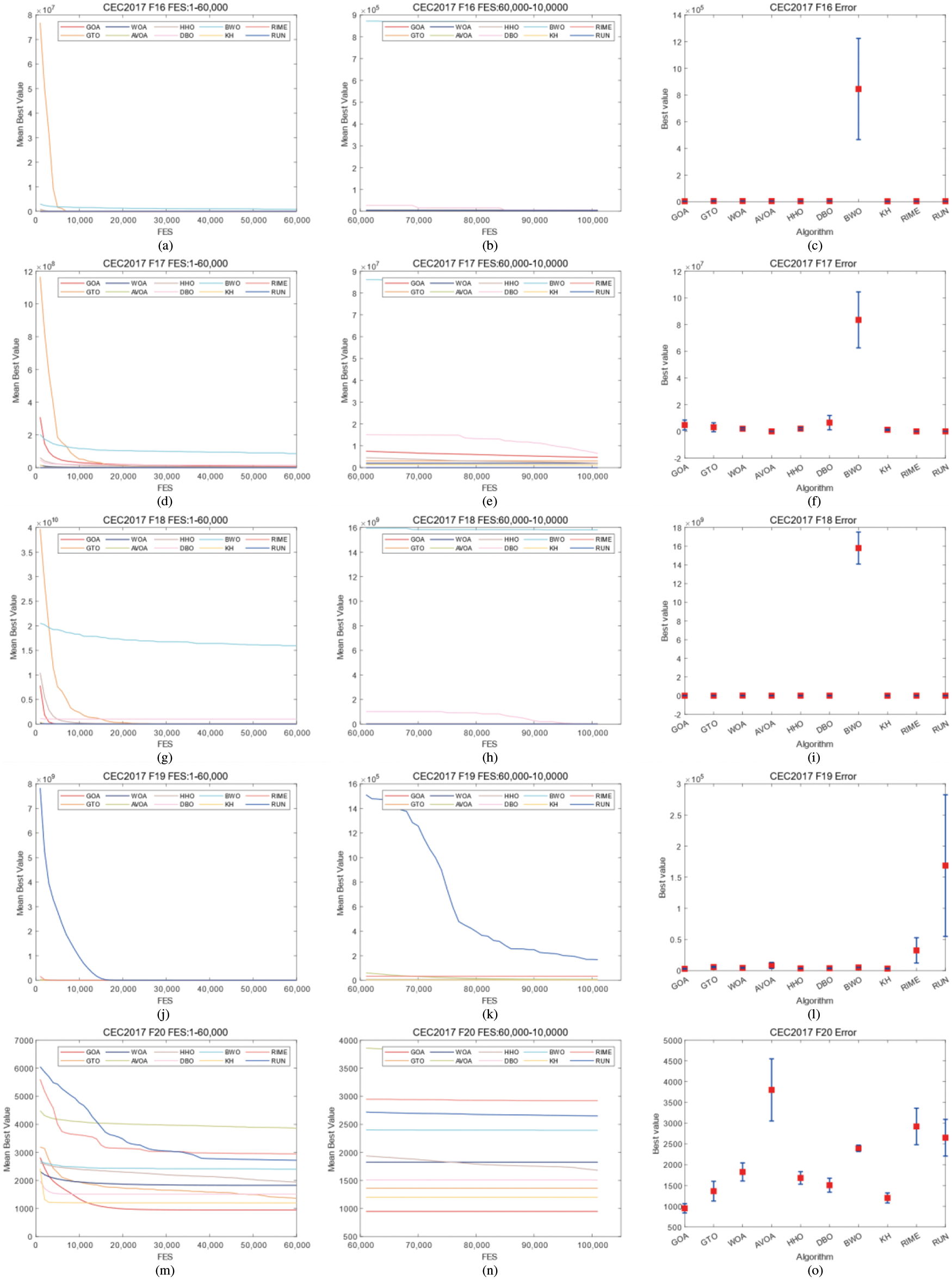
Figure 5: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2017 F16–F20

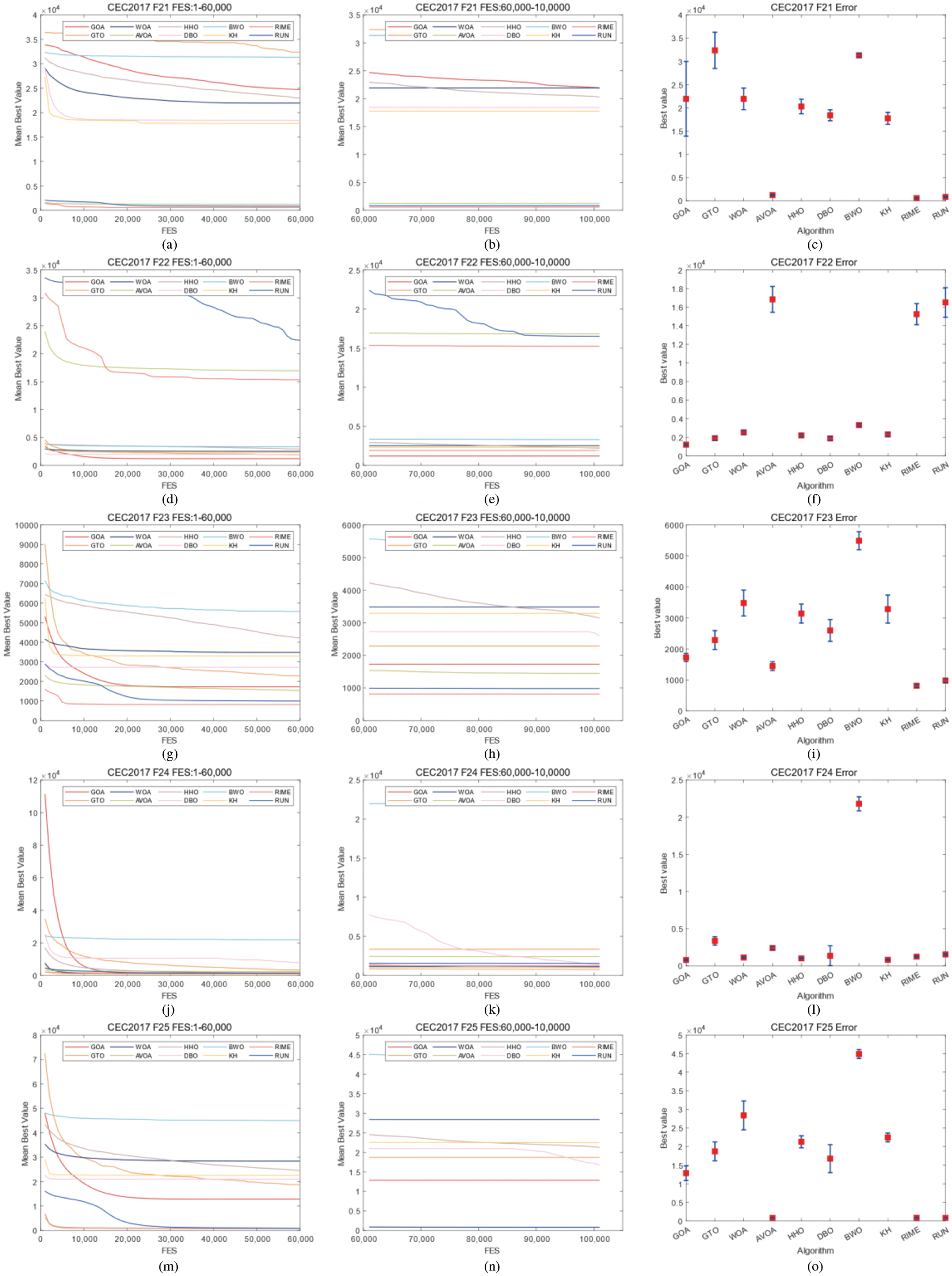
Figure 6: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2017 F21–F25

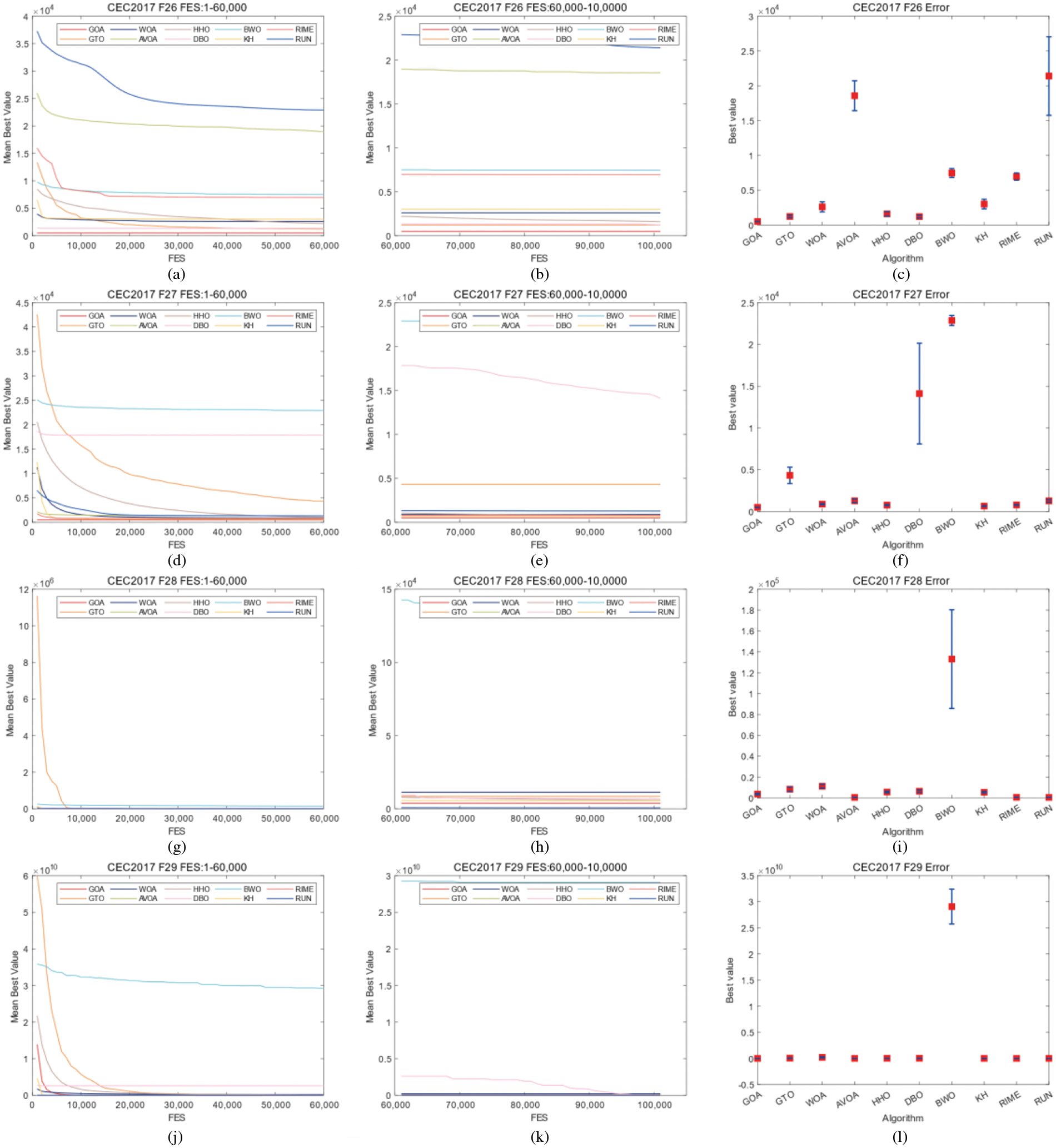
Figure 7: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2017 F26–F29

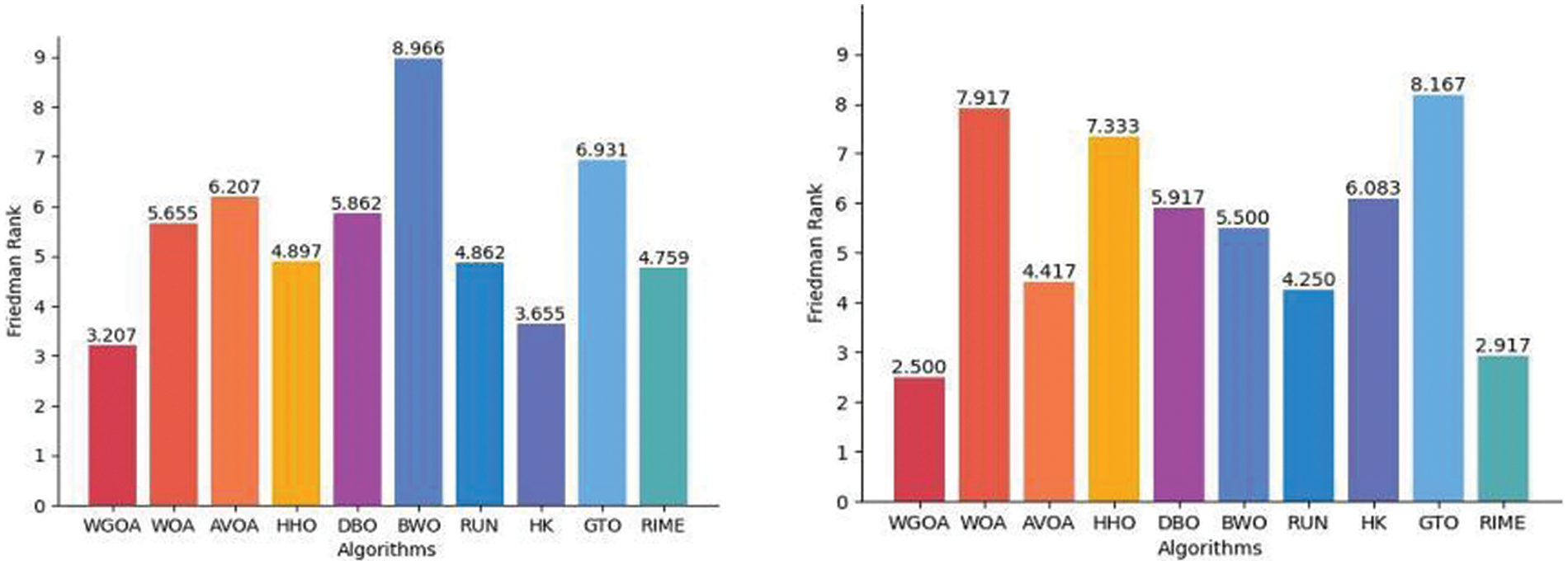
Figure 8: Friedman test results for the WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2017 (left) and CEC2022 (right)

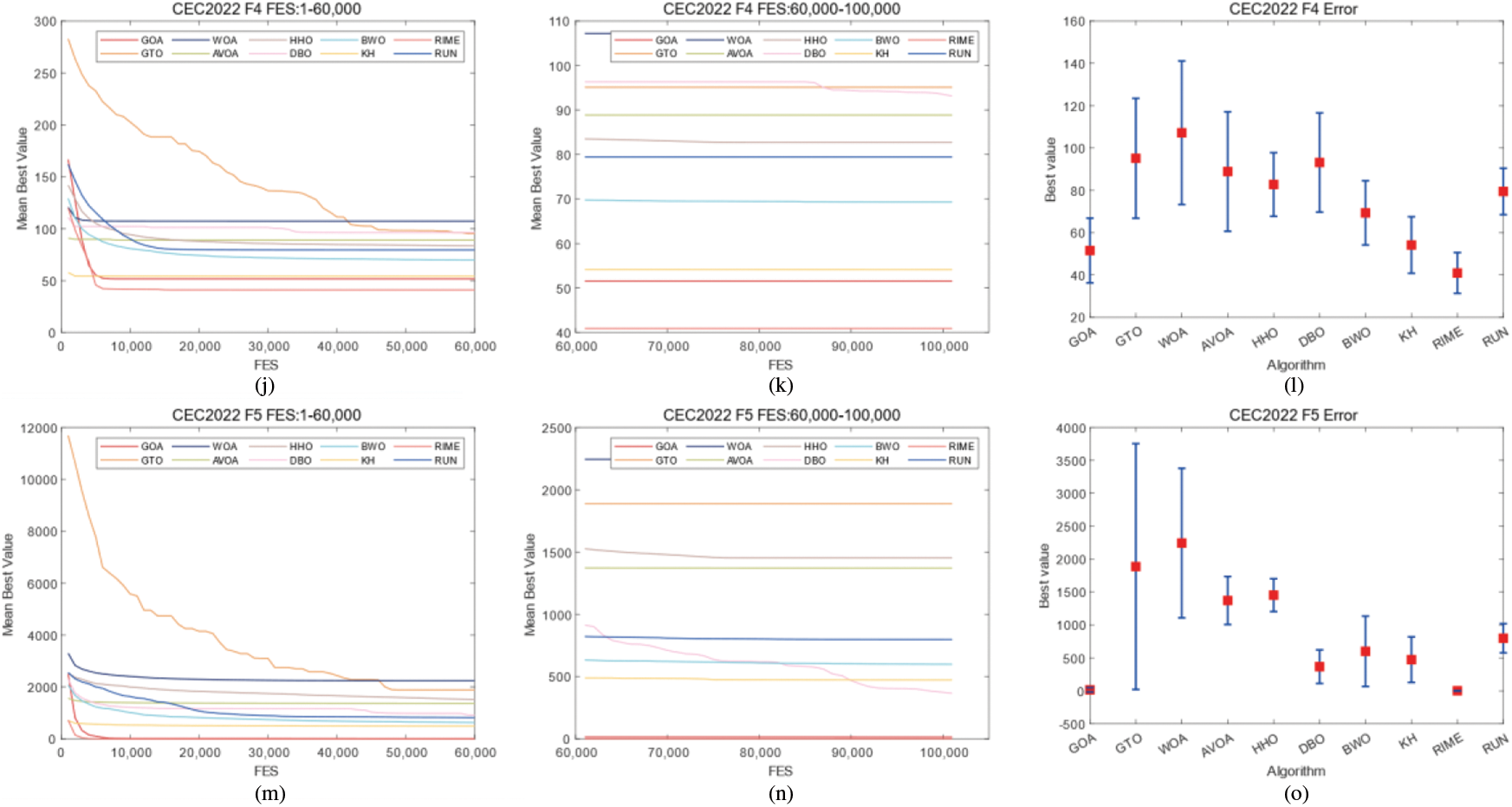
Figure 9: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2022 F1–F5

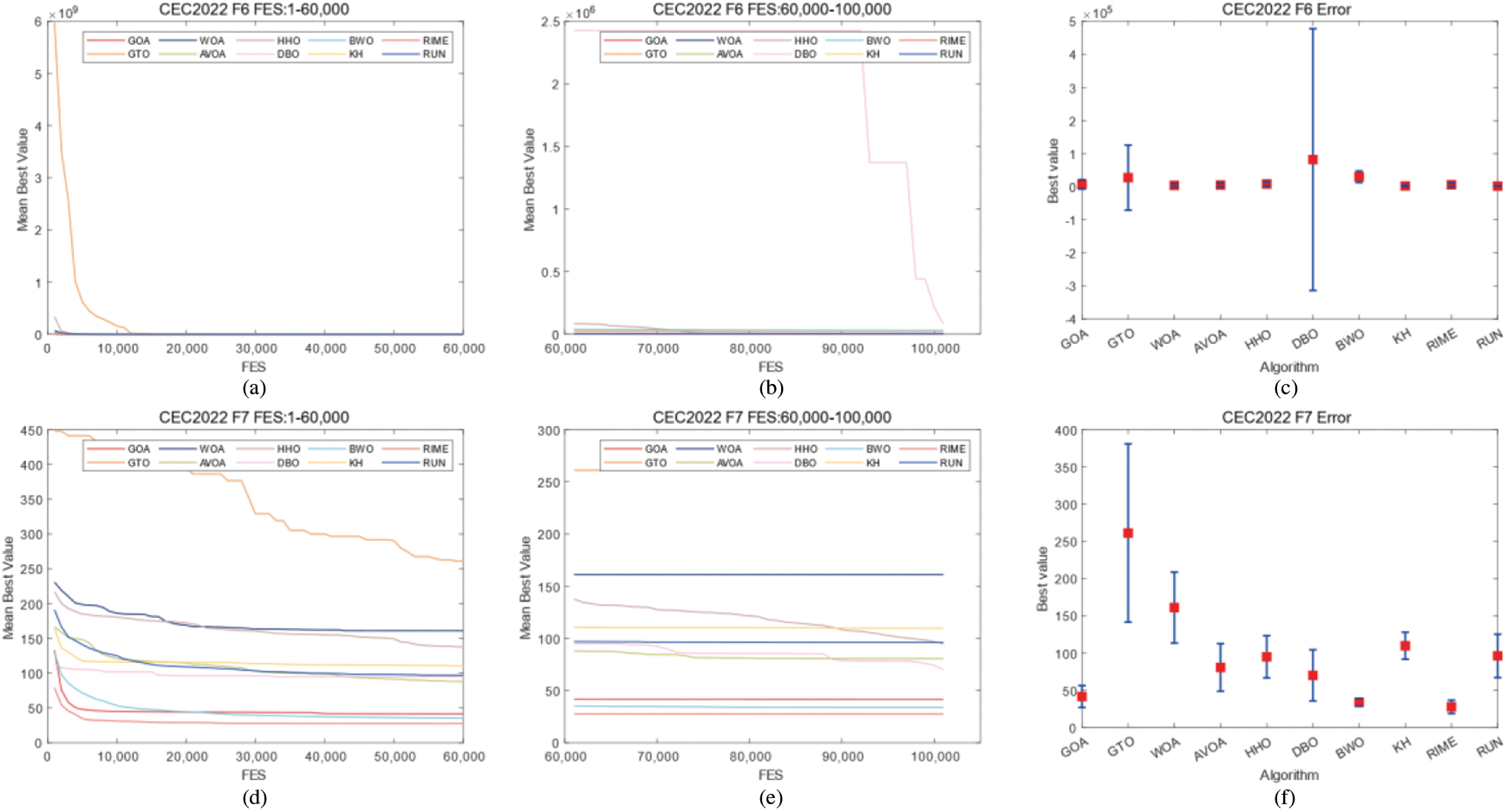
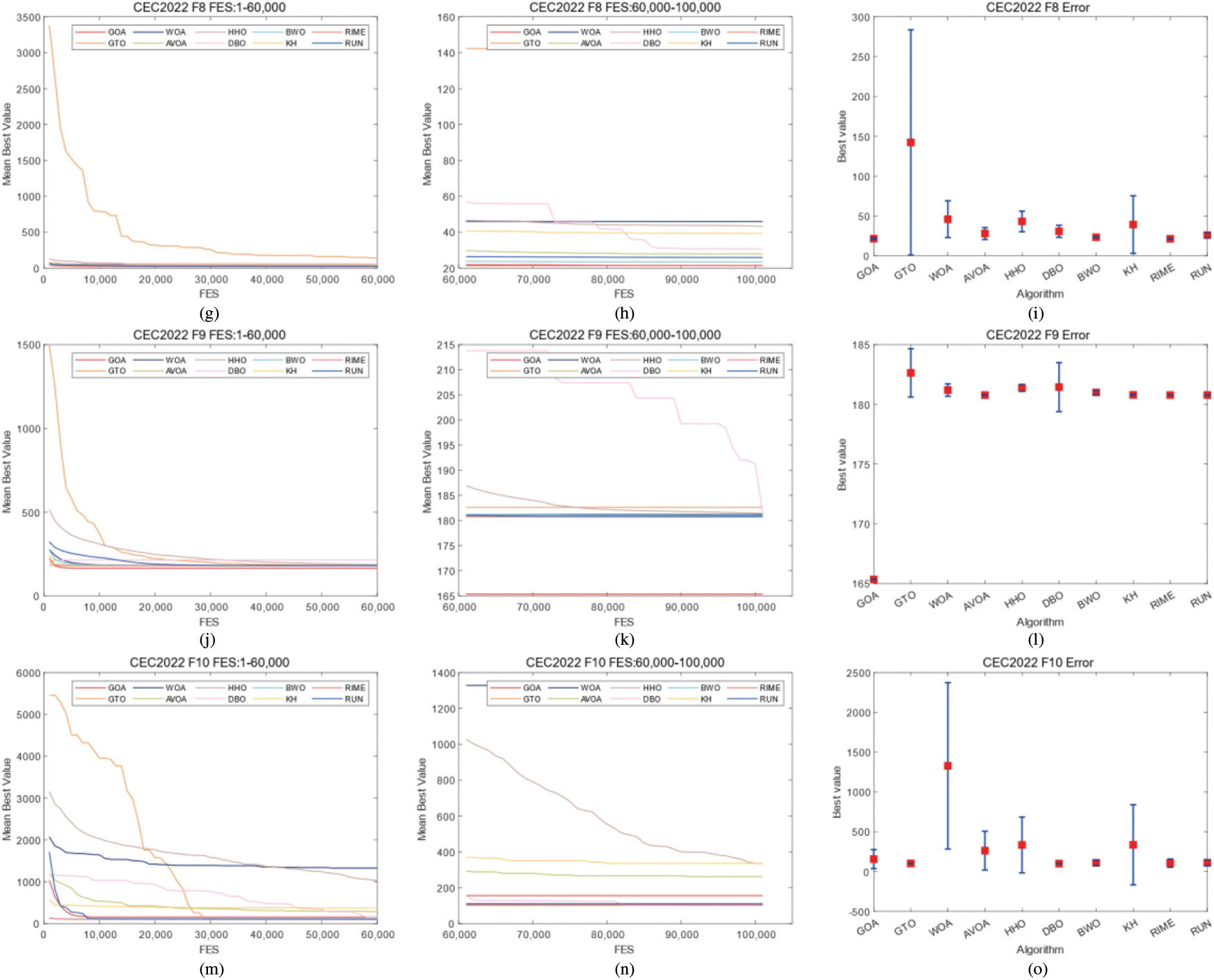
Figure 10: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2022 F6–F10

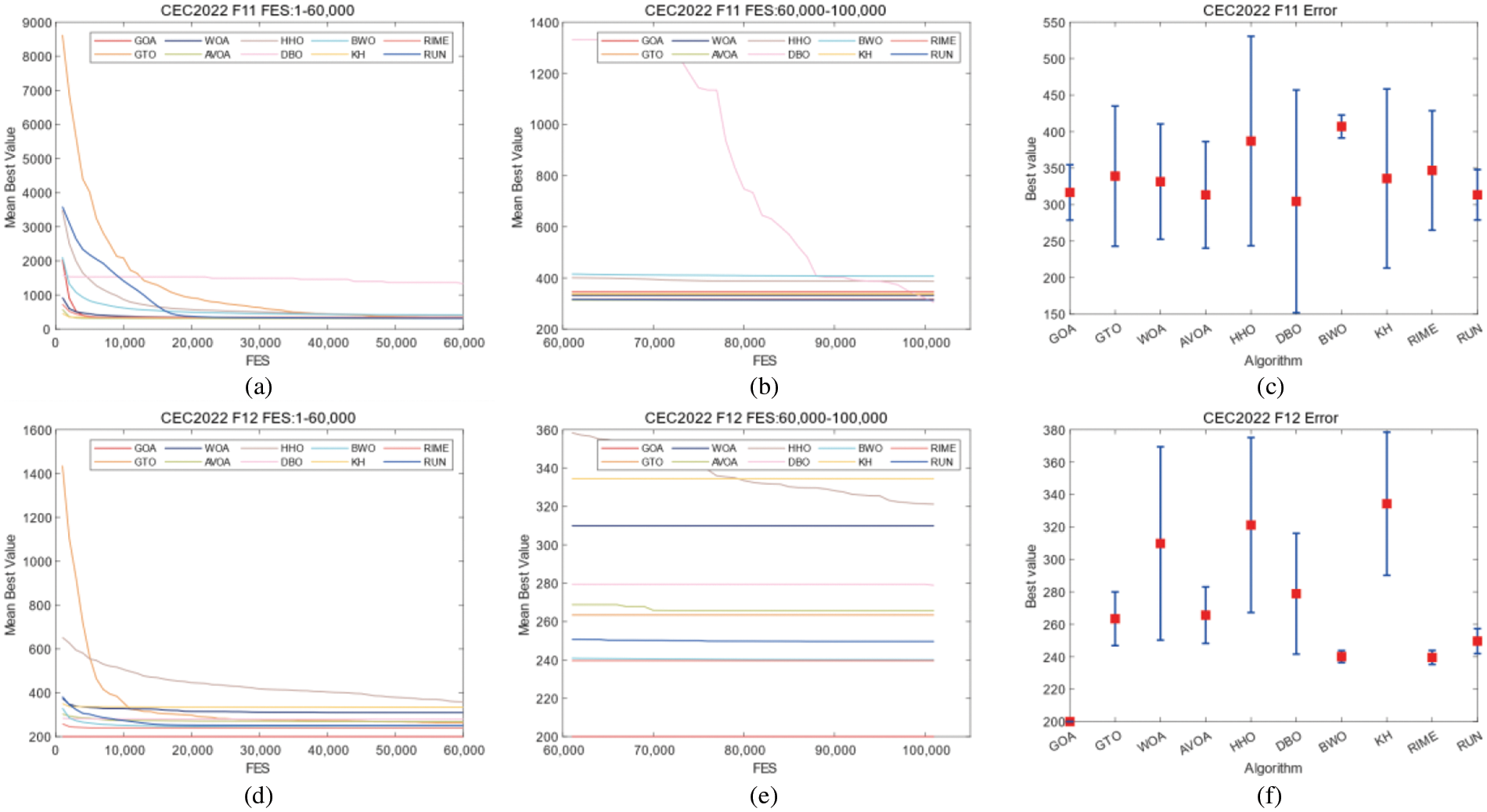
Figure 11: Convergence curves and error bars of WGOA, WOA, AVOA, HHO, DBO, BWO, RUN, KH, GTO and RIME on CEC2022 F11–F12

To further verify the performance of GWOA, a Wilcoxon rank-sum test under 0.05 level was conducted. The experimental results for CEC2017 are presented in Table 8, and the experimental results for CEC2022 are presented in Table 9.

4.3 Discussion

In the CEC2017 benchmark functions, WGOA ranked first in mean values among 10 functions and second among 6 functions. WGOA also achieved the first position in standard deviation among 5 functions and the second position among 4 functions. In a suite comprising 29 test functions and a selection of 10 competing algorithms, the WGOA achieved the foremost position with an average ranking of 3.207, marking it as the preeminent algorithm amongst all contenders.

In the CEC2022 benchmark functions, WGOA obtained the first rank in mean values among 5 functions and the second rank in mean values among 3 functions. WGOA achieved the first position in standard deviation among 3 functions and the second position in standard deviation among 2 functions. Across a total of 12 test functions and a cohort of 10 evaluation algorithms, the WGOA secured the leading average rank of 2.500, situating it at the apex of the algorithmic hierarchy.

The exceptional performance of the Wild Gibbon Optimization Algorithm (WGOA) is attributed to the synergistic interplay between community search and community competition strategies. The community search is dedicated to enhancing the algorithm’s diversity by furnishing it with a plethora of candidate positions in each iteration. Conversely, the community competition aims to augment the algorithm’s precision by exploring more promising solutions within the local search space.

In CEC2017, WGOA outputs best results in F3, F5, F12, F14, F19, F20, F22, F24, F26, and F27. In CEC2022, WGOA outputs best results in F1, F2, F3, F9, F12. However, During the processing of functions F6 and F10 of CEC2022, the WGOA exhibited slow convergence rates. This can be attributed to the algorithm’s search strategies failing to adequately balance exploitation and exploration when addressing such problems. Given the limitations of WGOA in handling these types of issues, integrating an adaptive mechanism into WGOA represents a significant avenue for future work.

5  Conclusions

In this paper, a novel meta-heuristic algorithm called the Wild Gibbon Optimization Algorithm (WGOA) is proposed. The algorithm is inspired by the competition among gibbon populations and is used to solve high-dimensional optimization problems. This algorithm combines a community search strategy and a community competition strategy. The community search strategy is used in the evolution of individual optima, and the community competition strategy is used in the evolution of global optima. The cooperation of these two strategies can be used to balance local search and global search, which can improve the high-dimensional search accuracy. Compared to the original algorithm, both strategies make only linear dimensional changes with O(N) time complexity in terms of computational complexity. In this study, the CEC2017 and CEC2022 benchmark function are selected to evaluate the algorithm, and nine excellent optimization algorithms are selected to compare with WGOA. In the CEC2017, the WGOA achieved the foremost position with an average ranking of 3.207, marking it as the preeminent algorithm amongst all contenders. In the CEC2022, the WGOA secured the leading average rank of 2.500, situating it at the apex of the algorithmic hierarchy. These experimental results indicate that the algorithm has a superior ability in solving optimization problems.

However, on some hybrid functions, the Wild Gibbon Optimization Algorithm (WGOA) does not achieve optimal performance and tends to fall into local optima. Furthermore, an increase in the computational burden may occur as the number of members in the gibbon family continues to grow. Therefore, incorporating an adaptive mechanism into WGOA constitutes an important area of future work. On another note, applying WGOA to real-world problems such as neural network parameter optimization and multi-objective feature selection represents a viable direction for future research.

Acknowledgement: The research was conducted under the auspices of the Hosei International Fund (HIF) Foreign Scholars Fellowship.

Funding Statement: This research was funded by Natural Science Foundation of Hubei Province Grant Numbers 2023AFB003, 2023AFB004; Education Department Scientific Research Program Project of Hubei Province of China Grant Number Q20222208; Natural Science Foundation of Hubei Province of China (No. 2022CFB076); Artificial Intelligence Innovation Project of Wuhan Science and Technology Bureau (No. 2023010402040016); JSPS KAKENHI Grant Number JP22K12185.

Author Contributions: Conceptualization, Jia Guo; methodology, Jia Guo and Jin Wang; software, Ke Yan; validation, Qiankun Zuo; formal analysis, Ruiheng Li; investigation, Zhou He; resources, Jia Guo and Jin Wang; data curation, Jia Guo; writing—original draft preparation, Jia Guo; writing—review and editing, Jin Wang; visualization, Zhou He and Dong Wang; supervision, Yuji Sato; project administration, Jia Guo and Qiankun Zuo; funding acquisition, Jia Guo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Dataset available on request from the authors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. W. Li, D. Y. Xu, J. Geng, and W. C. Hong, “A ship motion forecasting approach based on empirical mode decomposition method hybrid deep learning network and quantum butterfly optimization algorithm,” Nonlinear Dyn, vol. 107, no. 3, pp. 2447–2467, 2022. doi: 10.1007/s11071-021-07139-y. [Google Scholar] [CrossRef]

2. B. S. Yıldız et al., “A novel hybrid arithmetic optimization algorithm for solving constrained optimization problems,” Knowl.-Based Syst., vol. 271, pp. 110554, 2023. doi: 10.1016/j.knosys.2023.110554. [Google Scholar] [CrossRef]

3. S. Li, S. Zhao, Y. Zhang, J. Hong, and W. Chen, “Source-free unsupervised adaptive segmentation for knee joint MRI,” Biomed. Signal Process. Control, vol. 92, pp. 106028, 2024. doi: 10.1016/j.bspc.2024.106028. [Google Scholar] [CrossRef]

4. J. Hong, Y. D. Zhang, and W. Chen, “Source-free unsupervised domain adaptation for cross-modality abdominal multi-organ segmentation,” Knowl.-Based Syst., vol. 250, pp. 109155, 2022. doi: 10.1016/j.knosys.2022.109155. [Google Scholar] [CrossRef]

5. X. Li et al., “EAFP-Med: An efficient adaptive feature processing module based on prompts for medical image detection,” Expert. Syst. Appl., vol. 247, pp. 123334, 2024. doi: 10.1016/j.eswa.2024.123334. [Google Scholar] [CrossRef]

6. J. Wang, S. Y. Lu, S. H. Wang, and Y. D. Zhang, “RanMerFormer: Randomized vision transformer with token merging for brain tumor classification,” Neurocomputing, vol. 573, pp. 127216, 2024. doi: 10.1016/j.neucom.2023.127216. [Google Scholar] [CrossRef]

7. X. Li et al., “DBTN: An adaptive neural network for multiple-disease detection via imbalanced medical images distribution,” Appl. Intell., vol. 54, no. 2, pp. 2188–2210, 2024. doi: 10.1007/s10489-023-05165-4. [Google Scholar] [CrossRef]

8. J. Guo, G. Zhou, K. Yan, B. Shi, Y. Di and Y. Sato, “A novel hermit crab optimization algorithm,” Sci. Rep., vol. 13, pp. 9934, 2023. doi: 10.1038/s41598-023-37129-6. [Google Scholar] [PubMed] [CrossRef]

9. K. Sörensen, “Metaheuristics—The metaphor exposed,” Int. Trans. Operations Res., vol. 22, no. 1, pp. 3–18, 2015. doi: 10.1111/itor.12001. [Google Scholar] [CrossRef]

10. E. S. M. El-kenawy, N. Khodadadi, S. Mirjalili, A. A. Abdelhamid, M. M. Eid and A. Ibrahim, “Greylag goose optimization: Nature-inspired optimization algorithm,” Expert. Syst. Appl., vol. 238, pp. 122147, 2024. doi: 10.1016/j.eswa.2023.122147. [Google Scholar] [CrossRef]

11. B. Abdollahzadeh et al. “Puma optimizer (POA novel metaheuristic optimization algorithm and its application in machine learning,” Cluster Comput., 2024. doi: 10.1007/s10586-023-04221-5. [Google Scholar] [CrossRef]

12. S. Memarian, N. Behmanesh-Fard, P. Aryai, M. Shokouhifar, S. Mirjalili and M. del C. Romero-Ternero, “TSFIS-GWO: Metaheuristic-driven takagi-sugeno fuzzy system for adaptive real-time routing in WBANs,” Appl. Soft Comput., vol. 155, pp. 111427, 2024. doi: 10.1016/j.asoc.2024.111427. [Google Scholar] [CrossRef]

13. J. Guo et al., “A twinning bare bones particle swarm optimization algorithm,” PLoS One, vol. 17, no. 5 May, pp. 1–30, 2022. doi: 10.1371/journal.pone.0267197. [Google Scholar] [PubMed] [CrossRef]

14. C. Huang, X. Li, and Y. Wen, “AN OTSU image segmentation based on fruitfly optimization algorithm,” Alex. Eng. J., vol. 60, no. 1, pp. 183–188, 2021. doi: 10.1016/j.aej.2020.06.054. [Google Scholar] [CrossRef]

15. D. Chen, Y. Ge, Y. Wan, Y. Deng, Y. Chen and F. Zou, “Poplar optimization algorithm: A new meta-heuristic optimization technique for numerical optimization and image segmentation,” Expert. Syst. Appl., vol. 200, pp. 117118, 2022. doi: 10.1016/j.eswa.2022.117118. [Google Scholar] [CrossRef]

16. S. Chakraborty and K. Mali, “SuFMoFPA: A superpixel and meta-heuristic based fuzzy image segmentation approach to explicate COVID-19 radiological images,” Expert. Syst. Appl., vol. 167, pp. 114142, 2021. doi: 10.1016/j.eswa.2020.114142. [Google Scholar] [PubMed] [CrossRef]

17. X. Deng, R. Li, L. Zhao, K. Wang, and X. Gui, “Multi-obstacle path planning and optimization for mobile robot,” Expert. Syst. Appl., vol. 183, pp. 115445, 2021. doi: 10.1016/j.eswa.2021.115445. [Google Scholar] [CrossRef]

18. Md R. Islam, P. Protik, S. Das, and P. K. Boni, “Mobile robot path planning with obstacle avoidance using chemical reaction optimization,” Soft Comput., vol. 25, no. 8, pp. 6283–6310, 2021. doi: 10.1007/s00500-021-05615-6. [Google Scholar] [CrossRef]

19. R. Chen, H. Shen, and Y. Lai, “A metaheuristic optimization algorithm for energy efficiency in digital twin,” Internet of Things and Cyber-Phys. Syst., vol. 2, pp. 159–169, 2022. doi: 10.1016/j.iotcps.2022.08.001. [Google Scholar] [CrossRef]

20. M. Khanali et al. “Multi-objective optimization of energy use and environmental emissions for walnut production using imperialist competitive algorithm,” Appl. Energy, vol. 284, pp. 116342, 2021. doi: 10.1016/j.apenergy.2020.116342. [Google Scholar] [CrossRef]

21. A. F. Güven and M. M. Samy, “Performance analysis of autonomous green energy system based on multi and hybrid metaheuristic optimization approaches,” Energy Convers. Manag., vol. 269, pp. 116058, 2022. doi: 10.1016/j.enconman.2022.116058. [Google Scholar] [CrossRef]

22. H. Su et al. “RIME: A physics-based optimization,” Neurocomputing, vol. 532, pp. 183–214, 2023. doi: 10.1016/j.neucom.2023.02.010. [Google Scholar] [CrossRef]

23. P. C. Song, S. C. Chu, J. S. Pan, and H. Yang, “Simplified phasmatodea population evolution algorithm for optimization,” Complex Intell. Syst., vol. 8, no. 4, pp. 2749–2767, 2022. doi: 10.1007/s40747-021-00402-0. [Google Scholar] [CrossRef]

24. D. Połap and M. Woźniak, “Red fox optimization algorithm,” Expert. Syst. Appl., vol. 166, pp. 114107, 2021. doi: 10.1016/j.eswa.2020.114107. [Google Scholar] [CrossRef]

25. X. L. Li, R. Serra, and J. Olivier, “A multi-component PSO algorithm with leader learning mechanism for structural damage detection,” Appl. Soft Comput., vol. 116, pp. 108315, 2022. doi: 10.1016/j.asoc.2021.108315. [Google Scholar] [CrossRef]

26. H. Zhang and Q. Peng, “PSO and K-means-based semantic segmentation toward agricultural products,” Future Gener. Comput. Syst., vol. 126, pp. 82–87, 2022. doi: 10.1016/j.future.2021.06.059. [Google Scholar] [CrossRef]

27. D. Li, W. Guo, A. Lerch, Y. Li, L. Wang and Q. Wu, “An adaptive particle swarm optimizer with decoupled exploration and exploitation for large scale optimization,” Swarm Evol. Comput., vol. 60, 2021. doi: 10.1016/j.swevo.2020.100789. [Google Scholar] [CrossRef]

28. L. Zhang, T. Gao, G. Cai, and K. L. Hai, “Research on electric vehicle charging safety warning model based on back propagation neural network optimized by improved gray wolf algorithm,” J. Energy Storage, vol. 49, pp. 104092, 2022. doi: 10.1016/j.est.2022.104092. [Google Scholar] [CrossRef]

29. E. A. Atta, A. F. Ali, and A. A. Elshamy, “A modified weighted chimp optimization algorithm for training feed-forward neural network,” PLoS One, vol. 18, no. 3, pp. e0282514, Mar. 2023. doi: 10.1371/journal.pone.0282514. [Google Scholar] [PubMed] [CrossRef]

30. J. Guo, J. Li, Y. Sato, and Z. Yan, “A gated recurrent unit model with fibonacci attenuation particle swarm optimization for carbon emission prediction,” Processes, vol. 12, pp. 1063, 2024. doi: 10.3390/pr12061063. [Google Scholar] [CrossRef]

31. N. Bacanin et al., “Hybridized sine cosine algorithm with convolutional neural networks dropout regularization application,” Sci. Rep., vol. 12, no. 1, pp. 6302, 2022. doi: 10.1038/s41598-022-09744-2. [Google Scholar] [PubMed] [CrossRef]

32. M. Shokouhifar, “FH-ACO: Fuzzy heuristic-based ant colony optimization for joint virtual network function placement and routing,” Appl. Soft Comput., vol. 107, pp. 107401, 2021. doi: 10.1016/j.asoc.2021.107401. [Google Scholar] [CrossRef]

33. L. Qian, M. Khishe, Y. Huang, and S. Mirjalili, “SEB-ChOA: An improved chimp optimization algorithm using spiral exploitation behavior,” Neural Comput. Appl., vol. 36, no. 9, pp. 4763–4786, 2024. doi: 10.1007/s00521-023-09236-y. [Google Scholar] [CrossRef]

34. L. Jovanovic et al., “Multi-step crude oil price prediction based on LSTM approach tuned by salp swarm algorithm with disputation operator,” Sustainability, vol. 14, pp. 14616, Nov. 2022. doi: 10.3390/su142114616. [Google Scholar] [CrossRef]

35. C. Tang, W. Sun, M. Xue, X. Zhang, H. Tang and W. Wu, “A hybrid whale optimization algorithm with artificial bee colony,” Soft Comput., vol. 26, no. 5, pp. 2075–2097, 2022. doi: 10.1007/s00500-021-06623-2. [Google Scholar] [CrossRef]

36. S. Thawkar, S. Sharma, M. Khanna, and L. Kumar Singh, “Breast cancer prediction using a hybrid method based on butterfly optimization algorithm and ant lion optimizer,” Comput. Biol. Med., vol. 139, pp. 104968, 2021. doi: 10.1016/j.compbiomed.2021.104968. [Google Scholar] [PubMed] [CrossRef]

37. S. Deb and X. Z. Gao, “A hybrid ant lion optimization chicken swarm optimization algorithm for charger placement problem,” Complex Intell. Syst., vol. 8, no. 4, pp. 2791–2808, 2022. doi: 10.1007/s40747-021-00510-x. [Google Scholar] [CrossRef]

38. M. M. Emam, E. H. Houssein, and R. M. Ghoniem, “A modified reptile search algorithm for global optimization and image segmentation: Case study brain MRI images,” Comput. Biol. Med., vol. 152, pp. 106404, 2023. doi: 10.1016/j.compbiomed.2022.106404. [Google Scholar] [PubMed] [CrossRef]

39. F. MiarNaeimi, G. Azizyan, and M. RasKHi, “Horse herd optimization algorithm: A nature-inspired algorithm for high-dimensional optimization problems,” Knowl.-Based Syst., vol. 213, pp. 106711, 2021. doi: 10.1016/j.knosys.2020.106711. [Google Scholar] [CrossRef]

40. W. Ma, X. Zhou, H. Zhu, L. Li, and L. Jiao, “A two-stage hybrid ant colony optimization for high-dimensional feature selection,” Pattern Recognit., vol. 116, pp. 107933, 2021. doi: 10.1016/j.patcog.2021.107933. [Google Scholar] [CrossRef]

41. C. Zhong, G. Li, and Z. Meng, “Beluga whale optimization: A novel nature-inspired metaheuristic algorithm,” Knowl. Based Syst., vol. 251, pp. 109215, 2022. doi: 10.1016/j.knosys.2022.109215. [Google Scholar] [CrossRef]

42. B. Abdollahzadeh, F. S. Gharehchopogh, and S. Mirjalili, “African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems,” Comput. Ind. Eng., vol. 158, pp. 107408, 2021. doi: 10.1016/j.cie.2021.107408. [Google Scholar] [CrossRef]

43. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja and H. Chen, “Harris hawks optimization: Algorithm and applications,” Future Gener. Comput. Syst., vol. 97, pp. 849–872, 2019. doi: 10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]

44. J. Xue and B. Shen, “Dung beetle optimizer: A new meta-heuristic algorithm for global optimization,” J. Supercomput., vol. 79, no. 7, pp. 7305–7336, 2023. doi: 10.1007/s11227-022-04959-6. [Google Scholar] [CrossRef]

45. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

46. I. Ahmadianfar, A. A. Heidari, A. H. Gandomi, X. Chu, and H. Chen, “RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method,” Expert. Syst. Appl., vol. 181, pp. 115079, 2021. doi: 10.1016/j.eswa.2021.115079. [Google Scholar] [CrossRef]

47. A. H. Gandomi and A. H. Alavi, “Krill herd: A new bio-inspired optimization algorithm,” Commun. Nonlinear Sci. Numer. Simul., vol. 17, no. 12, pp. 4831–4845, 2012. doi: 10.1016/j.cnsns.2012.05.010. [Google Scholar] [CrossRef]

48. B. Abdollahzadeh, F. Soleimanian Gharehchopogh, S. Mirjalili, “Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems,” Int. J. Intell. Syst., vol. 36, no. 10, pp. 5887–5958, Oct. 2021. doi: 10.1002/int.22535. [Google Scholar] [CrossRef]

49. G. Zhou, J. Du, J. Guo, and G. Li, “A novel hippo swarm optimization: For solving high-dimensional problems and engineering design problems,” J. Comput. Des. Eng., 2024. doi: 10.1093/jcde/qwae035. [Google Scholar] [CrossRef]