QBIoT: A Quantum Blockchain Framework for IoT with an Improved Proof-of-Authority Consensus Algorithm and a Public-Key Quantum Signature

1  Introduction

The Internet of Things (IoT) has rapidly evolved, connecting many smart devices and thus becoming an integral part of our daily lives [1]. This expansion has led to extensive data collection and network communication, offering enhanced convenience and intelligence for individuals and industrial operations [2]. However, IoT systems’ diverse, distributed, and complex nature [3] has given rise to critical challenges, including privacy breaches and data security concerns [4].

The advent of blockchain technology provides an effective solution to address these challenges. Originally introduced by Nakamoto for Bitcoin [5], blockchain is a decentralized ledger technology that securely records transactions or data blocks chronologically, forming an immutable chain. Blockchain is not a new technology in itself; rather, it is an amalgamation of existing innovations, such as peer-to-peer (P2P) networking, hashing algorithms, consensus mechanisms, asymmetric cryptography, and smart contracts. It offers a robust foundation for establishing trust and ensuring data security among IoT devices through decentralized, secure data storage and automated smart contract execution. Fig. 1 illustrates a typical use case of blockchain in IoT scenarios.

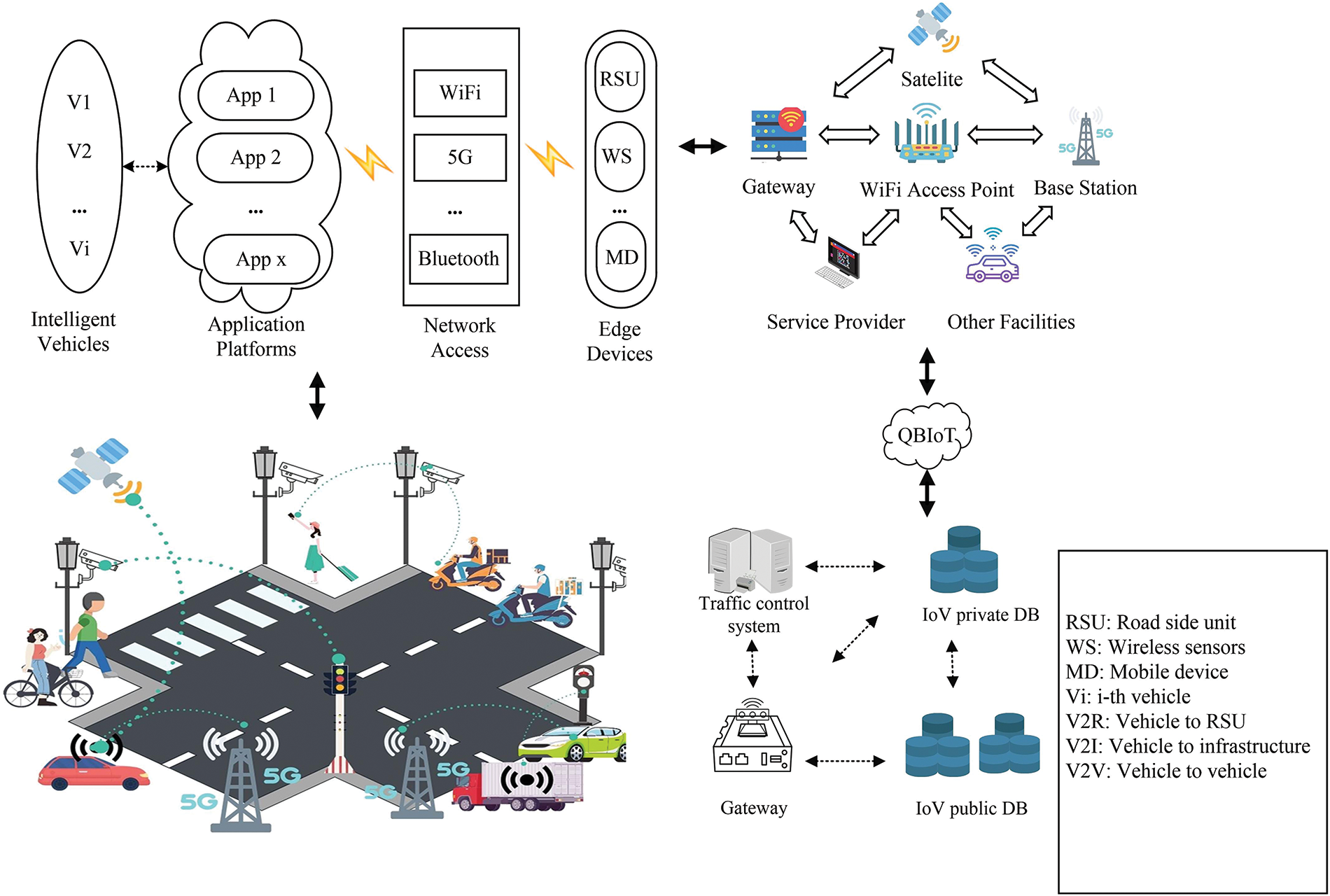
Fig. 1: A typical application of blockchain in IoT

Fig. 1 illustrates the communication links in a typical internet of vehicle (IoV) environment, highlighting the importance of IoT in enabling connectivity between vehicles and their surroundings. Smart vehicles establish various communication links like vehicle-to-vehicle (V2V), vehicle-to-roadside unit (V2R), and vehicle-to-infrastructure (V2I) through embedded processors in OBUs and wireless technology. Data flow starts in the vehicle, is processed by the application platform, and transmitted efficiently using technologies like WiFi, CarPlay, and 5G. Edge devices such as mobile devices and sensors collect and process data, sending it to satellites, base stations, and wider network nodes. The security of data flow is maintained through QBIoT technology, ensuring a secure connected car environment.

Numerous attempts have been made to integrate blockchain with IoT in recent years. In 2021, Rathee et al. [6] proposed a solution based on a hybrid blockchain method to enhance the security of multinational-scale Industrial Internet of Things (IIoT). The solution achieves significant efficiency improvements in dealing with DoS and DDoS threats, authentication delays and message tampering attacks, but neglects quantum computing attacks. In 2022, Kouanou et al. [7] proposed a blockchain method to secure data within an IoT architecture, developing an architecture for a smart home using blockchain. Data collected were stored in the EOS blockchain, demonstrating the ability to handle over 500 data points per second. However, their solution did not account for quantum adversaries. In 2023, Sharma et al. [8] designed a blockchain-based application for managing healthcare certificates, serving as a communication medium between the underlying blockchain network and user entities, such as IoT devices, for generating and verifying medical certificates. While their work effectively showcased blockchain’s applicability in the IoT, it did not address quantum computing attacks.

However, quantum computing breakthroughs have begun to threaten the security foundations of classical blockchain [9]. The Shor quantum algorithm [10–12] can efficiently break traditional encryption algorithms like RSA and Elliptic Curve Cryptography (ECC), potentially enabling attackers to exploit quantum computing to steal private keys or forge digital signatures, compromising data integrity and confidentiality within the blockchain ledger. The Grover search algorithm [13] can easily find collisions in hash functions, making hash collision attacks more accessible and compromising data integrity. In response to these emerging threats, researchers have started exploring quantum-resistant cryptographic algorithms and techniques to bolster blockchain security.

In 2018, Kiktenko et al. [14] designed a quantum-secured blockchain and implemented progressive, secure authentication using quantum key distribution over an urban fiber network. In 2021, Chen et al. [15] developed a post-quantum blockchain scheme for smart cities, which is capable of withstanding quantum computing attacks. Their scheme featured a novel post-quantum proof-of-work consensus protocol for record-keeping and an identity-based post-quantum signature for transaction verification. However, the detailed block structure was not presented in their work. Also, in 2021, Saha et al. [16] introduced a post-quantum blockchain solution that used lattice polynomials for identity-based encryption (IBE) and aggregate signatures for reaching consensus in blockchain applications. Their experiments demonstrated efficiency in delay, throughput, energy consumption, and complexity. In 2022, Ye et al. [17] proposed a quantum-assisted blockchain for IoT based on quantum signatures. However, their scheme had a flaw in the block structure design due to the use of a Merkle tree structure, rendering transaction records on the chain vulnerable to second pre-image attacks by quantum adversaries. In 2022, Qu et al. [18] developed a quantum blockchain-enabled model for securely sharing private electronic medical records in the Internet of Medical Things (IoMT), deploying entangled states for block linkage. Their novel block structure recorded the hash value of each block with just a single qubit. In 2023, Zhu et al. [19] introduced a data-sharing scheme for electronic medical records, combining quantum keys with blockchain. In the same year, Singh et al. [20] presented a secure scheme for transaction establishment in the blockchain using quantum teleportation and a quantum digital signature. Also, in 2023, Zhang et al. [21] proposed a secure energy scheme for the Internet of Vehicles (IoV) based on post quantum blockchain, which can improve energy utilization efficiency and enrich the application of blockchain technology in IoV.

While these works have made notable strides in achieving post-quantum secure blockchain solutions, research in this area remains limited, particularly in IoT. Despite the increasing threat of quantum computing to blockchain, few quantum-resistant blockchain solutions are designed specifically for IoT. Existing quantum-resistant blockchain solutions commonly face three key challenges: (1) Utilizing insecure data structures like the Merkle tree in the block architecture, exposing transaction records to potential cyberattacks by quantum adversaries. (2) Employing transaction signature schemes based on post-quantum cryptography consumes substantial computing and storage resources, leading to transaction inefficiency. Alternatively, using a quantum signature scheme, while secure, also consumes significant quantum resources, causing system inefficiencies. (3) Ignoring the risk of a single point of failure in the consensus mechanism due to the paralysis of the accounting node.

With the significant enhancement of quantum computing power, traditional computational secure systems and IoT protection face unprecedented challenges. This paper specifically investigates the emerging network security threats in the realm of IoT blockchain, while also addressing the pressing need to combat the obstacles posed by anti-quantum blockchain technology.

It proposes a blockchain solution based on public key quantum signatures and quantum hash functions tailored for IoT. Moreover, as the computational power of quantum computers increases, the ability to solve difficult problems such as lattice cryptography increases, which will reduce the security level of post-quantum cryptography. However, the security of quantum cryptography is guaranteed by the principles of quantum mechanics, and its security performance will remain changed. Therefore, the security of our proposed scheme is exceptionally high. The primary contributions of our work are as follows:

1.    Construction of the QBIoT Model: Introducing a QBIoT model to enhance IoT security using quantum methods, effectively defending against both quantum and classical cyberattacks.

2.    Complete Architecture of QBIoT: Detailing the QBIoT architecture, including the adoption of a quantum hash function for tamper-proof storage of published transaction records, the development of public key quantum signature for transaction verification. Additionally, we firstly give a novel consensus algorithm, Proof of Authority with Random Election (PoARE), to allocate the bookkeeping right and generate new blocks.

3.    Security Analysis of QBIoT: Conducting a thorough security analysis of QBIoT, demonstrating its correctness and security while highlighting its advantages compared to peer solutions.

The remainder of this paper is structured as follows: Section 2 provides background information and introduces related work and the underlying technologies we employ. Section 3 outlines the QBIoT Model and presents the QBIoT architecture, including a detailed explanation of the PoARE consensus mechanism. Section 4 offers a comprehensive transaction and block generation workflow, while Section 5 provides a detailed security analysis of QBIoT. Finally, Section 6 concludes our work.

2  Preliminary

In recent years, two significant developments have emerged that are pivotal to our understanding of the security landscape. Firstly, the rapid advancements in quantum computing technology have brought us closer to realizing large-scale quantum computers. This breakthrough has presented an increasingly severe security challenge to blockchain systems. Secondly, the field of quantum communication, notably quantum key distribution (QKD) and quantum cryptography, has evolved rapidly, offering a new arsenal of technologies to fortify blockchain security.

QKD is a quantum-mechanical approach for secure key transmission. It leverages the principles of quantum mechanics to achieve secure key distribution by exploiting the non-clonability of non-orthogonal quantum states. Since the inception of the first QKD protocol, BB84, in 1984, numerous executable QKD protocols have been proposed. Some companies have even begun to commercialize QKD technology to provide secure communication solutions.

A quantum hash function (QHF) [22] is designed to withstand attacks from quantum computers. It employs the principles of quantum mechanics to ensure that the hash function output remains resistant to collision and pre-image attacks, both from classical and quantum computers. There are two methods for researching quantum hash functions [23]. One is based on quantum one-way function and the other is based on quantum simulation. In recent years, quantum hash functions have gained prominence in quantum cryptography research. In 2021, Yang et al. [24] demonstrated a hash function based on controlled quantum walk (CQW) with broken-line-type decoherence on a cycle. In 2022, Zhou et al. [25] introduced a hash function utilizing controlled alternating quantum walks with memory. Additionally, in 2022, Shi et al. [26] created a quantum hash function through grouped coarse-grained boson sampling (GCGBS), offering predictable outputs and repeatability. For our work, we adopt the QHF as presented in the literature [27].

Quantum Digital Signature (QDS) is a cryptographic technique that deploys quantum methods to provide immunity to quantum computing attacks. It utilizes quantum mechanics principles to sign messages among multiple parties with unconditional security. Quantum digital signatures were initially proposed by Gottesman et al. in 2001 [28], and since then, several practical QDS schemes have been introduced and implemented [29–32]. Moreover, quantum signatures have seen substantial practical advancements. In 2023, Yin et al. [33] introduced the concept of “one hash at a time,” moving away from the classical GC01 signature paradigm and creating a new paradigm of quantum digital signatures. This approach achieves information-theoretically secure digital signatures, enhancing the efficiency of quantum digital signatures by orders of magnitude. Their groundbreaking work has propelled quantum digital signatures into the commercialization stage, providing robust protection for information authenticity, integrity, and non-repudiation. In the same year, Li et al. [34] introduced an efficient quantum signature scheme and conducted physical experiments.

Eq. (2) illustrates how a single qubit rotation operation transforms the state of a qubit from its initial state, |ζ⟩, to a new state, |ζ′⟩, after the operation.

|ζ⟩=α|0⟩+β|1⟩(1)

R(θ)|ζ⟩=R(θ)(α|0⟩+β|1⟩)=(αcos⁡θ−βsin⁡θ)|0⟩+(βcos⁡θ+αsin⁡θ)|1⟩(2)

Furthermore, insights from various studies on quantum blockchain technology have provided valuable guidance. In 2018, Fedorov et al. [35] summarized the quantum computing threat to traditional blockchains. In 2019, Sun et al. [36] introduced a quantum-secured private blockchain framework to resist quantum computing attacks. This framework incorporates a digital signature protocol based on QKD and employs a voting-based consensus algorithm to achieve blockchain consensus. In 2020, Coladangelo et al. [37] developed a hybrid classical-quantum payment scheme using quantum states as a form of “banknote”. This approach addresses the trust issues associated with quantum banknotes in public-key quantum currency systems. However, their approach primarily relied on classical blockchains and did not outline the design of a quantum blockchain. In 2021, Iovane [38] validated blocks and allocated new blocks in the blockchain using a multiscale approach combined with Quantum and Relativistic Mechanics. In 2022, Azzaoui et al. [39] enhanced the security and feasibility of their proposed IoMT architecture through Quantum Terminal Machines (QTM) and blockchain technology. Their work presented a secure and scalable solution for intelligent computing in medical scenarios. In 2024, Kumar et al. [40] proposed a quantum blockchain architecture using cyclic QSCD and QKD. They adopted the Quantum-Secured Yet Another Consensus (QSYAC) algorithm to ensure the reliability and fault tolerance of the framework. Also, in 2024, Jiang et al. [41] designed a novel medical data processing system based on quantum blockchain (QB-IMD). They proposed a quantum blockchain architecture and a novel electronic medical record algorithm (QEMR) to ensure that medical data is tamper-proof.

3  QBIoT

The proposed QBIoT architecture is divided into five layers: 1) Perception Layer; 2) Communication Layer; 3) Data Storage Layer; 4) Blockchain Layer; 5) Application Layer. Additionally, QBIoT utilizes a dual-network architecture that combines QKD networks with classical networks. The structural diagram of our QBIoT is presented in Fig. 2. The following will provide a detailed explanation of the functions of each layer:

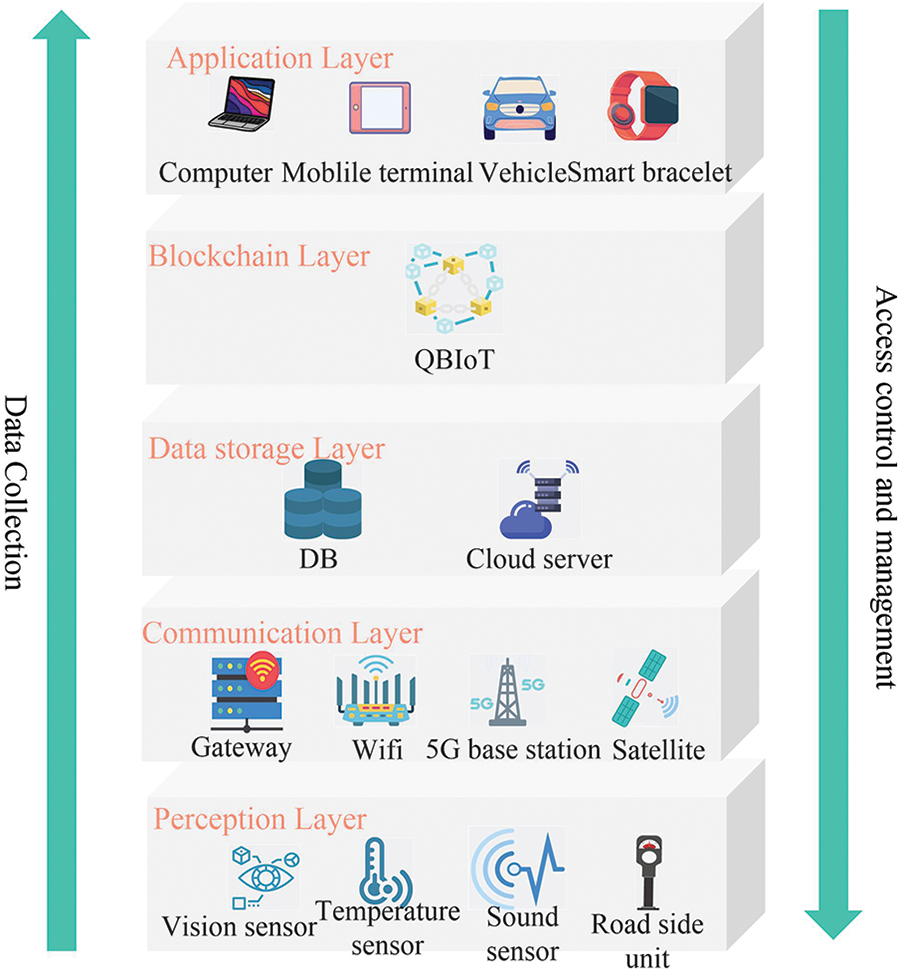
Fig. 2: The QBIoT-based framework for IoT

Perception Layer: This layer encompasses IoT devices, sensors, and physical entities responsible for sensing and data collection. Here, data generated by these devices is captured, stored, and subjected to initial processing.

Communication Layer: Data collected in the Perception Layer is transmitted to the blockchain network in this layer. This communication can be facilitated through various technologies, including both wired and wireless methods. Data is encrypted and securely transmitted within this layer.

Data Storage Layer: Validated data from the blockchain is stored in this layer using distributed storage platforms like the InterPlanetary File System (IPFS) or cloud servers. On-chain, only the data’s digest value, storage address, size, and other necessary information are retained, with the original data stored off-chain.

Blockchain Layer: This layer comprises the blockchain network, nodes, and smart contracts. The nodes refer to devices or systems participating in the blockchain network, including private databases, publicly accessible databases, and so on. Specifically, the communication between nodes is built upon a dual-layer network, which integrates the QKD network and the classical network. Here, IoT data is recorded onto the blockchain to ensure immutability and traceability. Smart contracts facilitate automated conditional logic, including data validation, authorization, and exchange. This layer transforms the traditional client-server (C-S) model of IoT communication into a distributed peer-to-peer model, providing enhanced privacy and security for data.

Application Layer: This layer houses various IoT services and applications for processing and analyzing data stored on the blockchain.

Fig. 3 illustrates the application of the QBIoT framework within a smart residential community. It features a range of network devices, including home gateways, public gateways, and data processing equipment such as cloud storage servers. The community’s IoT devices encompass smart door locks, cameras, environmental sensors, smart meters, and others used to monitor and collect diverse information within the community, such as access control, security monitoring, environmental parameters, and energy consumption.

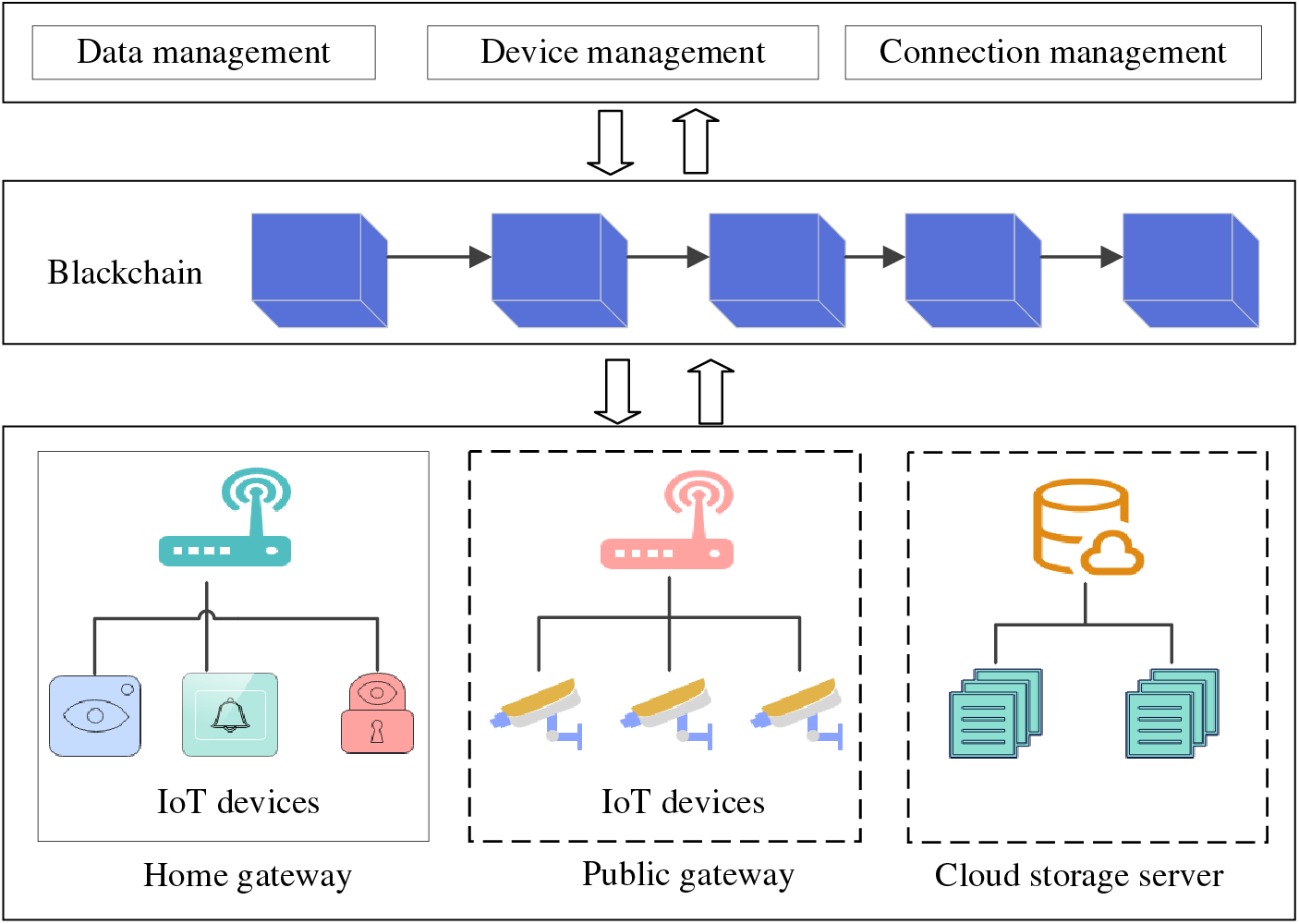
Figure 3: QBIoT framework in a smart residential community

The home gateway serves as a blockchain network node, bridging the public blockchain network and the terminal devices within households. The public gateway records data information collected by end devices within the neighborhood, and the cloud storage server connects to the blockchain network to provide on-chain permission verification and off-chain storage services.

3.1 The Block Structure of QBIoT

Data in a blockchain is structured into blocks, which are linked to ensure immutability. Each data block consists of a blockhead and body, as shown in Fig. 4. The block header contains essential information, such as the block number, the accounting node, the QHF value of the current block, the QHF value of the previous block, and the block’s creation timestamp. The block body holds transaction records that quantum signatures have verified.

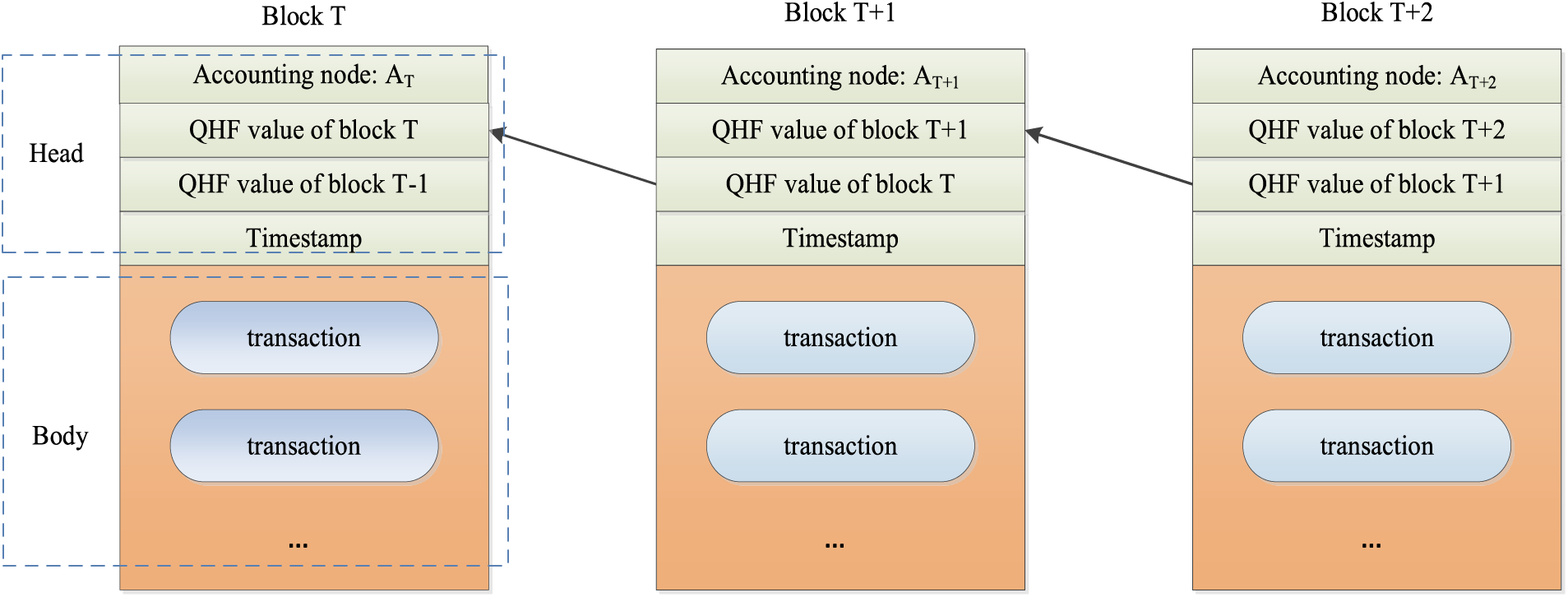
Figure 4: Block structure of QBIoT

In literature [17], Ye et al. used classical hash functions and Merkle tree structures to construct and verify blocks, ensuring the integrity and security of transactions. However, the Merkle tree structure is vulnerable to quantum computing attacks. As quantum computing advances, the susceptibility of the traditional hash function-based Merkle tree structure to pre-image collision attacks becomes increasingly evident [42]. To enhance blockchain security and protect against quantum computing attacks, specifically second pre-image attacks by the Grover algorithm, we incorporate a quantum hash function within QBIoT.

3.2 Blockchain Structure of QBIoT

Given the potential threat posed by quantum adversaries, QBIoT employs the quantum hash function to generate the QHF value for each block. These QHF values create interconnectivity among the blocks. In a transaction record, a third-party verifier can confirm the authenticity of the transaction content using the signer’s public key to verify the signature. Once enough transactions are collected, the leader node compiles them into a new block, initiates a vote, and broadcasts the valid block to other validator nodes in the blockchain network. The blockchain structure is depicted in Fig. 5.

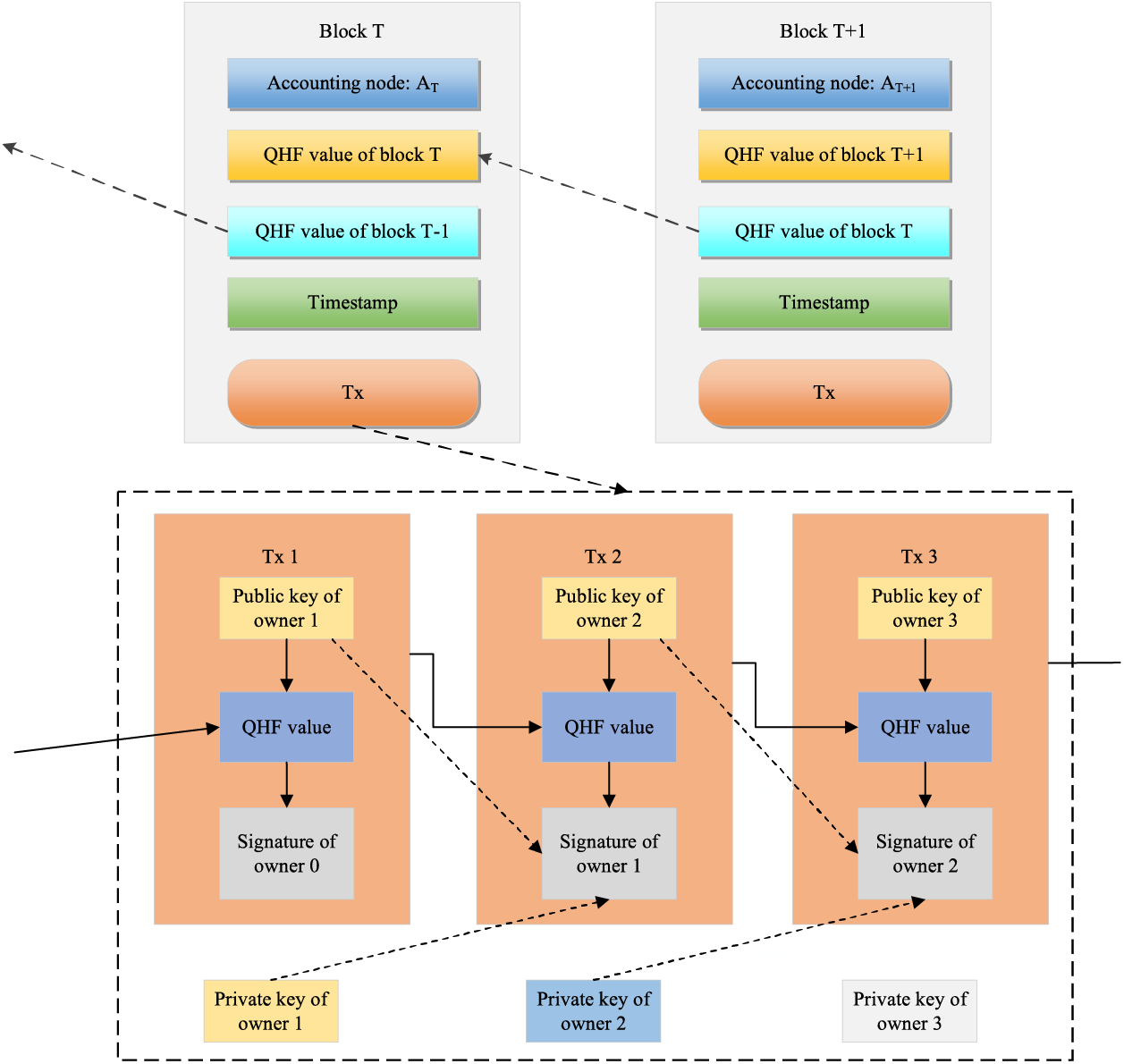
Figure 5: Blockchain structure of QBIoT

4  The Workflow in QBIoT

For better understanding, the following Table 1 lists some important symbols used in this paper.

4.1 New Block Generation in QBIoT

In a typical blockchain system, a jointly elected accounting node assumes responsibility for proposing and generating new blocks. In QBIoT, this process is governed by the PoARE consensus mechanism, which will be comprehensively described in this section.

The consensus mechanism is the linchpin of blockchain technology, ensuring that all nodes within the blockchain network achieve consensus on data and transactions. It significantly influences crucial blockchain characteristics such as security, scalability, and decentralization. Popular consensus mechanisms in use today include Proof of Work (PoW), Proof of Stake (PoS), Delegated Proof of Stake (DPoS), Proof of Authority (PoA), Practical Byzantine Fault Tolerance (PBFT), and more. Selecting an appropriate consensus mechanism depends on a blockchain project’s specific goals and requirements. Table 2 compares mainstream consensus protocols based on eight key aspects.

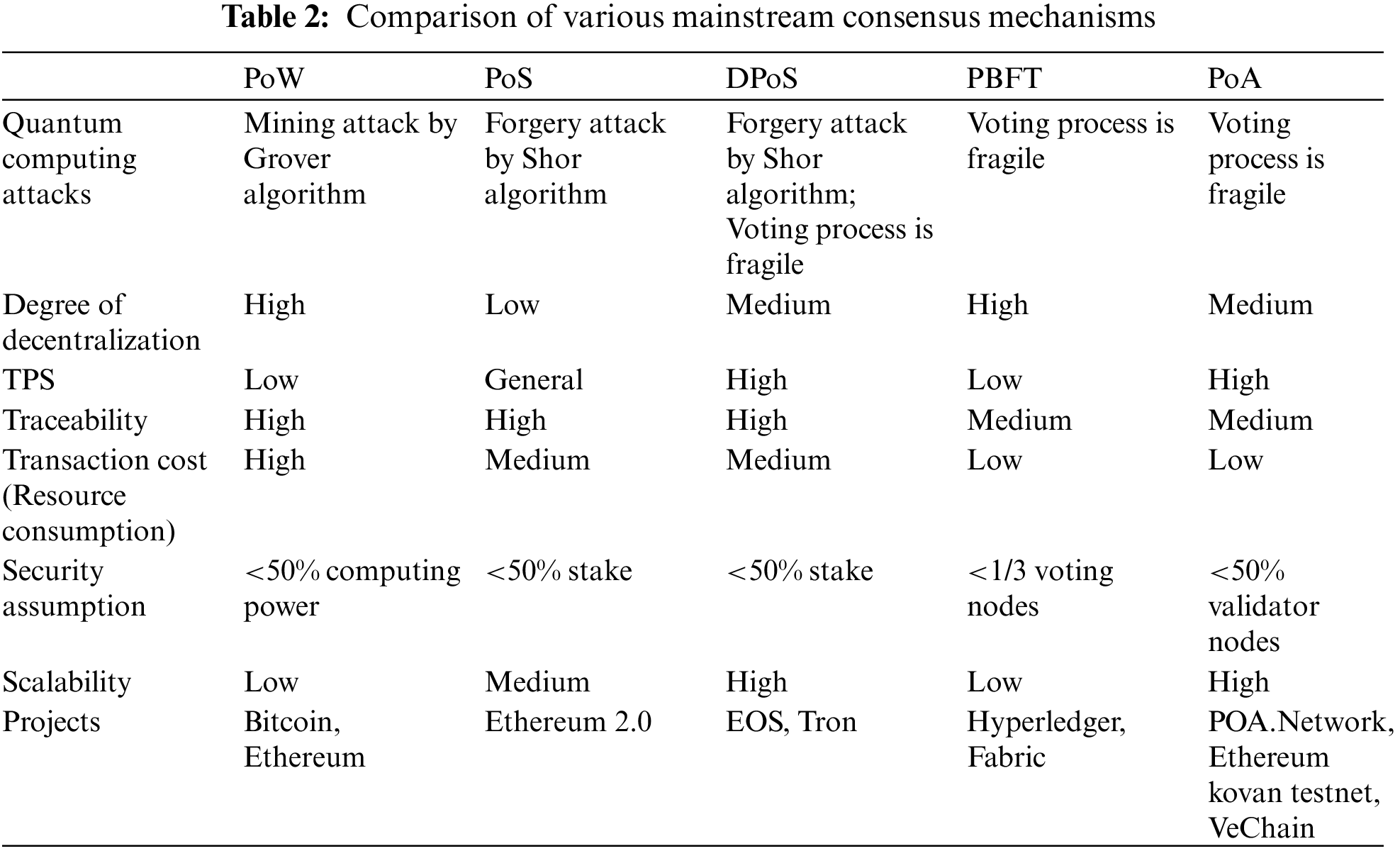
The PoW [43] consensus mechanism, initially proposed by Dwork et al., is utilized in cryptocurrencies like Bitcoin and Ethereum. PoW involves the selection of an accounting node through mining, where miners compete to find a nonce value that satisfies a specific condition (i.e., the hash value of the nonce meeting certain criteria). PoW is susceptible to mining attacks [44], as the Grover quantum algorithm accelerates the search for the pre-image of the hash function. This means that if a competitor with a quantum computer joins the mining activity, he gains a substantial advantage, leading to quicker mining rewards and bookkeeping rights. Literature [44] indicated that a quantum adversary employing the enhanced Grover algorithm can successfully mine on the Bitcoin platform in just 2 s, whereas an ordinary classical computer miner would take 465 days. Consequently, the PoW consensus mechanism is considered unfair due to quantum computing advancements. Furthermore, the PoW mining process is highly energy-intensive, consuming significant power and computing resources, which makes it inefficient.

In the PoS consensus mechanism, stakers compete for bookkeeping rights by pledging their stake, which involves public key signatures. These signatures are vulnerable to key recovery attacks by Shor’s algorithm. As a result, a quantum adversary can use Shor’s algorithm to deduce the staker’s private key from the existing signature and public key, leading to the loss of assets. Furthermore, the PoS consensus mechanism lacks sufficient fairness and decentralization, as large stakeholders can exploit their stake’s advantage to obtain near-monopoly bookkeeping rights, which contradicts the original decentralization concept in blockchain design.

Similar to PoS, in the DPoS [45] consensus mechanism, asset staking transactions are susceptible to quantum computing attacks by Shor’s algorithm. Moreover, DPoS necessitates elections that rely on voting algorithms often employing classical public-key signatures [46], making them vulnerable to quantum computing attacks.

The PBFT [47] consensus mechanism is hindered by poor scalability [48], limiting the scale of the blockchain network. Once the number of nodes reaches a certain threshold, the efficiency of reaching consensus decreases significantly, rendering PBFT unsuitable for our consideration.

The PoA [49] consensus mechanism, proposed by Gavin Wood, the founder of Ethereum, in 2004, is currently implemented in projects like Aura and Clique blockchains. PoA relies on the reputation of a real identity as collateral. It follows a rigorous vetting process for regular nodes seeking authority node status. Once nodes pass the qualification audit, they become authority nodes and publish their identity information on the public network, ensuring their honesty and trustworthiness. Authority nodes possess the privilege to validate transactions, and during a consensus round, the validating nodes on the validating node list take turns serving as the leader node, each with an equal time allocation. This setup promotes fairness and impartiality.

For QBIoT, the selected consensus mechanism must offer relatively high transactions per second (TPS), scalability, low transaction costs, and equitable distribution of bookkeeping rights. Consequently, we adopt an enhanced PoA mechanism known as proof of authority with random election (PoARE).

QBIoT utilizes the PoARE consensus mechanism for electing the accounting node. PoARE is a more secure consensus mechanism based on improving the PoA consensus mechanism.

In PoA, new block creation depends on a set of authenticated, validator nodes chosen through a trustable mechanism. At the beginning of each consensus cycle, certain rules govern the election of a leader node from among the validator nodes. This leader node is granted the privilege to create a new block. The leader node produces a candidate block within its designated time frame and broadcasts it throughout the network. Validator nodes receive the candidate block, collectively verifying its validity through voting. If the candidate block garners more than half of the votes in approval, it is accepted by the blockchain system. Subsequently, all validator nodes append it to their blockchain ledger. Due to the controlled identity of the leader node, PoA ensures the proper generation of blocks, thereby upholding the stability and security of the blockchain system.

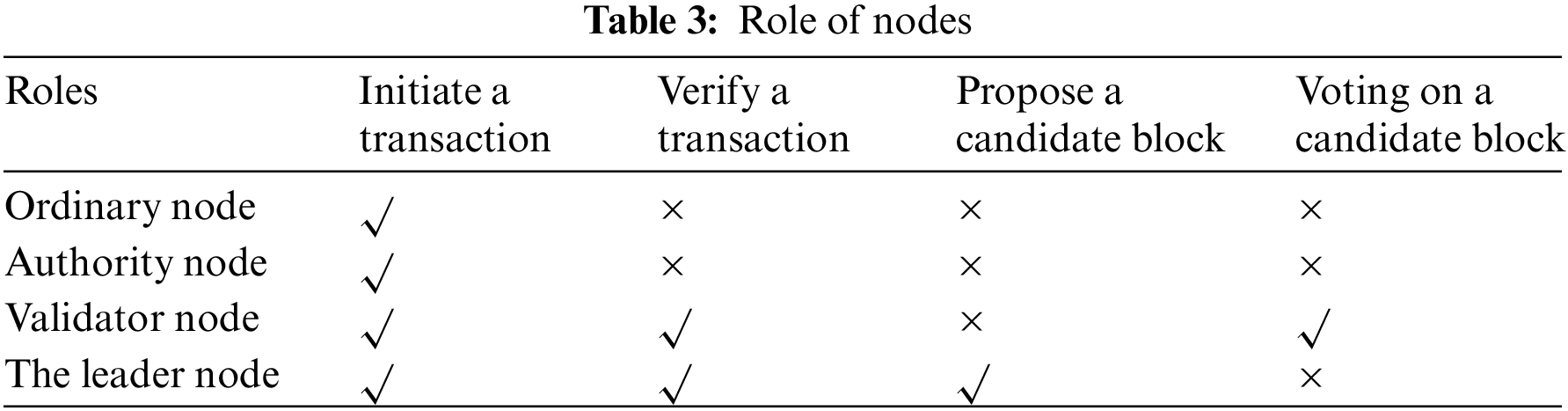
A PoA-based blockchain network comprises four node types: ordinary nodes, authority nodes, validator nodes, and leader nodes. Table 3 delineates the specific roles and permissions of these nodes.

PoARE inherits the security benefits of PoA grounded in identity management and introduces improvements in three key areas. (1) The identity of the leader node is concealed and confidentially shared among the validator nodes through the Quantum Secret Sharing Protocol (QSS) [50]. (2) PoARE introduces the leader node election algorithm based on the quantum random number generator (QRNG), making leader node election entirely randomized, more flexible, and efficient. (3) It implements a dynamic updating mechanism for the list of validator nodes, which limits the involvement of faulty or compromised nodes in bookkeeping, reducing their adverse impact on the blockchain system. This enhances the efficiency and robustness of the blockchain network. The comparison between PoA and PoARE is shown in Table 4.

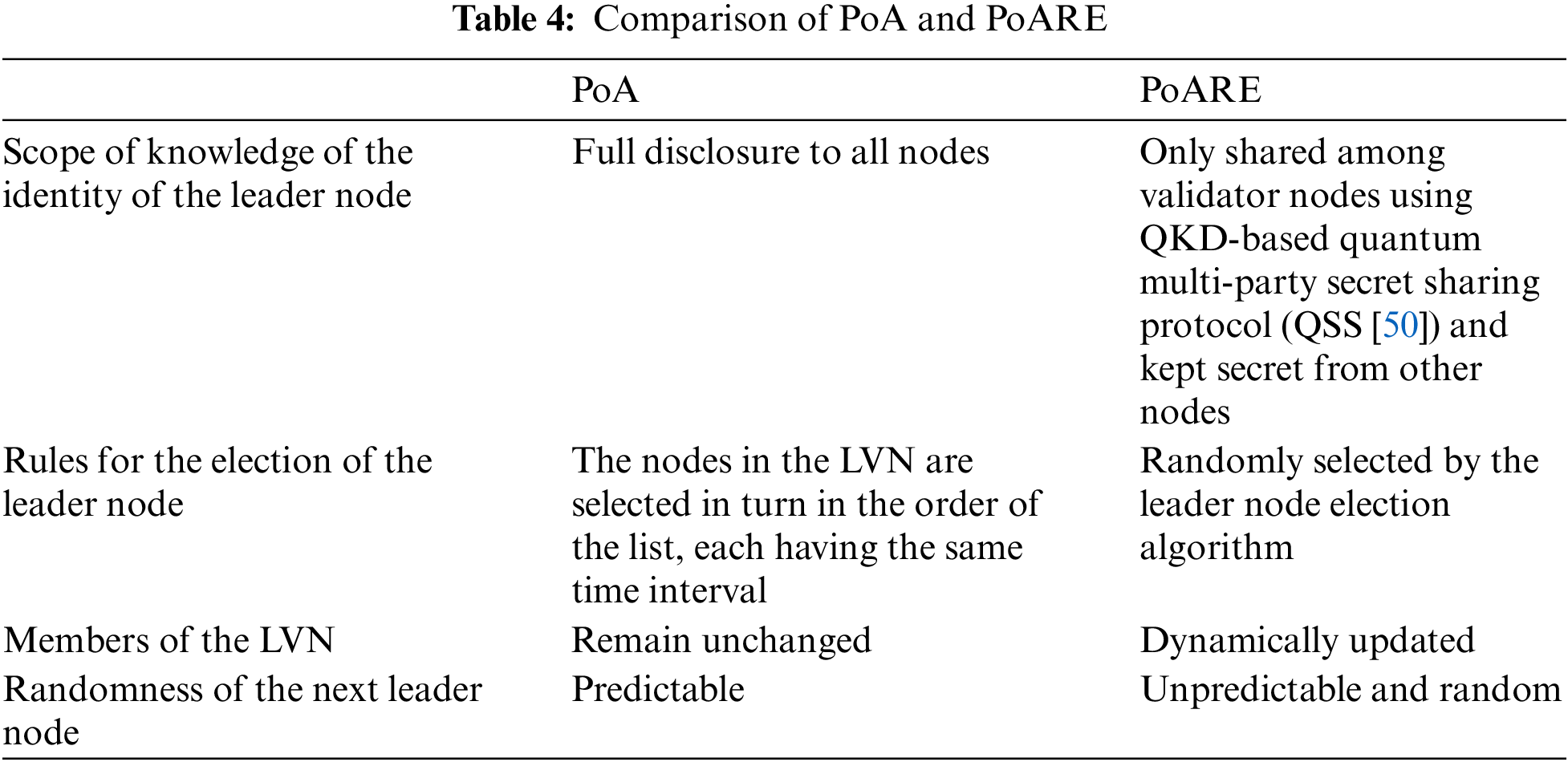
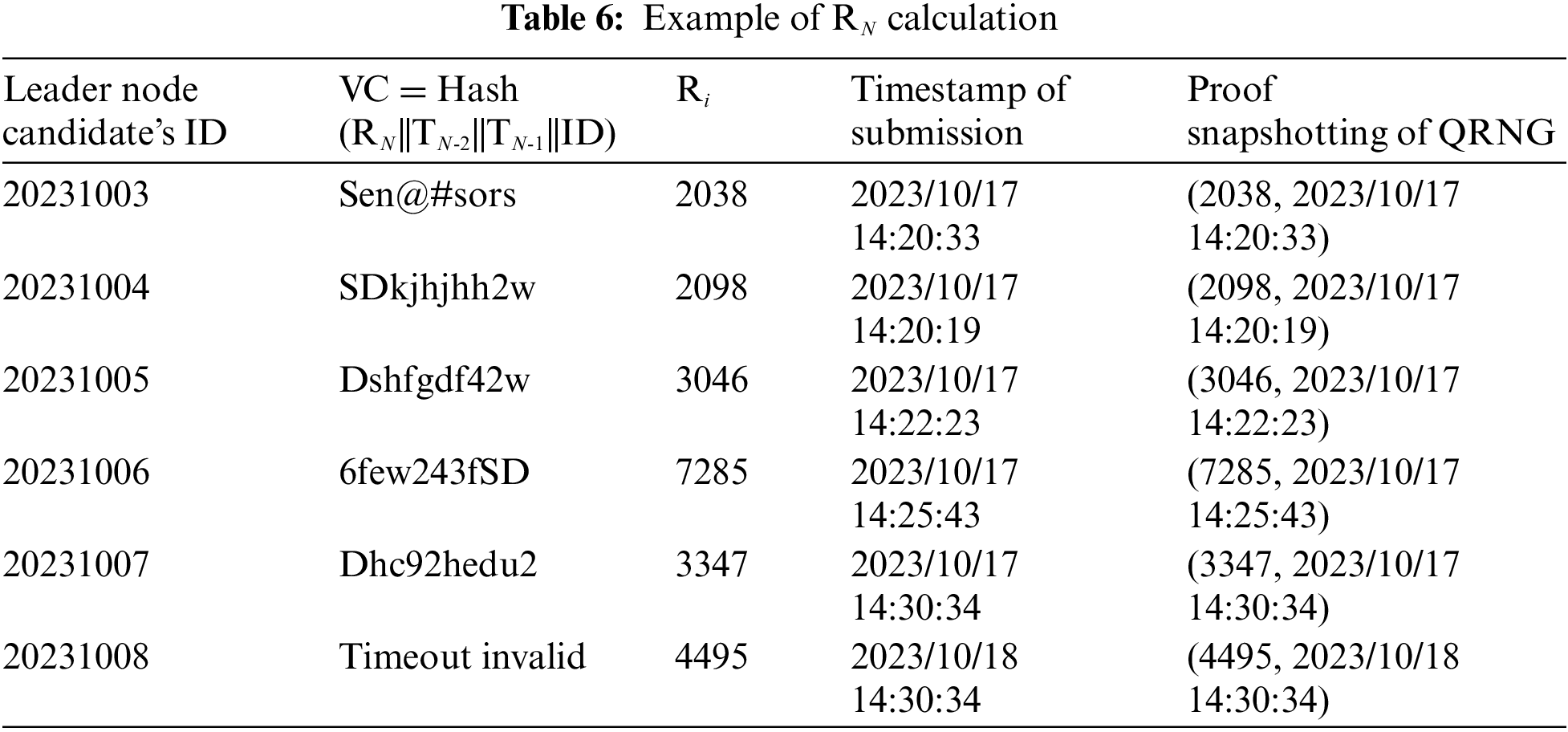
Table 5 outlines the leader node election algorithm used in the PoARE consensus mechanism. At the start of each consensus cycle, the leader node (AN) generates a random number (RN), which is secretly shared using the QSS. The RN is collaboratively generated by all candidate nodes seeking the leader node position supervised by all of them. Each candidate node submits a random number (R) using the quantum random number generator (QRNG) chip, and the RN is the sum of all submitted random numbers. It is important to note that random numbers can only be proposed during the interval Tstart-Tend after the vote for block BN is closed; random numbers submitted beyond this period are disregarded. Subsequently, AN calculates the competition value (VC) for each candidate node vying for the leader node role, where VC = Hash (RN||TN-2||TN-1||ID), with “||” representing the character concatenation symbol. The candidate node with the highest VC value becomes the leader node for the next consensus. The incumbent leader node (AN) shares the identity information of the subsequent leader node (AN+1) among the validator nodes through the QSS protocol. Once AN completes block voting, whether the block (BN) is accepted into the blockchain or discarded, AN proceeds to the leader node election process for the next consensus. An example of this algorithm is illustrated in Table 5.

In the following, we give an example to illustrate the leader node election process in PoARE-based QBIoT. The leader node election process can be divided into three phases according to the chronological order, which are (a) the random number submission phase, (b) the ballot processing phase, and (c) the leader node identity sharing phase.

In the random number submission phase, the leader node (AN), who has completed the bookkeeping task in the previous term, initiates the new leader node election and sets a time period, Tstart-Tend, for this phase, in which each leader node candidate (i.e., Vi, a member of the LVN that has not participated in bookkeeping) wishing to obtain the bookkeeping right, picks a random number, Ri, generated by the QRNG, and submits a sequence (ID, Ri, t, proof snapshotting of Ri) to the leader node (AN) as a ballot for winning the next leader node role.

When the time reaches Tend, the process automatically enters the ballot processing phase, in which AN generates the RN for this consensus and calculates VC for all the ballots and sorts them alphabetically. In this phase, AN stops receiving ballots from the candidate nodes, and checks all the received ballots, flags the invalid ballots, retains the valid ballots, and calculates the RN, which is the sum of Ri of all the valid ballots. After the value of RN has been calculated, AN calculates the corresponding VC for each valid ballot. Then all the VCs are sorted alphabetically, and the proposer of the ballot with the largest VC is identified as the leader node (AN+1) for the next consensus. AN stores identity of the leader node (AN+1), and would broadcast its ballot to all validator nodes in the forthcoming leader node identity sharing phase for verification. As shown in Table 6, after calculation, we can get the sum of Ri, Sum (Ri) = 14467.

After AN+1 has been determined by the AN, the identity of AN+1 is shared secretly in the leader node identity sharing phase within all validator nodes. AN shares the ballot with its VC attached to it containing the ID of the new leader node (AN+1) with all the validator nodes through the QSS. At this point, all validator nodes have known the identity of the new leader node (AN+1), and the system would enter into the (N + 1)th consensus, where AN hands over the transaction queue with the unpacked transactions from the Nth consensus to the new leader node (AN+1), who continues to collect transactions and performs the bookkeeping task.

After the new leader node (AN+1) is elected, the system enters into the (N + 1)th consensus, then all the validator nodes start submitting new transactions to (AN+1), and (AN+1) starts to perform transaction collection and validation. The specific process of a transaction, including signing and verification, is described in detail the following Section 4.2.

4.2 A Transaction Process

Drawing inspiration from [51], we have devised a Public Key Quantum Signature (PKQS) protocol, employing single-qubit rotation to facilitate transaction verification within the QBIoT framework. The PKQS protocol leverages qubit rotation applied to quantum particles as an encryption operation. To illustrate, if we have an initial quantum state denoted as |ξ⟩, then the qubit rotation operation can be represented as R(θ)|ξ⟩=|ξ|′⟩, with R(θ)=cos⁡θ|0⟩⟨0|+sin⁡θ|0⟩⟨1|−sin⁡θ|1⟩⟨0|+cos⁡θ|1⟩⟨1|. It is straightforward to derive |ξ′⟩ from |ξ⟩ and θ by applying the qubit rotation operation R(θ) to |ξ⟩. However, deducing θ from |ξ⟩ and |ξ′⟩ is infeasible, as |ξ⟩ and |ξ′⟩ are two unknown quantum states. Accurate information about |ξ⟩ and |ξ′⟩ cannot be obtained by measuring them using the appropriate basis. Consequently, θ cannot be ascertained. Therefore, the qubit rotation parameter θ is a private key, while |ξ′⟩ functions as the corresponding public key.

For clarity, let us set the stage: Alice initiates (signs) a transaction, Bob is the transaction recipient, Tx represents the transaction message, and Trent, acting as the transaction verifier, is considered a trusted entity. To enhance security and fairness, we have incorporated the PoARE consensus mechanism, where the validator node takes on the role of Trent. Trent’s primary responsibilities include validating the signature and ensuring the message’s legitimacy. In a transaction, Alice commences by computing the QHF value (h) of the transaction message (Tx), encodes h into a quantum sequence (|h⟩), and proceeds to sign |h⟩, generating the signature. We assume the quantum sequence |h⟩ comprises n particles, denoted as ⊗i=1n|hi⟩, where |hi⟩=αi|0⟩+βi|1⟩,|αi|2+|βi|2=1. The signature protocol unfolds as follows:

Step 1: Alice and Bob jointly agree on the secret QHF parameter KAB, and Alice uses QHF with QHF(Tx,KAB)=h to encrypt the message Tx. Subsequently, Alice forwards h and her identity ID={ID1,ID2,…,IDn} to Trent, who generates a private key sk=H(ID⊕h) for Alice, where H is a mapping function with uniformly distributed output, and sk={sk1,sk2,…,skn}={θi}n,θ∈(0,2π].

Step 2: Alice encodes h into |H⟩=⊗i=1n|hi⟩ based on the encoding table presented in Table 7. She prepares four identical quantum sequences, denoted as |H1⟩=⊗i=1n|hi⟩, |H2⟩=⊗i=1n|hi⟩, |H3⟩=⊗i=1n|hi⟩, |H4⟩=⊗i=1n|hi⟩.

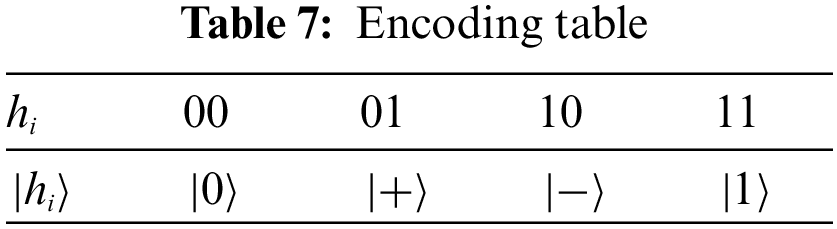
Step 3: Alice applies the qubit rotation operation R(ski)(i=1,2,…,n) to the particle |hi⟩ in |H1⟩, where R(ski)=cos⁡ski|0⟩⟨0|+sin⁡ski|0⟩⟨1|−sin⁡ski|1⟩⟨0|+cos⁡ski|1⟩⟨1|. This operation transforms the particle |hi⟩ into |hi′⟩. After the qubit rotation operation, |H1⟩=⊗i=1n|hi⟩ becomes |H1′⟩=⊗i=1n|hi′⟩.

Step 4: Alice sends |H2⟩ and |H1′⟩ to Trent. |H2⟩ is the quantum sequence that Alice will sign, while |H1′⟩ serves as Alice’s public key for the transaction Tx.

Step 5: Alice applies the qubit rotation operation R(ski)(i=1,2,…,n) to the particle |hi⟩ in |H3⟩, converting |H3⟩ into |H3′⟩.

Step 6: Alice prepares n Bell states, denoted as |ψi⟩=12(|00⟩+|11⟩),(i=1,2,…,n). |ψi⟩ consists of two quantum state particles, with one being |ai⟩, and the other being |bi⟩. Alice retains |ai⟩ and forwards |bi⟩ to Trent.

Step 7: Alice conducts n joint Bell measurements for |H3′⟩ and |ai⟩. In the ith joint Bell measurement, the two target particles to be measured are the ith particles of |H3′⟩, and |ai⟩, respectively. After the measurement, Alice obtains the measurement result R=(r1,r2,…,ri,…,rn),i∈{1,2,…,n}. The value of ri is {00,01,10,11} when the Bell states are |ψ+⟩=12(|00⟩+|11⟩),|ψ−⟩=12(|00⟩−|11⟩), |ϕ+⟩=12(|01⟩+|10⟩), and |ϕ−⟩=12(|01⟩−|10⟩), respectively.

Step 8: Alice retains (|H4⟩,R) as the signature pair and transmits them to Bob. Quantum sequence |H4⟩ represents the transaction message digest, and R is used as the signature for Tx.

Step 9: Upon receiving the signature pair (|H4⟩,R), Bob prepares a quantum sequence |H5⟩ by encoding h as per the encoding table (Table 7) in Step 2. He then compares |H5⟩ with |H4⟩. If |H5⟩ and |H4⟩ match, Bob forwards (|H4⟩,R) to Trent and proceeds to the next step. In case of any disparity between |H5⟩ and |H4⟩, the signature pair is deemed invalid, and Bob discards it, effectively terminating the protocol.

Step 10: Trent receives Bob’s signature pair (|H4⟩,R). Trent then performs unitary operation τ on the particle |bi⟩ based on the value of ri, as outlined in Table 8.

Step 11: After executing the unitary operations in Step 10, Trent employs the QSTC method [52] to compare the ith particle of |H1′⟩ with the particle |bi⟩. If |H1i′⟩=|bi⟩ for all i, values from 1 to n. Trent deems the signature valid and accepts the transaction Tx. Conversely, the signature is considered invalid and discarded if any discrepancies are found.

It is necessary to add that, during each transmission of a quantum sequence in the protocol, we will insert the decoy state particles into the original quantum sequence before transmission to form a hybrid quantum sequence, and after the transmission of the hybrid quantum sequence is completed, we will complete the eavesdropping detection by sender announcing the position of the decoy state particles, receiver selecting the suitable measurement basis for the measurement, and comparing the measurement results to make sure that there is no eavesdropping before recovering the original quantum sequence. The detailed process of transaction verification is visually represented in Fig. 6.

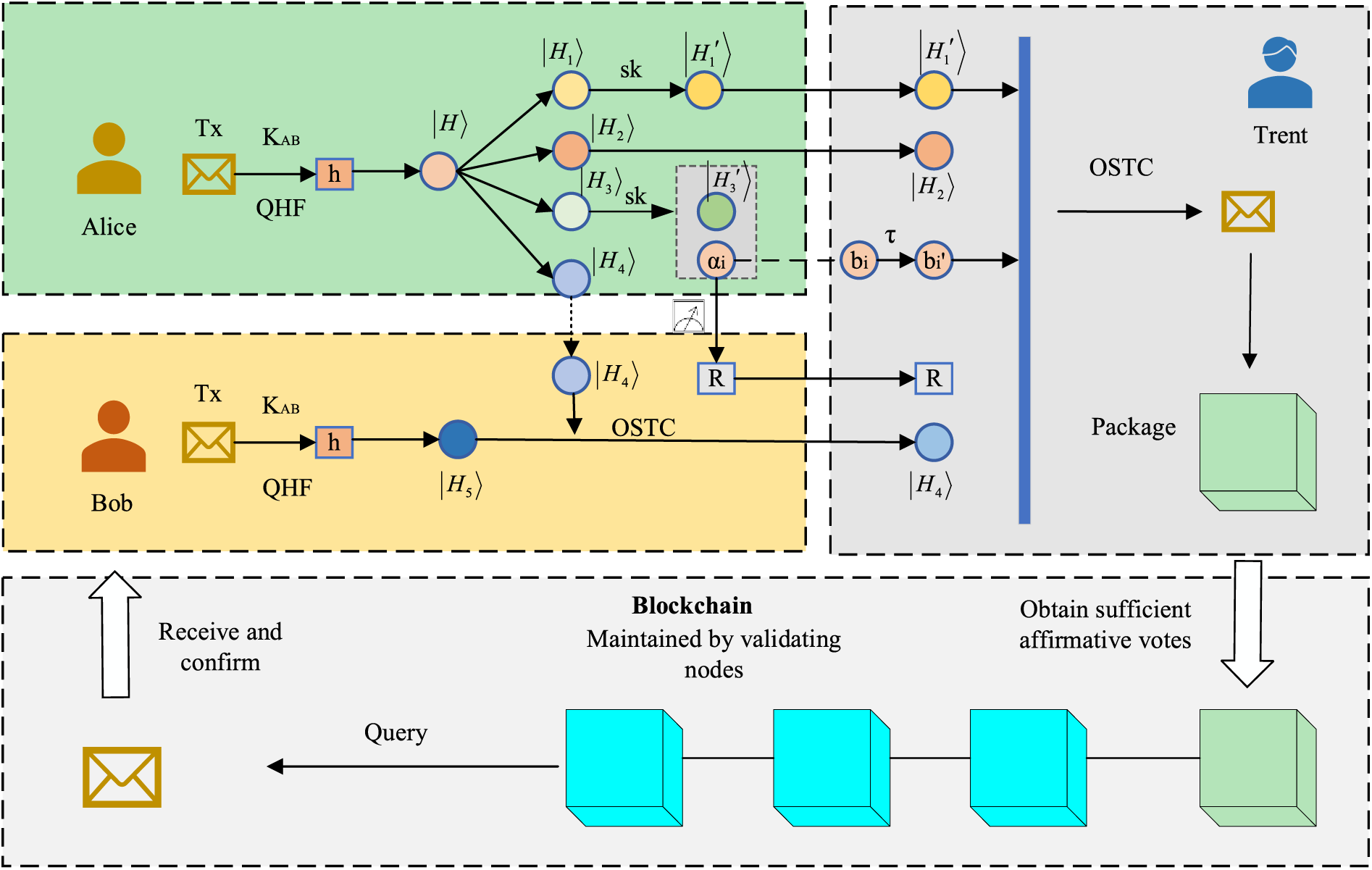
Figure 6: Transaction process

5  Security Analysis of QBIoT

5.1 Security Analysis of Transactions

5.1.1 Proof of Correctness of a Transaction

In this section, we delve into the proof of correctness for transactions within QBIoT. The process begins with transforming ith particle of |H3⟩ initially in the state |hi⟩=αi|0⟩+βi|1⟩. After Alice applies the single-qubit rotation operation R(ski) to |hi⟩, it transitions into the state |hi′⟩.

|hi′⟩=U(ski)(αi|0⟩+βi|1⟩)=[αcos⁡(ski)−βsin⁡(ski)]|0⟩+[βcos⁡(ski)+αsin⁡(ski)]|1⟩(3)

Subsequently, a joint Bell measurement is performed on |hi′⟩ and |ai⟩, leading to the transformation of |hi′⟩ into |hi′′⟩. Four possible scenarios can arise:

(1) (αcos⁡ski−βsin⁡ski)|0⟩+(βcos⁡ski+αsin⁡ski)|1⟩ with the result |ψ+⟩.

(2) (αcos⁡ski−βsin⁡ski)|1⟩+(βcos⁡ski+αsin⁡ski)|0⟩ with the result |ϕ+⟩.

(3) (αcos⁡ski−βsin⁡ski)|0⟩−(βcos⁡ski+αsin⁡ski)|1⟩ with the result |ϕ−⟩.

(4) (αcos⁡ski−βsin⁡ski)|0⟩−(βcos⁡ski+αsin⁡ski)|1⟩ with the result |ψ−⟩.

Following Trent’s unitary operation τ in Step 10, the particle |bi⟩ transforms, becoming |bi′⟩.

|bi′⟩=[αcos⁡(ski)−βsin⁡(ski)]|0⟩+[βcos⁡(ski)+αsin⁡(ski)]|1⟩(4)

Since the ith particle of |H1′⟩ is in the same state, in the case of a valid signature, particle |bi⟩ will remain identical to the ith particle of |H1′⟩. This is due to the inherent quantum properties of the Bell state. Hence, Trent can confirm the signature’s validity through QSTC [52], which guarantees 100% accuracy when comparing identical quantum states.

5.1.2 Security against Forgery for a Transaction

We consider two types of forgery attacks: transaction forgery and signature forgery.

Security against transaction forgery:

If Bob attempts to fabricate a transaction and sends an invalid (|H4∗⟩,R) to Trent, the forgery is easily detected by comparing |H4∗⟩ and |H2⟩ from Alice in Step 4 through QSTC.

Security against signature forgery:

In case Bob forges a signature R′ on a real transaction, this act leads to discrepancies between the particle |bi⟩ and the particle in |H1′⟩, which Trent detects in Step 11. If an external adversary like Eve tries to forge an invalid signature R′, she encounters the same challenge as Bob.

The critical aspect is that the signature is a classical bit string, easily reproduced, whereas the transaction digest |H4⟩ exists as quantum states, preventing replication due to the no-cloning theorem [53]. Even if Bob attempts to generate a forged signature using a real signature pair (|H4⟩,R) as mentioned earlier, his forgery is swiftly uncovered by Trent.

5.1.3 Undeniability

Undeniability in a transaction context means that Alice cannot deny receiving a valid signature pair (|H4⟩,R). As Step 4 illustrates, Alice transmits |H2⟩ to Trent, ensuring that no other party knows its contents before packaging it into a new block. Since the signature R is generated based on joint Bell measurement results, even if an adversary like Eve tries to fake measurement results through guesswork, the probability of success is P=14n, where n represents the number of qubits in |H⟩. With a sufficiently large n, P becomes negligible. Consequently, Alice alone can produce a valid R, and Alice cannot deny this. Furthermore, if Alice fails to perform the joint Bell measurement, the particle |ai⟩ cannot be separated from |ψi⟩, rendering the signature unverifiable. On the other hand, Bob cannot deny receiving the real signature because he must send |H4⟩ to Trent in Step 9, which Trent ultimately verifies.

5.1.4 Security against Eavesdropping

In QBIoT, security is bolstered through the use of decoy particles. These decoys are randomly introduced into the transmitted particles, making it impossible for an attacker to accurately distinguish between decoy and real particles. If an eavesdropper, like Eve, attempts to intercept and measure the transmitted particles, there is a chance they might inadvertently measure a decoy particle, resulting in a 14 error rate. With sufficient decoy particles (t), the attacker has a high probability of being detected. As t increases, the probability of successful eavesdropping converges to nearly impossible.

5.1.5 Transaction Efficiency

Examining transaction efficiency, taking a signature with n qubits as an example, the signer Alice must prepare 4n qubits and n Bell states. Additionally, Alice carries out 2n single-qubit rotation operations and n joint Bell state measurements. As the signature receiver, Bob performs n single-qubit rotation operations and n unitary operations. Trent, the verifier, conducts n unitary operations and 2n quantum state comparisons. These operations within the PKQS are all simple and executable, making the proposed signature protocol feasible with current technology. Notably, Trent’s operations in signature verification preserve the particles |bi⟩, allowing for repeated verification, ultimately enhancing the efficiency and practicality of QBIoT. QBIoT, therefore, overcomes a challenge faced by most quantum signatures where quantum state signatures cannot be repeatedly verified.

Moreover, in contrast to classical public key signatures, our QDS scheme does not require the intervention of an arbitrator to facilitate signature verification. This simplifies the transaction process and reduces reliance on external entities, significantly improving transaction efficiency within QBIoT.

5.2 Security Analysis of Transaction Records

Before Alice sends a transaction to Bob, she encrypts the transaction information using a quantum hash function. Quantum hash functions are tailored for quantum computing environments, offering resilience against attacks like Grover’s algorithm. Attempting to find an original input matching a particular hash would demand exponentially more computational resources, making second pre-image attacks exceedingly difficult. Moreover, Alice creates a signature pair (|H4⟩,R), transmits it to Bob, and Trent verifies it. During transmission, even if an attacker intercepts the transaction information and the signature, they cannot easily decipher the signature or obtain transaction details. The security of this signature pair relies on quantum physics, rendering it impervious to effective quantum attacks. Trent verifies the received transaction information and ensures its integrity by comparing the corresponding QHF values. Any tampering with the transaction information would result in a hash value mismatch, exposing the alteration.

5.3 Resistance to Quantum Computing Cyber Attacks

QBIoT demonstrates resilience against quantum computing attacks. Quantum cryptography is a part of quantum information science and is fundamentally secure, unlike classical cryptography [54]. Quantum mechanics principles such as the quantum no-cloning theorem [53] and the Heisenberg uncertainty principle [55] make it challenging for attackers to go unnoticed during an attack, enhancing the security of the QBIoT scheme. In summary, our proposed QBIoT scheme proves secure against quantum computing attacks.

5.4 Comprehensive Performance Evaluation for QBIoT

Quantum adversaries, equipped with quantum computers, have the ability to intercept, store, measure, and manipulate quantum-state particles, presenting a significant security challenge to quantum blockchain networks. IBM’s recent development of a 1121-qubit quantum computer [56] has further enhanced the capabilities of these adversaries. Therefore, QBIoT can be utilized to assess the security implications of a quantum adversary attack. Due to the scarcity of quantum resources, we use the number of quantum public keys consumed by a single blockchain transaction to evaluate the efficiency of the transaction.

The Blockchain Trilemma [57], coined by Vitalik Buterin, founder of Ethereum, represents the trade-off between decentralization, security, and scalability. Often, enhancing one aspect entails sacrificing another. Mainstream blockchain systems like Bitcoin, Ethernet, and EOS have all compromised in the Blockchain Trilemma. Bitcoin prioritizes decentralization and security at the expense of efficiency. Ethernet 2.0 adopts PoS for efficiency but faces performance issues and high transaction fees. EOS utilizes DPoS for scalability but sacrifices decentralization due to few nodes.

However, in the case of QBIoT, our solution introduces more nodes into the validation and consensus process through the PoARE consensus mechanism, maintaining decentralization while improving performance. PoARE optimizes block generation efficiency and transaction validation, reducing the complexity of the consensus algorithm and thus enhancing scalability. Furthermore, using quantum cryptography and communication techniques, such as QKD, QDS, QHF, QSS, etc., ensures QBIoT’s resistance to quantum computing attacks, bolstering IoT data security. Additionally, our solution resists quantum computing attacks, enhancing blockchain security. QBIoT strikes a nearly perfect balance between decentralization, security, and scalability, thus representing a significant advancement in this context.

Specifically, compared with literatures 14 and 46, our proposed quantum blockchain scheme exhibits superior efficiency and scalability.

As for the quantum-secured blockchain proposed by Kiktenko et al. [14], the validation of a single transaction requires all the other (n−1) nodes’ verification, therefore, (n−1) copies of quantum keys would be prepared by the transaction initiator for a single transaction. While in the quantum blockchain proposed by Li et al. [46], the verification of a single transaction requires the signer to prepare n (n−1) copies of quantum public keys in total. When it comes to QBIoT, the signature of a single transaction consumes 5 copies of quantum public keys only, which is rather resource-efficient. As shown in Fig. 7, in the schemes of literature [14,46], with the increase of the number of nodes, the number of quantum keys to be consumed to complete a single transaction increases rapidly, which will reduce the operational efficiency of the system and limit the scalability of the blockchain network. In our scheme, on the other hand, the number of quantum public keys consumed by a single transaction is constant, and thus our scheme is more quantum resource-efficient and thus achieved better scalability and practicality.

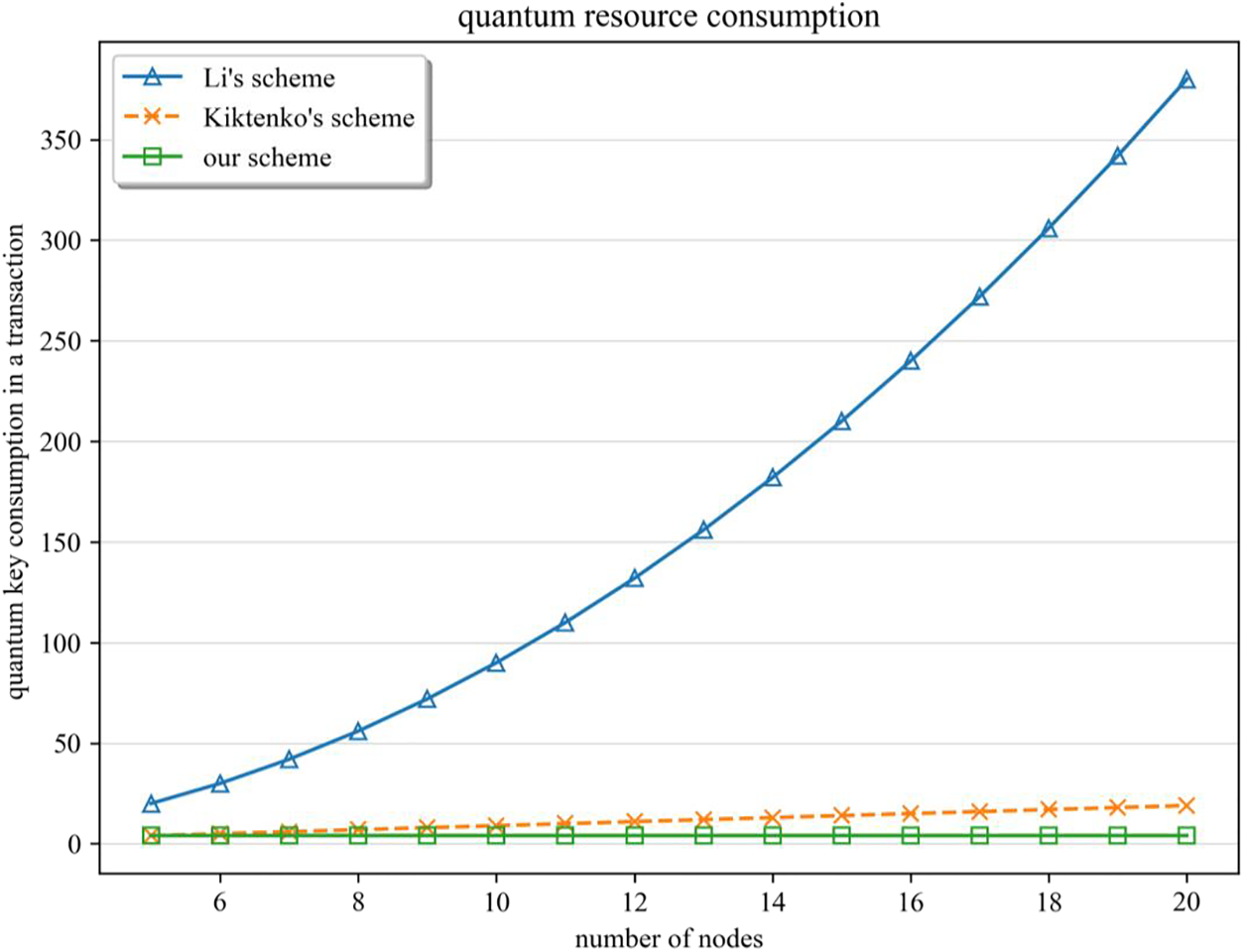
Figure 7: Comparison of the quantum key consumption in a transaction

For a blockchain network, resistance to cyberspace attacks is an essential indicator of its robustness. A PoA-based blockchain is rather fragile to centralized attacks when the adversaries know who is the real leader node. Because all the cyberspace attacks would be accurately implemented on the publicly available leader node. While in QBIoT, it is quite different. As QBIoT adopts the PoARE consensus algorithm that conceals the leader node’s identity, attacker could not distinguish the real leader node from other validator nodes, so the attacks intended for the leader node are implemented on all validator nodes evenly. As the number of authentication nodes increases, the advantage of PoARE over PoA in resisting attacks on the bookkeeping node becomes more and more significant. This is because when the number of attacks is certain (e.g., A), the leader node suffers A attacks in a general blockchain network employing PoA; whereas, in QBIoT employing PoARE, the real leader node will only suffer A/N attacks on average, since the identity of the leader node is inaccessible to the adversary. Fig. 8 shows the trend of the number of attacks with the number of validator nodes for conventional PoA-based blockchain system and PoARE-based QBIoT.

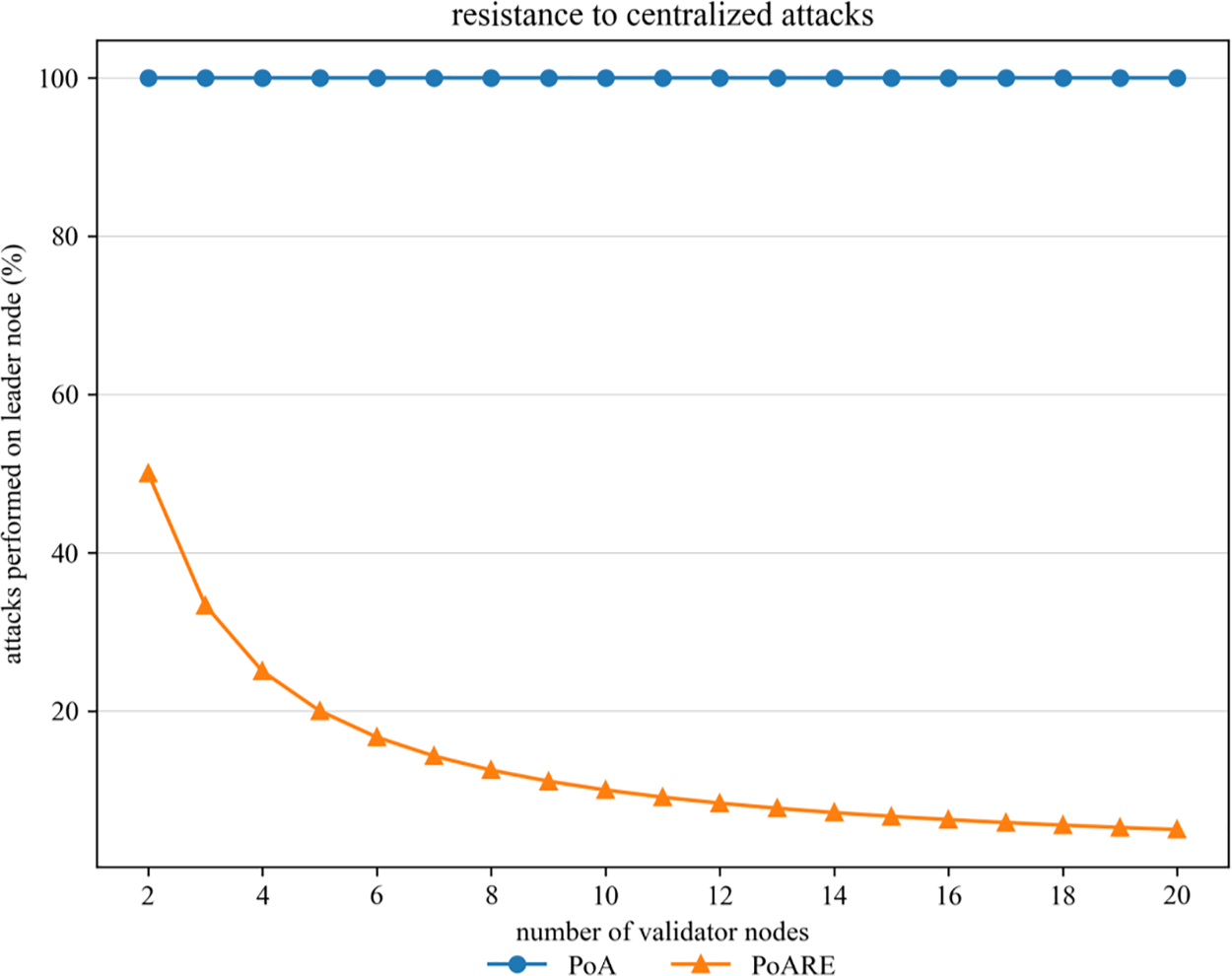
Figure 8: Comparison of the centralized cyberattacks implemented on the accounting node

5.5 Comparison with Other Quantum Blockchain Solutions

As shown in Table 9, a comprehensive comparison between our work and other quantum blockchain schemes is made from 4 aspects, demonstrating the comprehensive security of QBIoT.

Our QBIoT scheme is designed to employ quantum hash functions, ensuring resistance to quantum computing attacks for transaction records. It uses a quantum public key signature algorithm for transaction integrity and authenticity. The PoARE consensus mechanism brings notable scalability, transaction efficiency, and security advantages. In summary, our proposed scheme excels in security and efficiency.

By encompassing these aspects, QBIoT presents a comprehensive security framework and improved performance, distinguishing itself as a robust solution for blockchain implementation.

6  Conclusions

In this paper, we have discussed the security challenges that traditional IoT faces, particularly in terms of data privacy and device security. We have explored existing blockchain technologies and identified their vulnerabilities, especially when confronted with the emerging threat of quantum computing attacks. In response, we have introduced a groundbreaking blockchain solution, QBIoT, which leverages a public-key quantum signature and a quantum hash function to bolster the security of the Internet of Things.

The core elements of our proposed solution encompass block generation through an enhanced POA consensus mechanism, referred to as PoARE, and the application of a quantum hash function and a public key quantum signature for signing transaction information. This approach not only elevates the security of the blockchain system but also enhances its fairness and efficiency.

Looking ahead, we are committed to further refining and optimizing this solution to meet the future escalating demands for IoT security. We believe that in the foreseeable future, quantum blockchain will play a pivotal role in various facets of the financial and social domains, furnishing heightened security and trustworthiness in the digital realm.

The evolution of QBIoT and its incorporation into real-world applications is anticipated to contribute significantly to the realm of post-quantum era blockchain solutions, effectively countering quantum computing cyber-attacks and upholding the cybersecurity of the Internet of Things.

Acknowledgement: None.

Funding Statement: This research is supported by National Key RD Program of China (Grant No. 2022YFB3104402, the Research on Digital Identity Trust System for Massive Heterogeneous Terminals in Road Traffic System), the Fundamental Research Funds for the Central Universities (Grant Nos. 3282023015, 3282023035, 3282023051), National First-Class Discipline Construction Project of Beijing Electronic Science and Technology Institute (No. 3201012).

Author Contributions: Ang Liu performed the methodology and wrote the manuscript; Qing Zhang drew six figures, from Figs. 1 to 6; Shengwei Xu performed conceptualization; Huamin Feng reviewed and edited the manuscript; Xiubo Chen performed formal analysis for the scheme; and Wen Liu drew Figs. 7 to 8. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No new data or materials were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Sathish and C. Y. Rubavathi, “A survey on blockchain mechanisms (BCM) based on internet of things (IoT) applications,” Multimed. Tools Appl., vol. 81, no. 1, pp. 33419–33458, 2022. doi: 10.1007/s11042-022-12784-5. [Google Scholar] [CrossRef]

2. P. Cui, U. Guin, A. Skjellum, and D. Umphress, “Blockchain in IoT: Current trends, challenges, and future roadmap,” J. Hardw. Syst. Secur., vol. 3, no. 3, pp. 338–364, 2019. doi: 10.1007/s41635-019-00079-5. [Google Scholar] [CrossRef]

3. H. N. Dai, Z. Zheng, and Y. Zhang, “Blockchain for internet of things: A survey,” IEEE Internet Things J., vol. 6, no. 3, pp. 8076–8094, 2019. doi: 10.1109/JIOT.2019.2920987. [Google Scholar] [CrossRef]

4. W. Liang and N. Ji, “Privacy challenges of IoT-based blockchain: A systematic review,” Cluster Comput. J. Networks Softw. Tools Appl., vol. 25, no. 3, pp. 2203–2221, 2022. doi: 10.1007/s10586-021-03260-0. [Google Scholar] [CrossRef]

5. S. Nakamoto, “Bitcoin: A peer-to-peer electronic cash system,” Technical Report, 2019. Accessed: May 19, 2024. [Online]. Available: https://bitcoin.org/bitcoin.pdf [Google Scholar]

6. G. Rathee, F. Ahmad, R. Sandhu, C. A. Kerrache, and M. A. Azad, “On the design and implementation of a secure blockchain-based hybrid framework for industrial internet-of-things,” Inf. Process. Manag., vol. 58, no. 3, pp. 102526, 2021. doi: 10.1016/j.ipm.2021.102526. [Google Scholar] [CrossRef]

7. A. Kouanou et al., “Securing data in an internet of things network using blockchain technology: Smart home case,” SN Comput. Sci., vol. 3, no. 2, pp. 167–190, 2022. doi: 10.1007/s42979-022-01065-5. [Google Scholar] [CrossRef]

8. P. Sharma, S. Namasudra, R. G. Crespo, J. Parra-Fuente, and M. C. Trivedi, “EHDHE: Enhancing security of healthcare documents in IoT-enabled digital healthcare ecosystems using blockchain,” Inf. Sci., vol. 629, no. 3, pp. 703–718, 2023. doi: 10.1016/j.ins.2023.01.148. [Google Scholar] [CrossRef]

9. W. Wang, Y. Yu, and L. Du, “Quantum block chain based on asymmetric quantum encryption and a stake vote consensus algorithm,” Sci. Rep., vol. 12, no. 8606, pp. 456–468, 2022. [Google Scholar]

10. P. W. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms,” in Proc. 35th Annu. Symp. Foundations Comput. Sci., Santa Fe, NM, USA, 1994, vol. 12, pp. 124–134. [Google Scholar]

11. T. Monz, D. Nigg, E. A. Martinez, M. F. Brandl, and P. Schindler, “Realization of a scalable Shor algorithm,” Science, vol. 12351, no. 6277, pp. 1068–1070, 2016. doi: 10.1126/science.aad9480. [Google Scholar] [CrossRef]

12. O. Regev, “An efficient quantum factoring algorithm,” arXiv preprint arXiv:2308.06572, 2023. [Google Scholar]

13. L. K. Grover, “Quantum mechanics helps in searching for a needle in a haystack,” Phys. Rev. Lett., vol. 79, no. 2, pp. 703–718, 1997. doi: 10.1103/PhysRevLett.79.325. [Google Scholar] [CrossRef]

14. E. O. Kiktenko et al., “Quantum-secured blockchain,” Quant. Sci. Technol., vol. 3, no. 3, pp. 035004, 2018. doi: 10.1088/2058-9565/aabc6b. [Google Scholar] [CrossRef]

15. J. Chen, W. Gan, M. Hu, and C. M. Chen, “On the construction of a post-quantum blockchain for smart city,” J. Inf. Secur. Appl., vol. 58, no. 7, pp. 2203–2221, 2021. doi: 10.1016/j.jisa.2021.102780. [Google Scholar] [CrossRef]

16. A. Saha et al., “A blockchain framework in post-quantum decentralization,” IEEE Trans. Serv. Comput., vol. 12, no. 8606, pp. 456–468, 2021. doi: 10.1109/TSC.2021.3116896. [Google Scholar] [CrossRef]

17. F. Ye, Z. Zhou, and Y. Li, “Quantum-assisted blockchain for IoT based on quantum signature,” Quant. Inf. Process., vol. 21, no. 9, pp. 327–337, 2022. doi: 10.1007/s11128-022-03676-6. [Google Scholar] [CrossRef]

18. Z. Qu, Z. Zhang, and M. Zheng, “A quantum blockchain-enabled framework for secure private electronic medical records in internet of medical things,” Inf. Sci., vol. 612, no. 3, pp. 942–958, 2022. doi: 10.1016/j.ins.2022.09.028. [Google Scholar] [CrossRef]

19. D. Zhu, Y. Sun, N. Li, L. Song, and J. Zheng, “Secure electronic medical records sharing scheme based on blockchain and quantum key,” Cluster Comput., vol. 27, pp. 3037–3054, 2024. doi: 10.1007/s10586-023-04110-x [Google Scholar] [CrossRef]

20. S. Singh, N. K. Rajput, V. K. Rathi, H. M. Pandey, and A. K. Jaiswal, “Securing blockchain transactions using quantum teleportation and quantum digital signature,” Neural Process. Lett., vol. 55, no. 4, pp. 3827–3842, 2023. doi: 10.1007/s11063-020-10272-1. [Google Scholar] [CrossRef]

21. J. Zhang, Y. Xin, Y. Wang, X. Lei, and Y. Yang, “A secure energy internet scheme for IoV based on post-quantum blockchain,” Comput. Mater. Contin., vol. 75, no. 3, pp. 6323–6336, 2023. doi: 10.32604/cmc.2023.034668. [Google Scholar] [CrossRef]

22. D. Li, P. Ding, Y. Zhou, and Y. Yang, “Controlled alternate quantum walk-based block hash function,” Quantum Inf. Process, vol. 22, no. 10, pp. 363, 2023. doi: 10.1007/s11128-023-04123-w. [Google Scholar] [CrossRef]

23. P. Hou, T. Shang, Y. Zhang, Y. Tang, and J. Liu, “Quantum hash function based on controlled alternate lively quantum walks,” Sci. Rep., vol. 13, no. 1, pp. 5887, 2023. doi: 10.1038/s41598-023-33119-w. [Google Scholar] [CrossRef]

24. Y. G. Yang, J. R. Dong, Y. L. Yang, Y. H. Zhou, and W. M. Shi, “Usefulness of decoherence in quantum-walk-based hash function,” Int. J. Theor. Phys., vol. 60, no. 3, pp. 1025–1037, 2021. doi: 10.1007/s10773-021-04724-0. [Google Scholar] [CrossRef]

25. Q. Zhou and S. F. Lu, “Hash function based on controlled alternate quantum walks with memory,” IEEE Trans. Quantum Eng., vol. 3, pp. 1–10, 2022. [Google Scholar]

26. J. Shi et al., “A quantum hash function with grouped coarse-grained boson sampling,” Quant. Inf. Process., vol. 21, no. 2, pp. 73–98, 2022. doi: 10.1007/s11128-022-03416-w. [Google Scholar] [CrossRef]

27. A. El-Latif et al., “Quantum-inspired blockchain-based cybersecurity: Securing smart edge utilities in IoT-based smart cities,” Inf. Process. Manag., vol. 58, no. 4, pp. 102549–102578, 2021. doi: 10.1016/j.ipm.2021.102549. [Google Scholar] [CrossRef]

28. D. Gottesman and I. Chuang, “Quantum digital signatures,” arXiv preprint arXiv:quant-ph/0105032, 2001. [Google Scholar]

29. H. L. Yin et al., “Experimental quantum digital signature over 102 km,” Phys. Rev. A, vol. 95, no. 3, pp. 032334–032357, 2017. doi: 10.1103/PhysRevA.95.032334. [Google Scholar] [CrossRef]

30. M. Thornton, H. Scott, C. Croal, and N. Korolkova, “Continuous-variable quantum digital signature,” Quantum, vol. 4, pp. 297–321, 2020. [Google Scholar]

31. Y. S. Lu et al., “Efficient quantum digital signatures without symmetrization step,” Opt. Express, vol. 29, no. 7, pp. 10162–10171, 2021. doi: 10.1364/OE.420667. [Google Scholar] [CrossRef]

32. X. Ruan et al., “Orbital angular momentum-encoded quantum digital signature over atmospheric channel,” Quant. Inf. Process., vol. 21, no. 5, pp. 191–213, 2022. doi: 10.1007/s11128-022-03536-3. [Google Scholar] [CrossRef]

33. H. L. Yin et al., “Experimental quantum secure network with digital signatures and encryption,” Natl. Sci. Rev., vol. 10, no. 4, pp. 228–250, 2023. doi: 10.1093/nsr/nwac228. [Google Scholar] [CrossRef]

34. B. Li, Y. Xie, X. Cao, C. Li, and Y. Fu, “One-time universal hashing quantum digital signatures without perfect keys,” arXiv preprint arXiv:2301.01132, 2023. [Google Scholar]

35. A. K. Fedorov, E. O. Kiktenko, and A. I. Lvovsky, “Quantum computers put blockchain security at risk,” Nature, vol. 563, no. 7732, pp. 67–90, 2018. doi: 10.1038/d41586-018-07449-z. [Google Scholar] [CrossRef]

36. X. Sun, M. Sopek, Q. Wang, and P. Kulicki, “Towards quantum-secured permissioned blockchain: Signature, consensus, and logic,” Entropy, vol. 21, no. 9, pp. 1–15, 2019. doi: 10.3390/e21090887. [Google Scholar] [CrossRef]

37. A. Coladangelo and O. Sattath, “A quantum money solution to the blockchain scalability problem,” Quantum, vol. 4, pp. 297–330, 2020. doi: 10.22331/q. [Google Scholar] [CrossRef]

38. G. M. Iovane, “MuReQua chain: Multiscale relativistic quantum blockchain,” IEEE Access, vol. 9, pp. 39827–39838, 2021. doi: 10.1109/ACCESS.2021.3064297. [Google Scholar] [CrossRef]

39. A. E. Azzaoui, P. K. Sharma, and J. H. Park, “Blockchain-based delegated Quantum Cloud architecture for medical big data security,” J. Netw. Comput. Appl., vol. 198, no. 13, pp. 103304–103346, 2022. doi: 10.1016/j.jnca.2021.103304. [Google Scholar] [CrossRef]

40. M. Kumar and B. Mondal, “Quantum blockchain architecture using cyclic QSCD and QKD,” Quant. Inf. Process., vol. 23, no. 3, pp. 101, 2024. doi: 10.1007/s11128-024-04316-x. [Google Scholar] [CrossRef]

41. M. Jiang, Y. Li, W. Susilo, and D. Duong, “Quantum-safe puncturable signatures with their application in blockchain,” IEEE Trans. Inf. Forensics Secur., vol. 19, pp. 2761–2770, 2024. doi: 10.1109/TIFS.2024.3353074. [Google Scholar] [CrossRef]

42. A. Liu, X. B. Chen, G. Xu, Z. Wang, X. Feng and H. Feng, “Quantum-enhanced blockchain: A secure and practical blockchain scheme,” Comput. Mater. Contin., vol. 76, no. 1, pp. 259–277, 2023. doi: 10.32604/cmc.2023.039397. [Google Scholar] [CrossRef]

43. C. Dwork and M. Naor, “Pricing via processing or combatting junk mail,” in Advances in Cryptology—CRYPTO ’92, 1992, vol. 740, pp. 139–147. [Google Scholar]

44. F. M. Ablayev, D. A. Bulychkov, D. A. Sapaev, A. V. Vasilie, and M. T. Ziatdinov, “Quantum-assisted blockchain,” Lobachevskii J. Math., vol. 39, no. 7, pp. 957–960, 2018. doi: 10.1134/S1995080218070028. [Google Scholar] [CrossRef]

45. A. K. Yadav et al., “A comparative study on consensus mechanism with security threats and future scopes: Blockchain,” Comput. Commun., vol. 201, no. 2, pp. 102–115, 2023. doi: 10.1016/j.comcom.2023.01.018. [Google Scholar] [CrossRef]

46. Q. Li, J. Wu, J. Quan, J. Shi, and S. Zhang, “Efficient quantum blockchain with a consensus mechanism QDPoS,” IEEE Trans. Inf. Forensics Secur., vol. 17, no. 1, pp. 3264–3276, 2022. doi: 10.1109/TIFS.2022.3203316. [Google Scholar] [CrossRef]

47. Y. Chen et al., “An improved algorithm for practical byzantine fault tolerance to large-scale consortium chain,” Inf. Process. Manag., vol. 59, no. 2, pp. 102884, 2022. doi: 10.1016/j.ipm.2022.102884. [Google Scholar] [CrossRef]

48. A. Liu et al., “A secure scheme based on a hybrid of classical-quantum communications protocols for managing classical blockchains,” Entropy, vol. 25, no. 5, pp. 811–860, 2023. doi: 10.3390/e25050811. [Google Scholar] [CrossRef]

49. S. Joshi, “Feasibility of proof of authority as a consensus protocol model,” arXiv preprint arXiv:2109.02480, 2021. [Google Scholar]

50. A. Shen et al., “Experimental quantum secret sharing based on phase encoding of coherent states,” Sci. China Phys. Mech. Astron., vol. 66, no. 6, pp. 260311–260322, 2023. doi: 10.1007/s11433-023-2105-7. [Google Scholar] [CrossRef]

51. H. Qin, H. Xu, and W. K. S. Tang, “Public-key quantum signature based on phase shift operation,” Mod. Phys. Lett. B, vol. 17, no. 6, pp. 62–70, 2020. doi: 10.1142/S0217984920500840. [Google Scholar] [CrossRef]

52. H. Buhrman, R. Cleve, J. Watrous, and R. de Wolf, “Quantum fingerprinting,” Phys. Rev. Lett., vol. 87, no. 16, pp. 167902–167920, 2001. doi: 10.1103/PhysRevLett.87.167902. [Google Scholar] [CrossRef]

53. K. Nagata, T. Nakamura, A. Farouk, and D. N. Diep, “No-cloning theorem, kochen-specker theorem, and quantum measurement theories,” Int. J. Theor. Phys., vol. 58, no. 6, pp. 1845–1853, 2019. doi: 10.1007/s10773-019-04078-8. [Google Scholar] [CrossRef]

54. Y. Gao, X. B. Chen, G. Xu, K. Yuan, and W. Liu, “A novel quantum blockchain scheme base on quantum entanglement and DPoS,” Quant. Inf. Process., vol. 19, no. 12, pp. 420–431, 2019. doi: 10.1007/s11128-020-02915-y. [Google Scholar] [CrossRef]

55. S. Aristarhov, “Heisenberg’s uncertainty principle and particle trajectories,” Found. Phys., vol. 53, no. 4, pp. 7–11, 2019. doi: 10.1007/s10701-022-00646-x. [Google Scholar] [CrossRef]

56. S. Bravyi et al., “High-threshold and low-overhead fault-tolerant quantum memory,” Nature, vol. 627, no. 8005, pp. 778–782, 2024. doi: 10.1038/s41586-024-07107-7. [Google Scholar] [CrossRef]

57. S. Reno and M. M. Haque, “Solving blockchain trilemma using off-chain storage protocol,” IET Inf. Secur., vol. 17, no. 4, pp. 681–702, 2023. doi: 10.1049/ise2.12124. [Google Scholar] [CrossRef]