SMSTracker: A Self-Calibration Multi-Head Self-Attention Transformer for Visual Object Tracking

1  Introduction

Visual object tracking is a significant research field within computer vision, focusing on inferring object states throughout video sequences. The primary objective is to identify and track the target object in the initial frame, followed by estimating its state in subsequent frames. This task necessitates the utilization of diverse techniques and algorithms to ensure the consistent tracking of the target across various frames, enabling continuous monitoring and analysis. Over the years, a variety of techniques have been proposed to tackle this challenge, ranging from traditional methods based on handcrafted features to more recent approaches harnessing deep learning and Transformer.

Traditional target tracking algorithms include Mean Shift [1], Particle Filtering [1], Sparse Representation [2] and Optical Flow [3]. The traditional algorithms were proposed relatively early, have the disadvantages of large data volume and slow speed, and are gradually eliminated in the development of target tracking. Tracking algorithms based on correlation filtering have been widely researched due to higher tracking accuracy and faster computation. For example, Bolme et al. [4] introduced a Minimum Output Sum of Squared Error (MOSSE) filter to achieve target tracking. This marked the first instance of incorporating a correlation filter into object tracking, allowing the tracker to pause and resume its position when the object reappears. Montero et al. [5] introduced kernel techniques into correlation filters and proposed the CSK (Circulant Structure for Kernelized) tracker, which achieved superior object tracking performance by employing circular shift sampling to emulate the filter and optimizing coefficients. Danelljan et al. [6] focused their research on the detection and tracking framework and introduced a robust scale estimation method. Their approach relies on learning from a scale pyramid representation and employs independent filters for both translation and scale estimation, significantly enhancing the precision and real-time performance of object tracking. Li et al. [7] introduced a scale-adaptive scheme to address the issue of fixed template size in kernelized correlation filter tracking. By implementing this scale-adaptive scheme, they further enhanced the overall tracking performance. Bouraffa et al. [8] introduced an innovative adaptive manual feature fusion strategy, which is used to fuse multi-channel features into the peak strength context-aware CF (Correlation Filter) framework at the response level. Notably, this research creatively combines elastic network regression and context awareness into the optimization problem, making it the first tracking algorithm to embed multiple features simultaneously. While traditional object tracking methods are relatively mature, they exhibit limited performance and require substantial domain expertise when dealing with complex scenarios and variations in lighting conditions.

In recent years, deep learning methods have achieved excellent results in solving problems in the field of computer vision target tracking by virtue of their powerful feature extraction and modelling capabilities. Ma et al. [9] effectively leveraged features extracted from deep convolutional neural networks, thereby significantly improving the accuracy and robustness of object tracking. However, challenges persist in addressing issues such as low resolution and occlusion, which continue to pose challenges in mitigating tracking drift. Valmadre et al. [10] introduced innovative improvements to correlation filters by transforming them into a combination of differentiable layers and feature extraction networks, enabling end-to-end optimization. This transformation not only enhanced tracking performance but also opened up new possibilities for the automation and end-to-end training of object tracking methods. Gundogdu et al. [11] introduced an efficient backpropagation algorithm and concurrently developed a convolutional neural network that enables end-to-end training. This innovation not only enhances training efficiency but also reduces dependence on classification training networks. Wang et al. [12] introduced a lightweight end-to-end network architecture, DCFNet, designed to simultaneously learn convolutional features and perform the process of correlation tracking, resulting in improved object tracking performance. Fan et al. [13] introduced a motion stare prediction and localization network (MP-LN), which predicts and transforms a reasonable search area based on the continuous motion status of the target, enabling more accurate motion state estimation.

However, these methods often struggled with variations in object appearance, motion, and occlusion. The introduction of Transformers into visual object tracking offers a new paradigm, leveraging their self-attention mechanisms to handle these challenges more effectively. TransTrack [14] utilized the Transformer architecture, using the object features from the previous frame as queries for the current frame, and introduces learned object queries to detect targets. This simplifies complex multi-step configurations, enhancing tracking accuracy and efficiency. Chen et al. [15] introduced a simplified visual object tracking architecture named SimTrack. Its uniqueness lies in guiding serialized samples and searches into the Transformer backbone for joint feature learning and interaction. In contrast to traditional multi-branch frameworks, SimTrack comprises only a single branch backbone, eliminating the complex interaction heads. This simplification not only makes the model more straightforward but also enhances its learning capacity, effectively addressing feature inconsistency issues in the process. However, SimTrack also encounters a challenge, namely the issue of feature redundancy, which can lead to reduced real-time performance of the system. To address this issue, we propose introducing a tensor decomposition self-attention mechanism and a self-calibration attention fusion block based on SimTrack.

In conclusion, our contributions are summarized as follows:

a)   We propose a hybrid tensor decomposition self-organizing multi-head self-attention Transformer mechanism for visual object tracking, capable of compressing and accelerating the Transformer while effectively eliminating redundant information in a single-branch Transformer backbone.

b)   We propose a self-calibration attention fusion block as an external Transformer module to address attention ambiguities and inconsistencies, mitigating the performance degradation in object tracking and thereby achieving stable tracking of the target.

c)   We implement SMSTracker to conduct comprehensive experiments on the dataset, achieving competitive results.

2  Related Work

2.1 Traditional Visual Object Tracking Algorithms

Traditional visual object tracking algorithms are typically categorized into generative model approaches and discriminative model approaches [16]. The classification is based on the modeling approach used for the initial target model. The working mechanism of generative models involves modeling the target region in the current frame, then, in the next frame, using similarity measurement as a criterion to select the region most similar to the target model as the predicted location and updating it as the new target model. For example, Comaniciu et al. [1] constructed the Mean Shift vector for building the target model, which consistently points towards the region with the densest sample points and rapidly converges, thus facilitating efficient target tracking. Vojir et al. [17] introduced the Adaptive Scale Mean Shift (ASMS) algorithm, which incorporates classic color histogram features to improve scale estimation, effectively addressing scale expansion due to cluttered backgrounds and scale implosion issues when dealing with similar objects. Nummiaro et al. [18] proposed a particle filtering algorithm, which has a better ability to model nonlinear systems, thus achieving better results. By employing machine learning techniques, an optimal discriminative function is trained to search for the most matching solution region in subsequent frames, thereby determining the target region. For instance, Kernel Correlation Filter with Detection Proposals (KCFDP) [19] provided promising candidate frames with different scales and aspect ratios, which are then integrated into a correlation filter tracker with enhanced features and robust updates. Although traditional visual object tracking algorithms have achieved better results, they face the challenges of computational complexity, risk of overfitting and complex environments in practical applications.

2.2 Visual Object Tracking Based on Deep Learning

With the continuous development in the field of computer vision, target tracking algorithms based on deep learning are emerging and gradually occupying a mainstream position. Wang et al. [20] first attempted to apply deep learning to the field of target tracking, however, at that time, the performance of the algorithm was not satisfactory compared to other traditional algorithms. Multi-Domain Convolutional Neural Network (MDNet) [21] adopted VGG-M, a pre-trained model for image classification tasks, as the initial model for its network and achieved significant accuracy breakthroughs by training offline on different video sequences.

Inspired by Transformer, Zhao et al. [22] proposed visual Tracking with Transformer (TrTr), which not only improves the accuracy but also makes the framework more concise. Guo et al. [23] proposed a Siamese graph attention network for general object tracking (SiamGAT) that canceled the fixed feature region cropping and instead uses goal-awareness to determine the cropping region and introduced a graph attention mechanism to better capture the information relationship between images, thus improving the tracking accuracy. TransT [24] takes advantage of the self-attention mechanism and cross-attention mechanism in Transformer to globally model the template frame and search frame feature maps, which can avoid the problem of convolutional inter-correlation operations falling into local optimums during tracking. Cui et al. [25] proposed MixFormer, an end-to-end tracking framework that allows for the simultaneous extraction of discriminative features for a specific target and enables extensive communication between the target and the search. This approach provides significant improvements in short-term tracking compared to other trackers. Bai et al. [26] proposed introducing a Spatial Calibration Module (SCM) outside the Transformer to integrate semantically similar patch tokens and their spatial relationships into a unified diffusion model. This dynamic adjustment of spatial and semantic relationships enables the generated attention maps to capture object boundaries more clearly and filter out background regions unrelated to objects.

Due to the fact that the Transformer model can capture global contextual information [27], many researchers have proposed to use the multi-head attention mechanism of the Transformer model to solve the problem of restricted sensory field in convolutional neural networks, which can efficiently acquire global information, and the multi-head mechanism can map the coding vectors to multiple different spaces, thus enhancing the expressive power of the model.

3  Methodology

3.1 Overview of SMSTracker

To simplify the model framework and enhance its learning capabilities, we adopt a single-branch Transformer structure. To address the issue of feature information redundancy inherent in a single-branch Transformer backbone, we employ a self-organizing multi-head self-attention Transformer mechanism with hybrid tensor decomposition. To address the problem of ambiguous and inconsistent attention, we introduce an attention self-calibration block to mitigate tracking performance degradation due to environmental factors during target tracking. The architecture of the proposed Self-calibration Multi-head Self-Attention Transformer for Visual Object Tracking (SMSTracker) is shown in Fig. 1. The input sample and search images are first serialized and sent together to the Hybrid Tensor Decomposition Transformer for joint feature and interaction learning. A self-calibrating attention fusion block is integrated after the transformer to prevent degradation of the feature attention map. The block comprises numerous attention fusion blocks, enabling it to utilize attention maps derived from tensor decomposition multi-head self-attention mechanisms for weighted feature attention maps, ensuring the stable tracking of target objects.

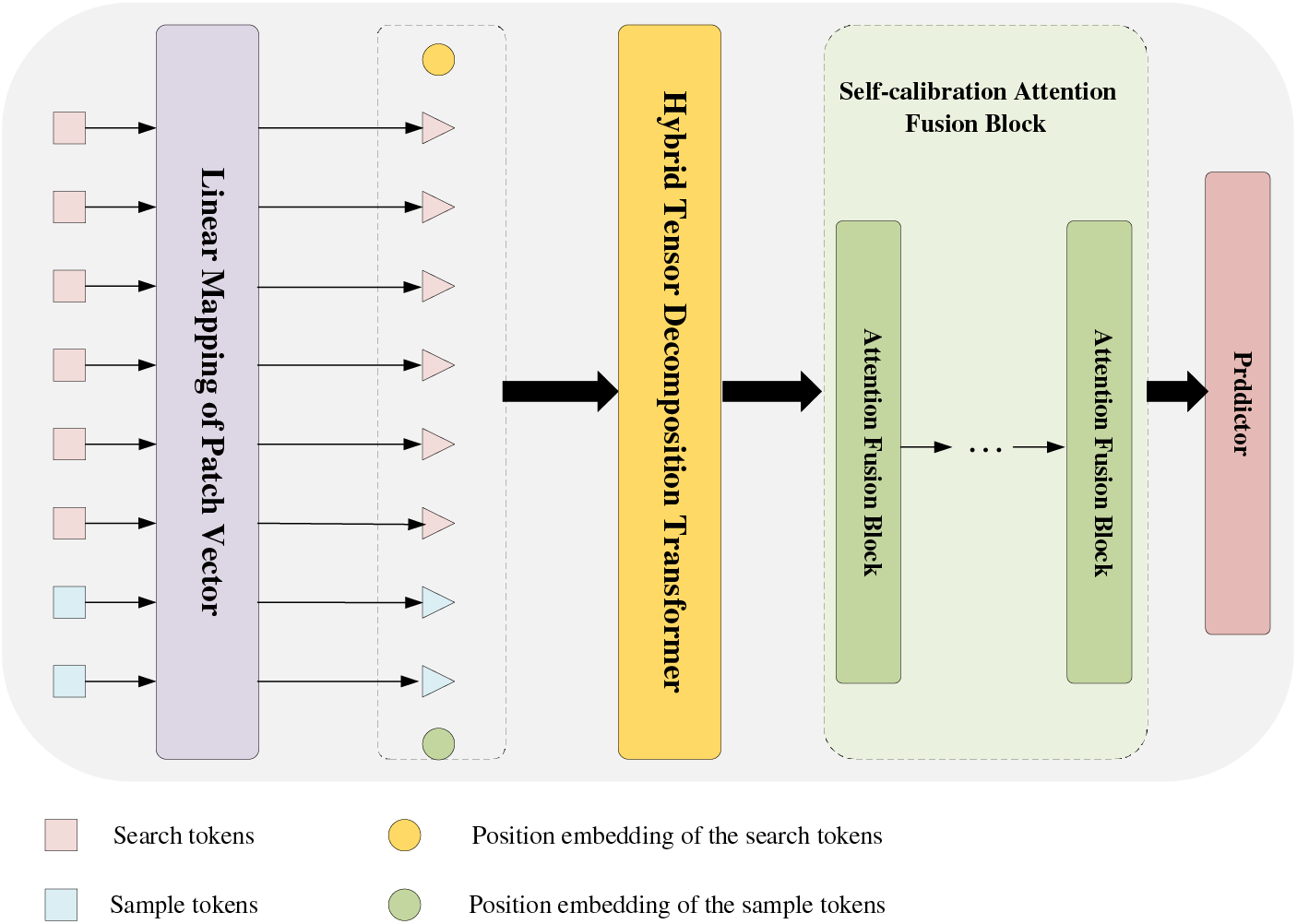
Figure 1: The architecture details of SMSTracker. First, the input sample and search images are serialized and sent together to the Hybrid Tensor Decomposition Transformer for joint feature and interaction learning. Then, the attention self-calibration fusion block comprising a plurality of attention fusion blocks is integrated after Transformer. Finally, the target-related attention features are utilized for target tracking through a predictor

3.2 Hybrid Tensor Decomposition Transformer

The overall structure of the Transformer and the Hybrid Tensor Decomposition Transformer is illustrated in Fig. 2. We will now introduce this model from two perspectives: Hybrid Tensor Embedding and Self-Attention, as well as the Hybrid Tensor Decomposition Transformer Feed-Forward Network.

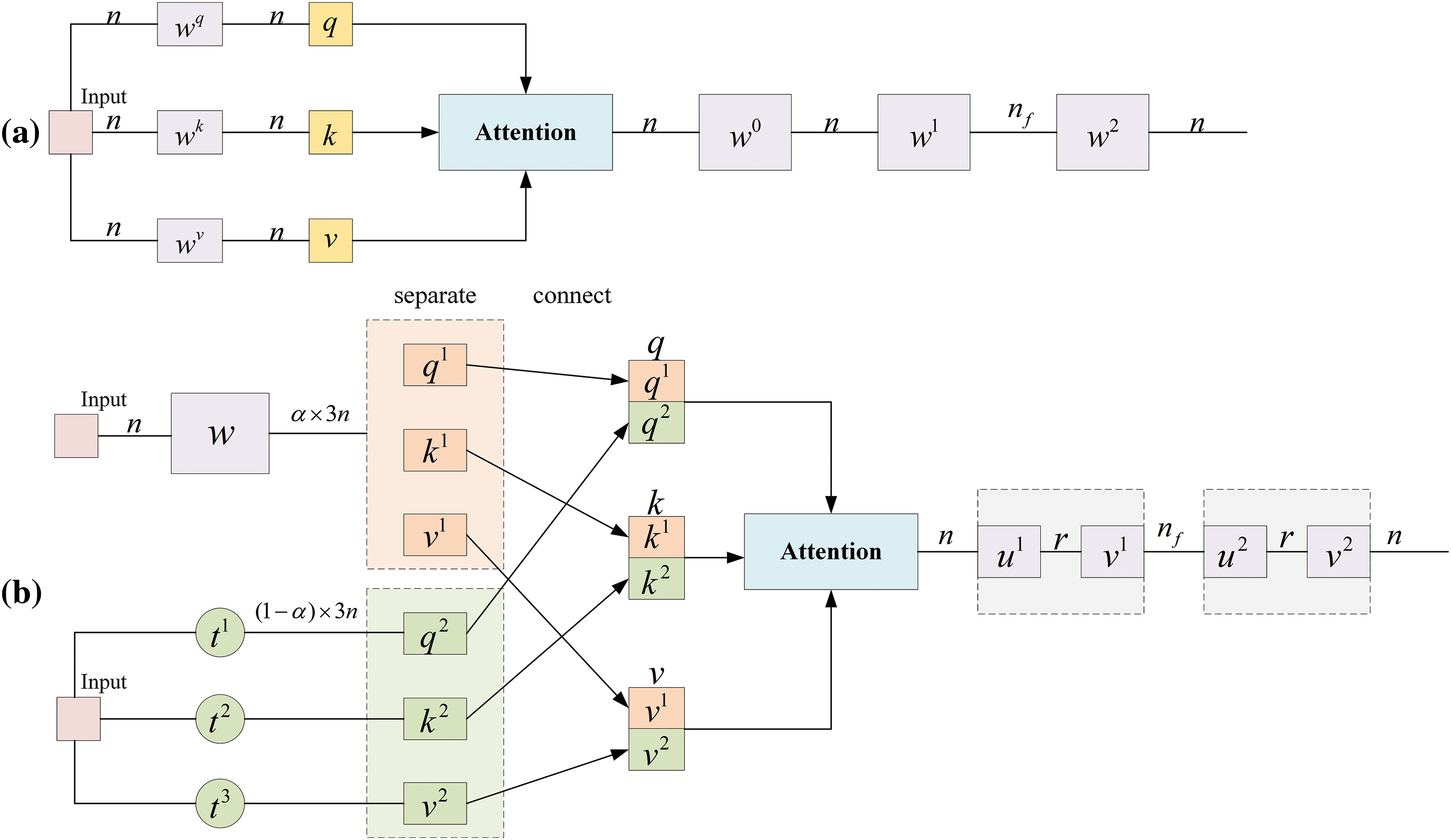
Figure 2: The structure of Hybrid Tensor Decomposition Transformer. (a) is the original Transformer structure and (b) is our proposed Hybrid Tensor Decomposition Transformer

3.2.1 Hybrid Tensor Embedding and Self-Attention

The embedding layer, often a somewhat overlooked yet pivotal component of the model architecture, deserves special attention. Traditionally, Wu et al. [28] employed a joint source-target vocabulary approach. Dimension size of the embedding matrix is s×n, where ‘s’ represents the vocabulary size, and ‘n’ denotes the embedding dimension. This strategy has proven effective in various natural language processing tasks. However, the potential pitfalls of using tensor-training embeddings as a direct replacement for the original embedding layer have been shown. It was observed that this approach could lead to a notable decline in the machine translation model’s performance, raising concerns about the effectiveness of such embeddings in certain contexts.

To address this challenge, we propose methods that combine dense and sparse embedding. Specifically, it does this by connecting a low-dimensional dense embedding matrix to a tensor-train matrix containing three tensor-train cores. The formula is shown below:

wE=concatenate(we,wtt)(1)

where we represents the low-dimensional dense embedding matrix, the dimension of we is s×αn, the dimension of wtt is s×(1−α)n, and α∈[0,1] is used to control the ratio of the two embeddings.

Self-attention enables the input X to undergo three distinct projection operations, obtaining representations for query, key and value respectively. These representations are crucial for constructing the attention matrix and computing the output. The formula is defined as:

Attention(q,k,v)=softmax(Xwq(wk)TXT(n)−12)Xwv(2)

where X is the input with dimension l×n, l is the sequence length and n is the model dimension. Concatenate weight matrices into a single matrix by columns, and the formula is as follows:

w=concatenate(wq,wk,wv)(3)

Then, the w matrix is divided into a dense part wd and a part with three tensor-train cores wtt. The definitions are as follows:

w=separate(wd,wtt)(4)

where wd has dimension n×3βn, wtt has dimension n×3(1−β)n, and β∈[0,1] is used to control the dense layer and the tensor-training cores layer.

The input initially passes through the dense component, resulting in the separation of the output into q1, k1 and v1. Simultaneously, the input also goes through the low-rank tensor-training cores component, leading to the separation of the output into q2, k2 and v2. Subsequently, q1 is concatenated with q2, k1 is concatenated with k2, and v1 is concatenated with v2, resulting in the complete representations of query, key and value.

3.2.2 Hybrid Tensor Decomposition Transformer Feed-Forward Network

Since the performance of the Transformer is relatively less affected by the feed-forward network compared to the self-attention network, we chose to build on the Hybrid Tensor Decomposition Transformer by introducing a Low-rank Matrix Factorized layer in the feed-forward network to enhance our model by introducing a Low-rank Matrix Factorized layer to improve the model processing speed. The primary role of the feed-forward network within our model is to facilitate a non-linear transformation of the input. This transformation is essential for capturing complex patterns and relationships within the data, ultimately contributing to the model’s overall performance and effectiveness. The formula is as follows:

feed−forward(X)=σ(Xw1+b1)w2+b2(5)

where σ(⋅) represents the activation function ReLU, w1 has dimension n×nf, w2 has dimension nf×n, b1 has dimension nf, b2 has dimension n. n is the dimension of our model and nf is the dimension of the feed-forward network. The variables such as w1, w2, b1 and b2 are retained from the original Transformer structure. Low-rank Matrix Factorized layer consists of four dense layers. The specific formula is as follows:

Lfeed−forward(X)=σ(Xu1v1+b1)u2v2+b2(6)

where σ(⋅) represents the activation function ReLU, u1 has dimension n×r, v1 has dimension r×nf, u2 has dimension nf×r, v2 has dimension r×n, b1 has dimension nf and b2 has dimension n. Furthermore, r is the order of the Matrix Factorization.

3.3 Self-Calibration Attention Fusion Block

During long time target tracking, the feature attention map is subject to visual impairment problems such as target occlusion and model degradation problems. To solve this problem, we adopt a self-calibration idea by inserting a Self-calibration Attention Fusion Block outside the Transformer to refine and fuse attention and TD attention maps.

3.3.1 Structure of the Self-Calibration Attention Fusion Block

The specific structure of the Self-calibration Attention Fusion Block is shown in Fig. 3. The input is processed by Transformer to produce an attention map, preserving the original discriminative features. This feature attention map represents the basic outline and structural information of the target. However, during extended target tracking, this feature attention map can be influenced by apparent issues such as target occlusion, making model degradation more likely. To tackle this problem, we adopt a self-calibration approach. We utilize a tensor decomposition self-attention mechanism to obtain a TD attention map, which is then used to weight the feature attention map, thereby achieving stable target tracking.

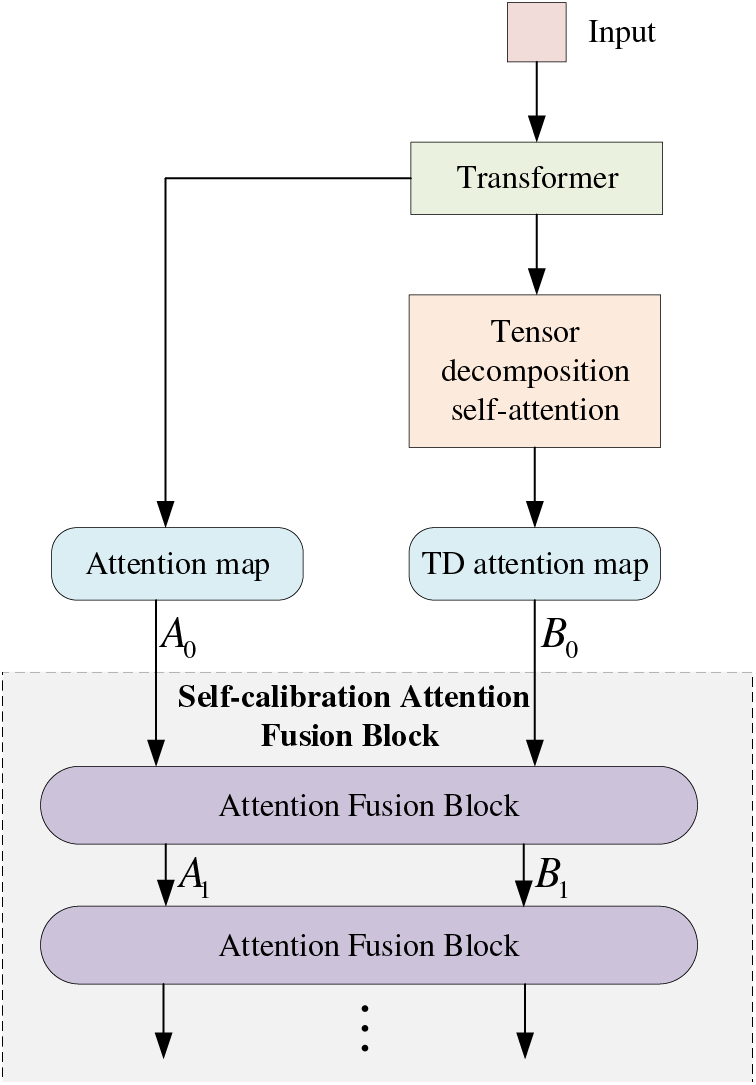
Figure 3: The structure of the self-calibration attention fusion block

As shown in Fig. 3, the (i+1)th Attention Fusion Block takes Ai and Bi as inputs and produces Ai+1 and Bi+1 as outputs. By stacking multiple Attention Fusion Blocks, the strengths of the two maps are dynamically adjusted through the weighted fusion of these two types of attention maps.

3.3.2 Attention Fusion Block

Attention fusion block consists of three sub-modules, including attention map measurement, Laplacian information calculation and thresholding filtering. The attention fusion block specific detail diagram is shown in Fig. 4.

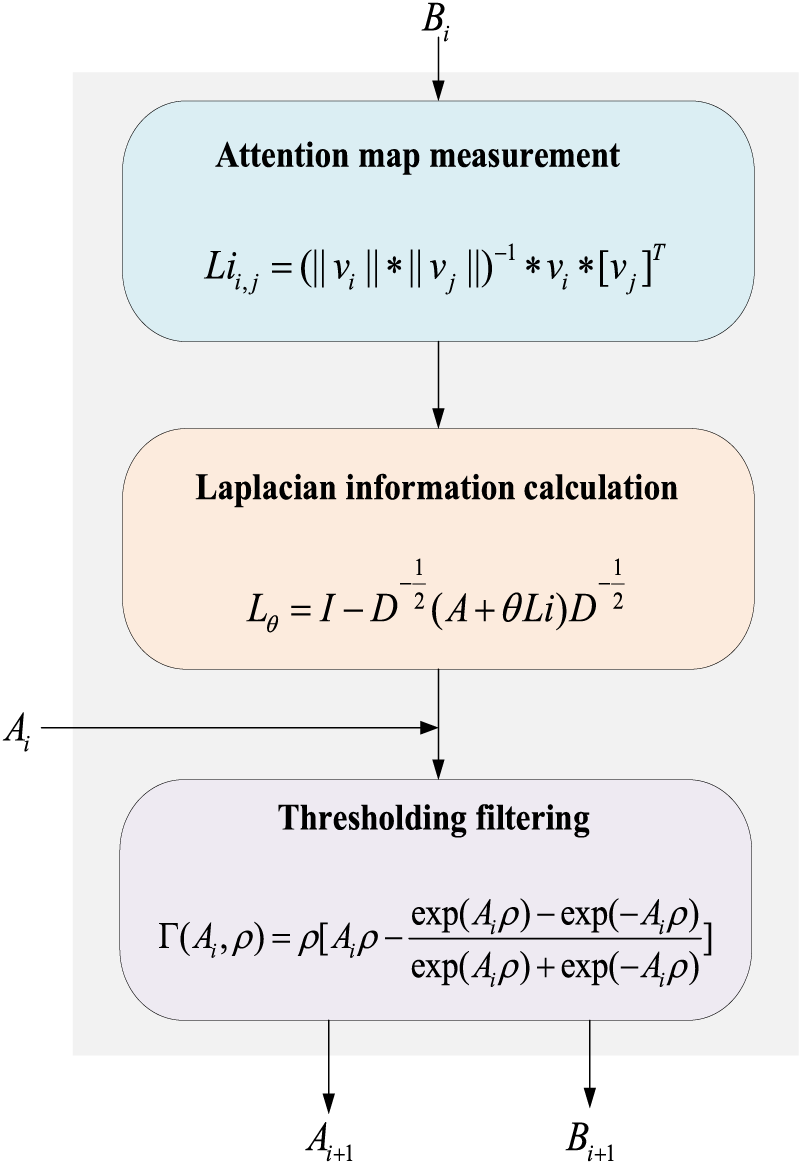
Figure 4: The structure of the attention fusion block

Attention map measurement: Attention map measurement is a key component of the attention fusion block that is used to evaluate and quantify the distribution of attention to inputs. Its main purpose is to help us understand how much attention the model pays to different input elements in order to better tune and optimize model performance. The following is a process for attention map measurement: First, we construct a graph G<V,E>, where V represents vertices and E represents edges. vi and vj are flat vectors, while Lii,j represents the cosine distance between vi and vj. To evaluate attention information in G we design a model to describe the inflow and outflow of traffic at vi. The traffic input is based on the initial attention map, where the attention score corresponds to the input rate, and the contribution of neighboring nodes is that vi shares traffic with them. In addition, traffic moves outward to nearby nodes simultaneously. In order to incorporate attention maps, we introduce a “meaning flow” out of the nodes. As a result, the rate of change of the flow of vi can be determined. Thus, we can measure the attention map Li, The formula is defined as follows:

Lii,j=(||vi||∗||vj||)−1∗vi∗[vj]T(7)

where the greater value Lii,j indicates a higher degree of similarity shared between vi and vj.

Laplacian information calculation: To capture attention relationships, we define an adjacency matrix A to represent the connectivity of the edges in G, and a degree matrix D, a diagonal matrix whose elements on the diagonal represent the degree of each node. Subsequently, we obtain the Laplacian matrix L¯=D−A, with each element (L¯)i,j−1 representing the correlation between vi and vj under equilibrium conditions. To resolve the problem of ambiguous and inconsistent attention, we incorporate L¯ with attention map measurement Li. We employ a tunable parameter θ to dynamically tunable the semantic influence, rendering the fusion process adaptable to a wide range of scenarios. The improved Laplacian matrix Lθ is defined as follows:

Lθ=I−D−12(A+θLi)D−12(8)

where I is the identity matrix. Then, the reallocated attention activation map is computed and the formula is defined as follows:

Ai+1=flatten(Ai)(Lθ)i(9)

where Ai+1 represents the output of the reallocated attention map, flatten(⋅) is a flattening operation that transforms Ai into a sequence, and i represents the ith attention fusion block.

But in practice there may be situations where 1(Lθ)i does not exist. To avoid this problem, we use Newton Schulz iteration [29] to solve for 1(Lθ)i to approximate the attention fusion result. The calculation process is as follows:

G0=β(Lθ)TGk=Gk−1+Fk−1Gk−1Fk=I−AGk(10)

where β is a constant value, G0 is the initialization matrix, k denotes the number of iterations, I is the identity matrix, Fk is the minimization of the estimation error.

Thresholding filtering: While the redistributed attention map Ai+1 provides a clearer picture of the target contours and boundaries, it can also appear to spread attentional fusion beyond the target boundaries, which can lead to an overevaluation of the bounding box. To address this issue, we introduce a threshold filter aimed at enhancing the distinction in density between the target object and the adjacent background, while concurrently diminishing external interference. The equation for the threshold filter is as follows:

Γ(Ai,ρ)=ρ[Aiρ−exp⁡(Aiρ)−exp⁡(−Aiρ)exp⁡(Aiρ)+exp⁡(−Aiρ)](11)

where ρ∈(0,1) is the threshold parameter. Then, Bi and Γ(Ai,ρ) perform an element-by-element multiplication operation:

Bi+1=Bi∘Γ(Ai,ρ)(12)

where ∘ denotes element-wise multiplication.

3.4 Loss Function

To train our SMSTracker, we calculate the loss between the prediction frame and the truth frame. Cross entropy loss is used as classification loss in training with the following formula:

Lcls=1N∑i−[yi×ln⁡(pi)+(1−yi)×ln⁡(1−pi)](13)

where N is the number of samples, yi denotes the true label of the ith sample, pi denotes the probability of predicting the correct result for the ith sample.

Additionally, L1 loss and GIoU (Generalized IoU) [30] are utilized for supervising the bounding box prediction results. The loss function is defined as follows:

L=λ1Lcls+λ2LL1+λ3LGIoU(14)

where Lcls is the classification loss, LL1 stands for 1-norm loss, and LGLoU stands for Generalised Intersection over Union (GIoU) loss. λ1, λ2 and λ3 are the weighting parameters for each loss to balance each component of the loss.

4  Experiments

4.1 Experimental Setting

4.1.1 Dataset

SMSTracker is trained using four publicly available datasets, including OTB2015 [31], TrackingNet [32], LaSOT [33] and GOT-10k [34]. In order to enhance the robustness and generalization ability of the model, we use data enhancement methods such as scale transformation and luminance dithering. In each round of training, SMSTracker randomly selects a total of 30,000 training sample pairs, which include a sample image and a search region image, and they belong to the same video sequence.

OTB2015 comprises a total of 100 videos, which have been categorized into 11 attributes such as Illumination Variation, Scale Variation, and Occlusion based on the different types of interference present in the videos. This dataset utilizes manually annotated real labels, and it also includes one-quarter of the videos in grayscale format.

TrackingNet is constructed by selecting 30,132 videos from the target detection dataset, YoutubeBoundingBoxes, to form the training video set. Additionally, 511 videos were chosen to create the testing video set. These training videos span across 23 different object categories and are divided into 12 training subsets, with each subset containing 2511 videos. The testing set of the TrackingNet dataset comprises 511 videos.

LaSOT is a long tracking dataset with high-quality annotations, consisting of 1400 video sequences. Out of these, 1120 are designated for training, and the remaining 280 are used for testing purposes. LaSOT provides superior target annotation data, including detailed information such as bounding boxes. It encompasses twelve challenging attributes, including illumination variation, full occlusion, and partial occlusion.

GOT-10k is a large dataset consisting of 10,000 video sequences for training and 180 video sequences for testing. Given that most videos in the GOT-10k dataset are relatively short in duration, it places a stronger emphasis on evaluating tracker performance in short-term tracking scenarios. The dataset includes a whopping 563 target categories, surpassing other tracking datasets by a wide margin.

4.1.2 Implementation Details

Our SMSTracker is implemented with Python 3.8.13 on PyTorch 1.7.1. The GPU used in our experiments is NVIDIA A40 (48 G) and the cuda version is 11.2. The optimizer is AdamW [35] and the batch size is set to be 16. The initial learning rate is set to 10−4 and the weight decay is set to 10−5 for a total of 300 iterations.

4.2 Qualitative Analysis

In order to better illustrate the difference between the SMSTracker algorithm and other algorithms, six video sequences from the GOT-10k dataset are selected for comparison with the SimTrack [15], STARK-S [36], and STMTrack [37] methods. The tracking results of the SMSTracker algorithm and other state-of-the-art algorithms are shown in Fig. 5, where red denotes the SMSTracker algorithm, green denotes the SimTrack algorithm, dark blue denotes the STMTrack algorithm, and light blue denotes the STARK-S algorithm.

Figure 5: Visualization of results on six video sequences

From Fig. 5, it can be observed that the SMSTracker algorithm accurately tracks the target when it undergoes rapid movement, occlusion, scale variations, motion blur, low resolution, and in-plane rotation. Compared to other algorithms, SMSTracker has higher target tracking accuracy. In addition, SMSTracker shows greater stability in long-term target tracking. Therefore, it can be concluded that SMSTracker achieves good results.

4.3 Quantitative Analysis

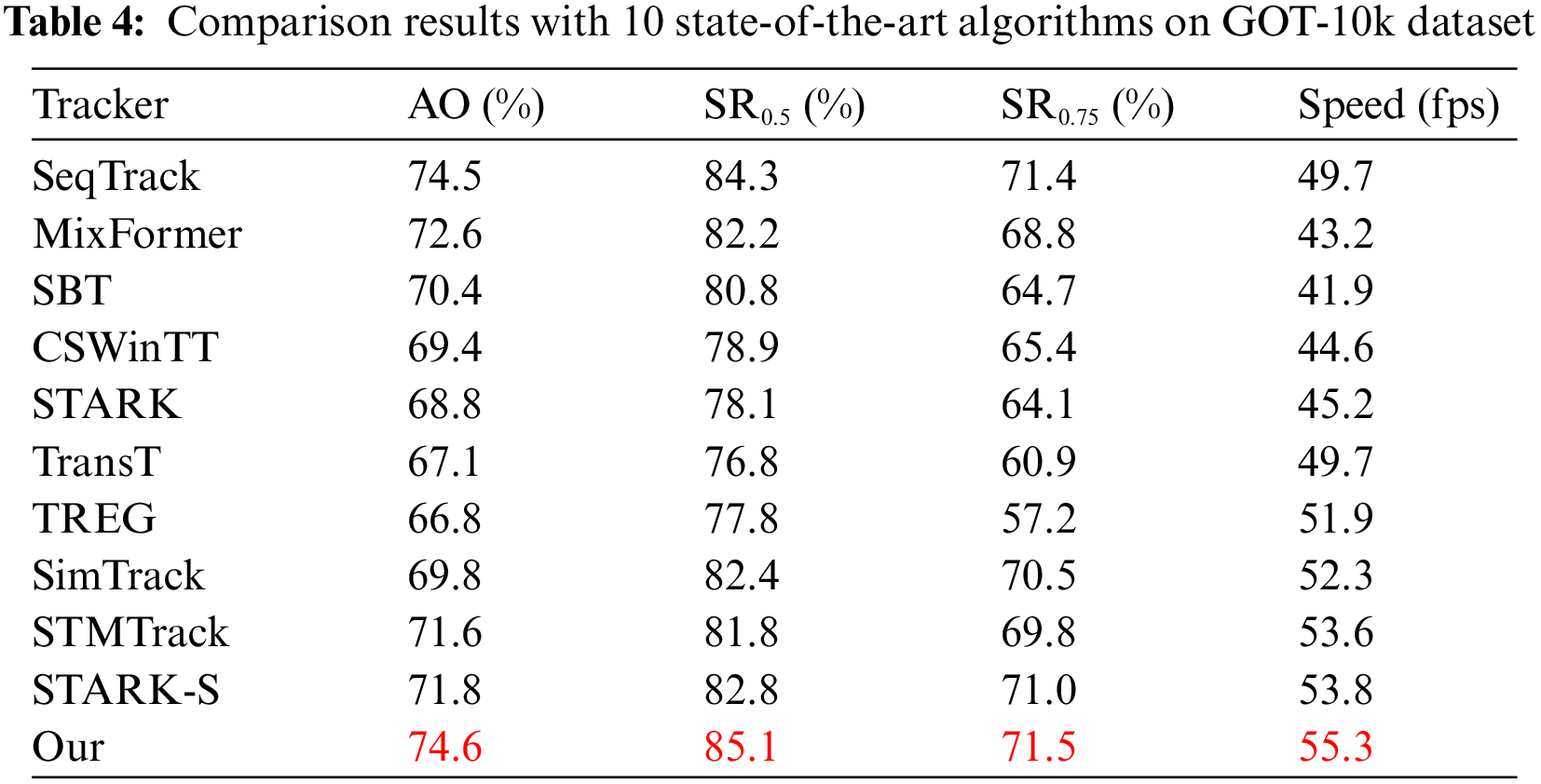
In order to verify the effectiveness of the tracking algorithm proposed in this paper, SMSTracker is compared with excellent algorithms at home and abroad in recent years, and the index scores of each algorithm on the four common datasets, namely, OTB2015, TrackingNet, LaSOT and GOT-10k, are listed in detail.

OTB2015 uses precision and success rates as evaluation metrics. Compare with seven currently advanced target tracking algorithms, SimTrack [15], MixFormer [25], ToMP [38], KeepTrack [39], SiamGAT [23], TransT [24], and KYS [40] on the OTB2015 dataset. The comparison results are shown in Table 1. We can conclude that the SMSTracker algorithm demonstrates excellent performance in two key performance metrics: precision and success rate. It achieves a precision of 93.9%, representing a 1.2% improvement compared to KeepTrack, and a success rate of 71.5%, indicating a 0.4% improvement over KeepTrack. These results strongly suggest the superiority of the SMSTracker algorithm. It effectively mitigates challenges such as target occlusion and interference from similar objects during the tracking process by analyzing the motion characteristics of the target.

TrackingNet uses Area Under the Curve (AUC) and Normalized Precision (PNorm) as evaluation metrics. Compare SMSTracker with seven other tracking algorithms on the TrackingNet dataset. The other seven trackers are SimTrack [15], STARK [36], TransT [24], Siam R-CNN [41], TrDiMP [42], PrDiMP-50 [43] and KYS [40]. The comparison results are shown in Table 2. From Table 2, it is evident that our algorithm outperforms current mainstream algorithms in both AUC and PNorm metrics. Compared to SimTrack, there is a 0.1% improvement in the AUC metric and a 0.9% improvement in the PNorm metric. This indicates that SMSTracker predicts target centers closer to the true target center, enabling precise localization of the target’s position.

LaSOT uses Area Under the Curve (AUC), Normalized Precision (PNorm) and Precision (P) as evaluation metrics. Compare SMSTracker with seven other tracking algorithms on the LaSOT dataset. The other seven trackers are SimTrack [15], SeqTrack [44], MixFormer [25], CSWinTT [45], TransT [24], KeepTrack [39], and DualTFR [46]. The comparison results are shown in Table 3. The AUC, PNorm, and P metrics for SMSTracker are 72.2%, 81.4%, and 77.9%, respectively. Compared to the baseline algorithm SimTrack, there are improvements of 2.9% in AUC, and 2.9% in PNorm. This suggests that SMSTracker also excels in the field of long video tracking.

GOT-10k introduces two metrics, Average Overlap (AO) and Success Rate (SR), as benchmarks for evaluating tracker performance on the GOT-10k dataset. AO represents the average overlap between all ground truth labels and the tracker’s predicted bounding boxes. SR is used to measure the percentage of frames in the test set where the overlap exceeds a certain threshold. Common thresholds include 0.5 and 0.75, corresponding to metrics known as SR0.5 and SR0.75. SR0.5 indicates the proportion of frames where the overlap between predicted and true bounding boxes exceeds 0.5, while SR0.75 represents the proportion of frames where the overlap exceeds 0.75. The success rate of SMSTrack on GOT-10k is 85.1%, which is 2.7% higher than that of the baseline model SimTrack, and the comparison results are plotted in Fig. 6. Conduct a comparative analysis of SMSTracker with ten other tracking algorithms using the GOT-10K dataset. The other ten trackers are SeqTrack [44], MixFormer [25], SBT [47], CSWinTT [45], STARK [36], TransT [24], TREG [48], SimTrack [15], STMTrack [37] and STARK-S [36]. The comparison results are shown in Table 4. As can be seen in Table 4, SMSTracker exhibits excellent performance, outperforming the current mainstream tracking algorithms, with metrics of 74.6% for AO, 85.1% for SR0.5, and 71.5% for SR0.75. Compared with SimTrack, there is an improvement of 4.8%, 2.7%, and 1.0% in AO, SR0.5, and SR0.75, respectively. In addition, our model also demonstrates strong advantages in tracking speed. This indicates a higher accuracy in regressing the target bounding box and a stronger ability to capture changes in target dynamics.

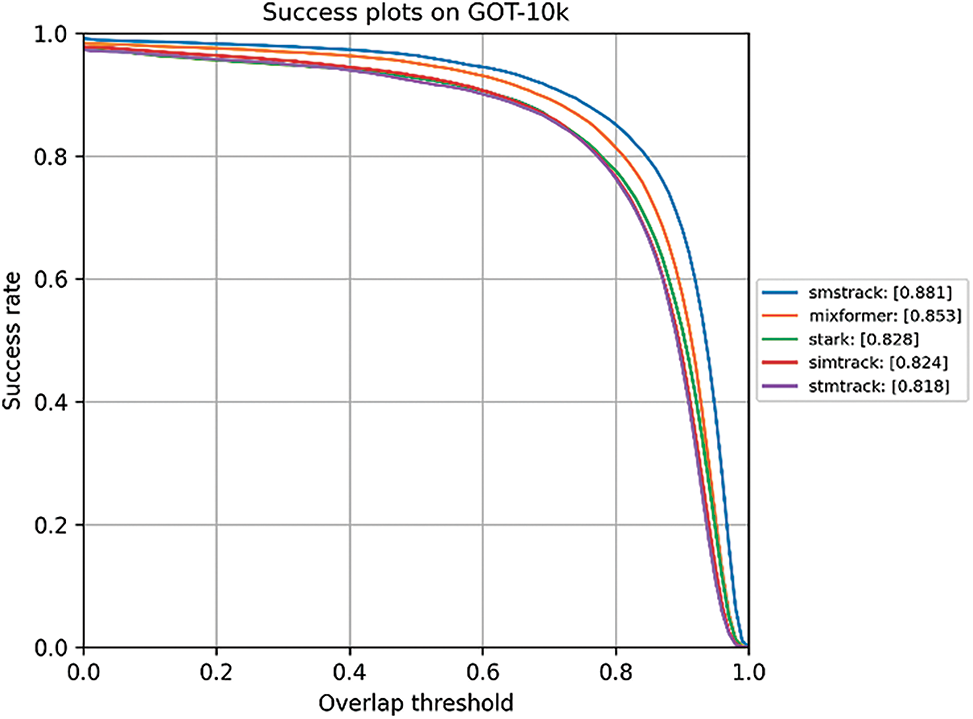
Figure 6: Comparison result on GOT-10k testing set in terms of success scores

4.4 Ablation Study

To assess the effectiveness of our proposed modules, we conducted comprehensive ablation experiments on the LaSOT dataset, systematically analyzing the results across four distinct network configurations. In these experiments, we employed SimTrack as our baseline model. For the second model, we introduced the Hybrid Tensor Decomposition Self-Attention Mechanism (HTDA) into SimTrack. This addition was aimed at mitigating redundancy within the transformer backbone network. In the third model, we integrated the Self-Calibration Attention Fusion Block (SCAF) with SimTrack. This incorporation was designed to address issues related to attention ambiguity and inconsistency within the baseline model. In the fourth and final model, we combined both the HTDA and SCAF modules into SimTrack, representing the comprehensive approach proposed in this study. Through these experiments, we systematically evaluated the impact of these modules on tracking performance. The four models were trained separately and the results of the ablation experiments are shown in Table 5.

From Table 5, it is evident that the inclusion of the HTDA module and the SCAF module has led to improvements in both AUC and PNorm when compared to the baseline algorithm. Upon integrating the HTDA module, the AUC, PNorm, and FLOPs metrics were measured at 71.8%, 80.9%, and 18.9 G, respectively. In comparison to SimTrack, this represents a 2.5% increase in AUC, a 2.4% increase in PNorm, and a simultaneous reduction of 6.1 G in FLOPs. These results indicate that the Hybrid Tensor Decomposition Self-attention Transformer significantly enhances tracking accuracy while substantially reducing complexity. In the third model, the AUC, PNorm, and FLOPs metrics were measured at 72.4%, 81.5%, and 26.5 G, respectively. Although complexity increased with a 1.5 G rise in FLOPs, substantial improvements in tracking performance were observed with a 3.1% increase in AUC and a 3% increase in PNorm. This indicates that the self-calibration attention fusion block can capture sharper boundaries of the target object, filtering out background regions unrelated to the target object, thereby achieving more precise target tracking. The proposed algorithm, which combines the strengths of the Hybrid Tensor Decomposition Self-attention Transformer and the Self-calibration Attention Fusion Block, achieved AUC, PNorm, and FLOPs metrics of 72.2%, 81.4%, and 21.2 G, respectively. Compared to the baseline algorithm, this represents a 2.9% increase in AUC, a 2.9% increase in PNorm, and a simultaneous reduction of 3.8 G in FLOPs. These findings indicate that the improved algorithm strikes a reasonable balance between computational complexity and tracking performance, making it highly relevant for practical target tracking tasks.

5  Conclusion

In this paper, we propose a target tracker called SMSTracker based on the Self-calibration Multi-head Self-Attention Transformer. By amalgamating hybrid tensor decomposition Transformer, we effectively eliminate redundancy while compressing and accelerating transformer operations, thus enhancing the real-time capability of target tracking. Additionally, we incorporate a self-calibration attention fusion block to capture sharper target boundaries, improving tracking performance stability. Experimental results demonstrate that this approach outperforms existing methods in terms of precision and success rate across multiple datasets, substantiating the superiority and applicability of our method.

Acknowledgement: We express our gratitude to the National Natural Science Foundation of China and the Postgraduate Research & Practice Innovation Program of Jiangsu Province for their support.

Funding Statement: This work is supported by the National Natural Science Foundation of China under Grant 62177029 and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX21_0740), China.

Author Contributions: All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Zhongyang Wang, Feng Liu and Hu Zhu. Methodology and experiments were operated by Zhongyang Wang. The first draft of the manuscript was written by Feng Liu, Hu Zhu and all authors commented on previous versions of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The code implementation of the proposed model is available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. Comaniciu, V. Ramesh, and P. Meer, “Real-time tracking of non-rigid objects using mean shift,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. CVPR 2000 (Cat. No.PR00662), Hilton Head, SC, USA, 2000, vol. 2, pp. 142–149. [Google Scholar]

2. X. Mei and H. Ling, “Robust visual tracking and vehicle classification via sparse representation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 33, no. 11, pp. 2259–2272, 2011. doi: 10.1109/TPAMI.2011.66. [Google Scholar] [PubMed] [CrossRef]

3. S. S. Beauchemin and J. L. Barron, “The computation of optical flow,” ACM Comput. Surv., vol. 27, no. 3, pp. 433–466, 1995. doi: 10.1145/212094.212141. [Google Scholar] [CrossRef]

4. D. S. Bolme, J. R. Beveridge, B. A. Draper, and Y. M. Lui, “Visual object tracking using adaptive correlation filters,” in 2010 IEEE Comput. Society Conf. Comput. Vis. Pattern Recognit., San Francisco, CA, USA, 2010, pp. 2544–2550. [Google Scholar]

5. A. Montero, J. Lang, and R. Laganiere, “Exploiting the circulant ` structure of tracking-by-detection with kernels,” in Proc. Int. Conf. Comput. Vis. Workshops, 2015, pp. 587–594. [Google Scholar]

6. M. Danelljan, G. Hager, F. Khan, and M. Felsberg, “Accurate scale estimation for robust visual tracking,” in Br. Mach. Vis. Conf., Nottingham, UK, Bmva Press, Sep. 1–5, 2014. [Google Scholar]

7. Y. Li and J. Zhu, “A scale adaptive kernel correlation filter tracker with feature integration,” in Comput. Vis.–ECCV 2014 Workshops, Zurich, Switzerland, Sep. 6–7, 2014, pp. 254–265. [Google Scholar]

8. T. Bouraffa, Z. Feng, L. Yan, Y. Xia, and B. Xiao, “Multi-feature fusion tracking algorithm based on peak-context learning,” Image Vis. Comput., vol. 123, no. 4, pp. 104468, 2022. doi: 10.1016/j.imavis.2022.104468. [Google Scholar] [CrossRef]

9. C. Ma, J. B. Huang, X. Yang, and M. H. Yang, “Hierarchical convolutional features for visual tracking,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Santiago, Chile, 2015, pp. 3074–3082. [Google Scholar]

10. J. Valmadre, L. Bertinetto, J. Henriques, A. Vedaldi, and P. H. Torr, “End-to-end representation learning for correlation filter based tracking,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit (CVPR), Honolulu, HI, USA, 2017, pp. 5000–5008. [Google Scholar]

11. E. Gundogdu and A. A. Alatan, “Good features to correlate for visual tracking,” IEEE Trans. Image Process., vol. 27, no. 5, pp. 2526–2540, 2018. doi: 10.1109/TIP.2018.2806280. [Google Scholar] [PubMed] [CrossRef]

12. Q. Wang, J. Gao, J. Xing, M. Zhang, and W. Hu, “DCFNet: Discriminant correlation filters network for visual tracking,” arXiv preprint arXiv:1704.04057, 2017. [Google Scholar]

13. C. Fan, R. Zhang, and Y. Ming, “MP-LN: Motion state prediction and localization network for visual object tracking,” Vis. Comput., vol. 38, no. 12, pp. 4291–4306, 2022. [Google Scholar]

14. P. Sun et al., “Transtrack: Multiple object tracking with transformer,” arXiv preprint arXiv:2012, 2012. [Google Scholar]

15. B. Chen et al., “Backbone is all your need: A simplified architecture for visual object tracking,” in European Conf. Comput. Vis., Tel Aviv, Israel, 2022, pp. 375–392. [Google Scholar]

16. J. Jia, Z. Lai, Y. Qian, and Z. Yao, “Aerial video trackers review,” Entropy, vol. 22, no. 12, pp. 1358, 2020. doi: 10.3390/e22121358. [Google Scholar] [PubMed] [CrossRef]

17. T. Vojir, J. Noskova, and J. Matas, “Robust scale-adaptive mean-shift for tracking,” Pattern Recognit. Lett., vol. 49, pp. 250–258, 2014. doi: 10.1016/j.patrec.2014.03.025. [Google Scholar] [CrossRef]

18. K. Nummiaro, E. K. Meier, and L. V. Gool, “An adaptive color-based particle filter,” Image Vis. Comput., vol. 21, no. 1, pp. 99–110, 2003. [Google Scholar]

19. D. Huang, L. Luo, M. Wen, Z. Chen, and C. Zhang, “Enable scale and aspect ratio adaptability in visual tracking with detection proposals,” in Proc. Br. Mach.Vis. Conf. (BMVC), Swansea, UK, Sep. 2015, pp. 185.1–185.12. [Google Scholar]

20. N. Wang and D. Y. Yeung, “Learning a deep compact image representation for visual tracking,” Adv. Neural Inf. Process. Syst., vol. 1, pp. 809–817, 2013. [Google Scholar]

21. H. Nam and B. Han, “Learning multi-domain convolutional neural networks for visual tracking,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, 2016, pp. 4293–4302. [Google Scholar]

22. M. Zhao, K. Okada, and M. Inaba, “TrTr: Visual tracking with transformer,” arXiv preprint arXiv:2105.03817, 2021. [Google Scholar]

23. D. Guo, Y. Shao, Y. Cui, Z. Wang, L. Zhang and C. Shen, “Graph attention tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Nashville, TN, USA, 2021, pp. 9543–9552. [Google Scholar]

24. X. Chen, B. Yan, J. Zhu, D. Wang, X. Yang and H. Lu, “Transformer tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognition, Nashville, TN, USA, 2021, pp. 8126–8135. [Google Scholar]

25. Y. Cui, C. Jiang, L. Wang, and G. Wu, “MixFormer: End-to-end tracking with iterative mixed attention,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, 2022, pp. 13608–13618. [Google Scholar]

26. H. Bai, R. Zhang, J. Wang, and X. Wan, “Weakly supervised object localization via transformer with implicit spatial calibration,” in Eur. Conf. Comput. Vis., Tel Aviv, Israel, 2022, pp. 612–628. [Google Scholar]

27. K. Islam, “Recent advances in vision transformer: A survey and outlook of recent work,” arXiv preprint arXiv:2203.01536, 2022. [Google Scholar]

28. F. Wu, A. Fan, A. Baevski, Y. N. Dauphin, and M. Auli, “Pay less attention with lightweight and dynamic convolutions,” arXiv preprint arXiv:1901.10430, 2019. [Google Scholar]

29. A. Stotsky, “Systematic review of newton-schulz iterations with unified factorizations: Integration in the richardson method and application to robust failure detection in electrical networks,” arXiv preprint arXiv:2208.04068, 2022. [Google Scholar]

30. H. Rezatofighi, N. Tsoi, J. Gwak, A. Sadeghian, I. Reid and S. Savarese, “Generalized intersection over union: A metric and a loss for bounding box regression,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, 2019, pp. 658–666. [Google Scholar]

31. Y. Wu, J. Lim, and M. H. Yang, “Online object tracking: A benchmark,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Portland, OR, USA, 2013, pp. 2411–2418. [Google Scholar]

32. M. Muller, A. Bibi, S. Giancola, S. Alsubaihi, and B. Ghanem, “TrackingNet: A large-scale dataset and benchmark for object tracking in the wild,” in Proc. Eur. Conf. Comput. Vis. (ECCV), Munich, Germany, 2018, pp. 300–317. [Google Scholar]

33. H. Fan et al., “LaSOT: A high-quality benchmark for large-scale single object tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, 2019, pp. 5374–5383. [Google Scholar]

34. L. Huang, X. Zhao, and K. Huang, “GOT-10k: A large high-diversity benchmark for generic object tracking in the wild,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 43, no. 5, pp. 1562–1577, 2019. [Google Scholar]

35. I. Loshchilov and F. Hutter, “Decoupled weight decay regularization,” arXiv preprint arXiv:1711.05101, 2017. [Google Scholar]

36. B. Yan, H. Peng, J. Fu, D. Wang, and H. Lu, “Learning spatio-temporal transformer for visual tracking,” in Proc. IEEE/CVF Int. Conf. Comput. Vis., Montreal, QC, Canada, 2021, pp. 10448–10457. [Google Scholar]

37. Z. Fu, Q. Liu, Z. Fu, and Y. Wang, “STMTrack: Template-free visual tracking with space-time memory networks,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Nashville, TN, USA, 2021, pp. 13774–13783. [Google Scholar]

38. C. Mayer et al., “Transforming model prediction for tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, 2022, pp. 8731–8740. [Google Scholar]

39. C. Mayer, M. Danelljan, D. P. Paudel, and L. van Gool, “Learning target candidate association to keep track of what not to track,” in Proc. IEEE/CVF Int. Conf. Comput. Vis., Montreal, QC, Canada, 2021, pp. 13444–13454. [Google Scholar]

40. G. Bhat, M. Danelljan, L. van Gool, and R. Timofte, “Know your surroundings: Exploiting scene information for object tracking,” in Comput. Vis.–ECCV 2020: 16th Eur. Conf., Proc., Glasgow, UK, Springer, Aug. 23–28, 2020, pp. 205–221. [Google Scholar]

41. P. Voigtlaender, J. Luiten, P. H. Torr, and B. Leibe, “Siam R-CNN: Visual tracking by re-detection,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, 2020, pp. 6578–6588. [Google Scholar]

42. N. Wang, W. Zhou, J. Wang, and H. Li, “Transformer meets tracker: Exploiting temporal context for robust visual tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Nashville, TN, USA, 2021, pp. 1571–1580. [Google Scholar]

43. M. Danelljan, L. V. Gool, and R. Timofte, “Probabilistic regression for visual tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, 2020, pp. 7183–7192. [Google Scholar]

44. X. Chen, H. Peng, D. Wang, H. Lu, and H. Hu, “SeqTrack: Sequence to sequence learning for visual object tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Vancouver, BC, Canada, 2023, pp. 14572–14581. [Google Scholar]

45. Z. Song, J. Yu, Y. P. P. Chen, and W. Yang, “Transformer tracking with cyclic shifting window attention,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, 2022, pp. 8791–8800. [Google Scholar]

46. F. Xie, C. Wang, G. Wang, W. Yang, and W. Zeng, “Learning tracking representations via dual-branch fully transformer networks,” in Proc. IEEE/CVF Int. Conf. Comput. Vis., Montreal, BC, Canada, 2021, pp. 2688–2697. [Google Scholar]

47. F. Xie, C. Wang, G. Wang, Y. Cao, W. Yang and W. Zeng, “Correlationaware deep tracking,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, 2022, pp. 8751–8760. [Google Scholar]

48. Y. Cui, C. Jiang, L. Wang, and G. Wu, “Target transformed regression for accurate tracking,” arXiv preprint arXiv:2104.00403, 2021. [Google Scholar]